title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python3] Priority Queue + Greedy + Couting - Simple Solution | construct-string-with-repeat-limit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def repeatLimitedString(self, s: str, repeatLimit: int) -> str:\n cnt = collections.Counter(s)\n chars = [(-ord(k), k, v) for k, v in cnt.items()]\n\n heapq.heapify(chars)\n res = []\n while chars:\n o, ch, ct = heapq.heappop(chars)\n add = 0\n if len(res) >= repeatLimit and res[-1] == ch:\n if not chars: break\n no, nch, nct = heapq.heappop(chars)\n res.append(nch)\n if nct - 1 != 0: heapq.heappush(chars, (no, nch, nct - 1))\n else:\n add = min(repeatLimit, ct)\n res.extend([ch for _ in range(add)])\n if ct - add != 0: heapq.heappush(chars, (o, ch, ct - add))\n return "".join(res)\n``` | 1 | You are given a string `s` and an integer `repeatLimit`. Construct a new string `repeatLimitedString` using the characters of `s` such that no letter appears **more than** `repeatLimit` times **in a row**. You do **not** have to use all characters from `s`.
Return _the **lexicographically largest**_ `repeatLimitedString` _possible_.
A string `a` is **lexicographically larger** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears later in the alphabet than the corresponding letter in `b`. If the first `min(a.length, b.length)` characters do not differ, then the longer string is the lexicographically larger one.
**Example 1:**
**Input:** s = "cczazcc ", repeatLimit = 3
**Output:** "zzcccac "
**Explanation:** We use all of the characters from s to construct the repeatLimitedString "zzcccac ".
The letter 'a' appears at most 1 time in a row.
The letter 'c' appears at most 3 times in a row.
The letter 'z' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "zzcccac ".
Note that the string "zzcccca " is lexicographically larger but the letter 'c' appears more than 3 times in a row, so it is not a valid repeatLimitedString.
**Example 2:**
**Input:** s = "aababab ", repeatLimit = 2
**Output:** "bbabaa "
**Explanation:** We use only some of the characters from s to construct the repeatLimitedString "bbabaa ".
The letter 'a' appears at most 2 times in a row.
The letter 'b' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "bbabaa ".
Note that the string "bbabaaa " is lexicographically larger but the letter 'a' appears more than 2 times in a row, so it is not a valid repeatLimitedString.
**Constraints:**
* `1 <= repeatLimit <= s.length <= 105`
* `s` consists of lowercase English letters. | The maximum distance must be the distance between the first and last critical point. For each adjacent critical point, calculate the difference and check if it is the minimum distance. |
[Python3] factors | count-array-pairs-divisible-by-k | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/793daa0aab0733bfadd4041fdaa6f8bdd38fe229) for solutions of weekly 281. \n\n```\nclass Solution:\n def coutPairs(self, nums: List[int], k: int) -> int:\n factors = []\n for x in range(1, int(sqrt(k))+1):\n if k % x == 0: factors.append(x)\n ans = 0 \n freq = Counter()\n for x in nums: \n x = gcd(x, k)\n ans += freq[k//x]\n for f in factors: \n if x % f == 0 and f <= x//f: \n freq[f] += 1\n if f < x//f: freq[x//f] += 1\n return ans \n``` | 6 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _such that:_
* `0 <= i < j <= n - 1` _and_
* `nums[i] * nums[j]` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 7
**Explanation:**
The 7 pairs of indices whose corresponding products are divisible by 2 are
(0, 1), (0, 3), (1, 2), (1, 3), (1, 4), (2, 3), and (3, 4).
Their products are 2, 4, 6, 8, 10, 12, and 20 respectively.
Other pairs such as (0, 2) and (2, 4) have products 3 and 15 respectively, which are not divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 0
**Explanation:** There does not exist any pair of indices whose corresponding product is divisible by 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 105` | Once x drops below 0 or goes above 1000, is it possible to continue performing operations on x? How can you use BFS to find the minimum operations? |
Just like Two-Sum hashmap | count-array-pairs-divisible-by-k | 1 | 1 | **It\'s just like two sum in that we were storing the remaining part if the target sum was 10 and we found 7 we were storing the 10-7 in hashmap so if we found 3 we will return it\'s index from there same we need to find the product which is divisible by k so for example if we need to make a pair which is divisible by 10 so by far we have found 12 so the [gcd](https://byjus.com/maths/greatest-common-divisor/) of 12,10 will be 2 now what is the other counter we need to find it is 5 hence if we find 5\'s multiple or 5 we will add this pair to answer**\n`So the time complexity here won\'t be O(n^2) because a number can only have limited factors hence for 10^5 the max will be (10^5)^1/2 so at max the loop will iterate upto 100 - 200 (roughly) `\n```py\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n counter = Counter() #hashmap dicitionary of python\n ans = 0\n n = len(nums)\n \n for i in range(n):\n x = math.gcd(k,nums[i]) #ex: 10 = k and we have nums[i] as 12 so gcd will be 2\n want = k // x #what do we want from upper ex: we need 5\n for num in counter:\n if num % want == 0: #so if we find a number that is divisible by 5 then we can multiply it to 12 and make it a factor of 10 for ex we find 20 so it will be 240 which is divisible by 10 hence we will add it to answer\n ans += counter[num] #we are adding the freq as we can find no of numbers that have same factor\n counter[x] += 1 #here we are increasing the freq of 2 so that if we find 5 next time we can add these to the answer\n return ans\n```\n```java\npublic class Solution {\n public int countPairs(int[] nums, int k) {\n // Create a HashMap to count the occurrences of numbers\n Map<Integer, Integer> counter = new HashMap<>();\n int ans = 0;\n int n = nums.length;\n\n for (int i = 0; i < n; i++) {\n int gcdResult = gcd(k, nums[i]); // Calculate the GCD of \'k\' and \'nums[i]\'\n int desiredFactor = k / gcdResult; // Calculate the desired factor to form a pair with \'nums[i]\'\n\n for (int num : counter.keySet()) {\n if (num % desiredFactor == 0) {\n // If \'num\' is divisible by the desired factor, it can form pairs with \'nums[i]\'\n // Add the frequency of \'num\' to the answer\n ans += counter.get(num);\n }\n }\n\n // Increase the count of \'gcdResult\' in the HashMap\n counter.put(gcdResult, counter.getOrDefault(gcdResult, 0) + 1);\n }\n\n return ans;\n }\n```\n | 11 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _such that:_
* `0 <= i < j <= n - 1` _and_
* `nums[i] * nums[j]` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 7
**Explanation:**
The 7 pairs of indices whose corresponding products are divisible by 2 are
(0, 1), (0, 3), (1, 2), (1, 3), (1, 4), (2, 3), and (3, 4).
Their products are 2, 4, 6, 8, 10, 12, and 20 respectively.
Other pairs such as (0, 2) and (2, 4) have products 3 and 15 respectively, which are not divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 0
**Explanation:** There does not exist any pair of indices whose corresponding product is divisible by 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 105` | Once x drops below 0 or goes above 1000, is it possible to continue performing operations on x? How can you use BFS to find the minimum operations? |
Python | O(N * (k^1/3)) | Easy code with explanation (Get all factors) | count-array-pairs-divisible-by-k | 0 | 1 | ## Explanation:\n1. We can get all factors of `k` first.\n2. For each `num` in `nums`, `k // gcd(num, k)` will be the multiplier that num needs that make the result is divisible by `k`.\n3. We use `counter` to maintain how many numbers is divisible by factors of `k`.\n\n\n## Solutions:\n```\nclass Solution:\n def coutPairs(self, nums: List[int], k: int) -> int:\n # Generate all factors of k\n factors = []\n for i in range(1, int(k ** 0.5) + 1):\n if k % i == 0:\n factors.append(i)\n\t\t\t\t# To prevent us from putting the same number into it\n if k // i != i:\n factors.append(k // i)\n \n res = 0\n counter = collections.Counter()\n for num in nums:\n # `k // math.gcd(num, k)` is the smallest factor that makes `num` multiply it will be divisible by k\n res += counter[k // math.gcd(num, k)]\n \n for factor in factors:\n # if num % factor == 0, means if can provide this factor for other `num` to multiply and make it divisible by k\n if num % factor == 0:\n counter[factor] += 1\n return res\n```\n\n## Complexcity\nTime Complexity: O(N * (k^1/3)) // N = len(nums)\nSpace Complexity: O(k^1/3)\n | 1 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _such that:_
* `0 <= i < j <= n - 1` _and_
* `nums[i] * nums[j]` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 7
**Explanation:**
The 7 pairs of indices whose corresponding products are divisible by 2 are
(0, 1), (0, 3), (1, 2), (1, 3), (1, 4), (2, 3), and (3, 4).
Their products are 2, 4, 6, 8, 10, 12, and 20 respectively.
Other pairs such as (0, 2) and (2, 4) have products 3 and 15 respectively, which are not divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 0
**Explanation:** There does not exist any pair of indices whose corresponding product is divisible by 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 105` | Once x drops below 0 or goes above 1000, is it possible to continue performing operations on x? How can you use BFS to find the minimum operations? |
Count Array Pairs Divisible by K | count-array-pairs-divisible-by-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe algorithm counts pairs of numbers in the list where their Greatest Common Divisor (GCD)is divisible by k. The GCD represents the largest common factor between two numbers.We can achieve this by calculating the GCD of each number with k and counting their frequencies.\n\n\n# Complexity\n- Time complexity:O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nfrom math import gcd\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n d = defaultdict(int)\n for i in nums:\n d[gcd(i, k)] += 1\n\n ans = 0\n\n for i in d.keys():\n for j in d.keys():\n if (i * j) % k == 0:\n if i < j:\n ans += d[i] * d[j]\n elif j == i:\n ans += d[i] * (d[i] - 1) // 2\n\n return ans\n\n\n\n\n``` | 0 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _such that:_
* `0 <= i < j <= n - 1` _and_
* `nums[i] * nums[j]` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\], k = 2
**Output:** 7
**Explanation:**
The 7 pairs of indices whose corresponding products are divisible by 2 are
(0, 1), (0, 3), (1, 2), (1, 3), (1, 4), (2, 3), and (3, 4).
Their products are 2, 4, 6, 8, 10, 12, and 20 respectively.
Other pairs such as (0, 2) and (2, 4) have products 3 and 15 respectively, which are not divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 5
**Output:** 0
**Explanation:** There does not exist any pair of indices whose corresponding product is divisible by 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 105` | Once x drops below 0 or goes above 1000, is it possible to continue performing operations on x? How can you use BFS to find the minimum operations? |
Simple solution in Python3 | counting-words-with-a-given-prefix | 0 | 1 | # Intuition\nHere we have:\n- `words` and `pref`\n- our goal is to find, **how many** words start from `pref`\n\n# Approach\n1. declare `ans`\n2. for each word check `startswith(pref)`\n\n# Complexity\n- Time complexity: **O(N*K)** since we iterate over `words` by length `K`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space\n\n# Code\n```\nclass Solution:\n def prefixCount(self, words: List[str], pref: str) -> int:\n ans = 0\n\n for word in words:\n if word.startswith(pref): ans += 1\n\n return ans\n``` | 1 | You are given an array of strings `words` and a string `pref`.
Return _the number of strings in_ `words` _that contain_ `pref` _as a **prefix**_.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** words = \[ "pay ", "**at**tention ", "practice ", "**at**tend "\], `pref` \= "at "
**Output:** 2
**Explanation:** The 2 strings that contain "at " as a prefix are: "**at**tention " and "**at**tend ".
**Example 2:**
**Input:** words = \[ "leetcode ", "win ", "loops ", "success "\], `pref` \= "code "
**Output:** 0
**Explanation:** There are no strings that contain "code " as a prefix.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length, pref.length <= 100`
* `words[i]` and `pref` consist of lowercase English letters. | null |
Simplest Python solution. Use startswith | counting-words-with-a-given-prefix | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def prefixCount(self, words: List[str], pref: str) -> int:\n cnt = 0\n for s in words:\n if s.startswith(pref):\n cnt += 1\n return cnt\n``` | 3 | You are given an array of strings `words` and a string `pref`.
Return _the number of strings in_ `words` _that contain_ `pref` _as a **prefix**_.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** words = \[ "pay ", "**at**tention ", "practice ", "**at**tend "\], `pref` \= "at "
**Output:** 2
**Explanation:** The 2 strings that contain "at " as a prefix are: "**at**tention " and "**at**tend ".
**Example 2:**
**Input:** words = \[ "leetcode ", "win ", "loops ", "success "\], `pref` \= "code "
**Output:** 0
**Explanation:** There are no strings that contain "code " as a prefix.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length, pref.length <= 100`
* `words[i]` and `pref` consist of lowercase English letters. | null |
Python one line simple solution | counting-words-with-a-given-prefix | 0 | 1 | **Python**\n\n```\ndef prefixCount(self, words: List[str], pref: str) -> int:\n\treturn sum([word.startswith(pref) for word in words])\n```\n\n**Like it ? please upvote !** | 15 | You are given an array of strings `words` and a string `pref`.
Return _the number of strings in_ `words` _that contain_ `pref` _as a **prefix**_.
A **prefix** of a string `s` is any leading contiguous substring of `s`.
**Example 1:**
**Input:** words = \[ "pay ", "**at**tention ", "practice ", "**at**tend "\], `pref` \= "at "
**Output:** 2
**Explanation:** The 2 strings that contain "at " as a prefix are: "**at**tention " and "**at**tend ".
**Example 2:**
**Input:** words = \[ "leetcode ", "win ", "loops ", "success "\], `pref` \= "code "
**Output:** 0
**Explanation:** There are no strings that contain "code " as a prefix.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length, pref.length <= 100`
* `words[i]` and `pref` consist of lowercase English letters. | null |
Python easy Solution | using Counter | minimum-number-of-steps-to-make-two-strings-anagram-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n cnt1=Counter(s)\n cnt2=Counter(t)\n sm=0\n cnt=cnt1-cnt2+(cnt2-cnt1)\n for i in cnt.values():\n sm+=i\n return sm\n``` | 3 | You are given two strings `s` and `t`. In one step, you can append **any character** to either `s` or `t`.
Return _the minimum number of steps to make_ `s` _and_ `t` _**anagrams** of each other._
An **anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "**lee**tco**de** ", t = "co**a**t**s** "
**Output:** 7
**Explanation:**
- In 2 steps, we can append the letters in "as " onto s = "leetcode ", forming s = "leetcode**as** ".
- In 5 steps, we can append the letters in "leede " onto t = "coats ", forming t = "coats**leede** ".
"leetcodeas " and "coatsleede " are now anagrams of each other.
We used a total of 2 + 5 = 7 steps.
It can be shown that there is no way to make them anagrams of each other with less than 7 steps.
**Example 2:**
**Input:** s = "night ", t = "thing "
**Output:** 0
**Explanation:** The given strings are already anagrams of each other. Thus, we do not need any further steps.
**Constraints:**
* `1 <= s.length, t.length <= 2 * 105`
* `s` and `t` consist of lowercase English letters. | While generating substrings starting at any index, do you need to continue generating larger substrings if you encounter a consonant? Can you store the count of characters to avoid generating substrings altogether? |
[Python3, Java, C++] Counter O(len(s) + (len(t)) | minimum-number-of-steps-to-make-two-strings-anagram-ii | 1 | 1 | * Count the number of characters in each string \n* Compare the counts for each character\n* If the counts of the characters don\'t match, add the difference of the counts to answer\n<iframe src="https://leetcode.com/playground/TrFoEYxb/shared" frameBorder="0" width="600" height="200"></iframe>\n\nTime complexity: `O(len(s) + (len(t))` | 43 | You are given two strings `s` and `t`. In one step, you can append **any character** to either `s` or `t`.
Return _the minimum number of steps to make_ `s` _and_ `t` _**anagrams** of each other._
An **anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "**lee**tco**de** ", t = "co**a**t**s** "
**Output:** 7
**Explanation:**
- In 2 steps, we can append the letters in "as " onto s = "leetcode ", forming s = "leetcode**as** ".
- In 5 steps, we can append the letters in "leede " onto t = "coats ", forming t = "coats**leede** ".
"leetcodeas " and "coatsleede " are now anagrams of each other.
We used a total of 2 + 5 = 7 steps.
It can be shown that there is no way to make them anagrams of each other with less than 7 steps.
**Example 2:**
**Input:** s = "night ", t = "thing "
**Output:** 0
**Explanation:** The given strings are already anagrams of each other. Thus, we do not need any further steps.
**Constraints:**
* `1 <= s.length, t.length <= 2 * 105`
* `s` and `t` consist of lowercase English letters. | While generating substrings starting at any index, do you need to continue generating larger substrings if you encounter a consonant? Can you store the count of characters to avoid generating substrings altogether? |
[Python3] freq table | minimum-number-of-steps-to-make-two-strings-anagram-ii | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/6f8a2c98f0feab59d2e0ec35f928e3ee1d3e4456) for solutions of weekly 282. \n\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n fs, ft = Counter(s), Counter(t)\n return sum((fs-ft).values()) + sum((ft-fs).values())\n``` | 6 | You are given two strings `s` and `t`. In one step, you can append **any character** to either `s` or `t`.
Return _the minimum number of steps to make_ `s` _and_ `t` _**anagrams** of each other._
An **anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "**lee**tco**de** ", t = "co**a**t**s** "
**Output:** 7
**Explanation:**
- In 2 steps, we can append the letters in "as " onto s = "leetcode ", forming s = "leetcode**as** ".
- In 5 steps, we can append the letters in "leede " onto t = "coats ", forming t = "coats**leede** ".
"leetcodeas " and "coatsleede " are now anagrams of each other.
We used a total of 2 + 5 = 7 steps.
It can be shown that there is no way to make them anagrams of each other with less than 7 steps.
**Example 2:**
**Input:** s = "night ", t = "thing "
**Output:** 0
**Explanation:** The given strings are already anagrams of each other. Thus, we do not need any further steps.
**Constraints:**
* `1 <= s.length, t.length <= 2 * 105`
* `s` and `t` consist of lowercase English letters. | While generating substrings starting at any index, do you need to continue generating larger substrings if you encounter a consonant? Can you store the count of characters to avoid generating substrings altogether? |
Counter | minimum-number-of-steps-to-make-two-strings-anagram-ii | 0 | 1 | For some reason, I misread the description, and tried to solve another problem.\n\n**Python 3**\n```python\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n cs, ct = Counter(s), Counter(t)\n return sum(cnt for ch, cnt in ((cs - ct) + (ct - cs)).items())\n```\n**C++**\n```cpp\nint minSteps(string s, string t) {\n int cnt[26] = {};\n for (char ch : s) \n ++cnt[ch - \'a\'];\n for (char ch : t) \n --cnt[ch - \'a\'];\n return accumulate(begin(cnt), end(cnt), 0, [](int sum, int n){ return sum + abs(n); });\n}\n``` | 6 | You are given two strings `s` and `t`. In one step, you can append **any character** to either `s` or `t`.
Return _the minimum number of steps to make_ `s` _and_ `t` _**anagrams** of each other._
An **anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "**lee**tco**de** ", t = "co**a**t**s** "
**Output:** 7
**Explanation:**
- In 2 steps, we can append the letters in "as " onto s = "leetcode ", forming s = "leetcode**as** ".
- In 5 steps, we can append the letters in "leede " onto t = "coats ", forming t = "coats**leede** ".
"leetcodeas " and "coatsleede " are now anagrams of each other.
We used a total of 2 + 5 = 7 steps.
It can be shown that there is no way to make them anagrams of each other with less than 7 steps.
**Example 2:**
**Input:** s = "night ", t = "thing "
**Output:** 0
**Explanation:** The given strings are already anagrams of each other. Thus, we do not need any further steps.
**Constraints:**
* `1 <= s.length, t.length <= 2 * 105`
* `s` and `t` consist of lowercase English letters. | While generating substrings starting at any index, do you need to continue generating larger substrings if you encounter a consonant? Can you store the count of characters to avoid generating substrings altogether? |
Self Understandable Python (2 methods) : | minimum-number-of-steps-to-make-two-strings-anagram-ii | 0 | 1 | **Method 1:**\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n a=Counter(s)\n b=Counter(t)\n c=(a-b)+(b-a)\n \n count=0\n for i in c:\n count+=c[i]\n return count\n```\n**Method 2:**\n```\nclass Solution:\n def minSteps(self, s: str, t: str) -> int:\n a=Counter(s)\n b=Counter(t)\n \n count=0\n for i in set(s + t):\n count+=abs(a[i]-b[i])\n \n return count\n``` | 3 | You are given two strings `s` and `t`. In one step, you can append **any character** to either `s` or `t`.
Return _the minimum number of steps to make_ `s` _and_ `t` _**anagrams** of each other._
An **anagram** of a string is a string that contains the same characters with a different (or the same) ordering.
**Example 1:**
**Input:** s = "**lee**tco**de** ", t = "co**a**t**s** "
**Output:** 7
**Explanation:**
- In 2 steps, we can append the letters in "as " onto s = "leetcode ", forming s = "leetcode**as** ".
- In 5 steps, we can append the letters in "leede " onto t = "coats ", forming t = "coats**leede** ".
"leetcodeas " and "coatsleede " are now anagrams of each other.
We used a total of 2 + 5 = 7 steps.
It can be shown that there is no way to make them anagrams of each other with less than 7 steps.
**Example 2:**
**Input:** s = "night ", t = "thing "
**Output:** 0
**Explanation:** The given strings are already anagrams of each other. Thus, we do not need any further steps.
**Constraints:**
* `1 <= s.length, t.length <= 2 * 105`
* `s` and `t` consist of lowercase English letters. | While generating substrings starting at any index, do you need to continue generating larger substrings if you encounter a consonant? Can you store the count of characters to avoid generating substrings altogether? |
Solution with clear explanation and example with a plot. | minimum-time-to-complete-trips | 0 | 1 | # Intuition\n--> Since number of trips possible for a given number of days with respect to time array is monotonic, we can use Binary search on the ouput limit.\n\n--> Output is monotonic because when output increases trips you can make is non decresing with respect to time array.\n\n--> Example to understand it is monotonic, if time = [5,10,10] ,totalTrips = 9 .\n\nTrips Vs Days is non decreasing or monotonic.\n\n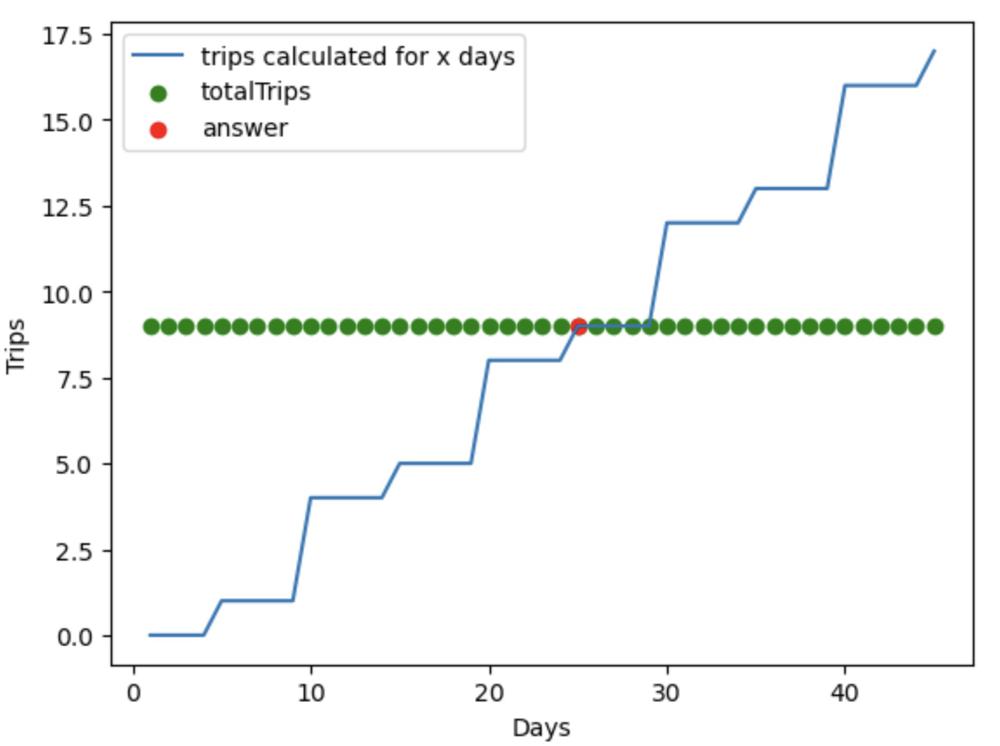\n\n\n\n\n# Approach\n--> Trip counter function is calculating number of trips you can make when you are given some number of days\n--> Since answer remains between 1 and totalTrips*min(time) we can use binary search.\n--> lets say you have time = [5,10,10] ,totalTrips = 9 , then your output limits are 1 and 9 multpipied by 5.\n\n\n# Complexity\n- Time complexity:\n--> Worst case complexity is O(Nlogk)\n--> N is number of elememts in time\n--> k is 10**14 in worst case\n\n- Space complexity:\n--> O(1)\n\n# Code\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n\n def trip_counter(num):\n\n i = 0\n\n trips = 0\n\n while i < len(time):\n\n trips += num // time[i]\n i+=1\n if trips > totalTrips:\n break\n\n return trips\n \n start = 1\n end = totalTrips*min(time) \n\n while start <= end:\n\n mid = (start+end)//2\n\n trips = trip_counter(mid)\n\n if trips >= totalTrips:\n end = mid-1\n \n else:\n start = mid+1\n \n\n return start\n\n\n\n\n\n\n\n``` | 3 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
[Python] One-liner, two-liner | minimum-time-to-complete-trips | 0 | 1 | # Approach\nBinary search (or rather, bisect) the minimum time required to fulfill all trips.\n\n# Code\n\n### Two liner\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n check = lambda t: sum(t // bus for bus in time) >= totalTrips\n return bisect_left(range(time[0] * totalTrips), True, key=check)\n\n```\n\n### One liner\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n return bisect_left(range(time[0] * totalTrips), True, key=lambda t: sum(t // bus for bus in time) >= totalTrips)\n\n```\n\n### Without bisect library\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n check = lambda t: sum(t // bus for bus in time) >= totalTrips\n\n lo, hi = 1, time[0] * totalTrips\n while lo < hi:\n mid = (lo + hi) // 2\n if check(mid):\n hi = mid\n else:\n lo = mid + 1\n \n return lo\n\n\n```\n\nBy the way, this is the article that solved binary search for me once and for all: http://coldattic.info/post/95/ | 2 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
📌📌Python3 || ⚡1737 ms, faster than 97.75% of Python3 | minimum-time-to-complete-trips | 0 | 1 | \n```\ndef minimumTime(self, time: List[int], totalTrips: int) -> int:\n def check(t):\n res = 0\n for e in time:\n res += t//e\n return res >= totalTrips\n maxt = max(time)\n left, right = 1, (totalTrips//sum([maxt//e for e in time]) + 1)*maxt\n while left < right:\n m = (left + right)//2\n if check(m):\n right = m\n else:\n left = m + 1\n return left\n```\nhere\'s a step-by-step explanation of the code:\n\n1. Define a function check(t) that takes an integer t and returns True if the number of trips that can be completed in t time is greater than or equal to the total number of trips needed (totalTrips), otherwise returns False.\n1. Initialize a variable maxt to the maximum value in the time list.\n1. Initialize left to 1 and right to a value that guarantees that there will be enough time to complete all the trips. This value is calculated as follows:\n\t1. For each element e in the time list, calculate the number of trips that can be completed in maxt time (i.e., maxt//e).\n\t1. Add up all these values to get the total number of trips that can be completed in maxt time.\n\t1. Divide totalTrips by this total number of trips to get an estimate of the minimum amount of time needed to complete all the trips.\n\t1. Multiply this estimate by maxt to get an upper bound on the time needed to complete all the trips.\n1. While left is less than right, do the following:\n\t1. Calculate the midpoint m between left and right.\n\t1. If check(m) returns True, set right to m.\n\t1. Otherwise, set left to m + 1.\n1. When the while loop terminates, return left, which represents the minimum amount of time needed to complete all the trips. | 2 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
Python Solution || Faster than 96% of other solutions | minimum-time-to-complete-trips | 0 | 1 | Please Upvote if you like it.\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n a, b = 1, totalTrips * min(time)\n\n def f(x):\n return sum(x // t for t in time) >= totalTrips\n \n while a < b:\n m = (a + b) // 2\n if not f(m): a = m + 1\n else: b = m\n return a | 2 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
beats 100% space complexity. | minimum-time-to-complete-trips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nas the question requires as to find the minimum time required to finish the total trip. first i needed to find the range in which the solution can lay and traverse through that inorder to reach an optimal solution. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI used binary search to solve the question in which i first looked for the left and right bound of the solution in which i found that the potential left boundary that is lowest possible answer is the minimum time taken to finish one trip. as the minimum amount of trip required can only be one. and also the maximum time taken is also can be calculated as (minimum time taken * the total trip required).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlog(n)) - for the sorting the values in descending order \nO(nlog(n)) - for the search for the valid trip\noverall - O(nlog(n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwe don\'t have addtional space to store value that grows as our answer changes hence :- O(1)\n# Code\n```\nclass Solution:\n def satisfiesTrip(self,mid, time, totalTrip):\n trip = 0\n for t in time:\n trip += mid//t\n if trip >= totalTrip:\n return True\n return False\n\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n time.sort(reverse=True)\n minimum = min(time)\n left = minimum\n right = minimum*totalTrips\n while left < right:\n mid = (left+ right)//2\n\n if self.satisfiesTrip(mid, time, totalTrips):\n right = mid\n else:\n left = mid + 1\n return right\n\n``` | 2 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
✅ All Binary Search Problems 🔥🔥 | minimum-time-to-complete-trips | 1 | 1 | **Good Binary Search Problems**\n* [1552. Magnetic Force Between Two Balls](https://leetcode.com/problems/magnetic-force-between-two-balls/)\n* [1870. Minimum Speed to Arrive on Time](https://leetcode.com/problems/minimum-speed-to-arrive-on-time/)\n* [875. Koko Eating Bananas](https://leetcode.com/problems/koko-eating-bananas/)\n* [1011. Capacity To Ship Packages Within D Days](https://leetcode.com/problems/capacity-to-ship-packages-within-d-days/)\n* [1283. Find the Smallest Divisor Given a Threshold](https://leetcode.com/problems/find-the-smallest-divisor-given-a-threshold/)\n* [1482. Minimum Number of Days to Make m Bouquets](https://leetcode.com/problems/minimum-number-of-days-to-make-m-bouquets/)\n* [2064. Minimized Maximum of Products Distributed to Any Store](https://leetcode.com/problems/minimized-maximum-of-products-distributed-to-any-store/)\n* [1231. Divide Chocolate](https://leetcode.com/problems/divide-chocolate/)\n* [774. Minimize Max Distance to Gas Station](https://leetcode.com/problems/minimize-max-distance-to-gas-station/)\n* [410. Split Array Largest Sum](https://leetcode.com/problems/split-array-largest-sum/)\n* [1539. Kth Missing Positive Number](https://leetcode.com/problems/kth-missing-positive-number/)\n* [162. Find Peak Element](https://leetcode.com/problems/find-peak-element/)\n* [441. Arranging Coins](https://leetcode.com/problems/arranging-coins/)\n* [378. Kth Smallest Element in a Sorted Matrix](https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/)\n* [287. Find the Duplicate Number](https://leetcode.com/problems/find-the-duplicate-number/)\n* [209. Minimum Size Subarray Sum](https://leetcode.com/problems/minimum-size-subarray-sum/)\n* [1760. Minimum Limit of Balls in a Bag](https://leetcode.com/problems/minimum-limit-of-balls-in-a-bag/)\n* [1631. Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/)\n* [2070. Most Beautiful Item for Each Query](https://leetcode.com/problems/most-beautiful-item-for-each-query/)\n* [475. Heaters](https://leetcode.com/problems/heaters/)\n* [1818. Minimum Absolute Sum Difference](https://leetcode.com/problems/minimum-absolute-sum-difference/)\n* [1838. Frequency of the Most Frequent Element](https://leetcode.com/problems/frequency-of-the-most-frequent-element/)\n* [778. Swim in Rising Water](https://leetcode.com/problems/swim-in-rising-water/)\n* [668. Kth Smallest Number in Multiplication Table](https://leetcode.com/problems/kth-smallest-number-in-multiplication-table/)\n* [878. Nth Magical Number](https://leetcode.com/problems/nth-magical-number/)\n* [719. Find K-th Smallest Pair Distance](https://leetcode.com/problems/find-k-th-smallest-pair-distance/)\n* [2141. Maximum Running Time of N Computers](https://leetcode.com/problems/maximum-running-time-of-n-computers/)\n* [1287. Element Appearing More Than 25% In Sorted Array](https://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array/)\n* [34. Find First and Last Position of Element in Sorted Array](https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/)\n* [774. Minimize Max Distance to Gas Station](https://leetcode.com/problems/minimize-max-distance-to-gas-station/)\n* [1150. Check If a Number Is Majority Element in a Sorted Array](https://leetcode.com/problems/check-if-a-number-is-majority-element-in-a-sorted-array/)\n* [1482. Minimum Number of Days to Make m Bouquets](https://leetcode.com/problems/minimum-number-of-days-to-make-m-bouquets/)\n* [981. Time Based Key-Value Store](https://leetcode.com/problems/time-based-key-value-store/)\n* [1201. Ugly Number III](https://leetcode.com/problems/ugly-number-iii/)\n* [704. Binary Search](https://leetcode.com/problems/binary-search/)\n* [69. Sqrt(x)](https://leetcode.com/problems/sqrtx/)\n* [35. Search Insert Position](https://leetcode.com/problems/search-insert-position/)\n* [278. First Bad Version](https://leetcode.com/problems/first-bad-version/)\n* https://leetcode.com/discuss/interview-question/777057/the-painters-partition-problem \n* https://www.codechef.com/problems/PREZ \n* For more problems you can refer to this page :- https://leetcode.com/problemset/all/?topicSlugs=binary-search&page=1 \n\n\n | 308 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
Clean Code Python | minimum-time-to-complete-trips | 0 | 1 | **Please upvote if u liked the solution**\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n return bisect_left(range(time[0] * totalTrips + 1), True, key=lambda t: sum(t // bus for bus in time) >= totalTrips)\n``` | 1 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
python3 || simple binary search | minimum-time-to-complete-trips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can reduce half the search space for time, in eac iteration of binary search.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nbinay search\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nLet n be the length of time, m be the upper limit of totalTrips and k be the maximum time taken by one trip.\nO(n.log(m.k))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n #binary search\n def checkIfTotalTripsCanHappen(timee):\n trips=0\n for i in time:\n trips+=(timee//i)\n return trips>=totalTrips\n #print(checkIfTotalTripsCanHappen(3))\n #print(checkIfTotalTripsCanHappen(2))\n #print(checkIfTotalTripsCanHappen(4))\n\n left=1\n right=max(time)*totalTrips\n while(left<right):\n mid=left+(right-left)//2\n if(checkIfTotalTripsCanHappen(mid)):\n right=mid\n else:\n left=mid+1\n return left\n``` | 1 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
O(n log(k)) solution | 1378 ms in Python3 | Beats 100% | minimum-time-to-complete-trips | 0 | 1 | Here is a solution which is more efficient that the solutions using only the minimum of `time` for computing the upper bound.\n\nEDIT: I added an improvement whose worst-case complexity only depends on $$n$$: no matter `totalTrips` and the values in `time`, it runs in at most $$O(n \\log(n))$$, and it can be faster depending on the values in `time`.\n\n# Intuition\n- Provide improved bounds on the time required before starting the binary search.\n\n# Approach\n\nThis assumes that you understood properly the simple solution.\n\n## Computation of the bounds\nLet $$x_1, ..., x_n$$ be the values in the array `time`, let $$p$$ be `totalTrips`, let $$T_0$$ be the result and let $$S = \\displaystyle \\sum_{i = 1}^{n} \\displaystyle \\frac{1}{x_i}$$.\n\nFor a given time $$t$$, the maximal number of trips is $$f(t) = \\displaystyle \\sum_{i = 1}^{n} \\left \\lfloor \\displaystyle \\frac{t}{x_i} \\right \\rfloor$$.\n\n**Lower bound** \n$$T_0 \\geqslant \\left \\lceil \\displaystyle \\frac{p}{S} \\right \\rceil$$\n\n**Proof of the lower bound**\nOn the one hand, $$f(T_0) = \\displaystyle \\sum_{i = 1}^{n} \\left \\lfloor \\displaystyle \\frac{T_0}{x_i} \\right \\rfloor \\leqslant \\displaystyle \\sum_{i = 1}^{n} \\displaystyle \\frac{T_0}{x_i} = T_0 S$$. \nOn the other hand, $$f(T_0) \\geqslant p$$ by definition of $$T_0$$.\nTherefore, $$T_0 \\geqslant \\displaystyle \\frac{p}{S}$$.\n\n\n**Upper bound**\n$$T_0 \\leqslant 1 + \\left \\lfloor \\displaystyle \\frac{p + n - 1}{S}\\right \\rfloor$$\n**Proof of the upper bound**\nFirst, $$f(T_0 - 1) = \\displaystyle \\sum_{i = 1}^{n} \\left \\lfloor \\displaystyle \\frac{T_0 - 1}{x_i} \\right \\rfloor > \\displaystyle \\sum_{i = 1}^{n} \\left( \\displaystyle \\frac{T_0 - 1}{x_i} - 1 \\right) = (T_0 - 1) S - n$$.\nBesides, $$f(T_0 - 1) \\leqslant p - 1$$ by definition of $$T_0$$.\nThen $$T_0 < 1 + \\displaystyle \\frac{p + n - 1}{S}$$.\n\n## Floating point caveat\nComputing the sum of the inverses of the elements of `time` is subject to rounding errors because it uses float. This is why in the code I use `fsum` instead of `sum` for a more accurate computation as well as `float_safety = 1e-3` so if that the result is really close to an integer I actually move pass that integer.\n\n## EDIT: An improvement with an even better complexity\nNote: this is slower in practice unless the integers in `time` are quite big.\n\n**Observation:** $$T_0$$ is necessarily a multiple of some $$x_i$$ (consequence of the minimality of $$T_0$$).\n\nWhat makes the binary search slow down when the $$x_i$$\'s get really big in comparision to $$n$$ is that we might do little steps whereas the multiples are sparse.\n\nHere is an example (not realistic, just to convey the idea):\n- We are looking for a multiple of $$2^{1000}$$\n- $$left = 5 \\times 2^{1000} - 42$$ and $$right = 6 \\times 2^{1000} - 42$$\n - Simple binary search would need 1000 iterations.\n - Jumping to multiples would require 2 iterations.\n\n**Algorithm: Modified binary search**\nInstead of updating `right` or `left` with the middle value, we use the following updating rule.\n\n- If we want to update `right` to `mid`, run through the array to find to largest multiple not greater than `mid` and use this value for the update.\n- If we want to update `left` to `mid + 1`, run through the array to find to smallest multiple greater than `mid` and use this value for the update.\n\nEach update runs in $$O(n)$$ so the complexity of each iteration of the binary search is still the same.\n\n# Complexity\nLet $$n$$ be the length of time, $$k$$ be the maximum time taken by one trip, and $$l$$ be the maximum time taken by one trip.\n- Time complexity: $$O(n \\log(\\min(k, nl))$$ (actually $$O(n \\log\\frac{n}{S})$$)\n - $$S \\geqslant \\displaystyle \\frac{n}{k}$$ and $$S \\geqslant \\displaystyle \\frac{1}{l}$$.\n - For the binary search, the size of the search space is less than $$ 1 + \\displaystyle \\frac{n}{S} \\leqslant 1 + \\min(k, nl)$$ so it requires $$O(\\log(\\min(k, nl)))$$ iterations.\n - Each binary search iteration runs in $$O(n)$$.\n - Computation of the bounds is done in $$O(n)$$.\n- EDIT: Time complexity of the improved version: $$O(n \\log(n \\min(1, S^{-1})))$$\n - The number of iteration of the modified binary search depends on the number of multiples of $$x_i$$\'s in the search interval which is less than $$length\\_of\\_interval \\times S + n$$, that is $$O(n)$$.\n\n\n# Code\nNote: this code is a simplified version of my submission for users who are not very familiar with python. My actual submission uses a python specific trick to have a faster running code although with the same complexity (see below).\n\n```python []\nfrom math import ceil, floor, fsum\n\n\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n n = len(time)\n # use fsum instead of sum for improved float accuracy\n sum_inv = fsum(1 / t for t in time)\n # add an extra margin because of rounding errors\n float_safety = 1e-3\n left = ceil(totalTrips / sum_inv - float_safety)\n right = floor((totalTrips + n - 1) / sum_inv + float_safety)\n\n while left != right:\n mid = (left + right) // 2\n if sum((mid // t for t in time)) >= totalTrips:\n right = mid\n else:\n left = mid + 1\n \n return left\n```\n\nMy actual code uses the map builtin with a dunder method twice because it is faster than a handwritten generator.\n\n```python []\nfsum(map((1).__truediv__, time))\n# instead of\nfsum(1 / t for t in time)\n\n# and\n\nsum(map(mid.__floordiv__, time))\n# instead of\nsum((mid // t for t in time))\n```\n | 1 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
Python solution | minimum-time-to-complete-trips | 0 | 1 | # Code\n```\nclass Solution:\n def minimumTime(self, time: List[int], totalTrips: int) -> int:\n left = 1\n right = max(time) * totalTrips\n\n while right > left:\n mid = (left + right)//2\n sums = sum([mid//t for t in time])\n if sums >= totalTrips:\n right = mid\n else:\n left = mid + 1\n \n return left \n``` | 1 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
Python short and clean. Binary Search. | minimum-time-to-complete-trips | 0 | 1 | # Approach\nNotice that the time needed can never be greater than `min(time) * total_trips`.\nLeveraging this, binary search for `min_time` in the range `[0, min(time) * total_trips]`\n\n# Complexity\n- Time complexity: $$O(n * log(n * k))$$\n\n- Space complexity: $$O(1)$$\n\nwhere,\n`n is length of time`,\n`k is total_trips`.\n\n# Code\n```python\nclass Solution:\n def minimumTime(self, time: list[int], total_trips: int) -> int:\n l, r = 0, min(time) * total_trips\n while l <= r:\n m = (l + r) // 2\n trips = sum(m // t for t in time)\n l, r = (l, m - 1) if trips >= total_trips else (m + 1, r)\n return l\n\n\n``` | 1 | You are given an array `time` where `time[i]` denotes the time taken by the `ith` bus to complete **one trip**.
Each bus can make multiple trips **successively**; that is, the next trip can start **immediately after** completing the current trip. Also, each bus operates **independently**; that is, the trips of one bus do not influence the trips of any other bus.
You are also given an integer `totalTrips`, which denotes the number of trips all buses should make **in total**. Return _the **minimum time** required for all buses to complete **at least**_ `totalTrips` _trips_.
**Example 1:**
**Input:** time = \[1,2,3\], totalTrips = 5
**Output:** 3
**Explanation:**
- At time t = 1, the number of trips completed by each bus are \[1,0,0\].
The total number of trips completed is 1 + 0 + 0 = 1.
- At time t = 2, the number of trips completed by each bus are \[2,1,0\].
The total number of trips completed is 2 + 1 + 0 = 3.
- At time t = 3, the number of trips completed by each bus are \[3,1,1\].
The total number of trips completed is 3 + 1 + 1 = 5.
So the minimum time needed for all buses to complete at least 5 trips is 3.
**Example 2:**
**Input:** time = \[2\], totalTrips = 1
**Output:** 2
**Explanation:**
There is only one bus, and it will complete its first trip at t = 2.
So the minimum time needed to complete 1 trip is 2.
**Constraints:**
* `1 <= time.length <= 105`
* `1 <= time[i], totalTrips <= 107` | Since generating substrings is not an option, can we count the number of substrings a vowel appears in? How much does each vowel contribute to the total sum? |
[Python] DP with pre-treatment to reduce time complexity | minimum-time-to-finish-the-race | 0 | 1 | Let t[n] denotes the minimum time to run n laps, the DP equation is thus:\nt[n] = min {r = 1 ~ min(maxt,n)} t[r] + changeTime + t[n-r]\n\nNow we add some pre-treatment:\n1) The default value of t[n] for any n can be set as changeTime * (n-1) + min(f) * n, i.e., change tire after every lap. \n2) We don\'t need to consider all tires. If tire1 and tire2 satisfies f1<=f2 and r1<=r2, then tire1 dominates tire2. Therefore, suppose (in a sorted list of tires) the last tire we consider is tire1, we only consider tire2 if f2>f1 and r2<r1. \n3) maxt is the largest possible number of laps to run without changing tires. Therefore, maxt can be quite small compared to numLaps. To get maxt, for every tire we consider in 2, try running it without changing tires until the time for running the next lap is greater than changeTime + f (and thus it\'s better to change tire). Or simply use maxt = 17 as 2^17 = 131072>10^5. \n\nThe current time complexity stands at O(T log T + (T+N) log C), where T = number of tires, N = numLaps and C = changeTime. O(T log T) from sorting the tires, O(T log C) to derive maxt (note that maxt < log2(changeTime)), and finally soving the DP for O(N log C). \n\nAlthough ignoring pre-treatment 2 and considering all tires would eliminate the O(T log T) part, it will actually make the (hidden) constant larger for the O(T log C) part later, and the runtime comparison is 2600+ ms w/ pre-treatment 2 compared to 8000+ ms w/o, suggesting that in the testcases many tires are dominated. \n\nMeanwhile, pre-treatment 3 is a huge improvement in terms of time complexity from O(N^2) of the usual DP to O(N log C). The runtime comparison is 2600+ ms w/ compared to 7500+ ms w/o. \n\nHere\'s my code. On second thought the newTires list is not necessary but I am lazy so I will just leave it be. \n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n tires.sort()\n newTires = []\n minTime = [changeTime*(i-1) + tires[0][0]*i for i in range(numLaps+1)]\n minTime[0] = 0\n maxi = 0\n for f,r in tires:\n if not newTires or f>newTires[-1][0] and r<newTires[-1][1]:\n newTires.append([f,r])\n t = f\n i = 1\n while i<numLaps and t*(r-1)<changeTime:\n t = t*r + f\n i += 1\n if minTime[i]>t:\n minTime[i]=t\n maxi = max(i,maxi)\n for lap in range(numLaps+1):\n for run in range(min(lap,maxi+1)):\n minTime[lap] = min(minTime[lap],minTime[lap-run]+changeTime+minTime[run])\n return minTime[numLaps]\n``` | 4 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
Hindsight is the Answer | Commented and Explained | minimum-time-to-finish-the-race | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRather than try to figure it out before or as you run the race, figure it out afterwards. The key is that we are trying to discern the best possible lap for the best possible set of tires from the sets of all tires that can be changed to including changeTime. Once we have that firmly in mind, the dp approach becomes more apparent. The key herein is that we are trying to determine at the end of the process the minimal time for a lap as either what it currently is, or if we would have been better off changing the tires earlier for a better lap (why I say hindsight is the answer). With this in mind the approach follows. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart by filtering out the useful from the useless tires. The useful tires will have minimal f_i and minimal r_i (these increase the least overtime). From this we can get to the useful tires most quickly since changeTime is universal. To do the filtering, sort the tires by f_i, and then filter by a decreasing minimum r_i. This will give us the best tires at the later times in the race. \n\nOnce we filter our tires, we need a listing of which tires we\'ve gotten the best use of in foresight, and get our time sums and previous time sums listings set up. We\'ll also make a minimum round times dictionary for minimal times around the track as a dictionary for a given lap. \n\nNow we race! \n- For each lap \n - set a minimum lap time at infinity \n - for each tire we have not used up \n - determine the add time as this tires f_i * its previous r_i amount\n - if we\'re not on the first lap and our minimum round times for the first lap + changeTime is now lte to our additional time \n - bench this tire and continue \n - otherwise,\n - time sums at this tire is incremented by add_time \n - previous time sums at this tire is multiplied by this tires rate (here\'s your previous r_i amount!) \n - minimum round time is min of self and time sums at t_i \n - if minimum lap time is lt infinity \n - we found some minimum lap time that is real, record it for this lap \n \nTime for the after action \nBuild a dpa of size of laps + 1 \nSet dpa[0] to 0 and all others to infinity \n\n- For each lap \n - for each lap index and lap record in minimum laps dictionary \n - if lap index is lte this lap \n - dpa at lap index is to be minimized between self and the dpa at lap - lap index + lap record + changeTime (would it have been better if we changed tires? If so, what would it be?) \n\nAt end, the dpa[-1] less changeTime is your answer (always once too many!) \n \n# Complexity\n- Time complexity : Total is O( Max (T log T, T * L, L^2)) \n - O(T log T) to sort Tires \n - O(T) to loop Tires\n - O(L) to loop laps \n - in which O(T) to loop tires \n - This is O(L * T) then \n - O(L) to loop laps \n - O(R) to loop records. Records must be O(L) to match set up. \n - This is O(L^2 then) \n - Total is O( Max (T log T, T * L, L^2)) \n\n- Space complexity : O( Max (T, L))\n - O(T) for finished, tires, time_sums, prev_time_sums\n - O(L) for minimum round times \n - O(L) for dpa \n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n # filter function of tires \n def filter_tires() : \n # min rate maximizes at 10^5 so 10^6 is sufficiently large to filter \n # output is the tires we care about \n min_rate, output = 1_000_000, []\n # for f_i, r_i in tires (sorting means it is in order of minimal f_i not r_i! This is important) \n for f_i, r_i in sorted(tires) : \n # if r_i is gte current min rate -> continue \n if r_i >= min_rate : \n continue \n else : \n # otherwise, append to the output and update the min rate \n output.append([f_i, r_i])\n min_rate = r_i \n # return output when completed \n return output \n \n # filter the tires out of the processing \n tires = filter_tires()\n # figure out your filtered length of tires \n tL = len(tires) \n # set up your finished list of tire components \n finished = [False] * tL \n # set up your time sums current \n time_sums = [0] * tL \n # set up your previous time sums (product multiples here so start with 1) \n prev_time_sums = [1] * tL\n # set a minimum round times dictionary \n minimum_round_times = dict() \n\n # from first to last lap \n for l_i in range(1, numLaps + 1) : \n # find the minimum round time for this lap \n minimum_round_time = float(\'inf\')\n # by considering all of our tires \n for t_i in range(tL) : \n # that we have not already used up \n if finished[t_i] : \n continue \n else : \n # the additional time is the tires at t_i at 0 multiplied by the previous time sums at t_i \n # we record and update the prev time sums as specified as we go along \n add_time = tires[t_i][0] * prev_time_sums[t_i] \n # if lap indix is gt 1 and add_time is gte minimum_round_times[1] + changeTime -> this tire is used\n if l_i > 1 and add_time >= minimum_round_times[1] + changeTime : \n # mark it as used and continue, we got the most out of it \n finished[t_i] = True \n else : \n # otherwise, increment time_sums by the add_time \n time_sums[t_i] += add_time \n # then multiple the previous time sums by the r_i as needed \n prev_time_sums[t_i] *= tires[t_i][1]\n # now minimize the minimum round time using time sums updated valuation \n minimum_round_time = min(minimum_round_time, time_sums[t_i])\n\n # at end of all t_i, if minimum round time is updated \n if minimum_round_time < float(\'inf\') : \n # mark it as such in the dictionary \n minimum_round_times[l_i] = minimum_round_time \n \n # set up a dynamic processing array \n dpa = [float(\'inf\')] * (numLaps + 1) \n # set the intital to 0 \n dpa[0] = 0 \n # for each lap \n for l_i in range(1, numLaps + 1) : \n # for the best of each lap minimum round times \n for l_j, l_t in minimum_round_times.items() : \n # if this lap is before the current lap or is the current lap \n if l_j <= l_i : \n # minimize in regards to the prior lap and its time + changeTime (should we have changed the tires?)\n dpa[l_i] = min(dpa[l_i - l_j] + l_t + changeTime, dpa[l_i])\n # at the end return the dpa at final lap less the changeTime (we\'ll always do one too many, sadly)\n return dpa[-1] - changeTime\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
Beat 100% submissions | minimum-time-to-finish-the-race | 0 | 1 | # Intuition\nProprocessing for reduce the computation, and then do a simple DP. \n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n def filter_tires():\n min_r, out = float(\'inf\'), []\n for f, r in sorted(tires):\n if r >= min_r:\n continue\n out.append([f, r])\n min_r = r\n return out\n\n tires = filter_tires()\n m = len(tires)\n done = [False] * m\n sum_times = [0] * m\n prev_times = [1] * m\n round_min_times = {}\n for i in range(1, numLaps + 1):\n round_min_time = float(\'inf\')\n for j in range(m):\n if done[j]:\n continue\n add_time = tires[j][0] * prev_times[j]\n if i > 1 and add_time >= round_min_times[1] + changeTime:\n done[j] = True\n else:\n sum_times[j] += add_time\n prev_times[j] *= tires[j][1]\n round_min_time = min(round_min_time, sum_times[j])\n if round_min_time < float(\'inf\'):\n round_min_times[i] = round_min_time\n dp = [float(\'inf\')] * (numLaps + 1)\n dp[0] = 0\n for i in range(1, numLaps + 1):\n for r, t in round_min_times.items():\n if r <= i:\n dp[i] = min(dp[i - r] + t + changeTime, dp[i])\n return dp[-1] - changeTime\n\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
beats 97% , simple DP | minimum-time-to-finish-the-race | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires, changeTime, numLaps):\n ans = [float("inf")]*20\n\n for f,r in tires:\n prefix = val = f\n for i in range(20):\n ans[i] = min(ans[i],prefix)\n val = val*r\n if val >= f + changeTime: break\n prefix += val\n\n @lru_cache(None)\n def dfs(n):\n min_val = ans[n-1] if n <= 20 else float("inf")\n\n for j in range(1,min(20,n//2)+1):\n min_val = min(min_val,dfs(j) + dfs(n-j) + changeTime)\n\n return min_val \n\n return dfs(numLaps)\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
DP ?>? easy shit no fancy shit fk that | minimum-time-to-finish-the-race | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], ct: int, nl: int) -> int:\n cn=[]\n dis=[float("inf")]*(nl+1)\n for x,y in tires:\n cnt=-1\n res=0\n while x*(pow(y,cnt+1))<ct+x:\n cnt+=1\n res+=x*(pow(y,cnt))\n if cnt+1<=nl:\n dis[cnt+1]=min(dis[cnt+1],res)\n cn.append((x,cnt+1,res))\n ans=float("inf")\n res=[]\n dp=[float("inf")]*(nl+1)\n dp[0]=0\n for i in range(1,nl+1):\n if dis[i]!=float("inf"):\n res.append((i,dis[i]))\n dp[i]=dis[i]\n for i in range(nl+1):\n for vl,cs in res:\n if i+vl<=nl:\n dp[i+vl]=min(dp[i+vl],dp[i]+ct+cs)\n return dp[-1]\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
Python (Simple DP) | minimum-time-to-finish-the-race | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires, changeTime, numLaps):\n ans = [float("inf")]*20\n\n for f,r in tires:\n prefix = val = f\n for i in range(20):\n ans[i] = min(ans[i],prefix)\n val = val*r\n if val >= f + changeTime: break\n prefix += val\n\n @lru_cache(None)\n def dfs(n):\n min_val = ans[n-1] if n <= 20 else float("inf")\n\n for j in range(1,min(20,n//2)+1):\n min_val = min(min_val,dfs(j) + dfs(n-j) + changeTime)\n\n return min_val \n\n return dfs(numLaps)\n\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
Easy Python solution for beginners with comments | minimum-time-to-finish-the-race | 0 | 1 | # Intuition\n\nSimilar idea to other solutions but I think this version is easier to understand for beginners. \n\nFirst, we use Dynamic Programming. Below is the recurrent equation.\n\n- `dp[i]` is optimal solution of `numLaps=i+1`\n- `dp[0] = best time to complete 1 lap without changing tires`\n- `dp[i] = min(b0, b1, b2, ..., bj)` where `j < i` and `bj = dp[j] + changeTime + best time to complete remaining i-j laps without changing tires`\n\nNow we see that we need *"best time to complete some laps without changing tires*". This can be easily pre-computed.\n\nFurther optimization is explained in-line, but this optimization doesn\'t change the time complexity.\n\n# Complexity\n- Time complexity\n max($$O(n^2)$$, $$O(nt)$$) where n is numLaps and t is number of tires\n\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n\n best = [math.inf] * numLaps # best time to complete i+1 lap without changing tires\n for f, r in tires:\n total_time = 0\n lap_time = f\n for i in range(numLaps):\n if lap_time > f + changeTime:\n break # optimization - if lap_time is longer than changeTime + f, no point to continue with the current tire\n total_time += lap_time\n best[i] = min(best[i], total_time)\n lap_time *= r\n\n dp = [best[0]] # dp[i] = optimal solution of i + 1 th lap\n for i in range(1, numLaps):\n dpi = best[i]\n for j in range(i-1,-1,-1):\n if best[i-j-1] == math.inf:\n break\n dpi = min(dpi, dp[j] + changeTime + best[i-j-1])\n dp.append(dpi)\n\n return dp[-1]\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
Python Comments easy DP to improved DP | minimum-time-to-finish-the-race | 0 | 1 | Solution: find all possible combinations, use DP\n- state: dp[i] the number of seconds after finish lap i, after changing tire, it is a new start.\n- policy: dp[i, new_tire] = min(dp[i - j, old_tire] + cost of time from change tire at i-j lap to i lap)\n- actions: 1. change to tire j after lap i - 1, 0<= j < n; 2. continue with the current tire\n\nBrutal Force DP:\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n \n # initialize the dp.\n n_tires = len(tires)\n dp = [0 for i in range(numLaps+1)]\n \n # save accumulate tire time: num_tires x laps (can be improved)\n tire_time = [[0] * (numLaps + 1) for _ in range(n_tires)]\n for t2 in range(n_tires):\n f = tires[t2][0]\n r = tires[t2][1]\n for lap in range(1, numLaps + 1):\n tire_time[t2][lap] = tire_time[t2][lap - 1] + f * r ** (lap - 1)\n \n for i in range(1, numLaps + 1):\n dp[i] = float(\'inf\')\n for j in range(i):\n for t2 in range(n_tires):\n time = dp[j] + tire_time[t2][i-j]\n if j > 0:\n time += changeTime\n dp[i] = min(dp[i], time)\n\n return dp[-1]\n```\n\nImprove the algorithm\n\nOnly need to consider \n1. use current tire lap time < changeTiretime, \n2. max number of laps is 16: 2^16 = 65536 > 10^5 (from problem constraints)\n\nnew DP:\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n # initialize the dp. dp[0] = 0\n n_tires = len(tires)\n dp = [0 for i in range(numLaps+1)]\n \n # save accumulate tire time: num_tires x laps\n min_tire_time = [float(\'inf\')] * (numLaps + 1)\n \n max_lap = min(16, numLaps)\n cur_lap = [0] * n_tires\n for f, r in tires:\n total_lap_time = 0\n lap = 1\n\t\t\t# only consider current tire lap time < changeTiretime\n while total_lap_time <= changeTime and lap <= max_lap:\n total_lap_time += f * r ** (lap - 1)\n # find the best tire\n min_tire_time[lap] = min(min_tire_time[lap], total_lap_time)\n lap += 1\n \n for i in range(1, numLaps + 1):\n dp[i] = float(\'inf\')\n for j in range(i-max_lap,i):\n time = dp[j] + min_tire_time[i-j]\n if j > 0:\n time += changeTime\n dp[i] = min(dp[i], time)\n\n return dp[-1]\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
DP : transit function | minimum-time-to-finish-the-race | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n transit function:\n f(i) = min(f(k) + changeTime + f(i - k)) when k = [1,i)) \n reduce the range of k for the symmetric of k and i-k\n f(i) = min(f(i), sum(f * power(r, j) for j in (0, i - 1)) when k == 0 \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(numLap * numLap * numTires)$$ for successivecost calculation\n$$O(numLap * numLap)$$ for dp\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minimumFinishTime(self, tires: List[List[int]], changeTime: int, numLaps: int) -> int:\n \'\'\'\n dp[i] stands for the minimum cost to finishish the number of i laps\n f(i) = min(f(k) + changeTime + f(i - k)) when k = [1,i)) \n f(i) = min(f(i), sum(f * power(r, j) for j in [0, i - 1]) when k == 0 \n \'\'\'\n\n dp = [math.inf] * (numLaps + 1)\n n = len(tires)\n successivecost = [tires[i][0] for i in range(n)]\n for i in range(1, min(numLaps + 1, 20)): #LTE if not constraint with 20\n dp[i] = min(successivecost)\n for j in range(n):\n successivecost[j] = tires[j][0]*((pow(tires[j][1], i + 1) - 1)//(tires[j][1] - 1))\n\n\n for i in range(2, numLaps + 1):\n for k in range(1, min(i , i//2 + 1)):\n dp[i] = min(dp[i], dp[k] + changeTime + dp[i-k])\n return dp[numLaps]\n``` | 0 | You are given a **0-indexed** 2D integer array `tires` where `tires[i] = [fi, ri]` indicates that the `ith` tire can finish its `xth` successive lap in `fi * ri(x-1)` seconds.
* For example, if `fi = 3` and `ri = 2`, then the tire would finish its `1st` lap in `3` seconds, its `2nd` lap in `3 * 2 = 6` seconds, its `3rd` lap in `3 * 22 = 12` seconds, etc.
You are also given an integer `changeTime` and an integer `numLaps`.
The race consists of `numLaps` laps and you may start the race with **any** tire. You have an **unlimited** supply of each tire and after every lap, you may **change** to any given tire (including the current tire type) if you wait `changeTime` seconds.
Return _the **minimum** time to finish the race._
**Example 1:**
**Input:** tires = \[\[2,3\],\[3,4\]\], changeTime = 5, numLaps = 4
**Output:** 21
**Explanation:**
Lap 1: Start with tire 0 and finish the lap in 2 seconds.
Lap 2: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Lap 3: Change tires to a new tire 0 for 5 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 0 and finish the lap in 2 \* 3 = 6 seconds.
Total time = 2 + 6 + 5 + 2 + 6 = 21 seconds.
The minimum time to complete the race is 21 seconds.
**Example 2:**
**Input:** tires = \[\[1,10\],\[2,2\],\[3,4\]\], changeTime = 6, numLaps = 5
**Output:** 25
**Explanation:**
Lap 1: Start with tire 1 and finish the lap in 2 seconds.
Lap 2: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 3: Change tires to a new tire 1 for 6 seconds and then finish the lap in another 2 seconds.
Lap 4: Continue with tire 1 and finish the lap in 2 \* 2 = 4 seconds.
Lap 5: Change tires to tire 0 for 6 seconds then finish the lap in another 1 second.
Total time = 2 + 4 + 6 + 2 + 4 + 6 + 1 = 25 seconds.
The minimum time to complete the race is 25 seconds.
**Constraints:**
* `1 <= tires.length <= 105`
* `tires[i].length == 2`
* `1 <= fi, changeTime <= 105`
* `2 <= ri <= 105`
* `1 <= numLaps <= 1000` | There exists a monotonic nature such that when x is smaller than some number, there will be no way to distribute, and when x is not smaller than that number, there will always be a way to distribute. If you are given a number k, where the number of products given to any store does not exceed k, could you determine if all products can be distributed? Implement a function canDistribute(k), which returns true if you can distribute all products such that any store will not be given more than k products, and returns false if you cannot. Use this function to binary search for the smallest possible k. |
Python dictionary | most-frequent-number-following-key-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mostFrequent(self, nums: List[int], key: int) -> int:\n d = {f"{key}": 0}\n list = []\n for i in range(1, len(nums)):\n if nums[i-1] == key:\n if nums[i] not in d:\n d[nums[i]] = 1\n else:\n d[nums[i]] += 1\n \n return max(d, key=d.get)\n``` | 0 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
Python3 O(N) solution with dictionary and heap (90.83% Runtime) | most-frequent-number-following-key-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nStore and retrieve value counts with dictionary. Then utilize heap with the counts as a priority for the value.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo store/update/access value counts with O(1), use a dictionary.\nThen use value counts as a priority of an element using a heap (priority queue).\n\n(Heap is min-heap by default. So put negative priorities for it to make it max-heap)\n\nThe first element will be the target \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nIt this solution is similar to yours of helpful, please consider an upvote for me.\n```\nclass Solution:\n def mostFrequent(self, nums: List[int], key: int) -> int:\n l = len(nums)\n d = defaultdict(int)\n\n for i in range(0, l-1):\n if nums[i] == key:\n target = nums[i+1]\n d[target] += 1\n\n import heapq\n h = []\n for k, v in d.items():\n heapq.heappush(h, (-v, k))\n\n return heapq.heappop(h)[1]\n``` | 1 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
[Java/Python 3] Simple code. | most-frequent-number-following-key-in-an-array | 1 | 1 | **Java**\n```java\n public int mostFrequent(int[] nums, int key) {\n Map<Integer, Integer> freq = new HashMap<>();\n int mostFreq = -1;\n for (int i = 0, n = nums.length, max = 0; i + 1 < n; ++i) {\n if (nums[i] == key) {\n int candidate = nums[i + 1];\n freq.put(candidate, 1 + freq.getOrDefault(candidate, 0));\n if (freq.get(candidate) > max) {\n max = freq.get(candidate);\n mostFreq = candidate;\n }\n }\n }\n return mostFreq;\n }\n```\nOr make the above simpler as follows:\n\n```java\n public int mostFrequent(int[] nums, int key) {\n Map<Integer, Integer> freq = new HashMap<>();\n int mostFreq = nums[0];\n for (int i = 0, n = nums.length; i + 1 < n; ++i) {\n if (nums[i] == key && \n freq.merge(nums[i + 1], 1, Integer::sum) > \n freq.get(mostFreq)) {\n mostFreq = nums[i + 1];\n }\n }\n return mostFreq;\n }\n```\n\n----\n\n**Python 3**\n\n```python\n def mostFrequent(self, nums: List[int], key: int) -> int:\n c = Counter()\n for i, n in enumerate(nums):\n if n == key and i + 1 < len(nums):\n c[nums[i + 1]] += 1\n return c.most_common(1)[0][0]\n```\n\nOne liner for fun: - credit to **@stefan4trivia**.\n\n```python\n def mostFrequent(self, nums: List[int], key: int) -> int:\n return statistics.mode(b for a, b in itertools.pairwise(nums) if a == key)\n``` | 26 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
Python 2 Lines Functional Style | most-frequent-number-following-key-in-an-array | 0 | 1 | # Intuition\nGet a list of all the values that come right after the keys\nThen return the most frequent one\n\n# Code\n```\nclass Solution:\n def mostFrequent(self, nums: List[int], key: int) -> int:\n l = [t for k,t in zip(nums, nums[1:]) if k == key]\n return max(set(l), key = l.count)\n``` | 2 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
Python - Multiple Solutions + One-Liners | Clean and Simple | most-frequent-number-following-key-in-an-array | 0 | 1 | **Solution - Count by hand**:\n```\nclass Solution:\n def mostFrequent(self, nums, key):\n counts = {}\n \n for i in range(1,len(nums)):\n if nums[i-1]==key:\n if nums[i] not in counts: counts[nums[i]] = 1\n else: counts[nums[i]] += 1\n \n return max(counts, key=counts.get)\n```\n\n**Solution - Counter**:\n```\nclass Solution:\n def mostFrequent(self, nums, key):\n arr = [nums[i] for i in range(1,len(nums)) if nums[i-1]==key]\n c = Counter(arr)\n return max(c, key=c.get)\n```\n\n**One-Liner - Counter**:\n```\nclass Solution:\n def mostFrequent(self, nums, key):\n return max(c := Counter([nums[i] for i in range(1,len(nums)) if nums[i-1]==key]), key=c.get)\n```\n\n**One-Liner - Mode**:\n```\nclass Solution:\n def mostFrequent(self, nums, key):\n return mode(nums[i] for i in range(1,len(nums)) if nums[i-1]==key)\n```\n\n**One-Liner - Mode with Pairwise** (Credit: [stefan4trivia](https://leetcode.com/stefan4trivia)):\n```\nclass Solution:\n def mostFrequent(self, nums, key):\n return mode(b for a, b in pairwise(nums) if a == key)\n``` | 8 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
Python3 Readable | most-frequent-number-following-key-in-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def mostFrequent(self, nums: List[int], key: int) -> int:\n targets = []\n\n for i in range(len(nums) - 1):\n if nums[i] == key:\n targets.append(nums[i + 1])\n \n count = collections.Counter(targets)\n\n return sorted(count, key = count.get, reverse = True)[0] \n \n``` | 0 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
ChatGTP 3.5 solution | most-frequent-number-following-key-in-an-array | 0 | 1 | # Intuition\nChatGTP 3.5 solution\n\n# Approach\n\nUsing a dictionary target_counts to keep track of the counts of targets that follow the key. The loop iterates through the elements of nums, and whenever it encounters an element equal to the key, it looks at the next element (target) and updates its count in the target_counts dictionary. The result is the target with the maximum count.\n\nHere\'s a breakdown of approach:\n\nInitialization: Initialize an empty dictionary target_counts, max_count to 0, and result_target to 0.\n\nIteration through the list: Iterate through the elements of nums using a for loop.\n\nUpdate counts: Whenever an element in nums is equal to the key, the next element is considered as a target, and its count is updated in the target_counts dictionary.\n\nUpdate result_target: If the count of the current target is greater than the current maximum count (max_count), update max_count and set result_target to the current target.\n\nReturn the result: After the loop, return the result_target, which represents the target with the maximum count following the key.\n\n\n# Complexity\n- Time complexity: O(N)\n\nThe time complexity of code is O(N), where N is the length of the input list nums. The for loop iterates through the elements of nums once, and within the loop, operations like dictionary lookups and updates take constant time.\n\n\n- Space complexity: O(N)\n\nThe space complexity is also O(N), where N is the length of the input list nums. The target_counts dictionary can have at most N/2 entries (assuming every element in nums is a potential target following a key), and other variables (max_count, result_target, target) take constant space.\n\n# Code\n```\nclass Solution:\n def mostFrequent(self, nums: List[int], key: int) -> int:\n target_counts = {} \n max_count = 0\n result_target = 0\n\n for i in range(len(nums) - 1):\n if nums[i] == key:\n target = nums[i + 1]\n target_counts[target] = target_counts.get(target, 0) + 1\n\n \n if target_counts[target] > max_count:\n max_count = target_counts[target]\n result_target = target\n\n return result_target\n``` | 0 | You are given a **0-indexed** integer array `nums`. You are also given an integer `key`, which is present in `nums`.
For every unique integer `target` in `nums`, **count** the number of times `target` immediately follows an occurrence of `key` in `nums`. In other words, count the number of indices `i` such that:
* `0 <= i <= nums.length - 2`,
* `nums[i] == key` and,
* `nums[i + 1] == target`.
Return _the_ `target` _with the **maximum** count_. The test cases will be generated such that the `target` with maximum count is unique.
**Example 1:**
**Input:** nums = \[1,100,200,1,100\], key = 1
**Output:** 100
**Explanation:** For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
**Example 2:**
**Input:** nums = \[2,2,2,2,3\], key = 2
**Output:** 2
**Explanation:** For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* The test cases will be generated such that the answer is unique. | Could you try every word? Could you use a hash map to achieve a good complexity? |
Python Simple Solution using sort() | sort-the-jumbled-numbers | 0 | 1 | \n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n def c(n):\n v=""\n for p in str(n):\n v+=str(mapping[int(p)])\n return int(v)\n k=[]\n for p in range(len(nums)):\n k.append([c(nums[p]),p,nums[p]])\n k.sort()\n return [p[2] for p in k]\n``` | 1 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
Python Simple Solution using sort() | sort-the-jumbled-numbers | 0 | 1 | \n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n def c(n):\n v=""\n for p in str(n):\n v+=str(mapping[int(p)])\n return int(v)\n k=[]\n for p in range(len(nums)):\n k.append([c(nums[p]),p,nums[p]])\n k.sort()\n return [p[2] for p in k]\n``` | 1 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
[Java/Python 3] Convert and sort indices accordingly. | sort-the-jumbled-numbers | 1 | 1 | **Q & A**\n*Q*: How is `Arrays.sort(indices, Comparator.comparing(i -> convert(nums[i], mapping)));` sorting the elements of `indices` array?\n\n*A*: Sort the `i`\'s in `indices` according to the corresponding value of `convert(nums[i], mapping)`. E.g.,\n\nInput: mapping = [8,9,4,0,2,1,3,5,7,6], nums = [991,338,38]\n\nThen we need to sort `indices = [0, 1, 2]`.\n\nExplanation: \nMap the number 991 as follows:\n1. mapping[9] = 6, so all occurrences of the digit 9 will become 6.\n2. mapping[1] = 9, so all occurrences of the digit 1 will become 9.\nTherefore, the mapped value of 991 is 669, and **index `0` is mapped to 669.**\n\n338 maps to 007, or 7 after removing the leading zeros, and **index `1` is mapped to 7**.\n38 maps to 07, which is also 7 after removing leading zeros, and **index `2` is mapped to 7**..\nSince 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38, and **index 1 should come before index 2**.\n\n**So the sorted indices is [1, 2, 0], and the corresponding values in nums are 338, 38, 991.**\n\n\nThus, the sorted array is [338,38,991].\n\n\n**End of Q & A**\n\n\n----\n\n\nSort the indices by the converted value first, if equal, then by original index.\n\nBoth java.util.Arrays.sort(T[] a, Comparator<? super T> c) and sorted() in Python are guaranteed to be stable, so no need to sub-sort by the index. -- credit to **@SunnyvaleCA**.\n\n```java\n public int[] sortJumbled(int[] mapping, int[] nums) {\n int n = nums.length, k = 0;\n Integer[] indices = new Integer[n];\n for (int i = 0; i < n; ++i)\n indices[i] = i;\n Arrays.sort(indices, Comparator.comparing(i -> convert(nums[i], mapping)));\n // return Stream.of(indices).mapToInt(i -> nums[i]).toArray();\n int[] ans = new int[n];\n for (int idx : indices)\n ans[k++] = nums[idx];\n return ans;\n }\n private int convert(int num, int[] mapping) {\n if (num == 0)\n return mapping[0];\n int n = 0, f = 1;\n while (num > 0) {\n n += mapping[num % 10] * f;\n f *= 10;\n num /= 10;\n }\n return n;\n }\n```\n\n----\n\n\n\n```python\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n \n def convert(num: int) -> int:\n if num == 0:\n return mapping[0]\n n, f = 0, 1\n while num > 0:\n num, r = divmod(num, 10)\n n += mapping[r] * f\n f *= 10\n return n\n \n indices = sorted(range(len(nums)), key=lambda i: convert(nums[i]))\n return [nums[i] for i in indices]\n```\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(n)`, where `n = nums.length`.\n\n-------\n\nPlease **upvote** if the post is helpful. | 24 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
[Java/Python 3] Convert and sort indices accordingly. | sort-the-jumbled-numbers | 1 | 1 | **Q & A**\n*Q*: How is `Arrays.sort(indices, Comparator.comparing(i -> convert(nums[i], mapping)));` sorting the elements of `indices` array?\n\n*A*: Sort the `i`\'s in `indices` according to the corresponding value of `convert(nums[i], mapping)`. E.g.,\n\nInput: mapping = [8,9,4,0,2,1,3,5,7,6], nums = [991,338,38]\n\nThen we need to sort `indices = [0, 1, 2]`.\n\nExplanation: \nMap the number 991 as follows:\n1. mapping[9] = 6, so all occurrences of the digit 9 will become 6.\n2. mapping[1] = 9, so all occurrences of the digit 1 will become 9.\nTherefore, the mapped value of 991 is 669, and **index `0` is mapped to 669.**\n\n338 maps to 007, or 7 after removing the leading zeros, and **index `1` is mapped to 7**.\n38 maps to 07, which is also 7 after removing leading zeros, and **index `2` is mapped to 7**..\nSince 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38, and **index 1 should come before index 2**.\n\n**So the sorted indices is [1, 2, 0], and the corresponding values in nums are 338, 38, 991.**\n\n\nThus, the sorted array is [338,38,991].\n\n\n**End of Q & A**\n\n\n----\n\n\nSort the indices by the converted value first, if equal, then by original index.\n\nBoth java.util.Arrays.sort(T[] a, Comparator<? super T> c) and sorted() in Python are guaranteed to be stable, so no need to sub-sort by the index. -- credit to **@SunnyvaleCA**.\n\n```java\n public int[] sortJumbled(int[] mapping, int[] nums) {\n int n = nums.length, k = 0;\n Integer[] indices = new Integer[n];\n for (int i = 0; i < n; ++i)\n indices[i] = i;\n Arrays.sort(indices, Comparator.comparing(i -> convert(nums[i], mapping)));\n // return Stream.of(indices).mapToInt(i -> nums[i]).toArray();\n int[] ans = new int[n];\n for (int idx : indices)\n ans[k++] = nums[idx];\n return ans;\n }\n private int convert(int num, int[] mapping) {\n if (num == 0)\n return mapping[0];\n int n = 0, f = 1;\n while (num > 0) {\n n += mapping[num % 10] * f;\n f *= 10;\n num /= 10;\n }\n return n;\n }\n```\n\n----\n\n\n\n```python\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n \n def convert(num: int) -> int:\n if num == 0:\n return mapping[0]\n n, f = 0, 1\n while num > 0:\n num, r = divmod(num, 10)\n n += mapping[r] * f\n f *= 10\n return n\n \n indices = sorted(range(len(nums)), key=lambda i: convert(nums[i]))\n return [nums[i] for i in indices]\n```\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(n)`, where `n = nums.length`.\n\n-------\n\nPlease **upvote** if the post is helpful. | 24 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Sorted Lambda | sort-the-jumbled-numbers | 0 | 1 | \nWe will use Python to leverage `@cache`.\n> Note: the solution is accepted without cahce (since constraints are relaxed).\n\nWatch for `0` edge case and convert it to a number using `mapping`.\n\n**Python**\n```python\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n @cache\n def convert(i: int):\n res, pow10 = 0, 1\n while i:\n res += pow10 * mapping[i % 10]\n i //= 10\n pow10 *= 10\n return res\n return sorted(nums, key=lambda i: mapping[i] if i < 10 else convert(i))\n```\n\nYou can also convert the array first, and sort it that way. Counter-intuitively, the runtime for this solution is a bit slower.\n**Python**\n```python\n nums = zip(nums, [mapping[i] if i < 10 else convert(i) for i in nums])\n return [a for a, b in sorted(nums, key = lambda i: i[1])]\n``` | 8 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
Sorted Lambda | sort-the-jumbled-numbers | 0 | 1 | \nWe will use Python to leverage `@cache`.\n> Note: the solution is accepted without cahce (since constraints are relaxed).\n\nWatch for `0` edge case and convert it to a number using `mapping`.\n\n**Python**\n```python\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n @cache\n def convert(i: int):\n res, pow10 = 0, 1\n while i:\n res += pow10 * mapping[i % 10]\n i //= 10\n pow10 *= 10\n return res\n return sorted(nums, key=lambda i: mapping[i] if i < 10 else convert(i))\n```\n\nYou can also convert the array first, and sort it that way. Counter-intuitively, the runtime for this solution is a bit slower.\n**Python**\n```python\n nums = zip(nums, [mapping[i] if i < 10 else convert(i) for i in nums])\n return [a for a, b in sorted(nums, key = lambda i: i[1])]\n``` | 8 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
python 1-line | sort-the-jumbled-numbers | 0 | 1 | ```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n \n return sorted(nums, key = lambda x: int("".join([str(mapping[int(digit)]) for digit in str(x)])))\n``` | 2 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
python 1-line | sort-the-jumbled-numbers | 0 | 1 | ```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n \n return sorted(nums, key = lambda x: int("".join([str(mapping[int(digit)]) for digit in str(x)])))\n``` | 2 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
[Python] - 10 Liner Solution ✔ | sort-the-jumbled-numbers | 0 | 1 | \tclass Solution:\n\t\tdef sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n\t\t\tres = []\n\t\t\tfor num in nums:\n\t\t\t\tans = ""\n\t\t\t\tfor char in str(num):\n\t\t\t\t\tans += str(mapping[int(char)])\n\t\t\t\tres.append(int(ans))\n\t\t\tfinal = list(zip(nums, res))\n\t\t\tfinal = sorted(final, key=lambda x: x[1])\n\t\t\treturn [tup[0] for tup in final]\n | 2 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
[Python] - 10 Liner Solution ✔ | sort-the-jumbled-numbers | 0 | 1 | \tclass Solution:\n\t\tdef sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n\t\t\tres = []\n\t\t\tfor num in nums:\n\t\t\t\tans = ""\n\t\t\t\tfor char in str(num):\n\t\t\t\t\tans += str(mapping[int(char)])\n\t\t\t\tres.append(int(ans))\n\t\t\tfinal = list(zip(nums, res))\n\t\t\tfinal = sorted(final, key=lambda x: x[1])\n\t\t\treturn [tup[0] for tup in final]\n | 2 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Easy Solution! || PYTHON || BEATS 98.8%|| SORTING | sort-the-jumbled-numbers | 0 | 1 | ```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n mapp = {ind:val for ind,val in enumerate(mapping)}\n # print(mapp)\n ans = []\n for num in nums:\n pre , alph = 1 , 0\n if num == 0:alph = mapp[num]\n org= num\n while num>0:\n left = num%10\n alph = mapp[left]*pre + alph\n pre,num = pre*10 ,num//10\n ans.append((alph,org))\n ans.sort(key = lambda x :x[0])\n # print(ans)\n return [ele[1] for ele in ans]\n``` | 0 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
Easy Solution! || PYTHON || BEATS 98.8%|| SORTING | sort-the-jumbled-numbers | 0 | 1 | ```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n mapp = {ind:val for ind,val in enumerate(mapping)}\n # print(mapp)\n ans = []\n for num in nums:\n pre , alph = 1 , 0\n if num == 0:alph = mapp[num]\n org= num\n while num>0:\n left = num%10\n alph = mapp[left]*pre + alph\n pre,num = pre*10 ,num//10\n ans.append((alph,org))\n ans.sort(key = lambda x :x[0])\n # print(ans)\n return [ele[1] for ele in ans]\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Python | Custom Sorting | Japanese | sort-the-jumbled-numbers | 0 | 1 | # Complexity\n## Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(NlogN + NlogD)$$, $N = nums$\u306E\u8981\u7D20\u6570 $$D = nums$$\u306B\u542B\u307E\u308C\u308B\u8981\u7D20\u306E\u6700\u5927\u5024\n\n\u524D\u534A\u306F\u30BD\u30FC\u30C8\u306E\u6642\u9593\u8A08\u7B97\u91CF\u306A\u306E\u3067\u81EA\u660E\u3067\u3059\u306D\u3002\u5F8C\u8005\u306F\u3084\u3084\u3053\u3057\u3044\u306E\u3067\u3059\u304C\u3001\u30BD\u30FC\u30C8\u3092\u3059\u308B\u305F\u3081\u306B\u6570\u5024\u3092mapping\u3059\u308B\u51E6\u7406\u304C\u3042\u308B\u306E\u3067\u3059\u304C\u305D\u3061\u3089\u306F\u30BD\u30FC\u30C8\u306E\u524D\u306B\u547C\u3070\u308C\u307E\u3059\u3002\u5909\u63DB\u306B\u306F\u6BCE\u56DE10\u3092\u5272\u3063\u3066\u3044\u304F\u306E\u3067\u6841\u6570\u5206\u30EB\u30FC\u30D7\u304C\u3042\u308B\u3068\u8003\u3048\u3066\u304F\u3060\u3055\u3044\u3002\u3064\u307E\u308A\u3001$$O(NlogD)$$\u3001 $$D = nums$$\u306B\u542B\u307E\u308C\u308B\u8981\u7D20\u306E\u6700\u5927\u5024\u3068\u306A\u308A\u307E\u3059\u3002\n\n## Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n\n# Code\n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n def mapping(num: int):\n # \u30A8\u30C3\u30B8\u30B1\u30FC\u30B9\u306E\u5BFE\u5FDC\n if num == 0:\n return mapping[num]\n mapped_number = 0\n factor = 1\n\n # \u6841\u3054\u3068\u306B\u53D6\u308A\u51FA\u3057\u3066\u3001digit\u3092\u30DE\u30C3\u30D4\u30F3\u30B0\u3057\u3066\u3044\u304F\n # 1\u306E\u4F4D\u306B\u306F1\u3092\u4E57\u7B97\u300110\u306E\u4F4D\u306B\u306F10\u3092\u4E57\u7B97 100\u306E\u4F4D\u306B\u306F100\u3092\u4E57\u7B97...\n # \u7B49\u3092\u7E70\u308A\u8FD4\u3059\n while num > 0:\n digit = num % 10\n mapped_digit = mapping[digit]\n mapped_number += mapped_digit * factor\n factor *= 10\n num = num // 10\n return mapped_number\n\n nums.sort(key=mapping)\n return nums\n``` | 0 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
Python | Custom Sorting | Japanese | sort-the-jumbled-numbers | 0 | 1 | # Complexity\n## Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(NlogN + NlogD)$$, $N = nums$\u306E\u8981\u7D20\u6570 $$D = nums$$\u306B\u542B\u307E\u308C\u308B\u8981\u7D20\u306E\u6700\u5927\u5024\n\n\u524D\u534A\u306F\u30BD\u30FC\u30C8\u306E\u6642\u9593\u8A08\u7B97\u91CF\u306A\u306E\u3067\u81EA\u660E\u3067\u3059\u306D\u3002\u5F8C\u8005\u306F\u3084\u3084\u3053\u3057\u3044\u306E\u3067\u3059\u304C\u3001\u30BD\u30FC\u30C8\u3092\u3059\u308B\u305F\u3081\u306B\u6570\u5024\u3092mapping\u3059\u308B\u51E6\u7406\u304C\u3042\u308B\u306E\u3067\u3059\u304C\u305D\u3061\u3089\u306F\u30BD\u30FC\u30C8\u306E\u524D\u306B\u547C\u3070\u308C\u307E\u3059\u3002\u5909\u63DB\u306B\u306F\u6BCE\u56DE10\u3092\u5272\u3063\u3066\u3044\u304F\u306E\u3067\u6841\u6570\u5206\u30EB\u30FC\u30D7\u304C\u3042\u308B\u3068\u8003\u3048\u3066\u304F\u3060\u3055\u3044\u3002\u3064\u307E\u308A\u3001$$O(NlogD)$$\u3001 $$D = nums$$\u306B\u542B\u307E\u308C\u308B\u8981\u7D20\u306E\u6700\u5927\u5024\u3068\u306A\u308A\u307E\u3059\u3002\n\n## Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n\n# Code\n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n def mapping(num: int):\n # \u30A8\u30C3\u30B8\u30B1\u30FC\u30B9\u306E\u5BFE\u5FDC\n if num == 0:\n return mapping[num]\n mapped_number = 0\n factor = 1\n\n # \u6841\u3054\u3068\u306B\u53D6\u308A\u51FA\u3057\u3066\u3001digit\u3092\u30DE\u30C3\u30D4\u30F3\u30B0\u3057\u3066\u3044\u304F\n # 1\u306E\u4F4D\u306B\u306F1\u3092\u4E57\u7B97\u300110\u306E\u4F4D\u306B\u306F10\u3092\u4E57\u7B97 100\u306E\u4F4D\u306B\u306F100\u3092\u4E57\u7B97...\n # \u7B49\u3092\u7E70\u308A\u8FD4\u3059\n while num > 0:\n digit = num % 10\n mapped_digit = mapping[digit]\n mapped_number += mapped_digit * factor\n factor *= 10\n num = num // 10\n return mapped_number\n\n nums.sort(key=mapping)\n return nums\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
Python Solution to the problem | sort-the-jumbled-numbers | 0 | 1 | # Intuition\nThe intuition behind the solution is to create a dictionary (new) to store the mapped values of each number in nums. Then, sort the dictionary keys to get the mapped values in non-decreasing order. Finally, concatenate the lists associated with each key to get the sorted array.\n\n# Approach\nInitialize an empty dictionary new to store the mapped values.\nIterate through each number in nums.\nFor each number, iterate through its digits, map each digit using the mapping array, and concatenate the mapped digits to form the new mapped number as a string.\nIf the mapped number is not in the dictionary, add it with a list containing the original number. Otherwise, append the original number to the existing list.\nExtract the keys from the dictionary and sort them.\nConcatenate the lists associated with each sorted key to get the final sorted array.\nReturn the sorted array.\n\n# Complexity\n- Time complexity:\nO(n * d * log(d)) where n is the number of elements in nums and d is the average number of digits in each element. The time complexity is dominated by sorting the dictionary keys.\n\n- Space complexity:\nO(n * d) where n is the number of elements in nums and d is the average number of digits in each element. The space complexity is due to storing the mapped values in the dictionary.\n\n# Code\n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n new = {}\n for i in nums:\n string = ""\n traverse = str(i)\n for j in traverse:\n idx = int(j)\n string+=str(mapping[idx])\n if int(string) not in new:\n new[int(string)] = [i]\n else:\n new[int(string)].append(i)\n lst = list(new.keys())\n lst.sort()\n fin = []\n for i in lst:\n fin+=new[i]\n return fin\n \n\n``` | 0 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
Python Solution to the problem | sort-the-jumbled-numbers | 0 | 1 | # Intuition\nThe intuition behind the solution is to create a dictionary (new) to store the mapped values of each number in nums. Then, sort the dictionary keys to get the mapped values in non-decreasing order. Finally, concatenate the lists associated with each key to get the sorted array.\n\n# Approach\nInitialize an empty dictionary new to store the mapped values.\nIterate through each number in nums.\nFor each number, iterate through its digits, map each digit using the mapping array, and concatenate the mapped digits to form the new mapped number as a string.\nIf the mapped number is not in the dictionary, add it with a list containing the original number. Otherwise, append the original number to the existing list.\nExtract the keys from the dictionary and sort them.\nConcatenate the lists associated with each sorted key to get the final sorted array.\nReturn the sorted array.\n\n# Complexity\n- Time complexity:\nO(n * d * log(d)) where n is the number of elements in nums and d is the average number of digits in each element. The time complexity is dominated by sorting the dictionary keys.\n\n- Space complexity:\nO(n * d) where n is the number of elements in nums and d is the average number of digits in each element. The space complexity is due to storing the mapped values in the dictionary.\n\n# Code\n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n new = {}\n for i in nums:\n string = ""\n traverse = str(i)\n for j in traverse:\n idx = int(j)\n string+=str(mapping[idx])\n if int(string) not in new:\n new[int(string)] = [i]\n else:\n new[int(string)].append(i)\n lst = list(new.keys())\n lst.sort()\n fin = []\n for i in lst:\n fin+=new[i]\n return fin\n \n\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
[Python3] Simple Sort Solution | sort-the-jumbled-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n hm = dict()\n newNums = []\n for i, e in enumerate(nums):\n newE = ""\n sNum = str(e)\n for ch in sNum:\n newE += str(mapping[int(ch)])\n hm[i] = e\n newNums.append((int(newE), i))\n \n newNums.sort(key=lambda tup: [tup[0], tup[1]])\n\n ans = []\n for e in newNums:\n ans.append(hm[e[1]])\n\n return ans\n``` | 0 | You are given a **0-indexed** integer array `mapping` which represents the mapping rule of a shuffled decimal system. `mapping[i] = j` means digit `i` should be mapped to digit `j` in this system.
The **mapped value** of an integer is the new integer obtained by replacing each occurrence of digit `i` in the integer with `mapping[i]` for all `0 <= i <= 9`.
You are also given another integer array `nums`. Return _the array_ `nums` _sorted in **non-decreasing** order based on the **mapped values** of its elements._
**Notes:**
* Elements with the same mapped values should appear in the **same relative order** as in the input.
* The elements of `nums` should only be sorted based on their mapped values and **not be replaced** by them.
**Example 1:**
**Input:** mapping = \[8,9,4,0,2,1,3,5,7,6\], nums = \[991,338,38\]
**Output:** \[338,38,991\]
**Explanation:**
Map the number 991 as follows:
1. mapping\[9\] = 6, so all occurrences of the digit 9 will become 6.
2. mapping\[1\] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is \[338,38,991\].
**Example 2:**
**Input:** mapping = \[0,1,2,3,4,5,6,7,8,9\], nums = \[789,456,123\]
**Output:** \[123,456,789\]
**Explanation:** 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is \[123,456,789\].
**Constraints:**
* `mapping.length == 10`
* `0 <= mapping[i] <= 9`
* All the values of `mapping[i]` are **unique**.
* `1 <= nums.length <= 3 * 104`
* `0 <= nums[i] < 109` | When is it impossible to collect the rainwater from all the houses? When one or more houses do not have an empty space adjacent to it. Assuming the rainwater from all previous houses is collected. If there is a house at index i and you are able to place a bucket at index i - 1 or i + 1, where should you put it? It is always better to place a bucket at index i + 1 because it can collect the rainwater from the next house as well. |
[Python3] Simple Sort Solution | sort-the-jumbled-numbers | 0 | 1 | # Code\n```\nclass Solution:\n def sortJumbled(self, mapping: List[int], nums: List[int]) -> List[int]:\n hm = dict()\n newNums = []\n for i, e in enumerate(nums):\n newE = ""\n sNum = str(e)\n for ch in sNum:\n newE += str(mapping[int(ch)])\n hm[i] = e\n newNums.append((int(newE), i))\n \n newNums.sort(key=lambda tup: [tup[0], tup[1]])\n\n ans = []\n for e in newNums:\n ans.append(hm[e[1]])\n\n return ans\n``` | 0 | Given the array `restaurants` where `restaurants[i] = [idi, ratingi, veganFriendlyi, pricei, distancei]`. You have to filter the restaurants using three filters.
The `veganFriendly` filter will be either _true_ (meaning you should only include restaurants with `veganFriendlyi` set to true) or _false_ (meaning you can include any restaurant). In addition, you have the filters `maxPrice` and `maxDistance` which are the maximum value for price and distance of restaurants you should consider respectively.
Return the array of restaurant _**IDs**_ after filtering, ordered by **rating** from highest to lowest. For restaurants with the same rating, order them by _**id**_ from highest to lowest. For simplicity `veganFriendlyi` and `veganFriendly` take value _1_ when it is _true_, and _0_ when it is _false_.
**Example 1:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 1, maxPrice = 50, maxDistance = 10
**Output:** \[3,1,5\]
**Explanation:**
The restaurants are:
Restaurant 1 \[id=1, rating=4, veganFriendly=1, price=40, distance=10\]
Restaurant 2 \[id=2, rating=8, veganFriendly=0, price=50, distance=5\]
Restaurant 3 \[id=3, rating=8, veganFriendly=1, price=30, distance=4\]
Restaurant 4 \[id=4, rating=10, veganFriendly=0, price=10, distance=3\]
Restaurant 5 \[id=5, rating=1, veganFriendly=1, price=15, distance=1\]
After filter restaurants with veganFriendly = 1, maxPrice = 50 and maxDistance = 10 we have restaurant 3, restaurant 1 and restaurant 5 (ordered by rating from highest to lowest).
**Example 2:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 50, maxDistance = 10
**Output:** \[4,3,2,1,5\]
**Explanation:** The restaurants are the same as in example 1, but in this case the filter veganFriendly = 0, therefore all restaurants are considered.
**Example 3:**
**Input:** restaurants = \[\[1,4,1,40,10\],\[2,8,0,50,5\],\[3,8,1,30,4\],\[4,10,0,10,3\],\[5,1,1,15,1\]\], veganFriendly = 0, maxPrice = 30, maxDistance = 3
**Output:** \[4,5\]
**Constraints:**
* `1 <= restaurants.length <= 10^4`
* `restaurants[i].length == 5`
* `1 <= idi, ratingi, pricei, distancei <= 10^5`
* `1 <= maxPrice, maxDistance <= 10^5`
* `veganFriendlyi` and `veganFriendly` are 0 or 1.
* All `idi` are distinct. | Map the original numbers to new numbers by the mapping rule and sort the new numbers. To maintain the same relative order for equal mapped values, use the index in the original input array as a tiebreaker. |
[Java/Python 3] 2 codes:Topological sort & DFS, w/ brief explanation and comments. | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 1 | 1 | **Topological Sort**\n\n1. Build graph from parent to kids, and compute in-degree for each node;\n2. Use topological to get direct parent and all ancestors of the direct parent of each node;\n\n```java\n public List<List<Integer>> getAncestors(int n, int[][] edges) {\n \n // Build graph, and compute in degree.\n int[] inDegree = new int[n];\n Map<Integer, List<Integer>> parentToKids = new HashMap<>();\n for (int[] e : edges) {\n parentToKids.computeIfAbsent(e[0], l -> new ArrayList<>()).add(e[1]);\n ++inDegree[e[1]];\n }\n \n // 1. Use a list of sets to save ancestors \n // and to avoid duplicates.\n // 2. Use a Queue to save 0-in-degree nodes as\n // the starting nodes for topological sort.\n List<Set<Integer>> sets = new ArrayList<>();\n Queue<Integer> q = new LinkedList<>();\n for (int i = 0; i < n; ++i) {\n sets.add(new HashSet<>());\n if (inDegree[i] == 0)\n q.offer(i);\n }\n \n // BFS to their neighbors and decrease \n // the in degrees, when reaching 0, add\n // it into queue;\n // During this procedure, get direct parent, add \n // all ancestors of direct parents\' of each kid.\n while (!q.isEmpty()) {\n int parent = q.poll();\n for (int kid : parentToKids.getOrDefault(parent, Arrays.asList())) {\n sets.get(kid).add(parent);\n sets.get(kid).addAll(sets.get(parent));\n if (--inDegree[kid] == 0)\n q.offer(kid);\n }\n }\n \n // Sort ancestors and put into return list. \n List<List<Integer>> ans = new ArrayList<>();\n for (Set<Integer> set : sets)\n ans.add(new ArrayList<>(new TreeSet<>(set)));\n return ans;\n }\n```\n```python\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n \n # Build graph, compute in degree and\n # get direct parent for each node. \n ans = [set() for _ in range(n)]\n in_degree = [0] * n\n parent_to_kids = defaultdict(set)\n for parent, kid in edges:\n ans[kid].add(parent)\n parent_to_kids[parent].add(kid)\n in_degree[kid] += 1\n \n # Use Topological sort to get direct parent\'s all ancestors \n dq = deque([u for u, degree in enumerate(in_degree) if degree == 0])\n while dq:\n parent = dq.popleft()\n for kid in parent_to_kids[parent]:\n ans[kid].update(ans[parent])\n in_degree[kid] -= 1\n if in_degree[kid] == 0:\n dq.append(kid)\n return [sorted(s) for s in ans] \n```\n\n----\n\n**DFS**\n\n**Q & A**\n*Q1*: In the DFS approach how are we sorting the sublists?\n*A1*: \n1) The recursion sequence of the dfs method \nand \n2) the traversal sequence in the last for loop in the `getAncestors` method \n\nguarantee that the ancestor list is sorted during adding process.\n\nYou can print out the methods names and nodes number to verify it.\n\n----\n\n\n1. Build graph from parent to kids, and save `n` empty list into return List `ans`; \n2. Traverse all nodes; for each node, recurse to the lowest offspring; During recursion, add the ancestor into the corresponding ancestors list for each offspring;\n3. The recursion terminates once the the ancestor list ends with current ancestor.\n\n```java\n public List<List<Integer>> getAncestors(int n, int[][] edges) {\n Map<Integer, List<Integer>> parentToKids = new HashMap<>();\n for (int[] e : edges) {\n parentToKids.computeIfAbsent(e[0], l -> new ArrayList<>()).add(e[1]);\n }\n List<List<Integer>> ans = new ArrayList<>();\n for (int i = 0; i < n; ++i) {\n ans.add(new ArrayList<>());\n }\n for (int i = 0; i < n; ++i) {\n dfs(i, i, ans, parentToKids);\n }\n return ans;\n }\n private void dfs(int ancestor, int kid, List<List<Integer>> ans, Map<Integer, List<Integer>> parentToKids) {\n List<Integer> ancestors = ans.get(kid);\n if (ancestors.isEmpty() || ancestors.get(ancestors.size() - 1) != ancestor) {\n if (ancestor != kid) {\n ancestors.add(ancestor);\n }\n for (int grandKid : parentToKids.getOrDefault(kid, Arrays.asList())) {\n dfs(ancestor, grandKid, ans, parentToKids);\n }\n }\n }\n```\n```python\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n \n def dfs(ancestor: int, kid: int) -> None:\n if not (ans[kid] and ans[kid][-1] == ancestor):\n if kid != ancestor:\n ans[kid].append(ancestor)\n for grand_child in parent_to_kids[kid]:\n dfs(ancestor, grand_child)\n\n parent_to_kids = defaultdict(list)\n for parent, kid in edges:\n parent_to_kids[parent].append(kid)\n ans = [[] for _ in range(n)]\n for i in range(n):\n dfs(i, i)\n return ans\n```\n\n**Analysis for both methods:**\n\nTime & space: `O(n ^ 2 + E)`, where `E = # of edges`.\n\n----\n\nPlease free feel to ask if you have any questions, and **Upovte** if it is helpful. Thanks. | 50 | You are given a positive integer `n` representing the number of nodes of a **Directed Acyclic Graph** (DAG). The nodes are numbered from `0` to `n - 1` (**inclusive**).
You are also given a 2D integer array `edges`, where `edges[i] = [fromi, toi]` denotes that there is a **unidirectional** edge from `fromi` to `toi` in the graph.
Return _a list_ `answer`_, where_ `answer[i]` _is the **list of ancestors** of the_ `ith` _node, sorted in **ascending order**_.
A node `u` is an **ancestor** of another node `v` if `u` can reach `v` via a set of edges.
**Example 1:**
**Input:** n = 8, edgeList = \[\[0,3\],\[0,4\],\[1,3\],\[2,4\],\[2,7\],\[3,5\],\[3,6\],\[3,7\],\[4,6\]\]
**Output:** \[\[\],\[\],\[\],\[0,1\],\[0,2\],\[0,1,3\],\[0,1,2,3,4\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1\],\[0,2\],\[0,3\],\[0,4\],\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Output:** \[\[\],\[0\],\[0,1\],\[0,1,2\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= edges.length <= min(2000, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi <= n - 1`
* `fromi != toi`
* There are no duplicate edges.
* The graph is **directed** and **acyclic**. | Irrespective of what path the robot takes, it will have to traverse all the rows between startRow and homeRow and all the columns between startCol and homeCol. Hence, making any other move other than traversing the required rows and columns will potentially incur more cost which can be avoided. |
[Java/Python 3] 2 codes:Topological sort & DFS, w/ brief explanation and comments. | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 1 | 1 | **Topological Sort**\n\n1. Build graph from parent to kids, and compute in-degree for each node;\n2. Use topological to get direct parent and all ancestors of the direct parent of each node;\n\n```java\n public List<List<Integer>> getAncestors(int n, int[][] edges) {\n \n // Build graph, and compute in degree.\n int[] inDegree = new int[n];\n Map<Integer, List<Integer>> parentToKids = new HashMap<>();\n for (int[] e : edges) {\n parentToKids.computeIfAbsent(e[0], l -> new ArrayList<>()).add(e[1]);\n ++inDegree[e[1]];\n }\n \n // 1. Use a list of sets to save ancestors \n // and to avoid duplicates.\n // 2. Use a Queue to save 0-in-degree nodes as\n // the starting nodes for topological sort.\n List<Set<Integer>> sets = new ArrayList<>();\n Queue<Integer> q = new LinkedList<>();\n for (int i = 0; i < n; ++i) {\n sets.add(new HashSet<>());\n if (inDegree[i] == 0)\n q.offer(i);\n }\n \n // BFS to their neighbors and decrease \n // the in degrees, when reaching 0, add\n // it into queue;\n // During this procedure, get direct parent, add \n // all ancestors of direct parents\' of each kid.\n while (!q.isEmpty()) {\n int parent = q.poll();\n for (int kid : parentToKids.getOrDefault(parent, Arrays.asList())) {\n sets.get(kid).add(parent);\n sets.get(kid).addAll(sets.get(parent));\n if (--inDegree[kid] == 0)\n q.offer(kid);\n }\n }\n \n // Sort ancestors and put into return list. \n List<List<Integer>> ans = new ArrayList<>();\n for (Set<Integer> set : sets)\n ans.add(new ArrayList<>(new TreeSet<>(set)));\n return ans;\n }\n```\n```python\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n \n # Build graph, compute in degree and\n # get direct parent for each node. \n ans = [set() for _ in range(n)]\n in_degree = [0] * n\n parent_to_kids = defaultdict(set)\n for parent, kid in edges:\n ans[kid].add(parent)\n parent_to_kids[parent].add(kid)\n in_degree[kid] += 1\n \n # Use Topological sort to get direct parent\'s all ancestors \n dq = deque([u for u, degree in enumerate(in_degree) if degree == 0])\n while dq:\n parent = dq.popleft()\n for kid in parent_to_kids[parent]:\n ans[kid].update(ans[parent])\n in_degree[kid] -= 1\n if in_degree[kid] == 0:\n dq.append(kid)\n return [sorted(s) for s in ans] \n```\n\n----\n\n**DFS**\n\n**Q & A**\n*Q1*: In the DFS approach how are we sorting the sublists?\n*A1*: \n1) The recursion sequence of the dfs method \nand \n2) the traversal sequence in the last for loop in the `getAncestors` method \n\nguarantee that the ancestor list is sorted during adding process.\n\nYou can print out the methods names and nodes number to verify it.\n\n----\n\n\n1. Build graph from parent to kids, and save `n` empty list into return List `ans`; \n2. Traverse all nodes; for each node, recurse to the lowest offspring; During recursion, add the ancestor into the corresponding ancestors list for each offspring;\n3. The recursion terminates once the the ancestor list ends with current ancestor.\n\n```java\n public List<List<Integer>> getAncestors(int n, int[][] edges) {\n Map<Integer, List<Integer>> parentToKids = new HashMap<>();\n for (int[] e : edges) {\n parentToKids.computeIfAbsent(e[0], l -> new ArrayList<>()).add(e[1]);\n }\n List<List<Integer>> ans = new ArrayList<>();\n for (int i = 0; i < n; ++i) {\n ans.add(new ArrayList<>());\n }\n for (int i = 0; i < n; ++i) {\n dfs(i, i, ans, parentToKids);\n }\n return ans;\n }\n private void dfs(int ancestor, int kid, List<List<Integer>> ans, Map<Integer, List<Integer>> parentToKids) {\n List<Integer> ancestors = ans.get(kid);\n if (ancestors.isEmpty() || ancestors.get(ancestors.size() - 1) != ancestor) {\n if (ancestor != kid) {\n ancestors.add(ancestor);\n }\n for (int grandKid : parentToKids.getOrDefault(kid, Arrays.asList())) {\n dfs(ancestor, grandKid, ans, parentToKids);\n }\n }\n }\n```\n```python\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n \n def dfs(ancestor: int, kid: int) -> None:\n if not (ans[kid] and ans[kid][-1] == ancestor):\n if kid != ancestor:\n ans[kid].append(ancestor)\n for grand_child in parent_to_kids[kid]:\n dfs(ancestor, grand_child)\n\n parent_to_kids = defaultdict(list)\n for parent, kid in edges:\n parent_to_kids[parent].append(kid)\n ans = [[] for _ in range(n)]\n for i in range(n):\n dfs(i, i)\n return ans\n```\n\n**Analysis for both methods:**\n\nTime & space: `O(n ^ 2 + E)`, where `E = # of edges`.\n\n----\n\nPlease free feel to ask if you have any questions, and **Upovte** if it is helpful. Thanks. | 50 | There are `n` kids with candies. You are given an integer array `candies`, where each `candies[i]` represents the number of candies the `ith` kid has, and an integer `extraCandies`, denoting the number of extra candies that you have.
Return _a boolean array_ `result` _of length_ `n`_, where_ `result[i]` _is_ `true` _if, after giving the_ `ith` _kid all the_ `extraCandies`_, they will have the **greatest** number of candies among all the kids__, or_ `false` _otherwise_.
Note that **multiple** kids can have the **greatest** number of candies.
**Example 1:**
**Input:** candies = \[2,3,5,1,3\], extraCandies = 3
**Output:** \[true,true,true,false,true\]
**Explanation:** If you give all extraCandies to:
- Kid 1, they will have 2 + 3 = 5 candies, which is the greatest among the kids.
- Kid 2, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
- Kid 3, they will have 5 + 3 = 8 candies, which is the greatest among the kids.
- Kid 4, they will have 1 + 3 = 4 candies, which is not the greatest among the kids.
- Kid 5, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
**Example 2:**
**Input:** candies = \[4,2,1,1,2\], extraCandies = 1
**Output:** \[true,false,false,false,false\]
**Explanation:** There is only 1 extra candy.
Kid 1 will always have the greatest number of candies, even if a different kid is given the extra candy.
**Example 3:**
**Input:** candies = \[12,1,12\], extraCandies = 10
**Output:** \[true,false,true\]
**Constraints:**
* `n == candies.length`
* `2 <= n <= 100`
* `1 <= candies[i] <= 100`
* `1 <= extraCandies <= 50` | Consider how reversing each edge of the graph can help us. How can performing BFS/DFS on the reversed graph help us find the ancestors of every node? |
Python3 | Solved using Topo Sort(Kahn Algo) with Queue(BFS) | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | ```\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n #Use Kahn\'s algorithm of toposort using a queue and bfs!\n graph = [[] for _ in range(n)]\n indegrees = [0] * n\n \n #Time: O(n^2)\n #Space: O(n^2 + n + n) -> O(n^2)\n \n #1st step: build adjacency list grpah and update the initial indegrees of every node!\n for edge in edges:\n src, dest = edge[0], edge[1]\n graph[src].append(dest)\n indegrees[dest] += 1\n \n \n queue = deque()\n ans = [set() for _ in range(n)]\n #2nd step: go through the indegrees array and add to queue for any node that has no ancestor!\n for i in range(len(indegrees)):\n if(indegrees[i] == 0):\n queue.append(i)\n \n #Kahn\'s algorithm initiation!\n #while loop will run for each and every node in graph!\n #in worst case, adjacency list for one particular node may contain all other vertices!\n while queue:\n cur = queue.pop()\n \n #for each neighbor\n for neighbor in graph[cur]:\n #current node is ancestor to each and every neighboring node!\n ans[neighbor].add(cur)\n #every ancestor of current node is also an ancestor to the neighboring node!\n ans[neighbor].update(ans[cur])\n indegrees[neighbor] -= 1\n if(indegrees[neighbor] == 0):\n queue.append(neighbor)\n \n #at the end, we should have set of ancestors for each and every node!\n #in worst case, set s for ith node could have all other vertices be ancestor to node i !\n ans = [(sorted(list(s))) for s in ans]\n return ans | 4 | You are given a positive integer `n` representing the number of nodes of a **Directed Acyclic Graph** (DAG). The nodes are numbered from `0` to `n - 1` (**inclusive**).
You are also given a 2D integer array `edges`, where `edges[i] = [fromi, toi]` denotes that there is a **unidirectional** edge from `fromi` to `toi` in the graph.
Return _a list_ `answer`_, where_ `answer[i]` _is the **list of ancestors** of the_ `ith` _node, sorted in **ascending order**_.
A node `u` is an **ancestor** of another node `v` if `u` can reach `v` via a set of edges.
**Example 1:**
**Input:** n = 8, edgeList = \[\[0,3\],\[0,4\],\[1,3\],\[2,4\],\[2,7\],\[3,5\],\[3,6\],\[3,7\],\[4,6\]\]
**Output:** \[\[\],\[\],\[\],\[0,1\],\[0,2\],\[0,1,3\],\[0,1,2,3,4\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1\],\[0,2\],\[0,3\],\[0,4\],\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Output:** \[\[\],\[0\],\[0,1\],\[0,1,2\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= edges.length <= min(2000, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi <= n - 1`
* `fromi != toi`
* There are no duplicate edges.
* The graph is **directed** and **acyclic**. | Irrespective of what path the robot takes, it will have to traverse all the rows between startRow and homeRow and all the columns between startCol and homeCol. Hence, making any other move other than traversing the required rows and columns will potentially incur more cost which can be avoided. |
Python3 | Solved using Topo Sort(Kahn Algo) with Queue(BFS) | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | ```\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n #Use Kahn\'s algorithm of toposort using a queue and bfs!\n graph = [[] for _ in range(n)]\n indegrees = [0] * n\n \n #Time: O(n^2)\n #Space: O(n^2 + n + n) -> O(n^2)\n \n #1st step: build adjacency list grpah and update the initial indegrees of every node!\n for edge in edges:\n src, dest = edge[0], edge[1]\n graph[src].append(dest)\n indegrees[dest] += 1\n \n \n queue = deque()\n ans = [set() for _ in range(n)]\n #2nd step: go through the indegrees array and add to queue for any node that has no ancestor!\n for i in range(len(indegrees)):\n if(indegrees[i] == 0):\n queue.append(i)\n \n #Kahn\'s algorithm initiation!\n #while loop will run for each and every node in graph!\n #in worst case, adjacency list for one particular node may contain all other vertices!\n while queue:\n cur = queue.pop()\n \n #for each neighbor\n for neighbor in graph[cur]:\n #current node is ancestor to each and every neighboring node!\n ans[neighbor].add(cur)\n #every ancestor of current node is also an ancestor to the neighboring node!\n ans[neighbor].update(ans[cur])\n indegrees[neighbor] -= 1\n if(indegrees[neighbor] == 0):\n queue.append(neighbor)\n \n #at the end, we should have set of ancestors for each and every node!\n #in worst case, set s for ith node could have all other vertices be ancestor to node i !\n ans = [(sorted(list(s))) for s in ans]\n return ans | 4 | There are `n` kids with candies. You are given an integer array `candies`, where each `candies[i]` represents the number of candies the `ith` kid has, and an integer `extraCandies`, denoting the number of extra candies that you have.
Return _a boolean array_ `result` _of length_ `n`_, where_ `result[i]` _is_ `true` _if, after giving the_ `ith` _kid all the_ `extraCandies`_, they will have the **greatest** number of candies among all the kids__, or_ `false` _otherwise_.
Note that **multiple** kids can have the **greatest** number of candies.
**Example 1:**
**Input:** candies = \[2,3,5,1,3\], extraCandies = 3
**Output:** \[true,true,true,false,true\]
**Explanation:** If you give all extraCandies to:
- Kid 1, they will have 2 + 3 = 5 candies, which is the greatest among the kids.
- Kid 2, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
- Kid 3, they will have 5 + 3 = 8 candies, which is the greatest among the kids.
- Kid 4, they will have 1 + 3 = 4 candies, which is not the greatest among the kids.
- Kid 5, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
**Example 2:**
**Input:** candies = \[4,2,1,1,2\], extraCandies = 1
**Output:** \[true,false,false,false,false\]
**Explanation:** There is only 1 extra candy.
Kid 1 will always have the greatest number of candies, even if a different kid is given the extra candy.
**Example 3:**
**Input:** candies = \[12,1,12\], extraCandies = 10
**Output:** \[true,false,true\]
**Constraints:**
* `n == candies.length`
* `2 <= n <= 100`
* `1 <= candies[i] <= 100`
* `1 <= extraCandies <= 50` | Consider how reversing each edge of the graph can help us. How can performing BFS/DFS on the reversed graph help us find the ancestors of every node? |
dfs from child to parent | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | # approach:\njust take transpose of the graph and call dfs for each node.\nAs graph edges are reversed and we are calling dfs, its like calling dfs from leaf to parent, and just keep appending the vertices which are not in ans[node]..... \n\n\n# Code\n```\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n\n ans = [[] for _ in range(n)]\n\n g = defaultdict(list)\n\n for u, v in edges:\n g[v].append(u)\n \n def dfs(node, curr):\n for v in g[curr]:\n if v not in ans[node]:\n dfs(node, v)\n ans[node].append(v) \n \n for i in range(n):\n dfs(i,i)\n\n for k in ans:\n k.sort()\n \n return ans \n\n``` | 4 | You are given a positive integer `n` representing the number of nodes of a **Directed Acyclic Graph** (DAG). The nodes are numbered from `0` to `n - 1` (**inclusive**).
You are also given a 2D integer array `edges`, where `edges[i] = [fromi, toi]` denotes that there is a **unidirectional** edge from `fromi` to `toi` in the graph.
Return _a list_ `answer`_, where_ `answer[i]` _is the **list of ancestors** of the_ `ith` _node, sorted in **ascending order**_.
A node `u` is an **ancestor** of another node `v` if `u` can reach `v` via a set of edges.
**Example 1:**
**Input:** n = 8, edgeList = \[\[0,3\],\[0,4\],\[1,3\],\[2,4\],\[2,7\],\[3,5\],\[3,6\],\[3,7\],\[4,6\]\]
**Output:** \[\[\],\[\],\[\],\[0,1\],\[0,2\],\[0,1,3\],\[0,1,2,3,4\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1\],\[0,2\],\[0,3\],\[0,4\],\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Output:** \[\[\],\[0\],\[0,1\],\[0,1,2\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= edges.length <= min(2000, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi <= n - 1`
* `fromi != toi`
* There are no duplicate edges.
* The graph is **directed** and **acyclic**. | Irrespective of what path the robot takes, it will have to traverse all the rows between startRow and homeRow and all the columns between startCol and homeCol. Hence, making any other move other than traversing the required rows and columns will potentially incur more cost which can be avoided. |
dfs from child to parent | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | # approach:\njust take transpose of the graph and call dfs for each node.\nAs graph edges are reversed and we are calling dfs, its like calling dfs from leaf to parent, and just keep appending the vertices which are not in ans[node]..... \n\n\n# Code\n```\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n\n ans = [[] for _ in range(n)]\n\n g = defaultdict(list)\n\n for u, v in edges:\n g[v].append(u)\n \n def dfs(node, curr):\n for v in g[curr]:\n if v not in ans[node]:\n dfs(node, v)\n ans[node].append(v) \n \n for i in range(n):\n dfs(i,i)\n\n for k in ans:\n k.sort()\n \n return ans \n\n``` | 4 | There are `n` kids with candies. You are given an integer array `candies`, where each `candies[i]` represents the number of candies the `ith` kid has, and an integer `extraCandies`, denoting the number of extra candies that you have.
Return _a boolean array_ `result` _of length_ `n`_, where_ `result[i]` _is_ `true` _if, after giving the_ `ith` _kid all the_ `extraCandies`_, they will have the **greatest** number of candies among all the kids__, or_ `false` _otherwise_.
Note that **multiple** kids can have the **greatest** number of candies.
**Example 1:**
**Input:** candies = \[2,3,5,1,3\], extraCandies = 3
**Output:** \[true,true,true,false,true\]
**Explanation:** If you give all extraCandies to:
- Kid 1, they will have 2 + 3 = 5 candies, which is the greatest among the kids.
- Kid 2, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
- Kid 3, they will have 5 + 3 = 8 candies, which is the greatest among the kids.
- Kid 4, they will have 1 + 3 = 4 candies, which is not the greatest among the kids.
- Kid 5, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
**Example 2:**
**Input:** candies = \[4,2,1,1,2\], extraCandies = 1
**Output:** \[true,false,false,false,false\]
**Explanation:** There is only 1 extra candy.
Kid 1 will always have the greatest number of candies, even if a different kid is given the extra candy.
**Example 3:**
**Input:** candies = \[12,1,12\], extraCandies = 10
**Output:** \[true,false,true\]
**Constraints:**
* `n == candies.length`
* `2 <= n <= 100`
* `1 <= candies[i] <= 100`
* `1 <= extraCandies <= 50` | Consider how reversing each edge of the graph can help us. How can performing BFS/DFS on the reversed graph help us find the ancestors of every node? |
Python Elegant & Short | Reverse edges | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | ```\nfrom collections import defaultdict\nfrom typing import Iterable, List\n\n\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> Iterable[List[int]]:\n def dfs(u: int) -> set:\n if not ancestors[u]:\n for v in graph[u]:\n if v not in ancestors[u]:\n ancestors[u].update({v} | dfs(v))\n return ancestors[u]\n\n graph = defaultdict(set)\n for u, v in edges:\n graph[v].add(u)\n\n ancestors = [set() for _ in range(n)]\n for u in range(n):\n if not ancestors[u]:\n dfs(u)\n\n return map(sorted, ancestors)\n``` | 2 | You are given a positive integer `n` representing the number of nodes of a **Directed Acyclic Graph** (DAG). The nodes are numbered from `0` to `n - 1` (**inclusive**).
You are also given a 2D integer array `edges`, where `edges[i] = [fromi, toi]` denotes that there is a **unidirectional** edge from `fromi` to `toi` in the graph.
Return _a list_ `answer`_, where_ `answer[i]` _is the **list of ancestors** of the_ `ith` _node, sorted in **ascending order**_.
A node `u` is an **ancestor** of another node `v` if `u` can reach `v` via a set of edges.
**Example 1:**
**Input:** n = 8, edgeList = \[\[0,3\],\[0,4\],\[1,3\],\[2,4\],\[2,7\],\[3,5\],\[3,6\],\[3,7\],\[4,6\]\]
**Output:** \[\[\],\[\],\[\],\[0,1\],\[0,2\],\[0,1,3\],\[0,1,2,3,4\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1\],\[0,2\],\[0,3\],\[0,4\],\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Output:** \[\[\],\[0\],\[0,1\],\[0,1,2\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= edges.length <= min(2000, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi <= n - 1`
* `fromi != toi`
* There are no duplicate edges.
* The graph is **directed** and **acyclic**. | Irrespective of what path the robot takes, it will have to traverse all the rows between startRow and homeRow and all the columns between startCol and homeCol. Hence, making any other move other than traversing the required rows and columns will potentially incur more cost which can be avoided. |
Python Elegant & Short | Reverse edges | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | ```\nfrom collections import defaultdict\nfrom typing import Iterable, List\n\n\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> Iterable[List[int]]:\n def dfs(u: int) -> set:\n if not ancestors[u]:\n for v in graph[u]:\n if v not in ancestors[u]:\n ancestors[u].update({v} | dfs(v))\n return ancestors[u]\n\n graph = defaultdict(set)\n for u, v in edges:\n graph[v].add(u)\n\n ancestors = [set() for _ in range(n)]\n for u in range(n):\n if not ancestors[u]:\n dfs(u)\n\n return map(sorted, ancestors)\n``` | 2 | There are `n` kids with candies. You are given an integer array `candies`, where each `candies[i]` represents the number of candies the `ith` kid has, and an integer `extraCandies`, denoting the number of extra candies that you have.
Return _a boolean array_ `result` _of length_ `n`_, where_ `result[i]` _is_ `true` _if, after giving the_ `ith` _kid all the_ `extraCandies`_, they will have the **greatest** number of candies among all the kids__, or_ `false` _otherwise_.
Note that **multiple** kids can have the **greatest** number of candies.
**Example 1:**
**Input:** candies = \[2,3,5,1,3\], extraCandies = 3
**Output:** \[true,true,true,false,true\]
**Explanation:** If you give all extraCandies to:
- Kid 1, they will have 2 + 3 = 5 candies, which is the greatest among the kids.
- Kid 2, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
- Kid 3, they will have 5 + 3 = 8 candies, which is the greatest among the kids.
- Kid 4, they will have 1 + 3 = 4 candies, which is not the greatest among the kids.
- Kid 5, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
**Example 2:**
**Input:** candies = \[4,2,1,1,2\], extraCandies = 1
**Output:** \[true,false,false,false,false\]
**Explanation:** There is only 1 extra candy.
Kid 1 will always have the greatest number of candies, even if a different kid is given the extra candy.
**Example 3:**
**Input:** candies = \[12,1,12\], extraCandies = 10
**Output:** \[true,false,true\]
**Constraints:**
* `n == candies.length`
* `2 <= n <= 100`
* `1 <= candies[i] <= 100`
* `1 <= extraCandies <= 50` | Consider how reversing each edge of the graph can help us. How can performing BFS/DFS on the reversed graph help us find the ancestors of every node? |
🐍 python, simple BFS solution with explanation; O(V+E) | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | # Intuition\nThis is a topoligical sort problem. Here we use the famous Kahn\'s algo. \n\n# Approach\n1) Like most of the graphs problem first we create and adjacency map and in_degree dictionary.\n2) Then we create a queue and add the nodes with no parent (in_degree[node]==0 or node not in_degree), we add that to the queue.\n3) We create a list of sets, which set_i contains the ancestors for node i\n4) we run a BFS to reduce the in_degree of each node we visit and once the the degree is zero we add that to the queue. Also, at each step, we update the set_i. \n\n# Complexity\n- Time complexity: O(V+E)\n\n- Space complexity: O(V+E) not including the space we need for the output. \n# Code\n```\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n adj_map = defaultdict(defaultdict)\n in_degree = defaultdict(int)\n for beg, end in edges:\n adj_map[beg][end]=None\n in_degree[end]+=1\n\n q = deque()\n for node in range(n):\n if node not in in_degree:\n q.append(node)\n\n ans = [set() for _ in range(n)]\n while q:\n node = q.popleft()\n for child in adj_map[node]:\n in_degree[child]-=1\n if in_degree[child]==0:\n q.append(child)\n ans[child].update(ans[node] | {node})\n return [sorted(list(i)) for i in ans]\n``` | 1 | You are given a positive integer `n` representing the number of nodes of a **Directed Acyclic Graph** (DAG). The nodes are numbered from `0` to `n - 1` (**inclusive**).
You are also given a 2D integer array `edges`, where `edges[i] = [fromi, toi]` denotes that there is a **unidirectional** edge from `fromi` to `toi` in the graph.
Return _a list_ `answer`_, where_ `answer[i]` _is the **list of ancestors** of the_ `ith` _node, sorted in **ascending order**_.
A node `u` is an **ancestor** of another node `v` if `u` can reach `v` via a set of edges.
**Example 1:**
**Input:** n = 8, edgeList = \[\[0,3\],\[0,4\],\[1,3\],\[2,4\],\[2,7\],\[3,5\],\[3,6\],\[3,7\],\[4,6\]\]
**Output:** \[\[\],\[\],\[\],\[0,1\],\[0,2\],\[0,1,3\],\[0,1,2,3,4\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
**Example 2:**
**Input:** n = 5, edgeList = \[\[0,1\],\[0,2\],\[0,3\],\[0,4\],\[1,2\],\[1,3\],\[1,4\],\[2,3\],\[2,4\],\[3,4\]\]
**Output:** \[\[\],\[0\],\[0,1\],\[0,1,2\],\[0,1,2,3\]\]
**Explanation:**
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
**Constraints:**
* `1 <= n <= 1000`
* `0 <= edges.length <= min(2000, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= fromi, toi <= n - 1`
* `fromi != toi`
* There are no duplicate edges.
* The graph is **directed** and **acyclic**. | Irrespective of what path the robot takes, it will have to traverse all the rows between startRow and homeRow and all the columns between startCol and homeCol. Hence, making any other move other than traversing the required rows and columns will potentially incur more cost which can be avoided. |
🐍 python, simple BFS solution with explanation; O(V+E) | all-ancestors-of-a-node-in-a-directed-acyclic-graph | 0 | 1 | # Intuition\nThis is a topoligical sort problem. Here we use the famous Kahn\'s algo. \n\n# Approach\n1) Like most of the graphs problem first we create and adjacency map and in_degree dictionary.\n2) Then we create a queue and add the nodes with no parent (in_degree[node]==0 or node not in_degree), we add that to the queue.\n3) We create a list of sets, which set_i contains the ancestors for node i\n4) we run a BFS to reduce the in_degree of each node we visit and once the the degree is zero we add that to the queue. Also, at each step, we update the set_i. \n\n# Complexity\n- Time complexity: O(V+E)\n\n- Space complexity: O(V+E) not including the space we need for the output. \n# Code\n```\nclass Solution:\n def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:\n adj_map = defaultdict(defaultdict)\n in_degree = defaultdict(int)\n for beg, end in edges:\n adj_map[beg][end]=None\n in_degree[end]+=1\n\n q = deque()\n for node in range(n):\n if node not in in_degree:\n q.append(node)\n\n ans = [set() for _ in range(n)]\n while q:\n node = q.popleft()\n for child in adj_map[node]:\n in_degree[child]-=1\n if in_degree[child]==0:\n q.append(child)\n ans[child].update(ans[node] | {node})\n return [sorted(list(i)) for i in ans]\n``` | 1 | There are `n` kids with candies. You are given an integer array `candies`, where each `candies[i]` represents the number of candies the `ith` kid has, and an integer `extraCandies`, denoting the number of extra candies that you have.
Return _a boolean array_ `result` _of length_ `n`_, where_ `result[i]` _is_ `true` _if, after giving the_ `ith` _kid all the_ `extraCandies`_, they will have the **greatest** number of candies among all the kids__, or_ `false` _otherwise_.
Note that **multiple** kids can have the **greatest** number of candies.
**Example 1:**
**Input:** candies = \[2,3,5,1,3\], extraCandies = 3
**Output:** \[true,true,true,false,true\]
**Explanation:** If you give all extraCandies to:
- Kid 1, they will have 2 + 3 = 5 candies, which is the greatest among the kids.
- Kid 2, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
- Kid 3, they will have 5 + 3 = 8 candies, which is the greatest among the kids.
- Kid 4, they will have 1 + 3 = 4 candies, which is not the greatest among the kids.
- Kid 5, they will have 3 + 3 = 6 candies, which is the greatest among the kids.
**Example 2:**
**Input:** candies = \[4,2,1,1,2\], extraCandies = 1
**Output:** \[true,false,false,false,false\]
**Explanation:** There is only 1 extra candy.
Kid 1 will always have the greatest number of candies, even if a different kid is given the extra candy.
**Example 3:**
**Input:** candies = \[12,1,12\], extraCandies = 10
**Output:** \[true,false,true\]
**Constraints:**
* `n == candies.length`
* `2 <= n <= 100`
* `1 <= candies[i] <= 100`
* `1 <= extraCandies <= 50` | Consider how reversing each edge of the graph can help us. How can performing BFS/DFS on the reversed graph help us find the ancestors of every node? |
Python + 2 pointers + Explanation. | minimum-number-of-moves-to-make-palindrome | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMovesToMakePalindrome(self, s: str) -> int:\n # At each point, we look at the first and the last elements\n # if they are the same, then we skip them, else we find\n # another element in the string that matches the left\n # element and then we make the necessary swaps to move it\n # to the right place. \n # if we can\'t find that element -- this means this is the middle element\n # in the palindrome, we just move it one position to the right and continue\n # over the next few iterations, it will be moved to the center automatically\n # run it for string = "dpacacp", answer should be 4\n # the character that should be in the middle is "d"\n l, r, res, st = 0, len(s)-1, 0, list(s)\n while l < r:\n if st[l] != st[r]:\n i = r\n while i > l and st[l] != st[i]:\n i -= 1\n if i == l:\n st[i], st[i+1] = st[i+1], st[i]\n res += 1\n continue\n else:\n while i < r:\n st[i], st[i+1] = st[i+1], st[i]\n i += 1\n res += 1\n l, r = l+1, r-1\n return res\n``` | 1 | You are given a string `s` consisting only of lowercase English letters.
In one **move**, you can select any two **adjacent** characters of `s` and swap them.
Return _the **minimum number of moves** needed to make_ `s` _a palindrome_.
**Note** that the input will be generated such that `s` can always be converted to a palindrome.
**Example 1:**
**Input:** s = "aabb "
**Output:** 2
**Explanation:**
We can obtain two palindromes from s, "abba " and "baab ".
- We can obtain "abba " from s in 2 moves: "a**ab**b " -> "ab**ab** " -> "abba ".
- We can obtain "baab " from s in 2 moves: "a**ab**b " -> "**ab**ab " -> "baab ".
Thus, the minimum number of moves needed to make s a palindrome is 2.
**Example 2:**
**Input:** s = "letelt "
**Output:** 2
**Explanation:**
One of the palindromes we can obtain from s in 2 moves is "lettel ".
One of the ways we can obtain it is "lete**lt** " -> "let**et**l " -> "lettel ".
Other palindromes such as "tleelt " can also be obtained in 2 moves.
It can be shown that it is not possible to obtain a palindrome in less than 2 moves.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists only of lowercase English letters.
* `s` can be converted to a palindrome using a finite number of moves. | Think about how dynamic programming can help solve the problem. For any fixed cell (r, c), can you calculate the maximum height of the pyramid for which it is the apex? Let us denote this value as dp[r][c]. How will the values at dp[r+1][c-1] and dp[r+1][c+1] help in determining the value at dp[r][c]? For the cell (r, c), is there a relation between the number of pyramids for which it serves as the apex and dp[r][c]? How does it help in calculating the answer? |
Python + 2 pointers + Explanation. | minimum-number-of-moves-to-make-palindrome | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMovesToMakePalindrome(self, s: str) -> int:\n # At each point, we look at the first and the last elements\n # if they are the same, then we skip them, else we find\n # another element in the string that matches the left\n # element and then we make the necessary swaps to move it\n # to the right place. \n # if we can\'t find that element -- this means this is the middle element\n # in the palindrome, we just move it one position to the right and continue\n # over the next few iterations, it will be moved to the center automatically\n # run it for string = "dpacacp", answer should be 4\n # the character that should be in the middle is "d"\n l, r, res, st = 0, len(s)-1, 0, list(s)\n while l < r:\n if st[l] != st[r]:\n i = r\n while i > l and st[l] != st[i]:\n i -= 1\n if i == l:\n st[i], st[i+1] = st[i+1], st[i]\n res += 1\n continue\n else:\n while i < r:\n st[i], st[i+1] = st[i+1], st[i]\n i += 1\n res += 1\n l, r = l+1, r-1\n return res\n``` | 1 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
[python3] easy to understand 2 pointer solution with comments | minimum-number-of-moves-to-make-palindrome | 0 | 1 | ```\n\'\'\'\nidea is to fix one side (left or right) and make other side equal to it\nfor e.g. \naabb , I will make right side equal to left.\n1. index[0] = a != index[3] = b \n2. now look for a from right to left \n3. once found swap with adjacent element till it reaches index[3].\n4. abba. is palindrome. took 2 swaps, \n\nfor cases like abb \n1. we fixed left side a. \n2. now from right we will move to left looking for a , we found it at index 0 which is our left\n3. now when left == right, just swap it with next adjacent element and continue.\n4. you will get your palindrome\n\n\'\'\'\n\nclass Solution:\n def minMovesToMakePalindrome(self, s: str) -> int:\n s = list(s)\n n = len(s)\n lt = 0\n rt = n-1\n ans = 0\n while lt < rt:\n l = lt\n r = rt\n while s[l] != s[r]:\n r -= 1\n # for abb like case\n # swap(s[r], s[r+1])\n # bab\n if l == r:\n s[r], s[r+1] = s[r+1], s[r]\n ans += 1\n continue\n else:\n\t\t\t# for aabb like case\n while r < rt:\n s[r], s[r+1] = s[r+1], s[r]\n ans += 1\n r += 1\n lt += 1\n rt -= 1\n return ans\n``` | 1 | You are given a string `s` consisting only of lowercase English letters.
In one **move**, you can select any two **adjacent** characters of `s` and swap them.
Return _the **minimum number of moves** needed to make_ `s` _a palindrome_.
**Note** that the input will be generated such that `s` can always be converted to a palindrome.
**Example 1:**
**Input:** s = "aabb "
**Output:** 2
**Explanation:**
We can obtain two palindromes from s, "abba " and "baab ".
- We can obtain "abba " from s in 2 moves: "a**ab**b " -> "ab**ab** " -> "abba ".
- We can obtain "baab " from s in 2 moves: "a**ab**b " -> "**ab**ab " -> "baab ".
Thus, the minimum number of moves needed to make s a palindrome is 2.
**Example 2:**
**Input:** s = "letelt "
**Output:** 2
**Explanation:**
One of the palindromes we can obtain from s in 2 moves is "lettel ".
One of the ways we can obtain it is "lete**lt** " -> "let**et**l " -> "lettel ".
Other palindromes such as "tleelt " can also be obtained in 2 moves.
It can be shown that it is not possible to obtain a palindrome in less than 2 moves.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists only of lowercase English letters.
* `s` can be converted to a palindrome using a finite number of moves. | Think about how dynamic programming can help solve the problem. For any fixed cell (r, c), can you calculate the maximum height of the pyramid for which it is the apex? Let us denote this value as dp[r][c]. How will the values at dp[r+1][c-1] and dp[r+1][c+1] help in determining the value at dp[r][c]? For the cell (r, c), is there a relation between the number of pyramids for which it serves as the apex and dp[r][c]? How does it help in calculating the answer? |
[python3] easy to understand 2 pointer solution with comments | minimum-number-of-moves-to-make-palindrome | 0 | 1 | ```\n\'\'\'\nidea is to fix one side (left or right) and make other side equal to it\nfor e.g. \naabb , I will make right side equal to left.\n1. index[0] = a != index[3] = b \n2. now look for a from right to left \n3. once found swap with adjacent element till it reaches index[3].\n4. abba. is palindrome. took 2 swaps, \n\nfor cases like abb \n1. we fixed left side a. \n2. now from right we will move to left looking for a , we found it at index 0 which is our left\n3. now when left == right, just swap it with next adjacent element and continue.\n4. you will get your palindrome\n\n\'\'\'\n\nclass Solution:\n def minMovesToMakePalindrome(self, s: str) -> int:\n s = list(s)\n n = len(s)\n lt = 0\n rt = n-1\n ans = 0\n while lt < rt:\n l = lt\n r = rt\n while s[l] != s[r]:\n r -= 1\n # for abb like case\n # swap(s[r], s[r+1])\n # bab\n if l == r:\n s[r], s[r+1] = s[r+1], s[r]\n ans += 1\n continue\n else:\n\t\t\t# for aabb like case\n while r < rt:\n s[r], s[r+1] = s[r+1], s[r]\n ans += 1\n r += 1\n lt += 1\n rt -= 1\n return ans\n``` | 1 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Straightforward Brute-Force in Python, Beating 100% | minimum-number-of-moves-to-make-palindrome | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIn each turn, it is necessary to match the first character `s[0]` and the last charactor `s[-1]` of the string `s`. Do nothing if the first and the last ones already match (i.e., `s[0] == s[-1]`). Otherwise, my greedy approach determines to replace the first or the last one by considering the cost. The cost to replace the first character `s[0]` is its distance to the leftmost occurrence of `s[-1]`; the cost to replace the last character `s[-1]` is its distance to the rightmost occurrence of `s[0]`. Pick up the choice with the lower cost and trim the first and the last characters from the string. \n\n# Complexity\n- Time complexity: $$O(n^2)$$, where $$n$$ is the length of the input string.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The input is $$O(n)$$. Only constant extra memeory is used.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMovesToMakePalindrome(self, s: str) -> int:\n l, r = 0, len(s)-1\n ans = 0\n while len(s) > 2:\n if s[0] != s[-1]:\n nl, nr = s.find(s[-1]), s.rfind(s[0])\n if nl < len(s) - nr - 1: \n ans += nl\n s = s[:nl] + s[nl+1:-1]\n else:\n ans += len(s) - nr - 1\n s = s[1:nr] + s[nr+1:]\n else:\n s = s[1:-1]\n return ans\n``` | 1 | You are given a string `s` consisting only of lowercase English letters.
In one **move**, you can select any two **adjacent** characters of `s` and swap them.
Return _the **minimum number of moves** needed to make_ `s` _a palindrome_.
**Note** that the input will be generated such that `s` can always be converted to a palindrome.
**Example 1:**
**Input:** s = "aabb "
**Output:** 2
**Explanation:**
We can obtain two palindromes from s, "abba " and "baab ".
- We can obtain "abba " from s in 2 moves: "a**ab**b " -> "ab**ab** " -> "abba ".
- We can obtain "baab " from s in 2 moves: "a**ab**b " -> "**ab**ab " -> "baab ".
Thus, the minimum number of moves needed to make s a palindrome is 2.
**Example 2:**
**Input:** s = "letelt "
**Output:** 2
**Explanation:**
One of the palindromes we can obtain from s in 2 moves is "lettel ".
One of the ways we can obtain it is "lete**lt** " -> "let**et**l " -> "lettel ".
Other palindromes such as "tleelt " can also be obtained in 2 moves.
It can be shown that it is not possible to obtain a palindrome in less than 2 moves.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists only of lowercase English letters.
* `s` can be converted to a palindrome using a finite number of moves. | Think about how dynamic programming can help solve the problem. For any fixed cell (r, c), can you calculate the maximum height of the pyramid for which it is the apex? Let us denote this value as dp[r][c]. How will the values at dp[r+1][c-1] and dp[r+1][c+1] help in determining the value at dp[r][c]? For the cell (r, c), is there a relation between the number of pyramids for which it serves as the apex and dp[r][c]? How does it help in calculating the answer? |
Straightforward Brute-Force in Python, Beating 100% | minimum-number-of-moves-to-make-palindrome | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nIn each turn, it is necessary to match the first character `s[0]` and the last charactor `s[-1]` of the string `s`. Do nothing if the first and the last ones already match (i.e., `s[0] == s[-1]`). Otherwise, my greedy approach determines to replace the first or the last one by considering the cost. The cost to replace the first character `s[0]` is its distance to the leftmost occurrence of `s[-1]`; the cost to replace the last character `s[-1]` is its distance to the rightmost occurrence of `s[0]`. Pick up the choice with the lower cost and trim the first and the last characters from the string. \n\n# Complexity\n- Time complexity: $$O(n^2)$$, where $$n$$ is the length of the input string.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The input is $$O(n)$$. Only constant extra memeory is used.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMovesToMakePalindrome(self, s: str) -> int:\n l, r = 0, len(s)-1\n ans = 0\n while len(s) > 2:\n if s[0] != s[-1]:\n nl, nr = s.find(s[-1]), s.rfind(s[0])\n if nl < len(s) - nr - 1: \n ans += nl\n s = s[:nl] + s[nl+1:-1]\n else:\n ans += len(s) - nr - 1\n s = s[1:nr] + s[nr+1:]\n else:\n s = s[1:-1]\n return ans\n``` | 1 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
Python Greedy 2 pointer | minimum-number-of-moves-to-make-palindrome | 0 | 1 | \tclass Solution:\n\t\tdef minMovesToMakePalindrome(self, s: str) -> int:\n\t\t\ts = list(s) #makes it easy for assignment op\n\n\t\t\tres = 0\n\t\t\tleft, right = 0, len(s) - 1\n\n\t\t\twhile left < right:\n\t\t\t\tl, r = left, right\n\n\t\t\t\t#find matching char\n\t\t\t\twhile s[l] != s[r]:\n\t\t\t\t\tr -= 1\n\n\t\t\t\t# if index dont match then swap\n\t\t\t\tif l != r:\n\t\t\t\t\t# swap one by one\n\t\t\t\t\twhile r < right:\n\t\t\t\t\t\ts[r], s[r + 1] = s[r + 1], s[r]\n\t\t\t\t\t\tres += 1\n\t\t\t\t\t\tr += 1\n\n\t\t\t\telse:\n\t\t\t\t\ts[r], s[r + 1] = s[r + 1], s[r]\n\t\t\t\t\tres += 1\n\t\t\t\t\tcontinue # get outside the main while loop\n\n\t\t\t\tleft += 1\n\t\t\t\tright -= 1\n\n\t\t\treturn res | 2 | You are given a string `s` consisting only of lowercase English letters.
In one **move**, you can select any two **adjacent** characters of `s` and swap them.
Return _the **minimum number of moves** needed to make_ `s` _a palindrome_.
**Note** that the input will be generated such that `s` can always be converted to a palindrome.
**Example 1:**
**Input:** s = "aabb "
**Output:** 2
**Explanation:**
We can obtain two palindromes from s, "abba " and "baab ".
- We can obtain "abba " from s in 2 moves: "a**ab**b " -> "ab**ab** " -> "abba ".
- We can obtain "baab " from s in 2 moves: "a**ab**b " -> "**ab**ab " -> "baab ".
Thus, the minimum number of moves needed to make s a palindrome is 2.
**Example 2:**
**Input:** s = "letelt "
**Output:** 2
**Explanation:**
One of the palindromes we can obtain from s in 2 moves is "lettel ".
One of the ways we can obtain it is "lete**lt** " -> "let**et**l " -> "lettel ".
Other palindromes such as "tleelt " can also be obtained in 2 moves.
It can be shown that it is not possible to obtain a palindrome in less than 2 moves.
**Constraints:**
* `1 <= s.length <= 2000`
* `s` consists only of lowercase English letters.
* `s` can be converted to a palindrome using a finite number of moves. | Think about how dynamic programming can help solve the problem. For any fixed cell (r, c), can you calculate the maximum height of the pyramid for which it is the apex? Let us denote this value as dp[r][c]. How will the values at dp[r+1][c-1] and dp[r+1][c+1] help in determining the value at dp[r][c]? For the cell (r, c), is there a relation between the number of pyramids for which it serves as the apex and dp[r][c]? How does it help in calculating the answer? |
Python Greedy 2 pointer | minimum-number-of-moves-to-make-palindrome | 0 | 1 | \tclass Solution:\n\t\tdef minMovesToMakePalindrome(self, s: str) -> int:\n\t\t\ts = list(s) #makes it easy for assignment op\n\n\t\t\tres = 0\n\t\t\tleft, right = 0, len(s) - 1\n\n\t\t\twhile left < right:\n\t\t\t\tl, r = left, right\n\n\t\t\t\t#find matching char\n\t\t\t\twhile s[l] != s[r]:\n\t\t\t\t\tr -= 1\n\n\t\t\t\t# if index dont match then swap\n\t\t\t\tif l != r:\n\t\t\t\t\t# swap one by one\n\t\t\t\t\twhile r < right:\n\t\t\t\t\t\ts[r], s[r + 1] = s[r + 1], s[r]\n\t\t\t\t\t\tres += 1\n\t\t\t\t\t\tr += 1\n\n\t\t\t\telse:\n\t\t\t\t\ts[r], s[r + 1] = s[r + 1], s[r]\n\t\t\t\t\tres += 1\n\t\t\t\t\tcontinue # get outside the main while loop\n\n\t\t\t\tleft += 1\n\t\t\t\tright -= 1\n\n\t\t\treturn res | 2 | You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
Return _the array after sorting it_.
**Example 1:**
**Input:** arr = \[0,1,2,3,4,5,6,7,8\]
**Output:** \[0,1,2,4,8,3,5,6,7\]
**Explantion:** \[0\] is the only integer with 0 bits.
\[1,2,4,8\] all have 1 bit.
\[3,5,6\] have 2 bits.
\[7\] has 3 bits.
The sorted array by bits is \[0,1,2,4,8,3,5,6,7\]
**Example 2:**
**Input:** arr = \[1024,512,256,128,64,32,16,8,4,2,1\]
**Output:** \[1,2,4,8,16,32,64,128,256,512,1024\]
**Explantion:** All integers have 1 bit in the binary representation, you should just sort them in ascending order.
**Constraints:**
* `1 <= arr.length <= 500`
* `0 <= arr[i] <= 104` | Consider a greedy strategy. Let’s start by making the leftmost and rightmost characters match with some number of swaps. If we figure out how to do that using the minimum number of swaps, then we can delete the leftmost and rightmost characters and solve the problem recursively. |
The Finest and Simple Solution | cells-in-a-range-on-an-excel-sheet | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def cellsInRange(self, s: str) -> List[str]:\n k,k1,l=int(s[1]),int(s[4]),[]\n for i in range(ord(s[0]),ord(s[3])+1):\n for j in range(int(s[1]),int(s[4])+1):\n l1=\'\'\n l1+=chr(i)\n l1+=str(j)\n l.append(l1)\n return l\n\n\n\n\n\n\n\n\n\n\n``` | 1 | A cell `(r, c)` of an excel sheet is represented as a string `" "` where:
* denotes the column number `c` of the cell. It is represented by **alphabetical letters**.
* For example, the `1st` column is denoted by `'A'`, the `2nd` by `'B'`, the `3rd` by `'C'`, and so on.
* is the row number `r` of the cell. The `rth` row is represented by the **integer** `r`.
You are given a string `s` in the format `": "`, where represents the column `c1`, represents the row `r1`, represents the column `c2`, and represents the row `r2`, such that `r1 <= r2` and `c1 <= c2`.
Return _the **list of cells**_ `(x, y)` _such that_ `r1 <= x <= r2` _and_ `c1 <= y <= c2`. The cells should be represented as **strings** in the format mentioned above and be sorted in **non-decreasing** order first by columns and then by rows.
**Example 1:**
**Input:** s = "K1:L2 "
**Output:** \[ "K1 ", "K2 ", "L1 ", "L2 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrows denote the order in which the cells should be presented.
**Example 2:**
**Input:** s = "A1:F1 "
**Output:** \[ "A1 ", "B1 ", "C1 ", "D1 ", "E1 ", "F1 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrow denotes the order in which the cells should be presented.
**Constraints:**
* `s.length == 5`
* `'A' <= s[0] <= s[3] <= 'Z'`
* `'1' <= s[1] <= s[4] <= '9'`
* `s` consists of uppercase English letters, digits and `':'`. | null |
[Java/Python 3] Simple code w/ analysis. | cells-in-a-range-on-an-excel-sheet | 1 | 1 | \n\n```java\n public List<String> cellsInRange(String s) {\n char c1 = s.charAt(0), c2 = s.charAt(3);\n char r1 = s.charAt(1), r2 = s.charAt(4);\n List<String> cells = new ArrayList<>();\n for (char c = c1; c <= c2; ++c) {\n for (char r = r1; r <= r2; ++r) {\n cells.add("" + c + r);\n }\n }\n return cells;\n }\n```\n```python\n def cellsInRange(self, s: str) -> List[str]:\n c1, c2 = ord(s[0]), ord(s[3])\n r1, r2 = int(s[1]), int(s[4])\n return [chr(c) + str(r) for c in range(c1, c2 + 1) for r in range(r1, r2 + 1)]\n```\nPython 3 Two liner: credit to **@stefan4trivia**:\n```python\ndef cellsInRange(self, s: str) -> List[str]:\n c1, r1, _, c2, r2 = map(ord, s)\n return [chr(c) + chr(r) for c in range(c1, c2 + 1) for r in range(r1, r2 + 1)]\n```\n**Analysis:**\n\nTime: `O((c2 - c1 + 1) * (r2 - r1 + 1))`, space: `O(1)` - excluding return space. | 43 | A cell `(r, c)` of an excel sheet is represented as a string `" "` where:
* denotes the column number `c` of the cell. It is represented by **alphabetical letters**.
* For example, the `1st` column is denoted by `'A'`, the `2nd` by `'B'`, the `3rd` by `'C'`, and so on.
* is the row number `r` of the cell. The `rth` row is represented by the **integer** `r`.
You are given a string `s` in the format `": "`, where represents the column `c1`, represents the row `r1`, represents the column `c2`, and represents the row `r2`, such that `r1 <= r2` and `c1 <= c2`.
Return _the **list of cells**_ `(x, y)` _such that_ `r1 <= x <= r2` _and_ `c1 <= y <= c2`. The cells should be represented as **strings** in the format mentioned above and be sorted in **non-decreasing** order first by columns and then by rows.
**Example 1:**
**Input:** s = "K1:L2 "
**Output:** \[ "K1 ", "K2 ", "L1 ", "L2 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrows denote the order in which the cells should be presented.
**Example 2:**
**Input:** s = "A1:F1 "
**Output:** \[ "A1 ", "B1 ", "C1 ", "D1 ", "E1 ", "F1 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrow denotes the order in which the cells should be presented.
**Constraints:**
* `s.length == 5`
* `'A' <= s[0] <= s[3] <= 'Z'`
* `'1' <= s[1] <= s[4] <= '9'`
* `s` consists of uppercase English letters, digits and `':'`. | null |
🔥[Python 3] Two loops + 1 line bonus, beats 97% 🥷🏼 | cells-in-a-range-on-an-excel-sheet | 0 | 1 | ```python3 []\nclass Solution:\n def cellsInRange(self, s: str) -> List[str]:\n res = []\n for ch in range(ord(s[0]), ord(s[3])+1):\n for i in range(int(s[1]), int(s[4])+1):\n res.append(f\'{chr(ch)}{i}\')\n return res\n```\n```python3 []\nclass Solution:\n def cellsInRange(self, s: str) -> List[str]:\n return [f\'{chr(ch)}{i}\' for ch in range(ord(s[0]), ord(s[3])+1) for i in range(int(s[1]), int(s[4])+1)]\n```\n\n\n\n | 4 | A cell `(r, c)` of an excel sheet is represented as a string `" "` where:
* denotes the column number `c` of the cell. It is represented by **alphabetical letters**.
* For example, the `1st` column is denoted by `'A'`, the `2nd` by `'B'`, the `3rd` by `'C'`, and so on.
* is the row number `r` of the cell. The `rth` row is represented by the **integer** `r`.
You are given a string `s` in the format `": "`, where represents the column `c1`, represents the row `r1`, represents the column `c2`, and represents the row `r2`, such that `r1 <= r2` and `c1 <= c2`.
Return _the **list of cells**_ `(x, y)` _such that_ `r1 <= x <= r2` _and_ `c1 <= y <= c2`. The cells should be represented as **strings** in the format mentioned above and be sorted in **non-decreasing** order first by columns and then by rows.
**Example 1:**
**Input:** s = "K1:L2 "
**Output:** \[ "K1 ", "K2 ", "L1 ", "L2 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrows denote the order in which the cells should be presented.
**Example 2:**
**Input:** s = "A1:F1 "
**Output:** \[ "A1 ", "B1 ", "C1 ", "D1 ", "E1 ", "F1 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrow denotes the order in which the cells should be presented.
**Constraints:**
* `s.length == 5`
* `'A' <= s[0] <= s[3] <= 'Z'`
* `'1' <= s[1] <= s[4] <= '9'`
* `s` consists of uppercase English letters, digits and `':'`. | null |
Simple Python3 | NO ord(), NO chr() | cells-in-a-range-on-an-excel-sheet | 0 | 1 | ```\nclass Solution:\n def cellsInRange(self, s: str) -> List[str]:\n start, end = s.split(\':\')\n start_letter, start_num = start[0], int(start[-1])\n end_letter, end_num = end[0], int(end[1])\n alphabet = list(\'ABCDEFGHIJKLMNOPQRSTUVWXYZ\')\n alphabet_slice = \\\n alphabet[alphabet.index(start_letter):alphabet.index(end_letter) + 1]\n res = list()\n for el in alphabet_slice:\n res += [el + str(num) for num in range(start_num, end_num + 1)]\n return res\n``` | 2 | A cell `(r, c)` of an excel sheet is represented as a string `" "` where:
* denotes the column number `c` of the cell. It is represented by **alphabetical letters**.
* For example, the `1st` column is denoted by `'A'`, the `2nd` by `'B'`, the `3rd` by `'C'`, and so on.
* is the row number `r` of the cell. The `rth` row is represented by the **integer** `r`.
You are given a string `s` in the format `": "`, where represents the column `c1`, represents the row `r1`, represents the column `c2`, and represents the row `r2`, such that `r1 <= r2` and `c1 <= c2`.
Return _the **list of cells**_ `(x, y)` _such that_ `r1 <= x <= r2` _and_ `c1 <= y <= c2`. The cells should be represented as **strings** in the format mentioned above and be sorted in **non-decreasing** order first by columns and then by rows.
**Example 1:**
**Input:** s = "K1:L2 "
**Output:** \[ "K1 ", "K2 ", "L1 ", "L2 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrows denote the order in which the cells should be presented.
**Example 2:**
**Input:** s = "A1:F1 "
**Output:** \[ "A1 ", "B1 ", "C1 ", "D1 ", "E1 ", "F1 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrow denotes the order in which the cells should be presented.
**Constraints:**
* `s.length == 5`
* `'A' <= s[0] <= s[3] <= 'Z'`
* `'1' <= s[1] <= s[4] <= '9'`
* `s` consists of uppercase English letters, digits and `':'`. | null |
[Python3] 1-line | cells-in-a-range-on-an-excel-sheet | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/bb5647e856ff11b072f9c51a140e0f243c100171) for solutions of weekly 283.\n\n```\nclass Solution:\n def cellsInRange(self, s: str) -> List[str]:\n return [chr(c)+str(r) for c in range(ord(s[0]), ord(s[3])+1) for r in range(int(s[1]), int(s[4])+1)]\n``` | 10 | A cell `(r, c)` of an excel sheet is represented as a string `" "` where:
* denotes the column number `c` of the cell. It is represented by **alphabetical letters**.
* For example, the `1st` column is denoted by `'A'`, the `2nd` by `'B'`, the `3rd` by `'C'`, and so on.
* is the row number `r` of the cell. The `rth` row is represented by the **integer** `r`.
You are given a string `s` in the format `": "`, where represents the column `c1`, represents the row `r1`, represents the column `c2`, and represents the row `r2`, such that `r1 <= r2` and `c1 <= c2`.
Return _the **list of cells**_ `(x, y)` _such that_ `r1 <= x <= r2` _and_ `c1 <= y <= c2`. The cells should be represented as **strings** in the format mentioned above and be sorted in **non-decreasing** order first by columns and then by rows.
**Example 1:**
**Input:** s = "K1:L2 "
**Output:** \[ "K1 ", "K2 ", "L1 ", "L2 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrows denote the order in which the cells should be presented.
**Example 2:**
**Input:** s = "A1:F1 "
**Output:** \[ "A1 ", "B1 ", "C1 ", "D1 ", "E1 ", "F1 "\]
**Explanation:**
The above diagram shows the cells which should be present in the list.
The red arrow denotes the order in which the cells should be presented.
**Constraints:**
* `s.length == 5`
* `'A' <= s[0] <= s[3] <= 'Z'`
* `'1' <= s[1] <= s[4] <= '9'`
* `s` consists of uppercase English letters, digits and `':'`. | null |
Python Solution using AP Sum Explained | append-k-integers-with-minimal-sum | 0 | 1 | **Idea Used:**\nHere we use the idea of adding the sum of values that exist b/w all consecutive values until we expire all k given to us. \n\n**Steps:**\n\n1. Sort the numbers and add 0 to the start and 2000000001 to the end of the list.\n2. Now go through all the n values of nums\n3. For each iteration select ith value as start and i+1th value as end\n4. In the current iteration we will be adding values b/w start and end as long as k does\'nt expire\n5. If start == end then continue\n6. Now we sill be using the values start+1, start+2 ... end -2, end-1. We would not use the values start and end themselves.\n7. We know that sum of consecutive integers is given by the AP formula with `d = 1`\n8. Add this sum to the result and remove the number of integers used from k\n\n**Why I added 0 and 2000000001:**\nSince the +ve integers start from 1, and it is not certain that the list might start from 1. We should manually take care of the smallest elements to add so as to minimize the possible sum. So I added 0 to allow it to blend in with the algorithm perfectly.\nThe reason I added 2000000001 is to prevent ourselves from running out of +ve numbers even when all k havent expired\n\n**Formula for sum in AP (arithmetic progression)**\nThe sum of given AP `a, a+d, a+2d, a+3d ... a+(i-1)d ... a+(n-1)d` is:\n`S = n/2[2a + (n \u2212 1) \xD7 d]` where a is the first term and n is the total number of terms in AP\n*In our case since we will be dealing with consecutive numbers `d = 1`*\n\n```\nclass Solution:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n nums.sort()\n res = 0\n nums.insert(0, 0)\n nums.append(2000000001)\n n = len(nums)\n for i in range(n-1):\n start = nums[i] # This is the lowerbound for current iteration\n end = nums[i+1] # This is the higherbound for current iteration\n if start == end:\n continue\n a = start + 1 # Starting value is lowerbound + 1\n n = min(end - start - 1, k) # Since the total number possible b/w start and end might be more than the k numbers left, so always choose the minimum.\n v = (n*(2*a + n - 1))//2 # n/2[2a + (n-1)d] with d = 1\n res += v # Add the sum of elements selected into res\n k -= n # n number of k\'s expired, thus k decrements\n return res\n``` | 8 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
[Java/Python 3] Two methods w/ brief explanation and analysis. | append-k-integers-with-minimal-sum | 1 | 1 | **Method 1:**\nSort and Track low missing bound and compute the arithmetic sequence.\n\n1. Sort the input;\n2. Starting from `1` as the lower bound of the missing range, then based on current `num` and `k`, determine current missing upper bound `hi`; Compute the subtotal in [lo, hi] and add it to `ans`.\n```java\n public long minimalKSum(int[] nums, int k) {\n Arrays.sort(nums);\n long ans = 0, lo = 1;\n for (int num : nums) {\n if (num > lo) {\n long hi = Math.min(num - 1, lo + k - 1);\n int cnt = (int)(hi - lo + 1);\n ans += (lo + hi) * cnt / 2;\n k -= cnt;\n if (k == 0) {\n return ans;\n }\n } \n lo = num + 1;\n }\n if (k > 0) {\n ans += (lo + lo + k - 1) * k / 2;\n }\n return ans;\n }\n```\n```python\n def minimalKSum(self, nums: List[int], k: int) -> int:\n ans, lo = 0, 1\n cnt = 0\n for num in sorted(nums):\n if num > lo:\n hi = min(num - 1, k - 1 + lo)\n cnt = hi - lo + 1\n ans += (lo + hi) * cnt // 2 \n k -= cnt\n if k == 0:\n return ans\n lo = num + 1\n if k > 0:\n ans += (lo + lo + k - 1) * k // 2\n return ans\n```\n\n----\n\n**Method 2:**\n\nStart from the sum of `1` to `k`, `ans`, then traverse the sorted distinct numbers of input array, `nums`; whenever find a `num` not greater than `k`, we need to deduct it from `ans` and add `++k`.\n\n\n```java\n public long minimalKSum(int[] nums, int k) {\n long ans = k * (k + 1L) / 2;\n TreeSet<Integer> unique = new TreeSet<>();\n for (int num : nums) {\n unique.add(num);\n }\n while (!unique.isEmpty()) {\n int first = unique.pollFirst();\n if (k >= first) {\n ans += ++k - first;\n }\n }\n return ans;\n }\n```\n\n```python\nfrom sortedcontainers import SortedSet\n\nclass class:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n ans = k * (k + 1) // 2\n for num in SortedSet(nums):\n if k >= num:\n k += 1\n ans += k - num\n return ans\n```\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(n)` - including sorting space, where `n = nums.length`. | 17 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
[Python3] swap | append-k-integers-with-minimal-sum | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/bb5647e856ff11b072f9c51a140e0f243c100171) for solutions of weekly 283.\n\n```\nclass Solution:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n ans = k*(k+1)//2\n prev = -inf \n for x in sorted(nums): \n if prev < x: \n if x <= k: \n k += 1\n ans += k - x\n else: break\n prev = x\n return ans \n``` | 10 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
Python Explanation || sort and add | append-k-integers-with-minimal-sum | 0 | 1 | **Idea:** \n* As we need samllest sum possible we need to choose smallest numbers that we can add.\n* To get smallest numbers we need to sort `nums` first.\n* Then append the numbers which are between suppose `(prev,curr)` or `(nums[i],nums[i+1])`.\n* This way we can get smallest numbers possible.\n* Now we need to take care of case when all numbers in array/list is finished but we still need to append some numbers.\n* Now in this case we will append numbers starting from `prev` till remaining numbers.\n\n**Example:**\nFirst Case:\n```\nnums = [1,4,25,10,25], k = 2\nSo let\'s first sort nums.\nnums=[1,4,10,25,25]\n\nNow prev=0 # starting point\ncurr=nums[0]=1 \nNow there is no number betwenn (prev,curr) that we can add in array/list.\nSo, move curr to next elemnt of nums and prev to curr.\n\nprev=1\ncurr=4\n(prev,curr)=2,3\nsum=2+3=5\nSo add 2 and 3. Now k become 0 so stop the process.\n\nAnd return sum.\n```\n\nSecond case:\n```\nnums = [5,6], k = 6\nso let\'s first sort nums.\nnums=[5,6]\n\nNow prev=0 # starting point\ncurr=nums[0]=5\n(prev,curr)=1,2,3,4\nsum=1+2+3+4=10\nk=2\nAs k is not 0 continue the process.\n\nNow prev=curr=5\ncurr=nums[1]=6\nNow there is no number betwenn (prev,curr) that we can add in array/list.\n\nnow prev=curr=6\nbut now we finished all numbers of nums. but still we need to add two more numbers.\nwe do not have number to update curr.\n\nSo, now start from prev and continue adding numbers untill k becomes zero.\nnumbers=7,8\n\nsum=sum+7+8\n =10+7+8\n =25\n\nand k=0\nreturn sum\n```\n\n**Note:**\nWe can\'t just iterate from all numbers between prev and curr to find sum of added number. As it might give TLE. So we can use formula for sum of Arithmetic Progression. As number between prev and curr will be in Arithmetic Progression with difference 1.\n\n**Formula for sum of AP:**\n```\nFormula 1: n/2(a + l)\nwhere,\nn = number of terms\na=first term\nl=last term\n\nFormula 2: n/2[2a + (n \u2212 1) \xD7 d]\nWhere, \nn = number of terms\na=first term\nd=difference between two term\n```\n\nWe will be using this formula to find sum betwenn (prev,curr).\n\n**Code:**\n```\nclass Solution:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n n=len(nums)\n curr=prev=0 # intialize both curr and prev \n nums.sort() # sort the nums\n sum=0 \n for i in range(n):\n curr=nums[i] # make curr equal to prev\n diff=curr-(prev+1) # find if there is any numbers in (prev,curr)\n if diff<=0: # if no then update prev and continue \n prev=curr\n continue\n if diff>k: # if yes then if number between (prev,curr) is more then k \n diff=k # then we will consider first k numbers only\n curr=prev+1+k # update curr to last number that we will add to use formula 1 of A.P.\n sum+=(diff*(curr+prev)//2) # formula 1 of A.P.\n prev=curr # update prev to curr\n k-=diff # update k\n if k==0: # if k is 0 then return\n break\n if k: # second case # we have finish nums but wnat to add more numbers\n sum+=(k*(2*prev+k+1)//2) # use formual 2 of A.P. we take d=1\n return sum\n```\nUpvote if you find it helpful :) | 8 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
Easy & explained python solution || faster than 99% | append-k-integers-with-minimal-sum | 0 | 1 | the idea is to find the last (biggest) number we gonna add to the list, by incrementing k by 1 each time we find a smaller number than it in the sorted list.\nafter that, we calculate the sum from 1 to the last added number, and remove the sum of the existing numbers (removable_sum).\nfor example, if k was 50 and the list contains 20 and 25, then k will become 52, and we calculate the sum of the 52 first numbers, then we remove 20 + 25 because they were already existing.\n```python\ndef minimalKSum(self, nums: List[int], k: int) -> int:\n\tnums = list(set(nums)) # to remove duplicated numbers\n\tnums.sort() # sorting the new list\n\tlast_term = k\n\tremovable_sum = 0\n\tfor num in nums :\n\t\tif (num <= last_term) : # if the current number is in the range of the k first numbers\n\t\t\tlast_term += 1 # we increment the last number we\'re going to add\n\t\t\tremovable_sum += num # adding the current number the sum of existing numbers\n\t\telse :\n\t\t\tbreak # if we found the k th number we break the loop\n\tsomme = (last_term * (1 + last_term) / 2) - removable_sum # we calculate the sum of the arithmetic sequence minus the sum of the existing numbers\n\treturn int(somme)\n``` | 5 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
Python | math solution with explanation | append-k-integers-with-minimal-sum | 0 | 1 | \n# Approach\nThe general idea is like: if element in array is <=k, we need to expand k to k+1 to make get first k element not in the array possible. If the element <=k, we need to sum them together, so the final result is k*(k+1)//2-sum of the appeared element.\n\nDetail is as follows:\nFirst let the element in the array be distinct.Then sort it, it is important because if we don\'t sort it, we may encounter some issue like this: we get an array [6,5], k=5, we found that 5 is <=k, so we expand k to k+1, which is 6, but actually 6 appears in the array so we can\'t use it.\nAfter this, we set object sums to sum all element which is <=k in the array, and then iterate the array, if element <=k: k+=1, sums+=nums[i].\n\n# Complexity\n- Time complexity:\nO(n)\n\n\n\n# Code\n```\nclass Solution:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n nums=list(set(nums))\n nums.sort()\n # print(nums)\n n=len(nums)\n sums=0\n for i in range(n):\n if nums[i]<=k:\n k+=1\n sums+=nums[i]\n # print(k,nums[i],sums)\n res=k*(k+1)//2-sums\n return res\n \n\n\n\n\n\n\n\n\n\n\n\n``` | 4 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
Python O(nlogn) solution with n(n+1) / 2 Range Sum | append-k-integers-with-minimal-sum | 0 | 1 | My first approach was the naive **O(n + k)** time but due to the large magnitude of k I was experiencing TLE.\n\n**New Approach: O(nlogn)**\n\n1) Sort nums: (The intution is that the "gaps" between adjacent sorted elements is space where we can add our k items"\n2) Define range sum n (n+1) / 2\n3) Iterate through these "gaps" and add the range sum to the solution. If the gap is larger than remaining k skip to next step.\n4) Once the gaps have been exhausted compute and add the range sum from the end to the end+remaining k\n5) Return this sum!\n\n```\nclass Solution:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n \n # define range sum\n def range_sum(start, stop, step=1):\n number_of_terms = (stop - start) // step\n sum_of_extrema = start + (stop - step)\n return number_of_terms * sum_of_extrema // 2\n \n nums = list(set(nums)) # remove repeats\n nums.sort() # O(nlogn)\n \n # total sum\n sol = 0\n \n prev = 0\n ptr = 0\n \n while k > 0:\n if ptr < len(nums):\n # potential window to add nums\n gap = nums[ptr] - prev - 1\n \n sol += range_sum(prev+1, min(nums[ptr], prev+k+1)) # add range sum O(1)\n \n k -= gap\n prev = nums[ptr]\n ptr += 1\n else: # draw numbers after all numbers in the list\n sol += range_sum(prev+1, prev + remaining + 1)\n k = 0\n \n return sol\n``` | 4 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
python | O(nlogn) solution using sort | 97.65% faster | append-k-integers-with-minimal-sum | 0 | 1 | A straightforward solution would be to initialize the sum with zero, search for the smallest integers that are not in `nums`, and add them to the sum. However, this approach would yield a TLE because the range we are searching within could be as big as `1e9`. \n\nTherefore, working within the range of `len(nums)` would be far more efficient because at most we would be working with `1e5` elements. This is why we can afford to sort and filter `nums` beforehand without getting TLE.\n\nThe idea behind this solution is that we initialize the sum with the sum of the first positive `k` integers, and when we find one of these integers in `nums`, we remove it from the sum (by subtracting) and add the next integer after `k`.\n\nAnother note is that after sorting, we can break the loop early when values become bigger than `k`, thus saving a bit more time.\n\n```python\nclass Solution:\n def minimalKSum(self, nums: List[int], k: int) -> int:\n k_sum = k * (k + 1) // 2\n nums = [*set(nums)]\n nums.sort()\n \n for num in nums:\n if num > k:\n break\n else:\n k += 1\n k_sum += k - num\n \n return k_sum\n```\n\n\n\n | 1 | You are given an integer array `nums` and an integer `k`. Append `k` **unique positive** integers that do **not** appear in `nums` to `nums` such that the resulting total sum is **minimum**.
Return _the sum of the_ `k` _integers appended to_ `nums`.
**Example 1:**
**Input:** nums = \[1,4,25,10,25\], k = 2
**Output:** 5
**Explanation:** The two unique positive integers that do not appear in nums which we append are 2 and 3.
The resulting sum of nums is 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70, which is the minimum.
The sum of the two integers appended is 2 + 3 = 5, so we return 5.
**Example 2:**
**Input:** nums = \[5,6\], k = 6
**Output:** 25
**Explanation:** The six unique positive integers that do not appear in nums which we append are 1, 2, 3, 4, 7, and 8.
The resulting sum of nums is 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36, which is the minimum.
The sum of the six integers appended is 1 + 2 + 3 + 4 + 7 + 8 = 25, so we return 25.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= 108` | Loop through the line of people and decrement the number of tickets for each to buy one at a time as if simulating the line moving forward. Keep track of how many tickets have been sold up until person k has no more tickets to buy. Remember that those who have no more tickets to buy will leave the line. |
Simple solution with HashMap in Python3 | create-binary-tree-from-descriptions | 0 | 1 | # Intuition\nHere we have:\n- list of `descriptions`, that consists with `[parent, child, isLeft]`\n- our goal is to **restore** a **Binary Search tree** from that list\n\nAn algorithm is **simple**: use **HashMap** to associate **node values** with nodes.\n\nThe catchiest thing is to find **a root**.\nBut remember, that root don\'t have a parent. We could **track** it with **HashSet**.\n\n# Approach\n1. declare `nodes` **HashMap**\n2. declare `hasParent` set to store **children**, that has parents\n3. iterate over `descriptions` and map `parent` node val to `child` according to `isLeft` edge (`0` - **right** edge, `1` - **left**)\n4. check for **root** in `nodes.keys` with `hasParent`\n5. return `nodes[root]` as a root of a **BST**\n\n# Complexity\n- Time complexity: **O(N)**, to iterate over `descriptons`\n\n- Space complexity: **O(N)**, to store `nodes` and `hasParent`\n\n# Code\n```\nclass Solution:\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n nodes = defaultdict(TreeNode)\n hasParent = set()\n\n for parent, child, isLeft in descriptions:\n if child not in nodes: nodes[child] = TreeNode(child)\n if parent not in nodes: nodes[parent] = TreeNode(parent)\n \n if isLeft: nodes[parent].left = nodes[child]\n else: nodes[parent].right = nodes[child]\n \n hasParent.add(child)\n \n for child in nodes.keys():\n if child not in hasParent:\n return nodes[child]\n``` | 1 | You are given a 2D integer array `descriptions` where `descriptions[i] = [parenti, childi, isLefti]` indicates that `parenti` is the **parent** of `childi` in a **binary** tree of **unique** values. Furthermore,
* If `isLefti == 1`, then `childi` is the left child of `parenti`.
* If `isLefti == 0`, then `childi` is the right child of `parenti`.
Construct the binary tree described by `descriptions` and return _its **root**_.
The test cases will be generated such that the binary tree is **valid**.
**Example 1:**
**Input:** descriptions = \[\[20,15,1\],\[20,17,0\],\[50,20,1\],\[50,80,0\],\[80,19,1\]\]
**Output:** \[50,20,80,15,17,19\]
**Explanation:** The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.
**Example 2:**
**Input:** descriptions = \[\[1,2,1\],\[2,3,0\],\[3,4,1\]\]
**Output:** \[1,2,null,null,3,4\]
**Explanation:** The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.
**Constraints:**
* `1 <= descriptions.length <= 104`
* `descriptions[i].length == 3`
* `1 <= parenti, childi <= 105`
* `0 <= isLefti <= 1`
* The binary tree described by `descriptions` is valid. | Consider the list structure ...A → (B → ... → C) → D..., where the nodes between B and C (inclusive) form a group, A is the last node of the previous group, and D is the first node of the next group. How can you utilize this structure? Suppose you have B → ... → C reversed (because it was of even length) so that it is now C → ... → B. What references do you need to fix so that the transitions between the previous, current, and next groups are correct? A.next should be set to C, and B.next should be set to D. Once the current group is finished being modified, you need to find the new A, B, C, and D nodes for the next group. How can you use the old A, B, C, and D nodes to find the new ones? The new A is either the old B or old C depending on if the group was of even or odd length. The new B is always the old D. The new C and D can be found based on the new B and the next group's length. You can set the initial values of A, B, C, and D to A = null, B = head, C = head, D = head.next. Repeat the steps from the previous hints until D is null. |
[Java/Python 3] 2 codes: HashMap and BFS, w/ brief explanation and analysis. | create-binary-tree-from-descriptions | 1 | 1 | **Q & A:**\nQ1: How to get root?\nA1: The node that does NOT have any parent is the root.\nUse `2` sets to store parents and kids respectively; from the `keySet()` of `valToNode`, `parents`, remove all `kids`, there must be one remaining, the root.\n\n**End of Q & A**\n\n**HashMap**\n\n```java\n public TreeNode createBinaryTree(int[][] descriptions) {\n Set<Integer> kids = new HashSet<>();\n Map<Integer, TreeNode> valToNode = new HashMap<>();\n for (int[] d : descriptions) {\n int parent = d[0], kid = d[1], left = d[2];\n valToNode.putIfAbsent(parent, new TreeNode(parent));\n valToNode.putIfAbsent(kid, new TreeNode(kid));\n kids.add(kid);\n if (left == 1) {\n valToNode.get(parent).left = valToNode.get(kid);\n }else {\n valToNode.get(parent).right = valToNode.get(kid);\n }\n }\n valToNode.keySet().removeAll(kids);\n return valToNode.values().iterator().next();\n }\n```\n```python\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n val_to_node, kids = {}, set()\n for parent, kid, left in descriptions:\n kids.add(kid)\n parent_node = val_to_node.setdefault(parent, TreeNode(parent))\n kid_node = val_to_node.setdefault(kid, TreeNode(kid))\n if left == 1:\n parent_node.left = kid_node\n else:\n parent_node.right = kid_node\n return val_to_node[(val_to_node.keys() - kids).pop()]\n```\n\n----\n\n**BFS**\n\n1. Build graph from parent to kids, and add parent and kids to `HashSet`s respectively;\n2. Remove all `kids` from `parents`, and the remaining is `root`;\n3. Starting from `root`, use BFS to construct binary tree according to the graph `parentsToKids` built in `1.`.\n\n```java\n public TreeNode createBinaryTree(int[][] descriptions) {\n Set<Integer> kids = new HashSet<>(), parents = new HashSet<>();\n Map<Integer, List<int[]>> parentToKids = new HashMap<>();\n for (int[] d : descriptions) {\n int parent = d[0], kid = d[1];\n parents.add(parent);\n kids.add(kid);\n parentToKids.computeIfAbsent(parent, l -> new ArrayList<>()).add(new int[]{kid, d[2]});\n }\n parents.removeAll(kids);\n TreeNode root = new TreeNode(parents.iterator().next());\n Deque<TreeNode> dq = new ArrayDeque<>();\n dq.offer(root);\n while (!dq.isEmpty()) {\n TreeNode parent = dq.poll();\n for (int[] kidInfo : parentToKids.getOrDefault(parent.val, Arrays.asList())) {\n int kid = kidInfo[0], left = kidInfo[1];\n dq.offer(new TreeNode(kid));\n if (left == 1) {\n parent.left = dq.peekLast();\n }else {\n parent.right = dq.peekLast();\n }\n }\n }\n return root;\n }\n```\n\n```python\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n g, kids, parents = defaultdict(list), set(), set()\n for parent, kid, left in descriptions:\n kids.add(kid)\n parents.add(parent)\n g[parent].append([kid, left])\n parents.difference_update(kids)\n root = TreeNode(parents.pop())\n dq = deque([root])\n while dq:\n parent = dq.popleft()\n for kid, left in g.pop(parent.val, []): \n dq.append(TreeNode(kid))\n if left == 1:\n parent.left = dq[-1]\n else:\n parent.right = dq[-1]\n return root\n```\n\n**Analysis:**\n\nEach node/value is visited at most twice, therefore,\n\nTime & space: `O(V + E)`, where `V = # of nodes, E = # of edges`. | 20 | You are given a 2D integer array `descriptions` where `descriptions[i] = [parenti, childi, isLefti]` indicates that `parenti` is the **parent** of `childi` in a **binary** tree of **unique** values. Furthermore,
* If `isLefti == 1`, then `childi` is the left child of `parenti`.
* If `isLefti == 0`, then `childi` is the right child of `parenti`.
Construct the binary tree described by `descriptions` and return _its **root**_.
The test cases will be generated such that the binary tree is **valid**.
**Example 1:**
**Input:** descriptions = \[\[20,15,1\],\[20,17,0\],\[50,20,1\],\[50,80,0\],\[80,19,1\]\]
**Output:** \[50,20,80,15,17,19\]
**Explanation:** The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.
**Example 2:**
**Input:** descriptions = \[\[1,2,1\],\[2,3,0\],\[3,4,1\]\]
**Output:** \[1,2,null,null,3,4\]
**Explanation:** The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.
**Constraints:**
* `1 <= descriptions.length <= 104`
* `descriptions[i].length == 3`
* `1 <= parenti, childi <= 105`
* `0 <= isLefti <= 1`
* The binary tree described by `descriptions` is valid. | Consider the list structure ...A → (B → ... → C) → D..., where the nodes between B and C (inclusive) form a group, A is the last node of the previous group, and D is the first node of the next group. How can you utilize this structure? Suppose you have B → ... → C reversed (because it was of even length) so that it is now C → ... → B. What references do you need to fix so that the transitions between the previous, current, and next groups are correct? A.next should be set to C, and B.next should be set to D. Once the current group is finished being modified, you need to find the new A, B, C, and D nodes for the next group. How can you use the old A, B, C, and D nodes to find the new ones? The new A is either the old B or old C depending on if the group was of even or odd length. The new B is always the old D. The new C and D can be found based on the new B and the next group's length. You can set the initial values of A, B, C, and D to A = null, B = head, C = head, D = head.next. Repeat the steps from the previous hints until D is null. |
[Python3] simulation | create-binary-tree-from-descriptions | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/bb5647e856ff11b072f9c51a140e0f243c100171) for solutions of weekly 283.\n\n```\nclass Solution:\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n mp = {}\n seen = set()\n for p, c, left in descriptions: \n if p not in mp: mp[p] = TreeNode(p)\n if c not in mp: mp[c] = TreeNode(c)\n if left: mp[p].left = mp[c]\n else: mp[p].right = mp[c]\n seen.add(c)\n for p, _, _ in descriptions: \n if p not in seen: return mp[p]\n``` | 13 | You are given a 2D integer array `descriptions` where `descriptions[i] = [parenti, childi, isLefti]` indicates that `parenti` is the **parent** of `childi` in a **binary** tree of **unique** values. Furthermore,
* If `isLefti == 1`, then `childi` is the left child of `parenti`.
* If `isLefti == 0`, then `childi` is the right child of `parenti`.
Construct the binary tree described by `descriptions` and return _its **root**_.
The test cases will be generated such that the binary tree is **valid**.
**Example 1:**
**Input:** descriptions = \[\[20,15,1\],\[20,17,0\],\[50,20,1\],\[50,80,0\],\[80,19,1\]\]
**Output:** \[50,20,80,15,17,19\]
**Explanation:** The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.
**Example 2:**
**Input:** descriptions = \[\[1,2,1\],\[2,3,0\],\[3,4,1\]\]
**Output:** \[1,2,null,null,3,4\]
**Explanation:** The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.
**Constraints:**
* `1 <= descriptions.length <= 104`
* `descriptions[i].length == 3`
* `1 <= parenti, childi <= 105`
* `0 <= isLefti <= 1`
* The binary tree described by `descriptions` is valid. | Consider the list structure ...A → (B → ... → C) → D..., where the nodes between B and C (inclusive) form a group, A is the last node of the previous group, and D is the first node of the next group. How can you utilize this structure? Suppose you have B → ... → C reversed (because it was of even length) so that it is now C → ... → B. What references do you need to fix so that the transitions between the previous, current, and next groups are correct? A.next should be set to C, and B.next should be set to D. Once the current group is finished being modified, you need to find the new A, B, C, and D nodes for the next group. How can you use the old A, B, C, and D nodes to find the new ones? The new A is either the old B or old C depending on if the group was of even or odd length. The new B is always the old D. The new C and D can be found based on the new B and the next group's length. You can set the initial values of A, B, C, and D to A = null, B = head, C = head, D = head.next. Repeat the steps from the previous hints until D is null. |
Python Solution using HashMap with Steps | create-binary-tree-from-descriptions | 0 | 1 | Here we use a HashMap to keep track of node values and their references along with the fact if that node has a parent or not. We develop the Binary Tree as we go along. Finally we check which node has no parent as that node is the root node.\n1. Maintain a hash map with the keys being node values and value being a list of its `REFERENCE` and a `HAS_PARENT` property which tells weather or not it has a parent or not (Represented by True if it has False if not)\n2. Traverse through the descriptions list.\n3. For every new node value found, add a new TreeNode into the list with its `HAS_PARENT` property being False.\n4. Now make the child node parents left/right child and update the `HAS_PARENT` property of child value in map to True.\n5. Now once the Binary Tree is made we traverse through the hash map to check which node still has no parent. This node is out root node.\n6. Return the root node.\n```\nclass Solution:\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n root = None\n table = {}\n for arr in descriptions:\n parent = arr[0]\n child = arr[1]\n isleft = arr[2]\n if table.get(parent, None) is None: # If key parent does not exist in table\n table[parent] = [TreeNode(parent), False]\n if table.get(child, None) is None: If key child does not exist in table\n table[child] = [TreeNode(child), False]\n table[child][1] = True # Since child is going to have a parent in the current iteration, set its has parent property to True\n if isleft == 1:\n table[parent][0].left = table[child][0]\n else:\n table[parent][0].right = table[child][0]\n\t\t# Now traverse the hashtable and check which node still has no parent\n for k, v in table.items():\n if not v[1]: # Has parent is False, so root is found.\n root = k\n\t\t\t\tbreak\n return table[root][0]\n``` | 5 | You are given a 2D integer array `descriptions` where `descriptions[i] = [parenti, childi, isLefti]` indicates that `parenti` is the **parent** of `childi` in a **binary** tree of **unique** values. Furthermore,
* If `isLefti == 1`, then `childi` is the left child of `parenti`.
* If `isLefti == 0`, then `childi` is the right child of `parenti`.
Construct the binary tree described by `descriptions` and return _its **root**_.
The test cases will be generated such that the binary tree is **valid**.
**Example 1:**
**Input:** descriptions = \[\[20,15,1\],\[20,17,0\],\[50,20,1\],\[50,80,0\],\[80,19,1\]\]
**Output:** \[50,20,80,15,17,19\]
**Explanation:** The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.
**Example 2:**
**Input:** descriptions = \[\[1,2,1\],\[2,3,0\],\[3,4,1\]\]
**Output:** \[1,2,null,null,3,4\]
**Explanation:** The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.
**Constraints:**
* `1 <= descriptions.length <= 104`
* `descriptions[i].length == 3`
* `1 <= parenti, childi <= 105`
* `0 <= isLefti <= 1`
* The binary tree described by `descriptions` is valid. | Consider the list structure ...A → (B → ... → C) → D..., where the nodes between B and C (inclusive) form a group, A is the last node of the previous group, and D is the first node of the next group. How can you utilize this structure? Suppose you have B → ... → C reversed (because it was of even length) so that it is now C → ... → B. What references do you need to fix so that the transitions between the previous, current, and next groups are correct? A.next should be set to C, and B.next should be set to D. Once the current group is finished being modified, you need to find the new A, B, C, and D nodes for the next group. How can you use the old A, B, C, and D nodes to find the new ones? The new A is either the old B or old C depending on if the group was of even or odd length. The new B is always the old D. The new C and D can be found based on the new B and the next group's length. You can set the initial values of A, B, C, and D to A = null, B = head, C = head, D = head.next. Repeat the steps from the previous hints until D is null. |
Python | Dictonary | Recursion | create-binary-tree-from-descriptions | 0 | 1 | create a tree dict to store all the child node\ncreate a dict to find the parent node\n\nuse recursion to form the tree. \n\n\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n tree = {}\n dp = {}\n for p,c,_ in descriptions:\n tree[p] = [None, None]\n \n dp[p] = True\n \n dp[c] = True\n for p,c,l in descriptions:\n dp[c] = False\n if l:\n tree[p][0] = c\n else:\n tree[p][1] = c\n pa = None\n for k,v in dp.items():\n if v:\n pa = k\n \n def create(parent):\n if not parent:\n return\n if parent not in tree:\n return TreeNode(parent)\n temp = TreeNode(parent)\n if tree[parent][0]:\n temp.left = create(tree[parent][0])\n if tree[parent][1]:\n temp.right = create(tree[parent][1])\n return temp\n \n return create(pa)\n``` | 4 | You are given a 2D integer array `descriptions` where `descriptions[i] = [parenti, childi, isLefti]` indicates that `parenti` is the **parent** of `childi` in a **binary** tree of **unique** values. Furthermore,
* If `isLefti == 1`, then `childi` is the left child of `parenti`.
* If `isLefti == 0`, then `childi` is the right child of `parenti`.
Construct the binary tree described by `descriptions` and return _its **root**_.
The test cases will be generated such that the binary tree is **valid**.
**Example 1:**
**Input:** descriptions = \[\[20,15,1\],\[20,17,0\],\[50,20,1\],\[50,80,0\],\[80,19,1\]\]
**Output:** \[50,20,80,15,17,19\]
**Explanation:** The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.
**Example 2:**
**Input:** descriptions = \[\[1,2,1\],\[2,3,0\],\[3,4,1\]\]
**Output:** \[1,2,null,null,3,4\]
**Explanation:** The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.
**Constraints:**
* `1 <= descriptions.length <= 104`
* `descriptions[i].length == 3`
* `1 <= parenti, childi <= 105`
* `0 <= isLefti <= 1`
* The binary tree described by `descriptions` is valid. | Consider the list structure ...A → (B → ... → C) → D..., where the nodes between B and C (inclusive) form a group, A is the last node of the previous group, and D is the first node of the next group. How can you utilize this structure? Suppose you have B → ... → C reversed (because it was of even length) so that it is now C → ... → B. What references do you need to fix so that the transitions between the previous, current, and next groups are correct? A.next should be set to C, and B.next should be set to D. Once the current group is finished being modified, you need to find the new A, B, C, and D nodes for the next group. How can you use the old A, B, C, and D nodes to find the new ones? The new A is either the old B or old C depending on if the group was of even or odd length. The new B is always the old D. The new C and D can be found based on the new B and the next group's length. You can set the initial values of A, B, C, and D to A = null, B = head, C = head, D = head.next. Repeat the steps from the previous hints until D is null. |
[ Python ] Faster then 100% solution | create-binary-tree-from-descriptions | 0 | 1 | ```\nclass Solution:\n def createBinaryTree(self, descriptions: List[List[int]]) -> Optional[TreeNode]:\n \n tree = dict()\n children = set()\n for parent, child, isLeft in descriptions:\n if parent not in tree : tree[parent] = TreeNode(parent)\n if child not in tree : tree[child] = TreeNode(child)\n \n if isLeft : tree[parent].left = tree[child]\n else : tree[parent].right = tree[child]\n \n children.add(child)\n \n for parent in tree:\n if parent not in children:\n return tree[parent]\n \n``` | 8 | You are given a 2D integer array `descriptions` where `descriptions[i] = [parenti, childi, isLefti]` indicates that `parenti` is the **parent** of `childi` in a **binary** tree of **unique** values. Furthermore,
* If `isLefti == 1`, then `childi` is the left child of `parenti`.
* If `isLefti == 0`, then `childi` is the right child of `parenti`.
Construct the binary tree described by `descriptions` and return _its **root**_.
The test cases will be generated such that the binary tree is **valid**.
**Example 1:**
**Input:** descriptions = \[\[20,15,1\],\[20,17,0\],\[50,20,1\],\[50,80,0\],\[80,19,1\]\]
**Output:** \[50,20,80,15,17,19\]
**Explanation:** The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.
**Example 2:**
**Input:** descriptions = \[\[1,2,1\],\[2,3,0\],\[3,4,1\]\]
**Output:** \[1,2,null,null,3,4\]
**Explanation:** The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.
**Constraints:**
* `1 <= descriptions.length <= 104`
* `descriptions[i].length == 3`
* `1 <= parenti, childi <= 105`
* `0 <= isLefti <= 1`
* The binary tree described by `descriptions` is valid. | Consider the list structure ...A → (B → ... → C) → D..., where the nodes between B and C (inclusive) form a group, A is the last node of the previous group, and D is the first node of the next group. How can you utilize this structure? Suppose you have B → ... → C reversed (because it was of even length) so that it is now C → ... → B. What references do you need to fix so that the transitions between the previous, current, and next groups are correct? A.next should be set to C, and B.next should be set to D. Once the current group is finished being modified, you need to find the new A, B, C, and D nodes for the next group. How can you use the old A, B, C, and D nodes to find the new ones? The new A is either the old B or old C depending on if the group was of even or odd length. The new B is always the old D. The new C and D can be found based on the new B and the next group's length. You can set the initial values of A, B, C, and D to A = null, B = head, C = head, D = head.next. Repeat the steps from the previous hints until D is null. |
Doubly-Linked List in Python | replace-non-coprime-numbers-in-array | 0 | 1 | By using doubly linked list, you can access the deletable pair in O(1) time.\nEvery time you delete some pair, you need to add a new node with the value of lcm. Also, it might be possible that one of the pair is already deleted, so you need to keep track of which nodes are already deleted. (`wasted` stores all the finished nodes.)\n\n```\nclass DoublyLinkedNode:\n def __init__(self, val=0):\n self.val = val\n self.prev = None\n self.next = None\n\nfrom math import gcd, lcm\nclass Solution:\n def replaceNonCoprimes(self, nums: List[int]) -> List[int]:\n def connect(node1, node2):\n node1.next, node2.prev = node2, node1\n \n def are_deletable(node1, node2):\n return node1.val != 0 and node2.val != 0 and gcd(node1.val, node2.val) > 1\n \n #Create doubly linked list\n dummy_head, dummy_tail = DoublyLinkedNode(), DoublyLinkedNode()\n nodes = [DoublyLinkedNode(num) for num in nums]\n N = len(nodes)\n deletables = []\n for i in range(1, N):\n connect(nodes[i - 1], nodes[i])\n if are_deletable(nodes[i - 1], nodes[i]):\n deletables.append((nodes[i - 1], nodes[i]))\n connect(dummy_head, nodes[0]); connect(nodes[-1], dummy_tail);\n \n #connect adjacent nodes while deletables exist\n wasted = set()\n while deletables:\n node1, node2 = deletables.pop()\n if node1 in wasted or node2 in wasted:\n continue\n new_node = DoublyLinkedNode(val=lcm(node1.val, node2.val))\n connect(node1.prev, new_node); connect(new_node, node2.next);\n wasted.add(node1); wasted.add(node2);\n if are_deletable(new_node.prev, new_node):\n deletables.append((new_node.prev, new_node))\n if are_deletable(new_node, new_node.next):\n deletables.append((new_node, new_node.next)) \n \n\t\t#output\n curr = dummy_head.next\n res = []\n while curr != dummy_tail:\n res.append(curr.val)\n curr = curr.next\n return res\n``` | 3 | You are given an array of integers `nums`. Perform the following steps:
1. Find **any** two **adjacent** numbers in `nums` that are **non-coprime**.
2. If no such numbers are found, **stop** the process.
3. Otherwise, delete the two numbers and **replace** them with their **LCM (Least Common Multiple)**.
4. **Repeat** this process as long as you keep finding two adjacent non-coprime numbers.
Return _the **final** modified array._ It can be shown that replacing adjacent non-coprime numbers in **any** arbitrary order will lead to the same result.
The test cases are generated such that the values in the final array are **less than or equal** to `108`.
Two values `x` and `y` are **non-coprime** if `GCD(x, y) > 1` where `GCD(x, y)` is the **Greatest Common Divisor** of `x` and `y`.
**Example 1:**
**Input:** nums = \[6,4,3,2,7,6,2\]
**Output:** \[12,7,6\]
**Explanation:**
- (6, 4) are non-coprime with LCM(6, 4) = 12. Now, nums = \[**12**,3,2,7,6,2\].
- (12, 3) are non-coprime with LCM(12, 3) = 12. Now, nums = \[**12**,2,7,6,2\].
- (12, 2) are non-coprime with LCM(12, 2) = 12. Now, nums = \[**12**,7,6,2\].
- (6, 2) are non-coprime with LCM(6, 2) = 6. Now, nums = \[12,7,**6**\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[12,7,6\].
Note that there are other ways to obtain the same resultant array.
**Example 2:**
**Input:** nums = \[2,2,1,1,3,3,3\]
**Output:** \[2,1,1,3\]
**Explanation:**
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**,3\].
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**\].
- (2, 2) are non-coprime with LCM(2, 2) = 2. Now, nums = \[**2**,1,1,3\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[2,1,1,3\].
Note that there are other ways to obtain the same resultant array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* The test cases are generated such that the values in the final array are **less than or equal** to `108`. | How can you use rows and encodedText to find the number of columns of the matrix? Once you have the number of rows and columns, you can create the matrix and place encodedText in it. How should you place it in the matrix? How should you traverse the matrix to "decode" originalText? |
Easiest Python Code | 7 Line Code | 99% faster | Stack | replace-non-coprime-numbers-in-array | 0 | 1 | # Complexity\n- Time complexity: $$O(nlogn)$$\n\n- Space complexity: $$O(nlogn)$$\n\n# Code\n```\nclass Solution:\n def replaceNonCoprimes(self, nums: List[int]) -> List[int]:\n stack = []\n for i in nums:\n toBeAppended = i\n while stack and gcd(stack[-1], toBeAppended) > 1:\n toBeAppended = lcm(toBeAppended, stack.pop())\n stack.append(toBeAppended)\n return stack \n``` | 4 | You are given an array of integers `nums`. Perform the following steps:
1. Find **any** two **adjacent** numbers in `nums` that are **non-coprime**.
2. If no such numbers are found, **stop** the process.
3. Otherwise, delete the two numbers and **replace** them with their **LCM (Least Common Multiple)**.
4. **Repeat** this process as long as you keep finding two adjacent non-coprime numbers.
Return _the **final** modified array._ It can be shown that replacing adjacent non-coprime numbers in **any** arbitrary order will lead to the same result.
The test cases are generated such that the values in the final array are **less than or equal** to `108`.
Two values `x` and `y` are **non-coprime** if `GCD(x, y) > 1` where `GCD(x, y)` is the **Greatest Common Divisor** of `x` and `y`.
**Example 1:**
**Input:** nums = \[6,4,3,2,7,6,2\]
**Output:** \[12,7,6\]
**Explanation:**
- (6, 4) are non-coprime with LCM(6, 4) = 12. Now, nums = \[**12**,3,2,7,6,2\].
- (12, 3) are non-coprime with LCM(12, 3) = 12. Now, nums = \[**12**,2,7,6,2\].
- (12, 2) are non-coprime with LCM(12, 2) = 12. Now, nums = \[**12**,7,6,2\].
- (6, 2) are non-coprime with LCM(6, 2) = 6. Now, nums = \[12,7,**6**\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[12,7,6\].
Note that there are other ways to obtain the same resultant array.
**Example 2:**
**Input:** nums = \[2,2,1,1,3,3,3\]
**Output:** \[2,1,1,3\]
**Explanation:**
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**,3\].
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**\].
- (2, 2) are non-coprime with LCM(2, 2) = 2. Now, nums = \[**2**,1,1,3\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[2,1,1,3\].
Note that there are other ways to obtain the same resultant array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* The test cases are generated such that the values in the final array are **less than or equal** to `108`. | How can you use rows and encodedText to find the number of columns of the matrix? Once you have the number of rows and columns, you can create the matrix and place encodedText in it. How should you place it in the matrix? How should you traverse the matrix to "decode" originalText? |
[Python 3] Stack solution | replace-non-coprime-numbers-in-array | 0 | 1 | ```\nclass Solution:\n def replaceNonCoprimes(self, nums: List[int]) -> List[int]: \n\n stack = nums[:1]\n \n for j in range(1, len(nums)):\n cur = nums[j]\n while stack and math.gcd(stack[-1], cur) > 1:\n prev = stack.pop()\n cur = math.lcm(prev, cur)\n stack.append(cur) \n \n return stack | 2 | You are given an array of integers `nums`. Perform the following steps:
1. Find **any** two **adjacent** numbers in `nums` that are **non-coprime**.
2. If no such numbers are found, **stop** the process.
3. Otherwise, delete the two numbers and **replace** them with their **LCM (Least Common Multiple)**.
4. **Repeat** this process as long as you keep finding two adjacent non-coprime numbers.
Return _the **final** modified array._ It can be shown that replacing adjacent non-coprime numbers in **any** arbitrary order will lead to the same result.
The test cases are generated such that the values in the final array are **less than or equal** to `108`.
Two values `x` and `y` are **non-coprime** if `GCD(x, y) > 1` where `GCD(x, y)` is the **Greatest Common Divisor** of `x` and `y`.
**Example 1:**
**Input:** nums = \[6,4,3,2,7,6,2\]
**Output:** \[12,7,6\]
**Explanation:**
- (6, 4) are non-coprime with LCM(6, 4) = 12. Now, nums = \[**12**,3,2,7,6,2\].
- (12, 3) are non-coprime with LCM(12, 3) = 12. Now, nums = \[**12**,2,7,6,2\].
- (12, 2) are non-coprime with LCM(12, 2) = 12. Now, nums = \[**12**,7,6,2\].
- (6, 2) are non-coprime with LCM(6, 2) = 6. Now, nums = \[12,7,**6**\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[12,7,6\].
Note that there are other ways to obtain the same resultant array.
**Example 2:**
**Input:** nums = \[2,2,1,1,3,3,3\]
**Output:** \[2,1,1,3\]
**Explanation:**
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**,3\].
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**\].
- (2, 2) are non-coprime with LCM(2, 2) = 2. Now, nums = \[**2**,1,1,3\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[2,1,1,3\].
Note that there are other ways to obtain the same resultant array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* The test cases are generated such that the values in the final array are **less than or equal** to `108`. | How can you use rows and encodedText to find the number of columns of the matrix? Once you have the number of rows and columns, you can create the matrix and place encodedText in it. How should you place it in the matrix? How should you traverse the matrix to "decode" originalText? |
[Python3] stack | replace-non-coprime-numbers-in-array | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/bb5647e856ff11b072f9c51a140e0f243c100171) for solutions of weekly 283.\n\n```\nclass Solution:\n def replaceNonCoprimes(self, nums: List[int]) -> List[int]:\n stack = []\n for x in nums: \n while stack and gcd(stack[-1], x) > 1: x = lcm(x, stack.pop())\n stack.append(x)\n return stack\n``` | 2 | You are given an array of integers `nums`. Perform the following steps:
1. Find **any** two **adjacent** numbers in `nums` that are **non-coprime**.
2. If no such numbers are found, **stop** the process.
3. Otherwise, delete the two numbers and **replace** them with their **LCM (Least Common Multiple)**.
4. **Repeat** this process as long as you keep finding two adjacent non-coprime numbers.
Return _the **final** modified array._ It can be shown that replacing adjacent non-coprime numbers in **any** arbitrary order will lead to the same result.
The test cases are generated such that the values in the final array are **less than or equal** to `108`.
Two values `x` and `y` are **non-coprime** if `GCD(x, y) > 1` where `GCD(x, y)` is the **Greatest Common Divisor** of `x` and `y`.
**Example 1:**
**Input:** nums = \[6,4,3,2,7,6,2\]
**Output:** \[12,7,6\]
**Explanation:**
- (6, 4) are non-coprime with LCM(6, 4) = 12. Now, nums = \[**12**,3,2,7,6,2\].
- (12, 3) are non-coprime with LCM(12, 3) = 12. Now, nums = \[**12**,2,7,6,2\].
- (12, 2) are non-coprime with LCM(12, 2) = 12. Now, nums = \[**12**,7,6,2\].
- (6, 2) are non-coprime with LCM(6, 2) = 6. Now, nums = \[12,7,**6**\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[12,7,6\].
Note that there are other ways to obtain the same resultant array.
**Example 2:**
**Input:** nums = \[2,2,1,1,3,3,3\]
**Output:** \[2,1,1,3\]
**Explanation:**
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**,3\].
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**\].
- (2, 2) are non-coprime with LCM(2, 2) = 2. Now, nums = \[**2**,1,1,3\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[2,1,1,3\].
Note that there are other ways to obtain the same resultant array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* The test cases are generated such that the values in the final array are **less than or equal** to `108`. | How can you use rows and encodedText to find the number of columns of the matrix? Once you have the number of rows and columns, you can create the matrix and place encodedText in it. How should you place it in the matrix? How should you traverse the matrix to "decode" originalText? |
One Trick to make this an LC Easy - Fastest O(n) python + Optimized for O(1) memory | replace-non-coprime-numbers-in-array | 0 | 1 | # Intuition\nAny result in the output will have to be a merge of a subarray or elements, what is that output value going to be?\nWell it has to be the LCM of all the numbers in the subarray that got merged.\n\n# Approach\nConceptually we use a stack to output the result greedily backtracking as when neccesary. We can then save space by modifying the input array using a pointer to emulate the stack.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$ extra space\n\n# Code\n```\nclass Solution:\n def replaceNonCoprimes(self, nums: List[int]) -> List[int]:\n i = 0\n for x in nums:\n while i and gcd(nums[i-1], x) > 1:\n x = lcm(nums[i-1], x)\n i -= 1\n nums[i] = x\n i += 1\n return nums[:i]\n``` | 0 | You are given an array of integers `nums`. Perform the following steps:
1. Find **any** two **adjacent** numbers in `nums` that are **non-coprime**.
2. If no such numbers are found, **stop** the process.
3. Otherwise, delete the two numbers and **replace** them with their **LCM (Least Common Multiple)**.
4. **Repeat** this process as long as you keep finding two adjacent non-coprime numbers.
Return _the **final** modified array._ It can be shown that replacing adjacent non-coprime numbers in **any** arbitrary order will lead to the same result.
The test cases are generated such that the values in the final array are **less than or equal** to `108`.
Two values `x` and `y` are **non-coprime** if `GCD(x, y) > 1` where `GCD(x, y)` is the **Greatest Common Divisor** of `x` and `y`.
**Example 1:**
**Input:** nums = \[6,4,3,2,7,6,2\]
**Output:** \[12,7,6\]
**Explanation:**
- (6, 4) are non-coprime with LCM(6, 4) = 12. Now, nums = \[**12**,3,2,7,6,2\].
- (12, 3) are non-coprime with LCM(12, 3) = 12. Now, nums = \[**12**,2,7,6,2\].
- (12, 2) are non-coprime with LCM(12, 2) = 12. Now, nums = \[**12**,7,6,2\].
- (6, 2) are non-coprime with LCM(6, 2) = 6. Now, nums = \[12,7,**6**\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[12,7,6\].
Note that there are other ways to obtain the same resultant array.
**Example 2:**
**Input:** nums = \[2,2,1,1,3,3,3\]
**Output:** \[2,1,1,3\]
**Explanation:**
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**,3\].
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**\].
- (2, 2) are non-coprime with LCM(2, 2) = 2. Now, nums = \[**2**,1,1,3\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[2,1,1,3\].
Note that there are other ways to obtain the same resultant array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* The test cases are generated such that the values in the final array are **less than or equal** to `108`. | How can you use rows and encodedText to find the number of columns of the matrix? Once you have the number of rows and columns, you can create the matrix and place encodedText in it. How should you place it in the matrix? How should you traverse the matrix to "decode" originalText? |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.