title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python easy solution with extend | partition-array-according-to-given-pivot | 0 | 1 | # Code\n```\nclass Solution:\n def pivotArray(self, nums: List[int], pivot: int) -> List[int]:\n res = [n for n in nums if n < pivot]\n res.extend([pivot] * nums.count(pivot))\n res.extend([n for n in nums if n > pivot])\n return res\n``` | 0 | You are given a stream of records about a particular stock. Each record contains a timestamp and the corresponding price of the stock at that timestamp. Unfortunately due to the volatile nature of the stock market, the records do not come in order. Even worse, some records may be incorrect. Another record with the same timestamp may appear later in the stream correcting the price of the previous wrong record. Design an algorithm that: Implement the StockPrice class: | How would you solve the problem for offline queries (all queries given at once)? Think about which data structure can help insert and delete the most optimal way. |
Easy to understand Python3 solution | partition-array-according-to-given-pivot | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pivotArray(self, nums: List[int], pivot: int) -> List[int]:\n mins = []\n maxs = []\n pivots=[]\n\n for i in nums:\n if i < pivot:\n mins.append(i)\n elif i > pivot:\n maxs.append(i)\n else:\n pivots.append(i)\n \n return mins + pivots + maxs\n \n``` | 0 | You are given a stream of records about a particular stock. Each record contains a timestamp and the corresponding price of the stock at that timestamp. Unfortunately due to the volatile nature of the stock market, the records do not come in order. Even worse, some records may be incorrect. Another record with the same timestamp may appear later in the stream correcting the price of the previous wrong record. Design an algorithm that: Implement the StockPrice class: | How would you solve the problem for offline queries (all queries given at once)? Think about which data structure can help insert and delete the most optimal way. |
4 pointers | partition-array-according-to-given-pivot | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pivotArray(self, nums, pivot):\n n = len(nums)\n left = 0\n right = n - 1\n result = [pivot] * n\n\n for i in range(n):\n j = n - 1 - i\n if nums[i] < pivot: # i set the value from left to right to maintain origin order\n result[left] = nums[i]\n left += 1\n if nums[j] > pivot: # j set the value from right to left to maintain origin order\n result[right] = nums[j]\n right -=1\n return result\n``` | 4 | You are given a stream of records about a particular stock. Each record contains a timestamp and the corresponding price of the stock at that timestamp. Unfortunately due to the volatile nature of the stock market, the records do not come in order. Even worse, some records may be incorrect. Another record with the same timestamp may appear later in the stream correcting the price of the previous wrong record. Design an algorithm that: Implement the StockPrice class: | How would you solve the problem for offline queries (all queries given at once)? Think about which data structure can help insert and delete the most optimal way. |
In place re-arrange numbers - T:O(N) , S: O(1)- 42/44 passed test cases | partition-array-according-to-given-pivot | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach \nIn Place rearranging numbers \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def pivotArray(self, nums: List[int], pivot: int) -> List[int]:\n\n left,right = 0, len(nums) - 1\n while left <= right:\n if(nums[left] < pivot):\n left += 1\n else:\n nums.append(nums[left])\n nums.pop(left)\n right -= 1\n left,right = 0, len(nums) - 1\n while left <= right:\n if(nums[left] < pivot):\n left += 1\n else:\n break\n while right >= left:\n if(nums[right] == pivot):\n nums.insert(left, nums[right])\n nums.pop(right + 1)\n left += 1\n else:\n right -= 1\n return nums\n \n \n\n \n \n``` | 1 | You are given a stream of records about a particular stock. Each record contains a timestamp and the corresponding price of the stock at that timestamp. Unfortunately due to the volatile nature of the stock market, the records do not come in order. Even worse, some records may be incorrect. Another record with the same timestamp may appear later in the stream correcting the price of the previous wrong record. Design an algorithm that: Implement the StockPrice class: | How would you solve the problem for offline queries (all queries given at once)? Think about which data structure can help insert and delete the most optimal way. |
Python 3 || 8 lines || T/M: 97% / 81% | minimum-cost-to-set-cooking-time | 0 | 1 | ```\nclass Solution:\n def minCostSetTime(self, startAt: int, moveCost: int, pushCost: int, targetSeconds: int) -> int:\n\n def cost(m: int,s: int)-> int:\n\n if not(0 <= m <= 99 and 0 <= s <= 99): return inf\n\n display = str(startAt)+str(100*m+s)\n\n moves = sum(display[i]!=display[i-1] for i in range(1,len(display)))\n pushes = len(display)-1\n \n return moveCost*moves + pushCost*pushes\n \n\n mins, secs = divmod(targetSeconds,60)\n \n return min(cost(mins,secs),cost(mins-1,secs+60))\n```\n[https://leetcode.com/problems/minimum-cost-to-set-cooking-time/submissions/925094755/](http://)\n\nI could be wrong, but I think that time complexity is *O*(1) and space complexity is *O*(1).\n | 3 | A generic microwave supports cooking times for:
* at least `1` second.
* at most `99` minutes and `99` seconds.
To set the cooking time, you push **at most four digits**. The microwave normalizes what you push as four digits by **prepending zeroes**. It interprets the **first** two digits as the minutes and the **last** two digits as the seconds. It then **adds** them up as the cooking time. For example,
* You push `9` `5` `4` (three digits). It is normalized as `0954` and interpreted as `9` minutes and `54` seconds.
* You push `0` `0` `0` `8` (four digits). It is interpreted as `0` minutes and `8` seconds.
* You push `8` `0` `9` `0`. It is interpreted as `80` minutes and `90` seconds.
* You push `8` `1` `3` `0`. It is interpreted as `81` minutes and `30` seconds.
You are given integers `startAt`, `moveCost`, `pushCost`, and `targetSeconds`. **Initially**, your finger is on the digit `startAt`. Moving the finger above **any specific digit** costs `moveCost` units of fatigue. Pushing the digit below the finger **once** costs `pushCost` units of fatigue.
There can be multiple ways to set the microwave to cook for `targetSeconds` seconds but you are interested in the way with the minimum cost.
Return _the **minimum cost** to set_ `targetSeconds` _seconds of cooking time_.
Remember that one minute consists of `60` seconds.
**Example 1:**
**Input:** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**Output:** 6
**Explanation:** The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
**Example 2:**
**Input:** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**Output:** 6
**Explanation:** The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.
**Constraints:**
* `0 <= startAt <= 9`
* `1 <= moveCost, pushCost <= 105`
* `1 <= targetSeconds <= 6039` | The target sum for the two partitions is sum(nums) / 2. Could you reduce the time complexity if you arbitrarily divide nums into two halves (two arrays)? Meet-in-the-Middle? For both halves, pre-calculate a 2D array where the kth index will store all possible sum values if only k elements from this half are added. For each sum of k elements in the first half, find the best sum of n-k elements in the second half such that the two sums add up to a value closest to the target sum from hint 1. These two subsets will form one array of the partition. |
[Python3, Java, C++] Combinations of Minutes and Seconds O(1) | minimum-cost-to-set-cooking-time | 1 | 1 | **Explanation**: \n* The maximum possible minutes are: `targetSeconds` / 60\n* Check for all possible minutes from 0 to `maxmins` and the corresponding seconds\n* `cost` function returns the cost for given minutes and seconds\n* `moveCost` is added to current cost if the finger position is not at the correct number\n* `pushCost` is added for each character that is pushed\n* Maintain the minimum cost and return it\n\n*Note*: We are multiplying `mins` by 100 to get it into the format of the microwave\nLet\'s say `mins` = 50,`secs` = 20\nOn the microwave we want 5020\nFor that we can do: 50 * 100 + 20 = 5020\n<iframe src="https://leetcode.com/playground/eJoNqmaV/shared" frameBorder="0" width="780" height="420"></iframe>\n\nOn further inspection we can deduce that we only really have 2 cases:\n`maxmins`, `secs`\n`maxmins - 1`, `secs + 60`\n<iframe src="https://leetcode.com/playground/VYzZV9Nh/shared" frameBorder="0" width="780" height="370"></iframe>\n\nSince maximum length of characters displayed on microwave = 4, `Time Complexity = O(1)` | 108 | A generic microwave supports cooking times for:
* at least `1` second.
* at most `99` minutes and `99` seconds.
To set the cooking time, you push **at most four digits**. The microwave normalizes what you push as four digits by **prepending zeroes**. It interprets the **first** two digits as the minutes and the **last** two digits as the seconds. It then **adds** them up as the cooking time. For example,
* You push `9` `5` `4` (three digits). It is normalized as `0954` and interpreted as `9` minutes and `54` seconds.
* You push `0` `0` `0` `8` (four digits). It is interpreted as `0` minutes and `8` seconds.
* You push `8` `0` `9` `0`. It is interpreted as `80` minutes and `90` seconds.
* You push `8` `1` `3` `0`. It is interpreted as `81` minutes and `30` seconds.
You are given integers `startAt`, `moveCost`, `pushCost`, and `targetSeconds`. **Initially**, your finger is on the digit `startAt`. Moving the finger above **any specific digit** costs `moveCost` units of fatigue. Pushing the digit below the finger **once** costs `pushCost` units of fatigue.
There can be multiple ways to set the microwave to cook for `targetSeconds` seconds but you are interested in the way with the minimum cost.
Return _the **minimum cost** to set_ `targetSeconds` _seconds of cooking time_.
Remember that one minute consists of `60` seconds.
**Example 1:**
**Input:** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**Output:** 6
**Explanation:** The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
**Example 2:**
**Input:** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**Output:** 6
**Explanation:** The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.
**Constraints:**
* `0 <= startAt <= 9`
* `1 <= moveCost, pushCost <= 105`
* `1 <= targetSeconds <= 6039` | The target sum for the two partitions is sum(nums) / 2. Could you reduce the time complexity if you arbitrarily divide nums into two halves (two arrays)? Meet-in-the-Middle? For both halves, pre-calculate a 2D array where the kth index will store all possible sum values if only k elements from this half are added. For each sum of k elements in the first half, find the best sum of n-k elements in the second half such that the two sums add up to a value closest to the target sum from hint 1. These two subsets will form one array of the partition. |
Simple Python Solution | minimum-cost-to-set-cooking-time | 0 | 1 | ```\nclass Solution:\n def minCostSetTime(self, startAt: int, moveCost: int, pushCost: int, targetSeconds: int) -> int:\n def count_cost(minutes, seconds): # Calculates cost for certain configuration of minutes and seconds\n time = f\'{minutes // 10}{minutes % 10}{seconds // 10}{seconds % 10}\' # mm:ss\n time = time.lstrip(\'0\') # since 0\'s are prepended we remove the 0\'s to the left to minimize cost\n t = [int(i) for i in time]\n current = startAt\n cost = 0\n for i in t:\n if i != current:\n current = i\n cost += moveCost\n cost += pushCost\n return cost\n ans = float(\'inf\')\n for m in range(100): # Check which [mm:ss] configuration works out\n for s in range(100):\n if m * 60 + s == targetSeconds: \n ans = min(ans, count_cost(m, s))\n return ans\n``` | 10 | A generic microwave supports cooking times for:
* at least `1` second.
* at most `99` minutes and `99` seconds.
To set the cooking time, you push **at most four digits**. The microwave normalizes what you push as four digits by **prepending zeroes**. It interprets the **first** two digits as the minutes and the **last** two digits as the seconds. It then **adds** them up as the cooking time. For example,
* You push `9` `5` `4` (three digits). It is normalized as `0954` and interpreted as `9` minutes and `54` seconds.
* You push `0` `0` `0` `8` (four digits). It is interpreted as `0` minutes and `8` seconds.
* You push `8` `0` `9` `0`. It is interpreted as `80` minutes and `90` seconds.
* You push `8` `1` `3` `0`. It is interpreted as `81` minutes and `30` seconds.
You are given integers `startAt`, `moveCost`, `pushCost`, and `targetSeconds`. **Initially**, your finger is on the digit `startAt`. Moving the finger above **any specific digit** costs `moveCost` units of fatigue. Pushing the digit below the finger **once** costs `pushCost` units of fatigue.
There can be multiple ways to set the microwave to cook for `targetSeconds` seconds but you are interested in the way with the minimum cost.
Return _the **minimum cost** to set_ `targetSeconds` _seconds of cooking time_.
Remember that one minute consists of `60` seconds.
**Example 1:**
**Input:** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**Output:** 6
**Explanation:** The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
**Example 2:**
**Input:** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**Output:** 6
**Explanation:** The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.
**Constraints:**
* `0 <= startAt <= 9`
* `1 <= moveCost, pushCost <= 105`
* `1 <= targetSeconds <= 6039` | The target sum for the two partitions is sum(nums) / 2. Could you reduce the time complexity if you arbitrarily divide nums into two halves (two arrays)? Meet-in-the-Middle? For both halves, pre-calculate a 2D array where the kth index will store all possible sum values if only k elements from this half are added. For each sum of k elements in the first half, find the best sum of n-k elements in the second half such that the two sums add up to a value closest to the target sum from hint 1. These two subsets will form one array of the partition. |
Python3 | Beats 100% time | minimum-cost-to-set-cooking-time | 0 | 1 | ```\nclass Solution:\n def minCostSetTime(self, startAt: int, moveCost: int, pushCost: int, targetSeconds: int) -> int:\n poss = [(targetSeconds // 60, targetSeconds % 60)] # store possibilities as (minutes, seconds)\n \n if poss[0][0] > 99: # for when targetSeconds >= 6000\n poss = [(99, poss[0][1]+60)]\n \n if poss[0][0] >= 1 and (poss[0][1]+60) <= 99:\n\t\t\t# adding a second possibility e.g. (01, 16) -> (0, 76)\n poss.append((poss[0][0]-1, poss[0][1]+60))\n \n costs = list()\n \n for i in poss:\n curr_start = startAt\n curr_cost = 0\n \n minutes = str(i[0])\n if i[0] != 0: # 0s are prepended, so no need to push 0s\n for j in minutes:\n if int(j) != curr_start:\n curr_cost += moveCost\n curr_start = int(j)\n curr_cost += pushCost\n \n seconds = str(i[1])\n if len(seconds) == 1 and i[0] != 0: # seconds is a single digit, prepend a "0" to it\n seconds = "0" + seconds\n \n for j in seconds:\n if int(j) != curr_start:\n curr_cost += moveCost\n curr_start = int(j)\n curr_cost += pushCost\n costs.append(curr_cost)\n \n return min(costs)\n``` | 2 | A generic microwave supports cooking times for:
* at least `1` second.
* at most `99` minutes and `99` seconds.
To set the cooking time, you push **at most four digits**. The microwave normalizes what you push as four digits by **prepending zeroes**. It interprets the **first** two digits as the minutes and the **last** two digits as the seconds. It then **adds** them up as the cooking time. For example,
* You push `9` `5` `4` (three digits). It is normalized as `0954` and interpreted as `9` minutes and `54` seconds.
* You push `0` `0` `0` `8` (four digits). It is interpreted as `0` minutes and `8` seconds.
* You push `8` `0` `9` `0`. It is interpreted as `80` minutes and `90` seconds.
* You push `8` `1` `3` `0`. It is interpreted as `81` minutes and `30` seconds.
You are given integers `startAt`, `moveCost`, `pushCost`, and `targetSeconds`. **Initially**, your finger is on the digit `startAt`. Moving the finger above **any specific digit** costs `moveCost` units of fatigue. Pushing the digit below the finger **once** costs `pushCost` units of fatigue.
There can be multiple ways to set the microwave to cook for `targetSeconds` seconds but you are interested in the way with the minimum cost.
Return _the **minimum cost** to set_ `targetSeconds` _seconds of cooking time_.
Remember that one minute consists of `60` seconds.
**Example 1:**
**Input:** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**Output:** 6
**Explanation:** The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
**Example 2:**
**Input:** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**Output:** 6
**Explanation:** The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.
**Constraints:**
* `0 <= startAt <= 9`
* `1 <= moveCost, pushCost <= 105`
* `1 <= targetSeconds <= 6039` | The target sum for the two partitions is sum(nums) / 2. Could you reduce the time complexity if you arbitrarily divide nums into two halves (two arrays)? Meet-in-the-Middle? For both halves, pre-calculate a 2D array where the kth index will store all possible sum values if only k elements from this half are added. For each sum of k elements in the first half, find the best sum of n-k elements in the second half such that the two sums add up to a value closest to the target sum from hint 1. These two subsets will form one array of the partition. |
Constant time and space (atmost 100 iterations) | minimum-cost-to-set-cooking-time | 0 | 1 | \n# Code\n```\nclass Solution:\n def minCostSetTime(self, startAt: int, moveCost: int, pushCost: int, targetSeconds: int) -> int:\n min_cost = float(\'inf\')\n \n def calculateCost(time_str, startAt, moveCost, pushCost):\n cost = 0\n for digit in time_str:\n if digit != \'0\' or cost > 0:\n cost += moveCost if startAt != int(digit) else 0\n cost += pushCost\n startAt = int(digit)\n return cost\n \n for minn in range(100):\n sec = targetSeconds - minn * 60\n if 0 <= sec < 100:\n time_str = f\'{minn:02d}{sec:02d}\'\n cost = calculateCost(time_str, startAt, moveCost, pushCost)\n min_cost = min(min_cost, cost)\n\n return min_cost\n\n``` | 0 | A generic microwave supports cooking times for:
* at least `1` second.
* at most `99` minutes and `99` seconds.
To set the cooking time, you push **at most four digits**. The microwave normalizes what you push as four digits by **prepending zeroes**. It interprets the **first** two digits as the minutes and the **last** two digits as the seconds. It then **adds** them up as the cooking time. For example,
* You push `9` `5` `4` (three digits). It is normalized as `0954` and interpreted as `9` minutes and `54` seconds.
* You push `0` `0` `0` `8` (four digits). It is interpreted as `0` minutes and `8` seconds.
* You push `8` `0` `9` `0`. It is interpreted as `80` minutes and `90` seconds.
* You push `8` `1` `3` `0`. It is interpreted as `81` minutes and `30` seconds.
You are given integers `startAt`, `moveCost`, `pushCost`, and `targetSeconds`. **Initially**, your finger is on the digit `startAt`. Moving the finger above **any specific digit** costs `moveCost` units of fatigue. Pushing the digit below the finger **once** costs `pushCost` units of fatigue.
There can be multiple ways to set the microwave to cook for `targetSeconds` seconds but you are interested in the way with the minimum cost.
Return _the **minimum cost** to set_ `targetSeconds` _seconds of cooking time_.
Remember that one minute consists of `60` seconds.
**Example 1:**
**Input:** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**Output:** 6
**Explanation:** The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
**Example 2:**
**Input:** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**Output:** 6
**Explanation:** The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.
**Constraints:**
* `0 <= startAt <= 9`
* `1 <= moveCost, pushCost <= 105`
* `1 <= targetSeconds <= 6039` | The target sum for the two partitions is sum(nums) / 2. Could you reduce the time complexity if you arbitrarily divide nums into two halves (two arrays)? Meet-in-the-Middle? For both halves, pre-calculate a 2D array where the kth index will store all possible sum values if only k elements from this half are added. For each sum of k elements in the first half, find the best sum of n-k elements in the second half such that the two sums add up to a value closest to the target sum from hint 1. These two subsets will form one array of the partition. |
Python (Simple Maths) | minimum-cost-to-set-cooking-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCostSetTime(self, startAt, moveCost, pushCost, targetSeconds):\n mins, secs = divmod(targetSeconds,60)\n\n def cost(m,s):\n ans = (moveCost + pushCost)*4\n\n if 0 <= m < 100 and 0 <= s < 100:\n str1 = str(startAt) + str(100*m + s)\n ans = sum(pushCost + moveCost*(str1[i] != str1[i+1]) for i in range(len(str1)-1))\n\n return ans\n\n return min(cost(mins,secs),cost(mins-1,secs+60))\n\n\n\n\n\n\n \n``` | 0 | A generic microwave supports cooking times for:
* at least `1` second.
* at most `99` minutes and `99` seconds.
To set the cooking time, you push **at most four digits**. The microwave normalizes what you push as four digits by **prepending zeroes**. It interprets the **first** two digits as the minutes and the **last** two digits as the seconds. It then **adds** them up as the cooking time. For example,
* You push `9` `5` `4` (three digits). It is normalized as `0954` and interpreted as `9` minutes and `54` seconds.
* You push `0` `0` `0` `8` (four digits). It is interpreted as `0` minutes and `8` seconds.
* You push `8` `0` `9` `0`. It is interpreted as `80` minutes and `90` seconds.
* You push `8` `1` `3` `0`. It is interpreted as `81` minutes and `30` seconds.
You are given integers `startAt`, `moveCost`, `pushCost`, and `targetSeconds`. **Initially**, your finger is on the digit `startAt`. Moving the finger above **any specific digit** costs `moveCost` units of fatigue. Pushing the digit below the finger **once** costs `pushCost` units of fatigue.
There can be multiple ways to set the microwave to cook for `targetSeconds` seconds but you are interested in the way with the minimum cost.
Return _the **minimum cost** to set_ `targetSeconds` _seconds of cooking time_.
Remember that one minute consists of `60` seconds.
**Example 1:**
**Input:** startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
**Output:** 6
**Explanation:** The following are the possible ways to set the cooking time.
- 1 0 0 0, interpreted as 10 minutes and 0 seconds.
The finger is already on digit 1, pushes 1 (with cost 1), moves to 0 (with cost 2), pushes 0 (with cost 1), pushes 0 (with cost 1), and pushes 0 (with cost 1).
The cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the minimum cost.
- 0 9 6 0, interpreted as 9 minutes and 60 seconds. That is also 600 seconds.
The finger moves to 0 (with cost 2), pushes 0 (with cost 1), moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12.
- 9 6 0, normalized as 0960 and interpreted as 9 minutes and 60 seconds.
The finger moves to 9 (with cost 2), pushes 9 (with cost 1), moves to 6 (with cost 2), pushes 6 (with cost 1), moves to 0 (with cost 2), and pushes 0 (with cost 1).
The cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
**Example 2:**
**Input:** startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76
**Output:** 6
**Explanation:** The optimal way is to push two digits: 7 6, interpreted as 76 seconds.
The finger moves to 7 (with cost 1), pushes 7 (with cost 2), moves to 6 (with cost 1), and pushes 6 (with cost 2). The total cost is: 1 + 2 + 1 + 2 = 6
Note other possible ways are 0076, 076, 0116, and 116, but none of them produces the minimum cost.
**Constraints:**
* `0 <= startAt <= 9`
* `1 <= moveCost, pushCost <= 105`
* `1 <= targetSeconds <= 6039` | The target sum for the two partitions is sum(nums) / 2. Could you reduce the time complexity if you arbitrarily divide nums into two halves (two arrays)? Meet-in-the-Middle? For both halves, pre-calculate a 2D array where the kth index will store all possible sum values if only k elements from this half are added. For each sum of k elements in the first half, find the best sum of n-k elements in the second half such that the two sums add up to a value closest to the target sum from hint 1. These two subsets will form one array of the partition. |
Python solution | O(nlogn) | explained with diagram | heap and dp solution | minimum-difference-in-sums-after-removal-of-elements | 0 | 1 | This solution is a combination of dp and heaps.\nTime: `O(nlogn)`\n\n# Explanation:\n\nWe can select in first part:\n* first `n` elements or\n* min `n` elements from first `n+1` elements\n* min `n` elements from first `n-2` elements\n* ...\n* min `n` elements from first `2n` elements\n\n\nIn other words,\nwe need to find a partition such that:\n* `n` minimum-value elements from `n+x` are in first part and\n* `n` maximum-value elements from `2n-x` are in second part\n\n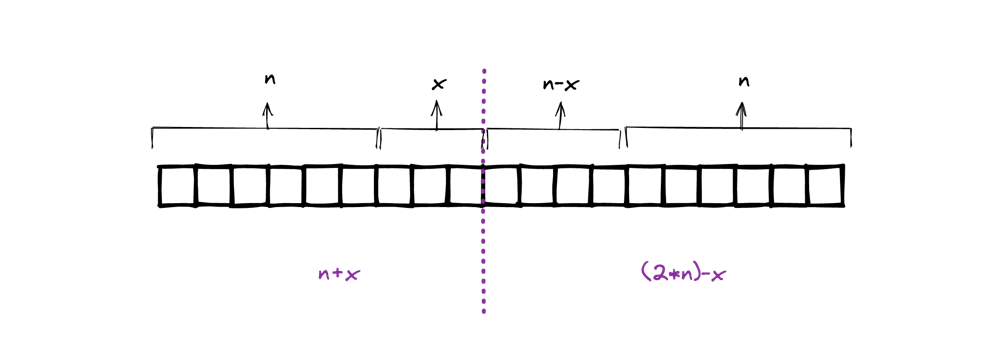\n\n\nHere,\n* difference would be minimum when we choose top minimum-value elements in first part and top maximum-value elements in second part\n* `x` can move from `[0, n]` \n\t* when `x` is `0`, we make sure there are `n` elements in first part \n\t (and from `2n` elements in second part -> `n` maximum-value elements will be selected and other `n` will be removed)\n\t* when `x` is `n` we make sure there are `n` elements in second part\n\nNow, we need `min_sum` for first part and `max_sum` for second part for all `x` values, then we can calculate the minimum difference (note: this is not absolute difference).\nWe will store these values in respective arrays and later calculate the minimum difference, shown below:\n\n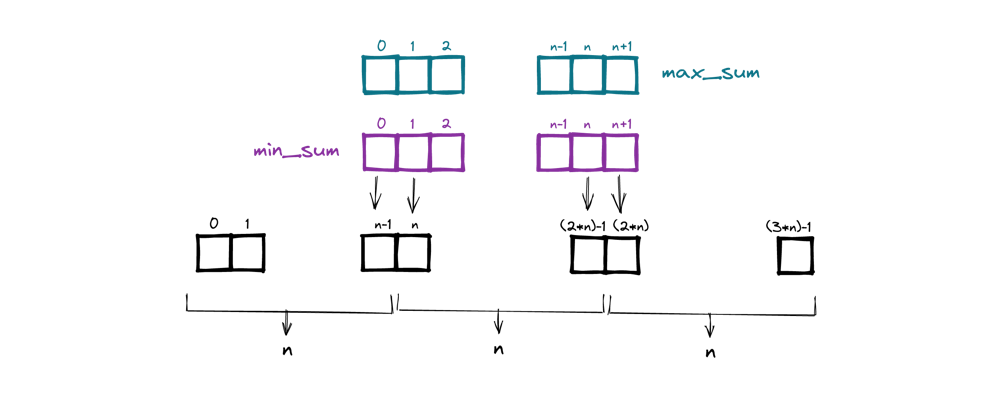\n\nTo calculate `min_sum` we will use `max_heap` to pop out maximum value for each iteration and insert the current element, \nsimilarly for calculating `max_sum` we will use `min_heap`\n\n# Solution\n\nSee code below:\n\n\n```python\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n n = len(nums) // 3\n\n # calculate max_sum using min_heap for second part\n min_heap = nums[(2 * n) :]\n heapq.heapify(min_heap)\n\n max_sum = [0] * (n + 2)\n max_sum[n + 1] = sum(min_heap)\n for i in range((2 * n) - 1, n - 1, -1):\n # push current\n heapq.heappush(min_heap, nums[i])\n # popout minimum from heap\n val = heapq.heappop(min_heap)\n # max_sum for this partition\n max_sum[i - n + 1] = max_sum[i - n + 2] - val + nums[i]\n\n\n # calculate min_sum using max_heap for first part\n max_heap = [-x for x in nums[:n]]\n heapq.heapify(max_heap)\n\n min_sum = [0] * (n + 2)\n min_sum[0] = -sum(max_heap)\n for i in range(n, (2 * n)):\n # push current\n heapq.heappush(max_heap, -nums[i])\n # popout maximum from heap\n val = -heapq.heappop(max_heap)\n # min_sum for this partition\n min_sum[i - n + 1] = min_sum[i - n] - val + nums[i]\n\n\n # find min difference bw second part (max_sum) and first part (min_sum)\n ans = math.inf\n for i in range(0, n + 1):\n print(i, min_sum[i], max_sum[i])\n ans = min((min_sum[i] - max_sum[i + 1]), ans)\n\n return ans\n\n```\n\n | 2 | You are given a **0-indexed** integer array `nums` consisting of `3 * n` elements.
You are allowed to remove any **subsequence** of elements of size **exactly** `n` from `nums`. The remaining `2 * n` elements will be divided into two **equal** parts:
* The first `n` elements belonging to the first part and their sum is `sumfirst`.
* The next `n` elements belonging to the second part and their sum is `sumsecond`.
The **difference in sums** of the two parts is denoted as `sumfirst - sumsecond`.
* For example, if `sumfirst = 3` and `sumsecond = 2`, their difference is `1`.
* Similarly, if `sumfirst = 2` and `sumsecond = 3`, their difference is `-1`.
Return _the **minimum difference** possible between the sums of the two parts after the removal of_ `n` _elements_.
**Example 1:**
**Input:** nums = \[3,1,2\]
**Output:** -1
**Explanation:** Here, nums has 3 elements, so n = 1.
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums\[0\] = 3, the array will be \[1,2\]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums\[1\] = 1, the array will be \[3,2\]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums\[2\] = 2, the array will be \[3,1\]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.
**Example 2:**
**Input:** nums = \[7,9,5,8,1,3\]
**Output:** 1
**Explanation:** Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums\[2\] = 5 and nums\[3\] = 8, the resultant array will be \[7,9,1,3\]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums\[1\] = 9 and nums\[4\] = 1. The resultant array becomes \[7,5,8,3\]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.
**Constraints:**
* `nums.length == 3 * n`
* `1 <= n <= 105`
* `1 <= nums[i] <= 105` | Try 'mapping' the strings to check if they are unique or not. |
Python: Heap + DP -- code is easy to read with comments | minimum-difference-in-sums-after-removal-of-elements | 0 | 1 | # Approach\nSimilar to many other answers. I\'m sharing my solution because I think my code is a bit clearer than other solutions I was seeing. I hope it\'s helpful!\n\nBy default we remove the middle n elements. The difference is `sum(nums[:n]) - sum([nums[2*n:]])`. However, we could choose to move one of the removes from the middle into the left group. This would replace the number we remove from the left group with the next number in the middle. Greedily, we always want to remove the largest element that hurts the difference the most. The opposite is true for the right group, except we want to remove the smallest element.\n\nWe record the best possible outcomes if we allow for x removes on the left or right. We then consider all possible allocations of the n removes between the left and right to find the minimum difference.\n\n- Time complexity: $$O(nlogn)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n n = len(nums) // 3\n \n # Build a max heap of the elements on the left side and a min heap of the elements on the right side\n left = [-num for num in nums[:n]]\n right = nums[2*n:]\n heapq.heapify(left)\n heapq.heapify(right)\n middle = nums[n:2*n]\n\n # Repeatedly remove the largest element from the left group and replace it with the next element from the middle\n left_sum = sum(nums[:n])\n left_remove = [left_sum]\n s = left_sum\n for i in range(n):\n largest = -1 * heapq.heappop(left)\n s -= largest\n s += middle[i]\n # Record the best option with i removes, regardless of if you actually use them to take new elements from the middle\n left_remove.append(min(left_remove[i], s))\n # Insert the new element from the middle into max heap since it\'s now part of the left group and could be chosen to remove in the future\n heapq.heappush(left, -1 * middle[i])\n\n # Do the same on the right side\n right_sum = sum(nums[2*n:])\n right_remove = [right_sum]\n s = right_sum\n for i in range(n):\n smallest = heapq.heappop(right)\n s -= smallest\n s += middle[-1-i]\n right_remove.append(max(right_remove[i], s))\n heapq.heappush(right, middle[-1-i])\n\n # Consider all options of how you allocate the n removes between the left and right side\n # We\'ve already calculated how each side uses those removes optimally\n # Return the allocation that leads to the smallest difference!\n return min(left_remove[i] - right_remove[n-i] for i in range(n+1))\n``` | 0 | You are given a **0-indexed** integer array `nums` consisting of `3 * n` elements.
You are allowed to remove any **subsequence** of elements of size **exactly** `n` from `nums`. The remaining `2 * n` elements will be divided into two **equal** parts:
* The first `n` elements belonging to the first part and their sum is `sumfirst`.
* The next `n` elements belonging to the second part and their sum is `sumsecond`.
The **difference in sums** of the two parts is denoted as `sumfirst - sumsecond`.
* For example, if `sumfirst = 3` and `sumsecond = 2`, their difference is `1`.
* Similarly, if `sumfirst = 2` and `sumsecond = 3`, their difference is `-1`.
Return _the **minimum difference** possible between the sums of the two parts after the removal of_ `n` _elements_.
**Example 1:**
**Input:** nums = \[3,1,2\]
**Output:** -1
**Explanation:** Here, nums has 3 elements, so n = 1.
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums\[0\] = 3, the array will be \[1,2\]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums\[1\] = 1, the array will be \[3,2\]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums\[2\] = 2, the array will be \[3,1\]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.
**Example 2:**
**Input:** nums = \[7,9,5,8,1,3\]
**Output:** 1
**Explanation:** Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums\[2\] = 5 and nums\[3\] = 8, the resultant array will be \[7,9,1,3\]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums\[1\] = 9 and nums\[4\] = 1. The resultant array becomes \[7,5,8,3\]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.
**Constraints:**
* `nums.length == 3 * n`
* `1 <= n <= 105`
* `1 <= nums[i] <= 105` | Try 'mapping' the strings to check if they are unique or not. |
[Python3|C++] Priority Queue | minimum-difference-in-sums-after-removal-of-elements | 0 | 1 | # Intuition\n`min(min_left[i] - max_right[i] | i = n, n+1, ... 2*n - 1, 2*n)`\n\n# Approach\nPlease refer to [this great post](https://leetcode.com/problems/minimum-difference-in-sums-after-removal-of-elements/solutions/1747003/python-o-nlogn-priority-queue-with-detailed-explanation/)\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python []\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n n = len(nums) // 3\n\n pq_mx = [-nums[i] for i in range(n)]\n heapq.heapify(pq_mx)\n mn_ss = -sum(pq_mx)\n mn_arr = [mn_ss] * (n+1)\n\n for i in range(n, 2*n):\n if nums[i] < -pq_mx[0]:\n mx = heapq.heapreplace(pq_mx, -nums[i])\n mn_ss += mx + nums[i]\n \n mn_arr[i-n + 1] = mn_ss\n\n pq_mn = [nums[i] for i in range(2*n, 3*n)]\n heapq.heapify(pq_mn)\n mx_ss = sum(pq_mn)\n mx_arr = [mx_ss] * (n+1)\n\n for i in range(2*n - 1, n-1, -1):\n if nums[i] > pq_mn[0]:\n mn = heapq.heapreplace(pq_mn, nums[i])\n mx_ss += -mn + nums[i]\n \n mx_arr[i-n] = mx_ss\n\n return min(mn-mx for mn, mx in zip(mn_arr, mx_arr))\n```\n```c++ []\nclass Solution {\npublic:\n long long minimumDifference(vector<int>& nums) {\n int m = nums.size();\n int n = m / 3;\n\n long mn_ss = 0;\n priority_queue<int> mx_pq;\n for (int i = 0; i < n; i++){\n mn_ss += nums[i];\n mx_pq.push(nums[i]);\n }\n vector<long> mn_arr(n+1, mn_ss);\n\n for (int i = n; i < 2*n; i++){\n if (nums[i] < mx_pq.top()){\n \n int mx = mx_pq.top();\n mx_pq.pop();\n mx_pq.push(nums[i]);\n mn_ss += -mx + nums[i];\n }\n mn_arr[i-n + 1] = mn_ss;\n }\n\n long mx_ss = 0;\n priority_queue<int, vector<int>, greater<>> mn_pq;\n for (int i = 2*n; i < m; i++){\n mx_ss += nums[i];\n mn_pq.push(nums[i]);\n }\n vector<long> mx_arr(n+1, mx_ss);\n\n for (int i = 2*n - 1; i >= n; i--){\n if (nums[i] > mn_pq.top()){\n int mn = mn_pq.top();\n mn_pq.pop();\n mn_pq.push(nums[i]);\n mx_ss += -mn + nums[i];\n }\n \n mx_arr[i-n] = mx_ss;\n }\n\n long ret = LONG_MAX;\n for (int i = 0; i <= n; i++){\n ret = min(mn_arr[i] - mx_arr[i], ret);\n }\n\n return ret;\n\n }\n};\n```\n | 0 | You are given a **0-indexed** integer array `nums` consisting of `3 * n` elements.
You are allowed to remove any **subsequence** of elements of size **exactly** `n` from `nums`. The remaining `2 * n` elements will be divided into two **equal** parts:
* The first `n` elements belonging to the first part and their sum is `sumfirst`.
* The next `n` elements belonging to the second part and their sum is `sumsecond`.
The **difference in sums** of the two parts is denoted as `sumfirst - sumsecond`.
* For example, if `sumfirst = 3` and `sumsecond = 2`, their difference is `1`.
* Similarly, if `sumfirst = 2` and `sumsecond = 3`, their difference is `-1`.
Return _the **minimum difference** possible between the sums of the two parts after the removal of_ `n` _elements_.
**Example 1:**
**Input:** nums = \[3,1,2\]
**Output:** -1
**Explanation:** Here, nums has 3 elements, so n = 1.
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums\[0\] = 3, the array will be \[1,2\]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums\[1\] = 1, the array will be \[3,2\]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums\[2\] = 2, the array will be \[3,1\]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.
**Example 2:**
**Input:** nums = \[7,9,5,8,1,3\]
**Output:** 1
**Explanation:** Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums\[2\] = 5 and nums\[3\] = 8, the resultant array will be \[7,9,1,3\]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums\[1\] = 9 and nums\[4\] = 1. The resultant array becomes \[7,5,8,3\]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.
**Constraints:**
* `nums.length == 3 * n`
* `1 <= n <= 105`
* `1 <= nums[i] <= 105` | Try 'mapping' the strings to check if they are unique or not. |
Two-direction scan with heap in Python, faster than 95% | minimum-difference-in-sums-after-removal-of-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is to find a pivot in between `n` and `2n` (inclusive) so that the sum of the mininum `n` elements in `nums[0:pivot]` - the sum of the maximum `n` elements in `nums[pivot:3n]` is minimized. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy soluton first scans the elements in from `2n` to `n` in the backward direction. A heap with the `n` maximum elemements can be found at each position is maintained during scanning, and the sum of the `n` elements is stored in a list `backward`. Then, the second scan is performed from `n` to `2n` in the forward direction. A heap with the `n` minimum elements at each poistion is maintained during the scanning, and the best solution can be obtained by using the precomputed information from the backward list. \n\n# Complexity\n- Time complexity: $$O(n \\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom heapq import heappush, heappop, heapify\n\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n n = len(nums) // 3\n left, right = [-v for v in nums[:n]], nums[-n:]\n backward = [0] * (n + 1)\n backward[n] = sum(right)\n heapify(left)\n heapify(right)\n \n for i in range(n-1, -1, -1):\n if nums[n + i] > right[0]:\n backward[i] = backward[i+1] - heappop(right) + nums[n+i]\n heappush(right, nums[n+i])\n else:\n backward[i] = backward[i+1]\n s = -sum(left)\n best = s - backward[0]\n for i in range(0, n):\n if nums[n+i] < -left[0]:\n s = s - (-heappop(left)) + nums[n+i]\n heappush(left, -nums[n+i])\n best = min(best, s - backward[i+1])\n return best\n``` | 0 | You are given a **0-indexed** integer array `nums` consisting of `3 * n` elements.
You are allowed to remove any **subsequence** of elements of size **exactly** `n` from `nums`. The remaining `2 * n` elements will be divided into two **equal** parts:
* The first `n` elements belonging to the first part and their sum is `sumfirst`.
* The next `n` elements belonging to the second part and their sum is `sumsecond`.
The **difference in sums** of the two parts is denoted as `sumfirst - sumsecond`.
* For example, if `sumfirst = 3` and `sumsecond = 2`, their difference is `1`.
* Similarly, if `sumfirst = 2` and `sumsecond = 3`, their difference is `-1`.
Return _the **minimum difference** possible between the sums of the two parts after the removal of_ `n` _elements_.
**Example 1:**
**Input:** nums = \[3,1,2\]
**Output:** -1
**Explanation:** Here, nums has 3 elements, so n = 1.
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums\[0\] = 3, the array will be \[1,2\]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums\[1\] = 1, the array will be \[3,2\]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums\[2\] = 2, the array will be \[3,1\]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.
**Example 2:**
**Input:** nums = \[7,9,5,8,1,3\]
**Output:** 1
**Explanation:** Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums\[2\] = 5 and nums\[3\] = 8, the resultant array will be \[7,9,1,3\]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums\[1\] = 9 and nums\[4\] = 1. The resultant array becomes \[7,5,8,3\]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.
**Constraints:**
* `nums.length == 3 * n`
* `1 <= n <= 105`
* `1 <= nums[i] <= 105` | Try 'mapping' the strings to check if they are unique or not. |
Python (Simple Heap) | minimum-difference-in-sums-after-removal-of-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDifference(self, nums):\n n = len(nums)//3\n\n left, right, mid = [-i for i in nums[:n]], nums[2*n:], nums[n:2*n]\n\n left_sum, right_sum = [-sum(left)], [sum(right)]\n\n heapq.heapify(left)\n heapq.heapify(right)\n\n for i in mid:\n heapq.heappush(left,-i)\n left_sum.append(left_sum[-1] + i + heapq.heappop(left))\n\n for i in mid[::-1]:\n heapq.heappush(right,i)\n right_sum.append(right_sum[-1] + i - heapq.heappop(right))\n\n right_sum = right_sum[::-1]\n\n return min([i-j for i,j in zip(left_sum,right_sum)])\n\n\n\n\n\n\n\n\n\n\n\n\n \n\n \n``` | 0 | You are given a **0-indexed** integer array `nums` consisting of `3 * n` elements.
You are allowed to remove any **subsequence** of elements of size **exactly** `n` from `nums`. The remaining `2 * n` elements will be divided into two **equal** parts:
* The first `n` elements belonging to the first part and their sum is `sumfirst`.
* The next `n` elements belonging to the second part and their sum is `sumsecond`.
The **difference in sums** of the two parts is denoted as `sumfirst - sumsecond`.
* For example, if `sumfirst = 3` and `sumsecond = 2`, their difference is `1`.
* Similarly, if `sumfirst = 2` and `sumsecond = 3`, their difference is `-1`.
Return _the **minimum difference** possible between the sums of the two parts after the removal of_ `n` _elements_.
**Example 1:**
**Input:** nums = \[3,1,2\]
**Output:** -1
**Explanation:** Here, nums has 3 elements, so n = 1.
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums\[0\] = 3, the array will be \[1,2\]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums\[1\] = 1, the array will be \[3,2\]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums\[2\] = 2, the array will be \[3,1\]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.
**Example 2:**
**Input:** nums = \[7,9,5,8,1,3\]
**Output:** 1
**Explanation:** Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums\[2\] = 5 and nums\[3\] = 8, the resultant array will be \[7,9,1,3\]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums\[1\] = 9 and nums\[4\] = 1. The resultant array becomes \[7,5,8,3\]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.
**Constraints:**
* `nums.length == 3 * n`
* `1 <= n <= 105`
* `1 <= nums[i] <= 105` | Try 'mapping' the strings to check if they are unique or not. |
[Python] O(n log n) Easy to Understand Explanation with pictures | minimum-difference-in-sums-after-removal-of-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe first thing we should always do when solving a problem is to carefully read the given examples. In this case, it is important to note that the goal is to find the minimum difference, not the minimum absolute difference. Once this detail is understood, the problem becomes more manageable.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nNow that we understand the actual problem, we can focus on approaching it. The first instinct might be to place the lowest elements in the first part of the array and the greatest elements in the second part. \n\n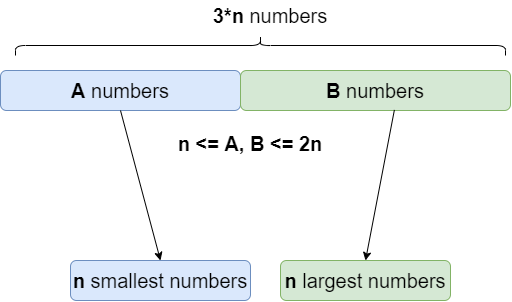\n\n\nWhile this is a good starting point, there are some refinements to be made before starting the implementation.\n\nIt should be noted that reordering the entire array is not allowed. Each element can only be shifted up to n positions. This means that the first element of the array cannot be part of the second part once the n elements are removed.\n\nTherefore, the first n elements of nums can only be either included in the first part or excluded. The same is true for the last n elements of nums, they can only be included in the second part.\n\nThe only remaining decision is whether the elements n+1 to 2n of nums should belong to the first part or the second part. If the first n+k elements belong to the first part and the rest to the second part, then it is clear that the problem reduces to finding this value of k.\n\nRemember that our objective is to make the sum of the first part as small as possible, while making the sum of the second part as large as possible. To achieve this, if the first part consists of n + k elements, we remove the k largest elements. Conversely, if the second part consists of 2n - k elements, we remove the n - k smallest elements. This way, we remove exactly n elements from the array, resulting in two parts with exactly n elements each.\n\nTo determine the value of k, the only option is to try k = 1, ..., n and determine the best solution by evaluating the difference between the first and second parts.\n\nThere are various methods to achieve this, but efficiency is key. One possible approach is to go through the elements of the array twice. The first pass involves finding the n largest elements in nums[:n + k], with k = 1, ..., n. In the second pass, we find the n smallest elements in nums[3n - k:], with k = 1, ..., n.\n\nThink of it as gradually increasing the size of a window, considering one more element in each step. In the first case, we are searching for larger numbers, while in the second case, we are searching for smaller numbers.\n\nA heap data structure can be used to efficiently find the n smallest or largest elements of the current window. As we consider each new element, we add it to the heap. To update the sum, we pop the first element in the heap and compare it with the newly considered element.\n\n\n\n# Complexity\n- Time complexity: $$\\mathcal{O}(n \\ log \\ n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$\\mathcal{O}(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n n = len(nums)//3\n # Max heap\n prefix_q = [-x for x in nums[:n]]\n heapq.heapify(prefix_q)\n \n # Initialize diff\n diff = [0]*(n+1)\n diff[0] = -sum(prefix_q)\n \n # Expand window rightwise -->\n for i in range(n):\n r = nums[i+n] \n # Update prefix sum: Consider r. Is it smaller than greatest in queue? \n greatest = -heapq.heappushpop(prefix_q, -r)\n diff[i+1] = diff[i] - greatest + r\n \n # Min heap\n suffix_q = nums[2*n:]\n heapq.heapify(suffix_q)\n \n prev_sum = sum(suffix_q)\n diff[-1] -= prev_sum\n \n #Expand window leftwise <--\n for i in range(n):\n l = nums[len(nums) - 1 - n - i]\n \n # Update suffix sum: Consider l. Is it greater than smallest in queue?\n smallest = heapq.heappushpop(suffix_q, l)\n prev_sum = prev_sum - smallest + l\n diff[n - 1 - i] -= prev_sum \n\n return min(diff)\n``` | 0 | You are given a **0-indexed** integer array `nums` consisting of `3 * n` elements.
You are allowed to remove any **subsequence** of elements of size **exactly** `n` from `nums`. The remaining `2 * n` elements will be divided into two **equal** parts:
* The first `n` elements belonging to the first part and their sum is `sumfirst`.
* The next `n` elements belonging to the second part and their sum is `sumsecond`.
The **difference in sums** of the two parts is denoted as `sumfirst - sumsecond`.
* For example, if `sumfirst = 3` and `sumsecond = 2`, their difference is `1`.
* Similarly, if `sumfirst = 2` and `sumsecond = 3`, their difference is `-1`.
Return _the **minimum difference** possible between the sums of the two parts after the removal of_ `n` _elements_.
**Example 1:**
**Input:** nums = \[3,1,2\]
**Output:** -1
**Explanation:** Here, nums has 3 elements, so n = 1.
Thus we have to remove 1 element from nums and divide the array into two equal parts.
- If we remove nums\[0\] = 3, the array will be \[1,2\]. The difference in sums of the two parts will be 1 - 2 = -1.
- If we remove nums\[1\] = 1, the array will be \[3,2\]. The difference in sums of the two parts will be 3 - 2 = 1.
- If we remove nums\[2\] = 2, the array will be \[3,1\]. The difference in sums of the two parts will be 3 - 1 = 2.
The minimum difference between sums of the two parts is min(-1,1,2) = -1.
**Example 2:**
**Input:** nums = \[7,9,5,8,1,3\]
**Output:** 1
**Explanation:** Here n = 2. So we must remove 2 elements and divide the remaining array into two parts containing two elements each.
If we remove nums\[2\] = 5 and nums\[3\] = 8, the resultant array will be \[7,9,1,3\]. The difference in sums will be (7+9) - (1+3) = 12.
To obtain the minimum difference, we should remove nums\[1\] = 9 and nums\[4\] = 1. The resultant array becomes \[7,5,8,3\]. The difference in sums of the two parts is (7+5) - (8+3) = 1.
It can be shown that it is not possible to obtain a difference smaller than 1.
**Constraints:**
* `nums.length == 3 * n`
* `1 <= n <= 105`
* `1 <= nums[i] <= 105` | Try 'mapping' the strings to check if they are unique or not. |
Reconstruction | sort-even-and-odd-indices-independently | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortEvenOdd(self, nums: List[int]) -> List[int]:\n odd = []\n eve = []\n for i in range(len(nums)):\n if i % 2 == 0:\n eve.append(nums[i])\n nums[i] = 1\n elif i % 2 == 1:\n odd.append(nums[i])\n nums[i] = 0\n\n eve.sort(reverse=True)\n odd.sort()\n\n for i in range(len(nums)):\n if nums[i] == 1:\n nums[i] = eve.pop()\n elif nums[i] == 0:\n nums[i] = odd.pop()\n\n return nums\n \n``` | 1 | You are given a **0-indexed** integer array `nums`. Rearrange the values of `nums` according to the following rules:
1. Sort the values at **odd indices** of `nums` in **non-increasing** order.
* For example, if `nums = [4,**1**,2,**3**]` before this step, it becomes `[4,**3**,2,**1**]` after. The values at odd indices `1` and `3` are sorted in non-increasing order.
2. Sort the values at **even indices** of `nums` in **non-decreasing** order.
* For example, if `nums = [**4**,1,**2**,3]` before this step, it becomes `[**2**,1,**4**,3]` after. The values at even indices `0` and `2` are sorted in non-decreasing order.
Return _the array formed after rearranging the values of_ `nums`.
**Example 1:**
**Input:** nums = \[4,1,2,3\]
**Output:** \[2,3,4,1\]
**Explanation:**
First, we sort the values present at odd indices (1 and 3) in non-increasing order.
So, nums changes from \[4,**1**,2,**3**\] to \[4,**3**,2,**1**\].
Next, we sort the values present at even indices (0 and 2) in non-decreasing order.
So, nums changes from \[**4**,1,**2**,3\] to \[**2**,3,**4**,1\].
Thus, the array formed after rearranging the values is \[2,3,4,1\].
**Example 2:**
**Input:** nums = \[2,1\]
**Output:** \[2,1\]
**Explanation:**
Since there is exactly one odd index and one even index, no rearrangement of values takes place.
The resultant array formed is \[2,1\], which is the same as the initial array.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | How can sorting the events on the basis of their start times help? How about end times? How can we quickly get the maximum score of an interval not intersecting with the interval we chose? |
You can specify steps when slicing a list :) | sort-even-and-odd-indices-independently | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortEvenOdd(self, nums: List[int]) -> List[int]:\n nums[0::2]=sorted(nums[0::2])\n nums[1::2]=sorted(nums[1::2],reverse=True)\n return nums\n\n\n \n``` | 2 | You are given a **0-indexed** integer array `nums`. Rearrange the values of `nums` according to the following rules:
1. Sort the values at **odd indices** of `nums` in **non-increasing** order.
* For example, if `nums = [4,**1**,2,**3**]` before this step, it becomes `[4,**3**,2,**1**]` after. The values at odd indices `1` and `3` are sorted in non-increasing order.
2. Sort the values at **even indices** of `nums` in **non-decreasing** order.
* For example, if `nums = [**4**,1,**2**,3]` before this step, it becomes `[**2**,1,**4**,3]` after. The values at even indices `0` and `2` are sorted in non-decreasing order.
Return _the array formed after rearranging the values of_ `nums`.
**Example 1:**
**Input:** nums = \[4,1,2,3\]
**Output:** \[2,3,4,1\]
**Explanation:**
First, we sort the values present at odd indices (1 and 3) in non-increasing order.
So, nums changes from \[4,**1**,2,**3**\] to \[4,**3**,2,**1**\].
Next, we sort the values present at even indices (0 and 2) in non-decreasing order.
So, nums changes from \[**4**,1,**2**,3\] to \[**2**,3,**4**,1\].
Thus, the array formed after rearranging the values is \[2,3,4,1\].
**Example 2:**
**Input:** nums = \[2,1\]
**Output:** \[2,1\]
**Explanation:**
Since there is exactly one odd index and one even index, no rearrangement of values takes place.
The resultant array formed is \[2,1\], which is the same as the initial array.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | How can sorting the events on the basis of their start times help? How about end times? How can we quickly get the maximum score of an interval not intersecting with the interval we chose? |
Best Easy Solution | sort-even-and-odd-indices-independently | 0 | 1 | # Intuition\nIteration\n\n# Approach\nBruteforce\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def sortEvenOdd(self, nums: List[int]) -> List[int]:\n lst=[]\n dst=[]\n bst=[]\n mst=[]\n cst=[0]*len(nums)\n for i in range(len(nums)):\n if i%2==0:\n lst.append(nums[i])\n dst.append(i)\n else:\n bst.append(nums[i])\n mst.append(i)\n lst.sort()\n bst.sort()\n bst=bst[::-1]\n for i in range(len(lst)):\n cst[dst[i]]=lst[i]\n for j in range(len(bst)):\n cst[mst[j]]=bst[j]\n return cst\n\n \n \n``` | 1 | You are given a **0-indexed** integer array `nums`. Rearrange the values of `nums` according to the following rules:
1. Sort the values at **odd indices** of `nums` in **non-increasing** order.
* For example, if `nums = [4,**1**,2,**3**]` before this step, it becomes `[4,**3**,2,**1**]` after. The values at odd indices `1` and `3` are sorted in non-increasing order.
2. Sort the values at **even indices** of `nums` in **non-decreasing** order.
* For example, if `nums = [**4**,1,**2**,3]` before this step, it becomes `[**2**,1,**4**,3]` after. The values at even indices `0` and `2` are sorted in non-decreasing order.
Return _the array formed after rearranging the values of_ `nums`.
**Example 1:**
**Input:** nums = \[4,1,2,3\]
**Output:** \[2,3,4,1\]
**Explanation:**
First, we sort the values present at odd indices (1 and 3) in non-increasing order.
So, nums changes from \[4,**1**,2,**3**\] to \[4,**3**,2,**1**\].
Next, we sort the values present at even indices (0 and 2) in non-decreasing order.
So, nums changes from \[**4**,1,**2**,3\] to \[**2**,3,**4**,1\].
Thus, the array formed after rearranging the values is \[2,3,4,1\].
**Example 2:**
**Input:** nums = \[2,1\]
**Output:** \[2,1\]
**Explanation:**
Since there is exactly one odd index and one even index, no rearrangement of values takes place.
The resultant array formed is \[2,1\], which is the same as the initial array.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | How can sorting the events on the basis of their start times help? How about end times? How can we quickly get the maximum score of an interval not intersecting with the interval we chose? |
PYTHON BEATS 100% OF RUNTIME✅ | smallest-value-of-the-rearranged-number | 0 | 1 | # Approach\n1- Check if num is **negative** or not\n\n2- **Store** all **digits** in num in an array **except** the **zeros**\n\n3- If num is **negative** -> you need to order the array in **descending** order and add all **zeros** to the **left**\nif num is **positive** -> you need to order the array in **ascending** order and add all **zeros** to the **right** in the **second** **position**. Not in the first because the number can\'t have any leading zeros.\n\nps: if you have any improvements, let me know :)\n\n\n# Code\n```\nclass Solution(object):\n def smallestNumber(self, num):\n\n if num == 0:\n return 0\n \n isNegative, nums, countZero, s = False, [], 0, str(num)\n \n if num < 0:\n isNegative = True\n s = s[1:]\n \n for i in range(len(s)):\n if s[i] != \'0\':\n nums.append(s[i])\n else:\n countZero += 1\n\n nums.sort(reverse=isNegative)\n newN = \'\'.join(nums)\n\n if isNegative:\n return int(\'-\' + newN + \'0\' * countZero)\n\n return int(newN[0] + \'0\' * countZero + newN[1:])\n \n``` | 1 | You are given an integer `num.` **Rearrange** the digits of `num` such that its value is **minimized** and it does not contain **any** leading zeros.
Return _the rearranged number with minimal value_.
Note that the sign of the number does not change after rearranging the digits.
**Example 1:**
**Input:** num = 310
**Output:** 103
**Explanation:** The possible arrangements for the digits of 310 are 013, 031, 103, 130, 301, 310.
The arrangement with the smallest value that does not contain any leading zeros is 103.
**Example 2:**
**Input:** num = -7605
**Output:** -7650
**Explanation:** Some possible arrangements for the digits of -7605 are -7650, -6705, -5076, -0567.
The arrangement with the smallest value that does not contain any leading zeros is -7650.
**Constraints:**
* `-1015 <= num <= 1015` | Can you find the indices of the most left and right candles for a given substring, perhaps by using binary search (or better) over an array of indices of all the bars? Once the indices of the most left and right bars are determined, how can you efficiently count the number of plates within the range? Prefix sums? |
Intuitive Python solution, not using str | smallest-value-of-the-rearranged-number | 0 | 1 | # Intuition\nThis problem is similar to sorting an array but in here you need to sort digits in ascending order if the number is positive and descending order if negative. (Technically, it\'s non descending for positive and non acending for negative since we can have duplicate digit)\n\nWe would like to operate as number instead of converting it to string at any point.\n\n# Approach\nLeverage stack data structure to store digits and sort it after.\n\nStep 1: Check edge case\nStep 2: Get number sign\nStep 3: Add all digits in stack\nStep 4: Sort in non descending order\nStep 5: Check if we need a negative number, reverse the stack. If positive number, check if we have leading zero and swap with the next non zero number.\nStep 6: Construct the final number\n\n# Complexity\n- Time complexity:\nO(n) we did 2 separated loop which is O(2n), sort is O(logn). So total would be O(2n+logn) = O(n)\n\n- Space complexity:\nO(n) for the stack\n\n# Code\n```\nclass Solution:\n def smallestNumber(self, num: int) -> int:\n if num == 0:\n return 0\n\n sign = 1 if num > 0 else -1\n num = num * -1 if num < 0 else num\n stack = []\n while num >= 10:\n stack.append(num%10)\n num = num // 10\n \n stack.append(num)\n stack.sort()\n \n res = 0\n if sign < 0:\n stack = stack[::-1]\n else:\n # check if there\'s 0 in stack:\n if 0 in stack:\n for i in range(len(stack)):\n if stack[i] != 0:\n stack[0], stack[i] = stack[i], stack[0]\n break\n\n for i in stack:\n res = res * 10 + i\n\n return res * sign\n``` | 0 | You are given an integer `num.` **Rearrange** the digits of `num` such that its value is **minimized** and it does not contain **any** leading zeros.
Return _the rearranged number with minimal value_.
Note that the sign of the number does not change after rearranging the digits.
**Example 1:**
**Input:** num = 310
**Output:** 103
**Explanation:** The possible arrangements for the digits of 310 are 013, 031, 103, 130, 301, 310.
The arrangement with the smallest value that does not contain any leading zeros is 103.
**Example 2:**
**Input:** num = -7605
**Output:** -7650
**Explanation:** Some possible arrangements for the digits of -7605 are -7650, -6705, -5076, -0567.
The arrangement with the smallest value that does not contain any leading zeros is -7650.
**Constraints:**
* `-1015 <= num <= 1015` | Can you find the indices of the most left and right candles for a given substring, perhaps by using binary search (or better) over an array of indices of all the bars? Once the indices of the most left and right bars are determined, how can you efficiently count the number of plates within the range? Prefix sums? |
Python solution || Easy to understand || string || bitset | design-bitset | 0 | 1 | ```\nclass Bitset:\n\n def __init__(self, size: int):\n\t\t# stores original bits True -> 1, False -> 0\n self.bit = [False for i in range(size)]\n\t\t# inverse list of self.bit\n self.bitinv = [True for i in range(size)]\n\t\t# counter of True\n self.ones = 0\n\t\t# counter of False (both are for self.bit)\n self.zeros = size\n\t\t# original size\n self.size = size\n\n def fix(self, idx: int) -> None:\n\t\t# if the bit is 0/False set the bit and update the counters bitinv stores opposite of self.bit every time\n if not self.bit[idx]:\n self.zeros -= 1\n self.ones += 1\n self.bit[idx] = True\n self.bitinv[idx] = False\n\n def unfix(self, idx: int) -> None:\n\t\t# if the bit is set unset the bit and update both the lists as mentioned above\n if self.bit[idx]:\n self.zeros += 1\n self.ones -= 1\n self.bit[idx] = False\n self.bitinv[idx] = True\n\n def flip(self) -> None:\n\t\t# changing the zeros counter to ones and vice versa.\n self.ones,self.zeros = self.zeros,self.ones\n\t\t# changing the list pointers now inverse list will be the main list i.e. self.bit will point towards self.bitinv and vice versa.\n self.bit,self.bitinv = self.bitinv,self.bit\n\n def all(self) -> bool:\n\t\t# return True if ones counter equal to size otherwise False.\n return self.ones == self.size\n\n def one(self) -> bool:\n\t\t# returns True if ones counter greater than zeros\n return self.ones > 0\n\n def count(self) -> int:\n\t\t# returns the number of ones\n return self.ones\n\n def toString(self) -> str:\n\t\t# appending 1 to string if it\'s True in self.bit otherwise 0\n ans = \'\'\n for bit in self.bit:\n if bit:\n ans += \'1\'\n else:\n ans += \'0\'\n return ans\n``` | 1 | A **Bitset** is a data structure that compactly stores bits.
Implement the `Bitset` class:
* `Bitset(int size)` Initializes the Bitset with `size` bits, all of which are `0`.
* `void fix(int idx)` Updates the value of the bit at the index `idx` to `1`. If the value was already `1`, no change occurs.
* `void unfix(int idx)` Updates the value of the bit at the index `idx` to `0`. If the value was already `0`, no change occurs.
* `void flip()` Flips the values of each bit in the Bitset. In other words, all bits with value `0` will now have value `1` and vice versa.
* `boolean all()` Checks if the value of **each** bit in the Bitset is `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `boolean one()` Checks if there is **at least one** bit in the Bitset with value `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `int count()` Returns the **total number** of bits in the Bitset which have value `1`.
* `String toString()` Returns the current composition of the Bitset. Note that in the resultant string, the character at the `ith` index should coincide with the value at the `ith` bit of the Bitset.
**Example 1:**
**Input**
\[ "Bitset ", "fix ", "fix ", "flip ", "all ", "unfix ", "flip ", "one ", "unfix ", "count ", "toString "\]
\[\[5\], \[3\], \[1\], \[\], \[\], \[0\], \[\], \[\], \[0\], \[\], \[\]\]
**Output**
\[null, null, null, null, false, null, null, true, null, 2, "01010 "\]
**Explanation**
Bitset bs = new Bitset(5); // bitset = "00000 ".
bs.fix(3); // the value at idx = 3 is updated to 1, so bitset = "00010 ".
bs.fix(1); // the value at idx = 1 is updated to 1, so bitset = "01010 ".
bs.flip(); // the value of each bit is flipped, so bitset = "10101 ".
bs.all(); // return False, as not all values of the bitset are 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "00101 ".
bs.flip(); // the value of each bit is flipped, so bitset = "11010 ".
bs.one(); // return True, as there is at least 1 index with value 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "01010 ".
bs.count(); // return 2, as there are 2 bits with value 1.
bs.toString(); // return "01010 ", which is the composition of bitset.
**Constraints:**
* `1 <= size <= 105`
* `0 <= idx <= size - 1`
* At most `105` calls will be made **in total** to `fix`, `unfix`, `flip`, `all`, `one`, `count`, and `toString`.
* At least one call will be made to `all`, `one`, `count`, or `toString`.
* At most `5` calls will be made to `toString`. | N is small, we can generate all possible move combinations. For each possible move combination, determine which ones are valid. |
[Python3, Java, C++] All Operations O(1) | Flipped String/Flip Flag | design-bitset | 1 | 1 | \n* Flipping can be done using a flipped string that contains the flipped version of the current bitset. C++ and Java solutions have been done using this method. All operations are O(1) in C++ at the cost of an extra string of length `size`\n* Python solution has been done using a flip flag. Flip flag stores whether the current bitset has to be flipped. `toString` is O(n)\n* Keep a count variable `ones` that counts the number of ones in the bitset. This has to be updated in `fix`, `unfix`, and `flip` functions.\n<iframe src="https://leetcode.com/playground/kUJV4c3B/shared" frameBorder="0" width="900" height="590"></iframe> | 92 | A **Bitset** is a data structure that compactly stores bits.
Implement the `Bitset` class:
* `Bitset(int size)` Initializes the Bitset with `size` bits, all of which are `0`.
* `void fix(int idx)` Updates the value of the bit at the index `idx` to `1`. If the value was already `1`, no change occurs.
* `void unfix(int idx)` Updates the value of the bit at the index `idx` to `0`. If the value was already `0`, no change occurs.
* `void flip()` Flips the values of each bit in the Bitset. In other words, all bits with value `0` will now have value `1` and vice versa.
* `boolean all()` Checks if the value of **each** bit in the Bitset is `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `boolean one()` Checks if there is **at least one** bit in the Bitset with value `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `int count()` Returns the **total number** of bits in the Bitset which have value `1`.
* `String toString()` Returns the current composition of the Bitset. Note that in the resultant string, the character at the `ith` index should coincide with the value at the `ith` bit of the Bitset.
**Example 1:**
**Input**
\[ "Bitset ", "fix ", "fix ", "flip ", "all ", "unfix ", "flip ", "one ", "unfix ", "count ", "toString "\]
\[\[5\], \[3\], \[1\], \[\], \[\], \[0\], \[\], \[\], \[0\], \[\], \[\]\]
**Output**
\[null, null, null, null, false, null, null, true, null, 2, "01010 "\]
**Explanation**
Bitset bs = new Bitset(5); // bitset = "00000 ".
bs.fix(3); // the value at idx = 3 is updated to 1, so bitset = "00010 ".
bs.fix(1); // the value at idx = 1 is updated to 1, so bitset = "01010 ".
bs.flip(); // the value of each bit is flipped, so bitset = "10101 ".
bs.all(); // return False, as not all values of the bitset are 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "00101 ".
bs.flip(); // the value of each bit is flipped, so bitset = "11010 ".
bs.one(); // return True, as there is at least 1 index with value 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "01010 ".
bs.count(); // return 2, as there are 2 bits with value 1.
bs.toString(); // return "01010 ", which is the composition of bitset.
**Constraints:**
* `1 <= size <= 105`
* `0 <= idx <= size - 1`
* At most `105` calls will be made **in total** to `fix`, `unfix`, `flip`, `all`, `one`, `count`, and `toString`.
* At least one call will be made to `all`, `one`, `count`, or `toString`.
* At most `5` calls will be made to `toString`. | N is small, we can generate all possible move combinations. For each possible move combination, determine which ones are valid. |
[Java/Python 3] Boolean array, time O(1) except init() and toString() | design-bitset | 1 | 1 | Use 2 boolean arrays to record current state and the corresponding flipped one.\n\n```java\n private boolean[] bits;\n private boolean[] flipped;\n private int sz, cnt;\n \n public BooleanArray2(int size) {\n sz = size;\n bits = new boolean[size];\n flipped = new boolean[size];\n Arrays.fill(flipped, true);\n }\n \n public void fix(int idx) {\n if (!bits[idx]) {\n bits[idx] ^= true;\n flipped[idx] ^= true;\n cnt += 1;\n }\n }\n \n public void unfix(int idx) {\n if (bits[idx]) {\n bits[idx] ^= true;\n flipped[idx] ^= true;\n cnt -= 1;\n }\n }\n \n public void flip() {\n boolean[] tmp = bits;\n bits = flipped;\n flipped = tmp;\n cnt = sz - cnt;\n }\n \n public boolean all() {\n return cnt == sz;\n }\n \n public boolean one() {\n return cnt > 0;\n }\n \n public int count() {\n return cnt;\n }\n \n public String toString() {\n StringBuilder sb = new StringBuilder();\n for (boolean b : bits) {\n sb.append(b ? \'1\' : \'0\');\n }\n return sb.toString();\n }\n```\n```python\n def __init__(self, size: int):\n self.sz = size\n self.bits = [False] * size\n self.flipped = [True] * size\n self.bitCount = 0\n \n def fix(self, idx: int) -> None:\n if not self.bits[idx]:\n self.bits[idx] ^= True\n self.flipped[idx] ^= True\n self.bitCount += 1\n\n def unfix(self, idx: int) -> None:\n if self.bits[idx]:\n self.bits[idx] ^= True\n self.flipped[idx] ^= True\n self.bitCount -= 1\n\n def flip(self) -> None:\n self.bits, self.flipped = self.flipped, self.bits\n self.bitCount = self.sz - self.bitCount \n\n def all(self) -> bool:\n return self.sz == self.bitCount\n\n def one(self) -> bool:\n return self.bitCount > 0\n\n def count(self) -> int:\n return self.bitCount\n\n def toString(self) -> str:\n return \'\'.join([\'1\' if b else \'0\' for b in self.bits])\n```\n\n----\n\nMinor optimization of the space: using only **one** boolean array and a boolean variable `flipAll` to indicate the flip.\n\n```java\n private boolean[] arr;\n private int sz, cnt;\n private boolean flipAll;\n \n public Bitset(int size) {\n sz = size;\n arr = new boolean[size];\n }\n \n public void fix(int idx) {\n if (!(arr[idx] ^ flipAll)) {\n arr[idx] ^= true;\n cnt += 1;\n }\n }\n \n public void unfix(int idx) {\n if (arr[idx] ^ flipAll) {\n arr[idx] ^= true;\n cnt -= 1;\n }\n }\n \n public void flip() {\n flipAll ^= true;\n cnt = sz - cnt;\n }\n \n public boolean all() {\n return cnt == sz;\n }\n \n public boolean one() {\n return cnt > 0;\n }\n \n public int count() {\n return cnt;\n }\n \n public String toString() {\n StringBuilder sb = new StringBuilder();\n for (boolean b : arr) {\n sb.append(b ^ flipAll ? \'1\' : \'0\');\n }\n return sb.toString();\n }\n```\n\n```python\n def __init__(self, size: int):\n self.sz = size\n self.arr = [False] * size\n self.cnt = 0\n self.flipAll = False\n \n def fix(self, idx: int) -> None:\n if not (self.arr[idx] ^ self.flipAll):\n self.cnt += 1\n self.arr[idx] ^= True\n\n def unfix(self, idx: int) -> None:\n if self.arr[idx] ^ self.flipAll:\n self.arr[idx] ^= True\n self.cnt -= 1\n\n def flip(self) -> None:\n self.flipAll ^= True\n self.cnt = self.sz - self.cnt \n\n def all(self) -> bool:\n return self.sz == self.cnt\n\n def one(self) -> bool:\n return self.cnt > 0\n\n def count(self) -> int:\n return self.cnt\n\n def toString(self) -> str:\n return \'\'.join([\'1\' if (v ^ self.flipAll) else \'0\' for v in self.arr])\n```\n\n**Analysis:**\n\nTime & space:\nInitialization and `toString()` are both `O(size)`; others are all `O(1)`; | 15 | A **Bitset** is a data structure that compactly stores bits.
Implement the `Bitset` class:
* `Bitset(int size)` Initializes the Bitset with `size` bits, all of which are `0`.
* `void fix(int idx)` Updates the value of the bit at the index `idx` to `1`. If the value was already `1`, no change occurs.
* `void unfix(int idx)` Updates the value of the bit at the index `idx` to `0`. If the value was already `0`, no change occurs.
* `void flip()` Flips the values of each bit in the Bitset. In other words, all bits with value `0` will now have value `1` and vice versa.
* `boolean all()` Checks if the value of **each** bit in the Bitset is `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `boolean one()` Checks if there is **at least one** bit in the Bitset with value `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `int count()` Returns the **total number** of bits in the Bitset which have value `1`.
* `String toString()` Returns the current composition of the Bitset. Note that in the resultant string, the character at the `ith` index should coincide with the value at the `ith` bit of the Bitset.
**Example 1:**
**Input**
\[ "Bitset ", "fix ", "fix ", "flip ", "all ", "unfix ", "flip ", "one ", "unfix ", "count ", "toString "\]
\[\[5\], \[3\], \[1\], \[\], \[\], \[0\], \[\], \[\], \[0\], \[\], \[\]\]
**Output**
\[null, null, null, null, false, null, null, true, null, 2, "01010 "\]
**Explanation**
Bitset bs = new Bitset(5); // bitset = "00000 ".
bs.fix(3); // the value at idx = 3 is updated to 1, so bitset = "00010 ".
bs.fix(1); // the value at idx = 1 is updated to 1, so bitset = "01010 ".
bs.flip(); // the value of each bit is flipped, so bitset = "10101 ".
bs.all(); // return False, as not all values of the bitset are 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "00101 ".
bs.flip(); // the value of each bit is flipped, so bitset = "11010 ".
bs.one(); // return True, as there is at least 1 index with value 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "01010 ".
bs.count(); // return 2, as there are 2 bits with value 1.
bs.toString(); // return "01010 ", which is the composition of bitset.
**Constraints:**
* `1 <= size <= 105`
* `0 <= idx <= size - 1`
* At most `105` calls will be made **in total** to `fix`, `unfix`, `flip`, `all`, `one`, `count`, and `toString`.
* At least one call will be made to `all`, `one`, `count`, or `toString`.
* At most `5` calls will be made to `toString`. | N is small, we can generate all possible move combinations. For each possible move combination, determine which ones are valid. |
✔️ PYTHON || EXPLAINED || ;] | design-bitset | 0 | 1 | **UPVOTE IF HELPFuuL**\n\n* Make an array for storing bits. *Initializing all the values to 0*\n* Keep a variable ```on``` to keep the count of number of ones.\n* Create another ```bool``` variable ```flipped = False``` to store condition of array. **[ If array is fliiped, variable is changed to ```True```, if flipped again change to ```False``` and keeping doing this ]** Hence we can perform flip operation in O ( 1 ). Also remember to change number of one ```on```\n* Other conditons can be derived and understood from the code below.\n\n**UPVOTE IF HELPFuuL**\n\n```\nclass Bitset:\n\n def __init__(self, size: int):\n self.a=[0]*size\n self.on=0;\n self.n = size;\n self.flipped=False\n\n \n def fix(self, idx: int) -> None:\n if self.flipped:\n if self.a[idx]==1:\n self.on+=1\n self.a[idx]=0\n else:\n if self.a[idx]==0:\n self.on+=1\n self.a[idx]=1\n\n \n def unfix(self, idx: int) -> None:\n if self.flipped:\n if self.a[idx]==0:\n self.on-=1\n self.a[idx]=1\n else:\n if self.a[idx]==1:\n self.on-=1\n self.a[idx]=0\n\n \n def flip(self) -> None:\n if self.flipped:\n self.flipped=False\n else:\n self.flipped=True\n self.on = self.n-self.on\n \n \n def all(self) -> bool:\n if self.n==self.on:\n return True\n return False\n\n \n def one(self) -> bool:\n if self.on>0:\n return True\n return False\n\n \n def count(self) -> int:\n return self.on\n \n \n def toString(self) -> str:\n s=""\n if self.flipped:\n for i in self.a:\n if i:\n s+="0"\n else:\n s+="1"\n return s\n for i in self.a:\n if i:\n s+="1"\n else:\n s+="0"\n return s\n```\n\n\n | 9 | A **Bitset** is a data structure that compactly stores bits.
Implement the `Bitset` class:
* `Bitset(int size)` Initializes the Bitset with `size` bits, all of which are `0`.
* `void fix(int idx)` Updates the value of the bit at the index `idx` to `1`. If the value was already `1`, no change occurs.
* `void unfix(int idx)` Updates the value of the bit at the index `idx` to `0`. If the value was already `0`, no change occurs.
* `void flip()` Flips the values of each bit in the Bitset. In other words, all bits with value `0` will now have value `1` and vice versa.
* `boolean all()` Checks if the value of **each** bit in the Bitset is `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `boolean one()` Checks if there is **at least one** bit in the Bitset with value `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `int count()` Returns the **total number** of bits in the Bitset which have value `1`.
* `String toString()` Returns the current composition of the Bitset. Note that in the resultant string, the character at the `ith` index should coincide with the value at the `ith` bit of the Bitset.
**Example 1:**
**Input**
\[ "Bitset ", "fix ", "fix ", "flip ", "all ", "unfix ", "flip ", "one ", "unfix ", "count ", "toString "\]
\[\[5\], \[3\], \[1\], \[\], \[\], \[0\], \[\], \[\], \[0\], \[\], \[\]\]
**Output**
\[null, null, null, null, false, null, null, true, null, 2, "01010 "\]
**Explanation**
Bitset bs = new Bitset(5); // bitset = "00000 ".
bs.fix(3); // the value at idx = 3 is updated to 1, so bitset = "00010 ".
bs.fix(1); // the value at idx = 1 is updated to 1, so bitset = "01010 ".
bs.flip(); // the value of each bit is flipped, so bitset = "10101 ".
bs.all(); // return False, as not all values of the bitset are 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "00101 ".
bs.flip(); // the value of each bit is flipped, so bitset = "11010 ".
bs.one(); // return True, as there is at least 1 index with value 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "01010 ".
bs.count(); // return 2, as there are 2 bits with value 1.
bs.toString(); // return "01010 ", which is the composition of bitset.
**Constraints:**
* `1 <= size <= 105`
* `0 <= idx <= size - 1`
* At most `105` calls will be made **in total** to `fix`, `unfix`, `flip`, `all`, `one`, `count`, and `toString`.
* At least one call will be made to `all`, `one`, `count`, or `toString`.
* At most `5` calls will be made to `toString`. | N is small, we can generate all possible move combinations. For each possible move combination, determine which ones are valid. |
Python | O(1) operations using one list only| 97.43% faster | design-bitset | 0 | 1 | ```python\nclass Bitset:\n def __init__(self, size: int):\n self.bitset = [0] * size\n self.size = size\n self.ones = 0\n self.flipped = False\n \n\t\t\n def fix(self, idx: int) -> None:\n if self.flipped and self.bitset[idx]:\n self.bitset[idx] = 0\n self.ones += 1\n\t\t\t\n elif not self.flipped and not self.bitset[idx]:\n self.bitset[idx] = 1\n self.ones += 1\n \n\t\t\n def unfix(self, idx: int) -> None:\n if self.flipped and not self.bitset[idx]:\n self.bitset[idx] = 1\n self.ones -= 1\n\t\t\t\n elif not self.flipped and self.bitset[idx]:\n self.bitset[idx] = 0\n self.ones -= 1\n \n\t\t\n def flip(self) -> None:\n self.flipped = not self.flipped\n self.ones = self.size - self.ones\n\n\n def all(self) -> bool:\n return self.ones == self.size\n \n\n def one(self) -> bool:\n return self.ones > 0\n \n\t\t\n def count(self) -> int:\n return self.ones\n \n\t\t\n def toString(self) -> str:\n if self.flipped:\n return "".join("0" if i else "1" for i in self.bitset)\n \n return "".join("1" if i else "0" for i in self.bitset)\n``` | 1 | A **Bitset** is a data structure that compactly stores bits.
Implement the `Bitset` class:
* `Bitset(int size)` Initializes the Bitset with `size` bits, all of which are `0`.
* `void fix(int idx)` Updates the value of the bit at the index `idx` to `1`. If the value was already `1`, no change occurs.
* `void unfix(int idx)` Updates the value of the bit at the index `idx` to `0`. If the value was already `0`, no change occurs.
* `void flip()` Flips the values of each bit in the Bitset. In other words, all bits with value `0` will now have value `1` and vice versa.
* `boolean all()` Checks if the value of **each** bit in the Bitset is `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `boolean one()` Checks if there is **at least one** bit in the Bitset with value `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `int count()` Returns the **total number** of bits in the Bitset which have value `1`.
* `String toString()` Returns the current composition of the Bitset. Note that in the resultant string, the character at the `ith` index should coincide with the value at the `ith` bit of the Bitset.
**Example 1:**
**Input**
\[ "Bitset ", "fix ", "fix ", "flip ", "all ", "unfix ", "flip ", "one ", "unfix ", "count ", "toString "\]
\[\[5\], \[3\], \[1\], \[\], \[\], \[0\], \[\], \[\], \[0\], \[\], \[\]\]
**Output**
\[null, null, null, null, false, null, null, true, null, 2, "01010 "\]
**Explanation**
Bitset bs = new Bitset(5); // bitset = "00000 ".
bs.fix(3); // the value at idx = 3 is updated to 1, so bitset = "00010 ".
bs.fix(1); // the value at idx = 1 is updated to 1, so bitset = "01010 ".
bs.flip(); // the value of each bit is flipped, so bitset = "10101 ".
bs.all(); // return False, as not all values of the bitset are 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "00101 ".
bs.flip(); // the value of each bit is flipped, so bitset = "11010 ".
bs.one(); // return True, as there is at least 1 index with value 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "01010 ".
bs.count(); // return 2, as there are 2 bits with value 1.
bs.toString(); // return "01010 ", which is the composition of bitset.
**Constraints:**
* `1 <= size <= 105`
* `0 <= idx <= size - 1`
* At most `105` calls will be made **in total** to `fix`, `unfix`, `flip`, `all`, `one`, `count`, and `toString`.
* At least one call will be made to `all`, `one`, `count`, or `toString`.
* At most `5` calls will be made to `toString`. | N is small, we can generate all possible move combinations. For each possible move combination, determine which ones are valid. |
[Python 3] Two Lists, Keep track of ones and zeroes | design-bitset | 0 | 1 | **Approach:** Keep two lists, one with the regular bits and other with flipped.\n\nAlso, keep track of the number of ones and zeroes in the regular.\nThen it is straightforward solution.\nWhen using flip, interchange the two lists and the number of ones and zeroes.\n\n**DO UPVOTE IF YOU FOUND IT HELPFUL.**\n\n```\nclass Bitset:\n\n def __init__(self, size: int):\n self.bits = [0 for i in range(size)]\n self.flipped = [1 for i in range(size)]\n self.size = size\n self.ones = 0\n self.zeroes = self.size\n\n def fix(self, idx: int) -> None:\n self.flipped[idx] = 0\n if self.bits[idx] == 1:\n return\n self.bits[idx] = 1\n self.ones += 1\n self.zeroes -= 1\n\n def unfix(self, idx: int) -> None:\n self.flipped[idx] = 1\n if self.bits[idx] == 0:\n return\n self.bits[idx] = 0\n self.zeroes += 1\n self.ones -= 1\n\n def flip(self) -> None:\n self.bits, self.flipped = self.flipped, self.bits\n self.ones = self.size-self.ones\n self.zeroes = self.size-self.zeroes\n\n def all(self) -> bool:\n return self.ones == self.size\n\n def one(self) -> bool:\n return self.ones > 0\n\n def count(self) -> int:\n return self.ones\n\n def toString(self) -> str:\n return "".join([str(i) for i in self.bits])\n\n\n# Your Bitset object will be instantiated and called as such:\n# obj = Bitset(size)\n# obj.fix(idx)\n# obj.unfix(idx)\n# obj.flip()\n# param_4 = obj.all()\n# param_5 = obj.one()\n# param_6 = obj.count()\n# param_7 = obj.toString()\n``` | 2 | A **Bitset** is a data structure that compactly stores bits.
Implement the `Bitset` class:
* `Bitset(int size)` Initializes the Bitset with `size` bits, all of which are `0`.
* `void fix(int idx)` Updates the value of the bit at the index `idx` to `1`. If the value was already `1`, no change occurs.
* `void unfix(int idx)` Updates the value of the bit at the index `idx` to `0`. If the value was already `0`, no change occurs.
* `void flip()` Flips the values of each bit in the Bitset. In other words, all bits with value `0` will now have value `1` and vice versa.
* `boolean all()` Checks if the value of **each** bit in the Bitset is `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `boolean one()` Checks if there is **at least one** bit in the Bitset with value `1`. Returns `true` if it satisfies the condition, `false` otherwise.
* `int count()` Returns the **total number** of bits in the Bitset which have value `1`.
* `String toString()` Returns the current composition of the Bitset. Note that in the resultant string, the character at the `ith` index should coincide with the value at the `ith` bit of the Bitset.
**Example 1:**
**Input**
\[ "Bitset ", "fix ", "fix ", "flip ", "all ", "unfix ", "flip ", "one ", "unfix ", "count ", "toString "\]
\[\[5\], \[3\], \[1\], \[\], \[\], \[0\], \[\], \[\], \[0\], \[\], \[\]\]
**Output**
\[null, null, null, null, false, null, null, true, null, 2, "01010 "\]
**Explanation**
Bitset bs = new Bitset(5); // bitset = "00000 ".
bs.fix(3); // the value at idx = 3 is updated to 1, so bitset = "00010 ".
bs.fix(1); // the value at idx = 1 is updated to 1, so bitset = "01010 ".
bs.flip(); // the value of each bit is flipped, so bitset = "10101 ".
bs.all(); // return False, as not all values of the bitset are 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "00101 ".
bs.flip(); // the value of each bit is flipped, so bitset = "11010 ".
bs.one(); // return True, as there is at least 1 index with value 1.
bs.unfix(0); // the value at idx = 0 is updated to 0, so bitset = "01010 ".
bs.count(); // return 2, as there are 2 bits with value 1.
bs.toString(); // return "01010 ", which is the composition of bitset.
**Constraints:**
* `1 <= size <= 105`
* `0 <= idx <= size - 1`
* At most `105` calls will be made **in total** to `fix`, `unfix`, `flip`, `all`, `one`, `count`, and `toString`.
* At least one call will be made to `all`, `one`, `count`, or `toString`.
* At most `5` calls will be made to `toString`. | N is small, we can generate all possible move combinations. For each possible move combination, determine which ones are valid. |
Two passes, min of removing everything in left plus removing all to the right | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | # Code\n```\nclass Solution:\n def minimumTime(self, s):\n left, res, n = 0, len(s), len(s)\n lefts = []\n for i,c in enumerate(s):\n left = min(left + (c == \'1\') * 2, i + 1)\n lefts.append(left)\n right = 0\n rights = []\n for i,c in enumerate(s[::-1]):\n right = min(right + (c == \'1\') * 2, i + 1)\n rights.append(right) \n rights = rights[::-1]\n res = rights[0]\n for i in range(n-1):\n res = min(res,lefts[i]+rights[i+1]) \n res = min(res,lefts[n-1])\n return res\n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
O(N) T and O(1) S | Commented and Explained | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe number of prefix to remove and number of suffix to remove suffice for this problem as we are only asked to minimize time. I had started out incorrectly trying to minimize time and maximize overall length delivered, realizing that that is in fact a harder problem. Once I did, it became clear that length and the overall removals are in fact tied together. With this we can propose a simple solution of counting the number of unnecessary removals on the left to right trip, and using that to calculate the maximal number of necessary removals. This then allows us to take a string length difference that optimizes the problem space conveniently. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet number of prefix removed unnecessarily to 0 \nSet number of prefix to remove to 0 \nGet the length of s as a variable \n- Loop over s in terms of indices\n - if s at current index is \'1\', decrement number of prefix removed unnecessarily \n - otherwise, increment number of prefix removed unnecessarily \n - if number of prefix removed unnecessarily is lt 0, this is a location where up to here we would want to remove on the prefix side. Reset the num prefix removed unnecessarily to 0 \n - set the num prefix to remove to max of self and num prefix removed unnecessarily \n\nAt the end, the difference of the string length and the number of prefix to remove is the answer, since we have maximized the num prefix to remove and in turn minimized the num suffix to remove to only those that are advantageous \n\n# Complexity\n- Time complexity: O(N) to loop over s \n\n- Space complexity: O(1) as only variables and no storage is used \n\n# Code\n```\nclass Solution:\n def minimumTime(self, s: str) -> int:\n # determine number of prefix spots that were valid that will be removed if only from the left \n num_prefix_removed_unnecessarily = 0 \n # determine num prefix to remove maximally \n num_prefix_to_remove = 0 \n # get length of s \n sL = len(s) \n # for each index in s \n for i in range(sL) : \n # if it is a valid removal, this means we can reduce num prefix removed unnecessarily \n # otherwise, we should increment it to reflect this cost in the state of prefix removals \n if s[i] == "1" : \n num_prefix_removed_unnecessarily -= 1 \n else : \n num_prefix_removed_unnecessarily += 1 \n # if we have trended negative, it means that up to here was all valid removal \n # in that case, we set num prefix removed unnecessarily to 0 \n if num_prefix_removed_unnecessarily < 0 : \n num_prefix_removed_unnecessarily = 0 \n # the number of prefix to remove is maximized as this goes along \n # the inherent number of removals total is then determined as the length less this number \n # the suffixes removals are inherent to this as the negation resets the num prefix removed \n # unnecessarily, which then contributes to an increase relatively to the number of suffixes \n # consider example 1 walkthrough : num prefix removed unnecessarily maximizes at 2 \n # num suffixes to remove then tops out at 3 respectively. This gives a total of 5, \n # which is by necessity 7 - 2 (length - num prefixes to remove) \n # example 2 works similarly, where the max is set at 2, so the difference is 4 - 2 = 2 \n num_prefix_to_remove = max(num_prefix_to_remove, num_prefix_removed_unnecessarily) \n # the difference in distance is necessarily less than s and is based on the best removal criteria \n # the difference also solves the amount of suffixes to remove, as the number of suffixes to remove \n # is necessarily tied to the number of prefixes removed unnecessarily and the num prefix to remove that\n # is calculated \n return sL - num_prefix_to_remove\n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Python Solution Using Kadane's algorithm O(N) and O(1) | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | \n# Code\n```\nclass Solution:\n def minimumTime(self, s: str) -> int:\n \'\'\'\n the technique that we use is find middle string which contain 0 and 1 which done by cost 2 so we have to minimize that so we find maximum sum so minimum number of ones that done by cost 2 and overall cost is minimized\n \'\'\'\n currentSum=0\n ans=0\n for i in range(len(s)):\n if(s[i]==\'1\'):\n currentSum-=1\n else:\n currentSum+=1\n if(currentSum<0):\n currentSum=0\n ans=max(ans,currentSum)\n return len(s)-ans\n\n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
100% memory and 60% in speed | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTime(self, s):\n left, min_time, n = 0, len(s), len(s)\n\n for i,c in enumerate(s):\n left = min(left + (c=="1")*2,i+1)\n min_time = min(min_time,left + n-1-i)\n\n return min_time\n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Python (Simple Maths) | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTime(self, s):\n left, min_time, n = 0, len(s), len(s)\n\n for i,c in enumerate(s):\n left = min(left + (c=="1")*2,i+1)\n min_time = min(min_time,left + n-1-i)\n\n return min_time\n\n\n\n\n \n\n \n\n\n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
DP ez | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | \n# Approach\nsimple dp states\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTime(self, s: str) -> int:\n n=len(s)\n ind=[i for i in range(len(s)) if s[i]=="1"]\n if len(ind)==0:\n return 0\n dp=[[0,0,0] for i in range(len(ind))] #left spot right\n ans=float("inf")\n for i in range(len(ind)):\n res=[0,0,0]\n if i:\n res=dp[i-1]\n dp[i][0]=ind[i]+1\n dp[i][1]=min(res[0],res[1])+2\n dp[i][2]=min(res[0],res[1])+(n-ind[i])\n ans=min(ans,dp[i][2])\n return min(ans,min(dp[-1]))\n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Python | Min sum of contiguous subsequence | minimum-time-to-remove-all-cars-containing-illegal-goods | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe trick is to convert this problem to:\n Remove the minimum sum of contiguous subsequence.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(N)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(N)$\n# Code\n```\nclass Solution:\n def minimumTime(self, s: str) -> int:\n pre = minS = -1 if s[0] == \'0\' else 0\n for i in range(1, len(s)):\n pre = min(0, pre + (1 if s[i] == \'1\' else -1)) \n minS = min(minS, pre)\n return len(s) + minS\n\n \n``` | 0 | You are given a **0-indexed** binary string `s` which represents a sequence of train cars. `s[i] = '0'` denotes that the `ith` car does **not** contain illegal goods and `s[i] = '1'` denotes that the `ith` car does contain illegal goods.
As the train conductor, you would like to get rid of all the cars containing illegal goods. You can do any of the following three operations **any** number of times:
1. Remove a train car from the **left** end (i.e., remove `s[0]`) which takes 1 unit of time.
2. Remove a train car from the **right** end (i.e., remove `s[s.length - 1]`) which takes 1 unit of time.
3. Remove a train car from **anywhere** in the sequence which takes 2 units of time.
Return _the **minimum** time to remove all the cars containing illegal goods_.
Note that an empty sequence of cars is considered to have no cars containing illegal goods.
**Example 1:**
**Input:** s = "**11**00**1**0**1** "
**Output:** 5
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end. Time taken is 1.
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2 + 1 + 2 = 5.
An alternative way is to
- remove a car from the left end 2 times. Time taken is 2 \* 1 = 2.
- remove a car from the right end 3 times. Time taken is 3 \* 1 = 3.
This also obtains a total time of 2 + 3 = 5.
5 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Example 2:**
**Input:** s = "00**1**0 "
**Output:** 2
**Explanation:**
One way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the left end 3 times. Time taken is 3 \* 1 = 3.
This obtains a total time of 3.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove the car containing illegal goods found in the middle. Time taken is 2.
This obtains a total time of 2.
Another way to remove all the cars containing illegal goods from the sequence is to
- remove a car from the right end 2 times. Time taken is 2 \* 1 = 2.
This obtains a total time of 2.
2 is the minimum time taken to remove all the cars containing illegal goods.
There are no other ways to remove them with less time.
**Constraints:**
* `1 <= s.length <= 2 * 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Simple solution in Python3 | count-operations-to-obtain-zero | 0 | 1 | # Intuition\nHere we have:\n- two integers `num1` and `num2` respectively\n- our goal is to find how many **decrementations** we should apply to make either `num1` or `num2` equal to `0`\n\nFollowing to the description we need to subtract `num1` from `num2`, if `num1 >= num2` and vice-versa.\nLet\'s simulate a process.\n\n# Approach\n1. declare `ans` to store a count of steps\n2. perform decrementations and increment `ans` until any of integer becomes `0`\n3. return `ans`\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(1**)\n\n\n# Code\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n ans = 0\n\n while num1 and num2:\n if num1 >= num2: num1 -= num2\n else: num2 -= num1\n\n ans += 1\n\n return ans\n``` | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Simple While Loop Solution || Python | count-operations-to-obtain-zero | 0 | 1 | # Code\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n cnt=0\n while(num1>0 and num2>0):\n if num1>=num2:\n num1-=num2\n else:\n num2-=num1\n cnt+=1\n return cnt\n```\n\n***Please Upvote*** | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Beats 57.77% || Count operations to obtain zero | count-operations-to-obtain-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n count=0\n while num1!=0 and num2!=0:\n if num1>=num2:\n num1=num1-num2\n count+=1\n else:\n num2=num2-num1\n count+=1\n return count\n\n``` | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Python Eazy to understand beat 94% and simple🚀 | count-operations-to-obtain-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n result = 0\n while num1 != 0 and num2 != 0:\n num1, num2 = max(num1, num2), min(num1, num2)\n result += (num1 // num2)\n num1 = num1 % num2\n\n return result\n \n``` | 2 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Python Easy Solution | count-operations-to-obtain-zero | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n ans = 0\n\n while num1 > 0 and num2 > 0:\n if num1>=num2:\n num1 -= num2\n else:\n num2 -= num1\n\n ans += 1\n\n return ans\n``` | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Python | Easy Solution✅ | count-operations-to-obtain-zero | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n count = 0\n while num1 != 0 and num2 != 0:\n if num1 >= num2:\n num1 -= num2\n else:\n num2 -= num1\n count +=1\n return count\n``` | 7 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Easy Python solution | count-operations-to-obtain-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n counter = 0\n while num1 and num2:\n if num1 >= num2:\n num1 -= num2\n else:\n num2 -= num1\n counter += 1\n return counter\n``` | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Python intuitive simple solution | count-operations-to-obtain-zero | 0 | 1 | **Python :**\n\n```\ndef countOperations(self, num1: int, num2: int) -> int:\n\toperations = 0\n\n\twhile num1 and num2:\n\t\tif num2 > num1:\n\t\t\tnum2 -= num1\n\t\t\toperations += 1\n\n\t\tif num1 > num2:\n\t\t\tnum1 -= num2\n\t\t\toperations += 1\n\n\t\tif num1 == num2:\n\t\t\treturn operations + 1\n\n\treturn operations\n```\n\n**Like it ? please upvote !** | 6 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
[Python3] simulation | count-operations-to-obtain-zero | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/2506277d2af78559a0e58d2130fdbe87beab42b5) for solutions of weekly 280. \n\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n ans = 0 \n while num1 and num2: \n ans += num1//num2\n num1, num2 = num2, num1%num2\n return ans \n``` | 6 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Count GCD steps (w/o recursion and if-else) | count-operations-to-obtain-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCount GCD steps.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIf there\'s `num1 < num2` here, no steps are added and `nums` are swapped.\n# Complexity\n- Time complexity: $$O(GCD)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n* You could find some other extraordinary solutions in my [profile](https://leetcode.com/almostmonday/) on the Solutions tab (I don\'t post obvious or not interesting solutions at all.)\n* If this was helpful, please upvote so that others can see this solution too.\n---\n\n# Code\n```\nclass Solution(object):\n def countOperations(self, num1, num2):\n res = 0\n while num2:\n res += num1 // num2\n num1, num2 = num2, num1 % num2\n \n return res\n``` | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Python3 | 2 approaches Normal and Optimized in time | count-operations-to-obtain-zero | 0 | 1 | **Normal Solution**\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n ct=0\n while num2 and num1:\n if num1>=num2:\n num1=num1-num2\n else:\n num2=num2-num1\n ct+=1\n return ct\n```\n\n**More Optimized Solution**\n```\nclass Solution:\n def countOperations(self, num1: int, num2: int) -> int:\n ans = 0\n if num1 < num2:\n num1, num2 = num2, num1\n while num2:\n num1, num2 = num2, num1 - num2\n if num1 < num2:\n num1, num2 = num2, num1\n ans += 1\n return ans\n``` | 4 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has n accounts numbered from 1 to n. The initial balance of each account is stored in a 0-indexed integer array balance, with the (i + 1)th account having an initial balance of balance[i]. Execute all the valid transactions. A transaction is valid if: Implement the Bank class: | How do you determine if a transaction will fail? Simply apply the operations if the transaction is valid. |
Python 3 hashmap solution O(N), no sort needed | minimum-operations-to-make-the-array-alternating | 0 | 1 | Key implementation step:\n* Create two hashmaps to count the frequencies of num with odd and even indices, respectively;\n* Search for the `num` in each hashmap with the maximum and second maximum frequencies:\n\t* If the two `num`\'s with the maximum frequencies are not equal, then return `len(nums) - (maxFreqOdd + maxFreqEven)`;\n\t* Otherwise return `len(nums) - max(maxFreqOdd + secondMaxFreqEven, maxFreqEven + secondMaxFreqOdd)`.\n\nOne thing to note in step 2 is that after getting the two hashmaps for odd and even indices, we **don\'t** need to sort the hashmap keys based on their values or using heaps, but only need to write a subroutine by scanning through all `num`\'s in the hashmap, so the overall time complexity is `O(N)` instead of `O(NlogN)`.\n\nBelow is my in-contest solution, though I could have made it a bit neater. Please upvote if you find this solution helpful.\n\n```\nclass Solution:\n def minimumOperations(self, nums: List[int]) -> int:\n n = len(nums)\n odd, even = defaultdict(int), defaultdict(int)\n for i in range(n):\n if i % 2 == 0:\n even[nums[i]] += 1\n else:\n odd[nums[i]] += 1\n topEven, secondEven = (None, 0), (None, 0)\n for num in even:\n if even[num] > topEven[1]:\n topEven, secondEven = (num, even[num]), topEven\n elif even[num] > secondEven[1]:\n secondEven = (num, even[num])\n topOdd, secondOdd = (None, 0), (None, 0)\n for num in odd:\n if odd[num] > topOdd[1]:\n topOdd, secondOdd = (num, odd[num]), topOdd\n elif odd[num] > secondOdd[1]:\n secondOdd = (num, odd[num])\n if topOdd[0] != topEven[0]:\n return n - topOdd[1] - topEven[1]\n else:\n return n - max(secondOdd[1] + topEven[1], secondEven[1] + topOdd[1])\n``` | 12 | You are given a **0-indexed** array `nums` consisting of `n` positive integers.
The array `nums` is called **alternating** if:
* `nums[i - 2] == nums[i]`, where `2 <= i <= n - 1`.
* `nums[i - 1] != nums[i]`, where `1 <= i <= n - 1`.
In one **operation**, you can choose an index `i` and **change** `nums[i]` into **any** positive integer.
Return _the **minimum number of operations** required to make the array alternating_.
**Example 1:**
**Input:** nums = \[3,1,3,2,4,3\]
**Output:** 3
**Explanation:**
One way to make the array alternating is by converting it to \[3,1,3,**1**,**3**,**1**\].
The number of operations required in this case is 3.
It can be proven that it is not possible to make the array alternating in less than 3 operations.
**Example 2:**
**Input:** nums = \[1,2,2,2,2\]
**Output:** 2
**Explanation:**
One way to make the array alternating is by converting it to \[1,2,**1**,2,**1**\].
The number of operations required in this case is 2.
Note that the array cannot be converted to \[**2**,2,2,2,2\] because in this case nums\[0\] == nums\[1\] which violates the conditions of an alternating array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Can we enumerate all possible subsets? The maximum bitwise-OR is the bitwise-OR of the whole array. |
[Python3] 4-line | minimum-operations-to-make-the-array-alternating | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/2506277d2af78559a0e58d2130fdbe87beab42b5) for solutions of weekly 280. \n\nUpdated implementation using `most_common()`\n```\nclass Solution:\n def minimumOperations(self, nums: List[int]) -> int:\n pad = lambda x: x + [(None, 0)]*(2-len(x))\n even = pad(Counter(nums[::2]).most_common(2))\n odd = pad(Counter(nums[1::2]).most_common(2))\n return len(nums) - (max(even[0][1] + odd[1][1], even[1][1] + odd[0][1]) if even[0][0] == odd[0][0] else even[0][1] + odd[0][1])\n```\n\n```\nclass Solution:\n def minimumOperations(self, nums: List[int]) -> int:\n odd, even = Counter(), Counter()\n for i, x in enumerate(nums): \n if i&1: odd[x] += 1\n else: even[x] += 1\n \n def fn(freq): \n key = None\n m0 = m1 = 0\n for k, v in freq.items(): \n if v > m0: key, m0, m1 = k, v, m0\n elif v > m1: m1 = v\n return key, m0, m1\n \n k0, m00, m01 = fn(even)\n k1, m10, m11 = fn(odd)\n return len(nums) - max(m00 + m11, m01 + m10) if k0 == k1 else len(nums) - m00 - m10\n``` | 22 | You are given a **0-indexed** array `nums` consisting of `n` positive integers.
The array `nums` is called **alternating** if:
* `nums[i - 2] == nums[i]`, where `2 <= i <= n - 1`.
* `nums[i - 1] != nums[i]`, where `1 <= i <= n - 1`.
In one **operation**, you can choose an index `i` and **change** `nums[i]` into **any** positive integer.
Return _the **minimum number of operations** required to make the array alternating_.
**Example 1:**
**Input:** nums = \[3,1,3,2,4,3\]
**Output:** 3
**Explanation:**
One way to make the array alternating is by converting it to \[3,1,3,**1**,**3**,**1**\].
The number of operations required in this case is 3.
It can be proven that it is not possible to make the array alternating in less than 3 operations.
**Example 2:**
**Input:** nums = \[1,2,2,2,2\]
**Output:** 2
**Explanation:**
One way to make the array alternating is by converting it to \[1,2,**1**,2,**1**\].
The number of operations required in this case is 2.
Note that the array cannot be converted to \[**2**,2,2,2,2\] because in this case nums\[0\] == nums\[1\] which violates the conditions of an alternating array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Can we enumerate all possible subsets? The maximum bitwise-OR is the bitwise-OR of the whole array. |
[Python3] Counter | minimum-operations-to-make-the-array-alternating | 0 | 1 | # Approach\nUse Python\'s `Counter` to get the most frequent elements in the even- and odd-indexed elements of `nums`. If the most frequent elements are different, we can just return the number of elements in `nums` that are _not_ their corresponding most frequent element.\n\nIf the most frequent elements _are_ the same, we instead need to use the 2nd-most-frequent element in either the odd- or even-indexed array.\n\n# Complexity\n- Time complexity: $$O(N)$$ for the construction of element frequencies\n\n- Space complexity: $$O(N)$$\n\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def minimumOperations(self, nums: List[int]) -> int:\n # if array only has a single value, no operations needed\n if len(nums) == 1:\n return 0\n \n # count elements at even and odd indices\n evens = Counter(nums[::2])\n odds = Counter(nums[1::2])\n\n # get the most frequent element out of the odd-\n # and even-indexed elements\n max1 = max([(f,c) for c,f in evens.items()])\n max2 = max([(f,c) for c,f in odds.items()])\n\n # if the most frequent elements are not equal,\n # just return the number of elements in the array\n # that are not their corresponding most frequent element\n if max1[1] != max2[1]:\n return len(nums) - max1[0] - max2[0]\n # if the most frequent elements ARE equal, we need to change\n # one of the arrays to be comprised of its next most frequent\n # element\n else:\n # remove most frequent element so we can get second most\n # frequent\n evens.pop(max1[1])\n odds.pop(max1[1])\n\n # add a dummy value with 0 frequency in case\n # there is no second most frequent element\n evens[\'a\'] = 0\n odds[\'a\'] = 0\n\n # return the fewest number of operations between:\n # 1) take most-frequent of even-indexed and 2nd-most-frequent\n # of odd-indexed, or\n # 2) vice versa\n return len(nums) - max(\n max1[0] + max(odds.values()),\n max2[0] + max(evens.values())\n )\n``` | 0 | You are given a **0-indexed** array `nums` consisting of `n` positive integers.
The array `nums` is called **alternating** if:
* `nums[i - 2] == nums[i]`, where `2 <= i <= n - 1`.
* `nums[i - 1] != nums[i]`, where `1 <= i <= n - 1`.
In one **operation**, you can choose an index `i` and **change** `nums[i]` into **any** positive integer.
Return _the **minimum number of operations** required to make the array alternating_.
**Example 1:**
**Input:** nums = \[3,1,3,2,4,3\]
**Output:** 3
**Explanation:**
One way to make the array alternating is by converting it to \[3,1,3,**1**,**3**,**1**\].
The number of operations required in this case is 3.
It can be proven that it is not possible to make the array alternating in less than 3 operations.
**Example 2:**
**Input:** nums = \[1,2,2,2,2\]
**Output:** 2
**Explanation:**
One way to make the array alternating is by converting it to \[1,2,**1**,2,**1**\].
The number of operations required in this case is 2.
Note that the array cannot be converted to \[**2**,2,2,2,2\] because in this case nums\[0\] == nums\[1\] which violates the conditions of an alternating array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Can we enumerate all possible subsets? The maximum bitwise-OR is the bitwise-OR of the whole array. |
Easy 3 line python | minimum-operations-to-make-the-array-alternating | 0 | 1 | # Intuition\nWe find 2 most common values in the odd and even lists. We append a dummy (0,0) to each in case those lists contain 1 unique number. We then find the maximum number of characters we can leave repeating and subtract it from len of nums to return all other characters which will need to be swapped. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nclass Solution:\n def minimumOperations(self, nums: List[int]) -> int:\n q1 = Counter(nums[::2]).most_common(2) + [(0,0)]\n q2 = Counter(nums[1::2]).most_common(2) + [(0,0)] \n return len(nums) - (q1[0][1] + q2[0][1] if q1[0][0] != q2[0][0] else (q1[1][1] + q2[0][1] if (q1[1][1] + q2[0][1]) > (q1[0][1] + q2[1][1]) else q1[0][1] + q2[1][1]))\n``` | 0 | You are given a **0-indexed** array `nums` consisting of `n` positive integers.
The array `nums` is called **alternating** if:
* `nums[i - 2] == nums[i]`, where `2 <= i <= n - 1`.
* `nums[i - 1] != nums[i]`, where `1 <= i <= n - 1`.
In one **operation**, you can choose an index `i` and **change** `nums[i]` into **any** positive integer.
Return _the **minimum number of operations** required to make the array alternating_.
**Example 1:**
**Input:** nums = \[3,1,3,2,4,3\]
**Output:** 3
**Explanation:**
One way to make the array alternating is by converting it to \[3,1,3,**1**,**3**,**1**\].
The number of operations required in this case is 3.
It can be proven that it is not possible to make the array alternating in less than 3 operations.
**Example 2:**
**Input:** nums = \[1,2,2,2,2\]
**Output:** 2
**Explanation:**
One way to make the array alternating is by converting it to \[1,2,**1**,2,**1**\].
The number of operations required in this case is 2.
Note that the array cannot be converted to \[**2**,2,2,2,2\] because in this case nums\[0\] == nums\[1\] which violates the conditions of an alternating array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | Can we enumerate all possible subsets? The maximum bitwise-OR is the bitwise-OR of the whole array. |
[Java/Python 3] Sort, then 1 pass find max rectangle, w/ graph explanation and analysis. | removing-minimum-number-of-magic-beans | 1 | 1 | **Intuition**\nThe problem asks us to get the minimum beans by removing part or all from any individual bean bag(s), in order to make remaining bean bags homogeneous in terms of the number of beans. \n\nTherefore, we can sort input first, then remove smallest bags by whole and largest bags by part, in order to get the biggest rectangle. After computing the area of biggest rectangle, we can subtract it from the total number of beans to get the required minimum beans.\n\n----\n\nAfter sorting the input, what we need is to find the largest rectangle from the histogram formed by the `beans`. Please refer to different rectangles (not show all of them, just several ones for illustration purpose) in the 2nd picture.\n\n\n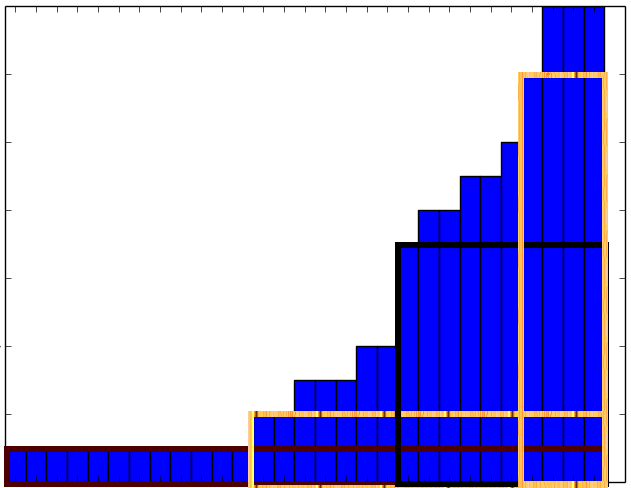\n\n\n**Java**\n\n```java\n public long minimumRemoval(int[] beans) {\n long mx = 0, sum = 0;\n Arrays.sort(beans)\n for (int i = 0, n = beans.length; i < n; ++i) {\n sum += beans[i];\n mx = Math.max(mx, (long)beans[i] * (n - i));\n }\n return sum - mx;\n }\n```\nAnother style of Java code:\n```java\n public long minimumRemoval(int[] beans) {\n long mx = 0, sum = 0, i = 0;\n Arrays.sort(beans);\n for (int bean : beans) {\n sum += bean;\n mx = Math.max(mx, bean * (beans.length - i++));\n }\n return sum - mx;\n }\n```\n\n----\n\n**Python 3**\n```python\n def minimumRemoval(self, beans: List[int]) -> int:\n mx, n = 0, len(beans)\n for i, bean in enumerate(sorted(beans)):\n mx = max(mx, bean * (n - i))\n return sum(beans) - mx\n```\n\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(n)` - including sorting space.\n\n----\n\n**Q & A**\n*Q1:* Why we have to find the "largest rectangle" from the histogram?\n*A1:* We are required to remove minimum # of beans to make the remaining bags having same #, and those remaining bags can form a "rectangle". There are `n` options to form rectangles, which one should we choose? The largest one, which need to remove only minimum # of beans.\n\n*Q2*: Which categories or tags does such a problem come from? Greedy or Math?\n*A2*: The purpose of sorting is to remove the whole of smallest bags and remove part of biggest bags. Hence the part of the sorting can be regarded as **Greedy**; The computing and finding the largest rectangle part can be regarded as **Math**.\n\n*Q3*: Is [453. Minimum Moves to Equal Array Elements](https://leetcode.com/problems/minimum-moves-to-equal-array-elements) similar to this problem?\n*A3*: It is a bit similar.\n\n1. For 453, after a brain teaser we only need to compute the area of the shortest (or lowest) and widest rectangle of dimension `min(nums) * n`;\n2. For this problem, we need to go one step further: compute the areas of all possible rectangles, `beans[i] * (number of beans[k] >= beans[i])`, where `n = beans.length, 0 <= i, k < n`, then find the max area out of them.\n\n**End of Q** | 67 | You are given an array of **positive** integers `beans`, where each integer represents the number of magic beans found in a particular magic bag.
**Remove** any number of beans (**possibly none**) from each bag such that the number of beans in each remaining **non-empty** bag (still containing **at least one** bean) is **equal**. Once a bean has been removed from a bag, you are **not** allowed to return it to any of the bags.
Return _the **minimum** number of magic beans that you have to remove_.
**Example 1:**
**Input:** beans = \[4,**1**,6,5\]
**Output:** 4
**Explanation:**
- We remove 1 bean from the bag with only 1 bean.
This results in the remaining bags: \[4,**0**,6,5\]
- Then we remove 2 beans from the bag with 6 beans.
This results in the remaining bags: \[4,0,**4**,5\]
- Then we remove 1 bean from the bag with 5 beans.
This results in the remaining bags: \[4,0,4,**4**\]
We removed a total of 1 + 2 + 1 = 4 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that remove 4 beans or fewer.
**Example 2:**
**Input:** beans = \[**2**,10,**3**,**2**\]
**Output:** 7
**Explanation:**
- We remove 2 beans from one of the bags with 2 beans.
This results in the remaining bags: \[**0**,10,3,2\]
- Then we remove 2 beans from the other bag with 2 beans.
This results in the remaining bags: \[0,10,3,**0**\]
- Then we remove 3 beans from the bag with 3 beans.
This results in the remaining bags: \[0,10,**0**,0\]
We removed a total of 2 + 2 + 3 = 7 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that removes 7 beans or fewer.
**Constraints:**
* `1 <= beans.length <= 105`
* `1 <= beans[i] <= 105` | How much is change actually necessary while calculating the required path? How many extra edges do we need to add to the shortest path? |
✅ Python | Clear and Concise + Explanation | removing-minimum-number-of-magic-beans | 0 | 1 | If you want to make all the numbers the same inside an array (only decreasing is allowed)\nyou need to make `sum(arr) - len(arr) * min(arr)` operations overall as you need to decrease all elements by `arr[i] - min(arr)` where `0<=i<len(arr)`\n\nAs described in problem statement we can decrease number of beans in the bag and when it becomes `0` we dont need to make all other bags `0` to make them equal (We just ignore `0` bags, which simply means length of array also decreases).\n\n\nApproach:\n-\n- Sort beans\n- Calculate number of operations for every element in beans\n\n```\ndef minimumRemoval(self, beans: List[int]) -> int:\n\tbeans.sort()\n\ts = sum(beans)\n\tl = len(beans)\n\tres = float(\'inf\')\n\n\tfor i in range(len(beans)):\n\t\tres = min(res, s - l * beans[i])\n\t\tl -= 1\n\t\t\n\treturn res\n``` | 21 | You are given an array of **positive** integers `beans`, where each integer represents the number of magic beans found in a particular magic bag.
**Remove** any number of beans (**possibly none**) from each bag such that the number of beans in each remaining **non-empty** bag (still containing **at least one** bean) is **equal**. Once a bean has been removed from a bag, you are **not** allowed to return it to any of the bags.
Return _the **minimum** number of magic beans that you have to remove_.
**Example 1:**
**Input:** beans = \[4,**1**,6,5\]
**Output:** 4
**Explanation:**
- We remove 1 bean from the bag with only 1 bean.
This results in the remaining bags: \[4,**0**,6,5\]
- Then we remove 2 beans from the bag with 6 beans.
This results in the remaining bags: \[4,0,**4**,5\]
- Then we remove 1 bean from the bag with 5 beans.
This results in the remaining bags: \[4,0,4,**4**\]
We removed a total of 1 + 2 + 1 = 4 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that remove 4 beans or fewer.
**Example 2:**
**Input:** beans = \[**2**,10,**3**,**2**\]
**Output:** 7
**Explanation:**
- We remove 2 beans from one of the bags with 2 beans.
This results in the remaining bags: \[**0**,10,3,2\]
- Then we remove 2 beans from the other bag with 2 beans.
This results in the remaining bags: \[0,10,3,**0**\]
- Then we remove 3 beans from the bag with 3 beans.
This results in the remaining bags: \[0,10,**0**,0\]
We removed a total of 2 + 2 + 3 = 7 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that removes 7 beans or fewer.
**Constraints:**
* `1 <= beans.length <= 105`
* `1 <= beans[i] <= 105` | How much is change actually necessary while calculating the required path? How many extra edges do we need to add to the shortest path? |
[Python3] 2-line | removing-minimum-number-of-magic-beans | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/2506277d2af78559a0e58d2130fdbe87beab42b5) for solutions of weekly 280. \n\n```\nclass Solution:\n def minimumRemoval(self, beans: List[int]) -> int:\n beans.sort()\n return sum(beans) - max((len(beans)-i)*x for i, x in enumerate(beans))\n``` | 4 | You are given an array of **positive** integers `beans`, where each integer represents the number of magic beans found in a particular magic bag.
**Remove** any number of beans (**possibly none**) from each bag such that the number of beans in each remaining **non-empty** bag (still containing **at least one** bean) is **equal**. Once a bean has been removed from a bag, you are **not** allowed to return it to any of the bags.
Return _the **minimum** number of magic beans that you have to remove_.
**Example 1:**
**Input:** beans = \[4,**1**,6,5\]
**Output:** 4
**Explanation:**
- We remove 1 bean from the bag with only 1 bean.
This results in the remaining bags: \[4,**0**,6,5\]
- Then we remove 2 beans from the bag with 6 beans.
This results in the remaining bags: \[4,0,**4**,5\]
- Then we remove 1 bean from the bag with 5 beans.
This results in the remaining bags: \[4,0,4,**4**\]
We removed a total of 1 + 2 + 1 = 4 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that remove 4 beans or fewer.
**Example 2:**
**Input:** beans = \[**2**,10,**3**,**2**\]
**Output:** 7
**Explanation:**
- We remove 2 beans from one of the bags with 2 beans.
This results in the remaining bags: \[**0**,10,3,2\]
- Then we remove 2 beans from the other bag with 2 beans.
This results in the remaining bags: \[0,10,3,**0**\]
- Then we remove 3 beans from the bag with 3 beans.
This results in the remaining bags: \[0,10,**0**,0\]
We removed a total of 2 + 2 + 3 = 7 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that removes 7 beans or fewer.
**Constraints:**
* `1 <= beans.length <= 105`
* `1 <= beans[i] <= 105` | How much is change actually necessary while calculating the required path? How many extra edges do we need to add to the shortest path? |
[Python3] Greedy + Sort - Simple Solution | removing-minimum-number-of-magic-beans | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nInspired from this [solution](https://leetcode.com/problems/removing-minimum-number-of-magic-beans/solutions/1766795/java-python-3-sort-then-1-pass-find-max-rectangle-w-graph-explanation-and-analysis/) \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumRemoval(self, beans: List[int]) -> int:\n s, max_rec_area, n = 0, 0, len(beans)\n beans.sort()\n for i, b in enumerate(beans):\n s += b\n max_rec_area = max(max_rec_area, b * (n - i))\n return s - max_rec_area\n``` | 0 | You are given an array of **positive** integers `beans`, where each integer represents the number of magic beans found in a particular magic bag.
**Remove** any number of beans (**possibly none**) from each bag such that the number of beans in each remaining **non-empty** bag (still containing **at least one** bean) is **equal**. Once a bean has been removed from a bag, you are **not** allowed to return it to any of the bags.
Return _the **minimum** number of magic beans that you have to remove_.
**Example 1:**
**Input:** beans = \[4,**1**,6,5\]
**Output:** 4
**Explanation:**
- We remove 1 bean from the bag with only 1 bean.
This results in the remaining bags: \[4,**0**,6,5\]
- Then we remove 2 beans from the bag with 6 beans.
This results in the remaining bags: \[4,0,**4**,5\]
- Then we remove 1 bean from the bag with 5 beans.
This results in the remaining bags: \[4,0,4,**4**\]
We removed a total of 1 + 2 + 1 = 4 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that remove 4 beans or fewer.
**Example 2:**
**Input:** beans = \[**2**,10,**3**,**2**\]
**Output:** 7
**Explanation:**
- We remove 2 beans from one of the bags with 2 beans.
This results in the remaining bags: \[**0**,10,3,2\]
- Then we remove 2 beans from the other bag with 2 beans.
This results in the remaining bags: \[0,10,3,**0**\]
- Then we remove 3 beans from the bag with 3 beans.
This results in the remaining bags: \[0,10,**0**,0\]
We removed a total of 2 + 2 + 3 = 7 beans to make the remaining non-empty bags have an equal number of beans.
There are no other solutions that removes 7 beans or fewer.
**Constraints:**
* `1 <= beans.length <= 105`
* `1 <= beans[i] <= 105` | How much is change actually necessary while calculating the required path? How many extra edges do we need to add to the shortest path? |
[Python3] Top-down DP without bitmask | maximum-and-sum-of-array | 0 | 1 | I think bitmask is unintuitive while the slots selection state can be stored as a string instead. Although the performance will be less than using bitmask but time complexity will be the same.\n\n# Code\n```\nclass Solution:\n def maximumANDSum(self, nums: List[int], numSlots: int) -> int:\n memo = {}\n def dfs(i, slots):\n if i == len(nums):\n return 0\n key = (i, \'\'.join(map(str, slots)))\n if key in memo:\n return memo[key]\n ans = 0\n for j in range(len(slots)):\n if slots[j] > 0:\n slots[j] -= 1\n ans = max(ans, dfs(i+1, slots) + (nums[i] & (j+1)))\n slots[j] += 1\n memo[key] = ans\n return ans\n slots = [2 for _ in range(numSlots)]\n return dfs(0, slots)\n``` | 3 | You are given an integer array `nums` of length `n` and an integer `numSlots` such that `2 * numSlots >= n`. There are `numSlots` slots numbered from `1` to `numSlots`.
You have to place all `n` integers into the slots such that each slot contains at **most** two numbers. The **AND sum** of a given placement is the sum of the **bitwise** `AND` of every number with its respective slot number.
* For example, the **AND sum** of placing the numbers `[1, 3]` into slot `1` and `[4, 6]` into slot `2` is equal to `(1 AND 1) + (3 AND 1) + (4 AND 2) + (6 AND 2) = 1 + 1 + 0 + 2 = 4`.
Return _the maximum possible **AND sum** of_ `nums` _given_ `numSlots` _slots._
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6\], numSlots = 3
**Output:** 9
**Explanation:** One possible placement is \[1, 4\] into slot 1, \[2, 6\] into slot 2, and \[3, 5\] into slot 3.
This gives the maximum AND sum of (1 AND 1) + (4 AND 1) + (2 AND 2) + (6 AND 2) + (3 AND 3) + (5 AND 3) = 1 + 0 + 2 + 2 + 3 + 1 = 9.
**Example 2:**
**Input:** nums = \[1,3,10,4,7,1\], numSlots = 9
**Output:** 24
**Explanation:** One possible placement is \[1, 1\] into slot 1, \[3\] into slot 3, \[4\] into slot 4, \[7\] into slot 7, and \[10\] into slot 9.
This gives the maximum AND sum of (1 AND 1) + (1 AND 1) + (3 AND 3) + (4 AND 4) + (7 AND 7) + (10 AND 9) = 1 + 1 + 3 + 4 + 7 + 8 = 24.
Note that slots 2, 5, 6, and 8 are empty which is permitted.
**Constraints:**
* `n == nums.length`
* `1 <= numSlots <= 9`
* `1 <= n <= 2 * numSlots`
* `1 <= nums[i] <= 15` | null |
[Python3] dp (top-down) | maximum-and-sum-of-array | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/2506277d2af78559a0e58d2130fdbe87beab42b5) for solutions of weekly 280. \n\n```\nclass Solution:\n def maximumANDSum(self, nums: List[int], numSlots: int) -> int:\n \n @cache\n def fn(k, m): \n """Return max AND sum."""\n if k == len(nums): return 0 \n ans = 0 \n for i in range(numSlots): \n if m & 1<<2*i == 0 or m & 1<<2*i+1 == 0: \n if m & 1<<2*i == 0: mm = m ^ 1<<2*i\n else: mm = m ^ 1<<2*i+1\n ans = max(ans, (nums[k] & i+1) + fn(k+1, mm))\n return ans \n \n return fn(0, 0)\n``` | 16 | You are given an integer array `nums` of length `n` and an integer `numSlots` such that `2 * numSlots >= n`. There are `numSlots` slots numbered from `1` to `numSlots`.
You have to place all `n` integers into the slots such that each slot contains at **most** two numbers. The **AND sum** of a given placement is the sum of the **bitwise** `AND` of every number with its respective slot number.
* For example, the **AND sum** of placing the numbers `[1, 3]` into slot `1` and `[4, 6]` into slot `2` is equal to `(1 AND 1) + (3 AND 1) + (4 AND 2) + (6 AND 2) = 1 + 1 + 0 + 2 = 4`.
Return _the maximum possible **AND sum** of_ `nums` _given_ `numSlots` _slots._
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6\], numSlots = 3
**Output:** 9
**Explanation:** One possible placement is \[1, 4\] into slot 1, \[2, 6\] into slot 2, and \[3, 5\] into slot 3.
This gives the maximum AND sum of (1 AND 1) + (4 AND 1) + (2 AND 2) + (6 AND 2) + (3 AND 3) + (5 AND 3) = 1 + 0 + 2 + 2 + 3 + 1 = 9.
**Example 2:**
**Input:** nums = \[1,3,10,4,7,1\], numSlots = 9
**Output:** 24
**Explanation:** One possible placement is \[1, 1\] into slot 1, \[3\] into slot 3, \[4\] into slot 4, \[7\] into slot 7, and \[10\] into slot 9.
This gives the maximum AND sum of (1 AND 1) + (1 AND 1) + (3 AND 3) + (4 AND 4) + (7 AND 7) + (10 AND 9) = 1 + 1 + 3 + 4 + 7 + 8 = 24.
Note that slots 2, 5, 6, and 8 are empty which is permitted.
**Constraints:**
* `n == nums.length`
* `1 <= numSlots <= 9`
* `1 <= n <= 2 * numSlots`
* `1 <= nums[i] <= 15` | null |
Python | DFS with memo | maximum-and-sum-of-array | 0 | 1 | # Intuition\n\nDFS with memo.\n\n# Complexity\n- Time complexity: $$O(2^{2*numSlots})*numSlots$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(2^{numSlots})$$\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom functools import cache\n\nclass Solution:\n def maximumANDSum(self, nums: List[int], numSlots: int) -> int:\n # mask:\n # 4 3 2 1 <- slot num\n # 00 | 00 | 11 | 00 <- bitmask\n @cache\n def dfs(i, mask):\n if i >= len(nums):\n return 0\n res = 0\n for j in range(1, numSlots + 1):\n slot_1 = 1 << (2*j-2)\n slot_2 = 1 << (2*j-1)\n if not (mask & slot_1):\n res = max(res, (nums[i] & j) + dfs(i + 1, mask | slot_1))\n elif not (mask & slot_2):\n res = max(res, (nums[i] & j) + dfs(i + 1, mask | slot_2))\n return res\n return dfs(0, 0)\n\n``` | 0 | You are given an integer array `nums` of length `n` and an integer `numSlots` such that `2 * numSlots >= n`. There are `numSlots` slots numbered from `1` to `numSlots`.
You have to place all `n` integers into the slots such that each slot contains at **most** two numbers. The **AND sum** of a given placement is the sum of the **bitwise** `AND` of every number with its respective slot number.
* For example, the **AND sum** of placing the numbers `[1, 3]` into slot `1` and `[4, 6]` into slot `2` is equal to `(1 AND 1) + (3 AND 1) + (4 AND 2) + (6 AND 2) = 1 + 1 + 0 + 2 = 4`.
Return _the maximum possible **AND sum** of_ `nums` _given_ `numSlots` _slots._
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6\], numSlots = 3
**Output:** 9
**Explanation:** One possible placement is \[1, 4\] into slot 1, \[2, 6\] into slot 2, and \[3, 5\] into slot 3.
This gives the maximum AND sum of (1 AND 1) + (4 AND 1) + (2 AND 2) + (6 AND 2) + (3 AND 3) + (5 AND 3) = 1 + 0 + 2 + 2 + 3 + 1 = 9.
**Example 2:**
**Input:** nums = \[1,3,10,4,7,1\], numSlots = 9
**Output:** 24
**Explanation:** One possible placement is \[1, 1\] into slot 1, \[3\] into slot 3, \[4\] into slot 4, \[7\] into slot 7, and \[10\] into slot 9.
This gives the maximum AND sum of (1 AND 1) + (1 AND 1) + (3 AND 3) + (4 AND 4) + (7 AND 7) + (10 AND 9) = 1 + 1 + 3 + 4 + 7 + 8 = 24.
Note that slots 2, 5, 6, and 8 are empty which is permitted.
**Constraints:**
* `n == nums.length`
* `1 <= numSlots <= 9`
* `1 <= n <= 2 * numSlots`
* `1 <= nums[i] <= 15` | null |
Python, maximal matching, 44ms, beats 100% | maximum-and-sum-of-array | 0 | 1 | # Intuition\n\nIt is maximal matching problem on a bipartite graph.\n\nOn one side are the given numbers on the other side are the slots from 1 to `numSlots`, twice each. It is a complete bipartite graph, where an edge `(a, b)` has weight `(a & b)` and we need to find a maximal matching. Or a minimal one if the edge weights are negated.\n\nSuch a problem can be solved using `scipy.optimize.linear_sum_assignment`. However it is suprisingly slow in this environment. I suspect that loading the library, might be slow.\n\n\nThis implementation beats `scipy.optimize`. \n\n\n# Complexity\n- Time complexity: $$O(n^4)$$\n\n- Space complexity: $$O(n)$$, where $n=2*numSlots$.\n\n# Code\n```\n# from scipy.optimize import linear_sum_assignment\n\ndef min_matching(cost):\n m, n = len(cost), len(cost[0])\n assert m <= n\n worker2job = [-1]*(n+1)\n job_pot = [0]*m\n worker_pot = [0]*(n+1)\n answer = []\n inf = int(10**9)\n dummy_worker = n\n\n for curr_job in range(m):\n curr_workers = [dummy_worker]\n worker2job[dummy_worker] = curr_job\n\n prev = [-1]*(n+1)\n in_Z = [False]*(n+1)\n\n while curr_workers and all(worker2job[worker] != -1 for worker in curr_workers):\n for worker in curr_workers:\n in_Z[worker] = True\n\n delta = inf\n min_reduced_cost = [inf] * (n + 1)\n for curr_worker in range(n+1):\n if not in_Z[curr_worker]:\n continue\n job = worker2job[curr_worker]\n for worker in range(n):\n if not in_Z[worker]:\n reduced_cost = cost[job][worker]-job_pot[job]-worker_pot[worker]\n if reduced_cost < min_reduced_cost[worker]:\n min_reduced_cost[worker] = reduced_cost\n prev[worker] = curr_worker\n if reduced_cost < delta:\n delta = reduced_cost\n\n curr_workers.clear()\n for worker in range(n+1):\n if in_Z[worker]:\n job_pot[worker2job[worker]] += delta\n worker_pot[worker] -= delta\n else:\n min_reduced_cost[worker] -= delta\n if min_reduced_cost[worker] == 0:\n curr_workers.append(worker)\n # print(f"{curr_workers=},\\n{worker2job=},\\n{prev=},\\n{in_Z=},\\n{min_reduced_cost=},\\n{delta=}")\n curr_workers = [worker for worker in curr_workers if worker2job[worker] == -1]\n # print(f"filtered {curr_workers=}")\n curr_worker = curr_workers[0]\n\n while curr_worker != -1:\n worker2job[curr_worker] = worker2job[prev[curr_worker]]\n curr_worker = prev[curr_worker]\n return [(worker2job[i], i) for i in range(n) if worker2job[i] != -1]\n \n\nclass Solution:\n def maximumANDSum(self, nums: List[int], numSlots: int) -> int:\n cost = [[-((1+(i%numSlots)) & num) for i in range(2*numSlots)] for num in nums]\n matching = min_matching(cost)\n return sum(-cost[i][j] for i, j in matching)\n``` | 0 | You are given an integer array `nums` of length `n` and an integer `numSlots` such that `2 * numSlots >= n`. There are `numSlots` slots numbered from `1` to `numSlots`.
You have to place all `n` integers into the slots such that each slot contains at **most** two numbers. The **AND sum** of a given placement is the sum of the **bitwise** `AND` of every number with its respective slot number.
* For example, the **AND sum** of placing the numbers `[1, 3]` into slot `1` and `[4, 6]` into slot `2` is equal to `(1 AND 1) + (3 AND 1) + (4 AND 2) + (6 AND 2) = 1 + 1 + 0 + 2 = 4`.
Return _the maximum possible **AND sum** of_ `nums` _given_ `numSlots` _slots._
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6\], numSlots = 3
**Output:** 9
**Explanation:** One possible placement is \[1, 4\] into slot 1, \[2, 6\] into slot 2, and \[3, 5\] into slot 3.
This gives the maximum AND sum of (1 AND 1) + (4 AND 1) + (2 AND 2) + (6 AND 2) + (3 AND 3) + (5 AND 3) = 1 + 0 + 2 + 2 + 3 + 1 = 9.
**Example 2:**
**Input:** nums = \[1,3,10,4,7,1\], numSlots = 9
**Output:** 24
**Explanation:** One possible placement is \[1, 1\] into slot 1, \[3\] into slot 3, \[4\] into slot 4, \[7\] into slot 7, and \[10\] into slot 9.
This gives the maximum AND sum of (1 AND 1) + (1 AND 1) + (3 AND 3) + (4 AND 4) + (7 AND 7) + (10 AND 9) = 1 + 1 + 3 + 4 + 7 + 8 = 24.
Note that slots 2, 5, 6, and 8 are empty which is permitted.
**Constraints:**
* `n == nums.length`
* `1 <= numSlots <= 9`
* `1 <= n <= 2 * numSlots`
* `1 <= nums[i] <= 15` | null |
simple.py | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n c=0\n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if nums[i]==nums[j] and (i*j)%k==0:\n c+=1\n return c\n``` | 1 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Beats 65.34% | Count equal and divisible pairs | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n count=0\n for i in range(len(nums)):\n for j in range(len(nums)):\n if i<j and nums[i]==nums[j] and (i*j)%k==0:\n count+=1\n return count\n``` | 1 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Simplest solution beat 80% | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | \n# Code\n```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n count = 0\n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if nums[i] == nums[j] and (i * j) % k == 0:\n count += 1\n \n return count\n \n``` | 1 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
[Java/Python 3] Traverse indices with same values. | count-equal-and-divisible-pairs-in-an-array | 1 | 1 | ```java\n public int countPairs(int[] nums, int k) {\n Map<Integer, List<Integer>> indices = new HashMap<>();\n for (int i = 0; i < nums.length; ++i) {\n indices.computeIfAbsent(nums[i], l -> new ArrayList<>()).add(i);\n } \n int cnt = 0;\n for (List<Integer> ind : indices.values()) {\n for (int i = 0; i < ind.size(); ++i) {\n for (int j = 0; j < i; ++j) {\n if (ind.get(i) * ind.get(j) % k == 0) {\n ++cnt;\n }\n }\n }\n }\n return cnt;\n }\n```\n```python\n def countPairs(self, nums: List[int], k: int) -> int:\n cnt, d = 0, defaultdict(list)\n for i, n in enumerate(nums):\n d[n].append(i)\n for indices in d.values(): \n for i, a in enumerate(indices):\n for b in indices[: i]:\n if a * b % k == 0:\n cnt += 1\n return cnt\n``` | 21 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
[PYTHON 3] EASY | 2 FOR LOOPS | LOW MEMORY | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | Runtime: **109 ms, faster than 81.87%** of Python3 online submissions for Count Equal and Divisible Pairs in an Array.\nMemory Usage: **13.8 MB, less than 98.09%** of Python3 online submissions for Count Equal and Divisible Pairs in an Array.\n```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int: \n\n c = 0 \n for i in range(len(nums)): \n for e in range(i+1, len(nums)): \n if nums[i] == nums[e] and i*e % k == 0:\n c += 1\n return c | 2 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Pyhton3 solution using dictionary beats 99.7% | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | # stats\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe have a dictionary to store the indices in a array by looping through the array \n We have function make which tries all combinations in the indices and checks if their product id dicvisible by k returning c\nif length of indices is 1 we can skip the iteration\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*N) due to make function\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) due to dictionary\n\n# Code\n```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n d={}\n for i,v in enumerate(nums):\n if v in d:\n d[v].append(i)\n else:\n d|={v:[i]}\n s=0\n def make(a,n):\n c=0\n for i in range(n-1):\n for j in range(i+1,n):\n if a[i]*a[j]%k==0:\n c+=1\n return c\n for i in d:\n if len(d[i])==1:\n continue\n s+=make(d[i],len(d[i]))\n return s\n``` | 3 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Python3 Solution fastest | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | ```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n n=len(nums)\n c=0\n for i in range(0,n):\n for j in range(i+1,n):\n if nums[i]==nums[j] and ((i*j)%k==0):\n c+=1\n return c \n``` | 5 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Easy to understand || O(n2) || Simple python | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | ```\ndef countPairs(self, nums: List[int], k: int) -> int:\n count = 0\n \n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if nums[i]==nums[j] and (i*j)%k==0:\n count+=1\n return count\n``` | 2 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Python 3 (80ms) | Easy Brute Force N^2 Approach | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | ```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n n=len(nums)\n c=0\n for i in range(0,n):\n for j in range(i+1,n):\n if nums[i]==nums[j] and ((i*j)%k==0):\n c+=1\n return c\n``` | 3 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
Count Equal and Divisible Pairs in an Array | count-equal-and-divisible-pairs-in-an-array | 0 | 1 | python 3 :\n```\nclass Solution:\n def countPairs(self, nums: List[int], k: int) -> int:\n count= 0\n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if (nums[i]==nums[j]) and (i*j)%k==0:\n count+=1\n return count\n``` | 1 | Given a **0-indexed** integer array `nums` of length `n` and an integer `k`, return _the **number of pairs**_ `(i, j)` _where_ `0 <= i < j < n`, _such that_ `nums[i] == nums[j]` _and_ `(i * j)` _is divisible by_ `k`.
**Example 1:**
**Input:** nums = \[3,1,2,2,2,1,3\], k = 2
**Output:** 4
**Explanation:**
There are 4 pairs that meet all the requirements:
- nums\[0\] == nums\[6\], and 0 \* 6 == 0, which is divisible by 2.
- nums\[2\] == nums\[3\], and 2 \* 3 == 6, which is divisible by 2.
- nums\[2\] == nums\[4\], and 2 \* 4 == 8, which is divisible by 2.
- nums\[3\] == nums\[4\], and 3 \* 4 == 12, which is divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 1
**Output:** 0
**Explanation:** Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], k <= 100` | What is the earliest time a course can be taken? How would you solve the problem if all courses take equal time? How would you generalize this approach? |
[Java/Python 3] Divisible by 3. | find-three-consecutive-integers-that-sum-to-a-given-number | 1 | 1 | ```java\n public long[] sumOfThree(long num) {\n if (num % 3 != 0) {\n return new long[0];\n }\n num /= 3;\n return new long[]{num - 1, num, num + 1};\n }\n```\n```python\n def sumOfThree(self, num: int) -> List[int]:\n if num % 3 == 0:\n num //= 3\n return [num - 1, num, num + 1]\n return []\n```\n**Analysis:**\n\nTime & space: `O(1)`. | 16 | Given an integer `num`, return _three consecutive integers (as a sorted array)_ _that **sum** to_ `num`. If `num` cannot be expressed as the sum of three consecutive integers, return _an **empty** array._
**Example 1:**
**Input:** num = 33
**Output:** \[10,11,12\]
**Explanation:** 33 can be expressed as 10 + 11 + 12 = 33.
10, 11, 12 are 3 consecutive integers, so we return \[10, 11, 12\].
**Example 2:**
**Input:** num = 4
**Output:** \[\]
**Explanation:** There is no way to express 4 as the sum of 3 consecutive integers.
**Constraints:**
* `0 <= num <= 1015` | What data structure can we use to count the frequency of each character? Are there edge cases where a character is present in one string but not the other? |
[Python3] 1-line | find-three-consecutive-integers-that-sum-to-a-given-number | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/97dff55b43563450a33c98f2a216954117100dfe) for solutions of weekly 72. \n\n```\nclass Solution:\n def sumOfThree(self, num: int) -> List[int]:\n return [] if num % 3 else [num//3-1, num//3, num//3+1]\n``` | 5 | Given an integer `num`, return _three consecutive integers (as a sorted array)_ _that **sum** to_ `num`. If `num` cannot be expressed as the sum of three consecutive integers, return _an **empty** array._
**Example 1:**
**Input:** num = 33
**Output:** \[10,11,12\]
**Explanation:** 33 can be expressed as 10 + 11 + 12 = 33.
10, 11, 12 are 3 consecutive integers, so we return \[10, 11, 12\].
**Example 2:**
**Input:** num = 4
**Output:** \[\]
**Explanation:** There is no way to express 4 as the sum of 3 consecutive integers.
**Constraints:**
* `0 <= num <= 1015` | What data structure can we use to count the frequency of each character? Are there edge cases where a character is present in one string but not the other? |
Simple Maths || Python || Divisibility by 3 | find-three-consecutive-integers-that-sum-to-a-given-number | 0 | 1 | ```\nif num%3!=0:\n\treturn []\nelse:\n b=num//3\n return [b-1,b,b+1]\n``` | 1 | Given an integer `num`, return _three consecutive integers (as a sorted array)_ _that **sum** to_ `num`. If `num` cannot be expressed as the sum of three consecutive integers, return _an **empty** array._
**Example 1:**
**Input:** num = 33
**Output:** \[10,11,12\]
**Explanation:** 33 can be expressed as 10 + 11 + 12 = 33.
10, 11, 12 are 3 consecutive integers, so we return \[10, 11, 12\].
**Example 2:**
**Input:** num = 4
**Output:** \[\]
**Explanation:** There is no way to express 4 as the sum of 3 consecutive integers.
**Constraints:**
* `0 <= num <= 1015` | What data structure can we use to count the frequency of each character? Are there edge cases where a character is present in one string but not the other? |
Python 4 line solution. | find-three-consecutive-integers-that-sum-to-a-given-number | 0 | 1 | ```\nclass Solution(object):\n def sumOfThree(self, num):\n """\n :type num: int\n :rtype: List[int]\n """\n if num%3==0:\n l=num//3\n return [l-1,l,l+1]\n return []\n \n \n``` | 1 | Given an integer `num`, return _three consecutive integers (as a sorted array)_ _that **sum** to_ `num`. If `num` cannot be expressed as the sum of three consecutive integers, return _an **empty** array._
**Example 1:**
**Input:** num = 33
**Output:** \[10,11,12\]
**Explanation:** 33 can be expressed as 10 + 11 + 12 = 33.
10, 11, 12 are 3 consecutive integers, so we return \[10, 11, 12\].
**Example 2:**
**Input:** num = 4
**Output:** \[\]
**Explanation:** There is no way to express 4 as the sum of 3 consecutive integers.
**Constraints:**
* `0 <= num <= 1015` | What data structure can we use to count the frequency of each character? Are there edge cases where a character is present in one string but not the other? |
[Java/Python 3] Greedy w/ brief explanation and analysis. | maximum-split-of-positive-even-integers | 1 | 1 | **Note:** For the rigorous proof of greedy algorithm correctness you can refer to \n\nsimilar problem: [881. Boats to Save People](https://leetcode.com/problems/boats-to-save-people/discuss/156855/javapython-3-onlogn-code-sorting-greedy-with-greedy-algorithm-proof) \n\nto prove it similarly.\n\n----\n\n1. Starting from smallest positive even, `2`, each iteration deduct it from the `finalSum` and increase by 2, till reach or go beyond `final sum`; \n2. Add the remaining part of the `finalSum` to the largest positive to make sure all are distinct.\n**Note:** if the remaining part is `0`, then adding it to the largest positive will NOT influence anything; if NOT, then the remaining part must be less than or equal to the largest one, if NOT adding it to the largest one, there will be a **duplicate** number since we have traversed all positive even numbers that are less than or equal to the largest one. e.g., \n\n\t`finalSum = 32`, and we have increased `i` from `2` to `10` and get `2 + 4 + 6 + 8 + 10 = 30`. Now `finalSum` has deducted `30` and now is `2`, which is less than the next value of `i = 12`. Since we must used up `finalSum`, but putting `finalSum = 2` back into the even number sequence will result duplicates of `2`; In addition, if we add `2` to any number other than the biggest `10`, there will be duplicates also. The only option is adding `2` to the largest one, `10`, to avoid duplicates.\n\n```java\n public List<Long> maximumEvenSplit(long f) {\n LinkedList<Long> ans = new LinkedList<>();\n if (f % 2 == 0) {\n long i = 2;\n while (i <= f) {\n ans.offer(i);\n f -= i;\n i += 2;\n } \n ans.offer(f + ans.pollLast());\n }\n return ans;\n }\n```\n```python\n def maximumEvenSplit(self, f: int) -> List[int]:\n ans, i = [], 2\n if f % 2 == 0:\n while i <= f:\n ans.append(i)\n f -= i\n i += 2\n ans[-1] += f\n return ans\n```\n\n**Analysis:**\n\nAssume there are totally `i` iterations, so `2 + 4 + ... + 2 * i = (2 + 2 * i) * i / 2 = i * (i + 1) = i + i`<sup>2</sup> `~ finalSum`, get rid of the minor term `i`, we have `i`<sup>2</sup> `~ finalSum`, which means `i ~ finalSum`<sup>0.5</sup>; therefore\n\nTime: `O(n`<sup>0.5</sup>`)`, where `n = finalSum`, space: `O(1)`- excluding return space. | 121 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
Greedy Approach (easy) | maximum-split-of-positive-even-integers | 0 | 1 | # Intuition\nConsider the example with the number 14. The strategy involves initiating the addition process with the smallest even number, as starting with smaller numbers tends to yield longer sequences. Continue adding even numbers until the sum surpasses or equals the target.\n\nCase 1: If the sum of even numbers matches the target, we can straightforwardly return the list of numbers obtained.\n\nCase 2: In situations where the sum exceeds the target, let\'s illustrate with a target of 14. Starting from 2, the sequence might be 2+4+6+8, resulting in a sum of 20, which is greater than 14. In such cases, we need to refine the sequence. For 14, the correct sequence is 14 -> 2+4+8, and it\'s the 6 that poses an issue and needs removal.\n\nLet\'s denote the sequence 14 -> 2+4+8 as \'x\'. The obtained value 20 can be treated as \'x+6\'. To rectify this and obtain the correct sum of 14, we subtract 6 from 20, i.e., x+6 - x = 6. We then remove this value from our list.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumEvenSplit(self, finalSum: int) -> List[int]:\n\n if finalSum%2:\n return []\n else:\n res = []\n curSum = 0\n i = 2\n while curSum < finalSum:\n curSum+=i\n res.append(i)\n i+=2\n if curSum == finalSum:\n return res\n if curSum > finalSum:\n val = curSum-finalSum\n res.remove(val)\n return res\n\n \n\n \n \n``` | 2 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
Simple Python Solution with Explanation || O(sqrt(n)) Time Complexity || O(1) Space Complexity | maximum-split-of-positive-even-integers | 0 | 1 | ```\n\'\'\'VOTE UP, if you like and understand the solution\'\'\'\n\'\'\'You are free to correct my time complexity if you feel it is incorrect.\'\'\' \n```\n```\n**If finalSum is odd then their is no possible way**\n1. If finalSum is even then take s=0 and pointer i=2.\n2. add i in sum till s < finalSum and add i in the set l.\n3. If s == finalSum then return l\n4. else delete s from the l and return l.\n```\n\n\n```\nclass Solution:\n def maximumEvenSplit(self, finalSum: int) -> List[int]:\n l=set()\n if finalSum%2!=0:\n return l\n else:\n s=0\n i=2 # even pointer 2, 4, 6, 8, 10, 12...........\n while(s<finalSum):\n s+=i #sum \n l.add(i) # append the i in list\n i+=2\n if s==finalSum: #if sum s is equal to finalSum then no modidfication required\n return l\n else:\n l.discard(s-finalSum) #Deleting the element which makes s greater than finalSum\n\t\t\t\treturn l\n```\n\n | 58 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
Python Solution by Splitting and Merging | maximum-split-of-positive-even-integers | 0 | 1 | Basically divide the numbers into sum of 2\'s and then join the 2\'s to make different even sized numbers by first taking one 2, then two 2\'s, then three 2\'s and so on. If we do not have the required number of 2\'s left, then just add the remaining 2\'s into the last integer in the array. We add them to the last element of arr and not in middle to avoid clashing of values since we need unique values.\n```\nclass Solution:\n def maximumEvenSplit(self, finalSum: int) -> List[int]:\n arr = []\n if finalSum % 2 == 0: # If finalSum is odd then we cannot ever divide it with the given conditions\n a, i = finalSum // 2, 1 # a is the number of 2\'s and i is the number of 2\'s that we will use to form a even number in the current iteration\n while i <= a: # Till we have sufficient number of 2\'s available\n arr.append(2*i) # Join the i number of 2\'s to form a even number\n a -= i # Number of 2\'s remaining reduces by i\n i += 1 # Number of 2\'s required in next itertation increases by 1\n s = sum(arr)\n arr[-1] += finalSum - s # This is done if their were still some 2\'s remaining that could not form a number due to insufficient count, then we add the remaining 2\'s into the last number.\n return arr\n``` | 10 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
[Python3] Easy Math with Arithmetic Sequence | maximum-split-of-positive-even-integers | 0 | 1 | To obtain the maximum split, it makes sense to adopt the greedy algorithm: **always pick the current least possible even integer first such that we finally obtain a longest split**. If the remaining target sum becomes smaller than the current least possible even integer, we simply go one step back, and add to the end of the previous remaining sum. Here are a few examples:\n\n\t2 => [2]\n\t4 => [2], then adding 4 would not work, as 2 + 4 > 4. So we move one step back, remove 2, and directly add 4 - 0 = 4 to the result. 4 => [4]\n\t\nLooking at more complicated examples:\n\n\t36 => starting with an empty list []\n\tstep 1: adding 2 to the result, we have [2], with a remaining sum of 34\n\tstep 2: adding 4 to the result, we have [2, 4], with a remaining sum of 30\n\tstep 3: adding 6 to the result, we have [2, 4, 6], with a remaining sum of 24\n\tstep 4: adding 8 to the result, we have [2, 4, 6, 8], with a remaining sum of 16\n\tstep 5: adding 10 to the result, we have [2, 4, 6, 8, 10], with a remaining sum of 6\n\tstep 6: We cannot add 12, because the remaining sum is 6. In this case, we move one step backward, with the result [2,4,6,8], and append the remaining sum of 16. Thus we will have the final result [2,4,6,8,16]. \n\t\nOf course, [2,4,6,10,14] would also be a solution to the previous example. But **no other solution would be longer than the one we obtain from greedy algorithm. As we have tried out best to use those smallest possible even numbers.**\n\t\nThen we spotted the result is simply an** Arithmetic Sequence** with a common difference of 2, plus the ending remaining sum. We know that from middle school math:\n\t\n\t2 + 4 + 6 + ... + 2*(n - 1) = n * (n - 1)\n\t\nTherefore, we simply want to find such an **n**, so that we can summarize our result as such an Arithmetic Sequence with the final remaining sum to the end. Taking a **square root of the finalSum** would be the quickest way to find such **n**, rather than iterating from 1. Then, calculating **n** would take roughly *O(1)* time (correct me if I am wrong about this), and formulating the result takes *O(sqrt(targetSum))* time. So the solution could be optimized in the following way:\n\n\n\timport math\n\tclass Solution:\n\n\t\tdef maximumEvenSplit(self, finalSum: int) -> List[int]:\n\t\t\tif finalSum % 2 == 1:\n\t\t\t\treturn []\n\n\t\t\ti = math.floor(math.sqrt(finalSum))\n\n\t\t\tif i * (i + 1) > finalSum:\n\t\t\t\ti -= 1\n\n\t\t\treturn [2 * j for j in range(1, i)] + [finalSum - (i * (i - 1))] | 2 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
Python - O(finalSum^0.5) Easy Solution | maximum-split-of-positive-even-integers | 0 | 1 | If finalSum is divisible by 2, we can divide it by 2 and try to find list of unique positive integers that sum to finalSum. We can multiply everything by 2 at the end to return result. Take the smallest consecutive sequence i.e. 1,2,3,...,n -> this will have a sum of n*(n+1)/2. If this sum == finalSum, we are done. This is trivial case.\n\nThe non-trivial case:\nIf we observe that 1+2+...+n < finalSum but 1+2+...+(n+1) > finalSum. Then, it is impossible to have a solution of size \'n+1\'. The smallest sequence of size n+1 exceeds finalSum. But, we can create a sequence of size \'n\' and this is a valid output. \n\nLet S = sum(1,2,...,n+1) and S-finalSum be the extra amount we don\'t need. So we can remove the number "S-finalSum" from the seq [1,2,...,n+1]. Observe, 1 <= S-finalSum <= n. Therefore, from the sequence [1,2,...,n+1] if we remove S-finalSum, we have the solution that is of size \'n\'. \n\nTime Complexity:\nWe are looking at the sequence of numbers [1,2,...,n] with the smallest \'n\' such that it\'s sum exceeds finalSum. This sequence will have sum = O(n^2). This sum should match finalSum, i.e. O(n^2) = finalSum. Therefore, n = O(finalSum^0.5). For example, if finalSum = 10^10, then the sequence [1,2,...,n] will be of size 10^5 and the loop in this algorithm will run for 10^5 iterations.\n\nPS: There are other ways to solve this too but they all revolve around the fact that if the smallest sequence of size \'n+1\' exceeds finalSum, you can always generate a sequence of size \'n\' whose sum equals finalSum.\n\n```\nclass Solution:\n def maximumEvenSplit(self, finalSum: int) -> List[int]:\n if(finalSum%2 != 0):\n return []\n \n finalSum = finalSum//2\n result = []\n total = 0\n remove = None\n for i in range(1, finalSum+1):\n result.append(i)\n total += i\n if(total == finalSum):\n break\n elif(total > finalSum):\n remove = total-finalSum\n break\n \n output = []\n for num in result:\n if(remove==None):\n output.append(2*num)\n else:\n if(num!=remove):\n output.append(2*num)\n \n return output\n``` | 7 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
65% TC and 83% SC easy python solution | maximum-split-of-positive-even-integers | 0 | 1 | ```\ndef maximumEvenSplit(self, finalSum: int) -> List[int]:\n\tif(finalSum % 2):\n\t\treturn []\n\tans = 0\n\ti = 2\n\ts = c = 0\n\tans = []\n\twhile(s != finalSum and i <= finalSum):\n\t\tif(i < (finalSum-s)//2 or i == finalSum-s):\n\t\t\tc += 1\n\t\t\tans.append(i)\n\t\t\ts += i\n\t\ti += 2\n\treturn ans\n``` | 2 | You are given an integer `finalSum`. Split it into a sum of a **maximum** number of **unique** positive even integers.
* For example, given `finalSum = 12`, the following splits are **valid** (unique positive even integers summing up to `finalSum`): `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`. Among them, `(2 + 4 + 6)` contains the maximum number of integers. Note that `finalSum` cannot be split into `(2 + 2 + 4 + 4)` as all the numbers should be unique.
Return _a list of integers that represent a valid split containing a **maximum** number of integers_. If no valid split exists for `finalSum`, return _an **empty** list_. You may return the integers in **any** order.
**Example 1:**
**Input:** finalSum = 12
**Output:** \[2,4,6\]
**Explanation:** The following are valid splits: `(12)`, `(2 + 10)`, `(2 + 4 + 6)`, and `(4 + 8)`.
(2 + 4 + 6) has the maximum number of integers, which is 3. Thus, we return \[2,4,6\].
Note that \[2,6,4\], \[6,2,4\], etc. are also accepted.
**Example 2:**
**Input:** finalSum = 7
**Output:** \[\]
**Explanation:** There are no valid splits for the given finalSum.
Thus, we return an empty array.
**Example 3:**
**Input:** finalSum = 28
**Output:** \[6,8,2,12\]
**Explanation:** The following are valid splits: `(2 + 26)`, `(6 + 8 + 2 + 12)`, and `(4 + 24)`.
`(6 + 8 + 2 + 12)` has the maximum number of integers, which is 4. Thus, we return \[6,8,2,12\].
Note that \[10,2,4,12\], \[6,2,4,16\], etc. are also accepted.
**Constraints:**
* `1 <= finalSum <= 1010` | The robot only moves along the perimeter of the grid. Can you think if modulus can help you quickly compute which cell it stops at? After the robot moves one time, whenever the robot stops at some cell, it will always face a specific direction. i.e., The direction it faces is determined by the cell it stops at. Can you precompute what direction it faces when it stops at each cell along the perimeter, and reuse the results? |
Python 3 SortedList solution, O(NlogN) | count-good-triplets-in-an-array | 0 | 1 | According to the question, first we obtain an index array `indices`, where `indices[i]` is the index of `nums1[i]` in `num2`, this can be done using a hashmap in `O(N)` time. For example, given `nums1 = [2,0,1,3], nums2 = [0,1,2,3]`, then `indices = [2,0,1,3]`; given `nums1 = [4,0,1,3,2], nums2 = [4,1,0,2,3]`, then `indices = [0,2,1,4,3]`.\n\nThen, the problem is essentially asking - find the total number of triplets `(x, y, z)` as a subsequence in `indices`, where `x < y < z`. To do this, we can scan through `indices` and locate the middle number `y`. Then, we count (1) how many numbers on the left of `y` in `indices` that are less than `y`; and (2) how many numbers on the right of `y` in `indices` that are greater than `y`. This can done using SortedList in Python or other data structures in `O(NlogN)` time.\n\nThe final step is to count the total number of **good triplets** as asked in the problem. This can be done by a linear scan in `O(N)` time.\n\nBelow is my in-contest solution, though I could have made it a bit neater. Please upvote if you find this solution helpful.\n```\nclass Solution:\n def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n hashmap2 = {}\n for i in range(n):\n hashmap2[nums2[i]] = i\n indices = []\n for num in nums1:\n indices.append(hashmap2[num])\n from sortedcontainers import SortedList\n left, right = SortedList(), SortedList()\n leftCount, rightCount = [], []\n for i in range(n):\n leftCount.append(left.bisect_left(indices[i]))\n left.add(indices[i])\n for i in range(n - 1, -1, -1):\n rightCount.append(len(right) - right.bisect_right(indices[i]))\n right.add(indices[i])\n count = 0\n for i in range(n):\n count += leftCount[i] * rightCount[n - 1 - i]\n return count\n``` | 15 | You are given two **0-indexed** arrays `nums1` and `nums2` of length `n`, both of which are **permutations** of `[0, 1, ..., n - 1]`.
A **good triplet** is a set of `3` **distinct** values which are present in **increasing order** by position both in `nums1` and `nums2`. In other words, if we consider `pos1v` as the index of the value `v` in `nums1` and `pos2v` as the index of the value `v` in `nums2`, then a good triplet will be a set `(x, y, z)` where `0 <= x, y, z <= n - 1`, such that `pos1x < pos1y < pos1z` and `pos2x < pos2y < pos2z`.
Return _the **total number** of good triplets_.
**Example 1:**
**Input:** nums1 = \[2,0,1,3\], nums2 = \[0,1,2,3\]
**Output:** 1
**Explanation:**
There are 4 triplets (x,y,z) such that pos1x < pos1y < pos1z. They are (2,0,1), (2,0,3), (2,1,3), and (0,1,3).
Out of those triplets, only the triplet (0,1,3) satisfies pos2x < pos2y < pos2z. Hence, there is only 1 good triplet.
**Example 2:**
**Input:** nums1 = \[4,0,1,3,2\], nums2 = \[4,1,0,2,3\]
**Output:** 4
**Explanation:** The 4 good triplets are (4,0,3), (4,0,2), (4,1,3), and (4,1,2).
**Constraints:**
* `n == nums1.length == nums2.length`
* `3 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= n - 1`
* `nums1` and `nums2` are permutations of `[0, 1, ..., n - 1]`. | Can we process the queries in a smart order to avoid repeatedly checking the same items? How can we use the answer to a query for other queries? |
[Python3] sortedlist & fenwick tree | count-good-triplets-in-an-array | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/97dff55b43563450a33c98f2a216954117100dfe) for solutions of weekly 72. \n\n\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n mp = {x : i for i, x in enumerate(nums1)}\n sl = SortedList()\n ans = 0 \n for i, x in enumerate(nums2):\n x = mp[x]\n left = sl.bisect_left(x)\n right = (len(nums2)-1-x) - (len(sl)-left)\n ans += left * right\n sl.add(x)\n return ans\n```\n\nAdded Fenwick tree solution\n```\nclass Fenwick: \n def __init__(self, n: int):\n self.nums = [0]*(n+1)\n\n def update(self, k: int, x: int) -> None: \n k += 1\n while k < len(self.nums): \n self.nums[k] += x\n k += k & -k \n\n def query(self, k: int) -> int: \n k += 1\n ans = 0\n while k:\n ans += self.nums[k]\n k -= k & -k\n return ans\n\n \nclass Solution:\n def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n mp = {x : i for i, x in enumerate(nums1)}\n fw = Fenwick(n)\n ans = 0 \n for i, x in enumerate(nums2):\n x = mp[x]\n left = fw.query(x)\n right = (n-1-x) - (fw.query(n-1)-left)\n ans += left * right\n fw.update(x, 1)\n return ans\n``` | 4 | You are given two **0-indexed** arrays `nums1` and `nums2` of length `n`, both of which are **permutations** of `[0, 1, ..., n - 1]`.
A **good triplet** is a set of `3` **distinct** values which are present in **increasing order** by position both in `nums1` and `nums2`. In other words, if we consider `pos1v` as the index of the value `v` in `nums1` and `pos2v` as the index of the value `v` in `nums2`, then a good triplet will be a set `(x, y, z)` where `0 <= x, y, z <= n - 1`, such that `pos1x < pos1y < pos1z` and `pos2x < pos2y < pos2z`.
Return _the **total number** of good triplets_.
**Example 1:**
**Input:** nums1 = \[2,0,1,3\], nums2 = \[0,1,2,3\]
**Output:** 1
**Explanation:**
There are 4 triplets (x,y,z) such that pos1x < pos1y < pos1z. They are (2,0,1), (2,0,3), (2,1,3), and (0,1,3).
Out of those triplets, only the triplet (0,1,3) satisfies pos2x < pos2y < pos2z. Hence, there is only 1 good triplet.
**Example 2:**
**Input:** nums1 = \[4,0,1,3,2\], nums2 = \[4,1,0,2,3\]
**Output:** 4
**Explanation:** The 4 good triplets are (4,0,3), (4,0,2), (4,1,3), and (4,1,2).
**Constraints:**
* `n == nums1.length == nums2.length`
* `3 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= n - 1`
* `nums1` and `nums2` are permutations of `[0, 1, ..., n - 1]`. | Can we process the queries in a smart order to avoid repeatedly checking the same items? How can we use the answer to a query for other queries? |
[Python] Simple O(NlogN) solution using bisect | count-good-triplets-in-an-array | 0 | 1 | ```\nclass Solution:\n def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n res = 0\n m2 = [0] * n\n q = []\n \n\t\t# Build index map of nums2\n for i in range(n):\n m2[nums2[i]] = i\n \n for p1 in range(n):\n p2 = m2[nums1[p1]] # Position of nums1[p1] in nums2\n idx = bisect.bisect(q, p2) # Position smaller than this one so far\n q.insert(idx, p2)\n before = idx\n after = n-1 - p1 - p2 + before # Based on number of unique values before and after are the same\n res += before * after\n \n return res\n``` | 2 | You are given two **0-indexed** arrays `nums1` and `nums2` of length `n`, both of which are **permutations** of `[0, 1, ..., n - 1]`.
A **good triplet** is a set of `3` **distinct** values which are present in **increasing order** by position both in `nums1` and `nums2`. In other words, if we consider `pos1v` as the index of the value `v` in `nums1` and `pos2v` as the index of the value `v` in `nums2`, then a good triplet will be a set `(x, y, z)` where `0 <= x, y, z <= n - 1`, such that `pos1x < pos1y < pos1z` and `pos2x < pos2y < pos2z`.
Return _the **total number** of good triplets_.
**Example 1:**
**Input:** nums1 = \[2,0,1,3\], nums2 = \[0,1,2,3\]
**Output:** 1
**Explanation:**
There are 4 triplets (x,y,z) such that pos1x < pos1y < pos1z. They are (2,0,1), (2,0,3), (2,1,3), and (0,1,3).
Out of those triplets, only the triplet (0,1,3) satisfies pos2x < pos2y < pos2z. Hence, there is only 1 good triplet.
**Example 2:**
**Input:** nums1 = \[4,0,1,3,2\], nums2 = \[4,1,0,2,3\]
**Output:** 4
**Explanation:** The 4 good triplets are (4,0,3), (4,0,2), (4,1,3), and (4,1,2).
**Constraints:**
* `n == nums1.length == nums2.length`
* `3 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= n - 1`
* `nums1` and `nums2` are permutations of `[0, 1, ..., n - 1]`. | Can we process the queries in a smart order to avoid repeatedly checking the same items? How can we use the answer to a query for other queries? |
Current Fastest Version Rewritten In Sensible Formatting | Commented and Explanation Attempted | count-good-triplets-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition here is not my own; my solution was way less elegant and involved binary search processing. This version is much cleaner and seems to use bitshifts and masking to accomplish a similar goal. Only intution is sparsely explained. To see print out of solutions and work through it on your own, several print(f\'\') statements are left commented. It WILL NOT submit with these uncommented as it will overflow output statements. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe first key in this verison and in my original version was to use a mapping of num values in nums1 to the index of occurrence, and have alongside that in this case a mapping of number of triplet occurrences at the various indices of nums2 for the nums1 values. \n\nThese are both built by enumerating over the respective nums list, but nums1 is straightforward. Nums2 however has the following during enumeration. \n\n- Get the nums1 index of the value in nums 2 and record it twice, once for a forward bitshifting and once for a backward bitshifting (more on that in a moment) \n- set a bitsum to 0 and then for one of the two nums1 indices recorded \n- while that nums1 indices recorded is not 0 \n - update the bit_sum by the number of triplets of nums2 at nums1 index according to the nums 1 indice currently used \n - remove the least significant bit of the nums1 indices currently being used (accomplished with a bitwise & operation of self and self - 1) \n- calculate the result increment multiple as the length of the lists, less the index in nums2 less the index in nums1 (the one you have not yet modified) to account for the positioning of the 3 triplet pair items. Then, increment this by the bit_sum calculated. Then, reduce this by 1 to account for an off by one factor. \n- result is then incremented by the bit_sum calculated * the result increment multiple. \n- Now that we\'ve done the backwards portion (removing least significant bit) do the forward portion. To start, increment the other nums1 index not yet used. \n- Then, while this index is less than the length of the list (basically, while valid) \n - increment the num triplets of nums2 at nums1 index by 1 at this index \n - shift this to the next most significant bit positioning (so 3 becomes 4 just as 2 becomes 4, but 5 becomes 8, and so on). This is done by the addition to self of self with bitwise and of negated self (this is an AWESOME trick!) \n\nWhen done, result is calculated appropriately and can be submitted \n\n# Complexity\n- Time complexity : O(n log n)\n - O(n) process on enumeration of nums1 or nums2 \n - in nums2 loop, for every enumeration step, we do O(log n) steps in each subloop (most significant bit and least significant bit operation)\n - total is then O(n log n) \n\n- Space complexity : O(n) \n - both mappings store O(n) valuations \n\n# Code\n```\nclass Solution:\n def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int : \n # get length of nums1 \n nL = len(nums1) \n # build a value to index listing of size nL \n nums1_val_to_index = [0] * nL \n # map value to index via enumeration \n for index, val in enumerate(nums1) : \n nums1_val_to_index[val] = index \n # build a number of triplets of nums2 value at nums1 indexing map \n num_triplets_nums2_at_nums1_index = [0] * nL \n # set a result = 0 \n result = 0 \n # for index, val in enumerate(nums2) \n for index, val in enumerate(nums2) : \n # uncomment to see processing \n # print(f\'for {index}, {val} in nums2\\n\')\n # get the pair index in nums1 and the nums1 index of the value in nums 2 (using it twice, so store twice)\n pair_index_in_nums1 = nums1_index = nums1_val_to_index[val]\n # print(f\'the value of pair_index_in_nums1 is {pair_index_in_nums1}. Bitsum starts at 0.\\n\')\n # print(f\'Current num_triplets_nums2_at_nums1_index is {num_triplets_nums2_at_nums1_index}\\n\')\n # we\'ll calculate a bitsum \n bit_sum = 0 \n # while we have the pair index \n while pair_index_in_nums1 : \n # update bit_sum by the number of triplets of nums2 value at nums1 index according to the pair index in nums 1\n bit_sum += num_triplets_nums2_at_nums1_index[pair_index_in_nums1]\n # remove the least significant bit from the binary form of pair index in nums1 \n # this is going back to front \n pair_index_in_nums1 &= pair_index_in_nums1 - 1 \n # print(f\'Bitsum is now {bit_sum} and pair_index_in_nums1 is now {pair_index_in_nums1}\\n\')\n # update result by bit_sum * (length - index in nums 2 - index in nums 1 + bit_sum - 1) \n # this calculates the number of triplets that are added to the total valuation as the length difference of the two \n # plus the bit sum of the number of triplets of nums2 at nums1 index (valid or not by positioning) must be 1 off from \n # the total of the valid pairings in terms of ordering according to the logic of bitmasks utilized herein \n result_increment_multiple = (nL - index - nums1_index + bit_sum - 1) \n # print(f\'Result increment multiple is {result_increment_multiple}\\n\')\n result += bit_sum * result_increment_multiple\n # print(f\'Result is now {result}.\\n\')\n # increment the nums1 index to account for 0 indexing \n nums1_index += 1 \n # while lt nL \n # print(f\'Starting from {nums1_index} until {nL}\\n\')\n while nums1_index < nL : \n # update the num_triplets_nums2_at_nums1_index by 1 \n num_triplets_nums2_at_nums1_index[nums1_index] += 1 \n # twos complement negation adds a singular bit in this case (next up value, so 3 -> 4 just as 2 -> 4)\n # then 2 -> 4 -> 8 on the next and so on and so forth \n nums1_index += nums1_index & -nums1_index\n # print(f\'num_triplets_nums2_at_nums1_index is now {num_triplets_nums2_at_nums1_index} and nums1_index is now {nums1_index}\\n\')\n # print(f\'Moving to next index value pairing.\\n\')\n # when done return result \n return result \n\n``` | 0 | You are given two **0-indexed** arrays `nums1` and `nums2` of length `n`, both of which are **permutations** of `[0, 1, ..., n - 1]`.
A **good triplet** is a set of `3` **distinct** values which are present in **increasing order** by position both in `nums1` and `nums2`. In other words, if we consider `pos1v` as the index of the value `v` in `nums1` and `pos2v` as the index of the value `v` in `nums2`, then a good triplet will be a set `(x, y, z)` where `0 <= x, y, z <= n - 1`, such that `pos1x < pos1y < pos1z` and `pos2x < pos2y < pos2z`.
Return _the **total number** of good triplets_.
**Example 1:**
**Input:** nums1 = \[2,0,1,3\], nums2 = \[0,1,2,3\]
**Output:** 1
**Explanation:**
There are 4 triplets (x,y,z) such that pos1x < pos1y < pos1z. They are (2,0,1), (2,0,3), (2,1,3), and (0,1,3).
Out of those triplets, only the triplet (0,1,3) satisfies pos2x < pos2y < pos2z. Hence, there is only 1 good triplet.
**Example 2:**
**Input:** nums1 = \[4,0,1,3,2\], nums2 = \[4,1,0,2,3\]
**Output:** 4
**Explanation:** The 4 good triplets are (4,0,3), (4,0,2), (4,1,3), and (4,1,2).
**Constraints:**
* `n == nums1.length == nums2.length`
* `3 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= n - 1`
* `nums1` and `nums2` are permutations of `[0, 1, ..., n - 1]`. | Can we process the queries in a smart order to avoid repeatedly checking the same items? How can we use the answer to a query for other queries? |
[Python] Straightforward binary search | count-good-triplets-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor triplet requirement, consider the middle one in the triplet, count how many "smaller" options in front and how many "bigger" options behind\n\n\n# Code\n```\nfrom bisect import bisect\n\nclass Solution:\n def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:\n dic = {num: i for i, num in enumerate(nums2)}\n n = len(nums1)\n idx_f, idx_b = [0], [0]\n front, back = [dic[nums1[0]]], [dic[nums1[-1]]]\n for num in nums1[1:]:\n idx = bisect(front, dic[num])\n front.insert(idx, dic[num])\n idx_f.append(idx)\n \n for num in nums1[n-2::-1]:\n \n idx = bisect(back, dic[num])\n idx_b.append(len(back) - idx)\n back.insert(idx, dic[num])\n \n \n idx_b = idx_b[::-1]\n \n return sum(a*b for a, b in zip(idx_f, idx_b))\n``` | 0 | You are given two **0-indexed** arrays `nums1` and `nums2` of length `n`, both of which are **permutations** of `[0, 1, ..., n - 1]`.
A **good triplet** is a set of `3` **distinct** values which are present in **increasing order** by position both in `nums1` and `nums2`. In other words, if we consider `pos1v` as the index of the value `v` in `nums1` and `pos2v` as the index of the value `v` in `nums2`, then a good triplet will be a set `(x, y, z)` where `0 <= x, y, z <= n - 1`, such that `pos1x < pos1y < pos1z` and `pos2x < pos2y < pos2z`.
Return _the **total number** of good triplets_.
**Example 1:**
**Input:** nums1 = \[2,0,1,3\], nums2 = \[0,1,2,3\]
**Output:** 1
**Explanation:**
There are 4 triplets (x,y,z) such that pos1x < pos1y < pos1z. They are (2,0,1), (2,0,3), (2,1,3), and (0,1,3).
Out of those triplets, only the triplet (0,1,3) satisfies pos2x < pos2y < pos2z. Hence, there is only 1 good triplet.
**Example 2:**
**Input:** nums1 = \[4,0,1,3,2\], nums2 = \[4,1,0,2,3\]
**Output:** 4
**Explanation:** The 4 good triplets are (4,0,3), (4,0,2), (4,1,3), and (4,1,2).
**Constraints:**
* `n == nums1.length == nums2.length`
* `3 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= n - 1`
* `nums1` and `nums2` are permutations of `[0, 1, ..., n - 1]`. | Can we process the queries in a smart order to avoid repeatedly checking the same items? How can we use the answer to a query for other queries? |
Python (BIT) | count-good-triplets-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BIT:\n def __init__(self,n):\n self.ans = [0]*(n+1)\n\n def query(self,i):\n res = 0\n while i > 0:\n res += self.ans[i]\n i -= i&-i\n return res\n\n def update(self,i,val):\n while i < len(self.ans):\n self.ans[i] += val\n i += i&-i\n\nclass Solution:\n def goodTriplets(self, nums1, nums2):\n dict1 = {x:i for i,x in enumerate(nums1)}\n n = len(nums1)\n arr = [dict1[nums2[i]] for i in range(n)]\n\n BIT1, BIT2, total = BIT(n), BIT(n), 0\n\n for i in arr:\n total += BIT2.query(i)\n BIT1.update(i+1,1)\n less = BIT1.query(i)\n BIT2.update(i+1,less)\n\n return total\n\n\n\n\n\n\n\n\n\n \n``` | 0 | You are given two **0-indexed** arrays `nums1` and `nums2` of length `n`, both of which are **permutations** of `[0, 1, ..., n - 1]`.
A **good triplet** is a set of `3` **distinct** values which are present in **increasing order** by position both in `nums1` and `nums2`. In other words, if we consider `pos1v` as the index of the value `v` in `nums1` and `pos2v` as the index of the value `v` in `nums2`, then a good triplet will be a set `(x, y, z)` where `0 <= x, y, z <= n - 1`, such that `pos1x < pos1y < pos1z` and `pos2x < pos2y < pos2z`.
Return _the **total number** of good triplets_.
**Example 1:**
**Input:** nums1 = \[2,0,1,3\], nums2 = \[0,1,2,3\]
**Output:** 1
**Explanation:**
There are 4 triplets (x,y,z) such that pos1x < pos1y < pos1z. They are (2,0,1), (2,0,3), (2,1,3), and (0,1,3).
Out of those triplets, only the triplet (0,1,3) satisfies pos2x < pos2y < pos2z. Hence, there is only 1 good triplet.
**Example 2:**
**Input:** nums1 = \[4,0,1,3,2\], nums2 = \[4,1,0,2,3\]
**Output:** 4
**Explanation:** The 4 good triplets are (4,0,3), (4,0,2), (4,1,3), and (4,1,2).
**Constraints:**
* `n == nums1.length == nums2.length`
* `3 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= n - 1`
* `nums1` and `nums2` are permutations of `[0, 1, ..., n - 1]`. | Can we process the queries in a smart order to avoid repeatedly checking the same items? How can we use the answer to a query for other queries? |
simple.py | count-integers-with-even-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n c=0\n for i in range(1,num+1):\n sum=0\n while(i>0):\n k=i%10\n sum=sum+k\n i=i//10\n if sum%2==0:\n c+=1\n return c\n``` | 2 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Best solution for beginners in leetcode | count-integers-with-even-digit-sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n count=0\n for i in range(1,num+1):\n digit=str(i)\n dsum=0\n for j in range(len(digit)):\n dsum+=int(digit[j])\n if dsum%2==0:\n count+=1\n\n return count \n\n \n``` | 1 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Easy Python Solution - countEven || Beats 97% | count-integers-with-even-digit-sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n c=0\n for i in range(2,num+1):\n sum,j = 0,i\n while j != 0:\n d = j % 10\n sum = sum + d\n j = j // 10\n if sum % 2 == 0:\n c += 1\n return c\n``` | 1 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
O(1) solution with 3 lines beats 95% | count-integers-with-even-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n n=sum(list(map(int,str(num).strip())))\n if n%2==0:\n return num//2\n else:\n return ceil(num/2)-1\n\n\n\n\n\n\n\n\n \n``` | 1 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
[Python3, Java, C++] 1 liners O(length(num)) | count-integers-with-even-digit-sum | 1 | 1 | **Brute force**:\nIterate through all the numbers from 1 to num inclusive and check if the sum of the digits of each number in that range is divisible by 2. \n<iframe src="https://leetcode.com/playground/jnt4pAME/shared" frameBorder="0" width="670" height="280"></iframe>\n\n\n**Observation**:\n```\nIntegers: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]\nSums: [1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 3, 4, 5, 6]\nSum is Even? : [0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1]\nCount(Even sums): [0, 1, 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 10, 10, 11, 11, 12] \n```\nFor a `num` with even sum of its digits, count of Integers With Even Digit Sum less than or equal to `num` is `num`/2\nFor a `num` with odd sum of its digits, count of Integers With Even Digit Sum less than or equal to `num` is (`num`-1)/2\n\n**Optimized solution:**\n<iframe src="https://leetcode.com/playground/RdZeyXuk/shared" frameBorder="0" width="830" height="190"></iframe>\n | 28 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
<Python3> O(1) - Discrete Formula - 100% faster - 1 LINE | count-integers-with-even-digit-sum | 0 | 1 | ### We sum the digits of num.\n\n##### if the sum is **even** -> return num // 2\n##### if the sum is **odd** -> return (num - 1) // 2\n\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n return num // 2 if sum([int(k) for k in str(num)]) % 2 == 0 else (num - 1) // 2\n```\n\t\t\n\t\t\n##### Since 1 <= num <= 1000 we will sum at most **4 digits**, hence the solution is **O(1)**. | 9 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Easy python solution. | count-integers-with-even-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe start a loop from range 1 till the num given to us,then we take digits one by one and check whether the sum of its digits are adding up to an even number.If yes we increase our count and finally return it.\n\n# Complexity\n- Time complexity:45 ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->Beats 68.16%of users with Python3\n\n- Space complexity:16.29MB\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->Beats 52.57%of users with Python3\n\n# Code\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n c=0\n for i in range(1,num+1):\n sum = 0\n while (i >0):\n sum = sum + int(i % 10)\n i = int(i/10)\n if(sum%2==0):\n c+=1\n return c\n``` | 1 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Count Integer with even digit sum | count-integers-with-even-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n countf = 0\n\n for i in range(1,num+1):\n s = str(i)\n count = 0\n for j in range(len(s)):\n a = int(s[j])\n # print(a)\n count = count+a\n if count%2==0:\n countf+=1\n return(countf)\n``` | 2 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Python | Easy Solution✅ | count-integers-with-even-digit-sum | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def countEven(self, num: int) -> int:\n count = 0\n for i in range(2,num+1):\n if sum(list(map(int, str(i).strip()))) % 2 == 0:\n count +=1\n return count\n``` | 6 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Python 3 (30ms) | Simple Maths Formula | Even Odd Solution | count-integers-with-even-digit-sum | 0 | 1 | ```\nclass Solution:\n def countEven(self, num: int) -> int:\n if num%2!=0:\n return (num//2)\n s=0\n t=num\n while t:\n s=s+(t%10)\n t=t//10\n if s%2==0:\n return num//2\n else:\n return (num//2)-1\n``` | 3 | Given a positive integer `num`, return _the number of positive integers **less than or equal to**_ `num` _whose digit sums are **even**_.
The **digit sum** of a positive integer is the sum of all its digits.
**Example 1:**
**Input:** num = 4
**Output:** 2
**Explanation:**
The only integers less than or equal to 4 whose digit sums are even are 2 and 4.
**Example 2:**
**Input:** num = 30
**Output:** 14
**Explanation:**
The 14 integers less than or equal to 30 whose digit sums are even are
2, 4, 6, 8, 11, 13, 15, 17, 19, 20, 22, 24, 26, and 28.
**Constraints:**
* `1 <= num <= 1000` | Is it possible to assign the first k smallest tasks to the workers? How can you efficiently try every k? |
Easy python solution | merge-nodes-in-between-zeros | 0 | 1 | ```\ndef mergeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\tcurr = head\n\twhile(curr):\n\t\tif(curr.val == 0):\n\t\t\ts = 0\n\t\t\ttar = curr\n\t\t\tcurr = curr.next\n\t\t\twhile(curr.val != 0):\n\t\t\t\ts += curr.val\n\t\t\t\tcurr = curr.next\n\t\t\ttar.val = s\n\t\t\tif(curr.next):\n\t\t\t\ttar.next = curr\n\t\t\telse:\n\t\t\t\ttar.next = None\n\t\t\t\tbreak\n\treturn head\n``` | 2 | You are given the `head` of a linked list, which contains a series of integers **separated** by `0`'s. The **beginning** and **end** of the linked list will have `Node.val == 0`.
For **every** two consecutive `0`'s, **merge** all the nodes lying in between them into a single node whose value is the **sum** of all the merged nodes. The modified list should not contain any `0`'s.
Return _the_ `head` _of the modified linked list_.
**Example 1:**
**Input:** head = \[0,3,1,0,4,5,2,0\]
**Output:** \[4,11\]
**Explanation:**
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 3 + 1 = 4.
- The sum of the nodes marked in red: 4 + 5 + 2 = 11.
**Example 2:**
**Input:** head = \[0,1,0,3,0,2,2,0\]
**Output:** \[1,3,4\]
**Explanation:**
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 1 = 1.
- The sum of the nodes marked in red: 3 = 3.
- The sum of the nodes marked in yellow: 2 + 2 = 4.
**Constraints:**
* The number of nodes in the list is in the range `[3, 2 * 105]`.
* `0 <= Node.val <= 1000`
* There are **no** two consecutive nodes with `Node.val == 0`.
* The **beginning** and **end** of the linked list have `Node.val == 0`. | Starting with i=0, check the condition for each index. The first one you find to be true is the smallest index. |
[ Python ] ✅✅ Simple Python Solution | Nested Loop 🥳✌👍 | merge-nodes-in-between-zeros | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 6310 ms, faster than 29.52% of Python3 online submissions for Merge Nodes in Between Zeros.\n# Memory Usage: 104.3 MB, less than 16.40% of Python3 online submissions for Merge Nodes in Between Zeros.\n\n\tclass Solution:\n\t\tdef mergeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n\n\t\t\tcurrent_node = head.next\n\n\t\t\tresult = new_node = ListNode(0)\n\n\t\t\twhile current_node:\n\n\t\t\t\tcurrent_sum = 0\n\n\t\t\t\twhile current_node.val != 0:\n\t\t\t\t\tcurrent_sum = current_sum + current_node.val\n\t\t\t\t\tcurrent_node = current_node.next\n\n\t\t\t\tnew_node.next = ListNode(current_sum)\n\t\t\t\tnew_node = new_node.next\n\n\t\t\t\tcurrent_node = current_node.next\n\n\t\t\treturn result.next\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D\n | 4 | You are given the `head` of a linked list, which contains a series of integers **separated** by `0`'s. The **beginning** and **end** of the linked list will have `Node.val == 0`.
For **every** two consecutive `0`'s, **merge** all the nodes lying in between them into a single node whose value is the **sum** of all the merged nodes. The modified list should not contain any `0`'s.
Return _the_ `head` _of the modified linked list_.
**Example 1:**
**Input:** head = \[0,3,1,0,4,5,2,0\]
**Output:** \[4,11\]
**Explanation:**
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 3 + 1 = 4.
- The sum of the nodes marked in red: 4 + 5 + 2 = 11.
**Example 2:**
**Input:** head = \[0,1,0,3,0,2,2,0\]
**Output:** \[1,3,4\]
**Explanation:**
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 1 = 1.
- The sum of the nodes marked in red: 3 = 3.
- The sum of the nodes marked in yellow: 2 + 2 = 4.
**Constraints:**
* The number of nodes in the list is in the range `[3, 2 * 105]`.
* `0 <= Node.val <= 1000`
* There are **no** two consecutive nodes with `Node.val == 0`.
* The **beginning** and **end** of the linked list have `Node.val == 0`. | Starting with i=0, check the condition for each index. The first one you find to be true is the smallest index. |
[Java/Python 3] One pass two pointers, copy sum to 0 nodes. | merge-nodes-in-between-zeros | 1 | 1 | Use zero nodes to store the sum of merged nodes, remove the last zero node, which is unused.\n\n1. Use `prev` to connect and move among all zero nodes;\n2. Use `head` to traverse nodes between zero nodes, and add their values to the previous zero node;\n3. Always use `prev` point to the node right before current zero node, hence we can remove the last zero node easily.\n\n```java\n public ListNode mergeNodes(ListNode head) {\n ListNode dummy = new ListNode(Integer.MIN_VALUE), prev = dummy;\n while (head != null && head.next != null) {\n prev.next = head; // prev connects next 0 node.\n head = head.next; // head forward to a non-zero node.\n while (head != null && head.val != 0) { // traverse all non-zero nodes between two zero nodes.\n prev.next.val += head.val; // add current value to the previous zero node.\n head = head.next; // forward one step.\n }\n prev = prev.next; // prev point to the summation node (initially 0).\n }\n prev.next = null; // cut off last 0 node.\n return dummy.next;\n }\n```\n```python\n def mergeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n dummy = prev = ListNode(-math.inf)\n while head and head.next:\n prev.next = head\n head = head.next\n while head and head.val != 0:\n prev.next.val += head.val\n head = head.next\n prev = prev.next\n prev.next = None \n return dummy.next\n```\n\n**Analysis:**\n\nTime: `O(n)`, extra space: `O(1)`, where `n` is the number of nodes. | 21 | You are given the `head` of a linked list, which contains a series of integers **separated** by `0`'s. The **beginning** and **end** of the linked list will have `Node.val == 0`.
For **every** two consecutive `0`'s, **merge** all the nodes lying in between them into a single node whose value is the **sum** of all the merged nodes. The modified list should not contain any `0`'s.
Return _the_ `head` _of the modified linked list_.
**Example 1:**
**Input:** head = \[0,3,1,0,4,5,2,0\]
**Output:** \[4,11\]
**Explanation:**
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 3 + 1 = 4.
- The sum of the nodes marked in red: 4 + 5 + 2 = 11.
**Example 2:**
**Input:** head = \[0,1,0,3,0,2,2,0\]
**Output:** \[1,3,4\]
**Explanation:**
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 1 = 1.
- The sum of the nodes marked in red: 3 = 3.
- The sum of the nodes marked in yellow: 2 + 2 = 4.
**Constraints:**
* The number of nodes in the list is in the range `[3, 2 * 105]`.
* `0 <= Node.val <= 1000`
* There are **no** two consecutive nodes with `Node.val == 0`.
* The **beginning** and **end** of the linked list have `Node.val == 0`. | Starting with i=0, check the condition for each index. The first one you find to be true is the smallest index. |
Python 3 Linked list - O(n) time and space - if you want to avoid the O(logN) heap push/pop | construct-string-with-repeat-limit | 0 | 1 | # Approach\nThis approach is similar to that of a priority queue / heap.\n\nHowever, using a linked list avoid the O(logN) time operations of heappush() and heappop().\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n"""\nImplementation of a Node in a linked list.\n"""\nclass Node:\n def __init__(self, chr, val):\n self.chr = chr # A letter\n self.val = val # Store count of a letter \n self.next = None\n\n"""\nSolution with a linked list\n"""\nclass Solution:\n def repeatLimitedString(self, s: str, repeatLimit: int) -> str:\n # Count the letters and store them in an array of 26 \n counts = [0] * 26\n for i in s:\n counts[ord(i)-97] += 1\n\n # Loop through the counts and construct a linked list that link letters\n # and their counts in descending order, ignoring letters that have 0 count.\n # We have as a result:\n # root = Node(dummy, -1) -> Node(z, 2) -> Node(c, 4) -> Node(a, 1)\n root = last = Node("dummy", -1)\n for i in range(len(counts)-1, -1, -1):\n if counts[i] != 0:\n last.next = Node(chr(i+97), counts[i])\n last = last.next\n root = root.next\n \n # We go through the linked list like we do with the priority queue and\n # add letters into the answer array.\n k = repeatLimit\n ans = []\n # As long as the list is not empty, we keep going.\n while root: \n # The current node has count > repeatLimit\n if root.val > k:\n # We add the letter into ans (repeatLimit) times and update\n # the remaining count in the Node.\n ans.extend([root.chr] * k)\n root.val -= k\n \n # We need to take away one from the next Node (the next largest\n # letter) and add to the ans as separator.\n if root.next is None:\n # There are no more smaller letters we can use and cannot\n # continue adding the letter from the current Node since\n # limit is reached.\n break\n else:\n # We add the next largest letter from the next Node and\n # update remaining count. If remaining count == 0, we remove \n # that Node and link Node.next to Node.next.next.\n ans.append(root.next.chr)\n root.next.val -= 1\n if root.next.val == 0:\n root.next = root.next.next\n \n # The current node has count <= repeatLimit\n else:\n # We simply add the letters (count) times into ans and move\n # on to the next Node. \n ans.extend([root.chr] * root.val)\n root = root.next\n\n return "".join(ans)\n \n \n``` | 2 | You are given a string `s` and an integer `repeatLimit`. Construct a new string `repeatLimitedString` using the characters of `s` such that no letter appears **more than** `repeatLimit` times **in a row**. You do **not** have to use all characters from `s`.
Return _the **lexicographically largest**_ `repeatLimitedString` _possible_.
A string `a` is **lexicographically larger** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears later in the alphabet than the corresponding letter in `b`. If the first `min(a.length, b.length)` characters do not differ, then the longer string is the lexicographically larger one.
**Example 1:**
**Input:** s = "cczazcc ", repeatLimit = 3
**Output:** "zzcccac "
**Explanation:** We use all of the characters from s to construct the repeatLimitedString "zzcccac ".
The letter 'a' appears at most 1 time in a row.
The letter 'c' appears at most 3 times in a row.
The letter 'z' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "zzcccac ".
Note that the string "zzcccca " is lexicographically larger but the letter 'c' appears more than 3 times in a row, so it is not a valid repeatLimitedString.
**Example 2:**
**Input:** s = "aababab ", repeatLimit = 2
**Output:** "bbabaa "
**Explanation:** We use only some of the characters from s to construct the repeatLimitedString "bbabaa ".
The letter 'a' appears at most 2 times in a row.
The letter 'b' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "bbabaa ".
Note that the string "bbabaaa " is lexicographically larger but the letter 'a' appears more than 2 times in a row, so it is not a valid repeatLimitedString.
**Constraints:**
* `1 <= repeatLimit <= s.length <= 105`
* `s` consists of lowercase English letters. | The maximum distance must be the distance between the first and last critical point. For each adjacent critical point, calculate the difference and check if it is the minimum distance. |
[Python3] priority queue | construct-string-with-repeat-limit | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/793daa0aab0733bfadd4041fdaa6f8bdd38fe229) for solutions of weekly 281. \n\n```\nclass Solution:\n def repeatLimitedString(self, s: str, repeatLimit: int) -> str:\n pq = [(-ord(k), v) for k, v in Counter(s).items()] \n heapify(pq)\n ans = []\n while pq: \n k, v = heappop(pq)\n if ans and ans[-1] == k: \n if not pq: break \n kk, vv = heappop(pq)\n ans.append(kk)\n if vv-1: heappush(pq, (kk, vv-1))\n heappush(pq, (k, v))\n else: \n m = min(v, repeatLimit)\n ans.extend([k]*m)\n if v-m: heappush(pq, (k, v-m))\n return "".join(chr(-x) for x in ans)\n``` | 29 | You are given a string `s` and an integer `repeatLimit`. Construct a new string `repeatLimitedString` using the characters of `s` such that no letter appears **more than** `repeatLimit` times **in a row**. You do **not** have to use all characters from `s`.
Return _the **lexicographically largest**_ `repeatLimitedString` _possible_.
A string `a` is **lexicographically larger** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears later in the alphabet than the corresponding letter in `b`. If the first `min(a.length, b.length)` characters do not differ, then the longer string is the lexicographically larger one.
**Example 1:**
**Input:** s = "cczazcc ", repeatLimit = 3
**Output:** "zzcccac "
**Explanation:** We use all of the characters from s to construct the repeatLimitedString "zzcccac ".
The letter 'a' appears at most 1 time in a row.
The letter 'c' appears at most 3 times in a row.
The letter 'z' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "zzcccac ".
Note that the string "zzcccca " is lexicographically larger but the letter 'c' appears more than 3 times in a row, so it is not a valid repeatLimitedString.
**Example 2:**
**Input:** s = "aababab ", repeatLimit = 2
**Output:** "bbabaa "
**Explanation:** We use only some of the characters from s to construct the repeatLimitedString "bbabaa ".
The letter 'a' appears at most 2 times in a row.
The letter 'b' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "bbabaa ".
Note that the string "bbabaaa " is lexicographically larger but the letter 'a' appears more than 2 times in a row, so it is not a valid repeatLimitedString.
**Constraints:**
* `1 <= repeatLimit <= s.length <= 105`
* `s` consists of lowercase English letters. | The maximum distance must be the distance between the first and last critical point. For each adjacent critical point, calculate the difference and check if it is the minimum distance. |
Greedy Python Solution | 100% Runtime | construct-string-with-repeat-limit | 0 | 1 | Upvote if you find this article helpful\u2B06\uFE0F.\n### STEPS:\n1. Basically we make a sorted table with freq of each character.\n2. Then we take the most lexicographically superior character (Call it A).\n3. If its freq is in limits, directly add it.\n4. If its freq is more than the limit. Add repeatLimit number of A\'s and then search for the next lexicographically superior character(Call it TEMP) and add it just once, as we will again add the remaining A\'s.\n5. Repeat this process until either all A\'s are consumed or we run out of TEMP characters.\n6. Repeat all these steps for all other remaining characters in lexicographic order.\n\n**NOTE: Here we make the Greedy choice of choosing a lexicographically superior character at each step, while selecting A and also while selecting TEMP.**\n**NOTE: I have not removed characters if a characters freq becomes 0. This is because random pop() operations in the middle of a list takes O(n) time. For pop() operations in default index(End of list) is O(1). Refer to this article \u27A1\uFE0F [Time Complexity of Python Library Functinons](https://wiki.python.org/moin/TimeComplexity)** \n\n### STATUS:\n\n\n### CODE:\n```\nclass Solution:\n def repeatLimitedString(self, s: str, repeatLimit: int) -> str:\n table = Counter(s)\n char_set = [\'0\', \'a\', \'b\', \'c\', \'d\', \'e\', \'f\', \'g\', \'h\', \'i\', \'j\', \'k\', \'l\', \'m\', \'n\', \'o\', \'p\', \'q\', \'r\', \'s\',\n \'t\', \'u\', \'v\', \'w\', \'x\', \'y\', \'z\']\n sorted_table = []\n for i in range(26,-1,-1):\n if char_set[i] in table:\n sorted_table.append((char_set[i],table[char_set[i]]))\n\n result = ""\n n = len(sorted_table)\n for i in range(n):\n char, curr_freq = sorted_table[i] # The lexicographically larger character and its frequency\n index_to_take_from = i + 1 # We take from this index the next lexicographically larger character(TEMP) if the repeatLimit for A is exceeded\n while curr_freq > repeatLimit: # Limit exceeded\n result += char*repeatLimit # Add repeatLimit number of character A\'s\n curr_freq -= repeatLimit # Decrease frequency of character A\n # Now we search for the next lexicographically superior character that can be used once\n while index_to_take_from < n: # Till we run out of characters\n ch_avail, freq_avail = sorted_table[index_to_take_from]\n if freq_avail == 0: # If its freq is 0 that means that it was previously used. This is done as we are not removing the character from table if its freq becomes 0. \n index_to_take_from += 1 # Check for next lexicographically superior character\n else:\n result += ch_avail # If found then add that character \n sorted_table[index_to_take_from] = (ch_avail,freq_avail-1) # Update the new characters frequency\n break\n else:\n break # We cannot find any lexicographically superior character\n else:\n result += char*curr_freq # If the freq is in limits then just add them\n return result\n```\n | 4 | You are given a string `s` and an integer `repeatLimit`. Construct a new string `repeatLimitedString` using the characters of `s` such that no letter appears **more than** `repeatLimit` times **in a row**. You do **not** have to use all characters from `s`.
Return _the **lexicographically largest**_ `repeatLimitedString` _possible_.
A string `a` is **lexicographically larger** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears later in the alphabet than the corresponding letter in `b`. If the first `min(a.length, b.length)` characters do not differ, then the longer string is the lexicographically larger one.
**Example 1:**
**Input:** s = "cczazcc ", repeatLimit = 3
**Output:** "zzcccac "
**Explanation:** We use all of the characters from s to construct the repeatLimitedString "zzcccac ".
The letter 'a' appears at most 1 time in a row.
The letter 'c' appears at most 3 times in a row.
The letter 'z' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "zzcccac ".
Note that the string "zzcccca " is lexicographically larger but the letter 'c' appears more than 3 times in a row, so it is not a valid repeatLimitedString.
**Example 2:**
**Input:** s = "aababab ", repeatLimit = 2
**Output:** "bbabaa "
**Explanation:** We use only some of the characters from s to construct the repeatLimitedString "bbabaa ".
The letter 'a' appears at most 2 times in a row.
The letter 'b' appears at most 2 times in a row.
Hence, no letter appears more than repeatLimit times in a row and the string is a valid repeatLimitedString.
The string is the lexicographically largest repeatLimitedString possible so we return "bbabaa ".
Note that the string "bbabaaa " is lexicographically larger but the letter 'a' appears more than 2 times in a row, so it is not a valid repeatLimitedString.
**Constraints:**
* `1 <= repeatLimit <= s.length <= 105`
* `s` consists of lowercase English letters. | The maximum distance must be the distance between the first and last critical point. For each adjacent critical point, calculate the difference and check if it is the minimum distance. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.