title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[We💕Simple] One Liner! (Regex) - Shorter than thought | largest-3-same-digit-number-in-string | 0 | 1 | I like solving problems in a simple way. Regex is one of the very good methods for solving problems simply. If you are curious about other solutions using Regex, please check my other solutions too.\n\n\n```Python []\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n return max(re.findall(r\'(\\d)\\1\\1\', num) or [""]) * 3\n```\n```Kotlin []\nclass Solution {\n companion object {\n private val pattern = Regex("(\\\\d)\\\\1{2}")\n }\n\n fun largestGoodInteger(num: String): String =\n pattern.findAll(num).map { it.value }.maxOrNull() ?: ""\n}\n```\n\nHere\'s a breakdown of how the code approaches this problem:\n\n1. **Regular Expression (Regex) Matching**: The method `re.findall(r\'(\\d)\\1\\1\', num)` is used. This regex pattern `r\'(\\d)\\1\\1\'` is designed to find all substrings in `num` where a digit (`\\d`) is followed by itself twice (`\\1\\1`). The `\\1` refers to the first captured group, which is the digit matched by `\\d`.\n2. **Finding the Maximum**: The `max` function is used to find the largest substring that matches the regex pattern. This works because the substrings are digits, and their natural ordering will give the highest numeric value. If there are no matches, the `max` function returns an empty string as default (`or [""]`).\n3. **Constructing the Result**: The resulting string (either a three-digit substring or an empty string) is then multiplied by 3. This might seem redundant for a three-digit substring, as it\'s already of the desired length, but it\'s crucial for the empty string case. Multiplying an empty string by 3 still results in an empty string, which is the expected output when no "good integer" is found.\n\nThe method effectively combines regular expressions and Python\'s built-in functions to find the largest substring of three identical digits in a string, returning it if found, or an empty string otherwise. This approach is concise and leverages Python\'s powerful string processing capabilities.\n\n\n---\n## See Also.\n* [Number of Ways to Divide a Long Corridor](https://leetcode.com/problems/number-of-ways-to-divide-a-long-corridor/solutions/4337246/wesimple-regexrsps-solution-shorter-than-thought/) <- Regex Solution\n* [Decode String](https://leetcode.com/problems/decode-string/solutions/4357829/wesimple-regexp-one-liner-shorter-than-thought/) <- Regex Solution | 2 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Sliding Window with fixed window size in Python | largest-3-same-digit-number-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Sliding Window with fixed window size\n- In this problem, the window size is 3\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Compare the current character with the previous character\n - If they are the same and the window size reaches 3, we can update the result\n - If they are not the same, we update the start index of the window \n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n candidate = ""\n start = 0\n for i in range(1, len(num)):\n current, prev = num[i], num[i-1]\n if current == prev:\n if i - start + 1 == 3:\n if candidate == "":\n candidate = current\n else:\n candidate = max(int(candidate), int(current))\n else:\n start = i \n return str(candidate) * 3\n```\n\n- Comment any questions or feedback that you guys have. If this is helpful to you guys, please upvote | 2 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
🚀✅🚀 Easy solution for Beginner Friendly [Python / C# / Java / Rust] 🔥🔥 | largest-3-same-digit-number-in-string | 1 | 1 | # Intuition\nThe goal of the code appears to be finding the largest three-digit substring in the given number `num` where all three digits are the same.\n\n# Approach\nThe approach taken in the code is to iterate through the given number `num` and check for consecutive three-digit substrings where all three digits are the same. If such a substring is found, the code updates the `target` variable with the maximum value of these substrings. Finally, if a valid `target` is found, the code returns it as a string.\n\n# Complexity\n- **Time complexity:** O(n), where n is the length of the input number `num`. The code iterates through each digit of the number once.\n- **Space complexity:** O(1), as the code uses a constant amount of extra space regardless of the input size.\n\n# Code\n```python []\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n target = -1\n for i in range(len(num)-2):\n if num[i] == num[i+1] == num[i+2]:\n if int(num[i] + num[i+1] + num[i+2]) > target:\n target = int(num[i] + num[i+1] + num[i+2])\n if target != -1:\n if target == 0:\n return str(target) + "00"\n return str(target)\n return ""\n```\n```C# []\npublic class Solution {\n public string LargestGoodInteger(string num) {\n int target = -1;\n for (int i = 0; i < num.Length - 2; i++) {\n if (num[i] == num[i + 1] && num[i] == num[i + 2]) {\n int current = int.Parse(num.Substring(i, 3));\n if (current > target) {\n target = current;\n }\n }\n }\n if (target != -1) {\n if (target == 0) {\n return target + "00";\n }\n return target.ToString();\n }\n return "";\n }\n}\n```\n```Java []\npublic class Solution {\n public String largestGoodInteger(String num) {\n int target = -1;\n for (int i = 0; i < num.length() - 2; i++) {\n if (num.charAt(i) == num.charAt(i + 1) && num.charAt(i) == num.charAt(i + 2)) {\n int current = Integer.parseInt(num.substring(i, i + 3));\n if (current > target) {\n target = current;\n }\n }\n }\n if (target != -1) {\n if (target == 0) {\n return target + "00";\n }\n return Integer.toString(target);\n }\n return "";\n }\n}\n```\n```Rust []\nimpl Solution {\n pub fn largest_good_integer(num: String) -> String {\n let mut target = -1;\n let num_chars: Vec<char> = num.chars().collect();\n for i in 0..num_chars.len() - 2 {\n if num_chars[i] == num_chars[i + 1] && num_chars[i] == num_chars[i + 2] {\n let current: i32 = num_chars[i..i + 3].iter().collect::<String>().parse().unwrap();\n if current > target {\n target = current;\n }\n }\n }\n if target != -1 {\n if target == 0 {\n return format!("{}00", target);\n }\n return target.to_string();\n }\n "".to_string()\n }\n}\n\n```\n\n\n- Please upvote me !!! | 13 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Easy Python Solution with basic Knowledge | largest-3-same-digit-number-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSolve Problem Easily\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n res=""\n\n l=0\n r=2\n\n while r<len(num):\n \n if num[l]==num[r] and num[l]==num[r-1]:\n res=res if res>num[l:r+1] else num[l:r+1]\n \n l+=1\n r+=1\n return(res)\n\n \n``` | 1 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Python Easiest Solution | 93% Faster | largest-3-same-digit-number-in-string | 0 | 1 | # Approach\n- Initialize two variable count (int) and l(list)\n- Initialize value of a counter at 1. If a streak of 3 is found, append it to the list (l)\n- If the list (l) is empty, return an empty string. \n- Otherwise, find the maximum in the list (l) and return it in form of string three times.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n l=[]\n count=1\n for i in range(1,len(num)) :\n if(num[i]==num[i-1]) :\n count+=1\n else:\n count=1\n if(count==3) :\n l+=[int(num[i])]\n if (len(l)==0):\n return ""\n return str(max(l))*3\n``` | 1 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
100% runtime | largest-3-same-digit-number-in-string | 0 | 1 | # Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n strike = 1\n biggest = -1\n for i in range(0, len(num) - 1):\n if num[i] == num[i + 1]:\n strike += 1\n if strike == 3:\n newStrike = int(num[i])\n if newStrike > biggest:\n biggest = newStrike\n else:\n strike = 1\n if biggest == -1:\n return ""\n biggest = str(biggest)\n return biggest + biggest + biggest\n``` | 1 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Largest 3-Same-Digit Number in String | largest-3-same-digit-number-in-string | 0 | 1 | \n\n# Approach\nIterate through the string to find a substring(largest) of length 3 that has same digit.\n\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n mgi = ""\n for i in range(len(num) - 2):\n if num[i] == num[i + 1] == num[i + 2]:\n cgi = num[i:i + 3]\n if cgi > mgi:\n mgi = cgi\n return mgi\n\n``` | 1 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
[Python3/Java/C++/Go/TypeScript] Enumeration | largest-3-same-digit-number-in-string | 1 | 1 | **Solution 1: Enumeration**\n\nWe can enumerate each digit $i$ from large to small, where $0 \\le i \\le 9$, and then check whether the string $s$ consisting of three consecutive $i$ is a substring of $num$. If it is, we directly return $s$.\n\nIf we have enumerated all the possible values of $i$ and still haven\'t found a substring that satisfies the condition, we return an empty string.\n\n\n```python [sol1-Python3]\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n for i in range(9, -1, -1):\n if (s := str(i) * 3) in num:\n return s\n return ""\n```\n\n\n```java [sol1-Java]\nclass Solution {\n public String largestGoodInteger(String num) {\n for (int i = 9; i >= 0; i--) {\n String s = String.valueOf(i).repeat(3);\n if (num.contains(s)) {\n return s;\n }\n }\n return "";\n }\n}\n```\n\n\n\n```cpp [sol1-C++]\nclass Solution {\npublic:\n string largestGoodInteger(string num) {\n for (char i = \'9\'; i >= \'0\'; --i) {\n string s(3, i);\n if (num.find(s) != string::npos) {\n return s;\n }\n }\n return "";\n }\n};\n```\n\n\n\n```go [sol1-Go]\nfunc largestGoodInteger(num string) string {\n\tfor c := \'9\'; c >= \'0\'; c-- {\n\t\tif s := strings.Repeat(string(c), 3); strings.Contains(num, s) {\n\t\t\treturn s\n\t\t}\n\t}\n\treturn ""\n}\n```\n\n\n\n```ts [sol1-TypeScript]\nfunction largestGoodInteger(num: string): string {\n for (let i = 9; i >= 0; i--) {\n const s = String(i).repeat(3);\n if (num.includes(s)) {\n return s;\n }\n }\n return \'\';\n}\n```\n\nThe time complexity is $O(10 \\times n)$, where $n$ is the length of the string $num$. The space complexity is $O(1)$.\n\n\n\n---\n\nYou can find all of my solutions here: https://github.com/doocs/leetcode\n\n\n | 1 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Vey Easy Solution using Python|| BruthForce solution⚡❤️ | largest-3-same-digit-number-in-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n ans=-1\n for i in range(2,len(num)):\n if (num[i]==num[i-1]==num[i-2]):\n ans=max(ans,int(num[i]))\n \n if ans==-1:\n return ""\n else:\n return 3*str(ans)\n\n\n \n \n \n\n``` | 1 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
✅ 89.45% Post-order traversal | count-nodes-equal-to-average-of-subtree | 1 | 1 | # Intuition\nThe problem asks us to count the number of nodes where the node\'s value is equal to the average of its subtree (including itself). To calculate the average, we need the sum and count of nodes in the subtree. Our first thought could be to traverse the tree and, for every node, calculate the sum and count of nodes in its subtree and then check if the average matches the node\'s value. However, this would lead to recalculating the sum and count for overlapping subtrees, resulting in a time complexity of $O(n^2)$. Instead, we can optimize our approach to calculate the sum and count while traversing the tree in a single pass.\n\n# Live Coding & More\nhttps://youtu.be/vCD1hGT5e8M?si=JfZ7YX5_VMeOETIa\n\n# Approach\n\nTo solve the problem, we employ a post-order traversal approach. In post-order traversal, the tree is traversed in such a way that we first explore the left subtree, then the right subtree, and finally the node itself. This method is particularly suitable for this problem because, to determine the average value of a subtree rooted at a node, we need information from its left and right subtrees first. \n\n## Base Case\nOur recursive function\'s first duty is to identify if it has reached a leaf node, i.e., a node that doesn\'t have children. If the node being processed is `None`, it indicates that it\'s a leaf, and as such, we return both a sum and count of 0. This is because, for non-existent children of leaf nodes, there\'s no value to add or count to increment.\n\n## Recursive Logic\n\nFor every node in the tree, we perform the following steps:\n\n1. **Left Subtree Processing**:\n We recursively calculate the sum and count of nodes for the left child of the current node. This gives us the total value of all nodes and the number of nodes in the left subtree.\n\n2. **Right Subtree Processing**:\n Similarly, we recursively calculate the sum and count of nodes for the right child of the current node. This provides the total value of all nodes and the number of nodes in the right subtree.\n\n3. **Current Node\'s Subtree Calculation**:\n - **Sum**: To calculate the sum of the values in the subtree rooted at the current node, we add the node\'s own value to the sums from the left and right subtrees. \n - **Count**: The count of nodes in the subtree rooted at the current node is found by adding 1 (for the current node itself) to the counts from the left and right subtrees.\n \n4. **Average Comparison**:\n We check if the average of the subtree rooted at the current node matches the node\'s value. The average is calculated by performing integer division of the sum by the count. If they match, it indicates that the node\'s value is indeed the average of its subtree, and we increment our result counter.\n\n5. **Return Values**:\n Finally, for the benefit of the parent node in the recursive chain, we return the current node\'s subtree sum and count. This ensures that as the recursion unwinds, each parent node gets the aggregate values of its children and can perform its own calculations.\n\nBy following this approach, the algorithm efficiently traverses the tree, calculating and checking averages in one pass, without needing to revisit nodes or perform redundant calculations.\n\n# Complexity\n- **Time complexity**: $O(n)$. We perform a single traversal of the tree, visiting each node exactly once.\n- **Space complexity**: $O(h)$, where $h$ is the height of the tree. This accounts for the space used by the call stack during the recursive traversal.\n\n\n# Code\n``` Python []\nclass Solution:\n def averageOfSubtree(self, root: TreeNode) -> int:\n result = 0\n\n def traverse(node):\n nonlocal result\n \n if not node:\n return 0, 0\n \n left_sum, left_count = traverse(node.left)\n right_sum, right_count = traverse(node.right)\n \n curr_sum = node.val + left_sum + right_sum\n curr_count = 1 + left_count + right_count\n \n if curr_sum // curr_count == node.val:\n result += 1\n \n return curr_sum, curr_count\n \n traverse(root)\n return result\n```\n``` C++ []\nclass Solution {\npublic:\n int averageOfSubtree(TreeNode* root) {\n int result = 0;\n traverse(root, result);\n return result;\n }\n\nprivate:\n pair<int, int> traverse(TreeNode* node, int& result) {\n if (!node) return {0, 0};\n \n auto [left_sum, left_count] = traverse(node->left, result);\n auto [right_sum, right_count] = traverse(node->right, result);\n \n int curr_sum = node->val + left_sum + right_sum;\n int curr_count = 1 + left_count + right_count;\n \n if (curr_sum / curr_count == node->val) result++;\n \n return {curr_sum, curr_count};\n }\n};\n```\n``` Java []\nclass Solution {\n public int averageOfSubtree(TreeNode root) {\n int[] result = new int[1];\n traverse(root, result);\n return result[0];\n }\n\n private int[] traverse(TreeNode node, int[] result) {\n if (node == null) return new int[]{0, 0};\n \n int[] left = traverse(node.left, result);\n int[] right = traverse(node.right, result);\n \n int currSum = node.val + left[0] + right[0];\n int currCount = 1 + left[1] + right[1];\n \n if (currSum / currCount == node.val) result[0]++;\n \n return new int[]{currSum, currCount};\n }\n}\n```\n``` Go []\nfunc averageOfSubtree(root *TreeNode) int {\n result := 0\n traverse(root, &result)\n return result\n}\n\nfunc traverse(node *TreeNode, result *int) (int, int) {\n if node == nil {\n return 0, 0\n }\n \n leftSum, leftCount := traverse(node.Left, result)\n rightSum, rightCount := traverse(node.Right, result)\n \n currSum := node.Val + leftSum + rightSum\n currCount := 1 + leftCount + rightCount\n \n if currSum / currCount == node.Val {\n *result++\n }\n \n return currSum, currCount\n}\n```\n``` Rust []\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn average_of_subtree(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {\n fn traverse(node: Option<Rc<RefCell<TreeNode>>>, result: &mut i32) -> (i32, i32) {\n if let Some(n) = node {\n let n = n.borrow();\n let (left_sum, left_count) = traverse(n.left.clone(), result);\n let (right_sum, right_count) = traverse(n.right.clone(), result);\n \n let curr_sum = n.val + left_sum + right_sum;\n let curr_count = 1 + left_count + right_count;\n \n if curr_sum / curr_count == n.val {\n *result += 1;\n }\n \n (curr_sum, curr_count)\n } else {\n (0, 0)\n }\n }\n \n let mut result = 0;\n traverse(root, &mut result);\n result\n }\n}\n```\n``` JavaScript []\nvar averageOfSubtree = function(root) {\n let result = 0;\n \n const traverse = node => {\n if (!node) return [0, 0];\n \n const [leftSum, leftCount] = traverse(node.left);\n const [rightSum, rightCount] = traverse(node.right);\n \n const currSum = node.val + leftSum + rightSum;\n const currCount = 1 + leftCount + rightCount;\n \n if (Math.floor(currSum / currCount) === node.val) result++;\n \n return [currSum, currCount];\n };\n \n traverse(root);\n return result;\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param TreeNode $root\n * @return Integer\n */\n function averageOfSubtree($root) {\n $result = 0;\n $this->traverse($root, $result);\n return $result;\n }\n \n function traverse($node, &$result) {\n if ($node === null) return [0, 0];\n \n list($leftSum, $leftCount) = $this->traverse($node->left, $result);\n list($rightSum, $rightCount) = $this->traverse($node->right, $result);\n \n $currSum = $node->val + $leftSum + $rightSum;\n $currCount = 1 + $leftCount + $rightCount;\n \n if (intval($currSum / $currCount) == $node->val) $result++;\n \n return [$currSum, $currCount];\n }\n}\n```\n``` C# []\npublic class Solution {\n public int AverageOfSubtree(TreeNode root) {\n int result = 0;\n Traverse(root, ref result);\n return result;\n }\n\n private (int, int) Traverse(TreeNode node, ref int result) {\n if (node == null) return (0, 0);\n \n var (leftSum, leftCount) = Traverse(node.left, ref result);\n var (rightSum, rightCount) = Traverse(node.right, ref result);\n \n int currSum = node.val + leftSum + rightSum;\n int currCount = 1 + leftCount + rightCount;\n \n if (currSum / currCount == node.val) result++;\n \n return (currSum, currCount);\n }\n}\n```\n\n# Performance\n\n| Language | Execution Time (ms) | Memory Usage |\n|------------|---------------------|--------------|\n| Java | 0 | 43.2 MB |\n| Rust | 2 | 2.3 MB |\n| C++ | 4 | 12.5 MB |\n| Go | 5 | 4.3 MB |\n| PHP | 17 | 19.8 MB |\n| Python3 | 44 | 17.8 MB |\n| JavaScript | 74 | 47.6 MB |\n| C# | 76 | 40.2 MB |\n\n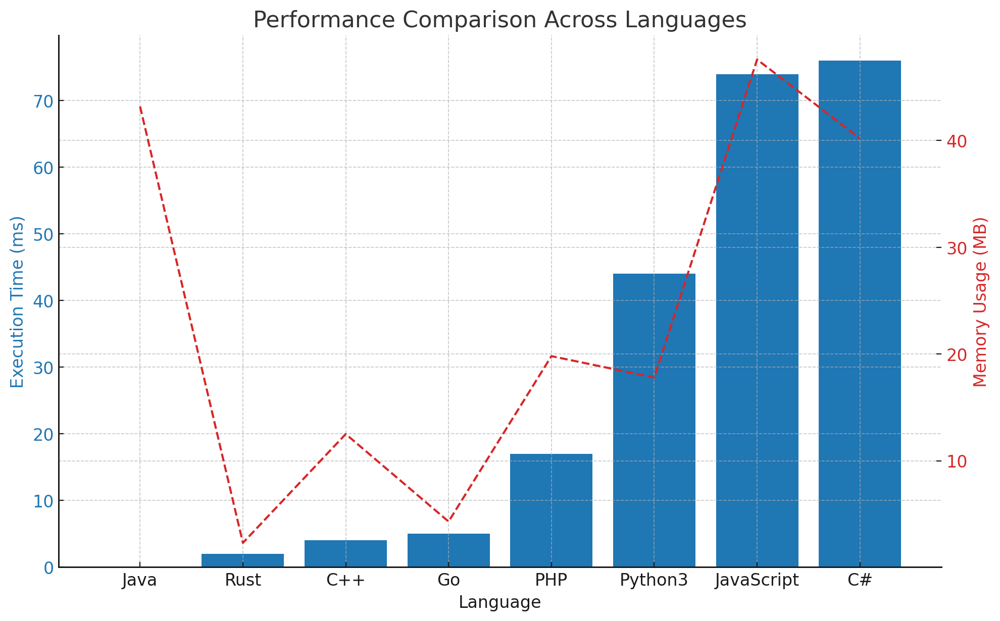\n\n\n# What We Learned\nThis problem teaches us the importance of optimizing our approach to avoid recalculating values for overlapping subtrees. By using a post-order traversal, we can calculate the sum and count for each subtree in a single pass, significantly improving the time complexity from $O(n^2)$ to $O(n)$. It also emphasizes the utility of using a nonlocal variable to keep track of the result during recursive traversal. | 68 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
【Video】Give me 8 minutes - How we think about a solution - Why we use postorder traversal? | count-nodes-equal-to-average-of-subtree | 1 | 1 | # Intuition\nCalculate subtree of left and right child frist\n\n---\n\n# Solution Video\n\nhttps://youtu.be/MV6NpUXCfUU\n\n\u25A0 Timeline of the video\n`0:05` Which traversal do you use for this question?\n`1:55` How do you calculate information you need?\n`3:34` How to write Inorder, Preorder, Postorder\n`4:16` Coding\n`7:50` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,919\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution.\n\nFirst of all, we know that we have to traverse the tree and have 3 well known traversal.\n\nTo be honest, I asked you about the same question in the yesterday\'s post. lol\n\n---\n\n\u25A0 Question\n\nWhich traversal do you use?\n\n---\n\nThinking time...\n\n... \uD83D\uDE29\n\n... \uD83D\uDE0F\n\n... \uD83D\uDE06\n\n... \uD83D\uDE04\n\nMy answer is postorder\n\n---\n\n\u2B50\uFE0F Points\n\nThe reason why we choose postorder traversal is that it processes child nodes (left and right subtrees) first to calculate the subtree\'s sum, number of nodes and number of results, then uses that information to check the condition at the parent node.\n\nTo calculate that information of a subtree including a parent, it is necessary to use information from the child nodes. That\'s why the left and right subtrees should be processed first.\n\nWhen we have\n```\n 5\n / \\\n 6 7\n\n```\n\nthe order of postorder process should be 6, 7 and 5.\n\nSo, we have information of subtree of 6 and information of subtree of 7, then finally we can calculate information of subtree of 5 which is including 6 and 7. \n\n---\n\n- How do you calculate information we need?\n\nTo get result, we need `total sum` and `total number of nodes` because we calculate average of each subtree. This is not complicated. just\n\n##### Total Sum\n---\n`sum of left subtree` + `sum of right subtree` + `current value`\n\n---\n##### Number of nodes\n---\n\n\n`number of nodes from left` + `number of nodes from right` + 1\n\n`+1` is for a current node\n\n---\n\nEasy!\n\nThen every time we calculate number of results with this condition\n\n##### Number of results\n---\n\n\u2B50\uFE0F Points\n\nres += `(node.val == total_sum // total_count)`\n\n---\n\n---\n\n\u25A0 Python Tips\n\nAbout calculation of number of results\n\nIn Python, `True` is equivalent to the integer `1`, and `False` is equivalent to the integer `0`. This is based on implicit conversion between Python\'s boolean type (`bool`) and integer type (`int`). Here are some examples:\n\n```python []\nbool_true = True\nint_one = 1\n\nbool_false = False\nint_zero = 0\n\n# True and 1 are equivalent\nprint(bool_true == int_one) # True\n\n# False and 0 are equivalent\nprint(bool_false == int_zero) # True\n```\n\nAs a result, if a condition is `True`, it is considered as satisfied and is treated as the integer `1`. The result is then added to the variable `res`, which counts the number of nodes that meet the condition.\n\nThat is just pretentious coding style. lol\nIt\'s the same as\n\n```Python []\nres += (node.val == total_sum // total_count)\n\u2193\nif node.val == total_sum // total_count:\n res += 1\n```\n\n---\n\n- How to write inorder, preorder, postorder\n\nAcutually, I wrote the same contents yesterday, but knowing how to write inorder, preorder, and postorder traversals might be helpful for other problems as well.\n\n```python []\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\ndef inorder(root):\n if not root:\n return []\n result = []\n result += inorder(root.left)\n result.append(root.val)\n result += inorder(root.right)\n return result\n\ndef preorder(root):\n if not root:\n return []\n result = []\n result.append(root.val)\n result += preorder(root.left)\n result += preorder(root.right)\n return result\n\ndef postorder(root):\n if not root:\n return []\n result = []\n result += postorder(root.left)\n result += postorder(root.right)\n result.append(root.val)\n return result\n```\n\nLet\'s focus on `result.append(root.val)` in each function.\n\n---\n\n\u2B50\uFE0F Points\n\nFor `Inorder`, we do something `between left and right`.\nFor `Preorder`, we do something `before left and right`.\nFor `Postorder`, we do something `after left and right`.\n\n---\n\nWe use `postorder` this time, so do the key point above after left and right.\n\nYou can compare `postorder` with `inorder` by yesterday\'s daily coding challenge. I put yesterday\'s video and post at bottom of the post.\n\nLet\'s see a real algorithm!\n\n### Algorithm Overview:\n\nThe algorithm calculates the number of nodes in a binary tree where the value of the node is equal to the average value of its subtree. It uses a post-order traversal to process the tree nodes.\n\n### Detailed Explanation:\n\n1. Initialize a variable `res` to 0. This variable will be used to keep track of the count of nodes that meet the specified condition.\n\n2. Define a recursive function `postorder(node)` that takes a `node` as an argument.\n\n3. Inside the `postorder` function:\n - Check if the current `node` is `None`, indicating an empty subtree or a leaf node. If it is, return a tuple `(0, 0)` representing the sum and number of nodes in the subtree.\n\n - Recursively call the `postorder` function on the left child of the current node and store the result in the `left` variable.\n\n - Recursively call the `postorder` function on the right child of the current node and store the result in the `right` variable.\n\n - Use a `nonlocal` statement to access and update the `res` variable in the outer scope. This variable keeps track of the count of nodes that meet the condition.\n\n - Calculate the `total_sum` as the sum of the values of the current node, the left subtree, and the right subtree: `total_sum = left[0] + right[0] + node.val`.\n\n - Calculate the `total_count` as the count of nodes in the current subtree: `total_count = 1 + left[1] + right[1]`.\n\n - Increment the `res` variable when the condition `node.val == total_sum // total_count` is true. This condition checks if the current node\'s value is equal to the average value of its subtree.\n\n - Return a tuple `(total_sum, total_count)` representing the updated sum and count for the current subtree.\n\n4. Call the `postorder(root)` function on the root of the binary tree to initiate the post-order traversal and accumulate the count of nodes that meet the condition in the `res` variable.\n\n5. Return the final value of `res`, which represents the count of nodes in the binary tree where the value of the node is equal to the average value of its subtree.\n\nThe code uses a post-order traversal to process the subtrees before processing the current node, which is essential for correctly computing the average values of subtrees.\n\n# Complexity\n- Time complexity: $$O(N)$$\nN is the number of nodes in the binary tree. This is because the code visits each node exactly once during the post-order traversal, and the work done at each node is constant.\n\n- Space complexity: $$O(N)$$\nThis space is used for the recursive call stack during the post-order traversal. In the worst case, if the binary tree is skewed and unbalanced, the space complexity can be O(N). \n\n```python []\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n res = 0\n\n def postorder(node):\n if not node:\n return (0, 0) # sum, number of nodes\n \n left = postorder(node.left)\n right = postorder(node.right)\n\n nonlocal res\n\n total_sum = left[0] + right[0] + node.val\n total_count = 1 + left[1] + right[1]\n res += (node.val == total_sum // total_count)\n\n return (total_sum, total_count)\n \n postorder(root)\n\n return res\n```\n```javascript []\nvar averageOfSubtree = function(root) {\n var res = 0;\n\n var postorder = function(node) {\n if (!node) {\n return [0, 0]; // sum, number of nodes\n }\n\n var left = postorder(node.left);\n var right = postorder(node.right);\n\n var totalSum = left[0] + right[0] + node.val;\n var totalCount = 1 + left[1] + right[1];\n res += node.val === Math.floor(totalSum / totalCount);\n\n return [totalSum, totalCount];\n };\n\n postorder(root);\n\n return res;\n};\n```\n```java []\nclass Solution {\n private int res = 0; \n\n public int averageOfSubtree(TreeNode root) {\n postorder(root);\n return res; \n }\n\n private int[] postorder(TreeNode node) {\n if (node == null) {\n return new int[]{0, 0}; // sum, number of nodes\n }\n\n int[] left = postorder(node.left);\n int[] right = postorder(node.right);\n\n int totalSum = left[0] + right[0] + node.val;\n int totalCount = 1 + left[1] + right[1];\n res += (node.val == totalSum / totalCount ? 1 : 0);\n\n return new int[]{totalSum, totalCount};\n } \n}\n```\n```C++ []\nclass Solution {\n int res = 0;\n\npublic:\n int averageOfSubtree(TreeNode* root) {\n postorder(root);\n return res;\n }\n\n pair<int, int> postorder(TreeNode* node) {\n if (!node) {\n return {0, 0}; // sum, number of nodes\n }\n\n auto left = postorder(node->left);\n auto right = postorder(node->right);\n\n int totalSum = left.first + right.first + node->val;\n int totalCount = 1 + left.second + right.second;\n res += (node->val == totalSum / totalCount);\n\n return {totalSum, totalCount};\n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/build-an-array-with-stack-operations/solutions/4244407/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/MCYiEw2zvNw\n\n\u25A0 Timeline of the video\n\n`0:04` Basic idea to solve this question\n`1:04` How do you operate each number from the steam of integers?\n`3:34` What operation we need for the two patterns\n`5:17` Coding\n`6:37` Time Complexity and Space Complexity\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-mode-in-binary-search-tree/solutions/4233557/video-give-me-5-minutes-how-we-think-about-a-solution-why-do-we-use-inorder-traversal/\n\nvideo\nhttps://youtu.be/0i1Ze62pTuU\n\n\u25A0 Timeline of the video\n`0:04` Which traversal do you use for this question?\n`0:34` Properties of a Binary Search Tree\n`1:31` Key point of my solution code\n`3:09` How to write Inorder, Preorder, Postorder\n`4:08` Coding\n`7:13` Time Complexity and Space Complexity\n\n\n\n\n | 44 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
🚀 Beats 100% | Easy To Understand 🚀🔥 | count-nodes-equal-to-average-of-subtree | 1 | 1 | # Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int ans = 0;\n\n pair<int,int> postorder(TreeNode* &root,int sum,int count)\n {\n if(root == 0) return {0,0};\n\n auto l = postorder(root->left,sum,count);\n auto r = postorder(root->right,sum,count);\n\n sum = l.first + root->val + r.first;\n count = l.second + 1 + r.second;\n\n if(sum / count == root->val) ans++;\n return {sum,count};\n }\n\n int averageOfSubtree(TreeNode* root) {\n postorder(root,0,0);\n return ans;\n }\n};\n``` | 3 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
Detailed Dry Run of DFS on Trees!! 😸 | count-nodes-equal-to-average-of-subtree | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n count = 0\n def dfs(root):\n nonlocal count\n if not root:\n return 0,0 \n ls , lc = dfs(root.left)\n rs , rc = dfs(root.right)\n if root.val == (root.val + ls + rs) // (lc + rc + 1) : count += 1 \n return root.val + ls + rs , lc + rc + 1\n dfs(root)\n return count\n``` | 2 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
g gun post-order traversal DFS solution for real men in python | count-nodes-equal-to-average-of-subtree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n self.cnt = 0\n \n def dfs(node):\n if not node:\n return 0, 0 # return sum and count of nodes as 0\n\n left_sum, left_count = dfs(node.left)\n right_sum, right_count = dfs(node.right)\n \n # Calculate total sum and count for current subtree\n total_sum = node.val + left_sum + right_sum\n total_count = 1 + left_count + right_count\n \n # Check if average of current subtree (rounded down) equals the node\'s value\n if total_sum // total_count == node.val:\n self.cnt += 1\n \n return total_sum, total_count\n \n dfs(root)\n return self.cnt\n\n``` | 1 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
🚀 100% || DFS || Explained Intuition🚀 | count-nodes-equal-to-average-of-subtree | 1 | 1 | # Problem Description\n\nGiven the **root** of a binary tree. The task is to determine the **number** of nodes in the tree whose value **matches** the floored **average** of all the values within their respective **subtrees**. In other words, you need to count the nodes where the node\'s value is equal to the integer average of all values in its subtree.\n\n- Here\'s some additional information to keep in mind:\n\n - The **average** of a set of elements is calculated by **summing** those elements and **dividing** the sum by the **number** of elements.\n - A **subtree** of a given node **includes** the node **itself** and all of its **descendant** nodes.\n\nThe **goal** is to find the count of nodes in the binary tree that **meet** this condition.\n\n- **Constraints:**\n - The number of nodes in the tree is in the range `[1, 1000]`.\n - `0 <= Node.val <= 1000`.\n \n---\n\n\n# Intuition\n\nHello there,\uD83D\uDE04\n\nLet\'s look\uD83D\uDC40 at today\'s problem.\nIn today\'s problem, We have a **tree**\uD83C\uDF32 and each node in it have a value and for each node we have to check if its value is **equal** to the average of values in its **subtree**. If so, calculate number of nodes with this description.\uD83E\uDD28\n\nBut before that what is a **subtree** of a node ?\uD83E\uDD14\nA subtree in general is a part of a tree\uD83C\uDF32 but for a specific node the subtree is the part of the tree that containing all of its children and descnedants going down to the **leaves**.\uD83C\uDF43\nlet\'s see an example.\n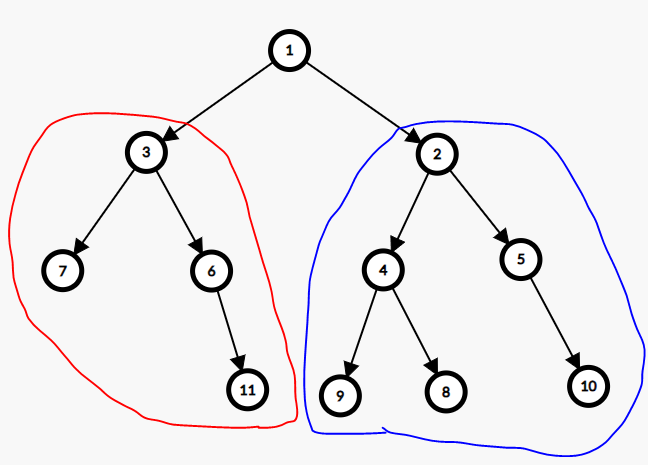\n\nHere the subtree of `node 2` is the part with **blue** color. the subtree of `node 3` is the part with **red** color and also we can consider the **whole tree** as a subtree for `node 1`.\n\nNow how we get the values and number of nodes for all of the node subtree?\uD83E\uDD14\nI will pretend that I didn\'t say the algorithm in the title.\uD83D\uDE02\nWe can do it with a simple algorithm that **traverses** the tree and there is no simpler tha **DFS**, Our hero today\uD83E\uDDB8\u200D\u2642\uFE0F.\n\n- And since any **tree**:\n - has only **one** **root**.\n - **doesn\'t** have **loops**.\n \nThen we can apply **DFS** at the only **root** of the tree and without concerning about the loops.\nThe **DFS** Function of any node will **check** for all nodes in its subtree that meet our requirements and return the number of nodes in its subtree and the sum of values for its subtree.\uD83D\uDCAA\n\n\nThis is an example how our DFS will look like for each node since it will return `(sum of values of subtree, number of nodes)`.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Approach\n1. Initialize an integer variable `matchingSubtreeCount` to keep track of subtrees with matching averages.\n2. Create a Depth-First Search **DFS** function `calculateSubtreeValues` that takes a `currentNode` as input and returns a pair of integers. These integers represent:\n - The **sum** of values within the current subtree.\n - The **number** of nodes within the current subtree.\n3. In the `calculateSubtreeValues` function:\n - **Base Case**: check if the `currentNode` is null. If it is, return `{0, 0}`, signifying that both the sum and number of nodes are zero for a null node.\n - The **sum** of values in the current subtree is the **sum** of values in the left and right subtrees **plus** the value of the `currentNode` and The **number** of nodes is **number** of nodes in the left and right subtrees then **increment** it by 1 for the `currentNode`.\n - **Increment** the `matchingSubtreeCount` if the current node\'s value matches the average of its subtree.\n - **Return** a pair of values `{sumOfValues, numberOfNodes}` representing the calculated values for the current subtree.\n11. In the main function, perform **DFS** from the root then return `matchingSubtreeCount` after traversing over all the nodes.\n\n\n# Complexity\n- **Time complexity:**$O(N)$\nSince the DFS **traverse** over all the nodes of the tree then the complexity is `O(N)` where `N` is the number of nodes within the tree.\n- **Space complexity:**$O(N)$\nSince the DFS is a **recursive** call and it reserves a **memory stack frame** for each call so the **maximum** number of calls it can make in the same time is `N` calls so complexity is `O(N)`;\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int matchingSubtreeCount = 0; // Initialize the count of subtrees with matching averages.\n\n // A Depth-First Search (DFS) function and returns a pair of values:\n // - The sum of values within the current subtree.\n // - The number of nodes within the current subtree.\n pair<int, int> calculateSubtreeValues(TreeNode* currentNode) {\n if (currentNode == nullptr)\n return {0, 0}; // Base case: Return 0 for both sum and number of nodes if the node is null.\n\n // Recursively calculate values for the left and right subtrees.\n auto leftSubtree = calculateSubtreeValues(currentNode->left);\n auto rightSubtree = calculateSubtreeValues(currentNode->right);\n\n // Calculate the sum of values and the number of nodes in the current subtree.\n int sumOfValues = leftSubtree.first + rightSubtree.first + currentNode->val;\n int numberOfNodes = leftSubtree.second + rightSubtree.second + 1;\n\n // Check if the current node\'s value matches the average of its subtree.\n if (sumOfValues / numberOfNodes == currentNode->val)\n matchingSubtreeCount++; \n\n return {sumOfValues, numberOfNodes}; // Return the calculated values for the current subtree.\n }\n\n int averageOfSubtree(TreeNode* root) {\n calculateSubtreeValues(root); // Start the DFS from the root node.\n return matchingSubtreeCount; \n }\n};\n```\n```Java []\nclass Solution {\n private int matchingSubtreeCount = 0; // Initialize the count of subtrees with matching averages.\n\n // A Depth-First Search (DFS) function that returns an array of two values:\n // - The sum of values within the current subtree.\n // - The number of nodes within the current subtree.\n private int[] calculateSubtreeValues(TreeNode currentNode) {\n if (currentNode == null)\n return new int[]{0, 0}; // Base case: Return 0 for both sum and number of nodes if the node is null.\n\n // Recursively calculate values for the left and right subtrees.\n int[] leftSubtree = calculateSubtreeValues(currentNode.left);\n int[] rightSubtree = calculateSubtreeValues(currentNode.right);\n\n // Calculate the sum of values and the number of nodes in the current subtree.\n int sumOfValues = leftSubtree[0] + rightSubtree[0] + currentNode.val;\n int numberOfNodes = leftSubtree[1] + rightSubtree[1] + 1;\n\n // Check if the current node\'s value matches the average of its subtree.\n if (sumOfValues / numberOfNodes == currentNode.val)\n matchingSubtreeCount++;\n\n return new int[]{sumOfValues, numberOfNodes}; // Return the calculated values for the current subtree.\n }\n\n public int averageOfSubtree(TreeNode root) {\n calculateSubtreeValues(root); // Start the DFS from the root node.\n return matchingSubtreeCount; \n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.matchingSubtreeCount = 0 # Initialize the count of subtrees with matching averages.\n\n # A Depth-First Search (DFS) function that returns a tuple of two values:\n # - The sum of values within the current subtree.\n # - The number of nodes within the current subtree.\n def calculateSubtreeValues(self, currentNode):\n if currentNode is None:\n return 0, 0 # Base case: Return 0 for both sum and number of nodes if the node is None.\n\n # Recursively calculate values for the left and right subtrees.\n leftSubtree = self.calculateSubtreeValues(currentNode.left)\n rightSubtree = self.calculateSubtreeValues(currentNode.right)\n\n # Calculate the sum of values and the number of nodes in the current subtree.\n sumOfValues = leftSubtree [0] + rightSubtree[0] + currentNode.val\n numberOfNodes = leftSubtree [1] + rightSubtree[1] + 1\n\n # Check if the current node\'s value matches the average of its subtree.\n if sumOfValues // numberOfNodes == currentNode.val:\n self.matchingSubtreeCount += 1\n\n return sumOfValues , numberOfNodes # Return the calculated values for the current subtree.\n\n\n def averageOfSubtree(self, root):\n self.calculateSubtreeValues(root) # Start the DFS from the root node.\n return self.matchingSubtreeCount \n\n```\n\n\n\n | 68 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
Beats 98% DFS Very Intuitive method | count-nodes-equal-to-average-of-subtree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEvery node requires the sum of its subtree and length, so as we work our way up the tree from the bottom, we return the sum as well as the length and sum of the left and right branches. We then add this to the node and determine whether the average matches the node value.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\na. If root is None (i.e., the current node is a leaf or an empty subtree), return 0 for the sum and 0 for the count.\nb. Recursively call dfs on the left and right subtrees, obtaining the sum and count of nodes for both left and right subtrees.\nc. Calculate the sum of the values in the current subtree as root.val + left + right, and calculate the count of nodes in the current subtree as ln + rn + 1.\nd. Check if the average value of the current subtree is an integer by comparing (root.val + left + right) // (ln + rn + 1) to root.val. If they are equal, increment the ans variable by 1.\n\nCall the dfs function on the input root node to initiate the traversal of the entire binary tree.\n\nReturn the value of ans, which represents the count of nodes in the tree for which the average value of the subtree is an integer.\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(height of tree)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n self.ans = 0\n def dfs(root):\n if not root: return 0,0\n left,ln = dfs(root.left)\n right,rn = dfs(root.right)\n if(root.val+left+right)//(ln+rn+1) == root.val:\n self.ans += 1\n return root.val+left+right,ln+rn+1\n dfs(root)\n return self.ans\n \n``` | 1 | Given the `root` of a binary tree, return _the number of nodes where the value of the node is equal to the **average** of the values in its **subtree**_.
**Note:**
* The **average** of `n` elements is the **sum** of the `n` elements divided by `n` and **rounded down** to the nearest integer.
* A **subtree** of `root` is a tree consisting of `root` and all of its descendants.
**Example 1:**
**Input:** root = \[4,8,5,0,1,null,6\]
**Output:** 5
**Explanation:**
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
**Example 2:**
**Input:** root = \[1\]
**Output:** 1
**Explanation:** For the node with value 1: The average of its subtree is 1 / 1 = 1.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 1000` | Could you put the elements smaller than the pivot and greater than the pivot in a separate list as in the sequence that they occur? With the separate lists generated, could you then generate the result? |
[Python3] group-by-group | count-number-of-texts | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/9aa0edb0815f3e0a75a47808e1690ca424f169e5) for solutions of weekly 292. \n\n```\nclass Solution:\n def countTexts(self, pressedKeys: str) -> int:\n MOD = 1_000_000_007 \n \n @cache \n def fn(n, k): \n """Return number of possible text of n repeated k times."""\n if n < 0: return 0\n if n == 0: return 1\n ans = 0\n for x in range(1, k+1): ans = (ans + fn(n-x, k)) % MOD\n return ans \n \n ans = 1\n for key, grp in groupby(pressedKeys): \n if key in "79": k = 4\n else: k = 3\n ans = (ans * fn(len(list(grp)), k)) % MOD \n return ans \n```\n\nAdded a shorter implementation \n```\nclass Solution:\n def countTexts(self, pressedKeys: str) -> int:\n dp = [0] * (len(pressedKeys)+1)\n dp[0] = 1\n for i, ch in enumerate(pressedKeys):\n dp[i+1] = dp[i]\n if i and pressedKeys[i-1] == ch: \n dp[i+1] += dp[i-1]\n if i >= 2 and pressedKeys[i-2] == ch: \n dp[i+1] += dp[i-2]\n if i >= 3 and pressedKeys[i-3] == ch and ch in "79": dp[i+1] += dp[i-3]\n dp[i+1] %= 1_000_000_007\n return dp[-1]\n``` | 9 | Alice is texting Bob using her phone. The **mapping** of digits to letters is shown in the figure below.
In order to **add** a letter, Alice has to **press** the key of the corresponding digit `i` times, where `i` is the position of the letter in the key.
* For example, to add the letter `'s'`, Alice has to press `'7'` four times. Similarly, to add the letter `'k'`, Alice has to press `'5'` twice.
* Note that the digits `'0'` and `'1'` do not map to any letters, so Alice **does not** use them.
However, due to an error in transmission, Bob did not receive Alice's text message but received a **string of pressed keys** instead.
* For example, when Alice sent the message `"bob "`, Bob received the string `"2266622 "`.
Given a string `pressedKeys` representing the string received by Bob, return _the **total number of possible text messages** Alice could have sent_.
Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** pressedKeys = "22233 "
**Output:** 8
**Explanation:**
The possible text messages Alice could have sent are:
"aaadd ", "abdd ", "badd ", "cdd ", "aaae ", "abe ", "bae ", and "ce ".
Since there are 8 possible messages, we return 8.
**Example 2:**
**Input:** pressedKeys = "222222222222222222222222222222222222 "
**Output:** 82876089
**Explanation:**
There are 2082876103 possible text messages Alice could have sent.
Since we need to return the answer modulo 109 + 7, we return 2082876103 % (109 + 7) = 82876089.
**Constraints:**
* `1 <= pressedKeys.length <= 105`
* `pressedKeys` only consists of digits from `'2'` - `'9'`. | Define a separate function Cost(mm, ss) where 0 <= mm <= 99 and 0 <= ss <= 99. This function should calculate the cost of setting the cocking time to mm minutes and ss seconds The range of the minutes is small (i.e., [0, 99]), how can you use that? For every mm in [0, 99], calculate the needed ss to make mm:ss equal to targetSeconds and minimize the cost of setting the cocking time to mm:ss Be careful in some cases when ss is not in the valid range [0, 99]. |
✅ Python Simple Memoisation/Caching | check-if-there-is-a-valid-parentheses-string-path | 0 | 1 | There are two main parts of the solution:\n1. Logic to determine whether a sequence is [Balanced Paranteses](https://leetcode.com/problems/valid-parentheses/). This can be achieved using `Stack`(`O(N) space`) or using a `counter` variable(`O(1) space`). I will be using the latter.\n2. A recursive function to check the existence of a valid parantheses sequence in the input `grid`.\n\n\n\n```\nclass Solution:\n def hasValidPath(self, grid: List[List[str]]) -> bool: \n m = len(grid)\n n = len(grid[0])\n @lru_cache(maxsize=None)\n def hasValidPathInner(x, y, cnt):\n # cnt variable would act as a counter to track \n # the balance of parantheses sequence\n if x == m or y == n or cnt < 0:\n return False\n \n # logic to check the balance of sequence\n cnt += 1 if grid[x][y] == \'(\' else -1\n \n # if balanced and end of grid, return True\n if x == m - 1 and y == n - 1 and not cnt:\n return True\n \n return hasValidPathInner(x + 1, y, cnt) or hasValidPathInner(x, y + 1, cnt)\n\n return hasValidPathInner(0, 0, 0)\n```\n\n**Time = O(mn(m+n))** - Due to memoization, the same path won\'t be visited twice. `M + N` is the max length of a sequence or max depth of recursive stack from `0,0` to `m-1,n-1` in the `grid` \n**Space = O(mn(m+n))**\n\n\n----\n***Please upvote if you find it useful*** | 15 | A parentheses string is a **non-empty** string consisting only of `'('` and `')'`. It is **valid** if **any** of the following conditions is **true**:
* It is `()`.
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid parentheses strings.
* It can be written as `(A)`, where `A` is a valid parentheses string.
You are given an `m x n` matrix of parentheses `grid`. A **valid parentheses string path** in the grid is a path satisfying **all** of the following conditions:
* The path starts from the upper left cell `(0, 0)`.
* The path ends at the bottom-right cell `(m - 1, n - 1)`.
* The path only ever moves **down** or **right**.
* The resulting parentheses string formed by the path is **valid**.
Return `true` _if there exists a **valid parentheses string path** in the grid._ Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[ "( ", "( ", "( "\],\[ ") ", "( ", ") "\],\[ "( ", "( ", ") "\],\[ "( ", "( ", ") "\]\]
**Output:** true
**Explanation:** The above diagram shows two possible paths that form valid parentheses strings.
The first path shown results in the valid parentheses string "()(()) ".
The second path shown results in the valid parentheses string "((())) ".
Note that there may be other valid parentheses string paths.
**Example 2:**
**Input:** grid = \[\[ ") ", ") "\],\[ "( ", "( "\]\]
**Output:** false
**Explanation:** The two possible paths form the parentheses strings "))( " and ")(( ". Since neither of them are valid parentheses strings, we return false.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 100`
* `grid[i][j]` is either `'('` or `')'`. | The lowest possible difference can be obtained when the sum of the first n elements in the resultant array is minimum, and the sum of the next n elements is maximum. For every index i, think about how you can find the minimum possible sum of n elements with indices lesser or equal to i, if possible. Similarly, for every index i, try to find the maximum possible sum of n elements with indices greater or equal to i, if possible. Now for all indices, check if we can consider it as the partitioning index and hence find the answer. |
100% Faster Code | C++ and Python | Sliding Window | String Handling | find-the-k-beauty-of-a-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSliding Window\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**C++ Solution:-**\n```\nclass Solution {\npublic:\n int divisorSubstrings(int num, int k) {\n int divisor = num;\n string str_div = to_string(num);\n int i = 0;\n int beauty = 0;\n while (i < str_div.size() - k + 1) {\n int dividend = stoi(str_div.substr(i, k));\n if(dividend > 0) {\n if( divisor % dividend == 0) beauty++;\n }\n i++;\n }\n return beauty;\n }\n};\n```\n**Python Solution:-**\n```\nclass Solution:\n def divisorSubstrings(self, num: int, k: int) -> int:\n beauty = 0\n divisor = num\n i = 0\n j = k\n str_div = str(num)\n n = len(str_div)\n while j <= n:\n dividend = int(str_div[i:j])\n print(dividend)\n if dividend > 0:\n if divisor % dividend == 0:\n beauty += 1\n i += 1\n j += 1\n return beauty\n\n``` | 1 | The **k-beauty** of an integer `num` is defined as the number of **substrings** of `num` when it is read as a string that meet the following conditions:
* It has a length of `k`.
* It is a divisor of `num`.
Given integers `num` and `k`, return _the k-beauty of_ `num`.
Note:
* **Leading zeros** are allowed.
* `0` is not a divisor of any value.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** num = 240, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "24 " from "**24**0 ": 24 is a divisor of 240.
- "40 " from "2**40** ": 40 is a divisor of 240.
Therefore, the k-beauty is 2.
**Example 2:**
**Input:** num = 430043, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "43 " from "**43**0043 ": 43 is a divisor of 430043.
- "30 " from "4**30**043 ": 30 is not a divisor of 430043.
- "00 " from "43**00**43 ": 0 is not a divisor of 430043.
- "04 " from "430**04**3 ": 4 is not a divisor of 430043.
- "43 " from "4300**43** ": 43 is a divisor of 430043.
Therefore, the k-beauty is 2.
**Constraints:**
* `1 <= num <= 109`
* `1 <= k <= num.length` (taking `num` as a string) | All the elements in the array should be counted except for the minimum and maximum elements. If the array has n elements, the answer will be n - count(min(nums)) - count(max(nums)) This formula will not work in case the array has all the elements equal, why? |
Simple Sliding Window implementation in O(n) | find-the-k-beauty-of-a-number | 0 | 1 | # Approach\n###### Fixed Sized Sliding Window\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def divisorSubstrings(self, num: int, k: int) -> int:\n \n sub_arr = str(num)[:k]\n count = 0\n\n if(num % int(sub_arr) == 0):\n count += 1\n\n for i in range(1,len(str(num))-k+1):\n sub_arr = str(num)[i:k+i]\n\n if(int(sub_arr) != 0 and num % int(sub_arr) == 0):\n count += 1\n \n return count\n```\n\n# Idea\n\nBasically, we have to find all the substrings of the given number (by converting it to string) such that the substring is a divisor of the original number and as same length as k.\n\n1) We can maintain a fixed sized Sliding Window of size k\n\n2) Slide the window and in each iteration, if the conditions are satisied then increment count by 1\n\n\n##### If you find my solution helpful and worthy, please consider upvoting my solution. Upvotes play a crucial role in ensuring that this valuable content reaches others and helps them as well.\n\n##### Only your support motivates me to continue contributing more solutions and assisting the community further.\n\n##### Thank You for spending your valuable time. | 1 | The **k-beauty** of an integer `num` is defined as the number of **substrings** of `num` when it is read as a string that meet the following conditions:
* It has a length of `k`.
* It is a divisor of `num`.
Given integers `num` and `k`, return _the k-beauty of_ `num`.
Note:
* **Leading zeros** are allowed.
* `0` is not a divisor of any value.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** num = 240, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "24 " from "**24**0 ": 24 is a divisor of 240.
- "40 " from "2**40** ": 40 is a divisor of 240.
Therefore, the k-beauty is 2.
**Example 2:**
**Input:** num = 430043, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "43 " from "**43**0043 ": 43 is a divisor of 430043.
- "30 " from "4**30**043 ": 30 is not a divisor of 430043.
- "00 " from "43**00**43 ": 0 is not a divisor of 430043.
- "04 " from "430**04**3 ": 4 is not a divisor of 430043.
- "43 " from "4300**43** ": 43 is a divisor of 430043.
Therefore, the k-beauty is 2.
**Constraints:**
* `1 <= num <= 109`
* `1 <= k <= num.length` (taking `num` as a string) | All the elements in the array should be counted except for the minimum and maximum elements. If the array has n elements, the answer will be n - count(min(nums)) - count(max(nums)) This formula will not work in case the array has all the elements equal, why? |
Easy Solution Python3 | find-the-k-beauty-of-a-number | 0 | 1 | ```\nclass Solution:\n def divisorSubstrings(self, num: int, k: int) -> int:\n \n ans = 0;\n for x in range(len(str(num))):\n substr = str(num)[x:x+k:];\n \n if len(substr) < k: break;\n elif int(substr) == 0: continue;\n\n ans += num % int(substr) == 0;\n \n return ans;\n``` | 0 | The **k-beauty** of an integer `num` is defined as the number of **substrings** of `num` when it is read as a string that meet the following conditions:
* It has a length of `k`.
* It is a divisor of `num`.
Given integers `num` and `k`, return _the k-beauty of_ `num`.
Note:
* **Leading zeros** are allowed.
* `0` is not a divisor of any value.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** num = 240, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "24 " from "**24**0 ": 24 is a divisor of 240.
- "40 " from "2**40** ": 40 is a divisor of 240.
Therefore, the k-beauty is 2.
**Example 2:**
**Input:** num = 430043, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "43 " from "**43**0043 ": 43 is a divisor of 430043.
- "30 " from "4**30**043 ": 30 is not a divisor of 430043.
- "00 " from "43**00**43 ": 0 is not a divisor of 430043.
- "04 " from "430**04**3 ": 4 is not a divisor of 430043.
- "43 " from "4300**43** ": 43 is a divisor of 430043.
Therefore, the k-beauty is 2.
**Constraints:**
* `1 <= num <= 109`
* `1 <= k <= num.length` (taking `num` as a string) | All the elements in the array should be counted except for the minimum and maximum elements. If the array has n elements, the answer will be n - count(min(nums)) - count(max(nums)) This formula will not work in case the array has all the elements equal, why? |
Python Elegant & Short | Sliding window | O(log10(n)) time | O(1) memory | find-the-k-beauty-of-a-number | 0 | 1 | ```\nclass Solution:\n """\n Time: O(log10(n)*k)\n Memory: O(log10(n))\n """\n\n def divisorSubstrings(self, num: int, k: int) -> int:\n str_num = str(num)\n return sum(\n num % int(str_num[i - k:i]) == 0\n for i in range(k, len(str_num) + 1)\n if int(str_num[i - k:i]) != 0\n )\n```\n```\nclass Solution:\n """\n Time: O(log10(n))\n Memory: O(1)\n """\n\n def divisorSubstrings(self, num: int, k: int) -> int:\n power = 10 ** (k - 1)\n tmp, window = divmod(num, 10 * power)\n\n count = int(window and not num % window)\n while tmp:\n tmp, digit = divmod(tmp, 10)\n window = digit * power + window // 10\n count += window and not num % window\n\n return count\n\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 5 | The **k-beauty** of an integer `num` is defined as the number of **substrings** of `num` when it is read as a string that meet the following conditions:
* It has a length of `k`.
* It is a divisor of `num`.
Given integers `num` and `k`, return _the k-beauty of_ `num`.
Note:
* **Leading zeros** are allowed.
* `0` is not a divisor of any value.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** num = 240, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "24 " from "**24**0 ": 24 is a divisor of 240.
- "40 " from "2**40** ": 40 is a divisor of 240.
Therefore, the k-beauty is 2.
**Example 2:**
**Input:** num = 430043, k = 2
**Output:** 2
**Explanation:** The following are the substrings of num of length k:
- "43 " from "**43**0043 ": 43 is a divisor of 430043.
- "30 " from "4**30**043 ": 30 is not a divisor of 430043.
- "00 " from "43**00**43 ": 0 is not a divisor of 430043.
- "04 " from "430**04**3 ": 4 is not a divisor of 430043.
- "43 " from "4300**43** ": 43 is a divisor of 430043.
Therefore, the k-beauty is 2.
**Constraints:**
* `1 <= num <= 109`
* `1 <= k <= num.length` (taking `num` as a string) | All the elements in the array should be counted except for the minimum and maximum elements. If the array has n elements, the answer will be n - count(min(nums)) - count(max(nums)) This formula will not work in case the array has all the elements equal, why? |
Prefix Sum | number-of-ways-to-split-array | 0 | 1 | **Python 3**\n```python\nclass Solution:\n def waysToSplitArray(self, n: List[int]) -> int:\n n = list(accumulate(n))\n return sum(n[i] >= n[-1] - n[i] for i in range(len(n) - 1))\n```\n\n**C++**\nWe could use a prefix sum, but in C++ we would need to store it in another `long long` vector (because of overflow). So, we are using a running sum here for efficiency.\n```cpp\nint waysToSplitArray(vector<int>& n) {\n long long right = accumulate(begin(n), end(n), 0LL), left = 0, res = 0;\n for (int i = 0; i < n.size() - 1; ++i) {\n left += n[i];\n right -= n[i];\n res += left >= right;\n }\n return res;\n}\n``` | 16 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
7 Lines Python Code || Beats 82 % | number-of-ways-to-split-array | 0 | 1 | # Intuition\nso you have to count the number of ways we can split array basically in two parts such that `sum of left Part >= right Part`\nso first find the total sum of the array\nand loop through your given array and add each element to left Part and subtract it from your totalSum (which is now your right Part)\nif the condition satisfies increase count\nreturn count of subarray as your ans\n\n# Code\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n summ = sum(nums)\n leftSum, count = 0, 0\n for i in range(len(nums) - 1):\n leftSum += nums[i]\n summ -= nums[i]\n if leftSum >= summ:\n count += 1\n return count\n \n``` | 2 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
[C++/Python3] Very Concise Prefix Sum O(1) | number-of-ways-to-split-array | 0 | 1 | **Python**\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n lsum, rsum, ans = 0, sum(nums), 0\n for i in range(len(nums) - 1):\n lsum += nums[i]\n rsum -= nums[i]\n ans += (lsum >= rsum)\n return ans\n\t\t\n```\n\n**C++**\n```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n long long lsum = 0, rsum = 0, ans = 0;\n for (int& num: nums) rsum += num;\n for (int i = 0; i < nums.size() - 1; ++i) {\n lsum += nums[i];\n rsum -= nums[i];\n ans += (lsum >= rsum);\n }\n return ans;\n }\n};\n``` | 4 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
Python3 || beats 99% || simple solution | number-of-ways-to-split-array | 0 | 1 | ```\nclass Solution:\n\tdef waysToSplitArray(self, nums: List[int]) -> int:\n s0 = sum(nums)\n s1, d = 0, 0\n for i in nums[:-1]:\n s1 += i\n if s1 >= (s0-s1):\n d += 1\n return d\n``` | 4 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
Simple O(n) Time and O(1) Space Solution || Python | number-of-ways-to-split-array | 0 | 1 | If you have any ***doubts*** or ***suggestion***, put in comments.\n```\nclass Solution(object):\n def waysToSplitArray(self, nums):\n lSum, rSum = 0, sum(nums)\n ans = 0\n for i in range(len(nums) - 1):\n lSum += nums[i]\n rSum -= nums[i]\n if lSum >= rSum: ans += 1\n return ans\n```\n**UpVote**, if you like it **:)** | 4 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
Python Easy Solution || Sliding Window | number-of-ways-to-split-array | 0 | 1 | # Code\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n cnt=0\n left=nums[0]\n right=sum(nums[1:])\n if left>=right:\n cnt+=1\n for i in range(1,len(nums)-1):\n left+=nums[i]\n right-=nums[i]\n if left>=right:\n cnt+=1\n return cnt\n\n```\n\n***Please Upvote*** | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
✅ [Python] ITS JUST PREFIX SUM !!! | number-of-ways-to-split-array | 0 | 1 | ```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n \n array = list(accumulate(nums, operator.add))\n count=0\n end = array[-1]\n for i in range (len(array)-1):\n \n left = array[i]-0\n right = end - array[i]\n \n if left >= right: count+=1\n \n return count\n``` | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
Fastest Python 3, Cumulative sum | number-of-ways-to-split-array | 0 | 1 | # Intuition\nCalculate half of array sum and compare cumalative sum\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def waysToSplitArray1(self, nums: List[int]) -> int:\n ans = 0\n half = (sum(nums) + 1) // 2\n total = 0\n for num in nums[:-1]:\n total += num\n if total >= half:\n ans += 1\n return ans\n \n def waysToSplitArray2(self, nums: List[int]) -> int:\n half = (sum(nums) + 1) // 2\n preSum = list(itertools.accumulate(nums))\n return sum([preSum[i] >= half for i in range(len(nums) - 1)])\n \n waysToSplitArray = waysToSplitArray1\n``` | 0 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
Beat 90% Runtime, friendly for begineers! | number-of-ways-to-split-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis code is very friendly for begineers. I\'ve introduced more local variables to make the code more reable.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe most efficient way to solve this problem is using prefix sum. The n-th element in the prefix sum array equals to the sum of the first n elements in the input list("nums" by default). \n\nExample:\n[10, 4, -8, 7] //input list\n[10, 14, 6, 13] //prefix sum array\n\n1st iteration:\nsum_left = 10 = arr[i]\nsum_right = 4-8+7 = sum_total - arr[i]\n\n2nd iteration:\nsum_left = 10+4 = arr[i]\nsum_right = -8+7 = sum_total - arr[i]\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n # prefix sum array\n arr = []\n res = 0\n for i in nums:\n res += i\n arr.append(res)\n \n res = 0\n sum_total = arr[-1]\n \n # find sum of elements\n for i in range(len(nums)-1):\n sum_left = arr[i]\n sum_right = sum_total - sum_left\n if sum_left >= sum_right:\n res += 1\n return res\n``` | 0 | You are given a **0-indexed** integer array `nums` of length `n`.
`nums` contains a **valid split** at index `i` if the following are true:
* The sum of the first `i + 1` elements is **greater than or equal to** the sum of the last `n - i - 1` elements.
* There is **at least one** element to the right of `i`. That is, `0 <= i < n - 1`.
Return _the number of **valid splits** in_ `nums`.
**Example 1:**
**Input:** nums = \[10,4,-8,7\]
**Output:** 2
**Explanation:**
There are three ways of splitting nums into two non-empty parts:
- Split nums at index 0. Then, the first part is \[10\], and its sum is 10. The second part is \[4,-8,7\], and its sum is 3. Since 10 >= 3, i = 0 is a valid split.
- Split nums at index 1. Then, the first part is \[10,4\], and its sum is 14. The second part is \[-8,7\], and its sum is -1. Since 14 >= -1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[10,4,-8\], and its sum is 6. The second part is \[7\], and its sum is 7. Since 6 < 7, i = 2 is not a valid split.
Thus, the number of valid splits in nums is 2.
**Example 2:**
**Input:** nums = \[2,3,1,0\]
**Output:** 2
**Explanation:**
There are two valid splits in nums:
- Split nums at index 1. Then, the first part is \[2,3\], and its sum is 5. The second part is \[1,0\], and its sum is 1. Since 5 >= 1, i = 1 is a valid split.
- Split nums at index 2. Then, the first part is \[2,3,1\], and its sum is 6. The second part is \[0\], and its sum is 0. Since 6 >= 0, i = 2 is a valid split.
**Constraints:**
* `2 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | For a given element x, how can you quickly check if x - 1 and x + 1 are present in the array without reiterating through the entire array? Use a set or a hash map. |
Easy short Python with explanation and example | maximum-white-tiles-covered-by-a-carpet | 0 | 1 | Brute force solution: For the start each tile, continue to iterate to the right until we run out of `carpetLen`. This runs in `O(n^2)`\n=> Better solution with runtime `O(nlogn)`:\n- We create a prefix sum array `dp` to store the TOTAL coverage from 0 to the start of each tile\n- For each tile with start `s`, we binary search the end of the carpet `s + carpetLen` to see which tile on the right would the carpet end belongs to\n- Finally, knowing the index of the right tile `r`, we subtract the TOTAL coverage of the right tile (memorized in the `dp` array) to the TOTAL coverage of the left tile (memorized in the `dp` array) and any offset (since the end may lie somewhere within the right tile, or on the right hand side of it if the right tile is the last one)\n- Example:\nInput: \n`tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10`\n=>\n`starts = [1, 10, 12, 20, 30]`\n`ends = [5, 11, 18, 25, 32]`\n`dp = [0, 5, 7, 14, 20, 23]`\n=> for each iteration:\n[e, l, r, cover] = \n[11 0 2 6]\n[20 1 4 9]\n[22 2 4 9]\n[30 3 5 6]\n[40 4 5 3]\n=> maxCover = 9\n```\ndef maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:\n\ttiles.sort()\n\tmaxCover = 0\n\tstarts, ends = zip(*tiles)\n\tdp = [0]*(len(tiles) + 1) # dp: total covered lengths from 0\n\tfor i in range(len(tiles)):\n\t\tdp[i+1] = dp[i] + ends[i] - starts[i] + 1 # length of each tile is end - start + 1\n\tfor l in range(len(tiles)):\n\t\te = starts[l] + carpetLen\n\t\tr = bisect_right(starts, e)\n\t\tcover = dp[r] - dp[l] - max(0, ends[r-1] - e + 1) # total cover on the right MINUS total cover on the left MINUS offset\n\t\tmaxCover = max(maxCover, cover)\n\treturn maxCover \n``` | 12 | You are given a 2D integer array `tiles` where `tiles[i] = [li, ri]` represents that every tile `j` in the range `li <= j <= ri` is colored white.
You are also given an integer `carpetLen`, the length of a single carpet that can be placed **anywhere**.
Return _the **maximum** number of white tiles that can be covered by the carpet_.
**Example 1:**
**Input:** tiles = \[\[1,5\],\[10,11\],\[12,18\],\[20,25\],\[30,32\]\], carpetLen = 10
**Output:** 9
**Explanation:** Place the carpet starting on tile 10.
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.
**Example 2:**
**Input:** tiles = \[\[10,11\],\[1,1\]\], carpetLen = 2
**Output:** 2
**Explanation:** Place the carpet starting on tile 10.
It covers 2 white tiles, so we return 2.
**Constraints:**
* `1 <= tiles.length <= 5 * 104`
* `tiles[i].length == 2`
* `1 <= li <= ri <= 109`
* `1 <= carpetLen <= 109`
* The `tiles` are **non-overlapping**. | Divide the array into two parts- one comprising of only positive integers and the other of negative integers. Merge the two parts to get the resultant array. |
[Python3] greedy | maximum-white-tiles-covered-by-a-carpet | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e134859baf16ddb9bd1645d01619449f3d067c14) for solutions of biweekly 78. \n\n```\nclass Solution:\n def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:\n tiles.sort()\n ans = ii = val = 0 \n for i in range(len(tiles)): \n hi = tiles[i][0] + carpetLen - 1\n while ii < len(tiles) and tiles[ii][1] <= hi:\n val += tiles[ii][1] - tiles[ii][0] + 1\n ii += 1\n partial = 0 \n if ii < len(tiles): partial = max(0, hi - tiles[ii][0] + 1)\n ans = max(ans, val + partial)\n val -= tiles[i][1] - tiles[i][0] + 1\n return ans \n``` | 1 | You are given a 2D integer array `tiles` where `tiles[i] = [li, ri]` represents that every tile `j` in the range `li <= j <= ri` is colored white.
You are also given an integer `carpetLen`, the length of a single carpet that can be placed **anywhere**.
Return _the **maximum** number of white tiles that can be covered by the carpet_.
**Example 1:**
**Input:** tiles = \[\[1,5\],\[10,11\],\[12,18\],\[20,25\],\[30,32\]\], carpetLen = 10
**Output:** 9
**Explanation:** Place the carpet starting on tile 10.
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.
**Example 2:**
**Input:** tiles = \[\[10,11\],\[1,1\]\], carpetLen = 2
**Output:** 2
**Explanation:** Place the carpet starting on tile 10.
It covers 2 white tiles, so we return 2.
**Constraints:**
* `1 <= tiles.length <= 5 * 104`
* `tiles[i].length == 2`
* `1 <= li <= ri <= 109`
* `1 <= carpetLen <= 109`
* The `tiles` are **non-overlapping**. | Divide the array into two parts- one comprising of only positive integers and the other of negative integers. Merge the two parts to get the resultant array. |
Python | Binary Search | maximum-white-tiles-covered-by-a-carpet | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom bisect import bisect_left\nclass Solution:\n def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:\n \n stc=[]\n pre=[]\n l=0\n tiles.sort()\n last=0\n maxx=0\n for i in tiles:\n stc.append(i[0])\n stc.append(i[1])\n pre.append(i[1]-i[0]+1+last)\n l+=2\n last=pre[-1]\n for i in range(l//2):\n K=bisect_left(stc,tiles[i][0]+carpetLen-1)\n ind=(K)//2\n tt=0\n if ind!=i:\n tt+=pre[ind-1]-pre[i]+(tiles[i][1]-tiles[i][0]+1)\n \n if K%2==1:\n tt+=(tiles[i][0]+carpetLen-stc[K-1])\n elif K<l and tiles[i][0]+carpetLen-1 == stc[K]:\n tt+=1\n maxx=max(maxx,tt)\n return maxx\n \n \n\n \n``` | 0 | You are given a 2D integer array `tiles` where `tiles[i] = [li, ri]` represents that every tile `j` in the range `li <= j <= ri` is colored white.
You are also given an integer `carpetLen`, the length of a single carpet that can be placed **anywhere**.
Return _the **maximum** number of white tiles that can be covered by the carpet_.
**Example 1:**
**Input:** tiles = \[\[1,5\],\[10,11\],\[12,18\],\[20,25\],\[30,32\]\], carpetLen = 10
**Output:** 9
**Explanation:** Place the carpet starting on tile 10.
It covers 9 white tiles, so we return 9.
Note that there may be other places where the carpet covers 9 white tiles.
It can be shown that the carpet cannot cover more than 9 white tiles.
**Example 2:**
**Input:** tiles = \[\[10,11\],\[1,1\]\], carpetLen = 2
**Output:** 2
**Explanation:** Place the carpet starting on tile 10.
It covers 2 white tiles, so we return 2.
**Constraints:**
* `1 <= tiles.length <= 5 * 104`
* `tiles[i].length == 2`
* `1 <= li <= ri <= 109`
* `1 <= carpetLen <= 109`
* The `tiles` are **non-overlapping**. | Divide the array into two parts- one comprising of only positive integers and the other of negative integers. Merge the two parts to get the resultant array. |
Same as 200 other Solutions 🙏🙏 | substring-with-largest-variance | 0 | 1 | # Code\n```\nclass Solution:\n def largestVariance(self, s: str) -> int:\n res=0\n for ch1 in set(s):\n for ch2 in set(s):\n if ch1==ch2: continue\n ch2_front=False; has_ch2=False; var=0\n for i in range(len(s)):\n if s[i]==ch1: var+=1\n if s[i]==ch2:\n has_ch2=True\n var-=1\n if ch2_front and var>=-1:\n ch2_front=False\n var+=1\n elif var<0:\n ch2_front=True\n var=-1\n res=max(res,var if has_ch2 else 0)\n return res \n``` | 4 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Python3 Solution | substring-with-largest-variance | 0 | 1 | \n```\nclass Solution:\n def largestVariance(self, s: str) -> int:\n chars = {}\n for c in s:\n chars[c] = chars.get(c, 0) + 1\n\n permutations = itertools.permutations(chars, 2)\n count = 0\n for a, b in permutations:\n count = max(self.kadene(a, b, s, chars), count)\n return count\n\n def kadene(self, a, b, s, chars):\n count = 0\n max_local = 0\n is_a = False\n is_b = False\n\n val_a = chars[a]\n val_b = chars[b]\n for c in s:\t\t\t\n if c != a and c != b:\n continue\n\n if max_local < 0 and val_a != 0 and val_b != 0:\n max_local = 0\n is_a = False\n is_b = False\n\n if c == a:\n max_local += 1\n val_a -= 1\n is_a = True\n\t\t\t\t\t\t\n if c == b:\n max_local -= 1\n val_b -=1\n is_b = True\n \n if is_a and is_b:\n count = max(count, max_local)\n return count\n``` | 2 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Modified Kadane's with Greedy Optimization | Commented and Explained | substring-with-largest-variance | 0 | 1 | # Intuition\nThe following intuition lays out the process generally. If you want to attempt it on your own, or are doing this for class as extra credit, you should read ONLY the Intuition. It should be enough to cover your problem.\n\nRemember, extra credit is on the honor system somewhat, as I\'m judging your code against any fundamental differences to mine. You should either try to improve it for extra credit, or show that you did implement it in a non-improved fashion for extra credit. Improvements are above and beyond, while non-improved fashion is meant to show honest work. You decide which matters more to you as part of the process.\n\nIt must also use the two stated ideas in the title, in this case Kadane\'s Algorithm with a Greedy Optimization. \n\nTo review Kadane\'s Algorithm, see [here](https://en.wikipedia.org/wiki/Maximum_subarray_problem). To review Greedy Optimizations, see [here](https://en.wikipedia.org/wiki/Greedy_algorithm)\n\nIn the general Kadane\'s algorithm, we are comparing a global max with a local max based on a subarray of values. In this case, we are concerned with the letters in the alphabet that are present, and are interested in the substring formation. The first examples findings for the last substring are the most important. Notice that they use \'babbb\' with a variance of 3. This is a key idea, as it shows that we are truly only concerned with any two characters at a given time. \n\nFrom this, we can make our way to a modification by considering the two character limitation as a minor and major key. We can count the major key incidences, and compare it to the largest size IF we have encountered at least one minor key. \n\nThis gives way to some rather nice optimization ideas before we continue with the details. For the greedy approach, what early stopping condition could we preface ourself with? Remember, we are looking for a global maximum, where the number of major counts is greater than the number of minor counts at some point in the string. If doing this for class, answer the following question : \n\n> Since we are concerned with the global maximum of major count - minor count, and since each character has some frequency in the original string, how should we sort our major keys and our minor keys? What greedy advantage does this give us? \n\nContinuing our intution from there, we should note that there are instances where we would wish to reset our count of major and minor in our string. Our limiting factor in that case is the presence of the minor keys yet to be seen. If we have a string, and have not seen any minor keys, we cannot update the global max as we do not have a substring. Similarly, if we have a string, and have no remaining minor keys, we can already calculate the maximum left for the major key in the string, and should update accordingly. If doing this for class, answer the following question : \n\n> What is the update criterion look like when minor keys remaining is 0? How can we facilitate this using known data structures? \n\nThis is the end of the intuition, feel free to reach out if in class and want help on where to go from here. Otherwise, if you read the approach, you\'re going to try for an improvement or your own implementation and comment on differences! \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nSet up a mapping for character frequency and indices of occurence in s \nThen, \n- For each index and value in s \n - update the frequency of this value\n - update the indices of this value to include this index \n\nGet the character keys as the characters that appear as keys in the mapping \n\nSet up your major and minor keys as this key list in a particular sorted order (check code if not in class to see what is meant, otherwise, this is part of your work!) \n\nSet global max to 0 \n\nThen, \n- For major key in major keys \n - if char_frequency of major key - 1 lte global max \n - break as no others will be greater as well \n - for minor key in minor keys \n - if minor key is major key -> continue \n - otherwise \n - set major and minor counts to 0 \n - set remaining major and minor counts as the frequency of each \n - get the indices of occurrence for each of your keys as the sorted indices of minor and major key \n - for index in total indices \n - if s[index] is major char \n - major count += 1 \n - remaining major -= 1 \n - otherwise \n - as above for minor \n \n - global max is max of global max and major - minor count if minor count > 0 else global max \n \n - if major count lt minor count \n - if remaining major - 1 lte global max -> break \n - else if remaining minor > 0 \n - major count = 0 \n - minor count = 0 \n - continue \n - otherwise \n - global max is max of global max and major count + remaining_major - minor count \n - break \n - else, continue \n\nWhen loop completes, return global max \n\n# Complexity\n- Time complexity : O(S + A log A + n * ( s log s + s\' ))\n - O(S) to traverse the string once\n - O(A log A) to sort the keys \n - O(mj) where mj is the subset of major keys such that a global max is established that lops off the remaining mj (note part about skipping out if char frequency of major key - 1 is lte global max at top of major char char loop) \n - within which we do O(MC), where MC is the minor char keys, for which we will consider them all \n - within which we need on average s log s time to sort their indices of occurrence \n - we then need s\' to go over indices while valid \n - all steps inside here are O(1) so do not need to be counted \n - In total then O(S) + O(mj * MC * (s log s + s\')) \n - S can be of size up to 10**4 \n - mj and MC at max are 26 \n - so either O(S) or O(mj * MC * (s log s + s\'))\n - if mj is 1/2 of MC, which holds for 137 of 138 test cases \n - and if MC at most 26 \n - then at most we get 338 * (s log s + s\') \n - as s is potentially as much or more than mj or MC, we can treat those as the main components \n - so we get O(S + n * (s log s + s\')) where n is the number of repetitions in total for the s log s sorting and s\' is the time to completion of the sorted list, S is the total string length, and s is the size of the indices of the characters in the string on average as a pairing. \n\n- Space complexity : O(A * s)\n - O(A) for the frequency of characters in S, where A is the size of the alphabet \n - O(A * s) where s is the size of the lists of the indices on average for each letter in the alphabet \n - All other space temporary assignment of size O(s) \n\n# Code\n```\nclass Solution:\n def largestVariance(self, s: str) -> int :\n # get each character frequency and indices \n char_frequency = collections.defaultdict(int)\n char_indices = collections.defaultdict(list)\n # get each index for each char as a list and track frequency \n for index, char in enumerate(s) : \n char_frequency[char] += 1 \n char_indices[char].append(index)\n # get the list of possible char keys \n char_keys = list(char_frequency.keys())\n # get the major and minor keys in order by their frequency, major sorted by highest frequency, minor by lowest \n char_keys_major = sorted(char_keys, key = lambda char_key : char_frequency[char_key], reverse=True)\n char_keys_minor = sorted(char_keys, key = lambda char_key : char_frequency[char_key])\n # track the global max \n global_max = 0 \n # use these to generate all pairings as major key in outerloop \n for major_char in char_keys_major : \n # skip useless major chars. Occurs greedily now. \n if char_frequency[major_char] - 1 <= global_max : \n break\n # minor key in inner loop \n for minor_char in char_keys_minor :\n # skip on matches \n if major_char == minor_char : \n continue \n else : \n # otherwise, get counts \n major_count = 0 \n minor_count = 0 \n # track remaining minor \n remaining_minor = char_frequency[minor_char]\n remaining_major = char_frequency[major_char]\n # get indices list of char matches (reduces time and space complexity greatly)\n total_indices = sorted([index_1 for index_1 in char_indices[major_char]] + [index_2 for index_2 in char_indices[minor_char]])\n # for each index in total indices \n for index in total_indices : \n # if s[index] is major char, increment major count \n if s[index] == major_char : \n major_count += 1 \n remaining_major -= 1 \n else : \n # otherwise, based on total indices, it must be minor char\n # increment minor count and decrement remaining minor \n minor_count += 1 \n remaining_minor -= 1 \n \n # then if minor count is gt 0, update global max \n global_max = max(global_max, major_count-minor_count) if minor_count > 0 else global_max\n\n # if major is lt minor count \n if (major_count < minor_count) : \n # if remaining major - 1 <= global max -> break \n if remaining_major - 1 <= global_max : \n break \n elif remaining_minor > 0 : \n # otherwise, if there\'s still a shot -> reset \n major_count = 0 \n minor_count = 0 \n else : \n # if major count lt minor count, but no remaining minor \n # if remaining major + major count - minor count <= global max break \n # otherwise, remaining major + major count - minor count gt global max \n # update then break. Either way, break. Due to this, use global update instead \n global_max = max(global_max, (major_count + remaining_major) - minor_count)\n break\n else : \n continue \n\n # return when done \n return global_max\n\n\n \n``` | 1 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Python Solution (Beats 99%) | substring-with-largest-variance | 0 | 1 | # Intuition\nThe main idea in this problem seems to be something a little bit like best subarray sums, except instead of having a singular array to explore, you must explore one with every combination of characters in the string.\n\n# Approach\nThe idea is to test every combination of characters $a,b \\in s$ with $a \\neq b$. And test how many more times $a$ appears than $b$. We can do this efficiently using the *Kadane* algorithm.\n\nBecause it would be very wasteful for strings with many different characters to test every position in the array, we can use a trick and instead do something similar to a *natural merge*, where we store the occurrences in the string of every character and we can then check them in order.\n\nThe last challenge is to deal with cases where $a$ appears in the candidate substring but $b$ doesn\'t. Since we know that $b \\in s$, we can *always* extend the substring to the nearest $b$, resulting in a substring with 1 less variance.\n\n# Complexity\nWith $n = len(s)$ and $c =$ number of unique characters in $s$.\nWe have some simple preprocessing which is $O(n)$\nThe following feels like $O(nc^2)$, but because of the optimization where we don\'t query 0s in the "array", we save on a lot of comparisons if we have many different characters.\n\nWe run the algorithm on every permutation $\\{a,b \\in s | a \\neq b\\}$, giving us $c^2$ executions.\n\nEach execution iterates over only the occurrences of $a$ and $b$ in $s$, which in average is ${2n}/{c}$.\n\nAfter simplifying, we get the final time complexity.\n\n- Time complexity:\n$$O(nc)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def largestVariance(self, s: str) -> int:\n letters = set(s)\n occurrences = {c: [] for c in letters}\n for i, c in enumerate(s):\n occurrences[c].append(i)\n \n # Alias\n occ = occurrences\n \n best = 0\n for a in letters:\n for b in letters:\n if a == b: continue\n ptr_a = 0\n ptr_b = 0\n occ_a = occ[a]\n occ_b = occ[b]\n len_a = len(occ_a)\n len_b = len(occ_b)\n found_a = False\n found_b = False\n\n best_sum = float(\'-inf\')\n max_curr = 0\n while ptr_a < len_a and ptr_b < len_b:\n if occ_a[ptr_a] < occ_b[ptr_b]:\n ptr_a += 1\n max_curr += 1\n if found_b: best_sum = max(max_curr, best_sum)\n else: best_sum = max(max_curr - 1, best_sum)\n else:\n found_b = True\n ptr_b += 1\n max_curr -= 1\n if max_curr < 0: \n max_curr = 0\n found_b = False\n \n max_curr += len_a - ptr_a\n best_sum = max(max_curr - (0 if found_b else 1), best_sum)\n print(f"max variance between {a} and {b} is {best_sum}")\n best = max(best_sum, best)\n return best\n\n\n\n\n \n \n``` | 1 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Explained Brute force with Sliding Window for beginners. | substring-with-largest-variance | 0 | 1 | # Intuition\nWe have to find maximum difference between occurences of two characters.\n\n\n# Approach\nI used hints to solve the problem.\nI have not used any external library so it must be easy to rewrite in any other language.\nAs there are only 26 chars in alphabets therefore at max 325 combinations or 650 permutation can be there.\n1).We first find all permutaions.\n\n2).Then for each combination treat one of char as +1 and other -1 and find maximum sum of subarray which include both .\nIf our maximum sum doesnot have any -1 or second char then we subtract -1 from sum bcoz the second char will surely be on immediate left or right of our maximum sum subarray.\nwe iterate through all permutations and find best result.\n\nInstead of Sliding Window you may be able to use Prefix sum.\n\n# Complexity\n- Time complexity:\n$$O(N^2)$$\n\nPlease corrent if wrong.\n- Space complexity:\n $$O(n)$$\n\n# Code\n```\nclass Solution:\n def largestVariance(self, s: str) -> int:\n res=0\n Combinations=[]\n Unique=[]\n for i in s:\n if i not in Unique:\n Unique.append(i)\n for i in range(len(Unique)):\n for j in range(i+1,len(Unique)):\n Combinations.append([Unique[i],Unique[j]])\n Combinations.append([Unique[j],Unique[i]])\n #Till now we have just found all the possible pair of two chars.\n for i in range(len(Combinations)):\n first=Combinations[i][0]\n second=Combinations[i][1]\n currSum=0\n ans=0\n start=0\n isSecond=0\n for j in range(len(s)):\n if s[j]!=first and s[j]!=second:\n start+=1\n continue\n if s[j]==first:\n currSum+=1\n elif s[j]==second:\n isSecond+=1\n currSum-=1\n if currSum>ans and isSecond>0:\n ans=max(currSum,ans)\n else:\n ans=max(currSum-1,ans)\n while currSum<0 and start<=j:\n if s[start]==first:\n currSum-=1\n elif s[start]==second:\n currSum+=1\n isSecond-=1\n start+=1\n res=max(res,ans)\n\n return res\n```\n\nI would appreciate if you can comment a cleaner version of code.\nThanks have an error free day.\n | 1 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Python short and clean. Functional programming. | substring-with-largest-variance | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/substring-with-largest-variance/editorial/) but written using functional programming.\n\n# Complexity\n- Time complexity: $$O(n \\cdot k^2)$$\n\n- Space complexity: $$O(k)$$\n\nwhere,\n`n is the length of s`,\n`k is the charset of s. i.e in this case 26`.\n\n# Code\n```python\nclass Solution:\n def largestVariance(self, s: str) -> int:\n def variance(major: str, minor: str, rem_minors: int) -> int:\n encoder = partial(getitem, defaultdict(int, {major: 1, minor: -1}))\n encoded_s = filter(bool, map(encoder, s))\n\n next_ = lambda st, x: tuple(map(add, (x > 0, x < 0, min(x, 0)), ((0, 0, st[2]) if st[0] < st[1] and st[2] > 0 else st)))\n states = accumulate(encoded_s, next_, initial=(0, 0, rem_minors)) # init_st = (major_count, minor_count, remaining_minor_count)\n\n return max((mjr - mnr for mjr, mnr, _ in states if mnr > 0), default=0)\n \n c = Counter(s)\n return max(variance(mjr, mnr, c[mnr]) for mjr, mnr in product(ascii_lowercase, ascii_lowercase))\n\n\n``` | 1 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Python 🔥Java 🔥C++ 🔥Simple Solution 🔥Easy to Understand | substring-with-largest-variance | 1 | 1 | # An Upvote will be encouraging \uD83D\uDC4D\n\n# Video Solution\n\n# Search \uD83D\uDC49 `Substring With Largest Variance By Tech Wired`\n\n# OR\n\n# Click the link in my profile\n\n# Intuition\n\n- Initialize count1, count2, and max_variance to 0. These variables will keep track of the counts and the maximum variance encountered.\n\n- Create a set of distinct characters from the input string s. This step ensures that we only consider unique characters for our pairs.\n\n- Iterate over the characters in the string s twice:\na. First, iterate in the original order.\nb. Then, iterate in the reverse order.\n\n- For each pair of distinct characters (l1 and l2) from the set:\na. Reset count1 and count2 to 0.\nb. Iterate over each character in the string s.\n\n- Inside the inner iteration:\na. If the current character is equal to l1, increment count1.\nb. If the current character is equal to l2, increment count2.\n\n- Check if count1 is less than count2. If so, reset count1 and count2 to 0. This step ensures that the counts are only considered if count1 >= count2.\n\n- If both count1 and count2 are greater than 0, calculate the variance (count1 - count2) and update max_variance if the calculated variance is greater than the current max_variance. This step keeps track of the maximum variance encountered so far.\n\n- After completing the iteration for the current string order, reverse the string s for the next iteration. Reversing the string allows us to consider the pairs in both the original and reverse order.\n\n- Finally, return the maximum variance (max_variance) found during the iterations.\n\n```Python []\nclass Solution:\n def largestVariance(self, s: str) -> int:\n count1 = 0\n count2 = 0\n max_variance = 0\n \n # create distinct list of character pairs\n pairs = [(l1, l2) for l1 in set(s) for l2 in set(s) if l1 != l2]\n\n # run once for original string order, then again for reverse string order\n for runs in range(2):\n for pair in pairs:\n count1 = count2 = 0\n for letter in s:\n # no reason to process letters that aren\'t part of the current pair\n if letter not in pair:\n continue\n if letter == pair[0]:\n count1 += 1\n elif letter == pair[1]:\n count2 += 1\n if count1 < count2:\n count1 = count2 = 0\n elif count1 > 0 and count2 > 0:\n max_variance = max(max_variance, count1 - count2)\n \n \n # reverse the string for the second time around\n s = s[::-1]\n \n return max_variance\n```\n```Java []\npublic class Solution {\n public int largestVariance(String s) {\n int count1 = 0;\n int count2 = 0;\n int maxVariance = 0;\n\n // Create a distinct set of character pairs\n HashSet<Character> distinctChars = new HashSet<>();\n for (char c : s.toCharArray()) {\n distinctChars.add(c);\n }\n\n // Run once for original string order, then again for reverse string order\n for (int runs = 0; runs < 2; runs++) {\n for (char l1 : distinctChars) {\n for (char l2 : distinctChars) {\n if (l1 == l2) {\n continue;\n }\n count1 = count2 = 0;\n for (char letter : s.toCharArray()) {\n if (letter == l1) {\n count1++;\n } else if (letter == l2) {\n count2++;\n }\n if (count1 < count2) {\n count1 = count2 = 0;\n } else if (count1 > 0 && count2 > 0) {\n maxVariance = Math.max(maxVariance, count1 - count2);\n }\n }\n }\n }\n\n // Reverse the string for the second time around\n s = new StringBuilder(s).reverse().toString();\n }\n\n return maxVariance;\n }\n}\n```\n```C++ []\n\nclass Solution {\npublic:\n int largestVariance(string s) {\n int count1 = 0;\n int count2 = 0;\n int max_variance = 0;\n\n // Create a distinct set of character pairs\n unordered_set<char> distinct_chars(s.begin(), s.end());\n\n // Run once for original string order, then again for reverse string order\n for (int runs = 0; runs < 2; runs++) {\n for (char l1 : distinct_chars) {\n for (char l2 : distinct_chars) {\n if (l1 == l2) {\n continue;\n }\n count1 = count2 = 0;\n for (char letter : s) {\n if (letter == l1) {\n count1++;\n } else if (letter == l2) {\n count2++;\n }\n if (count1 < count2) {\n count1 = count2 = 0;\n } else if (count1 > 0 && count2 > 0) {\n max_variance = max(max_variance, count1 - count2);\n }\n }\n }\n }\n\n // Reverse the string for the second time around\n reverse(s.begin(), s.end());\n }\n\n return max_variance;\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D\n\n | 64 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
"Weird Kadane" | Intuition + Solution Explained | substring-with-largest-variance | 0 | 1 | > **Note you can find the finalised Python3 Code at the very bottom. This post describes how you can start from a standard Kadane\'s Algorithm and end up at the solution [@votrubac describes in his post](https://leetcode.com/problems/substring-with-largest-variance/discuss/2039178/weird-kadane).** @NeosDeus suggested I make this a stand-alone post as this was initially a comment on that solution.\n>\n>Furthermore [this idea also really helped understand how you can solve this using @votrubac\'s approach](https://leetcode.com/problems/substring-with-largest-variance/discuss/2491331/Insights-into-Votrubac-soln)\n\n**The Solution**\n\nWe\'re trying to solve the problem by just taking two individual letters `a` and `b` from our allowed alphabet as per the question rules: "`s consists of lowercase English letters`", and solving the problem for `a` against `b`. We will also end up solving it for `b` against `a` due to the loop. The final solution is the max of all the possible letters in the string solved against each other.\n\nIdea being, you\'re solving:\n```python\nmax_variance = 0\nunique = list(set(s))\nfor a in unique: # see below\n for b in unique: # rules dictate these 2 loops would be no more than O(26*26)\n if a == b: continue\n a_against_b_var = solveOne(a, b, s) # <= you want to do this efficiently\n max_variance = max(a_against_b_var, max_variance)\n\nreturn max_variance \n```\n\nNow you want to solve one such problem `solveOne` efficiently. \n\nA naive solution for solving `a` against `b` and `b` against `a` simultaneously is a `O(N^2)` loop tracking the -1 and +1 as explained in the hint, and taking the abs value of `(countA - countB)`. \n\nBut you can see that what you\'re really trying to do, is maximise the count of `a` against `b` and `b` against `a` for both cases. This is really just [#53](https://leetcode.com/problems/3sum) **Maximum Subarray**, which you can do in O(N) (so 2*O(N) for both `a` against `b` and `b` against `a`: much better than O(N^2)), with a twist:\n\nYou can only consider your current running subarray as a valid solution if you were considering at least one `b` (= one `-1`) inside the solution. Solutions composed of just `a` are not valid. So you must ensure that you have `b`s, but you must also minimise their "impact" on the running sum.\n\nYou start with a solution not considering these bonus rules. Just basic Kadane\'s algorithm for the `a`s against the `b`s:\n\n```python \ndef solveOne(a, b, string):\n max_var = 0\n var = 0\n \n for c in string:\n if c == a:\n var += 1\n elif c == b:\n var -= 1\n \n var = max(0, var)\n max_var = max(max_var, var)\n \n return max_var\n```\n\nThen you add the simple rule of "you must have a b in the considered substring"\n```python\ndef solveOne(a, b, string):\n max_var = 0\n var = 0\n\n has_b = False\n \n for c in string:\n if c == a:\n var += 1\n elif c == b:\n has_b = True\n var -= 1\n\n var = max(0, var)\n if has_b:\n max_var = max(max_var, var)\n \n return max_var\n```\n\nNow for the more complex rules: \nConsider "baaaa". The correct solution is 3. The above algoritm would give us results: \n```\n+----------+---+---+---+---+---+\n| letter | b | a | a | a | a |\n+----------+---+---+---+---+---+\n| variance | 0 | 1 | 2 | 3 | 4 |\n+----------+---+---+---+---+---+\n```\nThis is an issue, so we must ensure we track the `b` properly. So we can\'t be resetting to 0 immediately as you do in the typical Kadane algorithm.\nLet\'s say we allow var to go to -1 (at least initially), so that seeing an `a` after a `b` will reset us back to 0 (which would be a correct result for the string "ba"). \n\nNow what did the `max(0, var)` in Kadane\'s algorithm really _mean_?\nWell, we were discarding a subarray and restarting at/after the current array item because the subarray up until the discarded number was no longer "saveable"; we would not get the max possible sum by continuing to add numbers to that running sum. Restarting from 0 with the other/remaining half *could* still give us a better result.\n\nLet\'s say we kept the -1 for the `b`s without resetting to 0, and consider:\n```\n+----------+----+---+---+---+---+\n| letter | b | b | a | a | a |\n+----------+----+---+---+---+---+\n| variance | -1 | ? | ? | ? | ? |\n+----------+----+---+---+---+---+\n```\n\nWe\'re considering the subarray `"[b]baaa"` and start that off with a decrement. Do we want `"[bb]aaa"` to be considered in its entirety? \nWell, `bb` would not give us the max sum of `a`s if we kept both `b`s and kept going trying to look for `a`s, similar to going to a negative value in the original Kadane\'s algorithm. \n\nE.g. `"[bba]aa"` would give us -1, `"[bbaa]a"` would give us 0, but `"b[baa]a"` would give us 1. Removing the first of those "b"s obviously doesn\'t break the rule of "all substrings must have at least one b" and maximises the sum for `a`.\n\nSo we want to cut off/restart our subarray start each time we get to -1 in this implementation. Such that in the example we\'d be considering:\n`"[b]baaa"` -> `"[bb]aaa"` becomes `"b[b]aaa"` -> `"b[ba]aa"` -> `"b[baa]a"` -> `"b[baaa]"` (this gives us the max!)\n```\n+----------+----+----+---+---+---+\n| letter | b | b | a | a | a |\n+----------+----+----+---+---+---+\n| variance | -1 | -1 | 0 | 1 | 2 |\n+----------+----+----+---+---+---+\n```\n\nTo summarise up until now:\n- if we have a positive var value and we see an `a` or a `b`, we just increment/decrement accordingly\n- we only consider a var value towards our maximum from the point we\'ve seen at least one `b` and that `b` is contained in our subarray\n- -1 indicates the start of a new subarray, if we get a var value under -1, we reset var to -1 which means we restart the subarray from that point\n\nWhat if we had some `a`s before we get another b like in `"baabbbaaaaa"\n```\n+----+---+---+---+---+---+---+---+---+---+---+\n| b | a | a | b | b | b | a | a | a | a | a |\n+----+---+---+---+---+---+---+---+---+---+---+\n| -1 | 0 | 1 | ? | | | | | | | |\n+----+---+---+---+---+---+---+---+---+---+---+\n```\nWell, observe that we wouldn\'t get the max value by considering `"[baab]bbbaaaaa"` (var = 0), rather `"b[aab]bbbaaaaa"` (var = 1) would be more optimal and continue following the rule of having to have at least one `b`. \nIt\'s pretty easy to say that if we knew we had a `b` as our first subarray member, then when we see our next `b` assuming we had some `a`s, we benefit by simply shifting our subarray range to the right by one, which results in the var value remaining unchanged, but us having the ability to extend into a larger sum with subsequent characters. \n\nWe can also know when we have such a `b` at the start of our range, because as we just saw it\'s whenever we restart the subarray: whenever we get to var <= -1.\n\nShould this rule take priority over the subarray restart rule? Throwback to the previous example: `"[b]baaaa"` -> `"[bb]aaaa"` becomes `"b[b]aaaa"` which kind of a special case of this idea, but we\'d like to be immediately aware that our first subarray member is `b` here so that we could apply the rule again later. \nSo in general, the main reason to do a right shift is when we are considering a non -1 valued subarray (= not a single item that is a `b`) to preserve the running sum.\n\nSo we\'d like to have:\n`"[b]aabbbaaaaa"` (-1) -> `"[ba]abbbaaaaa"` (0) -> `"[baa]bbbaaaaa"` (1) -> `"[baab]bbaaaaa"` would be 0 but we shift right to get `"b[aab]bbaaaaa"` (1) -> `"b[aabb]baaaaa"` (0) -> `"b[aabbb]aaaaa"` (-1) leading to a reset starting with that last `b`: `"baabb[b]aaaaa"` (-1) -> `"baabb[ba]aaaa"` (0) -> `"baabb[baa]aaa"` (1) -> `"baabb[baaa]aa"` (2) -> `"baabb[baaaa]a"` (3) -> `"baabb[baaaaa]"` (4)\n```\n+----+---+---+---+---+----+---+---+---+---+---+\n| b | a | a | b | b | b | a | a | a | a | a |\n+----+---+---+---+---+----+---+---+---+---+---+\n| -1 | 0 | 1 | 1 | 0 | -1 | 0 | 1 | 2 | 3 | 4 |\n+----+---+---+---+---+----+---+---+---+---+---+\n```\n\n**Final Rules**\n\nThe rules we\'ve found are, for any given char `c` being considered at any position in the string:\n- if we have any var value and we see that the current `c` == `a` we can just increment. There\'s no special rules relating to incrementing\n- if we see the current `c` == `b`:\n> - if we see that we have a non -1 var value (indicating a current substring containing not just `b`s) and assuming we could "shift right by one" to save our current var value, then we will do so. We would need to track if we do actually have a `b` at the start of our current substring to be able to do so.\n> - if for the new var value, `var - 1`, `(var - 1)` <= -1, we set it to -1 exactly and restart the substring from the current `b`. We now have a first `b` for the previous rule to use.\n> - otherwise the var value is currently positive, and adding the b would set var to 0 (minimum), not ever below 0.\n\n\n**Final Code**\nThis gets us to @votrubac\'s code, or here the python version of it:\n\n```python\ndef solveOne(a, b, string):\n max_var = 0\n \n var = 0\n has_b = False\n first_b = False # first element of the currently considered subarray is b\n \n for c in string:\n if c == a:\n var += 1\n \n elif c == b:\n has_b = True\n \n if first_b and var >= 0: # "shift right" and save a 1 in the current sum to be able to properly maximise it\n # we can only do this when we know that we have a `b` at the start of our current subarray, and we\'ll only ever have a single b at the start\n # always followed by an a, due to the next rule\n first_b = False \n elif (var - 1) < 0: # restart the subarray from this b (inclusive) onwards\n # this rule ensures we skip double-b\'s, every subarray will always end up being `ba....`, `[bb]a` would become `b[b]a` -> `b[ba]`\n first_b = True \n var = -1\n else:\n var -= 1 # var will always be >= 0 in this case\n \n if has_b and var > max_var:\n max_var = var\n \n return max_var\n``` \n | 110 | The **variance** of a string is defined as the largest difference between the number of occurrences of **any** `2` characters present in the string. Note the two characters may or may not be the same.
Given a string `s` consisting of lowercase English letters only, return _the **largest variance** possible among all **substrings** of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "aababbb "
**Output:** 3
**Explanation:**
All possible variances along with their respective substrings are listed below:
- Variance 0 for substrings "a ", "aa ", "ab ", "abab ", "aababb ", "ba ", "b ", "bb ", and "bbb ".
- Variance 1 for substrings "aab ", "aba ", "abb ", "aabab ", "ababb ", "aababbb ", and "bab ".
- Variance 2 for substrings "aaba ", "ababbb ", "abbb ", and "babb ".
- Variance 3 for substring "babbb ".
Since the largest possible variance is 3, we return it.
**Example 2:**
**Input:** s = "abcde "
**Output:** 0
**Explanation:**
No letter occurs more than once in s, so the variance of every substring is 0.
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of lowercase English letters. | You should test every possible assignment of good and bad people, using a bitmask. In each bitmask, if the person i is good, then his statements should be consistent with the bitmask in order for the assignment to be valid. If the assignment is valid, count how many people are good and keep track of the maximum. |
Python || Easy Solution || Stack | find-resultant-array-after-removing-anagrams | 0 | 1 | # Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def check(self,word1: str,word2: str)->bool:\n word1=list(word1)\n word1.sort()\n word2=list(word2)\n word2.sort()\n if word1==word2:\n return 1\n return 0\n\n def removeAnagrams(self, words: List[str]) -> List[str]:\n lis=[]\n for i in range(len(words)):\n if len(lis)==0 or Solution.check(self,lis[len(lis)-1],words[i])==0:\n lis.append(words[i])\n return lis \n``` | 1 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
Python counter || Solution | find-resultant-array-after-removing-anagrams | 0 | 1 | ```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n res=[words[0]] \n for i in range(1,len(words)):\n mp1,mp2=Counter(words[i-1]),Counter(words[i]) \n if mp1!=mp2:\n res.append(words[i]) \n return res\n\t\t#misread easy to medium\n # s=[]\n # ans=[]\n # for i in words:\n # mp=[0]*26 \n # for j in i:\n # mp[ord(j)-ord("a")]+=1\n # if str(mp) in s:\n # continue\n # else:\n # ans.append(i)\n # s.append(str(mp))\n # return ans\n | 1 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
itertools is awesome | find-resultant-array-after-removing-anagrams | 0 | 1 | Here\'s a one-liner\n\n```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n return (next(val) for _, val in groupby(words, key=sorted))\n``` | 1 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
Weird Description | find-resultant-array-after-removing-anagrams | 0 | 1 | Misread this question 2 times and wasted like 20 minutes. \n\n**Python 3**\nWanted to bubble-up this solution by one of our humble commenters below (whose name rhymes with batman). \n\nApparently, `itertools.groupby` groups *consecutive* elements by a key (which is `sorted` here). And `next` takes the first element from that group.\n\nIt pays to learn vast and powerful Python libraries.\n\n```python\nclass Solution:\n def removeAnagrams(self, w: List[str]) -> List[str]:\n return [next(g) for _, g in groupby(w, sorted)]\n```\n\nOriginal Solution\n```python\nclass Solution:\n def removeAnagrams(self, w: List[str]) -> List[str]:\n return [w[i] for i in range(0, len(w)) if i == 0 or sorted(w[i]) != sorted(w[i - 1])]\n```\n#### Silly Hash\nThis solution won\'t work if there are hash collisions (unless we add a check). The idea is to compute a hash using characters value but not position. \n\nIf the size of words is limited to 10, computing a hash would be faster than comparing counter for 26 characters.\n\n**C++**\n```cpp\nvector<string> removeAnagrams(vector<string>& words) {\n long long hash = -1;\n vector<string> res;\n for (auto &w : words)\n if (auto new_hash = accumulate(begin(w), end(w), 0LL, [](long long s, char ch){ return s + (1 << (ch - \'a\')); });\n hash != new_hash) {\n res.push_back(w);\n hash = new_hash;\n }\n return res;\n}\n``` | 48 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
Python | Easy Solution✅ | find-resultant-array-after-removing-anagrams | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n i = 0\n while True:\n if i == len(words)-1:\n break\n if \'\'.join(sorted(words[i])) == \'\'.join(sorted(words[i+1])):\n words.pop(i+1)\n i-=1\n i+=1\n return words\n``` | 6 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
⛔Remove anagrams || 😐4 liner code || 👍🏻Least complexity... | find-resultant-array-after-removing-anagrams | 0 | 1 | # KARRAR\n>Anagrams...\n>>Removing anagrams...\n>>>Low time complexity...\n>>>>Optimized and generalized solution...\n>>>>> Easy to understand...\n- PLEASE \uD83D\uDC4D\uD83C\uDFFB UPVOTE...\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach:\n Simplest approach...\n Sort the arrays and compare there indeces...\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Beats 88% (57 ms)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Beats 15% (16 MB)\n\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n ans=[words[0]]\n for i in range(1,len(words)):\n if(sorted(words[i-1])!=sorted(words[i])):\n ans.append(words[i])\n \n return ans\n``` | 5 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
C++ - Easiest Beginner Friendly Sol || O(n*m*26) time and O(n*m) space | find-resultant-array-after-removing-anagrams | 1 | 1 | # Intuition of this Problem:\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create a vector called "count" with 26 elements, all initialized to 0.\n2. Compare the length of two strings, if they are not equal, return false.\n3. Increment the count of elements in "count" corresponding to the characters in string s and decrement the count of elements corresponding to the characters in string t.\n4. Call the function "countAllZeroes" to check if all elements in "count" are 0, if yes return true, otherwise return false.\n5. Create a vector called "uniqueWords" and insert the first element of the "words" vector into it.\n6. Loop through the rest of the "words" vector and compare the current word with the previous word in "uniqueWords". If they are anagrams, skip this word and continue with the next word. If they are not anagrams, insert this word into "uniqueWords".\n7. Return "uniqueWords".\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n bool countAllZeroes(vector<int>& count) {\n for (int i = 0; i < 26; i++) {\n if (count[i] != 0)\n return false;\n }\n return true;\n }\n bool isAnagram(string s, string t) {\n int n = s.length();\n int m = t.length();\n if (n != m)\n return false;\n vector<int> count(26, 0);\n for (int i = 0; i < n; i++) {\n count[s[i] - \'a\']++;\n count[t[i] - \'a\']--;\n }\n if (countAllZeroes(count) == true)\n return true;\n return false;\n }\n vector<string> removeAnagrams(vector<string>& words) {\n vector<string> uniqueWords;\n uniqueWords.push_back(words[0]);\n for (int i = 1; i < words.size(); i++) {\n if (isAnagram(words[i-1], words[i]))\n continue;\n else\n uniqueWords.push_back(words[i]);\n }\n return uniqueWords;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean countAllZeroes(int[] count) {\n for (int i = 0; i < 26; i++) {\n if (count[i] != 0)\n return false;\n }\n return true;\n }\n public boolean isAnagram(String s, String t) {\n int n = s.length();\n int m = t.length();\n if (n != m)\n return false;\n int[] count = new int[26];\n for (int i = 0; i < n; i++) {\n count[s.charAt(i) - \'a\']++;\n count[t.charAt(i) - \'a\']--;\n }\n if (countAllZeroes(count) == true)\n return true;\n return false;\n }\n public List<String> removeAnagrams(String[] words) {\n List<String> uniqueWords = new ArrayList<>();\n uniqueWords.add(words[0]);\n for (int i = 1; i < words.length; i++) {\n if (isAnagram(words[i-1], words[i]))\n continue;\n else\n uniqueWords.add(words[i]);\n }\n return uniqueWords;\n }\n}\n\n```\n```Python []\nclass Solution:\n def countAllZeroes(self, count):\n for i in range(26):\n if count[i] != 0:\n return False\n return True\n \n def isAnagram(self, s, t):\n n = len(s)\n m = len(t)\n if n != m:\n return False\n count = [0] * 26\n for i in range(n):\n count[ord(s[i]) - ord(\'a\')] += 1\n count[ord(t[i]) - ord(\'a\')] -= 1\n if self.countAllZeroes(count) == True:\n return True\n return False\n \n def removeAnagrams(self, words):\n uniqueWords = []\n uniqueWords.append(words[0])\n for i in range(1, len(words)):\n if self.isAnagram(words[i-1], words[i]):\n continue\n else:\n uniqueWords.append(words[i])\n return uniqueWords\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n * m * 26)**, where n is the number of words in the given list and m is the maximum length of a word. This is because for each pair of words, the time taken to check if they are anagrams of each other is O(m * 26), and this operation is repeated for n-1 pairs, giving us a time complexity of O(n * m * 26).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n * m)**, where n is the number of words in the given list and m is the maximum length of a word. This is because we are using a list uniqueWords to store the unique words, and its length can be at most n.\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 8 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
Python 3 | Intuitive + How to approach | O(n) without sorting | find-resultant-array-after-removing-anagrams | 0 | 1 | # Goal\nReturn the list of words after removing anagrams\n\n\n# Approach\n## 1. How do we know if those words have the same anagram? \n\nThose words have the same anagram if the words have the same letters even though they have different orders of letters.\n\n"baby" and "ybba" are anagrams because they have 2b, 1a, and 1y. It means we count the letters in the word. So, to solve this problem, we need to store the counter of the letter of the word as a key tuple in the dictionary (hashmap) and the value will be the word itself. To make it easier, the counter of the letter will be the list of 26 integers with 0 as the initialized number.\n\ne.g \n- "ab" will be [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]\n- "bapak" will be [2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]\n\n## 2. What if the counter of letters as key tuple exists in anagram? \n\nCheck if the previous word doesn\'t have the same anagram, we can put the current word into result\n\nE.g words = ["ab", "c", "ba"]\n1. "ab", we will have dictionary:\n{(1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0): \'ab\'}\n2. "c" we will have dictionary: {(1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0): \'ab\', (0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0): \'c\'}\n3. We know that the counter of phrase "ba" will be (1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) which is already exist in the dictionary. \n\nSo, does it mean we exclude phrase "ba"? The answer is NO because we should check the previous word == the word already stored in the same tuple counter or not. You could take a look the rule in the problem description that `select any index i such that 0 < i < words.length and words[i - 1] and words[i] are anagrams, and delete words[i] from words`. Therefore, if it\'s not the same, we should include the word.\n\nCode:\n\n```python\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n res = []\n anagrams = {}\n\n for i in range(len(words)):\n word = words[i]\n counter = [0]*26\n for c in word:\n counter[ord(c)-ord(\'a\')] += 1\n\n if tuple(counter) not in anagrams:\n res.append(word)\n else:\n if anagrams[tuple(counter)] != words[i-1]:\n res.append(word)\n anagrams[tuple(counter)] = word\n return res\n```\n\nTime Complexity: O(n)\nSpace Complexity: O(n)\n\n# Can we do better?\nYes, we can improve the space complexity slightly better by getting rid of the dictionary (hashmap). We just need to store the previous into the previous list. Thanks @codebreaker176 for the better code.\n\n```python\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n res = []\n prev = []\n\n for i in range(len(words)):\n word = words[i]\n counter = [0]*26\n for c in word:\n counter[ord(c)-ord(\'a\')] += 1\n\n if counter != prev:\n res.append(word)\n prev = counter\n return res\n``` | 13 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
python - small & easy to understand solution | find-resultant-array-after-removing-anagrams | 0 | 1 | Runtime: 52 ms, faster than 96.66% of Python3 online submissions for Find Resultant Array After Removing Anagrams.\nMemory Usage: 13.8 MB, less than 75.32% of Python3 online submissions for Find Resultant Array After Removing Anagrams.\n```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n key = ""\n result = []\n \n for word in words:\n letters = list(word)\n letters.sort()\n new_key = "".join(letters)\n \n if new_key != key :\n key = new_key\n result.append(word)\n \n return result\n```\n\n**More understanding variant :**\n\n**idea of solution :**\n1. get first word from array and sorting it and retain as **key** and put first word in answer(**result**) \n2. in loop will give all words from array starting with index 1\n3. for each word will check : is the sorting rearranging of this word equal **key** or not ?\n a. is eqaul : ignore this word\n b. isn\'t equal : put this word in answer and update **key**\nRuntime: 56 ms, faster than 93.03% of Python3 online submissions for Find Resultant Array After Removing Anagrams.\nMemory Usage: 13.8 MB, less than 75.32% of Python3 online submissions for Find Resultant Array After Removing Anagrams.\n```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n def sort_construct(word):\n letters = list(word)\n letters.sort()\n return "".join(letters)\n \n key = sort_construct(words[0])\n result = [words[0]]\n \n for i in range(1, len(words)):\n new_key = sort_construct(words[i])\n if new_key != key :\n key = new_key\n result.append(words[i])\n \n return result\n``` | 3 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
Python: Faster than upto 97% quick hashmap/list answer | find-resultant-array-after-removing-anagrams | 0 | 1 | First code submission :D\n\nYou can substitute the hashMap with a list if you\'d like, gives around the same answer time at **77.8%** to as fast as **97%** in one case.\n\n```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n #automatically get first word\n hashMap ={0: words[0]} \n for i in range(1,len(words)):\n notAnagram = words[i]\n #sort words in alphabetical order\n #if not the same add to hashMap\n if sorted(words[i]) != sorted(words[i-1]):\n hashMap[i] = notAnagram\n return list(hashMap.values())\n``` | 1 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
Python Easy Solution with Comments | find-resultant-array-after-removing-anagrams | 0 | 1 | ```\nclass Solution:\n def removeAnagrams(self, words: List[str]) -> List[str]:\n if len(words) == 1:\n return words\n \n i = 1\n while i < len(words):\n anagram = "".join(sorted(words[i]))\n\t\t\t# check if words[i-1] and words[i] are anagrams\n if anagram == "".join(sorted(words[i - 1])):\n\t\t\t\t# if anagrams then remove second instance from the list of words\n words.pop(i)\n else:\n i += 1\n \n return words\n``` | 5 | You are given a **0-indexed** string array `words`, where `words[i]` consists of lowercase English letters.
In one operation, select any index `i` such that `0 < i < words.length` and `words[i - 1]` and `words[i]` are **anagrams**, and **delete** `words[i]` from `words`. Keep performing this operation as long as you can select an index that satisfies the conditions.
Return `words` _after performing all operations_. It can be shown that selecting the indices for each operation in **any** arbitrary order will lead to the same result.
An **Anagram** is a word or phrase formed by rearranging the letters of a different word or phrase using all the original letters exactly once. For example, `"dacb "` is an anagram of `"abdc "`.
**Example 1:**
**Input:** words = \[ "abba ", "baba ", "bbaa ", "cd ", "cd "\]
**Output:** \[ "abba ", "cd "\]
**Explanation:**
One of the ways we can obtain the resultant array is by using the following operations:
- Since words\[2\] = "bbaa " and words\[1\] = "baba " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "baba ", "cd ", "cd "\].
- Since words\[1\] = "baba " and words\[0\] = "abba " are anagrams, we choose index 1 and delete words\[1\].
Now words = \[ "abba ", "cd ", "cd "\].
- Since words\[2\] = "cd " and words\[1\] = "cd " are anagrams, we choose index 2 and delete words\[2\].
Now words = \[ "abba ", "cd "\].
We can no longer perform any operations, so \[ "abba ", "cd "\] is the final answer.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c ", "d ", "e "\]
**Output:** \[ "a ", "b ", "c ", "d ", "e "\]
**Explanation:**
No two adjacent strings in words are anagrams of each other, so no operations are performed.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters. | What is the range that the answer must fall into? The answer has to be in the range [0, max(buckets)] (inclusive). For a number x, is there an efficient way to check if it is possible to make the amount of water in each bucket x. Let in be the total amount of water that needs to be poured into buckets and out be the total amount of water that needs to be poured out of buckets to make the amount of water in each bucket x. If out - (out * loss) >= in, then it is possible. |
[Python 3] Sort and pairwise, 3 lines || beats 100% || 555ms 🥷🏼 | maximum-consecutive-floors-without-special-floors | 0 | 1 | ```python3 []\nclass Solution:\n def maxConsecutive(self, bottom: int, top: int, special: List[int]) -> int:\n special.sort()\n res = max((b-a-1 for a, b in pairwise(special)), default = 0)\n\n return max(res, special[0] - bottom, top - special[-1])\n```\n\n | 2 | Alice manages a company and has rented some floors of a building as office space. Alice has decided some of these floors should be **special floors**, used for relaxation only.
You are given two integers `bottom` and `top`, which denote that Alice has rented all the floors from `bottom` to `top` (**inclusive**). You are also given the integer array `special`, where `special[i]` denotes a special floor that Alice has designated for relaxation.
Return _the **maximum** number of consecutive floors without a special floor_.
**Example 1:**
**Input:** bottom = 2, top = 9, special = \[4,6\]
**Output:** 3
**Explanation:** The following are the ranges (inclusive) of consecutive floors without a special floor:
- (2, 3) with a total amount of 2 floors.
- (5, 5) with a total amount of 1 floor.
- (7, 9) with a total amount of 3 floors.
Therefore, we return the maximum number which is 3 floors.
**Example 2:**
**Input:** bottom = 6, top = 8, special = \[7,6,8\]
**Output:** 0
**Explanation:** Every floor rented is a special floor, so we return 0.
**Constraints:**
* `1 <= special.length <= 105`
* `1 <= bottom <= special[i] <= top <= 109`
* All the values of `special` are **unique**. | Repeatedly iterate through the array and check if the current value of original is in the array. If original is not found, stop and return its current value. Otherwise, multiply original by 2 and repeat the process. Use set data structure to check the existence faster. |
Python Easy Solution || 100% || Beats 98.95% || Beginners Friendly || | maximum-consecutive-floors-without-special-floors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxConsecutive(self, bottom: int, top: int, special: List[int]) -> int:\n mx= 0\n l = bottom\n special.sort()\n for idx, value in enumerate(special):\n if idx==0:\n mx=max(mx, value-l)\n l=value\n else:\n mx=max(mx, value-l-1)\n l=value\n mx=max(mx, top-value)\n return mx\n``` | 1 | Alice manages a company and has rented some floors of a building as office space. Alice has decided some of these floors should be **special floors**, used for relaxation only.
You are given two integers `bottom` and `top`, which denote that Alice has rented all the floors from `bottom` to `top` (**inclusive**). You are also given the integer array `special`, where `special[i]` denotes a special floor that Alice has designated for relaxation.
Return _the **maximum** number of consecutive floors without a special floor_.
**Example 1:**
**Input:** bottom = 2, top = 9, special = \[4,6\]
**Output:** 3
**Explanation:** The following are the ranges (inclusive) of consecutive floors without a special floor:
- (2, 3) with a total amount of 2 floors.
- (5, 5) with a total amount of 1 floor.
- (7, 9) with a total amount of 3 floors.
Therefore, we return the maximum number which is 3 floors.
**Example 2:**
**Input:** bottom = 6, top = 8, special = \[7,6,8\]
**Output:** 0
**Explanation:** Every floor rented is a special floor, so we return 0.
**Constraints:**
* `1 <= special.length <= 105`
* `1 <= bottom <= special[i] <= top <= 109`
* All the values of `special` are **unique**. | Repeatedly iterate through the array and check if the current value of original is in the array. If original is not found, stop and return its current value. Otherwise, multiply original by 2 and repeat the process. Use set data structure to check the existence faster. |
Simple python3 solution | iterate via special + pairwise | maximum-consecutive-floors-without-special-floors | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def maxConsecutive(self, bottom: int, top: int, special: List[int]) -> int:\n arr = special[:]\n arr.append(bottom - 1)\n arr.append(top + 1)\n arr.sort()\n\n result = 0\n for a, b in pairwise(arr):\n current = b - a - 1\n result = max(result, current)\n return result\n\n``` | 1 | Alice manages a company and has rented some floors of a building as office space. Alice has decided some of these floors should be **special floors**, used for relaxation only.
You are given two integers `bottom` and `top`, which denote that Alice has rented all the floors from `bottom` to `top` (**inclusive**). You are also given the integer array `special`, where `special[i]` denotes a special floor that Alice has designated for relaxation.
Return _the **maximum** number of consecutive floors without a special floor_.
**Example 1:**
**Input:** bottom = 2, top = 9, special = \[4,6\]
**Output:** 3
**Explanation:** The following are the ranges (inclusive) of consecutive floors without a special floor:
- (2, 3) with a total amount of 2 floors.
- (5, 5) with a total amount of 1 floor.
- (7, 9) with a total amount of 3 floors.
Therefore, we return the maximum number which is 3 floors.
**Example 2:**
**Input:** bottom = 6, top = 8, special = \[7,6,8\]
**Output:** 0
**Explanation:** Every floor rented is a special floor, so we return 0.
**Constraints:**
* `1 <= special.length <= 105`
* `1 <= bottom <= special[i] <= top <= 109`
* All the values of `special` are **unique**. | Repeatedly iterate through the array and check if the current value of original is in the array. If original is not found, stop and return its current value. Otherwise, multiply original by 2 and repeat the process. Use set data structure to check the existence faster. |
Python Simulation - Just sort the array special | maximum-consecutive-floors-without-special-floors | 0 | 1 | ```\nclass Solution:\n def maxConsecutive(self, bottom: int, top: int, special: list[int]) -> int:\n special.sort()\n res = special[0] - bottom\n \n for i in range(1, len(special)):\n res = max(res, special[i] - special[i - 1] - 1)\n \n return max(res, top - special[-1])\n``` | 7 | Alice manages a company and has rented some floors of a building as office space. Alice has decided some of these floors should be **special floors**, used for relaxation only.
You are given two integers `bottom` and `top`, which denote that Alice has rented all the floors from `bottom` to `top` (**inclusive**). You are also given the integer array `special`, where `special[i]` denotes a special floor that Alice has designated for relaxation.
Return _the **maximum** number of consecutive floors without a special floor_.
**Example 1:**
**Input:** bottom = 2, top = 9, special = \[4,6\]
**Output:** 3
**Explanation:** The following are the ranges (inclusive) of consecutive floors without a special floor:
- (2, 3) with a total amount of 2 floors.
- (5, 5) with a total amount of 1 floor.
- (7, 9) with a total amount of 3 floors.
Therefore, we return the maximum number which is 3 floors.
**Example 2:**
**Input:** bottom = 6, top = 8, special = \[7,6,8\]
**Output:** 0
**Explanation:** Every floor rented is a special floor, so we return 0.
**Constraints:**
* `1 <= special.length <= 105`
* `1 <= bottom <= special[i] <= top <= 109`
* All the values of `special` are **unique**. | Repeatedly iterate through the array and check if the current value of original is in the array. If original is not found, stop and return its current value. Otherwise, multiply original by 2 and repeat the process. Use set data structure to check the existence faster. |
✔️JAVA || PYTHON ||✔️ 100% || EASY | maximum-consecutive-floors-without-special-floors | 1 | 1 | **SORT THE ARRAY IN INCREASING ORDER**\n\nWE HAVE TO SELECT MAXIMUM VALUE FROM **:**\n* Difference between bottom and least value of array\n* Difference between largest value and top\n* Difference between consecutive values in sorted order -1\n\n\n\n**JAVA**\n```\nclass Solution {\n public int maxConsecutive(int x, int y, int[] a) {\n Arrays.sort(a);\n int r=Math.max(a[0]-x,y-a[a.length-1])+1;\n for (int i=0;i<a.length-1;i++){\n if (a[i+1]-a[i]>r){r=a[i+1]-a[i];}\n }return r-1;\n }\n}\n```\n**PYTHON**\n```\nclass Solution:\n def maxConsecutive(self, x: int, y: int, a: List[int]) -> int:\n a.sort()\n r=max(a[0]-x,y-a[-1])\n for i in range(len(a)-1):\n a[i]=a[i+1]-a[i]\n a[-1]=0\n r=max(max(a)-1,r)\n return r\n``` | 1 | Alice manages a company and has rented some floors of a building as office space. Alice has decided some of these floors should be **special floors**, used for relaxation only.
You are given two integers `bottom` and `top`, which denote that Alice has rented all the floors from `bottom` to `top` (**inclusive**). You are also given the integer array `special`, where `special[i]` denotes a special floor that Alice has designated for relaxation.
Return _the **maximum** number of consecutive floors without a special floor_.
**Example 1:**
**Input:** bottom = 2, top = 9, special = \[4,6\]
**Output:** 3
**Explanation:** The following are the ranges (inclusive) of consecutive floors without a special floor:
- (2, 3) with a total amount of 2 floors.
- (5, 5) with a total amount of 1 floor.
- (7, 9) with a total amount of 3 floors.
Therefore, we return the maximum number which is 3 floors.
**Example 2:**
**Input:** bottom = 6, top = 8, special = \[7,6,8\]
**Output:** 0
**Explanation:** Every floor rented is a special floor, so we return 0.
**Constraints:**
* `1 <= special.length <= 105`
* `1 <= bottom <= special[i] <= top <= 109`
* All the values of `special` are **unique**. | Repeatedly iterate through the array and check if the current value of original is in the array. If original is not found, stop and return its current value. Otherwise, multiply original by 2 and repeat the process. Use set data structure to check the existence faster. |
Python Simple Solution | Single Iteration | Optimized solution | Difference between floors | maximum-consecutive-floors-without-special-floors | 0 | 1 | ```\nclass Solution:\n def maxConsecutive(self, bottom: int, top: int, special: List[int]) -> int:\n c = 0 \n special.sort()\n c = special[0]-bottom\n bottom = special[0]\n for i in range(1,len(special)):\n if special[i]-bottom>1:\n c = max(c,special[i]-bottom-1)\n bottom = special[i]\n if top-bottom>1:\n c = max(c,top-bottom)\n return c\n``` | 2 | Alice manages a company and has rented some floors of a building as office space. Alice has decided some of these floors should be **special floors**, used for relaxation only.
You are given two integers `bottom` and `top`, which denote that Alice has rented all the floors from `bottom` to `top` (**inclusive**). You are also given the integer array `special`, where `special[i]` denotes a special floor that Alice has designated for relaxation.
Return _the **maximum** number of consecutive floors without a special floor_.
**Example 1:**
**Input:** bottom = 2, top = 9, special = \[4,6\]
**Output:** 3
**Explanation:** The following are the ranges (inclusive) of consecutive floors without a special floor:
- (2, 3) with a total amount of 2 floors.
- (5, 5) with a total amount of 1 floor.
- (7, 9) with a total amount of 3 floors.
Therefore, we return the maximum number which is 3 floors.
**Example 2:**
**Input:** bottom = 6, top = 8, special = \[7,6,8\]
**Output:** 0
**Explanation:** Every floor rented is a special floor, so we return 0.
**Constraints:**
* `1 <= special.length <= 105`
* `1 <= bottom <= special[i] <= top <= 109`
* All the values of `special` are **unique**. | Repeatedly iterate through the array and check if the current value of original is in the array. If original is not found, stop and return its current value. Otherwise, multiply original by 2 and repeat the process. Use set data structure to check the existence faster. |
Check Each Bit | largest-combination-with-bitwise-and-greater-than-zero | 0 | 1 | **Intuition:** we need to count integerts that share the same bit. Bitwise AND of those integers will be positive.\n\nWe count integers that share each bit, and return the maximum.\n\n**Python 3**\n```python\nclass Solution:\n def largestCombination(self, candidates: List[int]) -> int:\n return max(sum(n & (1 << i) > 0 for n in candidates) for i in range(0, 24))\n```\n\n**C++**\n```cpp\nint largestCombination(vector<int>& cs) {\n int res = 0, max_e = *max_element(begin(cs), end(cs));\n for (int b = 1; b <= max_e; b <<= 1) {\n int cnt = 0;\n for (auto n : cs)\n cnt += (n & b) > 0;\n res = max(res, cnt);\n }\n return res;\n}\n```\n\nAnother version using `bitset`.\n**C++**\n```cpp\nint largestCombination(vector<int>& cs) {\n int cnt[24] = {};\n for (auto n : cs)\n transform(begin(cnt), end(cnt), begin(bitset<24>(n).to_string()), begin(cnt), [](int s, char ch){ return s + (ch == \'1\'); });\n return *max_element(begin(cnt), end(cnt));\n}\n``` | 60 | The **bitwise AND** of an array `nums` is the bitwise AND of all integers in `nums`.
* For example, for `nums = [1, 5, 3]`, the bitwise AND is equal to `1 & 5 & 3 = 1`.
* Also, for `nums = [7]`, the bitwise AND is `7`.
You are given an array of positive integers `candidates`. Evaluate the **bitwise AND** of every **combination** of numbers of `candidates`. Each number in `candidates` may only be used **once** in each combination.
Return _the size of the **largest** combination of_ `candidates` _with a bitwise AND **greater** than_ `0`.
**Example 1:**
**Input:** candidates = \[16,17,71,62,12,24,14\]
**Output:** 4
**Explanation:** The combination \[16,17,62,24\] has a bitwise AND of 16 & 17 & 62 & 24 = 16 > 0.
The size of the combination is 4.
It can be shown that no combination with a size greater than 4 has a bitwise AND greater than 0.
Note that more than one combination may have the largest size.
For example, the combination \[62,12,24,14\] has a bitwise AND of 62 & 12 & 24 & 14 = 8 > 0.
**Example 2:**
**Input:** candidates = \[8,8\]
**Output:** 2
**Explanation:** The largest combination \[8,8\] has a bitwise AND of 8 & 8 = 8 > 0.
The size of the combination is 2, so we return 2.
**Constraints:**
* `1 <= candidates.length <= 105`
* `1 <= candidates[i] <= 107` | How can we update the hash value efficiently while iterating instead of recalculating it each time? Use the rolling hash method. |
[Java/Python 3] Bit manipulation w/ explanation and analysis. | largest-combination-with-bitwise-and-greater-than-zero | 1 | 1 | E.g. candidates = [16,17,71,62,12,24,14] \nconvert to binary:\n`[0b1 0000, 0b1 0001, 0b100 0111, 0b11 1110, 0b1100, 0b1 1000, 0b1110]`\n\n1. At `0-th` bit, we have only `17 = 0b1 0001` with `1`, others all have `0` at `0-th` bit, any combination including a number other than `17` in the `candidates` will result a bitwise AND `0` at `0-th` bit; The corresponding largest combination size is `1`;\n2. At `1-th` bit, we have `71 = 0b100 0111`, `62 = 0b11 1110` and `14 = 0b1110` with `1`, others all have `0` at `0-th` bit, any combination including a number other than `71, 62` or `14` in the `candidates` will result a bitwise AND `0` at `0-th` bit; The corresponding largest combination size is `3`;\n3. At `2-th` bit, we have `71 = 0b100 0111`, `62 = 0b11 1110`, `12 = 0b1100` and `14 = 0b1110` with `1`, others all have `0` at `0-th` bit, any combination including a number other than `71, 62, 12` or `14` in the `candidates` will result a bitwise AND `0` at `0-th` bit; The corresponding largest combination size is `4`;\n4. At `3-rd` bit, we have `62 = 0b11 1110`, `12 = 0b1100`, `24 = 0b1 1000` and `14 = 0b1110` with `1`, others all have `0` at `0-th` bit, any combination including a number other than `62, 12, 24` or `14` in the `candidates` will result a bitwise AND `0` at `0-th` bit; The corresponding largest combination size is `4`;\n5. At `4-th` bit, we have `16 = 0b1 0000`, `17 = 0b1 0001`, `62 = 0b11 1110`, and `24 = 0b1 1000` with `1`, others all have `0` at `0-th` bit, any combination including a number other than `16, 17, 62`, or `24` in the `candidates` will result a bitwise AND `0` at `0-th` bit; The corresponding largest combination size is `4`;\n6. At `5-th` bit, we have only `62 = 0b11 1110` with `1`, others all have `0` at `0-th` bit, any combination including a number other than `62` in the `candidates` will result a bitwise AND `0` at `0-th` bit; The corresponding largest combination size is `1`;\n7. At all other bits, any combination will will result a bitwise AND `0` at these bits; The corresponding largest combination size are all `0`;\n\nSince at any bit the bitwIse AND greater than `0` will reslut the overall integers bitwise AND greater than `0`, from above 7 steps we can conclude that the largest combination with bitwise AND greater than `0` is `4`.\n\nGiven the Constraints:\n\n`1 <= candidates[i] <= 10`<sup>7</sup>\n\nSince `10`<sup>7</sup> < `2`<sup>24</sup> = `16,777,216`, the integers in input at most have `24` bits.\n\nHence the algorithm is as follows:\n\nCheck the `i-th` (i < 24) bit of the integers in `candidates`, those with `1` at `i-th` bit must have bitwise AND greater than `0`. Traverse from `0-th` bit to `23-rd` bit and locate the largest size of combination.\n```java\n public int largestCombination(int[] candidates) {\n int largest = 0;\n for (int i = 0; i < 24; ++i) {\n int sum = 0;\n for (int c : candidates) {\n sum += (c >> i) & 1;\n }\n largest = Math.max(largest, sum);\n }\n return largest;\n }\n```\n```python\n def largestCombination(self, cand: List[int]) -> int:\n largest = 0\n for i in range(24):\n largest = max(largest, sum((c >> i) & 1 for c in cand)\n return largest\n```\n\nor make them 1 liners:\n```java\n public int largestCombination(int[] candidates) {\n return IntStream.range(0, 24)\n .map(i -> IntStream.of(candidates).map(c -> (c >> i) & 1).sum())\n .max()\n .getAsInt();\n }\n```\n```python\n def largestCombination(self, cand: List[int]) -> int:\n return max(sum((c >> i) & 1 for c in cand) for i in range(24))\n```\n\n**Analysis:**\n\nAssume `range = 2`<sup>x</sup> `= 0b100..00` (1 followed by x 0\'s), then we need to check `0-th` to `x-th` bit, where `x = `log<sub>2</sub>(range). Therefore, we can conclude as follows:\n\nThe outer loop traverse `range` binary bits from least significant bit to most significant bit, which cost `O(log(Range))`, where `Range = 10`<sup>7</sup>; the inner loop cost time `O(n)`, therefore\n\nTime: `O(nlog(Range))`, space: `O(1)`, where `n = candidates.length, Range = 10`<sup>7</sup>. | 14 | The **bitwise AND** of an array `nums` is the bitwise AND of all integers in `nums`.
* For example, for `nums = [1, 5, 3]`, the bitwise AND is equal to `1 & 5 & 3 = 1`.
* Also, for `nums = [7]`, the bitwise AND is `7`.
You are given an array of positive integers `candidates`. Evaluate the **bitwise AND** of every **combination** of numbers of `candidates`. Each number in `candidates` may only be used **once** in each combination.
Return _the size of the **largest** combination of_ `candidates` _with a bitwise AND **greater** than_ `0`.
**Example 1:**
**Input:** candidates = \[16,17,71,62,12,24,14\]
**Output:** 4
**Explanation:** The combination \[16,17,62,24\] has a bitwise AND of 16 & 17 & 62 & 24 = 16 > 0.
The size of the combination is 4.
It can be shown that no combination with a size greater than 4 has a bitwise AND greater than 0.
Note that more than one combination may have the largest size.
For example, the combination \[62,12,24,14\] has a bitwise AND of 62 & 12 & 24 & 14 = 8 > 0.
**Example 2:**
**Input:** candidates = \[8,8\]
**Output:** 2
**Explanation:** The largest combination \[8,8\] has a bitwise AND of 8 & 8 = 8 > 0.
The size of the combination is 2, so we return 2.
**Constraints:**
* `1 <= candidates.length <= 105`
* `1 <= candidates[i] <= 107` | How can we update the hash value efficiently while iterating instead of recalculating it each time? Use the rolling hash method. |
[Python] Count the Number of Ones at Each Bit, Clean & Concise | largest-combination-with-bitwise-and-greater-than-zero | 0 | 1 | Step 0. Define an array `s` to store the total number of `1`\'s at each bit (reversely);\nStep 1. Convert each `candidate` to binary string;\nStep 2. For each bit, if it is `1`, add it to the array at that bit;\nStep 3. Return the maximum number of 1\u2019s among all possible bits\n\nTime: `O(N * log(10^7))`\nSpace: `O(1)`\n\n```\nclass Solution:\n def largestCombination(self, candidates: List[int]) -> int:\n\t\ts = [0 for _ in range(30)]\n for c in candidates:\n b = bin(c)[2:][::-1]\n for i, d in enumerate(b):\n if d == \'1\':\n s[i] += 1\n return max(s)\n``` | 2 | The **bitwise AND** of an array `nums` is the bitwise AND of all integers in `nums`.
* For example, for `nums = [1, 5, 3]`, the bitwise AND is equal to `1 & 5 & 3 = 1`.
* Also, for `nums = [7]`, the bitwise AND is `7`.
You are given an array of positive integers `candidates`. Evaluate the **bitwise AND** of every **combination** of numbers of `candidates`. Each number in `candidates` may only be used **once** in each combination.
Return _the size of the **largest** combination of_ `candidates` _with a bitwise AND **greater** than_ `0`.
**Example 1:**
**Input:** candidates = \[16,17,71,62,12,24,14\]
**Output:** 4
**Explanation:** The combination \[16,17,62,24\] has a bitwise AND of 16 & 17 & 62 & 24 = 16 > 0.
The size of the combination is 4.
It can be shown that no combination with a size greater than 4 has a bitwise AND greater than 0.
Note that more than one combination may have the largest size.
For example, the combination \[62,12,24,14\] has a bitwise AND of 62 & 12 & 24 & 14 = 8 > 0.
**Example 2:**
**Input:** candidates = \[8,8\]
**Output:** 2
**Explanation:** The largest combination \[8,8\] has a bitwise AND of 8 & 8 = 8 > 0.
The size of the combination is 2, so we return 2.
**Constraints:**
* `1 <= candidates.length <= 105`
* `1 <= candidates[i] <= 107` | How can we update the hash value efficiently while iterating instead of recalculating it each time? Use the rolling hash method. |
Bitwise AND? Leave it to Python map->sum. | largest-combination-with-bitwise-and-greater-than-zero | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe obvious approach is to enumerate every combination, compute its bitwise-and, count the number of 1 bits, and take the maximum of that over all combinations. Just one problem with this: There are far too many combinations.\n\nFortunately, we can transform the problem into the following: Consider all the bits used for any of the ```candidates```. If we are going to find a non-zero bitwise-and of some combination, then that bitwise-and will have *some* bit that\'s non-zero and by inference that bit is 1 in all the candidates comprising a winning (largest) combination. \n\nThis means we can iterate over each of the bit positions for all the candidates, counting how many candidates have a 1 in that bit position and then taking the maximum over all possible bit positions.\n<!-- Describe your approach to solving the problem. -->\nThe code simply iterates over all single-1-bit numbers -- 1, 2, 4, 8, etc. -- between 1 and ```max(candidates)```. For each of those numbers, we use the Python ```map``` function to map each candidate into 1 if the bitwise-and of the single-1-bit number and the candidate is non-zero and 0 otherwise, so then we have a bunch of 0\'s and 1\'s. Then, we can count the 1\'s (via ```sum```) to determine how many numbers can be bitwise-anded together to produce a non-zero result, and then take the maximum of those counts over all the single-1-bit numbers.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe number of bits we need to examine is a constant related to the value of the largest candidate, but unrelated to the number of candidates, so $$O(1)$$. The ```sum``` and ```map``` iterate over all the candidates, so the overall time complexity is $$(n)$$ where $$n$$ is the number of candidates.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nConceptually, every time we do the ```map``` operation, we create a result list the same size as ```candidates```. However, I believe that Python is being pretty clever about pipelining the ```map``` and ```sum``` such that only a single intermediate value is retained; hence the space complexity is $$O(1)$$.\n# Code\n```\nclass Solution:\n def largestCombination(self, candidates: List[int]) -> int:\n max_cand = max( candidates )\n bit = 1\n biggest = 0\n while bit <= max_cand:\n biggest = max( biggest, sum( map( lambda candidate: 1 if bit & candidate else 0, candidates ) ) )\n bit <<= 1 # Shift to next higher bit\n return biggest\n``` | 0 | The **bitwise AND** of an array `nums` is the bitwise AND of all integers in `nums`.
* For example, for `nums = [1, 5, 3]`, the bitwise AND is equal to `1 & 5 & 3 = 1`.
* Also, for `nums = [7]`, the bitwise AND is `7`.
You are given an array of positive integers `candidates`. Evaluate the **bitwise AND** of every **combination** of numbers of `candidates`. Each number in `candidates` may only be used **once** in each combination.
Return _the size of the **largest** combination of_ `candidates` _with a bitwise AND **greater** than_ `0`.
**Example 1:**
**Input:** candidates = \[16,17,71,62,12,24,14\]
**Output:** 4
**Explanation:** The combination \[16,17,62,24\] has a bitwise AND of 16 & 17 & 62 & 24 = 16 > 0.
The size of the combination is 4.
It can be shown that no combination with a size greater than 4 has a bitwise AND greater than 0.
Note that more than one combination may have the largest size.
For example, the combination \[62,12,24,14\] has a bitwise AND of 62 & 12 & 24 & 14 = 8 > 0.
**Example 2:**
**Input:** candidates = \[8,8\]
**Output:** 2
**Explanation:** The largest combination \[8,8\] has a bitwise AND of 8 & 8 = 8 > 0.
The size of the combination is 2, so we return 2.
**Constraints:**
* `1 <= candidates.length <= 105`
* `1 <= candidates[i] <= 107` | How can we update the hash value efficiently while iterating instead of recalculating it each time? Use the rolling hash method. |
Bitwise checking | largest-combination-with-bitwise-and-greater-than-zero | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst find out the largest bit position, then iteratively check the number of 1\'s for each bit position.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestCombination(self, candidates: List[int]) -> int:\n if len(candidates) == 1:\n return 1\n m = max(candidates)\n n = 0 # the largest bit position\n while 2 ** n - 1 < m:\n n += 1\n res = 0\n for i in range(n):\n cur = 0 #count the number of 1\'s for bit position i\n for num in candidates:\n if num & (1<<i):\n cur += 1\n res = max(res, cur)\n return res \n``` | 0 | The **bitwise AND** of an array `nums` is the bitwise AND of all integers in `nums`.
* For example, for `nums = [1, 5, 3]`, the bitwise AND is equal to `1 & 5 & 3 = 1`.
* Also, for `nums = [7]`, the bitwise AND is `7`.
You are given an array of positive integers `candidates`. Evaluate the **bitwise AND** of every **combination** of numbers of `candidates`. Each number in `candidates` may only be used **once** in each combination.
Return _the size of the **largest** combination of_ `candidates` _with a bitwise AND **greater** than_ `0`.
**Example 1:**
**Input:** candidates = \[16,17,71,62,12,24,14\]
**Output:** 4
**Explanation:** The combination \[16,17,62,24\] has a bitwise AND of 16 & 17 & 62 & 24 = 16 > 0.
The size of the combination is 4.
It can be shown that no combination with a size greater than 4 has a bitwise AND greater than 0.
Note that more than one combination may have the largest size.
For example, the combination \[62,12,24,14\] has a bitwise AND of 62 & 12 & 24 & 14 = 8 > 0.
**Example 2:**
**Input:** candidates = \[8,8\]
**Output:** 2
**Explanation:** The largest combination \[8,8\] has a bitwise AND of 8 & 8 = 8 > 0.
The size of the combination is 2, so we return 2.
**Constraints:**
* `1 <= candidates.length <= 105`
* `1 <= candidates[i] <= 107` | How can we update the hash value efficiently while iterating instead of recalculating it each time? Use the rolling hash method. |
[Python3] SortedList | count-integers-in-intervals | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/5edf72d3865cd9791f0a89b968c0c1aeeaa381c3) for solutions of weekly 293. \n\n```\nfrom sortedcontainers import SortedList\n\nclass CountIntervals:\n\n def __init__(self):\n self.cnt = 0 \n self.intervals = SortedList()\n\n def add(self, left: int, right: int) -> None:\n k = self.intervals.bisect_left((left, right))\n while k < len(self.intervals) and self.intervals[k][0] <= right: \n l, r = self.intervals.pop(k)\n self.cnt -= r - l + 1\n right = max(right, r)\n if k and left <= self.intervals[k-1][1]: \n l, r = self.intervals.pop(k-1)\n self.cnt -= r - l + 1\n left = l\n right = max(right, r)\n self.cnt += right - left + 1\n self.intervals.add((left, right))\n\n def count(self) -> int:\n return self.cnt\n``` | 27 | Given an **empty** set of intervals, implement a data structure that can:
* **Add** an interval to the set of intervals.
* **Count** the number of integers that are present in **at least one** interval.
Implement the `CountIntervals` class:
* `CountIntervals()` Initializes the object with an empty set of intervals.
* `void add(int left, int right)` Adds the interval `[left, right]` to the set of intervals.
* `int count()` Returns the number of integers that are present in **at least one** interval.
**Note** that an interval `[left, right]` denotes all the integers `x` where `left <= x <= right`.
**Example 1:**
**Input**
\[ "CountIntervals ", "add ", "add ", "count ", "add ", "count "\]
\[\[\], \[2, 3\], \[7, 10\], \[\], \[5, 8\], \[\]\]
**Output**
\[null, null, null, 6, null, 8\]
**Explanation**
CountIntervals countIntervals = new CountIntervals(); // initialize the object with an empty set of intervals.
countIntervals.add(2, 3); // add \[2, 3\] to the set of intervals.
countIntervals.add(7, 10); // add \[7, 10\] to the set of intervals.
countIntervals.count(); // return 6
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 7, 8, 9, and 10 are present in the interval \[7, 10\].
countIntervals.add(5, 8); // add \[5, 8\] to the set of intervals.
countIntervals.count(); // return 8
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 5 and 6 are present in the interval \[5, 8\].
// the integers 7 and 8 are present in the intervals \[5, 8\] and \[7, 10\].
// the integers 9 and 10 are present in the interval \[7, 10\].
**Constraints:**
* `1 <= left <= right <= 109`
* At most `105` calls **in total** will be made to `add` and `count`.
* At least **one** call will be made to `count`. | Can we build a graph from words, where there exists an edge between nodes i and j if words[i] and words[j] are connected? The problem now boils down to finding the total number of components and the size of the largest component in the graph. How can we use bit masking to reduce the search space while adding edges to node i? |
[Python3] built-in List beats SortedList | count-integers-in-intervals | 0 | 1 | ### Idea\n1. Initialize list `interv` with `[(-inf, -inf), (inf, inf)]` to store the merged intervals and integer `cov = 0`, to be updated after addition of each interval\n2. Whenever an interval must be added, the following must be done\n- Using binary search, find the range of affected intervals in `interv`, denoted by `li` for left most, `ri` for right most + 1\n- the range of the new merged interval (`lval`, `rval`)\n- replace the range of [li, ri - 1], inclusive with the new merged interval `(lval, rval)`\n3. Update the coverege by\n- Finding and subtracting the coverage of deleted intervals `to_delete`\n- Adding the coverage of new interval `rval - lval + 1`\n\n### Code\n#### Built-in List\n```\nclass CountIntervals:\n\n def __init__(self):\n\t# initialize the merged intervals list as below to handle edge cases\n self.interv = [(-inf, -inf), (inf, inf)]\n self.cov = 0 \n\n def add(self, left: int, right: int) -> None:\n \n interv = self.interv\n \n\t\t# find the left most position for inserting of the new potentially merged interval\n\t\t# we use `left - 1` because the interval coverage is inclusive\n li = bisect.bisect_left(interv, left - 1, key=itemgetter(1))\n lval = min(interv[li][0], left)\n\t\t\n\t\t# find the right most position for inserting the new potentially merged interval\n\t\t# we use `right + 1` because the interval coverage is inclusive\n ri = bisect.bisect_right(interv, right + 1, key=itemgetter(0))\n rval = max(interv[ri - 1][1], right)\n\n\t\t# find the coverage of the intervals that will be replaced by the new interval\n to_delete = 0\n for _ in range(li, ri):\n to_delete += interv[_][1] - interv[_][0] + 1\n \n\t\t# udpate the coverage\n self.cov += rval - lval + 1 - to_delete\n interv[li: ri] = [(lval, rval)]\n\n def count(self) -> int:\n return self.cov\n```\n\n#### SortedList\n```\nfrom sortedcontainers import SortedList\n\nclass CountIntervals:\n\n def __init__(self):\n self.cov = 0 \n self.interv = SortedList([(-inf, -inf), (inf, inf)])\n\n def add(self, left: int, right: int) -> None:\n li = self.interv.bisect_left((left - 1, -inf))\n if self.interv[li - 1][1] >= left - 1:\n li -= 1\n lval = min(self.interv[li][0], left)\n ri = self.interv.bisect_right((right + 1, inf))\n rval = max(self.interv[ri - 1][1], right)\n \n \n to_delete = 0\n for _ in range(li, ri):\n to_delete += self.interv[_][1] - self.interv[_][0] + 1\n self.cov += rval - lval + 1 - to_delete\n del self.interv[li: ri]\n self.interv.add((lval, rval))\n\n def count(self) -> int:\n return self.cov\n```\n\n### Feedback\nI appreciate your feedback and support! :) | 44 | Given an **empty** set of intervals, implement a data structure that can:
* **Add** an interval to the set of intervals.
* **Count** the number of integers that are present in **at least one** interval.
Implement the `CountIntervals` class:
* `CountIntervals()` Initializes the object with an empty set of intervals.
* `void add(int left, int right)` Adds the interval `[left, right]` to the set of intervals.
* `int count()` Returns the number of integers that are present in **at least one** interval.
**Note** that an interval `[left, right]` denotes all the integers `x` where `left <= x <= right`.
**Example 1:**
**Input**
\[ "CountIntervals ", "add ", "add ", "count ", "add ", "count "\]
\[\[\], \[2, 3\], \[7, 10\], \[\], \[5, 8\], \[\]\]
**Output**
\[null, null, null, 6, null, 8\]
**Explanation**
CountIntervals countIntervals = new CountIntervals(); // initialize the object with an empty set of intervals.
countIntervals.add(2, 3); // add \[2, 3\] to the set of intervals.
countIntervals.add(7, 10); // add \[7, 10\] to the set of intervals.
countIntervals.count(); // return 6
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 7, 8, 9, and 10 are present in the interval \[7, 10\].
countIntervals.add(5, 8); // add \[5, 8\] to the set of intervals.
countIntervals.count(); // return 8
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 5 and 6 are present in the interval \[5, 8\].
// the integers 7 and 8 are present in the intervals \[5, 8\] and \[7, 10\].
// the integers 9 and 10 are present in the interval \[7, 10\].
**Constraints:**
* `1 <= left <= right <= 109`
* At most `105` calls **in total** will be made to `add` and `count`.
* At least **one** call will be made to `count`. | Can we build a graph from words, where there exists an edge between nodes i and j if words[i] and words[j] are connected? The problem now boils down to finding the total number of components and the size of the largest component in the graph. How can we use bit masking to reduce the search space while adding edges to node i? |
Python3 Sorted List | Merge Intervals in stream | FB follow-up for 56 | count-integers-in-intervals | 0 | 1 | Directly modified from my another post of solution: https://leetcode.com/problems/merge-intervals/discuss/1889983/python-binary-search-solution-for-fb-follow-up-merge-in-stream\n\n#### Original idea\nThis is the idea when I tried to come up with the solution for the follow-up question of 56 with out BST:\n\nThe basic idea of the solution is, when we merge intervals we are placing the points on a line segment. Let\'s denote start points as 0 and endpoints as 1 for separating different points, then we could get a representation. For instance, merged intervals: [1, 4], [7, 9], we could denote as\n[1,0], [4, 1], [7, 0], [9, 1]\n\nThen every time we have a new start and end, we could insert [st, 0], [ed, 1] to this list.\n\nThere are 2 key observations for this representations:\n\n1. we should not get 2 continous start or 2 continous end.\nFor instance, if after insert we get sth. like [1,0], [2, 0], [3, 1], [4,1], we know a merge should happens.\n\n2. If it is an insertion that will not trigger any merges, we could know that the place we insert start and end should differ only by 1.\nFor instance, we already have [1,0], [4,1] denotes the merged interval [1, 4] and we want to insert [5, 6] , we will get the index to insert is 2 and 3 which differs by 1\n\nBased on 1 and 2, let\'s denote the place to insert [st, 0] is idx1 and [ed, 1] is idx2, then:\n\n1. if idx2 - idx1 != 1, we know the elements between should be removed\n2. If we encounter invalid situation #1, we set idx1 = idx1 - 1 or idx2 = idx2 + 1 for further checks\n\n\n#### Update specified for this problem\nTo further modify for this question, we need to maintain a count variable and update it when new intervals come.\n\nWe added the number of [st, ed] for all new intervals to be added, and then remove the duplicates when we pop out the intervals that should cause duplicate additions.\n\n```Python\nfrom sortedcontainers import SortedList\nclass CountIntervals:\n\n def __init__(self):\n self.sorted_list = SortedList()\n self.num = 0\n\n def add(self, st: int, ed: int) -> None:\n self.sorted_list.add([st, 0])\n self.sorted_list.add([ed, 1])\n \n self.num += ed - st + 1\n # print(self.sorted_list)\n \n idx1 = self.sorted_list.index([st, 0])\n idx2 = self.sorted_list.index([ed, 1])\n \n \n if idx1 - 1 >= 0 and self.sorted_list[idx1 - 1][1] == 0:\n idx1 -= 1\n if idx2 + 1 < len(self.sorted_list) and self.sorted_list[idx2 + 1][1] == 1:\n idx2 += 1\n \n if idx2 - idx1 != 1:\n j = idx1 + 1\n for _ in range(idx1 + 1, idx2):\n if self.sorted_list[j][1] == 0: # encounter a start point need to be remove\n self.num -= (self.sorted_list[j + 1][0] - self.sorted_list[j][0] + 1) # so we need to decrease the duplicated addition to the total number\n self.sorted_list.pop(j)\n\n def count(self) -> int: # O(1)\n return self.num\n``` | 7 | Given an **empty** set of intervals, implement a data structure that can:
* **Add** an interval to the set of intervals.
* **Count** the number of integers that are present in **at least one** interval.
Implement the `CountIntervals` class:
* `CountIntervals()` Initializes the object with an empty set of intervals.
* `void add(int left, int right)` Adds the interval `[left, right]` to the set of intervals.
* `int count()` Returns the number of integers that are present in **at least one** interval.
**Note** that an interval `[left, right]` denotes all the integers `x` where `left <= x <= right`.
**Example 1:**
**Input**
\[ "CountIntervals ", "add ", "add ", "count ", "add ", "count "\]
\[\[\], \[2, 3\], \[7, 10\], \[\], \[5, 8\], \[\]\]
**Output**
\[null, null, null, 6, null, 8\]
**Explanation**
CountIntervals countIntervals = new CountIntervals(); // initialize the object with an empty set of intervals.
countIntervals.add(2, 3); // add \[2, 3\] to the set of intervals.
countIntervals.add(7, 10); // add \[7, 10\] to the set of intervals.
countIntervals.count(); // return 6
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 7, 8, 9, and 10 are present in the interval \[7, 10\].
countIntervals.add(5, 8); // add \[5, 8\] to the set of intervals.
countIntervals.count(); // return 8
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 5 and 6 are present in the interval \[5, 8\].
// the integers 7 and 8 are present in the intervals \[5, 8\] and \[7, 10\].
// the integers 9 and 10 are present in the interval \[7, 10\].
**Constraints:**
* `1 <= left <= right <= 109`
* At most `105` calls **in total** will be made to `add` and `count`.
* At least **one** call will be made to `count`. | Can we build a graph from words, where there exists an edge between nodes i and j if words[i] and words[j] are connected? The problem now boils down to finding the total number of components and the size of the largest component in the graph. How can we use bit masking to reduce the search space while adding edges to node i? |
Python Binary Search | count-integers-in-intervals | 0 | 1 | **Approach**\n1. If there is no intervals yet, just add it and keep track of the count. Otherwise:\n2. Search through intervals for where left of the new interval is less than the end of any interval.\n3. Search through intervals for where right of the new interval is greater than the start of any interval.\n4. If our found left index is inside an interval, take the minimum of it and the interval.\n5. If our found right index is inside of an interval, take hte maximum of it and the interval.\n6. Otherwise [left, right] will be inserted into the list. \n7. Keep track of counts as we go, we\'re going to add to counts the amount of the new interval\n8. We\'re going to remove from counts all intervals between our left index and right index. If we\'re just inserting, the space between left index and right index will be 0. So we\'ll only be adding.\n\n**Other Considerations**\nIn the competition two things caused my time limit exceeded:\n1. Not keeping track of counts and walking it instead. One of the test cases is, add add add... for 50+ iterations followed by count count count... for 100+ iterations. So if you have to walk count each time, you\'ll TLE.\n2. Even with that, updating the interval list afterwards with array slicing. This is confusing for me.\n\nHad to look at yag313\'s solution to see array slice + assignment which is much much faster. I think python does extra memory allocation and will add two arrays together followed by another addition of the third array in my naive attempt.\n\n***Would love a detailed explanation from anyone on what the time complexity between the two lines are please.***\n\n```\nimport bisect\nfrom operator import itemgetter\n\nclass CountIntervals:\n\n def __init__(self):\n self.intervals = []\n self.cur_count = 0\n\n def add(self, left: int, right: int) -> None:\n if not self.intervals:\n self.intervals.append([left, right])\n self.cur_count = right - left + 1\n return\n\n l = bisect.bisect_left(self.intervals, left, key=itemgetter(1))\n r = bisect.bisect_right(self.intervals, right, key=itemgetter(0))\n \n if l < len(self.intervals):\n left = min(left, self.intervals[l][0])\n \n if r > 0:\n right = max(right, self.intervals[r-1][1])\n \n to_add = right - left + 1\n \n to_remove = 0\n for i in range(l, r):\n to_remove += self.intervals[i][1] - self.intervals[i][0] + 1\n \n self.cur_count += to_add - to_remove\n \n # TOO SLOW!!\n # 15 seconds!!\n # self.intervals = self.intervals[:l] + [[left, right]] + self.intervals[r:]\n \n # 1.3 - 1.6 seconds\n self.intervals[l:r] = [[left, right]]\n\n def count(self) -> int:\n return self.cur_count\n\n\n# Your CountIntervals object will be instantiated and called as such:\n# obj = CountIntervals()\n# obj.add(left,right)\n# param_2 = obj.count()\n``` | 10 | Given an **empty** set of intervals, implement a data structure that can:
* **Add** an interval to the set of intervals.
* **Count** the number of integers that are present in **at least one** interval.
Implement the `CountIntervals` class:
* `CountIntervals()` Initializes the object with an empty set of intervals.
* `void add(int left, int right)` Adds the interval `[left, right]` to the set of intervals.
* `int count()` Returns the number of integers that are present in **at least one** interval.
**Note** that an interval `[left, right]` denotes all the integers `x` where `left <= x <= right`.
**Example 1:**
**Input**
\[ "CountIntervals ", "add ", "add ", "count ", "add ", "count "\]
\[\[\], \[2, 3\], \[7, 10\], \[\], \[5, 8\], \[\]\]
**Output**
\[null, null, null, 6, null, 8\]
**Explanation**
CountIntervals countIntervals = new CountIntervals(); // initialize the object with an empty set of intervals.
countIntervals.add(2, 3); // add \[2, 3\] to the set of intervals.
countIntervals.add(7, 10); // add \[7, 10\] to the set of intervals.
countIntervals.count(); // return 6
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 7, 8, 9, and 10 are present in the interval \[7, 10\].
countIntervals.add(5, 8); // add \[5, 8\] to the set of intervals.
countIntervals.count(); // return 8
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 5 and 6 are present in the interval \[5, 8\].
// the integers 7 and 8 are present in the intervals \[5, 8\] and \[7, 10\].
// the integers 9 and 10 are present in the interval \[7, 10\].
**Constraints:**
* `1 <= left <= right <= 109`
* At most `105` calls **in total** will be made to `add` and `count`.
* At least **one** call will be made to `count`. | Can we build a graph from words, where there exists an edge between nodes i and j if words[i] and words[j] are connected? The problem now boils down to finding the total number of components and the size of the largest component in the graph. How can we use bit masking to reduce the search space while adding edges to node i? |
Python || merge intervals | count-integers-in-intervals | 0 | 1 | 1. We save non-overlapping intervals by two arrays, `self.L` and `self.R`. `[self.L[i], self.R[i]]` is the `i`th interval.\n2. When a new interval `I = [left, right]` is added, use binary search to find:\n\t- `idx_l`: index of the first interval whose right endpoint >= `left`.\n\t- `idx_r`: index of the first interval whose left endpoint > `right` .\nHere are some examples:\n\n\t- case 1: `idx_l = 2, idx_r = 4`.\n\t- case 2: `idx_l = 1, idx_r = 4`.\n\t- case 3: `idx_l = 2, idx_r = 3`.\n3. From `idx_r-1` to `idx_l`, pop the interval one by one. Each time an interval is popped out, merge it with `I`.\n4. After all overlapping intervals are popped out, insert the merged `I`.\n```\nfrom bisect import bisect_left, bisect_right\n\nclass CountIntervals:\n def __init__(self):\n self.L = []\n self.R = []\n self.total = 0\n\n def add(self, left: int, right: int) -> None:\n if not self.L:\n self.L.append(left)\n self.R.append(right)\n self.total += right-left+1\n else:\n idx_l, idx_r = bisect_left(self.R, left), bisect_right(self.L, right)\n lm, rm = left, right\n while idx_l < idx_r:\n l1 = self.L.pop(idx_r-1)\n r1 = self.R.pop(idx_r-1)\n self.total -= r1-l1+1\n lm = min(lm, l1)\n rm = max(rm, r1)\n idx_r -= 1\n self.L.insert(idx_l, lm)\n self.R.insert(idx_l, rm)\n self.total += rm-lm+1\n \n def count(self) -> int:\n return self.total | 1 | Given an **empty** set of intervals, implement a data structure that can:
* **Add** an interval to the set of intervals.
* **Count** the number of integers that are present in **at least one** interval.
Implement the `CountIntervals` class:
* `CountIntervals()` Initializes the object with an empty set of intervals.
* `void add(int left, int right)` Adds the interval `[left, right]` to the set of intervals.
* `int count()` Returns the number of integers that are present in **at least one** interval.
**Note** that an interval `[left, right]` denotes all the integers `x` where `left <= x <= right`.
**Example 1:**
**Input**
\[ "CountIntervals ", "add ", "add ", "count ", "add ", "count "\]
\[\[\], \[2, 3\], \[7, 10\], \[\], \[5, 8\], \[\]\]
**Output**
\[null, null, null, 6, null, 8\]
**Explanation**
CountIntervals countIntervals = new CountIntervals(); // initialize the object with an empty set of intervals.
countIntervals.add(2, 3); // add \[2, 3\] to the set of intervals.
countIntervals.add(7, 10); // add \[7, 10\] to the set of intervals.
countIntervals.count(); // return 6
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 7, 8, 9, and 10 are present in the interval \[7, 10\].
countIntervals.add(5, 8); // add \[5, 8\] to the set of intervals.
countIntervals.count(); // return 8
// the integers 2 and 3 are present in the interval \[2, 3\].
// the integers 5 and 6 are present in the interval \[5, 8\].
// the integers 7 and 8 are present in the intervals \[5, 8\] and \[7, 10\].
// the integers 9 and 10 are present in the interval \[7, 10\].
**Constraints:**
* `1 <= left <= right <= 109`
* At most `105` calls **in total** will be made to `add` and `count`.
* At least **one** call will be made to `count`. | Can we build a graph from words, where there exists an edge between nodes i and j if words[i] and words[j] are connected? The problem now boils down to finding the total number of components and the size of the largest component in the graph. How can we use bit masking to reduce the search space while adding edges to node i? |
Easy python 3 Solution beats 85%🧑💻💻🤖 | percentage-of-letter-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def percentageLetter(self, s: str, letter: str) -> int:\n count=0\n start_index=0\n l=len(s)\n for i in range(l):\n j = s.find(letter,start_index)\n if(j!=-1):\n start_index = j+1\n count+=1\n per = math.floor((count/l)*100)\n return per\n\n\n``` | 1 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
python soln | percentage-of-letter-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def percentageLetter(self, s: str, letter: str) -> int:\n l=len(s)\n count=0\n for i in s:\n if i==letter:\n count+=1\n else:\n pass\n return int((count/l)*100) \n``` | 1 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
[Python ||O(N)] Runtime 50 ms Beats 56.36% Memory 13.9 MB Beats 10.66% | percentage-of-letter-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def percentageLetter(self, s: str, letter: str) -> int:\n c=0\n for i in s:\n if i==letter:\n c+=1\n n=len(s)\n return int(c/n*100)\n``` | 1 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
Simple solution with HashMap in Python3 | percentage-of-letter-in-string | 0 | 1 | # Intuition\nHere we have:\n- string `s` and a `letter` character\n- our goal is find how much percentage (rounded to down) `letter` allocates \n\n# Approach\n1. define a **HashMap**, to store frequencies and find a percentage as `freqOfLetterInS * 100 // len(s)`. \n\n# Complexity\n- Time complexity: **O(N)**, to create a **HashMap** `cache`\n\n- Space complexity: **O(N)**, the same for storing\n\n# Code\n```\nclass Solution:\n def percentageLetter(self, s: str, letter: str) -> int:\n cache = Counter(s)\n\n return cache[letter] * 100 // len(s) if letter in cache else 0\n``` | 1 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
Percentage of letter in string | percentage-of-letter-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n\nclass Solution:\n def percentageLetter(self, s: str, letter: str) -> int:\n if letter not in s:\n return 0\n return round(math.floor((s.count(letter)/len(s))*100)) \n``` | 1 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
Easy Python Solution | percentage-of-letter-in-string | 0 | 1 | ```\ndef percentageLetter(self, s: str, letter: str) -> int:\n return ("%d" %(s.count(letter)/len(s)*100))\n``` | 4 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
Python simple one liner solution | percentage-of-letter-in-string | 0 | 1 | # Code\n```\nclass Solution:\n def percentageLetter(self, s: str, letter: str) -> int:\n return int((s.count(letter) / len(s)) * 100)\n```\n\nLike it ? Please upvote ! | 6 | Given a string `s` and a character `letter`, return _the **percentage** of characters in_ `s` _that equal_ `letter` _**rounded down** to the nearest whole percent._
**Example 1:**
**Input:** s = "foobar ", letter = "o "
**Output:** 33
**Explanation:**
The percentage of characters in s that equal the letter 'o' is 2 / 6 \* 100% = 33% when rounded down, so we return 33.
**Example 2:**
**Input:** s = "jjjj ", letter = "k "
**Output:** 0
**Explanation:**
The percentage of characters in s that equal the letter 'k' is 0%, so we return 0.
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter. | Notice that if a solution exists, we can represent them as x-1, x, x+1. What does this tell us about the number? Notice the sum of the numbers will be 3x. Can you solve for x? |
[Python] Priority queue; Explained | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | We just need to calculate the number of missing rocks for each of the bag;\nPlace the additional rocks into the bag that need the least number of rocks.\n\nWe can use a min heap/priority queue to sort the bags based on the missing rocks.\n\n```\nimport heapq\n\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], additionalRocks: int) -> int:\n missing_rocks = []\n num_full_bags = 0\n \n for idx, bag in enumerate(capacity):\n heapq.heappush(missing_rocks, bag - rocks[idx])\n \n while missing_rocks:\n additionalRocks -= heapq.heappop(missing_rocks)\n if additionalRocks >= 0:\n num_full_bags += 1\n \n return num_full_bags\n``` | 2 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Python 1-liner | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | We always want to fill the bags closest to being full, so sort bags by the number of spaces left. Then compute prefix sum to find cumulative number of spaces left. Finally, perform a binary search to find the index where our cumulative sum is <= the number of additional rocks.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\ndef maximumBags(self, capacity: List[int], rocks: List[int], additionalRocks: int) -> int:\n return bisect(list(accumulate(sorted([capacity[i] - rocks[i] for i in range(len(capacity))]))), additionalRocks)\n``` | 2 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Python | Functional Style and Readability | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | # Intuition\n\nIt\'s easiest to fill up bags that are closest to being full.\n\n# Approach\n\n1. First of all, find the `free` space in each bag as `capacity[i] - rocks[i]`. It is rather obvious that one can use `zip` to avoid iteration by index. You may further recall that `operator.sub` can perform subtraction. The tricky part is that `operator.sub` takes two args, whereas `zip` produces tuples with two elements, so instead of a usual `map` you need `itertools.starmap` to unpack the tuples produced by `zip`:\n\n```python\nfree = itertools.starmap(operator.sub, zip(capacity, rocks))\n```\n\n2. As explained in the intuition, the cheapest (in terms of additional rocks placed) way of filling `i` bags is to take `i` smallest values from `free`. Therefore, after sorting `free` the `cost` to fill `i` bags is the `i`-th prefix sum which can be computed with `itertools.accumulate`:\n\n```python\ncosts = itertools.accumulate(sorted(free))\n```\n\n3. Each prefix sum that is less than or equal to `additional_rocks` represents a bag that we can fill fully. It therefore remains to count the number of such prefix sums. `sum(map(can_fill, costs))` comes to mind. \n\n```python\nreturn sum(map(can_fill, costs))\n```\n\n4. `can_fill` should somehow express `additional_rocks >= cost` in a functional way. This is an example of a context-dependent expression. A general way to incorporate context in a function is `functools.partial` that captures some of the function\'s arguments from the environment. In our case the function is `>=` a.k.a. `operator.ge` and the argument to capture is `additional_rocks`:\n\n```python\ncan_fill = functools.partial(operator.ge, additional_rocks)\n```\n\n# Complexity\n\n- Time complexity: $$O(n \\log n)$$ for sorting. $$O(n)$$ for prefix sums.\n\n- Space complexity: $$O(n)$$ for sorting. $$O(1)$$ for prefix sums thanks to generators.\n\n# Code\n\n```python\nimport functools\nimport itertools\nimport operator\n\n\nclass Solution:\n def maximumBags(self, capacity: list[int], rocks: list[int],\n additional_rocks: int) -> int:\n free = itertools.starmap(operator.sub, zip(capacity, rocks))\n costs = itertools.accumulate(sorted(free))\n can_fill = functools.partial(operator.ge, additional_rocks)\n return sum(map(can_fill, costs))\n```\n\nI think that the above code has the optimal percentage of functional style. Note that defining additional variables doesn\'t hurt the performance thanks to generators. Some people will prefer the following "inlined" version:\n\n```python\nimport functools\nimport itertools\nimport operator\n\n\nclass Solution:\n def maximumBags(self, capacity: list[int], rocks: list[int],\n additional_rocks: int) -> int:\n return sum(map(\n functools.partial(\n operator.ge, \n additional_rocks\n ),\n itertools.accumulate(sorted(itertools.starmap(\n operator.sub,\n zip(capacity, rocks)\n )))\n ))\n```\n\nI still find the above code to be readable, but only barely. You can go further and convert it into a one-liner:\n\n```python\nclass Solution:\n def maximumBags(self, c: list[int], r: list[int], a: int) -> int:\n return sum(map(partial(ge, a), accumulate(sorted(starmap(sub, zip(c, r))))))\n```\n\nNow this definitely isn\'t readable, but it\'s fun so why not? Let me know which of the above versions you find the most readable in the comments down below!\n | 2 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Beats 100% | CodeDominar Solution | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | # Code\n```\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], additionalRocks: int) -> int:\n # Calculate the vacant space in each bag\n vacant = []\n for a, b in zip(capacity, rocks):\n vacant.append(a - b)\n\n # Sort the list of vacant spaces in ascending order\n vacant.sort()\n\n # Initialize a counter for the number of filled bags\n ans = 0\n\n # Iterate over the list of vacant spaces\n for i in range(len(vacant)):\n # If the current bag has no rocks, increment the counter\n if vacant[i] == 0:\n ans += 1\n # If the current bag has some rocks, check if there are enough additional rocks to fill it\n else:\n # If there are enough additional rocks, fill the bag and decrement the additional rocks counter\n if additionalRocks >= vacant[i]:\n additionalRocks -= vacant[i]\n ans += 1\n # If there are not enough additional rocks, break the loop and return the current count\n else:\n break\n return ans\n\n``` | 2 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Fastest PYTHON SOLUTION | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | # Intuition\nMy thought behind this logic is that I want to fill up the bags first that needs less additional rocks to full the bags\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIt\'s the greedy approach, sort the bags with their difference between full capacity and current filled amount \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(NlogN)\n\n- Space complexity:O(N)\n\n# Code\n```\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], additionalRocks: int) -> int:\n dif=[capacity[i]-rocks[i] for i in range(len(rocks))]\n dif.sort()\n ct=0\n for i in range(len(dif)):\n if additionalRocks==0:\n break\n if additionalRocks>=dif[i]:\n ct+=1\n additionalRocks-=dif[i]\n else:\n break\n return ct\n``` | 2 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Easy solution | O(nlogn) TC | O(1) SC | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | ```\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], additionalRocks: int) -> int:\n for i in range(len(capacity)):\n capacity[i] -= rocks[i]\n \n capacity.sort()\n for i in range(len(capacity)):\n if capacity[i] > additionalRocks:\n return i\n additionalRocks -= capacity[i]\n \n return len(capacity)\n``` | 4 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Python 3-lines efficient solution | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | # Intuition\nIt\'s easy\n\n# Approach\nSort difference, iterate while we can use additionalRocks\n\n# Complexity\n- Time complexity:\n$$O(N*logN)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], aRocks=1) -> int:\n bags, n, l = sorted(y-x for x,y in zip(rocks, capacity)), -1, len(rocks)\n while (n:=n+1) < l and aRocks >= bags[n]: aRocks -= bags[n]\n return n\n\n``` | 1 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
✅ 100% beats || Python3 || ☢️ Sort ☢️ || understandable code | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | Link submission:\nhttps://leetcode.com/problems/maximum-bags-with-full-capacity-of-rocks/submissions/1125068163\n\n# Intuition\nReceiving the maximum number of bags which fulled with rocks is involved in the problem.There are $$capacity$$ and $$rocks$$ lists given.The former represents the capasity of n bags in rocks. Additionally, $$additionalRocks$$ integer is given in order to fill bags with given extra rocks.The aim is to fill as much as bags we can.\n\n# Approach\n1. Firstly, we need to find the deficiency between current rocks in a bag and how much it can again receive, list comprehension and iterating in foor loop is alternative way for this process since both of $$capacity$$ and $$rocks$$ have the same length\n2. As all differences of bags are present during the process,number of all 0 differences added to a new created variable by using $$count$$ and then it involves to iterate difference list again with a view to get only over 0 difference.\n3. Iterating sorted difference list in ascending order enables substracting every difference from $$additionalRocks$$ and checking every iteration if there is left enough rocks to fill coming bag.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumBags(self, capacity: list[int], rocks: list[int], additionalRocks: int) -> int:\n rock = [capacity[x] - rocks[x] for x in range(len(capacity))]\n bags = rock.count(0)\n rock = [x for x in rock if x != 0]\n rock.sort()\n\n for x in rock:\n if not additionalRocks - x < 0:\n bags += 1\n additionalRocks -= x\n else:\n break\n\n return bags\n```\n\n\n | 1 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
2279. Maximum Bags With Full Capacity of Rocks --> Python easy Soln | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\nn is the size of rocks array\n\n# Code\n```\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], ar: int) -> int:\n dif=[]\n n=len(rocks)\n for i in range(n):\n dif.append(capacity[i]-rocks[i]) #Number of rocks required to get full\n\n dif.sort() #sorting it in ascending order so that minimum requirement bags are filled first so that we can fill maximum number of bags\n i=0\n ans=0\n while i<n and ar:\n if dif[i]<=ar:\n ans+=1\n ar-=dif[i]\n i+=1\n return ans\n\n``` | 1 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Python Solution Explained ✅ | O(n) | maximum-bags-with-full-capacity-of-rocks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the problem asks us for the count off filed bags it is better to create an array of difference between current and max capacity\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe first create an array `diffBag` which is the difference between `capacity` and `rocks`. \nThen we sort the `diffBag`.\nFinaly we count the nummber of bags that can be filled from the `additionalRocks` variable.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumBags(self, capacity: List[int], rocks: List[int], additionalRocks: int) -> int:\n \n diffBag = []\n # determine the difference betwin max capacity and current rocks\n for c, r in zip(capacity,rocks):\n diffBag.append(c-r)\n \n diffBag.sort()\n \n filledbags = 0\n #count bags that can be filed\n for f in diffBag:\n if f == 0:\n filledbags += 1\n continue\n \n if additionalRocks <= 0:\n return filledbags\n \n if f <= additionalRocks:\n filledbags += 1\n additionalRocks -= f\n \n return filledbags\n \n``` | 1 | You have `n` bags numbered from `0` to `n - 1`. You are given two **0-indexed** integer arrays `capacity` and `rocks`. The `ith` bag can hold a maximum of `capacity[i]` rocks and currently contains `rocks[i]` rocks. You are also given an integer `additionalRocks`, the number of additional rocks you can place in **any** of the bags.
Return _the **maximum** number of bags that could have full capacity after placing the additional rocks in some bags._
**Example 1:**
**Input:** capacity = \[2,3,4,5\], rocks = \[1,2,4,4\], additionalRocks = 2
**Output:** 3
**Explanation:**
Place 1 rock in bag 0 and 1 rock in bag 1.
The number of rocks in each bag are now \[2,3,4,4\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that there may be other ways of placing the rocks that result in an answer of 3.
**Example 2:**
**Input:** capacity = \[10,2,2\], rocks = \[2,2,0\], additionalRocks = 100
**Output:** 3
**Explanation:**
Place 8 rocks in bag 0 and 2 rocks in bag 2.
The number of rocks in each bag are now \[10,2,2\].
Bags 0, 1, and 2 have full capacity.
There are 3 bags at full capacity, so we return 3.
It can be shown that it is not possible to have more than 3 bags at full capacity.
Note that we did not use all of the additional rocks.
**Constraints:**
* `n == capacity.length == rocks.length`
* `1 <= n <= 5 * 104`
* `1 <= capacity[i] <= 109`
* `0 <= rocks[i] <= capacity[i]`
* `1 <= additionalRocks <= 109` | First, check if finalSum is divisible by 2. If it isn’t, then we cannot split it into even integers. Let k be the number of elements in our split. As we want the maximum number of elements, we should try to use the first k - 1 even elements to grow our sum as slowly as possible. Thus, we find the maximum sum of the first k - 1 even elements which is less than finalSum. We then add the difference over to the kth element. |
Python Easy Solution || Cross Product | minimum-lines-to-represent-a-line-chart | 0 | 1 | # Code\n```\nclass Solution:\n def minimumLines(self, stockPrices: List[List[int]]) -> int:\n stockPrices.sort()\n line=1\n if len(stockPrices)==1:\n return 0\n for i in range(1,len(stockPrices)-1):\n if (stockPrices[i][1]-stockPrices[i-1][1])*(stockPrices[i+1][0]-stockPrices[i][0])!=(stockPrices[i+1][1]-stockPrices[i][1])*(stockPrices[i][0]-stockPrices[i-1][0]):\n line+=1\n return line\n``` | 1 | You are given a 2D integer array `stockPrices` where `stockPrices[i] = [dayi, pricei]` indicates the price of the stock on day `dayi` is `pricei`. A **line chart** is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:
Return _the **minimum number of lines** needed to represent the line chart_.
**Example 1:**
**Input:** stockPrices = \[\[1,7\],\[2,6\],\[3,5\],\[4,4\],\[5,4\],\[6,3\],\[7,2\],\[8,1\]\]
**Output:** 3
**Explanation:**
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.
**Example 2:**
**Input:** stockPrices = \[\[3,4\],\[1,2\],\[7,8\],\[2,3\]\]
**Output:** 1
**Explanation:**
As shown in the diagram above, the line chart can be represented with a single line.
**Constraints:**
* `1 <= stockPrices.length <= 105`
* `stockPrices[i].length == 2`
* `1 <= dayi, pricei <= 109`
* All `dayi` are **distinct**. | For every value y, how can you find the number of values x (0 ≤ x, y ≤ n - 1) such that x appears before y in both of the arrays? Similarly, for every value y, try finding the number of values z (0 ≤ y, z ≤ n - 1) such that z appears after y in both of the arrays. Now, for every value y, count the number of good triplets that can be formed if y is considered as the middle element. |
Python | Easy to Understand | minimum-lines-to-represent-a-line-chart | 0 | 1 | ```\nclass Solution:\n def minimumLines(self, stockPrices: List[List[int]]) -> int:\n # key point: never use devision to judge whether 3 points are on a same line or not, use the multiplication instead !!\n \n n = len(stockPrices)\n stockPrices.sort(key = lambda x: (x[0], x[1]))\n \n if n == 1:\n return 0\n \n pre_delta_y = stockPrices[0][1] - stockPrices[1][1]\n pre_delta_x = stockPrices[0][0] - stockPrices[1][0]\n num = 1\n \n for i in range(1, n-1):\n cur_delta_y = stockPrices[i][1] - stockPrices[i+1][1]\n cur_delta_x = stockPrices[i][0] - stockPrices[i+1][0]\n \n if pre_delta_y * cur_delta_x != pre_delta_x * cur_delta_y:\n num += 1\n pre_delta_x = cur_delta_x\n pre_delta_y = cur_delta_y\n \n return num | 12 | You are given a 2D integer array `stockPrices` where `stockPrices[i] = [dayi, pricei]` indicates the price of the stock on day `dayi` is `pricei`. A **line chart** is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:
Return _the **minimum number of lines** needed to represent the line chart_.
**Example 1:**
**Input:** stockPrices = \[\[1,7\],\[2,6\],\[3,5\],\[4,4\],\[5,4\],\[6,3\],\[7,2\],\[8,1\]\]
**Output:** 3
**Explanation:**
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.
**Example 2:**
**Input:** stockPrices = \[\[3,4\],\[1,2\],\[7,8\],\[2,3\]\]
**Output:** 1
**Explanation:**
As shown in the diagram above, the line chart can be represented with a single line.
**Constraints:**
* `1 <= stockPrices.length <= 105`
* `stockPrices[i].length == 2`
* `1 <= dayi, pricei <= 109`
* All `dayi` are **distinct**. | For every value y, how can you find the number of values x (0 ≤ x, y ≤ n - 1) such that x appears before y in both of the arrays? Similarly, for every value y, try finding the number of values z (0 ≤ y, z ≤ n - 1) such that z appears after y in both of the arrays. Now, for every value y, count the number of good triplets that can be formed if y is considered as the middle element. |
PYTHON SIMPLE SOLUTION | EASY TO UNDERSTAND LOGIC | SORTING | minimum-lines-to-represent-a-line-chart | 0 | 1 | ```\nclass Solution:\n def minimumLines(self, stockPrices: List[List[int]]) -> int:\n if len(stockPrices) == 1:\n return 0\n stockPrices.sort(key = lambda x: x[0])\n ans = 1\n for i in range(1,len(stockPrices)-1):\n if (stockPrices[i+1][1]-stockPrices[i][1])*(stockPrices[i][0]-stockPrices[i-1][0]) != (stockPrices[i+1][0]-stockPrices[i][0])*(stockPrices[i][1]-stockPrices[i-1][1]):\n ans += 1\n return ans\n``` | 2 | You are given a 2D integer array `stockPrices` where `stockPrices[i] = [dayi, pricei]` indicates the price of the stock on day `dayi` is `pricei`. A **line chart** is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:
Return _the **minimum number of lines** needed to represent the line chart_.
**Example 1:**
**Input:** stockPrices = \[\[1,7\],\[2,6\],\[3,5\],\[4,4\],\[5,4\],\[6,3\],\[7,2\],\[8,1\]\]
**Output:** 3
**Explanation:**
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.
**Example 2:**
**Input:** stockPrices = \[\[3,4\],\[1,2\],\[7,8\],\[2,3\]\]
**Output:** 1
**Explanation:**
As shown in the diagram above, the line chart can be represented with a single line.
**Constraints:**
* `1 <= stockPrices.length <= 105`
* `stockPrices[i].length == 2`
* `1 <= dayi, pricei <= 109`
* All `dayi` are **distinct**. | For every value y, how can you find the number of values x (0 ≤ x, y ≤ n - 1) such that x appears before y in both of the arrays? Similarly, for every value y, try finding the number of values z (0 ≤ y, z ≤ n - 1) such that z appears after y in both of the arrays. Now, for every value y, count the number of good triplets that can be formed if y is considered as the middle element. |
Python Solution || O(nlogn) | minimum-lines-to-represent-a-line-chart | 0 | 1 | ```\nfrom fractions import Fraction # For larger values it will give accurate answer\nclass Solution:\n def minimumLines(self, stockPrices: List[List[int]]) -> int:\n l=[]\n stockPrices.sort()\n c=None\n k=0\n for i,j in pairwise(stockPrices):\n x=Fraction(j[1]-i[1],j[0]-i[0]) #(j[1]-i[1]) // (j[0]-i[0])\n if x!=c:\n k+=1\n c=x\n return k\n```\n\n***Please Upvote if it helps.*** | 1 | You are given a 2D integer array `stockPrices` where `stockPrices[i] = [dayi, pricei]` indicates the price of the stock on day `dayi` is `pricei`. A **line chart** is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:
Return _the **minimum number of lines** needed to represent the line chart_.
**Example 1:**
**Input:** stockPrices = \[\[1,7\],\[2,6\],\[3,5\],\[4,4\],\[5,4\],\[6,3\],\[7,2\],\[8,1\]\]
**Output:** 3
**Explanation:**
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.
**Example 2:**
**Input:** stockPrices = \[\[3,4\],\[1,2\],\[7,8\],\[2,3\]\]
**Output:** 1
**Explanation:**
As shown in the diagram above, the line chart can be represented with a single line.
**Constraints:**
* `1 <= stockPrices.length <= 105`
* `stockPrices[i].length == 2`
* `1 <= dayi, pricei <= 109`
* All `dayi` are **distinct**. | For every value y, how can you find the number of values x (0 ≤ x, y ≤ n - 1) such that x appears before y in both of the arrays? Similarly, for every value y, try finding the number of values z (0 ≤ y, z ≤ n - 1) such that z appears after y in both of the arrays. Now, for every value y, count the number of good triplets that can be formed if y is considered as the middle element. |
This problem needs to labelled as "banished at interviews", "Ok for education/competions" | sum-of-total-strength-of-wizards | 0 | 1 | # Intuition(what I think about this problem)\n\nI think there should be a label on such problems like "Educational" or something like "Not a great interview problem unless you have 2 hours". I think the idea of asking coding problems at interviews should be to test weather a candidate can come up with multiple solutions each with differenet complexities and trade-offs to solve a problem. Yes one approach can borrow bits from the previous approach, but not use entirely new and overtly difficult ideas to get to a better solution.\n\nThere is really ONLY ONE way to do it in O(n) and on top of that you need to have 2-3 big intuitive leaps to get there. There seems to be no middle ground to solve this problem easily and no easy way to get from O(n^2) -> O(n log n) let alone O(n). There is no way to tradeoff more space to gain time unless you use a DP or combine other difficult concepts like Sparse Arrays and Binary trees which have overhead of their own. This problem allows for very little of that kind of thinking. \n\nUnless you know of some of these ideas upfront there is no way you can solve this in < 40 mins in an interview. \n\n# Approach(why do I feel this way)\n\nLeetCode\'s own submission data for approaches other than using prefix sums and monostacks demonstrates this problem. The only alternate solutions I could find that are not quite using the prefix sum approach were pretty hard DP ones (DP, mind you, is banned from some interview process like meta):\n\nhttps://leetcode.com/problems/sum-of-total-strength-of-wizards/solutions/2067907/bad-but-cool-and-educational-dp-solution/\n\nhttps://leetcode.com/problems/sum-of-total-strength-of-wizards/solutions/2062288/c-similar-as-lc907-one-pass-o-n-two-dp-simple-solution-with-explanation/\n\nThis one uses Binary trees and Sparse arrays(what!):\nhttps://leetcode.com/problems/sum-of-total-strength-of-wizards/solutions/3360654/c-sparse-table-prefix-sum-binary-search-o-n-log-n/\n\nConstructive Feedback: Submission data can also be a good way to summarize how many ways there are to solve a problem and how complex it is. And then to tag them as such to warn others befoe they try to solve such problems.\n\n# Complexity\n- Time complexity:\nO(n) if you can manage to convince yourself and the interviewer of the prefix sum and monotonic stack approach\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n """\n This is the editorial solution. NOT MINE.\n """\n def totalStrength(self, strength: List[int]) -> int:\n mod, n = 10 ** 9 + 7, len(strength)\n \n # Get the first index of the non-larger value to strength[i]\'s right.\n right_index = [n] * n\n stack = []\n for i in range(n):\n while stack and strength[stack[-1]] >= strength[i]:\n right_index[stack.pop()] = i\n stack.append(i)\n\n # Get the first index of the smaller value to strength[i]\'s left.\n left_index = [-1] * n\n stack = []\n for i in range(n - 1, -1, -1):\n while stack and strength[stack[-1]] > strength[i]:\n left_index[stack.pop()] = i\n stack.append(i)\n \n # prefix sum of the prefix sum array of strength.\n presum_of_presum = list(accumulate(accumulate(strength, initial = 0), initial = 0))\n answer = 0\n # For each element in strength, we get the value of R_term - L_term.\n for i in range(n):\n # Get the left index and the right index.\n left_bound = left_index[i]\n right_bound = right_index[i]\n \n # Get the left_count and right_count (marked as L and R in the previous slides)\n left_count = i - left_bound\n right_count = right_bound - i\n \n # Get positive presum and the negative presum.\n neg_presum = (presum_of_presum[i + 1] - presum_of_presum[i - left_count + 1]) % mod\n pos_presum = (presum_of_presum[i + right_count + 1] - presum_of_presum[i + 1]) % mod\n \n # The total strength of all subarrays that have strength[i] as the minimum.\n answer += strength[i] * (pos_presum * left_count - neg_presum * right_count)\n answer %= mod\n \n return answer\n``` | 1 | As the ruler of a kingdom, you have an army of wizards at your command.
You are given a **0-indexed** integer array `strength`, where `strength[i]` denotes the strength of the `ith` wizard. For a **contiguous** group of wizards (i.e. the wizards' strengths form a **subarray** of `strength`), the **total strength** is defined as the **product** of the following two values:
* The strength of the **weakest** wizard in the group.
* The **total** of all the individual strengths of the wizards in the group.
Return _the **sum** of the total strengths of **all** contiguous groups of wizards_. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** strength = \[1,3,1,2\]
**Output:** 44
**Explanation:** The following are all the contiguous groups of wizards:
- \[1\] from \[**1**,3,1,2\] has a total strength of min(\[1\]) \* sum(\[1\]) = 1 \* 1 = 1
- \[3\] from \[1,**3**,1,2\] has a total strength of min(\[3\]) \* sum(\[3\]) = 3 \* 3 = 9
- \[1\] from \[1,3,**1**,2\] has a total strength of min(\[1\]) \* sum(\[1\]) = 1 \* 1 = 1
- \[2\] from \[1,3,1,**2**\] has a total strength of min(\[2\]) \* sum(\[2\]) = 2 \* 2 = 4
- \[1,3\] from \[**1,3**,1,2\] has a total strength of min(\[1,3\]) \* sum(\[1,3\]) = 1 \* 4 = 4
- \[3,1\] from \[1,**3,1**,2\] has a total strength of min(\[3,1\]) \* sum(\[3,1\]) = 1 \* 4 = 4
- \[1,2\] from \[1,3,**1,2**\] has a total strength of min(\[1,2\]) \* sum(\[1,2\]) = 1 \* 3 = 3
- \[1,3,1\] from \[**1,3,1**,2\] has a total strength of min(\[1,3,1\]) \* sum(\[1,3,1\]) = 1 \* 5 = 5
- \[3,1,2\] from \[1,**3,1,2**\] has a total strength of min(\[3,1,2\]) \* sum(\[3,1,2\]) = 1 \* 6 = 6
- \[1,3,1,2\] from \[**1,3,1,2**\] has a total strength of min(\[1,3,1,2\]) \* sum(\[1,3,1,2\]) = 1 \* 7 = 7
The sum of all the total strengths is 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44.
**Example 2:**
**Input:** strength = \[5,4,6\]
**Output:** 213
**Explanation:** The following are all the contiguous groups of wizards:
- \[5\] from \[**5**,4,6\] has a total strength of min(\[5\]) \* sum(\[5\]) = 5 \* 5 = 25
- \[4\] from \[5,**4**,6\] has a total strength of min(\[4\]) \* sum(\[4\]) = 4 \* 4 = 16
- \[6\] from \[5,4,**6**\] has a total strength of min(\[6\]) \* sum(\[6\]) = 6 \* 6 = 36
- \[5,4\] from \[**5,4**,6\] has a total strength of min(\[5,4\]) \* sum(\[5,4\]) = 4 \* 9 = 36
- \[4,6\] from \[5,**4,6**\] has a total strength of min(\[4,6\]) \* sum(\[4,6\]) = 4 \* 10 = 40
- \[5,4,6\] from \[**5,4,6**\] has a total strength of min(\[5,4,6\]) \* sum(\[5,4,6\]) = 4 \* 15 = 60
The sum of all the total strengths is 25 + 16 + 36 + 36 + 40 + 60 = 213.
**Constraints:**
* `1 <= strength.length <= 105`
* `1 <= strength[i] <= 109` | null |
[Python] "Geometric" Solution | sum-of-total-strength-of-wizards | 0 | 1 | # Intuition\nI thought it would be fun to do an array-based solution that does not utilize a conventional stack approach. It isn\'t the fastest but I find it interesting. \n# Approach\nThe number of occurrences of a value across all contiguous subarrays is given with position index array $$pos$$ is given by:\n\n$$count = (1-median(pos))^2+max(pos)-(pos-median(pos))^2$$\n\nGraphically this looks something like: \n\n\n\n\nThe number of occurences of values that in contiguous subarrays that contain some value at some position $$focus$$ is given by a triangular function of peak $$count[focus]$$ with a rising leg from the nearest zero to the left of $$focus$$ and falling leg from the peak to the neartest zero to the right of $$focus$$. See the "build_line" function below. They look something like this:\n\n\n\nWith these two functions established, all we need to do is start with $$counts$$, select the largest strength value, determine the $$linevec$$ at that strength value, calculate strength as:\n\n$$strength_{total} = strength_{total} + \\Sigma(linevec*strength)*strength[focus]$$\n\nand the new counts is just:\n\n$$counts=counts-linevec$$\n\nWhich after the first pass may look like: \n\n\nThen we just repeat for the next largest strength and so on. \n\nThis solution works, but the main issue is that building these triangles isn\'t as fast as I would hope. \n\n# Code\n```\nimport numpy as np\n\nclass Solution:\n def build_line(self,counts, focus):\n lins = np.zeros(len(counts),dtype="int64")\n left_zeros = 0\n for i in range(focus-1, -1, -1):\n if counts[i] == 0:\n left_zeros = i + 1\n break\n left_dt = counts[focus] // (focus + 1 - left_zeros) # use integer division\n lins[(left_zeros):(focus+1)] = range(counts[focus] - ((focus-left_zeros + 1)- 1) * left_dt,counts[focus]+1,left_dt)\n \n right_zeros = len(counts) + 1\n for i in range(focus, len(counts)):\n if counts[i] == 0:\n right_zeros = i + 1\n break\n right_dt = counts[focus] // (right_zeros - focus - 1) # use integer division\n lins[focus:(right_zeros)] = range(counts[focus],counts[focus] - (right_zeros-focus-1) * right_dt - 1,-right_dt)[:len(lins[focus:(right_zeros+1)])]\n return lins\n \n def totalStrength(self, strength: List[int]) -> int:\n strength_sum = 0\n nparr=np.arange(1, len(strength) + 1)\n npmed=np.median(nparr)\n\n counts = np.array((1 - npmed) ** 2 + len(strength) - (nparr - npmed) ** 2,dtype="int64")\n mod = 10 ** 9 + 7\n strength=np.array(strength,dtype="int64")\n for focus in np.argsort(strength):\n linevec = self.build_line(counts, focus)\n strength_sum = strength_sum + np.dot(strength,linevec) * strength[focus]\n counts = counts - linevec\n \n return (int(strength_sum) % mod)\n``` | 1 | As the ruler of a kingdom, you have an army of wizards at your command.
You are given a **0-indexed** integer array `strength`, where `strength[i]` denotes the strength of the `ith` wizard. For a **contiguous** group of wizards (i.e. the wizards' strengths form a **subarray** of `strength`), the **total strength** is defined as the **product** of the following two values:
* The strength of the **weakest** wizard in the group.
* The **total** of all the individual strengths of the wizards in the group.
Return _the **sum** of the total strengths of **all** contiguous groups of wizards_. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** strength = \[1,3,1,2\]
**Output:** 44
**Explanation:** The following are all the contiguous groups of wizards:
- \[1\] from \[**1**,3,1,2\] has a total strength of min(\[1\]) \* sum(\[1\]) = 1 \* 1 = 1
- \[3\] from \[1,**3**,1,2\] has a total strength of min(\[3\]) \* sum(\[3\]) = 3 \* 3 = 9
- \[1\] from \[1,3,**1**,2\] has a total strength of min(\[1\]) \* sum(\[1\]) = 1 \* 1 = 1
- \[2\] from \[1,3,1,**2**\] has a total strength of min(\[2\]) \* sum(\[2\]) = 2 \* 2 = 4
- \[1,3\] from \[**1,3**,1,2\] has a total strength of min(\[1,3\]) \* sum(\[1,3\]) = 1 \* 4 = 4
- \[3,1\] from \[1,**3,1**,2\] has a total strength of min(\[3,1\]) \* sum(\[3,1\]) = 1 \* 4 = 4
- \[1,2\] from \[1,3,**1,2**\] has a total strength of min(\[1,2\]) \* sum(\[1,2\]) = 1 \* 3 = 3
- \[1,3,1\] from \[**1,3,1**,2\] has a total strength of min(\[1,3,1\]) \* sum(\[1,3,1\]) = 1 \* 5 = 5
- \[3,1,2\] from \[1,**3,1,2**\] has a total strength of min(\[3,1,2\]) \* sum(\[3,1,2\]) = 1 \* 6 = 6
- \[1,3,1,2\] from \[**1,3,1,2**\] has a total strength of min(\[1,3,1,2\]) \* sum(\[1,3,1,2\]) = 1 \* 7 = 7
The sum of all the total strengths is 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44.
**Example 2:**
**Input:** strength = \[5,4,6\]
**Output:** 213
**Explanation:** The following are all the contiguous groups of wizards:
- \[5\] from \[**5**,4,6\] has a total strength of min(\[5\]) \* sum(\[5\]) = 5 \* 5 = 25
- \[4\] from \[5,**4**,6\] has a total strength of min(\[4\]) \* sum(\[4\]) = 4 \* 4 = 16
- \[6\] from \[5,4,**6**\] has a total strength of min(\[6\]) \* sum(\[6\]) = 6 \* 6 = 36
- \[5,4\] from \[**5,4**,6\] has a total strength of min(\[5,4\]) \* sum(\[5,4\]) = 4 \* 9 = 36
- \[4,6\] from \[5,**4,6**\] has a total strength of min(\[4,6\]) \* sum(\[4,6\]) = 4 \* 10 = 40
- \[5,4,6\] from \[**5,4,6**\] has a total strength of min(\[5,4,6\]) \* sum(\[5,4,6\]) = 4 \* 15 = 60
The sum of all the total strengths is 25 + 16 + 36 + 36 + 40 + 60 = 213.
**Constraints:**
* `1 <= strength.length <= 105`
* `1 <= strength[i] <= 109` | null |
Python simplest O(n) full derivation | sum-of-total-strength-of-wizards | 0 | 1 | Let `s = strength`, `p[k]=s[0] + ... + s[k]` be the prefix sum of `s`, `pp[k]=p[0] + ... + p[k]` be the sum of prefix sums. We want to derive `t[k]` denoting total sum of strengths of wizards ending at index `k`. We would like to keep indices of `s` minimums in monotonic increasing stack e.g. `s = [1, 2, 3, 2, 5]` then `incr_stack = [0, 1, 3, 4]` (we could get rid of one of the 2s but not doing it simplifies code). We consider two cases \n\n1. we know `t[k]` and `s` at next index `s[k+1] > s[k]` then we calculate `t[k+1]` as follows:\n\n\n\nand append `s[k+1]` to `incr_stack`. \n\n2. Otherwise, we consider what happens if `s[l+1] < s[l]`. Then some of the values at indices in incr_stack ought to be popped out. We derive the equation for `t[l+1]` below:\n\n\n\n\nWe notice that in both cases we need to track sum of minimums for previous indices. Now we can write the code. \n\n```\nclass Solution:\n def totalStrength(self, strength: List[int]) -> int:\n \n s = strength\n \n p_sum = [s[0]]\n pp_sum = [p_sum[0]]\n for i in range(1, len(s)):\n p_sum.append((s[i] + p_sum[-1]))\n pp_sum.append((p_sum[i] + pp_sum[-1]))\n \n # we add two zeros so that when we access pp_sum[-2] (incorrectly) we get zero - this simplifies equations below\n pp_sum = pp_sum + [0, 0]\n \n # we add -1 so that we can know how many indices are from idx 0 \n # by incr_stack[-1] - incr_stack[-2] when incr_stack[-1] == 0\n incr_stack = [-1, 0]\n\n t = [0]*len(s)\n t[0] = s[0]**2\n t = t + [0]\n \n minimum_sum = s[0]\n total_sum = s[0]**2 % (10**9 + 7)\n \n for i in range(1, len(s)):\n # case 1\n if incr_stack[-1] == -1 or s[i] > s[incr_stack[-1]]:\n minimum_sum += s[i]\n t[i] = t[i-1] + minimum_sum * s[i]\n \n incr_stack.append(i)\n # case 2\n else:\n new_min_part = 0\n \n # because we have new minimum some minimums in stack are \n # no longer minimums so we need to update\n while incr_stack[-1] != -1 and s[incr_stack[-1]] > s[i]:\n last = incr_stack.pop()\n minimum_sum -= (last - incr_stack[-1]) * s[last]\n new_min_part += (last - incr_stack[-1]) * s[i]\n\n t[i] = t[incr_stack[-1]] + \\\n (p_sum[i] - p_sum[incr_stack[-1]]) * minimum_sum + \\\n s[i] * ((i - incr_stack[-1])*p_sum[i] - (pp_sum[i-1] - pp_sum[incr_stack[-1]-1]))\n \n minimum_sum += new_min_part + s[i]\n incr_stack.append(i)\n \n total_sum = (total_sum + t[i]) % (10**9 + 7)\n\n return total_sum\n``` | 0 | As the ruler of a kingdom, you have an army of wizards at your command.
You are given a **0-indexed** integer array `strength`, where `strength[i]` denotes the strength of the `ith` wizard. For a **contiguous** group of wizards (i.e. the wizards' strengths form a **subarray** of `strength`), the **total strength** is defined as the **product** of the following two values:
* The strength of the **weakest** wizard in the group.
* The **total** of all the individual strengths of the wizards in the group.
Return _the **sum** of the total strengths of **all** contiguous groups of wizards_. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** strength = \[1,3,1,2\]
**Output:** 44
**Explanation:** The following are all the contiguous groups of wizards:
- \[1\] from \[**1**,3,1,2\] has a total strength of min(\[1\]) \* sum(\[1\]) = 1 \* 1 = 1
- \[3\] from \[1,**3**,1,2\] has a total strength of min(\[3\]) \* sum(\[3\]) = 3 \* 3 = 9
- \[1\] from \[1,3,**1**,2\] has a total strength of min(\[1\]) \* sum(\[1\]) = 1 \* 1 = 1
- \[2\] from \[1,3,1,**2**\] has a total strength of min(\[2\]) \* sum(\[2\]) = 2 \* 2 = 4
- \[1,3\] from \[**1,3**,1,2\] has a total strength of min(\[1,3\]) \* sum(\[1,3\]) = 1 \* 4 = 4
- \[3,1\] from \[1,**3,1**,2\] has a total strength of min(\[3,1\]) \* sum(\[3,1\]) = 1 \* 4 = 4
- \[1,2\] from \[1,3,**1,2**\] has a total strength of min(\[1,2\]) \* sum(\[1,2\]) = 1 \* 3 = 3
- \[1,3,1\] from \[**1,3,1**,2\] has a total strength of min(\[1,3,1\]) \* sum(\[1,3,1\]) = 1 \* 5 = 5
- \[3,1,2\] from \[1,**3,1,2**\] has a total strength of min(\[3,1,2\]) \* sum(\[3,1,2\]) = 1 \* 6 = 6
- \[1,3,1,2\] from \[**1,3,1,2**\] has a total strength of min(\[1,3,1,2\]) \* sum(\[1,3,1,2\]) = 1 \* 7 = 7
The sum of all the total strengths is 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44.
**Example 2:**
**Input:** strength = \[5,4,6\]
**Output:** 213
**Explanation:** The following are all the contiguous groups of wizards:
- \[5\] from \[**5**,4,6\] has a total strength of min(\[5\]) \* sum(\[5\]) = 5 \* 5 = 25
- \[4\] from \[5,**4**,6\] has a total strength of min(\[4\]) \* sum(\[4\]) = 4 \* 4 = 16
- \[6\] from \[5,4,**6**\] has a total strength of min(\[6\]) \* sum(\[6\]) = 6 \* 6 = 36
- \[5,4\] from \[**5,4**,6\] has a total strength of min(\[5,4\]) \* sum(\[5,4\]) = 4 \* 9 = 36
- \[4,6\] from \[5,**4,6**\] has a total strength of min(\[4,6\]) \* sum(\[4,6\]) = 4 \* 10 = 40
- \[5,4,6\] from \[**5,4,6**\] has a total strength of min(\[5,4,6\]) \* sum(\[5,4,6\]) = 4 \* 15 = 60
The sum of all the total strengths is 25 + 16 + 36 + 36 + 40 + 60 = 213.
**Constraints:**
* `1 <= strength.length <= 105`
* `1 <= strength[i] <= 109` | null |
[Easty Python ] | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- wrost O(N^2)\n- best O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def digitCount(self, s: str) -> bool:\n for i in range(len(s)):\n c=s.count(str(i))\n if c==int(s[i]):\n continue\n else:\n return False\n return True\n\n``` | 1 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Easy Python3 Solution using Count | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | \n# Code\n```\nclass Solution:\n def digitCount(self, num: str) -> bool:\n for i in range(len(num)):\n if int(num[i]) != num.count(str(i)):\n return False\n return True\n``` | 7 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Python Beginner Friendly Explanation Beats - 91% | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | # Approach\nSimple Compare the count of current index with value at corrent index\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def digitCount(self, num: str) -> bool:\n for i in range(len(num)):\n if num.count(str(i)) != int(num[i]):\n return False\n return True \n``` | 1 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Easy Python solution | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def digitCount(self, num: str) -> bool:\n for i in range(len(num)):\n if num.count(str(i)) != int(num[i]):\n return False\n return True \n``` | 1 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Easy approach for beginners : time complexity : O(n) | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def digitCount(self, num: str) -> bool:\n for i in range(len(num)):\n if num.count(str(i))!=int(num[i]):\n return False\n return True\n``` | 1 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Easy Python Solution | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | ```\ndef digitCount(self, num: str) -> bool:\n for i in range(len(num)):\n if num.count(str(i))!=int(num[i]):\n return False\n return True\n``` | 4 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Python3 very elegant and straightforward | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | \n```\n c = Counter(num)\n for idx, x in enumerate(num):\n if c[str(idx)] != int(x):\n return False\n return True\n``` | 2 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.