title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python||Greedy||Fast||Easy to undestand|| With explanations | longest-binary-subsequence-less-than-or-equal-to-k | 0 | 1 | 1. As the answer is a **subsequence** then we understand that we MUST get ALL zeroes from string to maximize the answer(it depends on length)\n2. Another greedy thing to consider is position of 1 in a binary representation and the greedy thing -> we must decrease the k starting by least position of 1\n\n```\nclass Solution:\n def longestSubsequence(self, s: str, k: int) -> int:\n n = len(s)\n ones = []\n\t\t# Notice how I reversed the string,\n\t\t# because the binary representation is written from greatest value of 2**n\n for i, val in enumerate(s[::-1]):\n if val == \'1\':\n ones.append(i)\n\t\t# Initialize ans, there are already number of zeroes (num_of_zeroes = len(nums) - len(ones)\n ans = n - len(ones)\n i = 0\n\t\t# imagine k == 5 and binary string 001011\n\t\t# ones = [0, 1, 3]\n\t\t# first loop: 5 - 2**0 -> 4, ans += 1\n\t\t# second loop: 4 - 2**1 -> 2, ans +=1\n\t\t# Third loop does not occur because 2 - 2**3 -> -6 which is less than zero\n\t\t# So the ans is 3 + 2 = 5\n while i < len(ones) and k - 2 ** ones[i] >= 0:\n ans += 1\n k -= 2 ** ones[i]\n i += 1\n\t\n return ans\n``` | 6 | You are given a binary string `s` and a positive integer `k`.
Return _the length of the **longest** subsequence of_ `s` _that makes up a **binary** number less than or equal to_ `k`.
Note:
* The subsequence can contain **leading zeroes**.
* The empty string is considered to be equal to `0`.
* A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
**Example 1:**
**Input:** s = "1001010 ", k = 5
**Output:** 5
**Explanation:** The longest subsequence of s that makes up a binary number less than or equal to 5 is "00010 ", as this number is equal to 2 in decimal.
Note that "00100 " and "00101 " are also possible, which are equal to 4 and 5 in decimal, respectively.
The length of this subsequence is 5, so 5 is returned.
**Example 2:**
**Input:** s = "00101001 ", k = 1
**Output:** 6
**Explanation:** "000001 " is the longest subsequence of s that makes up a binary number less than or equal to 1, as this number is equal to 1 in decimal.
The length of this subsequence is 6, so 6 is returned.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 109` | Can you think of a DP solution? Let DP[i][j] denote the minimum number of white tiles still visible from indices i to floor.length-1 after covering with at most j carpets. The transition will be whether to put down the carpet at position i (if possible), or not. |
✅Python || Easy Approach || beats 90.00% Runtime | longest-binary-subsequence-less-than-or-equal-to-k | 0 | 1 | ```\nclass Solution:\n def longestSubsequence(self, s: str, k: int) -> int:\n \n ans = 0\n n = len(s)\n \n if k > int(s, 2):\n return n\n \n for i in range(n):\n if int(s[n - 1 - i:], 2) > k:\n curr = i\n break\n \n if i == n - 1:\n return n\n\n ans = i + s[:n - i].count("0")\n \n return ans\n``` | 2 | You are given a binary string `s` and a positive integer `k`.
Return _the length of the **longest** subsequence of_ `s` _that makes up a **binary** number less than or equal to_ `k`.
Note:
* The subsequence can contain **leading zeroes**.
* The empty string is considered to be equal to `0`.
* A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
**Example 1:**
**Input:** s = "1001010 ", k = 5
**Output:** 5
**Explanation:** The longest subsequence of s that makes up a binary number less than or equal to 5 is "00010 ", as this number is equal to 2 in decimal.
Note that "00100 " and "00101 " are also possible, which are equal to 4 and 5 in decimal, respectively.
The length of this subsequence is 5, so 5 is returned.
**Example 2:**
**Input:** s = "00101001 ", k = 1
**Output:** 6
**Explanation:** "000001 " is the longest subsequence of s that makes up a binary number less than or equal to 1, as this number is equal to 1 in decimal.
The length of this subsequence is 6, so 6 is returned.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= k <= 109` | Can you think of a DP solution? Let DP[i][j] denote the minimum number of white tiles still visible from indices i to floor.length-1 after covering with at most j carpets. The transition will be whether to put down the carpet at position i (if possible), or not. |
Simple Python Solution with explanation 🔥 | selling-pieces-of-wood | 0 | 1 | # Approach\n\n* Price Map -> \n\n Since prices is a list, it is costly to fetch the price of a specific height `h` and width `w`. \n Lets convert it to a map: `priceMap` where the first order key is height and second order key is width.\n\n ```\n height: h1\n width: w1\n price: priceMap[h1][w1]\n ```\n\n* Recursive approach ->\n\n Lets say we have a rectangle of height `h` and width `w`, \n\n * first, lets check if there is any price in our `priceMap` for this rectangle configuration (or initialise it to zero)\n * now lets say we make a horizontal cut, so that it divides the rectangle in two rectangles:\n Rectangle 1: height: `h1`, width: `w`\n Rectangle 2: height: `h-h1`, width: `w`\n\n \n * lets check where can we make a cut so that we get the maximum price, `h1` can be anywhere between `[1, h-1]` (inclusive)\n we will recursively check for each of this rectangle, and maximise the amount\n ```\n money = max(\n money, \n rec(h1, w) + rec(h-h1, w)\n )\n ```\n\n do the same vertically\n\n\n# Complexity\n- Time complexity:\n$$O(m * n)$$\n\n- Space complexity:\n$$O(m * n)$$ -> memoization and priceMap\n\n# Code\n```\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n\n priceMap = {}\n for p in prices:\n if p[0] in priceMap:\n priceMap[p[0]][p[1]] = p[2]\n else:\n priceMap[p[0]] = {p[1]: p[2]}\n\n def getPrice(h, w):\n if h in priceMap and w in priceMap[h]:\n return priceMap[h][w]\n return 0\n\n @cache\n def rec(h, w):\n money = getPrice(h, w)\n\n # cut horizontal\n for i in range(1, h):\n money = max(money, rec(i, w) + rec(h - i, w))\n\n # cut vertical\n for i in range(1, w):\n money = max(money, rec(h, i) + rec(h, w - i))\n\n return money\n\n return rec(m, n)\n\n``` | 3 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
Python bottom up DP faster than 99% | selling-pieces-of-wood | 0 | 1 | ```\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n dp = [[0]*(n+1) for _ in range(m+1)]\n for h, w, p in prices:\n dp[h][w] = p\n for i in range(1, m+1):\n for j in range(1, n+1):\n v = max(dp[k][j] + dp[i - k][j] for k in range(1, i // 2 + 1)) if i > 1 else 0\n h = max(dp[i][k] + dp[i][j - k] for k in range(1, j // 2 + 1)) if j > 1 else 0\n dp[i][j] = max(dp[i][j], v, h)\n return dp[m][n] | 1 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
93% Time and Memory | Commented and Explained | selling-pieces-of-wood | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a dp problem, where we need to build a cut profit chart to show profit attainable at a specific cutting combination which drives towards the profit of cutting the whole board or as much as possible. If printed, can show up to where to cut clearly and show maximal profit. \n\nThis is similar to number of coins to make change and other dp problems, where we are maximizing at each state the value of doing x or y a certain number of times. \n\nWe start by initializing each combination in prices \nThen, we consider both vertical cuts holding cols constant and horizontal cuts holding rows constant \n\nFrom there, we loop as needed over rows and cols to build row and col profits \n\nWe want to maximize each possible cutting by considering if we split along a col or split along a row and maximize as appropriate \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a chart of profits of size m+1 by n+1 with initial values of 0 \n\nFor each segment type in prices, at row and col maximize profit to initialize prices \n\nFor col in range 2 to cols + 1 \n- col profits is cut profit chart at 1 at k + cut profit chart at 1 at col-k for k in range 1 to col//2 + 1 -> basically, get your possible profits based on col current if you place a cut at k, holding rows as 1 \n- maximize the col profits \n- mark cut profit chart at 1 at col to max of self and the max col profits \n\nDo same but for rows in range 2 to rows + 1 \n\nWhy this works -> if we consider cutting at rows = 1 -> we will infact get 0 as possible row profits -> this is also true for cols. \n\nAs such, we know that for all rows = 1, row profits is 0, and similar for all cols = 1, col profits is 0. As such, we now know that we can do two additional linear passes to fill in col and row profits at the start (could have done other order, no issue with it) \n\nFinally, to build final chart, loop rows in range 2 to m+1 and cols in range 2 to n+1, during which \n- calculate row profits as list of cut profit chart at k at col + cut profit chart at row - k at col for k in range 1, row//2 + 1 \n- similar set up for col profits \n- maximize both \n- maximize cut profit chart at row at col as max of self and max row profits and max col profits \n\nWhen done, return cut profit chart at row at col \n\n# Complexity\n- Time complexity : O(m x n) \n - Takes O(m x n) to build cut profit chart initially \n - Takes O(p) to build all prices into profit chart \n - Takes O(m + n) to fill initial row and col held constant \n - Takes O(m x n) to iterate over the list \n - in which we fill a sub range of size 1 to m, n // 2\n - can be seen as taking time log m and log n via the div 2 \n - as log m and log n are subset to m and n, this is equivalent to a constant multiplier, and as such can be treated as a constant \n - big O drops this to O(m x n) \n\n- Space complexity: O(m x n) \n - We store m x n cut profits in the cut profit chart \n\n# Code\n```\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n # can sell rectangles at final total \n # to cut piece of wood, make vert or horizontal across entire width or height to split in two \n # After cutting into some number of pieces, can sell each piece at price \n # You can sell multiple pieces of the same shape \n # You do not have to sell all the shapes \n # Grain of wood matters, so you cannot rotate to swap width and height \n # Can cut as many times as you want \n # Example problem \n # 1 x 4 = 2, 2 x 2 = 7, 2 x 1 = 3, size is 3 x 5 \n # number of 1 x 4 obtainable -> 3 \n # number of 2 x 2 obtainable -> 2 \n # number of 2 x 1 obtainable -> 5 \n # max number of an item type attainable = 5 \n # max number of space => 15 \n # build a cut profit chart set to 0 for each row and col in the board \n cut_profit_chart = [[0] * (n + 1) for _ in range(m+1)] \n\n # for each segmentation, mark maximally \n for row, col, profit in prices : \n cut_profit_chart[row][col] = max(profit, cut_profit_chart[row][col]) \n\n # for each column on row == 1 mark maximally \n for col in range(2, n+1) : \n col_profits = [cut_profit_chart[1][k] + cut_profit_chart[1][col - k] for k in range(1, col//2 + 1)]\n max_col_profit = max(col_profits)\n cut_profit_chart[1][col] = max(cut_profit_chart[1][col], max_col_profit) \n \n # for each row on col == 1 mark maximally \n for row in range(2, m + 1) : \n row_profits = [cut_profit_chart[k][1] + cut_profit_chart[row - k][1] for k in range(1, row//2 + 1)]\n max_row_profit = max(row_profits)\n cut_profit_chart[row][1] = max(cut_profit_chart[row][1], max_row_profit) \n\n # for each row in range 2 to end \n for row in range(2, m + 1) : \n # print(f\'For row {row}\')\n # for each col in range col to end \n for col in range(2, n+1) : \n # print(f\'For col {col}\')\n # get profits of row cutting (aka make two pieces by cutting along row)\n row_profits = [cut_profit_chart[k][col] + cut_profit_chart[row - k][col] for k in range(1, row//2 + 1)]\n # get profits of col cutting (aka make two pieces by cutting along a col )\n col_profits = [cut_profit_chart[row][k] + cut_profit_chart[row][col - k] for k in range(1, col//2 + 1)]\n # maximize row and col profits \n max_row_profit = max(row_profits)\n max_col_profit = max(col_profits) \n # maximize cut profit at row and col via max of max row and max col profit \n cut_profit_chart[row][col] = max(cut_profit_chart[row][col], max_row_profit, max_col_profit) \n # print(f\'row profits were {row_profits} for k in {list((k, col, row-k, col) for k in range(1, row//2 + 1))}\')\n # print(f\'col profits were {col_profits} for k in {list((row, k, row, col-k) for k in range(1, col//2 + 1))}\')\n # print(f\'cut profit chart now {cut_profit_chart}\\n\\n\')\n \n # return when done \n # print(f\'Cut profit chart at end is {cut_profit_chart}\')\n return cut_profit_chart[row][col]\n\n``` | 0 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
py3 sol | selling-pieces-of-wood | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen facing an optimization problem like this, where we need to find the maximum value obtainable through a series of decisions (cuts, in this case), dynamic programming (DP) is a good fit. The problem has an optimal substructure, which means that the optimal solution to the whole problem can be constructed from the optimal solutions to its subproblems. Additionally, the problem has overlapping subproblems, meaning that the same subproblems are solved multiple times, making it ideal for memoization, which is a core concept of DP.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe dynamic programming approach involves solving the problem in a bottom-up manner by building up a solution using previously computed values. We create a 2D dp array, where dp[i][j] represents the maximum price we can get for a piece of wood with dimensions i x j. We start by filling this array with the given prices for specific sizes of the pieces, and then we iteratively find the optimal cuts for every size up to the input dimensions m x n.\n\nTo find the optimal solution for a piece of size i x j, we consider every possible cut:\n\nHorizontal cut: We cut the piece into two horizontally and calculate the sum of the values of the two resulting pieces for each possible cut.\nVertical cut: Similarly, we cut the piece into two vertically and calculate the sum for each possible cut.\nFor each dimension (i, j), the maximum price is the maximum between the price of selling it as is (if available), and the maximum obtainable prices from each possible cut. We continue this process until we\'ve computed the value for the full size, dp[m][n], which provides the maximum price for the entire wood piece.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is $$O(m \\cdot n \\cdot (m + n))$$. For each cell (i, j) in the dp matrix, we potentially make i horizontal cuts and j vertical cuts, where each cut involves a constant amount of work to update the dp value.\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(m \\cdot n)$$ as we use a 2D array to store the maximum price for each sub-piece of wood up to size m x n.\n\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n # Initialize the 2D array dp with zeros\n dp = [[0] * (n + 1) for _ in range(m + 1)]\n \n # Populate the dp array with given prices\n for h, w, price in prices:\n dp[h][w] = price\n \n # Use dynamic programming to fill in the rest of the dp array\n for i in range(1, m+1):\n for j in range(1, n+1):\n # Calculate maximum price for (i, j) by trying to cut horizontally\n for cut in range(1, i//2 + 1):\n dp[i][j] = max(dp[i][j], dp[cut][j] + dp[i - cut][j])\n # Calculate maximum price for (i, j) by trying to cut vertically\n for cut in range(1, j//2 + 1):\n dp[i][j] = max(dp[i][j], dp[i][cut] + dp[i][j - cut])\n \n # The maximum price for m x n piece of wood will be in dp[m][n]\n return dp[m][n]\n``` | 0 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
python3 solution for me bp | selling-pieces-of-wood | 0 | 1 | # Code\n```\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n prices_dict = {(h,w): p for h,w,p in prices}\n\n dp = {}\n\n for i in range(1, m+1):\n for j in range(1, n+1):\n val = dp.get((i,j) , prices_dict.get((i,j), 0))\n for k in range(1, i//2+1):\n val = max(val, dp.get((k,j), prices_dict.get((k,j), 0))+dp.get((i-k,j), prices_dict.get((i-k,j), 0)))\n \n for k in range(1,j//2+1):\n val = max(val, dp.get((i,k), prices_dict.get((i,k), 0))+dp.get((i,j-k), prices_dict.get((i,j-k), 0)))\n\n dp[(i,j)] = val\n \n return dp[(m,n)]\n\n\n\n\n\n \n``` | 0 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
Python 90% time and 57% space | selling-pieces-of-wood | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n\n\n P=[[0 for i in range(n+1)]for j in range(m+1)]\n\n for i in prices:\n P[i[0]][i[1]]=i[2]\n dp=[[False for i in range(n+1)]for j in range(m+1)]\n def sol(x,y):\n if dp[x][y] is not False:\n return dp[x][y]\n ret=P[x][y]\n for k in range(x//2):\n a=sol(k+1,y)+sol(x-(k+1),y)\n ret=max(ret,a)\n for k in range(y//2):\n a=sol(x,k+1)+sol(x,y-(k+1))\n ret=max(ret,a)\n dp[x][y]=ret\n return ret\n final=sol(m,n)\n return final\n\n \n``` | 0 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
Python, short and clean, memo+DP | selling-pieces-of-wood | 0 | 1 | # Intuition\nMain observation: we always cut <b>straight whole line</b> which splits rectangle into two. It gives fuel to DP solution over $m,n$: what is the maximal price we can get out of $$m*n$$ rectangle? We just try exact match in prices, each vertical and horizontal cut, and choose maximum option.\nDP formula: $f(m,n)=max(f(m,x)+f(m,n-x)_{1<=x<n},f(x,n)+f(m-x,n)_{1<=x<m},price(m,n))$\n\n# Approach\nImplement DP formula + use memoization via `@cache`. \n\n# Complexity\n- Time complexity: `O(m*n*(m+n))`\n- Space complexity: `O(m*n)`\n\n# Code\n```\nclass Solution:\n def sellingWood(self, m: int, n: int, prices: List[List[int]]) -> int:\n prices=defaultdict(int)|{(h,w):p for h,w,p in prices}\n @cache\n def f(m,n): \n hor = max((f(x,n)+f(m-x,n) for x in range(1,1+m//2)), default=0)\n ver = max((f(m,x)+f(m,n-x) for x in range(1,1+n//2)), default=0)\n return max(hor,ver, prices[m,n])\n return f(m,n)\n \n \n``` | 0 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
Python (Simple DP) | selling-pieces-of-wood | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sellingWood(self, m, n, prices):\n dict1 = collections.defaultdict(int)\n\n for i,j,k in prices:\n dict1[(i,j)] = k\n\n @lru_cache(None)\n def dfs(h,w):\n if h == 0 or w == 0: return 0\n\n max_val = dict1[(h,w)]\n\n for i in range(1,h//2+1):\n max_val = max(max_val,dfs(i,w) + dfs(h-i,w))\n\n for j in range(1,w//2+1):\n max_val = max(max_val,dfs(h,j) + dfs(h,w-j))\n\n return max_val \n\n return dfs(m,n)\n\n\n\n\n \n``` | 0 | You are given two integers `m` and `n` that represent the height and width of a rectangular piece of wood. You are also given a 2D integer array `prices`, where `prices[i] = [hi, wi, pricei]` indicates you can sell a rectangular piece of wood of height `hi` and width `wi` for `pricei` dollars.
To cut a piece of wood, you must make a vertical or horizontal cut across the **entire** height or width of the piece to split it into two smaller pieces. After cutting a piece of wood into some number of smaller pieces, you can sell pieces according to `prices`. You may sell multiple pieces of the same shape, and you do not have to sell all the shapes. The grain of the wood makes a difference, so you **cannot** rotate a piece to swap its height and width.
Return _the **maximum** money you can earn after cutting an_ `m x n` _piece of wood_.
Note that you can cut the piece of wood as many times as you want.
**Example 1:**
**Input:** m = 3, n = 5, prices = \[\[1,4,2\],\[2,2,7\],\[2,1,3\]\]
**Output:** 19
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 2 pieces of wood shaped 2 x 2, selling for a price of 2 \* 7 = 14.
- 1 piece of wood shaped 2 x 1, selling for a price of 1 \* 3 = 3.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 14 + 3 + 2 = 19 money earned.
It can be shown that 19 is the maximum amount of money that can be earned.
**Example 2:**
**Input:** m = 4, n = 6, prices = \[\[3,2,10\],\[1,4,2\],\[4,1,3\]\]
**Output:** 32
**Explanation:** The diagram above shows a possible scenario. It consists of:
- 3 pieces of wood shaped 3 x 2, selling for a price of 3 \* 10 = 30.
- 1 piece of wood shaped 1 x 4, selling for a price of 1 \* 2 = 2.
This obtains a total of 30 + 2 = 32 money earned.
It can be shown that 32 is the maximum amount of money that can be earned.
Notice that we cannot rotate the 1 x 4 piece of wood to obtain a 4 x 1 piece of wood.
**Constraints:**
* `1 <= m, n <= 200`
* `1 <= prices.length <= 2 * 104`
* `prices[i].length == 3`
* `1 <= hi <= m`
* `1 <= wi <= n`
* `1 <= pricei <= 106`
* All the shapes of wood `(hi, wi)` are pairwise **distinct**. | Count the number of times each target value follows the key in the array. Choose the target with the maximum count and return it. |
Python Easy Solution By Counting Number of "|" | count-asterisks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countAsterisks(self, s: str) -> int:\n count = 0\n ans = 0\n\n for i in range(len(s)):\n if s[i] == "|":\n count += 1\n if count % 2 == 0:\n if s[i] == "*":\n ans += 1\n \n return ans\n \n``` | 1 | You are given a string `s`, where every **two** consecutive vertical bars `'|'` are grouped into a **pair**. In other words, the 1st and 2nd `'|'` make a pair, the 3rd and 4th `'|'` make a pair, and so forth.
Return _the number of_ `'*'` _in_ `s`_, **excluding** the_ `'*'` _between each pair of_ `'|'`.
**Note** that each `'|'` will belong to **exactly** one pair.
**Example 1:**
**Input:** s = "l|\*e\*et|c\*\*o|\*de| "
**Output:** 2
**Explanation:** The considered characters are underlined: "l|\*e\*et|c\*\*o|\*de| ".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.
**Example 2:**
**Input:** s = "iamprogrammer "
**Output:** 0
**Explanation:** In this example, there are no asterisks in s. Therefore, we return 0.
**Example 3:**
**Input:** s = "yo|uar|e\*\*|b|e\*\*\*au|tifu|l "
**Output:** 5
**Explanation:** The considered characters are underlined: "yo|uar|e\*\*|b|e\*\*\*au|tifu|l ". There are 5 asterisks considered. Therefore, we return 5.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters, vertical bars `'|'`, and asterisks `'*'`.
* `s` contains an **even** number of vertical bars `'|'`. | null |
Easy Python Solution using Flag | count-asterisks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraversing the string and whenever \'|\' encounter in string reverse the flag value. And If the flag value is Flase i only count those \'*\'.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countAsterisks(self, s: str) -> int:\n c=0\n flag=False\n for i in s:\n if (i==\'|\'):\n flag=not(flag)\n if(i==\'*\' and flag==False):\n c=c+1\n return c\n``` | 2 | You are given a string `s`, where every **two** consecutive vertical bars `'|'` are grouped into a **pair**. In other words, the 1st and 2nd `'|'` make a pair, the 3rd and 4th `'|'` make a pair, and so forth.
Return _the number of_ `'*'` _in_ `s`_, **excluding** the_ `'*'` _between each pair of_ `'|'`.
**Note** that each `'|'` will belong to **exactly** one pair.
**Example 1:**
**Input:** s = "l|\*e\*et|c\*\*o|\*de| "
**Output:** 2
**Explanation:** The considered characters are underlined: "l|\*e\*et|c\*\*o|\*de| ".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.
**Example 2:**
**Input:** s = "iamprogrammer "
**Output:** 0
**Explanation:** In this example, there are no asterisks in s. Therefore, we return 0.
**Example 3:**
**Input:** s = "yo|uar|e\*\*|b|e\*\*\*au|tifu|l "
**Output:** 5
**Explanation:** The considered characters are underlined: "yo|uar|e\*\*|b|e\*\*\*au|tifu|l ". There are 5 asterisks considered. Therefore, we return 5.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters, vertical bars `'|'`, and asterisks `'*'`.
* `s` contains an **even** number of vertical bars `'|'`. | null |
Python O(n) | count-asterisks | 0 | 1 | \n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def countAsterisks(self, s: str) -> int:\n ans,t = 0,0\n for i in s:\n if i == "|":\n t += 1\n elif t % 2 ==0:\n ans += i=="*"\n\n return ans\n``` | 3 | You are given a string `s`, where every **two** consecutive vertical bars `'|'` are grouped into a **pair**. In other words, the 1st and 2nd `'|'` make a pair, the 3rd and 4th `'|'` make a pair, and so forth.
Return _the number of_ `'*'` _in_ `s`_, **excluding** the_ `'*'` _between each pair of_ `'|'`.
**Note** that each `'|'` will belong to **exactly** one pair.
**Example 1:**
**Input:** s = "l|\*e\*et|c\*\*o|\*de| "
**Output:** 2
**Explanation:** The considered characters are underlined: "l|\*e\*et|c\*\*o|\*de| ".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.
**Example 2:**
**Input:** s = "iamprogrammer "
**Output:** 0
**Explanation:** In this example, there are no asterisks in s. Therefore, we return 0.
**Example 3:**
**Input:** s = "yo|uar|e\*\*|b|e\*\*\*au|tifu|l "
**Output:** 5
**Explanation:** The considered characters are underlined: "yo|uar|e\*\*|b|e\*\*\*au|tifu|l ". There are 5 asterisks considered. Therefore, we return 5.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters, vertical bars `'|'`, and asterisks `'*'`.
* `s` contains an **even** number of vertical bars `'|'`. | null |
Python Elegant & Short | Two solutions | One pass / One line | count-asterisks | 0 | 1 | \tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(1)\n\t\t"""\n\n\t\tdef countAsterisks(self, s: str) -> int:\n\t\t\tis_closed = True\n\t\t\tcount = 0\n\n\t\t\tfor c in s:\n\t\t\t\tcount += is_closed * c == \'*\'\n\t\t\t\tis_closed ^= c == \'|\'\n\n\t\t\treturn count\n\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tdef countAsterisks(self, s: str) -> int:\n\t\t\treturn sum(chunk.count(\'*\') for chunk in s.split(\'|\')[0::2])\n | 3 | You are given a string `s`, where every **two** consecutive vertical bars `'|'` are grouped into a **pair**. In other words, the 1st and 2nd `'|'` make a pair, the 3rd and 4th `'|'` make a pair, and so forth.
Return _the number of_ `'*'` _in_ `s`_, **excluding** the_ `'*'` _between each pair of_ `'|'`.
**Note** that each `'|'` will belong to **exactly** one pair.
**Example 1:**
**Input:** s = "l|\*e\*et|c\*\*o|\*de| "
**Output:** 2
**Explanation:** The considered characters are underlined: "l|\*e\*et|c\*\*o|\*de| ".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.
**Example 2:**
**Input:** s = "iamprogrammer "
**Output:** 0
**Explanation:** In this example, there are no asterisks in s. Therefore, we return 0.
**Example 3:**
**Input:** s = "yo|uar|e\*\*|b|e\*\*\*au|tifu|l "
**Output:** 5
**Explanation:** The considered characters are underlined: "yo|uar|e\*\*|b|e\*\*\*au|tifu|l ". There are 5 asterisks considered. Therefore, we return 5.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters, vertical bars `'|'`, and asterisks `'*'`.
* `s` contains an **even** number of vertical bars `'|'`. | null |
[Java/Python 3] Count after bars reach even, w/ brief explanation and analysis. | count-asterisks | 1 | 1 | Traverse input `s` and check the number of bars (`|`), whenever it reaches even numbers, we are outside of the pairs, then count the stars (`*`) in.\n\n```java\n public int countAsterisks(String s) {\n int star = 0;\n boolean barEven = true;\n for (int i = 0; i < s.length(); ++i) {\n char c = s.charAt(i);\n if (c == \'|\') {\n barEven = !barEven;\n }else if (c == \'*\' && barEven) {\n ++star;\n }\n }\n return star;\n }\n```\n```python\n def countAsterisks(self, s: str) -> int:\n bar_even, star = True, 0\n for c in s:\n if c == \'|\':\n bar_even = not bar_even\n elif c == \'*\' and bar_even:\n star += 1 \n return star\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`, where `n = s.length()`.\n\n----\n\n1 liners: \n\nThe following codes: credit to **@stefan4trivia**\n\n```java\n public int countAsterisks(String s) {\n return s.replaceAll("\\\\|.*?\\\\||[^*]", "").length();\n }\n```\n```python\n def countAsterisks(self, s: str) -> int:\n return re.sub(r\'\\|.*?\\|\', \'\', s).count(\'*\')\n```\n----\n\nThe following Py 3 code: credit to **@WilmerKrisp**\n\n```python\n def countAsterisks(self, s: str) -> int:\n return (\'\'.join(s.split(\'|\')[::2])).count(\'*\')\n```\n\n**Analysis:**\n\nTime & space: `O(n)`, where `n = s.length()`.\n\t | 14 | You are given a string `s`, where every **two** consecutive vertical bars `'|'` are grouped into a **pair**. In other words, the 1st and 2nd `'|'` make a pair, the 3rd and 4th `'|'` make a pair, and so forth.
Return _the number of_ `'*'` _in_ `s`_, **excluding** the_ `'*'` _between each pair of_ `'|'`.
**Note** that each `'|'` will belong to **exactly** one pair.
**Example 1:**
**Input:** s = "l|\*e\*et|c\*\*o|\*de| "
**Output:** 2
**Explanation:** The considered characters are underlined: "l|\*e\*et|c\*\*o|\*de| ".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.
**Example 2:**
**Input:** s = "iamprogrammer "
**Output:** 0
**Explanation:** In this example, there are no asterisks in s. Therefore, we return 0.
**Example 3:**
**Input:** s = "yo|uar|e\*\*|b|e\*\*\*au|tifu|l "
**Output:** 5
**Explanation:** The considered characters are underlined: "yo|uar|e\*\*|b|e\*\*\*au|tifu|l ". There are 5 asterisks considered. Therefore, we return 5.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters, vertical bars `'|'`, and asterisks `'*'`.
* `s` contains an **even** number of vertical bars `'|'`. | null |
Python3 solution using for loop and continue | count-asterisks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo ignore the characters in between a pair of ```|```\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing a ```for``` loop and ```continue``` to skip the characters in between a pair of ```|```\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nWe are iterating the string once\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nA new list is created\n\n# Code\n```\nclass Solution:\n def countAsterisks(self, s: str) -> int:\n l = []\n temp = \'\'\n for i in s:\n if i == \'|\':\n temp += i\n # reset the temp, if a pair is closed\n if temp.count(\'|\') == 2:\n temp = \'\'\n # ignore the characters in between a pair\n if \'|\' in temp:\n continue\n # if none of the above conditions are met append the character into the list\n elif i != \'|\':\n l.append(i)\n return \'\'.join(l).count(\'*\')\n``` | 2 | You are given a string `s`, where every **two** consecutive vertical bars `'|'` are grouped into a **pair**. In other words, the 1st and 2nd `'|'` make a pair, the 3rd and 4th `'|'` make a pair, and so forth.
Return _the number of_ `'*'` _in_ `s`_, **excluding** the_ `'*'` _between each pair of_ `'|'`.
**Note** that each `'|'` will belong to **exactly** one pair.
**Example 1:**
**Input:** s = "l|\*e\*et|c\*\*o|\*de| "
**Output:** 2
**Explanation:** The considered characters are underlined: "l|\*e\*et|c\*\*o|\*de| ".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.
**Example 2:**
**Input:** s = "iamprogrammer "
**Output:** 0
**Explanation:** In this example, there are no asterisks in s. Therefore, we return 0.
**Example 3:**
**Input:** s = "yo|uar|e\*\*|b|e\*\*\*au|tifu|l "
**Output:** 5
**Explanation:** The considered characters are underlined: "yo|uar|e\*\*|b|e\*\*\*au|tifu|l ". There are 5 asterisks considered. Therefore, we return 5.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters, vertical bars `'|'`, and asterisks `'*'`.
* `s` contains an **even** number of vertical bars `'|'`. | null |
DFS approach | count-unreachable-pairs-of-nodes-in-an-undirected-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dfs(self,i,visited,graph,done,count):\n visited.add(i)\n count=1\n done.add(i)\n for j in graph[i]:\n if j not in visited:\n count+=self.dfs(j,visited,graph,done,count)\n return count \n def countPairs(self, n: int, edges: List[List[int]]) -> int:\n graph=[[] for _ in range(n)]\n for edge in edges:\n src1, des1 = edge\n src2, des2 = edge[::-1]\n graph[src1].append(des1)\n graph[src2].append(des2)\n done= set()\n b=n\n sums=0\n for i in range(n):\n if i not in done:\n visited=set()\n l=self.dfs(i,visited,graph,done,0)\n print(l)\n sums=sums+(l*(b-l))\n b=b-l\n return sums if sums>0 else 0 \n \n\n \n\n \n``` | 5 | You are given an integer `n`. There is an **undirected** graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array `edges` where `edges[i] = [ai, bi]` denotes that there exists an **undirected** edge connecting nodes `ai` and `bi`.
Return _the **number of pairs** of different nodes that are **unreachable** from each other_.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 0
**Explanation:** There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.
**Example 2:**
**Input:** n = 7, edges = \[\[0,2\],\[0,5\],\[2,4\],\[1,6\],\[5,4\]\]
**Output:** 14
**Explanation:** There are 14 pairs of nodes that are unreachable from each other:
\[\[0,1\],\[0,3\],\[0,6\],\[1,2\],\[1,3\],\[1,4\],\[1,5\],\[2,3\],\[2,6\],\[3,4\],\[3,5\],\[3,6\],\[4,6\],\[5,6\]\].
Therefore, we return 14.
**Constraints:**
* `1 <= n <= 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated edges. | For each index, could you find the closest non-equal neighbors? Ensure that adjacent indices that are part of the same hill or valley are not double-counted. |
O(n) Time and Space || Python || Disjoint Data Structure | count-unreachable-pairs-of-nodes-in-an-undirected-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOnly those nodes are unreachable that are not in the connected component of the graph.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsed disjoint set data structure to find the parent of each node.\nThen found pairs of nodes, that have different parent nodes.\nStored the total number of pairs in variable tot, and stored the number of disconnected parents in ct.\nMultiplying ct with the size of the parent, gives the total number of pairs assosiated with that particular parent and the previous disconnected parents.\n```\nif i == dsu.parents[i] :\n```\nLine is used so that each parent is used only once, as the parents array might have repetitions.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```\nclass DSU :\n def __init__(self,n) :\n self.parent = [0 for i in range(n)]\n self.size = [0 for i in range(n)]\n for i in range(n) :\n self.parent[i] = i\n self.size[i] = 1\n\n def findParent(self,node) :\n if node == self.parent[node] :\n return node\n return self.findParent(self.parent[node])\n\n def union(self,a,b) :\n x = self.findParent(a)\n y = self.findParent(b)\n if x == y :\n return\n if self.size[x] < self.size[y] :\n self.parent[x] = y\n self.size[y] += self.size[x]\n else :\n self.parent[y] = x\n self.size[x] += self.size[y]\nclass Solution:\n def countPairs(self, n: int, edges: List[List[int]]) -> int:\n dsu = DSU(n)\n for n1,n2 in edges :\n dsu.union(n1,n2)\n n = len(dsu.parent)\n ct,tot = 0,0\n for i in range(n) :\n if i == dsu.parent[i] :\n tot += (ct * dsu.size[i])\n ct += dsu.size[i]\n return tot\n```\n \n\n | 2 | You are given an integer `n`. There is an **undirected** graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array `edges` where `edges[i] = [ai, bi]` denotes that there exists an **undirected** edge connecting nodes `ai` and `bi`.
Return _the **number of pairs** of different nodes that are **unreachable** from each other_.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 0
**Explanation:** There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.
**Example 2:**
**Input:** n = 7, edges = \[\[0,2\],\[0,5\],\[2,4\],\[1,6\],\[5,4\]\]
**Output:** 14
**Explanation:** There are 14 pairs of nodes that are unreachable from each other:
\[\[0,1\],\[0,3\],\[0,6\],\[1,2\],\[1,3\],\[1,4\],\[1,5\],\[2,3\],\[2,6\],\[3,4\],\[3,5\],\[3,6\],\[4,6\],\[5,6\]\].
Therefore, we return 14.
**Constraints:**
* `1 <= n <= 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated edges. | For each index, could you find the closest non-equal neighbors? Ensure that adjacent indices that are part of the same hill or valley are not double-counted. |
Python BFS Solution beats 95% | Adj List | count-unreachable-pairs-of-nodes-in-an-undirected-graph | 0 | 1 | \n# Code\n```\n def countPairs(self, n: int, edges: List[List[int]]) -> int:\n # We find the nodes in the present connected component\n # that means all the other nodes that are not connected are\n # notconnectednodes = n-connectedNodes\n # therefores required pairs = (connectedNodes)*(n-connectedNodes)\n # since we will count a pair twice once from each end we divide with 2 \n\n graph = [ [] for _ in range(0,n) ]\n for x,y in edges:\n graph[x].append(y)\n graph[y].append(x)\n \n res = 0\n visited = [0 for _ in range(0,n)]\n dq = deque()\n for i in range(0,n):\n if(visited[i]==0):\n dq.append(i);\n visited[i] = 1\n curCount = 1\n while(len(dq)>0):\n v = dq.popleft()\n for neib in graph[v]:\n if(visited[neib]== 0 ):\n curCount += 1\n visited[neib]=1\n dq.append(neib)\n res+= curCount*(n-curCount)\n return res//2\n \n\n``` | 2 | You are given an integer `n`. There is an **undirected** graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array `edges` where `edges[i] = [ai, bi]` denotes that there exists an **undirected** edge connecting nodes `ai` and `bi`.
Return _the **number of pairs** of different nodes that are **unreachable** from each other_.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 0
**Explanation:** There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.
**Example 2:**
**Input:** n = 7, edges = \[\[0,2\],\[0,5\],\[2,4\],\[1,6\],\[5,4\]\]
**Output:** 14
**Explanation:** There are 14 pairs of nodes that are unreachable from each other:
\[\[0,1\],\[0,3\],\[0,6\],\[1,2\],\[1,3\],\[1,4\],\[1,5\],\[2,3\],\[2,6\],\[3,4\],\[3,5\],\[3,6\],\[4,6\],\[5,6\]\].
Therefore, we return 14.
**Constraints:**
* `1 <= n <= 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated edges. | For each index, could you find the closest non-equal neighbors? Ensure that adjacent indices that are part of the same hill or valley are not double-counted. |
Python short and clean. DSU (Disjoint-Set-Union) | Union-Find. Functional programming. | count-unreachable-pairs-of-nodes-in-an-undirected-graph | 0 | 1 | # Approach\n1. Create a `DSU (Disjoint-Set-Union)`.\n\n2. `Union` the edges one by one.\n\n3. Count the number of `nodes` in each `disjoint-set`, let\'s call this `counts` array with length `m`.\n\n4. Return `total` number of pairs possible. i.e\n $$ \\mathrm{total} = \\sum_{i=1}^{i=m-1} \\sum_{j=0}^{j=i-1} \\mathrm{counts}_j \\cdot \\mathrm{counts}_i $$\n\n5. Notice that the inner summation is `prefix_sum` and the outer summation is `prefix_sum[i] * counts[i]`. Hence the entire expression can be written as:\n `total = sum(map(mul, accumulate(counts, add, initial=0), counts))`\n\n# Complexity\n- Time complexity: $$O(n + e)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is the number of nodes`,\n`e is the number of edges`.\n\n# Code\n```python\nclass Solution:\n def countPairs(self, n: int, edges: list[list[int]]) -> int:\n dsu = DSU(range(n))\n for u, v in edges: dsu.union(u, v)\n counts = Counter(map(dsu.find, range(n))).values()\n return sum(map(mul, accumulate(counts, add, initial=0), counts))\n\n\nT = Hashable\nclass DSU:\n def __init__(self, xs: Iterable[T] = ()) -> None:\n self.parents: Mapping[T, T] = {x: x for x in xs}\n self.sizes: Mapping[T, int] = {x: 1 for x in xs}\n\n def find(self, u: T) -> T:\n self.parents[u] = u if self.parents[u] == u else self.find(self.parents[u])\n return self.parents[u]\n \n def union(self, u: T, v: T) -> None:\n ur, vr = self.find(u), self.find(v)\n if ur == vr: return\n low, high = (ur, vr) if self.sizes[ur] < self.sizes[vr] else (vr, ur)\n self.parents[low] = high\n self.sizes[high] += self.sizes[low]\n \n def is_connected(self, u: T, v: T) -> bool:\n return self.find(u) == self.find(v)\n\n\n``` | 3 | You are given an integer `n`. There is an **undirected** graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array `edges` where `edges[i] = [ai, bi]` denotes that there exists an **undirected** edge connecting nodes `ai` and `bi`.
Return _the **number of pairs** of different nodes that are **unreachable** from each other_.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 0
**Explanation:** There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.
**Example 2:**
**Input:** n = 7, edges = \[\[0,2\],\[0,5\],\[2,4\],\[1,6\],\[5,4\]\]
**Output:** 14
**Explanation:** There are 14 pairs of nodes that are unreachable from each other:
\[\[0,1\],\[0,3\],\[0,6\],\[1,2\],\[1,3\],\[1,4\],\[1,5\],\[2,3\],\[2,6\],\[3,4\],\[3,5\],\[3,6\],\[4,6\],\[5,6\]\].
Therefore, we return 14.
**Constraints:**
* `1 <= n <= 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated edges. | For each index, could you find the closest non-equal neighbors? Ensure that adjacent indices that are part of the same hill or valley are not double-counted. |
Python | BFS + prefix sum solution | count-unreachable-pairs-of-nodes-in-an-undirected-graph | 0 | 1 | # Approach\n1) Make graph using $$dictionary$$ with $$set$$\n2) Apply $$BFS$$ on this graph to count number of $$connectivity$$ $$components$$ (and number of nodes in each component)\n3) Count $$prefix-sum$$ of this components to calc answer fast\n\n# Complexity\n- Time complexity: $$O(N)$$\n\n- Space complexity: $$O(N)$$\n\n# Code\n```\nclass Solution:\n def countPairs(self, n: int, edges: List[List[int]]) -> int:\n graph = {i: set() for i in range(n)}\n for a, b in edges:\n graph[a].add(b)\n graph[b].add(a)\n\n cmps, used = [], set()\n for eg in graph:\n if eg in used:\n continue\n q, counter = deque([eg]), 0\n used.add(eg)\n while q:\n pp = q.popleft()\n counter += 1\n for nn in graph[pp]:\n if nn not in used:\n q.append(nn)\n used.add(nn)\n cmps.append(counter)\n prefix = [cmps[0]] + [0]*(len(cmps) - 1)\n for i in range(1, len(cmps)):\n prefix[i] = prefix[i - 1] + cmps[i]\n ans = 0\n for i in range(len(cmps)):\n ans += (n - prefix[i])*cmps[i]\n return ans\n\n\n \n``` | 1 | You are given an integer `n`. There is an **undirected** graph with `n` nodes, numbered from `0` to `n - 1`. You are given a 2D integer array `edges` where `edges[i] = [ai, bi]` denotes that there exists an **undirected** edge connecting nodes `ai` and `bi`.
Return _the **number of pairs** of different nodes that are **unreachable** from each other_.
**Example 1:**
**Input:** n = 3, edges = \[\[0,1\],\[0,2\],\[1,2\]\]
**Output:** 0
**Explanation:** There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.
**Example 2:**
**Input:** n = 7, edges = \[\[0,2\],\[0,5\],\[2,4\],\[1,6\],\[5,4\]\]
**Output:** 14
**Explanation:** There are 14 pairs of nodes that are unreachable from each other:
\[\[0,1\],\[0,3\],\[0,6\],\[1,2\],\[1,3\],\[1,4\],\[1,5\],\[2,3\],\[2,6\],\[3,4\],\[3,5\],\[3,6\],\[4,6\],\[5,6\]\].
Therefore, we return 14.
**Constraints:**
* `1 <= n <= 105`
* `0 <= edges.length <= 2 * 105`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* There are no repeated edges. | For each index, could you find the closest non-equal neighbors? Ensure that adjacent indices that are part of the same hill or valley are not double-counted. |
[Java/Python 3] Bit manipulations w/ brief explanation and analysis. | maximum-xor-after-operations | 1 | 1 | **Key observation: `nums[i] & (nums[i] ^ x) <= nums[i]`**. Therefoe, we can only set off the `1` bits of each number if necessary, in order to make greatest of the xor all numbers after operations.\n\nSince 2<sup>27</sup> > 10<sup>8</sup>, we can traverse the left-most `28` bits to count how many `1`\'s on each bits.\n1. Count each set bit (`1` bit) on the `0th`, `1st`, `2nd`, ..., `27th` bit; if greater than `0`, we can make it odd so that the xor of all elements on that bit will be `1`;\n2. For each bit, add it (use `|=`) to the result.\n\n```java\n public int maximumXOR(int[] nums) {\n int[] cnt = new int[28];\n int maxXor = 0;\n for (int i = 0; i < 28; ++i) {\n for (int num : nums) {\n if (((num >> i) & 1) != 0) {\n ++cnt[i];\n }\n }\n if (cnt[i] > 0) {\n maxXor |= 1 << i; \n }\n }\n return maxXor;\n }\n```\n\n```python\n def maximumXOR(self, nums: List[int]) -> int:\n cnt = [0] * 28\n maxXor = 0 \n for i in range(28):\n for num in nums:\n if (num & (1 << i)) > 0:\n cnt[i] += 1\n if cnt[i] > 0: \n maxXor |= (1 << i)\n return maxXor\n```\n\n-----\n\nBased from the above explanation, as long as there are at least `1` set bit on a certain bit (say `ith` bit) , we can set that bit (`ith` bit) `1`. Therefore, that is bitwise or `|` operation. Therefore, we can simplify the above codes as follows:\n\n```java\n public int maximumXOR(int[] nums) {\n return IntStream.of(nums).reduce(0, (a, b) -> a | b);\n }\n```\n```python\n def maximumXOR(self, nums: List[int]) -> int:\n return functools.reduce(operator.ior, nums, 0)\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`, where `n = nums.length`. | 8 | You are given a **0-indexed** integer array `nums`. In one operation, select **any** non-negative integer `x` and an index `i`, then **update** `nums[i]` to be equal to `nums[i] AND (nums[i] XOR x)`.
Note that `AND` is the bitwise AND operation and `XOR` is the bitwise XOR operation.
Return _the **maximum** possible bitwise XOR of all elements of_ `nums` _after applying the operation **any number** of times_.
**Example 1:**
**Input:** nums = \[3,2,4,6\]
**Output:** 7
**Explanation:** Apply the operation with x = 4 and i = 3, num\[3\] = 6 AND (6 XOR 4) = 6 AND 2 = 2.
Now, nums = \[3, 2, 4, 2\] and the bitwise XOR of all the elements = 3 XOR 2 XOR 4 XOR 2 = 7.
It can be shown that 7 is the maximum possible bitwise XOR.
Note that other operations may be used to achieve a bitwise XOR of 7.
**Example 2:**
**Input:** nums = \[1,2,3,9,2\]
**Output:** 11
**Explanation:** Apply the operation zero times.
The bitwise XOR of all the elements = 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11.
It can be shown that 11 is the maximum possible bitwise XOR.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 108` | In what circumstances does a moving car not collide with another car? If we disregard the moving cars that do not collide with another car, what does each moving car contribute to the answer? Will stationary cars contribute towards the answer? |
Python One Line (Detailed Explanation) | maximum-xor-after-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem relies on a few key observations made in sequence, which lend themselves to a very elegant solution.\n\nObservation 1: Since x is arbitrary, we can make (nums[i] XOR x) anything we like. For a given target number T = (nums[i] XOR x), we can construct x bit by bit. If the jth bit of T is 1, then the jth bit of x differs from the jth bit of nums[i]. If the jth bit of T is 0, then the jth bit of x is the same as the jth bit of nums[i].\n\nObservation 2: We can set nums[i] to anything using the bits ALREADY in nums[i]. We want to set nums[i] equal to nums[i] AND (nums[i] XOR x). We already know T = (nums[i] XOR x) is arbitrary. We can turn off any bits in nums[i] by making those bits in T zero, but we cannot produce any new bits, since they must be ANDed by zeros in nums[i].\n\nObservation 3: We can obtain any bit present in any of the nums[i] in our final XOR. All we need to do is leave one instance of each bit present in some nums[i], and turn off all other copies of that bit. Then when we XOR all of that bit together, we\'ll get 1 XOR 0 XOR 0... which is just 1. Note we can\'t produce any bit outside of the nums[i] since XORing zeros can only produce zero. \n\nObservation 4: Taking all the bits present in nums boils down to taking the bitwise OR of all the numbers. This operation will turn on a bit if at least one of the nums[i] has this bit set to 1.\n\n# Implementation\n<!-- Describe your approach to solving the problem. -->\nWe can write a simple for loop that maintains a solution variable starting at zero, and ORs every nums[i] with it. This will work, but we can express the same idea a little cleaner with functools.reduce()\n\nReduce takes in a function which maps 2 values down to 1 value, and applies it to our list. It will reduce the first 2 list values into 1 value, then reduce that and the next list value to 1 value, continuing to absorb the whole list. \n\nOur reducing funtion is simply the bitwise OR, as we want to OR the first 2 elements, then OR that with the next element, then OR that with the next element, and so on. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumXOR(self, nums: List[int]) -> int:\n return reduce(lambda x, y: x | y, nums)\n``` | 2 | You are given a **0-indexed** integer array `nums`. In one operation, select **any** non-negative integer `x` and an index `i`, then **update** `nums[i]` to be equal to `nums[i] AND (nums[i] XOR x)`.
Note that `AND` is the bitwise AND operation and `XOR` is the bitwise XOR operation.
Return _the **maximum** possible bitwise XOR of all elements of_ `nums` _after applying the operation **any number** of times_.
**Example 1:**
**Input:** nums = \[3,2,4,6\]
**Output:** 7
**Explanation:** Apply the operation with x = 4 and i = 3, num\[3\] = 6 AND (6 XOR 4) = 6 AND 2 = 2.
Now, nums = \[3, 2, 4, 2\] and the bitwise XOR of all the elements = 3 XOR 2 XOR 4 XOR 2 = 7.
It can be shown that 7 is the maximum possible bitwise XOR.
Note that other operations may be used to achieve a bitwise XOR of 7.
**Example 2:**
**Input:** nums = \[1,2,3,9,2\]
**Output:** 11
**Explanation:** Apply the operation zero times.
The bitwise XOR of all the elements = 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11.
It can be shown that 11 is the maximum possible bitwise XOR.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 108` | In what circumstances does a moving car not collide with another car? If we disregard the moving cars that do not collide with another car, what does each moving car contribute to the answer? Will stationary cars contribute towards the answer? |
Python3 || 1 line, bit operations, w/ explanation || T/M: 88%/87% | maximum-xor-after-operations | 0 | 1 | Points to consider:\n\n* The problem calls for choosing an integer x, selecting an element n of the list, applying the compound operator op(n,x) = (x&n)^n, and taking the bit-intersection of the modified set. Because of the associative and commutative properties of the XOR operator, it does not matter which n we choose in nums. \n\n* Below is the truth table for op(num,x)\n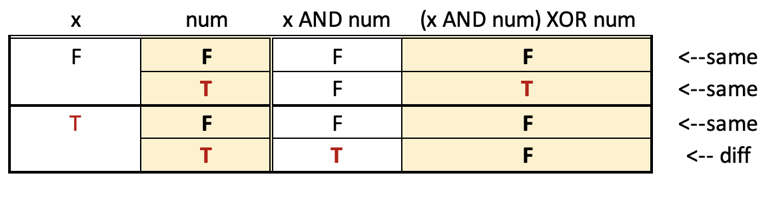\n The end result is that the op leaves num\'s bit unchanged unless x and num are both 1, in which case that bit of num becomes 0. It follows that by choosing x wisely, we can erase any bits in any of the elements of nums. \n\n* For example:\n _ _ _ _ _ _ _ _ _ 3 = 0x4 + 1x2 + 1x1 = 011 (base2)\n\t\t\t _ _ _ _ _ _ _ _ _ 2 = 0x4 + 1x2 + 0x1 = 010 (base2)\n\t\t\t _ _ _ _ _ _ _ _ _ 4 = 1x4 + 0x2 + 0x1 = 100 (base2)\n _ _ _ _ _ _ _ _ _ 6 = 1x4 + 1x2 + 0x1 = 110 (base2)\n\t\t\t \n_ _ _ _ _ _ XOR (3,2,4,6)\t= 0x4 + 1x2 + 1x1 = 011 (base2) = 3\n\nIn the base 2 representation of the XOR, the 4s digit is 0 because the bit-XOR of the 4s digits in nums,\nXOR(0,0,1,1) = 0 because there\'s an even number of 1s. And:\n 2s digits: XOR(1,1,0,1) => 2s digit of XOR(nums) = 1 because #of 1s is odd\n 1s digits: XOR(1,0,0,0) => 1s digit of XOR(nums) = 1 because #of 1s is odd\n \n* After applying Op(4,6) = 2 to nums[3]:\n _ _ _ _ _ _ _ _ _ 3 = 0x4 + 1x2 + 1x1 = 011 (base2)\n\t\t\t _ _ _ _ _ _ _ _ _ 2 = 0x4 + 1x2 + 0x1 = 010 (base2)\n\t\t\t _ _ _ _ _ _ _ _ _ 4 = 1x4 + 0x2 + 0x1 = 100 (base2)\n _ _ _ _ _ _ _ _ _ 2 = 0x4 + 1x2 + 0x1 = 110 (base2)\n\t\t\t \n_ _ _ _ _ XOR (3,2,4,2)\t= 1x4 + 1x2 + 1x1 = 111 (base2) = 7\n\n* The bottom line: choosing a value of x that will reduce columns with even 1s by one will maximize the value of XOR(nums). The only columns that cannot be changed are those with no 1s initially. Thus we can solve the problem by determining OR(nums).\n\nThree short solutions:\n \n ```\n class Solution:\n def maximumXOR(self, nums: List[int]) -> int:\n return reduce(lambda x,y: x|y, nums)\n\nclass Solution:\n def maximumXOR(self, nums: List[int]) -> int:\n return reduce(or_, nums)\n\nclass Solution:\n def maximumXOR(self, nums: List[int]) -> int:\n \n ans = 0\n for n in nums:\n ans |= n \n return ans | 8 | You are given a **0-indexed** integer array `nums`. In one operation, select **any** non-negative integer `x` and an index `i`, then **update** `nums[i]` to be equal to `nums[i] AND (nums[i] XOR x)`.
Note that `AND` is the bitwise AND operation and `XOR` is the bitwise XOR operation.
Return _the **maximum** possible bitwise XOR of all elements of_ `nums` _after applying the operation **any number** of times_.
**Example 1:**
**Input:** nums = \[3,2,4,6\]
**Output:** 7
**Explanation:** Apply the operation with x = 4 and i = 3, num\[3\] = 6 AND (6 XOR 4) = 6 AND 2 = 2.
Now, nums = \[3, 2, 4, 2\] and the bitwise XOR of all the elements = 3 XOR 2 XOR 4 XOR 2 = 7.
It can be shown that 7 is the maximum possible bitwise XOR.
Note that other operations may be used to achieve a bitwise XOR of 7.
**Example 2:**
**Input:** nums = \[1,2,3,9,2\]
**Output:** 11
**Explanation:** Apply the operation zero times.
The bitwise XOR of all the elements = 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11.
It can be shown that 11 is the maximum possible bitwise XOR.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 108` | In what circumstances does a moving car not collide with another car? If we disregard the moving cars that do not collide with another car, what does each moving car contribute to the answer? Will stationary cars contribute towards the answer? |
[Python3] top-down dp | number-of-distinct-roll-sequences | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7a67de4e975be771355e048bf8dde4cf0906e360) for solutions of biweekly 81. \n\n```\nclass Solution:\n def distinctSequences(self, n: int) -> int:\n \n @lru_cache\n def fn(n, p0, p1): \n """Return total number of distinct sequences."""\n if n == 0: return 1\n ans = 0\n for x in range(1, 7): \n if x not in (p0, p1) and gcd(x, p0) == 1: ans += fn(n-1, x, p0)\n return ans % 1_000_000_007\n \n return fn(n, -1, -1)\n``` | 5 | You are given an integer `n`. You roll a fair 6-sided dice `n` times. Determine the total number of **distinct** sequences of rolls possible such that the following conditions are satisfied:
1. The **greatest common divisor** of any **adjacent** values in the sequence is equal to `1`.
2. There is **at least** a gap of `2` rolls between **equal** valued rolls. More formally, if the value of the `ith` roll is **equal** to the value of the `jth` roll, then `abs(i - j) > 2`.
Return _the **total number** of distinct sequences possible_. Since the answer may be very large, return it **modulo** `109 + 7`.
Two sequences are considered distinct if at least one element is different.
**Example 1:**
**Input:** n = 4
**Output:** 184
**Explanation:** Some of the possible sequences are (1, 2, 3, 4), (6, 1, 2, 3), (1, 2, 3, 1), etc.
Some invalid sequences are (1, 2, 1, 3), (1, 2, 3, 6).
(1, 2, 1, 3) is invalid since the first and third roll have an equal value and abs(1 - 3) = 2 (i and j are 1-indexed).
(1, 2, 3, 6) is invalid since the greatest common divisor of 3 and 6 = 3.
There are a total of 184 distinct sequences possible, so we return 184.
**Example 2:**
**Input:** n = 2
**Output:** 22
**Explanation:** Some of the possible sequences are (1, 2), (2, 1), (3, 2).
Some invalid sequences are (3, 6), (2, 4) since the greatest common divisor is not equal to 1.
There are a total of 22 distinct sequences possible, so we return 22.
**Constraints:**
* `1 <= n <= 104` | To obtain points for some certain section x, what is the minimum number of arrows Bob must shoot? Given the small number of sections, can we brute force which sections Bob wants to win? For every set of sections Bob wants to win, check if we have the required amount of arrows. If we do, it is a valid selection. |
Python3] | Clear Top Down DP | number-of-distinct-roll-sequences | 0 | 1 | ## Idea\nUse memoization (e.g. `cache`, `lru_cache`) to store number of combinations of length `rem` that can come after each pair.\nHandle edge case of `n == 1` to return `6`.\n\n## FAQ\n- Why do we consider only two elements for memoization?\n-- because you only need to look back for the last two elements. Given by requirement `abs(i - j) > 2` for every `i` and `j` indices of the combination that has same roll. Also, considering 3 or more makes the problem more complicated and waste the effort.\n- Why do we use memoization?\n-- To avoid repeated calculation\n\n## Time and Memory Complexity\n`O(n)` for memory because we need to store constant * `n` combinations in the cache! (what is constant?)\nLet me know of the time-complexity in the comments!\n\n## Code\n```python\nclass Solution:\n def distinctSequences(self, n: int) -> int:\n mod = 1_000_000_007\n # edge case\n if n == 1: return 6\n # to create possible adjacent pairs\n next_option = {\n 1: (2, 3, 4, 5, 6),\n 2: (1, 3, 5),\n 3: (1, 2, 4, 5),\n 4: (1, 3, 5),\n 5: (1, 2, 3, 4, 6),\n 6: (1, 5)\n }\n # create dictionary where the key is allowed adjacent pairs and the value is list of third elment after the pair\n allowed_third = defaultdict(list)\n for i, j, k in product(list(range(1, 7)), repeat=3):\n if k != i and j in next_option[i] and k in next_option[j]:\n allowed_third[(i, j)] += k,\n # memoize the answers\n @cache\n def get_help(i, j, rem):\n ans = 0\n if rem == 0:\n return 1\n for k in allowed_third[(i, j)]:\n ans += get_help(j, k, rem - 1) % mod\n return ans\n ans = 0\n \n for i, j in allowed_third:\n ans += get_help(i, j, n - 2) % mod\n return ans % mod\n```\n\n## Feedback\nI appreciate your feedback and support!\n | 2 | You are given an integer `n`. You roll a fair 6-sided dice `n` times. Determine the total number of **distinct** sequences of rolls possible such that the following conditions are satisfied:
1. The **greatest common divisor** of any **adjacent** values in the sequence is equal to `1`.
2. There is **at least** a gap of `2` rolls between **equal** valued rolls. More formally, if the value of the `ith` roll is **equal** to the value of the `jth` roll, then `abs(i - j) > 2`.
Return _the **total number** of distinct sequences possible_. Since the answer may be very large, return it **modulo** `109 + 7`.
Two sequences are considered distinct if at least one element is different.
**Example 1:**
**Input:** n = 4
**Output:** 184
**Explanation:** Some of the possible sequences are (1, 2, 3, 4), (6, 1, 2, 3), (1, 2, 3, 1), etc.
Some invalid sequences are (1, 2, 1, 3), (1, 2, 3, 6).
(1, 2, 1, 3) is invalid since the first and third roll have an equal value and abs(1 - 3) = 2 (i and j are 1-indexed).
(1, 2, 3, 6) is invalid since the greatest common divisor of 3 and 6 = 3.
There are a total of 184 distinct sequences possible, so we return 184.
**Example 2:**
**Input:** n = 2
**Output:** 22
**Explanation:** Some of the possible sequences are (1, 2), (2, 1), (3, 2).
Some invalid sequences are (3, 6), (2, 4) since the greatest common divisor is not equal to 1.
There are a total of 22 distinct sequences possible, so we return 22.
**Constraints:**
* `1 <= n <= 104` | To obtain points for some certain section x, what is the minimum number of arrows Bob must shoot? Given the small number of sections, can we brute force which sections Bob wants to win? For every set of sections Bob wants to win, check if we have the required amount of arrows. If we do, it is a valid selection. |
🐍Python3 easiest solution🔥🔥 | check-if-matrix-is-x-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Traverse Diagonal and then whole matrix**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- traverse matrix by primary and secondary diagonal\n- check if any of diagonal element are 0 if yes then return False.\n- else make them zero.\n- now after doing this travse all elements and add them.\n- now at last if answer is 0 then return True otherwise False, because if answer is 0 then we have our \'X\' Matrix else not.\n\n# Complexity\n- Time complexity: O(N+N*2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkXMatrix(self, grid: List[List[int]]) -> bool:\n i, k, j, N = 0, len(grid) - 1, 0, len(grid)\n\n def isValid(r, c): # to check validity of co-ordinates\n return r in range(0, N) and c in range(0, N)\n \n while isValid(i,j): # traverse primary and secondary diagonal\n if grid[i][j] == 0: return 0 # checking \'X\' Condition\n if grid[k][j] == 0: return 0 # checking \'X\' Condition\n grid[i][j] = 0 # Falgging them 0\n grid[k][j] = 0 # Falgging them 0\n i += 1 # moving to next primary diagonal\n j += 1 # Common column factor\n k -= 1 # moving to next Secondary diagonal\n \n ans = 0\n# travsersing all the elements\n for r in range(N): \n for c in range(N): \n ans += grid[r][c] # adding to cherck \'X\' Condition at last\n return not ans # as said return "1 if 0" or "0 if otherwise"\n```\n# Please like and comment below :-) | 3 | A square matrix is said to be an **X-Matrix** if **both** of the following conditions hold:
1. All the elements in the diagonals of the matrix are **non-zero**.
2. All other elements are 0.
Given a 2D integer array `grid` of size `n x n` representing a square matrix, return `true` _if_ `grid` _is an X-Matrix_. Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[2,0,0,1\],\[0,3,1,0\],\[0,5,2,0\],\[4,0,0,2\]\]
**Output:** true
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
**Example 2:**
**Input:** grid = \[\[5,7,0\],\[0,3,1\],\[0,5,0\]\]
**Output:** false
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `0 <= grid[i][j] <= 105` | Use a segment tree to perform fast point updates and range queries. We need each segment tree node to store the length of the longest substring of that segment consisting of only 1 repeating character. We will also have each segment tree node store the leftmost and rightmost character of the segment, the max length of a prefix substring consisting of only 1 repeating character, and the max length of a suffix substring consisting of only 1 repeating character. Use this information to properly merge the two segment tree nodes together. |
Simple Python Solution | check-if-matrix-is-x-matrix | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def checkXMatrix(self, grid: List[List[int]]) -> bool:\n n=len(grid)\n for i in range(n):\n for j in range(n):\n if((i!=j and i+j!=n-1) and grid[i][j]!=0):\n return 0\n elif((i==j or i+j==n-1) and grid[i][j]==0):\n return 0\n return 1\n\n\n```\nLike? hit that button | 1 | A square matrix is said to be an **X-Matrix** if **both** of the following conditions hold:
1. All the elements in the diagonals of the matrix are **non-zero**.
2. All other elements are 0.
Given a 2D integer array `grid` of size `n x n` representing a square matrix, return `true` _if_ `grid` _is an X-Matrix_. Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[2,0,0,1\],\[0,3,1,0\],\[0,5,2,0\],\[4,0,0,2\]\]
**Output:** true
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
**Example 2:**
**Input:** grid = \[\[5,7,0\],\[0,3,1\],\[0,5,0\]\]
**Output:** false
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `0 <= grid[i][j] <= 105` | Use a segment tree to perform fast point updates and range queries. We need each segment tree node to store the length of the longest substring of that segment consisting of only 1 repeating character. We will also have each segment tree node store the leftmost and rightmost character of the segment, the max length of a prefix substring consisting of only 1 repeating character, and the max length of a suffix substring consisting of only 1 repeating character. Use this information to properly merge the two segment tree nodes together. |
Python 3 Beat 94% 263ms two pointer | check-if-matrix-is-x-matrix | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def checkXMatrix(self, grid: List[List[int]]) -> bool:\n i, j = 0, len(grid) - 1\n a, b = [], []\n while i < len(grid):\n if i != j and grid[i].count(0) != len(grid) - 2:\n return False\n if grid[i][i] and grid[i][j] != 0:\n a.append(grid[i][i])\n a.append(grid[i][j])\n i += 1\n j -= 1\n print(a, b)\n return len(a) == len(grid) * 2 \n``` | 1 | A square matrix is said to be an **X-Matrix** if **both** of the following conditions hold:
1. All the elements in the diagonals of the matrix are **non-zero**.
2. All other elements are 0.
Given a 2D integer array `grid` of size `n x n` representing a square matrix, return `true` _if_ `grid` _is an X-Matrix_. Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[2,0,0,1\],\[0,3,1,0\],\[0,5,2,0\],\[4,0,0,2\]\]
**Output:** true
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
**Example 2:**
**Input:** grid = \[\[5,7,0\],\[0,3,1\],\[0,5,0\]\]
**Output:** false
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `0 <= grid[i][j] <= 105` | Use a segment tree to perform fast point updates and range queries. We need each segment tree node to store the length of the longest substring of that segment consisting of only 1 repeating character. We will also have each segment tree node store the leftmost and rightmost character of the segment, the max length of a prefix substring consisting of only 1 repeating character, and the max length of a suffix substring consisting of only 1 repeating character. Use this information to properly merge the two segment tree nodes together. |
Easy Python Solution | check-if-matrix-is-x-matrix | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def checkXMatrix(self, grid: List[List[int]]) -> bool:\n n=len(grid)\n sum=0\n c=0\n for x in range(n):\n for y in range(n):\n if not(x==y) and not(x==n-y-1):\n sum+=grid[x][y]\n elif (x==y) or (x==n-y-1):\n if grid[x][y]!=0:\n c+=1\n if sum==0:\n if (n%2==0 and c==n*2) or (n%2!=0 and c==(n*2)-1):\n return True\n else:\n return False\n``` | 1 | A square matrix is said to be an **X-Matrix** if **both** of the following conditions hold:
1. All the elements in the diagonals of the matrix are **non-zero**.
2. All other elements are 0.
Given a 2D integer array `grid` of size `n x n` representing a square matrix, return `true` _if_ `grid` _is an X-Matrix_. Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[2,0,0,1\],\[0,3,1,0\],\[0,5,2,0\],\[4,0,0,2\]\]
**Output:** true
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
**Example 2:**
**Input:** grid = \[\[5,7,0\],\[0,3,1\],\[0,5,0\]\]
**Output:** false
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `0 <= grid[i][j] <= 105` | Use a segment tree to perform fast point updates and range queries. We need each segment tree node to store the length of the longest substring of that segment consisting of only 1 repeating character. We will also have each segment tree node store the leftmost and rightmost character of the segment, the max length of a prefix substring consisting of only 1 repeating character, and the max length of a suffix substring consisting of only 1 repeating character. Use this information to properly merge the two segment tree nodes together. |
Easiest Python solution you will find....... Single loop | check-if-matrix-is-x-matrix | 0 | 1 | \n```class Solution:\n def checkXMatrix(self, grid: List[List[int]]) -> bool:\n lst=[]\n a=0\n j=len(grid)-1\n for i in range(0,len(grid)):\n if grid[i][i]==0:\n return False\n if grid[i][j]==0:\n return False\n if i!=j:\n a=grid[i][i]+grid[i][j]\n lst.append(a)\n elif i==j:\n a=grid[i][i]\n lst.append(a)\n j-=1\n for i in range(0,len(grid)):\n if sum(grid[i])!=lst[i]:\n return False\n \n \n return True\n```\nAfter optimising.\n```\nclass Solution:\n def checkXMatrix(self, grid: List[List[int]]) -> bool:\n a=0\n j=len(grid)-1\n for i in range(0,len(grid)):\n if grid[i][i]==0 or grid[i][j]==0:\n return False\n else:\n if i!=j:\n a=grid[i][i]+grid[i][j]\n elif i==j:\n a=grid[i][i]\n if a!=sum(grid[i]):\n return False\n j-=1\n return True\n \n | 1 | A square matrix is said to be an **X-Matrix** if **both** of the following conditions hold:
1. All the elements in the diagonals of the matrix are **non-zero**.
2. All other elements are 0.
Given a 2D integer array `grid` of size `n x n` representing a square matrix, return `true` _if_ `grid` _is an X-Matrix_. Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[2,0,0,1\],\[0,3,1,0\],\[0,5,2,0\],\[4,0,0,2\]\]
**Output:** true
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
**Example 2:**
**Input:** grid = \[\[5,7,0\],\[0,3,1\],\[0,5,0\]\]
**Output:** false
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `0 <= grid[i][j] <= 105` | Use a segment tree to perform fast point updates and range queries. We need each segment tree node to store the length of the longest substring of that segment consisting of only 1 repeating character. We will also have each segment tree node store the leftmost and rightmost character of the segment, the max length of a prefix substring consisting of only 1 repeating character, and the max length of a suffix substring consisting of only 1 repeating character. Use this information to properly merge the two segment tree nodes together. |
[ Go , Python , C++ ] one pass w/ comments | check-if-matrix-is-x-matrix | 0 | 1 | <iframe src="https://leetcode.com/playground/j49mCxmw/shared" frameBorder="0" width="800" height="500"></iframe> | 6 | A square matrix is said to be an **X-Matrix** if **both** of the following conditions hold:
1. All the elements in the diagonals of the matrix are **non-zero**.
2. All other elements are 0.
Given a 2D integer array `grid` of size `n x n` representing a square matrix, return `true` _if_ `grid` _is an X-Matrix_. Otherwise, return `false`.
**Example 1:**
**Input:** grid = \[\[2,0,0,1\],\[0,3,1,0\],\[0,5,2,0\],\[4,0,0,2\]\]
**Output:** true
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
**Example 2:**
**Input:** grid = \[\[5,7,0\],\[0,3,1\],\[0,5,0\]\]
**Output:** false
**Explanation:** Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `0 <= grid[i][j] <= 105` | Use a segment tree to perform fast point updates and range queries. We need each segment tree node to store the length of the longest substring of that segment consisting of only 1 repeating character. We will also have each segment tree node store the leftmost and rightmost character of the segment, the max length of a prefix substring consisting of only 1 repeating character, and the max length of a suffix substring consisting of only 1 repeating character. Use this information to properly merge the two segment tree nodes together. |
[Python] Simple dp from index 0 to n | count-number-of-ways-to-place-houses | 0 | 1 | ```\nclass Solution:\n def countHousePlacements(self, n: int) -> int:\n # the two sides of the roads are identical. We just need to count one side\n self.dp = collections.defaultdict(lambda: None)\n self.dp[0, 0] = 1 # the number cases not building house at index 0\n self.dp[0, 1] = 2 # total cases: including building house and not building house at index 0\n \n idx = 1\n while idx < n:\n self.dp[idx, 0] = self.dp[idx - 1, 1]\n self.dp[idx, 1] = self.dp[idx - 1, 1] + self.dp[idx - 1, 0]\n idx += 1\n \n return (self.dp[n - 1, 1] * self.dp[n - 1, 1]) % 1000000007\n``` | 1 | There is a street with `n * 2` **plots**, where there are `n` plots on each side of the street. The plots on each side are numbered from `1` to `n`. On each plot, a house can be placed.
Return _the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street_. Since the answer may be very large, return it **modulo** `109 + 7`.
Note that if a house is placed on the `ith` plot on one side of the street, a house can also be placed on the `ith` plot on the other side of the street.
**Example 1:**
**Input:** n = 1
**Output:** 4
**Explanation:**
Possible arrangements:
1. All plots are empty.
2. A house is placed on one side of the street.
3. A house is placed on the other side of the street.
4. Two houses are placed, one on each side of the street.
**Example 2:**
**Input:** n = 2
**Output:** 9
**Explanation:** The 9 possible arrangements are shown in the diagram above.
**Constraints:**
* `1 <= n <= 104` | For every occurrence of key in nums, find all indices within distance k from it. Use a hash table to remove duplicate indices. |
Python | Easy to Understand | With Explanation | No Kadane | maximum-score-of-spliced-array | 0 | 1 | ```\nclass Solution:\n def maximumsSplicedArray(self, nums1: List[int], nums2: List[int]) -> int:\n # create a difference array between nums1 and nums2\n # idea: find two subarray(elements are contiguous) in the diff\n # one is the subarray that have the minimum negative sum\n # another one is the subarray that have the maximum positive sum\n # so there are four candidates for maximum score:\n # 1. original_sum1 \n # 2. original_sum \n # 3. original_sum1 - min_negative_sum\n # 4. original_sum2 + max_positive_sum\n \n original_sum1 = sum(nums1)\n original_sum2 = sum(nums2)\n diff = [num1 - num2 for num1, num2 in zip(nums1, nums2)]\n min_negative_sum = float(\'inf\')\n max_positive_sum = - float(\'inf\')\n cur_negative_sum = 0\n cur_positive_sum = 0\n \n for val in diff:\n cur_negative_sum += val\n\n if cur_negative_sum > 0:\n cur_negative_sum = 0\n \n cur_positive_sum += val\n \n if cur_positive_sum < 0:\n cur_positive_sum = 0\n \n min_negative_sum = min(min_negative_sum, cur_negative_sum)\n max_positive_sum = max(max_positive_sum, cur_positive_sum)\n\n return max(original_sum1 - min_negative_sum, original_sum2 + max_positive_sum, original_sum2, original_sum1)\n```\n\n**Feel free to ask if you have questions :)\nPlease upvote if you find it helpful, many thanks!** | 3 | You are given two **0-indexed** integer arrays `nums1` and `nums2`, both of length `n`.
You can choose two integers `left` and `right` where `0 <= left <= right < n` and **swap** the subarray `nums1[left...right]` with the subarray `nums2[left...right]`.
* For example, if `nums1 = [1,2,3,4,5]` and `nums2 = [11,12,13,14,15]` and you choose `left = 1` and `right = 2`, `nums1` becomes `[1,**12,13**,4,5]` and `nums2` becomes `[11,**2,3**,14,15]`.
You may choose to apply the mentioned operation **once** or not do anything.
The **score** of the arrays is the **maximum** of `sum(nums1)` and `sum(nums2)`, where `sum(arr)` is the sum of all the elements in the array `arr`.
Return _the **maximum possible score**_.
A **subarray** is a contiguous sequence of elements within an array. `arr[left...right]` denotes the subarray that contains the elements of `nums` between indices `left` and `right` (**inclusive**).
**Example 1:**
**Input:** nums1 = \[60,60,60\], nums2 = \[10,90,10\]
**Output:** 210
**Explanation:** Choosing left = 1 and right = 1, we have nums1 = \[60,**90**,60\] and nums2 = \[10,**60**,10\].
The score is max(sum(nums1), sum(nums2)) = max(210, 80) = 210.
**Example 2:**
**Input:** nums1 = \[20,40,20,70,30\], nums2 = \[50,20,50,40,20\]
**Output:** 220
**Explanation:** Choosing left = 3, right = 4, we have nums1 = \[20,40,20,**40,20**\] and nums2 = \[50,20,50,**70,30**\].
The score is max(sum(nums1), sum(nums2)) = max(140, 220) = 220.
**Example 3:**
**Input:** nums1 = \[7,11,13\], nums2 = \[1,1,1\]
**Output:** 31
**Explanation:** We choose not to swap any subarray.
The score is max(sum(nums1), sum(nums2)) = max(31, 3) = 31.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `1 <= nums1[i], nums2[i] <= 104` | Consider what the paths from src1 to dest and src2 to dest would look like in the optimal solution. It can be shown that in an optimal solution, the two paths from src1 and src2 will coincide at one node, and the remaining part to dest will be the same for both paths. Now consider how to find the node where the paths will coincide. How can algorithms for finding the shortest path between two nodes help us? |
[Python3] dfs | minimum-score-after-removals-on-a-tree | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/0cdc07e704aeceebd9f20162639cca47846e6641) for solutions of weekly 299. \n\n```\nclass Solution:\n def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int: \n n = len(nums)\n graph = [[] for _ in range(n)]\n for u, v in edges: \n graph[u].append(v)\n graph[v].append(u)\n \n def fn(u): \n score[u] = nums[u]\n child[u] = {u}\n for v in graph[u]: \n if seen[v] == 0: \n seen[v] = 1\n fn(v)\n score[u] ^= score[v]\n child[u] |= child[v]\n \n seen = [1] + [0]*(n-1)\n score = [0]*n\n child = [set() for _ in range(n)]\n fn(0)\n \n ans = inf \n for u in range(1, n): \n for v in range(u+1, n): \n if u in child[v]: \n uu = score[u]\n vv = score[v] ^ score[u]\n xx = score[0] ^ score[v]\n elif v in child[u]: \n uu = score[u] ^ score[v]\n vv = score[v]\n xx = score[0] ^ score[u]\n else: \n uu = score[u]\n vv = score[v]\n xx = score[0] ^ score[u] ^ score[v]\n ans = min(ans, max(uu, vv, xx) - min(uu, vv, xx))\n return ans \n```\n\nAdded an alternative implement (based on the solution of @cuiaoxiang). \n```\nclass Solution:\n def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int: \n n = len(nums)\n graph = [[] for _ in range(n)]\n for u, v in edges: \n graph[u].append(v)\n graph[v].append(u)\n \n def fn(u, p): \n nonlocal t\n score[u] = nums[u]\n tin[u] = (t := t+1) # time to enter\n for v in graph[u]: \n if v != p: \n fn(v, u)\n score[u] ^= score[v]\n tout[u] = t # time to exit \n \n t = 0 \n score = [0]*n\n tin = [0]*n \n tout = [0]*n \n fn(0, -1)\n \n ans = inf \n for u in range(1, n): \n for v in range(u+1, n): \n if tin[v] <= tin[u] and tout[v] >= tout[u]: # enter earlier & exit later == parent \n uu = score[u]\n vv = score[v] ^ score[u]\n xx = score[0] ^ score[v]\n elif tin[v] >= tin[u] and tout[v] <= tout[u]: \n uu = score[u] ^ score[v]\n vv = score[v]\n xx = score[0] ^ score[u]\n else: \n uu = score[u]\n vv = score[v]\n xx = score[0] ^ score[u] ^ score[v]\n ans = min(ans, max(uu, vv, xx) - min(uu, vv, xx))\n return ans \n``` | 6 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given a **0-indexed** integer array `nums` of length `n` where `nums[i]` represents the value of the `ith` node. You are also given a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Remove two **distinct** edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
1. Get the XOR of all the values of the nodes for **each** of the three components respectively.
2. The **difference** between the **largest** XOR value and the **smallest** XOR value is the **score** of the pair.
* For example, say the three components have the node values: `[4,5,7]`, `[1,9]`, and `[3,3,3]`. The three XOR values are `4 ^ 5 ^ 7 = **6**`, `1 ^ 9 = **8**`, and `3 ^ 3 ^ 3 = **3**`. The largest XOR value is `8` and the smallest XOR value is `3`. The score is then `8 - 3 = 5`.
Return _the **minimum** score of any possible pair of edge removals on the given tree_.
**Example 1:**
**Input:** nums = \[1,5,5,4,11\], edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\]\]
**Output:** 9
**Explanation:** The diagram above shows a way to make a pair of removals.
- The 1st component has nodes \[1,3,4\] with values \[5,4,11\]. Its XOR value is 5 ^ 4 ^ 11 = 10.
- The 2nd component has node \[0\] with value \[1\]. Its XOR value is 1 = 1.
- The 3rd component has node \[2\] with value \[5\]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.
**Example 2:**
**Input:** nums = \[5,5,2,4,4,2\], edges = \[\[0,1\],\[1,2\],\[5,2\],\[4,3\],\[1,3\]\]
**Output:** 0
**Explanation:** The diagram above shows a way to make a pair of removals.
- The 1st component has nodes \[3,4\] with values \[4,4\]. Its XOR value is 4 ^ 4 = 0.
- The 2nd component has nodes \[1,0\] with values \[5,5\]. Its XOR value is 5 ^ 5 = 0.
- The 3rd component has nodes \[2,5\] with values \[2,2\]. Its XOR value is 2 ^ 2 = 0.
The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0.
We cannot obtain a smaller score than 0.
**Constraints:**
* `n == nums.length`
* `3 <= n <= 1000`
* `1 <= nums[i] <= 108`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `edges` represents a valid tree. | A row of bricks can be represented uniquely by the points where two bricks are joined together. For a given row of bricks, how many configurations of bricks could you have put below this row such that the wall is sturdy? Use dynamic programming to store the number of possible sturdy walls with a given height and configuration of bricks on the top row. |
Solution without LCA and actual edge deleting. Simpler DFS. | minimum-score-after-removals-on-a-tree | 0 | 1 | # Approach\n1) Let\'s fix some edge *x-y*, imaginary delete it and consider two trees with roots *x* and *y*.\n2) Count subtrees xors for both of them (*xors* array).\n3) Let\'s fix some other node *v* - bottom end of second edge we delete.\n4) If *v* is in *x* tree, xors of components will be *[xors[v], xors[x] ^ xors[v], xors[y]]*. Another case is symmetrical.\n\n# Code\n```\nINF = 10**9\n\nclass Solution:\n def minimumScore(self, a: List[int], edges: List[List[int]]) -> int:\n n = len(a)\n g = [[] for _ in range(n)]\n for x, y in edges:\n g[x].append(y)\n g[y].append(x)\n\n def dfs(v, p):\n is_x_comp[v] = is_x_comp_flag\n for to in g[v]:\n if to == p:\n continue\n dfs(to, v)\n xors[v] ^= xors[to]\n\n \n res = INF\n\n for x, y in edges:\n xors = a.copy()\n is_x_comp = [False for _ in range(n)]\n is_x_comp_flag = True\n dfs(x, y)\n is_x_comp_flag = False\n dfs(y, x)\n\n for v in range(n):\n if v == x or v == y:\n continue\n vals = [\n xors[v],\n xors[x] ^ (xors[v] if is_x_comp[v] else 0),\n xors[y] ^ (0 if is_x_comp[v] else xors[v]),\n ]\n vals.sort()\n res = min(res, vals[2] - vals[0])\n \n return res\n``` | 0 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given a **0-indexed** integer array `nums` of length `n` where `nums[i]` represents the value of the `ith` node. You are also given a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Remove two **distinct** edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
1. Get the XOR of all the values of the nodes for **each** of the three components respectively.
2. The **difference** between the **largest** XOR value and the **smallest** XOR value is the **score** of the pair.
* For example, say the three components have the node values: `[4,5,7]`, `[1,9]`, and `[3,3,3]`. The three XOR values are `4 ^ 5 ^ 7 = **6**`, `1 ^ 9 = **8**`, and `3 ^ 3 ^ 3 = **3**`. The largest XOR value is `8` and the smallest XOR value is `3`. The score is then `8 - 3 = 5`.
Return _the **minimum** score of any possible pair of edge removals on the given tree_.
**Example 1:**
**Input:** nums = \[1,5,5,4,11\], edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\]\]
**Output:** 9
**Explanation:** The diagram above shows a way to make a pair of removals.
- The 1st component has nodes \[1,3,4\] with values \[5,4,11\]. Its XOR value is 5 ^ 4 ^ 11 = 10.
- The 2nd component has node \[0\] with value \[1\]. Its XOR value is 1 = 1.
- The 3rd component has node \[2\] with value \[5\]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.
**Example 2:**
**Input:** nums = \[5,5,2,4,4,2\], edges = \[\[0,1\],\[1,2\],\[5,2\],\[4,3\],\[1,3\]\]
**Output:** 0
**Explanation:** The diagram above shows a way to make a pair of removals.
- The 1st component has nodes \[3,4\] with values \[4,4\]. Its XOR value is 4 ^ 4 = 0.
- The 2nd component has nodes \[1,0\] with values \[5,5\]. Its XOR value is 5 ^ 5 = 0.
- The 3rd component has nodes \[2,5\] with values \[2,2\]. Its XOR value is 2 ^ 2 = 0.
The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0.
We cannot obtain a smaller score than 0.
**Constraints:**
* `n == nums.length`
* `3 <= n <= 1000`
* `1 <= nums[i] <= 108`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `edges` represents a valid tree. | A row of bricks can be represented uniquely by the points where two bricks are joined together. For a given row of bricks, how many configurations of bricks could you have put below this row such that the wall is sturdy? Use dynamic programming to store the number of possible sturdy walls with a given height and configuration of bricks on the top row. |
Python (Simple DFS) | minimum-score-after-removals-on-a-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumScore(self, nums, edges):\n dict1 = defaultdict(list)\n\n for i,j in edges:\n dict1[i].append(j)\n dict1[j].append(i)\n\n @lru_cache(None)\n def dfs(root,parent):\n res = []\n val = nums[root]\n\n for neighbor in dict1[root]:\n if neighbor != parent:\n cur = dfs(neighbor,root)\n res.extend(cur)\n val ^= cur[-1]\n\n res.append(val)\n\n return res\n\n min_val = float("inf")\n\n for x,y in edges:\n left_xors = dfs(x,y)\n right_xors = dfs(y,x)\n left_val = left_xors[-1]\n right_val = right_xors[-1]\n\n for l1 in left_xors[:-1]:\n l2 = left_val^l1\n min_val = min(min_val,max(l1,l2,right_val)-min(l1,l2,right_val))\n \n for r1 in right_xors[:-1]:\n r2 = right_val^r1\n min_val = min(min_val,max(r1,r2,left_val)-min(r1,r2,left_val))\n\n return min_val\n\n\n\n \n\n \n\n\n\n\n``` | 0 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given a **0-indexed** integer array `nums` of length `n` where `nums[i]` represents the value of the `ith` node. You are also given a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Remove two **distinct** edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
1. Get the XOR of all the values of the nodes for **each** of the three components respectively.
2. The **difference** between the **largest** XOR value and the **smallest** XOR value is the **score** of the pair.
* For example, say the three components have the node values: `[4,5,7]`, `[1,9]`, and `[3,3,3]`. The three XOR values are `4 ^ 5 ^ 7 = **6**`, `1 ^ 9 = **8**`, and `3 ^ 3 ^ 3 = **3**`. The largest XOR value is `8` and the smallest XOR value is `3`. The score is then `8 - 3 = 5`.
Return _the **minimum** score of any possible pair of edge removals on the given tree_.
**Example 1:**
**Input:** nums = \[1,5,5,4,11\], edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\]\]
**Output:** 9
**Explanation:** The diagram above shows a way to make a pair of removals.
- The 1st component has nodes \[1,3,4\] with values \[5,4,11\]. Its XOR value is 5 ^ 4 ^ 11 = 10.
- The 2nd component has node \[0\] with value \[1\]. Its XOR value is 1 = 1.
- The 3rd component has node \[2\] with value \[5\]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.
**Example 2:**
**Input:** nums = \[5,5,2,4,4,2\], edges = \[\[0,1\],\[1,2\],\[5,2\],\[4,3\],\[1,3\]\]
**Output:** 0
**Explanation:** The diagram above shows a way to make a pair of removals.
- The 1st component has nodes \[3,4\] with values \[4,4\]. Its XOR value is 4 ^ 4 = 0.
- The 2nd component has nodes \[1,0\] with values \[5,5\]. Its XOR value is 5 ^ 5 = 0.
- The 3rd component has nodes \[2,5\] with values \[2,2\]. Its XOR value is 2 ^ 2 = 0.
The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0.
We cannot obtain a smaller score than 0.
**Constraints:**
* `n == nums.length`
* `3 <= n <= 1000`
* `1 <= nums[i] <= 108`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* `edges` represents a valid tree. | A row of bricks can be represented uniquely by the points where two bricks are joined together. For a given row of bricks, how many configurations of bricks could you have put below this row such that the wall is sturdy? Use dynamic programming to store the number of possible sturdy walls with a given height and configuration of bricks on the top row. |
cccc | decode-the-message | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decodeMessage(self, key: str, message: str) -> str:\n decr_key = ""\n for ch in key:\n if ch not in decr_key:\n decr_key+=ch\n decr_key = decr_key.replace(" ", "")+" "\n out = ""\n alfa = "abcdefghijklmnopqrstuvwxyz "\n for char in message:\n out+= alfa[decr_key.index(char)]\n \n return out\n``` | 1 | You are given the strings `key` and `message`, which represent a cipher key and a secret message, respectively. The steps to decode `message` are as follows:
1. Use the **first** appearance of all 26 lowercase English letters in `key` as the **order** of the substitution table.
2. Align the substitution table with the regular English alphabet.
3. Each letter in `message` is then **substituted** using the table.
4. Spaces `' '` are transformed to themselves.
* For example, given `key = "**hap**p**y** **bo**y "` (actual key would have **at least one** instance of each letter in the alphabet), we have the partial substitution table of (`'h' -> 'a'`, `'a' -> 'b'`, `'p' -> 'c'`, `'y' -> 'd'`, `'b' -> 'e'`, `'o' -> 'f'`).
Return _the decoded message_.
**Example 1:**
**Input:** key = "the quick brown fox jumps over the lazy dog ", message = "vkbs bs t suepuv "
**Output:** "this is a secret "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**the** **quick** **brown** **f**o**x** **j**u**mps** o**v**er the **lazy** **d**o**g** ".
**Example 2:**
**Input:** key = "eljuxhpwnyrdgtqkviszcfmabo ", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb "
**Output:** "the five boxing wizards jump quickly "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**eljuxhpwnyrdgtqkviszcfmabo** ".
**Constraints:**
* `26 <= key.length <= 2000`
* `key` consists of lowercase English letters and `' '`.
* `key` contains every letter in the English alphabet (`'a'` to `'z'`) **at least once**.
* `1 <= message.length <= 2000`
* `message` consists of lowercase English letters and `' '`. | There are only 2 valid patterns: ‘101’ and ‘010’. Think about how we can construct these 2 patterns from smaller patterns. Count the number of subsequences of the form ‘01’ or ‘10’ first. Let n01[i] be the number of ‘01’ subsequences that exist in the prefix of s up to the ith building. How can you compute n01[i]? Let n0[i] and n1[i] be the number of ‘0’s and ‘1’s that exists in the prefix of s up to i respectively. Then n01[i] = n01[i – 1] if s[i] == ‘0’, otherwise n01[i] = n01[i – 1] + n0[i – 1]. The same logic applies to building the n10 array and subsequently the n101 and n010 arrays for the number of ‘101’ and ‘010‘ subsequences. |
Easy Python solution using Hashing | decode-the-message | 0 | 1 | ```python\nclass Solution:\n def decodeMessage(self, key: str, message: str) -> str:\n mapping = {\' \': \' \'}\n i = 0\n res = \'\'\n letters = \'abcdefghijklmnopqrstuvwxyz\'\n \n for char in key:\n if char not in mapping:\n mapping[char] = letters[i]\n i += 1\n \n for char in message:\n res += mapping[char]\n \n return res | 40 | You are given the strings `key` and `message`, which represent a cipher key and a secret message, respectively. The steps to decode `message` are as follows:
1. Use the **first** appearance of all 26 lowercase English letters in `key` as the **order** of the substitution table.
2. Align the substitution table with the regular English alphabet.
3. Each letter in `message` is then **substituted** using the table.
4. Spaces `' '` are transformed to themselves.
* For example, given `key = "**hap**p**y** **bo**y "` (actual key would have **at least one** instance of each letter in the alphabet), we have the partial substitution table of (`'h' -> 'a'`, `'a' -> 'b'`, `'p' -> 'c'`, `'y' -> 'd'`, `'b' -> 'e'`, `'o' -> 'f'`).
Return _the decoded message_.
**Example 1:**
**Input:** key = "the quick brown fox jumps over the lazy dog ", message = "vkbs bs t suepuv "
**Output:** "this is a secret "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**the** **quick** **brown** **f**o**x** **j**u**mps** o**v**er the **lazy** **d**o**g** ".
**Example 2:**
**Input:** key = "eljuxhpwnyrdgtqkviszcfmabo ", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb "
**Output:** "the five boxing wizards jump quickly "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**eljuxhpwnyrdgtqkviszcfmabo** ".
**Constraints:**
* `26 <= key.length <= 2000`
* `key` consists of lowercase English letters and `' '`.
* `key` contains every letter in the English alphabet (`'a'` to `'z'`) **at least once**.
* `1 <= message.length <= 2000`
* `message` consists of lowercase English letters and `' '`. | There are only 2 valid patterns: ‘101’ and ‘010’. Think about how we can construct these 2 patterns from smaller patterns. Count the number of subsequences of the form ‘01’ or ‘10’ first. Let n01[i] be the number of ‘01’ subsequences that exist in the prefix of s up to the ith building. How can you compute n01[i]? Let n0[i] and n1[i] be the number of ‘0’s and ‘1’s that exists in the prefix of s up to i respectively. Then n01[i] = n01[i – 1] if s[i] == ‘0’, otherwise n01[i] = n01[i – 1] + n0[i – 1]. The same logic applies to building the n10 array and subsequently the n101 and n010 arrays for the number of ‘101’ and ‘010‘ subsequences. |
Easy Python Solution | decode-the-message | 0 | 1 | # Intuition\nThis code creates a dictionary d that maps each unique character in key (excluding whitespace) to a lowercase letter of the alphabet (starting from \'a\'). It then iterates through each character in message, and if the character is in the dictionary d, it appends the corresponding letter to a string ans. If the character is a whitespace, it appends a whitespace to the string ans. The final string ans is then returned.\n\n# Approach\nThe first loop iterates through each character in key and checks if the character is not already in the dictionary d and is not a whitespace. If both conditions are satisfied, it adds the character to the dictionary with a value that corresponds to a lowercase letter of the alphabet (starting from \'a\'). The second loop iterates through each character in message, and if the character is in the dictionary d, it appends the corresponding letter to a string ans. If the character is a whitespace, it appends a whitespace to the string ans.\n\n# Complexity\n- Time complexity:\n O(k + m), where k is the length of key and m is the length of message.\n\n- Space complexity:\nO(26)\n\n# Code\n```\nclass Solution:\n def decodeMessage(self, key: str, message: str) -> str:\n d = {}\n ans = ""\n\n n = 0 \n for i in key:\n if i not in d and i != " ":\n d[i]=chr(ord(\'a\')+n)\n n += 1\n \n for i in message:\n if i in d:\n ans += d[i]\n elif i == " ":\n ans += " "\n \n return ans\n\n\n\n \n \n``` | 3 | You are given the strings `key` and `message`, which represent a cipher key and a secret message, respectively. The steps to decode `message` are as follows:
1. Use the **first** appearance of all 26 lowercase English letters in `key` as the **order** of the substitution table.
2. Align the substitution table with the regular English alphabet.
3. Each letter in `message` is then **substituted** using the table.
4. Spaces `' '` are transformed to themselves.
* For example, given `key = "**hap**p**y** **bo**y "` (actual key would have **at least one** instance of each letter in the alphabet), we have the partial substitution table of (`'h' -> 'a'`, `'a' -> 'b'`, `'p' -> 'c'`, `'y' -> 'd'`, `'b' -> 'e'`, `'o' -> 'f'`).
Return _the decoded message_.
**Example 1:**
**Input:** key = "the quick brown fox jumps over the lazy dog ", message = "vkbs bs t suepuv "
**Output:** "this is a secret "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**the** **quick** **brown** **f**o**x** **j**u**mps** o**v**er the **lazy** **d**o**g** ".
**Example 2:**
**Input:** key = "eljuxhpwnyrdgtqkviszcfmabo ", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb "
**Output:** "the five boxing wizards jump quickly "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**eljuxhpwnyrdgtqkviszcfmabo** ".
**Constraints:**
* `26 <= key.length <= 2000`
* `key` consists of lowercase English letters and `' '`.
* `key` contains every letter in the English alphabet (`'a'` to `'z'`) **at least once**.
* `1 <= message.length <= 2000`
* `message` consists of lowercase English letters and `' '`. | There are only 2 valid patterns: ‘101’ and ‘010’. Think about how we can construct these 2 patterns from smaller patterns. Count the number of subsequences of the form ‘01’ or ‘10’ first. Let n01[i] be the number of ‘01’ subsequences that exist in the prefix of s up to the ith building. How can you compute n01[i]? Let n0[i] and n1[i] be the number of ‘0’s and ‘1’s that exists in the prefix of s up to i respectively. Then n01[i] = n01[i – 1] if s[i] == ‘0’, otherwise n01[i] = n01[i – 1] + n0[i – 1]. The same logic applies to building the n10 array and subsequently the n101 and n010 arrays for the number of ‘101’ and ‘010‘ subsequences. |
EASY UNDERSTANDABLE | PYTHON O(N) SOLUTION | APPROACH | decode-the-message | 0 | 1 | \n**Bold**\n# Intuition\nMatch the characters of the key with the <index>+97 th ASCII value to it.\n\n# Approach\n* First try to remove all the spaces and the duplicate characters from the key and store it in str1\n* now itereate through the new string and find its index in the str1 now lets say "v" the index of "v in str1 is 22 . Add 97 with the index of it to get the character match of it.\n\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\nclass Solution:\n def decodeMessage(self, key: str, message: str) -> str:\n str1 = ""\n res = ""\n for i in key:\n if i != " " and i not in str1:\n str1+=i \n for i in message:\n if i != " ":\n res+= chr(str1.index(i)+97)\n else:\n res+=" "\n return res \n \n | 2 | You are given the strings `key` and `message`, which represent a cipher key and a secret message, respectively. The steps to decode `message` are as follows:
1. Use the **first** appearance of all 26 lowercase English letters in `key` as the **order** of the substitution table.
2. Align the substitution table with the regular English alphabet.
3. Each letter in `message` is then **substituted** using the table.
4. Spaces `' '` are transformed to themselves.
* For example, given `key = "**hap**p**y** **bo**y "` (actual key would have **at least one** instance of each letter in the alphabet), we have the partial substitution table of (`'h' -> 'a'`, `'a' -> 'b'`, `'p' -> 'c'`, `'y' -> 'd'`, `'b' -> 'e'`, `'o' -> 'f'`).
Return _the decoded message_.
**Example 1:**
**Input:** key = "the quick brown fox jumps over the lazy dog ", message = "vkbs bs t suepuv "
**Output:** "this is a secret "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**the** **quick** **brown** **f**o**x** **j**u**mps** o**v**er the **lazy** **d**o**g** ".
**Example 2:**
**Input:** key = "eljuxhpwnyrdgtqkviszcfmabo ", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb "
**Output:** "the five boxing wizards jump quickly "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**eljuxhpwnyrdgtqkviszcfmabo** ".
**Constraints:**
* `26 <= key.length <= 2000`
* `key` consists of lowercase English letters and `' '`.
* `key` contains every letter in the English alphabet (`'a'` to `'z'`) **at least once**.
* `1 <= message.length <= 2000`
* `message` consists of lowercase English letters and `' '`. | There are only 2 valid patterns: ‘101’ and ‘010’. Think about how we can construct these 2 patterns from smaller patterns. Count the number of subsequences of the form ‘01’ or ‘10’ first. Let n01[i] be the number of ‘01’ subsequences that exist in the prefix of s up to the ith building. How can you compute n01[i]? Let n0[i] and n1[i] be the number of ‘0’s and ‘1’s that exists in the prefix of s up to i respectively. Then n01[i] = n01[i – 1] if s[i] == ‘0’, otherwise n01[i] = n01[i – 1] + n0[i – 1]. The same logic applies to building the n10 array and subsequently the n101 and n010 arrays for the number of ‘101’ and ‘010‘ subsequences. |
Python Solution with comment | decode-the-message | 0 | 1 | **Time Complexcity O(N^2)\nspace complexcity O(N)**\n```\nclass Solution:\n def decodeMessage(self, key: str, message: str) -> str:\n st=[]\n # convert string to list \n lst1=key.split(" ")\n for words in lst1:\n for word in words:\n if word in st:\n continue\n else:\n st.append(word)\n # crate a list of alphabet\n a=[\'a\',\'b\',\'c\',\'d\',\'e\',\'f\',\'g\',\'h\',\'i\',\'j\',\'k\',\'l\',\'m\',\'n\',\'o\',\'p\',\'q\',\'r\',\'s\',\'t\',\'u\',\n \'v\',\'w\',\'x\',\'y\',\'z\']\n ans=[]\n # by index we cheak in both list \n lst=message.split(" ")\n for words in lst:\n c=\'\'\n print(words)\n for word in words:\n print(word)\n print(st.index(word))\n d=a[(st.index(word))]\n c+=d\n ans.append(c)\n return " ".join(ans)\n```\n**pls upvote if help full** | 1 | You are given the strings `key` and `message`, which represent a cipher key and a secret message, respectively. The steps to decode `message` are as follows:
1. Use the **first** appearance of all 26 lowercase English letters in `key` as the **order** of the substitution table.
2. Align the substitution table with the regular English alphabet.
3. Each letter in `message` is then **substituted** using the table.
4. Spaces `' '` are transformed to themselves.
* For example, given `key = "**hap**p**y** **bo**y "` (actual key would have **at least one** instance of each letter in the alphabet), we have the partial substitution table of (`'h' -> 'a'`, `'a' -> 'b'`, `'p' -> 'c'`, `'y' -> 'd'`, `'b' -> 'e'`, `'o' -> 'f'`).
Return _the decoded message_.
**Example 1:**
**Input:** key = "the quick brown fox jumps over the lazy dog ", message = "vkbs bs t suepuv "
**Output:** "this is a secret "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**the** **quick** **brown** **f**o**x** **j**u**mps** o**v**er the **lazy** **d**o**g** ".
**Example 2:**
**Input:** key = "eljuxhpwnyrdgtqkviszcfmabo ", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb "
**Output:** "the five boxing wizards jump quickly "
**Explanation:** The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "**eljuxhpwnyrdgtqkviszcfmabo** ".
**Constraints:**
* `26 <= key.length <= 2000`
* `key` consists of lowercase English letters and `' '`.
* `key` contains every letter in the English alphabet (`'a'` to `'z'`) **at least once**.
* `1 <= message.length <= 2000`
* `message` consists of lowercase English letters and `' '`. | There are only 2 valid patterns: ‘101’ and ‘010’. Think about how we can construct these 2 patterns from smaller patterns. Count the number of subsequences of the form ‘01’ or ‘10’ first. Let n01[i] be the number of ‘01’ subsequences that exist in the prefix of s up to the ith building. How can you compute n01[i]? Let n0[i] and n1[i] be the number of ‘0’s and ‘1’s that exists in the prefix of s up to i respectively. Then n01[i] = n01[i – 1] if s[i] == ‘0’, otherwise n01[i] = n01[i – 1] + n0[i – 1]. The same logic applies to building the n10 array and subsequently the n101 and n010 arrays for the number of ‘101’ and ‘010‘ subsequences. |
Beats 98.6% || Only LOOPS || Python 3 Explained | spiral-matrix-iv | 0 | 1 | # Intuition\nThe code is very similar to the SPIRAL MATRIX I / II but here you need to check if we reach at the end of head i.e head.next = None;\nif it is None return ans as we reached end and all other matrix coloumn will be -1 (ans matrix is prefilled with -1)\nIts a pretty long code and shorter codes are also available but its a good practice to know how loops work! ;)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def spiralMatrix(self, m: int, n: int, head: Optional[ListNode]) -> List[List[int]]:\n ans = [[-1]*(n) for _ in range(m)]\n first_row = 0\n first_col = 0\n last_row = m - 1\n last_col = n - 1\n while first_row < last_row and first_col < last_col:\n for j in range(first_col, last_col):\n ans[first_row][j] = head.val\n head = head.next\n if head == None:\n return ans\n \n for i in range(first_row, last_row):\n ans[i][last_col] = head.val\n head = head.next\n if head == None:\n return ans\n for j in range(last_col, first_col, -1):\n ans[last_row][j] = head.val\n head = head.next\n if head == None:\n return ans\n for i in range(last_row, first_row, -1):\n ans[i][first_col] = head.val\n head = head.next\n if head == None:\n return ans\n first_row += 1\n first_col += 1\n last_row -= 1\n last_col -= 1\n \n if head != None:\n for i in range(first_row, last_row + 1):\n for j in range(first_col, last_col + 1):\n ans[i][j] = head.val\n head = head.next \n if head == None:\n return ans \n return(ans)\n\n``` | 1 | You are given two integers `m` and `n`, which represent the dimensions of a matrix.
You are also given the `head` of a linked list of integers.
Generate an `m x n` matrix that contains the integers in the linked list presented in **spiral** order **(clockwise)**, starting from the **top-left** of the matrix. If there are remaining empty spaces, fill them with `-1`.
Return _the generated matrix_.
**Example 1:**
**Input:** m = 3, n = 5, head = \[3,0,2,6,8,1,7,9,4,2,5,5,0\]
**Output:** \[\[3,0,2,6,8\],\[5,0,-1,-1,1\],\[5,2,4,9,7\]\]
**Explanation:** The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.
**Example 2:**
**Input:** m = 1, n = 4, head = \[0,1,2\]
**Output:** \[\[0,1,2,-1\]\]
**Explanation:** The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.
**Constraints:**
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* The number of nodes in the list is in the range `[1, m * n]`.
* `0 <= Node.val <= 1000` | Each s_i is a suffix of the string s, so consider algorithms that can determine the longest prefix that is also a suffix. Could you use the Z array from the Z algorithm to find the score of each s_i? |
🔥🔥BEATS 90.46%🔥🔥||Easy Basic Solution | spiral-matrix-iv | 0 | 1 | \n# Approach\n\n---\n\nFill Matrix By traverssing Linked List\n\n# Complexity\n\n- Space complexity:\nO(N^2)\n\n# Code\n\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n\n---\n\n def spiralMatrix(self, m: int, n: int, head: Optional[ListNode]) -> List[List[int]]:\n mat=[[-1 for i in range(n)]for j in range(m)]\n colbegin=0\n rowbegin=0\n colend=n\n rowend=m\n while rowbegin<rowend and colbegin<colend and head!=None:\n for i in range(colbegin,colend):\n if head!=None:\n mat[rowbegin][i]=head.val\n head=head.next\n for j in range(rowbegin+1,rowend-1):\n if head!=None:\n mat[j][colend-1]=head.val\n head=head.next\n if rowbegin!=rowend-1:\n for i in range(colend-1,colbegin-1,-1):\n if head!=None:\n mat[rowend-1][i]=head.val\n head=head.next\n if colbegin!=colend-1:\n for j in range(rowend-2,rowbegin,-1):\n if head!=None:\n mat[j][colbegin]=head.val\n head=head.next\n colbegin+=1\n colend-=1\n rowbegin+=1\n rowend-=1\n return mat | 1 | You are given two integers `m` and `n`, which represent the dimensions of a matrix.
You are also given the `head` of a linked list of integers.
Generate an `m x n` matrix that contains the integers in the linked list presented in **spiral** order **(clockwise)**, starting from the **top-left** of the matrix. If there are remaining empty spaces, fill them with `-1`.
Return _the generated matrix_.
**Example 1:**
**Input:** m = 3, n = 5, head = \[3,0,2,6,8,1,7,9,4,2,5,5,0\]
**Output:** \[\[3,0,2,6,8\],\[5,0,-1,-1,1\],\[5,2,4,9,7\]\]
**Explanation:** The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.
**Example 2:**
**Input:** m = 1, n = 4, head = \[0,1,2\]
**Output:** \[\[0,1,2,-1\]\]
**Explanation:** The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.
**Constraints:**
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* The number of nodes in the list is in the range `[1, m * n]`.
* `0 <= Node.val <= 1000` | Each s_i is a suffix of the string s, so consider algorithms that can determine the longest prefix that is also a suffix. Could you use the Z array from the Z algorithm to find the score of each s_i? |
Simple Simulation very clear and easy to understand | spiral-matrix-iv | 0 | 1 | ```\n\nclass Solution:\n def spiralMatrix(self, m: int, n: int, head: Optional[ListNode]) -> List[List[int]]:\n result = [ [-1] * n for _ in range(m) ]\n node = head\n \n \n \n UP = 2\n DOWN = 3\n LEFT = 1\n RIGHT = 0\n \n directions = ( (0,1), (0,-1), (-1,0), (1,0))\n direction = RIGHT\n \n uB, dB, lB, rB = 0, m-1, 0, n-1\n row, col = 0, 0\n\n while node:\n result[row][col] = node.val \n node = node.next \n\n if direction == RIGHT and col == rB and row != dB:\n direction = DOWN\n uB += 1\n \n\n if direction == DOWN and col == rB and row == dB:\n direction = LEFT\n rB -= 1\n \n if direction == LEFT and col == lB and row != uB:\n direction = UP\n dB -= 1\n \n if direction == UP and col == lB and row == uB:\n direction = RIGHT\n lB += 1\n \n dr,dc = directions[direction]\n row,col = row+dr, col+dc\n\n return result\n\n``` | 2 | You are given two integers `m` and `n`, which represent the dimensions of a matrix.
You are also given the `head` of a linked list of integers.
Generate an `m x n` matrix that contains the integers in the linked list presented in **spiral** order **(clockwise)**, starting from the **top-left** of the matrix. If there are remaining empty spaces, fill them with `-1`.
Return _the generated matrix_.
**Example 1:**
**Input:** m = 3, n = 5, head = \[3,0,2,6,8,1,7,9,4,2,5,5,0\]
**Output:** \[\[3,0,2,6,8\],\[5,0,-1,-1,1\],\[5,2,4,9,7\]\]
**Explanation:** The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.
**Example 2:**
**Input:** m = 1, n = 4, head = \[0,1,2\]
**Output:** \[\[0,1,2,-1\]\]
**Explanation:** The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.
**Constraints:**
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* The number of nodes in the list is in the range `[1, m * n]`.
* `0 <= Node.val <= 1000` | Each s_i is a suffix of the string s, so consider algorithms that can determine the longest prefix that is also a suffix. Could you use the Z array from the Z algorithm to find the score of each s_i? |
🔥🔥One Way approach using spiral matrix traversal technique!!🔥🔥 | spiral-matrix-iv | 0 | 1 | \n# Approach\nFirst of all i created a 2-D matrix of size n*m . Then use spiral Matrix Traversal technique and assign the cur head value at each cell.\n\n\n# Complexity\n- Time complexity:\nO(N*M)\n\n- Space complexity:\nO(N*M)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def spiralMatrix(self, m: int, n: int, head: Optional[ListNode]) -> List[List[int]]:\n matrix=[[-1 for _ in range(n)]for _ in range(m)]\n top,left=0,0\n down,right=len(matrix)-1,len(matrix[0])-1\n direction=0\n cur=head\n while top<=down and left<=right:\n if direction==0:\n for i in range(left,right+1):\n if cur :\n matrix[top][i]=cur.val\n cur=cur.next\n \n top+=1\n elif direction==1:\n \n for i in range(top,down+1):\n if cur:\n matrix[i][right]=cur.val\n cur=cur.next\n \n right-=1\n elif direction==2:\n \n for i in range(right,left-1,-1):\n if cur:\n matrix[down][i]=cur.val\n cur=cur.next\n \n down-=1\n elif direction==3:\n \n for i in range(down,top-1,-1):\n if cur:\n matrix[i][left]=cur.val\n cur=cur.next\n \n left+=1\n direction=(direction+1)%4\n return matrix\n``` | 2 | You are given two integers `m` and `n`, which represent the dimensions of a matrix.
You are also given the `head` of a linked list of integers.
Generate an `m x n` matrix that contains the integers in the linked list presented in **spiral** order **(clockwise)**, starting from the **top-left** of the matrix. If there are remaining empty spaces, fill them with `-1`.
Return _the generated matrix_.
**Example 1:**
**Input:** m = 3, n = 5, head = \[3,0,2,6,8,1,7,9,4,2,5,5,0\]
**Output:** \[\[3,0,2,6,8\],\[5,0,-1,-1,1\],\[5,2,4,9,7\]\]
**Explanation:** The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.
**Example 2:**
**Input:** m = 1, n = 4, head = \[0,1,2\]
**Output:** \[\[0,1,2,-1\]\]
**Explanation:** The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.
**Constraints:**
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* The number of nodes in the list is in the range `[1, m * n]`.
* `0 <= Node.val <= 1000` | Each s_i is a suffix of the string s, so consider algorithms that can determine the longest prefix that is also a suffix. Could you use the Z array from the Z algorithm to find the score of each s_i? |
Two Queues or Rolling Array | number-of-people-aware-of-a-secret | 0 | 1 | The second solution below is the optimized version of the first one, though it could be hard to debug.\n\nTherefore, we will start with the two queues solution, which should be easier to code and build an intuition.\n\n#### Two Queues\n\nWe use separate queues to track how many people are ready to tell the secret each day (`d`), and how many people are going to forget the secret (`f`).\n\nWe track the current number of people who can share the secret in `sharing`.\n\nEach day, three things happen:\n1. We add people in the front of the `d` queue to `sharing` (if `d.size() >= delay`).\n2. We subtract people in the front of `f` queue from `sharing` (if `f.size() >= forget`).\n3. The resulting `sharing` people tell the secret to the same number of new people.\n\t- We add these new people to the back of the `d` and `f` queues.\n\n**C++**\n```cpp\nint peopleAwareOfSecret(int n, int delay, int forget) {\n long long sharing = 0, mod = 1000000007;\n deque<int> d{1}, f{1};\n while (--n > 0) {\n if (d.size() >= delay) {\n sharing = (sharing + d.front()) % mod;\n d.pop_front();\n }\n if (f.size() >= forget) {\n sharing = (mod + sharing - f.front()) % mod;\n f.pop_front();\n }\n d.push_back(sharing);\n f.push_back(sharing);\n }\n return accumulate(begin(f), end(f), 0LL) % mod;\n} \n```\n**Complexity Analysis**\n- Time: O(n)\n- Memory: O(delay + forget)\n\n#### Rolling Array\nThis solution does exactly the same as the one above, using one rolling array instead of two queues.\n**Python 3**\n```python\nclass Solution:\n def peopleAwareOfSecret(self, n: int, d: int, f: int) -> int:\n dp, md = [1] + [0] * (f - 1), 10**9 + 7\n for i in range(1, n):\n dp[i % f] = (md + dp[(i + f - d) % f] - dp[i % f] + (0 if i == 1 else dp[(i - 1) % f])) % md\n return sum(dp) % md\n```\n**C++**\n```cpp\nint peopleAwareOfSecret(int n, int d, int f) {\n vector<long long> dp(f);\n dp[0] = 1;\n int mod = 1000000007;\n for (int i = 1; i < n; ++i)\n dp[i % f] = (mod + (i - 1 ? dp[(i - 1) % f] : 0) + dp[(i + f - d) % f] - dp[i % f]) % mod;\n return accumulate(begin(dp), end(dp), 0LL) % mod;\n}\n```\n**Complexity Analysis**\n- Time: O(n)\n- Memory: O(forget) | 57 | On day `1`, one person discovers a secret.
You are given an integer `delay`, which means that each person will **share** the secret with a new person **every day**, starting from `delay` days after discovering the secret. You are also given an integer `forget`, which means that each person will **forget** the secret `forget` days after discovering it. A person **cannot** share the secret on the same day they forgot it, or on any day afterwards.
Given an integer `n`, return _the number of people who know the secret at the end of day_ `n`. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 6, delay = 2, forget = 4
**Output:** 5
**Explanation:**
Day 1: Suppose the first person is named A. (1 person)
Day 2: A is the only person who knows the secret. (1 person)
Day 3: A shares the secret with a new person, B. (2 people)
Day 4: A shares the secret with a new person, C. (3 people)
Day 5: A forgets the secret, and B shares the secret with a new person, D. (3 people)
Day 6: B shares the secret with E, and C shares the secret with F. (5 people)
**Example 2:**
**Input:** n = 4, delay = 1, forget = 3
**Output:** 6
**Explanation:**
Day 1: The first person is named A. (1 person)
Day 2: A shares the secret with B. (2 people)
Day 3: A and B share the secret with 2 new people, C and D. (4 people)
Day 4: A forgets the secret. B, C, and D share the secret with 3 new people. (6 people)
**Constraints:**
* `2 <= n <= 1000`
* `1 <= delay < forget <= n` | The bigger digit should appear first (more to the left) because it contributes more to the value of the number. Get all the even digits, as well as odd digits. Sort them separately. Reconstruct the number by giving the earlier digits the highest available digit of the same parity. |
Easy Simulation with Explanation | number-of-people-aware-of-a-secret | 0 | 1 | ##### Explanation\n* We could simulate the given requriements with an Array\n* Let\'s maintain an Array, `people`, where every index, `idx`, tracks the delay and forget timeline for everybody. Note that we do not care about people who forget about the secret, so the size could be `forget` for the Array \n* Initially, only 1 person will know the secret\n* Next, for the days between `(1, n - 1)`:\n\t* Everybody will move forward in their timeline. They will go closer to "the forgetting deadline". To simulate, let\'s shift the people to their next day\n\t* Everybody who is past their delay and present in the Array will share secrets with somebody new. To simulate, update the first day count by checking how many people may now share the secret (whether they\'ve passed the delay time)\t\n\n##### Complexities\n* Time: `O(n * forget)`\n* Space: `O(forget)`\n\n```\ndef mod_add(a: int, b: int) -> int:\n\tMOD = 1000000007\n\treturn ((a % MOD) + (b % MOD)) % MOD \n\n\nclass Solution:\n def peopleAwareOfSecret(self, n: int, delay: int, forget: int) -> int:\n people = [0] * forget\n people[0] = 1\n \n for _ in range(1, n):\n for idx in range(forget - 1, 0, -1):\n people[idx] = people[idx - 1] \n \n new = 0\n for idx in range(forget):\n if idx >= delay:\n new = mod_add(new, people[idx])\n \n people[0] = new\n \n total = 0\n for p in people:\n total = mod_add(total, p)\n \n return total \n``` | 11 | On day `1`, one person discovers a secret.
You are given an integer `delay`, which means that each person will **share** the secret with a new person **every day**, starting from `delay` days after discovering the secret. You are also given an integer `forget`, which means that each person will **forget** the secret `forget` days after discovering it. A person **cannot** share the secret on the same day they forgot it, or on any day afterwards.
Given an integer `n`, return _the number of people who know the secret at the end of day_ `n`. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 6, delay = 2, forget = 4
**Output:** 5
**Explanation:**
Day 1: Suppose the first person is named A. (1 person)
Day 2: A is the only person who knows the secret. (1 person)
Day 3: A shares the secret with a new person, B. (2 people)
Day 4: A shares the secret with a new person, C. (3 people)
Day 5: A forgets the secret, and B shares the secret with a new person, D. (3 people)
Day 6: B shares the secret with E, and C shares the secret with F. (5 people)
**Example 2:**
**Input:** n = 4, delay = 1, forget = 3
**Output:** 6
**Explanation:**
Day 1: The first person is named A. (1 person)
Day 2: A shares the secret with B. (2 people)
Day 3: A and B share the secret with 2 new people, C and D. (4 people)
Day 4: A forgets the secret. B, C, and D share the secret with 3 new people. (6 people)
**Constraints:**
* `2 <= n <= 1000`
* `1 <= delay < forget <= n` | The bigger digit should appear first (more to the left) because it contributes more to the value of the number. Get all the even digits, as well as odd digits. Sort them separately. Reconstruct the number by giving the earlier digits the highest available digit of the same parity. |
Python | DP | Dynamic Programming | number-of-people-aware-of-a-secret | 0 | 1 | Iterate from delay->forget for each time, increment one count, in addition to the current people who remember. For the day a user forgets, decrement one count\n\n```\nclass Solution:\n def peopleAwareOfSecret(self, n: int, delay: int, forget: int) -> int:\n \n dp = [0]*(n+1)\n \n for i in range(1, n+1):\n dp[i] += 1\n for k in range(i+delay, i+forget):\n if k < n+ 1:\n dp[k] += dp[i]\n if i+forget < n+1:\n dp[i+forget] -= 1\n \n return dp[-1] % (10**9+7)\n``` | 4 | On day `1`, one person discovers a secret.
You are given an integer `delay`, which means that each person will **share** the secret with a new person **every day**, starting from `delay` days after discovering the secret. You are also given an integer `forget`, which means that each person will **forget** the secret `forget` days after discovering it. A person **cannot** share the secret on the same day they forgot it, or on any day afterwards.
Given an integer `n`, return _the number of people who know the secret at the end of day_ `n`. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 6, delay = 2, forget = 4
**Output:** 5
**Explanation:**
Day 1: Suppose the first person is named A. (1 person)
Day 2: A is the only person who knows the secret. (1 person)
Day 3: A shares the secret with a new person, B. (2 people)
Day 4: A shares the secret with a new person, C. (3 people)
Day 5: A forgets the secret, and B shares the secret with a new person, D. (3 people)
Day 6: B shares the secret with E, and C shares the secret with F. (5 people)
**Example 2:**
**Input:** n = 4, delay = 1, forget = 3
**Output:** 6
**Explanation:**
Day 1: The first person is named A. (1 person)
Day 2: A shares the secret with B. (2 people)
Day 3: A and B share the secret with 2 new people, C and D. (4 people)
Day 4: A forgets the secret. B, C, and D share the secret with 3 new people. (6 people)
**Constraints:**
* `2 <= n <= 1000`
* `1 <= delay < forget <= n` | The bigger digit should appear first (more to the left) because it contributes more to the value of the number. Get all the even digits, as well as odd digits. Sort them separately. Reconstruct the number by giving the earlier digits the highest available digit of the same parity. |
[Python] Tabulation with visual explanation | number-of-people-aware-of-a-secret | 0 | 1 | The main idea is that on each i\'th day, every person who knows the secret, can tell one new person on every day within the range (lower, upper-1). where - \n\t1. Lower is calculated based on current day + delay\n\t2. Upper is the day before the person forgets which is i + forget (not inclusive)\n\nthus the main tabulation formula is dp[j] += dp[i] with some conditions. \n\nNote: The second dp[i] in the table below is the updated value. This is based on whether the specific `i` contributes to the final answer or not. This depends on whether people who knew the secret on the `i`th day will remember or forget on the `n`th day. \n\n\n```\nclass Solution:\n def peopleAwareOfSecret(self, n: int, delay: int, forget: int) -> int:\n \n dp = [0] * (n + 1)\n dp[0] = 0\n dp[1] = 1\n \n for i in range(1, n+1):\n if dp[i] > 0:\n lower = i + delay # 3\n upper = i + forget\n upper_bound = min(upper, n+1)\n for j in range(lower, upper_bound):\n dp[j] += dp[i]\n\n if upper <= n:\n dp[i] = 0\n \n print(dp)\n return sum(dp) % (10**9 + 7) | 6 | On day `1`, one person discovers a secret.
You are given an integer `delay`, which means that each person will **share** the secret with a new person **every day**, starting from `delay` days after discovering the secret. You are also given an integer `forget`, which means that each person will **forget** the secret `forget` days after discovering it. A person **cannot** share the secret on the same day they forgot it, or on any day afterwards.
Given an integer `n`, return _the number of people who know the secret at the end of day_ `n`. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 6, delay = 2, forget = 4
**Output:** 5
**Explanation:**
Day 1: Suppose the first person is named A. (1 person)
Day 2: A is the only person who knows the secret. (1 person)
Day 3: A shares the secret with a new person, B. (2 people)
Day 4: A shares the secret with a new person, C. (3 people)
Day 5: A forgets the secret, and B shares the secret with a new person, D. (3 people)
Day 6: B shares the secret with E, and C shares the secret with F. (5 people)
**Example 2:**
**Input:** n = 4, delay = 1, forget = 3
**Output:** 6
**Explanation:**
Day 1: The first person is named A. (1 person)
Day 2: A shares the secret with B. (2 people)
Day 3: A and B share the secret with 2 new people, C and D. (4 people)
Day 4: A forgets the secret. B, C, and D share the secret with 3 new people. (6 people)
**Constraints:**
* `2 <= n <= 1000`
* `1 <= delay < forget <= n` | The bigger digit should appear first (more to the left) because it contributes more to the value of the number. Get all the even digits, as well as odd digits. Sort them separately. Reconstruct the number by giving the earlier digits the highest available digit of the same parity. |
easy C++/Python DFS solutions|| w Explanation | number-of-increasing-paths-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse standard DFS to solve! After the DFS process, the value for visited[i][j] is the number of ways for starting from position (i, j) modulo the pretty prime number $10^9+7$!( since the if-condition is set to be grid[a][b]>grid[i][j] for (a, b) adjacent to (i, j) )\n# Approach\n<!-- Describe your approach to solving the problem. -->\nstandard DFS algoirhm \n```\nDFS(i, j):\n if visited(i, j)==-1:\n ans = 1\n for each (a, b) adjacent to (i, j) within the grid:\n if grid(a, b) > grid(i, j):\n ans += DFS(a, b)\n visited(i, j)=ans\n return ans\t\n```\nA 2D list called visited is created to track the visited state of each position in the grid. All positions are initialized to -1, indicating they have not been visited.\n\nThe dfs function performs a depth-first search. It takes the current position as input. If the current position has been visited before, it returns the previously calculated result. Otherwise, it calculates the number of paths from the current position to the destination by exploring valid adjacent positions and recursively calling dfs on them. The result is saved in the visited state for future reference and returned.\n\nA test case produced by me.\n```\n[[1,2,3,4,5,6,7,8,9,10],[2,3,4,5,6,7,8,9,10,11],[3,4,5,6,7,8,9,10,11,12],[4,5,6,7,8,9,10,11,12,13],[5,6,7,8,9,92,11,12,13,14],[1,2,3,4,5,6,7,8,9,10],[2,3,4,5,6,7,8,9,10,11],[3,4,5,6,7,8,9,10,11,12],[4,5,6,7,8,9,10,11,12,13],[5,6,7,689,9,10,11,12,13,14]]\n```\nThe array visited after DFS process\n```\nResult: 22623\n 2582 1777 1181 751 451 251 126 55 20 5\n 804 595 429 299 199 124 70 34 14 4\n 208 165 129 99 74 53 35 19 9 3\n 42 35 29 24 20 17 15 9 5 2\n 6 5 4 3 2 1 5 3 2 1\n 2859 1957 1287 806 476 263 136 61 23 6\n 895 664 476 326 210 125 69 34 14 4\n 230 187 149 115 84 55 34 19 9 3\n 42 37 33 30 28 20 14 9 5 2\n 4 3 2 1 7 5 4 3 2 1\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$ O(n * m)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$ O(n * m)$$\n# Code\n```\nclass Solution {\npublic:\n using int2=pair<int, int>;\n int countPaths(vector<vector<int>>& grid) {\n const int Mod=1e9+7;\n int n=grid.size(), m=grid[0].size();\n //cout<<n<<","<<m<<endl;\n vector<vector<int>> visited(n, vector<int>(m, -1));\n \n function<int(int, int)> dfs=[&](int i, int j){\n //\tcout<<"i="<<i<<",j="<<j<<"->"<<grid[i][j]<<endl;\n if (visited[i][j]!=-1) return visited[i][j];\n long result=1;\n vector<int2> adj={{i+1, j},{i, j+1}, {i-1, j}, {i, j-1}};\n for(auto& [a, b]: adj){\n \tif (a>=0 && a<n && b>=0 && b<m) \n if (grid[a][b]>grid[i][j]){\t//strictly increasing\n // cout<<"("<<a<<","<<b<<")\\n";\n result=(result+dfs(a, b))%Mod;\n } \n }\n return visited[i][j]=result;\n };\n\n long result=0;\n for(int i=0; i<n; i++)\n for(int j=0; j<m; j++){\n \tif (visited[i][j]==-1)\n dfs(i, j);\n result=(result+visited[i][j])%Mod;\n }\n return result;\n }\n};\n\n```\n# Python solution w Explanation in comments\n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n Mod = 10**9+7 # Define the modulus\n n, m = len(grid), len(grid[0]) # Get the size of the grid\n row = [-1 for _ in range(m)] # Initialize the visited state of each row as -1\n visited = [row[:] for _ in range(n)] # Initialize the visited state of the entire grid as -1\n\n def dfs(i, j):\n if visited[i][j] != -1: # If the position has been visited before, directly return the visited result\n return visited[i][j]\n result = 1 # Initial result is 1, representing the number of paths from the current position to the destination\n adj = [(i + 1, j), (i, j + 1), (i - 1, j), (i, j - 1)] # Define the four directions for adjacent positions\n for a, b in adj:\n if 0 <= a < n and 0 <= b < m: # Make sure the adjacent position is within the grid\n if grid[a][b] > grid[i][j]: # If the height of the adjacent position is greater than the current position, continue exploring in that direction\n result = (result + dfs(a, b)) % Mod # Update the result and take the modulus\n visited[i][j] = result # Save the result to the visited state to avoid duplicate calculations\n return result\n\n result = 0 # Initial result is 0\n for i in range(n):\n for j in range(m):\n if visited[i][j] == -1: # If the position has not been visited yet, perform depth-first search\n visited[i][j] = dfs(i, j) # Update the visited result of that position\n result = (result + visited[i][j]) % Mod # Add the visited result of that position to the final result and take the modulus\n\n # Uncomment the following line to print the visited state matrix\n # print(visited)\n\n return result # Return the final result\n\n``` | 3 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Python3 Solution | number-of-increasing-paths-in-a-grid | 0 | 1 | \n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n mod = 10**9+7 \n n = len(grid) \n m = len(grid[0]) \n dp = [[-1 for _ in range(m)] for _ in range(n)]\n \n def solve(row,col,grid,prev,dp):\n \n if row < 0 or col<0 or row >= len(grid) or col >= len(grid[0]) or grid[row][col] <= prev:\n return 0\n if dp[row][col] != -1: \n return dp[row][col]\n directions=[[1,0],[-1,0],[0,-1],[0,1]] \n total=1\n for dir in directions:\n new_row=row+dir[0]\n new_col=col+dir[1]\n total += solve(new_row,new_col,grid,grid[row][col],dp)\n dp[row][col] = total\n return total\n \n res=0\n for row in range(n):\n for col in range(m):\n res += solve(row,col,grid,-1,dp)\n return res % mod\n\n \n \n\n\n \n \n\n``` | 2 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Simple Python solution | number-of-increasing-paths-in-a-grid | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n mod = 10**9+7\n directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\n res = 0\n\n @lru_cache(maxsize = None)\n def dfs(i, j):\n ans = 0\n for dx, dy in directions:\n # if the next block is in bounds, and its value is greater than the prev\n if (0 <= i + dx < m) and (0 <= j + dy < n) and (grid[i+dx][j+dy] > grid[i][j]):\n ans += (1 + dfs(i+dx, j+dy))\n return ans\n \n for i in range(m):\n for j in range(n):\n res = (res + (dfs(i, j) % mod)) % mod\n \n return res+m*n\n \n``` | 2 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Faster than 89% , DFS, Python3 | number-of-increasing-paths-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n MOD = 10 ** 9 + 7\n m, n = len(grid), len(grid[0])\n dirxns = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n memo = [[-1] * n for _ in range(m)]\n res = 0\n def dfs(row, col):\n if memo[row][col] != -1:\n return memo[row][col]\n count = 1\n for dx, dy in dirxns:\n new_row, new_col = row + dx, col + dy\n if 0 <= new_row < m and 0 <= new_col < n and grid[new_row][new_col] > grid[row][col]:\n count += dfs(new_row, new_col)\n memo[row][col] = count\n return count\n for row in range(m):\n for col in range(n):\n res += dfs(row, col)\n return res % MOD\n``` | 1 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Python simple DP solution | number-of-increasing-paths-in-a-grid | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic programming.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(N\\cdot M)$ for calculating paths for each cell.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(N\\cdot M)$ for caching the counts for each cell.\n\n# Code\n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n DIRS = ((-1, 0), (1, 0), (0, 1), (0, -1))\n MOD = int(1e9+7)\n @cache\n def search(row: int, col: int) -> int:\n """Given this row and column, how many paths stem from here?"""\n count = 1 # Just visit the node itself\n for dr, dc in DIRS:\n if 0 <= row + dr < len(grid) and 0 <= col + dc < len(grid[0]):\n # Must be strictly increasing\n if not grid[row + dr][col + dc] > grid[row][col]:\n continue\n count += search(row + dr, col + dc)\n return count % MOD\n return sum(\n search(row, col)\n for row in range(len(grid))\n for col in range(len(grid[0]))\n ) % MOD\n``` | 1 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
[Python] Easy Understand Code, Bottom-up DP + Sorting | number-of-increasing-paths-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are caring about how many increasing sequences ending at each grid. The sum of number increasing sequences at each grid is the final answer.\n\nStarts from smallest number to the largest in the grid, if all surrounding numbers are larger than grid[i][j], then there\'s only one increasing sequence ends at grid[i][j], which is grid[i][j] itself. So dp[i][j] = 1.\n\nOtherwise, if grid[i][j] is larger than its neighbor, then each increasing sequence ends at its neighbor can append grid[i][j] to its tail. Thus, we add number of increasing sequences ending at grid[i][j]\'s neighbor to dp[i][j]. The same logic applies to four directions.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort values in grid together with their indices\n2. Initialize dp[i][j] with 0\n3. Implement the algorithm described above.\n4. Return sum of values in dp, remember mod 10 ** 9 + 7 \n\n# Complexity\n- Time complexity: O(mn\\*log(mn)) sorting m*n entries.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(mn)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n values = sorted([(grid[i][j], i, j) for i in range(len(grid)) for j in range(len(grid[0]))])\n dp = [[0] * len(grid[0]) for _ in range(len(grid))]\n for v, i, j in values:\n up = dp[i-1][j] if i > 0 and grid[i][j] > grid[i-1][j] else 0\n down = dp[i+1][j] if i < len(grid)-1 and grid[i][j] > grid[i+1][j] else 0\n left = dp[i][j-1] if j > 0 and grid[i][j] > grid[i][j-1] else 0\n right = dp[i][j+1] if j < len(grid[0])-1 and grid[i][j] > grid[i][j+1] else 0\n dp[i][j] = (up + down + left + right + 1) % (10 ** 9 + 7)\n return sum([sum(dp[i]) for i in range(len(dp))]) % (10 ** 9 + 7)\n\n``` | 1 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | number-of-increasing-paths-in-a-grid | 1 | 1 | # An Upvote will be encouraging \uD83D\uDC4D\n\n# Video Solution\n\n# Search \uD83D\uDC49` Number of Increasing Paths in a Grid By Tech Wired`\n# or\n# Click the Link in my Profile\n\n```Python []\nclass Solution:\n def countPaths(self, grid):\n rows = len(grid)\n cols = len(grid[0])\n mod = 10 ** 9 + 7\n\n @lru_cache(None)\n def count(row, col):\n res = 1\n for dx, dy in [[row, col + 1], [row, col - 1], [row + 1, col], [row - 1, col]]:\n if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] > grid[row][col]:\n res += count(dx, dy) % mod\n return res\n\n count_values = []\n for i in range(rows):\n for j in range(cols):\n count_values.append(count(i, j))\n path_sum = sum(count_values) % mod\n\n return path_sum\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n int mod = (int) Math.pow(10, 9) + 7;\n\n public int countPaths(int[][] grid) {\n int rows = grid.length;\n int cols = grid[0].length;\n\n int[][] dp = new int[rows][cols];\n for (int[] row : dp) {\n Arrays.fill(row, -1);\n }\n\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n if (dp[i][j] == -1) {\n helper(i, j, grid, dp, -1);\n }\n }\n }\n\n long pathSum = 0;\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n pathSum = (pathSum + dp[i][j]) % mod;\n }\n }\n return (int) pathSum;\n }\n\n public int helper(int row, int col, int[][] grid, int[][] dp, int parent) {\n int rows = grid.length;\n int cols = grid[0].length;\n\n if (row < 0 || row >= rows || col < 0 || col >= cols || grid[row][col] <= parent) {\n return 0;\n }\n\n if (dp[row][col] != -1) {\n return dp[row][col];\n }\n\n int down = helper(row + 1, col, grid, dp, grid[row][col]) % mod;\n int up = helper(row - 1, col, grid, dp, grid[row][col]) % mod;\n int right = helper(row, col + 1, grid, dp, grid[row][col]) % mod;\n int left = helper(row, col - 1, grid, dp, grid[row][col]) % mod;\n\n return dp[row][col] = (down + up + right + left + 1) % mod;\n }\n}\n\n```\n```C++ []\n#include <vector>\nusing namespace std;\n\nclass Solution {\npublic:\n int countPaths(vector<vector<int>>& grid) {\n int rows = grid.size();\n int cols = grid[0].size();\n int mod = 1e9 + 7;\n\n vector<vector<int>> dp(rows, vector<int>(cols, -1));\n\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n if (dp[i][j] == -1) {\n helper(i, j, grid, dp, -1);\n }\n }\n }\n\n long long pathSum = 0;\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n pathSum = (pathSum + dp[i][j]) % mod;\n }\n }\n return static_cast<int>(pathSum);\n }\n\n int helper(int row, int col, vector<vector<int>>& grid, vector<vector<int>>& dp, int parent) {\n int rows = grid.size();\n int cols = grid[0].size();\n\n if (row < 0 || row >= rows || col < 0 || col >= cols || grid[row][col] <= parent) {\n return 0;\n }\n\n if (dp[row][col] != -1) {\n return dp[row][col];\n }\n\n int down = helper(row + 1, col, grid, dp, grid[row][col]) % mod;\n int up = helper(row - 1, col, grid, dp, grid[row][col]) % mod;\n int right = helper(row, col + 1, grid, dp, grid[row][col]) % mod;\n int left = helper(row, col - 1, grid, dp, grid[row][col]) % mod;\n\n return dp[row][col] = (down + up + right + left + 1) % mod;\n }\n};\n\n```\n\n\n# An Upvote will be encouraging \uD83D\uDC4D\n | 20 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
✅✅Java✔ || C++✔ ||Python✔ || Solution Easy To Understand | number-of-increasing-paths-in-a-grid | 1 | 1 | # :) Guys Please VoteUp\nThe code provided seems to be solving a problem related to counting paths in a grid. However, without a clear problem statement, it\'s difficult to provide specific intuition.\n\n# Approach\nThe code uses a dynamic programming approach to count the number of paths in the given grid. It employs memoization to avoid redundant calculations. The countPaths method initializes a 2D array dp to store the number of paths for each grid cell. It then iterates through each cell in the grid and calls the solve method to calculate the number of paths starting from that cell.\n\nThe solve method takes the current grid, cell coordinates, the previous value (for comparison), and the memoization array dp. It first checks the base cases: if the current cell is out of bounds or has a value less than or equal to the previous value, it returns 0. If the result for the current cell is already calculated and stored in dp, it directly returns the stored value.\n\nIf the base cases are not met, the method recursively calls itself for the left, right, up, and down neighboring cells. It passes the current cell value as the new previous value to ensure that paths only move to cells with greater values. The results from these recursive calls are summed up, and 1 is added to account for the current cell. The sum is then stored in dp for memoization.\n\nFinally, the countPaths method returns the total number of paths calculated for all cells in the grid\n\n# Complexity\nTime complexity: The time complexity of the countPaths method is O(n * m), where n and m are the dimensions of the grid. This is because it iterates through each cell in the grid exactly once. The solve method has recursive calls, but each cell\'s result is memoized, ensuring that each cell is calculated only once.\n\nSpace complexity: The space complexity of the code is O(n * m) as well. It is determined by the memoization array dp, which has the same dimensions as the grid. The memory usage is proportional to the number of cells in the grid.\n\nOverall, the code uses a dynamic programming approach with memoization to efficiently calculate the number of paths in a grid.\n\n\n\n# Java Code\n```\nclass Solution {\n int mod = (int)(1e9+7);\n public int countPaths(int[][] grid) {\n int n = grid.length;\n int m = grid[0].length;\n \n int[][] dp = new int[n][m];\n for(int[] arr: dp){\n Arrays.fill(arr, -1);\n }\n int paths = 0;\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n paths = (paths+solve(grid, i, j, -1, dp))%mod;\n }\n }\n \n return paths;\n }\n \n public int solve(int[][] grid, int i, int j, int prev, int[][] dp){\n if(i<0 || j<0 || i>=grid.length || j>=grid[0].length || grid[i][j]<=prev){\n return 0;\n }\n \n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n \n int left = solve(grid, i, j-1, grid[i][j], dp);\n int right = solve(grid, i, j+1, grid[i][j], dp);\n int up = solve(grid, i-1, j, grid[i][j], dp);\n int down = solve(grid, i+1, j, grid[i][j], dp);\n \n return dp[i][j] = (1+left+right+up+down)%mod;\n }\n}\n```\n# C++ Code\n```\nclass Solution {\npublic:\n \n int Helper(vector<vector<int>>& grid, int i, int j, vector<vector<int>>& dp, int prev)\n {\n if(i<0 || j<0 || i>=grid.size() || j>=grid[0].size() || prev>=grid[i][j])\n return 0;\n \n if(dp[i][j]!=-1)\n return dp[i][j];\n \n int top = Helper(grid,i-1,j,dp,grid[i][j]);\n int bottom = Helper(grid,i+1,j,dp,grid[i][j]);\n int right = Helper(grid,i,j+1,dp,grid[i][j]);\n int left = Helper(grid,i,j-1,dp,grid[i][j]);\n \n dp[i][j] = (1 + top + bottom + right + left)%1000000007; // it will give signed integer overflow run time error if you do not modulo at this point of code\n return dp[i][j];\n }\n int countPaths(vector<vector<int>>& grid) {\n \n int m = grid.size();\n int n = grid[0].size();\n if(m==1 && n==1)\n return 1;\n vector<vector<int> > dp(m,vector<int> (n,-1));\n \n int ans =0;\n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(dp[i][j]==-1)\n ans = (ans + Helper(grid,i,j,dp,-1))%1000000007;\n else\n ans = (ans + dp[i][j])%1000000007;\n }\n }\n \n return ans;\n }\n};\n```\n\n# Python3 Code\n\n```\nclass Solution:\n def countPaths(self, grid: List[List[int]]) -> int:\n noOfRows, noOfCols, res = len(grid), len(grid[0]), 0\n dp = [[-1 for _ in range(noOfCols)] for _ in range(noOfRows)]\n \n def dfs(row: int, col: int, prev: int, dp: List[List[int]], grid: List[List[int]]) -> int:\n directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]\n if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]) or grid[row][col] <= prev:\n return 0\n if dp[row][col] != -1: \n return dp[row][col]\n ans = 1\n for direction in directions:\n newRow, newCol = row + direction[0], col + direction[1]\n ans += dfs(newRow, newCol, grid[row][col], dp, grid)\n dp[row][col] = ans\n return ans\n \n for row in range(noOfRows):\n for col in range(noOfCols):\n res += dfs(row, col, -1, dp, grid)\n return res % (10 ** 9 + 7)\n```\n\n# Java Code Explaination\nThe code represents a Solution class with two methods: countPaths and solve. Here\'s an explanation of each part:\n\nThe class-level variable mod is set to (int)(1e9+7), which is a common approach to store a large constant value for modulo operations.\n\nThe countPaths method takes a 2D grid as input and returns the total number of paths. It initializes variables n and m with the dimensions of the grid. It also creates a 2D array dp with the same dimensions to store the number of paths for each cell.\n\nThe dp array is initialized with -1 using the Arrays.fill method. This is done to indicate that the paths for each cell have not been calculated yet.\n\nThe paths variable is initialized to 0 to store the cumulative number of paths.\n\nThe nested for loops iterate through each cell in the grid using the variables i and j.\n\nWithin the loops, the solve method is called for each cell to calculate the number of paths starting from that cell. The solve method is passed the grid, the current cell coordinates (i and j), the previous value (initialized as -1), and the dp array.\n\nThe solve method first checks if the current cell is out of bounds or if its value is less than or equal to the previous value. If so, it returns 0 indicating that no paths are possible from that cell.\n\nIf the base cases are not met, the method checks if the result for the current cell has already been calculated and stored in the dp array. If so, it directly returns the stored value.\n\nIf the base cases are not met and the result is not stored in dp, the method proceeds to recursively call itself for the neighboring cells (left, right, up, and down). It passes the current cell\'s value as the new previous value to ensure that paths only move to cells with greater values.\n\nThe results from the recursive calls (left, right, up, and down) are summed up, and 1 is added to account for the current cell. The modulo operation % mod is applied to keep the result within the given modulo value.\n\nFinally, the calculated result is stored in the dp array for memoization, and it is also returned as the result of the solve method.\n\nThe cumulative paths variable in the countPaths method is updated by adding the result of the solve method for each cell. The modulo operation % mod is applied to keep the result within the given modulo value.\n\nAfter iterating through all the cells, the paths variable contains the total number of paths in the grid, and it is returned as the final result of the countPaths method.\n\nIn summary, the code uses a dynamic programming approach with memoization to efficiently calculate the number of paths in a grid. The solve method handles the recursive calculation for each cell, storing intermediate results in the dp array to avoid redundant calculations. The countPaths method orchestrates the process by iterating through each cell and accumulating the results.\n | 98 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Python short and clean. DP. DFS. Functional programming. | number-of-increasing-paths-in-a-grid | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution, Approach 2](https://leetcode.com/problems/number-of-increasing-paths-in-a-grid/editorial/) but using functional programming.\n\n# Complexity\n- Time complexity: $$O(m * n)$$\n\n- Space complexity: $$O(m * n)$$\n\nwhere, `m x n is the dimensions of grid.`\n\n# Code\n```python\nclass Solution:\n def countPaths(self, grid: list[list[int]]) -> int:\n M = 1_000_000_007\n m, n = len(grid), len(grid[0])\n dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))\n\n in_bounds = lambda i, j: 0 <= i < m and 0 <= j < n\n nbrs = lambda i, j: ((i + di, j + dj) for di, dj in dirs)\n starfilter = lambda f, xs: filter(lambda args: f(*args), xs)\n\n @cache\n def paths_to(i: int, j: int) -> int:\n valid_nbrs = starfilter(in_bounds, nbrs(i, j))\n increasing_nbrs = starfilter(lambda ni, nj: grid[ni][nj] > grid[i][j], valid_nbrs)\n return (sum(starmap(paths_to, increasing_nbrs)) + 1) % M\n \n return sum(starmap(paths_to, product(range(m), range(n)))) % M\n\n\n``` | 2 | You are given an `m x n` integer matrix `grid`, where you can move from a cell to any adjacent cell in all `4` directions.
Return _the number of **strictly** **increasing** paths in the grid such that you can start from **any** cell and end at **any** cell._ Since the answer may be very large, return it **modulo** `109 + 7`.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
**Example 1:**
**Input:** grid = \[\[1,1\],\[3,4\]\]
**Output:** 8
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[1\], \[3\], \[4\].
- Paths with length 2: \[1 -> 3\], \[1 -> 4\], \[3 -> 4\].
- Paths with length 3: \[1 -> 3 -> 4\].
The total number of paths is 4 + 3 + 1 = 8.
**Example 2:**
**Input:** grid = \[\[1\],\[2\]\]
**Output:** 3
**Explanation:** The strictly increasing paths are:
- Paths with length 1: \[1\], \[2\].
- Paths with length 2: \[1 -> 2\].
The total number of paths is 2 + 1 = 3.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 105` | The maximum length of expression is very low. We can try every possible spot to place the parentheses. Every possibility of expression is of the form a * (b + c) * d where a, b, c, d represent integers. Note the edge cases where a and/or d do not exist, in which case use 1 instead of them. |
Simple solution with using Post-order traversal in Python3 | evaluate-boolean-binary-tree | 0 | 1 | # Intuition\nThe problem descriprion is the following:\n- there\'s a **Full Binary Tree (FBT)**, whose values are in range **[0, 3]**\n- our goal is to **evaluate** the logical expressions over operands\n\n```py\n# Example\nroot = [2, 1, 3, null, null, 0, 1]\n\n# This tree can be interpreted as the next logical expression\nexpr = True || (False && True) => True || False => False\n\n# For this example we should use the POST-ORDER traversal.\n# This means, that all of the operations with node etc will \n# execute after all traversal in left and in right node.\n\n# Example of simple FBT\n# (2)\n# / \\\n# (1) (0)\n# The post-order traversal will give us the next list representation \nnums = [1, 0, 2]\n\n# And we represent the values as booleans, according to description\nnums = [True, False, ||]\n\n# After the traversal we should perform an operation (\n# the root node can represent operands and operators, \n# while leafs - only OPERANDS).\n# Thus returning value from that subtree is the evaluation\n# True || False == True\n``` \n\n# Approach\n1. initialize a `dfs` function with **post-order** traversal\n2. at each step initialize `left` and `right` as `False` values\n3. do the **post-order traversal**, if node has children from both sides\n4. match the `node.val` with corresponding values and do the operations, if it\'s needed\n5. return the result of logic expression as `dfs(root)`\n\n# Complexity\n- Time complexity: **O(n)**, because of iterating over `root`\n\n- Space complexity: **O(n)**, because of recursive call stack.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n def dfs(node):\n left, right = False, False\n \n if node.left:\n left = dfs(node.left)\n if node.right:\n right = dfs(node.right)\n\n match node.val:\n case 0:\n return False\n case 1:\n return True\n case 2:\n return left or right\n case _:\n return left and right\n\n return dfs(root)\n``` | 1 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Python recursion solution beats 85% | evaluate-boolean-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRecursive approach\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n if root.val == 2:\n return self.evaluateTree(root.left) or self.evaluateTree(root.right)\n elif root.val == 3:\n return self.evaluateTree(root.left) and self.evaluateTree(root.right)\n else:\n return root.val\n\n\n \n``` | 2 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
[ Go , Python , C++ ] w/ comments | evaluate-boolean-binary-tree | 0 | 1 | <iframe src="https://leetcode.com/playground/a8k3xokf/shared" frameBorder="0" width="800" height="500"></iframe> | 4 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Simple Python Solution | evaluate-boolean-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n if not root.left and not root.right:\n return root.val\n temp = root.val\n if temp ==2:\n return self.evaluateTree(root.left) | self.evaluateTree(root.right)\n else:\n return self.evaluateTree(root.left) & self.evaluateTree(root.right)\n\n``` | 1 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Python Elegant & Short | 94.5% faster | O(n) | Two lines | evaluate-boolean-binary-tree | 0 | 1 | \n\n```\nfrom operator import and_, or_\n\n\nclass Solution:\n\t"""\n\tTime: O(n)\n\tMemory: O(n)\n\t"""\n\n\tMAPPING = {\n\t\t0: lambda *_: False,\n\t\t1: lambda *_: True,\n\t\t2: or_,\n\t\t3: and_,\n\t}\n\n\tdef evaluateTree(self, root: Optional[TreeNode]) -> bool:\n\t\tif root is not None:\n\t\t\treturn self.MAPPING[root.val](\n\t\t\t\tself.evaluateTree(root.left),\n\t\t\t\tself.evaluateTree(root.right),\n\t\t\t)\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n\n | 14 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Python 3 lines | easiest | evaluate-boolean-binary-tree | 0 | 1 | # Upvote it :)\n```\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n if root.val == 2: return self.evaluateTree(root.left) or self.evaluateTree(root.right)\n elif root.val == 3: return self.evaluateTree(root.left) and self.evaluateTree(root.right)\n else: return root.val\n``` | 4 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
✅✅✅ 97.89% faster python solution | evaluate-boolean-binary-tree | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n if root.val==3:\n return self.evaluateTree(root.left) and self.evaluateTree(root.right)\n elif root.val==2:\n return self.evaluateTree(root.left) or self.evaluateTree(root.right)\n return root.val\n``` | 7 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Easy python 6 line solution | evaluate-boolean-binary-tree | 0 | 1 | ```\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n if root.val==0 or root.val==1:\n return root.val\n if root.val==2:\n return self.evaluateTree(root.left) or self.evaluateTree(root.right)\n if root.val==3:\n return self.evaluateTree(root.left) and self.evaluateTree(root.right)\n``` | 11 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Python straightforward recursion | evaluate-boolean-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe big picture is that you need to evalute the root with left subtree and right subtree.\nSo what is the termination condition? The answer is when you reach the leaf of the tree and return the boolean value of the leaf node.\nAnd then let the recursion do its job.\nIf the root value is 2, return an `or` between boolean values of left and right subtrees; `and` otherwise.\n\n\n# Complexity\n- Time complexity: `O(n)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n\n if not root.left and not root.right:\n return True if root.val else False\n\n if root.val == 2:\n return self.evaluateTree(root.left) or self.evaluateTree(root.right)\n elif root.val == 3:\n return self.evaluateTree(root.left) and self.evaluateTree(root.right)\n```\n**Please upvote if you found this helpful.** | 3 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Python3 || Recursion and boolean logic || 5 lines | evaluate-boolean-binary-tree | 0 | 1 | ```\nclass Solution:\n def evaluateTree(self, root: TreeNode) -> bool:\n #\n # Recursion:\n #\n # Base Case: node.val = 0 or 1. Return T or F\n # \n # Recursive Case: node.val = 2 or 3. Node value is determined\n\t\t\t\t\t\t\t\t# upon the values l = node.left.val, r = node.right.val, \n # and v = T if node.val = OR else F if node.val = AND\n #\n # From a Venn diagram or a truth table for l, r, v, one can\n # see the return from the recursive call is l&r or l&v or r&v\n #\n if root.val<2: return root.val\n l = self.evaluateTree(root.left)\n r = self.evaluateTree(root.right)\n v = root.val^1\n\n return l&r or l&v or r&v | 3 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Python || Inorder Traversal || Easy To Understand 🔥 | evaluate-boolean-binary-tree | 0 | 1 | # Code\n```\nclass Solution:\n def evaluateTree(self, root: Optional[TreeNode]) -> bool:\n def inorder(root):\n if root is None: return True\n val = root.val\n if root.left is not None and root.right is not None:\n if val == 2:\n return inorder(root.left) or inorder(root.right)\n elif val == 3:\n return inorder(root.left) and inorder(root.right)\n elif val == 1:\n return True\n return False\n return inorder(root) \n``` | 2 | You are given the `root` of a **full binary tree** with the following properties:
* **Leaf nodes** have either the value `0` or `1`, where `0` represents `False` and `1` represents `True`.
* **Non-leaf nodes** have either the value `2` or `3`, where `2` represents the boolean `OR` and `3` represents the boolean `AND`.
The **evaluation** of a node is as follows:
* If the node is a leaf node, the evaluation is the **value** of the node, i.e. `True` or `False`.
* Otherwise, **evaluate** the node's two children and **apply** the boolean operation of its value with the children's evaluations.
Return _the boolean result of **evaluating** the_ `root` _node._
A **full binary tree** is a binary tree where each node has either `0` or `2` children.
A **leaf node** is a node that has zero children.
**Example 1:**
**Input:** root = \[2,1,3,null,null,0,1\]
**Output:** true
**Explanation:** The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.
**Example 2:**
**Input:** root = \[0\]
**Output:** false
**Explanation:** The root node is a leaf node and it evaluates to false, so we return false.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `0 <= Node.val <= 3`
* Every node has either `0` or `2` children.
* Leaf nodes have a value of `0` or `1`.
* Non-leaf nodes have a value of `2` or `3`. | null |
Easiest one | the-latest-time-to-catch-a-bus | 0 | 1 | # Code\n```\nclass Solution:\n def latestTimeCatchTheBus(self, buses: List[int], passengers: List[int], capacity: int) -> int:\n buses.sort()\n passengers.sort()\n\n index = 0\n\n for start in buses:\n cap = capacity\n while index < len(passengers) and start >= passengers[index] and cap > 0:\n cap -= 1\n index += 1\n\n latest = start if cap > 0 else passengers[index-1] \n\n while latest in set(passengers):\n latest -= 1\n return latest \n``` | 1 | You are given a **0-indexed** integer array `buses` of length `n`, where `buses[i]` represents the departure time of the `ith` bus. You are also given a **0-indexed** integer array `passengers` of length `m`, where `passengers[j]` represents the arrival time of the `jth` passenger. All bus departure times are unique. All passenger arrival times are unique.
You are given an integer `capacity`, which represents the **maximum** number of passengers that can get on each bus.
When a passenger arrives, they will wait in line for the next available bus. You can get on a bus that departs at `x` minutes if you arrive at `y` minutes where `y <= x`, and the bus is not full. Passengers with the **earliest** arrival times get on the bus first.
More formally when a bus arrives, either:
* If `capacity` or fewer passengers are waiting for a bus, they will **all** get on the bus, or
* The `capacity` passengers with the **earliest** arrival times will get on the bus.
Return _the latest time you may arrive at the bus station to catch a bus_. You **cannot** arrive at the same time as another passenger.
**Note:** The arrays `buses` and `passengers` are not necessarily sorted.
**Example 1:**
**Input:** buses = \[10,20\], passengers = \[2,17,18,19\], capacity = 2
**Output:** 16
**Explanation:** Suppose you arrive at time 16.
At time 10, the first bus departs with the 0th passenger.
At time 20, the second bus departs with you and the 1st passenger.
Note that you may not arrive at the same time as another passenger, which is why you must arrive before the 1st passenger to catch the bus.
**Example 2:**
**Input:** buses = \[20,30,10\], passengers = \[19,13,26,4,25,11,21\], capacity = 2
**Output:** 20
**Explanation:** Suppose you arrive at time 20.
At time 10, the first bus departs with the 3rd passenger.
At time 20, the second bus departs with the 5th and 1st passengers.
At time 30, the third bus departs with the 0th passenger and you.
Notice if you had arrived any later, then the 6th passenger would have taken your seat on the third bus.
**Constraints:**
* `n == buses.length`
* `m == passengers.length`
* `1 <= n, m, capacity <= 105`
* `2 <= buses[i], passengers[i] <= 109`
* Each element in `buses` is **unique**.
* Each element in `passengers` is **unique**. | null |
Clean and Concise Greedy with Intuitive Explanation | the-latest-time-to-catch-a-bus | 0 | 1 | ##### Rationale\n* We could imagine the time given in the `passengers` Array to be a seat. A passenger may take a seat only if it is not taken already. The problem then boils down to finding the last possible seat for our candidate. This analogy makes it easier to visualize the problem\n* Since we would like our candidate to take the last seat, we could find the last possible seat number that they could take\n\t* Fit as many people as possible in every bus until you max out. We could sort the Arrays to make it easier\n\t* The maximum seat would either be the last seat in the last bus if it is maxed out or the bus capacity (buses[-1])\n* Iterate backwards from the last possible seat, if it is available, allocate it\n\n##### Complexities\n* Time: `O(blogb + plogp)`\n* Space: `O(p)`\n\n\n```\nclass Solution:\n def latestTimeCatchTheBus(self, buses: List[int], passengers: List[int], capacity: int) -> int:\n buses.sort()\n passengers.sort()\n \n passenger = 0\n for bus in buses:\n maxed_out = False\n cap = capacity\n \n while passenger < len(passengers) and passengers[passenger] <= bus and cap != 0:\n passenger += 1\n cap -= 1\n \n if cap == 0:\n maxed_out = True\n \n if maxed_out:\n max_seat = passengers[passenger - 1]\n else:\n max_seat = buses[-1]\n \n booked = set(passengers)\n for seat in range(max_seat, 0, -1):\n if seat not in booked:\n return seat\n``` | 7 | You are given a **0-indexed** integer array `buses` of length `n`, where `buses[i]` represents the departure time of the `ith` bus. You are also given a **0-indexed** integer array `passengers` of length `m`, where `passengers[j]` represents the arrival time of the `jth` passenger. All bus departure times are unique. All passenger arrival times are unique.
You are given an integer `capacity`, which represents the **maximum** number of passengers that can get on each bus.
When a passenger arrives, they will wait in line for the next available bus. You can get on a bus that departs at `x` minutes if you arrive at `y` minutes where `y <= x`, and the bus is not full. Passengers with the **earliest** arrival times get on the bus first.
More formally when a bus arrives, either:
* If `capacity` or fewer passengers are waiting for a bus, they will **all** get on the bus, or
* The `capacity` passengers with the **earliest** arrival times will get on the bus.
Return _the latest time you may arrive at the bus station to catch a bus_. You **cannot** arrive at the same time as another passenger.
**Note:** The arrays `buses` and `passengers` are not necessarily sorted.
**Example 1:**
**Input:** buses = \[10,20\], passengers = \[2,17,18,19\], capacity = 2
**Output:** 16
**Explanation:** Suppose you arrive at time 16.
At time 10, the first bus departs with the 0th passenger.
At time 20, the second bus departs with you and the 1st passenger.
Note that you may not arrive at the same time as another passenger, which is why you must arrive before the 1st passenger to catch the bus.
**Example 2:**
**Input:** buses = \[20,30,10\], passengers = \[19,13,26,4,25,11,21\], capacity = 2
**Output:** 20
**Explanation:** Suppose you arrive at time 20.
At time 10, the first bus departs with the 3rd passenger.
At time 20, the second bus departs with the 5th and 1st passengers.
At time 30, the third bus departs with the 0th passenger and you.
Notice if you had arrived any later, then the 6th passenger would have taken your seat on the third bus.
**Constraints:**
* `n == buses.length`
* `m == passengers.length`
* `1 <= n, m, capacity <= 105`
* `2 <= buses[i], passengers[i] <= 109`
* Each element in `buses` is **unique**.
* Each element in `passengers` is **unique**. | null |
Python Simple Solution 95.6% | the-latest-time-to-catch-a-bus | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def latestTimeCatchTheBus(self, buses: List[int], passengers: List[int], capacity: int) -> int:\n buses.sort()\n passengers.sort()\n index = 0\n l = len(passengers)\n for start in buses:\n cap = capacity\n while index < len(passengers) and start >= passengers[index] and cap > 0:\n cap -= 1\n index += 1\n\n latest = start if cap > 0 else passengers[index-1] \n\n while latest in set(passengers):\n latest -= 1\n return latest \n \n \n\n``` | 2 | You are given a **0-indexed** integer array `buses` of length `n`, where `buses[i]` represents the departure time of the `ith` bus. You are also given a **0-indexed** integer array `passengers` of length `m`, where `passengers[j]` represents the arrival time of the `jth` passenger. All bus departure times are unique. All passenger arrival times are unique.
You are given an integer `capacity`, which represents the **maximum** number of passengers that can get on each bus.
When a passenger arrives, they will wait in line for the next available bus. You can get on a bus that departs at `x` minutes if you arrive at `y` minutes where `y <= x`, and the bus is not full. Passengers with the **earliest** arrival times get on the bus first.
More formally when a bus arrives, either:
* If `capacity` or fewer passengers are waiting for a bus, they will **all** get on the bus, or
* The `capacity` passengers with the **earliest** arrival times will get on the bus.
Return _the latest time you may arrive at the bus station to catch a bus_. You **cannot** arrive at the same time as another passenger.
**Note:** The arrays `buses` and `passengers` are not necessarily sorted.
**Example 1:**
**Input:** buses = \[10,20\], passengers = \[2,17,18,19\], capacity = 2
**Output:** 16
**Explanation:** Suppose you arrive at time 16.
At time 10, the first bus departs with the 0th passenger.
At time 20, the second bus departs with you and the 1st passenger.
Note that you may not arrive at the same time as another passenger, which is why you must arrive before the 1st passenger to catch the bus.
**Example 2:**
**Input:** buses = \[20,30,10\], passengers = \[19,13,26,4,25,11,21\], capacity = 2
**Output:** 20
**Explanation:** Suppose you arrive at time 20.
At time 10, the first bus departs with the 3rd passenger.
At time 20, the second bus departs with the 5th and 1st passengers.
At time 30, the third bus departs with the 0th passenger and you.
Notice if you had arrived any later, then the 6th passenger would have taken your seat on the third bus.
**Constraints:**
* `n == buses.length`
* `m == passengers.length`
* `1 <= n, m, capacity <= 105`
* `2 <= buses[i], passengers[i] <= 109`
* Each element in `buses` is **unique**.
* Each element in `passengers` is **unique**. | null |
[Python] Easy to understand binary search solution | minimum-sum-of-squared-difference | 0 | 1 | This solution can be broken down into two parts:\n\n1. Find the new max for the array of diffs\n2. Find the index to first start replacing diffs with our new max\n\nWe can use binary search to solve both of these problems.\n\n```\nclass Solution:\n def minSumSquareDiff(self, nums1: List[int], nums2: List[int], k1: int, k2: int) -> int:\n n = len(nums1)\n k = k1+k2 # can combine k\'s because items can be turned negative\n diffs = sorted((abs(x - y) for x, y in zip(nums1, nums2)))\n \n # First binary search to find our new max for our diffs array\n l, r = 0, max(diffs)\n while l < r:\n mid = (l+r)//2\n \n # steps needed to reduce all nums greater than newMax\n steps = sum(max(0, num-mid) for num in diffs)\n \n if steps <= k:\n r = mid\n else:\n l = mid+1\n \n newMax = l\n k -= sum(max(0, num-newMax) for num in diffs) # remove used k\n\n # Second binary search to find first index to replace with max val\n l, r = 0, n-1\n while l < r:\n mid = (l+r)//2\n if diffs[mid] < newMax:\n l = mid+1\n else:\n r = mid\n\n # Replace items at index >= l with newMax\n diffs = diffs[:l]+[newMax]*(n-l)\n \n # Use remaining steps to reduce overall score\n for i in range(len(diffs)-1,-1,-1):\n if k == 0 or diffs[i] == 0: break\n diffs[i] -= 1\n k -= 1\n \n return sum(diff*diff for diff in diffs)\n```\nLC streams: https://twitch.tv/fomiee | 1 | You are given two positive **0-indexed** integer arrays `nums1` and `nums2`, both of length `n`.
The **sum of squared difference** of arrays `nums1` and `nums2` is defined as the **sum** of `(nums1[i] - nums2[i])2` for each `0 <= i < n`.
You are also given two positive integers `k1` and `k2`. You can modify any of the elements of `nums1` by `+1` or `-1` at most `k1` times. Similarly, you can modify any of the elements of `nums2` by `+1` or `-1` at most `k2` times.
Return _the minimum **sum of squared difference** after modifying array_ `nums1` _at most_ `k1` _times and modifying array_ `nums2` _at most_ `k2` _times_.
**Note**: You are allowed to modify the array elements to become **negative** integers.
**Example 1:**
**Input:** nums1 = \[1,2,3,4\], nums2 = \[2,10,20,19\], k1 = 0, k2 = 0
**Output:** 579
**Explanation:** The elements in nums1 and nums2 cannot be modified because k1 = 0 and k2 = 0.
The sum of square difference will be: (1 - 2)2 \+ (2 - 10)2 \+ (3 - 20)2 \+ (4 - 19)2 = 579.
**Example 2:**
**Input:** nums1 = \[1,4,10,12\], nums2 = \[5,8,6,9\], k1 = 1, k2 = 1
**Output:** 43
**Explanation:** One way to obtain the minimum sum of square difference is:
- Increase nums1\[0\] once.
- Increase nums2\[2\] once.
The minimum of the sum of square difference will be:
(2 - 5)2 \+ (4 - 8)2 \+ (10 - 7)2 \+ (12 - 9)2 = 43.
Note that, there are other ways to obtain the minimum of the sum of square difference, but there is no way to obtain a sum smaller than 43.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `0 <= nums1[i], nums2[i] <= 105`
* `0 <= k1, k2 <= 109` | null |
Python3. || Stack, 9 lines || T/M : 986 ms/28 MB | subarray-with-elements-greater-than-varying-threshold | 0 | 1 | ```\nclass Solution:\n def validSubarraySize(self, nums: List[int], threshold: int) -> int:\n # Stack elements are the array\'s indices idx, and montonic with respect to nums[idx].\n # When the index of the nearest smaller value to nums[idx] comes to the top of the \n # stack, we check whether the threshold criterion is satisfied. If so, we are done.\n # If not, we continue. Return -1 if we reach the end of nums without a winner.\n\t\t\t\t\t\t\t\n nums.append(0)\n stack = deque()\n\n for idx in range(len(nums)):\n\n while stack and nums[idx] <= nums[stack[-1]]: \n n = nums[stack.pop()] # n is the next smaller value for nums[idx]\n k = idx if not stack else idx - stack[-1] -1 \n if n > threshold //k: return k # threshold criterion. if n passes, all\n # elements of the interval pass\n stack.append(idx)\n\n return -1 | 8 | You are given an integer array `nums` and an integer `threshold`.
Find any subarray of `nums` of length `k` such that **every** element in the subarray is **greater** than `threshold / k`.
Return _the **size** of **any** such subarray_. If there is no such subarray, return `-1`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,3,4,3,1\], threshold = 6
**Output:** 3
**Explanation:** The subarray \[3,4,3\] has a size of 3, and every element is greater than 6 / 3 = 2.
Note that this is the only valid subarray.
**Example 2:**
**Input:** nums = \[6,5,6,5,8\], threshold = 7
**Output:** 1
**Explanation:** The subarray \[8\] has a size of 1, and 8 > 7 / 1 = 7. So 1 is returned.
Note that the subarray \[6,5\] has a size of 2, and every element is greater than 7 / 2 = 3.5.
Similarly, the subarrays \[6,5,6\], \[6,5,6,5\], \[6,5,6,5,8\] also satisfy the given conditions.
Therefore, 2, 3, 4, or 5 may also be returned.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], threshold <= 109` | null |
[Python3] monotonic stack | subarray-with-elements-greater-than-varying-threshold | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/04944f0a6a1f4d50ee6efd64fabfc227724cdc7a) for solutions of biweekly 82. \n\n```\nclass Solution:\n def validSubarraySize(self, nums: List[int], threshold: int) -> int:\n stack = []\n for hi, x in enumerate(nums + [0]): \n while stack and stack[-1][1] > x: \n val = stack.pop()[1]\n lo = stack[-1][0] if stack else -1 \n if val > threshold // (hi - lo - 1): return hi - lo - 1\n stack.append((hi, x))\n return -1 \n``` | 1 | You are given an integer array `nums` and an integer `threshold`.
Find any subarray of `nums` of length `k` such that **every** element in the subarray is **greater** than `threshold / k`.
Return _the **size** of **any** such subarray_. If there is no such subarray, return `-1`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,3,4,3,1\], threshold = 6
**Output:** 3
**Explanation:** The subarray \[3,4,3\] has a size of 3, and every element is greater than 6 / 3 = 2.
Note that this is the only valid subarray.
**Example 2:**
**Input:** nums = \[6,5,6,5,8\], threshold = 7
**Output:** 1
**Explanation:** The subarray \[8\] has a size of 1, and 8 > 7 / 1 = 7. So 1 is returned.
Note that the subarray \[6,5\] has a size of 2, and every element is greater than 7 / 2 = 3.5.
Similarly, the subarrays \[6,5,6\], \[6,5,6,5\], \[6,5,6,5,8\] also satisfy the given conditions.
Therefore, 2, 3, 4, or 5 may also be returned.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], threshold <= 109` | null |
[Python 3]Hint solution | subarray-with-elements-greater-than-varying-threshold | 0 | 1 | Again, hard needs hint...\n\n```\nclass Solution:\n def validSubarraySize(self, nums: List[int], t: int) -> int:\n n = len(nums)\n if t / n >= max(nums):\n return -1\n \n left = list(range(n))\n right = list(range(n))\n\n # leftmost boundary for the subarray for each index\n stack = []\n for i in range(n):\n while stack and nums[stack[-1]] >= nums[i]:\n left[i] = left[stack.pop()]\n stack.append(i)\n \n # rightmost boundary for the subarray for each index\n stack = []\n for i in reversed(range(n)):\n while stack and nums[stack[-1]] >= nums[i]:\n right[i] = right[stack.pop()]\n stack.append(i)\n\n # get size of subarray and if eligible then output\n for i in range(n):\n size = right[i] - left[i] + 1\n if nums[i] > t / size:\n return size\n \n return -1 | 1 | You are given an integer array `nums` and an integer `threshold`.
Find any subarray of `nums` of length `k` such that **every** element in the subarray is **greater** than `threshold / k`.
Return _the **size** of **any** such subarray_. If there is no such subarray, return `-1`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,3,4,3,1\], threshold = 6
**Output:** 3
**Explanation:** The subarray \[3,4,3\] has a size of 3, and every element is greater than 6 / 3 = 2.
Note that this is the only valid subarray.
**Example 2:**
**Input:** nums = \[6,5,6,5,8\], threshold = 7
**Output:** 1
**Explanation:** The subarray \[8\] has a size of 1, and 8 > 7 / 1 = 7. So 1 is returned.
Note that the subarray \[6,5\] has a size of 2, and every element is greater than 7 / 2 = 3.5.
Similarly, the subarrays \[6,5,6\], \[6,5,6,5\], \[6,5,6,5,8\] also satisfy the given conditions.
Therefore, 2, 3, 4, or 5 may also be returned.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], threshold <= 109` | null |
Python (Simple Stack Solution) | subarray-with-elements-greater-than-varying-threshold | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validSubarraySize(self, nums, threshold):\n nums.append(0)\n\n stack = []\n\n for i in range(len(nums)):\n while stack and nums[stack[-1]] >= nums[i]:\n n = nums[stack.pop()]\n size = i if not stack else i-stack[-1]-1\n if n > threshold/size: return size\n\n stack.append(i)\n\n return -1\n\n \n\n\n\n \n \n``` | 0 | You are given an integer array `nums` and an integer `threshold`.
Find any subarray of `nums` of length `k` such that **every** element in the subarray is **greater** than `threshold / k`.
Return _the **size** of **any** such subarray_. If there is no such subarray, return `-1`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,3,4,3,1\], threshold = 6
**Output:** 3
**Explanation:** The subarray \[3,4,3\] has a size of 3, and every element is greater than 6 / 3 = 2.
Note that this is the only valid subarray.
**Example 2:**
**Input:** nums = \[6,5,6,5,8\], threshold = 7
**Output:** 1
**Explanation:** The subarray \[8\] has a size of 1, and 8 > 7 / 1 = 7. So 1 is returned.
Note that the subarray \[6,5\] has a size of 2, and every element is greater than 7 / 2 = 3.5.
Similarly, the subarrays \[6,5,6\], \[6,5,6,5\], \[6,5,6,5,8\] also satisfy the given conditions.
Therefore, 2, 3, 4, or 5 may also be returned.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], threshold <= 109` | null |
Simple Python solution with explanation | minimum-amount-of-time-to-fill-cups | 0 | 1 | Sort the list. Every time take two max numbers and decrement them by one. Aslo increment count by one. If only one non zero element present then add that number to count and return the count. If all are zero then return count. \n\n```\nimport math\nclass Solution:\n def fillCups(self, l: List[int]) -> int:\n l.sort()\n c=0\n while(sum(l)!=0):\n if(l[-1]!=0 and l[-2]!=0):\n l[-1]-=1\n l[-2]-=1\n c+=1\n\t\t\t\t\n\t\t\t# If only one non zero element present then add that number to count and return the count.\n elif(l[-2]==0 and l[-3]==0):\n return c+l[-1]\n\t\t\t\t\n\t\t\t#If all are zero then return count\n elif(sum(l)==0):\n return c\n \n l.sort()\n return c\n```\n\nupvote if you like it | 3 | You have a water dispenser that can dispense cold, warm, and hot water. Every second, you can either fill up `2` cups with **different** types of water, or `1` cup of any type of water.
You are given a **0-indexed** integer array `amount` of length `3` where `amount[0]`, `amount[1]`, and `amount[2]` denote the number of cold, warm, and hot water cups you need to fill respectively. Return _the **minimum** number of seconds needed to fill up all the cups_.
**Example 1:**
**Input:** amount = \[1,4,2\]
**Output:** 4
**Explanation:** One way to fill up the cups is:
Second 1: Fill up a cold cup and a warm cup.
Second 2: Fill up a warm cup and a hot cup.
Second 3: Fill up a warm cup and a hot cup.
Second 4: Fill up a warm cup.
It can be proven that 4 is the minimum number of seconds needed.
**Example 2:**
**Input:** amount = \[5,4,4\]
**Output:** 7
**Explanation:** One way to fill up the cups is:
Second 1: Fill up a cold cup, and a hot cup.
Second 2: Fill up a cold cup, and a warm cup.
Second 3: Fill up a cold cup, and a warm cup.
Second 4: Fill up a warm cup, and a hot cup.
Second 5: Fill up a cold cup, and a hot cup.
Second 6: Fill up a cold cup, and a warm cup.
Second 7: Fill up a hot cup.
**Example 3:**
**Input:** amount = \[5,0,0\]
**Output:** 5
**Explanation:** Every second, we fill up a cold cup.
**Constraints:**
* `amount.length == 3`
* `0 <= amount[i] <= 100` | null |
Simple Python3 Solution|| Lists || Dictionaries || Upto 50% faster || | smallest-number-in-infinite-set | 0 | 1 | # Approach\nSimple Python3 code using Lists once and then dictionaries for the other.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n\n\n```python []\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.nums = list(range(1,1001))\n \n\n def popSmallest(self) -> int:\n self.nums.sort()\n n = self.nums[0]\n self.nums[:] = self.nums[1:]\n return n\n\n def addBack(self, num: int) -> None:\n if num not in self.nums:\n self.nums.append(num)\n\n\n# Your SmallestInfiniteSet object will be instantiated and called as such:\n# obj = SmallestInfiniteSet()\n# param_1 = obj.popSmallest()\n# obj.addBack(num)\n```\n\n```Py\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.nums = defaultdict(int)\n for i in range(1,1001):\n self.nums[i] = 1 \n \n\n def popSmallest(self) -> int:\n temp = sorted(self.nums.keys())\n n = temp[0]\n del self.nums[n]\n return n\n\n def addBack(self, num: int) -> None:\n self.nums[num] = 1\n\n\n# Your SmallestInfiniteSet object will be instantiated and called as such:\n# obj = SmallestInfiniteSet()\n# param_1 = obj.popSmallest()\n# obj.addBack(num)\n```\n | 2 | You have a set which contains all positive integers `[1, 2, 3, 4, 5, ...]`.
Implement the `SmallestInfiniteSet` class:
* `SmallestInfiniteSet()` Initializes the **SmallestInfiniteSet** object to contain **all** positive integers.
* `int popSmallest()` **Removes** and returns the smallest integer contained in the infinite set.
* `void addBack(int num)` **Adds** a positive integer `num` back into the infinite set, if it is **not** already in the infinite set.
**Example 1:**
**Input**
\[ "SmallestInfiniteSet ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest "\]
\[\[\], \[2\], \[\], \[\], \[\], \[1\], \[\], \[\], \[\]\]
**Output**
\[null, null, 1, 2, 3, null, 1, 4, 5\]
**Explanation**
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 is already in the set, so no change is made.
smallestInfiniteSet.popSmallest(); // return 1, since 1 is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 2, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 3, and remove it from the set.
smallestInfiniteSet.addBack(1); // 1 is added back to the set.
smallestInfiniteSet.popSmallest(); // return 1, since 1 was added back to the set and
// is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 4, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 5, and remove it from the set.
**Constraints:**
* `1 <= num <= 1000`
* At most `1000` calls will be made **in total** to `popSmallest` and `addBack`. | null |
python3 Solution | smallest-number-in-infinite-set | 0 | 1 | \n```\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.seen=[False]*1005\n\n\n def popSmallest(self) -> int:\n for i in range(1,1005):\n if not self.seen[i]:\n self.seen[i]=True\n return i\n\n def addBack(self, num: int) -> None:\n if num<len(self.seen):\n self.seen[num]=False\n\n\n# Your SmallestInfiniteSet object will be instantiated and called as such:\n# obj = SmallestInfiniteSet()\n# param_1 = obj.popSmallest()\n# obj.addBack(num)\n``` | 2 | You have a set which contains all positive integers `[1, 2, 3, 4, 5, ...]`.
Implement the `SmallestInfiniteSet` class:
* `SmallestInfiniteSet()` Initializes the **SmallestInfiniteSet** object to contain **all** positive integers.
* `int popSmallest()` **Removes** and returns the smallest integer contained in the infinite set.
* `void addBack(int num)` **Adds** a positive integer `num` back into the infinite set, if it is **not** already in the infinite set.
**Example 1:**
**Input**
\[ "SmallestInfiniteSet ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest "\]
\[\[\], \[2\], \[\], \[\], \[\], \[1\], \[\], \[\], \[\]\]
**Output**
\[null, null, 1, 2, 3, null, 1, 4, 5\]
**Explanation**
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 is already in the set, so no change is made.
smallestInfiniteSet.popSmallest(); // return 1, since 1 is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 2, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 3, and remove it from the set.
smallestInfiniteSet.addBack(1); // 1 is added back to the set.
smallestInfiniteSet.popSmallest(); // return 1, since 1 was added back to the set and
// is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 4, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 5, and remove it from the set.
**Constraints:**
* `1 <= num <= 1000`
* At most `1000` calls will be made **in total** to `popSmallest` and `addBack`. | null |
Python3 beats 🚀 95.5% and 99.45% 🚀 || quibler7 | smallest-number-in-infinite-set | 0 | 1 | \n# Code\n```\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.curr = 1\n self.set = set()\n\n def popSmallest(self) -> int:\n if self.set:\n ans = min(self.set)\n self.set.remove(ans)\n return ans\n else: \n self.curr += 1\n return self.curr -1\n\n def addBack(self, num: int) -> None:\n if self.curr > num:\n self.set.add(num)\n``` | 1 | You have a set which contains all positive integers `[1, 2, 3, 4, 5, ...]`.
Implement the `SmallestInfiniteSet` class:
* `SmallestInfiniteSet()` Initializes the **SmallestInfiniteSet** object to contain **all** positive integers.
* `int popSmallest()` **Removes** and returns the smallest integer contained in the infinite set.
* `void addBack(int num)` **Adds** a positive integer `num` back into the infinite set, if it is **not** already in the infinite set.
**Example 1:**
**Input**
\[ "SmallestInfiniteSet ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest "\]
\[\[\], \[2\], \[\], \[\], \[\], \[1\], \[\], \[\], \[\]\]
**Output**
\[null, null, 1, 2, 3, null, 1, 4, 5\]
**Explanation**
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 is already in the set, so no change is made.
smallestInfiniteSet.popSmallest(); // return 1, since 1 is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 2, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 3, and remove it from the set.
smallestInfiniteSet.addBack(1); // 1 is added back to the set.
smallestInfiniteSet.popSmallest(); // return 1, since 1 was added back to the set and
// is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 4, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 5, and remove it from the set.
**Constraints:**
* `1 <= num <= 1000`
* At most `1000` calls will be made **in total** to `popSmallest` and `addBack`. | null |
Python easy solution | smallest-number-in-infinite-set | 0 | 1 | \n# Complexity\n- Time complexity:\n```SmallestInfiniteSet().popSmallest()```: if ```len(SmallestInfiniteSet().added) == n > 0``` -> $$O(n)$$ else $$O(1)$$\n```SmallestInfiniteSet().addBack()```: $$O(1)$$\n```SmallestInfiniteSet()```: $$O(1)$$\n\n- Space complexity:\n```SmallestInfiniteSet().popSmallest()```: if ```len(SmallestInfiniteSet().added) == n > 0``` -> $$O(n)$$ else $$O(1)$$\n```SmallestInfiniteSet().addBack()```: $$O(1)$$\n```SmallestInfiniteSet()```: $$O(1)$$\n\n# Code\n```python\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.min = 1\n self.added = set()\n\n def popSmallest(self) -> int:\n to_pop = self.min\n if len(self.added) > 0:\n to_pop = min(min(self.added), to_pop)\n\n self.added.discard(to_pop)\n if to_pop == self.min:\n self.min += 1\n\n return to_pop\n\n def addBack(self, num: int) -> None:\n if num < self.min:\n self.added.add(num)\n\n```\n\n## OR\n\n# Code\n```python\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.min = 1\n self.added = set()\n\n def popSmallest(self) -> int:\n to_pop = self.min\n if len(self.added) > 0:\n to_pop = min(min(self.added), to_pop)\n\n if to_pop == self.min:\n self.min += 1\n else:\n self.added.remove(to_pop)\n\n return to_pop\n\n def addBack(self, num: int) -> None:\n if num < self.min:\n self.added.add(num)\n\n```\n\n | 1 | You have a set which contains all positive integers `[1, 2, 3, 4, 5, ...]`.
Implement the `SmallestInfiniteSet` class:
* `SmallestInfiniteSet()` Initializes the **SmallestInfiniteSet** object to contain **all** positive integers.
* `int popSmallest()` **Removes** and returns the smallest integer contained in the infinite set.
* `void addBack(int num)` **Adds** a positive integer `num` back into the infinite set, if it is **not** already in the infinite set.
**Example 1:**
**Input**
\[ "SmallestInfiniteSet ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest "\]
\[\[\], \[2\], \[\], \[\], \[\], \[1\], \[\], \[\], \[\]\]
**Output**
\[null, null, 1, 2, 3, null, 1, 4, 5\]
**Explanation**
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 is already in the set, so no change is made.
smallestInfiniteSet.popSmallest(); // return 1, since 1 is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 2, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 3, and remove it from the set.
smallestInfiniteSet.addBack(1); // 1 is added back to the set.
smallestInfiniteSet.popSmallest(); // return 1, since 1 was added back to the set and
// is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 4, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 5, and remove it from the set.
**Constraints:**
* `1 <= num <= 1000`
* At most `1000` calls will be made **in total** to `popSmallest` and `addBack`. | null |
[Python3] Heap approach | smallest-number-in-infinite-set | 0 | 1 | # Intuition\nWe need to maintain:\n1. Smallest number not yet retrieved\n2. Numbers that were already put back - in a heap and in a set\n\nWhen popping smallest - check if we have it pushed back - in the set - if it is present - then remove it from the set and from the heap, and return. \nOtherwise - return smallest and increment it. If after the increment it is present in the heap and set - remove it. \n\nWhen pushing back - check if it already present in the heap & set or is greater or equal than the smallest one - then ignore. \nOtherwise add it into the set and into the heap.\n\n\n# Code\n```\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.smallest = 1\n self.added = []\n self.added_set = set()\n\n def popSmallest(self) -> int:\n if self.added and self.added[0] < self.smallest:\n result = heapq.heappop(self.added)\n self.added_set.remove(result)\n return result\n result = self.smallest\n self.smallest += 1\n if self.added and self.smallest == self.added[0]:\n heapq.heappop(self.added)\n self.added_set.remove(self.smallest)\n return result\n\n def addBack(self, num: int) -> None:\n if num >= self.smallest or num in self.added_set:\n return\n heapq.heappush(self.added, num)\n self.added_set.add(num)\n``` | 1 | You have a set which contains all positive integers `[1, 2, 3, 4, 5, ...]`.
Implement the `SmallestInfiniteSet` class:
* `SmallestInfiniteSet()` Initializes the **SmallestInfiniteSet** object to contain **all** positive integers.
* `int popSmallest()` **Removes** and returns the smallest integer contained in the infinite set.
* `void addBack(int num)` **Adds** a positive integer `num` back into the infinite set, if it is **not** already in the infinite set.
**Example 1:**
**Input**
\[ "SmallestInfiniteSet ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest "\]
\[\[\], \[2\], \[\], \[\], \[\], \[1\], \[\], \[\], \[\]\]
**Output**
\[null, null, 1, 2, 3, null, 1, 4, 5\]
**Explanation**
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 is already in the set, so no change is made.
smallestInfiniteSet.popSmallest(); // return 1, since 1 is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 2, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 3, and remove it from the set.
smallestInfiniteSet.addBack(1); // 1 is added back to the set.
smallestInfiniteSet.popSmallest(); // return 1, since 1 was added back to the set and
// is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 4, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 5, and remove it from the set.
**Constraints:**
* `1 <= num <= 1000`
* At most `1000` calls will be made **in total** to `popSmallest` and `addBack`. | null |
Python short and clean. 2-solutions. | smallest-number-in-infinite-set | 0 | 1 | # Approach\nTL;DR, Similar to the [Editorial solution](https://leetcode.com/problems/smallest-number-in-infinite-set/editorial/).\n\n# Complexity\n- Time complexity: $$O((m + n) * log(n))$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`m is number of calls to popSmallest`,\n`n is number of calls to addBack`.\n\n# Code\nUsing SortedList:\n```python\nfrom sortedcontainers import SortedSet\n\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.k = 1\n self.added = SortedSet()\n\n def popSmallest(self) -> int:\n if self.added: return self.added.pop(0)\n else: self.k += 1; return self.k - 1\n\n def addBack(self, num: int) -> None:\n if num < self.k: self.added.add(num)\n\n\n```\n\nUsing heap and set:\n```python\nclass SmallestInfiniteSet:\n\n def __init__(self):\n self.k: int = 1\n self.added: set[int] = set()\n self.added_hq: list[int] = []\n\n def popSmallest(self) -> int:\n if self.added_hq:\n num = heappop(self.added_hq)\n self.added.remove(num)\n else:\n num = self.k\n self.k += 1\n return num\n\n def addBack(self, num: int) -> None:\n if num >= self.k or num in self.added: return\n heappush(self.added_hq, num)\n self.added.add(num)\n\n\n```\n\n | 2 | You have a set which contains all positive integers `[1, 2, 3, 4, 5, ...]`.
Implement the `SmallestInfiniteSet` class:
* `SmallestInfiniteSet()` Initializes the **SmallestInfiniteSet** object to contain **all** positive integers.
* `int popSmallest()` **Removes** and returns the smallest integer contained in the infinite set.
* `void addBack(int num)` **Adds** a positive integer `num` back into the infinite set, if it is **not** already in the infinite set.
**Example 1:**
**Input**
\[ "SmallestInfiniteSet ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest ", "addBack ", "popSmallest ", "popSmallest ", "popSmallest "\]
\[\[\], \[2\], \[\], \[\], \[\], \[1\], \[\], \[\], \[\]\]
**Output**
\[null, null, 1, 2, 3, null, 1, 4, 5\]
**Explanation**
SmallestInfiniteSet smallestInfiniteSet = new SmallestInfiniteSet();
smallestInfiniteSet.addBack(2); // 2 is already in the set, so no change is made.
smallestInfiniteSet.popSmallest(); // return 1, since 1 is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 2, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 3, and remove it from the set.
smallestInfiniteSet.addBack(1); // 1 is added back to the set.
smallestInfiniteSet.popSmallest(); // return 1, since 1 was added back to the set and
// is the smallest number, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 4, and remove it from the set.
smallestInfiniteSet.popSmallest(); // return 5, and remove it from the set.
**Constraints:**
* `1 <= num <= 1000`
* At most `1000` calls will be made **in total** to `popSmallest` and `addBack`. | null |
[Java/Python 3] Compare the sequences and the indices of 'L' and 'R'. | move-pieces-to-obtain-a-string | 1 | 1 | **Intuition:**\n\nSince `L`s and `R`s can ONLY move to empty spaces and can NOT swap, the sequences containing all `L`s and `R`s and only `L`s and `R`s of `start` and `target` must be same;\nSince `L`s and `R`s can move to left and right only respectively, all positions of `L`s in `start` must be no less than the corresponding ones in `target`, and all positions of `R`s in `start` must be no greater than the corresponding ones in `target`.\n\nBased on the above conclusion we can implement an algorithm as follows:\n\n**Algorithm:**\n\n1. Check if `start` and `target` are same if without `_`\'s;\n2. Check if all positions of `L`\'s in `start` are no less than those in `target`;\n3. Check if all positions of `R`\'s in `start` are no greater than those in `target`;\n4. If all above 3 are yes, return true; otherwise return false.\n\nCredit to **@Thoyajkiran** for removal of redundant code.\n```java\n public boolean canChange(String start, String target) {\n if (!(start.replaceAll("_", "")).equals(target.replaceAll("_", ""))) {\n return false;\n }\n for (int i = 0, j = 0, n = start.length(); i < n && j < n; ++i, ++j) {\n while (i < n && start.charAt(i) == \'_\') {\n ++i;\n }\n while (j < n && target.charAt(j) == \'_\') {\n ++j;\n }\n if (i < n && j < n && (start.charAt(i) == \'L\' && i < j || target.charAt(j) == \'R\' && i > j)) {\n return false;\n }\n }\n return true;\n }\n```\n```python\n def canChange(self, start: str, target: str) -> bool:\n if start.replace(\'_\', \'\') != target.replace(\'_\', \'\'):\n return False\n i = j = 0\n n = len(start)\n while i < n and j < n:\n while i < n and start[i] == \'_\':\n i += 1\n while j < n and target[j] == \'_\':\n j += 1\n if i < n and j < n and (start[i] == \'L\' and i < j or start[i] == \'R\' and i > j):\n return False\n i += 1\n j += 1\n return True\n```\n\n\n**Analysis:**\n\n`replace` and `for loop` contribute `O(n)` time complexity respectively. Each character at most visited twice, hence:\n\nTime & space: `O(n)`, where `n = start.length()`.\n\n----\n\nWe can optimize the space:\n\n```java\n public boolean canChange(String start, String target) {\n int i = 0, j = 0, n = start.length();\n while (i < n || j < n) {\n while (i < n && start.charAt(i) == \'_\') {\n ++i;\n }\n while (j < n && target.charAt(j) == \'_\') {\n ++j;\n }\n if (i == n || j == n) {\n return i == j;\n }\n if (start.charAt(i) != target.charAt(j)) {\n return false;\n }\n if (start.charAt(i) == \'L\') {\n if (i < j) {\n return false;\n }\n }else {\n if (i > j) {\n return false;\n }\n }\n ++i;\n ++j;\n }\n return true;\n }\n```\n```python\n def canChange(self, start: str, target: str) -> bool:\n n = len(start)\n i = j = 0\n while i < n or j < n:\n while i < n and start[i] == \'_\':\n i += 1\n while j < n and target[j] == \'_\':\n j += 1\n if n in (i, j):\n return i == j == n\n if start[i] != target[j]:\n return False\n if start[i] == \'L\':\n if i < j:\n return False\n else:\n if i > j:\n return False\n i += 1\n j += 1\n return True\n```\n\n**Analysis:**\n\n`for loop` contribute `O(n)` time complexity. Each character visited once, hence:\n\nTime: `O(n)`, space: `O(1)`, where `n = start.length()`. | 79 | You are given two strings `start` and `target`, both of length `n`. Each string consists **only** of the characters `'L'`, `'R'`, and `'_'` where:
* The characters `'L'` and `'R'` represent pieces, where a piece `'L'` can move to the **left** only if there is a **blank** space directly to its left, and a piece `'R'` can move to the **right** only if there is a **blank** space directly to its right.
* The character `'_'` represents a blank space that can be occupied by **any** of the `'L'` or `'R'` pieces.
Return `true` _if it is possible to obtain the string_ `target` _by moving the pieces of the string_ `start` _**any** number of times_. Otherwise, return `false`.
**Example 1:**
**Input:** start = "\_L\_\_R\_\_R\_ ", target = "L\_\_\_\_\_\_RR "
**Output:** true
**Explanation:** We can obtain the string target from start by doing the following moves:
- Move the first piece one step to the left, start becomes equal to "**L**\_\_\_R\_\_R\_ ".
- Move the last piece one step to the right, start becomes equal to "L\_\_\_R\_\_\_**R** ".
- Move the second piece three steps to the right, start becomes equal to "L\_\_\_\_\_\_**R**R ".
Since it is possible to get the string target from start, we return true.
**Example 2:**
**Input:** start = "R\_L\_ ", target = "\_\_LR "
**Output:** false
**Explanation:** The 'R' piece in the string start can move one step to the right to obtain "\_**R**L\_ ".
After that, no pieces can move anymore, so it is impossible to obtain the string target from start.
**Example 3:**
**Input:** start = "\_R ", target = "R\_ "
**Output:** false
**Explanation:** The piece in the string start can move only to the right, so it is impossible to obtain the string target from start.
**Constraints:**
* `n == start.length == target.length`
* `1 <= n <= 105`
* `start` and `target` consist of the characters `'L'`, `'R'`, and `'_'`. | null |
Python3 || 10 lines, w/ explanation || T/M: 96%/ 44% | move-pieces-to-obtain-a-string | 0 | 1 | ```\nclass Solution:\n # Criteria for a valid transormation:\n\n # 1) The # of Ls, # of Rs , and # of _s must be equal between the two strings\n #\n # 2) The ordering of Ls and Rs in the two strings must be the same.\n #\n # 3) Ls can only move left and Rs can only move right, so each L in start \n # cannot be to the left of its corresponding L in target, and each R cannot\n # be to the right of its corresponding R in target.\n\n def canChange(self, start: str, target: str) -> bool:\n \n if (len(start) != len(target) or \n start.count(\'_\') != target.count(\'_\')): return False # <-- Criterion 1\n\n s = [(ch,i) for i, ch in enumerate(start ) if ch != \'_\']\n t = [(ch,i) for i, ch in enumerate(target) if ch != \'_\']\n\n for i in range(len(s)):\n (sc, si), (tc,ti) = s[i], t[i]\n if sc != tc: return False # <-- Criteria 1 & 2\n if sc == \'L\' and si < ti: return False # <-- Criterion 3\n if sc == \'R\' and si > ti: return False # <--/\n\n return True # <-- It\'s a winner! | 3 | You are given two strings `start` and `target`, both of length `n`. Each string consists **only** of the characters `'L'`, `'R'`, and `'_'` where:
* The characters `'L'` and `'R'` represent pieces, where a piece `'L'` can move to the **left** only if there is a **blank** space directly to its left, and a piece `'R'` can move to the **right** only if there is a **blank** space directly to its right.
* The character `'_'` represents a blank space that can be occupied by **any** of the `'L'` or `'R'` pieces.
Return `true` _if it is possible to obtain the string_ `target` _by moving the pieces of the string_ `start` _**any** number of times_. Otherwise, return `false`.
**Example 1:**
**Input:** start = "\_L\_\_R\_\_R\_ ", target = "L\_\_\_\_\_\_RR "
**Output:** true
**Explanation:** We can obtain the string target from start by doing the following moves:
- Move the first piece one step to the left, start becomes equal to "**L**\_\_\_R\_\_R\_ ".
- Move the last piece one step to the right, start becomes equal to "L\_\_\_R\_\_\_**R** ".
- Move the second piece three steps to the right, start becomes equal to "L\_\_\_\_\_\_**R**R ".
Since it is possible to get the string target from start, we return true.
**Example 2:**
**Input:** start = "R\_L\_ ", target = "\_\_LR "
**Output:** false
**Explanation:** The 'R' piece in the string start can move one step to the right to obtain "\_**R**L\_ ".
After that, no pieces can move anymore, so it is impossible to obtain the string target from start.
**Example 3:**
**Input:** start = "\_R ", target = "R\_ "
**Output:** false
**Explanation:** The piece in the string start can move only to the right, so it is impossible to obtain the string target from start.
**Constraints:**
* `n == start.length == target.length`
* `1 <= n <= 105`
* `start` and `target` consist of the characters `'L'`, `'R'`, and `'_'`. | null |
[Python3] greedy | move-pieces-to-obtain-a-string | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/f00c06cefbc1b2305f127a8cde7ff9b010197930) for solutions of weekly 301. \n\n```\nclass Solution:\n def canChange(self, s: str, e: str) -> bool:\n dl = dr = 0 \n for ss, ee in zip(s, e): \n if dl > 0 or dl < 0 and ss == \'R\' or dr < 0 or dr > 0 and ss == \'L\': return False \n dl += int(ss == \'L\') - int(ee == \'L\')\n dr += int(ss == \'R\') - int(ee == \'R\')\n return dl == dr == 0 \n``` | 2 | You are given two strings `start` and `target`, both of length `n`. Each string consists **only** of the characters `'L'`, `'R'`, and `'_'` where:
* The characters `'L'` and `'R'` represent pieces, where a piece `'L'` can move to the **left** only if there is a **blank** space directly to its left, and a piece `'R'` can move to the **right** only if there is a **blank** space directly to its right.
* The character `'_'` represents a blank space that can be occupied by **any** of the `'L'` or `'R'` pieces.
Return `true` _if it is possible to obtain the string_ `target` _by moving the pieces of the string_ `start` _**any** number of times_. Otherwise, return `false`.
**Example 1:**
**Input:** start = "\_L\_\_R\_\_R\_ ", target = "L\_\_\_\_\_\_RR "
**Output:** true
**Explanation:** We can obtain the string target from start by doing the following moves:
- Move the first piece one step to the left, start becomes equal to "**L**\_\_\_R\_\_R\_ ".
- Move the last piece one step to the right, start becomes equal to "L\_\_\_R\_\_\_**R** ".
- Move the second piece three steps to the right, start becomes equal to "L\_\_\_\_\_\_**R**R ".
Since it is possible to get the string target from start, we return true.
**Example 2:**
**Input:** start = "R\_L\_ ", target = "\_\_LR "
**Output:** false
**Explanation:** The 'R' piece in the string start can move one step to the right to obtain "\_**R**L\_ ".
After that, no pieces can move anymore, so it is impossible to obtain the string target from start.
**Example 3:**
**Input:** start = "\_R ", target = "R\_ "
**Output:** false
**Explanation:** The piece in the string start can move only to the right, so it is impossible to obtain the string target from start.
**Constraints:**
* `n == start.length == target.length`
* `1 <= n <= 105`
* `start` and `target` consist of the characters `'L'`, `'R'`, and `'_'`. | null |
[Python3] freq table | count-the-number-of-ideal-arrays | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/f00c06cefbc1b2305f127a8cde7ff9b010197930) for solutions of weekly 301. \n\n**Intuition**\nIt is not hard to figure out that this is a DP problem. What\'s challenging is that due to the very tight time constraint, one has to come up with a linear-ish algorithm to solve this problem. So we have to play some math instead of running the naive DP. \n\nThe most important observation is that the number of ideal arrays of k distinct numbers are the same regardless of what the k numbers are. They are all (n-1, k-1) i.e. n-1 choose k-1. Here, you simply need to place the k-1 places where the numbers change among the n-1 candidates. \n\nWith this obsevation, the below DP setup can work in O(Nlog^2M) time. The states are \n1) number of changes `k` (or equivalently `k+1` unique values)\n2) the ending value which is used to generate ideal arrays with more unique values. \n\nSince there are multiple ways to end up at the same values e.g. `(1,2,6)`, `(1,3,6)`, I also need to maintain a counter to reflect this fact. \n\nI start with `{1:1, 2:1, ..., maxValue:1}` which indicates that `(1,1,..1)`, `(2,2,...,2)`, ... `(maxValue, maxValue, ..., maxValue)` each contributes 1 to the final answer. Then I enumerate the number of changes `k` as 1, 2, ..., n-1. At each `k`, I compute `freq[x]` which is the number of ways to arrive at `x` (with `k` changes). For example, with 2 changes, you can get 6 as `(1,2,6)` and `(1,3,6)`. Then, `comb(n-1, k) * freq[x]` is the contribution from the ideal arrays with `k` changes ending at `x`. \n\n```\nclass Solution:\n def idealArrays(self, n: int, maxValue: int) -> int:\n ans = maxValue\n freq = {x : 1 for x in range(1, maxValue+1)}\n for k in range(1, n): \n temp = Counter()\n for x in freq: \n for m in range(2, maxValue//x+1): \n ans += comb(n-1, k)*freq[x]\n temp[m*x] += freq[x]\n freq = temp\n ans %= 1_000_000_007\n return ans \n``` | 32 | You are given two integers `n` and `maxValue`, which are used to describe an **ideal** array.
A **0-indexed** integer array `arr` of length `n` is considered **ideal** if the following conditions hold:
* Every `arr[i]` is a value from `1` to `maxValue`, for `0 <= i < n`.
* Every `arr[i]` is divisible by `arr[i - 1]`, for `0 < i < n`.
Return _the number of **distinct** ideal arrays of length_ `n`. Since the answer may be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, maxValue = 5
**Output:** 10
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (5 arrays): \[1,1\], \[1,2\], \[1,3\], \[1,4\], \[1,5\]
- Arrays starting with the value 2 (2 arrays): \[2,2\], \[2,4\]
- Arrays starting with the value 3 (1 array): \[3,3\]
- Arrays starting with the value 4 (1 array): \[4,4\]
- Arrays starting with the value 5 (1 array): \[5,5\]
There are a total of 5 + 2 + 1 + 1 + 1 = 10 distinct ideal arrays.
**Example 2:**
**Input:** n = 5, maxValue = 3
**Output:** 11
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (9 arrays):
- With no other distinct values (1 array): \[1,1,1,1,1\]
- With 2nd distinct value 2 (4 arrays): \[1,1,1,1,2\], \[1,1,1,2,2\], \[1,1,2,2,2\], \[1,2,2,2,2\]
- With 2nd distinct value 3 (4 arrays): \[1,1,1,1,3\], \[1,1,1,3,3\], \[1,1,3,3,3\], \[1,3,3,3,3\]
- Arrays starting with the value 2 (1 array): \[2,2,2,2,2\]
- Arrays starting with the value 3 (1 array): \[3,3,3,3,3\]
There are a total of 9 + 1 + 1 = 11 distinct ideal arrays.
**Constraints:**
* `2 <= n <= 104`
* `1 <= maxValue <= 104` | null |
[Python] Freq Table Solution (by ye15) with Explanations | count-the-number-of-ideal-arrays | 0 | 1 | First, full credits to @ye15\'s [amazing solution](https://leetcode.com/problems/count-the-number-of-ideal-arrays/discuss/2261351/Python3-freq-table). Here are some explanations.\n\nInstead of counting the possible ideal arrays by different starting (or ending) values, we count the possible ideal arrays by the number of **unique values** in the array.\nStep 1a. Initialize `ans` as `maxValue`, representing ideal arrays with all of the same values (that is, the number of unique values in the array being 1)\nStep 1b. Initialize the `freq` table as a `Counter` object which represents the number of distinct ideal arrays ending with value `x` with the current number of unique values (which is 1 for now)\nStep 2. We iterate `k` which represents the current number of unique values. For each value of `k`, we define a `temp` as a `Counter` object for the next iteration of `freq`. Then, for each value `x` in the current `freq`, we consider the next possible value (i.e. `m * x`), different from `x`, such that there are `freq[x]` possible ways contributing to `nxt[m * x]`. In the meantime, `freq[x]` also contributes to the final output `ans` by a factor of `comb(n - 1, k)` (**key step**). This is because we have set the ending value to be *m * x*, so that among the first `n - 1` possible positions, there are `math.comb(n - 1, k)` possible ways to assign the `k` unique values to the `n - 1` positions. One thing to note is that since the ideal array is defined such that "every `arr[i]` is divisible by `arr[i - 1]`, for `0 < i < n`. After we have selected `k` positions out of `n - 1` possible positions, we can always work from the right to the left by keeping the current value as the same unless we encounter another selected position. For example, if `n = 5, k = 2, m = 2` and the two unique values are `1` and `2`, then `math.comb(n - 1, k) = math.comb(4, 2) = 6`. Below are the 6 possible ideal arrays contributing to `ans`.\n```\n(1, 2) -> [1, 2, 4, 4, 4]\n(1, 3) -> [1, 2, 2, 4, 4]\n(1, 4) -> [1, 2, 2, 2, 4]\n(2, 3) -> [1, 1, 2, 4, 4]\n(2, 4) -> [1, 1, 2, 2, 4]\n(3, 4) -> [1, 1, 1, 2, 4]\n```\nHence, we add `math.comb(n - 1, k) * freq[x]` to `ans`\nStep 3: Update `freq` by setting it to `temp`\nStep 4: Return `ans`\n\nFinally, adding an early stopping rule to the solution. If you find this explanation helpful, please feel free to upvote and also upvote the @ye15\'s post.\n```\nclass Solution:\n def idealArrays(self, n: int, maxValue: int) -> int:\n MOD = 10 ** 9 + 7\n ans = maxValue\n freq = {x: 1 for x in range(1, maxValue + 1)}\n for k in range(1, n):\n if not freq:\n break\n nxt = collections.defaultdict(int)\n for x in freq:\n for m in range(2, maxValue // x + 1):\n ans += math.comb(n - 1, k) * freq[x]\n nxt[m * x] += freq[x]\n freq = nxt\n ans %= MOD\n return ans\n``` | 3 | You are given two integers `n` and `maxValue`, which are used to describe an **ideal** array.
A **0-indexed** integer array `arr` of length `n` is considered **ideal** if the following conditions hold:
* Every `arr[i]` is a value from `1` to `maxValue`, for `0 <= i < n`.
* Every `arr[i]` is divisible by `arr[i - 1]`, for `0 < i < n`.
Return _the number of **distinct** ideal arrays of length_ `n`. Since the answer may be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, maxValue = 5
**Output:** 10
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (5 arrays): \[1,1\], \[1,2\], \[1,3\], \[1,4\], \[1,5\]
- Arrays starting with the value 2 (2 arrays): \[2,2\], \[2,4\]
- Arrays starting with the value 3 (1 array): \[3,3\]
- Arrays starting with the value 4 (1 array): \[4,4\]
- Arrays starting with the value 5 (1 array): \[5,5\]
There are a total of 5 + 2 + 1 + 1 + 1 = 10 distinct ideal arrays.
**Example 2:**
**Input:** n = 5, maxValue = 3
**Output:** 11
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (9 arrays):
- With no other distinct values (1 array): \[1,1,1,1,1\]
- With 2nd distinct value 2 (4 arrays): \[1,1,1,1,2\], \[1,1,1,2,2\], \[1,1,2,2,2\], \[1,2,2,2,2\]
- With 2nd distinct value 3 (4 arrays): \[1,1,1,1,3\], \[1,1,1,3,3\], \[1,1,3,3,3\], \[1,3,3,3,3\]
- Arrays starting with the value 2 (1 array): \[2,2,2,2,2\]
- Arrays starting with the value 3 (1 array): \[3,3,3,3,3\]
There are a total of 9 + 1 + 1 = 11 distinct ideal arrays.
**Constraints:**
* `2 <= n <= 104`
* `1 <= maxValue <= 104` | null |
[Python] Stars and Bars combinatorics, beats 100%, O(M log^2 M) | count-the-number-of-ideal-arrays | 0 | 1 | **Idea**\n\n* Count the number of ideal arrays without allowing repeats.\n* Use [Stars and Bars](https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)) to calculate the number of ideal arrays with repeats, given the unique counts. Each ideal array of length `x` without repeats can become `(n-1 choose x-1)` ideal arrays with repeats. \n****\nFor example, given an ideal array with no repeats of `[1,2,3]`, and a value of `n=6`, we can form (5 choose 2) = 10 different arrays of length 6 that contain only the digits (1, 2, 3) in that order.\n\nSince we only care about the length of the unique ideal arrays, we should iterate over divisors of each number.\n\nTo find the number of unique ideal arrays of length `k` that end on an integer `m`, sum the number of unique ideal arrays of length `k-1` that end on a divisor of `m`. \n\nWe can loop over the divisors instead for speed and to allow parallelization with numpy. The longest unique ideal array with a maximum value of M is at most `(log_2(M)+1)`, since each value in that array is twice as large as the previous. For us, 18 is large enough, since `log_2(10^4) < 14`\n\n****\n**Python (with numpy)** \n\n```python\nimport numpy as np\n\nclass Solution:\n def idealArrays(self, n: int, maxValue: int) -> int:\n MOD = 10 ** 9 + 7\n\n my_combs = [1] # n-1 choose k\n for k in range(1, 21):\n my_combs.append(((n - k) * my_combs[-1]) // k)\n\n my_lengths = np.zeros(shape=(maxValue + 1, 18), dtype=np.int32)\n my_lengths[:, 1] = 1\n my_lengths[:, 2] = 1\n\n for x in range(2, min((maxValue + 1) // 2, maxValue) + 1):\n my_lengths[2 * x: maxValue + 1: x, 1:] += my_lengths[x, :-1]\n\n my_lengths[0] = 0\n my_lengths[1, 2] = 0\n by_total_length = np.sum(my_lengths, axis=0)\n\n total = 0\n for k, v in enumerate(by_total_length):\n if k == 0 or v == 0:\n continue\n total += int(v) * my_combs[k - 1] % MOD\n\n return total % MOD\n```\nTime complexity: `O(maxValue * log^2(maxValue))`. \nSpace complexity: `O(maxValue * log(maxValue))`. \n\nUsing numpy, we can this run several times faster than an equivalent non-Numpy solution, and more competitive with compiled languages. However, a non-vectorized solution is still fast enough to pass Leetcode timing.\n\nEdit: Corrected variable names in time complexity | 1 | You are given two integers `n` and `maxValue`, which are used to describe an **ideal** array.
A **0-indexed** integer array `arr` of length `n` is considered **ideal** if the following conditions hold:
* Every `arr[i]` is a value from `1` to `maxValue`, for `0 <= i < n`.
* Every `arr[i]` is divisible by `arr[i - 1]`, for `0 < i < n`.
Return _the number of **distinct** ideal arrays of length_ `n`. Since the answer may be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, maxValue = 5
**Output:** 10
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (5 arrays): \[1,1\], \[1,2\], \[1,3\], \[1,4\], \[1,5\]
- Arrays starting with the value 2 (2 arrays): \[2,2\], \[2,4\]
- Arrays starting with the value 3 (1 array): \[3,3\]
- Arrays starting with the value 4 (1 array): \[4,4\]
- Arrays starting with the value 5 (1 array): \[5,5\]
There are a total of 5 + 2 + 1 + 1 + 1 = 10 distinct ideal arrays.
**Example 2:**
**Input:** n = 5, maxValue = 3
**Output:** 11
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (9 arrays):
- With no other distinct values (1 array): \[1,1,1,1,1\]
- With 2nd distinct value 2 (4 arrays): \[1,1,1,1,2\], \[1,1,1,2,2\], \[1,1,2,2,2\], \[1,2,2,2,2\]
- With 2nd distinct value 3 (4 arrays): \[1,1,1,1,3\], \[1,1,1,3,3\], \[1,1,3,3,3\], \[1,3,3,3,3\]
- Arrays starting with the value 2 (1 array): \[2,2,2,2,2\]
- Arrays starting with the value 3 (1 array): \[3,3,3,3,3\]
There are a total of 9 + 1 + 1 = 11 distinct ideal arrays.
**Constraints:**
* `2 <= n <= 104`
* `1 <= maxValue <= 104` | null |
Python (Simple Maths) | count-the-number-of-ideal-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def idealArrays(self, n, maxValue):\n ans = maxValue\n dict1 = {x:1 for x in range(1,maxValue+1)}\n\n for k in range(1,n):\n temp = Counter()\n for x in dict1:\n for m in range(2,maxValue//x+1):\n ans += comb(n-1,k)*dict1[x]\n temp[m*x] += dict1[x]\n dict1 = temp\n ans = ans%(10**9+7)\n\n return ans\n\n\n\n\n\n\n\n \n\n\n\n\n\n\n\n\n \n \n \n``` | 0 | You are given two integers `n` and `maxValue`, which are used to describe an **ideal** array.
A **0-indexed** integer array `arr` of length `n` is considered **ideal** if the following conditions hold:
* Every `arr[i]` is a value from `1` to `maxValue`, for `0 <= i < n`.
* Every `arr[i]` is divisible by `arr[i - 1]`, for `0 < i < n`.
Return _the number of **distinct** ideal arrays of length_ `n`. Since the answer may be very large, return it modulo `109 + 7`.
**Example 1:**
**Input:** n = 2, maxValue = 5
**Output:** 10
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (5 arrays): \[1,1\], \[1,2\], \[1,3\], \[1,4\], \[1,5\]
- Arrays starting with the value 2 (2 arrays): \[2,2\], \[2,4\]
- Arrays starting with the value 3 (1 array): \[3,3\]
- Arrays starting with the value 4 (1 array): \[4,4\]
- Arrays starting with the value 5 (1 array): \[5,5\]
There are a total of 5 + 2 + 1 + 1 + 1 = 10 distinct ideal arrays.
**Example 2:**
**Input:** n = 5, maxValue = 3
**Output:** 11
**Explanation:** The following are the possible ideal arrays:
- Arrays starting with the value 1 (9 arrays):
- With no other distinct values (1 array): \[1,1,1,1,1\]
- With 2nd distinct value 2 (4 arrays): \[1,1,1,1,2\], \[1,1,1,2,2\], \[1,1,2,2,2\], \[1,2,2,2,2\]
- With 2nd distinct value 3 (4 arrays): \[1,1,1,1,3\], \[1,1,1,3,3\], \[1,1,3,3,3\], \[1,3,3,3,3\]
- Arrays starting with the value 2 (1 array): \[2,2,2,2,2\]
- Arrays starting with the value 3 (1 array): \[3,3,3,3,3\]
There are a total of 9 + 1 + 1 = 11 distinct ideal arrays.
**Constraints:**
* `2 <= n <= 104`
* `1 <= maxValue <= 104` | null |
Simple solution with HashTable | maximum-number-of-pairs-in-array | 0 | 1 | # Intuition\nHere we have:\n- a list of `nums`\n- our goal is to find **the maximum count of pairs**, that has equal integers as `[1, 1], [2,2]` etc.\n\nWe don\'t need to **remove** integers, because it costs an auxillary **O(N)** time.\nInstead we define a **HashMap** to store frequencies of a particular integer.\n\n```\n# Example\n\n# What if you have 5 integers as [1,1,1,1,1].\n# How much pairs you could create to fulfill a condition above?\n# Only two => (1, 1), (1, 1) and there\'s 1 left.\n```\n\nTo create a pair, we should divide a frequency of integers by two.\n\n\n# Approach\n1. define `cache` and `pairs` count\n2. iterate over `nums`\n3. at each step check, if you have a new pair as `cache[num] % 2 == 0`, then increment `pairs` by one\n4. return `[pairs, len(pairs) - pairs * 2]`\n\n# Complexity\n- Time complexity: **O(N)**\n\n- Space complexity: **O(N)**\n\n# Code\n```\nclass Solution:\n def numberOfPairs(self, nums: List[int]) -> List[int]:\n cache = defaultdict(int)\n pairs = 0\n\n for num in nums:\n cache[num] += 1\n\n if cache[num] % 2 == 0:\n pairs += 1 \n\n return [pairs, len(nums) - pairs * 2]\n``` | 1 | You are given a **0-indexed** integer array `nums`. In one operation, you may do the following:
* Choose **two** integers in `nums` that are **equal**.
* Remove both integers from `nums`, forming a **pair**.
The operation is done on `nums` as many times as possible.
Return _a **0-indexed** integer array_ `answer` _of size_ `2` _where_ `answer[0]` _is the number of pairs that are formed and_ `answer[1]` _is the number of leftover integers in_ `nums` _after doing the operation as many times as possible_.
**Example 1:**
**Input:** nums = \[1,3,2,1,3,2,2\]
**Output:** \[3,1\]
**Explanation:**
Form a pair with nums\[0\] and nums\[3\] and remove them from nums. Now, nums = \[3,2,3,2,2\].
Form a pair with nums\[0\] and nums\[2\] and remove them from nums. Now, nums = \[2,2,2\].
Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[2\].
No more pairs can be formed. A total of 3 pairs have been formed, and there is 1 number leftover in nums.
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[1,0\]
**Explanation:** Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[\].
No more pairs can be formed. A total of 1 pair has been formed, and there are 0 numbers leftover in nums.
**Example 3:**
**Input:** nums = \[0\]
**Output:** \[0,1\]
**Explanation:** No pairs can be formed, and there is 1 number leftover in nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Python using Set 96% beats | maximum-number-of-pairs-in-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfPairs(self, nums: List[int]) -> List[int]:\n num_set=set()\n pair=0\n for num in nums:\n if num not in num_set:\n num_set.add(num)\n else:\n pair+=1\n num_set.remove(num)\n ans=[pair,len(num_set)]\n return ans\n``` | 1 | You are given a **0-indexed** integer array `nums`. In one operation, you may do the following:
* Choose **two** integers in `nums` that are **equal**.
* Remove both integers from `nums`, forming a **pair**.
The operation is done on `nums` as many times as possible.
Return _a **0-indexed** integer array_ `answer` _of size_ `2` _where_ `answer[0]` _is the number of pairs that are formed and_ `answer[1]` _is the number of leftover integers in_ `nums` _after doing the operation as many times as possible_.
**Example 1:**
**Input:** nums = \[1,3,2,1,3,2,2\]
**Output:** \[3,1\]
**Explanation:**
Form a pair with nums\[0\] and nums\[3\] and remove them from nums. Now, nums = \[3,2,3,2,2\].
Form a pair with nums\[0\] and nums\[2\] and remove them from nums. Now, nums = \[2,2,2\].
Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[2\].
No more pairs can be formed. A total of 3 pairs have been formed, and there is 1 number leftover in nums.
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[1,0\]
**Explanation:** Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[\].
No more pairs can be formed. A total of 1 pair has been formed, and there are 0 numbers leftover in nums.
**Example 3:**
**Input:** nums = \[0\]
**Output:** \[0,1\]
**Explanation:** No pairs can be formed, and there is 1 number leftover in nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Python | Easy Solution✅ | maximum-number-of-pairs-in-array | 0 | 1 | ```\ndef numberOfPairs(self, nums: List[int]) -> List[int]: \n output = [] # nums = [1,3,2,1,3,2,2]\n pair = 0\n unique = list(set(nums)) # [1,3,2] get unique elements from nums\n for i in range(len(unique)):\n count = nums.count(unique[i]) # count no of element in nums\n if count % 2 !=0:\n output.append(unique[i]) # if count is odd, after pairing one element will remain. Append that to output list \n pair += (count)//2 # get no of pairs\n return [pair,len(output)] # output = [2]\n``` | 4 | You are given a **0-indexed** integer array `nums`. In one operation, you may do the following:
* Choose **two** integers in `nums` that are **equal**.
* Remove both integers from `nums`, forming a **pair**.
The operation is done on `nums` as many times as possible.
Return _a **0-indexed** integer array_ `answer` _of size_ `2` _where_ `answer[0]` _is the number of pairs that are formed and_ `answer[1]` _is the number of leftover integers in_ `nums` _after doing the operation as many times as possible_.
**Example 1:**
**Input:** nums = \[1,3,2,1,3,2,2\]
**Output:** \[3,1\]
**Explanation:**
Form a pair with nums\[0\] and nums\[3\] and remove them from nums. Now, nums = \[3,2,3,2,2\].
Form a pair with nums\[0\] and nums\[2\] and remove them from nums. Now, nums = \[2,2,2\].
Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[2\].
No more pairs can be formed. A total of 3 pairs have been formed, and there is 1 number leftover in nums.
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[1,0\]
**Explanation:** Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[\].
No more pairs can be formed. A total of 1 pair has been formed, and there are 0 numbers leftover in nums.
**Example 3:**
**Input:** nums = \[0\]
**Output:** \[0,1\]
**Explanation:** No pairs can be formed, and there is 1 number leftover in nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Simple and Easy to Understand | Python | maximum-number-of-pairs-in-array | 0 | 1 | If you have any **doubt** or **suggestion,** put in comments **:)**\n```\nclass Solution(object):\n def numberOfPairs(self, nums):\n hashT = {}\n for n in nums:\n if n not in hashT: hashT[n] = 1\n else: hashT[n] += 1\n pairs, rem = 0, 0\n for n in hashT:\n pairs += (hashT[n] // 2)\n rem += (hashT[n] % 2)\n return [pairs, rem]\n```\n***UpVote***, if you like it ***:)*** | 5 | You are given a **0-indexed** integer array `nums`. In one operation, you may do the following:
* Choose **two** integers in `nums` that are **equal**.
* Remove both integers from `nums`, forming a **pair**.
The operation is done on `nums` as many times as possible.
Return _a **0-indexed** integer array_ `answer` _of size_ `2` _where_ `answer[0]` _is the number of pairs that are formed and_ `answer[1]` _is the number of leftover integers in_ `nums` _after doing the operation as many times as possible_.
**Example 1:**
**Input:** nums = \[1,3,2,1,3,2,2\]
**Output:** \[3,1\]
**Explanation:**
Form a pair with nums\[0\] and nums\[3\] and remove them from nums. Now, nums = \[3,2,3,2,2\].
Form a pair with nums\[0\] and nums\[2\] and remove them from nums. Now, nums = \[2,2,2\].
Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[2\].
No more pairs can be formed. A total of 3 pairs have been formed, and there is 1 number leftover in nums.
**Example 2:**
**Input:** nums = \[1,1\]
**Output:** \[1,0\]
**Explanation:** Form a pair with nums\[0\] and nums\[1\] and remove them from nums. Now, nums = \[\].
No more pairs can be formed. A total of 1 pair has been formed, and there are 0 numbers leftover in nums.
**Example 3:**
**Input:** nums = \[0\]
**Output:** \[0,1\]
**Explanation:** No pairs can be formed, and there is 1 number leftover in nums.
**Constraints:**
* `1 <= nums.length <= 100`
* `0 <= nums[i] <= 100` | null |
Simple Readable Python solution | max-sum-of-a-pair-with-equal-sum-of-digits | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maximumSum(self, nums: List[int]) -> int:\n a = [[sum([int(x) for x in str(nums[i])]), nums[i]] for i in range(len(nums))]\n mx = 0\n b = [a[i][0] for i in range(len(a))]\n if len(b) == len(set(b)): return -1\n\n d = defaultdict(list)\n for i in range(len(a)):\n d[a[i][0]].append(a[i][1])\n\n c = list(d.values())\n for ar in c:\n if len(ar) >= 2:\n mx = max(sorted(ar)[-1]+sorted(ar)[-2], mx)\n return mx\n \n\n``` | 1 | You are given a **0-indexed** array `nums` consisting of **positive** integers. You can choose two indices `i` and `j`, such that `i != j`, and the sum of digits of the number `nums[i]` is equal to that of `nums[j]`.
Return _the **maximum** value of_ `nums[i] + nums[j]` _that you can obtain over all possible indices_ `i` _and_ `j` _that satisfy the conditions._
**Example 1:**
**Input:** nums = \[18,43,36,13,7\]
**Output:** 54
**Explanation:** The pairs (i, j) that satisfy the conditions are:
- (0, 2), both numbers have a sum of digits equal to 9, and their sum is 18 + 36 = 54.
- (1, 4), both numbers have a sum of digits equal to 7, and their sum is 43 + 7 = 50.
So the maximum sum that we can obtain is 54.
**Example 2:**
**Input:** nums = \[10,12,19,14\]
**Output:** -1
**Explanation:** There are no two numbers that satisfy the conditions, so we return -1.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
python 3 with TC O(n), using defaultdict | max-sum-of-a-pair-with-equal-sum-of-digits | 0 | 1 | # Intuition\n- **First Thoughts**: Use a hash table to track numbers with the same digit sum. Since the goal is to find the maximum sum pair, the hash map needs to only record the highest value for each digit sum.\n\n# Approach\n- **Strategy**: Implement a Python defaultdict with a zero initial value, simplifying the conditional checks for updating the hash map. Iterate through the input list, calculating the digit sum for each integer. If the digit sum is already in the hash map, update the answer using the max function. Additionally, update the hash map\'s value for that digit sum if the current value is greater.\n\n# Complexity\n- **Time Complexity**: Iterating through the input list once results in a time complexity of O(n).\n- **Space Complexity**: The space complexity depends on the number of distinct digit sums.\n\n# Code\n```python\nfrom collections import defaultdict\n\nclass Solution:\n def maximumSum(self, nums: List[int]) -> int:\n max_seen = defaultdict(lambda: 0)\n ans = -float(\'inf\')\n for i in nums:\n digit_sum = sum(int(digit) for digit in str(i))\n if digit_sum in max_seen:\n ans = max(max_seen[digit_sum] + i, ans)\n if i > max_seen[digit_sum]:\n max_seen[digit_sum] = i\n return ans if ans != -float(\'inf\') else -1\n | 0 | You are given a **0-indexed** array `nums` consisting of **positive** integers. You can choose two indices `i` and `j`, such that `i != j`, and the sum of digits of the number `nums[i]` is equal to that of `nums[j]`.
Return _the **maximum** value of_ `nums[i] + nums[j]` _that you can obtain over all possible indices_ `i` _and_ `j` _that satisfy the conditions._
**Example 1:**
**Input:** nums = \[18,43,36,13,7\]
**Output:** 54
**Explanation:** The pairs (i, j) that satisfy the conditions are:
- (0, 2), both numbers have a sum of digits equal to 9, and their sum is 18 + 36 = 54.
- (1, 4), both numbers have a sum of digits equal to 7, and their sum is 43 + 7 = 50.
So the maximum sum that we can obtain is 54.
**Example 2:**
**Input:** nums = \[10,12,19,14\]
**Output:** -1
**Explanation:** There are no two numbers that satisfy the conditions, so we return -1.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[Python] two sum | max-sum-of-a-pair-with-equal-sum-of-digits | 0 | 1 | ```python\nclass Solution:\n def maximumSum(self, nums: List[int]) -> int:\n dict_map = {}\n \n res = -1\n for num in nums:\n temp = num\n new_num = 0\n while temp:\n new_num += temp % 10\n temp = temp // 10\n if new_num in dict_map:\n new_res = num + dict_map[new_num]\n res = max(res, new_res)\n dict_map[new_num] = max(num, dict_map[new_num])\n else:\n dict_map[new_num] = num\n return res\n``` | 3 | You are given a **0-indexed** array `nums` consisting of **positive** integers. You can choose two indices `i` and `j`, such that `i != j`, and the sum of digits of the number `nums[i]` is equal to that of `nums[j]`.
Return _the **maximum** value of_ `nums[i] + nums[j]` _that you can obtain over all possible indices_ `i` _and_ `j` _that satisfy the conditions._
**Example 1:**
**Input:** nums = \[18,43,36,13,7\]
**Output:** 54
**Explanation:** The pairs (i, j) that satisfy the conditions are:
- (0, 2), both numbers have a sum of digits equal to 9, and their sum is 18 + 36 = 54.
- (1, 4), both numbers have a sum of digits equal to 7, and their sum is 43 + 7 = 50.
So the maximum sum that we can obtain is 54.
**Example 2:**
**Input:** nums = \[10,12,19,14\]
**Output:** -1
**Explanation:** There are no two numbers that satisfy the conditions, so we return -1.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[Python 3] Quick Select - Simple solution | query-kth-smallest-trimmed-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(M)$$ for each queries in Average with M is length of nums\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N * M)$$ with M is length of nums and N is length of each string\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestTrimmedNumbers(self, nums: List[str], queries: List[List[int]]) -> List[int]:\n def partition(l: int, r: int, p: int, trim: int) -> int:\n tmp_trim = trim_arr[trim]\n pivot = tmp_trim[p]\n tmp_trim[p], tmp_trim[r] = tmp_trim[r], tmp_trim[p]\n new_p = l\n for i in range(l, r):\n if tmp_trim[i][0] < pivot[0] or \\\n (tmp_trim[i][0] == pivot[0] and tmp_trim[i][1] < pivot[1]):\n tmp_trim[i], tmp_trim[new_p] = tmp_trim[new_p], tmp_trim[i]\n new_p += 1\n \n tmp_trim[r], tmp_trim[new_p] = tmp_trim[new_p], tmp_trim[r]\n trim_arr[trim] = tmp_trim\n\n return new_p\n \n def select(l: int, r: int, k: int, trim: int) -> int:\n if l == r: return l\n p = random.randint(l, r)\n p = partition(l, r, p, trim)\n if p < k: return select(p + 1, r, k, trim)\n if p > k: return select(l, p - 1, k, trim)\n else: return p\n \n m, n = len(nums), len(nums[0])\n trim_arr = [[]]\n for i in range(n):\n trim_arr.append([(int(num[n - i - 1:]), j) for j, num in enumerate(nums)])\n \n res = []\n for k, trim in queries:\n i = select(0, m - 1, k - 1, trim)\n res.append(trim_arr[trim][i][1])\n \n return res\n``` | 3 | You are given a **0-indexed** array of strings `nums`, where each string is of **equal length** and consists of only digits.
You are also given a **0-indexed** 2D integer array `queries` where `queries[i] = [ki, trimi]`. For each `queries[i]`, you need to:
* **Trim** each number in `nums` to its **rightmost** `trimi` digits.
* Determine the **index** of the `kith` smallest trimmed number in `nums`. If two trimmed numbers are equal, the number with the **lower** index is considered to be smaller.
* Reset each number in `nums` to its original length.
Return _an array_ `answer` _of the same length as_ `queries`, _where_ `answer[i]` _is the answer to the_ `ith` _query._
**Note**:
* To trim to the rightmost `x` digits means to keep removing the leftmost digit, until only `x` digits remain.
* Strings in `nums` may contain leading zeros.
**Example 1:**
**Input:** nums = \[ "102 ", "473 ", "251 ", "814 "\], queries = \[\[1,1\],\[2,3\],\[4,2\],\[1,2\]\]
**Output:** \[2,2,1,0\]
**Explanation:**
1. After trimming to the last digit, nums = \[ "2 ", "3 ", "1 ", "4 "\]. The smallest number is 1 at index 2.
2. Trimmed to the last 3 digits, nums is unchanged. The 2nd smallest number is 251 at index 2.
3. Trimmed to the last 2 digits, nums = \[ "02 ", "73 ", "51 ", "14 "\]. The 4th smallest number is 73.
4. Trimmed to the last 2 digits, the smallest number is 2 at index 0.
Note that the trimmed number "02 " is evaluated as 2.
**Example 2:**
**Input:** nums = \[ "24 ", "37 ", "96 ", "04 "\], queries = \[\[2,1\],\[2,2\]\]
**Output:** \[3,0\]
**Explanation:**
1. Trimmed to the last digit, nums = \[ "4 ", "7 ", "6 ", "4 "\]. The 2nd smallest number is 4 at index 3.
There are two occurrences of 4, but the one at index 0 is considered smaller than the one at index 3.
2. Trimmed to the last 2 digits, nums is unchanged. The 2nd smallest number is 24.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `nums[i]` consists of only digits.
* All `nums[i].length` are **equal**.
* `1 <= queries.length <= 100`
* `queries[i].length == 2`
* `1 <= ki <= nums.length`
* `1 <= trimi <= nums[i].length`
**Follow up:** Could you use the **Radix Sort Algorithm** to solve this problem? What will be the complexity of that solution? | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.