title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 3 || 4 lines, fixed window || T/M: 99% / 99% | check-if-there-is-a-valid-partition-for-the-array | 0 | 1 | We use a sliding window of fixed length 3, checking element by element, whether any one of the three conditions is satisfied.\n```\nclass Solution:\n def validPartition(self, nums: List[int]) -> bool:\n\n checks = (True, False, nums[0] == nums[1])\n\n for curr, prev1, prev2 in zip(nums[2:], nums[1:], nums):\n\n checks = (checks[1], checks[2], # <-- slide the window\n (checks[1] and curr == prev1) or # <-- conditiion 1\n (checks[0] and curr == prev1 == prev2) or # <-- conditiion 2\n (checks[0] and curr == prev1+1 == prev2+2)) # <-- conditiion 3 \n\n return checks[2]\n```\n[https://leetcode.com/problems/check-if-there-is-a-valid-partition-for-the-array/submissions/1020355801/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~ `len(nums)`. | 3 | You are given a **0-indexed** integer array `nums`. You have to partition the array into one or more **contiguous** subarrays.
We call a partition of the array **valid** if each of the obtained subarrays satisfies **one** of the following conditions:
1. The subarray consists of **exactly** `2` equal elements. For example, the subarray `[2,2]` is good.
2. The subarray consists of **exactly** `3` equal elements. For example, the subarray `[4,4,4]` is good.
3. The subarray consists of **exactly** `3` consecutive increasing elements, that is, the difference between adjacent elements is `1`. For example, the subarray `[3,4,5]` is good, but the subarray `[1,3,5]` is not.
Return `true` _if the array has **at least** one valid partition_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[4,4,4,5,6\]
**Output:** true
**Explanation:** The array can be partitioned into the subarrays \[4,4\] and \[4,5,6\].
This partition is valid, so we return true.
**Example 2:**
**Input:** nums = \[1,1,1,2\]
**Output:** false
**Explanation:** There is no valid partition for this array.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | How can we use precalculation to efficiently calculate the average difference at an index? Create a prefix and/or suffix sum array. |
O(1) space in-place solution that isn't in Editorial | check-if-there-is-a-valid-partition-for-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse dynamic programming to solve this one.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNegate a number to mark a cell.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n* You could find some other extraordinary solutions in my [profile](https://leetcode.com/almostmonday/) on the Solutions tab (I don\'t post obvious or not interesting solutions at all.)\n* If this was helpful, please upvote so that others can see this solution too.\n---\n\n# Code\n```\nclass Solution(object):\n def validPartition(self, nums):\n nums[0] *= -1\n for i in range(len(nums) - 2):\n if nums[i] > -1: continue\n \n if abs(nums[i]) == abs(nums[i + 1]): nums[i + 2] = -abs(nums[i + 2])\n\n if (abs(nums[i]) == abs(nums[i + 1]) == abs(nums[i + 2]) or \n abs(nums[i]) + 1 == abs(nums[i + 1]) == abs(nums[i + 2]) - 1):\n if i + 3 == len(nums): return True\n else: nums[i + 3] = -abs(nums[i + 3])\n \n return nums[-2] < 0 and abs(nums[-2]) == abs(nums[-1])\n```\n\nYou could optimise it:\n```\nclass Solution(object):\n def validPartition(self, nums):\n nums[0] *= -1\n for i in range(len(nums) - 2):\n if nums[i] > -1: continue\n \n if abs(nums[i]) == abs(nums[i + 1]): \n nums[i + 2] = -abs(nums[i + 2])\n if abs(nums[i]) == abs(nums[i + 2]):\n if i + 3 == len(nums): return True\n else: nums[i + 3] = -abs(nums[i + 3])\n\n elif abs(nums[i]) + 1 == abs(nums[i + 1]) == abs(nums[i + 2]) - 1:\n if i + 3 == len(nums): return True\n else: nums[i + 3] = -abs(nums[i + 3])\n \n return nums[-2] < 0 and abs(nums[-2]) == abs(nums[-1])\n```\n\nif it\'s necessary, recover the values:\n```\nclass Solution(object):\n def validPartition(self, nums):\n nums[0] *= -1\n for i in range(len(nums) - 2):\n if nums[i] > -1: continue\n nums[i] *= -1\n \n if abs(nums[i]) == abs(nums[i + 1]): nums[i + 2] = -abs(nums[i + 2])\n\n if (abs(nums[i]) == abs(nums[i + 1]) == abs(nums[i + 2]) or \n abs(nums[i]) + 1 == abs(nums[i + 1]) == abs(nums[i + 2]) - 1):\n if i + 3 == len(nums): return True\n else: nums[i + 3] = -abs(nums[i + 3])\n \n res = nums[-2] < 0 and abs(nums[-2]) == abs(nums[-1])\n nums[-1], nums[-2] = abs(nums[-1]), abs(nums[-2])\n\n return res\n```\n\nYou could collect next steps, the number of which is limited:\n```\nclass Solution(object):\n def validPartition(self, nums):\n steps = {0}\n while steps:\n stepsNext = set()\n for i in steps:\n if i == len(nums): return True\n \n if (i + 1 < len(nums) and \n nums[i] == nums[i + 1] and \n (i + 2) not in steps): stepsNext.add(i + 2)\n \n if (i + 2 < len(nums) and \n (nums[i] == nums[i + 1] == nums[i + 2] or\n nums[i] + 1 == nums[i + 1] == nums[i + 2] - 1) and \n (i + 3) not in steps): stepsNext.add(i + 3)\n \n steps = stepsNext\n \n return False\n```\n\n---\n\nIf it\'s difficult to understand, you could start with this one:\n```\nclass Solution(object):\n def validPartition(self, nums):\n dp = [1] + [0] * len(nums)\n for i in range(len(nums) - 2):\n if not dp[i]: continue\n if nums[i] == nums[i + 1]: dp[i + 2] = 1\n if ((nums[i] == nums[i + 1] == nums[i + 2]) or\n (nums[i] + 1 == nums[i + 1] == nums[i + 2] - 1)): dp[i + 3] = 1\n \n return dp[-1] or (dp[-3] and nums[-1] == nums[-2])\n```\n\nAlso, you could check if there are any steps left:\n```\nclass Solution(object):\n def validPartition(self, nums):\n dp = [1] + [0] * len(nums)\n last = 0\n for i in range(len(nums) - 2):\n if i > last: return False\n if not dp[i]: continue\n if nums[i] == nums[i + 1]: dp[i + 2], last = 1, i + 2\n if ((nums[i] == nums[i + 1] == nums[i + 2]) or\n (nums[i] + 1 == nums[i + 1] == nums[i + 2] - 1)): dp[i + 3], last = 1, i + 3\n \n return dp[-1] or (dp[-3] and nums[-1] == nums[-2])\n```\n\n | 2 | You are given a **0-indexed** integer array `nums`. You have to partition the array into one or more **contiguous** subarrays.
We call a partition of the array **valid** if each of the obtained subarrays satisfies **one** of the following conditions:
1. The subarray consists of **exactly** `2` equal elements. For example, the subarray `[2,2]` is good.
2. The subarray consists of **exactly** `3` equal elements. For example, the subarray `[4,4,4]` is good.
3. The subarray consists of **exactly** `3` consecutive increasing elements, that is, the difference between adjacent elements is `1`. For example, the subarray `[3,4,5]` is good, but the subarray `[1,3,5]` is not.
Return `true` _if the array has **at least** one valid partition_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[4,4,4,5,6\]
**Output:** true
**Explanation:** The array can be partitioned into the subarrays \[4,4\] and \[4,5,6\].
This partition is valid, so we return true.
**Example 2:**
**Input:** nums = \[1,1,1,2\]
**Output:** false
**Explanation:** There is no valid partition for this array.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | How can we use precalculation to efficiently calculate the average difference at an index? Create a prefix and/or suffix sum array. |
Python3 Solution | check-if-there-is-a-valid-partition-for-the-array | 0 | 1 | \n```\nclass Solution:\n def validPartition(self, nums: List[int]) -> bool:\n n=len(nums)\n @cache\n def fn(index):\n if index==n:\n return True\n\n if index+1<n and nums[index]==nums[index+1] and fn(index+2):\n return True\n\n if index+2<n and nums[index]==nums[index+1]==nums[index+2] and fn(index+3):\n return True\n\n if index+2<n and nums[index]==nums[index+1]-1 and nums[index+1]==nums[index+2]-1 and fn(index+3):\n return True\n\n return False\n\n return fn(0) \n``` | 2 | You are given a **0-indexed** integer array `nums`. You have to partition the array into one or more **contiguous** subarrays.
We call a partition of the array **valid** if each of the obtained subarrays satisfies **one** of the following conditions:
1. The subarray consists of **exactly** `2` equal elements. For example, the subarray `[2,2]` is good.
2. The subarray consists of **exactly** `3` equal elements. For example, the subarray `[4,4,4]` is good.
3. The subarray consists of **exactly** `3` consecutive increasing elements, that is, the difference between adjacent elements is `1`. For example, the subarray `[3,4,5]` is good, but the subarray `[1,3,5]` is not.
Return `true` _if the array has **at least** one valid partition_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[4,4,4,5,6\]
**Output:** true
**Explanation:** The array can be partitioned into the subarrays \[4,4\] and \[4,5,6\].
This partition is valid, so we return true.
**Example 2:**
**Input:** nums = \[1,1,1,2\]
**Output:** false
**Explanation:** There is no valid partition for this array.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | How can we use precalculation to efficiently calculate the average difference at an index? Create a prefix and/or suffix sum array. |
Very Easy Code || Line by Line Explained || Memoization || C++ || java || Python | check-if-there-is-a-valid-partition-for-the-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExplore all the options and if any option returns true then answer is true.\n\nFor detailed explanation you can refer to my youtube channel (Hindi Language) \nhttps://youtu.be/lxpa98WWB-k\nor link in my profile.Here,you can find any solution in playlists monthwise from june 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. It initializes an array `dp` to store intermediate results.\n2. It defines a recursive function `solve` that takes an index `j` and the array `nums` as input and returns whether a valid partition can be formed starting from index `j`.\n3. The base case of the recursion is when `j` reaches the end of the array. In this case, it returns `1` indicating a valid partition.\n4. It checks if the result for the current index `j` is already computed and stored in the `dp` array. If yes, it returns the result directly.\n5. It checks for two conditions:\n - If the current element at index `j` is equal to the next element at index `j + 1`, it calls the `solve` function recursively for index `j + 2`.\n - If the current element at index `j` is equal to the next two elements at indices `j + 1` and `j + 2`, or if the elements form an incremental sequence (e.g., 1, 2, 3), it also calls the `solve` function recursively for index `j + 3`.\n6. It returns the result of the recursive calls and stores it in the `dp` array for memoization.\n7. The `validPartition` function initializes the `dp` array, then calls the `solve` function starting from index `0` of the input `nums` array.\n8. If the result of the `solve` function is `1`, it indicates a valid partition, so the function returns `true`. Otherwise, it returns `false`.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\nint dp[100005];\nint solve(int j,vector<int>&nums){\n if(j==nums.size()){\n return 1;\n }\n if(dp[j]!=-1)\n return dp[j];\n int c=0;\n if(j+1<nums.size()){\n if(nums[j]==nums[j+1])\n c=c|solve(j+2,nums);\n }\n if(j+2<nums.size()){\n if(nums[j]==nums[j+1]&&nums[j]==nums[j+2]){\n c=c|solve(j+3,nums);\n }\n if(nums[j]+1==nums[j+1]&&nums[j+1]+1==nums[j+2]){\n c=c|solve(j+3,nums);\n }\n }\n return dp[j]= c;\n}\n bool validPartition(vector<int>& nums) {\n memset(dp,-1,sizeof(dp));\n return solve(0,nums);\n }\n};\n```\n```java []\npublic class Solution {\n int[] dp = new int[100005];\n \n public int solve(int j, int[] nums) {\n if (j == nums.length) {\n return 1;\n }\n if (dp[j] != -1) {\n return dp[j];\n }\n int c = 0;\n if (j + 1 < nums.length) {\n if (nums[j] == nums[j + 1]) {\n c |= solve(j + 2, nums);\n }\n }\n if (j + 2 < nums.length) {\n if (nums[j] == nums[j + 1] && nums[j] == nums[j + 2]) {\n c |= solve(j + 3, nums);\n }\n if (nums[j] + 1 == nums[j + 1] && nums[j + 1] + 1 == nums[j + 2]) {\n c |= solve(j + 3, nums);\n }\n }\n return dp[j] = c;\n }\n \n public boolean validPartition(int[] nums) {\n Arrays.fill(dp, -1);\n return solve(0, nums) == 1;\n }\n}\n\n```\n```python []\nclass Solution:\n def __init__(self):\n self.dp = [-1] * 100005\n \n def solve(self, j, nums):\n if j == len(nums):\n return 1\n if self.dp[j] != -1:\n return self.dp[j]\n c = 0\n if j + 1 < len(nums):\n if nums[j] == nums[j + 1]:\n c |= self.solve(j + 2, nums)\n if j + 2 < len(nums):\n if nums[j] == nums[j + 1] and nums[j] == nums[j + 2]:\n c |= self.solve(j + 3, nums)\n if nums[j] + 1 == nums[j + 1] and nums[j + 1] + 1 == nums[j + 2]:\n c |= self.solve(j + 3, nums)\n self.dp[j] = c\n return c\n \n def validPartition(self, nums):\n self.dp = [-1] * 100005\n return self.solve(0, nums) == 1\n\n```\n# upvote if you understood the solution\n | 24 | You are given a **0-indexed** integer array `nums`. You have to partition the array into one or more **contiguous** subarrays.
We call a partition of the array **valid** if each of the obtained subarrays satisfies **one** of the following conditions:
1. The subarray consists of **exactly** `2` equal elements. For example, the subarray `[2,2]` is good.
2. The subarray consists of **exactly** `3` equal elements. For example, the subarray `[4,4,4]` is good.
3. The subarray consists of **exactly** `3` consecutive increasing elements, that is, the difference between adjacent elements is `1`. For example, the subarray `[3,4,5]` is good, but the subarray `[1,3,5]` is not.
Return `true` _if the array has **at least** one valid partition_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[4,4,4,5,6\]
**Output:** true
**Explanation:** The array can be partitioned into the subarrays \[4,4\] and \[4,5,6\].
This partition is valid, so we return true.
**Example 2:**
**Input:** nums = \[1,1,1,2\]
**Output:** false
**Explanation:** There is no valid partition for this array.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | How can we use precalculation to efficiently calculate the average difference at an index? Create a prefix and/or suffix sum array. |
Simple Recursion + Memoization solution Python 3 with comments! 😸 | check-if-there-is-a-valid-partition-for-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validPartition(self, nums):\n memo = {} #memoization to store the results of subproblems\n\n def solve(index):\n # Base case , return True when we reach end of the array\n if index == len(nums):\n return True\n\n valid_part = False # Initialize the result to False\n \n # if subproblem is already computed, return False\n if index in memo:\n return memo[index]\n \n # Check for a valid partition with exactly 2 equal elements\n if index < len(nums) - 1 and nums[index] == nums[index + 1]:\n valid_part = valid_part or solve(index + 2)\n \n # Check for a valid partition with exactly 3 equal elements\n if (\n index < len(nums) - 2\n and nums[index] == nums[index + 1] == nums[index + 2]\n ):\n valid_part = valid_part or solve(index + 3)\n \n # Check for a valid partition with 3 consecutive increasing elements\n if (\n index < len(nums) - 2\n and nums[index] + 1 == nums[index + 1]\n and nums[index + 1] + 1 == nums[index + 2]\n ):\n valid_part = valid_part or solve(index + 3)\n \n # Store the result in the memo\n memo[index] = valid_part\n return memo[index]\n return solve(0)\n\n``` | 1 | You are given a **0-indexed** integer array `nums`. You have to partition the array into one or more **contiguous** subarrays.
We call a partition of the array **valid** if each of the obtained subarrays satisfies **one** of the following conditions:
1. The subarray consists of **exactly** `2` equal elements. For example, the subarray `[2,2]` is good.
2. The subarray consists of **exactly** `3` equal elements. For example, the subarray `[4,4,4]` is good.
3. The subarray consists of **exactly** `3` consecutive increasing elements, that is, the difference between adjacent elements is `1`. For example, the subarray `[3,4,5]` is good, but the subarray `[1,3,5]` is not.
Return `true` _if the array has **at least** one valid partition_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[4,4,4,5,6\]
**Output:** true
**Explanation:** The array can be partitioned into the subarrays \[4,4\] and \[4,5,6\].
This partition is valid, so we return true.
**Example 2:**
**Input:** nums = \[1,1,1,2\]
**Output:** false
**Explanation:** There is no valid partition for this array.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | How can we use precalculation to efficiently calculate the average difference at an index? Create a prefix and/or suffix sum array. |
🔥 Beats 85% | Clean Code | DP + Memoization | ⚡️C++, Rust, Go, Java, Python, Javascript | check-if-there-is-a-valid-partition-for-the-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUltra Instinct \u26A1\uFE0F\n# Approach\n<!-- Describe your approach to solving the problem. -->\nExplore all possibilities and memoize explored! \uD83D\uDDFA\uFE0F\uD83C\uDF0D\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n bool chk(int i, int j, vector<int> &a) {\n if (j - i == 1) {\n return a[i] == a[j];\n }\n else {\n if (a[i] == a[i + 1] && a[i + 1] == a[i + 2]) return 1;\n return a[i + 1] - a[i] == 1 && a[i + 2] - a[i + 1] == 1;\n }\n return 0;\n }\n\n bool f(int i, vector<int> &a, vector<int> &dp) {\n if (i > a.size()) return 0;\n if (i == a.size()) return 1;\n\n if (dp[i] != -1) return dp[idx];\n bool two = 0, three = 0;\n if(i < a.size() - 1 && chk(i, i + 1, a)) two = f(i + 2, a, dp);\n if(i < a.size() - 2 && chk(i, i + 2, a)) three = f(i + 3, a, dp);\n\n return dp[i] = aa || b;\n }\n \n bool validPartition(vector<int>& nums) {\n vector<int> dp(nums.size(), -1);\n return f(0, nums, dp);\n }\n};\n```\n```Rust []\nimpl Solution {\n pub fn valid_partition(nums: Vec<i32>) -> bool {\n fn chk(i: usize, j: usize, a: &Vec<i32>) -> bool {\n if j - i == 1 { return a[i] == a[j]; } \n else {\n if a[i] == a[i + 1] && a[i + 1] == a[i + 2] { return true; }\n return a[i + 1] - a[i] == 1 && a[i + 2] - a[i + 1] == 1;\n }\n return false;\n }\n\n fn f(i: usize, a: &Vec<i32>, dp: &mut Vec<i32>) -> bool {\n if i > a.len() { return false; }\n if i == a.len() { return true; }\n\n if dp[i] != -1 { return dp[i] != 0; }\n\n let mut two = false;\n let mut three = false;\n if i < a.len() - 1 && chk(i, i + 1, a) { two = f(i + 2, a, dp); }\n if i < a.len() - 2 && chk(i, i + 2, a) { three = f(i + 3, a, dp); }\n\n dp[i] = (two || three) as i32;\n dp[i] != 0\n }\n\n let mut dp = vec![-1; nums.len()];\n f(0, &nums, &mut dp)\n }\n}\n\n```\n```Go []\nfunc validPartition(nums []int) bool {\n chk := func(i, j int, a []int) bool {\n if j-i == 1 {\n return a[i] == a[j]\n } else {\n if a[i] == a[i+1] && a[i+1] == a[i+2] {\n return true\n }\n return a[i+1]-a[i] == 1 && a[i+2]-a[i+1] == 1\n }\n }\n\n var f func(i int, a []int, dp []int) bool\n f = func(i int, a []int, dp []int) bool {\n if i > len(a) {\n return false\n }\n if i == len(a) {\n return true\n }\n\n if dp[i] != -1 {\n return dp[i] != 0\n }\n\n var two, three bool\n if i < len(a)-1 && chk(i, i+1, a) {\n two = f(i+2, a, dp)\n }\n if i < len(a)-2 && chk(i, i+2, a) {\n three = f(i+3, a, dp)\n }\n\n dp[i] = 0\n if two || three {\n dp[i] = 1\n }\n return dp[i] != 0\n }\n\n dp := make([]int, len(nums))\n for i := range dp {\n dp[i] = -1\n }\n\n return f(0, nums, dp)\n}\n\n```\n```Java []\nclass Solution {\n public boolean chk(int i, int j, int[] a) {\n if (j - i == 1) return a[i] == a[j];\n else {\n if (a[i] == a[i + 1] && a[i + 1] == a[i + 2]) return true;\n return a[i + 1] - a[i] == 1 && a[i + 2] - a[i + 1] == 1;\n }\n }\n\n public boolean f(int i, int[] a, int[] dp) {\n if (i > a.length) return false;\n if (i == a.length) return true;\n\n if (dp[i] != -1) return dp[i] == 1 ? true : false;\n\n boolean two = false, three = false;\n if (i < a.length - 1 && chk(i, i + 1, a)) two = f(i + 2, a, dp);\n if (i < a.length - 2 && chk(i, i + 2, a)) three = f(i + 3, a, dp);\n\n if (two || three) dp[i] = 1;\n else dp[i] = 0;\n\n return two || three;\n }\n \n public boolean validPartition(int[] nums) {\n int[] dp = new int[nums.length];\n Arrays.fill(dp, -1);\n return f(0, nums, dp);\n }\n}\n```\n```Python3 []\nclass Solution:\n def chk(self, i, j, a):\n if j - i == 1:return a[i] == a[j]\n\n else:\n if a[i] == a[i + 1] and a[i + 1] == a[i + 2]: return True\n return a[i + 1] - a[i] == 1 and a[i + 2] - a[i + 1] == 1\n\n return False\n \n def f(self, i, a, dp):\n if i > len(a): return False\n if i == len(a): return True\n \n if dp[i] != -1: return dp[i]\n \n two, three = False, False\n if i < len(a) - 1 and self.chk(i, i + 1, a): two = self.f(i + 2, a, dp)\n if i < len(a) - 2 and self.chk(i, i + 2, a): three = self.f(i + 3, a, dp)\n \n dp[i] = two or three\n return dp[i]\n \n def validPartition(self, nums: List[int]) -> bool:\n dp = [-1] * len(nums)\n return self.f(0, nums, dp)\n```\n```Javascript []\nconst validPartition = (nums) => {\n const chk = (i, j, a) => {\n if (j - i === 1) return a[i] === a[j];\n else {\n if (a[i] === a[i + 1] && a[i + 1] === a[i + 2]) return true;\n return a[i + 1] - a[i] === 1 && a[i + 2] - a[i + 1] === 1;\n }\n };\n\n const f = (i, a, dp) => {\n if (i > a.length) return false;\n if (i === a.length) return true;\n\n if (dp[i] !== -1) return dp[i];\n\n let two = false, three = false;\n if (i < a.length - 1 && chk(i, i + 1, a)) two = f(i + 2, a, dp);\n if (i < a.length - 2 && chk(i, i + 2, a)) three = f(i + 3, a, dp);\n\n return dp[i] = two || three;\n };\n\n const dp = new Array(nums.length).fill(-1);\n return f(0, nums, dp);\n};\n``` | 1 | You are given a **0-indexed** integer array `nums`. You have to partition the array into one or more **contiguous** subarrays.
We call a partition of the array **valid** if each of the obtained subarrays satisfies **one** of the following conditions:
1. The subarray consists of **exactly** `2` equal elements. For example, the subarray `[2,2]` is good.
2. The subarray consists of **exactly** `3` equal elements. For example, the subarray `[4,4,4]` is good.
3. The subarray consists of **exactly** `3` consecutive increasing elements, that is, the difference between adjacent elements is `1`. For example, the subarray `[3,4,5]` is good, but the subarray `[1,3,5]` is not.
Return `true` _if the array has **at least** one valid partition_. Otherwise, return `false`.
**Example 1:**
**Input:** nums = \[4,4,4,5,6\]
**Output:** true
**Explanation:** The array can be partitioned into the subarrays \[4,4\] and \[4,5,6\].
This partition is valid, so we return true.
**Example 2:**
**Input:** nums = \[1,1,1,2\]
**Output:** false
**Explanation:** There is no valid partition for this array.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | How can we use precalculation to efficiently calculate the average difference at an index? Create a prefix and/or suffix sum array. |
DP | longest-ideal-subsequence | 1 | 1 | For character `s[i]`, `dp[s[i]]` indicates the longest subsequence that ends at that character.\n \nFor character `s[i + 1]`, `dp[s[i + 1]] = 1 + max(dp[reachable])`, where `abs(s[i + 1] - reachable) <= k`.\n\n**Python 3**\n```python\nclass Solution:\n def longestIdealString(self, s: str, k: int) -> int:\n dp = [0] * 26\n for ch in s:\n i = ord(ch) - ord("a")\n dp[i] = 1 + max(dp[max(0, i - k) : min(26, i + k + 1)])\n return max(dp)\n```\n**C++**\n\'No raw loops\' version, just for fun.\n```cpp\nint longestIdealString(string s, int k) {\n int dp[26] = {};\n return k == 26 ? s.size() : accumulate(begin(s), end(s), 0, [&](int s, char ch){\n return max(s, dp[ch - \'a\'] = 1 + *max_element(\n begin(dp) + max(0, ch - \'a\' - k), begin(dp) + min(26, ch - \'a\' + k + 1)));\n });\n}\n```\n\n**Java**\n```java\npublic int longestIdealString(String s, int k) {\n int dp[] = new int[26];\n for (int i = 0; i < s.length(); ++i) {\n int a = s.charAt(i) - \'a\', mx = 0;\n for (int b = Math.max(0, a - k); b <= Math.min(25, a + k); ++b)\n mx = Math.max(mx, dp[b]);\n dp[a] = 1 + mx;\n }\n return Arrays.stream(dp).max().getAsInt();\n}\n```\n \n**Complexity Analysis**\n- Time: O(n); for each element, we check up to 26 characters.\n- Memory: O(1); we use a fixed-size `dp` array. | 35 | You are given a string `s` consisting of lowercase letters and an integer `k`. We call a string `t` **ideal** if the following conditions are satisfied:
* `t` is a **subsequence** of the string `s`.
* The absolute difference in the alphabet order of every two **adjacent** letters in `t` is less than or equal to `k`.
Return _the length of the **longest** ideal string_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
**Note** that the alphabet order is not cyclic. For example, the absolute difference in the alphabet order of `'a'` and `'z'` is `25`, not `1`.
**Example 1:**
**Input:** s = "acfgbd ", k = 2
**Output:** 4
**Explanation:** The longest ideal string is "acbd ". The length of this string is 4, so 4 is returned.
Note that "acfgbd " is not ideal because 'c' and 'f' have a difference of 3 in alphabet order.
**Example 2:**
**Input:** s = "abcd ", k = 3
**Output:** 4
**Explanation:** The longest ideal string is "abcd ". The length of this string is 4, so 4 is returned.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= k <= 25`
* `s` consists of lowercase English letters. | null |
[C++/Java/Python] Easy to understand | longest-ideal-subsequence | 1 | 1 | **Naive approach**: A brute force solution is to generate all the possible subsequences of various lengths and compute the maximum length of the valid subsequence. The time complexity will be exponential.\n\n**Efficient Approach**: An efficient approach is to use the concept **Dynamic Programming** \n\n* Create an array dp of 0\u2019s with size equal to length of string.\n* Create a supporting array max_length with 0\u2019s of size 26.\n* Iterate the string character by character and for each character determine the upper and lower bounds.\n* Iterate nested loop in the range of lower and upper bounds.\n* Fill the dp array with the maximum value between current dp indices and current max_length indices+1.\n* Fill the max_length array with the maximum value between current dp indices and current max_length indices.\n* Longest sub sequence length is the maximum value in dp array.\n\n**Let us consider an example:**\n\n\n**C++ program for the above approach**\n```\n#include <bits/stdc++.h>\nusing namespace std;\n\n// Function to find\n// the longest Special Sequence\nint longestIdealString(String s, int k)\n{\n\tint n = s.size();\n\t// Creating a list with\n\t// all 0\'s of size``\n\t// equal to the length of string\n\tvector<int> dp(n, 0);\n\n\t// Supporting list with\n\t// all 0\'s of size 26 since\n\t// the given string consists\n\t// of only lower case alphabets\n\tint max_length[26] = {0};\n\n\tfor (int i = 0; i < n; i++)\n\t{\n\n\t\t// Converting the ascii value to\n\t\t// list indices\n\t\tint curr = s[i] - \'a\';\n\n\t\t// Determining the lower bound\n\t\tint lower = max(0, curr - k);\n\n\t\t// Determining the upper bound\n\t\tint upper = min(25, curr + k);\n\n\t\t// Filling the dp array with values\n\t\tfor (int j = lower; j < upper + 1; j++)\n\t\t{\n\t\t\tdp[i] = max(dp[i], max_length[j] + 1);\n\t\t}\n\t\t//Filling the max_length array with max\n\t\t//length of subsequence till now\n\t\tmax_length[curr] = max(dp[i], max_length[curr]);\n\t}\n\n\tint ans = 0;\n\n\tfor(int i:dp) ans = max(i, ans);\n\n\t// return the max length of subsequence\n\treturn ans;\n}\n```\n\n**Java**\n```\npublic int longestIdealString(String s, int k) {\n\t\tint n = s.size();\n\t\t// Creating a list with\n\t\t// all 0\'s of size\n\t\t// equal to the length of String\n\t\tint []dp = new int[n];\n\n\t\t// Supporting list with\n\t\t// all 0\'s of size 26 since\n\t\t// the given String consists\n\t\t// of only lower case alphabets\n\t\tint []max_length = new int[26];\n\n\t\tfor (int i = 0; i < n; i++)\n\t\t{\n\n\t\t\t// Converting the ascii value to\n\t\t\t// list indices\n\t\t\tint curr = s.charAt(i) - \'a\';\n\n\t\t\t// Determining the lower bound\n\t\t\tint lower = Math.max(0, curr - k);\n\n\t\t\t// Determining the upper bound\n\t\t\tint upper = Math.min(25, curr + k);\n\n\t\t\t// Filling the dp array with values\n\t\t\tfor (int j = lower; j < upper + 1; j++)\n\t\t\t{\n\t\t\t\tdp[i] = Math.max(dp[i], max_length[j] + 1);\n\t\t\t}\n\n\t\t\t// Filling the max_length array with max\n\t\t\t// length of subsequence till now\n\t\t\tmax_length[curr] = Math.max(dp[i], max_length[curr]);\n\t\t}\n\n\t\tint ans = 0;\n\n\t\tfor(int i:dp) ans = Math.max(i, ans);\n\n\t\t// return the max length of subsequence\n\t\treturn ans;\n }\n```\n\n**Python3**\n```\n\tdef longestIdealString(self, s: str, k: int) -> int:\n\tn = len(s)\n\t# Creating a list with\n # all 0\'s of size\n # equal to the length of string\n dp = [0] * n\n \n # Supporting list with\n # all 0\'s of size 26 since\n # the given string consists\n # of only lower case alphabets\n max_length = [0] * 26\n \n for i in range(n):\n \n # Converting the ascii value to\n # list indices\n curr = ord(s[i]) - ord(\'a\')\n # Determining the lower bound\n lower = max(0, curr - k)\n # Determining the upper bound\n upper = min(25, curr + k)\n # Filling the dp array with values\n for j in range(lower, upper + 1):\n \n dp[i] = max(dp[i], max_length[j]+1)\n # Filling the max_length array with max\n # length of subsequence till now\n max_length[curr] = max(dp[i], max_length[curr])\n \n # return the max length of subsequence\n return max(dp)\n```\n\n\n\n\n | 9 | You are given a string `s` consisting of lowercase letters and an integer `k`. We call a string `t` **ideal** if the following conditions are satisfied:
* `t` is a **subsequence** of the string `s`.
* The absolute difference in the alphabet order of every two **adjacent** letters in `t` is less than or equal to `k`.
Return _the length of the **longest** ideal string_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
**Note** that the alphabet order is not cyclic. For example, the absolute difference in the alphabet order of `'a'` and `'z'` is `25`, not `1`.
**Example 1:**
**Input:** s = "acfgbd ", k = 2
**Output:** 4
**Explanation:** The longest ideal string is "acbd ". The length of this string is 4, so 4 is returned.
Note that "acfgbd " is not ideal because 'c' and 'f' have a difference of 3 in alphabet order.
**Example 2:**
**Input:** s = "abcd ", k = 3
**Output:** 4
**Explanation:** The longest ideal string is "abcd ". The length of this string is 4, so 4 is returned.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= k <= 25`
* `s` consists of lowercase English letters. | null |
Python 3. O(n) Solution - DP | longest-ideal-subsequence | 0 | 1 | ```\nclass Solution:\n def longestIdealString(self, s: str, k: int) -> int:\n \n # For storing the largest substring ending at that character \n psum=[0]*26\n ans=1\n for i in range(len(s)):\n element=ord(s[i])-97\n \n # Checking for k characters left to current element i.e. 2 characters left to c will be \'a\' and \'b\' \n \n j=element\n while j>-1 and j>=element-k:\n psum[element]=max(psum[element],psum[j]+1)\n j-=1\n \n # Checking for k characters right to current element i.e. 2 characters left to c will be \'d\' and \'e\' \n \n j=element+1\n while j<26 and j<=element+k:\n psum[element]=max(psum[element],psum[j]+1)\n j+=1\n \n ans=max(ans,psum[element])\n return ans\n | 1 | You are given a string `s` consisting of lowercase letters and an integer `k`. We call a string `t` **ideal** if the following conditions are satisfied:
* `t` is a **subsequence** of the string `s`.
* The absolute difference in the alphabet order of every two **adjacent** letters in `t` is less than or equal to `k`.
Return _the length of the **longest** ideal string_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
**Note** that the alphabet order is not cyclic. For example, the absolute difference in the alphabet order of `'a'` and `'z'` is `25`, not `1`.
**Example 1:**
**Input:** s = "acfgbd ", k = 2
**Output:** 4
**Explanation:** The longest ideal string is "acbd ". The length of this string is 4, so 4 is returned.
Note that "acfgbd " is not ideal because 'c' and 'f' have a difference of 3 in alphabet order.
**Example 2:**
**Input:** s = "abcd ", k = 3
**Output:** 4
**Explanation:** The longest ideal string is "abcd ". The length of this string is 4, so 4 is returned.
**Constraints:**
* `1 <= s.length <= 105`
* `0 <= k <= 25`
* `s` consists of lowercase English letters. | null |
[Python3] simulation | largest-local-values-in-a-matrix | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/abc9891d642b2454c148af46a140ff3497f7ce3c) for solutions of weekly 306. \n\n```\nclass Solution:\n def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:\n n = len(grid)\n ans = [[0]*(n-2) for _ in range(n-2)]\n for i in range(n-2): \n for j in range(n-2): \n ans[i][j] = max(grid[ii][jj] for ii in range(i, i+3) for jj in range(j, j+3))\n return ans \n``` | 25 | You are given an `n x n` integer matrix `grid`.
Generate an integer matrix `maxLocal` of size `(n - 2) x (n - 2)` such that:
* `maxLocal[i][j]` is equal to the **largest** value of the `3 x 3` matrix in `grid` centered around row `i + 1` and column `j + 1`.
In other words, we want to find the largest value in every contiguous `3 x 3` matrix in `grid`.
Return _the generated matrix_.
**Example 1:**
**Input:** grid = \[\[9,9,8,1\],\[5,6,2,6\],\[8,2,6,4\],\[6,2,2,2\]\]
**Output:** \[\[9,9\],\[8,6\]\]
**Explanation:** The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,1,1,1,1\],\[1,1,2,1,1\],\[1,1,1,1,1\],\[1,1,1,1,1\]\]
**Output:** \[\[2,2,2\],\[2,2,2\],\[2,2,2\]\]
**Explanation:** Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `1 <= grid[i][j] <= 100` | null |
🔥 [Python3] Short brute-force, using list comprehension | largest-local-values-in-a-matrix | 0 | 1 | ```python3 []\nclass Solution:\n def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:\n N = len(grid)-2\n res = [[0] * N for _ in range(N)]\n for i,j in product(range(N), range(N)):\n res[i][j] = max(grid[r][c] for r, c in product(range(i, i+3), range(j, j+3)))\n\n return res\n```\n```python3 []\nclass Solution:\n def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:\n N = len(grid)-2\n res = [[0] * N for _ in range(N)]\n for i in range(N):\n for j in range(N):\n res[i][j] = max([grid[r][c] for r in range(i, i+3) for c in range(j, j+3)])\n\n return res\n``` | 9 | You are given an `n x n` integer matrix `grid`.
Generate an integer matrix `maxLocal` of size `(n - 2) x (n - 2)` such that:
* `maxLocal[i][j]` is equal to the **largest** value of the `3 x 3` matrix in `grid` centered around row `i + 1` and column `j + 1`.
In other words, we want to find the largest value in every contiguous `3 x 3` matrix in `grid`.
Return _the generated matrix_.
**Example 1:**
**Input:** grid = \[\[9,9,8,1\],\[5,6,2,6\],\[8,2,6,4\],\[6,2,2,2\]\]
**Output:** \[\[9,9\],\[8,6\]\]
**Explanation:** The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,1,1,1,1\],\[1,1,2,1,1\],\[1,1,1,1,1\],\[1,1,1,1,1\]\]
**Output:** \[\[2,2,2\],\[2,2,2\],\[2,2,2\]\]
**Explanation:** Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `1 <= grid[i][j] <= 100` | null |
✅Python || Easy Approach || Brute force | largest-local-values-in-a-matrix | 0 | 1 | ```\nclass Solution:\n def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:\n\n n = len(grid)\n ans = []\n\n for i in range(n - 2):\n res = []\n\n for j in range(n - 2):\n k = []\n k.append(grid[i][j])\n k.append(grid[i][j + 1])\n k.append(grid[i][j + 2])\n k.append(grid[i + 1][j])\n k.append(grid[i + 1][j + 1])\n k.append(grid[i + 1][j + 2])\n k.append(grid[i + 2][j])\n k.append(grid[i + 2][j + 1])\n k.append(grid[i + 2][j + 2])\n m = max(k)\n res.append(m)\n\n ans.append(res)\n \n return ans\n``` | 16 | You are given an `n x n` integer matrix `grid`.
Generate an integer matrix `maxLocal` of size `(n - 2) x (n - 2)` such that:
* `maxLocal[i][j]` is equal to the **largest** value of the `3 x 3` matrix in `grid` centered around row `i + 1` and column `j + 1`.
In other words, we want to find the largest value in every contiguous `3 x 3` matrix in `grid`.
Return _the generated matrix_.
**Example 1:**
**Input:** grid = \[\[9,9,8,1\],\[5,6,2,6\],\[8,2,6,4\],\[6,2,2,2\]\]
**Output:** \[\[9,9\],\[8,6\]\]
**Explanation:** The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,1,1,1,1\],\[1,1,2,1,1\],\[1,1,1,1,1\],\[1,1,1,1,1\]\]
**Output:** \[\[2,2,2\],\[2,2,2\],\[2,2,2\]\]
**Explanation:** Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `1 <= grid[i][j] <= 100` | null |
Python Elegant & Short | 100% faster | largest-local-values-in-a-matrix | 0 | 1 | \n\n\n```\nclass Solution:\n\t"""\n\tTime: O(n^2)\n\tMemory: O(1)\n\t"""\n\n\tdef largestLocal(self, grid: List[List[int]]) -> List[List[int]]:\n\t\tn = len(grid)\n\t\treturn [[self.local_max(grid, r, c, 1) for c in range(1, n - 1)] for r in range(1, n - 1)]\n\n\t@staticmethod\n\tdef local_max(grid: List[List[int]], row: int, col: int, radius: int) -> int:\n\t\treturn max(\n\t\t\tgrid[r][c]\n\t\t\tfor r in range(row - radius, row + radius + 1)\n\t\t\tfor c in range(col - radius, col + radius + 1)\n\t\t)\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n\n | 7 | You are given an `n x n` integer matrix `grid`.
Generate an integer matrix `maxLocal` of size `(n - 2) x (n - 2)` such that:
* `maxLocal[i][j]` is equal to the **largest** value of the `3 x 3` matrix in `grid` centered around row `i + 1` and column `j + 1`.
In other words, we want to find the largest value in every contiguous `3 x 3` matrix in `grid`.
Return _the generated matrix_.
**Example 1:**
**Input:** grid = \[\[9,9,8,1\],\[5,6,2,6\],\[8,2,6,4\],\[6,2,2,2\]\]
**Output:** \[\[9,9\],\[8,6\]\]
**Explanation:** The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,1,1,1,1\],\[1,1,2,1,1\],\[1,1,1,1,1\],\[1,1,1,1,1\]\]
**Output:** \[\[2,2,2\],\[2,2,2\],\[2,2,2\]\]
**Explanation:** Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `1 <= grid[i][j] <= 100` | null |
✅ [Python] Two loop solution | largest-local-values-in-a-matrix | 0 | 1 | ```\nclass Solution:\n def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:\n n = len(grid)\n matrix = [[1]* (n-2) for i in range(n-2)]\n for i in range(1, n - 1):\n for j in range(1, n - 1):\n matrix[i-1][j-1] = max(grid[i-1][j-1], grid[i-1][j], grid[i-1][j+1],\n grid[i][j-1], grid[i][j], grid[i][j+1],\n grid[i+1][j-1], grid[i+1][j], grid[i+1][j+1])\n return matrix\n```\n | 8 | You are given an `n x n` integer matrix `grid`.
Generate an integer matrix `maxLocal` of size `(n - 2) x (n - 2)` such that:
* `maxLocal[i][j]` is equal to the **largest** value of the `3 x 3` matrix in `grid` centered around row `i + 1` and column `j + 1`.
In other words, we want to find the largest value in every contiguous `3 x 3` matrix in `grid`.
Return _the generated matrix_.
**Example 1:**
**Input:** grid = \[\[9,9,8,1\],\[5,6,2,6\],\[8,2,6,4\],\[6,2,2,2\]\]
**Output:** \[\[9,9\],\[8,6\]\]
**Explanation:** The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
**Example 2:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,1,1,1,1\],\[1,1,2,1,1\],\[1,1,1,1,1\],\[1,1,1,1,1\]\]
**Output:** \[\[2,2,2\],\[2,2,2\],\[2,2,2\]\]
**Explanation:** Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
**Constraints:**
* `n == grid.length == grid[i].length`
* `3 <= n <= 100`
* `1 <= grid[i][j] <= 100` | null |
SIMPLE PYTHON SOLUTION | node-with-highest-edge-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nArray Traversal\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def edgeScore(self, edges: List[int]) -> int:\n n=len(edges)\n sc=[0]*n\n mx=0\n ans=0\n for i in range(n):\n sc[edges[i]]+=i\n if sc[edges[i]]>mx:\n mx=sc[edges[i]]\n ans=edges[i]\n elif sc[edges[i]]==mx:\n if ans>edges[i]:\n ans=edges[i]\n return ans\n\n \n``` | 1 | You are given a directed graph with `n` nodes labeled from `0` to `n - 1`, where each node has **exactly one** outgoing edge.
The graph is represented by a given **0-indexed** integer array `edges` of length `n`, where `edges[i]` indicates that there is a **directed** edge from node `i` to node `edges[i]`.
The **edge score** of a node `i` is defined as the sum of the **labels** of all the nodes that have an edge pointing to `i`.
Return _the node with the highest **edge score**_. If multiple nodes have the same **edge score**, return the node with the **smallest** index.
**Example 1:**
**Input:** edges = \[1,0,0,0,0,7,7,5\]
**Output:** 7
**Explanation:**
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.
**Example 2:**
**Input:** edges = \[2,0,0,2\]
**Output:** 0
**Explanation:**
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.
**Constraints:**
* `n == edges.length`
* `2 <= n <= 105`
* `0 <= edges[i] < n`
* `edges[i] != i` | null |
[Java/Python 3] Iterative O(n) codes w/ brief explanation and analysis. | node-with-highest-edge-score | 1 | 1 | 1. Traverse the input `edges`, acculumate the score for each edge-pointed node;\n2. Traverse the `scores` array and find the solution.\n\n**Note:** Java code need a `long` type `scores` array, otherwise it would cause `int` overflow that will result wrong answer.\n```java\n public int edgeScore(int[] edges) {\n int n = edges.length, ans = 0;\n long[] scores = new long[n];\n for (int src = 0; src < n; ++src) {\n scores[edges[src]] += src;\n }\n for (int i = 0; i < n; ++i) {\n if (scores[i] > scores[ans]) {\n ans = i;\n }\n }\n return ans;\n }\n```\n```python\n def edgeScore(self, edges: List[int]) -> int:\n n, ans = len(edges), 0\n scores = [0] * n\n for src, tgt in enumerate(edges):\n scores[tgt] += src\n for i, score in enumerate(scores):\n if score > scores[ans]:\n ans = i\n return ans\n```\n\n**Analysis:**\n\nTime & space: `O(n)`, where `n = edges.length`. | 8 | You are given a directed graph with `n` nodes labeled from `0` to `n - 1`, where each node has **exactly one** outgoing edge.
The graph is represented by a given **0-indexed** integer array `edges` of length `n`, where `edges[i]` indicates that there is a **directed** edge from node `i` to node `edges[i]`.
The **edge score** of a node `i` is defined as the sum of the **labels** of all the nodes that have an edge pointing to `i`.
Return _the node with the highest **edge score**_. If multiple nodes have the same **edge score**, return the node with the **smallest** index.
**Example 1:**
**Input:** edges = \[1,0,0,0,0,7,7,5\]
**Output:** 7
**Explanation:**
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.
**Example 2:**
**Input:** edges = \[2,0,0,2\]
**Output:** 0
**Explanation:**
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.
**Constraints:**
* `n == edges.length`
* `2 <= n <= 105`
* `0 <= edges[i] < n`
* `edges[i] != i` | null |
✅Python || Easy Approach || Hashmap | node-with-highest-edge-score | 0 | 1 | ```\nclass Solution:\n def edgeScore(self, edges: List[int]) -> int:\n\n n = len(edges)\n cnt = defaultdict(int)\n ans = 0\n \n\t\t// we have the key stores the node edges[i], and the value indicates the edge score.\n for i in range(n):\n cnt[edges[i]] += i\n\n m = max(cnt.values())\n\n\t\t// In the second iteration, i is also the index of the node. So the first one meets == m, is the smallest index.\n for i in range(n):\n if cnt[i] == m:\n ans = i\n break\n \n return ans\n \n``` | 4 | You are given a directed graph with `n` nodes labeled from `0` to `n - 1`, where each node has **exactly one** outgoing edge.
The graph is represented by a given **0-indexed** integer array `edges` of length `n`, where `edges[i]` indicates that there is a **directed** edge from node `i` to node `edges[i]`.
The **edge score** of a node `i` is defined as the sum of the **labels** of all the nodes that have an edge pointing to `i`.
Return _the node with the highest **edge score**_. If multiple nodes have the same **edge score**, return the node with the **smallest** index.
**Example 1:**
**Input:** edges = \[1,0,0,0,0,7,7,5\]
**Output:** 7
**Explanation:**
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.
**Example 2:**
**Input:** edges = \[2,0,0,2\]
**Output:** 0
**Explanation:**
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.
**Constraints:**
* `n == edges.length`
* `2 <= n <= 105`
* `0 <= edges[i] < n`
* `edges[i] != i` | null |
Python | Simple counting | node-with-highest-edge-score | 0 | 1 | ```\nclass Solution:\n def edgeScore(self, edges: List[int]) -> int:\n n = len(edges)\n score = [0] * n\n \n for i, val in enumerate(edges):\n score[val] += i\n return score.index(max(score))\n``` | 2 | You are given a directed graph with `n` nodes labeled from `0` to `n - 1`, where each node has **exactly one** outgoing edge.
The graph is represented by a given **0-indexed** integer array `edges` of length `n`, where `edges[i]` indicates that there is a **directed** edge from node `i` to node `edges[i]`.
The **edge score** of a node `i` is defined as the sum of the **labels** of all the nodes that have an edge pointing to `i`.
Return _the node with the highest **edge score**_. If multiple nodes have the same **edge score**, return the node with the **smallest** index.
**Example 1:**
**Input:** edges = \[1,0,0,0,0,7,7,5\]
**Output:** 7
**Explanation:**
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.
**Example 2:**
**Input:** edges = \[2,0,0,2\]
**Output:** 0
**Explanation:**
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.
**Constraints:**
* `n == edges.length`
* `2 <= n <= 105`
* `0 <= edges[i] < n`
* `edges[i] != i` | null |
Short and intuitive solution NO stack, just count and string. | construct-smallest-number-from-di-string | 0 | 1 | Observations:\n1. Maximum digit in the output is the len of the pattern + 1. E.g. if pattern is "D\' or "I" the max digit will be 2 (2**1** or 1**2**). For DD or II we\'ll have max digit 3 and etc.\n2. We can use counter as a pattern and reverse it each time we find \'I\'. E.g. If we have pattern "DDD I DDD I" the counter "123 4 567 8" Reversed will be "4321 8765"\n3. We add \'I\' in the end of the pattern to make last reverse work and to make enumerate up to the required number\n\n\n\n\n# Code\n```\nclass Solution:\n def smallestNumber(self, pattern: str) -> str:\n pattern += \'I\'\n res = s = \'\'\n for i,p in enumerate(pattern):\n s += str(i+1)\n if p == \'I\':\n res += s[::-1]\n s =\'\'\n return res\n``` | 1 | You are given a **0-indexed** string `pattern` of length `n` consisting of the characters `'I'` meaning **increasing** and `'D'` meaning **decreasing**.
A **0-indexed** string `num` of length `n + 1` is created using the following conditions:
* `num` consists of the digits `'1'` to `'9'`, where each digit is used **at most** once.
* If `pattern[i] == 'I'`, then `num[i] < num[i + 1]`.
* If `pattern[i] == 'D'`, then `num[i] > num[i + 1]`.
Return _the lexicographically **smallest** possible string_ `num` _that meets the conditions._
**Example 1:**
**Input:** pattern = "IIIDIDDD "
**Output:** "123549876 "
**Explanation:**
At indices 0, 1, 2, and 4 we must have that num\[i\] < num\[i+1\].
At indices 3, 5, 6, and 7 we must have that num\[i\] > num\[i+1\].
Some possible values of num are "245639871 ", "135749862 ", and "123849765 ".
It can be proven that "123549876 " is the smallest possible num that meets the conditions.
Note that "123414321 " is not possible because the digit '1' is used more than once.
**Example 2:**
**Input:** pattern = "DDD "
**Output:** "4321 "
**Explanation:**
Some possible values of num are "9876 ", "7321 ", and "8742 ".
It can be proven that "4321 " is the smallest possible num that meets the conditions.
**Constraints:**
* `1 <= pattern.length <= 8`
* `pattern` consists of only the letters `'I'` and `'D'`. | null |
[Python3] greedy | construct-smallest-number-from-di-string | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/abc9891d642b2454c148af46a140ff3497f7ce3c) for solutions of weekly 306. \n\n```\nclass Solution:\n def smallestNumber(self, pattern: str) -> str:\n ans = [1]\n for ch in pattern: \n if ch == \'I\': \n m = ans[-1]+1\n while m in ans: m += 1\n ans.append(m)\n else: \n ans.append(ans[-1])\n for i in range(len(ans)-1, 0, -1): \n if ans[i-1] == ans[i]: ans[i-1] += 1\n return \'\'.join(map(str, ans))\n```\n\nFollowing @lee215\'s solution\n```\nclass Solution:\n def smallestNumber(self, pattern: str) -> str:\n ans = []\n stack = []\n for i in range(len(pattern)+1): \n stack.append(str(i+1))\n if i == len(pattern) or pattern[i] == \'I\': \n while stack: ans.append(stack.pop())\n return \'\'.join(ans) \n``` | 29 | You are given a **0-indexed** string `pattern` of length `n` consisting of the characters `'I'` meaning **increasing** and `'D'` meaning **decreasing**.
A **0-indexed** string `num` of length `n + 1` is created using the following conditions:
* `num` consists of the digits `'1'` to `'9'`, where each digit is used **at most** once.
* If `pattern[i] == 'I'`, then `num[i] < num[i + 1]`.
* If `pattern[i] == 'D'`, then `num[i] > num[i + 1]`.
Return _the lexicographically **smallest** possible string_ `num` _that meets the conditions._
**Example 1:**
**Input:** pattern = "IIIDIDDD "
**Output:** "123549876 "
**Explanation:**
At indices 0, 1, 2, and 4 we must have that num\[i\] < num\[i+1\].
At indices 3, 5, 6, and 7 we must have that num\[i\] > num\[i+1\].
Some possible values of num are "245639871 ", "135749862 ", and "123849765 ".
It can be proven that "123549876 " is the smallest possible num that meets the conditions.
Note that "123414321 " is not possible because the digit '1' is used more than once.
**Example 2:**
**Input:** pattern = "DDD "
**Output:** "4321 "
**Explanation:**
Some possible values of num are "9876 ", "7321 ", and "8742 ".
It can be proven that "4321 " is the smallest possible num that meets the conditions.
**Constraints:**
* `1 <= pattern.length <= 8`
* `pattern` consists of only the letters `'I'` and `'D'`. | null |
[Python] easy to understand greedy solution. | construct-smallest-number-from-di-string | 0 | 1 | This solution works by increasing the previous "I" by the total number of succeeding "D"s then decrementing 1 for every D. And then repeating the same process untill the loop ends. and check one last time out of the loop.\n```\nclass Solution:\n def smallestNumber(self, pattern: str) -> str:\n ans = []\n dec_count = 0\n for i in range(len(pattern)):\n if pattern[i] == "I":\n for j in range(i, i-dec_count-1,-1):\n ans.append(str(j+1))\n dec_count = 0\n elif pattern[i] == "D":\n dec_count += 1\n \n # for the remaining dec_count if there is any\n for j in range(len(pattern), len(pattern)-dec_count-1,-1):\n ans.append(str(j+1))\n return "".join(ans)\n``` | 5 | You are given a **0-indexed** string `pattern` of length `n` consisting of the characters `'I'` meaning **increasing** and `'D'` meaning **decreasing**.
A **0-indexed** string `num` of length `n + 1` is created using the following conditions:
* `num` consists of the digits `'1'` to `'9'`, where each digit is used **at most** once.
* If `pattern[i] == 'I'`, then `num[i] < num[i + 1]`.
* If `pattern[i] == 'D'`, then `num[i] > num[i + 1]`.
Return _the lexicographically **smallest** possible string_ `num` _that meets the conditions._
**Example 1:**
**Input:** pattern = "IIIDIDDD "
**Output:** "123549876 "
**Explanation:**
At indices 0, 1, 2, and 4 we must have that num\[i\] < num\[i+1\].
At indices 3, 5, 6, and 7 we must have that num\[i\] > num\[i+1\].
Some possible values of num are "245639871 ", "135749862 ", and "123849765 ".
It can be proven that "123549876 " is the smallest possible num that meets the conditions.
Note that "123414321 " is not possible because the digit '1' is used more than once.
**Example 2:**
**Input:** pattern = "DDD "
**Output:** "4321 "
**Explanation:**
Some possible values of num are "9876 ", "7321 ", and "8742 ".
It can be proven that "4321 " is the smallest possible num that meets the conditions.
**Constraints:**
* `1 <= pattern.length <= 8`
* `pattern` consists of only the letters `'I'` and `'D'`. | null |
Simple solution with using Stack DS | construct-smallest-number-from-di-string | 0 | 1 | # Intuition\nNote that problem can be solved by using `greedy`, `backtrack` or `stack` algorithm.\nFor this solution let me explain step-by-step `stack` - solution.\n\n\n---\n\nIf you haven\'t already familiar with [Stack DS](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)), than I **highly** recommend to know a little more! \n\n---\n\nThe problem explanation is quite simple as \n```\n# 0. the goal is to generate the smallest lexicographically \n# string with n-length, where 2 <= n <= 9 \n\n# 1. the initial string represents as \n# a sequence of \'I\'-s and \'D\'-s like \'IIDD\'\n\n# 2. the schema of placing number is \n# for I == num[i] > num[i - 1]\n# for D == num[i] < num[i + 1]\n\n```\nAt each step we need to **somehow** store the `i` **optimally** according to the schema above.\n\n```\n# Pseudocode\ns = \'IIDD\'\nstack = []\n\nfor i in range lengthof(s):\n add to stack s[index]\n\n if char == \'I\' or index == lengthof(s):\n while stack:\n pop from stack and add it to the output\n```\n\n\n# Approach\n1. initialize an empty `stack` and `ans` for storing numbers\n2. iterate over all chars in `pattern` - string\n3. add the current index `char + 1` to stack\n4. any time we\'re out of a string or the `pattern[i] == \'I\'`, pop all the chars from the `stack`\n5. return the `ans` variable\n\n# Complexity\n- Time complexity: **O(n)**, because of iterating over all chars in `pattern`\n\n- Space complexity: **O(n)**, because of storing elements in `stack` and inside `ans`.\n\n# Code\n```\nclass Solution:\n def smallestNumber(self, pattern: str) -> str:\n stack = []\n ans = []\n\n for i in range(len(pattern) + 1):\n stack.append(i + 1)\n\n if i == len(pattern) or pattern[i] == \'I\':\n while stack:\n ans.append(str(stack.pop()))\n\n return \'\'.join(ans)\n``` | 2 | You are given a **0-indexed** string `pattern` of length `n` consisting of the characters `'I'` meaning **increasing** and `'D'` meaning **decreasing**.
A **0-indexed** string `num` of length `n + 1` is created using the following conditions:
* `num` consists of the digits `'1'` to `'9'`, where each digit is used **at most** once.
* If `pattern[i] == 'I'`, then `num[i] < num[i + 1]`.
* If `pattern[i] == 'D'`, then `num[i] > num[i + 1]`.
Return _the lexicographically **smallest** possible string_ `num` _that meets the conditions._
**Example 1:**
**Input:** pattern = "IIIDIDDD "
**Output:** "123549876 "
**Explanation:**
At indices 0, 1, 2, and 4 we must have that num\[i\] < num\[i+1\].
At indices 3, 5, 6, and 7 we must have that num\[i\] > num\[i+1\].
Some possible values of num are "245639871 ", "135749862 ", and "123849765 ".
It can be proven that "123549876 " is the smallest possible num that meets the conditions.
Note that "123414321 " is not possible because the digit '1' is used more than once.
**Example 2:**
**Input:** pattern = "DDD "
**Output:** "4321 "
**Explanation:**
Some possible values of num are "9876 ", "7321 ", and "8742 ".
It can be proven that "4321 " is the smallest possible num that meets the conditions.
**Constraints:**
* `1 <= pattern.length <= 8`
* `pattern` consists of only the letters `'I'` and `'D'`. | null |
[Python3] dp | count-special-integers | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/abc9891d642b2454c148af46a140ff3497f7ce3c) for solutions of weekly 306. \n\n```\nclass Solution:\n def countSpecialNumbers(self, n: int) -> int:\n vals = list(map(int, str(n)))\n \n @cache\n def fn(i, m, on): \n """Return count at index i with mask m and profile flag (True/False)"""\n ans = 0 \n if i == len(vals): return 1\n for v in range(vals[i] if on else 10 ): \n if m & 1<<v == 0: \n if m or v: ans += fn(i+1, m ^ 1<<v, False)\n else: ans += fn(i+1, m, False)\n if on and m & 1<<vals[i] == 0: ans += fn(i+1, m ^ 1<<vals[i], True)\n return ans \n \n return fn(0, 0, True)-1\n``` | 5 | We call a positive integer **special** if all of its digits are **distinct**.
Given a **positive** integer `n`, return _the number of special integers that belong to the interval_ `[1, n]`.
**Example 1:**
**Input:** n = 20
**Output:** 19
**Explanation:** All the integers from 1 to 20, except 11, are special. Thus, there are 19 special integers.
**Example 2:**
**Input:** n = 5
**Output:** 5
**Explanation:** All the integers from 1 to 5 are special.
**Example 3:**
**Input:** n = 135
**Output:** 110
**Explanation:** There are 110 integers from 1 to 135 that are special.
Some of the integers that are not special are: 22, 114, and 131.
**Constraints:**
* `1 <= n <= 2 * 109` | null |
Python (Simple Digit DP) | count-special-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSpecialNumbers(self, n):\n ans = [int(i) for i in str(n)]\n n = len(ans)\n\n @lru_cache(None)\n def dp(pos,tight,mask):\n if pos == n:\n return 1\n\n total = 0\n\n upperlimit = ans[pos] if tight else 9\n\n for d in range(upperlimit+1):\n if mask&(1<<d):\n continue\n\n new_tight = tight and d == upperlimit\n new_mask = mask if mask == 0 and d == 0 else mask|(1<<d)\n\n total += dp(pos+1,new_tight,new_mask)\n\n return total\n\n return dp(0,True,0) - 1\n\n\n\n\n\n\n\n\n \n\n\n\n\n\n\n \n\n\n\n \n\n\n``` | 1 | We call a positive integer **special** if all of its digits are **distinct**.
Given a **positive** integer `n`, return _the number of special integers that belong to the interval_ `[1, n]`.
**Example 1:**
**Input:** n = 20
**Output:** 19
**Explanation:** All the integers from 1 to 20, except 11, are special. Thus, there are 19 special integers.
**Example 2:**
**Input:** n = 5
**Output:** 5
**Explanation:** All the integers from 1 to 5 are special.
**Example 3:**
**Input:** n = 135
**Output:** 110
**Explanation:** There are 110 integers from 1 to 135 that are special.
Some of the integers that are not special are: 22, 114, and 131.
**Constraints:**
* `1 <= n <= 2 * 109` | null |
[Java/Python 3] Sliding Window T O(n) S O(1), w/ brief explanation and analysis. | minimum-recolors-to-get-k-consecutive-black-blocks | 1 | 1 | Maintain a sliding window of size `k`, keep updating the count of `W` out of it and find the minimum.\n\nNote: `lo` and `hi` are the lower and upper bounds of the sliding window, exclusive and inclusive respectively.\n```java\n public int minimumRecolors(String blocks, int k) {\n int min = Integer.MAX_VALUE;\n for (int lo = -1, hi = 0, white = 0; hi < blocks.length(); ++hi) {\n white += blocks.charAt(hi) == \'W\' ? 1 : 0;\n if (hi - lo >= k) { // the window reaches size of k.\n min = Math.min(min, white); // update minimum.\n // slide 1 step right the lower bound of the sliding\n // window and update the value of white count.\n white -= blocks.charAt(++lo) == \'W\' ? 1 : 0;\n }\n }\n return min;\n }\n```\n```python\n def minimumRecolors(self, blocks: str, k: int) -> int:\n lo, white, mi = -1, 0, inf\n for hi, c in enumerate(blocks):\n if c == \'W\':\n white += 1\n if hi - lo >= k:\n mi = min(white, mi)\n lo += 1\n white -= blocks[lo] == \'W\' \n return mi\n```\nTime `O(k * n)` Python 3 code: - credit to **@chuhonghao01**\n```python\n def minimumRecolors(self, blocks: str, k: int) -> int:\n n, mi = len(blocks), inf\n for i in range(n - k + 1):\n white = blocks.count(\'W\', i, i + k)\n mi = min(white, mi)\n return mi\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`, where `n = blocks.length()`.\n\n----\n\nSimilar Problems: - Credit to **@haihoangdang91**.\n\n1151. Minimum Swaps to Group All 1\'s Together\n2134. Minimum Swaps to Group All 1\'s Together II\n | 25 | You are given a **0-indexed** string `blocks` of length `n`, where `blocks[i]` is either `'W'` or `'B'`, representing the color of the `ith` block. The characters `'W'` and `'B'` denote the colors white and black, respectively.
You are also given an integer `k`, which is the desired number of **consecutive** black blocks.
In one operation, you can **recolor** a white block such that it becomes a black block.
Return _the **minimum** number of operations needed such that there is at least **one** occurrence of_ `k` _consecutive black blocks._
**Example 1:**
**Input:** blocks = "WBBWWBBWBW ", k = 7
**Output:** 3
**Explanation:**
One way to achieve 7 consecutive black blocks is to recolor the 0th, 3rd, and 4th blocks
so that blocks = "BBBBBBBWBW ".
It can be shown that there is no way to achieve 7 consecutive black blocks in less than 3 operations.
Therefore, we return 3.
**Example 2:**
**Input:** blocks = "WBWBBBW ", k = 2
**Output:** 0
**Explanation:**
No changes need to be made, since 2 consecutive black blocks already exist.
Therefore, we return 0.
**Constraints:**
* `n == blocks.length`
* `1 <= n <= 100`
* `blocks[i]` is either `'W'` or `'B'`.
* `1 <= k <= n` | null |
Python Simple Solution | minimum-recolors-to-get-k-consecutive-black-blocks | 0 | 1 | # Intuition\nThink of slicing the string.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nReplace all \'W\' with \'B\' and append the count of \'W\' before replacing.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumRecolors(self, b: str, k: int) -> int:\n i = 0\n l = []\n while i < len(b):\n s = b[i:i + k]\n if len(s) == k:\n l.append(s.count(\'W\'))\n i += 1\n return min(l)\n``` | 1 | You are given a **0-indexed** string `blocks` of length `n`, where `blocks[i]` is either `'W'` or `'B'`, representing the color of the `ith` block. The characters `'W'` and `'B'` denote the colors white and black, respectively.
You are also given an integer `k`, which is the desired number of **consecutive** black blocks.
In one operation, you can **recolor** a white block such that it becomes a black block.
Return _the **minimum** number of operations needed such that there is at least **one** occurrence of_ `k` _consecutive black blocks._
**Example 1:**
**Input:** blocks = "WBBWWBBWBW ", k = 7
**Output:** 3
**Explanation:**
One way to achieve 7 consecutive black blocks is to recolor the 0th, 3rd, and 4th blocks
so that blocks = "BBBBBBBWBW ".
It can be shown that there is no way to achieve 7 consecutive black blocks in less than 3 operations.
Therefore, we return 3.
**Example 2:**
**Input:** blocks = "WBWBBBW ", k = 2
**Output:** 0
**Explanation:**
No changes need to be made, since 2 consecutive black blocks already exist.
Therefore, we return 0.
**Constraints:**
* `n == blocks.length`
* `1 <= n <= 100`
* `blocks[i]` is either `'W'` or `'B'`.
* `1 <= k <= n` | null |
[Python3] O(N) dp approach | time-needed-to-rearrange-a-binary-string | 0 | 1 | Please pull this git [commit](https://github.com/gaosanyong/leetcode/commit/e999ea07dc2ea2e8b7aad97696f67a3b965e496d) for solutions of biweekly 85. \n\n**Intuition**\nGiven the size of the problem, it is okay to run a simulation which takes `O(N^2)` to complete. However, a faster `O(N)` DP approach is available. \nHere, we consider the task as "moving 1s to the left". Two key observatoins are \n1) to move \'1\' at `i`th index it takes at least x steps if there are x \'0\'s preceeding it. \n2) if there is a \'1\' at \'i-1\'st index, it takes at least one more step to move this \'1\' to proper position. \n\n**Analysis**\nTime complexity `O(N)`\nSpace complexity `O(1)`\n```\nclass Solution: \n def secondsToRemoveOccurrences(self, s: str) -> int:\n ans = prefix = prev = 0 \n for i, ch in enumerate(s): \n if ch == \'1\': \n ans = max(prev, i - prefix)\n prefix += 1\n if ans: prev = ans+1\n return ans \n``` | 53 | You are given a binary string `s`. In one second, **all** occurrences of `"01 "` are **simultaneously** replaced with `"10 "`. This process **repeats** until no occurrences of `"01 "` exist.
Return _the number of seconds needed to complete this process._
**Example 1:**
**Input:** s = "0110101 "
**Output:** 4
**Explanation:**
After one second, s becomes "1011010 ".
After another second, s becomes "1101100 ".
After the third second, s becomes "1110100 ".
After the fourth second, s becomes "1111000 ".
No occurrence of "01 " exists any longer, and the process needed 4 seconds to complete,
so we return 4.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:**
No occurrence of "01 " exists in s, and the processes needed 0 seconds to complete,
so we return 0.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
**Follow up:**
Can you solve this problem in O(n) time complexity? | null |
✅Python || Easy Approach || Replace (5 lines) | time-needed-to-rearrange-a-binary-string | 0 | 1 | ```\nclass Solution:\n def secondsToRemoveOccurrences(self, s: str) -> int:\n\n ans = 0\n\n while \'01\' in s:\n ans += 1\n s = s.replace(\'01\', \'10\')\n \n return ans\n``` | 14 | You are given a binary string `s`. In one second, **all** occurrences of `"01 "` are **simultaneously** replaced with `"10 "`. This process **repeats** until no occurrences of `"01 "` exist.
Return _the number of seconds needed to complete this process._
**Example 1:**
**Input:** s = "0110101 "
**Output:** 4
**Explanation:**
After one second, s becomes "1011010 ".
After another second, s becomes "1101100 ".
After the third second, s becomes "1110100 ".
After the fourth second, s becomes "1111000 ".
No occurrence of "01 " exists any longer, and the process needed 4 seconds to complete,
so we return 4.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:**
No occurrence of "01 " exists in s, and the processes needed 0 seconds to complete,
so we return 0.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
**Follow up:**
Can you solve this problem in O(n) time complexity? | null |
Runtime 35ms, Memory 13.8mb Python Solution | time-needed-to-rearrange-a-binary-string | 0 | 1 | # Approach\n- The last "1" will take the longest time to travel to its destination in the string, which is the number of "0"s infront. \n- The special case is when "1" is right next to another "1", which will add one more step for the second 1 to move to the right.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def secondsToRemoveOccurrences(self, s: str) -> int:\n n = len(s)\n count, res = 0, 0\n\n for i in range(n):\n if (s[i] == \'0\'):\n count += 1\n else:\n if count > 0:\n res = max(res+1, count)\n\n return res\n``` | 1 | You are given a binary string `s`. In one second, **all** occurrences of `"01 "` are **simultaneously** replaced with `"10 "`. This process **repeats** until no occurrences of `"01 "` exist.
Return _the number of seconds needed to complete this process._
**Example 1:**
**Input:** s = "0110101 "
**Output:** 4
**Explanation:**
After one second, s becomes "1011010 ".
After another second, s becomes "1101100 ".
After the third second, s becomes "1110100 ".
After the fourth second, s becomes "1111000 ".
No occurrence of "01 " exists any longer, and the process needed 4 seconds to complete,
so we return 4.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:**
No occurrence of "01 " exists in s, and the processes needed 0 seconds to complete,
so we return 0.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
**Follow up:**
Can you solve this problem in O(n) time complexity? | null |
Python3 easy with string replace | time-needed-to-rearrange-a-binary-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def secondsToRemoveOccurrences(self, s: str) -> int:\n count = 0\n while "01" in s:\n s = s.replace("01", "10")\n count += 1\n return count\n\n \n``` | 1 | You are given a binary string `s`. In one second, **all** occurrences of `"01 "` are **simultaneously** replaced with `"10 "`. This process **repeats** until no occurrences of `"01 "` exist.
Return _the number of seconds needed to complete this process._
**Example 1:**
**Input:** s = "0110101 "
**Output:** 4
**Explanation:**
After one second, s becomes "1011010 ".
After another second, s becomes "1101100 ".
After the third second, s becomes "1110100 ".
After the fourth second, s becomes "1111000 ".
No occurrence of "01 " exists any longer, and the process needed 4 seconds to complete,
so we return 4.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:**
No occurrence of "01 " exists in s, and the processes needed 0 seconds to complete,
so we return 0.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
**Follow up:**
Can you solve this problem in O(n) time complexity? | null |
PYTHON | Beginner | Easy | 81% faster | time-needed-to-rearrange-a-binary-string | 0 | 1 | **Please upvode if it helps...**\n```\nclass Solution:\n def secondsToRemoveOccurrences(self, s: str) -> int:\n c=0\n for i in range(len(s)):\n if "01" in s:\n s=s.replace("01","10")\n c+=1\n return(c)\n\t\t``` | 1 | You are given a binary string `s`. In one second, **all** occurrences of `"01 "` are **simultaneously** replaced with `"10 "`. This process **repeats** until no occurrences of `"01 "` exist.
Return _the number of seconds needed to complete this process._
**Example 1:**
**Input:** s = "0110101 "
**Output:** 4
**Explanation:**
After one second, s becomes "1011010 ".
After another second, s becomes "1101100 ".
After the third second, s becomes "1110100 ".
After the fourth second, s becomes "1111000 ".
No occurrence of "01 " exists any longer, and the process needed 4 seconds to complete,
so we return 4.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:**
No occurrence of "01 " exists in s, and the processes needed 0 seconds to complete,
so we return 0.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
**Follow up:**
Can you solve this problem in O(n) time complexity? | null |
Python brute force step by step solution & small solution | time-needed-to-rearrange-a-binary-string | 0 | 1 | ### **Brute Force Solution**\n\n```\nclass Solution:\n\tdef secondsToRemoveOccurrences(self, s: str) -> int:\n\t\tcount = 0\n\t\ttemp = ""\n\t\tones = s.count("1") # get the count of 1\n\t\tfor _ in range(ones):\n\t\t\t"""\n\t\t\tmake a string with total number of 1\n\t\t\t"""\n\t\t\ttemp += "1"\n\n\t\twhile s[:ones] != temp:\n\t\t\t"""\n\t\t\tloop through index 0 to count of 1 while the string is not equal to temp string\n\t\t\t"""\n\n\t\t\tleft, right = 0, 1\n\t\t\twhile right < len(s):\n\t\t\t\t"""\n\t\t\t\tCompare the two index from left to right if\n\t\t\t\tthey both are equal to "01"\n\t\t\t\tif so then replace them\n\t\t\t\tand count the number of occurrence\n\t\t\t\t"""\n\t\t\t\tif s[left : left + 1] + s[right : right + 1] == "01":\n\t\t\t\t\ts = s.replace(s[left : left + 1] + s[right : right + 1], "10")\n\t\t\t\t\tcount += 1\n\t\t\t\tleft += 1\n\t\t\t\tright += 1\n\t\treturn count\n```\n\n### **Easy & Small Solution**\n\n```\nclass Solution:\n\tdef secondsToRemoveOccurrences(self, s: str) -> int:\n\t\tcount = 0\n\t\twhile "01" in s:\n\t\t\t"""\n\t\t\tWhile we are getting "01" in the string\n\t\t\twe will replace them into "10"\n\t\t\tand count the number of occurrence\n\t\t\t"""\n\t\t\ts = s.replace("01", "10")\n\t\t\tcount += 1\n\t\treturn count\n``` | 1 | You are given a binary string `s`. In one second, **all** occurrences of `"01 "` are **simultaneously** replaced with `"10 "`. This process **repeats** until no occurrences of `"01 "` exist.
Return _the number of seconds needed to complete this process._
**Example 1:**
**Input:** s = "0110101 "
**Output:** 4
**Explanation:**
After one second, s becomes "1011010 ".
After another second, s becomes "1101100 ".
After the third second, s becomes "1110100 ".
After the fourth second, s becomes "1111000 ".
No occurrence of "01 " exists any longer, and the process needed 4 seconds to complete,
so we return 4.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:**
No occurrence of "01 " exists in s, and the processes needed 0 seconds to complete,
so we return 0.
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'0'` or `'1'`.
**Follow up:**
Can you solve this problem in O(n) time complexity? | null |
[Python 3] Sweep Line - Difference Array | shifting-letters-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:\n n = len(s)\n d = [0 for _ in range(n + 1)]\n for start, end, direction in shifts:\n dir = 1 if direction else -1\n d[start] += dir\n d[end + 1] -= dir\n \n res = []\n for i in range(n):\n if i != 0: \n d[i] += d[i - 1]\n new_chr_ascii = (ord(s[i]) - ord("a") + d[i]) % 26 + ord("a")\n res.append(chr(new_chr_ascii))\n return "".join(res)\n``` | 4 | You are given a string `s` of lowercase English letters and a 2D integer array `shifts` where `shifts[i] = [starti, endi, directioni]`. For every `i`, **shift** the characters in `s` from the index `starti` to the index `endi` (**inclusive**) forward if `directioni = 1`, or shift the characters backward if `directioni = 0`.
Shifting a character **forward** means replacing it with the **next** letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Similarly, shifting a character **backward** means replacing it with the **previous** letter in the alphabet (wrapping around so that `'a'` becomes `'z'`).
Return _the final string after all such shifts to_ `s` _are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[\[0,1,0\],\[1,2,1\],\[0,2,1\]\]
**Output:** "ace "
**Explanation:** Firstly, shift the characters from index 0 to index 1 backward. Now s = "zac ".
Secondly, shift the characters from index 1 to index 2 forward. Now s = "zbd ".
Finally, shift the characters from index 0 to index 2 forward. Now s = "ace ".
**Example 2:**
**Input:** s = "dztz ", shifts = \[\[0,0,0\],\[1,1,1\]\]
**Output:** "catz "
**Explanation:** Firstly, shift the characters from index 0 to index 0 backward. Now s = "cztz ".
Finally, shift the characters from index 1 to index 1 forward. Now s = "catz ".
**Constraints:**
* `1 <= s.length, shifts.length <= 5 * 104`
* `shifts[i].length == 3`
* `0 <= starti <= endi < s.length`
* `0 <= directioni <= 1`
* `s` consists of lowercase English letters. | null |
✅ Python Cumulative Sum || Easy Solution | shifting-letters-ii | 0 | 1 | In this problem, we should be doing the exact same thing as in the first part of this problem (shifting letters) but there is an extra complexity of finding the final changes for each of the letters. \n\nA brute force approach would be to iterate through all of the letters that need to be changed for each shift in array shifts (e.g., from 0 to 2 in forward direction). However, this adds extra complexity if we have large ranges of letters that need to be changed. This is why we should be using a cumulative sum approach here. \n\nFor example, instead of iterating through the range, we can add a +1 if we are moving forward in the beginning of the range and -1 in the end of the range to make sure we are no longer applying the change. The same thing goes for the backward direction with the -1 at the beginning and +1 at the end.\n\n```\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:\n cum_shifts = [0 for _ in range(len(s)+1)]\n \n for st, end, d in shifts:\n if d == 0:\n cum_shifts[st] -= 1\n cum_shifts[end+1] += 1\n else:\n cum_shifts[st] += 1\n cum_shifts[end+1] -= 1\n \n cum_sum = 0\n for i in range(len(s)):\n cum_sum += cum_shifts[i]\n \n new_code = (((ord(s[i]) + cum_sum) - 97) % 26) + 97\n s = s[:i] + chr(new_code) + s[i+1:]\n \n return s\n``` | 20 | You are given a string `s` of lowercase English letters and a 2D integer array `shifts` where `shifts[i] = [starti, endi, directioni]`. For every `i`, **shift** the characters in `s` from the index `starti` to the index `endi` (**inclusive**) forward if `directioni = 1`, or shift the characters backward if `directioni = 0`.
Shifting a character **forward** means replacing it with the **next** letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Similarly, shifting a character **backward** means replacing it with the **previous** letter in the alphabet (wrapping around so that `'a'` becomes `'z'`).
Return _the final string after all such shifts to_ `s` _are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[\[0,1,0\],\[1,2,1\],\[0,2,1\]\]
**Output:** "ace "
**Explanation:** Firstly, shift the characters from index 0 to index 1 backward. Now s = "zac ".
Secondly, shift the characters from index 1 to index 2 forward. Now s = "zbd ".
Finally, shift the characters from index 0 to index 2 forward. Now s = "ace ".
**Example 2:**
**Input:** s = "dztz ", shifts = \[\[0,0,0\],\[1,1,1\]\]
**Output:** "catz "
**Explanation:** Firstly, shift the characters from index 0 to index 0 backward. Now s = "cztz ".
Finally, shift the characters from index 1 to index 1 forward. Now s = "catz ".
**Constraints:**
* `1 <= s.length, shifts.length <= 5 * 104`
* `shifts[i].length == 3`
* `0 <= starti <= endi < s.length`
* `0 <= directioni <= 1`
* `s` consists of lowercase English letters. | null |
[Python3] Line Sweep Method with Hashmap | shifting-letters-ii | 0 | 1 | Note that for one who doesn\'t know about line sweep technique, there will be a test case with enormous length giving TLE.\n\nFor knowing what character will become after shifting **n** position forward, we can use a list to achieve that purpose.\nAs there will be only lower letter, we can assign "a" ~ "z" to a list of length 26.\nFor instance, to know what character will be given after shifting "a" 3 times forward, the answer will be :\n**lettermap[ ( ord("a") - 97 + 3 ) % 26 ]** = "d"\n\nNext is to determine how to shift each character efficiently. It will be time-consuming if one goes to all characters between start and end of an interval then do the same to all intervals. \nBy applying line sweep, the time complexity could be reduced substantially to linear time.\n\nTo see the idea of line sweep : \n\n\nAfter iterating all shifting intervals and keep track of the shift offset starting at specific index,\nwe can get the number of shifts starting at each index then use this information to perform character shifting.\n\n\n\n\n```\nfrom collections import defaultdict\n\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:\n # As in Python string is immutable, so need to convert it into character list.\n arr = list(s)\n n = len(arr)\n \n # Since there are only lowercase letter, we can use a list to serve the need for referring shifting character.\n maplist = [chr(i) for i in range(97, 123)]\n shiftmap = defaultdict(int)\n \n # shiftmap[i] = d means all characters from ith index to the end of the string\n # need to be shifted forward d times (if d < 0, shift backward.)\n # For each interval, we only need to use start and (end + 1) index.\n for start, end, direct in shifts:\n d = 1 if direct == 1 else -1\n shiftmap[start] += d\n if end + 1 < n: # we only care about index < length of s\n shiftmap[end + 1] -= d\n \n # Iterate each index and check its shift offset from the map\n # update the offset continuously then find the character after shifting the accumulated offset.\n offset = 0\n for i in range(n):\n if shiftmap[i] != 0:\n offset += shiftmap[i]\n arr[i] = maplist[(ord(arr[i]) - 97 + offset) % 26]\n \n return "".join(arr)\n``` | 1 | You are given a string `s` of lowercase English letters and a 2D integer array `shifts` where `shifts[i] = [starti, endi, directioni]`. For every `i`, **shift** the characters in `s` from the index `starti` to the index `endi` (**inclusive**) forward if `directioni = 1`, or shift the characters backward if `directioni = 0`.
Shifting a character **forward** means replacing it with the **next** letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Similarly, shifting a character **backward** means replacing it with the **previous** letter in the alphabet (wrapping around so that `'a'` becomes `'z'`).
Return _the final string after all such shifts to_ `s` _are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[\[0,1,0\],\[1,2,1\],\[0,2,1\]\]
**Output:** "ace "
**Explanation:** Firstly, shift the characters from index 0 to index 1 backward. Now s = "zac ".
Secondly, shift the characters from index 1 to index 2 forward. Now s = "zbd ".
Finally, shift the characters from index 0 to index 2 forward. Now s = "ace ".
**Example 2:**
**Input:** s = "dztz ", shifts = \[\[0,0,0\],\[1,1,1\]\]
**Output:** "catz "
**Explanation:** Firstly, shift the characters from index 0 to index 0 backward. Now s = "cztz ".
Finally, shift the characters from index 1 to index 1 forward. Now s = "catz ".
**Constraints:**
* `1 <= s.length, shifts.length <= 5 * 104`
* `shifts[i].length == 3`
* `0 <= starti <= endi < s.length`
* `0 <= directioni <= 1`
* `s` consists of lowercase English letters. | null |
2 Python Solutions with explanation[BruteForce + LineSweep]✔ | shifting-letters-ii | 0 | 1 | \t**BRUTE-FORCE SOLUTION** (GIVING TLE)\n\tclass Solution:\n\t\tdef shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:\n\t\t\ttoshift = defaultdict(int)\n\n\t\t\tfor i in shifts:\n\t\t\t\tif i[2] == 0:\n\t\t\t\t\tc = -1\n\t\t\t\telse:\n\t\t\t\t\tc = 1\n\t\t\t\tfor j in range(i[0], i[1] + 1):\n\t\t\t\t\ttoshift[j] += c\n\t\t\t\t\t\n\t\t\tl = list(s)\n\t\t\tfor i in range(len(l)):\n\t\t\t\tif toshift[i]>0:\n\t\t\t\t\tacc= ord(l[i]) + (toshift[i]%26)\n\t\t\t\t\tif (acc) > 122:\n\t\t\t\t\t\tacc = 96 + (acc-122)\n\t\t\t\t\t\n\t\t\t\telse:\n\t\t\t\t\tacc= ord(l[i]) - (abs(toshift[i])%26)\n\t\t\t\t\tif (acc) < 97:\n\t\t\t\t\t\tacc = 123 - (97 - acc)\n\t\t\t\tl[i] = chr(acc)\n\n\t\t\treturn(\'\'.join(l))\n\t\n\t**OPTIMIZED SOLUTION**: (*LINE SWEEPING*)\n\t\n\tclass Solution:\n\t\tdef shiftingLetters(self, s: str, shifts: List[List[int]]) -> str:\n\t\t\ttoshift = [0]*(len(s) +1)\n\t\t\t\n\t\t\t#marking start and end points only for start and end points of each shift \n\t\t\tfor i in shifts:\n\t\t\t\tif i[2] == 1:\n\t\t\t\t\ttoshift[i[0]] += 1\n\t\t\t\t\ttoshift[i[1]+1] -= 1\n\t\t\t\telse:\n\t\t\t\t\ttoshift[i[0]] -= 1\n\t\t\t\t\ttoshift[i[1]+1] += 1\n\t\t\t\t\t\n\t\t\tfor j in range(1, len(s)): #calculating prefixSum\n\t\t\t\t\ttoshift[j] += toshift[j-1]\n\t\t\t\t\t\n\t\t\tl = list(s) #converting in list for doing modification\n\t\t\tfor i in range(len(l)):\n\t\t\t\tif toshift[i]>0: #for forward\n\t\t\t\t\tacc= ord(l[i]) + (toshift[i]%26) #doing modulo by 26 because we have 26 alphabets and if suppose we to shift alphabet by 43 ie(43 % 26 = 1) so we will shift by 1 \n\t\t\t\t\tif (acc) > 122:\n\t\t\t\t\t\tacc = 96 + (acc-122) #if range exceeds then first subtract by 122 then add it in 96 (if still you did\'nt get intution of it try doing dry run of it on some test cases)\n\t\t\t\t\t\t\n\t\t\t\telse: #for backward\n\t\t\t\t\tacc= ord(l[i]) - (abs(toshift[i])%26)\n\t\t\t\t\tif (acc) < 97:\n\t\t\t\t\t\tacc = 123 - (97 - acc)\n\t\t\t\t\t\t\n\t\t\t\tl[i] = chr(acc) #finally updating that character\n\n\t\t\treturn(\'\'.join(l))\n\t\t\t\nDo **UPVOTE** :)\n\n**COMPLEXITY :** O(N) time and O(N) space | 1 | You are given a string `s` of lowercase English letters and a 2D integer array `shifts` where `shifts[i] = [starti, endi, directioni]`. For every `i`, **shift** the characters in `s` from the index `starti` to the index `endi` (**inclusive**) forward if `directioni = 1`, or shift the characters backward if `directioni = 0`.
Shifting a character **forward** means replacing it with the **next** letter in the alphabet (wrapping around so that `'z'` becomes `'a'`). Similarly, shifting a character **backward** means replacing it with the **previous** letter in the alphabet (wrapping around so that `'a'` becomes `'z'`).
Return _the final string after all such shifts to_ `s` _are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[\[0,1,0\],\[1,2,1\],\[0,2,1\]\]
**Output:** "ace "
**Explanation:** Firstly, shift the characters from index 0 to index 1 backward. Now s = "zac ".
Secondly, shift the characters from index 1 to index 2 forward. Now s = "zbd ".
Finally, shift the characters from index 0 to index 2 forward. Now s = "ace ".
**Example 2:**
**Input:** s = "dztz ", shifts = \[\[0,0,0\],\[1,1,1\]\]
**Output:** "catz "
**Explanation:** Firstly, shift the characters from index 0 to index 0 backward. Now s = "cztz ".
Finally, shift the characters from index 1 to index 1 forward. Now s = "catz ".
**Constraints:**
* `1 <= s.length, shifts.length <= 5 * 104`
* `shifts[i].length == 3`
* `0 <= starti <= endi < s.length`
* `0 <= directioni <= 1`
* `s` consists of lowercase English letters. | null |
Do it backwards O(N) | maximum-segment-sum-after-removals | 0 | 1 | For nums = [1,2,5,6,1], removeQueries = [0,3,2,4,1], the reverse process will be \nadd 1 : [0, 2, 0 ,0 ,0]\nadd 4 : [0, 2, 0 ,0 ,1]\nadd 2 : [0, 2, 5 ,0 ,1]\nadd 3 : [0, 2, 5, 6, 1]\nadd 0 : [1, 2, 5, 6, 1]\n\nWhen an index q is added, extend the contiguous sequence by finding if q+1 or q-1 exists, and also record the value of the maximum segment sum. For example, before adding the 3rd element, there are two contiguous sequences, [2, 5] and [1], and we can extend it to a length 4 sequence after the 3rd element is added.\n```\nclass Solution:\n def maximumSegmentSum(self, nums: List[int], removeQueries: List[int]) -> List[int]:\n mp, cur, res = {}, 0, []\n for q in reversed(removeQueries[1:]):\n mp[q] = (nums[q], 1)\n rv, rLen = mp.get(q+1, (0, 0))\n lv, lLen = mp.get(q-1, (0, 0))\n \n total = nums[q] + rv + lv\n mp[q+rLen] = (total, lLen + rLen + 1)\n mp[q-lLen] = (total, lLen + rLen + 1)\n \n cur = max(cur, total)\n res.append(cur)\n \n return res[::-1] + [0]\n``` | 40 | You are given two **0-indexed** integer arrays `nums` and `removeQueries`, both of length `n`. For the `ith` query, the element in `nums` at the index `removeQueries[i]` is removed, splitting `nums` into different segments.
A **segment** is a contiguous sequence of **positive** integers in `nums`. A **segment sum** is the sum of every element in a segment.
Return _an integer array_ `answer`_, of length_ `n`_, where_ `answer[i]` _is the **maximum** segment sum after applying the_ `ith` _removal._
**Note:** The same index will **not** be removed more than once.
**Example 1:**
**Input:** nums = \[1,2,5,6,1\], removeQueries = \[0,3,2,4,1\]
**Output:** \[14,7,2,2,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 0th element, nums becomes \[0,2,5,6,1\] and the maximum segment sum is 14 for segment \[2,5,6,1\].
Query 2: Remove the 3rd element, nums becomes \[0,2,5,0,1\] and the maximum segment sum is 7 for segment \[2,5\].
Query 3: Remove the 2nd element, nums becomes \[0,2,0,0,1\] and the maximum segment sum is 2 for segment \[2\].
Query 4: Remove the 4th element, nums becomes \[0,2,0,0,0\] and the maximum segment sum is 2 for segment \[2\].
Query 5: Remove the 1st element, nums becomes \[0,0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[14,7,2,2,0\].
**Example 2:**
**Input:** nums = \[3,2,11,1\], removeQueries = \[3,2,1,0\]
**Output:** \[16,5,3,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 3rd element, nums becomes \[3,2,11,0\] and the maximum segment sum is 16 for segment \[3,2,11\].
Query 2: Remove the 2nd element, nums becomes \[3,2,0,0\] and the maximum segment sum is 5 for segment \[3,2\].
Query 3: Remove the 1st element, nums becomes \[3,0,0,0\] and the maximum segment sum is 3 for segment \[3\].
Query 4: Remove the 0th element, nums becomes \[0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[16,5,3,0\].
**Constraints:**
* `n == nums.length == removeQueries.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 109`
* `0 <= removeQueries[i] < n`
* All the values of `removeQueries` are **unique**. | null |
[Python3] Priority queue | maximum-segment-sum-after-removals | 0 | 1 | Please pull this git [commit](https://github.com/gaosanyong/leetcode/commit/e999ea07dc2ea2e8b7aad97696f67a3b965e496d) for solutions of biweekly 85. \n\n**Intuition**\nHere, I use \n1) a ordered set to store the points where `nums` are divided; \n2) a hash table mapping from left boundary to right boundary to validate if a triplet is still effective;\n3) a priority queue to the triplet of <range sum, left boundary, right boundary>.\n\nAt each query, I add the point to the set of dividers, adjust the mapping of its left and right boundary points, and add the new two pieces to the priority queue. While finding current maximum from the priority queue, I first validate if the triplet is still in effect by checking if the left boundary matches the right boundary in the hash table. If not, I discard the top element until a valid triplet. \n\n**Analysis**\nTime complexity `O(NlogN)`\nSpace complexity `O(N)`\n```\nclass Solution: \n def maximumSegmentSum(self, nums: List[int], removeQueries: List[int]) -> List[int]:\n n = len(nums)\n sl = SortedList([-1, n])\n prefix = list(accumulate(nums, initial=0))\n mp = {-1 : n}\n pq = [(-prefix[-1], -1, n)]\n \n ans = []\n for q in removeQueries: \n sl.add(q)\n i = sl.bisect_left(q)\n lo = sl[i-1]\n hi = sl[i+1]\n mp[lo] = q\n mp[q] = hi \n heappush(pq, (-(prefix[q]-prefix[lo+1]), lo, q))\n heappush(pq, (-(prefix[hi]-prefix[q+1]), q, hi))\n \n while mp[pq[0][1]] != pq[0][2]: heappop(pq)\n ans.append(-pq[0][0])\n return ans \n```\n | 8 | You are given two **0-indexed** integer arrays `nums` and `removeQueries`, both of length `n`. For the `ith` query, the element in `nums` at the index `removeQueries[i]` is removed, splitting `nums` into different segments.
A **segment** is a contiguous sequence of **positive** integers in `nums`. A **segment sum** is the sum of every element in a segment.
Return _an integer array_ `answer`_, of length_ `n`_, where_ `answer[i]` _is the **maximum** segment sum after applying the_ `ith` _removal._
**Note:** The same index will **not** be removed more than once.
**Example 1:**
**Input:** nums = \[1,2,5,6,1\], removeQueries = \[0,3,2,4,1\]
**Output:** \[14,7,2,2,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 0th element, nums becomes \[0,2,5,6,1\] and the maximum segment sum is 14 for segment \[2,5,6,1\].
Query 2: Remove the 3rd element, nums becomes \[0,2,5,0,1\] and the maximum segment sum is 7 for segment \[2,5\].
Query 3: Remove the 2nd element, nums becomes \[0,2,0,0,1\] and the maximum segment sum is 2 for segment \[2\].
Query 4: Remove the 4th element, nums becomes \[0,2,0,0,0\] and the maximum segment sum is 2 for segment \[2\].
Query 5: Remove the 1st element, nums becomes \[0,0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[14,7,2,2,0\].
**Example 2:**
**Input:** nums = \[3,2,11,1\], removeQueries = \[3,2,1,0\]
**Output:** \[16,5,3,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 3rd element, nums becomes \[3,2,11,0\] and the maximum segment sum is 16 for segment \[3,2,11\].
Query 2: Remove the 2nd element, nums becomes \[3,2,0,0\] and the maximum segment sum is 5 for segment \[3,2\].
Query 3: Remove the 1st element, nums becomes \[3,0,0,0\] and the maximum segment sum is 3 for segment \[3\].
Query 4: Remove the 0th element, nums becomes \[0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[16,5,3,0\].
**Constraints:**
* `n == nums.length == removeQueries.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 109`
* `0 <= removeQueries[i] < n`
* All the values of `removeQueries` are **unique**. | null |
[Python 3]Prefix Sum+Heap | maximum-segment-sum-after-removals | 0 | 1 | ```\n \nclass Solution:\n def maximumSegmentSum(self, nums: List[int], removeQueries: List[int]) -> List[int]:\n n = len(nums)\n acc = [0]\n # prefix sum\n for num in nums:\n acc.append(acc[-1] + num)\n \n # current max sum with boundries\n q = [(-sum(nums), 0, n - 1)]\n # removed index\n rm_idx = []\n \n \n ans = []\n for idx in removeQueries:\n bisect.insort(rm_idx, idx)\n while q:\n _, s, e = q[0]\n loc = bisect.bisect_left(rm_idx, s)\n idx = rm_idx[min(loc, len(rm_idx) - 1)]\n # if removed index fall between the boundry of largest sum\n if idx > e or idx < s: break\n heappop(q)\n if s < idx:\n heappush(q, (-(acc[idx] - acc[s]), s, idx - 1))\n if e > idx:\n heappush(q, (-(acc[e + 1] - acc[idx + 1]), idx + 1, e))\n if q:\n ans.append(-q[0][0])\n else:\n ans.append(0)\n \n \n return ans | 1 | You are given two **0-indexed** integer arrays `nums` and `removeQueries`, both of length `n`. For the `ith` query, the element in `nums` at the index `removeQueries[i]` is removed, splitting `nums` into different segments.
A **segment** is a contiguous sequence of **positive** integers in `nums`. A **segment sum** is the sum of every element in a segment.
Return _an integer array_ `answer`_, of length_ `n`_, where_ `answer[i]` _is the **maximum** segment sum after applying the_ `ith` _removal._
**Note:** The same index will **not** be removed more than once.
**Example 1:**
**Input:** nums = \[1,2,5,6,1\], removeQueries = \[0,3,2,4,1\]
**Output:** \[14,7,2,2,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 0th element, nums becomes \[0,2,5,6,1\] and the maximum segment sum is 14 for segment \[2,5,6,1\].
Query 2: Remove the 3rd element, nums becomes \[0,2,5,0,1\] and the maximum segment sum is 7 for segment \[2,5\].
Query 3: Remove the 2nd element, nums becomes \[0,2,0,0,1\] and the maximum segment sum is 2 for segment \[2\].
Query 4: Remove the 4th element, nums becomes \[0,2,0,0,0\] and the maximum segment sum is 2 for segment \[2\].
Query 5: Remove the 1st element, nums becomes \[0,0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[14,7,2,2,0\].
**Example 2:**
**Input:** nums = \[3,2,11,1\], removeQueries = \[3,2,1,0\]
**Output:** \[16,5,3,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 3rd element, nums becomes \[3,2,11,0\] and the maximum segment sum is 16 for segment \[3,2,11\].
Query 2: Remove the 2nd element, nums becomes \[3,2,0,0\] and the maximum segment sum is 5 for segment \[3,2\].
Query 3: Remove the 1st element, nums becomes \[3,0,0,0\] and the maximum segment sum is 3 for segment \[3\].
Query 4: Remove the 0th element, nums becomes \[0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[16,5,3,0\].
**Constraints:**
* `n == nums.length == removeQueries.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 109`
* `0 <= removeQueries[i] < n`
* All the values of `removeQueries` are **unique**. | null |
python 3 | union find | maximum-segment-sum-after-removals | 0 | 1 | ```\nclass Solution:\n def maximumSegmentSum(self, nums: List[int], removeQueries: List[int]) -> List[int]:\n n = len(nums)\n res = [0] * n\n parent = [i for i in range(n)]\n rank = [0] * n\n sums = [0] * n\n \n def union(i, j):\n i, j = find(i), find(j)\n if rank[i] < rank[j]:\n i, j = j, i \n parent[j] = i\n rank[i] += rank[j]\n sums[i] += sums[j]\n \n def find(i):\n while i != parent[i]:\n parent[i] = i = parent[parent[i]]\n return i\n \n for i in range(n - 1, 0, -1):\n j = removeQueries[i]\n sums[j] = nums[j]\n if j and sums[j - 1]:\n union(j, j - 1)\n if j != n - 1 and sums[j + 1]:\n union(j, j + 1)\n res[i - 1] = max(res[i], sums[find(j)])\n \n return res\n | 1 | You are given two **0-indexed** integer arrays `nums` and `removeQueries`, both of length `n`. For the `ith` query, the element in `nums` at the index `removeQueries[i]` is removed, splitting `nums` into different segments.
A **segment** is a contiguous sequence of **positive** integers in `nums`. A **segment sum** is the sum of every element in a segment.
Return _an integer array_ `answer`_, of length_ `n`_, where_ `answer[i]` _is the **maximum** segment sum after applying the_ `ith` _removal._
**Note:** The same index will **not** be removed more than once.
**Example 1:**
**Input:** nums = \[1,2,5,6,1\], removeQueries = \[0,3,2,4,1\]
**Output:** \[14,7,2,2,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 0th element, nums becomes \[0,2,5,6,1\] and the maximum segment sum is 14 for segment \[2,5,6,1\].
Query 2: Remove the 3rd element, nums becomes \[0,2,5,0,1\] and the maximum segment sum is 7 for segment \[2,5\].
Query 3: Remove the 2nd element, nums becomes \[0,2,0,0,1\] and the maximum segment sum is 2 for segment \[2\].
Query 4: Remove the 4th element, nums becomes \[0,2,0,0,0\] and the maximum segment sum is 2 for segment \[2\].
Query 5: Remove the 1st element, nums becomes \[0,0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[14,7,2,2,0\].
**Example 2:**
**Input:** nums = \[3,2,11,1\], removeQueries = \[3,2,1,0\]
**Output:** \[16,5,3,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 3rd element, nums becomes \[3,2,11,0\] and the maximum segment sum is 16 for segment \[3,2,11\].
Query 2: Remove the 2nd element, nums becomes \[3,2,0,0\] and the maximum segment sum is 5 for segment \[3,2\].
Query 3: Remove the 1st element, nums becomes \[3,0,0,0\] and the maximum segment sum is 3 for segment \[3\].
Query 4: Remove the 0th element, nums becomes \[0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[16,5,3,0\].
**Constraints:**
* `n == nums.length == removeQueries.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 109`
* `0 <= removeQueries[i] < n`
* All the values of `removeQueries` are **unique**. | null |
Python O(n) time complexity, easily understandable code | maximum-segment-sum-after-removals | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nUsing the example of nums = [1,2,5,6,1], removeQueries = [0,3,2,4,1].\n\nStarting from the empty list [0,0,0,0,0], add elements to the list until you obtain the original list.\n\n1. [0,2,0,0,0]\n2. [0,2,0,0,1]\n3. [0,2,5,0,1]\n4. [0,2,5,6,1]\n5. [1,2,5,6,1]\n\nMaking use of a dictionary to store each segment sum separately, we need to store 1.the value of the segment sum and 2.the range which the segment sum lies on.\n\nFrom step 3 for example, the dictionary will have three values, \n1: (7, [1,2])\n2: (7, [1,2])\n4: (1, [4,4])\n\nFrom step 4, the dictionary will have three values.\n1: (14, [1,4]) \n2: (7, [1,2])\n4: (14, [1,4]) \n\nEverytime you look at removeQueries, track index + 1 and index - 1 in the dictionary in order to update the value, and the new range of the segment sum.\n\nNotice that since 2 is between two "filled" indices, it will never be invoked in the code, and can be ignored.\n\nLastly, curr_max is used to track the maximum segment sum at all periods of time, before appending it to the return list. \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n+n) for ret and dct\n# Code\n```\nclass Solution:\n def maximumSegmentSum(self, nums: List[int], removeQueries: List[int]) -> List[int]:\n ret = [0] \n curr_max = 0\n dct = {}\n for index in removeQueries[:0:-1]:\n #In order to add queries one by one\n temp = nums[index]\n lower_index = upper_index = index\n\n if index - 1 in dct:\n temp += dct[index-1][0]\n lower_index = dct[index-1][1][0]\n \n if index + 1 in dct:\n temp += dct[index+1][0]\n upper_index = dct[index+1][1][1]\n \n dct[lower_index] = (temp, (lower_index, upper_index))\n dct[upper_index] = (temp, (lower_index, upper_index))\n curr_max = max(curr_max, temp)\n ret.append(curr_max)\n return ret[::-1]\n\n \n``` | 0 | You are given two **0-indexed** integer arrays `nums` and `removeQueries`, both of length `n`. For the `ith` query, the element in `nums` at the index `removeQueries[i]` is removed, splitting `nums` into different segments.
A **segment** is a contiguous sequence of **positive** integers in `nums`. A **segment sum** is the sum of every element in a segment.
Return _an integer array_ `answer`_, of length_ `n`_, where_ `answer[i]` _is the **maximum** segment sum after applying the_ `ith` _removal._
**Note:** The same index will **not** be removed more than once.
**Example 1:**
**Input:** nums = \[1,2,5,6,1\], removeQueries = \[0,3,2,4,1\]
**Output:** \[14,7,2,2,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 0th element, nums becomes \[0,2,5,6,1\] and the maximum segment sum is 14 for segment \[2,5,6,1\].
Query 2: Remove the 3rd element, nums becomes \[0,2,5,0,1\] and the maximum segment sum is 7 for segment \[2,5\].
Query 3: Remove the 2nd element, nums becomes \[0,2,0,0,1\] and the maximum segment sum is 2 for segment \[2\].
Query 4: Remove the 4th element, nums becomes \[0,2,0,0,0\] and the maximum segment sum is 2 for segment \[2\].
Query 5: Remove the 1st element, nums becomes \[0,0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[14,7,2,2,0\].
**Example 2:**
**Input:** nums = \[3,2,11,1\], removeQueries = \[3,2,1,0\]
**Output:** \[16,5,3,0\]
**Explanation:** Using 0 to indicate a removed element, the answer is as follows:
Query 1: Remove the 3rd element, nums becomes \[3,2,11,0\] and the maximum segment sum is 16 for segment \[3,2,11\].
Query 2: Remove the 2nd element, nums becomes \[3,2,0,0\] and the maximum segment sum is 5 for segment \[3,2\].
Query 3: Remove the 1st element, nums becomes \[3,0,0,0\] and the maximum segment sum is 3 for segment \[3\].
Query 4: Remove the 0th element, nums becomes \[0,0,0,0\] and the maximum segment sum is 0, since there are no segments.
Finally, we return \[16,5,3,0\].
**Constraints:**
* `n == nums.length == removeQueries.length`
* `1 <= n <= 105`
* `1 <= nums[i] <= 109`
* `0 <= removeQueries[i] < n`
* All the values of `removeQueries` are **unique**. | null |
Python Easy O(n) | minimum-hours-of-training-to-win-a-competition | 0 | 1 | \n# Code\n```\nclass Solution:\n def minNumberOfHours(self, initialEnergy: int, initialExperience: int, energy: List[int], experience: List[int]) -> int:\n\n \n exdif = 0\n ensum = 0\n for i in range(len(energy)):\n\n if initialExperience <= experience[i]:\n exdif = max(1,exdif,experience[i]+1-initialExperience)\n\n initialExperience += experience[i]\n ensum += energy[i]\n\n\n return max(ensum-initialEnergy+1,0) + exdif\n \n``` | 1 | You are entering a competition, and are given two **positive** integers `initialEnergy` and `initialExperience` denoting your initial energy and initial experience respectively.
You are also given two **0-indexed** integer arrays `energy` and `experience`, both of length `n`.
You will face `n` opponents **in order**. The energy and experience of the `ith` opponent is denoted by `energy[i]` and `experience[i]` respectively. When you face an opponent, you need to have both **strictly** greater experience and energy to defeat them and move to the next opponent if available.
Defeating the `ith` opponent **increases** your experience by `experience[i]`, but **decreases** your energy by `energy[i]`.
Before starting the competition, you can train for some number of hours. After each hour of training, you can **either** choose to increase your initial experience by one, or increase your initial energy by one.
Return _the **minimum** number of training hours required to defeat all_ `n` _opponents_.
**Example 1:**
**Input:** initialEnergy = 5, initialExperience = 3, energy = \[1,4,3,2\], experience = \[2,6,3,1\]
**Output:** 8
**Explanation:** You can increase your energy to 11 after 6 hours of training, and your experience to 5 after 2 hours of training.
You face the opponents in the following order:
- You have more energy and experience than the 0th opponent so you win.
Your energy becomes 11 - 1 = 10, and your experience becomes 5 + 2 = 7.
- You have more energy and experience than the 1st opponent so you win.
Your energy becomes 10 - 4 = 6, and your experience becomes 7 + 6 = 13.
- You have more energy and experience than the 2nd opponent so you win.
Your energy becomes 6 - 3 = 3, and your experience becomes 13 + 3 = 16.
- You have more energy and experience than the 3rd opponent so you win.
Your energy becomes 3 - 2 = 1, and your experience becomes 16 + 1 = 17.
You did a total of 6 + 2 = 8 hours of training before the competition, so we return 8.
It can be proven that no smaller answer exists.
**Example 2:**
**Input:** initialEnergy = 2, initialExperience = 4, energy = \[1\], experience = \[3\]
**Output:** 0
**Explanation:** You do not need any additional energy or experience to win the competition, so we return 0.
**Constraints:**
* `n == energy.length == experience.length`
* `1 <= n <= 100`
* `1 <= initialEnergy, initialExperience, energy[i], experience[i] <= 100` | null |
✅Python || Easy Approach | minimum-hours-of-training-to-win-a-competition | 0 | 1 | ```\nclass Solution:\n def minNumberOfHours(self, initialEnergy: int, initialExperience: int, energy: List[int], experience: List[int]) -> int:\n \n ans = 0\n n = len(energy)\n\n for i in range(n):\n while initialEnergy <= energy[i] or initialExperience <= experience[i]:\n if initialEnergy <= energy[i]:\n initialEnergy += 1\n ans += 1\n if initialExperience <= experience[i]:\n initialExperience += 1\n ans += 1\n initialEnergy -= energy[i]\n initialExperience += experience[i]\n \n return ans\n``` | 8 | You are entering a competition, and are given two **positive** integers `initialEnergy` and `initialExperience` denoting your initial energy and initial experience respectively.
You are also given two **0-indexed** integer arrays `energy` and `experience`, both of length `n`.
You will face `n` opponents **in order**. The energy and experience of the `ith` opponent is denoted by `energy[i]` and `experience[i]` respectively. When you face an opponent, you need to have both **strictly** greater experience and energy to defeat them and move to the next opponent if available.
Defeating the `ith` opponent **increases** your experience by `experience[i]`, but **decreases** your energy by `energy[i]`.
Before starting the competition, you can train for some number of hours. After each hour of training, you can **either** choose to increase your initial experience by one, or increase your initial energy by one.
Return _the **minimum** number of training hours required to defeat all_ `n` _opponents_.
**Example 1:**
**Input:** initialEnergy = 5, initialExperience = 3, energy = \[1,4,3,2\], experience = \[2,6,3,1\]
**Output:** 8
**Explanation:** You can increase your energy to 11 after 6 hours of training, and your experience to 5 after 2 hours of training.
You face the opponents in the following order:
- You have more energy and experience than the 0th opponent so you win.
Your energy becomes 11 - 1 = 10, and your experience becomes 5 + 2 = 7.
- You have more energy and experience than the 1st opponent so you win.
Your energy becomes 10 - 4 = 6, and your experience becomes 7 + 6 = 13.
- You have more energy and experience than the 2nd opponent so you win.
Your energy becomes 6 - 3 = 3, and your experience becomes 13 + 3 = 16.
- You have more energy and experience than the 3rd opponent so you win.
Your energy becomes 3 - 2 = 1, and your experience becomes 16 + 1 = 17.
You did a total of 6 + 2 = 8 hours of training before the competition, so we return 8.
It can be proven that no smaller answer exists.
**Example 2:**
**Input:** initialEnergy = 2, initialExperience = 4, energy = \[1\], experience = \[3\]
**Output:** 0
**Explanation:** You do not need any additional energy or experience to win the competition, so we return 0.
**Constraints:**
* `n == energy.length == experience.length`
* `1 <= n <= 100`
* `1 <= initialEnergy, initialExperience, energy[i], experience[i] <= 100` | null |
Build a Graph from the given tree, Use BFS to get the time to infect the nodes. | amount-of-time-for-binary-tree-to-be-infected | 0 | 1 | # Intuition\nsince we have to traverse back in the tree[top and bottom traversal]\nWe use Hashing. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can make use of a hashmap where we make the children and parent mapping.\nUse BFS for traversing the node. Insert the currently visited node to visited set increment the time by 1 each time you visit a node.Do this recursively till the queue is empty\nat last return the time.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:\n dict_ = defaultdict(list)\n def buildgraph(cur,parent):\n if cur and parent:\n dict_[cur.val].append(parent.val)\n dict_[parent.val].append(cur.val)\n if cur.left:\n buildgraph(cur.left,cur)\n if cur.right:\n buildgraph(cur.right,cur)\n buildgraph(root,0)\n \n infected = set()\n queue = [(start,0)]\n while queue:\n node,t=queue.pop(0)\n infected.add(node)\n for nei in dict_[node]:\n if nei not in infected:\n queue.append((nei,t+1))\n \n return t\n\n\n\n``` | 1 | You are given the `root` of a binary tree with **unique** values, and an integer `start`. At minute `0`, an **infection** starts from the node with value `start`.
Each minute, a node becomes infected if:
* The node is currently uninfected.
* The node is adjacent to an infected node.
Return _the number of minutes needed for the entire tree to be infected._
**Example 1:**
**Input:** root = \[1,5,3,null,4,10,6,9,2\], start = 3
**Output:** 4
**Explanation:** The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
**Example 2:**
**Input:** root = \[1\], start = 1
**Output:** 0
**Explanation:** At minute 0, the only node in the tree is infected so we return 0.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 105`
* Each node has a **unique** value.
* A node with a value of `start` exists in the tree. | How can we find the brightness at every position on the street? We can use a hash table to store the change in brightness from the previous position to the current position. |
Solution for Beginners : Amount of Time for Binary Tree to Be Infected (faster than 97% submission) | amount-of-time-for-binary-tree-to-be-infected | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nVery similar to the question https://leetcode.com/problems/all-nodes-distance-k-in-binary-tree/\nFirst Solve the previous question and then come to this.\nSteps are explained in comments.\nCode is pretty lengthy but very efficeint (faster than 97 % submissions).\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findNode(self, root, start):\n if root == None:\n return\n if root.val == start:\n return root\n else:\n return self.findNode(root.left, start) or self.findNode(root.right, start)\n\n def markParents(self, root, parentMap):\n queue = deque()\n queue.append(root)\n while queue:\n n = len(queue)\n for i in range(n):\n curr = queue.popleft()\n if curr.left != None:\n parentMap[curr.left] = curr\n queue.append(curr.left)\n if curr.right != None:\n parentMap[curr.right] = curr\n queue.append(curr.right)\n \n def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:\n # 1. Get the target Node first\n target = self.findNode(root, start)\n # 2. make the parentMap as done in previous question i.e all Nodes at distance k using the bfs traversal\n parentMap = defaultdict() # {child : parent}\n self.markParents(root, parentMap)\n queue = deque()\n queue.append(target)\n visited = defaultdict()\n visited[target] = True\n time = 0\n # 3. use a second bfs traversal to mark them all as visited and each time increase the time += 1\n while queue:\n n = len(queue)\n \n for i in range(n):\n curr = queue.popleft()\n if curr.left != None and visited.get(curr.left) == None:\n visited[curr.left] = True\n queue.append(curr.left)\n if curr.right != None and visited.get(curr.right) == None:\n visited[curr.right] = True\n queue.append(curr.right)\n if parentMap.get(curr) != None and visited.get(parentMap.get(curr)) == None:\n visited[parentMap.get(curr)] = True\n queue.append(parentMap.get(curr))\n # 4. After marking all of them , time is incremented to 1\n time += 1\n \n # Since we dont count the target Node time so final time is decremented by 1\n return time - 1 \n``` | 0 | You are given the `root` of a binary tree with **unique** values, and an integer `start`. At minute `0`, an **infection** starts from the node with value `start`.
Each minute, a node becomes infected if:
* The node is currently uninfected.
* The node is adjacent to an infected node.
Return _the number of minutes needed for the entire tree to be infected._
**Example 1:**
**Input:** root = \[1,5,3,null,4,10,6,9,2\], start = 3
**Output:** 4
**Explanation:** The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
**Example 2:**
**Input:** root = \[1\], start = 1
**Output:** 0
**Explanation:** At minute 0, the only node in the tree is infected so we return 0.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 105`
* Each node has a **unique** value.
* A node with a value of `start` exists in the tree. | How can we find the brightness at every position on the street? We can use a hash table to store the change in brightness from the previous position to the current position. |
[Python3] bfs | amount-of-time-for-binary-tree-to-be-infected | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/b7391a11acc4e9dbe563ebef84f8d78f7943a0f7) for solutions of weekly 307. \n\n**Intuition**\nI find it easier to treat the tree as a graph. First, I convert the tree to graph. Then I run a BFS to find the furthest away point which represents the answer. \n\n**Analysis**\nTime complexity O(N)\nSpace complexity O(N)\t\t\n\n```\nclass Solution: \t\t\n def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:\n graph = defaultdict(list)\n \n stack = [(root, None)]\n while stack: \n n, p = stack.pop()\n if p: \n graph[p.val].append(n.val)\n graph[n.val].append(p.val)\n if n.left: stack.append((n.left, n))\n if n.right: stack.append((n.right, n))\n \n ans = -1\n seen = {start}\n queue = deque([start])\n while queue: \n for _ in range(len(queue)): \n u = queue.popleft()\n for v in graph[u]: \n if v not in seen: \n seen.add(v)\n queue.append(v)\n ans += 1\n return ans \n``` | 39 | You are given the `root` of a binary tree with **unique** values, and an integer `start`. At minute `0`, an **infection** starts from the node with value `start`.
Each minute, a node becomes infected if:
* The node is currently uninfected.
* The node is adjacent to an infected node.
Return _the number of minutes needed for the entire tree to be infected._
**Example 1:**
**Input:** root = \[1,5,3,null,4,10,6,9,2\], start = 3
**Output:** 4
**Explanation:** The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
**Example 2:**
**Input:** root = \[1\], start = 1
**Output:** 0
**Explanation:** At minute 0, the only node in the tree is infected so we return 0.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 105`
* Each node has a **unique** value.
* A node with a value of `start` exists in the tree. | How can we find the brightness at every position on the street? We can use a hash table to store the change in brightness from the previous position to the current position. |
Python DFS Soln | Faster than 90% w/ Proof | Easy to Understand | amount-of-time-for-binary-tree-to-be-infected | 0 | 1 | Idea is that we can mutate the given tree node to hold parent pointers.\n1. Add parent pointer to all the nodes\n2. Calculate max depth from the start node\n```\ndef amountOfTime(self, root: Optional[TreeNode], start: int) -> int:\n\t# DFS function to add parent pointer to all nodes and get the start node\n\tdef addParent(node, parent):\n\t\tif not node:\n\t\t\treturn\n\n\t\tnode.parent = parent # mutating node and adding parent pointer\n\t\tif node.val == start: # get the start node\n\t\t\tnonlocal startNode \n\t\t\tstartNode = node\n\n\t\taddParent(node.left, node)\n\t\taddParent(node.right, node)\n\t\n\t# DFS function to calculate root to leaf maximum depth, here root is start node\n\tdef maxDepth(node):\n\t\tif not node or node in seen:\n\t\t\treturn 0\n\n\t\tseen.add(node)\n\n\t\treturn 1 + max(maxDepth(node.left), maxDepth(node.right), maxDepth(node.parent))\n\n\tseen = set()\n\tstartNode = None\n\taddParent(root, None)\n\n\treturn maxDepth(startNode) - 1 # -1 to exclude the startNode\n```\n\nTime: `O(n)` \nSpace: `O(n)`\n\n\n\n\n | 1 | You are given the `root` of a binary tree with **unique** values, and an integer `start`. At minute `0`, an **infection** starts from the node with value `start`.
Each minute, a node becomes infected if:
* The node is currently uninfected.
* The node is adjacent to an infected node.
Return _the number of minutes needed for the entire tree to be infected._
**Example 1:**
**Input:** root = \[1,5,3,null,4,10,6,9,2\], start = 3
**Output:** 4
**Explanation:** The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
**Example 2:**
**Input:** root = \[1\], start = 1
**Output:** 0
**Explanation:** At minute 0, the only node in the tree is infected so we return 0.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 105`
* Each node has a **unique** value.
* A node with a value of `start` exists in the tree. | How can we find the brightness at every position on the street? We can use a hash table to store the change in brightness from the previous position to the current position. |
Python3 || Recursive || Simple | amount-of-time-for-binary-tree-to-be-infected | 0 | 1 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n\n graph = []\n\n def init_graph(self, node):\n if node.left:\n self.graph[node.val].append(node.left.val)\n self.graph[node.left.val].append(node.val)\n self.init_graph(node.left)\n if node.right:\n self.graph[node.val].append(node.right.val)\n self.graph[node.right.val].append(node.val)\n self.init_graph(node.right)\n\n def height(self, v, p):\n if v == None:\n return -1\n else:\n m = -1\n for u in self.graph[v]:\n if u != p:\n m = max(m, self.height(u, v))\n return 1 + m\n\n def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:\n self.graph = [[] for _ in range(10**5 + 1)]\n self.init_graph(root)\n return self.height(start, -1)\n``` | 2 | You are given the `root` of a binary tree with **unique** values, and an integer `start`. At minute `0`, an **infection** starts from the node with value `start`.
Each minute, a node becomes infected if:
* The node is currently uninfected.
* The node is adjacent to an infected node.
Return _the number of minutes needed for the entire tree to be infected._
**Example 1:**
**Input:** root = \[1,5,3,null,4,10,6,9,2\], start = 3
**Output:** 4
**Explanation:** The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.
**Example 2:**
**Input:** root = \[1\], start = 1
**Output:** 0
**Explanation:** At minute 0, the only node in the tree is infected so we return 0.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 105]`.
* `1 <= Node.val <= 105`
* Each node has a **unique** value.
* A node with a value of `start` exists in the tree. | How can we find the brightness at every position on the street? We can use a hash table to store the change in brightness from the previous position to the current position. |
[Python3] Heap/Priority Queue, O(NlogN + klogk) | find-the-k-sum-of-an-array | 0 | 1 | **Initial Observation**\n1. Given `n` can be as large as `10^5`, the time complexity of this problem has to be no worse than log-linear.\n2. This problem is dealing with *subsequences* but not *subarrays*, indicating we can shuffle the order of the original array, e.g. by sorting it.\n3. Given `-10^9 <= nums[i] <= 10^9`, indicating we need to be *clever* when dealing with positive and negative numbers.\n4. Given we need to return the `k`-th largest subsequence sum, indicating we can use a min-heap to store the possible results.\n\n**Implementation**\n1. We find the sum of all positive numbers. This is the maximum possible sum among all subsequence sums. We initialize our min-heap `ans` to be `[maxSum]`.\n2. We create an array `absNums` of the absolute values, sorted from smallest to largest.\n3. We create a max-heap `maxHeap`. It will start with one pair in it. That pair will be `(maxSum - absNums[0], 0)`. The pairs are compared each time with largest sum first.\n4. Before we have `k` elements in `ans`, we will:\n```\npop (nextSum, i) from maxHeap\npush nextSum to ans\nif i + 1 < N:\n\tpush (nextSum + absNums[i] - absNums[i + 1], i + 1) to maxHeap\n\tpush (nextSum - absNums[i + 1], i + 1) to maxHeap\n```\n\n**Why we need two pushs following each pop from the max-heap?** (by @gonpachiro)\nIn this [post](https://stackoverflow.com/a/33220735), [David Eisenstat](https://stackoverflow.com/users/2144669/david-eisenstat) shared an intuitive explanation. Basically, we maintain a tree-structure via a min-heap to record the subsequence sums. Each time we delete a node, we insert its children. This way, we don\'t need to calculate every subsequence sum explicitly (i.e. by adding and subtracting rather than summing from scratch).\n\n**Complexity**\nTime Complexity: `O(NlogN + klogk)` for sorting and heap operations\nSpace Complexity: `O(N + k)`, for using `absNums`, `ans` and `maxHeap`\n \n **Solution**\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n maxSum = sum([max(0, num) for num in nums])\n absNums = sorted([abs(num) for num in nums])\n maxHeap = [(-maxSum + absNums[0], 0)]\n ans = [maxSum]\n while len(ans) < k:\n nextSum, i = heapq.heappop(maxHeap)\n heapq.heappush(ans, -nextSum)\n if i + 1 < len(absNums):\n heapq.heappush(maxHeap, (nextSum - absNums[i] + absNums[i + 1], i + 1))\n heapq.heappush(maxHeap, (nextSum + absNums[i + 1], i + 1))\n return ans[0]\n```\n\nPlease upvote if you find the solution helpful. Kudos to [btilly](https://stackoverflow.com/users/585411/btilly)\'s [post](https://stackoverflow.com/questions/72114300) for inspiration.\n\n**Cleaner Solution Using One Heap** (by @celestez)\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n maxSum = sum([max(0, num) for num in nums])\n absNums = sorted([abs(num) for num in nums])\n maxHeap, nextSum = [(-maxSum + absNums[0], 0)], -maxSum\n for _ in range(k - 1):\n nextSum, i = heapq.heappop(maxHeap)\n if i + 1 < len(absNums):\n heapq.heappush(maxHeap, (nextSum - absNums[i] + absNums[i + 1], i + 1))\n heapq.heappush(maxHeap, (nextSum + absNums[i + 1], i + 1))\n return -nextSum\n``` | 91 | You are given an integer array `nums` and a **positive** integer `k`. You can choose any **subsequence** of the array and sum all of its elements together.
We define the **K-Sum** of the array as the `kth` **largest** subsequence sum that can be obtained (**not** necessarily distinct).
Return _the K-Sum of the array_.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Note** that the empty subsequence is considered to have a sum of `0`.
**Example 1:**
**Input:** nums = \[2,4,-2\], k = 5
**Output:** 2
**Explanation:** All the possible subsequence sums that we can obtain are the following sorted in decreasing order:
- 6, 4, 4, 2, 2, 0, 0, -2.
The 5-Sum of the array is 2.
**Example 2:**
**Input:** nums = \[1,-2,3,4,-10,12\], k = 16
**Output:** 10
**Explanation:** The 16-Sum of the array is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= k <= min(2000, 2n)` | null |
[Python3] priority queue | find-the-k-sum-of-an-array | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/b7391a11acc4e9dbe563ebef84f8d78f7943a0f7) for solutions of weekly 307. \n\n**Intuition**\nHere, I will discuss a strategy to find the kth largest subsequence sum. \n* We start from the sum of all positive numbers in `nums` which is the largest one (say `m`); \n* To proceed, we subtract absolute values from `m`; \n\t* If the number is positive, this is equivalent to removing the number from the subsequence sum; \n\t* If the number is negative, this is equivalent to adding the number to the subsequence sum; \n* To enumerate all possitibilites, we generate a tree-ish path to cover different combinations;\n\t* This can be done by repeatedly generating two branches at each point with one always include a value at a given index `i` and the other always exclude the value. \n\nHere, I use a priority queue to control for the size so that the runtime won\'t explode. \n\n**Analysis**\nTime complexity O(NlogN + KlogK)\nSpace complexity O(N + K)\n\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n m = sum(x for x in nums if x > 0)\n pq = [(-m, 0)] \n vals = sorted(abs(x) for x in nums)\n for _ in range(k): \n x, i = heappop(pq)\n if i < len(vals): \n heappush(pq, (x+vals[i], i+1))\n if i: heappush(pq, (x-vals[i-1]+vals[i], i+1))\n return -x\n``` | 45 | You are given an integer array `nums` and a **positive** integer `k`. You can choose any **subsequence** of the array and sum all of its elements together.
We define the **K-Sum** of the array as the `kth` **largest** subsequence sum that can be obtained (**not** necessarily distinct).
Return _the K-Sum of the array_.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Note** that the empty subsequence is considered to have a sum of `0`.
**Example 1:**
**Input:** nums = \[2,4,-2\], k = 5
**Output:** 2
**Explanation:** All the possible subsequence sums that we can obtain are the following sorted in decreasing order:
- 6, 4, 4, 2, 2, 0, 0, -2.
The 5-Sum of the array is 2.
**Example 2:**
**Input:** nums = \[1,-2,3,4,-10,12\], k = 16
**Output:** 10
**Explanation:** The 16-Sum of the array is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= k <= min(2000, 2n)` | null |
Clear Py3 solution | find-the-k-sum-of-an-array | 0 | 1 | # Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n ps = sum([x for x in nums if x >= 0])\n al = sorted([x if x >= 0 else -x for x in nums])\n # print(al)\n q = SortedList()\n q.add((ps, 0))\n \n for i in range(k):\n # print(q, q[-1])\n s, idx = q.pop()\n # print(s)\n for j in range(idx, min(len(al), idx + k)):\n if len(q) > k and s - al[j] < q[-k][0]:\n break\n q.add((s - al[j], j + 1))\n return s\n \n``` | 0 | You are given an integer array `nums` and a **positive** integer `k`. You can choose any **subsequence** of the array and sum all of its elements together.
We define the **K-Sum** of the array as the `kth` **largest** subsequence sum that can be obtained (**not** necessarily distinct).
Return _the K-Sum of the array_.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Note** that the empty subsequence is considered to have a sum of `0`.
**Example 1:**
**Input:** nums = \[2,4,-2\], k = 5
**Output:** 2
**Explanation:** All the possible subsequence sums that we can obtain are the following sorted in decreasing order:
- 6, 4, 4, 2, 2, 0, 0, -2.
The 5-Sum of the array is 2.
**Example 2:**
**Input:** nums = \[1,-2,3,4,-10,12\], k = 16
**Output:** 10
**Explanation:** The 16-Sum of the array is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= k <= min(2000, 2n)` | null |
FSM + full binary tree + SortedList | find-the-k-sum-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n \n\n """\n 1: delete abs(nums[_]), 0: do not delete abs[nums[_]] from max_value\n FSM(\u6709\u9650\u72B6\u6001\u673A) is a full binary tree\n 1\n 11\n 111\n 101\n 01\n 011\n 001\n binary tree must satisfy:\n 1. child != father + "0"\n 2. each node at least one digit is "1"\n """\n from sortedcontainers import SortedList\n\n max_value = sum(_ for _ in nums if _ > 0)\n nums = sorted(abs(_) for _ in nums)\n sl = SortedList([(max_value, 0)]) # sub first element\n\n for _ in range(k):\n v, index = sl.pop(-1)\n if index < len(nums):\n sl.add((v - nums[index], index + 1))\n if index > 0:\n sl.add((v + nums[index - 1] - nums[index], index + 1))\n return v\n \n``` | 0 | You are given an integer array `nums` and a **positive** integer `k`. You can choose any **subsequence** of the array and sum all of its elements together.
We define the **K-Sum** of the array as the `kth` **largest** subsequence sum that can be obtained (**not** necessarily distinct).
Return _the K-Sum of the array_.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Note** that the empty subsequence is considered to have a sum of `0`.
**Example 1:**
**Input:** nums = \[2,4,-2\], k = 5
**Output:** 2
**Explanation:** All the possible subsequence sums that we can obtain are the following sorted in decreasing order:
- 6, 4, 4, 2, 2, 0, 0, -2.
The 5-Sum of the array is 2.
**Example 2:**
**Input:** nums = \[1,-2,3,4,-10,12\], k = 16
**Output:** 10
**Explanation:** The 16-Sum of the array is 10.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `-109 <= nums[i] <= 109`
* `1 <= k <= min(2000, 2n)` | null |
[Python] Straight forward solution; Explained | longest-subsequence-with-limited-sum | 0 | 1 | **Three steps**. See the details in the comments.\n\n```\nclass Solution:\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n # step 1: sort the nums, O(logn)\n nums.sort()\n # step 2: calculate the running sum of the nums, O(n)\n self.running_sum = []\n rs = 0\n for num in nums:\n rs += num\n self.running_sum.append(rs)\n \n # step 3: binary search the running sum value that is less than or equal to each query\n ans = []\n for q in queries:\n rs_idx = self.binarySearch(q)\n ans.append(rs_idx + 1)\n return ans\n \n \n def binarySearch(self, q):\n start = 0\n end = len(self.running_sum) - 1\n while start <= end:\n mid = (start + end) // 2\n if self.running_sum[mid] == q:\n return mid\n elif self.running_sum[mid] < q:\n start = mid + 1\n else:\n end = mid - 1\n # make sure that the returned index points to the less-than-or-equal-to value\n if self.running_sum[mid] > q:\n return mid - 1\n return mid\n``` | 1 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
[Python3] 2-line binary search | longest-subsequence-with-limited-sum | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/ea6bc01b091cbf032b9c7ac2d3c09cb4f5cd0d2d) for solutions of weekly 308. \n\n**Intuition**\nFor each query, we always try to use the smallest number availabel for the summation, which results in below binary search implementation. \n\n**Analysis**\nTime complexity `O((M+N)logN)`\nSpace complexity `O(M+N)`\n\n```\nclass Solution: \n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n prefix = list(accumulate(sorted(nums)))\n return [bisect_right(prefix, q) for q in queries]\n``` | 9 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
Prefix Sum | longest-subsequence-with-limited-sum | 1 | 1 | The minimal sum of any `k` elements of the array is the sum of `k` smallest elements.\n\nSo, we sort the array first. Then, we apply prefix sum so that the array `i`-th element of the array contains the minimal sum of `i` elements.\n\nFinally, we use a binary search to find the maximum number of elements for each query.\n\n**Python 3**\n```python\nclass Solution:\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n nums = list(accumulate(sorted(nums)))\n return [bisect_right(nums, q) for q in queries]\n```\n\n**Java**\n```java\npublic int[] answerQueries(int[] nums, int[] queries) {\n Arrays.sort(nums);\n Arrays.parallelPrefix(nums, Integer::sum);\n for (int i = 0; i < queries.length; ++i) {\n int pos = Arrays.binarySearch(nums, queries[i] + 1);\n queries[i] = pos < 0 ? ~pos : pos;\n }\n return queries;\n}\n```\n**C++**\n```cpp\nvector<int> answerQueries(vector<int>& nums, vector<int>& queries) {\n sort(begin(nums), end(nums));\n partial_sum(begin(nums), end(nums), begin(nums));\n transform(begin(queries), end(queries), begin(queries), [&](int q){ \n return upper_bound(begin(nums), end(nums), q) - begin(nums);\n });\n return queries;\n}\n``` | 21 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
✅Python || 2 Easy Approaches || Prefix Sum | longest-subsequence-with-limited-sum | 0 | 1 | ```\nclass Solution:\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n \n numsSorted = sorted(nums)\n res = []\n\t\t\n for q in queries:\n total = 0\n count = 0\n for num in numsSorted:\n total += num\n count += 1\n if total > q:\n count -= 1\n break\n res.append(count)\n \n return res\n```\n\n\nSolution 2 (Prefix Sum):\n```\nclass Solution:\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n \n ans = []\n\n nums.sort()\n sumx = []\n res = 0\n for x in nums:\n res += x\n sumx.append(res)\n\n for j in range(len(queries)):\n for i, y in enumerate(sumx):\n if y <= queries[j]:\n continue\n else:\n ans.append(i)\n break\n else:\n if len(ans) < j + 1:\n ans.append(len(nums))\n \n return ans\n``` | 2 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
✅ Python Solution | Easy Approach | longest-subsequence-with-limited-sum | 0 | 1 | ```\nclass Solution:\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n answer = [0] * len(queries)\n for id, query in enumerate(queries):\n spec_sum = 0\n for i, number in enumerate(sorted(nums)):\n spec_sum += number\n\n if spec_sum <= query:\n answer[id] += 1\n else:\n break\n\n return answer\n``` | 2 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
[Java/Python 3] Sort and Binary Search, w/ brief explanation and analysis. | longest-subsequence-with-limited-sum | 1 | 1 | Try to use small numbers in subsequence so that we can make it as long as possible. Therefore, it is logical to sort the input array and then use prefix sum array to binary search to locate the longest size.\n\n```java\n public int[] answerQueries(int[] nums, int[] queries) {\n int m = queries.length, n = nums.length, i = 0;\n Arrays.sort(nums);\n int[] prefixSum = new int[n + 1];\n for (int num : nums) {\n prefixSum[i + 1] = prefixSum[i++] + num;\n }\n i = 0;\n int[] ans = new int[m];\n for (int q : queries) {\n ans[i++] = binarySearch(prefixSum, q) - 1;\n }\n return ans;\n }\n private int binarySearch(int[] a, int k) {\n int lo = 0, hi = a.length;\n while (lo < hi) {\n int mid = lo + (hi - lo) / 2;\n if (a[mid] <= k) {\n lo = mid + 1;\n }else {\n hi = mid;\n }\n }\n return lo;\n }\n```\n\n----\n\n\n**Q & A**\n\nQ1: `ans.append(bisect.bisect_right(prefix_sum, q) - 1)` - what does this line mean?\nA1: `bisect.bisect_right(prefix_sum, q)` - Binary seach to find the largest index `idx` such that all `prefix_sum[ : idx] <= q` and all `prefix_sum[idx :] > q`. Since we put a dummy value `0` in the front of the prefix sum array `prefix_sum`, it is necessary to deduct `1` from `idx`. Therefore, `idx - 1` is the longest size of subsequence that is no greater than `q`.\n\n**End of Q & A**\n\n\n```python\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n prefix_sum = [0]\n for n in nums:\n prefix_sum.append(prefix_sum[-1] + n)\n ans = [] \n for q in queries:\n ans.append(bisect.bisect(prefix_sum, q) - 1)\n return ans\n```\nOr shorter\n\n```python\n def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:\n prefix_sum = [0]\n for n in sorted(nums):\n prefix_sum.append(prefix_sum[-1] + n)\n return [bisect_right(prefix_sum, q) - 1 for q in queries]\n```\n**Analysis:**\n\nTime: `O((m + n)logn)`, space: `O(m + n)` - including sorting space, where `m = queries.length, n = nums.length`. | 14 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
Python 1-liner functional programming. O((m + n) * log(n)), beats 97.88% runtime. | longest-subsequence-with-limited-sum | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- Sort `nums`\n- Calculate `prefix_sums`.\n- Binary search the `prefix_sums` for every `query`.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O((n + m)*log(n))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def answerQueries(self, nums: list[int], queries: list[int]) -> list[int]:\n return map(\n bisect.bisect,\n repeat(list(accumulate(sorted(nums)))),\n queries,\n )\n``` | 1 | You are given an integer array `nums` of length `n`, and an integer array `queries` of length `m`.
Return _an array_ `answer` _of length_ `m` _where_ `answer[i]` _is the **maximum** size of a **subsequence** that you can take from_ `nums` _such that the **sum** of its elements is less than or equal to_ `queries[i]`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[4,5,2,1\], queries = \[3,10,21\]
**Output:** \[2,3,4\]
**Explanation:** We answer the queries as follows:
- The subsequence \[2,1\] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer\[0\] = 2.
- The subsequence \[4,5,1\] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer\[1\] = 3.
- The subsequence \[4,5,2,1\] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer\[2\] = 4.
**Example 2:**
**Input:** nums = \[2,3,4,5\], queries = \[1\]
**Output:** \[0\]
**Explanation:** The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer\[0\] = 0.
**Constraints:**
* `n == nums.length`
* `m == queries.length`
* `1 <= n, m <= 1000`
* `1 <= nums[i], queries[i] <= 106` | null |
✅[Python3//C++//Java]✅ Easy and understand (Stack Simulation) | removing-stars-from-a-string | 1 | 1 | This code defines a function removeStars that takes a string s as input and returns a modified version of the input string with all asterisks (*) removed along with the preceding character.\n\nHere is a step-by-step explanation of the code:\n1. Initialize an empty list ans that will be used to build the modified string.\n2. Loop through each character i in the input string s.\n3. If the current character i is an asterisk, remove the last element from the ans list.\n4. If the current character i is not an asterisk, add it to the end of the ans list.\n5. Join the elements in the ans list into a string and return the result.\n\nFor example, if the input string is ``abc*d*ef*g*``, the function would first create an empty list ``ans = []``. Then, it would loop through each character in the string as follows:\n- i = \'a\': append \'a\' to ans (ans = [\'a\'])\n- i = \'b\': append \'b\' to ans (ans = [\'a\', \'b\'])\n- i = \'c\': append \'c\' to ans (ans = [\'a\', \'b\', \'c\'])\n- i = \'*\': remove the last element from ans (ans = [\'a\', \'b\'])\n- i = \'d\': append \'d\' to ans (ans = [\'a\', \'b\', \'d\'])\n- i = \'*\': remove the last element from ans (ans = [\'a\',\'b\'])\n- i = \'e\': append \'e\' to ans (ans = [\'a\',\'b\', \'e\'])\n- i = \'f\': append \'f\' to ans (ans = [\'a\',\'b\', \'e\', \'f\'])\n- i = \'*\': remove the last element from ans (ans = [\'a\',\'b\', \'e\'])\n- i = \'g\': append \'g\' to ans (ans = [\'a\',\'b\', \'e\', \'g\'])\n- i== \'*\': remove the last element from ans (ans = [\'a\',\'b\', \'e\'])\n\nFinally, the function would join the elements in ans into a string (\'abe\') and return the result.\n# Please Upvote \uD83D\uDE07\n# Code\n<iframe src="https://leetcode.com/playground/jEUgwsYM/shared" frameBorder="0" width="800" height="310"></iframe>\n\n\n | 266 | You are given a string `s`, which contains stars `*`.
In one operation, you can:
* Choose a star in `s`.
* Remove the closest **non-star** character to its **left**, as well as remove the star itself.
Return _the string after **all** stars have been removed_.
**Note:**
* The input will be generated such that the operation is always possible.
* It can be shown that the resulting string will always be unique.
**Example 1:**
**Input:** s = "leet\*\*cod\*e "
**Output:** "lecoe "
**Explanation:** Performing the removals from left to right:
- The closest character to the 1st star is 't' in "lee**t**\*\*cod\*e ". s becomes "lee\*cod\*e ".
- The closest character to the 2nd star is 'e' in "le**e**\*cod\*e ". s becomes "lecod\*e ".
- The closest character to the 3rd star is 'd' in "leco**d**\*e ". s becomes "lecoe ".
There are no more stars, so we return "lecoe ".
**Example 2:**
**Input:** s = "erase\*\*\*\*\* "
**Output:** " "
**Explanation:** The entire string is removed, so we return an empty string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters and stars `*`.
* The operation above can be performed on `s`. | null |
Beginner Friendly || Full explained || [Java/C++/Python] | removing-stars-from-a-string | 1 | 1 | # Intuition\n1. Use a stack to store the characters. Pop one character off the stack at each star. Otherwise, we push the character onto the stack\n\n# Approach\n1. **Base Case Check:**\n - If the input string is empty or null, the method returns an empty string.\n2. **Stack Initialization:**\n - A stack is initialized to store non-asterisk characters.\n3. **Iterate Through the Input String:**\n - The code iterates through each character in the input string. If the current character is not an asterisk, it is pushed onto the stack. If the current character is an asterisk and the stack is not empty, a character is popped from the stack, effectively removing the pair.\n4. **Build Result String:**\n - After processing the input string, a StringBuilder is used to build the result string by appending characters from the stack in reverse order.\n5. **Return Result:**\n - The final result is obtained by reversing the StringBuilder and converting it to a string.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public String removeStars(String s) {\n if(s.length()==0 || s==null) return "";\n Stack<Character> st = new Stack<>();\n\n for(int i=0; i<s.length(); i++) {\n char ch = s.charAt(i);\n if(ch!=\'*\') {\n st.push(ch);\n }\n else {\n if(!st.isEmpty()) {\n st.pop();\n }\n }\n }\n if(st.isEmpty()) return "";\n StringBuilder sb = new StringBuilder();\n while(!st.isEmpty()) {\n sb.append(st.pop());\n }\n return sb.reverse().toString();\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string removeStars(string s) {\n // Base Case Check\n if (s.length() == 0) return "";\n\n stack<char> st;\n\n // Iterate Through the Input String\n for (char ch : s) {\n if (ch != \'*\') {\n st.push(ch);\n } else {\n if (!st.empty()) {\n st.pop();\n }\n }\n }\n\n // Build Result String\n string result;\n while (!st.empty()) {\n result += st.top();\n st.pop();\n }\n\n // Reverse the Result String\n reverse(result.begin(), result.end());\n\n return result;\n }\n};\n```\n```Python []\nclass Solution:\n def removeStars(self, s: str) -> str:\n # Base Case Check\n if not s:\n return ""\n\n stack = []\n\n # Iterate Through the Input String\n for ch in s:\n if ch != \'*\':\n stack.append(ch)\n else:\n if stack:\n stack.pop()\n\n # Build Result String\n result = \'\'.join(stack[::-1])\n\n return result\n``` | 1 | You are given a string `s`, which contains stars `*`.
In one operation, you can:
* Choose a star in `s`.
* Remove the closest **non-star** character to its **left**, as well as remove the star itself.
Return _the string after **all** stars have been removed_.
**Note:**
* The input will be generated such that the operation is always possible.
* It can be shown that the resulting string will always be unique.
**Example 1:**
**Input:** s = "leet\*\*cod\*e "
**Output:** "lecoe "
**Explanation:** Performing the removals from left to right:
- The closest character to the 1st star is 't' in "lee**t**\*\*cod\*e ". s becomes "lee\*cod\*e ".
- The closest character to the 2nd star is 'e' in "le**e**\*cod\*e ". s becomes "lecod\*e ".
- The closest character to the 3rd star is 'd' in "leco**d**\*e ". s becomes "lecoe ".
There are no more stars, so we return "lecoe ".
**Example 2:**
**Input:** s = "erase\*\*\*\*\* "
**Output:** " "
**Explanation:** The entire string is removed, so we return an empty string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters and stars `*`.
* The operation above can be performed on `s`. | null |
Python!! Python3 Understandable and simplest solution. | removing-stars-from-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeStars(self, s: str) -> str:\n outputArr = []\n for chars in s:\n if chars == \'*\':\n outputArr.pop()\n else:\n outputArr.append(chars)\n \n return \'\'.join(outputArr)\n``` | 1 | You are given a string `s`, which contains stars `*`.
In one operation, you can:
* Choose a star in `s`.
* Remove the closest **non-star** character to its **left**, as well as remove the star itself.
Return _the string after **all** stars have been removed_.
**Note:**
* The input will be generated such that the operation is always possible.
* It can be shown that the resulting string will always be unique.
**Example 1:**
**Input:** s = "leet\*\*cod\*e "
**Output:** "lecoe "
**Explanation:** Performing the removals from left to right:
- The closest character to the 1st star is 't' in "lee**t**\*\*cod\*e ". s becomes "lee\*cod\*e ".
- The closest character to the 2nd star is 'e' in "le**e**\*cod\*e ". s becomes "lecod\*e ".
- The closest character to the 3rd star is 'd' in "leco**d**\*e ". s becomes "lecoe ".
There are no more stars, so we return "lecoe ".
**Example 2:**
**Input:** s = "erase\*\*\*\*\* "
**Output:** " "
**Explanation:** The entire string is removed, so we return an empty string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters and stars `*`.
* The operation above can be performed on `s`. | null |
🐍✅ Python3 easiest solution 🔥🔥 | removing-stars-from-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using Stack**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- push in stack till not found **\'*\'**\n- when found **"*"** this symbol pop from stack.\n- do this till end of s.\n- return stack in form of string\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeStars(self, s: str) -> str:\n stack = []\n i = 0\n n = len(s)\n while i < n :\n if s[i] != \'*\':\n stack.append(s[i])\n else:\n stack.pop()\n i += 1\n return \'\'.join(stack)\n```\n# Please like and comment below ( \u0361\u2688\u202F\u035C\u0296 \u0361\u2688) \uD83D\uDC49 | 1 | You are given a string `s`, which contains stars `*`.
In one operation, you can:
* Choose a star in `s`.
* Remove the closest **non-star** character to its **left**, as well as remove the star itself.
Return _the string after **all** stars have been removed_.
**Note:**
* The input will be generated such that the operation is always possible.
* It can be shown that the resulting string will always be unique.
**Example 1:**
**Input:** s = "leet\*\*cod\*e "
**Output:** "lecoe "
**Explanation:** Performing the removals from left to right:
- The closest character to the 1st star is 't' in "lee**t**\*\*cod\*e ". s becomes "lee\*cod\*e ".
- The closest character to the 2nd star is 'e' in "le**e**\*cod\*e ". s becomes "lecod\*e ".
- The closest character to the 3rd star is 'd' in "leco**d**\*e ". s becomes "lecoe ".
There are no more stars, so we return "lecoe ".
**Example 2:**
**Input:** s = "erase\*\*\*\*\* "
**Output:** " "
**Explanation:** The entire string is removed, so we return an empty string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters and stars `*`.
* The operation above can be performed on `s`. | null |
Stack.py | removing-stars-from-a-string | 0 | 1 | # Code\n```\nclass Solution:\n def removeStars(self, s: str) -> str:\n l=[]\n for i in s:\n if i==\'*\':l.pop()\n else:l.append(i)\n return "".join(l)\n \n\n``` | 1 | You are given a string `s`, which contains stars `*`.
In one operation, you can:
* Choose a star in `s`.
* Remove the closest **non-star** character to its **left**, as well as remove the star itself.
Return _the string after **all** stars have been removed_.
**Note:**
* The input will be generated such that the operation is always possible.
* It can be shown that the resulting string will always be unique.
**Example 1:**
**Input:** s = "leet\*\*cod\*e "
**Output:** "lecoe "
**Explanation:** Performing the removals from left to right:
- The closest character to the 1st star is 't' in "lee**t**\*\*cod\*e ". s becomes "lee\*cod\*e ".
- The closest character to the 2nd star is 'e' in "le**e**\*cod\*e ". s becomes "lecod\*e ".
- The closest character to the 3rd star is 'd' in "leco**d**\*e ". s becomes "lecoe ".
There are no more stars, so we return "lecoe ".
**Example 2:**
**Input:** s = "erase\*\*\*\*\* "
**Output:** " "
**Explanation:** The entire string is removed, so we return an empty string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters and stars `*`.
* The operation above can be performed on `s`. | null |
Python easy solution using stack | removing-stars-from-a-string | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nCreating Stack to maintain the characters of string. if any `*` is found we pop the previous character in stack.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def removeStars(self, s: str) -> str:\n stack = [] # stack to store characters\n for i in s:\n # if any \'*\' is found, pop previous \n if len(stack) >0 and i == \'*\':\n stack.pop()\n else:\n stack.append(i)\n # return the remaining characters to string\n return \'\'.join(stack)\n``` | 1 | You are given a string `s`, which contains stars `*`.
In one operation, you can:
* Choose a star in `s`.
* Remove the closest **non-star** character to its **left**, as well as remove the star itself.
Return _the string after **all** stars have been removed_.
**Note:**
* The input will be generated such that the operation is always possible.
* It can be shown that the resulting string will always be unique.
**Example 1:**
**Input:** s = "leet\*\*cod\*e "
**Output:** "lecoe "
**Explanation:** Performing the removals from left to right:
- The closest character to the 1st star is 't' in "lee**t**\*\*cod\*e ". s becomes "lee\*cod\*e ".
- The closest character to the 2nd star is 'e' in "le**e**\*cod\*e ". s becomes "lecod\*e ".
- The closest character to the 3rd star is 'd' in "leco**d**\*e ". s becomes "lecoe ".
There are no more stars, so we return "lecoe ".
**Example 2:**
**Input:** s = "erase\*\*\*\*\* "
**Output:** " "
**Explanation:** The entire string is removed, so we return an empty string.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters and stars `*`.
* The operation above can be performed on `s`. | null |
C++/Python loop & accumulate||94ms Beats 100% | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n```\ntotal time=time for collecting garbage + time for traveling\n```\nDivide the questions into 2 parts; it might make the solution easier.\ntime for collecting garbage is very easy; other is also not difficult.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nEach item costs 1 unit time to collect it. Count them.\nDuring the iteration find the last indices for items G, P, M.\nUsing accumulate/sum to sum up the travel time.\n\nThe instruction\n```\nif (tG==0 && x.find(\'G\')!=-1) tG=i;\n```\nchecks whether `tG==0`, if not, it does nothing; when `tG==0` then it checks whether ` x.find(\'G\')!=-1`, if yes, set `tG=i`.\n\nSince the iteration is backward, if the \'G\', \'P\', \'M\' are already found, the `x.find` will not proceed & it saves time.\n\nPython code is also provided in the same manner.\n\n[Please turn on English subtitles if necessary]\n[https://youtu.be/TveVxO7mdsI?si=ELYhMCD0em8d-BZk](https://youtu.be/TveVxO7mdsI?si=ELYhMCD0em8d-BZk)\n\nRevised code is faster & runs in 94ms beats 100%. The computing part for travel time uses a loop by one pass.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# C++ Code 107ms beats 100%\n```C++ []\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int garbageCollection(vector<string>& garbage, vector<int>& travel) \n {\n int n=garbage.size();\n int tG=0, tP=0, tM=0;\n int time=0; \n #pragma unroll\n for(int i=n-1; i>=0; i--){//time for collecting garbage\n string x=garbage[i];\n time+=x.size();\n if (tG==0 && x.find(\'G\')!=-1) tG=i;\n if (tP==0 && x.find(\'P\')!=-1) tP=i;\n if (tM==0 && x.find(\'M\')!=-1) tM=i;\n }\n // Add travel time\n time+=accumulate(travel.begin(), travel.begin()+(tG),0)\n +accumulate(travel.begin(), travel.begin()+(tP),0)\n +accumulate(travel.begin(), travel.begin()+(tM),0);\n return time;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n```python []\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n n=len(garbage)\n tG, tP, tM=0, 0, 0\n Time=0\n for i in range(n-1, -1, -1):\n x=garbage[i]\n Time+=len(x)\n if tG==0 and x.find(\'G\')!=-1: tG=i \n if tP==0 and x.find(\'P\')!=-1: tP=i\n if tM==0 and x.find(\'M\')!=-1: tM=i\n Time+=sum(travel[:tG])+sum(travel[:tP])+sum(travel[:tM])\n return Time\n\n \n```\n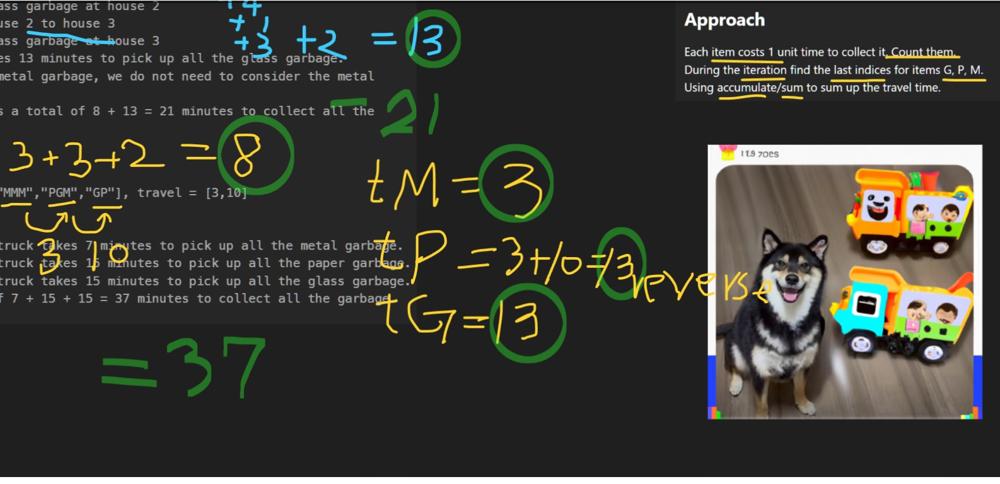\n\n# Revised code runs in 94ms & beats 100% \n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int garbageCollection(vector<string>& garbage, vector<int>& travel) \n {\n const int n=garbage.size();\n const char* GPM="GPM";\n int time=0, t[3]={0}; \n #pragma unroll\n for(int i=n-1; i>=0; i--){//time for collecting garbage\n string& x=garbage[i];\n time+=x.size();\n #pragma unroll\n for(int j=0; j<3; j++)\n if (t[j]==0 && x.find(GPM[j])!=-1) t[j]=i;\n \n }\n sort(t, t+3);\n // Add travel time\n #pragma unroll\n for(int i=0; i<t[2]; i++){\n int c=(i<t[0])?3:((i<t[1])?2:1);\n time+=c*travel[i];\n }\n return time;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n\n``` | 17 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | minimum-amount-of-time-to-collect-garbage | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(HashMaps)***\n1. **Prefix Sum Calculation:**\n\n - `prefixSum` vector stores the prefix sum of the `travel` vector.\n - It helps in calculating the distance traveled up to a certain point efficiently.\n1. **Garbage Collection Information:**\n\n - `garbageLastPos` is an unordered map that tracks the last house index for each type of garbage.\n - `garbageCount` stores the total count of each type of garbage across all houses.\n1. **Garbage Types:**\n\n - The `garbageTypes` array holds the three types of garbage: `M`, `P`, and `G`.\n1. **Main Calculation (Loop):**\n\n - For each garbage type, if there is at least one unit of this garbage:\n - The calculation involves adding the distance traveled to the last house where this garbage type was found (`prefixSum[garbageLastPos[c]]`) and the total count of this garbage type (`garbageCount[c]`).\n - The sum of these distances and counts is accumulated in `ans`.\n1. **Return:**\n\n - The function returns the final value of `ans`, which represents the calculated total for garbage collection considering the conditions mentioned in the code.\n\n# Complexity\n- *Time complexity:*\n $$O(N*K)$$\n \n\n- *Space complexity:*\n $$O(N)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int garbageCollection(vector<string>& garbage, vector<int>& travel) {\n // Vector to store the prefix sum in travel.\n vector<int> prefixSum(travel.size() + 1, 0);\n prefixSum[1] = travel[0];\n for (int i = 1; i < travel.size(); i++) {\n prefixSum[i + 1] = prefixSum[i] + travel[i];\n }\n \n // Map to store garbage type to the last house index.\n unordered_map<char, int> garbageLastPos;\n\n // Map to store the total count of each type of garbage in all houses.\n unordered_map<char, int> garbageCount;\n for (int i = 0; i < garbage.size(); i++) {\n for (char c : garbage[i]) {\n garbageLastPos[c] = i;\n garbageCount[c]++;\n }\n }\n \n // Array to store garbage types.\n char garbageTypes[3] = {\'M\', \'P\', \'G\'};\n int ans = 0;\n for (char c : garbageTypes) {\n // Add only if there is at least one unit of this garbage.\n if (garbageCount[c]) {\n ans += prefixSum[garbageLastPos[c]] + garbageCount[c];\n }\n }\n \n return ans;\n }\n};\n\n\n```\n\n```C []\nstruct GarbageInfo {\n char type;\n int count;\n};\n\nint garbageCollection(char** garbage, int* travel, int garbageSize, int travelSize) {\n int prefixSum[travelSize + 1];\n prefixSum[1] = travel[0];\n for (int i = 1; i < travelSize; i++) {\n prefixSum[i + 1] = prefixSum[i] + travel[i];\n }\n \n struct GarbageInfo garbageLastPos[256]; // Assuming ASCII characters\n struct GarbageInfo garbageCount[256]; // Assuming ASCII characters\n \n for (int i = 0; i < garbageSize; i++) {\n for (int j = 0; garbage[i][j] != \'\\0\'; j++) {\n char c = garbage[i][j];\n garbageLastPos[c].type = c;\n garbageLastPos[c].count = i;\n garbageCount[c].count++;\n }\n }\n \n char garbageTypes[3] = {\'M\', \'P\', \'G\'};\n int ans = 0;\n for (int i = 0; i < 3; i++) {\n char c = garbageTypes[i];\n if (garbageCount[c].count > 0) {\n ans += prefixSum[garbageLastPos[c].count] + garbageCount[c].count;\n }\n }\n \n return ans;\n}\n\n```\n\n```Java []\nclass Solution {\n public int garbageCollection(String[] garbage, int[] travel) {\n // Array to store the prefix sum in travel.\n int[] prefixSum = new int[travel.length + 1];\n prefixSum[1] = travel[0];\n for (int i = 1; i < travel.length; i++) {\n prefixSum[i + 1] = prefixSum[i] + travel[i];\n }\n\n // Map to store garbage type to the last house index.\n Map<Character, Integer>garbageLastPos = new HashMap<Character, Integer>();\n\n // Map to store the total count of each type of garbage in all houses.\n Map<Character, Integer>garbageCount = new HashMap<Character, Integer>();\n for (int i = 0; i < garbage.length; i++) {\n for (char c : garbage[i].toCharArray()) {\n garbageLastPos.put(c, i);\n garbageCount.put(c, garbageCount.getOrDefault(c, 0) + 1);\n }\n }\n\n String garbageTypes = "MPG";\n int ans = 0;\n for (char c : garbageTypes.toCharArray()) {\n // Add only if there is at least one unit of this garbage.\n if (garbageCount.containsKey(c)) {\n ans += prefixSum[garbageLastPos.get(c)] + garbageCount.get(c);\n }\n }\n\n return ans;\n }\n}\n\n```\n\n```python3 []\ndef garbage_collection(garbage, travel):\n prefix_sum = [0] * (len(travel) + 1)\n prefix_sum[1] = travel[0]\n for i in range(1, len(travel)):\n prefix_sum[i + 1] = prefix_sum[i] + travel[i]\n\n garbage_last_pos = {}\n garbage_count = {}\n for i in range(len(garbage)):\n for c in garbage[i]:\n garbage_last_pos[c] = i\n garbage_count[c] = garbage_count.get(c, 0) + 1\n\n garbage_types = [\'M\', \'P\', \'G\']\n ans = 0\n for c in garbage_types:\n if garbage_count.get(c):\n ans += prefix_sum[garbage_last_pos[c]] + garbage_count[c]\n\n return ans\n\n\n\n```\n```javascript []\nfunction garbageCollection(garbage, travel) {\n let prefixSum = Array(travel.length + 1).fill(0);\n prefixSum[1] = travel[0];\n for (let i = 1; i < travel.length; i++) {\n prefixSum[i + 1] = prefixSum[i] + travel[i];\n }\n\n let garbageLastPos = {};\n let garbageCount = {};\n for (let i = 0; i < garbage.length; i++) {\n for (let j = 0; j < garbage[i].length; j++) {\n let c = garbage[i][j];\n garbageLastPos[c] = i;\n garbageCount[c] = (garbageCount[c] || 0) + 1;\n }\n }\n\n let garbageTypes = [\'M\', \'P\', \'G\'];\n let ans = 0;\n for (let c of garbageTypes) {\n if (garbageCount[c]) {\n ans += prefixSum[garbageLastPos[c]] + garbageCount[c];\n }\n }\n\n return ans;\n}\n\n\n```\n\n---\n\n#### ***Approach 2(HashMap and In-place Modification)***\n\n1. **Prefix Sum Calculation:**\n - The code utilizes the `travel` vector to calculate the prefix sum by updating each element in the vector. It reassigns each element with the cumulative sum of all the elements up to that index.\n\n1. **Garbage Types and Positions:**\n\n - It uses an unordered map `garbageLastPos` to store the last house index for each garbage type (`M`, `P`, `G`) encountered in the input.\n - Additionally, it accumulates the total count of all characters in the `garbage` vector by iterating through each string in the vector. The variable `ans` stores this count initially.\n1. **Iterating through Garbage Types:**\n\n - Utilizes a string `garbageTypes` containing the characters `M`, `P`, `G`.\n - Iterates through each character in `garbageTypes` and checks the corresponding last house index for that type in the `garbageLastPos` map.\n - If the last house index for a particular garbage type is 0, it implies no travel time is required for that type. Otherwise, it calculates the travel time for that type using the prefix sum.\n1. **Returning the Total Answer:**\n - The function returns the accumulated value in `ans`, which represents the total calculated travel time required for garbage collection.\n\n\n# Complexity\n- *Time complexity:*\n $$O(N*K)$$\n \n\n- *Space complexity:*\n $$O(N)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int garbageCollection(vector<string>& garbage, vector<int>& travel) {\n // Store the prefix sum in travel itself.\n for (int i = 1; i < travel.size(); i++) {\n travel[i] = travel[i - 1] + travel[i];\n }\n \n // Map to store garbage type to the last house index.\n unordered_map<char, int> garbageLastPos;\n int ans = 0;\n for (int i = 0; i < garbage.size(); i++) {\n for (char c : garbage[i]) {\n garbageLastPos[c] = i;\n }\n ans += garbage[i].size();\n }\n \n string garbageTypes = "MPG";\n for (char c : garbageTypes) {\n // No travel time is required if the last house is at index 0.\n ans += (garbageLastPos[c] == 0 ? 0 : travel[garbageLastPos[c] - 1]);\n }\n \n return ans;\n }\n};\n\n```\n\n```C []\n\n#define MAX_GARBAGE_SIZE 1000\n\nint garbageCollection(char garbage[MAX_GARBAGE_SIZE][MAX_GARBAGE_SIZE], int travel[MAX_GARBAGE_SIZE], int garbageCount) {\n int travelSum[MAX_GARBAGE_SIZE] = {0};\n travelSum[0] = travel[0];\n\n for (int i = 1; i < garbageCount; i++) {\n travelSum[i] = travelSum[i - 1] + travel[i];\n }\n\n int garbageLastPos[256] = {0};\n int ans = 0;\n\n for (int i = 0; i < garbageCount; i++) {\n for (int j = 0; j < strlen(garbage[i]); j++) {\n garbageLastPos[garbage[i][j]] = i;\n }\n ans += strlen(garbage[i]);\n }\n\n char garbageTypes[] = "MPG";\n for (int i = 0; i < strlen(garbageTypes); i++) {\n ans += (garbageLastPos[garbageTypes[i]] == 0 ? 0 : travelSum[garbageLastPos[garbageTypes[i]] - 1]);\n }\n\n return ans;\n}\n\n```\n\n```Java []\nclass Solution {\n public int garbageCollection(String[] garbage, int[] travel) {\n // Store the prefix sum in travel itself.\n for (int i = 1; i < travel.length; i++) {\n travel[i] = travel[i - 1] + travel[i];\n }\n\n // Map to store garbage type to the last house index.\n Map<Character, Integer>garbageLastPos = new HashMap<Character, Integer>();\n int ans = 0;\n for (int i = 0; i < garbage.length; i++) {\n for (char c : garbage[i].toCharArray()) {\n garbageLastPos.put(c, i);\n }\n ans += garbage[i].length();\n }\n\n String garbageTypes = "MPG";\n for (char c : garbageTypes.toCharArray()) {\n // No travel time is required if the last house is at index 0.\n ans += (garbageLastPos.getOrDefault(c, 0) == 0 ? 0 : travel[garbageLastPos.get(c) - 1]);\n }\n\n return ans;\n }\n}\n\n```\n\n```python3 []\n\ndef garbage_collection(garbage, travel):\n for i in range(1, len(travel)):\n travel[i] += travel[i - 1]\n \n garbage_last_pos = {}\n ans = 0\n for i in range(len(garbage)):\n for c in garbage[i]:\n garbage_last_pos[c] = i\n ans += len(garbage[i])\n \n garbage_types = "MPG"\n for c in garbage_types:\n ans += travel[garbage_last_pos.get(c, 0) - 1] if garbage_last_pos.get(c, 0) != 0 else 0\n \n return ans\n\n\n```\n```javascript []\nfunction garbageCollection(garbage, travel) {\n for (let i = 1; i < travel.length; i++) {\n travel[i] += travel[i - 1];\n }\n\n const garbageLastPos = {};\n let ans = 0;\n for (let i = 0; i < garbage.length; i++) {\n for (const c of garbage[i]) {\n garbageLastPos[c] = i;\n }\n ans += garbage[i].length;\n }\n\n const garbageTypes = "MPG";\n for (const c of garbageTypes) {\n ans += (garbageLastPos[c] === 0 ? 0 : travel[garbageLastPos[c] - 1]);\n }\n\n return ans;\n}\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 4 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
【Video】Give me 10 minutes - Beats 98% - How we think about a solution | minimum-amount-of-time-to-collect-garbage | 1 | 1 | # Intuition\nIterate through from the last index.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/GZWR5cWZ3pw\n\n\u25A0 Timeline\n`0:05` Talk about time to pick up all garbages \n`1:44` Talk about time to travel to the next house\n`5:37` Demonstrate how it works\n`8:00` Coding\n`11:12` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,165\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nFirst of all, we have two types of time.\n\n---\n\n\u2B50\uFE0F Points\n\n- Time to pick up garbages\n- Time to travel to the next house\n\n---\n\nWe need to calculate total time of those two times.\n\n### Time to pick up garbages\n\nLet\'s think about this input.\n```\nInput: garbage = ["MMM","PGM","GP"], travel = [3,10]\n```\n\nThis is very simple. The description says "Picking up one unit of any type of garbage takes 1 minute", so total time to pick up all garbages is total number of `M`, `P` and `G`.\n\nIn this case,\n```\n4(= M) + 2(= P) + 1(= G) = 8 minutes\n```\n\n### Time to travel to the next house\n\nTravel time is a little bit tricky. The description says "Each garbage truck starts at house 0 and must visit each house in order; however, they do not need to visit every house".\n\nIn other words, the trucks don\'t have to go to the next house if they already picked up all garbages. On the other hand, they must visit all houses even if one particular garbage is only in the last house.\n\n(Seem like English test lol)\uD83D\uDE05\n\n\n---\n\nProblem\n\nProblem here is that we don\'t know where each truck can finish picking up all garbages.\n\n---\n\nTo solve this problem, my idea is to iterate through from the last house, because we can know where the last house is for each garbage.\n\nTo understand easily, I added extra garbage to the input. Let\'s think about `M` garbage.\n```\nInput: garbage = ["MMM","PGM","GP","M"], travel = [3,10,5]\n```\n\nThe last house has `M` garbage. At index 2 house, there is no `M`. At index 1 and 0 houses, there are `M`.\n\nIf we iterate through from the beginning, it\'s hard to know whether the `M` truck should go to `index 2` or not. But if we iterate through from the last, we are sure that the `M` truck must go to `index 2` because we know that there is `M` garbage in the last house. (As I explain eariler, each truck must visit each house **in order**, so the `M` truck must go to `index 2`).\n\n\n---\n\n\u2B50\uFE0F Points\n\nIterate through from the end, so that we are sure whether each truck goes next or not.\n\n---\n\nLet\'s see one by one.\n\n```\nInput: garbage = ["MMM","PGM","GP","M"], travel = [3,10,5]\n```\nCount number of garbages.\n```\nres = 9\n```\nIterate `travel` from the end (= iterate garbage from the end). The reason why we iterate `travel` is that we want to iterate `travel` and `garbage` at the same time but travel is always shorter than `garbage`, so we don\'t have to care about out of bounds.\n\nBetween the `index 3` and `index 2`, travel time is `5` and there is only `M`, so\n\n```\n["MMM","PGM","GP","M"]\n \u2191(= i)\n[3,10,5]\n \u2191(= i - 1)\nres += travel time * (M + P + G)\nres += 5 * (1 + 0 + 0)\nres = 14 (= 9 + 5)\n```\n`(M + P + G)` is number of each truck, `0` or `1`. In this case, Only `M` truck needs to go to the last house.\n\nTravel time index should be current index(i) - 1, because number of travel time is total number of houses - 1.\n\n```\n["MMM","PGM","GP","M"]\n 3 10 5\n```\n\nMove previous house. Travel time is `10`. There is `G` and `P`.\n\n```\n["MMM","PGM","GP","M"]\n \u2191(= i)\n[3,10,5]\n \u2191(= i - 1)\n\nres += travel time * (M + P + G)\nres += 10 * (1 + 1 + 1)\nres = 44\n```\nThere is no `M` garbage at `index 2`, but we know that `M` truck must go to the last house, so `M` truck is always `1`. More precisely, once the flags turn true, the flags are always true, because the trucks must go to the next house.\n\nMove previous house. Travel time is `3`. There are garbages of `P`, `G`, `M`.\n\n```\n["MMM","PGM","GP","M"]\n \u2191(= i)\n[3,10,5]\n \u2191(= i - 1)\n\nres += travel time *(M + P + G)\nres += 3 * (1 + 1 + 1)\nres = 53\n```\nThen finish iteration. We don\'t have to go to the first house because we already added number of garbages at `index 0` and travel time `3` * `3` trucks which is between `index 0` and `index 1`.\n\n```\nOutput: 53\n```\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n### Algorithm Overview:\n\nAt first, add number of garbages to result, then iterate through from the last index.\n\n### Detailed Explanation:\n\n1. **Initialization**: \n```\nres = 0\n```\nStart with initializing the total time (`res`) to 0.\n\n2. **Process Garbage Sizes**:\n```\nfor g in garbage:\n res += len(g)\n```\nFor each house, add the length of the garbage string to `res`. This step accounts for the time spent picking up garbage at each house.\n\n3. **Initialize Garbage Type Flags**:\n```\ng, p, m = False, False, False\n```\nSet boolean flags to track the presence of different types of garbage.\n\n4. **Update Garbage Type Flags**:\n```\nfor i in range(len(travel), 0, -1):\n m = m or \'M\' in garbage[i]\n p = p or \'P\' in garbage[i]\n g = g or \'G\' in garbage[i]\n\n res += travel[i-1] * (m + p + g)\n```\nBegin traversing the houses backward, starting from the last one. Check each garbage string for the presence of \'M\',\'P\', or \'G\', and update the corresponding boolean flags. For each house, calculate its contribution to the total time based on the travel time and the sum of boolean flags. Accumulate the calculated contribution to the total time.\n\n5. **Return Result**:\n```\nreturn res\n```\nOnce all houses are processed, return the final total time as the minimum number of minutes needed to pick up all the garbage.\n\nThis algorithm efficiently calculates the minimum time required for garbage collection based on the given conditions.\n\n\n# Complexity\n- Time complexity: $$O(T * G)$$\n`T` is length of `travel` variable and `G` is average time to find garbage in garbage string. But once we found the garbage, it will be $$O(T)$$. In reality, I think it\'s faster than this time complexity. In fact, this code beats more than 98%.\n\n- Space complexity: $$O(1)$$\n\n```python []\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n res = 0\n \n for g in garbage:\n res += len(g)\n\n m, p, g = False, False, False\n\n for i in range(len(travel), 0, -1):\n m = m or \'M\' in garbage[i]\n p = p or \'P\' in garbage[i]\n g = g or \'G\' in garbage[i]\n\n res += travel[i-1] * (m + p + g)\n \n return res\n```\n```javascript []\n/**\n * @param {string[]} garbage\n * @param {number[]} travel\n * @return {number}\n */\nvar garbageCollection = function(garbage, travel) {\n let res = 0;\n\n for (const g of garbage) {\n res += g.length;\n }\n\n let [m, p, g] = [false, false, false];\n\n for (let i = travel.length; i > 0; i--) {\n m = m || garbage[i].includes(\'M\');\n p = p || garbage[i].includes(\'P\');\n g = g || garbage[i].includes(\'G\');\n\n res += travel[i - 1] * (m + p + g);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int garbageCollection(String[] garbage, int[] travel) {\n int res = 0;\n\n for (String g : garbage) {\n res += g.length();\n }\n\n boolean m = false, p = false, g = false;\n\n for (int i = travel.length; i > 0; i--) {\n m = m || garbage[i].contains("M");\n p = p || garbage[i].contains("P");\n g = g || garbage[i].contains("G");\n\n res += travel[i-1] * ((m ? 1 : 0) + (p ? 1 : 0) + (g ? 1 : 0));\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int garbageCollection(std::vector<std::string>& garbage, std::vector<int>& travel) {\n int res = 0;\n\n for (const string& g : garbage) {\n res += g.length();\n }\n\n bool m = false, p = false, g = false;\n\n for (int i = travel.size(); i > 0; i--) {\n m = m || garbage[i].find("M") != string::npos;\n p = p || garbage[i].find("P") != string::npos;\n g = g || garbage[i].find("G") != string::npos;\n\n res += travel[i-1] * ((m ? 1 : 0) + (p ? 1 : 0) + (g ? 1 : 0));\n }\n\n return res;\n }\n};\n```\n\n---\n\n##### Python Tips\n\n`m`, `p` and `g` are boolean flags. Python considers `True` as `1` and `False` as `0`, so please execute this if you want to check.\n\n```\nprint(True + 1) # 2\nprint(False + 1) # 1\n```\nThat\'s why we can calculate like this.\n\n```\nres += travel[i-1] * (m + p + g)\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-nice-pairs-in-an-array/solutions/4312501/video-give-me-6-minutes-hashmap-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/424EOdu4TeY\n\n\u25A0 Timeline\u3000of the video\n\n`0:04` Think about how we calculate the answer\n`0:58` Demonstrate how it works\n`3:58` Coding\n`5:53` Time Complexity and Space Complexity\n`6:11` Summary of the algorithm with my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/reduction-operations-to-make-the-array-elements-equal/solutions/4306758/video-give-me-9-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/Tf69tOpE4GE\n\n\u25A0 Timeline of the video\n\n`0:05` Try to find a solution pattern\n`1:44` What if we have the same numbers in input array?\n`5:37` Why it works when we skip reduction\n`7:22` Coding\n`8:52` Time Complexity and Space Complexity | 48 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
Easy Intuitive solution using Hashmap and Prefix Sum | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ntravel time(taking prefix sum) will give us the time to travel to the particular index and travel_time[last_index[i] - 1] will give us the time to travel to the last index of the i -{\'M\', \'P\' , \'G\'} and adding that to the frequency will give us the total time for that particular i.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n travel_time , s = [] , 0 \n lis=\'\'.join(garbage)\n d = Counter(lis)\n for i in range(1,len(garbage)):\n s += travel[i-1]\n travel_time.append(s)\n last_index = defaultdict(int)\n for i in range(len(garbage)):\n if \'M\' in garbage[i]:\n last_index[\'M\'] = i\n if \'P\' in garbage[i]:\n last_index[\'P\'] = i\n if \'G\' in garbage[i]:\n last_index[\'G\'] = i\n ans = 0\n for i in d:\n ans += d[i]\n if last_index[i] > 0 : ans += travel_time[last_index[i] - 1]\n return ans\n``` | 2 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
✅ 100% || 🚀 Greedy Approach || | minimum-amount-of-time-to-collect-garbage | 1 | 1 | \n\n# C++ Result:\n\n\n# Python Result:\n\n\n# Java Result:\n\n\n# Intuition:\n**Here we are given a list of garbage and a list of travel times. We need to find the minimum time to pick up all the garbage. We can do this by iterating from the end of the garbage array and checking if the current house has any of the garbage. If it does, we add the travel time to the garbage. If all the garbage has been found, we break and return the sum of the garbage and the travel time.**\n\n# Approach: Using a greedy approach\n1. Iterate from the end of the garbage array\n2. Check if the current house has any of the garbage\n3. If it does, add the travel time to the garbage\n4. If all the garbage has been found, break\n5. Return the sum of the garbage and the travel time\n\n# Complexity\n- Time complexity: ***O(n)***\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ***O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n## UpVote\u2B06\uFE0F If this helps you:)\n\n# Code\n``` Python []\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n ans = 0\n\n n = len(garbage)\n\n m,p,g = False,False,False\n for i in range(n-1,-1,-1):\n if not g and "G" in garbage[i]:\n g=True\n ans+=sum(travel[:i])\n if not m and "M" in garbage[i]:\n m=True\n ans+=sum(travel[:i])\n if not p and "P" in garbage[i]:\n p=True\n ans+=sum(travel[:i])\n if all([m,p,g]):\n break\n\n return len("".join(garbage))+ans\n```\n``` C++ []\n#include <iostream>\n#include <vector>\n#include <numeric> // Include the numeric header for std::accumulate\n\nclass Solution {\npublic:\n int garbageCollection(std::vector<std::string>& garbage, std::vector<int>& travel) {\n int ans = 0;\n int n = garbage.size();\n bool m = false, p = false, g = false;\n for (int i = n - 1; i >= 0; --i) {\n if (!g && garbage[i].find(\'G\') != std::string::npos) {\n g = true;\n ans += std::accumulate(travel.begin(), travel.begin() + i, 0);\n }\n if (!m && garbage[i].find(\'M\') != std::string::npos) {\n m = true;\n ans += std::accumulate(travel.begin(), travel.begin() + i, 0);\n }\n if (!p && garbage[i].find(\'P\') != std::string::npos) {\n p = true;\n ans += std::accumulate(travel.begin(), travel.begin() + i, 0);\n }\n if (m && p && g) {\n break;\n }\n }\n return ans + std::accumulate(garbage.begin(), garbage.end(), 0, [](int sum, const std::string& str) {\n return sum + str.size();\n });\n }\n};\n```\n``` Java []\nimport java.util.Arrays;\n\nclass Solution {\n public int garbageCollection(String[] garbage, int[] travel) {\n int ans = 0;\n int n = garbage.length;\n boolean m = false, p = false, g = false;\n\n for (int i = n - 1; i >= 0; i--) {\n if (!g && garbage[i].contains("G")) {\n g = true;\n ans += Arrays.stream(travel, 0, i).sum();\n }\n if (!m && garbage[i].contains("M")) {\n m = true;\n ans += Arrays.stream(travel, 0, i).sum();\n }\n if (!p && garbage[i].contains("P")) {\n p = true;\n ans += Arrays.stream(travel, 0, i).sum();\n }\n if (m && p && g) {\n break;\n }\n }\n\n return Arrays.stream(garbage).mapToInt(String::length).sum() + ans;\n }\n}\n```\n | 2 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
[Python3] Greedy + prefix sum || beats 100% | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\n- Find last position (the most right house) for each type of garbage.\n- Find distance for every house using prefix sum (use [`itertools.accumulate`](https://docs.python.org/3/library/itertools.html#itertools.accumulate) to simplify code).\n- Don\'t forget to count the garbage (1 sek to peek 1 unit of any garbage).\n\n```The code below are almost the same, a difference only in type of iteration (while or for loops).```\n```python3 []\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n peekGarbageTime = endM = endP = endG = 0\n i = len(garbage) - 1\n\n while i >=0:\n peekGarbageTime += len(garbage[i])\n if not endM and \'M\' in garbage[i]: endM = i\n if not endP and \'P\' in garbage[i]: endP = i\n if not endG and \'G\' in garbage[i]: endG = i\n i -= 1\n\n dist = list(accumulate(travel, initial = 0))\n\n return dist[endM] + dist[endP] + dist[endG] + peekGarbageTime\n```\n```python3 []\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n peekGarbageTime = endM = endP = endG = 0\n\n for i, g in reversed(list(enumerate(garbage))):\n peekGarbageTime += len(g)\n if not endM and \'M\' in g: endM = i\n if not endP and \'P\' in g: endP = i\n if not endG and \'G\' in g: endG = i\n\n dist = list(accumulate(travel, initial = 0))\n\n return dist[endM] + dist[endP] + dist[endG] + peekGarbageTime\n```\n\n | 8 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
✅Python || Beats 100% || O(n) | minimum-amount-of-time-to-collect-garbage | 0 | 1 | \n\n# Problem\nThe problem is asking to minimize the time taken to collect all the garbage. We have three types of garbage and three trucks, each responsible for one type of garbage. The trucks can only move in one direction and cannot skip any houses. Therefore, we need to find the last occurrence of each type of garbage and calculate the total time taken to reach these houses and collect the garbage.\n# What we do\nWe first calculate the cumulative travel time for each house.\n```\nfib = [0]\nfor time in travel: fib.append(fib[-1] + time)\n```\n Then, we iterate over the garbage array in reverse order and keep track of the last occurrence of each type of garbage.\n```\nfor i in range(len(garbage)-1, -1, -1):\n v = garbage[i]\n if not memo[0] and "M" in v: memo[0] = i\n if not memo[1] and "P" in v: memo[1] = i\n if not memo[2] and "G" in v: memo[2] = i\n```\n ```all(memo)``` checks if all elements in the memo list are truthy (i.e., they have a value other than zero). If all elements in memo are non-zero, it means that we have found at least one occurrence of each type of garbage (metal, paper, and glass), and ```all(memo)``` will return ```True```. If any element in memo is zero, it means that we haven\u2019t found an occurrence of that type of garbage yet, and all(memo) will return ```False```.\n```\nif all(memo): break\n```\n Finally, we return the total amount of garbage plus the sum of the travel times to the last occurrence of each type of garbage. This ensures that all garbage is collected in the minimum amount of time.\n```\nreturn len("".join(garbage)) + (fib[memo[0]] + fib[memo[1]] + fib[memo[2]])\n```\n\n# Complexity\n- Time complexity: \n $$O(n)$$\n where $$n$$ is the number of houses. This is because we need to iterate over the garbage array once.\n- Space complexity: $$O(n)$$\n\n \n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n fib, memo = [0], [0] * 3\n\n for time in travel: fib.append(fib[-1] + time)\n \n for i in range(len(garbage)-1, -1, -1):\n v = garbage[i]\n if not memo[0] and "M" in v: memo[0] = i\n if not memo[1] and "P" in v: memo[1] = i\n if not memo[2] and "G" in v: memo[2] = i\n\n if all(memo): break\n\n return len("".join(garbage)) + (fib[memo[0]] + fib[memo[1]] + fib[memo[2]])\n\n \n```\n# CodeExplanation\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n # Initialize an array to store the cumulative travel time and an array to store the last occurrence of each type of garbage\n fib, memo = [0], [0] * 3\n\n # Calculate the cumulative travel time for each house\n for time in travel: fib.append(fib[-1] + time)\n \n \n # Iterate over the garbage array in reverse order\n for i in range(len(garbage)-1, -1, -1):\n v = garbage[i]\n # If the current house has metal garbage and it\'s the first occurrence, store its index\n if not memo[0] and "M" in v: memo[0] = i\n # If the current house has paper garbage and it\'s the first occurrence, store its index\n if not memo[1] and "P" in v: memo[1] = i\n # If the current house has glass garbage and it\'s the first occurrence, store its index\n if not memo[2] and "G" in v: memo[2] = i\n\n # If we have found at least one occurrence of each type of garbage, stop the iteration\n if all(memo): break\n\n # Return the total amount of garbage plus the sum of the travel times to the last occurrence of each type of garbage\n return len("".join(garbage)) + (fib[memo[0]] + fib[memo[1]] + fib[memo[2]])\n```\n# Upvote\n```\nUpvote = False\nif my_code == "Helpful":\n Upvote = True\nprint("Thank You")\n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
Easy python solution with comments! Time complexity O(n*m) | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*m): where n is no of houses to visit, m is the max length of garbage to collect at any house in our array.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n): dominated by space complexity of cum_sum, which is O(n-1)\n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n \n # create cumulative sum of cost to keep track of cost of visiting house i along the path\n # for instance if there is garbage G at index 3, then we need to travel from 0 -> 1 -> 2 -> 3 thereby adding total cost of travel\n # from 0 -> 3; our cum sum will keep track of this cost\n # i.e. what is the total cost of visiting house from source 0 index\n cum_sum = travel.copy() \n for i in range(1, len(cum_sum)):\n cum_sum[i] = cum_sum[i] + cum_sum[i-1]\n \n # map the frequency of the garbage across the houses; freq will simply be added; since the code is 1 min for picking up every garbage\n freq = defaultdict(int) \n last_index = defaultdict(int) # last house where garbage g exisited; this will be used to add total cost\n # update these hashmaps by visiting all the houses\n for i in range(len(garbage)):\n for g in "GMP":\n freq[g] += garbage[i].count(g)\n if g in garbage[i]:\n last_index[g] = i\n\n # iterate for every garbage category and keep adding cost\n # i.e. total_cost of visiting last house to collect garbage g + freq of garbage g\n time = 0\n for g in "GMP":\n time += (freq[g] + (cum_sum[last_index[g] - 1] if last_index[g]!=0 else 0))\n\n return time \n\n# Time complexity O(n*m); where n is no of houses to visit, m is the max length of garbage to collect at any house in our array.\n\n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
Easy Python Solution || Beats 94% in Runtime | minimum-amount-of-time-to-collect-garbage | 0 | 1 | \n\n# Approach\n1. Keep track of index of the last occurance of each garbage.\n2. Also keep track of frequency of Each letter. (You can maintain a single variable which stores total freq of each letter, here i have used variable `ans`).\n3. At the end sum up `travel` upto the last index of each letter and add them together.\n4. Also don\'t forget to add the total count of all the letters.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n \n lm = 0 # Last index at which "M" was seen\n lg = 0 # Last index at which "G" was seen\n lp = 0 # Last index at which "P" was seen\n ans = 0\n\n for i in range(len(garbage)):\n if "G" in garbage[i]:\n lg = i\n if "P" in garbage[i]:\n lp = i\n if "M" in garbage[i]:\n lm = i\n ans+=len(garbage[i])\n\n ans+=sum(travel[:lm])+sum(travel[:lg])+sum(travel[:lp])\n\n return ans\n \n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
🚀 Easy Iterative Approach || Explained Intuition🚀 | minimum-amount-of-time-to-collect-garbage | 1 | 1 | # Problem Description\n\nGiven an array `garbage` representing the types of garbage at each house (`M` for metal, `P` for paper, `G` for glass), and an array `travel` representing the travel time between consecutive houses, **determine** the **minimum** number of minutes needed for three garbage trucks to pick up all the garbage. Each truck is responsible for **one** type of garbage, and they must visit the houses **in order**, with only **one** truck operating at a time.\n\nThe time required to pick up `one` unit of any type of garbage is `1` minute. The trucks start at house `0` and move sequentially, but they don\'t need to visit every house. While one truck is in operation, the other two trucks are **idle**.\n\nReturn the **minimum** total time required to collect all the garbage, considering the travel time between houses and the time required to pick up the garbage at each house.\n\n- **Constraints:**\n - Only one truck operates at a time. \n - $2 <= garbage.length <= 10^5$\n - garbage[i] consists of only the letters \'M\', \'P\', and \'G\'.\n - $1 <= garbage[i].length <= 10$\n - $travel.length == garbage.length - 1$\n - $1 <= travel[i] <= 100$\n\n\n\n---\n\n\n\n# Intuition\n\nHi there, \uD83D\uDE04\n\nLet\'s dive\uD83E\uDD3F deep into our today\'s problem.\nIn today\'s problem we have array of `N` houses\uD83C\uDFE0 in the same town and we are required to collect garbage from all these houses. There are **three** types of garbages: `Metal`, `Paper` and `Glass`. Each type has its own truck and oen truck\uD83D\uDE9A\uD83D\uDE9B is operating at a time.\n\nSeems neat problem.\uD83D\uDE00\nHow can we start with this problem ?\uD83E\uDD14\nWe can notice that we have two arrays `garbage` which indicate sgarbages in each house and `travel` which indicates the required time to travel two consecutive houses.\n\n- There two important things we want to take care of:\uD83E\uDD28\n - a truck **do not need** to visit all houses.\uD83E\uDD2F\n - Let\'s say there is glass garbage in house 6, then glass truck must also visit house 0, 1, 2....5 until it reaches 6.\uD83D\uDE14\n\nFirst thing that we can think about is why not we see how far can each truck go?\uD83E\uDD14\nFor example for Glass truck if we have 10 houses and houses from 6 to 10 don\'t have glass garbage then this truck will stop at house 5 and not continue.\uD83E\uDD29\n\nGood what then ? \uD83E\uDD14\nWe can **accumulate** time needed to reach each house using the `travel` array and for each maximum house for each truck we add it to our total answer.\n\nWhat about the real garbage collecting ?\uD83E\uDD28\nWe didn\'t talk about this since it is the **easiest** part\uD83E\uDD29. Only **sum** number of garbage in each house. We don\'t have to handle it in special way since all the garbage are similar and it takes take one second to collect one unit.\n\nLet\'s see some examples.\n```\ngarbage = ["G","P","GP","GG"], travel = [2,4,3]\n\nTime to collect all garbage = 1 + 1 + 2 + 2 = 6\n\nMaximum distance for each truck:\nG -> 3\nP -> 2\nM -> 0\n\nTime for each truck to reah its maximum house:\nG -> 2 + 4 + 3 = 9\nP -> 2 + 4 = 6\nM -> 0\n\nTotal time = 6 + 9 + 6 + 0 = 21\n```\n\n\n```\ngarbage = ["P","M","G","GG","MM"], travel = [2,4,3,5]\n\nTime to collect all garbage = 1 + 1 + 1 + 2 + 2 = 7\n\nMaximum distance for each truck:\nG -> 3\nP -> 0\nM -> 4\n\nTime for each truck to reah its maximum house\nG -> 2 + 4 + 3 = 9\nP -> 0\nM -> 2 + 4 + 3 + 5 = 14\n\nTotal time = 9 + 14 + 0 + 7 = 30\n\n```\n\n### Note\nFor **determining** the time for each truck to reach its **maximum** house we can use **prefix sum** array and get the index for each house for each truck but since there are only **three** trucks, In my code implementation I didn\'t make an array and just **looped** over all the travel array to get the **maximum** time for each house which resulted in space complexity of `O(1)`. \uD83E\uDD29\nIf we had **large** number of trucks instead of `3` then it would be better to implement real prefix sum array.\uD83D\uDE03\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n# Approach\n\n1. **Initialize Variables:**\n - `totalMinutes`: Set to `0`, representing the **total** minutes needed for garbage collection.\n - `lastGarbageIndices`: Initialize a vector of size `3` with values `-1`, tracking the last occurrence indices of `M`, `P`, and `G` garbage types.\n2. **Calculate Initial Time:**\n - Add the size of the garbage at the first house to `totalMinutes` Since all the truck are at the first house initially.\n3. **Update Last Occurrence Indices:**\n - Iterate through each house starting from the second house.\n - Add the size of garbage at the current house to `totalMinutes`.\n - Update the last occurrence indices for \'M\', \'P\', and \'G\' garbage types based on their presence in the current house.\n4. **Travel Time Calculation:**\n - Iterate through each travel segment in the `travel` vector.\n - Add the current travel time to `currentTravelTime` as a **Prefix Sum**.\n - For each garbage truck type (`M`, `P`, `G`), check if its last occurrence index matches the current travel index.\n - If there is a match, add the current travel time to `totalMinutes`, representing the time spent collecting garbage during travel.\n6. **Return Result:**\n - Return the final value of `totalMinutes`, representing the minimum total time needed to pick up all the garbage.\n\n\n# Complexity\n- **Time complexity:** $O(N)$\nSince we are iterating over our garbage array to get last index of each garbage type then it takes `O(N)` then we are iterating over our travelling array which take also `O(N)` so total complexity is `2N` which is `O(N)`.\nWhere N is number of houses in garbage array.\n**FirstNote:** Complexity of first for-loop is `N*house_size` and since the house size is `10` then its complexity is `10*N` which is `O(N)`.\n**SecondNote:** Complexity of second for-loop is `N*garbage_type` and since the garpage type is `3` then its complexity is `3*N` which is `O(N)`.\n\n- **Space complexity:** $O(1)$\nSince we are only using constant space variables that doesn\'t depend on the input size.\n\n\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int garbageCollection(vector<string>& garbage, vector<int>& travel) {\n long long totalMinutes = 0; // Total minutes needed for garbage collection\n long long currentTravelTime = 0; // Current travel time\n\n // Add the initial minutes required to collect garbage at the first house\n totalMinutes += garbage[0].size();\n\n vector<int> lastGarbageIndices(3, -1); // Keep track of the last occurrence of each type of garbage\n\n // Iterate through each house starting from the second house\n for (int houseIndex = 1; houseIndex < garbage.size(); houseIndex++) {\n // Add the minutes required to collect garbage at the current house\n totalMinutes += garbage[houseIndex].size();\n\n // Update the indices of the last occurrence of each type of garbage\n if (garbage[houseIndex].find("M") != garbage[houseIndex].npos) \n lastGarbageIndices[0] = houseIndex - 1;\n if (garbage[houseIndex].find("P") != garbage[houseIndex].npos) \n lastGarbageIndices[1] = houseIndex - 1;\n if (garbage[houseIndex].find("G") != garbage[houseIndex].npos) \n lastGarbageIndices[2] = houseIndex - 1;\n }\n\n // Iterate through each travel segment\n for (int travelIndex = 0; travelIndex < travel.size(); travelIndex++) {\n // Add the current travel time\n currentTravelTime += travel[travelIndex];\n\n // Add the minutes required to collect garbage if a garbage truck is at the corresponding house\n for (int truckIndex = 0; truckIndex < 3; truckIndex++) {\n if (lastGarbageIndices[truckIndex] == travelIndex) {\n totalMinutes += currentTravelTime;\n }\n }\n }\n\n return totalMinutes;\n }\n};\n```\n```Java []\npublic class Solution {\n public int garbageCollection(String[] garbage, int[] travel) {\n long totalMinutes = 0; // Total minutes needed for garbage collection\n long currentTravelTime = 0; // Current travel time\n\n // Add the initial minutes required to collect garbage at the first house\n totalMinutes += garbage[0].length();\n \n // Keep track of the last occurrence of each type of garbage\n List<Integer> lastGarbageIndices = new ArrayList<>(List.of(-1, -1, -1)); \n\n // Iterate through each house starting from the second house\n for (int houseIndex = 1; houseIndex < garbage.length; houseIndex++) {\n // Add the minutes required to collect garbage at the current house\n totalMinutes += garbage[houseIndex].length();\n\n // Update the indices of the last occurrence of each type of garbage\n if (garbage[houseIndex].contains("M")) {\n lastGarbageIndices.set(0, houseIndex - 1);\n }\n if (garbage[houseIndex].contains("P")) {\n lastGarbageIndices.set(1, houseIndex - 1);\n }\n if (garbage[houseIndex].contains("G")) {\n lastGarbageIndices.set(2, houseIndex - 1);\n }\n }\n\n // Iterate through each travel segment\n for (int travelIndex = 0; travelIndex < travel.length; travelIndex++) {\n // Add the current travel time\n currentTravelTime += travel[travelIndex];\n\n // Add the minutes required to collect garbage if a garbage truck is at the corresponding house\n for (int truckIndex = 0; truckIndex < 3; truckIndex++) {\n if (lastGarbageIndices.get(truckIndex) == travelIndex) {\n totalMinutes += currentTravelTime;\n }\n }\n }\n\n return (int) totalMinutes;\n }\n}\n```\n```Python []\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n total_minutes = 0 # Total minutes needed for garbage collection\n current_travel_time = 0 # Current travel time\n\n # Add the initial minutes required to collect garbage at the first house\n total_minutes += len(garbage[0])\n\n last_garbage_indices = [-1, -1, -1] # Keep track of the last occurrence of each type of garbage\n\n # Iterate through each house starting from the second house\n for house_index in range(1, len(garbage)):\n # Add the minutes required to collect garbage at the current house\n total_minutes += len(garbage[house_index])\n\n # Update the indices of the last occurrence of each type of garbage\n if "M" in garbage[house_index]:\n last_garbage_indices[0] = house_index - 1\n if "P" in garbage[house_index]:\n last_garbage_indices[1] = house_index - 1\n if "G" in garbage[house_index]:\n last_garbage_indices[2] = house_index - 1\n\n # Iterate through each travel segment\n for travel_index in range(len(travel)):\n # Add the current travel time\n current_travel_time += travel[travel_index]\n\n # Add the minutes required to collect garbage if a garbage truck is at the corresponding house\n for truck_index in range(3):\n if last_garbage_indices[truck_index] == travel_index:\n total_minutes += current_travel_time\n\n return total_minutes\n```\n```C []\nint garbageCollection(char** garbage, int garbageSize, int* travel, int travelSize) {\n long long totalMinutes = 0; // Total minutes needed for garbage collection\n long long currentTravelTime = 0; // Current travel time\n\n // Add the initial minutes required to collect garbage at the first house\n totalMinutes += strlen(garbage[0]);\n\n int lastGarbageIndices[3] = {-1, -1, -1}; // Keep track of the last occurrence of each type of garbage\n\n // Iterate through each house starting from the second house\n for (int houseIndex = 1; houseIndex < garbageSize; houseIndex++) {\n // Add the minutes required to collect garbage at the current house\n totalMinutes += strlen(garbage[houseIndex]);\n\n // Update the indices of the last occurrence of each type of garbage\n if (strchr(garbage[houseIndex], \'M\') != NULL)\n lastGarbageIndices[0] = houseIndex - 1;\n if (strchr(garbage[houseIndex], \'P\') != NULL)\n lastGarbageIndices[1] = houseIndex - 1;\n if (strchr(garbage[houseIndex], \'G\') != NULL)\n lastGarbageIndices[2] = houseIndex - 1;\n }\n\n // Iterate through each travel segment\n for (int travelIndex = 0; travelIndex < travelSize; travelIndex++) {\n // Add the current travel time\n currentTravelTime += travel[travelIndex];\n\n // Add the minutes required to collect garbage if a garbage truck is at the corresponding house\n for (int truckIndex = 0; truckIndex < 3; truckIndex++) {\n if (lastGarbageIndices[truckIndex] == travelIndex) {\n totalMinutes += currentTravelTime;\n }\n }\n }\n\n return (int)totalMinutes;\n}\n```\n\n\n\n\n | 39 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
✅✅✅ Best-Optimized Solution 🌟Simple with Observation 💡🎯🏆 | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key insight here is that for each type of garbage (\'G\', \'P\', \'M\'), we want to find the last occurrence in the sequence of houses. This is because once a garbage truck picks up a particular type of garbage, it doesn\'t need to travel back to a house where that type of garbage occurred earlier. Therefore, you only need to consider the last occurrence of each type for minimizing travel time.\n\nBy identifying the last occurrence of each type of garbage, we can calculate the total travel time for each garbage truck by summing the travel times up to those last occurrences. This approach ensures an efficient collection of garbage by minimizing unnecessary travel between houses.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Iterate over Houses (in reverse order):**\nStart iterating from the last house to the first house (reverse order). For each house, increment the time (t) by the number of minutes needed to pick up the garbage at the current house.\n\n**Update Garbage Truck Times:**\nFor each house, if the type of garbage is glass (\'G\') and the time for glass (g) is 0(this implies that we have found the last occurence of glass).\nUpdate the time for glass (g) to be the sum of travel times up to the house where the last occurrence of metal was found.\nWe follow the same procedure for Paper (\'P\') and Metal (\'M\').\n\n**Return Result:**\nReturn the sum of time (t) and the times for metal (m), paper (p), and glass (g).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe dominant factor in the time complexity is the loop that iterates over the elements of the garbage list. The loop runs in reverse order, checking conditions and performing constant-time operations for each element. The loop\'s time complexity is O(len(garbage)), where len(garbage) is the number of elements in the list.\n\nThe sum(travel[:i]) operation inside the loop contributes an additional O(i) time complexity for each iteration. In the worst case, where i can be up to len(garbage), the overall time complexity becomes O(len(garbage)^2).\n\nTherefore, the overall time complexity is O(len(garbage)^2).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1), indicating constant space usage.\n\n# Code\n```\nclass Solution(object):\n def garbageCollection(self, garbage, travel):\n """\n :type garbage: List[str]\n :type travel: List[int]\n :rtype: int\n """\n t=0\n g=0\n p=0\n m=0\n for i in range(len(garbage)-1,-1,-1):\n t=t+len(garbage[i])\n if \'G\' in garbage[i] and g==0:\n g=sum(travel[:i])\n if \'P\' in garbage[i] and p==0:\n p=sum(travel[:i])\n if \'M\' in garbage[i] and m==0:\n m=sum(travel[:i])\n return t+g+p+m\n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
Reverse Loop With Prefix Sum Frequency Transform | Commented and Explained | 100% T and S | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA backwards loop can find the last index of each type of garbage \nA prefix sum of times can find the cost of the traversals needed \nA hashmap of the last indices then allows us to find the costs up to a specific point -> aka prefix sum up to point in travel \nWe can convert these into a frequency of the last stops to get the final form where we have used a frequency transform to limit the prefix sum calculation cost \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMake a position map and fill all with -1 of type of garbage to indice last found \nGet the length of the garbage route \nLoop i backwards over garbage route positioning \n- for each char in garbage at i \n - if position map[char] == -1 it is now equal to i \n - otherwise continue \n- if -1 is not in any position map values -> break \n\nCalculate travel cost as the length of the join of garbage -> O(1) operation \n\nBuild a prefix sum frequency dictionary \nThis stores the number of times that final indices matched in the list (more on why in time complexity) for any indice gt 0 \n\nThen, for each travel indice in prefix sum frequency \n- update total cost by the sum of travel up to travel indice * frequency this is the final stop \n\nWhen done return total cost \n\n# Complexity\n- Time complexity: O(G * g) at worst, O(g_i) at best \n - O(G) to loop backwards over garbage \n - early stopping is allowed \n - O(g) to loop over position map values where g is the unique type of trash in the problem \n - O(g_i) to loop over unique indices of g unique types of trash \n - Reason for doing so : in this problem, we are faced with only 3 types of trash. We could be faced with a similar problem with MANY types of trash. \n - As such, to reduce time complexity, we should reduce our number of prefix sums. We could further optimize via sorting the prefix sums, especially if the summation costs somehow were higher (can happen for prefix sums of object like structures, etc) \n - In our case here, we first reduce our types of traversal of G * g (number of garbage patches * size of garbage patches) to simply types of g \n - Then, we reduce by grouping types of g into prefix sum matched sets (g to g_i) \n - This gives a double frequency reduction in time complexity \n\n- Space complexity : O(g) \n - takes up O(g) to store positions \n - takes O(g_i) to store prefix sums \n - total is O(g + g_i)\n - g_i is either equal to or sub g \n - O(g) \n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n # set up position map of the final index at which a type of garbage was encountered\n position_map = {"G":-1, "M":-1, "P":-1}\n # get length of the garbage \n gL = len(garbage) \n # loop backwards \n for i in range(gL - 1, -1, -1) : \n # for each char in garbage at i -> if not yet marked, mark it, otherwise continue \n for char in garbage[i] : \n if position_map[char] == -1 : \n position_map[char] = i \n else : \n continue\n # if all marked, break \n if -1 not in position_map.values() : \n break \n # get travel cost set up as the total of the length of the garbage \n travel_cost = len("".join(garbage))\n # set up prefix sum frequency \n prefix_sum_frequency = dict() \n # for value in position map values \n for value in position_map.values() : \n # if gt 0 -> we have a prefix sum to calculate here \n if value > 0 : \n # if we have not considered it already, consider it at 1. Otherwise increment. \n if value not in prefix_sum_frequency : \n prefix_sum_frequency[value] = 1 \n else : \n prefix_sum_frequency[value] += 1 \n else : \n continue \n \n # for travel index in prefix sum frequency \n for travel_index in prefix_sum_frequency : \n # get the travel costs of any prefix sum frequency needed \n travel_costs = sum(travel[:travel_index]) * prefix_sum_frequency[travel_index]\n # then update travel cost based on this \n travel_cost += travel_costs \n \n # returning when done \n return travel_cost \n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
PYTHON3 FOR BEGINNERS || VERY EASY TO UNDERSTAND || BEST EFFICIENT | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\n**1)Cumulative Distance Calculation:**\n\nThe post list is used to store the cumulative sum of travel distances at each position. This is helpful for quickly determining the total distance traveled up to a certain point.\n\n**2)Iterating Backwards through Garbage Positions:**\n\nThe code iterates backward through the garbage list. This approach allows the algorithm to efficiently identify the last occurrences of "G", "M", and "P" in the garbage positions.\n\n**3)Tracking Last Occurrences:**\n\nThe variables g, m, and p are used to store the positions of the last occurrences of "G", "M", and "P" respectively. These positions are then used to calculate the total distance traveled for each type of garbage.\n\n**4)Counting Positions:**\n\nThe count variable is used to keep track of the total number of positions encountered during the iteration. This count is added to the total distance traveled.\n\n**5)Returning the Result:**\n\nThe function returns the sum of the distances traveled for "G", "M", and "P", along with the count of positions. This represents the total distance traveled during garbage collection.\n\nOverall, the code efficiently calculates the total distance traveled during garbage collection by considering the travel distances and types of garbage at each position. It utilizes cumulative sums and tracks the last occurrences of specific types of garbage.\n\n# Approach\nHere\'s a breakdown of the code:\n\n1)post is a list that stores the cumulative sum of travel distances. It is used to calculate the total distance traveled up to each position.\n\n2)Initialize variables g, m, and p to 0, which will be used to store the positions of the last occurrences of "G", "M", and "P" respectively.\n\n3)Initialize count to 0, which will be used to count the total number of positions.\n\n4)Iterate over the garbage list in reverse order using a for loop.\n\n5)Inside the loop, check if g, m, and p are not assigned and if the current position contains "G", "M", or "P" respectively. If true, assign the current post value to g, m, or p accordingly.\n\n6)Increment the count variable by the length of the current garbage position.\n\n7)Finally, return the sum of g, m, p, and count. This represents the total distance traveled during garbage collection.\n\nThe approach uses the cumulative sum of travel distances and tracks the positions of the last occurrences of "G", "M", and "P" to calculate the total distance traveled during garbage collection.\n\n# Complexity\n**- Time complexity:**\n\nThe time complexity of thecode is O(n), where \nn is the length of the garbage list. This is because the code iterates through the garbage list once in reverse order, and the operations inside the loop are constant time. The cumulative sum of travel distances is calculated in O(n) time, and the total time complexity is dominated by the loop that iterates through the positions in the garbage list.\n\n**- Space complexity:**\n\n\nThe space complexity of the given code is O(n), where n is the length of the travel list. This is primarily due to the space used by the post list, which stores the cumulative sum of travel distances at each position.\n\nAdditionally, there are some constant space variables such as g, m, p, and count, but these do not depend on the size of the input and contribute only a constant factor to the overall space complexity.\n\nTherefore, the dominant factor in the space complexity is the linear space required for the post list, resulting in a space complexity of O(n).\n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n post = [0]\n for i in range(len(travel)):\n post.append(post[-1]+travel[i])\n g =0;m=0;p=0;count=0\n for i in range(len(garbage)-1,-1,-1):\n if not g and "G" in garbage[i]:\n g = post[i]\n if not m and "M" in garbage[i]:\n m = post[i]\n if not p and "P" in garbage[i]:\n p = post[i]\n count += len(garbage[i])\n return (g+m+p+count)\n \n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
Python Easy & Brute force Solution | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Approach\nBrute force\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n join_garbage = "".join(garbage)\n count = 0\n for i in join_garbage:\n if i == \'M\':\n count += 1\n\n count_1 = 0\n for j in join_garbage:\n if j == \'P\':\n count_1 += 1 \n\n count_2 = 0\n for k in join_garbage:\n if k == \'G\':\n count_2 += 1 \n\n c = []\n for p in reversed(range(len(garbage))):\n if \'M\' in garbage[p]:\n c = travel[:p]\n break\n c_sum = sum(c) \n\n c_1 = []\n for q in reversed(range(len(garbage))):\n if \'P\' in garbage[q]:\n c_1 = travel[:q]\n break\n c_1_sum = sum(c_1)\n\n c_2 = []\n for r in reversed(range(len(garbage))):\n if \'G\' in garbage[r]:\n c_2 = travel[:r]\n break\n c_2_sum = sum(c_2)\n\n return count + count_1 + count_2 + c_sum + c_1_sum + c_2_sum \n\n\n\n\n\n \n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
Simple solution with Prefix Sum in Python3 | minimum-amount-of-time-to-collect-garbage | 0 | 1 | # Intuition\nHere we have:\n- `garbage`, that denotes to garbage for a particular home (G, P, M for glass, plastic and metal respectively)\n- `travel` as time to travel between homes\n- our goal is to define **how much** time trucks need to spend to collect all of the `garbage` **optimally**\n\nEach garbage collection spends `1` minute of time, and we **can\'t** use trucks **simultaneously**.\n\nFor this problem we\'re going to use a **Prefix Sum**, and associate **truck** with index to a `prefix`, since this\'s unnecessary to travel for a particular truck, if **there\'s no garbage** for it.\n\n# Approach\n1. define `g, p, m` to store indexes of trucks\n2. define `ans` to calculate amount of garbage to collect\n3. define `prefix` and fill it with `travel`\n4. iterate over `garbage`, check for each type of garbage and simply change an index, in that way a truck needs to travel from previous home to current (`0` initially)\n5. return `ans + prefix[g] + prefix[p] + prefix[m]`\n\n# Complexity\n- Time complexity: **O(N)**, to calculate `prefix` and collect `garbage`\n\n- Space complexity: **O(N)**, to store `prefix`\n\n# Code\n```\nclass Solution:\n def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:\n g = 0\n p = 0\n m = 0\n prefix = [0]\n ans = 0\n\n for t in travel: prefix.append(prefix[-1] + t)\n\n for i, target in enumerate(garbage):\n ans += len(target)\n\n if \'G\' in target: g = i\n if \'P\' in target: p = i\n if \'M\' in target: m = i\n\n return ans + prefix[g] + prefix[p] + prefix[m] \n``` | 1 | You are given a **0-indexed** array of strings `garbage` where `garbage[i]` represents the assortment of garbage at the `ith` house. `garbage[i]` consists only of the characters `'M'`, `'P'` and `'G'` representing one unit of metal, paper and glass garbage respectively. Picking up **one** unit of any type of garbage takes `1` minute.
You are also given a **0-indexed** integer array `travel` where `travel[i]` is the number of minutes needed to go from house `i` to house `i + 1`.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house `0` and must visit each house **in order**; however, they do **not** need to visit every house.
Only **one** garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks **cannot** do anything.
Return _the **minimum** number of minutes needed to pick up all the garbage._
**Example 1:**
**Input:** garbage = \[ "G ", "P ", "GP ", "GG "\], travel = \[2,4,3\]
**Output:** 21
**Explanation:**
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
**Example 2:**
**Input:** garbage = \[ "MMM ", "PGM ", "GP "\], travel = \[3,10\]
**Output:** 37
**Explanation:**
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
**Constraints:**
* `2 <= garbage.length <= 105`
* `garbage[i]` consists of only the letters `'M'`, `'P'`, and `'G'`.
* `1 <= garbage[i].length <= 10`
* `travel.length == garbage.length - 1`
* `1 <= travel[i] <= 100` | null |
[Python 3] Topological Sorting | build-a-matrix-with-conditions | 0 | 1 | \n\n\n```\n\ndef buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n ans = [[0] * k for _ in range(k)]\n\t\t\n def topological(condition):\n graph = defaultdict(list)\n indegree = [0] * k\n for a, b in condition:\n graph[a].append(b)\n indegree[b - 1] += 1\n \n que = deque()\n for i, val in enumerate(indegree):\n if val == 0:\n que.append(i + 1)\n \n order = []\n \n while que:\n temp = que.popleft()\n order.append(temp)\n \n for child in graph[temp]:\n indegree[child - 1] -= 1\n if indegree[child - 1] == 0:\n que.append(child)\n \n return order\n \n row_order = topological(rowConditions)\n col_order = topological(colConditions)\n \n #cycle detection\n if len(row_order) < k or len(col_order) < k:\n return []\n \n for row, val in enumerate(row_order):\n col = col_order.index(val)\n ans[row][col] = val\n \n return ans\n | 1 | You are given a **positive** integer `k`. You are also given:
* a 2D integer array `rowConditions` of size `n` where `rowConditions[i] = [abovei, belowi]`, and
* a 2D integer array `colConditions` of size `m` where `colConditions[i] = [lefti, righti]`.
The two arrays contain integers from `1` to `k`.
You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`.
The matrix should also satisfy the following conditions:
* The number `abovei` should appear in a **row** that is strictly **above** the row at which the number `belowi` appears for all `i` from `0` to `n - 1`.
* The number `lefti` should appear in a **column** that is strictly **left** of the column at which the number `righti` appears for all `i` from `0` to `m - 1`.
Return _**any** matrix that satisfies the conditions_. If no answer exists, return an empty matrix.
**Example 1:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[3,2\]\], colConditions = \[\[2,1\],\[3,2\]\]
**Output:** \[\[3,0,0\],\[0,0,1\],\[0,2,0\]\]
**Explanation:** The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.
**Example 2:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[2,3\],\[3,1\],\[2,3\]\], colConditions = \[\[2,1\]\]
**Output:** \[\]
**Explanation:** From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.
**Constraints:**
* `2 <= k <= 400`
* `1 <= rowConditions.length, colConditions.length <= 104`
* `rowConditions[i].length == colConditions[i].length == 2`
* `1 <= abovei, belowi, lefti, righti <= k`
* `abovei != belowi`
* `lefti != righti` | null |
[Python3] Topological Sort - Simple Solution | build-a-matrix-with-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFind the order for row and col respectively and then assign them to the matrix. Note that there are only `k` number need to assign which is also the side of square matrix. Thus we can assign each number in each unique row and col\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(M + N)$$ with `N` is number of `rowConditions` and `M` is number of `colConditions`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n matrix = [[0 for _ in range(k)] for _ in range(k)]\n \n def topo_sort(condition: List[List[int]]) -> dict:\n order = {}\n in_degree = [0 for _ in range(k)]\n g = collections.defaultdict(list)\n for start, end in condition:\n g[start - 1].append(end - 1)\n in_degree[end - 1] += 1\n \n dq = collections.deque()\n for i in range(k):\n if in_degree[i] == 0: dq.append(i)\n \n i = 0\n while dq:\n u = dq.popleft()\n order[u] = i\n for v in g[u]:\n in_degree[v] -= 1\n if in_degree[v] == 0: dq.append(v)\n i += 1\n \n return order\n \n row_order, col_order = topo_sort(rowConditions), topo_sort(colConditions)\n if len(row_order) != k or len(col_order) != k: return []\n for u in row_order:\n r, c = row_order[u], col_order[u]\n matrix[r][c] = u + 1\n return matrix\n``` | 2 | You are given a **positive** integer `k`. You are also given:
* a 2D integer array `rowConditions` of size `n` where `rowConditions[i] = [abovei, belowi]`, and
* a 2D integer array `colConditions` of size `m` where `colConditions[i] = [lefti, righti]`.
The two arrays contain integers from `1` to `k`.
You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`.
The matrix should also satisfy the following conditions:
* The number `abovei` should appear in a **row** that is strictly **above** the row at which the number `belowi` appears for all `i` from `0` to `n - 1`.
* The number `lefti` should appear in a **column** that is strictly **left** of the column at which the number `righti` appears for all `i` from `0` to `m - 1`.
Return _**any** matrix that satisfies the conditions_. If no answer exists, return an empty matrix.
**Example 1:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[3,2\]\], colConditions = \[\[2,1\],\[3,2\]\]
**Output:** \[\[3,0,0\],\[0,0,1\],\[0,2,0\]\]
**Explanation:** The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.
**Example 2:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[2,3\],\[3,1\],\[2,3\]\], colConditions = \[\[2,1\]\]
**Output:** \[\]
**Explanation:** From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.
**Constraints:**
* `2 <= k <= 400`
* `1 <= rowConditions.length, colConditions.length <= 104`
* `rowConditions[i].length == colConditions[i].length == 2`
* `1 <= abovei, belowi, lefti, righti <= k`
* `abovei != belowi`
* `lefti != righti` | null |
Topo_sort || python | build-a-matrix-with-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1)concept is to find topo_sort for row and col...\n2)iterate from topo_sort of row elements and find its corresponding pos in topo_sort of col\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Time complexity of topo sort\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: O(k*k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n \n\n# Code\n```\nclass Solution:\n def buildMatrix(self, k: int, row: List[List[int]], col: List[List[int]]) -> List[List[int]]:\n adj_l_A = [[] for i in range(k+1)]\n indegree_A = [0]*(k+1)\n for u,v in row:\n adj_l_A[u].append(v)\n indegree_A[v]+=1\n queue1 = []\n for i in range(1,k+1):\n if indegree_A[i]==0:\n queue1.append(i)\n adj_l_B = [[] for i in range(k+1)]\n indegree_B = [0]*(k+1)\n for u ,v in col:\n adj_l_B[u].append(v)\n indegree_B[v]+=1\n queue2 = []\n for i in range(1,k+1):\n if indegree_B[i]==0:\n queue2.append(i)\n\n\n \n def topo_sort(queue,res,adj_list,indegree):\n while queue:\n curr = queue.pop(0)\n res.append(curr)\n for i in adj_list[curr]:\n indegree[i]-=1\n if indegree[i]==0:\n queue.append(i)\n return res\n Row = topo_sort(queue1,[],adj_l_A,indegree_A)\n Col = topo_sort(queue2,[],adj_l_B,indegree_B)\n if len(Row)==k and len(Col)==k:\n grid = [[0 for i in range(k)] for j in range(k)]\n ind = {}\n for i in range(k):\n ind[Col[i]] = i\n for i in range(k):\n j = ind[Row[i]]\n grid[i][j] = Row[i]\n return grid\n return []\n\n\n \n``` | 1 | You are given a **positive** integer `k`. You are also given:
* a 2D integer array `rowConditions` of size `n` where `rowConditions[i] = [abovei, belowi]`, and
* a 2D integer array `colConditions` of size `m` where `colConditions[i] = [lefti, righti]`.
The two arrays contain integers from `1` to `k`.
You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`.
The matrix should also satisfy the following conditions:
* The number `abovei` should appear in a **row** that is strictly **above** the row at which the number `belowi` appears for all `i` from `0` to `n - 1`.
* The number `lefti` should appear in a **column** that is strictly **left** of the column at which the number `righti` appears for all `i` from `0` to `m - 1`.
Return _**any** matrix that satisfies the conditions_. If no answer exists, return an empty matrix.
**Example 1:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[3,2\]\], colConditions = \[\[2,1\],\[3,2\]\]
**Output:** \[\[3,0,0\],\[0,0,1\],\[0,2,0\]\]
**Explanation:** The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.
**Example 2:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[2,3\],\[3,1\],\[2,3\]\], colConditions = \[\[2,1\]\]
**Output:** \[\]
**Explanation:** From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.
**Constraints:**
* `2 <= k <= 400`
* `1 <= rowConditions.length, colConditions.length <= 104`
* `rowConditions[i].length == colConditions[i].length == 2`
* `1 <= abovei, belowi, lefti, righti <= k`
* `abovei != belowi`
* `lefti != righti` | null |
[Python3] topological sort | build-a-matrix-with-conditions | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/ea6bc01b091cbf032b9c7ac2d3c09cb4f5cd0d2d) for solutions of weekly 308. \n\n**Intuition**\nThe workhorse of this problem is topological sort. The orders in `aboveConditions` and `leftConditions` construct two graphs. Via topological sort, the order becomes apparent. \nSo the algo is summarized below:\n1) topological sort the two graphs to get the row orders and column orders; \n2) if no cycle is found in either row order or column order, an answer exists; otherwise, return empty matrix; \n3) for each number from 1 to k, find its row number and column number from the results of the sorting; \n4) fill the numbers into the matrix. \n\n**Analysis**\nTime complexity `O(K^2)`\nSpace complexity `O(K^2)`\n\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n \n def fn(cond): \n """Return topological sort"""\n graph = [[] for _ in range(k)]\n indeg = [0]*k\n for u, v in cond: \n graph[u-1].append(v-1)\n indeg[v-1] += 1\n queue = deque(u for u, x in enumerate(indeg) if x == 0)\n ans = []\n while queue: \n u = queue.popleft()\n ans.append(u+1)\n for v in graph[u]: \n indeg[v] -= 1\n if indeg[v] == 0: queue.append(v)\n return ans \n \n row = fn(rowConditions)\n col = fn(colConditions)\n \n if len(row) < k or len(col) < k: return []\n ans = [[0]*k for _ in range(k)]\n row = {x : i for i, x in enumerate(row)}\n col = {x : j for j, x in enumerate(col)}\n for x in range(1, k+1): ans[row[x]][col[x]] = x\n return ans \n``` | 15 | You are given a **positive** integer `k`. You are also given:
* a 2D integer array `rowConditions` of size `n` where `rowConditions[i] = [abovei, belowi]`, and
* a 2D integer array `colConditions` of size `m` where `colConditions[i] = [lefti, righti]`.
The two arrays contain integers from `1` to `k`.
You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`.
The matrix should also satisfy the following conditions:
* The number `abovei` should appear in a **row** that is strictly **above** the row at which the number `belowi` appears for all `i` from `0` to `n - 1`.
* The number `lefti` should appear in a **column** that is strictly **left** of the column at which the number `righti` appears for all `i` from `0` to `m - 1`.
Return _**any** matrix that satisfies the conditions_. If no answer exists, return an empty matrix.
**Example 1:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[3,2\]\], colConditions = \[\[2,1\],\[3,2\]\]
**Output:** \[\[3,0,0\],\[0,0,1\],\[0,2,0\]\]
**Explanation:** The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.
**Example 2:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[2,3\],\[3,1\],\[2,3\]\], colConditions = \[\[2,1\]\]
**Output:** \[\]
**Explanation:** From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.
**Constraints:**
* `2 <= k <= 400`
* `1 <= rowConditions.length, colConditions.length <= 104`
* `rowConditions[i].length == colConditions[i].length == 2`
* `1 <= abovei, belowi, lefti, righti <= k`
* `abovei != belowi`
* `lefti != righti` | null |
[Python 3] Topological Sort Ez To Understand | build-a-matrix-with-conditions | 0 | 1 | Intuition: For each row/col conditions, consider them as a directed edge. For example, in the given test case: \n\nrow_conditions could be represented as two edges: 1 -> 2 and 3 -> 2. This could work because there\'s no cycle in the graph (consider if we have 1 -> 2 and 2 -> 1, it is not possible to come up with a valid matrix because we end up in a cycle). Also we need to know the order in which the numbers could be placed, which algorithm could do both? -> topological sort! \n\nThe DFS code below could be an easy template for all source of topological sort problems. \n\n```\nclass Solution:\n def buildMatrix(self, n: int, rowC: List[List[int]], colC: List[List[int]]) -> List[List[int]]:\n\t\t# create two graphs, one for row and one for columns\n row_adj = {i: [] for i in range(1, n + 1)}\n col_adj = {i: [] for i in range(1, n + 1)}\n for u, v in rowC:\n row_adj[u].append(v)\n for u, v in colC:\n col_adj[u].append(v)\n \n # inorder to do topological sort, we need to maintain two visit lists: one marks which node \n # we have already processed (because not all nodes are connected to each other and we do not \n # want to end up in a infinite loop), the other one marks nodes we are currently visiting(or in \n # our recursion stack). If we visit a node that we are currently visiting, that means there is \n # a loop, so we return False; if it is not in our current visit but has already been visited, we \n # can safely travel to the next node and return True. \n\n row_stack = []\n row_visit = set()\n row_visiting = set()\n col_stack = []\n col_visit = set()\n col_visiting = set()\n \n def dfs(node, stack, visit, visiting, adj):\n if node in visiting:\n return False\n if node in visit:\n return True\n visit.add(node)\n visiting.add(node)\n for child in adj[node]:\n if not dfs(child, stack, visit, visiting, adj):\n return False\n visiting.remove(node)\n stack.append(node)\n return True\n \n # do dfs on each row/col graph\n for i in range(1, n + 1):\n if i not in row_visit:\n if not dfs(i, row_stack, row_visit, row_visiting, row_adj):\n return []\n if i not in col_visit:\n if not dfs(i, col_stack, col_visit, col_visiting, col_adj):\n return []\n\n\t\t \n\n # After the dfs, we also need a stack to store which node has been entirely explored. That\'s why we \n # append the current node to our stack after exploring all its neighbors. Remember we have to reverse \n # the stack after all DFS\'s, because the first-explored node gets appended first. \n row_stack, col_stack = row_stack[::-1], col_stack[::-1]\n \n \n # mark position for each element\n row_memo, col_memo = {}, {}\n for idx, num in enumerate(row_stack):\n row_memo[num] = idx\n for idx, num in enumerate(col_stack):\n col_memo[num] = idx\n \n # create an empty matrix as our ans\n ans = [[0]*n for _ in range(n)]\n \n # plug in values from what we have discovered\n for i in range(1, n + 1):\n ans[row_memo[i]][col_memo[i]] = i\n return ans\n``` | 1 | You are given a **positive** integer `k`. You are also given:
* a 2D integer array `rowConditions` of size `n` where `rowConditions[i] = [abovei, belowi]`, and
* a 2D integer array `colConditions` of size `m` where `colConditions[i] = [lefti, righti]`.
The two arrays contain integers from `1` to `k`.
You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`.
The matrix should also satisfy the following conditions:
* The number `abovei` should appear in a **row** that is strictly **above** the row at which the number `belowi` appears for all `i` from `0` to `n - 1`.
* The number `lefti` should appear in a **column** that is strictly **left** of the column at which the number `righti` appears for all `i` from `0` to `m - 1`.
Return _**any** matrix that satisfies the conditions_. If no answer exists, return an empty matrix.
**Example 1:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[3,2\]\], colConditions = \[\[2,1\],\[3,2\]\]
**Output:** \[\[3,0,0\],\[0,0,1\],\[0,2,0\]\]
**Explanation:** The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.
**Example 2:**
**Input:** k = 3, rowConditions = \[\[1,2\],\[2,3\],\[3,1\],\[2,3\]\], colConditions = \[\[2,1\]\]
**Output:** \[\]
**Explanation:** From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.
**Constraints:**
* `2 <= k <= 400`
* `1 <= rowConditions.length, colConditions.length <= 104`
* `rowConditions[i].length == colConditions[i].length == 2`
* `1 <= abovei, belowi, lefti, righti <= k`
* `abovei != belowi`
* `lefti != righti` | null |
3 Lines of Code | find-subarrays-with-equal-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubarrays(self, nums: List[int]) -> bool:\n list1=[]\n for i in range(len(nums)-1):\n list1.append(sum(nums[i:i+2%(len(nums))]))\n return sorted(set(list1))!=sorted(list1)\n\n``` | 1 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
beginner friendly code in python. | find-subarrays-with-equal-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubarrays(self, nums: List[int]) -> bool:\n dict1={}\n for i in range(len(nums)-1):\n x=sum(nums[i:i+2])\n dict1[i]=x\n list1=list(dict1.values())\n for i in range(len(list1)):\n j=i+1\n while j<len(list1):\n if list1[i]==list1[j]:\n return True\n j+=1\n return False\n\n\n``` | 1 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
Python3 || 3 (or 1) lines, T/M: 36ms/13.9MB | find-subarrays-with-equal-sum | 0 | 1 | ```\nclass Solution: # Let nums = [ 1,3,2,4,1,4],\n \n # Here\'s the plan: \n # 1) Compute all the sums: ((1,3),(3,2),(4,1),(1,4))\n # -->(1,5,5,5)\n # 2) Determine whether any sum occurs twice: \n # --> Counter({5: 3, 4: 1})\n # 3) Return the result.\n\n def findSubarrays(self, nums: List[int]) -> bool:\n\n sums = (x+y for x,y in zip(nums[1:], nums)) # <-- 1)\n\n counts = Counter(sums).values() # <-- 2)\n\n return max(counts) > 1 # <-- 3)\n\n # or (if you must):\n\n def findSubarrays(self, nums: List[int]) -> bool:\n return max(Counter([x+y for x,y in zip(nums[1:], nums)]).values()) > 1 | 4 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
Python || Sliding window || Bruteforce | find-subarrays-with-equal-sum | 0 | 1 | # Bruteforce \n# Sliding window\n## Time -> O(n)\n## Space -> O(n)\n\n```\nclass Solution:\n def findSubarrays(self, nums: List[int]) -> bool:\n """ \n\tBruteforce approch\n\t"""\n# for i in range(len(nums)-2):\n# summ1 = nums[i] + nums[i+1]\n# # for j in range(i+1,len(nums)):\n# for j in range(i+1,len(nums)-1):\n# summ = nums[j] + nums[j+1]\n# if summ == summ1:\n# return True\n# return False\n\t """\n\t Sliding Window\n\t """\n one ,two = len(nums)-2,len(nums)-1 // at end of list\n dic = {}\n while one >= 0:\n # print(one,two)\n summ = nums[one] + nums[two]\n if summ in dic:\n return True // if already there then there is 2 pairs\n else:\n dic[summ] = 1 // add summ in of window in dictonary\n one -=1\n two -=1\n return False\n```\n### \uD83D\uDE02 Random Dev Meme\n<img src="https://random-memer.herokuapp.com/" width="512px"/> | 4 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
Python | Easy Understanding | find-subarrays-with-equal-sum | 0 | 1 | ```\nclass Solution:\n def findSubarrays(self, nums: List[int]) -> bool:\n all_sums = []\n for i in range(0, len(nums) - 1):\n if nums[i] + nums[i + 1] in all_sums:\n return True\n else:\n all_sums.append(nums[i] + nums[i + 1])\n \n return False\n``` | 2 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
Optimum solution using python easy to understand. | find-subarrays-with-equal-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubarrays(self, nums: List[int]) -> bool:\n dict1={}\n for i in range(len(nums)-1):\n x=sum(nums[i:i+2])\n if x in dict1:\n return True\n else:\n dict1[x]=x \n return False\n\n\n``` | 3 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
✅ Python 99% Easy Simple Solution | Set | find-subarrays-with-equal-sum | 0 | 1 | #### Easy Solution:\n* Sum the two indexes `getSum`\n* If the `getSum` is in `sums` array then return true\n* Else add the summation into the array\n* After iterate through the array return false as there is no similar sum\n```\nclass Solution:\n\tdef findSubarrays(self, nums: list[int]) -> bool:\n\t\tsums = set()\n\n\t\tfor i in range(len(nums) - 1):\n\t\t\tgetSum = nums[i] + nums[i + 1]\n\t\t\tif getSum in sums:\n\t\t\t\treturn True\n\t\t\tsums.add(getSum)\n\t\treturn False\n``` | 1 | Given a **0-indexed** integer array `nums`, determine whether there exist **two** subarrays of length `2` with **equal** sum. Note that the two subarrays must begin at **different** indices.
Return `true` _if these subarrays exist, and_ `false` _otherwise._
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,2,4\]
**Output:** true
**Explanation:** The subarrays with elements \[4,2\] and \[2,4\] have the same sum of 6.
**Example 2:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** false
**Explanation:** No two subarrays of size 2 have the same sum.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** true
**Explanation:** The subarrays \[nums\[0\],nums\[1\]\] and \[nums\[1\],nums\[2\]\] have the same sum of 0.
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.
**Constraints:**
* `2 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109` | null |
simple solution | strictly-palindromic-number | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\njust google how to return false in what language you want thats all | 2 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
3 SECONDS ❌ EASY TO UNDERSTAND ❌ IMPORTANT VARIABLE ❌ BEATS SOME USERS ❌ HASHMAP ❌ GREEDY ALGORITHM | strictly-palindromic-number | 0 | 1 | # Intuition\nimplement hasmap\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 3 seconds\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \uD83E\uDD37\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n Importantvariable = 0\n hashmap = dict()\n for i in range(130000):\n if i % 2 == 0:\n print("lol")\n Importantvariable = abs((i**2) * (Importantvariable))\n return False\n``` | 1 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
professional cheater | python | strictly-palindromic-number | 0 | 1 | \n# Code\n```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n return False\n``` | 0 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
✔ Simple Python Code || Easily Understandable | strictly-palindromic-number | 0 | 1 | \n\n# Approach\n- Starting from ```base 2 to n```, find out the binary representation\n- Check for palindrom and count total no of palindroms\n- Check total no of palindroms ```if count == n-2:``` and if \u2714 return true\n- ```n-2``` is to exclude ```0,1``` as we\'r checking the base from 2\n\n\n# Code\n```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n count = 0\n for i in range(2,n+1):\n bit = \'\'\n dup = n\n while dup!=0:\n d = dup % i\n bit = str(d) + bit\n dup = dup // i\n\n rev = bit[::-1]\n \n if rev == bit:\n count += 1\n\n if count == n-2:\n return True\n\n``` | 3 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
Easy Python Solution | strictly-palindromic-number | 0 | 1 | \n# Code\n```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n for i in range(2,n-1):\n s=self.convert(n,i)\n if str(s)!=str(s)[::-1]:\n return False\n return True\n\n def convert(self, n,x):\n tem=""\n while n>0:\n tem+=str(n%x)\n if n//x in range(0,x):\n tem+=str(n//x)\n n//=x\n return tem[::-1]\n``` | 2 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
Python solution | strictly-palindromic-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n return False\n``` | 2 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
One Liner code that will beat 90% | strictly-palindromic-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n return False\n``` | 2 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
One Word Solution | Python | strictly-palindromic-number | 0 | 1 | ```\nclass Solution:\n def isStrictlyPalindromic(self, n: int) -> bool:\n pass\n``` | 1 | An integer `n` is **strictly palindromic** if, for **every** base `b` between `2` and `n - 2` (**inclusive**), the string representation of the integer `n` in base `b` is **palindromic**.
Given an integer `n`, return `true` _if_ `n` _is **strictly palindromic** and_ `false` _otherwise_.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** n = 9
**Output:** false
**Explanation:** In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.
**Example 2:**
**Input:** n = 4
**Output:** false
**Explanation:** We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.
**Constraints:**
* `4 <= n <= 105` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.