question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
painting-a-grid-with-three-different-colors | Rust | Bottom-up DP, 6ms, beats 100% | rust-bottom-up-dp-6ms-beats-100-by-soyfl-lvza | Intuition\nCompress each row into vertices, construct a graph and do DP on it.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\nrust\n#[derive(Debug, Clone, | soyflourbread | NORMAL | 2024-03-05T02:13:26.747999+00:00 | 2024-03-05T02:13:26.748032+00:00 | 5 | false | # Intuition\nCompress each row into vertices, construct a graph and do DP on it.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n# Code\n```rust\n#[derive(Debug, Clone, PartialOrd, Ord, PartialEq, Eq)]\npub enum Color {\n Blue,\n Pink,\n White,\n}\n\npub fn to_vertices(\n width: usize,\n) -> Vec<Vec<Color>> {\n fn backtrack(\n width: usize,\n parent_vec: &mut Vec<Color>,\n ret: &mut Vec<Vec<Color>>,\n ) {\n if parent_vec.len() >= width {\n return ret.push(parent_vec.clone());\n }\n\n for color_next in [\n Color::Blue, Color::Pink, Color::White,\n ] {\n if Some(&color_next) == parent_vec.last() {\n continue;\n }\n\n // BEGIN backtracking\n parent_vec.push(color_next);\n backtrack(width, parent_vec, ret);\n parent_vec.pop();\n // END backtracking\n }\n }\n\n let mut ret = vec![];\n backtrack(\n width,\n &mut Vec::with_capacity(width),\n &mut ret,\n );\n\n ret\n}\n\npub fn to_graph(\n vertices: Vec<Vec<Color>>,\n) -> Vec<Vec<usize>> {\n let n = vertices.len();\n\n let mut ret = vec![vec![]; n];\n \n for i in 0..n {\n for j in 0..n {\n let v = vertices[i].clone();\n let v_next = vertices[j].clone();\n if v.into_iter().zip(v_next.into_iter())\n .any(|(e0, e1)| e0 == e1) {\n continue;\n }\n\n ret[i].push(j);\n }\n }\n\n ret\n}\n\nconst MOD: usize = 1_000_000_007;\n\nimpl Solution {\n pub fn color_the_grid(m: i32, n: i32) -> i32 {\n let (m, n) = (m as usize, n as usize);\n let vertices = to_vertices(m);\n let dp_width = vertices.len();\n let graph = to_graph(vertices);\n\n let mut dp = vec![1usize; dp_width];\n for _ in 1..n {\n let mut dp_next = vec![usize::MIN; dp_width];\n\n for (v, count) in dp.into_iter().enumerate() {\n for &v_next in &graph[v] {\n dp_next[v_next] += count;\n }\n }\n for e in &mut dp_next { *e %= MOD; }\n\n dp = dp_next;\n }\n\n let mut ret = dp.into_iter().sum::<usize>();\n ret %= MOD;\n\n ret as i32\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Rust'] | 0 |
painting-a-grid-with-three-different-colors | C++ bitmask DP | c-bitmask-dp-by-sanzenin_aria-aa0p | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sanzenin_aria | NORMAL | 2024-02-21T02:40:28.726197+00:00 | 2024-02-21T02:41:34.456216+00:00 | 23 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int colorTheGrid(int m, int n) {\n const long long mod = 1e9+7;\n vector<Mask> masks(1);\n for(int i=0;i<m;i++){\n vector<Mask> new_masks;\n for(auto mask:masks){\n for(int c=1;c<4;c++){\n auto new_mask = mask;\n new_mask.set_color(i, c);\n if(new_mask.is_valid())\n new_masks.push_back(new_mask);\n }\n }\n masks = move(new_masks);\n }\n const int size = masks.size();\n vector v(size, 1LL);\n while(--n){\n vector new_v(size, 0LL);\n for(int i=0;i<size;i++){\n for(int j=0;j<size;j++){\n if(masks[i].can_be_neighbor(masks[j]))\n new_v[j] = (new_v[j] + v[i]) % mod;\n }\n }\n v = move(new_v);\n }\n return accumulate(v.begin(), v.end(), 0LL) % mod;\n }\n\n struct Mask{\n int get_color(int pos) const{\n return (bits >> (pos*2)) & 3;\n } \n void set_color(int pos, int color){\n bits |= (color << (pos*2));\n size = max(size, 1+pos);\n }\n\n bool can_be_neighbor(Mask rhs) const{\n for(int pos=0; pos<size; pos++){\n if(get_color(pos) == rhs.get_color(pos))\n return false;\n }\n return true;\n }\n\n bool is_valid() const{\n for(int i=1;i<size;i++){\n if(get_color(i-1) == get_color(i))\n return false;\n }\n return true;\n }\n\n int print() const{\n int x = 0;\n for(int i=0;i<size;i++){\n x*=10;\n x += get_color(i);\n }\n return x;\n }\n\n private:\n int size = 0;\n int bits = 0;\n };\n};\n``` | 0 | 0 | ['C++'] | 0 |
painting-a-grid-with-three-different-colors | DP on Counter() base (without recursion) (60% | 81%) | dp-on-counter-base-without-recursion-60-et98b | Code\n\nclass Solution:\n \n def colorTheGrid(self, m: int, n: int) -> int:\n mod = 10 ** 9 + 7\n\n def get_first_line(m) -> list[str]:\n | eshved | NORMAL | 2024-01-03T18:49:10.034401+00:00 | 2024-01-04T21:47:25.000592+00:00 | 16 | false | # Code\n```\nclass Solution:\n \n def colorTheGrid(self, m: int, n: int) -> int:\n mod = 10 ** 9 + 7\n\n def get_first_line(m) -> list[str]:\n """Returns all possible (24) variations of the first line.\n """\n res = [[], [""]]\n for i in range(m):\n for r in res[(1-i) % 2]:\n for c in \'rgb\':\n if not r or r[-1] != c:\n res[i % 2].append(r + c)\n res[(1-i) % 2].clear()\n return res[i % 2]\n\n \n @cache\n def get_lines(prev_line: str) -> tuple[str]:\n """Returns all possible variations of the\n next line based on the previous one.\n """\n return tuple(filter(\n lambda el: not set(enumerate(prev_line)) & set(enumerate(el)),\n first_line\n ))\n\n prev_counter = Counter(first_line := get_first_line(m))\n \n # find and count options for the following lines\n for _ in range(n - 1):\n cur_counter = Counter()\n for prev_line, cnt in prev_counter.items():\n cur_counter.update(\n {key: cnt % mod for key in get_lines(prev_line)}\n )\n prev_counter = cur_counter\n\n return sum(prev_counter.values()) % mod\n``` | 0 | 0 | ['Python3'] | 0 |
painting-a-grid-with-three-different-colors | easy with all steps | easy-with-all-steps-by-parwez0786-5tjn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | parwez0786 | NORMAL | 2024-01-02T12:49:33.462336+00:00 | 2024-01-02T12:49:33.462370+00:00 | 28 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution\n{\npublic:\n int dp[1001][1 << 10];\n int mod=1000000007;\n int solve(int row, int col, int preMask, int curMask, int n, int m)\n {\n if (col == m)\n {\n return 1;\n }\n if (dp[col][preMask] != -1)\n {\n return dp[col][preMask];\n }\n if (row == n)\n {\n return solve(0, col + 1, curMask, 0, n, m)%mod;\n }\n long long ans = 0;\n for (int k = 1; k <= 3; k++)\n {\n int colorAtPrevCol = 0;\n if ((1 << (2 * row)) & preMask)\n {\n colorAtPrevCol = colorAtPrevCol | (1 << 0);\n }\n if ((1 << (2 * row + 1)) & preMask)\n {\n colorAtPrevCol = colorAtPrevCol | (1 << 1);\n }\n \n\n int colorAtSameCol = 0;\n if (row > 0)\n {\n if ((1 << (2 * row - 2)) & curMask)\n {\n colorAtSameCol |= (1 << 0);\n }\n if ((1 << (2 * row - 1)) & curMask)\n {\n colorAtSameCol |= (1 << 1);\n }\n if (colorAtPrevCol != k && colorAtSameCol != k)\n {\n if (k == 1)\n {\n\n ans = (ans + solve(row + 1, col, preMask, curMask | (1 << (2 * row)), n, m))%mod;\n }\n else if (k == 2)\n {\n ans = (ans + solve(row + 1, col, preMask, curMask | (1 << (2 * row + 1)), n, m))%mod;\n }\n else\n {\n ans = (ans + solve(row + 1, col, preMask, (curMask | (1 << (2 * row)) | (1 << (2 * row + 1))), n, m))%mod;\n }\n }\n }\n else\n {\n if (colorAtPrevCol != k)\n {\n if (k == 1)\n {\n\n ans = (ans + solve(row + 1, col, preMask, curMask | (1 << (2 * row)), n, m))%mod;\n }\n else if (k == 2)\n {\n ans = (ans + solve(row + 1, col, preMask, curMask | (1 << (2 * row + 1)), n, m))%mod;\n }\n else\n {\n ans = (ans + solve(row + 1, col, preMask, (curMask | (1 << (2 * row)) | (1 << (2 * row + 1))), n, m))%mod;\n }\n }\n }\n }\n\n if (row == 0)\n {\n dp[col][preMask] = ans%mod;\n }\n return ans%mod;\n }\n int colorTheGrid(int m, int n)\n {\n memset(dp, -1, sizeof(dp));\n return solve(0, 0, 0, 0, m, n);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
painting-a-grid-with-three-different-colors | python DP top down | python-dp-top-down-by-harrychen1995-04nc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | harrychen1995 | NORMAL | 2023-11-13T19:25:12.504222+00:00 | 2023-11-13T19:25:12.504246+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n @functools.lru_cache(None)\n def generate(i):\n\n if i == m:\n return [""]\n ans = []\n for s in {"r", "b", "g"}:\n for j in generate(i+1):\n if not j or s != j[0]:\n ans.append(s+j)\n return ans\n \n @functools.lru_cache(None)\n def dp(i, prev):\n if i == n:\n return 1\n ans = 0\n if not prev:\n for p in generate(0):\n ans += dp(i+1, p)\n else:\n for p in generate(0):\n for k in range(len(p)):\n if p[k] == prev[k]:\n break\n else:\n ans += dp(i+1, p)\n return ans \n \n return dp(0, "") % (10**9 + 7)\n``` | 0 | 0 | ['Dynamic Programming', 'Python3'] | 0 |
painting-a-grid-with-three-different-colors | Dynamic programming | Top to bottom | Easy to understand code | dynamic-programming-top-to-bottom-easy-t-h843 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | geeknkta | NORMAL | 2023-11-01T15:13:38.051276+00:00 | 2023-11-01T15:13:38.051300+00:00 | 42 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int mod = 1000000007;\n vector<int> getAllPossibleMasks(int prevMask, int m) {\n vector<int> allPossibleMasks;\n dfs(0, prevMask, 0, m, allPossibleMasks);\n return allPossibleMasks;\n }\n\n void dfs(int row, int prevMask, int currentColMask, int m, vector<int>&allPossibleMasks) {\n if(row == m) { \n allPossibleMasks.push_back(currentColMask);\n return;\n } \n for(int i=1; i<=3; i++) {\n if((getColor(row, prevMask) != i ) && (row == 0 || getColor(row-1, currentColMask) != i)) {\n dfs(row + 1, prevMask, setCurrentColMask(currentColMask, row, i), m, allPossibleMasks);\n }\n }\n }\n\n int getColor(int row, int prevMask) {\n //cout << prevMask << " " << row << endl;\n return (prevMask >> (2*row)) & 3;\n }\n\n int setCurrentColMask(int mask, int pos, int color){\n return mask | (color << (2*pos));\n }\n\n\n int getResult(int col, int m, int n, int prevMask, vector<vector<int> > &dp) {\n if(col == n) {\n return 1;\n }\n\n if(dp[col][prevMask] != -1) {\n return dp[col][prevMask];\n }\n int ans = 0;\n\n vector<int> allPossibleMasks = getAllPossibleMasks(prevMask, m);\n for(int mask : allPossibleMasks) {\n ans = (ans + getResult(col + 1, m, n, mask, dp))%mod;\n }\n\n dp[col][prevMask] = ans;\n\n return ans;\n }\n\n int colorTheGrid(int m, int n) {\n vector<vector<int> > dp(n+1, vector<int>(1025, -1));\n return getResult(0, m, n, 0, dp);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
painting-a-grid-with-three-different-colors | C# Beats 100% in speed and memory usage | c-beats-100-in-speed-and-memory-usage-by-ug9o | \n\n\n# Complexity\n- Time complexity:\nO(n * (3^m)^2)\n\n- Space complexity:\nO(n * 3^m + (3^m)^2)\n\n# Code\n\npublic class Solution {\n public int ColorTh | junkmann | NORMAL | 2023-10-19T01:00:19.324638+00:00 | 2023-10-19T01:00:19.324672+00:00 | 7 | false | \n\n\n# Complexity\n- Time complexity:\n$$O(n * (3^m)^2)$$\n\n- Space complexity:\n$$O(n * 3^m + (3^m)^2)$$\n\n# Code\n```\npublic class Solution {\n public int ColorTheGrid(int m, int n) {\n var motif = new char[m];\n var motifs = new List<string>();\n\n motif[0] = \'R\';\n FindMotifs(1, motif, motifs);\n\n motif[0] = \'G\';\n FindMotifs(1, motif, motifs);\n\n motif[0] = \'B\';\n FindMotifs(1, motif, motifs);\n\n var stackables = FindStackables(motifs);\n var dp = new int[n, motifs.Count];\n\n for (var i = 0; i < motifs.Count; ++i) {\n dp[0, i] = 1;\n }\n\n for (var i = 1; i < n; ++i) {\n for (var j = 0; j < motifs.Count; ++j) {\n foreach (var stackable in stackables[j]) {\n dp[i, j] += dp[i - 1, stackable];\n dp[i, j] %= 1000000007;\n }\n }\n }\n\n var ans = 0;\n\n for (var i = 0; i < motifs.Count; ++i) {\n ans += dp[n - 1, i];\n ans %= 1000000007;\n }\n\n return ans;\n }\n\n private void FindMotifs(int i, char[] motif, List<string> motifs) {\n if (i == motif.Length) {\n motifs.Add(new string(motif));\n return;\n }\n\n switch (motif[i - 1]) {\n case \'R\':\n motif[i] = \'G\';\n FindMotifs(i + 1, motif, motifs);\n motif[i] = \'B\';\n FindMotifs(i + 1, motif, motifs);\n break;\n case \'G\':\n motif[i] = \'R\';\n FindMotifs(i + 1, motif, motifs);\n motif[i] = \'B\';\n FindMotifs(i + 1, motif, motifs);\n break;\n case \'B\':\n motif[i] = \'R\';\n FindMotifs(i + 1, motif, motifs);\n motif[i] = \'G\';\n FindMotifs(i + 1, motif, motifs);\n break;\n default:\n throw new Exception();\n }\n }\n\n private bool CanStack(string motifA, string motifB) {\n for (var i = 0; i < motifA.Length; ++i) {\n if (motifA[i] == motifB[i]) {\n return false;\n }\n }\n\n return true;\n }\n\n private List<int>[] FindStackables(List<string> motifs) {\n var ans = new List<int>[motifs.Count];\n\n for (var i = 0; i < motifs.Count; ++i) {\n ans[i] = new();\n \n for (var j = 0; j < motifs.Count; ++j) {\n if (CanStack(motifs[i], motifs[j])) {\n ans[i].Add(j);\n }\n }\n }\n\n return ans;\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
painting-a-grid-with-three-different-colors | Java solution | java-solution-by-pejmantheory-735x | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pejmantheory | NORMAL | 2023-09-16T07:48:46.672162+00:00 | 2023-09-16T07:48:46.672194+00:00 | 50 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int colorTheGrid(int m, int n) {\n this.m = m;\n this.n = n;\n return dp(0, 0, 0, 0);\n }\n\n private static final int kMod = 1_000_000_007;\n private int m;\n private int n;\n private int[][] memo = new int[1000][1024];\n\n private int dp(int r, int c, int prevColMask, int currColMask) {\n if (c == n)\n return 1;\n if (memo[c][prevColMask] != 0)\n return memo[c][prevColMask];\n if (r == m)\n return dp(0, c + 1, currColMask, 0);\n\n int ans = 0;\n\n // 1 := red, 2 := green, 3 := blue\n for (int color = 1; color <= 3; ++color) {\n if (getColor(prevColMask, r) == color)\n continue;\n if (r > 0 && getColor(currColMask, r - 1) == color)\n continue;\n ans += dp(r + 1, c, prevColMask, setColor(currColMask, r, color));\n ans %= kMod;\n }\n\n if (r == 0)\n memo[c][prevColMask] = ans;\n\n return ans;\n }\n\n // E.g. __ __ __ __ __\n // 01 10 11 11 11\n // R G B B B\n // GetColor(0110111111, 3) -> G\n private int getColor(int mask, int r) {\n return mask >> r * 2 & 3;\n }\n\n private int setColor(int mask, int r, int color) {\n return mask | color << r * 2;\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
painting-a-grid-with-three-different-colors | Top Down dp with bit masking Easy Complete Solution | top-down-dp-with-bit-masking-easy-comple-8aqo | My first thought was to just calculate No of possible paths to n-1, m-1 with given constrain but the thing went wrong was the other left remaining squires can f | demon_code | NORMAL | 2023-09-06T08:28:03.361289+00:00 | 2023-09-06T13:02:09.588904+00:00 | 7 | false | My first thought was to just calculate No of possible paths to n-1, m-1 with given constrain but the thing went wrong was the other left remaining squires can form different combination which is not part of selected path so it failed ``` :(```\n\nto colur any cell we need information about just upper sell and left cell``` ( if u plan to paint cells one after another sequencily from 0 to m-1th column till { 0 to row to n-1th row } ) ```\n\nSo the hint here is the m<=5 means we can effectively store the previous row colours and start painting by looking upper cell colur and just left painted cell\'s colur with following the constrain.\n``` Okey !```\n\n``` \nSo now we can start from 0th row with prev row intialised with\n"##... m times " (means first row has no such ristrictions of upper cell)\n\'0\' => red \'1\' =blue \'2\' => green\n``` \n\nwhen we enter in solve function we call a help function which genrates all possible next states for next i+1 row (see the implimenation of help it\'s very basic)\nthen for each state we call solve(i+1, state_i) and add all the solutions.\nto memoize the recursion we can transform this string into 3 base number which will help in space optimization and easy access to solved subproblems with O(1) complexcity\n\n``` \n i s next states\nTime : n* (3^m) * (3* 2^(m-1)) => n=no of rows, 3^m string different values(all possible) , inner loop next states< (3*2^(m-1)) \n```\n```\nSpace : n* (3^m)\n```\n```\nclass Solution {\npublic:\n \n int m=1e9+7;\n void help(string &s, string &t, vector<string> &a) // genrates next all next possible arrangement for next row, max next states :3*2*2*2*2 -> 48 it will \n {// very much less once we have upper cell and left cell contrain. 48 will only for 0th row \n \n if(t.size()==s.size())\n {\n a.push_back(t);\n return ;\n }\n char p;\n if(t.size()>0)\n p= t.back();\n else p=\'#\';\n int k=t.size();\n \n for(int i=\'0\'; i<=\'2\'; i++)\n {\n if(p!=i && s[k]!=i)\n {\n t.push_back(i);\n help(s,t,a);\n t.pop_back();\n }\n }\n \n return;\n }\n \n\n // map<pair<int,string>, int> mp;\n\n int n;\n int dp[1001][244];\n \n int change(string &s) // string to 3 based number for easy storage\n {\n if(s.back()==\'#\') return 0;\n int n=0;\n for(auto i: s) n=3*n+(i-\'0\');\n return n;\n }\n //curr row prev state \n int solve( int i, string &u )\n {\n if(i==n) return 1;\n \n // if(mp.find({i,u})!=mp.end()) return mp[{i,u}];\n \n int num= change(u);\n if(dp[i][num]!=-1) return dp[i][num];\n \n vector<string>a;\n string t="";\n help(u,t, a);\n long long ans=0;\n for(auto k: a) // at max (in i=0 ) 48 calls\n {\n ans+=solve(i+1, k)%m;\n ans%=m;\n }\n \n // return mp[{i,u}]=ans;\n \n return dp[i][num]=ans;\n \n \n \n }\n \n int colorTheGrid(int m, int n1) \n {\n // m=m1;\n n=n1;\n string s="";\n while(m--) s+=\'#\';\n memset(dp,-1,sizeof(dp));\n\t\t// s can have at max 48 different values for any row \n return solve(0,s);\n }\n};\n\n\n// ignore \n// my first approach to problem\n// possible path with constrain to reach destination \n// int mo= 1e9+7;\n// int dp[6][1001][4][4];\n// int n; int m;\n// int solve(int i, int j, int l, int u)\n// {\n// if(i==n-1 && j==m-1) \n// {\n \n// int t=0;\n// for(int c=0; c<=2; c++) if(c!=l && c!=u) t++;\n// return t;\n// }\n \n// if(i>=n || j>=m) return 0;\n \n// if(dp[i][j][l+1][u+1]!=-1) return dp[i][j][l+1][u+1];\n// long long ans=0;\n// for(int c=0; c<=2; c++)\n// {\n// if(c!=l && c!=u)\n// {\n// //down\n// ans+=solve(i+1,j,l,c);\n// //right\n// // ans%=mo;\n// ans+=solve(i, j+1,c,u);\n// // ans%=mo;\n// }\n// }\n// return dp[i][j][l+1][u+1]=ans; \n \n// }\n \n\n```\n\n\n\n\n\n\n\n\n\n\n\n | 0 | 0 | ['Dynamic Programming', 'Recursion', 'C', 'Bitmask'] | 0 |
painting-a-grid-with-three-different-colors | My Solution | my-solution-by-hope_ma-tdeg | \nclass Solution {\n public:\n int colorTheGrid(const int m, const int n) {\n constexpr int mod = 1000000007;\n constexpr int range = 2;\n constexpr i | hope_ma | NORMAL | 2023-07-12T15:01:22.873630+00:00 | 2023-07-12T15:01:22.873653+00:00 | 7 | false | ```\nclass Solution {\n public:\n int colorTheGrid(const int m, const int n) {\n constexpr int mod = 1000000007;\n constexpr int range = 2;\n constexpr int color_mask = 0b11;\n /**\n * `0b00` stands for red\n * `0b01` stands for green\n * `0b10` stands for blue\n * `0b11` is invalid\n */\n int layouts = 1 << (2 * m);\n vector<int> valid_layouts;\n for (int layout = 0; layout < layouts; ++layout) {\n bool valid = true;\n for (int i_color = 0; i_color < m; ++i_color) {\n const int previous_color = i_color == 0 ? color_mask : (layout >> 2 * (i_color - 1)) & color_mask;\n const int current_color = (layout >> 2 * i_color) & color_mask;\n if (current_color == color_mask || previous_color == current_color) {\n valid = false;\n break;\n }\n }\n if (valid) {\n valid_layouts.emplace_back(layout);\n }\n }\n \n int n_valid_layouts = static_cast<int>(valid_layouts.size());\n vector<int> compatibles[n_valid_layouts];\n for (int i = 0; i < n_valid_layouts - 1; ++i) {\n for (int j = i + 1; j < n_valid_layouts; ++j) {\n const int xor_result = valid_layouts[i] ^ valid_layouts[j];\n bool compatible = true;\n for (int i_color = 0; i_color < m; ++i_color) {\n const int item = (xor_result >> 2 * i_color) & color_mask;\n if (item == 0) {\n compatible = false;\n break;\n }\n }\n if (compatible) {\n compatibles[i].emplace_back(j);\n compatibles[j].emplace_back(i);\n }\n }\n }\n \n int dp[range][n_valid_layouts];\n memset(dp, 0, sizeof(dp));\n int previous = 0;\n int current = 1;\n fill(dp[previous], dp[previous] + n_valid_layouts, 1);\n for (int c = 1; c < n; ++c) {\n for (int layout = 0; layout < n_valid_layouts; ++layout) {\n for (const int previous_layout : compatibles[layout]) {\n dp[current][layout] = (dp[current][layout] + dp[previous][previous_layout]) % mod;\n }\n }\n \n previous ^= 1;\n current ^= 1;\n memset(dp[current], 0, sizeof(dp[current]));\n }\n \n int ret = 0;\n for (const int item : dp[previous]) {\n ret = (ret + item) % mod;\n }\n return ret;\n }\n};\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | No bitmask | no-bitmask-by-shivral-r0v2 | \n Add your space complexity here, e.g. O(n) \n\n# Code\n\nb=[]\ndef gen(s,n):\n global b\n if len(s)==n:\n fl=False\n for i in range(1,n):\ | shivral | NORMAL | 2023-05-18T13:08:26.440412+00:00 | 2023-05-18T13:08:26.440441+00:00 | 50 | false | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nb=[]\ndef gen(s,n):\n global b\n if len(s)==n:\n fl=False\n for i in range(1,n):\n fl|=s[i]==s[i-1]\n if not fl:\n b.append(s)\n return\n gen(s+"0",n)\n gen(s+"1",n)\n gen(s+"2",n)\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n global b\n dp=defaultdict(lambda :-1)\n mod=10**9+7\n b=[]\n gen("",m)\n # print(b)\n def rec(i,prev):\n if i==n:\n return 1\n if dp[i,prev]!=-1:\n return dp[i,prev]\n ans=0\n for cl in b:\n if prev==-1 :\n ans+=rec(i+1,cl)\n ans%=mod\n continue\n fl=False\n for id in range(len(cl)):\n fl|=prev[id]==cl[id]\n if fl==False:\n ans+=rec(i+1,cl)\n ans%=mod\n dp[i,prev]=ans\n return ans\n x=rec(0,-1)\n print(x)\n return x%mod\n``` | 0 | 0 | ['Python3'] | 0 |
painting-a-grid-with-three-different-colors | A concise solution with matrix ops only (beat 100% java submissions) | a-concise-solution-with-matrix-ops-only-i75mb | java\nclass Solution {\n public int colorTheGrid(int m, int n) {\n long mod = 1_000_000_007;\n long[][][] matrixs = {\n { { 2 } | safiir | NORMAL | 2023-05-06T07:36:44.273201+00:00 | 2023-05-06T10:07:50.976974+00:00 | 101 | false | ```java\nclass Solution {\n public int colorTheGrid(int m, int n) {\n long mod = 1_000_000_007;\n long[][][] matrixs = {\n { { 2 } },\n { { 3 } },\n { { 3, 2 }, { 2, 2 } },\n {\n { 3, 2, 1, 2 },\n { 2, 2, 1, 2 },\n { 1, 1, 2, 1 },\n { 2, 2, 1, 2 },\n },\n {\n { 3, 2, 2, 1, 0, 1, 2, 2 },\n { 2, 2, 2, 1, 1, 1, 1, 1 },\n { 2, 2, 2, 1, 0, 1, 2, 2 },\n { 1, 1, 1, 2, 1, 1, 1, 1 },\n { 0, 1, 0, 1, 2, 1, 0, 1 },\n { 1, 1, 1, 1, 1, 2, 1, 1 },\n { 2, 1, 2, 1, 0, 1, 2, 1 },\n { 2, 1, 2, 1, 1, 1, 1, 2 },\n },\n };\n int len = m == 1 ? 1 : (int) (Math.pow(2, m - 2));\n long[][] dp = new long[len][1];\n for (long[] row : dp) {\n row[0] = m == 1 ? 3 : 6;\n }\n long[][] matrix = matrixs[m - 1];\n dp = multiply(matrixPower(matrix, n - 1, mod), dp, mod);\n Long acc = 0l;\n for (long[] row : dp) {\n acc = (acc + row[0]) % mod;\n }\n return acc.intValue();\n }\n\n // matrix multiplication function\n private long[][] multiply(long[][] a, long[][] b, long mod) {\n int m = a.length, n = b[0].length, p = b.length;\n long[][] c = new long[m][n];\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n for (int k = 0; k < p; k++) {\n c[i][j] += a[i][k] * b[k][j] % mod;\n c[i][j] %= mod;\n }\n }\n }\n return c;\n }\n\n // matrix fast power function\n private long[][] matrixPower(long[][] matrix, long p, long mod) {\n long[][] res = new long[matrix.length][matrix.length];\n // initialized with the identity matrix\n for (int i = 0; i < matrix.length; i++) {\n res[i][i] = 1;\n }\n long[][] tmp = matrix;\n // power decomposition\n while (p != 0) {\n if ((p & 1) != 0) {\n res = multiply(res, tmp, mod);\n }\n tmp = multiply(tmp, tmp, mod);\n p >>= 1;\n }\n return res;\n }\n\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Java'] | 0 |
painting-a-grid-with-three-different-colors | Python Solution | python-solution-by-aurimas13-cd3y | \n\n# Approach\nHere\'s a step-by-step explanation of the solution:\n\n1. Generate all valid rows:\nThe generate_valid_rows function generates all valid rows of | aurimas13 | NORMAL | 2023-03-15T07:20:15.852852+00:00 | 2023-03-15T07:20:15.852906+00:00 | 82 | false | \n\n# Approach\nHere\'s a step-by-step explanation of the solution:\n\n1. Generate all valid rows:\nThe generate_valid_rows function generates all valid rows of length m, with no two adjacent cells having the same color. There are 3 ** m possible row combinations, and we iterate through all of them to find the valid ones. To check the validity of a row, we ensure that no two adjacent cells have the same color.\n\n2. Build an adjacency matrix:\nThe build_adjacency_matrix function constructs an adjacency matrix of size R x R, where R is the number of valid rows. The matrix represents the relationship between valid rows, with adj_matrix[i][j] being True if row i and row j can be adjacent in the grid, following the problem\'s constraints. The matrix will be used in the dynamic programming step to find the number of ways to paint the grid.\n\n3. Dynamic programming:\nThe dynamic programming approach is used to count the number of ways to paint the grid. We initialize a list dp of size R, where each entry represents the number of ways to paint the grid with that specific row at the last row of the grid. Initially, we set all entries in dp to 1, as there is only one way to paint the grid with a single row.\n\nThen, we iterate through the columns (n - 1 times) and update the dp list using the adjacency matrix information. For each valid row i, we check all valid adjacent rows j (using the adjacency matrix) and update the dp list accordingly. We keep track of the number of ways to paint the grid by taking the sum of the dp list at the end and applying the modulo operation.\n\n# Complexity\n- Time complexity:\nTime Complexity:\nThe time complexity of this solution is O(R^2 * n), where R is the number of valid rows. The majority of the time is spent on the dynamic programming step, where we iterate n - 1 times, and for each iteration, we perform R * R operations when updating the dp list.\n\n- Space complexity:\nThe space complexity of the solution is O(R^2 + R * n), which is mainly due to the adjacency matrix and the dynamic programming list dp. We also store a list of valid rows, but the overall space complexity is determined by the adjacency matrix and the dp list.\n\n# More \n\nMore of my LeetCode solutions at https://github.com/aurimas13/Solutions-To-Problems.\n\n# Code\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n MOD = 1000000007\n valid_rows = self.generate_valid_rows(m)\n adj_matrix = self.build_adjacency_matrix(valid_rows)\n dp = [1] * len(valid_rows)\n \n for _ in range(n - 1):\n dp_next = [0] * len(valid_rows)\n for i, row in enumerate(valid_rows):\n for j, adj_row in enumerate(valid_rows):\n if adj_matrix[i][j]:\n dp_next[j] += dp[i]\n dp_next[j] %= MOD\n dp = dp_next\n \n return sum(dp) % MOD\n\n def generate_valid_rows(self, m: int) -> list:\n valid_rows = []\n for i in range(3 ** m):\n row = []\n for j in range(m):\n row.append((i // (3 ** j)) % 3)\n if all(row[k] != row[k + 1] for k in range(m - 1)):\n valid_rows.append(tuple(row))\n return valid_rows\n\n def build_adjacency_matrix(self, valid_rows: list) -> list:\n adj_matrix = [[False] * len(valid_rows) for _ in range(len(valid_rows))]\n for i, row1 in enumerate(valid_rows):\n for j, row2 in enumerate(valid_rows):\n if all(row1[k] != row2[k] for k in range(len(row1))):\n adj_matrix[i][j] = True\n return adj_matrix\n\n``` | 0 | 0 | ['Dynamic Programming', 'Graph', 'Python3'] | 0 |
painting-a-grid-with-three-different-colors | [Python 3] Bitmask DP | python-3-bitmask-dp-by-gabhay-2ich | Intuition\nsince m is very small so it seems sensible to use Bitmask DP here\n\n# Approach\nwe use first 5 bits for red, next 5 for blue and next 5 bits for gre | gabhay | NORMAL | 2023-02-17T06:43:04.302906+00:00 | 2023-02-17T06:48:08.630739+00:00 | 56 | false | # Intuition\nsince m is very small so it seems sensible to use Bitmask DP here\n\n# Approach\nwe use first 5 bits for red, next 5 for blue and next 5 bits for green\nand continously check for each position if we can use a specific color.\n\n# Time Compexity:\nO(n\\*m\\*2^(2\\*m))\n\n# Code\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n colors=[0,5,10]\n def next(prev,curr,j):\n A=[]\n for color in colors:\n if prev&(1<<(j+color))==0 and (j==0 or curr&(1<<(j+color-1))==0):\n A.append(curr|1<<(j+color))\n return A\n\n mod=10**9+7\n @cache\n def solve(prev,curr,i,j):\n if i==n:\n return 1\n if j==m:return solve(curr,0,i+1,0)\n new=next(prev,curr,j)\n res=0\n if new:\n for final in new:\n res+=solve(prev,final,i,j+1)\n return res%mod\n return solve(0,0,0,0) \n \n``` | 0 | 0 | ['Python3'] | 0 |
painting-a-grid-with-three-different-colors | Python recursive DP, abstracted as a Graph counting problem | python-recursive-dp-abstracted-as-a-grap-b9pk | # Intuition \n\n\n\n\n\n# Complexity\nLet w := 3^m,\n- Time complexity: O(w^2m+w^2n)\n\n\n- Space complexity: O(w^2+wn)\n\n\n# Code\n\nM = 1_000_000_007\n\n\n | vWAj0nMjOtK33vIH0jpLww | NORMAL | 2023-02-11T05:25:49.750950+00:00 | 2023-02-12T13:49:11.029090+00:00 | 57 | false | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\nLet $$w := 3^m$$,\n- Time complexity: $$O(w^2m+w^2n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(w^2+wn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nM = 1_000_000_007\n\n\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n W = [x for x in product(range(3), repeat=m) if all(map(ne, x, x[1:]))]\n if n == 1:\n return len(W)\n adj = [[i for i, y in enumerate(W) if all(map(ne, x, y))] for x in W]\n\n @cache\n def dp(i, j):\n if j == n:\n return len(adj[i])\n return sum(dp(k, j+1) for k in adj[i]) % M\n\n return sum(dp(i, 2) for i in range(len(W))) % M\n``` | 0 | 0 | ['Dynamic Programming', 'Graph', 'Python3'] | 1 |
painting-a-grid-with-three-different-colors | Easy solution in c++ | easy-solution-in-c-by-doppelgangerofmeow-nxhv | Intuition\n Describe your first thoughts on how to solve this problem. \n1. Generateing all possible permutation using (m^3)\n2. Finding all permutation that co | doppelgangerOfMeow | NORMAL | 2022-12-22T11:00:50.001202+00:00 | 2022-12-22T11:00:50.001247+00:00 | 226 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Generateing all possible permutation using (m^3)\n2. Finding all permutation that could be promoted to\na. For example, 12 -> 21, 23 and etc.\n3. Using DP to record the value of transferring\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS, DP\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m^3^2) for finding all qualified promotion\nO(n * m^3^2) for moving stage by stage\n Since m is very small, we could ignore m as a constant.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n void createPermu(vector<int>& permu, int m, int current){\n if (m == 0) permu.push_back(current);\n else{\n int lastDigit = current % 10;\n createPermu(permu, m - 1, current * 10 + (lastDigit) % 3 + 1);\n createPermu(permu, m - 1, current * 10 + (lastDigit + 1) % 3 + 1);\n }\n }\n\n bool check(int a, int b){\n while (a > 0){\n if (a % 10 == b % 10) return false;\n a /= 10;\n b /= 10;\n }\n return true;\n }\n\n int colorTheGrid(int m, int n) {\n int mod(1e9 + 7);\n vector<int> permu;\n createPermu(permu, m - 1, 1);\n createPermu(permu, m - 1, 2);\n createPermu(permu, m - 1, 3);\n\n unordered_map<int, vector<int>> allowedNext;\n for (auto &a: permu) for (auto &b: permu) if (check(a, b)) allowedNext[a].push_back(b);\n unordered_map<int, vector<unsigned int>> dp;\n for (auto &permuToNext: allowedNext){\n dp[permuToNext.first].resize(n, 0);\n dp[permuToNext.first][0] = 1;\n }\n for (int i = 1; i < n; ++i){\n for (auto &permuToNext: allowedNext){\n for (auto &next: permuToNext.second){\n (dp[next][i] += dp[permuToNext.first][i - 1]) %= mod;\n }\n }\n }\n int ans(0);\n for (auto &pos: dp){\n (ans += pos.second[n - 1]) %= mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Combinatorics', 'C++'] | 0 |
painting-a-grid-with-three-different-colors | Bottom-Up DP solution, beats 98% of cpp solutions | bottom-up-dp-solution-beats-98-of-cpp-so-s6e8 | Beats 98.05% in Time and 99.35% in Space for cpp solutions\n\n\n\nclass Solution {\npublic:\n const int MOD = 1e9 + 7;\n void generateRows(vector<int> &ro | mosta7il | NORMAL | 2022-07-20T19:08:54.224660+00:00 | 2022-07-20T19:08:54.224703+00:00 | 165 | false | Beats **98.05%** in Time and **99.35%** in Space for cpp solutions\n\n\n```\nclass Solution {\npublic:\n const int MOD = 1e9 + 7;\n void generateRows(vector<int> &rows, int idx, int row, int last, int &M){\n if(idx == M){\n rows.push_back(row);\n return;\n }\n for(int i = 0;i<3;i++){\n if(idx == 0 || last != i)\n generateRows(rows, idx + 1, row * 10 + i, i, M);\n }\n }\n bool can(vector<int> &rows, int i, int j, int M){\n int rowi = rows[i], rowj = rows[j];\n while(M--){\n if(rowi % 10 == rowj %10)\n return 0;\n rowi /= 10; rowj /=10;\n }\n return 1;\n }\n void generateMoves(vector<int> &rows, vector<vector<int> > &Moves, int &m){\n int X = rows.size();\n for(int i = 0;i<X;i++){\n for(int j = 0;j < X;j++){\n if(i == j)continue;\n if(can(rows, i, j, m))\n Moves[i].push_back(j);\n }\n }\n }\n int colorTheGrid(int m, int N) {\n // Time: O(9^m + N * 3^m)\n vector< int > rows;\n generateRows(rows, 0, 0, 0, m);\n int X = rows.size();\n vector< vector<int> >Moves(X, vector<int>());\n generateMoves(rows, Moves, m);\n \n int dp[2][X];\n // Base case\n for(int i = 0;i<X;i++)\n dp[0][i] = 1;\n \n for(int idx = 1;idx<N;idx++){\n for(int lastRow = 0;lastRow<X;lastRow++){\n dp[idx&1][lastRow] = 0;\n for(int &i: Moves[lastRow]){\n dp[idx&1][lastRow] += dp[idx&1^1][i];\n dp[idx&1][lastRow] %= MOD;\n }\n }\n }\n \n int ans = 0;\n for(int i = 0;i<X;i++){\n ans += dp[N&1^1][i];\n ans %= MOD;\n }\n return ans;\n }\n};\n```\n\n | 0 | 0 | ['Dynamic Programming'] | 0 |
painting-a-grid-with-three-different-colors | C++ Recursion + Memo | c-recursion-memo-by-dhairya_sarin-i17a | \nclass Solution {\npublic:\n string color_scheme = "RYG";\n int mod;\n vector<string>valid_moves;\n unordered_map<string,int>dp;\n void generate | dhairya_sarin | NORMAL | 2022-07-17T03:18:22.445928+00:00 | 2022-07-17T03:18:22.445956+00:00 | 180 | false | ```\nclass Solution {\npublic:\n string color_scheme = "RYG";\n int mod;\n vector<string>valid_moves;\n unordered_map<string,int>dp;\n void generateValidMoves(int n , int taken , char last, string &cur)\n { if(taken==n)\n {valid_moves.push_back(cur);\n return;\n }\n for(auto x : color_scheme)\n { if(last!=x)\n { cur.push_back(x);\n generateValidMoves(n,taken+1,x,cur);\n cur.pop_back();\n }\n }\n }\n int solve(int n , int cur_len,string last_move)\n {\n if(cur_len==n)return 1;\n int ans =0;\n string hash = to_string(cur_len)+"#"+last_move;\n if(dp.find(hash)!=dp.end())return dp[hash];\n for(int i =0;i<valid_moves.size();i++)\n {\n auto cur_move = valid_moves[i];\n bool no_match =1;\n for(int i =0;i<last_move.size();i++)\n {\n if(last_move[i]==cur_move[i])no_match=0;\n }\n if(no_match)\n {\n ans= (ans%mod+solve(n,cur_len+1,cur_move))%mod;\n }\n }\n return dp[hash]= ans;\n }\n \n int colorTheGrid(int m, int n) {\n string cur ="";\n generateValidMoves(m,0,\'Z\',cur);\n string start = "";\n for(int i =0;i<m;i++)start+="B";\n mod=1e9+7;\n return solve(n,0,start);\n \n }\n};\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | Simple DP Implementation | simple-dp-implementation-by-day_tripper-45ea | \nclass Solution(object):\n def colorTheGrid(self, m, n):\n """\n :type m: int\n :type n: int\n :rtype: int\n """\n | Day_Tripper | NORMAL | 2022-07-03T04:03:06.582398+00:00 | 2022-07-03T04:03:06.582462+00:00 | 129 | false | ```\nclass Solution(object):\n def colorTheGrid(self, m, n):\n """\n :type m: int\n :type n: int\n :rtype: int\n """\n # m = 2\n\n patterns = ["a", "b", "c"]\n for i in range(m-1):\n new_patterns = []\n for p in patterns:\n for color in ["a","b","c"]:\n if color != p[-1]:\n new_patterns.append(p + color)\n patterns = new_patterns\n \n \n nxt_patterns = collections.defaultdict(list)\n for i in range(len(patterns)):\n for j in range(i+1, len(patterns)):\n p1 = patterns[i]\n p2 = patterns[j]\n if all(p1[k] != p2[k] for k in range(len(p1))):\n\n nxt_patterns[p1].append(p2)\n nxt_patterns[p2].append(p1)\n \n curcols = collections.defaultdict(int)\n for p in patterns:\n curcols[p] += 1\n for j in range(1, n):\n nxtcols = collections.defaultdict(int)\n for col in curcols:\n for nxtcol in nxt_patterns[col]:\n nxtcols[nxtcol] += curcols[col]\n curcols = nxtcols\n return sum(curcols.values()) % (10**9+7)\n \n``` | 0 | 0 | ['Dynamic Programming'] | 0 |
painting-a-grid-with-three-different-colors | This is meaningless | this-is-meaningless-by-stevefan1999-03wa | This question is just asking for the 3-coloring chromatic polynomial of the (n, m)-grid graph where n <= 5 and m <= 1000...Which is unfortunately an open proble | stevefan1999 | NORMAL | 2022-06-30T08:22:58.900665+00:00 | 2022-06-30T08:23:40.446255+00:00 | 120 | false | This question is just asking for the 3-coloring chromatic polynomial of the (n, m)-grid graph where n <= 5 and m <= 1000...Which is unfortunately an open problem.\n\nAnyone with Mathematica can brute force the formula. When the fuck did LC became an amalgamation of CodeForces and Project Euler? | 0 | 0 | [] | 1 |
painting-a-grid-with-three-different-colors | How can I improve my code. I've used backtracking but I run into TLE in some test cases | how-can-i-improve-my-code-ive-used-backt-m20w | class Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n matrix = [[0]*n for _ in range(m)]\n neighbors = [(-1,0),(0,-1)]\n de | teapea | NORMAL | 2022-06-30T04:28:57.875477+00:00 | 2022-06-30T04:28:57.875517+00:00 | 40 | false | ```class Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n matrix = [[0]*n for _ in range(m)]\n neighbors = [(-1,0),(0,-1)]\n def get_colors(r,c):\n colors = [1,2,3]\n ans = []\n if r==0 and c==0:\n return colors\n top = left = 0\n if r==0:\n left=matrix[r+neighbors[1][0]][c+neighbors[1][1]]\n elif c==0:\n top = matrix[r+neighbors[0][0]][c+neighbors[0][1]]\n else:\n \n [top,left] = [matrix[r+neighbors[0][0]][c+neighbors[0][1]],matrix[r+neighbors[1][0]][c+neighbors[1][1]]]\n for color in colors:\n if color not in [top,left]:\n ans.append(color)\n return ans\n \n @lru_cache(None)\n def backtrack(r,c,count):\n for color in get_colors(r,c):\n \n matrix[r][c] = color\n if r==m-1 and c==n-1:\n count+=1\n \n elif c<n-1:\n count = backtrack(r,c+1,count)\n else:\n count = backtrack(r+1,0,count)\n matrix[r][c]=0\n return count\n return backtrack(0,0,0)\n \n \n \n \n \n ``` | 0 | 0 | ['Backtracking'] | 0 |
painting-a-grid-with-three-different-colors | Python. Faster than 83%... | python-faster-than-83-by-nag007-1jpw | \nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n def f(i,p=-1,s=\'\'):\n if i==m:\n res.append(s)\n | nag007 | NORMAL | 2022-06-25T16:03:23.577373+00:00 | 2022-06-25T16:03:23.577408+00:00 | 84 | false | ```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n def f(i,p=-1,s=\'\'):\n if i==m:\n res.append(s)\n return\n for j in range(3):\n if j!=p:\n f(i+1,j,s+str(j))\n @lru_cache(None)\n def func(i,p):\n if i==n:\n return 1\n ans=0\n for j in pos[p]:\n ans+=func(i+1,j)\n return ans%(10**9+7)\n res=[]\n f(0)\n di={}\n pos=defaultdict(list)\n for i in range(len(res)):\n for j in range(i+1,len(res)):\n if all(res[i][k]!=res[j][k] for k in range(m)):\n pos[i].append(j)\n pos[j].append(i)\n pos[-1]=[i for i in range(len(res))]\n return func(0,-1)%(10**9+7)\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | Scala | scala-by-fairgrieve-4f02 | \nimport scala.util.chaining.scalaUtilChainingOps\n\nobject Solution {\n private object Color extends Enumeration {\n type Color = Value\n val Red, Blue, | fairgrieve | NORMAL | 2022-03-29T20:44:42.193528+00:00 | 2022-03-29T20:44:42.193554+00:00 | 53 | false | ```\nimport scala.util.chaining.scalaUtilChainingOps\n\nobject Solution {\n private object Color extends Enumeration {\n type Color = Value\n val Red, Blue, Green = Value\n }\n import Color._\n\n def colorTheGrid(m: Int, n: Int): Int = {\n val validCols = (1 to m).foldLeft(Iterable(List[Color]())) {\n case (cols, _) => cols.flatMap {\n case Nil => Color.values.iterator.map(List(_))\n case head :: tail => Color.values.iterator.collect {\n case color if color != head => color :: head :: tail\n }\n }\n }\n\n (2 to n)\n .foldLeft(validCols.map(_ -> 1)) {\n case (counts, _) => validCols.map { col1 =>\n counts\n .collect {\n case (col2, count) if col1.iterator.zip(col2).forall { case (color1, color2) => color1 != color2 } =>\n count\n }\n .fold(0)(add)\n .pipe(col1 -> _)\n }\n }\n .map(_._2)\n .fold(0)(add)\n }\n\n private def add(x: Int, y: Int) = (x + y) % 1000000007\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Scala'] | 0 |
painting-a-grid-with-three-different-colors | Fastest O(n) Python Solution | fastest-on-python-solution-by-vkarakchee-5e0i | The solution is completely similar to recurrent one of problem 1411. Memory complexity is O(1).\n\nclass Solution:\n def colorTheGrid(self, m: int, n: int) - | vkarakcheev | NORMAL | 2022-03-11T23:44:34.452308+00:00 | 2022-03-12T10:28:05.871929+00:00 | 181 | false | The solution is completely similar to recurrent one of problem 1411. Memory complexity is O(1).\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n\n if m == 1:\n return 3 * 2**(n-1) % 1000000007\n\n if m == 2:\n return 6 * 3**(n-1) % 1000000007\n\n if m == 3:\n (a, b) = (6, 6)\n for _ in range(n-1):\n a = 2*(a + b)\n b = a + b\n return (a + b) % 1000000007\n\n if m == 4:\n (a, b, c) = (6, 12, 6)\n for _ in range(n-1):\n (a, b, c) = (2*a + b + c, \n 2*a + 4*(b + c),\n a + 2*b + 3*c)\n return (a + b + c) % 1000000007\n\n if m == 5:\n (a, b, c, d, e, f) = (6, 12, 6, 12, 6, 6)\n for _ in range(n-1):\n (a, c, d, e) = (2*a + b + d, \n b + d + 2*(c + e + f),\n 2*(a + b + c) + 3*d + 4*(e + f),\n b + 2*(c + d + e + f))\n b += a + c\n f += e\n return (a + b + c + d + e + f) % 1000000007\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | [Python3] DP Rolling Array & Memo | 70% Time & 95% Space | python3-dp-rolling-array-memo-70-time-95-cvt3 | \nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n MOD = 10 ** 9 + 7\n # Get valid states for a column\n valid_states | pubghh01 | NORMAL | 2022-03-05T09:24:32.640384+00:00 | 2022-03-05T09:26:50.468718+00:00 | 162 | false | ```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n MOD = 10 ** 9 + 7\n # Get valid states for a column\n valid_states = generate_states(m)\n # Init rolling array dp\n dp = [[0] * len(valid_states) for _ in range(2)]\n # Init the first column of dp to all ones\n for i in range(len(dp[0])):\n dp[0][i] = 1\n\n # Memorize valid current and previous states pairs\n # memo: {(current state index, [previous valid state indexes])}\n memo = {}\n for i in range(1, n):\n for j in range(len(valid_states)):\n # Init the dp value of current column at this state to zero\n dp[i % 2][j] = 0\n # Iterate through all the valid states in previous column\n # First check if the current state index is in memo\n if j in memo:\n for k in memo[j]:\n dp[i % 2][j] = (dp[i % 2][j] + dp[(i - 1) % 2][k]) % MOD\n continue\n\n # If not, iterate through all the valid states in previous column\n valid_prev_states = []\n for k in range(len(valid_states)):\n # Accumulate to the dp value of current column at this state if the two states are valid\n if check_valid_states(valid_states[j], valid_states[k]):\n dp[i % 2][j] = (dp[i % 2][j] + dp[(i - 1) % 2][k]) % MOD\n valid_prev_states.append(k)\n\n # Save the current state index and previous valid state indexes list to memo\n memo[j] = valid_prev_states\n \n # Add up the dp values of the last column\n res = 0\n for i in range(len(dp[0])):\n res = (res + dp[(n - 1) % 2][i]) % MOD\n return res\n\ndef generate_states(m):\n states = []\n # Iterate over all possible states in 10 digit base\n for i in range(3 ** m):\n state_tmp = i\n state = []\n # Convert the state to 3 digit base\n for j in range(m):\n last_bit = state_tmp % 3\n if state and last_bit == state[-1]:\n break\n state.append(last_bit)\n state_tmp //= 3\n\n # Add the state to states if valid\n if len(state) == m:\n states.append(state)\n \n return states\n\ndef check_valid_states(state1, state2):\n for i in range(len(state1)):\n if state1[i] == state2[i]:\n return False\n return True\n``` | 0 | 0 | ['Dynamic Programming', 'Memoization'] | 0 |
painting-a-grid-with-three-different-colors | [Rust] DP & Mask runs in 88ms | rust-dp-mask-runs-in-88ms-by-bovinovain-flex | Realizing m <= 5 is crucial. It is possible to enuemrate all valid color permutation in a column and build dp based on it.\n\nuse std::collections::HashMap;\n\n | bovinovain | NORMAL | 2022-03-01T13:50:58.215642+00:00 | 2022-03-01T13:50:58.215683+00:00 | 107 | false | Realizing m <= 5 is crucial. It is possible to enuemrate all valid color permutation in a column and build dp based on it.\n```\nuse std::collections::HashMap;\n\nconst MOD: i32 = 1000_000_007;\nimpl Solution {\n pub fn color_the_grid(m: i32, n: i32) -> i32 {\n let mask = |mut x: usize| -> Vec<usize> {\n let mut res = vec![];\n for _ in 0..m {\n res.push(x % 3);\n x /= 3;\n }\n res\n };\n let mut candidate = vec![];\n let m = m as usize;\n let n = n as usize;\n \'outer: for x in 0usize..(3usize.pow(m as u32)) {\n let mut cur = mask(x);\n for w in cur.windows(2) {\n if w[0] == w[1] {\n continue \'outer;\n }\n }\n candidate.push(x);\n }\n let mut nxt: HashMap<usize, Vec<usize>> = HashMap::new();\n for cur in candidate.iter() {\n for next_cur in candidate.iter() {\n let c = mask(*cur);\n let nc = mask(*next_cur);\n if c.iter().zip(nc.iter()).all(|x| x.0 != x.1) {\n nxt.entry(*cur).or_default().push(*next_cur);\n }\n }\n }\n let mut dp: HashMap<usize, i32> = HashMap::new();\n for i in candidate.iter() {\n dp.insert(*i, 1);\n }\n for _ in 1..n {\n let mut ndp: HashMap<usize, i32> = HashMap::new();\n for (k, v) in dp.iter() {\n for next in nxt[k].iter() {\n if let Some(value) = ndp.get_mut(next) {\n *value = (*value + *v) % MOD;\n } else {\n ndp.insert(*next, *v);\n }\n }\n }\n dp = ndp;\n }\n let mut res = 0;\n for v in dp.values() {\n res = (res + *v) % MOD;\n }\n res\n }\n}\n\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | Solution using unordered map C++ | solution-using-unordered-map-c-by-aryan2-euvs | \nclass Solution {\npublic:\n //\n int mod=1e9+7;\n char arr[3]={\'R\',\'B\',\'G\'};\n vector<string>v;\n unordered_map<string,int>ans;\n void | aryan29 | NORMAL | 2022-02-22T18:07:23.834695+00:00 | 2022-02-22T18:07:23.834737+00:00 | 190 | false | ```\nclass Solution {\npublic:\n //\n int mod=1e9+7;\n char arr[3]={\'R\',\'B\',\'G\'};\n vector<string>v;\n unordered_map<string,int>ans;\n void get_v(int m, string s)\n {\n if(m==0)\n {\n v.push_back(s);\n return;\n }\n char ch=\'$\';\n if(s.size()>=1)\n ch=s[s.size()-1];\n for(int i=0;i<3;i++)\n {\n if(arr[i]!=ch)\n get_v(m-1,s+arr[i]);\n }\n \n }\n void recur(int curr,int n)\n {\n if(curr==n+1)\n return;\n unordered_map<string,int>newans;\n for(int i=0;i<v.size();i++) // our current ending\n {\n for(int j=0;j<v.size();j++) // checking wiht all prev endings\n {\n int fl=1;\n for(int l=0;l<v[i].size();l++)\n {\n if(v[i][l]==v[j][l])\n {\n fl=0;\n break;\n }\n }\n if(fl)\n {\n newans[v[i]]+=ans[v[j]];\n newans[v[i]]%=mod;\n // cout<<v[i]<<" "<<v[j]\n }\n }\n }\n ans=newans;\n recur(curr+1,n);\n }\n int colorTheGrid(int m, int n) {\n get_v(m,"");\n cout<<v.size()<<"\\n";\n for(auto it:v)\n ans[it]=1;\n recur(2,n);\n int myans=0;\n for(auto it:v)\n {\n myans+=ans[it];\n myans%=mod;\n } \n return myans;\n }\n};\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | DP with bitmask, similar to Prob 1349 Maximum Student Taking Exam | dp-with-bitmask-similar-to-prob-1349-max-s654 | Consider each column, since it has much less valid states as compared to each row.\nThe below algorithm can also be extended to work for more than 3 colors scen | finback | NORMAL | 2022-02-15T04:00:11.050004+00:00 | 2022-02-16T00:55:49.717974+00:00 | 172 | false | Consider each column, since it has much less valid states as compared to each row.\nThe below algorithm can also be extended to work for more than 3 colors scenario\n\n```\nclass Solution { \n long[] mask;\n int idx = 0;\n // RRR => 001001001, RGR => 001010001, RGB => 001010100\n public int colorTheGrid(int m, int n) {\n\t int K = 3; // Three colors in total\n int count = K;\n for (int i=0; i<m-1; ++i)\n count *= K;\n mask = new long[count];\n getMasks(0, m, K);\n \n // only consider valid mask value, neighbors do not have the samecolor\n boolean[] valid = new boolean[count];\n for (int i=0; i<count; ++i) {\n if ((mask[i] & (mask[i] << K)) == 0) {\n valid[i] = true;\n }\n }\n \n long[] dp = new long[count];\n for (int i=0; i<count; ++i) {\n dp[i] = valid[i] ? 1 : 0;\n }\n \n long mod = (long) (1e9+7);\n for (int i=1; i<=n-1; ++i) {\n // for each column\n long[] newDp = new long[count];\n for (int j=0; j<count; ++j) {\n if (valid[j]) {\n for (int k=0; k<count; ++k) {\n // each valid pairs of masks\n if (valid[k] && (mask[j] & mask[k]) == 0) {\n // if there is no "conflict"\n newDp[j] += dp[k];\n }\n }\n newDp[j] %= mod;\n }\n }\n dp = newDp;\n }\n long sum = 0;\n for (int i=0; i<count; ++i) {\n sum += dp[i];\n }\n return (int) (sum % mod);\n }\n \n void getMasks(long val, int m, int k) {\n if (m == 0) {\n mask[idx++] = val;\n return;\n }\n for (int i=0; i<k; ++i) {\n getMasks((val << k) | (1 << i), m-1, k);\n }\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask'] | 0 |
painting-a-grid-with-three-different-colors | c++ | dp | graph | c-dp-graph-by-srv-er-pgcl | \nclass Solution {\npublic:\n int md=1000000007;\n vector<string> st;\n int dp[50][1001];\n void fill(int m,char prev,string s){\n if(m==0)st | srv-er | NORMAL | 2022-02-15T01:19:25.558893+00:00 | 2022-02-15T01:19:25.558927+00:00 | 258 | false | ```\nclass Solution {\npublic:\n int md=1000000007;\n vector<string> st;\n int dp[50][1001];\n void fill(int m,char prev,string s){\n if(m==0)st.push_back(s);\n else{\n string t="RGB";\n for(auto&i:t){\n if(i!=prev) fill(m-1,i,s+i);\n } \n }\n \n }\n int dfs(vector<vector<int>> &gr,int i,int n){\n if(!n) return 1;\n if(dp[i][n]!=-1) return dp[i][n];\n int ans=0;\n for(auto&j:gr[i]) ans=(ans%md+dfs(gr,j,n-1)%md)%md;\n return dp[i][n]=ans%md;\n }\n int colorTheGrid(int m, int n) {\n fill(m,\'#\',"");\n memset(dp,-1,sizeof(dp));\n int sz=st.size();\n vector<vector<int>>gr(sz);\n for(int i=0;i<sz;i++){\n for(int j=i+1;j<sz;j++){ \n bool f=false;\n for(int k=0;k<m;k++){\n if(st[i][k]==st[j][k]){\n f=true;\n break;\n }\n }\n if(!f){\n gr[i].push_back(j);\n gr[j].push_back(i);\n }\n }\n }\n int ans=0;\n for(int i=0;i<sz;i++) ans=(ans%md+dfs(gr,i,n-1)%md)%md;\n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Graph', 'C'] | 0 |
painting-a-grid-with-three-different-colors | JAVA Intuitive Solution | java-intuitive-solution-by-krishna382nit-gtpo | \nclass Solution {\n public int colorTheGrid(int m, int n) {\n Map<String, Integer> map=new HashMap();\n populateMap(map, m,"");\n if(n= | krishna382nitjsr | NORMAL | 2022-02-06T20:47:52.531195+00:00 | 2022-02-06T20:48:20.154271+00:00 | 425 | false | ```\nclass Solution {\n public int colorTheGrid(int m, int n) {\n Map<String, Integer> map=new HashMap();\n populateMap(map, m,"");\n if(n==1){\n return map.size();\n }\n Map<String, List<String>> map1=new HashMap();\n for(String key:map.keySet()){\n populatePossibleCombinationsInDownRow(key, map1);\n }\n int tot=0;\n if(n==2){\n for(Map.Entry<String, List<String>> entry: map1.entrySet()){\n tot=tot+entry.getValue().size();\n }\n \n return tot;\n }\n for(Map.Entry<String, List<String>> entry: map1.entrySet()){\n map.put(entry.getKey(), entry.getValue().size());\n }\n Integer mod=1_000_000_007; \n for(int i=2;i<n;i++){\n Map<String, Integer> newMap=new HashMap();\n tot=0; \n for(Map.Entry<String, List<String>> entry: map1.entrySet()){\n int keySum=0;\n for(String val: entry.getValue()){\n keySum=(keySum+map.get(val)%mod)%mod;\n }\n newMap.put(entry.getKey(), keySum);\n tot=(tot+keySum)%mod; \n }\n map=newMap; \n }\n return tot;\n }\n \n private void populatePossibleCombinationsInDownRow(String key, Map<String, List<String>> map){\n map.put(key, new LinkedList()); \n populateInnerMap(map, "", key);\n }\n \n private void populateInnerMap( Map<String, List<String>> map, String prefix, String key){\n if(prefix.equals("")){\n if(key.charAt(0)==\'r\'){\n \n populateInnerMap(map,"g", key);\n populateInnerMap(map, "b", key); \n }else if(key.charAt(0)==\'g\'){\n populateInnerMap(map, "r", key);\n populateInnerMap(map, "b", key); \n }else{\n populateInnerMap(map, "r", key);\n populateInnerMap(map,"g", key); \n } \n \n }else{\n if(prefix.length()==key.length()){\n map.get(key).add(prefix);\n return;\n }\n \n char ls=prefix.charAt(prefix.length()-1);\n char ch=key.charAt(prefix.length()); \n if(ls==\'r\'){\n if(ch==\'b\'){\n populateInnerMap(map, prefix+"g", key); \n \n }else if(ch==\'g\'){\n populateInnerMap(map, prefix+"b", key); \n }else{\n populateInnerMap(map, prefix+"g", key); \n populateInnerMap(map, prefix+"b", key); \n } \n \n \n }else if(ls==\'g\'){\n \n if(ch==\'b\'){\n populateInnerMap(map, prefix+"r", key); \n \n }else if(ch==\'r\'){\n populateInnerMap(map, prefix+"b", key); \n }else{\n populateInnerMap(map, prefix+"r", key); \n populateInnerMap(map, prefix+"b", key); \n } \n \n }else{\n if(ch==\'r\'){\n populateInnerMap(map, prefix+"g", key); \n \n }else if(ch==\'g\'){\n populateInnerMap(map, prefix+"r", key); \n }else{\n populateInnerMap(map, prefix+"r", key); \n populateInnerMap(map, prefix+"g", key); \n } \n }\n } \n }\n \n private void populateMap( Map<String, Integer> map, int m, String prefix){\n if(prefix.equals("")){\n populateMap(map, m, "r");\n populateMap(map, m, "g");\n populateMap(map, m, "b"); \n }else{\n if(prefix.length()==m){\n map.put(prefix, 1);\n return;\n }\n \n char ls=prefix.charAt(prefix.length()-1);\n if(ls==\'r\'){\n populateMap(map, m, prefix+"b");\n populateMap(map, m, prefix+"g");\n }else if(ls==\'g\'){\n populateMap(map, m, prefix+"r");\n populateMap(map, m, prefix+"b");\n }else{\n populateMap(map, m, prefix+"r");\n populateMap(map, m, prefix+"g");\n }\n }\n }\n}\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | Golang DP solution | golang-dp-solution-by-tjucoder-7fcy | go\nfunc colorTheGrid(m int, n int) int {\n\tbase := make([]int, 0, m)\n\tfor i := 1; i <= 3; i++ {\n\t\tbase = append(base, i)\n\t}\n\tfor i := 2; i <= m; i++ | tjucoder | NORMAL | 2022-01-19T16:02:53.608334+00:00 | 2022-01-19T16:02:53.608365+00:00 | 119 | false | ```go\nfunc colorTheGrid(m int, n int) int {\n\tbase := make([]int, 0, m)\n\tfor i := 1; i <= 3; i++ {\n\t\tbase = append(base, i)\n\t}\n\tfor i := 2; i <= m; i++ {\n\t\tnewBase := make([]int, 0, 64)\n\t\tfor _, v := range base {\n\t\t\tfor j := 1; j <= 3; j++ {\n\t\t\t\tif j == v%10 {\n\t\t\t\t\tcontinue\n\t\t\t\t}\n\t\t\t\tnewBase = append(newBase, v*10+j)\n\t\t\t}\n\t\t}\n\t\tbase = newBase\n\t}\n\tmapping := make(map[int][]int, len(base))\n\tfor _, vf := range base {\n\tloop:\n\t\tfor _, vt := range base {\n\t\t\tdiv := 1\n\t\t\tfor i := 0; i < m; i++ {\n\t\t\t\tif (vf/div)%10 == (vt/div)%10 {\n\t\t\t\t\tcontinue loop\n\t\t\t\t}\n\t\t\t\tdiv *= 10\n\t\t\t}\n\t\t\tmapping[vf] = append(mapping[vf], vt)\n\t\t}\n\t}\n\tdp := make(map[int]int, len(mapping))\n\tfor k := range mapping {\n\t\tdp[k] = 1\n\t}\n\tfor i := 1; i < n; i++ {\n\t\tnext := make(map[int]int, len(mapping))\n\t\tfor k, vs := range mapping {\n\t\t\tfor _, v := range vs {\n\t\t\t\tnext[k] += dp[v]\n\t\t\t}\n\t\t\tnext[k] %= 1000000007\n\t\t}\n\t\tdp = next\n\t}\n\ttotal := 0\n\tfor _, v := range dp {\n\t\ttotal = (total + v) % 1000000007\n\t}\n\treturn total\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Go'] | 0 |
painting-a-grid-with-three-different-colors | Java Dp | java-dp-by-prathihaspodduturi-na4b | \nclass Solution {\n public void trav(int m,List<String>list,String s)\n {\n int len=s.length();\n if(len>1 && s.charAt(len-1)==s.charAt(len | prathihaspodduturi | NORMAL | 2021-12-15T12:04:25.634355+00:00 | 2021-12-15T12:04:25.634400+00:00 | 386 | false | ```\nclass Solution {\n public void trav(int m,List<String>list,String s)\n {\n int len=s.length();\n if(len>1 && s.charAt(len-1)==s.charAt(len-2))\n return;\n if(m==0)\n {\n list.add(s);\n return;\n }\n trav(m-1,list,s+"r");\n trav(m-1,list,s+"g");\n trav(m-1,list,s+"b");\n return;\n }\n public int comp(String s,String t)\n {\n for(int i=0;i<s.length();i++)\n {\n if(s.charAt(i)==t.charAt(i))\n return 0;\n }\n return 1;\n }\n public int colorTheGrid(int m, int n) {\n List<String>list=new ArrayList<>();\n trav(m,list,"");\n int mod=1000000007,s=list.size();\n int arr[][]=new int[s][s];\n for(int i=0;i<s;i++)\n {\n for(int j=0;j<s;j++)\n {\n arr[i][j]=comp(list.get(i),list.get(j));\n }\n }\n int dp[]=new int[s];\n for(int i=0;i<s;i++)\n dp[i]=1;\n for(int i=2;i<=n;i++)\n {\n int pres[]=new int[s];\n for(int j=0;j<s;j++)\n {\n for(int k=0;k<s;k++)\n {\n if(arr[j][k]==1)\n pres[j]=(pres[j]%mod+dp[k]%mod)%mod;\n }\n }\n dp=pres;\n }\n int ans=0;\n for(int i=0;i<s;i++)\n ans=(ans%mod+dp[i]%mod)%mod;\n return ans;\n }\n}\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | [JavaScript] DP with Bit masking | javascript-dp-with-bit-masking-by-tmohan-x1yq | Time O(n * (2^m) * (2^m))\nSpace O(n * 2^(2 * m))\n\nvar colorTheGrid = function (m, n) {\n let dp = Array.from({ length: n }, () => Array(1 << (2 * m)));\n\ | tmohan | NORMAL | 2021-09-15T16:23:18.950901+00:00 | 2021-09-15T16:23:18.950933+00:00 | 130 | false | **Time O(n * (2^m) * (2^m))\nSpace O(n * 2^(2 * m))**\n```\nvar colorTheGrid = function (m, n) {\n let dp = Array.from({ length: n }, () => Array(1 << (2 * m)));\n\n const mod = 1e9 + 7;\n\n const dfs = (rowIdx, colIdx, prevRowColor) => {\n if (rowIdx === n) return 1;\n\n if (colIdx === 0 && dp[rowIdx][prevRowColor])\n return dp[rowIdx][prevRowColor];\n\n let possibilities = 0;\n\n const topCell = (prevRowColor >> (2 * colIdx)) & 3,\n leftCell = (prevRowColor >> (2 * (colIdx - 1))) & 3;\n\n for (let i = 1; i <= 3; i++) {\n if (topCell !== i && leftCell !== i) {\n possibilities =\n (possibilities +\n dfs(\n rowIdx + (colIdx === m - 1),\n (colIdx + 1) % m,\n (prevRowColor ^ (topCell << (2 * colIdx))) | (i << (2 * colIdx))\n )) %\n mod;\n }\n }\n\n if (colIdx === 0) dp[rowIdx][prevRowColor] = possibilities;\n\n return possibilities;\n };\n\n return dfs(0, 0, 0);\n};\n\n``` | 0 | 0 | [] | 0 |
painting-a-grid-with-three-different-colors | Easy DP Approach using UnorderedMap | easy-dp-approach-using-unorderedmap-by-o-oh2l | \n#define ll long long int\nconst int mod=1e9+7;\nclass Solution {\n int r,c;\n string curr;\n vector<string> comb; // all possible valid combinations | ojha1111pk | NORMAL | 2021-09-12T16:30:30.160709+00:00 | 2021-09-12T16:30:30.160763+00:00 | 319 | false | ```\n#define ll long long int\nconst int mod=1e9+7;\nclass Solution {\n int r,c;\n string curr;\n vector<string> comb; // all possible valid combinations to color a column\n unordered_map<string,ll> dp[1003];\npublic:\n\t// finds all possible color combinations to color a given column\n void findCombinations(vector<int>& col){\n \n if(curr.length()==r){\n for(int i=r-1;i>0;i--){\n if(curr[i]==curr[i-1])\n return;\n }\n comb.push_back(curr);\n\t\t\treturn;\n }\n \n for(int i=0;i<3;i++){\n curr=curr+to_string(col[i]);\n findCombinations(col);\n curr.pop_back();\n }\n }\n \n\t// checks if ith coloumn can be colored as s and i+1th col can be colored as t\n bool check(string s,string t){\n for(int i=0;i<r;i++){\n if(s[i]==t[i])\n return 0;\n }\n return 1;\n }\n\n int colorTheGrid(int m, int n) {\n vector<int> col={1,2,3};\n r=m;\n c=n;\n curr="";\n\t\t\n\t\t// finds all valid combinations\n findCombinations(col);\n \n for(auto s:comb)\n dp[n-1][s]=1;\n \n\t\t// checks all combinations which can be used to color 2 consecutive columns\n vector<int> list[comb.size()+10];\n for(int i=0;i<comb.size();i++)\n for(int j=i;j<comb.size();j++){\n if(check(comb[i],comb[j])){\n list[i].push_back(j);\n list[j].push_back(i);\n }\n }\n \n for(int i=n-2;i>=0;i--)\n for(int j=0;j<comb.size();j++){\n ll nxt=0;\n for(auto ind:list[j])\n nxt=(nxt+dp[i+1][comb[ind]])%mod;\n dp[i][comb[j]]=nxt;\n }\n \n ll ans=0;\n for(auto e:dp[0])\n ans=(ans+e.second)%mod;\n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
largest-rectangle-in-histogram | 5ms O(n) Java solution explained (beats 96%) | 5ms-on-java-solution-explained-beats-96-skgtx | For any bar i the maximum rectangle is of width r - l - 1 where r - is the last coordinate of the bar to the right with height h[r] >= h[i] and l - is the last | anton4 | NORMAL | 2016-03-05T12:14:03+00:00 | 2018-10-21T01:39:43.212995+00:00 | 177,468 | false | For any bar `i` the maximum rectangle is of width `r - l - 1` where r - is the last coordinate of the bar to the **right** with height `h[r] >= h[i]` and l - is the last coordinate of the bar to the **left** which height `h[l] >= h[i]`\n\nSo if for any `i` coordinate we know his utmost higher (or of the same height) neighbors to the right and to the left, we can easily find the largest rectangle:\n\n int maxArea = 0;\n for (int i = 0; i < height.length; i++) {\n maxArea = Math.max(maxArea, height[i] * (lessFromRight[i] - lessFromLeft[i] - 1));\n }\n\nThe main trick is how to effectively calculate `lessFromRight` and `lessFromLeft` arrays. The trivial solution is to use **O(n^2)** solution and for each `i` element first find his left/right heighbour in the second inner loop just iterating back or forward:\n\n for (int i = 1; i < height.length; i++) { \n int p = i - 1;\n while (p >= 0 && height[p] >= height[i]) {\n p--;\n }\n lessFromLeft[i] = p; \n }\n\nThe only line change shifts this algorithm from **O(n^2)** to **O(n)** complexity: we don't need to rescan each item to the left - we can reuse results of previous calculations and "jump" through indices in quick manner:\n\n while (p >= 0 && height[p] >= height[i]) {\n p = lessFromLeft[p];\n }\n\nHere is the whole solution:\n\n public static int largestRectangleArea(int[] height) {\n if (height == null || height.length == 0) {\n return 0;\n }\n int[] lessFromLeft = new int[height.length]; // idx of the first bar the left that is lower than current\n int[] lessFromRight = new int[height.length]; // idx of the first bar the right that is lower than current\n lessFromRight[height.length - 1] = height.length;\n lessFromLeft[0] = -1;\n\n for (int i = 1; i < height.length; i++) {\n int p = i - 1;\n\n while (p >= 0 && height[p] >= height[i]) {\n p = lessFromLeft[p];\n }\n lessFromLeft[i] = p;\n }\n\n for (int i = height.length - 2; i >= 0; i--) {\n int p = i + 1;\n\n while (p < height.length && height[p] >= height[i]) {\n p = lessFromRight[p];\n }\n lessFromRight[i] = p;\n }\n\n int maxArea = 0;\n for (int i = 0; i < height.length; i++) {\n maxArea = Math.max(maxArea, height[i] * (lessFromRight[i] - lessFromLeft[i] - 1));\n }\n\n return maxArea;\n } | 1,357 | 12 | ['Dynamic Programming', 'Java'] | 125 |
largest-rectangle-in-histogram | AC Python clean solution using stack 76ms | ac-python-clean-solution-using-stack-76m-nmv1 | def largestRectangleArea(self, height):\n height.append(0)\n stack = [-1]\n ans = 0\n for i in xrange(len(height)):\n whi | dietpepsi | NORMAL | 2015-10-23T16:45:25+00:00 | 2018-10-24T11:02:29.968831+00:00 | 74,538 | false | def largestRectangleArea(self, height):\n height.append(0)\n stack = [-1]\n ans = 0\n for i in xrange(len(height)):\n while height[i] < height[stack[-1]]:\n h = height[stack.pop()]\n w = i - stack[-1] - 1\n ans = max(ans, h * w)\n stack.append(i)\n height.pop()\n return ans\n\n\n\n # 94 / 94 test cases passed.\n # Status: Accepted\n # Runtime: 76 ms\n # 97.34%\n\nThe stack maintain the indexes of buildings with ascending height. Before adding a new building pop the building who is taller than the new one. The building popped out represent the height of a rectangle with the new building as the right boundary and the current stack top as the left boundary. Calculate its area and update ans of maximum area. Boundary is handled using dummy buildings. | 646 | 6 | ['Python'] | 60 |
largest-rectangle-in-histogram | Short and Clean O(n) stack based JAVA solution | short-and-clean-on-stack-based-java-solu-s9u8 | For explanation, please see https://bit.ly/2we8Wfx\n\n\n public int largestRectangleArea(int[] heights) {\n int len = heights.length;\n Stack<I | legendaryengineer | NORMAL | 2015-01-19T20:51:19+00:00 | 2020-04-30T19:30:40.520578+00:00 | 120,429 | false | For explanation, please see https://bit.ly/2we8Wfx\n\n```\n public int largestRectangleArea(int[] heights) {\n int len = heights.length;\n Stack<Integer> s = new Stack<>();\n int maxArea = 0;\n for (int i = 0; i <= len; i++){\n int h = (i == len ? 0 : heights[i]);\n if (s.isEmpty() || h >= heights[s.peek()]) {\n s.push(i);\n } else {\n int tp = s.pop();\n maxArea = Math.max(maxArea, heights[tp] * (s.isEmpty() ? i : i - 1 - s.peek()));\n i--;\n }\n }\n return maxArea;\n }\n```\n\nOP\'s Note: Two years later I need to interview again. I came to this problem and I couldn\'t understand this solution. After reading the explanation through the link above, I finally figured this out again. \nTwo key points that I found helpful while understanding the solution: \n\n1. When a bar is popped, we calculate the area with the popped bar at index ``tp`` as shortest bar. Now we know the rectangle **height** is ``heights[tp]``, we just need rectangle width to calculate the area.\n2. How to determine rectangle **width**? The maximum width we can have here would be made of all connecting bars with height greater than or equal to ``heights[tp]``. ``heights[s.peek() + 1] >= heights[tp]`` because the index on top of the stack right now ``s.peek()`` is the first index left of ``tp`` with height smaller than tp\'s height (if ``s.peek()`` was greater then it should have already been poped out of the stack). ``heights[i - 1] >= heights[tp]`` because index ``i`` is the first index right of ``tp`` with height smaller than tp\'s height (if ``i`` was greater then ``tp`` would have remained on the stack). Now we multiply height ``heights[tp]`` by width ``i - 1 - s.peek()`` to get the **area**.\n\n | 369 | 12 | ['Java'] | 66 |
largest-rectangle-in-histogram | Video Explanation | video-explanation-by-niits-vacy | Solution Video\n\nhttps://youtu.be/WTbLeCP8rwM\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n\u25A0 Subs | niits | NORMAL | 2024-06-27T14:29:21.596748+00:00 | 2024-08-17T12:42:16.409320+00:00 | 22,922 | false | # Solution Video\n\nhttps://youtu.be/WTbLeCP8rwM\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 6,001\nThank you for your support!\n\n---\n\nhttps://youtu.be/bU_dXCOWHls\n\n---\n\n```python []\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n stack = [-1]\n max_area = 0\n\n for i in range(len(heights)):\n while stack[-1] != -1 and heights[i] <= heights[stack[-1]]:\n height = heights[stack.pop()]\n width = i - stack[-1] - 1\n max_area = max(max_area, height * width)\n stack.append(i)\n \n while stack[-1] != -1:\n height = heights[stack.pop()]\n width = len(heights) - stack[-1] - 1\n max_area = max(max_area, height * width)\n \n return max_area\n```\n```javascript []\n/**\n * @param {number[]} heights\n * @return {number}\n */\nvar largestRectangleArea = function(heights) {\n const stack = [-1];\n let max_area = 0;\n\n for (let i = 0; i < heights.length; i++) {\n while (stack[stack.length - 1] !== -1 && heights[i] <= heights[stack[stack.length - 1]]) {\n const height = heights[stack.pop()];\n const width = i - stack[stack.length - 1] - 1;\n max_area = Math.max(max_area, height * width);\n }\n stack.push(i);\n }\n\n while (stack[stack.length - 1] !== -1) {\n const height = heights[stack.pop()];\n const width = heights.length - stack[stack.length - 1] - 1;\n max_area = Math.max(max_area, height * width);\n }\n\n return max_area;\n};\n```\n```java []\nimport java.util.Stack;\n\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n Stack<Integer> stack = new Stack<>();\n stack.push(-1);\n int maxArea = 0;\n\n for (int i = 0; i < heights.length; i++) {\n while (stack.peek() != -1 && heights[i] <= heights[stack.peek()]) {\n int height = heights[stack.pop()];\n int width = i - stack.peek() - 1;\n maxArea = Math.max(maxArea, height * width);\n }\n stack.push(i);\n }\n\n while (stack.peek() != -1) {\n int height = heights[stack.pop()];\n int width = heights.length - stack.peek() - 1;\n maxArea = Math.max(maxArea, height * width);\n }\n\n return maxArea;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n stack<int> stack;\n stack.push(-1);\n int max_area = 0;\n\n for (int i = 0; i < heights.size(); i++) {\n while (stack.top() != -1 && heights[i] <= heights[stack.top()]) {\n int height = heights[stack.top()];\n stack.pop();\n int width = i - stack.top() - 1;\n max_area = max(max_area, height * width);\n }\n stack.push(i);\n }\n\n while (stack.top() != -1) {\n int height = heights[stack.top()];\n stack.pop();\n int width = heights.size() - stack.top() - 1;\n max_area = max(max_area, height * width);\n }\n\n return max_area; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\n##### \u2B50\uFE0F Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n##### \u2B50\uFE0F Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n##### \u2B50\uFE0F My recent video\n#33 Search in Rotated Sorted Array\n\nhttps://youtu.be/dO9OZJP_Hm8\n | 290 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 3 |
largest-rectangle-in-histogram | My concise C++ solution, AC 90 ms | my-concise-c-solution-ac-90-ms-by-sipipr-vlbv | I push a sentinel node back into the end of height to make the code logic more concise.\n \n\n class Solution {\n public:\n int largestR | sipiprotoss5 | NORMAL | 2014-10-09T01:18:19+00:00 | 2018-10-23T06:25:22.498889+00:00 | 89,874 | false | I push a sentinel node back into the end of height to make the code logic more concise.\n \n\n class Solution {\n public:\n int largestRectangleArea(vector<int> &height) {\n \n int ret = 0;\n height.push_back(0);\n vector<int> index;\n \n for(int i = 0; i < height.size(); i++)\n {\n while(index.size() > 0 && height[index.back()] >= height[i])\n {\n int h = height[index.back()];\n index.pop_back();\n \n int sidx = index.size() > 0 ? index.back() : -1;\n if(h * (i-sidx-1) > ret)\n ret = h * (i-sidx-1);\n }\n index.push_back(i);\n }\n \n return ret;\n }\n }; | 278 | 10 | [] | 39 |
largest-rectangle-in-histogram | [Java/C++] Explanation going from Brute to Optimal Approach | javac-explanation-going-from-brute-to-op-5m0n | \nWhat the Question is saying, \nGiven an array of integers heights representing the histogram\'s bar height where the width of each bar is 1, \nreturn the area | hi-malik | NORMAL | 2022-01-29T05:17:20.078713+00:00 | 2022-08-03T11:57:13.226306+00:00 | 22,120 | false | ```\nWhat the Question is saying, \nGiven an array of integers heights representing the histogram\'s bar height where the width of each bar is 1, \nreturn the area of the largest rectangle in the histogram.\n```\n\nUnderstand this problem with an example;\n**Input:** `heights = [2,1,5,6,2,3]`\n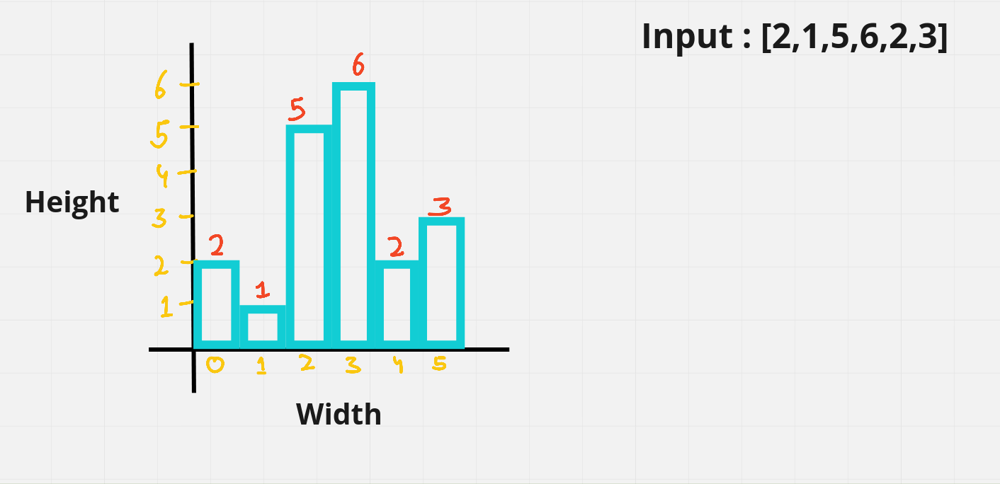\n\nLet\'s understand how we calculate this, let\'s took on index 4 height is 2. If we go to the left and see where the height is less then 2 and i.e. at index 1. So, that becomes the left Boundary. Similarly if we go to right and see where the height is less then 2 & i.e. at index 6 [which is end of the array].\n\nNow we have left & right boundary the area could be find out by height * width. And width will get by (right - left - 1) in case of 4 that will be 6 - 1 - 1 = 4. And we know the height already i.e. 2.\n\nThe Area we get is 2 * 4 i.e. 8\n\n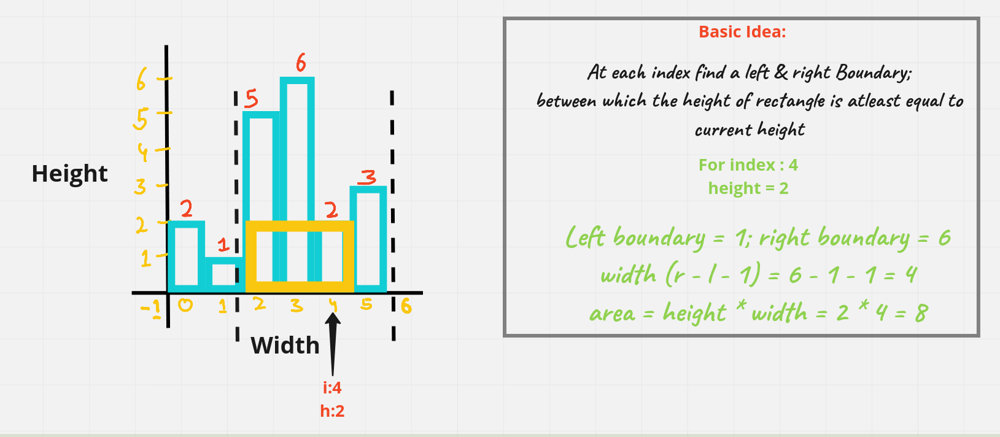\n\nThe main idea here would be how to find **left boundary & right boundary** for every index. The **brute way** is using an **ARRAY**\n`For left boundary array:`\n* Start with index 1, (left[0] = -1)\n* For each index -> go to left & find the nearest index where height [index] < height[curr]\n* Start with index 1,\n* Eg : Index 1 : left[1] = -1\n\n`For right boundary array:`\n* Start with index n - 2 right[n - 1] = n\n* For each index -> go to right & find the nearest index where height[index] < height[curr]\n* Start with index n - 2\n* Eg : Index 2 : right[2] = 4\n\nI hope you got the point and let\'s code this brute force Approach then we move to optimal Approach:\n**Java**\n```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int n = heights.length;\n if(n == 0) return 0; // Base Condition\n int maxArea = 0;\n int left[] = new int[n]; //fill left boundary\n int right[] = new int[n]; // fill right boundary\n \n left[0] = -1;\n right[n - 1] = n;\n \n for(int i = 1; i < n; i++){\n int prev = i - 1; // previous for comparing the heights\n while(prev >= 0 && heights[prev] >= heights[i]){\n prev = left[prev]; // we have done this to minimise the jumps we make to the left\n }\n left[i] = prev;\n }\n // Similarly we do for right\n for(int i = n - 2; i >= 0; i--){\n int prev = i + 1; \n while(prev < n && heights[prev] >= heights[i]){\n prev = right[prev]; \n }\n right[i] = prev;\n }\n // once we have these two arrays fill we need width & area\n for(int i = 0; i < n; i++){\n int width = right[i] - left[i] - 1;\n maxArea = Math.max(maxArea, heights[i] * width);\n }\n return maxArea;\n \n }\n}\n```\n**C++**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n if(n == 0) return 0; // Base Condition\n int maxArea = 0;\n vector<int> left(n); //fill left boundary\n vector<int> right(n); // fill right boundary\n \n left[0] = -1;\n right[n - 1] = n;\n \n for(int i = 1; i < n; i++){\n int prev = i - 1; // previous for comparing the heights\n while(prev >= 0 && heights[prev] >= heights[i]){\n prev = left[prev]; // we have done this to minimise the jumps we make to the left\n }\n left[i] = prev;\n }\n // Similarly we do for right\n for(int i = n - 2; i >= 0; i--){\n int prev = i + 1; \n while(prev < n && heights[prev] >= heights[i]){\n prev = right[prev]; \n }\n right[i] = prev;\n }\n // once we have these two arrays fill we need width & area\n for(int i = 0; i < n; i++){\n int width = right[i] - left[i] - 1;\n maxArea = max(maxArea, heights[i] * width);\n }\n return maxArea;\n }\n};\n```\nANALYSIS :\n* **Time Complexity :-** BigO(N^2)\n\n* **Space Complexity :-** BigO(N)\n\nNow, let\'s see our Optimize Approach i.e. **Using Stack**\nSo, what we do is we take a stack & keep on adding the indexes in the stack till we get a increasing sequence. Once the sequence becomes decreasing we need to pop the element and find the area `[That\'s the basic idea behind the stack]`\n\nSo, let\'s take the stack and we are at index 1. The height of current is less than that of top of stack which is the 0th index. As the height is decreasing. So, what we do here is find the area for elements in stack\n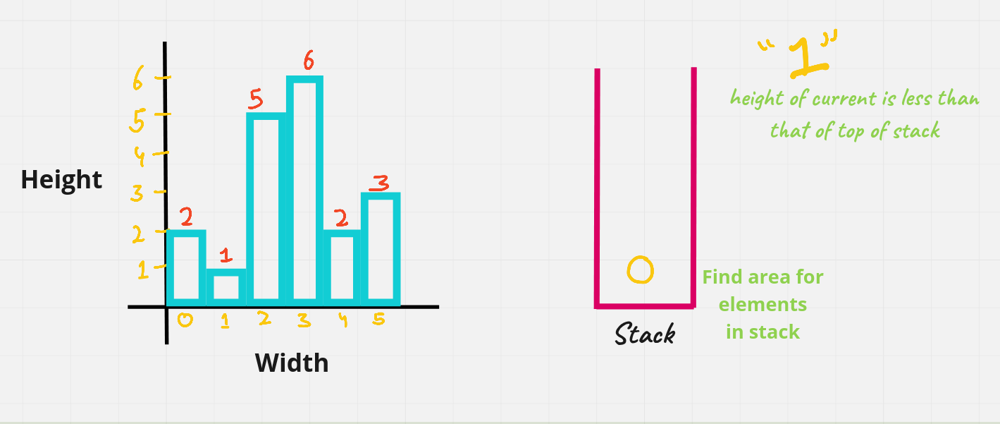\n\nNow, to find the area we pop the element from stack & then for that element the area becomes **height[top] * curr i.e. 1**\nIf the stack becomes empty i.e. if this is the only element present for that we find the width and multiply with the height of top element `[width would be curr - stack.peek - 1]` where curr is right & stack.peek() is left\n\nFor this case we **pop "0"** and stack becomes **empty**, so the area becomes **height[0] * curr = 2 * 1 = 2.** So, till now maxArea we have found is 2\n\n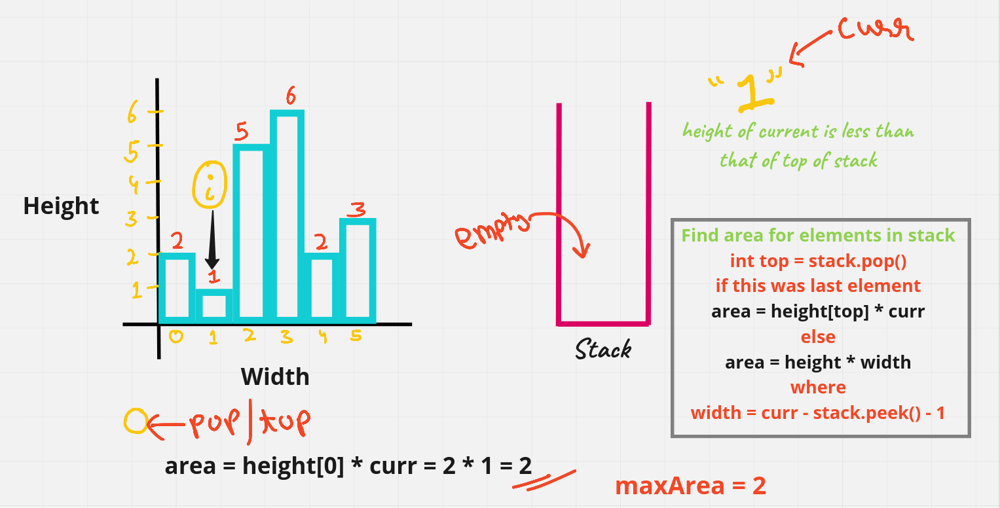\n\nWe will do this procedure for all the element\'s and we will get the **maxArea i.e. 10**\n\n*I hope you got the idea,* **So, let\'s code it up:**\n**Java**\n```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int n = heights.length;\n int maxArea = 0;\n Stack<Integer> st = new Stack<>();\n \n for(int i = 0; i <= n; i++){\n int currHeight = i == n ? 0 : heights[i];\n // check if currHeight becomes greater then height[top] element of stack. we do a push because it\'s an increasing sequence\n // otherwise we do pop and find area, so for that we write a while loop\n while(!st.isEmpty() && currHeight < heights[st.peek()]){\n int top = st.pop(); // current element on which we are working\n // now we need width & area\n int width = st.isEmpty() ? i : i - st.peek() - 1; // width differ, if stack is empty or not empty after we pop the element\n int area = heights[top] * width; // current height * width\n maxArea = Math.max(area, maxArea);\n }\n // if it doesn\'t enter in while loop, it means it\'s an increasing sequence & we need to push index\n st.push(i);\n }\n return maxArea;\n }\n}\n```\n**C++**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n int maxArea = 0;\n stack<int> st;\n \n for(int i = 0; i <= n; i++){\n int currHeight = i == n ? 0 : heights[i];\n // check if currHeight becomes greater then height[top] element of stack. we do a push because it\'s an increasing sequence\n // otherwise we do pop and find area, so for that we write a while loop\n while(!st.empty() && currHeight < heights[st.top()]){\n int top = st.top(); st.pop(); // current element on which we are working\n // now we need width & area\n int width = st.empty() ? i : i - st.top() - 1; // width differ if we stack is empty or not empty after we pop the element\n int area = heights[top] * width; // current height * width\n maxArea = max(area, maxArea);\n }\n // if it doesn\'t enter in while loop, it means it\'s an increasing sequence & we need to push index\n st.push(i);\n }\n return maxArea;\n }\n};\n```\nANALYSIS :\n* **Time Complexity :-** BigO(N)\n\n* **Space Complexity :-** BigO(N) | 264 | 56 | ['C', 'Java'] | 16 |
largest-rectangle-in-histogram | [Python] increasing stack, explained | python-increasing-stack-explained-by-dba-gzco | Key insight: for given bar i with value h, how to find the biggest rectangle, which is ending with this bar? We need to find the previous smallest place, where | dbabichev | NORMAL | 2020-12-31T10:24:02.552167+00:00 | 2020-12-31T13:01:27.646571+00:00 | 12,983 | false | **Key insight**: for given bar `i` with value `h`, how to find the biggest rectangle, which is ending with this bar? We need to find the previous smallest place, where value is less or equal than `h`: that is smallest `j`, such that `j < i` and `heights[j] >= heights[i]`. Ideal data structure for these type of problems is monostack: stack which has the following invariant: elements inside will be always in increasing order. To be more clear let us consired the following histogram `[1,4,2,5,6,3,2,6,6,5,2,1,3]`. Let us go element by element and understand what is going on.\n\n1. Stack is empty, so just put first bar of our histogram into stack: so we have `stack = [1]`. (actually what we put inside are indexes of bars, not values, but here we look at values for simplicity).\n2. Next we put bar `4`, and we have `[1, 4]` now. \n3. Next, we have bar `2`, which is less than `4`. So, first we evaluate When we evaluate `H` and `W`: width and height rectangle we can construct, using last element of stack as height: they equal to `4` and `1`. Next, we extract `4` and add `2` to stack, so we have `[1, 2]` bars in stack now.\n4. Next bar is bigger than `2`, so just add it and we have `[1, 2, 5]`\n5. Next bar is bigger than `5`, so just add it and we have `[1, 2, 5, 6]`\n6. Next bar is `3`, so we need to extract some stuff from our stack, until it becomes increasing one. We extract `6`, evaluate `(H, W) = (6, 1)` and extract `5` and evaluate `(H, W) = (5, 2)`. Now we have `[1, 2, 3]` in our stack.\n7. Next bar is `2`, it is smaller than `stack[-1]`, so we again need to extract some stuff: we extract `3` and have `(H, W) = (3, 3)` and also we extract `2` and have `(H, W) = (2, 5)`. Note here, why exactly we have `W = 5`: because we keep in stack indexes of our bars, and we can evaluate width as `i - stack[-1] - 1`. Now, we have `stack = [1, 2]`\n8. Next bar is `6`, so just put it to stack and we have `stack = [1, 2, 6]`.\n9. Next bar is `6` also, and we need to extract one last element from stack and put this new `6` to stack. `(H, W) = (6, 1)`. Note, that we have in stack `[1, 2, 6]` again, but it is values, for indexes last index was increased by one.\n10. Next bar is `5`, we extract last element from stack, have `(H, W) = (6, 2)` and put it to stack, so we have `[1, 2, 5]` now.\n11. Next bar is `2`, so we again start to pop elements to keep increasing order: `(H, W) = (5, 3)` for fisrt step and `(H, W) = (2, 9)` for second step, now `stack = [1, 2]`.\n12. Next bar is `1`, so we have `(H, W) = (2, 10)` and then `(H, W) = (1, 11)` and `stack = [1]`.\n13. Next bar is `3`, so we just put it to stack and have `[1, 3]` in stack.\n14. Next bar is `0` (we added it to process border cases), so we have `(H, W) = (3, 1)` and `(H, W) = (1, 13)` and finally stack is empty.\n\n**Complexity** is `O(n)`, where `n` is number of bars, space complexity is `O(n)` as well.\n\n```\nclass Solution:\n def largestRectangleArea(self, heights):\n stack, ans = [], 0\n for i, h in enumerate(heights + [0]):\n while stack and heights[stack[-1]] >= h:\n H = heights[stack.pop()]\n W = i if not stack else i-stack[-1]-1\n ans = max(ans, H*W)\n stack.append(i)\n return ans\n```\n\nSee also similar problems with monostack idea:\n\n**239.** Sliding Window Maximum https://leetcode.com/problems/sliding-window-maximum/discuss/951683/Python-Decreasing-deque-short-explained\n**496.** Next Greater Element I\n**739.** Daily Temperatures\n**862.** Shortest Subarray with Sum at Least K\n**901.** Online Stock Span\n**907.** Sum of Subarray Minimums\n**1687.** Delivering Boxes from Storage to Ports\n\n**Please let me know if you know more problems with this idea**\n\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 202 | 4 | ['Monotonic Stack'] | 18 |
largest-rectangle-in-histogram | Segment tree solution, just another idea, O(N*logN) Solution | segment-tree-solution-just-another-idea-4xuan | Inspired by this solution:\nhttp://www.geeksforgeeks.org/largest-rectangular-area-in-a-histogram-set-1/\n\nJust wanna to provide another idea of how to solve th | xiaohui5319 | NORMAL | 2016-05-20T05:40:14+00:00 | 2016-05-20T05:40:14+00:00 | 31,481 | false | Inspired by this solution:\nhttp://www.geeksforgeeks.org/largest-rectangular-area-in-a-histogram-set-1/\n\nJust wanna to provide another idea of how to solve this question in O(N*logN) theoretically, 40 ms solution:\n\n // Largest Rectangle in Histogram\n // Stack solution, O(NlogN) solution\n \n class SegTreeNode {\n public:\n int start;\n int end;\n int min;\n SegTreeNode *left;\n SegTreeNode *right;\n SegTreeNode(int start, int end) {\n this->start = start;\n this->end = end;\n left = right = NULL;\n }\n };\n \n class Solution {\n public:\n int largestRectangleArea(vector<int>& heights) {\n if (heights.size() == 0) return 0;\n // first build a segment tree\n SegTreeNode *root = buildSegmentTree(heights, 0, heights.size() - 1);\n // next calculate the maximum area recursively\n return calculateMax(heights, root, 0, heights.size() - 1);\n }\n \n int calculateMax(vector<int>& heights, SegTreeNode* root, int start, int end) {\n if (start > end) {\n return -1;\n }\n if (start == end) {\n return heights[start];\n }\n int minIndex = query(root, heights, start, end);\n int leftMax = calculateMax(heights, root, start, minIndex - 1);\n int rightMax = calculateMax(heights, root, minIndex + 1, end);\n int minMax = heights[minIndex] * (end - start + 1);\n return max( max(leftMax, rightMax), minMax );\n }\n \n SegTreeNode *buildSegmentTree(vector<int>& heights, int start, int end) {\n if (start > end) return NULL;\n SegTreeNode *root = new SegTreeNode(start, end);\n if (start == end) {\n root->min = start;\n return root;\n } else {\n int middle = (start + end) / 2;\n root->left = buildSegmentTree(heights, start, middle);\n root->right = buildSegmentTree(heights, middle + 1, end);\n root->min = heights[root->left->min] < heights[root->right->min] ? root->left->min : root->right->min;\n return root;\n }\n }\n \n int query(SegTreeNode *root, vector<int>& heights, int start, int end) {\n if (root == NULL || end < root->start || start > root->end) return -1;\n if (start <= root->start && end >= root->end) {\n return root->min;\n }\n int leftMin = query(root->left, heights, start, end);\n int rightMin = query(root->right, heights, start, end);\n if (leftMin == -1) return rightMin;\n if (rightMin == -1) return leftMin;\n return heights[leftMin] < heights[rightMin] ? leftMin : rightMin;\n }\n }; | 191 | 0 | ['C++'] | 112 |
largest-rectangle-in-histogram | AC clean Java solution using stack | ac-clean-java-solution-using-stack-by-je-e0le | public int largestRectangleArea(int[] h) {\n int n = h.length, i = 0, max = 0;\n \n Stack<Integer> s = new Stack<>();\n \n while (i | jeantimex | NORMAL | 2015-09-13T23:10:32+00:00 | 2018-10-01T15:36:57.399300+00:00 | 21,543 | false | public int largestRectangleArea(int[] h) {\n int n = h.length, i = 0, max = 0;\n \n Stack<Integer> s = new Stack<>();\n \n while (i < n) {\n // as long as the current bar is shorter than the last one in the stack\n // we keep popping out the stack and calculate the area based on\n // the popped bar\n while (!s.isEmpty() && h[i] < h[s.peek()]) {\n // tricky part is how to handle the index of the left bound\n max = Math.max(max, h[s.pop()] * (i - (s.isEmpty() ? 0 : s.peek() + 1)));\n }\n // put current bar's index to the stack\n s.push(i++);\n }\n \n // finally pop out any bar left in the stack and calculate the area based on it\n while (!s.isEmpty()) {\n max = Math.max(max, h[s.pop()] * (n - (s.isEmpty() ? 0 : s.peek() + 1)));\n }\n \n return max;\n } | 190 | 5 | ['Java'] | 12 |
largest-rectangle-in-histogram | Simple Divide and Conquer AC solution without Segment Tree | simple-divide-and-conquer-ac-solution-wi-9het | The idea is simple: for a given range of bars, the maximum area can either from left or right half of the bars, or from the area containing the middle two bars. | gildorwang | NORMAL | 2015-01-17T12:40:03+00:00 | 2018-08-29T06:19:37.340555+00:00 | 23,801 | false | The idea is simple: for a given range of bars, the maximum area can either from left or right half of the bars, or from the area containing the middle two bars. For the last condition, expanding from the middle two bars to find a maximum area is `O(n)`, which makes a typical Divide and Conquer solution with `T(n) = 2T(n/2) + O(n)`. Thus the overall complexity is `O(nlgn)` for time and `O(1)` for space (or `O(lgn)` considering stack usage). \n\nFollowing is the code accepted with 44ms. I posted this because I didn't find a similar solution, but only the RMQ idea which seemed less straightforward to me.\n\n class Solution {\n int maxCombineArea(const vector<int> &height, int s, int m, int e) {\n // Expand from the middle to find the max area containing height[m] and height[m+1]\n int i = m, j = m+1;\n int area = 0, h = min(height[i], height[j]);\n while(i >= s && j <= e) {\n h = min(h, min(height[i], height[j]));\n area = max(area, (j-i+1) * h);\n if (i == s) {\n ++j;\n }\n else if (j == e) {\n --i;\n }\n else {\n // if both sides have not reached the boundary,\n // compare the outer bars and expand towards the bigger side\n if (height[i-1] > height[j+1]) {\n --i;\n }\n else {\n ++j;\n }\n }\n }\n return area;\n }\n int maxArea(const vector<int> &height, int s, int e) {\n // if the range only contains one bar, return its height as area\n if (s == e) {\n return height[s];\n }\n // otherwise, divide & conquer, the max area must be among the following 3 values\n int m = s + (e-s)/2;\n // 1 - max area from left half\n int area = maxArea(height, s, m);\n // 2 - max area from right half\n area = max(area, maxArea(height, m+1, e));\n // 3 - max area across the middle\n area = max(area, maxCombineArea(height, s, m, e));\n return area;\n }\n public:\n int largestRectangleArea(vector<int> &height) {\n if (height.empty()) {\n return 0;\n }\n return maxArea(height, 0, height.size()-1);\n }\n }; | 144 | 1 | ['Divide and Conquer', 'C++'] | 15 |
largest-rectangle-in-histogram | Python solution without using stack. (with explanation) | python-solution-without-using-stack-with-sb7b | The algorithm using stack actually is not quite intuitive. At least I won't think about using it at first time.\n\nIt is more natural to think about this way. L | samuri | NORMAL | 2016-10-04T15:21:36.608000+00:00 | 2018-08-26T23:38:45.618608+00:00 | 11,670 | false | The algorithm using stack actually is not quite intuitive. At least I won't think about using it at first time.\n\nIt is more natural to think about this way. Let left[i] to indicate how many bars to the left (including the bar at index i) are equal or higher than bar[i], right[i] is that to the right of bar[i], so the the square of the max rectangle containing bar[i] is simply height[i] * (left[i] + right[i] - 1)\n\n class Solution:\n # @param height, a list of integer\n # @return an integer\n def largestRectangleArea(self, height):\n n = len(height)\n\n # left[i], right[i] represent how many bars are >= than the current bar\n\n left = [1] * n\n right = [1] * n\n max_rect = 0\n\n # calculate left\n for i in range(0, n):\n j = i - 1\n while j >= 0:\n if height[j] >= height[i]:\n left[i] += left[j]\n j -= left[j]\n else: break\n\n # calculate right\n for i in range(n - 1, -1, -1):\n j = i + 1\n while j < n:\n if height[j] >= height[i]:\n right[i] += right[j]\n j += right[j]\n else: break\n\n for i in range(0, n):\n max_rect = max(max_rect, height[i] * (left[i] + right[i] - 1))\n\n return max_rect\n\nNote, this algorithm runs O(n) not O(n^2)! The while loop in the for loop jumps forward or backward by the steps already calculated. | 117 | 2 | [] | 24 |
largest-rectangle-in-histogram | 44ms Easy Solution | C++ | 44ms-easy-solution-c-by-giriteja94495-suau | This method is not very intuitive ..i did this with some previous knowledge of similar problems\n\nclass Solution {\npublic:\n int largestRectangleArea(vecto | giriteja94495 | NORMAL | 2020-07-12T15:29:57.187789+00:00 | 2020-07-12T15:32:05.174240+00:00 | 12,091 | false | This method is not very intuitive ..i did this with some previous knowledge of similar problems\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n // this problem should be solved using stack .\n /* whenever you see a monotonic increase in the input which \n\t\twould yield the answer closest to \n\t\trequired you gotta understand that you should\n\t\tuse a stack datastructure to calculate the answer*/\n // so let\'s begin by creating a stack and ans that we return \n stack<int> st;\n int ans=0;\n //just to make our code understand better i\'m adding 0 at the end of\n //heights\n heights.push_back(0);\n /* how do you add the elements to the stack ? mmmmmm? okay \n\t\tlet us think \n way ,lets add all the ascending order elements to the stack so that \n\t\tit\n looks like climbing steps .coz in that way we can have atleast the \n\t\tmin\n size step * number of elements in the stack .if we encounter any \n\t\tbar with lesser height than the top element of the stack ,we \n\t\twill compute the \n existing stack element area and pop the top element just to check \n\t\tif the \n current top < bar height ,if it is so ..add it to the stack ..i think it \n\t\twill be more clearer if you go through the code*/\n //very important note .. we are adding indices ..not the values\n for(int i=0;i<heights.size();i++){\n while(!st.empty() && heights[st.top()]>heights[i]){\n //here we are checking if stack is empty or if we encounter \n\t\t\t\tany \n // number that doesn\'t satisfy our stack filling property\n int top=heights[st.top()];\n st.pop();\n int ran=st.empty()?-1:st.top();\n //this is to check if stack is empty, if so we will just take the //index\n ans=max(ans,top*(i-ran-1));\n // this is just to take the max area covered so far\n }\n st.push(i);\n //we push into the stack as long as it satsifies our stack condition\n }\n return ans;\n // i know it\'s not a very clever explanation ..but i tried to explain \n //whatever i can ...HAPPY CODING!!\n }\n};\n```\nHere in this problem stack can be replaced with vector and we can use popback and back methods which can implement the same functionality as stack but that one would take more time than the stack method\n | 100 | 4 | ['Stack', 'C', 'C++'] | 11 |
largest-rectangle-in-histogram | ✔️ [Python3] MONOTONIC STACK t(-_-t), Explained | python3-monotonic-stack-t-_-t-explained-jd0a8 | UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.\n\nThe idea is to use a monotonic stack. We iterate over bars a | artod | NORMAL | 2022-01-29T03:35:24.745577+00:00 | 2022-01-29T09:01:31.260792+00:00 | 11,526 | false | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe idea is to use a monotonic stack. We iterate over bars and add them to the stack as long as the last element in the stack is less than the current bar. When the condition doesn\'t hold, we start to calculate areas by popping out bars from the stack until the last element of the stack is greater than the current. The area is calculated as the number of pops multiplied by the height of the popped bar. On every pop, the height of the bar will be less or equal to the previous (since elements in the stack are always monotonically increasing).\n\nNow let\'s consider this example `[2,1,2]`. For this case the formula for the area (number of pops * current height) won\'t work because when we reach `1` we will pop out `2` from the stack and will not consider it later which is wrong since the largest area here is equal to `3 * 1`, i.e we somehow need to remember the previously discarded bars that still can form areas. We solve this problem by storing in the stack the width of the bar as well. So for our example, after discarding `2`, we push to the stack the `1` with the width equal to `2`.\n\nTime: **O(n)** - In the worst case we have 2 scans: one for the bars and one for the stack\nSpace: **O(n)** - in the wors case we push to the stack the whjole input array\n\nRuntime: 932 ms, faster than **51.27%** of Python3 online submissions for Largest Rectangle in Histogram.\nMemory Usage: 28.4 MB, less than **30.61%** of Python3 online submissions for Largest Rectangle in Histogram.\n\n```\ndef largestRectangleArea(self, bars: List[int]) -> int:\n\tst, res = [], 0\n\tfor bar in bars + [-1]: # add -1 to have an additional iteration\n\t\tstep = 0\n\t\twhile st and st[-1][1] >= bar:\n\t\t\tw, h = st.pop()\n\t\t\tstep += w\n\t\t\tres = max(res, step * h)\n\n\t\tst.append((step + 1, bar))\n\n\treturn res\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 90 | 5 | ['Monotonic Stack', 'Python3'] | 13 |
largest-rectangle-in-histogram | All 4 approaches shown || O(N^2) || O(NlogN) || O(N)(two pass) || O(N)(one pass) with explanation | all-4-approaches-shown-on2-onlogn-ontwo-cnl6w | I will try to explain all the three approaches I know for solving this problem : \n1) Brute Force O(n^2)(too slow TLE)\nwe can compute area of every subarray a | sharan_17 | NORMAL | 2022-01-29T08:21:30.900015+00:00 | 2022-01-29T08:22:08.092344+00:00 | 9,048 | false | I will try to explain all the three approaches I know for solving this problem : \n**1) Brute Force O(n^2)**(too slow **TLE**)\nwe can compute area of every subarray and return the max of them all.\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size() ; \n\t\tint max_area = 0 ; \n\t\tfor(int i = 0 ; i < n ; i++) {\n\t\t\tint curr_max = 0 ; \n\t\t\tint min_height = INT_MAX ; \n\t\t\tfor(int j = i ; j < n ; j++) {\n\t\t\t\tmin_height = min(min_height , heights[j]) ; \n\t\t\t\tcurr_max = max(curr_max , min_height * (j - i + 1)) ; \n\t\t\t}\n\t\t\tmax_area = max(max_area , curr_max) ; \n\t\t}\n\t\treturn max_area ; \n }\n};\n```\n\n**2) Divide n Conquer Approach O(NlogN)(using segment tree) O(N^2)(if we calculate range minimum naively)**\nWe can use Divide and Conquer to solve this in O(nLogn) time.\nThe idea is to find the minimum value in the given array.\nOnce we have index of the minimum value, the max area is maximum of following three values :\n1. Maximum area in left side of minimum value ( excluding the min value)\n2. Maximum area in right of minimum value ( excluding the min value)\n3. Minimum value * length of segment .\nThe areas on left and right can be calculated recursively.\nIf we use linear search to find the minimum value, then the worst case time complexity of this algorithm becomes O(n^2).**(TLE)**\n```\nclass SegmentTree {\npublic: \n int start , end , min ; \n SegmentTree *left ;\n SegmentTree *right ;\n \n SegmentTree (int start, int end) {\n this->start = start ;\n this->end = end ;\n left = right = NULL ;\n } \n};\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n SegmentTree* root = build(heights , 0 , heights.size() - 1) ;\n return maxAreaInThisSegment(heights , 0 , heights.size() - 1 , root) ;\n }\n \n SegmentTree* build(vector<int>& heights, int start, int end) {\n if (start > end) return NULL ;\n SegmentTree *root = new SegmentTree(start, end) ;\n if (start == end) {\n root->min = start ;\n return root ;\n } else {\n int middle = (start + end) / 2 ;\n root->left = build(heights, start, middle) ;\n root->right = build(heights, middle + 1, end) ;\n root->min = heights[root->left->min] < heights[root->right->min] ? root->left->min : root->right->min ;\n return root ;\n }\n }\n \n int query(vector<int> &heights , int start , int end , SegmentTree* root) {\n if(!root || end < root->start || start > root->end) return -1 ;\n if (start <= root->start && end >= root->end) {\n return root->min ;\n }\n int leftMin = query(heights , start , end , root->left) ;\n int rightMin = query(heights , start , end , root->right) ; \n if(leftMin == -1) return rightMin ;\n if(rightMin == -1) return leftMin ; \n return heights[leftMin] < heights[rightMin] ? leftMin : rightMin ; \n }\n //calculates the maximum possible area in the histogram between indexes start and end\n int maxAreaInThisSegment(vector<int> &heights , int start , int end , SegmentTree *root) {\n if(start > end) {\n return -1 ;\n } \n if(start == end) {\n return heights[start] ;\n }\n int wholeMin = query(heights , start , end , root) ; \n return max({heights[wholeMin] * (end - start + 1) , maxAreaInThisSegment(heights , start , wholeMin - 1 , root) , maxAreaInThisSegment(heights , wholeMin + 1 , end , root)}) ;\n }\n};\n```\n\n**3) Using left_smaller and right_smaller O(N)(2 pass)**\nwe use two arrays left and right which store the next smaller element to the left and right respectively.\nthen for every index we calculate area as `heights[i] * (right[i] - left[i] + 1)`\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size() ; \n vector<int> left(n , 0) , right(n , n) ; \n stack<int> s ; \n for(int i = 0 ; i < n ; i++) {\n while(!s.empty() && heights[i] <= heights[s.top()]) s.pop() ;\n if(s.empty()) left[i] = 0 ; //minimum element\n else left[i] = s.top() + 1 ;\n s.push(i) ; \n }\n while(!s.empty()) s.pop() ; \n for(int i = n - 1 ; i >= 0 ; i--) {\n while(!s.empty() && heights[i] <= heights[s.top()]) s.pop() ;\n if(s.empty()) right[i] = n - 1 ; //minimum element\n else right[i] = s.top() - 1 ;\n s.push(i) ; \n }\n int max_area = 0 ; \n for(int i = 0 ; i < n ; i++) {\n max_area = max(max_area , heights[i] * (right[i] - left[i] + 1)) ;\n }\n return max_area ;\n }\n};\n```\n**4) using only one stack O(N)(1 pass)**\nsame as approach 3 but better space complexity **(O(N) space)**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size() , max_area = INT_MIN , i = 0 ; \n stack<int> s ;\n while(i < n) {\n if(s.empty() || heights[s.top()] <= heights[i]) {\n s.push(i) ; \n i++ ; \n } else {\n int prev_top = s.top() ; \n s.pop() ; \n max_area = max(max_area , heights[prev_top] * (s.empty() ? i : i - s.top() - 1)) ;\n }\n }\n while(!s.empty()) {\n int prev_top = s.top() ; \n s.pop() ; \n max_area = max(max_area , heights[prev_top] * (s.empty() ? i : i - s.top() - 1)) ;\n } \n return max_area ;\n }\n};\n```\n\n | 81 | 2 | ['Divide and Conquer', 'Stack', 'Tree', 'Recursion', 'C'] | 3 |
largest-rectangle-in-histogram | 📊 Monotonique Stack Solution Intuition (Javascript) | monotonique-stack-solution-intuition-jav-ehn8 | Oh, hard problem it is, isn\'t it? \nLet\'s develop some intuition on how to access it.\n\n## Increasing \nWhen the heights are increasing, we can always build | avakatushka | NORMAL | 2021-08-28T10:20:59.953224+00:00 | 2021-08-28T10:24:12.689723+00:00 | 3,829 | false | Oh, **hard problem** it is, isn\'t it? \nLet\'s develop some intuition on how to access it.\n\n## Increasing \nWhen the heights are **increasing**, we can always build rectangle from a point there a previous height started, to the current point. \n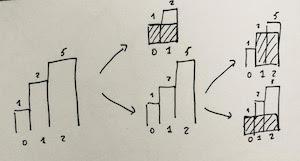\nE.g we have heights [1, 2, 5]. In point 2 we can build rectangle of the height 1. In the point 5 we can build rectangle of height 2, starting from index 1, or height 1, starting from index 0. \n\nLet\'s put the height, and the index, from where it\'s possible to build rectangle of this height, into a stack. \n\t```javascript\n\tstack.push([index, height])\n\t```\n## Decreasing \nWhen the height is **decreasing**, we couldn\'t build rectangle of any previous height, heigher than the current one. So it\'s the place to make evaluation. \n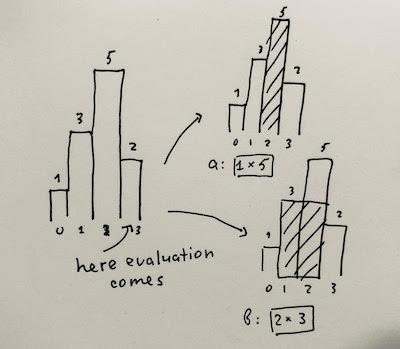\n\n\nWe\'ll pop all the heights bigger than the current one from the stack, and estimate the rectangles which could be build to this point:\n```javascript\nwhile (stack.length && stack[stack.length - 1][1] > heights[i]) {\n let [pos, height] = stack.pop();\n res = Math.max(res, (i - pos) * height);\n\t}\n```\n## What to put in the stack?\nIt\'s seems like we put in the stack the current index we are processing? \nAlmost. \nBut when we pop up all the heights which are bigger than the current one, guess where current height could start? From any of this points. \nImagine we have array [1, 3, 5, 2]. At the height of 2 we pop up 5 and 3, but rectangle of the height 2 can start from index 1, not from index 3!\nSo, we put in the stack the **earliest point, from there this height could start**. Which is either current index, or the last height poped from the stack. \n## Append 0 to heights\nTo make sure we processed all the heights, we can add additinal while statement in the end, or do more elegant solution - append 0 to the end of heights.\n\n## Full code\n```javascript\nheights.push(0) \nlet stack = [];\nlet res = 0;\nfor (let i = 0; i < heights.length; i++) {\n\tlet heightStart = i;\n\twhile (stack.length && stack[stack.length - 1][1] > heights[i]) {\n\t\t\tlet [pos, height] = stack.pop();\n\t\t\tres = Math.max(res, (i - pos) * height);\n\t\t\theightStart = pos; \n\t\t}\n\tstack.push([heightStart, heights[i]]);\n}\nreturn res;\n```\n\n\n | 68 | 0 | ['Stack', 'JavaScript'] | 8 |
largest-rectangle-in-histogram | My concise code (20ms, stack based, O(n)), one trick used | my-concise-code-20ms-stack-based-on-one-o622x | The idea is simple, use a stack to save the index of each vector entry in a ascending order; once the current entry is smaller than the one with the index s.top | lejas | NORMAL | 2015-05-21T01:59:00+00:00 | 2018-10-08T20:08:44.116083+00:00 | 15,181 | false | The idea is simple, use a stack to save the index of each vector entry in a ascending order; once the current entry is smaller than the one with the index s.top(), then that means the rectangle with the height height[s.top()] ends at the current position, so calculate its area and update the maximum. \nThe only trick I use to avoid checking whether the stack is empty (due to pop) and also avoiding emptying the stack at the end (i.e. after going through the vector, s is not empty and we have to consider those in the stack) is to put a dummy "0" at the beginning of vector "height" and the end of "height": the first one makes sure the stack will never be empty (since all the height entries are >=0) and the last one will flush all the remaining non-zero entries of the stack at the end of "for" iteration. This trick helps us keep the code concise.\n\n class Solution {\n public:\n int largestRectangleArea(vector<int>& height) {\n height.insert(height.begin(),0); // dummy "0" added to make sure stack s will never be empty\n height.push_back(0); // dummy "0" added to clear the stack at the end\n int len = height.size();\n int i, res = 0, idx;\n stack<int> s; // stack to save "height" index\n s.push(0); // index to the first dummy "0"\n for(i=1;i<len;i++)\n {\n while(height[i]<height[idx = s.top()]) // if the current entry is out of order\n {\n s.pop();\n res = max(res, height[idx] * (i-s.top()-1) ); // note how the width is calculated, use the previous index entry\n }\n s.push(i);\n }\n height.erase(height.begin()); // remove two dummy "0"\n height.pop_back();\n return res;\n }\n }; | 55 | 2 | [] | 7 |
largest-rectangle-in-histogram | [C++] Simple Solution | Brute Force ▶️ Optimal | W/ Explanation | c-simple-solution-brute-force-optimal-w-7oax0 | APPROACH 1 : BRUTE FORCE\n\n A Brute force approach would be to one by one consider all bars as starting points and calculate area of all rectangles starting wi | Mythri_Kaulwar | NORMAL | 2022-01-29T02:54:46.629012+00:00 | 2022-01-29T17:31:53.720248+00:00 | 5,796 | false | **APPROACH 1 : BRUTE FORCE**\n\n* A Brute force approach would be to one by one consider all bars as starting points and calculate area of all rectangles starting with every bar. \n* Finally return maximum of all possible areas. \n\n**Time complexity :** O(n^2)\n\n* We can use Divide and Conquer to solve this in O(nLogn) time. \n* The idea is to find the minimum value in the given array. \n* Once we have index of the minimum value, the max area is maximum of following three values :\n 1. Maximum area in left side of minimum value (w/o including the min value) \n 2. Maximum area in right of minimum value (not including the min value) \n 3. Number of bars multiplied by minimum value. \n* The areas on left & right can be calculated recursively. \n* If we use linear search to find the minimum value, then the worst case time complexity of this algorithm becomes O(n^2). (In the worst case, there are always ```n-1``` elements on one-side & 0 elements on the other)\n\n**APPROACH 2 : Using Left-Smaller & Right-Smaller Arrays**\n\n* First we will take two arrays left_smaller[] and right_smaller[] and initialize it with -1 and n respectively.\n* For every index, we will store the index of previous smaller and next smaller element in ```left_smaller``` and ```right_smaller``` arrays respectively. - ```O(n)``` time\n* Now for every element we will calculate area by taking this ith element as the smallest in the range left_smaller[i] and right_smaller[i] and multiplying it with the difference of left_smaller[i] and right_smaller[i].\n* Each time we update the max_area according to the area obtained in the previous step.\n\n**Time Complexity :** O(n) - 3-pass \n\n**Space Complexity :** O(n)\n\n**Code :**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n stack<int> s; \n vector<int> left_bound(n,0),right_bound(n,n); \n for(int i=0;i<n;i++) {\n while(!s.empty() && heights[i]<=heights[s.top()]) s.pop();\n if(s.empty()) left_bound[i]=0;\n else left_bound[i] = s.top()+1;\n\t\t\t\n s.push(i);\n }\n while(!s.empty()) s.pop();\n for(int i=n-1; i>=0; i--) {\n while(!s.empty() && heights[i]<=heights[s.top()]) s.pop();\n if(s.empty()) right_bound[i] = n-1;\n else right_bound[i] = s.top()-1;\n s.push(i);\n }\n int maxi = 0, area;\n for(int i=0; i<n; i++) {\n area = (right_bound[i]-left_bound[i]+1)*heights[i];\n maxi = max(maxi, area);\n }\n return maxi; \n }\n};\n```\n\n**APPROACH 3 : Using Only Stack**\n\n* For every bar \u2018x\u2019, we calculate the area with \u2018x\u2019 as the smallest bar in the rectangle.\n* We need to know index of the first smaller (smaller than \u2018x\u2019) bar on left of \u2018x\u2019 and index of first smaller bar on right of \u2018x\u2019.\n* We traverse all bars from left to right, maintain a stack of bars. \n* Every bar is pushed to stack once. \n* A bar is popped from stack when a bar of smaller height is seen. \n* When a bar is popped, we calculate the area with the popped bar as smallest bar - the current index tells us the \u2018right index\u2019 and index of previous item in stack is the \u2018left index\u2019.\n\n**ALGORITHM :**\n* Create an empty stack.\n* Start from first bar, and do following for every bar \u2018hist[i]\u2019 where \u2018i\u2019 varies from 0 to n-1. \n\t\t1. If stack is empty or hist[i] is higher than the bar at top of stack, then push \u2018i\u2019 to stack. \n\t\t2. If this bar is smaller than the top of stack, then keep removing the top of stack while top of the stack is greater. \n\t\t3. Let the removed bar be hist[tp]. \n\t\t4. Calculate area of rectangle with hist[tp] as smallest bar. For hist[tp], the \u2018left index\u2019 is previous (previous to tp) item in stack and \u2018right index\u2019 is \u2018i\u2019 (current index).\n Until the stack becomes empty, one by one remove all bars from stack and do steps 2-4 of the previous step for every removed bar.\n \n **Time Complexity :** O(n) - One-pass\n \n**Code :**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int ans=INT_MIN, area_with_top=0, top=0, i=0, n=heights.size();\n stack<int> s;\n \n while(i<n){\n if(s.empty() || heights[s.top()]<=heights[i]) s.push(i++);\n else{\n top = s.top(); s.pop();\n area_with_top = heights[top]*(s.empty() ? i : i-s.top()-1);\n ans = max(ans, area_with_top);\n }\n }\n \n while(!s.empty()){\n top = s.top(); s.pop();\n area_with_top = heights[top]*(s.empty() ? i : i-s.top()-1);\n ans = max(ans, area_with_top);\n } \n return ans;\n }\n};\n```\n\n**Do upvote if you like my solution :)**\n\n\n | 48 | 4 | ['Stack', 'C', 'C++'] | 3 |
largest-rectangle-in-histogram | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏 | beats-super-easy-beginners-by-codewithsp-83a9 | \n\n---\n\n\n---\n# Intuition\nThe problem can be visualized as calculating the largest rectangle that can be formed in a histogram. The intuition is to use a s | CodeWithSparsh | NORMAL | 2024-12-08T15:53:06.109952+00:00 | 2024-12-08T16:32:23.281582+00:00 | 5,178 | false | \n\n---\n\n\n---\n# Intuition\nThe problem can be visualized as calculating the largest rectangle that can be formed in a histogram. The intuition is to use a **stack** to keep track of indices of histogram bars that are not yet resolved. By ensuring that the heights in the stack are in increasing order, we can calculate the largest rectangle for each bar as soon as we encounter a bar of smaller height.\n\n---\n\n# Approach\n1. **Use a stack** to store indices of bars in increasing order of height.\n2. When a bar of smaller height is encountered, **calculate the maximum area** for all indices in the stack that are greater than the current bar\'s height.\n3. Use a **sentinel value** of `0` height at the end to ensure all bars are processed.\n4. For each resolved height, calculate the area using the width determined by the current index and the index of the previous smaller height.\n\n---\n\n# Complexity\n- **Time Complexity**: \n $$O(n)$$ because each bar is pushed and popped from the stack at most once.\n\n- **Space Complexity**: \n $$O(n)$$ for the stack.\n\n---\n\n\n```python []\nclass Solution:\n def largestRectangleArea(self, heights):\n stack = []\n max_area = 0\n n = len(heights)\n\n for i in range(n + 1):\n current_height = heights[i] if i < n else 0\n\n while stack and heights[stack[-1]] > current_height:\n height = heights[stack.pop()]\n width = i if not stack else i - stack[-1] - 1\n max_area = max(max_area, height * width)\n \n stack.append(i)\n \n return max_area\n```\n\n\n```cpp []\n#include <vector>\n#include <stack>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n stack<int> st;\n int maxArea = 0;\n int n = heights.size();\n\n for (int i = 0; i <= n; ++i) {\n int currentHeight = (i == n) ? 0 : heights[i];\n\n while (!st.empty() && heights[st.top()] > currentHeight) {\n int height = heights[st.top()];\n st.pop();\n int width = st.empty() ? i : i - st.top() - 1;\n maxArea = max(maxArea, height * width);\n }\n\n st.push(i);\n }\n\n return maxArea;\n }\n};\n```\n\n\n```java []\nimport java.util.Stack;\n\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n Stack<Integer> stack = new Stack<>();\n int maxArea = 0;\n int n = heights.length;\n\n for (int i = 0; i <= n; i++) {\n int currentHeight = (i == n) ? 0 : heights[i];\n\n while (!stack.isEmpty() && heights[stack.peek()] > currentHeight) {\n int height = heights[stack.pop()];\n int width = stack.isEmpty() ? i : i - stack.peek() - 1;\n maxArea = Math.max(maxArea, height * width);\n }\n\n stack.push(i);\n }\n\n return maxArea;\n }\n}\n```\n\n\n```go []\nfunc largestRectangleArea(heights []int) int {\n stack := []int{}\n maxArea := 0\n n := len(heights)\n\n for i := 0; i <= n; i++ {\n currentHeight := 0\n if i < n {\n currentHeight = heights[i]\n }\n\n for len(stack) > 0 && heights[stack[len(stack)-1]] > currentHeight {\n height := heights[stack[len(stack)-1]]\n stack = stack[:len(stack)-1]\n width := i\n if len(stack) > 0 {\n width = i - stack[len(stack)-1] - 1\n }\n maxArea = max(maxArea, height*width)\n }\n\n stack = append(stack, i)\n }\n\n return maxArea\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n\n\n```javascript []\nvar largestRectangleArea = function(heights) {\n let stack = [];\n let maxArea = 0;\n let n = heights.length;\n\n for (let i = 0; i <= n; i++) {\n let currentHeight = (i === n) ? 0 : heights[i];\n\n while (stack.length && heights[stack[stack.length - 1]] > currentHeight) {\n let height = heights[stack.pop()];\n let width = stack.length === 0 ? i : i - stack[stack.length - 1] - 1;\n maxArea = Math.max(maxArea, height * width);\n }\n\n stack.push(i);\n }\n\n return maxArea;\n};\n```\n\n\n```dart []\nclass Solution {\n int largestRectangleArea(List<int> heights) {\n int n = heights.length;\n List<int> stack = [];\n int maxArea = 0;\n\n for (int i = 0; i <= n; i++) {\n int currentHeight = (i == n) ? 0 : heights[i];\n\n while (stack.isNotEmpty && heights[stack.last] > currentHeight) {\n int height = heights[stack.removeLast()];\n int width = stack.isEmpty ? i : i - stack.last - 1;\n maxArea = max(maxArea, height * width);\n }\n\n stack.add(i);\n }\n\n return maxArea;\n }\n}\n```\n\n---\n\n {:style=\'width:250px\'} | 40 | 0 | ['Array', 'Stack', 'C', 'Monotonic Stack', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'Dart'] | 2 |
largest-rectangle-in-histogram | 6 Similar questions || Prev smaller - Next smaller || Monotonic stack || C++ | 6-similar-questions-prev-smaller-next-sm-0na3 | 1. Largest Rectangle in a Histogram: https://leetcode.com/problems/largest-rectangle-in-histogram/\n\n\nclass Solution {\npublic:\n int largestRectangleArea( | hyperVJ | NORMAL | 2021-11-30T07:38:37.092811+00:00 | 2021-11-30T07:38:37.092839+00:00 | 2,824 | false | **1. Largest Rectangle in a Histogram**: https://leetcode.com/problems/largest-rectangle-in-histogram/\n\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n vector<int> nsl(n),psl(n);\n \n stack<int> s;\n \n for(int i=n-1;i>=0;i--){\n while(!s.empty() && heights[s.top()]>=heights[i]){\n s.pop();\n }\n nsl[i] = s.empty() ? n : s.top();\n s.push(i);\n }\n \n while(!s.empty()){\n s.pop();\n }\n \n for(int i=0;i<n;i++){\n while(!s.empty() && heights[s.top()]>=heights[i]){\n s.pop();\n }\n psl[i] = s.empty() ? -1: s.top();\n s.push(i);\n }\n \n int ans = INT_MIN;\n for(int i=0;i<n;i++){\n ans = max(ans,(nsl[i]-psl[i]-1)*(heights[i]));\n }\n \n return ans;\n }\n};\n\n```\n\n**2. Maximal Rectangle** : https://leetcode.com/problems/maximal-rectangle/\n\n```\nclass Solution {\npublic:\n \n \n int histogram(vector<int>& heights){\n int n = heights.size();\n vector<int> nsl(n),psl(n);\n \n stack<int> s;\n \n for(int i=n-1;i>=0;i--){\n while(!s.empty() && heights[s.top()]>=heights[i]){\n s.pop();\n }\n nsl[i] = s.empty() ? n : s.top();\n s.push(i);\n }\n \n while(!s.empty()){\n s.pop();\n }\n \n for(int i=0;i<n;i++){\n while(!s.empty() && heights[s.top()]>=heights[i]){\n s.pop();\n }\n psl[i] = s.empty() ? -1: s.top();\n s.push(i);\n }\n \n int ans = INT_MIN;\n for(int i=0;i<n;i++){\n ans = max(ans,(nsl[i]-psl[i]-1)*(heights[i]));\n }\n \n return ans;\n }\n \n \n \n \n \n \n int maximalRectangle(vector<vector<char>>& matrix) {\n \n \n \n int n = matrix.size();\n \n if(n==0){\n return 0;\n }\n \n \n int m = matrix[0].size();\n \n int dup[n][m];\n \n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(matrix[i][j]==\'0\'){\n dup[i][j]=0;\n }\n else{\n dup[i][j]=1;\n }\n }\n }\n \n\n for(int i=0;i<n;i++){\n if(i==0) continue;\n \n for(int j=0;j<m;j++){\n if(matrix[i][j]==\'1\'){\n dup[i][j] = 1+dup[i-1][j];\n }\n else{\n dup[i][j] = 0;\n }\n }\n }\n \n \n int ans = INT_MIN;\n \n for(int i=0;i<n;i++){\n vector<int> each_row;\n for(int j=0;j<m;j++){\n each_row.push_back(dup[i][j]);\n }\n \n ans = max(ans,histogram(each_row));\n }\n \n \n return ans;\n }\n};\n\n```\n\n**3. Maximum score of a Good subarray**: https://leetcode.com/problems/maximum-score-of-a-good-subarray/\n\n```\nclass Solution {\npublic:\n int maximumScore(vector<int>& nums, int k) {\n int n=nums.size();\n int ans=0;\n vector<long long>nsr(n),nsl(n);\n //NSL\n stack<int>st;\n for(int i=0;i<n;i++){\n while(!st.empty() && nums[st.top()]>=nums[i])\n st.pop();\n nsl[i]=st.empty()?-1:st.top();\n st.push(i);\n }\n //NSR\n stack<int>tt;\n for(int i=n-1;i>=0;i--){\n while(!tt.empty() && nums[tt.top()]>=nums[i])\n tt.pop();\n nsr[i]=tt.empty()?n:tt.top();\n tt.push(i);\n }\n vector<long long>pref(n,0);\n pref[0]=nums[0];\n \n for(int i=1;i<n;i++){\n pref[i]=pref[i-1]+nums[i];\n }\n \n for(int i=0;i<n;i++){\n int mn = nums[i];\n int l=nsl[i]+1, r=nsr[i]-1;\n int len, prod;\n if(l<=k && r>=k){\n len = r-l+1;\n prod = mn*len;\n ans = max(ans,prod);\n }\n \n }\n return ans;\n }\n};\n```\n\n**4. Sum of subarray minimums** : https://leetcode.com/problems/sum-of-subarray-minimums/\n\n```\nclass Solution {\npublic:\n int sumSubarrayMins(vector<int>& arr) {\n \n int mod = 1000000007;\n int n = arr.size();\n vector<int> nsl(n);\n vector<int> psl(n);\n \n stack<int> s;\n \n for(int i=n-1;i>=0;i--){\n while(!s.empty() && arr[s.top()]>arr[i]){\n s.pop();\n }\n nsl[i] = s.empty() ? n : s.top();\n s.push(i);\n }\n \n while(!s.empty()){\n s.pop();\n }\n \n for(int i=0;i<n;i++){\n while(!s.empty() && arr[s.top()]>=arr[i]){\n s.pop();\n }\n psl[i] = s.empty() ? -1: s.top();\n s.push(i);\n }\n \n long long ans = 0;\n for(int i=0;i<n;i++){\n long long r = nsl[i]-i;\n long long l = i-psl[i];\n \n cout<<psl[i]<<" "<<nsl[i]<<endl;\n \n ans+= (l*r*arr[i]);\n ans = ans%mod;\n }\n \n return ans;\n }\n};\n```\n\n**5. Maximum subarray min-Product**: https://leetcode.com/problems/maximum-subarray-min-product/\n\n```\nclass Solution {\npublic:\n int maxSumMinProduct(vector<int>& nums) {\n int n = nums.size();\n \n vector<int> nsl(n);\n vector<int> psl(n);\n \n int mod = 1000000007;\n \n \n stack<int> s;\n for(int i=n-1;i>=0;i--){\n while(!s.empty() && nums[s.top()]>=nums[i]){\n s.pop();\n }\n nsl[i] = s.empty() ? n: s.top();\n s.push(i);\n }\n \n while(!s.empty()){\n s.pop();\n }\n \n for(int i=0;i<n;i++){\n while(!s.empty() && nums[s.top()]>=nums[i]){\n s.pop();\n }\n psl[i] = s.empty() ? -1: s.top();\n s.push(i);\n }\n \n long long prefix[n+1];\n prefix[0]=0;\n for(int i=1;i<=n;i++){\n prefix[i] = prefix[i-1]+nums[i-1];\n }\n \n long long ans = INT_MIN;\n for(int i=0;i<n;i++){\n ans = max(ans,nums[i]*(prefix[nsl[i]]-prefix[psl[i]+1]));\n }\n \n return ans%mod;\n \n }\n};\n\n```\n\n**6. Daily Temperatures**: https://leetcode.com/problems/daily-temperatures/\n\n```\nclass Solution {\npublic:\n vector<int> dailyTemperatures(vector<int>& temperatures) {\n stack<int> s;\n \n int n = temperatures.size();\n \n vector<int> ans(n);\n \n for(int i=n-1;i>=0;i--){\n if(s.empty()){\n ans[i] = 0;\n }\n else{\n while(!s.empty() && temperatures[i]>=temperatures[s.top()]){\n s.pop();\n }\n \n if(s.empty()){\n ans[i] = 0;\n }\n else{\n ans[i] = s.top()-i;\n }\n \n \n }\n \n s.push(i);\n }\n \n \n return ans;\n }\n};\n\n```\n\n | 39 | 0 | ['C', 'Monotonic Stack'] | 4 |
largest-rectangle-in-histogram | [Python] Monotone Increasing Stack, Similar problems attached | python-monotone-increasing-stack-similar-iivn | \nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n ## RC ##\n ## APPROACH : MONOTONOUS INCREASING STACK ##\n | 101leetcode | NORMAL | 2020-06-15T10:55:23.819071+00:00 | 2020-06-15T10:56:07.575536+00:00 | 6,365 | false | ```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n ## RC ##\n ## APPROACH : MONOTONOUS INCREASING STACK ##\n ## Similar to Leetcode: 1475. Final Prices With a Special Discount in a Shop ##\n ## Similar to Leetcode: 907. Sum Of Subarray Minimums ##\n ## Similar to Leetcode: 85. maximum Rectangle ##\n ## Similar to Leetcode: 402. Remove K Digits ##\n ## Similar to Leetcode: 456. 132 Pattern ##\n ## Similar to Leetcode: 1063. Number Of Valid Subarrays ##\n ## Similar to Leetcode: 739. Daily Temperatures ##\n ## Similar to Leetcode: 1019. Next Greater Node In LinkedList ##\n \n ## LOGIC ##\n ## 1. Before Solving this problem, go through Monotone stack.\n ## 2. Using Monotone Stack we can solve 1) Next Greater Element 2) Next Smaller Element 3) Prev Greater Element 4) Prev Smaller Element\n ## 3. Using \'NSE\' Monotone Stack concept, we can find width of rectangles, height obviously will be the minimum of those. Thus we can calculate the area\n ## 4. As we are using NSE concept, adding 0 to the end, will make sure that stack is EMPTY at the end. ( so all the areas can be calculated while popping )\n \n heights.append(0)\n stack = [-1]\n ans = 0\n for i in range(len(heights)):\n while heights[i] < heights[stack[-1]]:\n height = heights[stack.pop()]\n width = i - stack[-1] - 1\n ans = max(ans, height * width)\n stack.append(i)\n heights.pop()\n return ans\n``` | 39 | 0 | ['Python', 'Python3'] | 6 |
largest-rectangle-in-histogram | C++ solution, clean code | c-solution-clean-code-by-lchen77-j4x7 | int largestRectangleArea(vector<int>& height) {\n height.push_back(0);\n const int size_h = height.size();\n stack<int> stk;\n int i | lchen77 | NORMAL | 2015-08-09T19:53:20+00:00 | 2015-08-09T19:53:20+00:00 | 8,215 | false | int largestRectangleArea(vector<int>& height) {\n height.push_back(0);\n const int size_h = height.size();\n stack<int> stk;\n int i = 0, max_a = 0;\n while (i < size_h) {\n if (stk.empty() || height[i] >= height[stk.top()]) stk.push(i++);\n else {\n int h = stk.top();\n stk.pop();\n max_a = max(max_a, height[h] * (stk.empty() ? i : i - stk.top() - 1));\n }\n }\n return max_a;\n } | 38 | 2 | [] | 7 |
largest-rectangle-in-histogram | ✅C++ 100% || Worst to Best approaches with explanation || Easy to understand. | c-100-worst-to-best-approaches-with-expl-6px4 | Read the below solutions to understand the logic.\n\nPlease upvote if you like it\n\nSolution 1: Brute Force Approach (TLE)\n\nIntuition: The intuition behind t | pranjal9424 | NORMAL | 2022-09-15T11:48:43.784943+00:00 | 2022-09-15T16:37:23.034216+00:00 | 3,918 | false | **Read the below solutions to understand the logic.**\n\n***Please upvote if you like it***\n\n**Solution 1: Brute Force Approach (TLE)**\n\n**Intuition:** The intuition behind the approach is taking different bars and finding the maximum width possible using the bar.\n\n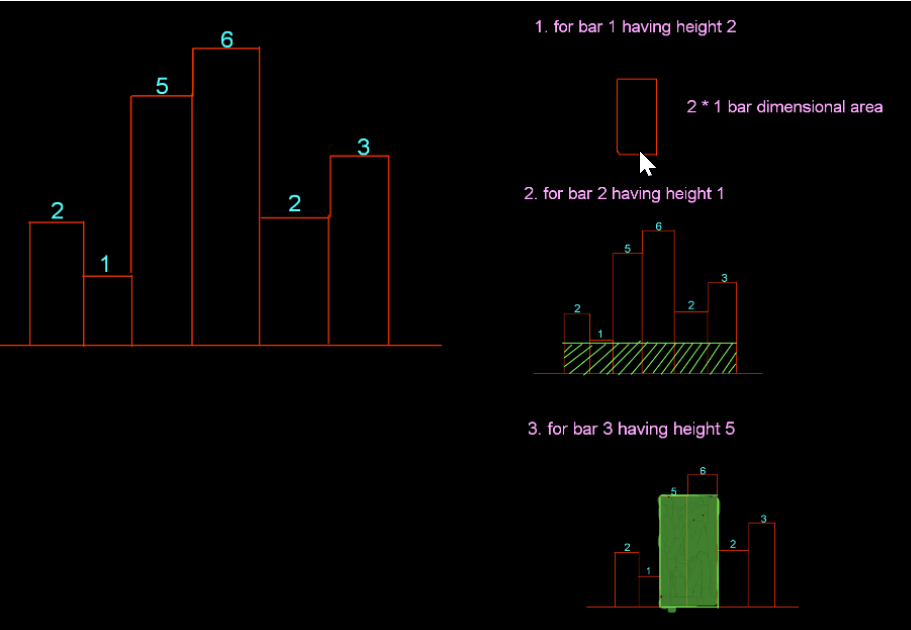\n\n**~Time Complexity: O(N*N )** \n\n**~Space Complexity: O(1)**\n\n**Code:-**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n=heights.size();\n int maxArea = 0;\n \n for (int i = 0; i < n; i++) {\n int minHeight = INT_MAX;\n for (int j = i; j < n; j++) {\n minHeight = min(minHeight, heights[j]);\n maxArea = max(maxArea, minHeight * (j - i + 1));\n }\n }\n \n return maxArea;\n }\n};\n```\n\n**Solution 2: Optimised Approach ( 100% Accepted )**\n\n**Intuition:** The intuition behind the approach is the same as finding the smaller element on both sides but in an optimized way using the concept of the next greater element and the next smaller element.\n\n**Approach: **\n\n1. Steps to be done for finding Left smaller element\n2. Steps to be done for finding the Right smaller element\n3. After finding the right smaller and left smaller of each subsequent array elements, after that find area for each bar using this formuula\n\n\t\n\t\n4. At the end return the maximum area.\n\n**Dry run:-**\n\n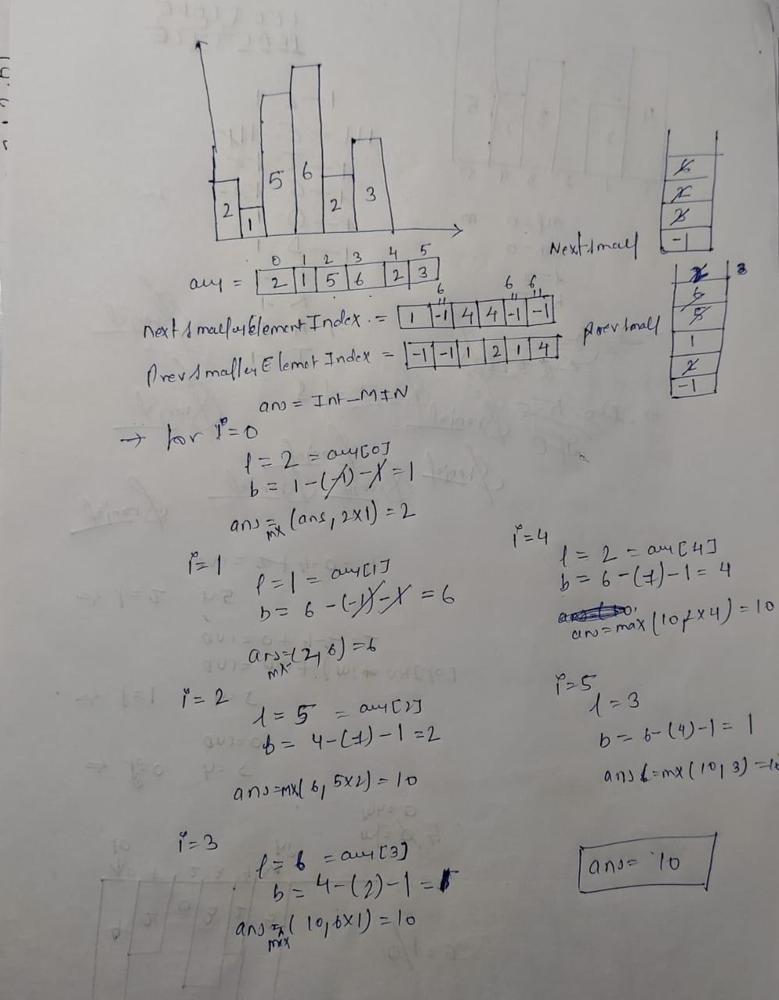\n\n\n**~Time Complexity: O( N )**\n\n**~Space Complexity: O(3N) where 3 is for the stack, left small array and a right small array**\n\n**Code:**\n```\nclass Solution {\npublic:\n vector<int> nextSmallerElementIndex(vector<int>& heights,int n){\n stack<int> st;\n vector<int> res(n);\n st.push(-1);\n for(int i=n-1;i>=0;i--){\n int curr=heights[i];\n while(st.top()!=-1 && heights[st.top()]>=curr){\n st.pop();\n }\n res[i]=st.top();\n st.push(i);\n }\n return res;\n }\n \n vector<int> prevSmallerElementIndex(vector<int>& heights,int n){\n stack<int> st;\n vector<int> res(n);\n st.push(-1);\n for(int i=0;i<n;i++){\n int curr=heights[i];\n while(st.top()!=-1 && heights[st.top()]>=curr){\n st.pop();\n }\n res[i]=st.top();\n st.push(i);\n }\n return res;\n }\n int largestRectangleArea(vector<int>& heights) {\n int n=heights.size();\n //Storing next smaller element index\n vector<int> next=nextSmallerElementIndex(heights,n);\n //Storing prev smaller element index\n vector<int> prev=prevSmallerElementIndex(heights,n);\n \n int ans=INT_MIN;\n for(int i=0;i<n;i++){\n int l=heights[i];\n if(next[i]==-1) next[i]=n;\n int b=next[i]-prev[i]-1;\n ans=max(ans,l*b);\n }\n return ans;\n }\n};\n```\n\n | 33 | 0 | ['Stack', 'C', 'Monotonic Stack', 'C++'] | 4 |
largest-rectangle-in-histogram | My modified answer from GeeksforGeeks, in JAVA | my-modified-answer-from-geeksforgeeks-in-bhd5 | I was stuck and took an eye on Geeks4Geeks. I got the idea and tried to figure it out by myself...\nIt takes me a lot of time to make it through....\n\nEDITED: | reeclapple | NORMAL | 2014-07-25T03:24:19+00:00 | 2014-07-25T03:24:19+00:00 | 18,683 | false | I was stuck and took an eye on Geeks4Geeks. I got the idea and tried to figure it out by myself...\nIt takes me a lot of time to make it through....\n\n**EDITED:** Now it is pretty concise....\n\n public class Solution {\n public int largestRectangleArea(int[] height) {\n if (height==null) return 0;//Should throw exception\n if (height.length==0) return 0;\n \n Stack<Integer> index= new Stack<Integer>();\n index.push(-1);\n int max=0;\n \n for (int i=0;i<height.length;i++){\n //Start calculate the max value\n while (index.peek()>-1)\n if (height[index.peek()]>height[i]){\n int top=index.pop(); \n max=Math.max(max,height[top]*(i-1-index.peek())); \n }else break;\n \n index.push(i);\n }\n while(index.peek()!=-1){\n \tint top=index.pop();\n max=Math.max(max,height[top]*(height.length-1-index.peek()));\n } \n return max;\n }\n} | 33 | 2 | ['Java'] | 7 |
largest-rectangle-in-histogram | ✔ C++ || 💯 Explanation using Stack || O(N) time, space | c-explanation-using-stack-on-time-space-6jg4z | Problem:\n- We are given an array of integers which represent the height of bars in a histogram.\n- The width of each bar is 1.\n- We need to form a rectangle w | GodOfm4a1 | NORMAL | 2023-04-20T06:45:02.441183+00:00 | 2023-04-20T06:47:15.047370+00:00 | 2,150 | false | Problem:\n- We are given an array of integers which represent the height of bars in a histogram.\n- The width of each bar is 1.\n- We need to form a rectangle with these bars with the largest area.\n\nExample :\n\n\n\n\n- Above we have a histogram, where value of bar represents the height of the bar.\n- We need to form rectangle using these which has the largest area.\n- Say, one rectangle which can be formed would be of ```height = 1```, and ```width = 6```, like below :\n\n\n\n\n- Another rectangle which can be formed is using the last 4 bars, as shown below:\n\n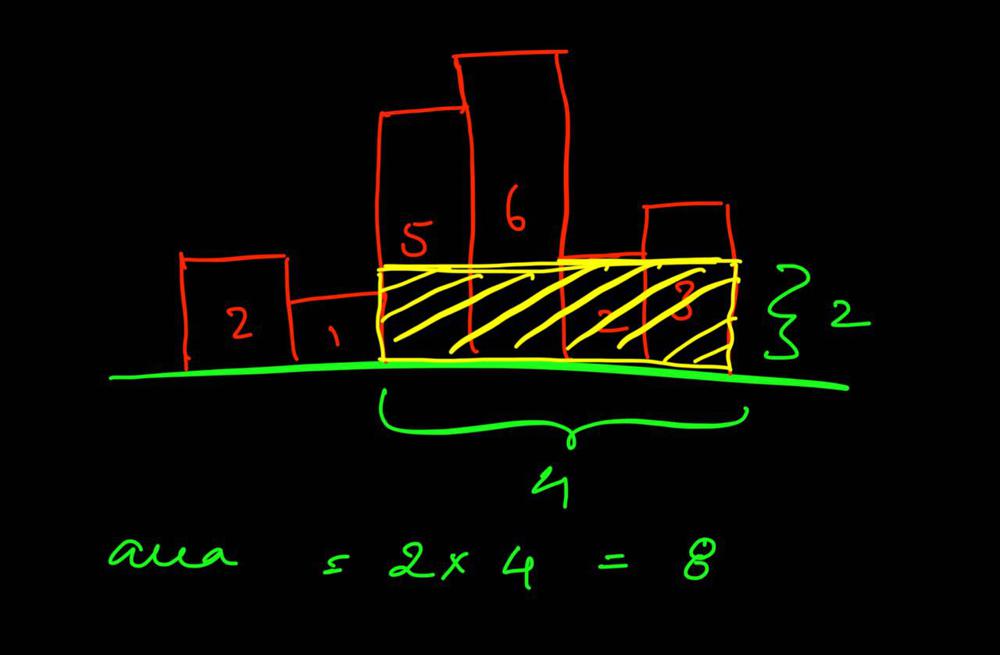\n\n\n- Since we need to find the rectangle with the largest area, it would be the one below : \n\n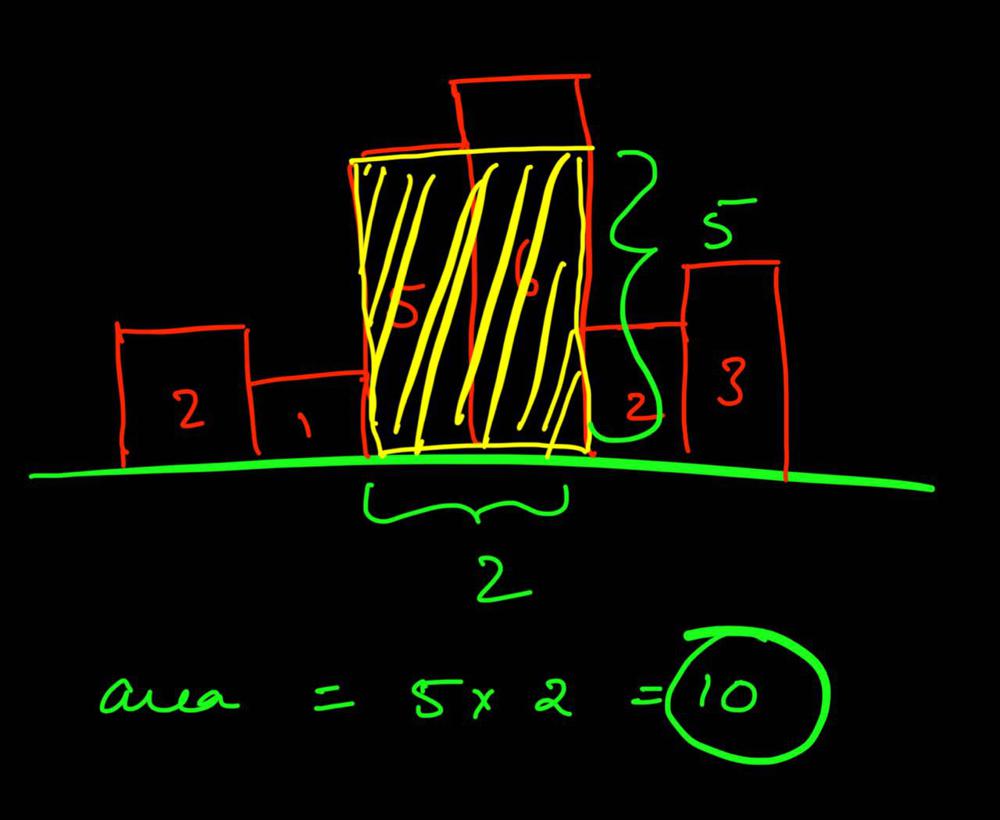\n\n\n# Solution explaination:\n\n- So the idea is to use stack, in such a way, that we push the indexes of bars with increasing heights into it.\n- If, at one point, we find a bar smaller than the bar in the top of stack, we will pop that bar, and use it as height of rectangle, and the width would be the the difference between the index of the popped bar and the index of the bar which we are currently at. \n- Let\'s understand through an example : ```[ 1 , 2 , 3 , 1]```\n\n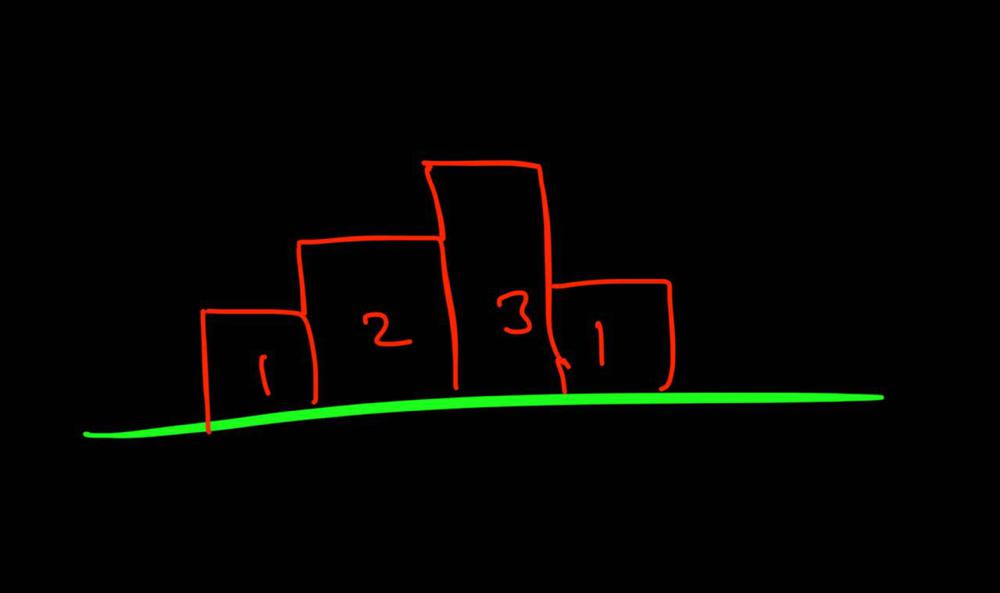\n\n\n- We will iterate through the bars one by one, through a variable, say ```i```. \n- Also, lets make a stack, initially empty.\n\n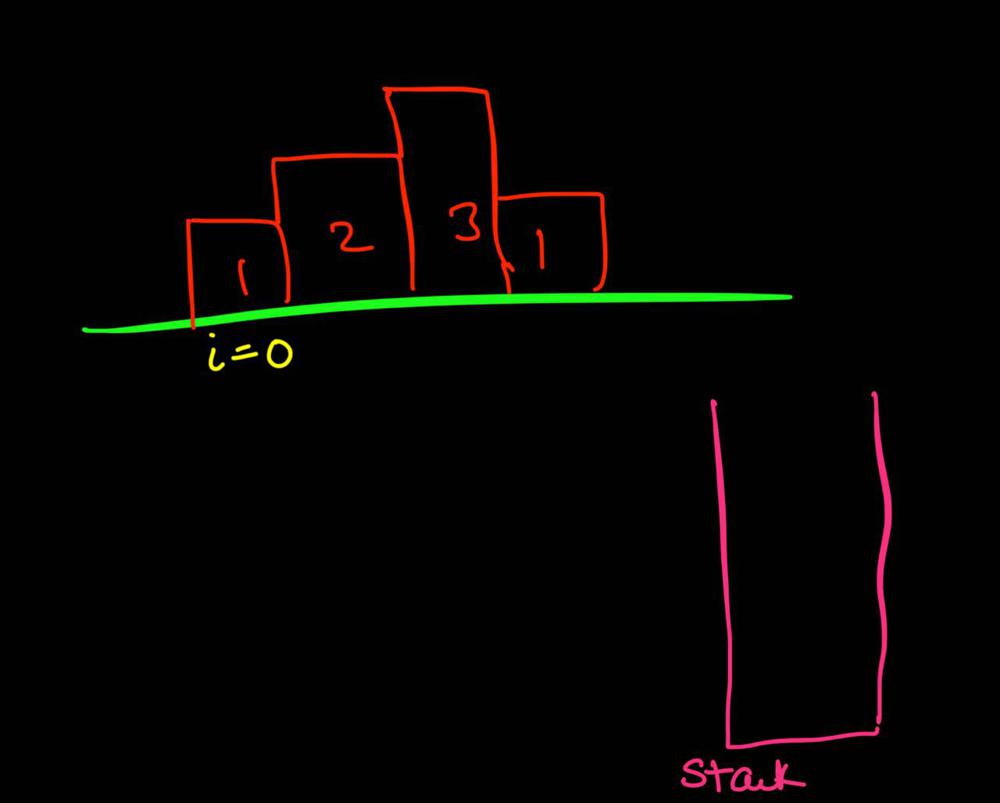\n\n\n- At , ```i = 0```, our stack is initially empty, so we push the index , ```i = 0``` into stack, and increment ```i```.\n\n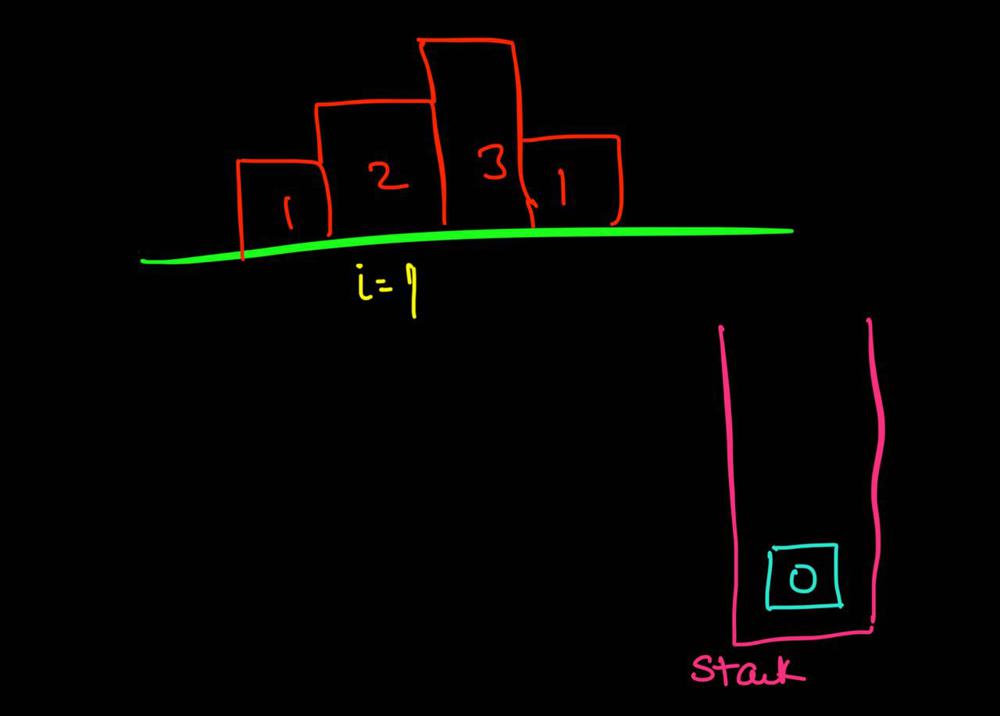\n\n\n- At, ```i = 1```, our stack is not empty.\n- As I had said, we will be pushing bars into stack, if the bar at which we are currently at (i = 1) is greater than the bar at the top of stack.\n- ```Top of stack = 0 , height[0] = 1```\n- ``` i = 1 , height [1] = 2 ```\n- ``` Since height[i] >= height[top of stack],therefore, push i=1 into stack```\n\n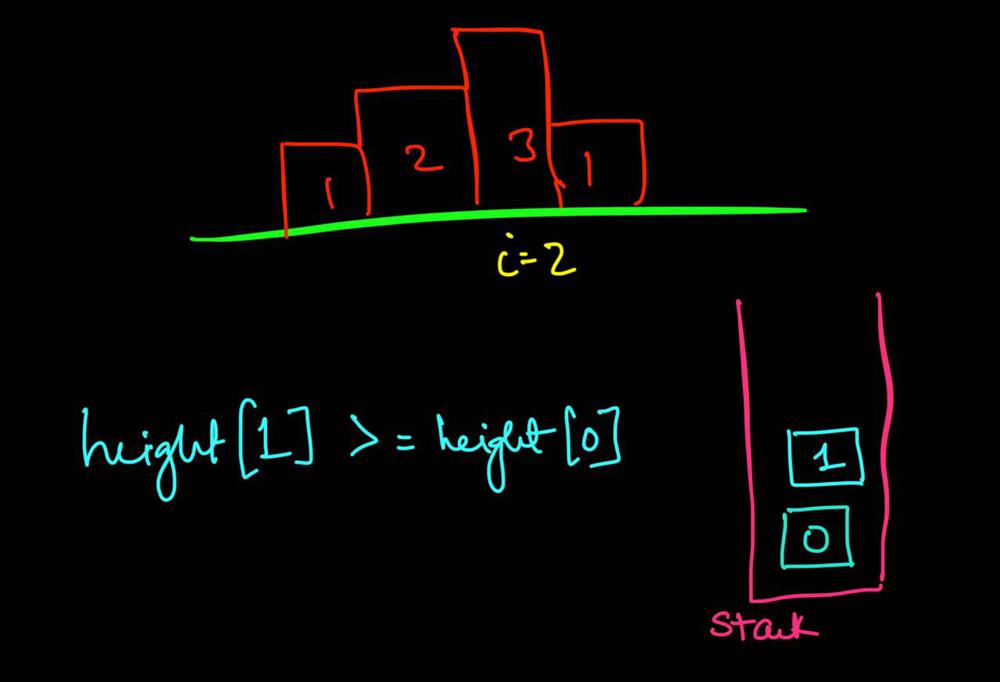\n\n\n- Similary, at ```i = 2``` \n- ```Top of stack = 1 , height[1] = 2```\n- ``` i = 2 , height [2] = 3 ```\n- ``` Since height[i] >= height[top of stack],therefore, push i = 2 , into stack```\n\n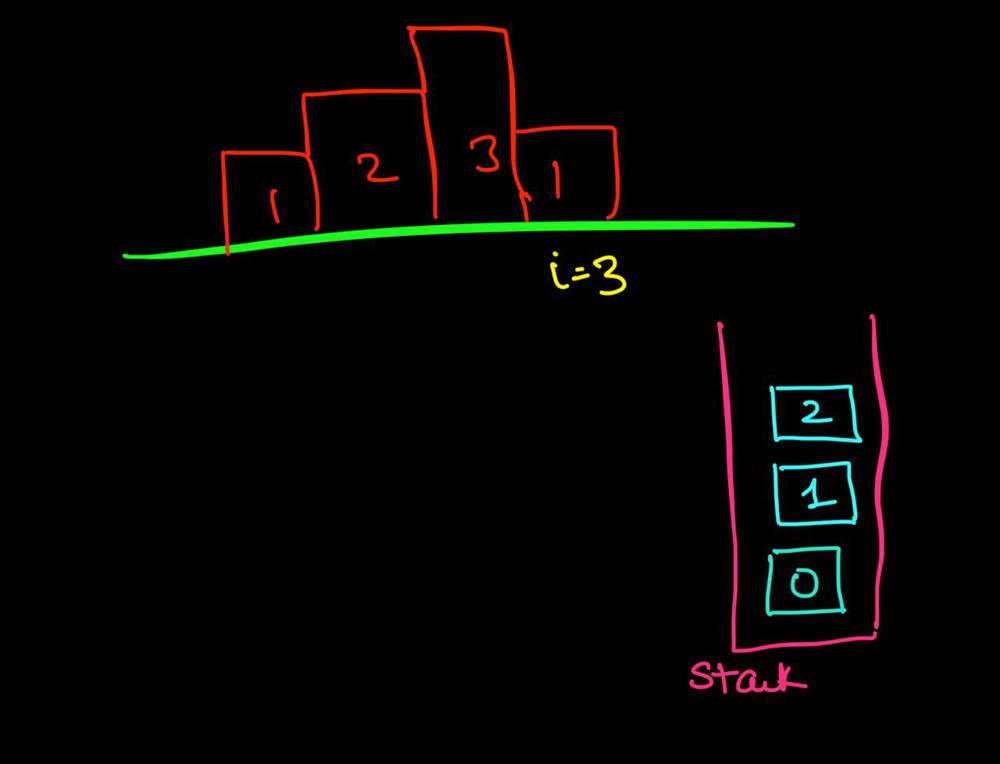\n\n\n- Now, at ``` i = 3 ``` , we see that ```height[i] < height[top of stack]```\n- ```height[i] = height[3] = 1```\n- ```height[top of stack] = height[2] = 3```\n- So, we cannot push this bar into stack.\n- We pop out the index at the top of the stack.\n- Now using this bar, we will form the ```height``` of rectangle.\n- So the question to form the ```width``` rectangle is : \n```\n What is the distance between the bars , top of stack, \n and the index \'i\' ?\n \n```\n- Important idea to note is, that while forming rectangle, we do not consider merging the bars behind the top of stack bar\n- This is because we have pushed them into the stack.Meaning they must already be less than this bar, so we cannot merge them with this bar to form rectangle.\n- So, we can can calculate our ```height``` and ```width``` of rectangle, and then calculate the area as shown below:\n\n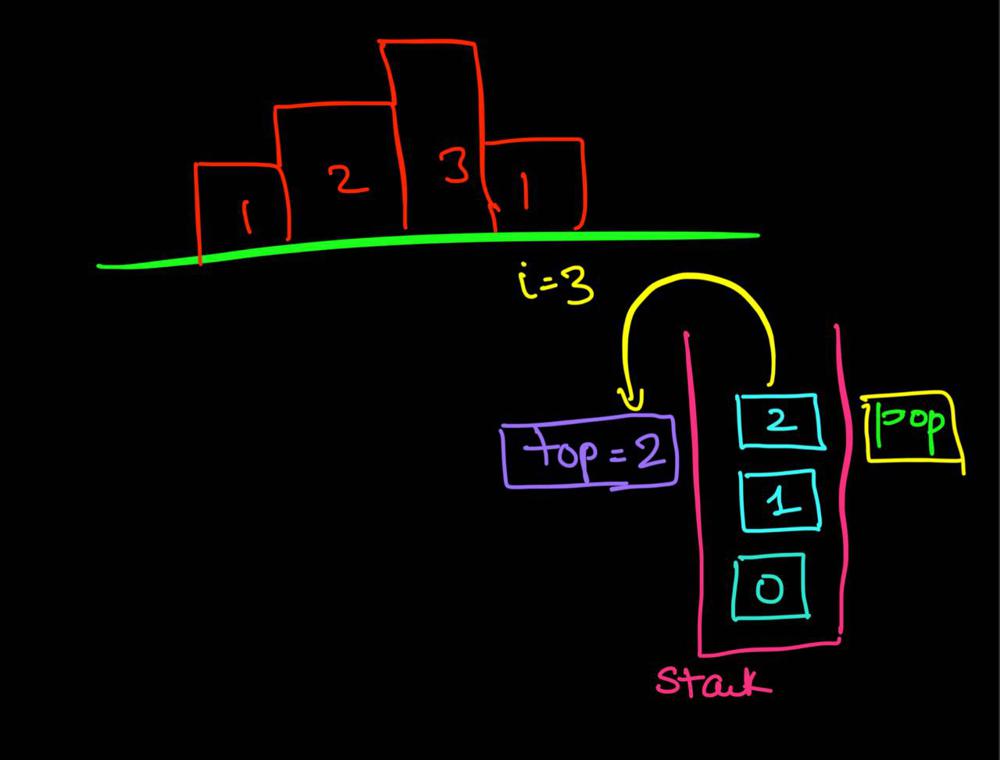\n\n\n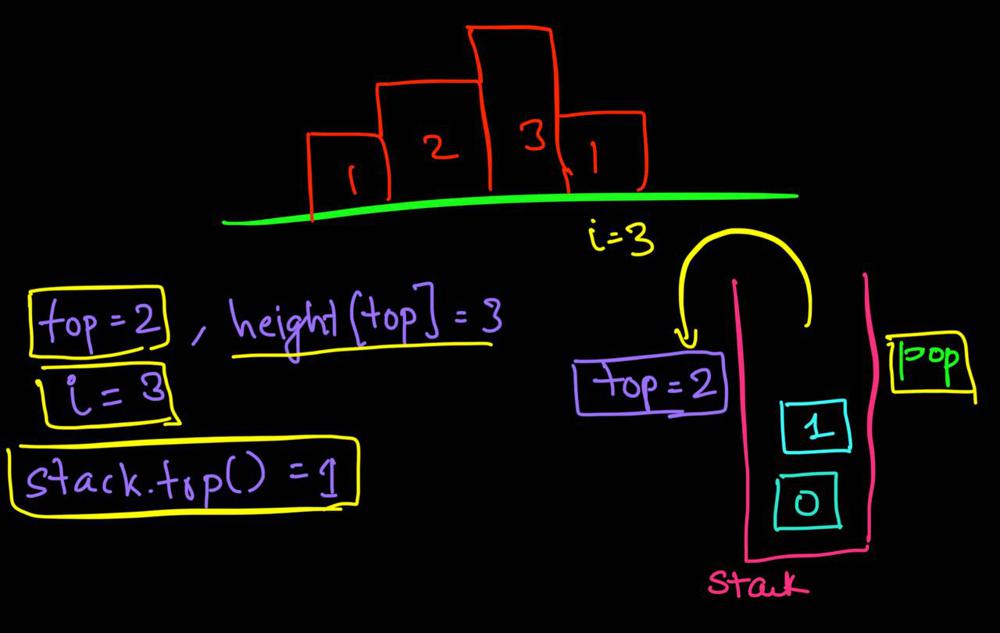\n\n\n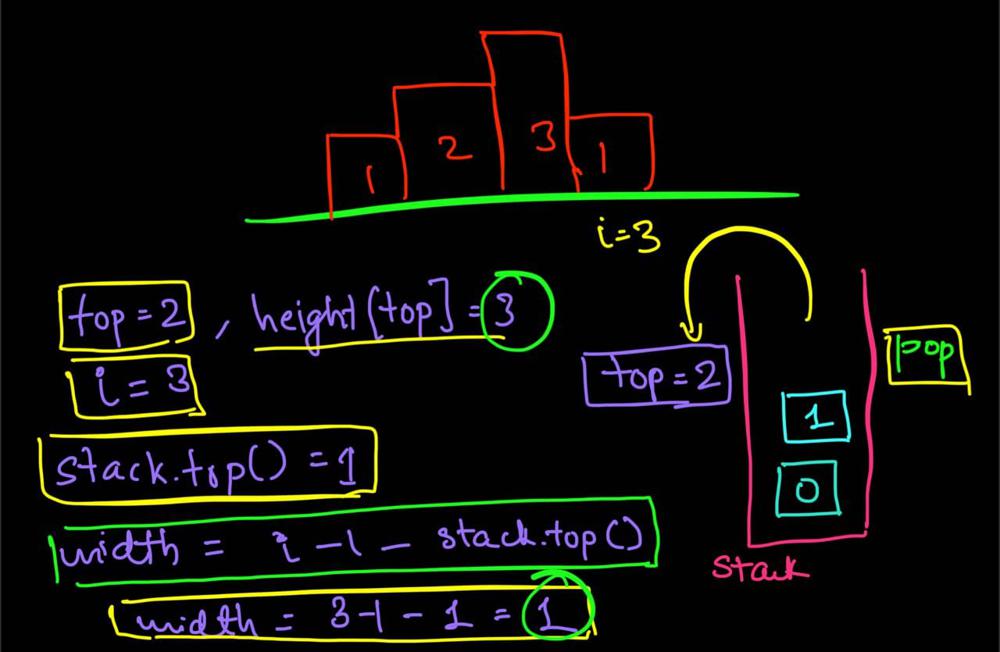\n\n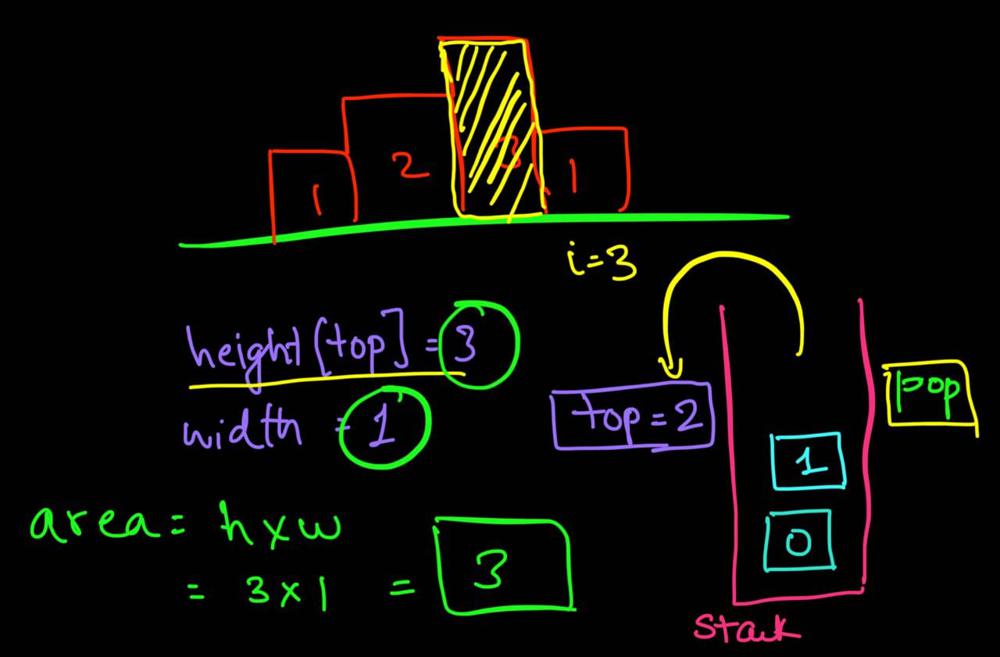\n\n- So , our ```max area = 3 ``` so far.\n- Again , we will compare the ```height[i]``` bar and ```height[top of stack]``` bar.\n- ```height[i] = height[3] = 1```\n- ```height[top of stack] = height[1] = 2```\n- Since ```height[i] <= height[top of stack] ``` we will pop from the stack, as shown below :\n\n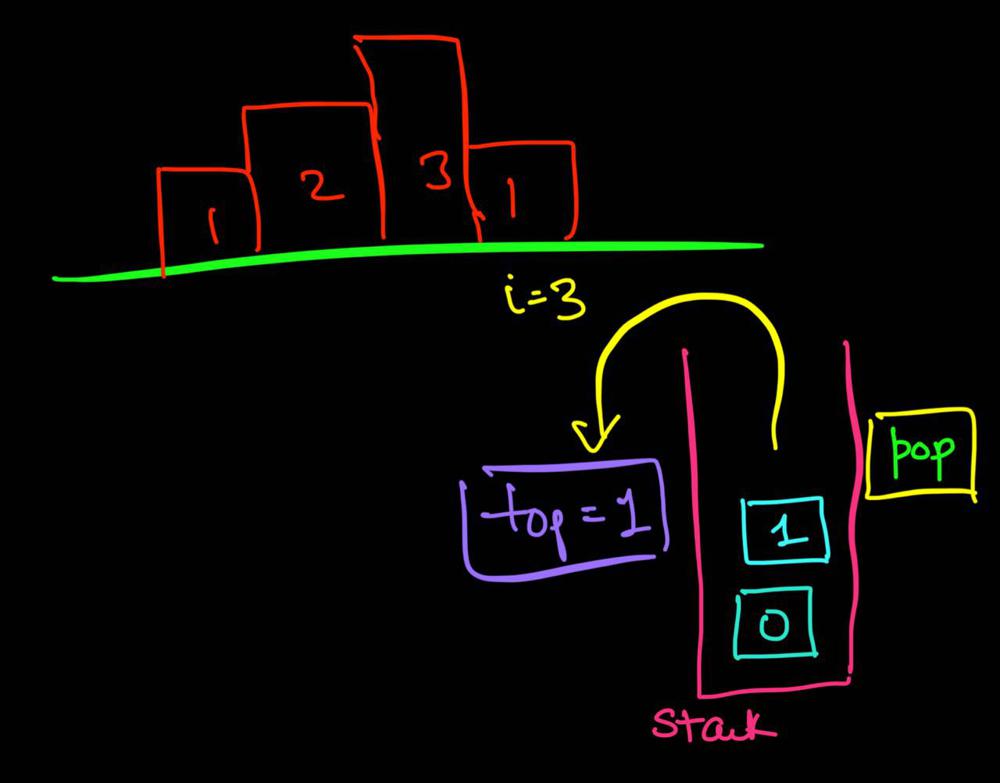\n\n\n- We will try forming a rectangle with ```height = height[top of stack] ```. \n\n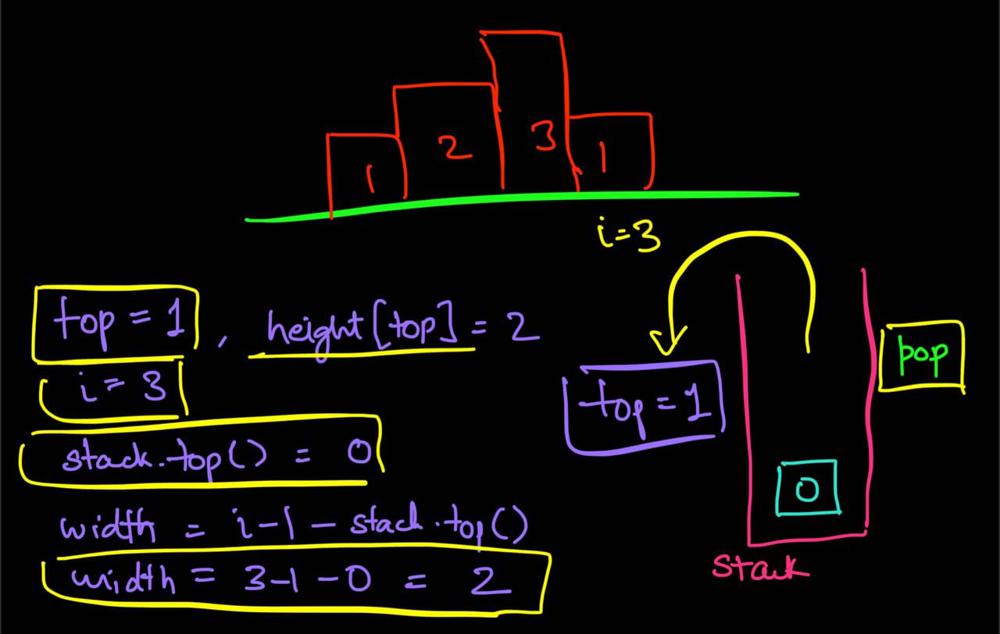\n\n\n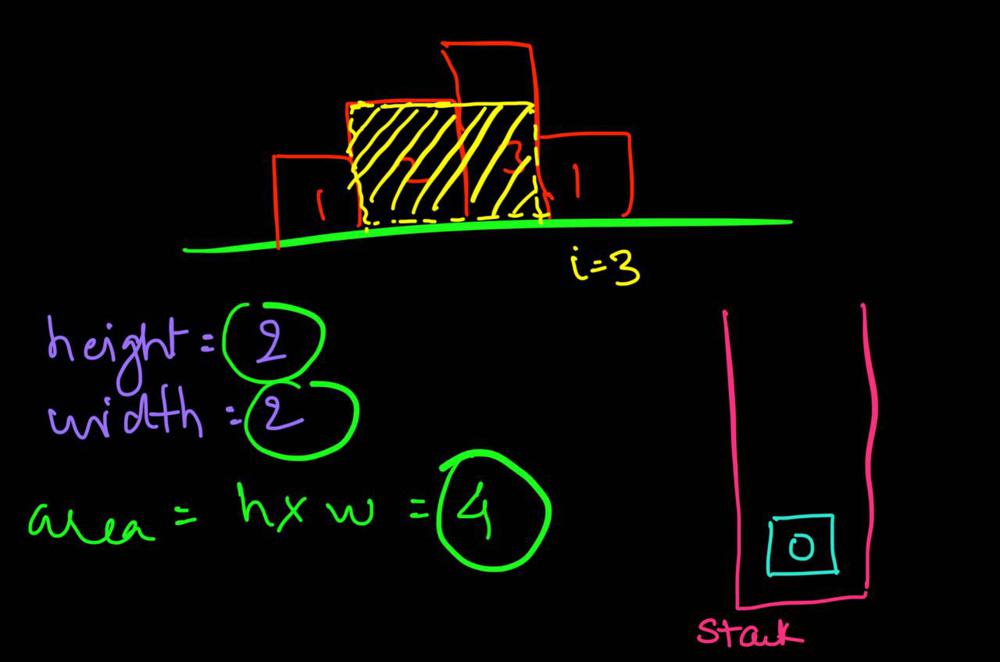\n\n\n- The area formed = 4, which is greater than ```max area = 3``` therefore, we will update ```max area = 4``` now.\n- Again, we will compare with ```height[i]``` and ```height[top of stack]```.\n- ```height[i] = height[3] = 1```\n- ```height[top of stack] = height[0] = 1 ```\n- ```height[i] <= height[top of stack]```, therefore pop from stack.\n\n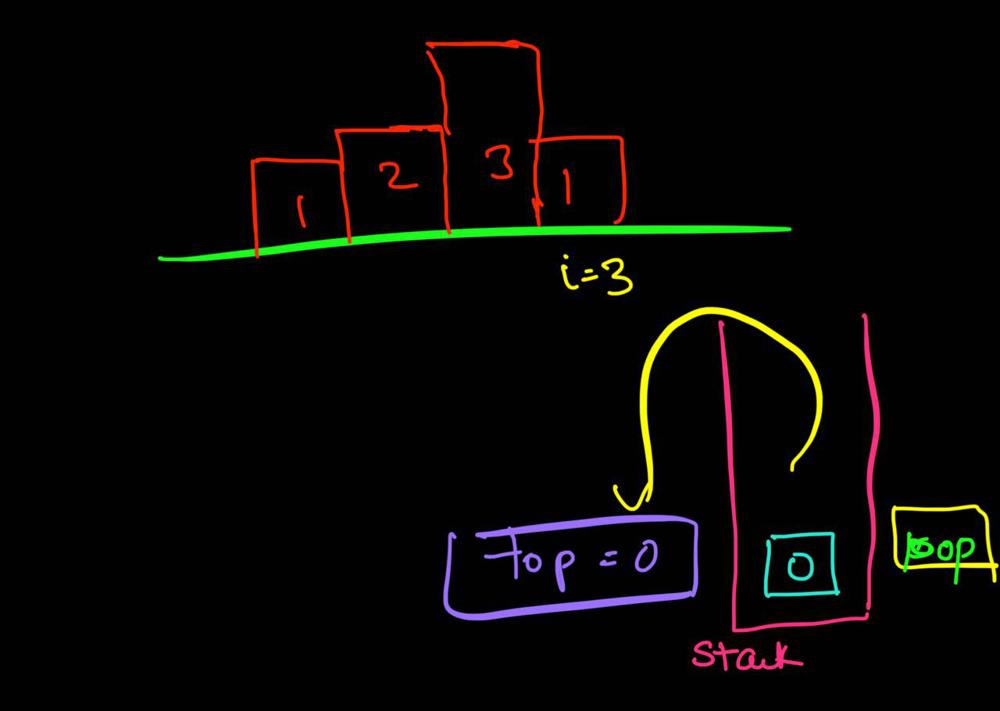\n\n\n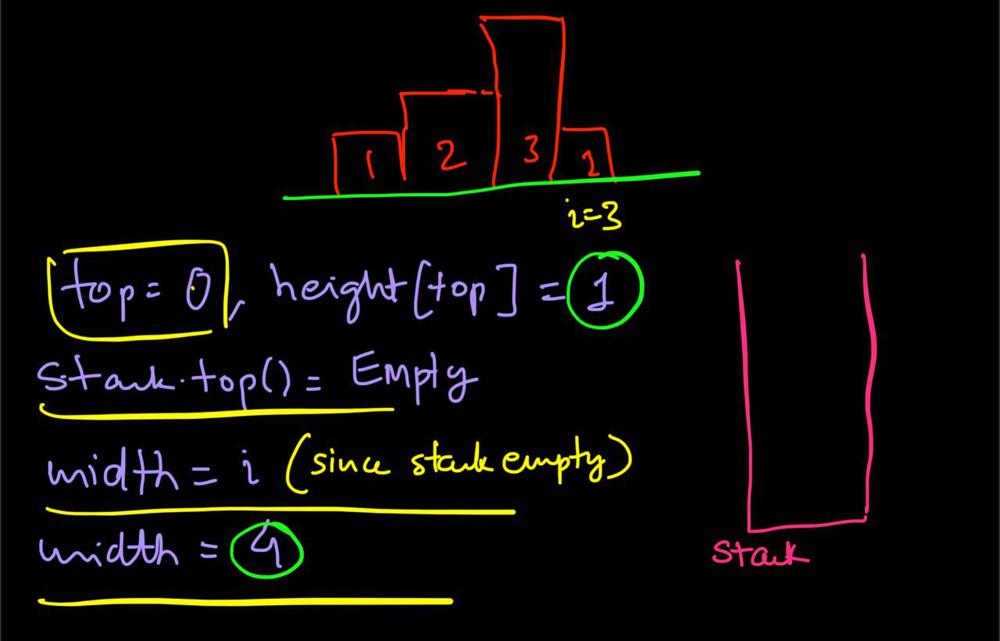\n\n\n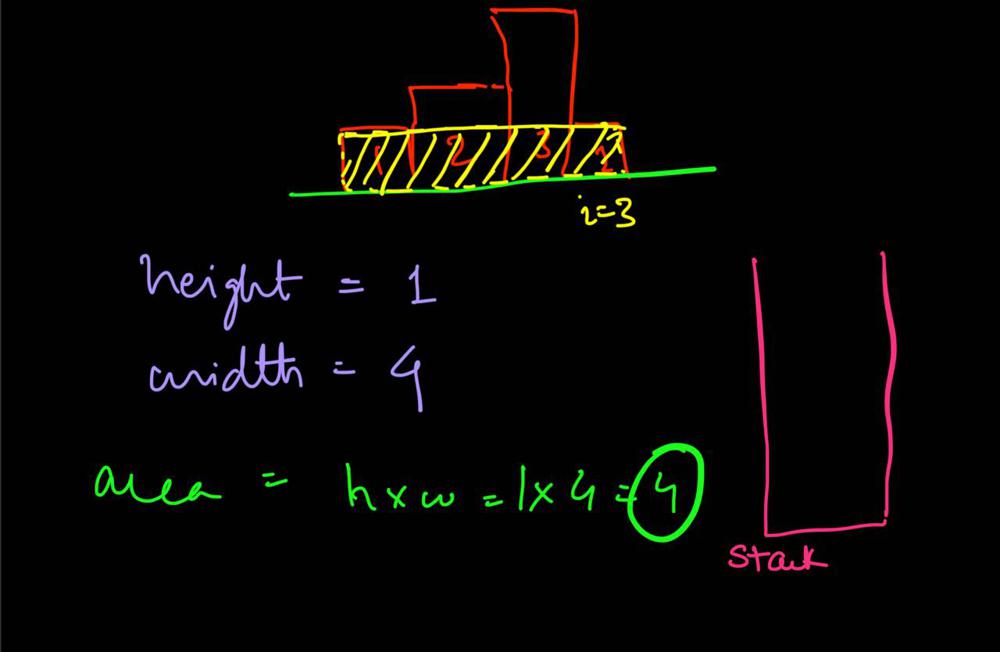\n\n\n- We have an empty stack, so we will push ```i=3``` bar into stack and increment ``i``.\n\n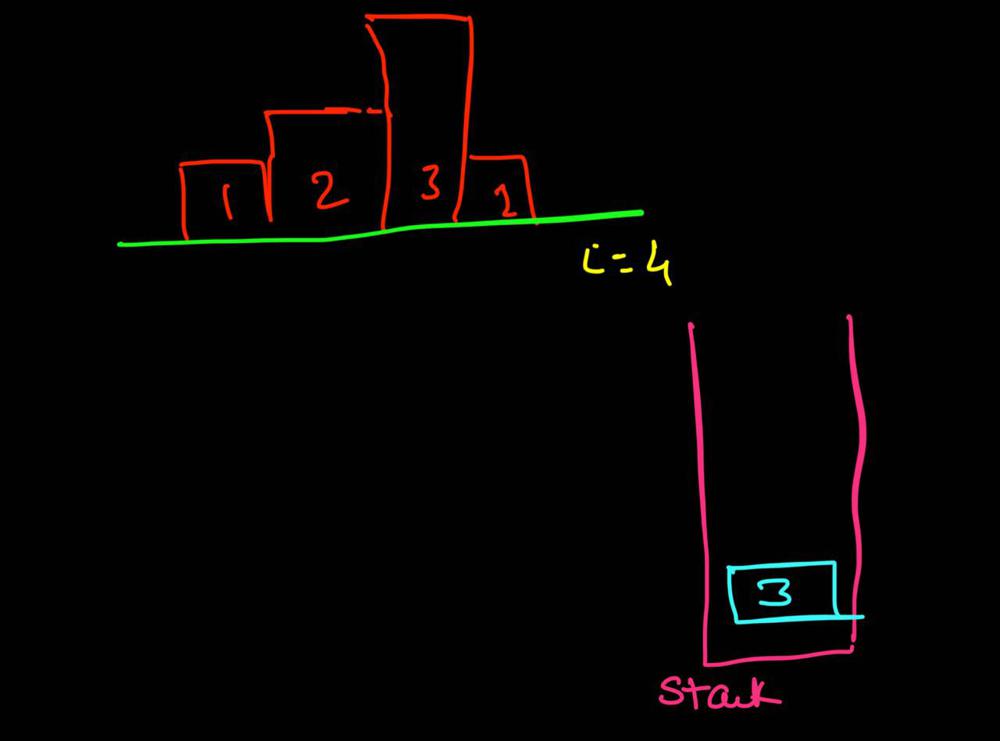\n\n\n- Since, we have tarversed all the bars, ```i=4```, there is no need to push more bars into the stack.\n- However, our stack is not yet empty.\n- So we will pop out the top of stack, and use it as ```height``` of rectangle.\n- So,\n\n\n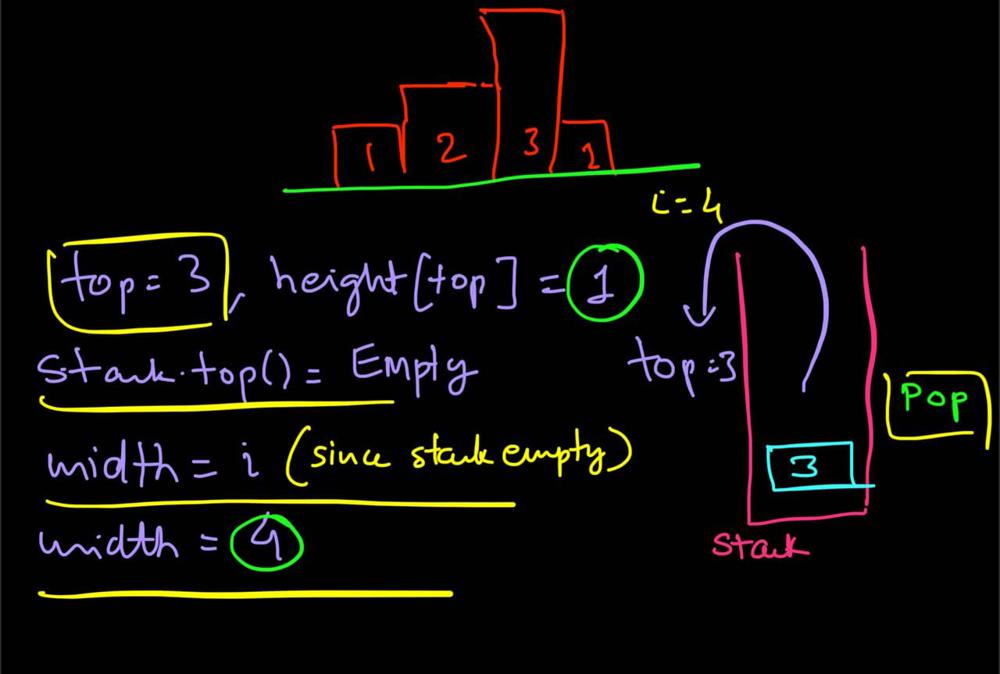\n\n\n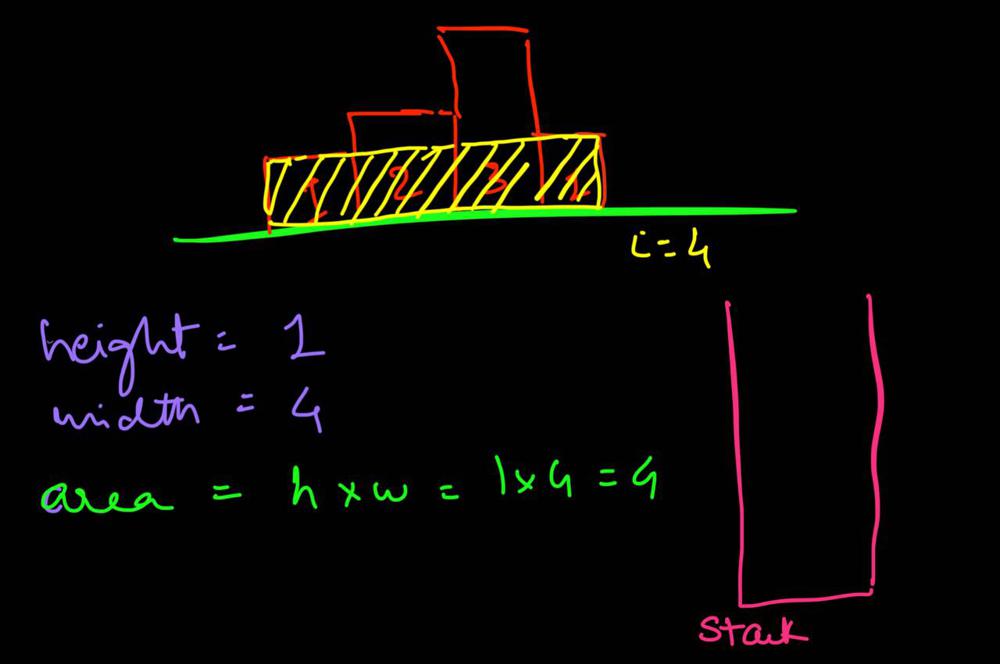\n\n\n- ```Thus the rectangle which can be formed with the max area would be = 4```.\n\n\n\n\n\n\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n stack<int>stk;\n int i=0;\n int n=heights.size();\n int maxArea = 0;\n while(i < n)\n { \n\n if(stk.empty() or( heights[stk.top()] <= heights[i] ))\n {\n stk.push(i++);\n }\n else\n {\n int minBarIndex = stk.top();\n stk.pop();\n int width = i;\n if(!stk.empty()) width = i - 1 - stk.top();\n int area = heights[minBarIndex] * width;\n maxArea = max(maxArea , area);\n }\n }\n\n while(!stk.empty())\n {\n int minBarIndex = stk.top();\n stk.pop();\n int width = i;\n if(!stk.empty()) width = i - 1 - stk.top();\n int area = heights[minBarIndex] * width;\n maxArea = max(maxArea , area);\n }\n return maxArea;\n }\n};\n``` | 28 | 0 | ['Stack', 'Monotonic Stack', 'Simulation', 'C++'] | 0 |
largest-rectangle-in-histogram | Beats 99%✅ | O( n )✅ | Python (Step by step explanation) | beats-99-o-n-python-step-by-step-explana-0oah | Intuition\nThe problem involves finding the largest rectangle that can be formed in a histogram of different heights. The approach is to iteratively process the | monster0Freason | NORMAL | 2023-10-16T17:09:51.462734+00:00 | 2023-11-05T20:28:52.990267+00:00 | 3,439 | false | # Intuition\nThe problem involves finding the largest rectangle that can be formed in a histogram of different heights. The approach is to iteratively process the histogram\'s bars while keeping track of the maximum area found so far.\n\n# Approach\n1. Initialize a variable `maxArea` to store the maximum area found, and a stack to keep track of the indices and heights of the histogram bars.\n\n2. Iterate through the histogram using an enumeration to access both the index and height of each bar.\n\n3. For each bar, calculate the width of the potential rectangle by subtracting the starting index (retrieved from the stack) from the current index.\n\n4. While the stack is not empty and the height of the current bar is less than the height of the bar at the top of the stack, pop elements from the stack to calculate the area of rectangles that can be formed.\n\n5. Update `maxArea` with the maximum of its current value and the area calculated in step 4.\n\n6. Push the current bar\'s index and height onto the stack to continue processing.\n\n7. After processing all bars, there may still be bars left in the stack. For each remaining bar in the stack, calculate the area using the height of the bar and the difference between the current index and the index at the top of the stack.\n\n8. Return `maxArea` as the result, which represents the largest rectangle area.\n\n# Complexity\n- Time complexity: O(n), where n is the number of bars in the histogram. We process each bar once.\n- Space complexity: O(n), as the stack can contain up to n elements in the worst case when the bars are in increasing order (monotonic).\n\n\n# Code\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n maxArea = 0\n stack = []\n\n for index , height in enumerate(heights):\n start = index\n \n while start and stack[-1][1] > height:\n i , h = stack.pop()\n maxArea = max(maxArea , (index-i)*h)\n start = i\n stack.append((start , height))\n\n for index , height in stack:\n maxArea = max(maxArea , (len(heights)-index)*height)\n\n return maxArea \n\n \n\n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 27 | 0 | ['Stack', 'Python3'] | 3 |
largest-rectangle-in-histogram | Javascript using stack (Detail breakdown) | javascript-using-stack-detail-breakdown-ilmb1 | Do I explain this good enough?``\njs\n/**\n * @param {number[]} heights\n * @return {number}\n */\nconst largestRectangleArea = function (heights) {\n let ma | harikirito | NORMAL | 2020-03-03T07:31:04.095360+00:00 | 2020-03-03T07:34:13.945507+00:00 | 2,729 | false | Do I explain this good enough?``\n```js\n/**\n * @param {number[]} heights\n * @return {number}\n */\nconst largestRectangleArea = function (heights) {\n let maxArea = 0;\n const stack = [];\n // Append shadow rectangle (height = 0) to both side\n heights = [0].concat(heights).concat([0]);\n for (let i = 0; i < heights.length; i++) {\n /**\n * Check if height of last element in the stack bigger than height at current position\n * Position in stack always smaller than current position at least 1\n * For example we have heights array [2,5,6,2]\n * 1: Add shadow rectangle to array => [0,2,5,6,2,0]\n * 2:\n * Expression: heights[stack[stack.length - 1]] > heights[i]\n * i = 0 => stack = [0],\n * i = 1 => heights[0] > heights[1] (0 > 2) => false => stack = [0,1]\n * i = 2 => heights[1] > heights[2] (2 > 5) => false => stack = [0,1,2]\n * i = 3 => heights[2] > heights[3] (5 > 6) => false => stack = [0,1,2,3]\n * i = 4 => heights[3] > heights[4] (6 > 2) => true\n * 3: Because the previous height bigger than the current height (6 > 2) so that we can confirm that the next rectangle\n * will only shrink area. Let calculate the result\n * First we get the position from the stack and assign to variable "j" from original stack = [0,1,2,3]\n * Expression: (i - stack[stack.length - 1] - 1) * heights[j]\n * j = 3 => stack = [0,1,2] => (i - stack[3 - 1] - 1) * => (4 - 2 - 1) * 6 = 6\n * Explain:\n * - We need to calculate area backward so that we take i - last stack (4 - 2) and because we already\n * get a value from stack before so that we need to subtract 1 => (4 - 2 - 1)\n * - The latest position in stack is the maximum height we can get (j = 3 => heights[3] = 6)\n * => Area calculate equal (4 - 2 - 1) * 6 = 6 (1 bar)\n * - Compare with the current max area (currently 0) => New max area = 6\n *\n * Expression: heights[stack[stack.length - 1]] > heights[i] | stack = [0,1,2]\n * heights[2] > heights[4] (5 > 2) => true\n * j = 2 => stack = [0, 1] => (i - stack[2 - 1] - 1) * 5 => (4 - 1 - 1) * 5 = 10\n * Area > MaxArea (10 > 6) => New max area = 10 (2 bar)\n * Explain: Because the height in stack are sorted (We stop add position to stack if the next height is lower)\n *\n * heights[1] > heights[4] (2 > 2) => false | stack = [0,1,2]\n * Keep running and the final answer it is the max area you need\n */\n while (stack && heights[stack[stack.length - 1]] > heights[i]) {\n const j = stack.pop();\n maxArea = Math.max((i - stack[stack.length - 1] - 1) * heights[j], maxArea);\n }\n stack.push(i);\n }\n return maxArea;\n};\n``` | 26 | 0 | ['JavaScript'] | 6 |
largest-rectangle-in-histogram | O(n) stack c++ solution 12ms 中文详细解释 | on-stack-c-solution-12ms-zhong-wen-xiang-s5wb | \u601D\u8DEF\u662F\n\n\u56E0\u4E3A\u76F8\u90BB\u7684\u6BD4curr\u9AD8\u7684\u5757\u80AF\u5B9A\u53EF\u4EE5\u4F5C\u4E3A \u9AD8\u5EA6\u4E3Aheights[curr]\u7684\u957F | alanzwy | NORMAL | 2019-01-12T07:08:22.886392+00:00 | 2019-01-12T07:08:22.886437+00:00 | 2,866 | false | \u601D\u8DEF\u662F\n\n\u56E0\u4E3A\u76F8\u90BB\u7684\u6BD4curr\u9AD8\u7684\u5757\u80AF\u5B9A\u53EF\u4EE5\u4F5C\u4E3A \u9AD8\u5EA6\u4E3Aheights[curr]\u7684\u957F\u65B9\u5F62\u7684\u4E00\u90E8\u5206\n\u6240\u4EE5\u89C2\u5BDF\u5230\u9AD8\u5EA6\u4E3Aheights[curr]\u7684\u957F\u65B9\u5F62\u7684\u6700\u5927\u9762\u79EF\u662F \n\n \uFF08\u540E\u4E00\u4E2A\u9AD8\u5EA6\u6BD4curr\u4F4E\u7684index - \u524D\u4E00\u4E2A\u9AD8\u5EA6\u6BD4curr\u4F4E\u7684index - 1\uFF09* \u5F53\u524D\u5757\u7684\u9AD8\u5EA6\n\n\u90A3\u4E48\u5C31\u8981\u627E\u5230\u524D\u4E00\u4E2A\u6BD4curr\u4F4E\u7684\u5757\u548C\u540E\u4E00\u4E2A\u6BD4curr\u4F4E\u7684\u5757\u7684index\n\n\u66F4\u8FDB\u4E00\u6B65\uFF0C \u5F53\u524D\u7684\u5757 \u662F \u524D\u9762\u6240\u6709\u6BD4\u4ED6\u9AD8\u7684\u5757 \u7684\u53F3\u754C\uFF0C\u5728\u8BA1\u7B97\u524D\u9762\u6240\u6709\u6BD4\u4ED6\u9AD8\u7684\u5757\u80FD\u5F62\u6210\u957F\u65B9\u5F62\u7684\u6700\u5927\u9762\u79EF\u65F6\u4E00\u5B9A\u4F1A\u7528\u5230\u3002\n\n\u53F3\u4FA7\u7684index\u627E\u5230\u4E86\uFF0C\u90A3\u4E48\u600E\u4E48\u627E\u5DE6\u4FA7\u6BD4\u5F53\u524D\u7684\u5757\u4F4E\u7684\u7B2C\u4E00\u4E2A\u5757\u7684index\u5462\uFF1F\n\n\u6211\u4EEC\u4F7F\u7528stack\u5B58\u5347\u5E8F\u6392\u5217\u7684index\uFF0C\u904D\u5386heights\uFF0C\u653E\u5165\u65B0\u7684height\u4E4B\u524Dpop\u6240\u6709\u6BD4\u4ED6\u9AD8\u7684\u5757\u7684index\u3002\n\uFF08\uFF01\uFF01\uFF01\uFF09\u540C\u65F6\uFF0C\u8BA1\u7B97\u88ABpop\u51FA\u53BB\u7684\u5757\u80FD\u5F62\u6210\u7684\u957F\u65B9\u5F62\u7684\u6700\u5927\u9762\u79EF\uFF0C\u56E0\u4E3A\u6B64\u65F6\u7684i\u662F\u53F3\u8FB9\u7B2C\u4E00\u4E2A\u6BD4\u5B83\u4F4E\u7684index\uFF0Cstack\u9876\u662F\u5DE6\u8FB9\u7B2C\u4E00\u4E2A\u6BD4\u5B83\u4F4E\u7684index\u3002\n\n\n```\nint largestRectangleArea(vector<int>& heights) {\n stack<int> indexes;\n int maxArea = 0;\n heights.push_back(0);\n indexes.push(0);\n for (int i = 1; i < heights.size(); i++){\n while(!indexes.empty() && heights[i] < heights[indexes.top()]){\n int h = heights[indexes.top()];\n indexes.pop();\n int prev = indexes.empty() ? -1 : indexes.top();\n maxArea = max(maxArea, (i - prev -1) * h);\n }\n indexes.push(i);\n }\n return maxArea;\n }\n``` | 23 | 3 | [] | 4 |
largest-rectangle-in-histogram | C++ | Stack | Next Smaller Element | c-stack-next-smaller-element-by-reetisha-bbtx | \nclass Solution {\npublic:\n vector<int> nextSmallerRight(vector<int> heights, int n){\n vector<int> res(n);\n stack<int> st;\n \n | reetisharma | NORMAL | 2021-10-07T13:30:04.364779+00:00 | 2021-10-24T17:50:23.039312+00:00 | 2,022 | false | ```\nclass Solution {\npublic:\n vector<int> nextSmallerRight(vector<int> heights, int n){\n vector<int> res(n);\n stack<int> st;\n \n for(int i=n-1; i>=0; i--){\n while(!st.empty() && heights[st.top()]>=heights[i])\n st.pop();\n if(st.empty())\n res[i] = -1;\n else\n res[i] = st.top();\n st.push(i);\n }\n return res;\n \n }\n vector<int> nextSmallerLeft(vector<int> heights, int n){\n vector<int> res(n);\n stack<int> st;\n \n for(int i=0; i<n; i++){\n while(!st.empty() && heights[st.top()]>=heights[i])\n st.pop();\n if(st.empty())\n res[i] = -1;\n else\n res[i] = st.top();\n st.push(i);\n }\n return res;\n \n }\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n \n vector<int> leftSmaller(n), rightSmaller(n);\n \n rightSmaller = nextSmallerRight(heights,n);\n leftSmaller = nextSmallerLeft(heights,n);\n\n \n int res = INT_MIN;\n \n for(int i=0; i<n; i++){\n int left = leftSmaller[i];\n int right = rightSmaller[i];\n int w;\n \n if(left==-1) left = -1;\n if(right==-1) right = n;\n \n w = (right-1)-(left+1)+1;\n res = max(res,heights[i]*w);\n }\n \n \n return res;\n }\n};\n\n``` | 20 | 1 | ['Stack', 'C'] | 4 |
largest-rectangle-in-histogram | C++/Java/Python/JavaScript || ✅🚀 Stack || ✔️🔥TC : O(n) | cjavapythonjavascript-stack-tc-on-by-dev-mbni | Intuition:\nThe intuition behind the solution is to use two arrays, nsr (nearest smaller to the right) and nsl (nearest smaller to the left), to determine the b | devanshupatel | NORMAL | 2023-05-13T13:52:30.722382+00:00 | 2023-05-13T13:52:30.722413+00:00 | 5,194 | false | # Intuition:\nThe intuition behind the solution is to use two arrays, `nsr` (nearest smaller to the right) and `nsl` (nearest smaller to the left), to determine the boundaries of the rectangle for each bar in the histogram. By calculating the area for each rectangle and keeping track of the maximum area, we can find the largest rectangle in the histogram.\n\n# Approach:\n1. Initialize an empty stack `s` to store the indices of the histogram bars.\n2. Create two arrays, `nsr` and `nsl`, each of size `n` (where `n` is the number of elements in the `heights` vector), and initialize all elements to 0.\n3. Process the histogram bars from right to left:\n - While the stack is not empty and the height of the current bar is less than or equal to the height of the bar at the top of the stack, pop the stack.\n - If the stack becomes empty, set `nsr[i]` (the nearest smaller to the right for the current bar) to `n`.\n - Otherwise, set `nsr[i]` to the index at the top of the stack.\n - Push the current index `i` onto the stack.\n4. Empty the stack.\n5. Process the histogram bars from left to right:\n - While the stack is not empty and the height of the current bar is less than or equal to the height of the bar at the top of the stack, pop the stack.\n - If the stack becomes empty, set `nsl[i]` (the nearest smaller to the left for the current bar) to -1.\n - Otherwise, set `nsl[i]` to the index at the top of the stack.\n - Push the current index `i` onto the stack.\n6. Initialize a variable `ans` to 0. This variable will store the maximum rectangle area.\n7. Iterate over the histogram bars:\n - Calculate the area of the rectangle for the current bar using the formula: `heights[i] * (nsr[i] - nsl[i] - 1)`.\n - Update `ans` with the maximum of `ans` and the calculated area.\n8. Return `ans` as the largest rectangle area in the histogram.\n\n# Complexity:\n- The time complexity of this solution is O(n), where n is the number of elements in the `heights` vector. This is because each bar is processed only once.\n- The space complexity is O(n) as well because we use two additional arrays of size n, `nsr` and `nsl`, and a stack to store indices.\n\n---\n# C++\n```cpp\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights){\n int n=heights.size();\n vector<int> nsr(n,0);\n vector<int> nsl(n,0);\n\n stack<int> s;\n\n for(int i=n-1;i>=0;i--){\n while(!s.empty() && heights[i]<=heights[s.top()]){\n s.pop();\n }\n if(s.empty()) nsr[i]=n;\n else nsr[i]=s.top();\n s.push(i);\n }\n\n while(!s.empty()) s.pop();\n\n for(int i=0;i<n;i++){\n while(!s.empty() && heights[i]<=heights[s.top()]){\n s.pop();\n }\n if(s.empty()) nsl[i]=-1;\n else nsl[i]=s.top();\n s.push(i);\n }\n\n int ans=0;\n\n for(int i=0;i<n;i++){\n ans=max(ans, heights[i]*(nsr[i]-nsl[i]-1));\n }\n return ans; \n }\n};\n```\n\n---\n# JAVA\n```java\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int n = heights.length;\n int[] nsr = new int[n];\n int[] nsl = new int[n];\n \n Stack<Integer> s = new Stack<>();\n\n for (int i = n - 1; i >= 0; i--) {\n while (!s.isEmpty() && heights[i] <= heights[s.peek()]) {\n s.pop();\n }\n if (s.isEmpty()) nsr[i] = n;\n else nsr[i] = s.peek();\n s.push(i);\n }\n\n while (!s.isEmpty()) s.pop();\n\n for (int i = 0; i < n; i++) {\n while (!s.isEmpty() && heights[i] <= heights[s.peek()]) {\n s.pop();\n }\n if (s.isEmpty()) nsl[i] = -1;\n else nsl[i] = s.peek();\n s.push(i);\n }\n\n int ans = 0;\n\n for (int i = 0; i < n; i++) {\n ans = Math.max(ans, heights[i] * (nsr[i] - nsl[i] - 1));\n }\n return ans;\n }\n}\n```\n\n---\n\n# Python\n```py\nclass Solution(object):\n def largestRectangleArea(self, heights):\n n = len(heights)\n nsr = [0] * n\n nsl = [0] * n\n\n s = []\n\n for i in range(n - 1, -1, -1):\n while s and heights[i] <= heights[s[-1]]:\n s.pop()\n if not s:\n nsr[i] = n\n else:\n nsr[i] = s[-1]\n s.append(i)\n\n while s:\n s.pop()\n\n for i in range(n):\n while s and heights[i] <= heights[s[-1]]:\n s.pop()\n if not s:\n nsl[i] = -1\n else:\n nsl[i] = s[-1]\n s.append(i)\n\n ans = 0\n\n for i in range(n):\n ans = max(ans, heights[i] * (nsr[i] - nsl[i] - 1))\n return ans\n\n```\n\n---\n\n# JavaScript\n```js\nvar largestRectangleArea = function(heights) {\n const n = heights.length;\n const nsr = new Array(n).fill(0);\n const nsl = new Array(n).fill(0);\n\n const stack = [];\n \n for (let i = n - 1; i >= 0; i--) {\n while (stack.length !== 0 && heights[i] <= heights[stack[stack.length - 1]]) {\n stack.pop();\n }\n if (stack.length === 0) {\n nsr[i] = n;\n } else {\n nsr[i] = stack[stack.length - 1];\n }\n stack.push(i);\n }\n\n while (stack.length !== 0) {\n stack.pop();\n }\n\n for (let i = 0; i < n; i++) {\n while (stack.length !== 0 && heights[i] <= heights[stack[stack.length - 1]]) {\n stack.pop();\n }\n if (stack.length === 0) {\n nsl[i] = -1;\n } else {\n nsl[i] = stack[stack.length - 1];\n }\n stack.push(i);\n }\n\n let ans = 0;\n\n for (let i = 0; i < n; i++) {\n ans = Math.max(ans, heights[i] * (nsr[i] - nsl[i] - 1));\n }\n \n return ans;\n};\n``` | 19 | 0 | ['Monotonic Stack', 'Python', 'C++', 'Java', 'JavaScript'] | 1 |
largest-rectangle-in-histogram | Java | TC: O(N) | SC: O(N) | Optimal Stack solution | java-tc-on-sc-on-optimal-stack-solution-tkik8 | java\n/**\n * Using stack to save the increasing height index.\n *\n * Time Complexity: O(N) --> Each element is visited maximum twice. (Once pushed\n * in stac | NarutoBaryonMode | NORMAL | 2021-10-13T10:00:52.891549+00:00 | 2021-10-13T10:09:07.735125+00:00 | 2,316 | false | ```java\n/**\n * Using stack to save the increasing height index.\n *\n * Time Complexity: O(N) --> Each element is visited maximum twice. (Once pushed\n * in stack and once popped for stack)\n *\n * Space Complexity: O(N)\n *\n * N = Length of the input array.\n */\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n if (heights == null) {\n throw new IllegalArgumentException("Input array is null");\n }\n\n int len = heights.length;\n if (len == 0) {\n return 0;\n }\n if (len == 1) {\n return heights[0];\n }\n\n Deque<Integer> stack = new ArrayDeque<>();\n int maxArea = 0;\n\n for (int i = 0; i <= len; i++) {\n while (!stack.isEmpty() && (i == len || heights[stack.peek()] >= heights[i])) {\n int h = heights[stack.pop()];\n int left = stack.isEmpty() ? -1 : stack.peek();\n /**\n * i-1 - left ==> This is calculating the width of the rectangle. Both ith and\n * left positions are excluded.\n */\n maxArea = Math.max(maxArea, (i - 1 - left) * h);\n }\n stack.push(i);\n }\n\n return maxArea;\n }\n}\n```\n\n---\n\nSolutions to other similar question on LeetCode:\n- [85. Maximal Rectangle](https://leetcode.com/problems/maximal-rectangle/discuss/1519263/Java-or-TC:-O(RC)-or-SC:-O(min(RC))-or-Optimal-Stack-solution)\n | 18 | 0 | ['Array', 'Stack', 'Java'] | 3 |
largest-rectangle-in-histogram | Share my 2ms Java solution. Beats 100% Java submissions | share-my-2ms-java-solution-beats-100-jav-tivk | public class Solution {\n public int largestRectangleArea(int[] heights) {\n if (heights == null || heights.length == 0) return 0;\n | ya_ah | NORMAL | 2016-03-13T19:38:49+00:00 | 2016-03-13T19:38:49+00:00 | 6,010 | false | public class Solution {\n public int largestRectangleArea(int[] heights) {\n if (heights == null || heights.length == 0) return 0;\n return getMax(heights, 0, heights.length);\n } \n int getMax(int[] heights, int s, int e) {\n if (s + 1 >= e) return heights[s];\n int min = s;\n boolean sorted = true;\n for (int i = s; i < e; i++) {\n if (i > s && heights[i] < heights[i - 1]) sorted = false;\n if (heights[min] > heights[i]) min = i;\n }\n if (sorted) {\n int max = 0;\n for (int i = s; i < e; i++) {\n max = Math.max(max, heights[i] * (e - i));\n }\n return max;\n }\n int left = (min > s) ? getMax(heights, s, min) : 0;\n int right = (min < e - 1) ? getMax(heights, min + 1, e) : 0;\n return Math.max(Math.max(left, right), (e - s) * heights[min]);\n }\n } | 17 | 2 | ['Java'] | 9 |
largest-rectangle-in-histogram | Solution Using Stack(C++) | solution-using-stackc-by-surabhi1997mitr-gc9x | This problem is particularly almost similar to Trapping Rainwater Problem.\nHere in this post I would like to highlight both their solutions so one could dop a | surabhi1997mitra | NORMAL | 2021-04-04T15:33:22.036940+00:00 | 2021-04-04T15:33:22.036974+00:00 | 1,717 | false | This problem is particularly almost similar to Trapping Rainwater Problem.\nHere in this post I would like to highlight both their solutions so one could dop a comparitive study of the approach and figure out their individual details.\n\n**Trapping Rainwater Problem (Approach Using Stack)**\n\n```\nint trap(vector<int>& height)\n{\n int ans = 0, current = 0;\n stack<int> st;\n while (current < height.size()) {\n while (!st.empty() && height[current] > height[st.top()]) {\n int top = st.top();\n st.pop();\n if (st.empty())\n break;\n int horizontal = current - st.top() - 1;\n int vertical = min(height[current], height[st.top()]) - height[top];\n ans += horizontal * vertical;\n }\n st.push(current++);\n }\n return ans;\n}\n```\n\n*Link: https://leetcode.com/problems/trapping-rain-water/solution/*\n\n**Largest Rectangle Problem (Approach Using Stack)**\n\n\n\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n stack<int>st;\n heights.push_back(0);\n int ret=0;\n for(int i = 0; i < heights.size(); i++)\n {\n while(st.size() > 0 && heights[st.top()] >= heights[i])\n {\n int vertical = heights[st.top()];\n st.pop();\n \n int right_upper_bound = st.size() > 0 ? st.top() : -1;\n int horizontal=(i-right_upper_bound-1);\n if(vertical * horizontal > ret)\n ret = vertical * horizontal;\n }\n st.push(i);\n }\n \n return ret;\n }\n };\n```\n\nHope this would help to make a comparision and help you to approach similar problems with ease!! | 15 | 3 | ['Stack', 'C'] | 0 |
largest-rectangle-in-histogram | ✔️ 100% Fastest Swift Solution, time: O(n), space: O(n). | 100-fastest-swift-solution-time-on-space-8gro | \nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the length of heights.\n // - space: O(n), where n is the length of heights.\n\ | sergeyleschev | NORMAL | 2022-04-07T05:44:40.681628+00:00 | 2022-04-07T05:44:40.681678+00:00 | 642 | false | ```\nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the length of heights.\n // - space: O(n), where n is the length of heights.\n\n func largestRectangleArea(_ heights: [Int]) -> Int {\n var stack = [Int]()\n let n = heights.count\n var ans = 0\n \n for i in 0..<n {\n while let curHeight = stack.last, heights[curHeight] >= heights[i] {\n stack.removeLast()\n let curWidth = stack.last ?? -1\n ans = max(ans, heights[curHeight] * (i - curWidth - 1))\n }\n stack.append(i)\n }\n \n while !stack.isEmpty {\n let curHeight = stack.removeLast()\n let curWidth = stack.last ?? -1\n ans = max(ans, heights[curHeight] * (n - curWidth - 1))\n }\n \n return ans\n }\n\n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful. | 14 | 0 | ['Swift'] | 0 |
largest-rectangle-in-histogram | Stack C++ - Easy to understand (180ms) [2 Approaches] | stack-c-easy-to-understand-180ms-2-appro-gnft | Here are two approaches for the problem:\n1. We use previous smaller element and next smaller element and compare those two to \n\tget our desired max rectangle | NeerajSati | NORMAL | 2022-01-29T04:31:26.395379+00:00 | 2022-01-29T05:26:16.505051+00:00 | 1,226 | false | Here are two approaches for the problem:\n1. We use previous smaller element and next smaller element and compare those two to \n\tget our desired max rectangle area.\n\t\n\tWe have to use two separate functions here to find the previous smaller and next smaller element.\n\tThe algorithm to make it happen is this:\n\t```\n\t curr += ( i - prevSmall[i]-1 ) * heights[i];\n curr += ( nextSmall[i] - i - 1 ) * heights[i];\n\t```\n\t\n\t**Time Complexity: O(n)\n\tSpace Complexity: O(n)**\n\t\n```\nclass Solution {\nprivate:\n vector<int> prevSmall;\n vector<int> nextSmall;\n\n void previousSmaller(vector<int> heights){\n stack<int> s;\n s.push(0);\n prevSmall.push_back(-1);\n for(int i=1;i<heights.size();i++){\n while(s.empty()==false && heights[s.top()]>=heights[i])\n s.pop();\n if(s.empty())\n prevSmall.push_back(-1);\n else\n prevSmall.push_back(s.top());\n s.push(i);\n }\n }\n void nextSmaller(vector<int> heights){\n stack<int> s;\n int n = heights.size();\n s.push(n-1);\n nextSmall.push_back(n);\n for(int i=n-2;i>=0;i--){\n while(s.empty()==false && heights[s.top()]>=heights[i])\n s.pop();\n if(s.empty())\n nextSmall.push_back(n);\n else\n nextSmall.push_back(s.top());\n s.push(i);\n }\n //We used the reverse of array to find the next Smaller\n //So we need to reverse the vector\n reverse(nextSmall.begin(),nextSmall.end());\n }\npublic:\n int largestRectangleArea(vector<int>& heights) {\n nextSmaller(heights);\n previousSmaller(heights);\n int res = 0;\n for(int i=0;i<heights.size();i++){\n int curr = heights[i];\n curr += (i-prevSmall[i]-1)*heights[i];\n curr += (nextSmall[i]-i-1)*heights[i];\n res=max(curr,res);\n }\n return res;\n }\n};\n```\n\n\n2. We can make the above approach more efficient by using the idea of just previous smaller element\n\tAnd it can be done in a single loop.\n\t**Time Complexity: O(n)\n\tSpace Complexity: O(n)**\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int res = 0, curr = 0, n = heights.size();\n stack<int> s;\n for(int i=0;i<n;i++){\n while(s.empty() == false && heights[s.top()]>=heights[i]){\n int top = s.top();\n s.pop();\n if(s.empty())\n curr = heights[top]*i;\n else\n curr = heights[top]*(i-s.top()-1);\n res = max(curr,res);\n }\n s.push(i);\n }\n //For the elements left in the stack\n while(s.empty() == false){\n int top = s.top();\n s.pop();\n if(s.empty())\n curr = heights[top]*n;\n else\n curr = heights[top]*(n-s.top()-1);\n res = max(curr,res);\n }\n return res;\n }\n};\n```\n\nHope you get it now :) | 14 | 0 | ['Stack', 'C'] | 2 |
largest-rectangle-in-histogram | Python Solution Using Monotonic Stack With Explanation | python-solution-using-monotonic-stack-wi-hfaj | Problem Description\n\nThe problem requires finding the area of the largest rectangle that can be formed in a histogram represented by an array of non-negative | KhadimHussainDev | NORMAL | 2024-04-13T07:29:36.314301+00:00 | 2024-04-14T11:40:50.533084+00:00 | 2,856 | false | ## Problem Description\n\nThe problem requires finding the area of the largest rectangle that can be formed in a histogram represented by an array of non-negative integers `heights`, where each bar\'s width is 1 unit.\n\n## Approach Explanation\n\nThis solution uses a stack-based approach to calculate the maximum rectangle area efficiently:\n- Initialize `max_area` to 0 to keep track of the maximum area encountered.\n- Initialize an empty stack to store indices and corresponding heights.\n- Iterate through each index `i` and height `h` in the `heights` array:\n - If the stack is empty or the height `h` is greater than or equal to the height at the top of the stack (`stack[-1][1]`):\n - Push the current index `i` and height `h` onto the stack.\n - Otherwise, while the stack is not empty and the height at the top of the stack (`stack[-1][1]`) is greater than the current height `h`:\n - Pop the top of the stack (`idx, he = stack.pop()`).\n - Calculate the area using the popped height `he` and the difference between the current index `i` and the popped index `idx` (`(i - idx) * he`).\n - Update `max_area` with the maximum of the current `max_area` and the calculated area.\n- After processing all heights in the `heights` array, handle any remaining heights in the stack to calculate potential areas.\n- Return the `max_area` as the result, which represents the area of the largest rectangle in the histogram.\n\n```python\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n max_area = 0\n stack = []\n for i , h in enumerate(heights):\n idx = i\n if not stack:\n stack.append([i , h])\n continue\n while stack and stack[-1][1] > h:\n idx , he = stack.pop()\n max_area = max(max_area , (i - idx ) * he)\n stack.append([idx , h])\n\n while stack:\n idx , he = stack.pop()\n max_area = max(max_area , (i - idx + 1) * he) \n return max_area\n```\n\n## Complexity Analysis\n\n- **Time Complexity**: O(n), where `n` is the number of elements in the `heights` array. Each element is processed a constant number of times (pushed and popped from the stack), resulting in linear time complexity.\n- **Space Complexity**: O(n), where `n` is the number of elements in the `heights` array. The stack can potentially hold all elements in the worst-case scenario (non-decreasing heights).\n---\nYou Should solve this now : [Leetcode 85](https://leetcode.com/problems/maximal-rectangle) [Leetcode 85 Solution](https://leetcode.com/problems/maximal-rectangle/solutions/5015357/python-solution-using-previous-technique-clearly-explained/)\n> #### ***If You Found it helpful, please upvote it. Thanks***\n\n\n | 13 | 1 | ['Stack', 'Monotonic Stack', 'Python3'] | 4 |
largest-rectangle-in-histogram | My C++ DP solution, 16ms, easy to understand! | my-c-dp-solution-16ms-easy-to-understand-z7k8 | I think it might be O(n), or very close to O(n), it cannot be O(n^2).\nCan anybody help to prove?\n\n\n int largestRectangleArea(vector& height) {\n i | phu1ku | NORMAL | 2015-07-21T09:57:29+00:00 | 2015-07-21T09:57:29+00:00 | 4,734 | false | I think it might be O(n), or very close to O(n), it cannot be O(n^2).\nCan anybody help to prove?\n\n\n int largestRectangleArea(vector<int>& height) {\n int n = height.size(), ans = 0, p;\n vector<int> left(n,0), right(n,n);\n for (int i = 1;i < n;++i) {\n p = i-1;\n while (p >= 0 && height[i] <= height[p])\n p = left[p] - 1;\n left[i] = p + 1;\n }\n for (int i = n-2;i >= 0;--i) {\n p = i+1;\n while (p < n && height[i] <= height[p])\n p = right[p];\n right[i] = p;\n }\n for (int i = 0;i < n;++i)\n ans = max(ans,height[i]*(right[i]-left[i]));\n return ans;\n } | 13 | 0 | ['C++'] | 7 |
largest-rectangle-in-histogram | Detailed explanation of this problem O(n) | detailed-explanation-of-this-problem-on-7xs0a | Idea 1:\n\tDivide and Conquer using segment tree search. Time & space O(nlgn)\n\thttp://www.geeksforgeeks.org/largest-rectangular-area-in-a-histogram-set-1/\n\t | zehua2 | NORMAL | 2016-08-19T23:54:49.344000+00:00 | 2016-08-19T23:54:49.344000+00:00 | 1,525 | false | Idea 1:\n\tDivide and Conquer using segment tree search. Time & space O(nlgn)\n\thttp://www.geeksforgeeks.org/largest-rectangular-area-in-a-histogram-set-1/\n\t\n\t\nIdea 2:\n\tFor each bar, we calculate maximum area with current bar as the smallest one in the rectangle. If we want to maximize the area of this rectangle, the two sides' bars right next to this rectangle (but not belonging to this rectangle) are smaller than current bar. \n\t\nIf we do this for every bar, and record the maximum, then this maximum is the result we want. (Since height of rectangle is determined by smallest bar in this rectangle, and width is determined by number of bars in this rectangle. Now we calculate all possible maximum rectangles whose height is one of the bars with largest possible width.)\n\t\nHow can we get left smaller bar and right smaller bar of each bar?\n\n(1) Brute force way: Traverse all bars, and use linear search to find. O(n^2) time O(1) space\n\t\n(2) Use two arrays to record known left, right bars of each bar. When we search for next bar, we might use this result to skip some bars. It is time O(n) and space O(n).\n\thttps://discuss.leetcode.com/topic/48127/java-o-n-left-right-arrays-solution-4ms-beats-96\n\t\n(3) Use a Stack to store indexes of all pending bars. What does 'pending' means here? It means we cannot find corresponding right bar for it. A valid corresponding right bar is defined as the first bar the smaller than this bar to the right.\n\nSo when we meet a higher bar than current top of stack, we push it. Otherwise, we pop out the top of current stack, because we find a valid right bar for this popped out bar. Then we look for its left bar which just located on the next layer of this stack. Now we have left bar and right bar of this popped out bar, we can calculate its maximum rectangle's area.\n\t\nSo stack always maintains indexes of ascending ordered bars.\n\t\nAfter we traverse all bars, if stack is not empty. Then it means there is no right bar for these remaining bars (an extreme example is increasing ordered bars), so we can just use heights.length as the index of right bar for them, and popped them out one by one.\n\t\nThis method time complexity is O(n) space O(n)\n\t\n\t\nSome corner cases during execution:\n\t1. Stack is empty when try to compare top of stack: Just push current bar.\n\t2. No left bar found after current bar is popped out: case like [3,1]. use -1 if stack is empty when looking for left bar.\n\t\t\nA small trick:\n\tWhen rightIndex == heights.length, use 0 as new bar's height so that we can pop out all remaining bars in the stack. (Since no bar's height will be smaller than 0. We won't need another while loop to handle it.)\n\n\n\n```java\npublic class Solution {\n public int largestRectangleArea(int[] heights) {\n Deque<Integer> stack = new ArrayDeque<>();\n int max = 0, rightIndex = 0;\n while(rightIndex <= heights.length) {\n int rightHeight = (rightIndex == heights.length ? 0 : heights[rightIndex]); // All new bars are seen as potential right bar\n if(stack.isEmpty() || heights[stack.peek()] < rightHeight) stack.push(rightIndex++); // Only increment rightIndex, when pushed\n else {\n int curHeight = heights[stack.pop()]; // Be careful that stack only store index, we still need heights[index] to get height\n int leftIndex = (stack.isEmpty() ? -1 : stack.peek()); // Be careful of case of no left bar\n max = Math.max(max, (rightIndex - leftIndex - 1) * curHeight);\n }\n }\n return max;\n }\n\t\n\t\n\t\n\t/*\n\t\tWithout trick version\n\t*/\n\tpublic int largestRectangleArea(int[] heights) {\n Deque<Integer> stack = new ArrayDeque<>();\n int max = 0, rightIndex = 0;\n while(rightIndex < heights.length) {\n int rightHeight = heights[rightIndex]; // All new bars are seen as potential right bar\n if(stack.isEmpty() || heights[stack.peek()] < rightHeight) stack.push(rightIndex++); // Only increment rightIndex, when pushed\n else {\n int curHeight = heights[stack.pop()]; // Be careful that stack only store index, we still need heights[index] to get height\n int leftIndex = (stack.isEmpty() ? -1 : stack.peek()); // Be careful of case of no left bar\n max = Math.max(max, (rightIndex - leftIndex - 1) * curHeight);\n }\n }\n while(!stack.isEmpty()) {\n int curHeight = heights[stack.pop()]; \n int leftIndex = (stack.isEmpty() ? -1 : stack.peek()); \n max = Math.max(max, (rightIndex - leftIndex - 1) * curHeight); // here rightIndex == heights.length\n }\n return max;\n }\n``` | 13 | 0 | [] | 2 |
largest-rectangle-in-histogram | Largest Rectangle in Histogram - Easy Approach explained with images | largest-rectangle-in-histogram-easy-appr-lqd0 | Problem Statement Explained\n Describe your first thoughts on how to solve this problem. \nThis question wants to find the largest rectangle (ie largest area) t | ak9807 | NORMAL | 2024-07-14T11:48:17.047177+00:00 | 2024-07-15T14:16:21.751520+00:00 | 3,137 | false | # Problem Statement Explained\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis question wants to find the largest rectangle (ie largest area) that can be formed in the given histogram.\nWe are given an array of heights of the histogram bars and width of all is supposed to be 1 unit.\n\n---\n\n\n# Understanding \n<!-- Describe your approach to solving the problem. -->\nOk , so let\'s start by looking closely at this figure\n\n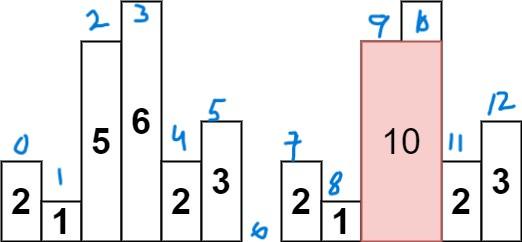\n\nThese numbers written in **blue** are indexes . We have to find the largest rectangle that can be formed using these bars. \nLet\'s start at index 0 , we have a bar of height 2 , this cannot alone make a rectangle ,right? So , we move on to the index 1 , and we get a bar of height 1 . Now look at the below image again.\n\n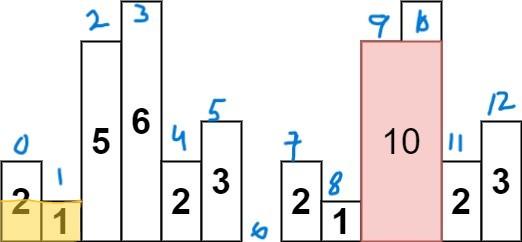\n\nYou can easily see that the current bar we are at , ie of height 1 can form a rectangle with bar at index 0 which was height 2.\nSo , now let\'s calculate the width of this rectangle .\nWidth will be `The current index we are on - The index present in the stack -1` (Will be explaining this formula in code walkthrough section.)\n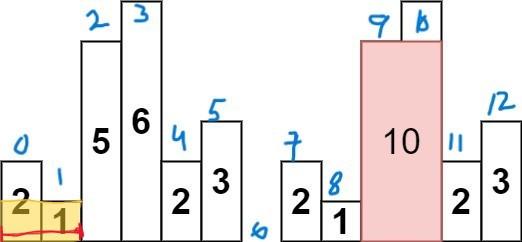\n\nThe red mark you see? that\'s the width of our new rectangle , since it is starting from 0 , we get our width as 1 directly without using the formula. The height will be 1 of course because that is the limiting height of the rectangle between the 0 th index bar and the 1st index bar. \n\nNow that we have both the height and the width , we can calculate the area of the rectangle.\n\nSuppose we are at index 4 and we are forming a rectangle with index 3 since it is longer. What will be the width then ? Let\'s see through an image again.\n\n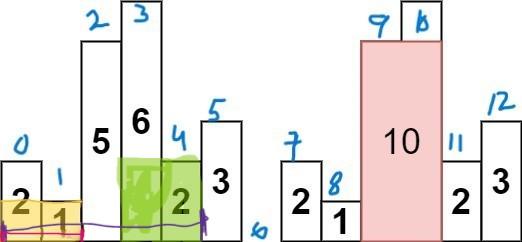\n\nLook at the pink and purple lines . Our width of the rectangle will be this entire `Purple line - the Pink line`. Now , since currently we are not including bar at index 2 and ( height 5 )\n,` we will subtract 1 from it` . And that is how the width of your rectangle is going to be calculated .\n\n\n \n\n---\n# Code WalkThrough and Approach\n\nThe approach is going to be quite simple. We will just loop through the heights of the bars and the moment we get a height which is less than the one present in the stack , we realize that we can form a rectangle now.\n\nOkay, so we first start with the initializations. \n1. **n** : initialized to the length of the heights array.\n\n2. **maxArea** : initialized to 0 , this will hold the maximum area we get as we traverse through the bars.\n\n3. **stack** : A stack to hold the indices of the bars.\n\nNow , after initializing , we put a for loop which runs until i<=n .\n\n**Why =n ?**\n-> See , when we get heights that are greater than the ones that are in the stack , we push those heights inside the stack too. right.\n\nBut , what if when we reach the last height , we have heights left in the stack , that were never processed? How do we deal with them?\nThat\'s why we put a condition that : `int currHeight = (i==n) ? 0 : heights[i];` we process one extra artificial bar at i==n , and assume that it\'s height is 0 . So now what will happen is that this artificial height will be less than all the heights in the stack , so we keep popping and processing them , until the stack becomes empty.\n\nNow , look at this part of the code. \n```\n while(!stack.isEmpty() && currHeight<heights[stack.peek()])\n {\n \n int top = stack.pop();\n int width = stack.isEmpty() ? i: i-stack.peek()-1;\n int area = heights[top]*width;\n maxArea = Math.max(maxArea , area);\n\n }//while\n```\n\nThis is the loop in which we traverse the array of heights until the stack is not empty , and the current height is less than the height in the stack (Why? Because ,when we encounter a height less than the previous one , we can form a rectangle from it)\n\n\n---\n\n\n# Code\n```java []\nimport java.util.Stack;\n\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int n = heights.length;\n int maxArea = 0;\n Stack<Integer>stack = new Stack<>();\n \n for(int i=0;i<=n;i++)\n {\n int currHeight = (i==n) ? 0 : heights[i];\n\n while(!stack.isEmpty() && currHeight<heights[stack.peek()])\n {\n \n int top = stack.pop();\n int width = stack.isEmpty() ? i: i-stack.peek()-1;\n int area = heights[top]*width;\n maxArea = Math.max(maxArea , area);\n\n }//while\n\n stack.push(i);\n\n }//for loop\n return maxArea;\n\n }//function ends\n}//class end \n```\n\n```python []\nclass Solution(object):\n def largestRectangleArea(self, heights):\n """\n :type heights: List[int]\n :rtype: int\n """\n n = len(heights)\n max_area = 0\n stack = []\n\n for i in range(n + 1):\n curr_height = 0 if i == n else heights[i]\n\n while stack and curr_height < heights[stack[-1]]:\n top = stack.pop()\n width = i if not stack else i - stack[-1] - 1\n area = heights[top] * width\n max_area = max(max_area, area)\n\n stack.append(i)\n\n return max_area\n```\n \n\n---\n# Complexity\n- Time complexity : $$O(n)$$\n<!-- Add your time complexity here, e.g. --> \n\n- Space complexity : $$O(n)$$\n<!-- Add your space complexity here, e.g. -->\n\n---\n**Feel free to ask any queries regarding this problem in the comments section**\n**Thankyou !**\n\n\n | 12 | 0 | ['Array', 'Stack', 'Monotonic Stack', 'Python', 'Java'] | 1 |
largest-rectangle-in-histogram | [JAVA] Clean Code, O(N) Solution Using Stack Data Structure | java-clean-code-on-solution-using-stack-wy9b9 | \nclass Solution {\n public int largestRectangleArea(int[] heights) {\n \n int maximumRectangle = 0;\n Stack<Integer> stack = new Stack< | anii_agrawal | NORMAL | 2020-09-24T19:05:43.440043+00:00 | 2021-04-28T19:35:10.095185+00:00 | 1,003 | false | ```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n \n int maximumRectangle = 0;\n Stack<Integer> stack = new Stack<> ();\n \n for (int i = 0; i <= heights.length; i++) {\n while (!stack.isEmpty () && (i == heights.length || heights[stack.peek ()] > heights[i])) {\n int length = heights[stack.pop ()];\n int width = stack.isEmpty () ? i : i - stack.peek () - 1;\n maximumRectangle = Math.max (maximumRectangle, length * width);\n }\n \n stack.push (i);\n }\n \n return maximumRectangle;\n }\n}\n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n**HAPPY CODING :)\nLOVE CODING :)**\n | 12 | 1 | ['Stack', 'Java'] | 1 |
largest-rectangle-in-histogram | faster than 88.25% [easy-understanding][c++][stack] | faster-than-8825-easy-understandingcstac-xy68 | \n class Solution {\n public:\n int largestRectangleArea(vector& heights) {\n stack s;\n in | rajat_gupta_ | NORMAL | 2020-08-20T06:47:31.067136+00:00 | 2020-08-20T07:02:14.060119+00:00 | 1,179 | false | \n class Solution {\n public:\n int largestRectangleArea(vector<int>& heights) {\n stack<int> s;\n int maxArea = 0;\n int area = 0;\n int i;\n for(i=0; i < heights.size();){\n if(s.empty() || heights[s.top()] <= heights[i]){\n s.push(i++);\n }else{\n int top = s.top();\n s.pop(); \n //if stack is empty means everything till i has to be\n //greater or equal to heights[top] so get area by\n //heights[top] * i;\n if(s.empty()){\n area = heights[top] * i;\n }\n //if stack is not empty then everythin from i-1 to heights.top() + 1\n //has to be greater or equal to heights[top]\n //so area = heights[top]*(i - stack.top() - 1);\n else{\n area = heights[top] * (i - s.top() - 1);\n }\n if(area > maxArea){\n maxArea = area;\n }\n }\n }\n while(!s.empty()){\n int top = s.top();\n s.pop();\n //if stack is empty means everything till i has to be\n //greater or equal to heights[top] so get area by\n //heights[top] * i;\n if(s.empty()){\n area = heights[top] * i;\n }\n //if stack is not empty then everything from i-1 to height.top() + 1\n //has to be greater or equal to heights[top]\n //so area = heights[top]*(i - stack.top() - 1);\n else{\n area = heights[top] * (i - s.top() - 1);\n }\n if(area > maxArea){\n maxArea = area;\n }\n }\n return maxArea;\n }\n };\n\t \n**Feel free to ask any question in the comment section.\nIf you like this solution, do UPVOTE.\nHappy Coding :)**\n\t | 12 | 1 | ['Stack', 'C', 'C++'] | 0 |
largest-rectangle-in-histogram | Java solution with explanations in Chinese | java-solution-with-explanations-in-chine-npra | S1:\u53CC\u91CD\u904D\u5386\u6CD5\n\n\u672C\u9898\u8981\u6C42\u7684\u662F\u4E00\u6BB5\u8FDE\u7EED\u7684\u77E9\u5F62\uFF0C\u80FD\u591F\u7EC4\u6210\u7684\u9762\u7 | wuruoye | NORMAL | 2019-01-25T06:56:33.228332+00:00 | 2019-01-25T06:56:33.228376+00:00 | 947 | false | S1:\u53CC\u91CD\u904D\u5386\u6CD5\n\n\u672C\u9898\u8981\u6C42\u7684\u662F\u4E00\u6BB5\u8FDE\u7EED\u7684\u77E9\u5F62\uFF0C\u80FD\u591F\u7EC4\u6210\u7684\u9762\u79EF\u6700\u5927\u7684\u77E9\u5F62\u7684\u9762\u79EF\uFF0C\u6240\u4EE5\uFF0C\u53EA\u8981\u80FD\u591F\u6C42\u51FA\u8FD9\u4E00\u6BB5\u77E9\u5F62\u7684\u4F4D\u7F6E\u7684\u5C31\u53EF\u4EE5\u4E86\u3002\u6700\u7B80\u5355\u7684\u60F3\u6CD5\uFF0C\u5C06\u6240\u6709\u7684\u53EF\u80FD\u7684\u7EC4\u5408\u90FD\u6C42\u89E3\u4E00\u904D\uFF0C\u6BD4\u8F83\u4E4B\u540E\u4FDD\u7559\u6700\u5927\u7684\u90A3\u4E00\u4E2A\u5C31\u597D\u4E86\uFF0C\u5982\u4E0B\uFF1A\n\n public static int largestRectangleArea(int[] heights) {\n int max = 0;\n for (int i = 0; i < heights.length; i++) {\n int min = heights[i];\n for (int j = i; j >= 0; j--) {\n if (heights[j] < min) {\n min = heights[j];\n }\n max = Math.max(max, min * (i-j+1));\n }\n }\n return max;\n }\n\n\u901A\u8FC7\u4E00\u4E2A\u53CC\u91CD\u904D\u5386\uFF0C\u5916\u5C42\u904D\u5386\u77E9\u5F62\u7684\u7ED3\u675F\u5730\u5740\uFF0C\u5185\u5C42\u904D\u5386\u77E9\u5F62\u8D77\u59CB\u5730\u5740\uFF0C\u901A\u8FC7\u6C42\u7B97\u6BCF\u4E00\u4E2A\u7EC4\u5408\u7684\u6700\u5927\u7EC4\u6210\u9762\u79EF\u6C42\u89E3\u3002\u65F6\u95F4\u590D\u6742\u5EA6\u4E3AO(n^2)\u3002\n\nS2:\u5206\u6CBB\u6CD5\n\n\u4E0A\u9762\u7684\u65B9\u6CD5\u6211\u4EEC\u662F\u4F9D\u636E\u77E9\u5F62\u7684\u8D77\u59CB\u3001\u7ED3\u675F\u4F4D\u7F6E\u8FDB\u884C\u5206\u7C7B\u3001\u6C42\u7B97\uFF0C\u90A3\u4E48\u6211\u4EEC\u8FD8\u53EF\u4EE5\u4F7F\u7528\u53E6\u4E00\u79CD\u65B9\u6CD5\u6C42\u7B97\uFF1A\u6309\u7167\u7EC4\u5408\u77E9\u9635\u7684\u9AD8\u5EA6\u4ECE\u4F4E\u5230\u9AD8\u6C42\u89E3\uFF0C\u7136\u540E\u53D6\u6700\u5927\u3002\u6211\u4EEC\u77E5\u9053\uFF0C\u5728\u7ED9\u5B9A\u7684\u4E00\u7EC4\u77E9\u9635\u4E2D\uFF0C\u5982\u679C\u53D6\u9AD8\u5EA6\u4E3A\u6700\u4F4E\u7684\u90A3\u4E00\u4E2A\uFF0C\u90A3\u4E48\u5BBD\u5EA6\u5FC5\u7136\u53EF\u53D6\u6570\u7EC4\u7684\u957F\u5EA6\u3002\u5982\uFF0C\u7ED9\u5B9A\u7684\u4E00\u4E2A\u6570\u7EC4[2,1,2]\uFF0C\u90A3\u4E48\u5F53\u6211\u4EEC\u53D6\u9AD8\u5EA6\u4E3A 1 \uFF0C\u90A3\u4E48\u5BBD\u5EA6\u5FC5\u7136\u53EF\u53D6 3 \u3002\u6B64\u65F6\u7EC4\u5408\u77E9\u9635\u7684\u9762\u79EF\u662F 3 \u3002\u8FD9\u65F6\uFF0C\u7EC4\u5408\u77E9\u9635\u53D6\u5F97\u662F\u6700\u4F4E\u9AD8\u5EA6 1 \u3002\u90A3\u4E48\u63A5\u4E0B\u6765\uFF0C\u5982\u679C\u53D6\u4E00\u4E2A\u66F4\u9AD8\u7684\u9AD8\u5EA6\uFF0C\u90A3\u4E48\u8FD9\u4E2A\u9AD8\u5EA6\u4E3A 1 \u7684\u5C0F\u77E9\u9635\u5FC5\u7136\u4E0D\u4F1A\u5305\u542B\u5728\u5185\uFF0C\u6240\u4EE5\u4E0B\u4E00\u6B65\u8981\u7EC4\u6210\u7684\u77E9\u9635\u5FC5\u7136\u5728\u8FD9\u4E2A 1 \u7684\u5DE6\u8FB9\u6216\u8005\u53F3\u8FB9\uFF0C\u8FD9\u6837\u4E00\u6765\uFF0C\u6211\u4EEC\u5C31\u53EF\u4EE5\u770B\u4F5C\uFF0C\u8FD9\u4E2A\u9AD8\u5EA6\u4E3A 1 \u7684\u5C0F\u77E9\u9635\u5C06\u6574\u4E2A\u77E9\u9635\u5E8F\u5217\u5206\u5272\u6210\u4E86\u4E24\u90E8\u5206\uFF0C\u6211\u4EEC\u4E0B\u4E00\u6B65\u8981\u5224\u65AD\u7684\u7EC4\u5408\u77E9\u9635\u5C31\u5728\u5DE6\u90E8\u6216\u8005\u53F3\u90E8\uFF0C\u5982\u6B64\u4E00\u4E0B\uFF0C\u6211\u4EEC\u53EA\u9700\u8981\u6C42\u5DE6\u53F3\u4E24\u90E8\u4E2D\u80FD\u591F\u7EC4\u6210\u7684\u6700\u5927\u9762\u79EF\u5C31\u597D\u4E86\uFF0C\u4E8E\u662F\uFF0C\u4E00\u4E2A\u6570\u7EC4[2,1,2]\u88AB\u6700\u5C0F\u503C1\u5206\u5272\u6210\u4E86\u4E24\u4E2A\u6570\u7EC4[2]\u548C[2]\uFF0C\u5982\u6B64\u4E00\u6765\uFF0C\u6C42[2,1,2]\u7684\u89E3\u7684\u95EE\u9898\u53D8\u6210\u4E86\u6C42[2]\u7684\u89E3\uFF0C\u800C[2]\u7684\u89E3\u53EA\u6709\u4E00\u4E2A 2 \uFF0C\u4EE5\u6B64\u7C7B\u63A8\uFF0C\u6211\u4EEC\u5C31\u53EF\u4EE5\u5C06\u4EFB\u610F\u4E00\u4E2A\u5927\u7684\u95EE\u9898\u5206\u89E3\u6210\u82E5\u5E72\u4E2A\u5C0F\u7684\u95EE\u9898\uFF0C\u7136\u540E\u5728\u8FD9\u51E0\u4E2A\u5C0F\u95EE\u9898\u4E2D\u6C42\u6700\u5927\u503C\u5373\u53EF\u3002\n\n\u4EE3\u7801\u5982\u4E0B\uFF1A\n\n public static int largestRectangleArea2(int[] heights) {\n return largest(heights, 0, heights.length-1);\n }\n public static int largest(int[] heights, int start, int end) {\n if (start > end) return 0;\n if (start == end) return heights[start];\n boolean sorted = true;\n int min = start;\n for (int i = start+1; i <= end; i++) {\n if (heights[i] < heights[i-1]) sorted = false;\n if (heights[i] < heights[min]) min = i;\n }\n if (sorted) {\n int max = heights[start] * (end - start + 1);\n for (int i = start+1; i <= end; i++) {\n max = Math.max(max, heights[i] * (end - i + 1));\n }\n return max;\n }\n return Math.max(Math.max(largest(heights, start, min-1), largest(heights, min+1, end)),\n heights[min] * (end - start + 1));\n }\n\n\u5BF9\u4E8E\u4E00\u4E2A\u6570\u7EC4\u800C\u8A00\uFF0C\u53EF\u80FD\u6210\u4E3A\u6700\u5927\u503C\u7684\u89E3\u6709\u4E09\u4E2A\uFF1A\n\n1. \u6700\u5C0F\u503C\u5DE6\u90E8\u7684\u67D0\u4E2A\u89E3\n2. \u6700\u5C0F\u503C\u53F3\u90E8\u7684\u67D0\u4E2A\u89E3\n3. \u5305\u542B\u5F53\u524D\u6700\u5C0F\u503C\u7684\u89E3\n\n\u53E6\u5916\uFF0C\u4E0A\u9762\u7684\u65B9\u6CD5\u4E2D\uFF0C\u901A\u8FC7\u5224\u65AD\u5F53\u524D\u7684\u5B50\u6570\u7EC4\u662F\u5426\u662F\u4E00\u4E2A\u6709\u5E8F\u6570\u7EC4\uFF0C\u6765\u7B80\u5316\u8FD9\u4E2A\u6570\u7EC4\u7684\u5224\u65AD\uFF0C\u4E0A\u9762\u4EC5\u5224\u65AD\u4E86\u7531\u5C0F\u5230\u5927\u7684\u987A\u5E8F\uFF0C\u8FD8\u53EF\u4EE5\u901A\u8FC7\u5224\u65AD\u662F\u5426\u662F\u4E00\u4E2A\u7531\u5927\u5230\u5C0F\u7684\u987A\u5E8F\u8FDB\u4E00\u6B65\u63D0\u9AD8\u5224\u65AD\u6548\u7387\u3002\u6B64\u7B97\u6CD5\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u4E3AO(n\\log n)\u3002\n\nS3:\u5229\u7528\u6808\n\n\u7B2C\u4E00\u79CD\u65B9\u6CD5\u7684\u5916\u5C42\u904D\u5386\uFF0C\u662F\u7EC4\u5408\u77E9\u9635\u7684\u7ED3\u675F\u4F4D\u7F6E\uFF0C\u7136\u540E\u5728\u5185\u5C42\u9010\u4E2A\u904D\u5386\u7EC4\u5408\u77E9\u9635\u7684\u5F00\u59CB\u4F4D\u7F6E\u3002\u901A\u8FC7\u5BF9\u8FD9\u6837\u4E00\u4E2A\u6A21\u578B\u7684\u5206\u6790\uFF0C\u5BF9\u4E8E\u4EE5\u4F4D\u7F6E i \u7ED3\u675F\u7684\u7EC4\u5408\u77E9\u9635\u6765\u8BF4\uFF0C\u5B83\u4E0E\u5F53\u524D\u4F4D\u7F6E\u4E4B\u524D\u7684\u77E9\u9635\u7684\u9AD8\u5EA6\u6709\u4E00\u5B9A\u5173\u7CFB\uFF1A\n\n1. \u5982\u679C i \u4F4D\u7F6E\u7684\u9AD8\u5EA6\u5927\u4E8E i-1 \u4F4D\u7F6E\u7684\u9AD8\u5EA6\uFF0C\u5219\u5728\u4E0E\u8FD9\u4E2A\u4F4D\u7F6E\u4E4B\u524D\u7684\u77E9\u9635\u7684\u7EC4\u5408\u4E2D\uFF0C\u4E0D\u80FD\u4EE5\u5F53\u524D\u4F4D\u7F6E\u7684\u9AD8\u5EA6\u4F5C\u4E3A\u7EC4\u5408\u77E9\u9635\u7684\u9AD8\u5EA6\u3002\u5982\u6570\u7EC4[1,2]\uFF0C\u90A3\u4E48\u5BF9\u4E8E\u4F4D\u7F6E 2 \u6765\u8BF4\uFF0C\u8FD9\u4E24\u4E2A\u4F4D\u7F6E\u7684\u7EC4\u5408\u4E0D\u80FD\u4EE5 2 \u4F5C\u4E3A\u7EC4\u5408\u77E9\u9635\u9AD8\u5EA6\u3002\n2. \u5982\u679C i \u4F4D\u7F6E\u7684\u9AD8\u5EA6\u4E0D\u5927\u4E8E i-1 \u4F4D\u7F6E\u7684\u9AD8\u5EA6\uFF0C\u5219\u5B58\u5728\u9AD8\u5EA6\u4E3A\u5F53\u524D\u9AD8\u5EA6\u7684\u7EC4\u5408\u77E9\u9635\u3002\u5982\u6570\u7EC4[2\uFF0C1]\uFF0C\u5BF9\u4E8E\u4F4D\u7F6E 1 \uFF0C\u6709\u4E00\u79CD\u7EC4\u5408\u65B9\u6CD5[1,1]\uFF0C\u6240\u4EE5\u5728\u8FD9\u79CD\u60C5\u51B5\u4E0B\u5E94\u8BE5\u5224\u65AD\u4E00\u4E0B\u3002\n\n\u53E6\u5916\uFF0C\u6211\u4EEC\u77E5\u9053\uFF0C\u5BF9\u4E8E\u4E00\u4E2A\u9AD8\u5EA6\u9012\u589E\u7684\u6570\u7EC4\u6765\u8BF4\uFF0C\u5F88\u5BB9\u6613\u6C42\u51FA\u5176\u7EC4\u5408\u77E9\u9635\u7684\u6700\u5927\u9762\u79EF\uFF0C\u90A3\u4E48\u662F\u5426\u53EF\u4EE5\u5C06\u4EFB\u610F\u4E00\u4E2A\u77E9\u9635\u8F6C\u5316\u4E3A\u4E00\u4E2A\u9AD8\u5EA6\u9012\u589E\u7684\u77E9\u9635\u5E8F\u5217\uFF1F\u5982\u5C06\u4E00\u4E2A\u6570\u7EC4[2,3,1,3,5]\u53D8\u6210[1,1,1,3,5]\uFF0C\u4F46\u662F\u8FD9\u4E2A\u8FC7\u7A0B\u4E2D\u5BF9 2 \u4F5C\u4E86\u6539\u53D8\uFF0C\u6211\u4EEC\u8981\u901A\u8FC7\u4E00\u5B9A\u529E\u6CD5\u5F25\u8865\u8FD9\u91CC\u7684\u6539\u53D8\uFF0C\u4E00\u79CD\u65B9\u6CD5\u662F\uFF0C\u5728\u4F5C\u6539\u53D8\u524D\uFF0C\u5C06\u5176\u80FD\u591F\u7EC4\u6210\u7684\u7EC4\u5408\u77E9\u9635\u7684\u6700\u5927\u9762\u79EF\u8BB0\u5F55\u4E0B\u6765\uFF0C\u5B8C\u4E86\u4E4B\u540E\u4FBF\u53EF\u4EE5\u5BF9\u5176\u505A\u51FA\u6539\u53D8\u4E86\u3002\u5BF9\u4E8E\u4E0A\u9762\u90A3\u4E2A\u4F8B\u5B50\uFF0C\u5B9E\u9645\u4E0A\u6211\u4EEC\u662F\u5BF9\u4E24\u4E2A\u9012\u589E\u7684\u6570\u7EC4\u6C42\u89E3\uFF1A[2,3]\u548C[1,1,1,3,5]\uFF0C\u800C\u5B83\u4EEC\u4E4B\u95F4\u7684\u6700\u5927\u89E3\u5FC5\u7136\u4E0E[2,3,1,3,5]\u7684\u89E3\u76F8\u540C\u3002\u4E8E\u662F\uFF0C\u5C06\u4E00\u4E2A\u4E0D\u89C4\u5219\u6570\u7EC4\u8F6C\u5316\u4E3A\u82E5\u5E72\u6709\u5E8F\u6570\u7EC4\uFF0C\u518D\u8FDB\u884C\u6C42\u89E3\uFF0C\u4FBF\u662F\u672C\u65B9\u6CD5\u7684\u601D\u60F3\u3002\n\n\u4E0B\u9762\u662F\u5229\u7528\u6808\u7684\u4E00\u79CD\u5B9E\u73B0\uFF0C\u5229\u7528\u6808\u7684\u8BDD\u4E0D\u9700\u8981\u5BF9\u539F\u6570\u636E\u8FDB\u884C\u4FEE\u6539\uFF0C\u800C\u662F\u76F4\u63A5\u5C06\u539F\u6570\u7EC4\u622A\u53D6\u6210\u591A\u4E2A\u6709\u5E8F\u6570\u7EC4\uFF0C\u901A\u8FC7\u4FDD\u5B58\u7D22\u5F15\u503C\u786E\u5B9A\u5F53\u524D\u7684\u7EC4\u5408\u77E9\u9635\u7684\u5BBD\u5EA6\uFF1A\n\n public static int largestRectangleArea3(int[] heights) {\n Stack<Integer> stack = new Stack<>();\n int n = heights.length;\n int max = 0;\n for (int i = 0; i <= n; i++) {\n while (!stack.empty() && (i >= n || heights[stack.peek()] > heights[i])) {\n int top = stack.pop();\n int h = heights[top];\n int w = stack.empty() ? i : (i-stack.peek()-1);\n max = Math.max(max, h*w);\n }\n stack.push(i);\n }\n return max;\n }\n\nS4:\u6700\u957F\u5BBD\u5EA6\u6CD5\n\n\u6211\u4EEC\u77E5\u9053\uFF0C\u7531\u591A\u4E2A\u77E9\u9635\u7EC4\u6210\u7684\u7EC4\u5408\u77E9\u9635\uFF0C\u5176\u5BBD\u5EA6\u4E3A\u77E9\u9635\u7684\u6570\u91CF\uFF0C\u9AD8\u5EA6\u4E3A\u77E9\u9635\u4E2D\u9AD8\u5EA6\u6700\u4F4E\u7684\u90A3\u4E00\u4E2A\u3002\u6240\u4EE5\uFF0C\u5BF9\u4E8E\u4EFB\u610F\u4E00\u4E2A\u4F4D\u7F6E\u7684\u77E9\u9635\uFF0C\u5047\u8BBE\u6B64\u65F6\u7684\u7EC4\u5408\u77E9\u9635\u9AD8\u5EA6\u4E3A\u5F53\u524D\u4F4D\u7F6E\u77E9\u9635\u7684\u9AD8\u5EA6\uFF0C\u6211\u4EEC\u53EA\u9700\u8981\u6C42\u51FA\u8FD9\u65F6\u7684\u7EC4\u5408\u77E9\u9635\u7684\u6700\u5927\u5BBD\u5EA6\uFF0C\u4FBF\u53EF\u4EE5\u6C42\u51FA\u4EE5\u5F53\u524D\u77E9\u9635\u7684\u9AD8\u5EA6\u4E3A\u9AD8\u5EA6\u7684\u7EC4\u5408\u77E9\u9635\u7684\u6700\u5927\u9762\u79EF\uFF0C\u90A3\u4E48\u6211\u4EEC\u53EA\u9700\u8981\u6C42\u51FA\u6BCF\u4E00\u4E2A\u4F4D\u7F6E\u80FD\u591F\u5F62\u6210\u7684\u6700\u5927\u89E3\uFF0C\u4FBF\u80FD\u591F\u5F97\u5230\u672C\u9898\u7684\u89E3\u3002\n\n\u8981\u6C42\u51FA\u67D0\u4E2A\u4F4D\u7F6E\u7684\u6700\u5927\u89E3\uFF0C\u5982 i \uFF0C\u53EF\u4EE5\u8FD9\u6837\u7406\u89E3\uFF0C\u4ECE\u6570\u7EC4[0,...,n]\u4E2D\u627E\u5230\u6700\u5927\u7684\u4E00\u6BB5[start,...,i,...end]\uFF0C\u5E76\u4E14\u5728\u8FD9\u6BB5\u4E2D\uFF0C\u4F4D\u7F6E i \u5904\u7684\u9AD8\u5EA6\u6700\u4F4E\uFF0C\u90A3\u4E48\u6B64\u65F6\u8FD9\u6BB5\u77E9\u9635\u7EC4\u6210\u7684\u7EC4\u5408\u77E9\u9635\u7684\u9762\u79EF\u5FC5\u7136\u662F(end-start) * heights[i]\u3002\u6240\u4EE5\u6211\u4EEC\u8981\u5728\u4F4D\u7F6E i \u7684\u5DE6\u8FB9\u627E\u5230\u4E00\u6BB5[start,...,i]\uFF0C\u662F\u7684\u8FD9\u91CC\u9762\u6BCF\u4E00\u4E2A\u77E9\u9635\u7684\u9AD8\u5EA6\u90FD\u5927\u4E8E\u7B49\u4E8E i \u5904\u7684\u9AD8\u5EA6\uFF0C\u540C\u7406\uFF0C\u8FD8\u8981\u5728 i \u7684\u53F3\u8FB9\u627E\u5230\u4E00\u6BB5[i,...end]\uFF0C\u627E\u5230\u8FD9\u4E9B\u4E4B\u540E\uFF0C\u4F4D\u7F6E i \u5904\u7684\u89E3\u5C31\u53EF\u4EE5\u6C42\u5F97\u4E86\u3002\n\n\u6240\u4EE5\uFF0C\u5BF9\u4E8E\u6BCF\u4E00\u4E2A\u4F4D\u7F6E\uFF0C\u53EA\u8981\u627E\u5230\u5728 i \u7684\u5DE6\u8FB9\u7B2C\u4E00\u4E2A\u5C0F\u4E8E i \u5904\u9AD8\u5EA6\u7684\u4F4D\u7F6E start \uFF0C\u518D\u627E\u5230 i \u7684\u53F3\u8FB9\u7B2C\u4E00\u4E2A\u5C0F\u4E8E i \u5904\u9AD8\u5EA6\u7684\u4F4D\u7F6E end \u4FBF\u53EF\u3002\u800C\u8FD9\u4E2A\u6570\u636E\u53EF\u4EE5\u901A\u8FC7\u4E24\u4E2A\u904D\u5386\u6C42\u89E3\u3002\n\n public static int largestRectangleArea4(int[] heights) {\n int n = heights.length;\n if (n == 0) return 0;\n int[] leftLess = new int[n], rightLess = new int[n];\n // find left\n leftLess[0] = 0;\n for (int i = 1; i < n; i++) {\n int p = i-1;\n while (true) {\n if (p >= 0 && heights[i] <= heights[p]) {\n p -= leftLess[p] + 1;\n } else {\n leftLess[i] = i - p - 1;\n break;\n }\n }\n }\n // find right\n rightLess[n-1] = 0;\n for (int i = n-2; i >= 0; i--) {\n int p = i+1;\n while (true) {\n if (p < n && heights[i] <= heights[p]) {\n p += rightLess[p] + 1;\n } else {\n rightLess[i] = p - 1 - i;\n break;\n }\n }\n }\n int max = 0;\n for (int i = 0; i < n; i++) {\n max = Math.max(max, heights[i] * (leftLess[i] + rightLess[i] + 1));\n }\n return max;\n }\n\n\u4F7F\u7528\u4E00\u4E2A\u6570\u7EC4 leftLess \u4FDD\u5B58\u6BCF\u4E2A\u4F4D\u7F6E\u7684\u5DE6\u8FB9\u9AD8\u5EA6\u5927\u4E8E\u5F53\u524D\u4F4D\u7F6E\u9AD8\u5EA6\u7684\u77E9\u9635\u6570\u91CF\uFF0CrightLess \u540C\u7406\u3002\u5177\u4F53\u7684\u6C42\u89E3\u65B9\u6CD5\u4E3A\uFF1A\u5BF9\u4E8E\u4F4D\u7F6E i \uFF0C\u5982\u679C i-1 \u5904\u7684\u9AD8\u5EA6\u5927\u4E8E i \u5904\u7684\u9AD8\u5EA6\uFF0C\u90A3\u4E48\u56E0\u4E3AleftLess[i-1]\u4FDD\u5B58\u7684\u662F\u5927\u4E8E\u4F4D\u7F6E i-1 \u5904\u9AD8\u5EA6\u7684\u6570\u91CF\uFF0C\u90A3\u4E48\u8FD9\u4E9B\u4F4D\u7F6E\u7684\u9AD8\u5EA6\u5FC5\u7136\u4E5F\u5927\u4E8E\u4F4D\u7F6E i \u5904\u7684\u9AD8\u5EA6\uFF0C\u6240\u4EE5\uFF0C\u6211\u4EEC\u53EF\u4EE5\u76F4\u63A5\u8DF3\u8FC71 + leftLess[i-1]\u4E2A\u4F4D\u7F6E\uFF0C\u5224\u65AD\u4E0B\u4E00\u4E2A\u4F4D\u7F6E p \u5904\u7684\u9AD8\u5EA6\u662F\u5426\u5927\u4E8E i \u5904\u7684\u9AD8\u5EA6\uFF0C\u5982\u679C\u8FD8\u662F\u5927\u4E8E\uFF0C\u90A3\u4E48\u8FD8\u8981\u7EE7\u7EED\u8DF3\u8FC7leftLess[p] + 1\u4E2A\u4F4D\u7F6E\uFF0C\u518D\u5224\u65AD......\u76F4\u5230 p \u5904\u7684\u9AD8\u5EA6\u5C0F\u4E8E i \u5904\u7684\u9AD8\u5EA6\uFF0C\u6B64\u65F6\u5728 i \u7684\u5DE6\u8FB9\u6BD4 i \u5904\u9AD8\u5EA6\u5927\u7684\u77E9\u9635\u7684\u6570\u91CF\u5C31\u662Fi - p - 1\u4E2A\u3002\u5BF9\u4E8E rightLess \u7684\u6C42\u89E3\u540C\u7406\u3002\n | 12 | 3 | [] | 6 |
largest-rectangle-in-histogram | [Python] Stack Solution O(N) Time - using approach of Next Smaller to Left and Right | python-stack-solution-on-time-using-appr-p92u | \nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n n = len(heights)\n # left boundary => next smaller element to | SamirPaulb | NORMAL | 2022-05-28T09:38:51.882768+00:00 | 2022-05-28T09:42:14.487702+00:00 | 2,418 | false | ```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n n = len(heights)\n # left boundary => next smaller element to left\n stack = []\n nextSmallerLeft = [0]*n\n for i in range(n):\n while stack and heights[stack[-1]] >= heights[i]:\n stack.pop()\n if stack:\n nextSmallerLeft[i] = stack[-1] + 1\n stack.append(i)\n \n # right boundary => next smaller element to right\n stack = []\n nextSmallerRight = [n-1]*n\n for i in range(n-1, -1, -1):\n while stack and heights[stack[-1]] >= heights[i]:\n stack.pop()\n if stack:\n nextSmallerRight[i] = stack[-1] - 1\n stack.append(i)\n \n res = heights[0]\n for i in range(n):\n height = heights[i]\n weidth = nextSmallerRight[i] - nextSmallerLeft[i] + 1\n area = height * weidth\n res = max(res, area)\n \n return res\n\t\t\n\t\t\n# Time: O(N)\n# Space: O(N)\n```\n | 11 | 0 | ['Stack', 'Monotonic Stack', 'Python', 'Python3'] | 3 |
largest-rectangle-in-histogram | [C++] O(n) Stack solution || Explaination with diagram | c-on-stack-solution-explaination-with-di-9en6 | Approach:\nArea of reactangle is height * width\nSince we want to maximise the area , we can either increase height or width. But since the heights are already | iShubhamRana | NORMAL | 2022-01-29T05:36:00.087881+00:00 | 2022-01-29T05:38:30.909711+00:00 | 629 | false | **Approach:**\nArea of reactangle is height * width\nSince we want to maximise the area , we can either increase height or width. But since the heights are already fixed , we need to find the maximum width for each height,\n\nThe naive approach to implement this is to traverse and for each height traverse to left and right and find the first block shorter than current . If we go beyond this , then we can form a rectangle only by \ntaking height of smaller block. \n**Time**: O(n^2), **Space**: O(1)\n\n**Optimisation**:\nWe can optimise the time to find smaller block on both sides by using a monotonic stack.\n1. We traverse from left and right seperately. \n2. The idea of monotonic stack is simple , if we find a smaller element than those in stack, then simply pop those greater elements from stack as if the new element is smaller than them , then it would be the first to cause any hinderance to further element and the elements in stack would be useless \n3. While doing so store the values in left and right arrays.\n4. Now traverse in array and now we can find left and right smaller blocks in constant time\n\n**Time: O(n)\nSpace: O(n)**\n\n\n\n\n```\nclass Solution {\npublic:\nint largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n vector<int> left(n, 0) , right(n, 0);\n\n stack<int> s;\n\n for (int i = 0; i < n; i++) {\n while (!s.empty() and heights[s.top()] >= heights[i]) {\n s.pop();\n }\n left[i] = (s.empty()) ? -1 : s.top();\n s.push(i);\n }\n\n while (!s.empty())\n s.pop();\n\n for (int i = n - 1; i >= 0; i--) {\n while (!s.empty() and heights[s.top()] >= heights[i]) {\n s.pop();\n }\n right[i] = (s.empty()) ? n : s.top();\n s.push(i);\n }\n\n int ans = INT_MIN;\n\n for (int i = 0; i < n; i++) {\n int distance = right[i] - left[i] - 1;\n ans = max(ans , heights[i] * distance);\n }\n\n\n return ans;\n\n}\n};\n``` | 11 | 0 | ['Monotonic Stack'] | 0 |
largest-rectangle-in-histogram | ✅C++ solution using Stack & Arrays with full explanations | c-solution-using-stack-arrays-with-full-0j6vx | If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!\u27 | dhruba-datta | NORMAL | 2022-01-22T13:06:46.186991+00:00 | 2022-01-22T17:45:09.380765+00:00 | 760 | false | > **If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!\u2764\uFE0F**\n> \n\n---\n## Explanation:\n\n### Solution 01\n\n- Here we\u2019ll take a stack & 2 arrays to solve it.\n- We\u2019ll find the left and right smaller of every index and store it in left and right array.\n- In the stack, we\u2019ll store the index which is in increasing order for the left array.\n- For the right array, we\u2019ll store decreasing indexes in the stack.\n- After iterating all elements we\u2019ll calculate the area using **`max(ans, heights[i]*(right[i]-left[i]+1))`**\n- **Time complexity:** O(n).\n\n---\n\n## Code:\n\n```cpp\n//Solution 01:\n**class Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size(), ans = 0, left[n], right[n];\n stack<int> st;\n \n for(int i=0; i<n; i++){\n while(!st.empty() && heights[st.top()] >= heights[i]) st.pop();\n if(st.empty()) left[i]=0;\n else left[i] = st.top() + 1;\n st.push(i);\n }\n \n while(!st.empty()) st.pop();\n \n for(int i=n-1; i>=0; i--){\n while(!st.empty() && heights[st.top()] >= heights[i]) st.pop();\n if(st.empty()) right[i] = n-1;\n else right[i] = st.top() - 1;\n st.push(i);\n }\n \n for(int i=0; i<n; i++)\n ans = max(ans, heights[i]*(right[i]-left[i]+1));\n \n return ans;\n }\n};**\n```\n\n---\n\n> **Please upvote this solution**\n> | 11 | 0 | ['C', 'C++'] | 1 |
largest-rectangle-in-histogram | Python solution | python-solution-by-zitaowang-fu9r | Initialize an empty stack and iterate over the elements in heights. Suppose we are at index i, we can construct stack in such a way that it contains all the rec | zitaowang | NORMAL | 2021-01-19T04:07:32.835863+00:00 | 2021-01-19T04:08:24.256004+00:00 | 846 | false | Initialize an empty `stack` and iterate over the elements in `heights`. Suppose we are at index `i`, we can construct `stack` in such a way that it contains all the rectangles that started at an index `j <= i`, and can survive `i` (i.e., `height[j] <= height[i]`). By construction, the rectangles in `stack` will have a monotonic non-decreasing height. More specifically, at index `i`, we have the following possibilities:\n1. The `stack` is empty, in which case, we add `(i, heights[i])` into `stack`, i.e., a rectangle starting at `i` of height `heights[i]`.\n2. The `stack` is non-empty, and `stack[-1][1] <= heights[i]`, in which case all rectangles in the `stack` will be able to survive `i`, and we don\'t need to do anything about existing elements in `stack`. We just need to append `(i, heights[i])` to the `stack`.\n3. The `stack` is non-empty, and `stack[-1][1] > heights[i]`, in which case rectangles in `stack` with height larger than `heights[i]` will not be able to survive `i`. So we keep popping the `stack` until it\'s empty or the last element of the stack has height no larger than `heights[i]`. Each time we pop `stack`, and get an element `(j, m)`, we need to update the `max_area`, because there is a rectangle of height `m` that started at `j` and end at `i - 1`, with area `(i - j) * m`, and it may well be the rectangle with the largest area. Finally, we need to append a rectangle `stack` of height `heights[i]`. To maximize its area, we want to make its starting point as small as possible. The smallest it can be is the starting point of the shortest rectangle that fails to survive `i`, which is the index of the last rectangle we popped from `stack`. So when finish `stack`, we just need to append `(j, heights[i])` to it.\n\nFinally, after iterating over `heights`, whatever that\'s left in `stack` are all the rectangles that managed to survive the last index of `heights`. So we just need to pop out each element `(j, m)` in `stack`, and check its area `(len(heights) - j) * m` is larger than `max_area`, and update `max_area` accordingly. After this, `max_area` is the desired solution to the problem.\n\nTime complexity: O(n), space complexity: O(n).\n\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n stack = []\n max_area = 0\n l = len(heights)\n for i, n in enumerate(heights):\n if not stack or stack[-1][1] <= n:\n stack.append((i, n))\n else:\n while stack and stack[-1][1] > n:\n j, m = stack.pop()\n max_area = max(max_area, (i - j) * m)\n stack.append((j, n))\n \n while stack:\n j, m = stack.pop()\n max_area = max(max_area, (l - j) * m)\n return max_area\n``` | 11 | 0 | [] | 1 |
largest-rectangle-in-histogram | TLE for test case 3000 consecutive 1s | tle-for-test-case-3000-consecutive-1s-by-ef9q | It passes the custom testcase in 24ms, but when I submit it's TLE..\n\nCode:\n\n public class Solution {\n public int largestRectangleArea(int[] heigh | arkansol | NORMAL | 2015-10-19T03:09:56+00:00 | 2015-10-19T03:09:56+00:00 | 1,445 | false | It passes the custom testcase in 24ms, but when I submit it's TLE..\n\nCode:\n\n public class Solution {\n public int largestRectangleArea(int[] height) {\n Stack<Integer> maxIdx = new Stack<Integer>();\n int area = 0;\n for (int i = 0; i < height.length; i++) {\n if (maxIdx.isEmpty() || height[maxIdx.peek()] <= height[i]) {\n maxIdx.push(i);\n } else {\n int idx = maxIdx.pop();\n int width = maxIdx.isEmpty() ? i : i - maxIdx.peek() - 1;\n area = Math.max(area, width * height[idx]);\n i--;\n }\n }\n while(!maxIdx.isEmpty()) {\n int idx = maxIdx.pop();\n int width = maxIdx.isEmpty() ? height.length : height.length - maxIdx.peek() - 1;\n area = Math.max(area, width * height[idx]);\n }\n return area;\n }\n }\n\nThanks! | 11 | 0 | [] | 2 |
largest-rectangle-in-histogram | Java Easy Solution | java-easy-solution-by-suryanshhbtu-1pko | \nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int ans=0;\n int ps[]=previousSmall(heights);\n int ns[]=nextSma | suryanshhbtu | NORMAL | 2022-02-05T19:20:22.559218+00:00 | 2022-02-05T19:20:22.559258+00:00 | 949 | false | ```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int ans=0;\n int ps[]=previousSmall(heights);\n int ns[]=nextSmall(heights);\n for(int i=0 ;i<heights.length ;i++){\n ans=Math.max(ans,(ns[i]-ps[i]-1)*heights[i]);\n }\n return ans;\n }\n public int[] previousSmall(int[] arr) {\n int n=arr.length;\n Stack<Integer> s= new Stack<>();\n int[] ans=new int[n];\n for(int i=0 ;i<n ;i++){\n while(!s.isEmpty() && arr[s.peek()]>=arr[i]) s.pop();\n if(s.isEmpty()) ans[i]=-1;\n else ans[i]=s.peek();\n \n s.push(i);\n }\n return ans;\n \n }\n public int[] nextSmall(int[] arr) {\n int n=arr.length;\n Stack<Integer> s= new Stack<>();\n int[] ans=new int[n];\n for(int i=n-1 ;i>=0 ;i--){\n while(!s.isEmpty() && arr[s.peek()]>=arr[i]) s.pop();\n if(s.isEmpty()) ans[i]=n;\n else ans[i]=s.peek();\n \n s.push(i);\n }\n return ans;\n \n }\n}\n\n``` | 10 | 0 | ['Stack', 'Java'] | 0 |
largest-rectangle-in-histogram | Easy C++ sol with just one traversal | easy-c-sol-with-just-one-traversal-by-by-cazx | Pre-requisite = Previous smaller element using stack.\n\nIdea :-The idea is to use the concept of next smaller element and previous smaller element, we will mai | byteZorvin | NORMAL | 2022-01-29T07:58:51.097926+00:00 | 2022-01-29T09:22:58.099945+00:00 | 301 | false | **Pre-requisite** = Previous smaller element using stack.\n\n**Idea** :-The idea is to use the concept of next smaller element and previous smaller element, we will maintain the index of previous smaller element in the stack and we can get the next smaller element when we pop the element from the stack as the element is popped only when we encounter a smaller element. If at the end the stack is not empty , then for those elements there was no next smaller element so we can consider the next smaller element to exist at the the index = size of the vector/ array, while the previous smaller element is always just below the element it in the stack given the stack had an element below it, otherwise consider the previous smaller element at -1. \n\n```\nint largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n stack<int> st;\n int maxArea = 0;\n \n for(int i = 0; i<n; i++) {\n while(!st.empty() && heights[i] <= heights[st.top()]) {\n int ind = st.top();\n st.pop();\n int currArea = heights[ind]*(st.empty() ? i : i - st.top() - 1);\n maxArea = max(maxArea, currArea);\n }\n st.push(i);\n }\n \n while(!st.empty()) {\n int ind = st.top();\n st.pop();\n int currArea = heights[ind]*(st.empty() ? n : n - st.top() - 1);\n maxArea = max(maxArea, currArea);\n }\n return maxArea;\n }\n``` | 10 | 0 | [] | 1 |
largest-rectangle-in-histogram | python using stack | python-using-stack-by-texasroh-0fcz | \nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n ans = 0\n stack = []\n heights = [0] + heights + [0]\n | texasroh | NORMAL | 2020-02-16T06:44:15.079848+00:00 | 2020-02-16T06:44:15.079884+00:00 | 1,729 | false | ```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n ans = 0\n stack = []\n heights = [0] + heights + [0]\n for i in range(len(heights)):\n while(stack and heights[stack[-1]] > heights[i]):\n j = stack.pop()\n ans = max(ans, (i-stack[-1]-1)*heights[j])\n stack.append(i)\n return ans\n```\t\t | 10 | 0 | ['Stack', 'Python'] | 2 |
largest-rectangle-in-histogram | 16ms [c++] 10-line code with stack | 16ms-c-10-line-code-with-stack-by-cq2159-e18b | int largestRectangleArea(vector<int>& height) {\n height.push_back(0); \n int len = height.size(),res = 0, cur=1;\n int s[len+1]={0};\n | cq2159 | NORMAL | 2015-10-03T20:35:45+00:00 | 2015-10-03T20:35:45+00:00 | 3,221 | false | int largestRectangleArea(vector<int>& height) {\n height.push_back(0); \n int len = height.size(),res = 0, cur=1;\n int s[len+1]={0};\n s[0]=-1;\n for(int i=1;i<len;i++){\n while(cur && height[i]<height[s[cur]])\n res = max(res, height[s[cur]] * (i-s[--cur]-1));\n s[++cur]=i;\n }\n return res;\n }\nThe idea is simply to insert position -1 to the beginning of the stack s, therefore we don't need to check whether the stack is empty or not. \nFor the height, push a "0" to the end to update the result until the last element in the height.\nHere I use an int array to simulate the stack for better time performance. | 10 | 1 | ['C++'] | 3 |
largest-rectangle-in-histogram | 10 line c++ solution | 10-line-c-solution-by-kenigma-wbkg | \n\n class Solution {\n public:\n int largestRectangleArea(vector& heights) {\n int res = 0;\n for (int i = 0; i < heights.si | kenigma | NORMAL | 2016-03-03T18:10:05+00:00 | 2018-09-12T13:20:56.131499+00:00 | 2,515 | false | \n\n class Solution {\n public:\n int largestRectangleArea(vector<int>& heights) {\n int res = 0;\n for (int i = 0; i < heights.size(); ++i) {\n if (i + 1 < heights.size() && heights[i] <= heights[i+1]) continue; // find the local max (greater than left and right)\n int minh = heights[i];\n for (int j = i; j >= 0; --j) {\n minh = min(minh, heights[j]);\n res = max(res, minh * (i - j + 1));\n }\n }\n return res;\n }\n }; | 10 | 1 | ['C++'] | 3 |
largest-rectangle-in-histogram | ✅ Simple clean stack approach with explanation | simple-clean-stack-approach-with-explana-0mx2 | Approach\n1. Monotonic Stack: Utilize a monotonic stack to keep track of heights and indices in ascending order. If the height encountered is less than the heig | MostafaAE | NORMAL | 2024-03-24T03:16:47.119682+00:00 | 2024-03-24T03:16:47.119710+00:00 | 1,185 | false | # Approach\n1. Monotonic Stack: Utilize a monotonic stack to keep track of heights and indices in ascending order. If the height encountered is less than the height at the top of the stack, pop elements from the stack and calculate the area of the rectangles until the current index.\n2. Compute Largest Area: While popping elements from the stack, calculate the area of the rectangle formed by the popped height and the current index, considering the width as the difference between the current index and the index at the top of the stack.\n\n# Complexity\n- Time complexity:\n`O(n)`\n\n- Space complexity:\n`O(n)`\n\n# Code\n```\nclass Solution {\npublic:\n /* \n * Approach:\n * 1. Monotonic Stack: Utilize a monotonic stack to keep track of heights and indices in ascending order. If the height encountered is less than the height at the top of the stack, pop elements from the stack and calculate the area of the rectangles until the current index.\n * 2. Compute Largest Area: While popping elements from the stack, calculate the area of the rectangle formed by the popped height and the current index, considering the width as the difference between the current index and the index at the top of the stack.\n * \n * Complexity:\n * Time Complexity : O(n)\n * Space Complexity : O(n)\n */\n int largestRectangleArea(vector<int>& heights) \n {\n heights.push_back(-1);\n stack<pair<int, int>> st;\n int largestArea{};\n \n for(int i = 0 ; i < (int)heights.size() ; i++)\n {\n int startIdx{i};\n while(!st.empty() && heights[i] < st.top().first)\n {\n auto [height, idx] = st.top();\n st.pop();\n largestArea = max(largestArea, height * (i - idx));\n startIdx = idx;\n }\n st.push({heights[i], startIdx});\n }\n \n return largestArea;\n }\n};\n```\n\n**Please consider upvoting \u2B06\uFE0F if you found this solution helpful! Thank you!** | 9 | 0 | ['Stack', 'Monotonic Stack', 'C++'] | 1 |
largest-rectangle-in-histogram | Easy understanding solution with monotonic stack C++ (image explanation included) | easy-understanding-solution-with-monoton-zk9g | Intuition\n Describe your first thoughts on how to solve this problem. \nTry to find the longest width w.r.t. height[i], which means we have to find the most le | sunskyxh | NORMAL | 2023-12-21T01:28:30.861537+00:00 | 2023-12-21T01:30:30.396734+00:00 | 663 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry to find the longest width w.r.t. `height[i]`, which means we have to find the most left (called `start`) and right (called `end`) positions where the all the heights between `[start, end]` are greater or equal to `height[i]`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing monotonic stack to find the first lower element in both left and right directions. If the index of the first lower element is `l`, it means from position `l + 1` to current position `i`, all the heights are greater or equal to current height `height[i]`. This is same for the right direction.\nAfter we find the first lower element in left (called `start`) and right(called `end`) directions, the width of this rectangle is `end - start + 1`, for each height, we can calculate the area respectively.\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nWhile building `starts` and `ends` and calculating the `max_area`, we traverse each element at most once.\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe `starts` and `ends` have the same size as `heights`.\n\n# Code\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int max_area = 0;\n int n = heights.size();\n vector<int> starts(n, 0);\n vector<int> ends(n, 0);\n \n stack<int> st;\n // Step 1: find the `start` for each height using monotonic stack.\n for (int i = n - 1; i >= 0; i--) {\n while (!st.empty() && heights[st.top()] > heights[i]) {\n starts[st.top()] = i + 1;\n st.pop();\n };\n st.push(i);\n }\n\n while(!st.empty()) {\n starts[st.top()] = 0;\n st.pop();\n }\n\n // Step 2: find the `end` for each height using monotonic stack.\n for (int i = 0; i < n; i++) {\n while (!st.empty() && heights[st.top()] > heights[i]) {\n ends[st.top()] = i - 1;\n st.pop();\n };\n st.push(i);\n }\n\n while(!st.empty()) {\n ends[st.top()] = n - 1;\n st.pop();\n }\n\n // Step 3: calcuate the area for each height. \n for (int i = 0; i < n; i++) {\n int width = ends[i] - starts[i] + 1;\n max_area = max(max_area, heights[i] * width);\n }\n return max_area;\n }\n};\n``` | 9 | 0 | ['Greedy', 'Monotonic Stack', 'C++'] | 0 |
largest-rectangle-in-histogram | Simplest C# solution with stack<int> | simplest-c-solution-with-stackint-by-sto-brey | \n\npublic class Solution {\n public int LargestRectangleArea(int[] heights) {\n int n = heights.Length;\n int max = 0;\n var stack = ne | stodorov | NORMAL | 2023-09-23T12:04:13.772142+00:00 | 2023-09-23T12:04:13.772161+00:00 | 591 | false | \n```\npublic class Solution {\n public int LargestRectangleArea(int[] heights) {\n int n = heights.Length;\n int max = 0;\n var stack = new Stack<int>();\n\n for(int i = 0; i <= n; i++)\n {\n var height = i < n ? heights[i] : 0;\n\n while(stack.Any() && heights[stack.Peek()] > height)\n {\n var currHeight = heights[stack.Pop()];\n var prevIndex = stack.Count == 0 ? -1 : stack.Peek();\n \n max = Math.Max(max, currHeight * (i - 1 - prevIndex));\n }\n\n stack.Push(i);\n }\n \n return max;\n }\n}\n\n``` | 9 | 0 | ['C#'] | 1 |
largest-rectangle-in-histogram | C++ || Stack Solution || Next smaller to left &Right | c-stack-solution-next-smaller-to-left-ri-2bi0 | \t// find the index vector for next smaller to left\n\t// find the index vector for next smaller to right \n\t// width will be right[i]-left[i]-1 \n\t// here st | anubhavsingh11 | NORMAL | 2022-06-24T17:55:28.808295+00:00 | 2022-06-24T17:55:28.808340+00:00 | 465 | false | \t// find the index vector for next smaller to left\n\t// find the index vector for next smaller to right \n\t// width will be right[i]-left[i]-1 \n\t// here stack<pair<int,int>> first element in pair denotes height[i] and \n\t// second element of pair corresponds to index i \n\n\tclass Solution {\n\tpublic:\n\t\t// next smaller to left --> traverse from left \n\t\t// here we will assume that one building is at index -1 of 0 height\n\t\tvector<int>NSL(vector<int>h)\n\t\t{\n\t\t\tvector<int>left;\n\t\t\tstack<pair<int,int>>st;\n\t\t\tint pseudo=-1; \n\t\t\tfor(int i=0;i<h.size();i++)\n\t\t\t{\n\t\t\t\tif(st.empty())\n\t\t\t\t left.push_back(pseudo);\n\n\t\t\t\telse if(st.size()>0 && st.top().first<h[i])\n\t\t\t\t\tleft.push_back(st.top().second);\n\n\t\t\t\telse if(st.size()>0 && st.top().first>=h[i])\n\t\t\t\t{\n\t\t\t\t\twhile(st.size()>0 && st.top().first>=h[i])\n\t\t\t\t\t\tst.pop();\n\t\t\t\t\tif(st.empty())\n\t\t\t\t\t\tleft.push_back(pseudo);\n\t\t\t\t\telse \n\t\t\t\t\t\tleft.push_back(st.top().second);\n\t\t\t\t}\n\t\t\t\tst.push({h[i],i});\n\t\t\t}\n\t\t\treturn left;\n\t\t}\n\n\t\t// next smaller to right traverse --> from right \n\t\t// here we will assume that one building is after lastmost index of 0 height\n\t\tvector<int>NSR(vector<int>h)\n\t\t{\n\t\t\tvector<int>right;\n\t\t\tstack<pair<int,int>>st;\n\t\t\tint pseudo=h.size(); \n\t\t\tfor(int i=h.size()-1;i>=0;i--)\n\t\t\t{\n\t\t\t\tif(st.empty())\n\t\t\t\t right.push_back(pseudo);\n\t\t\t\telse if(st.size()>0 && st.top().first<h[i])\n\t\t\t\t\tright.push_back(st.top().second);\n\t\t\t\telse if(st.size()>0 && st.top().first>=h[i])\n\t\t\t\t{\n\t\t\t\t\twhile(st.size()>0 && st.top().first>=h[i])\n\t\t\t\t\t\tst.pop();\n\t\t\t\t\tif(st.empty())\n\t\t\t\t\t\tright.push_back(pseudo);\n\t\t\t\t\telse \n\t\t\t\t\t\tright.push_back(st.top().second);\n\t\t\t\t}\n\t\t\t\tst.push({h[i],i});\n\t\t\t}\n\t\t\treturn right;\n\t\t}\n\n\t\tint largestRectangleArea(vector<int>& heights) {\n\t\t\tvector<int>left=NSL(heights);\n\t\t\tvector<int>right=NSR(heights);\n\t\t\tvector<int>width;\n\t\t\treverse(right.begin(),right.end()); // reversing to get the correct order of next smaller to right\n\n\t\t\tint maxarea=-1;\n\t\t\tfor(int i=0;i<heights.size();i++)\n\t\t\t{\n\t\t\t\tint width=right[i]-left[i]-1;\n\t\t\t\tmaxarea=max(maxarea,width*heights[i]);\n\t\t\t}\n\t\t\treturn maxarea;\n\t\t}\n\t}; | 9 | 0 | ['Stack', 'C'] | 1 |
largest-rectangle-in-histogram | JavaScript Using Stack Beat 97% | javascript-using-stack-beat-97-by-contro-3zwu | Time Complexity = O(N)\nSpace Complexity = O(N)\njavascript\nvar largestRectangleArea = function(heights) {\n // to deal with last element without going out | control_the_narrative | NORMAL | 2020-07-16T15:57:07.544484+00:00 | 2020-07-16T18:15:11.288860+00:00 | 1,562 | false | Time Complexity = O(N)\nSpace Complexity = O(N)\n```javascript\nvar largestRectangleArea = function(heights) {\n // to deal with last element without going out of bound\n heights.push(0)\n const stack = [];\n let maxArea = 0, curr, currH, top, topH, area;\n \n for(let i = 0; i < heights.length; i++) {\n top = stack[stack.length-1];\n topH = heights[top];\n // pop from stack as long as the top of the stack\n // is greater than the current height and\n // the stack has at least 2 items\n while(stack.length > 1 && topH > heights[i]) {\n curr = stack.pop();\n currH = heights[curr];\n top = stack[stack.length-1];\n topH = heights[top];\n area = currH * (i - 1 - top);\n maxArea = Math.max(area, maxArea);\n }\n \n // when only 1 item left in the stack\n if(stack.length && topH > heights[i]) {\n curr = stack.pop();\n currH = heights[curr];\n area = currH * i;\n maxArea = Math.max(area, maxArea);\n }\n stack.push(i);\n }\n return maxArea;\n};\n``` | 9 | 1 | ['JavaScript'] | 2 |
largest-rectangle-in-histogram | Short C++ solution use stack AC 28ms | short-c-solution-use-stack-ac-28ms-by-cc-lb52 | class Solution {\n public:\n int largestRectangleArea(vector<int>& height) {\n height.push_back(0);\n int result=0;\n | ccweikui | NORMAL | 2015-06-06T04:45:44+00:00 | 2018-08-15T22:53:27.420024+00:00 | 2,362 | false | class Solution {\n public:\n int largestRectangleArea(vector<int>& height) {\n height.push_back(0);\n int result=0;\n stack<int> indexStack;\n for(int i=0;i<height.size();i++){\n while(!indexStack.empty()&&height[i]<height[indexStack.top()]){\n int top=indexStack.top();\n indexStack.pop(); \n int nextTop=indexStack.size()==0?-1:indexStack.top();\n result=max((i-nextTop-1)*height[top],result);\n }\n indexStack.push(i);\n }\n return result;\n }\n }; | 9 | 0 | [] | 1 |
largest-rectangle-in-histogram | Explination of the stack solution (python solution) | explination-of-the-stack-solution-python-t8qk | To get the bigest rectangle area, we should check every rectangle with lowest point at i=1...n. \n\nDefine Si := the square with lowest point at i. \nTo calcu | jddymx | NORMAL | 2015-10-09T20:40:21+00:00 | 2015-10-09T20:40:21+00:00 | 2,804 | false | To get the bigest rectangle area, we should check every rectangle with lowest point at i=1...n. \n\nDefine `Si := the square with lowest point at i`. \nTo calculate faster this `Si` , we have to use a stack `stk` which stores some *indices*. \n\nThe elements in stk satisfy these **properties**: \n\n1. the indices as well as the corresponding heights are in ascending order \n2. for any adjecent indices i and j (eg. s=[...,i,j,...]), any index k between i and j are of height higher than j: \nheight[k]>height[j] \n\nWe loop through all indices, when we meet an index `k` with height lower than elements in stk (let's say, lower than index `i` in `stk`), we know that the right end of square `Si` is just `k-1`. And what is the left end of this square? Well it is just the index to the left of `i` in stk ! \n\nAnother important thing is that we should append a 0 to the end of height, so that all indices in stk will be checked this way. \n\n\n class Solution(object):\n def largestRectangleArea(self, height):\n """\n :type height: List[int]\n :rtype: int\n """\n mx = 0\n stk = []\n height.append(0) # very important!!\n for k in xrange(len(height)): \n while(stk and height[k]<height[stk[-1]]):\n rect = height[stk.pop()] * (k if not stk else k-stk[-1]-1)\n mx = max(mx, rect)\n stk.append(k)\n return mx | 9 | 0 | ['Python'] | 1 |
largest-rectangle-in-histogram | Python solution with detailed explanation | python-solution-with-detailed-explanatio-b89x | Solution with discussion https://discuss.leetcode.com/topic/77574/python-solution-with-detailed-explanation\n\nLargest Rectangle in Histogram https://leetcode.c | gabbu | NORMAL | 2017-02-02T17:34:57.476000+00:00 | 2018-08-27T02:01:09.537966+00:00 | 2,204 | false | **Solution with discussion** https://discuss.leetcode.com/topic/77574/python-solution-with-detailed-explanation\n\n**Largest Rectangle in Histogram** https://leetcode.com/problems/largest-rectangle-in-histogram/\n\nhttp://www.geeksforgeeks.org/largest-rectangle-under-histogram/\nhttp://www.geeksforgeeks.org/largest-rectangular-area-in-a-histogram-set-1/\n\n1. For every bar \u2018x\u2019, we calculate the area with \u2018x\u2019 as the smallest bar in the rectangle. \n2. If we calculate such area for every bar \u2018x\u2019 and find the maximum of all areas, our task is done. \n3. How to calculate area with \u2018x\u2019 as smallest bar? We need to know index of the first smaller (smaller than \u2018x\u2019) bar on left of \u2018x\u2019 and index of first smaller bar on right of \u2018x\u2019. Let us call these indexes as \u2018left index\u2019 and \u2018right index\u2019 respectively.\n4. We traverse all bars from left to right, maintain a stack of bars. Every bar is pushed to stack once. \n5. A bar is popped from stack when a bar of smaller height is seen. \n6. When a bar is popped, we calculate the area with the popped bar as smallest bar. \n7. **How do we get left and right indexes of the popped bar \u2013 the current index tells us the \u2018right index\u2019 and index of previous item in stack is the \u2018left index\u2019. Note index of previous item is important here.** \n8. Now using the above idea, we can make both an N^2 and NlgN algorithm.\n9. For N^2 algorithm, no stack is requried. We scan at each step in left and right direction.\n10. For NlgN algorithm, we find the minimum height m1. We then split at the minimum height.\n\n```\nclass Solution(object):\n def largestRectangleArea(self, heights):\n """\n :type heights: List[int]\n :rtype: int\n """\n max_area, st = 0, []\n for idx,x in enumerate(heights):\n if len(st) == 0:\n st.append(idx)\n elif x >= heights[st[-1]]:\n st.append(idx)\n else:\n while st and heights[st[-1]] > x:\n # For min_height, the right index is idx and the left index is st[-1].\n # Distance between them will be (right_index - left_index - 1). right & left index are not included in result.\n # If the stack is empty, then no bar on left is smaller. So width of base is idx.\n min_height = heights[st.pop()] \n max_area = max(max_area, min_height*(idx-1-st[-1])) if st else max(max_area, min_height*idx)\n st.append(idx)\n while st:\n min_height = heights[st.pop()] \n max_area = max(max_area, min_height*(len(heights)-1-st[-1])) if st else max(max_area, min_height*len(heights))\n return max_area\n``` | 9 | 1 | [] | 3 |
largest-rectangle-in-histogram | My 16ms C++ O(n) code without a stack | my-16ms-c-on-code-without-a-stack-by-bea-fqrm | Basically, I find the range (left[i], right[i]) within which the height of every element is at least height[i]. For each i, there is a rectangular with area hei | bear2015 | NORMAL | 2015-09-05T16:35:55+00:00 | 2015-09-05T16:35:55+00:00 | 2,534 | false | Basically, I find the range (left[i], right[i]) within which the height of every element is at least height[i]. For each i, there is a rectangular with area height[i] * (right[i]-left[i]+1), and the largest area must be one of them. Then run all i to find the largest area. Please notice it takes O(n) time to fill left[i] and right[i] if we use DP. We can use amortization analysis to find this out. If you think about the worst case for a certain i, if it takes k steps in the while loop to get left[i]. Then it means there are k indices (for each j update below) which only take 1 step each in the loop to find left item for these indices. Then the average number of steps of these k+1 indices is const. So it takes O(n) to fill left and right arrays.\n\n class Solution {\n public:\n int largestRectangleArea(vector<int>& height) {\n int N=height.size(), i, j, l, r, area=0, temp;\n if(N==0) return 0;\n vector<int> left(N), right(N);\n left[0]=0; //fill left[i] in the for loop\n for(i=1; i<N; ++i){\n l=i;\n j=i-1;\n while(j>=0&&height[j]>=height[i]){ // amortization shows const steps for this loop\n if(height[j]==height[i]){\n l=left[j];\n break;\n }\n l=left[j];\n j=left[j]-1;\n }\n left[i]=l;\n }\n right[N-1]=N-1; //fill right[i] in the for loop\n for(i=N-2; i>=0; --i){\n r=i;\n j=i+1;\n while(j<N && height[j]>=height[i]){ \n if(height[j]==height[i]){\n r=right[j];\n break;\n }\n r=right[j];\n j=right[j]+1;\n }\n right[i]=r;\n }\n for(i=0; i<N; ++i){\n temp=height[i]*(right[i]-left[i]+1);\n if(temp>area) area = temp;\n }\n return area;\n }\n }; | 9 | 0 | ['Dynamic Programming', 'C++'] | 2 |
largest-rectangle-in-histogram | TWO APPROACHES USING LEFT AND RIGHT MINIMUM || SINGLE PASS || O( N ) ✅✅ | two-approaches-using-left-and-right-mini-n6ad | Approach 1\n\n### Intuition:\nWe can solve this problem using a stack to efficiently calculate the left and right boundaries of each bar.\n\n### Approach:\n1. U | Sabari_Raj_004 | NORMAL | 2024-05-07T06:36:31.386832+00:00 | 2024-05-07T06:36:31.386865+00:00 | 1,004 | false | ## Approach 1\n\n### Intuition:\nWe can solve this problem using a stack to efficiently calculate the left and right boundaries of each bar.\n\n### Approach:\n1. Use two passes:\n - In the first pass, calculate the left boundary of each bar.\n - In the second pass, calculate the right boundary of each bar and simultaneously update the maximum area.\n2. To calculate the left boundary:\n - Use a stack to store the indices of bars.\n - Traverse the histogram from left to right.\n - For each bar, pop elements from the stack until finding a smaller bar.\n - The left boundary of the current bar is the index at the top of the stack.\n3. To calculate the right boundary and update the maximum area:\n - Repeat the same process as above, but traverse the histogram from right to left.\n - For each bar, pop elements from the stack until finding a smaller bar.\n - The right boundary of the current bar is the index at the top of the stack.\n - Update the maximum area by computing the area of the rectangle formed by the current bar.\n\n### Explanation: \n- We maintain two arrays, left[] and right[], to store the left and right boundaries of each bar.\n- In the first pass, we calculate the left boundaries using a stack.\n- In the second pass, we calculate the right boundaries and simultaneously update the maximum area.\n- The maximum area is updated by computing the area of the rectangle formed by each bar.\n\n### Time Complexity \nO(n), where n is the number of bars in the histogram.\n\n### Space Complexity:\nO(n), used for the stack and left/right arrays.\n\n### Example with Clear Explanation:\nConsider the histogram [2,1,5,6,2,3]. \nUsing Approach 1:\n - Calculate the left boundaries: [null,null,1,2,1,4]\n - Calculate the right boundaries and update maxArea:\n [4,5,2,4,4,6] => Max Area = 10\n\n### Code for Approach 1:\n\n```java\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n public int largestRectangleArea(int[] heights) {\n Stack<Integer> st=new Stack<>();\n int n=heights.length;\n int left[]=new int[n];\n int right[]=new int[n];\n Arrays.fill(left,-1);\n Arrays.fill(right,n);\n\n int i=0,c=0;\n while(i<n){\n while(!st.isEmpty()&&heights[st.peek()]>=heights[i]){\n st.pop();\n }\n if(!st.isEmpty()) left[i]=st.peek();\n st.add(i);\n i++;\n }\n st.clear();\n i=n-1;\n while(i>=0){\n while(!st.isEmpty()&&heights[st.peek()]>=heights[i]){\n st.pop();\n }\n if(!st.isEmpty()) right[i]=st.peek();\n st.add(i);\n c=Math.max(c,heights[i]*(right[i]-left[i]-1));\n i--;\n }\n return c;\n }\n}\n```\n## Approach 2\n\n### Intuition:\nSimilar to Approach 1, but with a slight optimization in how we handle the right boundaries.\n\n### Approach:\n1. Use a single pass:\n - Traverse the histogram from left to right.\n - For each bar, calculate its left boundary and simultaneously update the maximum area.\n - When calculating the right boundary, instead of another pass, we calculate the width directly.\n2. To calculate the left boundary:\n - Use a stack to store the indices of bars.\n - Traverse the histogram from left to right.\n - For each bar, pop elements from the stack until finding a smaller bar.\n - The left boundary of the current bar is the index at the top of the stack.\n3. To calculate the width and update the maximum area:\n - When calculating the right boundary, calculate the width directly using the current index and the index at the top of the stack.\n - Update the maximum area by computing the area of the rectangle formed by each bar.\n\n### Explanation: \n- Similar to Approach 1, but with a single pass and optimized calculation of the right boundary.\n\n### Time Complexity \nO(n), where n is the number of bars in the histogram.\n\n### Space Complexity:\nO(n), used for the stack and left array.\n\n### Example with Clear Explanation:\nConsider the histogram [2,1,5,6,2,3]. \nUsing Approach 2:\n - Calculate the left boundaries: [null,null,1,2,1,4]\n - Calculate the right boundaries and update maxArea:\n [null, 0, 1, 2, 1, 6] => Max Area = 10\n\n### Code for Approach 2:\n\n```java\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n Stack<Integer> st=new Stack<>();\n int n=heights.length;\n int left[]=new int[n];\n Arrays.fill(left,-1);\n int i=0,c=0;\n while(i<n){\n while(!st.isEmpty()&&heights[st.peek()]>=heights[i]){\n int t=st.pop();\n c=Math.max(c,heights[t]*(i-(!st.isEmpty()?st.peek():-1)-1));\n }\n if(!st.isEmpty()) left[i]=st.peek();\n st.add(i);\n i++;\n }\n while(!st.isEmpty()){\n int t=st.pop();\n c=Math.max(c,heights[t]*(n-(!st.isEmpty()?st.peek():-1)-1));\n }\n return c;\n }\n}\n```\n\n | 8 | 0 | ['Array', 'Stack', 'Monotonic Stack', 'Java'] | 1 |
largest-rectangle-in-histogram | ✅Easy✨||C++ || Beats 100% || With proper Explanation | easyc-beats-100-with-proper-explanation-g5zhb | Intuition\n Describe your first thoughts on how to solve this problem. \nWe will use two function next smaller and prev smaller element function and by getting | olakade33 | NORMAL | 2024-02-22T14:08:02.718362+00:00 | 2024-02-22T14:08:02.718396+00:00 | 1,199 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe will use two function next smaller and prev smaller element function and by getting that value we will find width and length is properly the height of histogram by simply just multiplying width and length we will get area and at the end using max function we will get maximun area in histogram.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The function largestRectangleArea takes a vector heights representing the heights of bars in a histogram.It initializes variables n to store the size of the heights vector and area to store the maximum area.It declares two vectors next and prev, which will be used to store the indices of the next smaller and previous smaller elements, respectively, for each element in the heights vector.\n\n2. The function then calls the helper functions nextelement and prevelement, which use a stack to find the next smaller and previous smaller elements\' indices for each element in the heights vector.After calculating the next and prev vectors, the function iterates through each element in the heights vector using a for loop.\n\n3. For each element, it calculates the width of the rectangle by subtracting the index of the previous smaller element from the index of the next smaller element and subtracting 1. This width represents the width of the rectangle formed by considering the current element as the height.The height of the rectangle is the value of the current element (heights[i]).\n\n4. The area of the rectangle is then calculated by multiplying the height and width.The function updates the area with the maximum value found so far.\n\n5. Finally, the function returns the maximum area found.\nThe algorithm essentially calculates the area of the largest rectangle that can be formed for each bar in the histogram by considering it as the height and extending it to the left and right until it encounters bars that are lower or of equal height.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(3N) -~= O(N)\n# Code\n```\nclass Solution {\npublic:\nvector<int> prevSmallerElement(vector<int>& input) {\n stack<int>s;\n s.push(-1);\n vector<int> ans(input.size());\n \n //left to right-> prev smaller element\n for(int i =0; i<input.size(); i++) {\n int curr = input[i];\n\n //your answer in stack\n while(s.top() != -1 && input[s.top()] >= curr) {\n s.pop();\n }\n\n //smallelemeent is found h ans store \n ans[i] = s.top();\n \n//push the curr elemen t\ns.push(i);\n }\nreturn ans;\n\n}\n\nvector<int> nextSmaller(vector<int> &input) {\n stack<int>s;\n s.push(-1);\n vector<int> ans(input.size());\n \n //left to right-> prev smaller element\n for(int i =input.size()-1; i>=0; i--) {\n int curr = input[i];\n\n //your answer in stack\n while(s.top() != -1 && input[s.top()] >= curr) {\n s.pop();\n }\n\n //smallelemeent is found h ans store \n ans[i] = s.top();\n \n//push the curr elemen t\ns.push(i);\n }\nreturn ans;\n}\n int largestRectangleArea(vector<int>& heights) {\n //step 1: prevSmaller output\n vector<int> prev = prevSmallerElement(heights);\n\n //step 2: nextSmaller call\n vector<int> next = nextSmaller(heights);\n\n int maxArea = INT_MIN;\n int size = heights.size();\n\n for(int i=0; i<heights.size(); i++) {\n int length = heights[i];\n \n //this is important step in code to ressign value to the size of histogram\n if(next[i] == -1) {\n next[i] = size;\n }\n\n int width = next[i] - prev[i] -1;\n\n int area = length*width;\n\n maxArea = max(maxArea, area);\n }\n return maxArea;\n }\n};\n``` | 8 | 0 | ['C++'] | 0 |
largest-rectangle-in-histogram | Shortest Code || Rat bhi skte ho | shortest-code-rat-bhi-skte-ho-by-surajma-l0vc | daalo -1 stack mein, aur 0 ko nums ke back mein\n2. jaldi se krlo pura yaad, interviewer ke saamne krdena anuvaad\n3. upvote kroge to milegi jrur, ldki nhi jo | surajmamgai | NORMAL | 2022-09-01T22:33:28.529643+00:00 | 2022-09-01T22:46:35.415497+00:00 | 424 | false | 1. **daalo -1 stack mein, aur 0 ko nums ke back mein**\n2. **jaldi se krlo pura yaad, interviewer ke saamne krdena anuvaad**\n3. **upvote kroge to milegi jrur, ldki nhi job huzur**\n\n\n\n\n```\n int largestRectangleArea(vector<int>& nums) {\n stack<int> st;\n st.push(-1);\n nums.push_back(0);\n int ans=0,n=nums.size();\n for(int i=0;i<n;i++)\n {\n while(!st.empty() && st.top()!=-1 && nums[i]<nums[st.top()]){\n int h=nums[st.top()],st.pop();\n ans=max(ans,h*(i-st.top()-1));\n }\n st.push(i);\n }\n return ans;\n }\n\n``` | 8 | 0 | [] | 1 |
largest-rectangle-in-histogram | Detailed explanation with diagrams and examples using pen and paper|| Brute-force and Optimized | detailed-explanation-with-diagrams-and-e-3tks | Explanation\n\n\n\n\n\n\n\nJAVA Code\n1. Brute force (To understand he concept)\n\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n | rachana_raut | NORMAL | 2022-01-29T17:03:19.883695+00:00 | 2022-01-29T17:03:19.883727+00:00 | 478 | false | **Explanation**\n\n\n\n\n\n\n\n**JAVA Code**\n1. Brute force (To understand he concept)\n```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int len = heights.length;\n if(len == 0) return 0;\n return helper(heights, len);\n }\n private int helper(int height[], int len){\n //We will check Nearest smallest to the left\n Stack <Integer> NSL = new Stack <>();\n //To check Nearest smallest to the right\n Stack <Integer> NSR = new Stack<>();\n int left[] = new int[len];\n int right[] = new int[len];\n //NSL\n for(int i = 0; i < len; i++){ \n if(NSL.isEmpty()) left[i] = -1;\n else if(!NSL.isEmpty() && height[NSL.peek()] >= height[i]){\n while(!NSL.isEmpty() && height[NSL.peek()] >= height[i])\n NSL.pop();\n if(NSL.isEmpty()) left[i] = -1;\n else left[i] = NSL.peek();\n }else left[i] = NSL.peek();\n // System.out.print("\\t" + left[i]); \n NSL.push(i); \n }\n // System.out.print("\\n");\n //NSR\n for(int i = len - 1; i >= 0; i--){\n if(NSR.isEmpty()) right[i] = len;\n else if(!NSR.isEmpty() && height[NSR.peek()] >= height[i]){\n while(!NSR.isEmpty() && height[NSR.peek()] >= height[i])\n NSR.pop();\n if(NSR.isEmpty()) right[i] = len;\n else right[i] = NSR.peek();\n }else right[i] = NSR.peek();\n // System.out.print("\\t" + right[i]); \n NSR.push(i); \n }\n int result = 0;\n// To find max distance from smallest element from left and smallest to it right\n for(int i = 0; i < len; i++){\n result = Math.max(result, (right[i] - left[i] - 1) * height[i]); \n }\n return result;\n }\n}\n```\n\n2. Optimized\n\n```\n public int largestRectangleArea(int[] heights) {\n int len = heights.length;\n Stack<Integer> s = new Stack<>();\n int maxArea = 0;\n for (int i = 0; i <= len; i++){\n int h = (i == len ? 0 : heights[i]);\n if (s.isEmpty() || h >= heights[s.peek()]) {\n s.push(i);\n } else {\n int top = s.pop();\n maxArea = Math.max(maxArea, heights[top] * (s.isEmpty() ? i : i - 1 - s.peek()));\n i--;\n }\n }\n return maxArea;\n }\n```\n\nNOTE: Try understanding concepts of Nearest smallest from left/ right && Nearest greatest from left/right for better understanding \n\n<br>\n<br>\n\nString yourReaction;\nif("understood".equals(yourReaction) || "liked it".equals(yourReaction))\nSystem.out.println(**"Please upvote!"**) | 8 | 0 | ['Java'] | 1 |
largest-rectangle-in-histogram | Easy Brute Force approach | C++ | easy-brute-force-approach-c-by-vaishnavi-p870 | \nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n=heights.size(),prev,next;\n long long maxi=0;\n f | vaishnavi_vv | NORMAL | 2022-01-29T12:10:01.750753+00:00 | 2022-01-29T12:10:01.750798+00:00 | 384 | false | ```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n=heights.size(),prev,next;\n long long maxi=0;\n for(int i=0;i<n;i++)\n {\n int c=1;\n prev=i-1;\n next=i+1;\n while(prev>=0 && heights[i]<=heights[prev]) //if prev>=current\n {\n c++;\n prev--;\n }\n while(next<n && heights[i]<=heights[next]) //if next>=current\n {\n c++;\n next++;\n }\n long long area=heights[i]*c;\n maxi=max(maxi,area);\n int t=heights[i];\n while(i<n && heights[i]==t) //for same heights\n {\n i++; \n }\n i--;\n \n }\n return maxi;\n }\n};\n``` | 8 | 1 | ['C'] | 2 |
largest-rectangle-in-histogram | Python3 O(N log(N)) divide and conquer approach explained | python3-on-logn-divide-and-conquer-appro-34wq | The first approach I came up with was to try every possible pair of start and end positions, keeping track of the minimum encountered height since the correspon | alexeir | NORMAL | 2020-04-04T10:59:16.952373+00:00 | 2020-04-04T14:58:34.490542+00:00 | 1,005 | false | The first approach I came up with was to try every possible pair of start and end positions, keeping track of the minimum encountered height since the corresponding starting position and pick the pair achieving maximum area. This can be implemented in O(N^2) time complexity. This approach exceeded the time limit (at least my Python3 implementation).\n\nI could not come up with an O(N) solution at the time. So decided to implement a divide and conquer recursive solution inspired by [this solution](https://leetcode.com/problems/maximum-subarray/discuss/561773/Divide-and-conquer-solution) to the follow up of the Maximum Subarray problem.\n\nWe take the full array and split it in half, the maximum Area achievable by the array is the largest of :\n* The maximum area achievable in the left half alone\n* The maximum area achievable in the right half alone\n* The maximum area achievable by combining both halves (in this case, we look at rectangles covering at least one bar from each half, anything else is already taken into account by the first two bullet points)\n\nThe first two points can be calculated in the same way recursively, with the base case of the recursion being a sub-array with one element.\nThe third one can be calculated in linear time. Start with the right most element in the left half and left most element in the right half (as said before we need at least one element from each half). And then add the bars one by one from the left or from the right, depending on which one is higher, until the boundaries of the subarray are reached. In the process, keep track of the minimum encountered height and of the largest obtained area.\n\nThe time complexity of this subroutine is linear and the overall complexity is O(N log(N)), since there are log(N) recursion depth levels and the subroutine is called 2^x times on subarrays of length N/2^x on each such level, where x is the level number, and the call on the full array is at level 0. \n\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n if len(heights) == 0:\n return 0\n self.heights = heights\n return self.largestArea(0, len(heights) - 1)\n \n def largestArea(self, l, r):\n if l == r:\n return self.heights[l]\n mid = (l + r) // 2\n leftArea = self.largestArea(l, mid)\n rightArea = self.largestArea(mid + 1, r)\n crossArea = self.crossLargestArea(l, mid, r)\n return max(leftArea, rightArea, crossArea)\n \n def crossLargestArea(self, l, mid, r):\n minH = min(self.heights[mid], self.heights[mid + 1])\n maxArea = 2 * minH\n i = mid\n j = mid + 1\n while i > l or j < r:\n if i <= l:\n j += 1\n minH = min(minH, self.heights[j])\n maxArea = max(maxArea, (j - l + 1) * minH)\n elif j >= r:\n i -= 1\n minH = min(minH, self.heights[i])\n maxArea = max(maxArea, (r - i + 1) * minH)\n elif self.heights[i - 1] > self.heights[j + 1]:\n i -= 1\n minH = min(minH, self.heights[i])\n maxArea = max(maxArea, (j - i + 1) * minH)\n else:\n j += 1\n minH = min(minH, self.heights[j])\n maxArea = max(maxArea, (j - i + 1) * minH)\n return maxArea\n``` | 8 | 0 | ['Divide and Conquer', 'Python3'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.