question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-number-of-work-sessions-to-finish-the-tasks | C++ || DP || Top Down | c-dp-top-down-by-rajat0301tajar-4btp | \nclass Solution {\npublic:\n typedef long long int64;\n int64 dp[1 << 15][16];\n int threshold;\n int64 solve(vector<int> &t, int mask, int currTim | rajat0301tajar | NORMAL | 2022-04-23T16:58:05.409728+00:00 | 2022-04-23T16:58:05.409756+00:00 | 332 | false | ```\nclass Solution {\npublic:\n typedef long long int64;\n int64 dp[1 << 15][16];\n int threshold;\n int64 solve(vector<int> &t, int mask, int currTime) {\n int n = t.size();\n if(mask == ((1 << n) - 1)) {\n return 1;\n }\n if(dp[mask][currTime] != -1) {\n return dp[mask][currTime];\n }\n int64 ans = 1 << 20;\n for(int i = 0; i < n; i++) {\n if((mask & (1 << i)) != 0) {\n continue;\n }\n // include in current session if possible\n if(currTime + t[i] <= threshold) {\n ans = min(ans, solve(t, mask | (1 << i), currTime + t[i]));\n }\n // use a new session\n ans = min(ans, (1LL + solve(t, mask | (1 << i), t[i])));\n }\n return dp[mask][currTime] = ans;\n }\n \n int minSessions(vector<int>& tasks, int sessionTime) {\n memset(dp, -1, sizeof(dp));\n threshold = sessionTime;\n return solve(tasks, 0, 0);\n }\n \n};\n``` | 1 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | sinkineben | C++ | Binary Search | State compression DP | sinkineben-c-binary-search-state-compres-1ka5 | Analysis\n\nWe should put the tasks into n boxes, the size of each box is sessionTime. And we want to minimize such n.\n\n\n\n## Binary Search\n\n- The min numb | sinkinben | NORMAL | 2022-04-07T12:43:14.673712+00:00 | 2022-04-07T12:43:14.673740+00:00 | 285 | false | **Analysis**\n\nWe should put the `tasks` into `n` boxes, the size of each box is `sessionTime`. And we want to minimize such `n`.\n\n\n\n## Binary Search\n\n- The min number of sessions we need is `l = SUM(tasks) / sessionTime`.\n- The max number of session we need is `n = tasks.size`.\n- Perform a binary search on this range `[l, n]`, to test each `m` whether if it\'s valid.\n\n```cpp\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n int total = accumulate(begin(tasks), end(tasks), 0);\n int l = total / sessionTime, r = n;\n while (l < r)\n {\n int m = l + (r - l) / 2;\n if (check(tasks, m, sessionTime)) r = m;\n else l = m + 1;\n }\n return l;\n }\n \n /* @sessions - The number of sessions.\n * @limit - Each session should have >= 1 task, but total time <= limit.\n */\n bool check(vector<int> &tasks, int sessions, int limit)\n {\n /* there are `sessions` work-sessions, and each session\n * `assign[i]` should be assigned with >= 1 task\n */\n vector<int> assign(sessions, 0);\n return backtrack(tasks, assign, 0, limit);\n }\n\n bool backtrack(vector<int> &tasks, vector<int> &assign, int idx, int limit)\n {\n /* When all the tasks have been assigned, then return true. */\n int n = tasks.size();\n if (idx >= n) return true;\n\n int task = tasks[idx];\n /* For each session `assign[i]`, try to put the `task` on it. */\n for (int &workload : assign)\n {\n if (workload + task <= limit)\n {\n workload += task;\n if (backtrack(tasks, assign, idx + 1, limit)) return true;\n workload -= task;\n }\n /* After assignments(backtracking), there is no task assigned to\n * current session, the false.\n */\n if (workload == 0) return false;\n }\n return false;\n }\n};\n```\n\n\n\n## State Compression DP\n\n**Get time of each subset**\n\n- Use an integer `x` to denote whether if `task[i]` is in the subset. If `(x >> j) & 1`, then `task[j]` is in the subset `x`.\n\n- Let `total[x]` denote the total time of tasks subset `x`, then we have\n\n ```cpp\n total[x] = tasks[j] + total[x - (1 << j)] where ((x >> j) & 1) != 0\n ```\n\n**DP**\n\nLet `dp[x]` denote the min number of sessions, when we have a subset of tasks (denoted by `x`) . \n\nFor each subset `s` of `x`, we can assign `s` with a new session (if the `sessionTime` is large enough to put `s` in).\n\nThen we have\n$$\ndp[x] = \\min_{s \\sube x}\\{ {dp[x -s]} + 1 \\ \\ | \\ \\ \\text{total}[s] \\le \\text{sessionTime} \\}\n$$\n\n```cpp\nclass Solution {\npublic:\n const int INF = INT_MAX / 2;\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n vector<int> total(1 << n, 0);\n for (int x = 1; x < (1 << n); ++x)\n {\n int j = x & (-x);\n int idx = __builtin__ctz(j);\n total[x] = tasks[idx] + total[x - j];\n }\n vector<int> dp(1 << n, INF);\n dp[0] = 0;\n for (int x = 1; x < (1 << n); ++x)\n {\n for (int s = x; s; s = (s - 1) & x)\n if (total[s] <= sessionTime)\n \tdp[x] = min(dp[x], dp[x - s] + 1);\n }\n return dp.back();\n }\n};\n```\n\n | 1 | 0 | ['Dynamic Programming', 'C'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | Backtracking with pruning | Beats 95% | c-backtracking-with-pruning-beats-95-by-rk4a3 | ```\nclass Solution {\nprivate:\n void backtrack(vector&tasks,vector&sessionTimes,int &ans,int index,int sessTime){\n if(sessionTimes.size()>=ans){\n | Diavolos | NORMAL | 2022-01-31T05:45:43.413448+00:00 | 2022-01-31T05:47:13.998140+00:00 | 557 | false | ```\nclass Solution {\nprivate:\n void backtrack(vector<int>&tasks,vector<int>&sessionTimes,int &ans,int index,int sessTime){\n if(sessionTimes.size()>=ans){\n return;\n } else if(index>=tasks.size()){\n ans=min(ans,(int)sessionTimes.size());\n } else {\n for(int i=0;i<sessionTimes.size();i++){\n if(sessionTimes[i]+tasks[index]<=sessTime){\n sessionTimes[i]=sessionTimes[i]+tasks[index];\n backtrack(tasks,sessionTimes,ans,index+1,sessTime);\n sessionTimes[i]=sessionTimes[i]-tasks[index];\n }\n }\n sessionTimes.push_back(tasks[index]);\n backtrack(tasks,sessionTimes,ans,index+1,sessTime);\n sessionTimes.pop_back();\n }\n}\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int ans=tasks.size();\n vector<int>sess;\n backtrack(tasks,sess,ans,0,sessionTime);\n return ans;\n }\n}; | 1 | 0 | ['Backtracking', 'C', 'C++'] | 2 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ Solution | Backtracking | Clean and Concise | c-solution-backtracking-clean-and-concis-sgs8 | \nclass Solution {\npublic:\n int mini;\n void backtrack(vector<int> tasks,int index,int st,int size,vector<int> count)\n {\n if(count.size()>mi | 1905759 | NORMAL | 2022-01-10T06:27:36.933131+00:00 | 2022-01-10T06:27:36.933177+00:00 | 231 | false | ```\nclass Solution {\npublic:\n int mini;\n void backtrack(vector<int> tasks,int index,int st,int size,vector<int> count)\n {\n if(count.size()>mini)\n return;\n if(index==size)\n {\n mini=min(mini,(int)count.size() );\n return;\n }\n int sum=accumulate(tasks.begin()+index,tasks.end(),0);\n for(int i=0;i<count.size();i++)\n {\n if(count[i]+sum<=st)\n {\n backtrack(tasks,size,st,size,count);\n return;\n }\n if(count[i]+tasks[index]<=st)\n {\n count[i]+=tasks[index];\n backtrack(tasks,index+1,st,size,count);\n count[i]-=tasks[index];\n }\n }\n count.push_back(tasks[index]);\n backtrack(tasks,index+1,st,size,count);\n count.pop_back();\n }\n int minSessions(vector<int>& tasks, int sessionTime) \n {\n int n=tasks.size();\n sort(tasks.begin(),tasks.end(),greater<int>());\n if(accumulate(tasks.begin(),tasks.end(),0)<=sessionTime)\n return 1;\n vector<int> count; \n mini=INT_MAX;\n backtrack(tasks,0,sessionTime,n,count);\n return mini;\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++] || Recursion + Memoization With BitMasking || ✅ | c-recursion-memoization-with-bitmasking-zux2m | \nclass Solution {\npublic:\n int n;\n vector<int> tasks;\n int sessionTime;\n\n int bitMask; //the standard BitMask\n \n vector<vector<int>> | tbne1905 | NORMAL | 2022-01-06T04:10:47.320986+00:00 | 2022-01-06T04:11:28.502250+00:00 | 161 | false | ```\nclass Solution {\npublic:\n int n;\n vector<int> tasks;\n int sessionTime;\n\n int bitMask; //the standard BitMask\n \n vector<vector<int>> f; // the memoization matrix \n\n int memo(int taskNo, int timeRemain){\n /*\n - taskNo: of all the remaining tasks, which task must be done as the \'taskNo\'th task\n Eg. TaskNo: 0, 1, 2, 3, 4, 5, 6....\n Tasks(i=) : 7, 10,5, 4, 13, 3,1...\n \n Note: taskNo is actually a function of bitMask\n \n ==> Note: taskNo = Number of 1\'s in the bitMask\n \n - timeRemain: time time remaining/available in the current session\n */\n \n if(f[bitMask][timeRemain] != -1) return f[bitMask][timeRemain];\n \n \n if(taskNo == n)\n return f[bitMask][timeRemain]= 0; // all tasks done!\n \n int mini = INT_MAX;\n\n \n //Which task should I do as the \'taskNo\'th task?\n \n for(int i=0;i<n;i++){\n \n //Is task[i] yet to be done?\n \n if( (bitMask & (1 << i)) == 0){ //Yes!, i\'th task has yet to be done \n \n \n //Can I do task[i] in the current session ?\n \n if(tasks[i] <= timeRemain){ //Yes, you can!\n \n bitMask = (bitMask | (1 << i)); //since we\'re doing task[i], set the i\'th LSB\n \n //Option1. Do task[i] as the \'taskNo\'th task in current session\n int a = memo(taskNo+1, timeRemain-tasks[i]);\n \n //Option2. End this session, and do task[i] as the \'taskNo\'th task in the next session\n int b = 1 + memo(taskNo+1, sessionTime - tasks[i]);\n \n bitMask = (bitMask & (~(1 << i))); //BackTracking!, unset the i\'th LSB\n \n //the minimum sessions needed b/w option1 & option2\n mini = min(mini, min(a, b));\n }\n else{ //No, I cannot do task[i] in the current session\n \n bitMask = (bitMask | (1 << i)); //since we\'re doing task[i], set the i\'th LSB\n \n //Hence, end this session here, and do it in the next session\n int c = 1 + memo(taskNo+1, sessionTime - tasks[i]);\n \n bitMask = (bitMask & (~(1 << i))); //BackTracking!, unset the i\'th LSB\n \n mini = min(mini, c); \n }\n }\n }\n \n \n return f[bitMask][timeRemain]= mini;\n }\n\n\n int minSessions(vector<int>& tasks, int sessionTime) {\n this->tasks = tasks;\n this->n = tasks.size();\n this->sessionTime = sessionTime;\n\n this->bitMask = 0;\n this->f.resize((1<<n), vector<int>(sessionTime + 1, -1));\n \n return 1 + memo(0,sessionTime);\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | c# : Easy Solution | c-easy-solution-by-rahul89798-vv6q | \tpublic class Solution\n\t{\n\t\tpublic int MinSessions(int[] tasks, int sessionTime)\n\t\t{\n\t\t\tint[,] dp = new int[(1 << tasks.Length), sessionTime + 1];\ | rahul89798 | NORMAL | 2021-12-13T14:05:28.700581+00:00 | 2021-12-13T14:05:28.700607+00:00 | 184 | false | \tpublic class Solution\n\t{\n\t\tpublic int MinSessions(int[] tasks, int sessionTime)\n\t\t{\n\t\t\tint[,] dp = new int[(1 << tasks.Length), sessionTime + 1];\n\t\t\treturn Solve(tasks, sessionTime, dp, 0, 0);\n\t\t}\n\n\t\tpublic int Solve(int[] tasks, int sessionTime, int[,] dp, int taken, int currTime)\n\t\t{\n\t\t\tif (taken == (1 << tasks.Length) - 1)\n\t\t\t\treturn 1;\n\n\t\t\tif (dp[taken, currTime] != 0)\n\t\t\t\treturn dp[taken, currTime];\n\n\t\t\tint ans = int.MaxValue;\n\t\t\tfor(int i = 0; i < tasks.Length; i++)\n\t\t\t{\n\t\t\t\tif ((taken & (1 << i)) > 0)\n\t\t\t\t\tcontinue;\n\n\t\t\t\tif (currTime + tasks[i] <= sessionTime)\n\t\t\t\t\tans = Math.Min(ans, Solve(tasks, sessionTime, dp, taken | (1 << i), currTime + tasks[i]));\n\t\t\t\telse\n\t\t\t\t\tans = Math.Min(ans, 1 + Solve(tasks, sessionTime, dp, taken | (1 << i), tasks[i]));\n\t\t\t}\n\n\t\t\tdp[taken, currTime] = ans;\n\t\t\treturn ans;\n\t\t}\n\t} | 1 | 0 | ['Backtracking', 'Bit Manipulation', 'Bitmask'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Py3/Py] Simple solution w/ comments | py3py-simple-solution-w-comments-by-sssh-90um | NOTE: Use cache instead of lru_cache for memoization\n> \n\n\n\nfrom math import inf\nfrom functools import cache\n\nclass Solution:\n def minSessions(self, | ssshukla26 | NORMAL | 2021-11-21T00:08:57.439441+00:00 | 2021-11-21T00:10:38.369296+00:00 | 271 | false | > NOTE: Use cache instead of lru_cache for memoization\n> \n\n\n```\nfrom math import inf\nfrom functools import cache\n\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n # Init\n n = len(tasks)\n \n @cache # NOTE: here use cache instead of lru_cache, otherwise TLE is encountered\n def recursion(mask, availableTime):\n \n # If all tasks are completed\n # return 0, as no session is\n # needed for anything to complete\n if mask == (1<<n) - 1:\n return 0\n \n else:\n \n # Init\n sessions = inf\n \n # Loop for each tasks and get minimum number of\n # sessions required to complete them\n for i in range(n):\n \n # Check if the current task is not yet complete\n if not (mask & (1<<i)):\n \n # if task can be completed in available time of the current session\n if tasks[i] <= availableTime:\n \n # Mark the current task complete, and update the available time\n num_sessions = recursion(mask | (1<<i), availableTime-tasks[i])\n \n else: # if task can\'t be completed in available time of the current session\n \n # Add new session to complete the current task\n # Mark the current task complete, and update the available time\n # in the new session\n num_sessions = 1 + recursion(mask | (1<<i), sessionTime-tasks[i])\n \n # Update minimum number of sessions needed\n sessions = min(sessions, num_sessions)\n \n # return minimum no. of sessions needed\n return sessions\n \n return recursion(0,0) \n``` | 1 | 1 | ['Dynamic Programming', 'Bit Manipulation'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | simple C++ using dp | simple-c-using-dp-by-luoyuf-1ido | \nint minSessions_(int idx, int mask, int left, vector<int>& tasks, int sessionTime, vector<vector<int>>& dp) {\n \n if (mask == ((1 << tasks.size()) - 1) | luoyuf | NORMAL | 2021-11-04T17:56:02.562985+00:00 | 2021-11-04T17:56:02.563022+00:00 | 311 | false | ```\nint minSessions_(int idx, int mask, int left, vector<int>& tasks, int sessionTime, vector<vector<int>>& dp) {\n \n if (mask == ((1 << tasks.size()) - 1))\n return 0;\n \n if (dp[left][mask] < INT_MAX) return dp[left][mask];\n \n int tot = INT_MAX;\n \n for (int i = 0; i < tasks.size(); ++i) {\n if (mask & (1 << i)) continue;\n if (tasks[i] > left) continue;\n tot = min(tot, minSessions_(i + 1, mask | (1 << i), left - tasks[i], tasks, sessionTime, dp));\n }\n \n if (tot == INT_MAX)\n tot = 1 + minSessions_(0, mask, sessionTime, tasks, sessionTime, dp);\n \n dp[left][mask] = tot;\n \n return tot;\n}\n\nint minSessions(vector<int>& tasks, int sessionTime) {\n \n vector<vector<int>> dp(sessionTime + 1, vector<int>(1 << tasks.size(), INT_MAX));\n \n return minSessions_(0, 0, 0, tasks, sessionTime, dp);\n \n}\n``` | 1 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python backtracking about 280ms and very low space complexity | python-backtracking-about-280ms-and-very-l6vw | This was directly inspired by this solution: https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1433054/Python-or-Backtr | shabie | NORMAL | 2021-10-23T18:41:37.399953+00:00 | 2021-11-06T22:20:43.282250+00:00 | 813 | false | This was directly inspired by this solution: https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1433054/Python-or-Backtracking-or-664ms-or-100-time-and-space-or-Explanation\n\nBasically the idea is to formulate it as a problem of finding least number of sessions such that their sum is at most equal to session time.\n\nSo for every value, we have two choices:\n\t1. add it to any one of the sessions we\'ve already made without exceeding the session time total\n\t2. put it in its own session\n\nWe try these choices in all combinations to find the least number.\n\nA couple of optimizations can be made to make the solution faster in certain cases.\n\nThe hardest part was figuring out looping over tasks will get you TLE. It is the sessions you need to loop over.\n\n```python\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n\t\n # if sum fully divisible, the answer can be directly calculated\n total_tasks = sum(tasks)\n quotient, remainder = divmod(total_tasks, sessionTime)\n \n sessions = []\n ans = len(tasks) # cant be more sessions so start with that\n least_num_sessions = quotient + (remainder > 0) # incase of a non-zero remainder, this is the least number of sessions possible\n \n def dfs(idx):\n nonlocal ans\n if len(sessions) >= ans:\n return\n \n if idx == len(tasks):\n if ans == least_num_sessions:\n return True # cant be lower so stop searching\n ans = min(ans, len(sessions))\n return\n \n # check if this value fits in any of the existing sessions\n for i in range(len(sessions)):\n if sessions[i] + tasks[idx] <= sessionTime:\n sessions[i] += tasks[idx]\n if dfs(idx + 1):\n return True\n sessions[i] -= tasks[idx]\n \n # give value its own session\n sessions.append(tasks[idx])\n if dfs(idx + 1):\n return True\n sessions.pop()\n \n dfs(0)\n return ans\n``` | 1 | 0 | ['Backtracking', 'Python', 'Python3'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ backtracking + dp | c-backtracking-dp-by-rohanjainbits-u6n8 | \nclass Solution {\npublic:\n \n int minSes(int session,long long int completedTasks,vector<int>& tasks,int sessionTime,vector<vector<int>>& dp)\n {\n | rohanjainbits | NORMAL | 2021-10-12T10:33:58.603753+00:00 | 2021-10-12T10:33:58.603788+00:00 | 280 | false | ```\nclass Solution {\npublic:\n \n int minSes(int session,long long int completedTasks,vector<int>& tasks,int sessionTime,vector<vector<int>>& dp)\n {\n int n = tasks.size();\n \n if(completedTasks==(pow(2,n)-1))\n {\n return dp[session][completedTasks]=1;\n }\n \n if(dp[session][completedTasks]!=-1)\n return dp[session][completedTasks];\n \n bool isAvail = false;\n int minSessions = INT_MAX;\n \n for(int i=0;i<n;i++)\n {\n if((completedTasks&(1<<i))==0 && tasks[i]<=session)\n {\n isAvail = true;\n minSessions = min(minSessions,minSes(session-tasks[i],completedTasks|(1<<i),tasks,sessionTime,dp));\n }\n }\n \n if(!isAvail)\n {\n return dp[session][completedTasks]=1+minSes(sessionTime,completedTasks,tasks,sessionTime,dp);\n }\n \n return dp[session][completedTasks]=minSessions;\n }\n \n int minSessions(vector<int>& tasks, int sessionTime)\n {\n long long int completedTasks = 0,n=tasks.size();\n vector<vector<int>> dp(sessionTime+5,vector<int>((1<<(n+1))+3,-1));\n \n return minSes(sessionTime,completedTasks,tasks,sessionTime,dp);\n }\n \n};\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++] DP with Bitmask | c-dp-with-bitmask-by-amsv_24-v2pa | \nclass Solution {\npublic:\n int dp[1<<14+1][16];\n int solve(vector<int>&tasks, int n, int mask, int time, int t){\n if(time>t)\n retu | amsv_24 | NORMAL | 2021-09-01T12:34:55.297816+00:00 | 2021-09-01T12:34:55.297845+00:00 | 370 | false | ```\nclass Solution {\npublic:\n int dp[1<<14+1][16];\n int solve(vector<int>&tasks, int n, int mask, int time, int t){\n if(time>t)\n return INT_MAX;\n if(mask==0)\n return 1;\n if(dp[mask][time]!=-1)\n return dp[mask][time];\n \n //for each task, there are 2 options\n //include in the ongoing session\n //start a new session\n \n int ans = INT_MAX;\n for(int i=0;i<n;i++){\n if(mask & (1<<i)){\n int ongoing = solve(tasks,n,mask^(1<<i),time+tasks[i],t);\n int newSession = 1+solve(tasks,n,mask^(1<<i),tasks[i],t);\n ans = min(ans,min(ongoing,newSession));\n }\n }\n return dp[mask][time] = ans;\n \n }\n int minSessions(vector<int>& tasks, int t) {\n int n=tasks.size();\n int mask=(1<<n)-1;\n memset(dp,-1,sizeof(dp));\n int ans=solve(tasks,n,mask,0,t);\n return ans;\n \n }\n};\n``` | 1 | 0 | ['Recursion', 'C', 'Bitmask', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ Short general code with O(3^n) | c-short-general-code-with-o3n-by-maximgo-1lyg | Create all possible subsets and keep assigning valid ones to sessions:\n\nclass Solution {\n // sumMap is for faster subSet sum lookup:\n int getSum(int m | maximgorkey | NORMAL | 2021-08-31T14:41:18.962847+00:00 | 2021-08-31T14:41:18.962891+00:00 | 115 | false | Create all possible subsets and keep assigning valid ones to sessions:\n```\nclass Solution {\n // sumMap is for faster subSet sum lookup:\n int getSum(int mask, const std::vector<int> &tasks, const int n)\n {\n int sum = 0;\n for(int i = 0; i < n && mask; ++i) {\n sum += (mask &1) ? tasks[i] : 0;\n mask >>= 1;\n }\n return sum;\n } \n int enumerate(int state, std::vector<int> &resultMap, const std::vector<int> &sumMap, const int sessionTime)\n {\n if(state == 0) return 0;\n if(resultMap[state] != -1) return resultMap[state];\n int result = INT_MAX;\n for (int s=state; s ; s=(s-1)&state) {\n if(sumMap[s] <= sessionTime) {\n result = std::min(result, 1+enumerate(state-s,resultMap,sumMap,sessionTime));\n }\n }\n return resultMap[state]=result;\n }\npublic:\t\n int minSessions(const std::vector<int> &tasks, const int sessionTime)\n {\n int n = tasks.size();\n int state = (1<<n)-1;\n \n std::vector<int> resultMap(std::vector<int>(1<<n, -1)); //result from each state\n std::vector<int> sumMap(1<<n,0); // sum for each state. \n for (int s=state; s ; s=(s-1)&state) sumMap[s] = getSum(s,tasks,n);\n return enumerate(state, resultMap,sumMap,sessionTime);\n }\n};\n```\nComplexity is O(3^n) .. See this for details: https://cp-algorithms.com/algebra/all-submasks.html .\n\nI think this general approach is more effective from learning point of view. \nLet me know if something is missing. | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | JAVA Binary Search 2ms Solution, same as Problem 1723. Find Minimum Time to Finish All Jobs | java-binary-search-2ms-solution-same-as-x7dbh | Minimum Number of Work Sessions to Finish the Tasks\n\n public int minSessions(int[] tasks, int sessionTime) {\n Arrays.sort(tasks);\n int lo = | chenzuojing | NORMAL | 2021-08-31T01:42:15.522373+00:00 | 2021-09-25T23:54:16.149686+00:00 | 165 | false | 1986. Minimum Number of Work Sessions to Finish the Tasks\n```\n public int minSessions(int[] tasks, int sessionTime) {\n Arrays.sort(tasks);\n int lo = 1, hi = tasks.length;\n\n while (lo < hi) {\n int numSessions = (lo + hi) / 2;\n if (canSchedule(tasks, new int[numSessions], tasks.length - 1, sessionTime))\n hi = numSessions;\n else\n lo = numSessions + 1;\n }\n return lo;\n }\n\n private boolean canSchedule(int[] tasks, int[] sessions, int taskIdx, int sessionTime) {\n if (taskIdx == -1) return true;\n\n Set<Integer> set = new HashSet<>();\n for (int i = 0; i < sessions.length; i++) {\n if (!set.add(sessions[i])) continue;\n if (tasks[taskIdx] + sessions[i] > sessionTime) continue;\n\n sessions[i] += tasks[taskIdx];\n if (canSchedule(tasks, sessions, taskIdx - 1, sessionTime))\n return true;\n sessions[i] -= tasks[taskIdx];\n }\n\n return false;\n }\n```\n\n1723. Find Minimum Time to Finish All Jobs\n```\n public int minimumTimeRequired(int[] jobs, int workers) {\n Arrays.sort(jobs);\n int n = jobs.length;\n int lo = jobs[n - 1], hi = Arrays.stream(jobs).sum();\n\n while (lo < hi) {\n int maxTime = lo + (hi - lo) / 2;\n if (canSchedule(jobs, new int[workers], n - 1, maxTime))\n hi = maxTime;\n else\n lo = maxTime + 1;\n }\n return lo;\n }\n\n private boolean canSchedule(int[] jobs, int[] workload, int jobIdx, int maxTime) {\n if (jobIdx == -1) return true;\n\n Set<Integer> set = new HashSet<>();\n for (int i = 0; i < workload.length; i++) {\n if (!set.add(workload[i])) continue;\n if (jobs[jobIdx] + workload[i] > maxTime) continue;\n\n workload[i] += jobs[jobIdx];\n if (canSchedule(jobs, workload, jobIdx - 1, maxTime))\n return true;\n workload[i] -= jobs[jobIdx];\n }\n\n return false;\n }\n``` | 1 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | Runtime- 0ms sometimes 4ms beats 100% | Size- 7.6 MB beats 100% | DP | Subset sum | | c-runtime-0ms-sometimes-4ms-beats-100-si-4mds | Time Complexity: O(s*n^2), s=sessionTime, n= tasks length\n\nLets take this example tasks=[2,3,4,4,5,6,7,10], sessionTime=12\n\nWe can store number of times an | lc_mb | NORMAL | 2021-08-30T15:28:36.198233+00:00 | 2021-08-30T15:28:36.198273+00:00 | 140 | false | **Time Complexity: O(s*n^2)**, s=sessionTime, n= tasks length\n\nLets take this example **tasks=[2,3,4,4,5,6,7,10], sessionTime=12**\n\nWe can store number of times an element is appearing in tasks, to a vector (like a hash map).\nLets create **hashVector=[0,0,1,1,2,1,1,1,0,0,1]** for elements 0 to 10 and initialise our answer as **ans=0**\n\nWe select elements from tasks having maximum sum upto **sessionTime** to create a new session for them. We can use DP to check **maxSum** and elements adding to **maxSum** as used in [Subset sum problem](http://leetcode.com/problems/partition-equal-subset-sum/) in a loop. We will update **hashVector** & loop until no task is remaining.\n\nUpdates after every loop:\n* **Loop 1:** tasks=[2,3,4,4,5,6,7,10], **maxSum**=12, elements taken out to form a new session=(2,10), **ans=1**\n* **Loop 2:** tasks=[3,4,4,5,6,7], **maxSum**=12, elements taken out to form a new session=(5,7), **ans=2**\n* **Loop 3:** tasks=[3,4,4,6], **maxSum**=11, elements taken out to form a new session=(3,4,4), **ans=3**\n* **Loop 4:** tasks=[6], **maxSum**=6, elements taken out to form a new session=(6), **ans=4**.\n* **Loop 5:** tasks=[], loop breaks.\n\nAfter tasks=[], loop will not run.\n\n```\nclass Solution {\npublic:\n bool tasksRemaining(vector<int>& v, int s){\n\t\t// Vector to store remaining tasks\n vector<int> vec;\n for(int i=1;i<v.size();i++){\n int count=v[i];\n while(count--) vec.push_back(i);\n }\n int n=vec.size();\n\t\t// If no tasks remaining\n if(n==0) return false;\n\t\t\n\t\t// DP like subset sum problem\n bool dp[n+1][s+1];\n\t\t// Max sum upto sessionTime from the remaining tasks\n int maxSum=0;\n for(int i=0;i<n+1;i++){\n for(int j=0;j<s+1;j++){\n if(j==0) dp[i][j]=true;\n else if(i==0) dp[i][j]=false;\n else{\n if(vec[i-1]>j) dp[i][j]=dp[i-1][j];\n else dp[i][j]=(dp[i-1][j]||dp[i-1][j-vec[i-1]]);\n }\n if(i==n && dp[i][j]) maxSum=j;\n }\n }\n\t\t\n\t\t// Selecting elements adding to "maxSum"\n int i=n;\n while(maxSum){\n while(vec[i-1]>maxSum) i--;\n if(dp[i-1][maxSum-vec[i-1]]){\n\t\t\t\t// Removing them from hashVector\n v[vec[i-1]]--;\n maxSum-=vec[i-1];\n }\n i--;\n }\n return true;\n }\n \n int minSessions(vector<int>& t, int s) {\n int n=t.size(),ans=0,m=0;\n for(int i=0;i<n;i++) \n\t\t\tm=max(m,t[i]);\n\t\t\n\t\t// Create hash vector of size "m+1"(max element of array+1)\n vector<int> v(m+1,0);\n for(int i=0;i<n;i++)\n v[t[i]]++;\n\t\t\t\n\t\t// Loop until all tasks are not done\n while(tasksRemaining(v,s)) ans++;\n return ans;\n }\n};\n```\n\nFeel free to correct me or add any improvements.\nThis is my first post, please upvote if you like the solution | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java - 1ms - bitmask & backtracking recursion - Easy recursive thinking | java-1ms-bitmask-backtracking-recursion-6ubr9 | Idea / Intuition\n I thought of having individual slots for each task as each of them is less than sessionTime, as that would be the requirement in worst case.\ | mystic13 | NORMAL | 2021-08-30T14:14:21.763442+00:00 | 2021-08-30T14:18:45.967898+00:00 | 386 | false | **Idea / Intuition**\n* I thought of having individual slots for each task as each of them is less than sessionTime, as that would be the requirement in worst case.\n* So for each new element we need to recur for an old slot with time>= current element time and one full empty slot.\n* To prune we can keep slotCount and when it is >= already found mincount we prune.\n\n***Improvement tip:***\nWithout sorting - 950ms\nSorting - 43ms\nDescending sort - 1ms\n\n\n```\nclass Solution {\n\t//simple reversing array logic ignore\n public static void reverse(int[] input) { int last = input.length - 1; int middle = input.length / 2; for (int i = 0; i <= middle; i++) { int temp = input[i]; input[i] = input[last - i]; input[last - i] = temp; } }\n static int minSlotsNeeded;\n public int minSessions(int[] tasks, int sessionTime) {\n int n=tasks.length;\n minSlotsNeeded = 10000;\n Arrays.sort(tasks);\n reverse(tasks); // descending\n int[] allSlots = new int[n];\n Arrays.fill(allSlots, sessionTime);\n rec(tasks, 0, allSlots, sessionTime, 0);\n return minSlotsNeeded;\n }\n static int rec(int[] tasks, int elems, int[] slots, int limit, int slotCount) {\n if(slotCount>=minSlotsNeeded) return 10000; // pruning if current slot utilization exceeds already found min\n int elem=-1;\n for(int i=0;i<tasks.length && elem==-1;i++) // finding out first unselected element\n if((elems>>i & 1)==0) elem=i;\n if(elem==-1) { // if no element unselected then see if the slot count can better minSlotsNeeded\n int count = 0;\n for(int a: slots)\n if(a<limit) count++;\n minSlotsNeeded = Math.min(minSlotsNeeded, count);\n return count;\n }\n elems = elems | 1<<elem;\n //all non full to be attempted for unselected task until incl first full slot\n int minSlots = 10000;\n for(int i=0;i<tasks.length;i++) {\n if(slots[i]>=tasks[elem]) {\n slots[i]-=tasks[elem];\n int slcount = slots[i]+tasks[elem] == limit? slotCount+1 : slotCount; // to inc slotCount if new slot otherwise old count stays\n minSlots = Math.min(minSlots, rec(tasks, elems, Arrays.copyOf(slots, slots.length), limit, slcount));\n slots[i]+=tasks[elem];\n if(slots[i]==limit) break; // if this is the first full slot we finished recursion for then we can stop\n }\n }\n \n return minSlots;\n }\n}\n``` | 1 | 0 | ['Backtracking', 'Java'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | track all possible combinations of open slots | python3 | track-all-possible-combinations-of-open-a7st9 | Approach\n Keep track of all possible options which will contain slots of time to fit in a given task\n Start with one option of one slot of sessionTime \n For | 495 | NORMAL | 2021-08-30T02:07:31.182086+00:00 | 2021-08-30T02:08:48.892178+00:00 | 111 | false | ### Approach\n* Keep track of all possible options which will contain slots of time to fit in a given `task`\n* Start with one option of one slot of `sessionTime` \n* For each new `task`, we have two choices:\n\t* Fit the `task` in one of the open slots in one of the available options, creating more opitons of slots\n\t* Allot an entirely new slot of `sessionTime`\n* Using tuples and sorting slot options by slot size allows us to avoid duplicate slot options and also break out of the inner loop sooner\n* At the end, the option with the least number of slots is the one that utilized all the slot in the most optimum way. So smallest length is the answer. \n* This approach essentially explores all possible ways to schedule the tasks, so it\'s an exhaustive search, similar to a DFS/BFS solution. \n\n\n```\ndef minSessions(self, tasks: List[int], sessionTime: int) -> int:\n tasks.sort(reverse=True)\n options = set([(sessionTime,)])\n for time in tasks:\n new_options = set()\n for slots in options:\n for i, slot in enumerate(slots):\n if slot >= time:\n new_option = list(slots)\n new_option[i] = slot-time\n new_options.add(tuple(sorted(new_option, reverse=True)))\n else:\n break\n new_options.add(tuple(sorted(slots + (sessionTime-time,), reverse=True)))\n options = new_options\n \n return min(map(len, options))\n```\n\n*This consistently runs faster than all Python3 solutions at the time of posting this.* | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python Top-Down DP and Thinking Process | python-top-down-dp-and-thinking-process-2kdns | Inspired by this top voted post:\nhttps://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1432155/Easier-than-top-voted-ones-o | shangpochou | NORMAL | 2021-08-29T22:29:24.586648+00:00 | 2021-08-29T22:29:24.586677+00:00 | 102 | false | Inspired by this top voted post:\nhttps://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1432155/Easier-than-top-voted-ones-or-LegitClickbait-or-c%2B%2B\nWhich has a great explanation of how does bit masks works for this problem.\n\nThe brutal recursive solution is finding all possible combinations. We take every un-taken task and pass it to the next level recursive call for any given list. There are two possibilities when we made the recursive call:\n1) Keep in the current working session\n2) Start a new working session\n\nAnd if all tasks are done, we return 1\n\n```\ndef recur_f(c_session_time, c_tasks):\n \n if(c_session_time > sessionTime):\n return math.inf\n \n if(sum(c_tasks) == len(c_tasks)*-1):\n return 1\n \n result = math.inf\n for i in range(0, len(c_tasks)):\n if(c_tasks[i] != -1):\n\t\t\t\t\t#avoid calling by reference so we made an copy of the current task list\n n_tasks = c_tasks.copy()\n n_tasks[i] = -1\n result = min(result, \n\t\t\t\t\tmin(\n\t\t\t\t\t\t#keep the current working session\n\t\t\t\t\t\trecur_f(c_session_time + tasks[i], n_tasks),\n\t\t\t\t\t\t#start a new working session\n\t\t\t\t\t\t1+recur_f(tasks[i], n_tasks))) \n\t\t\t\t\t\n return result\n \n return recur_f(0, tasks)\n```\n\nBut this will get TLE. So we need to optimize it by \n1) Using the bit string to represent the task status instead of using a list\n2) Using memorization (Top-Down DP)\n\nPlease check https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1432155/Easier-than-top-voted-ones-or-LegitClickbait-or-c%2B%2B for explanation for bit mask. \n\nBasically we use a binary representation of a integer, which is a bit string to represent the tasks status. E.g. 11111 means all five tasks are processed.\n\nAnd tasks | (1<<i) means set ith task as one, tasks & (1<<i) means check whether ith task is 1.\n\nSo we modified our brutal force recursive solution, and used an array with **current tasks bit string and current session time** as the variables. \n\nQuestions: Is anyone came up with a bottom-up version DP for this problem? \n\n```\nclass Solution:\n result = math.inf\n n_tasks = 0\n all_ones = 0\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n\n num_possible_schedule = (1 << 15)\n self.n_tasks = len(tasks)\n self.all_ones = (1<<self.n_tasks)-1\n \n def recur_f(c_session_time, c_tasks, dp_array):\n\n if(c_session_time > sessionTime):\n return math.inf\n \n if(c_tasks == self.all_ones):\n dp_array[c_tasks][c_session_time] = 1\n return 1\n \n if(dp_array[c_tasks][c_session_time] != -1):\n return dp_array[c_tasks][c_session_time]\n \n result = math.inf\n for i in range(0, self.n_tasks):\n if(c_tasks & (1<<i) == 0):\n \n n_tasks = c_tasks | (1<<i)\n \n result = min(result, \n min(recur_f(c_session_time + tasks[i], n_tasks, dp_array),1+recur_f(tasks[i], n_tasks, dp_array))) \n \n dp_array[c_tasks][c_session_time] = result\n return result\n\n dp_array = [[-1 for i in range(0, 16)] for j in range(0, num_possible_schedule)]\n\n return recur_f(0, 0, dp_array)\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [python] walk bucket solution, easy to understand | python-walk-bucket-solution-easy-to-unde-6op4 | this problem is similar to problem 1723.\nthe solution is straightforward. there are n tasks, so we create n bucket. each task[i] will be placed to one of the b | zyj5353 | NORMAL | 2021-08-29T18:07:20.953550+00:00 | 2021-08-29T18:07:20.953618+00:00 | 137 | false | this problem is similar to problem 1723.\nthe solution is straightforward. there are n tasks, so we create n bucket. each task[i] will be placed to one of the bucket. the non-empty bucket is the number of sessions and we want to find the min.\nBelow is the code. \nfunction walk will walk through every task and try to place it to one bucket(session), k is the current non empty bucket, which is the sessions we used so far.\nself.res is the current best result\nI did several pruning here\n1. if k larger than self.res, then we don\'t need to search forward anymore.\n2. for each task ,when we iterate all bucket, if the bucket value is the same, then we only need to calcuate one of them. this why I used seen set to track bucket value that has been used.\n\n\n\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n n=len(tasks)\n tasks.sort(reverse=True)\n self.res=n\n sessions=[0]*n\n def walk(i,k):\n if k>=self.res:\n return\n if i==n:\n self.res=min(self.res,k)\n return\n seen=set()\n for j in range(n):\n if sessions[j] in seen:\n continue\n if sessions[j]+tasks[i]<=sessionTime:\n seen.add(sessions[j])\n if sessions[j]==0:\n sessions[j]+=tasks[i]\n walk(i+1,k+1)\n else:\n sessions[j]+=tasks[i]\n walk(i+1,k)\n sessions[j]-=tasks[i]\n return \n walk(0,0)\n return self.res\n```\n\n\n | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Knapsack-like | 0 ms | O(s*n^2) Worst Case | knapsack-like-0-ms-osn2-worst-case-by-in-mmuw | Step 1: Build DP Matrix\n\nBuild a knapsack-like matrix to find how many ways we can spend X time with our current tasks.\n\nEx. [1,2,3] sessionTime = 3\n\n0 | IndievdB | NORMAL | 2021-08-29T17:03:28.626603+00:00 | 2021-08-29T17:13:42.049362+00:00 | 237 | false | **Step 1: Build DP Matrix**\n\nBuild a knapsack-like matrix to find how many ways we can spend X time with our current tasks.\n\nEx. [1,2,3] sessionTime = 3\n\n**0 1 2 3** \n1 0 0 0 | *looking at 0 tasks*\n1 1 0 0 | *including task 1*\n1 1 1 1 | *including task 2*\n1 1 1 2 | *including task 3*\n\n#Ways to spend s time with tasks 0->t =\n#Ways to spend s time with tasks 0->(t-1) +\n#Ways to spend s-(time of task t) time with tasks 0->(t-1).\n\n**Step 2: Extrapolate Tasks from Matrix**\n\nLook for the bottom-right-most, non-zero cell in our matrix (in this case [3,3]).\nFind the task that caused this cell to increase to its current value (task #3).\nAdd that task to the list of used tasks and decrease our column idx by that task\'s value.\n\n**Step 3: Remove Tasks, Increment Sessions, Repeat**\n\n[1,2,3] becomes [1,2]. Sessions = 1\nOur matrix becomes\n\n1 0 0 0 | *looking at 0 tasks*\n1 1 0 0 | *including task 1*\n1 1 1 1 | *including task 2*\n\nWe can extrapolate tasks 2 & 1 from this.\n\n[1,2] becomes []. Sessions = 2\n\n**Time Complexity**\n\nEach iteration has a complexity of O(sn), where s is sessionTime and n is the number of tasks.\nWorst case scenario, each session only includes one task, giving worst case O(s*n^2)\n\n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int sessions = 0;\n \n while (!tasks.empty()) {\n\t\t\t// Create dp matrix.\n vector<vector<int>> dp (tasks.size()+1, vector<int> (sessionTime+1, 0));\n \n for (auto& row : dp)\n row[0] = 1;\n \n for (int t=1; t<dp.size(); t++) {\n for (int s=1; s<dp[0].size(); s++) {\n int curTask = tasks[t-1];\n \n\t\t\t\t\tdp[t][s] = dp[t-1][s];\n\t\t\t\t\t\n\t\t\t\t\tif (curTask <= s)\n dp[t][s] += dp[t-1][s-curTask];\n }\n }\n \n\t\t\t// Build idx list from dp matrix.\n int row = dp.size()-1;\n int col = dp[0].size()-1;\n vector<int> indices;\n \n while (col>0 && row>0) {\n while (col > 0 && dp[row][col] == 0)\n col--;\n \n while (row > 0 && dp[row][col] == dp[row-1][col])\n row--;\n \n if (col==0 && row==0)\n continue;\n \n indices.push_back(row-1);\n col -= tasks[row-1];\n row--;\n }\n\t\t\t\n\t\t\t// Remove used tasks.\n for (auto idx : indices)\n tasks.erase(tasks.begin() + idx);\n \n sessions++;\n }\n \n return sessions;\n }\n};\n```\n | 1 | 0 | ['C', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | JavaScript and TypeScript Bitmask DP | javascript-and-typescript-bitmask-dp-by-jxzaw | DP[mask][time] = Minimum number of work sessions after assigning task by mask and it remains time session time\n\nJavaScript\njs\n/**\n * @param {number[]} task | menheracapoo | NORMAL | 2021-08-29T14:39:09.007836+00:00 | 2021-08-30T14:15:40.346428+00:00 | 324 | false | DP[mask][time] = Minimum number of work sessions after assigning task by `mask` and it remains `time` session time\n\nJavaScript\n```js\n/**\n * @param {number[]} tasks\n * @param {number} sessionTime\n * @return {number}\n */\nvar minSessions = function(tasks, sessionTime) {\n const n = tasks.length;\n const dp = Array(1 << n).fill().map(() => Array(16).fill(-1));\n \n const solve = (mask, time) => {\n if (mask === (1 << n) - 1) {\n return 1;\n }\n \n if (dp[mask][time] !== -1) {\n return dp[mask][time];\n }\n \n let min = Infinity;\n for (let i = 0; i < n; ++i) {\n if (mask & (1 << i)) {\n continue;\n }\n\n if (time >= tasks[i]) {\n min = Math.min(\n min,\n solve(mask | (1 << i), time - tasks[i]),\n );\n } else {\n min = Math.min(\n min,\n 1 + solve(mask | (1 << i), sessionTime - tasks[i]),\n );\n }\n }\n \n dp[mask][time] = min;\n return min;\n }\n \n return solve(0, sessionTime);\n};\n\n```\n\nTypeScript\n```ts\nfunction minSessions(tasks: number[], sessionTime: number): number {\n const n = tasks.length;\n const dp = Array(1 << n).fill(null).map(() => Array(16).fill(-1));\n \n const solve = (mask, time) => {\n if (mask === (1 << n) - 1) {\n return 1;\n }\n \n if (dp[mask][time] !== -1) {\n return dp[mask][time];\n }\n \n let min = Infinity;\n for (let i = 0; i < n; ++i) {\n if (mask & (1 << i)) {\n continue;\n }\n\n if (time >= tasks[i]) {\n min = Math.min(\n min,\n solve(mask | (1 << i), time - tasks[i]),\n );\n } else {\n min = Math.min(\n min,\n 1 + solve(mask | (1 << i), sessionTime - tasks[i]),\n );\n }\n }\n \n dp[mask][time] = min;\n return min;\n }\n \n return solve(0, sessionTime);\n};\n``` | 1 | 0 | ['TypeScript', 'JavaScript'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++] DP+Bitmasking | c-dpbitmasking-by-sahil_rajput_2000-7iti | \n/*\n Kind of Problem where we have the option to Pick now or Pick later but we definatley have to pick all items.\n We are using dp with bitmasking here w | sahil_rajput_2000 | NORMAL | 2021-08-29T12:30:58.620999+00:00 | 2021-11-10T12:37:40.364183+00:00 | 126 | false | ```\n/*\n Kind of Problem where we have the option to Pick now or Pick later but we definatley have to pick all items.\n We are using dp with bitmasking here where a ith bit in mask represents that element isPicked or not.\n if 1 that means picked if 0 means not picked Yet.\n We will do memoization to save time and store the result on two changing states mask(isTaken) and currTime\n The constraints given that array is of size 14 atMax and sessionTime is 15 atMax so that means we will only need mask of size 1<<15\n and second column is made of size 16 (1 grater than specified size of sessionTime)\n \n Approach : We are taking a mask intially and picking elements and setting ith bit of mask to represent we have picked and currTime should be atMax <= SessionTime\n so we are adding tasks values in this variable(currentTime) once it exceeds the sessionTime we will break recursion, we also have the option to not pick\n for that we are also setting the ith bit because it will also be picked (we are including this but including in next work session) and adding 1 that represents \n that we have created 1 more session by sending this element to be picked in next session and as we have created the next session so currentTime will be zero for this\n these recursion calls will give us work sessions which are created so we selecting minimum as asked in question and caching it with dp and returning min number of work \n sessions.\n we have One condition (isTaken == (1<<N)-1) that represents that we picked all elements (because Nth bit will be set only we reached last element of array and we subtracted 1\n beacuse we are accesding bits by N in number 1 which has already a set bit in simple terms to counter the effect of 1 we reduced this 1) \n will return 1 (as consider a case) - Input: tasks = [1,2,3,4,5], sessionTime = 15, in this all tasks will be counted in single work session so includeInNext will never be counted\n hence we never added 1 in whole program to represent that this is a session so for that we returned 1 in condition (isTaken == (1<<N)-1)\n*/\nclass Solution {\npublic:\n int dp[1<<15][16];\n int Sessions(vector<int> &tasks, int sessionTime, int isTaken, int currentTime, int N){\n //exceding the boundraies\n if(currentTime>sessionTime)\n return INT_MAX;\n //checking if all elements are selected\n if(isTaken == (1<<N)-1)\n return 1;\n //returning cached results if they are already calcultated\n if(dp[isTaken][currentTime] != -1)\n return dp[isTaken][currentTime];\n int ans = INT_MAX;\n for(int i=0; i<N; i++){\n //Means this index element is not picked yet\n if(!(isTaken&(1<<i))){\n //include in current work session so for that we added taks[i] in currentTime\n int includeNow = Sessions(tasks, sessionTime, isTaken|(1<<i), currentTime+tasks[i], N);\n //creating a new work session\n int includeInNext = 1 + Sessions(tasks, sessionTime, isTaken|(1<<i), 0+tasks[i], N);\n ans = min({ans, includeNow, includeInNext});\n }\n }\n dp[isTaken][currentTime] = ans;\n return dp[isTaken][currentTime];\n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n memset(dp, -1, sizeof(dp));\n return Sessions(tasks, sessionTime, 0, 0, tasks.size());\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | clean dp with memoization | clean-dp-with-memoization-by-youngsam-hjfs | credit to @shourabhpayal\nfor c++ https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1431836/C%2B%2B-Solution-or-Recursio | youngsam | NORMAL | 2021-08-29T09:49:58.856263+00:00 | 2021-08-29T09:49:58.856297+00:00 | 106 | false | credit to @shourabhpayal\nfor c++ https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1431836/C%2B%2B-Solution-or-Recursion-%2B-Memoization\n\n\nidea\n1. use bit mask to represent array \n 1) for selected element, set ith index to 1\n 2) for unselected element, is ith index is 0\n\t\n\te.g: [1,2,3,4,5,6] \n\t if 0 and 4th element selected , 100010\n\n2. use memoization to store interim result \n e.g: in #1 above example , \n 10010 binary equals to 18 , \n therefore, minimum value is in between memo[18][0] to memo[18][sessionTime]\n\t\t \n3. final result is in between memo[(1<<n)-1][0] and memo[(1<<n)-1][sessionTime]\n4. \n\t\t \n```\n\n\npublic int minSessions(int[] tasks, int sessionTime) { \n int n=tasks.length;\n Integer[][] memo= new Integer[1<<n][sessionTime+1]; \n return dp(tasks,memo,0,0,sessionTime,(1<<n)-1); \n }\n \n private int dp(int[] tasks,Integer[][] memo,int mask,int currTime,int sessionTime,int all){\n if(currTime>sessionTime)\n return Integer.MAX_VALUE;\n \n if(mask==all)\n return 1; \n \n if(memo[mask][currTime]!=null)\n return memo[mask][currTime];\n \n int res=Integer.MAX_VALUE;\n for(int i=0;i<tasks.length;i++){\n if((mask&(1<<i))==0){\n int a=dp(tasks,memo,mask|(1<<i),currTime+tasks[i],sessionTime,all); \n int b=dp(tasks,memo,mask|(1<<i),tasks[i],sessionTime,all)+1;\n res=Math.min(res,Math.min(a,b));\n } \n }\n \n return memo[mask][currTime]=res;\n }\n\n\n\n```\n\n\n\n | 1 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++] Dynamic Programming with bit-masking (commented) | c-dynamic-programming-with-bit-masking-c-ad0k | \nclass Solution\n{\n public:\n int n, k;\n vector<int> a;\n int dp[(1 << 14) + 5][16];\n int find(int mask, int left)\n {\n \t// mask = to s | __kaizen__ | NORMAL | 2021-08-29T09:03:14.020857+00:00 | 2021-08-29T09:03:14.020905+00:00 | 74 | false | ```\nclass Solution\n{\n public:\n int n, k;\n vector<int> a;\n int dp[(1 << 14) + 5][16];\n int find(int mask, int left)\n {\n \t// mask = to store the state of already selected items\n \t// left = how much sessionTime is still left to consume\n if (mask == (1 << n) - 1)\n return 0;\n int &mn = dp[mask][left];\n // memoization\n if (mn != -1)\n return mn;\n mn = 1e9;\n for (int i = 0; i < n; i++)\n {\n \t// if ith item is not selected in mask the select it\n if (((mask >> i) & 1) == 0)\n {\n \t// if sessionTime is still left to consume the simply subtract from it \n \t// and set the ith item in the mask\n if (left - a[i] >= 0)\n mn = min({mn, find((mask | (1 << i)), left - a[i])});\n // since every item is greater tha sessionTime i.e. (a[i]>=k), then\n // consume it from fresh sessionTime and increse the session by 1. \n mn = min(mn, 1 + find((mask | (1 << i)), k - a[i]));\n }\n }\n return mn;\n }\n int minSessions(vector<int> &tasks, int sessionTime)\n {\n a = tasks;\n n = size(a), k = sessionTime;\n for (auto &x : dp)\n for (auto &y : x)\n y = -1;\n return find(0, k) + 1;\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | sub-mask enumeration | O(3^n) | c-sub-mask-enumeration-o3n-by-hit7sh-93qz | We can reach a mask from all of its submasks.\n```\nclass Solution {\npublic:\n int minSessions(vector& tasks, int sessionTime) {\n int n = tasks.size | hit7sh | NORMAL | 2021-08-29T07:22:06.092450+00:00 | 2021-08-29T08:24:09.747232+00:00 | 102 | false | We can reach a mask from all of its submasks.\n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n vector<int> dp(1 << n, 100000);\n for (int mask = 0; mask < 1 << n; mask++) {\n int req = 0;\n for (int i = 0; i < n; i++) {\n if (mask & 1 << i) req += tasks[i];\n }\n if (req <= sessionTime) dp[mask] = 1;\n \n for (int smask = mask; ; smask = mask & (smask - 1)) {\n if (dp[smask] + dp[mask - smask] < dp[mask])\n dp[mask] = dp[smask] + dp[mask - smask];\n if (smask == 0) break;\n }\n }\n return dp[(1 << n) - 1];\n }\n}; | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++] Binary Search + DFS + Memo | c-binary-search-dfs-memo-by-dingdang2014-d0rg | If x is the minimum number of work sessions to finish the tasks, then any value of work sessions larger than x would also be enough to finish the tasks. Thus, | dingdang2014 | NORMAL | 2021-08-29T06:25:47.000372+00:00 | 2021-08-29T06:25:47.000402+00:00 | 161 | false | If x is the minimum number of work sessions to finish the tasks, then any value of work sessions larger than x would also be enough to finish the tasks. Thus, we can apply binary search to this question.\n\nThe initial `left` can be 0, and `right` is the size of the tasks (why?).\n\nThe first guess could be `mid = left + (right - left) / 2`.\n\nThen the question becomes: if we have `mid` work sesssions (each has sessionTime hours), can we finsih all the tasks?\n\nSo it becomes a multi-knapsack problem.\n\nThe good news is that the numbe rof tasks and sessionTime are very small, so we can memorize all the possible states. For example, the bits of an integer can be used to record whether each tasks has been finished or not.\n\nSee the code below:\n\n\n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size(), left = 0, right = n;\n sort(tasks.begin(), tasks.end(), greater());\n vector<vector<vector<int>>> memo(1<<n, vector<vector<int>>(n+1, vector<int>(sessionTime+1, -1)));\n while(left < right) {\n int mid = left + (right - left) / 2;\n if(!valid(tasks, 0, 0, sessionTime, mid, memo)) left = mid + 1;\n else right = mid;\n // cout<<mid<<" "<<left<<" "<<right<<endl;\n }\n return left;\n }\nprivate:\n bool valid(vector<int>& ts, int state, int sum, int& tm, int mid, vector<vector<vector<int>>>& memo) {\n int n = ts.size();\n if(state + 1 == (1<<n)) return sum > 0 ? mid > 0 : mid >= 0;\n if(mid<=0) return false;\n if(memo[state][mid][sum] != -1) return memo[state][mid][sum];\n for(int i=0; i<n; ++i) {\n if((state>>i) & 1) continue;\n if(tm < sum + ts[i]) continue;\n if(valid(ts, state | (1<<i), sum + ts[i], tm, mid, memo)) return memo[state][mid][sum] = 1;\n }\n return memo[state][mid][sum] = valid(ts, state, 0, tm, mid - 1, memo);\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ Solution | DP + Bit masking | c-solution-dp-bit-masking-by-hackaton172-swtv | We denote which tasks have been done and which are yet to be done by the binary representation of a variable mask (basic masking). Now everytime we have to sele | hackaton1729 | NORMAL | 2021-08-29T05:49:51.137733+00:00 | 2021-08-29T18:06:23.375269+00:00 | 229 | false | We denote which tasks have been done and which are yet to be done by the binary representation of a variable mask (basic masking). Now everytime we have to select a task to do, we have the following choices : \n1. If the current task requires time <= the time remaining in your current session, you can either select this task to be done or we can move on to some other undone task.\n2. If the current task requires time > the time remaining in your current session, to do this task, you need a new session.\n\nOur answer is the minimum of these three cases.\n\nIn this case a state of dp is defined by two variables, mask and time remaining in your current session, and stores the value of the number of new sessions required to do all tasks from current state.\n\n\'\'\'\n\nclass Solution {\npublic:\n int sto; \n\t\n int dp[(1<<14)-1][18]; int n;\n\t\n vector<int> tasks;\n\t\n int solve(int mask,int st){\n if(mask==(1<<n)-1){//If all the tasks are done, return 0;\n return 0;\n }\n if(dp[mask][st]!=-1) return dp[mask][st]; //If dp has the value of present state, no need to recalculate\n\t\t\n int ans=INT_MAX; \n\t\t\n for(int i=0;i<tasks.size();i++){\n if(tasks[i]<=st&&((mask&(1<<i))==0)){//case 1\n ans=min(ans,solve(mask|(1<<i),st-tasks[i]));\n }\n else if(((mask&(1<<i))==0)){//case 2\n ans=min(ans,solve(mask|(1<<i),sto-tasks[i])+1);\n }\n }\n return dp[mask][st]=ans;\n }\n \n int minSessions(vector<int>& task, int sessionTime) {\n tasks=task;\n sto=sessionTime; n=tasks.size();\n memset(dp,-1,sizeof(dp));\n int mask=0;\n return solve(mask,sto)+1; // + 1 for the initial session\n \n }\n};\n\n\'\'\'\n\n**If you found this helpful, please consider upvoting.** | 1 | 0 | ['Bit Manipulation', 'Recursion', 'Memoization'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | javascript bitmask dp 144ms | javascript-bitmask-dp-144ms-by-henrychen-jp1u | \nconst minSessions = (tasks, sessionTime) => {\n let n = tasks.length;\n let dp = Array(1 << n).fill(Number.MAX_SAFE_INTEGER);\n let valid = Array(1 < | henrychen222 | NORMAL | 2021-08-29T05:45:31.088337+00:00 | 2021-08-29T05:45:31.088399+00:00 | 336 | false | ```\nconst minSessions = (tasks, sessionTime) => {\n let n = tasks.length;\n let dp = Array(1 << n).fill(Number.MAX_SAFE_INTEGER);\n let valid = Array(1 << n).fill(false);\n for (let i = 0; i < 1 << n; i++) {\n let sum = 0;\n for (let j = 0; j < n; j++) {\n if (1 & (i >> j)) sum += tasks[j];\n // OR if (i << ~j < 0) sum += tasks[j];\n }\n valid[i] = sum <= sessionTime;\n }\n dp[0] = 0;\n for (let i = 0; i < 1 << n; i++) {\n for (let j = i; j > 0; j = (j - 1) & i) {\n if (valid[j]) {\n dp[i] = Math.min(dp[i], dp[i - j] + 1);\n }\n }\n }\n return dp[(1 << n) - 1];\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Bitmask', 'JavaScript'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C# - O(N * 2 ^ N + 3 ^ N) Dynamic Programming + Bit Masking | c-on-2-n-3-n-dynamic-programming-bit-mas-wqm7 | csharp\npublic int MinSessions(int[] tasks, int sessionTime)\n{\n\tint mask = 1 << tasks.Length;\n\tint[] sum = new int[mask];\n\tint[] d = new int[mask];\n\tAr | christris | NORMAL | 2021-08-29T05:07:07.942116+00:00 | 2021-08-29T05:17:19.542525+00:00 | 179 | false | ```csharp\npublic int MinSessions(int[] tasks, int sessionTime)\n{\n\tint mask = 1 << tasks.Length;\n\tint[] sum = new int[mask];\n\tint[] d = new int[mask];\n\tArray.Fill(d, 1000);\n\td[0] = 0;\n\n\tfor (int i = 1; i < mask; i++)\n\t{ \n\t\tfor (int j = 0; j < tasks.Length; j++)\n\t\t{\n\t\t\tif ((i & (1 << j)) != 0)\n\t\t\t{\n\t\t\t\tsum[i] += tasks[j];\n\t\t\t}\n\t\t}\n\t}\n\n\tfor (int i = 1; i < mask; i++)\n\t{ \n\t\t// Enumerate all submasks\n\t\tfor (int j = i; j != 0; j = (j - 1) & i)\n\t\t{\n\t\t\tif (sum[j] <= sessionTime)\n\t\t\t{\n\t\t\t\td[i] = Math.Min(d[i], d[j ^ i] + 1); \n\t\t\t}\n\t\t}\n\t}\n\n\treturn d[^1];\n}\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Java] Bitmask DP, O(N2^N) | java-bitmask-dp-on2n-by-blackpinklisa-hqlq | Let us let a bitmask represent the available tasks and the unavaliable tasks where a 1 bit represents that a task is still available and 0 bit represents a task | blackpinklisa | NORMAL | 2021-08-29T04:51:34.782355+00:00 | 2021-08-29T15:56:13.364921+00:00 | 154 | false | Let us let a bitmask represent the available tasks and the unavaliable tasks where a `1` bit represents that a task is still available and `0` bit represents a task that is unavailable. \n\nThen, we can let `dp[bitmask]` represent the minimum sessions required to fullfill all the tasks of that bitmask. \n\nTo solve for `dp[bitmask]`, we can iterate through all submasks, (subsets of the avaliable masks), and let all the available tasks of that submask be one session. We need to check first if that is a valid one session by summing up the task time and making sure its less than sessionTime. We can then recurse on `dp[bitmask ^ submask`].\n\n\n```\nclass Solution {\n int res = Integer.MAX_VALUE;\n Integer[] dp;\n \n // 1 == unused, 0 == used\n public int dp(int[] tasks, int sessionTime, int mask){\n if(mask == 0) return 0;\n if(dp[mask] != null) return dp[mask];\n int res = Integer.MAX_VALUE;\n int n = tasks.length;\n for (int submask = mask;; submask = (submask - 1) & mask) {\n if (submask == 0)\n break;\n int totalTime = 0;\n for(int i=0; i<n; i++){\n if((submask & (1 << i)) != 0){\n totalTime += tasks[i];\n }\n }\n if(totalTime <= sessionTime){\n int next_mask = mask ^ submask;\n res = Math.min(res, 1 + dp(tasks, sessionTime, next_mask));\n }\n }\n return dp[mask] = res;\n }\n \n public int minSessions(int[] tasks, int sessionTime) {\n int n = tasks.length;\n dp = new Integer[(1 << n)+1];\n return dp(tasks, sessionTime, (1 << n) - 1);\n }\n}\n``` | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Simple backtracking avoiding repeated recursive calls using hash set - C++ | simple-backtracking-avoiding-repeated-re-8heg | Just note that only backtracking will lead to TLE as there will be many repeated calls - you just need to skip those.\nHope this helps!\n\n void fun(vectorta | rajanyadg | NORMAL | 2021-08-29T04:36:32.466778+00:00 | 2021-08-29T04:36:32.466819+00:00 | 123 | false | Just note that only backtracking will lead to TLE as there will be many repeated calls - you just need to skip those.\nHope this helps!\n\n void fun(vector<int>tasks,int s,int k,int session,set<pair<vector<int>,int>>&st,vector<int>&v){\n if(tasks.empty()){\n v.push_back(k+1);\n return;\n }\n \n if(st.find(make_pair(tasks,s))!=st.end())\n return;\n \n st.insert(make_pair(tasks,s));\n \n if(!tasks.empty()){\n int flag=0;\n for(int i=0;i<tasks.size();i++){\n if(s+tasks[i]<=session){\n flag=1;\n int p=tasks[i];\n tasks.erase(tasks.begin()+i);\n if(s+p<=session)\n fun(tasks,s+p,k,session,st,v);\n\n tasks.insert(tasks.begin()+i,p);\n }\n }\n if(!flag){\n fun(tasks,0,k+1,session,st,v);\n }\n }\n }\n \n int minSessions(vector<int>& tasks, int sessionTime) {\n set<pair<vector<int>,int>>st;\n vector<int>v;\n fun(tasks,0,0,sessionTime,st,v);\n for(auto i:v)\n cout<<i<<" ";\n cout<<endl;\n return *min_element(v.begin(),v.end());\n } | 1 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Bottom up bitmask DP | bottom-up-bitmask-dp-by-changheng-uz6x | Let dp[state][sessionTimeLeft] equals to the number of session we need, example: dp[1101][10] (binary 1101) means the number of sessions we need when selecting | changheng | NORMAL | 2021-08-29T04:35:40.374027+00:00 | 2021-08-29T04:38:54.176247+00:00 | 163 | false | Let `dp[state][sessionTimeLeft]` equals to the number of session we need, example: `dp[1101][10]` (binary `1101`) means the number of sessions we need when selecting first, second and the third item, and there are 10 seconds left.\n\nNow, if `time >= tasks[i]`, `dp[state][time - tasks[i]] = dp[prevState][time]`.\nOtherwise, we need to start a new session, so `dp[state][sessionTime - tasks[i]] = min(dp[prevState][for t = 0 to sessionTime])`, (we choose the minimum amount of sessions required to transform from prevState to the current state)\n\n```cpp\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n const int N = tasks.size();\n vector<vector<int>> dp(1 << N, vector<int>(sessionTime + 1, INT_MAX / 2));\n dp[0][sessionTime] = 1;\n for (int state = 0; state < (1 << N); state++) {\n for (int t = 1; t <= sessionTime; t++) {\n for (int i = 0; i < tasks.size(); i++) {\n if (((state >> i) & 1) == 0) continue;\n const int prevState = state - (1 << i);\n if (t >= tasks[i]) {\n dp[state][t - tasks[i]] = min(\n dp[state][t - tasks[i]], \n dp[prevState][t]\n );\n } else {\n dp[state][sessionTime - tasks[i]] = min(\n dp[state][sessionTime - tasks[i]], \n *min_element(begin(dp[prevState]), end(dp[prevState])) + 1\n );\n }\n }\n }\n }\n return *min_element(begin(dp[(1 << N) - 1]), end(dp[(1 << N) - 1]));\n }\n};\n```\n\nTime complexity: `O(NT 2^N)`, where `N` is `tasks.size()`, `T` is `sessionTime` | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python3, Greedy + DP | python3-greedy-dp-by-wu1meng2-9jae | Finish large tasks first ==> Sort tasks reversely\n2. Use DP to put as many tasks as possible into one session\n3. Log the DP path such that those tasks done in | wu1meng2 | NORMAL | 2021-08-29T04:24:18.732852+00:00 | 2021-08-29T04:40:00.910610+00:00 | 586 | false | 1. Finish large tasks first ==> Sort tasks reversely\n2. Use DP to put as many tasks as possible into one session\n3. Log the DP path such that those tasks done in the current session can be removed before starting the next session\n\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n # dp[ntasks+1][sesstionTime+1]\n\t\t# Put large tasks first\n tasks.sort(reverse=True)\n \n tasks_ = [tasks[i] for i in range(len(tasks))]\n nSession = 0\n while len(tasks_) > 0:\n # Put as many task as possible into one session\n dp = [[0] * (sessionTime+1) for _ in range(len(tasks_)+1)]\n path = [[False] * (sessionTime+1) for _ in range(len(tasks_)+1)]\n \n delete = [False] * len(tasks_)\n nNew = len(tasks_)\n \n for i in range(1,len(tasks_)+1):\n for j in range(1,sessionTime+1):\n dp[i][j] = dp[i-1][j]\n if (j-tasks_[i-1] >= 0):\n # Put in tasks[i-1]\n if dp[i][j] < dp[i-1][j-tasks_[i-1]] + tasks_[i-1]:\n dp[i][j] = dp[i-1][j-tasks_[i-1]] + tasks_[i-1]\n path[i][j] = True\n nNew -= 1\n\n\t\t\t# Remove those tasks in the current session \n k = sessionTime;\n for i in range(len(tasks_), 0, -1):\n if path[i][k] and k >= 1:\n delete[i-1] = True\n k = k - tasks_[i-1]\n \n newtasks_ = []\n count = 0\n for i in range(len(tasks_)):\n if not delete[i]:\n newtasks_.append(tasks_[i])\n \n tasks_ = newtasks_\n \n nSession += 1\n \n return nSession\n``` | 1 | 0 | ['Python3'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | JAVA | Beat 100 % | Two Sum Idea | No bit-mask | No recursion | | java-beat-100-two-sum-idea-no-bit-mask-n-9sv9 | ```\n public int minSessions(int[] tasks, int sessionTime) {\n\t\t//reverse order sort\n tasks = Arrays.stream(tasks).boxed()\n .sorted(Col | uchihasasuke | NORMAL | 2021-08-29T04:22:31.839802+00:00 | 2021-08-29T04:25:04.737698+00:00 | 283 | false | ```\n public int minSessions(int[] tasks, int sessionTime) {\n\t\t//reverse order sort\n tasks = Arrays.stream(tasks).boxed()\n .sorted(Collections.reverseOrder())\n .mapToInt(Integer::intValue)\n .toArray();\n \n //Key is tasks[i], Value is counter\n Map<Integer, Integer> map = new HashMap<>();\n for(int t : tasks) {\n map.put(t, map.getOrDefault(t, 0) + 1);\n }\n \n int count = 0;\n for(int t : tasks) {\n if(map.get(t) > 0) {\n map.put(t, map.get(t) - 1);\n int cur = t;\n int temp = sessionTime - cur;\n while(cur < sessionTime) {\n if(map.getOrDefault(temp, 0) > 0) {\n cur += temp;\n map.put(temp, map.get(temp) - 1);\n } else {\n temp--;\n if(temp == 0) {\n break;\n }\n }\n }\n count++;\n }\n }\n return count; \n }\n\n\t | 1 | 3 | [] | 5 |
build-a-matrix-with-conditions | ✅💯🔥Explanations No One Will Give You🎓🧠VERY Detailed Approach🎯🔥Extremely Simple And Effective🔥 | explanations-no-one-will-give-youvery-de-6zdk | \n\n \n \n I am lucky that whatever fear I have inside me, my desire to win is always stronger.\n \n | heir-of-god | NORMAL | 2024-07-21T06:50:20.500352+00:00 | 2024-07-21T11:01:17.763787+00:00 | 19,845 | false | \n<blockquote>\n <p>\n <b>\n I am lucky that whatever fear I have inside me, my desire to win is always stronger.\n </b> \n </p>\n <p>\n --- Serena Williams ---\n </p>\n</blockquote>\n\n# \uD83D\uDC51Problem Explanation and Understanding:\n\n## \uD83C\uDFAF Problem Description\nYou are given an integer `k` and two 2d arrays `rowConditions` and `colConditions`. You need to create 2d matrix with sizes `k x k` where there\'s exactly k numbers from 1 to k and all other elements are 0. Elements in `rowConditions` and `colConditions` - arrays with 2 elements which just mean: `rowCondition[0] must be in a row ABOVE rowCondition[1]` and `colCondition[0] must be in a column LEFT to colCondition[1]`.\n\n## \uD83D\uDCE5\u2935\uFE0F Input:\n- Integer `k` representing sizes of the matrix\n- Integer 2d array `rowConditions` representing conditions for rows\n- Integer 2d array `colConditions` representing conditions for columns\n\n## \uD83D\uDCE4\u2934\uFE0F Output:\nThe valid matrix you created OR the empty array if such matrix doesn\'t exist\n\n---\n\n# 1\uFE0F\u20E3\uD83C\uDFC6 Approach: Topological Sorting With DFS\n\n# \uD83E\uDD14 Intuition\n**First of all - graphs is hard**. Okay, now forget about the graphs and let me explain how to think about this problem. \n- Let\'s make problem easier for us, what if we will consider only `rowConditions` and for a second forget about `colConditions`? Like imagine we have matrix `K x 1` so all we need to do is place numbers correctly according to row ordering in `rowConditions`. Let\'s say somehow we created this matrixes (now this doesn\'t matter how, because you want to understand the logic of the problem)\n\n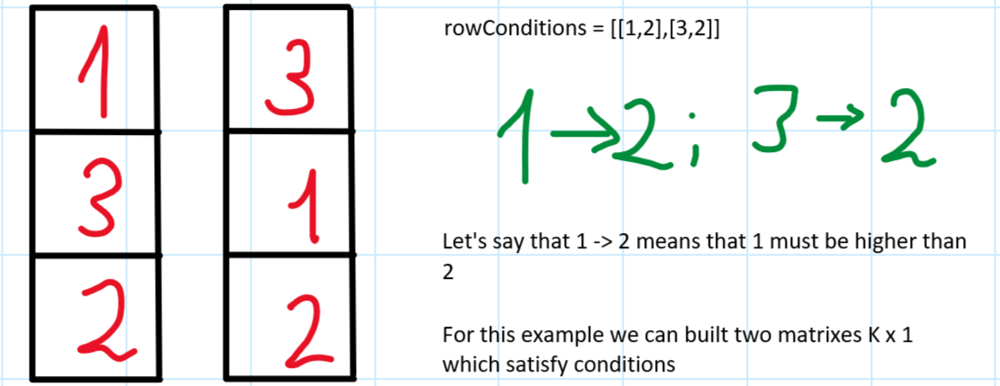\n\n- Okay, good, we know in which row every element will go, but what about columns? We want columns also to be *sorted* with `colConditions`. Can we do the same thing we did to rows? Absolutely, let\'s do this.\n\n\n\n- Let\'s say now we have correct orders for both rows and columns, we know for sure in which row element must be and in which column, can we now esaily construct matrix with this? Sure\n\n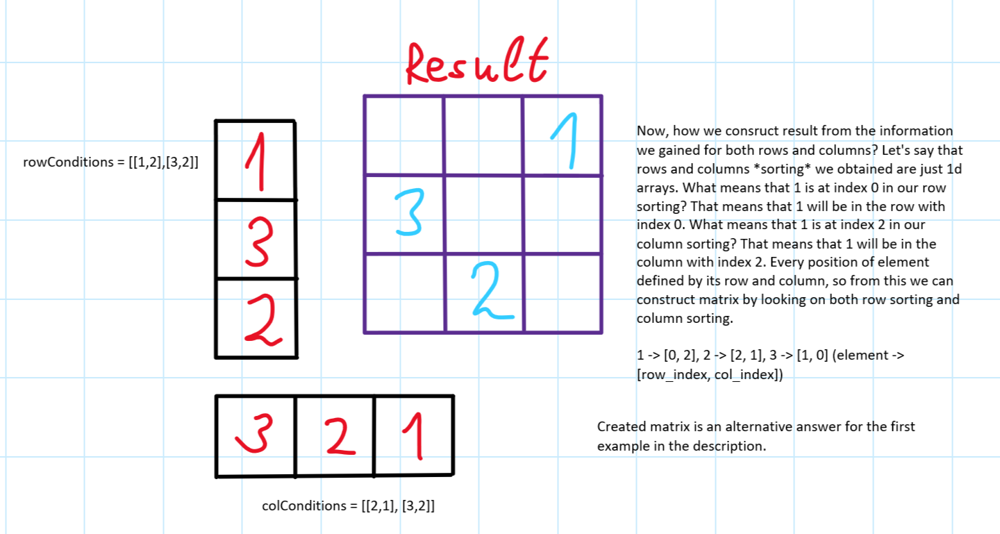\n\n- In fact, this is the whole logic for this problem. But let\'s think about some edge cases and implementing details.\n- First of all - we created these sortings for rows and columns by magic in the example but in fact behind this approach is algorithm *Topological Sorting*. Topological sorting - graph algorithm for directed graphs without cycles which just sort graph vertixes in manner `first comes my prerequisites (parents) then I come myself and only then come my childrens`\n\nThis is an example for topological sorting ([source](https://youtu.be/7J3GadLzydI?si=zpZ_A8oLRSNkGql4))\n\n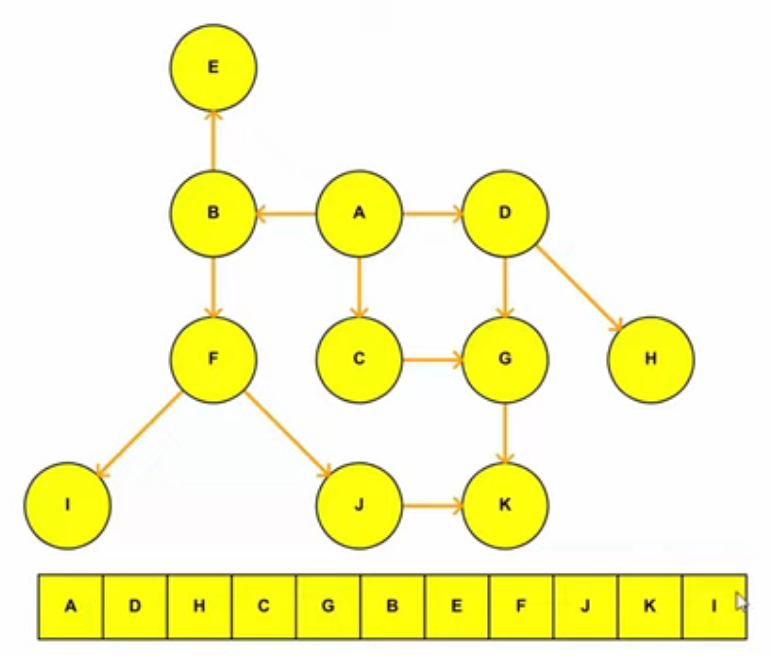\n\nThe sequence created above is just one of the possible sorting. Topological sort isn\'t unique which means that there can be multiple answers for one graph. \n\n- How we will apply topological sort to our problem? Well, look at the my pictures above where I\'ve drawn relations between values as arrows. In fact, we can imagine for both rows and columns conditions as graph where given to us `rowConditions` and `colConditions` are edges for graph. This will look like this:\n\n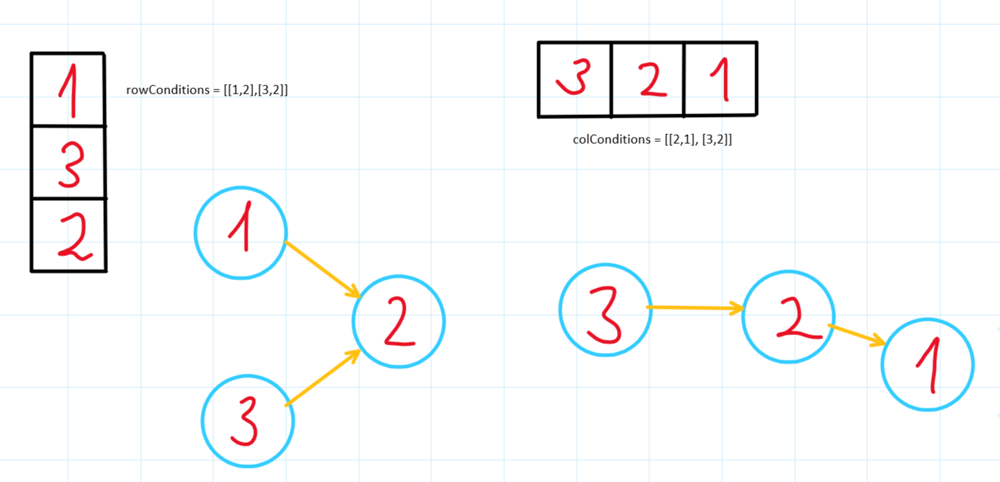\n\nAnd now if you think about topological sorting of the row graph you will see that in fact there\'s actually two possible sorting.\n\n- The one edge case I want to consider before we move on to the code - when there will be the case where matrix is impossible to create? Well, let\'s look on one more example from the description:\n\n\n\nDo you see the problem? When I was explaining topological sorting I mentioned that it works only for graphs with no cycle (Acyclic) but there\'s actually the cycle and also logic drawback if you think about it - 1 must be higher than 2, 2 must be higher than 3 (so this can be [1, 2, 3]) but now what?.... 3 must be higher than 1 which is impossible because of previous conditions.\n\nHope this all makes sense - if not or you have any doubts feel free to ask questions in the comments!\u2764\uFE0F\n\n# \uD83D\uDC69\uD83C\uDFFB\u200D\uD83D\uDCBB Coding \n- Define a nested helper function `dfs` for depth-first search:\n - `dfs` takes five arguments: `src` (current node), `graph` (adjacency list), `visited` (set of visited nodes), `cur_path` (current path nodes), and `res` (result list).\n - Return `False` if a cycle is detected (node is in `cur_path`) and `True` otherwise.\n - Mark the node as visited and add it to the current path.\n - Recursively call `dfs` for each neighbor; if any call returns `False`, return `False`.\n - Backtrack by removing the node from the current path and add it to the result list. (so last nodes visited will be first at list, that\'s why we reverse list in topo_sort)\n\n- Define another helper function `topo_sort` for topological sorting:\n - `topo_sort` takes `edges` (list of edges) as input.\n - Build an adjacency list `graph` from the edges.\n - Initialize `visited` and `cur_path` as empty sets, and `res` as an empty list.\n - Perform DFS on all nodes from 1 to `k` using the `dfs` function.\n - Return an empty list if a cycle is detected, otherwise return the result list reversed.\n\n- Perform topological sorting on `rowConditions` and `colConditions` using `topo_sort` and store the results in `row_sorting` and `col_sorting`.\n- If either sorting result is an empty list (there was a cycle), return an empty list.\n- Create a dictionary `value_position` to store the row and column indices for each value from 1 to `k`.\n- Assign row indices to the values based on `row_sorting`.\n- Assign column indices to the values based on `col_sorting`.\n- Initialize the result matrix `res` as a `k x k` matrix filled with zeros.\n- Populate the matrix `res` using the positions from `value_position`.\n- Return the populated matrix `res`.\n\n# \uD83D\uDCD5 Complexity Analysis\n- \u23F0 Time complexity: O(k), since you will run 2 dfs on `k` nodes and visit each exactly once -> O(2k) -> O(k) (You can also consider O(k^2) since you\'re created matrix k x k but there\'s no way to return matrix without creating it, so this doesn\'t make sense)\n- \uD83E\uDDFA Space complexity: O(k), since we use several data structures like arrays and hashmaps with size up to `k` and there\'s dfs call stack which is also linear for `k`\n\n# \uD83D\uDCBB Code (I\'ve saved comments for each language)\n``` python []\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: list[list[int]], colConditions: list[list[int]]) -> list[list[int]]:\n # return True if all okay and return False if cycle was found\n def dfs(src, graph, visited, cur_path, res) -> bool:\n if src in cur_path:\n return False # cycle detected\n\n if src in visited:\n return True # all okay, but we\'ve already visited this node\n\n visited.add(src)\n cur_path.add(src)\n\n for neighbor in graph[src]:\n if not dfs(neighbor, graph, visited, cur_path, res): # if any child returns false\n return False\n\n cur_path.remove(src) # backtrack path\n res.append(src)\n return True\n\n # if there will be cycle - return empty array, in other case return 1d array as described above\n def topo_sort(edges) -> list[int]:\n graph = defaultdict(list)\n for src, dst in edges:\n graph[src].append(dst)\n\n visited: set[int] = set()\n cur_path: set[int] = set()\n res: list[int] = []\n\n for src in range(1, k + 1, 1):\n if not dfs(src, graph, visited, cur_path, res):\n return []\n\n return res[::-1] # we will have res as reversed so we need to reverse it one more time\n\n row_sorting: list[int] = topo_sort(rowConditions)\n col_sorting: list[int] = topo_sort(colConditions)\n if [] in (row_sorting, col_sorting):\n return []\n\n value_position: dict[int, list[int]] = {\n n: [0, 0] for n in range(1, k + 1, 1)\n } # element -> [row_index, col_index]\n for ind, val in enumerate(row_sorting):\n value_position[val][0] = ind\n for ind, val in enumerate(col_sorting):\n value_position[val][1] = ind\n\n res: list[list[int]] = [[0 for _ in range(k)] for _ in range(k)]\n for value in range(1, k + 1, 1):\n row, column = value_position[value]\n res[row][column] = value\n\n return res\n```\n``` C++ []\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n unordered_map<int, vector<int>> graph;\n for (const auto& edge : rowConditions) {\n graph[edge[0]].push_back(edge[1]);\n }\n\n vector<int> row_sorting = topo_sort(graph, k);\n graph.clear();\n for (const auto& edge : colConditions) {\n graph[edge[0]].push_back(edge[1]);\n }\n vector<int> col_sorting = topo_sort(graph, k);\n\n if (row_sorting.empty() || col_sorting.empty()) {\n return {};\n }\n\n unordered_map<int, pair<int, int>> value_position;\n for (int i = 0; i < k; ++i) {\n value_position[row_sorting[i]].first = i;\n value_position[col_sorting[i]].second = i;\n }\n\n vector<vector<int>> res(k, vector<int>(k, 0));\n for (int value = 1; value <= k; ++value) {\n int row = value_position[value].first;\n int column = value_position[value].second;\n res[row][column] = value;\n }\n\n return res;\n }\n\nprivate:\n bool dfs(int src, unordered_map<int, vector<int>>& graph, unordered_set<int>& visited, unordered_set<int>& cur_path, vector<int>& res) {\n if (cur_path.count(src)) return false; // cycle detected\n if (visited.count(src)) return true; // all okay, but we\'ve already visited this node\n\n visited.insert(src);\n cur_path.insert(src);\n\n for (int neighbor : graph[src]) {\n if (!dfs(neighbor, graph, visited, cur_path, res)) // if any child returns false\n return false;\n }\n\n cur_path.erase(src); // backtrack path\n res.push_back(src);\n return true;\n }\n\n vector<int> topo_sort(unordered_map<int, vector<int>>& graph, int k) {\n unordered_set<int> visited;\n unordered_set<int> cur_path;\n vector<int> res;\n\n for (int src = 1; src <= k; ++src) {\n if (!dfs(src, graph, visited, cur_path, res))\n return {};\n }\n\n reverse(res.begin(), res.end()); // we will have res as reversed so we need to reverse it one more time\n return res;\n }\n};\n```\n``` JavaScript []\nvar buildMatrix = function(k, rowConditions, colConditions) {\n // return True if all okay and return False if cycle was found\n function dfs(src, graph, visited, cur_path, res) {\n if (cur_path.has(src)) return false; // cycle detected\n if (visited.has(src)) return true; // all okay, but we\'ve already visited this node\n\n visited.add(src);\n cur_path.add(src);\n\n for (let neighbor of (graph.get(src) || [])) {\n if (!dfs(neighbor, graph, visited, cur_path, res)) // if any child returns false\n return false;\n }\n\n cur_path.delete(src); // backtrack path\n res.push(src);\n return true;\n }\n\n // if there will be cycle - return empty array, in other case return 1d array as described above\n function topo_sort(edges) {\n let graph = new Map();\n for (let [src, dst] of edges) {\n if (!graph.has(src)) graph.set(src, []);\n graph.get(src).push(dst);\n }\n\n let visited = new Set();\n let cur_path = new Set();\n let res = [];\n\n for (let src = 1; src <= k; ++src) {\n if (!dfs(src, graph, visited, cur_path, res))\n return [];\n }\n\n return res.reverse(); // we will have res as reversed so we need to reverse it one more time\n }\n\n let row_sorting = topo_sort(rowConditions);\n let col_sorting = topo_sort(colConditions);\n if (!row_sorting.length || !col_sorting.length)\n return [];\n\n let value_position = {};\n for (let n = 1; n <= k; ++n) {\n value_position[n] = [0, 0]; // element -> [row_index, col_index]\n }\n row_sorting.forEach((val, ind) => value_position[val][0] = ind);\n col_sorting.forEach((val, ind) => value_position[val][1] = ind);\n\n let res = Array.from({ length: k }, () => Array(k).fill(0));\n for (let value = 1; value <= k; ++value) {\n let [row, column] = value_position[value];\n res[row][column] = value;\n }\n\n return res;\n};\n```\n``` Java []\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<Integer> row_sorting = topo_sort(rowConditions, k);\n List<Integer> col_sorting = topo_sort(colConditions, k);\n if (row_sorting.isEmpty() || col_sorting.isEmpty())\n return new int[0][0];\n\n Map<Integer, int[]> value_position = new HashMap<>();\n for (int n = 1; n <= k; ++n) {\n value_position.put(n, new int[2]); // element -> [row_index, col_index]\n }\n for (int ind = 0; ind < row_sorting.size(); ++ind) {\n value_position.get(row_sorting.get(ind))[0] = ind;\n }\n for (int ind = 0; ind < col_sorting.size(); ++ind) {\n value_position.get(col_sorting.get(ind))[1] = ind;\n }\n\n int[][] res = new int[k][k];\n for (int value = 1; value <= k; ++value) {\n int row = value_position.get(value)[0];\n int column = value_position.get(value)[1];\n res[row][column] = value;\n }\n\n return res;\n }\n\n // return True if all okay and return False if cycle was found\n private boolean dfs(int src, Map<Integer, List<Integer>> graph, Set<Integer> visited, Set<Integer> cur_path, List<Integer> res) {\n if (cur_path.contains(src)) return false; // cycle detected\n if (visited.contains(src)) return true; // all okay, but we\'ve already visited this node\n\n visited.add(src);\n cur_path.add(src);\n\n for (int neighbor : graph.getOrDefault(src, Collections.emptyList())) {\n if (!dfs(neighbor, graph, visited, cur_path, res)) // if any child returns false\n return false;\n }\n\n cur_path.remove(src); // backtrack path\n res.add(src);\n return true;\n }\n\n // if there will be cycle - return empty array, in other case return 1d array as described above\n private List<Integer> topo_sort(int[][] edges, int k) {\n Map<Integer, List<Integer>> graph = new HashMap<>();\n for (int[] edge : edges) {\n graph.computeIfAbsent(edge[0], x -> new ArrayList<>()).add(edge[1]);\n }\n\n Set<Integer> visited = new HashSet<>();\n Set<Integer> cur_path = new HashSet<>();\n List<Integer> res = new ArrayList<>();\n\n for (int src = 1; src <= k; ++src) {\n if (!dfs(src, graph, visited, cur_path, res))\n return Collections.emptyList();\n }\n\n Collections.reverse(res); // we will have res as reversed so we need to reverse it one more time\n return res;\n }\n}\n```\n\n## \uD83D\uDCA1\uD83D\uDCA1\uD83D\uDCA1I encourage you to check out [my profile](https://leetcode.com/heir-of-god/) and [Project-S](https://github.com/Heir-of-God/Project-S) project for detailed explanations and code for different problems (not only Leetcode). Happy coding and learning!\uD83D\uDCDA\n\n### Please consider *upvote*\u2B06\uFE0F\u2B06\uFE0F\u2B06\uFE0F because I try really hard not just to put here my code and rewrite testcase to show that it works but explain you WHY it works and HOW. Thank you\u2764\uFE0F\n\n## If you have any doubts or questions feel free to ask them in comments. I will be glad to help you with understanding\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n\n | 147 | 10 | ['Array', 'Hash Table', 'Graph', 'Topological Sort', 'Matrix', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 12 |
build-a-matrix-with-conditions | ✅Beats 100% -Explained with [ Video ] -C++/Java/Python/JS - Topological Sort - Explained in Detail | beats-100-explained-with-video-cjavapyth-qe4y | \n\n# YouTube Video Explanation:\n\n ### To watch the video please click on "Watch On Youtube" option available the left bottom corner of the thumbnail. \n\nIf | lancertech6 | NORMAL | 2024-07-21T01:13:02.889730+00:00 | 2024-07-21T01:43:49.144548+00:00 | 10,943 | false | \n\n# YouTube Video Explanation:\n\n<!-- ### To watch the video please click on "Watch On Youtube" option available the left bottom corner of the thumbnail. -->\n\n**If you want a video for this question please write in the comments**\n\n\n<!-- https://youtu.be/h_YTOvo65ng -->\n\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 2700 Subscribers*\n*Current Subscribers: 2641*\n\nFollow me on Instagram : https://www.instagram.com/divyansh.nishad/\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be viewed as a topological sorting problem. We need to order the rows and columns such that the conditions given in `rowConditions` and `colConditions` are met. This can be achieved by treating the conditions as directed edges in a graph and performing a topological sort.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Graph Construction**:\n - Construct a graph for row conditions and another graph for column conditions.\n - Nodes represent the numbers from 1 to k.\n - Directed edges represent the conditions, e.g., `rowConditions[i] = [a, b]` implies an edge from `a` to `b`.\n\n2. **Topological Sorting**:\n - Perform topological sorting on both graphs to determine the order of rows and columns.\n - Use Depth First Search (DFS) for topological sorting and detect any cycles which would make it impossible to satisfy the conditions.\n\n3. **Matrix Construction**:\n - Using the order obtained from the topological sort, place each number from 1 to k in the corresponding position in the k x k matrix.\n\n4. **Validation**:\n - If any cycle is detected during the topological sorting, return an empty matrix as it indicates that it is impossible to satisfy all conditions.\n\n\n# Complexity\n- **Time Complexity**:\n - Constructing the graph: O(n + m), where n and m are the lengths of `rowConditions` and `colConditions` respectively.\n - Topological Sorting: O(k + n) for rows and O(k + m) for columns.\n - Matrix construction: O(k^2).\n\n- **Space Complexity**:\n - Graph storage: O(k + n) for rows and O(k + m) for columns.\n - Additional space for topological sorting: O(k).\n - Matrix storage: O(k^2).\n\n\n# Step-by-Step Explanation\n\n#### Step 1: Construct Graphs for Conditions\n\nWe\'ll construct two directed graphs:\n1. `rowGraph` for `rowConditions`\n2. `colGraph` for `colConditions`\n\n**Example Input:**\n- \\( k = 3 \\)\n- `rowConditions = [[1, 2], [3, 2]]`\n- `colConditions = [[2, 1], [3, 2]]`\n\n**Row Graph:**\n\n| Node | Edges |\n|------|---------|\n| 1 | [2] |\n| 3 | [2] |\n\n**Column Graph:**\n\n| Node | Edges |\n|------|---------|\n| 2 | [1] |\n| 3 | [2] |\n\n#### Step 2: Perform Topological Sorting\n\nWe need to determine the order in which to place the numbers in the rows and columns using topological sorting.\n\n**Topological Sort for Rows:**\n\n| Node | Visited | DFS Path | Topological Order |\n|------|---------|----------|-------------------|\n| 1 | 0 | Start | |\n| 1 | 2 | Visit 1 | |\n| 2 | 2 | Visit 2 | |\n| 2 | 1 | Backtrack| |\n| 1 | 1 | Backtrack| 2 |\n| 3 | 0 | Start | |\n| 3 | 2 | Visit 3 | |\n| 2 | 1 | Skip | |\n| 3 | 1 | Backtrack| 3 |\n| | | | 1 |\n\n**Final Row Topological Order:** `[3, 1, 2]`\n\n**Topological Sort for Columns:**\n\n| Node | Visited | DFS Path | Topological Order |\n|------|---------|----------|-------------------|\n| 2 | 0 | Start | |\n| 2 | 2 | Visit 2 | |\n| 1 | 2 | Visit 1 | |\n| 1 | 1 | Backtrack| |\n| 2 | 1 | Backtrack| 1 |\n| 3 | 0 | Start | |\n| 3 | 2 | Visit 3 | |\n| 2 | 1 | Skip | |\n| 3 | 1 | Backtrack| 2 |\n| | | | 3 |\n\n**Final Column Topological Order:** `[3, 2, 1]`\n\n#### Step 3: Construct the Matrix\n\nUsing the topological orders, place each number in the corresponding position in the \\( k \\times k \\) matrix.\n\n**Row Indices:**\n\n| Number | Row Index |\n|--------|-----------|\n| 3 | 0 |\n| 1 | 1 |\n| 2 | 2 |\n\n**Column Indices:**\n\n| Number | Column Index |\n|--------|--------------|\n| 3 | 0 |\n| 2 | 1 |\n| 1 | 2 |\n\n**Matrix Construction:**\n\n- Place `3` at `(0, 0)`\n- Place `1` at `(1, 2)`\n- Place `2` at `(2, 1)`\n\n**Final Matrix:**\n\n| | 0 | 1 | 2 |\n|---|---|---|---|\n| 0 | 3 | 0 | 0 |\n| 1 | 0 | 0 | 1 |\n| 2 | 0 | 2 | 0 |\n\n---\n\n# Code\n```java []\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<Integer>[] rowGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < rowGraph.length; i ++) {\n rowGraph[i] = new ArrayList();\n }\n for(int [] rowCondition : rowConditions){ \n rowGraph[rowCondition[0]].add(rowCondition[1]); \n }\n\n List<Integer>[] colGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < colGraph.length; i ++) {\n colGraph[i] = new ArrayList();\n }\n for(int [] colCondition : colConditions){\n colGraph[colCondition[0]].add(colCondition[1]); \n }\n\n int[] visited = new int[k + 1];\n Deque<Integer> queue = new LinkedList<>(); \n for(int i = 1; i < rowGraph.length; i++){ \n if(!topSort(rowGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n \n int[] rowIndexMap = new int[k + 1]; \n for(int i = 0; i < k; i++){ \n int node = queue.pollLast(); \n rowIndexMap[node] = i;\n }\n\n visited = new int[k + 1];\n queue = new LinkedList();\n for(int i = 1; i < colGraph.length; i++){\n if(!topSort(colGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n int[] colOrder = new int[k];\n int[] colIndexMap = new int[k+1];\n for(int i = 0; i < k; i++){\n int node = queue.pollLast();\n colOrder[i] = node;\n colIndexMap[node] = i;\n }\n\n int[][] result = new int[k][k];\n \n for(int i = 1; i <= k; i++){\n result[rowIndexMap[i]][colIndexMap[i]] = i;\n }\n\n return result;\n\n }\n\n public boolean topSort(List<Integer>[] graph, int node, int[] visited, Deque<Integer> queue){\n if(visited[node] == 2) {\n return false;\n }\n if(visited[node] == 0){\n visited[node] = 2;\n for(int child : graph[node]){\n if(!topSort(graph, child, visited, queue)){\n return false;\n }\n }\n visited[node] = 1;\n queue.add(node);\n }\n return true;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> rowGraph(k + 1), colGraph(k + 1);\n for (auto& rc : rowConditions) {\n rowGraph[rc[0]].push_back(rc[1]);\n }\n for (auto& cc : colConditions) {\n colGraph[cc[0]].push_back(cc[1]);\n }\n \n vector<int> rowOrder = topoSort(rowGraph, k);\n vector<int> colOrder = topoSort(colGraph, k);\n \n if (rowOrder.empty() || colOrder.empty()) return {};\n \n vector<vector<int>> result(k, vector<int>(k, 0));\n unordered_map<int, int> rowMap, colMap;\n for (int i = 0; i < k; ++i) {\n rowMap[rowOrder[i]] = i;\n colMap[colOrder[i]] = i;\n }\n \n for (int i = 1; i <= k; ++i) {\n result[rowMap[i]][colMap[i]] = i;\n }\n \n return result;\n }\n \n vector<int> topoSort(vector<vector<int>>& graph, int k) {\n vector<int> inDegree(k + 1, 0), order;\n queue<int> q;\n for (int i = 1; i <= k; ++i) {\n for (int j : graph[i]) {\n ++inDegree[j];\n }\n }\n for (int i = 1; i <= k; ++i) {\n if (inDegree[i] == 0) q.push(i);\n }\n while (!q.empty()) {\n int node = q.front(); q.pop();\n order.push_back(node);\n for (int adj : graph[node]) {\n if (--inDegree[adj] == 0) q.push(adj);\n }\n }\n return order.size() == k ? order : vector<int>();\n }\n};\n```\n```Python []\nclass Solution(object):\n def buildMatrix(self, k, rowConditions, colConditions):\n rowGraph = defaultdict(list)\n for u, v in rowConditions:\n rowGraph[u].append(v)\n \n colGraph = defaultdict(list)\n for u, v in colConditions:\n colGraph[u].append(v)\n \n def topoSort(graph):\n inDegree = {i: 0 for i in range(1, k + 1)}\n for u in graph:\n for v in graph[u]:\n inDegree[v] += 1\n queue = deque([i for i in inDegree if inDegree[i] == 0])\n order = []\n while queue:\n node = queue.popleft()\n order.append(node)\n for v in graph[node]:\n inDegree[v] -= 1\n if inDegree[v] == 0:\n queue.append(v)\n return order if len(order) == k else []\n \n rowOrder = topoSort(rowGraph)\n colOrder = topoSort(colGraph)\n \n if not rowOrder or not colOrder:\n return []\n \n rowMap = {num: i for i, num in enumerate(rowOrder)}\n colMap = {num: i for i, num in enumerate(colOrder)}\n \n result = [[0] * k for _ in range(k)]\n for i in range(1, k + 1):\n result[rowMap[i]][colMap[i]] = i\n \n return result\n \n```\n```JavaScript []\n/**\n * @param {number} k\n * @param {number[][]} rowConditions\n * @param {number[][]} colConditions\n * @return {number[][]}\n */\nvar buildMatrix = function(k, rowConditions, colConditions) {\n \nconst rowGraph = Array.from({ length: k + 1 }, () => []);\n const colGraph = Array.from({ length: k + 1 }, () => []);\n \n for (const [u, v] of rowConditions) {\n rowGraph[u].push(v);\n }\n for (const [u, v] of colConditions) {\n colGraph[u].push(v);\n }\n \n const topoSort = (graph) => {\n const inDegree = Array(k + 1).fill(0);\n for (const u of graph) {\n for (const v of u) {\n inDegree[v]++;\n }\n }\n const queue = [];\n for (let i = 1; i <= k; i++) {\n if (inDegree[i] === 0) queue.push(i);\n }\n const order = [];\n while (queue.length) {\n const node = queue.shift();\n order.push(node);\n for (const v of graph[node]) {\n if (--inDegree[v] === 0) queue.push(v);\n }\n }\n return order.length === k ? order : [];\n };\n \n const rowOrder = topoSort(rowGraph);\n const colOrder = topoSort(colGraph);\n \n if (!rowOrder.length || !colOrder.length) return [];\n \n const rowMap = rowOrder.reduce((acc, num, i) => {\n acc[num] = i;\n return acc;\n }, {});\n \n const colMap = colOrder.reduce((acc, num, i) => {\n acc[num] = i;\n return acc;\n }, {});\n \n const result = Array.from({ length: k }, () => Array(k).fill(0));\n for (let i = 1; i <= k; i++) {\n result[rowMap[i]][colMap[i]] = i;\n }\n \n return result;\n};\n```\n\n | 107 | 4 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'Python', 'C++', 'Java', 'JavaScript'] | 7 |
build-a-matrix-with-conditions | [C++ with explanation] Simple Topological Sort Implementation | c-with-explanation-simple-topological-so-c1pp | Overview\nThis problem was a standard Topological Sort problem. THANKYOU Leetcode for covering such concept after a long time! \n\nHow I figured it out as Topol | Code-O-Maniac | NORMAL | 2022-08-28T04:00:49.330021+00:00 | 2022-08-28T04:13:20.622777+00:00 | 8,350 | false | **Overview**\nThis problem was a standard **Topological Sort** problem. THANKYOU Leetcode for covering such concept after a long time! \n\n**How I figured it out as Topological Sort?**\n* Ordering of numbers were required column wise and row wise.\n* Ordering were given in pairs `a -> b`, which means `a` should come before `b`. Looks like Directed Graph.\n\n**Pre-requisite:**\n* Knowledge of Topological Sort in Directed Acyclic Graph (DAG).\n* The resources I used were:\n\t* \t[First Video](https://www.youtube.com/watch?v=qQvylVxCgB4&list=PL5DyztRVgtRVLwNWS7Rpp4qzVVHJalt22&index=26)\n\t* \t[Second Video](https://www.youtube.com/watch?v=eJEpWBieUy4&list=PL5DyztRVgtRVLwNWS7Rpp4qzVVHJalt22&index=27)\n\t* \tThe above video is from [CodeNCode](https://www.youtube.com/channel/UCrR5BJxc1vZ0fmn0MOpuXQQ) Youtube Channel. You can look out his channel for the legendary Graph series (The best I could find).\n\t\n**Algorithm**\n1. Form Directed Graphs out of the orderings in `rowConditions` and `colConditions`\n2. Check these graphs for Acyclicity. If any of the graphs is cyclic, ordering is not possible. Hence, return `[]`.\n3. Now, we are confirmed that the graphs are DAG. Form topological sorts for the `rowConditions` and `colConditions`\n4. Let the topological sort from `rowConditions` be `rowSort` and that from `colConditions` be `colSort`.\n5. `rowSort` will determine the position of the element row-wise. \n6. `colSort` will determine the position of the element col-wise. \n\n**Code**\n```\nclass Solution {\n \n /* 1. Checking if cycle is present - If YES, Topological Sort is not possible */\n vector<char> color;\n bool dfs(int v, vector<vector<int>>& graph) {\n color[v] = 1;\n for (int u : graph[v]) {\n if (color[u] == 0) {\n if (dfs(u, graph))\n return true;\n } else if (color[u] == 1) {\n return true;\n }\n }\n color[v] = 2;\n return false;\n }\n bool find_cycle(vector<vector<int>>& graph, int n) {\n color.assign(n, 0);\n\n for (int v = 0; v < n; v++) {\n if (color[v] == 0 && dfs(v, graph))\n return true;\n }\n return false;\n }\n\n /* 2. Forming the Topological Sort for DAG */\n vector<bool> visited;\n void dfs2(int v, vector<vector<int>>& graph, vector<int>& ans) {\n visited[v] = true;\n for (int u : graph[v]) {\n if (!visited[u])\n dfs2(u, graph, ans);\n }\n ans.push_back(v);\n }\n\n void topological_sort(vector<vector<int>>& graph, int n, vector<int>& ans) {\n visited.assign(n, false);\n ans.clear();\n for (int i = 0; i < n; ++i) {\n if (!visited[i])\n dfs2(i, graph, ans);\n }\n reverse(ans.begin(), ans.end());\n }\n \npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> graph1(k);\n vector<vector<int>> graph2(k);\n \n for(auto x:rowConditions) {\n graph1[x[0] - 1].push_back(x[1] - 1);\n }\n for(auto x:colConditions) {\n graph2[x[0] - 1].push_back(x[1] - 1);\n }\n \n /* 3. Check if CYCLE present in any of the graphs */\n if(find_cycle(graph1, k) || find_cycle(graph2, k)) return vector<vector<int>>();\n \n /* 4. Forming Topological Sort for the DAGs */\n vector<int> ans1; vector<int> ans2;\n \n topological_sort(graph1, k, ans1);\n topological_sort(graph2, k, ans2);\n \n /* 5. Forming the answer from the rowPosition and colPosition for each element */\n vector<vector<int>> ans(k, vector<int>(k));\n \n map<int, int> m;\n for(int i = 0; i < k; i++) {\n m[ans2[i]] = i;\n }\n \n for(int i = 0; i < k; i++) {\n ans[i][m[ans1[i]]] = ans1[i] + 1;\n }\n \n return ans;\n }\n};\n```\n**Comments:**\n1. For faster implementation, I used the codes available from https://cp-algorithms.com/\n2. Codes are as follows: [Checking cycle in Directed Graph](https://cp-algorithms.com/graph/finding-cycle.html) and [Topological Sort](https://cp-algorithms.com/graph/topological-sort.html) | 85 | 0 | ['Graph', 'Topological Sort', 'C'] | 17 |
build-a-matrix-with-conditions | Kahn's topo sort/DFS rows & cols build matrix||66ms Beats 99.72% | kahns-topo-sortdfs-rows-cols-build-matri-djik | Intuition\n Describe your first thoughts on how to solve this problem. \nUse Kahn\'s algorthm, topological sort.\nApply for rowConditions, rowConditions to find | anwendeng | NORMAL | 2024-07-21T01:33:13.435225+00:00 | 2024-07-22T10:48:47.346364+00:00 | 7,874 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse Kahn\'s algorthm, topological sort.\nApply for rowConditions, rowConditions to find the ordering in row & in col.\nThen find pos (i, j) for x where 1<=x<=k\n\n2nd approach uses DFS+degree as visited instead of Kahn\'s algorithm. Moreover the output for the recursive function `f(int i)` is using `std::deque<int>` for push front the number `i` for avoiding of reversing the container.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTopological sort can solve the following questions\n[2192. All Ancestors of a Node in a Directed Acyclic Graph](https://leetcode.com/problems/all-ancestors-of-a-node-in-a-directed-acyclic-graph/solutions/5385071/topo-sort-kahn-s-algo-counting-sort-54ms-beats-100/)\n[207. Course Schedule](https://leetcode.com/problems/course-schedule/solutions/3756937/w-explanation-c-dfs-vs-bfs-kahn-s-algorithm/)\n[210. Course Schedule II](https://leetcode.com/problems/course-schedule-ii/)\n[1203. Sort Items by Groups Respecting Dependencies\n](https://leetcode.com/problems/sort-items-by-groups-respecting-dependencies/solutions/3933825/c-using-bfs-kahn-s-algorithm-vs-dfs-beats-97-67/)\n[1203. Sort Items by Groups Respecting Dependencies| Please Turn English Subtitles if Neceesary]\n[https://youtu.be/vdar3a_ZdCI](https://youtu.be/vdar3a_ZdCI)\nKahn\'s Algorithm is BFS method by removing the edges and decreasing the indegrees. \n1. Use Kahn\'salgorithm to define the function `vector<int> topo_sort(int k, vector<vector<int>>& conditions)`\n2. apply `order_row=topo_sort(k, rowConditions)`, `order_col=topo_sort(k, colConditions)`\n3. If `order_row.empty()|| order_col.empty()` some conflicts occur then return the empty array\n4. The rest is to build the answering matrix `arr`, to find pos (i, j) for each integer x where 1<=x<=k\n5. Use single for-loop to compute pos_i, pos_j & set `arr[pos_i[x]][pos_j[x]]=x`\n6. `arr` is the answer\n7. 2nd approach uses DFS+degree as visited instead of Kahn\'s algorithm. Moreover the output for the recursive function `f(int i)` is using `std::deque<int>` for push front the number `i` for avoiding of reversing the container.\n\n# Real RUN for testcase\n2 different approaches have different results; both are correct. Consider the testcase\n```\n8\n[[1,2], [1, 8]]\n[[5,7],[2,7],[4,3],[6,7],[4,3],[2,3],[6,2]]\n```\n\n\nUse topo_sort, one has\n```\norder_row=[ 1 3 4 5 6 7 2 8]\norder_col=[ 1 4 5 6 8 2 7 3]\n\narr=\n[ 1 0 0 0 0 0 0 0]\n[ 0 0 0 0 0 0 0 3]\n[ 0 4 0 0 0 0 0 0]\n[ 0 0 5 0 0 0 0 0]\n[ 0 0 0 6 0 0 0 0]\n[ 0 0 0 0 0 0 7 0]\n[ 0 0 0 0 0 2 0 0]\n[ 0 0 0 0 8 0 0 0]\n```\nUse dfs, one has\n```\norder_row=[ 7 6 5 4 3 1 8 2]\norder_col=[ 8 6 2 5 7 4 3 1]\n\narr=\n[ 0 0 0 0 0 0 7 0]\n[ 0 6 0 0 0 0 0 0]\n[ 0 0 5 0 0 0 0 0]\n[ 0 0 0 4 0 0 0 0]\n[ 0 0 0 0 0 3 0 0]\n[ 0 0 0 0 0 0 0 1]\n[ 8 0 0 0 0 0 0 0]\n[ 0 0 0 0 2 0 0 0]\n\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(k^2+|rowConditions|+|rowConditions|)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n $$O(k)$$ \n# Code|C++ 72ms Beats 99.72%\n```\nclass Solution {\npublic:\n //topological sort using BFS (Kahn\'s algorithm)\n static vector<int> topo_sort(int k, vector<vector<int>>& conditions){\n vector<int> deg(k+1, 0);\n vector<vector<int>> adj(k+1);\n for(auto& edge: conditions){\n int v=edge[0], w=edge[1];\n adj[v].push_back(w);\n deg[w]++;\n }\n queue<int> q;\n for (int i = 1; i<=k; i++) {\n if (deg[i] == 0) \n q.push(i);\n }\n\n int count=0;\n vector<int> ans;\n ans.reserve(k);\n while(!q.empty()){\n int j=q.front();\n q.pop();\n ans.push_back(j);\n count++;\n for(int k:adj[j]){\n deg[k]--;\n if (deg[k] == 0) {\n q.push(k);\n }\n }\n }\n if(count != k) return {};// has cycle\n else return ans ;\n\n }\n\n static void print(auto& c){\n cout<<"[";\n for(int x: c){\n cout<<x;\n if (x!=c.back()) cout<<", ";\n }\n cout<<"]\\n";\n }\n\n static vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n auto order_row=topo_sort(k, rowConditions);\n auto order_col=topo_sort(k, colConditions);\n\n // print out the ordering in row & in col\n // print(order_row), print(order_col);\n\n if (order_row.empty()|| order_col.empty())\n return {};// some conflict\n\n vector<vector<int>> arr(k, vector<int>(k));\n // Find pos for x where 1<=x<=k\n vector<int> pos_i(k+1, -1), pos_j(k+1, -1);\n for(int i=0; i<k; i++){\n pos_i[order_row[i]]=i;\n pos_j[order_col[i]]=i;\n }\n\n for(int x=1; x<=k; x++)\n arr[pos_i[x]][pos_j[x]]=x;\n \n return arr;\n }\n};\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# revised DFS+ deg as visited+ detect cycle||69ms beats 99.72%\n\nThere are some other versions.\n```\n //DFS+ degree as visited\n static deque<int> dfs(int k, vector<vector<int>>& conditions) {\n vector<int> deg(k + 1, 0);\n vector<vector<int>> adj(k + 1);\n for (auto& edge : conditions) {\n int v = edge[0], w = edge[1];\n adj[v].push_back(w);\n deg[w]++;\n }\n\n deque<int> ans;\n bool hasCycle= 0;\n // Use deg >=0 :unvisited, -1 = visiting, -2= visited\n function<void(int)> f = [&](int i) -> void {\n if (hasCycle) return;\n\n deg[i] = -1; // mark as visiting\n for (int j : adj[i]) {\n if (deg[j] >= 0) { // not visited\n f(j);\n } \n else if (deg[j]==-1) { //in the current path, so a cycle\n hasCycle = 1;\n return;\n }\n }\n deg[i]=-2; // mark as visited\n ans.push_front(i);\n };\n\n for (int i = 1; i <= k; i++) {\n if (deg[i]>=0) {\n f(i);\n if (hasCycle) return {}; // cycle detected\n }\n }\n return ans;\n }\n\n```\n | 64 | 0 | ['Array', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'Matrix', 'C++'] | 10 |
build-a-matrix-with-conditions | Kahn's Algo | Topological Sort | BFS | C++ | Short and Easy to Understand Code | kahns-algo-topological-sort-bfs-c-short-ldaxm | \nvector<int> khansAlgo(vector<vector<int>> &r, int k){\n vector<int> cnt(k+1, 0);\n vector<int> adj[k+1];\n for(auto x:r){\n cn | surajpatel | NORMAL | 2022-08-28T04:02:58.273097+00:00 | 2022-08-28T09:47:55.770139+00:00 | 4,023 | false | ```\nvector<int> khansAlgo(vector<vector<int>> &r, int k){\n vector<int> cnt(k+1, 0);\n vector<int> adj[k+1];\n for(auto x:r){\n cnt[x[1]]++;\n adj[x[0]].push_back(x[1]);\n }\n vector<int> row;\n queue<int> q;\n for(int i=1;i<=k;i++){\n if(cnt[i]==0){\n q.push(i);\n }\n }\n while(!q.empty()){\n int t = q.front();\n q.pop();\n row.push_back(t);\n for(auto x:adj[t]){\n cnt[x]--;\n if(cnt[x]==0){\n q.push(x);\n }\n }\n }\n return row;\n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& r, vector<vector<int>>& c) {\n vector<vector<int>> res(k, vector<int>(k, 0));\n \n vector<int> row = khansAlgo(r, k);\n if(row.size()!=k) return {};\n \n vector<int> col = khansAlgo(c, k);\n if(col.size()!=k) return {};\n \n vector<int> idx(k+1,0);\n for(int j=0;j<col.size();j++){\n idx[col[j]] = j;\n }\n for(int i=0;i<k;i++){\n res[i][idx[row[i]]] = row[i];\n }\n return res;\n }\n``` | 58 | 0 | ['Breadth-First Search', 'Topological Sort', 'C'] | 19 |
build-a-matrix-with-conditions | [Python 3] Explanation with pictures, Topological Sort | python-3-explanation-with-pictures-topol-2r40 | Detect if a circle exists in DAG\n\nHere is the BFS solution: start with dequeue of nodes with 0 indegree, update the indegree and add those nodes with 0 indegr | Bakerston | NORMAL | 2022-08-28T04:05:26.239710+00:00 | 2022-08-29T02:32:01.359657+00:00 | 2,563 | false | > Detect if a circle exists in DAG\n\nHere is the BFS solution: start with dequeue of nodes with 0 indegree, update the indegree and add those nodes with 0 indegree to dequeue. Once we are done, the sequence by which we pop the nodes are **one** workable order. \n\n\n\n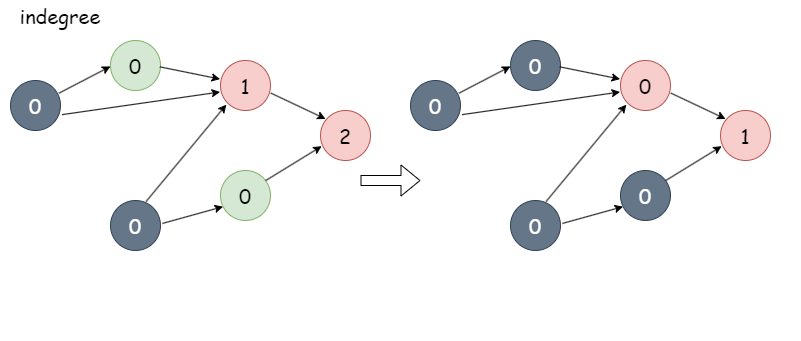\n\n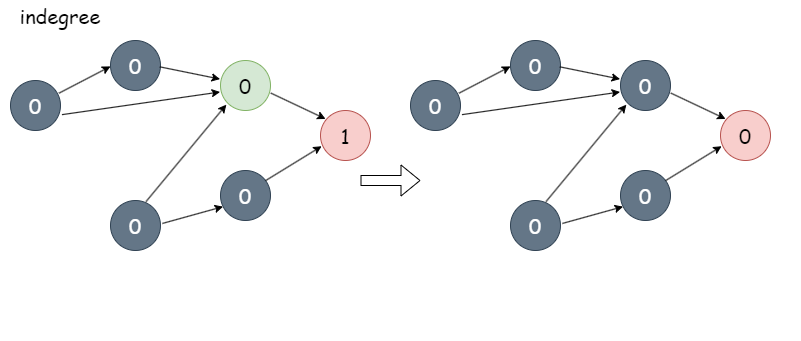\n\n> If there exists a circle, the nodes on circle will never be visited. Thus we end up with a sequence shorter than the total number of nodes.\n\n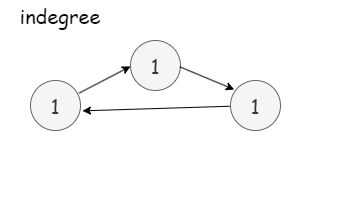\n\nOnce we find a proper order for both the rows and cols, just add the number back to an empty matrix accordingly.\n\n\n**python**\n\n```\ndef buildMatrix(self, k: int, R: List[List[int]], C: List[List[int]]) -> List[List[int]]:\n def helper(A):\n nxt, indegree = [set() for _ in range(k)], [0] * k\n dq, ans = collections.deque(), []\n A = set([tuple(a) for a in A]) \n for i, j in A:\n nxt[i - 1].add(j - 1)\n indegree[j - 1] += 1\n for i in range(k):\n if indegree[i] == 0:\n dq.append(i) \n while dq:\n cur = dq.popleft()\n ans.append(cur)\n for cand in nxt[cur]:\n indegree[cand] -= 1\n if indegree[cand] == 0:\n dq.append(cand) \n return ans if len(ans) == k else []\n \n ans1, ans2 = helper(R), helper(C)\n if not ans1 or not ans2: \n return []\n\n A = [[0] * k for _ in range(k)]\n for i in range(k): \n A[ans1.index(i)][ans2.index(i)] = i + 1\n return A\n``` | 44 | 0 | [] | 8 |
build-a-matrix-with-conditions | [C++, Python, Java] Topological Sort | c-python-java-topological-sort-by-tojuna-8wkg | Topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v i | tojuna | NORMAL | 2022-08-28T04:01:29.822043+00:00 | 2022-08-28T07:31:07.474441+00:00 | 2,776 | false | Topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.\n\nTopological sort steps:\n* Find a vertex that has indegree = 0 (no incoming edges)\n* Add that vertex to the array representing topological sorting of the graph\n* Since we have reached this node decrease the indegree of all the nodes that are supposed to come after this node\n* Repeat till there are no more vertices left.\n\n<iframe src="https://leetcode.com/playground/audDyjEZ/shared" frameBorder="0" width="900" height="600"></iframe> | 41 | 0 | ['Topological Sort', 'C', 'Python', 'Java'] | 6 |
build-a-matrix-with-conditions | Topological Sort | topological-sort-by-votrubac-jw46 | We apply topological sort independently for both conditions. \n\nAs a refresher, we build a directed graph with k nodes, and each condition is a directed link b | votrubac | NORMAL | 2022-08-28T04:01:24.978818+00:00 | 2022-08-28T04:14:28.828284+00:00 | 3,337 | false | We apply topological sort independently for both conditions. \n\nAs a refresher, we build a directed graph with `k` nodes, and each condition is a directed link between the corresponding nodes.\n\n> We represent the graph with the adjacency list (`al`). Note that we use a set to hold linked nodes as we may have duplicated conditions in the input.\n\nWe also track the number of conditions for each note in the `pre` array.\n\nTo get the sorted sequence, we do BFS starting from nodes with zero conditions.\n\nFor each node in the BFS queue `q`, we add it to the sequence, and then decrease the number of conditions for all connected notes. If the number of conditions for some node becomes zero, we add it to the BFS queue.\n\nIf there is a cycle, the topological sort would not produce all `k` elements.\n\nAfter we have an order of elements, we use it to sort indexes [0..k-1] to figure out where each element goes into the matrix.\n\n**C++**\n```cpp\nvector<int> top_sort(int k, vector<vector<int>>& conditions) {\n vector<int> sorted, id(k), pre(k + 1), q;\n vector<unordered_set<int>> al(k + 1);\n for (auto &c : conditions)\n if(al[c[0]].insert(c[1]).second)\n ++pre[c[1]];\n for (auto i = 1; i <= k; ++i)\n if (pre[i] == 0)\n q.push_back(i);\n while (!q.empty()) {\n vector<int> q1;\n for (auto i : q) {\n sorted.push_back(i);\n for (auto j : al[i])\n if (--pre[j] == 0)\n q1.push_back(j);\n }\n swap(q, q1);\n }\n if (sorted.size() != k)\n return {};\n iota(begin(id), end(id), 0);\n sort(begin(id), end(id), [&](int a, int b){ return sorted[a] < sorted[b]; }); \n return id;\n}\nvector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n auto rid = top_sort(k, rowConditions), cid = top_sort(k, colConditions);\n if (rid.empty() || cid.empty())\n return {};\n vector<vector<int>> res(k, vector<int>(k)); \n for (int i = 1; i <= k; ++i)\n res[rid[i - 1]][cid[i - 1]] = i;\n return res;\n}\n``` | 31 | 1 | [] | 10 |
build-a-matrix-with-conditions | [Python3] topological sort | python3-topological-sort-by-ye15-gwpv | Please pull this commit for solutions of weekly 308. \n\nIntuition\nThe workhorse of this problem is topological sort. The orders in aboveConditions and leftCon | ye15 | NORMAL | 2022-08-28T04:02:16.692070+00:00 | 2022-08-28T04:49:28.748106+00:00 | 1,291 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/ea6bc01b091cbf032b9c7ac2d3c09cb4f5cd0d2d) for solutions of weekly 308. \n\n**Intuition**\nThe workhorse of this problem is topological sort. The orders in `aboveConditions` and `leftConditions` construct two graphs. Via topological sort, the order becomes apparent. \nSo the algo is summarized below:\n1) topological sort the two graphs to get the row orders and column orders; \n2) if no cycle is found in either row order or column order, an answer exists; otherwise, return empty matrix; \n3) for each number from 1 to k, find its row number and column number from the results of the sorting; \n4) fill the numbers into the matrix. \n\n**Analysis**\nTime complexity `O(K^2)`\nSpace complexity `O(K^2)`\n\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n \n def fn(cond): \n """Return topological sort"""\n graph = [[] for _ in range(k)]\n indeg = [0]*k\n for u, v in cond: \n graph[u-1].append(v-1)\n indeg[v-1] += 1\n queue = deque(u for u, x in enumerate(indeg) if x == 0)\n ans = []\n while queue: \n u = queue.popleft()\n ans.append(u+1)\n for v in graph[u]: \n indeg[v] -= 1\n if indeg[v] == 0: queue.append(v)\n return ans \n \n row = fn(rowConditions)\n col = fn(colConditions)\n \n if len(row) < k or len(col) < k: return []\n ans = [[0]*k for _ in range(k)]\n row = {x : i for i, x in enumerate(row)}\n col = {x : j for j, x in enumerate(col)}\n for x in range(1, k+1): ans[row[x]][col[x]] = x\n return ans \n``` | 24 | 0 | ['Python3'] | 8 |
build-a-matrix-with-conditions | C++ | Topological Sort | c-topological-sort-by-_naaz-pp81 | Perform topological sort on rowConditions & colConditions\n The index of element in topological sort of rowConditions will be the rowIndex. Similarly, for the i | _naaz | NORMAL | 2022-08-28T04:01:56.772272+00:00 | 2022-08-28T11:53:26.270422+00:00 | 1,697 | false | * Perform **topological sort** on rowConditions & colConditions\n* The index of element in topological sort of rowConditions will be the rowIndex. Similarly, for the index of element in topological sort of colConditions will the colIndex of the element in the result grid\n* Time complexity of Topological sort is ```O(V + E)```, where V = No. of vertices = k and E = No. of Edges which can be atmost ```k * (k - 1) / 2``` \n* So, Time complexity: ```O(k ^ 2)``` | Space complexity: ```O(k ^ 2)```\n(Initialising the 2D vector also takes ```k ^ 2``` time complexity)\n\n\n\n```\nclass Solution {\npublic:\n // Same Code as Course Schedule - 2 \n vector<int> findOrder(int k, vector<vector<int>>& dependencies) {\n \n vector<vector<int>> adj(k + 1);\n vector<int> indegree(k + 1);\n for(auto dependency: dependencies) {\n adj[dependency[0]].push_back(dependency[1]);\n indegree[dependency[1]]++;\n }\n \n queue<int> q;\n for(int i = 1; i <= k; i++) {\n if(indegree[i] == 0) {\n q.push(i);\n }\n }\n \n int cnt = 0;\n vector<int> order;\n while(!q.empty()) {\n \n int cur = q.front();\n q.pop();\n \n cnt++;\n order.push_back(cur);\n \n for(int nbr: adj[cur]) {\n indegree[nbr]--;\n \n if(indegree[nbr] == 0) {\n q.push(nbr);\n }\n }\n }\n \n if(cnt == k) return order;\n return {};\n }\n \n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int> rowArray = findOrder(k, rowConditions); \n vector<int> colArray = findOrder(k, colConditions);\n \n // If one of the row conditions or col conditions has a cycle\n if(rowArray.size() == 0 || colArray.size() == 0) {\n return {};\n }\n \n vector<pair<int, int>> ind(k); // list of indices (i, j) for k values\n\t\t// from topological ordering deriving the indices for the values\n for(int i = 0; i < k; i++) {\n ind[rowArray[i] - 1].first = i; \n ind[colArray[i] - 1].second = i;\n }\n \n vector<vector<int>> result(k, vector<int>(k, 0));\n\t\t// iterate over the values and place then in the result grid\n for(int i = 0; i < k; i++) {\n result[ind[i].first][ind[i].second] = i + 1;\n }\n return result;\n }\n};\n```\n | 21 | 1 | ['Topological Sort', 'C'] | 7 |
build-a-matrix-with-conditions | No one can give such quality code... Bests 98.9% users.... #Quality code | no-one-can-give-such-quality-code-bests-lw8dn | \n\n# Python\n\nclass Solution:\n\n def buildMatrix(\n\n self,\n\n k: int,\n\n rowConditions: List[List[int]],\n\n colConditions: | Aim_High_212 | NORMAL | 2024-07-21T01:19:50.045407+00:00 | 2024-07-21T04:10:52.005083+00:00 | 2,100 | false | \n\n# Python\n```\nclass Solution:\n\n def buildMatrix(\n\n self,\n\n k: int,\n\n rowConditions: List[List[int]],\n\n colConditions: List[List[int]],\n\n ) -> List[List[int]]:\n\n # Store the topologically sorted sequences.\n\n order_rows = self.__topoSort(rowConditions, k)\n\n order_columns = self.__topoSort(colConditions, k)\n\n # If no topological sort exists, return empty array.\n\n if not order_rows or not order_columns:\n\n return []\n\n matrix = [[0] * k for _ in range(k)]\n\n pos_row = {num: i for i, num in enumerate(order_rows)}\n\n pos_col = {num: i for i, num in enumerate(order_columns)}\n\n for num in range(1, k + 1):\n\n if num in pos_row and num in pos_col:\n\n matrix[pos_row[num]][pos_col[num]] = num\n\n return matrix\n\n def __topoSort(self, edges: List[List[int]], n: int) -> List[int]:\n\n adj = defaultdict(list)\n\n order = []\n\n visited = [0] * (n + 1)\n\n has_cycle = [False]\n\n # Build adjacency list\n\n for x, y in edges:\n\n adj[x].append(y)\n\n # Perform DFS for each node\n\n for i in range(1, n + 1):\n\n if visited[i] == 0:\n\n self.__dfs(i, adj, visited, order, has_cycle)\n\n # Return empty if cycle detected\n\n if has_cycle[0]:\n\n return []\n\n # Reverse to get the correct order\n\n order.reverse()\n\n return order\n\n def __dfs(\n\n self,\n\n node: int,\n\n adj: defaultdict,\n\n visited: List[int],\n\n order: List[int],\n\n has_cycle: List[bool],\n\n ):\n\n # Mark node as visiting\n\n visited[node] = 1\n\n for neighbor in adj[node]:\n\n if visited[neighbor] == 0:\n\n self.__dfs(neighbor, adj, visited, order, has_cycle)\n\n # Early exit if a cycle is detected\n\n if has_cycle[0]:\n\n return\n\n elif visited[neighbor] == 1:\n\n # Cycle detected\n\n has_cycle[0] = True\n\n return\n\n # Mark node as visited\n\n visited[node] = 2\n\n # Add node to the order\n\n order.append(node)\n\n \n```\n\n# C++\n```\nclass Solution {\npublic:\n //topological sort using BFS (Kahn\'s algorithm)\n static vector<int> topo_sort(int k, vector<vector<int>>& conditions){\n vector<int> deg(k+1, 0);\n vector<vector<int>> adj(k+1);\n for(auto& edge: conditions){\n int v=edge[0], w=edge[1];\n adj[v].push_back(w);\n deg[w]++;\n }\n queue<int> q;\n for (int i = 1; i<=k; i++) {\n if (deg[i] == 0) \n q.push(i);\n }\n\n int count=0;\n vector<int> ans;\n ans.reserve(k);\n while(!q.empty()){\n int j=q.front();\n q.pop();\n ans.push_back(j);\n count++;\n for(int k:adj[j]){\n deg[k]--;\n if (deg[k] == 0) {\n q.push(k);\n }\n }\n }\n if(count != k) return {};// has cycle\n else return ans ;\n\n }\n\n static void print(auto& c){\n cout<<"[";\n for(int x: c){\n cout<<x;\n if (x!=c.back()) cout<<", ";\n }\n cout<<"]\\n";\n }\n\n static vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int> order_row=topo_sort(k, rowConditions);\n vector<int> order_col=topo_sort(k, colConditions);\n\n // print out the ordering in row & in col\n // print(order_row), print(order_col);\n\n if (order_row.empty()|| order_col.empty())\n return {};// some conflict\n\n vector<vector<int>> arr(k, vector<int>(k));\n // Find pos for x where 1<=x<=k\n vector<int> pos_i(k+1, -1), pos_j(k+1, -1);\n for(int i=0; i<k; i++)\n pos_i[order_row[i]]=i;\n\n for(int i=0; i<k; i++)\n pos_j[order_col[i]]=i;\n\n for(int x=1; x<=k; x++)\n arr[pos_i[x]][pos_j[x]]=x;\n \n return arr;\n }\n};\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n\n# Java\n```\nclass Solution {\n\n public int[][] buildMatrix(\n int k,\n int[][] rowConditions,\n int[][] colConditions\n ) {\n // Store the topologically sorted sequences.\n List<Integer> orderRows = topoSort(rowConditions, k);\n List<Integer> orderColumns = topoSort(colConditions, k);\n\n // If no topological sort exists, return empty array.\n if (orderRows.isEmpty() || orderColumns.isEmpty()) return new int[0][0];\n\n int[][] matrix = new int[k][k];\n for (int i = 0; i < k; i++) {\n for (int j = 0; j < k; j++) {\n if (orderRows.get(i).equals(orderColumns.get(j))) {\n matrix[i][j] = orderRows.get(i);\n }\n }\n }\n return matrix;\n }\n\n private List<Integer> topoSort(int[][] edges, int n) {\n // Build adjacency list\n List<List<Integer>> adj = new ArrayList<>();\n for (int i = 0; i <= n; i++) {\n adj.add(new ArrayList<>());\n }\n for (int[] edge : edges) {\n adj.get(edge[0]).add(edge[1]);\n }\n\n List<Integer> order = new ArrayList<>();\n // 0: not visited, 1: visiting, 2: visited\n int[] visited = new int[n + 1];\n boolean[] hasCycle = { false };\n\n // Perform DFS for each node\n for (int i = 1; i <= n; i++) {\n if (visited[i] == 0) {\n dfs(i, adj, visited, order, hasCycle);\n // Return empty if cycle detected\n if (hasCycle[0]) return new ArrayList<>();\n }\n }\n\n // Reverse to get the correct order\n Collections.reverse(order);\n return order;\n }\n\n private void dfs(\n int node,\n List<List<Integer>> adj,\n int[] visited,\n List<Integer> order,\n boolean[] hasCycle\n ) {\n visited[node] = 1; // Mark node as visiting\n for (int neighbor : adj.get(node)) {\n if (visited[neighbor] == 0) {\n dfs(neighbor, adj, visited, order, hasCycle);\n // Early exit if a cycle is detected\n if (hasCycle[0]) return;\n } else if (visited[neighbor] == 1) {\n // Cycle detected\n hasCycle[0] = true;\n return;\n }\n }\n // Mark node as visited\n visited[node] = 2;\n // Add node to the order\n order.add(node);\n }\n}\n``` | 19 | 3 | ['Array', 'Graph', 'Topological Sort', 'C', 'Matrix', 'Python', 'Java', 'Python3', 'JavaScript'] | 7 |
build-a-matrix-with-conditions | 💯✅🔥Detailed Easy Java ,Python3 ,C++ Solution|| 10 ms ||≧◠‿◠≦✌ | detailed-easy-java-python3-c-solution-10-1t51 | Intuition\nThe problem requires constructing a k x k matrix where each element must satisfy certain ordering constraints specified by rowConditions and colCondi | suyalneeraj09 | NORMAL | 2024-07-21T03:41:08.992190+00:00 | 2024-07-21T03:41:08.992219+00:00 | 2,522 | false | # Intuition\nThe problem requires constructing a `k x k` matrix where each element must satisfy certain ordering constraints specified by `rowConditions` and `colConditions`. The constraints dictate that if there is a condition like `[a, b]`, then `a` must appear before `b` in the respective row or column.\n\nTo solve this problem, we can leverage **topological sorting**, which is a method used to order the vertices of a directed graph such that for every directed edge `u -> v`, vertex `u` comes before vertex `v` in the ordering. This is particularly useful here since the row and column conditions can be represented as directed graphs.\n\n---\n# Approach\n1. **Graph Representation**: \n - Each condition is treated as a directed edge in a graph. For example, if we have a condition `[a, b]`, it means there is a directed edge from `a` to `b`.\n - We will maintain an adjacency list to represent the graph and an array to keep track of the in-degrees (number of incoming edges) for each node.\n\n2. **Topological Sorting**:\n - We perform topological sorting twice: once for the row conditions and once for the column conditions.\n - We use Kahn\'s algorithm for topological sorting, which involves:\n - Initializing a queue with all nodes that have an in-degree of zero (these can be placed in the matrix first).\n - Iteratively removing nodes from the queue, adding them to the sorted order, and decreasing the in-degree of their neighbors. If any neighbor\u2019s in-degree drops to zero, it is added to the queue.\n\n3. **Matrix Construction**:\n - After obtaining the topological orders for both row and column conditions, we create the `k x k` matrix.\n - We use a mapping from the column order to their respective indices to place elements in the correct positions according to the row order.\n\n4. **Edge Cases**:\n - If the size of either topological order is less than `k`, it indicates that it is impossible to satisfy the conditions, and we return an empty matrix.\n\n---\n# Time Complexity\n- **Topological Sorting**: The time complexity for each topological sort is $$O(V + E)$$, where $$V$$ is the number of vertices (equal to `k`) and $$E$$ is the number of edges (equal to the number of conditions).\n - In the worst case, if we assume that each condition is a unique edge, we can consider $$E$$ to be at most $$O(k^2)$$ (though typically it would be much less).\n- Therefore, the overall time complexity for both topological sorts is:\n $$\n O(k + E) + O(k + E) = O(k + E)\n $$\n\n- **Matrix Construction**: This takes $$O(k)$$ time to fill in the matrix.\n\nThus, the overall time complexity is:\n$$\nO(k + E)\n$$\n\n---\n# Space Complexity\n- **Graph Representation**: The adjacency list and the in-degree array both require $$O(k + E)$$ space.\n- **Other Data Structures**: The queue used for Kahn\'s algorithm and the list for storing the topological order also require $$O(k)$$ space.\n\nTherefore, the overall space complexity is:\n$$\nO(k + E)\n$$\n\n---\n# Step By Step Explantion\n\nThe provided code implements a solution to build a matrix based on specified row and column conditions using topological sorting. Let\'s break down the code step by step, particularly focusing on the input values `k = 3`, `rowConditions = [[1,2],[2,3],[3,1],[2,3]]`, and `colConditions = [[2,1]]`.\n\n### Step 1: Input Initialization\n\n1. **Input Parameters**:\n - `k = 3`: This indicates the size of the matrix we want to build, which will be a 3x3 matrix.\n - `rowConditions = [[1,2],[2,3],[3,1],[2,3]]`: This specifies that:\n - 1 must be before 2.\n - 2 must be before 3.\n - 3 must be before 1 (which creates a cycle).\n - 2 must be before 3 (redundant).\n - `colConditions = [[2,1]]`: This specifies that:\n - 2 must be before 1 in the columns.\n\n### Step 2: Topological Sorting for Row Conditions\n\n2. **Calling `GenerateTopologicalSort` for Row Conditions**:\n - The method is called with `rowConditions` and `k`.\n - An adjacency list (`graph`) is created to represent the directed graph based on the conditions.\n - The degree array (`deg`) is initialized to keep track of the number of incoming edges for each node.\n\n3. **Building the Graph**:\n - For each condition in `rowConditions`, edges are added to the graph and the degree array is updated:\n - From 1 to 2: `deg` becomes 1.\n - From 2 to 3: `deg` becomes 1.\n - From 3 to 1: `deg` becomes 1.\n - From 2 to 3 (redundant).\n\n The resulting graph and degree array will look like this:\n - `graph = [, , , []]` (1 -> 2, 2 -> 3, 3 -> 1)\n - `deg = [1, 1, 1]` (each node has one incoming edge).\n\n4. **Queue Initialization**:\n - Nodes with zero incoming edges are added to the queue. Since all nodes have at least one incoming edge, the queue remains empty.\n\n5. **Topological Sort Completion**:\n - Since the queue is empty, the topological sort cannot complete, and the method returns an empty list.\n\n### Step 3: Topological Sorting for Column Conditions\n\n6. **Calling `GenerateTopologicalSort` for Column Conditions**:\n - Similar steps are followed for `colConditions`.\n - The graph is initialized again, and the degree array is updated based on the column conditions.\n\n7. **Building the Graph for Columns**:\n - From 2 to 1: `deg` becomes 1.\n - The resulting graph for columns will be:\n - `graph = [, []]` (2 -> 1)\n - `deg = [1, 0]` (1 has one incoming edge, 2 has none).\n\n8. **Queue Initialization**:\n - Node 2 (index 1) is added to the queue since it has zero incoming edges.\n\n9. **Topological Sort Completion for Columns**:\n - The algorithm processes node 2, adds it to the order, and then processes node 1, resulting in the order: `[2, 1]`.\n\n### Step 4: Validating the Results\n\n10. **Checking Topological Sort Results**:\n - The result from the row conditions is empty, indicating that a cycle was detected.\n - The result from the column conditions is `[2, 1]`, which is valid.\n\n11. **Final Validation**:\n - Since the row order is empty (indicating that the matrix cannot be constructed due to the cycle), the method returns an empty matrix `new int`.\n\n### Conclusion\n\nThe final output of the `buildMatrix` function, given the input parameters, is an empty matrix because the row conditions create a cycle that prevents a valid topological sort. The code effectively detects this condition and handles it gracefully by returning an empty result. \n\nThis step-by-step explanation illustrates how the topological sorting process works and how it is applied to the given conditions to determine the feasibility of constructing the desired matrix.\n\n---\n\n```java []\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<Integer> order1 = GenerateTopologicalSort(rowConditions, k);\n List<Integer> order2 = GenerateTopologicalSort(colConditions, k);\n if (order1.size() < k || order2.size() < k)\n return new int[0][0];\n Map<Integer, Integer> m = new HashMap();\n for (int i = 0; i < k; i++)\n m.put(order2.get(i), i);\n int[][] ans = new int[k][k];\n for (int i = 0; i < k; i++)\n ans[i][m.get(order1.get(i))] = order1.get(i);\n return ans;\n }\n\n private List<Integer> GenerateTopologicalSort(int[][] A, int k) {\n int[] deg = new int[k];\n List<Integer> order = new ArrayList();\n List<List<Integer>> graph = new ArrayList();\n for (int i = 0; i < k; i++)\n graph.add(new ArrayList());\n Queue<Integer> q = new LinkedList();\n for (int[] c : A) {\n graph.get(c[0] - 1).add(c[1] - 1);\n deg[c[1] - 1]++;\n }\n for (int i = 0; i < k; i++)\n if (deg[i] == 0)\n q.add(i);\n while (!q.isEmpty()) {\n int x = q.poll();\n order.add(x + 1);\n for (int y : graph.get(x))\n if (--deg[y] == 0)\n q.add(y);\n }\n return order;\n }\n}\n```\n```python3 []\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n order1 = self.generate_topological_sort(rowConditions, k)\n order2 = self.generate_topological_sort(colConditions, k)\n \n if len(order1) < k or len(order2) < k:\n return []\n \n m = {order2[i]: i for i in range(k)}\n ans = [[0] * k for _ in range(k)]\n \n for i in range(k):\n ans[i][m[order1[i]]] = order1[i]\n \n return ans\n\n def generate_topological_sort(self, A: List[List[int]], k: int) -> List[int]:\n deg = [0] * k\n order = []\n graph = defaultdict(list)\n q = deque()\n \n for c in A:\n graph[c[0] - 1].append(c[1] - 1)\n deg[c[1] - 1] += 1\n \n for i in range(k):\n if deg[i] == 0:\n q.append(i)\n \n while q:\n x = q.popleft()\n order.append(x + 1)\n for y in graph[x]:\n deg[y] -= 1\n if deg[y] == 0:\n q.append(y)\n \n return order\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int> order1 = generateTopologicalSort(rowConditions, k);\n vector<int> order2 = generateTopologicalSort(colConditions, k);\n \n if (order1.size() < k || order2.size() < k) {\n return {};\n }\n \n unordered_map<int, int> m;\n for (int i = 0; i < k; i++) {\n m[order2[i]] = i;\n }\n \n vector<vector<int>> ans(k, vector<int>(k, 0));\n for (int i = 0; i < k; i++) {\n ans[i][m[order1[i]]] = order1[i];\n }\n \n return ans;\n }\n\nprivate:\n vector<int> generateTopologicalSort(const vector<vector<int>>& A, int k) {\n vector<int> deg(k, 0);\n vector<int> order;\n vector<vector<int>> graph(k);\n queue<int> q;\n \n for (const auto& c : A) {\n graph[c[0] - 1].push_back(c[1] - 1);\n deg[c[1] - 1]++;\n }\n \n for (int i = 0; i < k; i++) {\n if (deg[i] == 0) {\n q.push(i);\n }\n }\n \n while (!q.empty()) {\n int x = q.front();\n q.pop();\n order.push_back(x + 1);\n for (int y : graph[x]) {\n if (--deg[y] == 0) {\n q.push(y);\n }\n }\n }\n \n return order;\n }\n};\n```\n---\n\n\n\n---\n\n\n--- | 17 | 3 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'C++', 'Java', 'Python3'] | 3 |
build-a-matrix-with-conditions | Topological Sort & cycle detection using DFS | JAVA | 18ms | 100% | topological-sort-cycle-detection-using-d-384g | \nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n \n int[][] ans = new int[k][k];\n | akrchaubey | NORMAL | 2022-08-28T04:04:51.692761+00:00 | 2022-08-28T06:57:00.329541+00:00 | 923 | false | ```\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n \n int[][] ans = new int[k][k];\n \n // create adjacency List for the rows and columns\n Map<Integer, Set<Integer>> adjListRow = new HashMap<>();\n Map<Integer, Set<Integer>> adjListCol = new HashMap<>();\n for(int[] row : rowConditions){\n adjListRow.putIfAbsent(row[0], new HashSet<>());\n adjListRow.get(row[0]).add(row[1]);\n }\n for(int[] col : colConditions){\n adjListCol.putIfAbsent(col[0], new HashSet<>());\n adjListCol.get(col[0]).add(col[1]);\n }\n \n // run DFS with cycle detection while storing the finish order of the nodes\n Map<Integer, Integer> rowIndex = new HashMap<>();\n Map<Integer, Integer> colIndex = new HashMap<>();\n int[] visitedRow = new int[k+1];\n int[] visitedCol = new int[k+1];\n for(int i = 1; i <= k; i++){\n if(!(dfs(i, adjListRow, visitedRow, rowIndex) && dfs(i, adjListCol, visitedCol, colIndex)))\n return new int[0][0];\n }\n \n\t // assign the correct position to the nodes according to the finish order\n for( int i = 1; i <= k; i++){\n int r = rowIndex.size() - rowIndex.get(i) - 1;\n int c = colIndex.size() - colIndex.get(i) - 1;\n ans[r][c] = i;\n }\n \n return ans;\n }\n \n\t/** DFS with cycle detection (returns false in case of a cycle) \n\tState of a node can be one of the following\n\t\t0 -> unvisited\n\t\t1 -> visiting\n\t\t2 -> visited\n On the DFS path visiting a node with value 1 means we are visiting a node on the path we came from -> hence it is a cycle(DFS returns false). When a visited node is encountered, we can return back to the caller node.\n\t*/\n private boolean dfs(int node, Map<Integer, Set<Integer>> adjList, int[] visited, Map<Integer, Integer> map){\n\t \n if(visited[node] == 2) return true;\n if(visited[node] == 1) return false;\n visited[node] = 1;\n\t\t\n Set<Integer> list = adjList.get(node);\n if(list != null)\n for(int ele : list)\n if(visited[ele] != 2)\n if(!dfs(ele, adjList, visited, map)) return false;\n \n\t\t// mark the node visited and add to the map of finished nodes with the finish number\n visited[node] = 2;\n map.put(node, map.size());\n return true;\n } \n}\n``` | 10 | 1 | ['Depth-First Search', 'Topological Sort', 'Java'] | 2 |
build-a-matrix-with-conditions | Simple and Easy C++ | Kahn's Algorithm | Topological Sort | BFS | OOPS | simple-and-easy-c-kahns-algorithm-topolo-ph9y | Algorithm\n1. Create graph for both rowConditions and colConditions.\n2. Check if both graphs are acyclic using Kahn\'s Algorithm. If either graph is cyclic, th | neeleshgupta93 | NORMAL | 2022-08-30T18:34:08.327618+00:00 | 2022-08-30T18:34:08.327658+00:00 | 489 | false | **Algorithm**\n1. Create graph for both ```rowConditions``` and ```colConditions```.\n2. Check if both graphs are acyclic using Kahn\'s Algorithm. If either graph is cyclic, then return ```[]```.\n3. Kahn\'s Algorithm will give ```topological sorting (topo1 and topo2) ``` for both graphs.\n4. ```topo1``` will give position of element according to row.\n5. ```topo2``` will give position of element according to column.\n\n**Code**\n```\nclass graph{\n int n;\n vector<vector<int>> adj;\npublic:\n graph(int n){\n this->n = n;\n adj.resize(n);\n }\n \n void add_edge(int u, int v){\n adj[u].push_back(v);\n }\n \n void make_adj(vector<vector<int>> arr){\n for(auto& x:arr){\n this->add_edge(x[0], x[1]);\n }\n }\n \n vector<int> kahn_algo(){\n vector<int> indeg(this->n, 0);\n queue<int> q;\n vector<int> topo;\n \n for(auto &x : this->adj){\n for(int &y: x){\n indeg[y]++;\n } \n }\n\n for(int i=1; i<this->n; i++){\n if(indeg[i] == 0){\n q.push(i);\n }\n }\n\n while(!q.empty()){\n int cur = q.front();\n q.pop();\n\n topo.push_back(cur);\n \n for(auto& x : this->adj[cur]){\n indeg[x]--;\n if(indeg[x] == 0){\n q.push(x);\n }\n }\n }\n\n return topo;\n }\n};\n\nclass Solution {\npublic:\n vector<vector<int>> solve(int& n, vector<int>& topo1, vector<int>& topo2){\n if(topo1.size() != n || topo2.size() != n){\n return {};\n }\n \n vector<vector<int>> ans(n, vector<int>(n, 0));\n\n unordered_map<int, int> mp;\n \n for(int i=0; i<topo1.size(); i++){\n mp[topo1[i]] = i;\n }\n \n for(int i=0; i<topo2.size(); i++){\n ans[mp[topo2[i]]][i] = topo2[i];\n }\n \n return ans;\n }\n \n vector<vector<int>> buildMatrix(int n, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n \n graph g1(n+1), g2(n+1);\n \n g1.make_adj(rowConditions);\n g2.make_adj(colConditions);\n \n vector<int> topo1 = g1.kahn_algo(), topo2 = g2.kahn_algo();\n \n return solve(n, topo1, topo2); \n }\n};\n```\n\nPlease upvote if you find it helpful :) | 9 | 0 | ['Breadth-First Search', 'Graph', 'Topological Sort', 'C'] | 2 |
build-a-matrix-with-conditions | [LeetCode The Hard Way] Kahn's Algorithm with Explanation | leetcode-the-hard-way-kahns-algorithm-wi-0cv3 | Please check out LeetCode The Hard Way for more solution explanations and tutorials. If you like it, please give a star and watch my Github Repository.\n\n---\n | __wkw__ | NORMAL | 2022-08-29T12:10:47.741956+00:00 | 2022-08-29T12:11:00.952853+00:00 | 612 | false | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. If you like it, please give a star and watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way).\n\n---\n\n```cpp\nclass Solution {\npublic:\n // there is at least one vertex in the \u201Cgraph\u201D with an \u201Cin-degree\u201D of 0. \n // if all vertices in the \u201Cgraph\u201D have non-zero \u201Cin-degree\u201D, \n // then all vertices need at least one vertex as a predecessor. \n // In this case, no vertex can serve as the starting vertex.\n template<typename T_vector, typename T_vector_vector>\n T_vector kahn(int n, T_vector_vector &edges){\n vector<int> ordering, indegree(n, 0);\n vector<vector<int> > g(n);\n for (auto e : edges) {\n --e[0], --e[1];\n indegree[e[1]]++;\n g[e[0]].push_back(e[1]);\n }\n queue<int> q;\n for (int i = 0; i < n; i++) if (indegree[i] == 0) q.push(i);\n int visited = 0;\n while (!q.empty()) {\n int u = q.front(); q.pop();\n ordering.push_back(u);\n visited++;\n for (auto v : g[u]) {\n if (--indegree[v] == 0) q.push(v);\n }\n }\n if (visited != n) return T_vector{};\n return ordering;\n }\n \n // the idea is to topologically sort rowConditions & colConditions\n // then build the final matrix based on the order if possible\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> ans(k, vector<int>(k));\n // in example 1, rowOrders would be [1, 3, 2]\n vector<int> rowOrders = kahn<vector<int>>(k, rowConditions);\n // in example 1, colOrders would be [3, 2, 1]\n vector<int> colOrders = kahn<vector<int>>(k, colConditions);\n // since we need to map to a `k x k` matrix, \n // we need to make sure that both got exact k elements\n if ((int) rowOrders.size() == k && (int) colOrders.size() == k) {\n // used to map the index of the given row / col value\n // i.e. given the value, which row / col idx should it belong to\n vector<int> rowIdx(k), colIdx(k);\n for (int i = 0; i < k; i++) rowIdx[rowOrders[i]] = i, colIdx[colOrders[i]] = i;\n // update the final matrix\n for (int i = 0; i < k; i++) ans[rowIdx[i]][colIdx[i]] = i + 1;\n return ans;\n }\n // else we don\'t have a matrix that satisfies the conditions\n return vector<vector<int>>{};\n }\n};\n``` | 7 | 0 | ['Breadth-First Search', 'Topological Sort', 'C', 'C++'] | 2 |
build-a-matrix-with-conditions | Python | Topological Sorting | python-topological-sorting-by-khosiyat-br1b | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[Lis | Khosiyat | NORMAL | 2024-07-21T08:11:00.429213+00:00 | 2024-07-21T08:11:00.429240+00:00 | 511 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/build-a-matrix-with-conditions/submissions/1328224805/?envType=daily-question&envId=2024-07-21)\n\n# Code\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n def topological_sort(conditions):\n graph = defaultdict(list)\n indegree = {i: 0 for i in range(1, k + 1)}\n \n for u, v in conditions:\n graph[u].append(v)\n indegree[v] += 1\n \n zero_indegree = deque([i for i in range(1, k + 1) if indegree[i] == 0])\n order = []\n \n while zero_indegree:\n node = zero_indegree.popleft()\n order.append(node)\n \n for neighbor in graph[node]:\n indegree[neighbor] -= 1\n if indegree[neighbor] == 0:\n zero_indegree.append(neighbor)\n \n if len(order) != k:\n return []\n \n return order\n \n row_order = topological_sort(rowConditions)\n if not row_order:\n return []\n \n col_order = topological_sort(colConditions)\n if not col_order:\n return []\n \n row_pos = {num: i for i, num in enumerate(row_order)}\n col_pos = {num: i for i, num in enumerate(col_order)}\n \n matrix = [[0] * k for _ in range(k)]\n \n for num in range(1, k + 1):\n matrix[row_pos[num]][col_pos[num]] = num\n \n return matrix\n\n```\n\n# Steps\n\n## Topological Sorting\n\nFirst, we need to determine the order of the numbers for the rows and columns separately using the given conditions.\n\n## Matrix Construction\n\nUsing the sorted orders, we can then construct the matrix such that each number appears exactly once and the constraints are satisfied.\n\n# Step-by-step Approach\n\n## Topological Sorting for Rows and Columns\n\n- We need to perform a topological sort on the row conditions to determine the order in which the numbers should appear in the rows.\n- Similarly, we need to perform a topological sort on the column conditions to determine the order in which the numbers should appear in the columns.\n- If either of the conditions forms a cycle, it\'s impossible to satisfy the constraints, and we should return an empty matrix.\n\n## Construct the Matrix\n\nUsing the sorted orders from the topological sorts, place the numbers in their respective positions in a \\(k \\times k\\) matrix.\n\n# Explanation of the Code\n\n## Topological Sort Function\n\n- We create a graph and an in-degree count for each number.\n- We iterate through the conditions to build the graph and update the in-degree of each node.\n- We use a deque to process nodes with zero in-degree, appending them to the sorted order and reducing the in-degree of their neighbors.\n- If we process all numbers and the sorted order contains all \\(k\\) numbers, we return the order; otherwise, a cycle is present, and we return an empty list.\n\n## Building the Matrix\n\n- We get the row and column orders from the topological sort.\n- If either order is empty, we return an empty matrix.\n- We map each number to its position in the row and column orders.\n- We construct the matrix by placing each number at its corresponding position based on the sorted orders.\n\n\n | 6 | 0 | ['Python3'] | 0 |
build-a-matrix-with-conditions | easy c++ sol |Kahn's Algo | Topological Sort | BFS | C++ | Short and Easy to Understand Code | easy-c-sol-kahns-algo-topological-sort-b-vleh | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sarthakgoel84 | NORMAL | 2024-07-21T05:45:26.316507+00:00 | 2024-07-21T05:45:26.316540+00:00 | 1,126 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> khan(int k,vector<vector<int>>& Conditions){\n vector<int>graph[k+1];\n vector<int>degree(k+1);\n for(auto i:Conditions){\n graph[i[0]].push_back(i[1]);\n degree[i[1]]++;\n }\n queue<int>q;\n for(int i=1;i<k;i++){\n if(degree[i]==0){\n q.push(i);\n }\n }\n vector<int>ans;\n while(!q.empty()){\n int t=q.front();\n q.pop();\n ans.push_back(t);\n for(auto i:graph[t]){\n degree[i]--;\n if(degree[i]==0){\n q.push(i);\n }\n }\n }\n\n return ans;\n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int>row=khan(k+1,rowConditions);\n vector<int>col=khan(k+1,colConditions);\n if(row.size()<k || col.size()<k){\n return {};\n }\n unordered_map<int ,int>mp;\n for(int i=0;i<k;i++){\n mp[col[i]]=i;\n }\n vector<vector<int>>ans(k,vector<int>(k,0));\n for(int i=0;i<k;i++){\n int col_pos=mp[row[i]];\n ans[i][col_pos]=row[i];\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['C++'] | 6 |
build-a-matrix-with-conditions | Simple and Clean C++ solution using kahn's algorithm | simple-and-clean-c-solution-using-kahns-t7rg0 | Intuition\nSimple idea behind the solution is if we take projections of non zero elements of matrix along the row and column , those projected rows and colums s | Vaibhav_Potdar | NORMAL | 2023-03-15T20:12:58.084690+00:00 | 2023-03-15T20:26:13.347544+00:00 | 435 | false | # Intuition\nSimple idea behind the solution is if we take projections of non zero elements of matrix along the row and column , those projected rows and colums should be topologically sorted. \nSo we will first find valid orders of row and columns. seperately and then we will form the matrix. \n\n\n```\nclass Solution {\npublic:\n vector<int> validorder(vector<vector<int>> &conditions, int k){\n vector<int> indegree(k+1, 0);\n vector<vector<int>> adj(k+1);\n // we will first create an adj list\n for(int i = 0 ; i< conditions.size(); i++){\n int a = conditions[i][0];\n int b = conditions[i][1];\n indegree[b]++;\n adj[a].push_back(b);\n }\n //Kahn\'s algo\n vector<int> order;\n queue<int> q;\n for(int i=1;i<=k;i++){\n if(indegree[i]==0){\n q.push(i);\n }\n }\n while(!q.empty()){\n int node = q.front();\n q.pop();\n order.push_back(node);\n for(int i = 0 ; i<adj[node].size(); i++){\n int x=adj[node][i];\n indegree[x]--;\n if(indegree[x]==0){\n q.push(x);\n }\n }\n }\n return order;\n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int> validcol = validorder(rowConditions, k);\n vector<int> validrow = validorder(colConditions, k);\n\n if(validcol.size()!=k||validrow.size()!=k) return {};\n\n vector<vector<int>> validmatrix(k, vector<int>(k, 0));\n for(int i = 0;i<k;i++){\n for(int j = 0 ; j<k ; j++){\n if(validcol[i]==validrow[j]){\n validmatrix[i][j]=validcol[i];\n }\n }\n }\n return validmatrix;\n }\n};\n\n```\n\n\nSaw a lot of solutions using this approach to form matrix , thought it was a little complicated.\n```\nvector<int> idx(k+1,0);\n for(int j=0;j<validcol.size();j++){\n idx[validcol[j]] = j;\n }\n\n vector<vector<int>> validmatrix(k, vector<int>(k, 0));\n for(int i=0;i<k;i++){\n validmatrix[i][idx[validrow[i]]] = validrow[i];\n }\n```\n\n | 6 | 0 | ['Breadth-First Search', 'Graph', 'Topological Sort', 'C++'] | 4 |
build-a-matrix-with-conditions | Easy Explanation + Code with comments | Doubt of building matrix at end | Java | BFS | TopSort | easy-explanation-code-with-comments-doub-1o13 | From diffferent you might already know it is topological sort. But there is no harm in revising it.\nApproach:\nIn question, condition is given that a number sh | anuj0503 | NORMAL | 2022-09-02T16:50:13.760937+00:00 | 2022-09-02T16:50:13.760976+00:00 | 268 | false | From diffferent you might already know it is topological sort. But there is no harm in revising it.\nApproach:\nIn question, condition is given that a number should occur before other number in row/column and such conditions are many. This is cue for topological sort.\n\nNow, imagine we dont have to create 2D matrix at the end and simply a 1D matrix need to be form. Then only one array of conditions would be given in the question and we form a graph and perform topological sort.\n**Example 1:** if given: k = 3, rowConditions = [[1,2],[3,2]]\nthen this graph will be formed :\n1 ---> 2 <--- 3\nand its topological sorted array would be : 1, 3, 2 (we will use this further in explaination) or 3, 2, 1.\nIn this we know position of 1 is at 0 index, position of 3 is at 1 index, position of 2 will be at 2 index.\n\nTill now all good.\n\nNow, if above is given for column then also, can perform similar.\n**Example 2:** given inputs are : k = 3, colConditions = [[2,1],[3,2]]\nGraph will be:\n3 ---> 2 ---> 1\nTopological sort will be 3, 2, 1\nAlso, we know position of 3 is at 0 index, position of 2 is at 1 index, position of 1 will be at 2 index.\n\nNow comes the real question, **How to build matrix ?** \nSimply assume the positions in Example 1 are row numbers, means in which row these need to be inserted or we are forming a 1D array in vertical form like:\n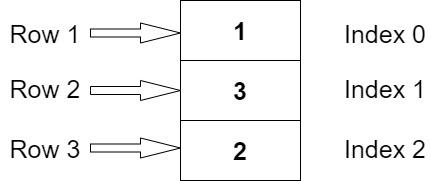\n\nFor Example 2 assume, positions are columns number and our 1D array will be in horizontal form like:\n\n\nNow for each number we know its row index and its column index, so we can create the matrix using that:\nPsuedoCode:\n```\nfor(int i = 1; i <=k ; i++){\n\tmatrix[position of i in row][position of i in column] = i\n}\n```\n```\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n Map<Integer, Set<Integer>> rowGraph = new HashMap<>();\n Map<Integer, Set<Integer>> colGraph = new HashMap<>();\n int[] inDegreeRow = new int[k+1];\n int[] inDegreeCol = new int[k+1];\n\n // Initalizing the map so that we dont have to check for null\n for(int i = 0; i <= k; i++) {\n rowGraph.put(i, new HashSet<>());\n colGraph.put(i, new HashSet<>());\n }\n\n // building a graph for row conditions along with populating the inDegree of each node.\n buildGraph(rowConditions, inDegreeRow, rowGraph);\n // building a graph for column conditions along with populating the inDegree of each node.\n buildGraph(colConditions, inDegreeCol, colGraph);\n\n // Finding Topological sort\n // or mapping of node/numbers to its position where it should be in row (index). \n Map<Integer, Integer> rowTopoSort = getTopologicalSort(rowGraph, inDegreeRow, k);\n \n // Finding Topological sort\n // or mapping of node/numbers to its position where it should be in column (index). \n Map<Integer, Integer> colTopoSort = getTopologicalSort(colGraph, inDegreeCol, k);\n\n // If we are not able to cover all nodes/numbers means there is cycle.\n if(rowTopoSort.size() != k || colTopoSort.size() != k) return new int[0][0];\n\n // Building tha metric usinbg the mapping we get from topological sort.\n return buildMatrix(k, rowTopoSort, colTopoSort);\n }\n\n private void buildGraph(int[][] conditions, int[] inDegree, Map<Integer, Set<Integer>> graph){\n for (int[] condition : conditions){\n int u = condition[0];\n int v = condition[1];\n\n Set<Integer> s = graph.get(u);\n s.add(v);\n graph.put(u, s);\n }\n\n for(int i = 1; i < inDegree.length; i++){\n for(int neighbour : graph.get(i)){\n inDegree[neighbour]++;\n }\n }\n }\n\n private Map<Integer, Integer> getTopologicalSort(Map<Integer, Set<Integer>> graph, int[] inDegree, int k){\n Map<Integer, Integer> numToPoistionMap = new HashMap<>();\n Queue<Integer> queue = new LinkedList<>();\n for(int i = 1; i <= k; i++){\n if(inDegree[i] == 0) queue.offer(i);\n }\n\n int position = 0;\n while(!queue.isEmpty()){\n int head = queue.poll();\n numToPoistionMap.put(head, position++);\n\n for(int neighbour : graph.get(head)){\n inDegree[neighbour]--;\n\n if(inDegree[neighbour] == 0) queue.offer(neighbour);\n }\n }\n\n return numToPoistionMap;\n }\n\n private int[][] buildMatrix(int k, Map<Integer, Integer> rowMap, Map<Integer, Integer> colMap){\n int[][] matrix = new int[k][k];\n\n for(int i = 1 ; i <= k; i++){\n matrix[rowMap.get(i)][colMap.get(i)] = i;\n }\n\n return matrix;\n }\n}\n```\n\nThanks for reading. If you like please upvote. | 6 | 0 | ['Breadth-First Search', 'Topological Sort', 'Java'] | 2 |
build-a-matrix-with-conditions | Graph solution and runtime beats 97.22% [EXPLAINED] | graph-solution-and-runtime-beats-9722-ex-qogb | IntuitionWe are given conditions that specify the relative positions of numbers in a matrix, both row-wise and column-wise. The goal is to arrange numbers such | r9n | NORMAL | 2024-12-23T22:20:08.949808+00:00 | 2024-12-23T22:20:08.949808+00:00 | 17 | false | # Intuition
We are given conditions that specify the relative positions of numbers in a matrix, both row-wise and column-wise. The goal is to arrange numbers such that these conditions are satisfied while filling a k x k matrix.
# Approach
Treat the row and column conditions as directed graphs and perform topological sorting on them to find a valid order for rows and columns, then place each number according to that order in the matrix.
This solution uses a graph to represent the conditions. Each condition (like "number a should be above number b in a row") forms a directed edge from a to b. The goal is to find a topological sort of the graph, which ensures that all conditions are satisfied, meaning numbers appear in the correct order in both rows and columns.
# Complexity
- Time complexity:
O(n + m + k), where n and m are the lengths of row and column conditions, and k is the size of the matrix.
- Space complexity:
O(k + n + m), as we store the graph, in-degree arrays, and topological orders.
# Code
```python3 []
class Solution:
def buildMatrix(self, k: int, rowConditions: list[list[int]], colConditions: list[list[int]]) -> list[list[int]]:
# Helper function to perform topological sorting using Kahn's algorithm
def topological_sort(conditions, k):
graph = defaultdict(list)
in_degree = [0] * (k + 1)
# Build graph and in-degree array
for u, v in conditions:
graph[u].append(v)
in_degree[v] += 1
# Queue for nodes with in-degree of 0
queue = deque([i for i in range(1, k + 1) if in_degree[i] == 0])
order = []
while queue:
node = queue.popleft()
order.append(node)
for neighbor in graph[node]:
in_degree[neighbor] -= 1
if in_degree[neighbor] == 0:
queue.append(neighbor)
# If the order does not contain all elements, a cycle exists
return order if len(order) == k else []
# Get the topological order for row and column conditions
row_order = topological_sort(rowConditions, k)
col_order = topological_sort(colConditions, k)
# If no valid order exists, return an empty matrix
if not row_order or not col_order:
return []
# Create an empty k x k matrix
matrix = [[0] * k for _ in range(k)]
# Map each number to its row and column position
row_pos = {num: idx for idx, num in enumerate(row_order)}
col_pos = {num: idx for idx, num in enumerate(col_order)}
# Fill the matrix
for num in range(1, k + 1):
matrix[row_pos[num]][col_pos[num]] = num
return matrix
``` | 5 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'Python3'] | 0 |
build-a-matrix-with-conditions | BFS - Intuition & Approach Explained C++ | bfs-intuition-approach-explained-c-by-re-iz2w | Intuition\n Describe your first thoughts on how to solve this problem. \nWhen I first read the problem, I noticed that there was a dependency involved. Whenever | reetisharma | NORMAL | 2024-07-21T12:22:40.677269+00:00 | 2024-07-21T12:25:20.137532+00:00 | 272 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen I first read the problem, I noticed that there was a dependency involved. Whenever we encounter dependency, we should think of graphs. Moreover, there was an additional constraint of ordering, which implies that we need to sort the elements in a specific order. Since we are given the conditions in the form of edges, we can simply apply topological sorting to resolve the dependencies and obtain the desired order\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Represent the condition dependency in the form of graph\n2. Sort the graph by topological sort\n3. Using the topological order obtained for rows and columns, construct the matrix such that each element is placed in the correct position respecting both row and column conditions.\n\n# Complexity\n- Time complexity: $$O(k+E)+O(k^2)=O(k^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n//topological sort, how?\n\n //use BFS Kahn\'s algorithm\n vector<int> topoSort(int k, vector<vector<int>> edges){\n vector<vector<int>> graph(k+1);\n vector<int> indegree(k+1,0);\n vector<int> res;\n\n\n //build graph & calculate indegrees\n for(vector<int>& edge: edges){\n graph[edge[0]].push_back(edge[1]);\n indegree[edge[1]]++;\n }\n\n queue<int> q;\n //push nodes with no dependency\n for(int i=1; i<=k; i++){\n if(indegree[i]==0){\n q.push(i);\n }\n }\n //BFS\n while(!q.empty()){\n int cur = q.front(); q.pop();\n res.push_back(cur);\n\n for(int neigh: graph[cur]){\n indegree[neigh]--;\n if(indegree[neigh]==0){\n q.push(neigh);\n }\n }\n }\n //check for cyle\n for(int i=1; i<=k; i++){\n if(indegree[i]!=0){\n return {};\n }\n }\n return res;\n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n\n vector<int> rowOrder = topoSort(k, rowConditions);\n vector<int> colOrder = topoSort(k, colConditions);\n\n //if we encountered a cycle in any condition, return empty array\n if(rowOrder.empty() || colOrder.empty()){\n return {};\n }\n\n vector<vector<int>> res(k, vector<int>(k,0));\n\n //build the result matrix\n for(int i=0; i<k; i++){\n int ele = rowOrder[i];\n for(int j=0; j<k; j++){\n if(colOrder[j]==ele){\n res[i][j] = ele;\n }\n }\n }\n return res;\n }\n};\n\n``` | 5 | 0 | ['Breadth-First Search', 'Graph', 'C++'] | 1 |
build-a-matrix-with-conditions | Easy Solution | Topological Sort | Python | C++ | easy-solution-topological-sort-python-c-gso83 | Approach\n1. Initialize and Populate the Graphs for rows and Columns:\n2. then create a topological sort function that sorts the given action in such a order th | Sachinonly__ | NORMAL | 2024-07-21T10:10:10.618486+00:00 | 2024-07-21T19:56:46.205797+00:00 | 267 | false | # Approach\n1. Initialize and Populate the Graphs for rows and Columns:\n2. then create a topological sort function that sorts the given action in such a order that if theres a dependency of child over a parent then child will always come after the parent. \n - Create a stack deque(why deque becuse it will help us append at 0 index in O(1) complexity whereas a normal list will take O(N) in worst time), visited set, check_cycle set and a 0 indexed cycle list defaulted at False ( will be update to True if found a cycle)\n - define a topoLogical_sort_helper function (in our case it is topoHelper) which is doing a recursive DFS in our topologicalsort function as well as checking for possible cycles.\n\n3. get the topological order of rows and columns using topologicalsort function.\n4. check wheather there is a cycle or not by checking wheather a valid rows and column are returned by the function.\n5. create a new dictionary d to store the indexed value of our row Position as it help us reduce the time for search of index in rows.\n6. update the matrix and then return it.\n\n# Complexity\n- Time complexity: O(N + M)\n\n- Space complexity: O(N + M)\n\n# Code\n```python []\nclass Solution(object):\n def buildMatrix(self, k, rowConditions, colConditions):\n rowgraph = defaultdict(list)\n colgraph = defaultdict(list)\n\n for x in rowConditions:\n rowgraph[x[0]].append(x[1])\n for x in colConditions:\n colgraph[x[0]].append(x[1])\n \n def topologicalsort(graph):\n stack = deque()\n visited = set()\n check_cycle = set()\n cycle = [False]\n\n def topoHelper(x):\n if cycle[0]:\n return\n\n visited.add(x)\n check_cycle.add(x)\n for i in graph[x]:\n if i in check_cycle:\n cycle[0] = True\n return\n\n if i not in visited:\n topoHelper(i)\n check_cycle.remove(x)\n stack.appendleft(x)\n \n for i in range(1,k+1):\n if cycle[0]:\n return []\n\n if i not in visited:\n topoHelper(i)\n return list(stack)\n \n rows = topologicalsort(rowgraph)\n columns = topologicalsort(colgraph)\n\n if not rows or not columns:\n return []\n\n d = {}\n for i,x in enumerate(rows):\n d[x] = i\n \n matrix = [[0]*k for _ in range(k)]\n for i,x in enumerate(columns):\n matrix[d[x]][i] = x\n return matrix\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n unordered_map<int, vector<int>> rowgraph;\n unordered_map<int, vector<int>> colgraph;\n\n for (const auto& x : rowConditions) {\n rowgraph[x[0]].push_back(x[1]);\n }\n for (const auto& x : colConditions) {\n colgraph[x[0]].push_back(x[1]);\n }\n\n auto topologicalsort = [&](unordered_map<int, vector<int>>& graph) {\n deque<int> stack;\n unordered_set<int> visited;\n unordered_set<int> check_cycle;\n bool cycle = false;\n\n function<void(int)> topoHelper = [&](int x) {\n if (cycle) return;\n\n visited.insert(x);\n check_cycle.insert(x);\n for (int i : graph[x]) {\n if (check_cycle.find(i) != check_cycle.end()) {\n cycle = true;\n return;\n }\n if (visited.find(i) == visited.end()) {\n topoHelper(i);\n }\n }\n check_cycle.erase(x);\n stack.push_front(x);\n };\n\n for (int i = 1; i <= k; ++i) {\n if (cycle) return vector<int>();\n if (visited.find(i) == visited.end()) {\n topoHelper(i);\n }\n }\n return vector<int>(stack.begin(), stack.end());\n };\n\n vector<int> rows = topologicalsort(rowgraph);\n vector<int> columns = topologicalsort(colgraph);\n\n if (rows.empty() || columns.empty()) {\n return {};\n }\n\n unordered_map<int, int> d;\n for (int i = 0; i < rows.size(); ++i) {\n d[rows[i]] = i;\n }\n\n vector<vector<int>> matrix(k, vector<int>(k, 0));\n for (int i = 0; i < columns.size(); ++i) {\n matrix[d[columns[i]]][i] = columns[i];\n }\n\n return matrix;\n }\n};\n```\n\n\n | 5 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'Python', 'C++', 'Python3'] | 0 |
build-a-matrix-with-conditions | JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-pa92 | https://youtu.be/HmnmBjjyZeo\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-07-21T08:39:24.767501+00:00 | 2024-07-21T08:39:24.767525+00:00 | 439 | false | https://youtu.be/HmnmBjjyZeo\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\n# Subscribe:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\n## Subscribe Goal:- 500\n## Current Subscriber:- 499\n\n# Complexity\n Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n - Constructing the graph: O(k + e), where e is the number of edges.\nTopological sorting: O(k + e) for each graph.\nConstructing the matrix: O(k^2) due to the nested loops for filling the matrix.\n\n Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- O(k + e) for storing the graph.\nO(k) for storing the topological sort result.\nO(k^2) for the final matrix.\n\n# Code\n```\nclass Solution {\n public List<Integer> topologicalOrder(int k, List<List<Integer>> gr) {\n int[] indeg = new int[k + 1];\n for (int node = 1; node <= k; node++) {\n for (int child : gr.get(node)) {\n indeg[child]++;\n }\n }\n Queue<Integer> q = new ArrayDeque<>();\n boolean[] vis = new boolean[k + 1];\n for (int node = 1; node <= k; node++) {\n if (indeg[node] == 0) {\n q.add(node);\n }\n }\n\n List<Integer> topoSort = new ArrayList<>();\n while (!q.isEmpty()) {\n int sz = q.size();\n while (sz-- > 0) {\n int node = q.poll();\n vis[node] = true;\n topoSort.add(node);\n\n for (int child : gr.get(node)) {\n if (!vis[child]) {\n indeg[child]--;\n if (indeg[child] == 0) {\n q.add(child);\n }\n }\n }\n }\n }\n for (int node = 1; node <= k; node++) {\n if (indeg[node] != 0) {\n return new ArrayList<>();\n }\n }\n return topoSort;\n }\n\n public List<List<Integer>> buildGraph(int k, int[][] conditions) {\n List<List<Integer>> gr = new ArrayList<>();\n for (int i = 0; i <= k; i++) {\n gr.add(new ArrayList<>());\n }\n\n for (int[] condition : conditions) {\n int u = condition[0], v = condition[1];\n gr.get(u).add(v);\n }\n return gr;\n }\n\n public void fillTopoArray(int k, List<Integer> rowTopo) {\n Set<Integer> vis = new HashSet<>(rowTopo);\n\n for (int el = 1; el <= k; el++) {\n if (!vis.contains(el)) {\n rowTopo.add(el);\n }\n }\n }\n\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<List<Integer>> rowGr = buildGraph(k, rowConditions);\n List<List<Integer>> colGr = buildGraph(k, colConditions);\n\n List<Integer> rowTopo = topologicalOrder(k, rowGr);\n List<Integer> colTopo = topologicalOrder(k, colGr);\n\n if (rowTopo.isEmpty() || colTopo.isEmpty()) {\n return new int[0][0];\n }\n\n fillTopoArray(k, rowTopo);\n fillTopoArray(k, colTopo);\n\n Map<Integer, Integer> colInd = new HashMap<>();\n for (int j = 0; j < k; j++) {\n colInd.put(colTopo.get(j), j);\n }\n\n int[][] ans = new int[k][k];\n for (int i = 0; i < k; i++) {\n ans[i][colInd.get(rowTopo.get(i))] = rowTopo.get(i);\n }\n return ans;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
build-a-matrix-with-conditions | ✅Beats 100% || Made it easy for you || C++/Java/Python/JS || Topological Sort || Explained in Detail | beats-100-made-it-easy-for-you-cjavapyth-2soc | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is about arranging integers from 1 to \uD835\uDC58\nk in a \uD835\uDC58 \xD | _Rachi | NORMAL | 2024-07-21T05:33:02.940219+00:00 | 2024-07-21T05:33:02.940244+00:00 | 503 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about arranging integers from 1 to \uD835\uDC58\nk in a \uD835\uDC58 \xD7 \uD835\uDC58 matrix such that: \n1. Specific integers appear in certain rows (based on rowConditions).\n2. Specific integers appear in certain columns (based on colConditions).\nThe constraints imply a topological sorting problem, where we need to arrange elements based on dependencies. We need to ensure that no circular dependencies exist (otherwise, the arrangement is impossible).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Graph Construction:**\n - Build two directed graphs (rowGraph and colGraph) based on rowConditions and colConditions, respectively.\n - Each graph represents dependencies (edges) between elements (nodes).\n\n2. **Topological Sorting:**\n - Perform topological sorting on both graphs.\n - If topological sorting fails (cycle detected), return an empty matrix because it\'s impossible to arrange the integers.\n\n3. **Matrix Construction:**\n - Use the results of topological sorts to determine the row and column positions of each integer.\n - Construct the final matrix based on these positions.\n\n# Complexity\n- Time complexity:\n - Constructing graphs: $$\uD835\uDC42(\uD835\uDC5F+\uD835\uDC50)$$, where \uD835\uDC5F is the number of rowConditions and \uD835\uDC50 is the number of colConditions.\n - Topological sorting: $$O(k+r)+O(k+c)$$ (for row and column graphs respectively).\n - Building the result matrix: $$O(k).$$\nOverall time complexity: $$O(k+r+c).$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n - Graph storage: O(k + n) for rows and O(k + m) for columns.\n - Additional space for topological sorting: O(k).\n - Matrix storage: O(k^2).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Example\n**Input**\n- k = 3\n- rowConditions = [[1, 2], [2, 3]]\n - colConditions = [[2, 1], [3, 2]]\n\n**Step-by-Step Solution**\n\n1. **Graph Construction:**\n - rowGraph:\n - 1 -> 2\n - 2 -> 3\n - colGraph:\n - 2 -> 1\n - 3 -> 2\n\n2. **Topological Sorting**:\n - Topological sort on rowGraph:\n - Start with 1 (in-degree 0), then 2, then 3.\n - rowOrder = [1, 2, 3].\n - Topological sort on colGraph:\n - Start with 3 (in-degree 0), then 2, then 1.\n - colOrder = [3, 2, 1].\n\n3. **Mapping Positions:**\n - rowMap:\n - 1 -> row 0\n - 2 -> row 1\n - 3 -> row 2\n - colMap:\n - 3 -> col 0\n - 2 -> col 1\n - 1 -> col 2\n\n4. **Matrix Construction:**\n - Position 1 at (0, 2)\n - Position 2 at (1, 1)\n - Position 3 at (2, 0)\n\n5. **Final matrix:**\n```\n[[0, 0, 1],\n [0, 2, 0],\n [3, 0, 0]]\n\n```\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> rowGraph(k + 1), colGraph(k + 1);\n for (auto& rc : rowConditions) {\n rowGraph[rc[0]].push_back(rc[1]);\n }\n for (auto& cc : colConditions) {\n colGraph[cc[0]].push_back(cc[1]);\n }\n \n vector<int> rowOrder = topoSort(rowGraph, k);\n vector<int> colOrder = topoSort(colGraph, k);\n \n if (rowOrder.empty() || colOrder.empty()) return {};\n \n vector<vector<int>> result(k, vector<int>(k, 0));\n unordered_map<int, int> rowMap, colMap;\n for (int i = 0; i < k; ++i) {\n rowMap[rowOrder[i]] = i;\n colMap[colOrder[i]] = i;\n }\n \n for (int i = 1; i <= k; ++i) {\n result[rowMap[i]][colMap[i]] = i;\n }\n \n return result;\n }\n \n vector<int> topoSort(vector<vector<int>>& graph, int k) {\n vector<int> inDegree(k + 1, 0), order;\n queue<int> q;\n for (int i = 1; i <= k; ++i) {\n for (int j : graph[i]) {\n ++inDegree[j];\n }\n }\n for (int i = 1; i <= k; ++i) {\n if (inDegree[i] == 0) q.push(i);\n }\n while (!q.empty()) {\n int node = q.front(); q.pop();\n order.push_back(node);\n for (int adj : graph[node]) {\n if (--inDegree[adj] == 0) q.push(adj);\n }\n }\n return order.size() == k ? order : vector<int>();\n }\n};\n```\n```python []\nclass Solution(object):\n def buildMatrix(self, k, rowConditions, colConditions):\n rowGraph = defaultdict(list)\n for u, v in rowConditions:\n rowGraph[u].append(v)\n \n colGraph = defaultdict(list)\n for u, v in colConditions:\n colGraph[u].append(v)\n \n def topoSort(graph):\n inDegree = {i: 0 for i in range(1, k + 1)}\n for u in graph:\n for v in graph[u]:\n inDegree[v] += 1\n queue = deque([i for i in inDegree if inDegree[i] == 0])\n order = []\n while queue:\n node = queue.popleft()\n order.append(node)\n for v in graph[node]:\n inDegree[v] -= 1\n if inDegree[v] == 0:\n queue.append(v)\n return order if len(order) == k else []\n \n rowOrder = topoSort(rowGraph)\n colOrder = topoSort(colGraph)\n \n if not rowOrder or not colOrder:\n return []\n \n rowMap = {num: i for i, num in enumerate(rowOrder)}\n colMap = {num: i for i, num in enumerate(colOrder)}\n \n result = [[0] * k for _ in range(k)]\n for i in range(1, k + 1):\n result[rowMap[i]][colMap[i]] = i\n \n return result\n \n```\n```java []\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<Integer>[] rowGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < rowGraph.length; i ++) {\n rowGraph[i] = new ArrayList();\n }\n for(int [] rowCondition : rowConditions){ \n rowGraph[rowCondition[0]].add(rowCondition[1]); \n }\n\n List<Integer>[] colGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < colGraph.length; i ++) {\n colGraph[i] = new ArrayList();\n }\n for(int [] colCondition : colConditions){\n colGraph[colCondition[0]].add(colCondition[1]); \n }\n\n int[] visited = new int[k + 1];\n Deque<Integer> queue = new LinkedList<>(); \n for(int i = 1; i < rowGraph.length; i++){ \n if(!topSort(rowGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n \n int[] rowIndexMap = new int[k + 1]; \n for(int i = 0; i < k; i++){ \n int node = queue.pollLast(); \n rowIndexMap[node] = i;\n }\n\n visited = new int[k + 1];\n queue = new LinkedList();\n for(int i = 1; i < colGraph.length; i++){\n if(!topSort(colGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n int[] colOrder = new int[k];\n int[] colIndexMap = new int[k+1];\n for(int i = 0; i < k; i++){\n int node = queue.pollLast();\n colOrder[i] = node;\n colIndexMap[node] = i;\n }\n\n int[][] result = new int[k][k];\n \n for(int i = 1; i <= k; i++){\n result[rowIndexMap[i]][colIndexMap[i]] = i;\n }\n\n return result;\n\n }\n\n public boolean topSort(List<Integer>[] graph, int node, int[] visited, Deque<Integer> queue){\n if(visited[node] == 2) {\n return false;\n }\n if(visited[node] == 0){\n visited[node] = 2;\n for(int child : graph[node]){\n if(!topSort(graph, child, visited, queue)){\n return false;\n }\n }\n visited[node] = 1;\n queue.add(node);\n }\n return true;\n }\n}\n```\n``` javascript []\n/**\n * @param {number} k\n * @param {number[][]} rowConditions\n * @param {number[][]} colConditions\n * @return {number[][]}\n */\nvar buildMatrix = function(k, rowConditions, colConditions) {\n \nconst rowGraph = Array.from({ length: k + 1 }, () => []);\n const colGraph = Array.from({ length: k + 1 }, () => []);\n \n for (const [u, v] of rowConditions) {\n rowGraph[u].push(v);\n }\n for (const [u, v] of colConditions) {\n colGraph[u].push(v);\n }\n \n const topoSort = (graph) => {\n const inDegree = Array(k + 1).fill(0);\n for (const u of graph) {\n for (const v of u) {\n inDegree[v]++;\n }\n }\n const queue = [];\n for (let i = 1; i <= k; i++) {\n if (inDegree[i] === 0) queue.push(i);\n }\n const order = [];\n while (queue.length) {\n const node = queue.shift();\n order.push(node);\n for (const v of graph[node]) {\n if (--inDegree[v] === 0) queue.push(v);\n }\n }\n return order.length === k ? order : [];\n };\n \n const rowOrder = topoSort(rowGraph);\n const colOrder = topoSort(colGraph);\n \n if (!rowOrder.length || !colOrder.length) return [];\n \n const rowMap = rowOrder.reduce((acc, num, i) => {\n acc[num] = i;\n return acc;\n }, {});\n \n const colMap = colOrder.reduce((acc, num, i) => {\n acc[num] = i;\n return acc;\n }, {});\n \n const result = Array.from({ length: k }, () => Array(k).fill(0));\n for (let i = 1; i <= k; i++) {\n result[rowMap[i]][colMap[i]] = i;\n }\n \n return result;\n};\n```\n\n\n | 5 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'Python', 'C++', 'Java', 'JavaScript'] | 5 |
build-a-matrix-with-conditions | 🔥🔥 ✅ Beats 100 %solutions with Detailed explanation || C++ || JAVA || Python | beats-100-solutions-with-detailed-explan-yr23 | Intuition Behind the Solution\n\nThe problem involves building a \( k \times k \) matrix with specific conditions on the ordering of rows and columns. The core | originalpandacoder | NORMAL | 2024-07-21T05:09:25.536822+00:00 | 2024-07-21T05:09:25.536849+00:00 | 511 | false | # Intuition Behind the Solution\n\nThe problem involves building a \\( k \\times k \\) matrix with specific conditions on the ordering of rows and columns. The core idea is to use topological sorting to determine a valid order of elements based on the given conditions.\n\nHere\u2019s a step-by-step breakdown of the intuition:\n\n1. **Understand the Problem Constraints**:\n - We need to place numbers \\( 1 \\) to \\( k \\) in a \\( k \\times k \\) matrix.\n - Each number should appear exactly once.\n - The matrix should satisfy both row and column conditions given in `rowConditions` and `colConditions`.\n\n2. **Graph Representation**:\n - We can represent the row conditions as a directed graph where each edge \\( (a, b) \\) means \\( a \\) must appear in a row above \\( b \\).\n - Similarly, we can represent the column conditions as another directed graph where each edge \\( (a, b) \\) means \\( a \\) must appear in a column to the left of \\( b \\).\n\n3. **Topological Sorting**:\n - Topological sorting of a directed graph gives a linear ordering of its vertices such that for every directed edge \\( (u, v) \\), vertex \\( u \\) comes before \\( v \\) in the ordering.\n - We perform topological sorting on the row graph to determine the row order of the elements.\n - Similarly, we perform topological sorting on the column graph to determine the column order of the elements.\n\n4. **Building the Matrix**:\n - Once we have the topological orders for rows and columns, we can place each element in the matrix according to these orders.\n - We create a mapping from each element to its row and column indices based on the topological sort results.\n\n5. **Check for Cycles**:\n - If there is a cycle in any of the graphs, a valid topological sort is not possible, which means the given conditions are contradictory, and we should return an empty matrix.\n\n\n# Approach and code breakdown\n\n##### Class Definition and Method Signature\n\n```java\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n```\n\nThis is the main method of the `Solution` class. It takes two parameters:\n- `k`: The number of elements to place in the matrix.\n- `rowConditions`: An array of conditions that specify the order of elements in the rows.\n- `colConditions`: An array of conditions that specify the order of elements in the columns.\n\n### Initialize Graphs\n\n```java\n List<Integer>[] rowGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < rowGraph.length; i ++) {\n rowGraph[i] = new ArrayList();\n }\n for(int [] rowCondition : rowConditions){ \n rowGraph[rowCondition[0]].add(rowCondition[1]); \n }\n\n List<Integer>[] colGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < colGraph.length; i ++) {\n colGraph[i] = new ArrayList();\n }\n for(int [] colCondition : colConditions){\n colGraph[colCondition[0]].add(colCondition[1]); \n }\n```\n\n- **rowGraph** and **colGraph**: These are adjacency lists representing the directed graphs for row and column conditions, respectively. The graphs are initialized to have `k + 1` vertices (1-based index).\n- The loops populate the adjacency lists based on the given conditions.\n\n### Topological Sorting for Rows\n\n```java\n int[] visited = new int[k + 1];\n Deque<Integer> queue = new LinkedList<>(); \n for(int i = 1; i < rowGraph.length; i++){ \n if(!topSort(rowGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n int[] rowIndexMap = new int[k + 1]; \n for(int i = 0; i < k; i++){ \n int node = queue.pollLast(); \n rowIndexMap[node] = i;\n }\n```\n\n- `visited`: Array to keep track of the visitation state of each node (0 = unvisited, 1 = visited, 2 = visiting).\n- `queue`: Used to store the topological order.\n- **Topological Sort**: The `topSort` method is called for each node to generate a topological order of the row conditions.\n- `rowIndexMap`: Maps each node to its position in the topological order for rows.\n\n### Topological Sorting for Columns\n\n```java\n visited = new int[k + 1];\n queue = new LinkedList();\n for(int i = 1; i < colGraph.length; i++){\n if(!topSort(colGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n int[] colOrder = new int[k];\n int[] colIndexMap = new int[k+1];\n for(int i = 0; i < k; i++){\n int node = queue.pollLast();\n colOrder[i] = node;\n colIndexMap[node] = i;\n }\n```\n\n- Resets `visited` and `queue` for the column conditions.\n- **Topological Sort**: Similar process as rows but for column conditions.\n- `colOrder` and `colIndexMap`: Store the topological order for columns and map each node to its position in the topological order.\n\n### Build the Result Matrix\n\n```java\n int[][] result = new int[k][k];\n \n for(int i = 1; i <= k; i++){\n result[rowIndexMap[i]][colIndexMap[i]] = i;\n }\n\n return result;\n }\n```\n\n- `result`: The final `k x k` matrix.\n- Places each number `i` at the correct position based on `rowIndexMap` and `colIndexMap`.\n\n### Topological Sort Helper Method\n\n```java\n public boolean topSort(List<Integer>[] graph, int node, int[] visited, Deque<Integer> queue){\n if(visited[node] == 2) {\n return false;\n }\n if(visited[node] == 0){\n visited[node] = 2;\n for(int child : graph[node]){\n if(!topSort(graph, child, visited, queue)){\n return false;\n }\n }\n visited[node] = 1;\n queue.add(node);\n }\n return true;\n }\n}\n```\n\n- **topSort**: Recursive method to perform topological sorting.\n- If a cycle is detected (`visited[node] == 2`), it returns false.\n- Marks the node as visiting (`visited[node] = 2`) and recursively visits all its children.\n- Once all children are visited, marks the node as visited (`visited[node] = 1`) and adds it to the queue.\n\nThis code ensures that the rows and columns of the matrix adhere to the given conditions by performing a topological sort and placing the elements accordingly.\n\n```C++ []\nclass Solution {\npublic:\n std::vector<std::vector<int>> buildMatrix(int k, std::vector<std::vector<int>>& rowConditions, std::vector<std::vector<int>>& colConditions) {\n std::vector<std::vector<int>> rowGraph(k + 1);\n for (const auto& rowCondition : rowConditions) {\n rowGraph[rowCondition[0]].push_back(rowCondition[1]);\n }\n\n std::vector<std::vector<int>> colGraph(k + 1);\n for (const auto& colCondition : colConditions) {\n colGraph[colCondition[0]].push_back(colCondition[1]);\n }\n\n std::vector<int> visited(k + 1, 0);\n std::deque<int> queue;\n for (int i = 1; i <= k; ++i) {\n if (!topSort(rowGraph, i, visited, queue)) {\n return {};\n }\n }\n\n std::vector<int> rowIndexMap(k + 1);\n for (int i = 0; i < k; ++i) {\n int node = queue.back(); queue.pop_back();\n rowIndexMap[node] = i;\n }\n\n visited.assign(k + 1, 0);\n queue.clear();\n for (int i = 1; i <= k; ++i) {\n if (!topSort(colGraph, i, visited, queue)) {\n return {};\n }\n }\n\n std::vector<int> colOrder(k);\n std::vector<int> colIndexMap(k + 1);\n for (int i = 0; i < k; ++i) {\n int node = queue.back(); queue.pop_back();\n colOrder[i] = node;\n colIndexMap[node] = i;\n }\n\n std::vector<std::vector<int>> result(k, std::vector<int>(k, 0));\n for (int i = 1; i <= k; ++i) {\n result[rowIndexMap[i]][colIndexMap[i]] = i;\n }\n\n return result;\n }\n\nprivate:\n bool topSort(const std::vector<std::vector<int>>& graph, int node, std::vector<int>& visited, std::deque<int>& queue) {\n if (visited[node] == 2) return false;\n if (visited[node] == 0) {\n visited[node] = 2;\n for (int child : graph[node]) {\n if (!topSort(graph, child, visited, queue)) {\n return false;\n }\n }\n visited[node] = 1;\n queue.push_back(node);\n }\n return true;\n }\n};\n\n```\n\n```JAVA []\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<Integer>[] rowGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < rowGraph.length; i ++) {\n rowGraph[i] = new ArrayList();\n }\n for(int [] rowCondition : rowConditions){ \n rowGraph[rowCondition[0]].add(rowCondition[1]); \n }\n\n List<Integer>[] colGraph = new ArrayList[k + 1]; \n for(int i = 1 ; i < colGraph.length; i ++) {\n colGraph[i] = new ArrayList();\n }\n for(int [] colCondition : colConditions){\n colGraph[colCondition[0]].add(colCondition[1]); \n }\n\n int[] visited = new int[k + 1];\n Deque<Integer> queue = new LinkedList<>(); \n for(int i = 1; i < rowGraph.length; i++){ \n if(!topSort(rowGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n \n int[] rowIndexMap = new int[k + 1]; \n for(int i = 0; i < k; i++){ \n int node = queue.pollLast(); \n rowIndexMap[node] = i;\n }\n\n visited = new int[k + 1];\n queue = new LinkedList();\n for(int i = 1; i < colGraph.length; i++){\n if(!topSort(colGraph, i, visited, queue)){\n return new int[0][0];\n }\n }\n\n int[] colOrder = new int[k];\n int[] colIndexMap = new int[k+1];\n for(int i = 0; i < k; i++){\n int node = queue.pollLast();\n colOrder[i] = node;\n colIndexMap[node] = i;\n }\n\n int[][] result = new int[k][k];\n \n for(int i = 1; i <= k; i++){\n result[rowIndexMap[i]][colIndexMap[i]] = i;\n }\n\n return result;\n\n }\n\n public boolean topSort(List<Integer>[] graph, int node, int[] visited, Deque<Integer> queue){\n if(visited[node] == 2) {\n return false;\n }\n if(visited[node] == 0){\n visited[node] = 2;\n for(int child : graph[node]){\n if(!topSort(graph, child, visited, queue)){\n return false;\n }\n }\n visited[node] = 1;\n queue.add(node);\n }\n return true;\n }\n}\n```\n```python []\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n rowGraph = defaultdict(list)\n for a, b in rowConditions:\n rowGraph[a].append(b)\n \n colGraph = defaultdict(list)\n for a, b in colConditions:\n colGraph[a].append(b)\n \n def topSort(graph):\n visited = [0] * (k + 1)\n stack = deque()\n \n def dfs(node):\n if visited[node] == 2:\n return False\n if visited[node] == 0:\n visited[node] = 2\n for child in graph[node]:\n if not dfs(child):\n return False\n visited[node] = 1\n stack.appendleft(node)\n return True\n \n for i in range(1, k + 1):\n if not dfs(i):\n return []\n return stack\n \n rowOrder = topSort(rowGraph)\n if not rowOrder:\n return []\n \n colOrder = topSort(colGraph)\n if not colOrder:\n return []\n \n rowIndex = {num: i for i, num in enumerate(rowOrder)}\n colIndex = {num: i for i, num in enumerate(colOrder)}\n \n result = [[0] * k for _ in range(k)]\n for num in range(1, k + 1):\n result[rowIndex[num]][colIndex[num]] = num\n \n return result\n\n```\n\n | 5 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'C++', 'Java'] | 2 |
build-a-matrix-with-conditions | Rust - Kahn's Algorithm with Matrix Manipulation | rust-kahns-algorithm-with-matrix-manipul-p2v1 | Solution - github\n\nProblem List\n#KahnsAlgorithm - github\n#MatrixManipulation - github\n\n#DirectedGraph - github\n#DetectCycle-Graph - github\n#Graph - gith | idiotleon | NORMAL | 2022-08-28T04:20:02.740471+00:00 | 2022-08-28T05:19:25.733728+00:00 | 321 | false | Solution - [github](https://github.com/An7One/lc_soln_rust_leon/tree/main/src/leetcode/lvl4/lc2392)\n\n<b>Problem List</b>\n#KahnsAlgorithm - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/blob/main/txt/by_algorithm/search/breath_first_search/by_algorithm/kahns_algorithm.txt)\n#MatrixManipulation - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/tree/main/txt/by_data_structure/array/by_topic/manipulation/matrix)\n\n#DirectedGraph - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/tree/main/txt/by_data_structure/graph/by_data_structure/directed_graph)\n#DetectCycle-Graph - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/blob/main/txt/by_data_structure/graph/by_topic/detect_cycle.txt)\n#Graph - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/tree/main/txt/by_data_structure/graph)\n\n```\nuse std::collections::{HashMap, VecDeque};\n\n/// @author: Leon\n/// https://leetcode.com/problems/build-a-matrix-with-conditions/\n/// Time Complexity: O(V + E) + O(`k`) ~ O(`k` + `_len_rcs` + `_len_ccs`)\n/// Space Complexity: O(V + E) + O(`k`) ~ O(`k` + `_len_rcs` + `_len_ccs`)\nimpl Solution {\n pub fn build_matrix(\n k: i32,\n row_conditions: Vec<Vec<i32>>,\n col_conditions: Vec<Vec<i32>>,\n ) -> Vec<Vec<i32>> {\n\t let _len_rcs: usize = row_conditions.len();\n let _len_ccs: usize = col_conditions.len();\n let k: usize = k as usize;\n let n: usize = k + 1;\n let (is_cyclic_r, map_r) = {\n let (graph, mut indegrees) = Self::build_graph(&row_conditions, n);\n Self::is_cyclic(&graph, &mut indegrees)\n };\n if is_cyclic_r {\n return Vec::new();\n }\n let (is_cyclic_c, map_c) = {\n let (graph, mut indegrees) = Self::build_graph(&col_conditions, n);\n Self::is_cyclic(&graph, &mut indegrees)\n };\n if is_cyclic_c {\n return Vec::new();\n }\n return Self::build_mat_simple(&map_r, &map_c, k);\n }\n /// to be improved\n /// this could pass for now,\n /// because of test cases being weak\n fn build_mat_simple(\n map_r: &HashMap<i32, usize>,\n map_c: &HashMap<i32, usize>,\n k: usize,\n ) -> Vec<Vec<i32>> {\n let mut ans: Vec<Vec<i32>> = vec![vec![0; k]; k];\n for num in 1..=k as i32 {\n let r: usize = *map_r.get(&num).unwrap();\n let c: usize = *map_c.get(&num).unwrap();\n ans[r][c] = num;\n }\n return ans;\n }\n fn is_cyclic(graph: &Vec<Vec<usize>>, indegrees: &mut Vec<u16>) -> (bool, HashMap<i32, usize>) {\n let len_vs: usize = indegrees.len();\n let mut queue: VecDeque<usize> = {\n let mut queue = VecDeque::with_capacity(len_vs);\n for idx in 1..len_vs {\n if indegrees[idx] == 0 {\n queue.push_back(idx);\n }\n }\n queue\n };\n let mut sorted: Vec<i32> = Vec::with_capacity(len_vs);\n while let Some(cur) = queue.pop_front() {\n sorted.push(cur as i32);\n for &nxt in &graph[cur] {\n indegrees[nxt] -= 1;\n if indegrees[nxt] == 0 {\n queue.push_back(nxt);\n }\n }\n }\n if sorted.len() < len_vs - 1 {\n return (true, HashMap::new());\n }\n let num_to_idx: HashMap<i32, usize> = {\n let mut map: HashMap<i32, usize> = HashMap::with_capacity(len_vs);\n for (idx, num) in sorted.into_iter().enumerate() {\n map.insert(num, idx);\n }\n map\n };\n return (false, num_to_idx);\n }\n fn build_graph(edges: &Vec<Vec<i32>>, n: usize) -> (Vec<Vec<usize>>, Vec<u16>) {\n let mut graph: Vec<Vec<usize>> = vec![Vec::with_capacity(n); n];\n let mut indegrees: Vec<u16> = vec![0; n];\n for edge in edges {\n let from: usize = edge[0] as usize;\n let to: usize = edge[1] as usize;\n graph[from].push(to);\n indegrees[to] += 1;\n }\n return (graph, indegrees);\n }\n}\n``` | 5 | 0 | ['Topological Sort', 'Rust'] | 2 |
build-a-matrix-with-conditions | [Python] Topological Sort Explained | python-topological-sort-explained-by-zsk-qa6b | rows and cols are independent, just run 2 topological sorts on each direction. time complexity is O(k^2)\n\n\nclass Solution:\n def buildMatrix(self, k: int, | zsk99881 | NORMAL | 2022-08-28T04:01:28.217401+00:00 | 2022-08-28T04:42:06.682923+00:00 | 352 | false | rows and cols are independent, just run 2 topological sorts on each direction. time complexity is O(k^2)\n\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n res = [[0 for _ in range(k)] for _ in range(k)]\n \n # build 2 graphs for row and col independently, count indegrees for each node \n # a node in each graph is a number between 1 to k\n row_graph, col_graph = defaultdict(set), defaultdict(set)\n row_indegrees, col_indegrees = defaultdict(int), defaultdict(int)\n for i, j in rowConditions:\n # note the input conditions could contain duplicates\n if j not in row_graph[i]:\n row_graph[i].add(j)\n row_indegrees[j] += 1\n for i, j in colConditions:\n if j not in col_graph[i]:\n col_graph[i].add(j)\n col_indegrees[j] += 1\n \n # run topological sort for nodes in row graph\n row_queue, col_queue = deque(), deque()\n row_order, col_order = {}, {}\n row_order_counter, col_order_counter = 0, 0\n row_visited, col_visited = set(), set()\n for i in range(1, k+1):\n # note that numbers did not appear in row conditions also have row_indegree = 0\n if row_indegrees[i] == 0:\n row_queue.append(i)\n row_visited.add(i)\n while row_queue:\n cur = row_queue.popleft()\n row_order[cur] = row_order_counter\n row_order_counter += 1\n for nxt in row_graph[cur]:\n if nxt in row_visited:\n continue\n row_indegrees[nxt] -= 1\n if row_indegrees[nxt] <= 0:\n row_visited.add(nxt)\n row_queue.append(nxt)\n \n # same topological sort for col graph\n for i in range(1, k+1):\n if col_indegrees[i] == 0:\n col_queue.append(i)\n col_visited.add(i)\n while col_queue:\n cur = col_queue.popleft()\n col_order[cur] = col_order_counter\n col_order_counter += 1\n for nxt in col_graph[cur]:\n if nxt in col_visited:\n continue\n col_indegrees[nxt] -= 1\n if col_indegrees[nxt] <= 0:\n col_visited.add(nxt)\n col_queue.append(nxt)\n\n # check if either row conditions or col conditions contains cycle\n if not (len(row_order) == k and len(col_order) == k):\n return []\n \n # no cycle, build result with row and col independently\n for i in range(1, k+1):\n res[row_order[i]][col_order[i]] = i\n return res\n \n \n \n \n``` | 5 | 1 | [] | 1 |
build-a-matrix-with-conditions | Topological Sort | BFS | DFS | Short and Easy to Understand C++ Code | topological-sort-bfs-dfs-short-and-easy-x81p1 | It can be easily observed that the problem can be solved independently for rows and columns. First we can find the row number for each number from 1 to K and th | shekabhi1208 | NORMAL | 2022-08-28T04:00:53.942540+00:00 | 2022-08-29T16:58:02.202964+00:00 | 539 | false | It can be easily observed that the problem can be solved independently for rows and columns. First we can find the row number for each number from 1 to K and then find the column number for each of them. \nHere, If we see the problem as a graph problem where we have nodes from 1 to K and edges as the dependencies given in **rowConditions** and **colConditions**. \nthen, after building the graph, we can see that there are a lot od dependencies like 2 should come before 3 and 3 should code after 5 and so on. So How can we find the order which can satisify these conditions. For this, we will use topological sort.\n\nSteps:\n1. Build the graph using **rowConditions**\n2. Find topological sorting order for this graph\n3. Build one more graph using **colConditions**\n4. Find topological sorting order for this graph\n5. fill the matrix using the sorting order given by topological sort. \n\n```\nclass Solution {\npublic:\n \n \n \n // return false if the graph formed is cyclic in nature. \n //normal graph building and topological sort code\n bool buildGraph(vector<vector<int> >& arr, int n, vector<int>& data) {\n vector<int> adj[n + 1];\n vector<int> indeg(n + 1, 0);\n for(auto& curr: arr) {\n adj[curr[0]].push_back(curr[1]);\n indeg[curr[1]]++;\n }\n queue<int> q;\n for(int i = 1; i <= n; i++) {\n if(indeg[i] == 0) {\n q.push(i);\n }\n }\n while(!q.empty()) {\n int node = q.front();\n q.pop();\n data.push_back(node);\n for(auto& x: adj[node]) {\n if(--indeg[x] == 0) {\n q.push(x);\n }\n }\n }\n return data.size() == n;\n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int> topoRow, topoCol;\n \n // if the graph formed by the two arrays is cyclic, then answer is not possible.\n if(!buildGraph(rowConditions, k, topoRow) || !buildGraph(colConditions, k, topoCol)) {\n return {};\n }\n \n int row[k + 1], col[k + 1];\n \n \n for(int i = 0; i < k; i++) {\n row[topoRow[i]] = i;\n col[topoCol[i]] = i;\n }\n \n vector<vector<int> > arr(k, vector<int>(k, 0));\n for(int i = 1; i <= k; i++) {\n arr[row[i]][col[i]] = i;\n }\n return arr;\n \n }\n};\n```\n | 5 | 1 | ['Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'C'] | 1 |
build-a-matrix-with-conditions | Easy Intuition||TOPO SORT|| | easy-intuitiontopo-sort-by-ankii09102003-t0sj | Intuition\nsince we have given the boundations like this should appear first than this like these.... so we can directly think of topological sort and then afte | ankii09102003 | NORMAL | 2024-08-23T16:18:44.500856+00:00 | 2024-08-23T16:18:44.500889+00:00 | 57 | false | # Intuition\nsince we have given the boundations like this should appear first than this like these.... so we can directly think of topological sort and then after getting order for row and column we can just use map to decide the actual row and column \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n unordered_map<int,list<int>>mp1;\n unordered_map<int,list<int>>mp2;\n vector<int>indegree1(k+1,0);\n vector<int>indegree2(k+1,0);\n\n for(int i=0;i<rowConditions.size();i++){\n mp1[rowConditions[i][0]].push_back(rowConditions[i][1]);\n indegree1[rowConditions[i][1]]++;\n }\n for(int i=0;i<colConditions.size();i++){\n mp2[colConditions[i][0]].push_back(colConditions[i][1]);\n indegree2[colConditions[i][1]]++;\n }\n vector<int>ans1;\n vector<int>ans2;\n queue<int>q1,q2;\n\n for(int i=1;i<indegree1.size();i++){\n if(indegree1[i]==0){\n q1.push(i);\n }\n }\n for(int i=1;i<indegree2.size();i++){\n if(indegree2[i]==0){\n q2.push(i);\n }\n }\n while(!q1.empty()){\n int element=q1.front();\n q1.pop();\n ans1.push_back(element);\n for(auto it:mp1[element]){\n indegree1[it]--;\n if(indegree1[it]==0){\n q1.push(it);\n }\n }\n }\n while(!q2.empty()){\n int element=q2.front();\n q2.pop();\n ans2.push_back(element);\n for(auto it:mp2[element]){\n indegree2[it]--;\n if(indegree2[it]==0){\n q2.push(it);\n }\n }\n }\n\n // for(int i=0;i<ans2.size();i++){\n // cout<<ans2[i]<<" ";\n // }\n vector<vector<int>>ans;\n if(ans1.size()<k || ans2.size()<k){\n return ans;\n }\n unordered_map<int,int>row,col;\n for(int i=0;i<ans1.size();i++){\n row[ans1[i]]=i;\n }\n for(int i=0;i<ans2.size();i++){\n col[ans2[i]]=i;\n }\n vector<vector<int>>final1(k,vector<int>(k,0));\n for(int i=1;i<=k;i++){\n final1[row[i]][col[i]]=i;\n }\n return final1;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
build-a-matrix-with-conditions | Easy to Understand | easy-to-understand-by-twasim-b2jx | Intuition\n Describe your first thoughts on how to solve this problem. \nTopological Ordering.\n# Approach\n Describe your approach to solving the problem. \nTh | twasim | NORMAL | 2024-07-21T19:53:01.301607+00:00 | 2024-07-21T19:53:01.301650+00:00 | 66 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTopological Ordering.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem is composition of two medium problem\n1.detecting cycle for edges case\n2.Degree vector is used to assign the topological ordering to elements.\n3.First I will check for node which have 0 indegree and place it in topologically(queue) available left end and then decrease the degree of all adjacent elements.\n4.Now again check which element is having currently zero indegree.\n5.put all those to the queue again. \n\nThe above steps(3,4,5) will continue until all the element has 0 indegree.\n\nDo this for row and coloumn seperately.\n\nrow vector is saying that particular element 1<=i<=k(1 based indexing)belongs to row[i] row in k*k matrix;\nsimilar for col.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2*(n+k) + 2*(n+k) + k*k)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO((n+k) + (k))\n# Code\n```\n#define fast ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL)\n#define ull unsigned long long int\n#define yes cout << "YES" << endl\n#define no cout << "NO" << endl\n#define ll long long int\n#define mii unordered_map<int,int>\n#define loop(i,s, e) for (int i = s; i < e; i++)\n#define show(x) cout<<x<<" ";\n#define pii pair<int,int>\n#define vi vector<int>\n#define pb push_back\n#define rr return\n#define s second\n#define f first\n#define inf 1e9\nconst int mod = 1e9+7;\nconst int N = 2e5+5;\n\nclass Solution {\n bool dfs(vector<int> adj[] , vector<int>& vis , vector<int>& pathvis ,int n){\n vis[n]=1;\n pathvis[n]=1;\n for(auto it:adj[n])\n if(!vis[it]){\n if(dfs(adj , vis , pathvis , it)== true){\n return true;\n }\n }\n else if (pathvis[it]){\n return true;\n } \n pathvis[n]=0;\n return false;\n }\nbool cycle(int V, vector<int> adj[]) {\n vector<int> vis(V+1,0);\n vector<int> pathvis(V+1,0);\n \n for(int i = 1 ; i<=V ; i ++){\n if(!vis[i]){\n if(dfs(adj , vis , pathvis , i)==true){\n return true;\n }\n }\n }\n return false;\n }\nvector<int> decide(vector<int> adj[],vector<int>& degree, int k){\n queue<int> q;\n vector<int> ans(k+1);\n loop(i,1,k+1){\n if (degree[i]==0)q.push(i);\n }\n int tt = 0;\n while(!q.empty()){\n int id = q.front();\n q.pop();\n ans[id]=tt++;\n for (auto x:adj[id]){\n degree[x]--;\n if (degree[x]==0)q.push(x);\n }\n }\n return ans;\n}\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int> adj[k+1];\n vector<int> degree(k+1);\n for (auto x:rowConditions){\n adj[x[0]].pb(x[1]);\n degree[x[1]]++;\n }\n if (cycle(k,adj)){return {};}\n vector<int> row = decide(adj,degree,k);\n loop(i,1,k+1){\n adj[i].clear();\n degree[i]=0;\n }\n for (auto x:colConditions){\n adj[x[0]].pb(x[1]);\n degree[x[1]]++;\n }\n if (cycle(k,adj)){return {};}\n vector<int> col= decide(adj,degree,k);\n vector<vector<int>> ans(k,vector<int>(k));\n loop(i,1,k+1){\n ans[row[i]][col[i]] = i;\n }\n return ans;\n }\n};\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 4 | 0 | ['Graph', 'Topological Sort', 'C++'] | 0 |
build-a-matrix-with-conditions | Beginner Friendly Solution with Graph and Topological Sort + Visualization (Step By Step) 😊😊 | beginner-friendly-solution-with-graph-an-m5pu | Intuition\nThe code aims to construct a matrix of size k x k based on two sets of conditions: rowConditions and colConditions. These conditions specify relation | briancode99 | NORMAL | 2024-07-21T07:33:57.320547+00:00 | 2024-07-21T07:33:57.320565+00:00 | 80 | false | # Intuition\nThe code aims to construct a matrix of size k x k based on two sets of conditions: rowConditions and colConditions. These conditions specify relationships between elements within rows and columns. The problem seems to involve finding a valid ordering of elements that satisfies these relationships, possibly using a topological sort algorithm.\n\n# Approach\n1. Build Graphs: Create directed graphs to represent the relationships specified by rowConditions and colConditions. Each node in the graph represents a row or column index, and an edge from node A to B indicates that element A should be placed above/left of element B in the final matrix.\n2. Topological Sort: Perform a topological sort on each graph to determine a valid ordering of rows and columns. If a cycle exists in either graph, it means the conditions are impossible to satisfy, and we return an empty matrix.\n3. Construct Matrix: Create an empty k x k matrix. Iterate through the sorted rows and columns, filling each cell with the corresponding element value.\n\n# Complexity\n- Time complexity: O(k\xB2 + m + n), where k is the size of the matrix, and m and n are the lengths of the rowConditions and colConditions arrays respectively.\n\n- Space complexity: O(k\xB2 + m + n), where k is the size of the matrix, and m and n are the lengths of the rowConditions and colConditions arrays respectively.\n\n# Visualization\n- rowConditions = [[1, 2],[3, 2]]\n- colConditions = [[2, 1],[3, 2]]\n\nCreate Row Conditions Graph and Row Indegree Table:\n```\n1 3 \n| / \n| /\n* * \n2 \n\n// 1 point to 2 and 3 point to 2\n// rowIndegree:\n1: 0\n2: 2\n3: 0\n```\n\nGet the row order using topological sort:\nWe start by initializing a stack and rowOrder array,\n- stack = []\n- rowOrder = []\n- rowIndegree:\n1: 0\n2: 2\n3: 0\n\nAfter that we fill the stack with the indegree value of zero, in this case we have 1 and 3 with indegree of zero,\nstack = [1, 3]\n\nWe do the topological sort using a while loop to check if there is any vertex/node in the stack, in this case there is 1 and 3 in the stack so we take the last item (since we use stack) so we pull out 3 and put it inside our rowOrder array,\n- stack = [1]\n- rowOrder = [3]\n\nThe next thing we need to do is to decrement the indegree value of the vertex/node we just pull out, in this case we pull out 3 and 3 point to 2, so we decrement 2 by 1.\n- rowIndegree:\n1: 0\n2: 1\n3: 0\n\nAfter that we pull out 1 since the stack is not empty and put it inside our rowOrder array,\n- stack = []\n- rowOrder = [3, 1]\n\nThe next thing we need to do is to decrement the indegree value of the vertex/node we just pull out, in this case we pull out 1 and 1 point to 1, so we decrement 2 by 1.\n- rowIndegree:\n1: 0\n2: 0\n3: 0\n\nSince the the indegree value of 2 is now 0, we can put it on our stack,\n- stack = [2]\n- rowOrder = [3, 1]\n\nAfter that we pull out 2 since the stack is not empty and put it inside our rowOrder array,\n- stack = []\n- rowOrder = [3, 1, 2]\n\nAfter that, our stack is finally empty and the last thing we need to check is whether or not the conditions can be satisfy. Meaning there is no cycle in our graph by check the length of the rowOrder and k value which in this case is equal, so no cycle.\n\nP.S. The thing that we do here is really similar with the thing that we need to do in "Course Schedule" question. (https://leetcode.com/problems/course-schedule/solutions/5510273/beginner-friendly-solution-with-graph-and-topological-sort/) - Check it out \uD83D\uDE0A\uD83D\uDE0A\n\nCreate Col Conditions Graph and Col Indegree Table:\n```\n2 * \n| \\ \n| \\\n* 3\n1 \n\n// 3 point to 2 and 2 point to 1\n// colIndegree:\n1: 1\n2: 1\n3: 0\n```\nGet the col order using topological sort:\nThe step to get the order for the column is really similar with what we do for the row, so in the end we will have row order of,\n- colOrder = [3, 2, 1]\n\nInsert value to matrix:\nAfter we done with our topological sort we have all the order for the row and col for the specific value (1 to k). We just need to combine this by mapping in the row and col.\n- rowOrder = [3, 1, 2]\n- rowMap = { \'1\': 1, \'2\': 2, \'3\': 0 }\nvalue of \'1\' is in index of 1\nvalue of \'2\' is in index of 2\nvalue of \'3\' is in index of 0\n\n- colOrder = [3, 2, 1]\n- colMap = { \'1\': 2, \'2\': 1, \'3\': 0 }\nvalue of \'1\' is in index of 2\nvalue of \'2\' is in index of 1\nvalue of \'3\' is in index of 0\n\nFinally, we just need to insert it inside the matrix by the coressponding map value we have. Value \'3\' is inserted in [0,0], value \'2\' is inserted in [2,1], and value \'1\' is inserted in [1,2]:\n- [3, 0, 0]\n[0, 0, 1]\n[0, 2, 0]\n\nThat\'s it, hopefully you find this useful and try to run it yourself. Thanks. \uD83D\uDE0A\uD83D\uDE0A\n\n```\n/**\n * @param {number} k\n * @param {number[][]} rowConditions\n * @param {number[][]} colConditions\n * @return {number[][]}\n */\nvar buildMatrix = function (k, rowConditions, colConditions) {\n // create rowConditions graph and rowIndegree\n const rowGraph = new Array(k).fill(null).map(() => new Array());\n const rowIndegree = new Array(k).fill(0);\n\n for (let rowCondition of rowConditions) {\n let [above, below] = rowCondition;\n above = above - 1; // we need to minus 1 because our array is indexed from 0 to 2, but the conditions is 1 to 3.\n below = below - 1;\n rowGraph[above].push(below);\n rowIndegree[below]++;\n }\n\n // create colConditions graph and colIndegree\n const colGraph = new Array(k).fill(null).map(() => new Array());\n const colIndegree = new Array(k).fill(0);\n\n for (let colCondition of colConditions) {\n let [left, right] = colCondition;\n left = left - 1;\n right = right - 1;\n colGraph[left].push(right);\n colIndegree[right]++;\n }\n\n // topological sort (get row order)\n const rowOrder = [];\n let stack = [];\n\n for (let i = 0; i < rowIndegree.length; i++) {\n if (rowIndegree[i] === 0) {\n stack.push(i);\n }\n }\n\n while (stack.length) {\n const current = stack.pop();\n rowOrder.push(current);\n\n for (let neighbor of rowGraph[current]) {\n rowIndegree[neighbor]--;\n if (rowIndegree[neighbor] === 0) {\n stack.push(neighbor);\n }\n }\n }\n\n // check if matrix can satisfy all the conditions\n if (rowOrder.length !== k) {\n return [];\n }\n\n // topological sort (get col order)\n const colOrder = [];\n stack = [];\n\n for (let i = 0; i < colIndegree.length; i++) {\n if (colIndegree[i] === 0) {\n stack.push(i);\n }\n }\n\n while (stack.length) {\n const current = stack.pop();\n colOrder.push(current);\n\n for (let neighbor of colGraph[current]) {\n colIndegree[neighbor]--;\n if (colIndegree[neighbor] === 0) {\n stack.push(neighbor);\n }\n }\n }\n\n // check if matrix can satisfy all the conditions\n if (colOrder.length !== k) {\n return [];\n }\n\n // create the matrix and fill it using the row order and col order\n const rowMap = rowOrder.reduce((acc, num, i) => {\n acc[num] = i;\n return acc;\n }, {});\n\n const colMap = colOrder.reduce((acc, num, i) => {\n acc[num] = i;\n return acc;\n }, {});\n\n const matrix = new Array(k).fill(null).map(() => new Array(k).fill(0));\n for (let i = 0; i < k; i++) {\n matrix[rowMap[i]][colMap[i]] = i + 1; // we need to add 1 again because before we decrement 1 to insert into graph.\n }\n\n return matrix;\n};\n``` | 4 | 0 | ['Graph', 'Topological Sort', 'JavaScript'] | 0 |
build-a-matrix-with-conditions | Java Clean Solution | Daily Challenge | java-clean-solution-daily-challenge-by-s-x2wr | Code\n\nclass Solution {\n\n private List<Integer> helperSort(int[][] arr, int k) {\n int[] deg = new int[k];\n List<List<Integer>> list = new | Shree_Govind_Jee | NORMAL | 2024-07-21T03:54:30.603155+00:00 | 2024-07-21T03:54:30.603185+00:00 | 317 | false | # Code\n```\nclass Solution {\n\n private List<Integer> helperSort(int[][] arr, int k) {\n int[] deg = new int[k];\n List<List<Integer>> list = new ArrayList<>();\n for (int i = 0; i < k; i++) {\n list.add(new ArrayList<>());\n }\n\n Queue<Integer> q = new LinkedList<>();\n for (int[] a : arr) {\n list.get(a[0] - 1).add(a[1] - 1);\n deg[a[1] - 1]++;\n }\n\n for (int i = 0; i < k; i++) {\n if (deg[i] == 0) {\n q.add(i);\n }\n }\n\n List<Integer> res = new ArrayList<>();\n while (!q.isEmpty()) {\n int temp = q.poll();\n res.add(temp + 1);\n for (int l : list.get(temp)) {\n if (--deg[l] == 0) {\n q.add(l);\n }\n }\n }\n return res;\n }\n\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n List<Integer> list1 = helperSort(rowConditions, k);\n List<Integer> list2 = helperSort(colConditions, k);\n\n if (list1.size() < k || list2.size() < k) {\n return new int[0][0];\n }\n\n Map<Integer, Integer> map = new HashMap<>();\n for (int i = 0; i < k; i++) {\n map.put(list2.get(i), i);\n }\n\n int[][] res = new int[k][k];\n for (int i = 0; i < k; i++) {\n res[i][map.get(list1.get(i))] = list1.get(i);\n }\n return res;\n }\n}\n``` | 4 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'Java'] | 2 |
build-a-matrix-with-conditions | [Python3] Topological Sort - Simple Solution | python3-topological-sort-simple-solution-zr3t | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nFind the order for row and col respectively and then assign them to the m | dolong2110 | NORMAL | 2023-09-07T18:39:37.684805+00:00 | 2023-09-07T18:39:37.684830+00:00 | 190 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFind the order for row and col respectively and then assign them to the matrix. Note that there are only `k` number need to assign which is also the side of square matrix. Thus we can assign each number in each unique row and col\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(M + N)$$ with `N` is number of `rowConditions` and `M` is number of `colConditions`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n matrix = [[0 for _ in range(k)] for _ in range(k)]\n \n def topo_sort(condition: List[List[int]]) -> dict:\n order = {}\n in_degree = [0 for _ in range(k)]\n g = collections.defaultdict(list)\n for start, end in condition:\n g[start - 1].append(end - 1)\n in_degree[end - 1] += 1\n \n dq = collections.deque()\n for i in range(k):\n if in_degree[i] == 0: dq.append(i)\n \n i = 0\n while dq:\n u = dq.popleft()\n order[u] = i\n for v in g[u]:\n in_degree[v] -= 1\n if in_degree[v] == 0: dq.append(v)\n i += 1\n \n return order\n \n row_order, col_order = topo_sort(rowConditions), topo_sort(colConditions)\n if len(row_order) != k or len(col_order) != k: return []\n for u in row_order:\n r, c = row_order[u], col_order[u]\n matrix[r][c] = u + 1\n return matrix\n``` | 4 | 0 | ['Greedy', 'Graph', 'Topological Sort', 'Matrix', 'Python3'] | 3 |
build-a-matrix-with-conditions | Heavely Commented || TopoSort || Khan's Algorithm || BFS || 100% Simple✅✅✅ | heavely-commented-toposort-khans-algorit-faul | \nclass Solution {\npublic:\n \n\t// Function to create adjacency List and indegree of the graph\n void adjListCreator(vector<vector<int>>&conditions,vect | C___vam2107 | NORMAL | 2023-07-12T09:42:15.124515+00:00 | 2023-07-12T09:42:15.124544+00:00 | 68 | false | ```\nclass Solution {\npublic:\n \n\t// Function to create adjacency List and indegree of the graph\n void adjListCreator(vector<vector<int>>&conditions,vector<vector<int>>&adj,vector<int>& indegree){\n for(auto &it:conditions){\n int u=it[0];\n int v=it[1];\n adj[v].push_back(u);\n indegree[u]++;\n }\n }\n //Function of Khan\'s Algorithm\n void kahnAlgo(vector<vector<int>>&adj,vector<int>& indegree,vector<int>&topoSort){\n queue<int>qu;\n for(int i=1;i<indegree.size();i++){\n if(indegree[i]==0)\n qu.push(i);\n }\n while(!qu.empty()){\n int k=qu.front();\n topoSort.push_back(k);\n qu.pop();\n for(auto &it:adj[k]){\n indegree[it]--;\n if(indegree[it]==0)qu.push(it);\n }\n }\n reverse(topoSort.begin(),topoSort.end());\n }\n \n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>>res(k,vector<int>(k,0));\n \n vector<vector<int>>adjRow(k+1);\n vector<vector<int>>adjCol(k+1);\n \n vector<int>indegreeRow(k+1,0);\n vector<int>indegreeCol(k+1,0);\n\t\t\n //Create adjacency List for both condition matrices\n\t\t//And calculate the indegree (i.e. number of incoming nodes) for each nodes\n adjListCreator(rowConditions,adjRow,indegreeRow);\n adjListCreator(colConditions,adjCol,indegreeCol);\n \n vector<int>topoSortRow,topoSortCol; //Store the REVERSE of topoSort (as work order is reverse of Topological sort) ordering of the two adjecency Lists\n\t\t\n\t\t//Apply khans algorithm to calculate the order of work\n kahnAlgo(adjRow,indegreeRow,topoSortRow); \n kahnAlgo(adjCol,indegreeCol,topoSortCol);\n\t\t\n\t\t// If the size of these two arrays are not equal to k (i.e. the number of nodes) it means there is a cycle present in the graph .Hence we return the empty vector \n if(topoSortRow.size()!=k or topoSortCol.size()!=k)return {};\n \n\t\t//Now we arrange the ordering of nodes into the resultant array by applying simple logic\n\t\t// index= 0 1 2\n\t\t// Lets say topoSortRow= 1 3 2\n\t\t// topoSortCol= 3 2 1\n\t\t// Since the topoSortRow[0]==topoSorCol[2]==1 , Hence our res[0][2]=1, Similarly we fill other \'res\' values\n for(int i=0;i<k;i++){\n for(int j=0;j<k;j++){\n if(topoSortRow[i]==topoSortCol[j]){\n res[i][j]=topoSortRow[i];\n break;\n }\n }\n }\n //Finally return the resultant array\n return res;\n }\n};\n```\n**Hope you find it helpful. If yes, kindly upvote!!** | 4 | 0 | ['Breadth-First Search', 'Graph', 'Topological Sort'] | 3 |
build-a-matrix-with-conditions | Topological Sort with Explanation and Complexity Analysis | topological-sort-with-explanation-and-co-2ef8 | Rationale\n The row and column dependencies could be established with a directed graph, where any edge from vertex A to vertex B denotes that vertex A should co | wickedmishra | NORMAL | 2022-08-28T04:01:55.609889+00:00 | 2022-08-28T04:08:16.420257+00:00 | 170 | false | ##### Rationale\n* The row and column dependencies could be established with a directed graph, where any edge from vertex A to vertex B denotes that vertex A should come before vertex B in the matrix\n* To resolve the dependencies, we could sort them topologically\n* If the relationship is acyclic, we would have all the elements ordered. Otherwise, the sort would stop early (see Kahn\'s Algorithm) with elements less than k\n* Post the topological sort for both the dependencies, we could find out the required indexes for all the elements and put them in the matrix. Note that the index at which the candidate is present in the topological order for the row relationship would be its row index. The same goes for its column index\n\n##### Complexities\n* Time: `O(k * k)`\n* Space: `O(k * k)`\n\nThese are loose bounds based upon the fact that the runtime for the sort is `O(V + E)`. For this problem, `V = k`. In the worse case, `E` could be `(V * (V - 1)) / 2` or `(k * (k - 1)) / 2`. Thus, the total runtime would be `O(k + (k * k))` or `O(k * k)`. (Note that the other operations that we\'ve done come under `O(k * k)` as well.)\n\n```\nclass Solution:\n def topological_sort(self, k: int, relations: List[List[int]]) -> List[int]:\n graph = [[] for _ in range(k)]\n indegrees = [0] * k\n order = []\n \n for _from, to in items:\n _from -= 1\n to -= 1\n \n graph[_from].append(to)\n indegrees[to] += 1\n\n queue = deque([vertex for vertex in range(k) if ind[vertex] == 0])\n \n while queue:\n curr = queue.popleft()\n \n order.append(curr)\n \n for neighbor in graph[curr]: \n indegrees[neighbor] -= 1\n if indegrees[neighbor] == 0:\n queue.append(neighbor)\n \n return order \n \n def buildMatrix(self, k: int, rows: List[List[int]], cols: List[List[int]]) -> List[List[int]]:\n topological_row = self.topological_sort(k, rows)\n topological_col = self.topological_sort(k, cols)\n \n # The dependencies couldn\'t be resolved. Return early.\n if len(top_row) != k or len(top_col) != k:\n return []\n\n # Based upon the relationships, find the row and column indices for every candidate.\n indexes = defaultdict(list)\n \n for row_index, candidate in enumerate(topological_row):\n indexes[candidate].append(row_index)\n \n for col_index, candidate in enumerate(topological_col):\n indexes[candidate].append(col_index)\n \n # Build the required matrix.\n matrix = [[0 for _ in range(k)] for __ in range(k)]\n for num in range(k):\n row, col = indexes[num]\n matrix[row][col] = num + 1\n \n return matrix\n```\n | 4 | 1 | ['Breadth-First Search', 'Topological Sort'] | 0 |
build-a-matrix-with-conditions | Java | Topological Sort | No Cycle -> No Conflict | java-topological-sort-no-cycle-no-confli-gdag | Model\nWe can model this as a directed graph, with above -> below and left -> right.\nWe will need to verify that there is no cycle and find out where its suppo | Student2091 | NORMAL | 2022-08-28T04:01:46.475812+00:00 | 2022-08-28T05:33:48.513511+00:00 | 535 | false | #### Model\nWe can model this as a directed graph, with `above -> below` and `left -> right`.\nWe will need to verify that there is no cycle and find out where its supposed `row` and `col` position is.\n\n#### Strategy\nOne crucial observation is that the grid size is `k x k` and we have `k` element to fill. \nAny row and column has enough spaces to host all `k` elements.\nThis means that if there is no cycle, then we will always be able to assign a unique `row` and a unique `col` value.\nHere I use topological sort to make sure there is no cycle, and populate the order in which we should place it. \nEach number will get its unique `row` and `column` value from `0` to `k-1`.\nRun this topological once for each direction - row, column.\n\n`Time O(k^2 + R + C)`\n`Space O(k^2 + max(R, C))`\n```Java\nclass Solution {\n public int[][] buildMatrix(int k, int[][] R, int[][] C) {\n int[][] ans = new int[k][k];\n int[] yp = new int[k+1]; // y position (col)\n int[] xp = new int[k+1]; // x position (row)\n Arrays.fill(xp, -1);\n Arrays.fill(yp, -1);\n if (!build(R, xp, k) || !build(C, yp, k)){ // if we can\'t build it, there is a cycle, return empty.\n return new int[0][0];\n }\n for (int i = 1; i <= k; i++){ // otherwise, we fill it.\n ans[xp[i]][yp[i]] = i;\n }\n return ans;\n }\n\n private boolean build(int[][] A, int[] pos, int k){\n List<Integer>[] map = new ArrayList[k+1];\n Arrays.setAll(map, o -> new ArrayList<>());\n int[] indg = new int[k+1];\n int depth = 0;\n for (int[] a : A){ // build the map and the indegree.\n map[a[0]].add(a[1]);\n indg[a[1]]++;\n }\n\t\t// here we enqueue all the nodes with indegree 0.\n Deque<Integer> queue = new ArrayDeque<>(IntStream.range(1, k+1).filter(o -> indg[o] == 0).boxed().toList());\n while(!queue.isEmpty()){\n int y = queue.poll();\n pos[y] = depth++; // set its depth. each value gets a unique depth.\n for (int next : map[y]){\n if (--indg[next] == 0){\n queue.offer(next);\n }\n }\n }\n if (Arrays.stream(indg).anyMatch(o -> o > 0)){\n return false; // If there is any node with indegree > 0, then there is a cycle.\n }\n for (int i = 1; i <= k; i++){\n if (pos[i] == -1){ // if there is any not filled yet, fill it\n pos[i] = depth++;\n }\n }\n return true;\n }\n}\n``` | 4 | 0 | ['Topological Sort', 'Java'] | 4 |
build-a-matrix-with-conditions | Find Topo sort and compare | Easy to understand | find-topo-sort-and-compare-easy-to-under-mg8j | \nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n int rowTopo[] = topoSort(k,rowConditions);\n | anilkumawat3104 | NORMAL | 2024-07-21T10:50:02.735714+00:00 | 2024-07-21T10:50:02.735755+00:00 | 27 | false | ```\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n int rowTopo[] = topoSort(k,rowConditions);\n int colTopo[] = topoSort(k,colConditions);\n int ans[][] = new int[k][k];\n if(rowTopo.length==0||colTopo.length==0)\n return new int[0][0];\n for(int i=1;i<=k;i++){\n for(int j=1;j<=k;j++){\n if(rowTopo[i]==colTopo[j]){\n ans[i-1][j-1] = rowTopo[i];\n }\n }\n }\n return ans;\n }\n public int[] topoSort(int V, int[][]node){\n \n ArrayList<ArrayList<Integer>> adj = new ArrayList<>();\n int []rank = new int[V+1];\n int ans[] = new int[V+1];\n for(int i=0;i<=V;i++){\n adj.add(new ArrayList<>());\n }\n for(int n[] : node){\n adj.get(n[0]).add(n[1]);\n rank[n[1]]++;\n }\n \n Queue<Integer> q = new LinkedList<>();\n for(int i=0;i<rank.length;i++){\n if(rank[i]==0){\n q.add(i);\n }\n }\n int len = 0;\n while(!q.isEmpty()){\n int temp = q.poll();\n ans[len++] = temp;\n for(int next : adj.get(temp)){\n rank[next]--;\n if(rank[next]==0){\n q.add(next);\n }\n }\n \n }\n if(len!=V+1)\n return new int[0];\n return ans;\n }\n}\n``` | 3 | 0 | ['Graph', 'Topological Sort', 'Matrix', 'Java'] | 0 |
build-a-matrix-with-conditions | A C Solution | a-c-solution-by-well_seasoned_vegetable-9tw4 | Code\n\n#define MAX_K 400\n\nstruct node {\n int val;\n struct node* next;\n};\n\nstruct graph {\n struct node* head[MAX_K + 1];\n int inDegree[MAX_ | well_seasoned_vegetable | NORMAL | 2024-07-21T08:08:18.373351+00:00 | 2024-07-21T13:22:04.234544+00:00 | 81 | false | # Code\n```\n#define MAX_K 400\n\nstruct node {\n int val;\n struct node* next;\n};\n\nstruct graph {\n struct node* head[MAX_K + 1];\n int inDegree[MAX_K + 1];\n};\n\nvoid addEdge(struct graph* graph, int from, int to) {\n struct node* new = malloc(sizeof(struct node));\n new->val = to;\n new->next = graph->head[from];\n graph->head[from] = new;\n graph->inDegree[to]++;\n}\n\nbool topologicalSort(int k, struct graph* graph, int* order) {\n int queue[MAX_K + 1];\n int front = 0, rear = 0;\n int orderIdx = 0;\n \n for(int i = 1; i <= k; i++) {\n if(graph->inDegree[i] == 0) {\n queue[rear++] = i;\n }\n } \n while(front < rear) {\n int node = queue[front++];\n order[orderIdx++] = node;\n \n struct node* current = graph->head[node];\n while (current) {\n graph->inDegree[current->val]--;\n if (graph->inDegree[current->val] == 0) {\n queue[rear++] = current->val;\n }\n current = current->next;\n }\n }\n \n return orderIdx == k;\n}\n\nint** buildMatrix(int k, int** rowConditions, int rowConditionsSize, int* rowConditionsColSize, int** colConditions, int colConditionsSize, int* colConditionsColSize, int* returnSize, int** returnColumnSizes) {\n struct graph rowGraph = {.head = {NULL}, .inDegree = {0}};\n struct graph colGraph = {.head = {NULL}, .inDegree = {0}};\n int rowOrder[MAX_K + 1];\n int colOrder[MAX_K + 1];\n \n for(int i = 0; i < rowConditionsSize; i++) {\n addEdge(&rowGraph, rowConditions[i][0], rowConditions[i][1]);\n }\n for(int i = 0; i < colConditionsSize; i++) {\n addEdge(&colGraph, colConditions[i][0], colConditions[i][1]);\n } \n if(!topologicalSort(k, &rowGraph, rowOrder) || !topologicalSort(k, &colGraph, colOrder)) {\n *returnSize = 0;\n return rowConditions;\n }\n\n int** ret = malloc(k * sizeof(int*));\n *returnColumnSizes = malloc(k * sizeof(int));\n *returnSize = k;\n\n for(int i = 0; i < k; i++) {\n (*returnColumnSizes)[i] = k;\n ret[i] = calloc(k, sizeof(int));\n }\n \n int rowPos[MAX_K + 1];\n int colPos[MAX_K + 1];\n \n for (int i = 0; i < k; i++) {\n rowPos[rowOrder[i]] = colPos[colOrder[i]] = i;\n }\n for (int num = 1; num <= k; num++) {\n ret[rowPos[num]][colPos[num]] = num;\n }\n \n return ret;\n}\n``` | 3 | 0 | ['C'] | 0 |
build-a-matrix-with-conditions | C++ || independent topological sort | c-independent-topological-sort-by-heder-wrtq | Topological sort for rows and cols independently and then combine the outcome.\n\n\n static vector<vector<int>> buildMatrix(int k,\n\t vector<vector<i | heder | NORMAL | 2022-08-29T19:54:37.860212+00:00 | 2022-08-29T19:54:37.860243+00:00 | 162 | false | Topological sort for rows and cols independently and then combine the outcome.\n\n```\n static vector<vector<int>> buildMatrix(int k,\n\t vector<vector<int>>& rowConditions,\n\t\t vector<vector<int>>& colConditions) {\n // Topological sort for rows and cols independently.\n const vector<int> row_order = tsort(k, rowConditions);\n if (empty(row_order)) return {};\n \n const vector<int> col_order = tsort(k, colConditions);\n if (empty(col_order)) return {};\n \n // Turnt the tsort into an index so we know in which column a\n // number should go.\n vector<int> col_index(k);\n for (int i = 0; i < size(col_order); ++i) {\n col_index[col_order[i] - 1] = i;\n }\n\n // Build the answer based on the above.\n vector<vector<int>> ans(k, vector<int>(k));\n for (int i = 0; i < size(row_order); ++i) {\n int n = row_order[i];\n ans[i][col_index[n - 1]] = n;\n }\n \n return ans;\n }\n```\t\n\nFor topological sort we use the classic Kahn\'s algorithm:\n\n```\n // Kahn\'s algorithm for topological sort.\n static vector<int> tsort(int k, const vector<vector<int>>& conds) {\n // Build adjacency list and in-degree vector.\n vector<vector<int>> adj(k + 1);\n vector<int> in_deg(k + 1);\n for (const vector<int>& cond : conds) {\n const int before = cond[0];\n const int after = cond[1];\n adj[before].push_back(after);\n ++in_deg[after];\n }\n \n // Topological sort.\n queue<int> q;\n for (int i = 1; i <= k; ++i) {\n if (!in_deg[i]) q.push(i);\n }\n \n vector<int> ans;\n ans.reserve(k);\n while (!empty(q)) {\n const int node = q.front(); q.pop();\n ans.push_back(node);\n for (int next : adj[node]) {\n if (!--in_deg[next]) {\n q.push(next);\n }\n }\n }\n \n if (size(ans) != k) return {};\n\n return ans;\n }\n``` | 3 | 0 | ['Topological Sort', 'C'] | 0 |
build-a-matrix-with-conditions | C++ - Topological Sort | beats 100% in both Time and Space Complexity | c-topological-sort-beats-100-in-both-tim-2noh | By using topo sort we are generating the order of sequence of numbers in row,column and here we also check whether there are any cycles in row,col directed grap | Naveen_kotha | NORMAL | 2022-08-29T05:25:36.240929+00:00 | 2022-08-29T05:25:36.240976+00:00 | 122 | false | By using topo sort we are generating the order of sequence of numbers in row,column and here we also check **whether there are any cycles in row,col directed graph**.\nIf there is any cycle in row or col directed graph, then we return an empty array\nWe are using topo sort because there is a **relation** between numbers. **eg: [1,2] means 1 must occur before 2, so there will be directed edge from 1 -> 2.**\n```\nbool findOrder(vector<vector<int>>& a, int k, unordered_map<int, int> &m){\n vector<int> adj[k+1];\n vector<int> indegree(k+1, 0);\n queue<int> q;\n int num = 0;\n \n for(int i=0;i< a.size();i++){\n adj[a[i][0]].push_back(a[i][1]);\n indegree[a[i][1]]++;\n }\n \n for(int i=1;i< k+1;i++){\n if(indegree[i] == 0) q.push(i);\n }\n \n if(!q.size()) return false;\n \n while(!q.empty()){\n int val = q.front();\n q.pop();\n indegree[val]--;\n \n m[val] = num;\n num++;\n \n for(auto i : adj[val]){\n indegree[i]--;\n if(indegree[i] == 0) q.push(i);\n }\n }\n \n return (m.size() != k) ? false : true;\n }\n \n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> ans(k, vector<int>(k, 0));\n vector<vector<int>> temp;\n \n unordered_map<int, int> row, col;\n \n bool a = findOrder(rowConditions,k,row);\n bool b = findOrder(colConditions,k,col);\n \n if(!a | !b) return temp;\n \n for(int i=1;i<= k;i++){\n ans[row[i]][col[i]] = i;\n }\n return ans;\n } | 3 | 1 | ['Topological Sort', 'C'] | 1 |
build-a-matrix-with-conditions | Topological sorting | Kahn's algorithm | topological-sorting-kahns-algorithm-by-n-ihl0 | We have hierarchy given to us by rowConditions and colConditions. We can map that hierarchy with a topological ordering algorithm.\n\nLet\'s find the order we c | nadaralp | NORMAL | 2022-08-28T09:04:25.123692+00:00 | 2022-08-28T09:08:45.398533+00:00 | 336 | false | We have hierarchy given to us by rowConditions and colConditions. We can map that hierarchy with a topological ordering algorithm.\n\nLet\'s find the order we can place rows and columns separately by running the Kahn\'s topsort algorithm. If there is a cycle detected we know we cannot have a valid order, we return `[]` as required.\n\nOtherwise we have a valid order, so for every node `[1,k]` we look it\'s index position in the rows order and cols order and put it in the matrix.\n\n```\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n try:\n row_conditions_topsort, row_node_to_index = self.top_sort(k, rowConditions)\n col_conditions_topsort, col_node_to_index = self.top_sort(k, colConditions)\n matrix = [[0 for _ in range(k)] for _ in range(k)]\n \n for n in range(1, k + 1):\n row, col = row_node_to_index[n], col_node_to_index[n]\n matrix[row][col] = n\n \n return matrix\n \n \n except:\n # If error thrown, kahn\'s algorithm detected a cycle\n return []\n \n def top_sort(self, k, edges: tuple[int, int]) -> list[int]:\n indegree = defaultdict(int)\n graph = defaultdict(list)\n \n for n in range(1, k + 1):\n indegree[n] = 0\n \n for u, v in edges:\n graph[u].append(v)\n indegree[v] += 1\n \n queue = deque()\n topsort = []\n for n in range(1, k + 1):\n if indegree[n] == 0:\n queue.append(n)\n \n while queue:\n node = queue.popleft()\n topsort.append(node)\n \n for nei in graph[node]:\n indegree[nei] -= 1\n if indegree[nei] == 0:\n queue.append(nei)\n \n if len(topsort) != k:\n raise Exception()\n \n node_to_index = {}\n for i, n in enumerate(topsort):\n node_to_index[n] = i\n \n return topsort, node_to_index\n```\n\n\n<hr />\nTook the virtual contest today :).\n\n<img src="https://nadarsandbox-videocontent-sandbox.s3.amazonaws.com/raw-thumbnails/WhatsApp+Image+2022-08-28+at+11.48.29+AM.jpeg" /> | 3 | 1 | ['Python'] | 1 |
build-a-matrix-with-conditions | Beats 99% | Easy Topological Sort | Cycle Detection | Simple Approach | beats-99-easy-topological-sort-cycle-det-zp01 | IntuitionThe problem requires constructing a 𝑘 × 𝑘 matrix such that two independent sets of conditions on rows and columns are satisfied. The key insight is tha | pranjaykapoor | NORMAL | 2025-01-24T10:50:56.794208+00:00 | 2025-01-24T10:50:56.794208+00:00 | 41 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires constructing a `𝑘 × 𝑘` matrix such that two independent sets of conditions on rows and columns are satisfied. The key insight is that the problem can be approached as two topological sorting tasks:
1. One for row constraints.
2. Another for column constraints.
The matrix construction is guided by these two topological orders.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Model the Problem as a Directed Graph:
- Treat each element from 1 to k as a node.
- Use the `rowConditions` and `colConditions` to create two directed graphs:
- One for row constraints (`adjRow`).
- One for column constraints (`adjCol`).
2. Topological Sorting:
- Use DFS-based topological sorting to find the order of elements in rows and columns.
- If a cycle is detected during topological sorting, return an empty matrix (`{}`), as the constraints cannot be satisfied.
3. Construct the Matrix:
- Map the topological orders into indices for rows and columns.
- Place the numbers in the matrix at their respective positions where the row index matches the topological order for rows and the column index matches the topological order for columns.
4. Edge Cases:
- If the constraints result in cycles, return `{}`.
Ensure all numbers from 1 to k are included in the topological sort.
- If any are missing, return `{}`.
# Complexity
- Time complexity:
- *Building the Graphs*: $$O(n+m)$$, where n is the size of `rowConditions` and m is the size of `colConditions`.
- *Topological Sorting*: $$O(k+E)$$, where E is the number of edges in the graph (proportional to n+m).
- *Constructing the Matrix*: $$O(k^2)$$, as we iterate over a k×k matrix.
- **Total**: $$O(n+m+k^2)$$.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(k + n + m)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool topoSort(stack<int> &s, vector<int> &vis, int node, vector<vector<int>> &adj,
vector<int> &dfsVis){
vis[node] = 1;
dfsVis[node] = 1;
for(auto neighbour : adj[node]){
if(!vis[neighbour]){
bool cycle = topoSort(s, vis, neighbour, adj, dfsVis);
if(cycle) return true;
}else if(dfsVis[neighbour]){
return true;
}
}
s.push(node);
dfsVis[node] = 0;
return false;
}
vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {
int n = rowConditions.size();
int m = colConditions.size();
vector<vector<int>> adjRow(k+1);
vector<vector<int>> adjCol(k+1);
for(int i = 0; i < n; i++){
adjRow[rowConditions[i][0]].push_back(rowConditions[i][1]);
}
for(int i = 0; i < m; i++){
adjCol[colConditions[i][0]].push_back(colConditions[i][1]);
}
stack<int> row, col;
vector<int> visRow(k+1, 0), visCol(k+1, 0);
vector<int> dfsVisRow(k+1, 0), dfsVisCol(k+1, 0);
for(int i = 1; i <= k; i++){
if(!visRow[i]){
bool cycle = topoSort(row, visRow, i, adjRow, dfsVisRow);
if(cycle) return {};
}
}
for(int i = 1; i <= k; i++){
if(!visCol[i]){
bool cycle = topoSort(col, visCol, i, adjCol, dfsVisCol);
if(cycle) return {};
}
}
vector<int> ansRow, ansCol;
while(!row.empty()){
ansRow.push_back(row.top());
row.pop();
}
while(!col.empty()){
ansCol.push_back(col.top());
col.pop();
}
/* if(ansRow.size() != k || ansCol.size() != k){
return {};
} */
vector<vector<int>> matrix(k, vector<int> (k, 0));
for(int i = 0; i < k; i++){
for(int j = 0; j < k; j++){
if(ansRow[i] == ansCol[j]){
matrix[i][j] = ansRow[i];
}
}
}
return matrix;
}
};
``` | 2 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'C++'] | 0 |
build-a-matrix-with-conditions | Simple || Easy ||Basic Understanding Approach || step by step || optimized ||Kahn algorithm||O(N) | simple-easy-basic-understanding-approach-x56q | Simple || Easy || Basic Understanding Approach || step by step || optimized|| Kahn algorithm || O(N) \n\nBuild a Matrix With Conditions\n\n# Intuition\n1. Intui | VaidyaPS | NORMAL | 2024-07-29T09:15:11.810868+00:00 | 2024-07-29T09:15:11.810901+00:00 | 5 | false | Simple || Easy || Basic Understanding Approach || step by step || optimized|| Kahn algorithm || O(N) \n\nBuild a Matrix With Conditions\n\n# Intuition\n1. Intuition in very simple we need to make a matrix by given condition where we have 2d matrix consist of row (above, bottom) and col (left,right). \n2. we can assume these 2 matrix in form of graph and try to execute a order of there arrival from (top to bottom) in row and (left to right) in col.\n3. Then this order will consider to making matix\n4. Simply put the element which appear in ith and jth position in row and col respectively in ans[i][j].\n5. remember that only 1 to k element are there. That means each row and col consist on only 1 element. which make it more simple to execute as we don\'t need to take care of other elements that would be 0.\n\n\n# Approach\n1. Execute a 2 vector of order (top to bottom) and (left to right).\n2. use concent of topology sort to get a perfet order of node which have visited 1st.\n3. After getting there order if there Present Cyclic nature in graph or we can say that given condition of row and col are not a DAG(direct acycylic graph) then we simply return empty vector as there is no such matrix present.\n ```\n if(r.size()==0||c.size()==0){\n return {};\n }\n4. we can simply put element in ans matix where r[i]=c[j] in ans[i][j]\n and remaining will be 0.\n ```\n for(int i=0;i<k;i++){\n for(int j=0;j<k;j++){\n if(r[i]==c[j]){\n ans[i][j]=r[i];\n }\n }\n }\n\nTOPOLOGY SORT (APPROCH)\n1. convert 2d vector to addecent array\n ```\n for(auto it: num){\n adj[it[0]].push_back(it[1]);\n }\n\n2. then execute indegree of size k+1 of each element from 1 to k.\n ```\n for(int i=1;i<=n;i++){\n for(auto it: adj[i]){\n indegree[it]++;\n }\n }\n3. where we get indegree as 0 push that in queue as it is note dependent on any other element\n ```\n for(int i=1;i<=n;i++){\n if(indegree[i]==0){\n q.push(i);\n }\n }\n3. now simply execute a BFS traversal and push the node =q.front() in ans array \n4. decrease the indegree count of all node dependent on node which was on front.\n ```\n while(q.size()!=0){\n auto node = q.front();\n q.pop();\n ans.push_back(node);\n for(auto it: adj[node]){\n indegree[it]--;\n if(indegree[it]==0){\n q.push(it);\n }\n }\n }\n5. if we get our array ans size = n that means no cyclic nature present in graph then we return ans. else empty array.\n ```\n if(ans.size()==n){\n return ans;\n }\n return {};\n\n# Complexity\n- Time complexity:\nO(K)\n\n- Space complexity:\nO(K+K);\n\n# Code\n```\nclass Solution {\npublic:\n \n vector<int> topology(vector<vector<int>> num, int n){\n vector<int> adj[n+1];\n for(auto it: num){\n adj[it[0]].push_back(it[1]);\n }\n vector<int> indegree(n+1,0);\n for(int i=1;i<=n;i++){\n for(auto it: adj[i]){\n indegree[it]++;\n }\n }\n queue<int> q;\n for(int i=1;i<=n;i++){\n if(indegree[i]==0){\n q.push(i);\n }\n }\n vector<int> ans;\n while(q.size()!=0){\n auto node = q.front();\n q.pop();\n ans.push_back(node);\n for(auto it: adj[node]){\n indegree[it]--;\n if(indegree[it]==0){\n q.push(it);\n }\n }\n }\n if(ans.size()==n){\n return ans;\n }\n return {};\n }\n\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& row, vector<vector<int>>& col) {\n int n = row.size();\n int m = col.size();\n vector<vector<int>> ans(k,vector<int>(k,0));\n\n vector<int> r= topology(row,k);\n vector<int> c = topology(col,k);\n if(r.size()==0||c.size()==0){\n return {};\n }\n for(int i=0;i<k;i++){\n for(int j=0;j<k;j++){\n if(r[i]==c[j]){\n ans[i][j]=r[i];\n }\n }\n }\n\n return ans;\n\n\n }\n};\n``` | 2 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'C++'] | 1 |
build-a-matrix-with-conditions | Simply Explained ✨ | simply-explained-by-aayushbharti-ue0s | Intuition\nTo solve this problem, we need to find a valid way to place each number from 1 to k in a k x k matrix such that all given row and column conditions a | AayushBharti | NORMAL | 2024-07-21T17:28:04.650798+00:00 | 2024-07-21T17:28:04.650833+00:00 | 25 | false | # Intuition\nTo solve this problem, we need to find a valid way to place each number from 1 to k in a k x k matrix such that all given row and column conditions are satisfied. This can be done using topological sorting. We first create the topological order for rows and columns separately using the given conditions and then place the numbers in the matrix accordingly.\n\n# Approach\n1. **Graph Construction**:\n - Construct two graphs, one for row conditions and one for column conditions, using the given `rowConditions` and `colConditions` arrays.\n - Each node represents a number from 1 to k, and directed edges represent the conditions.\n\n2. **Topological Sort**:\n - Perform topological sorting on both graphs to determine the order of placement for rows and columns.\n - If a cycle is detected during topological sorting, return an empty matrix since it is impossible to satisfy the conditions.\n\n3. **Matrix Construction**:\n - Using the topological orders obtained for rows and columns, place each number in the matrix at the position determined by its order.\n\n# Complexity\n- Time complexity: \\(O(k^2)\\), where \\(k\\) is the given integer, due to graph construction and topological sorting.\n- Space complexity: \\(O(k^2)\\) for storing the graphs and matrix.\n\n# Code\n```\nimport java.util.*;\n\nclass Solution {\n public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n // Get the topological order for rows and columns\n int[] rowOrder = topologicalSort(k, rowConditions);\n int[] colOrder = topologicalSort(k, colConditions);\n\n // If any order is null, it means there\'s a cycle and we can\'t construct the matrix\n if (rowOrder == null || colOrder == null) {\n return new int[0][0];\n }\n\n // Initialize the result matrix\n int[][] matrix = new int[k][k];\n \n // Create position arrays to store the position of each number in the row and column order\n int[] rowPos = new int[k + 1];\n int[] colPos = new int[k + 1];\n\n // Fill position arrays with the index positions from the topological order\n for (int i = 0; i < k; i++) {\n rowPos[rowOrder[i]] = i;\n colPos[colOrder[i]] = i;\n }\n\n // Place each number in the matrix according to the topological order positions\n for (int i = 1; i <= k; i++) {\n matrix[rowPos[i]][colPos[i]] = i;\n }\n\n return matrix;\n }\n\n private int[] topologicalSort(int k, int[][] conditions) {\n // Create an adjacency list for the graph\n List<Integer>[] graph = new ArrayList[k + 1];\n // Initialize indegree array to count the number of incoming edges for each node\n int[] indegree = new int[k + 1];\n\n // Initialize the adjacency list\n for (int i = 0; i <= k; i++) {\n graph[i] = new ArrayList<>();\n }\n\n // Build the graph from the conditions\n for (int[] condition : conditions) {\n int u = condition[0];\n int v = condition[1];\n graph[u].add(v);\n indegree[v]++;\n }\n\n // Initialize a queue to perform topological sorting\n Queue<Integer> queue = new LinkedList<>();\n // Add all nodes with no incoming edges to the queue\n for (int i = 1; i <= k; i++) {\n if (indegree[i] == 0) {\n queue.add(i);\n }\n }\n\n // Array to store the topological order\n int[] order = new int[k];\n int index = 0;\n\n // Perform BFS to get the topological order\n while (!queue.isEmpty()) {\n int node = queue.poll();\n order[index++] = node;\n\n // Reduce the indegree of the neighbors and add them to the queue if their indegree becomes 0\n for (int neighbor : graph[node]) {\n if (--indegree[neighbor] == 0) {\n queue.add(neighbor);\n }\n }\n }\n\n // If we have processed all nodes, return the order; otherwise, return null (indicating a cycle)\n return index == k ? order : null;\n }\n}\n\n``` | 2 | 0 | ['Java'] | 0 |
build-a-matrix-with-conditions | ✅💯🔥Explanations No One Will Give You🎓🧠Very Detailed Approach🎯🔥Extremely Simple And Effective🔥 | explanations-no-one-will-give-youvery-de-uq8z | \n# Code\n\nclass Solution {\npublic:\n vector<int> toposort(vector<vector<int>>& edges, int n) {\n unordered_map<int, vector<int>> adj;\n vect | ShivanshGoel1611 | NORMAL | 2024-07-21T15:10:14.997150+00:00 | 2024-07-21T15:11:21.371606+00:00 | 86 | false | \n# Code\n```\nclass Solution {\npublic:\n vector<int> toposort(vector<vector<int>>& edges, int n) {\n unordered_map<int, vector<int>> adj;\n vector<int> indegree(n + 1, 0);\n for (vector<int>& edge : edges) {\n int u = edge[0];\n int v = edge[1];\n adj[u].push_back(v);\n indegree[v]++;\n }\n queue<int> qu;\n for (int i = 1; i <= n; i++) {\n if (indegree[i] == 0) {\n qu.push(i);\n }\n }\n vector<int> topo;\n int count = 0;\n while (!qu.empty()) {\n int u = qu.front();\n qu.pop();\n topo.push_back(u);\n count++;\n for (auto& it : adj[u]) {\n indegree[it]--;\n if (indegree[it] == 0) {\n qu.push(it);\n \n }\n }\n }\n if (count != n) {\n return {};\n }\n return topo;\n }\n\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> matrix(k, vector<int>(k, 0));\n\n vector<int> toposort_row = toposort(rowConditions, k);\n vector<int> toposort_col = toposort(colConditions, k);\n\n if (toposort_row.empty() || toposort_col.empty()) {\n return {};\n }\n\n for(int i=0;i<k;i++)\n {\n for(int j=0;j<k;j++)\n {\n if(toposort_row[i]==toposort_col[j])\n {\n matrix[i][j]=toposort_row[i];\n }\n }\n }\n\n return matrix;\n }\n};\n\n``` | 2 | 1 | ['Graph', 'Topological Sort', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
build-a-matrix-with-conditions | Beats 100% || Easiest and Cleanest Logic || Topological Sort | beats-100-easiest-and-cleanest-logic-top-az3f | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | SPA111 | NORMAL | 2024-07-21T13:43:13.020670+00:00 | 2024-07-21T13:43:13.020701+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> getIndegree(vector<int> adj[], int k)\n {\n vector<int> indegree(k, 0);\n\n for (int i = 0; i < k; i++)\n {\n for (auto u : adj[i])\n indegree[u]++;\n }\n\n return indegree;\n }\n\n vector<int> topologicalSort(vector<vector<int>>& conditions, int k)\n {\n vector<int> adj[k];\n\n for (int i = 0; i < conditions.size(); i++)\n adj[conditions[i][0] - 1].push_back(conditions[i][1] - 1);\n\n vector<int> indegree = getIndegree(adj, k);\n queue<int> q;\n vector<int> order;\n\n for (int i = 0; i < k; i++)\n {\n if (indegree[i] == 0)\n q.push(i);\n }\n\n while (!q.empty())\n {\n int u = q.front();\n order.push_back(u);\n q.pop();\n\n for (auto v : adj[u])\n {\n indegree[v]--;\n if (indegree[v] == 0)\n q.push(v);\n }\n }\n\n if (order.size() != k)\n return {};\n\n return order;\n }\n\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowc, vector<vector<int>>& colc) {\n\n vector<int> horizontalOrder = topologicalSort(rowc, k);\n vector<int> verticalOrder = topologicalSort(colc, k);\n\n if (horizontalOrder.empty() || verticalOrder.empty()) \n return {};\n\n vector<vector<int>> matrix(k, vector<int>(k, 0));\n\n unordered_map<int, int> rowPos, colPos;\n\n for (int i = 0; i < k; i++) {\n rowPos[horizontalOrder[i]] = i;\n colPos[verticalOrder[i]] = i;\n }\n\n for (int i = 0; i < k; i++) {\n matrix[rowPos[i]][colPos[i]] = i + 1;\n }\n\n return matrix;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 0 |
build-a-matrix-with-conditions | Easy Approach and Clear Structure ! Beats 100% in runtime ! #TopologicalSort | easy-approach-and-clear-structure-beats-a75jx | Intuition\n Describe your first thoughts on how to solve this problem. \nThink is problem as a "GRAPH" problem. The first and second number in x-conditions just | alonza_0314 | NORMAL | 2024-07-21T10:59:58.134931+00:00 | 2024-07-21T10:59:58.134960+00:00 | 103 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThink is problem as a "GRAPH" problem. The first and second number in x-conditions just like a from u to v edge. Then, use topological sort to solve this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**First**, we can convert the x-conditions as a graph. I store the graph as four parts: number of vertices \\ adjacency list \\ roots whose indegree are \'0\' \\ indegree of each vertice.\n\n**Second**, go on topological sort on row-Graph and col-Graph. I store the result in a map which indicates {vertice: index in row / col}. In the \'for\' loop, g.Roots acts as the queue for BFS. The top of the queue as it is popped out will be put in the order map with the val is which index it would be. And if its adjacent vertice\'s indegree is decrease to zero, I push this vertice into the queue, i.e. g.Roots.\n\n**Last**, just put the result in the return matrix.\n\n**Be careful** that in each step you need to check whether there exist cycle or not, i.e. the error condition in each function.\n\n# Complexity\n- Time complexity: $$O(N + E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Code\n```\ntype Graph struct {\n Verts int\n AdjList map[int][]int\n Roots []int\n Indegree map[int]int\n}\n\nfunc NewGraph(k int, conditions [][]int) (*Graph, error) {\n g := Graph{\n Verts: k,\n AdjList: make(map[int][]int),\n Roots: make([]int, 0),\n Indegree: make(map[int]int),\n }\n for i := 1; i < k + 1; i += 1 {\n g.Indegree[i] = 0\n }\n for _, cond := range conditions {\n u, v := cond[0], cond[1]\n g.AdjList[u] = append(g.AdjList[u], v)\n g.Indegree[v] += 1\n }\n for key, val := range g.Indegree {\n if val == 0 {\n g.Roots = append(g.Roots, key)\n }\n }\n if len(g.Roots) == 0 {\n return nil, errors.New("")\n }\n return &g, nil\n}\n\nfunc (g *Graph) TopologicalSort() (map[int]int, error) {\n order, idx := make(map[int]int), 0\n for len(g.Roots) != 0 {\n top := g.Roots[0]\n g.Roots = g.Roots[1:]\n order[top] = idx\n idx += 1\n for _, adj := range g.AdjList[top] {\n g.Indegree[adj] -= 1\n if g.Indegree[adj] == 0 {\n g.Roots = append(g.Roots, adj)\n }\n }\n }\n if len(order) != g.Verts {\n return nil, errors.New("")\n }\n return order, nil\n}\n\nfunc buildMatrix(k int, rowConditions [][]int, colConditions [][]int) [][]int {\n rowGraph, err := NewGraph(k, rowConditions)\n if err != nil {\n return make([][]int, 0)\n }\n colGraph, err := NewGraph(k, colConditions)\n if err != nil {\n return make([][]int, 0)\n }\n\n rowTopo, err := rowGraph.TopologicalSort()\n if err != nil {\n return make([][]int, 0)\n }\n colTopo, err := colGraph.TopologicalSort()\n if err != nil {\n return make([][]int, 0)\n }\n rowGraph, colGraph = nil, nil\n\n ret := make([][]int, k)\n for i := 0; i < k; i += 1 {\n ret[i] = make([]int, k)\n }\n\n for i := 1; i < k + 1; i += 1 {\n ret[rowTopo[i]][colTopo[i]] = i\n }\n\n return ret\n}\n``` | 2 | 0 | ['Go'] | 1 |
build-a-matrix-with-conditions | Beats 100% || Made it easy for you || C++|| Topological Sort || Matrix Filling | beats-100-made-it-easy-for-you-c-topolog-hdh5 | \n### Problem Breakdown\n\n1. Topological Sorting: The problem can be translated into a graph problem where rowConditions and colConditions provide directed edg | itachiuchiha14 | NORMAL | 2024-07-21T08:11:58.770520+00:00 | 2024-07-21T08:11:58.770547+00:00 | 195 | false | \n### Problem Breakdown\n\n1. **Topological Sorting**: The problem can be translated into a graph problem where `rowConditions` and `colConditions` provide directed edges indicating the order of elements in rows and columns respectively.\n2. **Matrix Construction**: Once the topological orderings are obtained, we need to position each element in the matrix such that they conform to both row and column orderings.\n\n### Approach\n\n1. **Topological Sort**: For both `rowConditions` and `colConditions`, perform a topological sort to determine the order of elements in rows and columns.\n2. **Matrix Filling**: Using the obtained topological orders, fill the matrix such that each element \\(i\\) is placed at the intersection of its determined row and column.\n\n### Detailed Steps\n\n1. **Topological Sorting**:\n - **Adjacency List Construction**: For each condition, build an adjacency list.\n - **DFS for Cycle Detection and Order**: Use Depth-First Search (DFS) to detect cycles (which would imply an invalid ordering) and to produce a topological order.\n \n2. **Matrix Filling**:\n - **Create Matrix**: Initialize a \\(k \\times k\\) matrix filled with zeros.\n - **Position Elements**: Iterate through the topological orders and place each element at the intersection of its respective row and column order indices.\n\n### Code Explanation\n\n#### `buildMatrix` Function\nThis function coordinates the entire process:\n\n```cpp\nvector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n // Store the topologically sorted sequences.\n vector<int> orderRows = topoSort(rowConditions, k);\n vector<int> orderColumns = topoSort(colConditions, k);\n\n // If no topological sort exists, return empty array.\n if (orderRows.empty() or orderColumns.empty()) return {};\n\n vector<vector<int>> matrix(k, vector<int>(k, 0));\n for (int i = 0; i < k; i++) {\n for (int j = 0; j < k; j++) {\n if (orderRows[i] == orderColumns[j]) {\n matrix[i][j] = orderRows[i];\n }\n }\n }\n return matrix;\n}\n```\n\n1. **Topological Sorting**: Calls `topoSort` for rows and columns.\n2. **Matrix Initialization**: Creates an empty matrix of size \\(k \\times k\\).\n3. **Element Placement**: Places elements in the matrix based on their positions in `orderRows` and `orderColumns`.\n\n#### `topoSort` Function\nPerforms topological sorting using DFS:\n\n```cpp\nvector<int> topoSort(vector<vector<int>>& edges, int n) {\n vector<vector<int>> adj(n + 1);\n vector<int> order;\n vector<int> visited(n + 1, 0);\n bool hasCycle = false;\n\n // Build adjacency list\n for (auto& x : edges) {\n adj[x[0]].push_back(x[1]);\n }\n\n // Perform DFS for each node\n for (int i = 1; i <= n; i++) {\n if (visited[i] == 0) {\n dfs(i, adj, visited, order, hasCycle);\n if (hasCycle) return {};\n }\n }\n reverse(order.begin(), order.end());\n return order;\n}\n```\n\n1. **Adjacency List**: Builds adjacency list from edge list.\n2. **DFS Initialization**: Starts DFS for unvisited nodes.\n3. **Cycle Detection**: Returns empty order if a cycle is detected.\n\n#### `dfs` Function\nHandles the DFS traversal and cycle detection:\n\n```cpp\nvoid dfs(int node, vector<vector<int>>& adj, vector<int>& visited,\n vector<int>& order, bool& hasCycle) {\n visited[node] = 1; // Mark node as visiting\n for (int neighbor : adj[node]) {\n if (visited[neighbor] == 0) {\n dfs(neighbor, adj, visited, order, hasCycle);\n if (hasCycle) return;\n } else if (visited[neighbor] == 1) {\n // Cycle detected\n hasCycle = true;\n return;\n }\n }\n visited[node] = 2; // Mark node as visited\n order.push_back(node);\n}\n```\n\n1. **Mark as Visiting**: Marks the node as currently visiting.\n2. **Recurse on Neighbors**: Recursively visits all unvisited neighbors.\n3. **Cycle Check**: Checks for back edges indicating cycles.\n4. **Mark as Visited**: Marks the node as fully visited and adds it to the order list.\n\n### Complexity Analysis\n\n- **Time Complexity**:\n - **Topological Sorting**: \\(O(V + E)\\), where \\(V\\) is the number of nodes (in this case \\(k\\)) and \\(E\\) is the number of edges (conditions).\n - **Matrix Filling**: \\(O(k^2)\\) for positioning elements in the matrix.\n \n- **Space Complexity**:\n - **Adjacency List**: \\(O(V + E)\\).\n - **Visited Array and Order List**: \\(O(V)\\).\n\nThis approach ensures that the matrix is constructed correctly if valid topological orders exist for both rows and columns, and handles invalid cases by returning an empty matrix.\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions,\n vector<vector<int>>& colConditions) {\n // Store the topologically sorted sequences.\n vector<int> orderRows = topoSort(rowConditions, k);\n vector<int> orderColumns = topoSort(colConditions, k);\n\n // If no topological sort exists, return empty array.\n if (orderRows.empty() or orderColumns.empty()) return {};\n\n vector<vector<int>> matrix(k, vector<int>(k, 0));\n for (int i = 0; i < k; i++) {\n for (int j = 0; j < k; j++) {\n if (orderRows[i] == orderColumns[j]) {\n matrix[i][j] = orderRows[i];\n }\n }\n }\n return matrix;\n }\n\nprivate:\n vector<int> topoSort(vector<vector<int>>& edges, int n) {\n vector<vector<int>> adj(n + 1);\n vector<int> order;\n // 0: not visited, 1: visiting, 2: visited\n vector<int> visited(n + 1, 0);\n bool hasCycle = false;\n\n // Build adjacency list\n for (auto& x : edges) {\n adj[x[0]].push_back(x[1]);\n }\n\n // Perform DFS for each node\n for (int i = 1; i <= n; i++) {\n if (visited[i] == 0) {\n dfs(i, adj, visited, order, hasCycle);\n // Return empty if cycle detected\n if (hasCycle) return {};\n }\n }\n // Reverse to get the correct order\n reverse(order.begin(), order.end());\n return order;\n }\n\n void dfs(int node, vector<vector<int>>& adj, vector<int>& visited,\n vector<int>& order, bool& hasCycle) {\n visited[node] = 1; // Mark node as visiting\n for (int neighbor : adj[node]) {\n if (visited[neighbor] == 0) {\n dfs(neighbor, adj, visited, order, hasCycle);\n // Early exit if a cycle is detected\n if (hasCycle) return;\n } else if (visited[neighbor] == 1) {\n // Cycle detected\n hasCycle = true;\n return;\n }\n }\n // Mark node as visited\n visited[node] = 2;\n // Add node to the order\n order.push_back(node);\n }\n};\n```\n\n\n\n\n | 2 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'C++'] | 0 |
build-a-matrix-with-conditions | C++ / Python Solution | Matrix | Graph | Topological Sorting | Kahn's Algorithm | | c-python-solution-matrix-graph-topologic-zpon | Intuition\nTopological Sorting.\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nUse Kahn\'s Algorithm.\n Describe your approach to | Kaushik_Prajapati | NORMAL | 2024-07-21T05:55:07.746145+00:00 | 2024-07-21T05:55:07.746166+00:00 | 105 | false | # Intuition\nTopological Sorting.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUse Kahn\'s Algorithm.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(K^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(K^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n\n bool toposort(vector<vector<int>> &adj, vector<int> &tsort, vector<int> &ind)\n {\n int V = ind.size();\n queue<int> q;\n \n for(int i=0 ; i<V ; i++) if(ind[i] == 0) q.push(i);\n\n while(!q.empty())\n {\n int u = q.front();\n q.pop();\n tsort.push_back(u);\n\n for(auto &v: adj[u])\n {\n ind[v] -= 1;\n if(ind[v] == 0) q.push(v);\n }\n }\n\n if(tsort.size() != V) return false;\n return true;\n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n \n vector<vector<int>> adj_row(k, vector<int> ());\n vector<vector<int>> adj_col(k, vector<int> ());\n\n vector<int> ind_row(k, 0);\n vector<int> ind_col(k, 0);\n\n for(auto &edge: rowConditions) \n {\n adj_row[edge[0]-1].push_back(edge[1]-1);\n ind_row[edge[1]-1] += 1;\n }\n\n for(auto &edge: colConditions) \n {\n adj_col[edge[0]-1].push_back(edge[1]-1);\n ind_col[edge[1]-1] += 1;\n }\n \n vector<int> tsort_row;\n vector<int> tsort_col;\n\n bool notCycle_row = toposort(adj_row, tsort_row, ind_row);\n bool notCycle_col = toposort(adj_col, tsort_col, ind_col);\n\n if(!notCycle_row || !notCycle_col) return {};\n vector<vector<int>> ans(k, vector<int> (k, 0));\n\n for(int row = 0 ; row < k ; row++)\n {\n int col = find(tsort_col.begin(), tsort_col.end(), tsort_row[row]) - tsort_col.begin();\n ans[row][col] = tsort_row[row]+1;\n }\n\n return ans;\n }\n};\n```\n\n```Python []\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n \n def toposort(adj, tsort, ind):\n V = len(ind)\n q = deque()\n for i in range(V):\n if ind[i] == 0:\n q.append(i)\n\n while q:\n u = q.popleft()\n tsort.append(u)\n for v in adj[u]:\n ind[v] -= 1\n if ind[v] == 0:\n q.append(v)\n\n if len(tsort) != V: \n return False\n return True\n # End\n\n adj_row = [[] for i in range(k)]\n adj_col = [[] for i in range(k)]\n\n ind_row = [0] * k\n ind_col = [0] * k\n\n for edge in rowConditions: \n adj_row[edge[0]-1].append(edge[1]-1)\n ind_row[edge[1]-1] += 1\n\n for edge in colConditions: \n adj_col[edge[0]-1].append(edge[1]-1)\n ind_col[edge[1]-1] += 1\n \n tsort_row, tsort_col = [], []\n\n notCycle_row = toposort(adj_row, tsort_row, ind_row)\n notCycle_col = toposort(adj_col, tsort_col, ind_col)\n\n if not notCycle_row or not notCycle_col:\n return []\n \n ans = [[0] * k for i in range(k)]\n for row in range(k):\n col = tsort_col.index(tsort_row[row])\n ans[row][col] = tsort_row[row]+1\n\n return ans\n``` | 2 | 0 | ['Array', 'Graph', 'Topological Sort', 'Matrix', 'C++', 'Python3'] | 1 |
build-a-matrix-with-conditions | Kotlin Topological sort and build matrix | kotlin-topological-sort-and-build-matrix-f46a | Using topo sort Kann algorithm on row and column separately and then use that to rebuild matrix. Since only k number from 1..k in k * k matrix, each number can | james4388 | NORMAL | 2024-07-21T05:24:47.531243+00:00 | 2024-07-21T05:24:47.531289+00:00 | 29 | false | Using topo sort Kann algorithm on row and column separately and then use that to rebuild matrix. Since only k number from 1..k in k * k matrix, each number can be on one row and one column, no overlap\n```\nclass Solution {\n fun topologicalSort(edges: Array<IntArray>, n: Int): List<Int> {\n val graph = mutableMapOf<Int, MutableList<Int>>()\n val inDegree = IntArray(n + 1)\n val order = mutableListOf<Int>()\n for ((before, after) in edges) {\n graph[before] = graph.getOrDefault(before, mutableListOf<Int>())\n graph[before]!!.add(after)\n inDegree[after] += 1\n }\n val toVisit = ArrayDeque<Int>((1..n).filter({ inDegree[it] == 0 }))\n while (toVisit.isNotEmpty()) {\n val node = toVisit.removeFirst()\n order.add(node)\n for (nextNode in graph.getOrDefault(node, emptyList())) {\n inDegree[nextNode] -= 1\n if (inDegree[nextNode] == 0) {\n toVisit.add(nextNode)\n }\n } \n }\n if (order.size != n) {\n return emptyList()\n }\n return order\n }\n \n fun buildMatrix(k: Int, rowConditions: Array<IntArray>, colConditions: Array<IntArray>): Array<IntArray> {\n val rowOrder = topologicalSort(rowConditions, k)\n val colOrder = topologicalSort(colConditions, k)\n if (rowOrder.size == 0 || colOrder.size == 0) {\n return emptyArray()\n }\n val matrix = Array(k) { IntArray(k) }\n val colMap = colOrder.mapIndexed { index, num -> num to index }.toMap()\n for ((row, num) in rowOrder.withIndex()) {\n matrix[row][colMap[num]!!] = num\n }\n return matrix\n }\n}\n``` | 2 | 0 | ['Topological Sort', 'Kotlin'] | 0 |
build-a-matrix-with-conditions | C# Solution for Build a Matrix With Conditions Problem | c-solution-for-build-a-matrix-with-condi-a763 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe approach involves:\n\n\t1.\tTopological Sorting: Using Kahn\u2019s algorithm to fin | Aman_Raj_Sinha | NORMAL | 2024-07-21T04:17:20.789269+00:00 | 2024-07-21T04:17:20.789305+00:00 | 170 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe approach involves:\n\n\t1.\tTopological Sorting: Using Kahn\u2019s algorithm to find the order of elements based on the given constraints.\n\t2.\tMatrix Construction: Filling in the matrix based on the sorted row and column orders.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe solution is based on the concept of topological sorting and matrix construction:\n\n1.\tTopological Sorting:\n\t\u2022\tIntuition: Topological sorting is used to order vertices of a directed graph in such a way that for every directed edge uv from vertex u to vertex v , u comes before v in the ordering. This is particularly useful for resolving constraints that define ordering (like \u201Cnumber A must be above number B \u201D).\n\t\u2022\tApproach:\n\t \u2022\tGraph Construction: Build adjacency lists from constraints for rows and columns separately.\n\t \u2022\tIn-Degree Array: Track how many incoming edges each node has.\n\t \u2022\tKahn\u2019s Algorithm: Use a queue to process nodes with zero in-degrees and keep track of nodes whose ordering is resolved. Remove edges as you process nodes and update in-degrees of neighbors. If any nodes remain with non-zero in-degrees at the end, a cycle exists, making a valid ordering impossible.\n2.\tMatrix Construction:\n\t\u2022\tIntuition: Once we have the topological order for rows and columns, the next step is to place numbers into the matrix such that the order constraints are respected.\n\t\u2022\tApproach:\n\t \u2022\tMatrix Initialization: Create a k x k matrix initialized with zeros.\n\t \u2022\tPlacement: For each number, place it in the matrix based on its position in the topological order of rows and columns. The position in the row order determines the row, and the position in the column order determines the column.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tGraph Construction: O(E) , where E is the number of edges (constraints). This involves processing each edge once to build the adjacency list and update in-degrees.\n\u2022\tTopological Sorting: O(V + E) , where V is the number of vertices (numbers) and E is the number of edges. The time complexity for Kahn\u2019s algorithm is linear in terms of the number of vertices plus the number of edges.\n\u2022\tMatrix Filling: O(k^2) , where k is the matrix size. This involves iterating over the matrix to place numbers based on the sorted orders.\nOverall Time Complexity: O(k^2 + E) , since the matrix filling dominates for large k compared to the edge operations.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tGraph Representation: O(V + E) for storing adjacency lists and in-degrees.\n\u2022\tTopological Sorting Storage: O(V) for the sorted order and queue.\n\u2022\tMatrix Storage: O(k^2) for the matrix.\nOverall Space Complexity: O(k^2 + k + E) , which simplifies to O(k^2 + E) since k^2 will dominate for large k .\n\n# Code\n```\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution {\n public int[][] BuildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n int[] rowOrder = TopoSort(rowConditions, k);\n int[] colOrder = TopoSort(colConditions, k);\n \n if (rowOrder.Length == 0 || colOrder.Length == 0) {\n return new int[0][];\n }\n \n int[][] matrix = new int[k][];\n for (int i = 0; i < k; i++) {\n matrix[i] = new int[k];\n }\n \n // Fill the matrix based on the orders\n for (int i = 0; i < k; i++) {\n int rowPos = Array.IndexOf(rowOrder, i + 1);\n int colPos = Array.IndexOf(colOrder, i + 1);\n \n if (rowPos >= 0 && rowPos < k && colPos >= 0 && colPos < k) {\n matrix[rowPos][colPos] = i + 1;\n }\n }\n \n return matrix;\n }\n \n private int[] TopoSort(int[][] edges, int n) {\n List<int>[] adj = new List<int>[n + 1];\n for (int i = 0; i <= n; i++) {\n adj[i] = new List<int>();\n }\n \n int[] inDegree = new int[n + 1];\n foreach (var edge in edges) {\n int u = edge[0];\n int v = edge[1];\n adj[u].Add(v);\n inDegree[v]++;\n }\n \n Queue<int> queue = new Queue<int>();\n for (int i = 1; i <= n; i++) {\n if (inDegree[i] == 0) {\n queue.Enqueue(i);\n }\n }\n \n List<int> result = new List<int>();\n while (queue.Count > 0) {\n int node = queue.Dequeue();\n result.Add(node);\n foreach (int neighbor in adj[node]) {\n if (--inDegree[neighbor] == 0) {\n queue.Enqueue(neighbor);\n }\n }\n }\n \n if (result.Count != n) {\n return new int[0]; // Cycle detected or not all nodes are reachable\n }\n \n return result.ToArray();\n }\n}\n``` | 2 | 0 | ['C#'] | 2 |
build-a-matrix-with-conditions | Topological Sort (w/ Comments) | topological-sort-w-comments-by-alexplump-t6jy | Intuition\n Describe your first thoughts on how to solve this problem. \nDetermine what number has no numbers before it at any time.\n\n# Approach\n Describe yo | alexplump | NORMAL | 2024-07-21T02:46:21.050613+00:00 | 2024-07-21T02:46:21.050633+00:00 | 134 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDetermine what number has no numbers before it at any time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a dictionary of what numbers precede any number.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(k^2)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(k^2)$$\n\n# Code\n```\npublic class Solution {\n private int k;\n public int[][] BuildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n this.k = k;\n\n // Get positions of all numbers\n int[] row_positions = GetPositions(rowConditions);\n int[] column_positions = GetPositions(colConditions);\n\n // Check that there are no cycles\n if (row_positions == null || column_positions == null)\n return new int[0][];\n\n // Create 2-d array\n int[][] result = new int[k][];\n for (int i = 0; i < k; i++) {\n result[i] = new int[k];\n }\n\n // Put all number into their spots\n for (int i = 1; i <= k; i++) {\n result[row_positions[i]][column_positions[i]] = i;\n }\n\n return result;\n }\n\n private int[] GetPositions(int[][] conditions) {\n // Keep a dict of numbers that are before and after other numbers\n Dictionary<int, HashSet<int>> befores = new Dictionary<int, HashSet<int>>();\n Dictionary<int, HashSet<int>> afters = new Dictionary<int, HashSet<int>>();\n\n // Add all numbers as keys into the dictionaries\n for (int i = 1; i <= this.k; i++) {\n befores.Add(i, new HashSet<int>());\n afters.Add(i, new HashSet<int>());\n }\n\n // Populate dictionaries\n foreach (int[] condition in conditions) {\n int before = condition[0];\n int after = condition[1];\n\n befores[after].Add(before);\n afters[before].Add(after); \n }\n\n int[] order = new int[k+1];\n int position = 0;\n while (befores.Count > 0) {\n // Find the element with the least # of elements before it\n int next_key = -1;\n int next_count = Int32.MaxValue;\n foreach (var pair in befores) {\n if (pair.Value.Count < next_count) {\n next_key = pair.Key;\n next_count = pair.Value.Count;\n }\n }\n\n // Remove this number from all after\'s before list\n foreach (int after in afters[next_key])\n if (befores.ContainsKey(after))\n befores[after].Remove(next_key);\n else\n return null; // Cycle detected\n // known because a number after the current one\n // has already been placed before this one\n\n // Give this number a position in the matrix\n order[next_key] = position++;\n\n // Remove this number from the befores list\n befores.Remove(next_key);\n }\n\n return order;\n }\n}\n``` | 2 | 0 | ['C#'] | 2 |
build-a-matrix-with-conditions | Construct a 2D Matrix with Conditions. | construct-a-2d-matrix-with-conditions-by-a2iu | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this problem, we need to determine the relative positioning of numbers in a ma | pathik5 | NORMAL | 2024-07-21T02:12:46.798990+00:00 | 2024-07-21T02:12:46.799013+00:00 | 233 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, we need to determine the relative positioning of numbers in a matrix based on given row and column constraints. This is similar to a scheduling problem where tasks have dependencies. The dependencies in this case are the conditions given for rows and columns, which can be visualized as a directed graph. The topological sorting of this graph will give us the required order of numbers.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Graph Construction:\n - Construct directed graphs for both row conditions and column conditions.\n - Each node in the graph represents a number from 1 to k.\n - Directed edges in the graph represent the "above-below" and "left-right" conditions.\n2. Topological Sorting:\n - Perform topological sorting on both the row graph and the column graph.\n - If a cycle is detected in any of the graphs, it means that the conditions are contradictory, and thus, no valid matrix can be constructed.\n - If no cycles are detected, the topological sort will give us the order in which numbers should appear in rows and columns.\n3. Matrix Construction:\n - Use the order obtained from the topological sort to place the numbers in the matrix.\n - Initialize a k x k matrix with zeros.\n - Place each number in the matrix at the position derived from the topological sorting of rows and columns.\n# Complexity\n- Time complexity:\n - Constructing the graph takes $$O(n+m)$$, where $$n$$ is the number of row conditions and $$m$$ is the number of column conditions.\n - Topological sorting also takes $$O(k+E)$$, where $$k$$ is the number of nodes (which is equal to the given k) and $$E$$ is the number of edges in the graph.\n - Constructing the final matrix takes$$O(k^2)$$ since we are initializing a k x k matrix and placing k elements in it.\n - Overall time complexity is $$O(k+n+m+k 2)$$, which simplifies to $$O(k^2)$$ assuming k is large.\n- Space complexity:\n - Storing the graph takes $$O(k+E)$$.\n - Additional space for storing the in-degrees, the order of elements, and the final matrix results in $$O(k^2)$$ space.\n - Overall space complexity is $$O(k^2)$$.\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n // Helper function to perform topological sort\n auto topologicalSort = [](int k, const vector<vector<int>>& conditions) {\n vector<vector<int>> graph(k + 1);\n vector<int> inDegree(k + 1, 0);\n \n for (const auto& condition : conditions) {\n graph[condition[0]].push_back(condition[1]);\n inDegree[condition[1]]++;\n }\n \n queue<int> q;\n for (int i = 1; i <= k; ++i) {\n if (inDegree[i] == 0) {\n q.push(i);\n }\n }\n \n vector<int> order;\n while (!q.empty()) {\n int node = q.front();\n q.pop();\n order.push_back(node);\n \n for (int neighbor : graph[node]) {\n if (--inDegree[neighbor] == 0) {\n q.push(neighbor);\n }\n }\n }\n \n if (order.size() != k) return vector<int>(); // Cycle detected\n return order;\n };\n \n vector<int> rowOrder = topologicalSort(k, rowConditions);\n vector<int> colOrder = topologicalSort(k, colConditions);\n \n if (rowOrder.empty() || colOrder.empty()) return {}; // If there\'s a cycle\n \n unordered_map<int, int> rowPosition;\n unordered_map<int, int> colPosition;\n \n for (int i = 0; i < k; ++i) {\n rowPosition[rowOrder[i]] = i;\n colPosition[colOrder[i]] = i;\n }\n \n vector<vector<int>> result(k, vector<int>(k, 0));\n for (int num = 1; num <= k; ++num) {\n int row = rowPosition[num];\n int col = colPosition[num];\n result[row][col] = num;\n }\n \n return result;\n }\n};\n\n``` | 2 | 1 | ['Matrix', 'C++'] | 3 |
build-a-matrix-with-conditions | Python Topo Sort | python-topo-sort-by-hong_zhao-q9qc | Intuition\n Describe your first thoughts on how to solve this problem. \nUse topological sort to find the order of row and col\n\nIn the first example:\n\n[3,0, | hong_zhao | NORMAL | 2024-07-21T01:27:03.187761+00:00 | 2024-07-21T02:08:01.095391+00:00 | 524 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse topological sort to find the order of row and col\n\nIn the first example:\n```\n[3,0,0]\n[0,0,1]\n[0,2,0]\n```\nThe row order from top to bottom is `3 -> 1 -> 2`\nThe col order from left to right is `3 -> 2 -> 1`\n\nNow we know the position in (i, j) for each value [1, k]\nReturn an empty array if we can\'t build the matrix\n\n# Complexity\n- Time complexity: $$O(K * K)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(K * K)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n \n def order(conditions):\n adj = [[] for _ in range(k + 1)]\n deg = [0] * (k + 1)\n for u, v in conditions:\n adj[u].append(v)\n deg[v] += 1\n\n s = []\n for u, d in enumerate(deg):\n if u and d == 0:\n s.append(u)\n \n res = []\n while s:\n u = s.pop()\n res.append(u)\n for v in adj[u]:\n deg[v] -= 1\n if deg[v]:\n continue\n s.append(v)\n\n if any(deg):\n return []\n return res\n\n \n row = order(rowConditions)\n col = order(colConditions)\n \n col = {x: i for i, x in enumerate(col)}\n res = [[0] * k for _ in range(k)]\n for i, x in enumerate(row):\n if x not in col:\n break\n j = col[x]\n res[i][j] = x\n\n for r in res:\n if not any(r):\n return []\n return res\n\n``` | 2 | 0 | ['Python3'] | 4 |
build-a-matrix-with-conditions | Topo_sort || python | topo_sort-python-by-viishhnu-kdnr | Intuition\n Describe your first thoughts on how to solve this problem. \n1)concept is to find topo_sort for row and col...\n2)iterate from topo_sort of row elem | viishhnu | NORMAL | 2023-08-28T03:06:27.988623+00:00 | 2023-08-28T03:06:27.988645+00:00 | 104 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1)concept is to find topo_sort for row and col...\n2)iterate from topo_sort of row elements and find its corresponding pos in topo_sort of col\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: Time complexity of topo sort\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: O(k*k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n \n\n# Code\n```\nclass Solution:\n def buildMatrix(self, k: int, row: List[List[int]], col: List[List[int]]) -> List[List[int]]:\n adj_l_A = [[] for i in range(k+1)]\n indegree_A = [0]*(k+1)\n for u,v in row:\n adj_l_A[u].append(v)\n indegree_A[v]+=1\n queue1 = []\n for i in range(1,k+1):\n if indegree_A[i]==0:\n queue1.append(i)\n adj_l_B = [[] for i in range(k+1)]\n indegree_B = [0]*(k+1)\n for u ,v in col:\n adj_l_B[u].append(v)\n indegree_B[v]+=1\n queue2 = []\n for i in range(1,k+1):\n if indegree_B[i]==0:\n queue2.append(i)\n\n\n \n def topo_sort(queue,res,adj_list,indegree):\n while queue:\n curr = queue.pop(0)\n res.append(curr)\n for i in adj_list[curr]:\n indegree[i]-=1\n if indegree[i]==0:\n queue.append(i)\n return res\n Row = topo_sort(queue1,[],adj_l_A,indegree_A)\n Col = topo_sort(queue2,[],adj_l_B,indegree_B)\n if len(Row)==k and len(Col)==k:\n grid = [[0 for i in range(k)] for j in range(k)]\n ind = {}\n for i in range(k):\n ind[Col[i]] = i\n for i in range(k):\n j = ind[Row[i]]\n grid[i][j] = Row[i]\n return grid\n return []\n\n\n \n``` | 2 | 0 | ['Python3'] | 1 |
build-a-matrix-with-conditions | C++ Basic Topological Sort Approach | c-basic-topological-sort-approach-by-dav-xuk0 | Intuition\n Describe your first thoughts on how to solve this problem. \nIn this problem we are given \'k\' number of elements that is 1 through k\nalong with t | david_makhija | NORMAL | 2023-07-05T06:16:53.615545+00:00 | 2023-07-05T06:16:53.615582+00:00 | 45 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem we are given \'k\' number of elements that is 1 through k\nalong with the relative order between some of the elements\nthe order is given in two formats that is row-wise and column-wise which we need to maintain in the resultant matrix\nIf we assume these k elements to be a part of two graphs:-\nrowAdj & colAdj where rowConditions contains the directed edges {u, v} such that there is an edge from u to v for the graph rowAdj and colConditions contains the same for colAdj\nThen this problem can be seen as a topological sorting problem\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we create the graphs rowAdj and colAdj based on rowConditions and colConditions respectivly\nAfter that we check for cycles in both the graphs\nIf there exists any cycle in any of the newly obtained graphs, we will return an empty 2D matrix because topoSort is not possible in that case\nafter we have obtained the topological sort for both the graphs, we record the appropriate positions of these elements in the vector rowOrder for rowAdj and colOrder for colAdj\nNow that we have the positions for these elements in the matrix we can easily construct the matrix.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(rowConditions.length + colConditions.length + k)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(k * k)$$\n\n# Code\n```\nclass Compare {\npublic:\n bool operator()(vector<int> below, vector<int> above) {\n return above[0] > below[0];\n }\n};\n\nclass Solution {\n\n bool isCyclic(vector<int>* adj, int cur, vector<bool>& dfsvis, vector<bool>& vis) {\n if(dfsvis[cur]) {\n return true;\n }\n\n if(vis[cur]) {\n return false;\n }\n vis[cur] = true;\n\n bool cyclic = false;\n dfsvis[cur] = true;\n for(int x: adj[cur]) {\n cyclic |= isCyclic(adj, x, dfsvis, vis);\n }\n dfsvis[cur] = false;\n\n return cyclic;\n }\n\n void topoSort(stack<int>& sortedElements, vector<int>* adj, int curr, vector<bool>& vis) {\n if(vis[curr]) {\n return;\n }\n vis[curr] = true;\n\n for(int x: adj[curr]) {\n topoSort(sortedElements, adj, x, vis);\n }\n sortedElements.push(curr + 1);\n }\n\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n \n vector<vector<int>> temp;\n\n\n vector<int> rowAdj[k];\n vector<int> rowOutDegree(k, 0);\n priority_queue<vector<int>, vector<vector<int>>, Compare> rowPQ;\n vector<bool> row1Vis(k, false);\n vector<bool> row1DfsVis(k, false);\n for(auto x: rowConditions) {\n rowAdj[x[0] - 1].push_back(x[1] - 1);\n rowOutDegree[x[0] - 1]++;\n rowOutDegree[x[1] - 1]--;\n }\n\n for(int i = 0; i < k; i++) {\n if(isCyclic(rowAdj, i, row1DfsVis, row1Vis)) {\n return temp;\n }\n }\n\n for(int i = 0; i < k; i++) {\n rowPQ.push({rowOutDegree[i], i});\n }\n\n vector<int> colAdj[k];\n vector<int> colOutDegree(k, 0);\n priority_queue<vector<int>, vector<vector<int>>, Compare> colPQ;\n vector<bool> col1Vis(k, false);\n vector<bool> col1DfsVis(k, false);\n for(auto x: colConditions) {\n colAdj[x[0] - 1].push_back(x[1] - 1);\n colOutDegree[x[0] - 1]++;\n colOutDegree[x[1] - 1]--;\n }\n\n for(int i = 0; i < k; i++) {\n if(isCyclic(colAdj, i, col1DfsVis, col1Vis)) {\n return temp;\n }\n }\n\n for(int i = 0; i < k; i++) {\n colPQ.push({colOutDegree[i], i});\n }\n\n stack<int> rowSortedElements;\n vector<bool> rowVis(k, false);\n stack<int> colSortedElements;\n vector<bool> colVis(k, false);\n\n while(!rowPQ.empty()) {\n int node1 = rowPQ.top()[1];\n rowPQ.pop();\n if(!rowVis[node1]) {\n topoSort(rowSortedElements, rowAdj, node1, rowVis);\n }\n int node2 = colPQ.top()[1];\n colPQ.pop();\n if(!colVis[node2]) {\n topoSort(colSortedElements, colAdj, node2, colVis);\n }\n }\n\n vector<int> rowOrder(k+1);\n vector<int> colOrder(k+1);\n while(!rowSortedElements.empty()) {\n rowOrder[rowSortedElements.top()] = k - rowSortedElements.size();\n rowSortedElements.pop();\n colOrder[colSortedElements.top()] = k - colSortedElements.size();\n colSortedElements.pop();\n }\n \n vector<vector<int>> ans(k, vector<int>(k, 0));\n\n for(int i = 1; i <= k; i++) {\n ans[rowOrder[i]][colOrder[i]] = i;\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'Graph', 'Topological Sort', 'Matrix', 'C++'] | 1 |
build-a-matrix-with-conditions | TopoSort | toposort-by-recursive45-2jpm | \n\n# Code\n\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>> &rowConditions, vector<vector<int>> &colConditions)\ | Recursive45 | NORMAL | 2023-06-05T13:47:49.801340+00:00 | 2023-06-05T13:47:49.801381+00:00 | 225 | false | \n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>> &rowConditions, vector<vector<int>> &colConditions)\n{\n vector<int> adj1[k], adj2[k];\n vector<int> indegree1(k, 0), indegree2(k, 0);\n for (auto it : rowConditions)\n {\n int u = it[0] - 1;\n int v = it[1] - 1;\n adj1[u].push_back(v);\n indegree1[v]++;\n }\n\n for (auto it : colConditions)\n {\n int u = it[0] - 1;\n int v = it[1] - 1;\n adj2[u].push_back(v);\n indegree2[v]++;\n }\n\n vector<int> order1, order2;\n queue<int> q;\n for (int i = 0; i < k; i++)\n {\n if (indegree1[i] == 0)\n {\n q.push(i);\n }\n }\n\n while (!q.empty())\n {\n int node = q.front();\n q.pop();\n order1.push_back(node);\n\n for (auto it : adj1[node])\n {\n indegree1[it]--;\n if (indegree1[it] == 0)\n {\n q.push(it);\n }\n }\n }\n\n if (order1.size() < k)\n {\n return {};\n }\n\n for (int i = 0; i < k; i++)\n {\n if (indegree2[i] == 0)\n {\n q.push(i);\n }\n }\n\n while (!q.empty())\n {\n int node = q.front();\n q.pop();\n order2.push_back(node);\n\n for (auto it : adj2[node])\n {\n indegree2[it]--;\n if (indegree2[it] == 0)\n {\n q.push(it);\n }\n }\n }\n\n if (order2.size() < k)\n {\n return {};\n }\n\n vector<pair<int, int>> v(k);\n for (int i = 0; i < order1.size(); i++)\n {\n v[order1[i]].first = i;\n }\n\n for (int i = 0; i < order2.size(); i++)\n {\n v[order2[i]].second = i;\n }\n\n vector<vector<int>> ans(k, vector<int>(k, 0));\n for (int i = 0; i < k; i++)\n {\n int x = v[i].first;\n int y = v[i].second;\n ans[x][y] = i + 1;\n }\n\n return ans;\n}\n};\n``` | 2 | 0 | ['C++'] | 2 |
build-a-matrix-with-conditions | [Python 3] Topological Sorting | python-3-topological-sorting-by-bereket_-wiua | \n\n\n```\n\ndef buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n ans = [[0] * k for _ in | Bereket_sh | NORMAL | 2023-05-13T19:01:56.324203+00:00 | 2023-05-13T19:16:37.293953+00:00 | 555 | false | \n\n\n```\n\ndef buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:\n ans = [[0] * k for _ in range(k)]\n\t\t\n def topological(condition):\n graph = defaultdict(list)\n indegree = [0] * k\n for a, b in condition:\n graph[a].append(b)\n indegree[b - 1] += 1\n \n que = deque()\n for i, val in enumerate(indegree):\n if val == 0:\n que.append(i + 1)\n \n order = []\n \n while que:\n temp = que.popleft()\n order.append(temp)\n \n for child in graph[temp]:\n indegree[child - 1] -= 1\n if indegree[child - 1] == 0:\n que.append(child)\n \n return order\n \n row_order = topological(rowConditions)\n col_order = topological(colConditions)\n \n #cycle detection\n if len(row_order) < k or len(col_order) < k:\n return []\n \n for row, val in enumerate(row_order):\n col = col_order.index(val)\n ans[row][col] = val\n \n return ans\n | 2 | 0 | ['Topological Sort', 'Python3'] | 1 |
build-a-matrix-with-conditions | c++ | easy to undersatand | step by step | c-easy-to-undersatand-step-by-step-by-ve-4cws | ```\nclass Solution {\n vector top_sorting(vector> con, int k) {\n vector indegree(k+1, 0);\n vector> graph(k+1);\n for(auto &it: con) { | venomhighs7 | NORMAL | 2022-09-27T12:13:39.838741+00:00 | 2022-09-27T12:13:39.838779+00:00 | 96 | false | ```\nclass Solution {\n vector<int> top_sorting(vector<vector<int>> con, int k) {\n vector<int> indegree(k+1, 0);\n vector<vector<int>> graph(k+1);\n for(auto &it: con) {\n indegree[it[1]] += 1;\n graph[it[0]].push_back(it[1]);\n }\n \n vector<int> ans;\n queue<int> q;\n for(int i = 1; i <= k; i++) {\n if(indegree[i] == 0)\n q.push(i);\n }\n \n while(!q.empty()) {\n int u = q.front();\n q.pop();\n ans.push_back(u);\n for(int v: graph[u]) {\n indegree[v]--;\n if(indegree[v] == 0) \n q.push(v);\n }\n }\n \n return ans;\n }\n \npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowC, vector<vector<int>>& colC) {\n vector<int> rowOrder = top_sorting(rowC, k);\n vector<int> colOrder = top_sorting(colC, k);\n \n // check cycle\n if(rowOrder.size() != k || colOrder.size() != k)\n return {}; \n\t\t\t\n // row index and col index of i\n vector<int> r(k+1), c(k+1);\n for(int i = 0; i < k; i++) {\n r[rowOrder[i]] = i;\n c[colOrder[i]] = i;\n }\n \n vector<vector<int>> ans(k, vector<int>(k, 0));\n for(int i = 1; i <= k; i++) \n ans[r[i]][c[i]] = i;\n \n return ans;\n }\n}; | 2 | 0 | [] | 0 |
build-a-matrix-with-conditions | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-4k9o | Using Topological Sort With BFS\n\n Time Complexity :- O(V + E)\n\n Space Complexity :- O(V + E)\n\n\nclass Solution {\npublic:\n \n // function for findi | __KR_SHANU_IITG | NORMAL | 2022-09-01T11:27:19.754188+00:00 | 2022-09-01T11:27:19.754231+00:00 | 274 | false | * ***Using Topological Sort With BFS***\n\n* ***Time Complexity :- O(V + E)***\n\n* ***Space Complexity :- O(V + E)***\n\n```\nclass Solution {\npublic:\n \n // function for finding toposort of a graph\n \n vector<int> toposort(vector<vector<int>> adj)\n {\n int V = adj.size();\n \n // find the indegree of every node\n \n vector<int> indegree(V, 0);\n \n for(int u = 0; u < V; u++)\n {\n for(auto v : adj[u])\n {\n indegree[v]++;\n }\n }\n \n // res will store the toposort order of graph\n \n vector<int> res;\n \n // push the node with indegree = 0 into q\n \n queue<int> q;\n \n for(int u = 0; u < V; u++)\n {\n if(indegree[u] == 0)\n {\n q.push(u);\n }\n }\n \n while(!q.empty())\n {\n int size = q.size();\n \n for(int k = 0; k < size; k++)\n {\n int u = q.front();\n \n q.pop();\n \n res.push_back(u);\n \n // go to adjacent nodes\n \n for(auto v : adj[u])\n {\n indegree[v]--;\n \n if(indegree[v] == 0)\n {\n q.push(v);\n }\n }\n }\n }\n \n // res.size() != V, it means there is cycle\n \n if(res.size() != V)\n return {};\n \n return res;\n }\n \n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n \n int n = rowConditions.size();\n \n int m = colConditions.size();\n \n // create two adjacency list one for rowConditions and other for colConditions\n \n vector<vector<int>> adj_r(k);\n \n vector<vector<int>> adj_c(k);\n \n for(int i = 0; i < n; i++)\n {\n int u = rowConditions[i][0];\n \n int v = rowConditions[i][1];\n \n adj_r[u - 1].push_back(v - 1);\n }\n \n for(int i = 0; i < m; i++)\n {\n int u = colConditions[i][0];\n \n int v = colConditions[i][1];\n \n adj_c[u - 1].push_back(v - 1);\n }\n \n // call for toposort\n \n vector<int> row = toposort(adj_r);\n \n if(row.size() == 0)\n {\n return {};\n }\n \n // call for toposort\n \n vector<int> col = toposort(adj_c);\n \n if(col.size() == 0)\n {\n return {};\n }\n \n // create matrix\n \n // store the index of number of col in mp array\n \n vector<int> mp(k, 0);\n \n for(int i = 0; i < col.size(); i++)\n {\n mp[col[i]] = i;\n }\n \n vector<vector<int>> res(k, vector<int> (k, 0));\n \n for(int i = 0; i < row.size(); i++)\n {\n // find the val\n \n int val = row[i] + 1;\n \n // find the row and col\n \n int r = i;\n \n int c = mp[row[i]];\n \n // put in res matrix\n \n res[r][c] = val;\n }\n \n return res;\n }\n};\n``` | 2 | 0 | ['Breadth-First Search', 'Graph', 'Topological Sort', 'C', 'C++'] | 1 |
build-a-matrix-with-conditions | C++ | Topological sort | 100% Faster, 0ms | Easy Code to follow | c-topological-sort-100-faster-0ms-easy-c-dna9 | Please Upvote :)\n\n\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditio | ankit4601 | NORMAL | 2022-08-29T16:18:39.250779+00:00 | 2022-08-29T16:18:39.250816+00:00 | 231 | false | Please Upvote :)\n\n```\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<vector<int>> v(k,vector<int>(k,0));\n auto p=topo(rowConditions,k);\n auto q=topo(colConditions,k);\n if(p.size()==0 || q.size()==0)// if any of both have cycle\n return {};\n for(int i=1;i<p.size();i++)\n {\n // p[i] gives row topological index for i and q[i] gives column topological index for i\n v[p[i]][q[i]]=i;\n }\n return v;\n }\n vector<int> topo(vector<vector<int>>& v,int k)\n {\n vector<vector<int>> adj(k+1);\n for(auto x:v)\n {\n adj[x[0]].push_back(x[1]);\n }\n \n stack<int> s;\n vector<int> vis(k+1,0);\n for(int i=1;i<=k;i++)\n {\n if(vis[i]==0)\n dfs(adj,vis,s,i);\n }\n vector<int> res(k+1);\n int ind=0;\n while(!s.empty())\n {\n res[s.top()]=ind;\n s.pop();\n ind++;\n }\n // check if cycle is there or not\n for(int i=1;i<=k;i++)\n {\n for(auto x:adj[i])\n {\n if(res[i]>res[x])// cycle exist\n return {};\n }\n }\n return res;\n }\n void dfs(vector<vector<int>>& adj,vector<int>& vis,stack<int>& s,int i)\n {\n vis[i]=1;\n for(auto x:adj[i])\n {\n if(vis[x]==0)\n dfs(adj,vis,s,x);\n }\n s.push(i);// recursively put the parent in top of the child\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'Graph', 'Topological Sort', 'C', 'C++'] | 2 |
build-a-matrix-with-conditions | ✅C++|| Kahn's Algo || Topological Sort || Beginner friendly | c-kahns-algo-topological-sort-beginner-f-e2l7 | \nclass Solution {\npublic:\n vector<int> kahn(vector<vector<int>>conditions, int k)\n {\n vector<int>graph[k+1];\n vector<int>degree(k+1,0) | indresh149 | NORMAL | 2022-08-29T07:49:59.871538+00:00 | 2022-08-29T07:49:59.871764+00:00 | 59 | false | ```\nclass Solution {\npublic:\n vector<int> kahn(vector<vector<int>>conditions, int k)\n {\n vector<int>graph[k+1];\n vector<int>degree(k+1,0);\n vector<int>ans;\n queue<int>q;\n for(vector<int>condition : conditions)\n {\n graph[condition[0]].push_back(condition[1]);\n degree[condition[1]]++;\n }\n for(int i=1;i<k;i++) { if(degree[i]==0) q.push(i); }\n while(!q.empty())\n {\n int node = q.front(); \n ans.push_back(node); \n q.pop();\n for(int neighbour : graph[node]) \n { \n degree[neighbour]--; \n if(degree[neighbour]==0)\n {\n q.push(neighbour);\n }\n }\n }\n \n return ans; \n }\n vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {\n vector<int>row_order = kahn(rowConditions, k+1); \n vector<int>col_order = kahn(colConditions, k+1); \n \n unordered_map<int,int>m;\n if(row_order.size()<k || col_order.size() <k)return {};\n vector<vector<int>>ans(k,vector<int>(k,0));\n \n for(int i=0;i<k;i++)\n {\n m[col_order[i]] = i;\n }\n \n for(int i=0;i<k;i++)\n {\n int column_position = m[row_order[i]]; \n ans[i][column_position] = row_order[i];\n }\n return ans;\n }\n};\n```\n\n**Please upvote if it was helpful for you, thank you!** | 2 | 0 | ['Topological Sort', 'C'] | 0 |
build-a-matrix-with-conditions | Kotlin Topological Sort | Kahn's Algorithm | kotlin-topological-sort-kahns-algorithm-bgdcj | \nclass Solution {\n data class Node (var `val`: Int, val `in`: MutableList<Int>, val `out`: MutableList<Int>)\n fun buildMatrix(k: Int, rowConditions: Ar | Z3ROsum | NORMAL | 2022-08-29T04:37:15.967053+00:00 | 2022-08-29T04:37:15.967088+00:00 | 82 | false | ```\nclass Solution {\n data class Node (var `val`: Int, val `in`: MutableList<Int>, val `out`: MutableList<Int>)\n fun buildMatrix(k: Int, rowConditions: Array<IntArray>, colConditions: Array<IntArray>): Array<IntArray> {\n var rowSorted = listOf<Int>()\n var colSorted = listOf<Int>()\n for (curr in 0 until 2) {\n val topoSorted = mutableListOf<Node>()\n val nodes = Array(k + 1) { Node(it, mutableListOf(), mutableListOf()) }\n val conditions = if (curr == 0) rowConditions else colConditions\n \n for (i in conditions) {\n nodes[i[0]].out.add(i[1])\n nodes[i[1]].`in`.add(i[0])\n }\n val set = mutableSetOf<Node>()\n for (i in nodes.indices) {\n if (nodes[i].`in`.isEmpty()) set.add(nodes[i])\n }\n \n while (set.isNotEmpty()) {\n val n = set.first()\n set.remove(n)\n topoSorted.add(n)\n val out = n.out.toList()\n for (node in out) {\n val m = nodes[node]\n nodes[n.`val`].out.remove(m.`val`)\n nodes[m.`val`].`in`.remove(n.`val`)\n if (m.`in`.isEmpty()) set.add(m)\n }\n }\n \n var cycle = false\n for (i in nodes) {\n if (i.`in`.isNotEmpty() || i.out.isNotEmpty()) {\n cycle = true\n break\n }\n }\n if (cycle) return arrayOf()\n var assign = topoSorted.subList(1, topoSorted.size).map { it.`val` }\n if (curr == 0) rowSorted = assign\n else colSorted = assign\n }\n \n val matrix = Array(k) { IntArray(k) { 0 } }\n val y = HashMap<Int, Int>()\n val x = HashMap<Int, Int>()\n for (i in rowSorted.indices) {\n y[rowSorted[i]] = i\n }\n for (i in colSorted.indices) {\n x[colSorted[i]] = i\n }\n for (i in y) {\n val yVal = i.value\n val xVal = x[i.key]!!\n matrix[yVal][xVal] = i.key\n }\n return matrix\n }\n}\n``` | 2 | 0 | ['Topological Sort', 'Kotlin'] | 0 |
build-a-matrix-with-conditions | Step by Step Approach | Easy to Follow | C++ Implementation | step-by-step-approach-easy-to-follow-c-i-48ku | Here is an explanation from post contest discussion meeting.\n\nhttps://www.youtube.com/watch?v=LDNMlgBi5vg&list=PLQ9cQ3JqeqU_T-Ic3384j4uWDxUnXjlVO&index=4 | sandywadhwa | NORMAL | 2022-08-28T16:28:52.337219+00:00 | 2022-08-28T16:28:52.337251+00:00 | 26 | false | Here is an explanation from post contest discussion meeting.\n\nhttps://www.youtube.com/watch?v=LDNMlgBi5vg&list=PLQ9cQ3JqeqU_T-Ic3384j4uWDxUnXjlVO&index=4 | 2 | 0 | [] | 0 |
build-a-matrix-with-conditions | C++ Graph Solution | c-graph-solution-by-travanj05-8cu0 | cpp\nint rowIdx[500], colIdx[500];\n\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>> &rowConditions, vector<vector<in | travanj05 | NORMAL | 2022-08-28T06:15:33.346422+00:00 | 2022-08-28T06:15:33.346464+00:00 | 53 | false | ```cpp\nint rowIdx[500], colIdx[500];\n\nclass Solution {\npublic:\n vector<vector<int>> buildMatrix(int k, vector<vector<int>> &rowConditions, vector<vector<int>> &colConditions) {\n int n = rowConditions.size(), m = colConditions.size();\n fill(rowIdx, rowIdx + k + 1, 0);\n fill(colIdx, colIdx + k + 1, 0);\n vector<vector<int>> rGraph(k + 1), cGraph(k + 1);\n for (int i = 0; i < n; i++) {\n rowIdx[rowConditions[i][1]]++;\n rGraph[rowConditions[i][0]].push_back(rowConditions[i][1]);\n }\n for (int i = 0; i < m; i++) {\n colIdx[colConditions[i][1]]++;\n cGraph[colConditions[i][0]].push_back(colConditions[i][1]);\n }\n queue<int> cq, rq;\n for (int i = 1; i <= k; i++) {\n if (rowIdx[i] == 0) rq.push(i);\n if (colIdx[i] == 0) cq.push(i);\n }\n vector<int> rows(k + 1), cols(k + 1);\n int cnt = 0;\n while (!cq.empty()) {\n int i = cq.front();\n cq.pop();\n cols[i] = cnt++;\n for (int j : cGraph[i]) {\n colIdx[j]--;\n if (colIdx[j] == 0) {\n cq.push(j);\n }\n }\n }\n if (cnt != k) return {};\n cnt = 0;\n while (!rq.empty()) {\n int i = rq.front();\n rq.pop();\n rows[i] = cnt++;\n for (int j : rGraph[i]) {\n rowIdx[j]--;\n if (rowIdx[j] == 0) {\n rq.push(j);\n }\n }\n }\n if (cnt != k) return {};\n vector<vector<int>> res(k, vector<int>(k, 0));\n for (int i = 1; i <= k; i++) {\n res[rows[i]][cols[i]] = i;\n }\n return res;\n }\n};\n``` | 2 | 0 | ['Graph', 'C', 'C++'] | 1 |
build-a-matrix-with-conditions | C++ - Quick Explained Code - Topo Sort, Kahn's Algo | c-quick-explained-code-topo-sort-kahns-a-vy4b | Thought Process:\n This is an interesting problem, specially to see how graph helps solve this.\n Reading the problem with the rowConditions and columnCondition | geekykant | NORMAL | 2022-08-28T05:18:17.898189+00:00 | 2022-08-28T05:23:36.391181+00:00 | 98 | false | **Thought Process:**\n* This is an interesting problem, specially to see how graph helps solve this.\n* Reading the problem with the `rowConditions` and `columnConditions` does give the hint that applying topological sort would make sense here.\n* So we do the topo sort, and sparsely set the index across columns. Together, we apply it on rows and get one of the possible combinations.\n* **Edge case**: We can check if building matrix is not possible, which is when graph is cyclic i.e. `topo output size != N`.\n\n```cpp\nvector<int> topoSort(vector<vector<int>> conditions, int k){\n vector<int> indegree(k+1);\n unordered_map<int, vector<int>> graph;\n\n //building graph and indegree\n for(auto cond: conditions){\n graph[cond[0]].push_back(cond[1]);\n indegree[cond[1]]++;\n }\n\n //building the topo sort queue (0 degree nodes)\n queue<int> q;\n for(int i=1; i <= k; i++){\n if(indegree[i] == 0)\n q.push(i);\n }\n\n //building the topo ordered output\n vector<int> res;\n while(!q.empty()){\n int node = q.front(); q.pop();\n res.push_back(node);\n\n for(int child: graph[node]){\n indegree[child]--;\n if(indegree[child] == 0)\n q.push(child);\n }\n }\n return res;\n}\n\nvector<vector<int>> buildMatrix(int k, vector<vector<int>>& RowConditions, vector<vector<int>>& ColConditions) {\n vector<int> rows = topoSort(RowConditions, k),\n cols = topoSort(ColConditions, k);\n\n // Acc to Kahn\'s algo, if topo output size != N, then it\'s cyclic\n if(rows.size() != k || cols.size() != k) return {};\n\n vector<vector<int>> res(k, vector<int>(k, 0));\n vector<int> colIdx(k+1, 0);\n\n // The cols array has [most dependent,.. -> ..,least dependent elemts]\n // For colConditions = [[2,1],[3,2]], it will be [3,2,1]\n // val 3 -> idx 0\n // val 2 -> idx 1\n // val 1 -> idx 2\n for(int j=0; j < k; j++)\n colIdx[cols[j]] = j;\n\n // In each row, place the "row[i]" value at the j th index, \n // we sparsely allocated just above.\n for(int i=0; i < k; i++)\n res[i][colIdx[rows[i]]] = rows[i];\n\n return res;\n}\n``` | 2 | 0 | ['Graph', 'Topological Sort', 'C'] | 0 |
build-a-matrix-with-conditions | C# Solution | Graph, BFS | c-solution-graph-bfs-by-tonytroeff-g3bh | C#\npublic class Solution {\n public int[][] BuildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n Dictionary<int, HashSet<int>> rowMap | tonytroeff | NORMAL | 2022-08-28T05:10:52.567740+00:00 | 2022-08-28T05:10:52.567794+00:00 | 29 | false | ```C#\npublic class Solution {\n public int[][] BuildMatrix(int k, int[][] rowConditions, int[][] colConditions) {\n Dictionary<int, HashSet<int>> rowMap = new (), rowDepsMap = new (), colMap = new (), colDepsMap = new ();\n for (int i = 0; i < k; i++)\n {\n rowMap[i] = new ();\n rowDepsMap[i] = new ();\n colMap[i] = new ();\n colDepsMap[i] = new ();\n }\n\n FillData(rowConditions, rowMap, rowDepsMap);\n FillData(colConditions, colMap, colDepsMap);\n\n int[] rows = new int[k], cols = new int[k];\n if (Iterate(rowMap, rowDepsMap, rows) == false || Iterate(colMap, colDepsMap, cols) == false) return new int[0][];\n\n int[][] ans = new int[k][];\n for (int i = 0; i < k; i++) ans[i] = new int[k];\n for (int i = 0; i < k; i++) ans[rows[i]][cols[i]] = i + 1;\n\n return ans;\n\n void FillData(int[][] conditions, Dictionary<int, HashSet<int>> map, Dictionary<int, HashSet<int>> depsMap)\n {\n for (int i = 0; i < conditions.Length; i++)\n {\n map[conditions[i][0] - 1].Add(conditions[i][1] - 1);\n depsMap[conditions[i][1] - 1].Add(conditions[i][0] - 1);\n }\n }\n\n bool Iterate(Dictionary<int, HashSet<int>> map, Dictionary<int, HashSet<int>> depsMap, int[] res)\n {\n Queue<int> q = new ();\n foreach (var (num, deps) in depsMap)\n {\n if (deps.Count == 0) q.Enqueue(num);\n }\n\n if (q.Count == 0) return false;\n\n int index = 0;\n while (q.Count > 0)\n {\n int current = q.Dequeue();\n res[current] = index;\n\n foreach (var next in map[current])\n {\n depsMap[next].Remove(current);\n if (depsMap[next].Count == 0) q.Enqueue(next);\n }\n\n index++;\n }\n\n return index == k;\n }\n }\n}\n``` | 2 | 0 | ['Breadth-First Search', 'Graph'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.