question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
check-balanced-string | Beats 99% in java and One of the most easiest and simplest logic🔥 | beats-99-in-java-and-one-of-the-most-eas-k1cf | Complexity
Time complexity:
O(N)
Space complexity:
O(1)
Code | aryanxrajj | NORMAL | 2025-03-31T16:01:16.203544+00:00 | 2025-03-31T16:01:16.203544+00:00 | 1 | false |
# Complexity
- Time complexity:
- O(N)
- Space complexity:
- O(1)
# Code
```java []
class Solution {
public boolean isBalanced(String num) {
int even = 0, odd = 0;
for(int i = 0;i < num.length();i++){
char ch = num.charAt(i);
if(i % 2 == 0){
even+=ch - '0';
}else{
odd+=ch - '0';
}
}
if(even == odd){
return true;
}else{
return false;
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
check-balanced-string | 0 ms Beats 100.00% | Easy Typescript Solution with Explanation | 0-ms-beats-10000-easy-typescript-solutio-hba5 | IntuitionApproachComplexity
Time complexity: O(n) where n is the length of the input string num. This is because the function iterates through each character of | chetannada | NORMAL | 2025-03-31T11:26:19.461824+00:00 | 2025-03-31T11:26:43.891317+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(n)$$ where n is the length of the input string `num`. This is because the function iterates through each character of the string exactly once, performing constant-time operations (addition and comparison) for each character.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$ as the function uses a fixed amount of space for the variables `odd` and `even`, regardless of the size of the input string. No additional data structures that grow with the input size are used. Thus, the space used remains constant.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```typescript []
function isBalanced(num: string): boolean {
let odd: number = 0;
let even: number = 0;
for (let i = 0; i < num.length; i++) {
// if index is even then add current digit in even else in odd
if (i % 2 === 0) {
even += +num[i];
} else {
odd += +num[i];
}
}
// if odd is even is equal to odd then its balanced string
return even === odd;
};
``` | 0 | 0 | ['String', 'TypeScript'] | 0 |
check-balanced-string | 0 ms Beats 100.00% | Easy Javascript Solution with Explanation | 0-ms-beats-10000-easy-javascript-solutio-yic4 | IntuitionApproachComplexity
Time complexity: O(n) where n is the length of the input string num. This is because the function iterates through each character of | chetannada | NORMAL | 2025-03-31T11:23:18.805756+00:00 | 2025-03-31T11:23:43.620964+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(n)$$ where n is the length of the input string `num`. This is because the function iterates through each character of the string exactly once, performing constant-time operations (addition and comparison) for each character.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$ as the function uses a fixed amount of space for the variables `odd` and `even`, regardless of the size of the input string. No additional data structures that grow with the input size are used. Thus, the space used remains constant.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {string} num
* @return {boolean}
*/
var isBalanced = function (num) {
let odd = 0;
let even = 0;
for (let i = 0; i < num.length; i++) {
// if index is even then add current digit in even else in odd
if (i % 2 === 0) {
even += +num[i];
} else {
odd += +num[i];
}
}
// if odd is even is equal to odd then its balanced string
return even === odd;
};
``` | 0 | 0 | ['String', 'JavaScript'] | 0 |
check-balanced-string | Luke - checking whether string is balanced | luke-checking-whether-string-is-balanced-3oif | IntuitionApproachI used two variables (odd and even). I used a for loop and if the indice is even, I add the value of the index to the even, otherwise, I do tha | thunderlukey | NORMAL | 2025-03-30T13:39:08.706074+00:00 | 2025-03-30T13:39:08.706074+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
I used two variables (odd and even). I used a for loop and if the indice is even, I add the value of the index to the even, otherwise, I do that for the odd. Finally, I check if even and odd are equal. If so, return true. Otherwise, return false.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean isBalanced(String num) {
int odd = 0;
int even = 0;
for (int i=0; i<num.length(); i++){
if (i % 2 != 0){
odd += Character.getNumericValue(num.charAt(i));
}
else{
even += Character.getNumericValue(num.charAt(i));
}
}
return odd == even;
}
}
``` | 0 | 0 | ['Java'] | 0 |
check-balanced-string | O(N) Python3 solution easy peasy | on-python3-solution-easy-peasy-by-winsto-d0ep | IntuitionSimply sum the odd/even digitsApproach
Initialize two variables and a bool used as flag
Cycle chars in string
if flag is true add digit to first vari | WinstonWolf | NORMAL | 2025-03-29T17:23:20.359038+00:00 | 2025-03-29T17:23:20.359038+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Simply sum the odd/even digits
# Approach
<!-- Describe your approach to solving the problem. -->
- Initialize two variables and a bool used as flag
- Cycle chars in string
- - if flag is true add digit to first variable else add it in the second variable
- - Invert the flag
- Return true if first and second variable has the same value otherwise return false
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
one = 0
two = 0
flag = True
for it in num:
if flag:
one += ord(it) - ord('0')
else:
two += ord(it) - ord('0')
flag = not flag
return one == two
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | Scala solution with implicit and map | scala-solution-with-implicit-and-map-by-sqmnm | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | iyIeO99AmH | NORMAL | 2025-03-29T13:48:10.730969+00:00 | 2025-03-29T13:48:10.730969+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```scala []
object Solution {
def isBalanced(num: String): Boolean = {
num.toCharArray.zipWithIndex.map {
case (value, idx) =>
if (idx % 2 == 0) value.asNum else -value.asNum
}.sum == 0
}
implicit class CharNum(c: Char) {
def asNum: Int = c - '0'
}
}
``` | 0 | 0 | ['Scala'] | 0 |
check-balanced-string | Balanced or Busted? ⚖️🔢 Let’s Find Out! 😂 Python !! | balanced-or-busted-lets-find-out-python-b01zv | Intuition
The problem requires checking if the sum of digits at even indices
is equal to the sum of digits at odd indices.
Since we only need to traverse the st | Shahin1212 | NORMAL | 2025-03-29T05:16:07.090832+00:00 | 2025-03-29T05:16:07.090832+00:00 | 1 | false | # Intuition
- The problem requires checking if the sum of digits at even indices
- is equal to the sum of digits at odd indices.
- Since we only need to traverse the string once, a simple iteration
- with two counters (one for even indices and one for odd) will work efficiently.
# Approach
1. Initialize two variables: `even` for sum of digits at even indices and `odd` for sum at odd indices.
2. Iterate through the string:
# - If the index is even, add the digit to `even`.
# - If the index is odd, add the digit to `odd`.
3. Compare both sums and return `True` if they are equal, otherwise return `False`.
# Complexity
- Time complexity: O(n), where `n` is the length of the input string `num`, since we traverse it once.
- Space complexity: O(1), as we use only two integer variables for storage.
# Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
even = 0
odd = 0
for i in range(0, len(num), 2):
even += int(num[i])
for j in range(1, len(num), 2):
odd += int(num[j])
return odd == even
```

| 0 | 0 | ['Python3'] | 0 |
check-balanced-string | Balanced or Busted? ⚖️🔢 Let’s Find Out! 😂 Python !! | balanced-or-busted-lets-find-out-python-rrflu | Intuition
The problem requires checking if the sum of digits at even indices
is equal to the sum of digits at odd indices.
Since we only need to traverse the st | Shahin1212 | NORMAL | 2025-03-29T05:16:04.338184+00:00 | 2025-03-29T05:16:04.338184+00:00 | 1 | false | # Intuition
- The problem requires checking if the sum of digits at even indices
- is equal to the sum of digits at odd indices.
- Since we only need to traverse the string once, a simple iteration
- with two counters (one for even indices and one for odd) will work efficiently.
# Approach
1. Initialize two variables: `even` for sum of digits at even indices and `odd` for sum at odd indices.
2. Iterate through the string:
# - If the index is even, add the digit to `even`.
# - If the index is odd, add the digit to `odd`.
3. Compare both sums and return `True` if they are equal, otherwise return `False`.
# Complexity
- Time complexity: O(n), where `n` is the length of the input string `num`, since we traverse it once.
- Space complexity: O(1), as we use only two integer variables for storage.
# Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
even = 0
odd = 0
for i in range(0, len(num), 2):
even += int(num[i])
for j in range(1, len(num), 2):
odd += int(num[j])
return odd == even
```

| 0 | 0 | ['Python3'] | 1 |
check-balanced-string | Quick code loops | quick-code-loops-by-kunal_1310-weka | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kunal_1310 | NORMAL | 2025-03-28T07:05:09.978981+00:00 | 2025-03-28T07:05:09.978981+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isBalanced(string num) {
int e_sum=0,o_sum=0;
for(int i=0;i<num.size();i++){
if(i%2==0){
e_sum+=(num[i]-'0');
}
else{
o_sum+=(num[i]-'0');
}
}
return (e_sum==o_sum)?true:false;
}
};
``` | 0 | 0 | ['C++'] | 0 |
check-balanced-string | Simple Swift Solution | simple-swift-solution-by-felisviridis-2yh9 | Code | Felisviridis | NORMAL | 2025-03-27T11:23:00.923845+00:00 | 2025-03-27T11:23:00.923845+00:00 | 4 | false | 
# Code
```swift []
class Solution {
func isBalanced(_ num: String) -> Bool {
var digits = Array(num), evenSum = 0, oddSum = 0
for i in 0..<digits.count {
if i % 2 == 0 {
oddSum += digits[i].wholeNumberValue!
} else {
evenSum += digits[i].wholeNumberValue!
}
}
return evenSum == oddSum
}
}
``` | 0 | 0 | ['Swift'] | 0 |
check-balanced-string | O(n) easy to understand solution with JavaScript :) | on-easy-to-understand-solution-with-java-d9rn | IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(1)Code | bek-shoyatbek | NORMAL | 2025-03-27T00:05:34.041577+00:00 | 2025-03-27T00:05:34.041577+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$
# Code
```javascript []
/**
* @param {string} num
* @return {boolean}
*/
var isBalanced = function(num) {
let sumEvens = 0;
let sumOdds = 0;
let turn = 1;
for(let char of num){
if(turn%2==0) sumEvens+=parseInt(char);
else sumOdds+=parseInt(char);
turn++;
}
return sumEvens===sumOdds;
};
``` | 0 | 0 | ['JavaScript'] | 0 |
check-balanced-string | my solution | my-solution-by-leman_cap13-if96 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | leman_cap13 | NORMAL | 2025-03-24T14:44:22.305451+00:00 | 2025-03-24T14:44:22.305451+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
ev=[]
od=[]
for i in range(0,len(num),2):
ev.append(int(num[i]))
for j in range(1,len(num),2):
od.append(int(num[j]))
print(ev)
print(od)
if sum(ev)==sum(od):
return True
else:
return False
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | Something Interesting | something-interesting-by-shakhob-yr6x | Code | Shakhob | NORMAL | 2025-03-24T07:04:30.971248+00:00 | 2025-03-24T07:04:30.971248+00:00 | 1 | false | # Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
number = int(num)
even = 0
odd = 0
i = 0
while number > 0:
if i % 2 == 0:
even += number % 10
else:
odd += number % 10
number //= 10
i += 1
return even == odd
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | 0 ms Beats 100.00% | 0-ms-beats-10000-by-bvc01654-xi31 | IntuitionApproachComplexity
Time complexity:O(n)
Space complexity:O(1)
Code | bvc01654 | NORMAL | 2025-03-23T09:56:21.631912+00:00 | 2025-03-23T09:56:21.631912+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isBalanced(string num) {
int s1=0,s2=0;
for(int i=0;i<num.size();i++)
{
if(i%2==0)
s1+=(num[i]-'0');
else
s2+=(num[i]-'0');
}
return s1==s2;
}
};
``` | 0 | 0 | ['String', 'C++'] | 0 |
check-balanced-string | PYTHON WITH MK!! | python-with-mk-by-mohan_kumar_hd-k7td | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | MOHAN_KUMAR_HD | NORMAL | 2025-03-22T18:03:04.201367+00:00 | 2025-03-22T18:03:04.201367+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def isBalanced(self, s: str) -> bool:
even =0
odd=0
for i in range(0,len(s),2):
even=even+int(s[i])
for i in range(1,len(s),2):
odd+=int(s[i])
return (even==odd)
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | Check Balanced String | check-balanced-string-by-jyenduri-2qgb | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | jyenduri | NORMAL | 2025-03-22T07:41:44.522930+00:00 | 2025-03-22T07:41:44.522930+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {string} num
* @return {boolean}
*/
var isBalanced = function(num) {
const values = num.split('')
let eventCount= 0
let OddCount=0
for(let i=0 ; i < values.length ; i++){
if(i%2 ==0){
eventCount= eventCount+parseInt(values[i])
}else{
OddCount= OddCount+parseInt(values[i])
}
}
return OddCount==eventCount
};
``` | 0 | 0 | ['JavaScript'] | 0 |
check-balanced-string | Very Easy Solution | very-easy-solution-by-devanand8590-p2iw | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Devanand8590 | NORMAL | 2025-03-21T04:47:31.321491+00:00 | 2025-03-21T04:47:31.321491+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```dart []
class Solution {
bool isBalanced(String num) {
List<int> list = num.split('').map(int.parse).toList();
var addEven=0;
var addOdd=0;
for(int i=0;i<list.length;i++)
{
if(i%2==0)
{
addOdd += list[i];
}
else{
addEven += list[i];
}
}
return addOdd==addEven;
}
}
``` | 0 | 0 | ['Dart'] | 0 |
check-balanced-string | Solution | solution-by-omkarpatil_1304-3jej | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | omkarpatil_1304 | NORMAL | 2025-03-20T18:14:24.808750+00:00 | 2025-03-20T18:14:24.808750+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean isBalanced(String num) {
int evensum=0;
int oddsum=0;
for(int i=0;i<num.length();i++)
{
if(i%2==0)
{
evensum=evensum+num.charAt(i)-'0';
}
else
{
oddsum=oddsum+num.charAt(i)-'0';
}
}
return oddsum==evensum;
}
}
``` | 0 | 0 | ['Java'] | 0 |
check-balanced-string | Easy Solution | easy-solution-by-adhi_m_s-9rox | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Adhi_M_S | NORMAL | 2025-03-20T10:23:20.011189+00:00 | 2025-03-20T10:23:20.011189+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def isBalanced(self, num):
"""
:type num: str
:rtype: bool
"""
return sum([int(num[i]) for i in range(len(num)) if i%2!=0])==sum([int(num[i]) for i in range(len(num)) if i%2==0])
``` | 0 | 0 | ['Python'] | 0 |
check-balanced-string | Simple java Solution | simple-java-solution-by-pritdesa-9it8 | Code | pritdesa | NORMAL | 2025-03-19T19:52:54.281237+00:00 | 2025-03-19T19:52:54.281237+00:00 | 1 | false |
# Code
```java []
class Solution {
public boolean isBalanced(String num) {
int even = 0, odd = 0;
for(int i=0;i<num.length();i++){
if(i%2==0){
even += Character.getNumericValue(num.charAt(i));
}else{
odd += Character.getNumericValue(num.charAt(i));
}
}
if(even == odd){
return true;
}
return false;
}
}
``` | 0 | 0 | ['Java'] | 0 |
check-balanced-string | EASY SOLUTION 0ms /100 beats | easy-solution-0ms-100-beats-by-cookie_co-zise | IntuitionApproachMain approach is to first convert string to integer by subtracting the current string value to '0' ASCII value ...Complexity
Time complexity: | Cookie_coder | NORMAL | 2025-03-19T18:10:18.023861+00:00 | 2025-03-19T18:10:18.023861+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Main approach is to first convert string to integer by subtracting the current string value to '0' ASCII value ...
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
bool isBalanced(string num) {
int esum = 0, osum = 0;
for (int i = 0; i < num.length(); i++) {
int digit = num[i] - '0'; // Convert character to integer
if (i % 2 == 0) {
esum += digit; // Even index (0-based)
} else {
osum += digit; // Odd index (0-based)
}
}
return esum == osum; // Return true if sums are equal
}
};
``` | 0 | 0 | ['C++'] | 0 |
check-balanced-string | clear logic | clear-logic-by-sophie84-b0c0 | Code | sophie84 | NORMAL | 2025-03-19T17:02:10.816687+00:00 | 2025-03-19T17:02:10.816687+00:00 | 1 | false | # Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
sum_even = 0
sum_odd = 0
for i in range(len(num)):
if i%2==0:
sum_even += int(num[i])
else:
sum_odd += int(num[i])
return (sum_even==sum_odd)
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | easy solution | easy-solution-by-mukund_th04-odet | IntuitionWe need to check if a string of digits is balanced, meaning the sum of digits at even indices is equal to the sum of digits at odd indices. The simples | Mukund_TH04 | NORMAL | 2025-03-19T06:32:40.394077+00:00 | 2025-03-19T06:32:40.394077+00:00 | 1 | false | # Intuition
We need to check if a string of digits is balanced, meaning the sum of digits at even indices is equal to the sum of digits at odd indices. The simplest idea is to traverse the string once, summing digits at even and odd positions separately, and then compare the two sums.
---
# Approach
1. **Traverse the String:**
Iterate through each character in the input string.
2. **Convert Characters to Digits:**
For each character, subtract `'0'` to convert it from a character to its integer equivalent.
3. **Sum Based on Index Parity:**
- If the current index is even (i.e., `i % 2 == 0`), add the digit to the `even` sum.
- If the index is odd, add the digit to the `odd` sum.
4. **Compare Sums:**
After processing the entire string, check if the two sums are equal. If they are, the string is balanced; otherwise, it is not.
---
# Complexity
- **Time Complexity:**
\( O(n) \) where \( n \) is the length of the string, since we process each character exactly once.
- **Space Complexity:**
\( O(1) \) because we only use a few integer variables regardless of the input size.
---
# Code
```cpp
class Solution {
public:
bool isBalanced(string num) {
int even = 0, odd = 0;
for (int i = 0; i < num.size(); i++) {
int digit = num[i] - '0';
if (i % 2 == 0) {
even += digit;
} else {
odd += digit;
}
}
return even == odd;
}
};
``` | 0 | 0 | ['C++'] | 0 |
check-balanced-string | one liner... check it out | one-liner-check-it-out-by-senth-q1ye | Complexity
Time complexity:
O(n)
Space complexity:
O(n)
Code | senth | NORMAL | 2025-03-19T05:59:22.396325+00:00 | 2025-03-19T05:59:22.396325+00:00 | 1 | false | # Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
return sum(int(n) for n in num[::2]) == sum(int(n) for n in num[1::2])
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | simple... | simple-by-anakha123-ifbz | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | anakha123 | NORMAL | 2025-03-18T04:24:00.127779+00:00 | 2025-03-18T04:24:00.127779+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {string} num
* @return {boolean}
*/
var isBalanced = function(num) {
let arr=num.split('');
let odd=0,even=0;
for(let i=0;i<arr.length;i++){
let value= parseInt(arr[i])
if((i+1)%2==0){
even+=value;
}else{
odd+=value;
}
}
console.log(odd,even)
if(odd===even)return true;
return false
};
``` | 0 | 0 | ['JavaScript'] | 0 |
check-balanced-string | C++ Easiest approach | c-easiest-approach-by-aasthagupta_17-w1yn | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | aasthagupta_17 | NORMAL | 2025-03-16T07:57:13.648498+00:00 | 2025-03-16T07:57:13.648498+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isBalanced(string num) {
int sum1=0;
int sum2=0;
for(int i=0;i<num.size();i++){
if(i%2==0){
sum1+=num[i] -'0';
}
else{
sum2+=num[i] -'0';
}
}
return sum1==sum2;
}
};
``` | 0 | 0 | ['C++'] | 0 |
check-balanced-string | Java Solution beats 99.04% | java-solution-beats-9904-by-moreshivam20-9t9b | IntuitionFind even index and odd index then add sumApproachSo we will run two for loops first start from 0th index as even and will increment counter each time | moreshivam20 | NORMAL | 2025-03-16T06:18:20.092720+00:00 | 2025-03-16T06:18:20.092720+00:00 | 1 | false | # Intuition
Find even index and odd index then add sum
# Approach
So we will run two for loops first start from 0th index as even and will increment counter each time by i+2 for skip one odd index and for odd index we will start from 1st index and will keep addiing respeciveli in evenSum and OddSum and in last will
return evenSum == oddSum
Another approach we can use is that use if loop and find index of even digit by i%2 == 0 then add these digits in evenSum and else in oddSum bur for converting char into int we need to use this
oddSum = oddSum + (nums[i] -'0'); so we will get correct integer value
# Code
```java []
class Solution {
public boolean isBalanced(String num) {
int eSum = 0;
int oSum =0;
for(int i =0; i<num.length(); i=i+2){
eSum = eSum + (num.charAt(i) - '0');
}
for(int i =1 ; i<num.length(); i=i+2){
oSum = oSum + (num.charAt(i) -'0');
}
return eSum == oSum;
}
}
//2nd approach
class Solution {
public boolean isBalanced(String num) {
char[] nums = num.toCharArray();
int eSum = 0;
int oSum =0;
for(int i =0; i<nums.length; i++){
if( i%2 == 0){
eSum = eSum + (nums[i] - '0');
}else{
oSum = oSum + (nums[i] - '0');
}
}
System.out.println(eSum);
System.out.println(oSum);
return eSum == oSum;
}
}
```
| 0 | 0 | ['Java'] | 0 |
check-balanced-string | i think this is the easy way to understand for the beginner but not the optimize solution | i-think-this-is-the-easy-way-to-understa-catf | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | mdarizaman | NORMAL | 2025-03-15T08:47:43.842033+00:00 | 2025-03-15T08:47:43.842033+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def isBalanced(self, num: str) -> bool:
odd=''
even=''
for i in range(len(num)):
if i%2==0:
even+=num[i]
else:
odd+=num[i]
eSum=0
for i in even:
eSum+=int(i)
osum=0
for i in odd:
osum+=int(i)
if eSum == osum:
flag = True
else:
flag = False
return flag
``` | 0 | 0 | ['Python3'] | 0 |
check-balanced-string | 0ms Runtime with best Case Time Complexity using C Language and Suitable String Operations : ) | 0ms-runtime-with-best-case-time-complexi-8qxd | IntuitionThe problem requires checking whether the sum of digits at even indices equals the sum at odd indices. By iterating through the string of digits, you c | Vivek_Bartwal | NORMAL | 2025-03-15T06:12:24.812462+00:00 | 2025-03-15T06:12:24.812462+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires checking whether the sum of digits at even indices equals the sum at odd indices. By iterating through the string of digits, you can categorize the digits based on their indices and compute two separate sums. If these sums are equal, the string is considered "balanced."
# Approach
<!-- Describe your approach to solving the problem. -->
Initialize Variables:
Create two variables, sumeven and sumodd, both set to 0, to store the sums of digits at even and odd indices, respectively.
Iterate Through the String:
Traverse the string character by character using a loop.
Convert each character to its corresponding numeric value using num[i] - '0'.
Add the numeric value to either sumeven or sumodd based on the parity of the index (i % 2).
Comparison:
After the loop finishes, compare sumeven and sumodd.
Return true if the sums are equal; otherwise, return false.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
bool isBalanced(char* num) {
int sumeven = 0, sumodd = 0;
for(int i=0; num[i] != '\0'; i++)
{
if(i%2==0)
{
sumeven = sumeven + num[i] - '0';
}
else
{
sumodd = sumodd + num[i] - '0';
}
}
return sumeven == sumodd;
}
``` | 0 | 0 | ['C'] | 0 |
check-balanced-string | Beats 100% || C++ | beats-100-c-by-prem2907-gm2s | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | prem2907 | NORMAL | 2025-03-12T14:32:44.421229+00:00 | 2025-03-12T14:32:44.421229+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isBalanced(string num) {
int ev = 0, od = 0;
for (int i = 0; i < num.size(); i++) {
if (i % 2 == 0)
ev += num[i] - '0';
else
od += num[i] - '0';
}
return ev == od;
}
};
``` | 0 | 0 | ['C++'] | 0 |
check-balanced-string | Java | java-by-soumya_699-0fc5 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Soumya_699 | NORMAL | 2025-03-12T06:08:06.032818+00:00 | 2025-03-12T06:08:06.032818+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean isBalanced(String s) {
int sumEven = 0, sumOdd = 0;
for (int i = 0; i < s.length(); i++) {
if (i % 2 == 0) {
sumEven = sumEven + Character.getNumericValue(s.charAt(i));
} else {
sumOdd = sumOdd + Character.getNumericValue(s.charAt(i));
}
}
return sumOdd == sumEven;
}
}
``` | 0 | 0 | ['Java'] | 0 |
check-balanced-string | easy and best solution in c++ | easy-and-best-solution-in-c-by-ashish754-sfhm | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Ashish754937 | NORMAL | 2025-03-12T05:39:05.879263+00:00 | 2025-03-12T05:39:05.879263+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isBalanced(string num) {
int n=num.size();
int oddDigits=0;
int evenDigits=0;
for(int i=0;i<n;i++)
{
if((i+1)%2==0)
{
evenDigits+=num[i]-'0';
}
else
{
oddDigits+=num[i]-'0';
}
}
return oddDigits==evenDigits;
}
};
``` | 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) || Math | o1-math-by-fahad06-sdn7 | Intuition\n- Simplify the problem by understanding the cyclic nature of the ball passing. By calculating the number of complete back-and-forth trips and the rem | fahad_Mubeen | NORMAL | 2024-06-09T04:03:32.733818+00:00 | 2024-08-26T16:02:27.187913+00:00 | 8,139 | false | # Intuition\n- Simplify the problem by understanding the cyclic nature of the ball passing. By calculating the number of complete back-and-forth trips and the remaining steps, we can determine the final position of the ball. \n- If the total number of complete trips is even, the ball continues in the forward direction.\n- If odd, it reverses direction.\n\n# Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n n--; // Decrement n to simplify calculation (so range is now 0 to n-1)\n int rounds = k / n; // Calculate the number of complete back-and-forth trips\n int rem = k % n; // Calculate the remaining steps after the last complete trip\n\n if(rounds % 2 == 0) {\n // If the number of complete back-and-forth trips is even\n return rem; // The ball is passed forward from the start\n } else {\n // If the number of complete back-and-forth trips is odd\n return (n - rem); // The ball is passed backward from the end\n }\n }\n};\n```\n```Java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n n--; // Decrement n to simplify calculation (so range is now 0 to n-1)\n int rounds = k / n; // Calculate the number of complete back-and-forth trips\n int rem = k % n; // Calculate the remaining steps after the last complete trip\n\n if (rounds % 2 == 0) {\n // If the number of complete back-and-forth trips is even\n return rem; // The ball is passed forward from the start\n } else {\n // If the number of complete back-and-forth trips is odd\n return n - rem; // The ball is passed backward from the end\n }\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n n -= 1 # Decrement n to simplify calculation (so range is now 0 to n-1)\n rounds = k // n # Calculate the number of complete back-and-forth trips\n rem = k % n # Calculate the remaining steps after the last complete trip\n\n if rounds % 2 == 0:\n # If the number of complete back-and-forth trips is even\n return rem # The ball is passed forward from the start\n else:\n # If the number of complete back-and-forth trips is odd\n return n - rem # The ball is passed backward from the end\n\n```\n\n | 71 | 0 | ['Math', 'C++', 'Java', 'Python3'] | 11 |
find-the-child-who-has-the-ball-after-k-seconds | Easy Video Solution 🔥 || How to 🤔 in Interview || O(N)->O(1) 🔥 | easy-video-solution-how-to-in-interview-pq6kq | If you like the solution Please Upvote and subscribe to my youtube channel\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nDry Run | ayushnemmaniwar12 | NORMAL | 2024-06-09T04:04:18.588221+00:00 | 2024-06-09T06:33:24.740726+00:00 | 677 | false | ***If you like the solution Please Upvote and subscribe to my youtube channel***\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDry Run few examples and observe how you can derive a formula\n\n\n\n# ***Easy Video Explanation***\n\nhttps://youtu.be/lTD4AqpPxUA\n\n \n\n# Code (Brute Force)\n\n\n```C++ []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int p = 0;\n int f=0,i=0;\n while(k>0) {\n while(k>0 && i<n-1) {\n i++;\n k--;\n }\n if(k==0)\n return i;\n while(k>0 && i>0) {\n i--;\n k--;\n }\n if(k==0)\n return i;\n }\n return 0;\n }\n};\n```\n```python []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n i = 0\n while k > 0:\n while k > 0 and i < n - 1:\n i += 1\n k -= 1\n if k == 0:\n return i\n while k > 0 and i > 0:\n i -= 1\n k -= 1\n if k == 0:\n return i\n return 0\n\n```\n```Java []\n\nclass Solution {\n public int numberOfChild(int n, int k) {\n int i = 0;\n while (k > 0) {\n while (k > 0 && i < n - 1) {\n i++;\n k--;\n }\n if (k == 0) {\n return i;\n }\n while (k > 0 && i > 0) {\n i--;\n k--;\n }\n if (k == 0) {\n return i;\n }\n }\n return 0;\n }\n}\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(Max(N,k))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n\n# Code (Optimized)\n\n\n```C++ []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n n--; // Decrement n to simplify calculation (so range is now 0 to n-1)\n int rounds = k / n; // Calculate the number of complete back-and-forth trips\n int rem = k % n; // Calculate the remaining steps after the last complete trip\n\n if(rounds % 2 == 0) {\n // If the number of complete back-and-forth trips is even\n return rem; // The ball is passed forward from the start\n } else {\n // If the number of complete back-and-forth trips is odd\n return (n - rem); // The ball is passed backward from the end\n }\n }\n};\n```\n```python []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n n -= 1 # Decrement n to simplify calculation (so range is now 0 to n-1)\n rounds = k // n # Calculate the number of complete back-and-forth trips\n rem = k % n # Calculate the remaining steps after the last complete trip\n\n if rounds % 2 == 0:\n # If the number of complete back-and-forth trips is even\n return rem # The ball is passed forward from the start\n else:\n # If the number of complete back-and-forth trips is odd\n return n - rem # The ball is passed backward from the end\n\n```\n```Java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n n--; // Decrement n to simplify calculation (so range is now 0 to n-1)\n int rounds = k / n; // Calculate the number of complete back-and-forth trips\n int rem = k % n; // Calculate the remaining steps after the last complete trip\n\n if (rounds % 2 == 0) {\n // If the number of complete back-and-forth trips is even\n return rem; // The ball is passed forward from the start\n } else {\n // If the number of complete back-and-forth trips is odd\n return n - rem; // The ball is passed backward from the end\n }\n }\n}\n\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# ***If you like the solution Please Upvote and subscribe to my youtube channel***\n***It Motivates me to record more videos***\n\n*Thank you* \uD83D\uDE00 | 12 | 5 | ['Math', 'Iterator', 'Python', 'C++', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | ✅✅💯EASY SOLUTION || C++ 🔥🔥💯✅✅ | easy-solution-c-by-nikhil73995-0g7y | Intuition\n Describe your first thoughts on how to solve this problem. \nImagine children playing a game of "pass the ball" in a line.\nThe ball starts with the | nikhil73995 | NORMAL | 2024-06-09T04:22:28.127008+00:00 | 2024-06-09T05:35:26.186774+00:00 | 933 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nImagine children playing a game of "pass the ball" in a line.\nThe ball starts with the first child and moves one step right each second.\nWhen the ball reaches the last child, they throw it back (reverse direction).\nWhen the ball reaches the first child again, they throw it forward (reverse direction again).\nThe ball keeps moving like this: right, right, ..., reverse, left, left, ..., reverse, right, and so on.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart with position = 0 (first child) and direction = 1 (moving right).\nFor each of the k seconds:\nMove the ball: position += direction\n\nIf direction is 1, move right. If -1, move left.\nCheck if we need to reverse direction:\nIf position is n-1 (last child), set direction = -1 (start moving left).\nIf position is 0 (first child), set direction = 1 (start moving right).\n\n\n\n\nAfter k seconds, return the final position.\n# Complexity\n- Time complexity:O(k) - Depends on the number of seconds.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int position = 0;\n int direction = 1;\n \n for (int i = 0; i < k; ++i) {\n position += direction;\n \n // Reverse direction if the ball reaches either end\n if (position == n - 1) {\n direction = -1;\n } else if (position == 0) {\n direction = 1;\n }\n }\n \n return position;\n }\n};\n``` | 9 | 0 | ['C++'] | 4 |
find-the-child-who-has-the-ball-after-k-seconds | Python 3 || 2 lines, abs || T/S: 94% / 28% | python-3-2-lines-abs-ts-94-28-by-spauldi-nov4 | Here\'s the intuition:\n\n- After 2*n - 2 seconds, the ball is back to child 0, so we only need to be concerned with k%= 2*n -2.\n\n- The graph of f(k) = n-1 - | Spaulding_ | NORMAL | 2024-06-09T05:05:39.382770+00:00 | 2024-06-11T15:55:37.398543+00:00 | 237 | false | Here\'s the intuition:\n\n- After `2*n - 2` seconds, the ball is back to *child 0*, so we only need to be concerned with `k%= 2*n -2`.\n\n- The graph of ` f(k) = n-1 - abs(k-n+1)` is in the figure below, for the case in which *n* = 3. If *k* = 5, then *k* % 4 = 1 and *f*(1) = 1.\n\n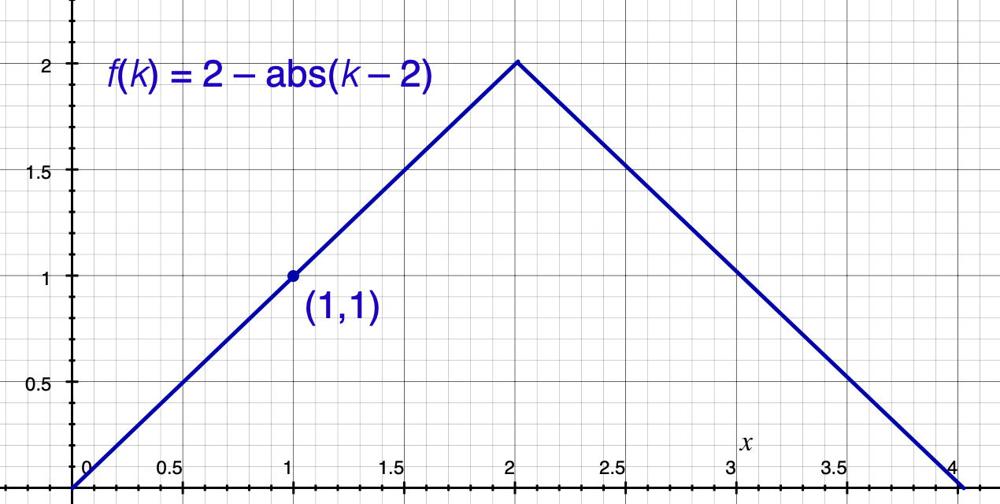\n\n\n\nIt\'s left to the mathematically prepared and motivated reader to verify the following code.\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n\n k%= 2*n -2\n\n return n-1 - abs(n-1 - k)\n```\nAnd we all know it could be a one-liner, but please don\'t post it here, even though it "might be interesting."\n\n[https://leetcode.com/problems/find-the-child-who-has-the-ball-after-k-seconds/submissions/1282445204/](https://leetcode.com/problems/find-the-child-who-has-the-ball-after-k-seconds/submissions/1282445204/)\n\nI could be wrong, but I think that time complexity is *O*(1) and space complexity is *O*(1).\n\n | 8 | 0 | ['Python3'] | 1 |
find-the-child-who-has-the-ball-after-k-seconds | 2-line O(1) sol||0ms beats 100% | 2-line-o1-sol0ms-beats-100-by-anwendeng-x70y | Intuition\n Describe your first thoughts on how to solve this problem. \nModular arithmetic with period N=2*(n-1)\n# Approach\n Describe your approach to solvin | anwendeng | NORMAL | 2024-06-09T04:33:13.325239+00:00 | 2024-06-09T04:33:13.325269+00:00 | 779 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nModular arithmetic with period `N=2*(n-1)`\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Modular arithmetic `x=k%N;`\n2. The answer is `(x<n)?x:N-x`\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code||0ms beats 100%\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int N=2*n-2, x=k%N;\n return (x<n)?x:N-x;\n }\n};\n\n``` | 7 | 0 | ['Math', 'C++'] | 3 |
find-the-child-who-has-the-ball-after-k-seconds | 5Lines simple code O(K) | 5lines-simple-code-ok-by-sumanth2328-3202 | \n\n# Code\n\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n posneg,j=1,0\n for i in range(k):\n j+=posneg\n | sumanth2328 | NORMAL | 2024-06-09T04:10:23.743711+00:00 | 2024-06-09T04:10:23.743760+00:00 | 980 | false | \n\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n posneg,j=1,0\n for i in range(k):\n j+=posneg\n if j==0 or j==n-1:\n posneg*=-1\n return j\n``` | 7 | 0 | ['Python3'] | 5 |
find-the-child-who-has-the-ball-after-k-seconds | 🔥Very Easy || 4 lines || Without Formula || Changing direction at the ends. | very-easy-4-lines-without-formula-changi-ae8m | Complexity\n- Time complexity:\nO(k) \n- Space complexity:\nO(1) \n\n# Code\n\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int dir | __esh_WAR_Amit | NORMAL | 2024-06-09T04:53:15.571067+00:00 | 2024-06-09T12:45:42.448970+00:00 | 356 | false | # Complexity\n- Time complexity:\n$$O(k)$$ \n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int direction = 1; // 1 means right, -1 means left\n int position = 0; // Starting position\n\n for (int steps = 0; steps < k; ++steps) {\n position += direction;\n\n // Change direction if at either end\n if (position == 0 || position == n - 1) {\n direction = -direction;\n }\n }\n return position;\n }\n};\n``` | 6 | 0 | ['C++'] | 1 |
find-the-child-who-has-the-ball-after-k-seconds | 💢☠💫Easiest👾Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅💥🔥💫Explained☠💥🔥 Beats 💯 | easiestfaster-lesser-cpython3javacpython-pisr | Intuition\n\n\n\n\n\n Describe your first thoughts on how to solve this problem. \nPython3 []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> i | Edwards310 | NORMAL | 2024-06-09T04:16:37.537885+00:00 | 2024-06-09T05:23:12.889569+00:00 | 209 | false | # Intuition\n\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n```Python3 []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n cycle_length = 2 * (n - 1) # Length of one cycle\n remainder = k % cycle_length # Remainder after k seconds\n \n if remainder < n: # Ball is within the range [0, n-1]\n return remainder\n else: # Ball is within the range [n, 2 * (n - 1)]\n return cycle_length - remainder\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int j = 0;\n int d = 1;\n while (k--) {\n j += d;\n if (j == n - 1 || j == 0)\n d *= -1;\n }\n return j;\n }\n};\n```\n```Java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n int j = 0, d = 1;\n while (k-- != 0) {\n j += d;\n if (j == n - 1 || j == 0)\n d *= -1;\n }\n return j;\n }\n}\n```\n```Python []\nclass Solution(object):\n def numberOfChild(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: int\n """\n c = 2 * (n -1)\n r = k % c\n return r if r < n else c - r\n```\n```C []\nint numberOfChild(int n, int k) {\n int c = 2 * (n - 1);\n int r = k % c;\n return r < n ? r : c - r;\n}\n```\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(1)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n cycle_length = 2 * (n - 1) # Length of one cycle\n remainder = k % cycle_length # Remainder after k seconds\n \n if remainder < n: # Ball is within the range [0, n-1]\n return remainder\n else: # Ball is within the range [n, 2 * (n - 1)]\n return cycle_length - remainder\n```\n# ***Please Upvote if it\'s useful for you***\n\n | 6 | 1 | ['Math', 'Brainteaser', 'C', 'Python', 'C++', 'Java', 'Python3'] | 2 |
find-the-child-who-has-the-ball-after-k-seconds | easy understanding solution beats 100% in time & space | easy-understanding-solution-beats-100-in-0yo7 | Code\n\njavascript []\nvar numberOfChild = function (n, k) {\n let ballPosition = 0; // Start with child 0 holding the ball\n let direction = 1; // Initially, | deleted_user | NORMAL | 2024-06-09T04:09:49.657188+00:00 | 2024-06-09T04:09:49.657214+00:00 | 1,468 | false | # Code\n\n```javascript []\nvar numberOfChild = function (n, k) {\n let ballPosition = 0; // Start with child 0 holding the ball\n let direction = 1; // Initially, the ball moves towards the right\n\n for (let i = 0; i < k; i++) {\n if (direction === 1) {\n if (ballPosition === n - 1) direction = -1; \n ballPosition += direction;\n } else {\n if (ballPosition === 0) direction = 1; \n ballPosition += direction;\n }\n } \n return ballPosition;\n};\n```\n```python []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n ball_position = 0 # Start with child 0 holding the ball\n direction = 1 # Initially, the ball moves towards the right\n\n for _ in range(k):\n if direction == 1:\n if ball_position == n - 1:\n direction = -1\n ball_position += direction\n else:\n if ball_position == 0:\n direction = 1\n ball_position += direction\n\n return ball_position\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int ballPosition = 0; // Start with child 0 holding the ball\n int direction = 1; // Initially, the ball moves towards the right\n\n for (int i = 0; i < k; i++) {\n if (direction == 1) {\n if (ballPosition == n - 1)\n direction = -1;\n ballPosition += direction;\n } else {\n if (ballPosition == 0)\n direction = 1;\n ballPosition += direction;\n }\n }\n return ballPosition;\n }\n};\n```\n```java []\nclass Solution {\n public int numberOfChild(int n, int k) { \n int ballPosition = 0; // Start with child 0 holding the ball\n int direction = 1; // Initially, the ball moves towards the right\n\n for (int i = 0; i < k; i++) {\n if (direction == 1) {\n if (ballPosition == n - 1) direction = -1; \n ballPosition += direction;\n } else {\n if (ballPosition == 0) direction = 1; \n ballPosition += direction;\n }\n } \n return ballPosition; \n }\n}\n``` \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n | 6 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 2 |
find-the-child-who-has-the-ball-after-k-seconds | DIRECT APPROACH || BASIC SIMULATION | direct-approach-basic-simulation-by-abhi-tllg | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nJUST KEEP ON ITERATIONG | Abhishekkant135 | NORMAL | 2024-06-09T04:22:51.831611+00:00 | 2024-06-09T04:22:51.831645+00:00 | 418 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJUST KEEP ON ITERATIONG AS IT SAYS AND YOU ARE DONE.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n int time=0;\n while(true){\n for(int i=1;i<=n-1;i++){\n time++;\n if(k==time){\n return i;\n } \n \n }\n for(int i=n-2;i>=0;i--){\n time++;\n if(k==time){\n return i;\n }\n }\n \n }\n }\n}\n``` | 4 | 0 | ['Simulation', 'Java'] | 3 |
find-the-child-who-has-the-ball-after-k-seconds | Java 1 Line simple code 🔥 O(1) Time and space | java-1-line-simple-code-o1-time-and-spac-kmii | Intuition\nsince time starts from 0 so K will always be related to n-1.\n\n# Approach\nSo firstly classify watch when ball reverses direction, If the final dire | hashed-meta | NORMAL | 2024-06-16T21:52:57.564119+00:00 | 2024-06-16T21:52:57.564143+00:00 | 99 | false | # Intuition\nsince time starts from ```0``` so `K` will always be related to n-1.\n\n# Approach\nSo firstly classify watch when ball reverses direction, If the final direction is same as the starting direction then it will be like 0 for 1st person, 1 for 2nd person and so on.\nAnd if the direction is reversed then change `K -> K%(n-1)` and return K.\n\n# Complexity\n- Time complexity : O(1)\n\n- Space complexity : O(1)\n\n# Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n // for easy understanding subtract n by 1;\n n--;\n return (k/n)%2==0 ? k%n : n-k%n;\n //return (k/(n-1))%2==0 ? k%(n-1) : (n-1)-k%(n-1);\n }\n}\n```\n\n# Upvote please \n\n | 3 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple O(1) || Solution fast | simple-o1-solution-fast-by-cs_balotiya-7xzw | Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int tem | cs_balotiya | NORMAL | 2024-06-09T12:22:23.169060+00:00 | 2024-06-09T12:22:23.169084+00:00 | 42 | false | # Complexity\n- Time complexity:\n$$O(1)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int temp1 = k / (n - 1);\n int temp2 = k % (n - 1);\n if (temp1 % 2 == 0) {\n // forward\n return temp2;\n }\n // backword\n return n - 1 - temp2;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) Solution | Beats 100💯 | o1-solution-beats-100-by-_rishabh_96-6zg2 | Number of Children in the Roundabout Game\n\n## Problem Statement\nGiven n children standing in a circle, you start counting them from 1 to k. Once you reach k, | _Rishabh_96 | NORMAL | 2024-06-09T09:42:41.373129+00:00 | 2024-06-09T09:42:41.373163+00:00 | 118 | false | # Number of Children in the Roundabout Game\n\n## Problem Statement\nGiven `n` children standing in a circle, you start counting them from 1 to `k`. Once you reach `k`, the count restarts from 1 again, but starting with the next child. After counting to `k` several times, determine which child will be the last one counted.\n\n## Intuition\nTo solve this problem, you can use the concept of rounds and remainders. Each complete round of counting `k` will cover all `n` children, and then the remainder will determine the final position.\n\n## Approach\n1. **Initialization**: Start by decrementing `n` by 1 to simplify calculations since we\'re dealing with 0-based indexing.\n2. **Rounds Calculation**: Determine the number of full rounds of `k` by integer division (`k / n`).\n3. **Remainder Calculation**: Find the remainder of `k` divided by `n` to get the position within the round.\n4. **Final Position Calculation**:\n - If the number of full rounds is even, the position remains as the remainder.\n - If the number of full rounds is odd, calculate the position from the other end of the circle.\n\n## Complexity\n- **Time complexity**: \\(O(1)\\), since the solution involves a constant number of arithmetic operations.\n- **Space complexity**: \\(O(1)\\), as no additional space is required other than a few integer variables.\n\n## Solution Code\n```cpp\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n n--; // Decrement n for 0-based indexing\n int rounds = k / n; // Calculate full rounds of k\n int rem = k % n; // Calculate remainder within the round\n\n if (rounds % 2 == 0) {\n return rem;\n } else {\n return (n - rem); \n }\n }\n};\n | 3 | 0 | ['Math', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Clean Simple Solution O(1) | clean-simple-solution-o1-by-lokeshsk1-j9un | Approach\n\nFor n = 5, k = 6\n\n0\t[0, 1, 2, 3, 4]\n1\t[0, 1, 2, 3, 4]\n2\t[0, 1, 2, 3, 4]\n3\t[0, 1, 2, 3, 4]\n4\t[0, 1, 2, 3, 4]\n5\t[0, 1, 2, 3, 4]\n6\t[0, 1 | lokeshsk1 | NORMAL | 2024-06-09T08:50:55.538841+00:00 | 2024-06-09T09:04:07.764326+00:00 | 99 | false | # Approach\n\nFor n = 5, k = 6\n\n0\t[```0```, 1, 2, 3, 4]\n1\t[0, ```1```, 2, 3, 4]\n2\t[0, 1, ```2```, 3, 4]\n3\t[0, 1, 2, ```3```, 4]\n4\t[0, 1, 2, 3, ```4```]\n5\t[0, 1, 2, ```3```, 4]\n6\t[0, 1, ```2```, 3, 4]\n7 [0, ```1```, 2, 3, 4]\n\nFor 8 it again comes to "0"\nand for 9 it comes to "1"\n\nWe should make k between 0 to 8\nSo we mod k with 8 (which is nothing but 2*(n-1))\n\nnow if k is less than n, we return k\nelse we subtract k from 8 (which is nothing but 2*(n-1))\n\nso for 7, 6 and 5 the answers are 1, 2 and 3 respectively\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n\n k = k % ((n-1)*2)\n \n if k < n:\n return k\n \n return (n-1)*2 - k\n``` | 3 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Iterative Solution | Python | iterative-solution-python-by-pragya_2305-vczv | Complexity\n- Time complexity: O(k)\n\n- Space complexity: o(1)\n\n# Code\n\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n child | pragya_2305 | NORMAL | 2024-06-09T04:19:07.108114+00:00 | 2024-06-09T04:19:07.108148+00:00 | 238 | false | # Complexity\n- Time complexity: O(k)\n\n- Space complexity: o(1)\n\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n child = 0\n reverse = 0\n while k:\n for i in range(n-1):\n if k==0:\n return child\n child=child+(-1 if reverse else 1)\n k-=1\n reverse=(reverse+1)%2\n \n return child\n \n \n \n``` | 3 | 0 | ['Array', 'Math', 'Python', 'Python3'] | 3 |
find-the-child-who-has-the-ball-after-k-seconds | TC: O(1) | SC: O(1) | BEATS 100% | SIMPLEST EXPLANATION | tc-o1-sc-o1-beats-100-simplest-explanati-qxf7 | Intuition\n Describe your first thoughts on how to solve this problem. \nIf k is less than n, then simply return the kth child (because ball is passing towards | vishwa-vijetha-g | NORMAL | 2024-06-09T04:03:35.034524+00:00 | 2024-06-09T04:06:03.097045+00:00 | 239 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf k is less than n, then simply return the kth child (because ball is passing towards right and it is the first time),\nif k is greater than n, then find the direction of ball pass by dividing k with the total children (n - 1).\nIf the quotient is an odd number that means ball is passing towards left (i.e, in the reverse direction), calculate the remainder and return rem th child from the back of the line (i.e, (n-1) - rem).\nIf the quotient is an even number that means ball is passing towards right (i.e, in the normal direction), calculate the remainder and return rem th child from the start of the line (i.e, rem).\n\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n if(k<n){\n return k;\n }else{\n int quo = k / (n - 1);\n int rem = k % (n - 1);\n if(quo%2==1){\n return (n - 1) - rem;\n }else{\n return rem;\n }\n }\n }\n}\n``` | 3 | 2 | ['Math', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | One line Solution 🚀|| 💡 Simple Math-Based Logic || 🔥 Beginner Friendly || 🧑💻 Clean Code | one-line-solution-simple-math-based-logi-fks6 | IntuitionThe problem can be solved using modular arithmetic to determine the position of a child after a given number of steps. The idea is to simulate the circ | Arunkarthick_k | NORMAL | 2025-01-28T22:34:21.827537+00:00 | 2025-01-28T22:34:21.827537+00:00 | 131 | false | # Intuition
The problem can be solved using modular arithmetic to determine the position of a child after a given number of steps. The idea is to simulate the circular behavior of counting, where positions wrap around after reaching the end.
# Approach
1. Calculate the effective position using the modulo operator to handle circular traversal.
2. Adjust the result to account for the symmetry caused by the bidirectional behavior of the counting.
# Complexity
- **Time complexity:** $$O(1)$$
The solution involves a constant number of operations.
- **Space complexity:** $$O(1)$$
No additional space is required.
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
return (n - 1) - Math.abs((n - 1) - k % ((n - 1) * 2));
}
}
``` | 2 | 0 | ['Math', 'Simulation', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple Easy to Understand Java Code || Beats 100% | simple-easy-to-understand-java-code-beat-0vqh | Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n# Code\njava []\nclass Solution {\n public int numberOfChild(int n, int k) {\n return | Saurabh_Mishra06 | NORMAL | 2024-09-21T06:09:56.941524+00:00 | 2024-09-21T06:09:56.941560+00:00 | 174 | false | # Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n# Code\n```java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n return (n-1) - Math.abs((n-1) - k%((n-1)*2));\n }\n}\n``` | 2 | 0 | ['Math', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Two Methods Math & pointer | two-methods-math-pointer-by-sangam_verma-pncg | FIRST METHOD - Using Maths\n# Code\n\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int d=k/(n-1);\n int r=k%(n-1);\n | sangam_verma | NORMAL | 2024-07-06T02:07:40.656156+00:00 | 2024-07-06T02:07:40.656179+00:00 | 278 | false | # FIRST METHOD - Using Maths\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int d=k/(n-1);\n int r=k%(n-1);\n if(d&1){\n return n-r-1; // odd then cournt from end side\n }\n else return r; // even then count from front\n }\n};\n```\n# SECOND METHOD - Using POINTER\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int i=0; // i indicate current position\n int p=0; // direction\n while(k--){\n if(i==0)p=1;\n if(i==n-1)p=-1;\n i+=p;\n }\n return i;\n }\n}; | 2 | 0 | ['Math', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Assembly with explanation and comparison with C | assembly-with-explanation-and-comparison-b7vg | \n# Rationale\n\nI\'ve solved this LeetCode problem using inline assembly in C. My goal isn\'t to showcase complexity, but rather to challenge myself and deepen | pcardenasb | NORMAL | 2024-06-14T01:24:00.009696+00:00 | 2024-06-14T01:24:00.009713+00:00 | 116 | false | \n# Rationale\n\nI\'ve solved this LeetCode problem using inline assembly in C. My goal isn\'t to showcase complexity, but rather to challenge myself and deepen my understanding of assembly language. \n\nAs a beginner in assembly, I welcome any improvements or comments on my code.\n\nAdditionally, I aim to share insights on practicing assembly on LeetCode.\n\n\n\n# Assembly Code\nThis mixed block shows the C code with inline assembly and the assembly code. View [Notes about assembly](#notes-about-assembly) for notes about the syntax used. Moreover, It shows the assembly code without comment for [comparision with C](#comparison-with-c). If you want to test this code you can [run locally](#run-locally).\n\n```c [C (inline asm)]\nint numberOfChild(int n, int k) {\n\tint ret;\n\t__asm__(\n".intel_syntax noprefix\\n"\n"\t## DIL: n\\n"\n"\t## sil: k\\n"\n"\tmov dl, 1\t\t\t\t\t# CL = 1 if ball going right, else -1\\n"\n"\txor eax, eax\t\t\t\t# AL will be the current position\\n"\n"\tdec dil\t\t\t\t\t\t# DIL = n-1\\n"\n"loop:\\n"\n"\tcmp al, dil\t\t\t\t\t# check if AL == n-1\\n"\n"\tjne not_rightmost\t\t\t# jump if AL != n-1\\n"\n"\tmov dl, -1\t\t\t\t\t# set direction to -1\\n"\n"not_rightmost:\\n"\n"\ttest al, al\t\t\t\t\t# check if AL == 0\\n"\n"\tjne not_leftmost\t\t\t# jump if AL != 0\\n"\n"\tmov dl, 1\t\t\t\t\t# set direction to 1\\n"\n"not_leftmost:\\n"\n"\tadd al, dl\t\t\t\t\t# pass the ball (update AL with DL)\\n"\n"\tdec sil\t\t\t\t\t\t# decrease the number of remain passes\\n"\n"\tjnz loop\t\t\t\t\t# come back to loop if remain passes\\n"\n"epilog:\t\\n"\n".att_syntax\\n"\n\t\t: "=a"(ret)\n\t);\n\treturn ret;\n}\n```\n```assembly [ASM (with comments)]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\n\t\nnumberOfChild:\n\t## DIL: n\n\t## sil: k\n\tmov dl, 1\t\t\t\t\t# CL = 1 if ball going right, else -1\n\txor eax, eax\t\t\t\t# AL will be the current position\n\tdec dil\t\t\t\t\t\t# DIL = n-1\nloop:\n\tcmp al, dil\t\t\t\t\t# check if AL == n-1\n\tjne not_rightmost\t\t\t# jump if AL != n-1\n\tmov dl, -1\t\t\t\t\t# set direction to -1\nnot_rightmost:\n\ttest al, al\t\t\t\t\t# check if AL == 0\n\tjne not_leftmost\t\t\t# jump if AL != 0\n\tmov dl, 1\t\t\t\t\t# set direction to 1\nnot_leftmost:\n\tadd al, dl\t\t\t\t\t# pass the ball (update AL with DL)\n\tdec sil\t\t\t\t\t\t# decrease the number of remain passes\n\tjnz loop\t\t\t\t\t# come back to loop if remain passes\nepilog:\t\n\tret\n```\n```assembly [ASM (without comments)]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\n\t\nnumberOfChild:\n\n\n\tmov dl, 1\n\txor eax, eax\n\tdec dil\nloop:\n\tcmp al, dil\n\tjne not_rightmost\n\tmov dl, -1\nnot_rightmost:\n\ttest al, al\n\tjne not_leftmost\n\tmov dl, 1\nnot_leftmost:\n\tadd al, dl\n\tdec sil\n\tjnz loop\nepilog:\t\n\tret\n```\n```assembly [ASM (without comments)]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tmov dl, 1\n\txor eax, eax\n\tdec dil\nloop:\n\tcmp al, dil\n\tjne not_rightmost\n\tmov dl, -1\nnot_rightmost:\n\ttest al, al\n\tjne not_leftmost\n\tmov dl, 1\nnot_leftmost:\n\tadd al, dl\n\tdec sil\n\tjnz loop\nepilog:\t\n\tret\n```\n\n# Notes about assembly\n\n- This code is written Intel syntax using the `.intel_syntax noprefix` directive.\n- This code uses `#` for comments because GAS (GNU Assembler) uses this syntax and Leetcode uses GCC for compiling.\n- The reason I return from the "function" by jumping to the `.epilog` is that it\'s easier to remove everything after the `.epilog` to obtain the C code with inline assembly. I am aware that in assembly I can have multiple ret instructions in my "function", but in inline assembly I need to replace those `ret` instructions with a jump to the end of the inline assembly block.\n\n# Comparison with C\n\nThis my solution using C and the assembly code generated by `gcc -S`. I removed unnecesary lines with the following shell command. I also generated the code with optimization level `-O0`, `-O1`, `-O2`, `-Os`, `-Oz` for comparison.\n\n```bash\n$ gcc -O2 -fno-asynchronous-unwind-tables -masm=intel -S code.c -o- | \n sed \'/^\\(.LCOLD\\|.LHOT\\|\\s*\\(\\.file\\|\\.type\\|\\.text\\|\\.p2align\\|\\.size\\|\\.ident\\|\\.section\\)\\)/d\'\n```\n\nNote that the C code may use `restrict`s, `const`s and type castings in order to get optimized code. Moreover, after the generated assembly code, I have also included my solution using assembly without comments for comparison.\n\n```C [-C code]\nint numberOfChild(const char n, char k) {\n\tchar pos = 0;\n\tchar direction = 1;\n\tdo {\n\t\tif (pos == n-1) {\n\t\t\tdirection = -1;\n\t\t}\n\t\tif (pos == 0) {\n\t\t\tdirection = 1;\n\t\t}\n\t\tpos += direction;\n\t\tk--;\n\t} while (k != 0);\n\n\treturn pos;\n}\n```\n```assembly [-gcc -O0]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tpush\trbp\n\tmov\trbp, rsp\n\tmov\tedx, edi\n\tmov\teax, esi\n\tmov\tBYTE PTR -20[rbp], dl\n\tmov\tBYTE PTR -24[rbp], al\n\tmov\tBYTE PTR -2[rbp], 0\n\tmov\tBYTE PTR -1[rbp], 1\n.L4:\n\tmovsx\tedx, BYTE PTR -2[rbp]\n\tmovsx\teax, BYTE PTR -20[rbp]\n\tsub\teax, 1\n\tcmp\tedx, eax\n\tjne\t.L2\n\tmov\tBYTE PTR -1[rbp], -1\n.L2:\n\tcmp\tBYTE PTR -2[rbp], 0\n\tjne\t.L3\n\tmov\tBYTE PTR -1[rbp], 1\n.L3:\n\tmovzx\tedx, BYTE PTR -2[rbp]\n\tmovzx\teax, BYTE PTR -1[rbp]\n\tadd\teax, edx\n\tmov\tBYTE PTR -2[rbp], al\n\tmovzx\teax, BYTE PTR -24[rbp]\n\tsub\teax, 1\n\tmov\tBYTE PTR -24[rbp], al\n\tcmp\tBYTE PTR -24[rbp], 0\n\tjne\t.L4\n\tmovsx\teax, BYTE PTR -2[rbp]\n\tpop\trbp\n\tret\n```\n```assembly [-gcc -O1]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tmov\tedx, 1\n\tmov\tecx, 0\n\tmovsx\tedi, dil\n\tsub\tedi, 1\n\tmov\tr10d, -1\n\tmov\tr9d, 1\n.L4:\n\tmovsx\teax, cl\n\tcmp\teax, edi\n\tcmove\tedx, r10d\n\ttest\tcl, cl\n\tcmove\tedx, r9d\n\tlea\teax, [rcx+rdx]\n\tmov\tecx, eax\n\tlea\tr8d, -1[rsi]\n\tmov\tesi, r8d\n\ttest\tr8b, r8b\n\tjne\t.L4\n\tmovsx\teax, al\n\tret\n```\n```assembly [-gcc -O2]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tmovsx\tedi, dil\n\tmov\tedx, 1\n\txor\teax, eax\n\tmov\tr8d, -1\n\tsub\tedi, 1\n.L4:\n\tmovsx\tecx, al\n\tcmp\tecx, edi\n\tcmove\tedx, r8d\n\tmov\tecx, edx\n\ttest\tal, al\n\tjne\t.L3\n\tmov\tecx, 1\n\tmov\tedx, 1\n.L3:\n\tadd\teax, ecx\n\tsub\tsil, 1\n\tjne\t.L4\n\tmovsx\teax, al\n\tret\n```\n```assembly [-gcc -Os]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tmovsx\tedi, dil\n\tmov\tdl, 1\n\txor\teax, eax\n\tdec\tedi\n.L4:\n\tmovsx\tecx, al\n\tcmp\tecx, edi\n\tjne\t.L2\n\tmov\tdl, -1\n.L2:\n\ttest\tal, al\n\tjne\t.L3\n\tmov\tdl, 1\n.L3:\n\tadd\teax, edx\n\tdec\tsil\n\tjne\t.L4\n\tmovsx\teax, al\n\tret\n```\n```assembly [-gcc -Oz]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tmovsx\tedi, dil\n\tmov\tdl, 1\n\txor\teax, eax\n\tdec\tedi\n.L4:\n\tmovsx\tecx, al\n\tcmp\tecx, edi\n\tjne\t.L2\n\tmov\tdl, -1\n.L2:\n\ttest\tal, al\n\tjne\t.L3\n\tmov\tdl, 1\n.L3:\n\tadd\teax, edx\n\tdec\tsil\n\tjne\t.L4\n\tmovsx\teax, al\n\tret\n```\n```assembly [-my ASM]\n\t.intel_syntax noprefix\n\t.globl\tnumberOfChild\nnumberOfChild:\n\tmov dl, 1\n\txor eax, eax\n\tdec dil\nloop:\n\tcmp al, dil\n\tjne not_rightmost\n\tmov dl, -1\nnot_rightmost:\n\ttest al, al\n\tjne not_leftmost\n\tmov dl, 1\nnot_leftmost:\n\tadd al, dl\n\tdec sil\n\tjnz loop\nepilog:\t\n\tret\n```\n\n\n# Run locally\n\nCompile locally the assembly code with GAS or the inline assembly with GCC.\n\n```bash\n$ as -o code.o assembly_code.s\n$ # or\n$ gcc -c -o code.o c_with_inline_assembly_code.c \n```\n\nThen, create a `main.c` file with the function prototype. Here you can include your tests.\n\n```c\n/* main.c */\n\nint numberOfChild(int n, int k);\n\nint main(int argc, const char *argv[]) {\n // Use numberOfChild function\n return 0;\n}\n```\n\nThen, compile `main.c` and link to create the executable\n\n```bash\n$ gcc main.c code.o -o main\n```\n\nFinally, execute\n\n```bash\n$ ./main\n```\n\n | 2 | 0 | ['C'] | 1 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) | Efficiently Finding the Child Who Holds the Ball After K Seconds | o1-efficiently-finding-the-child-who-hol-r42v | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve the problem of finding the child who has the ball after k seconds, we can leve | pushpitjain2006 | NORMAL | 2024-06-10T12:48:41.237805+00:00 | 2024-06-10T12:48:41.237840+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem of finding the child who has the ball after k seconds, we can leverage the observation that the ball\'s movement is periodic. The ball moves back and forth between the two ends of the line. Therefore, after a certain number of seconds, the ball\'s position starts to repeat in a predictable pattern. By understanding this pattern, we can determine the position of the ball without simulating each second.\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Identify the Periodicity:\n\nSince the ball changes direction at the ends of the line, the ball\'s position after k seconds can be found by considering the total length of movement before it starts repeating.\nThe ball travels from the start to the end and back again, forming a complete cycle. The length of this cycle is 2 * (n - 1).\n\n- Calculate Effective Position:\n\nThe effective number of moves is k % (2 * (n - 1)) because the position repeats every 2 * (n - 1) seconds.\nDepending on whether the ball is moving forward or backward within this effective number of moves, we can determine its exact position.\n\n- Determine Direction:\n\nIf the ball has moved past n - 1 moves in the effective number of moves, it means it is on its way back. Thus, we need to adjust the position accordingly.\n\n# Complexity\n- Time complexity:\nThe time complexity is O(1) since we are performing a constant number of operations regardless of the input size.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nThe space complexity is O(1) as we are using only a fixed amount of extra space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n n--;\n int op = k%(2*n);\n if(op/n){\n return 2*n-op;\n }\n return op;\n }\n};\n```\nIn this solution, we decrement n by 1 initially to simplify the calculation since we often reference n-1 in the process. The variable op represents the effective position within the cycle. If op is greater than or equal to n, it indicates the ball is on the return trip, and we adjust accordingly to find the correct child\'s position. This approach ensures that we determine the ball\'s position efficiently without unnecessary simulations.\n | 2 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) approach explained detailly | o1-approach-explained-detailly-by-hrushi-17q0 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem can be visualized as children sitting in a circle where the distribution of | Hrushi_7 | NORMAL | 2024-06-10T09:50:00.234706+00:00 | 2024-06-10T09:50:00.234742+00:00 | 35 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be visualized as children sitting in a circle where the distribution of items happens in a specific pattern, reversing direction after completing a round. By carefully calculating the direction and the remainder, we can determine which child receives the k-th item\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.Direction Calculation:\n\n*Every (n-1) items, the direction changes. The direction can be determined by dividing k by n-1.\n\n*If the result is even, it means the direction is still forward. If odd, the direction has reversed.\n\nRemainder Calculation:\n\n*The remainder when k is divided by n-1 tells us the position in the current segment.\n\n*If the direction is still forward (even number of complete rounds), the child can be directly determined by the remainder.\n\n*If the direction has reversed (odd number of complete rounds), the position must be calculated backwards from the end.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1) - The solution involves basic arithmetic operations that take constant time.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) - No extra space is used beyond the input variables.\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n \n int direction = k / (n - 1);\n int remainder = k % (n - 1);\n\n if(direction & 1){\n return n - remainder - 1;\n }\n return remainder;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple solution using Math || O(1) | simple-solution-using-math-o1-by-user745-xgz5 | Intuition\nAfter 2 * (n-1) seconds, ball ends up with the first child. After n-1 seconds, the ball is with the last child.\n\n# Approach\nSo take reminder of k | user7454af | NORMAL | 2024-06-09T22:49:58.446617+00:00 | 2024-06-09T22:49:58.446635+00:00 | 38 | false | # Intuition\nAfter $$2 * (n-1)$$ seconds, ball ends up with the first child. After $$n-1$$ seconds, the ball is with the last child.\n\n# Approach\nSo take reminder of k with $$2 * (n-1)$$. If k is less than $$n-1$$ return k, else return $$(n-1) - (k - (n-1))$$ as the ball reaches the end $$n-1$$ seconds and runs backward.\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimpl Solution {\n pub fn number_of_child(n: i32, k: i32) -> i32 {\n let k = k % (2 * (n - 1));\n if k > (n-1) {\n (n << 1) - 2 - k\n } else {\n k\n }\n }\n}\n``` | 2 | 0 | ['Rust'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | PYTHON🔥|| BEAT 100%🔥|| 100% EFFICIENT🔥|| BEGINNER'S APPROACH || EASY TO UNDERSTAND || | python-beat-100-100-efficient-beginners-q13c7 | if it\'s help, please up \u2B06vote!\u2764\uFE0F and comment\uD83D\uDD25\n# Intuition\n Describe your first thoughts on how to solve this problem. \n- My first | Adit_gaur | NORMAL | 2024-06-09T12:04:34.125402+00:00 | 2024-06-09T12:04:34.125433+00:00 | 34 | false | # if it\'s help, please up \u2B06vote!\u2764\uFE0F and comment\uD83D\uDD25\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- My first thought was to simulate the movement of the ball among the children in the queue. Given that the ball changes direction when it reaches either end of the line, I realized that the ball\'s movement forms a repeating pattern or period. This periodic behavior can be exploited to reduce the problem size and efficiently determine the final position of the ball after k seconds.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Period Identification:\n- - The ball completes one round trip (from the start to the end and back to the start) in 2 * (n - 1) seconds, where n is the number of children.\nThis period indicates that the ball\'s position after every 2 * (n - 1) seconds will be the same.\n- Effective Steps Calculation:\n- - To handle large values of k, compute the effective number of steps the ball moves within one period using k % (2 * (n - 1)). This reduces the problem size significantly.\nSimulate the Movement:\n- Initialize the ball\'s position at 0 and set the initial direction to the right.\n- Simulate the ball\'s movement for the calculated effective steps, adjusting the direction whenever the ball reaches either end of the line.\n- This approach ensures that we only simulate the minimal necessary steps to determine the final position, making the solution efficient.\n# Complexity\n- Time complexity: $$O(n)$$ --> The time complexity is O(effective_steps), which simplifies to O(n) in the worst case. However, since we reduce the problem using the period, the average case is much smaller and runs in constant time O(1) for large k.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we only use a few variables to keep track of the position, direction, and effective steps. No additional data structures are used that scale with the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def numberOfChild(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: int\n """\n # Calculate the effective number of steps within one period\n period = 2 * (n - 1)\n effective_steps = k % period\n \n # Simulate the ball\'s movement for effective_steps\n position = 0\n direction = 1 # 1 means right, -1 means left\n \n for _ in range(effective_steps):\n if position == 0:\n direction = 1\n elif position == n - 1:\n direction = -1\n position += direction\n \n return position\n```\n\n | 2 | 0 | ['Python'] | 1 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) Java solution using simple Math logic | o1-java-solution-using-simple-math-logic-oo9t | Intuition\nThe ball starts with child 0 and moves to the right. When it reaches the end (either child 0 or child n\u22121), the direction reverses. The problem | Sanjeev1903 | NORMAL | 2024-06-09T06:25:54.930669+00:00 | 2024-06-09T06:25:54.930700+00:00 | 130 | false | # Intuition\nThe ball starts with child 0 and moves to the right. When it reaches the end (either child 0 or child n\u22121), the direction reverses. The problem is to determine which child has the ball after k seconds. The key insight is to notice the periodic nature of the ball\'s movement.\n\n# Complexity\n- Time Complexity: $$O(1)$$ since all operations (modulus and division) are constant time.\n- Space Complexity: $$O(1)$$ since no additional space proportional to the input size is used.\n\n# Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n if(k < n) return k;\n int mod = k%(n-1);\n int times = (k-mod)/(n-1);\n if(times%2 == 0) return mod;\n return n-1-mod;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
find-the-child-who-has-the-ball-after-k-seconds | 100% BEATS || O(1) Complexity || Mathematical Approach | 100-beats-o1-complexity-mathematical-app-m2ir | If k is less than n:#\n - If k is less than the total number of children n, it means the ball won\'t reach either end of the line within k seconds. So, the ch | shubham6762 | NORMAL | 2024-06-09T04:40:18.140811+00:00 | 2024-06-09T04:40:18.140844+00:00 | 47 | false | 1. **If `k` is less than `n`:**#\n - If `k` is less than the total number of children `n`, it means the ball won\'t reach either end of the line within `k` seconds. So, the child who receives the ball after `k` seconds will simply be the `k`th child in the queue.\n\n2. **If `k` is greater than or equal to `n`:**\n - We imagine the ball moving through the queue in cycles. Each cycle consists of passing the ball from the first child to the last child and vice versa.\n - We calculate how many complete cycles (`a`) the ball completes and any remaining passes within the current cycle (`b`).\n - If the number of complete cycles `a` is odd, the direction of passing the ball reverses after each cycle. So, the child who receives the ball after `k` seconds is the child at position `n - 1 - b`.\n - If the number of complete cycles `a` is even, the direction of passing the ball remains the same after each cycle. So, the child who receives the ball after `k` seconds is the child at position `b`.\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n if (k < n)\n return k;\n \n int a = (k / (n - 1));\n int b = (k % (n - 1));\n \n if (a % 2 == 1)\n return n - 1 - b;\n return b;\n }\n};\n``` | 2 | 0 | ['Math', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Very Simple C Solution 100% | very-simple-c-solution-100-by-rajnarayan-17ev | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. when current reaches | rajnarayansharma110 | NORMAL | 2024-06-09T04:32:58.689312+00:00 | 2024-06-09T04:32:58.689342+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. when current reaches end then traverse in reverse direction else traverse forward\n# Complexity\n- Time complexity:O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint numberOfChild(int n, int k) {\n int cur=0;\n int time=0;\n while(time!=k){\n if(cur==n-1&&time<k){\n while(cur!=0&&time<k){\n cur--;\n time++;\n }\n }\n else{\n while(cur!=n-1&&time<k){\n time++;\n cur++;\n }\n }\n }\n return cur;\n}\n``` | 2 | 0 | ['C'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Best Solution Beats ✅100% --pkg | best-solution-beats-100-pkg-by-pradeepkr-mpgs | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nApproach is to traverse through the loop and if it reaches to the end of | pradeepkrgupta_39 | NORMAL | 2024-06-09T04:24:37.175010+00:00 | 2024-06-09T04:24:37.175041+00:00 | 192 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nApproach is to traverse through the loop and if it reaches to the end of the k then reverse it by using the codition (if pos==n-1 || pos==0)\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity : 0(k)\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n int pos = 0;\n int dir = 1;\n for(int i=0;i<k;i++){\n pos+=dir;\n if(pos==n-1 || pos==0){\n dir = -dir;\n }\n }\n return pos;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Contest Solution! | contest-solution-by-qatyayani-d24j | \n\n# Code\n\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n f=0\n i=0\n while True:\n if k==0:\n | Qatyayani | NORMAL | 2024-06-09T04:07:37.803023+00:00 | 2024-06-09T04:07:37.803046+00:00 | 30 | false | \n\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n f=0\n i=0\n while True:\n if k==0:\n return i\n if f==0:\n i+=1\n if i==n-1:\n f=1\n elif f==1:\n i-=1\n if i==0:\n f=0\n k-=1\n``` | 2 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | deque 🔥| C++ | deque-c-by-varuntyagig-a7xu | Code | varuntyagig | NORMAL | 2025-03-12T16:29:09.829468+00:00 | 2025-03-12T16:29:09.829468+00:00 | 16 | false | # Code
```cpp []
class Solution {
public:
int numberOfChild(int n, int k) {
deque<int> dq(1, 0);
bool flag1 = false;
for (int i = 1; i <= k; ++i) {
if (!flag1) {
dq.push_back(i);
if (dq.size() == n) {
flag1 = true;
}
} else if (flag1) {
dq.pop_back();
if (dq.size() == 1) {
flag1 = false;
}
}
}
return dq.size() - 1;
}
};
``` | 1 | 0 | ['Queue', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | ☑️ Finding the Child Who Has the Ball After K Seconds. ☑️ | finding-the-child-who-has-the-ball-after-f1rh | Code | Abdusalom_16 | NORMAL | 2025-02-24T04:50:38.965059+00:00 | 2025-02-24T04:50:38.965059+00:00 | 39 | false | # Code
```dart []
class Solution {
int numberOfChild(int n, int k) {
int max = n-1;
int number = 0;
bool isReverse = false;
while(k > 0){
k--;
if(isReverse){
number--;
if(number == 0){
isReverse = false;
}
}else{
number++;
if(number == max){
isReverse = true;
}
}
}
return number;
}
}
``` | 1 | 0 | ['Math', 'Simulation', 'Dart'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | C modulo O(1) | c-modulo-o1-by-michelusa-6v3y | null | michelusa | NORMAL | 2024-12-12T23:46:13.027458+00:00 | 2024-12-12T23:46:13.027458+00:00 | 20 | false | C modulo O(1)\nCount number of whole trips.\n\n# Code\n```c []\nint numberOfChild(int n, int k) {\n --n;\n const int trips = k / n ;\n const int left = k % n ;\n\n \n\n if ((trips & 1) == 1) { // at end\n return n - left ;\n } else {\n return left;\n }\n}\n``` | 1 | 0 | ['C'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Twister JS | twister-js-by-joelll-qr73 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Joelll | NORMAL | 2024-08-10T04:01:00.264690+00:00 | 2024-08-10T04:01:00.264720+00:00 | 78 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nvar numberOfChild = function(n, k) {\n const odi = parseInt(k/(n-1))\n const adi = k%(n-1)\n if(odi % 2 ==0){\n return adi\n }else{\n return (n-1) - adi\n }\n};\n\n``` | 1 | 0 | ['JavaScript'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | easy c++ solution || beats 100% | easy-c-solution-beats-100-by-yogeshwarib-y7yx | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yogeshwaribisht21 | NORMAL | 2024-06-15T15:20:22.439520+00:00 | 2024-06-15T15:20:22.439550+00:00 | 198 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n \n int i=0;\n bool vis=false;\n while(k>0)\n {\n if(i==0)\n {\n vis=false;\n }\n else if(i==n-1)\n {\n vis=true;\n }\n if(vis==false)\n {\n i++;\n }\n else\n {\n i--;\n }\n k--;\n } \n return i;\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
find-the-child-who-has-the-ball-after-k-seconds | Simple Java Code ☠️ | simple-java-code-by-abhinandannaik1717-akgp | Code\n\nclass Solution {\n public int numberOfChild(int n, int k) {\n if(k>=(2*(n-1))){\n k = k%(2*(n-1));\n }\n if(k>=(n-1)) | abhinandannaik1717 | NORMAL | 2024-06-15T14:11:13.971539+00:00 | 2024-06-19T13:07:21.114983+00:00 | 378 | false | # Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n if(k>=(2*(n-1))){\n k = k%(2*(n-1));\n }\n if(k>=(n-1)){\n k = k%(n-1);\n return (n-k-1);\n }\n else{\n return k;\n }\n }\n}\n```\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe problem involves determining the position of a ball passed among `n` children in a line, with the direction of passing reversing when the ball reaches either end. The objective is to find out which child will have the ball after `k` seconds.\n\n#### Key Insights:\n\n1. **Cyclic Nature of the Ball Passing**:\n - When the ball is passed from the first child (child 0) to the last child (child \\( n-1 \\)) and back to the first child, it forms a cycle.\n - The length of one complete cycle is \\( 2 \\times (n - 1) \\) seconds (moving to the right and then back to the left).\n\n2. **Normalization of `k`**:\n - If \\( k \\) is greater than or equal to the length of one complete cycle, we can reduce \\( k \\) using the modulo operation. This is because after every complete cycle, the position of the ball repeats.\n - Thus, `k = k % (2 times (n - 1))` gives us the effective number of seconds within a single cycle.\n\n3. **Determining the Ball\'s Position**:\n - After normalizing \\( k \\), we need to determine the ball\'s position within the current cycle:\n - If \\( k \\) is less than \\( n - 1 \\), the ball is moving to the right, and the position is directly \\( k \\).\n - If \\( k \\) is greater than or equal to \\( n - 1 \\), the ball has reached the end and is now moving back to the left. In this case, we compute the position as \\( (n - 1) - (k \\% (n - 1)) \\).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Cycle Length Calculation**:\n - The ball travels from child 0 to child \\( n-1 \\) and back to child 0. This round trip constitutes a complete cycle of length \\( 2 \\times (n - 1) \\) seconds.\n\n2. **Reduction of `k` within a Single Cycle**:\n - If `k` is larger than or equal to the length of a complete cycle, it can be reduced to within the cycle using the modulo operation. This is based on the observation that the ball\'s position repeats every \\( 2 \\times (n - 1) \\) seconds.\n - `k = k % (2 \\times (n - 1))` ensures that `k` falls within the range of one complete cycle.\n\n3. **Determining the Position within the Cycle**:\n - After normalizing `k`, we need to find out where the ball is in its current movement:\n - **Forward Movement**:\n - If `k` is less than \\( n - 1 \\), the ball is still moving towards the right (from child 0 towards child \\( n-1 \\)).\n - In this case, the position of the ball is simply `k`.\n - **Backward Movement**:\n - If `k` is greater than or equal to \\( n - 1 \\), the ball has reached the end (child \\( n-1 \\)) and is moving back towards the left (towards child 0).\n - To find the exact position during the backward movement, we use the expression `n - k - 1`. This accounts for the reverse traversal from child \\( n-1 \\) back to child 0.\n\nCertainly! Let\'s go through your code step-by-step with a specific example to illustrate how it determines which child has the ball after `k` seconds.\n\n### Example:\n\nLet\'s take `n = 5` children and `k = 12` seconds.\n\n### Step-by-Step Execution:\n\n#### Step 1: Calculate the Cycle Length\n- The cycle length is \\(2 \\times (n - 1)\\):\n \\[\n 2 \\times (5 - 1) = 8 \\text{ seconds}\n \\]\n- This means the ball travels from child 0 to child 4 and back to child 0 in 8 seconds.\n\n#### Step 2: Normalize `k` Within a Single Cycle\n- Given `k = 12`, which is larger than the cycle length:\n ```java\n if (k >= 2 * (n - 1)) {\n k = k % (2 * (n - 1));\n }\n ```\n- So, we reduce `k` using modulo operation:\n \\[\n 12 \\% 8 = 4\n \\]\n- Now, `k = 4` seconds, which is within a single cycle.\n\n#### Step 3: Determine the Ball\'s Position Within the Cycle\n- Compare `k` to `n - 1`:\n \\[\n n - 1 = 5 - 1 = 4\n \\]\n- Since `k = 4` is equal to `n - 1`, it means the ball is at the last child (child 4) and will start moving back to the left in the next second.\n\nHere\u2019s the relevant code segment:\n```java\nif (k >= n - 1) {\n k = k % (n - 1);\n return (n - k - 1);\n} else {\n return k;\n}\n```\n- Given `k = 4`:\n ```java\n k = 4 % 4 = 0;\n return (5 - 0 - 1) = 4;\n ```\n- The ball is with child 4 after `12` seconds.\n\n# Complexity\n\n- **Time Complexity**: \\( O(1) \\)\n - The code performs a constant number of operations regardless of the input size `n` and `k`. This includes arithmetic operations and conditional checks, all of which execute in constant time.\n\n- **Space Complexity**: \\( O(1) \\)\n - The code uses a constant amount of extra space, independent of the input size. It only requires space for a few variables (`n` and `k`), and does not use any additional data structures that would scale with the input.\n\n | 1 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | C++ Easy Code💯 || Beats 100% || Beginner friendly || Easy to understand || With explanation 💯💀 | c-easy-code-beats-100-beginner-friendly-pm385 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe numberOfChild function is designed to determine the position of a "child" in a sequ | Shodhan_ak | NORMAL | 2024-06-14T13:21:21.082716+00:00 | 2024-06-14T13:21:21.082757+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe numberOfChild function is designed to determine the position of a "child" in a sequence after k steps, given n total positions. Here\'s a step-by-step breakdown of the intuition behind the code:\n\nInitialization:\n\na represents the current position of the child, starting at position 0.\nb is a direction indicator, initialized to 1, meaning the child initially moves forward.\nMain Loop:\n\nThe loop runs k times, indicating the child will take k steps.\nIn each iteration, the child\'s position a is updated by adding b to it. This effectively moves the child one position forward if b is positive, or backward if b is negative.\nBoundary Checks:\n\nAfter updating a, the code checks if a has reached either end of the sequence (0 or n - 1).\nIf a is at one of the boundaries, the direction b is reversed (multiplied by -1). This causes the child to start moving in the opposite direction on the next step.\nReturn Value:\n\nAfter completing k steps, the function returns the final position a of the child.\nExample Walkthrough\nLet\'s walk through an example to understand how this works:\n\nSuppose n = 5 (positions 0 to 4) and k = 6 (6 steps).\nInitial state: a = 0, b = 1.\nSteps:\n\n1. a = 0 + 1 = 1\n2. a = 1 + 1 = 2\n3. a = 2 + 1 = 3\n4. a = 3 + 1 = 4 (boundary reached, reverse direction b = -1)\n5. a = 4 - 1 = 3\n6. a = 3 - 1 = 2\nAfter 6 steps, the child ends up at position 2.\n\nSummary\nThe numberOfChild function simulates a child moving back and forth in a sequence of positions, reversing direction each time a boundary is reached. This logic ensures that the child stays within the valid range of positions and allows for an easy calculation of the final position after a given number of steps.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the numberOfChild function is O(k), where k is the number of steps the child takes. This is because the loop runs exactly k times, performing a constant amount of work in each iteration (updating the position and checking boundaries).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the numberOfChild function is O(1). The function uses a fixed amount of additional space regardless of the input size. It only utilizes a few integer variables (a, b, i), which do not depend on the size of the input n or k.\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int a=0,b=1;\n for(int i=0;i<k;i++){\n a+=b;\n if(a==0 || a==n-1){\n b=-b;\n }\n }\n return a;\n\n\n \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | C++ | Circular Linked List | Easy and intuitive approach | c-circular-linked-list-easy-and-intuitiv-yaph | Intuition\nThe first thought to the question were recognising that this question involves a cyclic event where the ball goes from 0 to n-1 and then again comes | Anugrah_Gupta | NORMAL | 2024-06-13T09:04:53.885726+00:00 | 2024-06-13T09:04:53.885755+00:00 | 3 | false | # Intuition\nThe first thought to the question were recognising that this question involves a cyclic event where the ball goes from 0 to n-1 and then again comes back to 0. This led me to the idea of using Circular Linked List.\n\n# Approach\nSince the question says that there is a reversal of the passing order. So if there is a cirular linked list which has the head at 0, the starting point and goes to n-1 and then form n-1 comes back to 1 which would be the last node. Now, if we connect the node 1 to head we get our circular linked list representing the flow of passing.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n ListNode* head = new ListNode;\n ListNode* curr = head;\n for(int i=1;i<=n-1;i++) {\n curr->next = new ListNode(i);\n curr = curr->next;\n }\n for(int i=n-2;i>0;i--) {\n curr->next = new ListNode(i);\n curr = curr->next;\n }\n curr->next = head;\n curr = head;\n while(k--) {\n curr = curr->next;\n }\n return curr->val;\n }\n};\n``` | 1 | 0 | ['Linked List', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | simple solution with basic mathod | simple-solution-with-basic-mathod-by-vin-ezc7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vinay_kumar_swami | NORMAL | 2024-06-10T19:23:07.583768+00:00 | 2024-06-10T19:23:07.583794+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n n=n-1;\n int rem=k/n;\n int del=k%n;\n int ans;\n if(rem%2==0)\n {\n ans= del;\n }\n if(rem%2!=0)\n {\n ans=n-del;\n }\n \n return ans;\n // int i=0;\n // if(k<n)\n // {\n // return k;\n // }\n // while (i < n && k >= 0) {\n // if (i == n - 1&& k>=0) {\n \n // while (i >= 0 && k >= 0) {\n // k--;\n // i--;\n // cout<<"Hi"<<" "<<"i,k"<<endl;\n // }\n // } else {\n \n // i++;\n // k--;\n // cout<<"hellow"<<" "<<"i,k"<<endl;\n // }\n \n // }\n \n // return i+1;\n \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | ✅ O(1) Solution | o1-solution-by-eleev-0x0r | Solution\nswift\nstruct Solution {\n @_optimize(speed)\n func numberOfChild(_ n: Int, _ k: Int) -> Int {\n let n = n - 1\n // > Ifthe number | eleev | NORMAL | 2024-06-09T17:39:46.210726+00:00 | 2024-06-09T17:39:46.210750+00:00 | 9 | false | # Solution\n```swift\nstruct Solution {\n @_optimize(speed)\n func numberOfChild(_ n: Int, _ k: Int) -> Int {\n let n = n - 1\n // > Ifthe number of complete back-and-forth cycles is even:\n // -> calculate the remaining passings\n // > Otherwise (if odd):\n // -> the ball is passed backward, so we compute the remaining difference\n return k / n & 1 == 0 ? k % n : n - k % n\n }\n}\n``` | 1 | 0 | ['Math', 'Swift'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Day 253 Problem 2 Solved | day-253-problem-2-solved-by-lakshya311-slxe | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Code\n\nclass Solut | lakshya311 | NORMAL | 2024-06-09T13:15:44.500470+00:00 | 2024-06-09T13:15:44.500524+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int ans = k % (2 * n - 2);\n return (ans < n) ? ans : 2 * n - 2 - ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | ✅💯Very Easy Solution | Python 🔥🔥 | very-easy-solution-python-by-kg-profile-u313 | Code\n\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n eff = k % (2 * (n - 1))\n p = 0\n d = 1 \n \n | KG-Profile | NORMAL | 2024-06-09T13:04:22.727711+00:00 | 2024-06-09T13:04:22.727751+00:00 | 57 | false | # Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n eff = k % (2 * (n - 1))\n p = 0\n d = 1 \n \n for _ in range(eff):\n if p == 0:\n d = 1 \n elif p == n - 1:\n d = -1 \n \n p += d\n \n return p\n``` | 1 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | [Python] simple brute force | python-simple-brute-force-by-pbelskiy-01do | \nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n a = list(range(n))\n\n while len(a) < k*2:\n a.extend(list(ran | pbelskiy | NORMAL | 2024-06-09T09:56:12.804698+00:00 | 2024-06-09T09:56:12.804741+00:00 | 13 | false | ```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n a = list(range(n))\n\n while len(a) < k*2:\n a.extend(list(range(n - 2, -1, -1)))\n a.extend(list(range(1, n)))\n\n return a[k]\n``` | 1 | 0 | ['Python'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Easy One Liner Solution along with Intuition. | easy-one-liner-solution-along-with-intui-6be3 | Let\'s understand the intuition behind the solution with an example:\nGiven - \n\nn = 4\nk = 5\n\n\nNow let us look at all the solution from k=1 to k =12\n\n\n+ | OmGujarathi | NORMAL | 2024-06-09T09:45:35.859460+00:00 | 2024-06-09T09:45:56.967097+00:00 | 10 | false | **Let\'s understand the intuition behind the solution with an example:**\nGiven - \n```\nn = 4\nk = 5\n```\n\nNow let us look at all the solution from k=1 to k =12\n\n```\n+-----+-------+\n| k | Answer|\n+-----+-------+\n| 1 | 1 |\n| 2 | 2 |\n| 3 | 3 |\n| 4 | 2 |\n| 5 | 1 |\n| 6 | 0 |\n---------------\n| 7 | 1 |\n| 8 | 2 |\n| 9 | 3 |\n| 10 | 2 |\n| 11 | 1 |\n| 12 | 0 |\n+-----+-------+\n```\n***As you can see after every 2(n-1) values of \uD835\uDC58, the answers repeat in a pattern. So if we get the answer correct from k = 1 to 2(n-1) then we can deduce the solution for all values of \uD835\uDC58.***\n\n**Explaning the steps by which I arrived to the solution**\n\n1) The below solution works but only when `k <= n`\n\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n return k;\n }\n}\n```\n\n\n2. The below works only when `k <= 2n - 1.`\nThis formula adjusts the answer based on the distance from \uD835\uDC5B-1.\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n return n-1 - Math.abs(n - 1 - k);\n }\n}\n```\n\n3. Now mod k with 2 * (n-1) as the pattern repeats. \n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n return n-1 - Math.abs(n - 1 - k % (2*(n-1)));\n }\n}\n```\nThis approach ensures that the solution is efficient and works for all values of \uD835\uDC58.\n\n\n | 1 | 0 | ['Math'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | easy solution | beats 100% | easy-solution-beats-100-by-leet1101-jlcc | Intuition\nThe ball is passed back and forth between the children, reversing direction when it hits either end (child 0 or child n-1). This back-and-forth movem | leet1101 | NORMAL | 2024-06-09T08:52:32.119134+00:00 | 2024-06-09T08:52:32.119167+00:00 | 300 | false | ## Intuition\nThe ball is passed back and forth between the children, reversing direction when it hits either end (child 0 or child n-1). This back-and-forth movement can be tracked using a simple iterative approach.\n\n## Approach\n1. Start with the ball at position 0 and the direction set to 1 (moving to the right).\n2. Iterate `k` times, updating the position by the current direction.\n3. Whenever the ball reaches either end of the line (position 0 or n-1), reverse the direction.\n4. After `k` seconds, return the current position of the ball.\n\n## Complexity\n- Time complexity: $$O(k)$$, since we iterate `k` times.\n- Space complexity: $$O(1)$$, since we use only a constant amount of extra space.\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int position = 0; \n int direction = 1; \n\n for (int i = 0; i < k; ++i) {\n position += direction;\n \n if (position == 0 || position == n - 1) {\n direction *= -1;\n }\n }\n \n return position;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Easy Brute Force Approach | Easy to Understand | Beats 100% of users | easy-brute-force-approach-easy-to-unders-ak6a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nStep 1: \ntake an array | chaturvedialok44 | NORMAL | 2024-06-09T08:49:27.896989+00:00 | 2024-06-09T08:49:27.897042+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStep 1: \ntake an array arr[] of size n to hold the child.\nwill take a pointer p initially at arr[0] and variable count to couter the variable k and control the number of operation\n\nStep 2: \nwill make two while loop one will be for left to right direction, and as q reach to last element of arr[] then we come out of first while loop and then mark q = n-1 and now another while loop to change the direction if count is still less than k and then mark q = 0; and this process will be repeated till count != k.\n\nStep 3: \nOnce the count == k, we come out of while loop and return the value of p\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n int arr[] = new int[n];\n for(int i=0; i<n; i++){\n arr[i] = i;\n }\n int count = 0;\n int p = arr[0], q = 0;\n while(count != k){\n while(count != k && q < n-1){\n count++;\n q++;\n p = arr[q];\n } \n q = n-1;\n while(count != k && q > 0){\n count++;\n q--;\n p = arr[q];\n }\n q = 0;\n }\n return p;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 🔥Very Easy to understand and intuitive O(1)🔥approach.Beginner friendly | very-easy-to-understand-and-intuitive-o1-eh7b | \n\n# Complexity\n- Time complexity:\n O(1) \n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n | Saksham_Gulati | NORMAL | 2024-06-09T08:08:43.647910+00:00 | 2024-06-09T08:08:43.647948+00:00 | 142 | false | \n\n# Complexity\n- Time complexity:\n $$O(1)$$ \n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n if((k/(n-1))%2==0)\n return k%(n-1);\n return n-1-k%(n-1);\n \n }\n};\n``` | 1 | 0 | ['Math', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 🔥Simulation - Beginner Friendly | Clean Code | C++ | | simulation-beginner-friendly-clean-code-yt9k3 | Code\n\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n if (k == 1)\n return 1;\n \n int curr = 1;\n b | Antim_Sankalp | NORMAL | 2024-06-09T07:07:21.201885+00:00 | 2024-06-09T07:07:21.201920+00:00 | 78 | false | # Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n if (k == 1)\n return 1;\n \n int curr = 1;\n bool dir = false;\n k--;\n while (k--)\n {\n if (curr == n - 1)\n dir = true;\n if (curr == 0)\n dir = false;\n \n if (dir == false)\n curr++;\n if (dir == true)\n curr--;\n \n }\n \n return curr;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | ✅ Easy C++ Solution | easy-c-solution-by-moheat-5ur0 | Code\n\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int curr = 0;\n bool direction = true;\n while(k!=0)\n {\ | moheat | NORMAL | 2024-06-09T06:22:47.575151+00:00 | 2024-06-09T06:22:47.575175+00:00 | 91 | false | # Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int curr = 0;\n bool direction = true;\n while(k!=0)\n {\n if(direction)\n {\n if(curr == n-2)\n {\n direction = false;\n }\n curr++;\n }\n else if(!direction)\n {\n if(curr == 1)\n {\n direction = true;\n }\n curr--;\n }\n k--;\n }\n return curr;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | C++ || EASY | c-easy-by-abhishek6487209-dwen | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Abhishek6487209 | NORMAL | 2024-06-09T05:00:45.773161+00:00 | 2024-06-09T05:00:45.773185+00:00 | 75 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int pos = 0,dir = 1; \n for (int i = 0; i < k; ++i) {\n pos+= dir;\n if (pos == 0 or pos == n - 1) {\n dir *= -1;\n }\n }\n\n return pos; \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple Math || O(1) 100% Faster Solution | simple-math-o1-100-faster-solution-by-ya-3yv2 | Intuition\nFor a complete cycle there will be total of 2(n - 1) children and time will be k % 2(n - 1) because rest of the time complete cycles occur.\nNow if(t | yashvardhannn152004 | NORMAL | 2024-06-09T04:41:16.367546+00:00 | 2024-06-09T04:41:16.367580+00:00 | 5 | false | # Intuition\nFor a complete cycle there will be total of 2*(n - 1) children and time will be k % 2*(n - 1) because rest of the time complete cycles occur.\nNow if(time < n) means finally the ball was in left to right direction and answer would be k%l. Else it will be in right to left direction and answer would be 2*(n - 1) - k%l\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int l = 2 * (n - 1);\n int sec = k % l;\n \n if (sec < n) {\n return sec;\n } else {\n return l - sec;\n }\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) solution | o1-solution-by-ashis_kar-yazo | Approach\nBased on the quotient we can find the direction and the using the reminder we can find the result.\n\n# Complexity\n- Time complexity:O(1)\n\n- Space | ashis_kar | NORMAL | 2024-06-09T04:24:12.437097+00:00 | 2024-06-09T04:24:12.437183+00:00 | 69 | false | # Approach\nBased on the quotient we can find the direction and the using the reminder we can find the result.\n\n# Complexity\n- Time complexity:$$O(1)$$\n\n- Space complexity:$$O(1)$$\n\n# Code\n```\npublic class Solution {\n public int NumberOfChild(int n, int k) {\n n--;\n int q=k/n;\n int r=k%n;\n if((q&1)==1) //if odd, direction in reverse\n return n-r;\n return r;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Python O(n) Tc and o(1) Sc | python-on-tc-and-o1-sc-by-siva_manoj-qye0 | Intuition\nAfter every n-1 seconds the ball will change it\'s direction\nAfter every 2(n-1) seconds the ball will repeat it\'s previous cycle\n\n# Approach\n1 . | Siva_Manoj | NORMAL | 2024-06-09T04:11:49.060414+00:00 | 2024-06-09T04:11:49.060436+00:00 | 30 | false | # Intuition\nAfter every n-1 seconds the ball will change it\'s direction\nAfter every 2*(n-1) seconds the ball will repeat it\'s previous cycle\n\n# Approach\n1 . So we can update k value as k = k%(2*(n-1)) (bcz same cycle will repeat)\n\n2 . We can keep track of direction of ball by using direction variable which will change for (n-1) position\n\n# Complexity\n- Time complexity : O(n) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n total_steps = 2*(n-1)\n k = k % total_steps\n position = 0\n direction = 1\n for _ in range(k):\n position += direction\n if position == 0 or position == n - 1:\n direction *= -1\n \n return position\n``` | 1 | 0 | ['Math', 'Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Math solution | math-solution-by-prancinglynx-7223 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | prancingLynx | NORMAL | 2024-06-09T04:10:21.286476+00:00 | 2024-06-09T04:10:21.286525+00:00 | 292 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n s = k % (2 * (n - 1))\n return s if s < n else 2 * (n - 1) - s\n \n \n``` | 1 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Easy C++ Beginner Solution || O(1) || Beats 100% | easy-c-beginner-solution-o1-beats-100-by-tgu1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ravi_Prakash_Maurya | NORMAL | 2024-06-09T04:06:57.578541+00:00 | 2024-06-09T04:06:57.578565+00:00 | 94 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int m, int k) {\n int x = 0, n = 0;\n if((k % (m - 1)) % 2 == 0) n = 0;\n else n = m - 1;\n k = k % (m - 1);\n if(n == 0) n = k;\n else n = m - 1 - k;\n return n;\n }\n};\n``` | 1 | 0 | ['C++'] | 2 |
find-the-child-who-has-the-ball-after-k-seconds | C++ | O(1) | Intuition Explained in Detail | c-o1-intuition-explained-in-detail-by-me-2g6o | After n-1 seconds we reach right end \nAfter next n-1 seconds we reach left end\nAfter next n-1 seconds we right end again \n\n.... and so on \n\nSo,\nif n-1 / | mercer80 | NORMAL | 2024-06-09T04:04:35.217534+00:00 | 2024-06-09T05:01:06.172932+00:00 | 91 | false | After n-1 seconds we reach right end \nAfter next n-1 seconds we reach left end\nAfter next n-1 seconds we right end again \n\n.... and so on \n\nSo,\nif `n-1 / k` is an **odd** number we know for sure we are at **right end**.\n\nif `n-1/ k` is an **even** number then we know for sure we are at **left end.**\n\n\nOnce we figure out which end has the ball , we can use the remaining seconds calculate where the ball will end up .\n\nLets say n=4 , k=14\n\nk/n => 14/4 => 3\n3 is a odd number so ball is now at right end.\nfrom right end remaining seconds are `remainder` : `k % n` => 14%4 => 2\nso from right end move ball two steps i.e. \n `n-1 - remainder`\n4-1 - 2 = 1 which is the correct answer .\n\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n if(k/(n-1)%2==1){ //odd\n return n-1- k%(n-1);\n }\n else//even\n return k%(n-1);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Java Solution | java-solution-by-solved-nzih | \nclass Solution {\n public int numberOfChild(int n, int k) {\n int index = 0;\n char direction = \'r\';\n while (k != 0) {\n | solved | NORMAL | 2024-06-09T04:03:46.504134+00:00 | 2024-06-09T04:03:46.504166+00:00 | 37 | false | ```\nclass Solution {\n public int numberOfChild(int n, int k) {\n int index = 0;\n char direction = \'r\';\n while (k != 0) {\n if (index == n - 1) {\n direction = \'l\';\n }\n if (index == 0) {\n direction = \'r\';\n }\n if (direction == \'l\') {\n index--;\n } else {\n index++;\n }\n k = k - 1;\n }\n return index;\n }\n}\n``` | 1 | 0 | ['Simulation', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple O(1) solution | simple-o1-solution-by-0x4c0de-e28q | Intuition\n Describe your first thoughts on how to solve this problem. \nThe loop size is 2 * n - 2.\n\n### Approach\n Describe your approach to solving the pro | 0x4c0de | NORMAL | 2024-06-09T04:01:58.244466+00:00 | 2024-06-09T05:11:50.672408+00:00 | 128 | false | ### Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe loop size is `2 * n - 2`.\n\n### Approach\n<!-- Describe your approach to solving the problem. -->\nWe can query the remainder of the loop, forward or backward.\n\n### Complexity\n- Time complexity: $$O((1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n### Code\n```\nclass Solution {\n public int numberOfChild(int n, int k) {\n // loop size 2 * n - 2\n k = k % (2 * n - 2);\n if (k < n) {\n // forward\n return k;\n }\n\n // backward\n return n - 1 - (k - (n - 1));\n }\n}\n\n``` | 1 | 0 | ['Math', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Swift😎 | swift-by-upvotethispls-y4o3 | Math (accepted answer) | UpvoteThisPls | NORMAL | 2025-04-08T06:26:57.024427+00:00 | 2025-04-08T06:26:57.024427+00:00 | 2 | false | **Math (accepted answer)**
```
class Solution {
func numberOfChild(_ n: Int, _ k: Int) -> Int {
let (cycle, index) = k.quotientAndRemainder(dividingBy: n-1)
return cycle.isMultiple(of:2) ? index : n-1-index
}
}
``` | 0 | 0 | ['Swift'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | easy approach | easy-approach-by-sidgogia20-kz7a | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sidgogia20 | NORMAL | 2025-04-05T15:22:55.116220+00:00 | 2025-04-05T15:22:55.116220+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfChild(int n, int k) {
int ans=0,j=0,f=1;
for(int i=1;i<=k;i++){
if(j==n-1)f=-1;
else if(j==0)f=1;
ans=j+f;
j=ans;
}
return ans;
}
};
``` | 0 | 0 | ['Math', 'Simulation', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple Swift Solution | simple-swift-solution-by-felisviridis-51px | CodeCode | Felisviridis | NORMAL | 2025-04-02T10:42:49.116923+00:00 | 2025-04-02T11:48:07.132296+00:00 | 2 | false | 
# Code
```swift []
class Solution {
func numberOfChild(_ n: Int, _ k: Int) -> Int {
var pointer = 0, reverse = true
for i in 1...k {
if pointer == 0 || pointer == n - 1 {
reverse = !reverse
}
if reverse {
pointer -= 1
} else {
pointer += 1
}
}
return pointer
}
}
```
# Code
```swift []
class Solution {
func numberOfChild(_ n: Int, _ k: Int) -> Int {
let period = 2 * (n - 1)
let positionInPeriod = k % period
return positionInPeriod < n ? positionInPeriod : period - positionInPeriod
}
}
``` | 0 | 0 | ['Math', 'Swift', 'Simulation'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple and Easy Solution ( Runtime beats 100% and Memory beats 89%) | simple-and-easy-solution-runtime-beats-1-a04h | IntuitionThe problem involves passing a ball among n children arranged in a line. The ball starts at one end and moves sequentially until it reaches the other e | baytree1238 | NORMAL | 2025-03-11T09:23:30.975698+00:00 | 2025-03-11T09:23:30.975698+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves passing a ball among n children arranged in a line. The ball starts at one end and moves sequentially until it reaches the other end, at which point it reverses direction. By thinking of the ball’s path as a “back-and-forth” motion, we can determine the final position after k passes by figuring out:
How many complete “trips” (from one end to the other) have been made.
The direction of the ball on the current (incomplete) trip.
# Approach
<!-- Describe your approach to solving the problem. -->
Setup the children:
We create a list children that represents each child by their index (0 to n-1).
Determine complete trips:
A complete trip from one end to the other consists of n-1 passes.
The expression (k // (n-1)) gives the number of complete trips.
Taking modulo 2, i.e., (k // (n-1)) % 2, tells us the direction of the ball:
0 indicates that the ball is moving from left to right.
1 indicates that the ball is moving from right to left.
Determine position in the current trip:
The remainder order = k % (n-1) gives the number of passes made in the current trip.
Depending on the direction:
If moving left to right, the ball will be at the child with index order.
If moving right to left, the ball will be at the child with index -order-1 (which is equivalent to n - 1 - order).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
The algorithm involves creating a list of n children, which is an O(n) operation. The remaining arithmetic operations (division, modulo, and indexing) are all O(1).
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
The space used is O(n) due to the list of children.
# Code
```python []
class Solution(object):
def numberOfChild(self, n, k):
"""
:type n: int
:type k: int
:rtype: int
"""
# child_with_ball = 0
children = [i for i in range(n)]
left_end_right_end = (k // (n-1)) % 2
order = k % (n-1)
if left_end_right_end == 0:
child_with_ball = children[order]
else:
child_with_ball = children[-order-1]
return child_with_ball
``` | 0 | 0 | ['Python'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple solution in Java. Beats 100 % | simple-solution-in-java-beats-100-by-kha-co2e | Complexity
Time complexity:
O(1)
Space complexity:
O(1)
Code | Khamdam | NORMAL | 2025-03-08T04:54:07.632249+00:00 | 2025-03-08T04:54:07.632249+00:00 | 3 | false | # Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
n = n - 1;
int rounds = k / n;
int remainingSteps = k % n;
if (rounds % 2 == 0) {
return remainingSteps;
} else {
return n - remainingSteps;
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Repeating sequence can be solved with mathematical formulae for O(1) complexity [Kotlin] | repeating-sequence-can-be-solved-with-ma-ic9c | IntuitionThe problem describes a simple sequence of numbers that start from zero, increase to a maximum value and then decline again to zero.
The maximum value | user5661 | NORMAL | 2025-03-03T17:08:00.381915+00:00 | 2025-03-03T17:08:00.381915+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem describes a simple sequence of numbers that start from zero, increase to a maximum value and then decline again to zero.
The maximum value is the number of transitions in any direction before you reach the last child in the chain and are forced to reverse directions.
# Approach
<!-- Describe your approach to solving the problem. -->
The number of transtions before you reach the end of the chain is give by n - 1
max_transitions = n-1
Starting from zero, you return again to zero after doing two sets of transtitions, one going from left to right, and then going back from right to left. Let's call this the full loop length.
full_loop_length = 2* max_transitions
Take the modulus of k against the full loop length.
mod_val = k % full_loop_length
If the value returned is less than or equal to the max-transitions, the ball is in the forward leg of the loop, and hence the modulus itself gives the current location of the ball.
If the modules is greater than max-tranistion, the ball is on the reverse leg of the loop. Here you subtract the modulus value from the loop length to get the current location.
if mod_val <= max_transitions
return mod_val
else
return full_loop_length - mod_val
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(1) as it is a couple of simple mathematical calculations.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Three new variables are created to keep the code readable. So space complexity is also O(3) which simplifies to O(1)
# Code
```kotlin []
class Solution {
fun numberOfChild(n: Int, k: Int): Int {
val transitions = n - 1
val loopLength = 2*transitions
val modulus = k%loopLength
if(modulus < transitions)
return modulus
else
return loopLength - modulus
}
}
``` | 0 | 0 | ['Kotlin'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | O(n) Time Solution - Simple and Fast! | on-time-solution-simple-and-fast-by-ches-d3xe | ApproachChild 0 holds the ball, and passes it on to Child 1, who passes it on to Child 2, and so on. But whenever it reaches the n-1th child, the direction reve | ChessTalk890 | NORMAL | 2025-02-28T17:51:57.977636+00:00 | 2025-02-28T17:51:57.977636+00:00 | 3 | false | # Approach
<!-- Describe your approach to solving the problem. -->
Child 0 holds the ball, and passes it on to Child 1, who passes it on to Child 2, and so on. But whenever it reaches the n-1th child, the direction reverses. So, if n = 5, then the sequence will look something like this:
`0 -> 1 -> 2 -> 3 -> 4 -> 3 -> 2 -> 1 -> 0 -> 1 ...`
The key thing to take from this is that it goes from 0 to n, then from n-1 to 1, and then back to 0 again, meaning that we can represent one single cycle as
```
[a for a in range(n)] + [b for b in range(n-2, 0, -1)]
```
The first part of this, `[a for a in range(n)]` generates the part from 0 to n-1, and the second part, `[b for b in range(n-2, 0, -1)]` generates the reverse movement of the ball to complete the cycle.
Finally, we should return the item in position: k modulo the length of one complete cycle. This is how to do that:
```
return full_cycle[k%len(full_cycle)]
```
# Complexity
#### ***Time complexity:***
The construction of actual_n involves two list comprehensions:
- [a for a in range(n)], which takes 𝑂(𝑛) time to generate, and
- [b for b in range(n-2, 0, -1)], which takes 𝑂(𝑛) time to generate.
Together, this is 𝑂(𝑛) time.
The modulo operation and indexing into the list take 𝑂(1).
Thus, the overall time complexity is 𝑂(𝑛) due to the list construction.
#### ***Space complexity:***
The list full_cycle has
- 2𝑛−2 elements, which is 𝑂(𝑛) space.
- A few integer variables are used, which take 𝑂(1) space.
Thus, the overall space complexity is 𝑂(𝑛) due to the storage of the full_cycle list.
# Code
```python3 []
class Solution:
def numberOfChild(self, n: int, k: int) -> int:
if n<3:
return k%n
# For any n lower than 3, then the corresponding list will already loop back on itself.
full_cycle = [a for a in range(n)] + [b for b in range(n-2, 0, -1)]
# Generating the complete cycle list
return full_cycle[k%len(full_cycle)]
# Finally, we return the item in position k modulo the length of one complete cycle, or our actual_n list.
``` | 0 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | O(1) Solution fast as f*ck | o1-solution-fast-as-fck-by-yarikkotsur-kjyc | IntuitionApproachCyclic solution
Ecach children has bal: 0,1,2,3...n-1,n-2,...,3,2,1
CycleLen = 2n - 2
You need to take mod from cycle len
If k < n then k is so | yarikkotsur | NORMAL | 2025-02-25T16:45:19.454616+00:00 | 2025-02-25T16:45:19.454616+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Cyclic solution
Ecach children has bal: 0,1,2,3...n-1,n-2,...,3,2,1
CycleLen = 2n - 2
You need to take mod from cycle len
If k < n then k is solution otherwise you have to substract k from cycle len.
# Complexity
- Time complexity: O(1)
- Space complexity:
- Time complexity: O(1)
# Code
```golang []
func numberOfChild(n int, k int) int {
cycleLen := (2 * n - 2)
k = k % cycleLen
if k < n {
return k
} else {
return cycleLen - k
}
}
``` | 0 | 0 | ['Go'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Find the child who has the ball after k seconds📍 || Simple logic🎯|| Easy solution | find-the-child-who-has-the-ball-after-k-il5og | IntuitionThe problem simulates the movement of a child along a straight path of n positions. The child starts at position 0 and moves one step at a time. When r | palle_sravya | NORMAL | 2025-02-20T05:01:48.708438+00:00 | 2025-02-20T05:01:48.708438+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem simulates the movement of a child along a straight path of n positions. The child starts at position 0 and moves one step at a time. When reaching either end (0 or n-1), the direction reverses. The goal is to determine the child's position after k steps.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initialization: Start at position 0 with a direction of +1 (moving forward).
2. Iteration: Move the child one step in the current direction (+1 for forward, -1 for backward).
3. Boundary Handling:
- If the child reaches position 0, set the direction to +1.
- If the child reaches position n-1, set the direction to -1.
4. Repeat for k steps and return the final position.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(k)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int pos = 0;
int direction = 1;
int count = 0;
while(count < k){
// pos = i;
if(pos == 0){
direction = 1;
}
if(pos == n-1){
direction = -1;
}
pos = pos+direction;
count++;
}
return pos;
}
}
``` | 0 | 0 | ['Math', 'Simulation', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Easy Beginner friendly | Python code| Similar solution for Passing Pillow | easy-beginner-friendly-python-code-simil-ps5x | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | S-urjith_1001 | NORMAL | 2025-02-11T06:46:21.170691+00:00 | 2025-02-11T06:46:21.170691+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->Solve it like we solve passing pillow problem
# Approach
<!-- Describe your approach to solving the problem. -->See this similar solution
https://youtu.be/SR78dGOaxUs?si=WmiauViYAdmLrYAW
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1)
# Code
```python3 []
class Solution:
def numberOfChild(self, n: int, k: int) -> int:
direction = 1
winner_position = 0
for _ in range(k):
if winner_position == 0:
direction = 1
elif winner_position == (n-1):
direction = -1
winner_position += direction
return winner_position
``` | 0 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Java | O(1) | easy to understand | java-o1-easy-to-understand-by-lost_in_sk-635v | IntuitionApproachComplexity
Time complexity : O(1)
Space complexity : O(1)
Code | lost_in_sky | NORMAL | 2025-02-10T18:57:27.789092+00:00 | 2025-02-10T18:57:27.789092+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity : O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity : O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
k=k%(2*(n-1));
if(k/n==0){
return k%n;
}else{
return n-2-(k%n);
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.