question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-child-who-has-the-ball-after-k-seconds | java sol | java-sol-by-rrrautela-s0a2 | Code | rrrautela | NORMAL | 2025-02-10T03:51:59.575359+00:00 | 2025-02-10T03:51:59.575359+00:00 | 7 | false |
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int x = k;
if(k>=n){
x = k % (2*n - 2);
if(x>=n){
x = n-1 - (x%(n-1));
// x = x - x%(n-1) * 2;
}
}
return x;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 3178. Find the Child Who Has the Ball After K Seconds | 3178-find-the-child-who-has-the-ball-aft-cleo | IntuitionHard one to solve through optimal solution!ApproachFound internal logic of changing direction!Complexity
Time complexity: O(1)
Space complexity: O(1) | SPD-LEGEND | NORMAL | 2025-01-27T16:15:26.535991+00:00 | 2025-01-27T16:15:26.535991+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Hard one to solve through optimal solution!
# Approach
<!-- Describe your approach to solving the problem. -->
Found internal logic of changing direction!
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
if((k/(n-1))%2==0)
return k%(n-1);
return (n-1)-(k%(n-1));
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Array | Simple solution with 100% beaten | array-simple-solution-with-100-beaten-by-4n0v | IntuitionTo solve this problem, we can simulate the movement of the ball. Initially, the ball starts at child 0, and it moves in the right direction. When the b | Takaaki_Morofushi | NORMAL | 2025-01-27T03:39:37.917322+00:00 | 2025-01-27T03:39:37.917322+00:00 | 3 | false | # Intuition
To solve this problem, we can simulate the movement of the ball. Initially, the ball starts at child 0, and it moves in the right direction. When the ball reaches either end, it reverses direction. We need to compute the final child after `k` seconds of this movement.
# Approach
1. Initialize the ball's position at child 0 (`pos = 0`).
2. Use a boolean flag (`direction`) to track whether the ball is moving right (`true`) or left (`false`).
3. For each second, update the position based on the current direction:
- If moving right, increment the position. If the ball reaches the last child (position `n - 1`), reverse the direction.
- If moving left, decrement the position. If the ball reaches the first child (position `0`), reverse the direction.
4. After `k` seconds, return the final position.
# Complexity
- Time complexity: $$O(k)$$, as we simulate the ball passing for `k` seconds.
- Space complexity: $$O(1)$$, as only a few variables are used to store the current position and direction.
# Code
```cpp
class Solution {
public:
int numberOfChild(int n, int k) {
int pos = 0; // Ball starts at child 0
bool direction = true; // true = right, false = left
for (int i = 0; i < k; ++i) {
if (direction) {
pos++; // Move right
if (pos == n - 1) direction = false; // Reverse direction at right end
} else {
pos--; // Move left
if (pos == 0) direction = true; // Reverse direction at left end
}
}
return pos;
}
};
| 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | begineer friendly || 100% beat | begineer-friendly-100-beat-by-gyaneshkr-lg5h | IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(1)
Code | gyaneshkr | NORMAL | 2025-01-26T16:43:48.351999+00:00 | 2025-01-26T16:43:48.351999+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int dir=1; // 1->right -1->left
int children=0;
while(k-- > 0){
children+=dir;
if(children==n-1 || children==0) dir=-dir;
}
return children;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | numberOfChild: beautiful O(1) solution. BEAT 100%. ✅ | numberofchild-beautiful-o1-solution-beat-56vx | IntuitionTo determine which child will have the ball after k seconds, we need to consider the direction changes when the ball reaches the ends of the line. The | rTIvQYSHLp | NORMAL | 2025-01-23T20:14:14.307652+00:00 | 2025-01-23T20:14:14.307652+00:00 | 3 | false | # Intuition
To determine which child will have the ball after `k` seconds, we need to consider the direction changes when the ball reaches the ends of the line. The ball will move back and forth between the children based on the number of passes.
# Approach
1. Check if the quotient of \(k\) divided by \(n-1\) is even or odd to determine the final direction of the ball.
2. If even, the ball will move in the same direction as the initial direction.
3. If odd, the ball will move in the opposite direction after reaching the end.
4. Use the modulus operator to determine the position of the child based on the remaining passes.
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```c []
int numberOfChild(int n, int k) {
if((k/(n-1))%2==0) return k%(n-1);
else return n-k%(n-1)-1;
}
``` | 0 | 0 | ['Math', 'C'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | FORMULA BASED FULL EXPLAINATION | formula-based-full-explaination-by-prach-0l2x | IntuitionFor n students from 0 to n-1 , then from last to 1st notice a cycle !Hence ball goes in cycle be just get the effective shift in its initial Pos and de | PrachiKumari | NORMAL | 2025-01-18T11:19:33.320687+00:00 | 2025-01-18T11:19:33.320687+00:00 | 4 | false | # Intuition
For n students from 0 to n-1 , then from last to 1st notice a cycle !
Hence ball goes in cycle be just get the effective shift in its initial Pos and determine its Directions of motion either` L TO R `or `R TO L` .
# Approach
- Total cyclic shifts 0 to n-1 and back to 0th
(Take is as n vertices and n-1 edges to connect)
L to R : n-1 shifts/edges
R to L : n-1 shifts/edges
Hence `totalShifts = 2*(n-1) shifts
`
- `Effective pos `(take % of k as it give how many times balls shifts ) = `k%(totalShifts)`
- Now Direction :
1) `effPos from 0 to n-1 : L to R`
2) `effPos from n-1 to 2*(n-1) : R to L`
L to R . Effective pos give the children left on rightSide
R to L . totalShifts - Effective pos give the children on LeftSide
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int shifts = 2*(n-1) ;
int effPos = k%(shifts);
if ( effPos < n-1){// towards Right
return effPos;
}else {
return shifts - effPos;
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | FORMULA BASED FULL EXPLAINATION | formula-based-full-explaination-by-prach-06xh | IntuitionFor n students from 0 to n-1 , then from last to 1st notice a cycle !Hence ball goes in cycle be just get the effective shift in its initial Pos and de | PrachiKumari | NORMAL | 2025-01-18T11:19:30.721910+00:00 | 2025-01-18T11:19:30.721910+00:00 | 3 | false | # Intuition
For n students from 0 to n-1 , then from last to 1st notice a cycle !
Hence ball goes in cycle be just get the effective shift in its initial Pos and determine its Directions of motion either` L TO R `or `R TO L` .
# Approach
- Total cyclic shifts 0 to n-1 and back to 0th
(Take is as n vertices and n-1 edges to connect)
L to R : n-1 shifts/edges
R to L : n-1 shifts/edges
Hence `totalShifts = 2*(n-1) shifts
`
- `Effective pos `(take % of k as it give how many times balls shifts ) = `k%(totalShifts)`
- Now Direction :
1) `effPos from 0 to n-1 : L to R`
2) `effPos from n-1 to 2*(n-1) : R to L`
L to R . Effective pos give the children left on rightSide
R to L . totalShifts - Effective pos give the children on LeftSide
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int shifts = 2*(n-1) ;
int effPos = k%(shifts);
if ( effPos < n-1){// towards Right
return effPos;
}else {
return shifts - effPos;
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | FORMULA BASED FULL EXPLAINATION | formula-based-full-explaination-by-prach-joaq | IntuitionFor n students from 0 to n-1 , then from last to 1st notice a cycle !Hence ball goes in cycle be just get the effective shift in its initial Pos and de | PrachiKumari | NORMAL | 2025-01-18T11:19:29.238727+00:00 | 2025-01-18T11:19:29.238727+00:00 | 0 | false | # Intuition
For n students from 0 to n-1 , then from last to 1st notice a cycle !
Hence ball goes in cycle be just get the effective shift in its initial Pos and determine its Directions of motion either` L TO R `or `R TO L` .
# Approach
- Total cyclic shifts 0 to n-1 and back to 0th
(Take is as n vertices and n-1 edges to connect)
L to R : n-1 shifts/edges
R to L : n-1 shifts/edges
Hence `totalShifts = 2*(n-1) shifts
`
- `Effective pos `(take % of k as it give how many times balls shifts ) = `k%(totalShifts)`
- Now Direction :
1) `effPos from 0 to n-1 : L to R`
2) `effPos from n-1 to 2*(n-1) : R to L`
L to R . Effective pos give the children left on rightSide
R to L . totalShifts - Effective pos give the children on LeftSide
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int shifts = 2*(n-1) ;
int effPos = k%(shifts);
if ( effPos < n-1){// towards Right
return effPos;
}else {
return shifts - effPos;
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Easy Solution | easy-solution-by-choudhariaditya-vg2b | Code | choudhariaditya | NORMAL | 2025-01-14T17:53:31.605804+00:00 | 2025-01-14T17:53:31.605804+00:00 | 6 | false |
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
int i = 0;
while (k > 0) {
while (k > 0 && i < n - 1) {
i++;
k--;
}
if (k == 0) {
return i;
}
while (k > 0 && i > 0) {
i--;
k--;
}
if (k == 0) {
return i;
}
}
return 0;
}
}
``` | 0 | 0 | ['Math', 'Simulation', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | reduce by round/single side move | reduce-by-roundsingle-side-move-by-linda-8xg5 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | linda2024 | NORMAL | 2025-01-10T22:42:45.831434+00:00 | 2025-01-10T22:42:45.831434+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int NumberOfChild(int n, int k) {
int doubleSize = 2*(n-1);
k %= doubleSize; // calculate less than one round
if(k < n) // to right
return k;
k -= (n-1); // reduce from 0 to n-1
return n -1 -k; // return from n-1 to rest;
}
}
``` | 0 | 0 | ['C#'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 2 line | 2-line-by-sanzenin_aria-rit3 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sanzenin_aria | NORMAL | 2025-01-08T13:06:19.396368+00:00 | 2025-01-08T13:06:19.396368+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def numberOfChild(self, n: int, k: int) -> int:
k %= (n-1)*2
return k if k<=n-1 else (n-1)*2 -k
``` | 0 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 3178. Find the Child Who Has the Ball After K Seconds | 3178-find-the-child-who-has-the-ball-aft-0zyw | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-07T07:41:38.293212+00:00 | 2025-01-07T07:41:38.293212+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfChild(int n, int k) {
int position = 0; // Start with child 0
int direction = 1; // Ball is passing to the right initially
for (int i = 0; i < k; ++i) {
position += direction; // Move ball in the current direction
// Check if the ball has reached the boundary and reverse direction
if (position == 0 || position == n - 1) {
direction = -direction; // Reverse direction
}
}
return position;
}
};
``` | 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Java Best Solution 0ms | java-best-solution-0ms-by-trevorkmcintyr-82wr | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | trevorkmcintyre | NORMAL | 2025-01-07T05:01:33.551283+00:00 | 2025-01-07T05:01:33.551283+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfChild(int n, int k) {
boolean backwards = false;
int i = 0;
int timer = 0;
while(timer != k){
if(i==n-1){
backwards = true;
}
if(backwards && i == 0){
backwards = false;
}
if(!backwards){
i++;
}else{
i--;
}
timer++;
}
return i;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simplest Approach: Beats 100% | simplest-approach-beats-100-by-kajal_2-icd6 | IntuitionApproachComplexity
Time complexity: O(k)
Space complexity: O(1)
Code | Kajal_2 | NORMAL | 2025-01-03T10:03:02.697490+00:00 | 2025-01-03T10:03:02.697490+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(k)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numberOfChild(int n, int k) {
int position = 0; // Current position (child index)
int direction = 1; // Direction: 1 means forward, -1 means backward
for (int step = 1; step <= k; step++) {
position += direction; // Move in the current direction
// Change direction if we reach the first or last child
if (position == 0) {
direction = 1; // Move forward
} else if (position == n - 1) {
direction = -1; // Move backward
}
}
return position; // Final position after k steps
}
};
``` | 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 3178. Find the Child Who Has the Ball After K Seconds | 3178-find-the-child-who-has-the-ball-aft-6v84 | Time complexity: O(1)Space complexity: O(1)Code | Adarshjha | NORMAL | 2024-12-31T11:17:56.733855+00:00 | 2024-12-31T11:17:56.733855+00:00 | 3 | false |
# Time complexity: O(1)
# Space complexity: O(1)
# Code
```c []
int numberOfChild(int n, int k) {
int quo, rem, n2 = n - 1;
quo = k / n2;
rem = k % n2;
if(quo % 2){
return (n2-rem);
}
else{
return rem;
}
}
``` | 0 | 0 | ['C'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Find the Child Who Has the Ball After K Seconds - Simplified Solution | find-the-child-who-has-the-ball-after-k-14kgo | Problem OverviewWe have n children standing in a line, and a ball is passed between them every second. The ball starts with child 0 and moves to the right. When | JAHAGANAPATHI_SUGUMAR | NORMAL | 2024-12-29T13:27:15.317656+00:00 | 2024-12-29T13:27:15.317656+00:00 | 3 | false | # Problem Overview
We have `n` children standing in a line, and a ball is passed between them every second. The ball starts with child `0` and moves to the right. When the ball reaches either end of the line, the passing direction reverses. The task is to determine which child has the ball after `k` seconds.
# Intuition
The ball movement follows a repeating pattern:
- It takes `n-1` seconds for the ball to travel from one end of the line to the other.
- The direction of the ball's movement is determined by the number of complete cycles (`k / (n-1)`):
- If the cycle count is even, the ball moves forward.
- If the cycle count is odd, the ball moves backward.
- The position within the current cycle can be identified using the remainder (`k % (n-1)`).
# Approach
1. Calculate the number of complete cycles and the remainder using `k / (n-1)` and `k % (n-1)`.
2. If the cycle count is even, the ball's position is `rem`.
3. If the cycle count is odd, the ball's position is `n - rem - 1`.
# Complexity
- **Time complexity:** $$O(1)$$ — Only basic arithmetic operations are performed.
- **Space complexity:** $$O(1)$$ — No additional memory is used.
# Code
```java
class Solution {
public int numberOfChild(int n, int k) {
int rem = k % (n - 1);
int cycle = k / (n - 1);
if (cycle % 2 == 0) {
return rem;
} else {
return n - rem - 1;
}
}
}
| 0 | 0 | ['Math', 'Simulation', 'Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | One Line | one-line-by-khaled-alomari-i948 | null | khaled-alomari | NORMAL | 2024-12-25T22:02:00.371742+00:00 | 2024-12-25T22:02:00.371742+00:00 | 13 | false | # Complexity
- Time complexity:
$$O(1)$$
- Space complexity:
$$O(1)$$
# Code
```javascript []
const numberOfChild = (n, k) => (k %= n * 2 - 2) && k > n - 1 && 2 * n - 2 - k || k;
```
```typescript []
const numberOfChild = (n: number, k: number): number => (k %= n * 2 - 2) && k > n - 1 && 2 * n - 2 - k || k;
``` | 0 | 0 | ['Math', 'TypeScript', 'JavaScript'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple implementation in cpp without any math | simple-implementation-in-cpp-without-any-sec7 | IntuitionApproachComplexity
Time complexity:
O(k)
Space complexity:
O(1)
Code | aditya821 | NORMAL | 2024-12-23T17:05:04.713879+00:00 | 2024-12-23T17:05:04.713879+00:00 | 2 | false | # Intuition
# Approach
# Complexity
- Time complexity:
O(k)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
int numberOfChild(int n, int k) {
bool t=true;
int i=-1,cnt=-1;
while(cnt!=k){
if(i==n-1&&t==true){
t=!t;
}
if(i==0&&t==false){
t=!t;
}
if(t==true){
i++;
}
if(t==false){
i--;
}
cnt++;
}
return i;
}
};
``` | 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | simple solution | simple-solution-by-owenwu4-2uqy | Intuitionsimulate the process - this time, starting at 0, using a boolean flag to determine the upper and lower boundApproachComplexity
Time complexity:
Space | owenwu4 | NORMAL | 2024-12-22T15:03:59.372616+00:00 | 2024-12-22T15:03:59.372616+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
simulate the process - this time, starting at 0, using a boolean flag to determine the upper and lower bound
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def numberOfChild(self, n: int, k: int) -> int:
flag = True
start = 0
for i in range(k):
print(start)
if flag:
start += 1
if not flag:
start -= 1
if start == n - 1:
flag = False
if start == 0:
flag = True
print(start)
return start
``` | 0 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | solution | solution-by-ester45764-w9at | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ester45764 | NORMAL | 2024-12-20T18:38:14.946865+00:00 | 2024-12-20T18:38:14.946865+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def numberOfChild(self, n: int, k: int) -> int:
line=k//(n-1)
secondes=k%(n-1)
if line%2==0:
return secondes
else:
return n-secondes-1
``` | 0 | 0 | ['Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Revert Approach Solution | revert-approach-solution-by-sohan3das-rbyh | IntuitionI was thinking that how can i revert when i reach either of the end then i got this approach.Approach -> Revert ApproachComplexity
Time complexity: O(K | sohan3das | NORMAL | 2024-12-18T04:28:46.026454+00:00 | 2024-12-18T04:28:46.026454+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI was thinking that how can i revert when i reach either of the end then i got this approach.\n# Approach -> Revert Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity: O(K)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n int pointer = 0;\n boolean revert = false;\n for(int i=0;i<=k;i++){\n if(i>0){\n if(!revert){\n pointer = pointer + 1;\n if(pointer == n-1){\n revert = true;\n }\n }else{\n pointer = pointer - 1;\n if(pointer == 0){\n revert = false;\n }\n }\n } \n }\n return pointer;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | ✅🐍 Python simulation 🐍✅ | python-simulation-by-ninise-fwc9 | Code | Ninise | NORMAL | 2024-12-16T18:18:24.665677+00:00 | 2024-12-16T18:18:24.665677+00:00 | 5 | false | \n# Code\n```python3 []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n i = 0\n direction = True\n while k > 0:\n if direction and i == n - 1:\n direction = False\n i -= 1\n elif not direction and i == 0:\n direction = True\n i += 1\n elif direction:\n i += 1\n else:\n i -= 1\n k -= 1\n \n return i\n``` | 0 | 0 | ['Simulation', 'Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple Maths Solution C++ Beats 100% | simple-maths-solution-c-beats-100-by-tan-w7mx | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | tanishqj2005 | NORMAL | 2024-12-14T09:01:52.967243+00:00 | 2024-12-14T09:01:52.967243+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int comp = k / (n-1);\n int rem = k % (n-1);\n\n if(comp % 2 == 0){\n return rem;\n }\n else{\n return (n-1-rem);\n }\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Java Solution || Beats 100% | java-solution-beats-100-by-yashkesharwan-lr8l | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | yashkesharwani559 | NORMAL | 2024-12-13T16:02:11.192141+00:00 | 2024-12-13T16:02:11.192141+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n int t = (n-1)*2;\n k = k%t;\n\n if(k<n){\n return k;\n }\n\n return t-k;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 2 line code cpp || 100% time complexity | 2-line-code-cpp-100-time-complexity-by-p-kfs1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Prashant0100 | NORMAL | 2024-12-08T07:08:38.768767+00:00 | 2024-12-08T07:08:38.768797+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int ll=k%(2*(n-1));\n if(ll>n-1){\n return (2*(n-1))-ll;\n }\n return ll;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | One Line Solution: Time : O(1) & Space : O(1) | one-line-solution-time-o1-space-o1-by-bh-nflu | Intuition\nThe problem can be thought of as simulating the movement of the ball between the children while alternating directions when it reaches either end. In | bhardwajsameer7 | NORMAL | 2024-12-05T20:07:00.606041+00:00 | 2024-12-05T20:07:00.606073+00:00 | 1 | false | # Intuition\nThe problem can be thought of as simulating the movement of the ball between the children while alternating directions when it reaches either end. Instead of simulating every step explicitly, the key is recognizing the repetitive nature of the sequence.\n\nThe ball oscillates between the children in a predictable pattern, forming a "bounce-back" mechanism at the two ends (0 and n-1).\nUsing this insight, you can calculate the final position mathematically by reducing unnecessary calculations.\n\n**Example Walkthrough**\n```\nInput: n = 3, k = 5\nStep-by-step Calculation:\n\nThe total cycle length is 2 * (n - 1) = 4.\nk = 5 \u2192 Remainder when 5 is divided by 4 is 1.\nSince (5 / (n - 1)) % 2 == 1, the ball is in the "backward" phase.\nFinal position: (n - 1) - (k % (n - 1)) = 2 - (5 % 2) = 1.\n```\n\n# Approach\n**1. Observation of the Ball Movement:**\nEach complete traversal from 0 to n-1 and back takes 2 * (n-1) steps.\nThe position of the ball after k seconds depends on the remainder of k when divided by 2 * (n-1).\n\n**2. Handling Direction Reversal:**\nIf the ball moves to the right and reverses direction, the position in the second half of the cycle can be derived by subtracting from the last position.\n\n**3 Mathematical Computation:**\nDetermine which phase of the traversal the ball is in (moving forward or backward) using (k / (n-1)) % 2:\n\n- 0: Ball is moving forward.\n- 1: Ball is moving backward.\n\nCalculate the final position using modular arithmetic:\n- If moving forward: k % (n-1).\n- If moving backward: (n-1) - (k % (n-1)).\n\n**4. Implementation:** Using simple modular arithmetic, you can determine the final position of the ball after k seconds without simulating all steps.\n\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\n```java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n \n return (k / (n-1)) % 2 == 0 ? k % (n-1) : (n-1) - (k % (n-1));\n\n }\n}\n\n\n``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Video Explanation Solution easy to understand | Programming with Pirai | Half Moon Coder. | video-explanation-solution-easy-to-under-zifu | Video : https://youtu.be/lc5IuVczpNI\n\n# Code\npython3 []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n pos=0\n directi | Piraisudan_02 | NORMAL | 2024-12-05T16:24:39.761824+00:00 | 2024-12-05T16:24:39.761848+00:00 | 2 | false | # Video : https://youtu.be/lc5IuVczpNI\n\n# Code\n```python3 []\nclass Solution:\n def numberOfChild(self, n: int, k: int) -> int:\n pos=0\n direction=1\n for i in range(k):\n if direction==1:\n if pos==n-1:\n direction=-1\n pos+=direction\n else:\n if pos==0:\n direction=1\n pos+=direction\n return pos\n``` | 0 | 0 | ['Math', 'Simulation', 'Python3'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | 1ms solution. Pattern based logic | 1ms-solution-pattern-based-logic-by-that-ycmu | Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\njava []\n/**\n n=5, k=6\n 0->0\n 1->1\n 2->2\n 3 | ThatNinjaGuySpeaks | NORMAL | 2024-12-01T16:04:45.229672+00:00 | 2024-12-01T16:04:45.229714+00:00 | 1 | false | # Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```java []\n/**\n n=5, k=6\n 0->0\n 1->1\n 2->2\n 3->3\n 4->4\n \n 5->3\n 6->2\n 7->1\n 8->0\n\n 9->1\n 10->2\n 11->3\n 12->4\n\n 13->3\n 14->2\n 15->1\n 16->0\n\n 17->1\n 18->2\n 19->3\n 20->4\n\n Pattern goes through completely on the first try with n iterations. \n Forth that, it repeats iteself in batches of (n-1) \n */\nclass Solution {\n public int numberOfChild(int n, int k) {\n\n if(k<n)\n return k;\n k-=(n);\n if((k/(n-1))%2==0){\n return(n-2-(k%(n-1)));\n }else{\n return(1+(k%(n-1)));\n }\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | C++ Beats 100% | c-beats-100-by-muhammad-hussnain-gqnn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | muhammad-hussnain | NORMAL | 2024-11-27T13:56:27.848289+00:00 | 2024-11-27T13:56:27.848318+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numberOfChild(int n, int k) {\n int position=0;\n int direction=1;\n for(int i=0;i<k;i++){\n position=position+direction;\n if(position==0 || position==n-1){\n direction=direction*-1;\n }\n }\n return position;\n }\n};\n``` | 0 | 0 | ['Math', 'C++'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Easy Python beats 100% - 5 lines only | easy-python-beats-100-5-lines-only-by-pu-xgl5 | Intuition\nThere is no need for traversing the array. If k is equal to or less than n, its clear that we will end up on child k.\n\nOnce k hits n and the ball s | Puddle321 | NORMAL | 2024-11-25T21:39:44.125215+00:00 | 2024-11-25T21:39:44.125261+00:00 | 3 | false | # Intuition\nThere is no need for traversing the array. If k is equal to or less than n, its clear that we will end up on child k.\n\nOnce k hits n and the ball starts going backwards, the child that ends up with the ball is child number (n-1) - (k % (n-1)). This is because we count backwards from the last child (child n -1) the number of steps that we have taken since hitting the end of the line. \n\n# Approach\n\ntimes_traversed indicates the number of tims we have fully traversed the line. If times_traversed % 2 == 0 this means we have done one full cycle of the line (there and back once), and are at child 0 or greater. In this case we can calculate the child who receives the ball as child number k % (n-1).\n\nIf times_traversed % 2 is not 0, it means we have traversed the line an odd number of times (for example 3 times). This means we are either at child n, or are going backwards. Therefore we calculate the child with the ball as child number (n-1) - (k % (n-1)).\n\n# Complexity\n- Time complexity is O(1)\n- Space complexity is also O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution(object):\n def numberOfChild(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: int\n """\n \n times_traversed = k // (n-1)\n\n #this means we are going forwards \n if(times_traversed % 2 == 0):\n return k % (n-1)\n # this means we were going backwards\n else:\n return (n-1) - k % (n-1)\n \n\n \n``` | 0 | 0 | ['Python'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | Simple solution -> 0 ms | simple-solution-0-ms-by-developersuserna-x79f | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | DevelopersUsername | NORMAL | 2024-11-25T17:56:11.954622+00:00 | 2024-11-25T17:56:11.954662+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```java []\nclass Solution {\n public int numberOfChild(int n, int k) {\n\n k %= 2 * (n - 1);\n\n return k < n ? k : 2 * (n - 1) - k;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-child-who-has-the-ball-after-k-seconds | JavaScript Solution | javascript-solution-by-shriharimutalik96-czj0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shriharimutalik96 | NORMAL | 2024-11-24T17:46:52.199683+00:00 | 2024-11-24T17:46:52.199711+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number} n\n * @param {number} k\n * @return {number}\n */\nvar numberOfChild = function(n, k) {\n const odi = parseInt(k/(n-1))\n const adi = k%(n-1)\n if(odi % 2 ==0){\n return adi\n }else{\n return (n-1) - adi\n }\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
minimum-add-to-make-parentheses-valid | [C++/Java/Python] Straight Forward One Pass | cjavapython-straight-forward-one-pass-by-m7ix | Intuition:\nTo make a string valid,\nwe can add some ( on the left,\nand add some ) on the right.\nWe need to find the number of each.\n\n\n## Explanation:\nlef | lee215 | NORMAL | 2018-10-14T03:18:46.443556+00:00 | 2019-09-16T14:47:46.973592+00:00 | 42,412 | false | ## **Intuition**:\nTo make a string valid,\nwe can add some `(` on the left,\nand add some `)` on the right.\nWe need to find the number of each.\n<br>\n\n## **Explanation**:\n`left` records the number of `(` we need to add on the left of `S`.\n`right` records the number of `)` we need to add on the right of `S`,\nwhich equals to the number of current opened parentheses.\n<br>\n\nLoop char `c` in the string `S`:\n`if (c == \'(\')`, we increment `right`,\n`if (c == \')\')`, we decrement `right`.\nWhen `right` is already 0, we increment `left`\nReturn `left + right` in the end\n<br>\n\n## **Time Complexity**:\nTime `O(N)`\nSpace `O(1)`\n<br>\n\n**Java:**\n```java\n public int minAddToMakeValid(String S) {\n int left = 0, right = 0;\n for (int i = 0; i < S.length(); ++i) {\n if (S.charAt(i) == \'(\') {\n right++;\n } else if (right > 0) {\n right--;\n } else {\n left++;\n }\n }\n return left + right;\n }\n```\n\n**C++:**\n```cpp\n int minAddToMakeValid(string S) {\n int left = 0, right = 0;\n for (char c : S)\n if (c == \'(\')\n right++;\n else if (right > 0)\n right--;\n else\n left++;\n return left + right;\n }\n```\n\n**Python:**\n```python\n def minAddToMakeValid(self, S):\n left = right = 0\n for i in S:\n if right == 0 and i == \')\':\n left += 1\n else:\n right += 1 if i == \'(\' else -1\n return left + right\n```\n | 334 | 11 | [] | 43 |
minimum-add-to-make-parentheses-valid | [Java/Python 3] two one pass codes - space O(n) and O(1), respectively | javapython-3-two-one-pass-codes-space-on-omrv | Intuition:\n\nWe only need to count those unmatched parentheses. \nKey Observation:\n\nAfter removal of matched parentheses, the remainings must be ))...)(...(( | rock | NORMAL | 2018-10-14T03:03:02.786478+00:00 | 2024-10-09T08:37:14.008269+00:00 | 10,335 | false | **Intuition:**\n\nWe only need to count those unmatched parentheses. \n**Key Observation:**\n\nAfter removal of matched parentheses, the remainings must be `))...)(...(`(both numbers of open and close patheses can be `0`). Otherwise, there would be at least one pair of `()`.\n\n**Algorithm Description:**\n\nLoop through the input array.\n1. if encounter \'(\', push \'(\' into stack;\n2. otherwise, \')\', check if there is a matching \'(\' on top of stack; if no, increase the counter by 1; if yes, pop it out;\n3. after the loop, count in the un-matched characters remaining in the stack.\n\n\nMethod 1: \nTime & space: O(n).\n```java\n public int minAddToMakeValid(String S) {\n Deque<Character> stk = new ArrayDeque<>();\n int count = 0;\n for (char c : S.toCharArray()) {\n if (c == \'(\') { \n stk.push(c); \n }else if (stk.isEmpty()) { \n ++count; \n }else { \n stk.pop(); \n }\n }\n return count + stk.size();\n }\n```\nor, make the above the code shorter:\n\n```java\n public int minAddToMakeValid(String S) {\n Deque<Character> stk = new ArrayDeque<>();\n for (char c : S.toCharArray()) {\n if (c == \')\' && !stk.isEmpty() && stk.peek() == \'(\') { // pop out matched pairs.\n stk.pop(); \n }else { // push in unmatched chars.\n stk.push(c); \n } \n }\n return stk.size();\n }\n```\nMethod 2: \nSince there is only one kind of char, \'(\', in stack,only a counter will also work.\nTime: O(n), space: O(1).\n\n\n```java\n public int minAddToMakeValid(String S) {\n int count = 0, stk = 0;\n for (int i = 0; i < S.length(); ++i) {\n if (S.charAt(i) == \'(\') { \n ++stk; \n }else if (stk == 0) { \n ++count; \n }else {\n --stk; \n }\n }\n return count + stk;\n }\n```\n```python\n def minAddToMakeValid(self, S: str) -> int:\n stk = count = 0\n for c in S:\n if c == \'(\':\n stk += 1\n elif stk > 0:\n stk -= 1 \n else:\n count += 1\n return stk + count\n```\n\nSome may like variable namings such as `open` and `close` brackets, here are the corresponding codes:\n```java\n public int minAddToMakeValid(String s) {\n int unmatchedOpenBrackets = 0, unmatchedCloseBrackets = 0;\n for (int i = 0; i < s.length(); ++i) {\n if (s.charAt(i) == \'(\') {\n ++unmatchedOpenBrackets;\n }else if (unmatchedOpenBrackets > 0) {\n --unmatchedOpenBrackets;\n }else {\n ++unmatchedCloseBrackets;\n }\n }\n return unmatchedOpenBrackets + unmatchedCloseBrackets;\n }\n```\n\n```python\n def minAddToMakeValid(self, S: str) -> int:\n unmatched_open_brackets = unmatched_close_brackets = 0\n for c in S:\n if c == \'(\':\n unmatched_open_brackets += 1\n elif unmatched_open_brackets > 0:\n unmatched_open_brackets -= 1 \n else:\n unmatched_close_brackets += 1\n return unmatched_open_brackets + unmatched_close_brackets\n```\n\n | 82 | 2 | [] | 21 |
minimum-add-to-make-parentheses-valid | Beats 100% || Easy Self Explanatory Code || 3 Approaches | beats-100-easy-self-explanatory-code-3-a-afqw | 3 Approaches:\n\n\n# Approach 1\nTime O(N) Space O(N)\ncpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> S;\n | Garv_Virmani | NORMAL | 2024-10-09T03:10:29.239281+00:00 | 2024-10-09T03:26:52.807369+00:00 | 14,524 | false | # 3 Approaches:\n\n\n# Approach 1\n**Time O(N) Space O(N)**\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> S;\n int c = 0;\n for (char i : s) {\n if (i == \'(\')\n S.push(i);\n else {\n if (S.empty())\n c++;\n else\n S.pop();\n }\n }\n return c + S.size();\n }\n};\n```\n\n# Approach 2\n**Time O(N) Space O(N)**\n# Code\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n string stck;\n for (auto c : s) {\n if (stck.empty())\n stck.push_back(c);\n\n else if (stck.back() == \'(\' && c == \')\') {\n stck.pop_back();\n } else {\n stck.push_back(c);\n }\n }\n return stck.size();\n }\n};\n```\n\n# Approach 3\n**Time O(N) Space O(1)**\n``` cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int open = 0, close = 0;\n for (auto c : s) {\n if (c == \'(\') {\n open++;\n } else {\n if (open > 0)\n open--;\n else\n close++;\n }\n }\n return open + close;\n }\n};\n```\n\n\n\n | 76 | 4 | ['String', 'Stack', 'Greedy', 'C', 'Python', 'C++', 'Java', 'Rust', 'Ruby', 'JavaScript'] | 5 |
minimum-add-to-make-parentheses-valid | Java 4ms 100% straight-forward counting | java-4ms-100-straight-forward-counting-b-quh8 | Keep track of the number of unmatched open and closed parentheses.\n\n```\npublic int minAddToMakeValid(String S) {\n\tint unmatchedOpen = 0;\n\tint unmatchedCl | jebennett099 | NORMAL | 2019-01-30T06:57:08.508588+00:00 | 2019-01-30T06:57:08.508633+00:00 | 4,089 | false | Keep track of the number of unmatched open and closed parentheses.\n\n```\npublic int minAddToMakeValid(String S) {\n\tint unmatchedOpen = 0;\n\tint unmatchedClose = 0;\n \n\tfor (char c : S.toCharArray()) {\n\t\tif (c == \'(\') {\n unmatchedOpen++;\n } else if (unmatchedOpen > 0)\n\t\t\tunmatchedOpen--;\n } else {\n\t\t // This is a closed paren and there \n\t\t\t// isn\'t an open one to balance it out\n unmatchedClose++;\n }\n\t}\n \n return unmatchedClose + unmatchedOpen;\n} | 54 | 0 | [] | 5 |
minimum-add-to-make-parentheses-valid | Super simple approach, beats 100%, O(1) space and O(n) time, YouTube Video added | super-simple-approach-beats-100-o1-space-mm78 | Youtube Solution https://youtu.be/UojbHmdbj7Q\n# Intuition and approach\n keep it very very simple guys , just like below :- \n i have variable open = 0, mism | vinod_aka_veenu | NORMAL | 2024-10-09T01:47:07.779889+00:00 | 2024-10-09T05:38:03.826314+00:00 | 15,621 | false | # Youtube Solution https://youtu.be/UojbHmdbj7Q\n# Intuition and approach\n keep it very very simple guys , just like below :- \n i have variable **open = 0, mismatch = 0**\n now traverse in the string \nif **char = \'(\'** ==> open++;\nelse ===> **if(open>0)==> open--** ; (because we have to decrease open count as we found pairing close bracket)\n but **if(open==0)** that means we are finding closing bracket without having an open bracket ===> like below case\n**)()()** ===> we have a **leading close bracket** and no open one\n\nso we will increase **mismatch++**\n\nfinally we will return **(mismatch + open)** as answer.\n**now you might have question, how can i return as sum of both variable**\n\njust observe this string **)()()(((** ==> **mismatch = 1**\n ==> **open = 3** (total orphan open brackets)\n\nans = mismatch + open = 1 + 3 = 4\n\nwe need to add 4 operation ==> **(**)()()(((**)))** \n\n**still have doubt, will release Youtube video soon**\n\n\n \n\n\n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int open =0, mismatch=0;\n for(int i=0; i<s.length(); i++)\n {\n if(s.charAt(i)==\'(\')\n open++;\n else\n {\n if(open>0)\n open--;\n else\n mismatch++;\n }\n } \n return open+mismatch; \n }\n}\n```C++\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int open = 0, mismatch = 0;\n for (int i = 0; i < s.length(); i++) {\n if (s[i] == \'(\')\n open++;\n else {\n if (open > 0)\n open--;\n else\n mismatch++;\n }\n }\n return open + mismatch;\n }\n};\n```C# code\npublic class Solution {\n public int MinAddToMakeValid(string s) {\n int open = 0, mismatch = 0;\n for (int i = 0; i < s.Length; i++) {\n if (s[i] == \'(\')\n open++;\n else {\n if (open > 0)\n open--;\n else\n mismatch++;\n }\n }\n return open + mismatch;\n }\n}\n````Python code\nclass Solution(object):\n def minAddToMakeValid(self, s):\n """\n :type s: str\n :rtype: int\n """\n open_brackets = 0\n mismatch = 0\n for char in s:\n if char == \'(\':\n open_brackets += 1\n else:\n if open_brackets > 0:\n open_brackets -= 1\n else:\n mismatch += 1\n return open_brackets + mismatch\n\n | 34 | 11 | ['Array', 'String Matching', 'Python', 'C++', 'Java', 'C#'] | 15 |
minimum-add-to-make-parentheses-valid | C++ 0ms faster than 100% | c-0ms-faster-than-100-by-random_cpp-ji1t | Whenever we get open bracket we will increase count by 1 and when we get close bracket we will decrease count by 1. But If our count becomes less than 0 than we | random_cpp | NORMAL | 2021-05-18T06:31:00.049470+00:00 | 2021-05-18T06:31:00.049515+00:00 | 3,027 | false | Whenever we get open bracket we will increase count by 1 and when we get close bracket we will decrease count by 1. But If our count becomes less than 0 than we have to add open bracket before current position so just absolute value of count and make count 0. Now at last we will add count to ans as we have to close all opened bracket.\n\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int cnt = 0,ans = 0;\n \n for(int i =0;i<s.length();i++){\n if(s[i]==\'(\')cnt++;\n else cnt--;\n if(cnt<0){ans+=abs(cnt);cnt=0;}\n }\n ans+=abs(cnt); \n \n return ans;\n }\n};\n\n``` | 34 | 0 | [] | 9 |
minimum-add-to-make-parentheses-valid | python two lines code | python-two-lines-code-by-abcd28s-9nti | \nclass Solution(object):\n def minAddToMakeValid(self, S):\n """\n :type S: str\n :rtype: int\n """\n \n while "() | abcd28s | NORMAL | 2018-11-11T20:46:48.272614+00:00 | 2018-11-11T20:46:48.272654+00:00 | 3,012 | false | ```\nclass Solution(object):\n def minAddToMakeValid(self, S):\n """\n :type S: str\n :rtype: int\n """\n \n while "()" in S:\n S = S.replace("()", "")\n \n return len(S)\n``` | 31 | 1 | [] | 8 |
minimum-add-to-make-parentheses-valid | 2 solutions | Easy to Understand | Faster | Simple | Python Solution | 2-solutions-easy-to-understand-faster-si-yzfz | \n def without_stack(self, S):\n opening = count = 0\n for i in S:\n if i == \'(\': \n opening += 1\n else | mrmagician | NORMAL | 2020-04-10T04:10:47.963438+00:00 | 2020-04-10T04:10:47.963493+00:00 | 3,268 | false | ```\n def without_stack(self, S):\n opening = count = 0\n for i in S:\n if i == \'(\': \n opening += 1\n else:\n if opening: opening -= 1\n else: count += 1\n return count + opening\n \n def using_stack(self, S):\n stack = []\n for ch in S:\n if ch == \'(\': stack.append(ch)\n else:\n if len(stack) and stack[-1] == \'(\': stack.pop()\n else: stack.append(ch)\n return len(stack)\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 30 | 1 | ['Stack', 'Python', 'Python3'] | 3 |
minimum-add-to-make-parentheses-valid | Easy Solution (No Stack)🧠 Python | Java | C++ | C | C# | GO | Rust O(N), O(1) | easy-solution-no-stack-python-java-c-c-c-5dv8 | Intuition\n- Objective: Determine the minimum number of parentheses to add to make a string valid.\n\n- Goal: Keep two counters: one for open parentheses and on | violet_6 | NORMAL | 2024-10-09T00:14:15.864287+00:00 | 2024-10-09T00:30:05.001195+00:00 | 6,980 | false | # Intuition\n- **Objective**: Determine the minimum number of parentheses to add to make a string valid.\n\n- **Goal**: Keep two counters: one for open parentheses and one for the number of unmatched closing parentheses.\n\n# Approach\n1. Traverse the string character by character.\n2. Keep track of:\n- Open parentheses that still need to be matched.\n- Unmatched closing parentheses.\n3. For every open parenthesis \'(\', increase the count of open parentheses.\n4. For every closing parenthesis \')\', check if there\'s an unmatched open parenthesis available to pair it with:\n- If yes, decrease the open parenthesis count.\n- If not, increase the unmatched closing parenthesis count.\n5. At the end of the traversal, the result is the **sum** of `unmatched open` and `unmatched closing` parentheses, which indicates how many parentheses are needed to make the string valid.\n6. \n\n# Complexity\n- Time complexity: `O(N)`\n\n- Space complexity: `O(1)`\n\n# Code\n```python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n open_c = close_c = 0\n for c in s:\n if c == \'(\':\n open_c += 1\n elif c == \')\' and open_c > 0:\n open_c -= 1\n else:\n close_c += 1\n return open_c + close_c\n```\n\n``` java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int open_c = 0;\n int close_c = 0;\n\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n open_c++;\n } else if (c == \')\' && open_c > 0) {\n open_c--;\n } else {\n close_c++;\n }\n }\n return open_c + close_c;\n }\n}\n```\n\n``` C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int open_c = 0;\n int close_c = 0;\n\n for (char c : s) {\n if (c == \'(\') {\n open_c++;\n } else if (c == \')\' && open_c > 0) {\n open_c--;\n } else {\n close_c++;\n }\n }\n return open_c + close_c;\n }\n};\n```\n\n``` C# []\npublic class Solution {\n public int MinAddToMakeValid(string s) {\n int open_c = 0;\n int close_c = 0;\n\n foreach (char c in s) {\n if (c == \'(\') {\n open_c++;\n } else if (c == \')\' && open_c > 0) {\n open_c--;\n } else {\n close_c++;\n }\n }\n return open_c + close_c;\n }\n}\n```\n\n``` GO []\nfunc minAddToMakeValid(s string) int {\n open_c, close_c := 0, 0\n\n for _, c := range s {\n if c == \'(\' {\n open_c++\n } else if c == \')\' && open_c > 0 {\n open_c--\n } else {\n close_c++\n }\n }\n return open_c + close_c\n}\n```\n``` Rust []\nimpl Solution {\n pub fn min_add_to_make_valid(s: String) -> i32 {\n let mut open_c = 0;\n let mut close_c = 0;\n\n for c in s.chars() {\n if c == \'(\' {\n open_c += 1;\n } else if c == \')\' && open_c > 0 {\n open_c -= 1;\n } else {\n close_c += 1;\n }\n }\n open_c + close_c\n }\n}\n```\n\n``` C []\nint minAddToMakeValid(char* s) {\n int open_c = 0, close_c = 0;\n\n for (int i = 0; s[i] != \'\\0\'; i++) {\n if (s[i] == \'(\') {\n open_c++;\n } else if (s[i] == \')\' && open_c > 0) {\n open_c--;\n } else {\n close_c++;\n }\n }\n return open_c + close_c;\n}\n```\n# Congrats!! You\'ve learned something new today \u2B06\uFE0F\uD83E\uDD29\uD83D\uDC96\uD83D\uDC3E | 26 | 2 | ['C', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'C#'] | 8 |
minimum-add-to-make-parentheses-valid | Greedy string again||Beats 100% | greedy-string-againbeats-100-by-anwenden-3eth | Intuition\n Describe your first thoughts on how to solve this problem. \nGreedy string modifies the solution for yesterday\'s daily question\n1963. Minimum Num | anwendeng | NORMAL | 2024-10-09T01:57:52.993443+00:00 | 2024-10-09T08:27:46.821705+00:00 | 790 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGreedy string modifies the solution for yesterday\'s daily question\n[1963. Minimum Number of Swaps to Make the String Balanced](https://leetcode.com/problems/minimum-number-of-swaps-to-make-the-string-balanced/solutions/5884212/greedy-string42-ms-beats-9957/)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Set `r=0, l=0` to denote the unbalanced number for `(`, `)`\n2. Use a loop to proceed:\n```\nfor (char c: s){\n bool isLeft=(c==\'(\');\n l+=isLeft;\n (l>0)?l-=(!isLeft):r+=(!isLeft);\n}\n```\n3 `r+l` is the answer\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code||0ms beats 100%\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string& s) {\n int l=0, r=0;\n for (char c: s){\n bool isLeft=(c==\'(\');\n l+=isLeft;\n (l>0)?l-=(!isLeft):r+=(!isLeft);\n }\n return l+r;\n }\n};\n``` | 17 | 1 | ['String', 'Greedy', 'C++'] | 7 |
minimum-add-to-make-parentheses-valid | Python classic valid paranthesis solution | python-classic-valid-paranthesis-solutio-s7hr | \nclass Solution:\n def minAddToMakeValid(self, S):\n r, l = 0, []\n for s in S:\n if s == "(":\n l.append(s)\n | cenkay | NORMAL | 2018-10-14T07:40:38.573424+00:00 | 2018-10-18T16:04:18.198447+00:00 | 2,922 | false | ```\nclass Solution:\n def minAddToMakeValid(self, S):\n r, l = 0, []\n for s in S:\n if s == "(":\n l.append(s)\n elif l:\n l.pop()\n else:\n r += 1 \n return r + len(l)\n```\nor for fun =>\n```\nclass Solution:\n def minAddToMakeValid(self, S):\n l = r = 0\n for s in S: \n l, r = (l + 1, r) if s == "(" else (l - 1, r) if l else (l, r + 1)\n return l + r\n``` | 17 | 0 | [] | 3 |
minimum-add-to-make-parentheses-valid | [JAVA] [0MS] [100%] [STACK] | java-0ms-100-stack-by-trevor-akshay-5gwr | ```\nclass Solution {\n public int minAddToMakeValid(String S) {\n int res = 0;\n Stack stack = new Stack<>();\n for(char c : S.toCharArr | trevor-akshay | NORMAL | 2021-02-06T05:31:53.266341+00:00 | 2021-02-06T05:31:53.266377+00:00 | 2,000 | false | ```\nclass Solution {\n public int minAddToMakeValid(String S) {\n int res = 0;\n Stack<Character> stack = new Stack<>();\n for(char c : S.toCharArray()){\n if(c == \'(\'){\n stack.push(c);\n }\n else{\n if(stack.empty())\n res++;\n else\n stack.pop();\n }\n }\n return res+stack.size();\n }\n} | 16 | 0 | ['Stack', 'Java'] | 2 |
minimum-add-to-make-parentheses-valid | [Java] Easy to understand Stack Solution (8ms) | java-easy-to-understand-stack-solution-8-tzfp | Each time we come across an open paren '(', we add it to the stack. If we come across a closing paren ')' we check if the stack is empty and if not we pop off | ernie-h | NORMAL | 2018-10-18T04:18:06.733506+00:00 | 2018-10-21T11:55:15.996692+00:00 | 2,092 | false | Each time we come across an open paren '(', we add it to the stack.
If we come across a closing paren ')' we check if the stack is empty and if not we pop off the open paren.
Else if the stack is empty, we increment the counter for an amend needed.
In the case the stack is not empty when we complete the loop, we continually pop off the remaining items and increment the count till it is.
Solution:
```
public int minAddToMakeValid(String S) {
Stack<Character> stack = new Stack<Character> ();
int counter = 0;
for(int i = 0; i < S.length(); i++) {
char temp = S.charAt(i);
if(temp == '(') {
stack.push(temp);
}
else if(!stack.isEmpty()) {
stack.pop();
}
else counter++;
}
while(!stack.isEmpty()) {
counter ++;
stack.pop();
}
return counter;
}
| 16 | 1 | [] | 5 |
minimum-add-to-make-parentheses-valid | 🏗️ Two Approaches [SC: O(n) vs O(1)]: Stack vs. Greedy 🚀 | two-approaches-sc-on-vs-o1-stack-vs-gree-fq2l | Approach\n1. # First Approach:\n We traverse the string, and for each character:\n If it\'s an opening parenthesis (, we push it onto the stack.\n If i | AlgoArtisan | NORMAL | 2024-10-09T02:52:37.098389+00:00 | 2024-10-09T02:59:23.322369+00:00 | 932 | false | # Approach\n1. # First Approach:\n We traverse the string, and for each character:\n If it\'s an opening parenthesis (, we push it onto the stack.\n If it\'s a closing parenthesis ), we check if the top of the stack is an opening parenthesis (. If so, we pop the stack (since they balance each other). Otherwise, we push the closing parenthesis ) onto the stack.\n At the end, the size of the stack gives the number of unmatched parentheses.\n2. # Second Approach:\n Instead of using a stack, we maintain two variables:\n openingB counts unmatched opening parentheses (.\n closingB counts unmatched closing parentheses ).\n For each closing parenthesis ), we check if there is an unmatched opening parenthesis (. If so, we decrement the count of unmatched openings. If not, we increment the count of unmatched closings.\n For each opening parenthesis (, we increment the openingB count.\n The result is the sum of unmatched opening and closing parentheses.\n\n# Complexity\n1. # First Approach:\n- Time complexity:O(n), where n is the length of the string. We process each character once.\n\n- Space complexity:O(n), due to the stack storing unmatched parentheses in the worst case.\n\n2. # Second Approach:\n- Time complexity:O(n), where n is the length of the string. We process each character once.\n- Space complexity:O(1), as we only use two integer variables, regardless of the input size.\n\n\n# Code First Approach:\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char>st;\n for(const char& ch : s){\n bool isPoped = false;\n if(!st.empty()){\n char top = st.top();\n if(ch==\')\' && top == \'(\'){\n st.pop();\n isPoped = true;\n }\n }\n if(!isPoped){\n st.push(ch);\n }\n\n }\n return st.size();\n }\n};\n```\n\n# Code Second Approach\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int openingB = 0;\n int closingB = 0;\n for(const char& ch : s){\n if(ch == \')\'){\n if(openingB >=1){\n openingB--;\n }\n else{\n closingB++;\n }\n }\n else{\n openingB++;\n }\n }\n return openingB+closingB;\n }\n};\n```\n | 15 | 2 | ['String', 'Stack', 'Greedy', 'C++'] | 5 |
minimum-add-to-make-parentheses-valid | C++ Simple, Short and Easy Solution, O(n) time O(1) space, faster than 100% | c-simple-short-and-easy-solution-on-time-2see | \nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n int res = 0, n = S.size(), balance = 0;\n for (int i = 0; i < n; i++) {\n | yehudisk | NORMAL | 2021-02-19T10:02:40.267814+00:00 | 2021-02-19T10:02:40.267854+00:00 | 1,431 | false | ```\nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n int res = 0, n = S.size(), balance = 0;\n for (int i = 0; i < n; i++) {\n balance += S[i] == \'(\' ? 1 : -1;\n if (balance == -1) {\n res++;\n balance++;\n }\n }\n return res + balance;\n }\n};\n```\n**Like it? please upvote...** | 13 | 0 | ['C'] | 1 |
minimum-add-to-make-parentheses-valid | JavaScript Clean One Pass | javascript-clean-one-pass-by-control_the-n3zy | javascript\nvar minAddToMakeValid = function(S) {\n let open = 0, close = 0;\n \n for(let c of S) {\n if(c === \'(\') open++;\n else if(! | control_the_narrative | NORMAL | 2020-08-06T14:06:34.201741+00:00 | 2020-08-06T14:06:34.201771+00:00 | 1,090 | false | ```javascript\nvar minAddToMakeValid = function(S) {\n let open = 0, close = 0;\n \n for(let c of S) {\n if(c === \'(\') open++;\n else if(!open) close++;\n else open--;\n }\n return open + close;\n};\n``` | 13 | 1 | ['JavaScript'] | 1 |
minimum-add-to-make-parentheses-valid | Java simple solution 100% faster | java-simple-solution-100-faster-by-feyse-p4l9 | \nclass Solution {\n public int minAddToMakeValid(String S) {\n int openingNeeded = 0;\n int closingNeeded = 0;\n \n for(int i = | feyselmubarek | NORMAL | 2020-01-25T14:05:01.862774+00:00 | 2020-02-05T13:13:28.248113+00:00 | 869 | false | ```\nclass Solution {\n public int minAddToMakeValid(String S) {\n int openingNeeded = 0;\n int closingNeeded = 0;\n \n for(int i = 0; i < S.length(); i++){\n if(S.charAt(i) == \'(\'){\n closingNeeded++;\n }else{\n if(closingNeeded == 0){\n openingNeeded++;\n }else{\n closingNeeded--;\n }\n }\n }\n \n return openingNeeded + closingNeeded;\n }\n}\n``` | 12 | 0 | ['Java'] | 1 |
minimum-add-to-make-parentheses-valid | C++|| For Beginners..!!! || Stack | c-for-beginners-stack-by-ananya2023-slrk | \nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n int count=0;\n for(int i=0;i<s.size();i++){\n | ananya2023 | NORMAL | 2021-09-06T12:13:33.087288+00:00 | 2021-09-06T12:13:33.087323+00:00 | 1,969 | false | ```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n int count=0;\n for(int i=0;i<s.size();i++){\n if(s[i]==\')\'){\n if(st.empty())\n count++;\n else if(st.top()==\'(\')\n st.pop();\n else\n st.push(s[i]);\n }\n else if(s[i]==\'(\')\n st.push(s[i]);\n }\n return st.size()+count;\n }\n};\n``` | 11 | 0 | ['Stack', 'C', 'C++'] | 3 |
minimum-add-to-make-parentheses-valid | C++ 5 lines, O(n) | c-5-lines-on-by-votrubac-wgik | We can flip the question and ask how many "extra" parentheses the string has that makes it invalid. Then we can add (or remove) the same number of parentheses t | votrubac | NORMAL | 2018-10-14T03:45:06.431514+00:00 | 2018-10-15T06:48:23.729117+00:00 | 1,784 | false | We can flip the question and ask how many "extra" parentheses the string has that makes it invalid. Then we can add (or remove) the same number of parentheses to make it valid.\n\nWe increment the number of ```open``` parentheses when we see ```\'(\'```, and decrement otherwise. Every time that number is negative, that means that we have an extra ```\')\'```, and we increment ```closed```.\n\nThe result is the sum of extra open and extra closed parentheses.\n```\nint minAddToMakeValid(string S) {\n int open = 0, closed = 0;\n for (auto c : S) {\n open = c == \'(\' ? max(0, open) + 1 : open - 1;\n if (open < 0) ++closed;\n }\n return max(0, open) + closed;\n}\n``` | 11 | 0 | [] | 3 |
minimum-add-to-make-parentheses-valid | C++(Using Stack- 100% faster) | cusing-stack-100-faster-by-amit_singhh-1k32 | Please Upvote if you like the solution!\n\n class Solution {\n public:\n int minAddToMakeValid(string s) \n {\n stack st;//create a Stack\n | amit_singhh | NORMAL | 2022-03-26T18:30:45.458983+00:00 | 2022-03-26T18:30:45.459027+00:00 | 728 | false | **Please Upvote if you like the solution!**\n\n class Solution {\n public:\n int minAddToMakeValid(string s) \n {\n stack<char> st;//create a Stack\n \n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'(\')//whenever their is open bracket insert on stack\n st.push(\'(\');\n else \n {\n if(!st.empty() && st.top()==\'(\')//if their is open bracket on the top of stack and stack is not empty, then pop\n st.pop();\n else\n st.push(\')\');//otherwise push closing bracket on stack\n }\n }\n return st.size();//atlast return stack size\n }\n }; | 10 | 0 | ['String', 'Stack', 'C', 'C++'] | 0 |
minimum-add-to-make-parentheses-valid | Python 3-line mathematically optimal solution with explanation, one-pass O(n) time O(1) space | python-3-line-mathematically-optimal-sol-nakx | 3-liner:\npython\ndef minAddToMakeValid(self, S):\n a = b = 0\n for c in S: a, b = (a, b + 1) if c == \'(\' else (min(a, b - 1), b - 1)\n return b - a | zemer | NORMAL | 2018-10-14T07:01:08.771935+00:00 | 2018-10-20T12:21:51.389989+00:00 | 659 | false | 3-liner:\n```python\ndef minAddToMakeValid(self, S):\n a = b = 0\n for c in S: a, b = (a, b + 1) if c == \'(\' else (min(a, b - 1), b - 1)\n return b - a * 2\n```\nSome 1-liners with functional programming, just for fun:\n```python\ndef minAddToMakeValid(self, S):\n return (lambda a,b:b-a*2)(*reduce(lambda t,c:(t[0],t[1]+1)if c==\'(\'else(min(t[0],t[1]-1),t[1]-1),S,(0,0)))\n\ndef minAddToMakeValid(self, S):\n return (lambda a,b:b-a*2)(*reduce(lambda t,c:(lambda a,b:(a,b+1)if c==\'(\'else(min(a,b-1),b-1))(*t),S,(0,0)))\n```\nReadable version:\n```python\ndef minAddToMakeValid(self, S):\n height = lowest = 0\n for c in S:\n height += 1 if c == \'(\' else -1\n lowest = min(lowest, height)\n return -lowest * 2 + height\n```\n---\n\n### Explanation:\n\nA parentheses string can be drawn as a mountain range if you change `(` to `/` and `)` to `\\`. Examples:\n```\n /\\ /\\/\\\n() = /\\ ()() = /\\/\\ (()) = / \\ (()())() = / \\/\\\n```\nTake a moment to convince yourself that a parentheses string is valid if and only if (a) the mountain range ends on the ground and (b) the mountain range never goes underground. Condition (a) says that the number of left and right parentheses must be equal; condition (b) says you can\'t have more right parentheses than left ones for any substring `S[:whatever]`. Here are some examples of invalid strings (I\'ve added `__` on both sides to show where the ground is):\n```\n /\\/\\\n(()() = __/ __ <-- invalid because doesn\'t end on the ground\n\n\n /\\\n(()))( = __/ \\ __ <-- invalid because goes underground\n \\/ \n\n /\\\n))(((() = __ / __ <-- invalid because doesn\'t end on the ground and goes underground\n \\ /\n \\/\n```\nTo make an invalid mountain range valid again, we need to (a) make sure it ends on the ground and (b) lift it above the ground. To make sure it ends on the ground, we keep track of `height`. To lift the entire mountain range above the ground, we just need to find out how low it goes underground, so we keep track of `lowest`. In the last example shown above, this is what we do:\n```\n /\\ \n / \\\n /\\ /\\ /\\ / \\\n__ / __ ==> __ / \\__ ==> __/ \\/ \\__\n \\ / \\ / \n \\/ \\/ \n\n ))(((() ==> ))(((()) ==> (())(((())))\n ^ ^^ ^^\n | || ||\n | lift it above the ground\n |\n make it end on the ground\n```\nThe first (leftmost) picture shows that `height == 1` and `lowest == -2`. To make it end on the ground, we need to add a single `\\` (or `)`) at the end so that the mountain range starts and ends at the same height. Now we just need to lift the whole thing above the ground. Since the `lowest` point was `2` units below the ground, we need to add `//` (or `((`) on the left and `\\\\` (or `))`) on the right to lift the entire mountain range up. In total, we added `1 + 2 * 2` parentheses, which is `height + (-lowest) * 2`. | 10 | 0 | [] | 1 |
minimum-add-to-make-parentheses-valid | Let's Form Couples ❤️🔥 Part - II | Very Easy Explanation + Full Concept + illustrations | lets-form-couples-part-ii-very-easy-expl-htr6 | Youtube Explanation\nSoon to be on Channel : https://www.youtube.com/@Intuit_and_Code\nEdited:\nhttps://youtu.be/ZRr2UiHIBBA?si=kUm0zzURb2UkN91H\n\n> I would re | Rarma | NORMAL | 2024-10-09T07:30:33.964101+00:00 | 2024-10-09T08:56:14.597267+00:00 | 1,048 | false | # Youtube Explanation\nSoon to be on Channel : https://www.youtube.com/@Intuit_and_Code\nEdited:\nhttps://youtu.be/ZRr2UiHIBBA?si=kUm0zzURb2UkN91H\n\n> I would recommend to read this article first : **[Link](https://leetcode.com/problems/minimum-number-of-swaps-to-make-the-string-balanced/solutions/5886919/let-s-form-couples-very-easy-illustration-full-concept)**\nI Covered Nearly Same Concept as in that article, Let\'s Understand them again\n\n# Intuition & Approach\n \n\n\n\n\n> If Ya already read yesterday\'s article, then below feels similar\n\n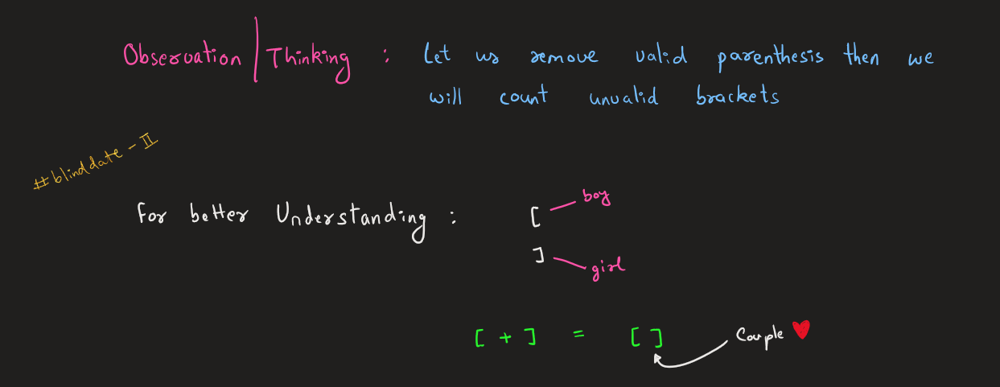\n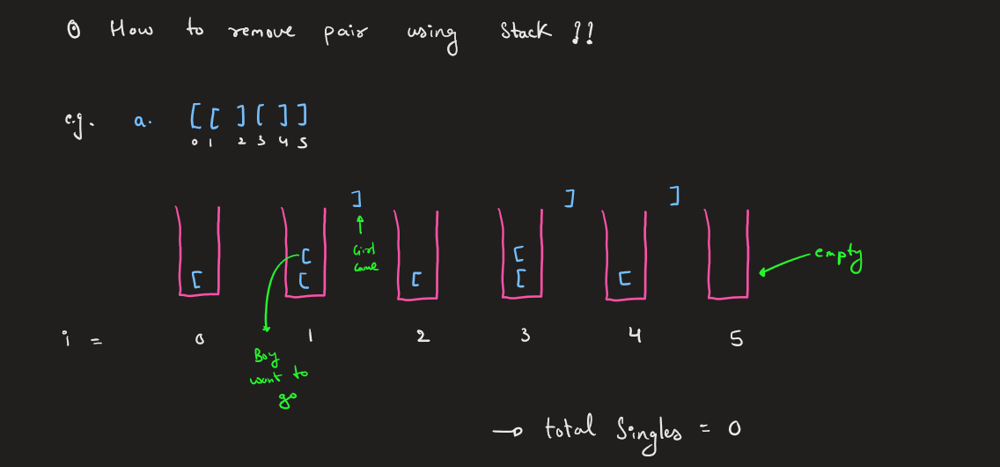\n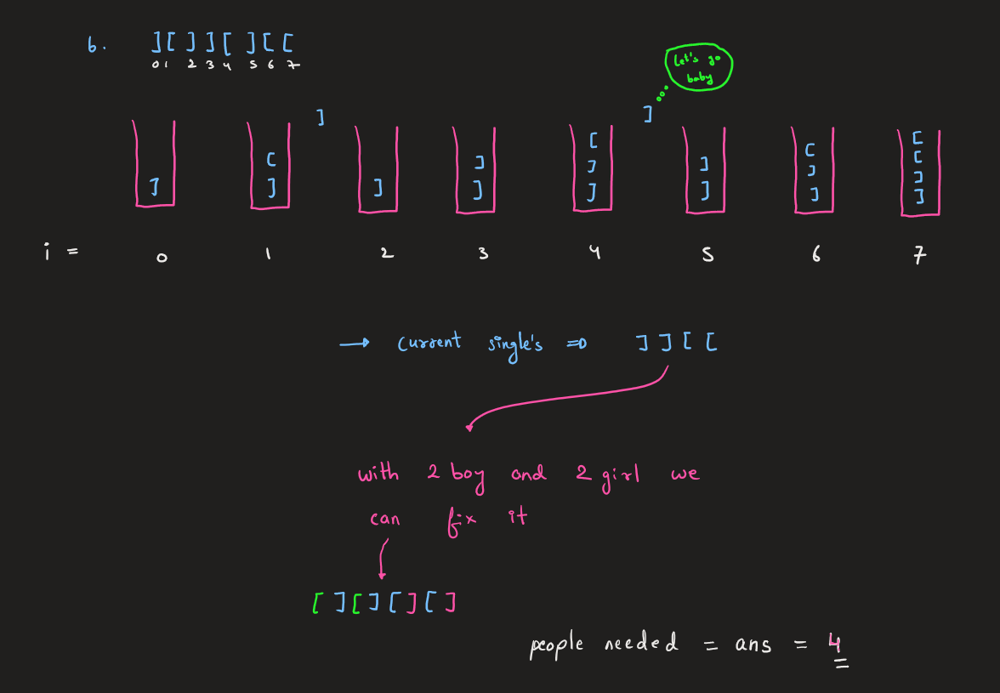\n\n# Code\n```c++ [ ]\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n\n for (auto& val : s) { // for(int i=0;i<s.size();i++)\n if (st.empty()) {\n st.push(val); // val = s[i]\n } \n else if (st.top() == \'(\' and val == \')\') {\n st.pop();\n } \n else {\n st.push(val); // val = s[i]\n }\n }\n\n return st.size();\n }\n};\n```\n``` java [ ]\nclass Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> st = new Stack<>();\n\n for (char val : s.toCharArray()) {\n if (st.isEmpty()) {\n st.push(val);\n } \n else if (st.peek() == \'(\' && val == \')\') {\n st.pop();\n } \n else {\n st.push(val);\n }\n }\n\n return st.size();\n }\n}\n```\n``` python [ ]\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n\n for val in s:\n if not stack:\n stack.append(val)\n elif stack[-1] == \'(\' and val == \')\':\n stack.pop()\n else:\n stack.append(val)\n\n return len(stack)\n```\n\n\n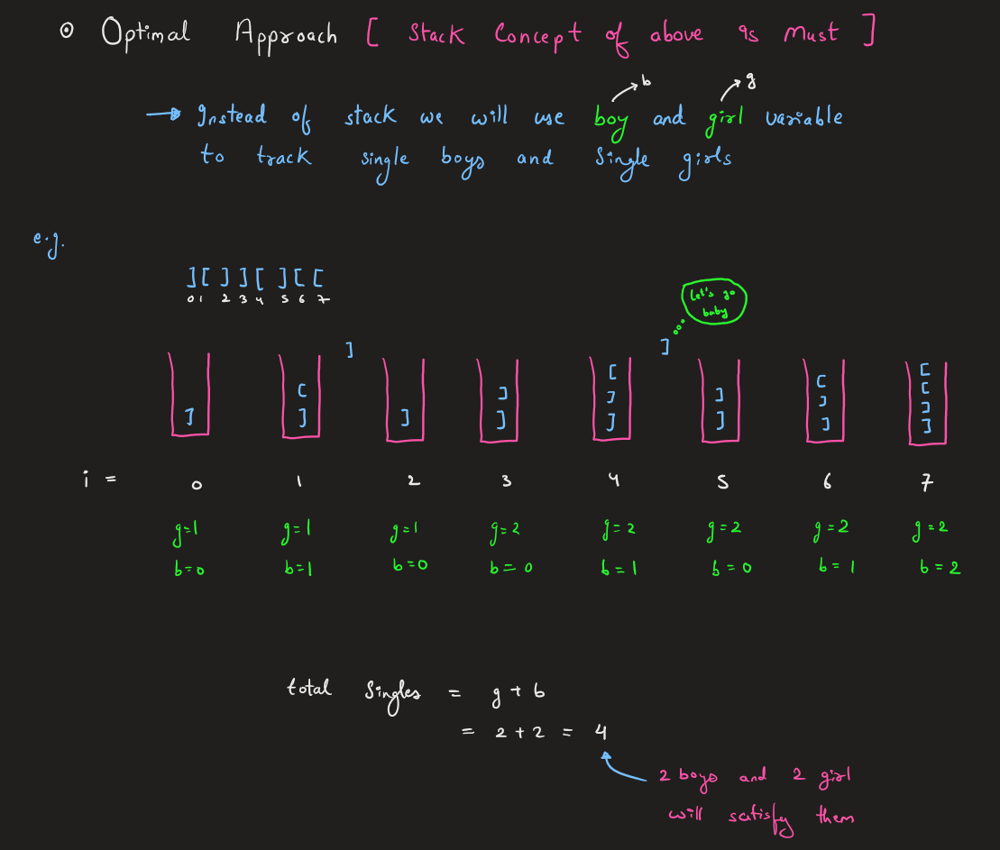\n\n\n# Complexity [ Optimized ]\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int girl=0, boys=0;\n\n for(int i=0;i<s.size();i++){\n if(boys>0 and s[i]==\')\'){\n // couple formed\n // no need to increase girl count\n // eventually boy decreased\n boys--;\n }\n else{\n if(s[i]==\'(\'){boys++;}\n else{girl++;}\n }\n }\n\n return girl+boys;\n }\n};\n```\n``` java [ ]\nclass Solution {\n public int minAddToMakeValid(String s) {\n int girl = 0, boys = 0;\n\n for (int i = 0; i < s.length(); i++) {\n if (boys > 0 && s.charAt(i) == \')\') {\n // Couple formed, decrease boys count\n boys--;\n } \n else {\n if (s.charAt(i) == \'(\') {\n boys++;\n } \n else {\n girl++;\n }\n }\n }\n\n return girl + boys;\n }\n}\n```\n``` python [ ]\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n girl, boys = 0, 0\n\n for i in range(len(s)):\n if boys > 0 and s[i] == \')\':\n # Couple formed, decrease boys count\n boys -= 1\n else:\n if s[i] == \'(\':\n boys += 1\n else:\n girl += 1\n\n return girl + boys\n``` | 9 | 0 | ['Math', 'String', 'Stack', 'Greedy', 'String Matching', 'Python', 'C++', 'Java', 'Python3'] | 3 |
minimum-add-to-make-parentheses-valid | Python | Greedy Pattern | python-greedy-pattern-by-khosiyat-y0rp | see the Successfully Accepted Submission\n\n# Code\npython3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n # Initialize balance v | Khosiyat | NORMAL | 2024-10-09T03:30:03.123427+00:00 | 2024-10-09T03:30:03.123466+00:00 | 1,011 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/minimum-add-to-make-parentheses-valid/submissions/1416537063/?envType=daily-question&envId=2024-10-09)\n\n# Code\n```python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n # Initialize balance variables for unmatched parentheses\n left_balance = 0 # Tracks unmatched \'(\'\n right_balance = 0 # Tracks unmatched \')\'\n \n # Traverse through the string\n for char in s:\n if char == \'(\':\n left_balance += 1 # Add an unmatched \'(\'\n elif char == \')\':\n if left_balance > 0:\n # If there is an unmatched \'(\', pair it with this \')\'\n left_balance -= 1\n else:\n # If no unmatched \'(\', this \')\' is unmatched\n right_balance += 1\n \n # The total moves needed is the sum of unmatched \'(\' and \')\'\n return left_balance + right_balance\n\n```\n\n## Approach:\nWe can solve this problem by using a greedy approach with a simple counter. The idea is to scan through the string and keep track of:\n\n- The number of unmatched opening parentheses `(`.\n- The number of unmatched closing parentheses `)`.\n\nWe maintain two variables:\n\n- **left_balance**: Tracks how many opening parentheses `(` are currently unmatched.\n- **right_balance**: Tracks how many closing parentheses `)` are unmatched due to either extra `)` or missing `(`.\n\n### Steps:\n1. **Iterate through the string**:\n - If we encounter an opening parenthesis `(`, we increment the `left_balance` because it means we have an additional opening parenthesis that needs to be matched.\n - If we encounter a closing parenthesis `)`, we need to check if there is an unmatched opening parenthesis in the `left_balance` to pair with. If there is, we decrement the `left_balance`. If not, we increment `right_balance` because this closing parenthesis is unmatched and needs an opening parenthesis to pair with.\n\n2. **Result**:\n - After processing the string, any remaining unmatched opening parentheses in `left_balance` will need closing parentheses to balance them.\n - Any remaining unmatched closing parentheses in `right_balance` will need opening parentheses to balance them.\n\n3. **The total number of parentheses needed** will be the sum of `left_balance` and `right_balance`.\n\n---\n\n## Explanation of the code:\n- `left_balance` keeps track of how many opening parentheses `(` are currently unmatched.\n- `right_balance` counts the number of unmatched closing parentheses `)`.\n- After processing the entire string, `left_balance` will hold the count of unmatched opening parentheses and `right_balance` will hold the count of unmatched closing parentheses.\n- The total number of insertions required is the sum of these two values.\n\n---\n\n### Time Complexity:\n- **O(n)** where `n` is the length of the string. We traverse the string once.\n\n### Space Complexity:\n- **O(1)**, as we only use a constant amount of extra space.\n\n\n | 9 | 0 | ['Python3'] | 4 |
minimum-add-to-make-parentheses-valid | Python3 || 10 lines, track ()s || T/S: 99% / 54% | python3-10-lines-track-s-ts-99-54-by-spa-m31j | Here\'s the intuition:\n\nFirst thoughts go right to using a stack, but we only need to determine the number the mis-balanced parenthesis pairs and return an in | Spaulding_ | NORMAL | 2024-10-09T00:18:25.677651+00:00 | 2024-10-09T04:38:00.379898+00:00 | 83 | false | Here\'s the intuition:\n\nFirst thoughts go right to using a stack, but we only need to determine the number the mis-balanced parenthesis pairs and return an integer. We can accomplish this task with simple counting.\n```python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n\n moves = tally = 0\n\n for ch in s:\n if ch ==\'(\':\n tally+= 1\n elif ch ==\')\' and tally > 0:\n tally-= 1\n else:\n tally = 0\n moves+= 1\n \n return tally + moves\n```\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int moves = 0, tally = 0;\n\n for (char ch : s) {\n if (ch == \'(\') {\n tally++;\n } else if (ch == \')\' && tally > 0) {\n tally--;\n } else {\n moves++;}}\n \n return tally + moves;}\n};\n```\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n\n int moves = 0, tally = 0;\n\n for (char ch : s.toCharArray()) {\n if (ch == \'(\') {\n tally++;\n } else if (ch == \')\' && tally > 0) {\n tally--;\n } else {\n moves++;}}\n \n return tally + moves;}}\n```\n[https://leetcode.com/problems/sorted-gcd-pair-queries/submissions/1416439710/?submissionId=1416439117](https://leetcode.com/problems/sorted-gcd-pair-queries/submissions/1416439710/?submissionId=1416439117)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~ `len(s)`. | 9 | 0 | ['C++', 'Java', 'Python3'] | 0 |
minimum-add-to-make-parentheses-valid | simple cpp solution | simple-cpp-solution-by-prithviraj26-6x3h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | prithviraj26 | NORMAL | 2023-02-10T04:59:51.774207+00:00 | 2023-02-10T04:59:51.774236+00:00 | 609 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n# Code\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char>st;\n for(int i=0;i<s.length();i++)\n {\n if(s[i]==\')\')\n {\n if(!st.empty()&&st.top()==\'(\')\n {\n st.pop();\n }\n else\n {\n st.push(\')\');\n }\n }\n else if(s[i]==\'(\')\n {\n st.push(\'(\');\n\n }\n }\n return st.size();\n }\n};\n```\n\n\n | 9 | 0 | ['String', 'Stack', 'C++'] | 0 |
minimum-add-to-make-parentheses-valid | Explaining One Pass | explaining-one-pass-by-gracemeng-viv6 | It is intuitive to count ( and ) and balance them on the fly.\n\nCases like )( should be disallowed, regardless of equal counts of ( and ) .\n\nThat is, count o | gracemeng | NORMAL | 2021-06-15T19:01:18.485141+00:00 | 2021-06-15T19:01:18.485172+00:00 | 426 | false | It is intuitive to count `(` and `)` and balance them on the fly.\n\nCases like `)(` should be disallowed, regardless of equal counts of `(` and `)` .\n\nThat is, count of `)` should `<=` count of `(` all the time.\n\nReferring to the code, when `right_expected == 0` and we hit `)`, we ought to add a `(` in the front immediately to maintain the above invariant.\n```\n def minAddToMakeValid(self, s: str) -> int:\n right_expected = added = 0\n for ch in s:\n if ch == \'(\':\n right_expected += 1\n else: # ch == \')\': \n if right_expected == 0: # Extra \')\' like \'())\'\n added += 1 # Add (\n else: # right_expected > 0\n right_expected -= 1\n\n return added + right_expected\n``` | 9 | 0 | [] | 1 |
minimum-add-to-make-parentheses-valid | BASIC IF ELSE STATEMENT ✅✅69_BEATS_100%✅✅🔥Easy Solution🔥With Explanation🔥 | basic-if-else-statement-69_beats_100easy-629h | Intuition\n Describe your first thoughts on how to solve this problem. \nwe need to count how many illegal paranthesis are there \na pair of paranthesis is lega | srinivas_bodduru | NORMAL | 2024-10-09T00:19:47.859025+00:00 | 2024-10-09T00:19:47.859058+00:00 | 1,352 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe need to count how many illegal paranthesis are there \na pair of paranthesis is legal only if it is like this ()\nmeans ) followed by (\nso we keep track of brackets encountered in a stack and we compare legal vs illegal \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe will have a stack \nfor every bracket we will check \nif it is ) we will see if the last bracket in our stack is (\n if yes we will pop our stack bcoz that is legal \nif not we will push onto stack as it has no partner bracket to pair up with \n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```javascript []\nvar minAddToMakeValid = function(s) {\n let stack=[]\n for(let x of s){\n if(stack[stack.length-1]==\'(\' && x==\')\')stack.pop()\n \n else stack.push(x)\n }\n return stack.length\n};\n```\n```python []\ndef minAddToMakeValid(s):\n stack = []\n for x in s:\n if stack and stack[-1] == \'(\' and x == \')\':\n stack.pop()\n else:\n stack.append(x)\n return len(stack)\n\n# Example usage\nprint(minAddToMakeValid("())"))\n\n```\n```java []\npublic class Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> stack = new Stack<>();\n for (char x : s.toCharArray()) {\n if (!stack.isEmpty() && stack.peek() == \'(\' && x == \')\') {\n stack.pop();\n } else {\n stack.push(x);\n }\n }\n return stack.size();\n }\n\n public static void main(String[] args) {\n Solution sol = new Solution();\n System.out.println(sol.minAddToMakeValid("())")); // Example usage\n }\n}\n\n```\n```c []\n#include <stdio.h>\n#include <string.h>\n\nint minAddToMakeValid(const char* s) {\n int top = -1;\n int n = strlen(s);\n char stack[n];\n \n for (int i = 0; i < n; i++) {\n if (top >= 0 && stack[top] == \'(\' && s[i] == \')\') {\n top--; // Pop stack\n } else {\n stack[++top] = s[i]; // Push stack\n }\n }\n \n return top + 1; // Stack size is top + 1\n}\n\nint main() {\n printf("%d\\n", minAddToMakeValid("())")); // Example usage\n return 0;\n}\n```\n```c++ []\n#include <iostream>\n#include <stack>\n#include <string>\n\nusing namespace std;\n\nint minAddToMakeValid(string s) {\n stack<char> stack;\n for (char x : s) {\n if (!stack.empty() && stack.top() == \'(\' && x == \')\') {\n stack.pop();\n } else {\n stack.push(x);\n }\n }\n return stack.size();\n}\n\nint main() {\n cout << minAddToMakeValid("())") << endl; // Example usage\n return 0;\n}\n```\n\n``` | 8 | 0 | ['String', 'Stack', 'Greedy', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 4 |
minimum-add-to-make-parentheses-valid | [Java] Stack Solution || With Explanation | java-stack-solution-with-explanation-by-9md8w | UPVOTE IF YOU LIKE THE EXPLANATION !!\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n Stack Data Structure\n# Approach\n Descr | Mjashwanth | NORMAL | 2023-04-24T15:42:47.280575+00:00 | 2023-04-24T15:43:40.325446+00:00 | 993 | false | # UPVOTE IF YOU LIKE THE EXPLANATION !!\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n Stack Data Structure\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Stack consists of **\'(\'** and **\')\'** symbols only.\n- In case of **\'(\'** you have to push it into the **Stack**.\n- In case of **\')\'** there are two conditions we have to handle.\n 1. Firstly when the stack is **empty**.\n 2. Secondly when the stack is **not empty** .\n- <h3>When Stack is empty!!</h3>\n 1. Increase the count value because we dont have enough **\'(\'** that equal to **\')\'**\n- <h3>When stack is not empty!!</h3>\n1. If stack is not empty definetly there will be a **\'(\'** at that time you can just pop it.\n- <h3>When Stack consists of only \'(\' !!</h3>\n 1. In this case we just have to add size of the **Stack** to the **count** variable.\n 2. **count** is the minimum additions to make parentheses valid.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n# Code\n```\nclass Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> stack = new Stack<>();\n int count = 0;\n for(char c : s.toCharArray()) {\n if(stack.isEmpty() ) {\n if(c == \'(\') stack.push(c);\n else count++;\n }\n else {\n if(c==\'(\') stack.push(c);\n else {\n stack.pop();\n }\n }\n\n }\n if(!stack.isEmpty() && stack.peek() == \'(\') {\n count += stack.size();\n }\n\n return count;\n }\n}\n``` | 8 | 0 | ['Stack', 'Java'] | 0 |
minimum-add-to-make-parentheses-valid | ✅C++ 100% faster & 90% memory efficient || easy single loop solution | c-100-faster-90-memory-efficient-easy-si-2516 | Please upvote if you find this helpful \uD83D\uDE4F\n\n# Code\n\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = 0;\n | underground_coder | NORMAL | 2023-01-03T04:44:54.147237+00:00 | 2023-01-03T04:44:54.147283+00:00 | 870 | false | # Please upvote if you find this helpful \uD83D\uDE4F\n\n# Code\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = 0;\n int open = 0;\n int close = 0;\n\n for(int j=0;j<s.length();j++){\n\n if((open - close) == 0 && s[j] == \')\'){\n ans++;\n }\n else if(s[j] == \'(\')\n open++;\n else\n close++;\n }\n ans += (open-close);\n return ans;\n }\n};\n```\n<B></B>\n<B></B>\n<B></B>\n##### Comment below if you didn\'t understand any steps\n | 8 | 0 | ['C++'] | 0 |
minimum-add-to-make-parentheses-valid | [Java] 100% [O(N) TC ][O(1) SC] || With Explanation | java-100-on-tc-o1-sc-with-explanation-by-i7pj | Please upvote if you like the solution !!\n# Intuition\n Describe your first thoughts on how to solve this problem. \n- If the symbol is \'(\' just increase the | Mjashwanth | NORMAL | 2023-04-25T01:18:53.584107+00:00 | 2023-04-25T01:18:53.584129+00:00 | 302 | false | # Please upvote if you like the solution !!\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- If the symbol is **\'(\'** just increase the count of **open** variable by 1.\n- If the symbol is **\')\'** check whether it\'s pair there or not. \n- If **open** variable is greater than zero we have the pair then decrement the count of **open** if not increase the **count** value by 1.\n- At last check **open** variable is greater than zero if it is then add to **count** variable.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution {\n public int minAddToMakeValid(String s) {\n int open = 0;\n int count = 0;\n for(char c : s.toCharArray()) {\n if(c == \'(\') {\n open++;\n }\n else if(c == \')\') {\n if(open > 0) open--;\n else count++;\n }\n }\n count += open;\n\n return count;\n }\n}\n``` | 7 | 0 | ['Java'] | 0 |
minimum-add-to-make-parentheses-valid | 2 pointer building up from Stack C++ solution | 2-pointer-building-up-from-stack-c-solut-lsvf | (1) Stack\n\nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n stack<char> stack;\n \n for(char s : S){\n if(s= | ankurharitosh | NORMAL | 2020-07-23T14:35:33.964808+00:00 | 2020-07-23T14:35:33.964850+00:00 | 406 | false | (1) Stack\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n stack<char> stack;\n \n for(char s : S){\n if(s==\'(\')\n stack.push(s);\n else{\n if(!stack.empty() && stack.top()==\'(\')\n stack.pop();\n else\n stack.push(s);\n }\n }\n return stack.size();\n }\n};\n\n```\n(2) 2 pointer\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n int balanceopen=0, balanceclose=0;\n \n for(int i=0; i<S.size(); i++){\n if(S[i]==\'(\')\n balanceopen++;\n else{\n if(balanceopen>0)\n balanceopen--;\n else\n balanceclose++;\n }\n }\n return balanceopen+balanceclose;\n }\n};\n``` | 7 | 0 | ['Two Pointers', 'Stack', 'C', 'C++'] | 0 |
minimum-add-to-make-parentheses-valid | python simple beats 100% (as of 22nd October, 2018) | python-simple-beats-100-as-of-22nd-octob-q8ve | The idea is to keep a separate counter for invalid left and right parenthesis. Whenever a new left parenthesis is encountered, the left counter is incremented b | keshavsarraf | NORMAL | 2018-10-22T11:24:19.546599+00:00 | 2018-10-25T01:38:16.622250+00:00 | 547 | false | The idea is to keep a separate counter for invalid left and right parenthesis. Whenever a new left parenthesis is encountered, the left counter is incremented by 1 (assuming it to be an invalid parenthesis). When a right parenthesis is encountered, the left counter is decremented by 1 (since we found a pair, we have one less invalid left parenthesis). But there is a catch, it may happen that we encounter a right parenthesis while the count of left count is 0, in which case we'll increment the right counter by 1 (because this is an invalid right parenthesis)
```
left = 0
right = 0
for p in S:
if p == "(":
left += 1
elif p == ")" and left <= 0:
right += 1
else:
left -= 1
return left + right
``` | 7 | 0 | [] | 0 |
minimum-add-to-make-parentheses-valid | Easy Python solution+ comments (12ms , 99% faster) | easy-python-solution-comments-12ms-99-fa-043y | \nclass Solution(object):\n def minAddToMakeValid(self, S):\n """\n :type S: str\n :rtype: int\n """\n stack =[]\n | pakilamak | NORMAL | 2020-08-07T07:03:18.873877+00:00 | 2020-08-07T07:11:42.513909+00:00 | 395 | false | ```\nclass Solution(object):\n def minAddToMakeValid(self, S):\n """\n :type S: str\n :rtype: int\n """\n stack =[]\n \n for i in range(len(S)):\n \n # if character is "(", then append to the stack\n if S[i] == "(":\n stack.append(S[i])\n else:\n if S[i] == ")":\n \n # check if stack has a character and also if the character is "(", then pop the character\n if stack and stack[-1] == \'(\':\n stack.pop()\n \n # else append ")" into the stack\n else:\n stack.append(S[i])\n \n # At the end return the length of the stack \n return len(stack)\n``` | 6 | 0 | ['Python'] | 1 |
minimum-add-to-make-parentheses-valid | Python | Beats 99% | Very easy to understand | python-beats-99-very-easy-to-understand-ysuw3 | Explaination:\nWhenever \'(\' comes, push it to stack.\nWhenever \')\' comes and stack is not empty, pop from stack.\nIf \')\' comes and stack is empty, add to | manasswami | NORMAL | 2020-04-16T10:20:13.250682+00:00 | 2020-04-16T10:20:13.250776+00:00 | 294 | false | **Explaination:**\nWhenever \'(\' comes, push it to stack.\nWhenever \')\' comes and stack is not empty, pop from stack.\nIf \')\' comes and stack is empty, add to count (count+=1)\n**Code:**\n```class Solution(object):\n def minAddToMakeValid(self, S):\n """\n :type S: str\n :rtype: int\n """\n stack = []\n count = 0\n for i in S:\n if i == \'(\':\n stack.append(i)\n elif stack:\n stack.pop()\n else:\n count += 1\n return (len(stack) + count) | 6 | 0 | [] | 3 |
minimum-add-to-make-parentheses-valid | 💡 C++ | O(n) | Space O(n) [Stack] -> O(1) [No Stack] | With Full Explanation ✏️ | c-on-space-on-stack-o1-no-stack-with-ful-5z2f | Intuition\nThe problem asks us to make a string of parentheses valid by adding the minimum number of parentheses. A valid string means every open parenthesis ( | Tusharr2004 | NORMAL | 2024-10-09T09:50:22.335325+00:00 | 2024-10-09T09:59:40.144334+00:00 | 18 | false | # Intuition\nThe problem asks us to make a string of parentheses valid by adding the minimum number of parentheses. A valid string means every open parenthesis `(` must have a corresponding close parenthesis `)`. The goal is to find how many parentheses need to be added to make the string valid.\n\nMy first thought is to use a stack or counters to keep track of unmatched parentheses as I iterate through the string.\n\n# Approach\nWe can use two approaches:\n\n1. **Using a Stack:**\n- Use a stack to store open parentheses `(`.\n- Traverse the string, and if we encounter a closing parenthesis `)` and the stack is not empty, we pop the open parenthesis from the stack (since it has a valid match).\n- If the stack is empty, we increment the answer because it means we have an unmatched closing parenthesis.\n- After traversing the string, the remaining unmatched open parentheses in the stack will need to be closed, so we add the size of the stack to our answer.\n2. **Space-Optimized Approach:**\n- Instead of using a stack, we can use a counter to keep track of open parentheses `(`.\n- Traverse the string, and for each open parenthesis, increment the counter. For each close parenthesis `)`, check if there is an unmatched open parenthesis to close. If yes, decrement the counter. If no, increment the answer (because it means we need an extra opening parenthesis).\n- After traversing the string, the counter will represent the number of unmatched open parentheses, which will need to be closed by adding the corresponding number of closing parentheses.\n\n# Complexity\n### Using a Stack :-\n- **Time complexity:** `O(n)` \u2014 We traverse the string once.\n- **Space complexity:** `O(n)` \u2014 In the worst case, all the parentheses are open, so the stack will store `n` elements.\n### Space-Optimized Approach :-\n- **Time complexity:** `O(n)` \u2014 We traverse the string once.\n- **Space complexity:** `O(1)` \u2014 Only two counters are used.\n\n# Code\n## Using a Stack\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = 0;\n stack<char> s1; // stack to track unmatched open parentheses\n for (int i = 0; s[i] != \'\\0\'; i++) {\n if (s[i] == \'(\') {\n s1.push(\'(\'); // push open parenthesis\n } else {\n if (!s1.empty() && s1.top() == \'(\') {\n s1.pop(); // valid match, pop from stack\n } else {\n ans++; // no match, increment answer\n }\n }\n }\n return ans + s1.size(); // add remaining unmatched open parentheses\n }\n};\n```\n## Space-Optimized Approach\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = 0;\n int lopen = 0; // counter for unmatched open parentheses\n \n for (int i = 0; s[i] != \'\\0\'; i++) {\n if (s[i] == \'(\') {\n lopen++; // increment for open parenthesis\n } else {\n if (lopen != 0) {\n lopen--; // valid match, decrement counter\n } else {\n ans++; // unmatched closing parenthesis\n }\n }\n }\n return ans + lopen; // add remaining unmatched open parentheses\n }\n};\n```\n\n\n\n\n# Ask any doubt !!!\nReach out to me \uD83D\uDE0A\uD83D\uDC47\n\uD83D\uDD17 https://tushar-bhardwaj.vercel.app/ | 5 | 1 | ['String', 'Stack', 'Greedy', 'C++'] | 1 |
minimum-add-to-make-parentheses-valid | Greedy Handling of Unbalanced Parentheses | Java | C++ | Video Solution | greedy-handling-of-unbalanced-parenthese-2ske | Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/aHp2Q6y0_Nw\n# Code\njava []\nclass Solution {\n public int minA | Lazy_Potato_ | NORMAL | 2024-10-09T05:36:46.958819+00:00 | 2024-10-09T05:36:46.958856+00:00 | 206 | false | # Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/aHp2Q6y0_Nw\n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int openReq = 0;\n int openCnt = 0;\n for(var chr : s.toCharArray()){\n if(chr == \'(\')openCnt++;\n else{\n if(openCnt > 0)openCnt--;\n else openReq++;\n }\n }\n int closeReq = openCnt;\n return openReq + closeReq;\n }\n}\n```\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int openReq = 0;\n int openCnt = 0;\n for(auto & chr : s){\n if(chr == \'(\')openCnt++;\n else{\n if(openCnt > 0)openCnt--;\n else openReq++;\n }\n }\n int closeReq = openCnt;\n return openReq + closeReq;\n }\n};\n``` | 5 | 0 | ['String', 'Stack', 'Greedy', 'C++', 'Java'] | 2 |
minimum-add-to-make-parentheses-valid | 💡| O(n) | C++ 0ms Beats 100.00% | Easy Solution🧠| Py3 23ms Beats 98.69% | Java 0ms Beats 100.00% | | on-c-0ms-beats-10000-easy-solution-py3-2-lzsb | \n#\n---\n\n> # Intuition\nTo determine the minimum number of insertions required to make the parentheses string valid, we need to track the number of unmatched | user4612MW | NORMAL | 2024-10-09T03:23:13.864355+00:00 | 2024-10-09T03:50:42.064038+00:00 | 585 | false | \n#\n---\n\n> # Intuition\nTo determine the minimum number of insertions required to make the parentheses string valid, we need to track the number of unmatched opening and closing parentheses. As we traverse the string, we increment counts based on whether the current character is an opening or closing parenthesis. When a closing parenthesis is found but no opening parenthesis is available to match, we increase the count of unmatched closing parentheses. At the end, the total unmatched parentheses are the result of adding unmatched opening and closing parentheses.\n\n> # Approach\nWe initialize two counters: one for unmatched opening parentheses and another for unmatched closing parentheses. As we traverse the string, we increment the opening counter when we find an opening parenthesis. When we find a closing parenthesis, if there are unmatched opening parentheses, we decrement the opening counter (indicating a match). Otherwise, we increment the closing counter (indicating an unmatched closing parenthesis). The result is the sum of unmatched opening and closing parentheses.\n\n> # Complexity\n- **Time Complexity** $$O(n)$$, where n is the length of the string. We process each character once.\n- **Space Complexity** $$O(1)$$, since we only use a few variables for tracking counts.\n\n---\n\n> # Code\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int o{0}, c{0};\n for (char ch : s) ch == \'(\' ? ++o : o ? --o : ++c;\n return o + c;\n }\n};\n```\n```Java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int o = 0, c = 0;\n for (char ch : s.toCharArray()) {\n if (ch == \'(\') {\n o++;\n } else if (o > 0) {\n o--;\n } else {\n c++;\n }\n }\n return o + c;\n }\n}\n```\n```python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n o = c = 0\n for ch in s:\n if ch == \'(\':\n o += 1\n elif o > 0:\n o -= 1\n else:\n c += 1\n return o + c\n```\n\n---\n\n> **CPP**\n> \n> **Java**\n> \n> **Python3**\n> \n\n\n---\n\n> ### Additional Notes\n> Note : The approach is highly efficient with a time complexity of $$\uD835\uDC42(\uD835\uDC5B)$$, making a single pass through the string, and constant space. This makes sure optimal performance for the given constraints.\n\n | 5 | 0 | ['C++', 'Java', 'Python3'] | 4 |
minimum-add-to-make-parentheses-valid | "💯 Beats 100% | No Stack Needed 🚫🧳 | Simple C++ Solution 🚀" | beats-100-no-stack-needed-simple-c-solut-j68e | Intuition\nThe problem asks for the minimum number of parentheses that need to be added to make a given string of parentheses valid. A string of parentheses is | geek_nik | NORMAL | 2024-10-09T02:12:50.584144+00:00 | 2024-10-09T02:12:50.584189+00:00 | 116 | false | # Intuition\nThe problem asks for the minimum number of parentheses that need to be added to make a given string of parentheses valid. A string of parentheses is valid when every open parenthesis $$($$ has a matching close parenthesis $$)$$. The idea is to keep track of unmatched open and close parentheses while iterating through the string.\n\n# Approach\nWe can solve this problem using a linear scan of the string while maintaining two variables:\n\n1. openCount: Tracks how many open parentheses ( are unmatched as we go through the string.\n2. closeCount: Tracks how many close parentheses ) do not have a matching open parenthesis.\n\nFor each character in the string:\n\n* If it is an open parenthesis (, we increment openCount.\n* If it is a close parenthesis ), we check:\n * If there\'s an unmatched open parenthesis (openCount > 0), we decrement openCount (since we\'ve found a match).\n * Otherwise, we increment closeCount (since it\'s an unmatched close parenthesis).\n3. At the end of the loop, the sum of openCount and closeCount gives us the minimum number of parentheses we need to add to make the string valid.\n\n\n\n# Complexity\n- Time complexity:\nThe time complexity is $$O(n)$$, where \n$$n$$ is the length of the string. This is because we are iterating through the string exactly once.\n\n- Space complexity:\nThe space complexity is $$O(1)$$ since we are only using two variables (openCount and closeCount) to track the state and are not using any additional space that scales with the input size.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int openCount = 0, closeCount = 0;\n \n for (char c : s) {\n if (c == \'(\') {\n openCount++;\n } else {\n if (openCount > 0) {\n openCount--;\n } else {\n closeCount++;\n }\n }\n }\n \n return openCount + closeCount;\n }\n};\n\n``` | 5 | 0 | ['String', 'Stack', 'Greedy', 'C++'] | 1 |
minimum-add-to-make-parentheses-valid | My solution beats 100% . simple solution in c++ | my-solution-beats-100-simple-solution-in-cnle | Intuition \uD83C\uDFAF\n Describe your first thoughts on how to solve this problem. \nThis problem focuses on finding the minimum number of parentheses addition | letsdoit5806 | NORMAL | 2024-10-09T02:06:03.104667+00:00 | 2024-10-09T02:06:03.104700+00:00 | 184 | false | # Intuition \uD83C\uDFAF\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem focuses on finding the minimum number of parentheses additions needed to make a string of parentheses (( and )) valid. A valid string of parentheses is one where every opening parenthesis (() has a corresponding closing parenthesis ()), and the pairs are properly nested.\n\nThe key idea here is to use a stack to track unmatched parentheses:\n\n<ul><li>If we encounter an opening parenthesis ((), we push it onto the stack.</li>\n<li>If we encounter a closing parenthesis ()), we check the top of the stack:</li></ul>\n<li>If the top is an unmatched opening parenthesis ((), we can form a valid pair, so we pop it.</li>\n<li>Otherwise, we push the closing parenthesis onto the stack as it is unmatched.</li></ul></ul>\nBy the end of the traversal, the stack will contain any unmatched parentheses, and the size of the stack will be the number of parentheses that need to be added to make the string valid.\n\n# Approach \uD83D\uDEB6\u200D\u2642\uFE0F\n<!-- Describe your approach to solving the problem. -->\n1. Stack Usage \uD83E\uDDEE:\n\n<ul><li>Traverse the string character by character.</li>\n<li>If the stack is not empty and the top of the stack is an unmatched opening parenthesis ((), and the current character is a closing parenthesis ()), pop the stack (this indicates a valid pair).</li>\n<li>Otherwise, push the current character (either ( or )) onto the stack.</li></ul>\n2. Unmatched Parentheses Count \uD83D\uDD04:\n\n<ul><li>By the end of the traversal, the stack will contain only unmatched parentheses (both ( and )).</li><li>\nThe size of the stack will give the total number of unmatched parentheses, and this is the minimum number of parentheses to add to make the string valid.</li></ul>\n3. Return Result \uD83C\uDFC1:\n\n<ul><li>The function returns the size of the stack, which represents the number of additions needed.</li></ul>\n\n4. Example \uD83D\uDCA1\nConsider the input string s = "())(":\n\n<li><ul>First ) matches with the first (, so the pair is valid and removed from the stack.</li>\n<li>The second ) is unmatched, so it\'s pushed onto the stack.</li>\n<li>The last ( is unmatched, so it also stays on the stack.</li>\n<li>In the end, the stack contains ) and (, which means we need to add 2 parentheses to balance them. The result is 2.</li></ul>\n# Complexity \uD83D\uDCCA\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n \n int minAddToMakeValid(string s) {\n stack<char> stac;\n for(char c : s)\n {\n if(!stac.empty() && stac.top()==\'(\' && c==\')\')stac.pop();\n else stac.push(c);\n }\n return stac.size();\n }\n};\n``` | 5 | 0 | ['Stack', 'C++'] | 1 |
minimum-add-to-make-parentheses-valid | ✅Efficient Easy to understand🔥Beginner Friendly🔥|| Stack|| | efficient-easy-to-understandbeginner-fri-9ds6 | Problem Understanding\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the minimum number of parentheses needed to be | anand_shukla1312 | NORMAL | 2024-10-09T01:09:11.943675+00:00 | 2024-10-09T01:09:11.943701+00:00 | 93 | false | # Problem Understanding\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the minimum number of parentheses needed to be added to make a given string of parentheses valid. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Stack-based Validation**: The code uses a stack to track unmatched opening parentheses \'(\'. For each character in the string:\n - If the character is \'(\', it is pushed onto the stack (indicating an unmatched opening parenthesis).\n - If the character is \')\':\n - If the stack is not empty (there is an unmatched \'(\'), it pops from the stack to indicate a match.\n - If the stack is empty (there is no unmatched \'(\'), it increments the ans counter to account for an unmatched closing parenthesis.\n1. **Final Step**:\n - At the end, the sum of len(stack) (which counts the unmatched opening parentheses) and ans (which counts the unmatched closing parentheses) is returned as the minimum number of parentheses that need to be added.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n ans = 0\n for i in s:\n if i == "(":\n stack.append(i)\n elif len(stack)>0 and i == ")":\n stack.pop()\n elif i == ")":\n ans += 1\n return len(stack) + ans \n```\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A | 5 | 0 | ['Stack', 'Python3'] | 0 |
minimum-add-to-make-parentheses-valid | Easy C++ Code, beats 100% time and 90% space complexity, 10 lines code | easy-c-code-beats-100-time-and-90-space-8wt6e | \n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nIterating once and counting all | Kyouma45 | NORMAL | 2023-05-31T11:56:05.656000+00:00 | 2023-05-31T11:56:05.656040+00:00 | 35 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIterating once and counting all the lose paranthesis in the string.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int opening=0,closing=0;\n std::string::iterator itr=s.begin();\n while(itr!=s.end())\n {\n if(*itr==\'(\'&&closing==0)\n opening++;\n else if(*itr==\')\'&&opening!=0)\n opening--;\n else if(*itr==\'(\')\n opening++;\n else\n closing++;\n itr++;\n }\n return opening+closing;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
minimum-add-to-make-parentheses-valid | Python | Easy Solution✅ | python-easy-solution-by-gmanayath-ogif | Solution 1:\n\ndef minAddToMakeValid(self, s: str) -> int:\n while "()" in s:\n s= s.replace("()","",1)\n return len(s)\n\nSolution 2:\ | gmanayath | NORMAL | 2022-08-28T07:45:11.292317+00:00 | 2022-12-22T16:46:56.687595+00:00 | 790 | false | Solution 1:\n```\ndef minAddToMakeValid(self, s: str) -> int:\n while "()" in s:\n s= s.replace("()","",1)\n return len(s)\n```\nSolution 2:\n```\ndef minAddToMakeValid(self, s: str) -> int:\n output=[]\n for i in range(len(s)):\n if s[i] == \'(\':\n output.append(s[i])\n elif s[i]==\')\':\n output.pop() if output and output[-1]==\'(\' else output.append(s[i])\n return len(output)\n``` | 5 | 0 | ['Python', 'Python3'] | 1 |
minimum-add-to-make-parentheses-valid | Javascript stack | javascript-stack-by-fbecker11-q8o7 | \nvar minAddToMakeValid = function(S) {\n const stack = []\n for(let s of S){\n if(s === \')\' && stack[stack.length-1] === \'(\')\n stack.pop()\n | fbecker11 | NORMAL | 2020-11-17T19:23:04.982168+00:00 | 2020-11-17T19:23:04.982200+00:00 | 506 | false | ```\nvar minAddToMakeValid = function(S) {\n const stack = []\n for(let s of S){\n if(s === \')\' && stack[stack.length-1] === \'(\')\n stack.pop()\n else\n stack.push(s)\n }\n return stack.length\n};\n``` | 5 | 1 | ['JavaScript'] | 0 |
minimum-add-to-make-parentheses-valid | 😍💯2 Lines of Codeeeee with 1 ms✅,Beats 90.31% in Memory📝 The Easiest Approach Ever🚀 | 2-lines-of-codeeeee-with-1-msbeats-9031-k11z7 | Appproach\nAaaaaaaaaaaaa.. I mean There\'s not much to explain. I\'m simply using contains() to check if any substring "()" is present in the main string. If I | ArcuLus | NORMAL | 2024-10-09T15:07:45.477961+00:00 | 2024-10-09T15:07:45.477984+00:00 | 18 | false | # Appproach\nAaaaaaaaaaaaa.. I mean There\'s not much to explain. I\'m simply using contains() to check if any substring "()" is present in the main string. If I find it, I remove it.\n\nFor example, let\'s say you have a string like "(((((())))))\')". In this case, everything is balanced except for the last \')\'.\n\nWith my approach, each time I find a valid pair "()", I remove it. In the end, I\'m left with just \')\'. To balance this, I need one more \'(\', which is exactly what the length of the remaining string represents.\n\n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n while(s.contains("()"))s=s.replace("()","");\n return s.length();\n }\n}\n``` | 4 | 0 | ['String', 'Stack', 'Greedy', 'Java'] | 1 |
minimum-add-to-make-parentheses-valid | Very easy......🔥🔥🔥🔥 | very-easy-by-pritambanik-z08r | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | PritamBanik | NORMAL | 2024-10-09T14:58:19.795406+00:00 | 2024-10-09T14:58:19.795441+00:00 | 42 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 100%\u2705\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\n\nint minAddToMakeValid(char *s) {\n int open = 0, close = 0;\n\n for (int i = 0; s[i] != \'\\0\'; i++) {\n if (s[i] == \'(\') {\n open++; // Count of unmatched opening brackets\n } else if (s[i] == \')\') {\n if (open > 0) {\n open--; // Match with an opening bracket\n } else {\n close++; // Unmatched closing brackets\n }\n }\n }\n\n // The result is the sum of unmatched open and close brackets\n return open + close;\n}\n\n``` | 4 | 0 | ['String', 'Stack', 'Greedy', 'C'] | 0 |
minimum-add-to-make-parentheses-valid | Simple 3 lines Code (Easy Approach) | simple-3-lines-code-easy-approach-by-tan-t2gb | \n# Approach\n1. Keep count of open and close bracket. \n2. if \'(\' encounter increesed open and else if \')\' encounter and open is greater than 0 means 1 ope | Tanmay_bhure | NORMAL | 2024-10-09T13:56:26.205198+00:00 | 2024-10-09T13:56:26.205238+00:00 | 133 | false | \n# Approach\n1. Keep count of open and close bracket. \n2. if \'(\' encounter increesed open and else if \')\' encounter and open is greater than 0 means 1 open open bracket is already happens so decreesed open else increese close\n3. return open + close\n\n# Complexity\n- Time complexity:\nO(n);\n\n- Space complexity:\nO(1)\n\n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int open= 0, close=0;\n for(char c: s.toCharArray()){\n if(c==\'(\') open++;\n else if (c==\')\' && open>0) open--;\n else close++;\n }\n return open+close;\n }\n}\n```\n# Code\n```C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int open = 0, close = 0;\n for (char c : s) {\n if (c == \'(\') open++;\n else if (c == \')\' && open > 0) open--;\n else close++;\n }\n return open + close;\n }\n};\n```\n# Code\n``` Python []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n open, close = 0, 0\n for c in s:\n if c == \'(\':\n open += 1\n elif c == \')\' and open > 0:\n open -= 1\n else:\n close += 1\n return open + close\n```\n | 4 | 0 | ['String', 'Greedy', 'Python', 'C++', 'Java'] | 0 |
minimum-add-to-make-parentheses-valid | Simple Java Code ☠️ | simple-java-code-by-abhinandannaik1717-84z2 | Code\njava []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int n = s.length();\n Stack<Character> stack = new Stack<>();\n | abhinandannaik1717 | NORMAL | 2024-10-09T13:21:45.968721+00:00 | 2024-10-09T13:21:45.968764+00:00 | 106 | false | # Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int n = s.length();\n Stack<Character> stack = new Stack<>();\n for(int i=0;i<n;i++){\n if(s.charAt(i) == \'(\'){\n stack.push(\'(\');\n }\n else{\n if(!stack.isEmpty() && stack.peek() == \'(\'){\n stack.pop();\n }\n else{\n stack.push(\')\');\n }\n }\n }\n return stack.size();\n }\n}\n```\n\n\n### Explanation:\n\n1. **Initialize a Stack:**\n - The stack will help track unmatched parentheses. We push opening parentheses `(` when we see them and try to match them with closing parentheses `)`.\n\n2. **Iterate Through the String:**\n - The loop goes through each character of the string one by one.\n\n3. **Handling Opening Parentheses `(`:**\n - If we encounter an opening parenthesis `(`, we simply push it onto the stack. This is because we need to find a closing parenthesis `)` to match it later.\n\n4. **Handling Closing Parentheses `)`**:\n - If we encounter a closing parenthesis `)`, we check whether the top of the stack is an opening parenthesis `(`. If the top of the stack is `(`, it means we found a matching pair, so we pop the stack to remove the matched `(`.\n - If the stack is either empty or the top of the stack is not `(`, it means that we don\u2019t have an unmatched opening parenthesis to balance the current `)`. In this case, we push the `)` onto the stack, indicating an unmatched closing parenthesis.\n\n5. **End of the Loop:**\n - By the end of the loop, the stack contains only unmatched parentheses (both opening `(` and closing `)` parentheses that couldn\u2019t be balanced).\n - The size of the stack tells us how many moves are required to make the string valid, as each unmatched parenthesis needs a corresponding matching one to become balanced.\n\n6. **Return the Stack Size:**\n - Finally, we return the size of the stack, which represents the minimum number of insertions needed to make the parentheses string valid.\n\n### Example:\n\n- Input: `"())"`\n - At index 0: We encounter `(` \u2192 Push `(` onto the stack.\n - At index 1: We encounter `)` \u2192 The top of the stack is `(`, so we pop the stack to balance this pair.\n - At index 2: We encounter `)` \u2192 The stack is empty, so we push `)` onto the stack.\n\n Stack: `[\')\']`\n\n The stack contains 1 unmatched closing parenthesis, so we return `1`.\n\n- Input: `"((("`\n - At each index (0, 1, 2), we encounter `(` and push them onto the stack.\n\n Stack: `[\'(\', \'(\', \'(\']`\n\n The stack contains 3 unmatched opening parentheses, so we return `3`.\n\n### Time Complexity:\n- **Time Complexity:** The time complexity is **O(n)**, where `n` is the length of the string. This is because we iterate through the string once and perform constant-time operations for each character.\n \n- **Space Complexity:** The space complexity is **O(n)** in the worst case, where all parentheses are unmatched and stored in the stack. \n\n\n\n\n\n\n\n | 4 | 0 | ['String', 'Stack', 'Java'] | 0 |
minimum-add-to-make-parentheses-valid | C++ || Easy Stack Approach✅✅ | c-easy-stack-approach-by-arunk_leetcode-7pq1 | Intuition\nThe goal is to determine how many parentheses must be added to make a given string valid. A valid parentheses string is one where every opening paren | arunk_leetcode | NORMAL | 2024-10-09T04:38:19.842561+00:00 | 2024-10-09T04:38:19.842606+00:00 | 170 | false | # Intuition\nThe goal is to determine how many parentheses must be added to make a given string valid. A valid parentheses string is one where every opening parenthesis `\'(\'` has a corresponding closing parenthesis `\')\'`. \n\nTo achieve this, we can use a stack to track unmatched opening parentheses and a counter to count unmatched closing parentheses.\n\n# Approach\n- Traverse through the string character by character.\n- If we encounter an opening parenthesis `\'(\'`, push it onto the stack.\n- If we encounter a closing parenthesis `\')\'`:\n - If the stack is empty, increment a counter `maxi` as it indicates an unmatched closing parenthesis.\n - If the stack is not empty and the top of the stack is an opening parenthesis `\'(\'`, we pop the stack to balance it.\n- Finally, the number of unmatched opening parentheses will be the size of the stack, and the number of unmatched closing parentheses will be stored in `maxi`. The total number of additions needed is the sum of these two values.\n\n# Complexity\n- **Time complexity:** O(n)\n- **Space complexity:** O(n)\n\n# Code\n\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int maxi = 0;\n stack<char> st;\n for(int i=0; i<s.length(); i++){\n if(s[i] == \')\' && st.empty()){\n maxi++;\n }\n else if(s[i] == \')\' && st.top() == \'(\') st.pop();\n else st.push(s[i]);\n }\n return st.size()+maxi;\n }\n};\n``` | 4 | 0 | ['Stack', 'C++'] | 1 |
minimum-add-to-make-parentheses-valid | Very Easy with O(1) Space 100% beat | very-easy-with-o1-space-100-beat-by-vira-hebv | \n\n\n# Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) \n | viratkohli_ | NORMAL | 2024-10-09T02:39:09.895274+00:00 | 2024-10-09T02:39:09.895322+00:00 | 20 | false | \n\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n if(s.empty()) return 0;\n int lcount = 0, rcount = 0;\n for(char ch:s){\n if(ch == \'(\'){\n lcount++;\n }\n else{\n if(lcount == 0){\n rcount++;\n }\n else{\n lcount--;\n }\n }\n }\n return lcount+rcount;\n }\n};\n``` | 4 | 0 | ['String', 'Greedy', 'C++'] | 0 |
minimum-add-to-make-parentheses-valid | JAVA | 100% Beats | Linear Approach with O(1) Space | java-100-beats-linear-approach-with-o1-s-krep | \n# Code\njava []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int set = 0;\n int res = 0;\n for (char c : s.toCharArr | SudhikshaGhanathe | NORMAL | 2024-09-08T08:32:12.667547+00:00 | 2024-09-08T08:32:12.667571+00:00 | 227 | false | \n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int set = 0;\n int res = 0;\n for (char c : s.toCharArray()) {\n switch (c) {\n case \'(\' -> set += 1;\n case \')\' -> set -= 1;\n }\n if (set == -1) {\n set += 1;\n res += 1;\n }\n }\n return res + set;\n }\n}\n``` | 4 | 0 | ['Java'] | 1 |
minimum-add-to-make-parentheses-valid | Java Simple Brute Force Solution Using Stack | java-simple-brute-force-solution-using-s-4btp | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is about finding the minimum number of parentheses that need to be added to | Chaitanya_91 | NORMAL | 2024-08-15T17:25:14.372129+00:00 | 2024-08-15T17:25:14.372166+00:00 | 191 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about finding the minimum number of parentheses that need to be added to make a string of parentheses valid. A valid string means that every opening parenthesis \'(\' has a corresponding closing parenthesis \')\'.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a stack to keep track of unmatched opening parentheses \'(\'.\nTraverse the string:\nIf the character is \'(\', push it onto the stack.\nIf the character is \')\', check if the stack is not empty:\nIf the stack is not empty, pop an element from the stack (indicating a match).\nIf the stack is empty, increment a counter c (indicating an unmatched closing parenthesis).\nAfter traversing the string, the size of the stack will represent the unmatched opening parentheses, and the counter c will represent the unmatched closing parentheses.\nThe result will be the sum of the stack size and the counter c.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minAddToMakeValid(String S) {\n Stack s = new Stack<>();\n int c = 0;\n for(int i=0; i<S.length(); i++){\n if(S.charAt(i) == \'(\'){\n s.add(S.charAt(i));\n }\n else{\n if(!s.isEmpty()){\n s.pop();\n }\n else{\n c++;\n }\n }\n }\n c = c + s.size();\n return c;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
minimum-add-to-make-parentheses-valid | SIMPLE STACK C++ COMMENTED SOLUTION | simple-stack-c-commented-solution-by-jef-1u5z | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Jeffrin2005 | NORMAL | 2024-07-26T12:37:55.292658+00:00 | 2024-07-26T12:41:12.626915+00:00 | 164 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> stk;\n int moves = 0;\n for(auto&c : s){\n if(c == \'(\'){\n // Push opening brackets onto the stack\n stk.push(c);\n }else{\n // If it\'s a closing bracket\n if (!stk.empty() && stk.top() == \'(\'){\n // Pop the stack if there\'s a matching opening bracket\n stk.pop();\n }else{\n // Otherwise, we need an extra opening bracket\n moves++;\n }\n }\n }\n // s = "(((" for this case we need 3 close brackets, moves = 0 , 0 + 3;\n // Add remaining unmatched opening brackets to the moves\n moves+=stk.size();\n return moves;\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
minimum-add-to-make-parentheses-valid | 100% beats, easy-peasy code. | 100-beats-easy-peasy-code-by-a_krisssh-nchs | \n#### I don\'t know why this problem is tagged as Medium. Easy-peasy code in O(N) time complexity and O(1) space complexity.\n\n\n# Code\n\nclass Solution {\np | a_krisssh | NORMAL | 2024-07-05T16:45:34.482992+00:00 | 2024-07-05T16:45:34.483021+00:00 | 321 | false | \n#### I don\'t know why this problem is tagged as Medium. Easy-peasy code in O(N) time complexity and O(1) space complexity.\n\n\n# Code\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int open = 0, close = 0;\n\n for(char ch: s){\n if(ch == \'(\') open++;\n else if(open == 0) close++;\n else open--;\n }\n\n return (open + close);\n }\n};\n```\n\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n### Intuition for the Solution:\n\n1. **Tracking Unmatched Parentheses**: The code uses two counters, `open` to track unmatched opening parentheses \'(\' and `close` to track unmatched closing parentheses \')\'.\n2. **Traversing the String**: As it iterates through each character in the string:\n - If it encounters an opening parenthesis \'(\', it increments the `open` counter.\n - If it encounters a closing parenthesis \')\', it checks if there are unmatched opening parentheses (`open` > 0). If there are, it decrements the `open` counter to match the current closing parenthesis. If there are no unmatched opening parentheses, it increments the `close` counter.\n3. **Result**: The total number of unmatched opening and closing parentheses (`open + close`) gives the minimum number of moves required to make the string valid. This is because each unmatched parenthesis needs to be matched by inserting the corresponding opposite parenthesis.\n\n### Explanation of the Example:\nFor the input "()))":\n- The first character is \'(\', so `open` is incremented to 1.\n- The next character is \')\', so `open` is decremented to 0 (matching the \'(\').\n- The next character is \')\', so `close` is incremented to 1 (no unmatched \'(\' to match it).\n- The last character is \')\', so `close` is incremented to 2 (no unmatched \'(\' to match it).\n\nThe total moves required are `open + close = 0 + 2 = 2`.\n\nThus, the minimum number of moves required to make the string valid is 2.\n | 4 | 0 | ['String', 'Greedy', 'C++'] | 0 |
minimum-add-to-make-parentheses-valid | ✔️✔️💯Brute Intuitive solution💯✅🔥 with and without stack beast time and Space | brute-intuitive-solution-with-and-withou-at2d | \n# Code\njava []\nclass Solution {\n public int minAddToMakeValid(String s) {\n\n int requiredAdditions = 0;\n Stack<Character> st = new Stack | Dixon_N | NORMAL | 2024-06-21T18:49:49.342356+00:00 | 2024-06-21T19:16:26.677586+00:00 | 209 | false | \n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n\n int requiredAdditions = 0;\n Stack<Character> st = new Stack<>();\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n st.push(c);\n } else if(st.isEmpty())\n {\n requiredAdditions++;\n }\n else{\n st.pop();\n }\n }\n return requiredAdditions+st.size();\n }\n}\n```\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int openCount = 0;\n int closeCount = 0;\n int requiredAdditions = 0;\n\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n openCount++;\n } else {\n if (closeCount < openCount) {\n closeCount++;\n } else {\n requiredAdditions++;\n }\n }\n }\n\n requiredAdditions += openCount - closeCount;\n return requiredAdditions;\n }\n}\n```\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int openCount = 0;\n int closeCount = 0;\n int requiredAdditions = 0;\n\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n openCount++;\n } else if (openCount > closeCount) {\n closeCount++; \n }else {\n requiredAdditions++;\n }\n }\n\n requiredAdditions += openCount - closeCount;\n return requiredAdditions;\n }\n}\n\n```\n\n[1541. Minimum Insertions to Balance a Parentheses String](https://leetcode.com/problems/minimum-insertions-to-balance-a-parentheses-string/solutions/5348641/the-parenthesis-template-question-brute-intuitive-interview/)\n[921. Minimum Add to Make Parentheses Valid](https://leetcode.com/problems/minimum-add-to-make-parentheses-valid/solutions/5348632/brute-intuitive-solution-with-and-without-stack-beast-time-and-space/)\n[20. Valid Parentheses](https://leetcode.com/problems/valid-parentheses/solutions/5159895/brute-intuitive-solution-beats-98/) --> *simple yet tricky*\n[301. Remove Invalid Parentheses](https://leetcode.com/problems/remove-invalid-parentheses/solutions/5305306/have-fun-solving-this-easy-problem/) -> **Important**\n[32. Longest Valid Parentheses](https://leetcode.com/problems/longest-valid-parentheses/solutions/5348623/simple-solution-in-java-must-read/)\n[1614. Maximum Nesting Depth of the Parentheses](https://leetcode.com/problems/maximum-nesting-depth-of-the-parentheses/solutions/5304994/the-parenthesis-problems/)\n[282. Expression Add Operators](https://leetcode.com/problems/expression-add-operators/solutions/5348619/brute-intuitive-recursive-solution-must-read/) --> **Important**\n[2232. Minimize Result by Adding Parentheses to Expression](https://leetcode.com/problems/minimize-result-by-adding-parentheses-to-expression/solutions/5304516/beats-98/)\n[241. Different Ways to Add Parentheses](https://leetcode.com/problems/different-ways-to-add-parentheses/solutions/5304322/java-simple-solution/)\n[856. Score of Parentheses](https://leetcode.com/problems/score-of-parentheses/solutions/5203496/scoreofparentheses/) --> **unique**\n[678. Valid Parenthesis String]()\n[1003. Check If Word Is Valid After Substitutions]()\n[1963. Minimum Number of Swaps to Make the String Balanced]() | 4 | 0 | ['Java'] | 3 |
minimum-add-to-make-parentheses-valid | PYTHON || OPTIMAL SOLUTION || 100% EFFICIENT || EASY TO UNDERSTAND || | python-optimal-solution-100-efficient-ea-tdk7 | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n- The intuition behind this pro | Adit_gaur | NORMAL | 2024-05-24T04:04:12.580876+00:00 | 2024-05-24T04:04:12.580897+00:00 | 88 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The intuition behind this problem is to determine the minimum number of parentheses (opening or closing) that need to be added to a given string to make it a valid parentheses expression. A valid parentheses expression is one where all opening parentheses have a matching closing parenthesis, and all closing parentheses have a matching opening parenthesis.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize two variables: count to keep track of the balance between opening and closing parentheses, and ans to store the minimum number of parentheses that need to be added.\nIterate through each character paran in the input string s:\n\n- If paran is an opening parenthesis \'(\', increment count by 1. \n- If paran is a closing parenthesis \')\', decrement count by 1.\n- If count becomes -1, it means we have encountered an extra closing parenthesis without a corresponding opening parenthesis. In this case, reset count to 0 and increment ans by 1 to account for the extra opening parenthesis that needs to be added.\n\n\n- After the loop finishes, add the final value of count to ans. The count variable represents the number of unmatched opening parentheses that need to be closed with closing parentheses.\n- Return ans, which represents the minimum number of parentheses that need to be added to make the string valid.\n\n# Complexity\n- Time complexity: O(n), where n is the length of the input string s. The code iterates through the string once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1), since the solution uses a constant amount of extra space to store temporary variables.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def minAddToMakeValid(self, s):\n """\n :type s: str\n :rtype: int\n """\n count = ans = 0\n for paran in s:\n if paran == \'(\':\n count += 1\n else:\n count -= 1\n if count == -1:\n count = 0\n ans += 1\n ans += count\n return ans\n \n```\nPLEASE UPVOTE ME, IF YOU LIKE THE SOLUTION.\n\n\n | 4 | 0 | ['String', 'Stack', 'Greedy', 'Python', 'Python3'] | 2 |
minimum-add-to-make-parentheses-valid | Java Easy Solution for Beginners | java-easy-solution-for-beginners-by-raja-gt11 | Approach\n1. Define a method minAddToMakeValid that takes a string s representing parentheses.\n2. Initialize a stack (Stack<Character> st) to keep track of ope | RajarshiMitra | NORMAL | 2024-05-13T05:39:39.890789+00:00 | 2024-06-16T07:03:45.945257+00:00 | 22 | false | # Approach\n1. Define a method `minAddToMakeValid` that takes a string `s` representing parentheses.\n2. Initialize a stack (`Stack<Character> st`) to keep track of opening parentheses.\n3. Initialize a counter (`count`) to count the number of additional parentheses needed.\n4. Iterate through each character in the string.\n5. If the current character is an opening parenthesis \'(\', push it onto the stack.\n6. If the current character is a closing parenthesis \')\':\n - If the stack is empty, increment the `count` to indicate a missing opening parenthesis.\n - If the stack is not empty, pop an opening parenthesis from the stack, matching it with the current closing parenthesis.\n7. After iterating through all characters, add the remaining unmatched opening parentheses in the stack to the `count`.\n8. Return the total count, which represents the minimum number of parentheses needed to make the string valid.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> st=new Stack<>();\n int count=0;\n for(int i=0; i<s.length(); i++){\n if(s.charAt(i) == \'(\') st.push(s.charAt(i));\n else{\n if(st.empty()) count++;\n else st.pop();\n }\n }\n return count+st.size();\n }\n}\n```\n\n\n | 4 | 0 | ['Java'] | 0 |
minimum-add-to-make-parentheses-valid | 🧠[C++/Java/Python]: One Pass Easy Solution | cjavapython-one-pass-easy-solution-by-hr-1fzc | Approach\n> 1. Initialize an empty stack st to keep track of unmatched opening parentheses.\n> 2. Iterate through each character i in the input string s.\n\n> 3 | hrishi13 | NORMAL | 2023-09-02T17:12:04.072681+00:00 | 2023-09-02T17:12:04.072721+00:00 | 373 | false | ## Approach\n> 1. Initialize an empty stack st to keep track of unmatched opening parentheses.\n> 2. Iterate through each character i in the input string s.\n\n> 3. For each character i:\n> * If the stack is empty, push the character onto the stack because there\'s nothing to match it with.\n> * If the stack is not empty and the current character i is a closing parenthesis \')\' and the top of the stack contains an opening parenthesis \'(\', then pop the opening parenthesis from the stack because a valid pair has been found.\n> * If none of the above conditions are met, push the current character i onto the stack.\n> 4. After processing all characters in the string, the remaining unmatched opening parentheses (if any) will be left on the stack. The size of the stack represents the minimum number of additions needed to make the string valid.\n> 5. Return the size of the stack as the result, which is the minimum number of additions required to make the string valid.\n\n---\n\n\n\n## Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n---\n\n\n\n## Code\n```C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n\n for(auto i: s){\n if(st.empty())\n st.push(i);\n else if(st.top() == \'(\' and i == \')\')\n st.pop();\n else\n st.push(i);\n }\n return st.size();\n }\n};\n```\n```Java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> stack = new Stack<>();\n\n for (char c : s.toCharArray()) {\n if (stack.isEmpty()) {\n stack.push(c);\n } else if (stack.peek() == \'(\' && c == \')\') {\n stack.pop();\n } else {\n stack.push(c);\n }\n }\n\n // At this point, the stack contains unmatched parentheses.\n // The size of the stack is the minimum number of additions required.\n return stack.size();\n }\n};\n```\n```Python []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n\n for char in s:\n if not stack:\n stack.append(char)\n elif stack[-1] == \'(\' and char == \')\':\n stack.pop()\n else:\n stack.append(char)\n\n # At this point, the stack contains unmatched parentheses.\n # The length of the stack is the minimum number of additions required.\n return len(stack)\n\n```\n\n---\n\n\n\n | 4 | 0 | ['Python', 'C++', 'Java', 'Python3'] | 0 |
minimum-add-to-make-parentheses-valid | 100% beats || c++ || stack | 100-beats-c-stack-by-ganeshkumawat8740-lr79 | Code\n\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = 0;\n vector<char> v;\n for(auto &i: s){\n i | ganeshkumawat8740 | NORMAL | 2023-06-22T03:39:35.471740+00:00 | 2023-06-22T03:39:35.471761+00:00 | 669 | false | # Code\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = 0;\n vector<char> v;\n for(auto &i: s){\n if(i==\'(\'){\n v.push_back(i);\n }else{\n if(v.empty())ans++;\n else{\n v.pop_back();\n }\n }\n }\n return ans+v.size();\n }\n};\n``` | 4 | 0 | ['String', 'Stack', 'Greedy', 'C++'] | 0 |
minimum-add-to-make-parentheses-valid | Simple Java Solution Using Stack | simple-java-solution-using-stack-by-vand-xj03 | \nclass Solution {\n public int minAddToMakeValid(String s) {\n \n Stack<Character> stk = new Stack();\n for(int i=0;i<s.length();i++){\n | vandittalwadia | NORMAL | 2023-02-03T07:54:44.899910+00:00 | 2023-02-03T07:59:38.023790+00:00 | 423 | false | ```\nclass Solution {\n public int minAddToMakeValid(String s) {\n \n Stack<Character> stk = new Stack();\n for(int i=0;i<s.length();i++){\n \n if(!stk.isEmpty() && s.charAt(i)==\')\' && stk.peek()==\'(\'){\n stk.pop();\n }\n else{\n stk.push(s.charAt(i));\n }\n }\n \n return stk.size();\n \n }\n}\n``` | 4 | 0 | ['Stack', 'Java'] | 0 |
minimum-add-to-make-parentheses-valid | C++ Solution in O(n) time | c-solution-in-on-time-by-lordmavles-3qmc | \nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int cc = 0, cur = 0;\n for(auto i: s){\n if(i == \'(\') ++cur;\n | lordmavles | NORMAL | 2022-07-21T09:34:14.012961+00:00 | 2022-07-21T09:34:14.013003+00:00 | 80 | false | ```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int cc = 0, cur = 0;\n for(auto i: s){\n if(i == \'(\') ++cur;\n else --cur;\n if(cur < 0) ++cc, ++cur;\n }\n cc += cur;\n return cc;\n }\n};\n``` | 4 | 0 | [] | 0 |
minimum-add-to-make-parentheses-valid | C++ || simple stack solution || faster than 100% | c-simple-stack-solution-faster-than-100-6ldr9 | \nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = s.length();\n stack<char> st;\n for(int i=0;i<s.length();i++ | ritamsadhu | NORMAL | 2022-03-06T21:09:02.798091+00:00 | 2022-03-06T21:09:45.045881+00:00 | 113 | false | ```\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n int ans = s.length();\n stack<char> st;\n for(int i=0;i<s.length();i++)\n {\n if(s[i]==\')\')\n {\n if(!st.empty() && st.top()==\'(\')\n {\n st.pop();\n ans-=2;\n }\n }\n else\n st.push(s[i]);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Stack'] | 0 |
minimum-add-to-make-parentheses-valid | Easy for Beginner in C++ || Stack | easy-for-beginner-in-c-stack-by-luciferr-exjw | class Solution {\npublic:\n\n\n int minAddToMakeValid(string s){\n stack st;\n int count=0;\n for(int i=0;i<s.length();i++){\n | luciferraturi | NORMAL | 2021-09-20T16:46:39.102306+00:00 | 2021-09-22T18:38:36.903629+00:00 | 65 | false | class Solution {\npublic:\n\n\n int minAddToMakeValid(string s){\n stack<int> st;\n int count=0;\n for(int i=0;i<s.length();i++){\n if(s[i]==\'(\'){\n st.push(i);\n }\n else if(s[i]==\')\'){\n if(st.empty()){\n count+=1;\n }\n else{\n st.pop();\n }\n }\n }\n return st.size()+count;\n }\n}; | 4 | 0 | [] | 0 |
minimum-add-to-make-parentheses-valid | [Python3] Simple Solution | python3-simple-solution-by-voidcupboard-p4ma | \nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n count = 0\n \n x = y = 0\n \n for i in s:\n i | VoidCupboard | NORMAL | 2021-05-26T01:50:57.147014+00:00 | 2021-05-26T01:50:57.147052+00:00 | 209 | false | ```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n count = 0\n \n x = y = 0\n \n for i in s:\n if(i == \'(\'):\n x += 1\n else:\n x -= 1\n \n if(x < 0):\n count += 1\n x = 0\n if(y < 0):\n count += 1\n y = 0\n \n return count + x + y\n``` | 4 | 1 | ['Python3'] | 1 |
minimum-add-to-make-parentheses-valid | 0-ms |100% faster | C++ Solution | 0-ms-100-faster-c-solution-by-emiya100-syps | ****\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n int i,n=S.size(),l=0,r=0,c=0;\n for(i=0;i<n;i++)\n {\n | emiya100 | NORMAL | 2021-01-08T09:47:28.416677+00:00 | 2021-01-08T09:47:28.416727+00:00 | 141 | false | ****\n```\nclass Solution {\npublic:\n int minAddToMakeValid(string S) {\n int i,n=S.size(),l=0,r=0,c=0;\n for(i=0;i<n;i++)\n {\n if(S[i]==\'(\')\n {\n l++;\n }\n else\n {\n if(l==0)\n {\n c++;\n }\n else\n {\n l--;\n }\n }\n }\n \n return l+c;\n \n }\n};\n\n\'\'\'\n | 4 | 0 | [] | 0 |
minimum-add-to-make-parentheses-valid | Python 3 using stack simple solution with explanation | python-3-using-stack-simple-solution-wit-h4pk | \nclass Solution:\n def minAddToMakeValid(self, S: str) -> int:\n _stack=[] #initilized a new stack\n for bracke | mintukrish | NORMAL | 2020-10-18T08:09:52.301325+00:00 | 2020-10-18T08:09:52.301358+00:00 | 291 | false | ```\nclass Solution:\n def minAddToMakeValid(self, S: str) -> int:\n _stack=[] #initilized a new stack\n for bracket in S: # looping through all the brackets in S, storing each in bracket variable\n if(len(_stack)==0): # checking if the stack is empty then\n _stack.append(bracket) # push the bracket to the empty stack\n else: # else\n curr=_stack[len(_stack)-1] #storing the top of the stack to the curr variable\n if curr ==\'(\' and bracket ==\')\': #checking if the curr has opening and the bracket has closing bracket then the bracket from the stack is poped \n _stack.pop()\n else: # else the bracket will be added to the stack\n _stack.append(bracket)\n \n return len(_stack) #returning the lenght of the stack - it contains all the invalid paranthesis \n\n``` | 4 | 0 | ['Stack', 'Python3'] | 0 |
minimum-add-to-make-parentheses-valid | Straightforward C++ (0 ms), O(N), with explanation | straightforward-c-0-ms-on-with-explanati-r3s4 | The idea is to keep track of number of unused \'(\' in addition to keep track of extra \')\'\nSo lets say we use open and cnt variables for this goal, respecti | ashkanxy | NORMAL | 2018-12-23T18:41:30.988846+00:00 | 2018-12-23T18:41:30.988890+00:00 | 707 | false | The idea is to keep track of number of unused \'(\' in addition to keep track of extra \')\'\nSo lets say we use open and cnt variables for this goal, respectively.\nMove forward through the string. \n* Once you reach a \'(\' , increament the open variable.\n* Once you reach the \')\', \n\t* If the open variable is equal to zero, that means the current \')\' is extra and we need one \')\' before the current position. Like if the strign is "( ) **)**". For the second \')\', we need to have a \'(\' before it, so increment the cnt.\n\t* If open variable is a positive number, means we have already visited some \'(\' which is not used yet. so lets decremenat open variable\n\nFInally we return sum of open and cnt variables.\n\n```\nint minAddToMakeValid(string S) {\n int len = S.length();\n if (len<=1)\n return len;\n int op=0; \n int cnt=0;\n for (int i=0;i<len; ++i){\n if (S[i]==\'(\' ) op++; \n else {\n if (op==0) cnt++; /*we rached an extra \')\' */\n else { op--; /*use one of previously visited \'(\' */\n }\n }\n }\n return (cnt+op);\n}\n```\n | 4 | 0 | [] | 0 |
minimum-add-to-make-parentheses-valid | Java clear one-pass stack solution with expalantion | java-clear-one-pass-stack-solution-with-d0ho3 | We need to add as many parentheses as left after finding and removing all valid pairs.\nFor example:\n()))((()())(\n\nlet\'s delete all valid pairs:\n()))((()() | olsh | NORMAL | 2018-10-14T18:20:47.521172+00:00 | 2018-10-14T18:20:47.521214+00:00 | 77 | false | We need to add as many parentheses as left after finding and removing all valid pairs.\nFor example:\n()))((()())(\n\nlet\'s delete all valid pairs:\n()))((()())( -> \n**()** ))((()())( ->\n))(( **()** ())( ->\n))(( **()** )( ->\n))( **()** ( ->\n))((\n\nWe can add 4 more parentheses to make it valid (one for each parenthes):\n**((** ))(( **))**\nThat\'s why, the number of needed parentheses will be always the same as the number of "invalid" parentheses in the input string:\n\n```\nclass Solution {\n public int minAddToMakeValid(String S) {\n Deque<Character> stack = new LinkedList<>();\n for (Character c: S.toCharArray()){\n\t\t\t\t// stack.isEmpty() means that current character is nothing to compare with\n\t\t\t\t// c.equals(stack.getLast()) means \')\'+\')\' or \'(\'+\'(\'\n\t\t\t\t// stack.getLast().equals(\')\') means that there\'s no pair for current parenthes\n if (stack.isEmpty() || c.equals(stack.getLast()) || stack.getLast().equals(\')\')){\n stack.add(c);\n }\n else {\n stack.removeLast();\n }\n }\n return stack.size();\n }\n}\n``` | 4 | 0 | [] | 0 |
minimum-add-to-make-parentheses-valid | Python Solution | python-solution-by-dipanjan0013-cpiu | IntuitionStack :)ApproachJust go through the string. If "(" comes, add it to the stack. In case of ")", if the stack is empty or the previous element is also ") | dipanjan0013 | NORMAL | 2025-04-06T19:08:31.626286+00:00 | 2025-04-06T20:18:21.745354+00:00 | 43 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Stack :)
# Approach
<!-- Describe your approach to solving the problem. -->
Just go through the string. If "(" comes, add it to the stack. In case of ")", if the stack is empty or the previous element is also ")", add it to the stack. And if not, just pop the last element cause it has to be a "(". Finally return the length of the stack.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```python3 []
class Solution:
def minAddToMakeValid(self, s: str) -> int:
s2 = []
for i in s:
if i == "(":
s2.append("(")
elif i == ")" and (s2 == [] or s2[-1] == ")"):
s2.append(")")
else:
s2.pop()
return len(s2)
``` | 3 | 0 | ['Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.