question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
count-subtrees-with-max-distance-between-cities | Bitmasking and FloyWarshall | bitmasking-and-floywarshall-by-ashishpat-cud1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AshishPatel17 | NORMAL | 2024-06-21T05:23:01.447721+00:00 | 2024-06-21T05:23:01.447756+00:00 | 29 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int solve(int mask , vector<vector<int>>&dist , int n)\n {\n // ab aap dekhiye \n // me vhi nodes include krunga jo link me h \n // complete tree ke liye har nodes ek dusre se connect honi chahiye \n int node =0 ;\n int edge = 0;\n int maxi = 0;\n for(int i = 0; i < n ; i++)\n {\n if(((mask>>i) & 1)==1)\n {\n node++;\n for(int j =i +1 ; j < n ; j++)\n {\n if(((mask>>j)&1)==1)\n {\n if(dist[i][j] == 1)edge++;\n maxi = max(maxi , dist[i][j]);\n }\n }\n }\n }\n if(node == edge +1 )return maxi;\n else return -1;\n \n }\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& e) {\n \n vector<int>a(n-1 , 0);\n vector<vector<int>>dist(15 , vector<int>(15 , INT_MAX));\n for(auto i : e)\n {\n dist[i[0]-1][i[1]-1] = dist[i[1]-1][i[0]-1] = 1;\n }\n // ab aap minimum distance nika lijiye floyd warshall algo se \n for(int i = 0 ; i < n ; i++)\n {\n for(int j = 0 ; j < n ; j++)\n {\n for(int k =0; k<n ; k++)\n {\n if(dist[j][i]!=INT_MAX and dist[i][k]!=INT_MAX)\n dist[j][k] = dist[k][j] = min({dist[j][k] , dist[j][i] + dist[i][k]});\n }\n }\n }\n // ab mere pass minimum distance aa gyi h basically me har subset of nodes\n // ke liye try krunga ki usme maximum distance between nodes kitni ho rhi h\n // aur us particular distance me ++ kr dunga \n for(int i = 0; i < (1<<n) ; i++)\n {\n // i denoting mask means 1111 -> denotes include node 1 ,2,3,4\n int ans = solve(i , dist , n);\n if(ans > 0)\n a[ans-1]++;\n }\n return a;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Bit mask + DFS step by step (best practices) | bit-mask-dfs-step-by-step-best-practices-b6p7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sulerhy | NORMAL | 2024-05-23T17:02:31.370334+00:00 | 2024-05-23T17:02:31.370372+00:00 | 41 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m * (2**n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:\n # TC: O(m * (2**n)) SP: O(n + m)\n diameters = defaultdict(int)\n # I hate node start with 1, so I decrease all of them\n for i in range(len(edges)):\n edges[i][0] -= 1\n edges[i][1] -= 1\n def is_tree(bitmask):\n if bitmask.bit_count() < 2: return False\n created_edges = 0\n for edge in edges:\n if (1 << edge[0]) & bitmask and (1 << edge[1]) & bitmask:\n created_edges += 1\n if created_edges == bitmask.bit_count() - 1:\n return True\n return False\n \n # create the tree:\n def create_tree(bitmask):\n tree = defaultdict(list)\n for edge in edges:\n if (1 << edge[0]) & bitmask and (1 << edge[1]) & bitmask:\n tree[edge[0]].append(edge[1])\n tree[edge[1]].append(edge[0])\n return tree\n\n # calculate the diameter;\n def dfs(tree, node) -> int:\n if not tree[node]: return 0\n max_height = 0\n second_height = 0\n visited.add(node)\n for child in tree[node]:\n if child in visited: continue\n height = 1 + dfs(tree, child)\n if max_height > height >= second_height:\n second_height = height\n elif height >= max_height:\n second_height = max_height\n max_height = height\n diameter = max_height + second_height\n longest_diameter[0] = max(longest_diameter[0], diameter)\n return max_height\n\n res = [0] * (n-1)\n for bitmask in range(1, 1<<n):\n if not is_tree(bitmask):\n continue\n # reset visited\n visited = set()\n # reset longest_diameter\n longest_diameter = [0]\n tree = create_tree(bitmask)\n # choose random node to start dfs\n root = list(tree.keys())[0]\n dfs(tree, root)\n # res start from 0 diameter, so -1 to be fit into res\n res[longest_diameter[0]-1] += 1\n return res\n \n\n\n \n\n\n``` | 0 | 0 | ['Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | Solution Count Subtrees With Max Distance Between Cities | solution-count-subtrees-with-max-distanc-rnat | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Suyono-Sukorame | NORMAL | 2024-05-23T01:19:11.358201+00:00 | 2024-05-23T01:19:11.358221+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public function countSubgraphsForEachDiameter($n, $edges) {\n $g = array_fill(0, $n, array_fill(0, $n, 999));\n \n foreach ($edges as $e) {\n $i = $e[0] - 1;\n $j = $e[1] - 1;\n $g[$i][$j] = $g[$j][$i] = 1;\n }\n \n for ($k = 0; $k < $n; $k++) {\n for ($i = 0; $i < $n; $i++) {\n for ($j = 0; $j < $n; $j++) {\n $g[$i][$j] = min($g[$i][$j], $g[$i][$k] + $g[$k][$j]);\n }\n }\n }\n \n $ans = array_fill(0, $n - 1, 0);\n for ($s = 0; $s < (1 << $n); $s++) {\n $k = substr_count(decbin($s), \'1\');\n $e = 0;\n $d = 0;\n for ($i = 0; $i < $n; $i++) {\n if ($s & (1 << $i)) {\n for ($j = $i + 1; $j < $n; $j++) {\n if ($s & (1 << $j)) {\n $e += $g[$i][$j] == 1;\n $d = max($d, $g[$i][$j]);\n }\n }\n }\n }\n if ($e == $k - 1 && $d > 0) {\n $ans[$d - 1]++;\n }\n }\n \n return $ans;\n }\n}\n\n``` | 0 | 0 | ['PHP'] | 0 |
count-subtrees-with-max-distance-between-cities | bitmask, dfs | bitmask-dfs-by-maxorgus-gifu | Code\n\nclass Solution:\n def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:\n graph = {i:set([]) for i in range(1, | MaxOrgus | NORMAL | 2024-05-10T03:11:39.434894+00:00 | 2024-05-10T03:11:39.434917+00:00 | 14 | false | # Code\n```\nclass Solution:\n def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:\n graph = {i:set([]) for i in range(1,n+1)}\n for u,v in edges:\n graph[u].add(v)\n graph[v].add(u)\n res = [0]*(n-1)\n for mask in range(1,2**n):\n ones = str(bin(mask)).count("1")\n if ones < 2:continue\n for j in range(1,n+1):\n if mask & (1 << (j-1)):\n queue = [j]\n seen = set([j])\n for d in queue:\n for dd in graph[d]:\n if mask & (1 << (dd-1)) and dd not in seen:\n queue.append(dd)\n seen.add(dd)\n feasible = len(seen) == ones\n break\n if not feasible:\n continue\n def helper(node,p):\n height,longest = 0,0\n heights = []\n for subnode in graph[node]:\n if mask & (1 << (subnode-1)) and subnode!=p:\n subh,subl = helper(subnode,node)\n heights.append(-subh)\n height = max(height,1+subh)\n longest = max(longest,subl)\n if len(heights)>1:\n heights.sort()\n longest = max(longest,2-heights[0]-heights[1])\n longest = max(longest,height)\n return height,longest\n for j in range(1,n+1):\n if mask & (1 << (j-1)):\n h,l = helper(j,-1)\n res[l-1]+=1\n break\n return res\n\n\n\n\n\n``` | 0 | 0 | ['Depth-First Search', 'Bitmask', 'Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | Golang + Tree Diameter (Double BFS) + Bitmask | golang-tree-diameter-double-bfs-bitmask-rahe6 | Approach\nUse bitmask to generate every city subset and then use double BFS to find tree diameter (max distance) for this city subset. Then increment the counte | michaeljank | NORMAL | 2024-04-28T04:52:35.455424+00:00 | 2024-04-28T04:52:35.455441+00:00 | 6 | false | # Approach\nUse bitmask to generate every city subset and then use double BFS to find tree diameter (max distance) for this city subset. Then increment the counter within the res slice. Basically combine Bitmasking to store state + Tree diameter (max distance)\n\n# Complexity\n- Time complexity:\nO(n * (2 ^ n))\n\n- Space complexity:\nO(n ^ 2) (Adjacency list)\n\n# Code\n```\nfunc countSubgraphsForEachDiameter(n int, edges [][]int) []int {\n adj := make([][]int, n)\n for _, edge := range edges {\n u := edge[0] - 1\n v := edge[1] - 1\n adj[u] = append(adj[u], v)\n adj[v] = append(adj[v], u)\n }\n\n res := make([]int, n - 1)\n\n var maxDistance func(mask int) int\n maxDistance = func(mask int) int {\n start := -1\n citiesInSubset := make(map[int]bool)\n for src := 0; src < n; src++ {\n if mask & (1 << src) == 0 {\n continue\n }\n start = src\n citiesInSubset[src] = true\n }\n if start == -1 {\n return -1\n }\n\n var bfs func(start int) (int, int, bool)\n bfs = func(start int) (int, int, bool) {\n visited := make(map[int]bool)\n var q []int\n q = append(q, start)\n visited[start] = true\n farthestNode := -1\n farthestDist := 0\n for len(q) != 0 {\n qSize := len(q)\n for i := 0; i < qSize; i++ {\n u := q[0]\n farthestNode = u\n q = q[1:]\n if adj[u] == nil {\n continue\n }\n for _, v := range adj[u] {\n if _, ok := citiesInSubset[v]; !ok {\n continue\n }\n if _, ok := visited[v]; ok {\n continue\n }\n visited[v] = true\n q = append(q, v)\n }\n }\n farthestDist++\n }\n isValid := len(visited) == len(citiesInSubset)\n return farthestNode, farthestDist - 1, isValid\n }\n\n // Tree diameter using BFS\n farthestNode, _, isValid := bfs(start)\n if !isValid {\n return -1\n }\n\n _, treeDiam, _ := bfs(farthestNode)\n return treeDiam\n }\n\n for mask := 0; mask < (1 << n); mask++ {\n d := maxDistance(mask)\n if d > 0 {\n res[d - 1]++\n }\n }\n return res\n}\n``` | 0 | 0 | ['Go'] | 0 |
count-subtrees-with-max-distance-between-cities | Bitmasking + Dijkstra's | bitmasking-dijkstras-by-mereddysujithred-837h | Approach\n Describe your approach to solving the problem. \nI solved this problem in 3 parts.\n1. Create a Tree.\n2. Get all possible subsets using bitmasking.\ | mereddysujithreddy | NORMAL | 2024-04-21T06:28:21.957339+00:00 | 2024-04-21T06:28:21.957387+00:00 | 25 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nI solved this problem in 3 parts.\n1. Create a Tree.\n2. Get all possible subsets using bitmasking.\n3. Check if the subset form a connected component or not. If yes, For each node in subset as source, get the maximum distance. Update it in the output list and return ans\n\nI solved the getting the maximum distance part using Dijkstra\'s.\nFor each node in subset, get the maximum distance for each node as source. \nWhenever the nodes traversed in Dijkstra\'s are less than no of nodes in subset, we know this is not a connected component. We skip this subset.\nIf the given subset forms a connected component, we find the maximum possible distance and update the result.\n\n# Code\n```\nclass Solution:\n def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:\n tree=defaultdict(list)\n for u,v in edges:\n tree[u].append(v)\n tree[v].append(u)\n def getDistances(src,nodes):\n heap=[[0,src]]\n minCost={}\n res=0\n while heap:\n cost,node=heappop(heap)\n if node in minCost:\n continue\n minCost[node]=cost\n if cost>res: res=cost\n for nei in tree[node]:\n if nei not in minCost and nei in nodes:\n heappush(heap,[1+cost,nei])\n if len(minCost)!=len(nodes): return [False,0]\n return [True,res]\n d=[0]* (n-1)\n for mask in range(1,2**n):\n nodes=set()\n for j in range(n):\n if mask & (1<<j):\n nodes.add(j+1)\n res=0\n if len(nodes)>1:\n for i in nodes:\n decide,val=getDistances(i,nodes)\n if not decide: break \n res=max(res,val)\n else: \n d[res-1]+=1\n return d\n``` | 0 | 0 | ['Shortest Path', 'Bitmask', 'Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | [C++] Solution with Very clear code, with sperate functions | c-solution-with-very-clear-code-with-spe-2xcq | \n# Approach\n Describe your approach to solving the problem. \n- create a graph to map all the edges\n- generate all subtrees, use bitmask to save memory.\n- n | ishitarakchhit | NORMAL | 2024-02-19T14:20:26.375280+00:00 | 2024-02-19T14:24:48.411023+00:00 | 44 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- create a graph to map all the edges\n- generate all subtrees, use bitmask to save memory.\n- now inside the `helper` function decode the subtrees one by one and then call `findMaxDist` function to find the max distance for that subtree and also check if that subtree is valid or i.e. the path from one city to another should go though the cities within that subtree.\n- and find the max distance for that subtree and store the result in `maxi` variable\n- `BFS` function finds the minimum distance to reach from one node to other and if `temp` is marked `-1`, it means that we cannot push that node to our queue. In the end if `temp` contains any value equal to `10^6`, it suggests that we were not able to visit that node and that particular subtree was invalid.\n# Complexity\n- Time complexity: O(2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n //function to create adjacency list using given edges, this will be an undirected graph\n void createGraph(vector<vector<int>> &graph, vector<vector<int>> &edges){\n for(int i=0; i<edges.size(); i++){\n graph[edges[i][0]].push_back(edges[i][1]);\n graph[edges[i][1]].push_back(edges[i][0]);\n }\n }\n \n //function to find the minimum distance to travel all the nodes from the current city\n vector<int> bfs(vector<vector<int>> &graph, int city, vector<int> &temp){\n int n = graph.size();\n temp[city] = 0;\n queue<pair<int,int>> q; //city, distance\n q.push({city, 0}); \n\n while(!q.empty()){\n int newCity= q.front().first;\n int dist = q.front().second;\n q.pop();\n\n for(int i=0; i<graph[newCity].size(); i++){\n int travel = graph[newCity][i];\n if(temp[travel] > dist+1){\n temp[travel] = dist+1;\n q.push({travel, dist+1});\n }\n if(temp[travel] == -1) continue;\n }\n }\n return temp;\n }\n\n \n\n //function to generate all subtrees or subsets. This function uses mask integer to store all subtrees\n void generateSubtrees(int mask, vector<int> &subtrees, int ind, int n){\n if(ind > n){\n subtrees.push_back(mask);\n return;\n }\n generateSubtrees(mask|(1<<ind), subtrees, ind+1, n);\n generateSubtrees(mask, subtrees, ind+1, n);\n }\n\n\n //function to find the maximum distance to travel from one city to another within a subtree\n int findMaxDist(vector<vector<int>> &graph, vector<int> &subtree){\n int maxi = 0;\n\n for(int i=0; i<subtree.size(); i++){\n vector<int> temp(graph.size(), -1);\n for(int i=0; i<subtree.size(); i++){\n temp[subtree[i]] = 1e6;\n }\n vector<int> dist = bfs(graph, subtree[i], temp);\n for(int j=0; j<dist.size(); j++){\n if(dist[j] == 1e6) return 0;\n maxi = max(maxi, dist[j]);\n }\n }\n \n return maxi;\n }\n \n//function to convert mask to a vector\n vector<int> decodeSubtree(int mask){\n vector<int> subtree;\n int i=0; \n while(mask>0){\n if((mask&1) == 1){\n subtree.push_back(i);\n }\n mask = mask>>1;\n i++;\n }\n return subtree;\n }\n\n //function to count required subtrees\n void helper(vector<vector<int>> &graph, vector<int> &ans, vector<int> &subtrees, int n){\n //store maximum distance for every subtree in the end of the subset\n for(int i=0; i<subtrees.size(); i++){\n vector<int> subtree = decodeSubtree(subtrees[i]);\n if(subtree.size()<2) continue;\n int dist = findMaxDist(graph, subtree);\n if(dist>=1 && dist<=n) ans[dist-1]++;\n }\n }\n\n\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<vector<int>> graph(n+1);\n vector<int> ans(n-1, 0);\n\n //create the graph using the given edges\n createGraph(graph, edges);\n\n //find all substrees of trees\n int mask = 0;\n vector<int> subtrees;\n generateSubtrees(mask, subtrees, 1, n);\n\n //function to find the final answer\n helper(graph, ans, subtrees, n);\n \n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | How to break this down in simple steps(91%Time)! | how-to-break-this-down-in-simple-steps91-auoa | Intuition\n Describe your first thoughts on how to solve this problem. \nEdges dict for faster access.\n\nMax dist can get caclulated via two bfs searches!\n\nL | lucasscodes | NORMAL | 2024-02-11T17:10:33.820676+00:00 | 2024-02-11T17:10:33.820709+00:00 | 25 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEdges dict for faster access.\n\nMax dist can get caclulated via two bfs searches!\n\nLast use recursion to shrink graph and get max dist for all smaller subgraphs also.\n\nReturn counter over different max dists found.\n# Code\n```\nclass Solution:\n def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:\n edges2 = defaultdict(list) #direct access node edges in O(1) instead of traversing all edges\n for a,b in edges:\n edges2[a].append(b)\n edges2[b].append(a)\n\n def bfs(root,nodes): #bfs returning max depth and first node on last layer\n level = [root] #bfs-queue\n seen = {root} #dont use again flags\n d = 0 #depth\n while True: #do while\n nextLevel = []\n for node in level: #bfs\n for other in edges2[node]: #children\n if nodes[other-1]==True and other not in seen: #children not deleted or used already\n seen.add(other) #mark as used\n nextLevel.append(other) #add to next bfs queue\n if nextLevel: #continue\n d += 1 #next depth reached\n level = nextLevel #take over children as bfs queue/layer\n else: break #done with bfs\n return level[0],d #first node + depth from root\n\n seen = set() #dont reuse same combinations\n def rec(nodes=[True for _ in range(n)]): #what dist is left with given connected nodes\n seen.add(str(nodes)) #never eval this combination again\n if sum(nodes)==1: return #deleted to much\n for i,b in enumerate(nodes):\n if b==True: #pick first node left as root\n root = i+1\n break\n #double bfs=>max-depth-node yiels max dist\n #also we have both reached nodes and the path between has the distance!\n other,_ = bfs(root,nodes) #first bfs\n _,dist = bfs(other,nodes) #second bfs\n res[dist-1] += 1 #save another subtree got this dist\n\n for i,b in enumerate(nodes): #try to delete nodes\n if b==True: #this one is left\n node = i+1 #the node value 1-indexed\n reaches = 0 #counter\n for other in edges2[node]: #connected nodes\n if nodes[other-1]==True: #is not yet deleted\n reaches += 1 #add as connected node\n #leafs can get deleted!\n if reaches==1: #leafs have exactly 1 connection\n new = list(nodes) #unlinked copy for more readable recursion\n new[node-1] = False #flip deletable => smaller nodes combination\n if str(new) not in seen: #this combination is new!\n rec(new) #get max dist for subset also\n\n\n res = [0 for _ in range(1,n)] #counts of max dists from 1 to n-1\n rec() #recursivley use all subtrees\n return res #return counts\n \n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nEach max dist calculation uses O(n) and traverses the graph twice.\nThis happens inside the memoized valid node combinations and will be called n(n+1)/2 => O(n\xB2) times.\nThus we reach O(n\xB3) in summary.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n\xB2) memo dominates bfs space.\n\n | 0 | 0 | ['Breadth-First Search', 'Recursion', 'Memoization', 'Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | Microsoft⭐ || Easy Solution🔥|| BEATS 100%✅ | microsoft-easy-solution-beats-100-by-pri-cj1j | #ReviseWithArsh #6Companies30Days challenge 2k24\nCompany 2 :- Google\n\n# Code\n\nclass Solution {\n vector<int> edges[16]; // edges[i] stores the neighbor | Priyanshi_gangrade | NORMAL | 2024-01-31T14:42:01.893455+00:00 | 2024-01-31T14:42:01.893486+00:00 | 51 | false | ***#ReviseWithArsh #6Companies30Days challenge 2k24\nCompany 2 :- Google***\n\n# Code\n```\nclass Solution {\n vector<int> edges[16]; // edges[i] stores the neighbors of city i\n int dists[16][16]{}; // dists[i][j] stores the distance between city i and city j\n int masks[16][16]{}; // masks[i][j] stores the mask of cities visited when going from i to j\n struct Data {\n int city;\n int dist;\n int mask;\n };\npublic:\n // Perform BFS starting at the current city\n void bfs(int curCity) {\n static std::deque<Data> q;\n static std::array<bool, 16> visited;\n visited.fill(false);\n q.clear();\n q.emplace_back(Data{curCity, 0, 1 << curCity});\n visited[curCity] = true;\n while (!q.empty()) {\n Data d = q.front();\n q.pop_front();\n for (auto neighbor : edges[d.city]) {\n if (!visited[neighbor]) {\n q.emplace_back(Data{neighbor, d.dist + 1, d.mask | (1 << neighbor)});\n visited[neighbor] = true;\n dists[neighbor][curCity] = dists[curCity][neighbor] = d.dist + 1;\n masks[neighbor][curCity] = masks[curCity][neighbor] = q.back().mask;\n }\n }\n }\n }\n\n vector<int> countSubgraphsForEachDiameter(const int n, vector<vector<int>>& ed) {\n for (const auto& pair: ed) {\n edges[pair[0] - 1].emplace_back(pair[1] - 1);\n edges[pair[1] - 1].emplace_back(pair[0] - 1);\n }\n vector<int> ans(n - 1, 0); // Initialize answer array\n // Calculate distances and masks for each city\n for (int j = 0; j < n; ++j) {\n bfs(j);\n }\n // Loop through every possible subset of cities\n for (int mask = 1; mask < (1 << n); ++mask) {\n int maxDist = 0;\n // Check distances between pairs of cities in the subset\n for (int i = 0; i < n; i++) {\n if (!(mask & (1 << i))) continue;\n for (int j = 0; j < i; j++) {\n if (mask & (1 << j)) {\n // Check if city i and city j are reachable within the subset\n if (dists[i][j] == 0 || (masks[i][j] & mask) != masks[i][j]) {\n i = j = n; // Break the loop\n maxDist = 0;\n break;\n }\n maxDist = std::max(maxDist, dists[i][j]);\n }\n }\n }\n if (maxDist) ans[maxDist - 1]++;\n }\n return ans;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | 1617. Count Subtrees With Max Distance Between Cities | 1617-count-subtrees-with-max-distance-be-mjaj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pgmreddy | NORMAL | 2024-01-30T15:29:18.788369+00:00 | 2024-01-30T15:29:18.788388+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n---\n\n```\nvar countSubgraphsForEachDiameter = function (n, edges) {\n const ad = Array.from({ length: n }, () => new Set());\n for (const [u, v] of edges) {\n ad[u - 1].add(v - 1);\n ad[v - 1].add(u - 1);\n }\n function getDepth_fromOneNodeToAllNodesInSubtree(U) {\n function dfs(u, visited) {\n if (!U.has(u)) return -Infinity;\n if (visited.has(u)) return -Infinity;\n visited.add(u);\n let d = 0;\n for (const v of ad[u]) {\n d = Math.max(d, 1 + dfs(v, visited));\n }\n return d;\n }\n if (!U.size) return -1;\n let max = -1;\n for (const u of U) {\n const visited = new Set();\n const d = dfs(u, visited);\n if (visited.size !== U.size) continue;\n max = Math.max(max, d);\n }\n return max;\n }\n const ans = Array(n - 1).fill(0);\n for (let i = 0; i < 1 << n; i++) {\n const subtree = new Set();\n for (let j = 0; j < n; j++) {\n if (i & (1 << j)) subtree.add(j);\n }\n const maxDepth = getDepth_fromOneNodeToAllNodesInSubtree(subtree);\n if (maxDepth > 0) ans[maxDepth - 1]++;\n }\n return ans;\n};\n```\n\n---\n | 0 | 0 | ['JavaScript'] | 0 |
count-subtrees-with-max-distance-between-cities | [Python] DFS and Bit solution with Japanese explanation | python-dfs-and-bit-solution-with-japanes-r083 | Intuition & Approach\n Describe your first thoughts on how to solve this problem. \n- \u6728\u306E\u76F4\u5F84\uFF08\u6700\u9577\u7D4C\u8DEF\uFF09\u306E\u6C42\u | tada_24 | NORMAL | 2024-01-15T13:04:29.234000+00:00 | 2024-01-15T13:04:29.234024+00:00 | 15 | false | # Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n- \u6728\u306E\u76F4\u5F84\uFF08\u6700\u9577\u7D4C\u8DEF\uFF09\u306E\u6C42\u3081\u65B9\u3092\u77E5\u3063\u3066\u3044\u308B\u5FC5\u8981\u304C\u3042\u308B\u3002\n- \u5168\u3066\u306E\u90E8\u5206\u6728\u306B\u3064\u3044\u3066\u8003\u3048\u308C\u308B\u3053\u3068\u304C\u3067\u304D\u308C\u3070\u826F\u3044\u3002\n- \u3053\u308C\u3092\u5B9F\u73FE\u3059\u308B\u305F\u3081\u306Bbit\u306B\u3088\u3063\u3066\u4F7F\u7528\u3059\u308B\u30A8\u30C3\u30B8\u3092\u8868\u73FE\u3059\u308B\n\n# Complexity\n$$N$$: ```n```\n- Time complexity: $$O(N2^N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u5168\u3066\u306E\u30A8\u30C3\u30B8\u306E\u4F7F\u7528\u30D1\u30BF\u30FC\u30F3\u304C$$(2^N)$$\u901A\u308A\u3002\u3000\u3000\n\u305D\u308C\u305E\u308C\u306E\u4F7F\u7528\u3059\u308B\u30A8\u30C3\u30B8\u30D1\u30BF\u30FC\u30F3\u3067\u306E`graph`\u4F5C\u6210\u3001`isTree`\u306B\u3088\u308B\u6728\u5224\u5B9A\u3001`diameter`\u306B\u3088\u308B\u76F4\u5F84\u306E\u8A08\u7B97\u306F\u5168\u3066$$O(N)$$\u3002\u3000\u3000\n\u3088\u3063\u3066\u5168\u4F53\u3067\u306F\u7A4D\u306E$$O(N2^N)$$\u3002\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`graph`\u3001`isTree`\u5185\u3067\u306Edfs\u306E\u30B9\u30BF\u30C3\u30AF\u3001`diameter`\u5185\u3067\u306Edfs\u306E\u30B9\u30BF\u30C3\u30AF\u305D\u308C\u305E\u308C\u3067$$O(N)$$\u4F7F\u7528\u3002\n\n# Code\n```python\ndef isTree(graph):\n N = len(graph)\n visited = set([])\n\n # \u9589\u8DEF\u304C\u3042\u308B\u304B\u3092\u8FD4\u3059\n def dfs(u, parent):\n visited.add(u)\n\n # \u9589\u8DEF\u304C\u3042\u308B\u304B\u3092\u5224\u5B9A\n hasCycle = False\n\n for v in graph[u]:\n # \u89AA\u306A\u306E\u3067\u30B9\u30EB\u30FC\n if v == parent:\n continue\n\n # \u5230\u9054\u6E08\u307F\u306E\u5B50\u30CE\u30FC\u30C9\u304C\u3042\u308B\u3068\u3044\u3046\u3053\u3068\u306F\u9589\u8DEF\u304C\u3042\u308B\u3053\u3068\u3092\u610F\u5473\u3059\u308B\n if v in visited:\n return True\n\n hasCycle |= dfs(v, u)\n\n return hasCycle\n\n # \u9589\u8DEF\u306A\u3057\u3067\u304B\u3064\u9023\u7D50\u304B\u3092\u78BA\u8A8D\n return (not dfs(0, -1)) and len(visited) == N\n\ndef diameter(tree_graph):\n global x, dis\n x, dis = 0, 0\n\n # x\u3092\u59CB\u70B9\u3068\u3059\u308B\n # p: u\u306E\u89AA\u3001d: x\u304B\u3089u\u3078\u306E\u8DDD\u96E2\n def dfs(u, p, d):\n global x, dis\n if d > dis:\n dis = d\n x = u\n for v in tree_graph[u]:\n if v == p:\n continue\n dfs(v, u, d+1) \n\n dfs(0, -1, 0) \n dis = 0\n dfs(x, -1, 0)\n return dis\n\nclass Solution:\n def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:\n ans = [0 for _ in range(n-1)]\n\n # \u3069\u306E\u30A8\u30C3\u30B8\u3092\u4F7F\u3046\u304B\u3092\u5168\u3066\u8003\u3048\u308B\u3001bit\u306B\u3088\u3063\u3066\u8868\u73FE\u3059\u308B\n for i in range(1 << (n-1)):\n # \u4F7F\u7528\u3059\u308B\u30A8\u30C3\u30B8\n use_edges = []\n nodes = set([])\n # j\u756A\u76EE\u306Ebit\u304C\u7ACB\u3063\u3066\u3044\u308B\u3068\u304Dedges[j]\u3092\u4F7F\u7528\u3059\u308B\n for j in range(n-1):\n if (i >> j) & 1:\n use_edges.append(edges[j])\n nodes.add(edges[j][0])\n nodes.add(edges[j][1])\n\n N = len(nodes)\n if N <= 1:\n continue\n\n node2node_id = {}\n for node_id, node in enumerate(list(nodes)):\n node2node_id[node] = node_id\n\n # use_edges\u306E\u4E2D\u306E\u30A8\u30C3\u30B8\u306E\u307F\u3067\u4F5C\u3089\u308C\u308B\u30B0\u30E9\u30D5\n graph = [[] for _ in range(N)] \n for edge in use_edges:\n a, b = edge\n a_id, b_id = node2node_id[a], node2node_id[b]\n graph[a_id].append(b_id)\n graph[b_id].append(a_id)\n\n # \u6728\u3067\u3042\u308B\u306A\u3089\u305D\u306E\u6700\u9577\u7D4C\u8DEF(\u76F4\u5F84)\u3092\u30AB\u30A6\u30F3\u30C8\n if isTree(graph):\n ans[diameter(graph)-1] += 1\n\n return ans \n``` | 0 | 0 | ['Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | bitmask + dfs | bitmask-dfs-by-parkcloud-udf4 | Intuition\nbitmask + find connected component + tree diameter \n\n# Approach\n\n\n# Complexity\n- Time complexity:O(n * 2^n)\n\n\n- Space complexity:O(n)\n\n# C | parkCloud | NORMAL | 2023-11-29T06:49:17.550984+00:00 | 2023-11-29T06:49:17.551017+00:00 | 9 | false | # Intuition\nbitmask + find connected component + tree diameter \n\n# Approach\n\n\n# Complexity\n- Time complexity:O(n * 2^n)\n\n\n- Space complexity:O(n)\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number[][]} edges\n * @return {number[]}\n */\nfunction getTreeDiameter(graph, nodes, n) {\n if (nodes.length === 1) return 0\n let root = nodes[0]\n let depths = Array(n).fill(0)\n let visited = new Set()\n function dfs(node, depth) {\n if (visited.has(node)) return\n visited.add(node)\n depths[node] = depth\n for (const to of graph.get(node) || []) {\n if (!visited.has(to) && nodes.includes(to)) {\n dfs(to, depth + 1)\n }\n }\n }\n function dfs2(node) {\n if (visited.has(node)) return\n visited.add(node)\n let dist = 0\n for (const to of graph.get(node) || []) {\n if (!visited.has(to) && nodes.includes(to)) {\n dist = Math.max(dist, dfs2(to) + 1)\n }\n }\n return dist\n }\n dfs(root, 0)\n let maxDepth = -1\n let furthestNode = -1\n for (const node of nodes) {\n if (depths[node] > maxDepth) {\n maxDepth = depths[node]\n furthestNode = node\n }\n }\n visited.clear()\n return dfs2(furthestNode)\n}\nfunction getComponentSize(graph, nodes, n) {\n let count = 0\n let visited = Array(n).fill(false)\n function dfs(node) {\n if (visited[node]) return\n visited[node] = true\n for (const to of graph.get(node) || []) {\n if (!visited[to] && nodes.includes(to)) {\n dfs(to)\n }\n }\n }\n for (const node of nodes) {\n if (!visited[node]) {\n dfs(node)\n count += 1\n }\n }\n return count\n}\nvar countSubgraphsForEachDiameter = function (n, edges) {\n let graph = new Map()\n let distMap = new Map()\n for (const [a, b] of edges) {\n u = a - 1\n v = b - 1\n if (!graph.has(u)) {\n graph.set(u, [])\n }\n if (!graph.has(v)) {\n graph.set(v, [])\n }\n graph.get(u).push(v)\n graph.get(v).push(u)\n }\n for (let mask = 0; mask < (1 << n); mask++) {\n let select = []\n for (let j = 0; j < n; j++) {\n if (mask & (1 << j)) {\n select.push(j)\n }\n }\n let size = getComponentSize(graph, select, n)\n if (size === 1) {\n let dist = getTreeDiameter(graph, select, n)\n if (!distMap.has(dist)) {\n distMap.set(dist, [])\n }\n distMap.get(dist).push(select)\n }\n }\n let ans = Array(n - 1).fill(0)\n for (let d = 1; d <= n - 1; d++) {\n let count = 0\n if (distMap.has(d)) {\n count = distMap.get(d).length\n }\n ans[d - 1] = count\n }\n return ans\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
count-subtrees-with-max-distance-between-cities | Floyd Warshall + Bitset + BFS | floyd-warshall-bitset-bfs-by-tangd6-k57y | Code\n\nclass Solution {\npublic:\n static const int MX = (int)20;\n int fw[MX][MX];\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<i | tangd6 | NORMAL | 2023-11-22T03:26:24.734630+00:00 | 2023-11-22T03:26:24.734661+00:00 | 32 | false | # Code\n```\nclass Solution {\npublic:\n static const int MX = (int)20;\n int fw[MX][MX];\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n int LG = 1 << (n);\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n fw[i][j] = (int)1e9;\n } \n }\n for (auto e : edges) {\n int u = e[0]-1, v = e[1]-1;\n fw[u][v] = 1;\n fw[v][u] = 1;\n }\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n for (int k = 0; k < n; k++) {\n fw[j][k] = min(fw[j][k], fw[j][i] + fw[i][k]);\n }\n }\n }\n vector<int> ans(n-1);\n for (int i = 0; i < LG; i++) {\n int flag = true;\n int md = 0;\n if (__builtin_popcount(i) == 1) continue;\n for (int j = 0; j < n; j++) {\n if (i & (1<<j)) {\n queue<int> q;\n int vis = 0;\n q.push(j);\n while (!q.empty()) {\n int fr = q.front();\n q.pop();\n if (vis & (1 << fr)) continue;\n vis |= 1 << fr;\n for (int k = 0; k < n; k++) {\n if (i & (1<<k) && fr != k) {\n if (fw[fr][k] == 1) q.push(k);\n }\n }\n }\n if (i != vis) flag = false;\n break;\n }\n }\n if (flag) {\n for (int j = 0; j < n; j++) {\n for (int k = j+1; k < n; k++) {\n if ((i & (1<<j)) && (i & (1<<k))) {\n md = max(md, fw[j][k]);\n }\n }\n }\n if (md > 0) ans[md-1]++;\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Short C++ DFS Code | short-c-dfs-code-by-tejasdesh18-sv12 | \n# Code\n\nclass Solution {\npublic:\n int max_depth = 0, farthest_node = 0;\n\n bool isConnected(int &nodes, unordered_map<int, vector<int>> &adj, int c | tejasdesh18 | NORMAL | 2023-10-13T20:23:22.205584+00:00 | 2023-10-13T20:23:22.205602+00:00 | 52 | false | \n# Code\n```\nclass Solution {\npublic:\n int max_depth = 0, farthest_node = 0;\n\n bool isConnected(int &nodes, unordered_map<int, vector<int>> &adj, int curr, int depth ){\n\n nodes = nodes^(1<<curr);\n\n if( depth>max_depth )\n max_depth = depth, farthest_node = curr; \n \n max_depth = max( max_depth, depth );\n\n if( !nodes ) return true;\n\n int ans = false;\n\n for( auto num: adj[curr] )\n if( nodes & 1<<num )\n ans |= isConnected( nodes, adj, num, depth+1 );\n\n return ans;\n }\n \n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n \n map<int,int> mp; unordered_map<int, vector<int>> adj;\n \n for( int i=0; i<edges.size(); i++ ){\n adj[edges[i][0]].push_back(edges[i][1]);\n adj[edges[i][1]].push_back(edges[i][0]);\n }\n \n for( int num=1; num<pow(2,n+1); num++ ){\n if(!(num%2)){\n int curr = 1, temp = num/2;\n\n while( !(temp%2) )\n curr++, temp /= 2;\n \n temp = num, max_depth = 0, farthest_node = curr;\n\n if(isConnected(temp, adj, curr, 0)){\n temp = num;\n isConnected(temp, adj, farthest_node, 0);\n mp[max_depth]++;\n }\n } \n }\n\n vector<int> ans(n-1,0);\n for( int i=1; i<n; i++ )\n if(mp[i]) ans[i-1]=mp[i];\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Floyd-Warshall || Bitmask || Explanation and Solution [C++] | floyd-warshall-bitmask-explanation-and-s-rw3f | *This problem is quite easy, just take two steps:\n+ First, I will find the length of any two vertices using the Floyd-Warshall algorithm.\n+ Browse all aggrega | doantrunghuy | NORMAL | 2023-09-07T23:20:44.483673+00:00 | 2023-09-07T23:20:44.483694+00:00 | 21 | false | ****This problem is quite easy, just take two steps:****\n+ First, I will find the length of any two vertices using the Floyd-Warshall algorithm.\n+ Browse all aggregations using Bitmask.\n\n****Vote if you think it\'s good****\n\n****Here is my C++ code you can refer to****\n\n```\nclass Solution {\npublic:\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n const int oo = n;\n vector<vector<int>> dp(n, vector<int>(n, oo));\n \n for (vector<int> edge : edges) {\n int u = edge[0] - 1;\n int v = edge[1] - 1;\n dp[u][v] = dp[v][u] = 1;\n }\n \n for (int k = 0; k < n; ++k) {\n for (int u = 0; u < n; ++u) {\n for (int v = 0; v < n; ++v) {\n if (u == v or k == v or k == u) {\n continue;\n }\n dp[u][v] = min(dp[u][v], dp[u][k] + dp[k][v]);\n }\n }\n }\n \n vector<int> ans(n - 1);\n \n for (int mask = 1; mask < (1 << n); ++mask) {\n int max_dist = 0;\n int cnt_vertex = 0, cnt_edge = 0;\n \n for (int i = 0; i < n; ++i) {\n if ((mask & (1 << i)) == 0) {\n continue;\n }\n cnt_vertex++;\n for (int j = i + 1; j < n; ++j) {\n if ((mask & (1 << j)) == 0) {\n continue;\n }\n cnt_edge += dp[i][j] == 1;\n max_dist = max(max_dist, dp[i][j]);\n }\n }\n \n if (max_dist != 0 and cnt_edge == cnt_vertex - 1) {\n ans[max_dist - 1]++;\n }\n }\n \n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Bitmask'] | 0 |
count-subtrees-with-max-distance-between-cities | Bitmask | Diameter of tree | C++ | clean code | easiest approach | bitmask-diameter-of-tree-c-clean-code-ea-yywv | Approach\n Describe your approach to solving the problem. \n1. Traverse through each possible subset using bitmask\n2. Ignore the mask which contains only one n | raj_keshari | NORMAL | 2023-08-31T12:31:30.082801+00:00 | 2023-08-31T12:31:30.082822+00:00 | 48 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Traverse through each possible subset using bitmask\n2. Ignore the mask which contains only one node or the graph is not connected.\n + for one node use : `(i&(i-1)) == 0` [mask must be in powers of 2]\n + for graph with more than one components : check the number of nodes which can be visited and it should be not be equal to number of set bits in mask\n3. Now the mask would surely be containing valid tree, just find diameter of it and increment the answer array.\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> g;\n vector<int> ans;\n int count_set_bits(int mask)\n {\n int count = 0;\n while(mask > 0) {count+= ((mask % 2) == 1);mask/=2;}\n return count;\n }\n int check_tree(int mask, int root, int par)\n {\n int ans = 1;\n for(auto &x:g[root])\n {\n if(x == par ||( (mask & (1<<x)) == 0)) continue;\n ans += check_tree(mask, x, root);\n }\n return ans;\n }\n int dfs(int mask ,int root, int par, vector<int> &lev)\n {\n int child = root;\n for(auto &x:g[root])\n {\n if(x == par || ((mask & (1<<x)) == 0)) continue;\n int temp_child = dfs(mask, x, root, lev);\n if(lev[root] < lev[x] + 1) \n {\n lev[root] = lev[x] + 1; \n child = temp_child;\n }\n }\n return child;\n }\n int diameter(int mask, int root, int n)\n {\n vector<int> lev(n,0);\n int deepest_node = dfs(mask, root, -1, lev);\n lev.assign(n,0);\n dfs(mask, deepest_node, -1, lev);\n return lev[deepest_node];\n }\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n g.resize(n);\n ans.resize(n-1);\n for(auto &x:edges) \n {\n g[x[0] - 1].push_back(x[1] - 1);\n g[x[1] - 1].push_back(x[0] - 1);\n }\n for(int i = 1;i<(1<<n);i++)\n {\n if((i&(i-1)) == 0 || check_tree(i, log2(i&(-i)), -1) != count_set_bits(i)) continue;\n int dia = diameter(i, log2(i&(-i)), n);\n ans[dia - 1]++;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | C++ solution | c-solution-by-pejmantheory-86fp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pejmantheory | NORMAL | 2023-08-29T08:09:38.145655+00:00 | 2023-08-29T08:09:38.145688+00:00 | 44 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public:\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n const int maxMask = 1 << n;\n const vector<vector<int>> dist = floydWarshall(n, edges);\n vector<int> ans(n - 1);\n\n // mask := subset of cities\n for (int mask = 0; mask < maxMask; ++mask) {\n const int maxDist = getMaxDist(mask, dist, n);\n if (maxDist > 0)\n ++ans[maxDist - 1];\n }\n\n return ans;\n }\n\n private:\n vector<vector<int>> floydWarshall(int n, const vector<vector<int>>& edges) {\n vector<vector<int>> dist(n, vector<int>(n, n));\n\n for (int i = 0; i < n; ++i)\n dist[i][i] = 0;\n\n for (const vector<int>& edge : edges) {\n const int u = edge[0] - 1;\n const int v = edge[1] - 1;\n dist[u][v] = 1;\n dist[v][u] = 1;\n }\n\n for (int k = 0; k < n; ++k)\n for (int i = 0; i < n; ++i)\n for (int j = 0; j < n; ++j)\n dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);\n\n return dist;\n }\n\n int getMaxDist(int mask, const vector<vector<int>>& dist, int n) {\n int maxDist = 0;\n int edgeCount = 0;\n int cityCount = 0;\n for (int u = 0; u < n; ++u) {\n if ((mask >> u & 1) == 0) // u is not in the subset.\n continue;\n ++cityCount;\n for (int v = u + 1; v < n; ++v) {\n if ((mask >> v & 1) == 0) // v is not in the subset.\n continue;\n if (dist[u][v] == 1) // u and v are connected.\n ++edgeCount;\n maxDist = max(maxDist, dist[u][v]);\n }\n }\n return edgeCount == cityCount - 1 ? maxDist : 0;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Easy to Understand | easy-to-understand-by-raj_tirtha-azsh | \n# Code\n\nclass Solution {\npublic:\n int dfs_cnt(int node,int mask,vector<vector<int>> &adj,vector<int> &vis){\n vis[node]=1;\n int cnt=1;\n | raj_tirtha | NORMAL | 2023-08-15T18:06:39.678435+00:00 | 2023-08-15T18:06:39.678460+00:00 | 23 | false | \n# Code\n```\nclass Solution {\npublic:\n int dfs_cnt(int node,int mask,vector<vector<int>> &adj,vector<int> &vis){\n vis[node]=1;\n int cnt=1;\n for(int it:adj[node]){\n if(vis[it]==1) continue;\n if(mask & (1<<it)){\n cnt+=dfs_cnt(it,mask,adj,vis);\n }\n }\n return cnt;\n }\n int diameter(int node,int mask,vector<vector<int>> &adj,vector<int> &vis,int &dm){\n vis[node]=1;\n int l=0,r=0;\n for(int it:adj[node]){\n if(vis[it]==1) continue;\n if(mask & (1<<it)){\n int h=diameter(it,mask,adj,vis,dm);\n if(h>r){\n l=r;\n r=h;\n }else{\n l=max(l,h);\n }\n }\n }\n dm=max(dm,l+r+1);\n return 1+max(l,r);\n }\n\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<vector<int>> adj(n);\n for(int i=0;i<edges.size();i++){\n int u=edges[i][0],v=edges[i][1];\n u--;\n v--;\n adj[u].push_back(v);\n adj[v].push_back(u);\n }\n vector<int> ans(n-1,0);\n for(int mask=0;mask<(1<<n);mask++){\n int cnt=__builtin_popcount(mask);\n vector<int> vis(n,-1);\n vector<int> vis1(n,-1);\n for(int i=0;i<n;i++){\n if(mask & (1<<i)){\n if(dfs_cnt(i,mask,adj,vis)!=cnt) continue;\n int dm=0;\n int d=diameter(i,mask,adj,vis1,dm);\n cout<<mask<<" "<<d<<"\\n";\n if(dm-2>=0) ans[dm-2]++;\n break;\n }\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Fastest C++ solution, beats 100%, smart brute force | fastest-c-solution-beats-100-smart-brute-hrt7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Tim | 1337beef | NORMAL | 2023-07-30T15:01:38.138758+00:00 | 2023-07-30T15:01:38.138776+00:00 | 79 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2 2^{n})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n // edges[i] is the neighbors of i\n vector<int> edges[16];\n // dists[i][j] is the dist between i and j\n int dists[16][16]{};\n // masks[i][j] is the mask of cities visited when going from i to j\n int masks[16][16]{};\n struct Data {\n int city;\n int dist;\n int mask;\n };\npublic:\n // do BFS starting at curCity\n void getCities(int curCity) {\n static std::deque<Data> q;\n static std::array<bool, 16> visited;\n visited.fill(false);\n q.clear();\n q.emplace_back(Data{curCity, 0, 1 << curCity});\n visited[curCity] = true;\n while (q.size()) {\n Data d = q.front();\n q.pop_front();\n for (auto neighbor : edges[d.city]) {\n if (!visited[neighbor]) {\n q.emplace_back(Data{neighbor, d.dist + 1, d.mask | (1<<(neighbor))});\n visited[neighbor] = true;\n dists[neighbor][curCity] = dists[curCity][neighbor] = d.dist + 1;\n masks[neighbor][curCity] = masks[curCity][neighbor] = q.back().mask;\n }\n }\n }\n }\n\n vector<int> countSubgraphsForEachDiameter(const int n, vector<vector<int>>& ed) {\n for (const auto& pair: ed) {\n edges[pair[0] - 1].emplace_back(pair[1] - 1);\n edges[pair[1] - 1].emplace_back(pair[0] - 1);\n }\n std::vector<int> ans(n - 1, 0);\n for (int j = 0; j < n; ++j) { // curCity\n getCities(j);\n }\n // loop thru every possible subset \n for (int mask = 1; mask < (1 << n); ++mask) {\n int maxDist = 0;\n for (int i = 0; i < n; i++) {\n if ((mask & (1 << i)) == 0) continue;\n for (int j = 0; j < i; j++) {\n // check i and j are reachable within the subset \n if (mask & (1 << j)) {\n if(dists[i][j]==0 || (masks[i][j] & mask) != masks[i][j] ) {i=j=n;maxDist=0;break;}\n maxDist = std::max(maxDist, dists[i][j]);\n }\n }\n }\n if (maxDist) ans[maxDist-1]++;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Bit Manipulation', 'Breadth-First Search', 'Graph', 'Bitmask', 'C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Bitmask+Floydd Warshall + Dsu | bitmaskfloydd-warshall-dsu-by-dijkstraal-v0m1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shadow2732 | NORMAL | 2023-06-16T15:57:39.229902+00:00 | 2023-06-16T15:57:39.229921+00:00 | 40 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(2^N *N)\n\n- Space complexity:\nO(N^2)\n\n# Code\n```\nclass Solution {\npublic:\nvoid make(int a,int parent[],int len[])\n{\n parent[a]=a;\n len[a]=1;\n}\n\nint find_(int a,int parent[])\n{\n if(a==parent[a])\n return a;\n //path compression\n int ans=find_(parent[a],parent);\n parent[a]=ans;\n return ans;\n}\n\nvoid Union(int a,int b,int parent[],int len[])\n{\n int x=find_(a,parent);\n int y=find_(b,parent);\n if(x==y)\n return;\n //union by size\n if(len[x]<len[y])\n swap(x,y);\n parent[y]=x;\n len[x]+=len[y];\n}\n\n\nbool connected(int n,vector<int>& temp,vector<vector<int>> matrix)\n{\n int parent[n],len[n];\n for(int i=0;i<n;i++)\n make(i,parent,len);\n for(int i=0;i<temp.size();i++)\n {\n for(int j=i+1;j<temp.size();j++)\n {\n int a=temp[i],b=temp[j];\n if(matrix[a][b])\n Union(a,b,parent,len);\n }\n }\n map<int,int> m;\n for(int x:temp)\n {\n int par=find_(x,parent);\n m[par]++;\n }\n return m.size()==1;\n}\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<vector<int>> matrix(n,vector<int>(n,0));\n vector<vector<int>> dist(n,vector<int>(n,1e9));\n for(int i=0;i<n;i++)\n dist[i][i]=0;\n for(auto v:edges)\n {\n int x=v[0]-1,y=v[1]-1;\n dist[x][y]=1;\n dist[y][x]=1;\n matrix[x][y]=1;\n matrix[y][x]=1;\n }\n for(int k=0;k<n;k++)\n {\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(dist[i][k]==1e9 || dist[k][j]==1e9)\n continue;\n dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);\n }\n }\n }\n vector<int> res(n-1,0);\n int sz=1<<n;\n for(int i=1;i<sz;i++)\n {\n vector<int> temp;\n for(int j=0;j<n;j++)\n {\n if(i&(1<<j))\n temp.push_back(j);\n }\n if(temp.size()==1)\n continue;\n if(!connected(n,temp,matrix))continue;\n int maxi=0;\n for(int a=0;a<temp.size();a++)\n {\n for(int b=a+1;b<temp.size();b++)\n {\n maxi=max(maxi,dist[temp[a]][temp[b]]);\n }\n }\n if(maxi)\n res[maxi-1]++;\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Very Hard | very-hard-by-aadityagautam-jt3c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aadityagautam | NORMAL | 2023-04-30T15:18:07.661777+00:00 | 2023-04-30T15:18:07.661814+00:00 | 159 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private List<Integer>[] g;\n private int msk;\n private int nxt;\n private int mx;\n\n public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {\n g = new List[n];\n Arrays.setAll(g, k -> new ArrayList<>());\n for (int[] e : edges) {\n int u = e[0] - 1, v = e[1] - 1;\n g[u].add(v);\n g[v].add(u);\n }\n int[] ans = new int[n - 1];\n for (int mask = 1; mask < 1 << n; ++mask) {\n if ((mask & (mask - 1)) == 0) {\n continue;\n }\n msk = mask;\n mx = 0;\n int cur = 31 - Integer.numberOfLeadingZeros(msk);\n dfs(cur, 0);\n if (msk == 0) {\n msk = mask;\n mx = 0;\n dfs(nxt, 0);\n ++ans[mx - 1];\n }\n }\n return ans;\n }\n\n private void dfs(int u, int d) {\n msk ^= 1 << u;\n if (mx < d) {\n mx = d;\n nxt = u;\n }\n for (int v : g[u]) {\n if ((msk >> v & 1) == 1) {\n dfs(v, d + 1);\n }\n }\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
count-subtrees-with-max-distance-between-cities | c++ 93% faster solution trying all subsets using bitmask | c-93-faster-solution-trying-all-subsets-1432e | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vedantnaudiyal | NORMAL | 2023-04-23T17:54:10.754531+00:00 | 2023-04-23T17:54:10.754570+00:00 | 94 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint answer=0;\nint nodes=0;\nint dfs(int node,int par,vector<vector<int>>& adj,int& mask){\n int a=INT_MIN;\n int b=INT_MIN;\n int maxi=0;\n nodes++;\n for(int & i: adj[node]){\n if(i!=par && mask & (1<<i)){\n int res=1+dfs(i,node,adj,mask);\n maxi=max(maxi,res);\n if(a<res){\n b=a;\n a=res;\n }\n else if(b<res){\n b=res;\n }\n \n }\n }\n if(a!=INT_MIN && b!=INT_MIN){\n answer=max(answer,a+b);\n }\n answer=max(answer,maxi);\n return maxi;\n}\nvoid subsets(int ind,int n,int s,vector<vector<int>>& adj,int mask,vector<int>& ans){\n if(ind==n){\n return;\n }\n // not_take\n subsets(ind+1,n,s,adj,mask,ans);\n // take\n s++;\n mask=mask | (1<<ind);\n if(s>1){\n answer=0;\n nodes=0;\n dfs(ind,-1,adj,mask);\n if(nodes==s){\n ans[answer-1]++;\n }\n }\n subsets(ind+1,n,s,adj,mask,ans);\n}\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<int> ans(n-1,0);\n vector<vector<int>> adj(n);\n for(auto& ele: edges){\n adj[ele[0]-1].push_back(ele[1]-1);\n adj[ele[1]-1].push_back(ele[0]-1);\n }\n subsets(0,n,0,adj,0,ans);\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | C++ | Submask Enumeration Bruteforce + BFS | c-submask-enumeration-bruteforce-bfs-by-mtfm4 | time~O(N * 2^N)\nspace~O(N + E)\n\nclass Solution {\npublic:\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector | crimsonX | NORMAL | 2023-04-12T05:59:14.141411+00:00 | 2023-04-12T06:00:23.577531+00:00 | 81 | false | time~O(N * 2^N)\nspace~O(N + E)\n```\nclass Solution {\npublic:\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<int> res(n-1);\n vector<vector<int>> adj(n+1);\n for(auto &a:edges){\n adj[a[0]].push_back(a[1]);\n adj[a[1]].push_back(a[0]);\n }\n int m=((1<<(n+1))-1)^1;\n for(int s=m;s;s=(s-1)&m){//2^N\n if(__builtin_popcount(s)==1)\n continue;\n int b,d1;\n for(int x=1;x<=15;x++){//N\n if(((s>>x)&1)==1){\n b=x;\n break;\n }\n }\n int visited=0;\n int c=1;\n queue<int> q;\n visited|=(1<<b);\n q.push(b);\n while(q.size()){//N\n int f=q.front();\n d1=f;\n q.pop();\n for(auto &a:adj[f]){\n if(((s>>a)&1)==0 or ((visited>>a)&1)==1)\n continue;\n visited|=(1<<a);\n c++;\n q.push(a);\n }\n }\n if(c!=__builtin_popcount(s))\n continue;\n c=0;\n visited=0;\n visited|=(1<<d1);\n q.push(d1);\n while(q.size()){//N\n int qlen=q.size();\n while(qlen-->0){\n int f=q.front();\n q.pop();\n for(auto &a:adj[f]){\n if(((s>>a)&1)==0 or ((visited>>a)&1)==1)\n continue;\n visited|=(1<<a);\n q.push(a);\n }\n }\n c++;\n }\n res[c-2]++;\n }\n return res;\n }\n};\n``` | 0 | 0 | ['Breadth-First Search', 'Queue', 'C', 'Bitmask', 'C++'] | 0 |
count-subtrees-with-max-distance-between-cities | C# bitmap | c-bitmap-by-rnajafi76-t9hn | Check the hints in description\n\n\npublic class Solution {\n public int[] CountSubgraphsForEachDiameter(int n, int[][] edges) {\n int[] res=new int[n | rnajafi76 | NORMAL | 2023-04-05T10:50:00.280644+00:00 | 2023-04-05T10:58:13.958032+00:00 | 30 | false | Check the hints in description\n\n```\npublic class Solution {\n public int[] CountSubgraphsForEachDiameter(int n, int[][] edges) {\n int[] res=new int[n-1];\n HashSet<int>[] g=BuildGraph(n,edges);\n for(int i=1;i<(1<<n);i++){\n int d=CalculateMaxDistance(n,g,i);\n if(d==0)\n continue;\n res[d-1]++;\n } \n return res;\n }\n \n int CalculateMaxDistance(int n, HashSet<int>[] g, int nodes){\n\n int root=1;\n int i=1;\n for(;root<=n;root++)\n if((i&nodes)>0)\n break;\n else\n i<<=1;\n int maxdist=0;\n dfs(-1,root,g,ref nodes, ref maxdist);\n\n return nodes==0 ? maxdist :0;\n }\n \n int dfs(int parent, int at, HashSet<int>[] g, ref int nodes, ref int maxdist){\n int d1=0,d2=0;\n int depth=0;\n // Console.WriteLine($"nodes={nodes} root={root}");\n\n nodes=nodes^(1<<(at-1));\n foreach(int to in g[at]){\n\n int p=(1<<(to-1))&nodes;\n if(p==0)\n continue;\n\n int dist=dfs(at,to,g,ref nodes, ref maxdist);\n if(dist>=d1){\n d2=d1;\n d1=dist;\n }else if(dist>d2)\n {\n d2=dist;\n }\n \n depth=Math.Max(depth,dist);\n \n }\n maxdist=Math.Max(maxdist,d1+d2);\n return depth+1;\n }\n \n HashSet<int>[] BuildGraph(int n, int[][] edges){\n HashSet<int>[] g =Enumerable.Range(0,n+1).Select (x=> new HashSet<int>()).ToArray();\n \n foreach(int[] e in edges){\n g[e[0]].Add(e[1]);\n g[e[1]].Add(e[0]);\n }\n \n return g;\n }\n}\n``` | 0 | 0 | ['Bit Manipulation'] | 0 |
count-subtrees-with-max-distance-between-cities | Python (Simple BFS + DP + BitMasking) | python-simple-bfs-dp-bitmasking-by-rnota-u558 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2023-03-09T16:14:28.273994+00:00 | 2023-03-09T16:14:28.274028+00:00 | 114 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubgraphsForEachDiameter(self, n, edges):\n def bfs(src,cities):\n stack, visited, max_dist = [(src,0)], {src}, 0\n\n while stack:\n node, dist = stack.pop(0)\n max_dist = dist\n\n for neighbor in dict1[node]:\n if neighbor not in visited and neighbor in cities:\n visited.add(neighbor)\n stack.append((neighbor,dist+1))\n\n return max_dist, visited\n\n\n def max_distance_two_nodes(state):\n cities = set()\n\n for i in range(n):\n if (state>>i)&1 == 1:\n cities.add(i)\n\n result = 0\n\n for i in cities:\n max_dist, visited = bfs(i,cities)\n if len(visited) < len(cities): return 0\n result = max(result,max_dist)\n\n return result \n\n\n dict1 = defaultdict(list)\n\n for i,j in edges:\n dict1[i-1].append(j-1)\n dict1[j-1].append(i-1)\n\n ans = [0]*(n-1)\n\n for j in range(1,2**n):\n d = max_distance_two_nodes(j)\n if d > 0: ans[d-1] += 1 \n\n return ans\n\n \n\n\n\n\n\n \n\n \n\n\n\n\n\n \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n \n \n \n``` | 0 | 0 | ['Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | Just a runnable solution | just-a-runnable-solution-by-ssrlive-9m03 | Code\n\nimpl Solution {\n pub fn count_subgraphs_for_each_diameter(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {\n let mut g = vec![vec![999; n as usize | ssrlive | NORMAL | 2023-02-13T17:41:12.798051+00:00 | 2023-02-13T17:47:15.780375+00:00 | 34 | false | # Code\n```\nimpl Solution {\n pub fn count_subgraphs_for_each_diameter(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {\n let mut g = vec![vec![999; n as usize]; n as usize];\n for e in edges.iter() {\n let i = (e[0] - 1) as usize;\n let j = (e[1] - 1) as usize;\n g[i][j] = 1;\n g[j][i] = 1;\n }\n for k in 0..n as usize {\n for i in 0..n as usize {\n for j in 0..n as usize {\n g[i][j] = g[i][j].min(g[i][k] + g[k][j]);\n }\n }\n }\n let mut ans = vec![0; n as usize - 1];\n for s in 0_i32..(1 << n) {\n let k = s.count_ones() as i32;\n let (mut e, mut d) = (0_i32, 0_i32);\n for (i, item) in g.iter().enumerate().take(n as usize) {\n if s & (1 << i) != 0 {\n for (j, &item_j) in item.iter().enumerate().take(n as usize).skip(i + 1) {\n if s & (1 << j) != 0 {\n e += i32::from(g[i][j] == 1);\n d = d.max(item_j);\n }\n }\n }\n }\n if e == k - 1 && d > 0 {\n ans[(d - 1) as usize] += 1;\n }\n }\n\n ans\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
count-subtrees-with-max-distance-between-cities | C++ bitmask + DFS, with explanation. | c-bitmask-dfs-with-explanation-by-geetes-bdq0 | Intuition\n Describe your first thoughts on how to solve this problem. \xA0\n \n# Approach\n Describe your approach to solving the problem. \n As n is small, | GeeteshSood | NORMAL | 2023-02-06T22:16:57.471947+00:00 | 2023-02-06T22:17:52.847893+00:00 | 120 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\xA0\n \n# Approach\n<!-- Describe your approach to solving the problem. -->\n As n is small, find all possible subsets and see if any of them can form a subtree. \n If it can form a subtree, find the greatest distance while treating any node in that subset as the root node.\n Once we visit a node, we clear the specific bit in the subtree, and after finishing dfs.\n if subtree == 0, that means it is a valid subtree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n 2^n for every subset and n for traversing that subset.\n so tc would be = O(n * 2 ^ n) solution\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n int dfs(int u,int par,vector<vector<int>> &adj,int &mask,int &ans){\n\n if(!(mask & (1<<u)))return 0; // if the current node is not present in the subset.\n\n mask = mask ^ (1<<u);\n\n int fmax = 0 , smax = 0;\n\n for(auto &v : adj[u]){\n if(v == par)continue;\n\n int val = dfs(v,u,adj,mask,ans);\n\n if(val >= fmax){\n smax = fmax;\n fmax = val;\n }\n else if(val > smax){\n smax = val;\n }\n }\n\n ans = max(ans,fmax+smax); // calculating the maximum distance at each node.\n\n return fmax + 1;\n }\n\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n\n vector<vector<int>> adj(n+1);\n\n for(auto &it : edges){\n int u = it[0] , v = it[1];\n adj[u].push_back(v);\n adj[v].push_back(u);\n }\n\n unordered_map<int,int> mp;\n \n for(int bit=1;bit<(1<<n);bit++){\n\n int mask = 0 , node = -1;\n \n for(int k=0;k<n;k++){\n if(bit & (1<<k)){\n mask |= (1<<(k+1));\n node = k+1;\n }\n }\n\n int ans = INT_MIN;\n\n dfs(node,-1,adj,mask,ans); // to determine whether or not our subset is connected, and to calculate the maximum distance\n \n if(mask == 0)mp[ans]++;\n }\n\n vector<int> ans;\n\n for(int i=1;i<n;i++){\n int val = mp[i];\n ans.push_back(val);\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['Bit Manipulation', 'Depth-First Search', 'Bitmask', 'C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Not a fast solution || C++ || Just working | not-a-fast-solution-c-just-working-by-re-z8t2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | recker2903 | NORMAL | 2022-12-25T17:35:22.913680+00:00 | 2022-12-25T17:35:22.913721+00:00 | 131 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n #define ll long long\n ll check(vector<ll>adj[],vector<ll>&path,int n){\n unordered_set<ll>ss(path.begin(),path.end());\n ll answer=INT_MIN,m=path.size();\n for(ll i=0;i<m;i++){\n ll mayank=path[i],length=0;\n vector<bool>visited(n);visited[mayank]=true;\n queue<ll>q;q.push(mayank);\n while(!q.empty()){\n ll size=q.size();\n while(size--){\n ll temp=q.front();q.pop();\n for(ll &x:adj[temp]){\n if(ss.find(x)!=ss.end() && visited[x]==false){\n visited[x]=true;\n q.push(x);\n }\n }\n }\n length++;\n }\n ll count=0;\n for(ll j=0;j<n;j++){\n if(visited[j]==true){\n count++;\n }\n }\n if(count!=path.size()){\n return -1;\n }\n else{\n answer=max(answer,length-1);\n }\n }\n return answer;\n }\n\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<ll>adj[n];\n vector<int>answer(n-1,0);\n for(auto &x:edges){\n adj[x[0]-1].push_back(x[1]-1);\n adj[x[1]-1].push_back(x[0]-1);\n }\n for(ll i=0;i<(1LL<<n);i++){\n vector<ll>path;\n for(ll j=0;j<n;j++){\n if(i&(1LL<<j)){\n path.push_back(j);\n }\n }\n if(path.size()<=1){\n continue;\n }\n ll temp=check(adj,path,n);\n if(temp!=-1){\n answer[temp-1]++;\n }\n }\n return answer;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-subtrees-with-max-distance-between-cities | Python3 easiest solution | python3-easiest-solution-by-avs-abhishek-o3nh | Code\n\nclass Solution(object):\n def countSubgraphsForEachDiameter(self, n, edges):\n def bfs(src, cities):\n visited = {src}\n | avs-abhishek123 | NORMAL | 2022-12-08T05:41:39.919738+00:00 | 2022-12-08T05:41:39.919772+00:00 | 164 | false | # Code\n```\nclass Solution(object):\n def countSubgraphsForEachDiameter(self, n, edges):\n def bfs(src, cities):\n visited = {src}\n q = deque([(src, 0)]) # Pair of (vertex, distance)\n farthestDist = 0 # Farthest distance from src to other nodes\n while len(q) > 0:\n u, d = q.popleft()\n farthestDist = d\n for v in graph[u]:\n if v not in visited and v in cities:\n visited.add(v)\n q.append((v, d+1))\n return farthestDist, visited\n\n def maxDistance(state): # return: maximum distance between any two cities in our subset. O(n^2)\n cities = set()\n for i in range(n):\n if (state >> i) & 1 == 1:\n cities.add(i)\n ans = 0\n for i in cities:\n farthestDist, visited = bfs(i, cities)\n if len(visited) < len(cities): return 0 # Can\'t visit all nodes of the tree -> Invalid tree\n ans = max(ans, farthestDist)\n return ans\n\n graph = defaultdict(list)\n for u, v in edges:\n graph[u-1].append(v-1)\n graph[v-1].append(u-1)\n \n ans = [0] * (n - 1)\n for state in range(1, 2 ** n):\n d = maxDistance(state)\n if d > 0: ans[d - 1] += 1\n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
count-subtrees-with-max-distance-between-cities | C++ | O(N log N * 2^N) | Bitmask & DFS | c-on-log-n-2n-bitmask-dfs-by-chawlasahil-949k | Algorithm:\n\nStep 1\nGenerate all subsets (or masks) -> O(2^N)\n\nStep 2\nFor every mask, check if the tree formed is valid or not.\nThis is done by finding th | chawlasahil565 | NORMAL | 2022-10-30T06:27:22.931639+00:00 | 2022-10-30T06:27:22.931681+00:00 | 127 | false | Algorithm:\n\nStep 1\nGenerate all subsets (or masks) -> O(2^N)\n\nStep 2\nFor every mask, check if the tree formed is valid or not.\nThis is done by finding the number of nodes reachable from one of the nodes using DFS -> O(number of edges in subtree) < O(N) (upper bound)\n\nStep 3\nFor every valid mask, find the diameter of that subtree using DFS + sorting -> O(N log N) (upper bound)\n\nOverall complexity -> O(2^N * NlogN)\n\nCode:\n```\nclass Solution {\npublic:\n void dfs_cnt(int idx, int par, int& cnt, int mask, vector<vector<int>>& adj_list)\n {\n cnt++;\n for(int i= 0; i< adj_list[idx].size(); i++)\n {\n int idx2 = adj_list[idx][i];\n if(par != idx2 && ((mask>>idx2)&1))\n {\n dfs_cnt(idx2, idx, cnt, mask, adj_list);\n }\n }\n return;\n }\n bool isMaskValid(int mask, int& idx, int n, vector<vector<int>>& adj_list)\n {\n idx=0;\n while(!(1 & (mask>>idx)))\n idx++;\n int exp_cnt = 0;\n for(int i= 0; i< n; i++)\n exp_cnt += ((mask>>i)&1);\n \n int cnt = 0;\n dfs_cnt(idx, -1, cnt, mask, adj_list);\n //cout << "For mask = " << mask << ", exp_cnt = " << exp_cnt << ", cnt = " << cnt << endl;\n if(cnt == exp_cnt && exp_cnt > 1)\n return true;\n return false;\n \n }\n int dfs(int idx, int par, int& d, int mask, vector<vector<int>>& adj_list)\n {\n //cout << "Inputs " << idx << ", " << par << endl;\n vector<int> dist;\n for(int i= 0; i< adj_list[idx].size(); i++)\n {\n int idx2 = adj_list[idx][i];\n if(par != idx2 && ((mask >> idx2) & 1))\n {\n int h = dfs(idx2, idx, d, mask, adj_list);\n dist.push_back(1+h);\n }\n }\n int ans = 0;\n \n if(!dist.empty())\n {\n if(dist.size() == 1)\n {\n d = max(d, dist[0]);\n ans = dist[0];\n }\n else\n {\n sort(dist.begin(), dist.end());\n int sz = dist.size();\n int h = dist[sz-1] + dist[sz-2];\n d = max(h, d);\n ans = dist[sz-1];\n }\n }\n //cout << "For idx = " << idx << ", par = " << par << ", ans = " << ans << ", d = " << d << endl;\n return ans;\n }\n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) \n {\n vector<vector<int>> adj_list(n, vector<int>());\n for(int i= 0; i< n-1; i++)\n {\n int x = edges[i][0]-1;\n int y = edges[i][1]-1;\n adj_list[x].push_back(y);\n adj_list[y].push_back(x);\n }\n \n vector<int> dp(n-1, 0);\n \n for(int mask = 1; mask < (1<<n); mask++)\n {\n int idx = 0;\n if(isMaskValid(mask, idx, n, adj_list))\n {\n int d = 0;\n dfs(idx, -1, d, mask, adj_list);\n if(d>0) dp[d-1]++;\n }\n }\n return dp;\n }\n};\n``` | 0 | 0 | ['Depth-First Search', 'C', 'Bitmask'] | 0 |
count-subtrees-with-max-distance-between-cities | C++ Simple Solution With Explanation Using Bitmask & Floyd Warshall Algorithm - O(2^N*N^2) | c-simple-solution-with-explanation-using-in2w | Firstly, we will use Floyd Warshall Algorithm to find the distance between every pair of nodes. Its time complexity will be O(N^3) \nHere, N is 15 so we can con | rahul-rj | NORMAL | 2022-10-20T09:45:39.953047+00:00 | 2022-10-20T09:45:39.953086+00:00 | 123 | false | Firstly, we will use Floyd Warshall Algorithm to find the distance between every pair of nodes. Its time complexity will be O(N^3) \nHere, N is 15 so we can consider every possible subset in O(2^N) and then\n1) check if it is a subtree: if it is a subtree then no of nodes (cities) - 1 = no of edges\n2) find the maximum distance between any two cities by the use of two loops i and j & finding max distance between cities i and j in O(N^2)\n```\nclass Solution {\npublic:\n int findDist(int bitmask, vector<vector<int>> &dist) {\n int numCities = 0, numEdges = 0, maxDist = 0;\n for(int i=0; i<dist.size(); i++) {\n if(((bitmask>>i)&1) == 0) continue; // skip if city i is not in subset\n numCities++;\n for(int j=i+1; j<dist.size(); j++) {\n if(((bitmask>>j)&1) == 0) continue; // skip if city j is not in subset\n numEdges += dist[i][j] == 1;\n maxDist = max(maxDist, dist[i][j]);\n }\n }\n if(numEdges != numCities - 1) maxDist = 0; // if no of edges not equal to no of cities - 1 then our subset is not a subtree so we return 0;\n return maxDist;\n }\n \n vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {\n vector<vector<int>> dist(n, vector<int> (n, n)); // dist[i][j] represent distance between nodes i and j which can be max n\n for(auto &e: edges) // updating distance between nodes that have an edge connecting them\n dist[e[0]-1][e[1]-1] = dist[e[1]-1][e[0]-1] = 1; \n \n for(int k=0; k<n; k++) // using floyd warshall algorithm to update distances\n for(int i=0; i<n; i++)\n for(int j=0; j<n; j++)\n dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]); \n \n vector<int> ans(n-1, 0);\n for(int bitmask = 0; bitmask < (1<<n); bitmask++) {\n int maxDist = findDist(bitmask, dist); // finding min distance between two nodes in the subset\n if(maxDist > 0) ans[maxDist-1]++;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Bitmask'] | 0 |
number-of-ways-to-arrive-at-destination | [C++/Python] Dijkstra - Clean & Concise | cpython-dijkstra-clean-concise-by-hiepit-5ww1 | Idea\n- We use Dijkstra algorithm to find the Shortest Path from src = 0 to dst = n - 1.\n- While dijkstra, we create additional ways array, where ways[i] keeps | hiepit | NORMAL | 2021-08-21T16:01:14.699252+00:00 | 2021-08-23T14:46:27.631003+00:00 | 34,461 | false | **Idea**\n- We use Dijkstra algorithm to find the Shortest Path from `src = 0` to `dst = n - 1`.\n- While dijkstra, we create additional `ways` array, where `ways[i]` keeps the number of shortest path from `src = 0` to `dst = i`. Then the answer is `ways[n-1]`.\n\n<iframe src="https://leetcode.com/playground/PhVJCRs6/shared" frameBorder="0" width="100%" height="700"></iframe>\n\n**Complexity**\n- Time: `O(M * logN + N)`, where `M <= N*(N-1)/2` is number of roads, `N <= 200` is number of intersections.\n- Space: `O(N + M)`\n\n**Question & Answer**\n1. Should I remove this line `if dist[u] < d: continue # Skip if d is not updated to latest version!`?\n\tIf you remove that line, the time complexity becomes `O(V^3 * logV)`, which can run pass all the testcases since `V <= 200`.\n\tBut if you keep that line, the time complexity reduces to `O(V^2 * logV)`.\n\tExplain: Other neightbors may visit node `u` multiple times (up to `O(V)` times) and push node `u` to the `minHeap`. In the worst case, node `u` will pop and process `O(V)` times, each time it takes `O(V)` to visit neighbors, there is up to `V` nodes like node `u`. So total time complexity is `O(V^3 * logV)`.\n\t\n\tCan check the following special graph (Not related to this problem)\n\t<img src="https://assets.leetcode.com/users/images/6e4e608c-950c-4606-ad37-3d38467cf67e_1629566004.4643087.png" alt="TLE Testcase Dijkstra" width="600"/>\n\tAnd this implementation https://ideone.com/lOoDHO will cause TLE.\n\t\n\t\nIf you think this **post is useful**, I\'m happy if you **give a vote**. Any **questions or discussions are welcome!** Thank a lot. | 548 | 6 | [] | 43 |
number-of-ways-to-arrive-at-destination | ✔️ DP + Dijkstra | Python | C++ | Java | JS | C# | Go | Rust | Kotlin | dp-shortest-path-python-by-otabek_kholmi-9eb0 | SUPPORT BY UPVOTING THE POST ⬆️IntuitionThis problem combines the shortest path algorithm with counting the number of ways to reach a destination using the shor | otabek_kholmirzaev | NORMAL | 2025-03-23T00:59:42.006959+00:00 | 2025-03-23T20:46:27.769866+00:00 | 17,501 | false | # SUPPORT BY UPVOTING THE POST ⬆️
# Intuition
This problem combines the shortest path algorithm with counting the number of ways to reach a destination using the shortest path. We use **Dijkstra's algorithm** to find the shortest paths and simultaneously count how many different ways we can reach each node with the current shortest distance.
# Approach
1. **Build the Graph:** Create an adjacency list representation of the graph where for each node, we store its neighbors and the time to reach them.
2. **Initialize:**
- Create a `dist` array to store the shortest distance to each node (initially infinity, except dist[0] = 0)
- Create a `ways` array to count the number of ways to reach each node via the shortest path (initially ways[0] = 1, others = 0)
3. **Dijkstra's Algorithm with DP:**
- Use a priority queue to explore nodes in order of increasing distance
- For each node, look at all its neighbors
- If we find a shorter path to a neighbor, update its distance and reset its count of ways
- If we find a path of equal length, add the current node's count to the neighbor's count
4. **Result:** After the algorithm completes, `ways[n-1]` contains the number of shortest paths from node 0 to node n-1.
The **dynamic programming** aspect comes from how we update the `ways` array. For each node, the number of ways to reach it is the sum of the ways to reach all its predecessors in the shortest path.
# Complexity
- Time Complexity: `O(E log V)`, where `E` is the number of edges (roads) and `V` is the number of vertices (intersections).
- Space complexity: `O(V + E)`.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
graph = [[] for _ in range(n)]
for u, v, time in roads:
graph[u].append((v, time))
graph[v].append((u, time))
dist = [float('inf')] * n
ways = [0] * n
dist[0] = 0
ways[0] = 1
pq = [(0, 0)]
MOD = 10**9 + 7
# Dijkstra's algorithm
while pq:
d, node = heapq.heappop(pq)
if d > dist[node]:
continue
for neighbor, time in graph[node]:
if dist[node] + time < dist[neighbor]:
dist[neighbor] = dist[node] + time
ways[neighbor] = ways[node]
heapq.heappush(pq, (dist[neighbor], neighbor))
elif dist[node] + time == dist[neighbor]:
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD
return ways[n-1]
```
```cpp []
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
vector<vector<pair<int, int>>> graph(n);
for (const auto& road : roads) {
int u = road[0], v = road[1], time = road[2];
graph[u].emplace_back(v, time);
graph[v].emplace_back(u, time);
}
vector<long long> dist(n, LLONG_MAX);
vector<int> ways(n, 0);
dist[0] = 0;
ways[0] = 1;
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> pq;
pq.emplace(0, 0);
const int MOD = 1e9 + 7;
while (!pq.empty()) {
auto [d, node] = pq.top();
pq.pop();
if (d > dist[node]) continue;
for (const auto& [neighbor, time] : graph[node]) {
if (dist[node] + time < dist[neighbor]) {
dist[neighbor] = dist[node] + time;
ways[neighbor] = ways[node];
pq.emplace(dist[neighbor], neighbor);
} else if (dist[node] + time == dist[neighbor]) {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
}
}
}
return ways[n - 1];
}
};
```
```java []
class Solution {
public int countPaths(int n, int[][] roads) {
List<List<int[]>> graph = new ArrayList<>();
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
for (int[] road : roads) {
int u = road[0], v = road[1], time = road[2];
graph.get(u).add(new int[]{v, time});
graph.get(v).add(new int[]{u, time});
}
long[] dist = new long[n];
int[] ways = new int[n];
Arrays.fill(dist, Long.MAX_VALUE);
dist[0] = 0;
ways[0] = 1;
PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(a -> a[0]));
pq.offer(new long[]{0, 0});
int MOD = 1_000_000_007;
while (!pq.isEmpty()) {
long[] curr = pq.poll();
long d = curr[0];
int node = (int) curr[1];
if (d > dist[node]) continue;
for (int[] neighbor : graph.get(node)) {
int nextNode = neighbor[0];
int time = neighbor[1];
if (dist[node] + time < dist[nextNode]) {
dist[nextNode] = dist[node] + time;
ways[nextNode] = ways[node];
pq.offer(new long[]{dist[nextNode], nextNode});
} else if (dist[node] + time == dist[nextNode]) {
ways[nextNode] = (ways[nextNode] + ways[node]) % MOD;
}
}
}
return ways[n - 1];
}
}
```
```javascript []
var countPaths = function(n, roads) {
const graph = Array.from({ length: n }, () => []);
for (const [u, v, time] of roads) {
graph[u].push([v, time]);
graph[v].push([u, time]);
}
const dist = Array(n).fill(Infinity);
const ways = Array(n).fill(0);
dist[0] = 0;
ways[0] = 1;
const pq = new MinHeap();
pq.push([0, 0]);
const MOD = 1e9 + 7;
while (!pq.isEmpty()) {
const [d, node] = pq.pop();
if (d > dist[node]) continue;
for (const [neighbor, time] of graph[node]) {
if (dist[node] + time < dist[neighbor]) {
dist[neighbor] = dist[node] + time;
ways[neighbor] = ways[node];
pq.push([dist[neighbor], neighbor]);
} else if (dist[node] + time === dist[neighbor]) {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
}
}
}
return ways[n - 1];
};
class MinHeap {
constructor() {
this.heap = [];
}
push(val) {
this.heap.push(val);
this._heapifyUp();
}
pop() {
if (this.heap.length === 1) return this.heap.pop();
const top = this.heap[0];
this.heap[0] = this.heap.pop();
this._heapifyDown();
return top;
}
isEmpty() {
return this.heap.length === 0;
}
_heapifyUp() {
let idx = this.heap.length - 1;
while (idx > 0) {
let parentIdx = Math.floor((idx - 1) / 2);
if (this.heap[parentIdx][0] <= this.heap[idx][0]) break;
[this.heap[parentIdx], this.heap[idx]] = [this.heap[idx], this.heap[parentIdx]];
idx = parentIdx;
}
}
_heapifyDown() {
let idx = 0;
while (2 * idx + 1 < this.heap.length) {
let leftIdx = 2 * idx + 1, rightIdx = 2 * idx + 2;
let smallest = leftIdx;
if (rightIdx < this.heap.length && this.heap[rightIdx][0] < this.heap[leftIdx][0]) {
smallest = rightIdx;
}
if (this.heap[idx][0] <= this.heap[smallest][0]) break;
[this.heap[idx], this.heap[smallest]] = [this.heap[smallest], this.heap[idx]];
idx = smallest;
}
}
}
```
```csharp []
public class Solution {
public int CountPaths(int n, int[][] roads) {
List<(int, int)>[] graph = new List<(int, int)>[n];
for (int i = 0; i < n; i++) graph[i] = new List<(int, int)>();
foreach (var road in roads) {
int u = road[0], v = road[1], time = road[2];
graph[u].Add((v, time));
graph[v].Add((u, time));
}
long[] dist = new long[n];
int[] ways = new int[n];
Array.Fill(dist, long.MaxValue);
Array.Fill(ways, 0);
dist[0] = 0;
ways[0] = 1;
int MOD = 1_000_000_007;
PriorityQueue<(long d, int v), (long d, int v)> pq = new();
pq.Enqueue((0, 0), (0, 0));
while (pq.Count > 0) {
var (d, node) = pq.Dequeue();
if (d > dist[node])
{
continue;
}
foreach (var (neighbor, time) in graph[node]) {
if (dist[node] + time < dist[neighbor]) {
dist[neighbor] = dist[node] + time;
ways[neighbor] = ways[node];
pq.Enqueue((dist[neighbor], neighbor), (dist[neighbor], neighbor));
} else if (dist[node] + time == dist[neighbor]) {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
}
}
}
return ways[n - 1];
}
}
```
```go []
func countPaths(n int, roads [][]int) int {
const MOD = 1_000_000_007
graph := make([][][2]int, n)
for _, road := range roads {
u, v, time := road[0], road[1], road[2]
graph[u] = append(graph[u], [2]int{v, time})
graph[v] = append(graph[v], [2]int{u, time})
}
dist := make([]int, n)
ways := make([]int, n)
for i := range dist {
dist[i] = math.MaxInt64
}
dist[0] = 0
ways[0] = 1
pq := &PriorityQueue{}
heap.Init(pq)
heap.Push(pq, &Item{node: 0, cost: 0})
for pq.Len() > 0 {
cur := heap.Pop(pq).(*Item)
if cur.cost > dist[cur.node] {
continue
}
for _, neighbor := range graph[cur.node] {
nextNode, time := neighbor[0], neighbor[1]
newDist := cur.cost + time
if newDist < dist[nextNode] {
dist[nextNode] = newDist
ways[nextNode] = ways[cur.node]
heap.Push(pq, &Item{node: nextNode, cost: newDist})
} else if newDist == dist[nextNode] {
ways[nextNode] = (ways[nextNode] + ways[cur.node]) % MOD
}
}
}
return ways[n-1]
}
// Priority Queue Implementation
type Item struct {
node int
cost int
}
type PriorityQueue []*Item
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool { return pq[i].cost < pq[j].cost }
func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*Item))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[:n-1]
return item
}
```
```rust []
use std::collections::BinaryHeap;
use std::cmp::Reverse;
const MOD: i32 = 1_000_000_007;
impl Solution {
pub fn count_paths(n: i32, roads: Vec<Vec<i32>>) -> i32 {
let n = n as usize;
let mut graph = vec![vec![]; n];
for road in &roads {
let (u, v, time) = (road[0] as usize, road[1] as usize, road[2]);
graph[u].push((v, time));
graph[v].push((u, time));
}
let mut dist = vec![i64::MAX; n];
let mut ways = vec![0; n];
dist[0] = 0;
ways[0] = 1;
let mut pq = BinaryHeap::new();
pq.push(Reverse((0, 0)));
while let Some(Reverse((cur_dist, node))) = pq.pop() {
if cur_dist > dist[node] {
continue;
}
for &(neighbor, time) in &graph[node] {
let new_dist = cur_dist + time as i64;
if new_dist < dist[neighbor] {
dist[neighbor] = new_dist;
ways[neighbor] = ways[node];
pq.push(Reverse((new_dist, neighbor)));
} else if new_dist == dist[neighbor] {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
}
}
}
ways[n - 1]
}
}
```
```kotlin []
class Solution {
fun countPaths(n: Int, roads: Array<IntArray>): Int {
val graph = Array(n) { mutableListOf<Pair<Int, Int>>() }
for (road in roads) {
val (u, v, time) = road
graph[u].add(Pair(v, time))
graph[v].add(Pair(u, time))
}
val dist = LongArray(n) { Long.MAX_VALUE }
val ways = IntArray(n) { 0 }
val MOD = 1_000_000_007
dist[0] = 0
ways[0] = 1
val pq = PriorityQueue(compareBy<Pair<Long, Int>> { it.first })
pq.add(Pair(0L, 0))
while (pq.isNotEmpty()) {
val (curDist, node) = pq.poll()
if (curDist > dist[node]) continue
for ((neighbor, time) in graph[node]) {
val newDist = curDist + time
if (newDist < dist[neighbor]) {
dist[neighbor] = newDist
ways[neighbor] = ways[node]
pq.add(Pair(newDist, neighbor))
} else if (newDist == dist[neighbor]) {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD
}
}
}
return ways[n - 1]
}
}
```
---

| 79 | 5 | ['Dynamic Programming', 'Shortest Path', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'Kotlin', 'JavaScript', 'C#'] | 6 |
number-of-ways-to-arrive-at-destination | [python] Almost Dijktra, explained | python-almost-dijktra-explained-by-dbabi-p7tw | The idea of this problem is to use Dijkstra algorithm, but also we need to keep not only distances to nodes, but counts as well.\n\n1. If we meet candidate == d | dbabichev | NORMAL | 2021-08-21T16:01:09.796183+00:00 | 2021-08-21T20:02:52.131449+00:00 | 7,036 | false | The idea of this problem is to use Dijkstra algorithm, but also we need to keep not only distances to nodes, but counts as well.\n\n1. If we meet `candidate == dist[neib]`, it means we found one more way to reach node with minimal cost.\n2. If `candidate < dist[neib]`, it means that we found better candidate, so we update distance and put `cnt[neib] = cnt[idx]`.\n\n#### Complexity\nIt is `O((E+V) log V)` for time as classical Dijkstra and `O(E+V)` for space\n\n```python\nclass Solution:\n def countPaths(self, n, roads):\n G = defaultdict(list)\n for x, y, w in roads:\n G[x].append((y, w))\n G[y].append((x, w))\n\n dist = [float(\'inf\')] * n\n dist[0] = 0\n cnt = [0]*n\n cnt[0] = 1\n heap = [(0, 0)]\n\n while heap:\n (min_dist, idx) = heappop(heap)\n if idx == n-1: return cnt[idx] % (10**9 + 7)\n for neib, weight in G[idx]:\n candidate = min_dist + weight\n if candidate == dist[neib]:\n cnt[neib] += cnt[idx]\n\n elif candidate < dist[neib]:\n dist[neib] = candidate\n heappush(heap, (weight + min_dist, neib))\n cnt[neib] = cnt[idx]\n``` | 58 | 2 | [] | 9 |
number-of-ways-to-arrive-at-destination | [C++] Dijkstra - Clean & Concise | c-dijkstra-clean-concise-by-arpit00nine-0r1j | \nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n int mod = 1e9+7;\n vector<vector<pair<int, int>>> graph(n); | Arpit00nine | NORMAL | 2021-08-21T16:51:21.110580+00:00 | 2021-08-21T16:51:21.110610+00:00 | 7,850 | false | ```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n int mod = 1e9+7;\n vector<vector<pair<int, int>>> graph(n);\n for(auto &road: roads) {\n graph[road[0]].push_back({road[1], road[2]});\n graph[road[1]].push_back({road[0], road[2]});\n }\n \n vector<long long> distance(n, LONG_MAX);\n vector<int> path(n, 0);\n \n priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;\n pq.push({0, 0});\n distance[0] = 0;\n path[0] = 1;\n \n while(!pq.empty()) {\n pair<long long, int> t = pq.top();\n pq.pop();\n \n for(auto &nbr: graph[t.second]) {\n long long vert = nbr.first;\n long long edge = nbr.second;\n \n if(distance[vert] > distance[t.second] + edge) {\n distance[vert] = distance[t.second] + edge;\n pq.push({distance[vert], vert});\n path[vert] = path[t.second] %mod;\n }\n else if(distance[vert] == t.first + edge) {\n path[vert] += path[t.second];\n path[vert] %= mod;\n }\n }\n }\n \n return path[n-1];\n }\n};\n``` | 46 | 1 | ['Dynamic Programming', 'C', 'C++'] | 4 |
number-of-ways-to-arrive-at-destination | JAVA STEP BY STEP EXPLAINED✅✅ || SIMPLEST SOLUTION😀✌️ | java-step-by-step-explained-simplest-sol-hw9c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhiyadav05 | NORMAL | 2023-08-30T06:55:17.684401+00:00 | 2023-08-30T06:55:17.684427+00:00 | 3,068 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(m + n log n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(m + n)\n\n\n\n# Code\n```\nclass Pair {\n long first;\n long second;\n\n Pair(long first, long second) {\n this.first = first;\n this.second = second;\n }\n}\n\nclass Solution {\n public int countPaths(int n, int[][] roads) {\n \n // Create an adjacency list to represent the graph\n ArrayList<ArrayList<Pair>> adj = new ArrayList<>();\n\n // Initialize the adjacency list\n for (int i = 0; i < n; i++) {\n adj.add(new ArrayList<>());\n }\n\n int m = roads.length;\n\n // Populate the adjacency list with road information\n for (int i = 0; i < m; i++) {\n adj.get(roads[i][0]).add(new Pair(roads[i][1], roads[i][2]));\n adj.get(roads[i][1]).add(new Pair(roads[i][0], roads[i][2]));\n }\n\n // Create a priority queue for Dijkstra\'s algorithm\n PriorityQueue<Pair> pq = new PriorityQueue<>((Pair1, Pair2) -> Long.compare(Pair1.first, Pair2.first));\n\n // Initialize arrays for distances and ways\n long dist[] = new long[n];\n long ways[] = new long[n];\n long mod = (int)(1e9 + 7);\n\n // Initialize distance and ways arrays\n for (int i = 0; i < n; i++) {\n dist[i] = Long.MAX_VALUE;\n ways[i] = 0;\n }\n\n // Starting node has distance 0 and one way to reach it\n dist[0] = 0;\n ways[0] = 1;\n\n pq.add(new Pair(0, 0));\n\n while (pq.size() != 0) {\n long dis = pq.peek().first;\n long node = pq.peek().second;\n pq.remove();\n\n // Explore neighboring nodes\n for (Pair it : adj.get((int) node)) {\n long adjNode = it.first;\n long edW = it.second;\n\n // If a shorter path is found, update distance and ways\n if (dis + edW < dist[(int) adjNode]) {\n dist[(int) adjNode] = dis + edW;\n pq.add(new Pair(dis + edW, adjNode));\n ways[(int) adjNode] = ways[(int) node];\n } else if (dis + edW == dist[(int) adjNode]) {\n // If multiple paths with the same length are found, add their ways\n ways[(int) adjNode] = (ways[(int) adjNode] + ways[(int) node]) % mod;\n }\n }\n }\n\n // Return the number of ways to reach the last node modulo mod\n return (int)(ways[n - 1] % mod);\n }\n}\n\n``` | 34 | 1 | ['Breadth-First Search', 'Graph', 'Shortest Path', 'Java'] | 3 |
number-of-ways-to-arrive-at-destination | Simple Java Solution | simple-java-solution-by-hxgxs1-gi0o | From the problem statement it was clear we need to apply dijkistra to find shortest path between source and dest.\n2. Well, dijkistra to rescue. Using dijkistra | hxgxs1 | NORMAL | 2021-08-21T16:26:33.697873+00:00 | 2022-03-05T03:32:41.909884+00:00 | 4,632 | false | 1. From the problem statement it was clear we need to apply dijkistra to find shortest path between source and dest.\n2. Well, dijkistra to rescue. Using dijkistra we can keep shortest path by keep relaxing the edges. (Cormen lingo).\n3. Catch is, whenver you find a better way to reach a particular vertex update the number of ways we can reach this vertex same as number of ways we can reach parent vertex.\n4. If we arrive at a vetrex, with same time from parent, we will add the parent\'s number of ways to the current vertex\'s number of ways i.e line dp[v[0]]+=dp[u] in the code\n5. In the End the last veretx will have total number of ways from origin i.e 0\n6. In my solution array named "dp" stores the number of ways from i-th vertex to 0th vertex.\n \n**Similar Problem**: https://leetcode.com/problems/minimum-cost-to-reach-city-with-discounts/\n\nclass Solution {\n int[] dist;\n long[] dp;\n\n public void findDis(Map<Integer, List<int[]>> graph){\n \n PriorityQueue<int[]> pq=new PriorityQueue<>((a, b) -> (a[1]- b[1]));\n pq.add(new int[]{0, 0});\n dist[0]=0;\n dp[0]=1;\n while(!pq.isEmpty()){\n int[] top=pq.poll();\n int u=top[0], d=top[1];\n\t\t\tif(dist[u]< d) // new edit\n\t\t\t\tcontinue;\n for(int[] v: graph.get(u)){\n if(dist[v[0]] > d + v[1]){\n dist[v[0]] = d+v[1];\n dp[v[0]]=dp[u];\n pq.offer(new int[]{v[0], dist[v[0]]});\n }else{\n if(dist[v[0]] == d+v[1]){\n dp[v[0]]+=dp[u];\n dp[v[0]]%= 1_000_000_007;\n }\n }\n }\n }\n }\n \n public int countPaths(int n, int[][] roads) {\n dist=new int[n];\n dp=new long[n];\n Map<Integer, List<int[]>> graph=new HashMap();\n Arrays.fill(dist, Integer.MAX_VALUE);\n for(int i=0;i<n;i++){\n graph.put(i, new ArrayList());\n \n }\n for(int[] e: roads){\n graph.get(e[0]).add(new int[]{e[1], e[2]});\n graph.get(e[1]).add(new int[]{e[0], e[2]});\n }\n findDis(graph);\n \n return (int)dp[n-1]%1_000_000_007;\n \n } \n}\n**Explanation for point 4 above:** \nlets say we had arrived at a vertex v previously and recorded its distance from 0 in dist array as dist[v]=40, which means its takes us time=40 from 0 to reach v. lets say the path it followed was 0 -> u1 -> u2 -> v . Here parent vertex of v was u2.\nNow when we arrive at v again but via a different parent, lets call this parent u3 via path 0 -> u1 -> u3 -> v, and the dist[u3]+ Time[u3, v] = 40, which mean this is a whole new way/path of arriving at v from 0 with same time (40), hence we will add the number ways of u3 to number of ways of v i.e dp[v] = dp[v] +dp[u3].\nHope this explanations helped.\nCheers! | 31 | 2 | [] | 4 |
number-of-ways-to-arrive-at-destination | Min heap | min-heap-by-votrubac-0k5d | This is just Vanila Dijkstra. I would only note that the min heap is required here not only for the performance, but also for the accuracy.\n\nWe process nodes | votrubac | NORMAL | 2021-08-22T23:35:09.905692+00:00 | 2021-08-22T23:37:49.008398+00:00 | 3,904 | false | This is just Vanila Dijkstra. I would only note that the min heap is required here not only for the performance, but also for the accuracy.\n\nWe process nodes in the queue from smallest to largest distance, so that we "wait" for all paths with the same distance to reach the node, accumulating the number of ways to reach that node (`cnt`), before moving further from that node.\n\n**C++**\n```cpp\nint countPaths(int n, vector<vector<int>>& roads) {\n vector<vector<pair<int, int>>> al(n);\n vector<long> time(n, 0), cnt(n, 1);\n for (auto &r : roads) {\n al[r[0]].push_back({r[1], r[2]});\n al[r[1]].push_back({r[0], r[2]});\n }\n priority_queue<pair<long, int>, vector<pair<long, int>>, greater<>> pq;\n pq.push({0, 0});\n while (!pq.empty()) {\n auto[dist, i] = pq.top(); pq.pop();\n for (auto [j, t] : al[i]) {\n if (time[j] == 0 || time[j] >= dist + t) {\n if (time[j] == dist + t)\n cnt[j] = (cnt[j] + cnt[i]) % 1000000007;\n else {\n time[j] = dist + t;\n cnt[j] = cnt[i];\n pq.push({time[j], j});\n }\n }\n }\n }\n return cnt[n - 1];\n}\n``` | 30 | 1 | [] | 3 |
number-of-ways-to-arrive-at-destination | C++ - Dijkstra algorithm + DP (Explained) | c-dijkstra-algorithm-dp-explained-by-sha-qpg6 | Idea:-\nDijkstra algorithm is being used to know the most optimal way to reach the target. \nWe are using an array to store the number of optimal ways to reach | sharmamayank94 | NORMAL | 2021-08-21T16:57:49.016334+00:00 | 2021-08-21T16:57:49.016383+00:00 | 2,461 | false | **Idea:-**\nDijkstra algorithm is being used to know the most optimal way to reach the target. \nWe are using an array to store the number of optimal ways to reach a node. Let us call this\n*paths[]*\n\nLet us consider an example only for DP logic:-\n\n\npaths[S] = 1 As there it is the starting node so there is only 1 way to reach it\npaths[A] = 1, paths[B] = 1, paths[C] = 1\n\nSo for the above example, there are 3 ways to reach D:-\nS->A->D (cost 3)\nS->B->D (cost 2)\nS->C->D (cost 2)\nNow there are two optimal ways which have cost of 2.\nThis can be calculated by knowing two things:-\n1) The least time taken to reach D that is 2 minutes \n2) How many ways were there to reach the predecessors through which we got the least time taken that is B and C\n\nNow as there are 2 optimal ways to reach D we can move forward to nodes E and F \nwhich follows the same principle and gives us \npaths[E] = paths[F] = 2 (Naturally because they have only one predecessor)\n\nFinally node G can be reached in two ways and both ways are optimal. \nTherefore again paths[G] = paths[E] + paths[F] = 4\nand this is how we get our answer. \n\nHere\'s the code:-\n\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n \n /*This is the preparation part of this problem, here we are simply \n\t\tconverting given data in the form of adjacency list which is required to\n\t\trun Dijkstra\'s algorithm */\n vector<pair<long long int, long long int>> adj[201];\n for(int i = 0; i < roads.size(); i++)\n {\n int u = roads[i][0];\n int v = roads[i][1];\n int w = roads[i][2];\n \n adj[u].push_back({v, w});\n adj[v].push_back({u, w});\n }\n\t\t\n priority_queue<pair<long long, long long>> pq;\n pq.push({0, 0});\n vector<long long> distance(201, LLONG_MAX);\n\t\t// Following is the dp array which stores the number of ways to reach a node\n vector<long long> paths(201, 0); \n vector<long long> visited(201, 0);\n \n distance[0] = 0; //because we are starting from 0\n paths[0] = 1;\n \n while(!pq.empty())\n {\n pair<long long, long long> p = pq.top(); pq.pop();\n long long dist = -p.first;\n int u = p.second;\n if(visited[u]) continue;\n visited[u] = 1;\n \n for(int i = 0; i < adj[u].size(); i++)\n {\n int v = adj[u][i].first;\n long long w = adj[u][i].second;\n \n\t\t\t\t/*this means that we\'ve found a better(less time consuming) \n\t\t\t\tway to reach v, now this better way will prevail and \n\t\t\t\twe now don\'t care about past ways therefore total number \n\t\t\t\tof ways to reach v is simply equal to the total number of ways \n\t\t\t\tto reach its parent which is u */\n if(dist + w < distance[v]) \n {\n distance[v] = dist + w;\n pq.push({-(dist+w), v});\n paths[v] = paths[u];\n }\n\t\t\t\t/*here we have a way to reach v which is taking same amount \n\t\t\t\tof time\tas the optimal path but this time parent of v \n\t\t\t\tis different therefore we ways to reach u to current ways \n\t\t\t\tof reaching v*/\n else if(dist+w == distance[v])\n {\n paths[v] = (paths[v] + paths[u])%1000000007;\n pq.push({-(dist+w), v});\n }\n }\n }\n \n return (int) paths[n-1];\n }\n};\n``` | 20 | 0 | [] | 4 |
number-of-ways-to-arrive-at-destination | Dijkstra once with DP||beats 100% | dijkstra-once-with-dpbeats-100-by-anwend-x66z | IntuitionShortest Path problem.
Apply Dijkstra's Agorithm once with considering DP, it can solve the problem.ApproachIt's my Dijkstra's collection https://leetc | anwendeng | NORMAL | 2025-03-23T00:44:39.513204+00:00 | 2025-03-23T01:52:24.051338+00:00 | 3,866 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Shortest Path problem.
Apply Dijkstra's Agorithm once with considering DP, it can solve the problem.
# Approach
<!-- Describe your approach to solving the problem. -->
It's my Dijkstra's collection [https://leetcode.com/problem-list/azox743c/](https://leetcode.com/problem-list/azox743c/)
Use Dijkstra's algorithm.
[LC 1631. [Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/solutions/4049711/c-dijkstra-s-algorithm-vs-dfs-binary-search-vs-union-find-pseudo-metric-91-ms-beats-98-93/). Please turn on English subtitles if necessary]
[https://youtu.be/IkpRzCICL_g?si=B4CSph1_mygXYB2w](https://youtu.be/IkpRzCICL_g?si=B4CSph1_mygXYB2w)
1. Let `vector<int2> adj[200]` be a global variable; due to my experience of allocation for 2D array is time consumming, let's perform only once.
2. define `dijkstra(int start, int n, unsigned long long* dist)` to find the distances for the shortest paths to all nodes & stored in `dist[]`. Using `unsigned long long way[n]` as DP state matrix.
3. In the implementation for Dijkstra's algo, a min heap ` pq` is used for which it contains the info pair `(distance, index)`. the whole process is proceeded by a BFS over `pq`. The DP part is using the argument `paths thru i & not thru i` when `newD==dist[j]`!!!!!
3. In `int countPaths(int n, vector<vector<int>>& roads)`, firstly clear `adj[i]` for every i
4. Build the adjacent list with the info pairs `(time, v) & (time, w)` for weighted edge (v, w) with weight `time`
5. Declare the array `dist[200]` & filled with `ULLONG_MAX`
6. Perform `dijkstra(0, n, dist)` once and return the answer.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O((n+|roads|)\log n)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(n)$
# Code||C++ 0ms beats 100%
```cpp []
const int mod=1e9+7;
using int2=pair<unsigned long long, int>;
vector<int2> adj[200];
class Solution {
public:
unsigned long long dijkstra(int start, int n, unsigned long long* dist){
unsigned long long way[n];
memset(way, 0, sizeof(way));
priority_queue<int2, vector<int2>, greater<int2>> pq;
pq.emplace(0, start);
dist[start]=0;
way[start]=1;
while(!pq.empty()){
auto [d0, i]=pq.top();
pq.pop();
for(auto [d2, j]:adj[i]){
unsigned long long newD=d0+d2;
if (newD<dist[j]){// path thru i, j
dist[j]=newD;
way[j]=way[i];
pq.emplace(newD, j);
}
else if( newD==dist[j]){
way[j]+=way[i]; // paths thru i & not thru i
way[j]%=mod;
}
}
}
return way[n-1];
}
int countPaths(int n, vector<vector<int>>& roads) {
for(int i=0; i<n; i++)
adj[i].clear();
for (auto& e: roads){
int u=e[0], v=e[1];
unsigned long long time=e[2];
adj[u].emplace_back(time, v);
adj[v].emplace_back(time, u);
}
unsigned long long dist[200];
fill(dist, dist+n, ULLONG_MAX);
return dijkstra(0, n, dist);
}
};
``` | 17 | 0 | ['Dynamic Programming', 'Shortest Path', 'C++'] | 6 |
number-of-ways-to-arrive-at-destination | C++ Solution O(n^3) || Floyd Warshall || DP | c-solution-on3-floyd-warshall-dp-by-kesh-jegj | \n#define ll long long int\nconst ll mod= 1e9+7;\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n ll dp[n][n][2]; \n | keshav_jain2161 | NORMAL | 2021-08-21T16:30:26.830000+00:00 | 2021-08-21T16:30:26.830062+00:00 | 1,419 | false | ```\n#define ll long long int\nconst ll mod= 1e9+7;\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n ll dp[n][n][2]; \n // dp[i][j][0] stores minimum distance and dp[i][j][1] stores number of ways to reach with the minimum distance dp[i][j][0]\n for(ll i=0; i<n; i++){\n for(ll j=0; j<n; j++){\n if(i!=j){\n dp[i][j][0] = 1e13;\n dp[i][j][1]=0;\n }\n else\n {\n dp[i][j][0]=0;\n dp[i][j][1]=1;\n }\n }\n }\n for(ll i=0; i<roads.size(); i++){\n dp[roads[i][0]][roads[i][1]][0]=roads[i][2];\n \n dp[roads[i][1]][roads[i][0]][0]=roads[i][2];\n dp[roads[i][0]][roads[i][1]][1]=1;\n \n dp[roads[i][1]][roads[i][0]][1]=1;\n }\n for(ll mid=0; mid<n; mid++){\n for(ll i=0; i<n; i++){\n for(ll j=0; j<n; j++){\n if(i!=mid && j!=mid){\n if(dp[i][mid][0]+dp[mid][j][0]<dp[i][j][0]){\n dp[i][j][0]=dp[i][mid][0]+dp[mid][j][0];\n dp[i][j][1] = (dp[i][mid][1]*dp[mid][j][1])%mod;\n }\n else if(dp[i][j][0]==dp[i][mid][0]+dp[mid][j][0]){\n dp[i][j][1] = (dp[i][j][1]+dp[i][mid][1]*dp[mid][j][1])%mod;\n }\n }\n }\n }\n }\n return dp[n-1][0][1];\n }\n};\n``` | 15 | 0 | [] | 3 |
number-of-ways-to-arrive-at-destination | Dijkstra's Algorithm | dijkstras-algorithm-by-zaidzack-4p6g | \nclass Solution {\n int mod = 1_000_000_007;\n public int countPaths(int n, int[][] roads) {\n List<int[]>[] graph = new ArrayList[n];\n \n | zaidzack | NORMAL | 2022-08-20T09:57:21.149159+00:00 | 2022-08-20T09:57:21.149191+00:00 | 3,142 | false | ```\nclass Solution {\n int mod = 1_000_000_007;\n public int countPaths(int n, int[][] roads) {\n List<int[]>[] graph = new ArrayList[n];\n \n for(int i = 0; i < n; i++)\n graph[i] = new ArrayList<int[]>();\n \n for(int[] edge: roads)\n {\n int src = edge[0], dest = edge[1], time = edge[2];\n \n graph[src].add(new int[]{dest, time});\n graph[dest].add(new int[]{src, time});\n }\n \n return shortestPath(graph, 0, n);\n }\n \n private int shortestPath(List<int[]>[] graph, int src, int target)\n {\n PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[1] - b[1]);\n \n int[] minCost = new int[target];\n Arrays.fill(minCost, Integer.MAX_VALUE);\n \n long[] ways = new long[target];\n ways[0] = 1;\n minCost[0] = 0;\n \n pq.offer(new int[]{0, 0});\n \n while(!pq.isEmpty())\n {\n int[] current = pq.poll();\n int city = current[0];\n int curCost = current[1];\n \n if(curCost > minCost[city]) \n continue;\n \n for(int[] neighbourData: graph[city])\n {\n int neighbour = neighbourData[0], time = neighbourData[1];\n \n if(curCost + time < minCost[neighbour])\n {\n minCost[neighbour] = curCost + time;\n pq.offer(new int[]{neighbour, minCost[neighbour]});\n ways[neighbour] = ways[city];\n }\n else if(curCost + time == minCost[neighbour])\n ways[neighbour] = (ways[neighbour] + ways[city]) % mod;\n }\n }\n return (int)ways[target - 1];\n }\n}\n``` | 13 | 1 | ['Java'] | 3 |
number-of-ways-to-arrive-at-destination | Python - Dijkstra's Algorithm (Min Heap Implementation) >90% time score | python-dijkstras-algorithm-min-heap-impl-as12 | ```\nfrom heapq import *\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n # create adjacency list\n adj_list = | kaustav43 | NORMAL | 2022-01-06T05:31:55.362029+00:00 | 2022-01-06T05:33:00.724816+00:00 | 2,596 | false | ```\nfrom heapq import *\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n # create adjacency list\n adj_list = defaultdict(list)\n for i,j,k in roads:\n adj_list[i].append((j,k))\n adj_list[j].append((i,k))\n \n start = 0\n end = n-1\n \n # set minimum distance of all nodes but start to infinity.\n # min_dist[i] = [minimum time from start, number of ways to get to node i in min time]\n min_dist = {i:[float(\'inf\'),0] for i in adj_list.keys()}\n min_dist[start] = [0,1]\n \n # Heap nodes in the format (elapsed time to get to that node, node index)\n # This is done so as to allow the heap to pop node with lowest time first\n # Push first node to heap.\n heap = [(0, start)]\n while heap:\n elapsed_time, node = heappop(heap)\n # if nodes getting popped have a higher elapsed time than minimum time required\n # to reach end node, means we have exhausted all possibilities\n # Note: we can do this only because time elapsed cannot be negetive\n if elapsed_time > min_dist[end][0]:\n break\n for neighbor, time in adj_list[node]:\n # check most expected condition first. Reduce check time for if statement\n if (elapsed_time + time) > min_dist[neighbor][0]:\n continue\n # if time is equal to minimum time to node, add the ways to get to node to\n # the next node in minimum time\n elif (elapsed_time + time) == min_dist[neighbor][0]:\n min_dist[neighbor][1] += min_dist[node][1]\n else: # node has not been visited before. Set minimum time \n min_dist[neighbor][0] = elapsed_time + time\n min_dist[neighbor][1] = min_dist[node][1]\n heappush(heap, (elapsed_time+time,neighbor))\n\n return min_dist[end][1]%(pow(10,9)+7)\n \n | 13 | 0 | ['Graph', 'Heap (Priority Queue)', 'Python', 'Python3'] | 1 |
number-of-ways-to-arrive-at-destination | C++ - Dijkstra algorithm || Easy Understanding | c-dijkstra-algorithm-easy-understanding-kch2k | Apply Dijkstra shortest path algorithm as the problem involves shortest distance from source to destination. We need to modify Dijkstra\'s algorithm so that it | sahooc029 | NORMAL | 2022-10-14T05:01:01.482358+00:00 | 2022-10-15T02:48:45.041467+00:00 | 2,315 | false | Apply **Dijkstra shortest path algorithm** as the problem involves shortest distance from source to destination. We need to modify **Dijkstra\'s algorithm** so that it can keep track of the path counts from node 0 to every other node in a way that it can keep track of the distance from every other node to node 0 with the shortest possible distance as the ultimate goal of the problem.\n\n* If you find a shortest distance then update the path with new value.\n* If you find a equal shortest distance then add the value of the parrent node path number to the current node.\n\n\n**P.S**: Use **`long long`** properly.\n\n\n**Time Complexity**: **```O(E * logV + N)```**, where **E** is number of roads, **V** is number of nodes.\n**Space Complexity**: **```O(E + V)```**\n\n**C++ code:**\n```\n\nclass Solution { \nprivate:\n int dijkstra(vector<pair<int, int>> adj[], int n) {\n\t\tint mod = 1e9 + 7;\n // priority queue for keep track of min distance \n priority_queue<pair<long long, long long>, vector<pair<long long, long long>>, greater<pair<long long, long long>>> pq;\n // store the distance and number of paths\n vector<long long> dis(n, 1e15), path(n, 0);\n\n // push the initial node and distance to reach start is 0\n pq.push({0, 0});\n // mark the distance to 0\n dis[0] = 0;\n // mark the path number to 1\n path[0] = 1;\n\n // until queue is not empty\n while (!pq.empty()) {\n // get the top (min distance) element from priority queue and remove\n long long dist = pq.top().first;\n int node = pq.top().second;\n pq.pop();\n\n // iterate on its adjacent nodes\n for (auto &child : adj[node]) {\n int adjNode = child.first;\n long long wt = child.second;\n\n // if it min distance to reach at a node then update it\n if (dist + wt < dis[adjNode]) {\n dis[adjNode] = dist + wt;\n path[adjNode] = path[node];\n pq.push({dist + wt, adjNode});\n }\n else if (dist + wt == dis[adjNode]) {\n //if it already visited with the shortest dis then increse the path with the current node path\n path[adjNode] = (path[node] + path[adjNode]) % mod;\n }\n }\n }\n\n return path[n - 1];\n }\n \npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n // adjacency list\n vector<pair<int, int>> adj[n];\n\n // create the graph\n for (auto &v : roads) {\n adj[v[0]].push_back({v[1], v[2]});\n adj[v[1]].push_back({v[0], v[2]});\n }\n \n return dijkstra(adj, n);\n }\n};\n\n```\n\nPlease **upvote** if you find this helpful. **:)**\nFeel free to comment in case of any doubt. | 11 | 0 | ['Graph', 'C', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | [Python] Dijkstra + DP solution (60-70% faster) | python-dijkstra-dp-solution-60-70-faster-o3c5 | Logic\n- Dijkstra algorithm can only get the shortest time from src to dst.\n- What we want to get is the number of ways with minimum time from src to dst.\n- W | lluB | NORMAL | 2022-06-02T13:08:01.235792+00:00 | 2022-06-02T13:10:48.407894+00:00 | 1,204 | false | ## Logic\n- Dijkstra algorithm can only get the shortest time from src to dst.\n- What we want to get is **the number of ways with minimum time from src to dst.**\n- We need\n\t1) **times** array : to check the minimum time to take from src to times[i].\n\t2) **ways** array : to check the total ways from src to ways[i] within minimum time.\n\n- if find same time path... update **ways** only \n ... because we don\'t need to update time \n ... and we don\'t need to go to that node(already in our heap)\n\n\n## EX1\n**times** [INF, INF, INF, INF, INF, INF] => [0, 2, 5, 5, 6, 7]\n**ways** [0, 0, 0, 0, 0, 0] => [1, 1, 1, 1, 1, 2, 4]\n\n\n## Reference\nIdea and code from ... #happycoding\nhttps://www.youtube.com/watch?v=1JCXqupyLoQ&t=465s\n\n\n\n```\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n\n #1. graph\n graph = collections.defaultdict(list)\n for u, v, t in roads:\n graph[u].append((v, t))\n graph[v].append((u, t))\n \n #2. times, ways array initializer\n times = [float(\'inf\')] * n\n ways = [0] * n\n \n times[0] = 0\n ways[0] = 1\n \n #3. dijkstra\n pq = [(0, 0)] # time, node\n \n while pq:\n old_t, u = heapq.heappop(pq) # current time, current node\n \n for v, t in graph[u]:\n new_t = old_t + t\n \n # casual logic: update shorter path\n if new_t < times[v]:\n times[v] = new_t\n ways[v] = ways[u]\n heapq.heappush(pq, (new_t, v))\n \n # if find same time path... update ways only\n elif new_t == times[v]:\n ways[v] += ways[u]\n \n modulo = 10 ** 9 + 7\n \n return ways[n-1] % modulo\n```\n\n**Please upvote if it helped! :)** | 11 | 0 | ['Dynamic Programming', 'Breadth-First Search', 'Python'] | 2 |
number-of-ways-to-arrive-at-destination | Dijkstra + Keeping Count of the number of ways | dijkstra-keeping-count-of-the-number-of-wdf3p | \ntypedef long long ll;\n typedef pair<long long, long long> ppl;\n int countPaths(int n, vector<vector<int>>& roads) {\n int mod = (1e9+7);\n | prakhar3099 | NORMAL | 2021-11-09T01:44:21.756800+00:00 | 2021-11-09T01:44:21.756850+00:00 | 1,381 | false | ```\ntypedef long long ll;\n typedef pair<long long, long long> ppl;\n int countPaths(int n, vector<vector<int>>& roads) {\n int mod = (1e9+7);\n vector<ll> dist(n,LLONG_MAX);\n vector<int> ways(n,0);\n priority_queue<ppl, vector<ppl>, greater<ppl>> pq;\n \n dist[0] = 0; ways[0]=1; pq.push({0,0});\n \n vector<ppl> adj[n];\n \n //making adjacency list\n for(auto x : roads){\n adj[x[0]].push_back({x[1],x[2]});\n adj[x[1]].push_back({x[0],x[2]});\n }\n \n while(!pq.empty()){\n ll distance = pq.top().first;\n ll node = pq.top().second;\n pq.pop();\n for(auto x : adj[node]){\n ll adjNode = x.first;\n ll nextDist = x.second;\n \n if(distance+nextDist < dist[adjNode]){\n dist[adjNode] = distance+nextDist;\n ways[adjNode] = ways[node];\n pq.push({dist[adjNode],adjNode});\n } else if(distance+nextDist == dist[adjNode]){\n ways[adjNode] = (ways[adjNode]+ways[node])%mod;\n }\n }\n }\n \n return ways[n-1];\n }\n``` | 10 | 0 | ['C'] | 0 |
number-of-ways-to-arrive-at-destination | C++ Dijkstra Solution O(V^2 LogV) | c-dijkstra-solution-ov2-logv-by-ahsan83-alki | Runtime: 96 ms, faster than 46.70% of C++ online submissions for Number of Ways to Arrive at Destination.\nMemory Usage: 40.5 MB, less than 7.91% of C++ online | ahsan83 | NORMAL | 2021-08-25T12:59:11.427986+00:00 | 2021-08-25T13:03:58.223589+00:00 | 1,347 | false | Runtime: 96 ms, faster than 46.70% of C++ online submissions for Number of Ways to Arrive at Destination.\nMemory Usage: 40.5 MB, less than 7.91% of C++ online submissions for Number of Ways to Arrive at Destination.\n\nNote: Solution taken from other post.\n\n```\nWe can find the shortest distance from any vertex to another using Dijkstra Algo in a weighted graph. \nHere we have to find the number of ways we can go from source to destination and so we keep an array\nto store the ways count for all nodes as we progress in Dijkstra Algo and use it for the neighbor nodes\nwhich is actually a DP approach. \n\nNow, each time we relax the cost of neighbor node we find a better distance for neighbor node and so \nthe number of way to go to neighbor node = number way to come to the current node and so we update \nthe ways[neighbor] = ways[node]. Also when we see that neighbor node cost and current node \ncost + edge cost is same then this is another way to go to the neighbor node with min cost and so we \nupdate neighbor node ways count as ways[neighbor] += ways[node]. Also when pop a node with cost \ngreater than the current cost of the node then we will ignore the furthur operations cause the cost \nis higher and we need to find min cost paths.\n```\n\n```\nclass Solution {\npublic:\n \n int countPaths(int n, vector<vector<int>>& roads) {\n \n // Adjacency list of the undirected graph\n vector<vector<vector<int>>>adjL(n);\n \n // distance vector of nodes\n vector<long>dist(n,LONG_MAX);\n \n // populate Adjacency List {node, cost} pair\n for(int i=0;i<roads.size();i++)\n {\n adjL[roads[i][0]].push_back({roads[i][1],roads[i][2]});\n adjL[roads[i][1]].push_back({roads[i][0],roads[i][2]});\n }\n \n int MOD = 1000000007;\n \n // track the number of ways to reach node with min cost\n vector<long>ways(n,0);\n \n // source node has way 1 \n ways[0] = 1;\n \n // push source node with distance 0, PQ stores {cost, node} pair\n priority_queue<pair<long,int>,vector<pair<long,int>>,greater<>>pQ;\n pQ.push({0,0});\n dist[0] = 0;\n \n long cost;\n int node; \n while(!pQ.empty())\n {\n cost = pQ.top().first;\n node = pQ.top().second;\n pQ.pop();\n \n // if cost is higher than current node distance then we ignroe furthur operations\n if(dist[node]<cost)continue;\n \n // loop through neighbors and relax the neighbor nodes\n for(auto &adj: adjL[node])\n { \n // relax neighbor nodes and push in to PQ\n // neighbor node ways will be updated with current node ways as\n // we find a better cost for neighbor node\n if(dist[node]+adj[1] < dist[adj[0]])\n {\n dist[adj[0]] = dist[node]+adj[1];\n ways[adj[0]] = ways[node];\n pQ.push({dist[adj[0]],adj[0]});\n }\n \n // if current node distance + edge cost = neighbor node cost then\n // this is another way to reach the neighbor node with min cost\n // so we update neighbor node ways as ways[neighbor] += ways[node]\n else if(dist[node]+adj[1] == dist[adj[0]])\n {\n ways[adj[0]] = (ways[adj[0]] + ways[node])%MOD;\n }\n }\n }\n\n // return the number of ways to reach destination node\n return ways[n-1];\n }\n};\n``` | 10 | 0 | ['Dynamic Programming', 'Graph', 'C'] | 1 |
number-of-ways-to-arrive-at-destination | 1976. Number of Ways to Arrive at Destination [C++] | 1976-number-of-ways-to-arrive-at-destina-lj9w | IntuitionTo find the number of shortest paths from node 0 to node n - 1, we need a way to not only compute the shortest distances but also count how many such p | moveeeax | NORMAL | 2025-03-23T18:36:13.224222+00:00 | 2025-03-23T18:36:13.224222+00:00 | 172 | false |
# Intuition
To find the number of shortest paths from node 0 to node n - 1, we need a way to not only compute the shortest distances but also count how many such paths exist. A modified Dijkstra's algorithm allows us to achieve both goals simultaneously.
# Approach
We represent the graph using an adjacency list and initialize the distance to all nodes as infinite except the start node (node 0), which is set to 0. We also keep a `ways` array to count the number of shortest paths to each node. As we run Dijkstra's algorithm using a min-heap (priority queue), we update both the shortest distances and the number of ways to reach each node. If we find a shorter path to a node, we update both its distance and path count. If we find an alternative path with the same minimum distance, we add to the path count modulo \(10^9 + 7\).
# Complexity
- Time complexity:
$$O((E + V) \log V)$$
where \(V\) is the number of nodes and \(E\) is the number of roads (edges). This is due to Dijkstra's algorithm with a min-heap.
- Space complexity:
$$O(E + V)$$
for the graph representation, distance array, ways array, and priority queue.
# Code
```cpp
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
const int MOD = 1e9 + 7;
vector<vector<pair<int, int>>> graph(n);
for (auto& road : roads) {
int u = road[0], v = road[1], t = road[2];
graph[u].emplace_back(v, t);
graph[v].emplace_back(u, t);
}
vector<long long> dist(n, LLONG_MAX);
vector<int> ways(n, 0);
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> pq;
dist[0] = 0;
ways[0] = 1;
pq.emplace(0, 0);
while (!pq.empty()) {
auto [d, u] = pq.top();
pq.pop();
if (d > dist[u]) continue;
for (auto& [v, t] : graph[u]) {
long long newDist = d + t;
if (newDist < dist[v]) {
dist[v] = newDist;
ways[v] = ways[u];
pq.emplace(newDist, v);
} else if (newDist == dist[v]) {
ways[v] = (ways[v] + ways[u]) % MOD;
}
}
}
return ways[n - 1];
}
};
``` | 9 | 0 | ['C++'] | 0 |
number-of-ways-to-arrive-at-destination | Python - Dijkstra's Algorithm | python-dijkstras-algorithm-by-ajith6198-j77u | \nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n graph = defaultdict(dict)\n for u, v, w in roads:\n | ajith6198 | NORMAL | 2021-08-21T17:33:21.696448+00:00 | 2021-08-21T17:33:21.696488+00:00 | 1,300 | false | ```\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n graph = defaultdict(dict)\n for u, v, w in roads:\n graph[u][v] = graph[v][u] = w\n dist = {i:float(inf) for i in range(n)}\n ways = {i:0 for i in range(n)}\n dist[0], ways[0] = 0, 1\n heap = [(0, 0)]\n while heap:\n d, u = heapq.heappop(heap)\n if dist[u] < d: \n continue\n for v in graph[u]:\n if dist[v] == dist[u] + graph[u][v]:\n ways[v] += ways[u]\n elif dist[v] > dist[u] + graph[u][v]:\n dist[v] = dist[u] + graph[u][v]\n ways[v] = ways[u]\n heapq.heappush(heap, (dist[v], v))\n return ways[n-1] % ((10 ** 9) + 7)\n``` | 9 | 0 | ['Python'] | 1 |
number-of-ways-to-arrive-at-destination | Simple Djikstra Approach✅✅ | simple-djikstra-approach-by-arunk_leetco-vvge | IntuitionTo count the number of different shortest paths from node 0 to node n - 1, we need more than just the shortest distances.
Dijkstra’s algorithm is ideal | arunk_leetcode | NORMAL | 2025-03-23T05:11:59.791662+00:00 | 2025-03-23T05:11:59.791662+00:00 | 2,027 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To count the number of different shortest paths from node 0 to node n - 1, we need more than just the shortest distances.
Dijkstra’s algorithm is ideal for finding shortest paths in weighted graphs, and we can enhance it to count the number
of ways we can reach each node with the shortest distance.
# Approach
<!-- Describe your approach to solving the problem. -->
- Build the graph using adjacency lists with edge weights.
- Use Dijkstra's algorithm to find the shortest distance from node 0 to all nodes.
- Maintain a ways[] array where ways[i] = number of shortest paths to node i.
- Use a min-heap (priority queue) to always process the node with the smallest known distance.
- For each neighbor:
- If a shorter path is found, update distance and ways.
- If an equally short path is found, add the number of ways.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(E * log V), where E is the number of edges and V is the number of nodes.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(V + E), for the graph, distance array, ways array, and priority queue.
# Code
```cpp []
#define ll long long
#define pll pair<ll, ll>
class Solution {
public:
int MOD = 1e9 + 7;
int countPaths(int n, vector<vector<int>>& roads) {
vector<vector<pll>> graph(n);
for(auto& road: roads) {
ll u = road[0], v = road[1], time = road[2];
graph[u].push_back({v, time});
graph[v].push_back({u, time});
}
return dijkstra(graph, n, 0);
}
int dijkstra(const vector<vector<pll>>& graph, int n, int src) {
vector<ll> dist(n, LONG_MAX);
vector<ll> ways(n);
ways[src] = 1;
dist[src] = 0;
priority_queue<pll, vector<pll>, greater<>> minHeap;
minHeap.push({0, 0}); // dist, src
while (!minHeap.empty()) {
auto[d, u] = minHeap.top(); minHeap.pop();
if (d > dist[u]) continue; // Skip if `d` is not updated to latest version!
for(auto [v, time] : graph[u]) {
if (dist[v] > d + time) {
dist[v] = d + time;
ways[v] = ways[u];
minHeap.push({dist[v], v});
} else if (dist[v] == d + time) {
ways[v] = (ways[v] + ways[u]) % MOD;
}
}
}
return ways[n-1];
}
};
| 8 | 0 | ['Graph', 'Topological Sort', 'Shortest Path', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | Optimizing Shortest Paths: Efficient Route Counting with Dijkstra’s Algorithm | 💯✔️ | optimizing-shortest-paths-efficient-rout-wxq3 | IntuitionThe problem is a variation of the shortest path problem in a weighted graph. Since we need to count the number of ways to reach the destination in the | iamanrajput | NORMAL | 2025-03-23T08:52:00.958473+00:00 | 2025-03-23T08:52:00.958473+00:00 | 1,244 | false | # Intuition
The problem is a variation of the shortest path problem in a weighted graph. Since we need to count the number of ways to reach the destination in the shortest time, Dijkstra’s algorithm is a natural choice. By tracking both distances and path counts, we can efficiently determine the result.
# Approach
1. **Graph Representation**: Construct an adjacency list from the given roads.
2. **Dijkstra's Algorithm**: Use a min-heap (priority queue) to find the shortest paths from node `0` to all other nodes.
3. **Path Counting**: Maintain an array `ways` where `ways[i]` stores the number of ways to reach node `i` in the shortest time.
4. **Heap Processing**:
- Pop the node with the smallest distance from the heap.
- If a shorter path to a neighboring node is found, update its distance and reset the path count.
- If an equal shortest path is found, add to the existing path count.
5. **Return Result**: The number of ways to reach node `n-1` modulo \(10^9 + 7\).
# Complexity
- **Time Complexity**: `O(E log V)`, where E is the number of roads and `V` is the number of intersections, due to Dijkstra’s algorithm with a priority queue.
- **Space Complexity**: `O(V + E)` for storing the graph, distances, and path counts.
# Code
```java []
class Solution {
public int countPaths(int n, int[][] roads) {
final long inf = Long.MAX_VALUE / 2;
final int mod = (int) 1e9 + 7;
long[][] g = new long[n][n];
for (var e : g) {
Arrays.fill(e, inf);
}
for (var r : roads) {
int u = r[0], v = r[1], t = r[2];
g[u][v] = t;
g[v][u] = t;
}
g[0][0] = 0;
long[] dist = new long[n];
Arrays.fill(dist, inf);
dist[0] = 0;
long[] f = new long[n];
f[0] = 1;
boolean[] vis = new boolean[n];
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 0; j < n; j++) {
if (!vis[j] && (t == -1 || dist[j] < dist[t])) {
t = j;
}
}
vis[t] = true;
for (int j = 0; j < n; j++) {
if (j == t) {
continue;
}
long ne = dist[t] + g[t][j];
if (dist[j] > ne) {
dist[j] = ne;
f[j] = f[t];
} else if (dist[j] == ne) {
f[j] = (f[j] + f[t]) % mod;
}
}
}
return (int) f[n - 1];
}
}
``` | 7 | 0 | ['Java'] | 1 |
number-of-ways-to-arrive-at-destination | ✅ C++ || Dijkstra || Priority_Queue || Easy to understand | c-dijkstra-priority_queue-easy-to-unders-wt06 | \n#define ll long long\nclass Solution {\npublic:\n int MOD = 1e9 + 7;\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<ll,ll>> | indresh149 | NORMAL | 2022-10-07T07:39:21.881492+00:00 | 2022-10-07T07:39:21.881528+00:00 | 1,244 | false | ```\n#define ll long long\nclass Solution {\npublic:\n int MOD = 1e9 + 7;\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<ll,ll>> adj[n];\n for(auto it:roads){\n adj[it[0]].push_back({it[1],it[2]});\n adj[it[1]].push_back({it[0],it[2]});\n }\n \n priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>> pq;\n vector<ll> dist(n,LONG_MAX), ways(n,0);\n dist[0] = 0;\n ways[0] = 1;\n \n pq.push({0,0});\n \n while(!pq.empty()){\n ll dis = pq.top().first;\n ll node = pq.top().second;\n pq.pop();\n \n for(auto it: adj[node]){\n ll adjNode = it.first;\n ll edW = it.second;\n //this is the first time I am coming\n //with the short distance\n if(dis + edW < dist[adjNode]){\n dist[adjNode] = dis + edW;\n pq.push({dis + edW,adjNode});\n ways[adjNode] = ways[node];\n }\n else if(dis +edW == dist[adjNode]){\n ways[adjNode] = (ways[adjNode] + ways[node])%MOD;\n }\n }\n }\n return ways[n-1];\n }\n};\n```\n**Don\'t forget to Upvote the post, if it\'s been any help to you** | 7 | 0 | ['C'] | 1 |
number-of-ways-to-arrive-at-destination | Graph, Dijkstra, Shortest Path, Dynamic Programming O((E+V)logV) | graph-dijkstra-shortest-path-dynamic-pro-9u8p | IntuitionTo find the number of ways to reach the destination node n - 1 from node 0 in the shortest possible time, we need more than just the shortest distance | Nyx_owl | NORMAL | 2025-03-23T12:04:25.614573+00:00 | 2025-03-23T12:04:25.614573+00:00 | 753 | false | # Intuition
To find the number of ways to reach the destination node `n - 1` from node `0` in the *shortest* possible time, we need more than just the shortest distance — we must also track **how many different paths** lead to that shortest distance.
A natural fit for shortest path problems is **Dijkstra’s algorithm**. By extending it with a `pathCount` array, we can track how many distinct paths reach each node using the current known shortest time.
# Approach
1. **Graph Representation:** First, we construct an adjacency list from the input `roads` array. Each edge is bidirectional and stores a pair `(neighbor, time)`.
2. **Dijkstra’s Algorithm:**
- Use a min-heap (priority queue) to explore the graph starting from node `0`.
- Track the shortest known time to reach each node using `shortest_time` array.
- Track the number of distinct paths that achieve this shortest time using `pathCount` array.
3. **Relaxation:** For each node processed:
- If a neighboring node can be reached in a strictly shorter time, update the shortest time and set its path count to that of the current node.
- If the neighboring node can be reached in **equal** shortest time, increment its path count by the current node’s count.
4. **Result:** Return the count of shortest paths to node `n - 1`, modulo \(10^9 + 7\).
# Complexity
- **Time complexity:**
$$O((E + V) \log V)$$
Where `V` is the number of intersections (nodes) and `E` is the number of roads (edges). The log factor comes from the priority queue operations.
- **Space complexity:**
$$O(V + E)$$
For the graph representation, heap, and auxiliary arrays (`shortest_time`, `pathCount`).
# Code
```python []
from typing import List
from collections import defaultdict
import heapq
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
MOD = 10**9 + 7
# Build the graph
graph = defaultdict(list)
for u, v, time in roads:
graph[u].append((v, time))
graph[v].append((u, time))
# Dijkstra's initialization
min_heap = [(0, 0)] # (time, node)
shortest_time = [float('inf')] * n
pathCount = [0] * n
shortest_time[0] = 0
pathCount[0] = 1
while min_heap:
curr_time, u = heapq.heappop(min_heap)
# Skip if we already found a better time
if curr_time > shortest_time[u]:
continue
for v, t in graph[u]:
new_time = curr_time + t
if new_time < shortest_time[v]:
shortest_time[v] = new_time
pathCount[v] = pathCount[u]
heapq.heappush(min_heap, (new_time, v))
elif new_time == shortest_time[v]:
pathCount[v] = (pathCount[v] + pathCount[u]) % MOD
return pathCount[n - 1] % MOD
| 6 | 0 | ['Graph', 'Shortest Path', 'Python3'] | 1 |
number-of-ways-to-arrive-at-destination | [C++] Dijkstra | Clean Code | Video Solution with Diagram | c-dijkstra-clean-code-video-solution-wit-ozjy | Complete Video Solution with full explanationIntuitionThe problem requires finding the shortest path from node 0 to node n-1 while also counting how many differ | abhinavbansal19961996 | NORMAL | 2025-03-23T10:16:48.094494+00:00 | 2025-03-23T10:16:48.094494+00:00 | 656 | false | # Complete Video Solution with full explanation
https://youtu.be/qJfun8H8T-A
# Intuition
The problem requires finding the shortest path from node 0 to node n-1 while also counting how many different ways exist to reach the destination in the shortest possible time.
Since the graph consists of weighted edges (time taken between intersections), the most efficient way to solve this problem is Dijkstra’s Algorithm, which finds the shortest path in a weighted graph.
However, we also need to track the number of ways to reach each node in the shortest time, which requires an additional count vector.
# Approach
1. Graph Representation
Convert the roads list into an adjacency list where each node stores its connected nodes along with the respective travel time.
2. Dijkstra’s Algorithm (Modified)
Use a min-heap (priority queue) to always process the node with the shortest known distance first.
Maintain an array shortestTime[i], which stores the minimum time required to reach node i.
Maintain another array ways[i] to track the number of ways to reach node i using the shortest time.
3. Processing Nodes
Start from node 0 with a time of 0 (shortestTime[0] = 0 and ways[0] = 1).
For each node u, check all its neighbors (v, time).
If reaching v via u results in a shorter time, update shortestTime[v] and set ways[v] = ways[u].
If reaching v via u results in the same shortest time, increment ways[v] by ways[u].
Continue until all nodes are processed.
4. Final Output
The value ways[n-1] gives the number of ways to reach the destination n-1 in the shortest time.
# Complexity
- Time complexity:
Since we use Dijkstra’s Algorithm with a priority queue, the time complexity is: 𝑂((𝑉+𝐸)log𝑉)
Extracting from the priority queue takes O(log V), and we do this for all nodes (O(V log V)).
Each edge is processed once (O(E log V)).
- Space complexity:
The adjacency list takes O(V+E).
The shortestTime and ways arrays take O(V).
The priority queue takes up to O(V).
# Code
```cpp []
class Solution {
public:
int MOD = 1e9 + 7;
int countPaths(int n, vector<vector<int>>& roads) {
// Graph Representation: Adjacency List
vector<vector<pair<int, int>>> graph(n);
for (auto& road : roads) {
graph[road[0]].emplace_back(road[1], road[2]);
graph[road[1]].emplace_back(road[0], road[2]);
}
// Min-Heap {shortestTime, node}
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> minHeap;
vector<long long> shortestTime(n, LLONG_MAX);
vector<int> ways(n, 0);
// Initial Conditions
shortestTime[0] = 0;
ways[0] = 1;
minHeap.emplace(0, 0);
while (!minHeap.empty()) {
auto [time, node] = minHeap.top();
minHeap.pop();
if (time > shortestTime[node]) continue; // Ignore outdated states
for (auto [neighbor, travelTime] : graph[node]) {
long long newTime = time + travelTime;
// Found a shorter path
if (newTime < shortestTime[neighbor]) {
shortestTime[neighbor] = newTime;
ways[neighbor] = ways[node]; // Reset the ways count
minHeap.emplace(newTime, neighbor);
}
// Found an equally short path
else if (newTime == shortestTime[neighbor]) {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
}
}
}
return ways[n - 1];
}
};
``` | 6 | 0 | ['C++'] | 1 |
number-of-ways-to-arrive-at-destination | ✅🚀easy Dijkstra+graph+friendly with explain code in all languages | easy-dijkstragraphfriendly-with-explain-94f5j | guys please upvote for support 😊🌟 Intuition and Approach — Shortest Path + Counting Paths1.🏙️ Problem:
We need to find the number of shortest paths from the st | thakur_saheb | NORMAL | 2025-03-23T02:14:23.984140+00:00 | 2025-03-23T17:52:44.841041+00:00 | 1,696 | false | # *guys please upvote for support 😊*
# 🌟 Intuition and Approach — Shortest Path + Counting Paths
# 1.🏙️ **Problem:**
- ###### We need to find the number of shortest paths from the starting node (0) to the destination node (n-1) in a weighted graph.
# 2. 🛣️ Graph Representation:
- ###### The graph is represented using an adjacency list (adj), where each node connects to its neighbors along with the travel time (edge weight).
# 3.⏳ Dijkstra's Algorithm:
- ###### We use Dijkstra’s algorithm to find the shortest paths.
- ###### Maintain shortesttime[] to store the minimum time to reach each node.
- ###### Use a priority queue (pq) to explore nodes based on the smallest travel time.
# 4.🔢 Counting Paths:
- ###### Maintain cnt[] to track the number of ways to reach each node via the shortest path.
- ###### If a shorter path is found, update the time and reset the count for that node.
- ###### If an equally short path is found, add the number of paths from the current node to the neighbor.
# 5.🔁 Process:
- ###### Explore neighbors of each node from the priority queue.
- ###### If a shorter path to a neighbor is found, update both the time and count.
- ###### If an equally short path is found, accumulate the count.
# 6.🎯 Result:
- ###### The result is stored in cnt[n-1], representing the number of shortest paths to the last node.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O((N+E)logN)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N+E)
# Code
```cpp []
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
int mod=1e9+7;
vector<vector<pair<int,int>>>adj(n);
for(auto r:roads){
adj[r[0]].push_back({r[1],r[2]});
adj[r[1]].push_back({r[0],r[2]});
}
priority_queue<pair<long long,int>,vector<pair<long long,int>>,greater<>>pq;
vector<long long>shortesttime(n,LLONG_MAX);
vector<int>cnt(n,0);
shortesttime[0]=0;
cnt[0]=1;
pq.push({0,0});
while(!pq.empty()){
long long time=pq.top().first;
int node=pq.top().second;
pq.pop();
if(time>shortesttime[node])continue;
for(auto [nbr,rtime]:adj[node]){
if(time+rtime<shortesttime[nbr]){
shortesttime[nbr]=time+rtime;
cnt[nbr]=cnt[node];
pq.push({shortesttime[nbr],nbr});
}
else if(time+rtime==shortesttime[nbr]){
cnt[nbr]=(cnt[nbr]+cnt[node])%mod;
}
}
}
return cnt[n-1];
}
};
```
```python []
import heapq
from collections import defaultdict
import sys
def countPaths(n, roads):
mod = 10**9 + 7
adj = defaultdict(list)
for u, v, t in roads:
adj[u].append((v, t))
adj[v].append((u, t))
shortesttime = [sys.maxsize] * n
cnt = [0] * n
pq = [(0, 0)] # (time, node)
shortesttime[0] = 0
cnt[0] = 1
while pq:
time, node = heapq.heappop(pq)
if time > shortesttime[node]:
continue
for nbr, rtime in adj[node]:
if time + rtime < shortesttime[nbr]:
shortesttime[nbr] = time + rtime
cnt[nbr] = cnt[node]
heapq.heappush(pq, (shortesttime[nbr], nbr))
elif time + rtime == shortesttime[nbr]:
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod
return cnt[-1]
```
``` java []
import java.util.*;
class Solution {
public int countPaths(int n, int[][] roads) {
int mod = 1_000_000_007;
List<int[]>[] adj = new ArrayList[n];
for (int i = 0; i < n; i++) adj[i] = new ArrayList<>();
for (int[] r : roads) {
adj[r[0]].add(new int[]{r[1], r[2]});
adj[r[1]].add(new int[]{r[0], r[2]});
}
long[] shortesttime = new long[n];
int[] cnt = new int[n];
Arrays.fill(shortesttime, Long.MAX_VALUE);
PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(a -> a[0]));
shortesttime[0] = 0;
cnt[0] = 1;
pq.offer(new long[]{0, 0});
while (!pq.isEmpty()) {
long[] top = pq.poll();
long time = top[0];
int node = (int) top[1];
if (time > shortesttime[node]) continue;
for (int[] edge : adj[node]) {
int nbr = edge[0], rtime = edge[1];
if (time + rtime < shortesttime[nbr]) {
shortesttime[nbr] = time + rtime;
cnt[nbr] = cnt[node];
pq.offer(new long[]{shortesttime[nbr], nbr});
} else if (time + rtime == shortesttime[nbr]) {
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod;
}
}
}
return cnt[n - 1];
}
}
```
```js []
var countPaths = function(n, roads) {
const mod = 1e9 + 7;
const adj = Array.from({ length: n }, () => []);
for (const [u, v, t] of roads) {
adj[u].push([v, t]);
adj[v].push([u, t]);
}
const shortestTime = Array(n).fill(Infinity);
const cnt = Array(n).fill(0);
const minHeap = [[0, 0]]; // [time, node]
shortestTime[0] = 0;
cnt[0] = 1;
while (minHeap.length) {
minHeap.sort((a, b) => a[0] - b[0]); // Ensure it's a min-heap
const [time, node] = minHeap.shift();
if (time > shortestTime[node]) continue;
for (const [nbr, rtime] of adj[node]) {
if (time + rtime < shortestTime[nbr]) {
shortestTime[nbr] = time + rtime;
cnt[nbr] = cnt[node];
minHeap.push([shortestTime[nbr], nbr]);
} else if (time + rtime === shortestTime[nbr]) {
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod;
}
}
}
return cnt[n - 1];
};
```
```C# []
using System;
using System.Collections.Generic;
public class Solution {
public int CountPaths(int n, int[][] roads) {
int mod = 1_000_000_007;
var adj = new List<(int, int)>[n];
for (int i = 0; i < n; i++) adj[i] = new List<(int, int)>();
foreach (var road in roads) {
adj[road[0]].Add((road[1], road[2]));
adj[road[1]].Add((road[0], road[2]));
}
long[] shortestTime = new long[n];
Array.Fill(shortestTime, long.MaxValue);
int[] cnt = new int[n];
var pq = new SortedSet<(long, int)> { (0, 0) };
shortestTime[0] = 0;
cnt[0] = 1;
while (pq.Count > 0) {
var (time, node) = pq.Min;
pq.Remove(pq.Min);
if (time > shortestTime[node]) continue;
foreach (var (nbr, rtime) in adj[node]) {
if (time + rtime < shortestTime[nbr]) {
pq.Remove((shortestTime[nbr], nbr));
shortestTime[nbr] = time + rtime;
cnt[nbr] = cnt[node];
pq.Add((shortestTime[nbr], nbr));
}
else if (time + rtime == shortestTime[nbr]) {
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod;
}
}
}
return cnt[n - 1];
}
}
```
```php []
function countPaths($n, $roads) {
$mod = 1e9 + 7;
$adj = array_fill(0, $n, []);
foreach ($roads as $road) {
$adj[$road[0]][] = [$road[1], $road[2]];
$adj[$road[1]][] = [$road[0], $road[2]];
}
$shortestTime = array_fill(0, $n, PHP_INT_MAX);
$cnt = array_fill(0, $n, 0);
$pq = new SplPriorityQueue();
$pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);
$shortestTime[0] = 0;
$cnt[0] = 1;
$pq->insert([0, 0], 0);
while (!$pq->isEmpty()) {
$current = $pq->extract();
[$time, $node] = $current['data'];
if ($time > $shortestTime[$node]) continue;
foreach ($adj[$node] as [$nbr, $rtime]) {
if ($time + $rtime < $shortestTime[$nbr]) {
$shortestTime[$nbr] = $time + $rtime;
$cnt[$nbr] = $cnt[$node];
$pq->insert([$shortestTime[$nbr], $nbr], -$shortestTime[$nbr]);
} elseif ($time + $rtime === $shortestTime[$nbr]) {
$cnt[$nbr] = ($cnt[$nbr] + $cnt[$node]) % $mod;
}
}
}
return $cnt[$n - 1];
}
```
```ruby []
def count_paths(n, roads)
mod = 1_000_000_007
adj = Array.new(n) { [] }
roads.each do |u, v, t|
adj[u] << [v, t]
adj[v] << [u, t]
end
shortest_time = Array.new(n, Float::INFINITY)
cnt = Array.new(n, 0)
pq = [[0, 0]] # [time, node]
shortest_time[0] = 0
cnt[0] = 1
until pq.empty?
time, node = pq.shift
next if time > shortest_time[node]
adj[node].each do |nbr, rtime|
if time + rtime < shortest_time[nbr]
shortest_time[nbr] = time + rtime
cnt[nbr] = cnt[node]
pq << [shortest_time[nbr], nbr]
elsif time + rtime == shortest_time[nbr]
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod
end
end
pq.sort_by!(&:first)
end
cnt[-1]
end
```
```kotlin []
import java.util.PriorityQueue
fun countPaths(n: Int, roads: Array<IntArray>): Int {
val mod = 1_000_000_007
val adj = Array(n) { mutableListOf<Pair<Int, Int>>() }
for (road in roads) {
adj[road[0]].add(Pair(road[1], road[2]))
adj[road[1]].add(Pair(road[0], road[2]))
}
val shortestTime = LongArray(n) { Long.MAX_VALUE }
val cnt = IntArray(n) { 0 }
val pq = PriorityQueue(compareBy<Pair<Long, Int>> { it.first })
shortestTime[0] = 0
cnt[0] = 1
pq.add(Pair(0L, 0))
while (pq.isNotEmpty()) {
val (time, node) = pq.poll()
if (time > shortestTime[node]) continue
for ((nbr, rtime) in adj[node]) {
if (time + rtime < shortestTime[nbr]) {
shortestTime[nbr] = time + rtime
cnt[nbr] = cnt[node]
pq.add(Pair(shortestTime[nbr], nbr))
} else if (time + rtime == shortestTime[nbr]) {
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod
}
}
}
return cnt[n - 1]
}
```
```swift []
import Foundation
func countPaths(_ n: Int, _ roads: [[Int]]) -> Int {
let mod = 1_000_000_007
var adj = Array(repeating: [(Int, Int)](), count: n)
for road in roads {
adj[road[0]].append((road[1], road[2]))
adj[road[1]].append((road[0], road[2]))
}
var shortestTime = Array(repeating: Int.max, count: n)
var cnt = Array(repeating: 0, count: n)
var pq = [(0, 0)]
shortestTime[0] = 0
cnt[0] = 1
while !pq.isEmpty {
let (time, node) = pq.removeFirst()
if time > shortestTime[node] { continue }
for (nbr, rtime) in adj[node] {
if time + rtime < shortestTime[nbr] {
shortestTime[nbr] = time + rtime
cnt[nbr] = cnt[node]
pq.append((shortestTime[nbr], nbr))
} else if time + rtime == shortestTime[nbr] {
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod
}
}
}
return cnt[n - 1]
}
```
```rust []
use std::collections::BinaryHeap;
use std::cmp::Reverse;
fn count_paths(n: i32, roads: Vec<Vec<i32>>) -> i32 {
let mod_val = 1_000_000_007;
let n = n as usize;
let mut adj = vec![vec![]; n];
for road in roads.iter() {
let u = road[0] as usize;
let v = road[1] as usize;
let t = road[2] as i64;
adj[u].push((v, t));
adj[v].push((u, t));
}
let mut shortest_time = vec![i64::MAX; n];
let mut cnt = vec![0; n];
let mut pq = BinaryHeap::new();
shortest_time[0] = 0;
cnt[0] = 1;
pq.push(Reverse((0, 0))); // (time, node)
while let Some(Reverse((time, node))) = pq.pop() {
if time > shortest_time[node] {
continue;
}
for &(nbr, rtime) in &adj[node] {
let new_time = time + rtime;
if new_time < shortest_time[nbr] {
shortest_time[nbr] = new_time;
cnt[nbr] = cnt[node];
pq.push(Reverse((new_time, nbr)));
} else if new_time == shortest_time[nbr] {
cnt[nbr] = (cnt[nbr] + cnt[node]) % mod_val;
}
}
}
cnt[n - 1] as i32
}
```
```GO []
package main
import (
"container/heap"
"fmt"
"math"
)
const MOD = 1_000_000_007
type Pair struct {
time, node int
}
type MinHeap []Pair
func (h MinHeap) Len() int { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i].time < h[j].time }
func (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(x interface{}) {
*h = append(*h, x.(Pair))
}
func (h *MinHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[:n-1]
return x
}
func countPaths(n int, roads [][]int) int {
adj := make([][]Pair, n)
for _, road := range roads {
u, v, t := road[0], road[1], road[2]
adj[u] = append(adj[u], Pair{t, v})
adj[v] = append(adj[v], Pair{t, u})
}
shortestTime := make([]int, n)
cnt := make([]int, n)
for i := range shortestTime {
shortestTime[i] = math.MaxInt64
}
shortestTime[0] = 0
cnt[0] = 1
pq := &MinHeap{{0, 0}}
heap.Init(pq)
for pq.Len() > 0 {
top := heap.Pop(pq).(Pair)
time, node := top.time, top.node
if time > shortestTime[node] {
continue
}
for _, neighbor := range adj[node] {
nbr, rtime := neighbor.node, neighbor.time
newTime := time + rtime
if newTime < shortestTime[nbr] {
shortestTime[nbr] = newTime
cnt[nbr] = cnt[node]
heap.Push(pq, Pair{newTime, nbr})
} else if newTime == shortestTime[nbr] {
cnt[nbr] = (cnt[nbr] + cnt[node]) % MOD
}
}
}
return cnt[n-1]
}
func main() {
roads := [][]int{{0, 1, 4}, {0, 2, 1}, {1, 2, 2}, {1, 3, 5}, {2, 3, 1}}
fmt.Println(countPaths(4, roads)) // Output: 2
}
```

| 6 | 0 | ['Swift', 'Python', 'C++', 'Java', 'Go', 'Rust', 'Ruby', 'Kotlin', 'JavaScript', 'C#'] | 2 |
number-of-ways-to-arrive-at-destination | Dijkstra Pattern | dijkstra-pattern-by-dixon_n-b8co | Important problem\nCheapest flight,minimum effort and more\n# Code\njava []\nclass Solution {\n public int countPaths(int numIntersections, int[][] roads) {\ | Dixon_N | NORMAL | 2024-06-18T00:58:11.775265+00:00 | 2024-06-18T00:58:11.775293+00:00 | 1,108 | false | Important problem\nCheapest flight,minimum effort and more\n# Code\n```java []\nclass Solution {\n public int countPaths(int numIntersections, int[][] roads) {\n ArrayList<ArrayList<Node>> adjacencyList = new ArrayList<>();\n for (int i = 0; i < numIntersections; i++) {\n adjacencyList.add(new ArrayList<>());\n }\n for (int[] road : roads) {\n int intersection1 = road[0], intersection2 = road[1], travelTime = road[2];\n adjacencyList.get(intersection1).add(new Node(travelTime, intersection2));\n adjacencyList.get(intersection2).add(new Node(travelTime, intersection1));\n }\n PriorityQueue<Node> minHeap = new PriorityQueue<>((x, y) -> Long.compare(x.distanceFromSource, y.distanceFromSource));\n long[] distanceFromSource = new long[numIntersections];\n int[] numWaysToReach = new int[numIntersections];\n for (int i = 0; i < numIntersections; i++) {\n distanceFromSource[i] = Long.MAX_VALUE;\n numWaysToReach[i] = 0;\n }\n distanceFromSource[0] = 0;\n numWaysToReach[0] = 1;\n minHeap.add(new Node(0, 0));\n int modulo = (int) (1e9 + 7);\n while (!minHeap.isEmpty()) {\n long currentDistance = minHeap.peek().distanceFromSource;\n int currentIntersection = minHeap.peek().intersection;\n minHeap.remove();\n for (Node neighbor : adjacencyList.get(currentIntersection)) {\n long neighborIntersection = neighbor.intersection;\n long travelTimeToNeighbor = neighbor.distanceFromSource;\n if (currentDistance + travelTimeToNeighbor < distanceFromSource[(int) neighborIntersection]) {\n distanceFromSource[(int) neighborIntersection] = currentDistance + travelTimeToNeighbor;\n minHeap.add(new Node(currentDistance + travelTimeToNeighbor, (int) neighborIntersection));\n numWaysToReach[(int) neighborIntersection] = numWaysToReach[currentIntersection];\n } else if (currentDistance + travelTimeToNeighbor == distanceFromSource[(int) neighborIntersection]) {\n numWaysToReach[(int) neighborIntersection] = (numWaysToReach[(int) neighborIntersection] + \n numWaysToReach[currentIntersection]) % modulo;\n }\n }\n }\n return numWaysToReach[numIntersections - 1] % modulo;\n }\n class Node {\n long distanceFromSource;\n int intersection;\n Node(long distanceFromSource, int intersection) {\n this.distanceFromSource = distanceFromSource;\n this.intersection = intersection;\n }\n }\n}\n``` | 6 | 0 | ['Java'] | 5 |
number-of-ways-to-arrive-at-destination | Dijkstra's Algo using Priority queue || C++ Solution | dijkstras-algo-using-priority-queue-c-so-60a2 | \n# Complexity\n- Time complexity: O(E logV)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(V) + O(N)\n Add your space complexity here, e. | aayu_t | NORMAL | 2023-06-18T19:45:07.923053+00:00 | 2023-06-18T19:45:42.424900+00:00 | 2,407 | false | \n# Complexity\n- Time complexity: **O(E logV)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(V) + O(N)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& a) {\n vector<pair<long long, long long>> adj[n];\n // it -> from to weight\n for(auto it:a){\n adj[it[0]].push_back({it[1], it[2]});\n adj[it[1]].push_back({it[0], it[2]});\n }\n vector<long long> ways(n, 0);\n vector<long long> dist(n, LONG_MAX);\n priority_queue<pair<long long, long long>, vector<pair<long long, long long>>, greater<pair<long long, long long>>> pq; // dist node\n pq.push({0, 0});\n dist[0] = 0;\n ways[0] = 1;\n while(!pq.empty()){\n long long d = pq.top().first;\n long long node = pq.top().second;\n pq.pop();\n for(auto it:adj[node]){\n long long wt = it.second;\n long long adjnode = it.first;\n if(d + wt < dist[adjnode]){\n dist[adjnode] = d + wt;\n ways[adjnode] = ways[node];\n pq.push({ dist[adjnode], adjnode});\n }\n else if(d + wt == dist[adjnode])\n ways[adjnode]=((ways[adjnode] % 1000000007 + ways[node]) % 1000000007) % 1000000007;\n }\n }\n return ways[n - 1] % 1000000007;\n }\n};\n``` | 6 | 0 | ['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | C++ || Dijkstra algorithm | c-dijkstra-algorithm-by-njyotiprakash189-gxu5 | Time Complexity=O(V+E)\nSpace Complexity=O(V+E)\nV=number of node\nE=number of edges\n\n\n \n #define ll long long\n class Solution {\n public:\n i | njyotiprakash189 | NORMAL | 2022-10-15T14:15:48.204911+00:00 | 2022-10-15T14:15:48.204948+00:00 | 671 | false | **Time Complexity=O(V+E)\nSpace Complexity=O(V+E)**\nV=number of node\nE=number of edges\n\n\n \n #define ll long long\n class Solution {\n public:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<ll,ll>> adj[n];\n for(auto it:roads){\n adj[it[0]].push_back({it[1],it[2]});\n adj[it[1]].push_back({it[0],it[2]});\n }\n \n priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>> pq;\n vector<ll> ways(n,0),dist(n,LONG_MAX);\n pq.push({0,0});\n dist[0]=0;\n ways[0]=1;\n int mod=1e9+7;\n \n while(!pq.empty()){\n ll dis=pq.top().first;\n ll node=pq.top().second;\n pq.pop();\n \n for(auto it:adj[node]){\n ll adjNode=it.first;\n ll edgeW=it.second;\n \n if(edgeW+dis< dist[adjNode]){\n dist[adjNode]=edgeW+dis;\n pq.push({edgeW+dis,adjNode});\n ways[adjNode]=ways[node];\n }\n else if(edgeW+dis==dist[adjNode]){\n ways[adjNode]=(ways[adjNode]+ways[node])%mod;\n }\n \n }\n }\n return ways[n-1]%mod;\n }\n };\n\t\n\t/**Please Don\'t forget to Upvote the post**/\n\n\n | 6 | 0 | ['Graph', 'C'] | 2 |
number-of-ways-to-arrive-at-destination | Clean Dijkstra implementation || c++ | clean-dijkstra-implementation-c-by-binay-xobx | \n#define ll long long\n#define pi pair<ll , ll>\nconst int mod = 1e9+7;\n\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n | binayKr | NORMAL | 2022-07-16T09:56:58.216080+00:00 | 2022-07-16T09:56:58.216125+00:00 | 433 | false | ```\n#define ll long long\n#define pi pair<ll , ll>\nconst int mod = 1e9+7;\n\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n \n \n vector<pi> adj[n]; // node-> pair< adjNode, distance>\n for(auto &it : roads)\n {\n adj[it[0]].push_back({it[1],it[2]});\n adj[it[1]].push_back({it[0],it[2]});\n }\n \n priority_queue<pi, vector<pi>, greater<pi>> pq;\n vector<ll> d(n,LONG_MAX), cnt(n,0);\n pq.push({0,0});\n d[0] = 0;\n cnt[0] = 1;\n \n while(!pq.empty())\n {\n ll node = pq.top().second;\n ll dist = pq.top().first;\n pq.pop();\n \n for(auto &it : adj[node])\n {\n ll nextNode = it.first;\n ll nextDist = it.second;\n \n if(dist + nextDist < d[nextNode])\n {\n cnt[nextNode] = cnt[node]; //just inherit the no. of shortest path found till node\n d[nextNode] = dist + nextDist;\n pq.push({d[nextNode],nextNode});\n }\n \n else if(dist + nextDist == d[nextNode])\n {\n cnt[nextNode] = (cnt[nextNode] + cnt[node])%mod; //(the no. of shortest path found till node + the no. of shortest path found till nextNode)\n }\n \n else continue;\n }\n }\n \n return cnt[n-1]%mod;\n }\n};\n``` | 6 | 0 | ['C'] | 0 |
number-of-ways-to-arrive-at-destination | Java, basic minHeap Dijkstra with minor changes | java-basic-minheap-dijkstra-with-minor-c-s1jv | Perform regular Dijkstra with some adjustments: \nadd one more ways[] array alongside to distance[] basic array.\nif there is an adjacent vertex with total time | dimitr | NORMAL | 2021-08-24T11:11:00.662068+00:00 | 2021-08-25T01:47:46.349710+00:00 | 1,190 | false | Perform regular Dijkstra with some adjustments: \nadd one more ways[] array alongside to distance[] basic array.\nif there is an adjacent vertex with total time less than currne time + edge distance, then update best distance and go ahead as usual, by adding edge into minHeap\nif same time already exists, then we have come from another vertex, but with the same overall time, so let sum both approaches ways count.\n\n```\n public int countPaths(int n, int[][] roads) {\n final int mod = 1000000007;\n int[][] adj = new int[n][n];\n for(int[] road : roads){\n adj[ road[0] ][ road[1] ] = road[2];\n adj[ road[1] ][ road[0] ] = road[2];\n }\n \n int[] time = new int[n], ways = new int[n];\n Arrays.fill(time,1,n, Integer.MAX_VALUE);\n ways[0]=1;\n \n Queue<int[]> q = new PriorityQueue<>((a,b)->a[1]-b[1]);\n q.offer(new int[]{0,0}); \n\n while(!q.isEmpty()){\n int[] e = q.poll();\n int v = e[0], t = e[1];\n if(t <= time[v]){\n for(int i=0;i<n;i++){\n if(adj[v][i]!=0){\n if(time[v]+adj[v][i] < time[i]){ \n time[i] = time[v]+adj[v][i]; \n \n q.offer(new int[]{i,time[i]});\n ways[i] = ways[v];\n }else if(time[v]+adj[v][i] == time[i]){ \n ways[i] = (ways[i]+ways[v])%mod; \n }\n }\n }\n }\n }\n return ways[n-1];\n }\n``` | 6 | 0 | [] | 3 |
number-of-ways-to-arrive-at-destination | [Python3] dfs + dp | python3-dfs-dp-by-ye15-bivb | \n\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n graph = {}\n for u, v, time in roads: \n graph. | ye15 | NORMAL | 2021-08-21T16:02:29.266918+00:00 | 2021-08-24T15:28:52.316273+00:00 | 1,807 | false | \n```\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n graph = {}\n for u, v, time in roads: \n graph.setdefault(u, {})[v] = time\n graph.setdefault(v, {})[u] = time\n \n dist = [inf]*n\n dist[-1] = 0\n stack = [(n-1, 0)]\n while stack: \n x, t = stack.pop()\n if t == dist[x]: \n for xx in graph.get(x, {}): \n if t + graph[x][xx] < dist[xx]: \n dist[xx] = t + graph[x][xx]\n stack.append((xx, t + graph[x][xx]))\n \n @cache\n def fn(x):\n """Return """\n if x == n-1: return 1 \n if dist[x] == inf: return 0 \n ans = 0 \n for xx in graph.get(x, {}): \n if graph[x][xx] + dist[xx] == dist[x]: ans += fn(xx)\n return ans % 1_000_000_007\n \n return fn(0)\n```\n\n```\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n graph = {}\n for u, v, time in roads: \n graph.setdefault(u, []).append((v, time))\n graph.setdefault(v, []).append((u, time))\n \n dist = [inf] * n\n dist[0] = 0\n ways = [0] * n\n ways[0] = 1\n \n pq = [(0, 0)]\n while pq: \n d, u = heappop(pq)\n if d > dist[-1]: break\n if d == dist[u]: \n for v, time in graph.get(u, []): \n if dist[u] + time < dist[v]: \n dist[v] = dist[u] + time\n ways[v] = ways[u]\n heappush(pq, (dist[v], v))\n elif dist[u] + time == dist[v]: ways[v] += ways[u]\n return ways[-1] % 1_000_000_007\n``` | 6 | 1 | ['Python3'] | 1 |
number-of-ways-to-arrive-at-destination | Striver's code that passes all TESTCASES | strivers-code-that-passes-all-testcases-2fns3 | Just change everything to long long.
and take mod=1e9+7Complexity
Time complexity: Simple Djkastra algo->ElogV
Space complexity: O(N)
Code | now_now123 | NORMAL | 2024-12-20T04:49:20.216480+00:00 | 2024-12-20T04:49:20.216480+00:00 | 1,396 | false | Just change everything to long long.
and take mod=1e9+7
# Complexity
- Time complexity: Simple Djkastra algo->ElogV
- Space complexity: O(N)
# Code
```cpp []
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
vector<vector<pair<long long, long long>>> adj(n);
for(auto it:roads){
adj[it[0]].push_back({it[1],it[2]});
adj[it[1]].push_back({it[0],it[2]});
}
priority_queue<pair<long long,long long>,
vector<pair<long long,long long> >,
greater<pair<long long,long long>>>pq;
vector<long long>dist(n,1e12) , ways(n,0);
dist[0]=0;
ways[0]=1; long long mod= 1e9+7;
pq.push({0,0}) ;//{dist,node};
while(!pq.empty()){
long long dis = pq.top().first;
long long node = pq.top().second;
pq.pop();
for(auto it:adj[node]){
long long adjNode=it.first;
long long edW=it.second;
//this is the 1st time i am coming with this short distance.
if(dis+edW<dist[adjNode]){
dist[adjNode]=dis+edW;
pq.push({dis+edW,adjNode});
ways[adjNode]=ways[node]%mod;
}
else if(dis+edW==dist[adjNode]){
ways[adjNode]=(ways[adjNode]+ways[node])%mod;
}
}
}
return ways[n-1]%mod;
}
};
``` | 5 | 0 | ['Graph', 'Shortest Path', 'C++'] | 2 |
number-of-ways-to-arrive-at-destination | Well Explained | well-explained-by-aayushagarwal001-ei1p | Intuition\nThe problem involves finding the number of distinct paths from the starting node 0 to the ending node n-1 in an undirected graph with weighted edges. | AayushAgarwal001 | NORMAL | 2024-06-16T13:38:10.961928+00:00 | 2024-06-16T13:38:10.961959+00:00 | 1,095 | false | # Intuition\nThe problem involves finding the number of distinct paths from the starting node `0` to the ending node `n-1` in an undirected graph with weighted edges. Each path\'s weight is calculated as the sum of edge weights along that path. Additionally, we need to keep track of the number of such paths because the weights might be the same for different paths.\n\n# Approach\n1. **Graph Representation:**\n - Use an adjacency list (`adj`) to represent the graph where each node points to a list of pairs representing its neighbors and the edge weights.\n\n2. **Dijkstra\'s Algorithm with Modifications:**\n - Use a priority queue (`pq`) to facilitate Dijkstra\'s algorithm. Each entry in the priority queue is a pair of `(time_to_reach_node, node)`.\n - Use two vectors, `time_to_reach` to store the minimum time to reach each node from the source node `0` and `ways` to store the number of distinct ways to reach each node.\n - Initialize `time_to_reach[0] = 0` and `ways[0] = 1`, indicating there is one way to reach the starting node with a weight of `0`.\n\n3. **Processing Nodes:**\n - Begin with the source node `0` in the priority queue with `time_to_reach[0] = 0` and `ways[0] = 1`.\n - Extract the node with the smallest `time_to_reach` from the priority queue. Update the `time_to_reach` and `ways` for its neighbors if a shorter path is found or if the same path weight can be reached through multiple ways.\n\n4. **Result Computation:**\n - After processing all nodes, return `ways[n-1] % MOD`, which represents the number of distinct paths to reach node `n-1`.\n\n5. **Edge Cases:**\n - Handle cases where nodes might be unreachable by checking if `ways[n-1]` remains `0`, indicating no valid path exists.\n\n# Complexity\n- **Time Complexity:** $$(O((n + m) \\log n))$$\n - Where \\(n\\) is the number of nodes and \\(m\\) is the number of edges (roads).\n - Each node and edge is processed once. Operations involving the priority queue have a logarithmic time complexity.\n\n- **Space Complexity:** $$(O(n))$$\n - Space is primarily used for the adjacency list (`adj`), priority queue (`pq`), `time_to_reach`, and `ways` vectors.\n\n\n# Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n const long long MOD = 1e9 + 7;\n vector<pair<int, int>> adj[n];\n\n for (int i = 0; i < roads.size(); i++) {\n adj[roads[i][0]].push_back({roads[i][1], roads[i][2]});\n adj[roads[i][1]].push_back({roads[i][0], roads[i][2]});\n }\n\n priority_queue<pair<long long, long long>, \n vector<pair<long long, long long>>, \n greater<pair<long long,long long>>> pq;\n\n vector<long long> time_to_reach(n, LONG_MAX);\n vector<long long> ways(n, 0);\n\n pq.push({0, 0});\n time_to_reach[0] = 0;\n ways[0] = 1;\n\n while(!pq.empty()){\n long long time = pq.top().first;\n long long node = pq.top().second;\n\n pq.pop();\n\n if (time > time_to_reach[node]) continue;\n\n\n for(auto it : adj[node]){\n long long nxt_node = it.first;\n long long new_time = it.second;\n\n if(time_to_reach[nxt_node] > time + new_time){\n time_to_reach[nxt_node] = time + new_time;\n ways[nxt_node] = ways[node];\n pq.push({time_to_reach[nxt_node], nxt_node});\n }\n else if (time_to_reach[nxt_node] == time + new_time) {\n ways[nxt_node] = (ways[nxt_node] + ways[node]) % MOD;\n\n }\n }\n }\n\n return ways[n-1]% MOD;\n }\n};\n``` | 5 | 1 | ['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'C++'] | 0 |
number-of-ways-to-arrive-at-destination | [C++] || Dijkstra Algorithm || DP | c-dijkstra-algorithm-dp-by-deleted_user-2vd2 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe minimum cost can be found using Dijkstra Algorithm and we can use DP array to store | deleted_user | NORMAL | 2023-07-26T14:41:53.249478+00:00 | 2023-07-26T14:41:53.249497+00:00 | 827 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe minimum cost can be found using Dijkstra Algorithm and we can use DP array to store the count value.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n-> Use Dijkstra to find the shortest amount of time.\n-> Use DP to keep states of shortest time fo a node (the count array)\n-> while finding shortest time\n-> when we find a shorter time we change dp by new value by the dp value of its parent (from where its coming from).\n-> when we find equal time we add value to current node\'s dp, i.e, adding the dp values of its parent or the adjacent where its coming from.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(E*log(N))\nE --> number of edges\nN --> number of vertices or nodes\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<vector<pair<int, int>>> adj(n);\n for(auto it : roads)\n {\n int from = it[0];\n int to = it[1];\n int time = it[2];\n adj[from].push_back({to, time});\n adj[to].push_back({from, time});\n }\n long long mod = 1e9 + 7;\n priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;\n pq.push({0, 0});\n vector<long long> dist(n, 1e15);\n vector<long long> count(n, 0);\n dist[0] = 0;\n count[0] = 1;\n while(pq.size())\n {\n long long timetaken = pq.top().first;\n int curr = pq.top().second;\n pq.pop();\n for(auto it : adj[curr])\n {\n int neigh = it.first;\n int traveltime = it.second;\n if(dist[neigh] == timetaken + traveltime)\n {\n count[neigh] = (count[neigh] + count[curr]) % mod;\n }\n else if(dist[neigh] > timetaken + traveltime)\n {\n dist[neigh] = timetaken + traveltime;\n pq.push({dist[neigh], neigh});\n count[neigh] = count[curr];\n }\n }\n }\n return count[n-1] % mod;\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Graph', 'C++'] | 0 |
number-of-ways-to-arrive-at-destination | C++ - Dijkstra algorithm || Easy Understanding || Beats 90 percent | c-dijkstra-algorithm-easy-understanding-85pmh | Code\n\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& r) {\n int mod=1e9+7;\n vector<vector<pair<long long,long long>> | anandmohit852 | NORMAL | 2023-01-18T12:03:08.356788+00:00 | 2023-01-18T12:03:08.356828+00:00 | 1,473 | false | # Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& r) {\n int mod=1e9+7;\n vector<vector<pair<long long,long long>>>adj(n);\n for(int i=0;i<r.size();i++){\n adj[r[i][0]].push_back({r[i][1],r[i][2]});\n adj[r[i][1]].push_back({r[i][0],r[i][2]});\n }\n vector<long long>c(n,0);\n c[0]=1;\n priority_queue<pair<long long,long long>, vector<pair<long long,long long>>, greater<pair<long long,long long>>> pq;\n vector<long long int>dist(n,1e15);\n dist[0]=0;\n pq.push({0,0});\n while(pq.empty()==false){\n auto x=pq.top();\n long long dis=x.first;\n long long node=x.second;\n pq.pop();\n for(auto it:adj[node]){\n long long wt=it.second;\n long long y=it.first; \n if(wt+dis<dist[y]){\n dist[y]=(wt+dis);\n pq.push({dist[y],y});\n c[y]=c[node];\n }\n else if((wt+dis)==dist[y]){\n c[y]=(c[y]+c[node])%mod;\n }\n \n }\n }\n return c[n-1];\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
number-of-ways-to-arrive-at-destination | Java Solution using Dijkstra Algorithm | java-solution-using-dijkstra-algorithm-b-lvvj | class Solution {\n \n private int dijkstra(int[][] roads,int n){\n long mod=(int)1e9+7;\n\t\t//PriorityQueue is used for sorting by time\n Q | vaibhavDiwan_1999 | NORMAL | 2022-02-09T15:57:48.387071+00:00 | 2022-02-09T16:05:18.373794+00:00 | 1,103 | false | class Solution {\n \n private int dijkstra(int[][] roads,int n){\n long mod=(int)1e9+7;\n\t\t//PriorityQueue is used for sorting by time\n Queue<long[]> pq = new PriorityQueue<>((l, r) -> Long.compare(l[1], r[1]));\n //Number of ways to reach a vertex from 0 in minimum time\n\t\tlong[] ways=new long[n];\n\t\t//Distance array to store the minimum time taken to reach a vertex\n long[] dist=new long[n];\n\t\t//Filling dist array with infinite distance.\n Arrays.fill(dist,(long)1e18);\n dist[0]=0;\n\t\t//Number of ways to reach 0 is 1.\n ways[0]=1;\n\t\t//We have to form graph roads array.\n ArrayList<long[]>[] graph=new ArrayList[n];\n for(int i=0;i<graph.length;i++) graph[i]=new ArrayList<>();\n for(int[] road:roads){\n graph[road[0]].add(new long[]{road[1],road[2]});\n graph[road[1]].add(new long[]{road[0],road[2]});\n }\n pq.add(new long[]{0,0});\n\t\t//Normal Dijkstra bfs is implemented.\n\t\twhile(pq.size()>0){\n long[] ele=pq.remove();\n long dis=ele[1];\n\t\t\t//Node value we are on(Parent Node).\n long node=ele[0];\n for(long[] e:graph[(int)node]){\n\t\t\t//Adjancent Node weight from parent.\n long wt=e[1];\n\t\t\t//Adjacent Node to parent\n long adjNode=e[0];\n\t\t\t\t//If the wt+dis (i.e time here) is less than already time taken then will update dist[(int)adjNode] and number of ways will be equal to ways[(int)node]\n if(wt+dis<dist[(int)adjNode]){\n dist[(int)adjNode]=wt+dis;\n ways[(int)adjNode]=ways[(int)node];\n pq.add(new long[]{adjNode,dist[(int)adjNode]});\n }\n\t\t\t\t//if wt+dis (i.e time here) is equal to already taken time then we will add it in ways array.\n else if(wt+dis==dist[(int)adjNode]){\n ways[(int)adjNode]=(ways[(int)node]+ways[(int)adjNode])%mod;\n }\n }\n }\n return (int)ways[n-1];\n }\n\n public int countPaths(int n, int[][] roads) {\n return dijkstra(roads,n); \n }\n} | 5 | 0 | ['Java'] | 1 |
number-of-ways-to-arrive-at-destination | Java / C++ Dijkstra Clean Effective Code with Explanation | java-c-dijkstra-clean-effective-code-wit-2qfc | Set up the classic Dijkstra algorithm keeping track of cost for each node and the number of paths with the smallest cost.\n\nA few tricks to make it work and ma | cosmopolitan | NORMAL | 2021-08-25T01:15:28.149082+00:00 | 2021-08-25T13:37:44.985969+00:00 | 1,992 | false | Set up the classic Dijkstra algorithm keeping track of cost for each node and the number of paths with the smallest cost.\n\nA few tricks to make it work and make it effective:\n\n1. Push to the queue only the nodes with the smallest cost. If you encounter the node with the same cost on a different path, update the paths but don\'t push the node to the queue again.\n2. If you encounter the node for the first time, or found a more cost-effective path, use the number of paths of the parent.\n3. If you encounter the node more than once with the optimal cost, increment the number of paths by the number of paths of the parent.\n\n**Java:**\n```\n public int countPaths(int n, int[][] roads) {\n final long MODULO = 1000000007;\n List<int[]>[] adj = new List[n];\n Arrays.setAll(adj, x -> new ArrayList<>());\n for (int[] r : roads) { // populate adjacency lists\n adj[r[0]].add(new int[]{r[1], r[2]});\n adj[r[1]].add(new int[]{r[0], r[2]});\n }\n long[] cost = new long[n], paths = new long[n];\n Arrays.fill(cost, -1); // -1 -> not visited\n Queue<long[]> q = new PriorityQueue<>((l, r) -> Long.compare(l[1], r[1])); // [node, cost]\n q.offer(new long[]{0,0});\n paths[0] = 1; // to make path accumulation work\n cost[0] = 0;\n \n while (!q.isEmpty()) {\n long[] f = q.poll();\n int fnode = (int) f[0];\n if (fnode == n - 1)\n return (int)(paths[fnode] % MODULO);\n for (int[] ch : adj[fnode]) {\n long newCost = f[1] + ch[1];\n if (newCost == cost[ch[0]]) // add all paths from the parent node\n paths[ch[0]] += paths[fnode] % MODULO;\n if (cost[ch[0]] == -1 || newCost < cost[ch[0]]) {\n paths[ch[0]] = paths[fnode]; // all previous paths are irrelevant\n q.offer(new long[]{ch[0], newCost});\n cost[ch[0]] = newCost;\n }\n }\n }\n return -1; // shouldn\'t get here\n }\n```\n**C++:**\n```\n int countPaths(int n, vector<vector<int>>& roads) {\n static constexpr long MODULO = 1000000007;\n vector<vector<pair<int,int>>> adj(n, vector<pair<int,int>>());\n for (const vector<int>& r : roads) { // populate adjacency lists with node and cost\n adj[r[0]].emplace_back(r[1], r[2]);\n adj[r[1]].emplace_back(r[0], r[2]);\n }\n vector<long> paths(n), cost(n, -1); // -1 -> not visited\n static constexpr auto comp = [](const pair<int,long>& l, const pair<int,long>& r) { return l.second > r.second; };\n priority_queue<pair<int,long>, vector<pair<int,long>>, decltype(comp)> q(comp); // [node, cost]\n q.emplace(0, 0);\n paths[0] = 1; // to make path accumulation work\n cost[0] = 0;\n \n while (!q.empty()) {\n auto [fnode, fCost] = q.top();\n q.pop();\n if (fnode == n - 1)\n return static_cast<int>(paths[fnode] % MODULO);\n for (const auto& [ chNode, chCost ] : adj[fnode]) {\n long newCost = fCost + chCost;\n if (newCost == cost[chNode]) // add all paths from the parent node\n paths[chNode] += paths[fnode] % MODULO;\n if (cost[chNode] == -1 || newCost < cost[chNode]) {\n paths[chNode] = paths[fnode]; // all previous paths are irrelevant\n q.emplace(chNode, newCost);\n cost[chNode] = newCost;\n }\n }\n }\n return -1; // shouldn\'t get here\n } | 5 | 0 | ['C', 'Java'] | 1 |
number-of-ways-to-arrive-at-destination | Simple Python Solution (Dijkstra algo) | simple-python-solution-dijkstra-algo-by-it17u | \'\'\'\n\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n \n\t\t//creating adgecency matrix\n mat = [[0] * n for _ in range(n)] | atul_iitp | NORMAL | 2021-08-21T16:33:15.048102+00:00 | 2021-08-21T17:45:37.470001+00:00 | 781 | false | \'\'\'\n\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n \n\t\t//creating adgecency matrix\n mat = [[0] * n for _ in range(n)]\n for i,j,k in roads:\n mat[i][j]= mat[j][i] = k\n \n\t\t// An array for keeping track of distance of last node from each node\n d = [float(\'inf\')] * (n)\n d[-1] = 0\n \t\t\n\t\t//count matrix for counting the no of paths from each node\n c = [1] * n\n\t\t\n for i in reversed(range(n-1)):\n incount = 0\n for j in range(i,n):\n if mat[i][j] > 0:\n if mat[i][j] + d[j] < d[i]:\n\t\t\t\t\t\t//updating the distace of ith node\n d[i] = mat[i][j] + d[j]\n\t\t\t\t\t\t//initializing the incount by the no of paths from node j\n incount = c[j]\n\t\t\t\t\t\t\n elif mat[i][j] + d[j] == d[i]:\n\t\t\t\t\t\t//updating the value of incount for samllest distance\n incount += c[j]\n \n\t\t\tc[i] = incount\n\t\t\t\n return c[0] % 1000000007\n \n \n \n\n \n\'\'\' | 5 | 2 | ['Python'] | 1 |
number-of-ways-to-arrive-at-destination | Effective Solution In C (yes, C and not C++) | BEATS 93% | USING DIJKSTRA’S ALGORITHM | | effective-solution-in-c-yes-c-and-not-c-40tbt | Intuition
The problem requires finding the number of shortest paths from node 0 to node n-1 in a weighted graph.
This suggests using Dijkstra’s algorithm to det | Delta7Actual | NORMAL | 2025-03-23T13:24:31.962846+00:00 | 2025-03-23T13:24:31.962846+00:00 | 102 | false | # Intuition
- The problem requires finding the number of shortest paths from node `0` to node `n-1` in a weighted graph.
- This suggests using **Dijkstra’s algorithm** to determine the shortest path and **dynamic programming** to count the number of ways to reach each node optimally.
---
# Approach
1. **Graph Representation**
- The graph is represented as an adjacency list, where each node stores a list of edges (neighboring nodes and weights).
2. **Dijkstra’s Algorithm for Shortest Path**
- Use a **distance array (`dist[i]`)** to store the shortest distance from node `0` to each node, initialized to `LLONG_MAX`.
- Use a **ways array (`ways[i]`)** to count the number of shortest paths leading to each node, initialized to `0`.
- Use a **priority queue (min-heap)** to process nodes in increasing order of distance.
3. **Relaxation of Edges**
- While processing a node, iterate through all its adjacent nodes.
- If a shorter path to a neighbor is found, update its distance and reset the number of ways.
- If an equal shortest path is found, add the number of ways from the current node to the neighbor.
4. **Final Result**
- The answer is stored in `ways[n-1]`, representing the number of shortest paths to the last node.
---
# Complexity
- **Time complexity:**
- Dijkstra’s algorithm runs in $$O((V + E) * log(V))$$ using a priority queue.
- Each edge is relaxed once, leading to an overall complexity of $$O(E*log(V))$$
- **Space complexity:**
- $$O(V + E)$$ for storing the graph.
- $$O(V)$$ for `dist` and `ways` arrays.
- $$O(V)$$ for the priority queue.
- Overall, $$O(V + E)$$
---
# Code
```c []
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MOD 1000000007
typedef long long ll;
// Structure to represent a node in the priority queue
typedef struct {
ll distance;
int node;
} HeapNode;
// Structure to represent the priority queue
typedef struct {
HeapNode* nodes;
int size;
int capacity;
} PriorityQueue;
// Function to create a priority queue
PriorityQueue* createPriorityQueue(int capacity) {
PriorityQueue* pq = (PriorityQueue*)malloc(sizeof(PriorityQueue));
pq->nodes = (HeapNode*)malloc(capacity * sizeof(HeapNode));
pq->size = 0;
pq->capacity = capacity;
return pq;
}
// Function to swap two nodes in the priority queue
void swap(HeapNode* a, HeapNode* b) {
HeapNode temp = *a;
*a = *b;
*b = temp;
}
// Function to heapify up
void heapifyUp(PriorityQueue* pq, int index) {
if (index && pq->nodes[index].distance < pq->nodes[(index - 1) / 2].distance) {
swap(&pq->nodes[index], &pq->nodes[(index - 1) / 2]);
heapifyUp(pq, (index - 1) / 2);
}
}
// Function to heapify down
void heapifyDown(PriorityQueue* pq, int index) {
int smallest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < pq->size && pq->nodes[left].distance < pq->nodes[smallest].distance)
smallest = left;
if (right < pq->size && pq->nodes[right].distance < pq->nodes[smallest].distance)
smallest = right;
if (smallest != index) {
swap(&pq->nodes[index], &pq->nodes[smallest]);
heapifyDown(pq, smallest);
}
}
// Function to push a node into the priority queue
void push(PriorityQueue* pq, ll distance, int node) {
if (pq->size == pq->capacity) {
pq->capacity *= 2;
pq->nodes = (HeapNode*)realloc(pq->nodes, pq->capacity * sizeof(HeapNode));
}
pq->nodes[pq->size].distance = distance;
pq->nodes[pq->size].node = node;
heapifyUp(pq, pq->size);
pq->size++;
}
// Function to pop the minimum node from the priority queue
HeapNode pop(PriorityQueue* pq) {
HeapNode root = pq->nodes[0];
pq->nodes[0] = pq->nodes[--pq->size];
heapifyDown(pq, 0);
return root;
}
// Function to check if the priority queue is empty
int isEmpty(PriorityQueue* pq) {
return pq->size == 0;
}
// Structure to represent an adjacency list node
typedef struct AdjListNode {
int dest;
ll weight;
struct AdjListNode* next;
} AdjListNode;
// Structure to represent an adjacency list
typedef struct {
AdjListNode** array;
int size;
} AdjList;
// Function to create an adjacency list node
AdjListNode* createAdjListNode(int dest, ll weight) {
AdjListNode* newNode = (AdjListNode*)malloc(sizeof(AdjListNode));
newNode->dest = dest;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
// Function to create an adjacency list
AdjList* createAdjList(int size) {
AdjList* adjList = (AdjList*)malloc(sizeof(AdjList));
adjList->array = (AdjListNode**)malloc(size * sizeof(AdjListNode*));
adjList->size = size;
for (int i = 0; i < size; i++)
adjList->array[i] = NULL;
return adjList;
}
// Function to add an edge to the adjacency list
void addEdge(AdjList* adjList, int src, int dest, ll weight) {
AdjListNode* newNode = createAdjListNode(dest, weight);
newNode->next = adjList->array[src];
adjList->array[src] = newNode;
newNode = createAdjListNode(src, weight);
newNode->next = adjList->array[dest];
adjList->array[dest] = newNode;
}
// Function to free the adjacency list
void freeAdjList(AdjList* adjList) {
for (int i = 0; i < adjList->size; i++) {
AdjListNode* node = adjList->array[i];
while (node) {
AdjListNode* temp = node;
node = node->next;
free(temp);
}
}
free(adjList->array);
free(adjList);
}
// Function to count the number of ways to arrive at the destination
int countPaths(int n, int** roads, int roadsSize, int* roadsColSize) {
// Create adjacency list
AdjList* adjList = createAdjList(n);
for (int i = 0; i < roadsSize; i++) {
int u = roads[i][0];
int v = roads[i][1];
ll time = roads[i][2];
addEdge(adjList, u, v, time);
}
// Initialize distances and ways
ll* dist = (ll*)malloc(n * sizeof(ll));
int* ways = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; i++) {
dist[i] = LLONG_MAX;
ways[i] = 0;
}
dist[0] = 0;
ways[0] = 1;
// Create priority queue
PriorityQueue* pq = createPriorityQueue(n);
push(pq, 0, 0);
// Dijkstra's algorithm
while (!isEmpty(pq)) {
HeapNode minNode = pop(pq);
ll distance = minNode.distance;
int node = minNode.node;
if (distance > dist[node])
continue;
AdjListNode* adj = adjList->array[node];
while (adj) {
int adjNode = adj->dest;
ll nextDist = adj->weight;
if (distance + nextDist < dist[adjNode]) {
dist[adjNode] = distance + nextDist;
ways[adjNode] = ways[node];
push(pq, dist[adjNode], adjNode);
} else if (distance + nextDist == dist[adjNode]) {
ways[adjNode] = (ways[adjNode] + ways[node]) % MOD;
}
adj = adj->next; // Move to the next adjacent node
}
}
int result = ways[n - 1];
// Free allocated memory
free(dist);
free(ways);
freeAdjList(adjList);
free(pq->nodes);
free(pq);
return result;
}
``` | 4 | 0 | ['Math', 'Dynamic Programming', 'Graph', 'Topological Sort', 'Memoization', 'Ordered Map', 'C', 'Combinatorics', 'Prefix Sum', 'Shortest Path'] | 1 |
number-of-ways-to-arrive-at-destination | C++ Solution || Detailed Explanation | c-solution-detailed-explanation-by-rohit-jwvm | IntuitionThe problem requires us to count the number of ways to reach the last node from the first node using the shortest path. This can be achieved using Dijk | Rohit_Raj01 | NORMAL | 2025-03-23T04:15:57.063280+00:00 | 2025-03-23T04:15:57.063280+00:00 | 625 | false | # Intuition
The problem requires us to count the number of ways to reach the last node from the first node using the shortest path. This can be achieved using Dijkstra's algorithm while maintaining a count of paths leading to each node via the shortest distance.
# Approach
1. **Graph Representation**: Represent the graph using an adjacency list where each node stores pairs of connected nodes and their respective edge weights.
2. **Priority Queue for Dijkstra's Algorithm**:
- Use a min-heap (`priority_queue`) to process nodes based on the shortest discovered distance.
- Maintain a `dist` array to store the shortest distance to each node.
- Maintain a `ways` array to store the number of ways to reach each node with the shortest path.
3. **Dijkstra's Algorithm Execution**:
- Initialize the source node (0) with a distance of `0` and `1` way to reach it.
- Process each node, and for each of its neighbors, update its shortest distance and count the number of ways if a new shortest path is found.
- If another shortest path is found to the same node, add the ways from the current node to the neighbor's `ways` value.
4. **Return the number of ways** to reach the last node `(n-1)`, ensuring results are modulo `1e9 + 7`.
# Complexity
- **Time Complexity**: $$O((V + E) \log V)$$, where `V` is the number of nodes and `E` is the number of edges. Dijkstra's algorithm processes each node and edge efficiently using a priority queue.
- **Space Complexity**: $$O(V + E)$$ for storing the adjacency list, distance array, and ways array.
# Code
```cpp
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
vector<pair<long long, long long>> adj[n];
for (auto it : roads) {
adj[it[0]].push_back({it[1], it[2]});
adj[it[1]].push_back({it[0], it[2]});
}
priority_queue<pair<long long, int>, vector<pair<long long, int>>,
greater<pair<long long, int>>>
pq;
pq.push({0, 0});
vector<long long> dist(n, LONG_MAX);
dist[0] = 0;
vector<long long> ways(n, 0);
ways[0] = 1;
long long mod = 1e9 + 7;
while (!pq.empty()) {
auto it = pq.top();
long long node = it.second;
long long dis = it.first;
pq.pop();
for (auto it : adj[node]) {
long long edjnode = it.first;
long long edjwt = it.second;
if (edjwt + dis < dist[edjnode]) {
dist[edjnode] = edjwt + dis;
pq.push({dist[edjnode], edjnode});
ways[edjnode] = ways[node];
} else if (dis + edjwt == dist[edjnode]) {
ways[edjnode] = (ways[edjnode] + ways[node]) % mod;
}
}
}
return ways[n - 1] % mod;
}
};
```
# Explanation
- **Graph Construction**: Convert input roads into an adjacency list.
- **Dijkstra's Algorithm**:
- Use a priority queue to always expand the shortest known path.
- Update distances and count paths when a new shortest distance is found.
- If another shortest path to the same node is found, accumulate the count of ways.
- **Final Result**: The number of ways to reach the last node with the shortest path.
## Edge Cases Considered
- Single-node graphs.
- Graphs with multiple shortest paths.
- Large graphs requiring modulo arithmetic to prevent overflow.

| 4 | 0 | ['Dynamic Programming', 'Graph', 'Shortest Path', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | Beat 99.5% || Well explained Java Solution with Dijkstra’s Algorithm | beat-995-well-explained-java-solution-wi-hnl6 | This Java program implements Dijkstra’s Algorithm to find the number of shortest paths from node 0 to node n-1 in a weighted undirected graph, where the edges a | princebhayani | NORMAL | 2025-02-02T19:18:14.565475+00:00 | 2025-02-02T19:18:14.565475+00:00 | 760 | false | This Java program implements **Dijkstra’s Algorithm** to find the **number of shortest paths** from node `0` to node `n-1` in a weighted undirected graph, where the edges are given in the form of a `roads` array.
---
## **Step-by-Step Explanation**
### **1. Understanding the Problem**
- The function `countPaths(int n, int[][] roads)` takes:
- `n`: The number of nodes (0 to `n-1`).
- `roads`: A list of edges, where each edge is represented as `[u, v, time]`, meaning there's a bidirectional road between node `u` and node `v` with a travel time of `time`.
- The goal is to determine **how many different shortest paths exist** from node `0` to node `n-1`.
---
### **2. Constants and Data Structures**
```java
final long INF = Long.MAX_VALUE / 2;
final int MOD = (int) 1e9 + 7;
```
- `INF`: Represents an infinitely large number to initialize the graph distances.
- `MOD`: Since the number of paths can be large, we take the result modulo \(10^9 + 7\) to avoid integer overflow.
---
### **3. Initialize the Graph as an Adjacency Matrix**
```java
long[][] graph = new long[n][n];
for (long[] row : graph) {
Arrays.fill(row, INF);
}
```
- The adjacency matrix `graph[i][j]` represents the travel time between node `i` and node `j`.
- It is initialized with `INF` since initially, no edges are present.
---
### **4. Populate the Graph with Given Roads**
```java
for (int[] road : roads) {
int u = road[0], v = road[1], time = road[2];
graph[u][v] = time;
graph[v][u] = time;
}
```
- Each edge `(u, v, time)` is bidirectional, so `graph[u][v]` and `graph[v][u]` are set to `time`.
---
### **5. Dijkstra’s Algorithm Setup**
```java
long[] dist = new long[n];
Arrays.fill(dist, INF);
dist[0] = 0;
int[] ways = new int[n];
ways[0] = 1;
```
- `dist[i]`: Stores the shortest time to reach node `i` from node `0`.
- `ways[i]`: Stores the **number of shortest paths** to reach node `i` from `0`.
- Initially, `dist[0] = 0` (distance to itself) and `ways[0] = 1` (one way to reach itself).
---
### **6. Priority Queue for Dijkstra’s Algorithm**
```java
PriorityQueue<Pair> pq = new PriorityQueue<>();
pq.offer(new Pair(0, 0));
```
- We use a **min-heap (priority queue)** to always process the node with the **smallest known distance**.
- Initially, we add `(0, 0)` meaning **start at node `0` with time `0`**.
---
### **7. Main Loop: Process Nodes in the Priority Queue**
```java
while (!pq.isEmpty()) {
Pair curr = pq.poll();
int u = curr.node;
long time = curr.time;
if (time > dist[u]) continue;
```
- Extract the node `u` with the smallest `time` from the priority queue.
- If the extracted time is greater than the stored shortest time `dist[u]`, **skip processing** (since a better path has already been found).
---
### **8. Explore All Neighbors of `u`**
```java
for (int v = 0; v < n; v++) {
if (graph[u][v] == INF) continue;
long newTime = time + graph[u][v];
```
- Iterate over all nodes `v` to check if there's a direct edge from `u` to `v`.
- Compute `newTime = time + graph[u][v]`, the potential new shortest distance to `v`.
---
### **9. Update Distances and Path Counts**
#### **(a) If `newTime` is shorter, update `dist[v]`**
```java
if (newTime < dist[v]) {
dist[v] = newTime;
ways[v] = ways[u];
pq.offer(new Pair(v, newTime));
}
```
- If we find a **shorter path** to `v`, update `dist[v]` and inherit the number of ways from `ways[u]`.
- Push `(v, newTime)` into the priority queue.
#### **(b) If `newTime` is equal to `dist[v]`, add to the path count**
```java
else if (newTime == dist[v]) {
ways[v] = (ways[v] + ways[u]) % MOD;
}
```
- If we find **another shortest path** to `v`, increase `ways[v]` by `ways[u]` (modulo `MOD`).
---
### **10. Return the Number of Shortest Paths to `n-1`**
```java
return ways[n - 1];
```
- `ways[n-1]` contains the number of ways to reach the last node `n-1` using the shortest path.
---
## **Helper Class: Pair**
```java
static class Pair implements Comparable<Pair> {
int node;
long time;
public Pair(int node, long time) {
this.node = node;
this.time = time;
}
public int compareTo(Pair other) {
return Long.compare(this.time, other.time);
}
}
```
- The `Pair` class stores `(node, time)`.
- Implements `Comparable<Pair>` so that the priority queue **sorts by `time` in ascending order**.
---
## **Time and Space Complexity Analysis**
### **Time Complexity:**
- **Building the graph**: \(O(E)\), where \(E\) is the number of edges.
- **Dijkstra’s Algorithm**:
- Each node is processed once: \(O(N)\).
- Each edge is relaxed once: \(O(E)\).
- The priority queue operations take \(O(\log N)\) time each.
- Overall, **\(O((N + E) \log N)\) ~ \(O(E \log N)\)**.
### **Space Complexity:**
- **Graph storage**: \(O(N^2)\) (adjacency matrix).
- **Distance and path arrays**: \(O(N)\).
- **Priority queue**: \(O(N)\).
- Overall, **\(O(N^2)\) in the worst case** (due to adjacency matrix).
---
## **Code**
```
class Solution {
public int countPaths(int n, int[][] roads) {
final long INF = Long.MAX_VALUE / 2;
final int MOD = (int) 1e9 + 7;
// Step 1: Initialize adjacency matrix with INF
long[][] graph = new long[n][n];
for (long[] row : graph) {
Arrays.fill(row, INF);
}
// Step 2: Fill the adjacency matrix with given roads
for (int[] road : roads) {
int u = road[0], v = road[1], time = road[2];
graph[u][v] = time;
graph[v][u] = time;
}
// Step 3: Dijkstra’s Algorithm
long[] dist = new long[n]; // Shortest time to each node
Arrays.fill(dist, INF);
dist[0] = 0;
int[] ways = new int[n]; // Number of shortest paths
ways[0] = 1;
PriorityQueue<Pair> pq = new PriorityQueue<>();
pq.offer(new Pair(0, 0)); // Start from node 0 with time 0
while (!pq.isEmpty()) {
Pair curr = pq.poll();
int u = curr.node;
long time = curr.time;
// If we’ve already found a shorter way, skip
if (time > dist[u]) continue;
// Step 4: Explore neighbors in the matrix
for (int v = 0; v < n; v++) {
if (graph[u][v] == INF) continue; // No direct edge
long newTime = time + graph[u][v];
if (newTime < dist[v]) { // Found a shorter path
dist[v] = newTime;
ways[v] = ways[u]; // Inherit path count
pq.offer(new Pair(v, newTime));
} else if (newTime == dist[v]) { // Found another shortest path
ways[v] = (ways[v] + ways[u]) % MOD;
}
}
}
return ways[n - 1]; // Number of ways to reach node (n-1)
}
// Pair class for Priority Queue
static class Pair implements Comparable<Pair> {
int node;
long time;
public Pair(int node, long time) {
this.node = node;
this.time = time;
}
public int compareTo(Pair other) {
return Long.compare(this.time, other.time);
}
}
}
```
| 4 | 0 | ['Dynamic Programming', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'Java'] | 0 |
number-of-ways-to-arrive-at-destination | 🛣️ Simple 🧠 Python Solution beats 93 % | Dijkstra algo | | simple-python-solution-beats-93-dijkstra-yr6m | \n\n---\n\n## \uD83D\uDEA6 Count Paths from Intersection 0 to n-1 in Shortest Time \u23F1\uFE0F\n\n### \uD83D\uDE80 Problem Statement:\n\nYou are in a city with | sagarsaini_ | NORMAL | 2024-08-21T07:37:48.357448+00:00 | 2024-08-21T07:37:48.357480+00:00 | 606 | false | \n\n---\n\n## \uD83D\uDEA6 Count Paths from Intersection 0 to n-1 in Shortest Time \u23F1\uFE0F\n\n### \uD83D\uDE80 Problem Statement:\n\nYou are in a city with `n` intersections numbered from `0` to `n - 1`. The city has some **bi-directional** roads between the intersections, where `roads[i] = [ui, vi, timei]` represents a road between intersection `ui` and intersection `vi` that takes `timei` minutes to travel. \uD83D\uDE97\uD83D\uDEE3\uFE0F\n\nYou want to know in how many ways you can **travel from intersection 0 to intersection n-1 in the shortest amount of time**.\n\nGiven `n` intersections and an array `roads`, return **the number of ways** to arrive at your destination in the shortest amount of time. Since the answer can be large, return it **modulo** `10^9 + 7`.\n\n### \uD83D\uDCA1 Intuition:\n\n- This problem is a twist on Dijkstra\'s algorithm! \uD83C\uDFAF\n- Instead of just finding the shortest path, we also need to **count how many ways** we can reach the destination intersection in the same shortest time.\n- **Dijkstra\'s Algorithm** helps us calculate the shortest time to reach each node.\n- We maintain a **ways array** to track the number of ways to reach each node in the shortest time.\n\n### \uD83E\uDDE0 Approach:\n\n1. **Adjacency List:** Build an adjacency list for the city where every road connects two intersections with a specific travel time.\n \n2. **Dijkstra\'s Algorithm:** Use a **min-heap** (priority queue) to explore nodes based on the shortest travel time.\n\n3. **Track Shortest Paths:** Maintain a `dis[]` array to store the shortest time to reach each node and a `ways[]` array to count the number of ways to reach that node in the shortest time.\n\n4. **Count Ways:** For each neighboring node, if the new calculated time matches the shortest time, add the number of ways from the current node to the neighbor. If the new time is shorter, update the shortest time and reset the ways to match the number of ways from the current node.\n\n5. **Final Answer:** Once all nodes have been processed, return the number of ways to reach the destination `n-1`, **modulo `10^9 + 7`**.\n\n### \uD83D\uDCDD Code:\n\n```python\nimport heapq\n\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n # Step 1\uFE0F\u20E3: Build the adjacency list for the graph\n adj = [[] for _ in range(n)]\n for u, v, w in roads:\n adj[u].append([v, w])\n adj[v].append([u, w])\n \n # Step 2\uFE0F\u20E3: Initialize arrays to store shortest distance and number of ways\n ways = [0] * n\n ways[0] = 1\n dis = [float("inf")] * n\n dis[0] = 0\n \n # Step 3\uFE0F\u20E3: Min-heap to store (time, node)\n heap = [(0, 0)] # (current time, node)\n \n while heap:\n time, node = heapq.heappop(heap)\n \n # Explore all neighbors of the current node\n for neighbor, travel_time in adj[node]:\n new_time = time + travel_time\n \n # Case 1\uFE0F\u20E3: If we found another way with the same shortest time\n if new_time == dis[neighbor]:\n ways[neighbor] += ways[node]\n \n # Case 2\uFE0F\u20E3: If we found a shorter time to reach the neighbor\n elif new_time < dis[neighbor]:\n dis[neighbor] = new_time\n heapq.heappush(heap, (new_time, neighbor))\n ways[neighbor] = ways[node]\n \n # Step 4\uFE0F\u20E3: Return the number of ways to reach the destination modulo 10^9 + 7\n MOD = 10**9 + 7\n return ways[n-1] % MOD\n```\n\n### \uD83D\uDD75\uFE0F\u200D\u2642\uFE0F Example Simulation:\n\nConsider an example:\n\n```\nn = 4\nroads = [[0,1,2],[0,2,4],[1,3,1],[2,3,1]]\n```\n\n- **Adjacency List** looks like this:\n - `0 -> [(1, 2), (2, 4)]`\n - `1 -> [(0, 2), (3, 1)]`\n - `2 -> [(0, 4), (3, 1)]`\n - `3 -> [(1, 1), (2, 1)]`\n\n- Start with the min-heap `[(0, 0)]` (i.e., 0 minutes at node 0).\n- Process nodes:\n - From node 0: Reach node 1 (time 2), and node 2 (time 4).\n - From node 1: Reach node 3 (time 3).\n - From node 2: Reach node 3 (time 5).\n- **Shortest time** to reach node `3` is `3` minutes. There is **1 way** to reach it.\n\n**Final Output:** `1`\n\n### \uD83D\uDD0D Complexity Analysis:\n\n- **Time Complexity:** `O(E log V)`, where `E` is the number of edges (roads) and `V` is the number of intersections. Each edge is processed once, and we push nodes into the heap with logarithmic complexity.\n- **Space Complexity:** `O(V + E)` for storing the adjacency list and the heap.\n\n### \uD83D\uDEA8 Edge Cases to Consider:\n\n1. **Isolated Intersections:** There should be no isolated intersections, as the inputs guarantee that all intersections are reachable.\n2. **Single Path:** If there is only one way to reach the destination, return `1`.\n3. **Multiple Shortest Paths:** Accurately count all ways to reach the destination in the same shortest time.\n\n---\n\nWith this approach, you can count all the ways to travel from intersection `0` to intersection `n-1` in the shortest time while keeping the solution efficient! \uD83C\uDF1F | 4 | 0 | ['Graph', 'Shortest Path', 'Python3'] | 0 |
number-of-ways-to-arrive-at-destination | Striver's Approach Passing all test cases | strivers-approach-passing-all-test-cases-o274 | Intuition\n Describe your first thoughts on how to solve this problem. \nWe start at one node (node 0) and want to figure out the best way to reach all other no | Priyanshi31487cs | NORMAL | 2024-05-15T17:24:47.084931+00:00 | 2024-05-15T17:24:47.084975+00:00 | 1,495 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe start at one node (node 0) and want to figure out the best way to reach all other nodes while also keeping track of the number of different paths we can take. To do this, we use a method called Dijkstra\'s algorithm, which helps us find the shortest routes efficiently. As we explore these routes, we also count how many ways we can reach each node. When we reach our destination node (node n\u22121), we have the total count of ways to get there.\n\n# Approach \nSimple Dijkstra\'s Algorithm + BFS + Heap(Priority Queue)\nThis approach uses Dijkstra\'s algorithm and additional data structures to efficiently count paths and update no of ways.\n# Complexity\n- Time complexity: O((n+E)logn) for Dijkstra\'s algorithm with a priority queue.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n+E) for storing the graph and ways count\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\nclass Solution {\n public int countPaths(int n, int[][] roads) {\n PriorityQueue<Pair> q = new PriorityQueue<>((x, y) -> Long.compare(x.a, y.a));\n List<List<Pair>> adj = new ArrayList<>();\n for (int i = 0; i < n; i++) {\n adj.add(new ArrayList<>());\n }\n for (int[] ar : roads) {\n adj.get(ar[0]).add(new Pair(ar[1], ar[2])); // node wt\n adj.get(ar[1]).add(new Pair(ar[0], ar[2]));\n }\n long[] dis = new long[n];\n int[] ways = new int[n];\n\n Arrays.fill(dis, Long.MAX_VALUE / 2);\n dis[0] = 0;\n ways[0] = 1;\n q.add(new Pair(0, 0));\n\n while (!q.isEmpty()) {\n long pd = q.peek().a;\n long node = q.peek().b;\n q.remove();\n for (Pair i : adj.get((int) node)) {\n long edgewt = i.b;\n long adjnode = i.a;\n if (edgewt + pd < dis[(int) adjnode]) {\n dis[(int) adjnode] = edgewt + pd;\n q.add(new Pair(dis[(int) adjnode], adjnode));\n ways[(int) adjnode] = ways[(int) node];\n } else if (edgewt + pd == dis[(int) adjnode]) {\n ways[(int) adjnode] = (ways[(int) adjnode] + ways[(int) node]) % ((int) 1e9 + 7); // Corrected ways count\n }\n }\n }\n\n return ways[n - 1] % ((int) 1e9 + 7);\n }\n}\n\nclass Pair {\n long a; // distance\n long b; // node\n\n Pair(long a, long b) {\n this.a = a;\n this.b = b;\n }\n}\n\n``` | 4 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Java'] | 2 |
number-of-ways-to-arrive-at-destination | Simple C++ solution | simple-c-solution-by-gcsingh1629-u7lh | Code\n\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<int, int>> adj[n];\n \n for(auto i | gcsingh1629 | NORMAL | 2023-09-02T09:52:01.507971+00:00 | 2023-09-02T09:52:01.507994+00:00 | 570 | false | # Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<int, int>> adj[n];\n \n for(auto it : roads)\n {\n adj[it[0]].push_back({it[1], it[2]});\n adj[it[1]].push_back({it[0], it[2]});\n }\n \n priority_queue<pair<long long, int>, vector<pair<long long, int>>,\n greater<pair<long long, int>>> pq;\n vector<long long> dist(n, 1e18);\n vector<long long> ways(n, 0);\n dist[0] = 0;\n ways[0] = 1;\n pq.push({0, 0});\n int mod = (1e9 + 7);\n \n while(!pq.empty())\n {\n long long dis = pq.top().first;\n int node = pq.top().second;\n pq.pop();\n \n for(auto it : adj[node])\n {\n long long edgeWeight = it.second;\n int adjNode = it.first;\n \n if(dis + edgeWeight < dist[adjNode])\n {\n dist[adjNode] = dis + edgeWeight;\n pq.push({dist[adjNode], adjNode});\n ways[adjNode] = ways[node];\n }\n else if(dis + edgeWeight == dist[adjNode])\n {\n ways[adjNode] = (ways[adjNode] + ways[node]) % mod;\n }\n }\n }\n return ways[n - 1] % mod;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
number-of-ways-to-arrive-at-destination | Python || 96.60% Faster || Easy || Dijkstra's | python-9660-faster-easy-dijkstras-by-pul-u9wo | \ndef countPaths(self, n: int, roads: List[List[int]]) -> int:\n adj=[[] for i in range(n)]\n for u,v,t in roads:\n adj[u].append((v,t) | pulkit_uppal | NORMAL | 2023-04-22T18:44:14.380325+00:00 | 2023-04-22T18:44:14.380376+00:00 | 1,313 | false | ```\ndef countPaths(self, n: int, roads: List[List[int]]) -> int:\n adj=[[] for i in range(n)]\n for u,v,t in roads:\n adj[u].append((v,t))\n adj[v].append((u,t))\n dist=[float(\'inf\')]*n\n ways=[0]*n\n ways[0]=1\n dist[0]=0\n pq=[]\n heapify(pq)\n heappush(pq,(0,0))\n mod=10**9+7\n while pq:\n time,node=heappop(pq)\n for v,t in adj[node]:\n if dist[v]>t+time:\n dist[v]=t+time\n heappush(pq,(dist[v],v))\n ways[v]=ways[node]\n elif dist[v]==t+time:\n ways[v]=(ways[v]+ways[node])%mod\n return ways[n-1]%mod\n```\n\n**An upvote will be encouraging** | 4 | 0 | ['Graph', 'Python', 'Java', 'Python3'] | 0 |
number-of-ways-to-arrive-at-destination | Best C++ Solution | best-c-solution-by-kumar21ayush03-icvk | Approach\nDijkstra\'s Algorithm\n\n# Complexity\n- Time complexity:\nO(ElogV)\n\n- Space complexity:\nO(V + E)\n\n# Code\n\nclass Solution {\npublic:\n int c | kumar21ayush03 | NORMAL | 2023-03-19T09:05:31.058901+00:00 | 2023-03-19T09:05:31.058933+00:00 | 1,602 | false | # Approach\nDijkstra\'s Algorithm\n\n# Complexity\n- Time complexity:\n$$O(ElogV)$$\n\n- Space complexity:\n$$O(V + E)$$\n\n# Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector <pair<long long, long long>> adj[n];\n for (auto it : roads) {\n adj[it[0]].push_back({it[1], it[2]});\n adj[it[1]].push_back({it[0], it[2]});\n }\n priority_queue <pair<long long, long long>, vector<pair<long long, long long>>, greater<>> pq;\n vector <long long> dist(n, LLONG_MAX), ways(n, 0);\n dist[0] = 0;\n ways[0] = 1;\n pq.push({0, 0});\n int mod = (int)(1e9 + 7);\n while (!pq.empty()) {\n long long dis = pq.top().first;\n long long node = pq.top().second;\n pq.pop();\n if (dist[node] < dis)\n continue;\n for (auto it : adj[node]) {\n long long adjNode = it.first;\n long long edW = it.second;\n if (dis + edW < dist[adjNode]) {\n dist[adjNode] = dis + edW;\n pq.push({dis + edW, adjNode});\n ways[adjNode] = ways[node];\n } else if (dis + edW == dist[adjNode]) {\n ways[adjNode] = (ways[adjNode] + ways[node]) % mod;\n }\n }\n }\n return ways[n - 1] % mod;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
number-of-ways-to-arrive-at-destination | [C++]Same as Dijkstra Alogrithm | csame-as-dijkstra-alogrithm-by-account_c-n33r | prerequisite: Dijkstra Algorithm\nvedio link :Dijkstra\'s Algorithm by Striver(Legend)\n\n#define ll long long\nconst int mod = 1e9+7;\nclass Solution {\npublic | account_changed | NORMAL | 2022-12-20T07:35:51.909697+00:00 | 2022-12-20T07:35:51.909734+00:00 | 849 | false | **prerequisite: Dijkstra Algorithm**\nvedio link :[Dijkstra\'s Algorithm by Striver(Legend)](https://youtu.be/V6H1qAeB-l4)\n```\n#define ll long long\nconst int mod = 1e9+7;\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n //First create an adjacency list\n vector<vector<pair<int,int>>> adj(n);\n for(int i = 0; i < roads.size(); i++){\n int u = roads[i][0];\n int v = roads[i][1];\n int w = roads[i][2];\n adj[u].push_back({v,w});\n adj[v].push_back({u,w});\n }\n //Now to calculate miminum time to reach the destination let create an array and initialize all the positions to LONG_INT\n // except starting index\n vector<ll> time(n,LONG_MAX);\n time[0] = 0;\n //Now to store the number of way to reach the node in min time let create another array named way\n //And initialize all the nodes to zero but the number of way to start from the staring index is 1 so initialize it\n vector<ll> way(n,0);\n way[0] = 1;\n //As usual create an priority queue of pair which stores node and time to reach the current node\n priority_queue <pair<ll,int>, vector<pair<ll,int>>, greater<pair<ll,int>> > pq;//{time,node}\n pq.push({0,0});\n while(!pq.empty()){\n ll currTime = pq.top().first;\n int node = pq.top().second;\n pq.pop();\n for(auto it: adj[node]){\n int adjNode = it.first;\n ll timeTotravel = it.second;\n // relax adjNode nodes and push in to priority queue\n // adjNode node ways will be updated with current node ways as\n // we find a lesser time for adjNode node\n if(currTime + timeTotravel < time[adjNode]){\n time[adjNode] = currTime + timeTotravel;\n pq.push({time[adjNode],adjNode});\n way[adjNode] = way[node]%mod;\n }\n // if current node time + timeTotravel = adjNode node cost then\n // this is another way to reach the adjNode node with min time\n // so we update adjNode node ways as ways[adjNode] = (ways[node]+way[adjNode])%mod\n else if(currTime + timeTotravel == time[adjNode])\n way[adjNode] = (way[adjNode]+way[node])%mod;\n }\n }\n return way[n-1];\n }\n};\n```\n**Time Complexity : O(Total Edge x log(Total Nodes))**\n**space complexity : O(Total Nodes)** | 4 | 0 | [] | 0 |
number-of-ways-to-arrive-at-destination | Java Solution Dijkstra using Min Heap with extensive Comments. Hope it helps... | java-solution-dijkstra-using-min-heap-wi-gl9k | \tclass Solution {\n\t\tpublic int countPaths(int n, int[][] roads) {\n\t\t\tList[] graph = constructGraph(n, roads); // returns adjacency List for given road[] | fameissrani | NORMAL | 2022-07-16T04:16:23.260099+00:00 | 2022-07-16T04:21:20.053368+00:00 | 515 | false | \tclass Solution {\n\t\tpublic int countPaths(int n, int[][] roads) {\n\t\t\tList<Edge>[] graph = constructGraph(n, roads); // returns adjacency List for given road[][]\n\n\t\t\tPriorityQueue<Pair> pq = new PriorityQueue<>();\n\t\t\tint[] dist = new int[n]; // dist array stores the min. cost/weight/time to reach from sourceVtx(0) to every other node in the graph\n\t\t\tArrays.fill(dist, Integer.MAX_VALUE); // since we want to calculate the Min. distance/time ..intialize each dist[i] with infinity.\n\n\t\t\tint[] path = new int[n]; // this is the extra storage which stores the count of paths from src to every other node in the graph\n\n\t\t\tpq.add(new Pair(0, 0)); // Pair(vtx, weight)\n\t\t\tdist[0] = 0; // we are starint from source : 0, therefore 0 distance/cost/time to reach 0 from 0.\n\t\t\tpath[0] = 1; // Initial/Base Value for source vtx : 1 path to reach source while standing on source.\n\n\t\t\tint modVal = (int)1e9 + 7; // required by question.\n\t\t\twhile(pq.size() > 0) {\n\t\t\t\tPair rem = pq.remove();\n\n\t\t\t\tfor(Edge e : graph[rem.vtx]) {\n\t\t\t\t\tint nbr = e.nbr; // V\n\t\t\t\t\tint nbrdist = e.wt; // nbrdist is the wt between rem.vtx(U) and its neighbour(V)\n\t\t\t\t\tif(rem.wsf + nbrdist < dist[nbr]) { // if this conditions is true : it means we are on a path which reach neighbour of rem.vtx i.e U at a lesser cost/time that what is stored in the distance array for this neighbour... so update it and add neighbour im queue\n\t\t\t\t\t\tdist[nbr] = rem.wsf + nbrdist;\n\t\t\t\t\t\tpath[nbr] = path[rem.vtx]; // this line means that if we can reach node : U in X ways then we can also reach the neighbours of U in X ways.... therefore path[nbr] = path[U] U here means rem.vtx\n\t\t\t\t\t\tpq.add(new Pair(nbr, dist[nbr]));\n\t\t\t\t\t} else if(rem.wsf + nbrdist == dist[nbr]) {\n\t\t\t\t\t// this check denotes that we came at this nbr previously and now again at same cost as previous time...\n\t\t\t\t\t// therefore we have explored a new path for reaching this nbr via current vtx i.e U....\n\t\t\t\t\t// therefore new ways of reaching nbr would be path[nbr] + path[rem.vtx] (Basic DP structure, dry run it once, you will get it)\n\t\t\t\t\t\tpath[nbr] += path[rem.vtx]; \n\t\t\t\t\t\tpath[nbr] = path[nbr] % modVal;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn path[n-1]; // n-1 is the destination vtx\n\t\t}\n\n\t\t// this class is for BFS traversing using MinHeap \n\t\tprivate class Pair implements Comparable<Pair>{ \n\t\t\tint vtx;\n\t\t\tint wsf;\n\t\t\tPair(int vtx, int wsf) {\n\t\t\t\tthis.vtx = vtx;\n\t\t\t\tthis.wsf = wsf; // weightSoFar\n\t\t\t}\n\n\t\t\tpublic int compareTo(Pair o) {\n\t\t\t\treturn this.wsf - o.wsf;\n\t\t\t}\n\t\t}\n\n\t\tprivate class Edge {\n\t\t\tint src; // U\n\t\t\tint nbr; // V\n\t\t\tint wt; // cost of travelling from U to V or vice versa\n\t\t\tEdge(int src, int nbr, int wt) {\n\t\t\t\tthis.src = src;\n\t\t\t\tthis.nbr = nbr;\n\t\t\t\tthis.wt = wt;\n\t\t\t}\n\t\t}\n\n\t\tprivate List<Edge>[] constructGraph(int n, int[][] roads) {\n\t\t\tList<Edge>[] graph = new ArrayList[n];\n\n\t\t\tfor(int i = 0; i < n; i++) { // initializing graph[] with empty arrayLists\n\t\t\t\tgraph[i] = new ArrayList<>();\n\t\t\t}\n\n\t\t\tfor(int i = 0; i < roads.length; i++) {\n\t\t\t\tint u = roads[i][0];\n\t\t\t\tint v = roads[i][1];\n\t\t\t\tint wt = roads[i][2];\n\n\t\t\t\tgraph[u].add(new Edge(u, v, wt)); // add Edge at Uth node which goes from U to V at wt cost\n\t\t\t\tgraph[v].add(new Edge(v, u, wt)); // add Edge at Vth node which goes from V to U at wt cost\n\t\t\t}\n\t\t\treturn graph;\n\t\t}\n\t} | 4 | 0 | [] | 0 |
number-of-ways-to-arrive-at-destination | [C++] : Using dikstra + toposort(DAG) + DP | c-using-dikstra-toposortdag-dp-by-zanhd-vd8x | \n#define ll long long int\nconst ll M = 1e9 + 7;\n#define MOD_ADD(a,b,m) ((a % m) + (b % m)) % m\n\nclass Solution {\npublic:\n \n static bool compare(pa | zanhd | NORMAL | 2022-04-15T16:30:56.466156+00:00 | 2022-04-15T16:30:56.466215+00:00 | 468 | false | ```\n#define ll long long int\nconst ll M = 1e9 + 7;\n#define MOD_ADD(a,b,m) ((a % m) + (b % m)) % m\n\nclass Solution {\npublic:\n \n static bool compare(pair<ll,ll> a, pair<ll,ll> b)\n {\n return a.second > b.second; // min heap\n }\n \n vector<ll> dikstra(ll src, vector<vector<pair<ll,ll>>> &adj, ll n)\n {\n vector<ll> dis(n, 1e18); //1e18 is imp here\n vector<bool> vis(n, 0);\n \n priority_queue<pair<ll,ll>, vector<pair<ll,ll>>, function<bool(pair<ll,ll>, pair<ll,ll>)>> Q(compare);\n \n Q.push({src, 0});\n \n while(!Q.empty())\n {\n pair<ll,ll> now = Q.top(); Q.pop();\n \n ll u = now.first;\n \n if(vis[u]) continue;\n vis[u] = 1;\n dis[u] = now.second;\n \n for(auto x : adj[u])\n {\n ll v = x.first;\n ll w = x.second;\n \n if(dis[v] > dis[u] + w)\n {\n dis[v] = dis[u] + w;\n Q.push({v, dis[v]});\n }\n }\n }\n \n return dis;\n }\n \n vector<ll> toposort(vector<vector<ll>> &adj, ll n)\n {\n vector<ll> ans;\n ll indegree[n]; memset(&indegree, 0x00, sizeof(indegree));\n for(int u = 0; u < n; u++)\n {\n for(auto v : adj[u])\n indegree[v]++;\n }\n \n \n queue<ll> q;\n for(int i = 0; i < n; i++) if(!indegree[i]) q.push(i);\n \n while(!q.empty())\n {\n ll u = q.front(); q.pop();\n ans.push_back(u);\n \n for(auto v : adj[u])\n {\n indegree[v]--;\n if(!indegree[v]) q.push(v);\n }\n }\n \n return ans;\n }\n \n int countPaths(int n, vector<vector<int>>& roads) \n {\n vector<vector<pair<ll,ll>>> adj(n);\n for(auto e : roads)\n {\n adj[e[0]].push_back({e[1], e[2]});\n adj[e[1]].push_back({e[0], e[2]});\n }\n \n vector<ll> dis = dikstra(0, adj, n);\n \n vector<vector<ll>> DAG(n);\n for(auto e : roads)\n {\n ll u = e[0];\n ll v = e[1];\n ll w = e[2];\n \n if(dis[u] + w == dis[v])\n {\n //include this edge u -> v\n DAG[u].push_back(v);\n }\n else if(dis[v] + w == dis[u])\n {\n //include this edge v -> u\n DAG[v].push_back(u);\n }\n }\n \n vector<ll> topo = toposort(DAG, n);\n \n ll dp[n]; memset(&dp, 0x00, sizeof(dp));\n dp[n - 1] = 1;\n \n for(int i = n - 1; i >= 0; i--)\n {\n ll u = topo[i];\n if(u == n - 1) continue;\n \n for(auto v : DAG[u]) dp[u] = MOD_ADD(dp[u], dp[v], M);\n }\n \n return dp[0];\n \n }\n};\n``` | 4 | 0 | ['Dynamic Programming', 'Topological Sort'] | 0 |
number-of-ways-to-arrive-at-destination | C++ || O(mlogn) || Approach Explained || Two solutions - i) Dijkstra ii) Dijkstra + DP | c-omlogn-approach-explained-two-solution-qxmm | I figured out Solution ii) first and then got to know that only Dijkstra would suffice and got Solution i) after seeing discussions. Both have same time complex | niksparmar22 | NORMAL | 2021-10-22T14:21:26.277551+00:00 | 2021-10-22T14:39:04.568212+00:00 | 326 | false | I figured out Solution ii) first and then got to know that only Dijkstra would suffice and got Solution i) after seeing discussions. Both have same time complexity and both passed all test cases.\n\nSolution i)\n\nApproach - Apply Dijkstra from n-1. Suppose waysToReachN1[i] denotes # of ways to reach n-1 from i. Our answer would be waysToReachN1[0].\n\nCases -\ni) i==n-1 | waysToReachN1[i] = 1\nii) If we find better distance for node i from node j then waysToReachN1[i]=waysToReachN1[j]\niii) If we find equal distance for node i from node j then waysToReachN1[i]+=waysToReachN1[j]\n\n```\nclass Solution {\npublic:\n struct cmp {\n bool operator()(const vector<long long> &left, const vector<long long> &right){\n return left[0] >= right[0];\n }\n };\n\n long long dijkstra(int n, vector<vector<vector<long long>>> &adj) {\n vector<long long> distances(n, LONG_MAX);\n priority_queue<vector<long long>, vector<vector<long long>>, cmp> Q;\n distances[n-1] = 0; \n vector<long long> waysToReachN1(n, 0);\n Q.push({distances[n-1], n-1}); \n waysToReachN1[n-1] = 1;\n while(!Q.empty()){\n vector<long long> vec = Q.top(); Q.pop();\n long long distanceSoFar = vec[0];\n int node = vec[1]; \n\t\t\tif(distanceSoFar > distances[node]) continue;\n for(vector<long long> vecNeigh: adj[node]){\n int node_neigh = vecNeigh[0];\n long long distanceBetweenTwo = vecNeigh[1]; \n if(distanceSoFar + distanceBetweenTwo < distances[node_neigh]){\n distances[node_neigh] = distanceSoFar + distanceBetweenTwo;\n Q.push({distances[node_neigh], node_neigh}); \n // found new way\n waysToReachN1[node_neigh] = waysToReachN1[node]; \n } else if(distanceSoFar + distanceBetweenTwo == distances[node_neigh]) {\n waysToReachN1[node_neigh]=(waysToReachN1[node_neigh] + waysToReachN1[node])%(1000000007); \n }\n } \n } \n\n return waysToReachN1[0]; \n } \n \n int countPaths(int n, vector<vector<int>>& roads) {\n vector<vector<vector<long long>>> adj(n);\n for(vector<int> road:roads){\n long long u = road[0];\n long long v = road[1];\n long long time = road[2];\n adj[u].push_back({v, time});\n adj[v].push_back({u, time});\n }\n \n return dijkstra(n,adj); \n }\n};\n```\nSolution ii)\n```\nclass Solution {\npublic:\n struct cmp {\n bool operator()(const vector<long long> &left, const vector<long long> &right){\n return left[0] >= right[0];\n }\n };\n\n vector<long long> dijkstra(int n, vector<vector<vector<long long>>> &adj) {\n vector<long long> distances(n, LONG_MAX);\n priority_queue<vector<long long>, vector<vector<long long>>, cmp> Q;\n distances[n-1] = 0; \n Q.push({distances[n-1], n-1}); \n while(!Q.empty()){\n vector<long long> vec = Q.top(); Q.pop();\n long long distanceSoFar = vec[0];\t\t\t\t\t\t\n int node = vec[1]; \n\t\t\tif(distanceSoFar > distances[node]) continue;\n for(vector<long long> vecNeigh: adj[node]){\n int node_neigh = vecNeigh[0];\n long long distanceBetweenTwo = vecNeigh[1]; \n if(distanceSoFar + distanceBetweenTwo < distances[node_neigh]){\n distances[node_neigh] = distanceSoFar + distanceBetweenTwo;\n Q.push({distances[node_neigh], node_neigh}); \n }\n } \n }\n\n return distances; \n }\n \n int countWays(int u, vector<vector<vector<long long>>> &adj, vector<long long> &distances, long long toCoverMore, vector<long long> &dp){\n int n = adj.size(); \n \n if(dp[u]!=-1) return dp[u];\n \n if(u==n-1){ \n if(toCoverMore == 0) return 1;\n return 0;\n }\n \n long long res = 0;\n \n for(vector<long long> vecNeigh: adj[u]){\n int node_neigh = vecNeigh[0];\n long long distanceBetweenTwo = vecNeigh[1];\n if(toCoverMore-distanceBetweenTwo == distances[node_neigh]){\n res=(res + countWays(node_neigh,adj,distances,toCoverMore-distanceBetweenTwo,dp))%(1000000007); \n } \n } \n \n return dp[u] = res;\n }\n \n \n int countPaths(int n, vector<vector<int>>& roads) {\n vector<vector<vector<long long>>> adj(n);\n for(vector<int> road:roads){\n long long u = road[0];\n long long v = road[1];\n long long time = road[2];\n adj[u].push_back({v, time});\n adj[v].push_back({u, time});\n }\n \n vector<long long> distances = dijkstra(n,adj); \n vector<long long> dp(n, -1);\n \n long long ways = countWays(0, adj, distances, distances[0], dp); \n return ways; \n \n }\n};\n``` | 4 | 0 | [] | 0 |
number-of-ways-to-arrive-at-destination | TestCases Wrong | testcases-wrong-by-lagahuahubro-ymqf | I am able to give custom test cases with time = 0. But in the constraints it is given\n1 <= timei <= 10^9.\nplease fix it.\n | lagaHuaHuBro | NORMAL | 2021-09-09T12:29:43.295410+00:00 | 2021-09-09T12:29:43.295455+00:00 | 129 | false | I am able to give custom test cases with time = 0. But in the constraints it is given\n```1 <= timei <= 10^9```.\nplease fix it.\n | 4 | 0 | [] | 0 |
number-of-ways-to-arrive-at-destination | C++ Dijkstra Two Solutions | c-dijkstra-two-solutions-by-shtanriverdi-5feu | Time Complexity: O(V^2 log V) where V is the number of node and E is the edges. \nSince we push each node to the minheap only once, that why we say log(V)\nSpac | shtanriverdi | NORMAL | 2021-08-31T17:10:39.367150+00:00 | 2021-08-31T17:19:18.450111+00:00 | 693 | false | **Time Complexity: O(V^2 log V)** where V is the number of node and E is the edges. \nSince we push each node to the minheap only once, that why we say log(V)\n**Space Complexity: O(V+ E)**\n\n**Optimized Solution**\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n // Build the weighted graph\n vector<vector<vector<int>>> graph(n);\n for (vector<int> &road : roads) {\n graph[road[0]].push_back({ road[2], road[1] }); // { time, node }\n graph[road[1]].push_back({ road[2], road[0] }); // { time, node }\n }\n \n // We will use a min-heap sorted by total time: { total time, node }\n priority_queue<vector<long long>, vector<vector<long long>>, greater<>> minheap;\n \n // Start with the initial node\n minheap.push({ 0, 0 }); // { time, node }\n \n // Distances table for Dijkstra, dist[i] gives the shortest path between src to node_i\n vector<long long> dist(n, LLONG_MAX);\n \n // Number of ways to reach a node via shortest path\n vector<long long> ways(n, 0);\n \n dist[0] = 0;\n ways[0] = 1;\n long long mod = 1000000007;\n \n while (!minheap.empty()) {\n // Get the current minimum time and node\n long long totalDist = minheap.top()[0];\n long long currentNode = minheap.top()[1];\n minheap.pop();\n \n // Optimization, we don\'t need the distances greater than the one previously found \n if (totalDist > dist[currentNode]) {\n continue;\n }\n \n // Check the neighbors and update dist value of the neighbors of the picked vertex\n for (vector<int> &neigh : graph[currentNode]) {\n // Relaxation, update the dist if neighbor is not visited and the new cost is smaller than the prev\n int neighbor = neigh[1];\n long long newDist = neigh[0] + totalDist;\n \n // Update the shortest path and ways\n if (newDist < dist[neighbor]) {\n dist[neighbor] = newDist;\n ways[neighbor] = ways[currentNode];\n minheap.push({ dist[neighbor], neighbor });\n }\n \n // Another shortest path found, increment the ways to node_i\n else if (newDist == dist[neighbor]) {\n ways[neighbor] = (ways[neighbor] + ways[currentNode]) % mod;\n }\n }\n }\n \n return ways[n - 1];\n }\n};\n```\n\n**Initial Solution**\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n // Build the weighted graph\n vector<vector<vector<int>>> graph(n);\n for (vector<int> &road : roads) {\n graph[road[0]].push_back({ road[2], road[1] }); // { time, node }\n graph[road[1]].push_back({ road[2], road[0] }); // { time, node }\n }\n \n // We will use a min-heap sorted by total time: { total time, node }\n priority_queue<vector<long long>, vector<vector<long long>>, greater<>> minheap;\n \n // Start with the initial node\n minheap.push({ 0, 0 }); // { time, node }\n \n // Distances table for Dijkstra, dist[i] gives the shortest path between src to node_i\n vector<long long> dist(n, LLONG_MAX);\n \n // Number of ways to reach a node via shortest path\n vector<long long> ways(n, 0);\n \n dist[0] = 0;\n ways[0] = 1;\n long long mod = 1000000007;\n \n while (!minheap.empty()) {\n // Get the current minimum time and node\n long long totalDist = minheap.top()[0];\n long long currentNode = minheap.top()[1];\n minheap.pop();\n \n // Check the neighbors and update dist value of the neighbors of the picked vertex\n for (vector<int> &neigh : graph[currentNode]) {\n // Relaxation, update the dist if neighbor is not visited and the new cost is smaller than the prev\n int neighbor = neigh[1];\n long long newDist = neigh[0] + totalDist;\n \n // Update the shortest path and ways\n if (newDist < dist[neighbor]) {\n dist[neighbor] = newDist;\n ways[neighbor] = ways[currentNode];\n minheap.push({ dist[neighbor], neighbor });\n }\n \n // Another shortest path found, increment the ways to node_i\n else if (newDist == dist[neighbor]) {\n ways[neighbor] = (ways[neighbor] + ways[currentNode]) % mod;\n }\n }\n }\n \n return ways[n - 1];\n }\n};\n``` | 4 | 0 | ['C'] | 1 |
number-of-ways-to-arrive-at-destination | JAVA SOLUTION USING DIJKSTRA AND DP | java-solution-using-dijkstra-and-dp-by-s-fnsn | The basic idea is to dijkstra algorithm and find the minimum path from 0 to (n - 1). The catch is that while traversing from one node to another if we encounter | Subhankar752 | NORMAL | 2021-08-26T06:21:29.492755+00:00 | 2021-08-26T06:21:29.492803+00:00 | 1,502 | false | The basic idea is to dijkstra algorithm and find the minimum path from 0 to (n - 1). The catch is that while traversing from one node to another if we encounter a node with more distance then we will initialise the number of ways to reach that node. Similarly, if we encounter a node with same distance as of previous count then we will increment the number of ways to reach that node by its count of previous node. In the end, we will return the number of ways to reach the (n - 1)th node. Hope this solution helps.\n```\nclass Solution {\n class Pair{\n int node;\n int dist;\n Pair(int node , int dist){\n this.node = node;\n this.dist = dist;\n }\n }\n public int countPaths(int n, int[][] roads) {\n int mod = (int)Math.pow(10 , 9) + 7;\n ArrayList<ArrayList<Pair>> adj = new ArrayList<>();\n int rows = roads.length;\n for(int i = 0 ; i < n ; i++)\n adj.add(new ArrayList<Pair>());\n for(int i = 0 ; i < rows ; i++){\n int from = roads[i][0];\n int to = roads[i][1];\n int dis = roads[i][2];\n adj.get(from).add(new Pair(to , dis));\n adj.get(to).add(new Pair(from , dis));\n }\n PriorityQueue<Pair> pq = new PriorityQueue<>((aa , bb) -> aa.dist - bb.dist);\n pq.add(new Pair(0 , 0));\n long[] ways = new long[n];\n ways[0] = 1;\n int[] dist = new int[n];\n Arrays.fill(dist , Integer.MAX_VALUE);\n dist[0] = 0;\n while(!pq.isEmpty()){\n Pair p = pq.remove();\n int node = p.node;\n int dis = p.dist;\n for(Pair pa : adj.get(node)){\n if((dis + pa.dist) < dist[pa.node]){\n ways[pa.node] = ways[node];\n dist[pa.node] = dis + pa.dist;\n pq.add(new Pair(pa.node , dist[pa.node]));\n }\n else if((dis + pa.dist) == dist[pa.node]){\n ways[pa.node] += ways[node];\n ways[pa.node] = ways[pa.node] % mod;\n }\n }\n }\n return (int)ways[n - 1];\n }\n}\n``` | 4 | 1 | ['Dynamic Programming', 'Java'] | 4 |
number-of-ways-to-arrive-at-destination | 0 ms C/C++, 1 ms JS. BFS and Dijkstra. Beats 100.00% | 0-ms-cc-1-ms-js-bfs-and-dijkstra-beats-1-kr5z | Approach
BFS 1 ms in JavaScript.
Dijkstra's Algorithm 40 ms in JavaScript.
Complexityv - vertices, e - edges.
Time complexity: BFS O(v3), Dijkstra O((v+e)logv) | nodeforce | NORMAL | 2025-03-24T03:48:57.130697+00:00 | 2025-03-24T03:51:12.938519+00:00 | 48 | false | # Approach
1. BFS `1 ms` in JavaScript.
2. Dijkstra's Algorithm `40 ms` in JavaScript.
# Complexity
$$v$$ - vertices, $$e$$ - edges.
- Time complexity: BFS $$O(v^3)$$, Dijkstra $$O((v + e) log v)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(v^2)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp [C++ BFS 0 ms]
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
if (n < 3) return 1;
const int mod = 1e9 + 7;
const int szn = n * sizeof(long);
const int sznn = n * n * sizeof(int);
unsigned long* time = (unsigned long*)alloca(szn);
unsigned long* count = (unsigned long*)alloca(szn);
int* m = (int*)alloca(sznn);
memset(time, 255, szn);
memset(count, 0, szn);
memset(m, 0, sznn);
for (const auto& r : roads)
m[r[0] * n + r[1]] = m[r[1] * n + r[0]] = r[2];
time[0] = 0;
count[0] = 1;
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n - 1; ++i) {
if (count[i] == 0) continue;
for (int j = 0; j < n; ++j) {
const int tj = m[i * n + j];
if (tj == 0) continue;
const int tij = time[i] + tj;
if (tij < time[j]) {
time[j] = tij;
count[j] = count[i];
} else if (tij == time[j]) {
count[j] = (count[j] + count[i]) % mod;
}
}
count[i] = 0;
}
}
return count[n - 1];
}
};
```
```c [C BFS 0 ms]
int countPaths(int n, int** roads, int rsize, int* _) {
if (n < 3) return 1;
const int mod = 1e9 + 7;
unsigned long time[n];
unsigned long count[n];
int m[n * n];
memset(time, 255, sizeof(time));
memset(count, 0, sizeof(count));
memset(m, 0, sizeof(m));
for (int i = 0; i < rsize; ++i) {
const int* r = roads[i];
m[r[0] * n + r[1]] = m[r[1] * n + r[0]] = r[2];
}
time[0] = 0;
count[0] = 1;
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n - 1; ++i) {
if (count[i] == 0) continue;
for (int j = 0; j < n; ++j) {
const int tj = m[i * n + j];
if (tj == 0) continue;
const int tij = time[i] + tj;
if (tij < time[j]) {
time[j] = tij;
count[j] = count[i];
} else if (tij == time[j]) {
count[j] = (count[j] + count[i]) % mod;
}
}
count[i] = 0;
}
}
return count[n - 1];
}
```
```javascript [JS BFS 1 ms]
const countPaths = (n, roads) => {
if (n < 3) return 1;
const mod = 1e9 + 7;
const time = new Array(n).fill(Infinity);
const count = new Array(n).fill(0);
const m = new Uint32Array(n * n);
for (const r of roads)
m[r[0] * n + r[1]] = m[r[1] * n + r[0]] = r[2];
time[0] = 0;
count[0] = 1;
for (let k = 0; k < n; ++k) {
for (let i = 0; i < n - 1; ++i) {
if (count[i] === 0) continue;
for (let j = 0; j < n; ++j) {
const tj = m[i * n + j];
if (tj === 0) continue;
const tij = time[i] + tj;
if (tij < time[j]) {
time[j] = tij;
count[j] = count[i];
} else if (tij === time[j]) {
count[j] = (count[j] + count[i]) % mod;
}
}
count[i] = 0;
}
}
return count[n - 1];
};
```
```javascript [JS Dijkstra 40 ms]
const countPaths = (n, roads) => {
if (n < 3) return 1;
const mod = 1e9 + 7;
const time = new Array(n).fill(Infinity);
const count = new Array(n).fill(0);
const q = new MinPriorityQueue((tn) => tn[0]);
const m = new Uint32Array(n * n);
for (const r of roads)
m[r[0] * n + r[1]] = m[r[1] * n + r[0]] = r[2];
time[0] = 0;
count[0] = 1;
q.push([0, 0]);
while (!q.isEmpty()) {
const tn = q.pop();
const ti = tn[0];
const i = tn[1];
if (ti > time[i]) continue;
for (let j = 0; j < n; ++j) {
const tj = m[i * n + j];
if (tj === 0) continue;
const tij = ti + tj;
if (tij < time[j]) {
time[j] = tij;
count[j] = count[i];
q.push([tij, j]);
} else if (tij === time[j]) {
count[j] = (count[j] + count[i]) % mod;
}
}
}
return count[n - 1];
};
``` | 3 | 0 | ['Array', 'Dynamic Programming', 'Breadth-First Search', 'Graph', 'C', 'Heap (Priority Queue)', 'Shortest Path', 'C++', 'TypeScript', 'JavaScript'] | 1 |
number-of-ways-to-arrive-at-destination | Dijkstra N log(n) | Greedy Logic | dijkstra-n-logn-greedy-logic-by-1_b3-d7p6 | IntuitionWe can observe that this is a shortest path problem. So Dijkstra or similar algorithm comes quickly to intuition. We will be using Dijkstra.
We can als | 1_b3 | NORMAL | 2025-03-23T10:30:13.336251+00:00 | 2025-03-23T10:30:13.336251+00:00 | 387 | false | # Intuition
We can observe that this is a shortest path problem. So Dijkstra or similar algorithm comes quickly to intuition. We will be using Dijkstra.
We can also notice one more thing , that all the ways which go from 0 to n-1 have same weighted distance which , overall is the shortest path from 0 to n-1.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
We can follow these sequential steps
1) Find the weight of shortest path between 0 to n-1;
2) A standard way of counting number of ways is to use this property,
( if we can reach a node 'A' using x ways and node 'B' using y ways , and we can reach node 'A' from 'B' or vice versa, then totl ways will be ways[A]+ways[B]( if both have same shortest distance in path), if node A gives shorter distance , then ways[B] = ways[A]).
3) By using this property , we can simply calculate the ways in Dijkstra loop using Priority Queue
4) For simplicity and overflow avoidance, I have used long long , and converted it to integer when returning.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(m log n) :
Where: m is the number of edges in the graph and n is the number of nodes.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n+m)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
int countPaths(int n, vector<vector<int>>& roads) {
ll mod = 1e9+7;
vector<vector<pair<ll,ll>>>adj(n);
for(ll i = 0;i<roads.size();i++){
ll u = roads[i][0];
ll v = roads[i][1];
ll wt = roads[i][2];
adj[u].push_back({wt,v});
adj[v].push_back({wt,u});
}
vector<ll>dist(n,LLONG_MAX);
dist[0]=0;
vector<ll>ways(n,0);
ways[0]=1;
priority_queue<pair<ll,ll>>pq;
pq.push({0,0});
while(!pq.empty()){
ll node = pq.top().second;
ll wt = -(pq.top().first);
pq.pop();
for(auto it:adj[node]){
ll newNode = it.second;
ll newWt = it.first;
if(wt+newWt <dist[newNode]){
dist[newNode] = newWt+wt;
pq.push({-(newWt+wt),newNode});
ways[newNode] = ways[node];
}
else if(wt+newWt == dist[newNode]){
ways[newNode] = (ways[newNode]+ways[node])%mod;
}
}
}
return (int)ways[n-1]%mod;
}
};
```
```java []
import java.util.*;
class Solution {
public int countPaths(int n, int[][] roads) {
final long MOD = 1000000007L;
List<List<long[]>> adj = new ArrayList<>();
for (long i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int i = 0; i < roads.length; i++) {
int u = roads[i][0];
int v = roads[i][1];
long wt = roads[i][2];
adj.get(u).add(new long[]{wt, v});
adj.get(v).add(new long[]{wt, u});
}
long[] dist = new long[n];
Arrays.fill(dist, Long.MAX_VALUE);
dist[0] = 0;
long[] ways = new long[n];
ways[0] = 1;
PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(a -> a[0]));
pq.offer(new long[]{0, 0});
while (!pq.isEmpty()) {
long[] current = pq.poll();
long node = current[1];
long wt = current[0];
for (long[] edge : adj.get((int) node)) {
long newNode = edge[1];
long newWt = edge[0];
if (wt + newWt < dist[(int) newNode]) {
dist[(int) newNode] = wt + newWt;
pq.offer(new long[]{wt + newWt, newNode});
ways[(int) newNode] = ways[(int) node];
} else if (wt + newWt == dist[(int) newNode]) {
ways[(int) newNode] = (ways[(int) newNode] + ways[(int) node]) % MOD;
}
}
}
return (int) (ways[n - 1] % MOD);
}
}
```
```python []
import heapq
MOD = 1000000007
class Solution:
def countPaths(self, n, roads):
adj = [[] for _ in range(n)]
# Build the graph
for u, v, wt in roads:
adj[u].append((wt, v))
adj[v].append((wt, u))
dist = [float('inf')] * n
dist[0] = 0
ways = [0] * n
ways[0] = 1
pq = [(0, 0)] # (distance, node)
while pq:
wt, node = heapq.heappop(pq)
for newWt, newNode in adj[node]:
if wt + newWt < dist[newNode]:
dist[newNode] = wt + newWt
heapq.heappush(pq, (dist[newNode], newNode))
ways[newNode] = ways[node]
elif wt + newWt == dist[newNode]:
ways[newNode] = (ways[newNode] + ways[node]) % MOD
return int(ways[n - 1] % MOD)
```
| 3 | 0 | ['Greedy', 'Shortest Path', 'C++', 'Java', 'Python3'] | 0 |
number-of-ways-to-arrive-at-destination | ✅✅ Dijkstra's Algorithm || Beginner Friendly || Easiest Code | dijkstras-algorithm-beginner-friendly-ea-ibtp | Approach1. Graph Representation
The given graph is an undirected weighted graph.
Construct an adjacency list adj using an unordered map.
2. Dijkstra’s Algorithm | Karan_Aggarwal | NORMAL | 2025-03-23T10:02:28.615192+00:00 | 2025-03-23T10:02:28.615192+00:00 | 171 | false | # Approach
### **1. Graph Representation**
- The given graph is an **undirected weighted graph**.
- Construct an **adjacency list** `adj` using an unordered map.
### **2. Dijkstra’s Algorithm**
- **Priority queue (Min-Heap)** is used to always process the node with the smallest distance first.
- Maintain a **`time[]`** array to store the shortest time to reach each node.
- Maintain a **`pathCount[]`** array to store the number of ways to reach each node with the shortest path.
### **3. Processing Nodes**
- Start from **node `0`**, set `time[0] = 0` and `pathCount[0] = 1`.
- For each adjacent node:
- If a **shorter path** is found, update `time[]` and reset `pathCount[]`.
- If an **equally short path** is found, add the number of ways to reach the current node (`pathCount[curr]`).
### **4. Modulo Operations**
- Since the number of paths can be large, **take modulo `1e9 + 7`** in calculations.
# Complexity Analysis
- **Time Complexity:**
- **`O((N + E) log N)`** (Dijkstra with min-heap).
- **Space Complexity:**
- **`O(N + E)`** (Adjacency list + Priority queue + Distance/Path arrays).
# 🔹 Edge Cases Considered
- ✔ Graph with **no roads** (only one node).
- ✔ Graph with **multiple shortest paths**.
- ✔ Graph with **large constraints** (to test efficiency of Dijkstra).
- ✔ **Disconnected nodes** (ensures no invalid access).
🚀 **Dijkstra ensures optimal paths, and path counting is done efficiently!**
# Code
```cpp []
class Solution {
public:
const int MOD=1e9+7;
typedef pair<long long,int>P;
int countPaths(int n, vector<vector<int>>& roads) {
unordered_map<int,vector<pair<int,int>>>adj;
for(auto &vec:roads){
int u=vec[0];
int v=vec[1];
int w=vec[2];
adj[u].push_back({v,w});
adj[v].push_back({u,w});
}
priority_queue<P,vector<P>,greater<P>>pq;
vector<long long>time(n,LLONG_MAX);
vector<int>pathCount(n,0);
time[0]=0;
pathCount[0]=1;
pq.push({0,0});
while(!pq.empty()){
long long currDist=pq.top().first;
int currNode=pq.top().second;
pq.pop();
for(auto &ngbr:adj[currNode]){
int ngbrNode=ngbr.first;
int ngbrDist=ngbr.second;
if(currDist+ngbrDist<time[ngbrNode]){
time[ngbrNode]=currDist+ngbrDist;
pq.push({currDist+ngbrDist,ngbrNode});
pathCount[ngbrNode]=pathCount[currNode];
}
else if(currDist+ngbrDist==time[ngbrNode]){
pathCount[ngbrNode]=(pathCount[ngbrNode]+pathCount[currNode])%MOD;
}
}
}
return pathCount[n-1];
}
};
```
# Have a Good Day 😊 UpVote? | 3 | 0 | ['Breadth-First Search', 'Graph', 'Shortest Path', 'C++'] | 0 |
number-of-ways-to-arrive-at-destination | 🎓Wave Relaxation Algorithm Explanation | 5~17ms (Beats 98~100) O(n×(n+m)) | 62.8~65.5 O(n+m) | wave-relaxation-algorithm-explanation-51-n7zt | IntuitionThe problem requires calculating the number of "shortest paths" from the starting node 0 to the destination node n - 1, with the final answer taken mod | whats2000 | NORMAL | 2025-03-23T09:15:32.743656+00:00 | 2025-03-24T01:33:24.257483+00:00 | 96 | false | # Intuition
The problem requires calculating the number of "shortest paths" from the starting node `0` to the destination node `n - 1`, with the final answer taken modulo $10^9+7$. We can visualize the problem as a map where:
- Each **node (intersection)** represents a junction.
- Each **edge (road)** represents a path connecting two intersections and is associated with a "travel time".
The goal is to determine the shortest travel time from the starting node to the destination and count how many different paths yield that minimum travel time.
---
# Approach
To solve the problem, we adopt the following steps:
### 1. Graph Representation
First, we clearly represent the city's road system:
- **Nodes and Edges**: Use an adjacency list to record which roads are available from each intersection.
For example, if it takes `3` units of time to go from intersection `A` to intersection `B`, we record it as:
`A → B (3)` and `B → A (3)` (since the roads are bidirectional).
This method allows each node to quickly access its adjacent nodes along with the travel time to reach them.
### 2. Wave Relaxation — Gradually Shortening Distances
The key idea here is to use multiple "waves" (iterations) to gradually update the shortest distance from the starting node to every other node.
#### Why Multiple Waves?
Since the road network might be complex and many potential paths exist, we cannot initially tell which route is the shortest. Therefore, we must repeatedly check and update to ensure we find the truly shortest path.
The specific process is as follows:
- Initially, we set the distance from the starting node (`0`) to itself as `0` (since no movement is required), and all other nodes are set to infinity (indicating that no path has yet been found).
- Then, we perform multiple iterations (waves). In each wave, we traverse every node:
- For each node, we attempt to propagate (relax) its current known shortest distance to its neighboring nodes.
- If a new, shorter path is found via this node, update the neighbor’s shortest distance.
- If the newly found path has the same travel time as the current shortest distance for the neighbor, it indicates that we have found an additional different shortest path; in this case, we add the number of paths from the current node to the neighbor’s path count.
- After processing all nodes in one wave, we check if any node’s distance was updated:
- If no updates occurred, then all shortest paths have been found and there is no need for further waves.
- If updates did occur, proceed with the next wave, with a maximum of `n` iterations (since at most `n-1` steps are needed to reach the destination).
#### A Detailed Example:
Assume that the distance from the starting node `0` to node `A` is currently `10`. Now, suppose we find another route from node `B` to node `A` that only takes `8` units of time.
- We then update the distance for node `A` to `8` and set the number of shortest paths for `A` equal to the number of paths reaching `B` (since this new, shorter path comes through `B`).
- Later, if we discover yet another route that takes `8` minutes to reach node `A`, we add the number of paths provided by this route to node `A`’s total, indicating that there are more ways to reach `A` in the shortest time.
### 3. Accumulating Path Counts and Modulo Operation
Since the number of paths can be very large, we need to perform a modulo operation while accumulating the path counts:
- At every update, we take the modulo $10^9+7$ of the path count to ensure the number stays within the required range and avoids overflow.
---
### Detailed Implementation Steps
#### Step 1: Initialization and Graph Construction
**Building the Graph**: Based on the input `roads` array, convert each edge into an adjacency list representation where each node records its neighboring nodes and the corresponding travel times.
```typescript
const graph: { edges: number[]; weights: number[] }[] = Array.from({ length: n }, () => ({
edges: [],
weights: [],
}));
for (const [u, v, w] of roads) {
graph[u].edges.push(v);
graph[u].weights.push(w);
graph[v].edges.push(u);
graph[v].weights.push(w);
}
```
**Initialization of Distances and Path Counts**
- Use an array `dist` to record the shortest distance from the starting node `0` to every other node. Initially, all distances are set to infinity, except for the starting node which is set to `0`.
- Use an array `ways` to record the number of shortest paths for each node. Initially, set the path count for the starting node as `1`.
```typescript
const dist = new Array(n).fill(Infinity);
dist[0] = 0;
const ways = new Array(n).fill(0);
ways[0] = 1;
const MOD = 1000000007;
```
#### Step 2: Wave Relaxation Algorithm
**Performing the Wave Iterations**: To ensure all shortest paths are updated correctly, we perform at most `n` waves. In each wave, traverse all nodes (except the destination) and for each neighboring edge, perform the following:
1. **Relaxation Operation**
For a given node `node` and its neighbor `neighbor`, calculate: $$newDist = dist[node] + travelTime$$
- If $$newDist < dist[neighbor],$$ update $$dist[neighbor] = newDist$$ and set $$ways[neighbor] = ways[node].$$
- If $$newDist === dist[neighbor],$$ it means an equivalent shortest path is found; hence, add $$ways[node]$$ to $$ways[neighbor]$$ and perform the modulo operation.
2. **Clearing the Current Node's Path Count**
To avoid re-propagating the same node’s path count in the same wave, reset $$ways[node]$$ to zero after processing all its adjacent edges.
```typescript
for (let wave = 0; wave < n; wave++) {
let updated = false; // Indicates whether any update occurred during this wave
for (let node = 0; node < n - 1; node++) {
if (ways[node] <= 0) {
continue;
}
const { edges, weights } = graph[node];
for (let k = 0; k < edges.length; k++) {
const neighbor = edges[k];
const newDist = dist[node] + weights[k];
if (newDist < dist[neighbor]) {
dist[neighbor] = newDist;
ways[neighbor] = ways[node];
updated = true;
} else if (newDist === dist[neighbor]) {
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
updated = true;
}
}
ways[node] = 0;
}
if (!updated) {
break;
}
}
```
#### Step 3: Returning the Result
After the iterations, $$ways[n - 1]$$ represents the total number of shortest paths from the starting node `0` to the destination node `n - 1` (already taken modulo $10^9+7$). Return this as the final answer.
```typescript
return ways[n - 1] % MOD;
```
---
# Complexity
- Time complexity:
- The wave traversal performs up to `n` iterations. In each iteration, all nodes and their adjacent edges are examined. In the worst-case scenario, the time complexity is $$O(n \times (n + m))$$.
- In practice, due to the early termination mechanism (breaking out when no updates occur), the algorithm typically does not execute all `n` iterations.
- **Final time complexity:** $$O(n \times (n + m))$$
- Space complexity:
- The space is mainly used for the graph representation, and the arrays for distances and path counts, resulting in a space complexity of $$O(n + m)$$.
- **Final space complexity:** $$O(n + m)$$
---
# Code
```typescript []
/**
* @param {number} n
* @param {number[][]} roads
* @return {number}
*/
function countPaths(n: number, roads: number[][]): number {
if (n === 1) {
return 1; // Only one node, so one path.
}
const MOD = 1000000007;
// Build the graph where each node stores its neighbors and corresponding travel times.
const graph: { edges: number[]; weights: number[] }[] = Array.from({ length: n }, () => ({
edges: [],
weights: [],
}));
for (const [u, v, w] of roads) {
graph[u].edges.push(v);
graph[u].weights.push(w);
graph[v].edges.push(u);
graph[v].weights.push(w);
}
// Initialize arrays for distances and the count of shortest paths.
const dist = new Array(n).fill(Infinity);
dist[0] = 0; // Start node has distance 0.
const ways = new Array(n).fill(0);
ways[0] = 1; // Only one way to reach the start node.
// Use wave relaxation: up to n waves are executed.
for (let wave = 0; wave < n; wave++) {
let updated = false; // Flag to check if any update happened in this wave.
// Process all nodes except the destination to propagate their current active path counts.
for (let node = 0; node < n - 1; node++) {
// Skip nodes that are not active in this wave (i.e., no new ways to propagate).
if (ways[node] <= 0) {
continue;
}
// For each neighbor of the current node...
const { edges, weights } = graph[node];
for (let k = 0; k < edges.length; k++) {
const neighbor = edges[k];
const newDist = dist[node] + weights[k]; // Calculate potential new distance.
if (newDist < dist[neighbor]) {
// Found a shorter path: update distance and reset path count.
dist[neighbor] = newDist;
ways[neighbor] = ways[node];
updated = true;
} else if (newDist === dist[neighbor]) {
// Found an alternative path with the same distance: accumulate the count.
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
updated = true;
}
}
// Mark the current node as processed in this wave.
ways[node] = 0;
}
// If no updates occurred in the entire wave, the distances and path counts won't change further.
if (!updated) {
break;
}
}
// The count of shortest paths to the destination node is returned.
return ways[n - 1] % MOD;
}
```
```javascript []
/**
* @param {number} n
* @param {number[][]} roads
* @return {number}
*/
function countPaths(n, roads) {
if (n === 1) {
return 1; // Only one node, so one path.
}
const MOD = 1000000007;
// Build the graph where each node stores its neighbors and corresponding travel times.
const graph = Array.from({ length: n }, () => ({
edges: [],
weights: [],
}));
for (const [u, v, w] of roads) {
graph[u].edges.push(v);
graph[u].weights.push(w);
graph[v].edges.push(u);
graph[v].weights.push(w);
}
// Initialize arrays for distances and the count of shortest paths.
const dist = new Array(n).fill(Infinity);
dist[0] = 0; // Start node has distance 0.
const ways = new Array(n).fill(0);
ways[0] = 1; // Only one way to reach the start node.
// Use wave relaxation: up to n waves are executed.
for (let wave = 0; wave < n; wave++) {
let updated = false; // Flag to check if any update happened in this wave.
// Process all nodes except the destination to propagate their current active path counts.
for (let node = 0; node < n - 1; node++) {
// Skip nodes that are not active in this wave (i.e., no new ways to propagate).
if (ways[node] <= 0) {
continue;
}
// For each neighbor of the current node...
const { edges, weights } = graph[node];
for (let k = 0; k < edges.length; k++) {
const neighbor = edges[k];
const newDist = dist[node] + weights[k]; // Calculate potential new distance.
if (newDist < dist[neighbor]) {
// Found a shorter path: update distance and reset path count.
dist[neighbor] = newDist;
ways[neighbor] = ways[node];
updated = true;
} else if (newDist === dist[neighbor]) {
// Found an alternative path with the same distance: accumulate the count.
ways[neighbor] = (ways[neighbor] + ways[node]) % MOD;
updated = true;
}
}
// Mark the current node as processed in this wave.
ways[node] = 0;
}
// If no updates occurred in the entire wave, the distances and path counts won't change further.
if (!updated) {
break;
}
}
// The count of shortest paths to the destination node is returned.
return ways[n - 1] % MOD;
}
```
# Result
| 3 | 0 | ['Dynamic Programming', 'Graph', 'Shortest Path', 'TypeScript', 'JavaScript'] | 2 |
number-of-ways-to-arrive-at-destination | Simple C++ | Beats 100% | Dijkstra Algo | Easy to Understand | simple-c-beats-100-dijkstra-algo-easy-to-356b | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | AK200199 | NORMAL | 2025-03-23T09:12:29.353871+00:00 | 2025-03-23T09:12:29.353871+00:00 | 240 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
// Logic is we can use Dijkstra’s algo for finding the shortest path between 0 to n-1 then we use DP to keep the counting of that path
int countPaths(int n, vector<vector<int>>& roads) {
vector<pair<int,int>>adj[n];
// creating adjacency list
for(auto& r:roads){
adj[r[0]].push_back({r[1],r[2]});
adj[r[1]].push_back({r[0],r[2]});
}
// distance vector
vector<long long>dist(n,1e18),ways(n,0);
priority_queue<pair<long long,int>,
vector<pair<long long,int>>,greater<>>pq;
int mod=1e9+7;
dist[0]=0;
ways[0]=1;
pq.push({0,0});
while(!pq.empty()){
auto [d,u]=pq.top(); pq.pop();
if(d>dist[u])continue;
for(auto&[v,w]:adj[u]){
if(dist[v]>d+w){
dist[v]=d+w;
ways[v]=ways[u];
pq.push({dist[v],v});
}else if(dist[v]==d+w){
ways[v]=(ways[v]+ways[u])%mod;
}
}
}
return ways[n-1];
}
};
``` | 3 | 0 | ['C++'] | 0 |
number-of-ways-to-arrive-at-destination | 🔥 Dijkstra's Algorithm | 🚀 Priority Queue | ⏱️ TC: O(E log V) 🎯 | dijkstras-algorithm-priority-queue-tc-oe-9m57 | IntuitionWe use Dijkstra's algorithm to find the shortest paths and simultaneously count how many different ways we can reach each node with the current shortes | Ashok_Kumar_25 | NORMAL | 2025-03-23T08:20:48.010089+00:00 | 2025-03-23T08:20:48.010089+00:00 | 362 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We use **Dijkstra's algorithm** to find the shortest paths and simultaneously count how many different ways we can reach each node with the current shortest distance.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Build the Graph: Create an adjacency list representation of the graph where for each node, we store its neighbors and the time to reach them.
2. Create a dist array to store the shortest distance to each node (initially infinity, except dist[0] = 0)
3. Create a ways array to count the number of ways to reach each node via the shortest path (initially ways[0] = 1, others = 0)
4. Use a priority queue to explore nodes in order of increasing distance
5. For each node, look at all its neighbors
- If we find a shorter path to a neighbor, update its distance and reset its count of ways
- If we find a path of equal length, add the current node's count to the neighbor's count
6. Result: After the algorithm completes, ways[n-1] contains the number of shortest paths from node 0 to node n-1.
# Complexity
- Time complexity: O(E log V)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(V + E)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
adj = defaultdict(list)
for u, v, time in roads:
adj[u].append((v, time))
adj[v].append((u, time))
dist = [0]+[float('inf')]*(n-1)
ways = [1]+[0]*(n-1)
pq = [(0, 0)] #(time, node)
MOD = 10**9 + 7
# Dijkstra's algorithm
while pq:
d, node = heapq.heappop(pq)
if d > dist[node]:
continue
for nei,t in adj[node]:
if dist[node]+t < dist[nei]:
dist[nei] = dist[node]+t
ways[nei] = ways[node]
heapq.heappush(pq, (dist[nei], nei))
elif dist[node]+t == dist[nei]:
ways[nei] = (ways[nei] + ways[node]) % MOD
return ways[n-1]
```

| 3 | 0 | ['Dynamic Programming', 'Graph', 'Shortest Path', 'Python3'] | 0 |
number-of-ways-to-arrive-at-destination | Dijkstra with a Twist: A Beginner-Friendly Editorial Guide to Count Shortest Paths 🛤️😏 | dijkstra-with-a-twist-a-beginner-friendl-lqs2 | Dijkstra with a Twist: A Beginner-Friendly Guide to Count Shortest Paths 🛤️😏Oh look, another graph problem where we need to find the shortest paths—how original | Ansh_Ghawri | NORMAL | 2025-03-23T07:12:59.124437+00:00 | 2025-03-23T07:22:03.703011+00:00 | 131 | false | # Dijkstra with a Twist: A Beginner-Friendly Guide to Count Shortest Paths 🛤️😏
Oh look, another graph problem where we need to find the shortest paths—how *original*! 🙄 This time, we’re tasked with counting the number of shortest paths from node 0 to node \(n-1\) in a graph, because apparently just finding the shortest path isn’t enough anymore. We’ll use **Dijkstra’s algorithm** (because of course we will), but with a little twist to count paths. Don’t worry, I’ll hold your hand through this with a beginner-friendly explanation—let’s see if we can make this graph problem less boring! 😏
## Intuition 🕵️♀️
When I first saw this problem, I thought: "Great, another shortest path problem—yawn! 🥱 But wait, they want the *number* of shortest paths? That’s… mildly interesting, I guess." Here’s how I broke it down:
- We have a graph with \(n\) nodes (0 to \(n-1\)) and `roads` (edges) where each road \([u, v, t]\) means there’s a path between nodes \(u\) and \(v\) that takes \(t\) time. Oh, and it’s undirected, so the road goes both ways—how convenient! 🚗
- We need to find the number of shortest paths from node 0 to node \(n-1\). A shortest path is a path that takes the least amount of time.
- Normally, Dijkstra’s algorithm would just give us the shortest time to reach each node, but this problem wants us to count how many ways we can get to \(n-1\) using that shortest time. Ugh, extra work! 🙄
- So, we’ll use Dijkstra’s to find the shortest times, but we’ll also keep track of how many paths lead to each node with that shortest time. Sounds like a job for some extra bookkeeping—let’s get to it! 📝
## Approach 🗺️
Here’s how I solved this problem in simple steps—because I know you’re probably new to this and need all the help you can get! 😏 Think of it like planning a road trip where you want the fastest route, but you also want to know how many different fastest routes there are. Let’s break it down:
1. **Build the Graph** 🏗️:
- First, we need to turn the `roads` into a graph. We’ll use an adjacency list because it’s the *cool* way to store graphs. For each road \([u, v, t]\), add \(v\) to \(u\)’s list and \(u\) to \(v\)’s list, with the time \(t\). So, `adj[u]` will have pairs like \((v, t)\), meaning you can go from \(u\) to \(v\) in \(t\) time. Easy peasy! 🛤️
2. **Set Up for Dijkstra’s** 🛠️:
- We’re going from node 0 (the source) to node \(n-1\) (the destination). Let’s call them `src` and `dest` because that’s what all the cool kids do. 😎
- We need two things:
- `time`: An array to store the shortest time to reach each node. Start with infinity for everyone except the source (set `time[src] = 0`—duh, it takes 0 time to reach the starting point!).
- `freq`: A map to count the number of shortest paths to each node. Since we start at `src`, set `freq[src] = 1` (there’s exactly 1 way to be at the starting point—by not moving, genius! 🙄).
3. **Run Dijkstra’s with a Twist** 🔄:
- Use a priority queue to process nodes in order of increasing time (because Dijkstra’s loves to be efficient). Start by pushing \((0, src)\) into the queue (time 0 to reach the source).
- While the queue isn’t empty:
- Pop the node with the smallest current time (`currT`) and its node (`node`).
- If `currT` is greater than the best time we already found for `node` (`time[node]`), skip it—Dijkstra’s doesn’t like wasting time on slow paths! ⏳
- For each neighbor of `node` (from `adj[node]`):
- Get the neighbor node (`nbrNode`) and the time to reach it (`edgeT`).
- **Case 1: Found a Faster Path** 🏎️:
- If `time[node] + edgeT` is less than `time[nbrNode]`, we’ve found a faster way to reach `nbrNode`! Update `time[nbrNode]` to this new time, set `freq[nbrNode] = freq[node]` (the number of ways to reach `nbrNode` is the same as the number of ways to reach `node`), and push the new time and node into the queue.
- **Case 2: Found Another Shortest Path** 🛤️:
- If `time[node] + edgeT` equals `time[nbrNode]`, we’ve found another path to `nbrNode` that takes the same time as the shortest path we already know. Add the number of ways to reach `node` to `freq[nbrNode]` (so `freq[nbrNode] += freq[node]`). Don’t forget to take the modulo because the problem says so—ugh, math! 🙄
4. **Get the Answer** 🎁:
- After Dijkstra’s finishes, `freq[n-1]` will tell us the number of shortest paths to node \(n-1\). Return it (with modulo, because the problem loves to make us jump through hoops). Done—finally! 🎉
This approach is beginner-friendly because we’re just using Dijkstra’s with a little extra step to count paths. It’s like Dijkstra’s decided to be extra and show off by counting paths too! Let’s see the complexity next. 📊
## Complexity 📈
Let’s figure out how much time and space this solution uses. I’ll explain it in a simple way, but don’t expect me to hold your hand through the math—you’re a big coder now! 😏
- **Time Complexity** ⏱️:
- **Building the Graph:** We loop through the `roads` list, which has \(E\) edges (where \(E\) is the number of roads). For each edge, we add it to the adjacency list twice (since it’s undirected). That takes **O(E)** time. Not bad! 🛤️
- **Dijkstra’s Setup:** Initializing the `time` array (size \(n\)) and `freq` map takes **O(n)** time. Pushing the source into the priority queue is **O(1)**—yawn! 🥱
- **Dijkstra’s Loop:** The priority queue processes each node at most once, so we pop \(n\) nodes. Popping from a priority queue takes **O(log n)** time, so that’s **O(n * log n)** for all nodes. For each node, we look at its neighbors. Across all nodes, we process each edge twice (since the graph is undirected), so that’s \(2E\) edge checks. Each edge check involves a push to the priority queue (which takes **O(log n)** time). So, processing edges takes **O(E * log n)**. Adding it up, Dijkstra’s takes **O(n * log n + E * log n)**, which simplifies to **O((n + E) * log n)**. Oh, and don’t forget the modulo operations—they’re **O(1)** but make us feel fancy! 😎
- **Overall:** The total time complexity is **O((n + E) * log n)**. Not terrible, I guess! 🕒
- **Space Complexity** 🗄️:
- **Adjacency List:** The `adj` map stores \(2E\) entries (since each edge is added twice). That’s **O(E)** space.
- **Priority Queue:** The priority queue can hold up to \(n\) nodes at a time, so that’s **O(n)** space.
- **Time and Freq Arrays:** The `time` array and `freq` map each take **O(n)** space.
- **Overall:** Adding it up, we get **O(E + n)** space. Pretty standard for a graph problem—nothing to write home about! 📦
This solution is efficient enough, and the path-counting twist makes it a bit more interesting than plain old Dijkstra’s. Now, let’s see the code—hope you’re ready to be impressed! 😏
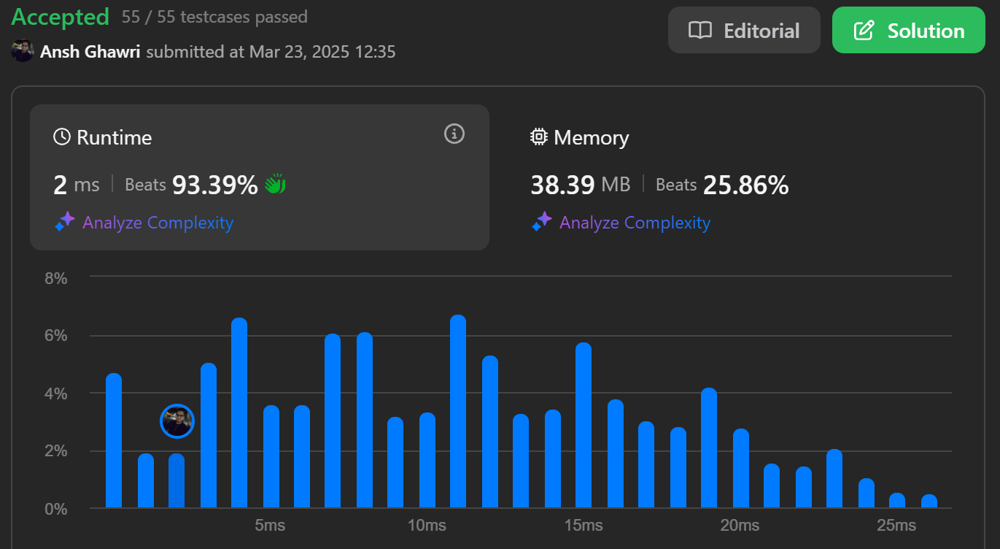
## Code 💻
Here’s the C++ code with comments to explain each part. I’ve kept it simple for beginners, but don’t expect me to spoon-feed you every line—you’ve got this! 😎
```cpp []
class Solution {
public:
typedef long long ll; // Because typing "long long" is too much work 🙄
typedef pair<ll, int> P; // Pair of (time, node) for the priority queue
int mod = 1e9 + 7; // Modulo because the problem loves big numbers
int countPaths(int n, vector<vector<int>>& roads) {
// Step 1: Build the graph—because we can’t do anything without it 🏗️
unordered_map<int, vector<P>> adj; // Adjacency list: node -> (neighbor, time)
for (auto& e : roads) {
adj[e[0]].push_back({e[1], e[2]}); // Add edge u -> v
adj[e[1]].push_back({e[0], e[2]}); // Add edge v -> u (undirected, duh!)
}
// Step 2: Set up the source and destination 🌍
int src = 0;
int dest = n - 1;
// Step 3: Set up for counting paths 📝
unordered_map<int, ll> freq; // Number of shortest paths to each node
freq[src] = 1; // There’s 1 way to reach the source—by standing still, genius!
// Step 4: Set up Dijkstra’s with a priority queue 🛠️
priority_queue<P, vector<P>, greater<P>> pq; // Min-heap: (time, node)
pq.push({0, src}); // Start at source with time 0
vector<ll> time(n, LLONG_MAX); // Shortest time to reach each node
time[src] = 0; // It takes 0 time to reach the source—shocking!
// Step 5: Run Dijkstra’s with a twist to count paths 🔄
while (!pq.empty()) {
ll currT = pq.top().first; // Current time
int node = pq.top().second; // Current node
pq.pop();
if (currT > time[node]) continue; // Skip if we found a faster path already—Dijkstra’s rules!
// Check all neighbors of the current node
for (auto& nbr : adj[node]) {
int nbrNode = nbr.first; // Neighbor node
ll edgeT = nbr.second; // Time to reach the neighbor
// Case 1: Found a faster path to the neighbor 🏎️
if (time[nbrNode] > time[node] + edgeT) {
time[nbrNode] = time[node] + edgeT; // Update shortest time
freq[nbrNode] = freq[node]; // Same number of paths as the current node
pq.push({time[nbrNode], nbrNode}); // Add to queue to explore further
}
// Case 2: Found another path with the same time 🛤️
else if (time[nbrNode] == time[node] + edgeT) {
freq[nbrNode] = (freq[nbrNode] + freq[node]) % mod; // Add the number of paths
}
}
}
// Step 6: Return the number of shortest paths to the destination 🎉
return freq[n-1] % mod; // Don’t forget the modulo—because big numbers are scary!
}
};
```
### 🎉 And that’s it! We’ve solved this graph problem with a beginner-friendly Dijkstra’s approach, added a twist to count paths, and thrown in some sarcasm to keep it spicy.
### If you’re new to Dijkstra’s or path counting, I hope this guide didn’t bore you to death! If you have any questions, feel free to ask—I might even answer without rolling my eyes! 😜 | 3 | 0 | ['Dynamic Programming', 'Graph', 'Shortest Path', 'C++'] | 0 |
number-of-ways-to-arrive-at-destination | Ultimate Graph Solution: Dijkstra + BFS-style + Path Counting + Min-Heap | Count All Shortest Paths | ultimate-graph-solution-dijkstra-bfs-sty-uv11 | Intuition
We want to find the number of different shortest paths from node 0 to node (n - 1).
This is a classic graph problem where we compute the shortest path | alperensumeroglu | NORMAL | 2025-03-23T00:20:22.416112+00:00 | 2025-03-23T00:20:22.416112+00:00 | 93 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. We want to find the number of *different shortest paths* from node 0 to node (n - 1).
2. This is a classic graph problem where we compute the shortest path using Dijkstra's algorithm,
3. but we also count how many different ways we can reach each node using that minimum time.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Build an adjacency list to represent the graph.
2. Use a modified Dijkstra algorithm:
- Track the shortest time to each node (time_to_node).
- Track the number of ways to reach each node using that shortest time (ways_to_node).
3. For each neighbor:
- If we found a shorter time, update both time and way count.
- If it's the same shortest time, increment the way count.
4. Return the number of ways to reach node (n - 1), modulo 1e9+7.
# Complexity
- Time: O((N + E) * log N), where N is the number of nodes and E is the number of edges.
- Space: O(N + E), for the graph and auxiliary arrays.
# Code
```python3 []
class Solution:
def countPaths(self, n, roads):
# Initialize adjacency list for the graph
graph = {}
for i in range(n):
graph[i] = []
for u, v, t in roads:
graph[u].append((v, t))
graph[v].append((u, t)) # because roads are bidirectional
# Initialize min-heap (priority queue): stores (travel_time, node)
min_heap = [(0, 0)]
# Shortest time to reach each node from source
time_to_node = [float('inf')] * n
time_to_node[0] = 0
# Number of ways to reach each node with the shortest time
ways_to_node = [0] * n
ways_to_node[0] = 1
MOD = int(1e9 + 7)
while min_heap:
# Pop the node with the smallest current travel time
current_time, current_node = self.heappop(min_heap)
for neighbor, travel_time in graph[current_node]:
total_time = current_time + travel_time
if total_time < time_to_node[neighbor]:
# Found a shorter path -> update
time_to_node[neighbor] = total_time
ways_to_node[neighbor] = ways_to_node[current_node]
self.heappush(min_heap, (total_time, neighbor))
elif total_time == time_to_node[neighbor]:
# Found another shortest path -> add ways
ways_to_node[neighbor] = (ways_to_node[neighbor] + ways_to_node[current_node]) % MOD
return ways_to_node[n - 1] % MOD
# Custom heappush (min-heap insert)
def heappush(self, heap, item):
heap.append(item)
self._siftup(heap, len(heap) - 1)
# Custom heappop (min-heap extract min)
def heappop(self, heap):
last_item = heap.pop()
if not heap:
return last_item
return_item = heap[0]
heap[0] = last_item
self._siftdown(heap, 0)
return return_item
# Maintain min-heap property after insert
def _siftup(self, heap, pos):
newitem = heap[pos]
while pos > 0:
parent = (pos - 1) >> 1
if newitem < heap[parent]:
heap[pos] = heap[parent]
pos = parent
else:
break
heap[pos] = newitem
# Maintain min-heap property after remove
def _siftdown(self, heap, pos):
end_pos = len(heap)
start_pos = pos
newitem = heap[pos]
child_pos = 2 * pos + 1
while child_pos < end_pos:
right_pos = child_pos + 1
if right_pos < end_pos and heap[right_pos] < heap[child_pos]:
child_pos = right_pos
heap[pos] = heap[child_pos]
pos = child_pos
child_pos = 2 * pos + 1
heap[pos] = newitem
self._siftup(heap, pos)
``` | 3 | 0 | ['Dynamic Programming', 'Greedy', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'Topological Sort', 'Heap (Priority Queue)', 'Prefix Sum', 'Shortest Path', 'Python3'] | 0 |
number-of-ways-to-arrive-at-destination | I was here | i-was-here-by-akuma-greyy-57ku | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Akuma-Greyy | NORMAL | 2024-06-20T16:52:44.422981+00:00 | 2024-06-20T16:52:44.423014+00:00 | 857 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPaths(self, n: int, roads: List[List[int]]) -> int:\n\n if n==1:\n return 1\n \n adjl = {}\n for road in roads:\n if road[0] not in adjl:\n adjl[road[0]] = { road[1] : road[2] }\n else:\n adjl[road[0]][road[1]] = road[2]\n if road[1] not in adjl:\n adjl[road[1]] = { road[0] : road[2] }\n else:\n adjl[road[1]][road[0]] = road[2]\n shortest = {}\n minHeap = []\n heapq.heappush(minHeap,(0,0))\n while minHeap and len(shortest)!=n:\n k=heapq.heappop(minHeap)\n if k[1] in shortest:\n continue\n shortest[k[1]]= k[0] \n for neighbour,weight in adjl[k[1]].items():\n if neighbour not in shortest:\n heapq.heappush(minHeap,(weight + k[0],neighbour))\n \n heap = []\n for a,b in shortest.items():\n heapq.heappush(heap,(b*-1,a))\n \n no_of_paths = [0]*n\n no_of_paths[n-1] = 1\n while heap:\n p = heapq.heappop(heap)\n for k,_ in adjl[p[1]].items():\n if ((p[0]*-1)-adjl[p[1]][k])==shortest[k]:\n no_of_paths[k] += no_of_paths[p[1]]\n return no_of_paths[0]%(10**9+7)\n \n \n \n``` | 3 | 0 | ['Dynamic Programming', 'Graph', 'Topological Sort', 'Shortest Path', 'Python3'] | 0 |
number-of-ways-to-arrive-at-destination | Efficient Shortest Path Computation and Path Counting using Dijkstra's Algorithm | efficient-shortest-path-computation-and-szxvl | Intuition\nWe use Dijkstra\'s algorithm to find the shortest paths from a given source node to all other nodes in a weighted undirected graph.\n\n# Approach\n1. | Stella_Winx | NORMAL | 2024-05-20T10:37:18.960252+00:00 | 2024-05-20T10:37:18.960285+00:00 | 1,330 | false | # Intuition\nWe use Dijkstra\'s algorithm to find the shortest paths from a given source node to all other nodes in a weighted undirected graph.\n\n# Approach\n1. Graph Representation: The graph is represented using an adjacency list, which is a collection of lists (in this case, implemented using an unordered map) where each list contains the neighbors of a particular node along with the corresponding edge weights.\n\n2. Dijkstra\'s Algorithm: Dijkstra\'s algorithm is employed to find the shortest paths from a given source node to all other nodes in the graph. The algorithm maintains two main data structures:\n\n1-> Distance Vector (dist): This vector stores the shortest distances from the source node to all other nodes. Initially, all distances are set to a maximum value (LLONG_MAX), indicating infinity.\n2-> Path Count Vector (pathCount): This vector keeps track of the number of shortest paths from the source node to each node in the graph.\n\n3. Priority Queue (Set): A set (st) is used as a priority queue to efficiently retrieve the node with the smallest tentative distance during each iteration of the algorithm. The set is ordered based on the tentative distances of the nodes.\n\n4. Main Loop: The main loop of the algorithm continues until there are no more nodes to explore in the set. During each iteration:\n1--> The node with the smallest tentative distance is extracted from the set.\n2--> Its neighbors are traversed, and if a shorter path is found to any neighbor, the distance and path count for that neighbor are updated accordingly.\n3--> If the distance to a neighbor is the same as the current shortest distance, the path count for that neighbor is incremented by the path count of the current node.\n\n5. Counting Paths: Once Dijkstra\'s algorithm completes execution, the countPaths function returns the path count for the destination node, which represents the number of shortest paths from the source node to the destination node.\n\n6. Modular Arithmetic: Modular arithmetic is employed to handle large numbers and prevent integer overflow. The path count is computed modulo M=1e9+7 to ensure that the result remains within the bounds of an integer.\n\nOverall, the approach efficiently finds the shortest paths and counts the number of such paths from the source node to the destination node using Dijkstra\'s algorithm and appropriate data structures.\n\n# Complexity\n- Time complexity:\nO((V + E) log V + n)\n\n- Space complexity:\nO(V + E)\n\n# Code\n```\nclass Solution {\npublic:\n const int M=1e9+7;\n vector<long long> dijkstra(vector<vector<int>> &roads, int n, int source, vector<int>& pathCount) {\n //adj list\n unordered_map<int,list<pair<int,int>>>adj;\n for(int i=0;i<roads.size();i++) \n {\n int u=roads[i][0];\n int v=roads[i][1];\n int w=roads[i][2]; //weights\n adj[u].push_back(make_pair(v,w));\n adj[v].push_back(make_pair(u,w));\n }\n\n vector<long long>dist(n,LLONG_MAX);\n pathCount.resize(n, 0); \n\n set<pair<long long,int>>st;\n dist[source]=0;\n pathCount[source]=1;\n st.insert(make_pair(0, source));\n\n while(!st.empty())\n {\n //fetch the top record\n auto top= *(st.begin());\n long long nodeDist=top.first;\n int node=top.second;\n\n //remove top now\n st.erase(st.begin());\n\n //ttraverse neighbors\n for(auto j:adj[node])\n {\n int neighbor=j.first;\n int weight=j.second;\n if(nodeDist+weight<dist[neighbor])\n {\n auto record=st.find(make_pair(dist[neighbor], neighbor));\n //if record found then erase it\n if(record!=st.end()) \n {\n st.erase(record);\n }\n //updatee in dist vector\n dist[neighbor]=nodeDist+weight;\n pathCount[neighbor]=pathCount[node]; \n\n // push record in set\n st.insert(make_pair(dist[neighbor],neighbor));\n } \n else if(nodeDist+weight==dist[neighbor]) \n {\n //pathCount[neighbor]+=pathCount[node];\n pathCount[neighbor]=(pathCount[neighbor]+pathCount[node])%M;\n }\n }\n }\n return dist;\n }\n\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<int>pathCount;\n vector<long long>dist =dijkstra(roads, n, 0, pathCount);\n \n //sinve last node is destination\n return pathCount[n-1];\n }\n};\n\n``` | 3 | 0 | ['Graph', 'Shortest Path', 'C++'] | 0 |
number-of-ways-to-arrive-at-destination | Striver's Easy C++ Approach | Solution | strivers-easy-c-approach-solution-by-ish-r11k | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves finding the number of different shortest paths from the source nod | ishajangir2002 | NORMAL | 2024-03-22T10:28:00.458239+00:00 | 2024-03-22T10:28:00.458262+00:00 | 528 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves finding the number of different shortest paths from the source node to the destination node in a graph with weighted edges. We can use Dijkstra\'s algorithm to find the shortest paths and keep track of the number of ways to reach each node.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate an adjacency list representation of the graph using the provided roads.\nUse Dijkstra\'s algorithm to find the shortest paths from the source node to all other nodes.\nWhile traversing the graph, keep track of the number of ways to reach each node by maintaining a ways vector.\nIf there is a shorter path to a node, update the shortest distance and the number of ways to reach that node.\nIf there are multiple shortest paths to a node, update the number of ways by adding the number of ways to reach the current node.\nFinally, return the number of ways to reach the destination node.\n\n# Complexity\n- Time complexity: \nO(VlogE), where \nV is the number of vertices and \n\nE is the number of edges. This is because we use Dijkstra\'s algorithm, which has a time complexity of \nO(VlogE).\n- Space complexity: \nO(V+E), where V is the number of vertices and \nE is the number of edges. We use extra space for storing the adjacency list, priority queue, distance vector, and ways vector.\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\nint M = 1e9 + 7;\n int countPaths(int n, vector<vector<int>>& roads) {\n ll src = 0;\n // create an adjancy list\n vector<pair<ll , ll>>adj[n];\n for(auto it : roads){\n int u = it[0];\n int v = it[1];\n int wt = it[2];\n adj[u].push_back({v ,wt});\n adj[v].push_back({u ,wt});\n }\n // time is very --> so we use the priority queue..\n priority_queue<pair<ll ,ll> , vector<pair<ll ,ll>> , greater<pair<ll ,ll>> >pq;\n // push the things--> {dis ,node}\n pq.push({0 ,0});\n\n\n // make the distance vector \n vector<ll>dist(n ,LLONG_MAX);\n dist[src] = 0;\n // make the ways vector\n vector<ll> ways(n ,0);\n ways[src] = 1;\n\n while(!pq.empty()){\n ll dis = pq.top().first;\n ll curr_node = pq.top().second;\n pq.pop();\n\n for(auto it : adj[curr_node]){\n ll neighnode = it.first;\n ll wt = it.second;\n\n if(dis + wt < dist[neighnode]){\n dist[neighnode] = dis + wt;\n pq.push({dist[neighnode] , neighnode});\n ways[neighnode] = ways[curr_node];\n } \n\n else if(dis + wt == dist[neighnode]){\n ways[neighnode] = (ways[neighnode] + ways[curr_node]) %M;\n }\n }\n \n }\n return ways[n-1 ]%M;\n\n }\n};\n```\n\n# Please Upvote !!! | 3 | 0 | ['C++'] | 1 |
number-of-ways-to-arrive-at-destination | Easy To Understand C++ Solution || Dijkstra | easy-to-understand-c-solution-dijkstra-b-4x49 | Intuition\nUse Dijkstra Algorithm to find the shortest distance between source node and destination node.Mean while maintain a seperate array/vector which takes | kashyap_25 | NORMAL | 2023-07-16T12:40:32.861808+00:00 | 2023-07-16T12:40:32.861830+00:00 | 1,501 | false | # Intuition\nUse Dijkstra Algorithm to find the shortest distance between source node and destination node.Mean while maintain a seperate array/vector which takes a note of number of shortest path to that particular node.\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nExcept for maintaining the seperate array/vector for number of shortest ways every thing is similar as Dijkstra\'s shortest path algo.\n**\nSo, For maintaining the seperate array/vector for number of shortest ways follow below instructions**:\n1).If the no of shortest paths for particulr node is empty or we are going to add for the first time directly add the number of shortest path from the parent node.\n**ways[adjNode]=ways[node]**\n2).And if already there is already entry for shortest path for particualr node then add the number of shortest path from parent and the current number of the shortest path of the node.\n** ways[adjNode]=(ways[adjNode]+ways[node])**\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(ElogV)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<int,int>>adj[n];\n for(int i=0;i<roads.size();i++)\n {\n adj[roads[i][0]].push_back({roads[i][1],roads[i][2]});\n adj[roads[i][1]].push_back({roads[i][0],roads[i][2]});\n }\n vector<long long>distance(n,1e15);\n vector<int>ways(n,0);\n\n priority_queue<pair<long long,int>,vector<pair<long long,int>>,greater<pair<long long,int>>>pq;\n\n ways[0]=1;\n distance[0]=0;\n pq.push({0,0});\n\n while(!pq.empty())\n {\n int node=pq.top().second;\n long long dis=pq.top().first;\n pq.pop();\n for(auto it:adj[node])\n {\n int adjNode=it.first;\n long long edgeWght=it.second;\n\n //New Entry\n if(dis+edgeWght<distance[adjNode])\n {\n ways[adjNode]=ways[node];\n distance[adjNode]=dis+edgeWght;\n pq.push({dis+edgeWght,adjNode});\n\n }\n else if(dis+edgeWght==distance[adjNode])\n {\n ways[adjNode]=(ways[adjNode]+ways[node])%((int)1e9+7);\n }\n }\n }\n return ways[n-1]%((int)1e9+7);\n\n \n }\n};\n``` | 3 | 0 | ['Breadth-First Search', 'Graph', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | C++ BFS Dijkastra 🔥🔥🔥 | c-bfs-dijkastra-by-abhishek6487209-ez71 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Abhishek6487209 | NORMAL | 2023-05-24T14:31:22.626468+00:00 | 2024-04-10T16:10:11.667746+00:00 | 1,604 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<pair<long long,long long>>adj[n];\n \n for(auto it: roads)\n {\n adj[it[0]].push_back({it[1],it[2]});\n adj[it[1]].push_back({it[0],it[2]});\n }\n \n priority_queue<pair<long long, long long>, vector<pair<long long, long long>>, greater<pair<long long, long long>>>pq;\n \n vector<long long> dist(n,LONG_MAX),ways(n,0);\n dist[0]=0;\n ways[0]=1;\n int mod=(1e9 +7);\n pq.push({0,0});\n while(!pq.empty())\n {\n long long d=pq.top().first;\n long long int node=pq.top().second;\n pq.pop();\n for(auto it:adj[node])\n {\n long long adjnode=it.first;\n long long int edgwt=it.second;\n //this is the first time i have entered with short distance \n if((d+edgwt)<dist[adjnode])\n {\n dist[adjnode]=d+edgwt;\n ways[adjnode]=ways[node];\n pq.push({dist[adjnode],adjnode});\n } else if((d+edgwt)==dist[adjnode])\n {\n ways[adjnode]=((ways[adjnode]%mod + ways[node])%mod)%mod;\n }\n }\n \n }\n return ways[n-1]%mod;\n }\n};\n``` | 3 | 0 | ['Breadth-First Search', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | Dijkstra + Top Down DP C++ ✌️ | dijkstra-top-down-dp-c-by-convexchull-m7xl | Intuition\nApplying dijkstra to find shortest distance then using a dfs to find number of paths having this shortest distance.\n\n\n# Approach\nFirst apply dijk | ConvexChull | NORMAL | 2022-10-26T14:26:37.250678+00:00 | 2022-10-26T14:26:37.250710+00:00 | 631 | false | # Intuition\nApplying dijkstra to find shortest distance then using a dfs to find number of paths having this shortest distance.\n\n\n# Approach\nFirst apply dijkstra from n-1 node then use the distance array generated in a dfs function which is memoized for optimization.\n\n\n# Complexity\n- Time complexity: O(ElogV) (Dijkstra) +O(V) DFS(memoized)\n\n\n- Space complexity:\nO(V)\n\n# Code\n```\nclass Solution {\n\n long long int shortest_distance;\n int mod=1e9+7;\n\n public:\n\n int dp[202];\n\n int dfs(vector<pair<int,int>> adj[],int node,vector<long long int>& dist)\n {\n if(node==dist.size()-1)return 1;\n\n if(dp[node]!=-1)return dp[node];\n\n long long int distance_to_dest=dist[node];\n\n int total=0;\n\n for(auto [nd,wt]:adj[node])\n {\n if(0LL+wt+dist[nd]==distance_to_dest)// the path must be shortest one \n {\n total=(0LL+total+dfs(adj,nd,dist))%mod;// counting all paths\n }\n }\n\n return dp[node]=total;\n\n }\n \n int countPaths(int n, vector<vector<int>>& roads) {\n\n memset(dp,-1,sizeof(dp));\n \n vector<pair<int,int>> adj[n];\n \n for(auto a:roads)\n {\n adj[a[0]].push_back({a[1],a[2]});\n adj[a[1]].push_back({a[0],a[2]}); \n }\n \n priority_queue< pair<long long int,int>,vector<pair<long long int,int>>,greater<pair<long long int,int>> > heap;\n \n vector<long long int> dist(n,LLONG_MAX);\n \n dist[n-1]=0;// dijkstra from reverse direction to find distan from node i to n-1 in O(1) during Dfs\n \n heap.push({0,n-1});\n \n while(heap.size())\n {\n auto [distance,node]=heap.top();\n \n heap.pop();\n\n if(distance>dist[node])continue;\n\n for(auto& [nd,wt]:adj[node])\n {\n long long int summer=(0LL+wt+distance);\n \n if(dist[nd]>summer)\n { \n dist[nd]=summer;\n \n heap.push({dist[nd],nd});\n }\n \n }\n }\n\n shortest_distance=dist[0];\n \n return dfs(adj,0,dist); \n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Depth-First Search', 'Graph', 'Shortest Path', 'C++'] | 1 |
number-of-ways-to-arrive-at-destination | C++ | Dijkstra | Number of ways to arrive at destination | c-dijkstra-number-of-ways-to-arrive-at-d-syh0 | \nclass Solution {\npublic:\n const int MOD = 1e9+7;\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<long long> dist(n,1e18), path(n | bits_069 | NORMAL | 2022-07-23T10:22:47.238441+00:00 | 2022-07-23T10:22:47.238488+00:00 | 433 | false | ```\nclass Solution {\npublic:\n const int MOD = 1e9+7;\n int countPaths(int n, vector<vector<int>>& roads) {\n vector<long long> dist(n,1e18), path(n,0);\n vector<vector<pair<int,int>>> g(n);\n for(int i=0; i<roads.size(); i++){\n g[roads[i][0]].push_back({roads[i][1],roads[i][2]});\n g[roads[i][1]].push_back({roads[i][0],roads[i][2]});\n\n }\n priority_queue<pair<long long,int>> pq;\n pq.push({0,0});\n dist[0]=0;\n path[0]=1;\n while(!pq.empty()){\n auto cur = pq.top();\n pq.pop();\n int node = cur.second;\n long long d = -cur.first;\n for(auto x: g[node]){\n if(dist[x.first]>d + x.second){\n dist[x.first]=d+x.second;\n pq.push({-dist[x.first],x.first});\n path[x.first]=path[node];\n }else if(dist[x.first]==d+x.second){\n path[x.first]= (path[x.first] + path[node]);\n if(path[x.first]>=MOD) path[x.first]-=MOD;\n }\n }\n }\n \n return path[n-1];\n }\n};\n``` | 3 | 0 | ['Math', 'C'] | 0 |
number-of-ways-to-arrive-at-destination | ✅✅C++ Dijkstra || BFS || | c-dijkstra-bfs-by-smilyface_123-7fqr | If Helpful Please Upvoke\n\n\n#define ll long long\nclass Solution{\n public:\n int mod = 1e9 + 7;\n int countPaths(int n, vector<vector < int>> &r | smilyface_123 | NORMAL | 2022-06-20T05:31:56.435271+00:00 | 2022-06-20T05:31:56.435309+00:00 | 354 | false | **If Helpful Please Upvoke**\n\n```\n#define ll long long\nclass Solution{\n public:\n int mod = 1e9 + 7;\n int countPaths(int n, vector<vector < int>> &roads){\n priority_queue<pair<ll, ll>, vector< pair<ll, ll>>, greater<pair<ll, ll>>> pq;\n pq.push({ 0,0 });\n vector<ll> dist(n, LLONG_MAX);\n dist[0] = 0;\n vector<ll> ways(n, 0);\n ways[0] = 1;\n\n vector<pair<ll, ll>> adj[n];\n for (auto &it: roads){\n adj[it[0]].push_back({ it[1],\n it[2] });\n adj[it[1]].push_back({ it[0],\n it[2] });\n }\n while (!pq.empty()){\n ll node = pq.top().second;\n ll dis = pq.top().first;\n pq.pop();\n for (auto it: adj[node]){\n ll wt = it.second;\n ll adjnode = it.first;\n if (wt + dis < dist[adjnode]){\n dist[adjnode] = wt + dis;\n ways[adjnode] = ways[node];\n pq.push({ dist[adjnode],\n adjnode });\n }\n else if (wt + dis == dist[adjnode])\n {\n ways[adjnode] = (ways[adjnode] + ways[node]) % mod;\n }\n }\n }\n\n return ways[n - 1];\n }\n };\n```\n\n**If Helpful PLease Like Or Upvoke** | 3 | 0 | [] | 0 |
number-of-ways-to-arrive-at-destination | [C++] | Dijkstra | c-dijkstra-by-makhonya-dueo | \nclass Solution {\npublic:\n int count = 0, MOD = 1e9 + 7;\n int countPaths(int n, vector<vector<int>>& r) {\n vector<pair<long long, long long>> | makhonya | NORMAL | 2022-06-15T05:51:48.568312+00:00 | 2022-06-15T05:51:48.568356+00:00 | 212 | false | ```\nclass Solution {\npublic:\n int count = 0, MOD = 1e9 + 7;\n int countPaths(int n, vector<vector<int>>& r) {\n vector<pair<long long, long long>> A[n];\n vector<long long> dist(n, LONG_MAX), ways(n);\n ways[0] = 1;\n priority_queue<pair<long long, long long>, vector<pair<long long, long long>>, greater<pair<long long, long long>>> pq;\n for(auto& a: r){\n A[a[0]].push_back({a[1], a[2]});\n A[a[1]].push_back({a[0], a[2]});\n }\n pq.push({0, 0});\n dist[0] = 0;\n while(!pq.empty()){\n auto [cost, node] = pq.top();\n pq.pop();\n if(cost > dist[node]) continue;\n for(auto& [to, time]: A[node]){\n if(dist[to] > time + dist[node]){\n dist[to] = time + dist[node];\n ways[to] = ways[node];\n pq.push({dist[to], to});\n }\n else if(dist[to] == time + dist[node])\n ways[to] += ways[node], ways[to] %= MOD;\n }\n }\n return max(1, (int)ways[n - 1]);\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.