question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
24-game | Short python solution | short-python-solution-by-lhengi-88st | Saw somebody is creating a whole num class and using operator overload to avoid double comparison error, but I think doing espilon comparison is good enough..\n | lhengi | NORMAL | 2019-02-11T19:27:49.915209+00:00 | 2019-02-11T19:27:49.915255+00:00 | 189 | false | Saw somebody is creating a whole num class and using operator overload to avoid double comparison error, but I think doing espilon comparison is good enough..\n"""\nclass Solution:\n def judgePoint24(self, nums: \'List[int]\') -> \'bool\':\n return self.helper(nums)\n \n def helper(self,lst):\n if len(lst) == 1:\n eps = 0.00000001\n if abs(lst[0]- 24) <= eps:\n return True\n return False\n \n for i in range(0,len(lst)):\n for j in range(0,len(lst)):\n if i == j:\n continue\n newLst = []\n for k in range(0,len(lst)):\n if k != i and k != j:\n newLst.append(lst[k])\n \n if self.helper(newLst + [ lst[i] + lst[j] ]):\n return True\n if self.helper(newLst + [lst[i] - lst[j]]):\n return True\n if self.helper(newLst + [lst[i] * lst[j]]):\n return True\n if lst[j] != 0 and self.helper(newLst + [lst[i] / lst[j]]):\n return True\n return False\n\n""" | 2 | 0 | [] | 0 |
24-game | Backtracking Simple Python Solution - Without Estimation | backtracking-simple-python-solution-with-6g9v | The logic behind this solution is that every number is stored as (numerator, denominator). \n From the array of length n, 2 numbers are picked\n\t All 4 operati | dewank | NORMAL | 2018-11-25T19:48:43.848131+00:00 | 2018-11-25T19:48:43.848214+00:00 | 410 | false | The logic behind this solution is that every number is stored as `(numerator, denominator)`. \n* From the array of length `n`, 2 numbers are picked\n\t* All 4 operations are done on the picked numbers\n\t* Answer is stored back in the array: array now becomes of length `n-1`\n* Repeated till array length is 1 -> Then the value is checked: `numerator/denominator == 24`\n```\nclass num():\n def __init__(self, n, d):\n self.n = n\n self.d = d\n \n def __add__(self, otherNum):\n n = (self.n * otherNum.d + self.d * otherNum.n)\n d = self.d * otherNum.d\n return num(n,d)\n \n def __sub__(self, otherNum):\n n = (self.n * otherNum.d - self.d * otherNum.n)\n d = self.d * otherNum.d\n return num(n,d)\n \n def __mul__(self, otherNum):\n n = self.n * otherNum.n\n d = self.d * otherNum.d\n return num(n,d)\n \n def __truediv__(self, otherNum):\n n = self.n * otherNum.d\n d = self.d * otherNum.n\n return num(n,d)\n \ndef helper(nums):\n \n if len(nums) == 1 and nums[0].d != 0:\n return True if nums[0].n/nums[0].d == 24 else False\n\n for i in range(0,len(nums)):\n for j in range(0, len(nums)):\n if i!=j:\n newArr = [nums[k] for k in range(0, len(nums)) if k!=i and k!=j]\n if helper(newArr + [nums[i] + nums[j]]):\n return True\n if helper(newArr + [nums[i] - nums[j]]):\n return True\n if helper(newArr + [nums[i] * nums[j]]):\n return True\n if helper(newArr + [nums[i] / nums[j]]):\n return True\n return False\n\nclass Solution:\n def judgePoint24(self, nums):\n """\n :type nums: List[int]\n :rtype: bool\n """\n for i in range(len(nums)):\n nums[i] = num(nums[i], 1)\n \n return helper(nums)\n``` | 2 | 0 | [] | 1 |
24-game | [Java][DFS] | javadfs-by-neruppu_da-r25x | Given: (a, b, c, d) - (A tuple of 4)\nGenerate: \nEdited: Thanks to @bellevue \n ((a+b),c,d) ((a-b),c,d) ((b-a),c,d) ((ab),c,d) ((a/b),c,d) ((b/a),c, | neruppu_da | NORMAL | 2017-09-17T06:03:32.798000+00:00 | 2017-09-17T06:03:32.798000+00:00 | 970 | false | **Given**: (a, b, c, d) - (A tuple of 4)\n**Generate**: \nEdited: Thanks to @bellevue \n* ((a+b),c,d) ((a-b),c,d) ((b-a),c,d) ((a*b),c,d) ((a/b),c,d) ((b/a),c,d)\n* ((a+c),b,d) ................................................................. ((c/a),b,d)\n* ((a+d),b,c) ................................................................. ((d/a),b,c)\n* (a,(b+c),d) ................................................................. (a,(c/b),d)\n* (a,(b+d),d) ................................................................. (a,(d/b),d)\n* (a,b,(c+d)) ................................................................. (a,b,(d/c))\n\nThere are 36 (6*6) such tuples. Of these, + & - are not order dependent. That is 2+3 = 3+2. But / & - are order dependent. i.e. 2/3 != 3/2. These look like (e,f,g) i.e. a tuple of 3 now.\n\n* Carrying out similar reductions gives 18 (6*3) tuples for each of the above-generated tuples. These now look like (h, i) i.e. a tuple of 2 now.\n\n* Similiar, the final reduction now yields 6 answers (a+b, a-b, a*b, a/b, b-a, b/a) for each of the above-generated tuple.\n\nThus in total 36x18x6 final values can be generated using the 4 operators and 4 initial values.\n\n**Algo**: Generate all such answers using dfs method and stop when it's 24.\n\n**Catches**:\n\n* Use ``` double ``` instead of ```int```\n* Be careful about the classical ``` divide by zero ``` error\n\n```\nclass Solution {\n enum ops{\n\tADD('+'), SUB('-'), MUL('*'), DIV('/');\n\tchar type;\n\tops(char c){\n\t\ttype = c;\n\t}\n\tpublic double doFunc(double a, double b){\n\t\tif(type=='+') return a+b;\n\t\tif(type=='-') return a-b;\n\t\tif(type=='*') return a*b;\n\t\telse return a/b;\n\t}\n}\n static ops[] operations;\n public static boolean judgePoint24(int[] nums) {\n\t\toperations = ops.values();\n\t\tdouble[] oops = new double[4];\n\t\tfor(int i=0;i<4;i++)\n\t\t\toops[i] = 1.0*nums[i];\n return doit(oops,4,new boolean[]{true,true,true,true});\n }\n public static boolean doit(double[] nums,int count,boolean[] use){\n \tif(count==1){\n \t\tfor(int i=0;i<4;i++)\n \t\t\tif(use[i] && nums[i]==24.0) return true;\n \t\treturn false;\n \t}\n for(int i=0;i<4;i++){\n \tif(use[i]){\n \t\tfor(int j=0;j<4;j++){\n \t\t\tif(j!=i && use[j]){\n \t\t\t\tdouble a = nums[i];\n \t\t\t\tuse[j] = false;\n \t\t\t\tboolean r = false;\n \t\t\t\tfor(int ai=0;ai<ops.values().length;ai++){\n \t\t\t\t\tif((operations[ai]==ops.ADD || operations[ai]==ops.MUL) && j<i) continue;\n \t\t\t\t\tif(operations[ai]==ops.DIV && nums[j]==0) continue;\n \t\t\t\t\tnums[i] = operations[ai].doFunc(a, nums[j]);\n \t\t\t\t\tr = r|| doit(nums,count-1,use);\n \t\t\t\t\tif(r) return r;\n \t\t\t\t}\n \t\t\t\tnums[i] = a;\n \t\t\t\tuse[j] = true;\n \t\t\t}\n \t\t}\n \t}\n \t\n }\n return false;\n }\n}\n```\nPS: Comments are appreciated. | 2 | 1 | [] | 1 |
24-game | Javascript recursive solution | javascript-recursive-solution-by-lccpc10-zmrm | \nvar judgePoint24 = function(cards) {\n if(cards.length===1) {\n var roundValue = Math.round(cards[0]*100)/100;\n return roundValue === 24;\n }\n\n fo | lccpc10 | NORMAL | 2017-11-25T16:31:30.257000+00:00 | 2017-11-25T16:31:30.257000+00:00 | 618 | false | ```\nvar judgePoint24 = function(cards) {\n if(cards.length===1) {\n var roundValue = Math.round(cards[0]*100)/100;\n return roundValue === 24;\n }\n\n for(var i=0; i<cards.length; i++) {\n for(var j=0; j<cards.length; j++) {\n if(i===j) continue;\n var small = Math.min(i,j);\n var large = Math.max(i,j);\n var thisCards = cards.slice();\n thisCards.splice(large,1);\n thisCards.splice(small,1);\n\n var iValue = cards[i];\n var jValue = cards[j];\n var isValid = false;\n isValid = isValid || judgePoint24( [iValue+jValue, ...thisCards] );\n isValid = isValid || judgePoint24( [iValue-jValue, ...thisCards] );\n isValid = isValid || judgePoint24( [iValue*jValue, ...thisCards] );\n if(jValue !==0) {\n isValid = isValid || judgePoint24( [iValue/jValue, ...thisCards] );\n }\n if(isValid) return true;\n }\n }\n return false;\n};\n``` | 2 | 0 | [] | 1 |
24-game | Simple & easy solution🔥🔥 | simple-easy-solution-by-aayu_t-8uxe | \n\n# Code\npython3 []\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n n = len(cards)\n if n == 1:\n if abs(2 | aayu_t | NORMAL | 2024-09-05T12:27:53.458754+00:00 | 2024-09-05T12:27:53.458788+00:00 | 58 | false | \n\n# Code\n```python3 []\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n n = len(cards)\n if n == 1:\n if abs(24 - cards[0]) < 0.001:\n return True\n return False\n \n for i in range(n):\n for j in range(i + 1, n):\n c1 = cards[i]\n c2 = cards[j]\n\n arr = [c1 + c2, c1 - c2, c2 - c1, c1 * c2]\n if c1:\n arr.append(c2 / c1)\n if c2:\n arr.append(c1 / c2)\n \n for val in arr:\n nextCards = [val]\n\n for k in range(n):\n if k not in (i, j):\n nextCards.append(cards[k])\n \n if self.judgePoint24(nextCards):\n return True\n return False\n \n``` | 1 | 0 | ['Array', 'Python3'] | 0 |
24-game | Backtracking | backtracking-by-rpsingh21-1xtx | Complexity\n- Time complexity: O(n!)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n^2)\n Add your space complexity here, e.g. O(n) \n\n# | rpsingh21 | NORMAL | 2024-05-20T18:46:12.161310+00:00 | 2024-05-20T18:46:12.161333+00:00 | 87 | false | # Complexity\n- Time complexity: $$O(n!)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n \n def generat_results(a, b):\n res = [a+b, a-b, b-a, a*b]\n if a:\n res.append(b/a)\n if b:\n res.append(a/b)\n return res\n\n\n def check(cards):\n if len(cards) == 1:\n return abs(cards[0] - 24.0) <= 0.1\n for i in range(len(cards)):\n for j in range(i+1, len(cards)):\n new_list = [num for k, num in enumerate(cards) if (k != i and k != j)]\n for res in generat_results(cards[i], cards[j]):\n new_list.append(res)\n if check(new_list):\n return True\n new_list.pop()\n return False\n \n return check(cards)\n\n\n \n\n``` | 1 | 0 | ['Backtracking', 'Python3'] | 0 |
24-game | Permutation + Backtracking | permutation-backtracking-by-coderpriest-npuf | Intuition\nTo solve this problem, we need to check if it\'s possible to combine the given numbers in such a way that they result in 24. We can achieve this by t | coderpriest | NORMAL | 2024-03-20T07:56:27.130481+00:00 | 2024-03-20T07:56:27.130509+00:00 | 390 | false | # Intuition\nTo solve this problem, we need to check if it\'s possible to combine the given numbers in such a way that they result in 24. We can achieve this by trying out all possible permutations of the numbers and applying mathematical operations to them. If any permutation yields 24, we return true; otherwise, we return false.\n\n# Approach\nWe\'ll define two functions: `valid` to check if given numbers can result in 24 when combined, and `get_perm` to generate all permutations of the given numbers and check if any permutation satisfies the condition.\n\nIn the `valid` function, we\'ll check if the given numbers can result in 24 by performing addition, subtraction, multiplication, and division while considering floating-point precision.\n\nIn the `get_perm` function, we\'ll generate all permutations of the given numbers using backtracking. We\'ll swap numbers at different positions to explore all possible combinations. Once we find a permutation that results in 24, we\'ll return true; otherwise, we\'ll return false.\n\n# Complexity\n- Time complexity: O(1) for the `valid` function as it performs a constant number of operations. For the `get_perm` function, it depends on the number of permutations, which is at most 4!, so it\'s also constant.\n- Space complexity: O(1) for the `valid` function as it uses constant space. For the `get_perm` function, it uses a set to track seen numbers during backtracking, which can have at most 4 elements, so it\'s also constant.\n\n# Code\n```cpp\nclass Solution {\npublic:\n bool valid(double a, double b) {\n return fabs(a + b - 24.0) < 0.0001 or fabs(a - b - 24.0) < 0.0001 or\n fabs(a * b - 24.0) < 0.0001 or (b != 0 and fabs(a / b - 24.0) < 0.0001);\n }\n \n bool valid(double a, double b, double c) {\n return valid(a + b, c) or valid(a, b + c) or valid(a - b, c) or\n valid(a, b - c) or valid(a * b, c) or valid(a, b * c) or\n valid(a / b, c) or valid(a, b / c);\n }\n \n bool get_perm(int idx, vector<double>& cards) {\n if (idx == 4) {\n return valid(cards[0] + cards[1], cards[2], cards[3]) or\n valid(cards[0], cards[1] + cards[2], cards[3]) or\n valid(cards[0], cards[1], cards[2] + cards[3]) or\n valid(cards[0] - cards[1], cards[2], cards[3]) or\n valid(cards[0], cards[1] - cards[2], cards[3]) or\n valid(cards[0], cards[1], cards[2] - cards[3]) or\n valid(cards[0] * cards[1], cards[2], cards[3]) or\n valid(cards[0], cards[1] * cards[2], cards[3]) or\n valid(cards[0], cards[1], cards[2] * cards[3]) or\n valid(cards[0] / cards[1], cards[2], cards[3]) or\n valid(cards[0], cards[1] / cards[2], cards[3]) or\n valid(cards[0], cards[1], cards[2] / cards[3]);\n }\n \n bool res = false;\n unordered_set<int> s;\n for (int i = idx; i < 4 and !res; i++) {\n if (s.count(cards[i]))\n continue;\n s.insert(cards[i]);\n swap(cards[idx], cards[i]);\n res |= get_perm(idx + 1, cards);\n swap(cards[idx], cards[i]);\n }\n return res;\n }\n \n bool judgePoint24(vector<int>& nums) {\n vector<double> cards;\n for (auto& x : nums)\n cards.push_back((double)x);\n return get_perm(0, cards);\n }\n};\n``` | 1 | 0 | ['Array', 'Math', 'Backtracking', 'C++'] | 1 |
24-game | Simple go solution | simple-go-solution-by-singhsaubhik-m17u | Code\n\nfunc abs(n float64) float64 { if n < 0 { return -n }; return n }\n\nfunc operationsResult(a, b float64) []float64 {\n res := []float64{a-b, a+b, b-a, | singhsaubhik | NORMAL | 2024-03-09T17:12:02.623227+00:00 | 2024-03-09T17:12:02.623254+00:00 | 13 | false | # Code\n```\nfunc abs(n float64) float64 { if n < 0 { return -n }; return n }\n\nfunc operationsResult(a, b float64) []float64 {\n res := []float64{a-b, a+b, b-a, a*b}\n if a > 0 {\n\t\tres = append(res, b / a)\n\t}\n\n\tif b > 0 {\n\t\tres = append(res, a / b)\n\t}\n\n return res\n}\n\nfunc helper(cards []float64) bool {\n n := len(cards)\n if n == 1 {\n return abs(cards[0] - 24) <= 0.1\n }\n\n for i := 0; i < n; i++ {\n for j := i + 1; j < n; j++ {\n var list []float64\n for k := 0; k < n; k++ {\n if k != i && k != j {\n list = append(list, cards[k])\n }\n }\n\n ops := operationsResult(cards[i], cards[j])\n for _, op := range ops {\n list = append(list, op)\n\n // Recur\n if helper(list) {\n return true\n }\n\n list = list[:len(list)-1]\n }\n }\n }\n\n return false\n}\n\nfunc judgePoint24(cards []int) bool {\n var list []float64\n\tfor _, c := range cards {\n\t\tlist = append(list, float64(c))\n\t}\n\n\treturn helper(list)\n}\n``` | 1 | 0 | ['Go'] | 0 |
24-game | DFS: traversing all permutations and all operations | dfs-traversing-all-permutations-and-all-io4i2 | \n# Code\n\nclass Solution {\npublic:\n vector<float> ops(float a, float b)\n {\n return {a+b,a-b,b-a,a*b,a/b,b/a};\n }\n bool dfs(vector<int | flyljx | NORMAL | 2023-06-05T04:45:46.099282+00:00 | 2023-06-05T04:45:46.099322+00:00 | 159 | false | \n# Code\n```\nclass Solution {\npublic:\n vector<float> ops(float a, float b)\n {\n return {a+b,a-b,b-a,a*b,a/b,b/a};\n }\n bool dfs(vector<int> nums, int k, float res)\n {\n if (k==3)\n {\n for (float f:ops(res,nums[3]))\n if (fabs(f-24.0)<0.001) return true;\n return false;\n }\n else if (k==1)\n {\n for (float f:ops(nums[0],nums[1]))\n if (dfs(nums,2,f)) return true;\n return false;\n }\n //k==2\n for (float f:ops(res,nums[2]))\n if (dfs(nums,3,f)) return true;\n for (float f:ops(nums[2],nums[3]))\n for(float g:ops(res,f))\n if (fabs(g-24)<0.001) return true;\n return false;\n }\n bool judgePoint24(vector<int>& cards) {\n for (int i=0;i<4;i++){\n for (int j=0;j<4;j++){\n if (j==i) continue;\n for (int k=0;k<4;k++){\n if (k==i || k==j) continue;\n for (int m=0;m<4;m++){\n if (m==i || m==j || m==k) continue;\n vector<int> v={cards[i],cards[j],cards[k],cards[m]};\n if (dfs(v,1,0)) return true;\n }\n }\n }\n \n }\n return false;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
24-game | Python || Solver can optionally print *all* solutions | python-solver-can-optionally-print-all-s-ip5s | Intuition\nPick any two numbers apply any operation, and replace the two numbers with their result. We now have a smaller problem.\n\n# Code\n\nclass Solution:\ | stomachion | NORMAL | 2023-06-02T17:52:33.841927+00:00 | 2023-08-23T05:32:50.005108+00:00 | 928 | false | # Intuition\nPick any two numbers apply any operation, and replace the two numbers with their result. We now have a smaller problem.\n\n# Code\n```\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n def compute(a,b,op):\n if op==0:\n return a+b\n if op==1:\n return a-b\n if op==2:\n return a*b\n return a/b\n\n def solve(nums: List[int]):\n nonlocal solCount\n n = len(nums)\n if n==1:\n if goal-e < nums[0] < goal+e:\n # print(sol)\n solCount += 1\n return\n # stop at one solution\n if solCount>0:\n return\n for i in range(n):\n for j in range(n):\n if i==j: continue\n for op in range(3 + (nums[j]!=0)):\n if i>j and op%2==0: continue\n x = compute(nums[i], nums[j], op)\n nums2 = [x]\n for k in range(n):\n if k!=i and k!=j:\n nums2.append(nums[k])\n # sol.append("%s = %s%s%s"%(x,nums[i],operator[op],nums[j]))\n solve(nums2)\n # sol.pop()\n\n e = 10**-5\n goal = 24\n operator = "+-*/"\n sol = []\n solCount = 0\n solve(cards)\n # print(solCount)\n return solCount>0\n\n``` | 1 | 0 | ['Python3'] | 1 |
24-game | A lot of solutions,A lot of people are copying | a-lot-of-solutionsa-lot-of-people-are-co-ug6c | I didn\'t have an idea at first\n Describe your first thoughts on how to solve this problem. \n\n# Use a backtracking method\n Describe your approach to solving | appleamzon | NORMAL | 2022-11-22T07:06:51.300290+00:00 | 2022-11-22T07:06:51.300339+00:00 | 200 | false | # I didn\'t have an idea at first\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Use a backtracking method\n<!-- Describe your approach to solving the problem. -->\n\n# Time:O(1) Space:O(n3)\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n boolean flag=false;\n double decimal=1e-6;\n List<Double> arr=new ArrayList<>();\n public boolean judgePoint24(int[] cards) {\n for(int num:cards) arr.add((double)num);\n read(arr);\n return flag;\n }\n private void read(List<Double> arr){\n if(flag) return;\n if(arr.size()==1 && Math.abs(arr.get(0)-24.0)<=decimal){\n flag=true;\n return;\n }\n for(int i=0;i<arr.size();i++){\n for(int j=0;j<i;j++){\n double p1=arr.get(i),p2=arr.get(j);\n List<Double> list=new ArrayList<>();\n list.addAll(Arrays.asList(p1+p2,p1-p2,p2-p1,p1*p2));\n if(p1>decimal) list.add(p2/p1);\n if(p2>decimal) list.add(p1/p2);\n arr.remove(i);\n arr.remove(j);\n for(double num:list){\n arr.add(num);\n read(arr);\n arr.remove(num);\n }\n arr.add(j,p2);\n arr.add(i,p1);\n }\n }\n }\n}\n``` | 1 | 0 | ['Math', 'Java'] | 0 |
24-game | Go. Backtracking | go-backtracking-by-sobik-q90b | \nvar epsilon = math.Pow10(-6)\n\nfunc judgePoint24(cards []int) bool {\n\n\tgenerateAllPossibleResults := func(a, b float64) []float64 {\n\t\tres := [] float64 | sobik | NORMAL | 2022-08-14T11:02:21.048267+00:00 | 2022-08-14T11:02:21.048308+00:00 | 365 | false | ```\nvar epsilon = math.Pow10(-6)\n\nfunc judgePoint24(cards []int) bool {\n\n\tgenerateAllPossibleResults := func(a, b float64) []float64 {\n\t\tres := [] float64 {a+b, a*b, a-b, b-a}\n\t if b != 0 {res = append(res, a/b) }\n\t if a != 0 {res = append(res, b/a) }\n\t\treturn res\n\t}\n\n\tisValid := func(a []float64) bool {\n\t\treturn math.Abs(a[0] - 24) <= epsilon\n\t}\n\n\tcardsWithoutIndexes := func(a []float64, index1, index2 int) []float64 {\n\t\tr := []float64{}\n\t\tfor i, v := range a {\n\t\t\tif i != index1 && i != index2 {\n\t\t\t\tr = append(r, v)\n\t\t\t}\n\t\t}\n\t\treturn r\n\t}\n\n\tvar backtrack func(a []float64) bool \n\n\tbacktrack = func(a []float64) bool {\n\t\tif len(a) == 1 { return isValid(a) }\n\t\tfor i:=0; i<len(a);i++ {\n\t\t\tfor j:=i+1; j<len(a); j++ {\n\t\t\t\tpossibleResults := generateAllPossibleResults(a[i], a[j])\n\t\t\t\tfor _,v := range possibleResults {\n\t\t\t\t\tnewA := cardsWithoutIndexes(a, i, j)\n\t\t\t\t\tnewA = append(newA, v)\n\t\t\t\t\tif backtrack(newA) { return true }\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn false\n\t}\n\t\n\tfCards := []float64{}\n\tfor _,v := range cards {\n\t\tfCards = append(fCards, float64(v))\t\n\t}\n\treturn backtrack(fCards)\n}\n``` | 1 | 0 | ['Backtracking', 'Go'] | 0 |
24-game | C++ + INTUTION + EASY | c-intution-easy-by-mistake1-bn61 | we take any two number and do operations( consider all pairs ) \n 1.a ->oprarion are a+b, a-b, b-a, a*b , a/b (if b!=0 ) and b/a if (b!=0).\n2. take | mistake1 | NORMAL | 2022-07-25T04:24:31.390904+00:00 | 2022-07-25T04:24:31.390937+00:00 | 200 | false | 1. we take any two number and do operations( consider all pairs ) \n 1.a ->oprarion are a+b, a-b, b-a, a*b , a/b (if b!=0 ) and b/a if (b!=0).\n2. take any operation and rest of the array element and do cheak for possible\n3. at the end size of the array will be 1 and if elenment is 24 return true else return false\n\n```\nclass Solution {\npublic:\n vector<double>getOperation(double & firstNo, double &secondNo)\n {\n vector<double>oper;\n oper.push_back(firstNo+secondNo);\n oper.push_back(firstNo-secondNo);\n oper.push_back(secondNo-firstNo);\n oper.push_back(firstNo*secondNo);\n if(firstNo>1e-9)\n oper.push_back(secondNo/firstNo);\n if(secondNo>1e-9)\n oper.push_back(firstNo/secondNo);\n return oper; \n }\n bool isPossible(vector<double>&arr)\n {\n int n=(int)arr.size();\n if(n==1)\n {\n return (abs(24.0-arr[0])<=1e-9);\n }\n \n for(int fi=0;fi<n;fi++)\n {\n for(int si=0;si<n;si++)\n {\n if(fi==si)continue;\n \n double firstNo=arr[fi];\n double secondNo=arr[si];\n vector<double>operation=getOperation(firstNo,secondNo);\n vector<double>nextArr;\n for(double & op:operation)\n {\n nextArr.clear();\n nextArr.push_back(op);\n for(int i=0;i<n;i++)\n {\n if(i==fi || i==si)continue;\n nextArr.push_back(arr[i]);\n }\n if(isPossible(nextArr)) return true;\n }\n }\n }\n return false;\n }\n bool judgePoint24(vector<int>& cards) {\n vector<double>arr(cards.begin(),cards.end());\n return isPossible(arr);\n \n }\n};\n``` | 1 | 0 | [] | 0 |
24-game | C++ Backtracking solution | c-backtracking-solution-by-uttu_dce-rva7 | \tif we have the array\n [a, b, c, d]\n\n and if we chose two numbers lets say we chose a and b, then all the possible operations are\n a + b (1)\n | uttu_dce | NORMAL | 2022-06-29T06:24:55.416754+00:00 | 2022-06-29T06:25:04.652933+00:00 | 216 | false | \tif we have the array\n [a, b, c, d]\n\n and if we chose two numbers lets say we chose a and b, then all the possible operations are\n a + b (1)\n a - b (2)\n b + a (3)\n b - a (4)\n a*b (5)\n b*a (6)\n a/b (7)\n b/a (8)\n\n but 1 and 3 are same and [5, 6] are same\n so we count them only once\n\n also for operations 7 and 8, we have to ensure that the denominator does not become 0\n so if we pick a and b, and we apply any of the above operations between them, let the resulting number be x\n so the newly generated array is\n [x, b, c]\n\n now again we apply the same on this array\n\n\n```\nclass Solution {\npublic:\n const int eps = 1e-4;\n vector<double> genPossibilities(double x, double y) {\n vector<double> res = {x + y, x - y, y - x, x * y};\n if (abs(y) > 0.000001) res.push_back(x / y);\n if (abs(x) > 0.000001) res.push_back(y / x);\n return res;\n }\n\n bool solve(vector<double> &a) {\n int n = a.size();\n if (n == 1) {\n return abs(a[0] - 24.0) <= 0.000001;\n }\n\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n vector<double> possibilities = genPossibilities(a[i], a[j]);\n vector<double> temp;\n for (int k = 0; k < n; k++) {\n if (k != i && k != j) temp.push_back(a[k]);\n }\n for (double x : possibilities) {\n vector<double> cur = temp;\n cur.push_back(x);\n bool res = solve(cur);\n if (res) return true;\n }\n }\n }\n\n return false;\n }\n bool judgePoint24(vector<int>& cards) {\n vector<double> a(cards.begin(), cards.end());\n return solve(a);\n }\n};\n``` | 1 | 0 | [] | 0 |
24-game | Easy Understanding Python DFS | easy-understanding-python-dfs-by-rtlc202-n052 | \n\n def dfs(cards):\n if len(cards) == 1:\n return math.isclose(cards[0], 24) # do NOT use \'==\'\n \n # | rtlc2020 | NORMAL | 2022-05-10T01:49:32.468282+00:00 | 2022-05-10T01:49:32.468311+00:00 | 277 | false | \n```\n def dfs(cards):\n if len(cards) == 1:\n return math.isclose(cards[0], 24) # do NOT use \'==\'\n \n # allow to start with any card\n for k in range(len(cards)):\n cards[k], cards[0] = cards[0], cards[k]\n \n # allow to combine with any card afterward\n for i in range(1, len(cards)):\n if dfs(cards[1:i] + cards[i+1:] + [cards[0] + cards[i]]):\n return True\n\n if dfs(cards[1:i] + cards[i+1:] + [cards[0] * cards[i]]):\n return True\n \n if dfs(cards[1:i] + cards[i+1:] + [cards[0] - cards[i]]):\n return True\n\n if dfs(cards[1:i] + cards[i+1:] + [cards[i] -cards[0]]):\n return True\n\n if cards[i] != 0 and dfs(cards[1:i] + cards[i+1:] + [cards[0]/cards[i]]):\n return True\n\n if cards[0] != 0 and dfs(cards[1:i] + cards[i+1:] + [cards[i]/cards[0]]):\n return True\n \n return False\n\n return dfs(cards)\n``` | 1 | 0 | ['Depth-First Search'] | 1 |
24-game | well commented easy to understand solution | well-commented-easy-to-understand-soluti-967o | \nclass Solution {\npublic:\n \n bool isPossible(vector<float>& cards) {\n int n = cards.size();\n // If we are left with only 1 cards then | vishalrathi02 | NORMAL | 2022-03-21T02:02:41.269666+00:00 | 2022-03-21T02:02:41.269694+00:00 | 225 | false | ```\nclass Solution {\npublic:\n \n bool isPossible(vector<float>& cards) {\n int n = cards.size();\n // If we are left with only 1 cards then it should be 24 else return false\n if (n == 1) {\n // max number can be 9*9*9*9 i.e 10 power 4 around, so we can float till 4 digits\n return ((cards[0] > 23.9999) && (cards[0] < 24.0001 ));\n }\n \n // Try for all possible permutation of the card\n for (int i = 0; i < n; i++) {\n for (int j = i+1; j < n; j++) {\n vector<float> newExpr;\n // push all the combination between 2 cards\n newExpr.push_back(cards[i]+cards[j]); // addition\n newExpr.push_back(abs(cards[i]-cards[j])); // substraction\n newExpr.push_back(cards[i]*cards[j]); // multiplication\n \n // division a/b\n if (cards[j] > 0)\n newExpr.push_back(cards[i]/cards[j]);\n \n // division b/a\n if (cards[i] > 0)\n newExpr.push_back(cards[j]/cards[i]);\n \n // Create a new card deck except 2 picked above for operation\n vector<float> newCards;\n for (int k = 0; k < n; k++) {\n if ((k != i) && (k != j)) \n newCards.push_back(cards[k]);\n }\n \n // Assume new card is the one with new possible sum calucuated \n // recurse with remaining cards with one card of possible sum\n for (auto e : newExpr) {\n newCards.push_back(e);\n if (isPossible(newCards))\n return true;\n newCards.pop_back();\n }\n }\n }\n return false;\n }\n bool judgePoint24(vector<int>& cards) {\n vector<float> newCards(cards.begin(), cards.end());\n return isPossible(newCards);\n }\n};\n``` | 1 | 0 | [] | 0 |
24-game | Python one line solution | python-one-line-solution-by-vanya_shkvir-jdko | Thanks to @karrenbel for his three loop solution\nhttps://leetcode.com/problems/24-game/discuss/1399166/Python3-clean-code\n\n\nfrom fractions import Fraction\n | vanya_shkvir | NORMAL | 2022-02-02T21:40:47.362657+00:00 | 2022-02-02T21:40:47.362685+00:00 | 730 | false | Thanks to @karrenbel for his three loop solution\nhttps://leetcode.com/problems/24-game/discuss/1399166/Python3-clean-code\n\n```\nfrom fractions import Fraction\n\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool: \n return any([any([True if f1(d, f2(c, f3(a, b))) == 24 or f1(f2(a, b), f3(c, d)) == 24 else False for (f1, f2, f3) in product([add, sub, mul, lambda x, y: x / y if y else 0], repeat=3)]) for (a, b, c, d) in set(permutations(map(Fraction, cards)))])\n``` | 1 | 0 | ['Python'] | 1 |
24-game | recursion and permutation Python code | recursion-and-permutation-python-code-by-8gzw | ```\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n def helper(nums, left, right):\n if left == right:\n | WaydeZ | NORMAL | 2022-01-03T15:57:40.879764+00:00 | 2022-01-03T15:59:09.769777+00:00 | 218 | false | ```\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n def helper(nums, left, right):\n if left == right:\n return set([nums[left]])\n res = set()\n for i in range(left, right):\n res1 = helper(nums, left, i)\n res2 = helper(nums, i+1, right)\n # merge\n for val1 in res1:\n for val2 in res2:\n res.add(val1 + val2) \n res.add(val1 - val2)\n res.add(val1 * val2)\n if val2 != 0:\n res.add(val1 / val2)\n return res\n \n for arr in permutations(cards):\n # each permutation\n cur_res = helper(arr, 0, 3)\n # edge case 3 3 8 8 ---> 8/(3-(8/3))\n #if 24 in cur_res:\n # return True\n for ans in cur_res:\n if abs(24 - ans) < 1.0e-5:\n return True\n \n return False | 1 | 0 | [] | 1 |
24-game | Python Backtracking with Explaination | python-backtracking-with-explaination-by-a1wm | python\nfrom itertools import permutations\n\nclass Solution:\n def __init__(self):\n self.eps = 0.001\n \n def judgePoint24(self, cards: List[i | taranthemonk | NORMAL | 2021-12-21T17:21:36.725475+00:00 | 2021-12-21T17:21:36.725518+00:00 | 267 | false | ```python\nfrom itertools import permutations\n\nclass Solution:\n def __init__(self):\n self.eps = 0.001\n \n def judgePoint24(self, cards: List[int]) -> bool:\n \n # solve the nums to get 24\n def solve(nums: int) -> bool:\n # no operation\n if len(nums) == 1:\n return abs(nums[0] - 24) <= self.eps\n \n # take any two and do an operation\n # test if the result can be formed to 24 with the rest\n return any(\n solve([x] + rest)\n for a, b, *rest in permutations(nums)\n for x in {a + b, a - b, a * b, 0 if b == 0 else a / b}\n )\n \n return solve(cards)\n``` | 1 | 0 | [] | 0 |
24-game | (C++) 679. 24 Game | c-679-24-game-by-qeetcode-6cr1 | \n\nclass Solution {\npublic:\n bool judgePoint24(vector<int>& cards) {\n \n function<bool(vector<double>&)> fn = [&] (vector<double>& nums) {\ | qeetcode | NORMAL | 2021-12-02T23:08:16.887620+00:00 | 2021-12-02T23:08:16.887648+00:00 | 201 | false | \n```\nclass Solution {\npublic:\n bool judgePoint24(vector<int>& cards) {\n \n function<bool(vector<double>&)> fn = [&] (vector<double>& nums) {\n if (nums.size() == 1) return abs(nums[0] - 24) < 1e-6; \n for (int i = 0; i < nums.size(); ++i) {\n for (int j = i+1; j < nums.size(); ++j) {\n vector<double> cand; \n for (int k = 0; k < nums.size(); ++k) \n if (k != i && k != j) cand.push_back(nums[k]); \n vector<double> vals = {nums[i]+nums[j], nums[i]-nums[j], nums[j]-nums[i], nums[i]*nums[j]}; \n if (nums[j]) vals.push_back(nums[i]/nums[j]); \n if (nums[i]) vals.push_back(nums[j]/nums[i]); \n for (auto& x : vals) {\n cand.push_back(x); \n if (fn(cand)) return true; \n cand.pop_back(); \n }\n }\n }\n return false; \n }; \n \n vector<double> nums(cards.begin(), cards.end()); \n return fn(nums); \n \n }\n};\n``` | 1 | 0 | ['C'] | 0 |
24-game | Cannot get this case to work [3,3,8,8] what combination would this be? | cannot-get-this-case-to-work-3388-what-c-g3t9 | class Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n \n #basically create a stack of operations and indices used and based \n | ariboi27 | NORMAL | 2021-11-04T03:48:50.286852+00:00 | 2021-11-04T03:50:27.819423+00:00 | 178 | false | class Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n \n #basically create a stack of operations and indices used and based \n self.s = []\n \n #initial condition\n for i,card in enumerate(cards):\n self.s.append(([i],card))\n \n self.list2 = []\n while(self.s):\n \n indices_used,total = self.s.pop(0)\n print(total)\n #do all operations with indices that are not seen\n if total == 24 and len(indices_used) == 4\n return True\n if len(indices_used) == 2:\n self.list2.append((indices_used,total))\n \n for i,v in enumerate(cards):\n if i not in indices_used:\n #do all operations\n indices_used_2 = indices_used.copy()\n indices_used_2.append(i)\n self.s.append( (indices_used_2.copy(), v + total) )\n self.s.append( (indices_used_2.copy(),v*total) )\n self.s.append( (indices_used_2.copy(),v - total) )\n self.s.append( (indices_used_2.copy(),total - v) )\n if total != 0:\n self.s.append( (indices_used_2.copy(), v/total) )\n if v != 0:\n self.s.append( (indices_used_2.copy(), total/v) )\n \n for tup in self.list2:\n indices_used,total = tup\n \n for tup in self.list2:\n indices_used_2,total2 = tup\n if indices_used[0] != indices_used_2[1] and indices_used[1] != indices_used_2[0] \\\n and indices_used[0] != indices_used_2[0] and indices_used[1] != indices_used_2[1]:\n if total + total2 == 24 or total2 - total == 24 or total - total2 == 24 or total*total2 == 24:\n return True\n if (total != 0 and total2/total == 24) or (total2 != 0 and total/total2 == 24):\n return True\n \n return False\n | 1 | 0 | [] | 4 |
24-game | Shortest and fastest solution in C++ | shortest-and-fastest-solution-in-c-by-ru-196g | Runtime 0ms, beats 100% of C++ submissions.\n\n\nclass Solution {\n bool eq24(double i) {\n return (i > 23.9999 && i < 24.0001);\n }\n double op | rufeng2000 | NORMAL | 2021-10-18T07:31:20.650737+00:00 | 2021-10-18T07:33:54.526646+00:00 | 420 | false | Runtime 0ms, beats 100% of C++ submissions.\n\n```\nclass Solution {\n bool eq24(double i) {\n return (i > 23.9999 && i < 24.0001);\n }\n double op(double a, double b, int op) {\n if (op == 0) return a + b;\n if (op == 1) return a - b;\n if (op == 2) return a * b;\n return a / b;\n }\npublic:\n bool judgePoint24(vector<int>& cards) {\n for (int a = 0; a < 4; a++)\n for (int b = 0; b < 4; b++)\n if (a != b)\n for (int c = 0; c < 4; c++)\n if (a != c && b != c)\n for (int d = 0; d < 4; d++)\n if (a != d && b != d && c != d) // permutation of 4 cards, index is a,b,c,d\n for (int x = 0; x < 4; x++)\n for (int y = 0; y < 4; y++)\n for (int z = 0; z < 4; z++) // 3 ops \'+-*/\', in x,y,z\n { // 5 possible RPN(Reverse Polish Notation) : N-Number, O-Ops\n if (eq24(op(cards[a],op(cards[b],op(cards[c],cards[d],x),y),z))) return true; // NNNNOOO\n if (eq24(op(cards[a],op(op(cards[b],cards[c],x),cards[d],y),z))) return true; // NNNONOO\n if (eq24(op(op(cards[a],op(cards[b],cards[c],x),y),cards[d],z))) return true; // NNNOONO\n if (eq24(op(op(cards[a],cards[b],x),op(cards[c],cards[d],y),z))) return true; // NNONNOO\n if (eq24(op(op(op(cards[a],cards[b],x),cards[c],y),cards[d],z))) return true; // NNONONO\n }\n return false;\n }\n};\n```\n | 1 | 0 | ['C'] | 3 |
24-game | [Python] 2 clean recursive solutions O(N^N) | python-2-clean-recursive-solutions-onn-b-71ww | Solution 1: Use itertools to get all the combinations. Then we recursively execute each possible operator in the list until we have one element leftover.\n\n\nd | quantum73 | NORMAL | 2021-10-09T17:15:56.747467+00:00 | 2021-10-09T17:19:03.373840+00:00 | 407 | false | __Solution 1__: Use itertools to get all the combinations. Then we recursively execute each possible operator in the list until we have one element leftover.\n\n```\ndef judgePoint24(self, cards: List[int]) -> bool:\n def dfs(pos):\n if len(pos) == 1 and round(pos[0], 1) == 24:\n return True\n for (i,a),(j,b) in itertools.combinations(enumerate(pos), 2):\n for x in [a+b, a-b, b-a, a*b, b and a/b, a and b/a]:\n if dfs([x]+[v for idx,v in enumerate(pos) if idx not in [i,j]]):\n return True\n return False\n return dfs(cards)\n```\n__Solution 2__: Instead of using itertools we can calculate the combinations ourselves. Again complexity is `O(N^N)`.\n```\ndef judgePoint24(self, cards: List[int]) -> bool:\n def dfs(pos):\n if len(pos) == 1 and round(pos[0],1) == 24: return True\n for i,a in enumerate(pos):\n pos_copy = pos[:i] + pos[i+1:]\n for j in range(i+1, len(pos)):\n b = pos[j]\n for x in [a+b, a-b, b-a, a*b, b and a/b, a and b/a]:\n pos_copy[j-1] = x\n if dfs(pos_copy): return True\n pos_copy[j-1] = b\n return False\n return dfs(cards)\n``` | 1 | 0 | ['Backtracking', 'Recursion', 'Combinatorics', 'Python'] | 0 |
24-game | C++ | Brute Force | c-brute-force-by-sonusharmahbllhb-l798 | \nclass Solution {\npublic:\n bool ans=0;\n void gun(vector<float> v,vector<char> ch){\n if(ans) return;\n if(v.size()==1){\n if( | sonusharmahbllhb | NORMAL | 2021-08-30T14:58:06.218624+00:00 | 2021-08-30T15:02:16.961599+00:00 | 545 | false | ```\nclass Solution {\npublic:\n bool ans=0;\n void gun(vector<float> v,vector<char> ch){\n if(ans) return;\n if(v.size()==1){\n if(abs(24-v[0])<0.1) ans=1;\n return;\n }\n for(int i=0;i<v.size()-1;i++){\n if(ans) return;\n vector<float> tmpv=v;\n vector<char> tmpc=ch;\n float n;\n if(tmpc[i]==\'+\')\n n=v[i]+v[i+1]; \n else if(tmpc[i]==\'-\')\n n=v[i]-v[i+1];\n else if(tmpc[i]==\'*\')\n n=v[i]*v[i+1];\n else\n \n n=v[i]/v[i+1]; \n tmpv.erase(tmpv.begin()+i);\n tmpv.erase(tmpv.begin()+i);\n tmpv.insert(tmpv.begin()+i,n);\n tmpc.erase(tmpc.begin()+i);\n gun(tmpv,tmpc);\n }\n }\n void fun(int mask,vector<float> val,vector<char> oper,vector<int>& cards){\n if(ans) return;\n if(val.size()==3){\n for(int i=0;i<4;i++){\n if((mask&(1<<i))==0){\n val.push_back(cards[i]);\n gun(val,oper);\n }\n }\n return;\n }\n for(int i=0;i<4;i++){\n if(ans) return;\n if((mask&(1<<i))==0){\n val.push_back(cards[i]);\n \n for(int j=0;j<4;j++){\n if(j==0) {oper.push_back(\'+\');fun(mask|(1<<i),val,oper,cards);}\n else if(j==1) {oper.push_back(\'-\');fun(mask|(1<<i),val,oper,cards);}\n else if(j==2) {oper.push_back(\'*\');fun(mask|(1<<i),val,oper,cards);}\n else {oper.push_back(\'/\');fun(mask|(1<<i),val,oper,cards);}\n oper.pop_back();\n }\n val.pop_back();\n }\n \n }\n }\n bool judgePoint24(vector<int>& cards) {\n fun(0,{},{},cards); \n return ans;\n }\n};\n``` | 1 | 1 | ['C', 'C++'] | 0 |
24-game | Simple DFS java solution without rounding issue | simple-dfs-java-solution-without-roundin-co6e | \n\nclass Solution {\n public boolean judgePoint24(int[] cards) {\n List<Number> nums = List.of(\n new Number(cards[0]),\n new N | fredking | NORMAL | 2021-08-18T05:49:55.513533+00:00 | 2021-08-18T05:55:35.973085+00:00 | 590 | false | \n```\nclass Solution {\n public boolean judgePoint24(int[] cards) {\n List<Number> nums = List.of(\n new Number(cards[0]),\n new Number(cards[1]),\n new Number(cards[2]),\n new Number(cards[3]));\n return dfs(nums);\n }\n \n private boolean dfs(List<Number> nums) {\n if (nums.size() == 1) {\n return nums.get(0).equals(24);\n }\n \n for (int i=0; i<nums.size(); i++) {\n for (int j=i+1; j<nums.size(); j++) {\n for (Number n : combine(nums.get(i), nums.get(j))) {\n List<Number> next = new ArrayList<>();\n next.add(n);\n for (int k=0; k<nums.size(); k++) {\n if (k != i && k != j) next.add(nums.get(k));\n }\n if (dfs(next)) return true;\n }\n }\n }\n return false;\n }\n \n private List<Number> combine(Number n1, Number n2) {\n List<Number> result = new ArrayList<>();\n if (n1.equals(0) || n2.equals(0)) {\n result.add(n1.equals(0) ? n2 : n1);\n return result;\n }\n result.add(n1.add(n2));\n result.add(n1.subtract(n2));\n result.add(n2.subtract(n1));\n result.add(n1.multiply(n2));\n result.add(n1.divide(n2));\n result.add(n2.divide(n1));\n return result;\n }\n \n private static class Number {\n private final int dividend;\n private final int divisor;\n \n public Number(int digit) {\n this.dividend = digit;\n this.divisor = 1;\n }\n \n private Number(int dividend, int divisor) {\n this.dividend = dividend;\n this.divisor = divisor;\n }\n \n public boolean equals(int num) {\n return dividend % divisor == 0 && dividend / divisor == num;\n }\n \n public Number add(Number o) {\n return new Number(dividend * o.divisor + o.dividend * divisor, \n divisor * o.divisor);\n }\n \n public Number subtract(Number o) {\n return new Number(dividend * o.divisor - o.dividend * divisor, \n divisor * o.divisor); \n }\n \n public Number multiply(Number o) {\n return new Number(dividend * o.dividend, divisor * o.divisor);\n }\n \n public Number divide(Number o) {\n if (o.dividend == 0) {\n throw new IllegalArgumentException("Invalid division by zero");\n }\n return new Number(dividend * o.divisor, divisor * o.dividend);\n }\n }\n}\n``` | 1 | 0 | [] | 0 |
24-game | Python Easy 95% Runtime Memoization with Comments | python-easy-95-runtime-memoization-with-pbjll | \nimport functools\n\nclass Solution:\n # Helper function to get the values for all possible cominations of num1 and num2 using different mathematical operat | mahaksarin21 | NORMAL | 2021-07-31T11:46:49.898328+00:00 | 2021-07-31T11:53:07.028181+00:00 | 335 | false | ```\nimport functools\n\nclass Solution:\n # Helper function to get the values for all possible cominations of num1 and num2 using different mathematical operators\n def getRes(self, num1, num2):\n res = [num1+num2, num1-num2, num2-num1, num1*num2]\n if num1 != 0:\n res.append(num2/num1)\n if num2 != 0:\n res.append(num1/num2)\n return res\n \n\t# Created a new function with tuple as input instead of list as lists are not hashable and cache cannot be used for them\n @functools.lru_cache(maxsize=None)\n\tdef jd(self, cards) -> bool:\n # If only two elements are left in cards, check if their combination can return 24\n\t\tif len(cards) == 2:\n for i in self.getRes(cards[0], cards[1]):\n # Need to round off as there can be cases like 23.99999 due to rounding off in previous steps\n\t\t\t\tif 24.0 == round(i, 5):\n return True\n return False\n \n for i in range(0, len(cards)):\n for j in range(i+1, len(cards)):\n # Creating a new list after removing the two elements in consideration\n\t\t\t\tc = [x for t, x in enumerate(cards) if i != t != j]\n vals = self.getRes(cards[i], cards[j])\n # Recursive call after replacing the elements removed above with their combination\n\t\t\t\tfor val in vals:\n if self.jd(tuple(c)+(val,)):\n return True\n return False\n \n def judgePoint24(self, cards: List[int]) -> bool:\n return self.jd(tuple(cards))\n``` | 1 | 0 | [] | 1 |
24-game | C++ iteration based | c-iteration-based-by-zehziur-3lv9 | Iterate every permutation and expression tree forms.\n\n\nclass Solution {\npublic:\n double eval(double a, double b, int op) {\n switch (op) {\n | zehziur | NORMAL | 2021-07-15T11:14:44.240383+00:00 | 2021-07-15T11:14:44.240431+00:00 | 219 | false | Iterate every permutation and expression tree forms.\n\n```\nclass Solution {\npublic:\n double eval(double a, double b, int op) {\n switch (op) {\n case 0: return a + b;\n case 1: return a - b;\n case 2: return a * b;\n case 3: return a / b;\n }\n return 0;\n }\n \n bool is24(double x) { return abs(x - 24.0) < 1e-6; }\n \n bool judgePoint24(vector<int>& cards) {\n sort(cards.begin(), cards.end());\n do {\n \n for (int i = 0; i < 4; i ++)\n for (int j = 0; j < 4; j ++)\n for (int k = 0; k < 4; k ++) {\n double a = cards[0], b = cards[1],\n c = cards[2], d = cards[3];\n \n // (((a b) c) d)\n double ans = eval(eval(eval(a, b, i), c, j), d, k);\n if (is24(ans))\n return true;\n // ((a b) (c d))\n ans = eval(eval(a, b, i), eval(c, d, k), j);\n if (is24(ans))\n return true;\n // (a (b (c d)))\n ans = eval(a, eval(b, eval(c, d, k), j), i);\n if (is24(ans))\n return true;\n // ((a (b c)) d)\n ans = eval(eval(a, eval(b, c, j), i), d, k);\n if (is24(ans))\n return true;\n // (a ((b c) d)))\n ans = eval(a, eval(eval(b, c, j), d, k), i);\n if (is24(ans))\n return true;\n }\n \n } while (next_permutation(cards.begin(), cards.end()));\n \n return false;\n }\n};\n``` | 1 | 0 | [] | 0 |
24-game | Python solution easy-understanding | python-solution-easy-understanding-by-fl-5r1l | class Solution:\n\n # calculte the different results of two numbers\n def two_number(a, b):\n s = set()\n s.add(a+b)\n s.add(a-b)\n | flyingspa | NORMAL | 2021-06-16T10:57:24.857486+00:00 | 2021-06-16T10:57:24.857529+00:00 | 409 | false | class Solution:\n\n # calculte the different results of two numbers\n def two_number(a, b):\n s = set()\n s.add(a+b)\n s.add(a-b)\n s.add(b-a)\n s.add(a*b)\n if b!=0:\n ans = a/b\n if abs(ans-round(ans))<10**(-3):\n s.add(round(ans))\n else:\n s.add(a/b)\n if a!=0:\n ans = b/a\n if abs(ans-round(ans))<10**(-3):\n s.add(round(ans))\n else:\n s.add(b/a)\n return s\n \n # calculte the different results of three numbers\n def three_number(l1):\n s = set()\n for i in range(3):\n rest = list(set(range(0,3))-set([i]))\n s1 = Solution.two_number(l1[rest[0]], l1[rest[1]])\n for x in s1:\n s = s.union(Solution.two_number(l1[i], x))\n return s\n\n def judgePoint24(self, cards: List[int]) -> bool:\n # 2-2\n for i in range(1,4):\n s1 = Solution.two_number(cards[0], cards[i])\n rest = list(set(range(0,4))-set([0, i]))\n s2 = Solution.two_number(cards[rest[0]], cards[rest[1]])\n for x in s1:\n for y in s2:\n if 24 in Solution.two_number(x, y):\n return True\n #1-3\n for i in range(4):\n three = Solution.three_number(cards[:i]+cards[i+1:])\n for x in three:\n if 24 in Solution.two_number(x, cards[i]):\n return True\n return False | 1 | 1 | ['Python'] | 0 |
24-game | Python - Backtracking on card permutations | python-backtracking-on-card-permutations-cgai | if we have N operands, we have N - 1 points where that would be the "last" operator\nSo for start st and end en, we iterate through all mid points and recursive | mahsaelyasi | NORMAL | 2021-06-02T01:59:09.398972+00:00 | 2021-06-02T02:00:23.405199+00:00 | 226 | false | if we have N operands, we have N - 1 points where that would be the "last" operator\nSo for start `st` and end `en`, we iterate through all `mid` points and recursively evaluate on `[st, mid]` and `[mid + 1, en]`. We apply all four operators. We add sub solutions to sets and return and expand the solution sets. 24 should exist in solution of `[0, n - 1]`.\nThis gets 85% time of all solutions\n```\ndef judgePoint24(self, nums: List[int]) -> bool:\n ops = {\'+\': lambda x, y: x + y,\n \'-\': lambda x, y: x - y,\n \'/\': lambda x, y: x / y if y != 0 else float(\'inf\'),\n \'*\': lambda x, y: x * y}\n \n def _eval(nums, st, en):\n if st == en:\n return set([nums[st]])\n n = len(nums)\n ans = []\n for mid in range(st, en):\n lefts = _eval(nums, st, mid)\n rights = _eval(nums, mid + 1, en)\n for left in lefts:\n for right in rights:\n for op in ops:\n ans.append(ops[op](left, right))\n return ans\n for perm_nums in itertools.permutations(nums):\n for x in _eval(perm_nums, 0, len(perm_nums) - 1):\n if abs(x - 24) < 0.00005:\n return True\n return False\n``` | 1 | 0 | [] | 1 |
count-sorted-vowel-strings | [Java/C++/Python] DP, O(1) Time & Space | javacpython-dp-o1-time-space-by-lee215-k5w0 | Explanation\ndp[n][k] means the number of strings constructed by at most k different characters.\n\nIf k = 1, use only u\nIf k = 2, use only o,u\nIf k = 3, use | lee215 | NORMAL | 2020-11-01T04:08:11.249862+00:00 | 2020-11-02T03:05:28.093641+00:00 | 41,521 | false | # **Explanation**\n`dp[n][k]` means the number of strings constructed by at most `k` different characters.\n\nIf `k = 1`, use only `u`\nIf `k = 2`, use only `o,u`\nIf `k = 3`, use only `i,o,u`\nIf `k = 4`, use only `e,i,o,u`\nIf `k = 5`, use only `a,e,i,o,u`\n<br>\n\n\n# Solution 1: Top Down\nTime `O(nk)`\nSpace `O(nk)`\nwhere k = 5\n\n**Python:**\n```py\n def countVowelStrings(self, n):\n seen = {}\n def dp(n, k):\n if k == 1 or n == 1: return k\n if (n, k) in seen:\n return seen[n, k]\n seen[n, k] = sum(dp(n - 1, k) for k in xrange(1, k + 1))\n return seen[n, k]\n return dp(n, 5)\n```\n\n# Solution 2: Bottom Up\nTime `O(nk)`\nSpace `O(nk)`\nwhere k = 5\n\n**Java:**\n```java\n public int countVowelStrings(int n) {\n int[][] dp = new int[n + 1][6];\n for (int i = 1; i <= n; ++i)\n for (int k = 1; k <= 5; ++k)\n dp[i][k] = dp[i][k - 1] + (i > 1 ? dp[i - 1][k] : 1);\n return dp[n][5];\n }\n```\n\n**C++:**\n```cpp\n int countVowelStrings(int n) {\n vector<vector<int>>dp(n + 1, vector<int>(6));\n for (int i = 1; i <= n; ++i)\n for (int k = 1; k <= 5; ++k)\n dp[i][k] = dp[i][k - 1] + (i > 1 ? dp[i - 1][k] : 1);\n return dp[n][5];\n }\n```\n\n**Python:**\n```py\n def countVowelStrings(self, n):\n dp = [[1] * 6] + [[0] * 6 for i in xrange(n)]\n for i in xrange(1, n + 1):\n for k in xrange(1, 6):\n dp[i][k] = dp[i][k - 1] + dp[i - 1][k]\n return dp[n][5]\n```\n<br>\n\n# Solution 3: Bottom up, 1D DP\nTime `O(nk)`\nSpace `O(k)`\nwhere k = 5\n\n**Java:**\n```java\n public int countVowelStrings(int n) {\n int[] dp = new int[] {0, 1, 1, 1, 1, 1};\n for (int i = 1; i <= n; ++i)\n for (int k = 1; k <= 5; ++k)\n dp[k] += dp[k - 1];\n return dp[5];\n }\n```\n\n**C++:**\n```cpp\n int countVowelStrings(int n) {\n vector<int> dp = {0,1,1,1,1,1};\n for (int i = 1; i <= n; ++i)\n for (int k = 1; k <= 5; ++k)\n dp[k] += dp[k - 1];\n return dp[5];\n }\n```\n**Python:**\n```py\n def countVowelStrings(self, n):\n dp = [0] + [1] * 5\n for i in xrange(1, n + 1):\n for k in xrange(1, 6):\n dp[k] += dp[k - 1]\n return dp[5]\n```\n**Python3**\n```py\n def countVowelStrings(self, n: int) -> int:\n dp = [1] * 5\n for i in range(n):\n dp = accumulate(dp)\n return list(dp)[-1]\n```\n<br>\n\n# Solution 4: Combination number\nNow we have `n` characters, we are going to insert 4 `l` inside.\nWe can add in the front, in the middle and in the end.\nHow many ways do we have?\nFor the 1st `l`, we have `n+1` position to insert.\nFor the 2nd `l`, we have `n+2` position to insert.\nFor the 3rd `l`, we have `n+3` position to insert.\nFor the 4th `l`, we have `n+4` position to insert.\nAlso 4 `l` are the same,\nthere are `(n + 1) * (n + 2) * (n + 3) * (n + 4) / 4!` ways.\n\nThe character before the 1st `l`, we set to `a`.\nThe character before the 2nd `l`, we set to `e`.\nThe character before the 3rd `l`, we set to `i`.\nThe character before the 4th `l`, we set to `o`.\nThe character before the 5th `l`, we set to `u`.\n\nWe get the one result for the oringinal problem.\n\nTime `O(1)`\nSpace `O(1)`\n\n**Java:**\n```java\n public int countVowelStrings(int n) {\n return (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24;\n }\n```\n**C++:**\n```cpp\n int countVowelStrings(int n) {\n return (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24;\n }\n```\n**Python:**\n```py\n def countVowelStrings(self, n):\n return (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24\n```\n**Python3**\n@imaginary_user\n```py\n def countVowelStrings(self, n: int) -> int:\n return comb(n + 4, 4)\n``` | 419 | 15 | [] | 41 |
count-sorted-vowel-strings | Java DP O(n) time Easy to understand | java-dp-on-time-easy-to-understand-by-fr-ente | time: O(n)\nspace: O(1)\njust think about the mathematical induction\nif we know all the string of len k, so the string of len k + 1 will be\n1 add a before all | FrankLu321 | NORMAL | 2020-11-01T04:09:17.365625+00:00 | 2020-11-01T04:22:58.465348+00:00 | 11,328 | false | time: O(n)\nspace: O(1)\njust think about the mathematical induction\nif we know all the string of len k, so the string of len k + 1 will be\n1 add a before all string of len k\n2 add e before the string of len k, which is starts with or after e\n3 add i before the string of len k, which starts with or after i\n4 add o before the string of len k, which starts with or after o\n5 add u before the string of len k, which starts with or after u\n```\nclass Solution {\n public int countVowelStrings(int n) {\n int a = 1, e = 1, i = 1, o = 1, u = 1;\n while(n > 1) {\n\t\t\t// add new char before prev string\n a = (a + e + i + o + u); // a, e, i, o, u -> aa, ae, ai, ao, au\n e = (e + i + o + u); // e, i, o, u -> ee, ei, eo, eu\n i = (i + o + u); // i, o, u -> ii, io, iu\n o = (o + u); // o, u -> oo, ou\n u = (u);; // u -> uu\n n--;\n }\n \n return a + e + i + o + u;\n }\n}\n``` | 353 | 10 | [] | 41 |
count-sorted-vowel-strings | ✅🔥DP & 5 Variables Approach - C++/Java/Python | dp-5-variables-approach-cjavapython-by-d-tkx1 | Intuition\n\n- Here we can observe a pattern to this problem.\n\n\n\t\t a e i o u\n n=1 1 1 1 1 1 /a, e, i, o, u\n n=2 5 4 3 2 1 /a-> a | dhruba-datta | NORMAL | 2022-05-11T02:59:40.146515+00:00 | 2023-12-03T22:24:44.675893+00:00 | 16,181 | false | # Intuition\n\n- Here we can observe a pattern to this problem.\n\n```\n\t\t a e i o u\n n=1 1 1 1 1 1 /a, e, i, o, u\n n=2 5 4 3 2 1 /a-> aa,ae,ai,ao,au | e-> ee,ei,eo,eu | i-> ii,io,iu | o-> oo,ou | u-> uu\n n=3 15 10 6 3 1\n```\n\n- If we observe from last there will be only 1 element which will start with u. Every other element will have the count of previous count + next element count. As example\nin n=2, i will be previous i(1) + count of next element, o(2) \u2192 3\nin n=3, e will be previous e(4) + count of next element, i(6) \u2192 10\n\n# Approach 01\n1. Using ***5 variables.***\n1. Initialize variables a, e, i, o, and u to 1, representing the count of strings ending with each vowel.\n2. Iterate from n-1 to 0 using a loop, updating the count for each vowel as follows:\n - Increment the count of strings ending with \'o\' (o += u).\n - Increment the count of strings ending with \'i\' (i += o).\n - Increment the count of strings ending with \'e\' (e += i).\n - Increment the count of strings ending with \'a\' (a += e).\n3. After the loop, the sum of counts for all vowels (a+e+i+o+u) represents the total count of strings of length n that consist only of vowels and are lexicographically sorted.\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(n), where algorithm iterates through the loop n times, and each iteration involves constant time operations.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we use a constant amount of space for variables regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n \n while(--n){\n o += u;\n i += o;\n e += i;\n a += e;\n }\n \n return a+e+i+o+u;\n }\n};\n```\n```Java []\nclass Solution {\n public int countVowelStrings(int n) {\n int a = 1, e = 1, i = 1, o = 1, u = 1;\n\n while (--n > 0) {\n o += u;\n i += o;\n e += i;\n a += e;\n }\n\n return a + e + i + o + u;\n }\n}\n```\n```python []\nclass Solution(object):\n def countVowelStrings(self, n):\n a, e, i, o, u = 1, 1, 1, 1, 1\n\n while n > 1:\n o += u\n i += o\n e += i\n a += e\n n -= 1\n\n return a + e + i + o + u\n```\n\n---\n\n\n\n# Approach 02\n\n1. Using ***Dynamic Programing(dp).***\n2. Initialize a vector dp of size 5 (representing the vowels) with all elements set to 1. This vector will store the count of strings ending with each vowel.\n3. Iterate n-1 times (since we already have the count for n=1).\n4. In each iteration, update the count in the dp vector by summing up the counts of strings ending with each vowel from right to left. This step corresponds to extending the strings by adding one more character.\n5. After the iterations, the sum of counts in the dp vector represents the total number of strings of length n that can be formed using vowels.\n6. Return the sum as the result.\n\n\n# Complexity\n- Time complexity: The time complexity of this solution is O(3n) - The algorithm iterates n-1 times, and each iteration involves updating the vector in constant time.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(1) since we use a constant amount of space for variables regardless of the input size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> dp(5, 1);\n int ans = 0;\n \n while(--n){\n for(int i=3; i>=0; i--){\n dp[i] += dp[i+1];\n }\n }\n \n for(auto x:dp) ans += x;\n \n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int countVowelStrings(int n) {\n int[] dp = new int[]{1, 1, 1, 1, 1};\n int ans = 0;\n\n while (--n > 0) {\n for (int i = 3; i >= 0; i--) {\n dp[i] += dp[i + 1];\n }\n }\n\n for (int x : dp) {\n ans += x;\n }\n\n return ans;\n }\n}\n```\n```python []\nclass Solution(object):\n def countVowelStrings(self, n):\n dp = [[0] * 5 for _ in range(n + 1)]\n\n for j in range(5):\n dp[1][j] = 1\n\n for i in range(2, n + 1):\n for j in range(5):\n for k in range(j, 5):\n dp[i][j] += dp[i - 1][k]\n\n result = sum(dp[n])\n return result\n```\n\n---\n\n> **Please upvote this solution**\n> | 217 | 2 | ['Dynamic Programming', 'Python', 'C++', 'Java', 'Python3'] | 14 |
count-sorted-vowel-strings | One-line solution | Math | No DP, no Big Integers | O(1) time, space | one-line-solution-math-no-dp-no-big-inte-plgi | Let me start with the answer itself, you just need to return the following:\n\n\n\nFor example, in Ruby:\n\ndef count_vowel_strings(n)\n (n + 1) * (n + 2) * (n | ykurmangaliyev | NORMAL | 2021-01-17T13:02:29.867847+00:00 | 2021-01-17T13:09:04.134852+00:00 | 8,954 | false | Let me start with the answer itself, you just need to return the following:\n\n\n\nFor example, in Ruby:\n```\ndef count_vowel_strings(n)\n (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24\nend\n```\n\nSee the explained solution further down.\n\n# 1. Simplify the problem\nThe "vowels" part in the problem statement makes it more confusing and makes it sound more complex, let\'s rephrase it using numbers:\n\n> Given an integer n, return the number of numbers of length n that consist only of digits 1 to 5 and all digits are non-decreasing.\n\nFor example, given `n = 2`, we need to count: 11, 12, 13, 14, 15, 22, 23, 24, 25, 33, 34, 35, 44, 45, 55.\n\nThe answer to the rephrased problem will be the same as to the original problem, these problems are equivalent. \n\n# 2. Solve the simple problem\nThe problem defined in part 1 is known as a problem counting the number of **combinations with repetitions**.\nIn particular, we need to choose **n** digits from the pool of **5** digits with repetitions.\n\nWhy combinations, but not permutations? Because the number needs to be sorted (the digits should be non-decreasing), so we need to only count "112", but not "121", "211".\n\nThe easiest way to calculate the number of combinations with repetitions is to use the folowing formula:\n\n\n\n\nIf we apply this formula to our problem where we choose n from 5 (k = n, n = 5), it can be then simplified to this:\n\n\n\n\nwhich is the answer!\n\nThank you for reading through :)\n | 198 | 4 | ['Math', 'Combinatorics'] | 16 |
count-sorted-vowel-strings | Vowels count - simple math - faster | vowels-count-simple-math-faster-by-suren-0nis | Hi,\n\nWhen we do some paper work for this we could see that vowel \'a\' will have all the values including \'a\', where as vowel \'e\' will have all the letter | Surendaar | NORMAL | 2022-05-11T05:28:54.739238+00:00 | 2022-05-11T06:47:28.822434+00:00 | 5,812 | false | Hi,\n\nWhen we do some paper work for this we could see that vowel \'a\' will have all the values including \'a\', where as vowel \'e\' will have all the letter except \'a\'.. as it is already covered in \'a\'.\n\na -> aa, ae, ai, ao, au\ne -> ee, ei, eo, eu\ni -> ii, io, iu\n0 -> oo, ou\nu -> uu\n\nBecause if we add e with a its again ae, so its already covered while sorting it lexicographically.\nSo we don\'t have to append the lexicographically smaller alphabet with bigger one.\n\nso the basic math for doing the same is ->\n1) Initially all the vowels will be 1\n2) Then each step vowels will go by following figure a = a+e+i+o+u, e = e+i+o+u, i=i+o+u.. etc., \n3) Till we reach the given number repeat the process\n\nKindly upvote if it helps, happy learning\n\n```\n\tint a=1, e=1, i=1, o=1, u=1;\n public int countVowelStrings(int n) { \n \tfor(int j=1; j<n; j++){\n \tincrement();\n }\n \treturn a+e+i+o+u;\n }\n\n private void increment() {\n\t\ta = a+e+i+o+u;\n\t\te = e+i+o+u;\n\t\ti = i+o+u;\n\t\to = o+u;\n\t} | 117 | 1 | ['Java'] | 13 |
count-sorted-vowel-strings | Dynamic Programming - Python [100%] [Explanation + code] | dynamic-programming-python-100-explanati-izpp | In this problem, the pattern I observed was prepending \'a\' to all the strings of length n-1 does not affect any order. Similarly, \'e\' can be prepended to st | mihirrane | NORMAL | 2020-11-01T06:08:56.406936+00:00 | 2021-01-17T22:20:12.898143+00:00 | 7,589 | false | In this problem, the pattern I observed was prepending \'a\' to all the strings of length n-1 does not affect any order. Similarly, \'e\' can be prepended to strings starting with \'e\' and greater vowels and so on.\n\nSo we have our subproblem.\n\n**How do we fill the DP Table?**\nLets, take an example of n = 3\n\n\n\nFor n = 1, number of strings starting with u is 1, with o is 2 (including the ones starting with u) and so on.\nFor n = 2, number of strings starting with u is 1, but for o its (number of strings of length 2 starting with u + number of strings of length 1 starting with o) and so on.\ndp[i][j] represents total no. of string of length i , starting with characters of column j and after j. (Thanks @[rkm_coder](https://leetcode.com/rkm_coder/) for the correction)\n\nThe recursive expression is : dp[i][j] = dp[i - 1][j] + dp[i][j + 1]\n\nFinally, we will get our answer at dp[n][0]\n\nThe running time of my algorithm is **O(n)**\n\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n dp = [[i for i in range(5,0,-1)] for _ in range(n)] # intialize dp matrix\n \n for i in range(1,n):\n for j in range(3,-1,-1):\n dp[i][j] = dp[i - 1][j] + dp[i][j + 1] # dp expression\n \n return dp[n-1][0]\n```\n\nAlso check out Java implementation here: https://leetcode.com/problems/count-sorted-vowel-strings/discuss/918728/java-dp-beats-100 | 106 | 2 | ['Dynamic Programming', 'Python3'] | 12 |
count-sorted-vowel-strings | Very Easy Solution | No DP | No Math Formula | Solving for n = 3 reveals the pattern | very-easy-solution-no-dp-no-math-formula-yjmf | \nThe problem seems like it will have a typical recursive solution,\nbut in reality it has a very trivial solution.\n\nImportant part of this problem is to rego | interviewrecipes | NORMAL | 2020-11-01T04:01:20.630165+00:00 | 2020-11-01T04:29:52.331516+00:00 | 8,191 | false | \nThe problem seems like it will have a typical recursive solution,\nbut in reality it has a very trivial solution.\n\nImportant part of this problem is to regonize the pattern.\n\nFor `n = 3`, let\'s see how many strings can be formed.\n\nIf start of the string is "aa", the third letter can be any of\n`{a, e, i, o, u}` and the string will still be lexicographically\nsorted. So there will be 5 strings. in total.\nSo, say` "aa" -> 5`.\nIf the start is "ae", the third letter can be `{e, i, o, u}`. \nNote that `a` can\'t be the third letter, otherwise the string \nwill not be lexicographically sorted. So count of strings will\nbe 4.\nSo, say` "ae" -> 4.`\nSimilarly, for `"ai" -> {i, o, u} -> 3`.\n```\n"ao" -> {o, u} -> 2.\n"au" -> {u} -> 1.\n```\n\nNow say start of the string is "ee".\n```\n"ee" -> {e, i, o, u} -> 4.\n"ei" -> {i, o, u} -> 3.\n"eo" -> {o, u} -> 2.\n"eu" -> {u} -> 1.\n```\n\nSimilarly,\n```\n"ii" -> {i, o, u} -> 3.\n"io" -> {o, u} -> 2.\n"iu" -> {u} -> 1.\n"oo" -> {o, u} -> 2.\n"ou" -> {u} -> 1.\n"uu" -> {u} -> 1.```\n```\n\n\nHence in total, there would be -\n\n```\n5 + 4 + 3 + 2 + 1 +\n4 + 3 + 2 + 1 +\n3 + 2 + 1 +\n2 + 1 +\n1 \n= 35 \n```\n\n\nYou can also try the above pattern n = 2.\n\nHere is the very simple code. It can certainly be optized with a mathematical formula.\nI kept it as is considering that n is very small anyway and not everyone would know the\nformula.\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int ans = 0;\n for (int j=1; j<=(n+1); j++) {\n int sum = 0;\n for (int i=1; i<=j; i++) {\n sum += i;\n ans += sum;\n }\n }\n return ans;\n }\n};\n```\n\n\n | 76 | 4 | [] | 14 |
count-sorted-vowel-strings | Intuitive C++ Solution (With explaination) | intuitive-c-solution-with-explaination-b-mlp2 | The solution uses DP but in a way that I found much more intuitive. We start the solution from the right i.e. generate suffixes and keep prepending it to either | yashjain | NORMAL | 2020-11-01T04:39:12.456477+00:00 | 2021-08-31T10:08:33.548537+00:00 | 3,544 | false | The solution uses DP but in a way that I found much more intuitive. We start the solution from the right i.e. generate suffixes and keep prepending it to either a, e, i, o, or u.\na = number of strings that start with a\ne = number of strings that start with e\ni = number of strings that start with i\no = number of strings that start with o\nu = number of strings that start with u\n\nSo, we can simply keep appending the string that starts with:\n1. a to only string that has a at the beginning.\n2. e to string that either has a or e at the beginning.\n3. i to string that has a, e or i at the beginning.\n.... And so on\n\n```\nint countVowelStrings(int n) {\n int a = 1, e = 1, i = 1, o = 1, u = 1;\n for(int j=2;j<=n;j++){\n a = a + e + i + o + u;\n e = e + i + o + u;\n i = i + o + u;\n o = o + u;\n u = u;\n }\n return a + e + i + o + u;\n }\n```\nIf you got this, try https://codeforces.com/problemset/problem/166/E, it uses a similar approach. | 73 | 0 | ['Dynamic Programming', 'C', 'C++'] | 7 |
count-sorted-vowel-strings | Count Sorted Vowel Strings | O(1) 1-Line Mathematical Solution w/ Explanation | count-sorted-vowel-strings-o1-1-line-mat-2sqq | Idea:\n\nThe mathematical solution is derived from Pascal\'s Triangle.\n\nThe formula for a triangular number is:\n\n x * (x + 1)\n\t -------------\n\t | sgallivan | NORMAL | 2021-01-17T11:47:17.505221+00:00 | 2021-01-17T12:21:34.532006+00:00 | 2,231 | false | ***Idea:***\n\nThe mathematical solution is derived from Pascal\'s Triangle.\n\nThe formula for a triangular number is:\n```\n x * (x + 1)\n\t -------------\n\t 1 * 2\n```\n...and the formula for a tetrahedral number is:\n```\n x * (x + 1) * (x + 2)\n\t -----------------------\n\t 1 * 2 * 3\n```\n...so the formula for the nth-simplex number is:\n```\n x * (x + 1) * (x + 2) * ... * (x + n - 1)\n\t -------------------------------------------\n\t n!\n```\nWe\'re dealing with a base of 5 vowels, so x = 5 and this formula starts to look like:\n```\n 5 * 6 * 7 * ... * (n + 4)\n\t ---------------------------\n\t n!\n```\n...but then we can realize that numbers start to cancel out from top to bottom, taking for example n = 10:\n```\n 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14\n\t ------------------------------------------------------------\n\t 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10\n```\nWe can factor out every number on the bottom greater than 4, and we\'ll also have the last four remaining numbers on the top, so the final formula ends up:\n```\n (n + 1) * (n + 2) * (n + 3) * (n + 4)\n\t ---------------------------------------\n\t 1 * 2 * 3 * 4\n```\n\n` `\n***Code:***\n\n```\nconst countVowelStrings = n => (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24\n``` | 58 | 3 | [] | 8 |
count-sorted-vowel-strings | [Python] simple DP solution - O(N) / O(1) | python-simple-dp-solution-on-o1-by-alanl-brnm | Python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n \n a = e = i = o = u = 1\n for _ in range(n - 1):\n a | alanlzl | NORMAL | 2020-11-01T04:01:34.889411+00:00 | 2020-11-01T04:01:34.889461+00:00 | 1,670 | false | ```Python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n \n a = e = i = o = u = 1\n for _ in range(n - 1):\n a, e, i, o, u = a+e+i+o+u, e+i+o+u, i+o+u, o+u, u\n \n return a+e+i+o+u\n``` | 55 | 11 | [] | 6 |
count-sorted-vowel-strings | ✅ Python 4 approaches (DP, Maths) | python-4-approaches-dp-maths-by-constant-n35m | DP Tabulation\n\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [[0] * 6 for _ in range(n+1)]\n for i in range(1, | constantine786 | NORMAL | 2022-05-11T00:47:21.808058+00:00 | 2022-05-12T00:58:43.761781+00:00 | 5,492 | false | 1. ##### DP Tabulation\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [[0] * 6 for _ in range(n+1)]\n for i in range(1, 6):\n dp[1][i] = i\n \n for i in range(2, n+1):\n dp[i][1]=1\n for j in range(2, 6):\n dp[i][j] = dp[i][j-1] + dp[i-1][j]\n \n return dp[n][5]\n```\n**Time = O(n)**\n**Space = O(n)**\n\n---\n2. ##### O(1) Space\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n dp = [1] * 5\n \n for i in range(2, n+1):\n for j in range(4, -1, -1):\n dp[j] += sum(dp[:j]) \n \n return sum(dp)\n```\n\nAlternative solution shared by [@koacosmos](https://leetcode.com/koacosmos/)\n\n```\nclass Solution:\n def countVowelStrings(self, k: int) -> int: \n dp = [1] * 5\n \n for _ in range(1, k):\n for i in range(1, 5): \n dp[i] = dp[i] + dp[i-1]\n \n return sum(dp)\n```\n**Time = O(n)**\n**Space = O(1)**\n\n---\n\n3. ##### Mathematical equation using [Combinations with repetition](https://en.wikipedia.org/wiki/Combination#Number_of_combinations_with_repetition)\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n return (n + 4) * (n + 3) * (n + 2) * (n + 1) // 24;\n```\n\n---\nSolution shared by [@nithinmanne1](https://leetcode.com/nithinmanne1/) using Python internal library.\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int: \n return math.comb(n + 4, 4)\n```\n\n**Time = O(1)\nSpace = O(1)**\n\n----\n\nOther contributers of this post:\n1. [@nithinmanne1](https://leetcode.com/nithinmanne1/)\n2. [@koacosmos](https://leetcode.com/koacosmos/)\n\n---\n\n***Please upvote if you find it useful*** | 52 | 1 | ['Python', 'Python3'] | 6 |
count-sorted-vowel-strings | Beautiful C++ solution (100% faster) | beautiful-c-solution-100-faster-by-pig14-s6a2 | (Updated)\n\nThe variable a, e, i, o, or u means the number of strings ended with an a, e, I, o, or u with a given length.\n\nIn each iteration, we expend the l | pig14726 | NORMAL | 2020-11-25T16:25:36.995497+00:00 | 2020-12-15T01:49:17.678458+00:00 | 3,288 | false | (Updated)\n\nThe variable a, e, i, o, or u means the number of strings ended with an a, e, I, o, or u with a given length.\n\nIn each iteration, we expend the length by 1. \u2018a\u2019 can only come after string ended with \u2018a\u2019, so the number of strings ended with an \'a\' remains unchanged. \u2018e\u2019 can be added to string ended with an \u2018a\u2019 or \u2018e\u2019, so we update the length using e\u2019 = e + a. And so forth.\n\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int a = 1;\n int e = 1;\n int i = 1;\n int o = 1;\n int u = 1;\n \n while (--n){\n e += a;\n i += e;\n o += i;\n u += o; \n }\n return a + e + i + o + u;\n }\n};\n``` | 48 | 1 | ['C'] | 6 |
count-sorted-vowel-strings | DP | C++ | Recursion->Memoization->Tabulation | Well commented | dp-c-recursion-memoization-tabulation-we-jdb1 | Recursive Solution [ Time-Complexity = O(n^2), Space-Complexity = O(n) ]\n\t\n \n\tint count(int i, int n, string &vowels){\n\n\t\t\tif(n==0) return 1; // if a | _walterwhite | NORMAL | 2022-05-11T04:23:34.888945+00:00 | 2022-05-11T04:32:02.711319+00:00 | 3,285 | false | **Recursive Solution** **[ Time-Complexity = O(n^2), Space-Complexity = O(n) ]**\n\t\n ```\n\tint count(int i, int n, string &vowels){\n\n\t\t\tif(n==0) return 1; // if a string of length n is formed\n\n\t\t\tif(i>=5) return 0; // if i exceeds the length of vowels\n\n\t\t\tint pick, notPick;\n\t\t\t// pick i.e. pick this alphabet\n\t\t\tpick= count(i, n-1, vowels);\n\t\t\t// notPick i.e. skip this alphabet\n\t\t\tnotPick= count(i+1, n, vowels);\n\n\t\t\treturn pick + notPick;\n\t}\n\n\tint countVowelStrings(int n) {\n\t\t string vowels= "aeiou"; // all vowels in lexicographically sorted order\n\t\t return count(0, n, vowels);\n\t}\n\t\n```\n\t\n**Memoization** **[ Time-Complexity = O(4 * n), Space-Complexity = O(5 * n) + O(n) ]**\n\n\n ```\n\tint count(int i, int n, string &vowels, vector<vector<int>> &dp){\n\n\t\t if(n==0) return 1; // if a string of length n is formed\n\n\t\t if(i>=5) return 0; // if i exceeds the length of vowels\n\n\t\t if(dp[i][n]!=-1) return dp[i][n]; // check if dp already contains the answer\n\n\t\t int pick, notPick;\n\t\t // pick i.e. pick this alphabet\n\t\t pick= count(i, n-1, vowels, dp);\n\t\t // notPick i.e. skip this alphabet\n\t\t notPick= count(i+1, n, vowels, dp);\n\n\t\t return dp[i][n]= pick + notPick; // store the value in dp\n\t}\n\n\tint countVowelStrings(int n) {\n\t\t string vowels= "aeiou"; // all vowels in lexicographically sorted order\n\t\t vector<vector<int>> dp(5, vector<int>(n+1, -1)); // declare dp vector\n\t\t return count(0, n, vowels, dp);\n\t}\n```\n\t\n**Tabulation** **[ Time-Complexity = O(4 * n), Space-Complexity = O(5 * n) ]**\n\n```\n\tint countVowelStrings(int n) {\n\n\t\tstring vowels= "aeiou"; // all vowels in lexicographically sorted order\n\n\t\tvector<vector<int>> dp(5, vector<int>(n+1)); // dp vector\n\n\t\t// base-case\n\t\tfor(int i=0; i<5; ++i) dp[i][0]= 1; // if n==0 return 1\n\n\t\t// tabulation\n\t\tfor(int i=4; i>=0; --i){\n\t\t for(int j=1; j<=n; ++j){\n\t\t\tint pick= 0, notPick= 0;\n\t\t\t// pick i.e. pick this alphabet\n\t\t\tpick= dp[i][j-1];\n\t\t\t// notPick i.e. skip this alphabet\n\t\t\tif(i<4) notPick= dp[i+1][j];\n\n\t\t\tdp[i][j]= pick+notPick;\n\t\t }\n\t\t}\n\n\t\treturn dp[0][n]; // return all strings possible starting from 0 index and of n length\n\t}\n``` | 45 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 3 |
count-sorted-vowel-strings | [Python] Start and bars, explained | python-start-and-bars-explained-by-dbabi-ndqj | Actually, this is very classical combinatorical problem, which can be solved, using so-called stars and bars method: https://en.wikipedia.org/wiki/Stars_and_bar | dbabichev | NORMAL | 2021-01-17T09:02:19.924795+00:00 | 2022-05-11T07:18:04.765601+00:00 | 7,342 | false | Actually, this is very classical combinatorical problem, which can be solved, using so-called **stars and bars** method: https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics). Imagine, that we have string `aa..aee..eii..ioo..ouu..u`, where we have some numbers of `a, e, i, o` and `u`. Then we can look at this problem in the following way: we have `n + 4`, places, and on some of them we need to put bars `|`, for example `aaaeeiuu` is corresponding to `***|**|*||**`. So, final number of solutions is number of combinations from `n+4` to `4,` which can be evaluated as `(n+4)!/n!/4!`.\n\n**Complexity**: time and space complexity is `O(1)`, because `n` is small. One quick optimization is to use `(n+4)*(n+3)*(n+2)*(n+1)//24` formula, which will work faster for big `n`, but given problem constraints different is negligible.\n\n```\nclass Solution:\n def countVowelStrings(self, n):\n return factorial(4+n)//factorial(4)//factorial(n)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 44 | 3 | [] | 4 |
count-sorted-vowel-strings | [Java/Python] Top Down DP - Clean & Concise | javapython-top-down-dp-clean-concise-by-758uk | Python 3\npython\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n @lru_cache(None)\n def dp(n, i):\n if n == 0: retu | hiepit | NORMAL | 2020-11-01T04:04:17.517363+00:00 | 2020-11-01T04:23:28.760786+00:00 | 3,555 | false | **Python 3**\n```python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n @lru_cache(None)\n def dp(n, i):\n if n == 0: return 1 # Found a valid answer\n if i == 5: return 0 # Reach to length of vowels [a, e, i, o, u]\n ans = dp(n, i + 1) # Skip vowels[i]\n ans += dp(n - 1, i) # Include vowels[i]\n return ans\n\n return dp(n, 0)\n```\n\n**Java**\n```java\nclass Solution {\n public int countVowelStrings(int n) {\n Integer[][] memo = new Integer[n + 1][5];\n return dp(n, 0, memo);\n }\n\n int dp(int n, int i, Integer memo[][]) {\n if (n == 0) return 1; // Found a valid answer\n if (i == 5) return 0; // Reach to length of vowels [a, e, i, o, u]\n if (memo[n][i] != null) return memo[n][i];\n \n int ans = dp(n, i+1, memo); // Skip vowels[i]\n ans += dp(n-1, i, memo); // Include vowels[i]\n \n return memo[n][i] = ans;\n }\n}\n```\n\n**Complexity:**\n- Time: `O(N * vowelsLen * 2)`, where `vowelsLen` is length of vowels (=5).\n- Space: `O(N* vowelsLen)` | 43 | 2 | [] | 3 |
count-sorted-vowel-strings | Python. One liner solution. O(1) time & space. | python-one-liner-solution-o1-time-space-4jhmt | Some combinatorics:\nIt is known that the characters should appear in ascending lexicographic order.\nIt is known that there are a total of 5 characters.\nConcl | m-d-f | NORMAL | 2021-01-17T10:14:15.381379+00:00 | 2021-01-17T15:42:31.873856+00:00 | 2,394 | false | Some combinatorics:\nIt is known that the characters should appear in ascending lexicographic order.\nIt is known that there are a total of 5 characters.\nConclusion: There are only 4 places where the character is replaced by the one followed by the sorted order.\nWe have n + 4 locations in total.\nHence, the answer is (using a binomial coefficient): n + 4 C 4\nAfter we simplify the above expression, we will get the solution in front of you.\n\n\t\n\tclass Solution:\n\t\tdef countVowelStrings(self, n: int) -> int:\n\t\t\treturn ((n + 1) * (n + 2) * (n + 3) * (n + 4)) // 24\n\nI sincerely hope you understood.\nIf there are any more questions, feel free to ask. | 36 | 7 | ['Python', 'Python3'] | 8 |
count-sorted-vowel-strings | 3 different solutions (backtracking, dynamic programming, math) | 3-different-solutions-backtracking-dynam-noou | \n\nBacktracking solution:\nTime complexity: O(n^5)\nWe try all the possibilities where adding the new vowel doesn\'t break the lexicographic order. For example | syph | NORMAL | 2021-05-06T03:29:20.045364+00:00 | 2021-05-06T20:15:17.408950+00:00 | 2,360 | false | \n\n**Backtracking solution:**\n**Time complexity:** `O(n^5)`\nWe try all the possibilities where adding the new vowel doesn\'t break the lexicographic order. For example, if the last character of our actual possibility is \'e\', we can\'t add an \'a\' after it.\n```\ndef count(n, last=\'\'):\n if n == 0:\n return 1\n else:\n nb = 0\n for vowel in [\'a\', \'e\', \'i\', \'o\', \'u\']:\n if last <= vowel:\n nb += count(n-1, vowel)\n return nb\n```\n\n\n**Dynamic programming solution:**\n**Time complexity:** `O(n)`\nWe use a dp matrix of n rows and 5 columns (one column for each vowel) where the number of strings of size k that start with a vowel v is the sum of strings of size k-1 with whom we can add the vowel v from the beginning without breaking the order\nWe can add \'a\' before any vowel string without breaking the order, so the number of strings of size k that start with \'a\' is the number of strings of size k-1 that start with \'a\', \'e\', \'i\', \'o\', or \'u\'\nWe can add \'e\' before strings that start with \'e\', \'i\', \'o\', or \'u\' without breaking the order, so the number of strings of size k that start with \'e\' is the number of strings of size k-1 that start with \'e\', \'i\', \'o\', or \'u\'\nSame logic with remaining vowels (\'i\' -> \'i\', \'o\', or \'u\' / \'o\' -> \'o\' or \'u\' / \'u\' -> \'u\')\nAfter filling the matrix, the last row will contain the numbers of strings of size n with each vowel, we do the sum\n```\ndef count(n):\n NB_VOWELS = 5\n dp = [[0]*NB_VOWELS for i in range(n)]\n dp[0] = [1]*NB_VOWELS\n for i in range(1, len(dp)):\n dp[i][0] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # a\n dp[i][1] = dp[i-1][1] + dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # e\n dp[i][2] = dp[i-1][2] + dp[i-1][3] + dp[i-1][4] # i\n dp[i][3] = dp[i-1][3] + dp[i-1][4] # o\n dp[i][4] = dp[i-1][4] # u\n return sum(dp[-1])\n```\n\n\n**Math solution:**\n**Time complexity:** `O(1)`\nThe number of possible sorted strings that we can get by taking n vowels from 5 possible vowels is the number of possible combinations with repetition that we can get by taking n elements from 5 possible elements, and we have a mathematical law for that\n\n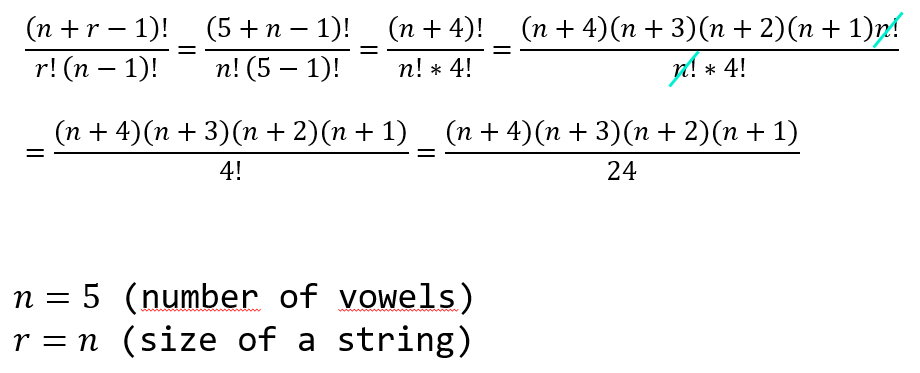\n\n```\ndef count(n):\n return (n+4)*(n+3)*(n+2)*(n+1)//24\n```\n\n\n\n\n\n | 31 | 0 | ['Math', 'Dynamic Programming', 'Backtracking', 'Python', 'Python3'] | 4 |
count-sorted-vowel-strings | C++ Backtracking vs Dynamic Programming beats 100.0% | c-backtracking-vs-dynamic-programming-be-vq9o | First I tried backtracking and find a solution but runtime is ~1200 ms and beats 5.0% only:\n\n\nclass Solution {\npublic:\n vector<char> vowels = {\'a\', \' | yilmaz | NORMAL | 2020-11-10T19:32:35.057390+00:00 | 2020-11-10T19:51:08.036312+00:00 | 2,895 | false | First I tried backtracking and find a solution but runtime is ~1200 ms and beats 5.0% only:\n\n```\nclass Solution {\npublic:\n vector<char> vowels = {\'a\', \'e\', \'i\', \'o\', \'u\'};\n int countVowelStrings(int n) {\n int count = 0;\n countVowelStringsHelper(n, \' \', count);\n return count;\n }\n void countVowelStringsHelper(int n, char last, int &count){\n if(n == 0){\n count++;\n }\n else{\n for(auto e: vowels){\n if(last <= e){\n countVowelStringsHelper(n-1, e, count);\n }\n }\n }\n }\n};\n```\nDP Solution:\n```\nn=1, dp = {1,2,3,4,5} return 5\nn=2, dp = {1,3,6,10,15} return 15\nn=3, dp = {1,4,10,20,35} return 35\n```\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> dp(5, 1);\n for(int i=0; i<n; i++){\n for(int j=1; j<5; j++){\n dp[j] = dp[j-1] + dp[j];\n }\n }\n return dp[4];\n }\n};\n``` | 29 | 3 | ['Dynamic Programming', 'Backtracking', 'C', 'C++'] | 6 |
count-sorted-vowel-strings | [C++] 4 lines DP solution | c-4-lines-dp-solution-by-rudy-zj6c | When n = 2, the only valid string starting with u is uu, valid strings starting with o are [oo, ou], and so on. The numbers (we use a vector cnt to store them) | rudy__ | NORMAL | 2020-11-01T04:41:21.902740+00:00 | 2020-11-04T06:19:30.905687+00:00 | 2,652 | false | When `n = 2`, the only valid string starting with `u` is `uu`, valid strings starting with `o` are `[oo, ou]`, and so on. The numbers (we use a vector `cnt` to store them) of valid strings starting with `a, e, i, o, u` are respectively `[5,4,3,2,1]`.
When `n = 3`, the only valid string starting with `u` is `uuu`, valid strings starting with `o` are `[ooo, oou, ouu]`, and so on. The numbers of valid strings starting with `a, e, i, o, u` are respectively `[15,10,6,3,1]`.
A typical DP problem, and you can find the pattern here: during each iteration over `1 ~ n`, the values of `cnt` can be calculated with its 'previous values'.
```c++
class Solution {
public:
int countVowelStrings(int n) {
vector<int64_t> cnt(5, 1);
for (int i = 1; i < n; i++)
for (int j = 3; j >= 0; j--) cnt[j] += cnt[j + 1];
return std::accumulate(cnt.begin(), cnt.end(), 0);
}
};
``` | 28 | 1 | [] | 0 |
count-sorted-vowel-strings | Java : 0 ms Faster than 100%, Easy to understand with explanation | java-0-ms-faster-than-100-easy-to-unders-nlxs | Time Complexity - O(n)\nSpace Complexity - O(1)\n\nOn carefully observing the sequence getting formed you will notice a pattern here:\n\nFor n = 1 : a , e , i, | anand004 | NORMAL | 2020-11-05T13:11:21.135839+00:00 | 2020-11-05T13:14:16.051475+00:00 | 1,321 | false | Time Complexity - O(n)\nSpace Complexity - O(1)\n\nOn carefully observing the sequence getting formed you will notice a pattern here:\n\nFor n = 1 : a , e , i, o, u \nString starting with a = 1, e = 1, i = 1, o = 1, u = 1 : Total = 5\n\nFor n = 2 : aa, ae, ai, ao, au, ee, ei, eo, eu, ii, io, iu, oo, ou, uu \nString starting with a = 5, e = 4, i = 3, o = 2, u = 1 : Total = 15\n\nFor n = 3 : aaa, aae, aai, aao, aau, aee, aei, aeo, aeu, aii, aio, aiu, aoo, aou, auu, eee, eei, eeo,eeu,eii, eio, eiu, eoo, eou, euu, iii, iio, iiu, ioo, iou, iuu, ooo, oou, ouu, uuu : Total = 35\n\nOn carefully observing :\nFor n = 2 : All the sequence formed count is equal to sum of previous sequences (i.e. n = 1) starting with a, e, i, o, u\n a = a + e + i + o + u (1 + 1 + 1 + 1+ 1) = 5\n\t\t\t\t e = e + i + o +u (1 + 1+ 1+ 1) = 4\n\t\t\t\t i = i + o + u (1 + 1 + 1) = 3\n\t\t\t\t o = o + u ( 1 + 1) = 2\n\t\t\t\t u = u (1) = 1\n\t\t\t\t Total = a + e + i + o + u = 5 + 4 + 3 + 2 + 1 = 15\n\t\t\t\t \nFor n = 3: All the sequence formed count is equal to sum of previous sequences (i.e. n = 2) starting with a, e, i, o, u \n a = a + e + i + o + u (5 + 4 + 3 + 2+ 1) = 15\n\t\t\t\t e = e + i + o +u (4 + 3+ 2+ 1) = 10\n\t\t\t\t i = i + o + u (3 + 2 + 1) = 6\n\t\t\t\t o = o + u ( 2 + 1) = 3\n\t\t\t\t u = u (1) = 1\n\t\t\t\t Total = a + e + i + o + u = 15 + 10 + 6 + 3 + 1 = 35\n\t\t\t\t \n\t\t\t\t \n\n```\nclass Solution {\n public int countVowelStrings(int n) {\n int a = 1;\n int e = 1;\n int i = 1;\n int o = 1;\n int u = 1;\n while(n-- > 1){\n a = a + e + i + o + u;\n e = e + i + o + u;\n i = i + o + u;\n o = o + u;\n u = u;\n }\n return a + e + i + o + u;\n \n }\n}\n```\n | 26 | 0 | ['Java'] | 4 |
count-sorted-vowel-strings | C++ | Faster than 100% | DP and MATH Approach | c-faster-than-100-dp-and-math-approach-b-hc14 | The problem can be solved with dynamic programming approach or from a direct math formula. Here I have solved using DP approach.\n dp[vowels[index] - 97] at eve | persistentBeast | NORMAL | 2022-05-11T05:05:38.916267+00:00 | 2022-05-16T07:42:24.682769+00:00 | 3,084 | false | * The problem can be solved with **dynamic programming approach** or from a **direct math formula**. Here I have solved using DP approach.\n* `dp[vowels[index] - 97]` at every value of `i` stores the number of lexicographically sorted strings which start from `vowels[index]` and is of length `i`.\n* `vowels[index]` can come before all the lexicographically sorted strings of length `i` starting from `vowels[idx]` **(idx > index)** to form new set of lexicographically sorted strings starting from `vowels[index`] having length `i + 1`. This is the logic for building answers.\n* Build upon this answer till `i == n` and in the end accumulate the answers for each vowel.\n\n**Dynamic Programming Approach :**\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n \n string vowels = "aeiou";\n int ans;\n \n vector<int> dp(26, 0);\n \n dp[\'a\' - 97] = 1;\n dp[\'e\' - 97] = 1;\n dp[\'i\' - 97] = 1;\n dp[\'o\' - 97] = 1;\n dp[\'u\' - 97] = 1;\n \n \n \n for(int i = 2; i <= n ; i++){\n \n for(int j = 0; j < 5; j++){\n \n for(int k = j + 1; k < 5; k++){\n \n dp[vowels[j] - 97] += dp[vowels[k] - 97];\n \n } \n \n }\n \n }\n \n ans = accumulate(dp.begin(), dp.end(), 0);\n \n return ans;\n \n }\n};\n```\n\n**Alternate Math Approach :**\n\n```\nclass Solution {\n \npublic:\n int countVowelStrings(int n) {\n \n return (n+4)*(n+3)*(n+2)*(n+1) / 24;\n }\n};\n``` | 24 | 1 | ['C'] | 4 |
count-sorted-vowel-strings | C++ Top Down DP and Formula | c-top-down-dp-and-formula-by-votrubac-v0xp | Top Down DP\nTop down DP was the easiest for me to get started. \n\ncpp\nint dp[51][5] = {};\nint countVowelStrings(int n, int prev = 0) {\n if (n == 1)\n | votrubac | NORMAL | 2020-11-01T22:08:31.698677+00:00 | 2020-11-01T23:07:07.702734+00:00 | 1,612 | false | #### Top Down DP\nTop down DP was the easiest for me to get started. \n\n```cpp\nint dp[51][5] = {};\nint countVowelStrings(int n, int prev = 0) {\n if (n == 1)\n return 5 - prev;\n if (dp[n][prev] == 0)\n for (int i = prev; i < 5; ++i)\n dp[n][prev] += countVowelStrings(n - 1, i);\n return dp[n][prev]\n```\n\n#### Formula\nWhile converting the solution above to bottom-up DP, I realized that there is a pattern we can describe with a simple formula.\n1) 1 + (1 + 2) | + 1\n2) 1 + (1 + 2) + (1 + 2 + 3) | + 1 + (1 + 2) | + 1\n3) 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) | + 1 + (1 + 2) + (1 + 2 + 3) | + 1 + (1 + 2) | + 1\n4) 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) + (1 + 2 + 3 + 4 + 5)| + (#3)\n- or\n4) 5 * (5 + 1) / 2 + #3\n5) 6 * (6 + 1) /2 + #4\n\n```cpp\nint countVowelStrings(int n) {\n int res = 0, sum = 0;\n for (int i = 1; i <= n + 1; ++i) {\n sum += i * (i + 1) / 2;\n res += sum;\n }\n return res;\n}\n``` | 24 | 1 | [] | 0 |
count-sorted-vowel-strings | Java O(n) | Visual Explanation | java-on-visual-explanation-by-raunaq21-s7we | The solution is pretty straightforward once a pattern is visible.\n\nFor n = 2\na => (a, e,i,o,u)\ne => (e,i,o,u)\ni => (i, o, u)\no => (o, u)\nu => (u) \n\n\nT | raunaq21 | NORMAL | 2022-05-11T11:56:04.853510+00:00 | 2022-07-28T17:59:37.290965+00:00 | 1,551 | false | The solution is pretty straightforward once a pattern is visible.\n```\nFor n = 2\na => (a, e,i,o,u)\ne => (e,i,o,u)\ni => (i, o, u)\no => (o, u)\nu => (u) \n```\n```\nThe resultant strings are:\naa, ae, ai, ao, au\nee, ei, eo, eu\t\t\t\t\nii, io, iu\t\t\t\t\t\t\noo, ou\t\t\t\t\t\nuu\n```\n```\nFor n = 3\naa => (a,e,i,o,u) 5 \nae => (e, i, o, u) 4 \nai => (i, o, u) 3 \nao => (o, u)\t 2 \nau => u\t\t 1 \n\nee => (e,i,o,u) 4 \nei => (i,o,u)\t 3 \neo => (o,u)\t\t 2 \neu => (u)\t\t 1 \n\n\nii => (i,o,u) 3 \nio => (o,u)\t 2 \niu =>\t (u) 1 \n\noo => (o,u) 2 \nou => (u) 1 \n\nuu => (u)\t 1 \n\n```\nThe total comes out to be 35 which is the desired output.\n```\nclass Solution {\n public int countVowelStrings(int n) {\n int a,e,i,o,u;\n a = e = i = o = u = 1;\n \n for(int t = 1; t < n; t++){\n \n a = a + e + i + o + u;\n e = e + i + o + u;\n i = i + o + u;\n o = o + u;\n u = u;\n }\n return a + e + i + o + u;\n }\n}\n``` | 19 | 0 | ['Java'] | 3 |
count-sorted-vowel-strings | Image Explanation: Distributing N Balls into 5 Boxes, Some Boxes May Be Empty | image-explanation-distributing-n-balls-i-4hrh | Leetcode 1641. Count Sorted Vowel Strings.\n\n# Math \n\nEvery vowel string is start by $a, e, i, o, u$, and there are $N$ strings. \n\nHow to distribute $N$ st | longluo | NORMAL | 2022-05-11T01:32:44.396196+00:00 | 2022-11-16T07:38:52.237591+00:00 | 1,620 | false | [Leetcode](https://leetcode.com/) [1641. Count Sorted Vowel Strings](https://leetcode.com/problems/count-sorted-vowel-strings/).\n\n# Math \n\nEvery vowel string is start by $a, e, i, o, u$, and there are $N$ strings. \n\nHow to distribute $N$ strings into the $5$ boxes, some boxes may be empty?\n\nImaging that there are $N$ balls, we have to put them in to $5$ boxes represented by the $5$ vowels, as the picture shows.\n\n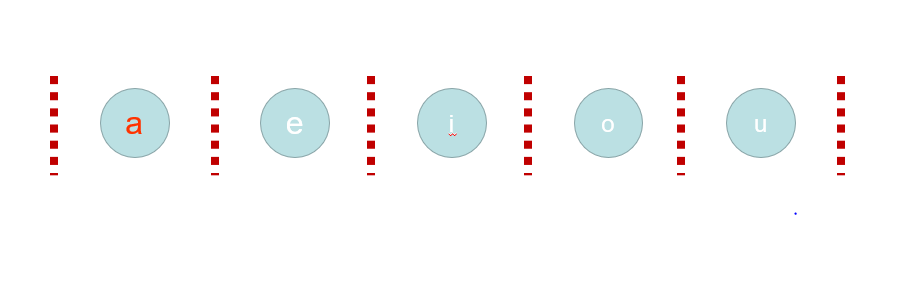\n\nOnce the number of characters in each box were fixed, the string is fixed.\n\nTherefore, how many ways are there to put $N$ balls in $5$ boxes, and the boxes can be empty?\n\nThe combinatorics explanation is [Pentatope number](https://en.wikipedia.org/wiki/Pentatope_number).\n\n1. $N$ balls in $M$ boxes, box can not empty: $C(n - 1, m - 1)$.\n2. $N$ balls in $M$ boxes, box can be empty: $C(n + m - 1, m - 1)$.\n\n```java\n public static int countVowelStrings(int n) {\n return (n + 4) * (n + 3) * (n + 2) * (n + 1) / 24;\n }\n```\n\n## Analysis\n\n- **Time Complexity**: $O(1)$.\n- **Space Complexity**: $O(1)$.\n\n------------\n\nAll suggestions are welcome. \nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\n\nExplore More [Leetcode Solutions](https://leetcode.com/discuss/general-discussion/1868912/My-Leetcode-Solutions-All-In-One). \uD83D\uDE09\uD83D\uDE03\uD83D\uDC97\n\n | 18 | 0 | ['Math', 'Dynamic Programming', 'Combinatorics', 'C++', 'Java'] | 1 |
count-sorted-vowel-strings | C++ code (Explained using permutation concept, faster than 100%) | c-code-explained-using-permutation-conce-tzbd | Code using permutation \nWe have total n places to fill with 5 vowels to fill with.In short we have n identical thigs to be distributed among 5 people for which | sakg | NORMAL | 2021-01-17T11:42:28.113454+00:00 | 2021-01-17T17:12:05.193417+00:00 | 948 | false | Code using permutation \nWe have total n places to fill with 5 vowels to fill with.In short we have n identical thigs to be distributed among 5 people for which the formulae is \n(n+5-1)C(5-1)= (n+4)C4=(n+1)*(n+2)*(n+3)*(n+4)/24\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n /// We can assume that there would be 4 transition states \n /// Ie from a->e->i->o->u\n /// and along with these transitions there would be n vowels in sorted order\n /// hence we have total n+4 locations and after choosing 4 of them \n /// (for the transitions to take place)\n /// the elements at all other positions got fixed \n /// hence the answer is n+4 C 4.\n return (n+1)*(n+2)*(n+3)*(n+4)/24;\n }\n};\n```\nCode using recursion :\nk denotes number of choices left for next character to be placed \nn denotes the number of characters left\nThe function is called recursively for all possible values of vowels \n```\nclass Solution {\npublic:\n int countVowelStrings(int n,int k=5) {\n if(k<=1)\n return k;\n if(n==1)\n return k;\n int ans=0;\n for(int i=0;i<k;i++)\n ans+=countVowelStrings(n-1,k-i);\n return ans;\n }\n};\n``` | 18 | 1 | [] | 1 |
count-sorted-vowel-strings | C++ two solutions DP and Math | c-two-solutions-dp-and-math-by-midnights-ob1z | Solved LIVE ON stream, link in profile. Math explained by a mathematician (not me) in my video\n\nHere is the DP solution:\n\nclass Solution {\n \n int d | midnightsimon | NORMAL | 2022-05-11T01:43:57.239134+00:00 | 2022-05-11T01:46:08.479019+00:00 | 1,543 | false | **Solved LIVE ON stream, link in profile. Math explained by a mathematician (not me) in my video**\n\nHere is the DP solution:\n```\nclass Solution {\n \n int dfs(int n, int i, vector<vector<int>>& memo) {\n if(n == 0) return 1;\n if(memo[n][i] != -1) return memo[n][i];\n int ret = 0;\n for(int j = i; j < 5; j++) {\n ret += dfs(n-1, j, memo);\n }\n \n return memo[n][i] = ret;\n \n }\n \npublic:\n int countVowelStrings(int n) {\n vector<vector<int>> memo(n+1, vector<int>(5, -1));\n return dfs(n, 0, memo);\n }\n};\n```\n\nHere is the math... Stars n Bars:\n```\nclass Solution {\n \npublic:\n int countVowelStrings(int n) {\n \n return (n+4)*(n+3)*(n+2)*(n+1) / 24;\n }\n};\n```\n | 15 | 0 | [] | 2 |
count-sorted-vowel-strings | C++ / 1 line / mathematical solution / with brief explanations | c-1-line-mathematical-solution-with-brie-40v0 | We have counts of a + e + i + o + u = n\nTherefore, we can use combination with repetition formula to solve it as:\nanswer = H(5, n) = C(5 + n - 1, n) = C(4 + n | liao119 | NORMAL | 2020-11-01T04:04:27.120269+00:00 | 2020-11-01T04:59:00.487879+00:00 | 497 | false | We have counts of a + e + i + o + u = n\nTherefore, we can use combination with repetition formula to solve it as:\nanswer = H(5, n) = C(5 + n - 1, n) = C(4 + n, n) = C(n + 4, 4) = (n+4) * (n+3) * (n+2) * (n+1) / 4!\n\nMore information of combination with repetition formula can be found here:\nhttps://en.wikipedia.org/wiki/Combination#Number_of_combinations_with_repetition\nThe notation of H above corresponds to the double parentheses in the link. The transformation of H and C is also included in the wiki page.\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n return (n+4) * (n+3) * (n+2) * (n+1) / 24;\n }\n};\n``` | 15 | 12 | [] | 5 |
count-sorted-vowel-strings | Python with Explanation (Dynamic Programming) | python-with-explanation-dynamic-programm-ud0s | Explanation:\nn = 1 -> 2 -> 3-> 4 ...\n____\na =\t 1 -> 5 -> 15 -> 35 ...\ne =\t 1 -> 4 -> 10 -> 20 ...\ni =\t 1 -> 3 -> 6 -> 10 ...\no =\t | prithuls | NORMAL | 2022-05-11T01:34:30.195247+00:00 | 2022-07-30T17:21:40.148986+00:00 | 1,129 | false | Explanation:\nn = 1 -> 2 -> 3-> 4 ...\n____________________________\na =\t 1 -> 5 -> 15 -> 35 ...\ne =\t 1 -> 4 -> 10 -> 20 ...\ni =\t 1 -> 3 -> 6 -> 10 ...\no =\t 1 -> 2 -> 3 -> 4 ...\nu =\t 1 -> 1 -> 1 -> 1 ...\n____________________________\nsum = 5 -> 15 -> 35 -> 70 ... (that\'s the answer)\n\nCode:\n\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n ## if n == 1: return 5 ##Edited: Actually don\'t need it!\n arr = [1, 1, 1, 1, 1] ## initial \n for i in range(2, n+1): ## for different values of n\n for j in range(5): ## for 5 vowels\n arr[j] = sum(arr[j:])\n return sum(arr) ## return sum of the array\n```\n\nPlease upvote if you like the answer! Happy coding!!\n | 14 | 0 | ['Dynamic Programming', 'Python'] | 1 |
count-sorted-vowel-strings | Beginner friendly [Java/JavaScript/Python] Solution | beginner-friendly-javajavascriptpython-s-dr2z | Time Complexity : O(n)\nJava\n\nclass Solution {\n public int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n while(n-- > 1){\n | HimanshuBhoir | NORMAL | 2022-02-22T04:54:57.690902+00:00 | 2022-08-13T13:09:51.346691+00:00 | 903 | false | **Time Complexity : O(n)**\n**Java**\n```\nclass Solution {\n public int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n while(n-- > 1){\n a = a + e + i + o + u;\n e = e + i + o + u;\n i = i + o + u;\n o = o + u;\n u = u;\n }\n return a + e + i + o + u;\n }\n}\n```\n**JavaScript**\n```\nvar countVowelStrings = function(n) {\n let a=1, e=1, i=1, o=1, u=1\n while(n-- > 1){\n a = a + e + i + o + u\n e = e + i + o + u\n i = i + o + u\n o = o + u\n u = u\n }\n return a + e + i + o + u\n};\n```\n**Python**\n```\nclass Solution(object):\n def countVowelStrings(self, n):\n a,e,i,o,u = 1,1,1,1,1\n for x in range(n-1):\n a = a + e + i + o + u\n e = e + i + o + u\n i = i + o + u\n o = o + u\n u = u\n return a + e + i + o + u\n``` | 14 | 0 | ['Python', 'Java', 'JavaScript'] | 1 |
count-sorted-vowel-strings | Most Simple solution with O(1) time complexity and 4 line of code in C++ | most-simple-solution-with-o1-time-comple-1z7g | In my solution I used a basic concept of Permuation and combination that we studied in 11th class for JEE exam. It is about counting the number of ways we can d | charan_is_king | NORMAL | 2021-02-15T05:27:38.618872+00:00 | 2021-02-15T05:27:38.618922+00:00 | 338 | false | In my solution I used a basic concept of Permuation and combination that we studied in 11th class for JEE exam. It is about counting the number of ways we can distribute \'n\' identical balls in \'k\' identical boxes. \n\nx1 + x2 + x3 + .......+ xk = n\n\nand the formula for this comes out to be (n+k-1)C(k-1) \n\nSo imagine here that you need to give some chance X of chance to each vowel so that it can appear in the string X times. \n\nhence it is : Xa +Xe +Xi + Xo + Xu = n\n\nand for each case there will only be one arrangement of the accending order of the string.\n\nso in this question we need to calculate (n+4-1) C (5-1) \n\nthe following is the code that is required. (please support me by upvoting this solution \uD83D\uDE42)\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int ans =1;\n for (int i=n; i>n-4;i--){\n ans *= (i+4);\n }\n return ans/24;\n }\n};\n```\n | 13 | 0 | [] | 0 |
count-sorted-vowel-strings | One line, O(1) space/time, no DP/strings | one-line-o1-spacetime-no-dpstrings-by-an-ppx3 | Solution\n\ncsharp\npublic int CountVowelStrings(int n) =>\n (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24;\n\n\nExplanation\n\nThis is a pure math exercise wit | anikit | NORMAL | 2022-05-11T12:55:23.159408+00:00 | 2023-01-03T21:50:52.444645+00:00 | 396 | false | **Solution**\n\n```csharp\npublic int CountVowelStrings(int n) =>\n (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24;\n```\n\n**Explanation**\n\nThis is a pure math exercise with a single variable, so using DP or actually constructing strings is an overkill. Here is the formula to count [combinations with repetitions](https://math.stackexchange.com/questions/208377/combination-with-repetitions):\n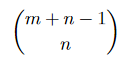\nwhere `m` is the number of distinct objects at our disposal and `n` is how many we can take.\n\nIn this case, we have 5 vowels to choose from, so `m = 5`. We proceed like this:\n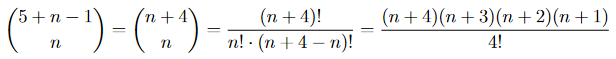\n\n | 12 | 0 | ['Math', 'Combinatorics', 'C#'] | 0 |
count-sorted-vowel-strings | C++ || 3 Approaches ||Recursion || DP || Combinations | c-3-approaches-recursion-dp-combinations-vpda | Approach 1 : Recursion\n\n\nclass Solution {\npublic:\n void dfs(int idx, int length, int n, int &count){\n ++length;\n \n if (length == | luvthakral247 | NORMAL | 2021-04-10T07:12:04.765738+00:00 | 2021-04-10T07:12:04.765768+00:00 | 1,211 | false | **Approach 1 : Recursion**\n\n```\nclass Solution {\npublic:\n void dfs(int idx, int length, int n, int &count){\n ++length;\n \n if (length == n){\n ++count;\n return;\n }\n \n for (int i = idx ; i < 5 ; i++){\n dfs(i,length,n,count);\n }\n }\n \n int countVowelStrings(int n) {\n int count = 0;\n for (int i = 0 ; i < 5 ; i++)\n dfs(i,0,n,count);\n return count;\n }\n};\n```\n\n**Approach 2 : Two Dimensional DP**\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int dp[n][5];\n \n // int dp[i][j] => Nummber of strings of length i+1 and ending at character j\n \n for (int i = 0 ; i < 5 ; i++)\n dp[0][i] = 1;\n \n for (int i = 1 ; i < n ; i++){\n dp[i][0] = dp[i-1][0];\n dp[i][1] = dp[i-1][1] + dp[i-1][0];\n dp[i][2] = dp[i-1][2] + dp[i-1][1] + dp[i-1][0];\n dp[i][3] = dp[i-1][3] + dp[i-1][2] + dp[i-1][1] + dp[i-1][0];\n dp[i][4] = dp[i-1][4] + dp[i-1][3] + dp[i-1][2] + dp[i-1][1] + dp[i-1][0];\n }\n \n int sum = 0;\n for (int i = 0 ; i < 5 ; i++)\n sum += dp[n-1][i];\n \n return sum;\n } \n};\n```\n\n**Approach 3: Combinations**\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n return (n+4)*(n+3)*(n+2)*(n+1)/24;\n } \n};\n``` | 12 | 0 | ['Dynamic Programming', 'Recursion', 'C', 'Combinatorics'] | 1 |
count-sorted-vowel-strings | Python 3 Dynamic Programming Explained | python-3-dynamic-programming-explained-b-odne | \nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n """\n Given a parameter n and assuming 5 vowels, this program\n uses d | hsweiner54 | NORMAL | 2021-01-17T17:57:40.863755+00:00 | 2021-01-18T19:56:35.115218+00:00 | 590 | false | ```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n """\n Given a parameter n and assuming 5 vowels, this program\n uses dynamic programming to determine the number of\n possible sorted vowel strings of length n.\n \n The theory behind the dynamic programming is based on:\n at length k, the number of times a vowel can be prefixed\n to a sorted vowel string of length k - 1. For example,\n to create the sorted vowel strings of length 2, we start\n with the sorted strings of length 1, which are:\n \n \'a\', \'e\', \'i\', \'o\', \'u\'\n \n To create the sorted strings of length 2, the vowels\n are prefixed to the strings of length 1 as follows:\n \n \'u\': \'uu\'\n \'o\': \'ou\', \'oo\'\n \'i\': \'iu\', \'io\', \'ii\'\n \'e\': \'eu\', \'eo\', \'ei\', \'ee\'\n \'a\': \'au\', \'ao\', \'ai\', \'ae\', \'aa\'\n \n The dynamic programming has a column for each vowel in\n reverse order and a row for each length starting with 1.\n The dp can be optimized by overwriting the same row for\n length k - 1 to create the dp for length k. For example,\n the dp for lengths 1 and 2 will look like:\n \n \'u\' \'o\' \'i\' \'e\' \'a\'\n 1 1 2 3 4 5\n 2 1 3 6 10 15\n\n :param n: length of vowel string\n :type n: int\n :return: number of possible sorted vowel strings of\n length n\n :rtype: int\n """\n dp = [1] * 5\n for k in range(n):\n for m in range(1, 5):\n dp[m] += dp[m - 1]\n return dp[-1]\n\n``` | 12 | 1 | ['Dynamic Programming', 'Python3'] | 0 |
count-sorted-vowel-strings | [C++] Super Easy Soln, with explaination. O(n) | O(1) | c-super-easy-soln-with-explaination-on-o-irkq | After working on this problem for quite some time, I figured out the following:\n1) The vowel \'a\' always has 5 children\n2) The vowel \'e\' always has 4 child | xxdil | NORMAL | 2020-12-03T18:24:21.730664+00:00 | 2021-01-18T08:14:40.633196+00:00 | 509 | false | After working on this problem for quite some time, I figured out the following:\n1) The vowel \'a\' always has 5 children\n2) The vowel \'e\' always has 4 children\n3) The vowel \'i\' always has 3 children\n4) and so on ...\n\n\n------\nSo if i was to draw a tree it would look like this:\n\n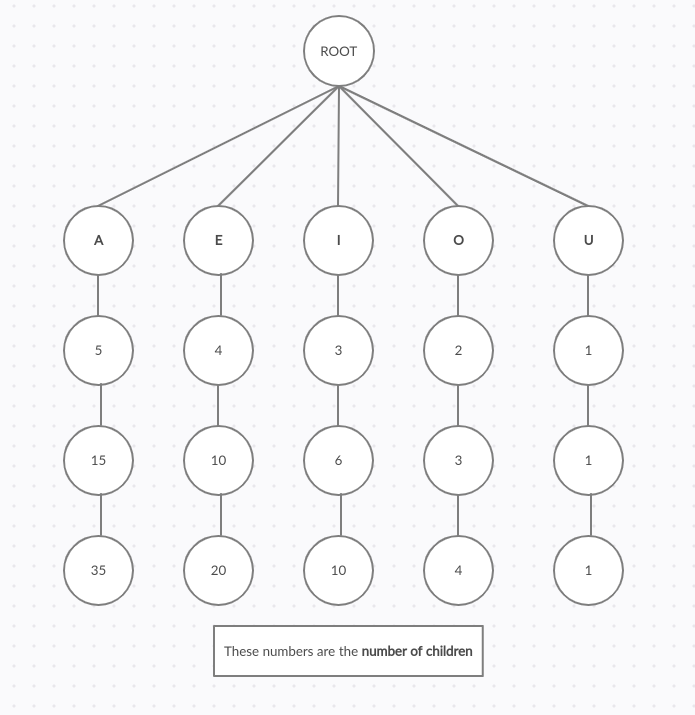\n\nIf you notice each layer of the tree, and analyse it we get the following arrays:\n\nDepth = 1 : [5, 4, 3, 2, 1]\nDepth = 2 : [15, 10, 6, 3, 1]\nDepth = 3 : [35, 20, 10, 4, 1]\nand so on..\n\n**At each depth the array is the presum array of the one before to it.**\n\n#### Presum function : \n```\nvoid presum(vector<int>& A)\n{\n\tfor(int i=1;i<5;++i)\n\t\tA[i] += A[i-1];\n}\n```\n\n------\n\nI will start with ``[1, 1, 1, 1, 1]``, say for layer 1.\n\n1) We run a loop from **1 to n-1**, to calculate the presum each time. \n2) Then simply find the sum of the array elements.\n\n#### Main function :\n\n```\nint countVowelStrings(int n)\n{\n\tvector<int> A(5, 1);\n\tfor(int i=1;i<n;++i)\n\t\tpresum(A);\n\n\tint sum = 0;\n\tfor(int i=0;i<5;++i)\n\t\tsum += A[i];\n\n\treturn sum;\n}\n```\n\n------\n### Full Code:\n```\nclass Solution {\npublic:\n void presum(vector<int>& A)\n {\n for(int i=1;i<5;++i)\n A[i] += A[i-1];\n }\n \n int countVowelStrings(int n)\n {\n vector<int> A(5, 1);\n for(int i=1;i<n;++i)\n presum(A);\n \n int sum = 0;\n for(int i=0;i<5;++i)\n sum += A[i];\n \n return sum;\n }\n};\n```\n\n*I realize that the code could be optimised a lot, but the point of this is to give a solution that makes sense to most people.* | 12 | 0 | [] | 1 |
count-sorted-vowel-strings | [Java] Solution + Intuition behind every possible DP solution here of this problem! | java-solution-intuition-behind-every-pos-wvvi | Let\'s take a generic example where we need to make n character long sorted stings :-\n[When I am telling first or second char then it is counted from right]\n\ | a_lone_wolf | NORMAL | 2020-11-02T20:50:15.237023+00:00 | 2020-11-03T15:33:41.309085+00:00 | 999 | false | Let\'s take a generic example where we need to make n character long sorted stings :-\n*[When I am telling first or second char then it is counted from right]*\n\nNow the possible strings possible for **n = 1** is :- a, e, i, o, u\n\nNow for **n = 2**, \nif the first character from end was \'a\' then the second char must be \'a\' only, right. [1 string possible]\nSimilarly, if the first character from end was \'e\' then the second char can be \'a\' and \'e\'. \n[2 strings possible]\nSimilarly, if the first character from end was \'i\' then the second char can be \'a\', \'e\' and \'i\'.\n[3 strings possible]\nSimilarly, if the first character from end was \'o\' then the second char can be \'a\', \'e\', \'i\' and \'o\'.\n[4 strings possible]\nSimilarly, if the first character from end was \'u\' then the second char can be \'a\', \'e\', \'i\', \'o\' and \'u\'.\n[5 strings possible]\n\n[At next Index from right i.e. At 2nd index]\n**a->** can be produced by all strings (As we have total 5 strings, Therefore 5)\n**e->** can be produced by all strings except which ends with \'a\'\n**i->** can be produced by all strings except which ends with \'a\', \'e\'\n**o->** can be produced by all strings except which ends with \'a\', \'e\', \'i\'\n**u->** can be produced by all strings except which ends with \'a\', \'e\', \'i\', \'o\'\n**5 + 4 + 3 + 2 + 1 = 15**\n\nNow for **n = 3**, \nif the second character from end was \'a\' then the third char must be \'a\' only, right. \nNow the possible string with \'a\' at second index when n was 2 is **5** [1*5 string possible]\nAgain take a took at n = 2, when total possible strings have \'a\' five times at index = 2. \n\nSimilary, \'e\' occurs 4 times when n was 2 and \'e\' for prev index will result into 2 possible chars \'a\' and \'e\' at current index, so [2*4 strings possible] \n\nSimilarly for other characters at second index we will have sum:-\n**(15) + (15-5) + (15-5-4) + (15-5-4-3) + (15-5-4-3-2) = 35**\n\nNow in similar fashion you can count possible strings of any length, Right.\nExample: for **n = 4** ->\n**(35) + (35-15) + (35-15-10) + (35-15-10-6) + (35-15-10-6-3) = 70**\n\n```\nclass Solution {\n public int countVowelStrings(int n) {\n int[] dp = new int[5]; // It will store count of each char [a, e, i, o, u]\n Arrays.fill(dp, 1);\n \n for(int i = 1; i < n; i++){\n int sum = 0;\n for(int j = 0; j < 5; j++){\n sum += dp[j];\n }\n \n int prev = 0;\n for(int idx = 0; idx < 5; idx++){\n int temp = dp[idx];\n sum -= prev;\n dp[idx] = sum;\n prev = temp;\n }\n }\n \n return dp[0] + dp[1] + dp[2] + dp[3] + dp[4];\n }\n}\n```\n\nIf it helps you then, Please upvote :)\nSuggestions are most welcome. :D | 12 | 0 | [] | 1 |
count-sorted-vowel-strings | Python Best Solution | python-best-solution-by-prajapati21-3tmz | \n# Code\n\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n mul=1\n j=1\n for i in range(5,5+n):\n mul=(mul*i | prajapati21 | NORMAL | 2023-11-19T05:30:43.172754+00:00 | 2023-11-19T05:30:43.172787+00:00 | 592 | false | \n# Code\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n mul=1\n j=1\n for i in range(5,5+n):\n mul=(mul*i)//j\n j+=1\n return mul\n \n``` | 11 | 0 | ['Python3'] | 1 |
count-sorted-vowel-strings | ✅C++ || EASY DP Solution 🚀 | c-easy-dp-solution-by-chiikuu-mzxu | Code\n\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<vector<int>>dp(n+1,vector<int>(5+1,0));\n for(int i=1;i<=5;i++)dp[1 | CHIIKUU | NORMAL | 2023-03-22T07:35:51.687183+00:00 | 2023-03-22T07:37:31.216748+00:00 | 1,075 | false | # Code\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<vector<int>>dp(n+1,vector<int>(5+1,0));\n for(int i=1;i<=5;i++)dp[1][i]=i;\n for(int i=2;i<=n;i++){\n for(int j=1;j<=5;j++){\n dp[i][j]= dp[i-1][j] + dp[i][j-1];\n }\n }\n return dp[n][5];\n }\n};\n```\n\n | 11 | 0 | ['Dynamic Programming', 'C++'] | 1 |
count-sorted-vowel-strings | ✅ 5 C++ Solutions || 1 Backtracking,1 Recursion(TLE), 1 DP and 2 other Approach || Easy | 5-c-solutions-1-backtracking1-recursiont-h7px | As you scroll down, there is a optimized solution given than the previous one.\n\n ##### Approach-1: Recursion (Shows TLE for n>40 and works for n<=40)\n\nHere | shivam-214 | NORMAL | 2022-05-11T09:28:15.391521+00:00 | 2022-05-11T09:28:15.391558+00:00 | 900 | false | ### **As you scroll down, there is a optimized solution given than the previous one.**\n\n* ##### **Approach-1**: **Recursion** *(Shows **TLE for n>40 and works for n<=40**)*\n\nHere, every next call for a decreased value of n gives us the required result and then we will add vowels at the start of result we get to get the strings of desired length. ( **i.e for n=2**, solver(n-1) or here, **solver(1) gives us the sorted vowels strings of length=1** and then we will **add up vowels again at the start of the sorted vowels strings we get, (maintaining the lexicographically sorted order) to get the sorted vowels strings of length=2**) \n\n***-->CODE:***\n```\nclass Solution\n{\nprivate:\n vector<char> vowels = {\'a\', \'e\', \'i\', \'o\', \'u\'};\npublic:\n vector<string> solver(int n)\n {\n if (n == 0)\n return {""};\n \n vector<string> asf = solver(n - 1);\n vector<string> ans;\n\n for (string i : asf)\n {\n for (char j : vowels)\n {\n\t\t\t \t//check that the character you want to insert \n\t\t\t\t//is smaller than the first character of asf(answer so far) string \n\t\t\t\t//to maintain lexicographically sorted order\n if (j <= i[0] || asf.size() == 1)\n ans.push_back(j + i);\n else\n break;\n }\n }\n return ans;\n }\n int countVowelStrings(int n)\n {\n vector<string> ans = solver(n);\n return ans.size();\n }\n};\n```\n\n* ##### **Approach-2**: **Backtrack** *(**Gets submitted**)*\n\n***-->CODE:***\n```\n void solver(vector<vector<char>> &ans, vector<char> &temp, vector<char> &vowels, int start, int n)\n {\n if (temp.size() == n)\n { ans.push_back(temp);\n return;\n }\n \n for (int i = start; i < vowels.size(); i++)\n {\n temp.push_back(vowels[i]);\n solver(ans, temp, vowels, i, n);\n temp.pop_back();\n }\n return;\n }\n\n int countVowelStrings(int n)\n { vector<char> vowels = {\'a\', \'e\', \'i\', \'o\', \'u\'};\n vector<char> temp;\n vector<vector<char>> ans;\n solver(ans, temp, vowels, 0, n);\n return ans.size();\n }\n```\n\n* ##### **Approach-3**: Dynamic Programming(**DP**), **Time:O(n), Space:O(n)**\n-Here, you can observe: \n```\nn=1, dp = {1,2,3,4,5} return 5\nn=2, dp = {1,3,6,10,15} return 15\nn=3, dp = {1,4,10,20,35} return 35\n```\n\n***-->CODE:***\n```\n int countVowelStrings(int n) {\n vector<int> dp(5, 1);\n for(int i=0; i<n; i++){\n for(int j=1; j<5; j++){\n dp[j] += dp[j-1];\n }\n }\n return dp[4];\n }\n```\n\n* ##### **Approach-4:** **Time:O(n), Space:O(1)**\n\n-Here, you can observe a pattern : \n```\n\t\t a e i o u\n -> n=1 1 1 1 1 1 \n -> n=2 5 4 3 2 1 \n -> n=3 15 10 6 3 1\n```\n\t\nIf we observe every other element will have the count of previous count value + next element count for the same n. As example\nn=2, a(in n=1) + count of next element, i.e e(in n=2) =5\nn=3, e(in n=2) + count of next element, i.e i(in n=3) =10\n\n***-->CODE:***\n ```\n int countVowelStrings(int n)\n {\n int a, e, i, o, u;\n a = e = i = o = u = 1;\n while (--n)\n {\n o += u;\n i += o;\n e += i;\n a += e;\n }\n return a + e + i + o + u;\n }\n```\n\n* ##### **Approach-5:** **Time:O(1), Space:O(1)**\n**Visit for detailed explanation**: [https://leetcode.com/problems/count-sorted-vowel-strings/discuss/1021493/One-line-solution-or-Math-or-No-DP-no-Big-Integers-or-O(1)-time-space](http://) \n\n***-->CODE:***\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n return (n+4)*(n+3)*(n+2)*(n+1) / 24;\n }\n};\n```\n | 11 | 0 | ['Math', 'Dynamic Programming', 'Backtracking', 'Recursion', 'C', 'Combinatorics'] | 3 |
count-sorted-vowel-strings | DP Solution [ Tabulation ] ✔ | dp-solution-tabulation-by-shivamishra21-kv6u | The solution has dynamic programming approach.\nWe have 5 vowels : [a,e,i,o,u]\nIf n = 1:\n\t\tsolution will have {a,e,i,o,u} as possible valid string\nIf n == | Shivamishra21 | NORMAL | 2022-02-19T17:28:40.994057+00:00 | 2022-02-19T17:28:40.994102+00:00 | 323 | false | The solution has **dynamic programming approach**.\nWe have 5 vowels : [a,e,i,o,u]\n*If n = 1:*\n\t\tsolution will have {a,e,i,o,u} as possible valid string\n*If n == 2*:\nsolution string will have ["aa","ae","ai","ao","au","ee","ei","eo","eu","ii","io","iu","oo","ou","uu"]\nthis can be explained as:\nfor a we can add :\naa, ae, ai, ao, au\nfor e:\nee, ei,eo, eu (we can\'t have \'ea\')\nsimilary for i, o , u\nNow I\'ve tried to show the patter with the help of below table.\n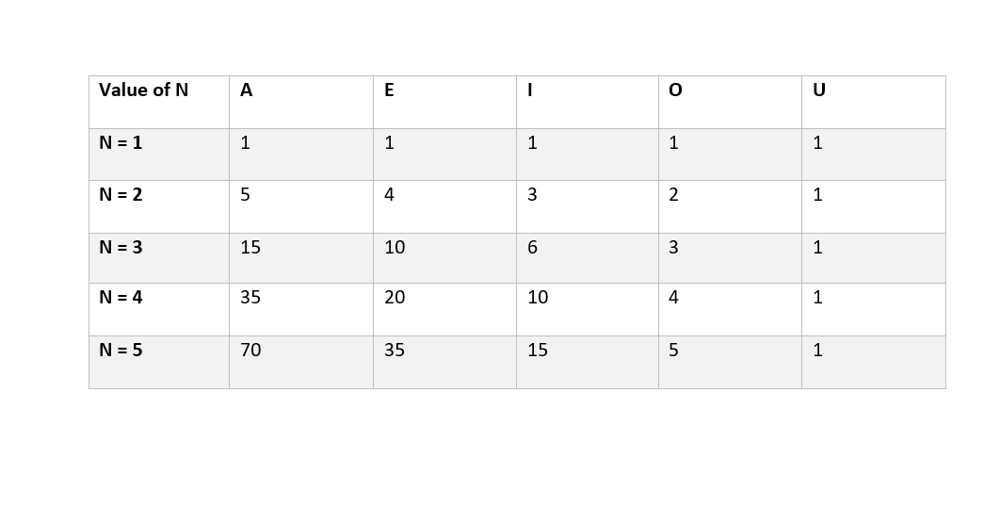\nfrom the table we can see then \ntable[i][j] = table[i][j+1]+table[i-1][j]\nNow, this will be the approach to move toward solution.\n\nComplete Solution:\n\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n if n == 1:\n return 5\n\t\t#initialised the table with 1\n dp = [[1]*5 for i in range(n+1)]\n\t\t\n for i in range(1,n+1):\n for j in range(3,-1,-1):\n dp[i][j] = dp[i][j+1]+dp[i-1][j]\n \n return dp[n][0]\n \n \n\n \n \n \n \n \n \n \n \n \n```\n\n\n | 11 | 0 | ['Dynamic Programming'] | 0 |
count-sorted-vowel-strings | C++| DP-Beats100% - 0ms Solution | PrefixSum | c-dp-beats100-0ms-solution-prefixsum-by-ex3jq | IDEA:- \nInitialise dp of size 5(u,o,i,e,a) with value 1.\n\nLogic:\nFor n = 1\nStrings possible "a","e","i","o","u".\n\nNow in case of n = 2 (i.e string length | garvitsharma05 | NORMAL | 2021-05-16T22:37:32.692364+00:00 | 2021-05-16T22:37:32.692402+00:00 | 509 | false | IDEA:- \nInitialise dp of size 5(u,o,i,e,a) with value 1.\n```\nLogic:\nFor n = 1\nStrings possible "a","e","i","o","u".\n\nNow in case of n = 2 (i.e string length == 2);\nFor "a" we have 5 choices to make it in sorted order i.e "a","e","i","o","u".\nFor "e", similarly we have 4 choices "e","i","o","u".\nSimilarly for "i" 3 choices, "o" 2 choices, "u" 1 choice.\nAdding up to 15 // that is where prefix sum logic comes from.\n\nFor n==3,\nfor "a", we have all 15 choices i.e including all previous choices of n=2;\nfor "e", we have total choices from "e"."i","o","u" = 10 (which is 15 - choice of "a" in n=2)\nSimilarly for all cases :)\n```\nInitially\n```\nu o i e a\n1 1 1 1 1\n```\nNow for n = 1\n```\nu o i e a\n1 2 3 4 5\nReturn dp[lastIndex];\n```\nNow for n = 2;\n```\nu o i e a\n1 3 6 10 15\nreturn dp[lastIndex];\n```\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> dp(5,1);\n for(int i = 0; i < n; i++){\n for(int j = 1; j <5; j++){\n dp[j] += dp[j-1];\n }\n }\n return dp[4];\n }\n};\n``` | 11 | 0 | ['Dynamic Programming', 'C', 'Prefix Sum'] | 4 |
count-sorted-vowel-strings | "Python" easy explanation blackboard | python-easy-explanation-blackboard-by-ha-g32y | The code is well explained in the image below\n Simple and easy python3 solution*\n\n\n\n\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n | harish_sahu | NORMAL | 2021-01-17T14:13:22.247633+00:00 | 2021-01-17T14:14:54.144808+00:00 | 1,114 | false | * **The code is well explained in the image below**\n* **Simple and easy python3 solution**\n\n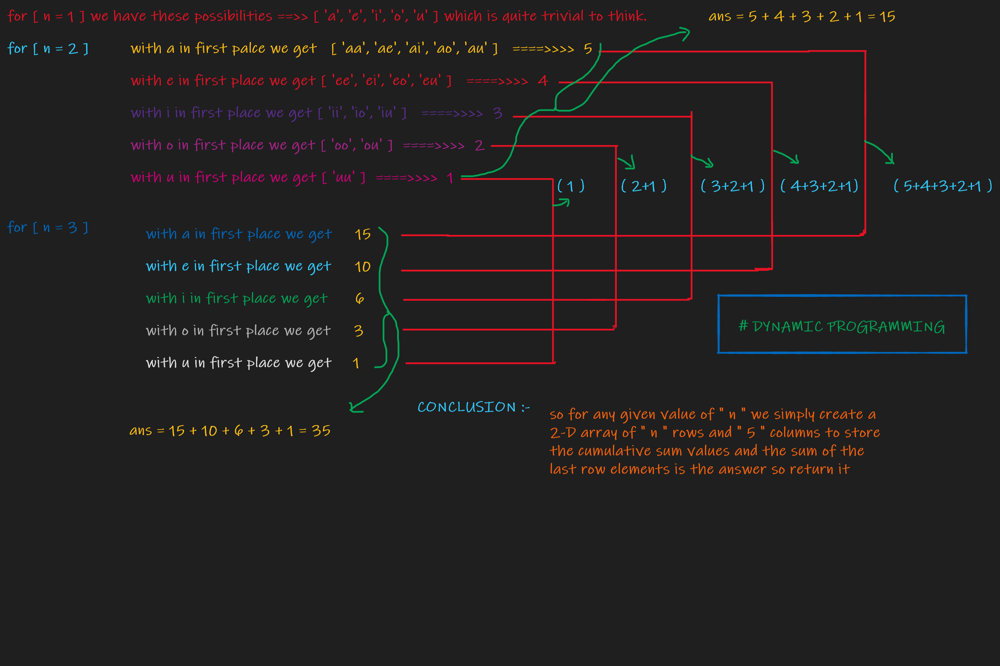\n\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n dp = [[0 for j in range(5)] for i in range(n)]\n for i in range(5):\n dp[0][i] = 1\n for i in range(n):\n dp[i][0] = 1\n for i in range(1, n):\n for j in range(5):\n dp[i][j] = dp[i][j - 1] + dp[i - 1][j]\n return sum(dp[n - 1])\n```\n | 11 | 0 | ['Dynamic Programming', 'Python', 'Python3'] | 3 |
count-sorted-vowel-strings | [JavaScript] Backtracking | javascript-backtracking-by-sma8282-uihg | This is basically the same as the other "generate permutations" problems with an extra constraint. (By the way, I quite literally learned 99% of my backtracking | sma8282 | NORMAL | 2020-11-01T11:23:39.068474+00:00 | 2020-12-04T14:21:19.535088+00:00 | 913 | false | This is basically the same as the other "generate permutations" problems with an extra constraint. (By the way, I quite literally learned 99% of my backtracking and "generate permutations" techniques from watching this video series: https://www.youtube.com/watch?v=RkXl5iYoQn4&ab_channel=happygirlzt)\n\nSo anyways, what would be the base case? I knew that we\'d be decrementing N, and that the base case is if the remaining N becomes 0.\n\nIt also occurred to me that we should keep track of what the start index is, so that we don\'t put an "e" before an "a."\n`a -> e -> i -> o -> u`\n\nHere is the first version of code that I wrote. In this case, I modelled it after the other permutation problems and actually generated all the different permutations.\n```js\nvar countVowelStrings = function(n) { \n const res = []\n const curr = []\n helper(res, curr, n, [\'a\',\'e\',\'i\',\'o\',\'u\'], 0)\n\n return res.length\n};\n\nfunction helper(res, curr, n, arr, startIdx) { \n // base case\n if (n === 0) {\n res.push([...curr]) // here I am creating a new copy of `curr` and adding it into `res`\n return\n }\n\n // recursive case\n for (let i = startIdx; i < arr.length; i++) {\n // choose \n curr.push(arr[i])\n helper(res, curr, n - 1, arr, i) // Here, it\'s important to pass in "i" as the new "startIdx," so that we make sure "e" does not go before "a," etc.\n \n // unchoose\n curr.pop()\n }\n}\n```\n\nThe above code is needlessly memory-intensive. And that is because the question doesn\'t actually require us to generate the actual permutations. So here is the code that I wrote, after removing all the part about actually generating the permutations.\n\n```js\nvar countVowelStrings = function(n) { \n let res = 0\n \n helper(n, 0)\n\n function helper(n, startIdx) { \n // base case\n if (n === 0) {\n res++\n return\n }\n\n // recursive case\n for (let i = startIdx; i < 5; i++) {\n helper(n - 1, i)\n }\n }\n\n return res\n};\n```\n\nI found the runtime complexity to be tricky to figure out, but I know for sure that it won\'t be over O(5^N) (O(branches^levels)). Space is O(N) because of the stack frames we are generating via recursion. | 11 | 0 | ['JavaScript'] | 1 |
count-sorted-vowel-strings | ✅Multiple C++ Solutions 🚀 | multiple-c-solutions-by-chiikuu-b942 | Code\n\n//Solution #1:\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n while(--n){\n o | CHIIKUU | NORMAL | 2023-03-22T07:45:37.957567+00:00 | 2023-03-22T07:45:37.957594+00:00 | 795 | false | # Code\n```\n//Solution #1:\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n int a=1, e=1, i=1, o=1, u=1;\n while(--n){\n o += u;\n i += o;\n e += i;\n a += e;\n }\n return a+e+i+o+u;\n }\n};\n\n//Solution #2\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<vector<int>>dp(n+1,vector<int>(5+1,0));\n for(int i=1;i<=5;i++)dp[1][i]=i;\n for(int i=2;i<=n;i++){\n for(int j=1;j<=5;j++){\n dp[i][j]= dp[i-1][j] + dp[i][j-1];\n }\n }\n return dp[n][5];\n }\n};\n\n//Solution #3\nclass Solution {\npublic:\n int t(vector<vector<int>>&dp,int n,int i){\n if(i==0){\n dp[n][i]=0;\n return dp[n][i];\n }\n if(n==1){\n dp[n][i]=i;\n return dp[n][i];\n }\n if(dp[n][i]!=-1)return dp[n][i];\n dp[n][i] = t(dp,n-1,i) + t(dp,n,i-1);\n return dp[n][i];\n }\n int countVowelStrings(int n) {\n vector<vector<int>>dp(n+1,vector<int>(5+1,-1));\n t(dp,n,5);\n return dp[n][5];\n }\n};\n```\n\n | 9 | 0 | ['C++'] | 0 |
count-sorted-vowel-strings | Java solution explanation with photos beats %100 of submissions | java-solution-explanation-with-photos-be-09ki | \nclass Solution {\n public int countVowelStrings(int n) {\n int[] arr = new int[5];\n for (int i = 0; i<5; i++)\n arr[i] = 1;\n | CS_OFM | NORMAL | 2021-01-17T16:12:50.576442+00:00 | 2021-01-17T16:12:50.576469+00:00 | 357 | false | ```\nclass Solution {\n public int countVowelStrings(int n) {\n int[] arr = new int[5];\n for (int i = 0; i<5; i++)\n arr[i] = 1;\n for (int k = 0; k<n; k++)\n for (int j = 1; j<5;j++)\n arr[j] = arr[j-1] + arr[j];\n return arr[4]; \n }\n}\n```\nI hope you understood. \n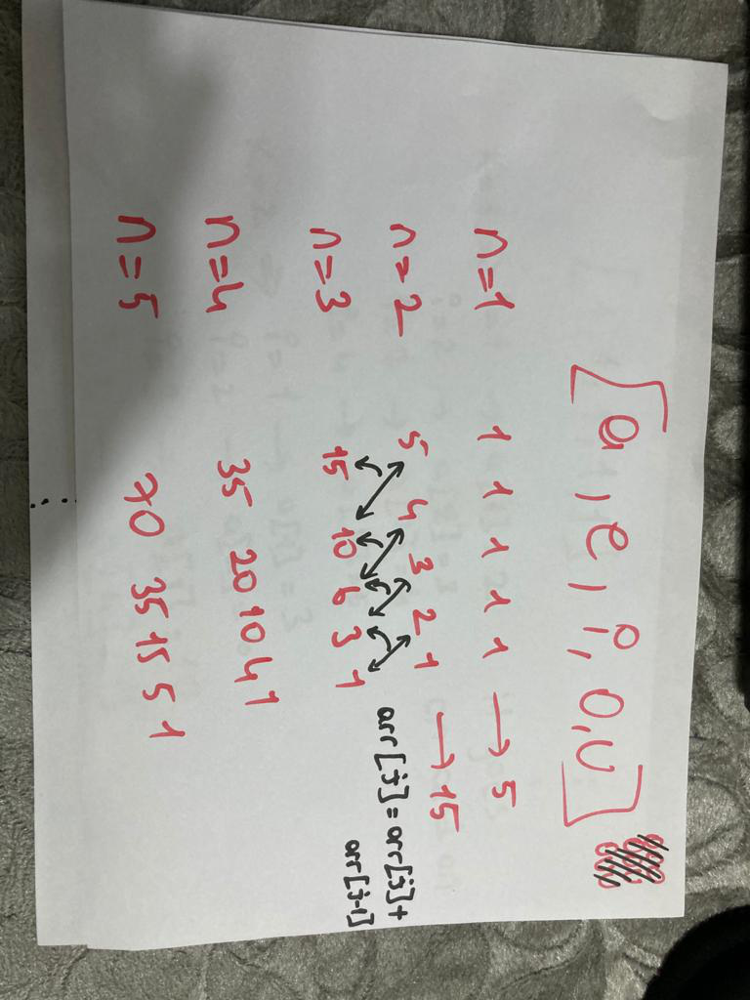\n\nFeel free to ask anything about the solution!\n\n | 9 | 0 | ['Java'] | 1 |
count-sorted-vowel-strings | C++ with comments. O(N) time O(1) space. Beats 100%. | c-with-comments-on-time-o1-space-beats-1-tbhn | The idea is to count the strings ending on a particular vowel. Here are how these counts go:\n\n\n a e i o u\n\t1 1 1 | 28gevu | NORMAL | 2020-12-17T02:06:00.053402+00:00 | 2020-12-17T02:20:29.857686+00:00 | 378 | false | The idea is to count the strings ending on a particular vowel. Here are how these counts go:\n\n```\n a e i o u\n\t1 1 1 1 1\n\t1 2 3 4 5\n\t1 3 6 10 15\n```\n\nYou get the idea: at each iteration there is a single string ending on \'a\', the one with \'a\' only. Starting with index 1, the number of strings ending with this letter is the sum off the previous line up to and including the index. We only need to keep the last row, and accumulate all the counts. This is constant space.\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n if(n == 0) return 0;\n \n // Number of strings of length 1 ending on: a, e, i, o, u\n array<int, 5> counts = { 1, 1, 1, 1, 1 };\n \n for(int i = 1; i < n; ++i) {\n // Only one string ending on \'a\' on each iteration. Start with 1.`\n for(int j = 1; j < 5; ++j) {\n counts[j] += counts[j-1];\n }\n }\n \n return accumulate(counts.begin(), counts.end(), 0);\n }\n};\n``` | 9 | 1 | [] | 1 |
count-sorted-vowel-strings | 0ms||100%||C++ Solution||O(1) Time Complexity | 0ms100c-solutiono1-time-complexity-by-ay-tv7m | \nclass Solution {\npublic:\n int countVowelStrings(int n) {\n return (n+1)*(n+2)*(n+3)*(n+4)/24;\n }\n};\n\n\n\nplease upvote!!! | Ayush_Modi43 | NORMAL | 2022-05-11T12:06:33.688551+00:00 | 2022-05-11T12:29:41.040289+00:00 | 390 | false | ```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n return (n+1)*(n+2)*(n+3)*(n+4)/24;\n }\n};\n```\n\n\nplease upvote!!! | 8 | 1 | [] | 1 |
count-sorted-vowel-strings | My Java Solutions 1) DP 2) Math formula | my-java-solutions-1-dp-2-math-formula-by-laqd | \n\nclass Solution {\n public int countVowelStrings(int n) {\n // create a dp array of size 6\n int [] dp = new int [6];\n // dp[0] must | vrohith | NORMAL | 2020-11-02T09:23:52.673008+00:00 | 2020-11-02T09:23:52.673053+00:00 | 751 | false | ```\n\nclass Solution {\n public int countVowelStrings(int n) {\n // create a dp array of size 6\n int [] dp = new int [6];\n // dp[0] must be 0 and the rest 1\n for (int i=1; i<dp.length; i++)\n dp[i] = 1;\n for (int i=1; i<=n; i++) {\n for (int k=1; k<=5; k++) {\n dp[k] += dp[k-1];\n }\n }\n return dp[5];\n }\n}\n\n\nclass Solution {\n public int countVowelStrings(int n) {\n // from discussions I found the answr is simply (n+4)C(4)\n return ((n+1) * (n+2) * (n+3) * (n+4)) / 24;\n }\n}\n``` | 8 | 0 | ['Math', 'Dynamic Programming', 'Java'] | 1 |
count-sorted-vowel-strings | C++| Intuitive Solution | DP and Memoization | c-intuitive-solution-dp-and-memoization-ib0r4 | Logic :\nThis problem is based on simple pick and non-pick concept. At every index we have a choice either to pick a vowel or skip it. So, here we get the idea | gojosaturo512 | NORMAL | 2022-07-13T19:23:54.072839+00:00 | 2022-07-14T14:52:35.567395+00:00 | 403 | false | **Logic :**\nThis problem is based on simple pick and non-pick concept. At every index we have a choice either to pick a vowel or skip it. So, here we get the idea of recursion, but while doing so we encounter overlapping problems and hence we go for the memoization part.\n\n```\nclass Solution {\npublic:\n int solve(int i,int sz,vector<vector<int>> &dp)\n {\n if(i<0)\n return 0;\n if(sz==0)\n {\n return 1;\n }\n \n if(dp[i][sz]!=-1)\n return dp[i][sz];\n \n int l = solve(i,sz-1,dp);\n \n int r = solve(i-1,sz,dp);\n \n return dp[i][sz] = l + r;\n }\n int countVowelStrings(int n) {\n \n vector<vector<int>> dp(5,vector<int> (n+1,-1));\n return solve(4,n,dp);\n }\n};\n```\n\nIf this solution helps you then, **Please Upvote!!** | 7 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
count-sorted-vowel-strings | DP Solution with Explanation | dp-solution-with-explanation-by-sai_pras-jw60 | It is an awesome problem. Lets deep dive in it.\n\nSo, they are asking the number of ways in which we can generate lexographically sorted strings of length n, | sai_prashant | NORMAL | 2022-05-11T15:26:18.804472+00:00 | 2022-05-11T15:32:48.025037+00:00 | 530 | false | It is an awesome problem. Lets deep dive in it.\n\nSo, they are asking the number of ways in which we can generate lexographically sorted strings of length n, which only contains vowels.\n\nNow lets think about it.\nSuppose if `n=1` then the possible strings would be ```"a","e","i","o","u"```.\n\n\nNow lets make an approach.\n\nLets create a 2-D array of size 5 * n and for our example lets take ```n=3```\nSo here is our array.\n\n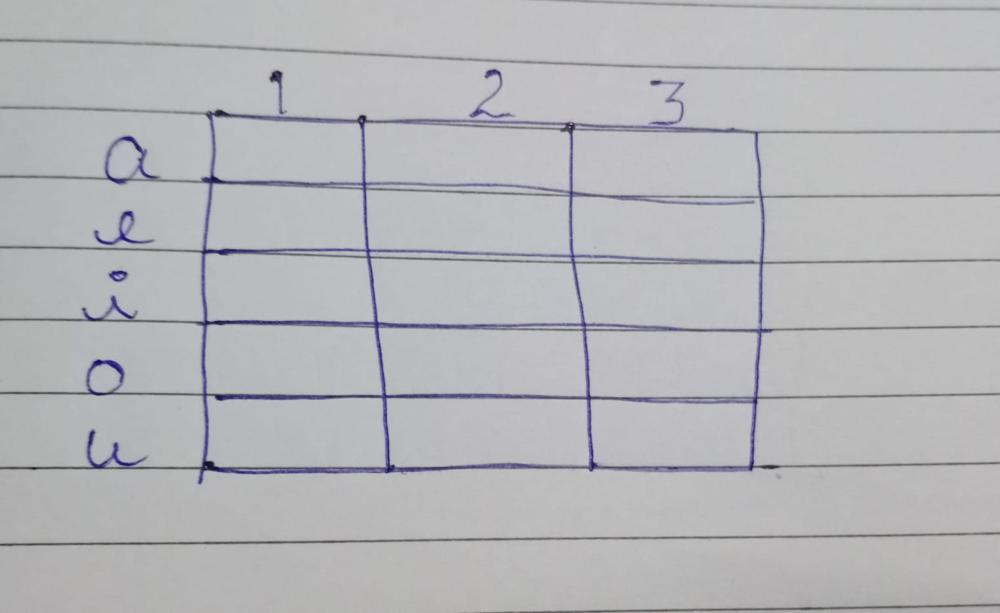\n\nHere we will store the number of strings we that will end on respective vowel for the given n.\nNow for n=1, all the values will be 1.\n\nLets fill it for n=2.\nFor string to be ending on ```a``` we have only one way i.e all the characters will be ```\'a\'```.\n\nFor string to be ending on ```b``` we have two options that either append ```\'b\'``` on string which previously ended on ```a``` or append ```\'b\'``` to the string which previously ended on ```b```.\n\nFor string to be ending on ```c``` we have three options that we append ```\'c\'``` on string ending with ```a``` or ```b``` or append ```\'c\'``` to the string which previously ended on ```c```.\n\nIt hope you got the idea :)\n\nNow lets fill our array.\n\n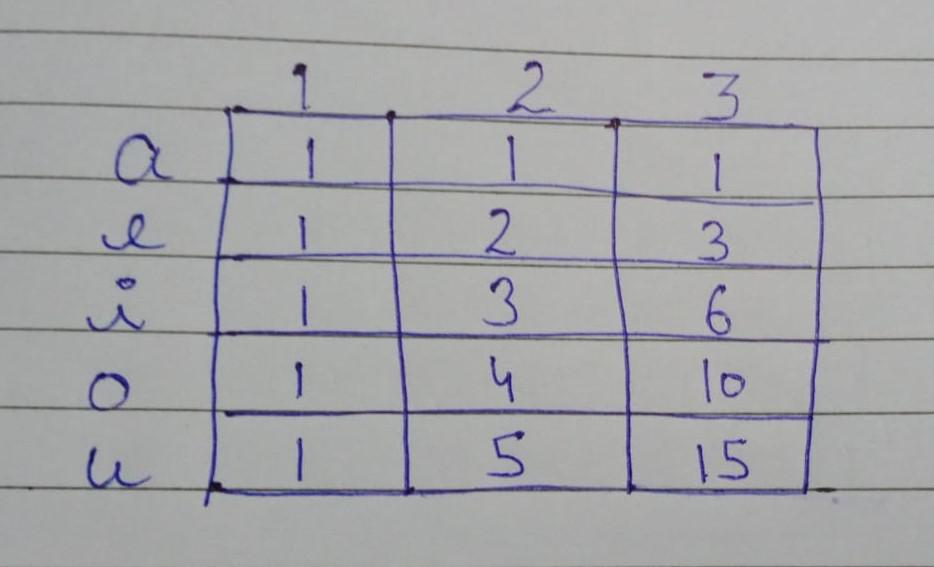\n\nAt last the sum of last column will be our answer.\n\nAwesome we solved it !!!\n\nBut can we do better? Can we do it in O(1) space?\n\nIf you look closely we are only using the previous values of the column. So there is no need to use this array we will replace it by 5 variables which will be storing the content of column values.\n\nHere is my code :\n\n```\nclass Solution {\n public int countVowelStrings(int n) {\n int a=1,e=1,i=1,o=1,u=1;\n for(int index=1;index<n;index++){\n int aNew=a,eNew=a+e,iNew=a+e+i,oNew=a+e+i+o,uNew=a+e+i+o+u;\n a=aNew;\n e=eNew;\n i=iNew;\n o=oNew;\n u=uNew;\n }\n return a+e+i+o+u;\n }\n}\n```\n\nHope u understood the solution.\n\n \n | 7 | 0 | ['Java'] | 1 |
count-sorted-vowel-strings | [C++] O(1), 1 Line Code | SIMPLEST SOLUTION | c-o1-1-line-code-simplest-solution-by-an-myji | \nclass Solution {\npublic:\n int countVowelStrings(int n) {\n \n return ((n+4)*(n+3)*(n+2)*(n+1))/24;\n \n }\n};\n\n\nExplanation :\ | anveshreddy18 | NORMAL | 2022-05-11T06:04:36.623569+00:00 | 2022-05-11T06:04:36.623593+00:00 | 145 | false | ```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n \n return ((n+4)*(n+3)*(n+2)*(n+1))/24;\n \n }\n};\n```\n\n**Explanation :**\n\nThink of the problem in this way. We have 5 objects and n slots to fill with these 5 objects (a,e,i,o,u). Objects can be repeated. Since we want only lexicographically smallest solution, we consider each combination as one solution only. \n\nSo, say p number of "a", q number of "e", r number of "i", s number of "o", t number of "u" we want to fill. Then it must happen that p+q+r+s+t = n\n\nAssume we have n stars, we want to split them into 5 segments, so for that we want to place 4 bars in between the stars.\nFor eg: n=12\nOne possible combination of bars and stars could be |***|***|***|***\nNow this is just one such combination where p=0, q=3, r=3, s=3, t=3.\nBut with these n stars and 4 bars, we can in total form (n+4)! permutations... out of which there are (n+4)!/(n!\\*4!) unique combinations.\n\nSo the answer is just (n+4)!/(n!\\*4!) = ((n+4)\\*(n+3)\\*(n+2)\\*(n+1))/24.\n\nPlease upvote if you found this helpful :)\n\n | 7 | 0 | ['Math', 'Probability and Statistics'] | 2 |
count-sorted-vowel-strings | [C++] Recursive Vs. Math Solutions Compared and Explained, 100% Time, 100% Space | c-recursive-vs-math-solutions-compared-a-ymbl | The core intuition here, came to me by just looking at the second example with n == 2.\n\ncpp\n"aa", "ae", "ai", "ao", "au", // all the combinations of {\'a\', | ajna | NORMAL | 2021-01-17T12:56:54.695810+00:00 | 2021-01-17T12:56:54.695839+00:00 | 521 | false | The core intuition here, came to me by just looking at the second example with `n == 2`.\n\n```cpp\n"aa", "ae", "ai", "ao", "au", // all the combinations of {\'a\', \'e\', \'i\', \'o\', \'u\'} from the level before with \'a\' prepended\n"ee", "ei", "eo", "eu", // all the combinations of {\'e\', \'i\', \'o\', \'u\'} from the level before with \'e\' prepended\n"ii", "io", "iu", // all the combinations of {\'i\', \'o\', \'u\'} from the level before with \'i\' prepended\n"oo", "ou", // all the combinations of {\'o\', \'u\'} from the level before with \'o\' prepended\n"uu" // all the combinations of {\'u\'} from the level before with \'u\' prepended\n```\n\nIf you consider `n == 3`, it is easier to think that you will get all the elements starting with `\'a\'` by just prepending that character in front of our previous results and so on.\n\nMore in general we will have `5` times all the combinations you can get with `5` elements for `n - 1`, plus `4` times all the combinations you can get with `4` elements and `n -1` and so on.\n\nWhen `n == 1` we can just return `k` (there are only `k` possible permutations of size `1` when you have `k` elements) and that is our base case; we also need to terminate the recursive calls when `k < 1`, since there are no possible combinations and we can add this as another base case, returning `0`.\n\nFinally, we can compose the general case as explained in 2 paragraphs above, as the result of calling `countVowelStrings` `5` times, decreasing `n` by `1` and further reducing `k` at each successive call.\n\nI know I could have used a loop, but I am a sucker for one-liner, so here it is!\n\nThe code, which scores about 5%, time, but almost 100% memory despite all the recursive call stack:\n\n```cpp\nclass Solution {\npublic:\n int countVowelStrings(int n, int k = 5) {\n return k < 1 ? 0 : n == 1 ? k : (countVowelStrings(--n, k--) + countVowelStrings(n, k--) + countVowelStrings(n, k--) + countVowelStrings(n, k--) + countVowelStrings(n, k--));\n }\n};\n```\n\nAnd this is if you could not figure out/remember the math in 30 mins (as I failed to d), otherwise you will just have to bow to the awesomely simplicity of combinatorics and compute the product of all the numbers in the `(n + 1) - (n+ 4)` range and divide it by the `4!`.\n\nIf you want to look a bit deeper at it, just consider that after picking `4` elements in our range, we only have one left and thus our solution can be computed at `n + 4` choose `4` - [formula and explanation](https://en.wikipedia.org/wiki/Binomial_coefficient).\n\nThe 100% Time, 100% Space code:\n\n```cpp\nclass Solution {\npublic:\n int countVowelStrings(int n, int k = 5) {\n return (n + 1) * (n + 2) * (n + 3) * (n + 4) / 24;\n }\n};\n``` | 7 | 2 | ['C', 'Combinatorics', 'Probability and Statistics', 'C++'] | 0 |
count-sorted-vowel-strings | [c++] commented | c-commented-by-vishwasgajawada-00s0 | \nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int>v(5,1); //[1,1,1,1,1] -> (a,e,i,o,u)\n //for the n=2 ,consider this, | vishwasgajawada | NORMAL | 2021-01-17T11:32:44.677011+00:00 | 2021-01-17T11:32:44.677041+00:00 | 228 | false | ```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int>v(5,1); //[1,1,1,1,1] -> (a,e,i,o,u)\n //for the n=2 ,consider this, \n // if starting is a, then the suffix can be any of the string in vector v from a\n // i.e aa,ae,ai,ao,au\n //for e, ee,ei,eo,eu and etc\n \n //for n=3\n // beside a any of the 2 character string from vector starting from a can be placed,like:-\n // a-> aaa,aae,.,.,aau\n // aee,aei,.,aeu\n // .\n // .\n // auu\n \n for(int i=2;i<=n;i++){\n v[0]=v[0]+v[1]+v[2]+v[3]+v[4];\n v[1]=v[1]+v[2]+v[3]+v[4];\n v[2]=v[2]+v[3]+v[4];\n v[3]=v[3]+v[4];\n v[4]=v[4];\n }\n return v[0]+v[1]+v[2]+v[3]+v[4];\n }\n};\n\n\n``` | 7 | 0 | [] | 0 |
count-sorted-vowel-strings | one line [C++]beats 100% in time | less memory than 98.67% | one-line-cbeats-100-in-time-less-memory-4huj1 | This probelm has a pattern you need to find,and when you did it would look like something like this:\n\nint countVowelStrings(int n) {\n return ((n+1)*(n | mkhasib1 | NORMAL | 2021-01-17T09:40:36.945542+00:00 | 2021-01-17T09:40:36.945582+00:00 | 331 | false | This probelm has a `pattern` you need to find,and when you did it would look like something like this:\n```\nint countVowelStrings(int n) {\n return ((n+1)*(n+2)*(n+3)*(n+4))/24;\n }\n```\nIf you have any questions drop them below \uD83D\uDC47 and if liked it ,kindly **Upvote** it \u2B06 | 7 | 1 | [] | 4 |
count-sorted-vowel-strings | JAVA 1-D DP beat 100% with explainations | java-1-d-dp-beat-100-with-explainations-5yjc0 | \n public int countVowelStrings(int n) {\n // dp[i][j]: for first i vowels of length j, what is the unique lexicon pattern count\n // divid int | 66dante | NORMAL | 2021-01-17T07:44:18.978564+00:00 | 2021-01-17T07:44:18.978595+00:00 | 562 | false | ```\n public int countVowelStrings(int n) {\n // dp[i][j]: for first i vowels of length j, what is the unique lexicon pattern count\n // divid into two groups, one with only i - vowels dp[i-1][j], the other that must contain at least 1 i-th vowel\n // the second group\'s last letter must be i-th vowel, because they all unique, the count of them is actually\n // dp[i][j - 1];\n // transformation func: dp[i][j] = dp[i -1][j] + dp[i][j-1]\n // for init, dp[1][*] = 1, dp[1][0] = 1\n // we can transfer the problem into 1-D dp, so dp[i] += dp[i - 1], scan from left to right\n // for init dp[0] = 1\n int[] dp = new int[n + 1];\n dp[0] = 1;\n for (int i = 0; i < 5; i++) {\n for (int j = 1; j <= n; j++) {\n dp[j] += dp[j - 1];\n }\n }\n return dp[n];\n \n }\n``` | 7 | 1 | [] | 0 |
count-sorted-vowel-strings | [C++] Clean O(n) code & Detailed Explanation | c-clean-on-code-detailed-explanation-by-n50m1 | When n = 1\na e i o u\n1 1 1 1 1\n\nWhen n = 2\naa \nae ee\nai ei ii\nao eo io oo\nau eu iu ou uu\n5 4 3 2 1\n\nWhen n = 3\nYou might realise, the # o | bluebirdy | NORMAL | 2020-11-01T05:19:36.303820+00:00 | 2020-11-01T05:27:06.898032+00:00 | 285 | false | **When n = 1**\n`a e i o u`\n`1 1 1 1 1 `\n\n**When n = 2**\n`aa` \n`ae ee`\n`ai ei ii`\n`ao eo io oo`\n`au eu iu ou uu`\n`5 4 3 2 1`\n\n**When n = 3**\nYou might realise, the # of three letter sequences begin as `aaa` and ends as `auu`, is exactly the same as the **sum** of all possible two letter sequences.\nShown here `aaa...auu` = `a` + `(aa...au,ee...eu,ii...iu,oo...ou,uu)` = 5 + 4 + 3 + 2 + 1 = 15\n\n\nThis actually applies to # of three letter sequences begin as `eee` and end as `euu` as well!\n`eee...euu` = `e` + `(ee...eu,ii...iu,oo...ou,uu)` = 4 + 3 + 2 + 1 = 10\n\nAnd for `iii...iuu`, `ooo...ouu`,` uuu` you gussed it!\n6 (3+2+1), 3 (2+1), and 1 (1) correspondingly\n\nThe final result will be\n`15 10 6 3 1`\n\n**When n = 4**\nYou can apply the same logic\nSince `aaaa` to `auuu` is same as `a` + `(aaa...uuu)`\n\nThe final result will be\n35 (15+10+6+3+1) 20 (10+6+3+1) 10 (6+3+1) 4 (3+1) 1 (1) or\n`35 20 10 4 1`\n\n**When n = 5**\nSame method and it gives\n`70 35 15 5 1`\n\nWe can now conclude an algorithmic pattern.\nFor a list `P`, 0-indexed. \n`P_0` represents the # of sequences length `n` begin with the letter `u`\n`P_1` represents the # of sequences length `n` begin with the letter `i`\n...\n`P_4` represents the # of sequences length `n` begin with the letter `a`\n\nTo find the # of sequences length `n+1`\nIt can be computed as follows, `0 <= i <= 4`\n`P_i = P_i + P_i-1 + ... + P_0`\n\nHere is the code I wrote in C++\n```class Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> sums(5,1);\n \n for (int i = 0; i < n; i++){\n for (int j = 1; j < 5; j++){\n sums[j] = sums[j] + sums[j-1];\n }\n }\n \n return sums[4];\n }\n};\n```\n\nThis is actually my first post with explanations!\nFeedbacks welcomed!\n | 7 | 0 | [] | 1 |
count-sorted-vowel-strings | JAVA Back Track | java-back-track-by-aoali77-xmf7 | \nclass Solution {\n //String vowels = "aeiou";\n int count = 0;\n public int countVowelStrings(int n) {\n backTrack(n, 0);\n return coun | aoali77 | NORMAL | 2020-11-01T04:06:31.631262+00:00 | 2021-02-09T01:07:17.486536+00:00 | 651 | false | ```\nclass Solution {\n //String vowels = "aeiou";\n int count = 0;\n public int countVowelStrings(int n) {\n backTrack(n, 0);\n return count;\n }\n private void backTrack(int n, int indexToStart){\n if(n == 0){\n count++;\n return;\n }\n for(int i = indexToStart; i < 5; i++){\n backTrack(n - 1, i);\n }\n }\n}\n``` | 7 | 0 | ['Backtracking', 'Java'] | 2 |
count-sorted-vowel-strings | Python one line (math.comb) - with explanation updated | python-one-line-mathcomb-with-explanatio-vnsb | Idea: \n\nWe can simplify the question to how many "vowel"-ending strings at each n. \n"-e" at n = 2: "ae", "ee"\n\nLet\'s see how many "vowel"-ending strings p | mp0530 | NORMAL | 2020-11-01T04:02:39.524210+00:00 | 2020-11-01T05:24:54.401974+00:00 | 530 | false | **Idea**: \n\nWe can simplify the question to how many "vowel"-ending strings at each n. \n"-e" at n = 2: "ae", "ee"\n\nLet\'s see how many "vowel"-ending strings possible at n:\n\nEx:\n```\nn = 1 2 3 4 5 \n------------------------\n"-a": 1 1 1 1 1 \n"-e": 1 2 3 4 5 \n"-i": 1 3 6 10 15 \n"-o": 1 4 10 20 35 \n"-u": 1 5 15 35 70 \n------------------------\nsum : 5 15 35 70 126\n```\nWe can see that this is a pascal triangle but it is oblique. Or we can see below:\n\n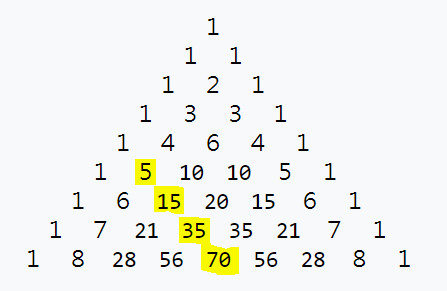\n\nTherefore, the sum of all strings at n is located at the **n+2th** element of **n+6th** row.\n\nAccording to Pascal Triangle: kth element at nth row is c(n-1, k-1)\n\n**Code:**\n```\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n return math.comb(n+4, n)\n```\n\n\n\n\n | 7 | 0 | [] | 1 |
count-sorted-vowel-strings | [C++]-1 LINER-EASY TO UNDERSTAND-BEGINNER-SHORT CONCISE-INTERVIEW-WITH EXPLANATION | c-1-liner-easy-to-understand-beginner-sh-vmwd | \n/*\n\nEXPLANATION: [C++]-1 LINER-EASY TO UNDERSTAND-BEGINNER-SHORT CONCISE-INTERVIEW-WITH EXPLANATION\n\nEXPLANATION:\n\nBasically n==1 - 5 combinations. Each | justcodingandcars | NORMAL | 2020-11-01T04:00:38.460237+00:00 | 2020-11-01T04:05:22.257437+00:00 | 794 | false | ```\n/*\n\nEXPLANATION: [C++]-1 LINER-EASY TO UNDERSTAND-BEGINNER-SHORT CONCISE-INTERVIEW-WITH EXPLANATION\n\nEXPLANATION:\n\nBasically n==1 - 5 combinations. Each ending with a vowel\n\nending with a-5,e-4,i-3,o-2,u-1\nn==2 = 5+4+3+2+1\n\nsimilarly n==3 == 35... 15+ (aa-5 , ae-4, ai-3,ao-2, au-1 and so on), which will lead to binomial coefficient of Binomial coefficient binomial(n,4) = n*(n-1)*(n-2)*(n-3)/24 starting from 5th term\n\nThus follows https://oeis.org/A000332\n*/\n\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n return ((n+4)*(n+3)*(n+2)*(n+1))/24;\n }\n};\n``` | 7 | 1 | [] | 0 |
count-sorted-vowel-strings | ✅C++ | Backtracking- recursion | Easy to Understand | c-backtracking-recursion-easy-to-underst-y36z | \nclass Solution {\npublic:\n \n void helper(int n, vector<char> &temp,int &count, int idx, vector<char> &vowels)\n {\n if(temp.size()==n)\n | Yash2arma | NORMAL | 2022-05-11T19:21:25.173952+00:00 | 2022-05-11T19:21:25.173998+00:00 | 287 | false | ```\nclass Solution {\npublic:\n \n void helper(int n, vector<char> &temp,int &count, int idx, vector<char> &vowels)\n {\n if(temp.size()==n)\n {\n count++;\n return;\n }\n \n for(int i=idx; i<vowels.size(); i++)\n {\n temp.push_back(vowels[i]);\n helper(n, temp, count, i, vowels);\n temp.pop_back();\n }\n return;\n }\n \n int countVowelStrings(int n) \n {\n vector<char> vowels{\'a\',\'e\',\'i\',\'o\',\'u\'};\n int count=0;\n vector<char> temp;\n helper(n, temp, count, 0, vowels);\n return count; \n }\n};\n``` | 6 | 0 | ['Backtracking', 'Recursion', 'C', 'C++'] | 0 |
count-sorted-vowel-strings | Easy Approach || Simple to understand | easy-approach-simple-to-understand-by-ka-ep0z | Hope you liked it :)\n\n```\nclass Solution {\npublic:\n void solve(vector &v, int n, int currindex, int &count, int l)\n {\n if(currindex >= n)\n | kajalgupta_0701 | NORMAL | 2022-05-11T05:02:09.975813+00:00 | 2022-05-11T05:03:17.122041+00:00 | 451 | false | **Hope you liked it :)**\n\n```\nclass Solution {\npublic:\n void solve(vector<char> &v, int n, int currindex, int &count, int l)\n {\n if(currindex >= n)\n {\n count++;\n return;\n }\n for(int i=l; i<v.size(); i++)\n {\n solve(v, n, currindex+1, count, i);\n }\n }\n \n int countVowelStrings(int n)\n {\n vector<char> v={\'a\',\'e\',\'i\',\'o\',\'u\'};\n int count = 0;\n solve(v, n, 0, count, 0);\n return count;\n }\n}; | 6 | 0 | ['Backtracking', 'C', 'C++'] | 0 |
count-sorted-vowel-strings | Count Sorted Vowel Strings | count-sorted-vowel-strings-by-chandakji2-y187 | i) proceed to build string recursively.\nii) insert next element in the string only if it is greater than the last element present and then decerease the n by 1 | chandakji2204 | NORMAL | 2022-05-11T00:30:29.846932+00:00 | 2022-05-11T00:30:29.846960+00:00 | 651 | false | i) proceed to build string recursively.\nii) insert next element in the string only if it is greater than the last element present and then decerease the n by 1.\niii) finally that will be our required string if n==0 i.e string of size n is form.\n\nremember : in recursion we have to write a base condition , recursion will handle all other cases.\n\nPlease Upvote :) !\n\n```\nclass Solution {\npublic:\n vector<char> vowels{\'a\',\'e\',\'i\',\'o\',\'u\'};\n \n void solve(int n,int last,int& count){\n if(n==0){\n count++;\n return;\n }\n for(int i=0;i<5;i++){\n if(i>=last){\n solve(n-1,i,count);\n }\n }\n }\n \n int countVowelStrings(int n) {\n int count=0;\n solve(n,0,count);\n return count;\n }\n};\n```\n\nMy other Solutions:\nhttps://leetcode.com/problems/partition-labels/discuss/1868704/partition-labels-on-solution-c-greedy-simple-solution\nhttps://leetcode.com/problems/power-of-four/discuss/1799832/power-of-four-c100bit-manipualtion-easy-solution\nhttps://leetcode.com/problems/partition-labels/discuss/1868704/partition-labels-on-solution-c-greedy-simple-solution\nhttps://leetcode.com/problems/binary-tree-level-order-traversal/discuss/1862025/binary-tree-level-order-traversal-queue-binary-tree-easy-solution\nhttps://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/discuss/1850726/minimum-remove-to-make-valid-parentheses-c-on-simple-logic-easy-solution\nhttps://leetcode.com/problems/maximum-number-of-vowels-in-a-substring-of-given-length/discuss/1849453/maximum-number-of-vowels-in-a-substring-of-given-length-csliding-window\nhttps://leetcode.com/problems/reverse-prefix-of-word/discuss/1840375/reverse-prefix-of-word-100-c\nhttps://leetcode.com/problems/find-n-unique-integers-sum-up-to-zero/discuss/1826246/find-n-unique-integers-sum-up-to-zero-100-simple-solution\nhttps://leetcode.com/problems/find-minimum-in-rotated-sorted-array/discuss/1814346/find-minimum-in-rotated-sorted-array-binary-search-100-ceasy-solution\nhttps://leetcode.com/problems/is-subsequence/discuss/1811098/is-subsequence-100-c-easy-solution\nhttps://leetcode.com/problems/search-in-rotated-sorted-array/discuss/1808021/search-in-rotated-sorted-array-ologn-solution-simple-solution-binary-search\nhttps://leetcode.com/problems/check-if-number-is-a-sum-of-powers-of-three/discuss/1799853/check-if-number-is-a-sum-of-powers-of-three-100-easy-solution\nhttps://leetcode.com/problems/sequential-digits/discuss/1751815/sequential-digits-c-100-easy-solution\nhttps://leetcode.com/problems/binary-gap/discuss/1749101/binary-gap-100-c-simple-solution\nhttps://leetcode.com/problems/kth-largest-element-in-an-array/discuss/1730888/kth-largest-element-in-an-array-c-sorting-simple-solution\nhttps://leetcode.com/problems/queries-on-number-of-points-inside-a-circle/discuss/1726527/queries-on-number-of-points-inside-a-circle-c-simple-mathematics\nhttps://leetcode.com/problems/integer-to-roman/discuss/1726042/integer-to-roman-c-easy-to-understand\nhttps://leetcode.com/problems/rings-and-rods/discuss/1724149/rings-and-rods-100-c-using-hashmap\nhttps://leetcode.com/problems/number-complement/discuss/1722669/number-compliment\nhttps://leetcode.com/problems/find-the-duplicate-number/discuss/1809351/find-the-duplicate-number-o1-space-binary-search-easy-solution\nhttps://leetcode.com/problems/smallest-string-with-a-given-numeric-value/discuss/1872424/Smallest-String-With-A-Given-Numeric-Value-oror-C%2B%2B-O(n)-oror-Simple-Solution-with-Explaination\nhttps://leetcode.com/problems/broken-calculator/discuss/1875269/Broken-Calculator-oror-C%2B%2B-100-O(n)-oror-Greedy-solution-with-Explanation-oror-Easy-Simple-Solution\nhttps://leetcode.com/problems/generate-parentheses/discuss/1875357/Generate-Parentheses-oror-C%2B%2B-recursive-Approach-with-explaination-oror-Easy-Approach\nhttps://leetcode.com/problems/boats-to-save-people/discuss/1877923/Boats-to-Save-People-oror-c%2B%2B-Greedy-oror-two-pointers-oror-sorting-oror-easy-Solution-with-explaination\nhttps://leetcode.com/problems/minimum-add-to-make-parentheses-valid/discuss/1901110/Minimum-Add-to-Make-Parentheses-Valid-oror-c%2B%2B-oror-100-oror-Simple-Solution-oror-String\nhttps://leetcode.com/problems/game-of-life/discuss/1937884/Game-of-Life-oror-100-oror-C%2B%2B-oror-Matrix-IMPLEMENTATION\nhttps://leetcode.com/problems/letter-case-permutation/discuss/2005077/Letter-Case-Permutation-oror-c%2B%2Boror-RecursionororEasy-Solution\nhttps://leetcode.com/problems/max-number-of-k-sum-pairs/discuss/2006992/Max-Number-of-K-Sum-Pairs-oror-C%2B%2Boror-HashMapororEasy-Solution\nhttps://leetcode.com/problems/implement-stack-using-queues/discuss/2009042/Implement-Stack-using-Queues-oror-c%2B%2B-oror-easySolutionoror-100 | 6 | 1 | ['Backtracking', 'Recursion', 'C'] | 1 |
count-sorted-vowel-strings | C++ | Dynamic Programming | 100% Faster | | c-dynamic-programming-100-faster-by-dhru-fr35 | \nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> v(n+1); v[0] = 1;\n for(int j = 0; j < 5; ++j){\n for | dhruv_73 | NORMAL | 2021-09-26T16:32:22.339919+00:00 | 2021-09-26T16:32:22.339957+00:00 | 355 | false | ```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n vector<int> v(n+1); v[0] = 1;\n for(int j = 0; j < 5; ++j){\n for(int i = 1; i <= n; ++i){\n v[i] += v[i-1];\n }\n }\n return v[n];\n }\n};\n```\n\n**Result-**\n```\nRuntime: 0 ms, faster than 100.00% of C++ online submissions for Count Sorted Vowel Strings.\nMemory Usage: 6.2 MB, less than 23.22% of C++ online submissions for Count Sorted Vowel Strings.\n``` | 6 | 0 | ['Dynamic Programming', 'C'] | 1 |
count-sorted-vowel-strings | Python DP O(N) time O(1) space w/ comment | python-dp-on-time-o1-space-w-comment-by-jyk32 | py\n\'\'\'\nw: dp\nh: when n = 1, we only have 5 choice,\n wheb n = 2, we have 15 options, how they related\n consider: [a, e, i, o, u]\n [aa, a | leovam | NORMAL | 2021-01-18T05:08:47.219347+00:00 | 2021-01-18T05:08:47.219399+00:00 | 290 | false | ```py\n\'\'\'\nw: dp\nh: when n = 1, we only have 5 choice,\n wheb n = 2, we have 15 options, how they related\n consider: [a, e, i, o, u]\n [aa, ae, ai, ao, au -- 5 strings\n ee, ei, eo, eu -- 4 strings\n ii, io, iu -- 3 strings\n oo, ou -- 2 strings\n uu] -- 1 strings\n \n we find a can be placed before any vowel, \n e can be place before e, i, o, u; \n i can be placed before i, o, u...\n \n so if n = 3, we can place a before any string when n = 2, which is 15\n we can place e before string not start with a, which is 10\n we can place i before strings not start with a, e, which is 6\n \n now see the pattern? \n\n let\'s present the valid number of string for each vowel in a list:\n n = 2, [5, 4, 3, 2, 1], 15 in total\n n = 3, [15, 10, 6, 3, 1], 35 in total\n n = 4, [35, 20, 10, 4, 1], 70 in total\n ...\n consider n = 2 and n = 3, from the end to the beginining, we can see\n 3 = 1 + 2, 6 = 3 + 3, 10 = 6 + 4, 15 = 10 + 5 \n \n now the pattern is clear, and you can try n=3 and n=4\n\'\'\'\n\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n # n = 1, base case\n dp = [1, 1, 1, 1, 1]\n # the valid number of string started with u is always 1\n # or you can say dp[-1] is always 1 \n u = 1\n for i in range(n-1):\n dp[4] = u\n for j in range(1, 5)[::-1]: \n dp[j-1] = dp[j-1] + dp[j]\n\n return sum(dp)\n``` | 6 | 0 | ['Dynamic Programming', 'Python'] | 0 |
count-sorted-vowel-strings | Count Sorted Vowel Strings: Python, 1-D DP | count-sorted-vowel-strings-python-1-d-dp-8v5o | python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n a = [1] * 5\n for _ in range(1, n):\n for i in range(1, 5):\ | sjoin | NORMAL | 2021-01-17T08:52:41.166666+00:00 | 2021-01-17T08:59:20.306092+00:00 | 422 | false | ```python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n a = [1] * 5\n for _ in range(1, n):\n for i in range(1, 5):\n a[i] += a[i-1]\n return sum(a)\n``` | 6 | 1 | ['Dynamic Programming', 'Python'] | 1 |
count-sorted-vowel-strings | java backtrack solution very simple | java-backtrack-solution-very-simple-by-o-12aj | \n int ans;\n public int countVowelStrings(int n) {\n // char[] ch ={\'a\',\'e\',\'i\',\'o\',\'u\'};\n ans=0;\n count(0,n);\n retu | osama010 | NORMAL | 2020-11-10T04:33:22.799369+00:00 | 2020-11-10T04:33:22.799471+00:00 | 646 | false | ```\n int ans;\n public int countVowelStrings(int n) {\n // char[] ch ={\'a\',\'e\',\'i\',\'o\',\'u\'};\n ans=0;\n count(0,n);\n return ans;\n }\n void count(int src,int n){\n if(n==0){ans++;return;}\n for(int i=src;i<5;i++){\n count(i,n-1);\n }\n }\n``` | 6 | 0 | ['Backtracking', 'Java'] | 3 |
count-sorted-vowel-strings | Python DP `O(1)` space, super EASY. | python-dp-o1-space-super-easy-by-herokil-h6dn | python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n a, e, i, o, u = 1, 1, 1, 1, 1\n for _ in range(n):\n a, e, i | herokillerever | NORMAL | 2020-11-09T13:10:04.566535+00:00 | 2020-11-09T13:10:04.566569+00:00 | 228 | false | ```python\nclass Solution:\n def countVowelStrings(self, n: int) -> int:\n a, e, i, o, u = 1, 1, 1, 1, 1\n for _ in range(n):\n a, e, i, o, u = a+e+i+o+u, e+i+o+u, i+o+u, o+u, u\n return a\n``` | 6 | 1 | [] | 1 |
count-sorted-vowel-strings | ✅C++ || DP Beats 100% 🚀 || (Memoization and Recursion) | c-dp-beats-100-memoization-and-recursion-0an7 | Code\n\nclass Solution {\npublic:\n int t(vector<vector<int>>&dp,int n,int i){\n if(i==0){\n dp[n][i]=0;\n return dp[n][i];\n | CHIIKUU | NORMAL | 2023-03-22T07:28:01.336628+00:00 | 2023-03-22T07:37:13.689948+00:00 | 1,606 | false | # Code\n```\nclass Solution {\npublic:\n int t(vector<vector<int>>&dp,int n,int i){\n if(i==0){\n dp[n][i]=0;\n return dp[n][i];\n }\n if(n==1){\n dp[n][i]=i;\n return dp[n][i];\n }\n if(dp[n][i]!=-1)return dp[n][i];\n dp[n][i] = t(dp,n-1,i) + t(dp,n,i-1);\n return dp[n][i];\n }\n int countVowelStrings(int n) {\n vector<vector<int>>dp(n+1,vector<int>(5+1,-1));\n t(dp,n,5);\n return dp[n][5];\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Combinatorics', 'C++'] | 0 |
count-sorted-vowel-strings | ✅C++ || Easy Recursion || Simple Explanation || 🗓️ Daily LeetCoding Challenge May, Day 11 | c-easy-recursion-simple-explanation-dail-2gjr | Please Upvote If It Helps\n\n\nclass Solution {\npublic:\n void helper(vector<char> &vowels, vector<char> &tmp, int &ans, int n, int start)\n {\n / | mayanksamadhiya12345 | NORMAL | 2022-05-11T16:56:00.197038+00:00 | 2022-05-11T19:32:50.601358+00:00 | 145 | false | **Please Upvote If It Helps**\n\n```\nclass Solution {\npublic:\n void helper(vector<char> &vowels, vector<char> &tmp, int &ans, int n, int start)\n {\n // if our tmp.size(), in which we are storing our combination reaches to the n then push that combination into our ans\n if(n==tmp.size())\n {\n ans++;\n return;\n }\n \n // start viisitng all the remaining vowels with the current vowel \n\t\t// beacuse it can make combination with itself and all the right vowels also\n // each time push current vowel to our temp and call the same function for current i\n for(int i=start;i<vowels.size();i++)\n {\n tmp.push_back(vowels[i]);\n helper(vowels,tmp,ans,n,i);\n tmp.pop_back(); // backtracking\n }\n return;\n }\n \n int countVowelStrings(int n) \n {\n // it is the vector by which we need to create all possible combination of strings\n vector<char> vowels = {\'a\',\'e\',\'i\',\'o\',\'u\'};\n \n // it will store the current string each time\n vector<char> tmp;\n \n // it will store all the possible combinations count\n int ans=0;\n \n // call the helper function\n helper(vowels,tmp,ans,n,0);\n \n return ans;\n }\n};\n``` | 5 | 0 | [] | 0 |
count-sorted-vowel-strings | Java || From recursion to memoization to tabulation || easy and explained | java-from-recursion-to-memoization-to-ta-h0tc | Recursion -->\n[ Time-Complexity = exponential, Space-Complexity = O(n) ]\n\nclass Solution {\n int count =0;\n public int countVowelStrings(int n) {\n | gourav02 | NORMAL | 2022-05-11T10:45:21.703225+00:00 | 2022-05-12T07:25:25.261567+00:00 | 351 | false | Recursion -->\n[ Time-Complexity = exponential, Space-Complexity = O(n) ]\n```\nclass Solution {\n int count =0;\n public int countVowelStrings(int n) {\n String[] s= new String[]{"a","e","i","o","u"};\n \n int ans = solve(0,n,s);\n return ans;\n }\n public int solve(int ind , int n ,String[] s){\n if(n==0){\n return 1;\n }\n if(ind>=s.length)return 0;\n \n int pick = solve(ind,n-1,s);\n int notPick = solve(ind+1,n,s);\n \n return (pick+notPick);\n }\n \n}\n```\n\nMemoization-->>\n[ Time-Complexity = O(4*N), Space-Complexity = O(5*n)+O(N) ]\n```\nclass Solution {\n int count = 0;\n\n public int countVowelStrings(int n) {\n String[] s = new String[] { "a", "e", "i", "o", "u" };\n int[][] dp = new int[5][n + 1];\n for (int[] x : dp) {\n Arrays.fill(x, -1);\n }\n int ans = solve(0, n, s,dp);\n return ans;\n }\n\n public int solve(int ind, int n, String[] s,int[][] dp) {\n if (n == 0) {\n return 1;\n }\n if (ind >= s.length) return 0;\n if(dp[ind][n]!=-1) return dp[ind][n];\n\n int pick = solve(ind, n - 1, s,dp);\n int notPick = solve(ind + 1, n, s,dp);\n\n return dp[ind][n] = (pick + notPick);\n }\n}\n```\n\nTabulation-->>\n[ Time-Complexity = O(4*N), Space-Complexity =O(N) ]\n```\nclass Solution {\n public int countVowelStrings(int n) {\n String[] s = new String[] { "a", "e", "i", "o", "u" };\n int[][] dp = new int[5][n + 1];\n for(int i=0;i<s.length;i++)\n dp[i][0] = 1;\n for(int i =4;i>=0;i--){\n for(int j=1;j<=n;j++){\n int pick = dp[i][j-1];\n int notPick = 0;\n if(i<4) notPick = dp[i+1][j];\n dp[i][j] = (pick+notPick);\n }\n }\n return dp[0][n];\n }\n}\n```\nplease upvote if helped. | 5 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 1 |
count-sorted-vowel-strings | python easy and a hard way | backtracking | DP | | python-easy-and-a-hard-way-backtracking-2v0xx | Using backtracking\n\n def countVowelStrings(self, n):\n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\']\n res = []\n idx = 0\n\n de | b44hrt | NORMAL | 2022-05-11T10:27:45.605475+00:00 | 2022-05-11T10:30:08.535878+00:00 | 415 | false | **Using backtracking**\n```\n def countVowelStrings(self, n):\n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\']\n res = []\n idx = 0\n\n def rec(s, idx):\n if len(s) == n:\n res.append(s)\n return\n for i in vowels[idx:]:\n rec(s + i, idx)\n idx += 1\n return res\n\t\t\t\n return len(rec(\'\', idx))\n```\n\n**Using DP array**\n```\ndef countVowelStrings(self, n):\n dp = [1] * 5 \n for x in range(n-1):\n for i in range(1, 5):\n dp[i] = dp[i] + dp[i - 1]\n \n return sum(dp)\n```\n\n | 5 | 0 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'Python'] | 0 |
count-sorted-vowel-strings | C++ logic based 2 line solution | c-logic-based-2-line-solution-by-nimesh-8h2aa | Logic based self explanatory code :\n\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n \n n += 4;\n \n int temp = n | Nimesh-Srivastava | NORMAL | 2022-05-11T05:37:29.594538+00:00 | 2022-05-11T05:43:23.688633+00:00 | 159 | false | Logic based self explanatory code :\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n \n n += 4;\n \n int temp = n * (n - 1) * (n - 2) * (n - 3);\n \n return temp / 24;\n }\n};\n```\n\nOR\n\n```\nclass Solution {\npublic:\n int countVowelStrings(int n) {\n \n int temp = (n + 1) * (n + 2) * (n + 3) * (n + 4);\n \n return temp / 24;\n }\n};\n``` | 5 | 0 | ['C', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.