question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
largest-rectangle-in-histogram | C++ stack solution | c-stack-solution-by-eplistical-l09m | The idea is simple: suppose a rectangle contains the column i and has a height heights[i], then the max area of the rectangle will be heights[i] * (rb[i] - lb[i | eplistical | NORMAL | 2020-01-01T19:26:39.392648+00:00 | 2020-01-01T19:26:39.392696+00:00 | 1,055 | false | The idea is simple: suppose a rectangle contains the column `i` and has a height `heights[i]`, then the max area of the rectangle will be `heights[i] * (rb[i] - lb[i] - 1)`. Here we define:\n\n- `lb[i]`: the index of first column on the left of `i` whose height is lower than `heights[i]`.\n- `rb[i]`: the index of first column on the right of `i` whose height is lower than `heights[i]`.\n\nWe first scan the `heights` array and use a stack to construct `lb[i]` and `rb[i]`. After that, we scan `heights` again and calculate `heights[i] * (rb[i] - lb[i] - 1)` to get the max possible area.\n\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int N = heights.size();\n stack<int> st;\n // construct lb[i]: idx of first col on the left that is lower than height[i]\n vector<int> lb(N);\n for (int i(0); i < N; ++i) {\n while (!st.empty() and heights[st.top()] >= heights[i]) {\n st.pop();\n }\n if (st.empty()) {\n lb[i] = -1;\n st.push(i);\n }\n else {\n lb[i] = st.top();\n st.push(i);\n }\n }\n \n // clear stack\n while (!st.empty()) st.pop();\n \n // construct rb[i]: idx of first col on the right that is lower than height[i]\n vector<int> rb(N);\n for (int i(N-1); i >= 0; --i) {\n while (!st.empty() and heights[st.top()] >= heights[i]) {\n st.pop();\n }\n if (st.empty()) {\n rb[i] = N;\n st.push(i);\n }\n else {\n rb[i] = st.top();\n st.push(i);\n }\n }\n \n // scan each col and get max area\n int rst = 0;\n for (int i(0); i < N; ++i) {\n rst = max(rst, \n heights[i] * (rb[i] - lb[i] - 1)\n );\n }\n return rst;\n }\n};\n``` | 8 | 0 | ['C++'] | 3 |
largest-rectangle-in-histogram | O(n) solution with clear code | on-solution-with-clear-code-by-kuskus87-y84p | The idea is very simple: for each bar find the area of the rectangle where this bar height defines the height of the whole rectangle.\nTo do that in O(n), we ne | kuskus87 | NORMAL | 2019-06-08T12:34:48.431335+00:00 | 2019-06-08T12:34:48.431376+00:00 | 1,127 | false | The idea is very simple: for each bar find the area of the rectangle where this bar height defines the height of the whole rectangle.\nTo do that in O(n), we need to find in O(1) the following indices:\n\t1) Index of the first element on the left from current `i` which is smaller than `heights[i]`\n\t2) Index of the first element on the right from current `i` which is smaller than `heights[i]`\n\n```C++\n vector<int> getNextSmaller(const vector<int>& heights) {\n stack<int> st;\n vector<int> res(heights.size(), heights.size());\n for (int i = 0; i < heights.size(); ++i) {\n while (!st.empty() && heights[st.top()] > heights[i]) {\n res[st.top()] = i;\n st.pop();\n }\n st.push(i);\n }\n \n return res;\n }\n // exactly the same as above except for the order\n // and the default element here is -1 (assume the the smaller element is before the start of the array)\n vector<int> getPrevSmaller(const vector<int>& heights) {\n stack<int> st;\n vector<int> res(heights.size(), -1);\n for (int i = heights.size() - 1; i >= 0; --i) {\n while (!st.empty() && heights[st.top()] > heights[i]) {\n res[st.top()] = i;\n st.pop();\n }\n st.push(i);\n }\n \n return res;\n }\n \n int largestRectangleArea(vector<int>& heights) {\n if (heights.size() == 0) return 0;\n \n auto nextSmaller = getNextSmaller(heights);\n auto prevSmaller = getPrevSmaller(heights);\n \n int res = 0;\n for (int i = 0; i < heights.size(); ++i) {\n int r = nextSmaller[i];\n int l = prevSmaller[i];\n res = max(res, heights[i]*(r - l - 1));\n }\n \n return res;\n }\n``` | 8 | 0 | ['C'] | 0 |
largest-rectangle-in-histogram | 16 ms beat 94% c++ solution | 16-ms-beat-94-c-solution-by-pkugoodspeed-i809 | class Solution {\n public:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size(),Area=0;\n vector<int> lef | pkugoodspeed | NORMAL | 2016-05-24T06:06:03+00:00 | 2016-05-24T06:06:03+00:00 | 844 | false | class Solution {\n public:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size(),Area=0;\n vector<int> left(n,0),right(n,0);\n for(int i=1;i<n;i++){ \n int j = i-1;\n while(j>=0 && heights[i]<=heights[j]){\n j -= (left[j]+1);\n }\n left[i] = i-j-1; //starts from i, how far the rectangle can go toward left\n }\n for(int i=n-2;i>=0;i--){\n int j=i+1;\n while(j<n && heights[i]<=heights[j]){\n j += (right[j]+1);\n }\n right[i] = j-i-1; //starts from i, how far the rectangle can go toward right\n }\n for(int i=0;i<n;i++) Area = max(Area,heights[i]*(right[i]+1+left[i])); //Bottom: left[i]+right[i]+1\n return Area;\n }\n }; | 8 | 0 | [] | 0 |
largest-rectangle-in-histogram | Most optimized Code in Java 💯 | most-optimized-code-in-java-by-no_one_ca-9cox | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | No_one_can_stop_me | NORMAL | 2023-03-06T08:10:10.076873+00:00 | 2023-03-06T08:10:28.788443+00:00 | 1,095 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int n = heights.length;\n int max = 0;\n int nr[] = new int[n];\n int nl[] = new int[n];\n\n Stack<Integer> s = new Stack<>();\n // Right\n for(int i = n-1; i>=0; i--){\n while(!s.empty() && heights[s.peek()]>=heights[i]){\n s.pop();\n }\n if(s.empty()){\n nr[i] = n;\n }\n else{\n nr[i] = s.peek();\n }\n s.push(i);\n }\n // Left\n s = new Stack<>();\n for(int i = 0; i<heights.length; i++){\n while(!s.empty() && heights[s.peek()]>=heights[i]){\n s.pop();\n }\n if(s.empty()){\n nl[i] = -1;\n }\n else{\n nl[i] = s.peek();\n }\n s.push(i);\n }\n\n for(int i = 0; i<n; i++){\n int hi = heights[i];\n int width = nr[i]-nl[i]-1;\n int curr = hi * width;\n max = Math.max(curr, max);\n }\n return max;\n }\n}\n``` | 7 | 0 | ['Java'] | 0 |
largest-rectangle-in-histogram | [Python] Simple Stack Solution | python-simple-stack-solution-by-rowe1227-26du | Key Insights:\n\nFor each index, the largest rectangle of heights h[i] that passes\nthrough the index will have a left bound at the first height lower\nthan h[i | rowe1227 | NORMAL | 2020-12-31T08:52:15.165243+00:00 | 2020-12-31T08:53:21.197945+00:00 | 361 | false | **Key Insights:**\n\nFor each index, the largest rectangle of heights h[i] that passes\nthrough the index will have a left bound at the first height lower\nthan h[i] to the left and a right bound at the first height lower than\nh[i] to the right.\n\n**Approach:**\n\nFor each index:\n1. Find the index of the first shorter building that is to the left\n2. Find the index of the first shorter building that is to the right\n3. The rectangle area is heights[i] * (right[i] - left[i] - 1)\n\n**Implementation:**\n\nUse a stack approach to find the index of the first building shorter\nthan heights[i] to the right of index i.\n\nThen reverse heights and repeat the process to find the first\nbuilding shorter than heights[i] to the left of i.\n\n<br>\n\n```python\ndef largestRectangleArea(self, heights: List[int]) -> int:\n\n\tif not heights: return 0\n\tn = len(heights)\n\t\n\t# 1. Index of the first building shorter than heights[i] to the right of i\n\tright = [n] * n\n\tstack = []\n\tfor i, h in enumerate(heights):\n\t\twhile stack and h < stack[-1][1]:\n\t\t\tright[stack.pop()[0]] = i\n\t\tstack.append((i, h))\n\n\t# 2. Index of the first building shorter than heights[i] to the left of i\n\tleft = [-1] * n\n\tstack = []\n\tfor i in range(n - 1, -1, -1):\n\t\th = heights[i]\n\t\twhile stack and h < stack[-1][1]:\n\t\t\tleft[stack.pop()[0]] = i\n\t\tstack.append((i, h))\n\n\tarea = [heights[i] * (right[i] - left[i] - 1) for i in range(n)]\n\treturn max(area)\n``` | 7 | 1 | [] | 0 |
largest-rectangle-in-histogram | [Python] A brief summary for Monotonous Stacks applications | python-a-brief-summary-for-monotonous-st-za5p | For this problem, an monotonously increasing stack is used to store the previous indices. Once current height < stack[-1]\'s height, a cadidate rectangler area | oldeelk | NORMAL | 2020-04-16T07:21:59.402199+00:00 | 2020-04-22T02:58:32.007124+00:00 | 322 | false | For this problem, an monotonously increasing stack is used to store the previous indices. Once `current height` < `stack[-1]\'s height`, a cadidate rectangler area can be calculated with `width: length between stack[-2] + 1 ~ current index - 1`, `height: stack[-1]\'s height`. Compare all candidates to get the final results. \n```\nclass Solution(object):\n def largestRectangleArea(self, heights):\n """\n :type heights: List[int]\n :rtype: int\n """\n heights.append(0)\n inStack, rst = [], 0\n for i in range(len(heights)):\n while inStack and heights[i] < heights[inStack[-1]]:\n\t\t\t # local regionMin\'s idx, where the `local region` is [last.last.idx + 1, cur.idx - 1]\n regionMinIdx = inStack.pop()\n h = heights[regionMinIdx]\n\t\t\t\t# width = endIdx - startIdx + 1 if there is a start, else endIdx - 0 + 1\n w = i - 1 - (inStack[-1] + 1) + 1 if inStack else i - 1 - 0 + 1\n rst = max(rst, h * w)\n inStack.append(i)\n return rst\n```\n\nBesides this one, monotonous stack can solve other problems with **a similiar template**. \n1. [Locate days between today and next warmer day](https://leetcode.com/problems/daily-temperatures/discuss/109832/Java-Easy-AC-Solution-with-Stack): it can be used when finding first largest element. \n```py\nclass Solution(object):\n def dailyTemperatures(self, T):\n """\n :type T: List[int]\n :rtype: List[int]\n """\n deStack = []\n rst = [0] * len(T)\n for i in range(len(T) - 1, -1, -1):\n while deStack and T[i] >= T[deStack[-1]]:\n deStack.pop()\n rst[i] = deStack[-1] - i if deStack else 0\n deStack.append(i)\n return rst\n```\n2. [Trapping rain water stack solution](https://leetcode.com/problems/trapping-rain-water/solution/): it can be used when finding `leftmost first larger element` **AND** the `rightmost first larger element` in one pass. \n```py\nclass Solution(object):\n def trap(self, height):\n """\n :type height: List[int]\n :rtype: int\n """\n # stack recording decreasing height\'s indices\n # each time cur height > last height, update the rectangular region last.last.Idx -> curIdx, last.Height -> min(last.last.Height, cur.Height)\n deStack = []\n rst = 0\n for curIdx, curHeight in enumerate(height):\n while deStack and curHeight > height[deStack[-1]]:\n lastIdx = deStack.pop()\n if deStack:\n rst += (curIdx - deStack[-1] - 1) * (min(curHeight, height[deStack[-1]]) - height[lastIdx])\n # Only processed prev rectangular blocks with left bar < curHeight, cur position might still able to keep \n # rain water so curIdx still need to be pushed in stack\n deStack.append(curIdx)\n return rst\n```\n3. [Minimum cost construct Tree from Leaf values](https://leetcode.com/problems/minimum-cost-tree-from-leaf-values/discuss/339959/One-Pass-O(N)-Time-and-Space): still, use it to find left and right first larger element. Also a, **wrong-result**, increasing instead of decreasing stack solution can be found [here](https://leetcode.com/problems/minimum-cost-tree-from-leaf-values/discuss/574870/Python-Two-Monotonous-Stack-solutions%3A-decreasing-and-increasing-stacks) for practice.\n```py\nclass Solution(object):\n def mctFromLeafValues(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n # Each number A can be removed by its left/right largest(or smallest depending on removing from small -> large or large -> small) adjacent number with cost A * left/right, \n # smallest cost to remove A would be A * min(left, right)\n # remove num with its min(left/right FIRST larger number)\n cost, n = 0, len(arr)\n arr.append(sys.maxsize) # add a large number at the end to pop out all final decreasing nums\n deStack = [] # decreasing stack\n for i, num in enumerate(arr):\n while deStack and num >= deStack[-1]:\n val = deStack.pop()\n if deStack or i != n:\n cost += val * min(num, deStack[-1]) if deStack else val * num\n deStack.append(num)\n return cost\n```\n4. [Asteroid merging](https://leetcode.com/problems/asteroid-collision/discuss/580582/Python-Stack-solution-WITHOUT-uninterpretable-nested-loops): monotonous stack is not limited to be used on finding first larger/smaller item. It can be extended on other tasks when only single direction expantion/updating is allowed and the `monotonous` feature can also mean for the increasing absolute value or other more abstract self-defined concepts.\n```py\nclass Solution(object):\n def asteroidCollision(self, asteroids):\n """\n :type asteroids: List[int]\n :rtype: List[int]\n Note: -5, 5, -3, 5 -> -5 5 5, the head wont merge with the tail\n """\n s = []\n def inner(cur):\n append_cur = True\n # inner loop is to backwardly delete s, cur is not moving at inner loop.\n while s and cur < 0 and s[-1] > 0:\n if abs(cur) > s[-1]:\n s.pop()\n continue # to delete more s\'s ending positive numbers\n elif abs(cur) == s[-1]:\n s.pop()\n append_cur = False # equal, cur is disposed\n break\n else:\n append_cur = False # |cur| < s[-1], cur is disposed\n break\n return append_cur\n \n \n for cur in asteroids:\n append_cur = inner(cur)\n if append_cur:\n s.append(cur)\n return s\n``` | 7 | 0 | [] | 0 |
largest-rectangle-in-histogram | python O(n) explained in detail | python-on-explained-in-detail-by-zxshuat-tmrz | \nclass Solution(object):\n def largestRectangleArea(self, heights):\n """\n :type heights: List[int]\n :rtype: int\n """\n | zxshuati | NORMAL | 2019-06-02T18:54:01.552346+00:00 | 2019-06-02T18:54:01.552387+00:00 | 807 | false | ```\nclass Solution(object):\n def largestRectangleArea(self, heights):\n """\n :type heights: List[int]\n :rtype: int\n """\n # for every bar, calc the area which uses this bar as the lowest bar\n # therefore we need to find the first lower bar towards the left and the \n # first lower bar towards the right\n # hence, we need a stack to keep stacking the higher bars\n # when a lower bar appears, thats the first lower bar towards the right\n # and the first lower bar towards the left will be the next bar in the stack\n stack = []\n max_area = 0\n for i in range(len(heights)):\n if not stack:\n stack.append(i)\n else:\n # if height not decreasing, just stack\n if heights[i] >= heights[stack[-1]]:\n stack.append(i)\n continue\n while stack and heights[i] < heights[stack[-1]]:\n # for the bar on top of the stack\n # we found the first lower bar towards the right\n this_bar = stack.pop()\n right_index = i\n left_index = stack[-1] if stack else -1 # no lower towards the left, so make it left of the leftmost, which makes it -1\n area = heights[this_bar] * (right_index - left_index -1)\n max_area = max(area, max_area)\n stack.append(i)\n while stack:\n this_bar = stack.pop()\n right_index = len(heights) # no lower towards the right, so make it right of the rightmost, which makes it len(heights)\n left_index = stack[-1] if stack else -1\n area = heights[this_bar] * (right_index - left_index -1)\n max_area = max(area, max_area)\n return max_area \n``` | 7 | 0 | [] | 0 |
largest-rectangle-in-histogram | Easy-to-understand 92ms Python solution, linear time and space. | easy-to-understand-92ms-python-solution-thvnm | class Solution(object):\n # Helper function calculating how far each bar can be extended to the right.\n def calmax(self, height):\n stack = []\n | pei11 | NORMAL | 2015-08-25T23:56:44+00:00 | 2015-08-25T23:56:44+00:00 | 2,299 | false | class Solution(object):\n # Helper function calculating how far each bar can be extended to the right.\n def calmax(self, height):\n stack = []\n n = len(height)\n rec = [0] * n\n for i in xrange(len(height)):\n while len(stack) > 0 and height[stack[-1]] > height[i]:\n top = stack.pop()\n rec[top] = i\n stack.append(i)\n for i in stack:\n rec[i] = n\n return rec\n def largestRectangleArea(self, height):\n # How far can each bar be extended to the right?\n rec1 = self.calmax(height)\n # How far can each bar be extended to the left?\n rec2 = self.calmax(height[::-1])[::-1]\n maxa = 0\n n = len(height)\n for i in xrange(n):\n # Add the left and right part together\n new = height[i] * (rec1[i] + rec2[i] - n)\n maxa = max(new, maxa)\n return maxa\n\nThis solution can be made faster. But who cares if the complexity is still \\Theta(n)? | 7 | 0 | [] | 2 |
largest-rectangle-in-histogram | 10 lines 🚀 Monotonic Stack | One pass | Dummy node technique | 10-lines-monotonic-stack-one-pass-dummy-cfexb | Intuition\n Describe your approach to solving the problem. \nUsing dummy nodes to avoid edge cases.\n\n# Complexity\n- Time complexity: O(n)\n Add your time com | sulerhy | NORMAL | 2024-10-10T14:55:48.621663+00:00 | 2024-11-21T05:39:40.040292+00:00 | 1,374 | false | # Intuition\n<!-- Describe your approach to solving the problem. -->\nUsing dummy nodes to avoid edge cases.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n stack = [-1] # dummy index, to prevent stack from empty error\n heights.append(0) # dummy node in the tail\n max_area = 0\n for i, cur_height in enumerate(heights):\n while stack and heights[stack[-1]] > cur_height:\n height = heights[stack.pop()]\n width = i - stack[-1] - 1\n max_area = max(max_area, width * height)\n stack.append(i)\n return max_area\n``` | 6 | 0 | ['Monotonic Stack', 'Python3'] | 0 |
largest-rectangle-in-histogram | Python Easy Solution (beats 96%) | python-easy-solution-beats-96-by-brianwu-drv2 | \n\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nUse ascending monotonic stack to solve this.\n\n# Approach\n Describe your appr | BrianWU-S | NORMAL | 2023-06-13T17:47:01.028964+00:00 | 2023-06-13T17:49:42.145482+00:00 | 1,830 | false | \n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse ascending monotonic stack to solve this.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- store a tuple: (index, val) in monotonic stack. This will make our idea clear and benefit our explanation\n- use ascending stack instead of descending stack\n- remember to record minStartIdx while poping stack. Otherwise, the solution can\'t tackle with inputs like: [2,1,2]. I saw many solutions are lack of this step, technically they are wrong. But it\'s weird that they can pass the submission. \n- when encounter the equal problem (current Height == height of stack top), we don\'t need to push it into the stack, since the area calculation will be coverd by the current stack top element.\n- appending a small number (0 or -1) at the end of the input array can efficiently solve non-empty stack problems. We can avoid writing extra code after the for/while loop to empty the stack.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n maxArea = 0\n stack = [] # startIdx, height\n heights.append(0) # allows us to clear out stack without extra logic\n for curI, curH in enumerate(heights):\n # don\'t need to append if we already have the value with a lower startIdx\n if stack and curH == stack[-1][1]:\n continue\n minStartIdx = curI\n while stack and curH < stack[-1][1]:\n startIdx, lastHeight = stack.pop()\n minStartIdx = startIdx\n maxArea = max(maxArea, lastHeight * (curI - startIdx))\n stack.append((minStartIdx, curH))\n return maxArea\n``` | 6 | 0 | ['Monotonic Stack', 'Python3'] | 0 |
largest-rectangle-in-histogram | C++ EasyToUnderstad Stack Solution || ⭐⭐⭐ | c-easytounderstad-stack-solution-by-shai-bvx5 | Intuition\n Describe your first thoughts on how to solve this problem. \nwe will consider heights[i] as a length and check both ways how much it extends to both | Shailesh0302 | NORMAL | 2023-03-29T12:35:21.801733+00:00 | 2023-03-29T12:35:21.801777+00:00 | 865 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe will consider heights[i] as a length and check both ways how much it extends to both ways \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor every heights[i] we will find its next smaller to the right and its next smaller to the left \n\nbecause till all elements are greater around heights[i], heights[i] length can be cut from them and added to its area, this way we calculate breadth of rectangle.\n\nfor every element of heights if we know how much we can extend its area to both sides, we can check for all heights[i] and return the maximum area as answer.\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights){\n int n=heights.size();\n vector<int> nsr(n,0);\n vector<int> nsl(n,0);\n\n stack<int> s;\n\n for(int i=n-1;i>=0;i--){\n while(!s.empty() && heights[i]<=heights[s.top()]){\n s.pop();\n }\n if(s.empty()) nsr[i]=n;\n else nsr[i]=s.top();\n s.push(i);\n }\n\n while(!s.empty()) s.pop();\n\n for(int i=0;i<n;i++){\n while(!s.empty() && heights[i]<=heights[s.top()]){\n s.pop();\n }\n if(s.empty()) nsl[i]=-1;\n else nsl[i]=s.top();\n s.push(i);\n }\n\n int ans=0;\n\n for(int i=0;i<n;i++){\n ans=max(ans, heights[i]*(nsr[i]-nsl[i]-1));\n }\n return ans; \n }\n};\n``` | 6 | 0 | ['Stack', 'C++'] | 0 |
largest-rectangle-in-histogram | Simple JavaScript Solution | simple-javascript-solution-by-nikki_khar-g2cq | Intuition\n Describe your first thoughts on how to solve this problem. \nJust Solve this Problem like any other stack problem of nearest minimum.\n\n# Approach\ | nikki_kharkwal | NORMAL | 2023-01-22T03:57:49.411003+00:00 | 2023-02-01T13:59:35.824851+00:00 | 862 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust Solve this Problem like any other stack problem of nearest minimum.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Find the nearest minimum elements for the left side of the given array.\n2. Find the nearest minimum elements for the right side of the given array. \n3. Find the area of all the elements.\n4. For Area you have to find length and breadth is given. So for length just Step 1 stack subtract Step 2 Stack, you will get the length.\n5. Then just take the maximum one out and return. \n\n# Complexity\n- Time complexity: N\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: N\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} heights\n * @return {number}\n */\nvar largestRectangleArea = function(heights) {\n let leftStack = [];\n let stack = [];\n \n//Left side nearest minimum element\n for(let i = 0;i < heights.length;i++){\n while(stack.length !== 0 && heights[stack[stack.length - 1]] >= heights[i]){\n stack.pop();\n }\n\n if(stack.length === 0){\n leftStack.push(-1);\n }\n else {\n leftStack.push(stack[stack.length - 1]);\n }\n stack.push(i);\n }\n\n//Right side nearest minimum element \n stack = [];\n let rightStack = [];\n\n for(let i = heights.length - 1;i >= 0; i--){\n while(stack.length !== 0 && heights[stack[stack.length - 1]] >= heights[i]){\n stack.pop();\n }\n\n if(stack.length === 0){\n rightStack.push(heights.length);\n }\n else {\n rightStack.push(stack[stack.length - 1]);\n }\n stack.push(i);\n }\n \n //Calculating maximum Area \n let max = -Infinity;\n let area;\n //Area = right - left - 1 (length) * heights[i](breadth)\n\n for(let i = 0;i < heights.length; i++){\n area = (rightStack[heights.length - i - 1] - leftStack[i] - 1) * heights[i];\n max = Math.max(area,max);\n }\n return max;\n};\n``` | 6 | 0 | ['Array', 'Stack', 'Monotonic Stack', 'JavaScript'] | 0 |
largest-rectangle-in-histogram | C++ || O(N) || Easy to Understand with In-Depth Explanation and Examples | c-on-easy-to-understand-with-in-depth-ex-qc0s | Table of Contents\n\n- TL;DR\n - Code\n - Complexity\n- In Depth Analysis\n - Intuition\n - Approach\n - Example\n\n# TL;DR\n\nPrecompute the next smallest | krazyhair | NORMAL | 2022-12-05T22:24:09.376537+00:00 | 2023-01-03T15:52:56.937840+00:00 | 583 | false | #### Table of Contents\n\n- [TL;DR](#tldr)\n - [Code](#code)\n - [Complexity](#complexity)\n- [In Depth Analysis](#in-depth-analysis)\n - [Intuition](#intuition)\n - [Approach](#approach)\n - [Example](#example)\n\n# TL;DR\n\nPrecompute the next smallest height for every height going from left to right and also from right to left. Then, we can go through these arrays and compute the largest area by finding the next smallest bar from left to right to determine the width and multiply it by the height of itself.\n\n## Code\n\n```c++\ntypedef long long ll;\n\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n const int n = heights.size();\n ll ans = 0;\n\n stack<int> elems;\n vector<int> next_smallest_height_to_left(n, -1),\n next_smallest_height_to_right(n, n);\n\n for (int i = 0; i < n; i++) {\n while (!elems.empty() && heights[elems.top()] > heights[i]) {\n next_smallest_height_to_right[elems.top()] = i;\n elems.pop();\n }\n elems.push(i);\n }\n\n // This is done because stack does not have a clear function\n while (!elems.empty()) elems.pop();\n\n for (int i = n - 1; i >= 0; i--) {\n while (!elems.empty() && heights[elems.top()] > heights[i]) {\n next_smallest_height_to_left[elems.top()] = i;\n elems.pop();\n }\n elems.push(i);\n }\n\n for (int i = 0; i < n; i++) {\n int width = next_smallest_height_to_right[i] - next_smallest_height_to_left[i] - 1;\n ans = max(ans, 1LL * width * heights[i]);\n }\n\n return ans;\n }\n};\n```\n\n## Complexity\n\n**Time Complexity:** $$O(N)$$ where $$N$$ is the length of the input array\n**Space Complexity:** $$O(N)$$\n\n**PLEASE UPVOTE IF YOU FIND MY POST HELPFUL!! \uD83E\uDD7A\uD83D\uDE01**\n\n---\n\n# In Depth Analysis\n\n## Intuition\n\nWe want to keep track of the next smallest height for each bar going from left to right and right to left, which we can precompute using a stack. When we have this, we know that for any given point that the way to figure out its area is finding the distance between the smallest value to the left of it and the smallest value to the right of it to give us the horizontal width of the rectangle and multiplying that by the height of the actual bar itself.\n\nFor example, take `[2,1,5,6,2,3]` as the heights. For index 0, the smallest value to the left of it is index -1 (since it doesn\'t exist, pretend the height is 0) and the smallest value to the right of it is at index 1 (height of 1). Then to find the distance it is 1 - (- 1) - 1 = 1 which is the correct width for the rectangle of this height. Then we multiply the height (2) times the width to get that with index 0, we can get a rectangle of area 2. If you are confused, take a look at the [bottom](#example) for a full walkthrough with this example\n\n## Approach \n\nUse 2 vectors: one to hold the index of the next smallest value to the left and the other one for the smallest value to the right. We can populate these arrays by using a stack and keeping it monotonically increasing. For finding the smallest height to the right,the way we do that is if the index at the top of the stack\'s height is greater than the current height, we have found the smallest height relatively to the previous height. Therefore, we pop off the stack and update its position in the array to contain the current index. The same process works when we go in reverse (from right to left).\n\nThen by the end, we just loop through all the heights and calculate the width, multiply it by the height, and update the largest area if it is greater than the answer so far.\n\n## Example\n\nLets use an example where `heights = [2,1,5,6,2,3]`\n\n**Compute from left to right**\n\n* i = 0\nStack = `[]` <-- TOP\nArray = `[-1,-1,-1,-1,-1,-1]`\n\nThere are no elements on the stack, so we just push the index `0`\n\n* i = 1\nStack = `[2]` <-- TOP\nArray = `[-1,-1,-1,-1,-1,-1]`\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[0] = 2` against `heights[i] = heights[1] = 1`. Since the top element is greater than current element, we update it\'s array index to hold `i = 1` and pop `0` off the stack. The while condition is now false and at the end, we always push the current index onto the stack\n\n* i = 2\nStack = `[1]` <-- TOP\nArray = `[1,-1,-1,-1,-1,-1]`\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[1] = 1` against `heights[i] = heights[2] = 5`. Since `1 < 5`, we just push the index `2`\n\n* i = 3\nStack = `[1,2]` <-- TOP\nArray = `[1,-1,-1,-1,-1,-1]`\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[2] = 5` against `heights[i] = heights[3] = 6`. Since `5 < 6`, we just push the index `3`\n\n* i = 4\nStack = `[1,2,3]` <-- TOP\nArray = `[1,-1,-1,-1,-1,-1]`\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[3] = 6` against `heights[i] = heights[4] = 2`. Since the top element is greater than current element, we update it\'s array index to hold `i = 4` and pop `3` off the stack. We check the while condition again\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[2] = 5` against `heights[i] = heights[4] = 2`. Since the top element is greater than current element, we update it\'s array index to hold `i = 4` and pop `2` off the stack. We check the while condition again.\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[1] = 1` against `heights[i] = heights[4] = 2`. Since `1 < 2`, we just push the index `4`\n\n* i = 5\nStack = `[1,4]` <-- TOP\nArray = `[1,-1,4,4,-1,-1]`\n\nSince the stack isn\'t empty, we compare `heights[elems.top()] = heights[4] = 2` against `heights[i] = heights[5] = 3`. Since `2 < 3`, we just push the index `5`\n\nThis generates the array `[1,-1,4,4,-1,-1]` which gives the index of the next smallest height\'s sindex of a particular height going from left to right\n\n*I am not doing it again for right to left, but it is the same idea*\n\n**Computing the largest area**\n\nHere are the two arrays:\n* Left to right = `[1,-1,4,4,-1,-1]`\n* Right to left = `[-1,-1,1,2,1,4]`\n\nNow we iterate and calculate the largest area for each\n\n* i = 0\nans = 0\n\nThe width is `left_to_right[i] - right_to_left[i] - 1 = left_to_right[0] - right_to_left[0] - 1 = 1 - (-1) - 1 = 1`. Therefore, the largest area is `1 * heights[i] = 1 * heights[0] = 1 * 2 = 2`. We update ans\n\n* i = 1\nans = 2\n\nThe width is `left_to_right[i] - right_to_left[i] - 1 = left_to_right[1] - right_to_left[1] - 1 = -1 - (-1) - 1 = -1`. Therefore, the largest area is `-1 * heights[i] = -1 * heights[1] = -1 * 1 = -1`. We do not update ans\n\n* i = 2\nans = 2\n\nThe width is `left_to_right[i] - right_to_left[i] - 1 = left_to_right[2] - right_to_left[2] - 1 = 4 - 1 - 1 = 2`. Therefore, the largest area is `2 * heights[i] = 2 * heights[2] = 2 * 5 = 10`. We update ans\n\n* i = 3\nans = 10\n\nThe width is `left_to_right[i] - right_to_left[i] - 1 = left_to_right[3] - right_to_left[3] - 1 = 4 - 2 - 1 = 1`. Therefore, the largest area is `1 * heights[i] = 1 * heights[3] = 1 * 6 = 6`. We do not update ans\n\n* i = 4\nans = 10\n\nThe width is `left_to_right[i] - right_to_left[i] - 1 = left_to_right[4] - right_to_left[4] - 1 = -1 - 1 - 1 = -3`. Therefore, the largest area is `-3 * heights[i] = -3 * heights[4] = -3 * 2 = -6`. We do not update ans\n\n* i = 5\nans = 10\n\nThe width is `left_to_right[i] - right_to_left[i] - 1 = left_to_right[5] - right_to_left[5] - 1 = -1 - 4 - 1 = -6`. Therefore, the largest area is `-6 * heights[i] = -6 * heights[5] = -6 * 3 = -18`. We do not update ans\n\n**PLEASE UPVOTE IF YOU FIND MY POST HELPFUL!! \uD83E\uDD7A\uD83D\uDE01** | 6 | 0 | ['Array', 'Stack', 'Monotonic Stack', 'C++'] | 0 |
largest-rectangle-in-histogram | [C++] Largest Rectangle in Histogram with Stack | c-largest-rectangle-in-histogram-with-st-5ugm | Description\n\nGet the Largest Area of Rectangle in a Histogram with a Monotonic Stack.\n\nProgram\n\ncpp []\nclass Solution {\npublic:\n int largestRectangl | harshcut | NORMAL | 2022-11-17T13:52:52.895890+00:00 | 2022-11-17T13:52:52.895926+00:00 | 1,446 | false | **Description**\n\nGet the Largest Area of Rectangle in a Histogram with a Monotonic Stack.\n\n**Program**\n\n```cpp []\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int result = 0;\n stack<pair<int, int>> stack;\n for (int i = 0; i < heights.size(); i++) {\n int start = i;\n while (!stack.empty() && stack.top().second > heights[i]) {\n int index = stack.top().first;\n int width = i - index;\n int height = stack.top().second;\n stack.pop();\n result = max(result, height * width);\n start = index;\n }\n stack.push({start, heights[i]});\n }\n while (!stack.empty()) {\n int width = heights.size() - stack.top().first;\n int height = stack.top().second;\n stack.pop();\n result = max(result, height * width);\n }\n return result;\n }\n};\n``` | 6 | 0 | ['Stack', 'Monotonic Stack', 'C++'] | 0 |
largest-rectangle-in-histogram | O(N) using single Stack in java | on-using-single-stack-in-java-by-tanx4-bf8u | \nclass Solution {\n public int largestRectangleArea(int[] heights) {\n \n /* Naive Solution \n \n int i;\n int max=height | tanx4 | NORMAL | 2022-09-24T16:38:39.752649+00:00 | 2022-09-24T16:38:39.752689+00:00 | 834 | false | ```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n \n /* Naive Solution \n \n int i;\n int max=heights[0];\n for(i=0;i<heights.length;i++)\n {\n int sum=heights[i];\n for(int j=i+1;j<heights.length;j++)\n {\n if(heights[j]>=heights[i])\n sum+=heights[i];\n else\n break;\n }\n for(int j=i-1;j>=0;j--)\n {\n if(heights[j]>=heights[i])\n sum+=heights[i];\n else\n break;\n }\n \n max=Math.max(max,sum);\n }\n return(max);\n \n */\n \n int i,n=heights.length;\n int res=0;\n int tb,cur;\n Stack<Integer> s=new Stack<>();\n \n for(i=0;i<heights.length;i++)\n {\n while(!s.isEmpty()&&heights[s.peek()]>=heights[i])\n {\n tb=s.pop();\n cur=heights[tb]*(s.isEmpty()?i:i-s.peek()-1);\n res=Math.max(res,cur);\n }\n s.push(i);\n }\n \n while(!s.isEmpty())\n {\n tb=s.pop();\n cur=heights[tb]*(s.isEmpty()?n:n-s.peek()-1);\n res=Math.max(res,cur);\n }\n return(res);\n \n \n \n \n }\n}\n``` | 6 | 0 | ['Stack', 'Java'] | 1 |
largest-rectangle-in-histogram | JAVA|| Array->(O(n^2)) || Easy To Undestand||TL | java-array-on2-easy-to-undestandtl-by-an-7h25 | \n | anmolnegi242 | NORMAL | 2022-08-13T08:57:29.955890+00:00 | 2023-07-01T14:46:49.817895+00:00 | 767 | false | \n | 6 | 0 | ['Array', 'Two Pointers', 'Java'] | 1 |
largest-rectangle-in-histogram | Stack based O(N) with detailed explanation | stack-based-on-with-detailed-explanation-112y | Solution intuition\n\nThe idea to efficiently solve this problem is very simple. Let\'s say we have heights as follows:\n\n\n\nFor any particular height which w | blueblazin | NORMAL | 2022-01-15T03:56:59.344242+00:00 | 2022-01-15T03:56:59.344293+00:00 | 683 | false | ## Solution intuition\n\nThe idea to efficiently solve this problem is very simple. Let\'s say we have heights as follows:\n\n\n\nFor any particular height which we choose,\n\n\n\nThe maximum area rectangle which includes this height is going to contain all heights to the left which are greater than or equal to the selected height and likewise for heights on the right. In this example, it would be:\n\n\n\nSo, if we can efficiently precompute, for each index `i`, the number of heights to the left which are greater than or equal to `heights[i]` and the number of heights to the right which are greater or equal to `heights[i]`:\n\n\n\nthen computing the area of the rectangle for each index `i` simply becomes:\n\n```\narea of rectangle of height heights[i] = heights[i] * (left[i] + right[i] + 1)\n```\nThe plus one is to include the bar for the selected height itself. If we have `left` and `right` precomputed then the max area can be computed in a single pass over `heights`.\n\n---\n\n## Computing left and right\n\nTo compute `left`, we can use a stack. The code is as follows:\n\n```py\nleft, stack = [0] * n, []\nfor i in range(n):\n h, start = heights[i], i\n while stack and h <= heights[stack[-1]]:\n start = stack.pop()\n\n left[i] = (i - start) + left[start]\n stack.append(i)\n```\nWe push each index onto a stack as we go over them. For each index we also want to compute the number of consecutive heights to the left of the index which are all greater or equal to the height at the index.\n\nTo do so we keep popping indices off the stack until their heights at greater or equal to `heights[i]`. We add the difference between the current index `i` and the last popped index `start` to `left[i]`.\n\nBut when we processed the index at `start`, we may have popped off further values from the stack so we also need to account for that by adding `left[start]`.\n\nIf we don\'t pop anything off the stack then `start = i` so we simply get `left[i] = (i - i) + left[i]` which is zero as one would expect.\n\nThe final code, including `right` is:\n\n```py\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n n = len(heights)\n\n left, stack = [0] * n, []\n for i in range(n):\n h, start = heights[i], i\n while stack and h <= heights[stack[-1]]:\n start = stack.pop()\n\n left[i] = (i - start) + left[start]\n stack.append(i)\n\n right, stack = [0] * n, []\n for i in reversed(range(n)):\n h, end = heights[i], i\n while stack and h <= heights[stack[-1]]:\n end = stack.pop()\n \n right[i] = (end - i) + right[end]\n stack.append(i)\n\n area = 0\n for i, height in enumerate(heights):\n width = right[i] + left[i] + 1\n area = max(area, width * height)\n return area\n```\n\n**Time complexity:** O(N)\n**Space complexity:** O(N)\n | 6 | 0 | ['Stack', 'Python'] | 2 |
largest-rectangle-in-histogram | Java | Stack | Detailed Explanation | O(N) | java-stack-detailed-explanation-on-by-ja-vavs | \nIntuition :\n1) Max area will always have atleast one full height on any index\n2) Find largest rectangle including each bar one by one.\n\ta) For each bar, W | javed_beingzero | NORMAL | 2021-11-30T04:32:33.513277+00:00 | 2022-01-29T17:16:32.658514+00:00 | 677 | false | ```\nIntuition :\n1) Max area will always have atleast one full height on any index\n2) Find largest rectangle including each bar one by one.\n\ta) For each bar, We have to find it\'s left limit & right limit (to know the maximum width)\n\tb) Find each index\'s left limit and store it in left array\n\t\ti) Traverse left to right, try to maximize the width in left side and we will expand until we find prev index\'s val is smaller than curr index\'s val\n\t\tii) We are using stack to check how much we can expand in left side for curr index to find the left limit.\n\t\tiii) Stack will check with the previous value to get to know the left limit but we are traversing right in loop\n\tc) Find it\'s right limit (where we find any index\'s value is smaller than current index in right side array of curr index\n\t\ti) Traverse right to left, try to maximize the width in right side with the help of stack & expand until we find prev index\'s val is smaller.\n\t\tii) Using stack to check how much we can expand in right side for curr index to find the right limit.\n3) Take the maximum of all the max area found by each bar.\n4) calculate area\n\t\twidth * height\nwhere \nwidth = right limit - left limit + 1\nheight = curr index\'s value\n5) Update max area & return it\n```\n```\n public int largestRectangleArea(int[] heights) {\n int len = heights.length;\n int[] left = new int[len];\n int[] right = new int[len];\n Stack<Integer> stack = new Stack<>();\n //traversing left to right and finding the left limit of each number with the help of stack\n for(int i=0;i<len;i++){\n if(stack.isEmpty()){\n stack.push(i);\n left[i] = 0;\n }else{\n //remove the index from stack if their height is greater or equal to curr number\'s height\n while(!stack.isEmpty() && heights[stack.peek()] >= heights[i])\n stack.pop();\n //when we found the index with less height that becomes left limit of curr number (index+1)\n left[i] = stack.isEmpty()?0:stack.peek()+1;\n stack.push(i);\n }\n }\n //removed old stored values\n stack = new Stack<>();\n \n //traversing from right to left and finding the right limit of each number with the help of stack\n for(int i=len-1;i>=0;i--){\n if(stack.isEmpty()){\n stack.push(i);\n right[i] = len-1;\n }else{\n //remove the index from stack if their height is greater or equal to curr number\'s height\n while(!stack.isEmpty() && heights[stack.peek()] >= heights[i])\n stack.pop();\n //when we found the index with less height that becomes right limit of curr number (index-1)\n right[i] = stack.isEmpty()?len-1:stack.peek()-1;\n stack.push(i);\n }\n }\n //calculating the area and finding max area\n int maxArea = Integer.MIN_VALUE;\n int[] area = new int[len];\n for(int i=0;i<len;i++){\n area[i] = (right[i] - left[i] + 1) * heights[i];\n maxArea = Math.max(maxArea, area[i]);\n }\n return maxArea;\n }\n``` | 6 | 0 | ['Stack', 'Java'] | 2 |
largest-rectangle-in-histogram | Standard Interview point of view Stack Solution | standard-interview-point-of-view-stack-s-1ziv | \nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n if(n == 0)\n return 0;\n | sauravgpt | NORMAL | 2021-03-16T08:54:30.049784+00:00 | 2021-03-16T08:54:30.049828+00:00 | 619 | false | ```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n int n = heights.size();\n if(n == 0)\n return 0;\n \n stack<int> S;\n \n int L[n];\n int R[n];\n \n for(int i=0; i<n; i++) {\n while(!S.empty() && heights[S.top()] >= heights[i]) \n S.pop();\n \n L[i] = S.empty() ? -1 : S.top();\n S.push(i);\n }\n \n while(!S.empty()) S.pop();\n \n for(int i=n-1; i>=0; i--) {\n while(!S.empty() && heights[S.top()] >= heights[i])\n S.pop();\n \n R[i] = S.empty() ? n : S.top();\n S.push(i);\n }\n \n int ans = 0;\n \n for(int i=0; i<n; i++) {\n ans = max(ans, (R[i]-L[i]-1) * heights[i]);\n }\n \n return ans;\n }\n};\n``` | 6 | 0 | ['C'] | 0 |
largest-rectangle-in-histogram | Python by monotone stack [w/ Comment] | python-by-monotone-stack-w-comment-by-br-f2zl | Python by monotone stack \n\n---\n\nImplementation:\n\n\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n \n # st | brianchiang_tw | NORMAL | 2021-02-26T10:30:43.319572+00:00 | 2021-02-26T10:30:43.319599+00:00 | 1,230 | false | Python by monotone stack \n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def largestRectangleArea(self, heights: List[int]) -> int:\n \n # store x coordination, init as -1\n stack = [ -1 ]\n \n # add zero as dummy tail \n heights.append( 0 )\n \n # top index for stack\n top = -1\n \n # area of rectangle\n rectangle = 0\n \n # scan each x coordination and y coordination\n for x_coord, y_coord in enumerate(heights):\n \n while heights[ stack[top] ] > y_coord:\n # current height is lower than previous\n # update rectangle area from previous heights\n \n # get height\n h = heights[ stack.pop() ]\n \n # compute width\n w = x_coord - stack[top] -1 \n \n # update maximal area\n rectangle = max(rectangle, h * w)\n \n # push current x coordination into stack\n stack.append( x_coord )\n \n \n return rectangle\n``` | 6 | 0 | ['Math', 'Monotonic Stack', 'Python', 'Python3'] | 0 |
largest-rectangle-in-histogram | [Java] Another thought using divide and conquer | java-another-thought-using-divide-and-co-aec3 | We can find the minimum height and the histogram can be divided into two part, left and right.\nThe ans must be among the mid(minimum) height times the length o | nanotrt2333 | NORMAL | 2020-07-27T04:48:27.622919+00:00 | 2020-09-06T23:42:58.856649+00:00 | 285 | false | We can find the minimum height and the histogram can be divided into two part, left and right.\nThe ans must be among the mid(minimum) height times the length of the interval, or the largest area from either side.\nThen we can come up with a working code,\n```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int n = heights.length;\n return largestRec(heights, 0, n - 1); \n }\n \n private int largestRec(int[] heights, int left, int right) {\n if (left > right) {\n return 0;\n }\n if (left == right) {\n return heights[left];\n }\n int mid = rangeMin(left, right, heights);\n int ans = heights[mid] * (right - left + 1);\n int l = largestRec(heights, left, mid - 1);\n int r = largestRec(heights, mid + 1, right);\n return Math.max(ans, Math.max(l, r));\n }\n \n private int rangeMin(int left, int right, int[] heights) {\n int curMin = left;\n for (int i = left; i <= right; ++i) {\n if (heights[i] < heights[curMin]) {\n curMin = i;\n }\n }\n return curMin;\n }\n}\n```\nwhich is slow because the time to find minimum is O(n), and the time complexity is O(n^2),\nWe can improve it by using RMQ, which gives us O(1) query on range minimums.\n```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n if (heights.length == 0) return 0;\n int n = heights.length;\n int w = (int) (Math.log(n) / Math.log(2) + 1e-10);\n int[][] rmq = new int[n][w + 1];\n for (int i = 0; i <= w; ++i) {\n for (int j = 0; j < n; ++j) {\n if (i == 0) {\n rmq[j][0] = j;\n } else {\n int r = Math.min(n - 1, j + (1 << (i - 1)));\n int a = rmq[j][i - 1], b = rmq[r][i - 1];\n rmq[j][i] = heights[a] <= heights[b] ? a : b;\n }\n }\n }\n return largestRec(heights, 0, n - 1, rmq); \n }\n \n private int largestRec(int[] heights, int left, int right, int[][] rmq) {\n if (left > right) {\n return 0;\n }\n if (left == right) {\n return heights[left];\n }\n int mid = rangeMin(rmq, left, right, heights);\n int ans = heights[mid] * (right - left + 1);\n int l = largestRec(heights, left, mid - 1, rmq);\n int r = largestRec(heights, mid + 1, right, rmq);\n return Math.max(ans, Math.max(l, r));\n }\n \n private int rangeMin(int[][] rmq, int left, int right, int[] heights) {\n int w = (int) (Math.log(right - left) / Math.log(2) + 1e-10);\n int a = rmq[left][w], b = rmq[right - (1 << w) + 1][w];\n return heights[a] <= heights[b] ? a : b;\n }\n}\n```\nRMQ need O(nlogn) time to construct. This method used a so-called technique, binary lifting. \nThe time complexity for find range minimum is now O(1). And the average time complexity is O(nlogn), similiar to quick sort. | 6 | 0 | [] | 0 |
largest-rectangle-in-histogram | My Accepted short Java Solution | my-accepted-short-java-solution-by-tatek-nemi | \nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int answer = 0;\n for(int i = 0; i < heights.length; i++){\n | tatek | NORMAL | 2019-11-14T02:53:58.626925+00:00 | 2019-11-14T02:53:58.626973+00:00 | 755 | false | ```\nclass Solution {\n public int largestRectangleArea(int[] heights) {\n int answer = 0;\n for(int i = 0; i < heights.length; i++){\n int currentHeight = heights[i];\n int left = i, right = i;\n while(left >= 0 && heights[left] >= currentHeight) left--;\n while(right < heights.length && heights[right] >= currentHeight) right++;\n answer = Math.max(answer,((right -1) - (left + 1) + 1 )*currentHeight );\n \n }\n \n return answer;\n }\n}\n``` | 6 | 0 | ['Java'] | 3 |
largest-rectangle-in-histogram | C# Solution | c-solution-by-leonhard_euler-v81q | \npublic class Solution \n{\n public int LargestRectangleArea(int[] heights) \n {\n int n = heights.Length, max = 0;\n var stack = new Stack | Leonhard_Euler | NORMAL | 2019-11-12T05:22:10.242176+00:00 | 2019-11-12T05:22:10.242257+00:00 | 426 | false | ```\npublic class Solution \n{\n public int LargestRectangleArea(int[] heights) \n {\n int n = heights.Length, max = 0;\n var stack = new Stack<int>();\n for(int i = 0; i <= n; i++)\n {\n var height = i < n ? heights[i] : 0;\n while(stack.Count != 0 && heights[stack.Peek()] > height)\n {\n var currHeight = heights[stack.Pop()];\n var prevIndex = stack.Count == 0 ? -1 : stack.Peek();\n max = Math.Max(max, currHeight * (i - 1 - prevIndex));\n }\n stack.Push(i);\n }\n \n return max;\n }\n}\n``` | 6 | 0 | [] | 0 |
largest-rectangle-in-histogram | Recursive JAVA solution in O(nLogn) | recursive-java-solution-in-onlogn-by-nis-qdf8 | \n\tprivate static int largestRectangleArea(int[] heights) {\n if (heights == null || heights.length == 0)\n return 0;\n\n //utility fu | nishantbhb | NORMAL | 2019-06-30T09:12:08.058352+00:00 | 2019-06-30T09:17:14.208101+00:00 | 775 | false | ```\n\tprivate static int largestRectangleArea(int[] heights) {\n if (heights == null || heights.length == 0)\n return 0;\n\n //utility function to divide and conquer\n return maxRectangle(heights, 0, heights.length - 1);\n }\n\n private static int maxRectangle(int[] arr, int l, int r) {\n\n //check if current array is out of bounds\n if (l > r)\n return 0;\n\n //check if it has only one element then that bar is the max area\n if (l == r)\n return arr[l];\n\n //find the minimum index in the current range\n int minIndex = findMinIndex(arr, l, r);\n\n //recursively find max area in the left sub-array\n int left = maxRectangle(arr, l, minIndex - 1);\n\n //recursively find max area in the right sub-array\n int right = maxRectangle(arr, minIndex + 1, r);\n\n //find max area among left and right sub-arrays\n int max = Math.max(left, right);\n\n //compare max with min_bar * curr_range\n return Math.max(max, arr[minIndex] * (r - l + 1));\n }\n\n private static int findMinIndex(int[] arr, int l, int r) {\n int min = Integer.MAX_VALUE;\n int minIndex = l;\n for (int i = l; i <= r; i++) {\n if (arr[i] < min) {\n min = arr[i];\n minIndex = i;\n }\n }\n return minIndex;\n }\n\t\n``` | 6 | 1 | ['Divide and Conquer', 'Recursion', 'Java'] | 5 |
largest-rectangle-in-histogram | (( Swift )) 100% Beaten - Using Stack Trick... O(N) RunTime ComPlexiTY | swift-100-beaten-using-stack-trick-on-ru-w4fz | \nclass Solution {\n func largestRectangleArea(_ heights: [Int]) -> Int {\n \n var heights = heights\n heights.append(0)\n \n | nraptis | NORMAL | 2019-06-20T23:24:42.423615+00:00 | 2019-06-20T23:24:42.423683+00:00 | 319 | false | ```\nclass Solution {\n func largestRectangleArea(_ heights: [Int]) -> Int {\n \n var heights = heights\n heights.append(0)\n \n var result = 0\n \n var stack = [Int]()\n \n for i in heights.indices {\n \n while stack.count > 0 && heights[i] <= heights[stack.last!] {\n \n var height = heights[stack.removeLast()]\n var span = i\n if stack.count > 0 {\n span = i - stack.last! - 1\n }\n result = max(result, span * height)\n }\n \n stack.append(i)\n \n }\n \n return result\n }\n}\n```\n\nBoom, baby, you are on the payroll. Insured and living large. Rollin\' like a big shot and giving back to the homies on the street. | 6 | 0 | [] | 1 |
largest-rectangle-in-histogram | 4ms Java solution, using O(n) stack space, O(n) time | 4ms-java-solution-using-on-stack-space-o-idtv | public class Solution {\n public int largestRectangleArea(int[] height) {\n if ((height == null) || (height.length == 0)) return 0;\n | gliangtao | NORMAL | 2015-11-22T19:17:01+00:00 | 2015-11-22T19:17:01+00:00 | 3,014 | false | public class Solution {\n public int largestRectangleArea(int[] height) {\n if ((height == null) || (height.length == 0)) return 0;\n final int N = height.length;\n int[] s = new int[N + 1];\n int i, top = 0, hi, area = 0;\n s[0] = -1;\n for (i = 0; i < N; i++) {\n hi = height[i];\n while ((top > 0) && (height[s[top]] > hi)) {\n area = Math.max(area, height[s[top]] * (i - s[top - 1] - 1));\n top--;\n }\n s[++top] = i;\n }\n while (top > 0) {\n area = Math.max(area, height[s[top]] * (N - s[top -1] - 1));\n top--;\n }\n return area;\n }\n } | 6 | 1 | ['Stack', 'Java'] | 7 |
largest-rectangle-in-histogram | Largest Rectangle in Histogram [C++] | largest-rectangle-in-histogram-c-by-move-ratb | IntuitionTo solve the problem of finding the largest rectangle area in a histogram, we need to consider how to efficiently calculate the area of the largest rec | moveeeax | NORMAL | 2025-01-22T15:31:26.331273+00:00 | 2025-01-22T15:31:26.331273+00:00 | 594 | false | # Intuition
To solve the problem of finding the largest rectangle area in a histogram, we need to consider how to efficiently calculate the area of the largest rectangle that can be formed within the bounds of the histogram. The key insight is to use a stack to keep track of the indices of the bars in the histogram, which allows us to calculate the area of rectangles in a systematic way.
# Approach
1. **Initialize a stack**: We use a stack to store the indices of the bars. This helps in keeping track of the bars that can form potential rectangles.
2. **Iterate through the bars**: We iterate through each bar in the histogram. For each bar, we check if it is smaller than the bar at the top of the stack.
3. **Calculate the area**: If the current bar is smaller, it means we have found the right boundary for the rectangle formed by the bar at the top of the stack. We then calculate the area of this rectangle and update the maximum area if this area is larger than the previously recorded maximum area.
4. **Push the current index to the stack**: After processing, we push the current index onto the stack.
5. **Handle remaining bars**: After processing all bars, we handle any remaining bars in the stack in a similar manner to ensure all possible rectangles are considered.
This approach ensures that we efficiently calculate the largest rectangle area by leveraging the stack to keep track of potential rectangles and their boundaries.
# Complexity
- **Time complexity**: The time complexity is \(O(n)\), where \(n\) is the number of bars in the histogram. This is because each bar is pushed and popped from the stack exactly once.
- **Space complexity**: The space complexity is \(O(n)\) due to the stack used to store the indices of the bars.
# Code
```cpp
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
stack<int> s;
int maxArea = 0;
for (int i = 0; i <= n; ++i) {
int h = (i == n) ? 0 : heights[i];
while (!s.empty() && h < heights[s.top()]) {
int height = heights[s.top()];
s.pop();
int width = s.empty() ? i : i - s.top() - 1;
maxArea = max(maxArea, height * width);
}
s.push(i);
}
return maxArea;
}
};
```
### Explanation
- **Initialization**: We start by initializing a stack and a variable `maxArea` to keep track of the maximum area found.
- **Iteration**: We iterate through each bar in the histogram. For each bar, we check if it is smaller than the bar at the top of the stack.
- **Area Calculation**: If the current bar is smaller, we calculate the area of the rectangle formed by the bar at the top of the stack. The height of the rectangle is the height of the bar at the top of the stack, and the width is the distance between the current index and the index of the previous bar in the stack.
- **Update Maximum Area**: We update `maxArea` if the calculated area is larger than the current `maxArea`.
- **Push to Stack**: After processing, we push the current index onto the stack.
- **Final Processing**: After processing all bars, we handle any remaining bars in the stack to ensure all possible rectangles are considered.
This method ensures that we efficiently find the largest rectangle area in the histogram using a stack-based approach. | 5 | 2 | ['C++'] | 0 |
largest-rectangle-in-histogram | NO STACK used, only vector!! | no-stack-used-only-vector-by-strange_qua-ij2h | Intuition \n Describe your first thoughts on how to solve this problem. \nSee this problem is little (un-intuitive) but pure logic. Just focus on the pattern of | strange_quark | NORMAL | 2024-09-20T12:03:51.656984+00:00 | 2024-09-21T18:34:04.676337+00:00 | 722 | false | # Intuition \n<!-- Describe your first thoughts on how to solve this problem. -->\nSee this problem is little (un-intuitive) but pure logic. Just focus on the pattern of given a height value at some position i, is the (i + 1)th position is bigger/equal or smaller than the current value.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach of this question is based on a simple intuition mentioned above and thus bifurcate in 2 cases.\n\n1. if a value smaller than the current value appear next in array then max-height of rectangle that can be formed with all future values will be limited by the smaller one. \nEg :- 2 1 5 6 ...\nat first we encounter 2, so 2 can expand only if next number is >= 2,\nbut its 1 so 2\'s ability is nerfed by 1, and 1 will take the place of 2, meaning if a new number 5 comes, it can form rectangle upto 2\'s place with height 1. So 1 replace everything that is bigger than its value that is already encountered.\n\n2. if number that comes next is bigger or equal to current that we just put its value and position.\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& h) {\n int n = h.size(), ans = h[0];\n vector<vector<int>> v;\n v.push_back({h[0], 0});\n for(int i = 1; i < n; i++)\n {\n if(h[i] > v[v.size() - 1][0]) v.push_back({h[i], i});\n else\n {\n int x;\n while(v.size() && v[v.size() - 1][0] >= h[i])\n {\n ans = max(ans, v[v.size() - 1][0] * (i - v[v.size() - 1][1]));\n x = v[v.size() - 1][1];\n v.pop_back();\n }\n v.push_back({h[i], x});\n }\n } \n\n while(!v.empty())\n {\n ans = max(ans, v[v.size() - 1][0] * (n - v[v.size() - 1][1]));\n v.pop_back();\n }\n\n return ans;\n }\n};\n``` | 5 | 0 | ['C++'] | 1 |
largest-rectangle-in-histogram | 💥[EXPLAINED] TypeScript. Runtime beats 99.47% | explained-typescript-runtime-beats-9947-i0x19 | Intuition\nUse a stack to efficiently track the indices of histogram bars. The stack helps determine the width of rectangles formed with each bar as the shortes | r9n | NORMAL | 2024-08-22T10:37:39.273273+00:00 | 2024-08-26T19:52:57.264604+00:00 | 121 | false | # Intuition\nUse a stack to efficiently track the indices of histogram bars. The stack helps determine the width of rectangles formed with each bar as the shortest bar in the rectangle.\n\n# Approach\nUse a stack to track bar indices. For each bar, pop from the stack when encountering a shorter bar, calculating the maximum rectangle area with the popped bar as the smallest height. Finally, pop remaining bars to compute the area.\n\n# Complexity\n- Time complexity:\nO(n), as each bar is pushed and popped from the stack exactly once.\n\n- Space complexity:\nO(n), for the stack used to store indices.\n\n# Code\n```typescript []\nfunction largestRectangleArea(heights: number[]): number {\n const stack: number[] = [];\n let maxArea = 0;\n let index = 0;\n\n while (index < heights.length) {\n if (stack.length === 0 || heights[stack[stack.length - 1]] <= heights[index]) {\n stack.push(index++);\n } else {\n const topOfStack = stack.pop()!;\n const height = heights[topOfStack];\n const width = stack.length === 0 ? index : index - stack[stack.length - 1] - 1;\n maxArea = Math.max(maxArea, height * width);\n }\n }\n\n while (stack.length > 0) {\n const topOfStack = stack.pop()!;\n const height = heights[topOfStack];\n const width = stack.length === 0 ? index : index - stack[stack.length - 1] - 1;\n maxArea = Math.max(maxArea, height * width);\n }\n\n return maxArea;\n}\n\n``` | 5 | 0 | ['TypeScript'] | 0 |
largest-rectangle-in-histogram | Simplest and Easiest Solution ️🔥 | O(n) | C++ | ️ | simplest-and-easiest-solution-on-c-by-va-5223 | Intuition\nTo find the largest rectangle in a histogram, we need to determine the largest possible rectangular area that can be formed using consecutive bars. T | vaib8557 | NORMAL | 2024-06-10T05:50:44.074508+00:00 | 2024-06-10T05:50:44.074547+00:00 | 1,799 | false | # Intuition\nTo find the largest rectangle in a histogram, we need to determine the largest possible rectangular area that can be formed using consecutive bars. The key idea is to efficiently find the next smaller element and the previous smaller element for each bar. Using these, we can compute the width of the rectangle where the current bar is the shortest bar in the rectangle, and thus calculate the maximum area for each bar as the shortest bar.\n\n# Approach\n1. Next Smaller Element (nxt array): Traverse the histogram from right to left. Use a stack to keep track of the indices of the bars. For each bar, pop elements from the stack until you find a bar shorter than the current bar. The index of this shorter bar is stored in the nxt array.\n2. Previous Smaller Element (prev array): Traverse the histogram from left to right. Use a stack to keep track of the indices of the bars. For each bar, pop elements from the stack until you find a bar shorter than the current bar. The index of this shorter bar is stored in the prev array.\n3. Calculate the Maximum Area: For each bar, calculate the width of the rectangle where the current bar is the shortest by using the nxt and prev arrays. The area of the rectangle is the height of the current bar multiplied by the width. Track the maximum area found.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n vector<int>nxt;\n vector<int>prev;\n stack<int>s;\n int n = heights.size();\n s.push(n);\n for(int i=n-1;i>=0;i--){\n while(s.top()!=n && heights[s.top()]>=heights[i]) s.pop();\n nxt.push_back(s.top());\n s.push(i);\n }\n while(!s.empty()) s.pop();\n s.push(-1);\n for(int i=0;i<n;i++){\n while(s.top()!=-1 && heights[s.top()]>=heights[i]) s.pop();\n prev.push_back(s.top());\n s.push(i);\n }\n int m=0;\n for(int i=0;i<n;i++)m = max(m,heights[i] * (nxt[n-1-i]-prev[i]-1));\n return m;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
largest-rectangle-in-histogram | Monotonic Stack Pattern deep understanding | monotonic-stack-pattern-deep-understandi-5n5u | Introduction To stack and NEG pattern - 4 variations covered in\n\n232. Implement Queue using Stacks\n225. Implement Stack using Queues\n155. Min Stack\n496. Ne | Dixon_N | NORMAL | 2024-05-17T19:44:27.714838+00:00 | 2024-05-24T21:30:46.802621+00:00 | 930 | false | Introduction To stack and NEG pattern - **4 variations** covered in\n\n[232. Implement Queue using Stacks](https://leetcode.com/problems/implement-queue-using-stacks/solutions/5203561/implement-queue-using-stacks/)\n[225. Implement Stack using Queues](https://leetcode.com/problems/implement-stack-using-queues/solutions/5203563/implement-stacks-using-queue/)\n[155. Min Stack](https://leetcode.com/problems/min-stack/solutions/4185675/java-simple-solution-using-two-stack-and-one-stack/)\n[496. Next Greater Element I](https://leetcode.com/problems/next-greater-element-i/solutions/5164552/must-read-intuitive-pattern-for-deep-understanding-of-nge-and-nsm/) **very very important**\n[503. Next Greater Element II](https://leetcode.com/problems/next-greater-element-ii/solutions/5201809/brute-intuitive-solution-beats-98-monotonic-pattern/)\n[907. Sum of Subarray Minimums](https://leetcode.com/problems/sum-of-subarray-minimums/solutions/5165808/monotonic-patter-continuation/) **pattern**\n[11. Container With Most Water](https://leetcode.com/problems/container-with-most-water/solutions/5165076/must-read-maximum-water-pattern/)\n[42. Trapping Rain Water](https://leetcode.com/problems/trapping-rain-water/solutions/5165626/building-intuitive-solution-one-step-at-a-time/)\n[1856. Maximum Subarray Min-Product](https://leetcode.com/problems/maximum-subarray-min-product/solutions/5167159/must-read-monotonic-stack-pattern-variations/)\n[735. Asteroid Collision](https://leetcode.com/problems/asteroid-collision/solutions/5166334/brute-solution/)\n[402. Remove K Digits](https://leetcode.com/problems/remove-k-digits/solutions/5166502/beast-intuitive-approach-step-by-step-nsg-to-right/)\n[2104. Sum of Subarray Ranges](https://leetcode.com/problems/sum-of-subarray-ranges/solutions/5166891/beastt-solution/)\n[84. Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram/solutions/5172029/monotonic-stack-pattern-deep-understanding/)\n[85. Maximal Rectangle](https://leetcode.com/problems/maximal-rectangle/solutions/5201947/brute-intuitive-solution-beats-98-monotonic-stack-pattern-deep-understanding/)\n[739. Daily Temperatures](https://leetcode.com/problems/daily-temperatures/solutions/5167031/must-read-monotonic-stack-pattern-variations/) **Fundamental**\n[853. Car Fleet](https://leetcode.com/problems/car-fleet/solutions/5167204/must-read-monotonic-stack-pattern-variations/)\n[150. Evaluate Reverse Polish Notation](https://leetcode.com/problems/evaluate-reverse-polish-notation/solutions/5172161/stack-intuitive-solution/)\n[895. Maximum Frequency Stack](https://leetcode.com/problems/maximum-frequency-stack/solutions/5172171/stack-implementation-problem/) **VVI** Implementation problem\n[173. Binary Search Tree Iterator](https://leetcode.com/problems/binary-search-tree-iterator/solutions/5172179/brute-solution/)\n[682. Baseball Game](https://leetcode.com/problems/baseball-game/solutions/5172183/straight-forward-approach/)\n[1209. Remove All Adjacent Duplicates in String II](https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii/solutions/5172210/stack-solution-pattern/) **Must Go through**\n[456. 132 Pattern](https://leetcode.com/problems/132-pattern/solutions/5202876/monotonic-stack/)\n[22. Generate Parentheses](https://leetcode.com/problems/generate-parentheses/solutions/5202882/monotonic-stack/)\n[460. LFU Cache]()\n[146. LRU Cache]()\n[901. Online Stock Span](https://leetcode.com/problems/online-stock-span/solutions/5172217/stack-nge-and-nse-deep-understanding/) **Must Read**\n[239. Sliding Window Maximum](https://leetcode.com/problems/sliding-window-maximum/solutions/5175931/nge-pattern/) **All three solution**\n[856. Score of Parentheses](https://leetcode.com/problems/score-of-parentheses/solutions/5203496/scoreofparentheses/)\n[844. Backspace String Compare](https://leetcode.com/problems/backspace-string-compare/solutions/5203544/brute-and-optimized-backspacecompare-beats-100/)\n[71. Simplify Path](https://leetcode.com/problems/simplify-path/solutions/5203538/simplifypath/)\n\n<br/>\n\n\n## 84. Largest Rectangle in Histogram\n# Code\n```java []\n//Next Smaller Element to the right pattern \n\n/*for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {\n ans[stack.pop()] = arr[i]; //Next Smaller Element to the right pattern \n }\n stack.push(i);\n}\n\n*/\nimport java.util.Stack;\n\npublic class Solution {\n\n\n public int largestRectangleArea(int[] heights) {\n int maxArea = 0;\n Stack<Pair> stack = new Stack<>();\n int n= heights.length;\n for (int i = 0; i <= n; i++) {\n int start = i;\n // Pop elements from stack while the current height is less than the height at stack\'s top\n while (!stack.isEmpty() && (i==n || stack.peek().height > heights[i])) {\n Pair pair = stack.pop();\n int index = pair.index;\n int height = pair.height;\n int length =i-index;\n maxArea = Math.max(maxArea, height * length);\n start = index; // Update start to the index of the popped element\n }\n if(i<n) stack.push(new Pair(start, heights[i])); // Push current index and height as a pair\n }\n\n return maxArea;\n }\n class Pair {\n int index;\n int height;\n\n Pair(int index, int height) {\n this.index = index;\n this.height = height;\n }\n }\n}\n\n````\n```java []\n//Next Smaller Element to the right pattern \n\n/*for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {\n ans[stack.pop()] = arr[i]; //Next Smaller Element to the right pattern \n }\n stack.push(i);\n}\n\n*/\nimport java.util.Stack;\n\npublic class Solution {\n\n\n public int largestRectangleArea(int[] heights) {\n int maxArea = 0;\n Stack<Pair> stack = new Stack<>();\n\n for (int i = 0; i < heights.length; i++) {\n int start = i;\n // Pop elements from stack while the current height is less than the height at stack\'s top\n while (!stack.isEmpty() && stack.peek().height > heights[i]) {\n Pair pair = stack.pop();\n int index = pair.index;\n int height = pair.height;\n int length =i-index;\n maxArea = Math.max(maxArea, height * length);\n start = index; // Update start to the index of the popped element\n }\n stack.push(new Pair(start, heights[i])); // Push current index and height as a pair\n }\n\n // Process remaining elements in the stack\n for (Pair pair : stack) {\n int index = pair.index;\n int height = pair.height;\n maxArea = Math.max(maxArea, height * (heights.length - index));\n }\n\n return maxArea;\n }\n class Pair {\n int index;\n int height;\n\n Pair(int index, int height) {\n this.index = index;\n this.height = height;\n }\n }\n}\n\n```\n\n## 739. Daily Temperatures\n```java []\nimport java.util.*;\n\nclass Pair {\n int index;\n int temperature;\n\n public Pair(int index, int temperature) {\n this.index = index;\n this.temperature = temperature;\n }\n}\n\nclass Solution {\n public int[] dailyTemperatures(int[] temperatures) {\n int[] res = new int[temperatures.length];\n Stack<Pair> stack = new Stack<>();\n\n for (int i = 0; i < temperatures.length; i++) {\n int t = temperatures[i];\n while (!stack.isEmpty() && t > stack.peek().temperature) {\n Pair stackTop = stack.pop();\n res[stackTop.index] = i - stackTop.index;//Pattern begins right-left.\n }\n stack.push(new Pair(i, t));\n }\n\n return res;\n }\n}\n\n```\n\n\n## 1856. Maximum Subarray Min-Product\n# Code\n```\nclass Solution {\n \n private static final int MOD = (int)(1e9+7);\n \n public int maxSumMinProduct(int[] nums) {\n long res = 0;\n Stack<Pair> stack = new Stack<>();\n long[] prefix = new long[nums.length + 1];\n \n // Compute the prefix sums\n for (int i = 0; i < nums.length; i++) {\n prefix[i + 1] = prefix[i] + nums[i];\n }\n \n // Traverse through the nums array\n for (int i = 0; i < nums.length; i++) {\n int newStart = i;\n \n while (!stack.isEmpty() && stack.peek().value > nums[i]) {\n Pair pair = stack.pop();\n int start = pair.index;\n int val = pair.value;\n long total = prefix[i] - prefix[start];\n res = Math.max(res, val * total);\n newStart = start;\n }\n \n stack.push(new Pair(newStart, nums[i]));\n }\n \n // Process the remaining elements in the stack\n while (!stack.isEmpty()) {\n Pair pair = stack.pop();\n int start = pair.index;\n int val = pair.value;\n long total = prefix[nums.length] - prefix[start];\n res = Math.max(res, val * total);\n }\n \n return (int)(res % (MOD));\n }\n class Pair {\n int index, value;\n \n Pair(int index, int value) {\n this.index = index;\n this.value = value;\n }\n }\n}\n\n``` | 5 | 0 | ['Java'] | 0 |
largest-rectangle-in-histogram | Easy to understand Backtracking and Stack Approach | easy-to-understand-backtracking-and-stac-euwe | Intuition\n Describe your first thoughts on how to solve this problem. \nEasy method to do the question.\n# Approach\n Describe your approach to solving the pro | ShivaanjayNarula | NORMAL | 2024-05-10T22:49:23.834256+00:00 | 2024-05-10T22:49:23.834287+00:00 | 169 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEasy method to do the question.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPrevious and Next Arrays: The previous and nexts functions are used to create two arrays, prev and next, which store the indices of the previous and next smaller elements for each element in the input array heights.\n\nCalculating Rectangle Area: For each element in heights, the code calculates the width of the rectangle that can be formed with that element as the height. The width is determined by the difference between the indices stored in prev and next arrays (minus one to exclude the current element).\n\nFinding Maximum Area: The code then calculates the area of each rectangle (height * width) and stores it in the ans array. Finally, it returns the maximum element from the ans array, which represents the largest rectangle that can be formed in the histogram.\n\nStack : The key idea behind this approach is to use a stack to keep track of increasing elements. When we encounter a smaller element, we pop elements from the stack until we find an element smaller than the current one. This helps us determine the previous and next smaller elements efficiently.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights)\n {\n int n = heights.size();\n vector<int> prev; // Stores the index of the previous smaller element for each element\n vector<int> next; // Stores the index of the next smaller element for each element\n previous(prev, heights.data(), n); // Calculate the previous array\n nexts(next, heights.data(), n); // Calculate the next array\n vector<int> ans; // Stores the area of each rectangle\n reverse(next.begin(), next.end()); // Reverse the next array for easier calculation\n for(int i = 0; i < n; i++)\n {\n ans.push_back(heights[i] * (next[i] - prev[i] - 1)); // Calculate area for each element\n }\n return *max_element(ans.begin(), ans.end()); // Return the maximum area\n }\n\n // Function to calculate the previous array\n void previous(vector<int>& prev, int *arr, int n)\n {\n stack<int> st;\n for(int i = 0; i < n; i++)\n {\n while(!st.empty() && arr[st.top()] >= arr[i])\n {\n st.pop(); // Remove elements greater than or equal to arr[i] from stack\n }\n if(st.empty())\n {\n prev.push_back(-1); // If stack is empty, there is no previous smaller element\n }\n else\n {\n prev.push_back(st.top()); // Otherwise, store the index of the previous smaller element\n }\n st.push(i); // Push current element index onto stack\n }\n }\n\n // Function to calculate the next array\n void nexts(vector<int>& next, int *arr, int n)\n {\n stack<int> st;\n for(int i = n-1; i >= 0; i--)\n {\n while(!st.empty() && arr[st.top()]>=arr[i])\n {\n st.pop(); // Remove elements greater than or equal to arr[i] from stack\n }\n if(st.empty())\n {\n next.push_back(n); // If stack is empty, there is no next smaller element, so n is used\n }\n else\n {\n next.push_back(st.top()); // Otherwise, store the index of the next smaller element\n }\n st.push(i); // Push current element index onto stack\n }\n }\n};\n\n```\nHope you all guys the best!!!!! | 5 | 0 | ['Backtracking', 'Stack', 'Recursion', 'C++'] | 0 |
largest-rectangle-in-histogram | Monotonic stack vs DP||37ms Beats 99.98% | monotonic-stack-vs-dp37ms-beats-9998-by-3ucng | Intuition\n Describe your first thoughts on how to solve this problem. \nThe same method can generalized to solve 85. Maximal Rectangle\n\n2 approaches are prov | anwendeng | NORMAL | 2024-04-18T12:29:11.136594+00:00 | 2024-04-18T12:29:11.136618+00:00 | 1,294 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe same method can generalized to solve [85. Maximal Rectangle](https://leetcode.com/problems/maximal-rectangle/solutions/5014468/monotonic-stackdpcount-successive-1s16ms-beats-9962/)\n\n2 approaches are provided. The monotonic stack method is 1-pass. DP method is a 2-pass method.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe part for monotonic stack is almost the same like in solving Leetcode 85. Maximal Rectangle which is harder.\n\nThe pattern for monotonic stack is used for many Leetcode\'s hard questions for which the variant is applied to LC 84 & LC 85 as follows (using C-style)\n```\nst={-1}; //let stack contain an element -1\ntop=0;\nfor (r=0; r<=col; r++){//Moving right index\n // Count the successive \'1\'s & store in h[j]\n h[j]=compute_for_h(j);\n\n // monotonic stack has at least element -1\n while(st has more than -1 and (j==col or h[j]<h[st[top]])){\n m=st[top--];//pop\n l=st[top];//left index\n w=r-l-1;\n area=h[m]*w;\n maxArea=max(maxArea, area);\n }\n st[++top]=j;//push\n}\n```\n\nThe following is generated by random data to show the maxArea for the histogram `h`. The green area is in fact the cells with \'1\' which are connected to the cells \'1\' in the row for considering.\n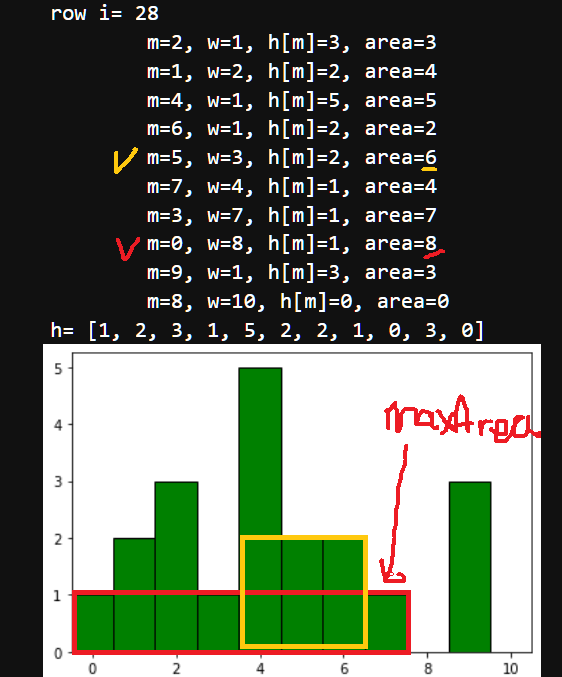\n[Please turn on english subtitles. Solving [42. Trapping Rain Water](https://leetcode.com/problems/trapping-rain-water/solutions/5010020/monotonic-stack-vs-priority-queueusing-pyplot-explain3ms-beats-9910/) use a similar way of monotonic stack, in the film is shown how to use pyplot.bar to visualize the data, especially for the area computing.]\n[https://youtu.be/IERpc-YJIT0?si=HaXCPOHz83goH3yf](https://youtu.be/IERpc-YJIT0?si=HaXCPOHz83goH3yf)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code using monotonic stack||37ms Beats 99.98%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int largestRectangleArea(vector<int>& heights) {\n if (heights.size()==0) return 0;\n heights.push_back(0);// easy for removing if-branch\n const int n=heights.size();\n int maxA=0;\n vector<int> st={-1};\n for(int r=0; r<n; r++){\n while(st.size()>1 && heights[st.back()]>=heights[r]){\n const int m=st.back();\n st.pop_back();\n const int w=r-st.back()-1;\n const int area=heights[m]*w;\n maxA=max(maxA, area);\n }\n st.push_back(r);\n }\n return maxA;\n }\n};\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# C++ using DP||45ms Beats 99.88%\n\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n //l: the x-coordinate of the bar to the left with height h[l] < h[i].\n //r: the x-coordinate of the bar to the right with height h[r] < h[i].\n int largestRectangleArea(vector<int>& heights) {\n const int n=heights.size();\n if (heights.size()==0) return 0;\n vector<int> l(n), r(n);\n r[n-1]=n, l[0]=-1;\n\n for(int i=1; i<n; i++){\n int p=i-1;\n while(p>=0 && heights[p]>=heights[i])\n p=l[p];\n l[i]=p;\n }\n\n int maxA=heights[n-1]*(r[n-1]-l[n-1]-1);\n for(int i=n-2; i>=0; i--){\n int p=i+1;\n while(p<n && heights[p]>=heights[i])\n p=r[p];\n r[i]=p;\n maxA=max(maxA, heights[i]*(r[i]-l[i]-1));\n }\n return maxA;\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Monotonic Stack', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++/Java/Python] From Straightforward to Optimized Bitmask DP - O(2^n * n) - Clean & Concise | cjavapython-from-straightforward-to-opti-yyjj | \u2714\uFE0F Solution 1: Straightforward Bitmask DP\n- Let dp(mask, remainTime) is the minimum of work sessions needed to finish all the tasks represent by mask | hiepit | NORMAL | 2021-08-31T13:34:07.662485+00:00 | 2021-09-01T03:15:46.029919+00:00 | 11,809 | false | **\u2714\uFE0F Solution 1: Straightforward Bitmask DP**\n- Let `dp(mask, remainTime)` is the minimum of work sessions needed to finish all the tasks represent by `mask` (where `i`th bit = 1 means tasks[i] need to proceed) with the `remainTime` we have for the current session.\n- Then `dp((1 << n) - 1, 0)` is our result\n\t- We use `mask` as `111...1111`, represent we need to process all `n` tasks.\n\t- We pass `remainTime = 0`, which means there is no remain time for the current session; ask them to create a new session.\n\n<iframe src="https://leetcode.com/playground/CQvMZRS9/shared" frameBorder="0" width="100%" height="530"></iframe>\n\nComplexity:\n- Time: `O(2^n * sessionTime * n)`, where `n <= 14` is length of tasks, `sessionTime <= 15`.\n Explain: There is total `2^n * sessionTime` dp states, they are `dp[0][0], dp[1][0]..., dp[2^n-1][remainTime]`. Each dp state needs an inner loop `O(n)` to calculate the result. \n- Space: `O(2^n * sessionTime)`\n\n---\n\n**\u2714\uFE0F Solution 2: Bitmask DP - Optimized (Independence with SessionTime)**\n- Let `dp(mask)` return `(the minimum of work sessions needed, remainTime)` to finish all the tasks represent by `mask` (where `i`th bit = 1 means tasks[i] need to proceed).\n- Then `dp((1 << n) - 1)[0]` is our result\n\t- We use `mask` as `111...1111`, represent we need to process all `n` tasks.\n\n<iframe src="https://leetcode.com/playground/MkXWVVw2/shared" frameBorder="0" width="100%" height="640"></iframe>\n\nComplexity:\n- Time: `O(2^n * n)`, where `n <= 14` is length of tasks.\n Explain: There is total `2^n` dp states, they are `dp[0], dp[1]..., dp[2^n-1]`. Each dp state needs an inner loop `O(n)` to calculate the result.\n- Space: `O(2^n)`\n\nIf you think this **post is useful**, I\'m happy if you **give a vote**. Any **questions or discussions are welcome!** Thank a lot. | 180 | 1 | [] | 12 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ Solution | Recursion + Memoization | c-solution-recursion-memoization-by-invu-9eiq | Wrong Greedy Approach:\n\n- Sort the tasks array and keep adding the task to the current session until the sum becomes equal to or more than the sessionTime.\n- | invulnerable | NORMAL | 2021-08-29T04:01:58.689715+00:00 | 2021-08-29T04:01:58.689760+00:00 | 17,293 | false | Wrong Greedy Approach:\n\n- Sort the `tasks` array and keep adding the task to the current session until the sum becomes equal to or more than the `sessionTime`.\n- This approach fails on test cases like `tasks` = {3, 4, 7, 8, 10} `sessionTime` = 12\n\n**Solution:**\n\nWe have created a vector named `sessions`. The length of which denotes the number of work sessions we currently have, and the value at `ith` index `sessions[i]` denotes the number of work hours we have completed in the `ith` session. Now in such scenerio\n\n- Each task in the `tasks` array has two options:\n 1. Get included in one of the session in `sessions`\n 2. Get included in a new session by adding one to the `sessions`.\n\nThe minimum of the two above choices will be the answer. The below code shows the Rercursive solution.\n\n**Recursion (TLE):**\n\n```\nclass Solution {\npublic:\n vector<int> sessions;\n\n int solve(vector<int>& tasks, int n, int sessionTime, int pos) {\n if (pos >= n )\n return 0;\n\n // adding the current task to a new session\n sessions.push_back(tasks[pos]);\n int ans = 1 + solve(tasks, n, sessionTime, pos + 1);\n sessions.pop_back();\n \n // trying to add it to the previous active session\n for (int i = 0; i < sessions.size();i++) {\n if (sessions[i] + tasks[pos] <= sessionTime) {\n sessions[i] += tasks[pos];\n ans = min(ans, solve(tasks, n, sessionTime, pos + 1));\n sessions[i] -= tasks[pos];\n }\n }\n \n return ans;\n }\n \n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n return solve(tasks, n, sessionTime, 0);\n }\n};\n```\n\n\nIn order to memoize the solution, we use a unordered map from String to int `dp`. The two states which we need to memoize are the `pos` and the `sessions`. We encode both these state by concating them as string with `$` as a delimeter.\n\nNote: We first sort the `sessions` to reduce the number of repeated states.\n\n**Recursion + Memoization Code (Accepted):**\n\n```\nclass Solution {\npublic:\n vector<int> sessions;\n unordered_map<string , int> dp;\n \n string encodeState(int pos, vector<int>& sessions) {\n vector<int> copy = sessions;\n sort(copy.begin(), copy.end());\n \n string key = to_string(pos) + "$";\n for (int i = 0; i < copy.size(); i++)\n key += to_string(copy[i]) + "$";\n \n return key;\n }\n \n int solve(vector<int>& tasks, int n, int sessionTime, int pos) {\n if (pos >= n )\n return 0;\n \n string key = encodeState(pos, sessions);\n \n if (dp.find(key) != dp.end())\n return dp[key];\n \n sessions.push_back(tasks[pos]);\n int ans = 1 + solve(tasks, n, sessionTime, pos + 1);\n sessions.pop_back();\n \n for (int i = 0; i < sessions.size();i++) {\n if (sessions[i] + tasks[pos] <= sessionTime) {\n sessions[i] += tasks[pos];\n ans = min(ans, solve(tasks, n, sessionTime, pos + 1));\n sessions[i] -= tasks[pos];\n }\n }\n \n return dp[key] = ans;\n }\n \n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n return solve(tasks, n, sessionTime, 0);\n }\n};\n```\n\n | 178 | 10 | [] | 32 |
minimum-number-of-work-sessions-to-finish-the-tasks | Easier than top voted ones | LegitClickbait | c++ | easier-than-top-voted-ones-legitclickbai-dezv | Algorithm\n1. We use 2 things -> mask to denote which elements are processed. If ith bit is 1 means ith element is processed. -> currentTime we start with 0 as | shourabhpayal | NORMAL | 2021-08-29T05:55:56.436519+00:00 | 2021-08-30T06:46:24.641428+00:00 | 7,108 | false | **Algorithm**\n1. We use 2 things -> ```mask``` to denote which elements are processed. If ```ith``` bit is 1 means ```ith``` element is processed. -> ```currentTime``` we start with 0 as current time.\n2. At each call go through all the unprocessed elements only.\n3. We can choose to include the ith unprocessed element in current session like this -> ```help(a, mask | (1<<i), currTime + a[i])```\n4. Or choose to include it in next session like this -> ```1 + help(a, mask | (1<<i), a[i])```\n5. Take minimum of step 3 and 4 across all unprocessed elements like this -> ```ans = min({ans, includeInCurrentSession, includeInNextSession})``` .\n2. If ```currentTime``` becomes more than targetTime it is invalid state.\n3. If all elements are processed then its the end of our algorithm.\n\n***Note***: \nWhen we do ```mask | (1<<i)``` we set the ith bit in mask to indicate element at ith position is processed.\nWhen we do ```mask & (1<<i)``` we are checking if ith bit in mask is set or not.\n\n**Code**\n```\nclass Solution {\npublic:\n int n, time, allOnes;\n int ans;\n int dp[1<<15][16];\n int minSessions(vector<int>& a, int t) {\n time = t;\n n = a.size();\n allOnes = (1<<n)-1;\n memset(dp, -1, sizeof dp);\n ans = help(a, 0, 0);\n return ans;\n }\n \n int help(vector<int> &a, int mask, int currTime){\n if(currTime > time) return INT_MAX;\n if(mask == allOnes) return 1;\n if(dp[mask][currTime] != -1) return dp[mask][currTime];\n int ans = INT_MAX;\n for(int i = 0 ; i < n ; i++){\n if( (mask & (1<<i)) == 0){\n int includeInCurrentSession = help(a, mask | (1<<i), currTime + a[i]);\n int includeInNextSession = 1 + help(a, mask | (1<<i), a[i]);\n ans = min({ans, includeInCurrentSession, includeInNextSession});\n }\n }\n return dp[mask][currTime] = ans;\n }\n};\n```\n**Time Complexity**: ```O(2^N * sessionTime * N)``` Here N is length of array ```a i.e tasks``` and sessionTime is ```time``` | 106 | 5 | ['Dynamic Programming', 'Bit Manipulation', 'C'] | 22 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Python] dynamic programming on subsets, explained | python-dynamic-programming-on-subsets-ex-d6rp | You can see that in this problem n <= 14, so we need to apply some kind of bruteforce algorithm. If we try just n! options, it will be too big, so the idea is t | dbabichev | NORMAL | 2021-08-29T04:01:33.963104+00:00 | 2021-08-29T09:28:38.249476+00:00 | 7,599 | false | You can see that in this problem `n <= 14`, so we need to apply some kind of bruteforce algorithm. If we try just `n!` options, it will be too big, so the idea is to use dynamic programming on subsets. Let `dp(mask)`, where `mask` is bitmask of already used jobs be the tuple of numbers: first one is number of sessions we took so far and the second one is how much time we spend for the last session.\n\nTo calculate `dp(mask)`, let us say `dp(10110)`, we need to look at all places we have `0`, that is `1-th, 2-th, 4-th` and look at positions `dp(00110), dp(10010), dp(10100)`. We calculate `full = last + tasks[j] > T` is indicator that last session is full and we need to start new one. So, total number of sessions we have is `pieces + full` and what we have in the last session is `tasks[j]` if session is full: we start new one and `tasks[j] + last` if it is not full.\n\n#### Complexity\nTime complexity is `O(2^n * n)`, because we have `2^n` masks and `O(n)` transitions from given mask. Space complexity is `O(2^n)`.\n\n```python\nclass Solution:\n def minSessions(self, tasks, T):\n n = len(tasks)\n\n @lru_cache(None)\n def dp(mask):\n if mask == 0: return (1, 0)\n ans = (float("inf"), float("inf"))\n for j in range(n):\n if mask & (1<<j):\n pieces, last = dp(mask - (1 << j))\n full = (last + tasks[j] > T)\n ans = min(ans, (pieces + full, tasks[j] + (1-full)*last)) \n return ans\n\n return dp((1<<n) - 1)[0]\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 86 | 8 | ['Dynamic Programming', 'Bitmask'] | 12 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Python] Clean & Simple, no bitmask | python-clean-simple-no-bitmask-by-yo1995-b5d9 | The full problem is NP-hard: https://en.wikipedia.org/wiki/Bin_packing_problem\n\nTo get the exact result, we have to recurse with some smart memorization techn | yo1995 | NORMAL | 2021-08-29T04:26:02.778483+00:00 | 2021-08-29T04:30:05.795818+00:00 | 4,814 | false | The full problem is NP-hard: https://en.wikipedia.org/wiki/Bin_packing_problem\n\nTo get the exact result, we have to recurse with some smart memorization techniques.\n\nI still find it challenging to use bitmask, so here is the dfs version.\n\nComparing to the default dfs which gets TLE, the trick here is to loop through the sessions, rather than the tasks themselves.\n\n```python\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n n = len(tasks)\n tasks.sort(reverse=True)\n sessions = []\n result = [n]\n \n def dfs(index):\n if len(sessions) > result[0]:\n return\n if index == n:\n result[0] = len(sessions)\n return\n for i in range(len(sessions)):\n if sessions[i] + tasks[index] <= sessionTime:\n sessions[i] += tasks[index]\n dfs(index + 1)\n sessions[i] -= tasks[index]\n sessions.append(tasks[index])\n dfs(index + 1)\n sessions.pop()\n \n dfs(0)\n return result[0]\n``` | 64 | 0 | ['Python'] | 11 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ & Java Bitmask DP with Explanation time: O(n * 2^n) space: O(2^n) | c-java-bitmask-dp-with-explanation-time-ac0yu | dp[mask] = {a, b} where\na - minimum number of session\nb - minimum time of last session\nThe idea is to go through all tasks who belong to mask and optimally c | felixhuang07 | NORMAL | 2021-08-29T04:01:03.912852+00:00 | 2021-09-04T06:08:58.259600+00:00 | 5,762 | false | dp[mask] = {a, b} where\na - minimum number of session\nb - minimum time of last session\nThe idea is to go through all tasks who belong to mask and optimally choose the last task \'t\' that was added to last session.\n\nSimilar problem: CSES Problem Set - Elevator Rides https://cses.fi/problemset/task/1653\nThis is exactly the same problem if you change the capacity of elevator to \'sessionTime\' and weights of people to \'task\'.\n```\n// C++ Solution\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n const int N = tasks.size();\n const int INF = 1e9;\n vector<pair<int, int>> dp(1 << N, {INF, INF});\n dp[0] = {0, INF};\n for(int mask = 1; mask < (1 << N); ++mask) {\n pair<int, int> best = {INF, INF};\n for(int i = 0; i < N; ++i) {\n if(mask & (1 << i)) {\n pair<int, int> cur = dp[mask ^ (1 << i)];\n if(cur.second + tasks[i] > sessionTime) {\n cur = {cur.first + 1, tasks[i]};\n } else\n cur.second += tasks[i];\n best = min(best, cur);\n }\n }\n dp[mask] = best;\n }\n return dp[(1 << N) - 1].first;\n }\n};\n```\n```\n// Java Solution\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n int n = tasks.length, MAX = Integer.MAX_VALUE;\n int[][] dp = new int[1<<n][2];\n dp[0][0] = 1;\n dp[0][1] = 0;\n \n for(int i = 1; i < (1 << n); i++) {\n dp[i][0] = MAX;\n dp[i][1] = 0;\n \n for(int t = 0; t < n; t++) {\n if(((1<<t) & i) == 0) continue;\n \n int[] prev = dp[(1<<t) ^ i];\n if(prev[1] + tasks[t] <= sessionTime) {\n dp[i] = min(dp[i], new int[]{prev[0], prev[1] + tasks[t]});\n }else{\n dp[i] = min(dp[i], new int[]{prev[0] + 1, tasks[t]});\n }\n } \n }\n \n return dp[(1<<n) - 1][0];\n }\n \n private int[] min(int[] d1, int[] d2) {\n if(d1[0] > d2[0]) return d2;\n if(d1[0] < d2[0]) return d1;\n if(d1[1] > d2[1]) return d2;\n \n return d1;\n }\n}\n``` | 50 | 1 | ['Dynamic Programming', 'C', 'Bitmask', 'Java'] | 10 |
minimum-number-of-work-sessions-to-finish-the-tasks | JAVA solution 15ms DFS + Pruning | java-solution-15ms-dfs-pruning-by-kge-oreo | The pruning - you only need to put the first k tasks in first k sessions.\n\nFor example, assume you are trying if the tasks can be assgiend to 5 sessions (i.e. | kge | NORMAL | 2021-08-29T05:49:01.058615+00:00 | 2021-08-30T06:15:16.389425+00:00 | 3,618 | false | The pruning - you only need to put the first k tasks in first k sessions.\n\nFor example, assume you are trying if the tasks can be assgiend to 5 sessions (i.e., n == 5).\n\n- When you run DFS for the first task, you see 5 empty sessions. It doesn\'t matter which session the task is assgiend to, becasue all of the 5 sessions are identical (/empty). If the DFS fails with the first taks assigned to session #1, there is no need to try the DFS with the first task assigned to session #2, #3, etc.\n- Similarly, for the first two tasks, you only need to consider assigning them to the first two sessions. For example, the following cases are all identical and there is no need to try all of them:\n\t- | session #1 | session #2 | session #3 | session #4 | session #5 |\n\t- |------------|------------|------------|------------|------------|\n\t- | task 1 | task 2 | | | |\n\t- | task 1 | | task 2 | | |\n\t- | | | | task 2 | task 1 |\n- For the first 3 tasks, you only need to consider assigning them to the first 3 sessions.\n- etc.\n\n```JAVA\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n for (int n = 1; n < tasks.length; n++) {\n int[] remain = new int[n];\n for (int i = 0; i < n; i++) {\n remain[i] = sessionTime;\n }\n if (canWork(tasks, 0, remain)) {\n return n;\n }\n }\n return tasks.length;\n }\n \n public boolean canWork(int[] tasks, int curr, int[] remain) {\n if (curr == tasks.length) {\n return true;\n }\n for (int i = 0; i < remain.length; i++) {\n if (i > curr) continue; // *pruning*\n if (remain[i] >= tasks[curr]) {\n remain[i] -= tasks[curr];\n if (canWork(tasks, curr + 1, remain)) {\n return true;\n }\n remain[i] += tasks[curr];\n }\n }\n return false;\n }\n}\n``` | 38 | 0 | [] | 10 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python | Backtracking | 664ms | 100% time and space | Explanation | python-backtracking-664ms-100-time-and-s-v68y | I think the test cases are little weak, because I just did backtracking and a little pruning and seems to be 4x faster than bitmask solutions.\n The question bo | detective_dp | NORMAL | 2021-08-29T14:54:17.225745+00:00 | 2021-08-30T20:36:52.024589+00:00 | 3,051 | false | * I think the test cases are little weak, because I just did backtracking and a little pruning and seems to be 4x faster than bitmask solutions.\n* The question boils down to finding minimum number of subsets such that each subset sum <= sessionTime. I maintain a list called subsets, where I track each subset sum. For each tasks[i] try to fit it into one of the existing subsets or create a new subset with this tasks[i] and recurse further. Once I reach the end of the list, I compare the length of the subsets list with current best and record minimum.\n* For pruning, I do the following - Once the length of subsets is larger than current best length, I backtrack. This doesn\'t decrease complexity in mathematical terms but I think in implementation, it helps a lot.\n\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n subsets = []\n self.ans = len(tasks)\n \n def func(idx):\n if len(subsets) >= self.ans:\n return\n \n if idx == len(tasks):\n self.ans = min(self.ans, len(subsets))\n return\n \n for i in range(len(subsets)):\n if subsets[i] + tasks[idx] <= sessionTime:\n subsets[i] += tasks[idx]\n func(idx + 1)\n subsets[i] -= tasks[idx]\n \n subsets.append(tasks[idx])\n func(idx + 1)\n subsets.pop()\n \n func(0)\n return self.ans | 30 | 0 | ['Backtracking', 'Python3'] | 2 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ DFS with pruning | c-dfs-with-pruning-by-mingrui-48x4 | \nclass Solution {\n vector<int> tasks;\n int sessionTime;\n int result;\n vector<int> sessions;\n void dfs(int idx) {\n if (sessions.size | mingrui | NORMAL | 2021-08-29T04:02:25.026920+00:00 | 2021-08-29T04:07:22.397882+00:00 | 2,824 | false | ```\nclass Solution {\n vector<int> tasks;\n int sessionTime;\n int result;\n vector<int> sessions;\n void dfs(int idx) {\n if (sessions.size() >= result) {\n return;\n }\n if (idx == tasks.size()) {\n result = sessions.size();\n return;\n }\n for (int i = 0; i < sessions.size(); i++) {\n if (sessions[i] + tasks[idx] <= sessionTime) {\n sessions[i] += tasks[idx];\n dfs(idx + 1);\n sessions[i] -= tasks[idx];\n }\n }\n sessions.push_back(tasks[idx]);\n dfs(idx + 1);\n sessions.pop_back();\n }\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n this->tasks = tasks;\n this->sessionTime = sessionTime;\n result = tasks.size();\n dfs(0);\n return result;\n }\n};\n``` | 26 | 1 | [] | 6 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | Backtracking | c-backtracking-by-believe_itt-314o | 1.Here we will create groups of hours whose sum is less than SessionTime .\n2.basically we will store only the sum of hours in grps array which is less than Ses | Believe_itt | NORMAL | 2021-08-29T07:34:29.970555+00:00 | 2021-08-29T07:35:51.274740+00:00 | 2,358 | false | 1.Here we will create **groups** of hours whose sum is less than `SessionTime` .\n2.basically we will store only the sum of hours in `grps` array which is less than `SessionTime` .\n3.Our aim is to minimize such number of groups to get minimum number of week sessions.\n\nSo, this is how we gonna create `grps` array : \ncase 1: if **current element + sum** is less than `SessionTime` , then we will add the element in previously created grps.\nelse \ncase 2: we will create new group in grps array.\n```\nclass Solution {\npublic:\n int ans=INT_MAX;\n void solve(int start, vector<int>& v, int target,vector<int>& grps){\n if(start>=v.size()){\n int temp = grps.size();\n ans=min(ans,temp);\n return ;\n }\n if(grps.size()>ans)return; // if grps size is greater than previously found size then we dont need to check this answer \n\t\t\n //Case 1\n int ans=INT_MAX;\n for(int i=0;i<grps.size();i++){\n if(grps[i]+v[start]<=target){\n grps[i]+=v[start];\n solve(start+1,v,target,grps);\n grps[i]-=v[start];\n }\n }\n //Case 2\n grps.push_back(v[start]);\n solve(start+1,v,target,grps);\n grps.pop_back(); \n }\n int minSessions(vector<int>& v, int target) {\n int n=v.size();\n vector<int>grps;\n solve(0,v,target,grps);\n return ans;\n }\n};\n``` | 22 | 1 | ['Backtracking', 'C', 'C++'] | 3 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ || TSP variation || simple explaination | c-tsp-variation-simple-explaination-by-k-6gix | variation of "Travelling salesman Problem"\n \n \n // we will choose a task from the set of un-completed task using bit-mask.\n // if t | kraabhi | NORMAL | 2021-08-29T04:02:51.344192+00:00 | 2021-08-29T04:02:51.344221+00:00 | 2,300 | false | variation of "Travelling salesman Problem"\n \n \n // we will choose a task from the set of un-completed task using bit-mask.\n // if time required to do this task + time exhuasted in prev task is less than or equal to sessionTime then we can do this task in same session .\n // otherwise, we have to start new session.\n \n \n \n \n int target;\n int fun(vector<int>&tasks,int mask,int curr_sum,int&T,vector<vector<int>>&dp){\n int n=tasks.size();\n if(mask==target){\n return 1;\n }\n \n // if already visited the current state then we will return from here only\n if(dp[mask][curr_sum]!=-1)\n return dp[mask][curr_sum];\n \n int ans= INT_MAX;\n int new_mask;\n \n for(int i=0;i<n;i++){\n if(mask&(1<<i)) continue;\n \n // if task[i] has not been done yet then.....\n new_mask=mask|(1<<i);\n if((curr_sum+tasks[i])>T){\n ans=min(ans,1+fun(tasks,new_mask,tasks[i],T,dp)); \n }\n else\n ans=min(ans,fun(tasks,new_mask,curr_sum+tasks[i],T,dp)); \n \n }\n \n dp[mask][curr_sum]=ans;\n return dp[mask][curr_sum];\n \n }\n int minSessions(vector<int>& tasks, int T) {\n int n=tasks.size();\n target=(1<<n)-1; \n int sum=0;\n for(auto& num:tasks){\n sum+=num;\n }\n \n \n vector<vector<int>>dp((1<<n)+5,vector<int>(sum+1,-1));\n return fun(tasks,0,0,T,dp);\n \n }\n}; | 20 | 2 | [] | 6 |
minimum-number-of-work-sessions-to-finish-the-tasks | DFS + Memo + Pruning (12 ms) | dfs-memo-pruning-12-ms-by-votrubac-j7xp | This is a multi-knapsack problem, which is very tough. Fortunately, it\u2019s constrained to 14 tasks. We won\u2019t have more than 14 sessions - each up to 15 | votrubac | NORMAL | 2021-08-29T04:17:07.424994+00:00 | 2021-08-29T04:32:29.731177+00:00 | 3,800 | false | This is a multi-knapsack problem, which is very tough. Fortunately, it\u2019s constrained to 14 tasks. We won\u2019t have more than 14 sessions - each up to 15 hours long. Therefore, we can represent the sessions state using 64-bit.\n\nThe most important optimization is to sort sessions before computing the state. The order of sessions does not matter - it only matters how long they are.\n\nTo speed it up even more, we can prune our search if it exceeds some number of sessions (which we can find greedily).\n\n**C++**\n```cpp\nunordered_map<long long, int> m;\nint dfs(vector<int>& tasks, vector<int> rem, int sessionTime, int i, int lim) {\n if (i >= tasks.size())\n return 0;\n if (rem.size() > lim)\n return 1000;\n long long cache = 0;\n sort(begin(rem), end(rem));\n for (auto r : rem)\n cache = (cache << 4) + r + 1;\n if (m.count(cache))\n return m[cache];\n rem.push_back(sessionTime - tasks[i]);\n int res = 1 + dfs(tasks, rem, sessionTime, i + 1, lim);\n rem.pop_back();\n for (int j = 0; j < rem.size(); ++j) {\n if (rem[j] >= tasks[i]) {\n rem[j] -= tasks[i];\n res = min(res, dfs(tasks, rem, sessionTime, i + 1, lim));\n rem[j] += tasks[i];\n }\n }\n return m[cache] = res;\n}\nint greedy(vector<int>& tasks, int sessionTime) {\n vector<int> sessions;\n for (int t : tasks) {\n bool found = false;\n for (int i = 0; !found && i < sessions.size(); ++i) {\n if (sessions[i] >= t) {\n sessions[i] -= t;\n found = true;\n }\n }\n if (!found)\n sessions.push_back(sessionTime - t);\n }\n return sessions.size();\n}\nint minSessions(vector<int>& tasks, int sessionTime) {\n sort(begin(tasks), end(tasks), greater<int>());\n return dfs(tasks, vector<int>() = {}, sessionTime, 0, greedy(tasks, sessionTime));\n}\n``` | 19 | 3 | ['C'] | 5 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ || DP + Bitmask || Recursion Memo BItmask || | c-dp-bitmask-recursion-memo-bitmask-by-i-p2w9 | Idea is to create a mask (n bits) to track if ith task has been performed or not. \nIf not, then we have 2 choices : \n1. Pick it and perform it in current runn | i_quasar | NORMAL | 2021-09-13T01:30:54.452950+00:00 | 2021-09-13T01:38:10.533479+00:00 | 1,390 | false | Idea is to create a mask (n bits) to track if *ith* task has been performed or not. \nIf not, then we have 2 choices : \n1. Pick it and perform it in current running session : \n2. Pick it and create a new session to perform it : \n\nHere dp(mask, time) is the minimum number of sessions needed to finish all the tasks represented by mask. Mask will have some/all bits set which means that tasks at that index of set bit are already performed. \n\nRemaining code is easy to understand. Just simple memoization and bitmask.\n\n```\nclass Solution {\npublic:\n int n;\n int dp[16][1<<14];\n int solve(vector<int>& tasks, int mask, int time, const int& sessionTime)\n {\n if(mask == 0) return 0; // mask is zero means all tasks are finished\n \n if(dp[time][mask] != -1) return dp[time][mask];\n \n int ans = INT_MAX;\n \n for(int i=0; i<n; i++)\n {\n if((mask&(1<<i))) // If ith task is available or not\n {\n if(time + tasks[i] <= sessionTime) // If this task can be performed\n ans = min(ans, solve(tasks, (mask^(1<<i)), time+tasks[i], sessionTime)); // Mark this as completed in ongoing session\n else \n ans = min(ans, 1 + solve(tasks, (mask^(1<<i)), tasks[i], sessionTime)); // Mark this as completed and create a new session\n }\n }\n return dp[time][mask] = ans;\n }\n \n int minSessions(vector<int>& tasks, int sessionTime) {\n n = tasks.size();\n memset(dp, -1, sizeof(dp));\n return solve(tasks, (1<<n)-1, 0, sessionTime) + 1;\n }\n};\n```\n**Time: O(2^n * sessionTime * n) \nSpace: O(2^n * sessionTime)** | 17 | 0 | ['Dynamic Programming', 'C', 'Bitmask'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python [k-subset sums] | python-k-subset-sums-by-gsan-qdwz | For a given value of k you can check if you can have k-subsets where none of the sums exceed T. Start from the lowest possible value of k and try if you can sol | gsan | NORMAL | 2021-08-29T04:04:52.349375+00:00 | 2021-08-29T04:04:52.349401+00:00 | 1,892 | false | For a given value of `k` you can check if you can have `k`-subsets where none of the sums exceed `T`. Start from the lowest possible value of `k` and try if you can solve. `k`-subset sums can be checked with backtracking.\n\n```python\nclass Solution:\n def minSessions(self, A, T):\n A.sort(reverse = True)\n \n if sum(A) <= T:\n return 1\n if min(A) == T:\n return len(A)\n\n k_min = sum(A) // T\n k_max = len(A)\n \n for k in range(k_min, k_max):\n ks = [0] * k\n \n def can_partition(j):\n if j == len(A):\n for i in range(k):\n if ks[i] > T:\n return False\n return True\n for i in range(k):\n if ks[i] + A[j] <= T:\n ks[i] += A[j]\n if can_partition(j + 1):\n return True\n ks[i] -= A[j]\n return False\n \n if can_partition(0):\n return k\n return len(A)\n``` | 17 | 2 | [] | 5 |
minimum-number-of-work-sessions-to-finish-the-tasks | Clean Java | clean-java-by-rexue70-afi7 | Use backtring and prune, we have a sessions buckets, we put each task into any one of "not full" one, we prefer to put into old buckets than into new empty buck | rexue70 | NORMAL | 2021-08-29T06:04:33.788221+00:00 | 2021-09-04T02:14:54.379268+00:00 | 1,735 | false | Use backtring and prune, we have a sessions buckets, we put each task into any one of "not full" one, we prefer to put into old buckets than into new empty buckets cause this would incrase speed.\n\n```\n//1ms Accept\nclass Solution {\n int res;\n int maxSessionTime;\n int[] tasks;\n int[] sessions;\n public int minSessions(int[] tasks, int sessionTime) {\n\t Arrays.sort(tasks);\n this.res = tasks.length;\n this.maxSessionTime = sessionTime;\n this.tasks = tasks;\n this.sessions = new int[tasks.length];\n dfs(tasks.length - 1, 0);\n return res;\n }\n \n private void dfs(int taskID, int sessionCount) {\n if (sessionCount > res) return; //prune, if we didn\'t use prune, it will be 2200ms, if lucky you get ac\n if (taskID == tasks.length) {\n res = Math.min(res, sessionCount);\n return;\n }\n for (int i = 0; i < sessionCount; i++)\n if (sessions[i] + tasks[taskID] <= maxSessionTime) { //put task into old session bucket\n sessions[i] += tasks[taskID];\n dfs(taskID - 1, sessionCount);\n sessions[i] -= tasks[taskID];\n }\n sessions[sessionCount] += tasks[taskID]; //put task into new empty session bucket\n dfs(taskID - 1, sessionCount + 1);\n sessions[sessionCount] -= tasks[taskID];\n }\n}\n``` | 14 | 3 | [] | 6 |
minimum-number-of-work-sessions-to-finish-the-tasks | Simple C++ Backtracking + DP solution with comments | simple-c-backtracking-dp-solution-with-c-ecyw | Basic Idea\nThe idea here is to use Backtracking + DP in order to solve this problem under the given constraints.\n\nIntution:\nThe basic intution we are going | rishabh_devbanshi | NORMAL | 2021-08-29T06:22:41.837288+00:00 | 2021-08-29T06:22:41.837318+00:00 | 857 | false | **Basic Idea**\nThe idea here is to use **Backtracking + DP** in order to solve this problem under the given constraints.\n\n**Intution:**\nThe basic intution we are going to use is that every element in the tasks array can either be included in its own separate session or in any one of the existing sessions. Whatever be the minimum of these two will be our answer.\nWe\'ll use a arr vector, where length of arr will denote the number of sessions we currently have and arr[i] will denote the number of hours we have worked in that ith session.\n\n**CODE:**\n```\n\tvector<int> arr;\n\t//unordered map for our dp table\n unordered_map<string,int> dp;\n \n\t//function to make key to be used in dp map\n\t// note: here we first sort copy array to reduce the repeated states\n string makeKey(vector<int> &arr,int pos)\n {\n string str = to_string(pos) + \'$\';\n vector<int> copy = arr;\n sort(copy.begin(),copy.end());\n for(auto val : copy) str += to_string(val) + \'$\';\n \n return str;\n }\n \n int recur(vector<int> &tasks,int sessionTime,int pos)\n {\n\t\t//if all tasks are finished , we return 0 indicating no more session is required\n if(pos >= tasks.size()) return 0;\n \n\t\t//getting key from the function above\n string key = makeKey(arr,pos);\n \n\t\t//if the key exists in our map, we\'ll simpy use it\'s value else we\'ll continue\n if(dp.find(key) != dp.end()) return dp[key];\n \n\t\t//Case 1: we make a separate session for our current task\n\t\t// and solve for rest of the array using backtracking\n arr.push_back(tasks[pos]);\n int ans = 1 + recur(tasks,sessionTime,pos+1);\n arr.pop_back();\n \n\t\t//Case 2: we try to include the current session in any one of the previous sessions\n\t\t// and try to solve for rest of array using backtracking, keeping track of the minm\n\t\t// value and storing it in our ans variable\n for(int i=0;i<arr.size();i++)\n {\n if(arr[i] + tasks[pos] <= sessionTime)\n {\n arr[i] += tasks[pos];\n ans = min(ans,recur(tasks,sessionTime,pos+1));\n arr[i] -= tasks[pos];\n }\n }\n \n\t\t//storing the ans for the current key and returning the ans calculated \n return dp[key] = ans;\n }\n\t\n\tint minSessions(vector<int>& tasks, int sessionTime) {\n return recur(tasks,sessionTime,0);\n }\n``` | 9 | 0 | ['Dynamic Programming', 'C'] | 5 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python 3 || 15 lines, dp, bisect_left || T/S: 97% / 52% | python-3-15-lines-dp-bisect_left-ts-97-5-mp0p | \npython3 []\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n\n def canFinish(x: int)-> bool:\n\n @lr | Spaulding_ | NORMAL | 2024-08-28T17:59:10.595880+00:00 | 2024-08-28T18:31:36.243932+00:00 | 242 | false | \n```python3 []\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n\n def canFinish(x: int)-> bool:\n\n @lru_cache(None)\n def dp(idx: int, slots: tuple)-> bool:\n\n if idx == n: return True\n update, task = list(slots), tasks[idx]\n\n for j, slot in enumerate(slots):\n if slot >= task:\n\n update[j]-= task\n if dp(idx + 1, tuple(sorted(update))): return True\n update[j]+= task\n\n return False\n\n return dp(0, tuple(sessionTime for _ in range(x)))\n\n\n n = len(tasks)\n tasks.sort(reverse=True)\n\n return bisect_left(range(n), True, key = canFinish)\n```\n\n[https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/submissions/1371416312/?submissionId=1371412635](https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/submissions/1371416312/?submissionId=1371412635)\n\nI could be wrong, but I think that, worst case, time complexity is *O*(*N* 2^*N)*) and space complexity is *O*(*N* 2^*N)), in which *N* ~ `len(nums)`. | 8 | 0 | ['Python3'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Simple C++ solution | simple-c-solution-by-rac101ran-yk05 | \nclass Solution {\npublic:\n int ans=INT_MAX;\n int minSessions(vector<int>& tasks, int sessions) {\n vector<int> subs;\n solve(0,tasks,s | rac101ran | NORMAL | 2021-09-10T11:12:50.283977+00:00 | 2021-09-10T11:12:50.284005+00:00 | 797 | false | ```\nclass Solution {\npublic:\n int ans=INT_MAX;\n int minSessions(vector<int>& tasks, int sessions) {\n vector<int> subs;\n solve(0,tasks,subs,sessions);\n return ans;\n }\n void solve(int pos,vector<int> &tasks,vector<int>&subs,int sessions) {\n if(pos>=tasks.size()) {\n ans=min(ans,(int)subs.size());\n return; \n }\n if(subs.size()>ans) return;\n for(int set=0; set<subs.size(); set++) {\n if(subs[set]+tasks[pos]<=sessions) {\n subs[set]+=tasks[pos];\n solve(pos+1,tasks,subs,sessions);\n subs[set]-=tasks[pos];\n }\n }\n subs.push_back(tasks[pos]);\n solve(pos+1,tasks,subs,sessions);\n subs.pop_back();\n }\n};\n``` | 7 | 0 | ['Backtracking'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java O(n! log(n)) Binary Search + Recursion (0ms, beats 100%) | java-on-logn-binary-search-recursion-0ms-zip3 | Instead of searching for the best answer using classic recursion + pruning, assume the aswer and check if it\'s possible to reach it. Search scope for given con | migfulcrum | NORMAL | 2021-08-29T22:09:54.211547+00:00 | 2021-08-31T08:53:31.533306+00:00 | 984 | false | Instead of searching for the best answer using classic recursion + pruning, assume the aswer and check if it\'s possible to reach it. Search scope for given constraints is very small. Sorting elements desc, allows to verify asserted value much faster.\n`sessions` store all times assigned to days `k` so far.\n`si `- index of current last session, so `si + 1` - number of sessions.\n\nComplexity analysis:\nIn recursive function, first task can go into first session only, second task can go to first session or new session, ... nth task can go to each `n` sessions. Recursion time complexity is then `O(n!)`. Binary search adds` log(n) `factor, so the overall time complexity is `O(n! log(n))`. \n\n```\n public int minSessions(int[] tasks, int sessionTime) {\n sortDescending(tasks);\n int l = 1;\n int r = tasks.length;\n while (l < r) {\n int maxSessions = (l + r) / 2;\n if (canSchedule(maxSessions, tasks, sessionTime, 0, 0, new int[tasks.length])) {\n r = maxSessions;\n } else {\n l = maxSessions + 1;\n }\n }\n return l;\n }\n\n boolean canSchedule(int max, int[] tasks, int sessionTime, int k, int si, int sessions[]) {\n if (si + 1 > max) return false;\n else if (k == tasks.length || max == tasks.length) return true;\n else {\n int t = tasks[k]; \n for (int i = 0; i <= si + 1; i++) { //iterate all current started sessions and si + 1 (new empty session)\n if (sessions[i] + t <= sessionTime) {\n sessions[i] += t;\n if (canSchedule(max, tasks, sessionTime, k + 1, Math.max(si, i), sessions)) return true;\n sessions[i] -= t;\n }\n }\n return false;\n }\n }\n\n private void sortDescending(int[] tasks) {\n Arrays.sort(tasks);\n int i = 0;\n while (i < tasks.length / 2) {\n int j = tasks.length - i - 1;\n int tmp = tasks[i];\n tasks[i] = tasks[j];\n tasks[j] = tmp;\n i++;\n }\n }\n``` | 7 | 0 | ['Recursion', 'Binary Tree'] | 3 |
minimum-number-of-work-sessions-to-finish-the-tasks | Tricky question leetcode well written 👏 and for the record Beats 100% | tricky-question-leetcode-well-written-an-tigv | Tricky question from 698. Partition to K Equal Sum Subsets leetcode well written \uD83D\uDC4F\n\nThe explanation may be lenthy .. but its woth explaining to the | Dixon_N | NORMAL | 2024-08-28T13:07:49.157251+00:00 | 2024-08-28T15:00:06.471210+00:00 | 362 | false | Tricky question from 698. Partition to K Equal Sum Subsets leetcode well written \uD83D\uDC4F\n\nThe explanation may be lenthy .. but its woth explaining to the interviewer \n\nHave fun with this one \uD83C\uDF40\uD83D\uDE80\n\n[For the record Beats 100% ](https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/submissions/1371119847)\n\n# Code\n```java []\n//Approach -1\nclass Solution {\n private int minSessions;\n\n public int minSessions(int[] tasks, int sessionTime) {\n minSessions = tasks.length;\n int[] sessions = new int[tasks.length];\n backtrack(tasks.length - 1, tasks, sessions, sessionTime);\n return minSessions;\n }\n\n private void backtrack(int index, int[] tasks, int[] sessions, int sessionTime) {\n if (index < 0) {\n int usedSessions = 0;\n for (int session : sessions) {\n if (session > 0) usedSessions++;\n }\n minSessions = Math.min(minSessions, usedSessions);\n return;\n }\n for (int i = 0; i < sessions.length; i++) {\n if (i > 0 && sessions[i] == sessions[i-1]) continue;\n if (sessions[i] + tasks[index] <= sessionTime) {\n sessions[i] += tasks[index];\n backtrack(index - 1, tasks, sessions, sessionTime);\n sessions[i] -= tasks[index];\n }\n if (sessions[i] == 0) break;\n }\n }\n}\n\n```\n```java []\n//Approach -2\nclass Solution {\n private int minSessions;\n\n public int minSessions(int[] tasks, int sessionTime) {\n minSessions = tasks.length; // Worst case: one session per task\n int[] sessions = new int[tasks.length];\n \n // Sort tasks in descending order\n //Arrays.sort(tasks);\n //reverse(tasks);\n \n backtrack(0, tasks, sessions, 0, sessionTime);\n return minSessions;\n }\n\n private void backtrack(int index, int[] tasks, int[] sessions, int usedSessions, int sessionTime) {\n if (usedSessions >= minSessions) {\n return; // Early termination\n }\n\n if (index == tasks.length) {\n minSessions = Math.min(minSessions, usedSessions);\n return;\n }\n\n for (int i = 0; i < sessions.length; i++) {\n if (i > 0 && sessions[i] == sessions[i-1]) continue; // Skip duplicate assignments\n \n if (sessions[i] + tasks[index] <= sessionTime) {\n sessions[i] += tasks[index];\n backtrack(index + 1, tasks, sessions, Math.max(usedSessions, i + 1), sessionTime);\n sessions[i] -= tasks[index];\n }\n \n if (sessions[i] == 0) break; // Optimization: no need to try empty sessions\n }\n }\n\n private void reverse(int[] arr) {\n int left = 0, right = arr.length - 1;\n while (left < right) {\n int temp = arr[left];\n arr[left] = arr[right];\n arr[right] = temp;\n left++;\n right--;\n }\n }\n}\n\n```\n\n```java []\n\n// Approach - 3\n\n\nclass Solution {\n private int minSessions;\n\n public int minSessions(int[] tasks, int sessionTime) {\n minSessions = tasks.length; // Worst case: one session per task\n int[] sessions = new int[tasks.length];\n \n // Sort tasks in descending order\n Arrays.sort(tasks);// Not mandatory\n reverse(tasks); // Not mandatory\n \n backtrack(0, tasks, sessions, 0, sessionTime);\n return minSessions;\n }\n\n private void backtrack(int index, int[] tasks, int[] sessions, int usedSessions, int sessionTime) {\n if (usedSessions >= minSessions) {\n return; // Early termination\n }\n\n if (index == tasks.length) {\n minSessions = Math.min(minSessions, usedSessions);\n return;\n }\n\n for (int i = 0; i < usedSessions + 1; i++) {\n if (i > 0 && sessions[i] == sessions[i-1]) continue; // Skip duplicate assignments\n \n if (sessions[i] + tasks[index] <= sessionTime) {\n sessions[i] += tasks[index];\n backtrack(index + 1, tasks, sessions, Math.max(usedSessions, i + 1), sessionTime);\n sessions[i] -= tasks[index];\n }\n \n if (sessions[i] == 0) break; // Optimization: no need to try empty sessions\n }\n }\n\n private void reverse(int[] arr) {\n int left = 0, right = arr.length - 1;\n while (left < right) {\n int temp = arr[left];\n arr[left] = arr[right];\n arr[right] = temp;\n left++;\n right--;\n }\n }\n}\n\n/*\nThe reason for using i < usedSessions + 1 instead of i < sessions.length is related to how we\'re managing the sessions in this backtracking approach. Here\'s the detailed explanation:\n\nusedSessions represents the number of sessions we\'re currently using.\nWhen we\'re deciding where to place the current task, we have two options:\na) Put it in one of the existing sessions (0 to usedSessions - 1)\nb) Start a new session (which would be at index usedSessions)\nBy using i < usedSessions + 1, we\'re allowing the algorithm to:\n\nTry all existing sessions (0 to usedSessions - 1)\nPotentially start one new session (at index usedSessions)\n\n\nIf we used i < sessions.length, we would be considering all possible sessions up to the maximum number of tasks, which is inefficient because:\n\nWe know we won\'t need more sessions than there are tasks\nMany of these sessions would be empty and unnecessary to consider\n\n\nBy limiting our search to usedSessions + 1, we\'re pruning the search space significantly, which improves the efficiency of the algorithm.\n\nThis approach ensures that we\'re only considering relevant sessions at each step of the backtracking process. It\'s a form of optimization that keeps the algorithm focused on the most promising solutions.\nTo illustrate with an example:\n\nIf we have 5 tasks and we\'re currently using 2 sessions\nusedSessions + 1 would be 3, so we\'d consider sessions 0, 1, and potentially start a new one at 2\nWe wouldn\'t need to consider sessions 3 and 4 at this point, as they would definitely be empty\n\nThis optimization is particularly effective when combined with the early termination checks and the strategy of trying to fill existing sessions before starting new ones.\n\n*/\n```\n\n**Updated** solution\n\n[698. Partition to K Equal Sum Subsets](https://leetcode.com/problems/partition-to-k-equal-sum-subsets/solutions/5559337/crazy-best-problem-to-solve-must-solve-this-pattern/)\n[2305. Fair Distribution of Cookies](https://leetcode.com/problems/fair-distribution-of-cookies/solutions/5559818/amazing-must-read-please-attach-more-question-of-this-template/)\n[1723. Find Minimum Time to Finish All Jobs](https://leetcode.com/problems/find-minimum-time-to-finish-all-jobs/solutions/5559845/add-more-of-this-template-question-here/)\n[473. Matchsticks to Square](https://leetcode.com/problems/matchsticks-to-square/solutions/5559911/please-add-more-question-that-can-be-solved-by-this-template/)\n\n# Code\n```java []\nclass Solution {\n public boolean canPartitionKSubsets(int[] nums, int k) {\n int sum = Arrays.stream(nums).sum();\n if (sum % k != 0) return false;\n \n int targetSum = sum / k;\n Arrays.sort(nums);\n // add a reverse it helps!\n return backtrack(nums.length - 1, nums, new int[k], targetSum);\n }\n \n private boolean backtrack(int index, int[] nums, int[] sums, int targetSum) {\n if (index < 0) return true;\n \n for (int i = 0; i < sums.length; i++) {\n if (sums[i] + nums[index] > targetSum) continue;\n \n sums[i] += nums[index];\n \n if (backtrack(index - 1, nums, sums, targetSum)) {\n return true;\n }\n \n sums[i] -= nums[index];\n \n if (sums[i] == 0) break;// why ? explanation given below\n }\n \n return false;\n }\n}\n/*\nGreat question! The line if (sums[i] == 0) break; is indeed a crucial optimization that can significantly reduce the time complexity in many cases. Let\'s break down why this is so effective:\n\nAvoiding Duplicate Work:\nWhen we backtrack and remove a number from a subset, if that subset becomes empty (sum becomes 0), it means we\'re back to the starting point for that subset. If we continue to the next iteration of the loop, we\'d be trying to add the current number to another empty subset. This would lead to exploring the same combinations we\'ve already explored or will explore in future recursive calls.\nSymmetry Breaking:\nAll empty subsets are identical from the perspective of our algorithm. Once we\'ve tried adding the current number to one empty subset and it didn\'t lead to a solution, there\'s no point in trying to add it to other empty subsets.\nPruning the Search Tree:\nBy breaking the loop when we encounter an empty subset, we\'re effectively pruning a large portion of the search tree. This can drastically reduce the number of recursive calls and iterations.\nReducing Permutations:\nWithout this break, the algorithm would consider all permutations of the subsets, which is unnecessary since we only care about the content of the subsets, not their order.\n\nTime Complexity Impact:\n\nIn the worst case (when no valid partition exists), the time complexity without this optimization could be O(k^n), where k is the number of subsets and n is the number of elements.\nWith this optimization, many redundant paths are eliminated, potentially reducing the time complexity significantly, although it remains exponential in the worst case.\n\nPractical Impact:\n\nFor inputs where many valid solutions exist, this optimization might not make a huge difference.\nHowever, for inputs where valid solutions are sparse or non-existent, this optimization can reduce the runtime from hours or days to seconds or minutes.\n\nExample:\nConsider an array [10, 10, 10, 7, 7, 7, 6, 6, 6] with k = 3. Without the optimization, the algorithm would try many permutations of how to distribute these numbers. With the optimization, once it tries [10, 10, 10] in one subset and backtracks, it immediately knows not to try 10 in the other empty subsets, significantly reducing the search space.\nIn summary, this simple optimization leverages the problem\'s structure to eliminate a vast number of unnecessary recursive calls, making the algorithm much more efficient in practice, especially for challenging inputs.\n*/\n\n```\n```java []\n// To print all such subsets\n\n// This is the very final result\n// To print all such subsets\n\n// This is the very final result\nimport java.util.*;\n\nclass Solution {\n public boolean canPartitionKSubsets(int[] nums, int k) {\n int sum = Arrays.stream(nums).sum();\n if (sum % k != 0) return false;\n \n int targetSum = sum / k;\n Arrays.sort(nums);\n reverse(nums); // Reverse the array to have larger numbers first\n \n List<List<Integer>> subsets = new ArrayList<>();\n for (int i = 0; i < k; i++) {\n subsets.add(new ArrayList<>());\n }\n \n boolean result = backtrack(0, nums, subsets, new int[k], targetSum);\n \n if (result) {\n System.out.println("Valid partition found:");\n for (int i = 0; i < subsets.size(); i++) {\n System.out.println("Subset " + (i + 1) + ": " + subsets.get(i));\n }\n } else {\n System.out.println("No valid partition found.");\n }\n \n return result;\n }\n \n private boolean backtrack(int index, int[] nums, List<List<Integer>> subsets, int[] sums, int targetSum) {\n if (index == nums.length) {\n return true; // All numbers have been used\n }\n \n for (int i = 0; i < subsets.size(); i++) {\n if (sums[i] + nums[index] > targetSum) continue;\n if(i>0 && sums[i]==sums[i-1]) continue;\n \n subsets.get(i).add(nums[index]); // Add to subset\n sums[i] += nums[index]; // Update sum\n \n if (backtrack(index + 1, nums, subsets, sums, targetSum)) {\n return true;\n }\n \n sums[i] -= nums[index]; // Revert sum\n subsets.get(i).remove(subsets.get(i).size() - 1); // Remove from subset\n \n if (sums[i] == 0) break; // Optimization: no need to try empty subsets\n }\n \n return false;\n }\n \n private void reverse(int[] nums) {\n int left = 0, right = nums.length - 1;\n while (left < right) {\n int temp = nums[left];\n nums[left] = nums[right];\n nums[right] = temp;\n left++;\n right--;\n }\n }\n}\n``` | 6 | 0 | ['Backtracking', 'Java'] | 4 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++|| very easy binary-search solution|| k subset partition prob | c-very-easy-binary-search-solution-k-sub-qnmh | \nclass Solution {\npublic:\n bool check(vector<int>&nums,vector<int>&vec,int step,int val)\n {\n if(step>=nums.size()) return true;\n int c | Blue_tiger | NORMAL | 2022-06-13T20:20:53.596004+00:00 | 2022-06-13T20:20:53.596047+00:00 | 617 | false | ```\nclass Solution {\npublic:\n bool check(vector<int>&nums,vector<int>&vec,int step,int val)\n {\n if(step>=nums.size()) return true;\n int cur=nums[step];\n for(int i=0;i<vec.size();i++)\n {\n if(vec[i]+cur<=val)\n {\n vec[i]+=cur;\n if(check(nums,vec,step+1,val)) return true;\n vec[i]-=cur;\n }\n if(vec[i]==0) break;\n }\n return false;\n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n \n int l=1,r=tasks.size();\n while(l<r)\n {\n int mid=(l+r)/2;\n vector<int>vec(mid,0);\n if(check(tasks,vec,0,sessionTime))\n {\n r=mid;\n }\n else\n l=mid+1;\n }\n return l;\n }\n};\n``` | 6 | 0 | ['Backtracking', 'Binary Search Tree'] | 2 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java DFS solution beating 100 % | java-dfs-solution-beating-100-by-shuashu-u8ez | ```\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n // sort desendingly\n // we know that the minSessionTimes is b | shuashuashua1997 | NORMAL | 2021-09-05T05:39:52.300686+00:00 | 2021-09-05T05:39:52.300728+00:00 | 794 | false | ```\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n // sort desendingly\n // we know that the minSessionTimes is between 1 to # number of tasks\n // then we can use dfs to find from 1 to n, which one works first\n // Copy Right to a classmate.\n Arrays.sort(tasks);\n int s = 0, t = tasks.length - 1;\n while (s <= t) {\n int temp = tasks[s];\n tasks[s] = tasks[t];\n tasks[t] = temp;\n s++;\n t--;\n }\n \n for (int n = 1; n < tasks.length; n++) {\n int[] remain = new int[n];\n for (int i = 0; i < n; i++) {\n remain[i] = sessionTime;\n }\n if (canWork(tasks, 0, remain)) return n;\n }\n return tasks.length;\n }\n \n private boolean canWork(int[] tasks, int curr, int[] remain) {\n if (curr == tasks.length) return true;\n for (int i = 0; i < remain.length; i++) {\n if (i > curr) continue; // if i th bucket\'s index is bigger that current task\'s index, we continue as it\'s impossible bc the worst east is that i == index when worksession is equal to task time.\n if (remain[i] >= tasks[curr]) {\n remain[i] -= tasks[curr];\n if (canWork(tasks, curr + 1, remain)) return true;\n remain[i] += tasks[curr];\n }\n }\n return false;\n }\n} | 6 | 1 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | 3ms | Greedy | Binary Search | DFS | c-3ms-greedy-binary-search-dfs-by-alex39-hus5 | we alway choose the max of the tasks to fill in the session.\nthen we use dfs to fill the remaining space in the session from the big to small,\nand we use Bina | alex391a | NORMAL | 2021-08-30T15:39:53.257444+00:00 | 2021-08-30T15:39:53.257488+00:00 | 265 | false | we alway choose the max of the tasks to fill in the session.\nthen we use dfs to fill the remaining space in the session from the big to small,\nand we use Binary Search to find the max one that less than remaining space.\n3ms\n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n sort(tasks.begin(),tasks.end());\n int ans=0;\n int nowleft=sessionTime;\n\n while (!tasks.empty()){\n vector<int> path;\n path.push_back(tasks.size()-1);\n int n=nowleft-int(*tasks.rbegin());\n dfs(tasks,tasks.size()-1,n,path,n,path);\n for(auto i:path){\n tasks.erase(tasks.begin()+i);\n }\n ans++;\n nowleft=sessionTime;\n }\n \n return(ans);\n \n \n }\n int lessmax(vector<int> tasks,int curr,int n){\n int l=0;\n int r=curr;\n if (tasks[curr]<=n){\n \n return r-1;\n } \n while (l<r){\n int mid=(l+r)/2;\n if (tasks[mid]<=n and tasks[mid+1]>n){\n return mid;\n }\n \n else if (tasks[mid]>n){\n \n r=mid;\n }\n \n else{\n l=mid;\n } \n } \n return -1;\n }\n void dfs(vector<int> tasks,int curr,int nowleft,vector<int> nowpath,int &minleft,vector<int>& minpath){\n\n int lm=lessmax(tasks,curr,nowleft);\n if (lm<0){\n if (nowleft<minleft){\n minleft=nowleft;\n minpath=nowpath;\n }\n return ;\n }\n for (int i=lm;i>=0;i--){\n nowpath.push_back(i);\n int tmp=nowleft-tasks[i];\n if (tmp==0){\n minleft=0;\n minpath=nowpath;\n return;\n }else{\n if (tmp<minleft){\n minleft=tmp;\n minpath=nowpath;\n } \n dfs(tasks,i,tmp,nowpath,minleft,minpath);\n if(minleft==0){\n return;\n }\n }\n nowpath.pop_back();\n }\n }\n};\n``` | 6 | 2 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Java] Bin Packing problem | java-bin-packing-problem-by-shk10-gbz0 | Problem at hand is essentially the well known Bin Packing Problem which is NP-hard.\ntasks[i] \u21D2 size of an item or items[i]\nsessionTime \u21D2 capacity of | shk10 | NORMAL | 2021-08-30T13:09:40.735713+00:00 | 2021-08-30T22:44:18.748462+00:00 | 2,846 | false | Problem at hand is essentially the well known [Bin Packing Problem](https://en.wikipedia.org/wiki/Bin_packing_problem) which is NP-hard.\ntasks[i] \u21D2 size of an item or items[i]\nsessionTime \u21D2 capacity of each bin\nGoal: minimize the number of sessions \u21D2 minimize the number of bins\n\nThere are couple of approximation algorithms for Bin packing like First-Fit, Best-Fit and Next-Fit which work well in practice but an efficient algorithm for optimal result is quite hard. This is where small input limits help us, we can just do a brute force i.e. enumerate all possibilities.\n\n**Basic approach**\n1. Maintain an array of ```bins``` of size ```n``` (because we don\'t need more than ```n``` bins for ```n``` items) and a counter ```used``` to keep track of bins used so far. ```bins[i]``` represents size occupied by all the items in ```i```\'th bin. ```bins[i]``` should never exceed ```capacity```.\n2. Do a backtracking and try to assign current item ```items[index]``` to all the available ```bins``` as long as they can accomodate it. Also explore the possibility of creating a new bin (```used++```) for this current item.\n3. Once all the items have been assigned to some bins, take the minimum of number of bins used (use a global variable for result). That is our answer.\n\n**Optimization**\n1. Use [Branch and bound](https://en.wikipedia.org/wiki/Branch_and_bound) technique. If we have already figured out through one of the terminal paths (i.e. valid assignments of all items) that **b** bins are sufficient, then we need not explore paths that we already know will lead to **>= b** bins as the result.\n2. No need to try assigning an item to multiple bins with the same size. 2 bins ```bins[i]``` and ```bins[j]``` of equal size are both identical as far as the backtracking for rest of the items goes, so we just try assign the current item to only one of them and explore that path only. We can use a Set for this in the code.\n3. Sort the items and try to assign items in larger to smaller order. This would help us to arrive at a reasonable estimate early.\n*Note:* I hate the fact that Java doesn\'t have ```Arrays.sort(int[], Comparator<Integer>)```. That\'s the only reason I had to iterate ```index``` in reverse order otherwise I had no intention to confuse readers. :)\n\n```\n// 2 ms. 100%\nclass Solution {\n private int best;\n private void assign(int[] bins, int used, int[] items, int index, int capacity) {\n if(used >= best) return;\n if(index < 0) {\n best = used;\n return;\n }\n\t\tSet<Integer> set = new HashSet<>();\n for(int i = 0; i < used; i++) {\n\t\t\tif(!set.add(bins[i]) continue;\n if(bins[i] + items[index] <= capacity) {\n bins[i] += items[index];\n assign(bins, used, items, index - 1, capacity);\n bins[i] -= items[index];\n }\n }\n bins[used] = items[index];\n assign(bins, used + 1, items, index - 1, capacity);\n bins[used] = 0;\n }\n public int minSessions(int[] tasks, int sessionTime) {\n Arrays.sort(tasks);\n best = tasks.length;\n assign(new int[tasks.length], 0, tasks, tasks.length - 1, sessionTime);\n return best;\n }\n}\n```\n\nTime complexity: O(n log n + n B<sub>n</sub>) = O(n B<sub>n</sub>) where B<sub>n</sub> represents n\'th [Bell number](https://en.wikipedia.org/wiki/Bell_number). B<sub>n</sub> counts the number of different ways to partition a set of n elements.\nSpace complexity: O(n<sup>2</sup>) [O(n) if we don\'t use Set optimization] | 6 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Python3] Bitmask DP - Detailed Explanation | python3-bitmask-dp-detailed-explanation-1w57k | Intuition\n Describe your first thoughts on how to solve this problem. \n- We have to try all possible cases to find minimum number of work session -> DP signal | dolong2110 | NORMAL | 2024-09-12T16:36:03.835408+00:00 | 2024-09-12T16:36:03.835439+00:00 | 170 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We have to try all possible cases to find minimum number of work session -> DP signal.\n- `1 <= n <= 14` the number of tasks is small enough to save all states using a bit number.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**1. Initialization:**\n- n = len(tasks): Calculates the number of tasks.\n\n**2. Dynamic Programming (Top-Down Approach):**\n- `@cache`: This decorator is used to memoize the `dp` function, avoiding redundant calculations.\n- `def dp(task_mask: int, remain_time: int) -> int:` Defines the recursive `dp` function.\n - if `task_mask == (1 << n) - 1: return 1`: If all tasks have been completed (the bitmask task_mask is full), return 1 as only one more session is needed to complete the remaining tasks.\n - `res = float("inf")`: Initializes the minimum number of sessions to infinity.\n - `for i in range(n):`: Iterates through all tasks.\n - `if task_mask & (1 << i) or tasks[i] > remain_time: continue`: Checks if the task is already completed or if it exceeds the remaining session time. If so, skip it.\n - `res = min(res, dp(task_mask | (1 << i), remain_time - tasks[i]), dp(task_mask | (1 << i), sessionTime) + 1)`: Recursively calculates the minimum number of sessions by considering two options:\n - Assigning the current task to the current session: `dp(task_mask | (1 << i)`, remain_time - tasks[i]).\n - Starting a new session for the current task: `dp(task_mask | (1 << i), sessionTime) + 1`.\n - `return res`: Returns the minimum number of sessions required to reach the current state.\n\n**3. Main Call:**\n\n- `return dp(0, sessionTime)`: Calls the dp function with initial values of 0 for the current state (no tasks completed) and the initial session time.\n\n**4. Explanation:**\n\n- The `dp` function uses a top-down dynamic programming approach to efficiently calculate the minimum number of sessions.\n- The state of the task completion is represented by the bitmask `task_mask`, and the remaining session time is represented by `remain_time`.\n- The `dp` function recursively explores different combinations of task assignments within sessions, considering the available time and the remaining tasks.\n- The memoization decorator ensures that the `dp` function avoids recalculating results for the same state, improving efficiency.\n- The final result is the minimum number of sessions required to complete all tasks.\n\n# Complexity\n- Time complexity: $$O(2 ^ N * S * N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(2 ^ N * S)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n n = len(tasks)\n @cache\n def dp(task_mask: int, remain_time: int) -> int:\n if task_mask == (1 << n) - 1: return 1\n res = float("inf")\n for i in range(n):\n if task_mask & (1 << i) or tasks[i] > remain_time: continue\n res = min(res, \n dp(task_mask | (1 << i), remain_time - tasks[i]), \n dp(task_mask | (1 << i), sessionTime) + 1)\n return res\n return dp(0, sessionTime))\n``` | 5 | 0 | ['Array', 'Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'Python3'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Python 3] DFS + Binary search, 32ms | python-3-dfs-binary-search-32ms-by-ladyk-eljn | ```\ndef minSessions(self, tasks: List[int], sessionTime: int) -> int:\n def dfs(i):\n if i == len(tasks):\n return True\n | ladykkk | NORMAL | 2021-11-18T06:37:26.445062+00:00 | 2021-11-18T06:46:09.147959+00:00 | 1,003 | false | ```\ndef minSessions(self, tasks: List[int], sessionTime: int) -> int:\n def dfs(i):\n if i == len(tasks):\n return True\n for j in range(mid):\n if cnt[j] >= tasks[i]:\n cnt[j] -= tasks[i]\n if dfs(i + 1):\n return True\n cnt[j] += tasks[i]\n if cnt[j] == sessionTime:\n break\n return False \n \n l, r = 1, len(tasks)\n tasks.sort(reverse=True)\n while l < r:\n mid = (l + r) // 2\n cnt = [sessionTime] * mid\n if not dfs(0):\n l = mid + 1\n else:\n r = mid\n return l | 5 | 0 | ['Binary Tree', 'Python'] | 3 |
minimum-number-of-work-sessions-to-finish-the-tasks | c++ random approach works | c-random-approach-works-by-dan_zhixu-t6lz | People have pointed out that sorting the tasks and then greedily add each task cannot solve the problem, but we can try randomly shuffle the tasks and use the g | dan_zhixu | NORMAL | 2021-08-31T11:09:20.402850+00:00 | 2021-08-31T11:09:20.402892+00:00 | 363 | false | People have pointed out that sorting the tasks and then greedily add each task cannot solve the problem, but we can try randomly shuffle the tasks and use the greedy approach. It works for this problem since the data set is not so large. \n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n \n int res = INT_MAX;\n \n for (int i = 0; i < 5000; ++i) {\n \n random_shuffle(tasks.begin(), tasks.end());\n \n res = min(res, calculate(tasks, sessionTime));\n }\n \n return res;\n }\n \n \n int calculate(vector<int> &tasks, int sessionTime) {\n \n int res = 1, crr = 0;\n \n for (auto &task : tasks) {\n \n if (crr + task <= sessionTime)\n crr += task;\n else {\n ++res;\n crr = task;\n }\n }\n return res;\n }\n};\n``` | 5 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ solution | Faster than 100% of C++ soltutions | No complex Algo | Easy to understand | c-solution-faster-than-100-of-c-soltutio-oyzo | Explanation:\nCreate an array state of size of sessionTime initialized as 1 for all the values in tasks and 0 elsewhere. Loop it out, trying to push as many tas | mag_14 | NORMAL | 2021-08-29T05:36:16.976264+00:00 | 2021-08-29T05:36:16.976308+00:00 | 499 | false | **Explanation:**\nCreate an array `state` of size of `sessionTime` initialized as 1 for all the values in `tasks` and 0 elsewhere. Loop it out, trying to push as many `tasks` as possible with sum not more than `sessionTime`, else break. Decrement all the values of `state` array that get executed to avoid repetitions. \n\n**Code:**\n\n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n if(tasks.size() == 1) return 1;\n int ans = 0;\n vector<int> state(15, 0);\n for(int i=0; i<tasks.size(); i++) {\n state[tasks[i]]++;\n }\n int i = 14;\n while(i > 0) {\n if(state[i] > 0) {\n int curr = i;\n int diff = sessionTime - curr;\n state[i]--;\n while(curr < sessionTime) {\n if(state[diff] > 0) {\n curr += diff;\n state[diff]--;\n }\n else {\n diff--;\n if(diff <= 0) {\n break;\n }\n }\n }\n ans++;\n }\n if(state[i] == 0) {\n i--;\n }\n }\n return ans;\n }\n};\n\n\n\n``` | 5 | 3 | ['Dynamic Programming', 'C'] | 4 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java || Beats 99.37% || 1ms || Binary Search || Backtracking || clear and simple Explanation | java-beats-9937-1ms-binary-search-backtr-j1dg | \n## Minimum Number of Work Sessions to Finish the Tasks\n\nProblem:\n\nYou are given a set of tasks represented by an integer array tasks, where tasks[i] repre | devchaitanya27 | NORMAL | 2023-07-01T11:49:43.096232+00:00 | 2023-07-01T11:49:43.096259+00:00 | 507 | false | \n## Minimum Number of Work Sessions to Finish the Tasks\n\n**Problem:**\n\nYou are given a set of tasks represented by an integer array `tasks`, where `tasks[i]` represents the number of hours required to finish the ith task. You work in sessions, where each session has a maximum duration of `sessionTime` hours. You need to find the minimum number of sessions required to finish all the tasks, while following these conditions:\n- Once you start a task in a session, you must complete it in the same session.\n- You can start a new task immediately after finishing the previous one.\n- You may complete the tasks in any order.\n\n**Solution:**\n\nWe can use a binary search approach to find the minimum number of sessions. We sort the tasks array in descending order to prioritize longer tasks. Then, we perform binary search on the range of possible session counts, from 1 to the total number of tasks.\n\nIn each iteration of the binary search, we simulate the distribution of tasks among sessions using a backtracking approach. We check if it is possible to complete all tasks within the given session count. If it is possible, we update the answer and continue searching for a smaller session count. Otherwise, we increase the session count and continue searching.\n\nHere\'s the Java implementation of the solution:\n\n```java\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n // Sort tasks in descending order to prioritize longer tasks\n Arrays.sort(tasks);\n reverse(tasks);\n\n int left = 1; // Minimum session count\n int right = tasks.length; // Maximum session count\n int answer = 0; // Minimum number of sessions required\n\n // Binary search on the range of possible session counts\n while (left <= right) {\n int mid = left + (right - left) / 2;\n int[] workSessions = new int[mid]; // Array to track tasks assigned to each session\n\n // Check if it\'s possible to complete all tasks within the given session count\n if (isPossible(0, mid, sessionTime, 0, tasks, workSessions, mid)) {\n answer = mid; // Update the answer\n right = mid - 1; // Continue searching for a smaller session count\n } else {\n left = mid + 1; // Increase the session count\n }\n }\n\n return answer;\n }\n\n // Backtracking function to simulate the distribution of tasks among sessions\n private static boolean isPossible(int idx, int k, int maxLen, int max, int[] tasks, int[] workSessions, int zeroCount) {\n if (tasks.length - idx < zeroCount) {\n return false; // Not enough tasks remaining to fill all sessions\n }\n\n if (idx == tasks.length) {\n if (max > maxLen) {\n return false; // Current session duration exceeds the maximum session time\n }\n return true; // All tasks have been assigned to sessions successfully\n }\n\n int currentTask = tasks[idx];\n\n for (int i = 0; i < k; i++) {\n if (workSessions[i] + currentTask > maxLen) {\n continue; // Current task cannot be assigned to this session\n }\n\n zeroCount -= workSessions[i] == 0 ? 1 : 0; // Decrement zeroCount if a session becomes non-empty\n workSessions[i] += currentTask; // Assign the task to the current session\n\n // Recursively check if it\'s possible to complete remaining tasks with the updated sessions\n if (isPossible(idx + 1, k, maxLen, Math.max(max, workSessions[i]), tasks, workSessions, zeroCount)) {\n return true; // Tasks can be completed with the current distribution of sessions\n }\n\n workSessions[i] -= currentTask; // Backtrack: Remove the task from the current session\n zeroCount += workSessions[i] == 0 ? 1 : 0; // Increment zeroCount if a session becomes empty again\n\n if (workSessions[i] == 0) {\n break; // Skip empty sessions to avoid redundant iterations\n }\n }\n\n return false; // Unable to complete all tasks with the current distribution of sessions\n }\n\n // Utility function to reverse an array\n private void reverse(int[] arr) {\n int i = 0, j = arr.length - 1;\n\n while (i < j) {\n int temp = arr[i];\n arr[i] = arr[j];\n arr[j] = temp;\n i++;\n j--;\n }\n }\n}\n\n```\n\n**Complexity Analysis:**\n\n- Time Complexity: O(N * log(N) * (2^N)), where N is the number of tasks. The algorithm performs binary search on the range of session counts, and for each iteration, it simulates the distribution of tasks using a backtracking approach. The backtracking has a complexity of O(2^N) in the worst case.\n- Space Complexity: O(N), where N is the number of tasks. We use additional space for the workSessions array.\n\n\n | 4 | 0 | ['Binary Search', 'Backtracking', 'Recursion', 'Java'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Bit Mask DP | C++ Solution | | bit-mask-dp-c-solution-by-solvedorerror-qcas | Intution\n1. We can Solve this question with Recusion ( But it Takes a lot higher time) (Generally T.C. -> O( N ! * N))\n2. In Recursive Solution of such type o | solvedORerror | NORMAL | 2023-06-12T07:55:32.324631+00:00 | 2023-06-12T07:55:32.324681+00:00 | 587 | false | **Intution**\n1. We can Solve this question with Recusion ( But it Takes a lot higher time) (Generally T.C. -> O( N ! * N))\n2. In Recursive Solution of such type of Problems, we need to modify the original array OR take a **Visited array** to Remember wich indices are visited.\n3. so essentially the if we wanna memoize the state of Recursion, It needs a **Map(which memoizes values for each a visited array)** (T.C. Slightly Reduces) (still -TLE May Come ).\n\n**NOTE**\n1. If the size of array (n<=22) we can mark visited indices in the first \'n\' bits of a mask (Integer) Instead of visited array.\n2. Which gives a lot quicker access, This is essentially The BIT_MASK DP.\n3. ** STORING THE VISITED INDICES IN THE BITS OF INREGER ** ( Which Represents the State).\n\n```\nclass Solution {\npublic:\n int mx;\n int dp[1<<14][16];\n int solve(int wd,int time ,vector<int>& tasks,int idx){\n int n=tasks.size(); \n if(idx==n){\n return time<mx;\n }\n if(dp[wd][time]!=-1)return dp[wd][time];\n int ans=INT_MAX;\n for(int i=0;i<n;i++){\n if((wd & (1<<i))){\n // wd[i]=true;\n wd=wd ^ (1<<i);\n if(tasks[i]>time){\n int curr=1+solve(wd,mx-tasks[i],tasks,idx+1);\n ans=min(ans,curr);\n }else if(tasks[i]==time){\n ans=min(ans,1+solve(wd,mx,tasks,idx+1));\n }else{\n ans=min(ans,solve(wd,time-tasks[i],tasks,idx+1));\n }\n wd=wd ^ (1<<i);\n }\n }\n return dp[wd][time]=ans;\n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n=tasks.size();\n // vector<bool> workdone(n,0);\n int workdone=1<<n;\n workdone--;\n mx=sessionTime;\n memset(dp,-1,sizeof(dp));\n return solve(workdone,sessionTime,tasks,0);\n }\n};\n``` | 4 | 0 | ['Dynamic Programming', 'Bitmask'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | Backtracking Solution | Java | Simpler to understand | backtracking-solution-java-simpler-to-un-ragy | The idea is to populate the tasks in such groups such that we can fit in optimal tasks together and at the same time maintain the threshold for a given session. | architgajpal | NORMAL | 2022-11-03T21:35:46.423901+00:00 | 2022-11-03T21:35:46.423940+00:00 | 1,368 | false | The idea is to populate the tasks in such groups such that we can fit in optimal tasks together and at the same time maintain the threshold for a given session. \n\nTo handle this, let us try to group them initially all independently and then backtrack to find space in any of the buckets and add the task to that bucket.\n```\nclass Solution {\n int minBucket = Integer.MAX_VALUE;\n public void helper(int[] tasks, int time, int index, List<Integer> buckets){\n \n //there has already been a setting when less buckets could satisfy requirements\n if(buckets.size() >= minBucket) \n return;\n if(index == tasks.length){\n minBucket = Math.min(minBucket, buckets.size());\n return;\n }\n \n buckets.add(tasks[index]);\n helper(tasks, time, index+1, buckets);\n buckets.remove(buckets.size() - 1);\n \n //now iterate over all the buckets and if there is space, put and backtrack again\n for(int i=0; i<buckets.size(); i++){\n if(tasks[index] + buckets.get(i) <= time){\n buckets.set(i, buckets.get(i) + tasks[index]);\n helper(tasks, time, index+1, buckets);\n buckets.set(i, buckets.get(i) - tasks[index]);\n }\n } \n }\n \n private void reverse(int[] tasks){\n int i=0, j=tasks.length-1;\n while(i < j){\n int temp = tasks[i];\n tasks[i] = tasks[j];\n tasks[j] = temp;\n i++;\n j--;\n }\n }\n public int minSessions(int[] tasks, int sessionTime) {\n Arrays.sort(tasks);\n reverse(tasks);\n helper(tasks, sessionTime, 0, new ArrayList<Integer>());\n return minBucket;\n }\n}\n``` | 4 | 0 | ['Backtracking', 'Java'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | JAVA|| BITMASKING + DP || RECURSIVELY | java-bitmasking-dp-recursively-by-asppan-rpze | SUPPOSE YOU HAVE [9,6,9] AND SEESIONTIME=14\nSO U CAN MAKE A BITMASK 000\nWHEN YOU TAKE 9 BIT MASK BECOMES 1000 AS 9 IS LESS THAN 14 YOU SEND recursive(9,1000)\ | asppanda | NORMAL | 2021-09-28T01:28:01.111542+00:00 | 2021-09-28T01:28:01.111587+00:00 | 1,005 | false | SUPPOSE YOU HAVE [9,6,9] AND SEESIONTIME=14\nSO U CAN MAKE A BITMASK 000\nWHEN YOU TAKE 9 BIT MASK BECOMES 1000 AS 9 IS LESS THAN 14 YOU SEND recursive(9,1000)\nthen you got 6 adding 6+9 you get 15 so u send 1+recursive(6,110)\nnow you have 9+6 you get 15 so u have greater than 14 so you send recursive(9,111)\nas you base condition 111 which is 7 so you see the sum which is not 0 which is greater than 0 so you send 1 if it was equal to 0 you must have send 0\n\nsee my code below\n\n\n```\n public static int val(int arr[],int sessionTime,int sum,int n,int mask,int dp[][])\n {\n if(mask==(1<<n)-1)//base condition\n {\n if(sum==0)\n {\n return 0;\n }\n else\n if(sum>0)\n {\n return 1;\n }\n }\n if(dp[mask][sum]!=-1)// taken dp of mask and sum\n {\n return dp[mask][sum];\n }\n int min=Integer.MAX_VALUE;\n for(int i=0;i<n;i++)\n {\n if((mask&(1<<i))==0)\n {\n if(sum+arr[i]==sessionTime)//if sum+9==14\n {\n int val1=val(arr,sessionTime,0,n,(mask|(1<<i)),dp);\n if(val1!=Integer.MAX_VALUE)\n {\n val1=val1+1;\n }\n min=Math.min(val1,min);\n }\n else\n if(sum+arr[i]<sessionTime)//if sum+9<14\n { \n int val1=val(arr,sessionTime,sum+arr[i],n,(mask|(1<<i)),dp);\n min=Math.min(val1,min);\n }\n else\n if(sum+arr[i]>sessionTime)//if sum+9>14\n {\n int val1=val(arr,sessionTime,arr[i],n,(mask|(1<<i)),dp);\n if(val1!=Integer.MAX_VALUE)\n {\n val1=val1+1;\n }\n min=Math.min(val1,min);\n }\n }\n }\n return dp[mask][sum]=min;\n }\n```\n```\n public int minSessions(int[] tasks, int sessionTime)\n {\n int n=tasks.length;\n int dp[][]=new int[1<<(n+1)-1][20];\n for(int i=0;i<(1<<n);i++)\n {\n for(int j=0;j<20;j++)\n {\n dp[i][j]=-1;\n }\n }\n```\n\n**IF U LIKE THE SOLUTION ITS YOUR WISH TO UPVOTE BUT PLS DONT DOWNVOTE** | 4 | 0 | ['Dynamic Programming', 'Backtracking', 'Bitmask', 'Java'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | Simple Backtracking | c-simple-backtracking-by-thangaraj1992-wu6x | Algorithm\nBacktracking:\nFor each task, we have two option\n1. To accomodate this task in one of the earlier sessions, given that earlier session time + cur_ta | Thangaraj1992 | NORMAL | 2021-08-29T09:19:35.657410+00:00 | 2021-08-29T09:19:35.657495+00:00 | 274 | false | **Algorithm**\nBacktracking:\nFor each task, we have two option\n1. To accomodate this task in one of the earlier sessions, given that earlier session time + cur_task_time <= max session time.\n2. To create a new session and allocate this task to that session.\n\nWe optimise the backtrack by breaking the recursion if our current session count exceeds that already calculated minimum session count\n\n```\nclass Solution {\npublic:\n int minSession = INT_MAX;\n vector<int> sessions;\n int minSessions(vector<int>& tasks, int sessionTime) \n {\n solve(0 ,tasks, sessionTime);\n return minSession;\n }\n \n void solve(int index, vector<int>& tasks, int target)\n {\n // All tasks are scheduled, if sessions is new minimum, update it.\n if(index >= tasks.size())\n {\n if(minSession > sessions.size())\n minSession = sessions.size();\n return ;\n }\n \n // if current session count is already greater than our min value, don\'t proceed \n if(sessions.size() > minSession)\n return; \n\t\t\n //Case 1: Try to fit this task in one of the possible previous sessions.\n for(int sessionNum = 0; sessionNum < sessions.size(); sessionNum++)\n {\n if(sessions[sessionNum] + tasks[index] <= target)\n {\n sessions[sessionNum] += tasks[index];\n solve(index+1, tasks, target);\n sessions[sessionNum] -= tasks[index];\n }\n }\n \n //Case 2: Put task as part of new session\n sessions.push_back(tasks[index]);\n solve(index+1, tasks, target);\n sessions.pop_back(); \n }\n};\n``` | 4 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | c++ solution with explanation backtrack/dfs type. | c-solution-with-explanation-backtrackdfs-58t0 | As we are checking for all positions/arrangements of a task to be done hence it always give min answer. Any doubt ask in comment else if you like? upvote.\n\ncl | abaddu_21 | NORMAL | 2021-08-29T04:26:57.818232+00:00 | 2021-08-29T04:34:51.525447+00:00 | 545 | false | As we are checking for all positions/arrangements of a task to be done hence it always give min answer. Any doubt ask in comment else if you like? upvote.\n```\nclass Solution {\npublic:\n int ans; //stores answer\n void help(vector<int>& tasks,int idx,vector<int>& v,int Time)\n {\n if(v.size()>=ans) // after this no optimal answer present\n return; \n if(idx>=tasks.size()) // if we come to this then it only means v.size()<ans\n {\n ans=v.size();\n return;\n }\n for(int i=0; i<v.size(); i++) // solving for each position in vector v to check \n\t\t// if this gives us optimal answer \n {\n if(v[i]+tasks[idx]<=Time)\n {\n v[i]+=tasks[idx];\n help(tasks,idx+1,v,Time);\n v[i]-=tasks[idx];\n }\n } \n // maybe optimal solution is after adding element to new position\n \t\tv.push_back(tasks[idx]);\n help(tasks,idx+1,v,Time);\n v.pop_back();\n }\n int minSessions(vector<int>& tasks, int Time) {\n if(tasks.size()==1)\n return 1;\n int sum=0,i=0;\n while(i<tasks.size())\n {\n sum+=tasks[i];\n i++;\n }\n if(sum<=Time)\n return 1;\n ans=tasks.size(); // max answer possible\n vector<int> v; // to get arrangements of tasks to do\n help(tasks,0,v,Time); // starting from 0\n return ans;\n }\n};\n``` | 4 | 0 | ['Backtracking', 'C'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | ✅✅Easy To Understand || C++ Code | easy-to-understand-c-code-by-__kr_shanu_-e3ne | Using Recursion && Memoization\n\n\nclass Solution {\npublic:\n \n // declare a dp\n \n unordered_map<string, int> dp;\n \n // sessions will s | __KR_SHANU_IITG | NORMAL | 2022-09-02T06:59:46.372963+00:00 | 2022-09-02T06:59:46.373002+00:00 | 1,824 | false | * ***Using Recursion && Memoization***\n\n```\nclass Solution {\npublic:\n \n // declare a dp\n \n unordered_map<string, int> dp;\n \n // sessions will store the no. of active sessions\n \n vector<int> sessions;\n \n // function for creating key\n \n // we are sorting the arr to avoid duplicate states, [10, 20, 10, 30] and [10, 10, 20, 30] will form the same key\n \n string create_key(int i)\n {\n vector<int> arr = sessions;\n \n sort(arr.begin(), arr.end());\n \n string res = "";\n \n for(int i = 0; i < arr.size(); i++)\n {\n res += to_string(arr[i]);\n \n res += \'#\';\n }\n \n res += to_string(i);\n \n return res;\n }\n \n // dfs function\n \n int dfs(vector<int>& nums, int i, int n, int time_limit)\n {\n if(i == n)\n {\n return 0;\n }\n \n // if already calculated\n \n string key = create_key(i);\n \n if(dp.count(key))\n return dp[key];\n \n int ans = INT_MAX;\n \n // create a new session\n \n sessions.push_back(nums[i]);\n \n ans = min(ans, 1 + dfs(nums, i + 1, n, time_limit));\n \n // backtrack part\n \n sessions.pop_back();\n \n // include the curr task in the previously active sessions\n \n for(int k = 0; k < sessions.size(); k++)\n {\n if(sessions[k] + nums[i] <= time_limit)\n {\n sessions[k] += nums[i];\n \n ans = min(ans, dfs(nums, i + 1, n, time_limit));\n \n // backtrack part\n \n sessions[k] -= nums[i];\n }\n }\n \n // store the res in dp and return it\n \n return dp[key] = ans;\n }\n \n int minSessions(vector<int>& nums, int sessionTime) {\n \n int n = nums.size();\n \n return dfs(nums, 0, n, sessionTime);\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [C++] Simple C++ Code | c-simple-c-code-by-prosenjitkundu760-bxu1 | \n\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n | _pros_ | NORMAL | 2022-08-16T14:55:35.115942+00:00 | 2022-08-16T14:55:35.115983+00:00 | 821 | false | \n\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n int n;\n int dfs(int ctime, vector<vector<int>> &dp, vector<int>& tasks, int stime, int bitmask)\n {\n if(bitmask == (1<<n)-1)\n return 0;\n if(dp[ctime][bitmask] != -1)\n return dp[ctime][bitmask];\n int val = INT_MAX;\n for(int i = 0; i < n; i++)\n {\n if(bitmask & (1 << i))\n continue;\n bitmask = (bitmask | (1<<i));\n if(ctime+tasks[i] <= stime)\n {\n val = min(val,dfs(ctime+tasks[i], dp, tasks, stime, bitmask));\n }\n else\n {\n val = min(val, 1+dfs(tasks[i], dp, tasks, stime, bitmask));\n }\n bitmask = (bitmask ^ (1<<i));\n }\n return dp[ctime][bitmask] = val;\n }\n \npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n n = tasks.size();\n vector<vector<int>> dp(sessionTime+1,vector<int>( (1<<tasks.size())-1 , -1));\n return 1+dfs(0, dp, tasks, sessionTime, 0);\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Backtracking', 'C', 'Bitmask', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | DP + Bitmasking | CPH | dp-bitmasking-cph-by-dy-123-f61q | Page no. 103 of https://cses.fi/book/book.pdf read from Permutations to subsets. \n\n\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int t | dy-123 | NORMAL | 2021-08-31T16:07:30.401910+00:00 | 2021-08-31T16:14:10.819555+00:00 | 196 | false | Page no. 103 of https://cses.fi/book/book.pdf read from Permutations to subsets. \n\n```\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int t) {\n int n=tasks.size();\n vector<pair<int,int>>best(1<<n,{n+1,t+1});\n // best[0]={1,0};\n best[0]={0,t+1};\n for(int i=1;i<(1<<n);++i){\n // best[i]={n+1,0};\n best[i]={n+1,t+1};\n for(int j=0;j<n;++j){\n if(i&(1<<j)){\n auto opt=best[i^(1<<j)];\n if(opt.second+tasks[j]<=t){\n opt.second+=tasks[j];\n }else{\n opt.first++;\n opt.second=tasks[j];\n }\n best[i]=min(best[i],opt);\n }\n }\n }\n return best[(1<<n)-1].first;\n }\n};\n```\n\n[felixhuang07 ](https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1431820/C++-Bitmask-DP-with-Explanation-time:-O(n-*-2n)-space:-O(2n)/1065585) \n\n | 3 | 0 | ['C'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java Solution | Backtrack + Recursion + Memoization | java-solution-backtrack-recursion-memoiz-smn1 | Solution:\n\n\nArrayList<Integer> sessions;\nHashMap<Pair<ArrayList<Integer>, Integer>,Integer> memo;\n\npublic int minSessions(int[] tasks, int sessionTime) {\ | gumptious33 | NORMAL | 2021-08-29T16:19:38.394887+00:00 | 2021-08-29T16:20:22.429742+00:00 | 786 | false | Solution:\n\n```\nArrayList<Integer> sessions;\nHashMap<Pair<ArrayList<Integer>, Integer>,Integer> memo;\n\npublic int minSessions(int[] tasks, int sessionTime) {\n\tsessions = new ArrayList();\n\tmemo = new HashMap();\n\treturn recursive(tasks, sessionTime, 0);\n}\n\nprivate int recursive(int[] tasks, int sessionTime, int currentPos){\n\t//Base case\n\tif(currentPos>=tasks.length){\n\t\treturn 0; //No tasks take zero sessions\n\t}\n\tPair<ArrayList<Integer>, Integer> pair = new Pair(new ArrayList(sessions), currentPos);\n\tif(memo.containsKey(pair)){\n\t\treturn memo.get(pair);\n\t}\n\n\t//We can always add a new session\n\tsessions.add(tasks[currentPos]);\n\tint result = 1 + recursive(tasks, sessionTime, currentPos+1);\n\t//Backtrack\n\tsessions.remove(sessions.size()-1);\n\n\t//Other cases are trying to add to current sessions\n\tfor(int i=0;i<sessions.size();i++){\n\t\tif(sessions.get(i)+tasks[currentPos]<=sessionTime){\n\t\t\tsessions.set(i, sessions.get(i)+tasks[currentPos]);\n\t\t\tresult = Math.min(result, recursive(tasks, sessionTime, currentPos+1));\n\t\t\tsessions.set(i, sessions.get(i)-tasks[currentPos]); //Backtrack\n\t\t}\n\t}\n\tmemo.put(pair, result);\n\treturn result;\n}\n```\n\nInspired by C++ solution by @Invulnerable: https://leetcode.com/problems/minimum-number-of-work-sessions-to-finish-the-tasks/discuss/1431836/C%2B%2B-Solution-or-Recursion-%2B-Memoization | 3 | 1 | ['Backtracking', 'Recursion', 'Memoization', 'Java'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Java] 1-ms Optimize backtracking solution using 3 techniques | java-1-ms-optimize-backtracking-solution-wpb7 | While trying my backtracking solution, I was getting TLE. The optimizations that helped me are shown below:\n\n1. Sort task array in descending order which help | chemEn | NORMAL | 2021-08-29T05:19:22.242583+00:00 | 2021-08-29T09:30:31.190299+00:00 | 874 | false | While trying my backtracking solution, I was getting TLE. The optimizations that helped me are shown below:\n\n1. Sort task array in descending order which helps in determining minimum number of sessions in less iterations.\n\n2. Create a global variable that stores the minimum number of sessions possible at any time. Before calling backtracking again, check that number of sessions must be less the the minimum till now. If it is not less than minimum, no need to call backtrack.\n\n3. Do not add a single task to multiple sessions with same timing till now. For example :\n\nSessions=[10,10,0,0,0] 5 sessions with 2 used and 3 unused. \n\nIf we have to add a task with time 3, we do not need to call two backtrack [13,10,0,0,0] and [10,13,0,0,0] by adding in each section, these both give same final answers. Only one is sufficient.\n\n\n```\nclass Solution {\n // 1st optimization\n int globe=Integer.MAX_VALUE;\n \n public int minSessions(int[] tasks, int sT) {\n \n // Sort the given tasks array in ascending order\n \n Arrays.sort(tasks);\n int n=tasks.length;\n int i=0,j=n-1;\n while(i<j){\n int temp=tasks[i];\n tasks[i]=tasks[j];\n tasks[j]=temp;\n i+=1;\n j-=1;\n }\n \n // create an array for maxium no. of sessions possible\n \n int[] session=new int[tasks.length+1];\n \n // call backtrack function\n return backtrack(session,tasks,sT,0);\n \n }\n public int backtrack(int[] session,int[] tasks,int sT,int index){\n \n if(index==tasks.length){\n \n int temp=count(session);\n globe=Math.min(globe,temp);\n return temp;\n \n }\n int ans=Integer.MAX_VALUE;\n \n //2nd optimization\n HashSet<Integer> done=new HashSet<>();\n \n for(int i=1;i<=tasks.length;i++){\n if(!done.contains(session[i]) && session[i]+tasks[index]<=sT){\n done.add(session[i]);\n session[i]=session[i]+tasks[index];\n if(count(session)<globe)\n ans=Math.min(ans,backtrack(session,tasks,sT,index+1));\n session[i]=session[i]-tasks[index];\n }\n }\n return ans;\n }\n \n // method to check the number of sessions\n public int count(int[] session){\n int count=0;\n for(int a:session){\n if(a!=0) count++;\n }\n return count;\n }\n}\n``` | 3 | 0 | ['Backtracking', 'Java'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | (DP + bit masking) Similar to travelling salesman problem with slight modification | dp-bit-masking-similar-to-travelling-sal-g1t7 | This problem can be easily solved using dynamic programming and bitmasking\n\nHere, the ith bit in mask is 1 if the ith task has been completed otherwise it is | hemantkr79 | NORMAL | 2021-08-29T04:24:18.974357+00:00 | 2021-08-29T05:08:09.874070+00:00 | 292 | false | This problem can be easily solved using dynamic programming and bitmasking\n\nHere, the ith bit in mask is 1 if the ith task has been completed otherwise it is 0\nwhen all the tasks are done, the value of mask will be equal to the value of \'done\'\n\n```\nclass Solution {\npublic:\n int solve(vector<int> &tasks,int n,vector<vector<int> > &dp,int sessionTime,int cur_session,int mask,int done) {\n if(mask==done) {\n return 0;\n }\n\t\t// if the value was calculated earlier, we return that value and save computation time\n if(dp[mask][cur_session]!=-1) {\n return dp[mask][cur_session];\n }\n int ans = INT_MAX; // let\'s assume INT_MAX sessions are required\n for(int i=0;i<n;i++) {\n if(((mask>>i)&1)==0) { // if the task has not been completed\n\t\t\t\t//cur_session stored the time used in the current session\n if(cur_session+tasks[i] <= sessionTime) { // if the task can be completed in current session\n int tmp = mask;\n mask = (mask|(1<<i)); // we mark that the task has been completed\n ans = min(ans,solve(tasks,n,dp,sessionTime,cur_session+tasks[i],mask,done));\n mask = tmp;\n }\n }\n }\n if(ans==INT_MAX) { // if no task can be completed in the current session, start a new session\n return dp[mask][cur_session] = 1 + solve(tasks,n,dp,sessionTime,0,mask,done);\n }\n\t\t// store and return answer\n return dp[mask][cur_session] = ans;\n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n int done = 0;\n for(int i=0;i<n;i++) {\n done = (done|(1<<i));\n }\n vector<vector<int> > dp((1<<n),vector<int>(sessionTime+1,-1));\n return 1+solve(tasks,n,dp,sessionTime,0,0,done);\n }\n};\n```\n\nTime complexity : ```(2^n)*n```\nspace compexity:``` (2^n)*sessionTime``` | 3 | 0 | [] | 3 |
minimum-number-of-work-sessions-to-finish-the-tasks | AC by lucky | ac-by-lucky-by-liketheflower-owxr | As the task length is pretty small, if we random shuffle a large number of times, we will have a high possibility to find the optimal result. The solution is si | liketheflower | NORMAL | 2021-08-29T04:24:12.263877+00:00 | 2021-08-29T04:31:39.825572+00:00 | 128 | false | As the task length is pretty small, if we random shuffle a large number of times, we will have a high possibility to find the optimal result. The solution is simple:\nRandom shuffle N times and find the minimum result.\n\nI guess the test cases are not that strong, so I can get the code AC by lucky.\n\n```python\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n ret = float("inf")\n for i in range(10000):\n random.shuffle(tasks)\n thisret = 0\n j, curr = 0, 0\n while j < len(tasks):\n if curr + tasks[j] <= sessionTime:\n curr += tasks[j]\n else:\n thisret += 1\n curr = tasks[j]\n j += 1\n if curr > 0:thisret += 1\n ret = min(ret, thisret)\n return ret\n``` | 3 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ Implementation using DP with Bitmasking | c-implementation-using-dp-with-bitmaskin-3p5f | \n\n# Code\n\nclass Solution {\npublic:\n int dp[16385][16];\n int f(int mask,vector<int>& tasks, int sessionTime,int curr=0){\n if(mask==((1<<task | ayushnautiyal1110 | NORMAL | 2023-10-27T14:30:47.439780+00:00 | 2023-10-27T14:30:47.439809+00:00 | 65 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int dp[16385][16];\n int f(int mask,vector<int>& tasks, int sessionTime,int curr=0){\n if(mask==((1<<tasks.size()) - 1)){\n return 1;\n }\n if(dp[mask][curr]!=-1){\n return dp[mask][curr];\n }\n int ans=1e9;\n for(int i=0;i<tasks.size();i++)\n {\n if(!((1<<i) & (mask))){\n if(curr+tasks[i]<=sessionTime){\n ans=min(ans,f((mask | (1<<i)),tasks,sessionTime,curr+tasks[i]));\n }\n else{\n ans=min(ans,1+f((mask | (1<<i)),tasks,sessionTime,tasks[i]));\n }\n }\n }\n return dp[mask][curr]=ans;\n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n int mask=0;\n memset(dp,-1,sizeof(dp));\n int ans= f(mask,tasks,sessionTime);\n return ans;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Golang subset traversal problem | golang-subset-traversal-problem-by-frank-ug1r | Intuition\n\u8FD9\u79CD\u5C5E\u4E8E\u904D\u5386\u5B50\u96C6\u7684\u95EE\u9898 \u6709\u56FA\u5B9A\u7684\u89E3\u6CD5\n# Complexity\n- Time complexity: O(3^n)\n Ad | franklinwen | NORMAL | 2022-12-22T00:50:12.409250+00:00 | 2022-12-22T00:50:12.409287+00:00 | 110 | false | # Intuition\n\u8FD9\u79CD\u5C5E\u4E8E\u904D\u5386\u5B50\u96C6\u7684\u95EE\u9898 \u6709\u56FA\u5B9A\u7684\u89E3\u6CD5\n# Complexity\n- Time complexity: O(3^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc minSessions(tasks []int, sessionTime int) int {\n /* \u904D\u5386\u5B50\u96C6\u7C7B\u578B\u95EE\u9898 state: 00100011 \u8868\u793Atask 2 6 7 \u88AB\u9009\u53D6\n dp[state]: Minimum Number of Work Sessions to Finish the state Tasks\n dp[state] = min(dp[state], dp[subset] + dp[state-subset])\n Time Complexity\uFF1A O(3^n) \u4EFB\u4F55\u4E00\u4E2Atask\u53EA\u6709\u53EF\u80FD\u5B58\u57283\u79CD\u72B6\u6001\uFF1A\n 1.\u5728state\u91CC\u9762 \u4E5F\u5728subset\u91CC 11\n 2.\u5728state\u91CC\u9762 \u4E0D\u5728subset\u91CC 10\n 3.\u4E0D\u5728state\u91CC \u4E0D\u5728subset\u91CC 00\n */\n num := len(tasks)\n dp := make([]int, 1 << num)\n for i := range dp {\n dp[i] = 15\n }\n // initialization \u6240\u6709\u53EF\u4EE5\u4E00\u4E2AsessionTime\u91CC\u5B8C\u6210\u7684sub tasks\n for state := 0; state < (1 << num); state++ {\n sumTime := 0\n for i := 0; i < num; i++ {\n if (state >> i) & 1 == 1 {\n sumTime += tasks[i]\n }\n }\n if sumTime <= sessionTime {\n dp[state] = 1\n }\n }\n /* \u8F6C\u79FB\u65B9\u7A0B substate\u6BCF\u6B21\u51CF1\uFF0C\u7136\u540E\u548Cstate\u53D6\u5171\u6709\u7684tasks\uFF0C\n \u56E0\u4E3A\u662F\u5728state\u91CC\u9762\u53D6substate\uFF0C state - substate\u5C31\u662F\u5269\u4E0B\u6CA1\u53D6\u7684task\n eg\uFF1A state\uFF1A10010011 substate\uFF1A10000001 \u5269\u4F59\u6CA1\u53D6\u7684\u5C31\u662F 00010010\n */\n for state := 0; state < (1 << num); state++ {\n for substate := state; substate > 0; substate = (substate - 1) & state {\n dp[state] = min(dp[state], dp[state-substate] + dp[substate])\n }\n }\n return dp[(1<<num)-1]\n}\n\nfunc min(i, j int) int {\n if i < j {\n return i\n }\n return j\n}\n``` | 2 | 0 | ['Go'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ || Fully Detailed Intuitions Explained ||No DP || Binary Search + Backtracking || Clean code | c-fully-detailed-intuitions-explained-no-ksg2 | Intuition -> We want to divide into minimum no of partitions such that all the tasks gets finished.\n\n## What we are looking to implement is , max size of part | KR_SK_01_In | NORMAL | 2022-08-18T13:47:30.223489+00:00 | 2022-08-18T14:00:39.869527+00:00 | 1,238 | false | ## Intuition -> We want to divide into minimum no of partitions such that all the tasks gets finished.\n\n## What we are looking to implement is , max size of partitions of time can be at max n & min will be 1.\n\n## So we will apply binary search on that, mid will be the our current no. of partitions we taken , we will create a array of size mid for storing the (possible time value ) in each partitions such that max value of each partitions should be less than or equal to sessionTime.\n\n#### By coincidence i have taken the name of array of size mid as dp , it is just for storing it . there is no as such dp (repition thing in this solution).\n\n## Now we will apply our approach of filling the mid no. of partitions , such that max value of partitions should be less than sessionTime , & each partitions must contain a non zero value in it (Some tasks must be done in each partionised set) , otherwise that case will be invalid .\n\n### so after computation , if dp[j]==0 ,we are return false (Invalid case).\n\n\n## Similar problem :- Minimum Time to finish the Task (Hard)\n\n```\n int ans=INT_MAX;\n \n bool func(vector<int> &nums , int mid , int time , int i , vector<int> &dp )\n {\n if(i>=nums.size())\n {\n return true;\n }\n \n int val=*max_element(nums.begin() , nums.end());\n \n if(val>time)\n {\n return false;\n }\n \n for(int j=0;j<mid;j++ )\n {\n if(dp[j] + nums[i] <= time)\n {\n dp[j]+=nums[i];\n \n if(func(nums , mid , time , i+1 , dp))\n {\n return true;\n }\n \n dp[j]-=nums[i];\n \n if(dp[j]==0)\n {\n // we can have all the partitions must have some non zero work value , if any partitions \n\t\t\t\t\t// value==0 , then no of partition is less than mid which is invalid as we have to have mid \n\t\t\t\t\t// number of partitons , then we have to return false \n return false;\n }\n }\n \n }\n \n return false;\n }\n \n int minSessions(vector<int>& nums, int time) {\n int n=nums.size();\n \n int l=1 , r=n;\n \n sort(nums.begin() , nums.end() , greater<int>());\n \n int ans=-1;\n \n while(l<=r)\n {\n int mid=(l+r)/2;\n \n vector<int> dp(mid , 0);\n \n if(func(nums , mid , time , 0 , dp))\n {\n ans=mid;\n r=mid-1;\n }\n else\n {\n l=mid+1;\n }\n }\n \n return ans;\n }\n``` | 2 | 0 | ['Backtracking', 'C', 'Binary Tree', 'C++'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ || DP + Bitmasking | c-dp-bitmasking-by-rosario1975-655u | class Solution {\npublic:\n \n vector> dp;\n \n int fun(int curTime,vector& arr,int t,int mask){\n if(mask == (1 << arr.size())-1)\n | rosario1975 | NORMAL | 2022-07-10T21:40:52.255987+00:00 | 2022-07-10T21:40:52.256031+00:00 | 356 | false | class Solution {\npublic:\n \n vector<vector<int>> dp;\n \n int fun(int curTime,vector<int>& arr,int t,int mask){\n if(mask == (1 << arr.size())-1)\n return 0;\n \n if(dp[curTime][mask] != -1)\n return dp[curTime][mask];\n \n \n int ans = 15;\n \n for(int i = 0; i < arr.size(); i++){\n \n if((mask & (1<<i)) == 0){\n mask = mask ^ (1 << i);\n \n if(curTime + arr[i] <= t)\n ans = min(ans , fun(curTime + arr[i], arr, t , mask));\n else\n ans = min(ans , 1+fun(arr[i], arr, t , mask));\n \n mask = mask ^ (1 << i);\n }\n }\n \n return dp[curTime][mask] = ans;\n }\n int minSessions(vector<int>& arr, int t) {\n int n = arr.size();\n \n dp = vector<vector<int>> (t+1,vector<int>( (1<<arr.size())-1 , -1));\n int mask = 0;\n return 1+fun(0,arr,t,mask);\n }\n}; | 2 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'C', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python Backtracking /w pruning | python-backtracking-w-pruning-by-hszh-nvtg | \nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n sessions = []\n \n self.ans = n = len( | hsZh | NORMAL | 2022-06-18T16:55:12.247224+00:00 | 2022-06-18T16:55:12.247259+00:00 | 230 | false | ```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n sessions = []\n \n self.ans = n = len(tasks)\n \n def backtracking(i):\n \n # pruning\n if len(sessions) >= self.ans:\n return\n \n if i == n:\n self.ans = min(self.ans, len(sessions))\n return\n\n # try to put it in every exist sesssions, or create a new one\n for s_idx in range(len(sessions)):\n if sessions[s_idx] + tasks[i] <= sessionTime:\n sessions[s_idx] += tasks[i]\n backtracking(i+1)\n sessions[s_idx] -= tasks[i]\n \n sessions.append(tasks[i])\n backtracking(i+1)\n sessions.pop()\n \n backtracking(0)\n return self.ans\n``` | 2 | 0 | [] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | O(n!logn) 0 ms 100% Faster Binary Search + Recursion C++ Solution | onlogn-0-ms-100-faster-binary-search-rec-9u6h | Problems for Idea Reference: https://leetcode.com/problems/partition-to-k-equal-sum-subsets/\n2. Book Alloction Problem (similiar to this https://leetcode.com/p | shubhamjha386 | NORMAL | 2022-04-29T07:01:38.526234+00:00 | 2022-06-05T10:26:45.129969+00:00 | 480 | false | Problems for Idea Reference: https://leetcode.com/problems/partition-to-k-equal-sum-subsets/\n2. Book Alloction Problem (similiar to this https://leetcode.com/problems/split-array-largest-sum/)\n\nSolution\n```\nclass Solution {\npublic:\n bool solve(vector<int> &nums,int &target,int idx,vector<int>&map)\n {\n if(idx==nums.size())\n return true;\n for(int i=0;i<map.size();i++)\n {\n if(map[i] + nums[idx]<=target)\n {\n map[i] += nums[idx];\n if(solve(nums,target,idx+1,map))\n return true;\n map[i] -= nums[idx];\n if(map[i]==0)\n break;\n }\n }\n return false;\n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n sort(tasks.begin(),tasks.end(),greater<int>());\n int l = 1,h = tasks.size(),m;\n while(l<h)\n {\n m = (l+h)/2;\n vector<int> map(m,0);\n if(solve(tasks,sessionTime,0,map))\n {\n h = m;\n }\n else\n l = m + 1;\n }\n return h;\n }\n};\n``` | 2 | 0 | ['Backtracking', 'Recursion', 'Binary Tree'] | 4 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Java] share my simple DFS backtracking solution with pruning, beats 91% | java-share-my-simple-dfs-backtracking-so-h896 | \n\nclass Solution {\n int min;\n public int minSessions(int[] tasks, int sessionTime) {\n min = tasks.length + 1; // upper bound, any result can\' | timmybeeflin | NORMAL | 2022-01-16T10:33:19.661536+00:00 | 2022-01-16T10:33:19.661563+00:00 | 797 | false | \n```\nclass Solution {\n int min;\n public int minSessions(int[] tasks, int sessionTime) {\n min = tasks.length + 1; // upper bound, any result can\'t over this upper bound\n \n Arrays.sort(tasks);\n reverse(tasks);\n dfs(tasks, 0, new int[tasks.length], sessionTime, 0);\n return min;\n }\n private void dfs(int[] tasks, int start, int[] bucket, int target, int count) {\n if(count >= min) {\n return; // pruning\n }\n \n if (start == tasks.length) {\n min = count;\n return;\n }\n \n // refer to this: https://leetcode.com/problems/find-minimum-time-to-finish-all-jobs/discuss/1009817/One-branch-cutting-trick-to-solve-three-LeetCode-questions\n Set<Integer> seen = new HashSet<>(); \n for (int i = 0; i < bucket.length; i++) {\n if (seen.contains(bucket[i])) {\n continue;\n }\n if (tasks[start] + bucket[i] > target) {\n continue;\n }\n if(bucket[i] == 0) {\n // new task period, count++\n count++;\n }\n seen.add(bucket[i]);\n \n bucket[i] += tasks[start];\n dfs(tasks, start+1, bucket, target, count);\n bucket[i] -= tasks[start];\n }\n \n }\n \n private void reverse(int[] nums) {\n int left = 0;\n int right = nums.length-1;\n while (left < right) {\n int temp = nums[left];\n nums[left] = nums[right];\n nums[right] = temp;\n left++;\n right--;\n }\n }\n}\n\n``` | 2 | 0 | ['Backtracking', 'Depth-First Search', 'Java'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | Solved without skills | solved-without-skills-by-imironhead-jnto | Honestly, I solved it by adding more and more conditions.\n\nThe basic idea is to check if N sessions are enough and do binary search on N.\n\nSome optimization | imironhead | NORMAL | 2021-09-05T18:19:45.040932+00:00 | 2021-09-05T18:19:45.040962+00:00 | 716 | false | Honestly, I solved it by adding more and more conditions.\n\nThe basic idea is to check if `N` sessions are enough and do binary search on `N`.\n\nSome optimizations are:\n- Sorts tasks. Processing heavy tasks first result in early rejections.\n- The minimum possible \'N\' is `max(1, sum(tasks) // sessionTime)`.\n- If a task is dispatched to an empty session, no need to check the other sessions. Because the remain (unchecked) sessions are also empty.\n\n```python\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n def process_task(idx_task, buckets):\n if idx_task == len(tasks):\n return True\n for i in range(len(buckets)):\n if buckets[i] + tasks[idx_task] <= sessionTime:\n buckets[i] += tasks[idx_task]\n if process_task(idx_task + 1, buckets):\n return True\n buckets[i] -= tasks[idx_task]\n if buckets[i] == 0:\n return False\n return False\n\n def possible(num_buckets):\n buckets = [0 for _ in range(num_buckets)]\n buckets[0] = tasks[0]\n return process_task(1, buckets)\n \n tasks.sort(reverse=True)\n \n l, r = max(1, sum(tasks) // sessionTime), len(tasks)\n\n while l < r:\n m = (l + r) // 2\n \n if possible(m):\n r = m\n else:\n l = m + 1\n\n return l\n``` | 2 | 0 | ['Binary Search', 'Python'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Example why sorting and greedy is not enough | example-why-sorting-and-greedy-is-not-en-zun9 | I see some examples like tasks = {3, 4, 7, 8, 10} sessionTime = 12, But sorting and greedy can give correct answer for that one. I manage to find on that greedy | fdsm_lhn | NORMAL | 2021-09-04T00:27:57.129128+00:00 | 2021-09-04T00:27:57.129160+00:00 | 658 | false | I see some examples like `tasks` = {3, 4, 7, 8, 10} `sessionTime` = 12, But sorting and greedy can give correct answer for that one. I manage to find on that greedy is not working right.\n\nthinking of case like `tasks` = {16, 9, 8, 7,6,6,3,2,2,1} `sessionTime` = 20,after first 6 tasks, u should have three session with 16/20, 17/20, 19/20 respectively, Now u have task with length of 3, if u use greedy u will choose to place it in the first one and ends up with 19/20, 17/20, 19/20. But obviously u can do better by put it in the second one.\n\nhope this is helpful. | 2 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | c++ dp solution using mask | c-dp-solution-using-mask-by-dilipsuthar6-lpvq | \nclass Solution {\npublic:\n long long dp[1<<15][180];\n int find(vector<int>&nums,int mask,int sum,int se,int n)\n {\n if(mask==(1<<n)-1)\n | dilipsuthar17 | NORMAL | 2021-08-30T15:26:00.994004+00:00 | 2021-08-30T15:26:00.994043+00:00 | 259 | false | ```\nclass Solution {\npublic:\n long long dp[1<<15][180];\n int find(vector<int>&nums,int mask,int sum,int se,int n)\n {\n if(mask==(1<<n)-1)\n {\n return 1;\n }\n int ans=INT_MAX;\n if(dp[mask][sum]!=-1)\n {\n return dp[mask][sum];\n }\n for(int i=0;i<n;i++)\n {\n if((mask&(1<<i))==0)\n {\n if(sum+nums[i]>se)\n {\n ans=min(ans,1+find(nums,mask|(1<<i),nums[i],se,n));\n }\n else\n {\n ans=min(ans,find(nums,mask|(1<<i),sum+nums[i],se,n));\n }\n }\n }\n return dp[mask][sum]=ans;\n }\n int minSessions(vector<int>&nums, int se)\n {\n memset(dp,-1,sizeof(dp));\n return find(nums,0,0,se,nums.size());\n }\n};\n``` | 2 | 0 | ['C', 'Bitmask', 'C++'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Python] recursion + tuple memoization, no bitmask, simple 64ms | python-recursion-tuple-memoization-no-bi-tske | I thought some of the other python recursion answers were not that intuitive. Here we simply try each possibility and cache what we\'ve done so far so no repeti | rjmcmc | NORMAL | 2021-08-29T19:27:53.457277+00:00 | 2021-08-29T19:34:08.294721+00:00 | 601 | false | I thought some of the other python recursion answers were not that intuitive. Here we simply try each possibility and cache what we\'ve done so far so no repetition. We take advantage of the tuple data structure which can be cached. The parameter x represents remaining sessiontime for this session. We reset it (plus add to session count) if we can\'t fit anymore tasks in it. \n\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n tasks = sorted(tasks)\n\n @lru_cache(None)\n def recur_fn(x,tasks):\n if len(tasks) == 0:\n return 1\n ans = 0\n result = []\n if tasks[0] > x:\n ans += 1 #on to the new session as can\'t fit anything in \n x = sessionTime #resets remaining session time to full session \n for i,val in enumerate(tasks):\n if val <= x:\n result.append(recur_fn(x-val,tasks[0:i] + tasks[i+1:]))\n else:\n break\n return ans + min(result)\n \n return recur_fn(sessionTime,tuple(tasks)) | 2 | 0 | ['Recursion', 'Memoization', 'Python3'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | [Python3] bit-mask dp | python3-bit-mask-dp-by-ye15-2cxc | Please see this commit for solutions of weekly 256.\n\n\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n | ye15 | NORMAL | 2021-08-29T17:06:03.423179+00:00 | 2021-08-30T04:23:14.708683+00:00 | 418 | false | Please see this [commit](https://github.com/gaosanyong/leetcode/commit/7abfd85d1a68e375fcc0be60558909fd98b270f3) for solutions of weekly 256.\n\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n @cache\n def fn(mask, rem):\n """Return minimum work sessions to finish tasks indicated by set bits in mask."""\n if not mask: return 0 # done \n ans = inf \n for i, x in enumerate(tasks): \n if mask & (1<<i): \n if x <= rem: ans = min(ans, fn(mask ^ (1<<i), rem - x))\n else: ans = min(ans, 1 + fn(mask ^ (1<<i), sessionTime - x))\n return ans\n \n return fn((1<<len(tasks))-1, 0)\n``` | 2 | 0 | ['Python3'] | 3 |
minimum-number-of-work-sessions-to-finish-the-tasks | Ruby/C# - Recursive solution | rubyc-recursive-solution-by-shhavel-24m3 | Solution\n\nAdd two arguments to the function: \n time - remainning time in the current session;\n spent - number of sessions already worked.\n \n# Explanation\ | shhavel | NORMAL | 2021-08-29T10:41:14.129143+00:00 | 2021-08-31T08:15:11.627782+00:00 | 176 | false | # Solution\n\nAdd two arguments to the function: \n `time` - remainning time in the current session;\n `spent` - number of sessions already worked.\n \n# Explanation\n\nCheck all tasks that can feet in remaining `time` and choose minimum posible value recursivelly \nor just start a new session if none feet (in remaining `time`).\n# Ruby\n\n```ruby\ndef min_sessions(tasks, session_time, time = 0, spent = 0)\n return spent if tasks.empty?\n return tasks[0] <= time ? spent : spent + 1 if tasks.one?\n\n candidates = tasks.uniq.select { _1 <= time }\n\n if candidates.empty?\n t = tasks.max\n arr = tasks.dup\n arr.delete_at(arr.index(t))\n min_sessions(arr, session_time, session_time - t, spent + 1)\n else\n candidates.map do |t|\n arr = tasks.dup\n arr.delete_at(arr.index(t))\n min_sessions(arr, session_time, time - t, spent)\n end.min\n end\nend\n```\n\n# C#\n\n```cs\npublic class Solution {\n public int MinSessions(int[] tasks, int sessionTime, int time = 0, int spent = 0) {\n if (tasks.Length == 0) return spent;\n if (tasks.Length == 1) return tasks[0] <= time ? spent : spent + 1;\n\n var candidates = tasks.Where(t => t <= time).Distinct().ToArray();\n\n if (candidates.Length == 0) {\n int t = tasks.Max();\n var arr = tasks.ToList();\n arr.RemoveAt(arr.IndexOf(t));\n return MinSessions(arr.ToArray(), sessionTime, sessionTime - t, spent + 1);\n } else {\n return candidates.Min(t => {\n var arr = tasks.ToList();\n arr.RemoveAt(arr.IndexOf(t));\n return MinSessions(arr.ToArray(), sessionTime, time - t, spent);\n });\n }\n }\n}\n``` | 2 | 0 | ['Recursion', 'Ruby'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java Bitmask | java-bitmask-by-ziwang0411-zzf1 | use bitmask to represent current works done. \nfor example, if current state = 101111 means second job is not done. \nTherefore, for the next state (111111), jo | ziwang0411 | NORMAL | 2021-08-29T04:24:10.004710+00:00 | 2021-08-29T04:24:10.004737+00:00 | 233 | false | use bitmask to represent current works done. \nfor example, if current state = 101111 means second job is not done. \nTherefore, for the next state (111111), job 2 is done and you will have :\n1. dp[111111][session+job2Time] = min(dp[111111][session+job2Time], dp[101111][session]) for currentJobsInTheSession+job2Time is smaller than sessionTime. \n\n2. Otherwise, you will start a new session and it will be dp[111111][job2Time] = min(dp[111111][job2Time], dp[101111][session]+1)\n```\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n Arrays.sort(tasks);\n int res = tasks.length;\n int n = tasks.length;\n int[][] dp = new int[1<<n][sessionTime+1];\n \n for (int i = 0; i<(1<<n); i++) {\n Arrays.fill(dp[i], 100); \n }\n dp[0][0] = 1;\n for (int i = 0; i<(1<<n); i++) {\n for (int t = 0; t<n; t++) {\n if (((1<<t) & i)==0) {\n int nextMask = i|(1<<t);\n for (int s = 0; s<sessionTime+1; s++) {\n if (s+tasks[t]<=sessionTime) {\n dp[nextMask][s+tasks[t]] = Math.min(dp[nextMask][s+tasks[t]], dp[i][s]);\n } else {\n dp[nextMask][tasks[t]] = Math.min(dp[nextMask][tasks[t]], dp[i][s]+1);\n }\n }\n }\n }\n }\n int len = dp.length;\n for (int i = 0; i<sessionTime+1; i++) {\n // System.out.println(dp[len-1][i]);\n res = Math.min(res, dp[len-1][i]);\n }\n return res;\n }\n \n}\n``` | 2 | 0 | [] | 2 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ | Explanation (Recursion + Memo + Bitmask) | c-explanation-recursion-memo-bitmask-by-5vls3 | We will keep adding to current untill task[pos]+cur <=SessionTime, ans remains same since we are not starting new session.\nIf cur+task[pos]>SessionTime, then w | codingsuju | NORMAL | 2021-08-29T04:13:34.032836+00:00 | 2021-08-29T05:18:15.430405+00:00 | 260 | false | We will keep adding to current untill task[pos]+cur <=SessionTime, ans remains same since we are not starting new session.\nIf cur+task[pos]>SessionTime, then we will start new session,and add 1 to ans since we are starting new session.\nEverytime we start new session , we should add 1 to ans.\n\nHere, in dp[mask][cur], mask stands for all task, that has been completed, and cur stands for elapsed time for current session.\n\n\nBonus point: Bitmasking works fine only for smaller input , for n<=16. Beacuse we have to iterate through every possible subset of size n. Number of subsets is 2^n, if n is the number of elements, and 2^16 is around 6 * 10^4\nSo, next time when you see n<=16. Go for approach with the Bitmask.\n```\nclass Solution {\npublic:\n int dp[1<<14][17];\n int INF=1e8;\n int m;\n int solve(int mask,int cur,vector<int> &t,int s)\n {\n if(mask==(1<<m)-1) // If all the task is included mask becomes 11111....(m times) which (2^m -1) =(1<<m)-1\n return 0;\n else if(dp[mask][cur]!=-1)\n return dp[mask][cur];\n int ans=INF;\n for(int i=0;i<t.size();i++)\n {\n if(mask&(1<<i)) // If already included in any session, we just continue.\n continue;\n else if(cur+t[i]<=s)\n ans=min(ans,solve(mask|(1<<i),cur+t[i],t,s)); //Add to current session\n else\n ans=min(ans,solve(mask|(1<<i),t[i],t,s)+1); // Start new session\n }\n return dp[mask][cur]=ans;\n }\n int minSessions(vector<int>& t, int s) {\n memset(dp,-1,sizeof dp);\n m=t.size();\n return solve(0,16,t,s);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Bitmask'] | 2 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python | Self-Inspired | Only work on Leetcode testcases. | python-self-inspired-only-work-on-leetco-659n | \nfrom itertools import combinations\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n tasks.sort()\n | yichonggoh99 | NORMAL | 2021-08-29T04:01:41.582923+00:00 | 2021-08-29T08:11:24.791544+00:00 | 523 | false | ```\nfrom itertools import combinations\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n \n tasks.sort()\n \n ans = 0\n i=1\n \n while tasks and i<=len(tasks): #get rid of all possible combination that results in sessionTime\n comb = combinations(tasks, i)\n \n for pairs in list(comb):\n if sum(pairs) == sessionTime:\n for val in pairs:\n tasks.remove(val)\n \n i=1\n ans+=1\n break\n \n i+=1\n \n while tasks: #for the remaining that is not perfect, selecting from the greatest to lowest\n quota = sessionTime\n ans+=1\n \n while quota > 0:\n i = bisect.bisect_right(tasks, quota) #right most item greater than quota\n if tasks and tasks[i-1] <= quota:\n quota -= tasks.pop(i-1)\n else:\n quota = -1\n \n return ans\n``` | 2 | 0 | [] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | Simple Solution | simple-solution-by-shlok1913-ir4z | Code | shlok1913 | NORMAL | 2025-04-10T11:06:30.526812+00:00 | 2025-04-10T11:06:30.526812+00:00 | 8 | false | # Code
```cpp []
class Solution {
public:
// map<pair <set <int> , int> , int> mp;
// i have to do bitmasking
// to chech if some bit in a number is 0 or not
// (num >> k) & 1 => 1/0
// to set some kth to one use this formulae
// num |= (1 << k)
// you can unset the bit using num &= ~(1 << k);
// and for the base case all those bits which are one will
// constitute a number which is equal to 2 ^ (size of tasks) - 1;
map <pair <int , int> , int> mp;
vector<vector<int>>dp;
int solve(vector<int>&tasks,int rem,int mask,int sT) {
// if (st.size() == tasks.size()) {
// return 0;
// }
if (mask == pow(2 , tasks.size()) - 1) {
return 0;
}
// if (mp.find({st,rem}) != mp.end()) return mp[{st,rem}];
// if (mp.count({mask , rem})) return mp[{mask,rem}];
if (dp[mask][rem] != -1) return dp[mask][rem];
int mn = INT_MAX;
for (int i = 0; i < tasks.size(); i++) {
// if (st.find(i) == st.end()) {
if (((mask >> i) & 1) == 0) {
if (tasks[i] <= rem) {
// st.insert(i);
mask = mask | (1 << i);
mn = min(mn,solve(tasks,rem-tasks[i],mask,sT));
// st.erase(i);
mask &= ~(1 << i);
}
// st.insert(i);
mask = mask | (1 << i);
mn = min(mn,1+solve(tasks,sT-tasks[i],mask,sT));
// st.erase(i);
mask &= ~(1 << i);
}
}
// return mp[{mask,rem}]=mn;
return dp[mask][rem] = mn;
}
int minSessions(vector<int>& tasks, int sT) {
vector<int>v;
// mn = INT_MAX;
// set <int> st;
// return 1 + solve(tasks,sT,st,sT);
dp.assign(pow(2 , tasks.size()) , vector<int>(sT+1 , -1));
return 1 + solve(tasks,sT,0,sT);
// return mn;
}
};
```

| 1 | 0 | ['Dynamic Programming', 'Backtracking', 'Bit Manipulation', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Straightforward Bitmask DP soln || Commented Solution | straightforward-bitmask-dp-soln-commente-7k2y | The approach is explained in the code.Code | Satyamjha_369 | NORMAL | 2025-02-05T18:31:47.612116+00:00 | 2025-02-05T18:31:47.612116+00:00 | 78 | false | The approach is explained in the code.
# Code
```cpp []
class Solution {
public:
int solve(vector<int>& t, int k, vector<vector<int>>& dp, int mask, int time){
if(mask == (1 << t.size()) - 1) //when completed all tasks
return 0;
if(dp[mask][time] != -1) //if subproblem solved before
return dp[mask][time];
int pick1 = 1e9, pick2 = 1e9; //large val to avoid selecting when choosing minimum
for(int i = 0; i < t.size(); i++){
if(mask & (1 << i)) //already completed this task
continue;
if(t[i] > time) //dont have enough time in current session so need to start a new one hence the +1
pick1 = min(pick1, 1 + solve(t, k, dp, mask | (1 << i), k - t[i]));
else //just complete this task in the curr remaining time
pick2 = min(pick2, solve(t, k, dp, mask | (1 << i), time - t[i]));
}
//since we want minimum time
return dp[mask][time] = min(pick1, pick2);
}
int minSessions(vector<int>& tasks, int k) {
vector<vector<int>> dp(1 << 14, vector<int>(16, -1));
return solve(tasks, k, dp, 0, k) + 1; //+1 because one session is active in the beginning of start of process
}
};
//since we can do it in any order then its better to bet on dp with this one
//what we can do is, we can try each task after all other tasks unless its not chosen (use a mask for that)
//about starting the solution, we should start with having k time on our hands as, we are alloed to use that much time and have two picks based on if, te remaining time can be used to finish a task or do we need a new session
``` | 1 | 0 | ['C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | C++ Easy To Read Memo Bitmask | c-easy-to-read-memo-bitmask-by-tristan23-ew3g | Code | Tristan232 | NORMAL | 2025-02-04T06:35:57.860087+00:00 | 2025-02-04T06:35:57.860087+00:00 | 55 | false |
# Code
```cpp []
class Solution {
public:
int set = 0;
int recur(vector<int>& tasks, int mask, int session, vector<vector<int>>& dp) {
if (mask==pow(2,tasks.size())-1) {
return 0;
}
if (dp[mask][session]!=-1) {
return dp[mask][session];
}
int res = INT_MAX-1000;
for (int i = 0;i<tasks.size();i++) {
if (!(mask&(1<<i))) {
if (session-tasks[i]<0) {
res = min(res,1+recur(tasks,mask|(1<<i),set-tasks[i],dp));
} else {
res = min(res,recur(tasks,mask|(1<<i),session-tasks[i],dp));
}
}
}
return dp[mask][session]=res;
}
int minSessions(vector<int>& tasks, int sessionTime) {
set = sessionTime;
vector<vector<int>> dp(pow(2,tasks.size()),vector<int>(sessionTime+1,-1));
return 1+recur(tasks,0,set,dp);
}
};
``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Backtracking', 'Bit Manipulation', 'Bitmask', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Binary Search & Backtracking | 100% | binary-search-backtracking-100-by-rockwe-26y0 | IntuitionSince the goal is to minimize work sessions lets binary search the number of sessions possible. So a basic binary search with the conditional being can | rockwell153 | NORMAL | 2025-02-03T18:12:47.337414+00:00 | 2025-02-03T18:35:39.397951+00:00 | 60 | false | # Intuition
Since the goal is to minimize work sessions lets binary search the number of sessions possible. So a basic binary search with the conditional being `canPartition`, where `canPartition` simply tries to fit all tasks into `mid` number of work sessions.
# Complexity
- Time complexity:
O( logn * k^n )
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
int minSessions(vector<int>& tasks, int sessionTime) {
sort(tasks.rbegin(), tasks.rend());
int left = 1, right = tasks.size();
while (left < right) {
int mid = (left + right) / 2;
vector<int> sessions(mid, 0);
if (canPartition(tasks, sessions, 0, sessionTime)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
bool canPartition(vector<int>& tasks, vector<int>& sessions, int index, int sessionTime) {
if (index == tasks.size()) return true;
unordered_set<int> seen;
for (int& session : sessions) {
if (seen.count(session)) continue;
if (session + tasks[index] <= sessionTime) {
session += tasks[index];
if (canPartition(tasks, sessions, index + 1, sessionTime)) return true;
session -= tasks[index];
seen.insert(session);
if (session == 0) break;
}
}
return false;
}
};
``` | 1 | 0 | ['Binary Search', 'Backtracking', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Bitmask dp | bitmask-dp-by-leofu-qds5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | leofu | NORMAL | 2024-10-11T10:35:11.204262+00:00 | 2024-10-11T11:54:31.672054+00:00 | 100 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n const int inf = 2e9;\n int n = tasks.size();\n vector<int> dp(1<<n, inf); // key: mask, value: minimum total time ( complete session * sessionTime + remainder)\n\n dp[0] = 0;\n for (int i = 1 ; i < (1<<n) ; ++i) {\n for (int j = 0 ; j < n ; ++j) {\n if ((i>>j)&1) {\n int prev_mask = i^(1<<j); // guaranteed < i, hence value already decided\n\n int complete_sessions = dp[prev_mask] / sessionTime;\n int remaining_usage = dp[prev_mask] % sessionTime;\n\n if (remaining_usage + tasks[j] <= sessionTime) {\n dp[i] = min(dp[i], dp[prev_mask] + tasks[j]);\n }\n\n else {\n dp[i] = min(dp[i], (complete_sessions + 1) * sessionTime + tasks[j]);\n }\n\n }\n }\n }\n\n if (dp.back() % sessionTime == 0) return dp.back() / sessionTime;\n return dp.back() / sessionTime + 1;\n }\n};\n```\n\n```cpp []\nclass Solution {\npublic:\n typedef pair<int,int> p;\n\n vector<p> dp;\n\n p solve(vector<int>& tasks, int sessionTime, int mask) { // output: first = sessions used, second = last session time\n int n = tasks.size();\n if (dp[mask].first != n + 1) { // we already calculated this\n return dp[mask];\n }\n\n for (int bit = 0 ; bit < n ; ++bit) {\n if ((mask>>bit)&1) {\n int prev_mask = mask^(1<<bit);\n p prev_value = solve(tasks, sessionTime, prev_mask);\n if (prev_value.second + tasks[bit] <= sessionTime) {\n prev_value.second += tasks[bit];\n dp[mask] = min(dp[mask], prev_value);\n }\n else {\n prev_value.first++;\n prev_value.second = tasks[bit];\n dp[mask] = min(dp[mask], prev_value);\n }\n }\n }\n\n return dp[mask];\n\n }\n\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n = tasks.size();\n\n // initialize dp\n dp = vector<p>(1<<n, make_pair(n + 1, 0));\n dp[0] = make_pair(1, 0); // it\'s using 1 session, and we use up 0 seconds in the last session \n return solve(tasks, sessionTime, (1<<n) - 1).first;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Very Simple Solution || Easy to understand | very-simple-solution-easy-to-understand-v9bwi | Complexity\n- Time complexity: O(2^n)\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\n void solve(int i, vector<int>& tasks, vector<int>& session, | coder_rastogi_21 | NORMAL | 2024-03-09T05:35:23.823084+00:00 | 2024-03-09T05:35:23.823119+00:00 | 81 | false | # Complexity\n- Time complexity: $$O(2^n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n void solve(int i, vector<int>& tasks, vector<int>& session, int sessionTime, int &ans)\n {\n if(i == tasks.size()) { //base case\n ans = min(ans,int(session.size())); //update the minimum sessions needed\n return;\n }\n\n if(session.size() > ans) //early exit (VERY IMPORTANT to avoid TLE) \n return;\n\n //CASE 1: add tasks[i] to any of the existing session\n for(int j=0; j<session.size(); j++) {\n if(session[j] + tasks[i] <= sessionTime) { //only add if it\'s possible\n session[j] += tasks[i];\n solve(i+1,tasks,session,sessionTime,ans);\n session[j] -= tasks[i];\n }\n }\n //CASE 2: add tasks[i] to a new session\n session.push_back(tasks[i]);\n solve(i+1,tasks,session,sessionTime,ans);\n session.pop_back();\n }\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int ans = INT_MAX;\n vector<int> session;\n solve(0,tasks,session,sessionTime,ans);\n return ans;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'C++'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | Python | DFS + Binary Search | ❌bitmask❌DP | Faster than 99% | python-dfs-binary-search-bitmaskdp-faste-vj2l | Intuition\n Describe your first thoughts on how to solve this problem. \nJust don\'t want to use bitmask and dynamic programming.\n# Approach\n Describe your ap | randaldong | NORMAL | 2022-11-18T08:42:40.575550+00:00 | 2022-11-18T08:42:58.465343+00:00 | 299 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust don\'t want to use bitmask and dynamic programming.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- How to find the minimum number of sessions? We can use binary search to do this. But different from typical binary search, we use `mid` as the number of sessions we\u2019ll have. If we can successfully allocate time for all the tasks with `mid` sessions, that means we still have the chance to minimize `mid`, i.e., upgrade `r = mid`; otherwise, we have to use larger `mid`, i.e., upgrade `l = mid + 1`. We stop when `l == r`.\n\n- How to determine whether the allocation of time is successful? We design a DFS function called `canFinish(i)`. It upgrades `remainTime` list each time and returns whether `tasks[i]` can be finished.\n- The base case is: if we\u2019ve reached the end of `tasks`, that means all the tasks can be finished, so we return True.\n- The basic idea of `canFinish` is that this function takes care of one task `tasks[i]` each time, allocating time to finish it. Specifically, we traverse the `remainTime` list, if the current `remainTime[j]` is still enough to finish the task `tasks[i]` that we\u2019re about to arrange, there are a few things we need to do:\n - allocate the time and upgrade the remain time (`remainTime[j] -= tasks[i]`) for next task\u2019s schedule.\n - since we\u2019ve done with task `tasks[i]`, it\u2019s time to think about whether we can allocate time for the next task `tasks[i+1]`, if it is, return `True`.\n - But if the deeper level returns `False` to the if statement (`canFinish[i+1]` returns `False`), we know that the allocation won\u2019t let the task been finished, so we have to add back `tasks[i]` to `remainTime[j]`. So only tasks that can be finished are allocated the time they need (subtract `tasks[i]` from remain time).\n - Then, `j` will move to the next index and use another session time for allocation, the remaining part is kind of repetitive.\n - After we add back `tasks[i]`, if `remainTime[j] == sessionTime`, we know that the next task cannot be finished and the remain time is only enough to finish the current task. So, we can just break from the loop and return `False`.\n# Complexity\nMaybe someone could help me with complexity analysis, I\'m really bad at this.\n\n# Code\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n def canFinish(i):\n if i == nTask:\n return True\n for j in range(mid):\n if remainTime[j] >= tasks[i]:\n remainTime[j] -= tasks[i]\n if canFinish(i + 1):\n return True\n remainTime[j] += tasks[i]\n if remainTime[j] == sessionTime:\n break\n return False \n \n nTask = len(tasks)\n l, r = 1, nTask\n tasks.sort(reverse=True)\n while l < r: \n mid = (l + r) // 2\n remainTime = [sessionTime] * mid\n if not canFinish(0):\n l = mid + 1\n else:\n r = mid\n return l\n```\n# Walk-through\nLet\u2019s walk through an example to help understanding.\n\n```python\ntasks = [5, 4, 5, 2, 1, 3]\nsessionTime = 15\n\n# reversely sorted tasks:\ntasks = [5, 5, 4, 3, 2, 1]\n\n# iter 1\nl = 1\nr = 6\nmid = 3\nremainTime = [15, 15, 15]\n\n#canFinish(0), tasks[0] = 5, j = 0\n remianTime = [10, 15, 15]\n#--canFinish(1), tasks[1] = 5, j = 0\n remianTime = [5, 15, 15]\n#----canFinish(2), tasks[2] = 4, j = 0\n remianTime = [1, 15, 15]\n#------canFinish(3), tasks[3] = 3, j = 0\n# remainTime[j] < tasks[i], j += 1\n#------canFinish(3), tasks[3] = 3, j = 1\n remianTime = [1, 12, 15]\n#--------canFinish(4), tasks[4] = 2, j = 0\n# remainTime[j] < tasks[i], j += 1\n#--------canFinish(4), tasks[4] = 2, j = 1\n remianTime = [1, 10, 15]\n#----------canFinish(5), tasks[5] = 1, j = 0\n remainTime[j] = [0, 10, 15] \n#------------canFinish(6), i == nTask, return True\n\n# upgrade r\nr = 3\n---------------------------------------------------\n# iter 2\nl = 1\nr = 3\nmid = 2\nremainTime = [15, 15]\n\n#canFinish(0), tasks[0] = 5, j = 0\n remianTime = [10, 15]\n#--canFinish(1), tasks[1] = 5, j = 0\n remianTime = [5, 15]\n#----canFinish(2), tasks[2] = 4, j = 0\n remianTime = [1, 15]\n#------canFinish(3), tasks[3] = 3, j = 0\n# remainTime[j] < tasks[i], j += 1\n#------canFinish(3), tasks[3] = 3, j = 1\n remianTime = [1, 12]\n#--------canFinish(4), tasks[4] = 2, j = 0\n# remainTime[j] < tasks[i], j += 1\n#--------canFinish(4), tasks[4] = 2, j = 1\n remianTime = [1, 10]\n#----------canFinish(5), tasks[5] = 1, j = 0\n remainTime[j] = [0, 10] \n#------------canFinish(6), i == nTask, return True\n\n# upgrade r\nr = 2\n---------------------------------------------------\n# iter 3\nl = 1\nr = 2\nmid = 1\nremainTime = [15]\n\n#canFinish(0), tasks[0] = 5, j = 0\n remianTime = [10]\n#--canFinish(1), tasks[1] = 5, j = 0\n remianTime = [5]\n#----canFinish(2), tasks[2] = 4, j = 0\n remianTime = [1]\n#------canFinish(3), tasks[3] = 3, j = 0\n remianTime = [1]\n# remainTime[j] < tasks[i], j += 1\n#------canFinish(3), tasks[3] = 3, j = 1\n# exit for loop, return False\n#----canFinish(2), tasks[2] = 4, j = 0\n\t remianTime = [5]\n#--canFinish(1), tasks[1] = 5, j = 0\n remianTime = [10] \n#canFinish(0), tasks[0] = 5, j = 0 \nremianTime = [15]\n\n# remainTime[j] == sessionTime\n# break for loop, return False\n\n# upgrade l\nl = 2 = r\n\n# exit while loop, return 2\n```\n\n\n | 1 | 0 | ['Binary Search', 'Depth-First Search', 'Python3'] | 1 |
minimum-number-of-work-sessions-to-finish-the-tasks | Java | Space O(2^n) | Bottom-Up 1D DP | java-space-o2n-bottom-up-1d-dp-by-studen-y4nb | Saw a lot of the posts on the front most-upvoted page with 2D dp with space complexity O(2^n * W). It\'s unnecssary. We can do it in O(2^n) space.\nBecause, for | Student2091 | NORMAL | 2022-07-30T23:27:24.195204+00:00 | 2022-07-30T23:40:58.039963+00:00 | 748 | false | Saw a lot of the posts on the front most-upvoted page with 2D dp with space complexity `O(2^n * W)`. It\'s unnecssary. We can do it in `O(2^n)` space.\nBecause, for a given subset of tasks, there is only 1 optimal way - the minimum number of bin required and then followed by the minimum weight.\nThere is no reason to try all the possible weights for the current bin subset. Try the best one will guarantee the optimal solution.\n\nFor example, bin `(0b101)` has a weight of `1`, and in another possibliity, bin `(0b101)`has a weight of 5. It is always more optimal to take the bin with weight of 1 and ignore the one with a weight of 5.\n\n#### Java\n```Java\n// Time Complexity O(2^n * n)\n// Space O(2^n)\nclass Solution {\n public int minSessions(int[] tasks, int sessionTime) {\n int n = tasks.length;\n int[] dp = new int[1<<n]; \n int[] w = new int[1<<n]; // best (min) weight for the current subset i\n Arrays.fill(dp, 100);\n Arrays.fill(w, 1000);\n dp[0]=0;\n for (int i = 1; i < 1<<n; i++){\n for (int j = 0; j < n; j++){\n if ((i & 1 << j) > 0){\n int extra = 0, wh = w[i^1<<j]+tasks[j];\n if (wh > sessionTime){ // need another bin\n extra = 1;\n wh=tasks[j];\n }\n dp[i] = Math.min(dp[i], dp[i^1<<j]+extra);\n if (dp[i^1<<j]+extra==dp[i]){ // update weight to min\n w[i]=Math.min(wh, w[i]);\n }\n }\n }\n }\n return dp[(1<<n)-1];\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Bitmask', 'Java'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | c++ | Backtraking Without DP and BitMasking 94% Faster | c-backtraking-without-dp-and-bitmasking-u4zbv | \nclass Solution {\npublic:\n int minSize = INT_MAX;\n void minHelper(vector<int> tasks,int time,int index,vector<int> assign){\n if(assign.size()> | bhagwat_singh_cse | NORMAL | 2022-07-13T04:25:40.423159+00:00 | 2022-07-13T04:25:40.423211+00:00 | 337 | false | ```\nclass Solution {\npublic:\n int minSize = INT_MAX;\n void minHelper(vector<int> tasks,int time,int index,vector<int> assign){\n if(assign.size()>=minSize)return;\n \n if(index==tasks.size()){\n int size = assign.size();\n minSize = size<minSize?size:minSize;\n return;\n }\n \n assign.push_back(tasks[index]);\n minHelper(tasks,time,index+1,assign);\n assign.pop_back();\n \n for(int i=0;i<assign.size();i++){\n int task = tasks[index];\n if(assign[i]+task<=time){\n assign[i]+=task;\n minHelper(tasks,time,index+1,assign);\n assign[i]-=task;\n }\n }\n \n }\n int minSessions(vector<int>& tasks, int sessionTime) {\n sort(tasks.begin(),tasks.end(),greater<int>());\n vector<int> assign;\n minHelper(tasks,sessionTime,0,assign);\n return minSize;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Recursion'] | 0 |
minimum-number-of-work-sessions-to-finish-the-tasks | 1986. Minimum Sessions ( c++ Dp with Bitmask using pairs) | 1986-minimum-sessions-c-dp-with-bitmask-86t4r | \ntypedef pair<int,int> pi;\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n=tasks.size();\n pi mask | 012_amar | NORMAL | 2022-06-25T13:01:55.959013+00:00 | 2022-06-25T13:01:55.959044+00:00 | 91 | false | ```\ntypedef pair<int,int> pi;\nclass Solution {\npublic:\n int minSessions(vector<int>& tasks, int sessionTime) {\n int n=tasks.size();\n pi masks[1<<n];\n masks[0]=make_pair(1,0);\n for(int i=1;i<1<<n;i++){\n masks[i]=pi{n+1,0};\n for(int j=0;j<n;j++){\n if((i&(1<<j)) > 0){\n int oldmask=i - (1<<j);\n pi t = masks[i];\n if(masks[oldmask].second+tasks[j] <= sessionTime){\n t.first = masks[oldmask].first;\n t.second=masks[oldmask].second+tasks[j];\n }else{\n t.first = masks[oldmask].first+1;\n t.second=tasks[j];\n }\n masks[i]=min(masks[i],t);\n }\n }\n }\n return masks[(1<<n) - 1].first;\n }\n};\n``` | 1 | 0 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.