question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
delete-columns-to-make-sorted-iii | NOT LIS intution | not-lis-intution-by-shivral-9kpx | \n Add your space complexity here, e.g. O(n) \n\n# Code\n\nclass Solution:\n def minDeletionSize(self, strs: List[str]) -> int:\n strs=list(map(list,s | shivral | NORMAL | 2023-04-28T06:43:26.467849+00:00 | 2023-04-28T06:43:26.467882+00:00 | 55 | false | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDeletionSize(self, strs: List[str]) -> int:\n strs=list(map(list,strs))\n n=len(strs[0])\n def check(i,last):\n if last==-1 or i>=n:\n return True\n for s in strs:\n if s[last]>s[i]:\n return False\n return True\n \n dp=[-1]*(n+1)\n def rec(last):\n if last>=n:\n return 0\n if dp[last]!=-1:\n return dp[last]\n ans=float("inf")\n for i in range(last+1,n+1):\n if check(i,last):\n cs=(i-last-1)\n if last==-1:\n cs=i+1\n ans=min(ans,(cs)+rec(i))\n dp[last]=ans\n return ans\n return rec(-1)-1\n\n``` | 0 | 0 | ['Python3'] | 0 |
delete-columns-to-make-sorted-iii | Python solution in 5 lines | python-solution-in-5-lines-by-metaphysic-b76q | Intuition\n Describe your first thoughts on how to solve this problem. \nThis problem is identical to the classic longest non-decreasing subsequence. \nThe prob | metaphysicalist | NORMAL | 2023-04-16T19:58:31.281754+00:00 | 2023-04-16T19:58:31.281786+00:00 | 64 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is identical to the classic longest non-decreasing subsequence. \nThe problem can be efficiently solved in binary search. \nDue to the small input size, the solution based on the slower DP algorithm can also be accepted. \nThe implementation can be very short with the `all()` function for comparing two indices. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n^2 * m) where n is the length of indices, and m is the number of strings. \n\n# Code\n```\nclass Solution:\n def minDeletionSize(self, strs: List[str]) -> int:\n m, n = len(strs), len(strs[0])\n dp = [0] * (n+1)\n for i in range(n):\n dp[i] = 1 + max([dp[j] for j in range(i) if all(strs[k][j] <= strs[k][i] for k in range(m))], default=0)\n return n - max(dp)\n\n\n \n``` | 0 | 0 | ['Dynamic Programming', 'Python3'] | 0 |
delete-columns-to-make-sorted-iii | DP LIS (beats 100%) | dp-lis-beats-100-by-n1shadh-u4n4 | Intuition\n- Use Longest Increasing subsequence concept.\n- Remember that this LIS must have the same index elements across all the strings. \n\n# Complexity\n- | N1shadh | NORMAL | 2023-04-02T10:43:03.043402+00:00 | 2023-04-02T10:43:03.043437+00:00 | 98 | false | # Intuition\n- Use Longest Increasing subsequence concept.\n- Remember that this LIS must have the same index elements across all the strings. \n\n# Complexity\n- Time complexity: O(n*m^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n int n = strs.size();\n int m = strs[0].length();\n int ans = 1;\n vector<int> lis(m,1);\n for(int i=1;i<m;i++) {\n for(int j=0;j<i;j++) {\n bool flg = 1;\n for(int k=0;k<n;k++) {\n if(strs[k][j] > strs[k][i]) {\n flg = 0; break;\n }\n }\n if(flg) {\n if(lis[i] < lis[j]+1) {\n lis[i] = lis[j]+1;\n }\n }\n }\n ans = max(ans,lis[i]);\n }\n\n return m-ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Greedy', 'C++'] | 0 |
delete-columns-to-make-sorted-iii | c++ simple and explained dp solution tabulation technique | c-simple-and-explained-dp-solution-tabul-i1x6 | Intuition\n Describe your first thoughts on how to solve this problem. \nI can consider a LIS only if it is made by same set of indices that\'swhy all strings | vedantnaudiyal | NORMAL | 2023-03-13T12:20:43.284875+00:00 | 2023-03-13T12:20:43.284911+00:00 | 59 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI can consider a LIS only if it is made by same set of indices that\'swhy all strings ith character must be greater than its prev character(jth which is being considered at a time from 0->i-1) to consider LIS of 1+ greater length than previous jth length\ndp vector is storing the maximum lis length with same set of indices\nat last n-ans will be the minimum no of deletions\npls upvote if it helped\n# Approach\n<!-- Describe your approach to solving the problem. -->\ndp (bottom up) tabulation\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*n*m);\nn-> no of indexes in one string\nm-> no of strings in vector\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n int ans=1;\n vector<int> dp(strs[0].size(),1);\n for(int i=1;i<strs[0].length();i++){\n int res=1;\n for(int j=0;j<i;j++){\n bool temp=1;\n for(int k=0;k<strs.size();k++){\n if(strs[k][i]<strs[k][j]){\n temp=0;\n break;\n }\n }\n if(temp){\n res=max(res,1+dp[j]);\n }\n } \n dp[i]=res;\n ans=max(ans,res);\n }\n return strs[0].size()-ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
delete-columns-to-make-sorted-iii | Javascript - DP | javascript-dp-by-faustaleonardo-kh0l | Code\n\n/**\n * @param {string[]} strs\n * @return {number}\n */\nvar minDeletionSize = function (strs) {\n const n = strs.length;\n const m = strs[0].length; | faustaleonardo | NORMAL | 2023-02-22T00:44:07.448055+00:00 | 2023-02-22T00:44:15.551201+00:00 | 41 | false | # Code\n```\n/**\n * @param {string[]} strs\n * @return {number}\n */\nvar minDeletionSize = function (strs) {\n const n = strs.length;\n const m = strs[0].length;\n const dp = new Array(m).fill(1);\n\n for (let colOne = 0; colOne < m; colOne++) {\n for (let colTwo = 0; colTwo < colOne; colTwo++) {\n for (let row = 0; row <= n; row++) {\n if (row === n) {\n dp[colOne] = Math.max(dp[colOne], dp[colTwo] + 1);\n } else if (strs[row][colTwo] > strs[row][colOne]) {\n break;\n }\n }\n }\n }\n\n return m - Math.max(...dp);\n};\n\n``` | 0 | 0 | ['Dynamic Programming', 'JavaScript'] | 0 |
delete-columns-to-make-sorted-iii | Best time complexity C++ solution | best-time-complexity-c-solution-by-85370-v3n2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | 8537046703 | NORMAL | 2023-02-20T18:31:41.529486+00:00 | 2023-02-20T18:31:41.529532+00:00 | 67 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& st) {\n \n vector<int> dp(st[0].size(), 1);\n for (auto i = 0; i < st[0].size(); ++i) {\n for (auto j = 0; j < i; ++j)\n for (auto k = 0; k <= st.size(); ++k) {\n if (k == st.size()) dp[i] = max(dp[i], dp[j] + 1);\n else if (st[k][j] > st[k][i]) break;\n }\n }\n return st[0].size() - *max_element(begin(dp), end(dp));\n }\n \n \n};\n``` | 0 | 0 | ['Array', 'Math', 'String', 'C++'] | 0 |
delete-columns-to-make-sorted-iii | [golang] dp | golang-dp-by-vl4deee11-r9ey | \nvar mem [102][102]int\n\nfunc minDeletionSize(strs []string) int {\n\n\tfor i := 0; i < 102; i++ {\n\t\tfor j := 0; j < 102; j++ {\n\t\t\tmem[i][j] = -1\n\t\t | vl4deee11 | NORMAL | 2023-02-03T03:54:32.002072+00:00 | 2023-02-03T03:54:32.002106+00:00 | 17 | false | ```\nvar mem [102][102]int\n\nfunc minDeletionSize(strs []string) int {\n\n\tfor i := 0; i < 102; i++ {\n\t\tfor j := 0; j < 102; j++ {\n\t\t\tmem[i][j] = -1\n\t\t}\n\t}\n\tvar dp func(i, pi int) int\n\tdp = func(i, pi int) int {\n\t\tif i >= len(strs[0]) {\n\t\t\treturn 0\n\t\t}\n\t\tl := pi\n\t\tif pi == -1 {\n\t\t\tl = 101\n\t\t}\n\t\tif mem[i][l] != -1 {\n\t\t\treturn mem[i][l]\n\t\t}\n\t\tf := true\n\t\tif pi != -1 {\n\t\t\tfor kk := 0; kk < len(strs); kk++ {\n\t\t\t\tif strs[kk][i] < strs[kk][pi] {\n\t\t\t\t\tf = false\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\n\t\tmem[i][l] = 1 + dp(i+1, pi)\n\t\tif f {\n\t\t\tn := dp(i+1, i)\n\t\t\tif n < mem[i][l] {\n\t\t\t\tmem[i][l] = n\n\t\t\t}\n\t\t}\n\t\treturn mem[i][l]\n\t}\n\treturn dp(0, -1)\n}\n\n``` | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | Same as LIS | same-as-lis-by-roboto7o32oo3-4l9h | Complexity\n- Time complexity: O(n^2*m)\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n | roboto7o32oo3 | NORMAL | 2023-01-13T11:17:17.441196+00:00 | 2023-01-13T11:17:17.441236+00:00 | 79 | false | # Complexity\n- Time complexity: $$O(n^2*m)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n int m=strs.size(), n=strs[0].size();\n\n vector<int> dp(n, 1);\n\n for(int i=1; i<n; i++) {\n for(int j=0; j<i; j++) {\n bool flag = true;\n for(int k=0; k<m; k++) {\n if(strs[k][i] < strs[k][j]) {\n flag = false;\n break;\n }\n }\n\n if(flag) {\n dp[i] = max(dp[i], 1 + dp[j]);\n }\n }\n }\n\n return n - *max_element(dp.begin(), dp.end());\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
delete-columns-to-make-sorted-iii | Just a runnable solution | just-a-runnable-solution-by-ssrlive-hwcy | Code\n\nimpl Solution {\n pub fn min_deletion_size(strs: Vec<String>) -> i32 {\n let m = strs.len();\n let n = strs[0].len();\n let mut | ssrlive | NORMAL | 2023-01-05T05:41:37.773881+00:00 | 2023-01-05T05:41:37.773931+00:00 | 43 | false | # Code\n```\nimpl Solution {\n pub fn min_deletion_size(strs: Vec<String>) -> i32 {\n let m = strs.len();\n let n = strs[0].len();\n let mut res = n as i32 - 1;\n let mut dp = vec![1; n];\n for j in 0..n {\n for i in 0..j {\n let mut k = 0;\n while k < m {\n if strs[k].as_bytes()[i] > strs[k].as_bytes()[j] {\n break;\n }\n k += 1;\n }\n if k == m && dp[i] + 1 > dp[j] {\n dp[j] = dp[i] + 1;\n }\n }\n res = res.min(n as i32 - dp[j]);\n }\n res\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
delete-columns-to-make-sorted-iii | C++, top-down DP approach | c-top-down-dp-approach-by-pavlot-w07y | \nclass Solution {\npublic:\n int minDeletionSize( vector<string>& strs ) {\n const int m = strs.size();\n const int n = strs[0].length();\ | pavlot | NORMAL | 2022-12-03T21:46:31.625999+00:00 | 2022-12-03T21:53:36.130016+00:00 | 116 | false | ```\nclass Solution {\npublic:\n int minDeletionSize( vector<string>& strs ) {\n const int m = strs.size();\n const int n = strs[0].length();\n\n std::vector<std::vector<int>> cache( n,std::vector<int>( n + 1,-1 ) );\n\n const std::function<int(int,int)> dfs = [&]( int idx, int prev_idx ) {\n if (idx == n)\n return ( 0 );\n \n if (cache[idx][prev_idx + 1] != -1)\n return ( cache[idx][prev_idx + 1] );\n\n // we have to delete the current column if it violates\n // lexicographic order - we don\'t have choice here, but if it \n // does not violate the order we have two choices\n // - delete or do not delete:\n bool del_f{ false };\n /* delete this column: */\n int best = dfs( idx + 1,prev_idx ) + 1;\n\n /* determine if we can hold this column without deletion: */\n for (int i = 0; i < m && prev_idx != -1; ++i) {\n if (strs[i][idx] < strs[i][prev_idx]) {\n del_f = true;\n break ;\n }\n }\n /* hold this column: */\n if (del_f == false)\n best = std::min( best,dfs( idx + 1,idx ) );\n cache[idx][prev_idx + 1] = best;\n return ( best );\n };\n\n return ( dfs( 0,-1 ) );\n``` | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
delete-columns-to-make-sorted-iii | [C++] longest path in a graph | c-longest-path-in-a-graph-by-ivan-2727-n224 | Build a graph where each vertex corresponds to an index and there is an edge between indices i and j if i < j and they are compatible, i.e. for all strings, s[i | ivan-2727 | NORMAL | 2022-09-27T22:39:00.130035+00:00 | 2022-09-27T22:39:00.130063+00:00 | 27 | false | Build a graph where each vertex corresponds to an index and there is an edge between indices `i` and `j` if `i < j` and they are compatible, i.e. for all strings, `s[i] <= s[j]`. This is a directed acycling graph and each resulting string after deletion of minimum amount of indices will have the length of the longest path in this graph, thus the answer is string size minus the length of the longest path.\n```\nclass Solution {\npublic:\n vector<vector<int>> g;\n vector<int> dp;\n vector<bool> vis;\n void dfs(int v) {\n vis[v] = true;\n for (int u : g[v]) {\n if (!vis[u]) dfs(u);\n dp[v] = max(dp[v], dp[u]+1); \n }\n }\n int minDeletionSize(vector<string>& strs) {\n int n = strs.size();\n int m = strs[0].size(); \n g = vector<vector<int>> (m);\n for (int i = 0; i < m; i++) {\n for (int j = i+1; j < m; j++) {\n bool ok = true;\n for (int k = 0; k < n; k++) {\n if (strs[k][j] < strs[k][i]) {ok = false; break;}\n }\n if (ok) g[i].push_back(j);\n }\n }\n vis = vector<bool> (m, false);\n dp = vector<int> (m); \n for (int v = 0; v < m; v++) {\n if (!vis[v]) dfs(v);\n }\n return m - 1 - *max_element(dp.begin(), dp.end()); \n }\n};\n``` | 0 | 0 | ['Depth-First Search', 'Graph'] | 0 |
delete-columns-to-make-sorted-iii | C++ Dynamic programming solution | Beats 97% | c-dynamic-programming-solution-beats-97-7n0um | Subproblems: S(index)=Minimum length for strs[i][index:] for all i in [0,strs[0].size()-1]\n\nRelation: S(index)=min{next-index-1+S(next) where next belongs to | Diavolos | NORMAL | 2022-09-13T07:23:41.607468+00:00 | 2022-09-13T07:24:15.745657+00:00 | 126 | false | Subproblems: S(index)=Minimum length for strs[i][index:] for all i in [0,strs[0].size()-1]\n\nRelation: S(index)=min{next-index-1+S(next) **where** next **belongs to** [index+1:end) **such that** strs[i][next]>=strs[i][index] **for all** i **belongs to** [0,strs.size())}\nThe reason why I have added next-index-1 to the recursive formula is because index and next will be a part of our subsequence and we have to delete everything **in between** them(not including them) therefore the -1.\n\nBase case: S(index)=0 **if** index>=strs[0].size()\n\nOriginal problem: We have to start at every possible starting position, when we start at the ith position, we would have deleted i characters that occured before that position: min{index+S(index)}\n\nTime complexity: O(NW^2)\n```\nclass Solution {\nprivate:\n vector<int>mem;\n int solve(vector<string>&strs,int index){\n if(index>=strs[0].size()){\n return 0;\n } else if(mem[index]!=-1){\n return mem[index];\n } else {\n int ans=strs[0].size()-index-1;\n for(int next=index+1;next<strs[0].size();next++){\n bool correct=true;\n for(int rows=0;rows<strs.size();rows++){\n if(strs[rows][next]<strs[rows][index]){\n correct=false;\n break;\n }\n }\n if(correct){\n ans=min(ans,next-index-1+solve(strs,next));\n }\n }\n return mem[index]=ans;\n }\n }\npublic:\n int minDeletionSize(vector<string>& strs) {\n mem=vector<int>(strs[0].size(),-1);\n int ans=strs[0].size();\n for(int index=0;index<strs[0].size();index++){\n ans=min(ans,index+solve(strs,index));\n }\n return ans;\n }\n}; | 0 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
delete-columns-to-make-sorted-iii | Python Recursive LIS: 96% time, 13% space | python-recursive-lis-96-time-13-space-by-06n6 | ```\nclass Solution:\n def minDeletionSize(self, strs: List[str]) -> int:\n n = len(strs[0])\n \n def checkRest(idx1, idx2):\n | hqz3 | NORMAL | 2022-09-09T03:16:38.039785+00:00 | 2022-09-09T03:16:38.039844+00:00 | 29 | false | ```\nclass Solution:\n def minDeletionSize(self, strs: List[str]) -> int:\n n = len(strs[0])\n \n def checkRest(idx1, idx2):\n for i in range(1, len(strs)):\n if not strs[i][idx1] <= strs[i][idx2]: return False\n return True\n \n @cache\n def lis(idx):\n longest = 1\n for i in range(idx + 1, n):\n if strs[0][idx] <= strs[0][i] and checkRest(idx, i):\n longest = max(longest, 1 + lis(i))\n return longest\n\n longest = 0\n for i in range(n):\n longest = max(longest, lis(i))\n \n return n - longest | 0 | 0 | ['Python'] | 0 |
delete-columns-to-make-sorted-iii | simpe dp | simpe-dp-by-innsharsh-qnvn | \nclass Solution {\npublic:\n int dp[102][102];\n int solve(vector<string> &strs,int ind,int prev_ind){\n int n=strs.size();\n if(ind<0){\n | innsharsh | NORMAL | 2022-09-07T05:39:27.591996+00:00 | 2022-09-07T05:39:27.592042+00:00 | 14 | false | ```\nclass Solution {\npublic:\n int dp[102][102];\n int solve(vector<string> &strs,int ind,int prev_ind){\n int n=strs.size();\n if(ind<0){\n return 0;\n }\n if(dp[ind][prev_ind+1]!=-1){\n return dp[ind][prev_ind+1];\n }\n if(prev_ind==-1){\n return dp[ind][prev_ind+1]=min(1+solve(strs,ind-1,prev_ind),solve(strs,ind-1,ind));\n }\n \n int opt1=1+solve(strs,ind-1,prev_ind);\n \n for(int i=0;i<n;i++){\n if(strs[i][ind]>strs[i][prev_ind]){\n return dp[ind][prev_ind+1]=opt1;\n }\n }\n return dp[ind][prev_ind+1]=min(opt1,solve(strs,ind-1,ind));\n }\n int minDeletionSize(vector<string>& strs) {\n memset(dp,-1,sizeof(dp));\n return solve(strs,strs[0].size()-1,-1);\n }\n};\n``` | 0 | 0 | ['Dynamic Programming'] | 0 |
delete-columns-to-make-sorted-iii | ✅CPP || Intuition + Comments || DFS | cpp-intuition-comments-dfs-by-ajinkyakam-hdcu | Intuition : For every index, iterate over all strings and find all valid character indexes. A valid character at index j for and index i (for j>i) is defined as | ajinkyakamble332 | NORMAL | 2022-08-26T07:06:20.046633+00:00 | 2022-08-26T07:06:20.046672+00:00 | 60 | false | Intuition : For every index, iterate over all strings and find all valid character indexes. A valid character at index j for and index i (for j>i) is defined as char[j] >=char[i] for all strings. \n\nThis is the preprocesing to find all valid indexes. Now, our problem is reduced to find largest such valid subsequence.\n\nPost that, do dfs to find the one with maximum depth. \n```\n unordered_map<int,int> dp;\n \n\t//dfs for maxDepth\n int dfsLen(int i, unordered_map<int,set<int>> &mp){ \n if(dp.find(i)!=dp.end()){\n return dp[i];\n }\n int mxLen=0;\n for(auto st:mp[i]){\n mxLen=max(1+dfsLen(st,mp),mxLen);\n }\n return dp[i]=mxLen;\n }\n \n int minDeletionSize(vector<string>& strs) {\n int n=strs.size();\n int m=strs[0].size();\n unordered_map<int,set<int>> mp;\n \n for(int j=0;j<m;++j){ \n for(int k=j+1;k<m;++k){\n\t\t\t\t//fixing a j and k s.t we can iterate over all strings to see if we can \n\t\t\t\t// go to k from j\n bool chk=true;\n for(int i=0;i<n;++i){\n if(strs[i][k]<strs[i][j]){\n chk=false;\n }\n }\n if(chk==true){\n mp[j].insert(k);\n } \n }\n }\n \n int ans=1;\n for (auto it:mp){\n ans=max(1+dfsLen(it.first,mp),ans);\n }\n return m-ans;\n }\n``` | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | ✅ Cpp || Recursion || Dfs + memoization | cpp-recursion-dfs-memoization-by-ferocio-xi6n | \nclass Solution {\npublic:\n int n;\n unordered_map<int,int> memo;\n long long dfs(vector<set<int>> &adj,string &vis,int i){\n long long temp=0 | ferociouscentaur | NORMAL | 2022-08-26T06:31:28.224842+00:00 | 2022-08-26T06:31:28.224877+00:00 | 56 | false | ```\nclass Solution {\npublic:\n int n;\n unordered_map<int,int> memo;\n long long dfs(vector<set<int>> &adj,string &vis,int i){\n long long temp=0;\n \n if(memo.find(i)!=memo.end()) return memo[i];\n for(int j = i;j<n;j++){\n if(!vis[j]){\n vis[j] = 1;\n vector<int> t;\n for(auto x:adj[j]){\n if(!vis[x]){\n vis[x] = 1;\n t.push_back(x);\n }\n }\n temp = max(temp,1+dfs(adj,vis,j+1));\n for(auto x:t){\n vis[x] = 0;\n }\n vis[j] = 0;\n }\n }\n return memo[i]=temp;\n }\n int minDeletionSize(vector<string>& strs) {\n n= strs[0].size();\n vector<set<int>> adj(n);\n for(int i = 0;i<strs.size();i++){\n for(int j=0;j<strs[i].size();j++){\n for(int k=j+1;k<strs[i].size();k++){\n if(strs[i][k]<strs[i][j]){\n adj[j].insert(k);\n }\n }\n }\n }\n \n long long ans = 1;\n string vis(n,0);\n int cnt= 0;\n for(int i=0;i<strs[0].size();i++){\n ans = max(ans,1+dfs(adj,vis,i));\n }\n return n-(ans-1);\n \n \n \n }\n};\n``` | 0 | 0 | ['Depth-First Search', 'Recursion', 'Memoization'] | 0 |
delete-columns-to-make-sorted-iii | Easy Java Solution | LIS Variation | Dp | easy-java-solution-lis-variation-dp-by-_-7g6e | \n\t\n\tpublic int minDeletionSize(String[] strs) {\n\t int n = strs.length;\n int m = strs[0].length();\n int[] dp = new int[m];\n \n | _shashank_ | NORMAL | 2022-08-14T09:41:06.987171+00:00 | 2022-08-14T09:45:37.174405+00:00 | 91 | false | \n\t\n\tpublic int minDeletionSize(String[] strs) {\n\t int n = strs.length;\n int m = strs[0].length();\n int[] dp = new int[m];\n \n int overallMax = 0;\n for(int i=0;i<m;i++){\n dp[i] = 1;\n for(int j=0;j<i;j++){\n \n if(isValid(strs,i,j)){\n dp[i] = Math.max(dp[i],dp[j]+1);\n }\n \n }\n overallMax = Math.max(dp[i],overallMax);\n }\n \n return m-overallMax;\n }\n \n private boolean isValid(String[] strs ,int i,int j){\n for(int k=0;k<strs.length;k++){\n if(strs[k].charAt(j)>strs[k].charAt(i))\n return false;\n }\n return true;\n }\n | 0 | 0 | ['Java'] | 0 |
delete-columns-to-make-sorted-iii | Python Longest Increasing Subsequence solution | python-longest-increasing-subsequence-so-bcxr | \n def minDeletionSize(self, strs: List[str]) -> int:\n m = len(strs[0])\n dp = [1]*m\n\t\t#dp[i] refers to the length of LIS beginning at i \n | vincent_great | NORMAL | 2022-06-30T02:41:49.976866+00:00 | 2022-06-30T02:41:49.976895+00:00 | 80 | false | ```\n def minDeletionSize(self, strs: List[str]) -> int:\n m = len(strs[0])\n dp = [1]*m\n\t\t#dp[i] refers to the length of LIS beginning at i \n for i in range(m):\n for j in range(i+1, m):\n incresing = True\n for s in strs:\n if s[i]>s[j]:\n incresing = False\n break\n if incresing:\n dp[j] = max(dp[j], dp[i]+1)\n \n return m-max(dp)\n``` | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | Simple variation of Longest Increasing Subsequence problem | simple-variation-of-longest-increasing-s-62a3 | \nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n \n int i, j, k, n = strs[0].size(), m = strs.size(), ans = 0;\n | kunalanand24154321 | NORMAL | 2022-05-26T19:00:59.632639+00:00 | 2022-05-26T19:00:59.632687+00:00 | 63 | false | ```\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n \n int i, j, k, n = strs[0].size(), m = strs.size(), ans = 0;\n \n vector<int>dp(n+1);\n \n for(i = 0; i < n; i++) {\n dp[i] = 1;\n for (j = i - 1; j >= 0; j--) {\n bool valid = true;\n for(k = 0; k < m; k++) {\n \n if (strs[k][i] < strs[k][j]) {\n valid = false;\n break;\n }\n }\n \n if (valid) {\n dp[i] = max(dp[i], 1 + dp[j]);\n }\n }\n \n ans = max(ans, dp[i]);\n }\n \n ans = n - ans;\n \n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming'] | 0 |
delete-columns-to-make-sorted-iii | Top-Down DP | top-down-dp-by-unluckyguy-ubc8 | \nclass Solution {\npublic:\n bool isGreater(vector<string> &strs, int prev, int curr){\n if(prev < 0){\n return true;\n }\n | UnLuckyGuy | NORMAL | 2022-03-26T05:41:27.340651+00:00 | 2022-03-26T05:41:27.340681+00:00 | 96 | false | ```\nclass Solution {\npublic:\n bool isGreater(vector<string> &strs, int prev, int curr){\n if(prev < 0){\n return true;\n }\n int sz = strs.size();\n for(int i = 0; i < sz; i++){\n int num1 = strs[i][prev] - \'a\';\n int num2 = strs[i][curr] - \'a\';\n if(num1 > num2){\n return false;\n }\n }\n return true;\n }\n int minDel(vector<vector<int>> &dp, vector<string> &strs, int prev, int curr){\n if(curr == dp.size()){\n return 0;\n } \n if(prev != -1 && dp[prev][curr] != -1) {\n return dp[prev][curr];\n }\n int dels = INT_MAX;\n \n if(isGreater(strs, prev, curr)){\n dels = min(dels, minDel(dp,strs,curr, curr+1));\n }\n dels = min(dels, 1+minDel(dp, strs, prev, curr+1));\n if(prev != -1){\n dp[prev][curr] = dels;\n }\n \n return dels;\n }\n int minDeletionSize(vector<string>& strs) {\n int sz = strs[0].length();\n vector<vector<int>> dp(sz, vector<int>(sz, -1));\n return minDel(dp,strs,-1,0);\n }\n};\n``` | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | c++(156ms 17%) bitset & dp | c156ms-17-bitset-dp-by-zx007pi-3llt | Runtime: 156 ms, faster than 17.04% of C++ online submissions for Delete Columns to Make Sorted III.\nMemory Usage: 23.5 MB, less than 17.05% of C++ online subm | zx007pi | NORMAL | 2022-01-15T10:12:37.249191+00:00 | 2022-01-15T10:12:37.249222+00:00 | 104 | false | Runtime: 156 ms, faster than 17.04% of C++ online submissions for Delete Columns to Make Sorted III.\nMemory Usage: 23.5 MB, less than 17.05% of C++ online submissions for Delete Columns to Make Sorted III.\n```\nclass Solution {\npublic:\n vector<bitset<100>>t;\n \n void fill_table(vector<string>& strs){\n for(auto &w: strs){\n vector<vector<int>>v(26, vector<int>());\n v[w.back() - \'a\'].push_back(w.size()-1);\n for(int j = w.size()-2; j >= 0; j--){\n bitset<100>b;\n int id = w[j] - \'a\';\n \n for(int k = id; k != 26; k++)\n for(auto id: v[k]) b[id] = 1;\n \n v[id].push_back(j);\n \n t[j] &= b;\n }\n }\n }\n \n int minDeletionSize(vector<string>& strs){\n int n = strs[0].size();\n t.resize(n-1);\n for(auto &b : t) b.set();\n fill_table(strs);\n \n vector<int>dp(n, 0); \n queue<pair<int, int>>;\n \n for(int i = 0; i != t.size(); i++)\n for(int j = 0; t[i].any(); j++)\n if(t[i][j]) dp[j] = max(dp[j], dp[i] + 1), t[i][j] = 0;\n \n return n - ( *max_element(dp.begin(), dp.end()) + 1);\n }\n};\n``` | 0 | 0 | ['C', 'C++'] | 0 |
delete-columns-to-make-sorted-iii | C++ || O(n^2*m) || Simple DP || Fast || Notes | c-on2m-simple-dp-fast-notes-by-aholtzman-74dg | \n// For every index in the string find the longest increasing substrings from 0 to the index (the check must be susseful for all the strings)\n// Find the long | aholtzman | NORMAL | 2021-12-24T18:55:51.950976+00:00 | 2021-12-25T22:37:02.823125+00:00 | 124 | false | ```\n// For every index in the string find the longest increasing substrings from 0 to the index (the check must be susseful for all the strings)\n// Find the longest substring for all the indexes\n// The minimum deletion equel to string length minus the largest substring\n// Use the DP array to keep the max substring for the index\n// Time complexity O(n^2*m), Space complexity O(n) n = string length, m vector size\n// Time 97.78%, Space 94.44%\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n int m = strs.size();\n int n = strs[0].length();\n int dp[n];\n int max_length = 1;\n dp[0] = 1;\n for(int i=1; i<n; i++)\n {\n int mx = 1; \n for(int j=i-1; j>=0; j--)\n {\n int k;\n if (dp[j]<mx) continue; // First check if it ptential new max for i index\n for(k=0; k<m; k++) // Check if all substrings in increasing order\n if (strs[k][j] > strs[k][i]) break;\n if (k==m) mx = dp[j]+1; // new max for index i\n }\n dp[i] = mx;\n max_length = max(max_length,mx); \n }\n return n-max_length;\n }\n};\n``` | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | Intuitive | intuitive-by-thinkinoriginal-ggx0 | \nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n int slen = strs[0].size();\n vector<int> dp(slen, 1);\n int | thinkinoriginal | NORMAL | 2021-10-15T15:52:27.243003+00:00 | 2021-10-15T15:52:27.243047+00:00 | 71 | false | ```\nclass Solution {\npublic:\n int minDeletionSize(vector<string>& strs) {\n int slen = strs[0].size();\n vector<int> dp(slen, 1);\n int res = 1;\n \n for (int i = 1; i < slen; i++) {\n for (int j = 0; j < i; j++) {\n\t\t \n\t\t // Bellow is the different from the one dimensional LIS\n\t\t // Others are equal\n bool update =true;\n for (auto x : strs) {\n if (x[i] < x[j]) {\n update = false;\n break;\n }\n }\n if (!update)\n continue;\n dp[i] = max(dp[j] + 1, dp[i]);\n res = max(dp[i], res);\n }\n }\n \n return slen - res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
delete-columns-to-make-sorted-iii | EASY C++ solution | easy-c-solution-by-aaditya-pal-0lu6 | c++\nclass Solution {\npublic:\n vector<string>str;\n vector<vector<int>>dp;\n int findmax(int id,int prev){\n //Base case\n if(id>=str[0 | aaditya-pal | NORMAL | 2021-06-29T05:41:13.490721+00:00 | 2021-06-29T05:41:13.490763+00:00 | 138 | false | ```c++\nclass Solution {\npublic:\n vector<string>str;\n vector<vector<int>>dp;\n int findmax(int id,int prev){\n //Base case\n if(id>=str[0].size()){\n return 0;\n }\n //if id==0\n int ans = 0;\n if(prev==-1){\n ans = max(ans,1 + findmax(id+1,id));\n ans = max(ans,findmax(id+1,prev));\n }\n else{\n if(dp[id][prev]!=-1) return dp[id][prev];\n bool flag = true;\n //if we take the current index if we can \n for(int i = 0;i<str.size();i++){\n if(str[i][id]<str[i][prev]){\n flag = false;\n break;\n } \n }\n if(flag) ans = max(ans,1 + findmax(id+1,id));\n \n //we dont take\n \n ans = max(ans,findmax(id+1,prev));\n }\n if(prev!=-1)\n return dp[id][prev] = ans;\n return ans;\n }\n int minDeletionSize(vector<string>& strs) {\n str = strs;\n dp.resize(strs[0].size()+1,vector<int>(strs[0].size()+1,-1));\n return strs[0].size() - findmax(0,-1);\n \n }\n};\n\n\n/*\n Either we can take the current index\n it is the 0th index\n the prev index taken is smaller than curr index for each string\n We will not or cannot take the current index \n*/\n``` | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | java 7ms solution | java-7ms-solution-by-shivam_gupta-7rqc | java code is:\n# \n\nclass Solution {\n public int minDeletionSize(String[] strs) {\n //0-current-delete,1-current-kept;\n int n=strs[0].length | shivam_gupta_ | NORMAL | 2021-05-20T03:38:08.592405+00:00 | 2021-05-20T03:38:08.592447+00:00 | 67 | false | java code is:\n# \n```\nclass Solution {\n public int minDeletionSize(String[] strs) {\n //0-current-delete,1-current-kept;\n int n=strs[0].length();\n int dp[][]=new int[n+1][2];\n for(int i=1;i<=n;i++){\n dp[i][0]=1+Math.min(dp[i-1][0],dp[i-1][1]);\n int j,min=i-1;\n for(j=i-1;j>0;j--){\n boolean lexico=true;\n for(String str : strs)if(str.charAt(i-1)<str.charAt(j-1)){\n lexico=false;\n break;\n }\n if(lexico)min=Math.min(min,dp[j][1]+i-j-1);\n }\n dp[i][1]=min;\n }\n return Math.min(dp[n][0],dp[n][1]);\n }\n}\n```\n***Please,Upvote if this is helpful*** | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | [C++] Solution DP | c-solution-dp-by-libbyxu-nce1 | \tclass Solution {\n\tpublic:\n\t\tint minDeletionSize(vector& strs) {\n\n\t\t\tint n=strs[0].size(), m=strs.size();\n\t\t\tvectordp(n,1);\n\n\t\t\t//lambda fun | libbyxu | NORMAL | 2021-05-16T21:52:28.730203+00:00 | 2021-05-16T21:52:28.730246+00:00 | 112 | false | \tclass Solution {\n\tpublic:\n\t\tint minDeletionSize(vector<string>& strs) {\n\n\t\t\tint n=strs[0].size(), m=strs.size();\n\t\t\tvector<int>dp(n,1);\n\n\t\t\t//lambda function\n\t\t\tauto checkTowS=[&](int i, int j)->bool{\n\t\t\t\tfor(int k=0;k<m;++k)\n\t\t\t\t\tif(strs[k][i]<strs[k][j])return false;\n\t\t\t\treturn true;\n\t\t\t};\n\n\t\t\tfor(int i=0;i<n;++i)\n\t\t\t\tfor(int j=0;j<i;++j)\n\t\t\t\t\tif(checkTowS(i,j))dp[i]=max(dp[i],dp[j]+1);\n\n\t\t\treturn n-*max_element(dp.begin(),dp.end()); \n\t\t}\n\t};\n | 0 | 0 | [] | 0 |
delete-columns-to-make-sorted-iii | 100% Efficient, T O(n*l*l) || S O(l), n = len of 'strs' & l = length of a word | 100-efficient-t-onll-s-ol-n-len-of-strs-seubt | Intution for algo is instead of keeping count of deleted columns we keep count of max columns we can keep\n * we use int array dp which has default value \'1\' | harsh007kumar | NORMAL | 2021-04-19T09:56:07.434021+00:00 | 2021-04-19T09:56:07.434053+00:00 | 85 | false | * Intution for algo is instead of keeping count of deleted columns we keep count of max columns we can keep\n * we use int array dp which has default value \'1\' for each columns as surely we can atleast keep 1 column for all rows\n * \n * Now we check for a given columns C considering we keep it, can we keep the next column \'D\',\n * and to make sure we check all the rows of \'strs\' should satisfy condition\n * strs[rowId][C] <= strs[rowId][D]\n * if not than we cannot keep column \'D\'\n * if all rows pass the check we can update max columns kept at given column C as Math.Max(dp[C],1+dp[D])\n * \n * we start with 2nd last columns as C & continue in above fashion till C is >= 0\n * at end we pull the max column kept from dp array\n * and return total columns - max columns kept to get \'min columns deleted\'\n```\npublic class Solution {\n // Time O(n*l*l) || Space O(l), n = len of \'strs\' & l = length of a word\n public int MinDeletionSize(string[] strs) {\n int len = strs[0].Length, i;\n int[] dp = new int[len]; // stores no of columns kept i.e. Not Deleted from current index\n for (i = 0; i < len; i++) dp[i] = 1; // as min 1 columns can be kept while still keep each word lexo-sorted in \'strs\'\n\n // start checking for max possible columns count we can keep from each index start from 2nd last column onwards\n for (int startingCol = len - 2; startingCol >= 0; startingCol--)\n for (int currCol = startingCol + 1; currCol < len; currCol++)\n {\n for (i = 0; i < strs.Length; i++)\n if (strs[i][startingCol] > strs[i][currCol]) // not lexo-sorted\n break;\n\n if (i == strs.Length) // all rows checks passed for curr column\n dp[startingCol] = Math.Max(dp[startingCol], 1 + dp[currCol]);\n }\n int ans = 0;\n for (i = 0; i < len; i++)\n ans = Math.Max(ans, dp[i]); // get maximum columns kept\n\n return len - ans; // returming min columns deleted\n }\n}\n```\n | 0 | 0 | ['Dynamic Programming'] | 0 |
count-nodes-with-the-highest-score | Python 3 | Graph, DFS, Post-order Traversal, O(N) | Explanation | python-3-graph-dfs-post-order-traversal-bayye | Explanation\n- Intuition: Maximum product of 3 branches, need to know how many nodes in each branch, use DFS to start with\n- Build graph\n- Find left, right, u | idontknoooo | NORMAL | 2021-10-24T04:15:53.346632+00:00 | 2021-10-24T04:15:53.346685+00:00 | 8,547 | false | ### Explanation\n- Intuition: Maximum product of 3 branches, need to know how many nodes in each branch, use `DFS` to start with\n- Build graph\n- Find left, right, up (number of nodes) for each node\n\t- left: use recursion\n\t- right: use recursion\n\t- up: `n - 1 - left - right`\n- Calculate score store in a dictinary\n- Return count of max key\n- Time: `O(n)`\n### Implementation \n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n graph = collections.defaultdict(list)\n for node, parent in enumerate(parents): # build graph\n graph[parent].append(node)\n n = len(parents) # total number of nodes\n d = collections.Counter()\n def count_nodes(node): # number of children node + self\n p, s = 1, 0 # p: product, s: sum\n for child in graph[node]: # for each child (only 2 at maximum)\n res = count_nodes(child) # get its nodes count\n p *= res # take the product\n s += res # take the sum\n p *= max(1, n - 1 - s) # times up-branch (number of nodes other than left, right children ans itself)\n d[p] += 1 # count the product\n return s + 1 # return number of children node + 1 (self)\n count_nodes(0) # starting from root (0)\n return d[max(d.keys())] # return max count\n``` | 110 | 4 | ['Depth-First Search', 'Graph', 'Python', 'Python3'] | 13 |
count-nodes-with-the-highest-score | DFS | dfs-by-votrubac-y3r9 | The value of a node is the product of:\n1. number of nodes in the left subtree, \n2. number of nodes in the right subtree,\n3. number of all other nodes, exclud | votrubac | NORMAL | 2021-10-24T04:00:40.284032+00:00 | 2021-10-24T18:11:34.864487+00:00 | 9,192 | false | The value of a node is the product of:\n1. number of nodes in the left subtree, \n2. number of nodes in the right subtree,\n3. number of all other nodes, excluding the current one (n - left - right - 1)\n\nWe can just use DFS to count child nodes for (1) and (2), and we can then compute (3) as we know the total nubers of nodes.\n\n**C++**\n```cpp\nint dfs(vector<vector<int>> &al, vector<long long> &s, int i) {\n long long prod = 1, sum = 1;\n for (int j : al[i]) {\n int cnt = dfs(al, s, j);\n prod *= cnt;\n sum += cnt;\n }\n s[i] = prod * (max(1ll, (long long)al.size() - sum));\n return i != 0 ? sum : count(begin(s), end(s), *max_element(begin(s), end(s)));\n}\nint countHighestScoreNodes(vector<int>& p) {\n vector<vector<int>> al(p.size());\n vector<long long> s(p.size());\n for (int i = 1; i < p.size(); ++i)\n al[p[i]].push_back(i);\n return dfs(al, s, 0);\n}\n```\n**Java**\n```java\nlong dfs(List<List<Integer>> al, long[] s, int i) {\n long prod = 1, sum = 1;\n for (int j : al.get(i)) {\n long cnt = dfs(al, s, j);\n prod *= cnt;\n sum += cnt;\n }\n s[i] = prod * (Math.max(1, al.size() - sum));\n return sum;\n} \npublic int countHighestScoreNodes(int[] p) {\n List<List<Integer>> al = new ArrayList<>();\n for (int i = 0; i < p.length; ++i)\n al.add(new ArrayList<Integer>()); \n long[] s = new long[p.length];\n for (int i = 1; i < p.length; ++i)\n al.get(p[i]).add(i);\n dfs(al, s, 0);\n long max_val = Arrays.stream(s).max().getAsLong();\n return (int)Arrays.stream(s).filter(v -> v == max_val).count();\n}\n``` | 77 | 3 | ['C', 'Java'] | 9 |
count-nodes-with-the-highest-score | [JAVA] Simple DFS Solution generalised for any tree with detailed comments. T=O(V+E), S=O(V+E) | java-simple-dfs-solution-generalised-for-pnh2 | \n/*\n This solution is generalised to perform for any tree, not only binary tree. \n To calculate score for each node, we need the number of nodes in the | pramitb | NORMAL | 2021-10-24T04:03:39.398159+00:00 | 2021-10-24T04:05:36.382340+00:00 | 4,155 | false | ```\n/*\n This solution is generalised to perform for any tree, not only binary tree. \n To calculate score for each node, we need the number of nodes in the subtrees whose root is a child of the current node \n and also the number of nodes in the remaining tree excluding the subtree with root at the current node.\n Once we have these values we find the product of the non-zero values among them and update the maximum score \n and the count of the number of nodes with the maximum score.\n*/\nclass Solution {\n long maxScore; // stores the maximum score\n int count; // store the count of maximum score\n public int countHighestScoreNodes(int[] parent) {\n int n=parent.length;\n \n // creating the tree\n List<Integer> list[]=new ArrayList[n];\n for(int i=0;i<n;i++)\n list[i]=new ArrayList<>();\n for(int i=1;i<n;i++){\n list[parent[i]].add(i);\n }\n \n maxScore=0l;\n count=0;\n \n dfs(0,list,n);\n \n return count;\n }\n \n // returns the number of nodes in the subtree with root u.\n public int dfs(int u, List<Integer> list[], int n){ \n \n int total=0; // stores total number of nodes in the subtree with root u, excluding u.\n long prod=1l,rem,val;\n \n // traversing children in the subtree\n for(int v:list[u]){\n val=dfs(v,list,n); // number of nodes in the subtree with root v.\n total+=val;\n prod*=val;\n }\n rem=(long)(n-total-1); // number of nodes in the remaining tree excluding the subtree with root u.\n \n if(rem>0)// only count the remaining part if there is at least one node.\n prod*=rem;\n \n // updating maxScore and count.\n if(prod>maxScore){\n maxScore=prod;\n count=1; \n }\n else if(prod==maxScore){\n count++;\n }\n \n return total+1; // returning total number of nodes in the subtree with node u.\n }\n}\n```\nT = O(V+E)\nS = O(V+E)\nPlease upvote if you find this helpful. | 49 | 5 | [] | 5 |
count-nodes-with-the-highest-score | [C++] DFS || Easy Solution with comments | c-dfs-easy-solution-with-comments-by-man-wd07 | \nclass Solution {\n int helper(int src,vector<vector<int>>& g,vector<int>& size){\n int ans = 1;\n for(auto child:g[src]){\n an | manishbishnoi897 | NORMAL | 2021-10-24T04:01:55.390152+00:00 | 2021-10-24T11:11:54.292800+00:00 | 3,705 | false | ```\nclass Solution {\n int helper(int src,vector<vector<int>>& g,vector<int>& size){\n int ans = 1;\n for(auto child:g[src]){\n ans += helper(child,g,size);\n }\n return size[src] = ans; \n }\n \n \npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size();\n vector<int> size(n,0); // size[i] indicates size of subtree(rooted at i node) + 1\n vector<vector<int>> g(n); // storing left and right child of a node\n for(int i=1;i<n;i++){\n g[parents[i]].push_back(i);\n }\n helper(0,g,size); // calculating size of each subtree\n long long cnt = 0, maxi = 0;\n for(int i=0;i<n;i++){\n long long pro = 1; \n pro = max(pro,(long long)n - size[i]); // calculating leftover nodes excluding child nodes \n for(auto node:g[i]){\n pro = pro * size[node]; // multiplying with size of subtree\n }\n if(pro > maxi){\n maxi = pro;\n cnt = 1;\n }\n else if(pro == maxi){\n cnt++;\n }\n }\n return cnt;\n }\n};\n```\n**Hit upvote if you like it :)** | 38 | 1 | [] | 3 |
count-nodes-with-the-highest-score | [Python3] post-order dfs | python3-post-order-dfs-by-ye15-09sb | \n\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n tree = [[] for _ in parents]\n for i, x in enumerate(paren | ye15 | NORMAL | 2021-10-24T04:02:10.708908+00:00 | 2021-10-24T15:51:16.397653+00:00 | 2,391 | false | \n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n tree = [[] for _ in parents]\n for i, x in enumerate(parents): \n if x >= 0: tree[x].append(i)\n \n freq = defaultdict(int)\n \n def fn(x): \n """Return count of tree nodes."""\n left = right = 0\n if tree[x]: left = fn(tree[x][0])\n if len(tree[x]) > 1: right = fn(tree[x][1])\n score = (left or 1) * (right or 1) * (len(parents) - 1 - left - right or 1)\n freq[score] += 1\n return 1 + left + right\n \n fn(0)\n return freq[max(freq)]\n```\n\nAlternatively \n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n tree = [[] for _ in parents]\n for i, x in enumerate(parents): \n if x >= 0: tree[x].append(i)\n \n def fn(x): \n """Return count of tree nodes."""\n count = score = 1\n for xx in tree[x]: \n cc = fn(xx)\n count += cc\n score *= cc\n score *= len(parents) - count or 1\n freq[score] += 1\n return count\n \n freq = defaultdict(int)\n fn(0)\n return freq[max(freq)]\n``` | 23 | 3 | ['Python3'] | 5 |
count-nodes-with-the-highest-score | ✅ C++ , Clean code | Graph + DFS | Easy Explanation with comments | c-clean-code-graph-dfs-easy-explanation-xduve | C++\n\nclass Solution {\npublic:\n \n \n // Steps : \n // 1 - For each node, you need to find the sizes of the subtrees rooted in each of its child | HustlerNitin | NORMAL | 2021-11-24T22:00:45.707116+00:00 | 2022-11-13T13:44:37.334264+00:00 | 1,629 | false | **C++**\n```\nclass Solution {\npublic:\n \n \n // Steps : \n // 1 - For each node, you need to find the sizes of the subtrees rooted in each of its children.\n \n // 2 - How to determine the number of nodes in the rest of the tree? \n\t// Can you subtract the size of the subtree rooted at the node from the total number of nodes of the tree?\n \n // 3 - Use these values to compute the score of the node. Track the maximum score, and how many nodes achieve such score. \n \n\t// calculating size of each subtree by standing at every node \'0\' to \'n-1\'\n int dfs(int src,vector<vector<int>>& g,vector<int>& size)\n {\n int ans = 1;// for curent node\n for(auto child : g[src]){\n ans += dfs(child,g,size);\n }\n return size[src] = ans; \n }\n \n // This code can also be work for generalized tree not only for Binary tree\n int countHighestScoreNodes(vector<int>& parents) \n { \n int n=parents.size();\n vector<int>size(n,0); // size[i] indicates size of subtree(rooted at i node) + 1\n vector<vector<int>>g(n); // storing left and right child of a node\n for(int i=1;i<n;i++){\n g[parents[i]].push_back(i); // \'There is no parent for 0th node\'\n }\n \n dfs(0,g,size); //calculating size of each subtree(rooted at ith node)\n\n long long int maxCount = 0; // To avoid overflow because perform product below you should take "long long int"\n long long int maxScore = 0;\n for(int i=0;i<n;i++) // Nodes from \'0\' to \'n-1\'\n {\n // calculate score of each node after removal their \'edge\' or \'node itself\'.\n long long int product = 1;\n product = max(product, (long long int)(n - size[i])); // calculating leftover nodes excluding child nodes \n for(auto x : g[i])\n {\n product = product*size[x];\n }\n \n if(product > maxScore){\n maxScore = product;\n maxCount = 1;\n }\n else if(product == maxScore){\n maxCount++; // store count of nodes which have maximum score equal to "maxScore"\n }\n }\n \n return maxCount;\n }\n};\n```\n**Hit the upvote if you like it : )**\n**Happy Coding** | 17 | 0 | ['C'] | 3 |
count-nodes-with-the-highest-score | Intuitive JAVA solution, faster than 100% | intuitive-java-solution-faster-than-100-oft88 | I used the most straightforward way to solve this problem.\nIt can be divided into 3 steps.\n Construct tree by using the parents[] array.\n Find the highest sc | ironpotato | NORMAL | 2021-10-24T07:06:15.698967+00:00 | 2021-10-24T19:08:24.359687+00:00 | 1,259 | false | I used the most straightforward way to solve this problem.\nIt can be divided into 3 steps.\n* Construct tree by using the parents[] array.\n* Find the highest score\n* Count nodes with the highest score\n\n```\nclass Solution {\n long highest = 0;\n \n public int countHighestScoreNodes(int[] parents) {\n int n = parents.length;\n int res = 0;\n Node[] arr = new Node[n];\n //construct tree\n for (int i = 0; i < parents.length; i++) {\n arr[i] = new Node();\n }\n \n for (int i = 1; i < parents.length; i++) {\n int parentId = parents[i];\n if (arr[parentId].left == null) {\n arr[parentId].left = arr[i];\n } else {\n arr[parentId].right = arr[i];\n }\n }\n\n findSize(arr[0]);\n \n\t\t//find the highest score\n for (int i = 0; i < parents.length; i++) {\n long product = 1; \n int leftCnt = arr[i].left == null ? 0 : arr[i].left.cnt;\n int rightCnt = arr[i].right == null ? 0 : arr[i].right.cnt;\n int restCnt = n - 1 - leftCnt - rightCnt;\n \n if (leftCnt > 0) {\n product *= leftCnt;\n }\n if (rightCnt > 0) {\n product *= rightCnt;\n }\n if (restCnt > 0) {\n product *= restCnt;\n }\n arr[i].product = product;\n highest = Math.max(highest, product);\n }\n \n\t\t//count nodes\n for (int i = 0; i < parents.length; i++) {\n if (arr[i].product == highest) {\n res++;\n }\n }\n return res;\n }\n \n class Node {\n Node left;\n Node right;\n long product = 0L;\n int cnt = 0; \n public Node() {}\n }\n \n private int findSize (Node root) {\n if (root == null) {\n return 0;\n }\n int size = findSize(root.left) + findSize(root.right) + 1;\n root.cnt = size;\n return size;\n } \n}\n``` | 17 | 0 | ['Recursion'] | 2 |
count-nodes-with-the-highest-score | C++ Post-order Traversal | c-post-order-traversal-by-lzl124631x-2f9f | See my latest update in repo LeetCode\n\n## Solution 1. Post-order Traversal\n\nPost-order traverse the tree. For each node, calculate its score by multiplying | lzl124631x | NORMAL | 2021-10-24T04:01:35.458120+00:00 | 2021-10-24T04:01:35.458148+00:00 | 1,743 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Post-order Traversal\n\nPost-order traverse the tree. For each node, calculate its score by multiplying the node count of its left subtree, right subtree and nodes not in the current subtree (ignoring `0`). Count the nodes with the maximum score.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-264/problems/count-nodes-with-the-highest-score/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(N)\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& P) {\n long N = P.size(), ans = 0, maxScore = 0;\n vector<vector<int>> G(N); // build the graph -- G[i] is a list of the children of node `i`.\n for (int i = 1; i < N; ++i) G[P[i]].push_back(i);\n function<int(int)> dfs = [&](int u) { // Post-order traversal. Returns the size of the subtree rooted at node `u`.\n long score = 1, cnt = 1;\n for (int v : G[u]) {\n int c = dfs(v);\n cnt += c;\n score *= c;\n }\n long other = N - cnt; // The count of nodes not in this subtree rooted at node `u`.\n if (other) score *= other;\n if (score > maxScore) {\n maxScore = score;\n ans = 0;\n }\n if (score == maxScore) ++ans;\n return cnt;\n };\n dfs(0);\n return ans;\n }\n};\n``` | 11 | 1 | [] | 0 |
count-nodes-with-the-highest-score | Java Solution | Subnodes Count | With Explanation | java-solution-subnodes-count-with-explan-aenu | Counts array is having the counts of subnodes for each node.\nNow removing a node , remaining can be easily get with product of subnodes of that node\'s subnode | surajthapliyal | NORMAL | 2021-10-24T06:03:10.358974+00:00 | 2021-10-24T06:32:02.008478+00:00 | 681 | false | Counts array is having the counts of subnodes for each node.\nNow removing a node , remaining can be easily get with product of subnodes of that node\'s subnodes and upper nodes (total - counts[node])\nIn case of parent we dont have any upper nodes so we dont do it when i==0.\nStore all products along with thier frequency in a HashMap then return the max one.\n```\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n int n = parents.length;\n List<Integer>[] tree = new ArrayList[n];\n \n\t\tfor(int i=0;i<n;i++)\n tree[i] = new ArrayList<>();\n \n\t for(int i=1;i<n;i++)\n tree[parents[i]].add(i);\n \n\t int counts[] = new int[n];\n Arrays.fill(counts,1);\n \n\t\tdfs(0,tree,counts);\n \n\t\tlong max = 0, res = 0;\n HashMap<Long,Long> map = new HashMap<>(); \n \n\t\tfor(int i=0;i<n;i++){\n long prod = 1;\n for(int u : tree[i]) {\n prod *= counts[u];\n }\n\t\t\t\n if(i!=0) prod *= n-counts[i];\n map.put(prod,map.getOrDefault(prod,0L)+1L);\n\t\t\t\n if(prod >= max) {\n max = prod;\n res = map.get(prod);\n }\n }\n\t\t\n return (int)res;\n }\n\t\n private int dfs(int node,List<Integer>[] tree,int counts[]){ \n\t\n for(int next : tree[node])\n counts[node] += dfs(next,tree,counts);\n \n\t return counts[node];\n\t\t\n }\n}\n``` | 8 | 0 | [] | 0 |
count-nodes-with-the-highest-score | ✔️ PYTHON || EXPLAINED || ;] | python-explained-by-karan_8082-9gme | UPVOTE IF HELPFuuL\n\nObservation : \nscore = number of above nodes * number of nodes of 1 child * number of nodes ofother child\n\nWe are provided with the par | karan_8082 | NORMAL | 2022-06-29T09:14:40.018016+00:00 | 2022-06-29T09:42:59.509025+00:00 | 744 | false | **UPVOTE IF HELPFuuL**\n\n**Observation** : \nscore = ```number of above nodes * number of nodes of 1 child * number of nodes ofother child```\n\nWe are provided with the parents of nodes, For convenience we keep mapping of chilren of nodes.\n\n* First task : Create a dictionary to keep the children of nodes.\n* Secondly, with recurssion we find number of nodes below and including itself for ```node i``` and store in ```nums```\n\nNow use formula :\n* Number of nodes above node i = Total nodes - ```nums[i]``` . -> nums [ i ] is number of nodes below it + 1.\n* Number of nodes for children are provided directly stored in nums dictionary.\n\n**UPVOTE IF HELPFuuL**\n\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n \n def fin(n):\n k=1\n for i in child[n]:\n k += fin(i)\n nums[n]=k\n return k\n \n child = {}\n for i in range(len(parents)):\n child[i]=[]\n for i in range(1,len(parents)):\n child[parents[i]].append(i)\n \n nums={}\n fin(0)\n k=1\n for i in child[0]:\n k*=nums[i]\n score=[k]\n for i in range(1,len(nums)):\n k=1\n k*=(nums[0]-nums[i])\n for j in child[i]:\n k*=nums[j]\n score.append(k)\n \n return score.count(max(score))\n```\n![Uploading file...]()\n | 7 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | Easy to understand C++ Solution | Post Order | DFS | O(n) | easy-to-understand-c-solution-post-order-nuym | Intuition\n Describe your first thoughts on how to solve this problem. \nWe are asked to count the nodes with highest score. \nScore of a node is nothing but pr | cstrasengan | NORMAL | 2024-02-01T06:28:14.701133+00:00 | 2024-02-01T06:28:14.701157+00:00 | 780 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are asked to count the nodes with highest score. \n**Score of a node** is nothing but product of number of nodes in the remaining forests after removing that node from the tree. \n\n**Important Observation**:\nWe can categorize the nodes into three cases\n1. **Root Node** - A score of a root node is just the product of number of nodes in left sub tree and number of nodes in right sub tree i.e `leftSubTreeNodes * rightSubTreeNodes`, Since a root node doesn\'t have a parents, we will have at most two forests when we remove the node \n2. **Leaf Node** - Since a leaf node doesn\'t have any children, on deleting a leaf node we get one forest. So, the score of the leaf node is `numberOfNodesInATree` - 1\n3. **Middle Node** - A Middle node can have both children and a parent. So, when we delete a middle node, we get 3 forests. Score of a middle node is `leftSubTreeNodes * rightSubTreeNodes *otherNodes`.\n\nOn careful observation cases 2 and 3 can be simplified and combined into one case.\n`leftSubTreeNodes * rightSubTreeNodes * (numberOfTreeNodes - (lefSubTreeNodes + rightSubtreeNodes +1))`, *because other nodes can be calculated as total no of nodes - no of child nodes + 1(including the current node). Also, for leafnodes, we don\'t include the child nodes while computing the score.*\n\n*For Root node however, since we don\'t have a parent, the other nodes will be 0, so we don\'t include that while computing the score for that node.*\n\nSince, we want to know the count in the left subtrees and right subtrees before computing the score every node, we use the postOrder traversal.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create an adjacency list for the tree from the parents array.\n2. Do a post order traversal. \n3. In the post order traversal, while traversing the node, compute the score according to the above algorithm, update the maximum score if it\'s greater than the previous max score and the set the maxScore Count to 1.\n4. If the score equal to maxScore, update the maxScore Frequency\n\n\n# Complexity\n- Time complexity: `O(n)`\nWe are traversing all the nodes in the Tree exactly once. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)` - to store the adjaceny list\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> graph;\n long long maxScore = 0;\n int root = -1;\n int maxScoreFrequency = 0;\n\n int dfs(int node) {\n int count = 0;\n long long score = 1;\n for(auto adj: graph[node]){\n auto child = dfs(adj);\n count += child;\n score *= child;\n }\n if(node != root) score *= (graph.size() -(count + 1));\n if(maxScore < score) {\n maxScore = score;\n maxScoreFrequency = 1;\n } else if(maxScore == score) {\n maxScoreFrequency++;\n }\n return count +1;\n }\n\n int countHighestScoreNodes(vector<int>& parents) {\n graph.resize(parents.size());\n for(int i = 0 ; i < parents.size(); i++) {\n if(parents[i] != -1) {\n graph[parents[i]].push_back(i);\n }else {\n root = i;\n }\n }\n dfs(root);\n return maxScoreFrequency;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
count-nodes-with-the-highest-score | C++ simple dfs with explanation | c-simple-dfs-with-explanation-by-shyamab-towf | class Solution {\npublic:\n \n \n int dfs(vector adj[], int n,int i, vector&dp)\n {\n int ans=1;\n \n // ans+=adj[i].size();\n | shyamabhishek115 | NORMAL | 2021-12-06T19:18:08.632365+00:00 | 2021-12-06T19:18:08.632413+00:00 | 415 | false | class Solution {\npublic:\n \n \n int dfs(vector<int> adj[], int n,int i, vector<int>&dp)\n {\n int ans=1;\n \n // ans+=adj[i].size();\n \n for(auto it:adj[i])\n {\n ans+= dfs(adj,n,it,dp);\n }\n \n return dp[i]=ans;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n \n int n=parents.size();\n \n vector<int>dp(n+1,-1);\n \n vector<int>adj[n+1];\n \n for(int i=0;i<n;i++)\n {\n if(parents[i]!=-1)\n {\n adj[parents[i]].push_back(i);\n }\n }\n long long mn=0;\n int id=0;\n \n dfs(adj,n,0,dp); // dfs for calculating the size of each subtree\n \n \n for(int i=0;i<n;i++)\n {\n long long a=0,b=0,prod=0;\n \n if(adj[i].size()==2) // if it has two size thn there will be three comp in prod\n {\n a= dp[adj[i][0]];\n b= dp[adj[i][1]];\n \n prod=a*b*(n-a-b-1);\n if(i==0){ prod=a*b;}\n }\n else if(adj[i].size()==1){ // else 2 comp would be there\n \n a=dp[adj[i][0]];\n prod=a*(n-a-1);\n if(i==0){ prod=a;}\n }\n else{ // if no size thn must be leaf, so size is n-1\n prod=n-1; \n }\n \n // cout<<a<<" "<<b<<" "<<prod<<endl;\n if(prod>mn){\n mn=prod; // cal mx prod\n id=1; // if new mx prod found,initiase it ti 1, as this is only elemnt\n }\n else if(prod==mn)\n {\n id++; // else increase its val\n }\n \n }\n \n \n return id;\n }\n}; | 5 | 1 | [] | 1 |
count-nodes-with-the-highest-score | Easy Java Solution With Comments | easy-java-solution-with-comments-by-pava-endq | \nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n //--build tree start--\n Node[] arr = new Node[parents.length];\n | pavankumarchaitanya | NORMAL | 2021-10-24T04:01:20.834694+00:00 | 2021-10-24T04:01:20.834729+00:00 | 800 | false | ```\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n //--build tree start--\n Node[] arr = new Node[parents.length];\n for(int i = 0;i<parents.length;i++)\n arr[i] = new Node();\n \n for(int i = 1;i<parents.length;i++){\n arr[i].parent = arr[parents[i]];\n arr[i].id = i;\n if(arr[parents[i]].left==null){\n arr[parents[i]].left = arr[i];\n }else\n arr[parents[i]].right = arr[i];\n }\n // --build tree complete---\n \n countLeftAndRightScoreNodes(arr[0]);// build node\'s left and right count maps\n\n for(Node node: arr){//calculate product of all subtrees for given node\n long parentSide = 1, rightSide = rcMap.getOrDefault(node.id,0), leftSide = lcMap.getOrDefault(node.id,0);\n parentSide = (rcMap.getOrDefault(0,0)+lcMap.getOrDefault(0,0)+1) - (rightSide+leftSide+1); // root\'s left count + root\'s right count - (current node and below count)\n long product = Math.max(parentSide,1)*Math.max(rightSide,1)*Math.max(leftSide,1);\n tm.put(product,tm.getOrDefault(product, 0)+1);\n }\n return tm.get(tm.lastKey());\n }\n \n TreeMap<Long, Integer> tm = new TreeMap<>();\n Map<Integer,Integer> lcMap = new HashMap<>();//left count\n Map<Integer,Integer> rcMap = new HashMap<>();\n\n void countLeftAndRightScoreNodes(Node root){//post order traversal to build left and right node counts\n if(root == null)\n return;\n countLeftAndRightScoreNodes(root.left);\n countLeftAndRightScoreNodes(root.right);\n\n int currentCount = (root.left!=null?lcMap.getOrDefault(root.id,0):0)+(root.right!=null?rcMap.getOrDefault(root.id,0):0)+1;\n if(root.parent==null)\n return;\n if(root==root.parent.left){\n lcMap.put(root.parent.id,currentCount);\n }else{\n rcMap.put(root.parent.id,currentCount);\n }\n }\n \n}\nclass Node{\n Node left;\n Node right;\n Node parent;\n int id = 0;//index\n public Node(){\n }\n public Node(Node left, Node right, Node parent){\n this.left = left;\n this.right = right;\n this.parent = parent;\n }\n}\n``` | 5 | 0 | [] | 2 |
count-nodes-with-the-highest-score | Easy C++ Solution || DFS || GRAPH | easy-c-solution-dfs-graph-by-bleedin_mar-xe7k | Intuition\nSince TreeNode class is not previously declared so it is a hint we dont need that. It is just a simple problem of graph and selecting the maximum.\n\ | bleedin_maroon | NORMAL | 2023-09-09T20:42:22.265253+00:00 | 2023-09-09T20:42:22.265282+00:00 | 610 | false | # Intuition\nSince TreeNode class is not previously declared so it is a hint we dont need that. It is just a simple problem of graph and selecting the maximum.\n\n# Approach\nCreate adjacency matrix and take the product of the components after disconnection. If its is max update max and reset count to 1, else update count.\n\n# Complexity\n- Time complexity:\nO(n)-->Since we are iterating each nodes only once.\n\n- Space complexity:\nO(n)-->For creating adjacency matrix.\n\n# Code\n```\nclass Solution {\npublic:\n int n;\n long long maxi=-1, count=0;\n int solver(vector<vector<int>>& adj, int node) {\n long long score = 1;\n int childs = adj[node].size();\n\n int leftNodes = 0, rightNodes = 0;\n if (childs > 0) leftNodes = solver(adj, adj[node][0]);\n if (childs > 1) rightNodes = solver(adj, adj[node][1]);\n\n if (leftNodes > 0) score *=leftNodes;\n if (rightNodes > 0) score *=rightNodes;\n\n int parentNodes = n-leftNodes-rightNodes-1;\n if (parentNodes > 0) score *= parentNodes;\n\n if (score > maxi) {\n maxi = score;\n count = 1;\n }\n\n else if (score == maxi) count++;\n\n return leftNodes + rightNodes + 1;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n n = parents.size();\n vector<vector<int>> adj(n);\n for (int i=1; i<n; i++) {\n adj[parents[i]].push_back(i);\n }\n\n solver(adj, 0);\n return count;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
count-nodes-with-the-highest-score | [Python] DFS Solution with Dictionary, Straightforward, No Zip | python-dfs-solution-with-dictionary-stra-onu7 | Runtime: 1816 ms, faster than 83.52% of Python3 online submissions for Count Nodes With the Highest Score.\nMemory Usage: 112.2 MB, less than 76.78% of Python3 | bbshark | NORMAL | 2022-10-22T02:37:45.316924+00:00 | 2022-10-22T02:37:45.316949+00:00 | 201 | false | *Runtime: 1816 ms, faster than 83.52% of Python3 online submissions for Count Nodes With the Highest Score.\nMemory Usage: 112.2 MB, less than 76.78% of Python3 online submissions for Count Nodes With the Highest Score.*\n\nMy solution is never fancy but it must be straightforward and understandable (hopefully).\n1. Create a dictionary of {parent node : its son nodes}\n2. Do a dfs search to find out the size of each node, save the results\n3. Calculate the score for each node (assume it\'s removed), record the frequency of each score in another dictionary, also record the max score.\n\n\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n \n dic = {} # parent : sons\n for i in range(n):\n if parents[i] not in dic:\n dic[parents[i]] = []\n dic[parents[i]].append(i)\n \n # dfs search the size of each node (number of subtrees + node itself)\n # save the result in tree_size\n tree_size = [0 for i in range(n)]\n def search(root: int):\n root_size = 1\n if root in dic: # if root is a parent\n for son in dic[root]:\n son_size = search(son)\n root_size += son_size\n \n tree_size[root] = root_size\n return root_size\n \n\t\t# search the root\n search(0)\n \n max_score = 0\n freq = {}\n for i in range(n):\n\t\t\t# initialization: if i is not a parent\n left_size = 0\n right_size = 0\n \n if i in dic: # if i is a parent\n if len(dic[i]) > 0:\n left_size = tree_size[dic[i][0]] # size of its left subtree\n if len(dic[i]) > 1:\n right_size = tree_size[dic[i][1]] # size of its right subtree\n \n # score = size of left subtree * size of right subtree * size the other trees (except i which is removed)\n score = max(left_size, 1) * max(right_size, 1) * max(n - 1 - left_size - right_size, 1)\n \n if score not in freq:\n freq[score] = 0\n freq[score] += 1\n max_score = max(max_score, score)\n \n return freq[max_score]\n```\n\nSome of the master solutions in discussion are too fancy for me to understand (as I only know basic functions), so I made my own.\nHope it can help! ( \u2022\u0300 \u03C9 \u2022\u0301 )y | 4 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 1 |
count-nodes-with-the-highest-score | Java | O(n) | DFS | Concise | java-on-dfs-concise-by-tyro-fupr | \n\nclass Solution {\n long max = 0, res = 0;\n public int countHighestScoreNodes(int[] parents) {\n Map<Integer, List<Integer>> hm = new HashMap() | tyro | NORMAL | 2021-10-24T12:05:22.193513+00:00 | 2021-12-18T00:20:39.052391+00:00 | 1,207 | false | \n```\nclass Solution {\n long max = 0, res = 0;\n public int countHighestScoreNodes(int[] parents) {\n Map<Integer, List<Integer>> hm = new HashMap();\n for(int i = 0; i < parents.length; i++) { // build the tree\n hm.computeIfAbsent(parents[i], x ->new ArrayList<>()).add(i);\n }\n dfs(0, parents.length, hm); // traverse the tree to get the result\n return (int)res;\n }\n int dfs(int s, int n, Map<Integer, List<Integer>> hm) {\n int sum = 1;\n long mult = 1L;\n for(int child : hm.getOrDefault(s, new ArrayList<>())) {\n int count = dfs(child, n, hm); // subtree node count\n sum += count;\n mult *= count; // multiply the result by children size\n } \n mult *= (s == 0 ? 1L : n - sum); // multiply the result by remain size except self and children size(the nodes through parent)\n if(mult > max) {\n max = mult;\n res = 1;\n } else if (mult == max) {\n res++;\n }\n return sum; // return the node count of the tree rooted at s\n }\n}\n``` | 4 | 0 | ['Depth-First Search', 'Java'] | 1 |
count-nodes-with-the-highest-score | C++ post-order solution | c-post-order-solution-by-chejianchao-7yca | \nGet the number of nodes of L subtree and R subtree. and score = l * r * rest. (if l, r, rest == 0 then set to 1)\n\nclass Solution {\npublic:\n long long a | chejianchao | NORMAL | 2021-10-24T04:00:51.211718+00:00 | 2021-10-24T16:06:06.920911+00:00 | 574 | false | \nGet the number of nodes of L subtree and R subtree. and score = l * r * rest. (if l, r, rest == 0 then set to 1)\n```\nclass Solution {\npublic:\n long long ans = 0;\n long long cnt = 0;\n vector<vector<int> > adj;\n int n;\n long long dfs(int node) {\n long long l = 0, r = 0;\n if(adj[node].size() >= 1) {\n l = dfs(adj[node][0]);\n }\n if(adj[node].size() >= 2) {\n r = dfs(adj[node][1]);\n }\n long long rest = n - 1 - r - l;\n long long score = (l == 0 ? 1 : l) * (r == 0 ? 1 : r) * (rest == 0 ? 1 : rest);\n if(score == ans) {\n ++cnt;\n }else if(score > ans) {\n ans = score;\n cnt = 1;\n }\n return l + r + 1;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n n = parents.size();\n adj.resize(n);\n for(int i = 1; i < parents.size(); i++ ){\n adj[parents[i]].push_back(i);\n }\n dfs(0);\n return cnt;\n }\n};\n```\n\nWe can also use for-loop:\n```\n\nclass Solution {\npublic:\n long long ans = 0;\n long long cnt = 0;\n vector<vector<int> > adj;\n int n;\n long long dfs(int node) {\n long long rest = n - 1;\n long long score = 1;\n for(int child : adj[node]) {\n long long subtreeCount = dfs(child);\n rest -= subtreeCount;\n score *= subtreeCount ? subtreeCount : 1;\n }\n score *= rest ? rest : 1;\n if(score == ans) {\n ++cnt;\n }else if(score > ans) {\n ans = score;\n cnt = 1;\n }\n return n - rest;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n n = parents.size();\n adj.resize(n);\n for(int i = 1; i < parents.size(); i++ ){\n adj[parents[i]].push_back(i);\n }\n dfs(0);\n return cnt;\n }\n};\n``` | 4 | 0 | [] | 2 |
count-nodes-with-the-highest-score | Easy Solution || Explained Well || java | easy-solution-explained-well-java-by-amr-dayr | Objective\nFor each node, we want to calculate a score. This score is the product of the sizes of the subtrees of its children and the remaining nodes outside t | Amritanshu23 | NORMAL | 2024-05-19T07:35:30.186143+00:00 | 2024-05-19T07:35:30.186173+00:00 | 104 | false | Objective\nFor each node, we want to calculate a score. This score is the product of the sizes of the subtrees of its children and the remaining nodes outside these subtrees. We need to find out how many nodes have the highest score.\n\nSteps to Solve the Problem\nCreate the Binary Tree:\n\nConvert the parents array into a tree structure so we can easily navigate and calculate subtree sizes.\nTraverse the Tree:\n\nVisit each node and calculate the size of its subtrees.\nCalculate the score for each node using the sizes of its subtrees and the remaining nodes.\nTrack Scores:\n\nKeep track of all scores and identify the maximum score.\nCount how many nodes have this maximum score.\nDetailed Steps\nStep 1: Create the Binary Tree\nWe need to create nodes and link them based on the parents array.\n\nEach node is represented by a TreeNode class.\nWe store all nodes in an array and then link them according to their parent indices.\nHere\'s a method to create the tree:\n\n```\n\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n\n TreeNode(int val) {\n this.val = val;\n this.left = null;\n this.right = null;\n }\n}\n\npublic TreeNode createTree(int[] parents) {\n int n = parents.length;\n TreeNode[] nodes = new TreeNode[n];\n \n // Create all nodes\n for (int i = 0; i < n; i++) {\n nodes[i] = new TreeNode(i);\n }\n\n TreeNode root = null;\n \n // Link nodes according to the parents array\n for (int i = 0; i < n; i++) {\n if (parents[i] == -1) {\n root = nodes[i]; // The root node\n } else {\n TreeNode parent = nodes[parents[i]];\n if (parent.left == null) {\n parent.left = nodes[i];\n } else {\n parent.right = nodes[i];\n }\n }\n }\n \n return root;\n}\n```\nStep 2: Traverse the Tree and Calculate Scores\nWe will use a post-order traversal (process left subtree, right subtree, then the node) to calculate the size of each subtree and the score for each node.\n\n```\n\nclass Solution {\n \n HashMap<Long, List<Long>> scoreMap = new HashMap<>();\n int totalNodes = 0;\n long maxScore = 0;\n\n public int countHighestScoreNodes(int[] parents) {\n TreeNode root = createTree(parents);\n totalNodes = parents.length;\n calculateScores(root);\n return scoreMap.get(maxScore).size();\n }\n\n public int calculateScores(TreeNode node) {\n if (node == null) return 0;\n \n int leftSize = calculateScores(node.left);\n int rightSize = calculateScores(node.right);\n \n long score = 1;\n if (leftSize != 0) score *= leftSize;\n if (rightSize != 0) score *= rightSize;\n if (totalNodes - leftSize - rightSize - 1 != 0) score *= (totalNodes - leftSize - rightSize - 1);\n\n maxScore = Math.max(score, maxScore);\n scoreMap.putIfAbsent(score, new ArrayList<>());\n scoreMap.get(score).add((long)node.val);\n\n return leftSize + rightSize + 1;\n }\n\n public TreeNode createTree(int[] parents) {\n int n = parents.length;\n TreeNode[] nodes = new TreeNode[n];\n \n for (int i = 0; i < n; i++) {\n nodes[i] = new TreeNode(i);\n }\n\n TreeNode root = null;\n \n for (int i = 0; i < n; i++) {\n if (parents[i] == -1) {\n root = nodes[i]; // The root node\n } else {\n TreeNode parent = nodes[parents[i]];\n if (parent.left == null) {\n parent.left = nodes[i];\n } else {\n parent.right = nodes[i];\n }\n }\n }\n \n return root;\n }\n}\n```\nExplanation of the Code\nTreeNode Class:\n\nRepresents each node with val, left, and right.\ncreateTree Method:\n\nConverts the parents array into a tree structure.\ncalculateScores Method:\n\nRecursively calculates the size of each subtree.\nComputes the score for each node and updates the maxScore.\nUses a HashMap scoreMap to keep track of scores and corresponding nodes.\ncountHighestScoreNodes Method:\n\nUses the above methods to create the tree, calculate scores, and return the count of nodes with the highest score.\nSummary\nThis solution involves creating the tree from the parents array, traversing it to calculate the scores for each node, and then determining how many nodes have the highest score. The use of a HashMap helps in efficiently counting nodes with the same score, and the traversal ensures all nodes are processed correctly. | 3 | 0 | ['Tree'] | 0 |
count-nodes-with-the-highest-score | simple java solution using hashmap | simple-java-solution-using-hashmap-by-ha-etxh | ```\n// if you found my solution usefull please upvote it\nclass Solution \n{\n public HashMap hash;\n public int dfs(int i,List[] adj,int totalNodes)\n | Haswanth_kumar | NORMAL | 2022-10-28T06:48:40.523976+00:00 | 2022-10-28T06:48:40.524019+00:00 | 296 | false | ```\n// if you found my solution usefull please upvote it\nclass Solution \n{\n public HashMap<Long,Integer> hash;\n public int dfs(int i,List<Integer>[] adj,int totalNodes)\n {\n int sumOfNodes=0;\n long product=1l;\n for(int curr : adj[i])\n {\n int currNodes=dfs(curr,adj,totalNodes);\n sumOfNodes+=currNodes;\n product*=currNodes;\n }\n int upNodes=(totalNodes-sumOfNodes-1);\n if(upNodes>0) product*=upNodes;\n hash.put(product,hash.getOrDefault(product,0)+1);\n return sumOfNodes+1;\n }\n public int countHighestScoreNodes(int[] parents) \n {\n List<Integer>[] adj=new ArrayList[parents.length];\n for(int i=0;i<parents.length;i++) adj[i]=new ArrayList();\n for(int i=1;i<parents.length;i++)\n {\n adj[parents[i]].add(i);\n }\n hash=new HashMap<>();\n dfs(0,adj,parents.length);\n long max=0;\n for(long i : hash.keySet()) max=Math.max(max,i);\n return hash.get(max);\n }\n} | 3 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | cpp easy solution using recursion | cpp-easy-solution-using-recursion-by-san-36ri | ```\nclass treeNode{\n public:\n treeNode left,right;\n int val;\n \n treeNode(int val){\n this->val=val;\n left=right=NULL | Sanket_Jadhav | NORMAL | 2022-09-06T13:43:10.451752+00:00 | 2022-09-06T13:43:10.451790+00:00 | 654 | false | ```\nclass treeNode{\n public:\n treeNode* left,*right;\n int val;\n \n treeNode(int val){\n this->val=val;\n left=right=NULL;\n }\n};\n\nclass Solution {\npublic:\n unordered_map<long long int,int>ans;\n int func(treeNode* root,int n){\n if(!root)return 0;\n \n int a=0,b=0;\n a=func(root->left,n);\n b=func(root->right,n);\n \n long long int t=1,m=n-(a+b+1);\n if(a!=0)t*=a;\n if(b!=0)t*=b;\n if(m!=0)t*=m;\n \n \n ans[t]++;\n \n return a+b+1;\n }\n \n int countHighestScoreNodes(vector<int>& parents) {\n int n=parents.size();\n unordered_map<int,treeNode*>m;\n \n for(int i=0;i<n;i++){\n treeNode* root=new treeNode(i);\n m[i]=root;\n }\n \n for(int i=1;i<n;i++){\n int ele=parents[i];\n if(m[ele]->left==NULL)m[ele]->left=m[i];\n else m[ele]->right=m[i];\n }\n \n func(m[0],n);\n \n long long int maxi=0,t=0;\n for(auto ele:ans){\n if(ele.first>=maxi){\n t=ele.second;\n maxi=ele.first;\n }\n }\n return t;\n }\n}; | 3 | 0 | ['C++'] | 0 |
count-nodes-with-the-highest-score | Calculate subtree size at every node | calculate-subtree-size-at-every-node-by-ggtzv | Calculate subtree size at every node.\nThen, score of a node = (product of size of subtree from every child) * (size of FULL tree - size of subtree at node).\n\ | srhd_dhrs | NORMAL | 2021-11-03T07:02:23.898378+00:00 | 2021-11-03T07:06:23.367935+00:00 | 2,346 | false | **Calculate subtree size at every node.**\nThen, score of a node = (product of size of subtree from every child) * (size of FULL tree - size of subtree at node).\n\n```\nclass Solution {\npublic:\n int getSize(int cur, vector<int> children[], int subSize[]) {\n subSize[cur] = 1;\n \n for(auto c : children[cur])\n subSize[cur] += getSize(c, children, subSize);\n \n return subSize[cur];\n } \n \n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size();\n int subSize[n];\n vector<int> children[n];\n \n for(int i=0; i<n; i++) \n if(parents[i]!=-1) children[parents[i]].push_back(i);\n \n getSize(0, children, subSize);\n \n long long int maxProduct = 0, ans = 0;\n \n for(int i=0; i<n; i++) {\n long long int curProduct = max(n - subSize[i], 1);\n // above condition given for root\n for(auto c : children[i]) curProduct *= subSize[c];\n \n if(curProduct > maxProduct) {\n maxProduct = curProduct;\n ans = 1;\n } else if(curProduct == maxProduct) ans++;\n }\n \n return ans;\n }\n}; | 3 | 0 | [] | 0 |
count-nodes-with-the-highest-score | Subtree size | Adjacency List | subtree-size-adjacency-list-by-esh_war12-oe6j | Intuition\n Describe your first thoughts on how to solve this problem. \nScore is product of subtree sizes so we should have a easier way to find subtree size w | esh_war12 | NORMAL | 2024-07-08T10:02:19.529794+00:00 | 2024-07-08T10:02:19.529827+00:00 | 351 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nScore is product of subtree sizes so we should have a easier way to find subtree size when each of node is removed in constant time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind subtree size of each node. (If you don\'t know search on cp algo or CodeNCode channel).\n\nTo find the answer we have to check score of each node removal and maintain max score.\n\nWhen a node is removed we will have atmost 3 different trees. \nTrees formed from left and right subtrees of current node , and another tree from parent node . \n\nlong long x = max(n-subtreesize[i],1); Gives subtree size for 3rd option . To understand this try checking on different nodes \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int>subtreesize;\n vector<int>vis;\n int dfs(int node,vector<int> adj[], int csize)\n {\n vis[node]=1;\n subtreesize[node] = csize;\n for(auto child : adj[node])\n {\n if(vis[child]==0)\n {\n subtreesize[node] += dfs(child,adj,1);\n }\n }\n return subtreesize[node];\n\n }\n int countHighestScoreNodes(vector<int>& parents)\n {\n int n = parents.size();\n vector<int>adj[n+1];\n for(int i=1;i<n;i++)\n {\n adj[parents[i]].push_back(i);\n adj[i].push_back(parents[i]);\n }\n subtreesize.resize(n+2,0);\n vis.resize(n+2,0);\n dfs(0,adj,1);\n\n for(int i=0;i<n;i++)\n {\n cout<<subtreesize[i]<<" ";\n }\n long long score = 0;\n int ans = 0;\n for(int i=0;i<n;i++)\n {\n long long x = max(n-subtreesize[i],1);\n\n for(auto child : adj[i])\n {\n if(child == parents[i])continue;\n x *= subtreesize[child];\n }\n if(x>score)\n {\n score = x;\n ans =1; \n }\n else if(x==score)\n {\n ans++;\n }\n }\n return ans;\n\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
count-nodes-with-the-highest-score | C++ Simple DFS On Binary Tree | c-simple-dfs-on-binary-tree-by-rishabhsi-9mhh | \nclass Solution {\npublic:\n long long N;\n long long maxi;\n long long count;\n int dfs(vector<vector<int>>& g, int src){\n \n int l | Rishabhsinghal12 | NORMAL | 2023-01-11T18:11:07.147904+00:00 | 2023-01-11T18:11:07.147950+00:00 | 861 | false | ```\nclass Solution {\npublic:\n long long N;\n long long maxi;\n long long count;\n int dfs(vector<vector<int>>& g, int src){\n \n int l = 0,r = 0;\n \n if(g[src].size() > 0){\n l = dfs(g,g[src][0]);\n }\n \n if(g[src].size() > 1){\n r = dfs(g,g[src][1]);\n }\n \n long long res = 1;\n \n if(l)res *= l;\n if(r)res *= r;\n \n long long left = N-(l+r)-1;\n \n if(left)res *= left;\n if(maxi < res){\n count=1;\n maxi=res;\n }\n \n else if(maxi == res){\n count++;\n }\n \n return l+r+1;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n \n int n = size(parents);\n \n maxi = -1;\n count = 0;\n N=n;\n \n vector<vector<int>> g(n);\n \n for(int i = 1; i < n; i++){\n \n g[parents[i]].push_back(i);\n }\n \n dfs(g,0);\n \n return count;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'C', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | ✔ Python3 Solution | DFS | O(n) | python3-solution-dfs-on-by-satyam2001-ln0u | Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n | satyam2001 | NORMAL | 2023-01-01T07:53:17.705749+00:00 | 2023-01-01T07:53:17.705791+00:00 | 934 | false | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n scores = [1] * n\n graph = [[] for _ in range(n)]\n for e, i in enumerate(parents):\n if e: graph[i].append(e)\n def dfs(i):\n res = 1\n for j in graph[i]:\n val = dfs(j)\n res += val\n scores[i] *= val\n if i: scores[i] *= (n - res)\n return res\n dfs(0)\n return scores.count(max(scores))\n``` | 2 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | 2 DFS | C++ | 2-dfs-c-by-tusharbhart-au0e | \nclass Solution {\n int dfs1(int node, int pre, vector<int> adj[], vector<int> &cnt) {\n int c = 1;\n for(int ad : adj[node]) {\n i | TusharBhart | NORMAL | 2022-12-23T10:04:50.412303+00:00 | 2022-12-23T10:04:50.412339+00:00 | 901 | false | ```\nclass Solution {\n int dfs1(int node, int pre, vector<int> adj[], vector<int> &cnt) {\n int c = 1;\n for(int ad : adj[node]) {\n if(ad == pre) continue;\n c += dfs1(ad, node, adj, cnt);\n }\n return cnt[node] = c;\n }\n void dfs2(int node, int pre, vector<int> adj[], vector<int> &cnt, int n, unordered_map<long long, int> &m) {\n long long p = 1;\n for(int ad : adj[node]) {\n if(ad == pre) {\n p *= n - cnt[node];\n continue;\n }\n p *= cnt[ad];\n dfs2(ad, node, adj, cnt, n, m);\n }\n m[p]++;\n }\n\npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size(), ans;\n long long mx = 0;\n vector<int> adj[n];\n for(int i=1; i<n; i++) adj[i].push_back(parents[i]), adj[parents[i]].push_back(i);\n\n vector<int> cnt(n);\n dfs1(0, -1, adj, cnt);\n \n unordered_map<long long, int> m;\n dfs2(0, -1, adj, cnt, n, m);\n\n for(auto i : m) {\n if(i.first > mx) ans = i.second, mx = i.first;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'C++'] | 0 |
count-nodes-with-the-highest-score | ✅ EZ Python || DFS | ez-python-dfs-by-0xsapra-q1lr | \nclass Node:\n \n \n def __init__(self, n):\n self.n = n\n self.left = None\n self.right = None\n\nclass Solution:\n def count | 0xsapra | NORMAL | 2022-10-18T18:12:52.455500+00:00 | 2022-10-18T18:12:52.455540+00:00 | 481 | false | ```\nclass Node:\n \n \n def __init__(self, n):\n self.n = n\n self.left = None\n self.right = None\n\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n \n MAX_COUNT = 0\n MAX_NUM = -inf\n TOTAL = len(parents)\n \n \n nodes = {}\n for i in range(TOTAL):\n nodes[i] = Node(i)\n \n for i in range(1, TOTAL):\n parent_node = nodes[parents[i]]\n if parent_node.left == None:\n parent_node.left = nodes[i]\n else:\n parent_node.right = nodes[i]\n \n \n def dfs(node):\n \n nonlocal MAX_NUM\n nonlocal MAX_COUNT\n nonlocal TOTAL\n \n if not node:\n return 0\n \n l = dfs(node.left)\n r = dfs(node.right)\n total_child = l+r\n top = TOTAL - total_child - 1\n \n l_temp = l if l !=0 else 1\n r_temp = r if r!=0 else 1\n top_temp = top if top !=0 else 1\n \n count = l_temp * r_temp * top_temp\n\n \n if count > MAX_NUM :\n MAX_NUM = count\n MAX_COUNT = 1\n elif count == MAX_NUM:\n MAX_COUNT += 1\n \n return 1 + l + r \n \n dfs(nodes[0])\n \n return MAX_COUNT\n \n``` | 2 | 0 | ['Depth-First Search', 'Python'] | 0 |
count-nodes-with-the-highest-score | JAVA SOLUTION || HASHMAP || DFS || DP || EASY TO UNDERSTAND | java-solution-hashmap-dfs-dp-easy-to-und-3s2t | \nclass Solution {\n public int countHighestScoreNodes(int[] parents) \n {\n int total_nodes=parents.length;\n \n //stores parent nod | 29nidhishah | NORMAL | 2022-09-03T12:11:02.375193+00:00 | 2022-09-03T12:11:02.375234+00:00 | 753 | false | ```\nclass Solution {\n public int countHighestScoreNodes(int[] parents) \n {\n int total_nodes=parents.length;\n \n //stores parent node---> child nodes\n Map<Integer,List<Integer>> parent_child=new HashMap<>();\n for(int i=0;i<total_nodes;i++)\n {\n if(!parent_child.containsKey(parents[i]))\n parent_child.put(parents[i],new ArrayList<>());\n \n List<Integer> temp=parent_child.get(parents[i]);\n temp.add(i);\n parent_child.put(parents[i],temp);\n }\n \n \n //count[i]=num of nodes with ith node as a subTree\n int count[]=new int[total_nodes];\n int x=1;\n for(int i=0;i<total_nodes;i++)\n {\n if(count[i]==0)\n x=fill_count_array(i,parent_child,count);\n }\n \n \n long max=0;int ans=0;\n \n for(int i=0;i<total_nodes;i++)\n {\n List<Integer> child=parent_child.get(i);\n long curr=1;\n \n if(child!=null)\n {\n for(int j=0;j<child.size();j++)\n curr=curr*(long)count[child.get(j)];\n }\n \n if(parents[i]!=-1)\n curr=curr*(long)(total_nodes-count[i]);\n \n \n if(curr>max)\n {\n max=curr;\n ans=1;\n }\n \n else if(curr==max)\n ans++;\n }\n \n return ans;\n }\n \n public int fill_count_array(int node,Map<Integer,List<Integer>> map,int count[])\n {\n if(count[node]!=0)\n return count[node];\n \n List<Integer> child=map.get(node);\n int total=1;\n \n if(child==null)\n return count[node]=1;\n \n for(int i=0;i<child.size();i++)\n {\n total+=fill_count_array(child.get(i),map,count);\n }\n \n count[node]=total;\n return total;\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Depth-First Search', 'Java'] | 1 |
count-nodes-with-the-highest-score | C++ solution using binary tree creation & then dfs for finding answer | c-solution-using-binary-tree-creation-th-m4vw | struct TreeNode\n {\n TreeNode left =NULL;\n TreeNode right=NULL ;\n int val;\n int totalcount=0;\n };\n | KR_SK_01_In | NORMAL | 2022-03-07T17:34:32.068324+00:00 | 2022-03-07T17:35:49.017269+00:00 | 165 | false | struct TreeNode\n {\n TreeNode* left =NULL;\n TreeNode* right=NULL ;\n int val;\n int totalcount=0;\n };\n \n int func(TreeNode* root , int n)\n {\n if(root==NULL)\n {\n return 0;\n }\n \n int x=func(root->left,n) + func(root->right,n)+1;\n root->totalcount=x;\n \n return x;\n }\n \n int countHighestScoreNodes(vector<int>& parents) {\n int n=parents.size();\n unordered_map<int ,TreeNode*> mp;\n \n //TreeNode* root=new TreeNode(0);\n for(int i=0;i<n;i++)\n {\n TreeNode* node=new TreeNode();\n node->val=i;\n mp[i]=node;\n }\n for(int i=0;i<parents.size();i++)\n {\n if(parents[i]!=-1)\n {\n TreeNode* node=mp[parents[i]];\n if(node->left==NULL)\n {\n node->left=mp[i];\n }\n else\n {\n node->right=mp[i];\n }\n \n }\n }\n TreeNode* root=mp[0];\n func(root,n);\n \n long long ans=0;\n int count=0;\n long long currval;\n int x1,x2;\n for(auto it=mp.begin();it!=mp.end();it++)\n {\n TreeNode* node=it->second;\n TreeNode* s1=node->left;\n TreeNode* s2=node->right;\n int nodeval=it->first;\n if(s1==NULL)\n x1=0;\n else\n x1=s1->totalcount;\n \n if(s2==NULL)\n x2=0;\n else\n x2=s2->totalcount;\n \n \n if(x1==0 && x2==0)\n {\n currval=n-1;\n if(nodeval==0)\n currval=1;\n }\n else\n if(x1==0)\n {\n currval=(long long)x2*(n-x2-1);\n if(nodeval==0)\n currval=x2;\n }\n else\n if(x2==0)\n {\n currval=(long long)x1*(n-x1-1);\n if(nodeval==0)\n currval=x1;\n }\n else\n {\n currval=(long long)((long long)x1*(x2)*(long long)(n-x1-x2-1));\n if(nodeval==0)\n currval=(long long)x1*x2;\n }\n \n \n if(currval==ans)\n {\n count++;\n }\n\t\t\t\t\t if(currval>ans)\n {\n ans=currval;\n count=1;\n }\n \n \n }\n \n return count;\n \n \n } | 2 | 0 | ['C', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | Dynamic Programming On Graphs | dynamic-programming-on-graphs-by-tamande-qlaa | I used dp on trees to solve this problem.\nThe concept is simple. \nFirst you calculate size of each subtree for every node. Here dp on trees is applied for tha | tamandeeps | NORMAL | 2022-03-01T10:58:23.227310+00:00 | 2022-03-01T10:58:23.227337+00:00 | 188 | false | I used dp on trees to solve this problem.\nThe concept is simple. \nFirst you calculate size of each subtree for every node. Here dp on trees is applied for that. Size of subtrees added and +1 to get total size of that current node.\nTo calculate score for current node, you subtract size of root node subtracted with size of current node and that is multiplied with sizes of subtree nodes.\n\n \n\t\tint countHighestScoreNodes(vector<int>& parent) {\n \n int n=parent.size();\n vector<vector<int>> adj(n);\n for(int i=1;i<n;i++)\n {\n adj[parent[i]].push_back(i);\n }\n vector<ll> sz(n,0),score(n,0);\n dfs(0,adj,sz);\n ll max_score=INT_MIN;\n ll s=1;\n for(auto j: adj[0])\n s*=sz[j];\n score[0]=s;\n for(int i=1;i<n;i++)\n {\n s=1;\n s*=(sz[0]-sz[i]);\n for(auto j: adj[i])\n {\n s*=sz[j];\n }\n score[i]=s;\n // cout<<score[i]<<" ";\n }\n int count=0;\n max_score=*max_element(score.begin(),score.end());\n for(auto i: score)\n {\n if(max_score==i)\n count++;\n }\n return count;\n \n }\n void dfs(int i, vector<vector<int>> &adj, vector<ll> &sz)\n {\n sz[i]++;\n for(auto j: adj[i])\n {\n dfs(j,adj,sz);\n sz[i]+=sz[j];\n }\n // cout<<sz[i]<<endl;\n } | 2 | 0 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'Graph'] | 0 |
count-nodes-with-the-highest-score | C++ DFS solution | c-dfs-solution-by-dan_zhixu-htpk | DFS solution. The first one uses a few maps to manage the countings. The second solution uses global variable and does the comparison in the DFS. \n\nSolution 1 | dan_zhixu | NORMAL | 2021-10-30T06:33:13.556172+00:00 | 2021-10-30T07:13:11.024945+00:00 | 193 | false | DFS solution. The first one uses a few maps to manage the countings. The second solution uses global variable and does the comparison in the DFS. \n\nSolution 1\n```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n \n unordered_map<int, vector<int>> graph;\n \n for (int i = 0; i < parents.size(); ++i)\n {\n int p = parents[i];\n if (graph.find(p) != graph.end())\n {\n graph[p].push_back(i);\n }\n else\n {\n vector<int> v { i };\n graph[p] = v;\n }\n }\n \n unordered_map<int, long long> productMap;\n unordered_map<int, int> totalMap;\n \n int sum = dfs(-1, graph, productMap, totalMap);\n \n long long max = 0;\n int count = 0;\n long long product = 1;\n \n for (int i = 0; i < parents.size(); ++i)\n {\n product = 1;\n \n if (i == 0)\n {\n product = productMap[0];\n }\n else\n {\n product = (sum - totalMap[i] - 1) * productMap[i];\n }\n \n if (product > max)\n {\n max = product;\n count = 1;\n }\n else if (product == max)\n {\n ++count;\n }\n }\n return count;\n }\n \n \n int dfs(int node, unordered_map<int, vector<int>> &graph, unordered_map<int, long long> &productMap, \n unordered_map<int, int> &totalMap)\n {\n int sum = 1;\n long long product = 1;\n \n if (graph.find(node) == graph.end())\n {\n totalMap[node] = sum;\n productMap[node] = product;\n \n return sum;\n }\n \n vector<int> nodes = graph[node];\n \n for (int &n : nodes)\n {\n int num = dfs(n, graph, productMap, totalMap);\n \n sum += num;\n product *= num;\n }\n \n totalMap[node] = sum;\n productMap[node] = product;\n \n return sum;\n }\n};\n```\n\nSolution 2\n```\nclass Solution {\n \n long max = 0;\n int count = 0;\n \npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n \n unordered_map<int, vector<int>> graph;\n \n for (int i = 0; i < parents.size(); ++i)\n {\n int p = parents[i];\n if (graph.find(p) != graph.end())\n {\n graph[p].push_back(i);\n }\n else\n {\n vector<int> v { i };\n graph[p] = v;\n }\n }\n \n int sum = parents.size();\n \n dfs(0, graph, sum);\n \n return count;\n }\n \n \n int dfs(int node, unordered_map<int, vector<int>> &graph, int &sum)\n {\n long product = 1;\n int total = 1;\n \n if (graph.find(node) == graph.end())\n {\n product = (long)(sum - 1);\n \n if (product > max)\n {\n max = product;\n count = 1;\n }\n else if (product == max)\n {\n ++count;\n }\n return total;\n }\n \n vector<int> nodes = graph[node];\n \n for (int &n : nodes)\n {\n int num = dfs(n, graph, sum);\n \n product *= num;\n total += num;\n }\n \n if (node != 0)\n {\n product *= (sum - total);\n }\n \n if (product > max)\n {\n max = product;\n count = 1;\n }\n else if (product == max)\n {\n ++count;\n }\n \n return total;\n }\n};\n``` | 2 | 1 | [] | 0 |
count-nodes-with-the-highest-score | c++ solution | c-solution-by-dilipsuthar60-xaf8 | \nclass Solution {\npublic:\n vector<vector<int>>dp;\n void find(int x,int p,vector<int>&sub)\n {\n for(auto it:dp[x])\n {\n i | dilipsuthar17 | NORMAL | 2021-10-30T06:10:11.627656+00:00 | 2021-10-30T06:11:53.446262+00:00 | 315 | false | ```\nclass Solution {\npublic:\n vector<vector<int>>dp;\n void find(int x,int p,vector<int>&sub)\n {\n for(auto it:dp[x])\n {\n if(it!=p)\n {\n find(it,x,sub);\n sub[x]+=sub[it];\n }\n }\n \n }\n int countHighestScoreNodes(vector<int>& parents)\n {\n int n=parents.size();\n dp.resize(n);\n for(int i=1;i<n;i++)\n {\n dp[parents[i]].push_back(i);\n }\n vector<int>subtree(n,1);\n find(0,-1,subtree);\n map<long long ,int,greater<long long>>mp;\n for(int i=0;i<n;i++)\n {\n long long pro=max(1,n-subtree[i]);\n for(auto it:dp[i])\n {\n pro=1ll*pro*subtree[it];\n }\n mp[pro]++;\n }\n return mp.begin()->second;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'C', 'C++'] | 0 |
count-nodes-with-the-highest-score | [Python] Simple DFS Solution with explanation | python-simple-dfs-solution-with-explanat-y35r | for each node, when we remove it, we have the following parts:\n1. child subtree if any\n2. parent subtree if any\n\nwe use dfs to count the number of node in e | nightybear | NORMAL | 2021-10-30T02:46:43.413614+00:00 | 2021-10-30T02:46:43.413645+00:00 | 534 | false | for each node, when we remove it, we have the following parts:\n1. child subtree if any\n2. parent subtree if any\n\nwe use dfs to count the number of node in each child subtree (no.1) and calculate the number of node in the parent subtree by `N - sum(child_subtree) - 1(node itself)`. We use `memo` to aovid duplicated calculation in dfs.\n\n```python\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n children = collections.defaultdict(list)\n for i, par in enumerate(parents):\n children[par].append(i)\n\n @lru_cache(None)\n def dfs(root):\n count = 1\n for child in children[root]:\n count += dfs(child)\n return count\n\n N = len(parents)\n max_score = 0\n score_counter = collections.defaultdict(int)\n\n for root in range(N):\n child = children[root]\n _sum = 0\n score = 1\n\n # score of the child tree\n for c in child:\n count = dfs(c)\n score *= count\n _sum += count\n\n curr_score = score * max(1, N-_sum-1) # score of the parent subtree\n score_counter[curr_score] += 1\n max_score = max(max_score, curr_score)\n\n return score_counter[max_score]\n``` | 2 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 0 |
count-nodes-with-the-highest-score | Golang postorder-traversal solution | golang-postorder-traversal-solution-by-t-8r74 | go\ntype cs struct {\n\tchildren []int\n\tsummary int\n}\n\nfunc countHighestScoreNodes(parents []int) int {\n\tmagic := make([]*cs, len(parents))\n\tfor i := | tjucoder | NORMAL | 2021-10-24T17:10:01.650213+00:00 | 2021-10-24T17:10:01.650258+00:00 | 91 | false | ```go\ntype cs struct {\n\tchildren []int\n\tsummary int\n}\n\nfunc countHighestScoreNodes(parents []int) int {\n\tmagic := make([]*cs, len(parents))\n\tfor i := range magic {\n\t\tmagic[i] = &cs{\n\t\t\tchildren: make([]int, 0, 2),\n\t\t\tsummary: 1,\n\t\t}\n\t}\n\tfor i := 1; i < len(parents); i++ {\n\t\tmagic[parents[i]].children = append(magic[parents[i]].children, i)\n\t}\n\tpostOrderTraversal(magic, 0)\n\thighestScore := 1\n\tfor _, v := range magic[0].children {\n\t\thighestScore *= magic[v].summary\n\t}\n\thighestCount := 1\n\tfor i := 1; i < len(parents); i++ {\n\t\tcurrentScore := 1\n\t\tfor _, v := range magic[i].children {\n\t\t\tcurrentScore *= magic[v].summary\n\t\t}\n\t\tcurrentScore *= magic[0].summary - magic[i].summary\n\t\tif currentScore > highestScore {\n\t\t\thighestScore = currentScore\n\t\t\thighestCount = 1\n\t\t} else if currentScore == highestScore {\n\t\t\thighestCount++\n\t\t}\n\t}\n\treturn highestCount\n}\n\nfunc postOrderTraversal(magic []*cs, i int) {\n\tfor _, v := range magic[i].children {\n\t\tpostOrderTraversal(magic, v)\n\t\tmagic[i].summary += magic[v].summary\n\t}\n}\n``` | 2 | 0 | ['Go'] | 0 |
count-nodes-with-the-highest-score | javascript dfs 372ms | javascript-dfs-372ms-by-henrychen222-tl8d | \nconst initializeGraph = (n) => { let G = []; for (let i = 0; i < n; i++) { G.push([]); } return G; };\n\nlet g, n, res, cnt;\nconst countHighestScoreNodes = ( | henrychen222 | NORMAL | 2021-10-24T04:54:46.451842+00:00 | 2021-10-24T05:02:15.226196+00:00 | 223 | false | ```\nconst initializeGraph = (n) => { let G = []; for (let i = 0; i < n; i++) { G.push([]); } return G; };\n\nlet g, n, res, cnt;\nconst countHighestScoreNodes = (parents) => {\n res = -1, cnt = 0, n = parents.length, g = initializeGraph(n);\n for (let i = 0; i < n; i++) {\n if (parents[i] == -1) continue;\n g[parents[i]].push(i);\n }\n dfs(0);\n return cnt;\n};\n\nconst dfs = (x) => {\n let subtree = 0, p = 1;\n for (const child of g[x]) {\n let tmp = dfs(child);\n subtree += tmp;\n p *= tmp;\n }\n if (subtree < n - 1) p *= n - 1 - subtree;\n if (p > res) { // larger score comes, update res and reset cnt = 1\n res = p;\n cnt = 1;\n } else if (p == res) { // equal largest score\n cnt++;\n }\n return subtree + 1;\n};\n``` | 2 | 0 | ['Depth-First Search', 'JavaScript'] | 1 |
count-nodes-with-the-highest-score | c# post-order dfs 100% 100% | c-post-order-dfs-100-100-by-canran-0byz | \npublic class Solution {\n \n int dfs(int[,] leaves, int[,] nums, int node)\n {\n int left = leaves[node, 0] == -1? 0: dfs(leaves, nums, leaves | canran | NORMAL | 2021-10-24T04:31:51.694359+00:00 | 2021-10-24T04:34:03.034854+00:00 | 120 | false | ```\npublic class Solution {\n \n int dfs(int[,] leaves, int[,] nums, int node)\n {\n int left = leaves[node, 0] == -1? 0: dfs(leaves, nums, leaves[node, 0]);\n int right = leaves[node, 1] == -1? 0: dfs(leaves, nums, leaves[node, 1]);\n nums[node, 0] = left;\n nums[node, 1] = right;\n return left + right + 1;\n }\n \n public int CountHighestScoreNodes(int[] parents) {\n int len = parents.Length;\n if (len < 2)\n return 0;\n \n int root = 0;\n int[,] nums= new int[len,2];\n int[,] leaves = new int[len, 2];\n \n for (int i = 0; i < len; i++){\n leaves[i,0] = -1;\n leaves[i,1] = -1;\n }\n \n for (int i = 0; i < len; i++){\n if (parents[i] == -1){\n root = i;\n continue;\n }\n \n if (leaves[parents[i], 0] == -1)\n leaves[parents[i], 0] = i;\n else\n leaves[parents[i], 1] = i;\n }\n \n dfs (leaves, nums, root);\n \n int result = 0;\n long max = 0;\n for (int i = 0; i < len; i++)\n {\n long left = nums[i,0];\n long right = nums[i,1];\n long rest = len - left - right - 1 == 0? 1 : len - left - right - 1;\n if (left == 0)\n left = 1;\n if (right == 0)\n right = 1;\n \n long p = left * right * rest;\n \n if (p > max){\n max = p;\n result = 1;\n }else if (p == max){\n result += 1;\n }\n }\n return result;\n }\n}\n```\n | 2 | 0 | ['Depth-First Search'] | 1 |
count-nodes-with-the-highest-score | O(n) solution using simple tree traversal (C++) with explanation comments | on-solution-using-simple-tree-traversal-p34dl | \nclass Solution {\npublic:\n\n// first form a tree data structure to build your tree later in the q.\n\n struct TreeNode\n {\n int val;\n T | pizza_slice | NORMAL | 2021-10-24T04:10:01.523034+00:00 | 2021-10-24T04:10:01.523065+00:00 | 102 | false | ```\nclass Solution {\npublic:\n\n// first form a tree data structure to build your tree later in the q.\n\n struct TreeNode\n {\n int val;\n TreeNode *left=NULL;\n TreeNode *right=NULL;\n };\n \n map<int,long long> score;\n long long maxScore=0;\n \n\t// use this function to return the size, however, also keep updating the score simulatneously\n\t// store the score corresponding to each node in a map called score, declared above, also \n\t// keep a note of the largest score so far!\n\t\n long long sizeHunt(TreeNode* node,int n)\n {\n if(!node) return 0;\n if(!node->left&&!node->right) // incase of a leaf node\n {\n score[node->val]=n-1;\n maxScore=max(maxScore,(long long) n-1);\n return 1;\n }\n \n\t\t// incase it\'s a non-leaf node, you need to get the size of the left and right subtree and also, the nodes, other than that.\n\t\t\n long long left=sizeHunt(node->left,n);\n long long right=sizeHunt(node->right,n);\n \n\t\t// remaining calculates the nodes other than the left and right subtrees.\n\t\t\n long long rem=n-(left+right+1);\n long long s=0;\n if(left&&right) s=left*right;\n else if(left) s=left;\n else s=right;\n \n if(rem) s*=rem;\n \n score[node->val]=s;\n maxScore=max(maxScore,score[node->val]);\n \n\t\t// return the size of this subtree\n\t\t\n return left+right+1;\n }\n \n int countHighestScoreNodes(vector<int>& parents) {\n int n=parents.size();\n map<int,TreeNode*> mp;\n \n\t\t// store the node correspoding to the node value in the map\n\t\t\n for(int i=0;i<n;i++)\n {\n TreeNode* node=new TreeNode();\n node->val=i;\n mp[i]=node;\n }\n \n\t\t// use the parent array to assign the children to its parent.\n\t\t\n for(int i=1;i<n;i++)\n {\n int p=parents[i];\n TreeNode* prt=mp[p];\n if(!prt->left) prt->left=mp[i];\n else prt->right=mp[i];\n \n mp[p]=prt;\n }\n \n TreeNode *root=mp[0];\n \n sizeHunt(root,n);\n int ans=0;\n \n\t\t// go through the whole score map to see how many nodes have got the maxScore.\n\t\t\n for(auto it=score.begin();it!=score.end();it++)\n {\n if(it->second==maxScore) ans++;\n }\n \n return ans;\n }\n};\n\n``` | 2 | 0 | [] | 0 |
count-nodes-with-the-highest-score | C++ | DP on Tree | Easy solution | DFS | c-dp-on-tree-easy-solution-dfs-by-chanda-v675 | Calculate size of subtree for each node using DFS\n Now we have to remove each vertex i* , there might be three possibility-\n 1. we remove leaf node\n | chandanagrawal23 | NORMAL | 2021-10-24T04:06:24.290507+00:00 | 2021-10-24T04:11:04.541576+00:00 | 515 | false | * Calculate size of subtree for each node using DFS\n* Now we have to remove each vertex **i** , there might be three possibility-\n 1. we remove leaf node\n 2. we remove node having one child\n 3. we remove node having two child \n```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& par) {\n long long int n = par.size();\n vector<long long int> adj[n];\n for(long long int i=1;i<par.size();i++)\n {\n adj[par[i]].push_back(i);\n }\n vector<long long int>dp(n,0);\n map<long long int,long long int>mp;\n dfs(adj,0,-1,dp);\n long long int ans = -1;\n for(long long int i=0;i<n;i++)\n {\n long long int left , right , rem;\n if(adj[i].size()==0)\n {\n left = 1;\n right = 1;\n rem = n-1;\n }\n if(adj[i].size()==1)\n {\n left = dp[adj[i][0]];\n right = 1;\n rem = n-1-left;\n if(rem==0)\n rem=1;\n }\n \n if(adj[i].size()==2)\n {\n left = dp[adj[i][0]];\n right = dp[adj[i][1]];\n rem = n-1-left-right;\n if(rem==0)\n rem=1;\n }\n // cout<<left*right*rem<<" ";\n mp[left*right*rem]++;\n }\n return mp.rbegin()->second;\n }\n \n void dfs(vector<long long int>adj[] ,long long int src , long long int par , vector<long long int>&dp )\n {\n dp[src]=1;\n for(auto xt : adj[src])\n {\n if(xt!=par)\n {\n dfs(adj,xt,src,dp);\n dp[src]+=dp[xt];\n }\n }\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'C'] | 2 |
count-nodes-with-the-highest-score | (C++) 2049. Count Nodes With the Highest Score | c-2049-count-nodes-with-the-highest-scor-dum9 | \n\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size(); \n vector<vector<int>> tree(n); \n | qeetcode | NORMAL | 2021-10-24T04:06:07.673611+00:00 | 2021-10-25T02:32:14.665483+00:00 | 268 | false | \n```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size(); \n vector<vector<int>> tree(n); \n for (int i = 0; i < n; ++i) \n if (parents[i] >= 0) tree[parents[i]].push_back(i); \n \n map<long, int> freq; \n \n function<int(int)> fn = [&](int x) {\n int left = 0, right = 0; \n if (tree[x].size()) left = fn(tree[x][0]); \n if (tree[x].size() > 1) right = fn(tree[x][1]); \n long score = 1; \n if (left) score *= left; \n if (right) score *= right; \n if (n - 1 - left - right) score *= n - 1 - left - right; \n ++freq[score]; \n return 1 + left + right; \n };\n \n fn(0); \n return freq.rbegin()->second; \n }\n};\n```\n\nAlternative implementation\n```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size(); \n vector<vector<int>> tree(n); \n for (int i = 0; i < n; ++i) \n if (parents[i] >= 0) tree[parents[i]].push_back(i); \n \n map<long, int> freq; \n \n function<int(int)> fn = [&](int x) {\n long count = 1, score = 1; \n for (auto& xx : tree[x]) {\n int cc = fn(xx); \n count += cc; \n score *= cc; \n }\n score *= max(1l, n - count); \n ++freq[score]; \n return count; \n };\n \n fn(0); \n return freq.rbegin()->second; \n }\n};\n``` | 2 | 0 | ['C'] | 1 |
count-nodes-with-the-highest-score | BFS Solution | Intuitive | Topological Sort Version | bfs-solution-intuitive-topological-sort-w782z | IntuitionStart with leaf nodes. As they dont have any out degree.Approach
Start with leaf node.
Count the children of nodes as u move above using topo sort algo | I_Hacker | NORMAL | 2025-03-31T19:51:49.427397+00:00 | 2025-04-09T04:13:32.505968+00:00 | 49 | false | # Intuition
Start with leaf nodes. As they dont have any out degree.
# Approach
1. Start with leaf node.
2. Count the children of nodes as u move above using topo sort algorithm with outdegree as O.
3. As you have count of children, just need to prod = (count of left children) * (count of right children) * (number of nodes left).
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
int countHighestScoreNodes(vector<int>& parents) {
int cn=parents.size();
unordered_map<int, int> mp;
for(int i=0;i<cn;i++){
// Map to store count of children of each parent.
mp[parents[i]]++;
}
queue<long long> q;
for(int i=0;i<cn;i++){
// Start with leaf node. They dont have outdegree.
if(mp[i]==0)q.push(i);
}
unordered_map<long long, pair<long long, long long>> v;
for(long long i=0;i<cn;i++){
// Keep count of left children & right children.
v[i]={0, 0};
}
unordered_map<long long, long long> ans;
long long m=0;
while(!q.empty()){
int n=q.size();
while(n-->0){
// Take First node out with outdegree 0
long long node=q.front();q.pop();
// If its 0 parent = -1, come out of loop
if(node==-1)break;
long long t=0;
// If node is not 0, prod of count of left & right children with number of nodes left.
if(node!=0)
t=(long long)(v[node].first==0?1:v[node].first)*(v[node].second==0?1:v[node].second)*(cn-v[node].first-v[node].second-1);
// If node is 0, prod of count of left & right children is enough.
else
t=(v[node].first==0?1:v[node].first)*(v[node].second==0?1:v[node].second);
m=max(m, t);
// Keep count of maximum times m appears.
ans[t]++;
// Storing count of children in parent v. (Order of left & right really doesnt matter
long long par = parents[node];
// Storing for left children first.
if(v[par].first==0)v[par]={v[node].first+v[node].second+1, v[par].second};
// Storing for right children next.
else v[par]={v[par].first, v[node].first+v[node].second+1};
mp[par]--;
if(mp[par]==0)q.push(par);
}
}
return ans[m];
}
};
``` | 1 | 0 | ['Breadth-First Search', 'Topological Sort', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | Simple C++ Solution || (Using DFS) ✅✅ | simple-c-solution-using-dfs-by-abhi242-nliv | Code\n\nclass Solution {\npublic:\n map<long long,int> mp;\n int dfs(vector<int> adj[],int node,int n){\n int ans=0;\n int i=0;\n int | Abhi242 | NORMAL | 2024-08-02T14:00:11.260500+00:00 | 2024-08-02T14:00:11.260527+00:00 | 71 | false | # Code\n```\nclass Solution {\npublic:\n map<long long,int> mp;\n int dfs(vector<int> adj[],int node,int n){\n int ans=0;\n int i=0;\n int sum1=0;\n int sum2=0;\n for(int a:adj[node]){\n if(i==0){\n sum1=(1+dfs(adj,a,n));\n }else{\n sum2=(1+dfs(adj,a,n));\n }\n i++;\n }\n mp[(long long)max(1,sum1)*max(1,sum2)*max(1,(n-1-sum1-sum2))]++;\n return sum1+sum2;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n int n=parents.size();\n vector<int> adj[n];\n for(int i=0;i<n;i++){\n if(parents[i]==-1) continue;\n adj[parents[i]].push_back(i);\n }\n dfs(adj,0,n);\n int ans=mp.rbegin()->second;\n return ans;\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | Easy Solution, simulation of recursion using queue | easy-solution-simulation-of-recursion-us-w9lf | Intuition\n Describe your first thoughts on how to solve this problem. \nIf the input was given in the form of TreeNode then the obvious way is to use postorder | mp_aka_sh | NORMAL | 2024-07-25T07:05:18.213102+00:00 | 2024-07-25T07:05:18.213124+00:00 | 45 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf the input was given in the form of TreeNode then the obvious way is to use postorder traversal. That is, a node receives number of left nodes from left child node and similary from right, then we can just multiply them with the remaining node to get the answer. \nIn postorder traversal, things to node:\n1. Start from leaf node\n2. return the value to parent\n3. parent operates when it receives data from all its child\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. vector<pair<int, int>> to track left and right child of each node values with default value 0. This is similar to the values returned by them in case of recursion.\n2. vector<int> - isleaf, given the tree is binary, n(children) can be 2,1,0. push this value on to the queue when it is 0, that is either the node is leaf node (in the beginning) or the node\'s all children have finshed with it calculation.\n3. queue<int> to simulate the backtracking of recursion\n4. left * right * (n-v[node].first-v[node].second-1) is the formula to calculate the score\n5. map to store the number of occurences\n6. Since we dont have pointers which explicitly tell whether the value is returned from left/right child, or are both of them present? \n - we will use isleaf to keep track of number of children.\n - parent receives value from either left or right, so once left is returned it is obvious that next return value will be right or vice-versa. So assign the first with the value(assuming left) and then fill second value. Simultaneously we will reduce the number in isleaf saying that a child has returned the value.\n - when the isleaf is 0, i.e., the node has received the values from both the child then the particular node is ready to return the value.\n\nwe are just multiplying values from left and right subtrees so its fair to assume first in pair holds left subtree value.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& parents) {\n int n=parents.size();\n vector<pair<int, int>>v(n, {0,0}); //store returned values from left and right subtree \n\n vector<int>isleaf(n, 0);\n for (int i=1;i<n;i++) isleaf[parents[i]]++;//store n(children)\n\n queue<int>q;\n for (int i=1;i<n;i++) if (isleaf[i]==0) q.push(i);\n\n map<long, long>mp;\n while (!q.empty() && q.front()) {\n int node=q.front();\n q.pop();\n\n long left=v[node].first ? v[node].first : 1, right=v[node].second ? v[node].second : 1;\n long val = (long) (left * right * (n-v[node].first-v[node].second-1)); //calulare the score\n mp[val]++;\n\n int parent=parents[node];\n if (v[parent].first==0) {v[parent].first = v[node].first+v[node].second+1;isleaf[parent]--;} // fill .first first, if isleaf[parent] is 1, then it all its child has finished the job so push the parent to the queue\n else {v[parent].second = v[node].first+v[node].second+1;isleaf[parent]--;} //if parent has second child, it comes down to else and then isleaf becomes 0, then push this parent on to stack\n\n if (isleaf[parent]==0) q.push(parent);\n \n }\n \n int left=v[0].first ? v[0].first : 1, right=v[0].second ? v[0].second : 1;\n mp[(long)left*right]++; // parent==0; all nodes will be in left or right sub tree, the part value is 0, so explicit calculation\n\n return mp.rbegin()->second;\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'Queue', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | Python - Recursive Post Order Traversal (DFS) Solution ✅ | python-recursive-post-order-traversal-df-35b1 | The idea is to first count how many nodes each node has on its left and right. This information will be helpful when we have to get the score of a node.\n\n\n\n | itsarvindhere | NORMAL | 2024-06-13T06:05:38.382799+00:00 | 2024-06-13T06:06:33.470607+00:00 | 67 | false | The idea is to first count how many nodes each node has on its left and right. This information will be helpful when we have to get the score of a node.\n\n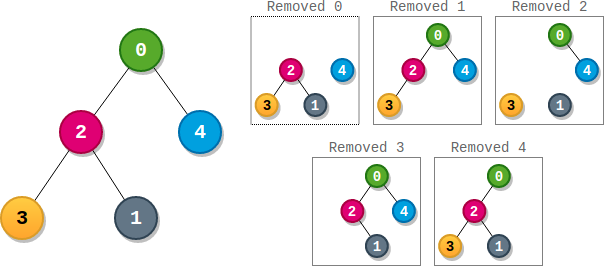\n\nIf you look at the above example, whenever we remove any node from the tree, its score is simply the product of \n\n\tnodesOnLeft * nodesOnRight * nodesOnTop\n\t\nTo get the nodes on left and nodes on right, we can simply traverse the tree in DFS (Post Order) and then get the count and save it somewhere.\n\nFor the top, it is pretty simple. If we know how many nodes are on the left and right, we can say that the nodes on top will be - \n\n\tTotal Nodes - (nodesOnLeft + 1 + nodesOnRight)\n\nAnd well, the last thing remaining will be to find the highest score and the count of nodes with that score.\n\n```\nclass Solution:\n \n # Recursive DFS function\n def dfs(self, i, parentNodes, nodeCount):\n \n # Base Case (It is a leaf node)\n if i not in parentNodes: \n nodeCount[i] = [0,0]\n return 1\n \n leftCount, rightCount = 0,0\n \n if len(parentNodes[i]) > 1:\n \n # Count of nodes in the left subtree\n leftCount = self.dfs(parentNodes[i][0], parentNodes, nodeCount)\n\n # Count of nodes in the right subtree\n rightCount = self.dfs(parentNodes[i][1], parentNodes, nodeCount)\n \n else:\n \n # Count of nodes in the left subtree\n leftCount = self.dfs(parentNodes[i][0], parentNodes, nodeCount)\n \n \n # Update the dictionary\n nodeCount[i] = [leftCount, rightCount]\n \n # Return the count for the previous recursive calls\n return leftCount + 1 + rightCount\n \n def countHighestScoreNodes(self, parents: List[int]) -> int:\n \n # Total Number of nodes\n n = len(parents)\n \n # A dictionary to keep track of the parent and the children of that parent node\n parentNodes = defaultdict(list)\n for i in range(n): parentNodes[parents[i]].append(i)\n \n # First, for each node, we need to find the count of nodes in each of the subtrees rooted at children nodes\n # A dictionary where key will be the node value and value will be a pair [leftCount, rightCount]\n nodeCount = {}\n \n # Call the recursive DFS function to count the nodes\n self.dfs(0, parentNodes, nodeCount)\n \n # Now, we have to find the highest score and the number of nodes with that highest score\n highestScore = 0\n count = 0\n \n # For each node\n for i in range(n):\n \n # What if this node is removed along with its edges?\n # We now have to find product of sizes of all the subtrees that are left\n # If current node is removed, we will get at most three different subtrees\n # One that is on the top of the node that we just removed\n # One will be the subtree rooted at the left child of the current node\n # One will be the subtree rooted at the right child of the current node\n \n # First, we check for the topCount\n # If we know how many nodes the left and right subtrees have\n # We can say the tree on top will have nodes = totalNodes - (leftCount + 1 + rightCount)\n topCount = n - (nodeCount[i][0] + 1 + nodeCount[i][1])\n \n # Now, we check for left and right children\n leftCount, rightCount = nodeCount[i][0], nodeCount[i][1]\n \n # To avoid issues due to multiplication with 0\n if leftCount == 0: leftCount = 1\n if rightCount == 0: rightCount = 1\n if topCount == 0: topCount = 1\n \n # What is the score of the node\n score = leftCount * rightCount * topCount\n \n # Check if the current score is greater than the highest score so far\n if score > highestScore:\n \n # Update the highest score\n highestScore = score\n \n # Rest the count\n count = 1\n \n # If it is equal to the highest score, update the node count\n elif score == highestScore: count += 1\n \n # Return the count of nodes with the highest score\n return count\n \n``` | 1 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'Python', 'Python3'] | 0 |
count-nodes-with-the-highest-score | Explaned well || fully commented || java || using HashMap || Creating tree | explaned-well-fully-commented-java-using-o1g7 | Intuition\n Describe your first thoughts on how to solve this problem. \nAs the parents value is given in the array where parents[i] is the parent of i. \nparen | codingWithAman | NORMAL | 2024-05-22T16:05:24.367201+00:00 | 2024-05-22T16:54:31.384024+00:00 | 228 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs the parents value is given in the array where parents[i] is the parent of i. \nparents =[-1,3,1,0,3]\nIn this case parent of 3 has two child, i.e, 1 and 4 as 3 is coming twice in the array at index 1 and 4. Parent 1 has 2 as the child and 0 as 3 as the child. So, it will look something like this -->\n\n 0\n /\n 3\n / \\\n 1 4\n\nSo, When we can decipher the Tree, then we need to find the size if we disconnect the parent node and then one or more than one subtree would be formed. So, we then need to find the product of the size of the subtree after removing a node.\nAlso, the twist is the we don\'t need to return the max score, rather than that, we need to return the size of the nodes with maximum score.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n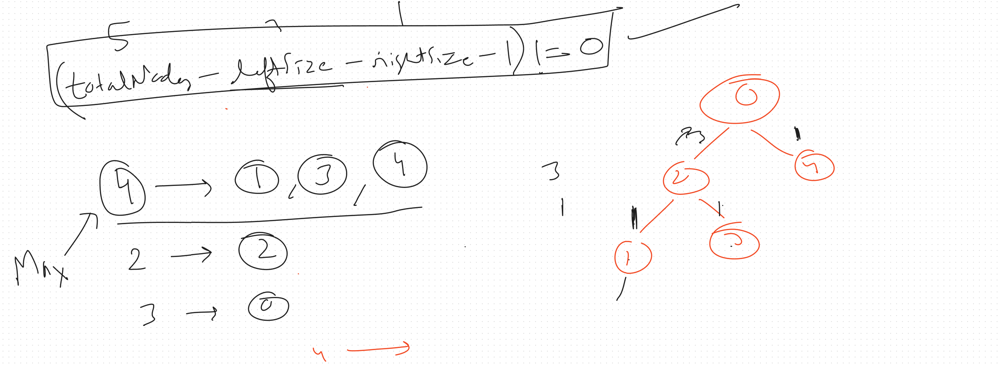\n\nFirstly, we will create a Tree using the parents array. So, we will create a Tree array and add the i index at every place.\nThen, we will find the node[parent[i]] and add the left or the right child of it with the node[i].\n\nThen, we will use another function to calculate scores where we will do the dfs post order traversal on the Tree which we made.\n\nMost important thing is to check the leftSize and rightSize and if they are not 0, then we will multiply it with the score.\n\n****totalNodes - leftSize - rightSize - 1 ==> this we will do to check the number of nodes if we remove one.\n\nThen, we will take a global variable maxScore and update the max score everytime in it.\n\nLast but not the least, we will add the score as the key and node.val as the value in the list in the HashMap and store it accordingly.\n\nP.s --> we need to use Long data type as we are multiplying and it can have Integer overflow. So, please use long.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\ncreating the tree will be O(n) as we are just going once to every node and adding it.\nCalculating scores will also be O(n) as we are storing the score with it value which are having the same score in the hashmap. So, we are avoiding the repeated counts in the recursion by storing it in the hashmap. So, it will be O(n).\nTherefore, time will be o(n);\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nAs the stack will take O(n) in the calculateScore function. Therefore, maximum will be O(n).\n\n# Code\n```\nclass Solution {\n\n //using long as we are multiplying and it can have (32bits)Integer overflow. So, long(64bits) will have more memory to store.\n HashMap<Long, List<Long>> map = new HashMap<>();\n int totalNodes = 0;\n long maxscore = 0;\n\n public int countHighestScoreNodes(int[] parents) {\n TreeNode root = createTree(parents);\n totalNodes = parents.length;\n calculateScores(root);\n return map.get(maxscore).size();\n }\n\n public int calculateScores(TreeNode node){\n if(node == null) return 0;\n\n int leftSize = calculateScores(node.left);\n int rightSize = calculateScores(node.right);\n\n long score = 1;\n if(leftSize != 0) score *= leftSize; //this is for the left side to multiply the value \n if(rightSize != 0) score *= rightSize;//this is for the right side to multiply the value \n\n //this tells us that if we remove parent node, then left side \n if(totalNodes - leftSize - rightSize -1 != 0){\n score *= (totalNodes - leftSize - rightSize -1); \n }\n\n\n maxscore = Math.max(score, maxscore);//to check the max out of the nodes.\n\n map.putIfAbsent(score, new ArrayList<>());//with every score add the number of does in the list.\n map.get(score).add((long)node.val);//add the val in it.\n\n return leftSize + rightSize +1;\n }\n\n public TreeNode createTree(int[] parents){\n int n = parents.length;\n TreeNode[] nodes = new TreeNode[n]; \n\n //will create a TreeNode of the index and use this index for the parents.\n for(int i = 0; i<n;i++){\n nodes[i] = new TreeNode(i);//[0,1,2,3,4]\n }\n\n TreeNode root = null;\n //[-1, 2, 0,2,0]\n for(int i = 0; i<n;i++){\n \n if(parents[i] == -1) root = nodes[i];//will add the 0 in the parent.\n else{\n TreeNode parent = nodes[parents[i]];//2 , 0 , 2, 0\n if(parent.left == null){\n parent.left = nodes[i];//2-->1 , 0-->2\n }else{\n parent.right = nodes[i];//2-->3, 0--> 4\n }\n }\n }\n\n return root;\n }\n\n}\n``` | 1 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Java with comments | java-with-comments-by-endlessjourney-0so6 | Code\n\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n int N = parents.length;\n\n // Initialize adjacency list and su | endlessjourney | NORMAL | 2024-01-22T00:44:52.293175+00:00 | 2024-01-22T00:44:52.293215+00:00 | 275 | false | # Code\n```\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n int N = parents.length;\n\n // Initialize adjacency list and subtree sizes array\n List<List<Integer>> al = new ArrayList<>();\n for (int i = 0; i < N; i++) {\n al.add(new ArrayList<>());\n }\n long[] subtreeSizes = new long[N];\n\n // Construct adjacency list\n for (int i = 1; i < N; i++) {\n al.get(parents[i]).add(i);\n }\n\n // Calculate subtree sizes using DFS\n dfs(al, subtreeSizes, 0);\n\n long maxSubtreeSize = Arrays.stream(subtreeSizes).max().getAsLong();\n return (int)Arrays.stream(subtreeSizes).filter(size -> size == maxSubtreeSize).count();\n }\n\n // DFS function to calculate subtree sizes and update the array s \n private long dfs(List<List<Integer>> al, long[] subtreeSizes, int currNode) {\n long productOfSizes = 1, sumOfSizes = 1;\n\n // Traverse neighbors of the current node\n for (int neighbor : al.get(currNode)) {\n long neighborSize = dfs(al, subtreeSizes, neighbor);\n productOfSizes *= neighborSize;\n sumOfSizes += neighborSize;\n }\n\n // Update subtreeSizes array for the current node\n subtreeSizes[currNode] = productOfSizes * Math.max(1, al.size() - sumOfSizes);\n\n // Return the sum of subtree sizes\n return sumOfSizes;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
count-nodes-with-the-highest-score | c# recursive solution | c-recursive-solution-by-sree_lakshmi-n3al | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sree_lakshmi | NORMAL | 2024-01-20T01:15:26.390626+00:00 | 2024-01-20T01:15:26.390668+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n Dictionary<int, int[]> parentDict = new();\n int result = 0;\n long maxScore = 0;\n \n public int CountHighestScoreNodes(int[] parents) {\n for(int i=0; i< parents.Length; i++){\n parentDict.TryAdd(i, new int[2]);\n }\n for(int i=1; i<parents.Length; i++){\n if(parentDict[parents[i]][0] == 0) parentDict[parents[i]][0] = i;\n else parentDict[parents[i]][1] = i;\n }\n\n CountScores(0, parents.Length);\n return result;\n }\n\n public int CountScores(int index, int totalSize){\n int left = 0, right = 0;\n long count =1;\n if(parentDict[index][0] != 0) left = CountScores(parentDict[index][0], totalSize);\n if(parentDict[index][1] != 0) right = CountScores(parentDict[index][1], totalSize);\n\n int subTree = left + right +1;\n int other = totalSize - subTree;\n if(left != 0) count *= (long)left;\n if(right != 0) count *= (long)right;\n if(other != 0) count *= (long)other;\n if(count == maxScore) result++;\n else if(count > maxScore){\n maxScore = count;\n result = 1;\n } \n return subTree;\n\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
count-nodes-with-the-highest-score | C++ | Single DFS O(n) | Easy Explanation | c-single-dfs-on-easy-explanation-by-adit-4adl | \n# Approach\n Describe your approach to solving the problem. \n1. Need the sizes of all the subtrees (subordinate as well as above one) to calculate each node\ | AdityaGiri | NORMAL | 2023-07-18T18:43:59.067702+00:00 | 2023-07-18T20:20:17.202208+00:00 | 53 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Need the sizes of all the subtrees (subordinate as well as above one) to calculate each node\'s score.\n\n2. Calculate sizes of left & right subordinate subtree as we run the dfs function for the current node.\n\n3. Now to get the size of above tree, we simply can deduct the `sum of sizes of subordinate tree + 1 (current node)` from the total number of nodes(N).\nTherefore, `size of above subtree = N - sum - 1`.\n\n4. Calculate score and store it in `allScores` array while keeping track of `maxScore`.Return count of `maxScore` in `allScores`.\n\n---\n\n\n# Complexity\n- Time complexity: **O(n)** - *dfs, traversing parent, allScores array*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n)** - *tree adjajency list, allScores array*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n# Code\n```\nclass Solution {\npublic:\n int N;\n long maxScore = 0;\n vector<long> allScores;\n\n long dfs(int node,vector<vector<int>>& tree){\n \n long score = 1;\n long sum = 0;\n for(int v:tree[node]){\n \n long res = dfs(v,tree);\n sum += res;\n score *= res;\n }\n sum++; // added current\n score *= (N-sum>0) ? N-sum : 1; // to check that score doesn\'t gets multiplied by 0 for root node\n maxScore = max(maxScore,score);\n allScores.push_back(score);\n\n return sum;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size();\n N = n;\n vector<vector<int>> tree(n);\n\n for(int i=1; i<n; i++){\n\n tree[parents[i]].push_back(i);\n }\n\n dfs(0,tree);\n int cntOfMax = 0;\n\n for(long& s: allScores){\n if(s==maxScore) cntOfMax++;\n }\n return cntOfMax;\n }\n};\n``` | 1 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | Python Easy Recursive Solution | python-easy-recursive-solution-by-sparsh-gi3k | Code\n\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n\n sizes = [[0]*2 for _ in range(len(parents))]\n dic = | sparshlodha04 | NORMAL | 2022-12-10T07:03:06.094195+00:00 | 2022-12-10T07:03:47.248155+00:00 | 1,076 | false | ## Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n\n sizes = [[0]*2 for _ in range(len(parents))]\n dic = defaultdict(list)\n\n def rec(root):\n\n if not dic[root]:\n return 1\n\n if len(dic[root]) == 1:\n sizes[root][0] = rec(dic[root][0])\n elif len(dic[root]) == 2:\n sizes[root][0] = rec(dic[root][0])\n sizes[root][1] = rec(dic[root][1])\n\n return 1 + sizes[root][0] + sizes[root][1]\n\n for i in range(1,len(parents)):\n dic[parents[i]].append(i)\n\n total = rec(0)\n\n res = []\n for x,y in sizes:\n res.append(max(x,1) * max(y,1) * max(total-x-y-1,1))\n\n return res.count(max(res))\n\n``` | 1 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | Java Solution || HashTables || DFS || O(n) time | java-solution-hashtables-dfs-on-time-by-kooi3 | ```java\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n int n = parents.length; // no. of nodes\n \n //for stor | nishant7372 | NORMAL | 2022-10-31T07:11:06.047526+00:00 | 2022-10-31T07:19:36.847192+00:00 | 140 | false | ```java\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n int n = parents.length; // no. of nodes\n \n //for storing left and right child of each node\n ArrayList<Integer>[] a = new ArrayList[n];\n \n for(int i=0;i<n;i++)\n a[i]=new ArrayList<Integer>();\n \n for(int i=1;i<n;i++)\n a[parents[i]].add(i);\n \n //store total number of children of each node\n int[] child = new int[n]; \n Arrays.fill(child,-1);\n \n dfs(0,a,child); //calculating all childrens at each node\n \n //storing scores of each node\n long[] scores = new long[a.length];\n \n long maxScore=0; //maxScore\n \n for(int i=0;i<n;i++)\n {\n long res=1; // calculating score for a particular node\n for(int y:a[i])\n res*=child[y]+1;\n \n res*=Math.max(1,n-child[i]-1);\n scores[i]=res;\n if(res>maxScore)\n maxScore=res;\n }\n \n int c=0; // count of maxScores\n for(long score:scores)\n if(score==maxScore)\n c++;\n \n return c;\n }\n \n private int dfs(int x,ArrayList<Integer>[] a,int[] child)\n {\n int c=0;\n for(int y:a[x])\n c+=dfs(y,a,child);\n\n return child[x]=c+a[x].size();\n }\n} | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | Python (Simple DFS) | python-simple-dfs-by-rnotappl-zxyl | \n def countHighestScoreNodes(self, parents):\n dict1 = defaultdict(list)\n \n for node, parent in enumerate(parents):\n dict | rnotappl | NORMAL | 2022-08-25T14:10:05.394212+00:00 | 2022-08-25T14:10:05.394252+00:00 | 73 | false | \n def countHighestScoreNodes(self, parents):\n dict1 = defaultdict(list)\n \n for node, parent in enumerate(parents):\n dict1[parent].append(node)\n \n n, dict2 = len(parents), defaultdict(int)\n \n def dfs(node):\n product, total = 1, 0\n \n for child in dict1[node]:\n res = dfs(child)\n product *= res\n total += res\n \n product *= max(1, n-1-total)\n \n dict2[product] += 1\n \n return total + 1\n \n dfs(0)\n \n return dict2[max(dict2.keys())]\n | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | [Java] 35ms DFS, 95% + explanations | java-35ms-dfs-95-explanations-by-stefane-ad41 | \nclass Solution {\n /** Algorithm/Theory\n 1. An efficient first step is to build the tree. This way, we can post-order traverse it and determine the | StefanelStan | NORMAL | 2022-06-28T00:42:06.357783+00:00 | 2022-06-28T21:18:33.949794+00:00 | 564 | false | ```\nclass Solution {\n /** Algorithm/Theory\n 1. An efficient first step is to build the tree. This way, we can post-order traverse it and determine the product of non-empty subtrees\n 2. Use a simple Node[] array to map node order/value to Node content.\n set node[0] to be the parent.\n loop from 1 to n and if the current node[i] is null, set it as new node. If the parent is null, initialize node[parent[i]].\n set node[parent[i]].left or .right to node[i], depending if left or right is already set.\n 3. Continue post-order traversal. \n - if on a leaf, that leaf will make a score of total -1. Check against the current highest score and set. Return 1 as that leaft has only 1 node\n - if not on a leaf, apply post-oder to left and right.\n 4. After 3b) for each parent node, determine its number of nodes from its subtree: 1 + left + right.\n 6. Once 5 is done, determine the highest score that node will generate.\n This will be Math.max(1, onLeft) * Math.max(1, onRight) * Math.max(1, (totalNodes - nrOfNodesFromSubtree)).\n Basically we are multiplying the remaining 3 groups of nodes that are formed from the removal of that node (left, right, above).\n Pay attention to multiply with 1 (not with 0). The root will have no "above" nodes so total - nodesOnSubtree will return 0.\n */\n public int countHighestScoreNodes(int[] parents) {\n Node[] nodes = buildTree(parents);\n long[] highestScore = {0,0};\n countHighestScore(nodes[0], highestScore, parents.length);\n return (int)highestScore[1];\n }\n\n private int countHighestScore(Node node, long[] highestScore, int total) {\n if (node != null) {\n if (node.left == null && node.right == null) {\n // a leaf will have 1 node under(itself) and will produce a total nodes - 1 score.\n if (highestScore[0] == total - 1) {\n highestScore[1]++;\n } else if (highestScore[0] < total - 1) {\n highestScore[0] = total - 1;\n highestScore[1] = 1;\n }\n return 1;\n } else {\n // apply post-order and see how many nodes are left and right\n int onLeft = countHighestScore(node.left, highestScore, total);\n int onRight = countHighestScore(node.right, highestScore, total);\n int totalSubtree = onLeft + onRight + 1;\n // if left or right is null, replace it with 1, multiplication by 1\n long possibleScore = (long) (Math.max(1, onLeft)) * Math.max(onRight, 1)\n * Math.max(1, total - totalSubtree);\n if (highestScore[0] == possibleScore) {\n highestScore[1]++;\n } else if (highestScore[0] < possibleScore) {\n highestScore[0] = possibleScore;\n highestScore[1] = 1;\n }\n return totalSubtree;\n }\n }\n return 0;\n }\n\n private Node[] buildTree(int[] parents) {\n Node[] nodes = new Node[parents.length];\n nodes[0] = new Node();\n for (int i = 1; i < parents.length; i++) {\n // create current node\n if (nodes[i] == null) {\n nodes[i] = new Node();\n }\n // create parent node\n if (nodes[parents[i]] == null) {\n nodes[parents[i]] = new Node();\n }\n // link parent node left or right to this child node.\n if (nodes[parents[i]].left == null) {\n nodes[parents[i]].left = nodes[i];\n } else {\n nodes[parents[i]].right = nodes[i];\n }\n }\n return nodes;\n }\n\n private static class Node {\n Node left;\n Node right;\n }\n}\n``` | 1 | 0 | ['Depth-First Search', 'Java'] | 0 |
count-nodes-with-the-highest-score | Simple Java Solution (DFS, Build Tree) | simple-java-solution-dfs-build-tree-by-m-ss9k | ```\nclass Solution {\n static class TreeNode {\n int val;\n TreeNode left,right;\n TreeNode() {\n \n }\n TreeN | mokshteng | NORMAL | 2022-06-08T06:35:37.820410+00:00 | 2022-06-08T06:35:37.820447+00:00 | 78 | false | ```\nclass Solution {\n static class TreeNode {\n int val;\n TreeNode left,right;\n TreeNode() {\n \n }\n TreeNode(int val) {\n this.val=val;\n }\n }\n public int countHighestScoreNodes(int[] parents) {\n int n=parents.length;\n HashMap<Integer,TreeNode> map=new HashMap<>();\n for(int i=0;i<n;i++) {\n map.put(i,new TreeNode(i));\n }\n TreeNode root=null;\n for(int i=0;i<n;i++) {\n if(parents[i]==-1) {\n root=map.get(i);\n }\n else {\n TreeNode parent=map.get(parents[i]);\n TreeNode child=map.get(i);\n if(parent.left==null) {\n parent.left=child;\n }\n else {\n parent.right=child;\n }\n \n }\n }\n Queue<Long> queue=new LinkedList<>();\n getScore(root,queue,n);\n long max=0;\n int count=0;\n while(n-->0) {\n long temp=queue.poll();\n max=Math.max(max,temp);\n queue.offer(temp);\n }\n while(!queue.isEmpty()) {\n if(max==queue.poll())\n ++count;\n }\n return count;\n \n \n }\n long getScore(TreeNode root,Queue<Long> queue,int size) {\n if(root==null)\n return 0;\n long left=getScore(root.left,queue,size);\n long right=getScore(root.right,queue,size);\n long up=size-left-right-1;\n long temp=0;\n if(left==0&&right==0&&up==0) {\n temp=0;\n }\n else {\n long tempLeft=left==0?1:left;\n long tempRight=right==0?1:right;\n up=up==0?1:up;\n temp=tempLeft*tempRight*up;\n }\n \n queue.offer(temp);\n return 1+left+right;\n }\n} | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | Two dfs O(n) | two-dfs-on-by-mayankmodi041998-954a | \nclass Solution {\npublic:\n vector<vector<int>>adj;\n vector<long long int>counter;\n long long int res=0;\n int countt=0;\n void dfs(int src)\ | mayankmodi041998 | NORMAL | 2022-05-24T14:45:46.408781+00:00 | 2022-05-24T14:45:46.408826+00:00 | 30 | false | ```\nclass Solution {\npublic:\n vector<vector<int>>adj;\n vector<long long int>counter;\n long long int res=0;\n int countt=0;\n void dfs(int src)\n {\n for(int i=0;i<adj[src].size();i++)\n {\n int u=adj[src][i];\n dfs(u);\n counter[src]+=counter[u];\n }\n counter[src]++;\n }\n \n void dfs2(int src,vector<int>& parents)\n {\n long long int p=1;\n for(int i=0;i<adj[src].size();i++)\n {\n int u=adj[src][i];\n p=p*counter[u];\n\n dfs2(u,parents);\n \n \n \n }\n if(parents[src] != -1)\n {\n p=p*(counter.size()-counter[src]);\n\n }\n \n \n if(p > res)\n {\n res=p;\n countt=1;\n }\n else if(p == res)\n {\n countt++;\n }\n \n \n }\n \n int countHighestScoreNodes(vector<int>& parents) {\n int n=parents.size();\n adj.resize(n);\n int root;\n for(int u=0;u<n;u++)\n {\n int v=parents[u];\n if(v == -1)\n {\n root=u;\n continue;\n }\n adj[v].push_back(u);\n }\n counter.resize(n,0);\n dfs(root);\n\n dfs2(root,parents);\n return countt;\n \n }\n};\n``` | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | C++ Easy Postorder Traversal (85% time beat) | c-easy-postorder-traversal-85-time-beat-okind | LOGIC : \n\nSimply get the count of left nodes and right nodes recursively and get the remaining nodes(after removing the current nodes by doing n-(l+r)-1. Now | SHUBHAMBRODY26 | NORMAL | 2022-03-29T06:33:54.476516+00:00 | 2022-03-29T06:33:54.476555+00:00 | 202 | false | **LOGIC : **\n\nSimply get the count of left nodes and right nodes recursively and get the remaining nodes(after removing the current nodes by doing n-(l+r)-1. Now we multiply them and check if it is same as our current multiplication or greater than. If equal, we just increase the counter and if greater, we update our ansvalue and set counter to 1.\nThere is a thing to keep in mind. \'l\', \'r\' and \'rem\' can be \'0\'. If so happens then set it to 1 so that when multiplying it won\'t make the answer \'0\'.\n\nHere\'s the code\n\n```\nclass Solution {\npublic:\n long long val = 0, cnt = 0;\n int traversal(TreeNode* root, int n)\n {\n if(!root) return 0;\n int l = traversal(root->left, n);\n int r = traversal(root->right, n);\n int nl = l, nr = r, rem = n-l-r-1;\n if(l == 0) \n {\n nl++;\n }\n if(r == 0)\n {\n nr++;\n }\n if(rem == 0)\n {\n rem++;\n }\n long long ans = 1L*nl*nr*rem;\n if(ans > val)\n {\n val = ans;\n cnt=1;\n }\n else if(ans == val)\n {\n cnt++;\n }\n return l+r+1;\n }\n int countHighestScoreNodes(vector<int>& parents) {\n TreeNode* root;\n vector<TreeNode*> temp(parents.size());\n for(int i = 0; i < temp.size(); i++)\n {\n temp[i] = new TreeNode(i);\n }\n for(int i = 1; i < temp.size(); i++)\n {\n if(temp[parents[i]]->left) temp[parents[i]]->right = temp[i];\n else temp[parents[i]]->left = temp[i];\n }\n root = temp[0];\n traversal(root, parents.size());\n return cnt;\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'Recursion'] | 0 |
count-nodes-with-the-highest-score | Easy and simple code || C++ || DFS || O(N) solution | easy-and-simple-code-c-dfs-on-solution-b-uucn | Step-1 We build a undirected graph using parent array.\nStep -2 For each node we need the count of left and right subtree size so ans for a node will be ( left | utsav___gupta | NORMAL | 2022-03-11T05:51:21.666189+00:00 | 2022-03-11T05:54:19.073692+00:00 | 177 | false | **Step-1** We build a undirected graph using parent array.\n**Step -2** For each node we need the count of left and right subtree size so ans for a node will be ( **left subtree size * right subtree size * (total nodes -left subtree size -right subtree size**) to get this we will make a dfs call with the root which will visit all its child nodes and return the subtree sizes which we will keep on adding.\n**Step -3** return the current subtree size (**left subtree size + right subtree size +1** ) .\n\nTC->O(N) //Since we are visiting each nodes only once.\nSC->O(N) //Visted array\n\n```\nint maxcnt=0;\nlong long maxans=-1;\nint total=0;\nint dfs(int src, vector<vector<int>>&g,vector<bool>&vis)\n{\n vis[src]=true;\n int sum=0;\n long long temp=1ll;\n for(auto ne:g[src])\n {\n if(vis[ne]==false)\n {\n int v1=dfs(ne,g,vis);\n sum+=v1; // Adding subtree size of all child nodes\n if(v1!=0)temp=temp*v1; // multiplying subtree sizes\n }\n }\n \n sum+=1; //including current node in current tree size\n if(total-sum>0)\n {\n temp=temp*(total-sum); //multiplying subtree size which is parent of current node\n }\n \n if(temp>=maxans)\n {\n if(temp==maxans)maxcnt++;\n else\n {\n maxans=temp;\n maxcnt=1;\n }\n }\n \n return sum; // returning size of current tree\n}\n\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& parents)\n {\n int root=0;\n int n=parents.size();\n total=n;\n vector<vector<int>>g(n);\n for(int i=0;i<parents.size();i++)\n {\n if(parents[i]==-1)\n {\n root=i;\n }\n else\n {\n g[parents[i]].push_back(i);\n g[i].push_back(parents[i]);\n }\n }\n maxcnt=0;\n maxans=-1;\n vector<bool>vis(n,false);\n dfs(root,g,vis);\n return maxcnt;\n }\n};\n```\n\n\n\nSimilar problem -[1519. Number of Nodes in the Sub-Tree With the Same Label](https://leetcode.com/problems/number-of-nodes-in-the-sub-tree-with-the-same-label/)\nLittle diff but same concept.\n\nPlease upvote if u like the post. It gives me motivation !!! | 1 | 0 | ['Depth-First Search', 'C'] | 0 |
count-nodes-with-the-highest-score | Java - O(N) space and time solution | java-on-space-and-time-solution-by-pathe-89gb | A cut score is multiplication of no of leftChildren, no of rightChidren and remaning nodes (Total nodes-leftChildren-rightChildren-1).\nBelow is Java Code for t | pathey | NORMAL | 2022-03-06T23:34:23.824840+00:00 | 2022-03-06T23:34:23.824871+00:00 | 96 | false | A cut score is multiplication of no of leftChildren, no of rightChidren and remaning nodes (Total nodes-leftChildren-rightChildren-1).\nBelow is Java Code for the solution with comments.\n\n```\n//TreeNode \nclass TreeNode\n{\n int val;\n TreeNode left;\n TreeNode right;\n int leftChilds=0;\n int rightChilds=0;\n TreeNode(int val)\n {\n this.val=val;\n }\n}\nclass Solution {\n HashMap<Long,Integer> costs;\n long max; //To store maximum cost value\n int n;\n public int countHighestScoreNodes(int[] parents) {\n costs=new HashMap<Long,Integer>(); //To store frequency of each cost value\n max=0;\n n=parents.length;\n HashMap<Integer,TreeNode> hm=new HashMap<Integer,TreeNode>();\n TreeNode root=new TreeNode(0); //Initializing root node\n hm.put(0,root);\n for(int i=1;i<parents.length;i++)\n {\n int parent=parents[i];\n TreeNode child=hm.getOrDefault(i,new TreeNode(i));\n TreeNode parentNode=hm.getOrDefault(parent,new TreeNode(parent));\n if(parentNode.left==null)\n {\n parentNode.left=child;\n }\n else\n {\n parentNode.right=child;\n }\n hm.put(i,child);\n hm.put(parent,parentNode);\n }//Loop to construct tree structure.\n postOrderTraverse(root); //postOrder traversal\n return costs.get(max); // Returning maximum frequency\n }\n public int postOrderTraverse(TreeNode root)\n {\n if(root==null)\n return 0;\n \n long one=1; \n root.leftChilds=postOrderTraverse(root.left); //Getting no of leftChilds\n root.rightChilds=postOrderTraverse(root.right); //Getting no of rightChilds\n long score=(one*Math.max(root.leftChilds,1)*(Math.max(root.rightChilds,1))*(Math.max(n-root.leftChilds-root.rightChilds-1,1))); // Calculating the score of the node\n costs.put(score,costs.getOrDefault(score,0)+1);\n max=Math.max(score,max);\n return root.leftChilds+root.rightChilds+1; \n }\n}\n``` | 1 | 0 | ['Depth-First Search', 'Binary Tree'] | 0 |
count-nodes-with-the-highest-score | Count Nodes With the Highest Score | C++ | SubTree Size + Maths | DFS | count-nodes-with-the-highest-score-c-sub-yhnc | \nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& p) {\n int n = p.size();\n vector<int> tree[n], subTreeSize(n, 0), vis(n, | renu_apk | NORMAL | 2022-01-12T07:59:51.092532+00:00 | 2022-01-12T08:01:07.100768+00:00 | 83 | false | ```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& p) {\n int n = p.size();\n vector<int> tree[n], subTreeSize(n, 0), vis(n, 0);\n for(int i = 0; i < n; i++){\n if(p[i] != -1){\n tree[p[i]].push_back(i);\n }\n }\n \n function<int(int)> dfs=[&](int u)-> int{\n vis[u] = 1;\n int currSize = 1;\n for(auto& next : tree[u]){\n if(!vis[next]){\n currSize += dfs(next);\n }\n }\n subTreeSize[u] = currSize;\n return currSize;\n };\n \n dfs(0);\n \n long ans = 0;\n unordered_map<long ,int> freq;\n for(int i = 0; i < n; i++){\n long val = 1, sum = 0;\n for(auto& c : tree[i]){\n if(p[c] == i) val *= subTreeSize[c], sum += subTreeSize[c];\n }\n val *= max(1L, n - sum - 1);\n ans = max(ans, val);\n freq[val]++;\n }\n \n return freq[ans];\n }\n};\n``` | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | Java solution fail. what's wrong? | java-solution-fail-whats-wrong-by-pvp-vm8b | \nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n HashMap<Integer, TreeNode> treeMap = new HashMap<Integer, TreeNode>();\n | pvp | NORMAL | 2021-12-15T13:46:09.845082+00:00 | 2021-12-15T13:46:09.845105+00:00 | 100 | false | ```\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n HashMap<Integer, TreeNode> treeMap = new HashMap<Integer, TreeNode>();\n for (int i = 0; i < parents.length; i++) {\n TreeNode node;\n if (!treeMap.containsKey(i)) {\n node = new TreeNode(i);\n treeMap.put(i, node);\n } else {\n node = treeMap.get(i);\n }\n if (parents[i] == -1) {\n continue;\n }\n if (!treeMap.containsKey(parents[i])) {\n TreeNode parent = new TreeNode(parents[i]);\n treeMap.put(parents[i], parent);\n parent.setChild(node);\n } else {\n TreeNode parent = treeMap.get(parents[i]);\n parent.setChild(node);\n }\n }\n\n TreeNode root = treeMap.get(0);\n int score = setScoreForNodes(root);\n System.out.println(score);\n System.out.println(parents.length);\n\n int cnt = 0;\n int maxProduct = 0;\n for (int i = 0; i < parents.length; i++) {\n TreeNode node = treeMap.get(i);\n int leftScore = node.left == null? 0 : node.left.score;\n int rightScore = node.right == null? 0 : node.right.score;\n int otherPartScore = score - node.score;\n leftScore = Math.max(leftScore, 1);\n rightScore = Math.max(rightScore, 1);\n otherPartScore = Math.max(otherPartScore, 1);\n int total = leftScore * rightScore * otherPartScore;\n if (total == maxProduct) {\n cnt += 1;\n } else if (total > maxProduct) {\n maxProduct = total;\n cnt = 1;\n }\n }\n return cnt;\n }\n\n public int setScoreForNodes(TreeNode root) {\n if (Objects.isNull(root)) {\n return 0;\n }\n int score = 1 + setScoreForNodes(root.left) + setScoreForNodes(root.right);\n root.score = score;\n return score;\n }\n\n class TreeNode {\n int val;\n int score;\n TreeNode left;\n TreeNode right;\n\n public TreeNode(int val) {\n this.val = val;\n return;\n }\n\n public void setChild(TreeNode node) {\n if (this.left == null) {\n this.left = node;\n } else {\n this.right = node;\n }\n return;\n }\n }\n}\n``` | 1 | 0 | [] | 2 |
count-nodes-with-the-highest-score | Java build tree and dfs | java-build-tree-and-dfs-by-nadabao-c9co | I really like this question, very suitable for real interview.\nTesting tree building, dfs, corner case, etc\n\n\nclass Solution {\n long max = 0;\n long | nadabao | NORMAL | 2021-11-13T06:06:32.238394+00:00 | 2021-11-13T06:07:38.287681+00:00 | 181 | false | I really like this question, very suitable for real interview.\nTesting tree building, dfs, corner case, etc\n\n```\nclass Solution {\n long max = 0;\n long cnt = 0;\n public int countHighestScoreNodes(int[] parents) {\n TreeNode root = buildTree(parents); \n dfs(root, parents.length);\n return (int) cnt;\n }\n \n private long dfs(TreeNode node, int n) {\n if (node == null) return 0;\n long l = dfs(node.left, n);\n long r = dfs(node.right, n);\n long remain = n - l - r - 1;\n long prod = (l > 0 ? l : 1) * (r > 0 ? r : 1) * (remain > 0 ? remain : 1); // tricky\n if (prod == max) {\n cnt++;\n } else if (prod > max) {\n max = prod;\n cnt = 1;\n }\n return l + r + 1;\n }\n \n private TreeNode buildTree(int[] parents) {\n int n = parents.length;\n TreeNode[] nodeArray = new TreeNode[n];\n TreeNode root = null;\n \n for (int i = 0; i < n; i++) {\n nodeArray[i] = new TreeNode(i);\n }\n \n for (int i = 0; i < n; i++) {\n if (parents[i] == -1) {\n root = nodeArray[i];\n continue;\n }\n TreeNode node = nodeArray[parents[i]]; // i = 1, node = 2\n if (node.left == null) {\n node.left = nodeArray[i];\n } else {\n node.right = nodeArray[i];\n }\n\n }\n return root;\n }\n}\n\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode(int val) {\n this.val = val;\n }\n}\n``` | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | Should be intuitive | should-be-intuitive-by-liqiangc-7mz4 | \tint dfs(const vector >& g, int i, long& maxScore, long& res){\n long score = 1, sum = 0;\n for(int x : g[i]){\n int cnt = dfs(g, x, m | liqiangc | NORMAL | 2021-10-30T00:10:43.918976+00:00 | 2021-11-13T15:45:20.524962+00:00 | 71 | false | \tint dfs(const vector<vector<int> >& g, int i, long& maxScore, long& res){\n long score = 1, sum = 0;\n for(int x : g[i]){\n int cnt = dfs(g, x, maxScore, res);\n score *= cnt;\n sum += cnt;\n }\n score *= g.size()-sum-(i!=0);\n if(score>maxScore) maxScore = score, res = 1;\n else if(score == maxScore) ++res;\n return sum+1;\n }\n int countHighestScoreNodes(const vector<int>& parents) {\n long n = parents.size(), res = 0, maxScore = 0;\n vector<vector<int> > g(n);\n for(int i=1; i<n; ++i) g[parents[i]].push_back(i);\n dfs(g, 0, maxScore, res);\n return res;\n } | 1 | 0 | [] | 1 |
count-nodes-with-the-highest-score | DSS based Solution || C++ | dss-based-solution-c-by-sj4u-w0t9 | \n\n\n\n#define ll long long\nclass Solution {\npublic:\n \n struct Node\n{\n Node* left;\n Node* right;\n int val;\n ll count;//to store coun | SJ4u | NORMAL | 2021-10-25T11:16:49.244339+00:00 | 2021-10-25T11:16:49.244413+00:00 | 92 | false | ```\n\n\n\n#define ll long long\nclass Solution {\npublic:\n \n struct Node\n{\n Node* left;\n Node* right;\n int val;\n ll count;//to store count(left)+count(right)\n Node(int c)\n {\n left=NULL;\n right=NULL;\n count=0;\n val=c;\n }\n};\n\n \n \n //normal dfs after tree construction\n vector<ll>v;\nint recurs(Node* root,int n)\n{\n if(!root)\n return 0;\n \n \n int left=recurs(root->left,n);\n int right=recurs(root->right,n);\n root->count=left+right;\n \n\n \n ll left1=left,right1=right;\n \n if(left1==0)\n left1=1;\n if(right1==0)\n right1=1;\n ll val=(n-1-left-right);\n if((n-1-left-right)==0)\n val=1;\n \n v.push_back(left1*right1*(val));\n return root->count+1;\n}\n \n int countHighestScoreNodes(vector<int>& parent) {\n v.clear();\n int n=parent.size();\n \n \n //tree construction\n vector<Node*>tree(n);\n \n for(int i=0;i<n;i++)\n {\n tree[i]=new Node(i);\n }\n \n for(int i=0;i<n;i++)\n {\n if(parent[i]!=-1)\n {\n if(tree[parent[i]]->left==NULL)\n tree[parent[i]]->left=tree[i];\n else\n tree[parent[i]]->right=tree[i];\n }\n }\n \n Node* root=tree[0];\n recurs(root,n);\n int c=0;\n \n sort(v.rbegin(),v.rend());\n \n for(int i=0;i<n;i++)\n {\n // cout<<i<<" : "<<v[i]<<endl;\n if(v[i]==v[0])\n c++;\n else\n break;\n }\n return c;\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'C'] | 1 |
count-nodes-with-the-highest-score | DFS solution Python | dfs-solution-python-by-jinghuayao-bovz | \nclass Solution:\n """\n Deleting a node can yield at most 3 branches\n """\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n | jinghuayao | NORMAL | 2021-10-24T23:06:32.776605+00:00 | 2021-10-24T23:06:32.776649+00:00 | 75 | false | ```\nclass Solution:\n """\n Deleting a node can yield at most 3 branches\n """\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n \n # build a graph representation\n graph = collections.defaultdict(set)\n for node, parent in enumerate(parents):\n graph[parent].add(node)\n \n # total number of nodes, to be used\n # to count the subtree obtained by removing\n # a node but not the subtrees of node.left or node.right\n n = len(parents)\n \n \n # use a dict to record product-frequency pairs\n d = collections.Counter()\n \n # a helper function\n def dfs(node):\n """\n return number of nodes of the subtree rooted at node\n """\n p, s = 1, 0\n # at most two children\n for child in graph[node]:\n res = dfs(child)\n p *= res\n s += res\n # a possible branch from top of the node\n p *= max(1, n - 1 - s)\n d[p] += 1\n return s + 1\n \n dfs(0)\n return d[max(d.keys())]\n \n```\n\nThis solution is motivated by \nhttps://leetcode.com/problems/count-nodes-with-the-highest-score/discuss/1537603/Python-3-or-Graph-DFS-Post-order-Traversal-O(N)-or-Explanation\n | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | [JAVA] Easy + Clear Explanation + Clean Code O(N) | java-easy-clear-explanation-clean-code-o-0594 | As shown in the image Below :\nwe Just need to find the No of Nodes in Left Sub-Tree , Right SubTree and the parent SubTree \nand multiply them to find the prod | embrane | NORMAL | 2021-10-24T14:34:05.703913+00:00 | 2021-10-24T14:34:05.703952+00:00 | 622 | false | As shown in the image Below :\nwe Just need to find the No of Nodes in Left Sub-Tree , Right SubTree and the parent SubTree \nand multiply them to find the product generated if we remove the current Node \n**Steps** :\n1. DFS to find the No of Nodes in each subTree \n2. no for i in Range 0 to N-1 cal the Above Product \n3. then Find the max among all the product and count No of times max occours;\n\nBelow is Code :\nSimple and Concise :\n```\nList<Integer>[] adj;\n int N;\n public int countHighestScoreNodes(int[] par) {\n N=par.length;\n adj=new List[N];\n for(int i=0;i<adj.length;i++)adj[i]=new Vector<Integer>();\n\n for(int i=0;i<par.length;i++) {//build Tree\n if(par[i]==-1) continue;\n adj[par[i]].add(i);\n }\n\n long mx=Long.MIN_VALUE;\n dp=new Integer[N];//arr for storing noOfNodes\n noOfNodes(0);\n\n List<Long> list=new Vector<>();\n for(int i=0;i<par.length;i++) {\n long product=1;\n int left=(adj[i].size()>=1)?dp[adj[i].get(0)]:1; //if left child exist then cal. else left=1\n int right=(adj[i].size()>=2)?dp[adj[i].get(1)]:1;\n if(par[i]==-1)\n product=product*left*right;\n else \n product=product*left*right*(dp[0]-dp[i]);\n\n mx=Math.max(mx, product);\n list.add(product);\n }\n int cnt=0;\n for(long x:list)\n if(x==mx)cnt++;\n\n return cnt;\n }\t\t\n\n Integer[] dp;\n int noOfNodes(int i) {\n if(dp[i]!=null) return dp[i]; \n\n int no=1;\n for(int child:adj[i]) {\n no+=noOfNodes(child);\n }\n return dp[i]=no;\n }\n```\nTime Complexity - O(N)\n**Please Upvote if you found Useful !!**\n\n\n\n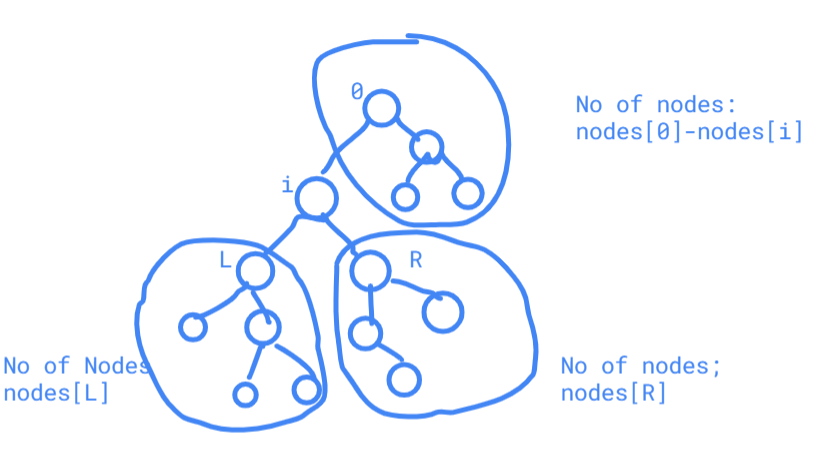\n\n | 1 | 8 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'Java'] | 0 |
count-nodes-with-the-highest-score | C++ DFS; Will work for n-ary tree also; Separate score and size count; | c-dfs-will-work-for-n-ary-tree-also-sepa-v4bo | I separate the computation of the score for each node from the computation of the size of the node. This code will also work for a N-ary tree.\n\n\nclass Soluti | equine | NORMAL | 2021-10-24T08:08:33.134881+00:00 | 2021-10-24T13:33:12.520870+00:00 | 123 | false | I separate the computation of the score for each node from the computation of the size of the node. This code will also work for a N-ary tree.\n\n```\nclass Solution {\npublic:\n int dfs(int u, vector<vector<int>>& graph,vector<int>& numNodes) {\n numNodes[u] = 1;\n for (int v : graph[u]) {\n numNodes[u] += dfs(v,graph,numNodes);\n }\n return numNodes[u];\n }\n int countHighestScoreNodes(vector<int>& parents) {\n int n = parents.size();\n \n vector<vector<int>> graph(n);\n for (int i = 1; i < n; i++) {\n graph[parents[i]].push_back(i);\n }\n \n vector<int> numNodes(n,-1);\n dfs(0,graph,numNodes);\n \n vector<long long> score(n,0L);\n long long maxScore = LLONG_MIN;\n for (int i = 0; i < n; i++) {\n score[i] = (i > 0) ? (numNodes[0] - numNodes[i]) : 1;\n for (int child : graph[i]) {\n score[i] *= numNodes[child];\n }\n maxScore = max(maxScore,score[i]);\n }\n \n return count_if(begin(score),end(score),[maxScore](long long x){return x == maxScore;});\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'C'] | 0 |
count-nodes-with-the-highest-score | [Python] DFS | python-dfs-by-waywardcc-vm8u | \nclass Solution(object):\n def countHighestScoreNodes(self, parents):\n """\n :type parents: List[int]\n :rtype: int\n """\n | waywardcc | NORMAL | 2021-10-24T05:59:37.792636+00:00 | 2021-10-24T05:59:37.792686+00:00 | 83 | false | ```\nclass Solution(object):\n def countHighestScoreNodes(self, parents):\n """\n :type parents: List[int]\n :rtype: int\n """\n hmap = collections.defaultdict(list)\n n = len(parents)\n for i in range(n):\n if parents[i] != -1:\n hmap[parents[i]].append(i)\n \n self.maxKey, self.res = 0, 0\n \n def dfs(node):\n score = 1\n count = 0\n for nxt in hmap[node]:\n subCount = dfs(nxt)\n score*=subCount\n count += subCount\n \n score *= n-1-count or 1\n \n if score > self.maxKey:\n self.maxKey = score\n self.res = 1\n elif score == self.maxKey:\n self.res += 1\n \n return count + 1\n \n dfs(0)\n\n return self.res\n``` | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | C++ Easy Solution Using DFS | c-easy-solution-using-dfs-by-saiteja_bal-h81h | \nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& p) {\n int n=p.size();\n vector<vector<int>> child(n);\n \n | saiteja_balla0413 | NORMAL | 2021-10-24T05:07:29.532271+00:00 | 2021-10-24T05:11:33.285915+00:00 | 176 | false | ```\nclass Solution {\npublic:\n int countHighestScoreNodes(vector<int>& p) {\n int n=p.size();\n vector<vector<int>> child(n);\n \n for(int i=1;i<n;i++)\n {\n child[p[i]].push_back(i);\n }\n int cnt=0;\n long long maxi=0;\n solve(0,child,n,maxi,cnt);\n return cnt;\n \n \n }\n int solve(int node,vector<vector<int>>& child,int& total,long long& maxi,int& cnt)\n {\n int left=0;\n int right=0;\n for(int i=0;i<child[node].size();i++)\n {\n if(i==0)\n left=solve(child[node][0],child,total,maxi,cnt);\n if(i==1)\n right=solve(child[node][1],child,total,maxi,cnt);\n }\n \n long long curr=1;\n if(left)\n curr*=left;\n if(right)\n curr*=right;\n if(node!=0)\n curr*=(total -( left +right +1));\n if(curr>maxi)\n {\n maxi=curr;\n cnt=1;\n }\n else if(curr==maxi)\n cnt++;\n return left+right+1;\n }\n};\n```\n**Upvote if this helps you :)** | 1 | 0 | ['C'] | 1 |
count-nodes-with-the-highest-score | Java | DFS | java-dfs-by-shubham242k-vvrv | \nclass Solution {\n int n;\n ArrayList<Integer>[] tree;\n long[] res;\n public int countHighestScoreNodes(int[] parents) {\n n = parents.len | shubham242k | NORMAL | 2021-10-24T04:21:18.256371+00:00 | 2021-10-24T04:22:14.405783+00:00 | 96 | false | ```\nclass Solution {\n int n;\n ArrayList<Integer>[] tree;\n long[] res;\n public int countHighestScoreNodes(int[] parents) {\n n = parents.length;\n tree = new ArrayList[n];\n for(int i = 0 ; i < n ; i++)tree[i] = new ArrayList<>();\n \n for(int i = 1 ; i < n ; i++){\n tree[parents[i]].add(i);\n }\n \n res = new long[n];\n \n depth(0);\n long max = 0;\n for(long v : res){\n max = Math.max(max,v);\n }\n int count = 0 ;\n for(long v : res) if(v == max) count++;\n return count;\n }\n \n \n public int depth(int src){\n int child = 1;\n long ma = 1;\n for(int nbr : tree[src]){\n int sc = depth(nbr);\n ma *= sc;\n child += sc;\n }\n if(src != 0)\n ma *= (n - child);\n \n res[src] = ma;\n return child;\n }\n}\n``` | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | [Python] DFS count nodes - 1,2,3 edges | python-dfs-count-nodes-123-edges-by-coco-9516 | User DFS to count all nodes for the tree.\nThen iterate through all nodes. There are 3 cases after removing a node:\n- it has 1 edge: n-1\n- it has 2 edges: chi | coco987 | NORMAL | 2021-10-24T04:07:42.414018+00:00 | 2021-10-24T04:07:42.414048+00:00 | 86 | false | User DFS to count all nodes for the tree.\nThen iterate through all nodes. There are 3 cases after removing a node:\n- it has 1 edge: n-1\n- it has 2 edges: child_count * (n - 1 - child_count)\n- it has 3 edges: L_count * R_count * (n-1-L_count-R_count)\n\nNote: root 0 is a special case. Treat it seperately.\n\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n # build tree\n children = collections.defaultdict(list)\n for i in range(1, n):\n children[parents[i]].append(i)\n \n # count nodes\n d = {}\n def dfs_count(node):\n cnt = 1\n for v in children[node]:\n cnt += dfs_count(v)\n d[node] = cnt\n return cnt\n \n dfs_count(0)\n \n # root\n max_cnt = 1\n if len(children[0]) == 1: # root has 1 child\n max_val = n-1\n else: # root has 2 children\n max_val = d[children[0][0]] * d[children[0][1]]\n \n # 1 to n-1\n for i in range(1, n):\n if len(children[i]) == 0: # 1 link\n val = n-1\n elif len(children[i]) == 1: # 2 links\n val = d[children[i][0]] * (n - 1 - d[children[i][0]])\n else: # 3 links\n val = d[children[i][0]] * d[children[i][1]] * (n - 1 - d[children[i][0]] - d[children[i][1]])\n if val > max_val:\n max_val = val\n max_cnt = 1\n elif val == max_val:\n max_cnt += 1\n \n return max_cnt\n \n \n``` | 1 | 0 | [] | 0 |
count-nodes-with-the-highest-score | 🎨 The ART of Dynamic Programming | the-art-of-dynamic-programming-by-clayto-8ffu | \uD83C\uDFA8 The ART of Dynamic Programming: let cnt[i] be the count of nodes for each ith subtree, then we can use deductive reasoning to calculate the cardina | claytonjwong | NORMAL | 2021-10-24T04:00:35.959289+00:00 | 2022-12-26T17:01:05.144743+00:00 | 336 | false | [\uD83C\uDFA8 The ART of Dynamic Programming:](https://leetcode.com/discuss/general-discussion/712010/The-ART-of-Dynamic-Programming-An-Intuitive-Approach%3A-from-Apprentice-to-Master) let `cnt[i]` be the count of nodes for each `i`<sup>th</sup> subtree, then we can use deductive reasoning to calculate the cardinality for the remaining connected components when each `i`<sup>th</sup> subtree root is removed, ie. the left/right subtree counts are trivial (the sum of `cnt[kids[i]]`), and we use inversion to the count of nodes "above" as the total node count minus the `i`<sup>th</sup> subtree count (`cnt[0] - cnt[i]`). Note: `cnt[0]` == `N`.\n\n**\uD83D\uDED1Base case:** leaf nodes have no kids, so the count of each leaf node is `1`.\n\n**\uD83E\uDD14 Recurrence relation:** post-order traversal of the tree, and the `i`<sup>th</sup> subtree count is accumulated as the recursive stack unwinds, ie. `1` plus the count of all `j`<sup>th</sup> kids subtree counts.\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun countHighestScoreNodes(P: IntArray): Int {\n var N = P.size\n var kid = Array(N){ mutableListOf<Int>() }\n var cnt = LongArray(N){ 1 }\n for (i in 1 until N)\n kid[P[i]].add(i)\n fun go(i: Int = 0): Long {\n for (j in kid[i])\n cnt[i] += go(j)\n return cnt[i]\n }\n go()\n var (best, hi) = Pair(mutableMapOf<Long, Int>(), 0L)\n for (i in 0 until N) {\n var t = Math.max(1L, N.toLong() - cnt[i])\n for (j in kid[i])\n t *= cnt[j]\n best[t] = 1 + (best[t] ?: 0); hi = Math.max(hi, t)\n }\n return best[hi]!!\n }\n}\n```\n\n*Javascript*\n```\nlet countHighestScoreNodes = (P, best = new Map(), hi = 0) => {\n let N = P.length;\n let kid = [...Array(N).keys()].map(i => []),\n cnt = Array(N).fill(1);\n for (let i = 1; i < N; ++i)\n kid[P[i]].push(i);\n let go = (i = 0) => {\n for (let j of kid[i])\n cnt[i] += go(j);\n return cnt[i];\n };\n go();\n for (let i = 0; i < N; ++i) {\n let t = Math.max(1, N - cnt[i]);\n for (let j of kid[i])\n t *= cnt[j];\n best.set(t, 1 + (best.get(t) || 0)), hi = Math.max(hi, t);\n }\n return best.get(hi);\n};\n```\n\n*Python3*\n```\nclass Solution:\n def countHighestScoreNodes(self, P: List[int]) -> int:\n N = len(P)\n kids = defaultdict(set)\n for i in range(1, N):\n kids[P[i]].add(i)\n cnt = [1] * N\n def go(i = 0):\n for j in kids[i]:\n cnt[i] += go(j)\n return cnt[i]\n go()\n best = Counter()\n for i in range(N):\n t = max(1, N - cnt[i])\n for j in kids[i]:\n t *= cnt[j]\n best[t] += 1\n return best[max(best.keys())]\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using LL = long long;\n using VI = vector<int>;\n using Map = unordered_map<int, int>;\n using Adj = unordered_map<int, VI>;\n using fun = function<int(int)>;\n int countHighestScoreNodes(VI& P, Adj kids = {}, Map cnt = {}, Map best = {}, LL hi = 0) {\n int N = P.size();\n for (auto i{ 1 }; i < N; ++i)\n kids[P[i]].push_back(i);\n fun go = [&](auto i) {\n for (auto j: kids[i])\n cnt[i] += go(j);\n return cnt[i] += 1;\n };\n go(0);\n for (auto i{ 0 }; i < N; ++i) {\n LL t = max(1, N - cnt[i]);\n for (auto j: kids[i])\n t *= cnt[j];\n ++best[t], hi = max(hi, t);\n }\n return best[hi];\n }\n};\n``` | 1 | 1 | [] | 0 |
count-nodes-with-the-highest-score | Simple Java solution with Approach and Proper comments | simple-java-solution-with-approach-and-p-l34g | IntuitionWe need to build the Tree and as mentioned in the problem remove each Node and see how many subtrees remnaining key point in this problem is how to fin | user5958h | NORMAL | 2025-04-06T13:11:13.693505+00:00 | 2025-04-06T13:11:13.693505+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to build the Tree and as mentioned in the problem remove each Node and see how many subtrees remnaining key point in this problem is how to find the parent level nodes
```
5
4. 3
1. 2
```
so in above when we remove 3 , we have 1 , 2 and 5-->4 so parent level nodes are Total(5) -( Left(1) + right(2) + 1(node itself)) = 2.
# Approach
Below code has been implemented using the same steps with comments .
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```java []
class Solution {
public int countHighestScoreNodes(int[] parents) {
int totalNodes = parents.length;
// STEP-1 Build the Tree
TreeNode[] tree = new TreeNode[totalNodes];
// STEP-2 Make sure that all Nodes are created in this array
for(int i=0; i<totalNodes; i++){
tree[i] = new TreeNode();
}
// STEP-3 Build the actual Tree , start with node 1 , since node 0 do not have parent
for(int node=1; node< totalNodes; node++) {
// This is the root Or Parent
TreeNode root = tree[parents[node]];
if(root.left == null){
root.left = tree[node];
}else if(root.right == null){
root.right = tree[node];
}
}
// STEP-4 Capture the count of nodes at each subtree level
countNodes(tree[0]);
// STEP-5 Caculate the maxScore
return maxScore(tree);
}
private int countNodes(TreeNode root){
if(root == null){
return 0;
}
root.count = 1 + countNodes(root.left) + countNodes(root.right);
return root.count;
}
private int maxScore(TreeNode[] tree){
int totalNodes = tree.length;
long maxScore = 0;
int count =0;
for(int node =0; node <tree.length; node++){
TreeNode root = tree[node];
int leftTreeNodes = root.left == null ? 0 : root.left.count;
int rightTreeNode = root.right == null ? 0 : root.right.count;
int parentNodes = totalNodes - (leftTreeNodes + rightTreeNode +1);
long product =1;
if(leftTreeNodes > 0){
product*=leftTreeNodes;
}
if(rightTreeNode > 0){
product*=rightTreeNode;
}
if(parentNodes > 0){
product*=parentNodes;
}
long currentScore = product;
if(currentScore > maxScore){
// Reset count to 1
maxScore = currentScore;
count=1;
}else if(currentScore == maxScore){
count++;
}
}
return count;
}
}
class TreeNode {
TreeNode left ;
TreeNode right;
int count;
}
``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Simple Java solution with Approach and Proper comments | simple-java-solution-with-approach-and-p-8a57 | IntuitionWe need to build the Tree and as mentioned in the problem remove each Node and see how many subtrees remnaining key point in this problem is how to fin | user5958h | NORMAL | 2025-04-06T13:11:10.796268+00:00 | 2025-04-06T13:11:10.796268+00:00 | 12 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to build the Tree and as mentioned in the problem remove each Node and see how many subtrees remnaining key point in this problem is how to find the parent level nodes
```
5
4. 3
1. 2
```
so in above when we remove 3 , we have 1 , 2 and 5-->4 so parent level nodes are Total(5) -( Left(1) + right(2) + 1(node itself)) = 2.
# Approach
Below code has been implemented using the same steps with comments .
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```java []
class Solution {
public int countHighestScoreNodes(int[] parents) {
int totalNodes = parents.length;
// STEP-1 Build the Tree
TreeNode[] tree = new TreeNode[totalNodes];
// STEP-2 Make sure that all Nodes are created in this array
for(int i=0; i<totalNodes; i++){
tree[i] = new TreeNode();
}
// STEP-3 Build the actual Tree , start with node 1 , since node 0 do not have parent
for(int node=1; node< totalNodes; node++) {
// This is the root Or Parent
TreeNode root = tree[parents[node]];
if(root.left == null){
root.left = tree[node];
}else if(root.right == null){
root.right = tree[node];
}
}
// STEP-4 Capture the count of nodes at each subtree level
countNodes(tree[0]);
// STEP-5 Caculate the maxScore
return maxScore(tree);
}
private int countNodes(TreeNode root){
if(root == null){
return 0;
}
root.count = 1 + countNodes(root.left) + countNodes(root.right);
return root.count;
}
private int maxScore(TreeNode[] tree){
int totalNodes = tree.length;
long maxScore = 0;
int count =0;
for(int node =0; node <tree.length; node++){
TreeNode root = tree[node];
int leftTreeNodes = root.left == null ? 0 : root.left.count;
int rightTreeNode = root.right == null ? 0 : root.right.count;
int parentNodes = totalNodes - (leftTreeNodes + rightTreeNode +1);
long product =1;
if(leftTreeNodes > 0){
product*=leftTreeNodes;
}
if(rightTreeNode > 0){
product*=rightTreeNode;
}
if(parentNodes > 0){
product*=parentNodes;
}
long currentScore = product;
if(currentScore > maxScore){
// Reset count to 1
maxScore = currentScore;
count=1;
}else if(currentScore == maxScore){
count++;
}
}
return count;
}
}
class TreeNode {
TreeNode left ;
TreeNode right;
int count;
}
``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Java simple solution beats 90%. With Explanations | java-simple-solution-beats-90-with-expla-1jd7 | IntuitionThe intuition is if we have a size aware binary tree then we can calculate the score of each node in constant time(linear overall). Once we remove a no | cutkey | NORMAL | 2025-04-04T05:59:34.925258+00:00 | 2025-04-06T16:51:41.399658+00:00 | 12 | false | # Intuition
The intuition is if we have a size aware binary tree then we can calculate the score of each node in constant time(linear overall). Once we remove a node then the size of the tree with remaining nodes is root.size - node.size. The left and right nodes of the node that are removed will have sizes left.size and right.size. The score is the product of left.size, right.size and root.size - node.size. Make sure that your floor is 1.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Define a TreeNode class that as left, right and parent pointers and also a field called size which is the size of the sub tree rooted at the node.
2. Convert the array to a binary tree by iterating through it.
3. Store reference to each node in an array too. (This is needed to buld the tree anyways).
4. Use DFS to calculate and set the size of each node.
5. Loop through the array of nodes and calculate the score. Score = left.size * right.size * (root.size-current.size). Make sure you use the floor value 1 for null children and when current is root.
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class TreeNode {
public TreeNode left;
public TreeNode right;
public TreeNode parent;
public int val;
public long size;
public TreeNode(int val) {
this.val = val;
this.size = 1;
}
}
class Solution {
TreeNode[] nodes;
int count = 0;
long max = 0;
public int countHighestScoreNodes(int[] parents) {
nodes = new TreeNode[parents.length];
TreeNode root = new TreeNode(0);
nodes[0] = root;
for (int i = 1; i < parents.length; i++) {
if (nodes[i] == null) nodes[i] = new TreeNode(i);
if (nodes[parents[i]] == null) nodes[parents[i]] = new TreeNode(parents[i]);
TreeNode parent = nodes[parents[i]];
if (parent.left == null) parent.left = nodes[i];
else parent.right = nodes[i];
nodes[i].parent = parent;
}
updatesize(root);
for (int i = 0; i < parents.length; i++) {
TreeNode current = nodes[i];
TreeNode left = current.left, right = current.right, parent = current.parent;
long lsize = left != null ? left.size : 1;
long rsize = right != null ? right.size : 1;
long psize = Math.max(root.size - current.size, 1);
long score = lsize*rsize*psize;
if (score > max) {
count = 1;
max = score;
}
else if (score == max) count++;
}
return count;
}
private long updatesize(TreeNode node) {
if (node != null) {
node.size += updatesize(node.left);
node.size += updatesize(node.right);
return node.size;
}
return 0;
}
}
``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Fast Python approach using two DFS's | fast-python-approach-using-two-dfss-by-y-o9ia | IntuitionNotice the problem requires an operation on each node, meaning DFS is applicable. Next, for each node, we need to know the size of the subtrees it is c | yunbo2016 | NORMAL | 2025-03-11T02:43:20.399462+00:00 | 2025-03-11T02:43:20.399462+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Notice the problem requires an operation on each node, meaning DFS is applicable. Next, for each node, we need to know the size of the subtrees it is connected to. This information can also be calcualted with a DFS.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Use an array named sizes to store the size of the subtree under each node, including the node itself.
2. Fill in this array by using a DFS that adds the count of all its neighbors and itself.
3. With this sizes array filled, begin a new DFS to calculate the scores. For each node, if the node has a parent, multiply the score by the size of the entire tree minus the size of the current node's subtree. Then multiply score by the sizes of the neighboring subtrees. If the score is larger than the greatest seen so far, update the result. Then recurse for all other nodes.
# Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```python3 []
class Solution:
def countHighestScoreNodes(self, parents: List[int]) -> int:
# Solve using two dfs's
# First dfs to count the size of the subtree of each node
# second dfs goes through and caluclates the score using previously counted sizes
# First, construct the tree
adj = [[] for i in range(len(parents))]
for i in range(1, len(parents)):
adj[parents[i]].append(i)
# First dfs to count the size of each subtree
sizes = [1 for i in range(len(parents))]
self.count(0, sizes, adj)
# Second dfs to calculate scores
resPair = [0, 0]
self.calculateScores(0, parents, adj, resPair, sizes)
return resPair[1]
def count(self, node, sizes, adj):
for neighbor in adj[node]:
self.count(neighbor, sizes, adj)
sizes[node] += sizes[neighbor]
def calculateScores(self, node, parents, adj, resPair, sizes):
score = 1
# If node has a parent, add to multiplication
if parents[node] != -1:
score *= sizes[0] - sizes[node]
for neighbor in adj[node]:
score *= sizes[neighbor]
if score > resPair[0]:
resPair[0] = score
resPair[1] = 1
elif score == resPair[0]:
resPair[1] += 1
for neighbor in adj[node]:
self.calculateScores(neighbor, parents, adj, resPair, sizes)
``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | Java | java-by-najmamd-sqoy | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | NajmaMd | NORMAL | 2025-03-05T17:37:26.331714+00:00 | 2025-03-05T17:37:26.331714+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
long totalNodes = 0;
List<ArrayList> children = new ArrayList<>();
long score = 0;
int outputNodesCount = 0;
public int countHighestScoreNodes(int[] parents) {
totalNodes = parents.length;
while (totalNodes >= 0) {
children.add(new ArrayList());
totalNodes -= 1;
}
totalNodes = parents.length;
for (int i = 1; i < totalNodes; i++) {
int tempParent = parents[i];
List tempList = children.get(tempParent);
tempList.add(i);
}
long max = navigate(parents, children, 0);
System.out.print(score+",");
return outputNodesCount;
}
public long navigate(int[] parents, List<ArrayList> children, int node) {
ArrayList<Integer> childrenList = children.get(node);
long childScoresSum = 0;
long childScoresProduct = 1;
long tempChildCount = 0;
if (childrenList == null || childrenList.size() == 0) {
childScoresProduct = totalNodes - 1;
} else {
for (int child : childrenList) {
tempChildCount = navigate(parents, children, child);
childScoresProduct *= tempChildCount;
childScoresSum += tempChildCount;
}
if (parents[node] >= 0) {
long parentSubtree = Math.abs(totalNodes - childScoresSum - 1);
childScoresProduct *= parentSubtree;
}
}
if (score < childScoresProduct) {
score = childScoresProduct;
outputNodesCount = 1;
} else if (score == childScoresProduct)
outputNodesCount++;
return childScoresSum+1;
}
}
``` | 0 | 0 | ['Java'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.