question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
count-nodes-with-the-highest-score | Python3: clear and simple DFS solution | python3-clear-and-simple-dfs-solution-by-qatx | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sleepingbear | NORMAL | 2025-03-04T18:08:56.684076+00:00 | 2025-03-04T18:08:56.684076+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countHighestScoreNodes(self, parents: List[int]) -> int:
n = len(parents)
tree = defaultdict(list)
for i, p in enumerate(parents):
if p >= 0:
tree[p].append(i)
highest_score = 0
highest_nodes = 0
def update_score(node, score):
nonlocal highest_score, highest_nodes
if score > highest_score:
highest_nodes = 1
highest_score = score
elif score == highest_score:
highest_nodes += 1
def visit(node): # return size of subtree rooted at node
children = tree.get(node, [])
score = 1
sizes = 1
for child in children:
s = visit(child)
score *= s
sizes += s
if n > sizes:
score *= n - sizes
update_score(node, score)
return sizes
visit(0)
return highest_nodes
``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | [Java] Topology order to calculate sub tree size | java-topology-order-to-calculate-sub-tre-mrgv | IntuitionUse topology order to calculate sub tree size for each nodeComplexity
Time complexity: O(N)
Space complexity: O(N)
Code | joyforce | NORMAL | 2025-02-23T01:22:57.735015+00:00 | 2025-02-23T01:22:57.735015+00:00 | 15 | false | # Intuition
Use topology order to calculate sub tree size for each node
# Complexity
- Time complexity: O(N)
- Space complexity: O(N)
# Code
```java []
class Solution {
public int countHighestScoreNodes(int[] parents) {
// topology order to calculate sub tree size
int n = parents.length;
int[] inDegree = new int[n];
for (int p : parents) {
if (p != -1) inDegree[p]++;
}
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (inDegree[i] == 0) q.offer(i);
}
int[] subTreeSize = new int[n];
Arrays.fill(subTreeSize, 1);
while (!q.isEmpty()) {
int top = q.poll();
if (top == 0) continue;
int parent = parents[top];
if (--inDegree[parent] == 0) {
q.offer(parent);
}
subTreeSize[parent] += subTreeSize[top];
}
long[] score = new long[n];
Arrays.fill(score, 1);
for (int i = 1; i < n; i++) {
score[i] *= (subTreeSize[0] - subTreeSize[i]);
int p = parents[i];
score[p] *= subTreeSize[i];
}
long maxScore = -1;
int count = 0;
for (int i = 0; i < n; i++) {
if (score[i] > maxScore) {
count = 1;
maxScore = score[i];
} else if (score[i] == maxScore) {
count++;
}
}
return count;
}
}
``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Adjacency List | DFS | Binary Tree | Hash Map | Easy Solution | adjacency-list-dfs-binary-tree-hash-map-xd5l3 | IntuitionTo find the size of sub-forests connected to given node. Sub-forests formed by children can be found using dfs traversal and sub-forest formed by remai | mynk_mishra | NORMAL | 2025-02-08T11:55:59.171329+00:00 | 2025-02-08T11:55:59.171329+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To find the size of sub-forests connected to given node. Sub-forests formed by children can be found using dfs traversal and sub-forest formed by remaining is (size of total tree) - (size of all children sub-forest) - 1(for current node).
# Code
```java []
class Solution {
int total;
long res = -1;
Map<Long, Integer> scoreMap;
public int countHighestScoreNodes(int[] parents) {
total = parents.length;
scoreMap = new HashMap<Long, Integer>();
Map<Integer, ArrayList<Integer>> tree = new HashMap<Integer, ArrayList<Integer>>();
for(int i = 0; i < total; i++){
tree.put(i, new ArrayList<Integer>());
}
for(int i = 1; i < total; i++){
int el = i;
int p = parents[i];
tree.get(p).add(el);
}
solve(0, tree);
return scoreMap.get(res);
}
public long solve(int n, Map<Integer, ArrayList<Integer>> tree){
List<Long> ans = new ArrayList<Long>();
for(int v: tree.get(n)){
ans.add(solve(v, tree));
}
long mul = 1;
long sum = 0;
for(long el: ans){
mul *= el;
sum += el;
}
if(n != 0){
if(ans.size() == 0){
mul *= (total - 1);
}else{
mul *= (total - sum - 1);
}
}
scoreMap.put(mul, scoreMap.getOrDefault(mul, 0) + 1);
res = Math.max(res, mul);
return sum + 1;
}
}
``` | 0 | 0 | ['Array', 'Hash Table', 'Tree', 'Depth-First Search', 'Binary Tree', 'Java'] | 0 |
count-nodes-with-the-highest-score | Easy to read and understand solution. O(n) time and space complexity | easy-to-read-and-understand-solution-on-8lq3z | IntuitionWe need to calculate sum of subtrees on every node, than we can find out how many nodes will be in the tree without any one.ApproachBuild a map of node | vladpron2016 | NORMAL | 2025-02-06T18:54:48.544301+00:00 | 2025-02-06T18:54:48.544301+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to calculate sum of subtrees on every node, than we can find out how many nodes will be in the tree without any one.
# Approach
<!-- Describe your approach to solving the problem. -->
Build a map of nodes, than calculcate number of nodes on every one by dfs, than findout number of nodes without current one, and count how many times deleting node gives us the maximum number of nodes.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```java []
class Solution {
public int countHighestScoreNodes(int[] parents) {
long[] result = new long[parents.length];
long max = 0;
int[][] map = new int[parents.length][2];
for (int i = 0; i < parents.length; i++) {
Arrays.fill(map[i], -1);
}
for (int i = 1; i < parents.length; i++) {
int to = parents[i];
if (map[to][0] == -1) {
map[to][0] = i;
} else {
map[to][1] = i;
}
}
int[] count = new int[parents.length];
dfs(count, 0, map);
for (int i = 0; i < result.length; i++) {
int left = map[i][0];
int right = map[i][1];
int leftSum = left == - 1 ? 0 : count[left];
int rightSum = right == - 1 ? 0 : count[right];
int topSum = count[0] - leftSum - rightSum - 1;
result[i] = 1;
result[i] *= leftSum == 0 ? 1 : leftSum;
result[i] *= rightSum == 0 ? 1 : rightSum;
result[i] *= topSum == 0 ? 1 : topSum;
max = Math.max(max, result[i]);
}
int res = 0;
for (int i = 0; i < result.length; i++) {
res += result[i] == max ? 1 : 0;
}
return res;
}
private int dfs(int[] count, int idx, int[][] map) {
int left = map[idx][0] == -1 ? 0 : dfs(count, map[idx][0], map);
int right = map[idx][1] == -1 ? 0 : dfs(count, map[idx][1], map);
count[idx] = left + right + 1;
return count[idx];
}
}
``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | 2049. Count Nodes With the Highest Score | 2049-count-nodes-with-the-highest-score-q9jck | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-17T14:34:50.206454+00:00 | 2025-01-17T14:34:50.206454+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countHighestScoreNodes(self, parents: List[int]) -> int:
n = len(parents)
tree = defaultdict(list)
for i, p in enumerate(parents):
if p != -1:
tree[p].append(i)
def dfs(node):
size = 1
score = 1
for child in tree[node]:
s = dfs(child)
score *= s
size += s
self.scores[node] = score * (n - size if node != 0 else 1)
return size
self.scores = {}
dfs(0)
max_score = max(self.scores.values())
return sum(1 for score in self.scores.values() if score == max_score)
``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | Beats 100% ---> Simple Approach | beats-100-simple-approach-by-vatan999-oj21 | IntuitionThe goal is to calculate the number of nodes in the tree whose removal maximizes the product of the sizes of its disconnected components. This requires | vatan999 | NORMAL | 2025-01-17T07:03:43.894808+00:00 | 2025-01-17T07:03:43.894808+00:00 | 10 | false | # Intuition
The goal is to calculate the number of nodes in the tree whose removal maximizes the product of the sizes of its disconnected components. This requires traversing the tree, computing the product for each node's removal, and determining the maximum product and its frequency.
# Approach
1. **Tree Construction**:
- Convert the `parents` array into a tree structure using `TreeNode` objects.
- Each `TreeNode` object represents a node in the tree with references to its left and right children.
2. **Recursive Calculation**:
- Implement a recursive function to traverse the tree and calculate the size of the subtree for each node.
- During the traversal, calculate the product of the sizes of three components:
- Left subtree
- Right subtree
- The remaining nodes excluding the current subtree
3. **Tracking Maximum Product**:
- Keep track of the maximum product encountered.
- Maintain a count of how many nodes yield the maximum product.
4. **Type Handling**:
- Use `long long` to handle large intermediate product values and prevent overflow.
5. **Memory Management**:
- Clean up dynamically allocated nodes to avoid memory leaks.
# Complexity
- **Time Complexity**:
- Tree construction takes \(O(n)\).
- Recursive traversal of the tree also takes \(O(n)\).
- Overall time complexity is \(O(n)\).
- **Space Complexity**:
- Space for the tree is \(O(n)\).
- Recursive stack depth is \(O(h)\), where \(h\) is the height of the tree. In the worst case (skewed tree), \(h = O(n)\).
# Code
```cpp
class Solution {
public:
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int val) {
this->val = val;
this->left = nullptr;
this->right = nullptr;
}
};
int solve(TreeNode* root, long long& ans, int total, int& count) {
if (!root) return 0;
int left = solve(root->left, ans, total, count);
int right = solve(root->right, ans, total, count);
int rest = total - left - right - 1;
int ret = left + right + 1;
long long leftVal = max(static_cast<long long>(left), 1LL);
long long rightVal = max(static_cast<long long>(right), 1LL);
long long restVal = max(static_cast<long long>(rest), 1LL);
long long currentScore = leftVal * rightVal * restVal;
if (ans < currentScore) {
ans = currentScore;
count = 1;
} else if (ans == currentScore) {
count++;
}
return ret;
}
int countHighestScoreNodes(vector<int>& parents) {
int n = parents.size();
vector<TreeNode*> nodes(n);
for (int i = 0; i < n; i++) {
nodes[i] = new TreeNode(i);
}
for (int i = 1; i < n; i++) {
if (!nodes[parents[i]]->left)
nodes[parents[i]]->left = nodes[i];
else
nodes[parents[i]]->right = nodes[i];
}
long long ans = 0;
int count = 0;
solve(nodes[0], ans, n, count);
for (auto node : nodes) {
delete node;
}
return count;
}
};
``` | 0 | 0 | ['C++'] | 0 |
count-nodes-with-the-highest-score | DFS | dfs-by-up41guy-goqr | null | Cx1z0 | NORMAL | 2025-01-15T08:16:20.813363+00:00 | 2025-01-15T08:16:20.813363+00:00 | 5 | false | ```javascript []
/**
* @param {number[]} parents
* @return {number}
*/
const countHighestScoreNodes = function (parents) {
const tree = Array.from({ length: parents.length }, () => []);
for (let i = 1; i < parents.length; i++) {
tree[parents[i]].push(i);
}
let maxScore = 0, count = 0;
const dfs = (node) => {
let size = 1, product = 1;
const total = parents.length - 1;
for (const child of tree[node]) {
const childSize = dfs(child);
size += childSize;
product *= childSize;
}
const score = node === 0 ? product : product * (total - size + 1);
if (score > maxScore) {
maxScore = score;
count = 1;
} else if (score === maxScore) {
count++;
}
return size;
};
dfs(0);
return count;
};
``` | 0 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Binary Tree', 'JavaScript'] | 0 |
count-nodes-with-the-highest-score | Proper DFS Solution || C++ most intuitive Solution | proper-dfs-solution-c-most-intuitive-sol-iu5d | Intuitionjust keep track of the number of nodes in the left subtree and right subtree of a node and the number of nodes in the upper part
number of nodes in the | reggie_ledoux | NORMAL | 2025-01-10T19:28:24.853296+00:00 | 2025-01-10T19:28:24.853296+00:00 | 17 | false | # Intuition
just keep track of the number of nodes in the left subtree and right subtree of a node and the number of nodes in the upper part
`number of nodes in the upper part = n - (left subtree nodes+ right subtree nodes +1(the node itself))` perform the dfs just like we do in tree and update populate the nodes in a map , at last find the max score and number of nodes having that score .
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(N)
- Space complexity:O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int dfs(unordered_map<int ,int>& left, unordered_map<int,int>& right , unordered_map<int,int>& parent,vector<int> adj[] , int node, int n){
if(adj[node].size()==0){
left[node]=0;
right[node]=0;
parent[node]=n-1;
return 1;
}
vector<int> ref = adj[node];
if(ref.size()!=1){
int lft = dfs(left, right ,parent ,adj, ref[0], n);
left[node]= lft;
int rght = dfs(left, right, parent ,adj, ref[1],n );
right[node] = rght ;
parent[node] = n-(lft+rght+1);
return lft+rght +1;
}
else{
int lft = dfs(left, right, parent ,adj, ref[0],n);
left[node]= lft;
right [node]=0;
parent[node] = n-(lft+1);
return lft+1;
}
}
int countHighestScoreNodes(vector<int>& parents) {
int n = parents.size();
vector<int> adj[100001];
for(int i=0;i<n;i++){
int u = parents[i];
int v =i;
if (u !=-1) adj[u].push_back(i);
}
unordered_map<int,int> left;
unordered_map<int, int > right ;
unordered_map<int,int> parent ;
dfs(left , right, parent , adj,0,n);
long long ans = INT_MIN;
for(int i=0;i<n;i++){
long long lft = 1LL*left[i];
long long rght = 1LL*right[i];
long long Parent= 1LL*parent[i];
lft!=0?:lft=1LL*1;
rght!=0?:rght=1LL*1;
Parent!=0?:Parent=1LL*1;
ans = max(ans , 1LL*lft*rght*Parent);
}
int count =0;
for(int i=0;i<n;i++){
long long lft = 1LL*left[i];
long long rght = 1LL*right[i];
long long Parent= 1LL*parent[i];
lft!=0?:lft=1LL*1;
rght!=0?:rght=1LL*1;
Parent!=0?:Parent=1LL*1;
if(1LL*lft*rght*Parent == ans) count++;
}
return count ;
}
};
``` | 0 | 0 | ['C++'] | 0 |
count-nodes-with-the-highest-score | The bigger picture | the-bigger-picture-by-tonitannoury01-f8zt | IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(n)
Code | tonitannoury01 | NORMAL | 2025-01-03T16:28:51.913440+00:00 | 2025-01-03T16:28:51.913440+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```javascript []
/**
* @param {number[]} parents
* @return {number}
*/
var countHighestScoreNodes = function (parents) {
let n = parents.length;
let adj = Array(n)
.fill(0)
.map(() => []);
for (let i = 1; i < n; i++) {
adj[parents[i]].push(i);
}
let scores = new Map();
let dfs = (node) => {
if (!node && node !== 0) {
return 0;
}
let children = adj[node];
let left = children[0];
let right = children[1];
let leftCount = 0;
let rightCount = 0;
if (left) {
leftCount = 1 + dfs(left);
}
if (right) {
rightCount = 1 + dfs(right);
}
let rem = n - 1 - leftCount - rightCount;
let score = (leftCount || 1) * (rightCount || 1) * (rem || 1);
if (scores.has(score)) {
scores.set(score, scores.get(score) + 1);
} else {
scores.set(score, 1);
}
return leftCount + rightCount;
};
dfs(0);
let maxScore = Math.max(...Array.from(scores.keys()))
return scores.get(maxScore);
};
``` | 0 | 0 | ['JavaScript'] | 0 |
count-nodes-with-the-highest-score | Python dfs simple | python-dfs-simple-by-vineel97-442o | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | vineel97 | NORMAL | 2025-01-03T04:14:11.191507+00:00 | 2025-01-03T04:14:11.191507+00:00 | 13 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countHighestScoreNodes(self, parents: List[int]) -> int:
n = len(parents)
adj = { i : [] for i in range(n)}
for i in range(n):
if parents[i] != -1:
adj[parents[i]].append(i)
sizes = [0] * n
def dfs(i):
if not adj[i]:
sizes[i] = 1
return 1
size = 0
for n in adj[i]:
size += dfs(n)
sizes[i] = size + 1
return sizes[i]
dfs(0)
scores = [0] * n
for i in range(n):
score = 1
for n in adj[i]:
score *= sizes[n]
score *= max(1, sizes[0] - sizes[i])
scores[i] = score
#print(scores)
c = Counter(scores)
max_score = max(c)
return c[max_score]
``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | My DAG Solution, | my-dag-solution-by-jackson1-0hqc | IntuitionUse DAG iterative not DFS with recursion.ApproachComplexity
Time complexity:
Space complexity:
Code | Jackson1 | NORMAL | 2025-01-02T17:41:51.125386+00:00 | 2025-01-02T17:41:51.125386+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Use DAG iterative not DFS with recursion.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
import java.util.*;
class Solution {
public int countHighestScoreNodes(int[] parents) {
int n = parents.length;
int[] childCount = new int[n]; // Tracks the number of children for each node
int[][] subtreeSizes = new int[n][2]; // Stores sizes of left and right subtrees
Map<Integer, List<Integer>> graph = new HashMap<>();
// Build the DAG (parent-to-children relationship)
for (int i = 0; i < n; i++) {
graph.putIfAbsent(i, new ArrayList<>());
}
for (int i = 1; i < n; i++) {
graph.get(parents[i]).add(i);
childCount[parents[i]]++;
}
// Find all leaf nodes
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (childCount[i] == 0) {
queue.add(i);
}
}
// Bottom-up traversal to calculate subtree sizes
while (!queue.isEmpty()) {
int current = queue.poll();
int parent = parents[current];
if (parent == -1) continue; // Skip the root node
// Calculate subtree size for parent
if (subtreeSizes[parent][0] == 0) {
subtreeSizes[parent][0] = subtreeSizes[current][0] + subtreeSizes[current][1] + 1;
} else {
subtreeSizes[parent][1] = subtreeSizes[current][0] + subtreeSizes[current][1] + 1;
}
// Reduce the child count of the parent
if (--childCount[parent] == 0) {
queue.add(parent);
}
}
// Calculate scores and determine the highest score
long maxScore = 0;
int countMaxScore = 0;
for (int i = 0; i < n; i++) {
long score = 1;
int remainingNodes = n - 1 - subtreeSizes[i][0] - subtreeSizes[i][1];
if (remainingNodes > 0) score *= remainingNodes;
if (subtreeSizes[i][0] > 0) score *= subtreeSizes[i][0];
if (subtreeSizes[i][1] > 0) score *= subtreeSizes[i][1];
if (score > maxScore) {
maxScore = score;
countMaxScore = 1;
} else if (score == maxScore) {
countMaxScore++;
}
}
return countMaxScore;
}
}
``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Simple DFS backtracking solution | simple-dfs-backtracking-solution-by-kulk-nxi6 | IntuitionTypical problem of backtracking. In the question the binary tree isn't given in the nodal form. Thus create graph#nodes=#nodes.left+#nodes.right+1Compl | kulkarnipinaki | NORMAL | 2024-12-28T16:58:22.254759+00:00 | 2024-12-28T16:58:22.254759+00:00 | 10 | false | # Intuition
Typical problem of backtracking. In the question the binary tree isn't given in the nodal form. Thus create graph
#nodes=#nodes.left+#nodes.right+1
# Complexity
- Time complexity: **O(n)**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(n)**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countHighestScoreNodes(self, parents: List[int]) -> int:
n=len(parents)
graph=[[] for i in range(n)]
for i in range(1,n):
graph[parents[i]].append(i)
def dfs(source,graph,res=None,visited=None):
n=len(graph)
if not res or not visited:
res,visited=[1]*n,[False]*n
if not graph[source]:
return res
visited[source]=True
for i in graph[source]:
if not visited[i]:
dfs(i,graph,res,visited)
res[source]+=res[i]
return res
a=dfs(0,graph)
res=[]
kmax=0
for i in range(n):
left,right=1,1
if graph[i]:
left=a[graph[i][0]]
if len(graph[i])==2:
right=a[graph[i][1]]
k=max(a[0]-a[i],1)*left*right
kmax=max(k,kmax)
res.append(k)
x=0
for i in range(n):
if(kmax==res[i]):
x+=1
return x
``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | DFS + node counting + freq | Easy | dfs-node-counting-freq-easy-by-krystek-ign6 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Krystek | NORMAL | 2024-12-25T23:38:11.930938+00:00 | 2024-12-25T23:38:11.930938+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countHighestScoreNodes(self, parents: List[int]) -> int:
n = len(parents)
adj = defaultdict(list)
for child, parent in enumerate(parents):
if child == 0: continue
adj[parent].append(child)
occur = defaultdict(int)
def dfs(node):
if not node in adj: #leaf node
occur[n-1] += 1
return 1
curr = 1
size = 0
for nei in adj[node]:
res = dfs(nei)
size += res
curr *= max(1, res)
curr *= max(1, n - size - 1)
occur[curr] += 1
return size + 1
dfs(0)
return occur[max(occur.keys())]
``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | Easy 2 DFS | Very Intuitive | easy-2-dfs-very-intuitive-by-akashkumari-pehd | Code | akashkumariitian360 | NORMAL | 2024-12-23T20:13:35.210920+00:00 | 2024-12-23T20:14:05.541053+00:00 | 9 | false |
# Code
```cpp []
#define ll long long
class Solution {
public:
vector<int>v;
ll ans;
void dfs(int node,int par,vector<vector<int>>&adj){
v[node]=1;
for(auto child:adj[node]){
if(child!=par){
dfs(child,node,adj);
v[node]+=v[child];
}
}
}
void dfs1(int node,int par,vector<vector<int>>&adj,vector<int>&nums,map<ll,int>&mp){
//parent
ll temp=1;
if(nums[node]!=-1){
temp = v[0];
temp-= v[node];
}
for(auto child:adj[node]){
//int temp1=1;
if(child!=par){
temp= 1LL*temp*v[child];
}
}
mp[temp]++;
ans = max(1LL*ans,temp);
for(auto child:adj[node]){
if(child!=par){
dfs1(child,node,adj,nums,mp);
}
}
}
int countHighestScoreNodes(vector<int>& nums) {
int n = nums.size();
vector<vector<int>>adj(n);
for(int i=1;i<n;i++){
adj[nums[i]].push_back(i);
adj[i].push_back(nums[i]);
}
v.resize(n+1);
dfs(0,-1,adj);
ans = 0;
map<ll,int>mp;
dfs1(0,-1,adj,nums,mp);
return mp[ans];
}
};
``` | 0 | 0 | ['Array', 'Depth-First Search', 'Binary Tree', 'C++'] | 0 |
count-nodes-with-the-highest-score | C++ Postorder traversal | c-postorder-traversal-by-galster-6ioh | IntuitionThe score of a node is the multiplication of the number of children on its right and his left and the tree which its parent belongs to.ApproachFirst cr | galster | NORMAL | 2024-12-21T06:29:41.186880+00:00 | 2024-12-21T06:29:41.186880+00:00 | 6 | false | # Intuition
The score of a node is the multiplication of the number of children on its right and his left and the tree which its parent belongs to.
# Approach
First create an array Children which will have for each node a pair of left childe, right child.
Do a post order traversal of the Children array and for each node calculate the number of children (including itself) in the tree rooted at it. Then for traverse the tree from 1 to N. for each node find the number of children on the left, the right, and for the parent tree just use nodeCount[0] - nodeCount[i]
multiply them and store the score.
Finally, sort the scores in decending order, and return how many have the highest count.
# Complexity
- Time complexity:
$$O(NLogN)$$
- Space complexity:
$$O(N)$$
# Code
```cpp []
class Solution {
int getNodesCounts(int root, const vector<pair<int,int>>& ch, vector<int> &nodeCount){
if(root == -1){
return 0;
}
auto [ch1,ch2] = ch[root];
int l = getNodesCounts(ch1,ch,nodeCount);
int r = getNodesCounts(ch2,ch,nodeCount);
nodeCount[root] = l + r + 1;
return nodeCount[root];
}
public:
int countHighestScoreNodes(vector<int>& parents) {
vector<pair<int,int>> children(parents.size(),{-1,-1});
for(int i = 1; i < parents.size(); ++i){
auto &[ch1, ch2] = children[parents[i]];
if(ch1 == -1){
ch1 = i;
}else{
ch2 = i;
}
}
vector<int> nodeCounts(parents.size(),0);
getNodesCounts(0,children,nodeCounts);
vector<long long> scores(parents.size(),0);
for(int i = 0; i < parents.size(); ++i){
long long ch1Count = children[i].first == -1 ? 1 : nodeCounts[children[i].first];
long long ch2Count = children[i].second == -1 ? 1 : nodeCounts[children[i].second];
long long pcount = parents[i] == -1 ? 1 : nodeCounts[0] - nodeCounts[i];
scores[i] = pcount* ch1Count * ch2Count;
}
sort(begin(scores),end(scores),[](const long long &i, const long long &j){
return i > j;
});
long long topScore = scores[0];
int result = 1;
for(int i = 1; i < scores.size(); ++i){
if(scores[i] != topScore){
break;
}
result++;
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
count-nodes-with-the-highest-score | Clean Python code with easy to understand explanation. | clean-python-code-with-easy-to-understan-t6y2 | Intuition\n Describe your first thoughts on how to solve this problem. \nThree Cases\nRoot node\nLeaf node\nMid node (neither noot nor leaf node)\nn = length of | git_cat_99 | NORMAL | 2024-11-10T22:01:21.610637+00:00 | 2024-11-10T22:01:21.610664+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThree Cases\nRoot node\nLeaf node\nMid node (neither noot nor leaf node)\nn = length of parents array\n1. Leaf node leaves behind (n - 1) nodes\n2. Root node leaves behind nodes in left subtree and right subtree\n3. Mid node leaves behind nodes in left subtree and right subtree and n - (nodes in subtree with mid node as local root)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create a graph dictionary with key = node integer value and val = list of children integer values\n2. DFS to find number of nodes in subtree of each node -> store in a dictionary\n3. Use the insight in the intuition section to calculate each node\'s score\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n \n n = len(parents)\n graph = defaultdict(list)\n for node, parent in enumerate(parents):\n graph[parent].append(node)\n \n def dfs(node):\n visited.add(node)\n res = 1\n for nei in graph[node]:\n if nei not in visited:\n res += dfs(nei)\n nodes_in_subtree[node] = res\n return res\n \n nodes_in_subtree = defaultdict(int)\n visited = set()\n dfs(0)\n\n score_to_num_nodes = defaultdict(int)\n\n for node in range(n):\n if len(graph[node]) == 0:\n score_to_num_nodes[n - 1] += 1\n \n elif node == 0:\n score = 1\n for child in graph[node]:\n score *= nodes_in_subtree[child]\n score_to_num_nodes[score] += 1\n \n else:\n score = 1\n for child in graph[node]:\n score *= nodes_in_subtree[child]\n score *= (n - nodes_in_subtree[node])\n score_to_num_nodes[score] += 1\n \n max_score = max(score_to_num_nodes.keys())\n return score_to_num_nodes[max_score] | 0 | 0 | ['Depth-First Search', 'Recursion', 'Binary Tree', 'Python3'] | 0 |
count-nodes-with-the-highest-score | pure C | pure-c-by-ekko3add-qssr | Intuition\nMy first thought was to use DFS in a post-order traversal manner to compute the number of nodes in each subtree.\nBy traversing each node\'s left and | ekko3add | NORMAL | 2024-11-05T13:18:25.134780+00:00 | 2024-11-05T13:18:25.134811+00:00 | 3 | false | # Intuition\nMy first thought was to use DFS in a post-order traversal manner to compute the number of nodes in each subtree.\nBy traversing each node\'s left and right children, we can calculate the number of nodes in the left and right subtrees, then compute the "score" using the below formula:\n```\nscore = left * right * (total - left - right - 1)\n```\nThe term ```total - left - right - 1``` represents the remaining nodes outside of the current subtree\n\n\n# Approach\nUse two arrays leftChild and rightChild:\n>to represent the left and right children of each node by parsing the parents array.\n\nA DFS function that:\n> 1. Return the size of the subtrees.\n> 2. Calculate the score for the current node using the formula: left * right * (total - left - right - 1).\n> 3. Track the maximum score and count how many nodes achieve this maximum score.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ (ignore constant factors)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\nint dfs(int node, int *leftChild, int *rightChild, int totalNodes, long *maxScore, int *maxCount) {\n if (node == -1) return 0;\n\n int left = dfs(leftChild[node], leftChild, rightChild, totalNodes, maxScore, maxCount);\n int right = dfs(rightChild[node], leftChild, rightChild, totalNodes, maxScore, maxCount);\n\n long score = 1;\n int subtreeSize = left + right + 1;\n\n if (left > 0) score *= left;\n if (right > 0) score *= right;\n if (totalNodes - subtreeSize > 0) score *= (totalNodes - subtreeSize);;\n\n if (score > *maxScore) {\n *maxCount = 1;\n *maxScore = score;\n } else if (score == *maxScore){\n (*maxCount) += 1;\n }\n\n return subtreeSize;\n}\n\nint countHighestScoreNodes(int* parents, int parentsSize) {\n int totalNodes = parentsSize;\n long maxScore = 0, maxCount = 0;\n\n int *leftChild = malloc(sizeof(int) * parentsSize);\n int *rightChild = malloc(sizeof(int) * parentsSize);\n\n // init\n for (int i = 0; i < parentsSize; ++i) {\n leftChild[i] = -1;\n rightChild[i] = -1;\n }\n\n // construct the left and right child\n for (int i = 1; i < parentsSize; ++i) {\n int parent = parents[i];\n\n if (leftChild[parent] == -1) {\n leftChild[parent] = i;\n } else {\n rightChild[parent] = i;\n }\n }\n\n dfs(0, leftChild, rightChild, totalNodes, &maxScore, &maxCount);\n \n free(leftChild);\n free(rightChild);\n\n return maxCount;\n}\n``` | 0 | 0 | ['Depth-First Search', 'C', 'Binary Tree', 'Counting'] | 0 |
count-nodes-with-the-highest-score | DFS || O(N) Time and space | dfs-on-time-and-space-by-bhaskarv2000-iye1 | Intuition\nUse DFS, recursively move to the leaf nodes, calculate score, and return total child nodes from there.\n\n# Approach\nScore of a node = Non-zero Numb | BhaskarV2000 | NORMAL | 2024-10-31T07:50:21.124125+00:00 | 2024-10-31T07:50:21.124158+00:00 | 2 | false | # Intuition\nUse DFS, recursively move to the leaf nodes, calculate score, and return total child nodes from there.\n\n# Approach\nScore of a node = Non-zero Number of Left child nodes * Non-zero Number of right child nodes * Non-zero Number of remaiming nodes except child nodes and self node.\n\n# Complexity\n- Time complexity:\nO(N)\nEach node we are visiting only once.\nAnd returning the total child nodes from there.\n\n- Space complexity:\nO(N)\n\n# Code\n```python3 []\nfrom typing import List\n\n\nclass Solution:\n\n def update_score_and_count(self, score):\n print(score)\n if self.max_score < score:\n self.max_score = score\n self.max_score_nodes = 1\n elif self.max_score == score:\n self.max_score_nodes += 1\n\n def travserse(self, root: int):\n if self.adj.get(root) == None:\n score = self.total_nodes-1\n self.update_score_and_count(score)\n # left child of leaf = 0, right child of leaf = 0, total childs of caller node = 0+1(self)+0\n return 1\n\n total_child = 0\n score = 1\n for child in self.adj[root]:\n # find the number of left and right childs.\n count = self.travserse(child)\n # if there is no left child then 0 will not be multiplied to score, similarly, for right and head node.\n # only sub-trees with non-zero number of nodes will be multiplied.\n if count != 0:\n total_child += count\n score *= count\n\n # Suppose if there is node whose left, child, and parent(total nodes - left - child -1(self)), all 3 are present.\n # So, the score due to left and right child is already calculated above,\n # With the below operation we update the score with remaining nodes\n if self.total_nodes-(1+total_child) != 0:\n score *= (self.total_nodes-(1+total_child))\n self.update_score_and_count(score)\n total_nodes = total_child + 1 # total nodes = left childs + right childs + self node\n return total_nodes\n\n def create_adjacency_list(self, parents: List[int]):\n self.adj: dict[int, List] = {}\n for node in range(len(parents)):\n if self.adj.get(parents[node]) == None:\n self.adj[parents[node]] = []\n self.adj[parents[node]].append(node)\n\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n self.max_score = 0\n self.max_score_nodes = 0\n self.total_nodes = len(parents)\n\n self.create_adjacency_list(parents)\n\n self.travserse(0)\n return self.max_score_nodes\n\n``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | count-nodes-with-the-highest-score C# Solution | count-nodes-with-the-highest-score-c-sol-s7cx | \n\n# Code\ncsharp []\npublic class Solution {\n Dictionary<int, int[]> parentDict = new();\n int result = 0;\n long maxScore = 0;\n \n public in | himashusharma | NORMAL | 2024-10-18T06:36:55.998027+00:00 | 2024-10-18T06:36:55.998065+00:00 | 8 | false | \n\n# Code\n```csharp []\npublic class Solution {\n Dictionary<int, int[]> parentDict = new();\n int result = 0;\n long maxScore = 0;\n \n public int CountHighestScoreNodes(int[] parents) {\n for(int i=0; i< parents.Length; i++){\n parentDict.TryAdd(i, new int[2]);\n }\n for(int i=1; i<parents.Length; i++){\n if(parentDict[parents[i]][0] == 0) parentDict[parents[i]][0] = i;\n else parentDict[parents[i]][1] = i;\n }\n\n CountScores(0, parents.Length);\n return result;\n }\n\n public int CountScores(int index, int totalSize){\n int left = 0, right = 0;\n long count =1;\n if(parentDict[index][0] != 0) left = CountScores(parentDict[index][0], totalSize);\n if(parentDict[index][1] != 0) right = CountScores(parentDict[index][1], totalSize);\n\n int subTree = left + right +1;\n int other = totalSize - subTree;\n if(left != 0) count *= (long)left;\n if(right != 0) count *= (long)right;\n if(other != 0) count *= (long)other;\n if(count == maxScore) result++;\n else if(count > maxScore){\n maxScore = count;\n result = 1;\n } \n return subTree;\n\n }\n}\n``` | 0 | 0 | ['Array', 'Tree', 'Depth-First Search', 'Binary Tree', 'C#'] | 0 |
count-nodes-with-the-highest-score | Easy Solution || DFS | easy-solution-dfs-by-abhi5114-7dii | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Abhi5114 | NORMAL | 2024-10-15T14:48:12.856316+00:00 | 2024-10-15T14:48:32.196647+00:00 | 32 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n long max = 0;\n\n public int countHighestScoreNodes(int[] parents) {\n List<List<Integer>> adj = new ArrayList<>();\n int n = parents.length;\n for (int i = 0; i < n; i++) {\n adj.add(new ArrayList<>());\n }\n\n for (int i = 1; i < n; i++) {\n\n adj.get(parents[i]).add(i);\n }\n int subtree[] = new int[n];\n long score[] = new long[n];\n Subtree(adj, 0, subtree,parents,score,n);\n System.out.println(Arrays.toString(subtree));\n // System.out.println(adj);\n int cnt = 0;\n for (int i = 0; i < n; i++) {\n if (score[i] == max)\n cnt++;\n }\n return cnt;\n\n }\n\n public int Subtree(List<List<Integer>> adj, int i, int subtree[], int parents[], long score[],int n) {\n if (adj.get(i).size() == 0) // leaf node\n {\n subtree[i] = 1;\n score[i] = (n - subtree[i]);\n max = Math.max(max, score[i]);\n return 1;\n }\n int size = 0;\n long prod = 1;\n\n for (int neighbor : adj.get(i)) {\n size += Subtree(adj, neighbor, subtree,parents,score,n);\n prod *= subtree[neighbor];\n }\n\n subtree[i] = 1 + size;\n if (parents[i] != -1) {\n prod *= (n - subtree[i]);\n }\n score[i] = prod;\n max = Math.max(max, prod);\n return subtree[i];\n }\n \n}\n``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | Simple Java Solution | simple-java-solution-by-sakshikishore-rgar | Code\njava []\npublic class Node {\n int x;\n int y;\n\n public Node(int i, int j) {\n x = i;\n y = j;\n }\n}\n\nclass Solution {\n | sakshikishore | NORMAL | 2024-10-14T03:35:29.072838+00:00 | 2024-10-14T03:35:29.072868+00:00 | 13 | false | # Code\n```java []\npublic class Node {\n int x;\n int y;\n\n public Node(int i, int j) {\n x = i;\n y = j;\n }\n}\n\nclass Solution {\n public int countHighestScoreNodes(int[] parents) {\n long max=0;\n HashMap<Integer,Node> map=new HashMap<Integer,Node>();\n HashMap<Integer,Integer> h=new HashMap<Integer,Integer>();\n Queue<Integer> q=new LinkedList<Integer>();\n HashSet<Integer> hset=new HashSet<Integer>();\n for(int i=0;i<parents.length;i++)\n {\n if(!h.containsKey(parents[i]))\n {\n\n h.put(parents[i],1);\n }\n else\n {\n h.put(parents[i],2);\n }\n hset.add(parents[i]); \n }\n for(int i=0;i<parents.length;i++)\n {\n if(!hset.contains(i))\n {\n Node node=new Node(0,0);\n map.put(i,node);\n q.add(i);\n }\n }\n hset=new HashSet<Integer>();\n int count=0;\n while(q.size()>0)\n {\n int m=q.poll();\n Node node=map.get(m);\n long p=1;\n int c=node.x+node.y+1;\n if(node.x!=0)\n {\n p=p*node.x;\n }\n if(node.y!=0)\n {\n p=p*node.y;\n }\n if(parents.length-c!=0)\n {\n p=p*(parents.length-c);\n }\n if(p>max)\n {\n count=1;\n max=p;\n }\n else if(p==max)\n {\n count++;\n }\n if(parents[m]!=-1)\n {\n if(map.containsKey(parents[m]))\n {\n Node n=map.get(parents[m]);\n n.y=node.x+node.y+1;\n map.put(parents[m],n);\n q.add(parents[m]);\n }\n else\n {\n int z=node.x+node.y+1;\n Node n=new Node(z,0);\n map.put(parents[m],n);\n if(h.get(parents[m])==1)\n {\n q.add(parents[m]);\n }\n }\n }\n \n }\n return count;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
count-nodes-with-the-highest-score | DFS | dfs-by-drk-89zg | python3 []\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n graph = defaultdict(list)\n for i in range(len(par | drk_ | NORMAL | 2024-10-05T18:29:45.418492+00:00 | 2024-10-05T18:29:45.418512+00:00 | 1 | false | ```python3 []\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n graph = defaultdict(list)\n for i in range(len(parents)) :\n graph[parents[i]].append(i)\n \n total = len(parents) - 1 \n answer = defaultdict(int)\n\n def dfs(node) :\n if node is None :\n return 0\n\n if node not in graph :\n answer[total] += 1\n return 1\n\n left, right = (graph[node] + [None for _ in range(2)])[ : 2]\n left_count, right_count = dfs(left), dfs(right)\n\n score = (\n (right_count * (\n total - right_count if node else 1)) if not left_count else \n (left_count * (\n total - left_count if node else 1)) if not right_count else \n (left_count * right_count * (\n total - (left_count + right_count) if node else 1\n ))\n ) \n\n answer[score] += 1\n return left_count + right_count + 1\n \n dfs(0)\n max_score = max(answer.keys())\n return answer[max_score]\n \n``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | Python3 Recursive DFS Solution with Explanation | python3-recursive-dfs-solution-with-expl-uin4 | Approach\n Describe your approach to solving the problem. \nBuild a tree using the parents array. Keep track of maxScore and frequency with a dictionary. Track | sage_ | NORMAL | 2024-10-03T16:34:59.659648+00:00 | 2024-10-03T16:34:59.659685+00:00 | 7 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nBuild a tree using the parents array. Keep track of maxScore and frequency with a dictionary. Track number of nodes in a subtree with `countNodes` DFS. \n\nThere are 3 subtrees that we will need to count and multiply:\n1 Parent subtree up to node removed\n2 Left subtree of node removed\n3 Right subtree of node removed\n\nTreat this almost like a prefix sum problem when calculating how many nodes for each subtree. Multiply the 3 totals.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n\n def countNodes(root):\n total = 1 + sum(countNodes(child) for child in tree[root])\n nodes[root] = total\n return total\n\n #Build binary tree\n tree = {i: [] for i in range(len(parents))}\n for i, parent in enumerate(parents):\n if parent != -1: tree[parent].append(i)\n\n #Keep track of scores\n maxScore = float(\'-inf\')\n scores = defaultdict(int)\n nodes = [0] * len(parents)\n \n #Build nodes array to track how many nodes in a subtree given a root\n #Use this calculate the number of nodes in the conn components when a node is removed\n if parents:\n countNodes(0)\n\n for node in range(len(parents)):\n\n #There are 3 subtrees that we will need to count and multiply\n #[1] Parent subtree up to node removed\n #[2] Left subtree of node removed\n #[3] Right subtree of node removed\n score = max(1, nodes[0] - nodes[node])\n for child in tree[node]:\n score *= max(1, nodes[child]) #[2], [3]\n\n #Count how many times we see this score\n scores[score] += 1\n maxScore = max(maxScore, score)\n \n return scores[maxScore]\n``` | 0 | 0 | ['Python3'] | 0 |
count-nodes-with-the-highest-score | TreeNode + PostOrder to calculate left and right subtree sums | treenode-postorder-to-calculate-left-and-nad0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | lex217 | NORMAL | 2024-10-03T03:14:31.779088+00:00 | 2024-10-03T03:14:31.779122+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass TreeNode:\n def __init__(self, val):\n self.val = val\n self.left = None\n self.right = None\n self.leftSize = 0\n self.rightSize = 0\n \nclass Solution(object):\n def countHighestScoreNodes(self, parents):\n """\n :type parents: List[int]\n :rtype: int\n """\n\n n = len(parents)\n val_to_node = {i:TreeNode(i) for i in range(n)}\n\n # build tree\n for c, p in enumerate(parents):\n if c != 0:\n parent = val_to_node[p]\n child = val_to_node[c]\n if not parent.left:\n parent.left = child\n else:\n parent.right = child\n\n def postOrder(node): # returns Size of subtress where we store in the nodes\n if node is None:\n return 0\n node.leftSize = postOrder(node.left)\n node.rightSize = postOrder(node.right)\n return 1 + node.leftSize + node.rightSize\n postOrder(val_to_node[0])\n \n score_to_number = defaultdict(int)\n highest_score = float("-inf")\n for i in range(n):\n node = val_to_node[i]\n left, right = node.leftSize, node.rightSize\n remaining = max(1, n - left - right - 1)\n score = max(1,left)*max(1,right)*remaining\n score_to_number[score] += 1\n highest_score = max(highest_score, score)\n return score_to_number[highest_score] \n``` | 0 | 0 | ['Python'] | 0 |
count-nodes-with-the-highest-score | C# Tree Traversal and Subtree Size Calculation Solution using DFS | c-tree-traversal-and-subtree-size-calcul-616t | Intuition\n Describe your first thoughts on how to solve this problem. The problem can be approached by leveraging tree traversal techniques, specifically DFS, | GetRid | NORMAL | 2024-09-25T14:37:36.023492+00:00 | 2024-09-25T14:37:36.023536+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->The problem can be approached by leveraging tree traversal techniques, specifically DFS, to gather essential information about the tree structure, such as subtree sizes. This data allows simulating the removal of each node efficiently, which is the core requirement to compute scores. The solution is built upon a clear understanding of tree properties and the use of DFS as a powerful tool for recursive calculations, making it a systematic and logical approach to solving the problem. The main idea is to transform the problem into manageable parts: calculate subtree sizes, compute scores, and compare scores to identify the nodes with the maximum score.\n___\n\n# Approach\n<!-- Describe your approach to solving the problem. -->// Tree Construction: The adjacency list tree is created to store the child nodes for each parent.\n// DFS to Calculate Subtree Sizes: The DFS function computes the size of each subtree rooted at a given \n// node, which is crucial for score calculations.\n// Score Calculation:\n// *For each node, compute the product of the sizes of its child subtrees.\n// *Multiply this product by the size of the remaining nodes (if any).\n// *Update the maximum score and count of nodes achieving this score.\n// Result: the function returns the count of nodes with the highest score.\n___\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n), where \'n\' is the number of nodes.\n___\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(n).\n___\n\n# Code\n```csharp []\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution {\n public int CountHighestScoreNodes(int[] parents) {\n int n = parents.Length;\n \n // Create an adjacency list to represent the tree\n List<int>[] tree = new List<int>[n];\n for (int i = 0; i < n; i++) {\n tree[i] = new List<int>();\n }\n \n // Build the tree structure\n for (int i = 1; i < n; i++) {\n tree[parents[i]].Add(i);\n }\n \n // Array to store subtree sizes\n int[] subtreeSizes = new int[n];\n \n // Use DFS to calculate the size of each subtree\n DFS(0, tree, subtreeSizes);\n \n long maxScore = 0;\n int count = 0;\n \n // Calculate the score for each node\n for (int i = 0; i < n; i++) {\n long score = 1;\n int remainingNodes = n - 1; // Total nodes excluding the current node\n \n // Multiply the sizes of each child subtree\n foreach (int child in tree[i]) {\n score *= subtreeSizes[child];\n remainingNodes -= subtreeSizes[child];\n }\n \n // Multiply by the size of the remaining tree if it\'s not empty\n if (remainingNodes > 0) {\n score *= remainingNodes;\n }\n \n // Update maxScore and count\n if (score > maxScore) {\n maxScore = score;\n count = 1;\n } else if (score == maxScore) {\n count++;\n }\n }\n \n return count;\n }\n \n // DFS to calculate the size of each subtree\n private int DFS(int node, List<int>[] tree, int[] subtreeSizes) {\n int size = 1; // Counting the current node itself\n foreach (int child in tree[node]) {\n size += DFS(child, tree, subtreeSizes);\n }\n subtreeSizes[node] = size;\n return size;\n }\n}\n``` | 0 | 0 | ['Array', 'Tree', 'Depth-First Search', 'C#'] | 0 |
count-nodes-with-the-highest-score | Python 3 | Graph, DFS, O(N) | python-3-graph-dfs-on-by-anik_mahmud-jljs | \nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n graph: List[List[int]] = [[] for _ in ran | anik_mahmud | NORMAL | 2024-09-16T07:31:49.570173+00:00 | 2024-09-16T07:31:49.570211+00:00 | 1 | false | ```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n graph: List[List[int]] = [[] for _ in range(n)]\n\n\n for idx, val in enumerate(parents):\n if val == -1: \n continue\n graph[idx].append(val)\n graph[val].append(idx)\n\n def dfs(node: int, parent: int) -> int:\n cnt = 1 \n for child in graph[node]:\n if child != parent:\n cnt += dfs(child, node) \n subtree[node].append(child)\n res[node] = cnt\n return cnt \n\n res: Dict[int, int] = defaultdict(int)\n subtree: Dict[int, List] = defaultdict(list)\n\n dfs(0, -1)\n\n maxList = [\n (res[0] - res[i]) * math.prod([res[val] for val in subtree[i]])\n if i != 0 else math.prod([res[val] for val in subtree[i]])\n for i in range(n)\n ]\n\n mx = max(maxList)\n ans: int = 0\n for val in maxList:\n if val == mx:\n ans += 1\n\n return ans\n``` | 0 | 0 | ['Depth-First Search'] | 0 |
permutation-sequence | "Explain-like-I'm-five" Java Solution in O(n) | explain-like-im-five-java-solution-in-on-il4e | EDIT: I\'m tired of some of you commenting on the O(n)-ness of this and especially those of you with snarky condescending tones. It\'s not difficult to implemen | tso | NORMAL | 2015-06-28T18:07:10+00:00 | 2021-10-09T06:29:48.514211+00:00 | 131,719 | false | **EDIT: I\'m tired of some of you commenting on the O(n)-ness of this and especially those of you with snarky condescending tones. It\'s not difficult to implement your own data structure that can do O(1) "list" remove. I\'m not going to put all that code here and dilute the the main solution which is the pattern of solving the permutations. The description on the pattern is already long enough as it is. If you can\'t figure out how to do an O(1) remove, then you shouldn\'t be doing this problem in the first place. Those of you commenting condescendingly, take a freaking break from leetcoding all day. Those of you with kind words and thanks, you\'re welcome and thanks for taking the time to read through the somewhat long description.**\n\nI\'m sure somewhere can be simplified so it\'d be nice if anyone can let me know. The pattern was that:\n\nsay n = 4, you have {1, 2, 3, 4}\n\nIf you were to list out all the permutations you have \n\n1 + (permutations of 2, 3, 4)\n<br>2 + (permutations of 1, 3, 4)\n<br>3 + (permutations of 1, 2, 4)\n<br>4 + (permutations of 1, 2, 3)\n\n<br>We know how to calculate the number of permutations of n numbers... n! So each of those with permutations of 3 numbers means there are 6 possible permutations. Meaning there would be a total of 24 permutations in this particular one. So if you were to look for the (k = 14) 14th permutation, it would be in the \n\n3 + (permutations of 1, 2, 4) subset. \n\nTo programmatically get that, you take k = 13 (subtract 1 because of things always starting at 0) and divide that by the 6 we got from the factorial, which would give you the index of the number you want. In the array {1, 2, 3, 4}, k/(n-1)! = 13/(4-1)! = 13/3! = 13/6 = 2. The array {1, 2, 3, 4} has a value of 3 at index 2. So the first number is a 3.\n\nThen the problem repeats with less numbers.\n\nThe permutations of {1, 2, 4} would be:\n\n1 + (permutations of 2, 4)\n<br>2 + (permutations of 1, 4)\n<br>4 + (permutations of 1, 2)\n\nBut our k is no longer the 14th, because in the previous step, we\'ve already eliminated the 12 4-number permutations starting with 1 and 2. So you subtract 12 from k.. which gives you 1. Programmatically that would be...\n\nk = k - (index from previous) * (n-1)! = k - 2*(n-1)! = 13 - 2*(3)! = 1\n\nIn this second step, permutations of 2 numbers has only 2 possibilities, meaning each of the three permutations listed above a has two possibilities, giving a total of 6. We\'re looking for the first one, so that would be in the 1 + (permutations of 2, 4) subset. \n\nMeaning: index to get number from is k / (n - 2)! = 1 / (4-2)! = 1 / 2! = 0.. from {1, 2, 4}, index 0 is 1\n\n<br>so the numbers we have so far is 3, 1... and then repeating without explanations.\n\n<br>{2, 4}\n<br>k = k - (index from pervious) * (n-2)! = k - 0 * (n - 2)! = 1 - 0 = 1;\n<br>third number\'s index = k / (n - 3)! = 1 / (4-3)! = 1/ 1! = 1... from {2, 4}, index 1 has 4\n<br>Third number is 4\n\n<br>{2}\n<br>k = k - (index from pervious) * (n - 3)! = k - 1 * (4 - 3)! = 1 - 1 = 0;\n<br>third number\'s index = k / (n - 4)! = 0 / (4-4)! = 0/ 1 = 0... from {2}, index 0 has 2\n<br>Fourth number is 2\n\n<br>Giving us 3142. If you manually list out the permutations using DFS method, it would be 3142. Done! It really was all about pattern finding.\n\n\n\n public class Solution {\n public String getPermutation(int n, int k) {\n int pos = 0;\n List<Integer> numbers = new ArrayList<>();\n int[] factorial = new int[n+1];\n StringBuilder sb = new StringBuilder();\n \n // create an array of factorial lookup\n int sum = 1;\n factorial[0] = 1;\n for(int i=1; i<=n; i++){\n sum *= i;\n factorial[i] = sum;\n }\n // factorial[] = {1, 1, 2, 6, 24, ... n!}\n \n // create a list of numbers to get indices\n for(int i=1; i<=n; i++){\n numbers.add(i);\n }\n // numbers = {1, 2, 3, 4}\n \n k--;\n \n for(int i = 1; i <= n; i++){\n int index = k/factorial[n-i];\n sb.append(String.valueOf(numbers.get(index)));\n numbers.remove(index);\n k-=index*factorial[n-i];\n }\n \n return String.valueOf(sb);\n }\n\n | 1,487 | 20 | [] | 160 |
permutation-sequence | C++ | Very Easy and Detailed Explanation (Idea + code) | c-very-easy-and-detailed-explanation-ide-ury6 | Let us first take an example to under the idea:\nSuppose n = 4.\nSo we have elements - 1,2,3,4\nThere are total n!= 4! = 24 permutations possible. We can see a | ashwinfury1 | NORMAL | 2020-06-20T10:22:04.767459+00:00 | 2020-06-20T10:29:53.964163+00:00 | 21,865 | false | Let us first take an example to under the idea:\nSuppose n = 4.\nSo we have elements - 1,2,3,4\nThere are total n!= 4! = 24 permutations possible. We can see a specific pattern here:\n\n```\narr\n[ 1 2 3 4]\n1 2 3 4 2 1 3 4 3 1 2 4 4 1 2 3\n1 2 4 3 2 1 4 3 3 1 4 2 4 1 3 2\n1 3 2 4 2 3 1 4 3 2 1 4 4 2 1 3\n1 3 4 2 2 3 4 1 3 2 4 1 4 2 3 1\n1 4 2 3 2 4 1 3 3 4 1 2 4 3 1 2\n1 4 3 2 2 4 3 1 3 4 2 1 4 3 2 1\nSo we have 4 block with 6 elements each.\n\nn = 4 we can take an array [1,2,3,4] , initital ans = ""\nlets say we have k =15, the 15 th permutation is "3 2 1 4":\n\nAs we can see the first value is 3 that means out of the four blocks we need the 3rd block. \nEach blocks has n-1! = 3! = 6 elements --> 15 = 6*2 + 3 i.e. we skip 2 blocks and our ans is the third element in the 3rd block\nLet us assume the blocks are zero indexed.\nNow 15 / 6 = 2; So we select the 2nd block (0-indexed) that means 2nd index in our array - 3\nNow ans = "3"\nRemove this element from the array and our array becomes: [1,2,4]\n---------------------------------------------------------------------------------------------\nNow we are in this block:\n3 1 2 4 - 1 \n3 1 4 2 - 2 Block 0\n ------ \n3 2 1 4 - 3 (ans)\n3 2 4 1 - 4 Block 1\n ------\n3 4 1 2 - 5 \n3 4 2 1 - 6 Block 2\nNow we have 3 blocks each of with 2 elements \ni,e. n = n-1 = 3blocks and n-1! = 2! = 2 elements\nn = 3, what will be the k? As we passed 12 elements we have k = 15-12 => the third element in this large block.\nk = 3\nelement in partition (p) = 2;\nk / p = 3 / 2 = 1 => ans is in block 1, value to add to ans = 2\narr[1] = 2;\nans = "32"\nremove 2 from array => [1,4]\nNow we have 2 elements left(n-1 = 3-1) \n-----------------------------------------------------------------------------\n32 1 4 Block 0\n32 4 1 Block 1\n\nn=2, k = 1\n1 will be added ans = "321" arr= [4]\nAs we only have one value value in array append it to ans. ans = "3214"\n\nOne very important note:(Corner case)\nWhen we have k as a multiple of elements in partition for e.g. k = 12 Then we want to be in block with index 1\nbut as index = 12 / 6 = 2; we have to keep index = index-1;\nOnly when we are aiming at the last element we will hit this case.\nHere the blocks are zero indexed but the elements inside them are 1 index.\n\nI\'m sure after you look at the code you will completely understand it\n```\n\nCode:\n\n```\nclass Solution {\npublic:\n // Our recursive function that will complete the ans string.\n\t// v - is our current array = [1,2,3,4]\n\t// ans is the answer string, n and k are current values of n and k\n\t// factVal is an array containing the factorial of all integers from 0-9 to get factorial in O(1) time.\n\t// That means I have stored all the factorials in this array before hand to avoid calculation. You can also write factorial funciton if you want.\n\t\n void setPerm(vector<int>& v,string& ans,int n,int k,vector<int>& factVal){\n // if there is only one element left append it to our ans (Base case)\n\t if(n==1){\n ans+=to_string(v.back());\n return;\n }\n\t\t\n\t\t// We are calculating the required index. factVal[n-1] means for n = 4 => factVal[3] = 6.\n // 15 / 6 = 2 will the index for k =15 and n = 4.\n\t\tint index = (k/factVal[n-1]);\n // if k is a multiple of elements of partition then decrement the index (Corner case I was talking about)\n\t\tif(k % factVal[n-1] == 0){\n index--;\n }\n\t\t\n\t\tans+= to_string(v[index]); // add value to string\n v.erase(v.begin() + index); // remove element from array\n k -= factVal[n-1] * index; // adjust value of k; k = 15 - 6*2 = 3.\n\t\t// Recursive call with n=n-1 as one element is added we need remaing.\n setPerm(v,ans,n-1,k,factVal);\n }\n \n string getPermutation(int n, int k) {\n if(n==1) return "1";\n\t\t//Factorials of 0-9 stored in the array. factVal[3] = 6. (3! = 6)\n vector<int>factVal = {1,1,2,6,24,120,720,5040,40320,362880};\n string ans = "";\n vector<int> v;\n\t\t// Fill the array with all elements\n for(int i=1;i<=n;i++) v.emplace_back(i);\n setPerm(v,ans,n,k,factVal);\n return ans;\n }\n};\n```\n\nI hope you enjoyed it. If there is any blunder kindly let me know.\nHappy Coding! | 244 | 3 | [] | 23 |
permutation-sequence | Share my Python solution with detailed explanation | share-my-python-solution-with-detailed-e-kc2j | The idea is as follow:\n\nFor permutations of n, the first (n-1)! permutations start with 1, next (n-1)! ones start with 2, ... and so on. And in each group of | dasheng2 | NORMAL | 2015-07-20T15:59:53+00:00 | 2018-10-26T05:51:06.071872+00:00 | 26,484 | false | The idea is as follow:\n\nFor permutations of n, the first (n-1)! permutations start with 1, next (n-1)! ones start with 2, ... and so on. And in each group of (n-1)! permutations, the first (n-2)! permutations start with the smallest remaining number, ...\n\ntake n = 3 as an example, the first 2 (that is, (3-1)! ) permutations start with 1, next 2 start with 2 and last 2 start with 3. For the first 2 permutations (123 and 132), the 1st one (1!) starts with 2, which is the smallest remaining number (2 and 3). So we can use a loop to check the region that the sequence number falls in and get the starting digit. Then we adjust the sequence number and continue.\n\n import math\n class Solution:\n # @param {integer} n\n # @param {integer} k\n # @return {string}\n def getPermutation(self, n, k):\n numbers = range(1, n+1)\n permutation = ''\n k -= 1\n while n > 0:\n n -= 1\n # get the index of current digit\n index, k = divmod(k, math.factorial(n))\n permutation += str(numbers[index])\n # remove handled number\n numbers.remove(numbers[index])\n \n return permutation | 168 | 5 | ['Python'] | 21 |
permutation-sequence | An iterative solution for reference | an-iterative-solution-for-reference-by-a-7nwq | Recursion will use more memory, while this problem can be solved by iteration. I solved this problem before, but I didn't realize that using k = k-1 would avoid | adeath | NORMAL | 2014-11-13T22:02:06+00:00 | 2018-10-02T21:45:40.797903+00:00 | 35,695 | false | Recursion will use more memory, while this problem can be solved by iteration. I solved this problem before, but I didn't realize that using k = k-1 would avoid dealing with case k%(n-1)!==0. Rewrote this code, should be pretty concise now. \n\nOnly thing is that I have to use a list to store the remaining numbers, neither linkedlist nor arraylist are very efficient, anyone has a better idea?\n\nThe logic is as follows: for n numbers the permutations can be divided to (n-1)! groups, for n-1 numbers can be divided to (n-2)! groups, and so on. Thus k/(n-1)! indicates the index of current number, and k%(n-1)! denotes remaining index for the remaining n-1 numbers.\nWe keep doing this until n reaches 0, then we get n numbers permutations that is kth. \n\n public String getPermutation(int n, int k) {\n List<Integer> num = new LinkedList<Integer>();\n for (int i = 1; i <= n; i++) num.add(i);\n int[] fact = new int[n]; // factorial\n fact[0] = 1;\n for (int i = 1; i < n; i++) fact[i] = i*fact[i-1];\n k = k-1;\n StringBuilder sb = new StringBuilder();\n for (int i = n; i > 0; i--){\n int ind = k/fact[i-1];\n k = k%fact[i-1];\n sb.append(num.get(ind));\n num.remove(ind);\n }\n return sb.toString();\n } | 140 | 2 | ['Java'] | 21 |
permutation-sequence | ✔️C++🔥100%✅Fastest solution || Best approach with good explanation || Easy to understand. 1 | c100fastest-solution-best-approach-with-zc3z8 | Intution:-\n\nSince this is permutaion we can assume that there are four positions that need to be filled using the four numbers of the sequence. First, we need | pranjal9424 | NORMAL | 2022-08-30T01:22:37.376807+00:00 | 2022-12-12T19:00:10.183413+00:00 | 7,993 | false | **Intution:-**\n\nSince this is permutaion we can assume that there are four positions that need to be filled using the four numbers of the sequence. First, we need to decide which number is to be placed at the first index. Once the number at the first index is decided we have three more positions and three more numers. Now the problem is shorter. We can repeat the technique that was used previously untl all the positions are filled.\n\n**On Paper Dry run:-**\n\n\n\n\n**Approach**\n\n**STEP 1:**\n\nMathematically speaking there can be 4 variations while generating the permutation. We can have our permutation starting with either 1 or 2 or 3 or 4. If the first position is already occupied by one number there are three more positions left. The remaining three numbers can be permuted among themselves while filling the 3 positions and will generate 3! = 6 sequences. Hence each block will have 6 permutations adding up to a total of 6*4 = 24 permutations. If we consider the sequences as 0-based and in the sorted form we observe:- \n\n* The 0th \u2013 5th permutation will start with 1 \n* The 6th \u2013 11th permutation will start with 2\n* The 12th \u2013 17th permutation will start with 3 \n* The 18th \u2013 23rd permutation will start with 4.\n\n\t(For better understanding refer to the picture below.) \n\n\nWe make K = 17-1 considering 0-based indexing. Since each of the four blocks illustrated above comprises 6 permutations, therefore, the 16th permutation will lie in (16 / 6 ) = 2nd block, and our answer is the (16 % 6) = 4th sequence from the 2nd block. Therefore 3 occupies the first position of the sequence and K = 4.\n\n\n**STEP 2:**\n\nOur new search space comprises three elements {1,2,4} where K = 4 . Using the previous technique we can consider the second position to be occupied can be any one of these 3 numbers. Again one block can start with 1, another can start with 2 and the last one can start with 4 . Since one position is fixed, the remaining two numbers of each block can form 2! = 2 sequences. In sorted order :\n\n* The 0th \u2013 1st sequence starts with 1 \n* The 2nd \u2013 3rd sequence starts with 2 \n* The 4th \u2013 5th sequence starts with 4\n\n\n\nThe 4th permutation will lie in (4/2) = 2nd block and our answer is the 4%2 = 0th sequence from the 2nd block. Therefore 4 occupies the second position and K = 0.\n\n\n\n**STEP 3:**\n\nThe new search space will have two elements {1 ,2} and K = 0. One block starts with 1 and the other block starts with 2. The other remaining number can form only one 1! = 1 sequence. In sorted form \u2013\n\n* The 0th sequence starts with 1 \n* The 1st sequence. starts with 2\n\n\n\nThe 0th permutation will lie in the (0/1) = 0th block and our answer is the 0%1 = 0th sequence from the 0th block. Therefore 1 occupies the 3rd position and K = 0.\n\n\n\n**STEP 4:** \n\nNow the only block has 2 in the first position and no remaining number is present.\n\nThis is the point where we place 2 in the last position and stop.\n\n**The final answer is 3412.**\n\n**Code:-**\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact=1;\n vector<int> nums;\n for(int i=1;i<n;i++){\n fact=fact*i;\n nums.push_back(i);\n }\n nums.push_back(n);\n k=k-1;\n string ans="";\n while(true){\n ans=ans+to_string(nums[k/fact]);\n nums.erase(nums.begin()+k/fact);\n if(nums.size()==0){\n break;\n }\n k=k%fact;\n fact=fact/nums.size();\n }\n return ans;\n }\n};\n```\n\n**Code Dry run:-**\n\n | 106 | 0 | ['Math', 'Backtracking', 'Recursion', 'C', 'Iterator', 'C++'] | 10 |
permutation-sequence | Easy understand, Most concise C++ solution, minimal memory required | easy-understand-most-concise-c-solution-tr47n | This problem is recursive like dynamic programming.\nKth Permutation sequence can be formed by choosing the 1st digit and then the rest of the digits one by one | 1337beef | NORMAL | 2014-09-13T13:37:26+00:00 | 2020-02-01T03:27:46.977059+00:00 | 31,022 | false | This problem is recursive like dynamic programming.\nKth Permutation sequence can be formed by choosing the 1st digit and then the rest of the digits one by one.\nVisually:\n1 + (permutations of rest of digits)\n2 + (permutations of ...)\nso on...\n\nFor N=3,\nwe have the permutations:\n1|2,3\n1|3,2\n2|1,3\n2|3,1\n3|1,2\n3|2,1\n\nI put a bar "|" to separate first digit from the rest of digits.\nThere are a total of N! = 3! = 6 perms. Each 1st digit is "attached" to (n-1)! =2! = 2 permutations formed by rest of digits. \nThus , to choose 1st digit, simply calculate (k-1) / (n-1)! and use it to index into an array of digits 1,2,3,\nOnce 1st digit is chosen, we choose 2nd and so on recursively.\n\nWe remove 1st digit from the array of digits , so the remaining are the "rest of digits".\nThere are 2 ways to remove: \n1) pull the chosen digit from its current place to the right place in the permutation and shift rest of digits accordingly. (this is the in-place method chosen in my code so left part is partially formed permuation and right part is the candidates)\n2) mark the chosen digit as "used" so you don\'t use it again. (need an array of booleans to track)\n\nNotice the candidates always remain sorted regardless of which digit is removed. This is an important property to solve the problem recursively. \n\n\n\n\n\n\n\n\n\tstring getPermutation(int n, int k) {\n int i,j,f=1;\n // left part of s is partially formed permutation, right part is the leftover chars.\n string s(n,\'0\');\n for(i=1;i<=n;i++){\n f*=i;\n s[i-1]+=i; // make s become 1234...n\n }\n for(i=0,k--;i<n;i++){\n f/=n-i;\n j=i+k/f; // calculate index of char to put at s[i]\n char c=s[j];\n // remove c by shifting to cover up (adjust the right part).\n for(;j>i;j--)\n s[j]=s[j-1];\n k%=f;\n s[i]=c;\n }\n return s;\n } | 85 | 4 | [] | 16 |
permutation-sequence | Clean Java Solution | clean-java-solution-by-mo10-1mpm | The basic idea is to decide which is the correct number starting from the highest digit.\nUse k divide the factorial of (n-1), the result represents the ith not | mo10 | NORMAL | 2015-08-12T00:13:01+00:00 | 2018-10-02T20:57:08.496107+00:00 | 12,686 | false | The basic idea is to decide which is the correct number starting from the highest digit.\nUse k divide the factorial of (n-1), the result represents the ith not used number.\nThen update k and the factorial to decide next digit.\n\n\n public String getPermutation(int n, int k) {\n\n LinkedList<Integer> notUsed = new LinkedList<Integer>();\n\n\t\tint weight = 1;\n\n\t\tfor (int i = 1; i <= n; i++) {\n\t\t\tnotUsed.add(i);\n\t\t\tif (i == n)\n\t\t\t\tbreak;\n\t\t\tweight = weight * i;\n\t\t}\n\n\t\tString res = "";\n\t\tk = k - 1;\n\t\twhile (true) {\n\t\t\tres = res + notUsed.remove(k / weight);\n\t\t\tk = k % weight;\n\t\t\tif (notUsed.isEmpty())\n\t\t\t\tbreak;\n\t\t\tweight = weight / notUsed.size();\n\t\t}\n\n\t\treturn res;\n } | 78 | 0 | [] | 8 |
permutation-sequence | C++ | 100% time, space efficient | Iterative Solution | Detailed Explanation with Example | c-100-time-space-efficient-iterative-sol-1ra2 | The approach is mathematical. The idea is to keep selecting a digit and eliminating it from further selection based on value of K. \n\nFor example:\n\nGiven, N | dimpleryp | NORMAL | 2020-06-20T15:17:22.565346+00:00 | 2020-06-21T19:50:13.454958+00:00 | 6,703 | false | The approach is mathematical. The idea is to keep selecting a digit and eliminating it from further selection based on value of K. \n\nFor example:\n\n**Given, N = 4, K = 9**\n\nThere are 6 numbers starting with 1: 1234, 1243, 1324, 1342, 1423, 1432\nThere are 6 numbers starting with 2: 2134, 2143, 2314, 2341, 2413, 2431\nSimilarly, there are 6 numbers starting with 3 and 6 numbers starting with 4.\n\n**This is because when we have chosen one place out of 4 places (as N=4), there are 3 places remaining to be filled and those 3 places can be filled in 6 ways or (N-1)! ways.**\n\nSo, we have to keep identifying which digit to choose. \n\nInitially, we have to choose a digit from **{1,2,3,4}.**\n\nSince K = 9, meaning it belongs to second set of six numbers and hence, would begin with 2.\n\n**Now, first place is chosen as 2 and output string becomes "2". \nThis means we have eliminated 6 choices starting with 1 (1234, 1243, 1324, 1342, 1423, 1432).**\n\nNow, K would be updated as **K = 9 - 6 = 3.**\n\nWe now have to identify remaining 3 places with the digits **{1,3,4}** and with **K = 3.**\n\nThere are 2 numbers starting with 1: 134, 143\nThere are 2 numbers starting with 3: 314, 341\nThere are 2 numbers starting with 4: 413, 431\n\nThis is because when we have chosen one place out of 3 available places, there are 2 places remaining to be filled and those 2 places can be filled in 2 ways.\n\n**Since, K = 3, meaning it belongs to second set of two numbers and hence, answer would be appended with "3" and output string becomes "23". \nThis means we have eliminated 2 choices starting with 1 (134, 143).**\n\nNow, K would be updated as K = 3 - 2 = 1.\n\nWe now have to identify remaining 2 places with the digits **{1,4}** with **K = 1.**\n\nThere is 1 number starting with 1: 14\nThere is 1 number starting with 4: 41\n\nThis is because when we have chosen one place out of 2 available places, there is only 1 place remaining to be filled and that 1 place can be only be filled in 1 ways.\n\n**Since, K = 1, meaning it belongs to first set of one number and hence, answer would be appended with "14" and output string becomes "2314".**\n\n**Therefore, final answer becomes "2314".**\n\nHope it helps! :)\n\n```\nclass Solution {\npublic:\n vector<int> fact;\n \n void findfact(int n)\n {\n fact = vector<int>(n);\n \n fact[0] = 1;\n \n if(n==1) return;\n \n fact[1] = 1;\n for(int i=2; i<n; i++)\n fact[i] = i*fact[i-1];\n }\n \n string getPermutation(int N, int K) {\n int n = N-1, k = K-1, nt, kt;\n \n findfact(N);\n vector<int> num(N);\n for(int i=0; i<N; i++)\n num[i] = i+1;\n vector<int>::iterator it; \n \n string ans = "";\n \n while(n>=0)\n {\n nt = k/fact[n];\n kt = k%fact[n];\n\n ans += (num[nt]+\'0\');\n it = num.begin(); \n num.erase(it+nt);\n n--;\n k = kt; \n }\n\n return ans;\n }\n};\n``` | 73 | 1 | ['Math', 'C', 'Iterator', 'C++'] | 4 |
permutation-sequence | [Python] Math solution + Oneliner, both O(n^2), expained | python-math-solution-oneliner-both-on2-e-1nji | The simplest way to solve this problem is use backtracking, where you just generate all sequences, with complexity O(k) = O(n!). We can do better. Let us consid | dbabichev | NORMAL | 2020-06-20T07:41:57.029541+00:00 | 2020-06-20T16:28:50.210321+00:00 | 3,901 | false | The simplest way to solve this problem is use backtracking, where you just generate all sequences, with complexity `O(k) = O(n!)`. We can do better. Let us consider an example: `n=6`, `k=314`. How we can find the first digit? There are `5! = 120` permutations, which start with `1`, there are also `120` permutations, which start with `2`, and so on. `314 > 2*120` and `314 < 3*120`, so it means, that the fist digit we need to take is `3`. So we build first digit of our number, remove it from list of all digits `digits` and continue:\n\n1. `k = 314-2*5! = 74`, `n - 1 = 5`, `d = 3`, build number so far `3`, `digits = [1,2,4,5,6]`\n2. `k = 74-3*4! = 2`, `n - 1 = 4`, `d = 0`, build number so far `35`, `digits = [1,2,4,6]`\n3. `k = 2-0*3! = 2`, `n - 1 = 3`, `d = 0`, build number so far `351`, `digits = [2,4,6]`\n4. `k = 2-1*2! = 0`, `n - 1 = 2`, `d = 2`, build number so far `3512`, `digits = [4,6]`\n5. `k = 0-1*1! = 0`, `n - 1 = 1`, `d = 2`, build number so far `35126`, `digits = [4]`\n6. Finally, we have only one digit left, output is `351264`.\n\n**Complexity**. I keep list of `n` digits, and then delete them one by one. Complexity of one deletion is `O(n)`, so overall complexity is `O(n^2)`. Note, that it can be improved to `O(n log n)` if we use SortedList, but it just not worth it, `n` is too small.\n\n```\nclass Solution:\n def getPermutation(self, n, k):\n numbers = list(range(1,n+1))\n answer = ""\n \n for n_it in range(n,0,-1):\n d = (k-1)//factorial(n_it-1)\n k -= d*factorial(n_it-1)\n answer += str(numbers[d])\n numbers.remove(numbers[d])\n \n return answer\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**\n\n### Oneliner\nHere it is, with `O(n^2)` complexity!\n\n```\nreturn reduce(lambda s,n:(s[0]+s[2][(d:=s[1]//(f:=factorial(n)))],s[1]%f,s[2][:d]+s[2][d+1:]),range(n-1,-1,-1),(\'\',k-1,\'123456789\'))[0]\n``` | 68 | 6 | ['Math'] | 6 |
permutation-sequence | Sharing my straightforward C++ solution with explanation | sharing-my-straightforward-c-solution-wi-lxzs | string getPermutation(int n, int k) {\n int pTable[10] = {1};\n for(int i = 1; i <= 9; i++){\n pTable[i] = i * pTable[i - 1];\n | zxyperfect | NORMAL | 2015-01-08T23:12:28+00:00 | 2015-01-08T23:12:28+00:00 | 17,435 | false | string getPermutation(int n, int k) {\n int pTable[10] = {1};\n for(int i = 1; i <= 9; i++){\n pTable[i] = i * pTable[i - 1];\n }\n string result;\n vector<char> numSet;\n numSet.push_back('1');\n numSet.push_back('2');\n numSet.push_back('3');\n numSet.push_back('4');\n numSet.push_back('5');\n numSet.push_back('6');\n numSet.push_back('7');\n numSet.push_back('8');\n numSet.push_back('9');\n while(n > 0){\n int temp = (k - 1) / pTable[n - 1];\n result += numSet[temp];\n numSet.erase(numSet.begin() + temp);\n k = k - temp * pTable[n - 1];\n n--;\n }\n return result;\n }\n\nIn this program, `pTable` refers to permutation table and `numSet` refers to a set of numbers from 1 to 9. Before while loop, we need to initialize `pTable` and `numSet`, which is trivial.\n\nIn while loop, we do these following things.\n\n1 calculate which number we will use.\n\n2 remove that number from `numSet`.\n\n3 recalculate k.\n\n4 `n--`. \n\nFinally, we return result. | 61 | 2 | ['Hash Table', 'C++'] | 17 |
permutation-sequence | Backtrack Summary: General Solution for 10 Questions!!!!!!!! Python (Combination Sum, Subsets, Permutation, Palindrome) | backtrack-summary-general-solution-for-1-i2fn | For Java version, please refer to isssac3's answer.\n\n39. Combination Sum\nhttps://leetcode.com/problems/combination-sum/\n\n def combinationSum(self, candi | dichen001 | NORMAL | 2016-12-24T05:18:39.108000+00:00 | 2018-10-10T04:30:27.984809+00:00 | 6,892 | false | For Java version, please refer to [isssac3's answer.](https://discuss.leetcode.com/topic/46162/a-general-approach-to-backtracking-questions-in-java-subsets-permutations-combination-sum-palindrome-partioning)\n\n**39. Combination Sum**\nhttps://leetcode.com/problems/combination-sum/\n```\n def combinationSum(self, candidates, target):\n def backtrack(tmp, start, end, target):\n if target == 0:\n ans.append(tmp[:])\n elif target > 0:\n for i in range(start, end):\n tmp.append(candidates[i])\n backtrack(tmp, i, end, target - candidates[i])\n tmp.pop()\n ans = [] \n candidates.sort(reverse= True)\n backtrack([], 0, len(candidates), target)\n return ans\n```\n\n**40. Combination Sum II**\nhttps://leetcode.com/problems/combination-sum-ii/\n```\n def combinationSum2(self, candidates, target):\n def backtrack(start, end, tmp, target):\n if target == 0:\n ans.append(tmp[:])\n elif target > 0:\n for i in range(start, end):\n if i > start and candidates[i] == candidates[i-1]:\n continue\n tmp.append(candidates[i])\n backtrack(i+1, end, tmp, target - candidates[i])\n tmp.pop()\n ans = []\n candidates.sort(reverse= True)\n backtrack(0, len(candidates), [], target)\n return ans\n```\n\n**78. Subsets**\nhttps://leetcode.com/problems/subsets/\n```\n def subsets(self, nums):\n def backtrack(start, end, tmp):\n ans.append(tmp[:])\n for i in range(start, end):\n tmp.append(nums[i])\n backtrack(i+1, end, tmp)\n tmp.pop()\n ans = []\n backtrack(0, len(nums), [])\n return ans\n```\n\n**90. Subsets II**\nhttps://leetcode.com/problems/subsets-ii/\n```\n def subsetsWithDup(self, nums):\n def backtrack(start, end, tmp):\n ans.append(tmp[:])\n for i in range(start, end):\n if i > start and nums[i] == nums[i-1]:\n continue\n tmp.append(nums[i])\n backtrack(i+1, end, tmp)\n tmp.pop()\n ans = []\n nums.sort()\n backtrack(0, len(nums), [])\n return ans\n```\n\n**46. Permutations**\nhttps://leetcode.com/problems/permutations/\n```\n def permute(self, nums):\n def backtrack(start, end):\n if start == end:\n ans.append(nums[:])\n for i in range(start, end):\n nums[start], nums[i] = nums[i], nums[start]\n backtrack(start+1, end)\n nums[start], nums[i] = nums[i], nums[start]\n \n ans = []\n backtrack(0, len(nums))\n return ans\n```\n\n**47. Permutations II**\nhttps://leetcode.com/problems/permutations-ii/\n```\n def permuteUnique(self, nums):\n def backtrack(tmp, size):\n if len(tmp) == size:\n ans.append(tmp[:])\n else:\n for i in range(size):\n if visited[i] or (i > 0 and nums[i-1] == nums[i] and not visited[i-1]):\n continue\n visited[i] = True\n tmp.append(nums[i])\n backtrack(tmp, size)\n tmp.pop()\n visited[i] = False\n ans = []\n visited = [False] * len(nums)\n nums.sort()\n backtrack([], len(nums))\n return ans\n```\n\n**60. Permutation Sequence**\nhttps://leetcode.com/problems/permutation-sequence/\n```\n def getPermutation(self, n, k):\n nums = [str(i) for i in range(1, n+1)]\n fact = [1] * n\n for i in range(1,n):\n fact[i] = i*fact[i-1]\n k -= 1\n ans = []\n for i in range(n, 0, -1):\n id = k / fact[i-1]\n k %= fact[i-1]\n ans.append(nums[id])\n nums.pop(id)\n return ''.join(ans)\n```\n\n**131. Palindrome Partitioning**\nhttps://leetcode.com/problems/palindrome-partitioning/\n```\n def partition(self, s):\n def backtrack(start, end, tmp):\n if start == end:\n ans.append(tmp[:])\n for i in range(start, end):\n cur = s[start:i+1]\n if cur == cur[::-1]:\n tmp.append(cur)\n backtrack(i+1, end, tmp)\n tmp.pop()\n ans = []\n backtrack(0, len(s), [])\n return ans\n```\n\n****\n\n\n**267. Palindrome Permutation II**\nhttps://leetcode.com/problems/palindrome-permutation-ii/\nRelated to this two:\n`31. Next Permutation`: https://leetcode.com/problems/next-permutation/\n`266. Palindrome Permutation`: https://leetcode.com/problems/palindrome-permutation/\n\n```\n def generatePalindromes(self, s):\n kv = collections.Counter(s)\n mid = [k for k, v in kv.iteritems() if v%2]\n if len(mid) > 1:\n return []\n mid = '' if mid == [] else mid[0]\n half = ''.join([k * (v/2) for k, v in kv.iteritems()])\n half = [c for c in half]\n \n def backtrack(end, tmp):\n if len(tmp) == end:\n cur = ''.join(tmp)\n ans.append(cur + mid + cur[::-1])\n else:\n for i in range(end):\n if visited[i] or (i>0 and half[i] == half[i-1] and not visited[i-1]):\n continue\n visited[i] = True\n tmp.append(half[i])\n backtrack(end, tmp)\n visited[i] = False\n tmp.pop()\n \n ans = []\n visited = [False] * len(half)\n backtrack(len(half), [])\n return ans\n``` | 52 | 0 | [] | 5 |
permutation-sequence | 0ms C++ 12-line concise solution (no recursion, no helper function) | 0ms-c-12-line-concise-solution-no-recurs-h4iv | Attached please find my solution.\n\nIdea:\n\n- For an n-element permutation, there are (n-1)! permutations started with '1', (n-1)! permutations started with ' | zhiqing_xiao | NORMAL | 2015-07-19T15:03:20+00:00 | 2015-07-19T15:03:20+00:00 | 7,400 | false | Attached please find my solution.\n\nIdea:\n\n- For an n-element permutation, there are (n-1)! permutations started with '1', (n-1)! permutations started with '2', and so forth. Therefore we can determine the value of the first element.\n\n- After determining the first element, there are (n-1) candidates left. Then there are (n-2)! permutations started with the minimum element within the remaining set, and so forth.\n\nComplexities:\n\n- Time complexity: O(n^2) \n\n- Space complexity: O(n)\n\n==\n\n class Solution {\n public:\n string getPermutation(int n, int k) {\n // initialize a dictionary that stores 1, 2, ..., n. This string will store the permutation.\n string dict(n, 0);\n iota(dict.begin(), dict.end(), '1');\n \n // build up a look-up table, which stores (n-1)!, (n-2)!, ..., 1!, 0!\n vector<int> fract(n, 1);\n for (int idx = n - 3; idx >= 0; --idx) {\n fract[idx] = fract[idx + 1] * (n - 1 - idx);\n }\n \n // let k be zero base\n --k;\n \n // the main part.\n string ret(n, 0);\n for (int idx = 0; idx < n; ++idx) {\n int select = k / fract[idx];\n k %= fract[idx];\n ret[idx] = dict[select];\n dict.erase(next(dict.begin(), select)); // note that it is an O(n) operation\n }\n return ret;\n }\n }; | 32 | 0 | [] | 1 |
permutation-sequence | Simple 0s C++ solution | simple-0s-c-solution-by-kenigma-4vgm | since n will be between 1 and 9 inclusive. pre-calculate the factorials is faster.\n\n class Solution {\n public:\n string getPermutation(int n, in | kenigma | NORMAL | 2016-02-21T19:33:16+00:00 | 2016-02-21T19:33:16+00:00 | 5,752 | false | since n will be between 1 and 9 inclusive. pre-calculate the factorials is faster.\n\n class Solution {\n public:\n string getPermutation(int n, int k) {\n string res;\n string nums = "123456789";\n int f[10] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n --k;\n for (int i = n; i >= 1; --i) {\n int j = k / f[i - 1];\n k %= f[i - 1];\n res.push_back(nums[j]);\n nums.erase(nums.begin() + j);\n }\n return res;\n }\n }; | 29 | 0 | ['C++'] | 4 |
permutation-sequence | C++ Recursive Solution | Maths Explained | 0ms | Faster than 100 % | c-recursive-solution-maths-explained-0ms-3efi | Question is to find the Kth permutation of a given number.\n\nNaive approach to solve this problem is to store all the possible permutations in an array and the | dhairyabahl | NORMAL | 2021-06-29T22:59:57.768611+00:00 | 2021-06-29T23:03:10.428518+00:00 | 2,342 | false | **Question is to find the Kth permutation of a given number.**\n\nNaive approach to solve this problem is to store all the possible permutations in an array and then simply return the kth one. This approach works perfectly fine but is having poor time complexity \uD83D\uDE11\n\nThe most optimised approach of this question (according me) is rather than traversing on each and every possible permutation, we should only go to the kth one !! Rather than making an array, recursive function should just return the perfect one i.e. the kth one. \uD83D\uDE42\uD83D\uDD25\n\nNow the question is, How can we do that ?? How can we reach directly to the kth permutation ? And the answer to this question is, by simply using a little bit of maths \uD83D\uDD22 .\n\n**MATHS EXPLANATION**\n\nWe know that number of permutations of a given number is simply calculated as n! where n is the number of digits of number n. To conclude, we can assure that number with n digits will have n! permutations and we can further say that it will have n groups of (n-1)! permutations.\n\nWe can simply see in this figure that we can make n groups of (n-1)! and we can check in which group kth permutation will lie.\n\n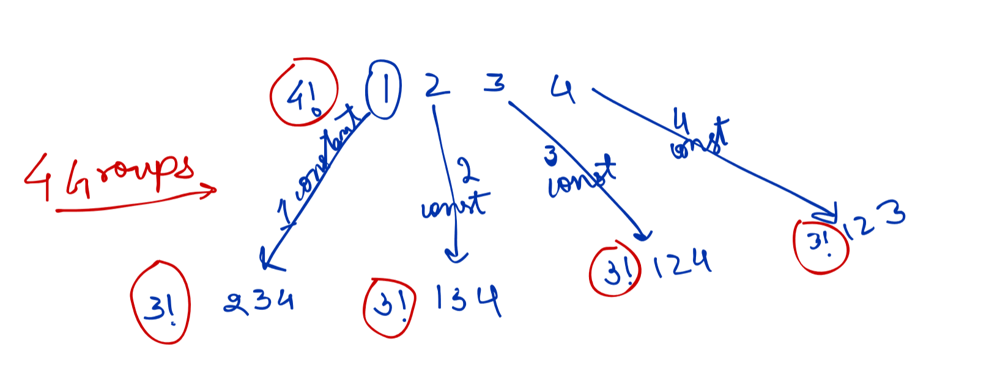\n\nAfter finding the most suitable group for the kth permutation, we will then do the same for that group as well and in that case, there will be (n-1) groups for (n-2)! permutations.\n\nWe will keep doing the same recursively until we find the best result i.e kth permutation.\n\nHere is the code for the problem : \n\n```\nclass Solution {\npublic:\n \n\t// this function is called to calculate possible number\n\t// of permutations for a given point through which, we will \n\t// calculate number of possible groups\n\t\n int fact(int num)\n {\n if(num==0)\n return 1 ;\n \n return num*fact(num-1);\n }\n \n string ans ;\n int count = 0 ;\n \n void permute(string str , int k, string finalAns)\n {\n \n if(str.length()==0)\n {\n ans = finalAns ;\n return ;\n }\n \n int number = str.length() - 1 ;\n int factNum = fact(number) ;\n \n for(int ctr = 0 ; ctr < str.length() ; ctr++ )\n {\n \n if( factNum < k )\n {\n k-=factNum;\n continue;\n }\n \n string sub = str.substr(0,ctr) + str.substr(ctr+1);\n permute(sub,k,finalAns+str[ctr]);\n break;\n \n }\n \n }\n \n string getPermutation(int n, int k) {\n \n string str = "" ;\n \n for(int ctr = 1 ; ctr <=n ; ctr++ ) \n str+=to_string(ctr);\n \n permute(str,k,"");\n \n return ans ;\n \n }\n};\n```\n\nI am still not sure if this is the best solution even after 0ms and faster than 100 % . Do upvote if you liked my approach ! All the best ! Happy Learning. | 26 | 1 | ['Math', 'Backtracking', 'C++'] | 4 |
permutation-sequence | Solution | solution-by-deleted_user-1ewv | C++ []\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> v={0};\n int tmp=1;\n for(int i=1;i<=n;i++){\n | deleted_user | NORMAL | 2023-01-03T14:04:02.442857+00:00 | 2023-03-06T13:23:22.368110+00:00 | 3,927 | false | ```C++ []\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> v={0};\n int tmp=1;\n for(int i=1;i<=n;i++){\n v.push_back(i);\n tmp*=i;\n }\n string s;\n cout<<tmp<<" ";\n for(int i=n;i>=2;i--){\n tmp/=i;\n int fl=(k+tmp-1)/tmp;\n s.push_back(v[fl]+\'0\');\n k-=(fl-1)*tmp;\n for(int j=fl;j<v.size()-1;j++){\n v[j]=v[j+1];\n }\n }\n s.push_back(v[1]+\'0\'); \n return s;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n nums = [i for i in range(1, n+1)] # list of numbers from 1 to n\n factorial = [1] * n\n for i in range(1, n):\n factorial[i] = factorial[i-1] * i\n \n k -= 1\n result = []\n for i in range(n-1, -1, -1):\n index = k // factorial[i]\n result.append(str(nums[index]))\n nums.pop(index)\n k = k % factorial[i]\n \n return \'\'.join(result)\n```\n\n```Java []\nclass Solution {\n private static int[] fact = {0, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n \n private String getPermutation(int n, int k, boolean[] nums, char[] str, int index) {\n int i = 0, m = nums.length;\n if(n == 1) {\n while(i < m && nums[i]) ++i;\n str[index++]=(char)(\'0\'+i+1);\n return String.valueOf(str);\n }\n if(k == 0) {\n while(i < m) {\n if(!nums[i]) str[index++]=(char)(\'0\'+i+1);\n ++i;\n }\n return String.valueOf(str);\n }\n \n int div = k/fact[n-1], mod = k%fact[n-1], j = -1;\n while(i < m-1 && div != j) {\n if(!nums[i]) ++j;\n if(j == div) break;\n ++i;\n }\n str[index++]=(char)(\'0\'+i+1);\n if(i < m) nums[i]=true;\n return getPermutation(n-1, mod, nums, str, index); \n }\n\n public String getPermutation(int n, int k) {\n boolean[] nums = new boolean[n];\n char[] charArr = new char[n];\n return getPermutation(n, k-1, nums, charArr, 0);\n }\n}\n```\n | 25 | 0 | ['C++', 'Java', 'Python3'] | 1 |
permutation-sequence | Permutation Sequence Java Solution|| 1.Bruteforce Approach || 2.Optimal Approach | permutation-sequence-java-solution-1brut-9gxn | \n1. First Approach\n//generate all permutation for 1 to n\n//store all permutation in some data structure\n//return kth term from data structure\n\n//Example : | palpradeep | NORMAL | 2022-11-04T08:58:21.839763+00:00 | 2022-11-06T18:06:03.033198+00:00 | 2,896 | false | ```\n1. First Approach\n//generate all permutation for 1 to n\n//store all permutation in some data structure\n//return kth term from data structure\n\n//Example :- n=3 , k=4\n//Generate permutations(LeetCode Qus. 46 :- Permutations) 1 to 3 i.e. \n123\n132\n213\n231\n312\n321\n//k=4th term is 231\n//our ans will be 231\n\nimport java.util.*;\nclass Solution {\n public String getPermutation(int n, int k) {\n int num[] = new int[n];\n for(int i=0; i<n; i++)\n {\n num[i] = i+1;\n }\n List<String> Tans = new ArrayList<>();\n help(0,num,n,k,Tans);\n Collections.sort(Tans);\n return Tans.get(k-1);\n }\n void help(int index, int[] num, int n, int k, List<String> Tans)\n {\n \n if(index==num.length){\n StringBuffer store = new StringBuffer();\n for(int i=0; i<n; i++)\n {\n store.append(num[i]);\n }\n Tans.add(store.toString());\n return;\n }\n \n for(int i=index; i<n; i++)\n {\n swap(i,index,num);\n help(index+1,num,n,k,Tans);\n swap(i,index,num);\n }\n }\n void swap(int i, int j, int[] num)\n {\n int temp = num[i];\n num[i] = num[j];\n num[j] = temp;\n }\n //T.C :- n!(for generating permutation) * n(for looping i=0 to nums.length) * n!logn(for sorting n! permutation)\n}\n\n2. Optimal Approach :- using Mathematics\n//Example :- n=4 ,k=17\n /////////STEP 1\n//We can have our permutation starting with either 1 or 2 or 3 or 4.\n//If first position is occupied by one number then there are three more positions left.\n//Then remaining three numbers can be permuted among themselves 3! = 6 sequences.\n\n//if we consider sequences as 0-based index in sorted form \n0th block |0th \u2013 5th permutation will start with 1 | {2,3,4} i.e. 0th{1,2,3,4}, 1st{1,2,4,3}, 2nd{1,3,2,4}, 3rd{1,3,4,2}, 4th{1,4,2,3}, 5th{1,4,3,2}\n1st block |6th \u2013 11th permutation will start with 2 | {1,3,4} i.e. 6th{2,1,3,4}, 7th{2,1,4,3}, 8th{2,3,1,4}, 9th{2,3,4,1}, 10th{2,4,1,3}, 11th{2,4,3,1}\n2nd block |12th \u2013 17th permutation will start with 3 | {1,2,4} i.e. 12th{3,1,2,4}, 13th{3,1,4,2}, 14th{3,2,1,4}, 15th{3,2,4,1}, 16th{3,4,1,2}, 17th{3,4,2,1}\n3rd block |18th \u2013 23rd permutation will start with 4 | {1,2,3} i.e. 18th{4,1,2,3}, 19th{4,1,3,2}, 20th{4,2,1,3}, 21st{4,2,3,1}, 22nd{4,3,1,2}, 23rd{4,3,2,1}\n\n//make K = 17-1 considering 0-based indexing\n//Since each of the four blocks illustrated above comprises 6 permutations, therefore the 16th permutation will lie in (16 / 6 ) = 2nd block i.e. 3 ans={3---}\n/and our answer is the (16 % 6) = 4th sequence from the 2nd block.\n \n //////////STEP 2\n //Our new search space comprises three elements {1,2,4} where K = 4 \n //If first position is occupied by one number then there are two more positions left.\n //Then remaining two numbers can be permuted among themselves 2! = 2 sequences.\n\n0th block |0th \u2013 1st sequence starts with 1 | {2,4} \n1st block |2nd \u2013 3rd sequence starts with 2 | {1,4}\n2nd block |4th \u2013 5th sequence starts with 4 | {1,2}\n\n//(4/2) = 2nd block i.e 4 ans={34--}\n//4%2 = 0th sequence from 2nd block\n\n /////////STEP 3\n //Our new search space comprises three elements {1,2} where K = 0\n //If first position is occupied by one number then there are one more positions left.\n //Then remaining one numbers can be permuted among themselves 1! = 1 sequences.\n0th block |0th sequence starts with 1 | {2} \n1st block |1st sequence. starts with 2 | {1}\n\n//(0/1) = 0th block i.e. ans={341}\n//0%1 = 0th sequence from 0th block\n\n /////////STEP 4\n//only 2 is remaining \nans = {3412}\n\nclass Solution {\n public String getPermutation(int n, int k) {\n int fact = 1;\n ArrayList < Integer > numbers = new ArrayList < > ();\n for (int i = 1; i < n; i++) {\n fact = fact * i;\n numbers.add(i);\n }\n numbers.add(n);\n String ans = "";\n k = k - 1;\n while (true) {\n ans = ans + numbers.get(k / fact);\n numbers.remove(k / fact);\n if (numbers.size() == 0) {\n break;\n }\n\n k = k % fact;\n fact = fact / numbers.size();\n }\n return ans;\n }\n}\nT.C:- n(for placing n numbers in n positions) * n(for every number we are reducingthe search space by removing one element, 1234-->124-->12-->1)\n\n``` | 25 | 0 | ['Math', 'Backtracking', 'Recursion', 'Java'] | 2 |
permutation-sequence | C++ | Solution with Comments | Brute Force and Optimal || Easy Understanding | c-solution-with-comments-brute-force-and-zkgy | Please Upvote if it helps you...\n\n\n\nSolution 1: Brute Force Solution\n\n\nApproach:\n\nThe extreme naive solution is to generate all the possible permutatio | Tejender_Upadhyay | NORMAL | 2022-07-09T05:54:14.865103+00:00 | 2022-07-10T05:25:00.946215+00:00 | 1,659 | false | ***Please Upvote if it helps you...***\n\n\n***\n***Solution 1: Brute Force Solution***\n***\n***\n***Approach:***\n***\nThe extreme naive solution is to generate all the possible permutations of the given sequence. This is achieved using recursion and every permutation generated is stored in some other data structure (here we have used a vector). Finally, we sort the data structure in which we have stored all the sequences and return the Kth sequence from it.\n***\n***\n***C++ Code:-***\n***\n```\nclass Solution {\n public:\n //function to generate all possible permutations of a string\n void solve(string & s, int index, vector < string > & res) {\n if (index == s.size()) {\n res.push_back(s);\n return;\n }\n for (int i = index; i < s.size(); i++) {\n swap(s[i], s[index]);\n solve(s, index + 1, res);\n swap(s[i], s[index]);\n }\n }\nstring getPermutation(int n, int k) {\n string s;\n vector < string > res;\n //create string\n for (int i = 1; i <= n; i++) {\n s.push_back(i + \'0\');\n }\n solve(s, 0, res);\n //sort the generated permutations\n sort(res.begin(), res.end());\n //make k 0-based indexed to point to kth sequence\n auto it = res.begin() + (k - 1);\n return *it;\n }\n};\n```\n***\n***\n***Time complexity: O(N! N) +O(N! Log N!)***\n\n***Reason:*** The recursion takes O(N!) time because we generate every possible permutation and another O(N) time is required to make a deep copy and store every sequence in the data structure. Also, O(N! Log N!) time required to sort the data structure\n\n***Space complexity: O(N)*** \n\n***Reason:*** Result stored in a vector, we are auxiliary space taken by recursion\n***\n***\n***Solution 2:(Optimal Approach)***\n\nSay we have N = 4 and K = 17. Hence the number sequence is {1,2,3,4}. \n***\n***Intuition:***\n\nSince this is a permutation we can assume that there are four positions that need to be filled using the four numbers of the sequence. First, we need to decide which number is to be placed at the first index. Once the number at the first index is decided we have three more positions and three more numbers. Now the problem is shorter. We can repeat the technique that was used previously until all the positions are filled. The technique is explained below.\n***\n***\n***Approach:***\n\n***STEP 1:***\n\nMathematically speaking there can be 4 variations while generating the permutation. We can have our permutation starting with either 1 or 2 or 3 or 4. If the first position is already occupied by one number there are three more positions left. The remaining three numbers can be permuted among themselves while filling the 3 positions and will generate 3! = 6 sequences. Hence each block will have 6 permutations adding up to a total of 6*4 = 24 permutations. If we consider the sequences as 0-based and in the sorted form we observe:- \n\nThe 0th \u2013 5th permutation will start with 1 \nThe 6th \u2013 11th permutation will start with 2\nThe 12th \u2013 17th permutation will start with 3 \nThe 18th \u2013 23rd permutation will start with 4.\n\n (For better understanding refer to the picture below.) \n\n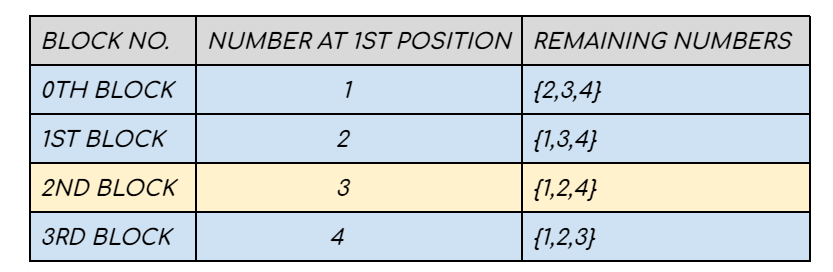\n\n\nWe make K = 17-1 considering 0-based indexing. Since each of the four blocks illustrated above comprises 6 permutations, therefore, the 16th permutation will lie in (16 / 6 ) = 2nd block, and our answer is the (16 % 6) = 4th sequence from the 2nd block. Therefore 3 occupies the first position of the sequence and K = 4.\n\n\n***\n\n***STEP 2:***\n\nOur new search space comprises three elements {1,2,4} where K = 4 . Using the previous technique we can consider the second position to be occupied can be any one of these 3 numbers. Again one block can start with 1, another can start with 2 and the last one can start with 4 . Since one position is fixed, the remaining two numbers of each block can form 2! = 2 sequences. In sorted order :\n\nThe 0th \u2013 1st sequence starts with 1 \nThe 2nd \u2013 3rd sequence starts with 2 \nThe 4th \u2013 5th sequence starts with 4\n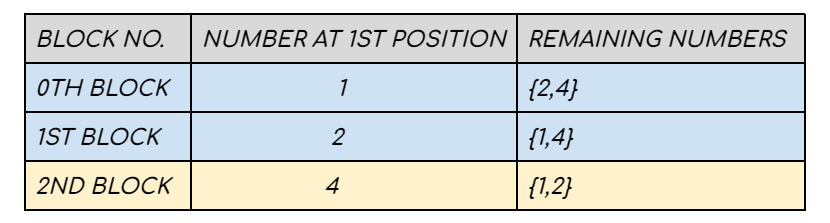\n\n\nThe 4th permutation will lie in (4/2) = 2nd block and our answer is the 4%2 = 0th sequence from the 2nd block. Therefore 4 occupies the second position and K = 0.\n\n***\n\n***STEP 3:***\n\nThe new search space will have two elements {1 ,2} and K = 0. One block starts with 1 and the other block starts with 2. The other remaining number can form only one 1! = 1 sequence. In sorted form \u2013\n\nThe 0th sequence starts with 1 \nThe 1st sequence. starts with 2\n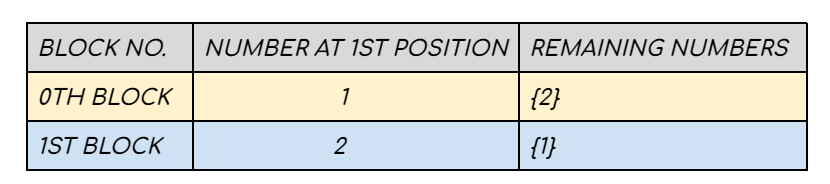\n\n\nThe 0th permutation will lie in the (0/1) = 0th block and our answer is the 0%1 = 0th sequence from the 0th block. Therefore 1 occupies the 3rd position and K = 0.\n***\n\n\n***STEP 4:***\n\nNow the only block has 2 in the first position and no remaining number is present.\n\n\n\nThis is the point where we place 2 in the last position and stop.\n***\n\n***The final answer is 3412.***\n***\n***\n\nC++ Code:-\n***\n```\nstring getPermutation(int n, int k) {\n int fact = 1;\n vector < int > numbers;\n for (int i = 1; i < n; i++) {\n fact = fact * i;\n numbers.push_back(i);\n }\n numbers.push_back(n);\n string ans = "";\n k = k - 1;\n while (true) {\n ans = ans + to_string(numbers[k / fact]);\n numbers.erase(numbers.begin() + k / fact);\n if (numbers.size() == 0) {\n break;\n }\n\n k = k % fact;\n fact = fact / numbers.size();\n }\n return ans;\n }\n```\n***\n***\n***Time Complexity: O(N) O(N) = O(N^2)***\n\n***Reason:*** We are placing N numbers in N positions. This will take O(N) time. For every number, we are reducing the search space by removing the element already placed in the previous step. This takes another O(N) time.\n\n***Space Complexity: O(N)***\n\n***Reason:*** We are storing the numbers in a data structure(here vector)\n***\n*** | 24 | 0 | ['Recursion', 'C', 'C++'] | 2 |
permutation-sequence | Does anyone have a better idea? Share my accepted python code here | does-anyone-have-a-better-idea-share-my-93uas | It's obvious that if we try to come up with n! solutions one by one until it reach kth element - O(k), it will exceed the time limit. Therefore, I tried to impl | paullo | NORMAL | 2014-05-25T10:19:12+00:00 | 2014-05-25T10:19:12+00:00 | 12,961 | false | It's obvious that if we try to come up with n! solutions one by one until it reach kth element - O(k), it will exceed the time limit. Therefore, I tried to implement a mathematical solution as follows:\n\n class Solution:\n # @return a string\n def getPermutation(self, n, k):\n \n ll = [str(i) for i in range(1,n+1)] # build a list of ["1","2",..."n"]\n \n divisor = 1\n for i in range(1,n): # calculate 1*2*3*...*(n-1)\n divisor *= i\n \n answer = ""\n while k>0 and k<=divisor*n: # there are only (divisor*n) solutions in total \n group_num = k/divisor\n k %= divisor\n \n if k>0: # it's kth element of (group_num+1)th group\n choose = ll.pop(group_num)\n answer += choose\n else: # it's last element of (group_num)th group\n choose = ll.pop(group_num-1) \n answer += choose\n ll.reverse() # reverse the list to get DESC order for the last element\n to_add = "".join(ll)\n answer += to_add\n break\n \n divisor/=len(ll)\n \n return answer\n \nBriefly take **(n,k) = (4,21)** for example, in the first iteration we divide the solution set into 4 groups: "1xxx", "2xxx", "3xxx", and "4xxx", while each group has 3! = 6 members. \n\nFrom 21/6 = 3...3, we know that the 21th element is the 3rd element in the (3+1)th group. In this group, we can divide it into 3 sub-groups again: "41xx", "42xx" and "43xx", and each group has 2!=2 members. \n\nThen, we calculate 3/2 and get 1...1, so it's the 1st element of (1+1)nd sub-group - "421x", and now it reach the base case with only one possibility - **"4213"**.\n\nAnyone pass the problem with different ideas? | 24 | 1 | ['Probability and Statistics', 'Python'] | 12 |
permutation-sequence | Python3 Solution Explained With a Tip For Faster Execution | Beats 99.8% | python3-solution-explained-with-a-tip-fo-r7uu | My solution is basically the same with the many others but here is another explanation:\n\nLet\'s go over an example:\n\nn=4 k=9\n1234 ------ start here\n1243 | aysusayin | NORMAL | 2020-06-20T13:26:24.604251+00:00 | 2020-06-20T21:20:05.257458+00:00 | 2,448 | false | My solution is basically the same with the many others but here is another explanation:\n\nLet\'s go over an example:\n```\nn=4 k=9\n1234 ------ start here\n1243 ------ third digit changes here \n1324 ------ second digit changes here \n1342\n1423\n1432 \n2134 ------ first digit changes here \n2143\n2314 -> k=9\n2341\n2413\n2431\n3124 ------ first digit changes here \n.\n.\n.\n```\nAs you can see first digit changes after 6 occurances which is (n-1)! and the second digit changes after 2 occurances which is (n-2)!. Similarly third digit changes after 1 occurances which is (n-3)!. Is this a coincidance? Of course not. Since it is a permutation we compute it like this:\n```(n)(n-1)(n-2)...(1)``` each paranthesis represents a digit. for the first place, we have n options. After using one of the numbers, we cannot use it again. So we have n-1 number options for the second place. In the end we multiply them to get the total number of permutations. Let\'s say we picked \'1\' for the first place. now we have (n-1)! options for the rest of the number. This is why at each step a number is repeated that many time. \n\nLet\'s go back to our example:\n\nSince the first digit is repeated (n-1)! times, by dividing the k by n we can find our first digit. Division must be integer division because we are only interested in the integer part.\n``` \nk=9, n=4\n(n-1)! = 6\nk /(n-1)! = 1\nremainder = 3\n```\nNumbers that we can use as digits are = ```[1,2,...,n]```\n\nSo, our first digit is the digit at index 1 which is ```2```. We take the digit at 1 because our list is sorted so we are sure that the second smallest digit is at index 1.\n\nSince we used ```2```, we need to remove it from our list and k takes the value of the remainder. You can think of lit ike this: we decided on our first digit so we can discard that part and deal with the rest of the number. As you can see the problem is the same! but this time we have (n-2)! instead of (n-1)!, k=remainder and we have one less number in our list. \n\n\n\nHere is my code:\n```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n factor = factorial(n-1)\n k -= 1 # index starts from 1 in the question but our list indexs starts from 0\n ans = []\n numbers_left = list(range(1,n+1))\n \n for m in range(n-1,0,-1):\n index = int(k // factor)\n ans += str(numbers_left[index])\n numbers_left.pop(index)\n k %= factor\n factor /= m\n \n ans += str(numbers_left[0])\n return \'\'.join(ans)\n```\n\n**Tips:**\n* Don\'t make ```ans``` a string because strings are not modified in place. It creates another copy of the string which makes your code slower. Instead of string, use a list which is pretty easy to append at the end, and then concatenate them in the end with join function. | 23 | 0 | ['Python', 'Python3'] | 2 |
permutation-sequence | Java Solution With Complete Explanation | java-solution-with-complete-explanation-f9o1f | \nSolution 1: Brute Force Solution\n\nApproach: \n\nThe extreme naive solution is to generate all the possible permutations of the given sequence. This is ach | ananya19 | NORMAL | 2022-09-10T12:05:34.147469+00:00 | 2022-09-17T18:34:26.379859+00:00 | 1,589 | false | \n**Solution 1: Brute Force Solution**\n\n**Approach:** \n\nThe extreme naive solution is to generate all the possible permutations of the given sequence. This is achieved using recursion and every permutation generated is stored in some other data structure (here we have used a vector). Finally, we sort the data structure in which we have stored all the sequences and return the Kth sequence from it.\n\n```\nimport java.util.*;\npublic class Main {\n static void swap(char s[], int i, int j) {\n char ch = s[i];\n s[i] = s[j];\n s[j] = ch;\n }\n static void permutationHelper(char s[], int index, ArrayList < String > res) {\n if (index == s.length) {\n String str = new String(s);\n\n res.add(str);\n return;\n }\n for (int i = index; i < s.length; i++) {\n swap(s, i, index);\n permutationHelper(s, index + 1, res);\n swap(s, i, index);\n }\n }\n\n static String getPermutation(int n, int k) {\n String s = "";\n ArrayList < String > res = new ArrayList < > ();\n for (int i = 1; i <= n; i++) {\n s += i;\n }\n permutationHelper(s.toCharArray(), 0, res);\n Collections.sort(res);\n\n return res.get(k);\n\n }\n public static void main(String args[]) {\n int n = 3, k = 3;\n String ans = getPermutation(n, k);\n System.out.println("The Kth permutation sequence is " + ans);\n }\n}\n```\n\n**Output:**\n\nThe Kth permutation sequence is 213\n\n**Time complexity: O(N! * N) +O(N! Log N!)**\n\n**Reason**: The recursion takes O(N!) time because we generate every possible permutation and another O(N) time is required to make a deep copy and store every sequence in the data structure. Also, O(N! Log N!) time required to sort the data structure\n\n**Space complexity: O(N) **\n\n*Reason: Result stored in a vector, we are auxiliary space taken by recursion*\n\n**Solution 2: (Optimal Approach)**\n\nSay we have N = 4 and K = 17. Hence the number sequence is {1,2,3,4}. \n\n**Intuition -**\n\nI am following 0 - indexing so if K = 17, i.e., the answer is 16th permutation.\nStore n numbers in a list -> [1, 2, 3, 4]\nSince this is a permutation we can assume that there are four positions that need to be filled using the four numbers of the sequence. \nFirst, we need to decide which number is to be placed at the first index. Once the number at the first index is decided we have three more positions and three more numbers. Now the problem is shorter\nWe can repeat the technique that was used previously until all the positions are filled.\n\n**Approach:** \n\n**STEP 1**:\n\nMathematically speaking there can be 4 variations while generating the permutation. We can have our permutation starting with either 1 or 2 or 3 or 4. If the first position is already occupied by one number there are three more positions left. The remaining three numbers can be permuted among themselves while filling the 3 positions and will generate 3! = 6 sequences. Hence each block will have 6 permutations adding up to a total of 6*4 = 24 permutations. If we consider the sequences as 0-based and in the sorted form we observe:- \n\nThe 0th \u2013 5th permutation will start with 1 \nThe 6th \u2013 11th permutation will start with 2\nThe 12th \u2013 17th permutation will start with 3 \nThe 18th \u2013 23rd permutation will start with 4.\n (For better understanding refer to the picture below.) \n\n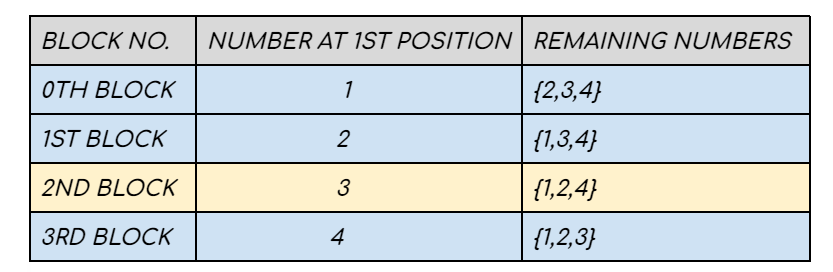\n\n\nWe make K = 17-1 considering 0-based indexing. Since each of the four blocks illustrated above comprises 6 permutations, therefore, the 16th permutation will lie in (16 / 6 ) = 2nd block, and our answer is the (16 % 6) = 4th sequence from the 2nd block. Therefore 3 occupies the first position of the sequence and K = 4.\n\n\n\n**STEP 2:**\n\nOur new search space comprises three elements {1,2,4} where K = 4 . Using the previous technique we can consider the second position to be occupied can be any one of these 3 numbers. Again one block can start with 1, another can start with 2 and the last one can start with 4 . Since one position is fixed, the remaining two numbers of each block can form 2! = 2 sequences. In sorted order :\n\nThe 0th \u2013 1st sequence starts with 1 \nThe 2nd \u2013 3rd sequence starts with 2 \nThe 4th \u2013 5th sequence starts with 4\n[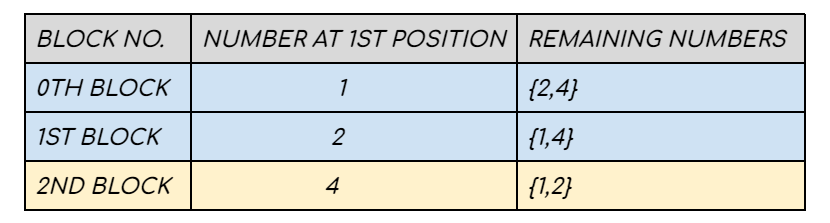\n](http://)\n\nThe 4th permutation will lie in (4/2) = 2nd block and our answer is the 4%2 = 0th sequence from the 2nd block. Therefore 4 occupies the second position and K = 0.\n\n\n\n**STEP 3:**\n\nThe new search space will have two elements {1 ,2} and K = 0. One block starts with 1 and the other block starts with 2. The other remaining number can form only one 1! = 1 sequence. In sorted form \u2013\n\nThe 0th sequence starts with 1 \nThe 1st sequence. starts with 2\n\n\nThe 0th permutation will lie in the (0/1) = 0th block and our answer is the 0%1 = 0th sequence from the 0th block. Therefore 1 occupies the 3rd position and K = 0.\n[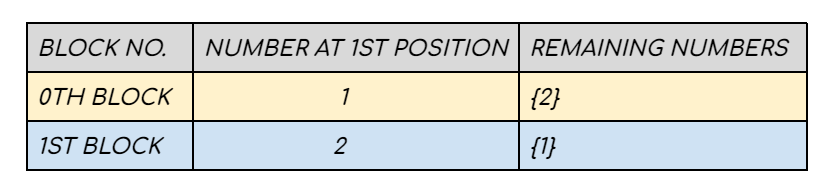\n](http://)\n\n\n**STEP 4**: \n\nNow the only block has 2 in the first position and no remaining number is present.\n\n[\n](http://)\nThis is the point where we place 2 in the last position and stop.\n\n\nThe final answer is "3412".\n\n**Code-**\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n\t k = k - 1; // following 0 indexing if k = 3 it means 2nd permutation is the ans\n String ans = "";\n // create a list to store all the numbers till n\n List<Integer> list = new ArrayList<>();\n int fact = 1; \n for(int i = 1; i <= n-1; i++) {\n fact = fact * i;\n list.add(i); // this will store numbers from 1 to n-1\n }\n list.add(n); // add n to list\n // running an infinte loop\n while (true) {\n ans = ans + list.get (k / fact);\n list.remove (k / fact);\n if (list.size() == 0) {\n break;\n }\n k = k % fact;\n fact = fact / list.size();\n }\n return ans;\n }\n}\n```\n\n**Time Complexity: O(N) * O(N) = O(N^2)**\n\nReason: We are placing N numbers in N positions. This will take O(N) time. For every number, we are reducing the search space by removing the element already placed in the previous step. This takes another O(N) time.\n\n**Space Complexity: O(N) **\n\nReason: We are storing the numbers in a data structure(here vector)\n\n**Do Upvote :)** | 19 | 0 | ['Java'] | 3 |
permutation-sequence | ✅C++✅||😁Hinglish||👍Easy-Explanation👌|| Recursion😍 || Interview Prep👨💻🔥 | chinglisheasy-explanation-recursion-inte-fwae | Approach\n- Explained properly in the code\n\n# Code\n\nclass Solution\n{\n public:\n \t//Logics\n\n \t//Naive Solution\n \t//1. Maanlo 1,2 | modisanskar5 | NORMAL | 2023-07-13T22:26:38.715468+00:00 | 2023-07-13T22:26:38.715509+00:00 | 1,450 | false | # Approach\n- Explained properly in the code\n\n# Code\n```\nclass Solution\n{\n public:\n \t//Logics\n\n \t//Naive Solution\n \t//1. Maanlo 1,2,3,4 diya hain to ek tareeka to apna tha ki saare permutations nikal lenge like (Permutations 2) then we will find the K the one.\n \t//2. But it is very naive solution so we will look for some optimal solution.\n\n \t//Optimal Solution\n \t//1. Agar ham dhyan se dekhe to hame ek pattern dikhayi dega.\n \t//2. For some range in permuations the position of the numbers are fixed.\n \t//3. So with this pattern we can start from the first index all the way to last index.\n \t//4. Kth sequence pe pata lagayenge ki 1st index pe kya tha, Fir wo num ab use ho gaya to aage use nahin hoga to use erase kar diya.\n \t//5. Yeh saari ranges ke ham blockSize banayenge aur un blockSize mein k ki subpositioning hoti rahegi.\n \t//6. Jab tak K=0 nahin ho jata tab tak yeh sub positioning chalti rahegi.\n //7. blockSize = (n-1)!\n \t//8. Num ki position for some index numbers[k/blockSize] and k = k%blockSize(subpositioning in the bloc), fir num jo use ho gaya use remove karenge to blockSize =(num-2)! use karenge aage.\n \t//blockSize bhi change hoga as the numbers are being removed.\n \t//9.Isi process se ham all the 4 indexes bhar lenge.\n\n \t//EXAMPLE: 1,2,3,4, k=17\n string getPermutation(int n, int k)\n {\n string ans = "";\n vector<int> numbers;\n \t//1-n tak saare numbers store karlenge\n int fact = 1;\n \t//This is the factorial\n for (int i = 1; i <= n; i++)\n {\n fact = fact * i;\t//4!=24\n numbers.push_back(i);\n }\n \t//Now the value of fact is the number of permutations or total ranges.\n \t//Now these ranges can be divided in blocks of blockSizes\n int blockSize = fact / n;\t//blockSize = 24/4 = 6 size ke 4 blocks\n k = k - 1;\t//For 0 based indexing//16\n while (true)\n {\n ans += to_string(numbers[k / blockSize]);\t\n //3,_,_,_\n //3,4,_,_\n //3,4,1,_\n //3,4,1,2\n \t//Index by index answers mein push karenge\n numbers.erase(numbers.begin() + k / blockSize);\n \t//Jo index use ho gayi use remove kar denge\n if (numbers.size() == 0)\n \t//Agar koi index use karne ko hain hi nahin\n {\n break;\n }\n k = k % blockSize;\t//16->4->0\n \t//K is repositioned for remaining numbers \n blockSize = blockSize / numbers.size();\t//6->2->1\n \t//Blocks are also changed according to remaining numbers\n }\n return ans;\n }\n};\n```\n# Complexity\n- Time complexity: $O(n^2)$ `n for placing them in n positions` and another `n for removing from vector`.\n\n- Space complexity: $O(n)$ just a `vector`.\n\nIf you *like* \uD83D\uDC4D this solution do *upvote* \u2B06\uFE0F and if there is any *improvement or suggestion* do mention it in the *comment* section \uD83D\uDE0A.\n\n<p align="center">\n<img src="https://assets.leetcode.com/users/images/1b604300-df68-46aa-a267-71f38463bb89_1684820402.7869222.jpeg" width=\'350\' alt="Upvote Image">\n</p> | 17 | 0 | ['Math', 'Recursion', 'C++'] | 1 |
permutation-sequence | c++ 0ms 100% with algorithm explanation | c-0ms-100-with-algorithm-explanation-by-svhq7 | as we know 4! = 24 = 4*(3!) that means the first layer looks like '1'[][][],'2'[][][],'3'[][][],'4'[][][] then we can search which position number 9 w | somone23412 | NORMAL | 2018-11-09T08:59:18.121727+00:00 | 2018-11-09T08:59:18.121765+00:00 | 2,002 | false | as we know
4! = 24 = 4*(3!)
that means the first layer looks like
'1'[][][],'2'[][][],'3'[][][],'4'[][][]
then we can search which position number 9 will be at this layer:
position = 9/3! = 1.5
and we know the first number position will be [1.5] = 2, which represent '2'[][][],we know the first number is '2'
the remainder is 9%3! = 3
then we use this number enter next layer:
'1'[][],'3'[][],'4'[][]
position = 3/2! = 1.5
[1.5] = 2 which represent '3'[][], we know the second number is '3'
......
repeat until we get remainder 0, that means we need to take Maximum arrangement in this layer.
so reverse and append to result.
sorry my english is pool

```
class Solution {
public:
string getPermutation(int n, int k) {
int d = n-1;
int t = k;
list<char> nums;
string result = "";
for(int i = 1; i <= n; i++){
nums.push_back(i+48);
}
while(t!=0){
int jd = jiecheng(d);
int position = ceil((double)t/jd);
auto it = nums.begin();
for(int i = 0; i< position-1 && it != nums.end(); i++, it++);
result += *it;
nums.remove(*it);
//cout<<t<<" "<<jd<<" "<<position<<" "<<t<<endl;
t = t%jd;
d--;
}
nums.reverse();
for(auto it = nums.begin(); it != nums.end(); it++){
result += *it;
}
return result;
}
int jiecheng(int n){
if(n == 0)return 1;
int sum = n;
while(--n > 0) sum*=n;
return sum;
}
};
```
| 16 | 0 | [] | 4 |
permutation-sequence | Editorial Easy Explanation! | editorial-easy-explanation-by-akshay0406-r3x6 | *using some maths\n*for ex: you have n = 4\nthen there will be 4! permutations and k=17\nthen if we are using 0 based index then we have to find 16th index\nNow | Akshay0406 | NORMAL | 2021-07-01T19:31:33.576811+00:00 | 2021-07-01T19:31:33.576857+00:00 | 891 | false | # ****using some maths\n**for ex: you have n = 4\nthen there will be 4! permutations and k=17\nthen if we are using 0 based index then we have to find 16th index\nNow as it is lexicographically sorted\nthen first digit 1 , other digits {2,3,4} permutations then\nfirst digit 2 , other digits {1,3,4} perm then\nfirst digit 3 , other digits{1,2,4}+ {}\nfirst digit 4 , other digits{1,2,3}**\n**Now for {1,3,4} there will be 3! = 6 perm\nand so on for other 3\nso if we have to find 16 it will start from 3 as 0-5 start from 1\n6-11 start from 2 12-17 start from 3 and 18-23 from 4\nNow as we fixed first place as 3,___,___,___\nWe will find second place digit which will be \n1 {2,4} perms + 2{1,4} perms + 4{1,2} perms\nNow {2,4} will be 2! perms i.e 2 so first two will start from 1 next two from 2 and last two from 4 we have to find 16-12 ->4th term which will start from 4 because 0based indexing(0,1,2,3,4)\nso Now 3,4,___,____ two digits left to find \n1{2} and 2{1} NOw 12 + 4 16 gone 17th term is 1{2} \nso 3,4,1,2\nSimple formula if n=4 start from 3! ,2!,1!\n k=17 first index will be k/3!\n\t\t\t\t\tand next k will be k%3!\n\t\t\t\t\tNow you can see from code you will understand it easily:**\n\n\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n ArrayList<Integer> arr = new ArrayList<>();\n int fact=1;\n for(int i=1;i<n;i++){\n fact=fact*i;\n arr.add(i);\n }\n arr.add(n);\n k=k-1;\n String ans="";\n while(true){\n int i1 = k/fact;\n int i2 = k%fact;\n ans+=arr.get(i1);\n arr.remove(i1);\n k=i2;\n if(arr.size()==0){\n break;\n }\n fact=fact/arr.size();\n }\n return ans;\n }\n}\n```\n# ****Do upvote!!\n | 15 | 0 | ['Math', 'Java'] | 2 |
permutation-sequence | C++ easy with next_permutation | c-easy-with-next_permutation-by-oleksam-fmya | \n// Please, Upvote :-)\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string s = "";\n for (int i = 1; i <= n; i++)\n | oleksam | NORMAL | 2020-06-20T09:40:26.596592+00:00 | 2020-06-20T09:40:26.596628+00:00 | 1,158 | false | ```\n// Please, Upvote :-)\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string s = "";\n for (int i = 1; i <= n; i++)\n s += to_string(i);\n int curPerm = 1;\n while (curPerm < k) {\n curPerm++;\n next_permutation(s.begin(), s.end());\n }\n return s;\n }\n};\n```\n | 15 | 5 | ['C', 'C++'] | 1 |
permutation-sequence | Python concise solution | python-concise-solution-by-oldcodingfarm-x2p9 | \n # TLE\n def getPermutation(self, n, k):\n nums = range(1, n+1)\n for i in xrange(k-1):\n self.nextPermutation(nums)\n r | oldcodingfarmer | NORMAL | 2015-09-08T11:14:16+00:00 | 2015-09-08T11:14:16+00:00 | 3,339 | false | \n # TLE\n def getPermutation(self, n, k):\n nums = range(1, n+1)\n for i in xrange(k-1):\n self.nextPermutation(nums)\n return "".join(map(str, nums))\n \n def nextPermutation(self, nums):\n l = d = m = len(nums)-1\n while l > 0 and nums[l] <= nums[l-1]:\n l -= 1\n if l == 0:\n nums.reverse()\n return \n k = l-1\n while nums[k] >= nums[d]:\n d -= 1\n nums[k], nums[d] = nums[d], nums[k]\n while l < m:\n nums[l], nums[m] = nums[m], nums[l]\n l += 1; m -= 1\n \n # AC\n def getPermutation(self, n, k):\n res, nums = "", range(1, n+1)\n k -= 1\n while n:\n n -= 1\n index, k = divmod(k, math.factorial(n))\n res += str(nums.pop(index))\n return res | 14 | 1 | ['Python'] | 0 |
permutation-sequence | C++, backtracking / STL / Math solutions | c-backtracking-stl-math-solutions-by-zef-0vii | Solution 1. Backtracking\n\nRun Time: 266ms\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string s = "", res = "";\n f | zefengsong | NORMAL | 2017-09-06T04:15:21.964000+00:00 | 2017-09-06T04:15:21.964000+00:00 | 1,511 | false | **Solution 1.** Backtracking\n\nRun Time: 266ms\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string s = "", res = "";\n for(int i = 1; i <= n; i++) s.push_back(i + '0');\n string path = s;\n int count = 0;\n DFS(s, 0, count, n, k, path, res);\n return res;\n }\n \n void DFS(string& s, int pos, int& count, int n, int k, string& path, string& res){\n if(count >= k || pos == n){\n if(++count == k) res = path;\n return;\n }\n for(int i = 0; i < n; i++){\n if(s[i] == '0') continue;\n path[pos] = s[i];\n s[i] = '0';\n DFS(s, pos + 1, count, n, k, path, res);\n s[i] = path[pos];\n }\n }\n};\n```\n***\n**Solution 2.** Using STL\n\nRun Time: 119ms\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string s = "";\n for(int i = 1; i <= n; i++) s.push_back(i + '0');\n while(--k) next_permutation(s.begin(), s.end());\n return s;\n }\n};\n```\n***\n**Solution 3.** Math. C++ version of this [thread](https://discuss.leetcode.com/topic/17348/explain-like-i-m-five-java-solution-in-o-n)\n\nRun Time: 3ms\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string s = "", res = "";\n vector<int>factorial(n + 1, 1);\n int sum = 1;\n for(int i = 1; i <= n; i++){\n s.push_back(i + '0');\n sum *= i;\n factorial[i] = sum;\n }\n k--;\n for(int i = 1; i <= n; i++){\n int index = k / factorial[n - i];\n res.push_back(s[index]);\n s.erase(s.begin() + index);\n k %= factorial[n - i];\n }\n return res;\n }\n};\n``` | 14 | 0 | ['C++'] | 0 |
permutation-sequence | ✅ [Solution] Swift: Permutation Sequence (+ test cases) | solution-swift-permutation-sequence-test-kua2 | swift\nclass Solution {\n func getPermutation(_ n: Int, _ k: Int) -> String {\n var numbers = [Int](1...n)\n var k = k, factorial = 1, diff = n | AsahiOcean | NORMAL | 2022-02-02T08:58:24.340469+00:00 | 2022-02-02T08:58:24.340496+00:00 | 935 | false | ```swift\nclass Solution {\n func getPermutation(_ n: Int, _ k: Int) -> String {\n var numbers = [Int](1...n)\n var k = k, factorial = 1, diff = n - 1, result = ""\n \n for i in 1..<n { factorial *= i }\n \n for _ in 0..<n {\n for (i, num) in numbers.enumerated() {\n if k > factorial {\n k -= factorial\n } else {\n result += String(num)\n numbers.remove(at: i)\n break\n }\n }\n if diff > 1 {\n factorial /= diff\n diff -= 1\n }\n }\n return result\n }\n}\n```\n\n---\n\n<p>\n<details>\n<summary>\n<img src="https://git.io/JDblm" height="24">\n<b>TEST CASES</b>\n</summary>\n\n<p><pre>\n<b>Result:</b> Executed 3 tests, with 0 failures (0 unexpected) in 0.012 (0.014) seconds\n</pre></p>\n\n```swift\nimport XCTest\n\nclass Tests: XCTestCase {\n \n private let solution = Solution()\n \n func test0() {\n let value = solution.getPermutation(3, 3)\n XCTAssertEqual(value, "213")\n }\n \n func test1() {\n let value = solution.getPermutation(4, 9)\n XCTAssertEqual(value, "2314")\n }\n \n func test2() {\n let value = solution.getPermutation(3, 1)\n XCTAssertEqual(value, "123")\n }\n}\n\nTests.defaultTestSuite.run()\n```\n\n</details>\n</p> | 12 | 0 | ['Swift'] | 0 |
permutation-sequence | 💡JavaScript Solution | javascript-solution-by-aminick-bovz | The idea\n1. Some facts about permutation:\n\t* For n, it has n! permutations\n2. Use k to find which permutation set it\'s in, and keep deciding inner permutat | aminick | NORMAL | 2020-02-06T07:03:02.321497+00:00 | 2020-02-06T07:03:02.321551+00:00 | 1,281 | false | ### The idea\n1. Some facts about permutation:\n\t* For `n`, it has `n!` permutations\n2. Use `k` to find which permutation set it\'s in, and keep deciding inner permutation sets.\n\n```\nn = 4, k = 9\n```\n\n| Current K: 9 | | | |\n|--------------|-------------|-------------------|--------|\n| Lead Number | Permutation | # of Permutations | |\n| 1 | [2,3,4] | 3! = 6 | |\n| 2 | [1,3,4] | 3! = 6 | <----- |\n| 3 | [1,2,4] | 3! = 6 | |\n| 4 | [1,2,3] | 3! = 6 | |\n\n| Current K: 3 | | | |\n|--------------|-------------|-------------------|--------|\n| Lead Number | Permutation | # of Permutations | |\n| 1 | [3,4] | 2! = 2 | |\n| 3 | [1,4] | 2! = 2 | <----- |\n| 4 | [1,2] | 2! = 2 | |\n\n| Current K: 1 | | | |\n|--------------|-------------|-------------------|--------|\n| Lead Number | Permutation | # of Permutations | |\n| 1 | [4] | 1! = 1 | <----- |\n| 4 | [1] | 1! = 1 | |\n\n| Current K: 0 | | | |\n|--------------|-------------|-------------------|--------|\n| Lead Number | Permutation | # of Permutations | |\n| 4 | [] | | <----- |\n\n``` javascript\n/**\n * @param {number} n\n * @param {number} k\n * @return {string}\n */\nvar getPermutation = function(n, k) {\n let factorial = [1];\n for (let i=1;i<=n;i++) factorial[i]= i * factorial[i-1];\n\n let nums = Array.from({length: n}, (v, i) => i+1);\n let res = "";\n for (let i=n;i>0;i--) {\n index = Math.ceil(k / factorial[i - 1]); // decide to use which permutation set\n res+=nums[index - 1];\n nums.splice(index - 1, 1);\n k -= (factorial[i-1] * (index - 1));\n }\n return res;\n};\n``` | 11 | 0 | ['JavaScript'] | 3 |
permutation-sequence | PYTHON3 CLEAN CODE| BEAT 90% TIME AND SPACE| MATH | python3-clean-code-beat-90-time-and-spac-kve7 | Intuition\n Describe your first thoughts on how to solve this problem. \nThis is one of the most interesting problems I\'ve ever solved. Using mathematical, rec | vietz22 | NORMAL | 2024-04-02T04:36:16.868702+00:00 | 2024-04-02T04:36:16.868734+00:00 | 825 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is one of the most interesting problems I\'ve ever solved. Using mathematical, recursion and greedy effectively. You can jump into the Dry Run for a better understand\nThis is a more detail explaination from @UtkarshDubey_19\n\n# Formula\n\n\n\n\n# Approach\n1. Make a function ```factorial(n)``` to find n!\n2. One more function ```get_sequence(n,k)``` to find index sequence. It will help us to find the index of elements in the result. \n+ ```seq``` : the result requence \n+ Reverse iterable (n-1) times to find each quotient corresspoding each ```factorial(i)```, then append it to ```seq```\n+ Return ```seq```\n3. Initialize empty string ```res``` to save result, ```array = [\'1\', \'2\', \'3\', ..., \'n\']``` to choice what char will next add to res by ```seq```\n4. Run while loop when ```seq``` is not empty :\n+ Pop left the ```seq``` to get the current index\n+ Add ```array[index]``` to ```res``` , then delete it from the array\n5. After the loop, the ```array``` will contain one last element, add it to the end of ```res``` and return \n\n# Dry run \nWith ```n = 5 ```and ``k = 35``. We need to find the 35th permuation of the five character of the set ```[1,2,3,4,5]```\n\n\n\n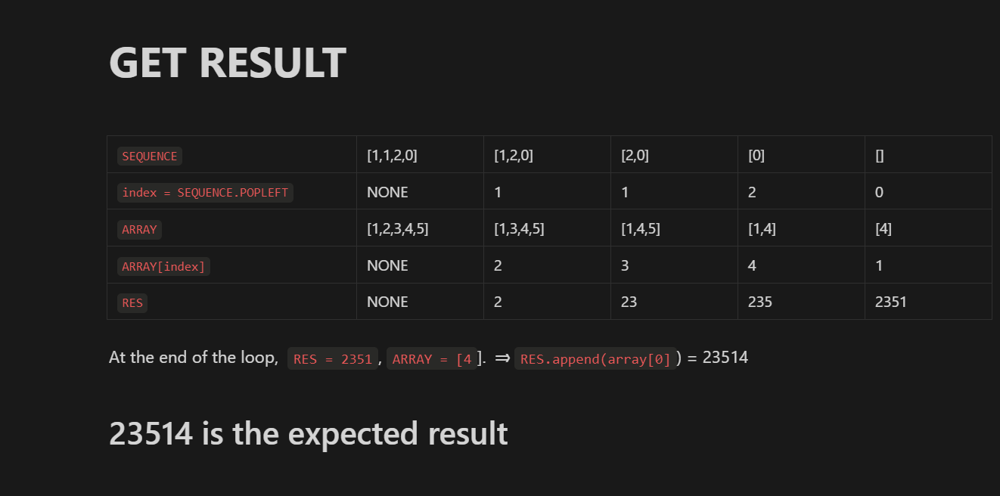\n# Code\n```\ndef factorial(n):\n if n == 0 : return 1\n return n*factorial(n-1)\n\ndef get_sequence(n,k):\n seq = []\n k = k - 1\n for i in range(n-1,0,-1):\n quotient,remainder = k//factorial(i),k%factorial(i)\n seq.append(quotient)\n k = remainder\n return seq\n\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n sequene = get_sequence(n,k)\n res = \'\'\n array = [str(i) for i in range(1,n+1)]\n while sequene :\n index = sequene.pop(0)\n res +=array[index]\n del array[index]\n res +=array[0]\n return res \n \n\n```\n\n | 10 | 0 | ['Math', 'Greedy', 'Recursion', 'Python3'] | 2 |
permutation-sequence | C++ next_permutation||Best O(n log n) by set beats 100% | c-next_permutationbest-on-log-n-by-set-b-ck2u | Intuition\n Describe your first thoughts on how to solve this problem. \nC++ STL makes such question so easy. Use iota to create a char array.\nThen use next_pe | anwendeng | NORMAL | 2023-08-28T11:44:21.031888+00:00 | 2023-08-29T04:17:54.877464+00:00 | 1,623 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nC++ STL makes such question so easy. Use iota to create a char array.\nThen use next_permutation k-1 times to find the answer!\n\nnext_permutation takes $O(n)$ time to find the next permutation.\n\nThe second method does not use next_permutation, but calculates the permutations by successively using divisions over factorials. \n\nFor fast performance, the C++ set (ordered set) is used A recurive version and an iterative version are provided. Both of them beat 100% with runtime 0 ms!\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English if necessary]\n[https://youtu.be/D__GqhWbfQQ?si=b49DiSKWli7U-2UV](https://youtu.be/D__GqhWbfQQ?si=b49DiSKWli7U-2UV)\n# Why using set not array?\nBecause in the code, it is necessary to erase elements from container in the middle. If array is used, the time for it is $O(n)$ which is too costly. An erase and an insert cost $O(\\log n)$, it is the right data structure for implementation.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n \\log n)$$ for 2nd and 3rd solutions\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code using next_permutation which is slow but accepted\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<char> S(n);\n iota(S.begin(), S.end(), \'1\');\n for(int i=1; i<k; i++)\n next_permutation(S.begin(), S.end()); \n return string(S.begin(), S.end());\n }\n};\n```\n# Code computing the permutations by successively using divisions over factorials beats 100% with runtime 0 ms\n```\nclass Solution {\npublic:\n vector<int> factorial;\n string Permutation(set<int>& nums, int n, int k) {\n if (n == 1) \n return to_string(*nums.begin());\n\n int index =k/ factorial[n-1];\n k %= factorial[n-1];\n\n auto it = nums.begin();\n advance(it, index); // Move iterator to the index\n int num = *it;\n nums.erase(it);\n\n return to_string(num) + Permutation(nums, n-1, k);\n }\n\n string getPermutation(int n, int k) {\n factorial.assign(n, 1);\n for (int i = 1; i < n; i++) {\n factorial[i]= i*factorial[i-1];\n }\n\n set<int> nums;\n for (int i = 1; i <= n; i++) {\n nums.insert(i);\n }\n --k; // Adjust k to 0-based index\n return Permutation(nums, n, k);\n }\n};\n\n```\n# Code for iterative version\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n\n set<int> nums;\n vector<int> factorial(n+1, 1);\n\n for (int i = 1; i <= n; i++) {\n nums.insert(i);\n factorial[i] = i*factorial[i-1];\n }\n\n --k; // Adjust k to 0-based index\n\n string perm;\n for (int i=n; i >= 1; i--) {\n int index = k/factorial[i-1];\n k%= factorial[i-1];\n auto it=nums.begin();\n advance(it, index); // Move iterator to the index\n perm+= to_string(*it);\n nums.erase(it);//O(log n) time\n }\n return perm;\n }\n};\n\n```\n\n | 10 | 0 | ['Ordered Set', 'C++'] | 1 |
permutation-sequence | ✔️ 100% Fastest Swift Solution | 100-fastest-swift-solution-by-sergeylesc-f4de | \nclass Solution {\n func getPermutation(_ n: Int, _ k: Int) -> String {\n var digitals: [Int] = []\n var res: String = ""\n var val = k | sergeyleschev | NORMAL | 2022-04-04T05:32:51.028128+00:00 | 2022-04-04T05:32:51.028154+00:00 | 263 | false | ```\nclass Solution {\n func getPermutation(_ n: Int, _ k: Int) -> String {\n var digitals: [Int] = []\n var res: String = ""\n var val = k\n var m = n\n\n for i in 1...n { digitals.append(i) }\n\n while res.count < n && val > 0 {\n let i = Int(ceil(Double(val) / Double(permutation(m - 1))))\n res += "\\(digitals[i-1])"\n print(i, digitals)\n digitals.remove(at: i - 1)\n val -= (i - 1) * permutation(m - 1)\n m -= 1\n }\n return res\n }\n\n\n func permutation(_ n: Int) -> Int {\n guard n > 1 else { return 1 }\n var res = 1\n for i in 1...n { res *= i }\n return res\n }\n \n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful. | 10 | 1 | ['Swift'] | 0 |
permutation-sequence | Java beats 100% | java-beats-100-by-deleted_user-sfu8 | Java beats 100%\n\n\n\n\n# Code\n\nclass Solution {\n private static int[] fact = {0, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n \n private String | deleted_user | NORMAL | 2024-05-14T11:21:30.349569+00:00 | 2024-05-14T11:21:30.349601+00:00 | 1,332 | false | Java beats 100%\n\n\n\n\n# Code\n```\nclass Solution {\n private static int[] fact = {0, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n \n private String getPermutation(int n, int k, boolean[] nums, char[] str, int index) {\n int i = 0, m = nums.length;\n if(n == 1) {\n while(i < m && nums[i]) ++i;\n str[index++]=(char)(\'0\'+i+1);\n return String.valueOf(str);\n }\n if(k == 0) {\n while(i < m) {\n if(!nums[i]) str[index++]=(char)(\'0\'+i+1);\n ++i;\n }\n return String.valueOf(str);\n }\n \n int div = k/fact[n-1], mod = k%fact[n-1], j = -1;\n while(i < m-1 && div != j) {\n if(!nums[i]) ++j;\n if(j == div) break;\n ++i;\n }\n str[index++]=(char)(\'0\'+i+1);\n if(i < m) nums[i]=true;\n return getPermutation(n-1, mod, nums, str, index); \n }\n\n public String getPermutation(int n, int k) {\n boolean[] nums = new boolean[n];\n char[] charArr = new char[n];\n return getPermutation(n, k-1, nums, charArr, 0);\n }\n}\n``` | 9 | 0 | ['Java'] | 0 |
permutation-sequence | O(1) time complexity god solution | o1-time-complexity-god-solution-by-suraj-xjzv | \nclass Solution {\n public String getPermutation(int n, int k) {\n\t\tint[] a3={123, 132, 213, 231, 312, 321};\n\t\tint[] a4={1234, 1243, 1324, 1342, 1423, | SurajAg | NORMAL | 2023-06-27T20:31:40.119321+00:00 | 2023-06-27T20:35:58.827472+00:00 | 2,285 | false | ```\nclass Solution {\n public String getPermutation(int n, int k) {\n\t\tint[] a3={123, 132, 213, 231, 312, 321};\n\t\tint[] a4={1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321};\n\t\tint[] a5={12345, 12354, 12435, 12453, 12534, 12543, 13245, 13254, 13425, 13452, 13524, 13542, 14235, 14253, 14325, 14352, 14523, 14532, 15234, 15243, 15324, 15342, 15423, 15432, 21345, 21354, 21435, 21453, 21534, 21543, 23145, 23154, 23415, 23451, 23514, 23541, 24135, 24153, 24315, 24351, 24513, 24531, 25134, 25143, 25314, 25341, 25413, 25431, 31245, 31254, 31425, 31452, 31524, 31542, 32145, 32154, 32415, 32451, 32514, 32541, 34125, 34152, 34215, 34251, 34512, 34521, 35124, 35142, 35214, 35241, 35412, 35421, 41235, 41253, 41325, 41352, 41523, 41532, 42135, 42153, 42315, 42351, 42513, 42531, 43125, 43152, 43215, 43251, 43512, 43521, 45123, 45132, 45213, 45231, 45312, 45321, 51234, 51243, 51324, 51342, 51423, 51432, 52134, 52143, 52314, 52341, 52413, 52431, 53124, 53142, 53214, 53241, 53412, 53421, 54123, 54132, 54213, 54231, 54312, 54321};\n\t\tint[] a6={.........tooo long for leetcode to handle.........};\n\t\tint[] a71={.......... Array in Comment section Down Below.........};\n\t\tint[] a72={........Fun Fact...........};\n\t\tint[] a73={.........Leetcode Array can only store about 1110 elements in it..........};\n\t\tint[] a74={...........thats why i had to devide the permutation of 7 in 5 different arrays......};\n\t\tint[] a75={........do message me on instagram for more codes like this ( @ mr.suraj.agarwal ) ..........};\n if(n==3)return Integer.toString(a3[k-1]);\n if(n==4)return Integer.toString(a4[k-1]);\n if(n==5)return Integer.toString(a5[k-1]);\n if(n==6)return Integer.toString(a6[k-1]);\n if(n==7)\n {\n if(k<a71.length)return Integer.toString(a71[k-1]);\n if(k<a71.length+a72.length)return Integer.toString(a72[k-1-a71.length]);\n if(k<a71.length+a72.length+a73.length)return Integer.toString(a73[k-1-a71.length-a72.length]);\n if(k<a71.length+a72.length+a73.length+a74.length)return Integer.toString(a74[k-1-a71.length-a72.length-a73.length]);\n if(k<a71.length+a72.length+a73.length+a74.length+a75.length)return Integer.toString(a75[k-1-a71.length-a72.length-a73.length-a74.length]);\n }\n if(n==1&&k==1)return "1";\n if(n==2&&k==1)return "12";\n if(n==2&&k==2)return "21";\n if(n==8&&k==31492)return "72641583";\n if(n==9&&k==54494)return "248716395";\n if(n==8&&k==11483)return "32864715";\n if(n==8&&k==15485)return "41623857";\n if(n==9&&k==24)return "123459876";\n if(n==8&&k==37565)return "84213756";\n if(n==9&&k==94626)return "348567921";\n if(n==9&&k==171669)return "531679428";\n if(n==8&&k==13122)return "36247851";\n if(n==9&&k==13531)return "147869235";\n if(n==8&&k==38790)return"85721643" ;\n if(n==9&&k==17223)return "154967328";\n if(n==9&&k==273815)return "783269514";\n if(n==9&&k==2678)return "126847395";\n if (n==8&&k==6593)return "24186735";\n if (n==8 && k==27891) return "64731528";\n if (n==8 && k==17198) return "43826175";\n if (n == 8 && k == 3193) return "16472358";\n if (n == 8 && k == 20545) return "51632478";\n if (n == 8 && k == 39532) return "86731452";\n if (n == 8 && k == 35784) return "81627543";\n if (n == 9 && k == 278082) return "792346851";\n if(n==8&&k==15025)return "38721456";\n if(n==8&&k==13801)return "37214568";\n if(n==9&&k==331987)return "928157346";\n if(n==8&&k==5081)return"21357846" ;\n if(n==9&&k==135401)return "439157826";\n if(n==9&&k==219601)return"647123589" ;\n if(n==9&&k==199269)return "594738216";\n if(n==8&&k==30654)return"71542863" ;\n if(n==9&&k==37098)return "194627853";\n if(n==9&&k==206490)return "619754832";\n if(n==8&&k==1715)return "14536827";\n if(n==8&&k==6927)return "24715863";\n if(n==8&&k==6972)return "24715863";\n if(n==9&&k==62716)return "265183794";\n if(n==8&&k==4266)return "17845632";\n if(n==8&&k==12528)return "35428761";\n if(n==8&&k==13219)return "36418257";\n if(n==8&&k==29805)return "68327415";\n if(n==8&&k==39705)return "87163425";\n if(n==9&&k==136371)return "451672839";\n if(n==9&&k==24479)return"168975423" ;\n if(n==9&&k==78494)return "296137485";\n if(n==9&&k==305645)return "856412937";\n if(n==9&&k==278621)return "792861534";\n if(n==8&&k==27104)return "63582174";\n if(n==8&&k==33856)return "76125483";\n if(n==9&&k==196883)return "591473826";\n if(n==9&&k==116907)return "392541768";\n if(n==9&&k==138270)return "456132987";\n if(n==9&&k==161191)return "498723156";\n if(n==9&&k==15198)return "41273865";\n if(n==8&&k==15198)return "41273865";\n if(n==8&&k==6192)return "23658741";\n if(n==8&&k==1907)return "14683725";\n if(n==8&&k==16959)return "43625871";\n if(n==8&&k==16956)return "43625871";\n if(n==9&&k==217778)return "642591387";\n if(n==9&&k==13596)return "147935862";\n if(n==8&&k==27428)return "64158273";\n if(n==8&&k==33720)return "75684321";\n if(n==9&&k==353955)return "972561438";\n if(n==9&&k==278893)return "793416258";\n if(n==9&&k==155915)return "489523716";\n if(n==8&&k==29382)return "67581432";\n if(n==8&&k==26592)return "62847531";\n if(n==9&&k==28533)return "176589324";\n if(n==9&&k==25996)return "173284695";\n if(n==9&&k==296662)return "839127564";\n if(n==8&&k==15700)return "41782563";\n if(n==8&&k==1047)return "13576428";\n if(n==8&&k==29499)return "67851324";\n if(n==9&&k==101134)return "361589472";\n if(n==8&&k==39545)return "86734512";\n if(n==9&&k==233794)return "683724591";\n if(n==8&&k==3656)return "17254386";\n if(n==8&&k==22602)return "54327861";\n if(n==8&&k==25212)return "61235874";\n if(n==8&&k==21092)return "52378164";\n if(n==9&&k==214267)return "635749128";\n if(n==8&&k==8590)return "26847351";\n return "213";\n }\n}\n```\n\n[]https://leetcode.com/problems/pascals-triangle/discuss/3638748/O(1)-time-complexity-god-solution\nprevious code leetcode 118. Pascal\'s Triangle | 9 | 2 | ['Java'] | 20 |
permutation-sequence | An efficient Java solution, without extra space or previous calculation of factorial | an-efficient-java-solution-without-extra-6v6p | This problem consists of two parts.\n\nPart one, find the array A[0..n-1] that satisfies:\n\nk-1 = (n-1)!A[0] + (n-2)!A[1] + ... + 2!A[n-3] + 1!A[n-2] | vision57 | NORMAL | 2014-12-24T08:31:27+00:00 | 2014-12-24T08:31:27+00:00 | 4,246 | false | This problem consists of two parts.\n\nPart one, find the array A[0..n-1] that satisfies:\n\n**k-1 = (n-1)!*A[0] + (n-2)!*A[1] + ... + 2!*A[n-3] + 1!*A[n-2] + 0!*A[n-1]**\n\nand **0 <= A[i] < n-i** (so the last item in the formula above is always 0).\n\nIt's obvious that the array A[0..n-1] can be calculated either from 0 to n-1 or reversely. In order to avoid previous calculation of factorial, A[0..n-1] is calculated from end to start here.\n\nPart two, translate A[0..n-1] into final sequence number. A[0..n-1] can be translated from end to start step by step, just like the mathematical solution of Joseph Circle.\n\n public class Solution {\n public String getPermutation(int n, int k) {\n \t\tk--;\n \t\tint fact = 1;\n \t\tchar[] result = new char[n];\n \t\tresult[n - 1] = '1';\n \t\tfor (int i = 2; i <= n; i++) {\n \t\t\tfact *= i;\n \t\t\tresult[n - i] = (char) (k % fact * i / fact + '1');\n \t\t\tfor (int j = n - i + 1; j < n; j++) {\n \t\t\t\tresult[j] += result[j] >= result[n - i] ? 1 : 0;\n \t\t\t}\n \t\t\tk -= k % fact;\n \t\t}\n \t\treturn new String(result);\n }\n } | 9 | 0 | ['Java'] | 1 |
permutation-sequence | Permutation Sequence [C++] | permutation-sequence-c-by-moveeeax-vy1r | IntuitionThe problem involves generating permutations of numbers in lexicographic order, and the key is to directly compute the k-th permutation without generat | moveeeax | NORMAL | 2025-01-18T09:31:45.262009+00:00 | 2025-01-18T09:31:45.262009+00:00 | 1,233 | false | # Intuition
The problem involves generating permutations of numbers in lexicographic order, and the key is to directly compute the k-th permutation without generating all permutations explicitly. This is achieved using factorials to determine the placement of digits.
# Approach
1. Precompute factorials for efficient computation of permutations.
2. Create a list of numbers from `1` to `n`.
3. Adjust `k` to be zero-indexed.
4. Iteratively:
- Compute the index of the current digit by dividing `k` by the factorial of remaining positions.
- Append the corresponding number to the result.
- Remove the used number from the list.
- Update `k` using the modulo operation and recompute the factorial for the next iteration.
5. Continue until all numbers are used.
# Complexity
- **Time complexity**:
- $$O(n^2)$$: Factorial computation is $$O(1)$$, but removing elements from a list is $$O(n)$$, which is repeated for all digits.
- **Space complexity**:
- $$O(n)$$: Space is used for the `nums` vector and the result string.
# Code
```cpp
class Solution {
public:
string getPermutation(int n, int k) {
int fact = 1;
vector<int> nums;
for (int i = 1; i < n; i++) {
fact *= i;
nums.push_back(i);
}
nums.push_back(n);
k -= 1;
string ans = "";
while (!nums.empty()) {
int index = k / fact;
ans += to_string(nums[index]);
nums.erase(nums.begin() + index);
if (nums.empty()) break;
k %= fact;
fact /= nums.size();
}
return ans;
}
};
``` | 8 | 0 | ['C++'] | 0 |
permutation-sequence | Backtracking recursion base solution in C++ | backtracking-recursion-base-solution-in-oqhcc | class Solution {\npublic:\n int cnt = 0; // counting the number of permutations done\nint helper(int n, int k, string &s, int p[])\n {\n if(s.size( | animesh_karmakar-46 | NORMAL | 2019-09-28T16:09:57.878941+00:00 | 2019-09-28T16:09:57.878991+00:00 | 1,627 | false | ``` class Solution {\npublic:\n int cnt = 0; // counting the number of permutations done\nint helper(int n, int k, string &s, int p[])\n {\n if(s.size() == n) {\n cnt += 1;\n // cnt is receive to k so flash all function from call stack \n if(cnt == k) {\n return 0;\n }\n return 1;\n }\n \n for(int i = 0; i < n; i++) {\n if(p[i]) continue;\n p[i] = 1;\n s.push_back(char(i + 1 + 48));\n if(helper(n, k, s, p) == 0) return 0;\n p[i] = 0;\n s.pop_back();\n }\n return 1;\n }\n string getPermutation(int n, int k) {\n string ans;\n int p[n] = {0}; // to trace the position\n helper(n, k, ans, p);\n return ans;\n }\n};``` | 8 | 0 | ['Backtracking', 'Recursion'] | 2 |
permutation-sequence | Share my easy understand solution with comments - Java | share-my-easy-understand-solution-with-c-j8tk | public int nFatorial(int n ) {\n \tif(n == 0)\n \t\treturn 1;\n \treturn n * nFatorial(n - 1);\n }\n \n public String getPermuta | liwang | NORMAL | 2015-02-25T19:45:55+00:00 | 2015-02-25T19:45:55+00:00 | 4,827 | false | public int nFatorial(int n ) {\n \tif(n == 0)\n \t\treturn 1;\n \treturn n * nFatorial(n - 1);\n }\n \n public String getPermutation(int n, int k) {\n \tif(n == 0)\n \t\treturn "";\n \t\n \tString res = "";\n \n \t// numbers to be added to result string\n List<Integer> num = new ArrayList<Integer>();\n \n // initialization, 0 just for padding\n for(int i = 0; i <= n; i++)\n \tnum.add(i);\n \n int factorial;\n int index;\n \n for(int i = n; i > 0; i--) {\n \tfactorial = nFatorial(i - 1);\n \n \t// calculate current number index\n \tindex = (int) Math.ceil(k / (double) factorial);\n \t\n \tres += num.get(index);\n \t\n \t// after adding, delete it from rest set\n \tnum.remove(index);\n \t\n \t// update k for the next loop\n \tk = k % factorial;\n \tif(k == 0)\n \t\tk = factorial;\n }\n return res;\n } | 8 | 0 | [] | 2 |
permutation-sequence | Beats 100% | Explained mathematics in detail | beats-100-explained-mathematics-in-detai-3b3b | IntuitionCode | dikshamehta4214 | NORMAL | 2025-03-25T18:23:35.931207+00:00 | 2025-03-25T18:23:35.931207+00:00 | 433 | false | # Intuition


# Code
```cpp []
class Solution {
public:
string getPermutation(int n, int k) {
vector<int> numbers; //to store all the numers from 1->n
int fact = 1; //factorial calculation
for(int i=1; i<n; i++){
fact = fact * i;
numbers.push_back(i);
}
numbers.push_back(n);
string ans = "";
//to align with 0 index based
k = k-1;
while(1){
// to select the fixed ith index
ans = ans + to_string(numbers[k/fact]);
//delete the chosen number
numbers.erase(numbers.begin() + k/fact);
//break the loop if nothing is left in numbers
if(numbers.size()==0){
break;
}
//to get next iteration k, fact
k = k%fact;
fact= fact / numbers.size();
}
return ans;
}
};
``` | 7 | 0 | ['C++'] | 4 |
permutation-sequence | 2 MS | JAVA | EXPLAINED ✔ | 2-ms-java-explained-by-4ryangautam-fcpu | Intuition\nDivide and conquer\u274C\nRemove and conquer\u2714\n\n# Approach\nIn this code you have to only understand three lines \nlets start with \n1. ans = a | 4ryangautam | NORMAL | 2023-07-23T20:46:01.936891+00:00 | 2023-07-23T20:46:01.936917+00:00 | 1,051 | false | # Intuition\nDivide and conquer\u274C\nRemove and conquer\u2714\n\n# Approach\nIn this code you have to only understand three lines \nlets start with \n1. ans = ans + num.get(k/fact); \nSo lets take an example 1 as example , we have given n = 3 and k = 3\nif we pick 1 then we left with 2 , 3;\nif we pick 2 then we left with 1 , 3;\nas we know permutation of n is n!,when we pick any number then picked number is not counted factorial of remaing number is stored, thats why \n for(int i = 1;i<n;i++){\n fact=fact*i;\nby this our factorial is 2 .\nthere is factorial of n-1.\nlets reduce the k by 1 because we have 0-based indexing , according to 0 based index we need now 2nd permutation\nk = 2.\nnow if we say what is k/fact , which gives us the starting value of our kth permutaion , which means 2/2 is 1 and we have to add 1th index value to our ans , now our ans is updated to 2.\n2. lets understand this k = k % fact, \nas we added 1 th index value to our ans , we have surity that if we pick 1th index then the permutations of remaining 2 elements give us next index to our ans , means\nif we pick 2 then remaing is [1,3] then we have to find kth permutataion from this and so how can we update our k , so can it gives us value what we needed ,\ncurrect k = 2 and fact = 2,after 2 = 2 % 2, we have k = 0,which means we have our remaining value in 0th permutaion of remaining element [1,3].\n3. fact = fact / num.size();\nas we get our first value , so we have to remove it from our list , as we added num.get(k/fact) to our ans , we have to remove it now ,\nby this we removed it num.remove(k/fact); as in previous step we updated our k and elements left 2 so we have to also update our factorial also .\nsee uf we have n =3 then factorial is 6\nn = 2 then factorial is 2\nn= 1 factorial is 1 , \nand we know we will choose 1 value from our n then there is n-1 left , so we have to find factorial of n-1 , you will understand this after this,as we removed 2 we have remaing elements \n[1,3] and k =0\nwe know we will choose one element from this and find permutaions of remaining elements,\n0th = we will choose 1 and find permutaion of [3]\n1th = we will choose 3 and find permutation of [1]\nso why we need factorial of n-1, by this current fact = 2 and after removing 1th index from num size of our list is also 2 .\n2 = 2 / 2 , nothing but 1.\n- Now we are ready to pick our next value new k = 0 , new list size is 2 and fact = 1.\nans = ans + num.get(0/1), so we choose 0th index value from our list and remove it from list , now updated ans is 21.\nAfter this we again update the value of k and fact , by steps i mention earlier new k is also 0 new fact is also 1 and new size of list is 1 , after this only one remaing value in our list is 1 we add it to ans and remove it from list which make list 0 \n if(num.size()==0)break; and when this condition is checkec it break the infintie loop and return the ans .\n\nThank You , if any step i am wrong or unable to make clear concept forgive me \uD83D\uDE4F.\n# Code\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n String ans = "";\n ArrayList<Integer> num = new ArrayList<>();\n int fact = 1;\n for(int i = 1;i<n;i++){\n fact=fact*i;\n num.add(i);\n }\n num.add(n);\n k=k-1;\n while(true){\n ans = ans + num.get(k/fact);\n num.remove(k/fact);\n if(num.size()==0)break;\n k = k % fact;\n fact = fact / num.size();\n }\n return ans;\n }\n}\n``` | 7 | 0 | ['Java'] | 0 |
permutation-sequence | python 20ms clean code. | python-20ms-clean-code-by-texasroh-qg4z | \nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n def fact(n):\n r = 1\n for i in range(2,n+1):\n | texasroh | NORMAL | 2020-02-06T05:03:50.064223+00:00 | 2020-02-06T05:03:50.064265+00:00 | 919 | false | ```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n def fact(n):\n r = 1\n for i in range(2,n+1):\n r *= i\n return r\n \n nums = [str(i) for i in range(1,n+1)]\n s=\'\'\n while(nums):\n div = fact(len(nums)-1)\n idx = 0\n while(k>div):\n idx += 1\n k -= div\n \n s += nums.pop(idx)\n \n return s\n``` | 7 | 0 | ['Python'] | 2 |
permutation-sequence | Java 100%/100% | O(n^2)/O(n) With Explanation | java-100100-on2on-with-explanation-by-ft-9gyh | See code comments for explanation\n\nclass Solution {\n public String getPermutation(int n, int k) {\n // Idea: calculate this by math\n //\n | ftkftw | NORMAL | 2020-01-15T07:33:38.808897+00:00 | 2020-01-15T18:44:16.969736+00:00 | 1,126 | false | See code comments for explanation\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n // Idea: calculate this by math\n //\n // Observation 1: (k - 1) / (n - 1)! + 1 determines\n // which number in [1, n] comes first\n // E.g. If n = 3, k = 3,\n // then (3 - 1) / (3 - 1)! + 1\n // = 2 / 2 + 1\n // = 2\n // Thus, "2xx" would be the answer\n //\n // Observation 2: The "xx" part in "2xx" can be calculated\n // similarly as a subproblem. This is therefore a recursion problem,\n // solvable with the usual dynamic programming/iterative techniques.\n //\n // First, let\'s calculate all factorials from 0 to n - 1\n // Not really needed to calculate 0!, but\n // 1) it helps to calculate 1! and\n // 2) it eliminates the need for special case code\n // when finding the last number in the answer.\n int[] factorials = new int[n];\n factorials[0] = 1;\n \n for (int i = 1; i < factorials.length; ++i) {\n factorials[i] = i * factorials[i - 1];\n }\n \n // Use an array to mark which numbers in [1, n] have already\n // been used in the answer\n // Be mindful of 1-based indexing in question vs. zero-based\n // indexing in code\n boolean[] used = new boolean[n];\n \n // This is the recursive part, solved iteratively\n //\n // Observation 3: Since 0th (first) num can be found via\n // (k - 1) / (n - 1)!, the 1th (second) num can be found\n // similarly using a k\'\n // k\' is the remainder of (k - 1) / (n - 1)!, e.g., what is\n // left over after using the quotient of (k - 1) / (n - 1)!\n // to find the previous index.\n // Let\'s start with k - 1 as the remainder to find the 0th num.\n // Use k - 1 because k is 1-based indexing as phrased in the\n // question but in code we use zero-based indexing.\n int remainder = k - 1;\n \n // Accumulator for answer\n // Use StringBuilder if you want further optimization\n String answer = "";\n \n // Iterate from n - 1 down to 0\n // From observation 2 above\n for (int i = n - 1; i >= 0; --i) {\n // offset is the index of the list of unused nums in [1, n]\n // This is from observation 1 above.\n // For example, if n = 3, k = 3,\n // offset = (3 - 1) / (3 - 1)! = 1\n // 1th num in the list [1, 2, 3] is 2\n int offset = remainder / factorials[i];\n \n // iterate through the used array and find the offset-th unused num\n for (int j = 0; j < used.length; ++j) {\n if (used[j]) {\n continue;\n }\n \n // Algorithm guarantees this will be matched once per loop\n // through the used array.\n //\n // Proof: offset is upper-bounded by i, which decreases by 1\n // every iteration of the outer loop. This is true because\n // remainder cannot exceed factorials[i + 1]. Also, we use one\n // num each iteration of the outer loop, so offset is always\n // less than or equal to the number of unused nums left.\n if (offset == 0) {\n // j is zero-based index, but [1,n] is 1-based\n answer += j + 1;\n used[j] = true;\n break;\n }\n \n --offset;\n }\n \n // From observation 3 above\n remainder %= factorials[i];\n }\n \n return answer;\n }\n}\n```\nTime complexity: O(n^2). Calculating factorials is O(n). Getting the correct num based on offset is upper-bounded at n + (n - 1) + ... + 1 or O(n^2).\nSpace complexity: O(n). Both factorials and used arrays are n length. | 7 | 0 | ['Math', 'Java'] | 0 |
permutation-sequence | Share my 0ms C++ solution with explanation | share-my-0ms-c-solution-with-explanation-mai1 | The question is:\n\nThe set [1,2,3,\u2026,n] contains a total of n ! unique permutations.\n\nBy listing and labeling all of the permutations in order,\nWe get t | kjer | NORMAL | 2016-03-13T04:29:04+00:00 | 2016-03-13T04:29:04+00:00 | 1,358 | false | The question is:\n\nThe **set *[1,2,3,\u2026,n]*** contains a total of ***n !*** ***unique* permutations**.\n\nBy listing and labeling all of the permutations ***in order***,\nWe get the following sequence (ie, for ***n = 3***):\n\n - 1 "***1*** 23"\n - 2 "***1*** 32"\n - 3 "***2*** 13"\n - 4 "***2*** 31"\n - 5 "***3*** 12"\n - 6 "***3*** 21"\n\nGiven ***n*** and ***k***, return the ***kth*** permutation sequence.\n\n**IMPORTANT : note the equation *N ! = N \xd7 (N - 1) !***\n\nHere, ***3 ! = 3 \xd7 2 !***, Let's get into the problem when ***n = 3***.\n\n***First***, we need to get the ***TOP DIGIT***. As listed above, the ***TOP DIGIT*** can be ***1, 2 or 3***.\n\n***1st*** and ***2nd*** 's ***TOP DIGIT*** is ***1***.\n\n***3rd*** and ***4th*** 's ***TOP DIGIT*** is ***2***.\n\n***5th*** and ***6th*** 's ***TOP DIGIT*** is ***3***.\n\nThe total ***n !*** is divided into ***3 parts***.\n\nDo you find some ***regularities*** when ***n = 3***?\n\nIf not, we can ***minus k by 1***, set p = k - 1, and then? \n\n - If ***p / (n - 1) ! = 0 (k = 1 and 2)*** , ***TOP DIGIT*** is ***1***.\n - If ***p/ (n - 1) ! = 1 (k = 3 and 4)*** , ***TOP DIGIT*** is ***2***.\n - If ***p / (n - 1) ! = 2 (k = 5 and 6)*** , ***TOP DIGIT*** is ***3***.\n\nAnd this is the ***FIRST RULE***. \n\n----------\n## FIRST RULE ##\n\n***n !*** can be ***DIVIDED*** into ***n PARTS***, and the ***TOP DIGIT*** of ***pth (starts with 0) PART*** equals to ***p / (n - 1) ! + 1***\n\n----------\n**Q** : how about the ***REST***?\n\n**A** : If the ***FIRST TOP DIGIT*** is determined, the same method can be used to find the ***SECOND TOP DIGIT***, and the ***THIRD TOP DIGIT ......***, but a little bit ***DIFFERENT***.\n\nFor example, if the ***FIRST TOP DIGIT A0*** is determined, \n\nthe total number of ***unique* permutations *STARTS WITH A0*** is ***(n - 1) !***.\n\nAs the ***FIRST RULE***, ***(n - 1) !*** can be ***DIVIDED*** into ***n - 1 PARTS***, and the ***TOP DIGIT*** of ***p' th PART*** equals to ***p' / (n - 2) ! + 1***\n\n**NOTICE**: here ***p'*** is the **INTERNAL** sequence number of the unique permutations which ***starts with A0***\n\n----------\n## SECOND RULE ##\n\n***p'*** is ***p*** in the ***SECOND ROUND***, and ***p' = p % (n - 1) !***\n\nWe can find the ***SECOND TOP DIGIT A1*** by calculate ***p' / (n - 2) ! + 1***,\n\nand ***p*** in the ***THIRD ROUND*** is ***p''***, and ***p'' = p' % (n - 2) !***\n\n***..............................***\n\nThis is the ***SECOND RULE***.\n\n----------\n**Q** : Which number will be used as ***A0, A1, ...* (the *TOP DIGITS*)**?\n\n**A** : At the ***FIRST ROUND***, ***TOP DIGIT A0*** equals to ***p / (n - 1) ! + 1***.\n\nWhen a number in [1,9] is ***USED*** as ***A0***, \n\nwe need to find the ***p' / (n - 2) ! + 1* SMALLEST** number in the ***REST*** to be ***A1***,\n\nand we need to find the ***p'' / (n - 3) ! + 1* SMALLEST** number in the ***REST*** to be ***A2***,\n\n***...................................***\n\n**IMPORTANCE** : To get this, a **size of *9 VECTOR*** should be set as a ***GLOBAL VARIABLE*** (or ***DATA MEMBER***), and let its ***q th*** element to be ***q + 1***\n\nNo matter which number is removed from the vector, its ***q th*** element will ***ALWAYS*** be the ***q th*** ***SMALLEST*** of the rest.\n\n----------\n**Q** : When will the loop ***STOPs***?\n\n**A** : Each round we calculate ***p(m) = p(m - 1) % (n - m) !***,\n\nand there are ***n - m* *DIGITs*** which are **NOT** determined.\n\nIf ***n - m = 2***, there will be ***2* *DIGITs*** which are **NOT** determined,\n\nwhich means there are ***ONLY 2*** numbers left in the ***VECTOR***.\n\nNow, we can directly set the ***LAST DIGIT*** and the ***2nd LAST DIGIT***.\n\nWhen ***n - m = 2***, if p(m) = 0, the ***SMALLER of the two (A0A1...AB and A0A1...BA)*** will be returned,\n\nso ***LAST DIGIT*** is set as the ***1st element of the vector*** and the ***2nd LAST DIGIT*** the ***0th***.\n\nif p(m) = 1, the ***LARGER of the two (A0A1...AB and A0A1...BA)*** will be returned,\n\nso ***LAST DIGIT*** is set as the ***0th element of the vector*** and the ***2nd LAST DIGIT*** the ***1st***.\n\n----------\n\n***My code:***\n\n class Solution {\n public:\n\n int factorial(int n)\n {\n if(n == 1) return 1;\n return n * factorial(n - 1);\n }\n\n void numberStrList(int n)\n {\n rtn = string (n, '0');\n record = vector<int>(n,1);\n for(int i = 0; i < record.size(); i++)\n {\n record[i] += i;\n }\n }\n\n string getPermutation(int n, int k) {\n numberStrList(n);\n //start from 0\n k = k - 1;\n \n if(n == 1)\n {\n if(k == 0)\n {\n return "1";\n }\n return "";\n }\n for(int i = 1; i < n - 1; i++)\n {\n rtn[i - 1] += record[k / factorial(n - i)];\n record.erase (record.begin() + k / factorial(n - i));\n k = k % factorial(n - i);\n }\n rtn[n - 2] += record[k^0];\n rtn[n - 1] += record[k^1];\n return rtn;\n }\n private:\n vector<int> record;\n string rtn;\n }; | 7 | 1 | ['Math', 'C++'] | 1 |
permutation-sequence | Best O(N*N) Solution | best-onn-solution-by-kumar21ayush03-803b | Approach\nMath\n\n# Complexity\n- Time complexity:\nO(n*n)\n\n- Space complexity:\nO(n)\n\n# Code\n\nclass Solution {\npublic:\n string getPermutation(int n, | kumar21ayush03 | NORMAL | 2023-08-24T12:45:43.224274+00:00 | 2023-08-26T05:52:34.562830+00:00 | 683 | false | # Approach\nMath\n\n# Complexity\n- Time complexity:\n$$O(n*n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector <int> nums;\n int fact = 1;\n for (int i = 1; i <= n; i++) {\n nums.push_back(i);\n fact *= i;\n }\n k--;\n string ans = "";\n while (n != 0) {\n fact /= n;\n int ind = k / fact;\n k -= ind * fact;\n ans += to_string(nums[ind]);\n nums.erase(nums.begin() + ind);\n n--;\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['C++'] | 0 |
permutation-sequence | C++ | Recursion | Backtracking | Easy | Brute Force | ~21% Space ~5% Time | c-recursion-backtracking-easy-brute-forc-f18q | \nclass Solution {\npublic:\n void recur(string s, string temp, vector<bool> &vis, vector<string> &ans, int &cnt, int k){\n if(temp.size() == s.size()){ | amanswarnakar | NORMAL | 2023-03-01T09:32:53.637459+00:00 | 2023-03-01T09:32:53.637503+00:00 | 3,250 | false | ```\nclass Solution {\npublic:\n void recur(string s, string temp, vector<bool> &vis, vector<string> &ans, int &cnt, int k){\n if(temp.size() == s.size()){\n ans.emplace_back(temp);\n cnt++;\n if(cnt == k) return;\n }\n for(int i = 0; i < s.size(); i++){\n if(!vis[i]){\n vis[i] = true;\n temp += s[i];\n recur(s, temp, vis, ans, cnt, k);\n temp.pop_back();\n vis[i] = false;\n }\n if(cnt == k) return;\n }\n }\n string getPermutation(int n, int k) {\n vector<string> ans;\n string s = "", temp = "";\n for(int i = 1; i < n + 1; i++)\n s += to_string(i);\n vector<bool> vis(n, false);\n int cnt = 0;\n recur(s, temp, vis, ans, cnt, k);\n return ans.back();\n }\n};\n``` | 6 | 0 | ['Backtracking', 'Recursion', 'C', 'C++'] | 1 |
permutation-sequence | ✅Accepted | | ✅Easy solution || ✅Short & Simple || ✅Best Method | accepted-easy-solution-short-simple-best-dcbt | \n# Code\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact=1;\n vector<int> v;\n for(int i=1;i<=n;i++)\n | sanjaydwk8 | NORMAL | 2023-01-23T17:10:42.006082+00:00 | 2023-01-23T17:10:42.006128+00:00 | 567 | false | \n# Code\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact=1;\n vector<int> v;\n for(int i=1;i<=n;i++)\n {\n v.push_back(i);\n if(i!=n)\n fact*=i;\n }\n k-=1;\n string s;\n for(int i=0;i<n;i++)\n {\n int j=k/fact;\n k%=fact;\n if(n-i-1)\n fact/=(n-i-1);\n s+=(\'0\'+v[j]);\n v.erase(v.begin()+j);\n }\n return s;\n }\n};\n```\nPlease **UPVOTE** if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 6 | 0 | ['C++'] | 0 |
permutation-sequence | ✅ [Python] just 6 lines to build it digit by digit (with detailed comments) | python-just-6-lines-to-build-it-digit-by-ajpu | \u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs remainder calculation to get permutation\'s most significant digit on each iteration. | stanislav-iablokov | NORMAL | 2022-11-03T20:35:15.644966+00:00 | 2022-11-04T18:50:56.755767+00:00 | 695 | false | **\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs remainder calculation to get permutation\'s most significant digit on each iteration. Time complexity is quadratic: **O(N\\*N)**. Space complexity is linear: **O(N)**.\n\n**Comment**. Every time we generate yet another `(n-1)!` permutations, the digit in the n-th position (starting from the left, 1-based indexing) increases by 1. Thus, to obtain digits in all positions, we simply reverse this logic.\n\n```\nfrom math import factorial as f\n\nclass Solution:\n def getPermutation(self, n: int, k: int, perm = "") -> str:\n \n digits = list(range(1,n+1))\n k -= 1\n\n for m in reversed(range(n)):\n i, k = divmod(k, f(m))\n perm += str(digits.pop(i))\n \n return perm\n``` | 6 | 0 | [] | 2 |
permutation-sequence | Java Mathy Solution Explained 100% Recursive thinking | java-mathy-solution-explained-100-recurs-6dms | Given n = 4, k = 9, we know that there at 6 permutation sequences that start with 1\n\nThere are 6 because after the first number there are 3 numbers for the 2n | qwerjkl112 | NORMAL | 2020-10-15T04:13:34.065466+00:00 | 2020-10-15T04:14:06.725839+00:00 | 279 | false | Given n = 4, k = 9, we know that there at 6 permutation sequences that start with `1`\n\nThere are **6** because after the first number there are 3 numbers for the `2nd` position and 2 numbers for the `3th` position and 1 number for the `4th`\n\n`1XXX`\n`1XXX`\n`1XXX`\n`1XXX`\n`1XXX`\n`1XXX`\n`2XXX`\n`2XXX`\n`2XXX`\n`2XXX`\n`2XXX`\n...\n`4XXX`\n\nKnowing this, we know we need to find the 9th sequence in this 24 sequences.\nSince we know for k,\n\n`0-5` starts with 1\n`6-11` starts with 2\n`12-18` starts with 3\n`19-24` starts with 4\n\nSince 9 in the range of `6-12` we know the first character will be 2. We can calculate this with `k/(current_sample_size) * (groups of number)` (8/24 * 4) = 1\n*since our list is 0 indexed we subtract 1 from k initally*\n\n*The tricky part here is figuring out the rest of the numbers*. \n\nNote that we after using the number `2`, we are left with `[1,3,4]` we just need to know where `9` lives on the second level\n\nGiven we are in the second quadrant, we know the first 2 numbers starts with first element in `[1,3,4]`, 2 for second element and so now.\n\n`1XX`\n`1XX`\n`3XX`\n`3XX`\n`4XX`\n`4XX`\nfor k,\n`0-1` starts with 1\n`2-3` starts with 4\n`4-5` starts with 3\n\nto find where 9 (really 8) sits between `6 -11`. We can subtract `8` by the left boundry `6` to transform `6 < 8 < 11` to `0 < 2 < 5`. We can reuse the last index we\'ve calculated to find the left boundry by `(product/n * index)`\nResize our product because now our sample size is reduced to 6. Our index 2 in this sample size correspond to the first instance of `3XX`\nReusing previous method to calculate index `(2/6) * 3 = 1`. Now we can go back to our List, grab and remove the element with index = 1. Which leaves us with `[1,4]`\n\nRepeat for next iteration: \nrecalculate k: `2 - (2 * 2) = 0` (transform previous`(2 < 2< 3)` -> `0 < 0 < 1`)\nresize product to 2 or *(2 * 1)*\ncalculate for index in list: `0/2 * 2 = 0`\nlist is now [4]\nOur String is now 231\n\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n List<Integer> numbers = new ArrayList<>();\n k = k-1;\n StringBuilder sb = new StringBuilder();\n for (int i = 1; i <= n; i++) {\n numbers.add(i);\n }\n int product = 1;\n for (int i = 1; i <= n; i++) {\n product *= i;\n }\n \n while (n > 0) {\n int index = (k*n/product);\n sb.append(numbers.get(index));\n numbers.remove(index);\n k -= (index * (product/n));\n product /= n;\n n--;\n }\n \n return sb.toString();\n }\n \n // cacl n*(n-1)*(n-2)...1 as $product\n // k--\n // while (n > 0) O(N)\n // $k/$product * $n = list.get($firstNumber) O(1)\n // list.remove($firstNumber) O(N)\n // $k -= (firstNumber * product / n) \n // $product /= n\n // n--;\n \n // O(n^2)\n}\n```\n\n`Time: O(n^2)`\n\n | 6 | 0 | [] | 2 |
permutation-sequence | [C++] 100% time 80% space, fully explained and easy to understand iterative solution | c-100-time-80-space-fully-explained-and-mxb1s | The base idea is that the first character can be found knowing that it is repeated (n - 1)! times.\n\nIf you have 1234 as your own base, for example, all the pe | ajna | NORMAL | 2020-06-20T14:41:28.466401+00:00 | 2020-06-20T14:44:21.192843+00:00 | 1,004 | false | The base idea is that the first character can be found knowing that it is repeated `(n - 1)!` times.\n\nIf you have `1234` as your own base, for example, all the permutations starting with, say, `2`, are going to be like this:\n\n`2134`\n`2143`\n`2314`\n`2341`\n`2413`\n`2431`\n\nSince you can indeed only permutate remaining `n - 1` elements `(n - 1)!` times.\n\nSo you will have 6 permutations startins with `1`, 6 starting with `2` and so on.\n\nOnce you get the first character, the problem is just a replica of itself (being careful to remove the first character you just found, in the above case would be `2`) and considering a new `k` as the remainder of the division by `(n - 1)!`, so, in my code: `k %= fact[n]`.\n\nRinse and repeat until you either have no more characters left to assign (in my code it would have been `!chars.size()`) or slightly more efficient to compute at each loop, until `n`).\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n // we know 1 <= n <= 9 - so storing pre-computed results is fine\n vector<int> fact = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n \n string getPermutation(int n, int k) {\n string res = "";\n vector<char> chars(n);\n int pos;\n k--; //adjusting for 1 based counting\n\t\t// prepopulating our base vector of available chars\n for (int i = 1; i <= n;) chars[i++ - 1] = \'0\' + i;\n while (n) {\n pos = k / fact[--n];\n res += chars[pos];\n chars.erase(begin(chars) + pos);\n k %= fact[n];\n }\n return res;\n }\n};\n```\n\nIt might be fun also to turn it into recursive, although I guess it will take more memory for no significant gain; also, \nI am wondering if I can avoid having a vector at all - probably so, but would complicate my logic significantly. | 6 | 0 | ['C', 'Combinatorics', 'Iterator', 'C++'] | 1 |
permutation-sequence | Python I think this is clean code. with some of my explanation | python-i-think-this-is-clean-code-with-s-ak3q | If we have n numbers then the total combinations would be factorial(n) which means same starting number should have (n - 1)! sequences. \n\nIf we do k mod (n - | winstonchi | NORMAL | 2016-02-16T15:46:22+00:00 | 2016-02-16T15:46:22+00:00 | 1,981 | false | If we have n numbers then the total combinations would be factorial(n) which means same starting number should have (n - 1)! sequences. \n\nIf we do k mod (n - 1)! then we can get the corresponding starting number and append to the result.\n\nNote that we need to maintain another array to mark visited numbers(I take remove to make sure we will not revisit the number again, each remove takes O(n) time )\n\nThe total time complexity would be O(n^2).\n\n class Solution(object):\n def getPermutation(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: str\n """\n nums = map(str, range(1, 10))\n k -= 1\n factor = 1\n for i in range(1, n):\n factor *= i\n res = []\n for i in reversed(range(n)):\n res.append(nums[k / factor])\n nums.remove(nums[k / factor])\n if i != 0:\n k %= factor\n factor /= i\n return "".join(res) | 6 | 1 | [] | 4 |
permutation-sequence | Java Recursive and Iterative | java-recursive-and-iterative-by-crickey1-hd76 | Iterative:\n\n public String getPermutation(int n, int k) {\n \n // e.g n = 5\n // [1][1][2][6][24]\n int[] factorial = new int[n | crickey180 | NORMAL | 2016-10-31T08:35:21.280000+00:00 | 2016-10-31T08:35:21.280000+00:00 | 2,389 | false | Iterative:\n```\n public String getPermutation(int n, int k) {\n \n // e.g n = 5\n // [1][1][2][6][24]\n int[] factorial = new int[n];\n factorial[0] = 1;\n \n for(int i = 1; i < n; i++) {\n factorial[i] = factorial[i-1] * i;\n }\n \n ArrayList<Integer> numbers = new ArrayList<>();\n for(int i = 1; i <= n; i++) {\n numbers.add(i);\n }\n \n String res = "";\n for(int i = n-1; i >= 0; i--) {\n \n int num = (k-1)/factorial[i];\n res += numbers.get(num);\n k -= num * factorial[i];\n numbers.remove(num);\n }\n \n return res;\n }\n```\n\nRecursive:\n```\n public String getPermutation(int n, int k) {\n \n // recursive\n // how do you make the problem smaller?\n List<Integer> list = new ArrayList<>();\n // 1,1,2,6\n int[] factorials = new int[n];\n factorials[0] = 1;\n for(int i = 1; i < n; i++) {\n factorials[i] = factorials[i-1] * i;\n }\n \n for(int i = 1; i <= n; i++) {\n list.add(i);\n }\n \n return helper(list, k, factorials);\n }\n \n private String helper(List<Integer> list, int k, int[] factorials) {\n \n if(list.size() == 0) {\n return "";\n }\n\n int num = (k-1)/factorials[list.size()-1];\n String str = "" + list.get(num);\n k -= num * factorials[list.size()-1];\n list.remove(num);\n\n return str+helper(list, k, factorials);\n }\n``` | 6 | 1 | [] | 2 |
permutation-sequence | [C++] Clean Code with Explanation | c-clean-code-with-explanation-by-alexand-fnik | Given n digits there will be total of (n * (n-1) * ... * 2 * 1) different permutations. - the 1st digit you have n options, 2nd digit you have n-1, ... last dig | alexander | NORMAL | 2017-12-20T01:34:13.392000+00:00 | 2017-12-20T01:34:13.392000+00:00 | 866 | false | 1. Given n digits there will be total of `(n * (n-1) * ... * 2 * 1)` different permutations. - the 1st digit you have `n` options, 2nd digit you have `n-1`, ... last digit you only have `1` option.\n2. Your choices to pick different number at each digit will form different groups of permutations. Example: Your choice for the `n` different number at the `1st` digit will result in `n` groups of permutations, start with `1` ~ `n`. and each group will contain `(n-1) * ... * 2 * 1)` permutations which can be further divided into n-1 groups, and so on...\n3. Given `0-based` sequence index `k`, what is the 1st `number` of the `k`th permutation depend on which `group` it is in, and this can be calculated by `k / $group_size`, which is `k / ((n-1)*...*2*1)`, and within that group, its index will be `k % ((n-1)*...*2*1)`, and `k` should be updated as that.\n4. Once 1st number is determined, the 2nd number can be determined by which sub-group it belongs to within the first level group, which again can be calculated by `k / $group_size`.\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n string digits = "123456789"; // digits pool, as numbers being picked 1 by 1, options will be reduced, pool will shrink\n /* Calculate the weight as n factorial, it is actaully the weight on the n+1 th digit */\n int weight = 1; // total number of permutations will be (n*...*2*1)\n for (int d = 1; d <= n; d++) weight *= d; // k options for kth digit\n --k %= weight; // use 0-based k, and module to weight;\n string s(n, '\\0');\n for (int i = 0; i < n; i++) {\n weight /= (n - i); // digit[0] have n options, digit[i] have n - i options\n int d = k / weight; // calculate digit id\n s[i] = digits[d];\n digits.erase(d, 1); // reduce digit from the pool, for it can only be used 1 time\n k %= weight;\n }\n\n return s;\n }\n};\n``` | 6 | 0 | [] | 0 |
permutation-sequence | SIMPLE CODE || CLEAN AND GREEN IN DEPTH EXPLAINED. | simple-code-clean-and-green-in-depth-exp-wmmt | Intuition\n Describe your first thoughts on how to solve this problem. \nProblem:\n\n- The code takes two integers n and k as input.\n- n represents the total n | Abhishekkant135 | NORMAL | 2024-06-07T10:25:12.916054+00:00 | 2024-06-07T10:25:12.916102+00:00 | 1,004 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Problem:**\n\n- The code takes two integers `n` and `k` as input.\n- `n` represents the total number of elements (1 to n).\n- `k` represents the index (1-based) of the desired permutation among all possible permutations of numbers from 1 to n.\n- The code outputs a string representing the k-th permutation.\n\n**Nutshell:**\n\n- The algorithm calculates the k-th permutation by iteratively determining digits at each position (from left to right) based on the value of `k`.\n- It leverages the fact that there are `n!` (n factorial) total permutations, and k-th permutation can be found mathematically without generating all permutations explicitly.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n\n\n**Steps:**\n\n1. **Preprocessing:**\n - `int fact=1;`: Initializes a variable `fact` to 1, which will store the factorial of `n-1` (used for calculations).\n - `List<Integer> numbers=new ArrayList<>();`: Creates an `ArrayList` named `numbers` to store the digits (1 to n) used for building the permutation.\n - `for(int i=1;i<n;i++){ ... }`: Fills the `numbers` list with digits 1 to n (excluding n as it\'s added next).\n - `fact=fact*i;`: Calculates `fact` (factorial of n-1) iteratively.\n - `numbers.add(n);`: Adds n to the `numbers` list to include all digits from 1 to n.\n - `String ans="";`: Initializes an empty string `ans` to store the final permutation string.\n - `k--;`: Decrements `k` by 1 to convert it to a 0-based index for easier calculations.\n\n2. **Iterative Digit Selection:**\n - `while(true){ ... }`: Enters a loop that continues until all digits are selected for the permutation string (`numbers` becomes empty).\n - `ans+=numbers.get(k/fact);`: Calculates the digit to be placed at the current position in the permutation string:\n - `k/fact` gives the index of the digit to be used from the `numbers` list based on the current value of `k` and `fact`.\n - The digit at the calculated index is retrieved from `numbers` and appended to `ans`.\n - `numbers.remove(k/fact);`: Removes the used digit from the `numbers` list to avoid using it again in subsequent selections.\n - `if(numbers.size()==0){ ... }`: Breaks out of the loop if all digits have been used (list becomes empty).\n - `k=k%fact;`: Updates `k` for the next digit selection. It removes the contribution of the previous factorial term (used digit\'s position) from `k`.\n - `fact=fact/numbers.size();`: Updates `fact` by dividing by the current number of remaining digits (reduced factorial for next digit selection).\n\n3. **Return Result:**\n - `return ans;`: After the loop exits (all digits used), the `ans` string containing the permutation digits in the correct order is returned.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N^2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n int fact=1;\n List<Integer> numbers=new ArrayList<>();\n for(int i=1;i<n;i++){\n fact=fact*i;\n numbers.add(i);\n }\n numbers.add(n);\n String ans="";\n k--;\n while(true){\n ans+=numbers.get(k/fact);\n numbers.remove(k/fact);\n if(numbers.size()==0){\n break;\n }\n k=k%fact;\n fact=fact/numbers.size();\n }\n return ans;\n }\n}\n``` | 5 | 0 | ['Math', 'Java'] | 0 |
permutation-sequence | Java beats 100% | C++ beats 100% | java-beats-100-c-beats-100-by-deleted_us-vz0x | Java beats 100% | C++ beats 100%\n\n\n\n\n\n\n\n# Code\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> v={0};\n | deleted_user | NORMAL | 2024-05-14T11:12:45.289361+00:00 | 2024-05-14T11:12:45.289401+00:00 | 1,528 | false | Java beats 100% | C++ beats 100%\n\n\n\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> v={0};\n int tmp=1;\n for(int i=1;i<=n;i++){\n v.push_back(i);\n tmp*=i;\n }\n string s;\n cout<<tmp<<" ";\n for(int i=n;i>=2;i--){\n tmp/=i;\n int fl=(k+tmp-1)/tmp;\n s.push_back(v[fl]+\'0\');\n k-=(fl-1)*tmp;\n for(int j=fl;j<v.size()-1;j++){\n v[j]=v[j+1];\n }\n }\n s.push_back(v[1]+\'0\'); \n return s;\n }\n};\n\n\n# Code\n```\nclass Solution {\n private static int[] fact = {0, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};\n \n private String getPermutation(int n, int k, boolean[] nums, char[] str, int index) {\n int i = 0, m = nums.length;\n if(n == 1) {\n while(i < m && nums[i]) ++i;\n str[index++]=(char)(\'0\'+i+1);\n return String.valueOf(str);\n }\n if(k == 0) {\n while(i < m) {\n if(!nums[i]) str[index++]=(char)(\'0\'+i+1);\n ++i;\n }\n return String.valueOf(str);\n }\n \n int div = k/fact[n-1], mod = k%fact[n-1], j = -1;\n while(i < m-1 && div != j) {\n if(!nums[i]) ++j;\n if(j == div) break;\n ++i;\n }\n str[index++]=(char)(\'0\'+i+1);\n if(i < m) nums[i]=true;\n return getPermutation(n-1, mod, nums, str, index); \n }\n\n public String getPermutation(int n, int k) {\n boolean[] nums = new boolean[n];\n char[] charArr = new char[n];\n return getPermutation(n, k-1, nums, charArr, 0);\n }\n}\n``` | 5 | 0 | ['C++', 'Java'] | 0 |
permutation-sequence | C++ Brute Force ->Optimal Solution (backtracking and Math) 🔥🔥🔥 | c-brute-force-optimal-solution-backtrack-pk1w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\nB | hk342064 | NORMAL | 2024-02-07T16:47:43.170057+00:00 | 2024-02-07T16:47:43.170083+00:00 | 742 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\nBrute Force(Backtracking)\n- Time complexity: O(n! x n + n!*log n!)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n!)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nOptimal Solution\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n\n# Code\n```\n\n\n--------------------------Backtracking-----------------------------\n\n\nclass Solution {\npublic:\n void func(int size,vector<int> &perm,vector<int> &ds,vector<vector<int>> &comb,vector<int> freq){\n if(ds.size()==size){\n comb.push_back(ds);\n return ;\n }\n for(int i=0;i<size;i++){\n if(!freq[i]){\n ds.push_back(perm[i]);\n freq[i]=1;\n \n func(size,perm,ds,comb,freq);\n freq[i]=0;\n ds.pop_back();\n }\n }\n }\n string getPermutation(int n, int k) {\n //recursion\n vector<int> perm;\n vector<int> ds;\n string ans;\n vector<vector<int>> comb;\n vector<int> freq(n,0);\n for(int i=1;i<=n;i++){\n perm.push_back(i);\n }\n func(n,perm,ds,comb,freq);\n //sort(comb.begin(),comb.end());\n for(int i=0;i<comb.size();i++){\n for(int j=0;j<comb[0].size();j++){\n cout<<comb[i][j]<<" ";\n }\n cout<<endl;\n }\n for (int i=0;i<n;i++) {\n ans = ans + to_string(comb[k-1][i]);\n }\n return ans;\n }\n};\n\n\n\n-------------------------OPTIMAL SOLUTION--------------------------\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact=1;\n vector<int> arr;\n\n for(int i=1;i<n;i++){\n fact=fact*i;\n arr.push_back(i);\n }\n arr.push_back(n);\n string ans="";\n k=k-1;\n while(true){\n ans+=to_string(arr[k/fact]);\n arr.erase(arr.begin()+k/fact);\n if(arr.size()==0) break;\n k=k%fact;\n fact=fact/arr.size();\n }\n return ans;\n }\n};\n``` | 5 | 0 | ['Math', 'Backtracking', 'C++'] | 0 |
permutation-sequence | 5 line code c++ | 5-line-code-c-by-ayumsh-ln96 | \nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> vec;\n for(int i=0;i<n;i++) vec.push_back(i+1);\n for( | ayumsh | NORMAL | 2023-07-31T13:39:40.492753+00:00 | 2023-07-31T13:39:40.492777+00:00 | 751 | false | ```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n vector<int> vec;\n for(int i=0;i<n;i++) vec.push_back(i+1);\n for(int i=0;i<k-1;i++) next_permutation(vec.begin(),vec.end());\n string s;\n for(int i=0;i<n;i++) s+=\'0\'+vec[i];\n return s;\n }\n};\n``` | 5 | 0 | ['C++'] | 2 |
permutation-sequence | ✅Accepted | | ✅Easy solution || ✅Short & Simple || ✅Best Method | accepted-easy-solution-short-simple-best-pj5i | \n# Code\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact=1;\n vector<int> v;\n for(int i=1;i<=n;i++)\n | sanjaydwk8 | NORMAL | 2023-01-23T17:06:05.930961+00:00 | 2023-01-23T17:06:05.931011+00:00 | 724 | false | \n# Code\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n int fact=1;\n vector<int> v;\n for(int i=1;i<=n;i++)\n {\n v.push_back(i);\n if(i!=n)\n fact*=i;\n }\n k-=1;\n string s;\n for(int i=0;i<n;i++)\n {\n int j=k/fact;\n k%=fact;\n if(n-i-1)\n fact/=(n-i-1);\n s+=(\'0\'+v[j]);\n v.erase(v.begin()+j);\n }\n return s;\n }\n};\n```\nPlease **UPVOTE** if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 5 | 0 | ['C++'] | 0 |
permutation-sequence | Easy solution by using STL, Permutation Sequence | easy-solution-by-using-stl-permutation-s-hyjs | \n\n# Code\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n \n string s;\n for(int i=1; i<=n; i++){\n s | Ashish_49 | NORMAL | 2023-01-07T13:02:40.943626+00:00 | 2023-01-07T13:02:40.943672+00:00 | 29 | false | \n\n# Code\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n \n string s;\n for(int i=1; i<=n; i++){\n s+=to_string(i);\n }\n vector<string>ans;\n do\n {\n ans.push_back(s);\n }while(next_permutation(s.begin(),s.end()));\n return ans[k-1];\n }\n};\n``` | 5 | 0 | ['C++'] | 2 |
permutation-sequence | 15 ms 🫡Easy Understanding | 15-ms-easy-understanding-by-ayon_ssp-4i3f | Complexity\n- Time complexity: O(n) -> Linear\n- Space complexity: O(n) -> To store the list[]\n\n# Code\n\nimport math\nclass Solution(object):\n def getPer | ayon_ssp | NORMAL | 2022-12-17T12:26:59.095370+00:00 | 2022-12-17T12:26:59.095414+00:00 | 995 | false | # Complexity\n- Time complexity: O(n) -> Linear\n- Space complexity: O(n) -> To store the list[]\n\n# Code\n```\nimport math\nclass Solution(object):\n def getPermutation(self, n, k):\n stToRet = ""\n lst = [str(i) for i in range(1,n+1)]\n \n while len(lst):\n n = len(lst)\n n1Fac = math.factorial(n-1)\n idxToRem = k/n1Fac-1 if (k%n1Fac==0) else k/n1Fac\n stToRet+= lst.pop(idxToRem)\n k = k%n1Fac\n return stToRet\n```\nYou Can also Look At My SDE Prep Repo [*`\uD83E\uDDE2 GitHub`*](https://github.com/Ayon-SSP/The-SDE-Prep) | 5 | 0 | ['Python'] | 0 |
permutation-sequence | C++ Solution || 4 Approaches || STL|| Backtracking || Iterative ||Recursion | c-solution-4-approaches-stl-backtracking-gq08 | 1st Appraoch\n(USING STL - next_permutation)\n\n\tstring getPermutation(int n, int k) {\n string s;\n for( int i=1; i<=n; i++)\n s.push | 9891YKYASH | NORMAL | 2022-08-04T02:38:31.219629+00:00 | 2022-08-04T02:39:42.731955+00:00 | 534 | false | **1st Appraoch\n(USING STL - next_permutation)**\n```\n\tstring getPermutation(int n, int k) {\n string s;\n for( int i=1; i<=n; i++)\n s.push_back( i+\'0\');\n \n while( k!=1){\n next_permutation(s.begin(), s.end());\n k--;\n }\n return s;\n }\n```\n\n***2nd Approach- Backtracking (TLE)***\n```\n\tvoid permut( string &s, int ind, set<string> &s1){\n if( ind == s.size()){\n s1.insert(s);\n return;\n }\n \n for( int i=ind; i<s.size(); i++){\n swap( s[i], s[ind]);\n permut( s, ind+1, s1);\n swap( s[i], s[ind]);\n }\n }\n string getPermutation(int n, int k) {\n string s;\n for( int i=1; i<n+1; i++) s.push_back( i+\'0\');\n set<string> s1;\n permut( s, 0, s1);\n for( auto i: s1){\n if( k==1){\n return i;\n }\n --k;\n }\n return "";\n }\n```\n\n***Optimal Approach ( RECURSIVE)***\n```\n void solve( int fact, vector<int> & v, int k, string &s){\n if( v.size()==0){\n return ; \n }\n \n s = s+ to_string(v[k/fact]);\n v.erase(v.begin() + k/fact);\n if( v.size()!=0)\n solve( fact/v.size(), v, k%fact, s);\n }\n string getPermutation(int n, int k) {\n //calculating the factorial of n-1 numbers and making an array of numbers 1->n\n int fact =1;\n vector<int> v;\n for( int i=1; i<n;i++){\n fact *= i;\n v.push_back(i);\n }v.push_back(n);\n k= k-1; //for 0-based indexing\n string s ="";\n solve( fact, v, k, s);\n return s;\n }\n```\n\n***Optimal Approach (Iterative)***\n```\nstring getPermutation(int n, int k) {\n //calculating the factorial of n-1 numbers and making an array of numbers 1->n\n int fact =1;\n vector<int> v;\n for( int i=1; i<n;i++){\n fact *= i;\n v.push_back(i);\n }v.push_back(n);\n k= k-1; //for 0-based indexing\n string s ="";\n while( true){\n s += to_string( v[ k/fact]);\n v.erase( v.begin()+ k/fact);\n k= k%fact;\n if( v.size()==0) break;\n fact /=v.size();\n \n }\n \n return s;\n }\n``` | 5 | 0 | ['Backtracking', 'Recursion', 'C', 'Iterator', 'C++'] | 0 |
permutation-sequence | Python O(N^2) 96% faster | python-on2-96-faster-by-abhigamez-c05r | \nimport math\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n ans = ""\n nums = [i for i in range(1,n+1)]\n for i | abhigamez | NORMAL | 2021-09-05T06:29:54.119769+00:00 | 2021-09-05T06:30:37.492599+00:00 | 927 | false | ```\nimport math\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n ans = ""\n nums = [i for i in range(1,n+1)]\n for i in range(1,n+1):\n index = 0\n c = math.factorial(n-i)\n \n while c < k:\n index +=1\n k -= c\n \n ans += str(nums[index])\n del nums[index]\n \n return ans\n \n \n```\nIf you find it usefull ,do upvote | 5 | 0 | ['Python', 'Python3'] | 0 |
permutation-sequence | 0ms C++ solution explained | 0ms-c-solution-explained-by-swathi_venne-xp1e | This problem can be solved with recursive approach. \n\n### OBSERVATION:\n Given n, we\'ll be having (n-1)! permutations starting with 1, (n-1)! permutations st | swathi_vennela | NORMAL | 2020-06-21T15:20:14.562043+00:00 | 2020-06-21T17:51:41.614748+00:00 | 203 | false | This problem can be solved with recursive approach. \n\n### OBSERVATION:\n* Given n, we\'ll be having (n-1)! permutations starting with 1, (n-1)! permutations starting with 2, and so on.. So, each block is of size (n-1!).\n* So, this can be used to find out the first digit of the required sequence. Say, n=4 and k=15, then, k/(n-1!) = 2.5 so, the required permutation will be lying somewhere in the 3rd block. So, the number starts with 3.\n\n### APPROACH:\n* Kth Permutation sequence can be formed by choosing the 1st digit and then the rest of the digits one by one.\n* We can find the first digit in the sequence, and then apply the same technique to keep finding the first digit of the remaining part of the sequence until the whole sequence is found.\n\n### EXAMPLE:\n* We can find the first digit in the number and keep updating n and k to find the first digit in the remaining part of the number.\n* Say, n=4 and k=15. Now, nums = {1,2,3,4}. ind = ceil(k/(n-1!) = 3. So, num is 3{}{}{}. \n* k = k%(n-1!), n=n-1\n* Now, n=3, k=3. nums={1,2,4}. ind = ceil(3/2) = 2. So, num is 32{}{}.\n* n=2,k=1, nums={1,4}. ind = ceil(1/2) = 1. So, num is 321{}.\n* n=1, k=1, nums = {4}. ind=ceil(1/1)=1. So, nums is 3214.\n\n#### NOTE: \n* Think about the case when k becomes zero before n. When does this happen? k becomes zero when n-1!=k (coz, k = k%n-1!). This means that this is the last element in the corresponding block, and obviously in this case, the remaining part of the permutation is going to be all the remaining digits arranged in descending order. \n* eg: n=3,k=2. \n\n### PSEUDOCODE:\n``` l = {1,2,3,..,N}\n result=0\n while(k&&n)\n {\n\t ind = ceil(k/(n-1!) //finding the first digit\n\t result = result*10 + l[ind] //appending it to result\n\t l.remove(l[ind]) //removing the found digit from l\n\t k = k%(n-1!) //updating k and n\n\t n = n-1\n }\n if(k==0)\n\t reverse the list l and append it to result\n\treturn result\n```\n\n### MY CODE:\n```\nstring getPermutation(int n, int k) {\n vector<int> numSet(n);\n for(int i=0;i<n;i++)\n numSet[i]=i+1;\n int fact[10] = {1};\n for(int i=1;i<=9;i++)\n fact[i] = fact[i-1]*(i);\n \n int ind,result=0;\n while(n&&k)\n {\n ind = ceil((double)k/fact[n-1]);\n result = (result*10)+numSet[ind-1];\n numSet.erase(numSet.begin()+(ind-1));\n k = k%(fact[n-1]);\n n = n-1;\n }\n if(k==0)\n {\n int t=numSet.size();\n for(int i=t-1;i>=0;i--)\n result = (result*10)+numSet[i]; \n }\n string st;\n st = st+to_string(result);\n return st;\n }\n```\n\nPS: This is not O(n) solution... It takes O(n^2) coz the erase() function of vector will always create a new vector array and copy the original value to it except the erased one...\n\n\n | 5 | 0 | [] | 0 |
permutation-sequence | Python 3 - Just a function composition, fully explained | python-3-just-a-function-composition-ful-uman | \nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n return \'\'.join(next(dropwhile(lambda t: t[0] < k, enumerate(permutations(list | geandbe | NORMAL | 2020-06-20T14:23:13.997882+00:00 | 2020-06-20T14:48:39.863149+00:00 | 804 | false | ```\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n return \'\'.join(next(dropwhile(lambda t: t[0] < k, enumerate(permutations(list("123456789"[0:n])))))[1])\n```\n\nThe solution just get composed from the existing function toolset following the thought train:\n\n`list("123456789"[0:n])` elements of a permutation\n\n`permutations(list("123456789"[0:n]))` **lazy** sequence of all permutations\n\n`enumerate(permutations(list("123456789"[0:n])), start=1)` the same, but now each permutation is wrapped into a tuple with its order number, starting with `1`\n\n`dropwhile(lambda t: t[0] < k, enumerate(permutations(list("123456789"[0:n]))))` the same, but with first `k - 1` permutations skipped\n\n`next(dropwhile(lambda t: t[0] < k, enumerate(permutations(list("123456789"[0:n])))))` the tuple having number `k` and the associated sought permutation\n\n`\'\'.join(next(dropwhile(lambda t: t[0] < k, enumerate(permutations(list("123456789"[0:n])))))[1])` converting the permutation from this tuple to string, mission accomplished!\n\n | 5 | 0 | ['Python3'] | 1 |
permutation-sequence | Java Solution With Explanation | java-solution-with-explanation-by-skakol-bikm | I was searching for proper answer got explanation in the below link. I just added code and improved on explanation\ncourtesy : https://www.lintcode.com/problem | skakollu | NORMAL | 2019-08-01T02:08:34.928892+00:00 | 2019-08-01T02:14:49.723648+00:00 | 634 | false | I was searching for proper answer got explanation in the below link. I just added code and improved on explanation\ncourtesy : https://www.lintcode.com/problem/permutation-sequence/note/187602\nSince we need to fix one position each time me need next we need to get permutations for (n-1)!\n\n\nwhen n = 4, the list is 1, 2, 3, 4 and k = 18\nthe total number of permutations is\nrow1: 1 + {2, 3, 4}: 1234, 1243, 1324, 1342, 1423, 1432\n==> 3! = 6 (factor) (from 0 to 5)\nrow2: 2 + {1, 3, 4}: 2134, 2143, 2314, 2341, 2413, 2431\n==> 3! = 6 (from 6 to 11)\nrow3: 3 + {1, 2, 4}: 3! (from 12 to 17)\nrow4: 4 + {1, 2, 3}: 3! (from 18 to 23)\nwhen k = 18, it means find the item from 0, then 17th is the permutation we want.\n\nSince K =18 means we need to go to 17th index \nso \nK--\n\nFind out the number on each position\nwhile i = n = 4\nlist: 1,2,3,4\nindex = (k - 1)/ (i - 1)! = 17/6 = 2. index 2 means it is row3 beginning with 3, then remove 3 from the list {1,2,3,4}, then the list becomes {1,2,4}. update k = (k-1) % 6 = 5.**** Add 3 to output.****\n\nWhen n = 3 \nrow 1 \n1,2,4\n1,4,2\n\nrow 2\n2,1,4\n2,4,1\n\nrow 3\n4,1,2\n4,2,1\n\nwhile i = n = 3, k = 5\nlist: 1, 2, 4\nindex = k / (i - 1)! = 5/2 = 2. index 2 means it is row3 beginning with 4, then remove 4 from the list {1, 2, 4}, then the list becomes {1, 4}. update k = k % 2 = 1. **** Add 4 to output.****\n\nWhen n = 2\n1,2\n\nwhile i = n = 2, k = 1\nlist: 1,2\nindex = k/(i-1)! = 1/1 = 1. index 1 means it is row2 beginning with 2, then remove 2 from the list {1, 2}, then the list becomes {1}. update k = k % 1 = 0. Add 2 to the output.\n\nWhen n = 1\n\n1\nwhile i = n = 1, k = 0\nindex = 0, index 0 means it is row1 beginning with 1. Add 1 to the output\n\nEventually, the output is 3421\n\nWhy to Divide by Factorial ? \n\nThink about a simple case where you are finding the digits of a decimal number e.g. 4836. You can compute rightmost place by dividing 4836 by 1 then modulo 10 to get 6. Then 4836 by 10 modulo 10 to get 3, then 4836 by 100 modulo 10 to get 8 etc. We don\'t need to change the number 4836 each time. Permutation case is similar but we use factorials instead of powers of 10 and modulus value changes.\n\nhttps://stackoverflow.com/questions/31216097/given-n-and-k-return-the-kth-permutation-sequence\n\nprivate String getPermutation3(int n, int k) {\n\n List<Integer> list = new ArrayList<>();\n\n for(int i =1; i <= n ; i++){\n list.add(i);\n }\n\n int[] fact = new int[n];\n\n // Since we cannot divide a number by 0 we are fixing index 0 to 1\n fact[0] =1;\n\n // Storing factorials for (n-1)!\n\n for(int i = 1; i < n; i++){\n fact[i] = i*fact[i-1];\n }\n // if position is 3 we need index 2 so k--\n k--;\n\n String s = "";\n\n // We are coming from back as we need to get the position of character for (n-1)! and we have put factorial in\n // increasing order in our factorial array so to get last character we need to come from reverse\n\n for(int i = n-1; i >=0 ; i--){\n\n int index = k/fact[i];\n\n s = s+ list.remove(index);\n // To go to next index\n k = k%fact[i];\n }\n return s;\n }\n\t\n\tHope This helps | 5 | 0 | [] | 0 |
permutation-sequence | Python two solutions backtracking(40ms) and math(36ms). | python-two-solutions-backtracking40ms-an-q4uf | Approach 1: backtracking.\nfirstly, we permute and count, got one and k-=1, when k==0, that is the kth. But it\'s too slow, consider that, we permute1234, whe | darktiantian | NORMAL | 2019-04-04T06:04:56.596073+00:00 | 2019-04-04T06:04:56.596150+00:00 | 874 | false | Approach 1: backtracking.\nfirstly, we permute and count, got one and `k-=1`, when k==0, that is the kth. But it\'s too slow, consider that, we permute`1234`, when choose `1`, there are `a = factorial(len(rest))` permutations, if k > a, we don\'t need permute starts with `1`. And minus the total `a`.\n\u6B64\u9898\u548C 46.Permutations \u5F88\u50CF\uFF0C\u4F46\u662F\u4F60\u4E0D\u80FD\u5168\u6392\u51FA\u6765\u518D\u901A\u8FC7\u7D22\u5F15\u6C42\uFF0C\u90A3\u6837\u4F1A\u8D85\u65F6\u3002\n\n```python\ndef getPermutation(self, n: int, k: int) -> str:\n self.k = k\n \n def backtrack(s, rest):\n if not rest:\n self.k -= 1\n if self.k == 0:\n return s\n return \'\'\n \n for i in range(len(rest)):\n if self.k > math.factorial(len(rest)-1):\n self.k -= math.factorial(len(rest)-1)\n continue\n old = s\n s += rest[i]\n ans = backtrack(s, rest[:i]+rest[i+1:])\n if ans: return ans\n s = old\n return \'\'\n nums = list(map(str, range(1, n+1)))\n return backtrack(\'\', nums)\n```\n\nApproach 2: math\n\n```python\ndef getPermutation(self, n: int, k: int) -> str:\n ans = \'\'\n nums = list(map(str, range(1, n+1)))\n fact = math.factorial(len(nums)-1)\n k -= 1\n while k:\n i, k = divmod(k, fact)\n ans += nums.pop(i)\n fact //= len(nums) \n ans += \'\'.join(nums)\n return ans\n``` | 5 | 0 | ['Math', 'Backtracking', 'Python3'] | 0 |
permutation-sequence | Easy to understand solution with sample | easy-to-understand-solution-with-sample-c1uy8 | class Solution {\n int getPermutationNumber(int n) {\n int result = 1;\n for(int i=1;i<=n;++i) {\n result *=i;\n | like2 | NORMAL | 2015-11-29T13:15:18+00:00 | 2015-11-29T13:15:18+00:00 | 1,651 | false | class Solution {\n int getPermutationNumber(int n) {\n int result = 1;\n for(int i=1;i<=n;++i) {\n result *=i;\n }\n \n return result;\n }\n \n public:\n string getPermutation(int n, int k) {\n // 1234, 1243, 1324, 1342, 1423,1432,\n // n*(n-1)!\n // k/(n-1)!\n // k= k%(n-1)!\n // 123: n=3, k=4 => k=4-1 (for indexing from 0)\n // 3/(2!)=1, head[1]==2, k%(2!) = 1\n // 1/(1!)=1, head[1]==3, k%(1!) = 0\n // 0/(0!)=0, head[0]=1\n vector<int> result; \n vector<int> nums;\n for(int i=1;i<=n;++i) {\n nums.push_back(i);\n }\n \n k=k-1;\n for(int i=0;i<n;++i) {\n int perms = getPermutationNumber(n-1-i);\n int index = k/perms;\n result.push_back(nums[index]);\n k%=perms;\n nums.erase(nums.begin()+index);\n }\n \n string s="";\n for(int i=0;i<result.size();++i) {\n s += std::to_string(result[i]);\n }\n \n return s;\n }\n }; | 5 | 0 | [] | 0 |
permutation-sequence | 44ms python solution | 44ms-python-solution-by-janejingya-v3zb | from math import factorial \n class Solution(object):\n \n def getPermutation(self, n, k):\n """\n :type n: int\n | janejingya | NORMAL | 2015-12-22T19:26:11+00:00 | 2015-12-22T19:26:11+00:00 | 2,215 | false | from math import factorial \n class Solution(object):\n \n def getPermutation(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: str\n """\n res = []\n nums = [i for i in xrange(1, n+1)]\n while n-1 >= 0:\n num, k = k/factorial(n-1), k % factorial(n-1)\n if k > 0:\n res.append(str(nums[num]))\n nums.remove(nums[num])\n else:\n res.append(str(nums[num-1]))\n nums.remove(nums[num-1])\n \n n -= 1\n \n return ''.join(res) | 5 | 1 | ['Python'] | 1 |
permutation-sequence | || Permutation Sequence || 3ms || TC: O(n²) || SC: O(n) || best explanation in detail || | permutation-sequence-3ms-tc-on2-sc-on-be-p5s3 | IntuitionThe problem asks us to find the k-th permutation sequence of the numbers from 1 to n.
Instead of generating all permutations (which is computationally | Ritik-Saxena | NORMAL | 2025-01-24T19:18:00.413687+00:00 | 2025-01-24T19:18:00.413687+00:00 | 1,042 | false | # Intuition
The problem asks us to find the k-th permutation sequence of the numbers from 1 to n.
Instead of generating all permutations (which is computationally expensive), we can directly construct the k-th permutation using factorials to determine the block in which the k-th permutation lies.
The permutations of n numbers can be grouped into (n-1)! blocks, where each block starts with a fixed number.
For example, for n = 4, the permutations are divided into:
Block 1: 1xxx (6 permutations starting with 1)
Block 2: 2xxx (6 permutations starting with 2)
Block 3: 3xxx (6 permutations starting with 3)
Block 4: 4xxx (6 permutations starting with 4) Each block contains
(n-1)! = 6 permutations.
Using this property, we can find the block where the k-th permutation lies and recursively reduce the problem to a smaller size.
# Approach
Pre-compute Factorials:
1) Calculate (n-1)! for n.
This tells us the number of permutations in each block.
Maintain an Array of Numbers (1 to n):
2) Keep a list of the available numbers to build the k-th permutation.
3) Iteratively Build the k-th Permutation:
Determine the block index using k / fact and append the corresponding number to the result string.
Update k as k % fact to focus on the specific position within the block.
Update fact to handle the reduced size (divide by the size of the remaining numbers).
4) Stop When All Numbers Are Used:
Once the list of numbers is empty, the permutation is complete.
# Complexity
- Time complexity:
O(n²)
- Space complexity:
O(n)
# Code
```java []
class Solution {
public String getPermutation(int n, int k) {
// Calculate (n-1)!
int fact = 1;
ArrayList<Integer> ds = new ArrayList<>();
for (int i = 1; i < n; i++) {
fact *= i; // Compute factorial
ds.add(i); // Add numbers 1 to (n-1) to the list
}
ds.add(n); // Add the last number (n)
// Convert k to 0-based index for easier calculations
k = k - 1;
String ans = ""; // Store the k-th permutation
// Construct the permutation
while (true) {
// Append the number at index (k / fact) in ds to the answer
ans = ans + ds.get(k / fact);
ds.remove(k / fact); // Remove the used number from the list
// If all numbers are used, break
if (ds.size() == 0) {
break;
}
// Update k and fact for the remaining numbers
k = k % fact;
fact = fact / ds.size();
}
return ans;
}
}
``` | 4 | 0 | ['Java'] | 3 |
permutation-sequence | Used recursion -- Time com = O(n) | used-recursion-time-com-on-by-satya78550-j7e7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | satya78550 | NORMAL | 2024-10-18T06:38:56.864752+00:00 | 2024-10-18T06:38:56.864801+00:00 | 414 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def getPermutation(self, n: int, k: int) -> str:\n result = []\n combo = []\n fac = 1\n st = set() # To track used numbers\n\n # Step 1: Initialize the combo array and compute factorial of n\n for i in range(1, n + 1):\n combo.append(i)\n fac *= i\n \n # Step 2: Recursive function to build the permutation\n def recursion(N, K):\n nonlocal result, n, st\n \n if n == 0: # Base case: no numbers left to choose\n return\n \n fac = N // n # Get factorial of (n-1)\n idx = K // fac # Determine which number to choose\n \n # Find the idx-th unused number in the combo\n count = 0\n for num in combo:\n if num not in st:\n if count == idx:\n result.append(num) # Add the number to the result\n st.add(num) # Mark this number as used\n break\n count += 1\n \n # Update K and N for the next recursion\n n -= 1\n recursion(fac, K % fac) # Recurse with updated values\n \n recursion(fac, k - 1)\n \n # Convert the result list to a string\n return \'\'.join(map(str, result))\n\n``` | 4 | 0 | ['Python3'] | 0 |
permutation-sequence | AFTER LOOKING THIS YOU WON'T BELIVE THIS IS HARD☠️🤯 | after-looking-this-you-wont-belive-this-xca2k | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhiyadav05 | NORMAL | 2023-05-01T13:51:46.455902+00:00 | 2023-05-01T13:51:46.455963+00:00 | 578 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(N)\n\n\n\n# Code\n```\nclass Solution {\n public String getPermutation(int n, int k) {\n \n int fact = 1; // initialize a variable to store the factorial of n\n\n List<Integer> numbers = new ArrayList<>(); // create a list to store the numbers from 1 to n\n\n // calculate the factorial of n and add numbers from 1 to n to the list\n for(int i = 1; i < n; i++){\n fact = fact * i;\n numbers.add(i);\n }\n numbers.add(n);\n\n String ans = ""; // initialize an empty string to store the answer\n\n k = k - 1; // since indexing starts from 0, subtract 1 from k\n\n // loop until all numbers have been used\n while(true){\n ans = ans + numbers.get(k / fact); // add the number at index k/fact to the answer\n numbers.remove(k / fact); // remove the used number from the list\n\n // if all numbers have been used, break out of the loop\n if(numbers.size() == 0){\n break;\n }\n\n k = k % fact; // calculate the remainder of k/fact and assign it to k\n fact = fact / numbers.size(); // divide the factorial by the size of the remaining list\n }\n return ans; // return the answer\n }\n}\n\n\n``` | 4 | 1 | ['String', 'Java'] | 0 |
permutation-sequence | Easy solution by using STL, Permutation Sequence | easy-solution-by-using-stl-permutation-s-apyc | \n\n# Code\n\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n \n string s;\n for(int i=1; i<=n; i++){\n s | Ashish_49 | NORMAL | 2023-01-07T13:02:37.066976+00:00 | 2023-01-07T13:02:37.067073+00:00 | 15 | false | \n\n# Code\n```\nclass Solution {\npublic:\n string getPermutation(int n, int k) {\n \n string s;\n for(int i=1; i<=n; i++){\n s+=to_string(i);\n }\n vector<string>ans;\n do\n {\n ans.push_back(s);\n }while(next_permutation(s.begin(),s.end()));\n return ans[k-1];\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
permutation-sequence | C++ math solution | c-math-solution-by-iamdon-nesd | \nclass Solution {\npublic:\n string getPermutation(int n, int k) \n {\n int fact[10] = {1,1,2,6,24,120,720,5040,40320,362880};\n string ans | IamDon | NORMAL | 2020-07-15T21:52:40.782051+00:00 | 2020-07-15T21:52:40.782104+00:00 | 404 | false | ```\nclass Solution {\npublic:\n string getPermutation(int n, int k) \n {\n int fact[10] = {1,1,2,6,24,120,720,5040,40320,362880};\n string ans="";\n string num="123456789";\n k--;\n for(int i=n; i>0; i--)\n {\n int j=k/fact[i-1];\n k = k%fact[i-1];\n ans += num[j];\n num.erase(num.begin()+j);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Math', 'C', 'C++'] | 1 |
permutation-sequence | [JAVA] Clean Code, O(N) Time Complexity, 0 ms Time, 98.57% Faster | java-clean-code-on-time-complexity-0-ms-bbugm | \nclass Solution {\n \n\tpublic String getPermutation (int n, int k) {\n\t\n\t\tint[] factorial = new int[n];\n\t\tList<Integer> nums = new ArrayList<>();\n\t\t | anii_agrawal | NORMAL | 2020-06-20T20:20:21.855369+00:00 | 2020-06-20T20:22:15.167211+00:00 | 214 | false | ```\nclass Solution {\n \n\tpublic String getPermutation (int n, int k) {\n\t\n\t\tint[] factorial = new int[n];\n\t\tList<Integer> nums = new ArrayList<>();\n\t\t\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tnums.add (i + 1);\n\t\t\tfactorial[i] = i == 0 ? 1 : i * factorial[i - 1];\n\t\t}\n\t\t\n\t\tStringBuilder ans = new StringBuilder ();\n\t\twhile (n-- != 0) {\n\t\t\tans.append (nums.remove ((k - 1) / factorial[n]));\n\t\t\tk = (k - 1) % factorial[n] + 1;\n\t\t}\n\t\n\t\treturn ans.toString ();\n\t}\n}\n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n**HAPPY CODING :)\nLOVE CODING :)** | 4 | 0 | [] | 1 |
permutation-sequence | 1ms Easy to understand solution | 1ms-easy-to-understand-solution-by-gorks-dzqo | ```\npublic String getPermutation(int n, int k) {\n List num = new LinkedList();\n for (int i = 1; i <= n; i++) \n \tnum.add(i);\n in | gorkshaozar | NORMAL | 2020-06-20T07:25:28.790947+00:00 | 2020-06-20T07:25:28.790984+00:00 | 583 | false | ```\npublic String getPermutation(int n, int k) {\n List<Integer> num = new LinkedList<Integer>();\n for (int i = 1; i <= n; i++) \n \tnum.add(i);\n int[] fact = new int[n]; // factorial\n fact[0] = 1;\n for (int i = 1; i < n; i++) \n \tfact[i] = i*fact[i-1];\n k = k-1;\n StringBuilder sb = new StringBuilder();\n for (int i = n; i > 0; i--){\n int ind = k/fact[i-1];\n k = k%fact[i-1];\n sb.append(num.get(ind));\n num.remove(ind);\n }\n return sb.toString(); \n } | 4 | 0 | ['Java'] | 1 |
permutation-sequence | Simple Java Solution using Backtracking | simple-java-solution-using-backtracking-wj0gn | \npublic String getPermutation(int n, int k) {\n List<String> result = new ArrayList<>();\n recursion(result,"", n, k,new boolean[n+1]);\n | erels | NORMAL | 2019-11-17T10:21:31.973615+00:00 | 2019-11-17T10:23:11.323559+00:00 | 686 | false | ```\npublic String getPermutation(int n, int k) {\n List<String> result = new ArrayList<>();\n recursion(result,"", n, k,new boolean[n+1]);\n return result.get(k-1);\n }\n \nprivate void recursion(List<String> result, String temp, int max, int k, boolean[] seen){\n \n if(temp.length()==max){\n result.add(new String(temp));\n }else{\n for(int i =1;i<=max;i++){\n if(result.size()==k)break;\n if(seen[i]) continue;\n seen[i] =true;\n String newStr = temp+i;\n recursion(result,newStr,max,k,seen);\n seen[i] = false;\n }\n }\n}\n``` | 4 | 0 | ['Backtracking'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.