licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1550 | using MultipleScattering
using Plots
## Define parameters
spatial_dimension = 2
medium = Acoustic(spatial_dimension; ρ = 1.0, c = 1.0);
# define the lattice vectors
v1 = [2.0,3.0]
v2 = [-2.0,1.0]
N = 15 # 2N is the number of points along each lattice vector
radius = 0.5
particle_medium = Acoustic(spatial_dimension; ρ = 0.3, c = 0.2);
particles = [
Particle(particle_medium, Circle(v1 * i + v2 * j, radius))
for i = -N:N, j = -2N:2N][:]
# let's create a defect by removing particles at near the origin
particles = filter(
p -> !(p ⊆ Circle(7*radius)) && p ⊆ Circle(100*radius)
, particles)
plot(particles)
# define a radially symmetric source that is smooth
source = regular_spherical_source(medium, [1.0]; position = [0.0,0.0])
source = point_source(medium, [0.0,0.0])
# Define region to plot
bottomleft = [-50*radius;-40*radius]
topright = [50*radius;40*radius]
region = Box([bottomleft, topright])
# choose the angular frequency
ω = 1.5
# You can skip the step of defining FrequencySimulation
result = run(particles, source, region, [ω]; exclude_region = Circle(0.2), res=200)
ts = LinRange(0.,2pi/ω,30)
maxc = floor(200*maximum(real.(field(result))))/200
minc = ceil(200*minimum(real.(field(result))))/200
t = ts[1]
anim = @animate for t in ts
plot(result,ω; seriestype = :heatmap,
phase_time=t, clim=(minc,maxc)
# , ylims = (-15.0,15.0) , c=:balance
)
plot!(particles)
plot!(colorbar=false, title="",axis=false, xguide ="",yguide ="")
end
gif(anim,"periodic-defect-outgoing.gif", fps = 7)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1908 | # # Simple random particles example
# ```
# ## Define particle properties
# Define the volume fraction of particles, the region to place the particles, and their radius
# ```julia
using MultipleScattering
num_particles = 4
radius = 1.0
particle_medium = Acoustic(2; ρ=0.2, c=0.1) # 2D particle with density ρ = 0.2 and soundspeed c = 0.1
particle_shape = Circle(radius)
max_width = 20*radius
bottomleft = [0.,-max_width]
topright = [max_width,max_width]
region_shape = Box([bottomleft,topright])
particles = random_particles(particle_medium, particle_shape; region_shape = region_shape, num_particles = num_particles)
# ```
# Now choose the receiver position `x`, the host medium, set plane wave as a source wave, and choose the angular frequency range `ωs`
# ```julia
x = [-10.,0.]
host_medium = Acoustic(2; ρ=1.0, c=1.0)
source = plane_source(host_medium; position = x, direction = [1.0,0.])
ωs = LinRange(0.01,1.0,100)
simulation = FrequencySimulation(particles, source)
result = run(simulation, x, ωs)
# ```
# We use the `Plots` package to plot both the response at the listener position x
# ```julia
using Plots; #pyplot(linewidth = 2.0)
plot(result, field_apply=real) # plot result
plot!(result, field_apply=imag)
#savefig("plot_result.png")
# ```
# 
# And plot the whole field inside the region_shape `bounds` for a specific wavenumber (`ω=0.8`)
# ```julia
bottomleft = [-15.,-max_width]
topright = [max_width,max_width]
bounds = Box([bottomleft,topright])
#plot(simulation,0.8; res=80, bounds=bounds)
#plot!(region_shape, linecolor=:red)
#plot!(simulation)
#scatter!([x[1]],[x[2]], lab="receiver")
#savefig("plot_field.png")
# ```
# 
# ## Things to try
# - Try changing the volume fraction, particle radius and ω values we evaluate
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1056 | using MultipleScattering
function run_time_response_single_particle(;
ωs = LinRange(0.0,50.0,2000),
particle_x = 100.0
)
# Define the particle
radius = 1.0
particle_medium = Acoustic(2; ρ = 10.0, c = 0.5)
# Define positions and radii of particle
particles = [Particle(particle_medium, Sphere([particle_x,0.0],radius))]
# Define source wave
host_medium = Acoustic(1.0, 1.0, 2)
source = plane_source(host_medium; position = [0.0,0.0], direction = [1.0,0.0])
# Simulate a single particle in frequency space
freq_result = run(particles, source, [0.0,0.0], ωs; min_basis_order = 1, basis_order = 14)
# Convert the frequency simulation into a time simulation
time_result = frequency_to_time(freq_result; impulse = GaussianImpulse(1.0; σ = 10/maximum(ωs)^2))
return freq_result, time_result
end
function plot_time_response_single_particle()
freq_result, time_result = run_time_response_single_particle()
plot(
plot(freq_result),
plot(time_result)
)
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 746 | import StaticArrays: SVector
using MultipleScattering
a2 = Acoustic(0.1,0.1 + 0.0im,2)
a2_host = Acoustic(1.0,1.0 + 0.0im,2)
# Create a finite transducer by adding point sources
n = 100
amp = 10.0/n
transducer = sum(point_source(a2_host, [-2.,y], amp) for y in LinRange(-2.,2.,n))
sim = FrequencySimulation(transducer)
using Plots; gr()
bounds = Box([[-1.9,-5.],[10.,5.]])
plot(sim, 4., seriestype=:contour, bounds=bounds, res=60)
ω_vec = 0.0:0.02:8.01
simres = run(sim, bounds, ω_vec, res=50)
timres = frequency_to_time(simres);
plot(timres, 10., seriestype=:contour)
ts = filter(t -> t<16, timres.t)
anim = @animate for t in ts
plot(timres,t,seriestype=:contour, clim=(0.,1.25), c=:balance)
end
gif(anim,"transducer.gif", fps = 6)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1244 | using MultipleScattering
using Plots
# define two particles to scatter the wave
# the first is centered at [1.,-2.], with radius 1.0, sound speed 2. and density 10.
p1 = Particle(Acoustic(2; c = 20.0, ρ = 10.),Sphere([1.,-4.], 1.0))
p2 = Particle(Acoustic(2; c = 1.0, ρ = 0.1),Sphere([3.,3.], 3.0))
particles = [p1,p2]
# specify the angular frequency of the incident wave
w_arr = collect(0.1:0.01:1.)
source = plane_source(Acoustic(1.0, 1.0, 2));
# calculate and plot the frequency response at x
x = [[-10.0,0.0]];
simulation = run(particles, source, x, w_arr)
plot(simulation)
# the above plot used the reciever/listener position is [-10.0, 0.0] and incident plane wave in the default position, [0.0,0.0], and direction direction, [1.0,0.0]
# to change these defaults use
x = [[-10.0,-10.0]]
source = plane_source(Acoustic(1.0, 1.0, 2); direction = [1.0,1.0], position = [0.0,0.0]);
simulation = run(particles, source, x, w_arr)
# to plot the frequency response over a region that includes the particles
# Define region to plot
region = Box([[-11.;-11.], [6.;6.]])
# Define frequency, run the simulation and plot the field
w = 3.2
result = run(particles, source, region, [w]; res=80)
plot(result, w; field_apply=abs, seriestype = :contour)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3150 | __precompile__()
module MultipleScattering
## Symmetries
export Symmetry, AbstractSymmetry, AbstractPlanarSymmetry, AbstractAzimuthalSymmetry
export WithoutSymmetry, PlanarSymmetry, PlanarAzimuthalSymmetry, AzimuthalSymmetry, RadialSymmetry, TranslationSymmetry
## Shapes
export Shape, Circle, Sphere, SphericalHelmholtz, Rectangle, Box, EmptyShape, Halfspace, Plate, TimeOfFlightPlaneWaveToPoint, TimeOfFlightPointWaveToPoint
export outer_radius, volume, name, iscongruent, (≅), congruent, in, issubset, origin, shape, (==), isequal, show
export boundary_functions, boundary_points, boundary_data, bounding_box, corners
export points_in_shape, bottomleft, topright
## Physical mediums
export PhysicalMedium, ScalarMedium, outgoing_basis_function, regular_basis_function, outgoing_radial_basis, regular_radial_basis, outgoing_translation_matrix, regular_translation_matrix, estimate_regular_basisorder, estimate_outgoing_basisorder, basisorder_to_basislength, basis_coefficients, basislength_to_basisorder, internal_field, check_material
export spatial_dimension, field_dimension
## Electromagnetic
export Electromagnetic
## Acoustics
export Acoustic, AcousticCapsule, sound_hard, hard, rigid, zero_neumann, sound_soft, soft, zero_dirichlet, pressure_release, impedance
## Particles
export AbstractParticle, Particle, CapsuleParticle, AbstractParticles
## RegularSources
export AbstractSource, RegularSource, source_expand, regular_spherical_coefficients, self_test, constant_source, point_source, plane_source, regular_spherical_source, (*), (+)
export PlaneSource
## Main simulation and results
export Simulation, run, overlapping_pairs, TimeSimulation, forcing, field
export SimulationResult, FrequencySimulation, FrequencySimulationResult, size
## Impulses for time response
export ContinuousImpulse, TimeDiracImpulse, FreqDiracImpulse, GaussianImpulse
export DiscreteImpulse, continuous_to_discrete_impulse, DiscreteTimeDiracImpulse, DiscreteGaussianImpulse
export TimeSimulationResult, frequency_to_time, time_to_frequency
export ω_to_t, t_to_ω, firstnonzero
export random_particles, statistical_moments
export t_matrix, get_t_matrices
export scattering_matrix
import Printf: @printf
using StaticArrays: SVector
using OffsetArrays: OffsetArray
using SpecialFunctions: besselj, hankelh1
using WignerSymbols, GSL
using Random, LinearAlgebra, RecipesBase, Statistics
using ProgressMeter
using AssociatedLegendrePolynomials: Plm, Nlm
# Generic machinery common to all physical models
include("types.jl")
include("shapes/shapes.jl")
include("physics/special_functions.jl") # Special functions missing from Base library
include("physics/physical_medium.jl")
include("particle.jl")
include("source.jl")
include("result.jl")
include("simulation.jl")
include("impulse.jl")
include("time_simulation.jl")
include("random/random.jl")
include("t_matrix.jl")
include("scattering_matrix.jl")
# Specific physical models
include("physics/diffbessel.jl")
include("physics/acoustics/export.jl")
include("physics/electromagnetism.jl")
#Plotting and graphics
include("plot/plot.jl")
# Precompile hints
include("precompile.jl")
end # module
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6636 | """
See also: [`ContinuousImpulse`](@ref), [`frequency_to_time`](@ref), [`DiscreteGaussianImpulse`](@ref)
DiscreteImpulse{T<:AbstractFloat}
A struct used to represent a numerical impulse. Only the fields: `in_freq` which is the frequency response vector, and the frequency vector `ω` are required to use this struct to use in the function `frequency_to_time`.
"""
struct DiscreteImpulse{T<:AbstractFloat}
t::Vector{T}
in_time::Vector{Complex{T}}
ω::Vector{T}
in_freq::Vector{Complex{T}}
function DiscreteImpulse{T}(t_vec::AbstractArray{T}, in_time::AbstractVector{Complex{T}}, ω_vec::AbstractArray{T}, in_freq::AbstractVector{Complex{T}}, do_self_test=true) where {T}
impulse = new{T}(t_vec,collect(in_time),ω_vec,collect(in_freq))
if do_self_test self_test(impulse) end
return impulse
end
end
"""
Check that the discrete impulse vectors are the right sizes
"""
function self_test(impulse::DiscreteImpulse{T}) where {T}
right_size = length(impulse.t) == length(impulse.in_time)
right_size = right_size && length(impulse.ω) == length(impulse.in_freq)
return right_size
end
function DiscreteImpulse(t_vec::AbstractArray{T}, in_time::Union{AbstractArray{Complex{T}},AbstractArray{T}},
ω_vec::AbstractArray{T} = t_to_ω(t_vec),
in_freq::Union{AbstractArray{Complex{T}},AbstractArray{T}} = Complex{T}[];
kws... ) where {T}
if isempty(in_freq)
in_freq = collect(time_to_frequency(Vector{T}(in_time), Vector{T}(t_vec), ω_vec; kws...))[:]
end
return DiscreteImpulse{T}(
Vector{T}(t_vec), Vector{Complex{T}}(in_time), Vector{T}(ω_vec), Vector{Complex{T}}(in_freq)
)
end
"""
See also: [`DiscreteImpulse`](@ref), [`frequency_to_time`](@ref)
ContinuousImpulse{T<:AbstractFloat}
A struct used to represent an analytic impulse function. Has two fields: `in_time` a function of time `t`, and `in_freq` a function of the angular frequency `ω`. `in_freq` should be the Fourier transform of `in_time`, though this is not enforced.
We use the Fourier transform convention:
F(ω) = ∫ f(t)*exp(im*ω*t) dt,
f(t) = (2π)^(-1) * ∫ F(ω)*exp(-im*ω*t) dω.
An impluse f(t) is convoluted in time with the field u(t), however we avoid the convolution by working with the fourier transform F(ω) of the impulse f(t), which results in
frequency to time: (2π)^(-1) * ∫ F(ω)*U(ω)*exp(-im*ω*t) dω
"""
struct ContinuousImpulse{T<:AbstractFloat}
in_time::Function
in_freq::Function
# Enforce that the Types are the same
function ContinuousImpulse{T}(in_time::Function, in_freq::Function, do_self_test=true) where {T}
impulse = new{T}(in_time,in_freq)
if do_self_test self_test(impulse) end
return impulse
end
end
"""
continuous_to_discrete_impulse(impulse::ContinuousImpulse, t_vec, ω_vec = t_to_ω(t_vec); t_shift = 0.0, ω_shift = 0.0)
Returns a [`DiscreteImpulse`](@ref) by sampling `impulse`. The signal can be shifted in time and frequency by choosing `t_shit` and `ω_shift`.
"""
function continuous_to_discrete_impulse(impulse::ContinuousImpulse{T}, t_vec::AbstractArray{T}, ω_vec::AbstractArray{T} = t_to_ω(t_vec); t_shift::T = zero(T), ω_shift::T = zero(T)) where {T}
# shift in frequency then in time
in_time = impulse.in_time.(t_vec .- t_shift) .* cos.(ω_shift .* (t_vec .- t_shift))
# shift in frequency then in time
in_freq = (impulse.in_freq.(ω_vec .- ω_shift) .+ impulse.in_freq.(ω_vec .+ ω_shift)) .* exp.(im .* ω_vec .* t_shift) ./ T(2)
return DiscreteImpulse(t_vec, in_time, ω_vec, in_freq)
end
"""
Check that the continuous impulse functions return the correct types
"""
function self_test(impulse::ContinuousImpulse{T}) where {T}
t = one(T)
impulse.in_time(t)::Union{T,Complex{T}}
ω = one(T)
impulse.in_freq(ω)::Union{T,Complex{T}}
return true
end
import Base.(+)
function +(i1::ContinuousImpulse{T},i2::ContinuousImpulse{T})::ContinuousImpulse{T} where {T}
in_time(t) = i1.in_time(t) + i2.in_time(t)
in_freq(ω) = i1.in_freq(ω) + i2.in_freq(ω)
ContinuousImpulse{T}(in_time,in_freq)
end
import Base.(*)
function *(a,impulse::ContinuousImpulse{T})::ContinuousImpulse{T} where {T}
if typeof(one(Complex{T})*a) != Complex{T}
throw(DomainError(a, "Multiplying impulse by $a would cause impulse type to change, please explicitly cast $a to same type as RegularSource ($T)"))
end
in_time(t) = a*impulse.in_time(t)
in_freq(ω) = a*impulse.in_freq(ω)
ContinuousImpulse{T}(in_time,in_freq)
end
*(i::ContinuousImpulse,a) = *(a,i)
"""
TimeDiracImpulse(t0::T)
Dirac Delta function of unit area in the time domain centred at t=t0.
Warning: in the time domain this is a singuarity and so may lead to unexpected behaviour.
"""
function TimeDiracImpulse(t0::T) where {T<:AbstractFloat}
in_time(t::T) = (t==t0) ? T(Inf) : zero(T)
in_freq(ω::T) = exp(im*ω*t0)
ContinuousImpulse{T}(in_time, in_freq, false)
end
function DiscreteTimeDiracImpulse(t0::T, t_vec::AbstractArray{T}, ω_vec::AbstractArray{T} = t_to_ω(t_vec)) where {T}
return continuous_to_discrete_impulse(TimeDiracImpulse(t0), t_vec, ω_vec)
end
"""
Dirac Delta function of unit area in the frequency domain centred at ω=ω0.
Warning: in frequency space this is a singuarity and so may lead to unexpected behaviour.
"""
function FreqDiracImpulse(ω0::T, dω::T = one(T)) where {T<:AbstractFloat}
in_time(t::T) = exp(-im*ω0*t) / (T(2)*π)
in_freq(ω::T) = (ω==ω0) ? T(Inf) : zero(ω)
ContinuousImpulse{T}(in_time, in_freq, false)
end
"""
See also: [`ContinuousImpulse`](@ref), [`TimeDiracImpulse`](@ref)
GaussianImpulse(maxω[; σ = 3.0/maxω^2])
Returns a gaussian impulse function, which in the frequency domain is `exp(-σ*ω^2)*(2sqrt(σ*pi))`.
"""
function GaussianImpulse(maxω::T; σ::T = T(3.0)/maxω^2, t_shift = zero(T), ω_shift = zero(T)) where T<:AbstractFloat
# shift in frequency then in time
in_time(t::T) = exp(-(t - t_shift)^2 / (4σ)) * cos(ω_shift * (t - t_shift))
# shift in frequency then in time
gauss_freq(ω::T) = exp(-σ*ω^2) * (2sqrt(σ*pi))
in_freq(ω::T) = (gauss_freq(ω - ω_shift) + gauss_freq(ω + ω_shift)) * exp.(im * ω * t_shift) / 2
ContinuousImpulse{T}(in_time, in_freq)
end
"""
See also: [`ContinuousImpulse`](@ref), [`TimeDiracImpulse`](@ref)
DiscreteGaussianImpulse(t_vec[, ω_vec])
Returns a discretised gaussian impulse.
"""
function DiscreteGaussianImpulse(t_vec::AbstractArray{T}, ω_vec::AbstractArray{T} = t_to_ω(t_vec);
kws...) where {T}
return continuous_to_discrete_impulse(GaussianImpulse(one(T); kws...), t_vec, ω_vec)
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 5519 | """
Particle(medium::PhysicalMedium, shape::Shape)
Create particle with inner medium and shape (dimensions must agree).
"""
struct Particle{Dim,P<:PhysicalMedium,S<:Shape} <: AbstractParticle{Dim}
medium::P
shape::S
# Enforce that the Dims are all the same
function Particle{Dim,P,S}(medium::P,shape::S) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim},S<:Shape{Dim}}
new{Dim,P,S}(medium,shape)
end
end
import Base.show
function show(io::IO, p::Particle)
# Particle paramaters can be determined entirely from the medium and shape so we do not need to print them
write(io, "Particle(")
show(io, p.medium)
write(io, ", ")
show(io, p.shape)
write(io, ")")
return
end
"""
CapsuleParticle(outer::Particle, inner::Particle)
A particle within another particle, both with the same shape type and origin.
"""
struct CapsuleParticle{Dim,P<:PhysicalMedium,S<:Shape} <: AbstractParticle{Dim}
outer::Particle{Dim,P,S}
inner::Particle{Dim,P,S}
# Enforce that particles are concentric
function CapsuleParticle{Dim,P,S}(p2::Particle{Dim,P,S},p1::Particle{Dim,P,S}) where {Dim,P<:PhysicalMedium{Dim},S<:Shape}
if origin(p1) != origin(p2) error("outer and inner particles should share the same origin") end
if outer_radius(p1) >= outer_radius(p2)
new{Dim,P,S}(p1,p2)
else
new{Dim,P,S}(p2,p1)
end
end
end
# Shorthand for all Vectors of particles
AbstractParticles{Dim} = Vector{Pt} where Pt<:AbstractParticle{Dim}
# Convenience constructor which does not require explicit types/parameters
function Particle(medium::P,s::S) where {Dim,P<:PhysicalMedium{Dim},S<:Shape{Dim}}
Particle{Dim,P,S}(medium,s)
end
"""
Particle(medium, radius)
Returns a particle shaped like a sphere or circle, when the particle shape is not given and with the specified `radius`.
"""
function Particle(medium::P, radius) where {Dim, P <: PhysicalMedium{Dim}}
Particle{Dim,P,Sphere{typeof(radius),Dim}}(medium,Sphere(Dim,radius))
end
function CapsuleParticle(p1::Particle{Dim,P,S},p2::Particle{Dim,P,S}) where {Dim,S<:Shape,P<:PhysicalMedium}
CapsuleParticle{Dim,P,S}(p1,p2)
end
shape(p::Particle) = p.shape
shape(p::CapsuleParticle) = p.outer.shape
# Shape holds infomation about origin of Particle
origin(p::AbstractParticle) = origin(shape(p))
boundary_points(p::AbstractParticle, num_points::Int = 3; kws...) = boundary_points(shape(p),num_points; kws...)
CircleParticle{T,P} = Particle{2,P,Sphere{T,2}}
outer_radius(p::AbstractParticle) = outer_radius(shape(p))
volume(p::AbstractParticle) = volume(shape(p))
bounding_box(p::AbstractParticle) = bounding_box(shape(p))
bounding_box(ps::AbstractParticles) = bounding_box([shape(p) for p in ps])
function volume(particles::AbstractParticles)
mapreduce(volume, +, particles)
end
import Base.(==)
function ==(p1::Particle, p2::Particle)
p1.medium == p2.medium &&
p1.shape == p2.shape
end
function ==(p1::CapsuleParticle, p2::CapsuleParticle)
p1.outer == p2.outer &&
p1.inner == p2.inner
end
import Base.isequal
function isequal(p1::Particle, p2::Particle)
isequal(p1.medium, p2.medium) &&
isequal(p1.shape, p2.shape)
end
"""
iscongruent(p1::AbstractParticle, p2::AbstractParticle)::Bool
≅(p1::AbstractParticle, p2::AbstractParticle)::Bool
Returns true if medium and shape of particles are the same, ignoring origin, false otherwise.
"""
iscongruent(p1::AbstractParticle, p2::AbstractParticle) = false # false by default, overload in specific examples
# Define synonym for iscongruent ≅, and add documentation
≅(p1::AbstractParticle, p2::AbstractParticle) = iscongruent(p1, p2)
@doc (@doc iscongruent(::AbstractParticle, ::AbstractParticle)) (≅(::AbstractParticle, ::AbstractParticle))
function iscongruent(p1::Particle, p2::Particle)
p1.medium == p2.medium &&
iscongruent(p1.shape, p2.shape)
end
function iscongruent(p1::CapsuleParticle, p2::CapsuleParticle)
iscongruent(p1.inner, p2.inner) && iscongruent(p1.outer, p2.outer)
end
import Base.in
"""
in(vector, particle)::Bool
Returns true if vector is in interior of shape of particle, false otherwise.
"""
in(x::AbstractVector, particle::AbstractParticle) = in(x, shape(particle))
import Base.issubset
issubset(s::Shape, particle::AbstractParticle) = issubset(s, shape(particle))
issubset(particle::AbstractParticle, s::Shape) = issubset(shape(particle), s)
issubset(particle1::AbstractParticle, particle2::AbstractParticle) = issubset(shape(particle1), shape(particle2))
# NOTE that medium in both functions below is only used to get c and to identify typeof(medium)
regular_basis_function(p::Particle{Dim,P}, ω::T) where {Dim,T, P<:PhysicalMedium{Dim}} = regular_basis_function(p.medium, ω)
"""
estimate_regular_basis_order(medium::P, ω::Number, radius::Number; tol = 1e-6)
"""
function estimate_outgoing_basisorder(medium::PhysicalMedium, p::Particle, ω::Number; tol = 1e-6)
k = ω / real(medium.c)
# A large initial guess
L = Int(round(4 * abs(k*outer_radius(p)))) + 1
ts = [
norm(diag(t_matrix(p, medium, ω, l)))
for l = 1:L]
ts = ts ./ ts[1];
l = findfirst(diff(ts) .< tol)
return l
end
# Add generic documentation from shape
@doc (@doc issubset(::Shape, ::Shape)) issubset(::Shape, ::AbstractParticle)
@doc (@doc issubset(::Shape, ::Shape)) issubset(::AbstractParticle, ::Shape)
@doc (@doc issubset(::Shape, ::Shape)) issubset(::AbstractParticle, ::AbstractParticle)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 503 |
# Precompile most objects in Float64, as it will be most commonly used
circle1 = Sphere((1.0,2.0), 0.5)
circle2 = Sphere((0.0,1.0), 0.5)
particle_medium = Acoustic(0.1, 0.2+0.5im, 2)
host_medium = Acoustic(1.0, 1.0+0.0im, 2)
particles = [Particle(particle_medium, circle1), Particle(particle_medium, circle2)]
source = plane_source(host_medium, SVector(-10.0,0.0), SVector(1.0,0.0), 1.0)
sim = FrequencySimulation(particles, source)
x = [SVector(1.0,1.0), SVector(0.0,0.0)]
ω = 0.5
run(sim, x, ω)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 4872 |
"Abstract class for Results of Simulations"
abstract type SimulationResult{T,Dim,FieldDim} end
"""
Struct to hold results of a FrequencySimulation
"""
struct FrequencySimulationResult{T<:Real,Dim,FieldDim} <: SimulationResult{T,Dim,FieldDim}
"Values of field through space (rows) and angular frequencies (columns)"
field::Matrix{SVector{FieldDim,Complex{T}}}
"Positions"
x::Vector{SVector{Dim,T}}
"Angular frequencies"
ω::Vector{T}
end
function FrequencySimulationResult(field::Union{AbstractArray{Complex{T}},AbstractMatrix{A} where A<:AbstractVector{Complex{T}}}, x::AbstractVector{V}, ω::AbstractVector{T}) where {T, V<:AbstractVector{T}}
if size(field,2) == 1 # if field is a vector we cast it to a Matrix
field = reshape(field, size(field,1), size(field,2))
end
# We expect size(field) == (length(ω),length(x)), if it's the other way around, we assume the user just input the transpose.
if size(field) == (length(ω), length(x))
field = transpose(field)
elseif size(field) != (length(x),length(ω))
@error "we expect size(field) == (length(x),length(ω))"
end
x = [SVector(xi...) for xi in x]
field = [SVector(d...) for d in field]
FieldDim = size(field[1],1)
Dim = length(x[1])
FrequencySimulationResult{T,Dim,FieldDim}(field, Vector(x), Vector(ω))
end
"""
Struct to hold results of a simulation through time
"""
struct TimeSimulationResult{T<:AbstractFloat,Dim,FieldDim} <: SimulationResult{T,Dim,FieldDim}
"Values of field through space (rows) and time (columns)"
field::Matrix{SVector{FieldDim,T}}
"Positions"
x::Vector{SVector{Dim,T}}
"Times"
t::Vector{T}
end
function TimeSimulationResult(time_field::Union{AbstractArray{T}, AbstractMatrix{A} where A<:AbstractVector{T}}, x::AbstractVector{V}, t::AbstractVector{T}) where {T,V<:AbstractVector{T}}
if typeof(time_field) <: AbstractVector # if field is a vector we cast it to a Matrix
time_field = reshape(time_field, size(time_field,1), size(time_field,2))
end
x = [SVector(xi...) for xi in x]
time_field = [SVector(d...) for d in time_field]
FieldDim = size(time_field[1],1)
Dim = length(x[1])
TimeSimulationResult{T,Dim,FieldDim}(time_field, Vector(x), Vector(t))
end
"""
field(result::SimulationResult, [i::Integer, j::Integer])
Get field from result, optionally specifying indices.
Returns single value of/matrix of complex SVectors() if vector field, and complex float if scalar field.
"""
function field(result::SimulationResult, i::Integer, j::Integer)
result.field[i,j]
end
function field(result::SimulationResult{T,Dim,1}) where {Dim, T}
map(x->x[1], result.field)
end
field(result::SimulationResult) = result.field
function field(result::SimulationResult{T,Dim,1}, i::Integer, j::Integer) where {Dim, T}
result.field[i,j][1]
end
import Base.size
size(r::FrequencySimulationResult) = (length(r.x),length(r.ω))
size(r::TimeSimulationResult) = (length(r.x),length(r.t))
# import Base.union
# """
# Combine two FrequencyResults intelligently, allows user to optionally sort ω
# and x
# """
# function union(r1::FrequencySimulationResult, r2::FrequencySimulationResult; sort::Function = identity)
# if r1.x == r2.x
# elseif r1.ω == r2.ω
# end
# end
#
# function union(r1::SimulationResult,r2::SimulationResult)
# error("No implementation of union found for Simulation Results of type $(typeof(r1)) and $(typeof(r2))")
# end
import Base.(+)
function +(s1::SimulationResult,s2::SimulationResult)::SimulationResult
if typeof(s1) != typeof(s2)
error("Can not sum different types $(typeof(s1)) and $(typeof(s2))")
end
return typeof(s1)(s1.field + s2.field, s1.x, getfield(s1,3))
end
function +(s::SimulationResult,a::Union{Complex{T},T})::SimulationResult where T <: Number
if length(s.field[1]) > 1
error("Can not add a number to a vector field")
elseif typeof(s.field[1] .+ a) != typeof(s.field[1])
error("Summing SimulationResult with $a would cause SimulationResult.field to change its type.")
end
return typeof(s)([f .+ a for f in s.field], s.x, getfield(s,3))
end
function +(s::SimulationResult,a)::SimulationResult
if typeof(s.field[1] .+ a) != typeof(s.field[1])
error("Summing SimulationResult with $a would cause SimulationResult.field to change its type.")
end
return typeof(s)([f .+ a for f in s.field], s.x, getfield(s,3))
end
+(a,s1::SimulationResult) = +(s1::SimulationResult,a)
import Base.(*)
function *(a,s::SimulationResult)::SimulationResult
if typeof(s.field .* a) != typeof(s.field)
error("Multiplying SimulationResult by $a would cause the field of SimulationResult to change type.")
end
return typeof(s)([f .* a for f in s.field], s.x, getfield(s,3))
end
*(s::SimulationResult,a) = *(a,s)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1255 |
"Create the matrix S which will be inverted to find the scattering coefficients."
function scattering_matrix(medium::PhysicalMedium, particles::AbstractParticles, t_matrices::Vector, ω::T, basis_order::Integer)::Matrix{Complex{T}} where T
# Generate response for one specific k
# Number of particles
P = length(particles)
# Length of scattering basisfor each particle
N = basisorder_to_basislength(typeof(medium),basis_order)
# No particles means no scattering
if P == 0
return Matrix{Complex{T}}(undef,0,0)
end
# Faire: this could potentially return an MMatrix
function S_block(j,l)
if j == l
return zeros(Complex{T}, N, N)
else
x_lj = origin(particles[j]) .- origin(particles[l])
U = outgoing_translation_matrix(medium, basis_order, basis_order, ω, x_lj)
return - transpose(U) * t_matrices[l]
end
end
# Evaluates all the blocks in the big matrix
S_blocks = [S_block(j,l) for j in 1:P, l in 1:P]
# Reshape S_blocks into big matrix
S = zeros(Complex{T}, P*N, P*N)
for i in 1:P
for j in 1:P
S[((i-1)*N+1):(i*N), ((j-1)*N+1):(j*N)] .= S_blocks[i,j]
end
end
return S
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 10289 | abstract type Simulation{Dim} end
spatial_dimension(::Simulation{Dim}) where {Dim} = Dim
"""
FrequencySimulation([particles::AbstractParticles=[],]
source::AbstractSource)
Build a FrequencySimulation. If particles are not provided, an empty array is used.
After building, you can [`run`](@ref) the simulation to get a [`FrequencySimulationResult`](@ref).
"""
mutable struct FrequencySimulation{Dim,P<:PhysicalMedium} <: Simulation{Dim}
"Vector of particles, can be of different types."
particles::AbstractParticles
"RegularSource wave, where source.medium is the background medium of the simulation."
source::AbstractSource{P}
end
field_dimension(::FrequencySimulation{Dim,P}) where {Dim,P} = field_dimension(P)
# Constructor which infers parametric types from input arguments, note that we don't need to do much type checking as the struct will error is inconsistent
function FrequencySimulation(particles::AbstractParticles{Dim}, source::AbstractSource{P}) where {Dim,P<:PhysicalMedium{Dim}}
FrequencySimulation{Dim,P}(particles, source)
end
# A simulation with just sources is perfectly reasonable
function FrequencySimulation(source::AbstractSource{P}) where {Dim,P<:PhysicalMedium{Dim}}
FrequencySimulation{Dim,P}(AbstractParticle{Dim}[], source)
end
import Base.show
function show(io::IO, mime::MIME"text/plain", s::FrequencySimulation{T}) where {T}
# text/plain is repl type
# FrequencySimulation paramaters can be determined entirely from the medium and shape so we do not need to print them
println(io, "FrequencySimulation{$T}")
print(io, "medium = ")
show(io, s.source.medium)
println(io)
println(io, "particles = ")
for particle in s.particles
show(io, particle)
end
return
end
import Base.run
run(particles::AbstractParticles, source::AbstractSource, x::Union{Shape,AbstractVector}, ω; kws...) = run(FrequencySimulation(particles,source), x, ω; kws...)
run(particle::AbstractParticle, source::AbstractSource, x::Union{Shape,AbstractVector}, ω; kws...) = run(FrequencySimulation([particle],source), x, ω; kws...)
run(source::AbstractSource, x::Union{Shape,Vector}, ω; kws...) = run(FrequencySimulation(source), x, ω; kws...)
function run(sim::FrequencySimulation, x::AbstractVector{<:Number}, ωs::AbstractVector{<:Number}=eltype(x)[];
kws...)::SimulationResult
run(sim,[x],ωs; kws...)
end
function run(sim::FrequencySimulation, x::AbstractVector{<:Number}, ω::Number;
kws...)::SimulationResult
run(sim,[x],[ω]; kws...)
end
# Function to check if particles are overlapping: return pairs of overlapping particles
function overlapping_pairs(origins,radii)
nb_particles = length(radii)
output = Vector{Int64}[]
for i=1:nb_particles
for j=i+1:nb_particles
if norm(origins[i] - origins[j]) < (radii[i] + radii[j])
push!(output,[i,j])
end
end
end
return output
end
function overlapping_pairs(p::AbstractParticles)
origins = origin.(p)
radii = outer_radius.(p)
overlapping_pairs(origins,radii)
end
# Main run function, all other run functions use this
function run(sim::FrequencySimulation, x_vec::Vector{V}, ω::Number;
basis_order::Integer = 5,
only_scattered_waves::Bool = false, kws...) where V<:AbstractVector
# Return an error if any particles are overlapping
overlapping_pairs_vec = overlapping_pairs(sim.particles)
if !isempty(overlapping_pairs_vec)
nb_overlaps = size(overlapping_pairs_vec,1)
error("Error: particles are overlapping ($nb_overlaps overlaps). The function overlapping_pairs(p::AbstractParticles) can be used to obtain the list of overlapping pairs.")
end
Dim = spatial_dimension(sim)
# FieldDim = field_dimension(sim)
x_vec = [SVector{Dim}(x) for x in x_vec]
# return just the source if there are no particles
field_vec = if isempty(sim.particles)
f = field(sim.source)
f.(x_vec,ω)
else
# Calculate the outgoing basis coefficients around each particle, this is where most of the maths happens
a_vec = basis_coefficients(sim, ω; basis_order=basis_order)
if only_scattered_waves # remove source wave
sim = FrequencySimulation(sim.particles,
constant_source(sim.source.medium)
)
end
# Evaluate the total field at the requested x positions
field(sim, ω, x_vec, a_vec)
end
# Construct results object
# T = real(eltype(field_vec))
field_vec = reshape(map(f->SVector(f...), field_vec), :, 1)
return FrequencySimulationResult(field_vec, x_vec, Vector([ω]))
end
function run(sim::FrequencySimulation, x_vec::Vector{V}, ωs::AbstractArray=[];
ts::AbstractArray = [], result_in_time = !isempty(ts),
basis_order::Int = 5,
min_basis_order::Int = basis_order,
basis_order_vec::AbstractVector{Int} = [-1],
kws...)::SimulationResult where V<:AbstractVector
Dim = spatial_dimension(sim)
if isempty(ωs) ωs = t_to_ω(ts) end
x_vec = [SVector{Dim}(x) for x in x_vec]
# Considering basis_order to be the maximum basis order, then to avoid too much truncation error we use smaller basis orders on the smaller frequencies.
if basis_order_vec == [-1]
max_basis_order = max(basis_order,min_basis_order)
basis_order_vec = Int.(round.(
LinRange(min_basis_order, max_basis_order, length(ωs))
))
basis_order_vec = basis_order_vec[sortperm(ωs)]
end
# if user asks for ω = 0, then we provide
if first(ωs) == 0
# Compute for each angular frequency, then join up all the results
fields = mapreduce(
i -> run(sim,x_vec,ωs[i]; basis_order = basis_order_vec[i], kws...).field,
hcat, eachindex(ωs)[2:end])
# extrapolate field at ω = 0, which should be real when the time signal is real
zeroresponse = real(ωs[3].*fields[:,1] - ωs[2].*fields[:,2]) ./ (ωs[3]-ωs[2])
fields = reshape([zeroresponse; fields[:]], length(zeroresponse), size(fields,2)+1)
else
fields = mapreduce(
i -> run(sim,x_vec,ωs[i]; basis_order = basis_order_vec[i], kws...).field,
hcat, eachindex(ωs))
end
if !result_in_time
FrequencySimulationResult(fields,x_vec,Vector(ωs))
else
@error "Using `result_in_time=true` in `run` is depricated and will be removed in later versions. Please instead use `frequency_to_time` on the results of `run`."
# if isempty(ts) ts = ω_to_t(ωs) end
#
# # better to use the defaults of TimeSimulationResult's Constructor.
# frequency_to_time(FrequencySimulationResult(fields,x_vec,Vector(ωs)); t_vec = reshape(ts,length(ts)), time_kws...)
end
end
# Add docstring to run functions
"""
run(sim::FrequencySimulation, x, ω; basis_order=5)
Run the simulation `sim` for the position `x` and angular frequency `ω`.
Position can be an SVector or Vector{SVector} and frequency can be a float or
vector of floats.
"""
function run(s::FrequencySimulation) throw(MethodError(run, (s,))) end
run(sim::FrequencySimulation, region::Shape, ω::AbstractFloat; kws...) = run(sim, region, [ω]; kws...)
"""
run(sim::FrequencySimulation, region::Shape;
res=20, xres=res, yres=res, basis_order=5)
Run the simulation `sim` for a grid of positions in region and for angular frequency `ω`.
Frequency can be a float or vector of floats. The resolution of the grid points is defined
by xres and yres.
"""
function run(sim::FrequencySimulation, region::Shape, ω_vec::AbstractVector;
kws...)
x_vec, inds = points_in_shape(region; kws...)
# x_vec is a square grid of points and x_vec[inds] are the points in the region.
result = run(sim, x_vec[inds], ω_vec; kws...)
field_mat = zeros(typeof(result.field[1]), length(x_vec), length(ω_vec))
field_mat[inds,:] = result.field
return FrequencySimulationResult(field_mat, x_vec, ω_vec)
end
"""
basis_coefficients(sim::FrequencySimulation, ω::AbstractFloat; basis_order::Int=5)::Matrix{Complex}
Return coefficients for bases around each particle for a given simulation and angular frequency (ω).
"""
function basis_coefficients(sim::FrequencySimulation{Dim,P}, ω::Number; basis_order::Int = 5) where {Dim,P}
# Precompute T-matrices for these particles
t_matrices = get_t_matrices(sim.source.medium, sim.particles, ω, basis_order)
# Compute scattering matrix for all particles
S = scattering_matrix(sim.source.medium, sim.particles, t_matrices, ω, basis_order)
# Get forcing vector from source, forms the right hand side of matrix equation to find basis_coefficients
source_coefficient = regular_spherical_coefficients(sim.source)
forcing = reduce(vcat, [source_coefficient(basis_order,origin(p),ω)[:] for p in sim.particles])
# forcing = reduce(vcat, [
# (source_coefficient(basis_order,origin(p),ω) |> transpose)[:]
# for p in sim.particles])
# Find scattering coefficients by solving this forcing
a = (S + I) \ forcing
# reshape and multiply by t-matrix to get the scattering coefficients
a = reshape(a,basisorder_to_basislength(P,basis_order),length(sim.particles))
for i in axes(a,2)
a[:,i] = t_matrices[i] * a[:,i]
end
return a
end
function field(sim::FrequencySimulation{Dim,P}, ω::Number, x_vec::Vector{V}, a_vec) where {Dim, P<:PhysicalMedium, T<:Number, V<:AbstractArray{T}}
N = basislength_to_basisorder(P,size(a_vec,1))
num_particles = length(sim.particles)
basis = outgoing_basis_function(sim.source.medium, ω)
FieldDim = field_dimension(sim)
function sum_basis(x)
sum(eachindex(sim.particles)) do i
p = sim.particles[i]
# basis(N, x-origin(p)) * (reshape(a_vec[:,i],FieldDim,:) |> transpose)[:]
basis(N, x-origin(p)) * a_vec[:,i]
end
end
map(x_vec) do x
j = findfirst(p -> x ∈ p, sim.particles)
if typeof(j) === Nothing
field(sim.source)(x,ω) + sum_basis(x)
else
p = sim.particles[j]
internal_field(x, p, sim.source, ω, collect(a_vec[:,j]))
end
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 8652 | """
Represent any source (incident) wave
Subtypes may have a symmetry (such as [`PlaneSource`](@ref)) and will contain information about physical medium.
"""
abstract type AbstractSource{P} end
"""
PlaneSource(medium::P, amplitude::SVector, direction::SVector)
Is a struct type which describes a plane-wave source that drives/forces the whole system. It has three fields: a physical `medium`, an `amplitude` of the source, and the direction the propagate in `direction`.
For any given angular frequency ω, the PlaneSource has the value ``e^{i ω/c \\mathbf v \\cdot \\mathbf x }`` at the point ``\\mathbf x``, where ``c`` is the medium wavespeed and ``\\mathbf v`` is the direction.
"""
struct PlaneSource{T<:Real,Dim,FieldDim,P<:PhysicalMedium} <: AbstractSource{P}
medium::P
direction::SVector{Dim,T}
position::SVector{Dim,T}
amplitude::SVector{FieldDim,Complex{T}}
# Check that P has same Dim and FieldDim
function PlaneSource(medium::P, direction::AbstractArray, position = SVector(zeros(eltype(direction),Dim)...), amplitude = SVector{FieldDim}(ones(eltype(direction),FieldDim))) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim}}
normw = sqrt(sum(direction .^2)) # note if direction is complex this is different from norm(direction)
if !(normw ≈ 1)
@warn "The direction will be normalised so that sum(direction .^2) == 1.0"
end
if length(direction) != Dim || length(position) != Dim
throw(DimensionMismatch("The spatial dimensions of the medium do not match dimensions of the direction or position vector."))
elseif length(amplitude) != FieldDim
throw(DimensionMismatch("The dimensions of the field in the medium (i.e. always 1 for acoustics) do not match the dimension of the amplitude vector."))
end
T = promote_type(eltype(direction), eltype(position), real(eltype(amplitude)))
new{T,Dim,FieldDim,P}(medium, SVector{Dim}(direction ./ normw), SVector{Dim}(position), complex(SVector{FieldDim}(amplitude)))
end
end
field(s::PlaneSource{T}) where T = function (x::AbstractArray{T}, ω::T)
s.amplitude * exp(im * (ω / s.medium.c) * dot(x - s.position,s.direction))
end
field(s::PlaneSource{T,Dim,1}) where {T, Dim} = function (x::AbstractArray{T}, ω::T)
s.amplitude[1] * exp(im * (ω / s.medium.c) * dot(x - s.position,s.direction))
end
field(s::PlaneSource{T}, x::AbstractArray{T}, ω::T) where T = field(s)(x,ω)
function PlaneSource(medium::P;
direction = vcat(SVector(1), SVector{Dim-1}(zeros(Float64,Dim-1))),
position = zeros(eltype(direction),Dim),
amplitude = SVector{FieldDim}(ones(eltype(direction),FieldDim))
) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim}}
PlaneSource(medium,direction,position,amplitude)
end
Symmetry(s::PlaneSource{T,Dim}) where {Dim,T} = (abs(dot(s.direction,azimuthalnormal(Dim))) == norm(s.direction)) ? PlanarAzimuthalSymmetry{Dim}() : PlanarSymmetry{Dim}()
"""
RegularSource(medium::P, field::Function, coef::Function)
Is a struct type which describes the source field that drives/forces the whole system. It is also known as an incident wave. It has three fields `RegularSource.medium`, `RegularSource.field`, and `RegularSource.coef`.
The source field at the position 'x' and angular frequency 'ω' is given by
```julia-repl
x = [1.0,0.0]
ω = 1.0
RegularSource.field(x,ω)
```
The field `RegularSource.coef`
regular_basis_function(medium::Acoustic{T,2}, ω::T)
"""
struct RegularSource{P<:PhysicalMedium,S<:AbstractSymmetry} <: AbstractSource{P}
medium::P
"Use: field(x,ω)"
field::Function
"Use: coefficients(n,x,ω)"
coefficients::Function
# Enforce that the Types are the same
function RegularSource{P,S}(medium::P,field::Function,coefficients::Function) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim},S<:AbstractSymmetry{Dim}}
s = new{P,S}(medium,field,coefficients)
self_test(s)
return s
end
end
function RegularSource(medium::P,field::Function,coefficients::Function; symmetry::AbstractSymmetry{Dim} = WithoutSymmetry{Dim}()) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim}}
return RegularSource{P,typeof(symmetry)}(medium,field,coefficients)
end
Symmetry(reg::RegularSource{P,S}) where {P,S} = S()
"""
regular_spherical_coefficients(source::RegularSource)
return a function which can calculate the coefficients of a regular spherical wave basis.
"""
function regular_spherical_coefficients(source::RegularSource)
source.coefficients
end
"""
Check that the source functions return the correct types
"""
function self_test(source::RegularSource{P}) where {P}
ω = 1.0
# choose rand postion, hopefully not the source position/origin
x = SVector(rand(0.1:0.1:1.0,spatial_dimension(P))...)
# Check that the result of field has the same dimension as field dimension of P
if field_dimension(P) == 1
length(first(source.coefficients(1,x,ω))) == field_dimension(P)
# else # this else is not necessarily correct..
# source.coefficients(1,x,ω)::SVector{field_dimension(P),Complex{T}}
end
return true
end
field(s::RegularSource) = s.field
field(s::RegularSource, x::AbstractArray, ω::Number) = field(s)(x,ω)
function constant_source(medium::PhysicalMedium{Dim,FieldDim}, num = zeros(Float64,FieldDim) .* im) where {Dim, FieldDim}
return RegularSource(medium, (x,ω) -> num, (order,x,ω) -> num)
end
function constant_source(medium::PhysicalMedium{Dim,1}, num = zero(Float64) .* im) where {Dim}
return RegularSource(medium, (x,ω) -> num, (order,x,ω) -> [num])
end
"""
regular_spherical_source(PhysicalMedium,regular_coefficients; amplitude = one(T), position = zeros(T,Dim))
``c_n = ```regular_coefficients[n]`, ``x_o=```position`, and let ``v_n(kx)`` represent the regular spherical basis with wavenumber ``k`` at position ``x``. The above returns a `source` where `source.field(x,ω) =```\\sum_n c_n v_n(kx -k x_0)``
"""
function regular_spherical_source(medium::PhysicalMedium{Dim},regular_coefficients::AbstractVector{CT};
symmetry::AbstractSymmetry{Dim} = WithoutSymmetry{Dim}(),
amplitude::Union{T,Complex{T}} = one(T),
position::AbstractArray{T} = SVector(zeros(T,Dim)...)) where {T,Dim,CT<:Union{T,Complex{T}}}
coeff_order = basislength_to_basisorder(typeof(medium),length(regular_coefficients))
function source_field(x,ω)
vs = regular_basis_function(medium, ω)(coeff_order,x-position)
return amplitude * (vs * regular_coefficients)
end
function source_coef(order,centre,ω)
k = ω / medium.c
# for the translation matrix below, order is the number columns and coeff_order is the number rows
V = regular_translation_matrix(medium, order, coeff_order, ω, centre - position)
return amplitude .* (transpose(V) * regular_coefficients)
end
return RegularSource(medium, source_field, source_coef; symmetry = symmetry)
end
"""
source_expand(RegularSource, centre; basis_order = 4)
Returns a function of `(x,ω)` which approximates the value of the source at `(x,ω)`. That is, the source is written in terms of a regular basis expansion centred at `centre`.
"""
function source_expand(source::AbstractSource, centre::AbstractVector{T}; basis_order::Int = 4) where T
# Convert to SVector for efficiency and consistency
centre = SVector(centre...)
return function (x::AbstractVector{T}, ω::T)
vs = regular_basis_function(source.medium, ω)
regular_coefficients = regular_spherical_coefficients(source)
res = vs(basis_order, x - centre) * regular_coefficients(basis_order,centre,ω)
# res = sum(regular_coefficients(basis_order,centre,ω) .* vs(basis_order, x - centre), dims = 1)[:]
if length(res) == 1
res = res[1]
end
return res
end
end
import Base.(+)
function +(s1::RegularSource{P},s2::RegularSource{P})::RegularSource{P} where {P}
if s1.medium != s2.medium
error("Can not add sources from different physical mediums.")
end
field(x,ω) = s1.field(x,ω) + s2.field(x,ω)
coef(n,centre,ω) = s1.coefficients(n,centre,ω) + s2.coefficients(n,centre,ω)
sym1 = Symmetry(s1)
sym2 = Symmetry(s2)
S = typeof(Symmetry(sym1,sym2))
RegularSource{P,S}(s1.medium,field,coef)
end
import Base.(*)
function *(a,s::RegularSource{P,S})::RegularSource{P,S} where {P,S}
field(x,ω) = a * s.field(x,ω)
coef(n,centre,ω) = a .* s.coefficients(n,centre,ω)
RegularSource{P,S}(s.medium,field,coef)
end
*(s::RegularSource,a) = *(a,s)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1837 | """
t_matrix(particle, medium, ω, order)
Returns a finite T-matrix, with size depending on `order`, for a specific `particle` within a `medium` with specific physical properties.
"""
function t_matrix(p::AbstractParticle{Dim}, medium::PhysicalMedium{Dim}, ω::T, order::Integer)::AbstractMatrix{T} where {T<:AbstractFloat,Dim}
error("T-matrix function is not yet written for $(name(p.medium)) $(name(p.shape)) in a $(name(medium)) medium")
end
"""
get_t_matrices(PhysicalMedium, Vector{Particles}, ω, basis_order::Integer)
Returns vector of T-matrices from a vector of particles in a specific domain.
Can save computation if multiple of the same kind of particle are present in the
vector.
"""
function get_t_matrices(medium::PhysicalMedium, particles::AbstractParticles, ω::AbstractFloat, basis_order::Integer)::Vector
t_matrices = Vector{AbstractMatrix}(undef, length(particles))
# Vector of particles unique up to congruence, and the respective T-matrices
unique_particles = Vector{AbstractParticle}(undef, 0)
unique_t_matrices = Vector{AbstractMatrix}(undef, 0)
for p_i in eachindex(particles)
p = particles[p_i]
# If we have calculated this T-matrix before, just point to that one
found = false
for cp_i in eachindex(unique_particles)
cp = unique_particles[cp_i]
if iscongruent(p, cp)
t_matrices[p_i] = unique_t_matrices[cp_i]
found = true
break
end
end
# Congruent particle was not found, we must calculate this t-matrix
if !found
t_matrices[p_i] = t_matrix(p, medium, ω, basis_order)
push!(unique_particles, particles[p_i])
push!(unique_t_matrices, t_matrices[p_i])
end
end
return t_matrices
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6857 |
"""
Convert a FrequencySimulationResult into a TimeSimulationResult by using the inverse fourier transform.
Assumes only positive frequencies and a real time signal
"""
function frequency_to_time(simres::FrequencySimulationResult{T,Dim,FieldDim};
t_vec::AbstractVector{T} = ω_to_t(simres.ω),
impulse::ContinuousImpulse{T} = TimeDiracImpulse(zero(T)), #GaussianImpulse(maximum(simres.ω)),
discrete_impulse::DiscreteImpulse{T} = continuous_to_discrete_impulse(impulse, t_vec, simres.ω),
method = :DFT
) where {Dim,FieldDim,T}
t_vec = discrete_impulse.t
f = transpose(field(simres))
dims = size(f)
if FieldDim > 1
f = hcat([vcat(f[:,j]...) for j in 1:dims[2]]...)
end
time_field = frequency_to_time(f, simres.ω, t_vec;
discrete_impulse = discrete_impulse, method = method)
if FieldDim > 1
time_field = reshape(time_field,(:,FieldDim,dims[2]))
time_field = [
SVector(time_field[i,:,j]...)
for i in 1:size(time_field,1), j in 1:size(time_field,3)]
end
return TimeSimulationResult(permutedims(time_field,(2,1)), simres.x, t_vec)
end
"""
Convert a TimeSimulationResult into a FrequencySimulationResult by using the fourier transform.
Assumes only positive frequencies and a real time signal
"""
function time_to_frequency(timres::TimeSimulationResult{T,Dim,FieldDim};
ω_vec = t_to_ω(timres.t),
impulse::ContinuousImpulse{T} = TimeDiracImpulse(zero(T)), #GaussianImpulse(maximum(ω_vec)),
discrete_impulse::DiscreteImpulse{T} = continuous_to_discrete_impulse(impulse,timres.t, ω_vec),
method =:DFT
) where {Dim,FieldDim,T}
ω_vec = discrete_impulse.ω
f = transpose(field(timres))
dims = size(f)
if FieldDim > 1
f = hcat([vcat(f[:,j]...) for j in 1:dims[2]]...)
end
freq_field = time_to_frequency(f, timres.t, ω_vec;
discrete_impulse = discrete_impulse, method = method)
if FieldDim > 1
freq_field = reshape(freq_field,(:,FieldDim,dims[2]))
freq_field = [
SVector(freq_field[i,:,j]...)
for i in 1:size(freq_field,1), j in 1:size(freq_field,3)]
end
return FrequencySimulationResult(permutedims(freq_field,(2,1)), deepcopy(timres.x), ω_vec)
end
"""
returns an array of time from the frequency array ω_vec.
Uses the same convention for sampling the time as the discrete Fourier transfrom.
Assumes ω_vec is ordered and non-negative.
"""
function ω_to_t(ω_arr::AbstractArray{T}) where T <: AbstractFloat
N = length(ω_arr)
if ω_arr[1] == zero(T)
N -= 1
elseif minimum(ω_arr) < zero(T)
error("expected only non-negative values for the frequencies")
end
dω = median(abs.((circshift(ω_arr,1) - ω_arr)[2:end]))
t_arr = LinRange(zero(T),2π/dω,2N+2)[1:(2N+1)]
return t_arr
end
"The inverse of ω_to_t if ω_vec[1] == 0"
function t_to_ω(t_arr::AbstractArray{T}) where T <: AbstractFloat
N = Int(round((length(t_arr)-one(T))/T(2)))
maxt = t_arr[2] - t_arr[1] + t_arr[end] - t_arr[1] # subtract t_arr[1] in case t_arr[1] != zero(T)
maxω = N*2π/maxt
ω_vec = LinRange(zero(T),maxω,N+1)
return ω_vec
end
"""
Returns the first element of array which isn't zero (assumes elements are
increasing and distinct)
"""
function firstnonzero(arr::AbstractArray{T}) where T <: AbstractFloat
if arr[1] != 0
return arr[1]
else
return arr[2]
end
end
"""
See also: [`DiscreteImpulse`](@ref), [`ContinuousImpulse`](@ref)
Calculates the time response from the frequency response by approximating an
inverse Fourier transform. The time signal is assumed to be real and the
frequenices ω_vec are assumed to be positive (can include zero) and sorted. The
result is convoluted in time ωith the user specified impulse.
We use the Fourier transform convention:
F(ω) = ∫ f(t)*exp(im*ω*t) dt
f(t) = (2π)^(-1) * ∫ F(ω)*exp(-im*ω*t) dt
To easily sample any time, the default is not FFT, but a discrete version of the transform above.
"""
function frequency_to_time(field_mat::AbstractArray{Complex{T}}, ω_vec::AbstractVector{T},
t_vec::AbstractArray{T} = ω_to_t(ω_vec);
impulse::ContinuousImpulse{T} = TimeDiracImpulse(zero(T)),
discrete_impulse::DiscreteImpulse{T} = continuous_to_discrete_impulse(impulse, t_vec, ω_vec),
method=:DFT) where T <: AbstractFloat
# In case the used specifies discrete_impulse but not t_vec
t_vec = discrete_impulse.t
if size(field_mat,1) != size(ω_vec,1) error("Vector of frequencies ω_vec expected to be same size as size(field_mat,1)") end
function f(t::T,j::Int)
fs = discrete_impulse.in_freq .* field_mat[:,j] .* exp.(-(im*t) .* ω_vec)
if method == :DFT && ω_vec[1] == zero(T)
fs[1] = fs[1]/T(2) # so as to not add ω=0 tωice in the integral of ω over [-inf,inf]
end
fs
end
inverse_fourier_integral = (t,j) -> numerical_integral(ω_vec, f(t,j), method)
u = [inverse_fourier_integral(t,j) for t in discrete_impulse.t, j in axes(field_mat,2)]
return real.(u)/pi # a constant 1/(2pi) appears due to our Fourier convention, but because we only use positive frequencies, and assume a real time signal, this becomes 1/pi.
end
"""
The inverse of the function frequency_to_time (only an exact inverse when using
:DFT integration). We use the Fourier transform convention:
F(ω) = ∫ f(t)*exp(im*ω*t) dt
"""
function time_to_frequency(field_mat::Union{AbstractArray{T},AbstractArray{Complex{T}}}, t_vec::AbstractVector{T},
ω_vec::AbstractArray{T} = t_to_ω(t_vec);
impulse::ContinuousImpulse{T} = TimeDiracImpulse(zero(T)),
discrete_impulse::DiscreteImpulse{T} = continuous_to_discrete_impulse(impulse, t_vec, ω_vec),
method=:DFT) where T <: AbstractFloat
# In case the used specifies discrete_impulse but not ω_vec
ω_vec = discrete_impulse.ω
# to use an impulse below in time we would need to do a discrete convolution, which we decided against.
f(ω::T, j::Int) = field_mat[:,j] .* exp.((im*ω) .* t_vec)
fourier_integral = (ω,j) -> numerical_integral(t_vec, f(ω,j), method)
uhat = [discrete_impulse.in_freq[i]*fourier_integral(discrete_impulse.ω[i],j) for i in eachindex(discrete_impulse.ω), j in axes(field_mat,2)]
return uhat
end
function numerical_integral(xs::AbstractArray{T}, fs::Union{AbstractArray{T},AbstractArray{Complex{T}}}, method = :DFT) where T <: AbstractFloat
if method == :trapezoidal
sum(1:(length(xs)-1)) do xi
(fs[xi] + fs[xi+1])*(xs[xi+1] - xs[xi])/T(2)
end
elseif method == :DFT
fs[1]*(xs[2] - xs[1]) +
sum(2:length(xs)) do xi
fs[xi]*(xs[xi] - xs[xi-1])
end
else
error("The method $method for numerical integration is not known.")
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 4660 | # This file contains most all abstract types, or types that are widely used.
"""
Object we can scatter waves off
Subtypes will contain information about shape and material properties. Most
crucially, they will implement the [`t_matrix`](@ref) function
"""
abstract type AbstractParticle{Dim} end
"""
AbstractSymmetry
An abstract types which dictates the symmetry of the setup. That is, the symmetry shared between the incident wave and the shape of the material.
"""
abstract type AbstractSymmetry{Dim} end
"""
WithoutSymmetry
A type used to describe materials and incident waves which share no common symmetry. This will lead to the most general regular wave expansion for the eignvectors.
"""
struct WithoutSymmetry{Dim} <: AbstractSymmetry{Dim} end
"""
An incident plane-wave and infinite cylinder material will result in all fields being cylindrical Bessel waves with a phase.
"""
abstract type AbstractTranslationSymmetry{Dim} <: AbstractSymmetry{Dim} end
"""
TranslationSymmetry
A type used to describe materials and incident waves that both share a translation symmetry.
"""
struct TranslationSymmetry{Dim,T} <: AbstractTranslationSymmetry{Dim}
direction::SVector{Dim,T}
end
TranslationSymmetry{Dim}(vector::AbstractVector{T}) where {Dim,T} = TranslationSymmetry{Dim,T}(vector)
"""
An incident plane-wave and halfspace material will result in all fields being plane-waves.
"""
abstract type AbstractPlanarSymmetry{Dim} <: AbstractSymmetry{Dim} end
"""
PlanarSymmetry
A type used to describe materials and incident waves that both share a planar symmetry.
"""
struct PlanarSymmetry{Dim} <: AbstractPlanarSymmetry{Dim} end
"""
For spatial dimension > 2, we can consider problems that have azimuthal symmetry. For example, a plane-wave incident on a sphere.
"""
abstract type AbstractAzimuthalSymmetry{Dim} <: AbstractSymmetry{Dim} end
"""
AzimuthalSymmetry
A type used to describe materials and incident waves in 3 spatial dimensions that share a symmetry about the azimuth.
"""
struct AzimuthalSymmetry{Dim} <: AbstractAzimuthalSymmetry{Dim} end
AzimuthalSymmetry() = AzimuthalSymmetry{3}()
"""
RadialSymmetry
A type used to describe materials and incident waves in that are both radially symmetric. That is, the material is a sphere, and the incident wave is radially symmetric around the center of this spherical material.
"""
struct RadialSymmetry{Dim} <: AbstractAzimuthalSymmetry{Dim} end
"""
PlanarAzimuthalSymmetry
A type used to describe a materail and incident wave which have both [`PlanarSymmetry`](@ref) and [`AzimuthalSymmetry`](@ref).
"""
struct PlanarAzimuthalSymmetry{Dim} <: AbstractPlanarSymmetry{Dim} end
PlanarAzimuthalSymmetry() = PlanarAzimuthalSymmetry{3}()
function azimuthalnormal(dim::Int)
if dim == 2
return [1,0]
elseif dim == 3
return [0,0,1]
else
return [zeros(dim-1);1]
end
end
# If T1 is a shape, source, or material, first calculate its symmetry
"""
Symmetry(T)
returns the symmetry of the object T. Some possible symmetries include [`PlanarSymmetry`](@ref), [`RadialSymmetry`](@ref), and [`WithoutSymmetry`](@ref).
"""
"""
Symmetry(T1,T2)
returns the combined symmetry of the two objects T1 and T2.
"""
Symmetry(T1,T2) = Symmetry(Symmetry(T1),Symmetry(T2))
Symmetry(sym1::AbstractSymmetry{Dim},sym2::AbstractSymmetry{Dim}) where Dim = WithoutSymmetry{Dim}()
Symmetry(sym1::S,sym2::S) where S<:AbstractSymmetry = sym1
function Symmetry(sym1::TranslationSymmetry{Dim},sym2::TranslationSymmetry{Dim}) where Dim
if abs(dot(sym1.direction,sym2.direction)) > 0
PlanarSymmetry{Dim}()
else sym1
end
end
Symmetry(sym1::AbstractPlanarSymmetry{Dim},sym2::AbstractPlanarSymmetry{Dim}) where Dim = PlanarSymmetry{Dim}()
Symmetry(sym1::PlanarAzimuthalSymmetry{Dim},sym2::PlanarAzimuthalSymmetry{Dim}) where Dim = PlanarAzimuthalSymmetry{Dim}()
Symmetry(sym1::AzimuthalSymmetry{Dim},sym2::PlanarAzimuthalSymmetry{Dim}) where Dim = AzimuthalSymmetry{Dim}()
Symmetry(sym1::PlanarAzimuthalSymmetry{Dim},sym2::AzimuthalSymmetry{Dim}) where Dim = AzimuthalSymmetry{Dim}()
Symmetry(sym1::AbstractAzimuthalSymmetry{Dim},sym2::RadialSymmetry{Dim}) where Dim = AzimuthalSymmetry{Dim}()
Symmetry(sym1::RadialSymmetry{Dim},sym2::AbstractAzimuthalSymmetry{Dim}) where Dim = AzimuthalSymmetry{Dim}()
Symmetry(sym1::RadialSymmetry{Dim},sym2::RadialSymmetry{Dim}) where Dim = RadialSymmetry{Dim}()
Symmetry(sym1::PlanarAzimuthalSymmetry{Dim},sym2::RadialSymmetry{Dim}) where Dim = AzimuthalSymmetry{Dim}()
Symmetry(sym1::RadialSymmetry{Dim},sym2::PlanarAzimuthalSymmetry{Dim}) where Dim = AzimuthalSymmetry{Dim}()
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 417 | # "Derivative of Hankel function of zeroth kind"
# function diffhankelh1(n, z)
# if n != 0
# (hankelh1(-1 + n, z) - hankelh1(1 + n, z)) / 2
# else
# -hankelh1(one(n), z)
# end
# end
#
# "Derivative of Bessel function of first kind"
# function diffbesselj(n, z)
# if n != 0
# (besselj(-1 + n, z) - besselj(1 + n, z)) / 2
# else
# -besselj(one(n), z)
# end
# end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 392 |
"""
Electromagnetic
Represents the physical properties for a homogenous isotropic electromagnetic medium. Produces
a three dimensional vector field.
"""
struct Electromagnetic{Dim,T} <: PhysicalMedium{Dim,3}
μ::Complex{T} # Permeability
ε::Complex{T} # Permittivity
σ::Complex{T} # Conductivity
end
name(e::Electromagnetic{Dim,T}) where {Dim,T} = "$(Dim)D Electromagnetic"
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 8541 | """
PhysicalMedium{Dim,FieldDim}
An abstract type used to represent the physical medium, the dimension of
the field, and the number of spatial dimensions. We expect every sub-type of PhysicalMedium{Dim,1} to have a field c which is the complex wave speed.
"""
abstract type PhysicalMedium{Dim,FieldDim} end
"Extract the dimension of the field of this physical property"
field_dimension(p::PhysicalMedium{Dim,FieldDim}) where {Dim,FieldDim} = FieldDim
"Extract the dimension of the field of this type of physical property"
field_dimension(p::Type{P}) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim}} = FieldDim
"Extract the dimension of the space that this physical property lives in"
spatial_dimension(p::PhysicalMedium{Dim,FieldDim}) where {Dim,FieldDim} = Dim
"Extract the dimension of the space that this type of physical property lives in"
spatial_dimension(p::Type{P}) where {Dim,FieldDim,P<:PhysicalMedium{Dim,FieldDim}} = Dim
"""
ScalarMedium{Dim}
An type used to represent a scalar wave which satisfies a Helmoholtz equations. Dim represents the number of spatial dimensions.
"""
struct ScalarMedium{T,Dim} <: PhysicalMedium{Dim,1}
c::Complex{T} # complex wavespeed
end
"""
A basis for regular functions, that is, smooth functions. A series expansion in this basis should converge to any regular function within a ball.
"""
regular_basis_function
"""
Basis of outgoing wave when the dependance on the angles has been removed.
"""
outgoing_radial_function
"""
Basis of outgoing wave. A series expansion in this basis should converge to any scattered field outside of a ball which contains the scatterer.
"""
outgoing_basis_function
"""
the field inside an AbstractParticle a some given point x.
"""
internal_field
"""
A tuples of vectors of the field close to the boundary of the shape. The field is calculated from sim::FrequencySimulation, but the PhysicalMedium inside and outside of the shape are assumed to be given by inside_medium and outside_medium.
"""
boundary_data
## Below are many of the essential functions for scalar wave potentials (i.e. PhysicalMedium{Dim,1}) which are used to build all other types of vector waves (as we strict ourselves to isotropy.)
# basisorder_to_linearindices(::Type{Acoustic{T,3}}, order::Int) where T = (order^2 + 1):(order+1)^2
# basisorder_to_linearindices(::Type{Acoustic{T,2}}, order::Int) where T = 1:(2*order + 1)
basisorder_to_basislength(::Type{P}, order::Int) where P <: PhysicalMedium{3,1} = (order+1)^2
basisorder_to_basislength(::Type{P}, order::Int) where P <: PhysicalMedium{2,1} = 2*order + 1
basislength_to_basisorder(::Type{P},len::Int) where P <: PhysicalMedium{3,1} = Int(sqrt(len) - 1)
basislength_to_basisorder(::Type{P},len::Int) where P <: PhysicalMedium{2,1} = Int((len - 1) / 2.0)
function outgoing_radial_basis(medium::PhysicalMedium{2,1}, ω::T, order::Integer, r::T) where {T<:Number}
k = ω/medium.c
return transpose(hankelh1.(-order:order,k*r))
end
function outgoing_basis_function(medium::PhysicalMedium{2,1}, ω::T) where {T<:Number}
return function (order::Integer, x::AbstractVector{T})
r, θ = cartesian_to_radial_coordinates(x)
k = ω/medium.c
[hankelh1(m,k*r)*exp(im*θ*m) for m = -order:order] |> transpose
end
end
function outgoing_radial_basis(medium::PhysicalMedium{3,1}, ω::T, order::Integer, r::T) where {T<:Number}
k = ω/medium.c
hs = shankelh1.(0:order,k*r)
return [hs[l+1] for l = 0:order for m = -l:l] |> transpose
end
function outgoing_basis_function(medium::PhysicalMedium{3,1}, ω::T) where {T<:Number}
return function (order::Integer, x::AbstractVector{T})
r, θ, φ = cartesian_to_radial_coordinates(x)
k = ω/medium.c
Ys = spherical_harmonics(order, θ, φ)
hs = [shankelh1(l,k*r) for l = 0:order]
lm_to_n = lm_to_spherical_harmonic_index
return [hs[l+1] * Ys[lm_to_n(l,m)] for l = 0:order for m = -l:l] |> transpose
end
end
function outgoing_translation_matrix(medium::PhysicalMedium{2,1}, in_order::Integer, out_order::Integer, ω::T, x::AbstractVector{T}) where {T<:Number}
translation_vec = outgoing_basis_function(medium, ω)(in_order + out_order, x)
U = [
translation_vec[n-m + in_order + out_order + 1]
for n in -out_order:out_order, m in -in_order:in_order]
return U
end
function regular_translation_matrix(medium::PhysicalMedium{2,1}, in_order::Integer, out_order::Integer, ω::T, x::AbstractVector{T}) where {T<:Number}
translation_vec = regular_basis_function(medium, ω)(in_order + out_order, x)
V = [
translation_vec[n-m + in_order + out_order + 1]
for n in -out_order:out_order, m in -in_order:in_order]
return V
end
function outgoing_translation_matrix(medium::PhysicalMedium{3,1}, in_order::Integer, out_order::Integer, ω::T, x::AbstractVector{T}) where {T<:Number}
us = outgoing_basis_function(medium, ω)(in_order + out_order,x)
c = gaunt_coefficient
ind(order::Int) = basisorder_to_basislength(Acoustic{T,3},order)
U = [
begin
i1 = abs(l-dl) == 0 ? 1 : ind(abs(l-dl)-1) + 1
i2 = ind(l+dl)
cs = [c(T,l,m,dl,dm,l1,m1) for l1 = abs(l-dl):(l+dl) for m1 = -l1:l1]
sum(us[i1:i2] .* cs)
end
for dl = 0:in_order for dm = -dl:dl for l = 0:out_order for m = -l:l];
# U = [
# [(l,m),(dl,dm)]
# for dl = 0:order for dm = -dl:dl for l = 0:order for m = -l:l]
U = reshape(U, ((out_order+1)^2, (in_order+1)^2))
return U
end
# NOTE that medium in both functions below is only used to get c and to identify typeof(medium)
regular_basis_function(medium::PhysicalMedium{Dim,1}, ω::Union{T,Complex{T}}) where {Dim,T} = regular_basis_function(ω/medium.c, medium)
function regular_radial_basis(medium::PhysicalMedium{2,1}, ω::T, order::Integer, r::T) where {T<:Number}
k = ω / medium.c
return transpose(besselj.(-order:order,k*r))
end
function regular_basis_function(wavenumber::Union{T,Complex{T}}, ::PhysicalMedium{2,1}) where T
return function (order::Integer, x::AbstractVector{T})
r, θ = cartesian_to_radial_coordinates(x)
k = wavenumber
return [besselj(m,k*r)*exp(im*θ*m) for m = -order:order] |> transpose
end
end
function regular_radial_basis(medium::PhysicalMedium{3,1}, ω::T, order::Integer, r::T) where {T<:Number}
k = ω / medium.c
js = sbesselj.(0:order,k*r)
return [js[l+1] for l = 0:order for m = -l:l] |> transpose
end
function regular_basis_function(wavenumber::Union{T,Complex{T}}, ::PhysicalMedium{3,1}) where T
return function (order::Integer, x::AbstractVector{T})
r, θ, φ = cartesian_to_radial_coordinates(x)
Ys = spherical_harmonics(order, θ, φ)
js = [sbesselj(l,wavenumber*r) for l = 0:order]
lm_to_n = lm_to_spherical_harmonic_index
return [js[l+1] * Ys[lm_to_n(l,m)] for l = 0:order for m = -l:l] |> transpose
end
end
function regular_translation_matrix(medium::PhysicalMedium{3,1}, in_order::Integer, out_order::Integer, ω::T, x::AbstractVector{T}) where {T<:Number}
vs = regular_basis_function(medium, ω)(in_order + out_order,x)
c = gaunt_coefficient
ind(order::Int) = basisorder_to_basislength(Acoustic{T,3},order)
V = [
begin
i1 = (abs(l-dl) == 0) ? 1 : ind(abs(l-dl)-1) + 1
i2 = ind(l+dl)
cs = [c(T,l,m,dl,dm,l1,m1) for l1 = abs(l-dl):(l+dl) for m1 = -l1:l1]
sum(vs[i1:i2] .* cs)
end
for dl = 0:in_order for dm = -dl:dl for l = 0:out_order for m = -l:l];
V = reshape(V, ((out_order+1)^2, (in_order+1)^2))
return V
end
"""
estimate_regular_basis_order(medium::PhysicalMedium, ω::Number, radius::Number; tol = 1e-6)
"""
function estimate_regular_basisorder(medium::PhysicalMedium, ω::Number, radius::Number; tol = 1e-6)
@error "This is not complete"
k = ω / real(medium.c)
vs = regular_basis_function(medium, ω)
# A large initial guess
L = Int(round(4 * abs(k*radius)))
xs = radius .* rand(spatial_dimension(medium),10)
l = nothing
while isnothing(l)
meanvs = [
mean(norm(vs(l, xs[:,i])) for i in axes(xs,2))
for l = 1:L]
meanvs = mean(abs.(vs(L, xs[:,i])) for i in axes(xs,2))
normvs = [
norm(meanvs[basisorder_to_basislength(P,i-1):basisorder_to_basislength(P,i)])
for i = 1:L]
l = findfirst(normvs .< tol)
L = L + Int(round(abs(k * radius / 2.0))) + 1
end
return l
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 12626 | export sbesselj, shankelh1, diffsbessel, diffbessel
export diffbesselj, diffhankelh1, diffsbesselj, diffshankelh1, diff3sbesselj, diff2sbesselj, diff2shankelh1, diff3shankelh1
export gaunt_coefficient
export associated_legendre_indices, spherical_harmonics_indices, lm_to_spherical_harmonic_index
export complex_legendre_array
export spherical_harmonics, spherical_harmonics_dθ
export cartesian_to_radial_coordinates, radial_to_cartesian_coordinates
export cartesian_to_spherical_coordinates, spherical_to_cartesian_coordinates
export spherical_to_cartesian_transform, cartesian_to_spherical_transform
export spherical_to_cartesian_vector, cartesian_to_spherical_vector
export atan
#NOTE should use https://github.com/JuliaMath/Bessels.jl instead of SpecialFunctions.jl
#NOTE atan(x,y) is defined here but will likely be added to base soon.
import Base.atan
atan(y::Complex,x::Complex) = - im * log( (x+y*im) / sqrt(x^2+y^2) )
"""
sbesselj(m,x)
Returns the spherical besselj function. The order is 'm' and the argument is 'x'. Note 'x' can be a complex number.
"""
# function sbesselj(m::Number,x::T) where T<: Union{F,Complex{F}} where F <: AbstractFloat
# if (abs(x) > eps(F))
# return sqrt(pi/(T(2)*x)) * besselj(m+1/2,x)
# else
# return (m > 0 ? zero(T) : one(T))
# end
# end
function sbesselj(nu::Number, x::T) where {T}
besselj_nuhalf_x = besselj(nu + one(nu)/2, x)
if abs(x) ≤ sqrt(eps(real(zero(besselj_nuhalf_x))))
nu == 0 ? one(besselj_nuhalf_x) : zero(besselj_nuhalf_x)
else
√((float(T))(π)/2x) * besselj_nuhalf_x
end
end
"""
shankelh1(m,x)
Returns the spherical hankel function of the first kind. The order is 'm' and the argument is 'x'. Note 'x' can be a complex number.
"""
shankelh1(nu::Number,x::T) where T = √((float(T))(π)/2x) * hankelh1(nu+one(nu)/2,x)
"""
diffsbessel(f::Function,m,x)
Differentiates the spherical bessel function 'f' (for any spherical bessel). The order is 'm' and the argument is 'x'. Note 'x' can be a complex number.
"""
function diffsbessel(f::Function,n::Number,z::Number)
return f(n-1,z) - (n+1) * f(n,z) / z
end
# """
# diffsbessel(f::Function,m,x,n::Int)
# Differentiates 'n' times any spherical Bessel function 'f' of order 'm' and at the argument 'x'. Uses the formula
# ``(1/z d/dz)^n (z^{m+1} f_m(z)) = z^{m-n+1} f_{m-n}``
# which leads to
# ``(1/z d/dz)^{n} (z^{m+1} f_m(z)) = (1/z d/dz)^{n-1} (1/z d/dz) (z^{m+1} f_m(z))``
# """
# function diffsbessel(f::Function,m::Number,z,n::Int)
# if n == 0
# return f(m, z)
# elseif n > 0
# n = n - 1
# return diffsbessel(f,m,z)
# else
# error("Can not differentiate a negative number of times")
# end
# end
function diffsbesselj(n::Number,z::Number)
return if n == 0
- sbesselj(1,z) # case due to numerical stability
elseif z ≈ 0
(n == 1) ? typeof(z)(1/3) : typeof(z)(0)
else
sbesselj(n-1,z) - (n+1) * sbesselj(n,z) / z
end
end
function diff2sbesselj(n::Number,z::Number)
return if z ≈ 0
if n == 0
-typeof(z)(1/3)
elseif n == 2
-typeof(z)(2/15)
else
typeof(z)(0)
end
else
2sbesselj(n+1,z) / z + (n^2 - n - z^2) * sbesselj(n,z) / z^2
end
end
function diff2shankelh1(n::Number,z::Number)
return 2shankelh1(n+1,z) / z + (n^2 - n - z^2) * shankelh1(n,z) / z^2
end
function diff3sbesselj(n::Number,z::Number)
return ((-2 + n) * (-n + n^2 - z^2) * sbesselj(n,z) -
z * (6 + n + n^2 - z^2) * sbesselj(n+1,z))/z^3
end
function diff3shankelh1(n::Number,z::Number)
return ((-2 + n) * (-n + n^2 - z^2) * shankelh1(n,z) -
z * (6 + n + n^2 - z^2) * shankelh1(n+1,z))/z^3
end
function diffshankelh1(n::Number,z::Number)
return shankelh1(n-1,z) - (n+1) * shankelh1(n,z) / z
end
"""
diffbessel(f::Function,m,x,n::Int)
Differentiates 'n' times any bessel function 'f' of order 'm' and at the argument 'x'.
"""
function diffbessel(f::Function,m::Number,z,n::Int)
if n == 0
return f(m, z)
elseif n > 0
n = n - 1
return 0.5*(diffbessel(f,m-1,z,n) - diffbessel(f,m+1,z,n))
else
error("Can not differentiate a negative number of times")
end
end
"""
diffhankelh1(m,x,n::Int)
Differentiates 'n' times the hankelh1 function of order 'm' and at the argument 'x'.
"""
function diffhankelh1(m::Number,z::T,n::Int) where T<:Number
if n == 0
return hankelh1(m, z)
elseif n > 0
n = n - 1
return 0.5*(diffhankelh1(m-1,z,n) - diffhankelh1(m+1,z,n))
else
error("Can not differentiate a negative number of times")
end
end
"Derivative of Hankel function of the first kind"
diffhankelh1(n,z) = 0.5*(hankelh1(-1 + n, z) - hankelh1(1 + n, z))
"Derivative of Bessel function of first kind"
diffbesselj(n::Number,z::T) where T<:Number = 0.5*(besselj(-1 + n, z) - besselj(1 + n, z))
"m-th Derivative of Hankel function of the first kind"
function diffbesselj(n::Number,z::T,m::Int) where T<:Number
if m == 0
return besselj(n, z)
elseif m > 0
m = m - 1
return T(0.5)*(diffbesselj(n-1,z,m) - diffbesselj(n+1,z,m))
else
error("Can not differentiate a negative number of times")
end
end
"""
gaunt_coefficient(l1,m1,l2,m2,l3,m3)
A version of the Gaunt coefficients which are used to write the product of two spherical harmonics. If Y_{l,m} is a complex spherical harmonic, with the typical phase conventions from quantum mechanics, then:
gaunt_coefficient(l1,m1,l2,m2,l3,m3) = 4*π*im^{l2+l3-l1} Integral[Y_{l1,m1}*conj(Y_{l2,m2})*conj(Y_{l3,m3})]
where the integral is over the solid angle.
The most standard gaunt coefficients `G(l1,m1;l2,m2;l3)` are related through the identity:
4pi * G(l1,m1;l2,m2;l3) = im^(l1-l2-l3) * (-1)^m2 * gaunt_coefficient(l1,m1,l2,-m2,l3,m1+m2)
"""
function gaunt_coefficient(T::Type{<:AbstractFloat},l1::Int,m1::Int,l2::Int,m2::Int,l3::Int,m3::Int)
# note the wigner3j has only one convention, and is highly symmetric.
return (one(T)*im)^(l2+l3-l1) * (-T(1))^m1 * sqrt(4pi*(2*l1+1)*(2*l2+1)*(2*l3+1)) *
wigner3j(T,l1,l2,l3,0,0,0) * wigner3j(T,l1,l2,l3,m1,-m2,-m3)
end
gaunt_coefficient(l1::Int,m1::Int,l2::Int,m2::Int,l3::Int,m3::Int) = gaunt_coefficient(Float64,l1,m1,l2,m2,l3,m3)
function lm_to_spherical_harmonic_index(l::Int,m::Int)::Int
if l < abs(m)
error("The order m of a spherical harmonic must be great or equal than the degree l.")
end
return l^2 + m + l + 1
end
function spherical_harmonics_indices(l_max::Int)
ls = [l for l in 0:l_max for m in -l:l]
ms = [m for l in 0:l_max for m in -l:l]
return ls, ms
end
function associated_legendre_indices(l_max::Int)
ls = [l for l in 0:l_max for m in 0:l]
ms = [m for l in 0:l_max for m in 0:l]
return ls, ms
end
"""
`complex_legendre_array(l_max::Int, z::Complex{T})`
returns a vector of all associated legendre functions with degree `l <= l_max`. The degree and order (indices) of the elements of the vector are given by `spherical_harmonics_indices(l_max::Int)`.
The associated legendre polynomials are taken from the package AssociatedLegendrePolynomials.jl.
"""
function complex_legendre_array(l_max::Int, z::Union{T,Complex{T}}) where {T<:AbstractFloat}
leg_array = zeros(Complex{T}, (l_max + 1)^2)
ind = 0
for l in 0:l_max
for m in -l:l
ind += 1
if m < 0
leg_array[ind] = (-1)^m * Nlm(l, -m) * conj(Plm(l, -m, z))
else
leg_array[ind] = Nlm(l, m) * Plm(l, m, z)
end
end
end
return leg_array
end
"""
`spherical_harmonics(l_max::Int, θ::Complex{T}, φ::Union{T,Complex{T}})`
returns a vector of all spherical harmonics with degree `l <= l_max` with complex arguments. The degree and order (indices) of the elements of the vector are given by `spherical_harmonics_indices(l_max::Int)`.
"""
function spherical_harmonics(l_max::Int, θ::Complex{T}, φ::Union{T,Complex{T}}) where {T<:AbstractFloat}
Plm_arr = complex_legendre_array(l_max, cos(θ))
Ylm_vec = Vector{Complex{T}}(undef, (l_max + 1)^2)
ind = 0
for l in 0:l_max
for m in -l:l
ind += 1
Ylm_vec[ind] = Plm_arr[ind] * exp(m * im * φ)
end
end
return Ylm_vec
end
"""
spherical_harmonics_dθ(l_max::Int, θ::T, φ::T)
Returns a vector of all ``\\partial Y_{(l,m)}(\\theta,\\phi) / \\partial \\theta`` for all the degrees `l` and orders `m`.
"""
function spherical_harmonics_dθ(l_max::Int, θ::T, φ::T) where T <: AbstractFloat
c(l, m) = sqrt(Complex{T}(l^2 - m^2)) / sqrt(Complex{T}(4l^2 - 1))
Ys = spherical_harmonics(l_max+1, θ, φ)
lm_to_n = lm_to_spherical_harmonic_index
dY1s = [
(l == 0) ? zero(Complex{T}) : l * c(l + 1, m) * Ys[lm_to_n(l+1,m)]
for l = 0:l_max for m = -l:l]
dY2s = [
(l == abs(m)) ? zero(Complex{T}) : (l + 1) * c(l, m) * Ys[lm_to_n(l-1,m)]
for l = 0:l_max for m = -l:l]
return (dY1s - dY2s) ./ sin(θ)
end
"""
spherical_harmonics(l_max::Int, θ::T, φ::T)
Returns a vector of all the spherial harmonics ``Y_{(l,m)}(\\theta,\\phi)`` for all the degrees `l` and orders `m`. The degree and order (indices) of the elements of the vector are given by `spherical_harmonics_indices(l_max::Int)`.
"""
function spherical_harmonics(l_max::Int, θ::T, φ::Union{T,Complex{T}}) where {T<:AbstractFloat}
ls, ms = associated_legendre_indices(l_max)
Plm_arr = sf_legendre_array(GSL_SF_LEGENDRE_SPHARM, l_max, cos(θ))[eachindex(ls)]
Ylm_vec = Vector{Complex{T}}(undef, (l_max+1)^2)
Ylm_vec[1] = Plm_arr[1]
ind1 = 1
ind2 = 1
for i = 1:l_max
inds1 = (ind1+i):(ind1+2i)
Ylm_vec[(ind2+i):(ind2+3i)] = [reverse((-1).^ms[inds1[2:end]] .* conj(Plm_arr[inds1[2:end]])); Plm_arr[inds1]]
ind1 += i
ind2 += 2i
end
ls, ms = spherical_harmonics_indices(l_max)
Ylm_vec = (-one(T)) .^ ms .* exp.(ms .* (im*φ)) .* Ylm_vec
return Ylm_vec
end
cartesian_to_radial_coordinates(x::AbstractVector) = cartesian_to_radial_coordinates(SVector(x...))
radial_to_cartesian_coordinates(θ::AbstractVector) = radial_to_cartesian_coordinates(SVector(θ...))
cartesian_to_spherical_coordinates(x::AbstractVector) = cartesian_to_radial_coordinates(x)
spherical_to_cartesian_coordinates(θ::AbstractVector) = radial_to_cartesian_coordinates(θ)
spherical_to_cartesian_vector(v::AbstractVector,θ::AbstractVector) = spherical_to_cartesian_vector(SVector(v...),SVector(θ...))
cartesian_to_spherical_vector(v::AbstractVector,x::AbstractVector) = cartesian_to_spherical_vector(SVector(v...),SVector(x...))
spherical_to_cartesian_transform(θ::AbstractVector) = spherical_to_cartesian_transform(SVector(θ...))
cartesian_to_spherical_transform(x::AbstractVector) = cartesian_to_spherical_transform(SVector(x...))
function spherical_to_cartesian_transform(rθφ::SVector{3})
r, θ, φ = rθφ
M = [
[sin(θ) * cos(φ) cos(θ) * cos(φ) -sin(φ)];
[sin(θ) * sin(φ) cos(θ) * sin(φ) cos(φ)];
[cos(θ) -sin(θ) 0]
]
return M
end
function cartesian_to_spherical_transform(xyz::SVector{3})
r, θ, φ = cartesian_to_spherical_coordinates(xyz)
M = [
[ sin(θ) * cos(φ) sin(θ) * sin(φ) cos(θ)];
[ cos(θ) * cos(φ) cos(θ) * sin(φ) -sin(θ)];
[-sin(φ) cos(φ) 0]
]
return M
end
function spherical_to_cartesian_vector(v::SVector{3}, rθφ::SVector{3})
return spherical_to_cartesian_transform(rθφ) * v
end
function cartesian_to_spherical_vector(v::SVector{3}, xyz::SVector{3})
return cartesian_to_spherical_transform(xyz) * v
end
function cartesian_to_radial_coordinates(x::SVector{3,CT}) where CT
r = sqrt(sum(x .^2)) # note this is, and should be, a complex number when x is a complex vector
θ = atan(sqrt(x[1]^2+x[2]^2),x[3])
φ = (!iszero(x[1]) || !iszero(x[2])) ? atan(x[2], x[1]) : zero(CT)
return [r,θ,φ]
end
function cartesian_to_radial_coordinates(x::SVector{2,CT}) where CT
r = sqrt(sum(x .^2)) # note this should be complex if x is complex
θ = atan(x[2], x[1])
return [r,θ]
end
function radial_to_cartesian_coordinates(rθφ::SVector{3,CT}) where CT
r, θ, φ = rθφ
x = r * sin(θ) * cos(φ)
y = r * sin(θ) * sin(φ)
z = r * cos(θ)
return [x,y,z]
end
function radial_to_cartesian_coordinates(rθ::SVector{2,CT}) where CT
r, θ = rθ
x = r * cos(θ)
y = r * sin(θ)
return [x,y]
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 5380 | """
Acoustic{T<:AbstractFloat,Dim}(ρ::T, c::Complex{T})
Acoustic(ρ::T, c::Union{T,Complex{AbstractFloat}}, Dim::Integer)
Physical properties for a homogenous isotropic acoustic medium with wavespeed (c) and density (ρ)
Simulations in this medium produce scalar (1D) fields in Dim dimensions.
"""
struct Acoustic{T,Dim} <: PhysicalMedium{Dim,1}
ρ::T # Density
c::Complex{T} # Phase velocity
end
# Constructor which supplies the dimension without explicitly mentioning type
Acoustic(ρ::T,c::Union{T,Complex{T}},Dim::Integer) where {T<:Number} = Acoustic{T,Dim}(ρ,Complex{T}(c))
Acoustic(Dim::Integer; ρ::T = 0.0, c::Union{T,Complex{T}} = 0.0) where {T<:Number} = Acoustic{T,Dim}(ρ,Complex{T}(c))
import Base.show
function show(io::IO, p::Acoustic)
# Acoustic template paramaters can be determined entirely from the medium and shape so we do not need to print them
# Print is the style of the first constructor
write(io, "Acoustic($(p.ρ), $(p.c), $(spatial_dimension(p)))")
return
end
# Type aliases for convenience
TwoDimAcoustic{T} = Acoustic{T,2}
name(a::Acoustic{T,Dim}) where {Dim,T} = "$(Dim)D Acoustic"
"""
impedance(medium::Acoustic)
Characteristic specific acoustic impedance (z₀) of medium
"""
impedance(medium::Acoustic) = medium.ρ * medium.c
# Check for material properties that don't make sense or haven't been implemented
"""
check_material(p::Particle, outer_medium::Acoustic)
Checks if wave scattering from the particle `p` is physically viable given the material properties of `p` and its surrounding medium `outer_medium`.
"""
function check_material(p::Particle, outer_medium::Acoustic)
if isnan(abs(p.medium.c)*p.medium.ρ)
throw(DomainError("Particle's phase speed times density is not a number!"))
elseif isnan(abs(outer_medium.c)*outer_medium.ρ)
throw(DomainError("The medium's phase speed times density is not a number!"))
elseif iszero(outer_medium.c)
throw(DomainError("Wave propagation in a medium with zero phase speed is not defined"))
elseif iszero(outer_medium.ρ) && iszero(p.medium.c*p.medium.ρ)
throw(DomainError("Scattering in a medium with zero density from a particle with zero density or zero phase speed is not defined"))
elseif iszero(outer_radius(p))
throw(DomainError("Scattering from a circle of zero radius is not implemented yet"))
end
return true
end
"""
sound_hard([T::Type = Float64,] Dim::Integer)
Construct physical properties of a sound hard acoustic object with type T and dimension Dim.
Also known as [`rigid`](@ref) and equivalent to a [`zero_neumann`](@ref) pressure boundary condition.
"""
sound_hard(T::Type, Dim::Integer) = Acoustic{T,Dim}(T(Inf), one(T))
# If no type is given, assume Float64
sound_hard(Dim::Integer) = sound_hard(Float64, Dim)
"""
hard(host_medium::Acoustic)
See [`sound_hard`](@ref).
"""
hard(host_medium::Acoustic{T,Dim}) where {Dim,T} = sound_hard(T, Dim)
"""
rigid(host_medium::Acoustic)
See [`sound_hard`](@ref).
"""
rigid(host_medium::Acoustic{T,Dim}) where {Dim,T} = sound_hard(T, Dim)
"""
zero_neumann(host_medium::Acoustic)
See [`sound_hard`](@ref).
"""
zero_neumann(host_medium::Acoustic{T,Dim}) where {Dim,T} = sound_hard(T, Dim)
"""
sound_soft([T::Type = Float64,] Dim::Integer)
Construct physical properties of a sound hard acoustic object with type T and dimension Dim.
Equivalent to a [`zero_dirichlet`](@ref) pressure boundary condition.
"""
sound_soft(T::Type, Dim::Integer) = Acoustic{T,Dim}(zero(T), one(T))
# If no type is given, assume Float64
sound_soft(Dim::Integer) = sound_soft(Float64, Dim)
"""
soft(host_medium::Acoustic)
See [`sound_soft`](@ref).
"""
soft(host_medium::Acoustic{T,Dim}) where {Dim,T} = sound_soft(T, Dim)
"""
pressure_release(host_medium::Acoustic)
See [`sound_soft`](@ref).
"""
pressure_release(host_medium::Acoustic{T,Dim}) where {Dim,T} = sound_soft(T, Dim)
"""
zero_dirichlet(host_medium::Acoustic)
See [`sound_soft`](@ref).
"""
zero_dirichlet(host_medium::Acoustic{T,Dim}) where {Dim,T} = sound_soft(T, Dim)
"""
internal_field(x::AbstractVector, p::Particle{Dim,Acoustic{T,Dim}}, source::RegularSource, ω::T, scattering_coefficients::AbstractVector{Complex{T}})
The internal field for an acoustic particle in an acoustic medium. For a sphere and circular cylinder the result is exact, for everything else it is an approximation which assumes smooth fields.
"""
function internal_field(x::AbstractVector{T}, p::Particle{Dim,Acoustic{T,Dim}}, source::RegularSource{Acoustic{T,Dim}}, ω::T, scattering_coefficients::AbstractVector{Complex{T}}) where {Dim,T}
if !(x ∈ p)
@error "Point $x is not inside the particle with shape $(p.shape)"
end
if iszero(p.medium.c) || isinf(abs(p.medium.c))
return zero(Complex{T})
else
fs = scattering_coefficients
order = basislength_to_basisorder(Acoustic{T,Dim},length(fs))
r = outer_radius(p)
t_mat = t_matrix(p, source.medium, ω, order)
vs = regular_radial_basis(source.medium, ω, order, r)
vos = regular_radial_basis(p.medium, ω, order, r)
us = outgoing_radial_basis(source.medium, ω, order, r)
internal_coefs = (vs[:] .* (inv(t_mat) * fs) + us[:] .* fs) ./ vos[:]
inner_basis = regular_basis_function(p, ω)
return inner_basis(order, x-origin(p)) * internal_coefs
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1792 | function boundary_data(shape1::Shape{Dim}, inside_medium::Acoustic{TI,Dim}, outside_medium::Acoustic{TO,Dim},
sim::FrequencySimulation, ωs::Vector;
dr = 10^(3*Dim) * eps(number_type(shape1)), kws...) where {Dim,TI,TO}
in_m = inside_medium
out_m = outside_medium
T = number_type(shape1)
# points just inside particles
inside1_points = boundary_points(shape1; dr = - dr - 10*eps(T))[:]
inside2_points = boundary_points(shape1; dr = - 10*eps(T))[:]
inside_points = mean([inside1_points,inside2_points])
# points just outside particles
outside1_points = boundary_points(shape1; dr = 10*eps(T))[:]
outside2_points = boundary_points(shape1; dr = dr + 10*eps(T))[:]
outside_points = mean([outside1_points,outside2_points])
# results from just inside particles
L = length(inside1_points)
N = 6; #number of sets of points
all_points = [inside1_points; inside2_points; inside_points; outside1_points; outside2_points; outside_points]
results = run(sim, all_points, ωs; kws...)
in1 = field(results)[1:L,:]
in2 = field(results)[L+1:2L,:]
in = field(results)[2L+1:3L,:]
out1 = field(results)[3L+1:4L,:]
out2 = field(results)[4L+1:5L,:]
out = field(results)[5L+1:6L,:]
in_pressure = FrequencySimulationResult(in, inside_points, Vector(ωs))
out_pressure = FrequencySimulationResult(out, outside_points, Vector(ωs))
fields = (in2 - in1)/(dr * in_m.ρ)
in_displace = FrequencySimulationResult(fields, (inside1_points + inside2_points) ./ 2, Vector(ωs))
fields = (out2 - out1)/(dr * out_m.ρ)
out_displace = FrequencySimulationResult(fields, (outside1_points + outside2_points) ./ 2, Vector(ωs))
return ([in_pressure, out_pressure], [in_displace, out_displace])
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1678 | AcousticCircleParticle{T} = Particle{2,Acoustic{T,2},Sphere{T,2}}
"""
t_matrix(Particle{2,Acoustic{T,2},Sphere{T,2}}, Acoustic{T,2}, ω, order)
The T-matrix for a 2D circlular acoustic particle in a 2D acoustic medium.
"""
function t_matrix(p::Particle{2,Acoustic{T,2},Sphere{T,2}}, outer_medium::Acoustic{T,2}, ω::T, basis_order::Integer)::Diagonal{Complex{T}} where T <: AbstractFloat
# Check for material properties that don't make sense or haven't been implemented
check_material(p, outer_medium)
"Returns a ratio used in multiple scattering which reflects the material properties of the particles"
function Zn(m::Integer)::Complex{T}
m = T(abs(m))
ak = outer_radius(p)*ω/outer_medium.c
# set the scattering strength and type
if isinf(p.medium.c) || isinf(p.medium.ρ)
numer = diffbesselj(m, ak)
denom = diffhankelh1(m, ak)
elseif iszero(outer_medium.ρ)
numer = diffbesselj(m, ak)
denom = diffhankelh1(m, ak)
elseif iszero(p.medium.ρ) || iszero(p.medium.c)
numer = besselj(m, ak)
denom = hankelh1(m, ak)
else
q = impedance(p.medium)/impedance(outer_medium) # Impedance ratio
γ = outer_medium.c/p.medium.c #speed ratio
numer = q * diffbesselj(m, ak) * besselj(m, γ * ak) - besselj(m, ak)*diffbesselj(m, γ * ak)
denom = q * diffhankelh1(m, ak) * besselj(m, γ * ak) - hankelh1(m, ak)*diffbesselj(m, γ * ak)
end
return numer / denom
end
# Get Zns for positive m
Zns = map(Zn,0:basis_order)
return - Diagonal(vcat(reverse(Zns), Zns[2:end]))
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3759 |
"""
t_matrix(CapsuleParticle{2,Acoustic{T,2},Sphere{T,2}}, Acoustic{T,2}, ω, order)
The T-matrix for a 2D circlular capsule particle in an acoustic medium.
"""
function t_matrix(cap::CapsuleParticle{2,Acoustic{T,2},Sphere{T,2}}, medium::Acoustic{T,2}, ω::T, M::Integer)::Diagonal{Complex{T}} where T <: AbstractFloat
k = ω / medium.c
k0 = ω / cap.inner.medium.c
k1 = ω / cap.outer.medium.c
a0 = outer_radius(cap.inner)
a1 = outer_radius(cap.outer)
q = (medium.ρ*medium.c)/(cap.outer.medium.ρ*cap.outer.medium.c)
q0 = (cap.inner.medium.ρ*cap.inner.medium.c)/(cap.outer.medium.ρ*cap.outer.medium.c)
Yn(n::Integer) = hankelh1(n,k1*a1)*besselj(n,k1*a0) - hankelh1(n,k1*a0)*besselj(n,k1*a1)
Yddn(n::Integer) = diffhankelh1(n,k1*a1)*diffbesselj(n,k1*a0) - diffhankelh1(n,k1*a0)*diffbesselj(n,k1*a1)
Ydn(n::Integer,x::Complex{T},y::Complex{T}) = hankelh1(n,x)*diffbesselj(n,y) - diffhankelh1(n,y)*besselj(n,x)
function Tn(n::Integer)::Complex{T}
numer = Ydn(n,k*a1,k*a1) * (q0*besselj(n,k0*a0)*Ydn(n,k1*a1,k1*a0) - Yn(n)*diffbesselj(n,k0*a0))
denom = diffbesselj(n,k0*a0)*
(q*hankelh1(n,k*a1)*Ydn(n,k1*a0,k1*a1) + diffhankelh1(n,k*a1)*Yn(n)) +
q0*besselj(n,k0*a0)*
(q*hankelh1(n,k*a1)*Yddn(n) - diffhankelh1(n,k*a1)*Ydn(n,k1*a1,k1*a0))
return (numer - denom*besselj(n,k*a1)) / (denom*hankelh1(n,k*a1))
end
# Get Tns for positive m
Tns = map(Tn,0:M)
return Diagonal(vcat(reverse(Tns), Tns[2:end]))
end
function internal_field(x::AbstractArray{T}, p::CapsuleParticle{2,Acoustic{T,2},Sphere{T,2}}, source::RegularSource{Acoustic{T,2}}, ω::T, scattering_coefficients::AbstractVector) where T
Nh = Int((length(scattering_coefficients) - one(T))/T(2.0)) #shorthand
if iszero(p.outer.medium.c) || isinf(abs((p.outer.medium.c)))
return zero(Complex{T})
elseif norm(x - origin(p)) > outer_radius(p)
@warn "point $x not insider particle $p. Returning zero."
return zero(Complex{T})
end
k = ω / source.medium.c
k0 = ω / p.inner.medium.c
k1 = ω / p.outer.medium.c
a0 = outer_radius(p.inner)
a1 = outer_radius(p.outer)
q0 = (p.inner.medium.ρ*p.inner.medium.c) / (p.outer.medium.ρ*p.outer.medium.c)
q = (source.medium.ρ*source.medium.c) / (p.outer.medium.ρ*p.outer.medium.c)
Yn(n::Integer) = hankelh1(n,k1*a1)*besselj(n,k1*a0) - hankelh1(n,k1*a0)*besselj(n,k1*a1)
Yddn(n::Integer) = diffhankelh1(n,k1*a1)*diffbesselj(n,k1*a0) - diffhankelh1(n,k1*a0)*diffbesselj(n,k1*a1)
Ydn(n::Integer,x::Complex{T},y::Complex{T}) = hankelh1(n,x)*diffbesselj(n,y) - diffhankelh1(n,y)*besselj(n,x)
denom(n::Integer) = q0 * besselj(n,a0*k0) *
(q*besselj(n,a1*k)*Yddn(n) - diffbesselj(n,a1*k)*Ydn(n,a1*k1,a0*k1)) + diffbesselj(n,a0*k0) * (q*besselj(n,k*a1)*Ydn(n,a0*k1,a1*k1) + diffbesselj(n,k*a1)*Yn(n))
forces = scattering_coefficients .* [Ydn(n,k*a1,k*a1)/denom(n) for n = -Nh:Nh];
if norm(x - origin(p)) <= outer_radius(p.inner)
coefs = - q0 * forces .* Ydn.(-Nh:Nh, a0*k1, a0*k1)
basis = regular_basis_function(p.inner, ω)
return basis(Nh,x-origin(p)) * coefs
else # calculate field in the mid region
J_coefs = forces .* [
q0*besselj(n, a0*k0)*diffhankelh1(n, a0*k1) - hankelh1(n, a0*k1)*diffbesselj(n, a0*k0)
for n = -Nh:Nh]
H_coefs = forces .* [
besselj(n, a0*k1)*diffbesselj(n,a0*k0) - q0*besselj(n, a0*k0)*diffbesselj(n,a0*k1)
for n = -Nh:Nh]
J_basis = regular_basis_function(p.outer, ω)
H_basis = outgoing_basis_function(p.outer.medium, ω)
return J_basis(Nh,x-origin(p)) * J_coefs + H_basis(Nh,x-origin(p)) * H_coefs
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 179 | include("acoustics.jl")
include("circle.jl")
include("helmholtz_circle.jl")
include("concentric_capsule.jl")
include("sphere.jl")
include("source.jl")
include("boundary_data.jl")
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1480 | """
t_matrix(Particle{2,Acoustic{T,2},Sphere{T,2}}, Acoustic{T,2}, ω, order)
The T-matrix for a 2D circlular Helmholtz resonator in a 2D acoustic medium.
"""
function t_matrix(p::Particle{2,Acoustic{T,2},SphericalHelmholtz{T,2}}, outer_medium::Acoustic{T,2}, ω::T, basis_order::Integer)::Diagonal{Complex{T}} where T <: AbstractFloat
M = basis_order
ε = p.shape.aperture
γe = 0.5772156649
k = ω/outer_medium.c
kb = k*outer_radius(p)
Qsum = sum([(besselj(m, kb)*diffhankelh1(m, kb) + diffbesselj(m, kb)*hankelh1(m, kb))^2/(diffbesselj(m, kb)*diffhankelh1(m, kb)) for m in -2M:2M])
hε = (4im / pi) * (γe - 1im*pi/2 + log(k*ε/4)) - Qsum / 2
# Check for material properties that don't mkbe sense or haven't been implemented
check_material(p, outer_medium)
if p.medium.ρ < Inf || real(p.medium.c) < Inf
@warn "Theory not done for general Helmholtz resonators, using Newmann boundaries instead."
end
"Returns a ratio used in multiple scattering which reflects the material properties of the particles"
function Zn(m::Integer)::Complex{T}
m = T(abs(m))
# set the scattering strength and type
numer = diffbesselj(m, kb)
denom = diffhankelh1(m, kb)
resonance_term = 2 / (hε * (pi * kb * diffhankelh1(m, kb))^2)
return (numer / denom) - resonance_term
end
# Get Zns for positive m
Zns = map(Zn,0:M)
return - Diagonal(vcat(reverse(Zns), Zns[2:end]))
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6414 | """
point_source(medium::Acoustic, source_position, amplitude=1)::RegularSource
Create 2D [`Acoustic`](@ref) point [`RegularSource`](@ref) (zeroth Hankel function of first type)
"""
function point_source(medium::Acoustic{T,2}, source_position::AbstractVector, amplitude::Union{T,Complex{T},Function} = one(T))::RegularSource{Acoustic{T,2}} where T <: AbstractFloat
# Convert to SVector for efficiency and consistency
source_position = SVector{2,T}(source_position)
if typeof(amplitude) <: Number
amp(ω) = amplitude
else
amp = amplitude
end
source_field(x,ω) = (amp(ω)*im)/4 * hankelh1(0,ω/medium.c * norm(x-source_position))
function source_coef(order,centre,ω)
k = ω/medium.c
r, θ = cartesian_to_radial_coordinates(centre - source_position)
# using Graf's addition theorem
return (amp(ω)*im)/4 * [hankelh1(-n,k*r) * exp(-im*n*θ) for n = -order:order]
end
return RegularSource{Acoustic{T,2},WithoutSymmetry{2}}(medium, source_field, source_coef)
end
# If we replaced 3 with Dim below this could should work for all dimensions! Test carefully after changing.
function point_source(medium::Acoustic{T,3}, source_position, amplitude::Union{T,Complex{T},Function} = one(T))::RegularSource{Acoustic{T,3}} where T <: AbstractFloat
# Convert to SVector for efficiency and consistency
source_position = SVector{3,T}(source_position)
if typeof(amplitude) <: Number
amp(ω) = amplitude
else
amp = amplitude
end
# source_field(x,ω) = amp(ω) / (T(4π) * norm(x-source_position)) * exp(im * ω/medium.c * norm(x-source_position))
# source_field(x,ω) = amp(ω)/sqrt(4π) * shankelh1(0, ω/medium.c * norm(x-source_position))
source_field(x,ω) = amp(ω) * outgoing_basis_function(medium, ω)(0,x-source_position)[1]
# centre = 12.0 .* rand(3)
# x = centre + rand(3)
# order = 5
# U = outgoing_translation_matrix(medium, order, ω, centre);
# vs = regular_basis_function(medium, ω)(order, x - centre);
# us = outgoing_basis_function(medium, ω)(0, x);
# sum(U[1,:] .* vs) - us[1]
function source_coef(order,centre,ω)
U = outgoing_translation_matrix(medium, order, 1, ω, centre);
return amp(ω) .* U[1,:]
end
return RegularSource{Acoustic{T,3},WithoutSymmetry{3}}(medium, source_field, source_coef)
end
function plane_source(medium::Acoustic{T,Dim}; position::AbstractArray{T} = SVector(zeros(T,Dim)...),
direction = SVector(one(T), zeros(T,Dim-1)...),
amplitude::Union{T,Complex{T},Function} = one(T),
kws...
)::RegularSource{Acoustic{T,Dim}} where {T, Dim}
plane_source(medium, position, direction, amplitude; kws...)
end
"""
plane_source(medium::Acoustic, source_position, source_direction=[1,0], amplitude=1)::RegularSource
Create an [`Acoustic`](@ref) planar wave [`RegularSource`](@ref)
"""
function plane_source(medium::Acoustic{T,2}, position::AbstractArray{T},
direction::AbstractArray{T} = SVector(one(T),zero(T)),
amplitude::Union{T,Complex{T}} = one(T);
causal::Bool = false,
beam_width::T = T(Inf)
)::RegularSource{Acoustic{T,2}} where {T}
# Convert to SVector for efficiency and consistency
position = SVector(position...)
direction = SVector((direction ./ norm(direction))...) # unit direction
S = (abs(dot(direction,azimuthalnormal(2))) == one(T)) ? PlanarAzimuthalSymmetry{2} : PlanarSymmetry{2}
# This pseudo-constructor is rarely called, so do some checks and conversions
if iszero(norm(direction))
throw(DomainError("RegularSource direction must not have zero magnitude."))
end
if typeof(amplitude) <: Number
amp(ω) = amplitude
else
amp = amplitude
end
function source_field(x,ω)
x_width = norm((x - position) - dot(x - position, direction)*direction)
if (causal && dot(x - position,direction) < 0) || x_width > beam_width/2
zero(Complex{T})
else
amp(ω)*exp(im*ω/medium.c * dot(x-position, direction))
end
end
function source_coef(order,centre,ω)
# Jacobi-Anger expansion
θ = atan(direction[2],direction[1])
source_field(centre,ω) * [exp(im * n *(T(pi)/2 - θ)) for n = -order:order]
end
return RegularSource{Acoustic{T,2},S}(medium, source_field, source_coef)
end
function plane_source(medium::Acoustic{T,3}, position::AbstractArray{T},
direction::AbstractArray{T} = SVector(zero(T),zero(T),one(T)),
amplitude::Union{T,Complex{T}} = one(T);
causal::Bool = false,
beam_width::T = T(Inf)
) where {T}
# Convert to SVector for efficiency and consistency
position = SVector(position...)
direction = SVector( (direction ./ norm(direction))...) # unit direction
S = (abs(dot(direction,azimuthalnormal(3))) == one(T)) ? PlanarAzimuthalSymmetry{3} : PlanarSymmetry{3}
# This pseudo-constructor is rarely called, so do some checks and conversions
if iszero(norm(direction))
throw(DomainError("RegularSource direction must not have zero magnitude."))
end
if typeof(amplitude) <: Number
amp(ω) = amplitude
else
amp = amplitude
end
function source_field(x,ω)
x_width = norm((x - position) - dot(x - position, direction)*direction)
if (causal && dot(x - position,direction) < 0) || x_width > beam_width/2
zero(Complex{T})
else
amp(ω)*exp(im*ω/medium.c*dot(x - position, direction))
end
end
function source_coef(order,centre,ω)
# plane-wave expansion for complex vectors
r, θ, φ = cartesian_to_radial_coordinates(direction)
Ys = spherical_harmonics(order, θ, φ)
lm_to_n = lm_to_spherical_harmonic_index
return T(4pi) * source_field(centre,ω) .*
[
Complex{T}(im)^l * (-one(T))^m * Ys[lm_to_n(l,-m)]
for l = 0:order for m = -l:l]
end
return RegularSource{Acoustic{T,3},S}(medium, source_field, source_coef)
end
function regular_spherical_coefficients(psource::PlaneSource{T,Dim,1,Acoustic{T,Dim}}) where {Dim,T}
source = plane_source(psource.medium;
amplitude = psource.amplitude[1],
position = psource.position,
direction = psource.direction
)
source.coefficients
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1637 | """
t_matrix(Particle{3,Acoustic{T,3},Sphere{T,3}}, Acoustic{T,3}, ω, order)
The T-matrix for a 3D spherical acoustic particle in a 3D acoustic medium.
"""
function t_matrix(p::Particle{3,Acoustic{T,3},Sphere{T,3}}, outer_medium::Acoustic{T,3}, ω::T, basis_order::Integer)::Diagonal{Complex{T}} where T <: AbstractFloat
# Check for material properties that don't make sense or haven't been implemented
check_material(p, outer_medium)
"Returns a ratio used in multiple scattering which reflects the material properties of the particles"
function Zn(m::Integer)::Complex{T}
m = T(abs(m))
ak = outer_radius(p)*ω/outer_medium.c
# set the scattering strength and type
if isinf(p.medium.c) || isinf(p.medium.ρ) || iszero(outer_medium.ρ)
numer = diffsbesselj(m, ak)
denom = diffshankelh1(m, ak)
elseif iszero(p.medium.ρ) || iszero(p.medium.c)
numer = sbesselj(m, ak)
denom = shankelh1(m, ak)
else
q = impedance(p.medium)/impedance(outer_medium) # Impedance ratio
γ = outer_medium.c/p.medium.c #speed ratio
numer = q * diffsbesselj(m, ak) * sbesselj(m, γ * ak) - sbesselj(m, ak) * diffsbesselj(m, γ * ak)
denom = q * diffshankelh1(m, ak) * sbesselj(m, γ * ak) - shankelh1(m, ak) * diffsbesselj(m, γ * ak)
end
return numer / denom
end
Zns = Zn.(0:basis_order)
len(order::Int) = basisorder_to_basislength(Acoustic{T,3},order)
T_vec = - vcat(Zns[1],[repeat(Zns[l+1:l+1],len(l)-len(l-1)) for l = 1:basis_order]...)
return Diagonal(T_vec)
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1117 | include("plot_domain.jl")
include("plot_field.jl")
include("plot_moments.jl")
# Plot the result across angular frequency for a specific position (x)
@recipe function plot(simres::SimulationResult;
x = simres.x,
x_indices = [findmin([norm(z - y) for z in simres.x])[2] for y in x],
ω_indices = Colon(), field_apply = real)
for x_ind in x_indices
fs = field_apply.(field(simres)[x_ind, ω_indices])
xguide = ((typeof(simres) <: FrequencySimulationResult) ? "ω" : "t")
@series begin
label --> "$field_apply x=$(simres.x[x_ind])"
xguide --> xguide
(getfield(simres, 3)[ω_indices], fs)
end
end
end
"Plot just the particles"
@recipe function plot(sim::FrequencySimulation; bounds = :none)
# println("Plotting a simulation on its own")
@series begin
if bounds != :none
# bounds = bounding_box(sim.particles)
xlims --> (bottomleft(bounds)[1], topright(bounds)[1])
ylims --> (bottomleft(bounds)[2], topright(bounds)[2])
end
sim.particles
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 916 | @recipe function plot(p::CapsuleParticle)
@series shape(p.outer)
@series shape(p.inner)
end
# Plot a vector of particles
@recipe function plot(particles::AbstractParticles)
for particle in particles
@series begin
particle
end
end
end
# Plot the shape of a particle
@recipe function plot(particle::AbstractParticle)
shape(particle)
end
@recipe function plot(shape::Shape{2})
grid --> false
xguide --> "x"
yguide --> "y"
aspect_ratio := 1.0
label --> ""
linecolor --> :grey
x, y = boundary_functions(shape)
(x, y, 0.0, 1.0)
end
@recipe function plot(shape::Shape{3})
println("Only the (x,z) coordinates of this shape will be drawn")
grid --> false
xguide --> "x"
yguide --> "y"
aspect_ratio := 1.0
label --> ""
linecolor --> :grey
x, y, z = boundary_functions(shape)
(x, z, 0.0, 1.0)
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6932 |
"Plot the field for a particular wavenumber"
@recipe function plot(sim::FrequencySimulation{3}, ω::Number;
resolution = 10, res = resolution, xres=res, yres=res,
y = :auto,
field_apply=real,
region_shape = :auto,
bounds = :auto,
exclude_region = EmptyShape{3}(),
drawparticles=false)
# If user wants us to, generate bounding rectangle around particles
region_shape = (region_shape != :auto) ? region_shape :
if isempty(sim.particles)
if bounds == :auto
@warn "What region to plot? For example, use keyword bounds = Box([[-1.0,-1.0],[1.0,1.0]])"
Box([[-1,-1],[1,1]])
else bounds
end
else
region_shape = bounding_box(sim.particles)
end
bounds = bounding_box(region_shape)
# If user has not set xlims and ylims, set them to the rectangle
cs = corners(bounds)
xlims --> (cs[1][1], cs[end][1])
ylims --> (cs[1][end], cs[end][end])
if y == :auto
y = cs[1][2]
end
# Incase the user did set the xlims and ylims, generate a new bounding box with them
# p_xlims = plotattributes[:xlims]
# p_ylims = plotattributes[:ylims]
# bounds = Box([[T(p_xlims[1]),T(p_ylims[1])], [T(p_xlims[2]),T(p_ylims[2])]])
#
# region_shape = (bounds ⊆ region_shape) ? bounds : region_shape
field_sim = run(sim, region_shape, [ω];
y=y, xres=xres, zres=yres,
exclude_region=exclude_region
)
xy_mat = reshape(field_sim.x, (xres+1, yres+1))
x_pixels = [x[1] for x in xy_mat[:,1]]
y_pixels = [x[end] for x in xy_mat[1,:]]
@series begin
# Turn the responses (a big long vector) into a matrix, so that the heatmap will understand us
response_mat = transpose(reshape(field(field_sim), (xres+1, yres+1)))
seriestype --> :contour
fill --> true
grid --> false
aspect_ratio := 1.0
seriescolor --> :balance
title --> "Field at ω=$ω"
(x_pixels, y_pixels, field_apply.(response_mat))
end
if drawparticles
@series begin
sim.particles
end
end
end
"Plot the field for a particular wavenumber"
@recipe function plot(sim::FrequencySimulation{2}, ω::Number;
resolution = 10, res = resolution, xres=res, yres=res,
field_apply=real,
region_shape = :auto,
bounds = :auto,
exclude_region = EmptyShape{2}(),
drawparticles=true)
# If user wants us to, generate bounding rectangle around particles
region_shape = (region_shape != :auto) ? region_shape :
if isempty(sim.particles)
if bounds == :auto
@warn "What region to plot? For example, use keyword bounds = Box([[-1.0,-1.0],[1.0,1.0]])"
Box([[-1.0,-1.0],[1.0,1.0]])
else bounds
end
else
region_shape = bounding_box(sim.particles)
end
bounds = bounding_box(region_shape)
# If user has not set xlims and ylims, set them to the rectangle
xlims --> (bottomleft(bounds)[1], topright(bounds)[1])
ylims --> (bottomleft(bounds)[2], topright(bounds)[2])
# Incase the user did set the xlims and ylims, generate a new bounding
# rectangle with them
p_xlims = plotattributes[:xlims]
p_ylims = plotattributes[:ylims]
bounds = Box([[p_xlims[1],p_ylims[1]], [p_xlims[2],p_ylims[2]]])
region_shape = (bounds ⊆ region_shape) ? bounds : region_shape
field_sim = run(sim, region_shape, [ω]; xres=xres, yres=yres, zres=yres, exclude_region=exclude_region)
xy_mat = reshape(field_sim.x, (xres+1, yres+1))
x_pixels = [x[1] for x in xy_mat[:,1]]
y_pixels = [x[2] for x in xy_mat[1,:]]
@series begin
# Turn the responses (a big long vector) into a matrix, so that the heatmap will understand us
response_mat = transpose(reshape(field(field_sim), (xres+1, yres+1)))
seriestype --> :contour
fill --> true
grid --> false
aspect_ratio := 1.0
seriescolor --> :balance
title --> "Field at ω=$ω"
(x_pixels, y_pixels, field_apply.(response_mat))
end
if drawparticles
@series begin
sim.particles
end
end
end
"Plot the source field for a particular wavenumber"
@recipe function plot(s::RegularSource, ω)
(FrequencySimulation(s), ω)
end
# Plot the result in space (across all x) for a specific angular frequency
@recipe function plot(simres::FrequencySimulationResult, ω::AbstractFloat;
phase_time = 0.0, # does not except "t" as name of variable..
x_indices = axes(simres.x,1),
ω_index = findmin(abs.(getfield(simres, 3) .- ω))[2],
field_apply = real, seriestype = :surface,
region_shape = :empty)
x = [x[1] for x in simres.x[x_indices]]
# y will actually be z for 3D...
y = [x[end] for x in simres.x[x_indices]]
ω = getfield(simres, 3)[ω_index]
phase = exp(-im*ω*phase_time)
seriestype --> seriestype
seriescolor --> :balance
title --> "Field for ω = $ω"
aspect_ratio --> 1.0
if seriestype != :surface
# We could check here to see if x and y have the right structure
x = unique(x)
y = unique(y)
n_x = length(x)
n_y = length(y)
fill --> true
if region_shape != :empty
bounds = bounding_box(region_shape)
# If user has not set xlims and ylims, set them to the rectangle
xlims --> (bottomleft(bounds)[1], topright(bounds)[1])
ylims --> (bottomleft(bounds)[2], topright(bounds)[2])
else
xlims --> (minimum(x), maximum(x))
ylims --> (minimum(y), maximum(y))
end
x, y, field_apply.(phase.*transpose(reshape(field(simres)[x_indices,ω_index],n_x,n_y)))
else
(x, y, field_apply.(phase.*field(simres)[x_indices,ω_index]))
end
end
# Plot the result in space (across all x) for a specific angular frequency
@recipe function plot(timres::TimeSimulationResult, t::AbstractFloat;
x_indices = axes(timres.x,1),
t_index = findmin(abs.(getfield(timres, 3) .- t))[2],
field_apply = real, seriestype = :surface)
x = [x[1] for x in timres.x[x_indices]]
y = [x[2] for x in timres.x[x_indices]]
t = getfield(timres, 3)[t_index]
seriescolor --> :balance
title --> "Field for time = $t"
seriestype --> seriestype
aspect_ratio --> 1.0
if seriestype != :surface
# We should really check here to see if x and y have the right structure
x = unique(x)
y = unique(y)
n_x = length(x)
n_y = length(y)
fill --> true
x, y, field_apply.(transpose(reshape(field(timres)[x_indices,t_index],n_y,n_x)))
else
(x, y, field_apply.(field(timres)[x_indices,t_index]))
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2131 | # function plot{T}(mnts::StatisticalMoments{T}; ribbon=false, X = mnts.x_arr, use_moments = [1,2,4]) #, kws...)
# # if ribbon == true
# # plot_ribbon(mnts)
# plot_ribbon(mnts; X=X, use_moments=use_moments)
# # else
# # plot_graph(mnts; kws...)
# # end
# # println("well hello mister put me nose in other peoples code")
# end
# # woud have liked a user series plot:
# """
# plot(x, y, seriestype = :moments; kws...)
#
# A failed attempt a creating a user defined series plot for the moments `y` with x-axis `x`.
# """
@recipe function plot_ribbon(results::AbstractVector{SimRes};
field_apply = real,
num_moments = 2,
use_moments = 1:min(num_moments,length(results)),
Y = statistical_moments(results, num_moments; field_apply=field_apply)[use_moments],
x = results[1].ω,
labs = ["mean" "std" "skew" "kurt"]) where {T,SimRes<:SimulationResult{T}}
# must include mean
use_moments = sort(union([1; use_moments]))
if labs == [] labs = repeat([""], inner = length(y)) end
colors =[:black, :green, :orange, :red]
m = Y[1]
Ys = map(2:length(Y)) do i
Y_down = if iseven(use_moments[i])
Y[i]
# Y[i]/T(2)
else
map(y-> (y< zero(T)) ? -y : zero(T), Y[i])
end
Y_up = if iseven(use_moments[i])
Y[i]
# Y[i]/T(2)
else
map(y-> (y> zero(T)) ? y : zero(T), Y[i])
end
(Y_down, Y_up)
end
for i = 1:(length(Ys)-1)
Ys[i+1] = (Ys[i+1][1] + Ys[i][1], Ys[i+1][2] + Ys[i][2])
end
for i in reverse(1:length(Ys))
@series begin
seriestype := :line
ribbon := Ys[i]
lab --> labs[use_moments[i+1]]
c --> colors[use_moments[i+1]]
(x, m[:])
end
end
for i in 1:min(6,length(results))
@series begin
linealpha --> 0.2
lab --> ""
c --> :grey
results[i]
end
end
@series begin
seriestype := :line
c --> :black
linewidth --> 2
lab --> labs[1]
(x, m[:])
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3521 | "Plot the response across time"
@recipe function plot(simulation::TimeSimulation)
xguide --> "Time (t)"
yguide --> "Response"
grid --> false
title --> "Response from particles of radius $(signif(simulation.frequency_simulation.particles[1].r,2)) contained in a $(lowercase(name(simulation.frequency_simulation.shape)))\n with volfrac=$(signif(calculate_volfrac(simulation.frequency_simulation),2)) measured at ($(simulation.frequency_simulation.listener_positions[1,1]), $(simulation.frequency_simulation.listener_positions[2,1]))"
(simulation.time_arr, simulation.response)
end
# "Plot the field for an array of time"
# @recipe function plot{T}(TimeSimulation::TimeSimulation{T}; res=res)
# map(axes(TimeSimulation.time_arr,1)) do i
# simulation = deepcopy(TimeSimulation)
# simulation.response = reshape(TimeSimulation.response[i,:],1,:)
# plot(simulation,TimeSimulation.time_arr[i]; res=res, build_field=false)
# end
# end
"Plot the field for one time"
@recipe function plot{T}(TimeSimulation::TimeSimulation{T}, t::Union{T,Vector{T}};
res=20, xres=res, yres=res, resp_fnc=real,
drawshape = false, build_field=true, drawlisteners = build_field)
simulation = TimeSimulation.frequency_simulation
if isa(t,T) t_arr = [t]
else t_arr = t end
@series begin
# find a box which covers everything
shape_bounds = bounding_box(simulation.shape)
listeners_as_particles = map(
l -> Particle(simulation.listener_positions[:,l],mean_radius(simulation)/2),
1:size(simulation.listener_positions,2)
)
particle_bounds = bounding_box([simulation.particles; listeners_as_particles])
bounds = bounding_box(shape_bounds, particle_bounds)
if build_field
field_simulation = run(simulation, bounds; xres=xres, yres=yres)
field_TimeSimulation = deepcopy(TimeSimulation) # to use all the same options/fields as TimeSimulation
field_TimeSimulation.frequency_simulation = field_simulation
generate_responses!(field_TimeSimulation, t_arr)
else
field_TimeSimulation = TimeSimulation
end
# For this we sample at the centre of each pixel
x_pixels = LinRange(bounds.bottomleft[1], bounds.topright[1], xres+1)
y_pixels = LinRange(bounds.bottomleft[2], bounds.topright[2], yres+1)
# NOTE only plots the first time plot for now...
response_mat = transpose(reshape(field_TimeSimulation.response[1,:], (xres+1, yres+1)))
linetype --> :contour
fill --> true
fillcolor --> :balance
title --> "Field at time=$(t_arr[1])"
(x_pixels, y_pixels, resp_fnc.(response_mat))
end
if drawshape
@series begin
simulation.shape
end
end
for i=1:length(simulation.particles) @series simulation.particles[i] end
if drawlisteners
@series begin
line --> 0
fill --> (0, :lightgreen)
grid --> false
colorbar --> true
aspect_ratio --> 1.0
legend --> false
r = mean_radius(simulation.particles)/2
x(t) = r * cos(t) + simulation.listener_positions[1, 1]
y(t) = r * sin(t) + simulation.listener_positions[2, 1]
(x, y, -2π/3, 2π/3)
end
end
# clims --> (-0.65,0.65) # so that white is always = 0, these values are suitable when using default gaussian impulse
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 992 | """
statistical_moments(results, n; field_apply=real)::Vector{Matrix}
Calculate moments up to `n` of results at each position and wavenumber/time, after applying `field_apply`.
"""
function statistical_moments(results::AbstractVector{SimRes}, num_moments::Int; field_apply=real) where {T,SimRes<:SimulationResult{T}}
# Number of positions and wavenumbers/time points sampled
X, K = size(results[1])
# Number of realisations
R = length(results)
moments = [Matrix{T}(undef,X,K) for i=1:num_moments]
# For each wavenumber or timestep, calculate each moment up to num_moments
for i = 1:X
for j = 1:K
responses = [field_apply(field(results[r],i,j)) for r=1:R]
μ = mean(responses)
moments[1][i,j] = μ
for m=2:num_moments
moment = sum((responses .- μ).^m)/(R-1)
moments[m][i,j] = sign(moment) * abs(moment)^(1.0/m)
end
end
end
return moments
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 54 |
include("random_particles.jl")
include("moments.jl")
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6342 |
random_particles(particle_medium::PhysicalMedium{Dim}, particle_shape::Shape{Dim}; kws...) where {Dim} = random_particles(particle_medium, [particle_shape]; kws...)
function random_particles(particle_medium::PhysicalMedium{Dim}, particle_shapes::Vector{S};
num_particles::Integer = length(particle_shapes), volume_fraction = 0,
region_shape::Shape{Dim} = Box(fill(10*sum(outer_radius.(particle_shapes)),Dim)),
current_particles::AbstractParticles{Dim} = AbstractParticle{Dim}[],
kws...
) where {Dim, S<:Shape{Dim}}
particles = if volume_fraction == 0
num_each = Int(round(num_particles / length(particle_shapes)))
for s in particle_shapes
add_particles = random_particles(particle_medium, s, region_shape, num_each; current_particles = current_particles, kws...)
current_particles = [current_particles; add_particles]
end
current_particles
else
vol_each = volume_fraction / length(particle_shapes)
for s in particle_shapes
add_particles = random_particles(particle_medium, s, region_shape, vol_each; current_particles = current_particles, kws...)
current_particles = [current_particles; add_particles]
end
current_particles
end
return particles
end
# random_particles(particle_medium, particle_shapes)
#
# a = 1
# function f1(; a = [])
# if volume_fraction != zero(T)
# volume_fraction_each = volume_fraction / length(particle_shapes)
# for s in particle_shapes
# b = a
# a = [a; b]
# println(a)
# end
# println(a)
# end
# println(a)
# end
# f1(; a = [2])
# a
# function random_particles(particle_medium::PhysicalMedium{Dim}, particle_shape::Shape{Dim};
# region_shape::Shape{Dim} = Rectangle(zeros(T,2), T(10)*outer_radius(particle_shape), T(10)*outer_radius(particle_shape)),
# num_particles::Int = 0, volume_fraction::T = zero(T), kws...) where {T<:AbstractFloat,Dim}
#
# if volume_fraction == zero(T)
# if num_particles == 0 num_particles = 5 end
# random_particles(particle_medium, particle_shape,
# region_shape, num_particles; kws...)
# else
# random_particles(particle_medium, particle_shape,
# region_shape, volume_fraction; kws...)
# end
#
# end
function random_particles(particle_medium::P, particle_shape::S,
region_shape::Shape{Dim}, volfrac::AbstractFloat; kws...
) where {Dim,P<:PhysicalMedium{Dim},S<:Shape{Dim}}
N = Int(round(volfrac * volume(region_shape) / volume(particle_shape)))
return random_particles(particle_medium, particle_shape, region_shape, N; kws...)
end
"""
random_particles(particle_medium, particle_shapes::Vector{Shape}, region_shape, volume_fraction::Number;
seed=Random.make_seed())
random_particles(particle_medium, particle_shape::Shape, region_shape, volume_fraction::Number;
seed=Random.make_seed())
random_particles(particle_medium, particle_shape::Shape, region_shape, N::Integer;
seed=Random.make_seed())
Generate `N` random particles that fit inside `region_shape` (or fill with `volume_fraction`)
Specify seed to make output deterministic. Algorithm places particles unifomly randomly inside
the bounding box of `region_shape` and discards particle if it overlaps (based on outer radius)
or does not lies completely in box.
When passing particle_shapes::Vector{Shape} we assume each element is equally likely to occur. Repeating the same shape will lead to it being placed more often.
"""
function random_particles(particle_medium::P, particle_shape::S, region_shape::Shape{Dim}, N::Int;
seed=Random.make_seed(),
verbose::Bool = false,
separation_ratio = 1.0, # Min distance between particle centres relative to their outer radiuses.
max_attempts_to_place_particle::Int = 3000, # Maximum number of attempts to place a particle
current_particles::AbstractParticles{Dim} = AbstractParticle{Dim}[] # Particles already present.
) where {Dim,P<:PhysicalMedium{Dim},S<:Shape{Dim}}
# Check volume fraction is not impossible
volfrac = N * volume(particle_shape) / volume(region_shape)
max_packing = if length(current_particles) > 0
0.7854 - sum(volume.(current_particles))/volume(region_shape)
else 0.7854
end
if volfrac > max_packing
error("Specified volume fraction is larger than optimal packing of circles.")
end
# Create pseudorandom device with specified seed
randgen = MersenneTwister(seed)
box = bounding_box(region_shape)
if verbose
@printf("""\n
Generating %d randomly positioned %s shaped particles
Total particle volume: %0.5g
Inside %s of volume: %0.5g
Particle volume fraction: %0.5g
Bounding box volume: %0.5g
""", N, name(particle_shape), N*volume(particle_shape), name(region_shape),
volume(region_shape), volfrac, volume(box)
)
end
# Allocate memory for particles
L = length(current_particles)
particles = Vector{Particle{Dim,P,S}}(undef, N + L)
particles[1:L] = current_particles
for n = L+1:L+N
num_attempts = 0
overlapping = true
while overlapping
outside_box = true
while outside_box
x = (box.dimensions ./ 2) .* (1 .- 2 .* rand(randgen,typeof(origin(box)))) + origin(box)
particles[n] = Particle(particle_medium, congruent(particle_shape, x))
outside_box = !(particles[n] ⊆ region_shape)
end
overlapping = false
for i = 1:(n-1) #compare with previous particles
if norm(origin(particles[n]) - origin(particles[i])) < separation_ratio * (outer_radius(particles[n]) + outer_radius(particles[i]))
overlapping = true
break
end
end
num_attempts += 1
if num_attempts > max_attempts_to_place_particle
error("Tried to place a scatterer $max_attempts_to_place_particle times unsuccessfully. You could try increasing max_attempts_to_place_particle")
end
end
end
return particles[L+1:L+N]
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3813 | """
Box([origin::AbstractVector{T}=zeros(),] dimensions::AbstractVector{T})
A [`Box`](@ref) for 2D and 3D with axis aligned sides, defined by dimensions and origin (at the center).
"""
struct Box{T,Dim} <: Shape{Dim}
origin::SVector{Dim,T}
dimensions::SVector{Dim,T}
end
function Box(origin::AbstractVector{T}, dimensions::AbstractVector{T}) where T <: AbstractFloat
Dim = length(origin)
Box{T,Dim}(origin, dimensions)
end
function Box(origin::NTuple{Dim,T}, dimensions::NTuple{Dim,T}) where {Dim,T}
Box{T,Dim}(origin, dimensions)
end
Box(dimensions::AbstractVector{T}) where T <: AbstractFloat = Box(zeros(T,length(dimensions)),dimensions)
"""
Box(points::Vector{v} where v <: AbstractVector)
A [`Box`](@ref) for any dimension with axis aligned sides, that is a minimal cover for the points.
"""
function Box(points::Vector{v} where v <: AbstractVector)
ind = CartesianIndices(points[1])
xs = [p[i] for p in points, i in ind]
xmin = minimum(xs; dims = 1)
xmax = maximum(xs; dims = 1)
c = (xmin + xmax)[:] ./ 2.0;
dims = (xmax - xmin)[:];
return Box(c,dims)
end
Rectangle(bottomleft::Union{AbstractVector{T},NTuple{2,T}}, topright::Union{AbstractVector{T},NTuple{2,T}}) where T = Box([bottomleft,topright])
function Shape(b::Box{T,Dim};
addtodimensions = zeros(T,Dim),
vector_translation::AbstractVector{T} = zeros(T,Dim)
) where {T,Dim}
Box(b.origin + vector_translation, b.dimensions .+ addtodimensions)
end
name(shape::Box) = "Box"
name(shape::Box{T,2}) where T = "Rectangle"
outer_radius(r::Box) = sqrt(sum(r.dimensions .^ 2))
volume(box::Box) = prod(box.dimensions)
import Base.issubset
function issubset(inner::Box, outer::Box)
boxcorners = corners(inner)
return all(c ∈ outer for c in boxcorners)
end
import Base.in
function in(x::AbstractVector, b::Box)::Bool
all(abs.(x .- b.origin) .<= b.dimensions ./ 2)
end
import Base.(==)
function ==(r1::Box, r2::Box)
r1.origin == r2.origin &&
r1.dimensions == r2.dimensions
end
import Base.isequal
function isequal(r1::Box, r2::Box)
isequal(r1.origin, r2.origin) &&
isequal(r1.dimensions , r2.dimensions )
end
function iscongruent(r1::Box, r2::Box)
r1.dimensions == r2.dimensions
end
function congruent(r::Box, x)
Box(x, r.dimensions)
end
# Box bounds itself
bounding_box(b::Box) = b
"Returns a vector of SVector with the coordinates of the corners of the box"
function corners(b::Box{T,Dim}) where {T,Dim}
d1 = origin(b) - b.dimensions ./ T(2)
d2 = origin(b) + b.dimensions ./ T(2)
ds =[d1,d2]
boxcorners = map(0:(2^Dim-1)) do i
switches = 1 .+ [parse(Int,c) for c in bitstring(i)[end-Dim+1:end]]
[ds[switches[j]][j] for j in eachindex(switches)]
end
return boxcorners
end
"Return SVector with the coordinates of the bottom left of a rectangle"
bottomleft(rect::Box{T,2}) where T = origin(rect) .- SVector(rect.dimensions) ./ 2
"Return SVector with the coordinates of the top right of a rectangle"
topright(rect::Box{T,2}) where T = origin(rect) .+ SVector(rect.dimensions) ./ 2
function boundary_functions(rect::Box{T,2}) where T
w, h = rect.dimensions
function x(t)
check_boundary_coord_range(t)
if t <= 1//4 x = bottomleft(rect)[1] + 4t * w
elseif t <= 2//4 x = topright(rect)[1]
elseif t <= 3//4 x = topright(rect)[1] - 4*(t-2//4) * w
else x = bottomleft(rect)[1]
end
end
function y(t)
check_boundary_coord_range(t)
if t <= 1//4 y = bottomleft(rect)[2]
elseif t <= 2//4 y = bottomleft(rect)[2] + 4*(t-1//4) * h
elseif t <= 3//4 y = topright(rect)[2]
else y = topright(rect)[2] - 4*(t-3//4) * h
end
end
return x, y
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 468 | """
EmptyShape{Dim}
An empty shape with no points.
"""
struct EmptyShape{Dim} <: Shape{Dim} end
EmptyShape(s::Shape{Dim}) where {Dim} = EmptyShape{Dim}()
name(shape::EmptyShape) = "EmptyShape"
outer_radius(c::EmptyShape{Dim}) where {Dim} = 0
volume(shape::EmptyShape{Dim}) where {Dim} = 0
import Base.issubset
issubset(c1::Shape, c2::EmptyShape) = false
issubset(c1::EmptyShape, c2::Shape) = false
import Base.in
in(x::AbstractVector, c::EmptyShape) = false
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2440 | """
Halfspace(normal::AbstractVector{T} [, origin::AbstractVector{T}=zeros()])
A halfspace defined by all the points ``\\mathbf x`` that satify ``(\\mathbf x - \\mathbf o) \\cdot \\mathbf n < 0`` where ``\\mathbf n`` is the unit normal and ``\\mathbf o`` is the origin.
"""
struct Halfspace{T,Dim} <: Shape{Dim}
normal::SVector{Dim,T} # outward pointing normal vector
origin::SVector{Dim,T}
end
# Constructors
Halfspace(normal::AbstractVector{T}, origin::AbstractVector{T} = zeros(T,length(normal))) where {T} = Halfspace{T,length(normal)}(normal ./ norm(normal), origin)
Halfspace(normal::NTuple{Dim,T}, origin::AbstractVector{T} = zeros(T,Dim)) where {T,Dim} = Halfspace{T,Dim}(normal ./ norm(normal), origin)
function Shape(h::Halfspace{T,Dim};
addtodimensions = zero(T),
vector_translation = zeros(T,Dim)
) where {T,Dim}
return Halfspace(h.normal, h.origin + h.normal .* addtodimensions + vector_translation)
end
name(shape::Halfspace) = "Halfspace"
function Symmetry(shape::Halfspace{T,Dim}) where {T,Dim}
return (abs(dot(shape.normal,azimuthalnormal(Dim))) == one(T)) ? PlanarAzimuthalSymmetry{Dim}() : PlanarSymmetry{Dim}()
end
volume(shape::Halfspace) = Inf
outer_radius(hs::Halfspace{T}) where T = T(Inf)
# import Base.issubset
# function issubset(inner_rect::Halfspace{T}, outer_rect::Halfspace{T}) where T
# all(topright(inner_rect) .<= topright(outer_rect)) &&
# all(bottomleft(inner_rect) .>= bottomleft(outer_rect))
# end
import Base.in
function in(x::AbstractVector, hs::Halfspace)::Bool
dot(x - hs.origin, hs.normal) < 0
end
import Base.(==)
function ==(h1::Halfspace{T}, h2::Halfspace{T}) where T
h1.origin == h2.origin &&
h1.normal == h2.normal
end
import Base.isequal
function isequal(h1::Halfspace{T}, h2::Halfspace{T}) where T
isequal(h1.origin, h2.origin) &&
isequal(h1.normal, h2.normal)
end
function iscongruent(h1::Halfspace{T}, h2::Halfspace{T}) where T
h1.normal == h2.normal
end
function congruent(h::Halfspace{T}, x) where T
Halfspace(h.normal, x)
end
function boundary_functions(h::Halfspace{T,2}, scale::T = 10.0) where T
surface_vec = [-h.normal[2], h.normal[1]]
function x(t)
check_boundary_coord_range(t)
h.origin[1] + t * scale * surface_vec[1]
end
function y(t)
check_boundary_coord_range(t)
h.origin[2] + t * scale * surface_vec[2]
end
return x, y
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2558 | """
Plate(normal::AbstractVector{T}, width::T, [, origin::AbstractVector{T}=zeros()])
A plate defined by all the points ``\\mathbf x`` that satify ``|(\\mathbf x - \\mathbf o) \\cdot \\mathbf n| < w /2`` where ``\\mathbf n`` is the unit normal, ``\\mathbf o`` is the origin, and ``w`` is the width.
"""
struct Plate{T,Dim} <: Shape{Dim}
normal::SVector{Dim,T} # a unit vector which is orthogonal to the plate
width::T # the width
origin::SVector{Dim,T}
end
# Constructors
Plate(normal::AbstractVector{T}, width::T, origin::AbstractVector{T} = zeros(T,length(normal))) where {T} = Plate{T,length(normal)}(normal ./ norm(normal), width, origin)
Plate(normal::NTuple{Dim,T}, width::T, origin::AbstractVector{T} = zeros(T,Dim)) where {T,Dim} = Plate{T,Dim}(normal ./ norm(normal), width, origin)
function Shape(p::Plate{T,Dim};
addtodimensions = zero(T),
vector_translation = zeros(T,Dim)
) where {T,Dim}
return Plate(p.normal, p.width + addtodimensions, p.origin + vector_translation)
end
name(shape::Plate) = "Plate"
function Symmetry(shape::Plate{T,Dim}) where {T,Dim}
return (abs(dot(shape.normal,azimuthalnormal(Dim))) == one(T)) ? PlanarAzimuthalSymmetry{Dim}() : PlanarSymmetry{Dim}()
end
volume(shape::Plate) = Inf
outer_radius(hs::Plate{T}) where T = T(Inf)
# import Base.issubset
# function issubset(inner_rect::Plate{T}, outer_rect::Plate{T}) where T
# all(topright(inner_rect) .<= topright(outer_rect)) &&
# all(bottomleft(inner_rect) .>= bottomleft(outer_rect))
# end
import Base.in
function in(x::AbstractVector, p::Plate)::Bool
abs(dot(x - p.origin, p.normal)) < p.width / 2
end
import Base.(==)
function ==(h1::Plate, h2::Plate)
h1.origin == h2.origin &&
h1.width == h2.width &&
h1.normal == h2.normal
end
import Base.isequal
function isequal(h1::Plate, h2::Plate)
isequal(h1.origin, h2.origin) &&
isequal(h1.width, h2.width) &&
isequal(h1.normal, h2.normal)
end
function iscongruent(h1::Plate, h2::Plate)
(h1.normal == h2.normal) && (h1.width == h2.width)
end
function congruent(h::Plate, x)
Plate(h.normal, h.width, x)
end
# function boundary_functions(h::Plate{T,2}, scale::T = 10.0) where T
# surface_vec = [-h.normal[2], h.normal[1]]
#
# function x(t)
# check_boundary_coord_range(t)
# h.origin[1] + surface_vec[1] * width/2 + t * scale * surface_vec[1]
# end
#
# function y(t)
# check_boundary_coord_range(t)
# h.origin[2] + t * scale * surface_vec[2]
# end
#
# return x, y
# end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 5428 | """
Abstract idea which defines the external boundary of object.
"""
abstract type Shape{Dim} end
Symmetry(::Shape{Dim}) where {Dim} = WithoutSymmetry{Dim}()
dim(::S) where {Dim,S<:Shape{Dim}} = Dim
"""
origin(shape::Shape)::SVector
Origin of shape, typically the center
"""
origin(shape::Shape) = shape.origin
"""
number_type(shape::Shape)::DataType
Number type which is used to describe shape, defaults to the eltype of the origin vector.
"""
number_type(shape::Shape) = eltype(origin(shape))
"""
Shape(shape::Shape; addtodimensions = 0.0, vector_translation = zeros(...), kws...)
Alter the shape depending on the keywords.
"""
Shape(shape::Shape) = shape
"""
iscongruent(p1::Shape, p2::Shape)::Bool
≅(p1::Shape, p2::Shape)::Bool
True if shapes are the same but in different positions (origins), standard mathematical definition.
"""
iscongruent(s1::Shape, s2::Shape) = false # false by default, overload in specific examples
# Define synonym for iscongruent ≅, and add documentation
≅(s1::Shape, s2::Shape) = iscongruent(s1, s2)
@doc (@doc iscongruent(::Shape, ::Shape)) (≅(::Shape, ::Shape))
"""
congruent(s::Shape, x)::Shape
Create shape congruent to `s` but with origin at `x`
"""
function congruent end
"Generic helper function which tests if boundary coordinate is between 0 and 1"
function check_boundary_coord_range(t)
if t < 0 || t > 1
throw(DomainError("Boundary coordinate must be between 0 and 1"))
end
end
# Concrete shapes
# include("rectangle.jl")
include("box.jl")
include("sphere.jl")
include("halfspace.jl")
include("plate.jl")
include("time_of_flight.jl")
include("time_of_flight_from_point.jl")
include("empty_shape.jl")
"""
points_in_shape(Shape; resolution = 20, xres = resolution, yres = resolution,
exclude_region = EmptyShape(region), kws...)
returns `(x_vec, region_inds)` where `x_vec` is a vector of points that cover a box which bounds `Shape`, and `region_inds` is an array of linear indices such that `x_vec[region_inds]` are points contained `Shape`. For 3D we use `zres` instead of `yres`.
"""
function points_in_shape(region::Shape{2};
resolution::Number = 20, res::Number = resolution, xres::Number = res, yres::Number = res,
exclude_region::Shape = EmptyShape(region),
kws...)
rect = bounding_box(region)
#Size of the step in x and y direction
x_vec_step = rect.dimensions ./ [xres, yres]
bl = bottomleft(rect)
x_vec = [SVector{2}(bl + x_vec_step .* [i,j]) for i=0:xres, j=0:yres][:]
region_inds = findall(x -> !(x ∈ exclude_region) && x ∈ region, x_vec)
return x_vec, region_inds
end
function points_in_shape(region::Shape{3};
y = zero(number_type(region)),
resolution::Number = 20,
res::Number = resolution, xres::Number = res, zres::Number = res,
exclude_region::Shape = EmptyShape(region))
box = bounding_box(region)
#Size of the step in x and z direction
x_vec_step = [box.dimensions[1] / xres, zero(number_type(region)), box.dimensions[3] / zres]
bl = corners(box)[1]
x_vec = [SVector{3}(bl + x_vec_step .* [i,y,j]) for i = 0:xres, j = 0:zres][:]
region_inds = findall(x -> !(x ∈ exclude_region) && x ∈ region, x_vec)
return x_vec, region_inds
end
"Returns a set of points on the boundary of a 2D shape."
function boundary_points(shape2D::Shape{2}, num_points::Int = 4; dr = 0)
T = number_type(shape2D)
x, y = boundary_functions(shape2D)
v(τ) = SVector(x(τ),y(τ)) + dr * (SVector(x(τ),y(τ)) - origin(shape2D))
return [ v(τ) for τ in LinRange(zero(T),one(T),num_points+1)[1:end-1] ]
end
"Returns a set of points on the boundary of a 3D shape."
function boundary_points(shape3D::Shape{3}, num_points::Int = 4; dr = 0)
T = number_type(shape3D)
x, y, z = boundary_functions(shape3D)
v(τ,s) = SVector(x(τ,s),y(τ,s),z(τ,s)) + dr * (SVector(x(τ,s),y(τ,s),z(τ,s)) - origin(shape3D))
mesh = LinRange(zero(T),one(T),num_points+1)[1:end-1]
return [v(τ,s) for τ in mesh, s in mesh]
end
"Returns box which completely encloses the shapes"
bounding_box(shape1::Shape, shape2::Shape) = bounding_box([shape1, shape2])
# Create a box which bounds an array of shapes
function bounding_box(shapes::Vector{S}) where S<:Shape
boxes = bounding_box.(shapes)
corners_mat = hcat(vcat((corners.(boxes))...)...)
maxdims = maximum(corners_mat, dims=2)
mindims = minimum(corners_mat, dims=2)
c = (maxdims + mindims) ./ 2
dimensions = maxdims - mindims
return Box(c[:], dimensions[:])
end
# Docstrings
"""
name(shape::Shape)::String
Name of a shape
"""
function name end
"""
outer_radius(shape::Shape)
The radius of a circle which completely contains the shape
"""
function outer_radius end
"""
volume(shape::Shape)
Volume of a shape
"""
function volume end
"""
volume(shape::Shape)::NTuple{Function,Dim)
Returns Tuple of Dim Functions which define outer boundary of shape when given boundary coordinate t∈[0,1]
"""
function boundary_functions end
"""
issubset(shape1, shape2)::Bool
Returns true if shape1 is entirely contained within shape2, false otherwise (also works with particles).
"""
function issubset(s1::Shape,s2::Shape) throw(MethodError(issubset, (s1,s2))) end
"""
in(vector, shape)::Bool
Returns true if vector is in interior of shape, false otherwise.
"""
function in(::AbstractVector,::Shape) end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6323 | """
All abstract spheres will have an origin and a radius
"""
abstract type AbstractSphere{Dim} <: Shape{Dim} end
"""
Sphere([origin=zeros(),] radius)
A [`Shape`](@ref) where boundary is a fixed distance from the origin. In 2D this is a circle, in 3D the usual sphere, and in higher dimensions if difficult to visualise.
"""
struct Sphere{T,Dim} <: AbstractSphere{Dim}
origin::SVector{Dim,T}
radius::T
end
"""
SphericalHelmholtz([origin=zeros(),] radius, aperture)
A [`Shape`](@ref) which represents a 2D thin-walled isotropic Helmholtz resonator.
"""
struct SphericalHelmholtz{T,Dim} <: AbstractSphere{Dim}
origin::SVector{Dim,T}
radius::T
inner_radius::T
aperture::T
orientation::T
end
# Alternate constructors, where type is inferred naturally
Sphere(origin::NTuple{Dim}, radius::T) where {T,Dim} = Sphere{T,Dim}(origin, radius)
Sphere(origin::AbstractVector, radius::T) where {T} = Sphere{T,length(origin)}(origin, radius)
SphericalHelmholtz(origin::NTuple{Dim}, radius::T, inner_radius::T, aperture::T, orientation::T) where {T, Dim} = SphericalHelmholtz{T,Dim}(origin, radius, inner_radius, aperture, orientation)
SphericalHelmholtz(origin::NTuple{Dim}, radius::T; inner_radius::T = zero(T), aperture::T = zero(T), orientation::T = zero(T)) where {T, Dim} = SphericalHelmholtz{T,Dim}(origin, radius, inner_radius, aperture, orientation)
Sphere(Dim, radius::T) where {T} = Sphere{T,Dim}(zeros(T,Dim), radius)
function SphericalHelmholtz(Dim::Int, radius::T;
origin::T = zeros(T,Dim),
aperture::T = zero(T),
inner_radius::T = zero(T),
orientation::T = zero(T)) where {T}
return SphericalHelmholtz{T,Dim}(origin, radius, inner_radius, aperture, orientation)
end
Circle(origin::Union{AbstractVector{T},NTuple{2,T}}, radius::T) where T <: AbstractFloat = Sphere{T,2}(origin, radius::T)
Circle(radius::T) where T <: AbstractFloat = Sphere(2, radius::T)
Sphere(radius::T) where {T} = Sphere{T,3}(zeros(T,3), radius)
name(shape::Sphere) = "Sphere"
name(shape::Sphere{T,2}) where T = "Circle"
name(shape::SphericalHelmholtz) = "SphericalHelmholtz"
Symmetry(shape::AbstractSphere{Dim}) where {Dim} = RadialSymmetry{Dim}()
outer_radius(sphere::AbstractSphere) = sphere.radius
volume(shape::AbstractSphere{3}) = 4//3 * π * shape.radius^3
volume(shape::AbstractSphere{2}) = π * shape.radius^2
function Shape(sp::Sphere{T,Dim};
addtodimensions::T = 0.0,
vector_translation::AbstractVector{T} = zeros(T,Dim)
) where {T,Dim}
Sphere(sp.origin + vector_translation, sp.radius + addtodimensions)
end
# bounding_box(sphere::Sphere{T,3}; kws...) where T = bounding_box(Circle(sphere; kws...))
function bounding_box(sphere::AbstractSphere)
return Box(origin(sphere), fill(2*sphere.radius, dim(sphere)))
end
import Base.in
function in(x::AbstractVector, sphere::AbstractSphere)::Bool
norm(origin(sphere) .- x) <= sphere.radius
end
import Base.issubset
function issubset(inner_sphere::AbstractSphere, outer_sphere::AbstractSphere)
norm(origin(outer_sphere) - origin(inner_sphere)) <= outer_sphere.radius - inner_sphere.radius
end
function issubset(sphere::AbstractSphere, box::Box)
sphere_box = bounding_box(sphere)
return issubset(sphere_box,box)
end
function issubset(box::Box, sphere::AbstractSphere)
issubset(Sphere(origin(box),outer_radius(box)), sphere)
end
import Base.(==)
==(c1::AbstractSphere, c2::AbstractSphere) = false
function ==(c1::Sphere, c2::Sphere)
c1.origin == c2.origin && c1.radius == c2.radius
end
function ==(c1::SphericalHelmholtz, c2::SphericalHelmholtz)
c1.origin == c2.origin && c1.radius == c2.radius && c1.inner_radius == c2.inner_radius && c1.aperture == c2.aperture && c1.orientation == c2.orientation
end
import Base.isequal
function isequal(c1::AbstractSphere, c2::AbstractSphere)
false
end
function isequal(c1::Sphere, c2::Sphere)
isequal(c1.origin, c2.origin) && isequal(c1.radius, c2.radius)
end
function isequal(c1::SphericalHelmholtz, c2::SphericalHelmholtz)
isequal(c1.origin, c2.origin) && isequal(c1.radius, c2.radius) && s1.aperture == s2.aperture
end
function iscongruent(c1::AbstractSphere, c2::AbstractSphere)
false
end
function iscongruent(s1::Sphere, s2::Sphere)
s1.radius == s2.radius
end
function iscongruent(s1::SphericalHelmholtz, s2::SphericalHelmholtz)
s1.radius == s2.radius && s1.aperture == s2.aperture && s1.inner_radius == s2.inner_radius && s1.orientation == s2.orientation
end
function congruent(s::Sphere, x)
Sphere(x, s.radius)
end
function congruent(s::SphericalHelmholtz, x)
SphericalHelmholtz(x, s.radius, s.aperture)
end
function Circle(sphere::AbstractSphere; y = sphere.origin[2])
if abs(y - sphere.origin[2]) > sphere.radius
return EmptyShape(sphere)
else
r = sqrt(sphere.radius^2 - (sphere.origin[2] - y)^2)
return Sphere{number_type(sphere),2}(sphere.origin[[1,3]], r)
end
end
# boundary_functions(sphere::AbstractSphere; kws...) = boundary_functions(Circle(sphere; kws...))
function boundary_functions(sphere::Sphere{T,3}) where T
function x(t,s=0)
check_boundary_coord_range(t)
check_boundary_coord_range(s)
sphere.radius * sin(t * π) * cos(s * 2π) + origin(sphere)[1]
end
function y(t,s=0)
check_boundary_coord_range(t)
check_boundary_coord_range(s)
sphere.radius * sin(t * π) * sin(s * 2π) + origin(sphere)[2]
end
function z(t,s=0)
check_boundary_coord_range(t)
check_boundary_coord_range(s)
sphere.radius * cos(t * π) + origin(sphere)[3]
end
return x, y, z
end
function boundary_functions(circle::Sphere{T,2}) where T
function x(t)
check_boundary_coord_range(t)
circle.radius * cos(2π * t) + origin(circle)[1]
end
function y(t)
check_boundary_coord_range(t)
circle.radius * sin(2π * t) + origin(circle)[2]
end
return x, y
end
function boundary_functions(circle::SphericalHelmholtz{T,2}) where T
function x(t)
check_boundary_coord_range(t)
circle.radius * cos(2π * t) + origin(circle)[1]
end
function y(t)
check_boundary_coord_range(t)
circle.radius * sin(2π * t) + origin(circle)[2]
end
return x, y
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3190 | """
A shape which contains all particles,``x > x_0``, necessary to simulate a plane-wave scattering from an infinite medium, for a reciever at the focal point, for time ``t < D / c``, where ``c`` is the sound speed of the background medium, and ``D`` is some chosen focal distance. The plane-wave travels towards the positive direction of the ``x`` axis.
More precisely, if the focal point is at ``(x_f,y_f)`` then the interior of the shape
is defined as
``(y - y_f)^2 < (D + x_0)^2 - x_f^2 - 2(D + x_0 - x_f)x`` and ``x > min(x_0, x_f)``
where ``D`` is the focal distance.
"""
struct TimeOfFlightPlaneWaveToPoint{T <: AbstractFloat,Dim} <: Shape{Dim}
focal_point::AbstractVector{T}
focal_distance::T
minimum_x::T
end
TimeOfFlightPlaneWaveToPoint(focal_point::AbstractVector{T}, focal_distance::T; minimum_x::T = zero(eltype(focal_point))) where T <:AbstractFloat = TimeOfFlightPlaneWaveToPoint{T,length(focal_point)}(focal_point, focal_distance, minimum_x)
name(shape::TimeOfFlightPlaneWaveToPoint) = "Time of flight from planar source to the focal point"
# NOTE: this needs to be redone
function volume(shape::TimeOfFlightPlaneWaveToPoint{T}) where T <: AbstractFloat
D = shape.focal_distance
xf = shape.focal_point[1]
x_min = shape.minimum_x
x_max = (x_min + xf + D) / T(2)
a = D + x_min + xf
b = D + x_min - xf
return 2/3*(sqrt(b*(a - 2*x_min)^3) - sqrt(b*(a - 2*x_max)^3))
end
import Base.issubset
function issubset(sphere::Sphere{T,Dim}, shape::TimeOfFlightPlaneWaveToPoint{T,Dim}) where {T, Dim}
return (origin(sphere)[1] > shape.minimum_x) && (norm(origin(sphere) - shape.focal_point) <= shape.focal_distance - (origin(sphere)[1] - shape.minimum_x) - T(2) * outer_radius(sphere))
end
function bounding_box(shape::TimeOfFlightPlaneWaveToPoint{T,Dim}) where {T,Dim}
D = shape.focal_distance
xf = shape.focal_point[1]
y_f = shape.focal_point[2]
x_min = shape.minimum_x
x_max = (x_min + xf + D) / T(2)
centre = zeros(Dim)
centre[1] = (x_min + x_max) / T(2)
centre[2] = y_f
dimensions = ones(Dim) * T(2) * sqrt((D + x_min)^2 - xf^2 - 2*(D + x_min - xf)*x_min)
dimensions[1] = x_max - x_min
return Box(centre, dimensions)
end
function boundary_functions(shape::TimeOfFlightPlaneWaveToPoint{T,2}) where T
D = shape.focal_distance
xf = shape.focal_point[1]
y_f = shape.focal_point[2]
x_min = shape.minimum_x
x_max = (x_min + xf + D) / T(2)
function x(τ)
check_boundary_coord_range(τ)
if τ <= 1//3
return (1 - 3*τ)*x_min + 3*τ*x_max
elseif τ <= 2//3
return (3*τ - 1)*x_min + (2 - 3*τ)*x_max
else
return x_min
end
end
function y(τ)
check_boundary_coord_range(τ)
if τ <= 1//3
return y_f + sqrt((D + x_min)^2 - xf^2 - 2*(D + x_min - xf)*((1 - 3*τ)*x_min + 3*τ*x_max))
elseif τ <= 2//3
return y_f - sqrt((D + x_min)^2 - xf^2 - 2*(D + x_min - xf)*((3*τ - 1)*x_min + 3*(2//3 - τ)*x_max))
else
return y_f + (6*τ - 5)*sqrt((D + x_min)^2 - xf^2 - 2*(D + x_min - xf)*x_min)
end
end
return x, y
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1936 | """
A shape where anything inside could cause a disturbance at the listener position
from a point source wavefront starting at the listener. Also everything inside
has a positive `x` coordinate. It is equivalent to a segment of a circle.
More precisely, if the listener is at (l_x,l_y) then the interior of the shape
is defined as
sqrt((x-l_x)^2+(y-l_y)^2)<time and x>0
"""
struct TimeOfFlightPointWaveToPoint{T <: AbstractFloat} <: Shape{2}
listener_position::Vector{T}
time::T
end
name(shape::TimeOfFlightPointWaveToPoint) = "Time of flight from point source"
function volume(shape::TimeOfFlightPointWaveToPoint)
θ = 2acos(-shape.listener_position[1] / shape.time)
return shape.time^2 * (θ - sin(θ))/2
end
import Base.issubset
function issubset(circle::Sphere{2}, shape::TimeOfFlightPointWaveToPoint)
(origin(circle)[1] - circle.radius) > 0 &&
norm(origin(circle) - shape.listener_position) < (shape.time - 2circle.radius)
end
function bounding_box(shape::TimeOfFlightPointWaveToPoint)
box_height = 2sqrt(shape.time^2 - shape.listener_position[1]^2)
box_width = max(shape.time + shape.listener_position[1], 0)
return Box([SVector(zero(box_width), -box_height/2), SVector(box_width, box_height/2)])
end
function boundary_functions(shape::TimeOfFlightPointWaveToPoint)
function x(t)
check_boundary_coord_range(t)
if t <= 1//2
θ = acos(-shape.listener_position[1] / shape.time)
return shape.time*cos(θ*(4t-1)) + shape.listener_position[1]
else
return zero(t)
end
end
function y(t)
check_boundary_coord_range(t)
if t <= 1//2
θ = acos(-shape.listener_position[1] / shape.time)
return shape.time*sin(θ*(4t-1)) + shape.listener_position[2]
else
return 2*(3//4-t)*2*sqrt(shape.time^2 - shape.listener_position[1]^2)
end
end
return x, y
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3628 | @testset "Acoustic constructors" begin
# 2D Acoustic
a2 = Acoustic(0.1, 0.1+0.0im, 2)
@test spatial_dimension(a2) == 2
@test field_dimension(a2) == 1
# 3D Acoustic
a3 = Acoustic(1.0, 1.0+0.0im, 3)
@test spatial_dimension(a3) == 3
@test field_dimension(a3) == 1
# Boundary condition constuctors
@test sound_hard(2) == hard(a2)
@test sound_hard(2) == rigid(a2)
@test sound_hard(2) == zero_neumann(a2)
@test sound_soft(2) == soft(a2)
@test sound_soft(2) == pressure_release(a2)
@test sound_soft(2) == zero_dirichlet(a2)
@test sound_hard(2) != sound_soft(2)
end
@testset "Acoustic special functions" begin
T = Float64
ms = 0:4
map(2:3) do Dim
L1 = basisorder_to_basislength(Acoustic{T,Dim},ms[1])
L2 = basisorder_to_basislength(Acoustic{T,Dim},ms[end])
m = basislength_to_basisorder(Acoustic{T,Dim}, L2)
@test m == ms[end]
@test L1 == 1
end
# import EffectiveWaves: regular_translation_matrix
# import EffectiveWaves: outgoing_translation_matrix
# Test 3D outgoing translation matrix
ω = rand() + 0.1
medium = Acoustic(3; ρ = 1.0, c = 1.0)
r = rand(3) - [0.5,0.5,0.5];
d = rand(3) - [0.5,0.5,0.5];
d = 10 * d * norm(r) / norm(d)
order = 2
U = outgoing_translation_matrix(medium, 4*order, order, ω, d)
vs = regular_basis_function(medium, ω)(4*order,r)
us = outgoing_basis_function(medium, ω)(order,r + d)
@test maximum(abs.(U * vs[:] - us[:]) ./ abs.(us[:])) < 3e-6 # for linux: 4e-7
V = regular_translation_matrix(medium, 4*order, order, ω, d)
v1s = regular_basis_function(medium, ω)(4*order,r)
v2s = regular_basis_function(medium, ω)(order,r + d)
@test maximum(abs.(V * v1s[:] - v2s[:]) ./ abs.(v2s[:])) < 1e-8 # for linux: 4e-7
# Test 2D outgoing translation matrix
ω = rand() + 0.1
medium = Acoustic(2; ρ = 1.0, c = 1.0)
r = rand(2) - [0.5,0.5];
d = rand(2) - [0.5,0.5];
d = 10 * d * norm(r) / norm(d)
# Note that to be accurate the order of vs
order = 4
larger_order = 3order
U = outgoing_translation_matrix(medium, larger_order, order, ω, d)
vs = regular_basis_function(medium, ω)(larger_order,r)
us = outgoing_basis_function(medium, ω)(order,r + d)
@test maximum(abs.(U * vs[:] - us[:]) ./ abs.(us[:])) < 1e-9
V = regular_translation_matrix(medium, larger_order, order, ω, d)
v1s = regular_basis_function(medium, ω)(larger_order,r)
v2s = regular_basis_function(medium, ω)(order,r + d)
@test maximum(abs.(V * v1s[:] - v2s[:]) ./ abs.(v2s[:])) < 1e-10
end
@testset "Acoustic circle T-matrix" begin
circle = Sphere((0.0,0.0), 2.0)
a2 = Acoustic(0.1, 0.1+0.0im, 2)
a2_host = Acoustic(1.0, 1.0+0.0im, 2)
ω = 0.5
N_basis = estimate_outgoing_basisorder(a2_host, Particle(a2,circle), ω)
# Test return type is satisfied for valid input
t = t_matrix(Particle(a2,circle), a2_host, ω, N_basis)
@test typeof(t) <: Diagonal{Complex{Float64}}
p = Particle(Acoustic(Inf, 0.0im, 2),circle)
@test_throws DomainError t_matrix(p, Acoustic(1.0, 1.0+0.0im, 2), ω, N_basis)
p = Particle(Acoustic(1.0, 1.0+0.0im, 2),circle)
@test_throws DomainError t_matrix(p, Acoustic(0.0, Inf*im, 2), ω, N_basis)
@test_throws DomainError t_matrix(p, Acoustic(1.0, 0.0im, 2), ω, N_basis)
p = Particle(Acoustic(0.0, 1.0im, 2),circle)
@test_throws DomainError t_matrix(p, Acoustic(0.0, 1.0+0.0im, 2), ω, N_basis)
p = Particle(a2, Sphere([1.0, 1.0], 0.0))
@test_throws DomainError t_matrix(p, a2_host, ω, N_basis)
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 8093 | @testset "boundary conditions" begin
@testset "Circle Particle" begin
ωs = [0.1,0.2,0.3]
Nh = 8
basis_order = Nh
medium = Acoustic(1.,1.,2)
# Choose particles
soft_medium = Acoustic(0.,0.0 + 0.0im,2)
p_soft = Particle(soft_medium, Sphere([1.0,2.0], .5))
hard_medium = Acoustic(Inf,Inf + 0.0im,2)
p_hard = Particle(hard_medium, Sphere([-3.0,-2.0], 0.3))
sound = Acoustic(medium.ρ, 4. + 0.0im,2)
p1 = Particle(sound, Sphere([-10.0,0.0], .2))
particles = [p_soft, p_hard, p1]
# Create two point sources
source_position = [0.0,0.2]
amplitude = 1.0
source1 = point_source(medium, source_position, amplitude);
source2 = plane_source(medium, [0.0,0.0], [1.0,0.0], amplitude);
# source2 = point_source(medium, -source_position, amplitude)
source = 0.5*source1 + 0.5*source2;
sim = FrequencySimulation(particles, source)
sim_source = FrequencySimulation(source)
result = run(sim_source, [1.0,2.0], 0.1)
pressure_results, displace_results = boundary_data(
shape(particles[1]), particles[1].medium, medium, sim, ωs;
min_basis_order = 8, basis_order = 16
)
pressure_source_results, displace_source_results = boundary_data(
shape(particles[1]), particles[1].medium, medium, sim_source, ωs;
min_basis_order = 6,
basis_order = 10
)
# Zero pressure (Dirichlet) boundary condition
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field)) < 1e-6 * mean(norm.(pressure_source_results[2].field))
pressure_results, displace_results = boundary_data(
shape(particles[2]), particles[2].medium, medium, sim, ωs;
min_basis_order = 8,
basis_order = 16
)
pressure_source_results, displace_source_results = boundary_data(
shape(particles[2]), particles[2].medium, medium, sim_source, ωs;
basis_order = 6,
min_basis_order = 8
);
# Zero displacement (Neuman) boundary condition
@test maximum(norm.(displace_results[1].field - displace_results[2].field)) < 5e-5 * mean(norm.(displace_source_results[2].field))
pressure_results, displace_results = boundary_data(shape(particles[3]), particles[3].medium, medium, sim, ωs; min_basis_order = 8, basis_order = 14, dr = 8e-6);
pressure_source_results, displace_source_results = boundary_data(shape(particles[3]), particles[3].medium, medium, sim_source, ωs; min_basis_order = 6, basis_order = 10, dr = 1e-6);
# Continuous pressure and displacement accross particl boundary
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field)) < 2e-6 * mean(norm.(pressure_source_results[2].field))
@test maximum(norm.(displace_results[1].field - displace_results[2].field)) < 6e-5 * mean(norm.(displace_source_results[1].field))
# The source pressure should always be continuous across any interface, however the displacement is only continuous because p1.medium.ρ == medium.ρ
@test mean(norm.(pressure_source_results[1].field - pressure_source_results[2].field)) < 4e-8 * mean(norm.(pressure_source_results[2].field))
@test mean(norm.(displace_source_results[1].field - displace_source_results[2].field)) < 5e-7 * mean(norm.(displace_source_results[1].field))
end
@testset "CapsuleParticle" begin
concen_particles1 = [
Particle(Acoustic(2.0,2.0,2),Sphere((0.0,0.0),1.0)),
Particle(Acoustic(1.0,1.,2),Sphere((0.0,0.0),2.0))
]
concen_particles2 = [
Particle(Acoustic(2.0,1.0,2),Sphere((6.0,3.0),1.)),
Particle(Acoustic(0.4,0.8,2),Sphere((6.0,3.0),1.4))
]
particle = Particle(Acoustic(1.5,1.5,2),Sphere((-6.0,-3.0),0.8))
ps = [CapsuleParticle(concen_particles2...), CapsuleParticle(concen_particles1...), particle]
medium = Acoustic(0.8, 0.5 + 0.0im,2)
source = plane_source(medium, [0.0,0.0], [1.0,0.0], 1.)
sim = FrequencySimulation(ps, source)
ωs = [0.01,0.2,0.3,1.]
basis_vec = [8,16,16,24]
pressure_results, displace_results = boundary_data(shape(ps[1].outer), ps[1].outer.medium, medium, sim, ωs; basis_order_vec = basis_vec, dr = 1e9 * eps(Float64))
# Continuous pressure and displacement accross particl boundary
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field)) / mean(norm.(pressure_results[2].field)) < 1e-6
@test maximum(norm.(displace_results[1].field - displace_results[2].field)) / mean(norm.(displace_results[2].field)) < 5e-6
pressure_results, displace_results = boundary_data(shape(ps[1].inner), ps[1].inner.medium, ps[1].outer.medium, sim, ωs; basis_order_vec = basis_vec, dr = 1e9 * eps(Float64))
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field)) / mean(norm.(pressure_results[2].field)) < 1e-6
@test maximum(norm.(displace_results[1].field - displace_results[2].field)) / mean(norm.(displace_results[2].field)) < 5e-6
pressure_results, displace_results = boundary_data(shape(ps[2].outer), ps[2].outer.medium, medium, sim, ωs; basis_order_vec = basis_vec .+ 2, dr = 1e9 * eps(Float64))
# Continuous pressure and displacement accross particl boundary
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field)) / mean(norm.(pressure_results[2].field)) < 5e-6
@test maximum(norm.(displace_results[1].field - displace_results[2].field)) / mean(norm.(displace_results[2].field)) < 1e-5
pressure_results, displace_results = boundary_data(shape(ps[3]), ps[3].medium, medium, sim, ωs; basis_order_vec = basis_vec, dr = 1e9 * eps(Float64))
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field)) / mean(norm.(pressure_results[2].field)) < 1e-6
@test maximum(norm.(displace_results[1].field - displace_results[2].field)) / mean(norm.(displace_results[2].field)) < 5e-6
end
@testset "Spherical Particles" begin
# ωs = [0.1,0.2,0.3]
ωs = [0.3]
medium = Acoustic(3,ρ=1.1,c=0.5)
# Choose particles
soft_medium = Acoustic(3; ρ = 0.2, c= 0.3 + 0.0im)
p1 = Particle(soft_medium,Sphere([1.0,2.0,0.0], .5))
hard_medium = Acoustic(3; ρ = 3.2, c= 6.3 + 0.0im)
p2 = Particle(hard_medium,Sphere([-1.0,-2.0,0.0], 0.3))
sound = Acoustic(3,ρ=medium.ρ,c=1.5)
p3 = Particle(sound,Sphere([-4.0,0.0,0.0], .2))
particles = [p1, p2, p3]
os = origin.(particles)
[norm(o-u) for o in os, u in os]
# Create two point sources
# source_position = [0.0,0.2]
amplitude = 1.0
# source1 = point_source(medium, source_position, amplitude);
source2 = plane_source(medium, [0.0,0.0,0.0], [0.0,0.0,1.0], amplitude);
# source2 = point_source(medium, -source_position, amplitude)
# source = 0.5*source1 + 0.5*source2;
source = 1.5*source2;
sim = FrequencySimulation(particles, source);
sim_source = FrequencySimulation(source);
# result = run(sim_source, [1.0,2.0,1.0], ωs)
dr = 1e-7
map(particles) do p
pressure_results, displace_results = boundary_data(
shape(p), p.medium, medium, sim, ωs;
dr = dr, basis_order = 8 #,min_basis_order = 5
);
pressure_source_results, displace_source_results = boundary_data(
shape(p), p.medium, medium, sim_source, ωs;
dr = dr, basis_order = 8 #,min_basis_order = 5
);
@test maximum(norm.(pressure_results[1].field - pressure_results[2].field) ./ norm.(pressure_results[2].field)) < 1e-7
@test maximum(norm.(displace_results[1].field - displace_results[2].field) ./ norm.(displace_results[2].field)) < 4e-6
end
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2211 | # Run like a user might run it
@testset "End-to-end" begin
@testset "Particles with same shape" begin
# 2D acoustics
circle1 = Sphere((0.0,0.0),1.0)
circle2 = Sphere((0.0,5.0),2.0)
a_p = Acoustic(2; ρ = 1.0, c = 1.0)
a = Acoustic(2; ρ = 0.3, c = 0.2)
particles = [Particle(a_p,circle1), Particle(a_p,circle2)]
source = plane_source(a; position = [0.0,0.0], direction = [1.0,0.0])
sim = FrequencySimulation(particles,source)
# show(sim);
result = run(sim, [1.0,2.0], 0.1)
result = run(particles, source, [1.0,2.0], 0.1)
result = 3.2*result + result*4.0im + 0.3+4.0im # changes result.field
@test field(result)[1] == result.field[1][1] # returns
@test field(result,1,1) == result.field[1][1] # returns
# run simulation over a region rather than a specif set of x points
ω = 0.1
region = bounding_box([p.shape for p in particles])
result = run(particles, source, region, [ω]; res=10, only_scattered_waves = true)
# 3D acoustics
s1 = Sphere((1.0,-1.0,2.0),1.0)
s2 = Sphere((0.0,3.0,0.0),2.0)
a_p = Acoustic(3; ρ = 1.0, c = 1.0)
a = Acoustic(3; ρ = 0.3, c = 0.2)
particles = [Particle(a_p,s1), Particle(a_p,s2)]
source = plane_source(a; position = [0.0,0.0,0.0], direction = [0.0,0.0,1.0])
x = [-3.0,2.0,3.0]
ω = 0.1
sim = FrequencySimulation(particles,source)
result = run(particles, source, x, ω)
result = 3.2*result + result*4.0im + 0.3+4.0im # changes result.field
3.2 + result
@test field(result)[1] == result.field[1][1] # returns
@test field(result,1,1) == result.field[1][1] # returns
end
@testset "Particles with different shape" begin
circle = Sphere((0.0,0.0),1.0)
rect = Box((2.0,2.0),(3.0,2.0))
a_p = Acoustic(1.0,1.0,2)
a = Acoustic(0.3,0.2,2)
particles = [Particle(a_p,circle), Particle(a_p,rect)]
source = plane_source(a,[0.0,0.0],[1.0,0.0])
sim = FrequencySimulation(particles,source)
@test true
end
include("time_one_particle.jl")
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2574 | import Test: @testset, @test, @test_throws
import Statistics: mean
using MultipleScattering
using LinearAlgebra
@testset "Fourier transform" begin
ω_arr = collect(LinRange(0.0,100.0,200))
t_arr = ω_to_t(ω_arr)
N = length(ω_arr) - 1
t0 = t_arr[N]
# test invertablity
@test ω_arr ≈ t_to_ω(ω_to_t(ω_arr))
fs = rand(-1:0.01:1.,2N+1,1)
@test fs ≈ frequency_to_time(time_to_frequency(fs,t_arr),ω_arr)
# Gaussian to Gaussian
as = [0.5];
Fs = [exp(-a*ω^2)*exp(im*t0*ω) for ω in ω_arr, a in as]
fs = frequency_to_time(Fs,ω_arr,t_arr);
true_fs = (1/(2pi))*[sqrt(pi/a)*exp(-(t-t0)^2/(4*a)) for t in t_arr, a in as]
@test fs ≈ true_fs
@test Fs ≈ time_to_frequency(fs,t_arr,ω_arr)
# sinc to rectangle
rect(t) = (abs(t)<0.5) ? 1.0 : 0.
as = [0.7]; #only positive values
Fs = [ (ω == 0.0im) ? 1.0+0.0im : sin(a*pi*ω)*exp(im*t0*ω)/(a*pi*ω) for ω in ω_arr, a in as]
fs = frequency_to_time(Fs,ω_arr,t_arr) # only correct for half of time_arr
true_fs = (1/(2pi))*[(1/abs(a))*rect((t-t0)/(2*pi*a)) for t in t_arr, a in as]
@test mean(abs.(fs-true_fs)) < 0.02*mean(abs.(true_fs))
# trapezoidal integration
ω_arr = LinRange(0.0,130.0,600)
t_arr = ω_to_t(ω_arr)
fs = cos.(t_arr).*exp.(-(t_arr .- t_arr[end]/2).^2/(t_arr[end]^2/25))
fs = reshape(fs,length(fs),1)
Fs_trap = time_to_frequency(fs, t_arr; method=:trapezoidal)
Fs = time_to_frequency(fs, t_arr)
# plot(ω_arr,[real(Fs),real(Fs_trap)])
@test mean(abs.(Fs-Fs_trap)) < 0.0012*mean(abs.(Fs))
fs_trap = frequency_to_time(Fs_trap,ω_arr; method=:trapezoidal)
@test mean(abs.(fs-fs_trap))< 1e-5*mean(abs.(fs))
## rectangle to sinc
# as = [1/(2*(maximum(ω_arr)+ω_arr[2]))]; #only positive values
# # t0 = t_arr[end]/3
# Fs = Complex{Float64}[ rect(a*ω)*exp(im*t0*ω) for ω in ω_arr, a in as]
# fs = frequency_to_time(Fs, ω_arr, t_arr)
# true_fs = [ (t==t0) ? 1/(2pi*a) : sin((t-t0)/(2a))/(pi*(t-t0)) for t in t_arr, a in as]
# @test maximum(abs.(fs-true_fs)) < 1e-3*maximum(abs.(true_fs))
# pole to wavy heaviside
# ω_arr = collect(LinRange(0.0,10.0,4000)) # need fine mesh near ω=0
# dω = (ω_arr[2]-ω_arr[1])
# N = length(ω_arr)-1;
# time_arr = LinRange(0,2π/dω,2N+2)[1:(2N+1)]
# as = [0.1]; #only positive values
# Fs = Complex{Float64}[1/(a-im*ω) for ω in ω_arr, a in as]
# fs = frequency_to_time(Fs,ω_arr,time_arr);
# true_fs = [exp(-a*t) for t in time_arr, a in as]
# mean(abs.(fs-true_fs))
# 1e-3*mean(abs.(true_fs))
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 738 | @testset "Moments" begin
begin
# Fake results, with mean 4.0, standard deviation 2.0 and skew 0.0
fields = [2.0, 4.0, 6.0]
results_freq = [FrequencySimulationResult(reshape([complex(f)],1,1),[[0.0]],[0.0]) for f in fields]
results_time = [TimeSimulationResult(reshape([f],1,1),[[0.0]],[0.0]) for f in fields]
moments_freq = statistical_moments(results_freq, 3)
@test moments_freq[1][1,1] ≈ 4.0 &&
moments_freq[2][1,1] ≈ 2.0 &&
moments_freq[3][1,1] ≈ 0.0
moments_time = statistical_moments(results_time, 3)
@test moments_time[1][1,1] ≈ 4.0 &&
moments_time[2][1,1] ≈ 2.0 &&
moments_time[3][1,1] ≈ 0.0
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 5359 | @testset "Particle" begin
a = Acoustic(1.0, 1.0, 2)
a2 = Acoustic(1.0, 2.0, 2)
@testset "Types" begin
circle1 = Sphere((0.0,0.0),1.0)
circle2 = Circle((0.0,5.0),2.0)
a = Acoustic(1.0,1.0,2)
homog_particles = [Particle(a,circle1), Particle(a,circle2)]
# Check types comparisons work as user would expect
@test typeof(homog_particles) <: AbstractParticles
@test typeof(homog_particles) <: AbstractParticles{2}
circle = Sphere((0.0,0.0),1.0)
rect = Box((2.0,2.0),(3.0,2.0))
diff_shape_particles = [Particle(a,circle), Particle(a,rect)]
# Check types comparisons work as user would expect
@test typeof(diff_shape_particles) <: AbstractParticles
@test typeof(diff_shape_particles) <: AbstractParticles{2}
a2 = Acoustic(1.0,1.0,2)
a3 = Acoustic(1.0,1.0,3)
sphere = Sphere((0.0,0.0,0.0),1.0)
circular_particle = Particle(a2,circle)
@test typeof(circular_particle) <: Particle{2}
spherical_particle = Particle(a3,sphere)
@test typeof(spherical_particle) <: AbstractParticle{3}
# Dimension mismatch throws error
@test_throws MethodError Particle(a3,circle)
@test_throws MethodError Particle(a2,sphere)
# This is a valid vector of valid particles, but not of type Particles
# because the dimensions don't match
invalid_particles = [circular_particle, spherical_particle]
@test_throws TypeError invalid_particles::(Vector{Pt} where {Dim, Pt <: AbstractParticle{Dim}})
# does not throw an error
diff_shape_particles::(Vector{Pt} where {Dim, Pt <: AbstractParticle{Dim}})
@test true
end
@testset "Comparisons" begin
circle = Sphere((1.0,3.0),2.0)
circle_identical = Sphere((1.0,3.0),2.0)
circle_congruent = Sphere((4.0,7.0),2.0)
rect = Box((1.0,2.0),(2.0,4.0))
resonator = SphericalHelmholtz((1.0,3.0),2.0, 0.2, 0.01, -1.3)
resonator_kws = SphericalHelmholtz((1.0,3.0),2.0; inner_radius = 0.2, aperture = 0.1, orientation = -1.3)
resonator_dif_aperture = SphericalHelmholtz((1.0,3.0),2.0; aperture = 0.1)
resonator_identical = SphericalHelmholtz((1.0,3.0), 2.0; orientation = -1.3, inner_radius = 0.2, aperture = 0.01)
resonator_congruent = SphericalHelmholtz((4.0,7.0), 2.0; orientation = -1.3, inner_radius = 0.2, aperture = 0.01)
# Construct four particles, with two the same
p = Particle(a2,circle)
p_reference = p
p_identical = Particle(a2,circle_identical)
p_different = Particle(a2, rect)
p_congruent = Particle(a2,circle_congruent)
# Construct three resonator particles
pr = Particle(a2, resonator)
pr_reference = pr
pr_dif_aperture = Particle(a2, resonator_dif_aperture)
pr_identical = Particle(a2, resonator_identical)
pr_different = p_different
pr_congruent = Particle(a2, resonator_congruent)
# Test comparison operators
@test p == p_identical
@test p != p_different
@test !(p == p_different)
@test pr != pr_dif_aperture
@test !(pr == pr_dif_aperture)
@test p != pr
@test !(p == pr)
@test iscongruent(p, p_congruent)
@test !iscongruent(p, p_different)
@test !iscongruent(p, pr)
@test pr == pr_identical
@test pr != pr_different
@test !(pr == pr_different)
@test iscongruent(pr, pr_congruent)
@test !iscongruent(pr, pr_dif_aperture)
@test !iscongruent(pr, pr_different)
# Check that Julia fallback === works
@test p === p_reference
@test pr === pr_reference
# Particles are immutable, so are compared at the bit levelS
@test p === p_identical
@test pr === pr_identical
# Construct two almost identical particles
p1 = Particle(a, Sphere((0.0,0.0),1.0))
p1b = Particle(a, Sphere((-0.0,0.0),1.0))
# isequal is strict about +/-0.0 but IEEE compliant == is not strict
@test p1 == p1b
@test !isequal(p1,p1b)
end
@testset "Plot" begin
# Just run it to see if we have any errors (yes thats a very low bar)
# Single particle
particle = Particle(a, Sphere((1.0,0.0), 2.0))
plot(particle)
# Vector of particles of same shape
particles = [
Particle(a, Sphere((1.0,0.0), 2.0)),
Particle(a, Sphere((3.0,-1.0), 1.0))
]
plot(particles)
# Vector of particles of different shape
particles = [
CapsuleParticle(
Particle(Acoustic(2.0,2.0,2),Sphere((5.0,3.0),1.0)),
Particle(Acoustic(1.0,1.,2),Sphere((5.0,3.0),2.0))
),
Particle(a, Box((1.0,0.0),(2.0, 3.0))),
Particle(a, Sphere((3.0,-1.0), 1.0))
]
plot(particles)
@test true
end
end
@testset "Capsule Particle" begin
circle_in = Sphere((0.0,0.0),1.0)
circle_out = Sphere((0.0,0.0),2.0)
a_out = Acoustic(3.0,3.0,2)
a = Acoustic(1.0,1.0,2)
concen_particles = [ Particle(a_out,circle_out),Particle(a,circle_in)]
@test typeof(CapsuleParticle(concen_particles...)) <: AbstractParticle{2}
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1069 | import Base.Test: @testset, @test, @test_throws
using MultipleScattering
sound_p = Acoustic(1., 4. + 0.0im,2)
particles = [Particle(sound_p,Sphere([x,0.0], .5)) for x =0.:2.:10.]
sound_sim = Acoustic(1., 0.5 + 0.0im,2)
source = plane_source(sound_sim, [0.0,0.0], [1.0,0.0], 1.)
sim = FrequencySimulation(particles, source)
ω = 0.5
bounds = Box([[-0.,-1.], [10.,1.]])
ωs = 0.:0.1:1.
simres = run(sim, bounds, ωs)
timres = run(sim, bounds, ωs; ts = [30.], result_in_time=true)
using Plots ; #pyplot()
plot(sim,ω)
plot!(sim)
plot(simres; x = [[1,1]])
plot(simres,0.3)
plot(simres, 0.3, seriestype=:contour)
# include("plot_field.jl")
# plot_field(simres, linetype=:contour)
# plot_field(timres, linetype=:contour)
# plot!(sim)
amplitude = 1.0
# Create new souce as a linear combination of two other sources
s1 = point_source(sound_sim, [8.0,0.6], amplitude)
s2 = point_source(sound_sim, [2.0,-0.6], amplitude)
source = s1 + s2
sound_sim = Acoustic(1., 0.5 + 0.0im,2)
sim = FrequencySimulation(particles, source)
ω = 1.
# pyplot()
plot(sim,ω;res=60)
plot!(sim)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 804 | @testset "Print/show" begin
# Test whether we can reconstruct the objects from their show values
"Simulates a user printing an object in the REPL, copying and pasting the result and pressing enter"
function show_and_eval(object)
io = IOBuffer()
show(io, object)
io |> take! |> String |> Meta.parse |> eval
end
acoustic = Acoustic(1.89, 1.5, 2)
circle = Circle(2.0)
particle = Particle(acoustic, circle)
simulation = FrequencySimulation([particle], plane_source(acoustic))
@test acoustic == show_and_eval(acoustic)
@test circle == show_and_eval(circle)
@test particle == show_and_eval(particle)
# Currently can't do this with FrequencySimulations because of RegularSource type
@test show(devnull, simulation) == nothing
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2266 | @testset "Random generation" begin
# Make two random seeds, extremely low probability they will be the same
seed1 = 1
seed2 = 2
volfrac = 0.1
radius = 0.5
region_shape = Sphere(2, 20.0)
particle_shape = Circle(radius)
medium = Acoustic(2; ρ = 0.2, c = 0.2)
particles1 = random_particles(medium, particle_shape, region_shape, volfrac; seed=seed1)
particles1a = random_particles(medium, particle_shape, region_shape, volfrac; seed=seed1)
particles2 = random_particles(medium, particle_shape, region_shape, volfrac; seed=seed2)
# Particles should be determined solely by the seed
@test particles1 == particles1a
@test particles1 != particles2
@test_throws ErrorException random_particles(medium, particle_shape, region_shape, 0.9)
@test_throws ErrorException random_particles(medium, particle_shape, region_shape, 0.5; seed=3)
region_shape = Sphere(3, 20.0)
particle_shape = Sphere(radius)
medium = Acoustic(3; ρ = 0.2, c = 0.2)
# If a seed is not provided, then a different seed will be used everytime
particles2 = random_particles(medium, particle_shape, region_shape, volfrac)
end
@testset "Box around particles" begin
seed1 = 1
volfrac = 0.1
radius = 0.5
particle_shape = Sphere(radius)
medium = Acoustic(3; ρ = 0.2, c = 0.2)
region_shape = Box([0.0,0.0,0.0],[10.0,12.0,7.0])
particles = random_particles(medium, particle_shape, region_shape, volfrac; seed=seed1)
box = bounding_box(particles)
# check that all particles are within the bounding box
@test all(p ⊆ box for p in particles)
# check that moving all particles makes at least one particle leave the box
particles2 = [
Particle(medium,
congruent(particle_shape, origin(p) + 100 .* [eps(Float64),eps(Float64), eps(Float64)])
)
for p in particles]
@test any(!(p ⊆ box) for p in particles2)
# create a box around particle centres
points = origin.(particles)
box = Box(points)
@test all(p ∈ box for p in points)
@test !all(p ⊆ box for p in particles)
points = [
p + 100 .* [eps(Float64), eps(Float64), eps(Float64)]
for p in points]
@test !all(p ∈ box for p in points)
end | MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 494 | using MultipleScattering, Test
@testset "run examples and generate README.md" begin
examplestoconvert = ["random_particles", "particles_in_circle"]
folder = "../docs/src/example/"
for str in examplestoconvert
include(string(folder,str,"/",str,".jl"))
@test true
end
# auto generate their README.md to guarantee the code in these READMEs works.
include(folder*"generate-READMEs.jl")
generate_README(examplestoconvert, folder)
@test true
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 539 | import Test: @testset, @test, @test_throws
using MultipleScattering
using LinearAlgebra
using Plots
import Statistics: mean
include("special_functions.jl")
include("shapetests.jl")
include("particle_tests.jl")
include("random.jl")
include("print_tests.jl")
include("fourier_tests.jl")
include("acoustic_physics_tests.jl")
include("source_test.jl")
include("symmetrytests.jl")
include("boundary_conditions_tests.jl")
include("end_to_end_tests.jl")
include("time_tests.jl")
include("moments_tests.jl")
include("run_examples.jl")
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 7725 | @testset "Shape" begin
@testset "general properties" begin
shapetypes = [
Box, Halfspace, Plate, Sphere
]
shapes3D = [
Box([2.0, 3.0, 4.0]),
Halfspace([0.0,0.0,1.0]),
Plate([0.0,0.0,1.0],2.0),
Sphere([1.0,2.0,3.0],2.0)
]
shapes2D = [
Box([2.0, 3.0]),
Halfspace([1.0,0.0]),
Plate([1.0,0.0],1.0),
Sphere([1.0,2.0],1.0)
]
shapes2D = map(shapes2D) do s
MultipleScattering.Shape(s;
addtodimensions = 2.1,
vector_translation = [1.0,1.0]
)
end
# bitvec = typeof.(shapes2D) .<: shapetypes
bitvec = [
typeof(shapes2D[i]) <: shapetypes[i]
for i in eachindex(shapes2D)]
@test sum(bitvec) == length(shapes2D)
shapes3D = map(shapes3D) do s
MultipleScattering.Shape(s;
addtodimensions = 1.1,
vector_translation = [1.0,1.0,1.0]
)
end
# bitvec = typeof.(shapes3D) .<: shapetypes
bitvec = [
typeof(shapes3D[i]) <: shapetypes[i]
for i in eachindex(shapes3D)]
@test sum(bitvec) == length(shapes3D)
end
@testset "2D Box" begin
rectangle = Box([[0.0,0.0], [2.0, 3.0]])
o = origin(rectangle)
@test volume(rectangle) ≈ 6.0
@test name(rectangle) == "Rectangle"
@test o ∈ rectangle
@test (o+[0.0,3.1]) ∉ rectangle
@test iscongruent(rectangle, congruent(rectangle, [3.0,4.0]))
@test rectangle ≅ congruent(rectangle, [3.0,4.0]) # test infix
smaller_rectangle = Box(o, [1.0, 2.0])
@test smaller_rectangle ⊆ rectangle
@test rectangle == bounding_box(rectangle)
@test rectangle ⊆ Sphere(o, outer_radius(rectangle)) # a 2D sphere is a circle
# Test different ways to construct Rectangle produce same results
@test Box((0.0,0.0), (1.0, 2.0)) == Box([0.0,0.0], [1.0, 2.0]) # Tuple or Vector
@test Box((0.0,0.0), (1.0, 2.0)) == Box([1.0, 2.0]) # Assumes origin at zero
@testset "Boundary functions" begin
x, y = boundary_functions(rectangle)
@test x.(0:0.1:1) ≈ [0.0, 0.8, 1.6, 2.0, 2.0, 2.0, 1.2, 0.4, 0.0, 0.0, 0.0]
@test y.(0:0.1:1) ≈ [0.0, 0.0, 0.0, 0.6, 1.8, 3.0, 3.0, 3.0, 2.4, 1.2, 0.0]
@test_throws(DomainError,x(-eps(Float64)))
@test_throws(DomainError,x(1.0 + eps(Float64)))
@test_throws(DomainError,y(-eps(Float64)))
@test_throws(DomainError,y(1.0 + eps(Float64)))
end
end
@testset "Circle" begin
radius = 2.0
o = [6.7,8.9]
circle = Sphere(o, radius)
circle_bounding_box = bounding_box(circle)
@test volume(circle) / volume(circle_bounding_box) ≈ 0.7853981633974483
@test name(circle) == "Circle"
@test outer_radius(circle) == radius
@test o ∈ circle
@test (o+[0.0,radius+0.1]) ∉ circle
@test iscongruent(circle, congruent(circle,[3.0,4.0]))
@test circle ≅ congruent(circle,[3.0,4.0])
@test volume(circle) ≈ 12.566370614359172
smaller_circle = Sphere(o, radius-2)
@test smaller_circle ⊆ circle
@test circle ⊆ circle_bounding_box
# Test different ways to construct Circle produce same results
@test Sphere((0.0,0.0), 1.0) == Sphere([0.0,0.0], 1.0) # Tuple or Vector
@test Sphere((0.0,0.0), 1.0) == Sphere(2, 1.0) # Assumes origin at zero
@testset "Boundary functions" begin
x, y = boundary_functions(Sphere([-1.0,2.0],3.0))
@test x.(0:0.1:1) ≈
[2.0, 1.4270509831248424, -0.07294901687515765, -1.927050983124842, -3.427050983124842, -4.0, -3.4270509831248424, -1.9270509831248428, -0.07294901687515831, 1.427050983124842, 2.0]
@test y.(0:0.1:1) ≈
[2.0, 3.763355756877419, 4.853169548885461, 4.853169548885461, 3.7633557568774196, 2.0000000000000004, 0.2366442431225808, -0.8531695488854605, -0.8531695488854609, 0.23664424312257992, 1.9999999999999993]
@test_throws(DomainError,x(-eps(Float64)))
@test_throws(DomainError,x(1.0 + eps(Float64)))
@test_throws(DomainError,y(-eps(Float64)))
@test_throws(DomainError,y(1.0 + eps(Float64)))
end
end
@testset "Time of flight" begin
time_of_flight = TimeOfFlightPlaneWaveToPoint([-10.0,0.0], 40.0; minimum_x = 0.0)
time_of_flight_bounding_box = bounding_box(time_of_flight)
ratio = volume(time_of_flight) / volume(time_of_flight_bounding_box)
# Geometric arguments dictate that the ratio must be between 0.5 and 1.0
@test ratio > 0.5
@test ratio < 1.0
@test name(time_of_flight) == "Time of flight from planar source to the focal point"
end
@testset "Time of flight from point" begin
time_of_flight = TimeOfFlightPointWaveToPoint([-10.0,0.0],40.0)
time_of_flight_bounding_box = bounding_box(time_of_flight)
ratio = volume(time_of_flight) / volume(time_of_flight_bounding_box)
# Geometric arguments dictate that the ratio must be between 0.5 and 1.0
@test ratio > 0.5
@test ratio < 1.0
@test name(time_of_flight) == "Time of flight from point source"
@testset "Boundary functions" begin
x, y = boundary_functions(TimeOfFlightPointWaveToPoint([-1.0,0.0],3.0))
@test x.(0:0.1:1) ≈ [0.0,1.2182846930812632,1.9095426112571139,1.9095426112571139,1.2182846930812632,0.0,0.0,0.0,0.0,0.0,0.0]
@test y.(0:0.1:1) ≈ [-2.82842712474619,-2.019706171808505,-0.7311373286046446,0.7311373286046446,2.0197061718085054,2.82842712474619,1.6970562748477145,0.5656854249492386,-0.5656854249492386,-1.6970562748477145,-2.8284271247461903]
@test_throws(DomainError,x(-eps(Float64)))
@test_throws(DomainError,x(1.0 + eps(Float64)))
@test_throws(DomainError,y(-eps(Float64)))
@test_throws(DomainError,y(1.0 + eps(Float64)))
end
end
@testset "Sphere" begin
radius = 4.2
o = [3.4, -2.1, 2.0]
sphere = Sphere(o, radius)
@test name(sphere) == "Sphere"
@test outer_radius(sphere) == radius
@test o ∈ sphere
@test (o+[0.0,radius+0.1,0.0]) ∉ sphere
@test iscongruent(sphere, congruent(sphere,[3.0,4.0,1.0]))
@test volume(sphere) ≈ 310.33908869221415
smaller_sphere = Sphere(o, radius-2)
@test smaller_sphere ⊆ sphere
# Test different ways to construct Rectangle produce same results
@test Sphere((0.0,0.0,0.0), 1.0) == Sphere([0.0,0.0,0.0], 1.0)
end
# Causing Segmentation fault on Julia 1.1
@testset "Plot Shapes" begin
# Just try each to see if we have any errors (yes thats a very low bar)
rectangle = Box([[0.0,0.0],[2.0,3.0]])
plot(rectangle)
circle = Sphere([-1.0,2.0],2.0)
plot!(circle)
# timeofflight = TimeOfFlightPlaneWaveToPoint([-1.0,0.0],3.0)
# plot!(timeofflight)
timeofflightfrompoint = TimeOfFlightPointWaveToPoint([-1.0,0.0],3.0)
plot!(timeofflightfrompoint)
@test true
end
@testset "Infinite volume shapes" begin
normal = rand(3);
origin = rand(3);
width = 1.0 + rand();
p = Plate(normal, width, origin)
h = Halfspace(normal, origin)
shapes = [p,h];
@test isempty(findall( (volume.(shapes) .== Inf) .== 0))
xs = [rand(3) for i = 1:10];
[[x ∈ s for x in xs] for s in shapes]
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 3381 | @testset "acoustic sources" begin
a2 = Acoustic(0.1,0.1 + 0.0im,2)
a2_host = Acoustic(1.3,1.5 + 0.0im,2)
# Create two point sources
source_position = [0.0,1.0]
amplitude = 1.0
s1 = point_source(a2, source_position, amplitude)
s2 = point_source(a2, 2.0*source_position, amplitude)
# Create new souce as a linear combination of two other sources
s3 = 2*s1 + s2;
# Check that the field is indeed a linear conbination
x = [1.0, 1.0]
@test field(s3,x,1.0) == 2*field(s1,x,1.0) + field(s2,x,1.0)
# Test regular basis expansion of the source
ω = 0.8
basis_order = 7
centre = [1.0,0.0]
s3_expand = source_expand(s3, centre; basis_order = 7)
xs = [centre + 0.1 .* [cos(τ),sin(τ)] for τ = 0.0:0.3:1.5]
@test norm([field(s3,x,ω) - s3_expand(x,ω) for x in xs]) < 1e-7*norm([field(s3,x,ω) for x in xs])
source = plane_source(a2_host; position = [-10.0,0.0], direction = [1.0,0.0], amplitude = 1.0)
s_expand = source_expand(source, centre; basis_order = 4)
@test norm([field(source,x,ω) - s_expand(x,ω) for x in xs]) < 2e-9*norm([field(source,x,ω) for x in xs])
# Test DimensionMismatch between 3D and 2D
direction = [-10.0,1.0]
position = [rand(2)...]
amplitude = rand() + rand() * im
a3_host = Acoustic(3, ρ = 1.3, c = 1.5 + 0.0im)
@test_throws(DimensionMismatch,PlaneSource(a3_host; direction = direction))
@test_throws(DimensionMismatch,PlaneSource(a3_host; amplitude = [1.0,2.0]))
# Test equivalence between plane-sources
psource = PlaneSource(a2_host; direction = direction, position = position, amplitude = amplitude)
source = plane_source(a2_host; direction = direction, position = position, amplitude = amplitude)
pf = field(psource)
sf = field(source)
xs = [rand(2) for i = 1:10]
ωs = [rand() for i = 1:10]
errs = map(xs,ωs) do x,ω
abs(pf(x,ω) - sf(x,ω))
end
@test maximum(errs) < 2.0 * eps(Float64)
# test constructors for 3D acoustics checks
a3_host = Acoustic(3, ρ = 1.3, c = 1.5 + 0.0im)
direction = rand(3)
position = rand(3)
amplitude = rand() + 0.1
# check expansion in regular spherical waves
psource = plane_source(a3_host; direction = direction, position = position, amplitude = amplitude)
pointsource = point_source(a3_host, position, amplitude)
# Check that the field converges to its regular basis expansion around centre
k = real(ω / psource.medium.c)
centre = position + (4.0pi / k) .* rand(3)
x = centre + (0.1 / k) .* rand(3)
s_expand = source_expand(psource, x; basis_order = 4)
# test if the source is equal to its series expansion in a regular basis.
@test norm(field(psource,x,ω) - s_expand(x,ω)) < 1e-10 * abs(field(psource,x,ω))
# create source through a regular expansion of spherical waves
order = 3
len = basisorder_to_basislength(typeof(a3_host),order)
position = rand(3)
source = regular_spherical_source(a3_host, rand(len) ./ (1:len);
amplitude = rand(Complex{Float64}),
position = position
);
k = real(ω / source.medium.c)
centre = position + (4.0pi / k) .* rand(3)
x = centre + (0.1 / k) .* rand(3)
s_expand = source_expand(source, x; basis_order = 4)
@test norm(field(source,x,ω) - s_expand(x,ω)) < 1e-10 * abs(field(source,x,ω))
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 9384 | using GSL, SpecialFunctions
using Test, LinearAlgebra
@testset "Special functions" begin
@testset "bessel functions" begin
x = rand() - 0.5 + (rand() - 0.5) * im
@test diffbessel(besselj,2,x,2) ≈ diffbesselj(2,x,2)
@test diffbessel(hankelh1,2,x,2) ≈ diffhankelh1(2,x,2)
@test diffbessel(besselj,4,x,3) ≈ diffbesselj(4,x,3)
@test diffbessel(hankelh1,4,x,3) ≈ diffhankelh1(4,x,3)
# spherical bessel functions
@test shankelh1(1, x) ≈ - exp(im*x) * (x + im) / (x^2)
@test sbesselj(1, x) ≈ sin(x)/x^2 - cos(x)/x
@test sbesselj(1, eps(zero(Float64))) ≈ 0.0
@test sbesselj(0, eps(zero(Float64))) ≈ 1.0
n = 1
@test 2 * diffsbessel(shankelh1,n,x) ≈ shankelh1(n-1, x) - (shankelh1(n, x) + x*shankelh1(n+1, x))/x
@test diffsbessel(shankelh1,n,x) ≈ diffshankelh1(n,x)
@test diffsbessel(sbesselj,n,x) ≈ diffsbesselj(n,x)
n = 2
@test 2 * diffsbessel(shankelh1,n,x) ≈ shankelh1(n-1, x) - (shankelh1(n, x) + x*shankelh1(n+1, x))/x
xs = 0.01:0.9:11.0;
zs = xs + (collect(xs) .* 1im)
n = 15; ns = 0:n
ε = eps(Float64) * 10^7
maxerror = [
abs(diffsbesselj(n,x) - (sbesselj(n,x+ε) - sbesselj(n,x-ε)) / (2ε)) / abs(diffsbesselj(n,x))
for n in ns, x in zs] |> maximum
@test maxerror < 1e-4
maxerror = [
abs(diffshankelh1(n,x) - (shankelh1(n,x+ε) - shankelh1(n,x-ε)) / (2ε)) / abs(diffshankelh1(n,x))
for n in ns, x in zs] |> maximum
@test maxerror < 1e-5
maxerror = [
abs(diff2sbesselj(n,x) - (diffsbesselj(n,x+ε) - diffsbesselj(n,x-ε)) / (2ε)) / abs(diff2sbesselj(n,x))
for n in ns, x in zs] |> maximum
@test maxerror < 1e-4
maxerror = [
abs(diff2shankelh1(n,x) - (diffshankelh1(n,x+ε) - diffshankelh1(n,x-ε)) / (2ε)) / abs(diff2shankelh1(n,x))
for n in ns, x in zs] |> maximum
@test maxerror < 1e-5
maxerror = [
abs(diff3sbesselj(n,x) - (diff2sbesselj(n,x+ε) - diff2sbesselj(n,x-ε)) / (2ε)) / abs(diff3sbesselj(n,x))
for n in ns, x in zs] |> maximum
@test maxerror < 1e-4
maxerror = [
abs(diff3shankelh1(n,x) - (diff2shankelh1(n,x+ε) - diff2shankelh1(n,x-ε)) / (2ε)) / abs(diff3shankelh1(n,x))
for n in ns, x in zs] |> maximum
@test maxerror < 1e-5
# Compare with spherical bessel from GSL, which can only accept real arguments..
errs = map(xs) do x
maximum(abs.(sf_bessel_jl_array(n,x) - [sbesselj(n,x) for n in ns]))
end;
@test maximum(errs) < 20*eps(Float64)
errs = map(xs) do x
maximum(
abs.(
im .* sf_bessel_yl_array(n,x) -
[shankelh1(n,x) for n in ns] +
sf_bessel_jl_array(n,x)
) ./ abs.(sf_bessel_yl_array(n,x))
)
end;
@test maximum(errs) < 1e4*eps(Float64)
end
@testset "Associated legendre functions" begin
x = rand(1)[1] * 0.99
l_max = 2
# a few associated legendre functions without the Condon-Shortly factor
Plm_arr = [1,x,sqrt(1-x^2),(3x^2-1)/2, 3x*sqrt(1-x^2),3*(1-x^2)]
ls, ms = associated_legendre_indices(l_max)
@test sf_legendre_array(GSL_SF_LEGENDRE_NONE, l_max, x)[1:length(ls)] ≈ Plm_arr
sph_factors = (-1).^ms .* sqrt.((2 .* ls .+ 1) ./ (4pi) .* factorial.(ls-ms) ./ factorial.(ls+ms))
condon_phase = (-1).^ms
@test condon_phase .* sf_legendre_array(GSL_SF_LEGENDRE_SPHARM, l_max, x)[1:length(ls)] ≈ sph_factors .* Plm_arr
# test for the complex case
y = rand(1)[1] * 0.99
z = x + y*1im
# a few complex associated legendre functions
Plm_arr_complex = [1,conj(sqrt(1-z^2))/2,z,-sqrt(1-z^2),conj(1-z^2)/8,conj(z*sqrt(1-z^2))/2,(3z^2-1)/2,-3z*sqrt(1-z^2),3*(1-z^2)]
ls, ms = spherical_harmonics_indices(l_max)
norm_factors = sqrt.((2 .* ls .+ 1) ./ (4pi) .* factorial.(ls - ms) ./ factorial.(ls + ms))
@test complex_legendre_array(l_max, z) ≈ Plm_arr_complex .* norm_factors
end
@testset "Spherical harmonics" begin
θ = rand(1)[1] * 0.99
φ = rand(1)[1] * 0.99
l_max = 8 # small l_max due to factorial formula below
ls, ms = spherical_harmonics_indices(l_max)
sphs = spherical_harmonics(l_max, θ, φ)
sphs_dθ = spherical_harmonics_dθ(l_max, θ, φ)
@test sphs_dθ[1] == Complex{Float64}(0)
h = 1e5 * eps(Float64)
θ1 = θ - h
sph1s = spherical_harmonics(l_max, θ1, φ)
θ2 = θ + h
sph2s = spherical_harmonics(l_max, θ2, φ)
sphs_dθ_approx = (sph2s - sph1s) ./ (2h)
@test maximum(abs.(sphs_dθ_approx - sphs_dθ)[2:end] ./ abs.(sphs_dθ[2:end])) < 5e-4
@test maximum(i - lm_to_spherical_harmonic_index(ls[i],ms[i]) for i in eachindex(ls)) == 0
# check special case l == abs(m)
is = findall(ls .== abs.(ms))
for i in is
@test sphs[i] ≈ (- sign(ms[i]))^ls[i] / (2^ls[i] * factorial(ls[i])) *
sqrt(factorial(2*ls[i] + 1) / (4pi)) * sin(θ)^ls[i] * exp(im * ms[i] * φ)
end
l_max = 30
ls, ms = spherical_harmonics_indices(l_max)
sphs = spherical_harmonics(l_max, θ, φ)
# special case m == 0, reduce to just Legendre polynomials
Ps = sf_legendre_Pl_array(l_max, cos(θ))
is = findall(ms .== 0)
for l in 0:l_max
@test sphs[is][l+1] ≈ sqrt((2l+1)/(4pi)) * Ps[l+1]
end
#sphs[inds] .≈ sqrt.((2 .* (0:l_max) .+ 1) ./ (4pi)) .* Ps
# special case, north pole
θ = 0.0
sphs = spherical_harmonics(l_max, θ, φ)
for i in eachindex(sphs)
if ms[i] == 0
@test sphs[i] ≈ sqrt((2*ls[i] + 1)/(4pi))
else
@test sphs[i] ≈ 0.0
end
i += 1
end
# Test complex argument spherical harmonics
sphs_complex = spherical_harmonics(l_max, θ+0.0im, φ)
@test sphs ≈ sphs_complex
end
@testset "Gaunt and Wigner symbols" begin
l1 = rand(1:100)
l2 = rand(1:100)
l3 = rand(abs(l1-l2):2:(l1+l2)) # guarantees that iseven(l1+l2+l3)
@test iseven(l1+l2+l3)
m1 = rand(-l1:l1)
m2 = rand(-l2:l2)
m3 = m1-m2
@test_throws(DomainError,gaunt_coefficient(l1,2*l1,l2,m2,l3,m3))
@test_throws(MethodError,gaunt_coefficient(l1,m1,l2,m2,0.1,m3))
# the spherical harmonics linearisation formula
θ, φ = rand(2) .* pi
l_small = 6
l_max = 2*l_small # needs to be larger than l_small
ls, ms = spherical_harmonics_indices(l_max);
Ys = spherical_harmonics(l_max, θ, φ);
cs = reshape(
[
gaunt_coefficient(l1,m1,l2,m2,l3,m3)
for l3 = 0:l_max for m3 = -l3:l3
for l2 = 0:l_small for m2 = -l2:l2
for l1 = 0:l_small for m1 = -l1:l1]
, ((l_small + 1)^2,(l_small + 1)^2,(l_max+1)^2));
for n2 in 1:(l_small + 1)^2, n3 in 1:(l_small + 1)^2
@test 4pi * (-1)^(ms[n3]+ms[n2]) * (1.0im)^(ls[n3]-ls[n2]) * Ys[n3] * conj(Ys[n2]) ≈
sum( (1.0im).^(-ls) .* (-1.0).^ms .* conj.(Ys) .* cs[n2,n3,:]) atol = 1e-12
end
end
@testset "complex radial coordinates" begin
# Test 3-dimensional transforms
xs = [rand(-1.01:0.1:1.0,3) + rand(-1.01:0.1:1.0,3)*im for i = 1:100]
rθφs = cartesian_to_radial_coordinates.(xs)
@test maximum(norm.(xs - radial_to_cartesian_coordinates.(rθφs))) < 2e-14
rθφs = cartesian_to_spherical_coordinates.(xs)
vs = [rand(-1.01:0.1:1.0,3) + rand(-1.01:0.1:1.0,3)*im for i = 1:100]
svs = [
cartesian_to_spherical_vector(vs[i],xs[i])
for i in eachindex(vs)]
v2s = [
spherical_to_cartesian_vector(svs[i],rθφs[i])
for i in eachindex(vs)]
@test maximum(norm.(vs - v2s)) < 5e-14
# In a Cartesian representation
rθφ = cartesian_to_spherical_coordinates(xs[1])
r, θ, φ = rθφ
er = [cos(φ) * sin(θ), sin(φ) * sin(θ), cos(θ)]
eθ = [cos(φ) * cos(θ), sin(φ) * cos(θ), -sin(θ)]
eϕ = [-sin(φ), cos(φ), 0.0]
@test [1.0,0.0,0.0] - cartesian_to_spherical_vector(er,xs[1]) |> norm < 1e-14
@test [0.0,1.0,0.0] - cartesian_to_spherical_vector(eθ,xs[1]) |> norm < 1e-14
@test [-.0,0.0,1.0] - cartesian_to_spherical_vector(eϕ,xs[1]) |> norm < 1e-14
xs = [rand(-1.01:0.1:1.0,3) for i = 1:100]
rθφs = cartesian_to_radial_coordinates.(xs)
@test maximum(rθφ[2] for rθφ in rθφs) <= pi
@test minimum(rθφ[2] for rθφ in rθφs) >= 0.0
@test pi/2 < maximum(rθφ[3] for rθφ in rθφs) <= pi
@test -pi <= minimum(rθφ[3] for rθφ in rθφs) < -pi/2
# Test 2-dimensional transforms
xs = [rand(-1.01:0.1:1.0,2) + rand(-1.01:0.1:1.0,2)*im for i = 1:100]
rθs = cartesian_to_radial_coordinates.(xs)
@test maximum(norm.(xs - radial_to_cartesian_coordinates.(rθs))) < 1e-14
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2133 | @testset "Symmetries" begin
rectangle = Box([[0.0,0.0], [2.0, 3.0]])
circle = Sphere(rand(2), 2.0)
h2Dazi = Halfspace([1.0,0.0], [0.0,0.0])
shapes2D = [rectangle,circle,h2Dazi]
a2 = Acoustic(0.1,0.1 + 0.0im,2)
source_position = [0.0,1.0]
s1 = point_source(a2, source_position)
s2 = plane_source(a2; position = source_position, direction = [1.0,0.0])
# NOTE: should use the function regular_spherical_source, but for 2D one of the translation matrices has not been implemented yet
s3 = RegularSource{Acoustic{Float64,2},RadialSymmetry{2}}(a2, (x,ω) -> norm(x)+1.0im, (order,centre,ω) -> [1.0+1.0im for m = -order:order])
sources2D = [s1,s2,s3]
syms = [Symmetry(sh,s) for sh in shapes2D, s in sources2D]
@test syms == AbstractSymmetry{2}[
WithoutSymmetry{2}() WithoutSymmetry{2}() WithoutSymmetry{2}();
WithoutSymmetry{2}() AzimuthalSymmetry{2}() RadialSymmetry{2}();
WithoutSymmetry{2}() PlanarAzimuthalSymmetry{2}() AzimuthalSymmetry{2}()
]
check_commute = [Symmetry(sh,s) == Symmetry(s,sh) for s in sources2D, sh in shapes2D]
@test count(check_commute) == length(sources2D) * length(shapes2D)
sphere = Sphere(rand(3), 2.0)
p = Plate([1.0,1.0,1.0], 1.0)
hazi = Halfspace([0.0,0.0,1.0])
shapes3D = [p,sphere,hazi]
a3 = Acoustic(3, ρ = 1.3, c = 1.5)
psource = plane_source(a3; direction = [0.0,0.0,1.0])
pointsource = point_source(a3, [0.0,0.0,0.0])
radsource = regular_spherical_source(a3, [1.0+0.0im];
symmetry = RadialSymmetry{3}()
);
sources3D = [pointsource,psource,radsource];
syms = [Symmetry(sh,s) for sh in shapes3D, s in sources3D];
@test syms == AbstractSymmetry{3}[
WithoutSymmetry{3}() PlanarSymmetry{3}() WithoutSymmetry{3}();
WithoutSymmetry{3}() AzimuthalSymmetry{3}() RadialSymmetry{3}();
WithoutSymmetry{3}() PlanarAzimuthalSymmetry{3}() AzimuthalSymmetry{3}()
]
check_commute = [Symmetry(sh,s) == Symmetry(s,sh) for s in sources3D, sh in shapes3D]
@test count(check_commute) == length(sources3D) * length(shapes3D)
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 891 | @testset "TimeSimulation" begin
# Time response from a single particle
include("../docs/src/example/time_response_single_particle/time_response_single_particle.jl")
freq_result, time_result = run_time_response_single_particle()
# Spike at start and then two diffracted spikes later, then
# not much else
# incident plane wave
@test abs( maximum(field(time_result)) - 1.0) < 1e-2
# first diffraction
i1 = findmin(abs.(time_result.t .- 198.5))[2]
m, i = findmax(field(time_result)[i1-50:i1])
t = time_result.t[i1-50:i1][i]
@test abs(m - 0.046) < 2e-2
@test abs(t - 198) < 1e-1
# second diffraction
i2 = findmin(abs.(time_result.t .- 210.0))[2]
m, i = findmax(field(time_result)[i1+5:i2])
t = time_result.t[i1+5:i2][i]
@test abs(m - 0.05) < 2e-2
@test abs(t - 206) < 2e-1
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 6466 | @testset "Impulse operations" begin
# test adding analytic impulses
ω_vec = 0.0:0.1:1.01
t_vec = 0.0:0.1:1.01
gauss = GaussianImpulse(maximum(ω_vec))
dirac = FreqDiracImpulse(ω_vec[1])
impulse = gauss + dirac * 2.0
@test_throws(DomainError,[1]*dirac)
@test all(impulse.in_freq.(ω_vec) .== gauss.in_freq.(ω_vec) + 2.0 .* dirac.in_freq.(ω_vec))
@test all(impulse.in_time.(t_vec) .== gauss.in_time.(t_vec) + 2.0 .* dirac.in_time.(t_vec))
# test a shifted discrete impulse
t_vec = 0.0:0.1:10.01
ω_vec = t_to_ω(t_vec)
gauss = GaussianImpulse(maximum(ω_vec) / 2)
discrete_impulse = continuous_to_discrete_impulse(gauss, t_vec, ω_vec; t_shift = 4.2, ω_shift = maximum(ω_vec) / 2);
time_response = frequency_to_time(discrete_impulse.in_freq, ω_vec, t_vec);
freq_response = time_to_frequency(real.(discrete_impulse.in_time), t_vec, ω_vec);
@test maximum(abs.(time_response - discrete_impulse.in_time)) < 1e-2
@test maximum(abs.(freq_response - discrete_impulse.in_freq)) < 1e-2
# compare with the analytic shifts
gauss_shift = GaussianImpulse(maximum(ω_vec) / 2; t_shift = 4.2, ω_shift = maximum(ω_vec) / 2)
discrete_impulse2 = continuous_to_discrete_impulse(gauss_shift, t_vec, ω_vec);
@test maximum(abs.(discrete_impulse2.in_time - discrete_impulse.in_time)) < 1e-10
@test maximum(abs.(discrete_impulse2.in_freq - discrete_impulse.in_freq)) < 1e-10
end
@testset "Time Result" begin
sound_p = Acoustic(.1, 0.1 + 0.0im,2)
particles = [Particle(sound_p,Sphere([10.5,0.0], .5))]
sound_sim = Acoustic(1., 1. + 0.0im,2)
source = plane_source(sound_sim, [0.0,0.0], [1.0,0.0], 1.)
sim = FrequencySimulation(particles, source)
ω_vec = 0.0:0.01:5.01
@test LinRange(ω_vec) ≈ t_to_ω(ω_to_t(ω_vec)) # only exact for length(ω_vec) = even number
# invertability of dft
x_vec = [ [0.0,0.0], [3.0,0.0]]
ω_vec = 0.0:0.1:1.01
t_vec = ω_to_t(ω_vec)
simres = run(sim, x_vec, ω_vec)
# choose an impulse which does nothing and so can be inverted
discrete_impulse = DiscreteTimeDiracImpulse(0.0, t_vec, ω_vec)
timres = frequency_to_time(simres; method=:DFT, discrete_impulse = discrete_impulse)
simres2 = time_to_frequency(timres; method=:DFT, discrete_impulse = discrete_impulse)
@test norm(field(simres) - field(simres2)) / norm(field(simres)) < 1e-14
timres2 = frequency_to_time(simres2; method=:DFT, impulse = TimeDiracImpulse(0.0));
@test norm(field(timres2) - field(timres))/norm(field(timres)) < 1e-14
# test impulse consistency by seeing if we get the same result when going from freq to time, and when going from time to freq.
impulse = GaussianImpulse(maximum(ω_vec))
timres2 = frequency_to_time(simres; method=:DFT, impulse = impulse)
simres2 = time_to_frequency(timres; method=:DFT, impulse = impulse)
# invert without an impulse
timres3 = frequency_to_time(simres2; method=:DFT, discrete_impulse = discrete_impulse)
@test norm(field(timres2) - field(timres3))/norm(field(timres2)) < 1e-14
# Compare dft and trapezoidal integration
ω_vec = 0.0:0.1:100.01 # need a high frequency to match a delta impluse function!
simres = run(sim, x_vec, ω_vec)
timres1 = frequency_to_time(simres; method=:trapezoidal, impulse = TimeDiracImpulse(0.0))
timres2 = frequency_to_time(simres; method=:DFT, discrete_impulse = DiscreteTimeDiracImpulse(0.0, ω_to_t(simres.ω)))
@test norm(field(timres1) - field(timres2))/norm(field(timres1)) < 0.02
ω_vec = 0.0:0.0001:2.01 # need a high sampling to match a delta impluse function!
t_vec = 0.:0.5:20.
impulse = GaussianImpulse(maximum(ω_vec))
simres = run(sim, x_vec, ω_vec)
timres1 = frequency_to_time(simres; t_vec = t_vec, method=:trapezoidal, impulse = impulse)
timres2 = frequency_to_time(simres; t_vec = t_vec, method=:DFT, impulse = impulse)
@test norm(field(timres1) - field(timres2))/norm(field(timres1)) < 2e-5
# plot(timres1.t, [field(timres1)[1,:]-field(timres2)[1,:]])
end
@testset "Time shift signal" begin
sound_sim = Acoustic(2., 5.2 + 0.0im,2)
# suppose we measure in time the signal
t = 0.1:0.01:30.
t0 = 5.
impulse_func(t) = exp( -10000.0 .* (t - t0)^4)
measured_response = impulse_func.(t)
plot(t, measured_response)
ω = t_to_ω(t)
measured_f = time_to_frequency(measured_response, t, ω)
# at the point
source_x = [-3.0,2.0]
source_direction = [1.0,1.0]
x_measure = source_x + 4.0*source_direction
# then can we reverse-engineer what plane wave source (of the form below) would create this measured_response
travel_time = norm(x_measure - source_x)/real(sound_sim.c)
impulse_time = t .- travel_time;
impulse_response = impulse_func.(t);
amp0 = 1.0
source = plane_source(sound_sim, source_x, source_direction, amp0)
sim = FrequencySimulation(source)
simres = run(sim, [x_measure, x_measure + source_direction], ω)
short_time = 1.:0.00005:1.5
timres = frequency_to_time(simres; t_vec = short_time)
i1 = findmax(abs.(field(timres)[1,:]))[2]
i2 = findmax(abs.(field(timres)[2,:]))[2]
# test wave peak propagation speed
@test (short_time[i2] - short_time[i1] - norm(source_direction/sound_sim.c)) < 1e-4*norm(source_direction/sound_sim.c)
amps = measured_f./field(simres)[1,:]
# predict the source impulse
predict_impulse = frequency_to_time(amps, ω, impulse_time[300:600])
# correct mistake from ω=0
predict_impulse = predict_impulse .- mean(predict_impulse[1:2])
@test norm(predict_impulse - impulse_response[300:600]) < 1e-12*norm(impulse_response[300:600])
end
@testset "Vector field frequency to time" begin
## test invertablity
FieldDim = 4 # a 4D vector field in a 6 dimensional space!
Dim = 6
x = [rand(Dim) for i = 1:20]
t = LinRange(0.0,1.0,25)
fs = [rand(FieldDim) for i = 1:20, j = 1:25]
timeres = TimeSimulationResult(fs,x,t)
simres = time_to_frequency(timeres)
timeres2 = frequency_to_time(simres)
norm.(field(timeres2) - field(timeres))
@test timeres2.t == timeres.t
@test norm(norm.(field(timeres2) - field(timeres))) / norm(norm.(field(timeres))) < 1e-13
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2919 | import Base.Test: @testset, @test, @test_throws
using MultipleScattering
concen_particles1 = [
Particle(Acoustic(2.0,2.0,2),Sphere((0.0,0.0),2.0)),
Particle(Acoustic(0.2,0.2,2),Sphere((0.0,0.0),1.0))
]
concen_particles2 = [
Particle(Acoustic(2.0,1.0,2),Sphere((6.0,3.0),1.)),
Particle(Acoustic(0.4,0.8,2),Sphere((6.0,3.0),1.4))
]
particle = Particle(Acoustic(1.5,1.5,2),Sphere((-6.0,-3.0),0.8))
ps = [CapsuleParticle(concen_particles2...), CapsuleParticle(concen_particles1...), particle]
# plot(ps)
medium = Acoustic(0.8, 0.5 + 0.0im,2)
ps = [CapsuleParticle(concen_particles1...)]
source = plane_source(medium, [-3.0,0.0], [1.0,0.0], 1.)
sim = FrequencySimulation(ps, source)
using Plots; #pyplot()
ω = 1.4
bounds = Rectangle([-3.,-2.],[3.,2.]);
simres = run(sim,bounds,[ω]; res=40, basis_order=8)
plot(simres,ω,seriestype=:contour)
plot!(sim)
ωs = 0.:0.01:2.0
# simres = run(sim,bounds,ωs; res=30, basis_order =8);
simres = run(sim,bounds,ωs; res=15, basis_order = 26);
ts = 0.:0.4:50.
timres = TimeSimulationResult(simres; t_vec = ts)
#timres = run(sim,bounds,0.:0.02:2.0; ts = ts, res=20)
t=10.0
anim = @animate for t in ts
# plot(timres,t,seriestype=:contour, clim=(-0.8,0.8), c=:balance)
plot(timres,t,seriestype=:contour, clim=(0.0,0.8), c=:balance)
plot!(sim)
end
#
gif(anim,"time_capsule_balance.gif", fps = 4)
# gif(anim,"time_capsule.gif", fps = 4)
concen = CapsuleParticle(
Particle(Acoustic(2.0,2.0,2),Sphere((0.0,0.0),2.0)),
Particle(Acoustic(0.2,0.2,2),Sphere((0.0,0.0),1.0))
)
n=12
ps = [Particle(Acoustic(0.1,0.1,2),Sphere((4*cos(θ),4*sin(θ)),0.5)) for θ in LinRange(0.,2pi,n+1)[1:n] ]
ps = [concen; ps]
plot(ps)
ω = 1.4
source_position = [0.0,-3.0]
amplitude = 1.0
source = point_source(medium, source_position, amplitude)
sim = FrequencySimulation(ps, source)
sim_source = FrequencySimulation(source)
ω = 0.01
# checkout: ω = 0.63, strange resonance
bounds = Rectangle([-5.,-4.5],[5.,5.]);
simres = run(sim,bounds,[ω]; res=45, basis_order=3)
plot(simres,ω,seriestype=:contour)
plot!(sim)
ωs = 0.:0.0005:3.0
# simres = run(sim,bounds,ωs; res=57, min_basis_order = 4, basis_order = 14);
simres = run(sim,bounds,ωs; res=57, min_basis_order = 5, basis_order = 14);
ts = 0.:0.4:50.
timres = TimeSimulationResult(simres; t_vec = ts)
#timres = run(sim,bounds,0.:0.02:2.0; ts = ts, res=20)
timres2 = TimeSimulationResult(timres.field .+ 0.008, timres.x, timres.t)
t=0.0
anim = @animate for t in ts
# plot(timres,t,seriestype=:contour, clim=(-0.8,0.8), c=:balance)
plot(timres2,t,seriestype=:contour, clim=(-0.05,0.15), c=:balance)
plot!(sim)
end
gif(anim,"capsulse_dance.gif", fps = 4)
ω = 0.65
anim = @animate for ω in 0.:0.01:2.
# plot(timres,t,seriestype=:contour, clim=(-0.8,0.8), c=:balance)
plot(simres,ω,seriestype=:contour, clim=(-1.1,1.1), c=:balance)
plot!(sim)
end
gif(anim,"capsulse_dance_modes.gif", fps = 4)
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 1430 | using MultipleScattering
using Base.Test
using Plots
@testset "Summary" begin
include("shapetests.jl")
include("particle_tests.jl")
include("time_simulation_tests.jl")
include("moments_tests.jl")
# test our discretised Fourier transforms
@testset "Fourier tranforms" begin
include("fourier_test.jl")
@test fourier_test()
end
@testset "Type stability" begin
# Define everything as a Float32
volfrac = 0.01f0
radius = 1.0f0
k_arr = collect(LinRange(0.01f0,1.0f0,100))
simulation = FrequencySimulation(volfrac,radius,k_arr)
@test typeof(simulation.response[1]) == Complex{Float32}
end
@testset "Single scatterer" begin
include("single_scatter.jl")
# Test against analytic solution
@test single_scatter_test()
end
@testset "Boundary conditions" begin
include("boundary_conditions.jl")
# Test boundary conditions for 4 particles with random properties and positions.
@test boundary_conditions_test()
end
@testset "Plot FrequencySimulation" begin
# Just run it to see if we have any errors (yes thats a very low bar)
volfrac = 0.01
radius = 2.0
k_arr = collect(LinRange(0.2,1.0,5))
simulation = FrequencySimulation(volfrac,radius,k_arr)
plot(simulation)
plot(simulation,0.2)
@test true
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | code | 2216 | function single_scatter_test()
print("Testing single scatterer against an analytic solution with a random position and two random radii across a range of wavenumbers...")
listener = [-10.0, 0.0];
xp = 10*rand(2);
a1 = 10*rand();
a2 = 10*rand();
k_arr = LinRange(0.01,2.0,200)
M1 = Int(round(a1)); #largest hankelh1 order
M2 = Int(round(a2)); #largest hankelh1 order
# incident plane wave
uin(x,k) = exp(im * k * (x[1] - listener[1]))
# known solution for the scattering coefficients for a single scattering
function exact_single_scatter(x, k, a, M)
A(n,k) = -exp(im * k * (xp[1] - listener[1]) + im * n * pi / 2);
θ = atan(x[2] - xp[2], x[1] - xp[1])
r = norm(x - xp)
u = 0.0im
for m = -M:M
u += A(m, k) * besselj(m, a * k) / hankelh1(m, a * k) * hankelh1(m, k * r) * exp(im * m * θ)
end
return u
end
u1(x,k) = exact_single_scatter(x, k, a1, M1)
u2(x,k) = exact_single_scatter(x, k, a2, M2)
resp1 = [u1(listener, k) for k in k_arr];
resp2 = [u2(listener, k) for k in k_arr];
# Add on incoming wave for the total solution
resp1 += [uin(listener, k) for k in k_arr];
resp2 += [uin(listener, k) for k in k_arr];
# Using the MultipleScattering package
simulation1 = FrequencySimulation([Particle(xp,a1)], collect(k_arr);
listener_positions=listener,
source_direction=[1.0, 0.0],
hankel_order=M1
);
# Build a similar simulation with a different radius and hankel_order
simulation2 = FrequencySimulation([Particle(xp,a2)], collect(k_arr);
listener_positions=listener,
source_direction=[1.;0.],
hankel_order=M2
);
# Take the L^2 error between the analytic solution and our simulation
err1 = mean(abs.(resp1 - simulation1.response[:]));
err2 = mean(abs.(resp2 - simulation2.response[:]));
print("completed for radius=$a1 and $a2 with errors $err1 and $err2 \n")
if err1 < 1e-9 && err2 < 1e-9
return true
else
return false
end
end
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 155 | Even though initial commit and structure were committed by Jonathan, these were
based on work mostly by Artur.
.Artur Gower
.Jonathan Deakin
.Robert Gower | MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 7202 | # MultipleScattering
<!-- [![][docs-stable-img]][docs-stable-url] -->
[![][docs-dev-img]][docs-dev-url] [![][doi-img]][doi-url] [![CI][ci-img]][ci-url] [![][codecov-img]][codecov-url] [![][coveralls-img]][coveralls-url]
*A Julia library for simulating, processing, and plotting multiple scattering of waves.*
The library focuses on multipole methods (addition translation theorems) to solve the inhomogeneous Helmholtz equation
(time-harmonic waves). Multipole methods are particularly efficient at solving scattering from particles in an infinite domain. This library is configured to use T-matrices (also known as scattering matrices) to represent scattering from particles with any shape and properties (currently implemented for acoustics).
The package is setup to deal with different spatial dimensions and types of waves which satisfy Helmholtz equation's, e.g. acoustics, electromagnetism, elasticity. For details on some of the maths see [Martin (1995)](https://pdfs.semanticscholar.org/8bd3/38ec62affc5c89592a9d6d13f1ee6a7d7e53.pdf) and [Gower et al. (2017)](https://arxiv.org/abs/1712.05427).
<!-- If you are here to learn about
[Near Surface Backscattering](example/near_surface_backscattering), then [click here](example/near_surface_backscattering) to see an example. For details on the maths see [Gower et al. (2018)](https://arxiv.org/abs/1801.05490). To see how to take the [moments](example/moments) of the backscattering [click here](example/moments). -->
## Installation
This package is available for Julia 1.0.5 and beyond. To get started, just add the package by typing
```julia
julia> ]
pkg> add MultipleScattering
```
then press the backspace key followed by
```julia
julia> using MultipleScattering
```
## Documentation
- [**Latest Documentation**][docs-dev-url] — *documentation of the in-development version.*
## Simple example
Define the properties of your host medium:
```julia
dimension = 2 # could also be 3, but then all 2D vectors need to be 3D vectors
host_medium = Acoustic(dimension; ρ = 1.0, c = 1.0); # 2D acoustic medium with density ρ = 1.0 and soundspeed c = 1.0
```
An acoustic medium in 2D with density 1 and wavespeed 1.
Next, define two dense, circular acoustic particles, the first centred at [-2,2] with radius 2 and the second at [-2,-2] with radius 0.5,
```julia
particle_medium = Acoustic(dimension; ρ = 10.0, c = 2.0); # 2D acoustic particle with density ρ = 10.0 and soundspeed c = 2.0
p1 = Particle(particle_medium, Sphere([-2.0,2.0], 2.0));
p2 = Particle(particle_medium, Sphere([-2.0,-2.0], 0.5));
particles = [p1,p2];
```
Lastly we define the source, for example an incident plane wave (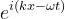) using a helper function.
```julia
source = plane_source(host_medium; direction = [1.0,0.0])
```
Once we have these three components, we can build our `FrequencySimulation` object
```julia
simulation = FrequencySimulation(particles, source)
```
To get numerical results, we run our simulation for specific positions and angular frequencies,
```julia
x = [[-10.0,0.0], [0.0,0.0]]
max_ω = 1.0
ω = 0.01:0.01:max_ω
result = run(simulation, x, ω)
```
### Plot
The package also provides recipes to be used with the `Plots` package for plotting simulations after they have been run.
In our above simulation we ran the simulation for 100 different wavenumbers, and measured the response at the location (-10,0).
To plot the time-harmonic response across these wavenumbers type:
```julia
using Plots
plot(result)
```

For a better overview you can plot the whole field in space for a specific angular frequency by typing:
```julia
ω = 0.8
plot(simulation,ω)
```

This shows the field over a spatial domain for one particular angular frequency `ω`.
Note: most things in the package can be plotted by typing `plot(thing)` if you need an insight into a specific part of your simulation.
To calculate an incident plane wave pulse in time use:
```julia
time_result = frequency_to_time(result)
plot(time_result)
```

Or for a Gaussian impulse in time:
```julia
t_vec = LinRange(0.,700.,400)
time_result = frequency_to_time(result; t_vec = t_vec, impulse = GaussianImpulse(max_ω))
plot(time_result)
```

## Examples
One way to learn the different features of this package is through the following examples.
<!-- For all examples see [here](docs/src/example/README.md). -->
| Examples | |
| ----------- | ----------- |
| [Helmholtz resonator](docs/src/example/helmholtz-resonator/resonator.md) | [Random particles](docs/src/example/random_particles/README.md) |
|  |  |
| [Choosing basis order](docs/src/example/hankel_convergence/README.md) | [Particles in a circle](docs/src/example/particles_in_circle/README.md) |
|  |  |
| [Times response lens](https://juliawavescattering.github.io/MultipleScattering.jl/dev/manual/time_response/#lens_example) | [Statistical moments](docs/src/example/moments/README.md) |
|  |  |
## Acknowledgements and contributing
This library was originally restructured from one written by
[Artur L Gower](https://arturgower.github.io/) and
[Jonathan Deakin](http://jonathan.thedeakin.net).
Contributions are welcome, and the aim is to expand this package to elasticity and electromagnetism.
[docs-dev-img]: https://img.shields.io/badge/docs-dev-blue.svg
[docs-dev-url]: https://JuliaWaveScattering.github.io/MultipleScattering.jl/dev
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: https://JuliaWaveScattering.github.io/MultipleScattering.jl/stable
[doi-img]: https://zenodo.org/badge/96763392.svg
[doi-url]: https://zenodo.org/badge/latestdoi/96763392
[ci-img]: https://github.com/JuliaWaveScattering/MultipleScattering.jl/actions/workflows/ci.yml/badge.svg
[ci-url]: https://github.com/JuliaWaveScattering/MultipleScattering.jl/actions/workflows/ci.yml
[codecov-img]: http://codecov.io/github/JuliaWaveScattering/MultipleScattering.jl/coverage.svg?branch=master
[codecov-url]: http://codecov.io/github/JuliaWaveScattering/MultipleScattering.jl?branch=master
[coveralls-img]: https://coveralls.io/repos/github/JuliaWaveScattering/MultipleScattering.jl/badge.svg?branch=master
[coveralls-url]: https://coveralls.io/github/JuliaWaveScattering/MultipleScattering.jl?branch=master
[issues-url]: https://github.com/JuliaWaveScattering/MultipleScattering.jl/issues
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 1229 | # MultipleScattering.jl Documentation
*A Julia library for simulating, processing, and plotting multiple scattering of acoustic waves.*
The library uses the multipole method to solve the Helmholtz equation
(time-harmonic waves). The multipole method is particularly efficient at solving scattering problems for particles in an infinite domain. This library is configured to use T-matrices to represent scattering from particles with any shape and properties. The package is setup to deal with different spatial dimensions and types of waves which satisfy Helmholtz equation's, e.g. acoustics, electromagnetism, elasticity. For details on some of the maths see [Martin (1995)](https://pdfs.semanticscholar.org/8bd3/38ec62affc5c89592a9d6d13f1ee6a7d7e53.pdf) and [Gower et al. (2017)](https://arxiv.org/abs/1712.05427).
## Installation
Install Julia v1.0 or later, then run
```julia
] # to enter the package mode
add MultipleScattering
```
Press backspace to exit the package mode.
## Manual
You can learn to use this package through [examples](example/README.md) or through our manual, which starts with a simple [Introduction](@ref).
## Contents
```@contents
Pages = ["base.md", "acoustics.md","random.md"]
Depth = 2
```
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 612 | # Overview
## [Simple random particles](random_particles/README.md)
- Simple example of random particles in rectangle
## [Random particles in a circle](particles_in_circle/README.md)
- Generate random particles in a circle
## [StatisticalMoments](moments/README.md)
- How to extract statistical information from a batch of simulations, in this
case: mean, standard deviation, skew and kurtosis (also known as moments).
## [Near surface backscattering](near_surface_backscattering/README.md)
- A method to calculate the backscattering from an infinite halfspace.
- See backscattering in frequency and time.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 195 | # Box size
If we are only interested in the response at a specific location for a certain
time interval, we need only simulate particles which are this distance (or time)
away from the listener. | MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 660 | # Convergence when increasing the number of Hankel functions
The code [convergence.jl](convergence.jl) tests how fast does the scattered wave (in frequency) converge when increasing the number of Hankel functions. To describe the scattered wave from each particle we use a series of Hankel functions (of the first kind).
```julia
include("convergence.jl")
simulations = hankel_order_convergence()
plot_hankel_order_convergence(simulations)
```

In the figures above `m` is the maximum order of the Hankel functions. The top left figure shows the configuration of particles considered.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 3254 | # Helmholtz resonator
---
The code [Resonator.jl](Resonator.jl) simulates a 2D Helmlholtz resonator by aligning particles in the shape of a bottle.
A Helmholtz resonator is made of a cavity with a small opening mouth. When illuminated with an acoustic waves at its specific resonant frequencies, the scattered field inside the cavity reaches high amplitudes. Those frequencies of course depend on the dimensions of the resonator that we set below.
```julia
using MultipleScattering
using Plots
# The four parameters below are all the required dimensions of the resonator.
cavity_radius = 1.0;
cavity_length = 2.5;
mouth_radius = 0.3;
mouth_length = 0.5;
```
To simulate the resonator, we align small circular particles to form a cavity. In the code below, the positions of the particles are stored in the vector X.
```julia
radius = .1; # radius of the particles
d_particle = 2.001*radius; # distance between centers
# define the cavity of the resonator
cavity_up = [
[x,cavity_radius+radius]
for x = radius:d_particle:cavity_length];
cavity_down = [
[x,-cavity_radius-radius]
for x = radius:d_particle:cavity_length]
cavity_right = [
[cavity_length+.05*radius,y]
for y = (- cavity_radius - radius):d_particle:(cavity_radius+2*radius)]
# define the mouth of the resonator
mouth_connect_down = [
[radius-d_particle,y]
for y=(-cavity_radius-radius):d_particle:(-mouth_radius)]
mouth_connect_up = [
[radius-d_particle,y]
for y=(mouth_radius+radius):d_particle:(cavity_radius+2*radius)]
mouth_up = [
[x,mouth_radius+radius]
for x = radius-2*d_particle:-d_particle:-mouth_length-radius]
mouth_down = [
[x,-mouth_radius-radius]
for x = radius-2*d_particle:-d_particle:-mouth_length-radius]
# put the different pieces together
X = [cavity_up; cavity_down; cavity_right; mouth_connect_down; mouth_connect_up; mouth_up; mouth_down];
X = [x - [cavity_length/2,cavity_radius/2-0.5] for x in X];
```
Now we can define the resonator:
```julia
particle_medium = Acoustic(2; ρ = 0., c = 0.);
Resonator = [
Particle(particle_medium, Circle(x, radius))
for x in X];
plot(Resonator)
savefig("Resonator.png")
```

Next we calculate the scattered field for an incoming plane wave at different frequencies.
```julia
host_medium = Acoustic(2; ρ=1.0, c=1.0); # medium of the background, 2 is the dimension of the setting.
source = plane_source(host_medium; direction = [1.0,0.0])
# region where the result will be plot
M=N=5.0;
bottomleft = [-M;-N]; topright = [M;N];
region = Box([bottomleft, topright]);
sim = FrequencySimulation(Resonator, source);
list_ω = [1.99,3.99,2.74]
result = run(sim, region, list_ω, basis_order=5, only_scattered_waves = true; res=200)
```
We plot the results for the different frequencies and observe that $\omega_0=1.99$ and $\omega_1=3.99$ correspond to resonant frequencies.
```julia
for p=1:3 # loop on the different frequencies
plot(result, list_ω[p]; seriestype = :heatmap) # clim=(-5.0,5.0)
colormap("RdBu")
plot!(Resonator,colorbar=true,
title="Field at ω="*string(list_ω[p]),axis=false, xguide ="", yguide ="")
savefig("plot_"*string(p)*".png")
end
```
The following plots are obtained:



| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 94 | # [Go to introductory example](https://github.com/JuliaWaveScattering/MultipleScattering.jl).
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 3098 | # StatisticalMoments
```@meta
DocTestSetup = quote
using MultipleScattering
end
```
Here we are going to simulate the scattered wave for many different configurations of particles. We can then take the average and standard deviation (the moments) of the scattered wave. In statistical mechanics this process is called [ensemble average](https://en.wikipedia.org/wiki/Ensemble_average_(statistical_mechanics)).
## Region and particles properties
First we choose the region to place particles and the receiver position:
```jldoctest moments; output = false, filter = r".*"s
using MultipleScattering
bottomleft = [0.0;-25.0]
topright = [50.0;25.0]
shape = Box([bottomleft, topright])
x = [-10.0,0.0]
# output
```
```julia
using Plots
plot(shape);
scatter!([x[1]],[x[2]], label="");
plot_shape = annotate!([(x[1], x[2] -2., "Receiver")])
```

Next we fill this `shape` with a random (uniform distribution) configuration of particles:
```jldoctest moments
volfrac = 0.05
radius = 1.0
particles = random_particles(Acoustic(2; ρ=0.0, c=0.0), Circle(radius);
region_shape = shape,
volume_fraction = volfrac,
seed=2
);
length(particles)
# output
40
```
To see the position of the chosen particles:
```julia
plot(plot_shape)
plot!(particles);
plot!()
```

Scattering a plane-wave from these particles
```julia
ωs = LinRange(0.01,1.0,100)
plane_wave = plane_source(Acoustic(1.0, 1.0, 2);
direction = [1.0,0.0], position = x);
```
```julia
plot(run(particles, plane_wave,x,ωs))
```

## The moments of the scattered wave
Now we will do simulations for particles placed in many different configurations and take the moments:
```julia
results = map(1:20) do i
particles = random_particles(Acoustic(2; ρ=0.0, c=0.0), Circle(radius);
region_shape = shape,
volume_fraction = volfrac,
seed=i
)
run(FrequencySimulation(particles, plane_wave), x, ωs)
end
# package Plots changed it's argument, the below no longer works..
# num_moments = 3
# plot(results; field_apply = real, num_moments = num_moments)
# plot!(xlabel="wavenumbers", title="Moments of the real part")
```

## Calculate the moments of the scattered wave in time
```julia
time_simulations = frequency_to_time.(results)
time_simulations[1].t # the time_arr chosen will be based on the discrete Fourier transform of simulations[1].k_arr
# real_time_moments = StatisticalMoments(time_simulations; response_apply=real) # moments of the real part
# plot(real_time_moments,xlims=(0,300));
# plot!(xlabel="time", title="Moments of the real part of the time wave")
```

## References
A. L. Gower, R. M. Gower, J. Deakin, W. J. Parnell, I. D. Abrahams,
Learning about random media from near-surface backscattering:
using machine learning to measure particle size and concentration,
arXiv preprint,
(2018)1801.05490
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 6992 | # Near-surface backscattering
Near-surface backscattering is a method of accurately calculating the backscattering from an infinite halfspace. For just the code see [backscattering.jl](backscattering.jl)
First, let us see why it is difficult to approximate the scattering from a halfspace filled with particles. That is, let us find out how many particles are required before the backscattering converges.
## Generate a large material filled with particles.
```julia
using MultipleScattering
host_medium = Acoustic(1.0, 1.0, 2)
radius = 0.8
volfrac = 0.10
max_width = 70.
particle_medium = Acoustic(0.2, 0.1, 2)
particle_shape = Circle(radius)
bottomleft = [0.,-max_width]
topright = [max_width,max_width]
shape = Box([bottomleft,topright])
particles = random_particles(particle_medium, particle_shape; region_shape = shape, volume_fraction = volfrac)
```
We send an incoming harmonic plane wave and receive the backscattering at `x`:
```julia
using Plots
pyplot(linewidth=2)
x = [-10.,0.]
source = plane_source(host_medium; position = x,
direction = [1.0,0.],
amplitude = 1.0)
plot(particles)
scatter!([x[1]],[x[2]], lab="")
annotate!([(x[1], x[2] -max_width/10., "Receiver")])
plot!(shape, linecolor = :red)
```

## Calculate backscattering for different quantity of particles
We will shave off particles on the right of this group of particles (above), and then calculate the backscattered waves for a range of angular frequencies `ωs`.
```julia
ωs = collect(0.01:0.01:1.)
widths = 10.:5.:max_width
num_particles = zeros(length(widths))
results = map(eachindex(widths)) do i
bottomleft = [0.,-widths[i]]
topright = [widths[i],widths[i]]
shape = Box([bottomleft, topright])
ps = filter(p -> p ⊆ shape, particles) # select particles that are inside shape
num_particles[i] = Int(length(ps))
simulation = FrequencySimulation(ps, source)
run(simulation, x, ωs)
end
backscattered_waves = field.(results)
M = length(backscattered_waves)
bM = backscattered_waves[M] # backscattering from largest material
differences = [norm(b - bM) for b in backscattered_waves[1:(M-1)]]./norm(bM)
plot_converge = plot(num_particles[1:(M-1)], differences,
xlabel = "number of particles", yguide ="error %",
label="frequency convergence"
)
```

The graph shows the rate of convergence, that is, how much the backscattering changes when including more particles (making the material deeper). The graph has not clearly converged, so we can only conclude that more than 400 particles are needed to accurately approximate the backscattering from an infinite halfspace.
We can accelerate this convergence by considering backscattering in time.
## Calculate backscattering in time
```julia
time_simulations = frequency_to_time.(results)
receiver = results[1].x[1]
times = 2*(widths .- receiver[1]) # time it takes for an incident plane wave to reach the furthest particles and then return to the receiver
plot()
for i in [1,3,6,9,12,13]
plot!(time_simulations[i],label="$(num_particles[i]) particles"
, xlims=(0,maximum(times)+10.), ylims=(-0.2,0.1)
, xticks = [0.; 30.; times]
)
end
gui()
```

We see that the responses in time diverge from each other more and more as time goes by. Meaning that if we only calculate the response for a short amount of time `34`, then the convergence will be accelerated.
```julia
time_vec = 0.:pi:34.2
time_results = frequency_to_time.(results; t_vec = time_vec, impulse = GaussianImpulse(maximum(ωs)))
backscattered_waves = field.(time_results)
bM = backscattered_waves[M] # backscattering from largest material
differences = [norm(b - bM) for b in backscattered_waves[1:(M-1)]]./norm(bM)
plot(plot_converge)
plot!(num_particles[1:(M-1)], differences, xlabel = "number of particles", yguide ="error %", label="time convergence")
```

The convergence of the time response, for time `0<t<34`, is much faster. In fact, less than 100 particles are needed to accurately approximate the backscattering from an infinite halfspace. The reason we don't show these as log plots is because there is a small constant error (about `0.01%`) due to the discrete Fourier transform. This error is caused by the Gibbs phenomena and by assuming the backscattering is periodic (when it is not). Both these errors are well understood and can be controlled.
## Calculate backscattering only from near-surface particles
This last step is about efficiency. We want to only include particle which contribute to the backscattering for short time intervals. To do this we created a region called `TimeOfFlightPlaneWaveToPoint(listener,time)`, where every particle in this shape takes less than `time` for their first scattered wave (due to an incident plane wave) to return to the `listener.` More precisely, if `listener = (lx,ly)`, then every point `(x,y)` inside this shape satisfies:
`x-lx+((x-lx)^2+(y-ly)^2)^(1/2)<time` and `x>0`.
For example, look at the largest quantity of particle we used
```julia
listener_position = [-10.,0.]
shape = TimeOfFlightPlaneWaveToPoint(listener_position,80.0)
scatter([listener_position[1]],[listener_position[2]]);
annotate!([(listener_position[1], listener_position[2] -max_width/10., "Receiver")])
plot!.(particles);
plot!(shape)
```

For time `0<t<80` the backscattering from these particles is the same as an infinite halfspace filled with particles. To achieve this result we need only the particles inside the shape `TimeOfFlightPlaneWaveToPoint` (region with the red outline). The particles outside this shape were unnecessary. To see this inaction:
```julia
times = 40.:15.:80.
near_surface_simulations = map(times) do t
shape = TimeOfFlightPlaneWaveToPoint(receiver,t) # choose a material with particles only in the near surface region
ps = filter(p -> p ⊆ shape, particles) # select particles that are inside shape
run(FrequencySimulation(ps, source), x, ωs) # calculate backscattering
end
time_near_simulations = frequency_to_time.(near_surface_simulations; impulse = GaussianImpulse(maximum(ωs)))
plot()
for i in 1:length(times)
plot!(time_near_simulations[i],label="time of flight $(times[i])"
, xlims=(0,maximum(times)+10.), ylims=(-0.6,0.3)
, xticks = [0.; times], title=""
)
end
gui()
```

Note the incident pulse has a thickness of about `10` in time, which is why the `time of flight 40` diverges from the other curves slightly before time `40`, and likewise for the other curves.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 2340 | # Random particles in a circle
The code [particles_in_circle.jl](particles_in_circle.jl) compares the scattered wave from one big circle, with the scattered wave from a circle filled with small particles.
```julia
using MultipleScattering
#You can also pick your own shape, an generate random particles inside it
#with a certain radius ands volume fraction
radius = 0.3
volfrac = 0.45
centre = [0.,0.]
big_radius = 3.0
particle_medium = Acoustic(2; ρ=0.0, c=0.0) # 2D particle with density ρ = 0.0 and soundspeed c = 0.0
particle_shape = Circle(radius)
circle = Sphere(centre, big_radius)
particles = random_particles(particle_medium, particle_shape; region_shape = circle, volume_fraction = volfrac, seed=1)
x = [-10.,0.] # position to receive the reflected wave
host_medium = Acoustic(2; ρ=1.0, c=1.0)
source = plane_source(host_medium; position = x, direction = [1.0,0.])
simulation = FrequencySimulation(particles, source)
```
The particles chosen are impenetrable, i.e. the wave is 100\% reflected. So this circle filled with scatterers should act like one big particle.
```julia
big_particle = Particle(particle_medium, circle)
big_particle_simulation = FrequencySimulation([big_particle], source)
#define a bounding box for plot
bottomleft = [-10, -2*big_radius]
topright = [big_radius, 2*big_radius]
box = Box([bottomleft, topright])
using Plots
height = 300
#gr(size=(1.4*height,height))
#pyplot(leg=false, size=(1.4*height,height))
ω = 0.5
#plot(big_particle_simulation, ω; res=15, bounds = box);
#plot!(big_particle)
#savefig("plot_field_big.png")
#plot(simulation, ω; res=15, bounds = box);
#plot!(particles, linecolor = :green)
#savefig("plot_field.png")
```
Resulting in the figures:


If we compare the response measured at the listener `[-10., 0.]`, they should be very similar:
```julia
#define angular frequency range
ωs = collect(LinRange(0.1,1.0,10))
result = run(simulation, x, ωs)
big_result = run(big_particle_simulation, x, ωs)
#plot(result, lab = "scattering from particles")
#plot!(big_result,
#lab = "scattering from big particle",
#title="Compare scattered wave from one big particle, \n and a circle filled with small particles")
```

| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 1871 | # Simple random particles example
```
## Define particle properties
Define the volume fraction of particles, the region to place the particles, and their radius
```julia
using MultipleScattering
num_particles = 4
radius = 1.0
particle_medium = Acoustic(2; ρ=0.2, c=0.1) # 2D particle with density ρ = 0.2 and soundspeed c = 0.1
particle_shape = Circle(radius)
max_width = 20*radius
bottomleft = [0.,-max_width]
topright = [max_width,max_width]
region_shape = Box([bottomleft,topright])
particles = random_particles(particle_medium, particle_shape; region_shape = region_shape, num_particles = num_particles)
```
Now choose the receiver position `x`, the host medium, set plane wave as a source wave, and choose the angular frequency range `ωs`
```julia
x = [-10.,0.]
host_medium = Acoustic(2; ρ=1.0, c=1.0)
source = plane_source(host_medium; position = x, direction = [1.0,0.])
ωs = LinRange(0.01,1.0,100)
simulation = FrequencySimulation(particles, source)
result = run(simulation, x, ωs)
```
We use the `Plots` package to plot both the response at the listener position x
```julia
using Plots; #pyplot(linewidth = 2.0)
plot(result, field_apply=real) # plot result
plot!(result, field_apply=imag)
#savefig("plot_result.png")
```

And plot the whole field inside the region_shape `bounds` for a specific wavenumber (`ω=0.8`)
```julia
bottomleft = [-15.,-max_width]
topright = [max_width,max_width]
bounds = Box([bottomleft,topright])
#plot(simulation,0.8; res=80, bounds=bounds)
#plot!(region_shape, linecolor=:red)
#plot!(simulation)
#scatter!([x[1]],[x[2]], lab="receiver")
#savefig("plot_field.png")
```

## Things to try
- Try changing the volume fraction, particle radius and ω values we evaluate
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 37 | # Time response from single particle
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 1535 | # Two particles
Define two particles with the first centred at [1.0,-4.0], with radius 1.0, sound speed 20.0, and density 10.0. The second particle is centered at [3.0,3.0], with radius 3.0, sound speed 1.0, and density 0.1.
```julia
using MultipleScattering
using Plots
pyplot()
p1 = Particle(Acoustic(2; c = 20.0, ρ = 10.0),Sphere([1.0,-4.0], 1.0))
p2 = Particle(Acoustic(2; c = 1.0, ρ = 0.1),Sphere([3.0,3.0], 3.0))
particles = [p1,p2]
```
Specify the angular frequency of the incident wave and calculate the response.
```julia
ωs = collect(0.1:0.01:1.0)
source = plane_source(Acoustic(1.0, 1.0, 2));
# Calculate and plot the frequency response at x.
x = [[-10.0,0.0]];
simulation = run(particles, source, x, ωs)
plot(simulation)
```

The above used an incident plane with the default position at [0.0, 0.0] and was simultated in the x direction. To change these defaults use:
```julia
x = [[-10.0,-10.0]]
source = plane_source(Acoustic(1.0, 1.0, 2); direction = [1.0,1.0], position = [0.0,0.0]);
simulation = run(particles, source, x, ωs)
```
Then plot the response around the particles and receiver.
```julia
region = Box([[-11.0;-11.0], [6.0;6.0]])
ω = 3.2
result = run(particles, source, region, [ω]; res=80)
plot(result, ω; field_apply=abs, seriestype = :contour)
```

The green circle in the plot is the receiver position. Looking at the region between the particles we see the complicated results of multiple scatttering.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 375 | # Acoustic
```@meta
CurrentModule = MultipleScattering
```
Acoustic type and functions.
```@autodocs
Modules = [MultipleScattering]
Order = [:constant, :type, :function]
Pages = ["src/physics/acoustics/acoustics.jl", "src/physics/acoustics/circle.jl", "src/physics/acoustics/sphere.jl", "src/physics/acoustics/source.jl", "src/physics/acoustics/boundary_data.jl"]
```
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 1707 | # Base
```@meta
CurrentModule = MultipleScattering
```
```@contents
Pages = ["base.md"]
```
## [Physical mediums](@id base_physical_property)
The types and functions shared between all different types of physical mediums.
```@autodocs
Modules = [MultipleScattering]
Order = [:type, :function]
Pages = ["src/physics/physical_medium.jl", "src/physics/special_functions.jl"]
```
## [Shapes and domains](@id base_shapes)
Shapes are used to define the shape of particles, and to define containers (or configurations) where all particles are placed. It is also used in plotting.
```@autodocs
Modules = [MultipleScattering]
Order = [:type, :function]
Pages = ["src/shapes/shapes.jl", "src/shapes/sphere.jl", "src/shapes/halfspace.jl", "src/shapes/plate.jl", "src/shapes/box.jl", "src/shapes/empty_shape.jl", "src/shapes/time_of_flight.jl"]
```
## [Particle](@id base_particle)
Particle types and functions.
```@docs
AbstractParticle
Particle
CapsuleParticle
iscongruent(::AbstractParticle,::AbstractParticle)
```
## [RegularSource](@id source_base)
RegularSource types and functions for all physical mediums.
```@autodocs
Modules = [MultipleScattering]
Order = [:type, :function]
Pages = ["src/source.jl"]
```
## [Impulse](@id impulse_base)
For convert to the time domain.
```@autodocs
Modules = [MultipleScattering]
Order = [:type, :function]
Pages = ["src/impulse.jl", "src/time_simulation.jl"]
```
## [Simulation](@id simulation_base)
Simulation types and functions.
```@docs
FrequencySimulation
run(::FrequencySimulation)
run(::FrequencySimulation, ::Shape, ::AbstractVector)
FrequencySimulationResult
basis_coefficients
field
scattering_matrix
t_matrix
get_t_matrices
```
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 156 | # Random
```@meta
CurrentModule = MultipleScattering
```
## Random particles
```@docs
random_particles
```
## Moments
```@docs
statistical_moments
```
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 5065 | # Introduction
### [Physical properties wave](@id into_physical_properties)
First define the host medium, for example for an acoustic medium in 2D
```@meta
DocTestSetup = quote
using MultipleScattering
end
```
```jldoctest intro
julia> using MultipleScattering;
julia> spatial_dim = 2; # could also be 3, but then all 2D vectors below would need to be 3D
julia> host_medium = Acoustic(spatial_dim; ρ = 1.0, c = 1.0) # density ρ = 1.0 and soundspeed c = 1.0
Acoustic(1.0, 1.0 + 0.0im, 2)
```
At this step we have restricted the physics to acoustics, that is, solutions to the Helmholtz equation: $\nabla^2 u(x,y,\omega) + k^2 u(x,y,\omega) = 0$, where $k = \dfrac{\omega}{c}$, $\omega$ is the angular frequency and $c$ the sound speed of the medium.
### [RegularSource wave](@id into_source)
The host medium will determine the types of waves that can propagate. For example an incident plane wave $\mathrm e^{ \mathrm i k x}$ there is a convenient constructor
```jldoctest intro
julia> source = plane_source(host_medium; direction = [1.0, 0.0]);
```
!!! note
Often $\mathrm e^{ \mathrm i k x - \mathrm i \omega t}$ is considered to be a harmonic plane-wave travelling along the $x-$axis. We omit the part $ - \mathrm i \omega t$ as is common in frequency space.
We generally call the incident wave a source. See [RegularSources](@ref) for details, and see [Acoustic](@ref) for some functions for the `Acoustic` medium.
### [Particles](@id into_particles)
Next, we define some particles to scatter an acoustic wave. We choose two filled circles, the first centred at [-2, 2] with radius 2 and the second at [-2, -2] with radius 0.5,
```jldoctest intro
julia> particle_medium = Acoustic(spatial_dim; ρ = 10.0, c = 2.0); # 2D acoustic particle with density ρ = 10.0 and soundspeed c = 2.0
julia> p1 = Particle(particle_medium, Sphere([-2.0, 2.0], 2.0));
julia> p2 = Particle(particle_medium, Sphere([-2.0, -2.0], 0.5));
julia> particles = [p1, p2];
```
See [Shapes](@ref) and [Particles](@ref) for details on different shapes and particles.
If you have the package `Plots` installed you can plot the particles. Note that although they appear hollow, we consider them to filled with the same homogenous material.
```julia
julia> using Plots;
julia> plot(particles)
```
!!! note
Most things in this package can be plotted just by typing `plot(thing)`. However you need to have `Plots` installed, and you may need to use the backend `pyplot()`. See [Plotting](@ref) for details on plotting.

### Simulation and results
Once we know the medium, the particles, and the have these three components, we can build our `FrequencySimulation` object
```jldoctest intro; output = false
julia> simulation = FrequencySimulation(particles, source);
```
To get numerical results, we run our simulation for specific positions and angular frequencies,
```jldoctest intro; output = false
julia> x = [[-10.0, 0.0], [0.0, 0.0]];
julia> max_ω = 1.0;
julia> ωs = 0.01:0.01:max_ω;
julia> result = run(simulation, x, ωs);
```
We can plot the time-harmonic response across the frequencies `ωs` wavenumbers and at the location (-10,0) by typing:
```julia
julia> plot(result)
```

For a better overview you can calculate the response for lots of points `x` in the domain and then plot the whole field for one frequency `ω` by typing:
```julia
julia> ω = 0.8;
julia> plot(simulation, ω);
julia> plot!(particles)
```

For details on plot fields and videos see [Plotting](@ref).
### Results in time
If we have calculated a frequency response $\hat u(\omega)$ over a range of frequencies $\omega$, then we can use a Fourier transform to calculate the response in time $u(t)$. That is, we can calculate $u(t)$ by approximating the Fourier transform:
$u(t) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat u(\omega)\mathrm e^{-\mathrm i \omega t} d\omega.$
For details see the section on [Time response](@ref). For example, taking a Discrete Fourier transform of the previous response leads to an incident plane wave pulse in time:
```julia
julia> time_result = frequency_to_time(result);
julia> plot(time_result)
```

In the image above the first peak on the left is due to the incident wave (the source), and the second peak is the wave scattered by the`particles`. Note how both peaks are quite jagged. This is due to [Gibb's phenomena](https://en.wikipedia.org/wiki/Gibbs_phenomenon). To resolve this we can use a Gaussian impulse function shown below. See [Time response](@ref) for more details.
```julia
julia> t_vec = LinRange(0.,700.,400);
julia> gauss_time_result = frequency_to_time(result; t_vec = t_vec, impulse = GaussianImpulse(max_ω));
julia> plot(gauss_time_result)
```

| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 2006 | # New particles
If you are feeling very adventurous, you can define a new type of particle.
A particle is define by its shape and physical properties. The simplest example being a circular acoustics particle: `Particle(Acoustic(1.0,1.0,2),Circle(1.0))`. To define a new particle you need to either use a new shape or a new physical medium.
## New shape
Suppose we want to define a new shape, which is very much like a rectangle.
```julia
using MultipleScattering
struct MyRectangle{T} <: Shape{2}
origin::Vector{T}
width::T
height::T
end
```
To be able to place particles in `MyRectangle` you need to extend the functions defined in the package you need to explicitly import them:
```julia
import MultipleScattering: volume, name, bounding_box
volume(shape::MyRectangle) = shape.width * shape.height
name(shape::MyRectangle) = "MyRectangle"
# every shape needs a bounding rectangle, this is where particles are first placed.
bounding_box(shape::MyRectangle) = Box(shape.origin, [shape.width, shape.height])
import Base.in, Base.issubset
function in(x::AbstractVector, r::MyRectangle)::Bool
all(abs.(x .- r.origin) .<= [r.width, r.height])
end
function issubset(circle::Sphere{T,2}, r::MyRectangle{T}) where {T}
all((origin(circle) .- circle.radius) .>= r.origin - [r.width/2.0, r.height/2.0]) &&
all((origin(circle) .+ circle.radius) .<= r.origin + [r.width/2.0, r.height/2.0])
end
```
!!! note
Using other packages with MultipleScattering may result in a naming conflict for functions like `volume`. In this case you will have to explicitly call `MultipleScattering.volume`.
With these definitions you can now fill this shape with circular particles, as shown in [Placing particles in a region](@ref).
To define a new particle from `MyRectangle` you need to extend the functions [`outer_radius`](@ref), `Base.(==)`, [`iscongruent`](@ref), then supposing you will use a predefined `PhysicalProperty` (such as `Acoustic`), you then need to extend [`t_matrix`](@ref).
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 3864 | # Particles
```@meta
DocTestSetup = quote
using MultipleScattering
end
```
[`Particle`](@ref) is a `struct` which define a scatterer, obstacle, or simply particle, which can scatter waves. See [Particle](@ref base_particle) for a list of relevant types and functions.
A `Particle` have two fields: `medium` and `shape`. The `medium` defines what kind of waves can propagate inside `Particle`, and what type of `RegularSource` can be used to scatter waves from `Particle`. One example `medium` is [Acoustic](@ref). The `shape` completely defines the geometry and position of the particle, see [Shapes](@ref) for details.
For an example we can define a circular particle with acoustics medium:
```jldoctest intro; output = false, filter = r".*"s
using MultipleScattering;
mymedium = Acoustic(2; ρ = 10.0, c = 2.0); # 2D acoustics with density ρ = 10.0 and soundspeed c = 2.0
myshape = Sphere([-2.0, 2.0], 2.0);
p1 = Particle(mymedium, myshape);
# output
Sphere{Float64, 2}([-2.0, 2.0], 2.0)
```
## Placing particles in a region
Suppose we want to place many circular particles in a region. The region has to be a pre-defined `Shape`, for example a `Circle`:
```julia
# Define the region
centre = [0.0, 0.0];
big_radius = 3.0;
circle = Sphere(centre, big_radius);
# Define the particle geometry and medium
p_radius = 0.3;
myshape = Circle(p_radius); # we do not specify centre as it is not used by random_particles
mymedium = Acoustic(2; ρ = 10.0, c = 2.0);
# Generate particles inside circle
volfrac = 0.2;
particles = random_particles(mymedium, myshape;
region_shape = circle,
volume_fraction = volfrac,
seed = 1
);
using Plots;
plot(particles)
plot!(circle, linecolor = :red)
```

## Placing polydisperse particles in a region
Similar to the above, we can place particles with a range of shapes.
Suppose we want to add to the above example a range of smaller particles:
```julia
# Define a range of particles sizes
rs = [0.05, 0.15, 0.15, 0.2]; # by repeating the radius 0.15 twice, there will be twice as many particles with this radius.
myshapes = Circle.(rs);
mymedium = Acoustic(2; ρ = 0.2, c = 0.2);
# Generate particles inside circle
volfrac = 0.15
polydisperse_particles = random_particles(mymedium, myshapes;
current_particles = particles,
region_shape = circle,
volume_fraction = volfrac,
seed = 1
);
plot(polydisperse_particles, linecolor = :green)
plot!(particles, linewidth = 2.0)
plot!(circle, linecolor = :red)
```

## Removing particles
Say we want to place a point-source within region filled with particles. To avoid placing the source inside any particle, we can remove a small region of particles:
```julia
small_circle = Circle(1.2);
filter!(p -> !(p ⊆ small_circle), polydisperse_particles)
plot(polydisperse_particles, linecolor = :green)
plot!(circle, linecolor = :red)
```

Next we place a point source in the centre and plot the result, while excluding a small region `Circle(0.1)` to avoid the singularity caused by a point source:
```julia
ω = 0.4;
point_wave = point_source(Acoustic(2; ρ = 1.0, c = 1.0), [0.0, 0.0]);
sim = FrequencySimulation(polydisperse_particles, point_wave);
plot(sim, ω;
resolution = 20,
exclude_region = Circle(0.1),
drawparticles = true
)
```

## Particle internals
To define the scattering from a particle we use the T-matrix method. This package only exports T-matrix for circular [`Particle`](@ref) and circular [`CapsuleParticle`](@ref). To understand how to define new T-matrix read [Notes on the T-matrix](../maths/multiplescattering.pdf) and see the source code of [`t_matrix`](@ref).
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 4719 | # Plotting
The plotting for this package is supplied by the package [Plots](http://docs.juliaplots.org). The options and keywords used for the package Plots can be used for the plots in this package.
Below are examples of plotting the whole field in frequency (harmonic wave) and time. The examples require the package `Plots` and, mostly, `PyPlot`.
## Field - Harmonic two gaps
```julia
using MultipleScattering
using Plots; gr(size = (800,300))
radius = 1
ω = 2.0
host_medium = Acoustic(1.0, 1.0, 2)
particle_medium = Acoustic(0.0, 0.0, 2)
# Create a wall of particles
particles = [
Particle(particle_medium, Sphere([0.,y],1.0))
for y = -40:2*radius:40.]
# Make two gaps in the wall
deleteat!(particles,[18,19,23,24])
# Define region to plot
bottomleft = [-10.;-15.]
topright = [30.;15.]
region = Box([bottomleft, topright])
# Calculating scattering for a plane wave
source = plane_source(host_medium; direction = [1.0,0.0])
# You can skip the step of defining FrequencySimulation
result = run(particles, source, region, [ω]; res=100)
plot(result,ω;
field_apply = abs, seriestype = :heatmap,
title = "Absolute value"
);
p1 = plot!(particles, ylims = (-15.0,15.0));
plot(result,ω;
field_apply = real, seriestype = :heatmap,
title = "Real part"
);
p2 = plot!(particles, ylims = (-15.0,15.0));
plot(p1, p2)
# savefig("gap-diffraction.png")
```

## Movie - Harmonic two gaps
Continuing from [Field - Harmonic two gaps](@ref), the previous example, we can plot how the harmonic field oscillates in time. That is, to get the harmonic field at time $t$ we just multiple the field by $\mathrm e^{-\mathrm i \omega t}$ for every $\mathbf x$. For example, the plane wave $\mathrm e^{\mathrm i x k}$ would become $\mathrm e^{\mathrm i x k -\mathrm i \omega t}$.
```julia
gr(size = (450,300))
ts = LinRange(0.,2pi/ω,30)
maxc = round(10*maximum(real.(field(result))))/10
minc = round(10*minimum(real.(field(result))))/10
anim = @animate for t in ts
plot(result,ω; seriestype = :heatmap,
phase_time=t, clim=(minc,maxc),
ylims = (-15.0,15.0) , c=:balance
)
plot!(particles)
plot!(colorbar=false, title="",axis=false, xguide ="",yguide ="")
end
# gif(anim,"gap-diffraction.gif", fps = 7)
```

## Movie - Time impulse plane-wave - two gaps
Continuing from [Field - Harmonic two gaps](@ref), we can plot how an impulse plave-wave in time passes through two gaps. See [Time response](@ref) for more details on the code used below.
```julia
gr(size = (450,300))
ωs = LinRange(0.0,2.0,300)[2:end] # avoid using ω = 0
# We use a lower resolution (resolution = 50) as this is a heavier calculation
result = run(particles, source, region, ωs; res = 50)
# Calculate time response over rect
t_max = 0.75 .* real(region.dimensions[1] / host_medium.c)
ts = LinRange(0.0,t_max,75)
impulse = GaussianImpulse(maximum(ωs)*0.6)
timres = frequency_to_time(result; t_vec = ts, impulse = impulse)
maxc = round(10*maximum(field(timres)))/10
minc = round(10*minimum(field(timres)))/10
# timres = TimeSimulationResult(timres.field .+ max_c/100.0 , timres.x, timres.t)
ylimits = (-region.dimensions[2]/2,region.dimensions[2]/2)
anim = @animate for t in ts
plot(timres,t, seriestype=:heatmap,
clim = (minc, maxc),
leg = false, ylims = ylimits
)
plot!(particles)
plot!(frame = :none, title="", xguide ="",yguide ="")
end
# gif(anim,"gap-diffraction.gif", fps = 7)
```

## Movie - Harmonic from random particles
```julia
using MultipleScattering
using Plots;
num_particles = 70
radius = 1.0
ω = 1.0
host_medium = Acoustic(1.0, 1.0, 2)
particle_medium = Acoustic(0.2, 0.3, 2)
particle_shape = Circle(radius)
max_width = 50*radius
bottomleft = [0.,-max_width]
topright = [max_width,max_width]
shape = Box([bottomleft,topright])
particles = random_particles(particle_medium, particle_shape; region_shape = shape, num_particles = num_particles)
source = plane_source(host_medium; direction = [1.0,0.5])
simulation = FrequencySimulation(particles, source)
bottomleft = [-25.,-max_width]
bounds = Box([bottomleft,topright])
result = run(simulation, bounds, [ω]; res=100)
ts = LinRange(0.,2pi/ω,30)
maxc = round(10*maximum(real.(field(result))))/10
minc = round(10*minimum(real.(field(result))))/10
anim = @animate for t in ts
plot(result,ω; seriestype = :heatmap, phase_time=t, clim=(minc,maxc), c=:balance)
plot!(simulation)
plot!(colorbar=false, title="",axis=false, xguide ="",yguide ="")
end
# gif(anim,"backscatter_harmonic.gif", fps = 7)
```

| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 1030 | # Shapes
```@meta
DocTestSetup = quote
using MultipleScattering
end
```
Shape is an abstract type which represents the shape of particles, and also the domain to place particles. See [Shape](@ref base_shapes) for a list of relevant types and functions.
## Existing shapes
The package provides three basic shapes. You can plot them using:
```jldoctest intro; output = false, filter = r".*"s
using MultipleScattering;
rectangle = Box([[0.0, -1.0],[1.0, 2.0]]);
circle = Sphere([-1.0, 0.0], 1.0);
timeofflight = TimeOfFlightPlaneWaveToPoint([1.0, 0.0], 3.0)
# output
```
```julia
using Plots;
plot(rectangle, linecolor = :red)
plot!(circle, linecolor = :green)
plot!(timeofflight, linecolor = :blue)
```

The `Box` and `TimeOfFlightPlaneWaveToPoint` are usually region where particles are placed. Time of flight is a shape which contains shapes from a half space which take at most `t` time to reach from the listener. The `Circle` is also used to define circular particles.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 6360 | # RegularSources
```@meta
DocTestSetup = quote
using MultipleScattering
end
```
[`RegularSource`](@ref) is a `struct` which represents any source, also called an incident wave. See [RegularSource](@ref source_base) for a list of relevant types and functions.
## Acoustics
For acoustics, any wave field $u_{\text{in}}(x,y)$ that satisfies $\nabla^2 u_{\text{in}}(x,y) + k^2 u_{\text{in}}(x,y) = 0$, with $k = \dfrac{\omega}{c}$, can be a source.
Two commonly used sources are a plane wave and point source. These can then be added together to create more complicated sources, like immitating a finite sized transducer / source.
For a plane-wave of the form $u_{\text{in}}(x,y) = A \mathrm e^{\mathrm i k \mathbf n \cdot (\mathbf x - \mathbf x_0)}$, where $A$ is the amplitude, $\mathbf n = (n_1,n_2,n_2)$ is unit vector which points in the direction of propagation, and $\mathbf x_0 = (x_0,y_0,z_0)$ is the initially position (or origin) of the source, we can use
```jldoctest intro
julia> using MultipleScattering;
julia> dimension = 3;
julia> medium = Acoustic(dimension; ρ = 1.0, c = 1.0);
julia> A = 1.0;
julia> n = [1.0, 1.0, 1.0];
julia> x0 = [1.0, 0.0, 0.0];
julia> plane_wave = plane_source(medium; amplitude = A, direction = n, position = x0);
```
We can plot this source wave one frequency ω by using
```julia
julia> ω = 1.0;
julia> plot_origin = zeros(3); plot_dimensions = 2 .* ones(3);
julia> plot_domain = Box(plot_origin, plot_dimensions);
julia> using Plots; pyplot();
julia> plot(plane_wave, ω; region_shape = plot_domain, y = 0.0) # in 3d currently only x-z slices are plotted for a given fixed y
```

Another useful source is the point source. In any dimension we consider the point source to be the zero order of the [`outgoing_basis_function`](@ref), which are the basis for all outgoing waves.
The point source for 2D is $u_{\text{in}}(x,y) = \frac{\mathrm i A}{4} \mathrm H_0^{(1)}(k \|(x-x_0,y-y_0)\|)$ and for
for 3D it is $u_{\text{in}}(x,y) = \frac{A}{4 \pi} \frac{e^{i k \| x - x_0\|)}}{\| x - x_0\|}$ where $A$ is the amplitude, $\mathbf x_0$ is the origin of the point source, and $\mathrm H_0^{(1)}$ is the Hankel function of the first kind.
```julia
julia> x0 = [0.0,-1.2, 0.0];
julia> point_wave = point_source(medium, x0, A);
```
```julia
julia> plot(point_wave, ω; region_shape = plot_domain)
```

> **_NOTE:_** Because the point source has a singularity at $x_0$ it is best to avoid plotting, and evaluating the field, close to $x_0$.
> This can be achieved by using `run(point_wave, ω; region_shape = plot_domain, exclude_region=some_region)` or `plot(point_wave, ω; region_shape = plot_domain, exclude_region=some_region)` both of which rely on the function [`points_in_shape`](@ref).
## Creating new sources
The easiest way to create new sources is to just sum together predefined sources:
```julia
julia> source = (3.0 + 1.0im) * point_wave + plane_wave;
julia> plot(source, ω; bounds = plot_domain)
```

For example, we can use this to create a finite emitter/transducer source,
```julia
julia> xs = LinRange(-0.7, 0.7, 30);
julia> source = sum(xs) do x point_source(medium, [x, 0.0, -1.1]) end;
```
```julia
julia> plot(source, 4.0; y = 0.0, bounds = plot_domain, field_apply = abs, resolution = 40)
```

where `field_apply` is applied to the wave field at every point, the default is `field_apply = real`, and `res` is the resolution along both the $x$ and $y$ axis. Note, this is not computationally very efficient. See [source.jl](../../../src/source.jl) for the very abstract code behind the scenes.
To define a new source you will need to understand the internals below.
## RegularSource internals
The `struct` [`RegularSource`](@ref) has three fields: `medium`, `field`, and `coef`, explained with examples below:
```jldoctest intro
julia> plane_wave = plane_source(Acoustic(1.0, 1.0, 2); direction = [1.0,0.0]);
julia> plane_wave.medium # the physical medium
Acoustic(1.0, 1.0 + 0.0im, 2)
julia> x = [1.0, 1.0]; ω = 1.0;
julia> plane_wave.field(x,ω) # the value of the field
0.5403023058681398 + 0.8414709848078965im
```
To calculate the scattering from a particle due to a source, we need the coefficients $$a_n(\mathbf x_0, \omega) = \text{RegularSource.coefficients(n, x0, ω)}.$$ We use these coefficients to represent the source in a radial coordinate system. That is, for any origin $\mathbf x_0$, we need to represent the incident wave $u_{\text{in}}(\mathbf x)$ using a series or regular waves
$$u_{\text{in}}(\mathbf x) = \sum_n a_n (\mathbf x_0, \omega) \mathrm v_n (\mathbf x - \mathbf x_0),$$
where for the scalar wave equation:
$$ \mathrm v_{n} (\mathbf x) = \begin{cases}
\mathrm J_{n}(k r) \mathrm e^{\mathrm i \theta n} & \text{for } \mathbf x \in \mathbb R^2, \\
\mathrm j_{\ell}(k r) \mathrm Y_{\ell}^m (\hat{\mathbf x}) & \text{for } \mathbf x \in \mathbb R^3, \\
\end{cases} $$
where for the first case $(r,\theta)$ are the polar coordinates and $n$ sums over $-N,-N+1, \cdots, N$, where $N$ is the basis order, and $\mathrm J_n$ is a Bessel function.
For the second case, we use a spherical coordinates with $r = \| \mathbf x\|$ and $\hat{\mathbf x} = \mathbf x/\|\mathbf x\|$, $n$ denotes the multi-index $n=\{\ell,m\}$ with summation over $\ell = 0, 1, \cdots,N$ and $m=-\ell,-\ell+1,\ell$, $\mathrm j_\ell$ is a spherical Bessel function, and $\mathrm Y_\ell^m$ is a spherical harmonic.
Both the inbuilt plane and point sources have functions `coef` which satisfy the above identity, for example
```julia
julia> using LinearAlgebra, SpecialFunctions;
julia> medium = Acoustic(2.0, 0.1, 2);
julia> source = plane_source(medium);
julia> x0 = [1.0, 1.0]; ω = 0.9;
julia> x = x0 + 0.1*rand(2); basis_order = 10;
julia> vs = regular_basis_function(medium, ω);
julia> source.field(x, ω) ≈ sum(source.coefficients(basis_order, x0, ω) .* vs(basis_order, x - x0))
true
```
The package also supplies a convenience function `source_expand`, which represents the source in terms of regular waves, for example:
```julia
julia> source2 = source_expand(source, x0; basis_order = 10);
julia> source.field(x, ω) ≈ source2(x, ω)
true
```
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 9998 | # Time response
```@meta
DocTestSetup = quote
using MultipleScattering
end
```
This package calculates all scattering in the frequency domain, and we call the resulting field the frequency response $\hat u(\mathbf x,\omega)$, which satisfies $\nabla^2 \hat u(\mathbf x,\omega) + k^2 \hat u(\mathbf x,\omega) = 0$, where $k = \dfrac{\omega}{c}$. We can transform the frequency response $\hat u(\mathbf x,\omega)$ into a time response $u(\mathbf x,t)$ using a Fourier transform, where $u(\mathbf x,t)$ satisfies $\nabla^2 u(\mathbf x,t) - \frac{1}{c^2} \frac{\partial^2}{\partial t^2}u(\mathbf x,t) = 0$. For a minimal example see [Results in time](@ref), or see [Technical details](@ref impulse_details) for more maths.
!!! note
The package assumes the time response $u(\mathbf x,t)$ is always real, this simplifies the Fourier transform.
## [Intro](@id impulse_intro)
As an example, let use a plane-wave source $\mathrm e^{\mathrm i \omega x}$ and measure the response at origin of the source $x = (0,0)$,
```jldoctest time; output = false, filter = r".*"s
using MultipleScattering;
plane_wave = plane_source(Acoustic(1.0, 1.0, 2); direction = [1.0, 0.0], position = [0.0, 0.0]);
x = [[0.0, 0.0]];
ωs = LinRange(0.0, 1.0, 100);
freq_response = run(plane_wave, x, ωs);
t_vec = LinRange(-20.0, 80.0, 110);
time_response = frequency_to_time(freq_response; t_vec = t_vec);
# output
```
where we specified the times `t_vec` to calculate `time_response`. If no `t_vec` is given, the default times would be `t_vec = ω_to_t(ωs)` which is the standard choice for the Discrete Fourier Transform.
Let us have a look at these responses:
```julia
using Plots;
p1 = plot(freq_response, xlims = (0, 2), ylims = (0.0, 1.5), field_apply = real);
p2 = plot(time_response);
plot(p1, p2)
```

Note how the time response has lobes after and before the largest signal. This is often undesirable, as we usually want signal which are compact in the time domain, i.e. zero before and after the largest signal. These lobes are called Gibbs Phenomena. They are caused by only calculating the frequency response $\hat u(\mathbf x,\omega)$ up to $\omega \leq 1$, and then (usually), taking $\hat u(\mathbf x,\omega) = 0$ for $\omega > 1$ when calculating the Fourier transform.
We can alter the response, in time and frequency, by specifying an impulse function $\hat f(\omega)$ which will use $\hat \phi(\mathbf x, \omega) = \hat f(\omega) u(\mathbf x \omega)$ as the frequency response. For example, we can choose $\hat f(\omega)$ to smooth out the drastic drop in $\hat u(\mathbf 0,\omega)$ when $\omega$ passes over $\omega = 1$.
## Gaussian impulse
The simplest way to avoid unwanted lobes (and Gibbs phenomena) is to use a Gaussian impulse function:
```jldoctest time
maxω = maximum(ωs);
gauss_impulse = GaussianImpulse(maxω);
typeof(gauss_impulse)
# output
ContinuousImpulse{Float64}
```
The argument `maxω` passed to [`GaussianImpulse`](@ref) will return an Gaussian impulse which will (mostly) avoid the lobes given by calculating only `ω <= maxω`. The Gaussian impulse in frequency and time is
```julia
ωs_all = -2.0:0.01:2.0;
p1 = plot(ω -> real(gauss_impulse.in_freq(ω)), ωs_all, title="Gaussian in frequency");
p2 = plot(gauss_impulse.in_time, t_vec, title="Gaussian in time");
plot(p1, p2)
```

The analytic expression for these functions are $\hat f(\omega) = 2 \sqrt{3 \pi / \Omega^2} \mathrm e^{-3 (\omega/\Omega)^2}$ and $f(t) = \mathrm e^{-(t \Omega)^2 / 12}$, where we used $\Omega = \mathrm{max}\,\omega$.
To use this impulse we simply:
```julia
gauss_time_response = frequency_to_time(freq_response; t_vec = t_vec, impulse = gauss_impulse);
p1 = plot(time_response);
p2 = plot(gauss_time_response);
plot(p1, p2)
```

There are still some lobes present because again `freq_response` only calculates `ω<=1.0`, but this time the drop is much less pronounced, which we can demonstrate with a plot of $\hat \phi(\mathbf 0, \omega)$:
```julia
φs = field(freq_response)[:] .* gauss_impulse.in_freq.(ωs);
plot(ωs, real.(φs), title="Frequency response φ")
```

## Discrete impulse
The only impulse the package provides is the Gaussian, both its discrete [`DiscreteGaussianImpulse`](@ref) and analytic form [`GaussianImpulse`](@ref). But all this is not necessary to use your own defined impulse function. You only need to define an impulse sampled in frequency. For example suppose we want a triangle impulse in frequency:
```jldoctest time; output = false, filter = r".*"s
# we need only define for ω > 0.0
triangle_freq(ω) = 5 - 5*ω;
# we only need the sampled frequency response.
in_freq = triangle_freq.(ωs);
# as we have specified in_freq we do not need to specify in_time.
in_time = 0.0*t_vec;
discrete_impulse = DiscreteImpulse(t_vec, in_time, ωs, in_freq);
time_response = frequency_to_time(freq_response; t_vec = t_vec, discrete_impulse = discrete_impulse);
# output
```
```julia
plot(time_response)
```

Alternatively, we can attempt to produce a triangle wave in the time domain, for which there is a convenient constructor:
```julia
triangle_time(t) = (abs(t/15) < 1) ? 1 - abs(t/15) : 0.0;
in_time = triangle_time.(t_vec);
# the function DiscreteImpulse below will calculate in_freq
discrete_impulse = DiscreteImpulse(t_vec, in_time, ωs);
time_response = frequency_to_time(freq_response; t_vec = t_vec, discrete_impulse = discrete_impulse);
plot!(time_response)
```

## [Lens example](@id lens_example)
As an example, we will make a reflective lens out of particles. To achieve this we will place the particles into a region with the shape [`TimeOfFlightPlaneWaveToPoint`](@ref).
First we choose the properties of the lens:
```julia
p_radius = 0.1;
volfrac = 0.3;
x = [-10.0; 0.0];
outertime = 34.8;
innertime = 34.0;
# Generate particles which are at most outertime away from our listener
outershape = TimeOfFlightPlaneWaveToPoint(x, outertime)
outerparticles = random_particles(Acoustic(2; ρ=0.0, c=0.0), Circle(p_radius);
region_shape = outershape,
volume_fraction = volfrac,
seed=2
);
# Filter out particles which are less than innertime away
innershape = TimeOfFlightPlaneWaveToPoint(x, innertime + 4*p_radius); # the + 4*p_radius is to account for double the particle diameter
particles = filter(p -> p⊈innershape, outerparticles);
plot(particles)
```

Next we simulate an impulse plane-wave starting at $x = -10$:
```julia
ωs = LinRange(0.01, 2.0, 100);
plane_wave = plane_source(Acoustic(1.0, 1.0, 2); direction = [1.0, 0.0], position = x);
sim = FrequencySimulation(particles, plane_wave);
freq_response = run(sim, x, ωs);
t_vec = -10.:0.2:81.
time_response = frequency_to_time(freq_response; t_vec=t_vec, impulse = GaussianImpulse(1.5; σ = 1.0));
xticks = [0.0, 20.0, 34.0, 40.0, 60.0, 80.0];
plot(time_response, title="Time response from lens", label="", xticks=xticks)
```

The first peak is the incident wave, and the next peak is the wave scattered from the lens which should arrive close to `t = 34`.
## [Technical details](@id impulse_details)
We can calculate the time response $u(\mathbf x,t)$, from the frequency response $\hat u(\mathbf x, \omega)$ by approximating the Fourier transform:
$u(\mathbf x,t) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat u(\mathbf x, \omega)\mathrm e^{-\mathrm i \omega t} d\omega,
\quad \hat u(\mathbf x, \omega) = \int_{-\infty}^\infty u(\mathbf x, t)\mathrm e^{\mathrm i \omega t} dt,$
where the second equation is the inverse transform. To modify the time response $u$, we can specify an impulse function $\hat f(\omega)$ which gives an new time response function $\phi(\mathbf x, t)$:
$\phi(\mathbf x, t) = \frac{1}{2\pi} \int_{-\infty}^\infty \hat f(\omega) \hat u(\mathbf x, \omega)\mathrm e^{-\mathrm i \omega t} d\omega = \frac{1}{\pi}\mathrm{Re}\, \int_0^\Omega \hat f(\omega) \hat u(\mathbf x, \omega)\mathrm e^{-\mathrm i \omega t} d\omega$
where the second identity results from assuming that $\phi(\mathbf x, t)$ is real, with $\mathrm Re$ being the real part. Also note that $\phi(\mathbf x,t) = (f * u)(\mathbf x, t)$, where $*$ is a convolution in time.
To approximate the above integral as finite integral, one option is to assume that $|\hat f(\omega) \hat u(\mathbf x, \omega)| \to 0$ as $|\omega| \to 0$, which would allow us to truncate the integration domain between $\omega \in [-\Omega, \Omega]$. We also need to discretise the integral. Putting both of these together results in
$\phi(\mathbf x, t) \approx \frac{1}{\pi}\mathrm{Re}\, \sum_{m=0}^M \hat f(\omega_m) \hat u(\mathbf x, \omega_m)\mathrm e^{-\mathrm i \omega_m t} \Delta \omega_m,$
where $\omega_M = \Omega$ and $\Delta \omega_m$ depends on the scheme used, with the simplest being $\Delta \omega_m = \omega_{m+1} - \omega_{m}$.
To learn more see the notes [Discrete Fourier Transform](../maths/DiscreteFourier.pdf) or the tests in the folder test of the source code.
!!! tip
The standard way to sample the frequencies is to take $\omega_m = m \Delta \omega$ and $\Delta \omega_m = \Delta \omega$ for some constant $\Delta \omega$. If we substitute this sampling into the approximation for $\phi(\mathbf x, t)$, shown above, we find that $\phi(\mathbf x,t)$ becomes periodic in time $t$ with period $T = 2\pi / \Delta \omega$. That is $\phi(\mathbf x, t + T) = \phi(\mathbf x, t)$ for every $t$. Suppose you were calculating a scattered wave that arrives at time $t = T + \tau$, what would happen? The answer is you would see this scattered wave arrive at time $t = \tau$, assuming $\tau < T$. This wrong arrival time occurs often when waves get trapped due to strong multiple scattering.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"MIT"
] | 0.1.21 | 3df28a341378af006306b3a60cf5df63f8d5b76c | docs | 782 | # Theory
Below are papers and notes that explain the theory behind this package.
## [The equations of Multiple Scattering](multiplescattering.pdf)
These short notes introduce the T-matrix, which defines how a particle scatters waves, and shows how it used in multiple scattering from many particles.
## [Multiple Scattering in the context of acoustics](acoustics.pdf)
These notes present the T-matrix construction in the context of acoustics, giving insight into the previous notes.
## [Discrete Fourier Transform](DiscreteFourier.pdf)
These notes give details on Green’s functions and Fourier transforms. We mostly
focus on using discrete impulse functions.
## [T-matrix Software](a9-ganesh.pdf)
This paper describes a method to calculate the T-matrix for new particles.
| MultipleScattering | https://github.com/JuliaWaveScattering/MultipleScattering.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 1030 | examples_dir = examples_dir = joinpath.(pkgdir(Geant4), ("examples","ext/G4Vis/examples"))
notebooks = [joinpath(item[1],notebook) for exdir in examples_dir for item in walkdir(exdir) for notebook in item[3]
if splitext(notebook)[2] == ".ipynb" && !Base.contains(notebook, "checkpoint") ]
vis_examples_dir = joinpath(pkgdir(Geant4), "ext/G4Vis/examples")
output_dir = joinpath(pkgdir(Geant4), "docs", "src", "notebooks")
#---Run all Jupyter notebooks (`.ipynb` files) in `examples` and write outputs to MD files---------
function build()
println("Building notebooks")
for notebook in notebooks
run(`jupyter nbconvert --execute --to=markdown --output-dir=$output_dir $notebook`)
end
return
end
#---Return Markdown file links which can be passed to Documenter.jl--------------------------------
function markdown_files()
md_files = map(notebooks) do notebook
file = splitext(basename(notebook))[1]
return joinpath("notebooks", "$file.md")
end
return md_files
end
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 725 | using Documenter, Geant4
include("build.jl")
build()
md_files = markdown_files()
T = ["Example $(splitext(basename(f))[1])" => f for f in md_files]
makedocs(;
modules=[Geant4],
format = Documenter.HTML(
prettyurls = Base.get(ENV, "CI", nothing) == "true",
size_threshold = 8000000,
size_threshold_warn = 4000000
),
pages=[
"Introduction" => "index.md",
"Public API" => "api.md",
"Examples" => T,
"Release Notes" => "releases.md",
],
repo="https://github.com/JuliaHEP/Geant4.jl/blob/{commit}{path}#L{line}",
sitename="Geant4.jl",
authors="Pere Mato",
)
deploydocs(;
repo="github.com/JuliaHEP/Geant4.jl",
push_preview = true
)
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 1811 | module G4Hist
using Geant4
using FHist
using Geant4.SystemOfUnits
const Hist1DType = typeof(Hist1D(;binedges=range(0,1,10)))
const Hist2DType = typeof(Hist2D(;binedges=(range(0,1,10),range(0,1,10))))
_getvalue(unit::Symbol) = getfield(Geant4.SystemOfUnits, unit)
_getvalue(units::Tuple{Symbol,Symbol}) = (getfield(Geant4.SystemOfUnits, units[1]), getfield(Geant4.SystemOfUnits, units[2]))
"""
H1D(title::String, nbins::Int, min::Float, max::Float, unit::Symbol)
Create a 1-dimentional histgram carrying the title and units
"""
struct H1D
title::String
hist::Hist1DType
unit::Symbol
unitval::Float64
end
Geant4.H1D(title, nbins, min, max, unit=:nounit) = H1D(title, Hist1D(;counttype=Float64,binedges=range(min,max,nbins+1),overflow=true), unit, _getvalue(unit))
Base.push!(h::H1D, v, w=1) = push!(h.hist, v/h.unitval, w)
Base.merge!(h1::H1D, h2::H1D) = merge!(h1.hist, h2.hist)
Base.empty!(h1::H1D) = empty!(h1.hist)
"""
H2D(title::String, xbins::Int, xmin::Float, xmax::Float, ybins::Int, ymin::Float, ymax::Float, unit::Tuple{Symbol,Symbol})
Create a 2-dimentional histgram carrying the title and units
"""
struct H2D
title::String
hist::Hist2DType
unit::Tuple{Symbol,Symbol}
unitval::Tuple{Float64,Float64}
end
Geant4.H2D(title, xbins, xmin, xmax, ybins, ymin, ymax, units=(:nounit, :nounit)) = H2D(title, Hist2D(;counttype=Float64,binedges=(range(xmin,xmax,xbins+1),range(ymin,ymax, ybins+1)),overflow=true), units, _getvalue(units))
Base.push!(h::H2D, u, v, w=1) = push!(h.hist, u/h.unitval[1], v/h.unitval[2], w)
Base.merge!(h1::H2D, h2::H2D) = merge!(h1.hist, h2.hist)
Base.empty!(h1::H2D) = empty!(h1.hist)
end
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 3939 | using IGLWrap_jll
#---A mesh type to capture what is returned by IGL functions---------------------------------------
mutable struct Cmesh
nv::Cint
nf::Cint
vertices::Ptr{Cdouble}
faces::Ptr{Cint}
@inline Cmesh() = new()
end
#---Functions to convert from Julia/C elements of the structure------------------------------------
@inline unsafe_array(T, p, n) = unsafe_wrap(Array, convert(Ptr{T}, p), n; own=true)
@inline fieldpointer(m::T, name) where{T} = pointer_from_objref(m) + fieldoffset(T, findfirst(==(name), fieldnames(T)))
@inline ncoors(m::Cmesh) = fieldpointer(m, :nv)
@inline nfaces(m::Cmesh) = fieldpointer(m, :nf)
@inline vpointer(m::Cmesh) = fieldpointer(m, :vertices)
@inline fpointer(m::Cmesh) = fieldpointer(m, :faces)
@inline vpointer(c::Vector{Point3{Float64}}) = convert(Ptr{Cdouble}, pointer(c))
@inline fpointer(f::Vector{TriangleFace{Int32}}) = convert(Ptr{Cint}, pointer(f))
@inline ncoors(c::Vector{Point3{Float64}}) = Base.size(c, 1) |> Int32
@inline nfaces(f::Vector{TriangleFace{Int32}}) = Base.size(f, 1) |> Int32
function boolean(op, m1::GeometryBasics.Mesh, m2::GeometryBasics.Mesh, t::Transformation3D{Float64}=one(Transformation3D{Float64}))
c1 = GeometryBasics.coordinates(m1)
f1 = GeometryBasics.decompose(TriangleFace{Int32}, GeometryBasics.faces(m1))
c2 = map(c -> c * t, GeometryBasics.coordinates(m2))
f2 = GeometryBasics.decompose(TriangleFace{Int32}, GeometryBasics.faces(m2))
cm = Cmesh()
j = Ref(Ptr{Cint}(0));
ret = @ccall libiglwrap.mesh_boolean(op::Cint,
ncoors(c1)::Cint, nfaces(f1)::Cint,
vpointer(c1)::Ref{Cdouble}, fpointer(f1)::Ref{Cint},
ncoors(c2)::Cint, nfaces(f2)::Cint,
vpointer(c2)::Ref{Cdouble}, fpointer(f2)::Ref{Cint},
ncoors(cm)::Ptr{Cint}, nfaces(cm)::Ptr{Cint},
vpointer(cm)::Ptr{Ptr{Cdouble}}, fpointer(cm)::Ptr{Ptr{Cint}},
j::Ref{Ptr{Cint}})::Cint
if ret == 0
c = unsafe_array(Point3{Float64}, cm.vertices, cm.nv)
f = unsafe_array(TriangleFace{Int32}, cm.faces, cm.nf)
return GeometryBasics.Mesh(c,f)
else
return
end
end
function GeometryBasics.mesh(psolid::CxxPtr{G4VSolid})
tsolid = GetEntityType(psolid)
shape = getproperty(Geant4, Symbol(tsolid))
solid = CxxRef{shape}(psolid)
GeometryBasics.mesh(solid[])
end
const operation = Dict("G4UnionSolid" => 0, "G4IntersectionSolid" => 1, "G4SubtractionSolid" => 2)
function GeometryBasics.mesh(s::G4BooleanSolid)
if isdefined(IGLWrap_jll, :libiglwrap)
op = operation[GetEntityType(s)]
left = GetConstituentSolid(s, 0)
right = GetConstituentSolid(s, 1)
boolean(op, GeometryBasics.mesh(left), GeometryBasics.mesh(right))
else
println("IGLWrap_jll is not available for currrent platform $(Sys.MACHINE) and is needed for drawing boolean solids")
GeometryBasics.Mesh(Point3{Float64}[], QuadFace{Int32}[])
end
end
function GeometryBasics.mesh(s::G4DisplacedSolid)
g4t = GetObjectTranslation(s)
g4r = GetObjectRotation(s)
t = Transformation3D{Float64}(convert(RotMatrix3{Float64}, CxxPtr(g4r)), convert(Vector3{Float64}, g4t))
m = GeometryBasics.mesh(GetConstituentMovedSolid(s))
points = GeometryBasics.coordinates(m)
faces = GeometryBasics.faces(m)
map!(c -> c * t, points, points)
GeometryBasics.Mesh(points, faces)
end
function Geant4.draw(solid::G4BooleanSolid; wireframe::Bool=false, kwargs...)
#---Needs library libigl for drawing booleans and this is not available in all platforms
if isdefined(IGLWrap_jll, :libiglwrap)
m = GeometryBasics.mesh(solid)
if wireframe
Makie.wireframe(m; linewidth=1, kwargs...)
else
Makie.mesh(m; kwargs...)
end
else
println("IGLWrap_jll is not available for currrent platform $(Sys.MACHINE) and is needed for drawing boolean solids")
return
end
end
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 5143 | #---G4Cons--------------------------------------------------------------------------------------
function GeometryBasics.coordinates(cone::G4Cons, facets=36)
rmin1 = GetInnerRadiusMinusZ(cone)
rmax1 = GetOuterRadiusMinusZ(cone)
rmin2 = GetInnerRadiusPlusZ(cone)
rmax2 = GetOuterRadiusPlusZ(cone)
z = GetZHalfLength(cone)
ϕ₀ = GetStartPhiAngle(cone)
Δϕ = GetDeltaPhiAngle(cone)
issector = Δϕ < 2π
ishollow = rmin1 > 0 || rmin2 > 0
issector ? facets = round(Int64, (facets/2π) * Δϕ) : nothing
isodd(facets) ? facets = 2 * div(facets, 2) : nothing
facets < 8 ? facets = 8 : nothing
nbf = Int(facets / 2) # Number of faces
nbv = issector ? nbf + 1 : nbf # Number of vertices
nbc = ishollow ? nbv : 1 # Number of centers
range = 1:(2*nbv + 2*nbc)
function inner(i)
return if i <= 2*nbv
ϕ = ϕ₀ + (Δϕ * (((i + z) ÷ 2) - z)) / nbf
isodd(i) ? Point(rmax2 * cos(ϕ), rmax2 * sin(ϕ), z) : Point(rmax1 * cos(ϕ), rmax1 * sin(ϕ), -z)
elseif ishollow
ϕ = ϕ₀ + (Δϕ * (((i - 2 * nbv + z) ÷ 2) - z)) / nbf
isodd(i) ? Point(rmin2 * cos(ϕ), rmin2 * sin(ϕ), z) : Point(rmin1 * cos(ϕ), rmin1 * sin(ϕ), -z)
elseif i == length(range)
Point(0., 0., -z)
elseif i == length(range) - 1
Point(0., 0., z)
end
end
return [inner(i) for i in range]
end
function GeometryBasics.faces(cone::G4Cons, facets=36)
rmin1 = GetInnerRadiusMinusZ(cone)
rmin2 = GetInnerRadiusPlusZ(cone)
Δϕ = GetDeltaPhiAngle(cone)
issector = Δϕ < 2π
ishollow = rmin1 > 0 || rmin2 > 0
issector ? facets = round(Int64, (facets/2π) * Δϕ) : nothing
isodd(facets) ? facets = 2 * div(facets, 2) : nothing
facets < 8 ? facets = 8 : nothing
nbf = Int(facets / 2) # Number of faces
nbv = issector ? nbf + 1 : nbf # Number of vertices
nbc = ishollow ? nbv : 1 # Number of centers
indexes = Vector{QuadFace{Int64}}()
for j in 1:nbf
a,b = 2j-1, 2j
c,d = !issector && j == nbf ? (1, 2) : (2j+1, 2j+2)
push!(indexes, (a,b,d,c))
if ishollow
a′,b′ = 2j-1+2nbv, 2j+2nbv
c′,d′ = !issector && j == nbf ? (2nbv+1, 2nbv+2) : (2j+1+2nbv, 2j+2+2nbv)
# inner wall
push!(indexes, (a′,b′,d′,c′))
# top
push!(indexes, (c, c′, a′, a))
# bottom
push!(indexes, (b, b′, d′, d))
else
a′,b′ = 2nbv+1, 2nbv+2
# top
push!(indexes, (a′,a, c, c))
# bottom
push!(indexes, (b′,d, b, b))
end
end
if issector
# wedge walls
a, b, c, d = ( 1, 2, 2nbv-1, 2nbv)
a′,b′,c′,d′ = ishollow ? (2nbv+1, 2nbv+2, 4nbv-1, 4nbv ) : (2nbv+1, 2nbv+2, 2nbv+1, 2nbv+2)
push!(indexes, (a, b, b′, a′))
push!(indexes, (c′, d′, d, c ))
end
return indexes
end
#---G4Polycone-------------------------------------------------------------------------------------
mutable struct SideRZ
r::Float64
z::Float64
end
mutable struct PolyconeParams
ϕ₀::Float64
Δϕ::Float64
n::Int32
z::Ptr{Float64}
rmin::Ptr{Float64}
rmax::Ptr{Float64}
end
function GeometryBasics.coordinates(pcon::G4Polycone, facets=24)
ϕ₀ = GetStartPhi(pcon)
ϕₑ = GetEndPhi(pcon)
n = GetNumRZCorner(pcon)
issector = !(ϕₑ-ϕ₀ ≈ 2π)
rz = [unsafe_load(Ptr{SideRZ}(GetPolyCorner(pcon, i-1).cpp_object)) for i in 1:n]
ϕfacets = round(Int64, (facets/2π) * (ϕₑ-ϕ₀))
ϕ = LinRange(ϕ₀, ϕₑ, ϕfacets)
inner(ϕ, r, z) = Point(r * cos(ϕ), r * sin(ϕ), z)
points = vec([inner(ϕ, rz[j].r, rz[j].z) for ϕ in ϕ, j in 1:n])
if issector
params = unsafe_load(Ptr{PolyconeParams}(GetOriginalParameters(pcon).cpp_object))
nz = params.n
z = unsafe_wrap(Array, params.z, nz; own = false)
rmin = unsafe_wrap(Array, params.rmin, nz; own = false)
rmax = unsafe_wrap(Array, params.rmax, nz; own = false)
for ϕ in (ϕ₀, ϕₑ)
for i in 1:nz
push!(points, Point(rmin[i] * cos(ϕ), rmin[i] * sin(ϕ), z[i]))
push!(points, Point(rmax[i] * cos(ϕ), rmax[i] * sin(ϕ), z[i]))
end
end
end
return points
end
function GeometryBasics.faces(pcon::G4Polycone, facets=24)
ϕ₀ = GetStartPhi(pcon)
ϕₑ = GetEndPhi(pcon)
n = GetNumRZCorner(pcon)
issector = !(ϕₑ-ϕ₀ ≈ 2π)
ϕfacets = round(Int64, (facets/2π) * (ϕₑ-ϕ₀))
idx = LinearIndices((ϕfacets, n))
quad(i, j) = QuadFace{Int}(idx[i, j], idx[i + 1, j], idx[i + 1, cyc(j + 1,n)], idx[i, cyc(j + 1,n)])
faces = vec([quad(i, j) for i in 1:(ϕfacets - 1), j in 1:n])
if issector
nz = unsafe_load(Ptr{PolyconeParams}(GetOriginalParameters(pcon).cpp_object)).n
offset = ϕfacets * n
for c in 0:1
for i in 0:nz-2
odx = offset + 2*i + 2*nz*c
push!(faces, QuadFace{Int}(odx+1, odx+2, odx+4, odx+3))
end
end
end
return faces
end
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 3712 | #---Event Display----------------------------------------------------------------------------------
mutable struct G4JLEventDisplay <: G4JLDisplay
const settings::NamedTuple
const stateChange::Function
const initDisplay::Function
# mutable attributes
lscene::LScene
figure::Figure
G4JLEventDisplay(settings, statech, initdisp) = new(settings, statech, initdisp)
end
"""
G4JLEventDisplay(settings_file)
Create a G4JLEventDisplay with all settings from .jl file
# Arguments
"""
function Geant4.G4JLEventDisplay(settings_file=nothing)
settings = eval(Meta.parse(read(joinpath(@__DIR__, "settings.jl"), String)))
if ! isnothing(settings_file)
user_settings = eval(Meta.parse(read(settings_file, String)))
settings = settings_merge(settings, user_settings)
end
G4JLEventDisplay(settings, stateChange, initDisplay)
end
#---State change notify----------------------------------------------------------------------------
function stateChange(from::G4ApplicationState, to::G4ApplicationState, app::G4JLApplication)::Bool
eventdisplay = app.evtdisplay
if from == G4State_Init && to == G4State_Idle
elseif from == G4State_Idle && to == G4State_GeomClosed
elseif from == G4State_GeomClosed && to == G4State_EventProc
clearEvent(eventdisplay)
elseif from == G4State_EventProc && to == G4State_GeomClosed
drawEvent(eventdisplay)
elseif from == G4State_GeomClosed && to == G4State_Idle
end
return true
end
#--------------------------------------------------------------------------------------------------
function initDisplay(evtdisp::G4JLEventDisplay)
settings = evtdisp.settings
if ! isdefined(evtdisp, :scene)
ui`/tracking/storeTrajectory 1`
# create the scene
set_theme!(backgroundcolor = settings.display.backgroundcolor)
fig = Figure(size=settings.display.resolution)
sc = LScene(fig[1,1], show_axis=settings.display.show_axis)
#display(fig)
evtdisp.lscene = sc
evtdisp.figure = fig
end
# draw the detector
if settings.detector.show_detector
sc = evtdisp.lscene
world = GetWorldVolume()
draw!(sc, world)
end
end
function clearEvent(evtdisp::G4JLEventDisplay)
s = evtdisp.lscene.scene
tobe = [p for p in plots(s) if p isa Lines || p isa Makie.Text] # The event is made of lines and text
for p in tobe
delete!(s,p)
end
end
function drawEvent(evtdisp::G4JLEventDisplay)
s = evtdisp.lscene.scene
settings = evtdisp.settings
trajectories = G4EventManager!GetEventManager() |> GetConstCurrentEvent |> GetTrajectoryContainer
if trajectories != C_NULL
points = Point3{Float64}[]
for t in trajectories
for i in 1:GetPointEntries(t)
push!(points, convert(Point3{Float64}, GetPoint(t, i-1) |> GetPosition))
end
push!(points, Point3{Float64}(NaN, NaN, NaN))
end
lines!(s, points, color=settings.trajectories.color, transparency=false, overdraw=false)
end
#wait_for_key("Press any key to continue with next event")
end
#---Settings (nested NamedTuple) merge fnction-----------------------------------------------------
function settings_merge(s1::NamedTuple, s2::NamedTuple)
for k in intersect(keys(s1), keys(s2))
v1, v2 = getfield(s1,k), getfield(s2,k)
if v1 isa NamedTuple
if v2 isa NamedTuple
v = settings_merge(v1, v2)
s2 = merge(s2, (; k => v))
else
error("$k in not of type NamedTuple in both NamedTuples")
end
end
end
merge(s1, s2)
end | Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 6877 | module G4Vis
using Geant4
using Makie
using Colors
import Base: convert
include("Transformation3D.jl")
function convert(::Type{Vector3{Float64}}, v::G4ThreeVector)
Vector3{Float64}(x(v), y(v), z(v))
end
function convert(::Type{Point3{Float64}}, v::G4ThreeVector)
Point3{Float64}(x(v), y(v), z(v))
end
function convert(::Type{RotMatrix3{Float64}}, r::CxxPtr{G4RotationMatrix})
if r == C_NULL
one(RotMatrix3{Float64})
else
RotMatrix3{Float64}(xx(r[]), yx(r[]), zx(r[]), xy(r[]), yy(r[]), zy(r[]), xz(r[]), yz(r[]), zz(r[]))
end
end
function convert(::Type{Tuple{RGB, Float64}}, c::ConstCxxRef{G4Colour})
return (RGB(GetRed(c),GetGreen(c), GetBlue(c)),GetAlpha(c))
end
function GeometryBasics.Tesselation(s::G4VSolid, nvertices::NTuple{N,<:Integer}) where N
return Tesselation{3,Float64,typeof(s),N}(s, Int.(nvertices))
end
GeometryBasics.mesh(s::G4VSolid) = GeometryBasics.mesh(Tesselation(s, 36), facetype=QuadFace{Int})
colors = colormap("Grays", 8)
function Geant4.draw(pv::G4VPhysicalVolume; wireframe::Bool=false, maxlevel::Int64=999)
lv = GetLogicalVolume(pv)
fig = Figure(size=(1280, 720))
s = LScene(fig[1,1])
draw!(s, lv[], one(Transformation3D{Float64}), 1, wireframe, maxlevel)
return fig
end
function Geant4.draw(lv::G4LogicalVolume; wireframe::Bool=false, maxlevel::Int64=999)
fig = Figure(size=(1280, 720))
s = LScene(fig[1,1])
draw!(s, lv, one(Transformation3D{Float64}), 1, wireframe, maxlevel)
return fig
end
function Geant4.draw(solid::G4VSolid; wireframe::Bool=false, kwargs...)
if wireframe
m = GeometryBasics.mesh(solid)
img = Makie.wireframe(m; linewidth=1, kwargs...)
else
points = GeometryBasics.coordinates(solid)
faces = GeometryBasics.faces(solid)
#normals = GeometryBasics.normals(solid)
m = GeometryBasics.normal_mesh(points, faces)
img = Makie.mesh(m; kwargs...)
end
#display("image/png", img)
end
function Geant4.draw!(s, pv::G4VPhysicalVolume; wireframe::Bool=false, maxlevel::Int64=999)
lv = GetLogicalVolume(pv)
draw!(s, lv[], one(Transformation3D{Float64}), 1, wireframe, maxlevel)
end
using Geant4.SystemOfUnits:cm3,g
function GetReplicaParameters(pv::CxxPtr{G4VPhysicalVolume})
axis = Ref{EAxis}(kYAxis)
nReplicas = Ref{Int32}(0)
width = Ref{Float64}(0.)
offset = Ref{Float64}(0.)
consuming = Ref{UInt8}(0)
GetReplicationData(pv, axis, nReplicas, width, offset, consuming)
return (axis[], nReplicas[], width[])
end
const UnitOnAxis = [( 1,0,0), (0,1,0), (0,0,1)]
function Geant4.draw!(s, lv::G4LogicalVolume, t::Transformation3D{Float64}, level::Int64, wireframe::Bool, maxlevel::Int64)
vsolid = GetSolid(lv)
tsolid = GetEntityType(vsolid)
shape = getproperty(Geant4,Symbol(tsolid))
solid = CxxRef{shape}(vsolid)
m = GeometryBasics.mesh(solid[])
g4vis = GetVisAttributes(lv)
if ! isempty(m)
if ! isone(t)
points = GeometryBasics.coordinates(m)
faces = GeometryBasics.faces(m)
map!(c -> c * t, points, points)
m = GeometryBasics.Mesh(meta(points; normals=normals(points, faces)), faces)
end
color = g4vis != C_NULL ? convert(Tuple{RGB, Float64}, GetColour(g4vis)) : (colors[level], GetDensity(GetMaterial(lv))/(12g/cm3))
visible = g4vis != C_NULL ? IsVisible(g4vis) : true
if wireframe
wireframe!(s, m, linewidth=1, visible=visible)
else
mesh!(s, m, color=color, transparency=true, visible=visible )
end
end
# Go down to the daughters (eventually)
level >= maxlevel && return
g4vis != C_NULL && IsDaughtersInvisible(g4vis) && return
for idx in 1:GetNoDaughters(lv)
daughter = GetDaughter(lv, idx-1)
if IsReplicated(daughter)
volume = GetLogicalVolume(daughter)
axis, nReplicas, width = GetReplicaParameters(daughter)
unitV = G4ThreeVector(UnitOnAxis[axis+1]...)
for i in 1:nReplicas
g4t = unitV * (-width*(nReplicas-1)*0.5 + (i-1)*width)
transformation = Transformation3D{Float64}(one(RotMatrix3{Float64}), convert(Vector3{Float64}, g4t))
draw!(s, volume[], transformation * t, level+1, wireframe, maxlevel)
end
else
g4t = GetTranslation(daughter)
g4r = GetRotation(daughter)
transformation = Transformation3D{Float64}(convert(RotMatrix3{Float64}, g4r), convert(Vector3{Float64}, g4t))
volume = GetLogicalVolume(daughter)
draw!(s, volume[], transformation * t, level+1, wireframe, maxlevel)
end
end
end
#---Testing functions------------------------------------------------------------
@inline Base.:*(a::G4ThreeVector, b::Vector3{Float64}) = G4ThreeVector(x(a)*b[1], y(a)*b[2], z(a)*b[3])
function Geant4.drawDistanceToOut(solid::G4VSolid, N::Int)
lo = G4ThreeVector()
hi = G4ThreeVector()
BoundingLimits(solid, lo, hi)
dim = hi - lo
points = (lo + dim * rp for rp in rand(Vector3{Float64}, N))
result = Vector{Point3{Float64}}()
for point in points
if Geant4.Inside(solid, point) == kInside
dir = normalize(rand(Point3) + Point3(-.5,-.5,-.5))
#push!(result, convert(Point3{Float64}, point))
push!(result, convert(Point3{Float64}, point) + dir * DistanceToOut(solid, point, G4ThreeVector(dir...)))
end
end
fig = Figure()
s = LScene(fig[1, 1])
scatter!(s, result, color=:black, markersize=1)
#scatter!(s, [lo, hi], color=:blue, markersize=10)
return fig
end
#---Utility functions--------------------------------------------------------------------------
cyc(x,n) = mod(x-1, n) + 1
#---Basic solids--------------------------------------------------------------------------------
include("Tubes.jl")
include("Traps.jl")
include("Torus.jl")
include("Cones.jl")
include("Sphere.jl")
include("PGon.jl")
#---Boolean solids------------------------------------------------------------------------------
include("Boolean.jl")
#---Event Display-------------------------------------------------------------------------------
include("G4Display.jl")
end # module G4Visualization
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 2061 | #---G4Polyhedra-------------------------------------------------------------------------------------
mutable struct PolyhedraParams
ϕ₀::Float64
Δϕ::Float64
ns::Int32
nz::Int32
z::Ptr{Float64}
rmin::Ptr{Float64}
rmax::Ptr{Float64}
end
function GeometryBasics.coordinates(pgon::G4Polyhedra, facets=24)
ϕ₀ = GetStartPhi(pgon)
ϕₑ = GetEndPhi(pgon)
n = GetNumRZCorner(pgon)
sides = GetNumSide(pgon)
issector = !(ϕₑ-ϕ₀ ≈ 2π)
rz = [unsafe_load(Ptr{SideRZ}(GetPolyCorner(pgon, i-1).cpp_object)) for i in 1:n]
ϕ = LinRange(ϕ₀, ϕₑ, sides + 1)
inner(ϕ, r, z) = Point(r * cos(ϕ), r * sin(ϕ), z)
points = vec([inner(ϕ, rz[j].r, rz[j].z) for ϕ in ϕ, j in 1:n])
if issector
params = unsafe_load(Ptr{PolyhedraParams}(GetOriginalParameters(pgon).cpp_object))
nz = params.nz
z = unsafe_wrap(Array, params.z, nz; own = false)
rmin = unsafe_wrap(Array, params.rmin, nz; own = false)
rmax = unsafe_wrap(Array, params.rmax, nz; own = false)
for ϕ in (ϕ₀, ϕₑ)
for i in 1:nz
push!(points, Point(rmin[i] * cos(ϕ), rmin[i] * sin(ϕ), z[i]))
push!(points, Point(rmax[i] * cos(ϕ), rmax[i] * sin(ϕ), z[i]))
end
end
end
return points
end
function GeometryBasics.faces(pgon::G4Polyhedra, facets=24)
ϕ₀ = GetStartPhi(pgon)
ϕₑ = GetEndPhi(pgon)
n = GetNumRZCorner(pgon)
sides = GetNumSide(pgon)
issector = !(ϕₑ-ϕ₀ ≈ 2π)
idx = LinearIndices((sides + 1, n))
quad(i, j) = QuadFace{Int}(idx[i, j], idx[i + 1, j], idx[i + 1, cyc(j + 1,n)], idx[i, cyc(j + 1,n)])
faces = vec([quad(i, j) for i in 1:sides, j in 1:n])
if issector
nz = unsafe_load(Ptr{PolyhedraParams}(GetOriginalParameters(pgon).cpp_object)).nz
offset = (sides + 1) * n
for c in 0:1
for i in 0:nz-2
odx = offset + 2*i + 2*nz*c
push!(faces, QuadFace{Int}(odx+1, odx+2, odx+4, odx+3))
end
end
end
return faces
end | Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 4023 | #---G4Orb----------------------------------------------------------------------------------------
function GeometryBasics.coordinates(orb::G4Orb, nvertices=24)
r = GetRadius(orb)
θ = LinRange(0, π, nvertices)
ϕ = LinRange(0, 2π, nvertices)
inner(θ, ϕ) = Point(cos(ϕ) * sin(θ), sin(ϕ) * sin(θ), cos(θ)) .* r
return vec([inner(θ, ϕ) for θ in θ, ϕ in ϕ])
end
function GeometryBasics.faces(::G4Orb, nvertices=24)
idx = LinearIndices((nvertices, nvertices))
quad(i, j) = QuadFace{Int}(idx[i, j], idx[i + 1, j], idx[i + 1, j + 1], idx[i, j + 1])
return vec([quad(i, j) for i in 1:(nvertices - 1), j in 1:(nvertices - 1)])
end
function GeometryBasics.normals(::G4Orb, nvertices=24)
return GeometryBasics.coordinates(G4Orb("",1), nvertices)
end
#---G4Sphere--------------------------------------------------------------------------------------
function GeometryBasics.coordinates(sph::G4Sphere, nvertices=24)
rmin = GetInnerRadius(sph)
rmax = GetOuterRadius(sph)
ϕ₀ = GetStartPhiAngle(sph)
Δϕ = GetDeltaPhiAngle(sph)
θ₀ = GetStartThetaAngle(sph)
Δθ = GetDeltaThetaAngle(sph)
ϕfacets = round(Int64, (nvertices/2π) * Δϕ)
θfacets = round(Int64, (nvertices/π) * Δθ)
θ = LinRange(θ₀, θ₀+Δθ, θfacets)
ϕ = LinRange(ϕ₀, ϕ₀+Δϕ, ϕfacets)
inner(θ, ϕ) = Point(cos(ϕ) * sin(θ), sin(ϕ) * sin(θ), cos(θ))
oshell = [inner(θ, ϕ) * rmax for θ in θ, ϕ in ϕ]
ishell = rmin > 0 ? [inner(θ, ϕ) * rmin for θ in θ, ϕ in ϕ] : (Δϕ < 2π || Δθ < π) ? [Point(0,0,0)] : []
return [vec(oshell); vec(ishell)]
end
function GeometryBasics.faces(sph::G4Sphere, nvertices=24)
rmin = GetInnerRadius(sph)
Δϕ = GetDeltaPhiAngle(sph)
Δθ = GetDeltaThetaAngle(sph)
ϕfacets = round(Int64, (nvertices/2π) * Δϕ)
θfacets = round(Int64, (nvertices/π) * Δθ)
idx = LinearIndices((θfacets, ϕfacets))
nf = ϕfacets * θfacets
quad(i, j) = QuadFace{Int}(idx[i, j], idx[i + 1, j], idx[i + 1, j + 1], idx[i, j + 1])
faces = vec([quad(i, j) for i in 1:(θfacets - 1), j in 1:(ϕfacets - 1)])
if rmin > 0
for q in vec([quad(i,j) .+ nf for i in 1:(θfacets - 1), j in 1:(ϕfacets - 1)])
push!(faces, q)
end
if π - Δϕ > 0 || π - Δθ > 0
bidx = [idx[1,1:end-1];idx[1:end-1,end];idx[end,end:-1:2];idx[end:-1:1,1]]
for i in 1:2(ϕfacets + θfacets)-4
push!(faces, QuadFace{Int}(bidx[i], bidx[i+1], bidx[i+1]+nf, bidx[i]+nf))
end
end
else
if 2π - Δϕ > 0 || π - Δθ > 0
bidx = [idx[1,1:end-1];idx[1:end-1,end];idx[end,end:-1:2];idx[end:-1:1,1]]
for i in 1:2(ϕfacets + θfacets)-4
push!(faces, QuadFace{Int}(bidx[i], bidx[i+1], nf+1, nf+1))
end
end
end
return faces
end
#---G4Ellipsoid------------------------------------------------------------------------------------
function GeometryBasics.coordinates(ellip::G4Ellipsoid, nvertices=24)
dx = GetDx(ellip)
dy = GetDy(ellip)
dz = GetDz(ellip)
topz = GetZTopCut(ellip)
botz = GetZBottomCut(ellip)
ϕfacets = nvertices
θfacets = nvertices ÷ 2
θ = LinRange(acos(topz/dz), acos(botz/dz), θfacets)
ϕ = LinRange(0, 2π, ϕfacets)
inner(θ, ϕ) = Point(dx * cos(ϕ) * sin(θ), dy * sin(ϕ) * sin(θ), dz * cos(θ))
points = vec([inner(θ, ϕ) for θ in θ, ϕ in ϕ])
push!(points, Point(0,0,topz), Point(0,0,botz))
return points
end
function GeometryBasics.faces(::G4Ellipsoid, nvertices=24)
ϕfacets = nvertices
θfacets = nvertices ÷ 2
idx = LinearIndices((θfacets, ϕfacets))
quad(i, j) = QuadFace{Int}(idx[i, j], idx[i + 1, j], idx[i + 1, j + 1], idx[i, j + 1])
faces = vec([quad(i, j) for i in 1:(θfacets - 1), j in 1:(ϕfacets - 1)])
for j in 1:(ϕfacets - 1)
push!(faces, QuadFace{Int}(idx[1,j], length(idx)+1, length(idx)+1, idx[1,j+1]),
QuadFace{Int}(idx[end,j], length(idx)+2, length(idx)+2, idx[end,j+1]))
end
return faces
end
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 1970 | #---G4Sphere--------------------------------------------------------------------------------------
function GeometryBasics.coordinates(tor::G4Torus, nvertices=48)
rmin = GetRmin(tor)
rmax = GetRmax(tor)
rtor = GetRtor(tor)
ϕ₀ = GetSPhi(tor)
Δϕ = GetDPhi(tor)
ϕfacets = round(Int64, (nvertices/2π) * Δϕ)
θfacets = round(Int64, nvertices/2)
θ = LinRange(0, 2π, θfacets)
ϕ = LinRange(ϕ₀, ϕ₀+Δϕ, ϕfacets)
inner(θ, ϕ, r, R) = Point((R + r * cos(θ))* cos(ϕ), (R + r * cos(θ)) * sin(ϕ), r * sin(θ))
oshell = [inner(θ, ϕ, rmax, rtor) for θ in θ, ϕ in ϕ]
ishell = rmin > 0 ? [inner(θ, ϕ, rmin, rtor) for θ in θ, ϕ in ϕ] : Δϕ < 2π ? [Point(rtor*cos(ϕ₀),rtor*sin(ϕ₀), 0), Point(rtor*cos(ϕ₀+Δϕ),rtor*sin(ϕ₀+Δϕ), 0)] : []
return [vec(oshell); vec(ishell)]
end
function GeometryBasics.faces(tor::G4Torus, nvertices=48)
rmin = GetRmin(tor)
Δϕ = GetDPhi(tor)
ϕfacets = round(Int64, (nvertices/2π) * Δϕ)
θfacets = round(Int64, nvertices/2)
idx = LinearIndices((θfacets, ϕfacets))
nf = ϕfacets * θfacets
quad(i, j) = QuadFace{Int}(idx[i, j], idx[i + 1, j], idx[i + 1, j + 1], idx[i, j + 1])
faces = vec([quad(i, j) for i in 1:(θfacets - 1), j in 1:(ϕfacets - 1)])
if rmin > 0
for q in vec([quad(i,j) .+ nf for i in 1:(θfacets - 1), j in 1:(ϕfacets - 1)])
push!(faces, q)
end
if Δϕ < 2π
for i in 1:(θfacets - 1)
push!(faces, QuadFace{Int}(idx[i, 1], idx[i+1, 1], idx[i+1, 1]+nf, idx[i, 1]+nf))
push!(faces, QuadFace{Int}(idx[i, end], idx[i+1, end], idx[i+1, end]+nf, idx[i+1, end]+nf))
end
end
else
if Δϕ < 2π
for i in 1:(θfacets - 1)
push!(faces, QuadFace{Int}(idx[i, 1], idx[i + 1, 1], nf + 1, nf + 1))
push!(faces, QuadFace{Int}(idx[i, end], idx[i + 1, end], nf + 2, nf + 2))
end
end
end
return faces
end | Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
|
[
"Apache-2.0"
] | 0.1.17 | 6936b20a42124581c88a5b0d9cc8b5c234eec682 | code | 3819 | #---Basic Geometry------------------------------------------------------------------------
using StaticArrays, GeometryBasics, Rotations, LinearAlgebra
const Vector3 = SVector{3}
const Vector2 = SVector{2}
Base.:*(x::Vector3, y::Vector3) = Vector3(x[1]*y[1], x[2]*y[2], x[3]*y[3])
Base.:*(x::Point3, y::Vector3) = Point3(x[1]*y[1], x[2]*y[2], x[3]*y[3])
Base.:*(x::Vector3, n::Number) = Vector3(x[1]*n, x[2]*n, x[3]*n)
Base.:*(n::Number, x::Vector3) = x * n
Base.:/(p::Point3, n::Number) = Point3(p[1]/n, p[2]/n, p[3]/n)
LinearAlgebra.:⋅(x::Vector3, y::Vector3) = x[1]*y[1] + x[2]*y[2] + x[3]*y[3]
Base.:-(p1::Point3, p2::Point3) = Vector3(p1[1]-p2[1], p1[2]-p2[2], p1[3]-p2[3])
Base.:+(p1::Point3, p2::Point3) = Vector3(p1[1]+p2[1], p1[2]+p2[2], p1[3]+p2[3])
LinearAlgebra.:×(x::Vector3, y::Vector3) = Vector3(x[2]*y[3]-x[3]*y[2], -x[1]*y[3]+x[3]*y[1], x[1]*y[2]-x[2]*y[1])
unitize(v::Vector3) = v/sqrt(v⋅v)
#---Transformation3D----------------------------------------------------------------------
struct Transformation3D{T<:AbstractFloat}
rotation::RotMatrix3{T}
translation::Vector3{T}
# optimization
has_rot::Bool
has_trans::Bool
Transformation3D{T}(rot::RotMatrix3{T}, trans::Vector3{T}) where T = new(rot, trans, !isone(rot), !iszero(trans))
end
Transformation3D() = Transformation3D{Float64}()
# Usefull constructors
Transformation3D{T}(dx, dy, dz) where T<:AbstractFloat = Transformation3D{T}(one(RotMatrix3{T}), Vector3{T}(dx, dy, dz))
Transformation3D{T}(dx, dy, dz, rotx, roty, rotz) where T<:AbstractFloat = Transformation3D{T}(RotMatrix3{T}(RotXYZ{T}(rotx, roty, rotz)), Vector3{T}(dx, dy, dz))
Transformation3D{T}(dx, dy, dz, rot::Rotation{3,T}) where T<:AbstractFloat = Transformation3D{T}(RotMatrix3{T}(rot), Vector3{T}(dx, dy, dz))
# Transforms
@inline transform(t::Transformation3D{T}, p::Point3{T}) where T<:AbstractFloat = t.has_rot ? t.rotation * (t.has_trans ? (p - t.translation) : p) : (t.has_trans ? (p - t.translation) : p)
@inline transform(t::Transformation3D{T}, d::Vector3{T}) where T<:AbstractFloat = t.has_rot ? t.rotation * d : d
@inline invtransform(t::Transformation3D{T}, p::Point3{T}) where T<:AbstractFloat = t.has_trans ? ((t.has_rot ? (p' * t.rotation)' : p) + t.translation) : ( t.has_rot ? (p' * t.rotation)' : p)
@inline invtransform(t::Transformation3D{T}, d::Vector3{T}) where T<:AbstractFloat = t.has_rot ? (d' * t.rotation)' : d
@inline Base.:*(t::Transformation3D{T}, p::Point3{T}) where T<:AbstractFloat = transform(t,p)
@inline Base.:*(t::Transformation3D{T}, d::Vector3{T}) where T<:AbstractFloat = transform(t,d)
@inline Base.:*(p::Point3{T}, t::Transformation3D{T}) where T<:AbstractFloat = invtransform(t,p)
@inline Base.:*(d::Vector3{T}, t::Transformation3D{T}) where T<:AbstractFloat = invtransform(t,d)
# Compose
Base.:*(t1::Transformation3D{T}, t2::Transformation3D{T}) where T<:AbstractFloat =
Transformation3D{T}(t1.rotation * t2.rotation, (t1.translation' * t2.rotation)' + t2.translation)
Base.inv(t::Transformation3D{T}) where T<:AbstractFloat = Transformation3D{T}(t.rotation', - t.rotation * t.translation)
Base.isapprox(t1::Transformation3D{T}, t2::Transformation3D{T}; atol::Real=0, rtol::Real=atol>0 ? 0 : √eps, nans::Bool=false) where T<:AbstractFloat =
isapprox(t1.rotation, t2.rotation; atol=atol, rtol=rtol, nans=nans) && isapprox(t1.translation, t2.translation; atol=atol, rtol=rtol, nans=nans)
# Utilities
Base.one(::Type{Transformation3D{T}}) where T<:AbstractFloat = Transformation3D{T}(one(RotMatrix3{T}), Vector3{T}(0,0,0))
Base.isone(t::Transformation3D{T}) where T<:AbstractFloat = isone(t.rotation) && iszero(t.translation)
hasrotation(t::Transformation3D{T}) where T<:AbstractFloat = !isone(t.rotation)
hastranslation(t::Transformation3D{T}) where T<:AbstractFloat = !iszero(t.translation)
| Geant4 | https://github.com/JuliaHEP/Geant4.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.