licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 23454 | # # [Attractors.jl Tutorial](@id tutorial)
# ```@raw html
# <video width="auto" controls loop>
# <source src="../attracont.mp4" type="video/mp4">
# </video>
# ```
# [`Attractors`](@ref) is a component of the **DynamicalSystems.jl** library.
# This tutorial will walk you through its main functionality.
# That is, given a `DynamicalSystem` instance, find all its attractors and their basins
# of attraction. Then,
# continue these attractors, and their stability properties, across a parameter value.
# It also offers various functions that compute nonlocal stability properties for an
# attractor, any of which can be used in the continuation to quantify stability.
# Besides this main functionality, there are plenty of other stuff,
# like for example [`edgestate`](@ref) or [`basins_fractal_dimension`](@ref),
# but we won't cover anything else in this introductory tutorial.
# See the [examples](@ref examples) page instead.
# ### Package versions used
import Pkg
#nb # Activate an environment in the folder containing the notebook
#nb Pkg.activate(dirname(@__DIR__))
#nb Pkg.add(["DynamicalSystems", "CairoMakie", "GLMakie", "OrdinaryDiffEq"])
Pkg.status(["Attractors", "CairoMakie", "OrdinaryDiffEq"])
#nb # ## Attractors.jl summary
#nb using Attractors # re=exported by `DynamicalSystems`
#nb @doc Attractors
# ## Tutorial - copy-pasteable version
# _Gotta go fast!_
# ```julia
# using Attractors, CairoMakie, OrdinaryDiffEq
# ## Define key input: a `DynamicalSystem`
# function modified_lorenz_rule(u, p, t)
# x, y, z = u; a, b = p
# dx = y - x
# dy = - x*z + b*abs(z)
# dz = x*y - a
# return SVector(dx, dy, dz)
# end
# p0 = [5.0, 0.1] # parameters
# u0 = [-4.0, 5, 0] # state
# diffeq = (alg = Vern9(), abstol = 1e-9, reltol = 1e-9, dt = 0.01) # solver options
# ds = CoupledODEs(modified_lorenz_rule, u0, p0; diffeq)
# ## Define key input: an `AttractorMaper` that finds
# ## attractors of a `DynamicalSystem`
# grid = (
# range(-15.0, 15.0; length = 150), # x
# range(-20.0, 20.0; length = 150), # y
# range(-20.0, 20.0; length = 150), # z
# )
# mapper = AttractorsViaRecurrences(ds, grid;
# consecutive_recurrences = 1000,
# consecutive_lost_steps = 100,
# )
# ## Find attractors and their basins of attraction state space fraction
# ## by randomly sampling initial conditions in state sapce
# sampler, = statespace_sampler(grid)
# algo = AttractorSeedContinueMatch(mapper)
# fs = basins_fractions(mapper, sampler)
# attractors = extract_attractors(mapper)
# ## found two attractors: one is a limit cycle, the other is chaotic
# ## visualize them
# plot_attractors(attractors)
# ## continue all attractors and their basin fractions across any arbigrary
# ## curve in parameter space using a global continuation algorithm
# algo = AttractorSeedContinueMatch(mapper)
# params(θ) = [1 => 5 + 0.5cos(θ), 2 => 0.1 + 0.01sin(θ)]
# pcurve = params.(range(0, 2π; length = 101))
# fractions_cont, attractors_cont = global_continuation(
# algo, pcurve, sampler; samples_per_parameter = 1_000
# )
# ## and visualize the results
# fig = plot_basins_attractors_curves(
# fractions_cont, attractors_cont, A -> minimum(A[:, 1]), pcurve; add_legend = false
# )
# ```
# ## Input: a `DynamicalSystem`
# The key input for most functionality of Attractors.jl is an instance of
# a `DynamicalSystem`. If you don't know how to make
# a `DynamicalSystem`, you need to consult the main tutorial of the
# [DynamicalSystems.jl library](https://juliadynamics.github.io/DynamicalSystemsDocs.jl/dynamicalsystems/stable/tutorial/).
# For this tutorial we will use a modified Lorenz-like system with equations
# ```math
# \begin{align*}
# \dot{x} & = y - x \\
# \dot{y} &= -x*z + b*|z| \\
# \dot{z} &= x*y - a \\
# \end{align*}
# ```
# which we define in code as
using Attractors # part of `DynamicalSystems`, so it re-exports functionality for making them!
using OrdinaryDiffEq # for accessing advanced ODE Solvers
function modified_lorenz_rule(u, p, t)
x, y, z = u; a, b = p
dx = y - x
dy = - x*z + b*abs(z)
dz = x*y - a
return SVector(dx, dy, dz)
end
p0 = [5.0, 0.1] # parameters
u0 = [-4.0, 5, 0] # state
diffeq = (alg = Vern9(), abstol = 1e-9, reltol = 1e-9, dt = 0.01) # solver options
ds = CoupledODEs(modified_lorenz_rule, u0, p0; diffeq)
# ## Finding attractors
# There are two major methods for finding attractors in dynamical systems.
# Explanation of how they work is in their respective docs.
# 1. [`AttractorsViaRecurrences`](@ref).
# 2. [`AttractorsViaFeaturizing`](@ref).
# You can consult [Datseris2023](@cite) for a comparison between the two.
# As far as the user is concerned, both algorithms are part of the same interface,
# and can be used in the same way. The interface is extendable as well,
# and works as follows.
# First, we create an instance of such an "attractor finding algorithm",
# which we call `AttractorMapper`. For example, [`AttractorsViaRecurrences`](@ref)
# requires a tesselated grid of the state space to search for attractors in.
# It also allows the user to tune some meta parameters, but in our example
# they are already tuned for the dynamical system at hand. So we initialize
grid = (
range(-10.0, 10.0; length = 150), # x
range(-15.0, 15.0; length = 150), # y
range(-15.0, 15.0; length = 150), # z
)
mapper = AttractorsViaRecurrences(ds, grid;
consecutive_recurrences = 1000, attractor_locate_steps = 1000,
consecutive_lost_steps = 100,
)
# This `mapper` can map any initial condition to the corresponding
# attractor ID, for example
mapper([-4.0, 5, 0])
# while
mapper([4.0, 2, 0])
# the fact that these two different initial conditions got assigned different IDs means
# that they converged to a different attractor.
# The attractors are stored in the mapper internally, to obtain them we
# use the function
attractors = extract_attractors(mapper)
# In Attractors.jl, all information regarding attractors is always a standard Julia
# `Dict`, which maps attractor IDs (positive integers) to the corresponding quantity.
# Here the quantity are the attractors themselves, represented as `StateSpaceSet`.
# We can visualize them with the convenience plotting function
using CairoMakie
plot_attractors(attractors)
# (this convenience function is a simple loop over scattering the values of
# the `attractors` dictionary)
# In our example system we see that for the chosen parameters there are two coexisting attractors:
# a limit cycle and a chaotic attractor.
# There may be more attractors though! We've only checked two initial conditions,
# so we could have found at most two attractors!
# However, it can get tedious to manually iterate over initial conditions, which is why
# this `mapper` is typically given to higher level functions for finding attractors
# and their basins of attraction. The simplest one
# is [`basins_fractions`](@ref). Using the `mapper`,
# it finds "all" attractors of the dynamical system and reports the state space fraction
# each attractors attracts. The search is probabilistic, so "all" attractors means those
# that at least one initial condition converged to.
# We can provide explicitly initial conditions to [`basins_fraction`](@ref),
# however it is typically simpler to provide it with with a state space sampler instead:
# a function that generates random initial conditions in the region of the
# state space that we are interested in. Here this region coincides with `grid`,
# so we can simply do:
sampler, = statespace_sampler(grid)
sampler() # random i.c.
#
sampler() # another random i.c.
# and finally call
fs = basins_fractions(mapper, sampler)
# The returned `fs` is a dictionary mapping each attractor ID to
# the fraction of the state space the corresponding basin occupies.
# With this we can confirm that there are (likely) only two attractors
# and that both attractors are robust as both have sufficiently large basin fractions.
# To obtain the full basins, which is computationally much more expensive,
# use [`basins_of_attraction`](@ref).
# You can use alternative algorithms in [`basins_fractions`](@ref), see
# the documentation of [`AttractorMapper`](@ref) for possible subtypes.
# [`AttractorMapper`](@ref) defines an extendable interface and can be enriched
# with other methods in the future!
# ## Different Attractor Mapper
# Attractors.jl utilizes composable interfaces throughout its functionality.
# In the above example we used one particular method to find attractors,
# via recurrences in the state space. An alternative is [`AttractorsViaFeaturizing`](@ref).
# For this method, we need to provide a "featurizing" function that given an
# trajectory (which is likely an attractor), it returns some features that will
# hopefully distinguish different attractors in a subsequent grouping step.
# Finding good features is typically a trial-and-error process, but for our system
# we already have some good features:
using Statistics: mean
function featurizer(A, t) # t is the time vector associated with trajectory A
xmin = minimum(A[:, 1])
ycen = mean(A[:, 2])
return SVector(xmin, ycen)
end
# from which we initialize
mapper2 = AttractorsViaFeaturizing(ds, featurizer; Δt = 0.1)
# [`AttractorsViaFeaturizing`](@ref) allows for a third input, which is a
# "grouping configuration", that dictates how features will be grouped into
# attractors, as features are extracted from (randomly) sampled state space trajectories.
# In this tutorial we leave it at its default value, which is clustering using the DBSCAN
# algorithm. The keyword arguments are meta parameters which control how long
# to integrate each initial condition for, and what sampling time, to produce
# a trajectory `A` given to the `featurizer` function. Because one of the two attractors
# is chaotic, we need denser sampling time than the default.
# We can use `mapper2` exactly as `mapper`:
fs2 = basins_fractions(mapper2, sampler)
attractors2 = extract_attractors(mapper2)
plot_attractors(attractors2)
# This mapper also found the attractors, but we should warn you: this mapper is less
# robust than [`AttractorsViaRecurrences`](@ref). One of the reasons for this is
# that [`AttractorsViaFeaturizing`](@ref) is not auto-terminating. For example, if we do not
# have enough transient integration time, the two attractors will get confused into one:
mapper3 = AttractorsViaFeaturizing(ds, featurizer; Ttr = 10, Δt = 0.1)
fs3 = basins_fractions(mapper3, sampler)
attractors3 = extract_attractors(mapper3)
plot_attractors(attractors3)
# On the other hand, the downside of [`AttractorsViaRecurrences`](@ref) is that
# it can take quite a while to converge for chaotic high dimensional systems.
# ## [Global continuation](@id global_cont_tutorial)
# If you have heard before the word "continuation", then you are likely aware of the
# **traditional continuation-based bifurcation analysis (CBA)** offered by many software,
# such as AUTO, MatCont, and in Julia [BifurcationKit.jl](https://github.com/bifurcationkit/BifurcationKit.jl).
# Here we offer a completely different kind of continuation called **global continuation**.
# The traditional continuation analysis continues the curves of individual _fixed
# points (and under some conditions limit cycles)_ across the joint state-parameter space and
# tracks their _local (linear) stability_.
# This approach needs to manually be "re-run" for every individual branch of fixed points
# or limit cycles.
# The global continuation in Attractors.jl finds _all_ attractors, _including chaotic
# or quasiperiodic ones_,
# in the whole of the state space (that it searches in), without manual intervention.
# It then continues all of these attractors concurrently along a parameter axis.
# Additionally, the global continuation tracks a _nonlocal_ stability property which by
# default is the basin fraction.
# This is a fundamental difference. Because all attractors are simultaneously
# tracked across the parameter axis, the user may arbitrarily estimate _any_
# property of the attractors and how it varies as the parameter varies.
# A more detailed comparison between these two approaches can be found in [Datseris2023](@cite).
# See also the [comparison page](@ref bfkit_comparison) in our docs
# that attempts to do the same analysis of our Tutorial with traditional continuation software.
# To perform the continuation is extremely simple. First, we decide what parameter,
# and what range, to continue over:
prange = 4.5:0.01:6
pidx = 1 # index of the parameter
# Then, we may call the [`global_continuation`](@ref) function.
# We have to provide a continuation algorithm, which itself references an [`AttractorMapper`](@ref).
# In this example we will re-use the `mapper` to create the "flagship product" of Attractors.jl
# which is the geenral [`AttractorSeedContinueMatch`](@ref).
# This algorithm uses the `mapper` to find all attractors at each parameter value
# and from the found attractors it continues them along a parameter axis
# using a seeding process (see its documentation string).
# Then, it performs a "matching" step, ensuring a "continuity" of the attractor
# label across the parameter axis. For now we ignore the matching step, leaving it to the
# default value. We'll use the `mapper` we created above and define
ascm = AttractorSeedContinueMatch(mapper)
# and call
fractions_cont, attractors_cont = global_continuation(
ascm, prange, pidx, sampler; samples_per_parameter = 1_000
)
# the output is given as two vectors. Each vector is a dictionary
# mapping attractor IDs to their basin fractions, or their state space sets, respectively.
# Both vectors have the same size as the parameter range.
# For example, the attractors at the 34-th parameter value are:
attractors_cont[34]
# There is a fantastic convenience function for animating
# the attractors evolution, that utilizes things we have
# already defined:
animate_attractors_continuation(
ds, attractors_cont, fractions_cont, prange, pidx;
);
# ```@raw html
# <video width="auto" controls loop>
# <source src="../attracont.mp4" type="video/mp4">
# </video>
# ```
# Hah, how cool is that! The attractors pop in and out of existence like out of nowhere!
# It would be incredibly difficult to find these attractors in traditional continuation software
# where a rough estimate of the period is required! (It would also be too hard due to the presence
# of chaos for most of the parameter values, but that's another issue!)
# Now typically a continuation is visualized in a 2D plot where the x axis is the
# parameter axis. We can do this with the convenience function:
fig = plot_basins_attractors_curves(
fractions_cont, attractors_cont, A -> minimum(A[:, 1]), prange,
)
# In the top panel are the basin fractions, by default plotted as stacked bars.
# Bottom panel is a visualization of the tracked attractors.
# The argument `A -> minimum(A[:, 1])` is simply a function that maps
# an attractor into a real number for plotting.
# ## Different matching procedures
# By default attractors are matched by their distance in state space.
# The default matcher is [`MatchBySSSetDistance`](@ref), and is given implicitly
# as a default 2nd argument when creating [`AttractorSeedContinueMatch`](@ref).
# But like anything else in Attractors.jl, "matchers" also follow a well-defined
# and extendable interface, see [`IDMatchers`](@ref) for that.
# Let's say that the default matching that we chose above isn't desirable.
# For example, one may argue that the attractor that pops up
# at the end of the continuation should have been assigned the same ID
# as attractor 1, because they are both to the left (see the video above).
# In reality one wouldn't really request that, because looking
# the video of attractors above shows that the attractors labelled "1", "2", and "3"
# are all completely different. But we argue here for example that "3" should have been
# the same as "1".
# Thankfully during a global continuation the "matching" step is completely
# separated from the "finding and continuing" step. If we don't like the
# initial matching, we can call [`match_sequentially!`](@ref) with a new
# instance of a matcher, and match again, without having to recompute
# the attractors and their basin fractions.
# For example, using this matcher:
matcher = MatchBySSSetDistance(use_vanished = true)
# will compare a new attractor with the latest instance of attractors
# with a given ID that have ever existed, irrespectively if they exist in the
# current parameter or not. This means, that the attractor "3" would in fact be compared
# with both attractor "2" and "1", even if "1" doesn't exist in the parameter "3"
# started existing at. And because "3" is closer to "1" than to "2", it will get
# matched to attractor "1" and get the same ID.
# Let's see this in action:
attractors_cont2 = deepcopy(attractors_cont)
match_sequentially!(attractors_cont2, matcher)
fig = plot_attractors_curves(
attractors_cont2, A -> minimum(A[:, 1]), prange,
)
# and as we can see, the new attractor at the end of the parameter range got
# assigned the same ID as the original attractor "1".
# For more ways of matching attractors see [`IDMatcher`](@ref).
# %% #src
# ## Enhancing the continuation
# The biggest strength of Attractors.jl is that it is not an isolated software.
# It is part of **DynamicalSystems.jl**. Here, we will use the full power of
# **DynamicalSystems.jl** and enrich the above continuation with various other
# measures of nonlocal stability, in particular Lyapunov exponents and
# the minimal fatal shock. First, let's plot again the continuation
# and label some things or clarity
fig = plot_basins_attractors_curves(
fractions_cont, attractors_cont, A -> minimum(A[:, 1]), prange; add_legend = false
)
ax1 = content(fig[2,1])
ax1.ylabel = "min(A₁)"
fig
# First, let's estimate the maximum Lyapunov exponent (MLE) for all attractors,
# using the `lyapunov` function that comes from the ChaosTools.jl submodule.
using ChaosTools: lyapunov
lis = map(enumerate(prange)) do (i, p) # loop over parameters
set_parameter!(ds, pidx, p) # important! We use the dynamical system!
attractors = attractors_cont[i]
## Return a dictionary mapping attractor IDs to their MLE
Dict(k => lyapunov(ds, 10000.0; u0 = A[1]) for (k, A) in attractors)
end
# The above `map` loop may be intimidating if you are a beginner, but it is
# really just a shorter way to write a `for` loop for our example.
# We iterate over all parameters, and for each we first update the dynamical
# system with the correct parameter, and then extract the MLE
# for each attractor. `map` just means that we don't have to pre-allocate a
# new vector before the loop; it creates it for us.
# We can visualize the LE with the other convenience function [`plot_continuation_curves!`](@ref),
ax2 = Axis(fig[3, 1]; ylabel = "MLE")
plot_continuation_curves!(ax2, lis, prange; add_legend = false)
fig
# This reveals crucial information for tha attractors, whether they are chaotic or not, that we would otherwise obtain only by visualizing the system dynamics at every single parameter.
# The story we can see now is that the dynamics start with a limit cycle (0 Lyapunov exponent), go into bi-stability of chaos and limit cycle, then there is only one limit cycle again, and then a chaotic attractor appears again, for a second bistable regime.
# The last piece of information to add is yet another measure of nonlocal stability: the minimal fatal shock (MFS), which is provided by [`minimal_fatal_shock`](@ref).
# The code to estimate this is similar with the `map` block for the MLE.
# Here however we re-use the created `mapper`, but now we must not forget to reset it inbetween parameter increments:
using LinearAlgebra: norm
search_area = collect(extrema.(grid ./ 2)) # smaller search = faster results
search_algorithm = MFSBlackBoxOptim(max_steps = 1000, guess = ones(3))
mfss = map(enumerate(prange)) do (i, p)
set_parameter!(ds, pidx, p)
reset_mapper!(mapper) # reset so that we don't have to re-initialize
## We need a special clause here: if there is only 1 attractor,
## then there is no MFS. It is undefined. We set it to `NaN`,
## which conveniently, will result to nothing being plotted by Makie.
attractors = attractors_cont[i]
if length(attractors) == 1
return Dict(k => NaN for (k, A) in attractors)
end
## otherwise, compute the actual MFS from the first point of each attractor
Dict(k =>
norm(minimal_fatal_shock(mapper, A[1], search_area, search_algorithm))
for (k, A) in attractors
)
end
# In a real application we wouldn't use the first point of each attractor,
# as the first point is completely random on the attractor (at least, for the
# [`AttractorsViaRecurrences`] mapper we use here).
# We would do this by examining the whole `A` object in the above block
# instead of just using `A[1]`. But this is a tutorial so we don't care!
# Right, so now we can visualize the MFS with the rest of the other quantities:
ax3 = Axis(fig[4, 1]; ylabel = "MFS", xlabel = "parameter")
plot_continuation_curves!(ax3, mfss, prange; add_legend = false)
## make the figure prettier
for ax in (ax1, ax2,); hidexdecorations!(ax; grid = false); end
resize!(fig, 500, 500)
fig
# ## Continuation along arbitrary parameter curves
# One of the many advantages of the global continuation is that we can choose
# what parameters to continue over. We can provide any arbitrary curve
# in parameter space. This is possible because (1) finding and matching attractors
# are two completely orthogonal steps, and (2) it is completely fine for
# attractors to dissapear (and perhaps re-appear) during a global continuation.
#For example, we can probe an elipsoid defined as
params(θ) = [1 => 5 + 0.5cos(θ), 2 => 0.1 + 0.01sin(θ)]
pcurve = params.(range(0, 2π; length = 101))
# here each component maps the parameter index to its value.
# We can just give this `pcurve` to the global continuation,
# using the same mapper and continuation algorithm,
# but adjusting the matching process so that vanished attractors
# are kept in "memory"
matcher = MatchBySSSetDistance(use_vanished = true)
ascm = AttractorSeedContinueMatch(mapper, matcher)
fractions_cont, attractors_cont = global_continuation(
ascm, pcurve, sampler; samples_per_parameter = 1_000
)
# and animate the result
animate_attractors_continuation(
ds, attractors_cont, fractions_cont, pcurve;
savename = "curvecont.mp4"
);
# ```@raw html
# <video width="auto" controls loop>
# <source src="../curvecont.mp4" type="video/mp4">
# </video>
# ```
# ## Conclusion and comparison with traditional local continuation
# We've reached the end of the tutorial! Some aspects we haven't highlighted is
# how most of the infrastructure of Attractors.jl is fully extendable.
# You will see this when reading the documentation strings of key structures
# like [`AttractorMapper`](@ref). All documentation strings are in the [API](@ref) page.
# See the [examples](@ref examples) page for more varied applications.
# And lastly, see the [comparison page](@ref bfkit_comparison) in our docs
# that attempts to do the same analysis of our Tutorial with traditional local continuation and bifurcation analysis software
# showing that (at least for this example) using Attractors.jl is clearly beneficial
# over the alternatives. | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 85 | module AttractorsVisualizations
using Attractors, Makie
include("plotting.jl")
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 17612 | ##########################################################################################
# Auto colors/markers
##########################################################################################
using Random: shuffle!, Xoshiro
function colors_from_keys(ukeys)
# Unfortunately, until `to_color` works with `Cycled`,
# we need to explicitly add here some default colors...
COLORS = [
"#7143E0",
"#191E44",
"#0A9A84",
"#AF9327",
"#5F166D",
"#6C768C",
]
if length(ukeys) ≤ length(COLORS)
colors = [COLORS[i] for i in eachindex(ukeys)]
else # keep colorscheme, but add extra random colors
n = length(ukeys) - length(COLORS)
colors = shuffle!(Xoshiro(123), collect(cgrad(COLORS, n+1; categorical = true)))
colors = append!(to_color.(COLORS), colors[1:(end-1)])
end
return Dict(k => colors[i] for (i, k) in enumerate(ukeys))
end
function markers_from_keys(ukeys)
MARKERS = [:circle, :dtriangle, :rect, :star5, :xcross, :diamond,
:hexagon, :cross, :pentagon, :ltriangle, :rtriangle, :hline, :vline, :star4,]
markers = Dict(k => MARKERS[mod1(i, length(MARKERS))] for (i, k) in enumerate(ukeys))
return markers
end
##########################################################################################
# Attractors
##########################################################################################
function Attractors.plot_attractors(a; kw...)
fig = Figure()
ax = Axis(fig[1,1])
plot_attractors!(ax, a; kw...)
return fig
end
function Attractors.plot_attractors!(ax, attractors;
ukeys = sort(collect(keys(attractors))), # internal argument just for other keywords
colors = colors_from_keys(ukeys),
markers = markers_from_keys(ukeys),
labels = Dict(ukeys .=> ukeys),
add_legend = length(ukeys) < 7,
access = SVector(1, 2),
sckwargs = (strokewidth = 0.5, strokecolor = :black,)
)
for k in ukeys
k ∉ keys(attractors) && continue
A = attractors[k]
x, y = columns(A[:, access])
scatter!(ax, x, y;
color = (colors[k], 0.9), markersize = 20,
marker = markers[k],
label = "$(labels[k])",
sckwargs...
)
end
add_legend && axislegend(ax)
return
end
##########################################################################################
# Basins
##########################################################################################
function Attractors.heatmap_basins_attractors(grid, basins::AbstractArray, attractors; kwargs...)
if length(size(basins)) != 2
error("Heatmaps only work in two dimensional basins!")
end
fig = Figure()
ax = Axis(fig[1,1])
heatmap_basins_attractors!(ax, grid, basins, attractors; kwargs...)
return fig
end
function Attractors.heatmap_basins_attractors!(ax, grid, basins, attractors;
ukeys = unique(basins), # internal argument just for other keywords
colors = colors_from_keys(ukeys),
markers = markers_from_keys(ukeys),
labels = Dict(ukeys .=> ukeys),
add_legend = length(ukeys) < 7,
access = SVector(1, 2),
sckwargs = (strokewidth = 1.5, strokecolor = :white,)
)
sort!(ukeys) # necessary because colormap is ordered
# Set up the (categorical) color map and colormap values
cmap = cgrad([colors[k] for k in ukeys], length(ukeys); categorical = true)
# Heatmap with appropriate colormap values. We need to transform
# the basin array to one with values the sequential integers,
# because the colormap itself also has as values the sequential integers
ids = 1:length(ukeys)
replace_dict = Dict(k => i for (i, k) in enumerate(ukeys))
basins_to_plot = replace(basins, replace_dict...)
heatmap!(ax, grid..., basins_to_plot;
colormap = cmap,
colorrange = (ids[1]-0.5, ids[end]+0.5),
)
# Scatter attractors
plot_attractors!(ax, attractors;
ukeys, colors, access, markers,
labels, add_legend, sckwargs
)
return ax
end
##########################################################################################
# Shaded basins
##########################################################################################
function Attractors.shaded_basins_heatmap(grid, basins::AbstractArray, attractors, iterations;
show_attractors = true,
maxit = maximum(iterations),
kwargs...)
if length(size(basins)) != 2
error("Heatmaps only work in two dimensional basins!")
end
fig = Figure()
ax = Axis(fig[1,1]; kwargs...)
shaded_basins_heatmap!(ax, grid, basins, iterations, attractors; maxit, show_attractors)
return fig
end
function Attractors.shaded_basins_heatmap!(ax, grid, basins, iterations, attractors;
ukeys = unique(basins),
show_attractors = true,
maxit = maximum(iterations))
sort!(ukeys) # necessary because colormap is ordered
ids = 1:length(ukeys)
replace_dict = Dict(k => i for (i, k) in enumerate(ukeys))
basins_to_plot = replace(basins.*1., replace_dict...)
access = SVector(1,2)
cmap, colors = custom_colormap_shaded(ukeys)
markers = markers_from_keys(ukeys)
labels = Dict(ukeys .=> ukeys)
add_legend = length(ukeys) < 7
it = findall(iterations .> maxit)
iterations[it] .= maxit
for i in ids
ind = findall(basins_to_plot .== i)
mn = minimum(iterations[ind])
mx = maximum(iterations[ind])
basins_to_plot[ind] .= basins_to_plot[ind] .+ 0.99.*(iterations[ind].-mn)/mx
end
# The colormap is constructed in such a way that the first color maps
# from id to id+0.99, id is an integer describing the current basin.
# Each id has a specific color associated and the gradient goes from
# light color (value id) to dark color (value id+0.99). It produces
# a shading proportional to a value associated to a specific pixel.
heatmap!(ax, grid..., basins_to_plot;
colormap = cmap,
colorrange = (ids[1], ids[end]+1),
)
# Scatter attractors
if show_attractors
for (i, k) ∈ enumerate(ukeys)
k ≤ 0 && continue
A = attractors[k]
x, y = columns(A[:, access])
scatter!(ax, x, y;
color = colors[k], markersize = 20,
marker = markers[k],
strokewidth = 1.5, strokecolor = :white,
label = "$(labels[k])"
)
end
# Add legend using colors only
add_legend && axislegend(ax)
end
return ax
end
function custom_colormap_shaded(ukeys)
# Light and corresponding dark colors for shading of basins of attraction
colors = colors_from_keys(ukeys)
n = length(colors)
# Note that the factor to define light and dark color
# is arbitrary.
LIGHT_COLORS = [darken_color(colors[k],0.3) for k in ukeys]
DARK_COLORS = [darken_color(colors[k],1.7) for k in ukeys]
v_col = Array{typeof(LIGHT_COLORS[1]),1}(undef,2*n)
vals = zeros(2*n)
for k in eachindex(ukeys)
v_col[2*k-1] = LIGHT_COLORS[k]
v_col[2*k] = DARK_COLORS[k]
vals[2*k-1] = k-1
vals[2*k] = k-1+0.9999999999
end
return cgrad(v_col, vals/maximum(vals)), colors
end
"""
darken_color(c, f = 1.2)
Darken given color `c` by a factor `f`.
If `f` is less than 1, the color is lightened instead.
"""
function darken_color(c, f = 1.2)
c = to_color(c)
return RGBAf(clamp.((c.r/f, c.g/f, c.b/f, c.alpha), 0, 1)...)
end
##########################################################################################
# Continuation
##########################################################################################
function Attractors.plot_basins_curves(fractions_cont, args...; kwargs...)
fig = Figure()
ax = Axis(fig[1,1])
ax.xlabel = "parameter"
ax.ylabel = "basins %"
plot_basins_curves!(ax, fractions_cont, args...; kwargs...)
return fig
end
function Attractors.plot_basins_curves!(ax, fractions_cont, prange = 1:length(fractions_cont);
ukeys = unique_keys(fractions_cont), # internal argument
colors = colors_from_keys(ukeys),
labels = Dict(ukeys .=> ukeys),
separatorwidth = 1, separatorcolor = "white",
add_legend = length(ukeys) < 7,
axislegend_kwargs = (position = :lt,),
series_kwargs = NamedTuple(),
markers = markers_from_keys(ukeys),
style = :band,
)
if !(prange isa AbstractVector{<:Real})
error("!(prange <: AbstractVector{<:Real})")
end
bands = fractions_series(fractions_cont, ukeys)
if style == :band
# transform to cumulative sum
for j in 2:length(bands)
bands[j] .+= bands[j-1]
end
for (j, k) in enumerate(ukeys)
if j == 1
l, u = 0, bands[j]
l = fill(0f0, length(u))
else
l, u = bands[j-1], bands[j]
end
band!(ax, prange, l, u;
color = colors[k], label = "$(labels[k])", series_kwargs...
)
if separatorwidth > 0 && j < length(ukeys)
lines!(ax, prange, u; color = separatorcolor, linewidth = separatorwidth)
end
end
ylims!(ax, 0, 1)
elseif style == :lines
for (j, k) in enumerate(ukeys)
scatterlines!(ax, prange, bands[j];
color = colors[k], label = "$(labels[k])", marker = markers[k],
markersize = 5, linewidth = 3, series_kwargs...
)
end
else
error("Incorrect style specification for basins fractions curves")
end
xlims!(ax, minimum(prange), maximum(prange))
add_legend && axislegend(ax; axislegend_kwargs...)
return
end
function fractions_series(fractions_cont, ukeys = unique_keys(fractions_cont))
bands = [zeros(length(fractions_cont)) for _ in ukeys]
for i in eachindex(fractions_cont)
for (j, k) in enumerate(ukeys)
bands[j][i] = get(fractions_cont[i], k, 0)
end
end
return bands
end
function Attractors.plot_attractors_curves(attractors_cont, attractor_to_real, prange = 1:length(attractors_cont); kwargs...)
fig = Figure()
ax = Axis(fig[1,1])
ax.xlabel = "parameter"
ax.ylabel = "attractors"
plot_attractors_curves!(ax, attractors_cont, attractor_to_real, prange; kwargs...)
return fig
end
function Attractors.plot_attractors_curves!(ax, attractors_cont, attractor_to_real, prange = 1:length(attractors_cont);
kwargs...
)
# make the continuation info values and just propagate to the main function
continuation_info = map(attractors_cont) do dict
Dict(k => attractor_to_real(A) for (k, A) in dict)
end
plot_continuation_curves!(ax, continuation_info, prange; kwargs...)
end
function Attractors.plot_continuation_curves!(ax, continuation_info, prange = 1:length(continuation_info);
ukeys = unique_keys(continuation_info), # internal argument
colors = colors_from_keys(ukeys),
labels = Dict(ukeys .=> ukeys),
add_legend = length(ukeys) < 7,
markers = markers_from_keys(ukeys),
axislegend_kwargs = (position = :lt,)
)
for i in eachindex(continuation_info)
info = continuation_info[i]
for (k, val) in info
scatter!(ax, prange[i], val;
color = colors[k], marker = markers[k], label = string(labels[k]),
)
end
end
xlims!(ax, minimum(prange), maximum(prange))
add_legend && axislegend(ax; axislegend_kwargs..., unique = true)
return
end
function Attractors.plot_continuation_curves(args...; kw...)
fig = Figure()
ax = Axis(fig[1,1])
plot_continuation_curves!(ax, args...; kw...)
return fig
end
# Mixed: basins and attractors
function Attractors.plot_basins_attractors_curves(fractions_cont, attractors_cont, a2r::Function, prange = 1:length(attractors_cont);
kwargs...
)
return Attractors.plot_basins_attractors_curves(fractions_cont, attractors_cont, [a2r], prange; kwargs...)
end
# Special case with multiple attractor projections:
function Attractors.plot_basins_attractors_curves(
fractions_cont, attractors_cont,
a2rs::Vector, prange = 1:length(attractors_cont);
ukeys = unique_keys(fractions_cont), # internal argument
colors = colors_from_keys(ukeys),
labels = Dict(ukeys .=> ukeys),
markers = markers_from_keys(ukeys),
kwargs...
)
# generate figure and axes; add labels and stuff
fig = Figure()
axb = Axis(fig[1,1])
A = length(a2rs)
axs = [Axis(fig[1+i, 1]; ylabel = "attractors_$(i)") for i in 1:A]
linkxaxes!(axb, axs...)
if A == 1 # if we have only 1, make it pretier
axs[1].ylabel = "attractors"
end
axs[end].xlabel = "parameter"
axb.ylabel = "basins %"
hidexdecorations!(axb; grid = false)
for i in 1:A-1
hidexdecorations!(axs[i]; grid = false)
end
# plot basins and attractors
plot_basins_curves!(axb, fractions_cont, prange; ukeys, colors, labels, kwargs...)
for (axa, a2r) in zip(axs, a2rs)
plot_attractors_curves!(axa, attractors_cont, a2r, prange;
ukeys, colors, markers, add_legend = false, # coz its true for fractions
)
end
return fig
end
# This function is kept for backwards compatibility only, really.
function Attractors.plot_basins_attractors_curves!(axb, axa, fractions_cont, attractors_cont,
attractor_to_real, prange = 1:length(attractors_cont);
ukeys = unique_keys(fractions_cont), # internal argument
colors = colors_from_keys(ukeys),
labels = Dict(ukeys .=> ukeys),
kwargs...
)
if length(fractions_cont) ≠ length(attractors_cont)
error("fractions and attractors don't have the same amount of entries")
end
plot_basins_curves!(axb, fractions_cont, prange; ukeys, colors, labels, kwargs...)
plot_attractors_curves!(axa, attractors_cont, attractor_to_real, prange;
ukeys, colors, add_legend = false, # coz its true for fractions
)
return
end
##########################################################################################
# Videos
##########################################################################################
function Attractors.animate_attractors_continuation(
ds::DynamicalSystem, attractors_cont, fractions_cont, prange, pidx; kw...)
pcurve = [[pidx => p] for p in prange]
return animate_attractors_continuation(ds, attractors_cont, fractions_cont, pcurve; kw...)
end
function Attractors.animate_attractors_continuation(
ds::DynamicalSystem, attractors_cont, fractions_cont, pcurve;
savename = "attracont.mp4", access = SVector(1, 2),
limits = auto_attractor_lims(attractors_cont, access),
framerate = 4, markersize = 10,
ukeys = unique_keys(attractors_cont),
colors = colors_from_keys(ukeys),
markers = markers_from_keys(ukeys),
Δt = isdiscretetime(ds) ? 1 : 0.05,
T = 100,
figure = NamedTuple(), axis = NamedTuple(), fracaxis = NamedTuple(),
legend = NamedTuple(),
add_legend = length(ukeys) ≤ 6
)
length(access) ≠ 2 && error("Need two indices to select two dimensions of `ds`.")
K = length(ukeys)
fig = Figure(; figure...)
ax = Axis(fig[1,1]; limits, axis...)
fracax = Axis(fig[1,2]; width = 50, limits = (0,1,0,1), ylabel = "fractions",
yaxisposition = :right, fracaxis...
)
hidedecorations!(fracax)
fracax.ylabelvisible = true
# setup attractor axis (note we change colors to be transparent)
att_obs = Dict(k => Observable(Point2f[]) for k in ukeys)
plotf! = isdiscretetime(ds) ? scatter! : scatterlines!
for k in ukeys
plotf!(ax, att_obs[k]; color = (colors[k], 0.75), label = "$k", markersize, marker = markers[k])
end
if add_legend
axislegend(ax; legend...)
end
# setup fractions axis
heights = Observable(fill(0.1, K))
barcolors = [colors[k] for k in ukeys]
barplot!(fracax, fill(0.5, K), heights; width = 1, gap = 0, stack=1:K, color = barcolors)
record(fig, savename, eachindex(pcurve); framerate) do i
p = pcurve[i]
ax.title = "p: $p" # TODO: Add compat printing here.
attractors = attractors_cont[i]
fractions = fractions_cont[i]
set_parameters!(ds, p)
heights[] = [get(fractions, k, 0) for k in ukeys]
for (k, att) in attractors
tr, tvec = trajectory(ds, T, first(vec(att)); Δt)
att_obs[k][] = vec(tr[:, access])
notify(att_obs[k])
end
# also ensure that attractors that don't exist are cleared
for k in setdiff(ukeys, collect(keys(attractors)))
att_obs[k][] = Point2f[]; notify(att_obs[k])
end
end
return fig
end
function auto_attractor_lims(attractors_cont, access)
xmin = ymin = Inf
xmax = ymax = -Inf
for atts in attractors_cont
for (k, A) in atts
P = A[:, access]
mini, maxi = minmaxima(P)
xmin > mini[1] && (xmin = mini[1])
ymin > mini[2] && (ymin = mini[2])
xmax < maxi[1] && (xmax = maxi[1])
ymax < maxi[2] && (ymax = maxi[2])
end
end
dx = xmax - xmin
dy = ymax - ymin
return (xmin - 0.1dx, xmax + 0.1dx, ymin - 0.1dy, ymax + 0.1dy)
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 737 | module Attractors
# Use the README as the module docs
@doc let
path = joinpath(dirname(@__DIR__), "README.md")
include_dependency(path)
read(path, String)
end Attractors
using Reexport
@reexport using StateSpaceSets
@reexport using DynamicalSystemsBase
# main files that import other files
include("dict_utils.jl")
include("mapping/attractor_mapping.jl")
include("basins/basins.jl")
include("continuation/basins_fractions_continuation_api.jl")
include("matching/matching_interface.jl")
include("boundaries/edgetracking.jl")
include("deprecated.jl")
include("tipping/tipping.jl")
# Visualization (export names extended in the extension package)
include("plotting.jl")
# minimal fatal shock algo
end # module Attractors
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 3211 | # This function is deprecated, however it will NEVER be removed.
# In the future, this call signature will remain here but its source code
# will simply be replaced by an error message.
function basins_of_attraction(grid::Tuple, ds::DynamicalSystem; kwargs...)
@warn("""
The function `basins_of_attraction(grid::Tuple, ds::DynamicalSystem; ...)` has
been replaced by the more generic
`basins_of_attraction(mapper::AttractorMapper, grid::Tuple)` which works for
any instance of `AttractorMapper`. The `AttractorMapper` itself requires as
input an kind of dynamical system the user wants, like a `StroboscopicMap` or
`CoupledODEs` or `DeterministicIteratedMap` etc.
For now, we do the following for you:
```
mapper = AttractorsViaRecurrences(ds, grid; sparse = false)
basins_of_attraction(mapper)
```
and we are completely ignoring any keywords you provided (which could be about the
differential equation solve, or the metaparameters of the recurrences algorithm).
We strongly recommend that you study the documentation of Attractors.jl
and update your code. The only reason we provide this backwards compatibility
is because our first paper "Effortless estimation of basins of attraction"
uses this function signature in the script in the paper (which we can't change anymore).
""")
mapper = AttractorsViaRecurrences(ds, grid; sparse = false)
return basins_of_attraction(mapper)
end
function continuation(args...; kwargs...)
@warn("""
The function `Attractors.continuation` is deprecated in favor of
`global_continuation`, in preparation for future developments where both
local/linearized and global continuations will be possible within DynamicalSystems.jl.
""")
return global_continuation(args...; kwargs...)
end
export continuation
@deprecate AttractorsBasinsContinuation GlobalContinuationAlgorithm
@deprecate RecurrencesSeededContinuation RecurrencesFindAndMatch
@deprecate GroupAcrossParameterContinuation FeaturizeGroupAcrossParameter
@deprecate match_attractor_ids! match_statespacesets!
@deprecate GroupAcrossParameter FeaturizeGroupAcrossParameter
@deprecate rematch! match_continuation!
@deprecate replacement_map matching_map
function match_statespacesets!(as::Vector{<:Dict}; kwargs...)
error("This function was incorrect. Use `match_sequentially!` instead.")
end
export match_continuation!, match_statespacesets!, match_basins_ids!
function match_continuation!(args...; kwargs...)
@warn "match_continuation! has been deprecated for `match_sequentially!`,
which has a more generic name that better reflects its capabilities."
return match_sequentially!(args...; kwargs...)
end
function match_statespacesets!(a_afte, a_befo; kwargs...)
@warn "match_statespacesets! is deprecated. Use `matching_map!` with `MatchBySSSetDistance`."
return matching_map!(a_afte, a_befo, MatchBySSSetDistance(kwargs...))
end
function match_basins_ids!(b₊::AbstractArray, b₋; threshold = Inf)
@warn "`match_basins_ids!` is deprecated, use `matching_map` with `MatchByBasinOverlap`."
matcher = MatchByBasinOverlap(threshold)
return matching_map!(b₊, b₋, matcher)
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 3506 | export unique_keys, swap_dict_keys!, next_free_id
# Utility functions for managing dictionary keys that are useful
# in continuation and attractor matching business
# Thanks a lot to Valentin (@Seelengrab) for generous help in the key swapping code.
# Swapping keys and ensuring that everything works "as expected" is,
# surprising, one of the hardest things to code in Attractors.jl.
"""
swap_dict_keys!(d::Dict, matching_map::Dict)
Swap the keys of a dictionary `d` given a `matching_map`
which maps old keys to new keys. Also ensure that a swap can happen at most once,
e.g., if input `d` has a key `4`, and `rmap = Dict(4 => 3, 3 => 2)`,
then the key `4` will be transformed to `3` and not further to `2`.
"""
function swap_dict_keys!(fs::Dict, _rmap::AbstractDict)
isempty(_rmap) && return
# Transform rmap so it is sorted in decreasing order,
# so that double swapping can't happen
rmap = sort!(collect(_rmap); by = x -> x[2])
cache = Tuple{keytype(fs), valtype(fs)}[]
for (oldkey, newkey) in rmap
haskey(fs, oldkey) || continue
oldkey == newkey && continue
tmp = pop!(fs, oldkey)
if !haskey(fs, newkey)
fs[newkey] = tmp
else
push!(cache, (newkey, tmp))
end
end
for (k, v) in cache
fs[k] = v
end
return fs
end
"""
overwrite_dict!(old::Dict, new::Dict)
In-place overwrite the `old` dictionary for the key-value pairs of the `new`.
"""
function overwrite_dict!(old::Dict, new::Dict)
empty!(old)
for (k, v) in new
old[k] = v
end
end
"""
additive_dict_merge!(d1::Dict, d2::Dict)
Merge keys and values of `d2` into `d1` additively: the values of the same keys
are added together in `d1` and new keys are given to `d1` as-is.
"""
function additive_dict_merge!(d1::Dict, d2::Dict)
z = zero(valtype(d1))
for (k, v) in d2
d1[k] = get(d1, k, z) + v
end
return d1
end
"""
retract_keys_to_consecutive(v::Vector{<:Dict}) → rmap
Given a vector of dictionaries with various positive integer keys, retract all keys so that
consecutive integers are used. So if the dictionaries have overall keys 2, 3, 42,
then they will transformed to 1, 2, 3.
Return the replacement map used to replace keys in all dictionaries with
[`swap_dict_keys!`](@ref).
As this function is used in attractor matching in [`global_continuation`](@ref)
it skips the special key `-1`.
"""
function retract_keys_to_consecutive(v::Vector{<:Dict})
ukeys = unique_keys(v)
ukeys = setdiff(ukeys, [-1]) # skip key -1 if it exists
rmap = Dict(k => i for (i, k) in enumerate(ukeys) if i != k)
return rmap
end
"""
unique_keys(v::Iterator{<:AbstractDict})
Given a vector of dictionaries, return a sorted vector of the unique keys
that are present across all dictionaries.
"""
function unique_keys(v)
unique_keys = Set(keytype(first(v))[])
for d in v
for k in keys(d)
push!(unique_keys, k)
end
end
return sort!(collect(unique_keys))
end
"""
next_free_id(new::Dict, old::Dict)
Return the minimum key of the "new" dictionary
that doesn't exist in the "old" dictionary.
"""
function next_free_id(a₊::AbstractDict, a₋::AbstractDict)
s = setdiff(keys(a₊), keys(a₋))
nextid = isempty(s) ? maximum(keys(a₋)) + 1 : minimum(s)
return nextid
end
function next_free_id(keys₊, keys₋)
s = setdiff(keys₊, keys₋)
nextid = isempty(s) ? maximum(keys₋) + 1 : minimum(s)
return nextid
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 7119 | ##########################################################################################
# Attractors
##########################################################################################
"""
plot_attractors(attractors::Dict{Int, StateSpaceSet}; kwargs...)
Plot the attractors as a scatter plot.
## Keyword arguments
- All the [common plotting keywords](@ref common_plot_kwargs).
Particularly important is the `access` keyword.
- `sckwargs = (strokewidth = 0.5, strokecolor = :black,)`: additional keywords
propagated to the `Makie.scatter` function that plots the attractors.
"""
function plot_attractors end
function plot_attractors! end
export plot_attractors, plot_attractors!
##########################################################################################
# Basins
##########################################################################################
"""
heatmap_basins_attractors(grid, basins, attractors; kwargs...)
Plot a heatmap of found (2-dimensional) `basins` of attraction and corresponding
`attractors`, i.e., the output of [`basins_of_attraction`](@ref).
## Keyword arguments
- All the [common plotting keywords](@ref common_plot_kwargs) and
`sckwargs` as in [`plot_attractors`](@ref).
"""
function heatmap_basins_attractors end
function heatmap_basins_attractors! end
export heatmap_basins_attractors, heatmap_basins_attractors!
"""
shaded_basins_heatmap(grid, basins, attractors, iterations; kwargs...)
Plot a heatmap of found (2-dimensional) `basins` of attraction and corresponding
`attractors`. A matrix `iterations` with the same size of `basins` must be provided
to shade the color according to the value of this matrix. A small value corresponds
to a light color and a large value to a darker tone. This is useful to represent
the number of iterations taken for each initial condition to converge. See also
[`convergence_time`](@ref) to store this iteration number.
## Keyword arguments
- `show_attractors = true`: shows the attractor on plot
- `maxit = maximum(iterations)`: clip the values of `iterations` to
the value `maxit`. Useful when there are some very long iterations and keep the
range constrained to a given interval.
- All the [common plotting keywords](@ref common_plot_kwargs).
"""
function shaded_basins_heatmap end
function shaded_basins_heatmap! end
export shaded_basins_heatmap, shaded_basins_heatmap!
##########################################################################################
# Continuation
##########################################################################################
"""
animate_attractors_continuation(
ds::DynamicalSystem, attractors_cont, fractions_cont, pcurve;
kwargs...
)
Animate how the found system attractors and their corresponding basin fractions
change as the system parameter is increased. This function combines the input
and output of the [`global_continuation`](@ref) function into a video output.
The input dynamical system `ds` is used to evolve initial conditions sampled from the
found attractors, so that the attractors are better visualized.
`attractors_cont, fractions_cont` are the output of [`global_continuation`](@ref)
while `ds, pcurve` are the input to [`global_continuation`](@ref).
## Keyword arguments
- `savename = "attracont.mp4"`: name of video output file.
- `framerate = 4`: framerate of video output.
- `Δt, T`: propagated to `trajectory` for evolving an initial condition sampled
from an attractor.
- Also all [common plotting keywords](@ref common_plot_kwargs).
- `figure, axis, fracaxis, legend`: named tuples propagated as keyword arguments to the
creation of the `Figure`, the `Axis`, the "bar-like" axis containing the fractions,
and the `axislegend` that adds the legend (if `add_legend = true`).
- `add_legend = true`: whether to display the axis legend.
"""
function animate_attractors_continuation end
export animate_attractors_continuation
"""
plot_basins_curves(fractions_cont [, prange]; kw...)
Plot the fractions of basins of attraction versus a parameter range/curve,
i.e., visualize the output of [`global_continuation`](@ref).
See also [`plot_basins_attractors_curves`](@ref) and
[`plot_continuation_curves`](@ref).
## Keyword arguments
- `style = :band`: how to visualize the basin fractions. Choices are
`:band` for a band plot with cumulative sum = 1 or `:lines` for a lines
plot of each basin fraction
- `separatorwidth = 1, separatorcolor = "white"`: adds a line separating the fractions
if the style is `:band`
- `axislegend_kwargs = (position = :lt,)`: propagated to `axislegend` if a legend is added
- `series_kwargs = NamedTuple()`: propagated to the band or scatterline plot
- Also all [common plotting keywords](@ref common_plot_kwargs).
"""
function plot_basins_curves end
function plot_basins_curves! end
export plot_basins_curves, plot_basins_curves!
"""
plot_attractors_curves(attractors_cont, attractor_to_real [, prange]; kw...)
Same as in [`plot_basins_curves`](@ref) but visualize the attractor dependence on
the parameter(s) instead of their basin fraction.
The function `attractor_to_real` takes as input a `StateSpaceSet` (attractor)
and returns a real number so that it can be plotted versus the parameter axis.
See also [`plot_basins_attractors_curves`](@ref).
Same keywords as [`plot_basins_curves`](@ref common_plot_kwargs).
See also [`plot_continuation_curves`](@ref).
"""
function plot_attractors_curves end
function plot_attractors_curves! end
export plot_attractors_curves, plot_attractors_curves!
"""
plot_continuation_curves(continuation_info [, prange]; kwargs...)
Same as in [`plot_basins_curves`](@ref) but visualize any arbitrary quantity characterizing
the continuation. Hence, the `continuation_info` is of exactly the same format as
`fractions_cont`: a vector of dictionaries, each dictionary mapping attractor IDs to real numbers.
`continuation_info` is meant to accompany `attractor_info` in [`plot_attractors_curves`](@ref).
To produce `continuation_info` from `attractor_info` you can do something like:
```julia
continuation_info = map(attractors_cont) do attractors
Dict(k => f(A) for (k, A) in attractors)
end
```
with `f` your function of interest that returns a real number.
"""
function plot_continuation_curves end
function plot_continuation_curves! end
export plot_continuation_curves, plot_continuation_curves!
"""
plot_basins_attractors_curves(
fractions_cont, attractors_cont, a2rs [, prange]
kwargs...
)
Convenience combination of [`plot_basins_curves`](@ref) and [`plot_attractors_curves`](@ref)
in a multi-panel plot that shares legend, colors, markers, etc.
This function allows `a2rs` to be a `Vector` of functions, each mapping
attractors into real numbers. Below the basins fractions plot, one additional
panel is created for each entry in `a2rs`.
`a2rs` can also be a single function, in which case only one panel is made.
"""
function plot_basins_attractors_curves end
function plot_basins_attractors_curves! end
export plot_basins_attractors_curves, plot_basins_attractors_curves!
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 90 | include("basins_utilities.jl")
include("fractality_of_basins.jl")
include("wada_test.jl")
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 5649 | # It works for all mappers that define a `basins_fractions` method.
"""
basins_of_attraction(mapper::AttractorMapper, grid::Tuple) → basins, attractors
Compute the full basins of attraction as identified by the given `mapper`,
which includes a reference to a [`DynamicalSystem`](@ref) and return them
along with (perhaps approximated) found attractors.
`grid` is a tuple of ranges defining the grid of initial conditions that partition
the state space into boxes with size the step size of each range.
For example, `grid = (xg, yg)` where `xg = yg = range(-5, 5; length = 100)`.
The grid has to be the same dimensionality as the state space expected by the
integrator/system used in `mapper`. E.g., a [`ProjectedDynamicalSystem`](@ref)
could be used for lower dimensional projections, etc. A special case here is
a [`PoincareMap`](@ref) with `plane` being `Tuple{Int, <: Real}`. In this special
scenario the grid can be one dimension smaller than the state space, in which case
the partitioning happens directly on the hyperplane the Poincaré map operates on.
`basins_of_attraction` function is a convenience 5-lines-of-code wrapper which uses the
`labels` returned by [`basins_fractions`](@ref) and simply assigns them to a full array
corresponding to the state space partitioning indicated by `grid`.
See also [`convergence_and_basins_of_attraction`](@ref).
"""
function basins_of_attraction(mapper::AttractorMapper, grid::Tuple; kwargs...)
basins = zeros(Int32, map(length, grid))
I = CartesianIndices(basins)
A = StateSpaceSet([generate_ic_on_grid(grid, i) for i in vec(I)])
fs, labels = basins_fractions(mapper, A; kwargs...)
attractors = extract_attractors(mapper)
vec(basins) .= vec(labels)
return basins, attractors
end
# Type-stable generation of an initial condition given a grid array index
@generated function generate_ic_on_grid(grid::NTuple{B, T}, ind) where {B, T}
gens = [:(grid[$k][ind[$k]]) for k=1:B]
quote
Base.@_inline_meta
@inbounds return SVector{$B, Float64}($(gens...))
end
end
"""
basins_fractions(basins::AbstractArray [,ids]) → fs::Dict
Calculate the state space fraction of the basins of attraction encoded in `basins`.
The elements of `basins` are integers, enumerating the attractor that the entry of
`basins` converges to (i.e., like the output of [`basins_of_attraction`](@ref)).
Return a dictionary that maps attractor IDs to their relative fractions.
Optionally you may give a vector of `ids` to calculate the fractions of only
the chosen ids (by default `ids = unique(basins)`).
In [Menck2013](@cite) the authors use these fractions to quantify the stability of a basin of
attraction, and specifically how it changes when a parameter is changed.
For this, see [`global_continuation`](@ref).
"""
function basins_fractions(basins::AbstractArray, ids = unique(basins))
fs = Dict{eltype(basins), Float64}()
N = length(basins)
for ξ in ids
B = count(isequal(ξ), basins)
fs[ξ] = B/N
end
return fs
end
"""
convergence_and_basins_of_attraction(mapper::AttractorMapper, grid)
An extension of [`basins_of_attraction`](@ref).
Return `basins, attractors, convergence`, with `basins, attractors` as in
`basins_of_attraction`, and `convergence` being an array with same shape
as `basins`. It contains the time each initial condition took
to converge to its attractor.
It is useful to give to [`shaded_basins_heatmap`](@ref).
See also [`convergence_time`](@ref).
# Keyword arguments
- `show_progress = true`: show progress bar.
"""
function convergence_and_basins_of_attraction(mapper::AttractorMapper, grid; show_progress = true)
if length(grid) != dimension(referenced_dynamical_system(mapper))
@error "The mapper and the grid must have the same dimension"
end
basins = zeros(length.(grid))
iterations = zeros(Int, length.(grid))
I = CartesianIndices(basins)
progress = ProgressMeter.Progress(
length(basins); desc = "Basins and convergence: ", dt = 1.0
)
for (k, ind) in enumerate(I)
show_progress && ProgressMeter.update!(progress, k)
u0 = Attractors.generate_ic_on_grid(grid, ind)
basins[ind] = mapper(u0)
iterations[ind] = convergence_time(mapper)
end
attractors = extract_attractors(mapper)
return basins, attractors, iterations
end
"""
convergence_and_basins_fractions(mapper::AttractorMapper, ics::StateSpaceSet)
An extension of [`basins_fractions`](@ref).
Return `fs, labels, convergence`. The first two are as in `basins_fractions`,
and `convergence` is a vector containing the time each initial condition took
to converge to its attractor.
Only usable with mappers that support `id = mapper(u0)`.
See also [`convergence_time`](@ref).
# Keyword arguments
- `show_progress = true`: show progress bar.
"""
function convergence_and_basins_fractions(mapper::AttractorMapper, ics::AbstractStateSpaceSet;
show_progress = true,
)
N = size(ics, 1)
progress = ProgressMeter.Progress(N;
desc="Mapping initial conditions to attractors:", enabled = show_progress
)
fs = Dict{Int, Int}()
labels = Vector{Int}(undef, N)
iterations = Vector{typeof(current_time(mapper.ds))}(undef, N)
for i ∈ 1:N
ic = _get_ic(ics, i)
label = mapper(ic; show_progress)
fs[label] = get(fs, label, 0) + 1
labels[i] = label
iterations[i] = convergence_time(mapper)
show_progress && ProgressMeter.next!(progress)
end
# Transform count into fraction
ffs = Dict(k => v/N for (k, v) in fs)
return ffs, labels, iterations
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 10882 | export uncertainty_exponent, basins_fractal_dimension, basins_fractal_test, basin_entropy
"""
basin_entropy(basins::Array{Integer}, ε = size(basins, 1)÷10) -> Sb, Sbb
Return the basin entropy [Daza2016](@cite) `Sb` and basin boundary entropy `Sbb`
of the given `basins` of attraction by considering `ε`-sized boxes along each dimension.
## Description
First, the n-dimensional input `basins`
is divided regularly into n-dimensional boxes of side `ε`.
If `ε` is an integer, the same size is used for all dimensions, otherwise `ε` can be
a tuple with the same size as the dimensions of `basins`.
The size of the basins has to be divisible by `ε`.
Assuming that there are ``N`` `ε`-boxes that cover the `basins`, the basin entropy is estimated
as [Daza2016](@cite)
```math
S_b = \\tfrac{1}{N}\\sum_{i=1}^{N}\\sum_{j=1}^{m_i}-p_{ij}\\log(p_{ij})
```
where ``m_i`` is the number of unique IDs (integers of `basins`) in box ``i``
and ``p_{ij}`` is the relative frequency (probability) to obtain ID ``j``
in the ``i`` box (simply the count of IDs ``j`` divided by the total in the box).
`Sbb` is the boundary basin entropy.
This follows the same definition as ``S_b``, but now averaged over only
only boxes that contains at least two
different basins, that is, for the boxes on the boundaries.
The basin entropy is a measure of the uncertainty on the initial conditions of the basins.
It is maximum at the value `log(n_att)` being `n_att` the number of unique IDs in `basins`. In
this case the boundary is intermingled: for a given initial condition we can find
another initial condition that lead to another basin arbitrarily close. It provides also
a simple criterion for fractality: if the boundary basin entropy `Sbb` is above `log(2)`
then we have a fractal boundary. It doesn't mean that basins with values below cannot
have a fractal boundary, for a more precise test see [`basins_fractal_test`](@ref).
An important feature of the basin entropy is that it allows
comparisons between different basins using the same box size `ε`.
"""
function basin_entropy(basins::AbstractArray{<:Integer, D}, ε::Integer = size(basins, 1)÷10) where {D}
es = ntuple(i -> ε, Val(D))
return basin_entropy(basins, es)
end
function basin_entropy(basins::AbstractArray{<:Integer, D}, es::NTuple{D, <: Integer}) where {D}
if size(basins) .% es ≠ ntuple(i -> 0, D)
throw(ArgumentError("The basins are not fully divisible by the sizes `ε`"))
end
Sb = 0.0; Nb = 0
εranges = map((d, ε) -> 1:ε:d, size(basins), es)
box_iterator = Iterators.product(εranges...)
for box_start in box_iterator
box_ranges = map((d, ε) -> d:(d+ε-1), box_start, es)
box_values = view(basins, box_ranges...)
uvals = unique(box_values)
if length(uvals) > 1
Nb += 1
# we only need to estimate entropy for boxes with more than 1 val,
# because in other cases the entropy is zero
Sb = Sb + _box_entropy(box_values, uvals)
end
end
return Sb/length(box_iterator), Sb/Nb
end
function _box_entropy(box_values, unique_vals = unique(box_values))
h = 0.0
for v in unique_vals
p = count(x -> (x == v), box_values)/length(box_values)
h += -p*log(p)
end
return h
end
"""
basins_fractal_test(basins; ε = 20, Ntotal = 1000) -> test_res, Sbb
Perform an automated test to decide if the boundary of the basins has fractal structures
based on the method of Puy et al. [Puy2021](@cite).
Return `test_res` (`:fractal` or `:smooth`) and the mean basin boundary entropy.
## Keyword arguments
* `ε = 20`: size of the box to compute the basin boundary entropy.
* `Ntotal = 1000`: number of balls to test in the boundary for the computation of `Sbb`
## Description
The test "looks" at the basins with a magnifier of size `ε` at random.
If what we see in the magnifier looks like a smooth boundary (onn average) we decide that
the boundary is smooth. If it is not smooth we can say that at the scale `ε` we have
structures, i.e., it is fractal.
In practice the algorithm computes the boundary basin entropy `Sbb` [`basin_entropy`](@ref)
for `Ntotal`
random boxes of radius `ε`. If the computed value is equal to theoretical value of a smooth
boundary
(taking into account statistical errors and biases) then we decide that we have a smooth
boundary. Notice that the response `test_res` may depend on the chosen ball radius `ε`.
For larger size,
we may observe structures for smooth boundary and we obtain a *different* answer.
The output `test_res` is a symbol describing the nature of the basin and the output `Sbb` is
the estimated value of the boundary basin entropy with the sampling method.
"""
function basins_fractal_test(basins; ε = 20, Ntotal = 1000)
dims = size(basins)
# Sanity check.
if minimum(dims)/ε < 50
@warn "Maybe the size of the grid is not fine enough."
end
if Ntotal < 100
error("Ntotal must be larger than 100 to gather enough statistics.")
end
v_pts = zeros(Float64, length(dims), prod(dims))
I = CartesianIndices(basins)
for (k,coord) in enumerate(I)
v_pts[:, k] = [Tuple(coord)...]
end
tree = searchstructure(KDTree, v_pts, Euclidean())
# Now get the values in the boxes.
Nb = 1
N_stat = zeros(Ntotal)
while Nb < Ntotal
p = [rand()*(sz-ε)+ε for sz in dims]
idxs = isearch(tree, p, WithinRange(ε))
box_values = basins[idxs]
bx_ent = _box_entropy(box_values)
if bx_ent > 0
Nb = Nb + 1
N_stat[Nb] = bx_ent
end
end
Ŝbb = mean(N_stat)
σ_sbb = std(N_stat)/sqrt(Nb)
# Table of boundary basin entropy of a smooth boundary for dimension 1 to 5:
Sbb_tab = [0.499999, 0.4395093, 0.39609176, 0.36319428, 0.33722572]
if length(dims) ≤ 5
Sbb_s = Sbb_tab[length(dims)]
else
Sbb_s = 0.898*length(dims)^-0.4995
end
# Systematic error approximation for the disk of radius ε
δub = 0.224*ε^-1.006
tst_res = :smooth
if Ŝbb < (Sbb_s - σ_sbb) || Ŝbb > (σ_sbb + Sbb_s + δub)
# println("Fractal boundary for size of box ε=", ε)
tst_res = :fractal
else
# println("Smooth boundary for size of box ε=", ε)
tst_res = :smooth
end
return tst_res, Ŝbb
end
# as suggested in https://github.com/JuliaStats/StatsBase.jl/issues/398#issuecomment-417875619
linreg(x, y) = hcat(fill!(similar(x), 1), x) \ y
"""
basins_fractal_dimension(basins; kwargs...) -> V_ε, N_ε, d
Estimate the fractal dimension `d` of the boundary between basins of attraction using
a box-counting algorithm for the boxes that contain at least two different basin IDs.
## Keyword arguments
* `range_ε = 2:maximum(size(basins))÷20` is the range of sizes of the box to
test (in pixels).
## Description
The output `N_ε` is a vector with the number of the balls of radius `ε` (in pixels)
that contain at least two initial conditions that lead to different attractors. `V_ε`
is a vector with the corresponding size of the balls. The output `d` is the estimation
of the box-counting dimension of the boundary by fitting a line in the `log.(N_ε)`
vs `log.(1/V_ε)` curve. However it is recommended to analyze the curve directly
for more accuracy.
It is the implementation of the popular algorithm of the estimation of the box-counting
dimension. The algorithm search for a covering the boundary with `N_ε` boxes of size
`ε` in pixels.
"""
function basins_fractal_dimension(basins::AbstractArray; range_ε = 3:maximum(size(basins))÷20)
dims = size(basins)
num_step = length(range_ε)
N_u = zeros(Int, num_step) # number of uncertain box
N = zeros(Int, num_step) # number of boxes
V_ε = zeros(1, num_step) # resolution
# Naive box counting estimator
for (k,eps) in enumerate(range_ε)
Nb, Nu = 0, 0
# get indices of boxes
bx_tuple = ntuple(i -> range(1, dims[i] - rem(dims[i],eps), step = eps), length(dims))
box_indices = CartesianIndices(bx_tuple)
for box in box_indices
# compute the range of indices for the current box
ind = CartesianIndices(ntuple(i -> range(box[i], box[i]+eps-1, step = 1), length(dims)))
c = basins[ind]
if length(unique(c))>1
Nu = Nu + 1
end
Nb += 1
end
N_u[k] = Nu
N[k] = Nb
V_ε[k] = eps
end
N_ε = N_u
# remove zeros in case there are any:
ind = N_ε .> 0.0
N_ε = N_ε[ind]
V_ε = V_ε[ind]
# get exponent via liner regression on `f_ε ~ ε^α`
b, d = linreg(vec(-log10.(V_ε)), vec(log10.(N_ε)))
return V_ε, N_ε, d
end
"""
uncertainty_exponent(basins; kwargs...) -> ε, N_ε, α
Estimate the uncertainty exponent[Grebogi1983](@cite) of the basins of attraction. This exponent
is related to the final state sensitivity of the trajectories in the phase space.
An exponent close to `1` means basins with smooth boundaries whereas an exponent close
to `0` represent completely fractalized basins, also called riddled basins.
The output `N_ε` is a vector with the number of the balls of radius `ε` (in pixels)
that contain at least two initial conditions that lead to different attractors.
The output `α` is the estimation of the uncertainty exponent using the box-counting
dimension of the boundary by fitting a line in the `log.(N_ε)` vs `log.(1/ε)` curve.
However it is recommended to analyze the curve directly for more accuracy.
## Keyword arguments
* `range_ε = 2:maximum(size(basins))÷20` is the range of sizes of the ball to
test (in pixels).
## Description
A phase space with a fractal boundary may cause a uncertainty on the final state of the
dynamical system for a given initial condition. A measure of this final state sensitivity
is the uncertainty exponent. The algorithm probes the basin of attraction with balls
of size `ε` at random. If there are a least two initial conditions that lead to different
attractors, a ball is tagged "uncertain". `f_ε` is the fraction of "uncertain balls" to the
total number of tries in the basin. In analogy to the fractal dimension, there is a scaling
law between, `f_ε ~ ε^α`. The number that characterizes this scaling is called the
uncertainty exponent `α`.
Notice that the uncertainty exponent and the box counting dimension of the boundary are
related. We have `Δ₀ = D - α` where `Δ₀` is the box counting dimension computed with
[`basins_fractal_dimension`](@ref) and `D` is the dimension of the phase space.
The algorithm first estimates the box counting dimension of the boundary and
returns the uncertainty exponent.
"""
function uncertainty_exponent(basins::AbstractArray; range_ε = 2:maximum(size(basins))÷20)
V_ε, N_ε, d = basins_fractal_dimension(basins; range_ε)
return V_ε, N_ε, length(size(basins)) - d
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 5066 | export test_wada_merge, haussdorff_distance
"""
test_wada_merge(basins, r) -> p
Test if the 2D array `basins` has the [Wada
property](https://en.wikipedia.org/wiki/Lakes_of_Wada)
using the merging technique of [Daza2018](@cite).
## Description
The technique consists in computing the generalized basins
of each attractor. These new basins are formed with on of the basins
and the union of the other basins. A new boundary is defined by
these two objects. The algorithm then computes the distance between
each boundaries of these basins pairwise. If all the boundaries are
within some distance `r`, there is a unique boundary separating
the basins and we have the wada property.
The algorithm returns the maximum proportion of pixels of a boundary
with distance strictly greater than `r` from another boundary.
If `p == 0`, we have the Wada property for this value of `r`.
If `p > 0`, the criteria to decide if
the basins are Wada is left to the user. Numerical inaccuracies
may be responsible for a small percentage of points with distance larger than `r`
"""
function test_wada_merge(basins,r)
ids = unique(basins)
if length(ids) < 3
@error "There must be at least 3 attractors"
return Inf
end
M = Vector{BitMatrix}(undef,length(ids))
for k in ids
M[k] = merged_basins(basins,k)
end
v = Vector{Float64}()
for k in 1:length(M)-1, j in k+1:length(M)
push!(v,wada_fractions(M[k],M[j],r))
end
return maximum(v)
end
"""
haussdorff_distance(M1, M2) -> hd
Compute the Hausdorff distance between two binary matrices of
the same size. First a distance matrix is computed using
`distance_matrix` for each matrix M1 and M2. The entries
of this matrix are the distance in L1 metric to the
closest 0 pixel in the initial matrix. The distance being
0 if it belongs to the basin with id 0.
"""
function haussdorff_distance(M1::BitMatrix, M2::BitMatrix)
bd1 = distance_matrix(M1)
bd2 = distance_matrix(M2)
hd1 = maximum(bd1.*M2)
hd2 = maximum(bd2.*M1)
return max(hd1,hd2)
end
# wada_fractions computes the distance between
# boundaries using the hausdorff distance.
# The distance is computed using the Shonwilker
# algorithm. The result is a matrix with the distance
# of the pixels from one boundary to the other.
# The algorithm returns the number of pixels
# that are at a distance strictly more than r
# (with the hausdorff distance).
function wada_fractions(bas1::BitMatrix, bas2::BitMatrix, r::Int)
bnd1 = get_boundary(bas1)
bd1 = distance_matrix(bnd1)
bnd2 = get_boundary(bas2)
bd2 = distance_matrix(bnd2)
c1 = count(bd1.*bnd2 .> r)
c2 = count(bd2.*bnd1 .> r)
return max(c1,c2)./length(bnd1)
end
# Return a matrix with two basins: the first is the basins
# from the attractor in `id` and the other basin is formed
# with the union of all others basins.
# The function returns a BitMatrix such that the basins of
# `id` is mapped to 0 and the other basins to 1.
function merged_basins(basins, id)
mrg_basins = fill!(BitMatrix(undef,size(basins)), false)
ids = setdiff(unique(basins), id)
for k in ids
I = findall(basins .== k)
mrg_basins[I] .= 1
end
return mrg_basins
end
# Generate all pairs of the number in ids without
# repetition
function generate_pairs(ids)
p = Vector{Tuple{Int,Int}}()
for (k,n1) in enumerate(ids)
for (j,n2) in enumerate(ids[k+1:end])
push!(p,(n1,n2))
end
end
return p
end
# This function returns the boundary between two basins:
# First we compute the distance matrix of the basins and its
# complementary. The pixels at distance 1 from a basin are
# the closest to the boundary. We compute the union the
# pixels computed from one basins and its complementary.
# We get the boundary in L1 distance!
function get_boundary(basins::BitMatrix)
bd1 = distance_matrix(basins)
bdd1 = distance_matrix( .! basins)
bnd = (bd1 .== 1) .| (bdd1 .== 1)
return bnd
end
# Function for L1 metric
w(M) = min(M[1,2]+1, M[2,1]+1, M[2,2])
w2(M) = min(M[1,2]+1, M[2,1]+1, M[1,1])
# R. Shonkwilker, An image algorithm for computing the Hausdorff distance efficiently in linear time.
# https://doi.org/10.1016/0020-0190(89)90114-2
# This compute the Distance transform matrix.
# Given a matrix, we compute the distance from the
# basin with label 0. The result is a matrix whose
# entry is the distance to the closest 0 pixel in the
# L1 metric (Manhattan).
function distance_matrix(basins::BitMatrix)
r,c = size(basins)
basdist = ones(Int32,r+2,c+2)*(r+c+4)
# Assign the maximum distance to the pixels not in the basin
basdist[2:r+1,2:c+1] .= (1 .- basins) .*(r+c+4)
# first pass right to left, up to bottom
for j in 2:c+1, k in 2:r+1
basdist[j,k] = w(view(basdist,j-1:j,k-1:k))
end
# second pass left to right, bottom up
for j in c+1:-1:1, k in r+1:-1:1
basdist[j,k] = w2(view(basdist,j:j+1,k:k+1))
end
# Remove the extra rows and cols necessary to the alg.
return basdist[2:r+1,2:c+1]
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 13237 | export edgetracking, bisect_to_edge, EdgeTrackingResults
"""
EdgeTrackingResults(edge, track1, track2, time, bisect_idx)
Data type that stores output of the [`edgetracking`](@ref) algorithm.
## Fields
* `edge::StateSpaceSet`: the pseudo-trajectory representing the tracked edge segment
(given by the average in state space between `track1` and `track2`)
* `track1::StateSpaceSet`: the pseudo-trajectory tracking the edge within basin 1
* `track2::StateSpaceSet`: the pseudo-trajectory tracking the edge within basin 2
* `time::Vector`: time points of the above `StateSpaceSet`s
* `bisect_idx::Vector`: indices of `time` at which a re-bisection occurred
* `success::Bool`: indicates whether the edge tracking has been successful or not
"""
struct EdgeTrackingResults{D, T}
edge::StateSpaceSet{D, T}
track1::StateSpaceSet{D, T}
track2::StateSpaceSet{D, T}
time::Vector{Float64}
bisect_idx::Vector{Int}
success::Bool
end
EdgeTrackingResults(nothing) = EdgeTrackingResults(StateSpaceSet([NaN]),
StateSpaceSet([NaN]), StateSpaceSet([NaN]), [NaN], [0], false)
"""
edgetracking(ds::DynamicalSystem, attractors::Dict; kwargs...)
Track along a basin boundary in a dynamical system `ds` with two or more attractors
in order to find an *edge state*. Results are returned in the form of
[`EdgeTrackingResults`](@ref), which contains the pseudo-trajectory `edge` representing the track on
the basin boundary, along with additional output (see below).
The system's `attractors` are specified as a `Dict` of `StateSpaceSet`s, as in
[`AttractorsViaProximity`](@ref) or the output of [`extract_attractors`](@ref). By default, the
algorithm is initialized from the first and second attractor in `attractors`. Alternatively,
the initial states can be set via keyword arguments `u1`, `u2` (see below). Note that the
two initial states must belong to different basins of attraction.
## Keyword arguments
* `bisect_thresh = 1e-7`: distance threshold for bisection
* `diverge_thresh = 1e-6`: distance threshold for parallel integration
* `u1`: first initial state (defaults to first point in first entry of `attractors`)
* `u2`: second initial state (defaults to first point in second entry of `attractors`)
* `maxiter = 100`: maximum number of iterations before the algorithm stops
* `abstol = 0.0`: distance threshold for convergence of the updated edge state
* `T_transient = 0.0`: transient time before the algorithm starts saving the edge track
* `tmax = Inf`: maximum integration time of parallel trajectories until re-bisection
* `Δt = 0.01`: time step passed to [`step!`](@ref) when evolving the two trajectories
* `ϵ_mapper = nothing`: `ϵ` parameter in [`AttractorsViaProximity`](@ref)
* `show_progress = true`: if true, shows progress bar and information while running
* `verbose = true`: if false, silences print output and warnings while running
* `kwargs...`: additional keyword arguments to be passed to [`AttractorsViaProximity`](@ref)
## Description
The edge tracking algorithm is a numerical method to find
an *edge state* or (possibly chaotic) saddle on the boundary between two basins of
attraction. Introduced by [Battelino1988](@cite) and further described by
[Skufca2006](@cite), the
algorithm has been applied to, e.g., the laminar-turbulent boundary in plane Couette
flow [Schneider2008](@cite), Wada basins [Wagemakers2020](@cite), as well as Melancholia
states in conceptual [Mehling2023](@cite) and intermediate-complexity [Lucarini2017](@cite)
climate models.
Relying only on forward integration of the system, it works even in
high-dimensional systems with complicated fractal basin boundary structures.
The algorithm consists of two main steps: bisection and tracking. First, it iteratively
bisects along a straight line in state space between the intial states `u1` and `u2` to find
the separating basin boundary. The bisection stops when the two updated states are less than
`bisect_thresh` (Euclidean distance in state space) apart from each other.
Next, a `ParallelDynamicalSystem` is initialized
from these two updated states and integrated forward until the two trajectories diverge
from each other by more than `diverge_thresh` (Euclidean distance). The two final states of
the parallel integration are then used as new states `u1` and `u2` for a new bisection, and
so on, until a stopping criterion is fulfilled.
Two stopping criteria are implemented via the keyword arguments `maxiter` and `abstol`.
Either the algorithm stops when the number of iterations reaches `maxiter`, or when the
state space position of the updated edge point changes by less than `abstol` (in
Euclidean distance) compared to the previous iteration. Convergence below `abstol` happens
after sufficient iterations if the edge state is a saddle point. However, the edge state
may also be an unstable limit cycle or a chaotic saddle. In these cases, the algorithm will
never actually converge to a point but (after a transient period) continue populating the
set constituting the edge state by tracking along it.
A central idea behind this algorithm is that basin boundaries are typically the stable
manifolds of unstable sets, namely edge states or saddles. The flow along the basin boundary
will thus lead to these sets, and the iterative bisection neutralizes the unstable
direction of the flow away from the basin boundary. If the system possesses multiple edge
states, the algorithm will find one of them depending on where the initial bisection locates
the boundary.
## Output
Returns a data type [`EdgeTrackingResults`](@ref) containing the results.
Sometimes, the AttractorMapper used in the algorithm may erroneously identify both states
`u1` and `u2` with the same basin of attraction due to being very close to the basin
boundary. If this happens, a warning is raised and `EdgeTrackingResults.success = false`.
"""
function edgetracking(ds::DynamicalSystem, attractors::Dict;
bisect_thresh=1e-6,
diverge_thresh=1e-5,
u1=collect(values(attractors))[1][1],
u2=collect(values(attractors))[2][1],
maxiter=100,
abstol=0.0,
T_transient=0.0,
tmax=Inf,
Δt=0.01,
ϵ_mapper=nothing,
show_progress=true,
verbose=true,
kwargs...)
pds = ParallelDynamicalSystem(ds, [u1, u2])
mapper = AttractorsViaProximity(ds, attractors, ϵ_mapper; kwargs...)
edgetracking(pds, mapper;
bisect_thresh, diverge_thresh, maxiter, abstol, T_transient, Δt, tmax,
show_progress, verbose)
end
"""
edgetracking(pds::ParallelDynamicalSystem, mapper::AttractorMapper; kwargs...)
Low-level function for running the edge tracking algorithm, see [`edgetracking`](@ref)
for a description, keyword arguments and output type.
`pds` is a `ParallelDynamicalSystem` with two states. The `mapper` must be an
`AttractorMapper` of subtype `AttractorsViaProximity` or `AttractorsViaRecurrences`.
"""
function edgetracking(pds::ParallelDynamicalSystem, mapper::AttractorMapper;
bisect_thresh=1e-6,
diverge_thresh=1e-5,
maxiter=100,
abstol=0.0,
T_transient=0.0,
Δt=0.01,
tmax=Inf,
show_progress=true,
verbose=true)
if bisect_thresh >= diverge_thresh
error("diverge_thresh must be larger than bisect_thresh.")
end
# initial bisection
u1, u2, success = bisect_to_edge(pds, mapper; bisect_thresh, verbose)
if !success
return EdgeTrackingResults(nothing)
end
edgestate = (u1 + u2)/2
track1, track2 = [u1], [u2]
time, bisect_idx = Float64[], Int[1]
progress = ProgressMeter.Progress(maxiter; desc = "Running edge tracking algorithm",
enabled = show_progress)
# edge track iteration loop
displacement, counter, T = Inf, 1, 0.0
while (displacement > abstol) && (maxiter > counter)
t = 0
set_state!(pds, u1, 1)
set_state!(pds, u2, 2)
distance = diffnorm(pds)
# forward integration loop
while (distance < diverge_thresh) && (t < tmax)
step!(pds, Δt)
distance = diffnorm(pds)
t += Δt
T += Δt
if T >= T_transient
push!(track1, current_state(pds, 1))
push!(track2, current_state(pds, 2))
push!(time, T)
end
end
# re-bisect
u1, u2, success = bisect_to_edge(pds, mapper; bisect_thresh, verbose)
if ~success
track1 = StateSpaceSet(track1)
track2 = StateSpaceSet(track2)
return EdgeTrackingResults(
StateSpaceSet((vec(track1) .+ vec(track2))./2),
track1, track2, time, bisect_idx, false)
end
T += Δt
if T >= T_transient
push!(track1, current_state(pds, 1))
push!(track2, current_state(pds, 2))
push!(time, T)
push!(bisect_idx, length(time))
end
displacement = diffnorm(edgestate, (u1 + u2)/2)
edgestate = (u1 + u2)/2
counter += 1
ProgressMeter.next!(progress;
showvalues = [(:Iteration, counter), (:"Edge point", edgestate)])
if verbose && (counter == maxiter)
@warn("Reached maximum number of $(maxiter) iterations.")
end
end
if verbose && (counter < maxiter)
println("Edge-tracking converged after $(counter) iterations.")
end
track1 = StateSpaceSet(track1)
track2 = StateSpaceSet(track2)
return EdgeTrackingResults(
StateSpaceSet((vec(track1) .+ vec(track2))./2),
track1,
track2,
time,
bisect_idx,
true)
end
"""
bisect_to_edge(pds::ParallelDynamicalSystem, mapper::AttractorMapper; kwargs...) -> u1, u2
Finds the basin boundary between two states `u1, u2 = current_states(pds)` by bisecting
along a straight line in phase space. The states `u1` and `u2` must belong to different
basins.
Returns a triple `u1, u2, success`, where `u1, u2` are two new states located on either side
of the basin boundary that lie less than `bisect_thresh` (Euclidean distance in state space)
apart from each other, and `success` is a Bool indicating whether the bisection was
successful (it may fail if the `mapper` maps both states to the same basin of attraction,
in which case a warning is raised).
## Keyword arguments
* `bisect_thresh = 1e-7`: The maximum (Euclidean) distance between the two returned states.
## Description
`pds` is a `ParallelDynamicalSystem` with two states. The `mapper` must be an
`AttractorMapper` of subtype `AttractorsViaProximity` or `AttractorsViaRecurrences`.
!!! info
If the straight line between `u1` and `u2` intersects the basin boundary multiple
times, the method will find one of these intersection points. If more than two attractors
exist, one of the two returned states may belong to a different basin than the initial
conditions `u1` and `u2`. A warning is raised if the bisection involves a third basin.
"""
function bisect_to_edge(pds::ParallelDynamicalSystem, mapper::AttractorMapper;
bisect_thresh=1e-6,
verbose=true)
u1, u2 = current_states(pds)
idx1, idx2 = mapper(u1), mapper(u2)
if (idx1 == idx2)
if idx1 == -1
error("AttractorMapper returned label -1 (could not match the initial condition with any attractor).
Try changing the settings of the `AttractorMapper` or increasing bisect_thresh, diverge_thresh.")
else
if verbose
@warn "Both initial conditions belong to the same basin of attraction.
Attractor label: $(idx1)
u1 = $(u1)
u2 = $(u2)"
end
return u1, u2, false
end
end
distance = diffnorm(u1, u2)
while distance > bisect_thresh
u_new = (u1 + u2)/2
idx_new = mapper(u_new)
# slightly shift u_new if it lands too close to the boundary
retry_counter = 1
while (idx_new == -1) && retry_counter < 3 # ToDO: make kwarg
if verbose
@warn "Shifting new point slightly because AttractorMapper returned -1"
end
u_new += bisect_thresh*(u1 - u2)
idx_new = mapper(u_new)
retry_counter += 1
end
# update u1 or u2
if idx_new == idx1
u1 = u_new
else
if idx_new != idx2
if idx_new == -1
error("AttractorMapper returned label -1 (could not match the initial condition with any attractor.)
Try changing the settings of AttractorsViaProximity or increasing bisect_thresh, diverge_thresh.")
else
if verbose
@warn "New bisection point belongs to a third basin of attraction."
end
end
end
u2 = u_new
end
distance = diffnorm(u1, u2)
end
return u1, u2, true
end
function diffnorm(u1, u2)
d = zero(eltype(u1))
@inbounds for i in eachindex(u1)
d += (u1[i] - u2[i])^2
end
sqrt(d)
end
function diffnorm(pds::ParallelDynamicalSystem)
diffnorm(current_state(pds, 1), current_state(pds, 2))
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 6976 | export aggregate_attractor_fractions
"""
aggregate_attractor_fractions(
fractions_cont, attractors_cont, featurizer, group_config [, info_extraction]
)
Aggregate the already-estimated curves of fractions of basins of attraction of similar
attractors using the same pipeline used by [`GroupingConfig`](@ref).
The most typical application of this function is to transform the output of a [`global_continuation`](@ref) with
[`RecurrencesFindAndMatch`](@ref) so that similar attractors, even across parameter
space, are grouped into one "attractor". Thus, the fractions of their basins are aggregated.
You could also use this function to aggregate attractors and their fractions even in
a single parameter configuration, i.e., using the output of [`basins_fractions`](@ref).
This function is useful in cases where you want the accuracy and performance of
[`AttractorsViaRecurrences`](@ref), but you also want the convenience of "grouping"
similar attractrors like in [`AttractorsViaFeaturizing`](@ref) for presentation or
analysis purposes. For example, a high dimensional model of competition dynamics
across multispecies may have extreme multistability. After finding this multistability
however, one may care about aggregating all attractors into two groups: where a given
species is extinct or not. This is the example highlighted in our documentation,
in [Extinction of a species in a multistable competition model](@ref).
## Input
1. `fractions_cont`: a vector of dictionaries mapping labels to basin fractions.
2. `attractors_cont`: a vector of dictionaries mapping labels to attractors.
1st and 2nd argument are exactly like the return values of
[`global_continuation`](@ref) with [`RecurrencesFindAndMatch`](@ref)
(or, they can be the return of [`basins_fractions`](@ref)).
3. `featurizer`: a 1-argument function to map an attractor into an appropriate feature
to be grouped later. Features expected by [`GroupingConfig`](@ref) are `SVector`.
4. `group_config`: a subtype of [`GroupingConfig`](@ref).
5. `info_extraction`: a function accepting a vector of features and returning a description
of the features. I.e., exactly as in [`FeaturizeGroupAcrossParameter`](@ref).
The 5th argument is optional and defaults to the centroid of the features.
## Return
1. `aggregated_fractions`: same as `fractions_cont` but now contains the fractions of the
aggregated attractors.
2. `aggregated_info`: dictionary mapping the new labels of `aggregated_fractions` to the
extracted information using `info_extraction`.
## Clustering attractors directly
_(this is rather advanced)_
You may also use the DBSCAN clustering approach here to group attractors
based on their state space distance (the [`set_distance`](@ref)) by making a distance
matrix as expected by the DBSCAN implementation.
For this, use `identity` as `featurizer`, and choose [`GroupViaClustering`](@ref)
as the `group_config` with `clust_distance_metric = set_distance` and provide a numerical
value for `optimal_radius_method` when initializing the [`GroupViaClustering`](@ref),
and also, for the `info_extraction` argument, you now need to provide a function that
expects a _vector of `StateSpaceSet`s_ and outputs a descriptor.
E.g., `info_extraction = vector -> mean(mean(x) for x in vector)`.
"""
function aggregate_attractor_fractions(
fractions_cont::Vector, attractors_cont::Vector, featurizer, group_config,
info_extraction = mean_across_features # function from grouping continuation
)
original_labels, unlabeled_fractions, parameter_idxs, features =
refactor_into_sequential_features(fractions_cont, attractors_cont, featurizer)
grouped_labels = group_features(features, group_config)
aggregated_fractions = reconstruct_joint_fractions(
fractions_cont, original_labels, grouped_labels, parameter_idxs, unlabeled_fractions
)
remove_minus_1_if_possible!(aggregated_fractions)
aggregated_info = info_of_grouped_features(features, grouped_labels, info_extraction)
return aggregated_fractions, aggregated_info
end
# convenience wrapper for only single input
function aggregate_attractor_fractions(fractions::Dict, attractors::Dict, args...)
aggregated_fractions, aggregated_info = aggregate_attractor_fractions(
[fractions], [attractors], args...
)
return aggregated_fractions[1], aggregated_info[1]
end
function refactor_into_sequential_features(fractions_cont, attractors_cont, featurizer)
# Set up containers
P = length(fractions_cont)
example_feature = featurizer(first(values(attractors_cont[1])))
features = typeof(example_feature)[]
original_labels = keytype(first(fractions_cont))[]
parameter_idxs = Int[]
unlabeled_fractions = zeros(P)
# Transform original data into sequential vectors
for i in eachindex(fractions_cont)
fs = fractions_cont[i]
ai = attractors_cont[i]
A = length(ai)
append!(parameter_idxs, (i for _ in 1:A))
unlabeled_fractions[i] = get(fs, -1, 0.0)
for k in keys(ai)
push!(original_labels, k)
push!(features, featurizer(ai[k]))
end
end
# `parameter_idxs` is the indices of the parameter a given feature maps to.
# necessary because for some parameter values we may have more or less attractors
# and hence more or less features
return original_labels, unlabeled_fractions, parameter_idxs, features
end
function reconstruct_joint_fractions(
fractions_cont, original_labels, grouped_labels, parameter_idxs, unlabeled_fractions
)
aggregated_fractions = [Dict{Int,Float64}() for _ in 1:length(fractions_cont)]
current_p_idx = 0
for j in eachindex(grouped_labels)
new_label = grouped_labels[j]
p_idx = parameter_idxs[j]
if p_idx > current_p_idx
current_p_idx += 1
aggregated_fractions[current_p_idx][-1] = unlabeled_fractions[current_p_idx]
end
d = aggregated_fractions[current_p_idx]
orig_frac = get(fractions_cont[current_p_idx], original_labels[j], 0)
d[new_label] = get(d, new_label, 0) + orig_frac
end
return aggregated_fractions
end
function info_of_grouped_features(features, grouped_labels, info_extraction)
ids = sort!(unique(grouped_labels))
# remove -1 if it's there
if ids[1] == -1; popfirst!(ids); end
# extract the infos
Dict(
id => info_extraction(
view(features, findall(isequal(id), grouped_labels))
) for id in ids
)
end
function remove_minus_1_if_possible!(afs)
isthere = false
for fs in afs
isthere = get(fs, -1, 0) > 0
isthere && return
end
# no `-1`, we remove from everywhere
for fs in afs
delete!(fs, -1)
end
return
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 3513 | export global_continuation, GlobalContinuationAlgorithm
"""
GlobalContinuationAlgorithm
Supertype of all algorithms used in [`global_continuation`](@ref).
Each algorithm typically references an [`AttractorMapper`](@ref),
as well as contains more information for how to continue/track/match attractors
across a parameter range.
See [`global_continuation`](@ref) for more.
"""
abstract type GlobalContinuationAlgorithm end
"""
global_continuation(gca::GlobalContinuationAlgorithm, prange, pidx, ics; kwargs...)
global_continuation(gca::GlobalContinuationAlgorithm, pcurve, ics; kwargs...)
Find and continue attractors (or representations of attractors)
and the fractions of their basins of attraction across a parameter range.
`global_continuation` is the central function of the framework for global stability analysis
illustrated in [Datseris2023](@cite).
The global continuation algorithm typically references an [`AttractorMapper`](@ref)
which is used to find the attractors and basins of a dynamical system. Additional
arguments that control how to continue/track/match attractors across a parameter range
are given when creating `gca`.
The basin fractions and the attractors (or some representation of them) are continued
across the parameter range `prange`, for the parameter of the system with index `pidx`
(any index valid in `DynamicalSystems.set_parameter!` can be used). In contrast to
traditional continuation (see online Tutorial for a comparison), global continuation
can be performed over arbitrary user-defined curves in parameter space.
The second call signature with `pcurve` allows for this possibility. In this case
`pcurve` is a vector of iterables, where each itereable maps parameter indices
to parameter values. These iterables can be dictionaries, named tuples, `Vector{Pair}`,
etc., and the sequence of the iterables defines a curve in parameter space.
In fact, the version with `prange, pidx` simply defines
`pcurve = [[pidx => p] for p in prange]` and calls the second method.
`ics` are the initial conditions to use when globally sampling the state space.
Like in [`basins_fractions`](@ref) it can be either a set vector of initial conditions,
or a 0-argument function that generates random initial conditions.
Possible subtypes of `GlobalContinuationAlgorithm` are:
- [`AttractorSeedContinueMatch`](@ref)
- [`FeaturizeGroupAcrossParameter`](@ref)
## Return
1. `fractions_cont::Vector{Dict{Int, Float64}}`. The fractions of basins of attraction.
`fractions_cont[i]` is a dictionary mapping attractor IDs to their basin fraction
at the `i`-th parameter combination.
2. `attractors_cont::Vector{Dict{Int, <:Any}}`. The continued attractors.
`attractors_cont[i]` is a dictionary mapping attractor ID to the
attractor set at the `i`-th parameter combination.
## Keyword arguments
- `show_progress = true`: display a progress bar of the computation.
- `samples_per_parameter = 100`: amount of initial conditions sampled at each parameter
combination from `ics` if `ics` is a function instead of set initial conditions.
"""
function global_continuation(alg::GlobalContinuationAlgorithm, prange::AbstractVector, pidx, sampler; kw...)
# everything is propagated to the curve setting
pcurve = [[pidx => p] for p in prange]
return global_continuation(alg, pcurve, sampler; kw...)
end
include("continuation_ascm_generic.jl")
include("continuation_recurrences.jl")
include("continuation_grouping.jl")
include("aggregate_attractor_fractions.jl") | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 9929 | export AttractorSeedContinueMatch
import ProgressMeter
using Random: MersenneTwister
"""
AttractorSeedContinueMatch(mapper, matcher = MatchBySSSetDistance(); seeding)
A global continuation method for [`global_continuation`](@ref).
`mapper` is any subtype of [`AttractorMapper`](@ref) which implements
[`extract_attractors`](@ref), i.e., it finds the actual attractors.
`matcher` is a configuration of how to match attractor IDs, see [`IDMatcher`](@ref)
for more options.
## Description
This is a general/composable global continuation method based on a 4-step process:
1. Seed initial conditions from previously found attractors
2. Propagate those forwards to "continue" previous attractors
3. Estimate basin fractions and potentially find new attractors
4. Match attractors
### Step 0 - Finding initial attractors
At the first parameter slice of the global continuation process, attractors and their fractions
are found using the given `mapper` and [`basins_fractions`](@ref).
See the `mapper` documentation and [`AttractorMapper`](@ref)
for details on how this works. Then, from the second parameter onwards the continuation occurs.
### Step 1 - Seeding initial conditions
Initial conditions can be seeded from previously found attractors.
This is controlled by the `seeding` keyword, which must be a function that given
a `StateSpaceSet` (an attractor), it returns an iterator of initial conditions.
By default the first point of an attractor is provided as the only seed.
Seeding can be turned off by providing the dummy function `seeding = A -> []`,
i.e., it always returns an empty iterator and hence no seeds and we skip to step 2.
### Step 2 - Continuing the seeds
The dynamical system referenced by the `mapper` is now set to the new parameter value.
The seeds are run through the `mapper` to converge to attractors at the new parameter value.
Seeding initial conditions close to previous attractors increases the probability
that if an attractor continues to exist in the new parameter, it is found.
Additionally, for some `mappers` this seeding process improves the accuracy as well as
performance of finding attractors, see e.g. discussion in [Datseris2023](@cite).
This seeding works for any `mapper`, regardless of if they can map individual initial conditions
with the `mapper(u0)` syntax! If this syntax isn't supported, steps 2 and 3 are done together.
### Step 3 - Estimate basins fractions
After the special seeded initial conditions are mapped to attractors,
attractor basin fractions are computed by sampling additional initial conditions
using the provided `ics` in [`global_continuation`](@ref).
I.e., exactly as in [`basins_fractions`](@ref).
Naturally, during this step new attractors may be found, besides those found
using the "seeding from previous attractors".
### Step 4 - Matching
Normally the ID an attractor gets assigned is somewhat a random integer.
Therefore, to ensure a logical output of the global continuation process,
attractors need to be "matched".
This means: attractor and fractions must have their _IDs changed_,
so that attractors that are "similar" to those at a
previous parameter get assigned the same ID.
What is "similar enough" is controlled by the `matcher` input.
The default `matcher` [`MatchBySSSetDistance`](@ref) matches
sets which have small distance in state space.
The matching algorithm itself can be quite involved,
so read the documentation of the `matcher` for how matching works.
A note on matching: the [`MatchBySSSetDistance`](@ref) can also be used
after the continuation is completed, as it only requires as input
the state space sets (attractors), without caring at which parameter each attractor
exists at. If you don't like the final matching output,
you may use a different instance of [`MatchBySSSetDistance`](@ref)
and call [`match_sequentially!`](@ref) again on the output,
without having to recompute the whole global continuation!
### Step 5 - Finish
After matching the parameter is incremented.
Steps 1-4 repeat until all parameter values are exhausted.
### Further note
This global continuation method is a generalization of the "RAFM" continuation
described in [Datseris2023](@cite). This continuation method is still exported
as [`RecurrencesFindAndMatch`](@ref).
"""
struct AttractorSeedContinueMatch{A, M, S} <: GlobalContinuationAlgorithm
mapper::A
matcher::M
seeding::S
end
const ASCM = AttractorSeedContinueMatch
ASCM(mapper, matcher = MatchBySSSetDistance(); seeding = _default_seeding) =
ASCM(mapper, matcher, seeding)
# TODO: This is currently not used, and not sure if it has to be.
function _scaled_seeding(attractor::AbstractStateSpaceSet; rng = MersenneTwister(1))
max_possible_seeds = 6
seeds = round(Int, log(max_possible_seeds, length(attractor)))
seeds = clamp(seeds, 1, max_possible_seeds)
return (rand(rng, vec(attractor)) for _ in 1:seeds)
end
# This is the one used
function _default_seeding(attractor::AbstractStateSpaceSet)
return (attractor[1],) # must be iterable
end
function global_continuation(acam::AttractorSeedContinueMatch, pcurve, ics;
samples_per_parameter = 100, show_progress = true,
)
N = samples_per_parameter
progress = ProgressMeter.Progress(length(pcurve);
desc = "Continuing attractors and basins:", enabled=show_progress
)
mapper = acam.mapper
reset_mapper!(mapper)
# first parameter is run in isolation, as it has no prior to seed from
set_parameters!(referenced_dynamical_system(mapper), pcurve[1])
if ics isa Function
fs = basins_fractions(mapper, ics; show_progress = false, N = samples_per_parameter)
else # we ignore labels in this continuation algorithm
fs, = basins_fractions(mapper, ics; show_progress = false)
end
# At each parmaeter `p`, a dictionary mapping attractor ID to fraction is created.
fractions_cont = [fs]
# The attractors are also stored (and are the primary output)
prev_attractors = deepcopy(extract_attractors(mapper))
attractors_cont = [deepcopy(prev_attractors)] # we need the copy
ProgressMeter.next!(progress)
# Continue loop over all remaining parameters
for p in @view(pcurve[2:end])
set_parameters!(referenced_dynamical_system(mapper), p)
reset_mapper!(mapper)
# Seed initial conditions from previous attractors
# Notice that one of the things that happens here is some attractors have
# really small basins. We find them with the seeding process here, but the
# subsequent random sampling in `basins_fractions` doesn't. This leads to
# having keys in `mapper.bsn_nfo.attractors` that do not exist in the computed
# fractions. The fix is easy: we add the initial conditions mapped from
# seeding to the fractions using an internal argument.
fs = if allows_mapper_u0(mapper)
seed_attractors_to_fractions_individual(mapper, prev_attractors, ics, N, acam.seeding)
else
seed_attractors_to_fractions_grouped(mapper, prev_attractors, ics, N, acam.seeding)
end
current_attractors = deepcopy(extract_attractors(mapper))
# we don't match attractors here, this happens directly at the end.
# here we just store the result
push!(fractions_cont, fs)
push!(attractors_cont, current_attractors)
# This is safe due to the deepcopies
overwrite_dict!(prev_attractors, current_attractors)
ProgressMeter.next!(progress)
end
rmaps = match_sequentially!(
attractors_cont, acam.matcher; pcurve, ds = referenced_dynamical_system(mapper)
)
match_sequentially!(fractions_cont, rmaps)
return fractions_cont, attractors_cont
end
function seed_attractors_to_fractions_individual(mapper, prev_attractors, ics, N, seeding)
# actual seeding
seeded_fs = Dict{Int, Int}()
for att in values(prev_attractors)
for u0 in seeding(att)
# We map the initial condition to an attractor, but we don't care
# about which attractor we go to. This is just so that the internal
# array of `AttractorsViaRecurrences` registers the attractors
label = mapper(u0; show_progress = false)
seeded_fs[label] = get(seeded_fs, label, 0) + 1
end
end
# Now perform basin fractions estimation as normal, utilizing found attractors
# (the function comes from attractor_mapping.jl)
if ics isa Function
fs = basins_fractions(mapper, ics;
additional_fs = seeded_fs, show_progress = false, N
)
else
fs, = basins_fractions(mapper, ics;
additional_fs = seeded_fs, show_progress = false
)
end
return fs
end
function seed_attractors_to_fractions_grouped(mapper, prev_attractors, ics, N, seeding)
# what makes this version different is that we can't just use `mapper(u0)`,
# so we need to store the seeded initial conditions and then combine them with
# the the ones generated from `ics`.
u0s = typeof(current_state(referenced_dynamical_system(mapper)))[]
# collect seeds
for att in values(prev_attractors)
for u0 in seeding(att)
push!(u0s, u0)
end
end
# now combine these with the rest of the initial conditions
if ics isa Function
for _ in 1:N
push!(u0s, copy(ics()))
end
else
append!(u0s, vec(ics))
end
# with these extra u0s we now perform fractions estimation as normal
fs, = basins_fractions(mapper, StateSpaceSet(u0s); show_progress = false)
return fs
end
allows_mapper_u0(::AttractorMapper) = true
function allows_mapper_u0(mapper::AttractorsViaFeaturizing)
if mapper.group_config isa GroupViaClustering
return false
elseif mapper.group_config isa GroupViaPairwiseComparison
return false
else
return true
end
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 4971 | export FeaturizeGroupAcrossParameter
import ProgressMeter
import Mmap
struct FeaturizeGroupAcrossParameter{A<:AttractorsViaFeaturizing, E} <: GlobalContinuationAlgorithm
mapper::A
info_extraction::E
par_weight::Float64
end
"""
FeaturizeGroupAcrossParameter <: GlobalContinuationAlgorithm
FeaturizeGroupAcrossParameter(mapper::AttractorsViaFeaturizing; kwargs...)
A method for [`global_continuation`](@ref).
It uses the featurizing approach discussed in [`AttractorsViaFeaturizing`](@ref)
and hence requires an instance of that mapper as an input.
When used in [`global_continuation`](@ref), features are extracted
and then grouped across a parameter range. Said differently, all features
of all initial conditions across all parameter values are put into the same "pool"
and then grouped as dictated by the `group_config` of the mapper.
After the grouping is finished the feature label fractions are distributed
to each parameter value they came from.
This continuation method is based on, but strongly generalizes, the approaches
in the papers [Gelbrecht2020](@cite) and [Stender2021](@cite).
## Keyword arguments
- `info_extraction::Function` a function that takes as an input a vector of feature-vectors
(corresponding to a cluster) and returns a description of the cluster.
By default, the centroid of the cluster is used.
This is what the `attractors_cont` contains in the return of `global_continuation`.
"""
function FeaturizeGroupAcrossParameter(
mapper::AttractorsViaFeaturizing;
info_extraction = mean_across_features,
par_weight = 0.0,
)
return FeaturizeGroupAcrossParameter(
mapper, info_extraction, par_weight
)
end
function mean_across_features(fs)
means = zeros(length(first(fs)))
N = length(fs)
for f in fs
for i in eachindex(f)
means[i] += f[i]
end
end
return means ./ N
end
function global_continuation(
continuation::FeaturizeGroupAcrossParameter, pcurve, ics;
show_progress = true, samples_per_parameter = 100
)
(; mapper, info_extraction, par_weight) = continuation
spp, n = samples_per_parameter, length(pcurve)
features = _get_features_pcurve(mapper, ics, n, spp, pcurve, show_progress)
# This is a special clause for implementing the MCBB algorithm (weighting
# also by parameter value, i.e., making the parameter value a feature)
# It calls a special `group_features` function that also incorporates the
# parameter value (see below). Otherwise, we call normal `group_features`.
# TODO: We have deprecated this special clause. In the next version we need to cleanup
# the source code and remove the `par_weight` and its special treatment in `group_features`.
if mapper.group_config isa GroupViaClustering && par_weight ≠ 0
labels = group_features(features, mapper.group_config; par_weight, plength = n, spp)
else
labels = group_features(features, mapper.group_config)
end
fractions_cont, attractors_cont =
label_fractions_across_parameter(labels, 1features, n, spp, info_extraction)
return fractions_cont, attractors_cont
end
function _get_features_pcurve(mapper::AttractorsViaFeaturizing, ics, n, spp, pcurve, show_progress)
progress = ProgressMeter.Progress(n;
desc="Generating features", enabled=show_progress, offset = 2,
)
# Extract the first possible feature to initialize the features container
feature = extract_features(mapper, ics; N = 1)
features = Vector{typeof(feature[1])}(undef, n*spp)
# Collect features
for (i, p) in enumerate(pcurve)
set_parameters!(mapper.ds, p)
current_features = extract_features(mapper, ics; show_progress, N = spp)
features[((i - 1)*spp + 1):i*spp] .= current_features
ProgressMeter.next!(progress)
end
return features
end
function label_fractions_across_parameter(labels, features, n, spp, info_extraction)
# finally we collect/group stuff into their dictionaries
fractions_cont = Vector{Dict{Int, Float64}}(undef, n)
dummy_info = info_extraction([first(features)])
attractors_cont = Vector{Dict{Int, typeof(dummy_info)}}(undef, n)
for i in 1:n
# Here we know which indices correspond to which parameter value
# because they are sequentially increased every `spp`
# (steps per parameter)
current_labels = view(labels, ((i - 1)*spp + 1):i*spp)
current_features = view(features, ((i - 1)*spp + 1):i*spp)
current_ids = unique(current_labels)
# getting fractions is easy; use API function that takes in arrays
fractions_cont[i] = basins_fractions(current_labels, current_ids)
attractors_cont[i] = Dict(
id => info_extraction(
view(current_features, findall(isequal(id), current_labels))
) for id in current_ids
)
end
return fractions_cont, attractors_cont
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2131 | export RecurrencesFindAndMatch, RAFM
"""
RecurrencesFindAndMatch <: GlobalContinuationAlgorithm
RecurrencesFindAndMatch(mapper::AttractorsViaRecurrences; kwargs...)
A method for [`global_continuation`](@ref) as in [Datseris2023](@cite) that is based on the
recurrences algorithm for finding attractors ([`AttractorsViaRecurrences`](@ref))
and then matching them according to their state space distance.
## Keyword arguments
- `distance = Centroid(), threshold = Inf`: passed to [`MatchBySSSetDistance`](@ref).
- `seeds_from_attractor`: A function that takes as an input an attractor and returns
an iterator of initial conditions to be seeded from the attractor for the next
parameter slice. By default, we sample only the first stored point on the attractor.
## Description
`RecurrencesFindAndMatch` is a wrapper type. It is has been generalized by
[`AttractorSeedContinueMatch`](@ref). It is still exported for backwards compatibility
and to have a clear reference to the original algorithm developed in [Datseris2023](@cite).
The source code of `RecurrencesFindAndMatch` is trival:
it takes the given mapper, it initializes a [`MatchBySSSetDistance`](@ref),
and along with `seeds_from_attractor` it makes the [`AttractorSeedContinueMatch`](@ref)
instance. This is the process described in [Datseris2023](@cite),
whereby attractors are found using the recurrences algorithm [`AttractorsViaRecurrences`](@ref)
and they are then matched by their distance in state space [`MatchBySSSetDistance`](@ref).
"""
function RecurrencesFindAndMatch(
mapper::AttractorsViaRecurrences; distance = Centroid(), threshold = Inf,
info_extraction = nothing, seeds_from_attractor = _default_seeding,
)
if info_extraction !== nothing
@warn "`info_extraction` is ignored in `RecurrencesFindAndMatch`.
You can extract info after the attractors have been found."
end
matcher = MatchBySSSetDistance(; distance, threshold)
return AttractorSeedContinueMatch(mapper, matcher, seeds_from_attractor)
end
"Alias for [`RecurrencesFindAndMatch`](@ref)."
const RAFM = RecurrencesFindAndMatch
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 7271 | # Definition of the attracting mapping API and exporting
# At the end it also includes all files related to mapping
export AttractorMapper,
AttractorsViaRecurrences,
AttractorsViaProximity,
AttractorsViaFeaturizing,
ClusteringConfig,
basins_fractions,
convergence_and_basins_of_attraction,
convergence_and_basins_fractions,
convergence_time,
basins_of_attraction,
automatic_Δt_basins,
extract_attractors,
subdivision_based_grid,
SubdivisionBasedGrid,
reset_mapper!
#########################################################################################
# AttractorMapper structure definition
#########################################################################################
"""
AttractorMapper(ds::DynamicalSystem, args...; kwargs...) → mapper
Subtypes of `AttractorMapper` are structures that map initial conditions of `ds` to
attractors. The found attractors are stored inside the `mapper`, and can be obtained
by calling `attractors = extract_attractors(mapper)`.
Currently available mapping methods:
* [`AttractorsViaProximity`](@ref)
* [`AttractorsViaRecurrences`](@ref)
* [`AttractorsViaFeaturizing`](@ref)
All `AttractorMapper` subtypes can be used with [`basins_fractions`](@ref)
or [`basins_of_attraction`](@ref).
In addition, some mappers can be called as a function of an initial condition:
```julia
label = mapper(u0)
```
and this will on the fly compute and return the label of the attractor `u0` converges at.
The mappers that can do this are:
* [`AttractorsViaProximity`](@ref)
* [`AttractorsViaRecurrences`](@ref)
* [`AttractorsViaFeaturizing`](@ref) with the [`GroupViaHistogram`](@ref) configuration.
## For developers
`AttractorMapper` defines an extendable interface. A new type needs to subtype
`AttractorMapper` and implement [`extract_attractors`](@ref), `id = mapper(u0)`
and the internal function `Attractors.referenced_dynamical_system(mapper)`.
From these, everything else in the entire rest of the library just works!
If it is not possible to implement `id = mapper(u0)`, then instead extend
`basins_fractions(mapper, ics)` with `ics` a vector of initial conditions.
"""
abstract type AttractorMapper end
referenced_dynamical_system(mapper::AttractorMapper) = mapper.ds
# Generic pretty printing
function generic_mapper_print(io, mapper)
ps = 14
println(io, "$(nameof(typeof(mapper)))")
println(io, rpad(" system: ", ps), nameof(typeof(referenced_dynamical_system(mapper))))
return ps
end
Base.show(io::IO, mapper::AttractorMapper) = generic_mapper_print(io, mapper)
#########################################################################################
# Generic basin fractions method structure definition
#########################################################################################
# It works for all mappers that define the function-like-object behavior
"""
basins_fractions(
mapper::AttractorMapper,
ics::Union{StateSpaceSet, Function};
kwargs...
)
Approximate the state space fractions `fs` of the basins of attraction of a dynamical
system by mapping initial conditions to attractors using `mapper`
(which contains a reference to a [`DynamicalSystem`](@ref)).
The fractions are simply the ratios of how many initial conditions ended up
at each attractor.
Initial conditions to use are defined by `ics`. It can be:
* a `StateSpaceSet` of initial conditions, in which case all are used.
* a 0-argument function `ics()` that spits out random initial conditions.
Then `N` random initial conditions are chosen.
See [`statespace_sampler`](@ref) to generate such functions.
## Return
The function will always return `fractions`, which is
a dictionary whose keys are the labels given to each attractor
(always integers enumerating the different attractors), and whose
values are the respective basins fractions. The label `-1` is given to any initial condition
where `mapper` could not match to an attractor (this depends on the `mapper` type).
If `ics` is a `StateSpaceSet` the function will also return `labels`, which is a
_vector_, of equal length to `ics`, that contains the label each initial
condition was mapped to.
See [`AttractorMapper`](@ref) for all possible `mapper` types, and use
[`extract_attractors`](@ref) (after calling `basins_fractions`) to extract
the stored attractors from the `mapper`.
See also [`convergence_and_basins_fractions`](@ref).
## Keyword arguments
* `N = 1000`: Number of random initial conditions to generate in case `ics` is a function.
* `show_progress = true`: Display a progress bar of the process.
"""
function basins_fractions(mapper::AttractorMapper, ics::Union{AbstractStateSpaceSet, Function};
show_progress = true, N = 1000, additional_fs::Dict = Dict(),
)
used_StateSpaceSet = ics isa AbstractStateSpaceSet
N = used_StateSpaceSet ? size(ics, 1) : N
progress = ProgressMeter.Progress(N;
desc="Mapping initial conditions to attractors:", enabled = show_progress
)
fs = Dict{Int, Int}()
used_StateSpaceSet && (labels = Vector{Int}(undef, N))
for i ∈ 1:N
ic = _get_ic(ics, i)
label = mapper(ic; show_progress)
fs[label] = get(fs, label, 0) + 1
used_StateSpaceSet && (labels[i] = label)
show_progress && ProgressMeter.next!(progress)
end
# the non-public-API `additional_fs` i s used in the continuation methods
additive_dict_merge!(fs, additional_fs)
N = N + (isempty(additional_fs) ? 0 : sum(values(additional_fs)))
# Transform count into fraction
ffs = Dict(k => v/N for (k, v) in fs)
if used_StateSpaceSet
return ffs, labels
else
return ffs
end
end
_get_ic(ics::Function, i) = ics()
_get_ic(ics::AbstractStateSpaceSet, i) = ics[i]
_get_ic(ics::AbstractVector, i) = ics[i]
"""
extract_attractors(mapper::AttractorsMapper) → attractors
Return a dictionary mapping label IDs to attractors found by the `mapper`.
This function should be called after calling [`basins_fractions`](@ref)
with the given `mapper` so that the attractors have actually been found first.
For `AttractorsViaFeaturizing`, the attractors are only stored if
the mapper was called with pre-defined initial conditions rather than
a sampler (function returning initial conditions).
"""
extract_attractors(::AttractorMapper) = error("not implemented")
"""
convergence_time(mapper::AttractorMapper) → t
Return the approximate time the `mapper` took to converge to an attractor.
This function should be called just right after `mapper(u0)` was called with
`u0` the initial condition of interest. Hence it is only valid with `AttractorMapper`
subtypes that support this syntax.
Obtaining the convergence time is computationally free,
so that [`convergence_and_basins_fractions`](@ref) can always
be used instead of [`basins_fractions`](@ref).
"""
function convergence_time end
#########################################################################################
# Includes
#########################################################################################
include("attractor_mapping_proximity.jl")
include("recurrences/attractor_mapping_recurrences.jl")
include("grouping/attractor_mapping_featurizing.jl")
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 7696 | """
AttractorsViaProximity(ds::DynamicalSystem, attractors::Dict [, ε]; kwargs...)
Map initial conditions to attractors based on whether the trajectory reaches `ε`-distance
close to any of the user-provided `attractors`. They have to be in a form of a dictionary
mapping attractor labels to `StateSpaceSet`s containing the attractors.
The system gets stepped, and at each step the distance of the current state to all
attractors is computed. If any of these distances is `< ε`, then the label of the nearest
attractor is returned. The distance is defined by the `distance` keyword.
`attractors` do not have to be "true" attractors. Any arbitrary sets
in the state space can be provided.
If an `ε::Real` is not provided by the user, a value is computed
automatically as half of the minimum distance between all `attractors`.
This operation can be expensive for large `StateSpaceSet`s.
If `length(attractors) == 1`, then `ε` becomes 1/10 of the diagonal of the box containing
the attractor. If `length(attractors) == 1` and the attractor is a single point,
an error is thrown.
## Keywords
* `Ttr = 100`: Transient time to first evolve the system for before checking for proximity.
* `Δt = 1`: Step time given to `step!`.
* `horizon_limit = 1e3`: If the maximum distance of the trajectory from any of the given
attractors exceeds this limit, it is assumed
that the trajectory diverged (gets labelled as `-1`).
* `consecutive_lost_steps = 1000`: If the `ds` has been stepped this many times without
coming `ε`-near to any attractor, it is assumed
that the trajectory diverged (gets labelled as `-1`).
* `distance = StrictlyMinimumDistance()`: Distance function for evaluating the distance
between the trajectory end-point and the given attractors. Can be anything given to
[`set_distance`](@ref).
"""
struct AttractorsViaProximity{DS<:DynamicalSystem, AK, SSS<:AbstractStateSpaceSet, N, K, M, SS<:AbstractStateSpaceSet} <: AttractorMapper
ds::DS
attractors::Dict{AK, SSS}
ε::Float64
Δt::N
Ttr::N
consecutive_lost_steps::Int
horizon_limit::Float64
search_trees::K
dist::Vector{Float64}
idx::Vector{Int}
maxdist::Float64
distance::M
cset::SS # current state of dynamical system as `StateSpaceSet`.
end
function AttractorsViaProximity(ds::DynamicalSystem, attractors::Dict, ε = nothing;
Δt=1, Ttr=100, consecutive_lost_steps=1000, horizon_limit=1e3, verbose = false,
distance = StrictlyMinimumDistance(),
)
if keytype(attractors) <: AbstractStateSpaceSet
error("The input attractors must be a dictionary of `StateSpaceSet`s.")
end
if dimension(ds) ≠ dimension(first(attractors)[2])
error("Dimension of the dynamical system and candidate attractors must match")
end
if distance isa Union{Hausdorff, StrictlyMinimumDistance}
# We pre-initialize `KDTree`s for performance
search_trees = Dict(k => KDTree(vec(att), distance.metric) for (k, att) in attractors)
else
search_trees = Dict(k => nothing for (k, att) in attractors)
end
if isnothing(ε)
ε = _deduce_ε_from_attractors(attractors, search_trees, verbose)
else
ε isa Real || error("ε must be a Real number")
end
mapper = AttractorsViaProximity(
ds, attractors,
ε, Δt, eltype(Δt)(Ttr), consecutive_lost_steps, horizon_limit,
search_trees, [Inf], [0], 0.0, distance, StateSpaceSet([current_state(ds)]),
)
return mapper
end
function _deduce_ε_from_attractors(attractors, search_trees, verbose = false)
if length(attractors) != 1
verbose && @info("Computing minimum distance between attractors to deduce `ε`...")
# Minimum distance between attractors
# notice that we do not use `StateSpaceSet_distance` because
# we have more than two StateSpaceSets and want the absolute minimum distance
# between one of them.
dist, idx = [Inf], [0]
minε = Inf
for (k, A) in attractors
for (m, tree) in search_trees
k == m && continue
for p in A # iterate over all points of attractor
Neighborhood.NearestNeighbors.knn_point!(
tree, p, false, dist, idx, Neighborhood.NearestNeighbors.always_false
)
dist[1] < minε && (minε = dist[1])
end
end
end
verbose && @info("Minimum distance between attractors computed: $(minε)")
ε = minε/2
else
attractor = first(attractors)[2] # get the single attractor
mini, maxi = minmaxima(attractor)
ε = sqrt(sum(abs, maxi .- mini))/10
if ε == 0
throw(ArgumentError("""
Computed `ε = 0` in automatic estimation, probably because there is
a single attractor that also is a single point. Please provide `ε` manually.
"""))
end
end
return ε
end
# TODO: Implement `show_progress`
function (mapper::AttractorsViaProximity)(u0; show_progress = false)
reinit!(mapper.ds, u0)
maxdist = 0.0
mapper.Ttr > 0 && step!(mapper.ds, mapper.Ttr)
lost_count = 0
while lost_count < mapper.consecutive_lost_steps
step!(mapper.ds, mapper.Δt)
lost_count += 1
u = current_state(mapper.ds)
# first check for Inf or NaN
any(x -> (isnan(x) || isinf(x)), u) && return -1
# then update the stored set
mapper.cset[1] = u
# then compute all distances
for (k, tree) in mapper.search_trees # this is a `Dict`
A = mapper.attractors[k]
# we use internal method from StateSpaceSets.jl
d = set_distance(mapper.cset, A, mapper.distance; tree2 = tree)
if d < mapper.ε
return k
elseif maxdist < d
maxdist = d
# exit if the distance is too large
maxdist > mapper.horizon_limit && return -1
end
end
end
return -1
end
# function (mapper::AttractorsViaProximity)(u0; show_progress = false)
# reinit!(mapper.ds, u0)
# maxdist = 0.0
# mapper.Ttr > 0 && step!(mapper.ds, mapper.Ttr)
# lost_count = 0
# while lost_count < mapper.consecutive_lost_steps
# step!(mapper.ds, mapper.Δt)
# lost_count += 1
# u = current_state(mapper.ds)
# # first check for Inf or NaN
# any(x -> (isnan(x) || isinf(x)), u) && return -1
# for (k, tree) in mapper.search_trees # this is a `Dict`
# Neighborhood.NearestNeighbors.knn_point!(
# tree, u, false, mapper.dist, mapper.idx, Neighborhood.NearestNeighbors.always_false
# )
# if mapper.dist[1] < mapper.ε
# return k
# elseif maxdist < mapper.dist[1]
# maxdist = mapper.dist[1]
# maxdist > mapper.horizon_limit && return -1
# end
# end
# end
# return -1
# end
function Base.show(io::IO, mapper::AttractorsViaProximity)
ps = generic_mapper_print(io, mapper)
println(io, rpad(" ε: ", ps), mapper.ε)
println(io, rpad(" Δt: ", ps), mapper.Δt)
println(io, rpad(" Ttr: ", ps), mapper.Ttr)
attstrings = split(sprint(show, MIME"text/plain"(), mapper.attractors), '\n')
println(io, rpad(" attractors: ", ps), attstrings[1])
for j in 2:length(attstrings)
println(io, rpad(" ", ps), attstrings[j])
end
return
end
extract_attractors(mapper::AttractorsViaProximity) = mapper.attractors
convergence_time(mapper::AttractorsViaProximity) = current_time(mapper.ds) - initial_time(mapper.ds)
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2254 | export GroupingConfig, group_features
"""
GroupingConfig
Supertype for configuration structs on how to group features together.
Used in several occasions such as [`AttractorsViaFeaturizing`](@ref)
or [`aggregate_attractor_fractions`](@ref).
Currently available grouping configurations are:
- [`GroupViaClustering`](@ref)
- [`GroupViaNearestFeature`](@ref)
- [`GroupViaHistogram`](@ref)
- [`GroupViaPairwiseComparison`](@ref)
## For developers
`GroupingConfig` defines an extendable interface.
The only thing necessary for a new grouping configuration is to:
1. Make a new type and subtype `GroupingConfig`.
2. If the grouping allows for mapping individual features to group index,
then instead extend the **internal function** `feature_to_group(feature, config)`.
This will also allow doing `id = mapper(u0)` with [`AttractorsViaFeaturizing`](@ref).
3. Else, extend the function `group_features(features, config)`.
You could still extend `group_features` even if (2.) is satisfied,
if there are any performance benefits.
4. Include the new grouping file in the `grouping/all_grouping_configs.jl` and list it in
this documentation string.
"""
abstract type GroupingConfig end
"""
group_features(features, group_config::GroupingConfig) → labels
Group the given iterable of "features" (anything that can be grouped, typically vectors of real numbers)
according to the configuration and return the labels (vector of equal length as `features`).
See [`GroupingConfig`](@ref) for possible grouping configuration configurations.
"""
function group_features(features, group_config::GroupingConfig)
return map(f -> feature_to_group(f, group_config), features)
end
"""
feature_to_group(feature::AbstractVector, group_config::GroupingConfig) → group_label
Map the given feature vector to its group label (integer).
This is an internal function. It is strongly recommended that `feature isa SVector`.
"""
function feature_to_group(feature, group_config::GroupingConfig)
throw(ArgumentError("""
`feature_to_group` not implemented for config $(nameof(typeof(group_config))).
"""))
end
include("cluster_config.jl")
include("histogram_config.jl")
include("nearest_feature_config.jl")
include("pairwise_comparison.jl")
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 9027 | export AttractorsViaFeaturizing, extract_features
# Flexible mapping of initial conditions into "attractors" by featurizing
# and grouping using arbitrary grouping configurations.
#####################################################################################
# Structs and documentation string
#####################################################################################
include("all_grouping_configs.jl")
struct AttractorsViaFeaturizing{DS<:DynamicalSystem, G<:GroupingConfig, F, T, SSS<:AbstractStateSpaceSet} <: AttractorMapper
ds::DS
featurizer::F
group_config::G
Ttr::T
Δt::T
total::T
threaded::Bool
attractors::Dict{Int, SSS}
end
"""
AttractorsViaFeaturizing(
ds::DynamicalSystem, featurizer::Function,
grouping_config = GroupViaClustering(); kwargs...
)
Initialize a `mapper` that maps initial conditions to attractors using a featurizing and
grouping approach. This is a supercase of the featurizing and clustering approach that
is utilized by bSTAB [Stender2021](@cite) and MCBB [Gelbrecht2020](@cite).
See [`AttractorMapper`](@ref) for how to use the `mapper`.
This `mapper` also allows the syntax `mapper(u0)` but only if the `grouping_config`
is _not_ `GroupViaClustering`.
`featurizer` is a function `f(A, t)` that takes as an input an integrated trajectory
`A::StateSpaceSet` and the corresponding time vector `t` and returns a vector
`v` of features describing the trajectory.
For better performance, it is strongly recommended that `v isa SVector{<:Real}`.
`grouping_config` is an instance of any subtype of [`GroupingConfig`](@ref) and decides
how features will be grouped into attractors, see below.
See also the intermediate functions [`extract_features`](@ref) and [`group_features`](@ref),
which can be utilized when wanting to work directly with features.
## Keyword arguments
* `T=100, Ttr=100, Δt=1`: Propagated to `DynamicalSystems.trajectory` for integrating
an initial condition to yield `A, t`.
* `threaded = true`: Whether to run the generation of features over threads by integrating
trajectories in parallel.
## Description
The trajectory `X` of an initial condition is transformed into features. Each
feature is a number useful in _characterizing the attractor_ the initial condition ends up
at, and **distinguishing it from other attractors**. Example features are the mean or standard
deviation of some the dimensions of the trajectory, the entropy of some of the
dimensions, the fractal dimension of `X`, or anything else you may fancy.
All feature vectors (each initial condition = 1 feature vector) are then grouped using one of the
sevaral available grouping configurations. Each group is assumed to be a unique attractor,
and hence each initial condition is labelled according to the group it is part of.
The method thus relies on the user having at least some basic idea about what attractors
to expect in order to pick the right features, and the right way to group them,
in contrast to [`AttractorsViaRecurrences`](@ref).
Attractors are stored and can be accessed with [`extract_attractors`](@ref),
however it should be clear that this mapper never actually finds attractors.
They way we store attractors is by picking the first initial condition that belongs
to the corresponding "attractor group", and then recording its trajectory
with the same arguments `T, Ttr, Δt`. This is stored as the attractor,
but of course there is no guarantee that this is actually an attractor.
"""
function AttractorsViaFeaturizing(ds::DynamicalSystem, featurizer::Function,
group_config::GroupingConfig = GroupViaClustering();
T=100, Ttr=100, Δt=1, threaded = true,
)
D = dimension(ds)
V = eltype(current_state(ds))
T, Ttr, Δt = promote(T, Ttr, Δt)
# For parallelization, the dynamical system is deepcopied.
return AttractorsViaFeaturizing(
ds, featurizer, group_config, Ttr, Δt, T, threaded, Dict{Int, StateSpaceSet{D,V}}(),
)
end
function reset_mapper!(mapper::AttractorsViaFeaturizing)
empty!(mapper.attractors)
return
end
DynamicalSystemsBase.rulestring(m::AttractorsViaFeaturizing) = DynamicalSystemsBase.rulestring(m.ds)
function Base.show(io::IO, mapper::AttractorsViaFeaturizing)
ps = generic_mapper_print(io, mapper)
println(io, rpad(" Ttr: ", ps), mapper.Ttr)
println(io, rpad(" Δt: ", ps), mapper.Δt)
println(io, rpad(" T: ", ps), mapper.total)
println(io, rpad(" group via: ", ps), nameof(typeof(mapper.group_config)))
println(io, rpad(" featurizer: ", ps), nameof(mapper.featurizer))
return
end
ValidICS = Union{AbstractStateSpaceSet, Function}
#####################################################################################
# Extension of `AttractorMapper` API
#####################################################################################
# We only extend the general `basins_fractions`, because the clustering method
# cannot map individual initial conditions to attractors
function basins_fractions(mapper::AttractorsViaFeaturizing, ics::ValidICS;
show_progress = true, N = 1000
)
# we always collect the initial conditions because we need their reference
# to extract the attractors
icscol = if ics isa Function
StateSpaceSet([copy(ics()) for _ in 1:N])
else
ics
end
features = extract_features(mapper, icscol; show_progress, N)
group_labels = group_features(features, mapper.group_config)
fs = basins_fractions(group_labels) # Vanilla fractions method with Array input
# we can always extract attractors because we store all initial conditions
extract_attractors!(mapper, group_labels, icscol)
if typeof(ics) <: AbstractStateSpaceSet
return fs, group_labels
else
return fs
end
end
#####################################################################################
# featurizing and grouping source code
#####################################################################################
import ProgressMeter
# TODO: This functionality should be a generic parallel evolving function...
"""
extract_features(mapper, ics; N = 1000, show_progress = true)
Return a vector of the features of each initial condition in `ics` (as in
[`basins_fractions`](@ref)), using the configuration of `mapper::AttractorsViaFeaturizing`.
Keyword `N` is ignored if `ics isa StateSpaceSet`.
"""
function extract_features(mapper::AttractorsViaFeaturizing, args...; kwargs...)
if !(mapper.threaded)
extract_features_single(mapper, args...; kwargs...)
else
extract_features_threaded(mapper, args...; kwargs...)
end
end
function extract_features_single(mapper, ics; show_progress = true, N = 1000)
N = (typeof(ics) <: Function) ? N : size(ics, 1) # number of actual ICs
first_feature = extract_feature(mapper.ds, _get_ic(ics, 1), mapper)
feature_vector = Vector{typeof(first_feature)}(undef, N)
feature_vector[1] = first_feature
progress = ProgressMeter.Progress(N; desc = "Integrating trajectories:", enabled=show_progress)
for i ∈ 1:N
ic = _get_ic(ics,i)
feature_vector[i] = extract_feature(mapper.ds, ic, mapper)
ProgressMeter.next!(progress)
end
return feature_vector
end
function (mapper::AttractorsViaFeaturizing)(u0)
f = extract_features_single(mapper, [u0])
return feature_to_group(f[1], mapper.group_config)
end
# TODO: We need an alternative to deep copying integrators that efficiently
# initializes integrators for any given kind of system. But that can be done
# later in the DynamicalSystems.jl 3.0 rework.
function extract_features_threaded(mapper, ics; show_progress = true, N = 1000)
N = (typeof(ics) <: Function) ? N : size(ics, 1) # number of actual ICs
systems = [deepcopy(mapper.ds) for _ in 1:(Threads.nthreads() - 1)]
pushfirst!(systems, mapper.ds)
first_feature = extract_feature(mapper.ds, _get_ic(ics, 1), mapper)
feature_vector = Vector{typeof(first_feature)}(undef, N)
feature_vector[1] = first_feature
progress = ProgressMeter.Progress(N; desc = "Integrating trajectories:", enabled=show_progress)
Threads.@threads for i ∈ 2:N
ds = systems[Threads.threadid()]
ic = _get_ic(ics, i)
feature_vector[i] = extract_feature(ds, ic, mapper)
ProgressMeter.next!(progress)
end
return feature_vector
end
function extract_feature(ds::DynamicalSystem, u0::AbstractVector{<:Real}, mapper)
A, t = trajectory(ds, mapper.total, u0; Ttr = mapper.Ttr, Δt = mapper.Δt)
return mapper.featurizer(A, t)
end
function extract_attractors!(mapper::AttractorsViaFeaturizing, labels, ics)
uidxs = unique(i -> labels[i], eachindex(labels))
attractors = Dict(labels[i] => trajectory(mapper.ds, mapper.total, ics[i];
Ttr = mapper.Ttr, Δt = mapper.Δt)[1] for i in uidxs if i > 0)
overwrite_dict!(mapper.attractors, attractors)
return
end
extract_attractors(mapper::AttractorsViaFeaturizing) = mapper.attractors
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 12397 | using Distances, Clustering, Distributions
import Optim
export GroupViaClustering
"""
GroupViaClustering(; kwargs...)
Initialize a struct that contains instructions on how to group features in
[`AttractorsViaFeaturizing`](@ref). `GroupViaClustering` clusters features into
groups using DBSCAN, similar to the original work by bSTAB [Stender2021](@cite) and
MCBB [Gelbrecht2020](@cite). Several options on clustering are available, see keywords below.
The defaults are a significant improvement over existing literature, see Description.
## Keyword arguments
* `clust_distance_metric = Euclidean()`: A metric to be used in the clustering.
It can be any function `f(a, b)` that returns the distance between real-valued vectors
`a, b`. All metrics from Distances.jl can be used here.
* `rescale_features = true`: if true, rescale each dimension of the extracted features
separately into the range `[0,1]`. This typically leads to more accurate clustering.
* `min_neighbors = 10`: minimum number of neighbors (i.e. of similar features) each
feature needs to have, including counting its own self,
in order to be considered in a cluster (fewer than this, it is
labeled as an outlier, `-1`).
* `use_mmap = false`: whether to use an on-disk map for creating the distance matrix
of the features. Useful when the features are so many where a matrix with side their
length would not fit to memory.
### Keywords for optimal radius estimation
* `optimal_radius_method::Union{Real, String} = "silhouettes_optim"`: if a real number, it
is the radius used to cluster features. Otherwise, it determines the method used to
automatically determine that radius. Possible values are:
- `"silhouettes"`: Performs a linear (sequential) search for the radius that maximizes a
statistic of the silhouette values of clusters (typically the mean). This can be chosen
with `silhouette_statistic`. The linear search may take some time to finish. To
increase speed, the number of radii iterated through can be reduced by decreasing
`num_attempts_radius` (see its entry below).
- `"silhouettes_optim"`: Same as `"silhouettes"` but performs an optimized search via
Optim.jl. It's faster than `"silhouettes"`, with typically the same accuracy (the
search here is not guaranteed to always find the global maximum, though it typically
gets close).
- `"knee"`: chooses the the radius according to the knee (a.k.a. elbow,
highest-derivative method) and is quicker, though generally leading to much worse
clustering. It requires that `min_neighbors` > 1.
* `num_attempts_radius = 100`: number of radii that the `optimal_radius_method` will try
out in its iterative procedure. Higher values increase the accuracy of clustering,
though not necessarily much, while always reducing speed.
* `silhouette_statistic::Function = mean`: statistic (e.g. mean or minimum) of the
silhouettes that is maximized in the "optimal" clustering. The original implementation
in [Stender2021](@cite) used the `minimum` of the silhouettes, and typically performs less
accurately than the `mean`.
* `max_used_features = 0`: if not `0`, it should be an `Int` denoting the max amount of
features to be used when finding the optimal radius. Useful when clustering a very large
number of features (e.g., high accuracy estimation of fractions of basins of
attraction).
## Description
The DBSCAN clustering algorithm is used to automatically identify clusters of similar
features. Each feature vector is a point in a feature space. Each cluster then basically
groups points that are closely packed together. Closely packed means that the points have
at least `min_neighbors` inside a ball of radius `optimal_radius` centered on them. This
method typically works well if the radius is chosen well, which is not necessarily an easy
task. Currently, three methods are implemented to automatically estimate an "optimal"
radius.
### Estimating the optimal radius
The default method is the **silhouettes method**, which includes keywords `silhouette` and
`silhouette_optim`. Both of them search for the radius that optimizes the clustering,
meaning the one that maximizes a statistic `silhouette_statistic` (e.g. mean value) of a
quantifier for the quality of each cluster. This quantifier is the silhouette value of
each identified cluster. A silhouette value measures how similar a point is to the cluster
it currently belongs to, compared to the other clusters, and ranges from -1 (worst
matching) to +1 (ideal matching). If only one cluster is found, the assigned silhouette is
zero. So for each attempted radius in the search the clusters are computed, their silhouettes
calculated, and the statistic of these silhouettes computed. The algorithm then finds the
radius that leads to the maximum such statistic. For `optimal_radius_method =
"silhouettes"`, the search is done linearly, from a minimum to a maximum candidate radius
for `optimal_radius_method = "silhouettes"`; `optimal_radius_method = silhouettes_optim`,
it is done via an optimized search performed by Optim.jl which is typically faster and
with similar accuracy. A third alternative is the`"elbow"` method, which works by
calculating the distance of each point to its k-nearest-neighbors (with `k=min_neighbors`)
and finding the distance corresponding to the highest derivative in the curve of the
distances, sorted in ascending order. This distance is chosen as the optimal radius. It is
described in [Ester1996](@cite) and [Schubert2017](@cite). It typically performs considerably worse
than the `"silhouette"` methods.
"""
struct GroupViaClustering{R<:Union{Real, String}, M, F<:Function} <: GroupingConfig
clust_distance_metric::M
min_neighbors::Int
rescale_features::Bool
optimal_radius_method::R
num_attempts_radius::Int
silhouette_statistic::F
max_used_features::Int
use_mmap::Bool
end
function GroupViaClustering(;
clust_distance_metric=Euclidean(), min_neighbors = 10,
rescale_features=true, num_attempts_radius=100,
optimal_radius_method::Union{Real, String} = "silhouettes_optim",
silhouette_statistic = mean, max_used_features = 0,
use_mmap = false,
)
return GroupViaClustering(
clust_distance_metric, min_neighbors,
rescale_features, optimal_radius_method,
num_attempts_radius, silhouette_statistic, max_used_features,
use_mmap,
)
end
#####################################################################################
# API function (group features)
#####################################################################################
# The keywords `par_weight, plength, spp` enable the "for-free" implementation of the
# MCBB algorithm (weighting the distance matrix by parameter value as well).
# The keyword version of this function is only called in
# `GroupingAcrossParametersContinuation` and is not part of public API!
function group_features(
features, config::GroupViaClustering;
par_weight::Real = 0, plength::Int = 1, spp::Int = 1,
)
nfeats = length(features); dimfeats = length(features[1])
if dimfeats ≥ nfeats
throw(ArgumentError("""
Not enough features. The algorithm needs the number of features
$nfeats to be greater or equal than the number of dimensions $dimfeats
"""))
end
if config.rescale_features
features = _rescale_to_01(features)
end
ϵ_optimal = _extract_ϵ_optimal(features, config)
distances = _distance_matrix(features, config; par_weight, plength, spp)
labels = _cluster_distances_into_labels(distances, ϵ_optimal, config.min_neighbors)
return labels
end
function _distance_matrix(features, config::GroupViaClustering;
par_weight::Real = 0, plength::Int = 1, spp::Int = 1
)
metric = config.clust_distance_metric
L = length(features)
if config.use_mmap
pth, s = mktemp()
dists = Mmap.mmap(s, Matrix{Float32}, (L, L))
else
dists = zeros(L, L)
end
if metric isa Metric # then the `pairwise` function is valid
# ensure that we give the vector of static vectors to pairwise!
pairwise!(metric, dists, vec(features); symmetric = true)
else # it is any arbitrary distance function, e.g., used in aggregating attractors
@inbounds for i in eachindex(features)
Threads.@threads for j in i:length(features)
v = metric(features[i], features[j])
dists[i, j] = dists[j, i] = v # utilize symmetry
end
end
end
if par_weight ≠ 0 # weight distance matrix by parameter value
par_vector = kron(range(0, 1, plength), ones(spp))
length(par_vector) ≠ size(dists, 1) && error("Feature size doesn't match.")
@inbounds for k in eachindex(par_vector)
# We can optimize the loop here due to symmetry of the metric.
# Instead of going over all `j` we go over `(k+1)` to end,
# and also add value to transpose. (also assume that if j=k, distance is 0)
for j in (k+1):size(dists, 1)
pdist = par_weight*abs(par_vector[k] - par_vector[j])
dists[k,j] += pdist
dists[j,k] += pdist
end
end
end
return dists
end
function _extract_ϵ_optimal(features, config::GroupViaClustering)
(; min_neighbors, clust_distance_metric, optimal_radius_method,
num_attempts_radius, silhouette_statistic, max_used_features) = config
if optimal_radius_method isa String
# subsample features to accelerate optimal radius search
if max_used_features == 0 || max_used_features > length(features)
features_for_optimal = vec(features)
else
features_for_optimal = sample(vec(features), max_used_features; replace = false)
end
# get optimal radius (function dispatches on the radius method)
ϵ_optimal, v_optimal = optimal_radius_dbscan(
features_for_optimal, min_neighbors, clust_distance_metric,
optimal_radius_method, num_attempts_radius, silhouette_statistic
)
elseif optimal_radius_method isa Real
ϵ_optimal = optimal_radius_method
else
error("Specified `optimal_radius_method` is incorrect. Please specify the radius
directly as a Real number or the method to compute it as a String")
end
return ϵ_optimal
end
# Already expecting the distance matrix, the output of `pairwise`
function _cluster_distances_into_labels(distances, ϵ_optimal, min_neighbors)
dbscanresult = dbscan(distances, ϵ_optimal; min_neighbors, metric=nothing)
cluster_labels = cluster_assignment(dbscanresult)
return cluster_labels
end
"""
Do "min-max" rescaling of vector of feature vectors so that its values span `[0,1]`.
"""
_rescale_to_01(features::Vector{<:AbstractVector}) = _rescale_to_01(StateSpaceSet(features))
function _rescale_to_01(features::AbstractStateSpaceSet)
mini, maxi = minmaxima(features)
rescaled = map(f -> (f .- mini) ./ (maxi .- mini), features)
return typeof(features)(rescaled) # ensure it stays the same type
end
#####################################################################################
# Utilities
#####################################################################################
"""
Util function for `classify_features`. Returns the assignment vector, in which the i-th
component is the cluster index of the i-th feature.
"""
function cluster_assignment(clusters, data; include_boundary=true)
assign = zeros(Int, size(data)[2])
for (idx, cluster) in enumerate(clusters)
assign[cluster.core_indices] .= idx
if cluster.boundary_indices != []
if include_boundary
assign[cluster.boundary_indices] .= idx
else
assign[cluster.boundary_indices] .= -1
end
end
end
return assign
end
function cluster_assignment(dbscanresult::Clustering.DbscanResult)
labels = dbscanresult.assignments
return replace!(labels, 0=>-1)
end
#####################################################################################
# Finding optimal ϵ
#####################################################################################
include("cluster_optimal_ϵ.jl")
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 7578 | #####################################################################################
# Calculate Silhouettes
#####################################################################################
"""
Calculate silhouettes. A bit slower than the implementation in `Clustering.jl` but seems
to be more robust. The latter seems to be incorrect in some cases.
"""
function silhouettes_new(dbscanresult::Clustering.DbscanResult, dists::AbstractMatrix)
labels = dbscanresult.assignments
clusters = [findall(x->x==i, labels) for i=1:maximum(labels)] #all clusters
if length(clusters) == 1 return zeros(length(clusters[1])) end #all points in the same cluster -> sil = 0
sils = zeros(length(labels))
outsideclusters = findall(x->x==0, labels)
for (idx_c, cluster) in enumerate(clusters)
@inbounds for i in cluster
a = sum(@view dists[i, cluster])/(length(cluster)-1) #dists should be organized s.t. dist[i, cluster] i= dist from i to idxs in cluster
b = _calcb!(i, idx_c, dists, clusters, outsideclusters)
sils[i] = (b-a)/(max(a,b))
end
end
return sils
end
function _calcb!(i, idx_c_i, dists, clusters, outsideclusters)
min_dist_to_clstr = typemax(eltype(dists))
for (idx_c, cluster) in enumerate(clusters)
idx_c == idx_c_i && continue
dist_to_clstr = mean(@view dists[cluster,i]) #mean distance to other clusters
if dist_to_clstr < min_dist_to_clstr min_dist_to_clstr = dist_to_clstr end
end
min_dist_to_pts = typemax(eltype(dists))
for point in outsideclusters
dist_to_pts = dists[point, i] # distance to points outside clusters
if dist_to_pts < min_dist_to_pts
min_dist_to_pts = dist_to_pts
end
end
return min(min_dist_to_clstr, min_dist_to_pts)
end
#####################################################################################
# Optimal radius dbscan
#####################################################################################
function optimal_radius_dbscan(features, min_neighbors, metric, optimal_radius_method,
num_attempts_radius, silhouette_statistic)
if optimal_radius_method == "silhouettes"
ϵ_optimal, v_optimal = optimal_radius_dbscan_silhouette(
features, min_neighbors, metric, num_attempts_radius, silhouette_statistic
)
elseif optimal_radius_method == "silhouettes_optim"
ϵ_optimal, v_optimal = optimal_radius_dbscan_silhouette_optim(
features, min_neighbors, metric, num_attempts_radius, silhouette_statistic
)
elseif optimal_radius_method == "knee"
ϵ_optimal, v_optimal = optimal_radius_dbscan_knee(features, min_neighbors, metric)
elseif optimal_radius_method isa Real
ϵ_optimal = optimal_radius_method
v_optimal = NaN
else
error("Unknown `optimal_radius_method`.")
end
return ϵ_optimal, v_optimal
end
"""
Find the optimal radius ε of a point neighborhood to use in DBSCAN, the unsupervised
clustering method for `AttractorsViaFeaturizing`. Iteratively search
for the radius that leads to the best clustering, as characterized by quantifiers known as
silhouettes. Does a linear (sequential) search.
"""
function optimal_radius_dbscan_silhouette(features, min_neighbors, metric,
num_attempts_radius, silhouette_statistic
)
feat_ranges = features_ranges(features)
ϵ_grid = range(
minimum(feat_ranges)/num_attempts_radius, minimum(feat_ranges);
length=num_attempts_radius
)
s_grid = zeros(size(ϵ_grid)) # silhouette statistic values (which we want to maximize)
# vary ϵ to find the best one (which will maximize the mean silhouette)
dists = pairwise(metric, features)
for i in eachindex(ϵ_grid)
clusters = dbscan(dists, ϵ_grid[i]; min_neighbors, metric = nothing)
sils = silhouettes_new(clusters, dists)
s_grid[i] = silhouette_statistic(sils)
end
optimal_val, idx = findmax(s_grid)
ϵ_optimal = ϵ_grid[idx]
return ϵ_optimal, optimal_val
end
function features_ranges(features)
d = StateSpaceSet(features) # zero cost if `features` is a `Vector{<:SVector}`
mini, maxi = minmaxima(d)
return maxi .- mini
end
"""
Same as `optimal_radius_dbscan_silhouette`,
but find minimum via optimization with Optim.jl.
"""
function optimal_radius_dbscan_silhouette_optim(
features, min_neighbors, metric, num_attempts_radius, silhouette_statistic
)
feat_ranges = features_ranges(features)
# vary ϵ to find the best radius (which will maximize the mean silhouette)
dists = pairwise(metric, features)
f = (ϵ) -> Attractors.silhouettes_from_distances(
ϵ, dists, min_neighbors, silhouette_statistic
)
opt = Optim.optimize(
f, minimum(feat_ranges)/100, minimum(feat_ranges); iterations=num_attempts_radius
)
ϵ_optimal = Optim.minimizer(opt)
optimal_val = -Optim.minimum(opt) # we minimize using `-`
return ϵ_optimal, optimal_val
end
function silhouettes_from_distances(ϵ, dists, min_neighbors, silhouette_statistic=mean)
clusters = dbscan(dists, ϵ; min_neighbors, metric = nothing)
sils = silhouettes_new(clusters, dists)
# We return minus here because Optim finds minimum; we want maximum
return -silhouette_statistic(sils)
end
"""
Find the optimal radius ϵ of a point neighborhood for use in DBSCAN through the elbow method
(knee method, highest derivative method).
"""
function optimal_radius_dbscan_knee(_features::Vector, min_neighbors, metric)
features = StateSpaceSet(_features)
tree = searchstructure(KDTree, features, metric)
# Get distances, excluding distance to self (hence the Theiler window)
d, n = size(features)
features_vec = [features[:,j] for j=1:n]
_, distances = bulksearch(tree, features_vec, NeighborNumber(min_neighbors), Theiler(0))
meandistances = map(mean, distances)
sort!(meandistances)
maxdiff, idx = findmax(diff(meandistances))
ϵ_optimal = meandistances[idx]
return ϵ_optimal, maxdiff
end
# The following function is left here for reference. It is not used anywhere in the code.
# It is the original implementation we have written based on the bSTAB paper.
"""
Find the optimal radius ε of a point neighborhood to use in DBSCAN, the unsupervised clustering
method for `AttractorsViaFeaturizing`. The basic idea is to iteratively search for the radius that
leads to the best clustering, as characterized by quantifiers known as silhouettes.
"""
function optimal_radius_dbscan_silhouette_original(features, min_neighbors, metric; num_attempts_radius=200)
d,n = size(features)
feat_ranges = maximum(features, dims = d)[:,1] .- minimum(features, dims = d)[:,1];
ϵ_grid = range(minimum(feat_ranges)/num_attempts_radius, minimum(feat_ranges), length=num_attempts_radius)
s_grid = zeros(size(ϵ_grid)) # average silhouette values (which we want to maximize)
# vary ϵ to find the best one (which will maximize the minimum silhouette)
for i in eachindex(ϵ_grid)
clusters = dbscan(features, ϵ_grid[i]; min_neighbors)
dists = pairwise(metric, features)
class_labels = cluster_assignment(clusters, features)
if length(clusters) ≠ 1 # silhouette undefined if only one cluster
sils = silhouettes(class_labels, dists)
s_grid[i] = minimum(sils)
else
s_grid[i] = 0; # considers single-cluster solution on the midpoint (following Wikipedia)
end
end
max, idx = findmax(s_grid)
ϵ_optimal = ϵ_grid[idx]
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 1170 | using ComplexityMeasures: FixedRectangularBinning, RectangularBinEncoding, encode
export GroupViaHistogram
export FixedRectangularBinning
"""
GroupViaHistogram(binning::FixedRectangularBinning)
Initialize a struct that contains instructions on how to group features in
[`AttractorsViaFeaturizing`](@ref). `GroupViaHistogram` performs a histogram
in feature space. Then, all features that are in the same histogram bin get the
same label. The `binning` is an instance of [`FixedRectangularBinning`](@ref)
from ComplexityMeasures.jl. (the reason to not allow `RectangularBinning` is because
during continuation we need to ensure that bins remain identical).
"""
struct GroupViaHistogram{E<:RectangularBinEncoding} <: GroupingConfig
encoding::E
end
function GroupViaHistogram(binning::FixedRectangularBinning)
enc = RectangularBinEncoding(binning)
return GroupViaHistogram(enc)
end
function feature_to_group(feature, config::GroupViaHistogram)
# The `encode` interface perfectly satisfies the grouping interface.
# How convenient. It's as if someone had the foresight to make these things work...
return encode(config.encoding, feature)
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2714 | using Neighborhood, Distances
export GroupViaNearestFeature
"""
GroupViaNearestFeature(templates; kwargs...)
Initialize a struct that contains instructions on how to group features in
[`AttractorsViaFeaturizing`](@ref). `GroupViaNearestFeature` accepts a `template`,
which is a vector of features. Then, generated features from initial conditions in
[`AttractorsViaFeaturizing`](@ref) are labelled according to the feature in
`templates` that is closest (the label is the index of the closest template).
`templates` can be a vector or dictionary mapping keys to templates. Internally
all templates are converted to `SVector` for performance. Hence, it is strongly recommended
that both `templates` and the output of the `featurizer` function in
[`AttractorsViaFeaturizing`](@ref) return `SVector` types.
## Keyword arguments
- `metric = Euclidean()`: metric to be used to quantify distances in the feature space.
- `max_distance = Inf`: Maximum allowed distance between a feature and its nearest
template for it to be assigned to that template. By default, `Inf` guarantees that a
feature is assigned to its nearest template regardless of the distance.
Features that exceed `max_distance` to their nearest template get labelled `-1`.
"""
struct GroupViaNearestFeature{D, T, K <: KDTree, X} <: GroupingConfig
templates::Vector{SVector{D,T}}
tree::K # KDTree with templates
max_distance::T
dummy_idxs::Vector{Int}
dummy_dist::Vector{T}
keys::X
end
function GroupViaNearestFeature(
templates; metric = Euclidean(), max_distance = Inf
)
k, v = collect(keys(templates)), values(templates)
x = first(v)
D = length(x); T = eltype(x)
t = map(x -> SVector{D,T}(x), v)
# The tree performs the nearest neighbor searches efficiently
tree = searchstructure(KDTree, t, metric)
dummy_idxs = [0]; dummy_dist = T[0]
return GroupViaNearestFeature(t, tree, T(max_distance), dummy_idxs, dummy_dist, k)
end
# The following function comes from the source code of the `bulksearch` function
# from Neighborhood.jl. It's the most efficient way to perform one knn search,
# and makes it unnecessary to also implement `group_features`. The bulk version
# has the same performance!
@inbounds function feature_to_group(feature, config::GroupViaNearestFeature)
(; tree, max_distance, dummy_idxs, dummy_dist) = config
skip = Neighborhood.NearestNeighbors.always_false
sort_result = false
Neighborhood.NearestNeighbors.knn_point!(
tree, feature, sort_result, dummy_dist, dummy_idxs, skip
)
label = dummy_idxs[1]
d = dummy_dist[1]
if d > max_distance
return -1
else
return config.keys[label]
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 4798 | export GroupViaPairwiseComparison
"""
GroupViaPairwiseComparison <: GroupingConfig
GroupViaPairwiseComparison(; threshold::Real, metric...)
Initialize a struct that contains instructions on how to group features in
[`AttractorsViaFeaturizing`](@ref). `GroupViaPairwiseComparison` groups features and
identifies clusters by considering the pairwise distance between features. It can be used
as an alternative to the clustering method in `GroupViaClustering`, having the
advantage that it is simpler, typically faster and uses less memory.
## Keyword arguments
* `threshold = 0.1`: A real number defining the maximum distance two features can have to
be considered in the same cluster - above the threshold, features are different. This
value simply needs to be large enough to differentiate clusters.
A good value for `threshold` depends on the feature variability within a cluster
the chosen metric, and whether features are rescaled. See description below for more.
* `metric = Euclidean()`: A function `metric(a, b)` that returns the distance between two
features `a` and `b`, outputs of `featurizer`. Any `Metric` from Distances.jl can be used
here.
* `rescale_features = true`: if true, rescale each dimension of the extracted features
separately into the range `[0, 1]`. This typically leads to more accurate grouping
for the default `metric`.
## Description
This algorithm assumes that the features are well-separated into distinct clouds, with the
maximum radius of the cloud controlled by `threshold`. Since the systems are
deterministic, this is achievable with a good-enough `featurizer` function, by removing
transients, and running the trajectories for sufficiently long. It then considers that
features belong to the same attractor when their pairwise distance, computed using
`metric`, is smaller than or equal to `threshold`, and that they belong
to different attractors when the distance is bigger. Attractors correspond to each
grouping of similar features. In this way, the key parameter `threshold` is
basically the amount of variation permissible in the features belonging to the same
attractor. If they are well-chosen, the value can be relatively small and does not need to
be fine tuned.
The `threshold` should achieve a balance: one one hand, it should be large enough
to account for variations in the features from the same attractor - if it's not large
enough, the algorithm will find duplicate attractors. On the other hand, it should be
small enough to not group together features from distinct attractors. This requires some
knowledge of how spread the features are. If it's too big, the algorithm will miss some
attractors, as it groups 2+ distinct attractors together. Therefore, as a rule of thumb,
one can repeat the procedure a few times, starting with a relatively large value and
reducing it until no more attractors are found and no duplicates appear.
The method scales as O(N) in memory and performance with N the number of features.
This is a huge difference versus the O(N^2) of [`GroupViaClustering`](@ref).
"""
@kwdef struct GroupViaPairwiseComparison{R<:Real, M} <: GroupingConfig
threshold::R = 0.1
metric::M = Euclidean()
rescale_features::Bool = true
end
function group_features(features, config::GroupViaPairwiseComparison)
if config.rescale_features
features = _rescale_to_01(features)
end
labels = _cluster_features_into_labels(features, config)
return labels
end
function _cluster_features_into_labels(features, config::GroupViaPairwiseComparison)
labels = ones(length(features))
metric = config.metric
threshold = config.threshold
# Assign feature 1 as a new cluster center
labels[1] = 1
cluster_idxs = [1] # idxs of the features that define each cluster
cluster_labels = [1] # labels for the clusters, going from 1 : num_clusters
next_cluster_label = 2
for idx_feature = 2:length(features)
feature = features[idx_feature]
# because here the cluster labels are always the positive integers,
# we don't need a dictionary. `Vector` keys are the IDs we need.
dist_to_clusters = [metric(feature, features[idx]) for idx in cluster_idxs]
min_dist, closest_cluster_label = findmin(dist_to_clusters)
if min_dist > threshold # bigger than threshold: new attractor
# assign feature as new cluster center
feature_label = next_cluster_label
push!(cluster_idxs, idx_feature)
push!(cluster_labels, next_cluster_label)
next_cluster_label += 1
else # smaller than threshold: assign to closest cluster
feature_label = closest_cluster_label
end
labels[idx_feature] = feature_label
end
return labels
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 16748 | #####################################################################################
# Type definition and documentation
#####################################################################################
"""
AttractorsViaRecurrences(ds::DynamicalSystem, grid; kwargs...)
Map initial conditions of `ds` to attractors by identifying attractors on the fly based on
recurrences in the state space, as outlined in [Datseris2022](@cite).
However, the Description section below for has a more accurate (and simpler)
exposition to the algorithm than the paper.
`grid` is instructions for partitioning the state space into finite-sized cells
so that a finite state machine can operate on top of it. Possibilities are:
1. A tuple of sorted `AbstractRange`s for a regular grid.
Example is `grid = (xg, yg)` where `xg = yg = range(-5, 5; length = 100)`
for a two-dimensional system.
2. A tuple of sorted `AbstractVector`s for an irregular grid, for example
`grid = (xg, yg)` with `xg = range(0, 10.0^(1/2); length = 200).^2,
yg = range(-5, 5; length = 100)`.
3. An instance of the special grid type
[`SubdivisionBasedGrid`](@ref), which can be created either manually or by using
[`subdivision_based_grid`](@ref).
This automatically analyzes and adapts grid discretization
levels in accordance with state space flow speed in different regions.
The grid has to be the same dimensionality as
the state space, use a [`ProjectedDynamicalSystem`](@ref) if you
want to search for attractors in a lower dimensional subspace.
## Keyword arguments
* `sparse = true`: control the storage type of the state space grid. If true,
uses a sparse array, whose memory usage is in general more efficient than a regular
array obtained with `sparse=false`. In practice, the sparse representation should
always be preferred when searching for [`basins_fractions`](@ref). Only for very low
dimensional systems and for computing the full [`basins_of_attraction`](@ref) the
non-sparse version should be used.
### Time evolution configuration
* `Ttr = 0`: Skip a transient before the recurrence routine begins.
* `Δt`: Approximate integration time step (second argument of the `step!` function).
The keyword `Dt` can also be used instead if `Δ` (`\\Delta`) is not accessible.
It is `1` for discrete time systems.
For continuous systems, an automatic value is calculated using
[`automatic_Δt_basins`](@ref). For very fine grids, this can become very small,
much smaller than the typical integrator internal step size in case of adaptive
integrators. In such cases, use `force_non_adaptive = true`.
* `force_non_adaptive = false`: Only used if the input dynamical system is `CoupledODEs`.
If `true` the additional keywords `adaptive = false, dt = Δt` are given as `diffeq`
to the `CoupledODEs`. This means that adaptive integration is turned off and `Δt` is
used as the ODE integrator timestep. This is useful in (1) very fine grids, and (2)
if some of the attractors are limit cycles. We have noticed that in this case the
integrator timestep becomes commensurate with the limit cycle period, leading to
incorrectly counting the limit cycle as more than one attractor.
### Finite state machine configuration
* `consecutive_recurrences = 100`: Number of consecutive visits to previously visited
unlabeled cells (i.e., recurrences) required before declaring we have converged to a new attractor.
This number tunes the accuracy of converging to attractors and should generally be high
(and even higher for chaotic systems).
* `attractor_locate_steps = 1000`: Number of subsequent steps taken to locate accurately the new
attractor after the convergence phase is over. Once `attractor_locate_steps` steps have been
taken, the new attractor has been identified with sufficient accuracy and iteration stops.
This number can be very high without much impact to overall performance.
* `store_once_per_cell = true`: Control if multiple points in state space that belong to
the same cell are stored or not in the attractor, when a new attractor is found.
If `true`, each visited cell will only store a point once, which is desirable for fixed
points and limit cycles. If `false` then `attractor_locate_steps` points are
stored per attractor, leading to more densely stored attractors,
which may be desirable for instance in chaotic attractors.
* `consecutive_attractor_steps = 2`: Μaximum checks of consecutives hits of an existing attractor cell
before declaring convergence to that existing attractor.
* `consecutive_basin_steps = 10`: Number of consecutive visits of the same basin of
attraction required before declaring convergence to an existing attractor.
This is ignored if `sparse = true`, as basins are not stored internally in that case.
* `consecutive_lost_steps = 20`: Maximum check of iterations outside the defined grid before we
declare the orbit lost outside and hence assign it label `-1`.
* `horizon_limit = 1e6`: If the norm of the integrator state reaches this
limit we declare that the orbit diverged to infinity.
* `maximum_iterations = Int(1e6)`: A safety counter that is always increasing for
each initial condition. Once exceeded, the algorithm assigns `-1` and throws a warning.
This clause exists to stop the algorithm never halting for inappropriate grids. It may happen
when a newly found attractor orbit intersects in the same cell of a previously found attractor (which leads to infinite resetting of all counters).
## Description
An initial condition given to an instance of `AttractorsViaRecurrences` is iterated
based on the integrator corresponding to `ds`. Enough recurrences in the state space
(i.e., a trajectory visited a region it has visited before) means
that the trajectory has converged to an attractor. This is the basis for finding attractors.
A finite state machine (FSM) follows the
trajectory in the state space, and constantly maps it to a cell in the given `grid`.
The grid cells store information: they are empty, visited, basins, or attractor cells.
The state of the FSM is decided based on the cell type and the previous state of the FSM.
Whenever the FSM recurs its state, its internal counter is increased, otherwise it is
reset to 0. Once the internal counter reaches a threshold, the FSM terminates or changes its state.
The possibilities for termination are the following:
- The trajectory hits `consecutive_recurrences` times in a row previously visited cells:
it is considered that an attractor is found and is labelled with a new ID. Then,
iteration continues for `attractor_locate_steps` steps. Each cell visited in this period stores
the "attractor" information. Then iteration terminates and the initial condition is
numbered with the attractor's ID.
- The trajectory hits an already identified attractor `consecutive_attractor_steps` consecutive times:
the initial condition is numbered with the attractor's basin ID.
- The trajectory hits a known basin `consecutive_basin_steps` times in a row: the initial condition
belongs to that basin and is numbered accordingly. Notice that basins are stored and
used only when `sparse = false` otherwise this clause is ignored.
- The trajectory spends `consecutive_lost_steps` steps outside the defined grid or the norm
of the dynamical system state becomes > than `horizon_limit`: the initial
condition is labelled `-1`.
- If none of the above happens, the initial condition is labelled `-1` after
`maximum_iterations` steps.
There are some special internal optimizations and details that we do not describe
here but can be found in comments in the source code.
(E.g., a special timer exists for the "lost" state which does not interrupt the main
timer of the FSM.)
A video illustrating how the algorithm works can be found in the online documentation,
under the [recurrences animation](@ref recurrences_animation) page.
"""
struct AttractorsViaRecurrences{DS<:DynamicalSystem, B, G, K} <: AttractorMapper
ds::DS
bsn_nfo::B
grid::G
kwargs::K
end
function AttractorsViaRecurrences(ds::DynamicalSystem, grid;
Dt = nothing, Δt = Dt, sparse = true, force_non_adaptive = false, kwargs...
)
if grid isa Tuple # regular or irregular
if all(t -> t isa AbstractRange, grid) && all(axis -> issorted(axis), grid) # regular
finalgrid = RegularGrid(grid)
elseif any(t -> t isa AbstractVector, grid) && all(axis -> issorted(axis), grid) # irregular
finalgrid = IrregularGrid(grid)
else
error("Incorrect grid specification!")
end
elseif grid isa SubdivisionBasedGrid
finalgrid = grid
else
error("Incorrect grid specification!")
end
bsn_nfo = initialize_basin_info(ds, finalgrid, Δt, sparse)
if ds isa CoupledODEs && force_non_adaptive
newdiffeq = (ds.diffeq..., adaptive = false, dt = bsn_nfo.Δt)
ds = CoupledODEs(ds, newdiffeq)
end
return AttractorsViaRecurrences(ds, bsn_nfo, finalgrid, kwargs)
end
function (mapper::AttractorsViaRecurrences)(u0; show_progress = true)
# Call low level code. Notice that in this
# call signature the internal basins info array of the mapper is NOT updated
# with the basins of attraction info. Only with the attractors info.
lab = recurrences_map_to_label!(mapper.bsn_nfo, mapper.ds, u0; show_progress, mapper.kwargs...)
# Transform to integers indexing from odd-even indexing
return iseven(lab) ? (lab ÷ 2) : (lab - 1) ÷ 2
end
function Base.show(io::IO, mapper::AttractorsViaRecurrences)
ps = generic_mapper_print(io, mapper)
println(io, rpad(" grid: ", ps), mapper.grid)
println(io, rpad(" attractors: ", ps), mapper.bsn_nfo.attractors)
return
end
extract_attractors(m::AttractorsViaRecurrences) = m.bsn_nfo.attractors
function convergence_time(m::AttractorsViaRecurrences)
i = m.bsn_nfo.safety_counter
kw = m.kwargs
if m.bsn_nfo.return_code == :new_att
# in this scenario we have an addition amount of iterations that is
# equal to the recurrences steps. We subtract this for more correct
# estimation of convergence time that will be closer to the convergence
# time of neighboring grid cells.
x = get(kw, :consecutive_recurrences, 100) + get(kw, :attractor_locate_steps, 1000)
elseif m.bsn_nfo.return_code == :bas_hit
return NaN
else
x = get(kw, :consecutive_attractor_steps, 2)
end
return (i - x + 1)*m.bsn_nfo.Δt
end
"""
basins_of_attraction(mapper::AttractorsViaRecurrences; show_progress = true)
This is a special method of `basins_of_attraction` that using recurrences does
_exactly_ what is described in the paper by Datseris & Wagemakers [Datseris2022](@cite).
By enforcing that the internal grid of `mapper` is the same as the grid of initial
conditions to map to attractors, the method can further utilize found exit and attraction
basins, making the computation faster as the grid is processed more and more.
"""
function basins_of_attraction(mapper::AttractorsViaRecurrences; show_progress = true)
basins = mapper.bsn_nfo.basins
if basins isa SparseArray;
throw(ArgumentError("""
Sparse version of AttractorsViaRecurrences is incompatible with
`basins_of_attraction(mapper)`."""
))
end
if (mapper.bsn_nfo.grid_nfo isa SubdivisionBasedGrid)
grid = mapper.grid.max_grid
else
grid = mapper.grid.grid
end
I = CartesianIndices(basins)
progress = ProgressMeter.Progress(
length(basins); desc = "Basins of attraction: ", dt = 1.0
)
# TODO: Here we can have a slightly more efficient iteration by
# iterating over `I` in different ways. In this way it always starts from the edge of
# the grid, which is the least likely location for attractors. We need to
# iterate I either randomly or from its center.
for (k, ind) in enumerate(I)
if basins[ind] == 0
show_progress && ProgressMeter.update!(progress, k)
y0 = generate_ic_on_grid(grid, ind)
basins[ind] = recurrences_map_to_label!(
mapper.bsn_nfo, mapper.ds, y0; show_progress, mapper.kwargs...
)
end
end
# remove attractors and rescale from 1 to max number of attractors
ind = iseven.(basins)
basins[ind] .+= 1
basins .= (basins .- 1) .÷ 2
return basins, mapper.bsn_nfo.attractors
end
#####################################################################################
# Definition of `BasinInfo` and initialization
#####################################################################################
# we need the abstract grid type because of the type parameterization in `BasinsInfo`
# the grid subtypes are in the grids file.
abstract type Grid end
mutable struct BasinsInfo{D, G<:Grid, Δ, T, V, A <: AbstractArray{Int, D}}
basins::A # sparse or dense
grid_nfo::G
Δt::Δ
state::Symbol
current_att_label::Int
visited_cell_label::Int
consecutive_match::Int
consecutive_lost::Int
prev_label::Int
safety_counter::Int
attractors::Dict{Int, StateSpaceSet{D, T, V}}
visited_cells::Vector{CartesianIndex{D}}
return_code::Symbol
end
function initialize_basin_info(ds::DynamicalSystem, grid_nfo, Δtt, sparse)
Δt = if isnothing(Δtt)
isdiscretetime(ds) ? 1 : automatic_Δt_basins(ds, grid_nfo)
else
Δtt
end
grid = grid_nfo.grid # this is always a Tuple irrespectively of grid type
D = dimension(ds)
T = eltype(current_state(ds))
G = length(grid)
if D ≠ G && (ds isa PoincareMap && G ∉ (D, D-1))
error("Grid and dynamical system do not have the same dimension!")
end
if grid_nfo isa SubdivisionBasedGrid
multiplier = maximum(keys(grid_nfo.grid_steps))
else
multiplier = 0
end
basins_array = if sparse
SparseArray{Int}(undef, (map(length, grid ).*(2^multiplier)))
else
zeros(Int, (map(length, grid).*(2^multiplier))...)
end
V = SVector{G, T}
bsn_nfo = BasinsInfo(
basins_array,
grid_nfo,
Δt,
:att_search,
2,4,0,1,0,0,
Dict{Int, StateSpaceSet{G, T, V}}(),
Vector{CartesianIndex{G}}(),
:search,
)
reset_basins_counters!(bsn_nfo)
return bsn_nfo
end
using LinearAlgebra: norm
"""
automatic_Δt_basins(ds::DynamicalSystem, grid; N = 5000) → Δt
Calculate an optimal `Δt` value for [`basins_of_attraction`](@ref).
This is done by evaluating the dynamic rule `f` (vector field) at `N` randomly chosen
points within the bounding box of the grid.
The average `f` is then compared with the average diagonal length of a grid
cell and their ratio provides `Δt`.
Notice that `Δt` should not be too small which happens typically if the grid resolution
is high. It is okay if the trajectory skips a few cells.
Also, `Δt` that is smaller than the internal step size of the integrator will cause
a performance drop.
"""
function automatic_Δt_basins(ds, grid_nfo::Grid; N = 5000)
isdiscretetime(ds) && return 1
if ds isa ProjectedDynamicalSystem
error("Automatic Δt finding is not implemented for `ProjectedDynamicalSystem`.")
end
# Create a random sampler with min-max the grid range
mins, maxs = minmax_grid_extent(grid_nfo)
sampler, = statespace_sampler(HRectangle([mins...], [maxs...]))
# Sample velocity at random points
f, p, t0 = dynamic_rule(ds), current_parameters(ds), initial_time(ds)
udummy = copy(current_state(ds))
dudt = 0.0
for _ in 1:N
point = sampler()
deriv = if !isinplace(ds)
f(point, p, t0)
else
f(udummy, point, p, t0)
udummy
end
dudt += norm(deriv)
end
s = mean_cell_diagonal(grid_nfo)
Δt = 10*s*N/dudt
return Δt
end
"""
reset_mapper!(mapper::AttractorsMapper)
Reset all accumulated information of `mapper` so that it is
as if it has just been initialized. Useful in `for` loops
that loop over a parameter of the dynamical system stored in `mapper`.
"""
function reset_mapper!(mapper::AttractorsViaRecurrences)
empty!(mapper.bsn_nfo.attractors)
if mapper.bsn_nfo.basins isa Array
mapper.bsn_nfo.basins .= 0
else
empty!(mapper.bsn_nfo.basins)
end
mapper.bsn_nfo.state = :att_search
mapper.bsn_nfo.consecutive_match = 0
mapper.bsn_nfo.consecutive_lost = 0
mapper.bsn_nfo.prev_label = 0
mapper.bsn_nfo.current_att_label = 2
mapper.bsn_nfo.visited_cell_label = 4
return
end
include("sparse_arrays.jl")
include("finite_state_machine.jl")
include("grids.jl")
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 13263 | #####################################################################################
# Implementation of the Finite State Machine (low level code)
#####################################################################################
"""
recurrences_map_to_label!(bsn_nfo::BasinsInfo, ds, u0; kwargs...) -> ic_label
Return the label of the attractor that the initial condition `u0` converges to,
or `-1` if it does not convergence anywhere (e.g., divergence to infinity or exceeding
`maximum_iterations`).
Notice the numbering system `cell_label` is as in `finite_state_machine!`.
Even numbers are attractors, odd numbers are basins.
"""
function recurrences_map_to_label!(bsn_nfo::BasinsInfo, ds::DynamicalSystem, u0;
# `mx_chk_safety` is deprecated
mx_chk_safety = Int(1e6), maximum_iterations = mx_chk_safety, Ttr = 0, kwargs...
)
# This routine identifies the attractor using the previously defined basin.
# reinitialize everything
reinit!(ds, u0)
Ttr > 0 && step!(ds, Ttr)
reset_basins_counters!(bsn_nfo)
cell_label = 0
bsn_nfo.safety_counter = 0
while cell_label == 0
step!(ds, bsn_nfo.Δt)
# This clause here is added because sometimes the algorithm will never halt
# for e.g., an ill conditioned grid where two or more attractors intersect
# within the same grid cell. In such a case, when starting on the second attractor
# the trajectory will forever reset between locating a new attractor and recurring
# on the previously found one...
bsn_nfo.safety_counter += 1
if bsn_nfo.safety_counter ≥ maximum_iterations
# TODO: Set up some debugging framework here via environment variable
# @warn """
# `AttractorsViaRecurrences` algorithm exceeded safety count without halting.
# It may be that the grid is not fine enough and attractors intersect in the
# same cell, or `maximum_iterations` is not high enough for a very fine grid.
# Here are some info on current status:\n
# state: $(current_state(ds)),\n
# parameters: $(current_parameters(ds)).
# """
cleanup_visited_cells!(bsn_nfo)
return -1
end
if !successful_step(ds)
cleanup_visited_cells!(bsn_nfo)
return -1
end
new_y = current_state(ds)
# The internal function `_possibly_reduced_state` exists solely to
# accommodate the special case of a Poincare map with the grid defined
# directly on the hyperplane, `plane::Tuple{Int, <: Real}`.
y = _possibly_reduced_state(new_y, ds, bsn_nfo)
n = basin_cell_index(y, bsn_nfo.grid_nfo)
cell_label = finite_state_machine!(bsn_nfo, n, y; kwargs...)
end
return cell_label
end
_possibly_reduced_state(y, ds, grid) = y
function _possibly_reduced_state(y, ds::PoincareMap, bsn_nfo)
grid = bsn_nfo.grid_nfo.grid
if ds.planecrossing.plane isa Tuple && length(grid) == dimension(ds)-1
return y[ds.diffidxs]
else
return y
end
end
"""
Main procedure which performs one step of the finite state machine.
Directly implements the algorithm of Datseris & Wagemakers 2021,
see the flowchart (Figure 2).
I.e., it obtains current state, updates state with respect to the cell
code the trajectory it is currently on, performs the check of counters,
and sets the f.s.m. to the new state, or increments counter if same state.
The basins and attractors are coded in the array with odd numbers for the basins and
even numbers for the attractors. The attractor `2n` has the corresponding basin `2n+1`.
This codification is changed when the basins and attractors are returned to the user.
Diverging trajectories and the trajectories staying outside the grid are coded with -1.
The label `1` (initial value) outlined in the paper is `0` here instead.
The function returns `0` unless the FSM has terminated its operation.
"""
function finite_state_machine!(
bsn_nfo::BasinsInfo, n::CartesianIndex, u;
# These are deprecated names:
mx_chk_att = 2,
mx_chk_hit_bas = 10,
mx_chk_fnd_att = 100,
mx_chk_loc_att = 1000,
mx_chk_lost = 20,
# These are the new names. They currently have the values of the
# deprecated names, so that existing code does not break. In the future,
# the deprecated names are removed and the new names get the values directly
consecutive_attractor_steps = mx_chk_att,
consecutive_basin_steps = mx_chk_hit_bas,
consecutive_recurrences = mx_chk_fnd_att,
attractor_locate_steps = mx_chk_loc_att,
consecutive_lost_steps = mx_chk_lost,
# other non-changed keywords
show_progress = true, # show_progress can be used when finding new attractor.
horizon_limit = 1e6,
store_once_per_cell = true,
)
# if n[1] == -1 means we are outside the grid,
# otherwise, we retrieve the label stored at the grid
# (which by default is 0 unless we have visited the cell before)
ic_label = n[1] == -1 ? -1 : bsn_nfo.basins[n]
update_finite_state_machine!(bsn_nfo, ic_label)
# This state means that we have visited a cell that contains a recorded attractor
if bsn_nfo.state == :att_hit
if ic_label == bsn_nfo.prev_label
bsn_nfo.consecutive_match += 1
end
if bsn_nfo.consecutive_match ≥ consecutive_attractor_steps
# We've hit an existing attractor `consecutive_attractor_steps` times in a row
# so we assign the initial condition directly to the attractor
hit_att = ic_label + 1
cleanup_visited_cells!(bsn_nfo)
reset_basins_counters!(bsn_nfo)
bsn_nfo.return_code = :att_hit
return hit_att
end
bsn_nfo.prev_label = ic_label
bsn_nfo.return_code = :search
return 0
end
# This state is "searching for an attractor". It is the initial state.
if bsn_nfo.state == :att_search
if ic_label == 0
# unlabeled box, label it with current odd label and reset counter
bsn_nfo.basins[n] = bsn_nfo.visited_cell_label
# also keep track of visited cells. This makes it easier to clean
# up the basin array later!
push!(bsn_nfo.visited_cells, n) # keep track of visited cells
bsn_nfo.consecutive_match = 0
elseif ic_label == bsn_nfo.visited_cell_label
# hit a previously visited box with the current label, possible attractor?
bsn_nfo.consecutive_match += 1
end
# If we accumulated enough recurrences, we claim that we
# have found an attractor, and we switch to `:att_found`.
if bsn_nfo.consecutive_match >= consecutive_recurrences
bsn_nfo.basins[n] = bsn_nfo.current_att_label
store_attractor!(bsn_nfo, u)
bsn_nfo.state = :att_found
bsn_nfo.consecutive_match = 0
end
bsn_nfo.prev_label = ic_label
bsn_nfo.return_code = :search
return 0
end
# This state can only be reached from `:att_search`. It means we have
# enough recurrences to claim we have found an attractor.
# We then locate the attractor by recording enough cells.
if bsn_nfo.state == :att_found
if ic_label == bsn_nfo.current_att_label
# Visited a cell already labelled as new attractor; check `store_once_per_cell`
store_once_per_cell || store_attractor!(bsn_nfo, u)
elseif ic_label == 0 || ic_label == bsn_nfo.visited_cell_label
# Visited a cells that was not labelled as the new attractor
# label it and store it as part of the attractor
bsn_nfo.basins[n] = bsn_nfo.current_att_label
store_attractor!(bsn_nfo, u)
elseif iseven(ic_label) && ic_label ≠ bsn_nfo.current_att_label
# Visited a cell labelled as an *existing* attractor! We have
# attractors intersection in the grid! The algorithm can't handle this,
# so we throw an error.
error("""
During the phase of locating a new attractor, found via sufficient recurrences,
we encountered a cell of a previously-found attractor. This means that two
attractors intersect in the grid, or that the precision with which we find
and store attractors is not high enough. Either decrease the grid spacing,
or increase `consecutive_recurrences` (or both).
Index of cell that this occured at: $(n).
""")
end
# in the `:att_found` phase, the consecutive match is always increasing
bsn_nfo.consecutive_match += 1
if bsn_nfo.consecutive_match ≥ attractor_locate_steps
# We have recorded the attractor with sufficient accuracy.
# We now set the empty counters for the new attractor.
current_basin = bsn_nfo.current_att_label + 1
cleanup_visited_cells!(bsn_nfo)
bsn_nfo.visited_cell_label += 2
bsn_nfo.current_att_label += 2
reset_basins_counters!(bsn_nfo)
bsn_nfo.return_code = :new_att
# We return the label corresponding to the *basin* of the attractor
return current_basin
end
return 0
end
# We've hit a cell labelled as a basin of an existing attractor.
# Note, this clause can only trigger if the basin array is NOT sparse.
if bsn_nfo.state == :bas_hit
if bsn_nfo.prev_label == ic_label
bsn_nfo.consecutive_match += 1
else
bsn_nfo.consecutive_match = 0
end
if bsn_nfo.consecutive_match > consecutive_basin_steps
cleanup_visited_cells!(bsn_nfo)
reset_basins_counters!(bsn_nfo)
bsn_nfo.return_code = :bas_hit
return ic_label
end
bsn_nfo.prev_label = ic_label
return 0
end
# This state occurs when the dynamical system state is outside the grid
if bsn_nfo.state == :lost
bsn_nfo.consecutive_lost += 1
if bsn_nfo.consecutive_lost > consecutive_lost_steps || norm(u) > horizon_limit
cleanup_visited_cells!(bsn_nfo)
reset_basins_counters!(bsn_nfo)
# problematic IC: diverges or wanders outside the defined grid
bsn_nfo.return_code = :diverge
return -1
end
bsn_nfo.prev_label = ic_label
return 0
end
end
function store_attractor!(bsn_nfo::BasinsInfo{D, G, Δ, T}, u) where {D, G, Δ, T}
# bsn_nfo.current_att_label is the number of the attractor multiplied by two
attractor_id = bsn_nfo.current_att_label ÷ 2
V = SVector{D, T}
if haskey(bsn_nfo.attractors, attractor_id)
push!(bsn_nfo.attractors[attractor_id], V(u))
else
# initialize container for new attractor
bsn_nfo.attractors[attractor_id] = StateSpaceSet([V(u)])
end
end
function cleanup_visited_cells!(bsn_nfo::BasinsInfo)
old_label = bsn_nfo.visited_cell_label
basins = bsn_nfo.basins
while !isempty(bsn_nfo.visited_cells)
ind = pop!(bsn_nfo.visited_cells)
if basins[ind] == old_label
if basins isa SparseArray # The `if` clause is optimized away
delete!(basins.data, ind)
else # non-sparse
basins[ind] = 0 # 0 is the unvisited label / empty label
end
end
end
end
function reset_basins_counters!(bsn_nfo::BasinsInfo)
bsn_nfo.consecutive_match = 0
bsn_nfo.consecutive_lost = 0
bsn_nfo.prev_label = 0
bsn_nfo.state = :att_search
end
function update_finite_state_machine!(bsn_nfo, ic_label)
current_state = bsn_nfo.state
if current_state == :att_found
# this is a terminal state, once reached you don't get out
return
end
# Decide the next state based on the input cell
next_state = :undef
if ic_label == 0 || ic_label == bsn_nfo.visited_cell_label
# unlabeled box or previously visited box with the current label
next_state = :att_search
elseif iseven(ic_label)
# hit an attractor box
next_state = :att_hit
elseif ic_label == -1
# out of the grid
# remember that when out of the grid we do not reset the counter of other state
# since the trajectory can follow an attractor that spans outside the grid
next_state = :lost
elseif isodd(ic_label)
# hit an existing basin box
next_state = :bas_hit
end
# Take action if the state has changed.
if next_state != current_state
# The consecutive_match counter is reset when we switch states.
# However if we enter or leave the :lost state
# we do not reset the counter consecutive_match
# since the trajectory can follow an attractor
# that spans outside the grid
if current_state == :lost || next_state == :lost
bsn_nfo.consecutive_lost = 1
else
bsn_nfo.consecutive_match = 1
end
end
bsn_nfo.state = next_state
return
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 7765 | #####################################################################################
# Grid construction
#####################################################################################
struct RegularGrid{D, R <: AbstractRange} <: Grid
grid_steps::SVector{D, Float64}
grid_minima::SVector{D, Float64}
grid_maxima::SVector{D, Float64}
grid::NTuple{D, R}
end
function RegularGrid(grid::NTuple)
D = length(grid)
grid_steps = SVector{D,Float64}(step.(grid))
grid_maxima = SVector{D,Float64}(maximum.(grid))
grid_minima = SVector{D,Float64}(minimum.(grid))
return RegularGrid(grid_steps, grid_minima, grid_maxima, grid)
end
minmax_grid_extent(g::RegularGrid) = g.grid_minima, g.grid_maxima
mean_cell_diagonal(g::RegularGrid{D}) where {D} = norm(g.grid_steps)
struct IrregularGrid{D, T <: Tuple} <: Grid
grid::T
end
IrregularGrid(tuple::T) where {T} = IrregularGrid{length(tuple), T}(tuple)
minmax_grid_extent(g::IrregularGrid) = minmax_grid_extent(g.grid)
minmax_grid_extent(g::NTuple) = map(minimum, g), map(maximum, g)
function mean_cell_diagonal(g::NTuple)
steps = map(r -> mean(diff(r)), g)
return norm(steps)
end
mean_cell_diagonal(g::IrregularGrid) = mean_cell_diagonal(g.grid)
"""
SubdivisionBasedGrid(grid::NTuple{D, <:AbstractRange}, lvl_array::Array{Int, D})
Given a coarse `grid` tesselating the state space, construct a `SubdivisionBasedGrid`
based on the given level array `lvl_array` that should have the same dimension as `grid`.
The level array has non-negative integer values, with 0 meaning that the
corresponding cell of the coarse `grid` should not be subdivided any further.
Value `n > 0` means that the corresponding cell will be subdivided
in total `2^n` times (along each dimension), resulting in finer cells
within the original coarse cell.
"""
struct SubdivisionBasedGrid{D, R <: AbstractRange} <:Grid
grid_steps::Dict{Int, Vector{Int}}
grid_minima::SVector{D, Float64}
grid_maxima::SVector{D, Float64}
lvl_array::Array{Int, D}
grid::NTuple{D, R}
max_grid::NTuple{D, R}
end
minmax_grid_extent(g::SubdivisionBasedGrid) = g.grid_minima, g.grid_maxima
mean_cell_diagonal(g::SubdivisionBasedGrid) = mean_cell_diagonal(g.grid)
"""
subdivision_based_grid(ds::DynamicalSystem, grid; maxlevel = 4, q = 0.99)
Construct a grid structure [`SubdivisionBasedGrid`](@ref) that can be directly passed
as a grid to [`AttractorsViaRecurrences`](@ref). The input `grid` is an
originally coarse grid (a tuple of `AbstractRange`s).
The state space speed is evaluate in all cells of the `grid`. Cells with small speed
(when compared to the "max" speed) resultin in this cell being subdivided more.
To avoid problems with spikes in the speed, the `q`-th quantile of the velocities
is used as the "max" speed (use `q = 1` for true maximum).
The subdivisions in the resulting grid are clamped to at most value `maxlevel`.
This approach is designed for _continuous time_ systems in which different areas of
the state space flow may have significantly different velocity. In case of
originally coarse grids, this may lead [`AttractorsViaRecurrences`](@ref)
being stuck in some state space regions with
a small motion speed and false identification of attractors.
"""
function subdivision_based_grid(ds::DynamicalSystem, grid; maxlevel = 4, q = 0.99)
lvl_array = make_lvl_array(ds, grid, maxlevel, q)
return SubdivisionBasedGrid(grid, lvl_array)
end
function SubdivisionBasedGrid(grid::NTuple{D, <:AbstractRange}, lvl_array::Array{Int, D}) where {D}
unique_lvls = unique(lvl_array)
any(<(0), unique_lvls) && error("Level array cannot contain negative values!")
grid_steps = Dict{Int, Vector{Int}}()
for i in unique_lvls
grid_steps[i] = [length(axis)*2^i for axis in grid]
end
grid_maxima = SVector{D, Float64}(maximum.(grid))
grid_minima = SVector{D, Float64}(minimum.(grid))
function scale_axis(axis, multiplier)
new_length = length(axis) * (2^multiplier)
return range(first(axis), last(axis), length=new_length)
end
multiplier = maximum(keys(grid_steps))
scaled_axis = [scale_axis(axis, multiplier) for axis in grid]
max_grid = Tuple(scaled_axis)
return SubdivisionBasedGrid(grid_steps, grid_minima, grid_maxima, lvl_array, grid, max_grid)
end
function make_lvl_array(ds::DynamicalSystem, grid, maxlevel, q)
isdiscretetime(ds) && error("Dynamical system must be continuous time.")
indices = CartesianIndices(length.(grid))
f, p = dynamic_rule(ds), current_parameters(ds)
udummy = copy(current_state(ds))
velocities = zeros(length.(grid))
for ind in indices
u0 = Attractors.generate_ic_on_grid(grid, ind)
velocity = if !isinplace(ds)
f(u0, p, 0.0)
else
f(udummy, u0, p, 0.0)
udummy
end
speed = norm(velocity)
if isnan(speed)
velocities[ind] = Inf
else
velocities[ind] = speed
end
end
maxvel = quantile(filter(x -> x != Inf, velocities), q)
# large ratio means small velocity means high subdivision
ratios = maxvel ./ velocities
# subdivision is just the log2 of the ratio. We do this fancy
# computation because this way zeros are handled correctly
# (and we also clamp the values of the level array correctly in 0-maxlevel)
result = [round(Int,log2(clamp(x, 1, 2^maxlevel))) for x in ratios]
return result
end
#####################################################################################
# Mapping a state to a cartesian index according to the grid
#####################################################################################
function basin_cell_index(u, grid_nfo::RegularGrid)
D = length(grid_nfo.grid_minima) # compile-type deduction
@inbounds for i in eachindex(grid_nfo.grid_minima)
if !(grid_nfo.grid_minima[i] ≤ u[i] ≤ grid_nfo.grid_maxima[i])
return CartesianIndex{D}(-1)
end
end
# Snap point to grid
ind = @. round(Int, (u - grid_nfo.grid_minima)/grid_nfo.grid_steps) + 1
return CartesianIndex{D}(ind...)
end
function basin_cell_index(u, grid_nfo::IrregularGrid)
D = length(grid_nfo.grid) # compile-type deduction
for (axis, coord) in zip(grid_nfo.grid, u)
if coord < first(axis) || coord > last(axis)
return CartesianIndex{D}(-1)
end
end
cell_indices = map((x, y) -> searchsortedlast(x, y), grid_nfo.grid, u)
return CartesianIndex{D}(cell_indices...)
end
function basin_cell_index(u, grid_nfo::SubdivisionBasedGrid)
D = length(grid_nfo.grid) # compile-type deduction
initial_index = basin_cell_index(u, RegularGrid(SVector{D,Float64}(step.(grid_nfo.grid)), grid_nfo.grid_minima, grid_nfo.grid_maxima, grid_nfo.grid))
if initial_index == CartesianIndex{D}(-1)
return initial_index
end
cell_area = grid_nfo.lvl_array[initial_index]
grid_maxima = grid_nfo.grid_maxima
grid_minima = grid_nfo.grid_minima
grid_steps = grid_nfo.grid_steps
max_level = maximum(keys(grid_steps))
grid_step = (grid_maxima - grid_minima .+ 1) ./ grid_steps[cell_area]
ind = @. round(Int, (u - grid_minima)/grid_step, RoundDown) * (2^(max_level-cell_area)) + 1
return CartesianIndex{D}(ind...)
end
#####################################################################################
# Pretty printing
#####################################################################################
Base.show(io::IO, g::RegularGrid) = Base.show(io, g.grid)
Base.show(io::IO, g::IrregularGrid) = Base.show(io, g.grid)
function Base.show(io::IO, g::SubdivisionBasedGrid)
println(io, "SubdivisionBasedGrid with $(maximum(g.lvl_array)) subdivisions")
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2881 | # This file contains parts of the source from SparseArrayKit.jl, which in all honestly
# is very similar to how we used to compute histograms in the old Entropies.jl package,
# but nevertheless here is the original license:
# MIT License
# Copyright (c) 2020 Jutho Haegeman <[email protected]> and Maarten Van Damme <[email protected]>
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
#########################################################################################
# Basic struct
#########################################################################################
struct SparseArray{T,N} <: AbstractArray{T,N}
data::Dict{CartesianIndex{N},T}
dims::NTuple{N,Int64}
end
function SparseArray{T,N}(::UndefInitializer, dims::Dims{N}) where {T,N}
return SparseArray{T,N}(Dict{CartesianIndex{N},T}(), dims)
end
SparseArray{T}(::UndefInitializer, dims::Dims{N}) where {T,N} =
SparseArray{T,N}(undef, dims)
SparseArray{T}(::UndefInitializer, dims...) where {T} = SparseArray{T}(undef, dims)
Base.empty!(x::SparseArray) = empty!(x.data)
Base.size(a::SparseArray) = a.dims
#########################################################################################
# Indexing
#########################################################################################
@inline function Base.getindex(a::SparseArray{T,N}, I::CartesianIndex{N}) where {T,N}
return get(a.data, I, zero(T))
end
Base.@propagate_inbounds Base.getindex(a::SparseArray{T,N}, I::Vararg{Int,N}) where {T,N} =
getindex(a, CartesianIndex(I))
@inline function Base.setindex!(a::SparseArray{T,N}, v, I::CartesianIndex{N}) where {T,N}
a.data[I] = v
return v
end
Base.@propagate_inbounds function Base.setindex!(
a::SparseArray{T,N}, v, I::Vararg{Int,N}) where {T,N}
return setindex!(a, v, CartesianIndex(I))
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 6779 | export MatchByBasinEnclosure
"""
MatchByBasinEnclosure(; kw...) <: IDMatcher
A matcher that matches attractors by whether they are enclosed in
the basin of a new attractor or not.
## Keyword arguments
- `ε = nothing`: distance threshold given to [`AttractorsViaProximity`](@ref).
If `nothing`, it is estimated as a quarter of the minimum distance of centroids
(in contrast to the default more accurate estimation in [`AttractorsViaProximity`](@ref)).
- `Δt = 1, consecutive_lost_steps = 1000`: also given to [`AttractorsViaProximity`](@ref).
We have not yet decided what should happen to attractors that did not converge to one of the current attractors
within this number of steps. At the moment they
get assigned the next available free ID but this may change in future releases.
- `distance = Centroid()`: metric to estimate distances between state space sets
in case there are co-flowing attractors, see below.
- `seeding = A -> A[end]`: how to select a point from the attractor to see if
it is enclosed in the basin of a new attractor.
## Description
An attractor `A₋` is a set in a state space that occupies a particular region
(or, a single point, if it is a fixed point).
This region is always within the basin of attraction of said attractor.
When the parameter of the dynamical system is incremented,
the attractors `A₊` in the new parameter have basins that may have changed in shape and size.
The new attractor `A₊` is "matched" (i.e., has its ID changed)
to the old attractor `A₋` attractor if `A₋` is located inside the basin of attraction of `A₊`.
To see if `A₋` is in the basin of `A₊`, we first pick a point from `A₋` using the `seeding`
keyword argument. By default this is the last point on the attractor, but it could be anything
else, including the centroid of the attractor (`mean(A)`).
This point is given as an initial condition to an [`AttractorsViaProximity`](@ref) mapper
that maps initial conditions to the `₊` attractors when
the trajectories from the initial conditions are `ε`-close to the `₊` attractors.
There can be the situation where multiple `₋` attractors converge to the same `₊`
attractor, which we call "coflowing attractors". In this scenario matching is prioritized
for the `₋` attractor that is closest to the `₊` in terms of state space set distance,
which is estimated with the `distance` keyword, which can be anything
[`MatchBySSSetDistance`](@ref) accepts. The closest `₊` attractor gets the
ID of the `₋` closest attractor that converge to it.
Basin enclosure is a concept similar to "basin (in)stability" in [Ritchie2023](@cite):
attractors that quantify as "basin stable" are matched.
"""
@kwdef struct MatchByBasinEnclosure{E, D, S, T} <: IDMatcher
ε::E = nothing
distance::D = Centroid()
seeding::S = A -> A[end]
Δt::T = 1
consecutive_lost_steps::Int = 1000
end
function matching_map(
current_attractors, prev_attractors, matcher::MatchByBasinEnclosure;
ds, p, pprev = nothing, next_id = next_free_id(current_attractors, prev_attractors)
)
if matcher.ε === nothing
e = ε_from_centroids(current_attractors)
else
e = matcher.ε
end
set_parameters!(ds, p)
proximity = AttractorsViaProximity(ds, current_attractors, e;
horizon_limit = Inf, Ttr = 0, consecutive_lost_steps = matcher.consecutive_lost_steps
)
# we start building the "flow" map mapping previous attractors
# to where they flowed to in current attractors
# (notice that `proximity(u)` returns IDs of current attractors)
flow = Dict(k => proximity(matcher.seeding(A)) for (k, A) in prev_attractors)
# of course, the matching map is the inverse of `flow`
rmap = Dict{Int, Int}()
# but we need to take care of diverging and co-flowing attractors.
# Let's start with diverging ones
for (old_ID, new_ID) in flow
if new_ID < 0 # diverged attractors get -1 ID
# but here we assign them just to the next available integer
rmap[new_ID] = next_id
next_id += 1
delete!(flow, old_ID) # and remove from flow map
end
end
# next up are the co-flowing attractors
allnewids = keys(current_attractors) #needed because flow only includes new ids that prev attractors flowed onto
grouped_flows = _grouped_flows(flow, allnewids) #map all current ids to prev ids that flowed onto them (if the att is new, no prev ids flowed, and the corresponding entry is empty)
# notice the keys of `grouped_flows` are new IDs, same as with `rmap`.
for (new_ID, old_flowed_to_same) in grouped_flows
if length(old_flowed_to_same) == 0 # none of the old IDs converged to the current `new_ID`
rmap[new_ID] = next_id #necessary to make rmap complete and avoid skipping keys
next_id += 1
elseif length(old_flowed_to_same) == 1
rmap[new_ID] = only(old_flowed_to_same)
else # need to resolve coflowing using distances
a₊ = Dict(new_ID => current_attractors[new_ID])
a₋ = Dict(old_ID => prev_attractors[old_ID] for old_ID in old_flowed_to_same)
ssmatcher = MatchBySSSetDistance(; distance = matcher.distance)
matched_rmap = matching_map(a₊, a₋, ssmatcher)
# this matcher has only one entry, so we use it to match
# (we don't care what happens to the rest of the old_IDs, as the `rmap`
# only cares about what adjustments need to happen to the new_IDs)
new_ID, old_ID = only(matched_rmap)# our main `rmap`
rmap[new_ID] = old_ID
end
end
return rmap
end
function ε_from_centroids(attractors::AbstractDict)
if length(attractors) == 1 # `attractors` has only 1 attractor
attractor = first(attractors)[2] # get the single attractor
mini, maxi = minmaxima(attractor)
ε = sqrt(sum(abs, maxi .- mini))/10
if ε == 0
throw(ArgumentError("""
Computed `ε = 0` in automatic estimation for `AttractorsViaFeaturizing`, probably because there is
only a single attractor that also is a single point. Please provide `ε` manually.
"""))
end
return ε
end
# otherwise compute cross-distances
distances = setsofsets_distances(attractors, attractors, Centroid())
alldists = sort!(vcat([collect(values(d)) for (k,d) in distances]...))
filter!(!iszero, alldists)
return minimum(alldists)/4
end
# group flows so that all old IDs that go to same new ID are in one vector
# i.e., new id => [prev ids that flowed to new id]
function _grouped_flows(flows, allnewids) # separated into
grouped = Dict(newid=>[k for (k,v) in flows if v==newid] for newid in allnewids)
return grouped
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 4167 | export MatchByBasinOverlap
"""
MatchByBasinOverlap(threshold = Inf)
A matcher that matches IDs given full basins of attraction.
## Description
This matcher cannot be used in with the generic global continuation
method of [`AttractorSeedContinueMatch`](@ref).
This matcher matches IDs of attractors whose basins of attraction before and after `b₋, b₊`
have the most overlap (in pixels). This overlap is normalized in 0-1 (with 1 meaning
100% of a basin in `b₋` is overlaping with some other basin in `b₊`).
Therefore, the values this matcher compares are _full basins of attraction_,
not attractors themselves (hence why it can't be given to [`AttractorSeedContinueMatch`](@ref)).
Rather, you may use this matcher with [`matching_map`](@ref).
The `threshold` can dissallow matching between basins that do not have enough overlap.
Basins whose overlap is less than `1/threshold` are guaranteed
to get assined different IDs.
For example: for `threshold = 2` basins that have ≤ 50% overlap get
different IDs guaranteed. By default, there is no threshold.
The information of the basins of attraction is typically an `Array`,
i.e., the direct output of [`basins_of_attraction`](@ref).
For convenience, as well as backwards compatibility, when using
[`matching_map`](@ref) with this mapper you may provide two `Array`s `b₊, b₋`
representing basins of attraction after and before, and the conversion to dictionaries
will happen internally as it is supposed to.
To replace the `IDs` in `b₊` given the replacement map just call `replace!(b₊, rmap...)`,
or use the in-place version [`matching_map!`](@ref) directly.
A lower-level input for this matcher in [`matching_map`](@ref)
can be dictionaries mapping IDs to vectors of cartesian indices,
where the indices mean which parts of the state space belong to which ID
"""
struct MatchByBasinOverlap
threshold::Float64
end
MatchByBasinOverlap() = MatchByBasinOverlap(Inf)
"""
matching_map(b₊::AbstractArray, b₋::AbstractArray, matcher::MatchByBasinOverlap)
Special case of `matching_map` where instead of having as input dictionaries
mapping IDs to values, we have `Array`s which represent basins of
attraction and whose elements are the IDs.
See [`MatchByBasinOverlap`](@ref) for how matching works.
"""
function matching_map(b₊::AbstractArray, b₋::AbstractArray, matcher::MatchByBasinOverlap; kw...)
a₊, a₋ = _basin_to_dict.((b₊, b₋))
matching_map(a₊, a₋, matcher; kw...)
end
function matching_map!(b₊::AbstractArray, b₋::AbstractArray, matcher::MatchByBasinOverlap; kw...)
rmap = matching_map(b₊, b₋, matcher; kw...)
replace!(b₊, rmap...)
return rmap
end
# actual implementation
function matching_map(a₊::AbstractDict, a₋, matcher::MatchByBasinOverlap; kw...)
# input checks
if !(valtype(a₊) <: Vector{<:CartesianIndex})
throw(ArgumentError("Incorrect input given. For matcher `MatchByBasinOverlap`,
the dictionaries values should be vectors of `CartesianIndex`."))
end
if sum(length, values(a₊)) ≠ sum(length, values(a₋))
throw(ArgumentError("The sizes of the two basins to be matched must be the same."))
end
# The source code of this matcher is beautiful. It computes a "dissimilarity"
# metric, which is the inverse of the basin overlaps. This "dissimilarity" is
# just a "distance" between basins of attraction. Thus, it actually
# propagates this "distance" to the matching code of `MatchBySSSetDistance`!
keys₊, keys₋ = keys.((a₊, a₋))
distances = Dict{eltype(keys₊), Dict{eltype(keys₋), Float64}}()
for i in keys₊
Bi = a₊[i]
d = valtype(distances)() # d is a dictionary of distances
# Compute normalized overlaps of each basin with each other basis
for j in keys₋
Bj = a₋[j]
overlap = length(Bi ∩ Bj)/length(Bj)
d[j] = 1 / overlap # distance is inverse overlap
end
distances[i] = d
end
_matching_map_distances(keys₊, keys₋, distances, matcher.threshold; kw...)
end
function _basin_to_dict(b::AbstractArray{Int})
ukeys = unique(b)
d = Dict(k => findall(isequal(k), b) for k in ukeys)
return d
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 9035 | # Matching is part of an extendable interface. However, as we have not been able to
# create more matchers than just the `MatchBySSSetDistance`, we do not expose this
# interface to the users. Perhaps in the future we will expose this!
# For now, the only parts exposed are these functions:
export matching_map, matching_map!, match_sequentially!, IDMatcher
# all of which take as input the treshold and distance of the
# `MatchBySSSetDistance` matcher.
"""
IDMatcher
Supertype of all "matchers" that match can IDs labelling attractors.
Currently available matchers:
- [`MatchBySSSetDistance`](@ref)
- [`MatchByBasinEnclosure`](@ref)
- [`MatchByBasinOverlap`](@ref)
Matchers implement an extendable interface based on the function [`matching_map`](@ref).
This function is used by the higher level function [`match_sequentially!`](@ref),
which can be called after any call to a global continuation to match attractors
differently, if the matching used originally during the continuation was not the best.
"""
abstract type IDMatcher end
"""
matching_map(
a₊::Dict, a₋::Dict, matcher;
ds::DynamicalSystem, p, pprev, next_id
) → rmap
Given dictionaries `a₊, a₋` mapping IDs to values,
return a _replacement map_: a dictionary mapping the IDs (keys) in dictionary `a₊`
to IDs (keys) in dictionary `a₋`, so that
so that values in `a₊` that are the "closest" to values in `a₋` get assigned the
same key as in `a₋`. In this way keys of `a₊` are "matched" to keys of `a₋`.
Use [`swap_dict_keys`](@ref) to apply `rmap` to `a₊`
or to other dictionaries with same keys as `a₊`.
How matching happens, i.e., how "closeness" is defined, depends on the algorithm `matcher`.
The values contained in `a₊, a₋` can be anything supported by `matcher`.
Within Attractors.jl they are typically `StateSpaceSet`s representing attractors.
Typically the +,- mean after and before some change of parameter of a dynamical system.
## Keyword arguments
- `ds`: the dynamical system that generated `a₊, a₋`.
- `p, pprev`: the parameters corresponding to `a₊, a₋`. Both need to be iterables mapping
parameter index to parameter value (such as `Dict, Vector{Pair}`, etc., so whatever
can be given as input to `DynamicalSystems.set_parameters!`).
- `next_id = next_free_id(a₊, a₋)`: the ID to give to values of `a₊` that cannot be
matched to `a₋` and hence must obtain a new unique ID.
Some matchers like [`MatchBySSSetDistance`](@ref) do not utilize `ds, p, pprev` in any way
while other matchers like [`MatchByBasinEnclosure`](@ref) do, and those require
expliticly giving values to `ds, p, pprev` as their default values
is just `nothing`.
"""
function matching_map(a₊, a₋, matcher::IDMatcher; kw...)
# For developers: a private keyword `next_id` is also given to `matching_map`
# that is utilized in the `match_sequentially!` function.
throw(ArgumentError("Not implemented for $(typeof(matcher))"))
end
"""
matching_map!(a₊, a₋, matcher; kw...) → rmap
Convenience function that first calls [`matching_map`](@ref) and then
replaces the IDs in `a₊` with this `rmap`.
"""
function matching_map!(a₊::AbstractDict, a₋, matcher::IDMatcher; kw...)
rmap = matching_map(a₊, a₋, matcher; kw...)
swap_dict_keys!(a₊, rmap)
return rmap
end
"""
match_sequentially!(dicts::Vector{Dict{Int, Any}}, matcher::IDMatcher; kw...)
Match the `dicts`, a vector of dictionaries mapping IDs (integers) to values,
according to the given `matcher` by sequentially applying the
[`matching_map`](@ref) function to all elements of `dicts` besides the first one.
In the context of Attractors.jl `dicts` are typically dictionaries mapping
IDs to attractors (`StateSpaceSet`s), however the function is generic and would
work for any values that `matcher` works with.
Return `rmaps`, which is a vector of dictionaries.
`rmaps[i]` contains the [`matching_map`](@ref) for `attractors[i+1]`,
i.e., the pairs of `old => new` IDs.
## Keyword arguments
- `pcurve = nothing`: the curve of parameters along which the continuation occured,
from which to extract the `p, pprev` values given to [`matching_map`](@ref).
See [`global_continuation`](@ref) if you are unsure what this means.
- `ds = nothing`: propagated to [`matching_map`](@ref).
- `retract_keys::Bool = true`: If `true` at the end the function will "retract" keys (i.e., make the
integers smaller integers) so that all unique IDs
are the 1-incremented positive integers. E.g., if the IDs where 1, 6, 8, they will become
1, 2, 3. The special ID -1 is unaffected by this.
- `use_vanished = false`: If `use_vanised = true`, then
IDs (and their corresponding sets) that existed before but have vanished are kept in "memory"
when it comes to matching: the current dictionary values (the attractor sets) are compared
to the latest instance of all values that have ever existed, each with a unique ID,
and get matched to their closest ones. The value of this keyword is obtained from the `matcher`.
"""
function match_sequentially!(
attractors::AbstractVector{<:Dict}, matcher::IDMatcher;
retract_keys = true, use_vanished = _use_vanished(matcher),
kw... # parameter and ds keywords
)
# this generic implementation works for any matcher!!!
# the matcher also provides the `use_vanished` keyword if it makes sense!
rmaps = Dict{Int,Int}[]
if !use_vanished # matchers implement this!
rmaps = _rematch_ignored!(attractors, matcher; kw...)
else
rmaps = _rematch_with_past!(attractors, matcher; kw...)
end
if retract_keys
retracted = retract_keys_to_consecutive(attractors) # already matched input
for (rmap, attrs) in zip(rmaps, attractors)
swap_dict_keys!(attrs, retracted)
# for `rmap` the situation is more tricky, because we have to change the
# value of the _values_ of the dictionary, not the keys!
for (k, v) in rmap
if v ∈ keys(retracted)
# so we make that the replacement map points to the
# retracted key instead of whatever it pointed to originally,
# if this key exists in the retracted mapping
rmap[k] = retracted[v]
end
end
end
# `attractors` have 1 more element than `rmaps`
swap_dict_keys!(attractors[end], retracted)
end
return rmaps
end
"""
match_sequentially!(continuation_quantity::Vector{Dict}, rmaps::Vector{Dict})
Do the same as in `match_sequentially!` above, now given the vector of matching maps,
and for any arbitrary quantity that has been tracked in the global_continuation.
`continuation_quantity` can for example be `fractions_cont` from [`global_continuation`](@ref).
"""
function match_sequentially!(continuation_quantity::AbstractVector{<:Dict}, rmaps::Vector{Dict{Int, Int}})
if length(rmaps) ≠ length(continuation_quantity) - 1
throw(ArgumentError("the matching maps should be 1 less than the global_continuation quantities"))
end
for (i, rmap) in enumerate(rmaps)
quantity = continuation_quantity[i+1]
swap_dict_keys!(quantity, rmap)
end
return rmaps
end
# Concrete implementation of `match_sequentially!`:
function _rematch_ignored!(attractors_cont, matcher;
ds = nothing, pcurve = eachindex(attractors_cont),
)
next_id = 1
rmaps = Dict{keytype(attractors_cont[1]), keytype(attractors_cont[1])}[]
for i in 1:length(attractors_cont)-1
a₊, a₋ = attractors_cont[i+1], attractors_cont[i]
p, pprev = pcurve[i+1], pcurve[i]
# If there are no attractors, skip the matching
(isempty(a₊) || isempty(a₋)) && continue
# Here we always compute a next id. In this way, if an attractor disappears
# and reappears, it will get a different (incremented) ID as it should!
next_id_a = max(maximum(keys(a₊)), maximum(keys(a₋)))
next_id = max(next_id, next_id_a) + 1
rmap = matching_map!(a₊, a₋, matcher; next_id, ds, p, pprev)
push!(rmaps, rmap)
end
return rmaps
end
function _rematch_with_past!(attractors_cont, matcher;
ds = nothing, pcurve = eachindex(attractors_cont),
)
# this dictionary stores all instances of previous attractors and is updated
# at every step. It is then given to the matching function as if it was
# the current attractors
latest_ghosts = deepcopy(attractors_cont[1])
rmaps = Dict{keytype(attractors_cont[1]), keytype(attractors_cont[1])}[]
for i in 1:length(attractors_cont)-1
a₊, a₋ = attractors_cont[i+1], attractors_cont[i]
p, pprev = pcurve[i+1], pcurve[i]
# update ghosts
for (k, A) in a₋
latest_ghosts[k] = A
end
rmap = matching_map!(a₊, latest_ghosts, matcher; pprev, p, ds)
push!(rmaps, rmap)
end
return rmaps
end
_use_vanished(matcher) = false
include("basin_overlap.jl")
include("sssdistance.jl")
include("basin_enclosure.jl") | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 5001 | export MatchBySSSetDistance
"""
MatchBySSSetDistance(; distance = Centroid(), threshold = Inf, use_vanished = false)
A matcher type that matches IDs by the distance of their corresponding state space sets.
## Keyword arguments
- `distance = Centroid()`: distance to match by, given to [`setsofsets_distances`](@ref).
- `threshold = Inf`: sets with distance larger than the `threshold` are guaranteed
to not be mapped to each other.
- `use_vanished = !isinf(threshold)`: value of the keyword `use_vanished` when
used in [`match_sequentially!`](@ref).
## Description
In this matcher the values compared are [`StateSpaceSet`](@ref)s
which in most cases represent attractors in the state space, but may also
represent any other set such as a group of features.
Here is how this matcher works:
(recall in this conversation that sets/attractors are stored in dictionaries,
mapping keys/IDs to the sets, and we want to match keys in the "new" dictionary (`a₊`)
to those in the "old" dictionary (`a₋`)).
The distance between all possible pairs of sets between the "old" sets and "new" sets
is computed as a formal distance between sets.
This is controlled by the `distance` option, itself given to the lower-level
[`setsofsets_distances`](@ref) function, so `distance` can be whatever that function accepts.
That is, one of [`Centroid`](@ref), [`Hausdorff`](@ref), [`StrictlyMinimumDistance`](@ref),
or any arbitrary user-provided function `f` that given two sets `f(A, B)` it returns a
positive number (their distance).
Sets (in particular, their corresponding IDs) are then matched according to this distance.
First, all possible ID pairs (old, new) are sorted according to the distance of their corresponding sets.
The pair with smallest distance is matched. IDs in matched pairs are removed from the
matching pool to ensure a unique mapping. Then, the next pair with least
remaining distance is matched, and the process repeats until all pairs are exhausted.
Additionally, you can provide a `threshold` value. If the distance between two sets
is larger than this `threshold`, then it is guaranteed that the two sets will get assigned
different ID in the replacement map, and hence, the set in `a₊` gets the next available
integer as its ID.
"""
@kwdef struct MatchBySSSetDistance{M, T<:Real} <: IDMatcher
distance::M = Centroid()
threshold::T = Inf
use_vanished::Bool = !isinf(threshold)
end
_use_vanished(m::MatchBySSSetDistance) = m.use_vanished
function matching_map(a₊::AbstractDict, a₋::AbstractDict, matcher::MatchBySSSetDistance;
kw...
)
distances = setsofsets_distances(a₊, a₋, matcher.distance)
keys₊, keys₋ = sort.(collect.(keys.((a₊, a₋))))
_matching_map_distances(keys₊, keys₋, distances::Dict, matcher.threshold; kw...)
end
function _matching_map_distances(keys₊, keys₋, distances::Dict, threshold;
next_id = next_free_id(keys₊, keys₋), kw... # rest of keywords aren't used.
)
# Transform distances to sortable collection. Sorting by distance
# ensures we prioritize the closest matches
sorted_keys_with_distances = Tuple{Int, Int, Float64}[]
for i in keys(distances)
for j in keys(distances[i])
push!(sorted_keys_with_distances, (i, j, distances[i][j]))
end
end
sort!(sorted_keys_with_distances; by = x -> x[3])
# Iterate through distances, find match with least distance, and "remove" (skip)
# all remaining same indices a'la Eratosthenis sieve
# In the same loop we match keys according to distance of values,
# but also ensure that keys that have too high of a value distance are guaranteed
# to have different keys, and ensure that there is unique mapping happening!
rmap = Dict{eltype(keys₊), eltype(keys₋)}()
done_keys₊ = eltype(keys₊)[] # stores keys of a₊ already processed
used_keys₋ = eltype(keys₋)[] # stores keys of a₋ already used
for (oldkey, newkey, dist) in sorted_keys_with_distances
# used keys can't be re-used to match again
(oldkey ∈ done_keys₊ || newkey ∈ used_keys₋) && continue
if dist < threshold
# If the distance is small enough, we store the "new" key
# in the replacement map (see after `if`), and we also
# ensure that this new key is marked as "used"
push!(used_keys₋, newkey)
else
# If the distance is too large, we assign a new key
# (notice that this assumes the sorting by distance we did above,
# otherwise it wouldn't work!)
newkey = next_id
next_id += 1
end
push!(done_keys₊, oldkey)
rmap[oldkey] = newkey
end
# if not all keys were processed, we map them to the next available integers
if length(done_keys₊) ≠ length(keys₊)
unprocessed = setdiff(collect(keys₊), done_keys₊)
for oldkey in unprocessed
rmap[oldkey] = next_id
next_id += 1
end
end
return rmap
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 12694 | using BlackBoxOptim: bboptimize, best_candidate
using Random: GLOBAL_RNG
import LinearAlgebra
export minimal_fatal_shock, MFSBruteForce, MFSBlackBoxOptim
export excitability_threshold
"""
minimal_fatal_shock(mapper::AttractorMapper, u0, search_area, algorithm; kw...)
Return the _minimal fatal shock_ (also known as _excitability threshold_
or _stability threshold_) for the initial point `u0` according to the
specified `algorithm` given a `mapper` that satisfies the `id = mapper(u0)` interface
(see [`AttractorMapper`](@ref) if you are not sure which mappers do that).
The output `mfs` is a vector like `u0`.
The `mapper` contains a reference to a [`DynamicalSystem`](@ref).
The options for `algorithm` are: [`MFSBruteForce`](@ref) or [`MFSBlackBoxOptim`](@ref).
For high dimensional systems [`MFSBlackBoxOptim`](@ref) is likely more accurate.
The `search_area` dictates the state space range for the search of the `mfs`.
It can be a 2-tuple of (min, max) values, in which case the same values are used
for each dimension of the system in `mapper`. Otherwise, it can be a vector of 2-tuples,
each for each dimension of the system. The search area is defined w.r.t. to `u0`
(i.e., it is the search area for perturbations of `u0`).
An alias to `minimal_fatal_shock` is `excitability_threshold`.
## Keyword arguments
- `metric = LinearAlgebra.norm`: a metric function that gives the norm of a perturbation vector.
This keyword is ignored for the [`MFSBruteForce`](@ref) algorithm.
- `target_id = nothing`: when not `nothing`, it should be an integer or a vector of
integers corresponding to target attractor label(s).
Then, the MFS is estimated based only on perturbations that lead to the target
attractor(s).
## Description
The minimal fatal shock is defined as the smallest-norm perturbation of the initial
point `u0` that will lead it a different basin of attraction than the one it was originally in.
This alternative basin is not returned, do `mapper(u0 .+ mfs)` if you need the ID.
The minimal fatal shock has many names. Many papers computed this quantity without explicitly
naming it, or naming it something simple like "distance to the threshold".
The first work that proposed the concept as a nonlocal stability quantifier
was by [Klinshov2015](@cite) with the name "stability threshold".
Here we use the name of [Halekotte2020](@cite).
Our implementation is generic and works for _any_ dynamical system,
using either black box optimization or brute force searching approaches
and the unique interface of Attractors.jl for mapping initial conditions to attractors.
In contrast to [Klinshov2015](@cite) or [Halekotte2020](@cite), our implementation
does not place any assumptions on the nature of the dynamical system, or whether
the basin boundaries are smooth.
The _excitability threshold_ is a concept nearly identical, however, instead of looking
for a perturbation that simply brings us out of the basin, we look for the smallest
perturbation that brings us into specified basin(s). This is enabled via the keyword
`target_id`.
"""
function minimal_fatal_shock(mapper::AttractorMapper, u0, search_area, algorithm;
metric = LinearAlgebra.norm, target_id = nothing
)
dim = length(u0)
if typeof(search_area) <: Tuple{<:Real,<:Real}
search_area = [search_area for _ in 1:dim]
elseif length(search_area) != dim
error("Input search area does not match the dimension of the system")
end
# generate a function that returns `true` for ids that that are in the target basin
id_u0 = mapper(u0)
idchecker = id_check_function(id_u0, target_id)
return _mfs(algorithm, mapper, u0, search_area, idchecker, metric)
end
const excitability_threshold = minimal_fatal_shock
id_check_function(id::Int, ::Nothing) = i -> i != id
function id_check_function(id::Integer, ti::Integer)
id == ti && error("target id and attractor id of u0 are the same.")
return i -> i == ti
end
function id_check_function(id::Integer, ti::AbstractVector{<:Integer})
id ∈ ti && error("attractor id of u0 belongs in target ids.")
return i -> i ∈ ti
end
"""
MFSBruteForce(; kwargs...)
The brute force randomized search algorithm used in [`minimal_fatal_shock`](@ref).
It consists of
two steps: random initialization and sphere radius reduction. On the first step,
the algorithm generates random perturbations within the search area and records
the perturbation that leads to a different basin but with the smallest magnitude.
With this
obtained perturbation it proceeds to the second step. On the second step, the algorithm
generates random perturbations on the surface of the hypersphere with radius equal to the
norm of the perturbation found in the first step.
It reduces the radius of the hypersphere and continues searching for the better result
with a smaller radius. Each time a better result is found, the radius is reduced further.
The algorithm records the perturbation with smallest radius that leads to a different basin.
Because this algorithm is based on hyperspheres, it assumes the Euclidean norm as the metric.
## Keyword arguments
- `initial_iterations = 10000`: number of random perturbations to try in the first step of the
algorithm.
- `sphere_iterations = 10000`: number of steps while initializing random points on hypersphere and
decreasing its radius.
- `sphere_decrease_factor = 0.999` factor by which the radius of the hypersphere is decreased
(at each step the radius is multiplied by this number). Number closer to 1 means
more refined accuracy
"""
Base.@kwdef struct MFSBruteForce
initial_iterations::Int64 = 10000
sphere_iterations::Int64 = 10000
sphere_decrease_factor::Float64 = 0.999
end
function _mfs(algorithm::MFSBruteForce, mapper, u0, search_area, idchecker, _metric)
metric = LinearAlgebra.norm
algorithm.sphere_decrease_factor ≥ 1 && error("Sphere decrease factor cannot be ≥ 1.")
dim = length(u0)
best_shock, best_dist = crude_initial_radius(
mapper, u0, search_area, idchecker, metric, algorithm.initial_iterations
)
best_shock, best_dist = mfs_brute_force(
mapper, u0, best_shock, best_dist, dim, idchecker, metric,
algorithm.sphere_iterations, algorithm.sphere_decrease_factor
)
return best_shock
end
"""
This function generates a random perturbation of the initial point `u0` within
specified "search_area" and checks if it is in the same basin of attraction.
It does so by generating a random vector of length dim and then adding it to u0.
If the perturbation is not in the same basin of attraction, it calculates the norm
of the perturbation and compares it to the best perturbation found so far.
If the norm is smaller, it updates the best perturbation found so far.
It repeats this process total_iterations times and returns the best perturbation found.
"""
function crude_initial_radius(mapper::AttractorMapper, u0, search_area, idchecker, metric, total_iterations)
best_dist = Inf
region = StateSpaceSets.HRectangle([s[1] for s in search_area], [s[2] for s in search_area])
generator, _ = statespace_sampler(region)
best_shock = copy(generator())
shock = copy(best_shock)
for _ in 1:total_iterations
perturbation = generator()
@. shock = perturbation + u0
new_id = mapper(shock)
if idchecker(new_id)
dist = metric(perturbation)
if dist < best_dist
best_dist = dist
best_shock .= perturbation
end
end
end
return best_shock, best_dist
end
"""
This function works on the results obtained by `crude_initial_radius`. It starts from
the best shock found so far and tries to find a better one by continuously reducing
the radius of the sphere on the surface of which it generates random perturbations.
If perturbation with the same basin of attraction is found, it updates the best shock found
so far and reduces the radius of the sphere. It repeats this process total_iterations times
and returns the best perturbation found.
"""
function mfs_brute_force(mapper::AttractorMapper, u0,
best_shock, best_dist, dim, idchecker, metric,
total_iterations, sphere_decrease_factor
)
temp_dist = best_dist*sphere_decrease_factor
region = HSphereSurface(temp_dist, dim)
generator, = statespace_sampler(region)
i = 0
new_shock = zeros(dim)
while i < total_iterations
perturbation = generator()
@. new_shock = perturbation + u0
new_id = mapper(new_shock)
# if perturbation leading to another basin:
if idchecker(new_id)
# record best
best_shock .= perturbation
best_dist = temp_dist
# update radius
temp_dist = temp_dist*sphere_decrease_factor
region = HSphereSurface(temp_dist, dim)
generator, = statespace_sampler(region)
end
i += 1
end
return best_shock, best_dist
end
"""
MFSBlackBoxOptim(; kwargs...)
The black box derivative-free optimization algorithm used in [`minimal_fatal_shock`](@ref).
## Keyword arguments
- `guess = nothing`: a initial guess for the minimal fatal shock given to the
optimization algorithm. If not `nothing`, `random_algo` below is ignored.
- `max_steps = 10000`: maximum number of steps for the optimization algorithm.
- `penalty = 1000.0`: penalty value for the objective function for perturbations that do
not lead to a different basin of attraction. This value is added to the norm of the
perturbation and its value should be much larger than the typical sizes of the basins of
attraction.
- `print_info`: boolean value, if true, the optimization algorithm will print information on
the evaluation steps of objective function, `default = false`.
- `random_algo = MFSBruteForce(100, 100, 0.99)`: an instance of [`MFSBruteForce`](@ref)
that can be used to provide an initial guess.
- `bbkwargs = NamedTuple()`: additional keyword arguments propagated to
`BlackBoxOptim.bboptimize` for selecting solver, accuracy, and more.
## Description
The algorithm uses BlackBoxOptim.jl and a penalized objective function to minimize.
y function used as a constraint function.
So, if we hit another basin during the search we encourage the algorithm otherwise we
punish it with some penalty. The function to minimize is (besides some details):
```julia
function mfs_objective(perturbation, u0, mapper, penalty)
dist = norm(perturbation)
if mapper(u0 + perturbation) == mapper(u0)
# penalize if we stay in the same basin:
return dist + penalty
else
return dist
end
end
```
Using an initial guess can be beneficial to both performance and accuracy,
which is why the output of a crude [`MFSBruteForce`](@ref) is used to provide a guess.
This can be disabled by either passing a `guess` vector explicitly or
by giving `nothing` as `random_algo`.
"""
Base.@kwdef struct MFSBlackBoxOptim{G, RA, BB}
guess::G = nothing
max_steps::Int64 = 10_000
penalty::Float64 = 0.999
print_info::Bool = false
random_algo::RA = MFSBruteForce(100, 100, 0.99)
bbkwargs::BB = NamedTuple()
end
function _mfs(algorithm::MFSBlackBoxOptim, mapper, u0, search_area, idchecker, metric)
function objective_function(perturbation)
return mfs_objective(perturbation, u0, idchecker, metric, mapper, algorithm.penalty)
end
dim = length(u0)
if algorithm.print_info == true
TraceMode = :compact
else
TraceMode = :silent
end
if isnothing(algorithm.random_algo) && isnothing(algorithm.guess)
result = bboptimize(objective_function;
MaxSteps = algorithm.max_steps, SearchRange = search_area,
NumDimensions = dim, TraceMode
)
else
if !isnothing(algorithm.guess)
guess = algorithm.guess
else
guess = minimal_fatal_shock(mapper, u0, search_area, algorithm.random_algo)
end
result = bboptimize(objective_function, guess;
MaxSteps = algorithm.max_steps,
SearchRange = search_area,
NumDimensions = dim, TraceMode,
algorithm.bbkwargs...
)
end
best_shock = best_candidate(result)
return best_shock
end
function mfs_objective(perturbation, u0, idchecker, metric, mapper::AttractorMapper, penalty)
dist = metric(perturbation)
if dist == 0
return penalty
end
new_shock = perturbation + u0
new_id = mapper(new_shock)
if idchecker(new_id) # valid shock, it brings us to a desired basin
return dist
else
return dist + penalty
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 53 | include("mfs.jl")
include("tipping_probabilities.jl") | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2288 | export tipping_probabilities
"""
tipping_probabilities(basins_before, basins_after) → P
Return the tipping probabilities of the computed basins before and after a change
in the system parameters (or time forcing), according to the definition of [Kaszas2019](@cite).
The input `basins` are integer-valued arrays, where the integers enumerate the attractor,
e.g. the output of [`basins_of_attraction`](@ref).
## Description
Let ``\\mathcal{B}_i(p)`` denote the basin of attraction of attractor ``A_i`` at
parameter(s) ``p``. Kaszás et al [Kaszas2019](@cite) define the tipping probability
from ``A_i`` to ``A_j``, given a parameter change in the system of ``p_- \\to p_+``, as
```math
P(A_i \\to A_j | p_- \\to p_+) =
\\frac{|\\mathcal{B}_j(p_+) \\cap \\mathcal{B}_i(p_-)|}{|\\mathcal{B}_i(p_-)|}
```
where ``|\\cdot|`` is simply the volume of the enclosed set.
The value of `` P(A_i \\to A_j | p_- \\to p_+)`` is `P[i, j]`.
The equation describes something quite simple:
what is the overlap of the basin of attraction of ``A_i`` at ``p_-`` with that of the
attractor ``A_j`` at ``p_+``.
If `basins_before, basins_after` contain values of `-1`, corresponding to trajectories
that diverge, this is considered as the last attractor of the system in `P`.
"""
function tipping_probabilities(basins_before::AbstractArray, basins_after::AbstractArray)
@assert size(basins_before) == size(basins_after)
bid, aid = unique.((basins_before, basins_after))
P = zeros(length(bid), length(aid))
N = length(basins_before)
# Make -1 last entry in bid, aid, if it exists
put_minus_1_at_end!(bid); put_minus_1_at_end!(aid)
# Notice: the following loops could be optimized with smarter boolean operations,
# however they are so fast that everything should be done within milliseconds even
# on a potato
for (i, ι) in enumerate(bid)
B_i = findall(isequal(ι), basins_before)
μ_B_i = length(B_i) # μ = measure
for (j, ξ) in enumerate(aid)
B_j = findall(isequal(ξ), basins_after)
μ_overlap = length(B_i ∩ B_j)
P[i, j] = μ_overlap/μ_B_i
end
end
return P
end
function put_minus_1_at_end!(bid)
if -1 ∈ bid
sort!(bid)
popfirst!(bid)
push!(bid, -1)
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 1490 | # Additional tests may be run in this test suite according to an environment variable
# `ATTRACTORS_EXTENSIVE_TESTS` which can be true or false.
# If false, a smaller, but representative subset of tests is used.
# ENV["ATTRACTORS_EXTENSIVE_TESTS"] = true or false (set externally)
using Test
defaultname(file) = uppercasefirst(replace(splitext(basename(file))[1], '_' => ' '))
testfile(file, testname=defaultname(file)) = @testset "$testname" begin; include(file); end
@testset "Attractors.jl" begin
@testset "mapping" begin
testfile("mapping/grouping.jl")
testfile("mapping/recurrence.jl")
testfile("mapping/proximity.jl")
testfile("mapping/attractor_mapping.jl")
testfile("mapping/basins_of_attraction.jl")
testfile("mapping/histogram_grouping.jl")
testfile("mapping/irregular_grid.jl")
end
@testset "basins analysis" begin
testfile("basins/tipping_points_tests.jl")
testfile("basins/uncertainty_tests.jl")
testfile("basins/wada_tests.jl")
end
@testset "continuation" begin
testfile("continuation/matching_attractors.jl")
testfile("continuation/recurrences_continuation.jl")
testfile("continuation/grouping_continuation.jl")
testfile("continuation/seed_continue_generic.jl")
end
@testset "mfs" begin
testfile("mfs/mfstest.jl")
end
@testset "boundaries" begin
testfile("boundaries/edgetracking_tests.jl")
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 769 | using Attractors
using Test
@testset "basins_fractions(::Array)" begin
b₋ = rand(Random.MersenneTwister(1234), Int16.(1:3), (10, 10, 10))
fs = basins_fractions(b₋)
@test keytype(fs) == Int16
@test all(v -> 0.31 < v < 0.35, values(fs))
# Also test analytically resolved just to be sure
ba = [1 2; 2 1]
fs = basins_fractions(ba)
@test fs[1] == 0.5
@test fs[2] == 0.5
end
@testset "Tipping probabilities (overlap)" begin
basins_before = ones(20, 20)
basins_before[1:10, 1:10] .= -1
basins_after = ones(20, 20)
basins_after[:, 11:20] .= 2
P = tipping_probabilities(basins_before, basins_after)
@test size(P) == (2,2)
@test P[1,1] ≈ 1/3
@test P[2,1] == 1
@test P[1,2] ≈ 2/3
@test P[2,2] == 0
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2500 | using Attractors
using Test
function grebogi_map()
function grebogi_map_rule(u, p, n)
θ = u[1]; x = u[2]
a,b,J₀ = p
dθ= θ + a*sin(2*θ) - b*sin(4*θ) -x*sin(θ)
dθ = mod(dθ,2π) # to avoid problems with attractor at θ=π
dx=-J₀*cos(θ)
return SVector{2}(dθ,dx)
end
p = (a = 1.32, b=0.9, J₀=0.3)
return DeterministicIteratedMap(grebogi_map_rule, rand(2), p)
end
@testset "original paper" begin
ds = grebogi_map()
θg = range(0, 2π, length = 251)
xg = range(-0.5, 0.5, length = 251)
mapper = AttractorsViaRecurrences(ds, (θg, xg); sparse = false)
bsn, att = basins_of_attraction(mapper; show_progress = false)
e, f, α = uncertainty_exponent(bsn; range_ε = 3:15)
# In the paper the value is roughly 0.2
@test (0.2 ≤ α ≤ 0.3)
end
@testset "Newton map" begin
function newton_map(dz,z, p, n)
f(x) = x^p[1]-1
df(x)= p[1]*x^(p[1]-1)
z1 = z[1] + im*z[2]
dz1 = f(z1)/df(z1)
z1 = z1 - dz1
dz[1]=real(z1)
dz[2]=imag(z1)
return
end
ds = DiscreteDynamicalSystem(newton_map,[0.1, 0.2], [3])
xg = yg = range(-1.,1.,length=300)
mapper = AttractorsViaRecurrences(ds, (xg, yg); sparse = false)
bsn,att = basins_of_attraction(mapper; show_progress = false)
e,f,α = uncertainty_exponent(bsn; range_ε = 5:30)
# Value (published) from the box-counting dimension is 1.42. α ≃ 0.6
@test (0.55 ≤ α ≤ 0.65)
end
@testset "Basin entropy and Fractal test" begin
ds = grebogi_map()
θg=range(0,2π,length = 300)
xg=range(-0.5,0.5,length = 300)
mapper = AttractorsViaRecurrences(ds, (θg, xg); sparse = false)
basin, attractors = basins_of_attraction(mapper; show_progress = false)
Sb, Sbb = basin_entropy(basin, 6)
@test 0.4 ≤ Sb ≤ 0.42
@test 0.6 ≤ Sbb ≤ 0.61
test_res, Sbb = basins_fractal_test(basin; ε = 5)
@test test_res == :fractal
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
henon() = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
ds = henon()
xg = yg = range(-2.,2.,length = 300)
mapper = AttractorsViaRecurrences(ds, (xg, yg); sparse = false)
basin, attractors = basins_of_attraction(mapper; show_progress = false)
test_res, Sbb = basins_fractal_test(basin; ε = 5)
@test test_res == :smooth
end
@testset "Basin entropy API" begin
basins = rand(Int, 50, 50)
@test_throws ArgumentError basin_entropy(basins, 7)
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 354 | using Test
@testset "Wada property test" begin
# Artificial smooth boundary
M = [1 1 1 1 2 2 2 2 3 3 3 3]'*ones(Int, 1,12)
@test test_wada_merge(M, 1) == 12*2/12^2
@test test_wada_merge(M, 2) == 12*2/12^2
# Artificial fractal boundary
M = [1 2 3 1 2 3 1 2 3 1 2 3]'*ones(Int, 1,12)
@test test_wada_merge(M, 1) == 0.
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 3233 | using Attractors
using Test
using OrdinaryDiffEq
using LinearAlgebra
@testset "Saddle point of cubic map" begin
cubicmap(u, p, n) = SVector{1}(p[1]*u[1] - u[1]^3)
ds = DeterministicIteratedMap(cubicmap, [1.0], [2.0])
attrs = Dict(1 => StateSpaceSet([1.0]), 2 => StateSpaceSet([-1.0]))
saddle = edgetracking(ds, attrs; Δt=1, abstol=1e-8).edge[end]
@test saddle[1] < 1e-5
end
@testset "Saddle point of FitzHugh-Nagumo system" begin
fhn(u, p, t) = SVector{2}([10*(u[1] - u[1]^3 - u[2]), -3*u[2] + u[1]])
ds = CoupledODEs(fhn, ones(2), diffeq=(;alg = Vern9()))
fp = [sqrt(2/3), sqrt(2/27)]
attrs = Dict([1 => StateSpaceSet([fp]), 2 => StateSpaceSet([-fp])])
bisect_thresh, diverge_thresh, maxiter, abstol = 1e-8, 1e-7, 100, 1e-9
edge = edgetracking(ds, attrs; u1=[-1.0, 0.2], u2=[1.0, 0.2],
bisect_thresh, diverge_thresh, maxiter, abstol).edge
println(edge[end], edge[end-1])
@test sqrt(sum(abs, (edge[end]-zeros(2)).^2)) < 1e-5
end
@testset "Thomas' rule" begin
# Chaotic dynamical system
function thomas_rule(u, p, t)
x,y,z = u
b = p[1]
xdot = sin(y) - b*x
ydot = sin(z) - b*y
zdot = sin(x) - b*z
return SVector{3}(xdot, ydot, zdot)
end
ds = CoupledODEs(thomas_rule, [1.0, 0, 0], [0.16]; diffeq=(reltol=1e-12,))
# Find attractors on a 3D grid
xg = yg = yz = range(-6.0, 6.0; length = 101)
grid = (xg, yg, yz)
mapper = AttractorsViaRecurrences(ds, grid; consecutive_recurrences = 1000)
sampler, = statespace_sampler(grid)
basins_fractions(mapper, sampler)
attractors = extract_attractors(mapper)
# Run edgetracking between pairs of points lying on different attractors
n_sample = 25
pairs12, pairs13, pairs23 = [], [], []
for i in 1:Int(sqrt(n_sample))
_pairs12, _pairs13, _pairs23 = [], [], []
for j in 1:Int(sqrt(n_sample))
et12 = edgetracking(ds, attractors;
u1=attractors[1][i], u2=attractors[2][j], bisect_thresh=1e-4,
diverge_thresh=1e-3, maxiter=10000, abstol=1e-5, verbose=false)
et13 = edgetracking(ds, attractors;
u1=attractors[1][i], u2=attractors[3][j], bisect_thresh=1e-4,
diverge_thresh=1e-3, maxiter=10000, abstol=1e-5, verbose=false)
et23 = edgetracking(ds, attractors;
u1=attractors[2][i], u2=attractors[3][j], bisect_thresh=1e-4,
diverge_thresh=1e-3, maxiter=10000, abstol=1e-5, verbose=false)
et12.success ? push!(_pairs12, et12.edge[end]) : nothing
et13.success ? push!(_pairs13, et13.edge[end]) : nothing
et23.success ? push!(_pairs23, et23.edge[end]) : nothing
end
push!(pairs12, _pairs12)
push!(pairs13, _pairs13)
push!(pairs23, _pairs23)
end
edgestates = reduce(vcat, [pairs12 pairs13 pairs23])
# Verify that all found edge states have the same Euclidean norm of `norm_value`
# (due to the symmetry of the system `ds`)
norm_value = 4.06585
norm_deviations = [norm(edgestates[i]) - norm_value for i in 1:length(edgestates)]
@test maximum(norm_deviations) < 1e-3
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 4127 | DO_EXTENSIVE_TESTS = get(ENV, "ATTRACTORS_EXTENSIVE_TESTS", "false") == "true"
using Test, Attractors
using Random
# TODO: Add a Histogram test with the competition dynamics model
@testset "Dummy bistable map" begin
function dumb_map(dz, z, p, n)
x, y = z
r = p[1]
if r < 0.5
dz[1] = dz[2] = 0.0
else
if x > 0
dz[1] = r
dz[2] = r
else
dz[1] = -r
dz[2] = -r
end
end
return
end
r = 3.833
ds = DiscreteDynamicalSystem(dumb_map, [0., 0.], [r])
sampler, = statespace_sampler(HRectangle([-3.0, -3.0], [3.0, 3.0]), 1234)
rrange = range(0, 2; length = 21)
ridx = 1
featurizer(a, t) = a[end]
clusterspecs = Attractors.GroupViaClustering(optimal_radius_method = "silhouettes", max_used_features = 200)
mapper = Attractors.AttractorsViaFeaturizing(ds, featurizer, clusterspecs; T = 20, threaded = true)
gap = FeaturizeGroupAcrossParameter(mapper; par_weight = 0.0)
fractions_cont, attractors_cont = global_continuation(
gap, rrange, ridx, sampler; show_progress = false
)
for (i, r) in enumerate(rrange)
fs = fractions_cont[i]
infos = attractors_cont[i]
if r < 0.5
k = sort!(collect(keys(fs)))
@test sort!(collect(keys(infos))) == k
@test length(k) == 1
@test infos[1] == [0, 0]
else
k = sort!(collect(keys(fs)))
@test sort!(collect(keys(infos))) == k
@test length(k) == 2
v = values(fs)
for f in v
# each fraction is about 50% but we have so small sampling that
# we need to allow huge errors
@test (0.3 < f < 0.7)
end
# one attractor is -r the other +r, but we don't know which in advance
if infos[2][1] < 0
infom = infos[2]
infop = infos[3]
else
infom = infos[3]
infop = infos[2]
end
@test all(infom .≈ [-r, -r])
@test all(infop .≈ [r, r])
end
@test sum(values(fs)) ≈ 1
end
end
if DO_EXTENSIVE_TESTS
@testset "Henon period doubling" begin
# Notice special parameter values:
b, a = -0.9, 1.1 # notice the non-default parameters
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
ds = DeterministicIteratedMap(henon_rule, ones(2), [a,b])
ps = range(0.6, 1.1; length = 11)
pidx = 1
sampler, = statespace_sampler(HRectangle([-2,-2], [2,2]), 1234)
# Feature based on period.
function featurizer(a, t) # feature based on period!
tol = 1e-5
L = length(a)
if abs(a[L-1,1] - a[L,1]) < tol
# period 1
return [1]
elseif abs(a[L-3,1] - a[L,1]) < tol
# period 3
return [3]
else
return [100]
end
end
clusterspecs = Attractors.GroupViaClustering(rescale_features = false, optimal_radius_method = 1.0)
mapper = Attractors.AttractorsViaFeaturizing(ds, featurizer, clusterspecs;
T = 10, Ttr = 2000, threaded = true
)
gap = FeaturizeGroupAcrossParameter(mapper; par_weight = 0.0)
fractions_cont, attractors_cont = global_continuation(
gap, ps, pidx, sampler;
samples_per_parameter = 100, show_progress = false
)
for (i, p) in enumerate(ps)
fs = fractions_cont[i]
if p < 0.9
k = sort!(collect(keys(fs)))
@test length(k) == 2
elseif p > 1.0 # (coexistence of period 1 and 3)
k = sort!(collect(keys(fs)))
@test length(k) == 3
end
@test sum(values(fs)) ≈ 1
infos = attractors_cont[i]
@test all(v -> v ∈ ([1.0], [3.0], [100.0]), values(infos))
end
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 10971 | using Test, Attractors
DO_EXTENSIVE_TESTS = get(ENV, "ATTRACTORS_EXTENSIVE_TESTS", "false") == "true"
@testset "matching utils" begin
@testset "No double duplication" begin
rmap = Dict(4 => 3, 3 => 2)
a = Dict(4 => 1)
swap_dict_keys!(a, rmap)
@test haskey(a, 3)
@test !haskey(a, 2)
end
end
@testset "MatchBySSSetDistance" begin
default = MatchBySSSetDistance()
@testset "analytic" begin
a_befo = Dict(1 => [SVector(0.0, 0.0)], 2 => [SVector(1.0, 1.0)])
a_befo = Dict(keys(a_befo) .=> StateSpaceSet.(values(a_befo)))
@testset "infinite threshold" begin
a_afte = Dict(2 => [SVector(0.0, 0.0)], 1 => [SVector(2.0, 2.0)])
a_afte = Dict(keys(a_afte) .=> StateSpaceSet.(values(a_afte)))
rmap = matching_map!(a_afte, a_befo, default)
@test rmap == Dict(1 => 2, 2 => 1)
@test a_afte[1] == a_befo[1] == StateSpaceSet([SVector(0.0, 0.0)])
@test haskey(a_afte, 2)
@test a_afte[2] == StateSpaceSet([SVector(2.0, 2.0)])
end
@testset "separating threshold" begin
a_afte = Dict(2 => [SVector(0.0, 0.0)], 1 => [SVector(2.0, 2.0)])
a_afte = Dict(keys(a_afte) .=> StateSpaceSet.(values(a_afte)))
matcher = MatchBySSSetDistance(threshold = 0.1)
rmap = matching_map!(a_afte, a_befo, matcher)
@test rmap == Dict(1 => 3, 2 => 1)
@test a_afte[1] == a_befo[1] == StateSpaceSet([SVector(0.0, 0.0)])
@test !haskey(a_afte, 2)
@test a_afte[3] == StateSpaceSet([SVector(2.0, 2.0)])
end
end
@testset "synthetic multistable matching" begin
attractors_cont_simple = Dict{Int64, SVector{1, Float64}}[Dict(1 => [0.0]), Dict(1 => [0.0]), Dict(2 => [2.0], 1 => [0.0]), Dict(2 => [0.0], 1 => [2.0]), Dict(2 => [2.0], 3 => [4.0], 1 => [-5.0]), Dict(2 => [4.0], 3 => [-5.0], 1 => [2.0]), Dict(4 => [6.0], 2 => [0.0], 3 => [2.0], 1 => [4.0]), Dict(4 => [4.0], 2 => [0.0], 3 => [2.0], 1 => [6.0]), Dict(5 => [8.0], 4 => [6.0], 2 => [0.0], 3 => [2.0], 1 => [4.0])]
attractors_cont = [Dict(k=>StateSpaceSet(Vector(v)) for (k,v) in atts) for atts in attractors_cont_simple]
mapped_atts = deepcopy(attractors_cont)
rmaps = match_sequentially!(mapped_atts, default)
fractions_cont = [Dict(1 => 1.0), Dict(1 => 1.0), Dict(2 => 0.8, 1 => 0.2), Dict(2 => 0.2, 1 => 0.8), Dict(2 => 0.2, 3 => 0.6, 1 => 0.2), Dict(2 => 0.6, 3 => 0.2, 1 => 0.2), Dict(4 => 0.4, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(4 => 0.2, 2 => 0.2, 3 => 0.2, 1 => 0.4), Dict(5 => 0.2, 4 => 0.2, 2 => 0.2, 3 => 0.2, 1 => 0.2)]
mapped_fracs = deepcopy(fractions_cont)
match_sequentially!(mapped_fracs, rmaps)
@test all(keys.(attractors_cont) .== keys.(mapped_atts) )
@test all(keys.(attractors_cont) .== keys.(mapped_fracs) )
@test all(Set.(values.(fractions_cont)) .== Set.(values.(mapped_fracs)))
end
@testset "global_continuation matching" begin
# Make fake attractors with points that become more "separated" as "parameter"
# is increased
jrange = 0.1:0.1:1
allatts = [Dict(1 => [SVector(0.0, 0.0)], 2 => [SVector(j, j)]) for j in jrange]
allatts = [Dict(keys(d) .=> StateSpaceSet.(values(d))) for d in allatts]
for i in eachindex(jrange)
if isodd(i) && i ≠ 1
# swap key of first attractor to from 1 to i
allatts[i][i] = allatts[i][1]
delete!(allatts[i], 1)
end
end
# Test with distance not enough to increment
match_sequentially!(allatts, MatchBySSSetDistance(threshold = 100.0)) # all odd keys become 1
@test all(haskey(d, 1) for d in allatts)
@test all(haskey(d, 2) for d in allatts)
# Test with distance enough to increment
allatts2 = deepcopy(allatts)
match_sequentially!(allatts2, MatchBySSSetDistance(threshold = 0.1)) # all keys there were `2` get incremented
@test all(haskey(d, 1) for d in allatts2)
for i in 2:length(jrange)
@test haskey(allatts2[i], i+1)
@test !haskey(allatts2[i], 2)
end
@test haskey(allatts2[1], 2)
end
@testset "global_continuation matching advanced" begin
jrange = 0.1:0.1:1
allatts = [Dict(1 => [SVector(0.0, 0.0)], 2 => [SVector(1.0, 1.0)], 3 => [SVector((10j)^2, 0)]) for j in jrange]
allatts = [Dict(keys(d) .=> StateSpaceSet.(values(d))) for d in allatts]
# delete attractors every other parameter
for i in eachindex(jrange)
if iseven(i)
delete!(allatts[i], 3)
end
end
@testset "ignore vanished" begin
@testset "no retract" begin
atts = deepcopy(allatts)
rmaps = match_sequentially!(atts, default; retract_keys = false)
# After the first 3 key, all subsequent keys 3 become the next integer,
# and since we started cutting away keys 3 from `i = 2` we have
# 4 extra 3 keys to add.
@test unique_keys(atts) == [1, 2, 3, 5, 7, 9, 11]
end
@testset "with retract" begin
# with retraction it becomes nice
atts = deepcopy(allatts)
rmaps = match_sequentially!(atts, default; retract_keys = true)
@test unique_keys(atts) == 1:7
end
end
@testset "use vanished" begin
@testset "Inf thresh" begin
atts = deepcopy(allatts)
match_sequentially!(atts, MatchBySSSetDistance(use_vanished = true))
@test unique_keys(atts) == 1:3
for i in eachindex(jrange)
if iseven(i)
@test sort!(collect(keys(atts[i]))) == 1:2
else
@test sort!(collect(keys(atts[i]))) == 1:3
end
end
end
@testset "finite thresh" begin
# okay here we test the case that the threshold becomes too large
threshold = 10.0 # at the 5th index, we cannot match anymore
atts = deepcopy(allatts)
match_sequentially!(atts, MatchBySSSetDistance(; use_vanished = true, threshold))
@testset "i=$(i)" for i in eachindex(jrange)
if iseven(i)
@test sort!(collect(keys(atts[i]))) == 1:2
else
if i < 5
@test sort!(collect(keys(atts[i]))) == 1:3
else
@test sort!(collect(keys(atts[i]))) == [1, 2, i÷2 + 2]
end
end
end
end
end
end
end # Matcher by distance tests
@testset "basin overlap" begin
b1 = ones(Int, 10, 10)
b1[:, 6:10] .= 2
b2 = copy(b1)
b2[:, 1:2] .= 2
b2[:, 3:10] .= 3 # 3 has more overlap to 2, while 2 has more overlap to 1
b3 = copy(b2)
b3[:, 1:10] .= 3 # so now this would be teh same as the previous 3, which is will become 2
m1 = MatchByBasinOverlap()
rmap = matching_map(b2, b1, m1)
@test rmap[3] == 2
@test rmap[2] == 1
bx = copy(b2)
matching_map!(bx, b1, m1)
@test sort(unique(bx)) == [1, 2]
rmap = matching_map(b3, bx, m1)
@test length(rmap) == 1
@test rmap[3] == 2
# test that there won't be matching with threshold
m2 = MatchByBasinOverlap(1.99)
rmap = matching_map(b2, b1, m2)
# here 3 should go to 2, as it overlaps all of 2
# while 2 cannot go to 1, as it doesn't 50% or more of 1.
# The next available ID is not 4 though, it is 3, as this is
# the next available integer given the previous keys (1, 2)
@test length(rmap) == 2
@test rmap[2] == 3
@test rmap[3] == 2
end
@testset "BasinEncloure" begin
@testset "synthetic multistable continuation" begin
function dummy_multistable_equilibrium!(dx, x, p, n)
r = p[1]
num_max_atts = 5
x_max_right = 10
x_pos_atts = [x_max_right*(i-1)/num_max_atts for i=1:num_max_atts]
if 3 <=r < 4 && (x[1] <= 2)
x_pos_atts[1] = -5
end
num_atts = r < (num_max_atts + 1) ? floor(Int, r) : ceil(Int, 2*num_max_atts - r)
x_atts = [x_pos_atts[i] for i=1:num_atts]
att_of_x = findlast(xatt->xatt<=x[1], x_atts)
if x[1] < 0 att_of_x = 1 end
dx .= x_atts[att_of_x]
return nothing
end
ds = DeterministicIteratedMap(dummy_multistable_equilibrium!, [0.], [1.0])
featurizer(A,t) = A[end]
grouping_config = GroupViaPairwiseComparison(; threshold=0.2)
mapper = AttractorsViaFeaturizing(ds, featurizer, grouping_config)
xg = range(0, 10, length = 100)
grid = (xg,)
sampler, = statespace_sampler(grid, 1234)
samples_per_parameter = 1000
ics = StateSpaceSet([deepcopy(sampler()) for _ in 1:samples_per_parameter])
rrange = range(1, 9.5; step=0.5)
ridx = 1
mapper = AttractorsViaFeaturizing(ds, featurizer, grouping_config; T=10, Ttr=1)
matcher = MatchByBasinEnclosure(;ε=0.1)
assc = AttractorSeedContinueMatch(mapper, matcher)
fs_curves, atts_all = global_continuation(assc, rrange, ridx, ics; show_progress = true)
atts_all_endpoint_solution = Dict{Int64, SVector{1, Float64}}[Dict(1 => [0.0]), Dict(1 => [0.0]), Dict(2 => [2.0], 1 => [0.0]), Dict(2 => [2.0], 1 => [0.0]), Dict(2 => [2.0], 3 => [4.0], 1 => [-5.0]), Dict(2 => [2.0], 3 => [4.0], 1 => [-5.0]), Dict(4 => [6.0], 2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(4 => [6.0], 2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(5 => [8.0], 4 => [6.0], 2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(5 => [8.0], 4 => [6.0], 2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(4 => [6.0], 2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(4 => [6.0], 2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(2 => [2.0], 3 => [4.0], 1 => [0.0]), Dict(2 => [2.0], 1 => [0.0]), Dict(2 => [2.0], 1 => [0.0]), Dict(1 => [0.0]), Dict(1 => [0.0])]
atts_all_endpoint = [Dict(k=>v[end] for (k,v) in atts) for atts in atts_all]
@test atts_all_endpoint == atts_all_endpoint_solution
fs_curves_solution = [Dict(1 => 1.0), Dict(1 => 1.0), Dict(2 => 0.8, 1 => 0.2), Dict(2 => 0.8, 1 => 0.2), Dict(2 => 0.2, 3 => 0.6, 1 => 0.2), Dict(2 => 0.2, 3 => 0.6, 1 => 0.2), Dict(4 => 0.4, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(4 => 0.4, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(5 => 0.2, 4 => 0.2, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(5 => 0.2, 4 => 0.2, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(4 => 0.4, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(4 => 0.4, 2 => 0.2, 3 => 0.2, 1 => 0.2), Dict(2 => 0.2, 3 => 0.6, 1 => 0.2), Dict(2 => 0.2, 3 => 0.6, 1 => 0.2), Dict(2 => 0.8, 1 => 0.2), Dict(2 => 0.8, 1 => 0.2), Dict(1 => 1.0), Dict(1 => 1.0)]
@test all(keys.(fs_curves_solution) .== keys.(fs_curves) )
for (fs_curve, fs_curve_solution) in zip(fs_curves, fs_curves_solution)
for (k, fs) in fs_curve
@test isapprox(fs, fs_curve_solution[k], atol=1e-1)
end
end
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 8272 | # This file also tests `aggregate_attractor_fractions`!
DO_EXTENSIVE_TESTS = get(ENV, "ATTRACTORS_EXTENSIVE_TESTS", "false") == "true"
using Test, Attractors
using Random
@testset "analytic bistable map" begin
# This is a fake bistable map that has two equilibrium points
# for r > 0.5. It has predictable fractions.
function dumb_map(dz, z, p, n)
x,y = z
r = p[1]
if r < 0.5
dz[1] = dz[2] = 0.0
else
if x > 0
dz[1] = r
dz[2] = r
else
dz[1] = -r
dz[2] = -r
end
end
return
end
r = 1.0
ds = DeterministicIteratedMap(dumb_map, [0., 0.], [r])
yg = xg = range(-10., 10, length = 100)
grid = (xg,yg)
mapper = AttractorsViaRecurrences(ds, grid; sparse = true, show_progress = false)
sampler, = statespace_sampler(grid, 1234)
rrange = range(0, 2; length = 20)
ridx = 1
rsc = RecurrencesFindAndMatch(mapper; threshold = 0.3)
fractions_cont, a = global_continuation(
rsc, rrange, ridx, sampler;
show_progress = false, samples_per_parameter = 1000
)
for (i, r) in enumerate(rrange)
fs = fractions_cont[i]
k = sort!(collect(keys(fs)))
@test k == sort!(collect(keys(a[i]))) # no -1 ID, so keys must match
if r < 0.5
k = sort!(collect(keys(fs)))
@test length(k) == 1
else
k = sort!(collect(keys(fs)))
@test length(k) == 2
v = values(fs)
for f in v
@test (0.4 < f < 0.6)
end
end
@test sum(values(fs)) ≈ 1
end
end
@testset "Multistable aggregating map" begin
# This is a fake multistable map helps at testing the grouping
# capabilities. We know what it does analytically!
function dumb_map(dz, z, p, n)
x,y = z
r = p[1]
θ = mod(angle(x + im*y),2pi)
rr = abs(x+ im*y)
# This map works as follows: for the parameter r< 0.5 there are
# 8 attractors close to the origin (radius 0.1)
# For r > 0.5 there are 8 attractors very close to the origin (radius 0.01
# and 8 attractors far away and well separated.
if r < 0.5
rr = 0.1
else
if rr > 1
rr = 3
else
rr = 0.01
end
end
if 0 < θ ≤ π/4
x = rr*cos(π/8); y = rr*sin(π/8)
elseif π/4 < θ ≤ π/2
x = rr*cos(3π/8); y = rr*sin(3π/8)
elseif π/2 < θ ≤ 3π/4
x = rr*cos(5π/8); y = rr*sin(5π/8)
elseif 3π/4 < θ ≤ π
x = rr*cos(7π/8); y = rr*sin(7π/8)
elseif π < θ ≤ 5π/4
x = rr*cos(9π/8); y = rr*sin(9π/8)
elseif 5π/4 < θ ≤ 6π/4
x = rr*cos(11π/8); y = rr*sin(11π/8)
elseif 6π/4 < θ ≤ 7π/4
x = rr*cos(13π/8); y = rr*sin(13π/8)
elseif 7π/4 < θ ≤ 8π/4
x = rr*cos(15π/8); y = rr*sin(15π/8)
end
dz[1]= x; dz[2] = y
return
end
function test_fs(fractions_cont, rrange, frac_results)
# For Grouping there should be one cluster for r < 0.5 and then 9 groups of attractors
# For matching, all attractors are detected and matched
# for r < 0.5 there are 4 attractors and for r > 0.5 there are 12
for (i, r) in enumerate(rrange)
fs = fractions_cont[i]
# non-zero keys
k = sort!([k for k in keys(fs) if fs[k] > 0])
if r < 0.5
@test length(k) == frac_results[1]
else
@test length(k) == frac_results[2]
end
@test sum(values(fs)) ≈ 1
end
end
r = 0.3
ds = DeterministicIteratedMap(dumb_map, [0.0, 0.0], [r])
yg = xg = range(-10., 10, length = 100)
grid = (xg, yg)
sampler, = statespace_sampler(grid, 1234)
rrange = range(0, 2; length = 21)
ridx = 1
# First, test the normal function of finding attractors
mapper = AttractorsViaRecurrences(ds, grid; sparse = true, show_progress = false)
rsc = RecurrencesFindAndMatch(mapper; threshold = 0.1)
fractions_cont, attractors_cont = global_continuation(
rsc, rrange, ridx, sampler;
show_progress = false, samples_per_parameter = 1000,
)
test_fs(fractions_cont, rrange, [4, 12])
# Then, test the aggregation of features via featurizing and histogram
using Statistics
featurizer = (x) -> mean(x)
hconfig = GroupViaHistogram(
FixedRectangularBinning(range(-4, 4; step = 0.005), 2)
)
aggr_fracs, aggr_info = aggregate_attractor_fractions(
fractions_cont, attractors_cont, featurizer, hconfig
)
test_fs(aggr_fracs, rrange, [4, 12])
end
if DO_EXTENSIVE_TESTS
@testset "Henon map" begin
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
ds = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
ps = range(1.2, 1.25; length = 101)
# In these parameters we go from a chaotic attractor to a period 7 orbit at a≈1.2265
# (you can see this by launching our wonderful `interactive_orbitdiagram` app).
# So we can use this to test different matching processes
# (because "by distance" matches the two kind of attractors already)
# Notice that the length=101 is rather sensitive and depending on it, some
# much smaller periodic windows exist in the range.
# (For 101, a period-14 window exists in the second parameter entry)
acritical = 1.2265
xg = yg = range(-2.5, 2.5, length = 500)
pidx = 1
sampler, = statespace_sampler(HRectangle([-2,-2], [2,2]), 1234)
distance_function = function (A, B)
# length of attractors within a factor of 2, then distance is ≤ 1
return abs(log(2, length(A)) - log(2, length(B)))
end
# notice that without this special distance function, even with a
# really small threshold like 0.2 we still get a "single" attractor
# throughout the range. Now we get one with period 14, a chaotic,
# and one with period 7 that spans the second half of the parameter range
mapper = AttractorsViaRecurrences(ds, (xg, yg); sparse=false,
consecutive_recurrences = 3000,
attractor_locate_steps = 3000
)
rsc = RecurrencesFindAndMatch(mapper;
threshold = 0.99, distance = distance_function
)
fractions_cont, attractors_cont = global_continuation(
rsc, ps, pidx, sampler;
show_progress = false, samples_per_parameter = 100
)
for (i, p) in enumerate(ps)
fs = fractions_cont[i]
attractors = attractors_cont[i]
@test sum(values(fs)) ≈ 1
# Test that keys are the same (-1 doesn't have attractor)
k = sort!(collect(keys(fs)))
-1 ∈ k && deleteat!(k, 1)
attk = sort!(collect(keys(attractors)))
@test k == attk
end
# unique keys
ukeys = Attractors.unique_keys(attractors_cont)
# We must have 3 attractors: initial chaotic, period 14 in the middle,
# chaotic again, and period 7 at the end. ALl of these should be matched to each other.
# Notice that due to the storage of "ghost" attractors in `RAFM`, the
# first and second chaotic attractors are mapped to each other.
@test ukeys == 1:3
# # Animation of henon attractors
# animate_attractors_continuation(ds, attractors_cont, fractions_cont, ps, pidx)
end
@testset "non-found attractors" begin
# This is standard henon map
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
ds = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
ps = range(1.2, 1.25; length = 3)
# This grid is chosen such that no attractors are in there!
xg = yg = range(-25, -5; length = 500)
pidx = 1
sampler, = statespace_sampler(HRectangle([-2,-2], [2,2]), 1234)
mapper = AttractorsViaRecurrences(ds, (xg, yg); sparse=false)
rsc = RecurrencesFindAndMatch(mapper)
fractions_cont, attractors_cont = global_continuation(
rsc, ps, pidx, sampler;
show_progress = false, samples_per_parameter = 100
)
@test all(i -> isempty(i), attractors_cont)
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2622 | # Testing the generalized `AttractorSeedContinueMatch`.
# We don't test recurrences combo because it is already tested
# in another file
using Test, Attractors
using Random
@testset "analytic bistable: featurizing" begin
# This is a fake bistable map that has two equilibrium points
# for r > 0.5. It has analytically resolved fractions for any box.
function dumb_map(dz, z, p, n)
x, y = z
r, q = p
if r < 0.5
dz[1] = dz[2] = 0.0
else
if x > 0
dz[1] = r
dz[2] = r
else
dz[1] = -r
dz[2] = -r
end
end
return
end
r = 1.0; q = 0.5
ds = DeterministicIteratedMap(dumb_map, [0., 0.], [r, q])
yg = xg = range(-10., 10, length = 100)
grid = (xg,yg)
mapper1 = AttractorsViaRecurrences(ds, grid; sparse = true, show_progress = false)
sampler, = statespace_sampler(grid, 1234)
rrange = range(0, 2; length = 20)
ridx = 1
function featurizer(A, t)
return A[end]
end
# in all honesty, we don't have to test 2 grouping configs,
# as the algorithm is agnostic to the grouping. But oh well!
group1 = GroupViaClustering(optimal_radius_method = 0.1)
mapper2 = AttractorsViaFeaturizing(ds, featurizer, group1; Ttr = 2, T = 2)
group2 = GroupViaPairwiseComparison(threshold = 0.1)
mapper3 = AttractorsViaFeaturizing(ds, featurizer, group2; Ttr = 2, T = 2)
mappers = [mapper1, mapper2, mapper3, mapper1]
@testset "case: $(i)" for (i, mapper) in enumerate(mappers)
algo = AttractorSeedContinueMatch(mapper)
if i < 4
fractions_cont, a = global_continuation(
algo, rrange, ridx, sampler;
show_progress = false, samples_per_parameter = 1000
)
else # test parameter curve version
pcurve = [[1 => r, 2 => 1.1] for r in rrange]
fractions_cont, a = global_continuation(
algo, pcurve, sampler;
show_progress = false, samples_per_parameter = 1000
)
end
for (i, r) in enumerate(rrange)
fs = fractions_cont[i]
if r < 0.5
k = sort!(collect(keys(fs)))
@test length(k) == 1
else
k = sort!(collect(keys(fs)))
@test length(k) == 2
v = values(fs)
for f in v
@test (0.4 < f < 0.6)
end
end
@test sum(values(fs)) ≈ 1
end
end
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 12474 | # This is an extensive test file. Its goal is to test all combination of mappers
# with all combinations of dynamical systems. However, this can take
# several years to complete. So, the environment parameter
# `ATTRACTORS_EXTENSIVE_TESTS` controls whether the tests should be done extensively or not.
# If not, a small, but representative subset of mappers and dynamical systems is used.
DO_EXTENSIVE_TESTS = get(ENV, "ATTRACTORS_EXTENSIVE_TESTS", "false") == "true"
using Test
using Attractors
using LinearAlgebra
using OrdinaryDiffEq: Vern9
using Random
using Statistics
# Define generic testing framework
function test_basins(ds, u0s, grid, expected_fs_raw, featurizer;
rerr = 1e-3, ferr = 1e-3, aerr = 1e-15, ε = nothing, max_distance = Inf,
proximity_test = true, pairwise_comparison_matrix_test = false, featurizer_matrix = nothing,
threshold_pairwise = 1,
kwargs... # kwargs are propagated to recurrences
)
# u0s is Vector{Pair}
sampler, = statespace_sampler(grid, 1234)
ics = StateSpaceSet([copy(sampler()) for i in 1:1000])
expected_fs = sort!(collect(values(expected_fs_raw)))
known_ids = collect(u[1] for u in u0s)
# reusable testing function
function test_basins_fractions(mapper;
err = 1e-3, known=false, single_u_mapping = true,
known_ids = known_ids, expected_fs = expected_fs,
)
if single_u_mapping
for (k, u0) in u0s
@test k == mapper(u0)
end
end
# Generic test
fs = basins_fractions(mapper, sampler; N = 100, show_progress = false)
for k in keys(fs)
@test 0 ≤ fs[k] ≤ 1
end
@test sum(values(fs)) ≈ 1 atol=1e-14
# Precise test with known initial conditions
fs, labels = basins_fractions(mapper, ics; show_progress = false)
# @show nameof(typeof(mapper))
# @show fs
approx_atts = extract_attractors(mapper)
found_fs = sort(collect(values(fs)))
# @show found_fs
if length(found_fs) > length(expected_fs)
# drop -1 key if it corresponds to just unidentified points
found_fs = found_fs[2:end]
end
@test length(found_fs) == length(expected_fs) #number of attractors
errors = abs.(expected_fs .- found_fs)
for er in errors
@test er .≤ err
end
if known # also test whether the attractor index is correct
for k in known_ids
@test abs(fs[k] - expected_fs_raw[k]) ≤ err
end
end
end
@testset "Recurrences" begin
mapper = AttractorsViaRecurrences(ds, grid; kwargs...)
test_basins_fractions(mapper; err = rerr)
end
@testset "Featurizing, clustering" begin
optimal_radius_method = "silhouettes_optim"
config = GroupViaClustering(; num_attempts_radius=20, optimal_radius_method)
mapper = AttractorsViaFeaturizing(ds, featurizer, config; Ttr = 500)
test_basins_fractions(mapper;
err = ferr, single_u_mapping = false, known_ids = [-1, 1, 2, 3]
)
end
@testset "Featurizing, pairwise comparison" begin
config = GroupViaPairwiseComparison(; threshold=threshold_pairwise,
metric=Euclidean(), rescale_features=false)
mapper = AttractorsViaFeaturizing(ds, featurizer, config; Ttr = 500)
test_basins_fractions(mapper;
err = ferr, single_u_mapping = false, known_ids = [-1, 1, 2, 3]
)
end
if pairwise_comparison_matrix_test
@testset "Featurizing, pairwise comparison, matrix features" begin
function metric_hausdorff(A,B)
set_distance(A, B, Hausdorff())
end
config = GroupViaPairwiseComparison(; threshold=threshold_pairwise,
metric=metric_hausdorff, rescale_features=false)
mapper = AttractorsViaFeaturizing(ds, featurizer_matrix, config; Ttr = 500)
test_basins_fractions(mapper;
err = ferr, single_u_mapping = false, known_ids = [-1, 1, 2, 3]
)
end
end
@testset "Featurizing, nearest feature" begin
# First generate the templates
function features_from_u(u)
A, t = trajectory(ds, 100, u; Ttr = 1000, Δt = 1)
featurizer(A, t)
end
# t = [features_from_u(x[2]) for x in u0s]
# templates = Dict([u0[1] for u0 ∈ u0s] .=> t) # keeps labels of u0s
templates = Dict(k => features_from_u(u) for (k, u) in u0s)
config = GroupViaNearestFeature(templates; max_distance)
mapper = AttractorsViaFeaturizing(ds, featurizer, config; Ttr=500)
# test the functionality mapper(u0) -> label
@test isinteger(mapper(current_state(ds))) == true
test_basins_fractions(mapper; err = ferr, single_u_mapping = false)
end
if DO_EXTENSIVE_TESTS && proximity_test
# Proximity method is the simplest and not crucial to test due to the limited
# practical use of not being able to find attractors
@testset "Proximity" begin
known_attractors = Dict(
k => trajectory(ds, 1000, v; Δt = 1, Ttr=100)[1] for (k,v) in u0s if k ≠ -1
)
mapper = AttractorsViaProximity(ds, known_attractors, ε; Ttr = 100, consecutive_lost_steps = 1000)
test_basins_fractions(mapper; known = true, err = aerr)
end
end
end
# %% Actual tests
@testset "Analytic dummy map" begin
function dumb_map(z, p, n)
x, y = z
r = p[1]
if r < 0.5
return SVector(0.0, 0.0)
else
if x ≥ 0
return SVector(r, r)
else
return SVector(-r, -r)
end
end
end
r = 1.0
ds = DeterministicIteratedMap(dumb_map, [0., 0.], [r])
u0s = [1 => [r, r], 2 => [-r, -r]] # template ics
xg = yg = range(-2.0, 2.0; length=100)
grid = (xg, yg)
expected_fs_raw = Dict(1 => 0.5, 1 => 0.5)
featurizer(A, t) = SVector(A[1][1])
test_basins(ds, u0s, grid, expected_fs_raw, featurizer;
max_distance = 20, ε = 1e-1, proximity_test = false, threshold_pairwise=1,
rerr = 1e-1, ferr = 1e-1, aerr = 1e-15)
end
@testset "Henon map: discrete & divergence" begin
u0s = [1 => [0.0, 0.0], -1 => [0.0, 2.0]] # template ics
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
ds = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
xg = yg = range(-2.0, 2.0; length=100)
grid = (xg, yg)
expected_fs_raw = Dict(-1 => 0.575, 1 => 0.425)
function featurizer(A, t)
# Notice that unsupervised clustering cannot support "divergence to infinity",
# which it identifies as another attractor (in fact, the first one).
x = SVector(mean(A[:, 1]), mean(A[:, 2]))
return any(isinf, x) ? SVector(200.0, 200.0) : x
end
test_basins(ds, u0s, grid, expected_fs_raw, featurizer;
max_distance = 20, ε = 1e-3, proximity_test = false, threshold_pairwise=1)
end
@testset "Magnetic pendulum: projected system" begin
mutable struct MagneticPendulumParams
γs::Vector{Float64}
d::Float64
α::Float64
ω::Float64
magnets::Vector{SVector{2, Float64}}
end
function magnetic_pendulum_rule(u, p, t)
x, y, vx, vy = u
γs::Vector{Float64}, d::Float64, α::Float64, ω::Float64 = p.γs, p.d, p.α, p.ω
dx, dy = vx, vy
dvx, dvy = @. -ω^2*(x, y) - α*(vx, vy)
for (i, ma) in enumerate(p.magnets)
δx, δy = (x - ma[1]), (y - ma[2])
D = sqrt(δx^2 + δy^2 + d^2)
dvx -= γs[i]*(x - ma[1])/D^3
dvy -= γs[i]*(y - ma[2])/D^3
end
return SVector(dx, dy, dvx, dvy)
end
function magnetic_pendulum(u = [sincos(0.12553*2π)..., 0, 0];
γ = 1.0, d = 0.3, α = 0.2, ω = 0.5, N = 3, γs = fill(γ, N), diffeq)
m = [SVector(cos(2π*i/N), sin(2π*i/N)) for i in 1:N]
p = MagneticPendulumParams(γs, d, α, ω, m)
return CoupledODEs(magnetic_pendulum_rule, u, p; diffeq)
end
diffeq = (alg = Vern9(), reltol = 1e-9, abstol = 1e-9)
ds = magnetic_pendulum(γ=1, d=0.2, α=0.2, ω=0.8, N=3; diffeq)
xg = range(-2,2; length = 201)
yg = range(-2,2; length = 201)
grid = (xg, yg)
ds = ProjectedDynamicalSystem(ds, 1:2, [0.0, 0.0])
u0s = [
1 => [-0.5, 0.857],
2 => [-0.5, -0.857],
3 => [1. , 0.],
]
expected_fs_raw = Dict(2 => 0.314, 3 => 0.309, 1 => 0.377)
function featurizer(A, t)
return SVector(A[end][1], A[end][2])
end
function featurizer_matrix(A, t)
return A
end
test_basins(ds, u0s, grid, expected_fs_raw, featurizer; ε = 0.2, Δt = 1.0, ferr=1e-2, featurizer_matrix, pairwise_comparison_matrix_test=true, threshold_pairwise=1)
end
# Okay, all of these aren't fundamentally new tests.
if DO_EXTENSIVE_TESTS
@testset "Lorenz-84 system: interlaced close-by" begin # warning, super expensive test
F = 6.886; G = 1.347; a = 0.255; b = 4.0
function lorenz84_rule(u, p, t)
F, G, a, b = p
x, y, z = u
dx = -y^2 -z^2 -a*x + a*F
dy = x*y - y - b*x*z + G
dz = b*x*y + x*z - z
return SVector{3}(dx, dy, dz)
end
diffeq = (alg = Vern9(), reltol = 1e-9, abstol = 1e-9)
ds = CoupledODEs(lorenz84_rule, fill(0.1, 3), [F, G, a, b]; diffeq)
u0s = [
1 => [2.0, 1, 0], # periodic
2 => [-2.0, 1, 0], # chaotic
3 => [0, 1.5, 1.0], # fixed point
]
M = 200; z = 3
xg = yg = zg = range(-z, z; length = M)
grid = (xg, yg, zg)
expected_fs_raw = Dict(2 => 0.18, 3 => 0.645, 1 => 0.175)
using ComplexityMeasures
function featurizer(A, t)
# `g` is the number of boxes needed to cover the set
probs = probabilities(ValueHistogram(0.1), A)
g = exp(entropy(Renyi(; q = 0), probs))
return SVector(g, minimum(A[:,1]))
end
test_basins(ds, u0s, grid, expected_fs_raw, featurizer;
ε = 0.01, ferr=1e-2, Δt = 0.2, consecutive_attractor_steps = 5, Ttr = 100, threshold_pairwise=100) #threshold is very high because features haven't really converged yet here
end
@testset "Duffing oscillator: stroboscopic map" begin
@inbounds function duffing_rule(x, p, t)
ω, f, d, β = p
dx1 = x[2]
dx2 = f*cos(ω*t) - β*x[1] - x[1]^3 - d * x[2]
return SVector(dx1, dx2)
end
diffeq = (alg = Vern9(), reltol = 1e-9, abstol = 1e-9)
ds = CoupledODEs(duffing_rule, [0.1, 0.25], [1.0, 0.2, 0.15, -1]; diffeq)
xg = yg = range(-2.2, 2.2; length=200)
grid = (xg, yg)
T = 2π/1.0
ds = StroboscopicMap(ds, T)
u0s = [
1 => [-2.2, -2.2],
2 => [2.2, 2.2],
]
expected_fs_raw = Dict(2 => 0.488, 1 => 0.512)
function featurizer(A, t)
return SVector(A[end][1], A[end][2])
end
test_basins(ds, u0s, grid, expected_fs_raw, featurizer;
ε = 1.0, ferr=1e-2, rerr = 1e-2, aerr = 5e-3, threshold_pairwise=1)
end
@testset "Thomas cyclical: Poincaré map" begin
function thomas_rule(u, p, t)
x,y,z = u
b = p[1]
xdot = sin(y) - b*x
ydot = sin(z) - b*y
zdot = sin(x) - b*z
return SVector{3}(xdot, ydot, zdot)
end
ds = CoupledODEs(thomas_rule, [1.0, 0, 0], [0.1665]; diffeq=(reltol=1e-9,))
xg = yg = range(-6.0, 6.0; length = 100) # important, don't use 101 here, because
# the dynamical system has some fixed points ON the hyperplane.
grid = (xg, yg)
pmap = PoincareMap(ds, (3, 0.0);
Tmax = 1e6,
rootkw = (xrtol = 1e-8, atol = 1e-8),
)
u0s = [
1 => [1.83899, -4.15575, 0],
2 => [1.69823, -0.0167188, 0],
3 => [-4.08547, -2.26516, 0],
]
expected_fs_raw = Dict(2 => 0.28, 3 => 0.266, 1 => 0.454)
function thomas_featurizer(A, t)
x, y = columns(A)
return SVector(minimum(x), minimum(y))
end
test_basins(pmap, u0s, grid, expected_fs_raw, thomas_featurizer; ε = 1.0, ferr=1e-2)
end
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 1106 | using Attractors, Test
# This is a fake bistable map that has two equilibrium points
# for r > 0.5. It has predictable fractions.
function dumb_map(z, p, n)
x, y = z
r = p[1]
if r < 0.5
return SVector(0.0, 0.0)
else
if x ≥ 0
return SVector(r, r)
else
return SVector(-r, -r)
end
end
end
r = 1.0
ds = DeterministicIteratedMap(dumb_map, [0., 0.], [r])
# deterministic grid, we know exactly the array layout
xg = yg = range(-1.5, 2.5; length=3)
grid = (xg, yg)
attrs = Dict(1 => StateSpaceSet([SVector(r, r)]), 2 => StateSpaceSet([SVector(-r, -r)]))
mapper = AttractorsViaProximity(ds, attrs; Ttr = 0)
basins, atts = basins_of_attraction(mapper, grid; show_progress=false)
@test basins[1, :] == fill(2, 3)
@test basins[2, :] == fill(1, 3)
@test basins[3, :] == fill(1, 3)
basins, atts, iterations = convergence_and_basins_of_attraction(mapper, grid; show_progress=false)
@test basins[1, :] == fill(2, 3)
@test basins[2, :] == fill(1, 3)
@test basins[3, :] == fill(1, 3)
@test length(atts) == 2
@test iterations == fill(1,3,3)
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2827 | DO_EXTENSIVE_TESTS = get(ENV, "ATTRACTORS_EXTENSIVE_TESTS", "false") == "true"
if DO_EXTENSIVE_TESTS
# The functionality tested here has been resolved and is only added as a test
# for future security. It has no need to be tested in every commit.
using Attractors
using Statistics, Random, Test
@testset "Clustering" begin
## prepare test (three possible attractors)
function featurizer(A, t)
return SVector(maximum(A[:,1]), maximum(A[:,2]))
end
function cluster_StateSpaceSets(featurizer, t, StateSpaceSets, clusterspecs)
features = [featurizer(StateSpaceSets[i], t) for i=1:length(StateSpaceSets)]
return group_features(features, clusterspecs)
end
attractor_pool = [[0 0], [10 10], [20 20]];
correct_labels = [1,1,1,1, 2,2,2,1,2,3,3,3,3,1]
a = attractor_pool[correct_labels]
correct_labels_infinite_threshold = deepcopy(correct_labels)
a[end] = [50 5]
correct_labels[end] = -1
correct_labels_infinite_threshold[end] = 3
attractors = Dict(1:length(a) .=> StateSpaceSet.(a; warn = false));
### silhouettes and real
@testset "method=$(optimal_radius_method)" for optimal_radius_method in ["silhouettes", "silhouettes_optim", 5.0]
for silhouette_statistic in [mean, minimum]
clusterspecs = GroupViaClustering(; num_attempts_radius=20, silhouette_statistic,
optimal_radius_method=optimal_radius_method, min_neighbors=2, rescale_features=false)
clust_labels = cluster_StateSpaceSets(featurizer, [], attractors, clusterspecs)
@test clust_labels == correct_labels
end
end
### knee method
@testset "method=knee" begin
correct_labels_knee = [1,1,1,1,2,2,2,1,2,3,3,3,3,1,2,2,2,2,2,3,3,3,3,3,3,1,1,1,1,1] #smaller number of features works even worse
Random.seed!(1)
a = [attractor_pool[label] + 0.2*rand(Float64, (1,2)) for label in correct_labels_knee]
attractors_knee = Dict(1:length(a) .=> StateSpaceSet.(a; warn = false));
clusterspecs = GroupViaClustering( optimal_radius_method="knee",
min_neighbors=4, rescale_features=false)
clust_labels = cluster_StateSpaceSets(featurizer, [], attractors_knee, clusterspecs)
# at least check if it finds the same amount of attractors;
# note this does not work for any value of `min_neighbors`.
# TODO: Test here is wrong.
# @test maximum(clust_labels) == maximum(correct_labels)
@test 1 ≤ maximum(clust_labels) ≤ 3
end
@testset "Mmap" begin
clusterspecs = GroupViaClustering(; num_attempts_radius=20, use_mmap=true,
min_neighbors=2, rescale_features=false)
clust_labels = cluster_StateSpaceSets(featurizer, [], attractors, clusterspecs)
@test clust_labels == correct_labels
end
end
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 1387 | using Test
using Attractors
import Random
using Statistics: mean
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
henon() = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
ds = henon()
xg = yg = range(-2.0, 2.0; length=100)
grid = (xg, yg)
expected_fs_raw = Dict(1 => 0.451, -1 => 0.549)
function featurizer(A, t)
# Notice that unsupervised clustering cannot support "divergence to infinity",
# which it identifies as another attractor (in fact, the first one).
x = SVector(mean(A[:, 1]), mean(A[:, 2]))
if any(x -> (isinf(x) || isnan(x) || x > 10), x)
SVector(200.0, 200.0)
else
x
end
end
binning = FixedRectangularBinning(range(-10, 240; step = 50), 2)
gconfig = GroupViaHistogram(binning)
mapper = AttractorsViaFeaturizing(ds, featurizer, gconfig)
xg = yg = range(-2.0, 2.0; length=100)
grid = (xg, yg)
expected_fs_raw = Dict(1 => 0.451, -1 => 0.549)
sampler, _ = statespace_sampler(grid, 12444)
ics = StateSpaceSet([copy(sampler()) for _ in 1:1000])
fs, = basins_fractions(mapper, ics; show_progress = false)
@test length(keys(fs)) == 2
@test fs[1] ≈ 0.45 rtol = 1e-1
# the divergent points go to last bin, which is 25 = 5x5
@test fs[25] ≈ 0.55 rtol = 1e-1
# Test that attractors have been stored.
# the second "attractor" is infinity
atts = extract_attractors(mapper)
@test atts[25][end] == [-Inf, -Inf] | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2698 | using Attractors
using Test
function predator_prey_ds()
function predator_prey_fastslow(u, p, t)
α, γ, ϵ, ν, h, K, m = p
N, P = u
du1 = α*N*(1 - N/K) - γ*N*P / (N+h)
du2 = ϵ*(ν*γ*N*P/(N+h) - m*P)
return SVector(du1, du2)
end
γ = 2.5
h = 1
ν = 0.5
m = 0.4
ϵ = 1.0
α = 0.8
K = 15
u0 = rand(2)
p0 = [α, γ, ϵ, ν, h, K, m]
ds = CoupledODEs(predator_prey_fastslow, u0, p0)
return ds
end
@testset "Different grids" begin
ds = predator_prey_ds()
u0 = [0.03, 0.5]
d = 21
xg = yg = range(0, 18; length = d)
grid_reg = (xg, yg)
pow = 8
xg = range(0, 18.0^(1/pow); length = d).^pow
grid_irreg = (xg, yg)
grid_subdiv = subdivision_based_grid(ds, grid_reg)
function test_grid(grid, bool)
ds = predator_prey_ds()
mapper = AttractorsViaRecurrences(ds, grid;
Dt = 0.05, sparse = true, force_non_adaptive = true,
consecutive_recurrences = 20, attractor_locate_steps = 100,
store_once_per_cell = true,
maximum_iterations = 1000,
)
id = mapper(u0)
A = extract_attractors(mapper)[1]
@test (length(A) > 1) == bool
end
@testset "regular fail" begin
test_grid(grid_reg, false)
end
@testset "irregular" begin
test_grid(grid_irreg, true)
end
@testset "subdivision" begin
test_grid(grid_subdiv, true)
end
end
@testset "basin cell index" begin
ds = predator_prey_ds()
xg = yg = range(0, 5, length = 6)
grid = subdivision_based_grid(ds, (xg, yg); maxlevel = 3)
lvl_array = grid.lvl_array
@test (Attractors.basin_cell_index((2, 1.1) , grid) == CartesianIndex((17,9)))
@test (Attractors.basin_cell_index((3.6, 2.1) , grid) == CartesianIndex((29,17)))
@test (Attractors.basin_cell_index((4.9, 4.9) , grid) == CartesianIndex((33,33)))
@test (Attractors.basin_cell_index((0.5, 0.5) , grid) == CartesianIndex((5,5)))
@test (Attractors.basin_cell_index((3.4, 1.6) , grid) == CartesianIndex((27,13)))
@test (Attractors.basin_cell_index((4.7, 2.2) , grid) == CartesianIndex((37,17)))
end
@testset "automatic Δt" begin
ds = predator_prey_ds()
xg = yg = range(0, 18, length = 30)
grid0 = (xg, yg)
xg = yg = range(0, 18.0^(1/2); length = 20).^2
grid1 = (xg, yg)
grid2 = SubdivisionBasedGrid(grid0, rand([0, 1, 2], (30, 30)))
using Attractors: RegularGrid, IrregularGrid
Dt0 = automatic_Δt_basins(ds, RegularGrid(grid0))
Dt1 = automatic_Δt_basins(ds, IrregularGrid(grid1))
Dt2 = automatic_Δt_basins(ds, grid2)
@test Dt0 > 0
@test Dt1 > 0
@test Dt2 > 0
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 2459 | using Attractors
using Test
@testset "Proximity set distance" begin
# This is a fake bistable map that has two equilibrium points
# for r > 0.5 and one for r < 0.5. It has predictable fractions.
function dumb_map(z, p, n)
x, y = z
r = p[1]
if r < 0.5
return SVector(0.0, 0.0)
else
u = SVector(r, r)
if x > 0
return u
else
return -u
end
end
end
r = 1.0
ds = DeterministicIteratedMap(dumb_map, [0., 0.], [r])
yg = xg = range(-10, 10, length = 101)
attractors = Dict(i => SSSet([SVector(r*x, r*x)]) for (i, x) in enumerate((1, -1)))
sampler, = statespace_sampler((xg, yg))
f = (A, B) -> abs(A[1][1] - B[1][1])
@testset "distance: $(distance)" for distance in (f, Centroid(), StrictlyMinimumDistance())
mapper = AttractorsViaProximity(ds, attractors, 0.1; Ttr = 2, distance)
fs = basins_fractions(mapper, sampler)
@test length(fs) == 2
@test 0.4 < fs[1] < 0.6
@test 0.4 < fs[2] < 0.6
end
end
@testset "Proximity deduce ε" begin
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
henon() = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
ds = henon()
@testset "single attractor, no ε" begin
attractors = Dict(1 => trajectory(ds, 10000, [0.0, 0.0]; Δt = 1, Ttr=100)[1])
mapper = AttractorsViaProximity(ds, attractors)
@test trunc(mapper.ε, digits = 2) ≈ 0.18 # approximate size of attractor here
end
@testset "two attractors, analytically known ε" begin
attractors = Dict(
1 => StateSpaceSet([0 1.0]; warn = false),
2 => StateSpaceSet([0 2.0]; warn = false)
)
mapper = AttractorsViaProximity(ds, attractors)
@test mapper.ε == 0.5
end
@testset "one attractor, single point (invalid)" begin
attractors = Dict(
1 => StateSpaceSet([0 1.0]; warn = false),
)
@test_throws ArgumentError AttractorsViaProximity(ds, attractors)
end
end
@testset "Fix #61" begin
cubicmap(u, p, n) = SVector{1}(p[1]*u[1] - u[1]^3)
ds = DeterministicIteratedMap(cubicmap, [1.0], [2.0])
fp = SVector(sqrt(2))
attrs = Dict(1 => StateSpaceSet([fp]), 2 => StateSpaceSet([-fp]))
mapper = AttractorsViaProximity(ds, attrs)
label = mapper([2.0])
@test label == -1
end | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 5145 | # This file performs more extensive tests specifically for `AttractorsViaRecurrences`
DO_EXTENSIVE_TESTS = get(ENV, "ATTRACTORS_EXTENSIVE_TESTS", "false") == "true"
if DO_EXTENSIVE_TESTS
# The functionality tested here has been resolved and is only added as a test
# for future security. It has no need to be tested in every commit.
using Attractors
using Test
using OrdinaryDiffEq: Vern9
using Random
@testset "point saving limit cycles" begin
@inbounds function morris_lecar_rule(u, p, t)
I, V3, V1, V2, V4, VCa, VL, VK, gCa, gK, gL, τ = p
V, N = u
M = 0.5*(1 + tanh((V-V1)/V2))
G = 0.5*(1 + tanh((V-V3)/V4))
du1 = -gCa*M*(V - VCa) -gK*N*(V - VK) -gL*(V-VL) + I
du2 = 1/τ*(-N + G)
return SVector{2}(du1, du2)
end
function test_morrislecar(; store_once_per_cell, stop_at_Δt, Δt = 0.15)
u0=[0.1, 0.1];
p = (I = 0.115, V3 = 0.1, V1 = -0.00, V2 = 0.15, V4 = 0.1,
VCa = 1 , VL = -0.5, VK = -0.7, gCa = 1.2, gK = 2,
gL = 0.5, τ = 3)
# p = [I, V3, V1, V2, V4, VCa, VL, VK, gCa, gK, gL, τ]
diffeq = (reltol = 1e-9, alg = Vern9())
df = CoupledODEs(morris_lecar_rule, u0, p; diffeq)
xg = yg = range(-1,1,length = 2000)
mapper = AttractorsViaRecurrences(df, (xg, yg);
attractor_locate_steps = 1000,
consecutive_recurrences = 2,
store_once_per_cell,
sparse = true,
Δt,
Ttr = 10,
force_non_adaptive = stop_at_Δt,
)
sampler, = statespace_sampler(HRectangle([-0.5, 0], [0.5, 1]), 155)
ics = StateSpaceSet([copy(sampler()) for i in 1:1000])
fs, labels = basins_fractions(mapper, ics; show_progress=false)
num_att = length(fs)
return num_att
end
@testset "Sparse limit cycles" begin
# how many times we store per cell doesn't change anything
# however breaking the orbit commensurability does!
num_att = test_morrislecar(; store_once_per_cell=true, stop_at_Δt = false)
@test num_att > 1
num_att = test_morrislecar(; store_once_per_cell=false, stop_at_Δt = false)
@test num_att > 1
num_att = test_morrislecar(; store_once_per_cell=false, stop_at_Δt = true)
@test num_att == 1
num_att = test_morrislecar(; store_once_per_cell=true, stop_at_Δt = true)
@test num_att == 1
end
end
@testset "Compatibility sparse and nonsparse" begin
function test_compatibility_sparse_nonsparse(ds, grid; kwargs...)
sampler, = statespace_sampler(grid, 1244)
ics = StateSpaceSet([copy(sampler()) for i in 1:1000])
mapper = AttractorsViaRecurrences(ds, grid; sparse=true, show_progress = false, kwargs...)
fs_sparse, labels_sparse = basins_fractions(mapper, ics; show_progress = false)
approx_atts_sparse = extract_attractors(mapper)
mapper = AttractorsViaRecurrences(ds, grid; sparse=false, show_progress = false, kwargs...)
fs_non, labels_non = basins_fractions(mapper, ics; show_progress = false)
approx_atts_non = extract_attractors(mapper)
@test fs_sparse == fs_non
@test labels_sparse == labels_non
@test approx_atts_sparse == approx_atts_non
end
@testset "Henon map: discrete & divergence" begin
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
ds = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
xg = yg = range(-2.0, 2.0; length=100)
grid = (xg, yg)
test_compatibility_sparse_nonsparse(ds, grid)
end
end
@testset "Escape to -1 test" begin
# This is for testing if the chk safety keyword is working
# as intended. The output should be only -1.
function dissipative_standard_map_rule(u, p, n)
x, y = u
ν, f₀ = p
s = x + y
xn = mod2pi(s)
yn = (1 - ν)*y + f₀*(sin(s))
return SVector(xn, yn)
end
p0 = (ν = 0.02, f0 = 4.0)
u0 = [0.1, 0.1]
ds = DeterministicIteratedMap(dissipative_standard_map_rule, u0, p0)
density = 10
xg = range(0, 2π; length = density+1)[1:end-1]
ymax = 2
yg = range(-ymax, ymax; length = density)
grid = (xg, yg)
mapper_kwargs = (
maximum_iterations = 10,
sparse = false, # we want to compute full basins
)
mapper = AttractorsViaRecurrences(ds, grid; mapper_kwargs...)
basins, attractors = basins_of_attraction(mapper)
ids = sort!(unique(basins))
@test ids... == -1
end
@testset "continuing lost state" begin
# see discussion in https://github.com/JuliaDynamics/Attractors.jl/pull/103#issuecomment-1754617229
henon_rule(x, p, n) = SVector{2}(1.0 - p[1]*x[1]^2 + x[2], p[2]*x[1])
henon() = DeterministicIteratedMap(henon_rule, zeros(2), [1.4, 0.3])
ds = henon()
xg = yg = range(-1.0, 1.0; length=100)
grid = (xg, yg)
mapper = AttractorsViaRecurrences(ds, grid)
id = mapper([0. ,0.])
@test id == 1 # we resume going into the attractor outside the grid
id2 = mapper([10. ,10.])
@test id2 == -1 # actual divergence to infinity is still detected
end
end # extensive tests clause
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | code | 6139 | using Attractors
using Test
using LinearAlgebra
@testset "Newton 2d" begin
function newton_map(z, p, n)
z1 = z[1] + im*z[2]
dz1 = newton_f(z1, p[1])/newton_df(z1, p[1])
z1 = z1 - dz1
return SVector(real(z1), imag(z1))
end
newton_f(x, p) = x^p - 1
newton_df(x, p)= p*x^(p-1)
ds = DiscreteDynamicalSystem(newton_map, [0.1, 0.2], [3.0])
xg = yg = range(-1.5, 1.5; length = 400)
newton = AttractorsViaRecurrences(ds, (xg, yg);
sparse = false, consecutive_lost_steps = 1000
)
attractors = [[1.0, 0.0], [-0.5, 0.8660254037844386], [-0.5, -0.8660254037844386]]
algo_r = Attractors.MFSBruteForce(sphere_decrease_factor = 0.96)
randomised = Dict([atr => minimal_fatal_shock(newton, atr, (-1.5, 1.5), algo_r) for atr in attractors])
algo_bb = Attractors.MFSBlackBoxOptim()
blackbox = Dict([atr => (minimal_fatal_shock(newton, atr, (-1.5, 1.5), algo_bb)) for atr in attractors])
random_seed = [[rand([-1,1])*rand()/2, rand([-1,1])*rand()/2] for _ in 1:20]
randomised_r = Dict([atr => (minimal_fatal_shock(newton, atr, (-1.5, 1.5), algo_r)) for atr in random_seed])
blackbox_r = Dict([atr => (minimal_fatal_shock(newton, atr, (-1.5, 1.5), algo_bb)) for atr in random_seed])
test = true
for i in (keys(randomised))
if norm(randomised[i]) >= 0.65 || norm(randomised[i]) <= 0.60 || newton(randomised[i] + i) == newton(i)
test = false
end
end
@test test
test = true
for i in (keys(blackbox))
if norm(blackbox[i]) >= 0.629 || norm(blackbox[i]) <= 0.62009 || newton(blackbox[i] + i) == newton(i)
test = false
end
end
@test test
test = true
for i in (keys(randomised_r))
if norm(randomised_r[i]) >= 0.5 || newton(randomised_r[i] + i) == newton(i)
test = false
end
end
@test test
test = true
for i in (keys(blackbox_r))
if norm(blackbox_r[i]) >= 0.5 || newton(blackbox_r[i] + i) == newton(i)
test = false
end
end
@test test
@testset "target id" begin
atrdict = Dict(i => StateSpaceSet([a]) for (i, a) in enumerate(attractors))
mapper = AttractorsViaProximity(ds, atrdict, 0.01)
algo_bb = Attractors.MFSBlackBoxOptim()
# multiple target attractors
mfs_1 = [
i => minimal_fatal_shock(mapper, a, (-1.5, 1.5), algo_bb; target_id = setdiff(1:3, [i]))
for (i, a) in enumerate(attractors)
]
# specific target attractors
mfs_2 = [
i => minimal_fatal_shock(mapper, a, (-1.5, 1.5), algo_bb; target_id = setdiff(1:3, [i])[1])
for (i, a) in enumerate(attractors)
]
# due to the symmetries of the system all mfs should be identical in magnitude
for mfs in (mfs_1, mfs_2)
for f in mfs
@test norm(f[2]) ≈ 0.622 rtol = 1e-2
end
end
end
end
###############################################
# Magnetic 2D #
###############################################
@testset "Magnetic 2D" begin
struct MagneticPendulum
magnets::Vector{SVector{2, Float64}}
end
mutable struct MagneticPendulumParams2
γs::Vector{Float64}
d::Float64
α::Float64
ω::Float64
end
function (m::MagneticPendulum)(u, p, t)
x, y, vx, vy = u
γs::Vector{Float64}, d::Float64, α::Float64, ω::Float64 = p.γs, p.d, p.α, p.ω
dx, dy = vx, vy
dvx, dvy = @. -ω^2*(x, y) - α*(vx, vy)
for (i, ma) in enumerate(m.magnets)
δx, δy = (x - ma[1]), (y - ma[2])
D = sqrt(δx^2 + δy^2 + d^2)
dvx -= γs[i]*(x - ma[1])/D^3
dvy -= γs[i]*(y - ma[2])/D^3
end
return SVector(dx, dy, dvx, dvy)
end
function magnetic_pendulum(u = [sincos(0.12553*2π)..., 0, 0];
γ = 1.0, d = 0.3, α = 0.2, ω = 0.5, N = 3, γs = fill(γ, N))
m = MagneticPendulum([SVector(cos(2π*i/N), sin(2π*i/N)) for i in 1:N])
p = MagneticPendulumParams2(γs, d, α, ω)
return CoupledODEs(m, u, p)
end
ds = magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)
psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])
attractors_m = Dict(i => StateSpaceSet([dynamic_rule(ds).magnets[i]]) for i in 1:3)
mapper_m = AttractorsViaProximity(psys, attractors_m)
xg = yg = range(-4, 4; length = 201)
grid = (xg, yg)
algo_r = Attractors.MFSBruteForce(sphere_decrease_factor = 0.99)
algo_bb = Attractors.MFSBlackBoxOptim()
attractor3 = vec((collect(values(attractors_m)))[3])
attractor2 = vec((collect(values(attractors_m)))[2])
attractor1 = vec((collect(values(attractors_m)))[1])
randomised_r = Dict([atr => norm(minimal_fatal_shock(mapper_m, atr, [(-4, 4), (-4, 4)], algo_r))
for atr in [attractor1[1], attractor2[1], attractor3[1]]])
blackbox_r = Dict([atr => norm(minimal_fatal_shock(mapper_m, atr, [(-4, 4), (-4, 4)], algo_bb))
for atr in [attractor1[1], attractor2[1], attractor3[1]]])
@test map(x -> (x <= 0.4) && (x) > 0.39, values(randomised_r)) |> all
@test map(x -> (x <= 0.395) && (x) > 0.39, values(blackbox_r)) |> all
end
###############################################
# Thomas 3D #
###############################################
@testset "3D symmetry" begin
using LinearAlgebra: norm
function thomas_rule(u, p, t)
x,y,z = u
b = p[1]
xdot = sin(y) - b*x
ydot = sin(z) - b*y
zdot = sin(x) - b*z
return SVector{3}(xdot, ydot, zdot)
end
thomas_cyclical(u0 = [1.0, 0, 0]; b = 0.2) = CoupledODEs(thomas_rule, u0, [b])
ds = thomas_cyclical(b = 0.1665)
xg = yg = zg = range(-6.0, 6.0; length = 251)
mapper_3d = AttractorsViaRecurrences(ds, (xg, yg, zg))
ux = SVector(1.5, 0, 0)
uy = SVector(0, 1.5, 0)
algo_bb = Attractors.MFSBlackBoxOptim(max_steps = 50000)
ux_res = minimal_fatal_shock(mapper_3d, ux, (-6.0,6.0), algo_bb)
uy_res = minimal_fatal_shock(mapper_3d, uy, (-6.0,6.0), algo_bb)
@test norm(ux_res) - norm(uy_res) < 0.0001
end
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 9162 | # v1.20
- `AttractorsViaProximity` has been significantly improved: it now allows for a keyword `distance`. This keyword decides how the distance between the trajectory end-point and the attractors is decided. The function has further been simplified and re-uses the existing `set_distance` function. The default `distance` keeps the previous behavior unaltered.
# v1.19
- Global continuation can now be performed across any arbitrary curve
in parameter space. This is something completely novel
and we'll likely work on a paper on this!
# v1.18
This is a big release, with (hopefully) nothing breaking, but lots of deprecations!
## New stuff
- New central Tutorial for Attractors.jl. It also highlights how to enrich a continuation output with other measures of nonlocal stability.
- New global continuation algorithm that generalizes RAFM: `AttractorSeedContinueMatch`.
- There is now an extendable API for "matchers", ways to match state spaces sets across a continuation. See `IDMatcher` for the API.
- New matcher `MatchBySSSetDistance` that does matching used to do in previous versions.
- New matcher `MatchByBasinOverlap` that does what `match_basins!` used to do.
- New matcher `MatchByBasinEnclosure` that is truly brand new.
- New plotting function `plot_continuation_curves!` to add additional information to the `plot_basins_attractors_curves` type plots.
- New exported function `reset_mapper!` to clear all stored information in an `AttractorMapper`.
- `AttractorsViaFeaturizing` now always stores the attractors and implements `extract_attractors`.
- New plotting function `plot_attractors`.
## Deprecations and renaming
- Function `continuation` has been deprecated for `global_continuation` in preparation for a future where both local/linear/tradiational continuation as well as our "attractors and basins continuation" are both provided by DynamicalSystems.jl.
- `match_continuation!` has been deprecated for `match_sequentially!`.
- Option `par_weight` is deprecated in `FeaturizeGroupAcrossParameter`. Part of the developer team (`@Datseris`, `@KalelR`) discussed this an concluded that `par_weight` doesn't make much scientific sense to include. Since it obfuscates the code and the documentation, it is no longer documented but still exported. It will be unavailable in the next breaking release.
# v1.17
- New function `convergence_and_basins_fractions`
- improved the algorithm
counting the convergence iterations for `AttractorsViaRecurrences` to give
more accurate results, by taking into account the user-provided convergence criteria, and multiplying with `Δt` to obtain the time in correct units.
- New function `test_wada_merge` to test the Wada property in 2D basins of attraction.
- New function `haussdorff_distance` to compute distance between two binary matrices.
# v1.16
The function `plot_basins_attractors_curves` can now take a vector of functions for mapping attractors to real numbers. Each makes a new panel with the chosen projection.
# v1.15
Improvements in the `minimal_fatal_shock` algorithm:
- Can now chose target attractors to shock towards, enabling computation
of the excitability threshold
- Can give in custom metric function for estimating the norm
- Exported alias `excitability_threshold` for `minimal_fatal_shock`
- New argument `bbkwargs` can be given to `MFSBlackBoxOptim` to propagate more keywords
to BlackBoxOptimization.jl
# v1.14
- New function `edgetrack` for finding saddles.
- New function `convergence_and_basins_of_attraction` for obtaining the iterates each initial condition took to reach the attractor.
- New plotting function `shaded_basins_heatmap`.
# v1.13
- The algorithm of `AttractorsViaRecurrences` has been simplified a bit. The action of the keyword `mx_chk_loc_att` has been changed which may lead to different results in some usage cases. Now `mx_chk_loc_att` counts how many steps to take after collecting enough recurrences, and this step count is only increasing.
- Additional benefit of this change is that incorrect algorithm behaviour can be caught eagerly. Now an error is thrown when we know in advance the algorithm will fail. (This also affects `continuation` with `RAFM`)
- The documentation of `AttractorsViaRecurrences` has been improved and clarified. Additionally a video illustrating algorithm behaviour has been added.
- A renaming of some of the options (keyword arguments) of `AttractorsViaRecurrences` has been done in line with the clarity increase of the algorithm. The following renames are in place and currently deprecated:
- `mx_chk_fnd_att -> consecutive_recurrences`
- `mx_chk_loc_att -> attractor_locate_steps`
- `mx_chk_att -> consecutive_attractor_steps`
- `mx_chk_hit_bas -> consecutive_basin_steps`
- `mx_chk_lost -> consecutive_lost_steps`
- `mx_chk_safety -> maximum_iterations`
# v1.12
- New algorithm `GroupViaPairwiseComparison` to group features in `AttractorsViaFeaturizing`. Simpler, typically faster and using less memory than DBSCAN, it can be useful in well-behaved systems.
# v1.11
- New algorithm `subdivision_based_grid`. Allows user to automatically construct the grid which simulates subdivision into regions with different discretization levels in accordance with state space flow speed.
# v1.10
- Added support of irregular grids to `AttractorsViaRecurrences`, now user can provide ranges without fixed step along the same axis.
# v1.9
- Matching attractors during the continuation with `RAFM` has been improved and is done by the function `match_continuation!` which has two options regarding how to handle attractors of previous parameters that have vanished.
# v1.8
- New algorithm `minimal_fatal_shock` that finds the minimal perturbation for arbitrary initial condition `u0` which will kick the system into different from the current basin.
# v1.7.1
- Fixed issue where poincare map was not working with basins of attraction as intended (sampling points directly on the hyperplane)
# v1.7
- Some functions have been renamed for higher level of clarity (deprecations have been put in place):
- `match_attractor_ids!` -> `match_statespacesets!`
- `GroupAcrossParameter` -> `FeaturizeGroupAcrossParameter`.
# v1.6
- Attractors.jl moved to Julia 1.9+
- Plotting utility functions are now part of the API using package extensions. They are exported, documented, and used in the examples.
# v1.5
- Our pre-print regarding the global stability analysis framework offered by Attractors.jl is now online: https://arxiv.org/abs/2304.12786
- Package now has a CITATION.bib file.
# v1.4
- New function `rematch!` that can be used after `continuation` is called with `AttractorsViaRecurrences`, if the original matching performed was not ideal.
# v1.3
- More plotting functions have been added and plotting has been exposed as API. After Julia 1.9 it will also be documented and formally included in the built docs.
# v1.2
- Add option `force_non_adaptive` to `AttractorsViaRecurrences`. This option is of instrumental importance when the grid is too fine or when limit cycle attractors are involved.
# v1.1
- `basins_fractions` no longer returns the attractors. Instead, a function `extract_attractors(mapper::AttractorMapper)` is provided that gives the attractors. This makes an overall more convenient experience that doesn't depend on the type of the initial conditions used.
# v1
- Added the `continuation` function and the two types `RecurrencesFindAndMatch` and `GroupAcrossParameterContinuation`
# v0.1.0
This is the first release. It continues from ChaosTools.jl v2.9, and hence, the comparison of attractor-related features is w.r.t to that version.
## Finding attractors
- New attractor mapping algorithm `AttractorsViaRecurrencesSparse` that uses sparse arrays to find attractors of arbitrarily high dimensional dynamical systems, eliminating the main drawback of `AttractorsViaRecurrences`.
- Clustering (used in `AttractorsViaFeaturizing`) has been completely overhauled. Now, a `ClusteringConfig` instances must be created and then passed on to `AttractorsViaFeaturizing`.
- `AttractorsViaFeaturizing` no longer has keywords about clustering.
- A new function `cluster_features` is exported to the public API.
- Multithreading is now an option in `AttractorsViaFeaturizing`. It is enabled by default.
- Added a new clause in automatic `ε` estimation in `AttractorsViaProximity` for when there is only a single attractor passed in by the user.
## Basin fractions continuation
- New function `continuation` that calculates basins fractions and how these change versus a parameter (given a continuation method)
- New basins fraction continuation method `RecurrencesFindAndMatch` that utilizes a brand new algorithm to continuate basins fractions of arbitrary systems.
- `match_attractor_ids!` has been fully overhauled to be more flexible, allow more ways to match, and also allow arbitrary user-defined ways to match.
- New function `match_basins_ids!` for matching the output of basins_of_attraction`.
- New exported functions `swap_dict_keys!, unique_keys, replacement_map` used in code that matches attractors and could be useful to front-end users.
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 2363 | # Attractors.jl
[](https://juliadynamics.github.io/DynamicalSystemsDocs.jl/attractors/dev/)
[](https://juliadynamics.github.io/DynamicalSystemsDocs.jl/attractors/stable/)
[](https://arxiv.org/abs/2304.12786)
[](https://github.com/JuliaDynamics/Attractors.jl/actions?query=workflow%3ACI)
[](https://codecov.io/gh/JuliaDynamics/Attractors.jl)
[](http://juliapkgstats.com/pkg/Attractors)
Attractors.jl is a Julia package for
- Finding all attractors, and all types of attractors, of arbitrary dynamical systems. An extendable interface allows for new algorithms for finding attractors.
- Finding their basins of attraction or the state space fractions of the basins.
This includes finding exit basins (divergence to infinity).
- Analyzing nonlocal stability of attractors (also called global stability or resilience).
- Performing **global continuation** of attractors and their basins (or other measures of stability), over a parameter range. Global continuation is a new, cutting-edge type of continuation that offers several advantages over traditional local continuation (AUTO, MatCont, BifurcationKit.jl, etc.), see the comparison in our docs.
- Finding the basin boundaries and edges states and analyzing their fractal properties.
- Tipping points related functionality for systems with known dynamic rule.
- And more!
It can be used as a standalone package, or as part of
[DynamicalSystems.jl](https://juliadynamics.github.io/DynamicalSystemsDocs.jl/dynamicalsystems/stable/).
To install it, run `import Pkg; Pkg.add("Attractors")`.
All further information is provided in the documentation, which you can either find [online](https://juliadynamics.github.io/DynamicalSystemsDocs.jl/attractors/stable/) or build locally by running the `docs/make.jl` file.
_Previously, Attractors.jl was part of ChaosTools.jl_ | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 537 | ---
name: Bug report
about: Create a report to help us improve
title: ''
labels: ''
assignees: ''
---
**Describe the bug**
A clear and concise description of what the bug is.
**Minimal Working Example**
Please provide a piece of code that leads to the bug you encounter.
If the code is **runnable**, it will help us identify the problem faster.
**Package versions**
Please provide the versions you use. To do this, run the code:
```julia
using Pkg
Pkg.status([
"Package1", "Package2"]; # etc.
mode = PKGMODE_MANIFEST
)
```
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 268 | ---
name: Feature request
about: Suggest an idea for this project
title: ''
labels: ''
assignees: ''
---
**Describe the feature you'd like to have**
**Cite scientific papers related to the feature/algorithm**
**If possible, sketch out an implementation strategy**
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 5856 | # API
## Finding attractors
Attractors.jl defines a generic interface for finding attractors of dynamical systems. One first decides the instance of [`DynamicalSystem`](@ref) they need. Then, an instance of [`AttractorMapper`](@ref) is created from this dynamical system. This `mapper` instance can be used to compute e.g., [`basins_of_attraction`](@ref), and the output can be further analyzed to get e.g., the [`basin_entropy`](@ref).
```@docs
AttractorMapper
extract_attractors
```
### Recurrences
```@docs
AttractorsViaRecurrences
automatic_Δt_basins
SubdivisionBasedGrid
subdivision_based_grid
```
### Proximity
```@docs
AttractorsViaProximity
```
### Featurizing
```@docs
AttractorsViaFeaturizing
```
## Grouping configurations
Grouping configurations that can be given to [`AttractorsViaFeaturizing`](@ref)
are part of a generic and extendable interface based on the [`group_features`](@ref)
function.
The grouping configuration sets how the features describing the trajectories will be grouped together.
Nevertheless, this grouping infrastructure can also be used and extended completely independently of finding attractors of dynamical systems!
### Grouping interface
```@docs
group_features
GroupingConfig
```
### Grouping types
```@docs
GroupViaClustering
GroupViaHistogram
GroupViaNearestFeature
GroupViaPairwiseComparison
```
### Grouping utils
```@docs
extract_features
```
## Basins of attraction
Calculating basins of attraction, or their state space fractions, can be done with the functions:
- [`basins_fractions`](@ref)
- [`basins_of_attraction`](@ref).
```@docs
basins_fractions
basins_of_attraction
statespace_sampler
```
## Convergence times
```@docs
convergence_and_basins_fractions
convergence_and_basins_of_attraction
convergence_time
```
## Final state sensitivity / fractal boundaries
Several functions are provided related with analyzing the fractality of the boundaries of the basins of attraction:
- [`basins_fractal_dimension`](@ref)
- [`basin_entropy`](@ref)
- [`basins_fractal_test`](@ref)
- [`uncertainty_exponent`](@ref)
- [`test_wada_merge`](@ref)
```@docs
basins_fractal_dimension
basin_entropy
basins_fractal_test
uncertainty_exponent
test_wada_merge
```
## Edge tracking and edge states
The edge tracking algorithm allows to locate and construct so-called edge states (also referred to as *Melancholia states*) embedded in the basin boundary separating different basins of attraction. These could be saddle points, unstable periodic orbits or chaotic saddles. The general idea is that these sets can be found because they act as attractors when restricting to the basin boundary.
```@docs
edgetracking
EdgeTrackingResults
bisect_to_edge
```
## Tipping points
This page discusses functionality related with tipping points in dynamical systems with known rule. If instead you are interested in identifying tipping points in measured timeseries, have a look at [TransitionIndicators.jl](https://github.com/JuliaDynamics/TransitionIndicators.jl).
```@docs
tipping_probabilities
```
## Minimal Fatal Shock
The algorithm to find minimal perturbation for arbitrary initial condition `u0` which will kick the system into different from the current basin.
```@docs
minimal_fatal_shock
MFSBlackBoxOptim
MFSBruteForce
```
## Global continuation
```@docs
global_continuation
```
### General seeding-based continuation
```@docs
AttractorSeedContinueMatch
```
### Recurrences continuation
```@docs
RecurrencesFindAndMatch
```
### Aggregating attractors and fractions
```@docs
aggregate_attractor_fractions
```
### Grouping continuation
```@docs
FeaturizeGroupAcrossParameter
```
## Matching attractors
Matching attractors follow an extendable interface based on [`IDMatcher`](@ref).
The available matchers are:
```@docs
MatchBySSSetDistance
MatchByBasinEnclosure
MatchByBasinOverlap
```
### Matching interface
```@docs
IDMatcher
matching_map
matching_map!
match_sequentially!
```
### Low-level distance functions
```@docs
Centroid
Hausdorff
StrictlyMinimumDistance
set_distance
setsofsets_distances
```
### Dict utils
```@docs
unique_keys
swap_dict_keys!
next_free_id
```
## Visualization utilities
Several plotting utility functions have been created to make the visualization of the output of Attractors.jl seamless. See the examples page for usage of all these plotting functions.
Note that all functions have an out-of-place and an in-place form, the in-place form always taking as a first input a pre-initialized `Axis` to plot in while the out-of-place creates and returns a new figure object.
E.g.,
```julia
fig = heatmap_basins_attractors(grid, basins, attractors; kwargs...)
heatmap_basins_attractors!(ax, grid, basins, attractors; kwargs...)
```
### [Common plotting keywords](@id common_plot_kwargs)
Common keywords for plotting functions in Attractors.jl are:
- `ukeys`: the basin ids (unique keys, vector of integers) to use. By default all existing keys are used.
- `access = [1, 2]`: indices of which dimensions of an attractor to select and visualize in a two-dimensional plot (as in [`animate_attractors_continuation`](@ref)).
- `colors`: a dictionary mapping basin ids (i.e., including the `-1` key) to a color. By default the JuliaDynamics colorscheme is used if less than 7 ids are present, otherwise random colors from the `:darktest` colormap.
- `markers`: dictionary mapping attractor ids to markers they should be plotted as
- `labels = Dict(ukeys .=> ukeys)`: how to label each attractor.
- `add_legend = length(ukeys) < 7`: whether to add a legend mapping colors to labels.
### Basins related
```@docs
plot_attractors
heatmap_basins_attractors
shaded_basins_heatmap
```
### Continuation related
```@docs
plot_basins_curves
plot_attractors_curves
plot_basins_attractors_curves
```
### Video output
```@docs
animate_attractors_continuation
``` | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 32002 | # [Examples for Attractors.jl](@ref examples)
Note that the examples utilize some convenience plotting functions offered by Attractors.jl which come into scope when using `Makie` (or any of its backends such as `CairoMakie`), see the [visualization utilities](@ref) for more.
## Newton's fractal (basins of a 2D map)
```@example MAIN
using Attractors
function newton_map(z, p, n)
z1 = z[1] + im*z[2]
dz1 = newton_f(z1, p[1])/newton_df(z1, p[1])
z1 = z1 - dz1
return SVector(real(z1), imag(z1))
end
newton_f(x, p) = x^p - 1
newton_df(x, p)= p*x^(p-1)
ds = DiscreteDynamicalSystem(newton_map, [0.1, 0.2], [3.0])
xg = yg = range(-1.5, 1.5; length = 400)
grid = (xg, yg)
# Use non-sparse for using `basins_of_attraction`
mapper_newton = AttractorsViaRecurrences(ds, grid;
sparse = false, consecutive_lost_steps = 1000
)
basins, attractors = basins_of_attraction(mapper_newton; show_progress = false)
basins
```
```@example MAIN
attractors
```
Now let's plot this as a heatmap, and on top of the heatmap, let's scatter plot the attractors. We do this in one step by utilizing one of the pre-defined plotting functions offered by Attractors.jl
```@example MAIN
using CairoMakie
fig = heatmap_basins_attractors(grid, basins, attractors)
```
Instead of computing the full basins, we could get only the fractions of the basins of attractions using [`basins_fractions`](@ref), which is typically the more useful thing to do in a high dimensional system.
In such cases it is also typically more useful to define a sampler that generates initial conditions on the fly instead of pre-defining some initial conditions (as is done in [`basins_of_attraction`](@ref). This is simple to do:
```@example MAIN
sampler, = statespace_sampler(grid)
basins = basins_fractions(mapper_newton, sampler)
```
in this case, to also get the attractors we simply extract them from the underlying storage of the mapper:
```@example MAIN
attractors = extract_attractors(mapper_newton)
```
## Shading basins according to convergence time
Continuing from above, we can utilize the [`convergence_and_basins_of_attraction`](@ref) function, and the [`shaded_basins_heatmap`](@ref) plotting utility function, to shade the basins of attraction based on the convergence time, with lighter colors indicating faster convergence to the attractor.
```@example MAIN
mapper_newton = AttractorsViaRecurrences(ds, grid;
sparse = false, consecutive_lost_steps = 1000
)
basins, attractors, iterations = convergence_and_basins_of_attraction(
mapper_newton, grid; show_progress = false
)
shaded_basins_heatmap(grid, basins, attractors, iterations)
```
## Minimal Fatal Shock
Here we find the Minimal Fatal Shock (MFS, see [`minimal_fatal_shock`](@ref)) for the attractors (i.e., fixed points) of Newton's fractal
```@example MAIN
shocks = Dict()
algo_bb = Attractors.MFSBlackBoxOptim()
for atr in values(attractors)
u0 = atr[1]
shocks[u0] = minimal_fatal_shock(mapper_newton, u0, (-1.5,1.5), algo_bb)
end
shocks
```
To visualize results we can make use of previously defined heatmap
```@example MAIN
ax = content(fig[1,1])
for (atr, shock) in shocks
lines!(ax, [atr, atr + shock]; color = :orange, linewidth = 3)
end
fig
```
## Fractality of 2D basins of the (4D) magnetic pendulum
In this section we will calculate the basins of attraction of the four-dimensional magnetic pendulum. We know that the attractors of this system are all individual fixed points on the (x, y) plane so we will only compute the basins there. We can also use this opportunity to highlight a different method, the [`AttractorsViaProximity`](@ref) which works when we already know where the attractors are. Furthermore we will also use a `ProjectedDynamicalSystem` to project the 4D system onto a 2D plane, saving a lot of computational time!
### Computing the basins
First we need to load in the magnetic pendulum from the predefined dynamical systems library
```@example MAIN
using Attractors, CairoMakie
using PredefinedDynamicalSystems
ds = PredefinedDynamicalSystems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)
```
Then, we create a projected system on the x-y plane
```@example MAIN
psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])
```
For this systems we know the attractors are close to the magnet positions. The positions can be obtained from the equations of the system, provided that one has seen the source code (not displayed here), like so:
```@example MAIN
attractors = Dict(i => StateSpaceSet([dynamic_rule(ds).magnets[i]]) for i in 1:3)
```
and then create a
```@example MAIN
mapper = AttractorsViaProximity(psys, attractors)
```
and as before, get the basins of attraction
```@example MAIN
xg = yg = range(-4, 4; length = 201)
grid = (xg, yg)
basins, = basins_of_attraction(mapper, grid; show_progress = false)
heatmap_basins_attractors(grid, basins, attractors)
```
### Computing the uncertainty exponent
Let's now calculate the [`uncertainty_exponent`](@ref) for this system as well.
The calculation is straightforward:
```@example MAIN
using CairoMakie
ε, f_ε, α = uncertainty_exponent(basins)
fig, ax = lines(log.(ε), log.(f_ε))
ax.title = "α = $(round(α; digits=3))"
fig
```
The actual uncertainty exponent is the slope of the curve (α) and indeed we get an exponent near 0 as we know a-priory the basins have fractal boundaries for the magnetic pendulum.
### Computing the tipping probabilities
We will compute the tipping probabilities using the magnetic pendulum's example
as the "before" state. For the "after" state we will change the `γ` parameter of the
third magnet to be so small, its basin of attraction will virtually disappear.
As we don't know _when_ the basin of the third magnet will disappear, we switch the attractor finding algorithm back to [`AttractorsViaRecurrences`](@ref).
```@example MAIN
set_parameter!(psys, :γs, [1.0, 1.0, 0.1])
mapper = AttractorsViaRecurrences(psys, (xg, yg); Δt = 1)
basins_after, attractors_after = basins_of_attraction(
mapper, (xg, yg); show_progress = false
)
# matching attractors is important!
rmap = match_statespacesets!(attractors_after, attractors)
# Don't forget to update the labels of the basins as well!
replace!(basins_after, rmap...)
# now plot
heatmap_basins_attractors(grid, basins_after, attractors_after)
```
And let's compute the tipping "probabilities":
```@example MAIN
P = tipping_probabilities(basins, basins_after)
```
As you can see `P` has size 3×2, as after the change only 2 attractors have been identified
in the system (3 still exist but our state space discretization isn't fine enough to
find the 3rd because it has such a small basin).
Also, the first row of `P` is 50% probability to each other magnet, as it should be due to
the system's symmetry.
## 3D basins via recurrences
To showcase the true power of [`AttractorsViaRecurrences`](@ref) we need to use a system whose attractors span higher-dimensional space. An example is
```@example MAIN
using Attractors
using PredefinedDynamicalSystems
ds = PredefinedDynamicalSystems.thomas_cyclical(b = 0.1665)
```
which, for this parameter, contains 3 coexisting attractors which are entangled
periodic orbits that span across all three dimensions.
To compute the basins we define a three-dimensional grid and call on it
[`basins_of_attraction`](@ref).
```julia
# This computation takes about an hour
xg = yg = zg = range(-6.0, 6.0; length = 251)
mapper = AttractorsViaRecurrences(ds, (xg, yg, zg); sparse = false)
basins, attractors = basins_of_attraction(mapper)
attractors
```
```
Dict{Int16, StateSpaceSet{3, Float64}} with 5 entries:
5 => 3-dimensional StateSpaceSet{Float64} with 1 points
4 => 3-dimensional StateSpaceSet{Float64} with 379 points
6 => 3-dimensional StateSpaceSet{Float64} with 1 points
2 => 3-dimensional StateSpaceSet{Float64} with 538 points
3 => 3-dimensional StateSpaceSet{Float64} with 537 points
1 => 3-dimensional StateSpaceSet{Float64} with 1 points
```
_Note: the reason we have 6 attractors here is because the algorithm also finds 3 unstable fixed points and labels them as attractors. This happens because we have provided initial conditions on the grid `xg, yg, zg` that start exactly on the unstable fixed points, and hence stay there forever, and hence are perceived as attractors by the recurrence algorithm. As you will see in the video below, they don't have any basin fractions_
The basins of attraction are very complicated. We can try to visualize them by animating the 2D slices at each z value, to obtain:
```@raw html
<video width="75%" height="auto" controls autoplay loop>
<source src="https://raw.githubusercontent.com/JuliaDynamics/JuliaDynamics/master/videos/attractors/cyclical_basins.mp4?raw=true" type="video/mp4">
</video>
```
Then, we visualize the attractors to obtain:
```@raw html
<video width="75%" height="auto" controls autoplay loop>
<source src="https://raw.githubusercontent.com/JuliaDynamics/JuliaDynamics/master/videos/attractors/cyclical_attractors.mp4?raw=true" type="video/mp4">
</video>
```
In the animation above, the scattered points are the attractor values the function [`AttractorsViaRecurrences`](@ref) found by itself. Of course, for the periodic orbits these points are incomplete. Once the function's logic understood we are on an attractor, it stops computing. However, we also simulated lines, by evolving initial conditions colored appropriately with the basins output.
The animation was produced with the code:
```julia
using GLMakie
fig = Figure()
display(fig)
ax = fig[1,1] = Axis3(fig; title = "found attractors")
cmap = cgrad(:dense, 6; categorical = true)
for i in keys(attractors)
tr = attractors[i]
markersize = length(attractors[i]) > 10 ? 2000 : 6000
marker = length(attractors[i]) > 10 ? :circle : :rect
scatter!(ax, columns(tr)...; markersize, marker, transparency = true, color = cmap[i])
j = findfirst(isequal(i), bsn)
x = xg[j[1]]
y = yg[j[2]]
z = zg[j[3]]
tr = trajectory(ds, 100, SVector(x,y,z); Ttr = 100)
lines!(ax, columns(tr)...; linewidth = 1.0, color = cmap[i])
end
a = range(0, 2π; length = 200) .+ π/4
record(fig, "cyclical_attractors.mp4", 1:length(a)) do i
ax.azimuth = a[i]
end
```
## Basins of attraction of a Poincaré map
[`PoincareMap`](@ref) is just another discrete time dynamical system within the DynamicalSystems.jl ecosystem. With respect to Attractors.jl functionality, there is nothing special about Poincaré maps. You simply initialize one use it like any other type of system. Let's continue from the above example of the Thomas cyclical system
```@example MAIN
using Attractors
using PredefinedDynamicalSystems
ds = PredefinedDynamicalSystems.thomas_cyclical(b = 0.1665);
```
The three limit cycles attractors we have above become fixed points in the Poincaré map (for appropriately chosen hyperplanes). Since we already know the 3D structure of the basins, we can see that an appropriately chosen hyperplane is just the plane `z = 0`. Hence, we define a Poincaré map on this plane:
```@example MAIN
plane = (3, 0.0)
pmap = PoincareMap(ds, plane)
```
We define the same grid as before, but now only we only use the x-y coordinates. This is because we can utilize the special `reinit!` method of the `PoincareMap`, that allows us to initialize a new state directly on the hyperplane (and then the remaining variable of the dynamical system takes its value from the hyperplane itself).
```@example MAIN
xg = yg = range(-6.0, 6.0; length = 250)
grid = (xg, yg)
mapper = AttractorsViaRecurrences(pmap, grid; sparse = false)
```
All that is left to do is to call [`basins_of_attraction`](@ref):
```@example MAIN
basins, attractors = basins_of_attraction(mapper; show_progress = false);
```
```@example MAIN
heatmap_basins_attractors(grid, basins, attractors)
```
_just like in the example above, there is a fourth attractor with 0 basin fraction. This is an unstable fixed point, and exists exactly because we provided a grid with the unstable fixed point exactly on this grid_
## Irregular grid for `AttractorsViaRecurrences`
It is possible to provide an irregularly spaced grid to `AttractorsViaRecurrences`. This can make algorithm performance better for continuous time systems where the state space flow has significantly different speed in some state space regions versus others.
In the following example the dynamical system has only one attractor: a limit cycle. However, near the origin (0, 0) the timescale of the dynamics becomes very slow. As the trajectory is stuck there for quite a while, the recurrences algorithm may identify this region as an "attractor" (incorrectly). The solutions vary and can be to increase drastically the max time checks for finding attractors, or making the grid much more fine. Alternatively, one can provide a grid that is only more fine near the origin and not fine elsewhere.
The example below highlights that for rather coarse settings of grid and convergence thresholds, using a grid that is finer near (0, 0) gives correct results:
```@example MAIN
using Attractors, CairoMakie
function predator_prey_fastslow(u, p, t)
α, γ, ϵ, ν, h, K, m = p
N, P = u
du1 = α*N*(1 - N/K) - γ*N*P / (N+h)
du2 = ϵ*(ν*γ*N*P/(N+h) - m*P)
return SVector(du1, du2)
end
γ = 2.5
h = 1
ν = 0.5
m = 0.4
ϵ = 1.0
α = 0.8
K = 15
u0 = rand(2)
p0 = [α, γ, ϵ, ν, h, K, m]
ds = CoupledODEs(predator_prey_fastslow, u0, p0)
fig = Figure()
ax = Axis(fig[1,1])
# when pow > 1, the grid is finer close to zero
for pow in (1, 2)
xg = yg = range(0, 18.0^(1/pow); length = 200).^pow
mapper = AttractorsViaRecurrences(ds, (xg, yg);
Dt = 0.1, sparse = true,
consecutive_recurrences = 10, attractor_locate_steps = 10,
maximum_iterations = 1000,
)
# Find attractor and its fraction (fraction is always 1 here)
sampler, _ = statespace_sampler(HRectangle(zeros(2), fill(18.0, 2)), 42)
fractions = basins_fractions(mapper, sampler; N = 100, show_progress = false)
attractors = extract_attractors(mapper)
scatter!(ax, vec(attractors[1]); markersize = 16/pow, label = "pow = $(pow)")
end
axislegend(ax)
fig
```
## Subdivision Based Grid for `AttractorsViaRecurrences`
To achieve even better results for this kind of problematic systems than with previuosly introduced `Irregular Grids` we provide a functionality to construct `Subdivision Based Grids` in which
one can obtain more coarse or dense structure not only along some axis but for a specific regions where the state space flow has
significantly different speed. [`subdivision_based_grid`](@ref) enables automatic evaluation of velocity vectors for regions of originally user specified
grid to further treat those areas as having more dense or coarse structure than others.
```@example MAIN
using Attractors, CairoMakie
function predator_prey_fastslow(u, p, t)
α, γ, ϵ, ν, h, K, m = p
N, P = u
du1 = α*N*(1 - N/K) - γ*N*P / (N+h)
du2 = ϵ*(ν*γ*N*P/(N+h) - m*P)
return SVector(du1, du2)
end
γ = 2.5
h = 1
ν = 0.5
m = 0.4
ϵ = 1.0
α = 0.8
K = 15
u0 = rand(2)
p0 = [α, γ, ϵ, ν, h, K, m]
ds = CoupledODEs(predator_prey_fastslow, u0, p0)
xg = yg = range(0, 18, length = 30)
# Construct `Subdivision Based Grid`
grid = subdivision_based_grid(ds, (xg, yg))
grid.lvl_array
```
The constructed array corresponds to levels of discretization for specific regions of the grid as a powers of 2,
meaning that if area index is assigned to be `3`, for example, the algorithm will treat the region as one being
`2^3 = 8` times more dense than originally user provided grid `(xg, yg)`.
Now upon the construction of this structure, one can simply pass it into mapper function as usual.
```@example MAIN
fig = Figure()
ax = Axis(fig[1,1])
# passing SubdivisionBasedGrid into mapper
mapper = AttractorsViaRecurrences(ds, grid;
Dt = 0.1, sparse = true,
consecutive_recurrences = 10, attractor_locate_steps = 10,
maximum_iterations = 1000,
)
# Find attractor and its fraction (fraction is always 1 here)
sampler, _ = statespace_sampler(HRectangle(zeros(2), fill(18.0, 2)), 42)
fractions = basins_fractions(mapper, sampler; N = 100, show_progress = false)
attractors_SBD = extract_attractors(mapper)
scatter!(ax, vec(attractors_SBD[1]); label = "SubdivisionBasedGrid")
# to compare the results we also construct RegularGrid of same length here
xg = yg = range(0, 18, length = 30)
mapper = AttractorsViaRecurrences(ds, (xg, yg);
Dt = 0.1, sparse = true,
consecutive_recurrences = 10, attractor_locate_steps = 10,
maximum_iterations = 1000,
)
sampler, _ = statespace_sampler(HRectangle(zeros(2), fill(18.0, 2)), 42)
fractions = basins_fractions(mapper, sampler; N = 100, show_progress = false)
attractors_reg = extract_attractors(mapper)
scatter!(ax, vec(attractors_reg[1]); label = "RegularGrid")
axislegend(ax)
fig
```
## Basin fractions continuation in the magnetic pendulum
Perhaps the simplest application of [`global_continuation`](@ref) is to produce a plot of how the fractions of attractors change as we continuously change the parameter we changed above to calculate tipping probabilities.
### Computing the fractions
This is what the following code does:
```@example MAIN
# initialize projected magnetic pendulum
using Attractors, PredefinedDynamicalSystems
using Random: Xoshiro
ds = Systems.magnetic_pendulum(; d = 0.3, α = 0.2, ω = 0.5)
xg = yg = range(-3, 3; length = 101)
ds = ProjectedDynamicalSystem(ds, 1:2, [0.0, 0.0])
# Choose a mapper via recurrences
mapper = AttractorsViaRecurrences(ds, (xg, yg); Δt = 1.0)
# What parameter to change, over what range
γγ = range(1, 0; length = 101)
prange = [[1, 1, γ] for γ in γγ]
pidx = :γs
# important to make a sampler that respects the symmetry of the system
region = HSphere(3.0, 2)
sampler, = statespace_sampler(region, 1234)
# continue attractors and basins:
# `Inf` threshold fits here, as attractors move smoothly in parameter space
rsc = RecurrencesFindAndMatch(mapper; threshold = Inf)
fractions_cont, attractors_cont = global_continuation(
rsc, prange, pidx, sampler;
show_progress = false, samples_per_parameter = 100
)
# Show some characteristic fractions:
fractions_cont[[1, 50, 101]]
```
### Plotting the fractions
We visualize them using a predefined function that you can find in `docs/basins_plotting.jl`
```@example MAIN
# careful; `prange` isn't a vector of reals!
plot_basins_curves(fractions_cont, γγ)
```
### Fixed point curves
A by-product of the analysis is that we can obtain the curves of the position of fixed points for free. However, only the stable branches can be obtained!
```@example MAIN
using CairoMakie
fig = Figure()
ax = Axis(fig[1,1]; xlabel = L"\gamma_3", ylabel = "fixed point")
# choose how to go from attractor to real number representation
function real_number_repr(attractor)
p = attractor[1]
return (p[1] + p[2])/2
end
for (i, γ) in enumerate(γγ)
for (k, attractor) in attractors_cont[i]
scatter!(ax, γ, real_number_repr(attractor); color = Cycled(k))
end
end
fig
```
as you can see, two of the three fixed points, and their stability, do not depend at all on the parameter value, since this parameter value tunes the magnetic strength of only the third magnet. Nevertheless, the **fractions of basin of attraction** of all attractors depend strongly on the parameter. This is a simple example that highlights excellently how this new approach we propose here should be used even if one has already done a standard linearized bifurcation analysis.
## Extinction of a species in a multistable competition model
In this advanced example we utilize both [`RecurrencesFindAndMatch`](@ref) and [`aggregate_attractor_fractions`](@ref) in analyzing species extinction in a dynamical model of competition between multiple species.
The final goal is to show the percentage of how much of the state space leads to the extinction or not of a pre-determined species, as we vary a parameter. The model however displays extreme multistability, a feature we want to measure and preserve before aggregating information into "extinct or not".
To measure and preserve this we will apply [`RecurrencesFindAndMatch`](@ref) as-is first. Then we can aggregate information. First we have
```julia
using Attractors, OrdinaryDiffEq
using PredefinedDynamicalSystems
using Random: Xoshiro
# arguments to algorithms
samples_per_parameter = 1000
total_parameter_values = 101
diffeq = (alg = Vern9(), reltol = 1e-9, abstol = 1e-9, maxiters = Inf)
recurrences_kwargs = (; Δt= 1.0, consecutive_recurrences=9, diffeq);
# initialize dynamical system and sampler
ds = PredefinedDynamicalSystems.multispecies_competition() # 8-dimensional
ds = CoupledODEs(ODEProblem(ds), diffeq)
# define grid in state space
xg = range(0, 60; length = 300)
grid = ntuple(x -> xg, 8)
prange = range(0.2, 0.3; length = total_parameter_values)
pidx = :D
sampler, = statespace_sampler(grid, 1234)
# initialize mapper
mapper = AttractorsViaRecurrences(ds, grid; recurrences_kwargs...)
# perform continuation of attractors and their basins
alg = RecurrencesFindAndMatch(mapper; threshold = Inf)
fractions_cont, attractors_cont = global_continuation(
alg, prange, pidx, sampler;
show_progress = true, samples_per_parameter
)
plot_basins_curves(fractions_cont, prange; separatorwidth = 1)
```
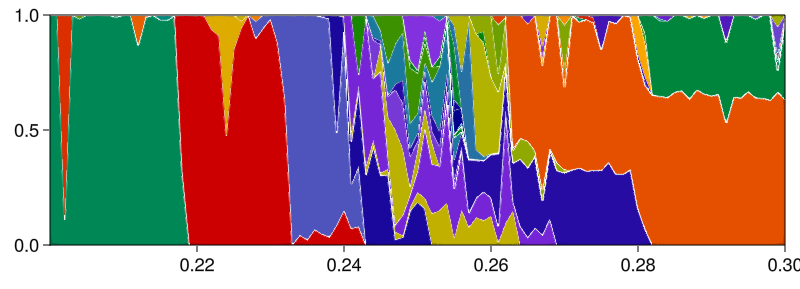
_this example is not actually run when building the docs, because it takes about 60 minutes to complete depending on the computer; we load precomputed results instead_
As you can see, the system has extreme multistability with 64 unique attractors
(according to the default matching behavior in [`RecurrencesFindAndMatch`](@ref); a stricter matching with less than `Inf` threshold would generate more "distinct" attractors).
One could also isolate a specific parameter slice, and do the same as what we do in
the [Fractality of 2D basins of the (4D) magnetic pendulum](@ref) example, to prove that the basin boundaries are fractal, thereby indeed confirming the paper title "Fundamental Unpredictability".
Regardless, we now want to continue our analysis to provide a figure similar to the
above but only with two colors: fractions of attractors where a species is extinct or not. Here's how:
```julia
species = 3 # species we care about its existence
featurizer = (A) -> begin
i = isextinct(A, species)
return SVector(Int32(i))
end
isextinct(A, idx = unitidxs) = all(a -> a <= 1e-2, A[:, idx])
# `minneighbors = 1` is crucial for grouping single attractors
groupingconfig = GroupViaClustering(; min_neighbors=1, optimal_radius_method=0.5)
aggregated_fractions, aggregated_info = aggregate_attractor_fractions(
fractions_cont, attractors_cont, featurizer, groupingconfig
)
plot_basins_curves(aggregated_fractions, prange;
separatorwidth = 1, colors = ["green", "black"],
labels = Dict(1 => "extinct", 2 => "alive"),
)
```
(in hindsight, the labels are reversed; attractor 1 is the alive one, but oh well)
## Trivial featurizing and grouping for basins fractions
This is a rather trivial example showcasing the usage of [`AttractorsViaFeaturizing`](@ref). Let us use once again the magnetic pendulum example. For it, we have a really good idea of what features will uniquely describe each attractor: the last points of a trajectory (which should be very close to the magnetic the trajectory converged to). To provide this information to the [`AttractorsViaFeaturizing`](@ref) we just create a julia function that returns this last point
```@example MAIN
using Attractors
using PredefinedDynamicalSystems
ds = Systems.magnetic_pendulum(d=0.2, α=0.2, ω=0.8, N=3)
psys = ProjectedDynamicalSystem(ds, [1, 2], [0.0, 0.0])
function featurizer(X, t)
return X[end]
end
mapper = AttractorsViaFeaturizing(psys, featurizer; Ttr = 200, T = 1)
xg = yg = range(-4, 4; length = 101)
region = HRectangle([-4, 4], [4, 4])
sampler, = statespace_sampler(region)
fs = basins_fractions(mapper, sampler; show_progress = false)
```
As expected, the fractions are each about 1/3 due to the system symmetry.
## Featurizing and grouping across parameters (MCBB)
Here we showcase the example of the Monte Carlo Basin Bifurcation publication.
For this, we will use [`FeaturizeGroupAcrossParameter`](@ref) while also providing a `par_weight = 1` keyword.
However, we will not use a network of 2nd order Kuramoto oscillators (as done in the paper by Gelbrecht et al.) because it is too costly to run on CI.
Instead, we will use "dummy" system which we know analytically the attractors and how they behave versus a parameter.
the Henon map and try to group attractors into period 1 (fixed point), period 3, and divergence to infinity. We will also use a pre-determined optimal radius for clustering, as we know a-priory the expected distances of features in feature space (due to the contrived form of the `featurizer` function below).
```@example MAIN
using Attractors, Random
function dumb_map(dz, z, p, n)
x, y = z
r = p[1]
if r < 0.5
dz[1] = dz[2] = 0.0
else
if x > 0
dz[1] = r
dz[2] = r
else
dz[1] = -r
dz[2] = -r
end
end
return
end
r = 3.833
ds = DiscreteDynamicalSystem(dumb_map, [0., 0.], [r])
```
```@example MAIN
sampler, = statespace_sampler(HRectangle([-3.0, -3.0], [3.0, 3.0]), 1234)
rrange = range(0, 2; length = 21)
ridx = 1
featurizer(a, t) = a[end]
clusterspecs = GroupViaClustering(optimal_radius_method = "silhouettes", max_used_features = 200)
mapper = AttractorsViaFeaturizing(ds, featurizer, clusterspecs; T = 20, threaded = true)
gap = FeaturizeGroupAcrossParameter(mapper; par_weight = 1.0)
fractions_cont, clusters_info = global_continuation(
gap, rrange, ridx, sampler; show_progress = false
)
fractions_cont
```
Looking at the information of the "attractors" (here the clusters of the grouping procedure) does not make it clear which label corresponds to which kind of attractor, but we can look at the:
```@example MAIN
clusters_info
```
## Using histograms and histogram distances as features
One of the aspects discussed in the original MCBB paper and implementation was the usage of histograms of the means of the variables of a dynamical system as the feature vector. This is useful in very high dimensional systems, such as oscillator networks, where the histogram of the means is significantly different in synchronized or unsychronized states.
This is possible to do with current interface without any modifications, by using two more packages: ComplexityMeasures.jl to compute histograms, and Distances.jl for the Kullback-Leibler divergence (or any other measure of distance in the space of probability distributions you fancy).
The only code we need to write to achieve this feature is a custom featurizer and providing an alternative distance to `GroupViaClustering`. The code would look like this:
```julia
using Distances: KLDivergence
using ComplexityMeasures: ValueHistogram, FixedRectangularBinning, probabilities
# you decide the binning for the histogram, but for a valid estimation of
# distances, all histograms must have exactly the same bins, and hence be
# computed with fixed ranges, i.e., using the `FixedRectangularBinning`
function histogram_featurizer(A, t)
binning = FixedRectangularBinning(range(-5, 5; length = 11))
ms = mean.(columns(A)) # vector of mean of each variable
p = probabilities(ValueHistogram(binning), ms) # this is the histogram
return vec(p) # because Distances.jl doesn't know `Probabilities`
end
gconfig = GroupViaClustering(;
clust_distance_metric = KLDivergence(), # or any other PDF distance
)
```
You can then pass the `histogram_featurizer` and `gconfig` to an [`AttractorsViaFeaturizing`](@ref) and use the rest of the library as usual.
## Edge tracking
To showcase how to run the [`edgetracking`](@ref) algorithm, let us use it to find the
saddle point of the bistable FitzHugh-Nagumo (FHN) model, a two-dimensional ODE system
originally conceived to represent a spiking neuron.
We define the system in the following form:
```@example MAIN
using OrdinaryDiffEq: Vern9
function fitzhugh_nagumo(u,p,t)
x, y = u
eps, beta = p
dx = (x - x^3 - y)/eps
dy = -beta*y + x
return SVector{2}([dx, dy])
end
params = [0.1, 3.0]
ds = CoupledODEs(fitzhugh_nagumo, ones(2), params, diffeq=(;alg = Vern9(), reltol=1e-11))
```
Now, we can use Attractors.jl to compute the fixed points and basins of attraction of the
FHN model.
```@example MAIN
xg = yg = range(-1.5, 1.5; length = 201)
grid = (xg, yg)
mapper = AttractorsViaRecurrences(ds, grid; sparse=false)
basins, attractors = basins_of_attraction(mapper)
attractors
```
The `basins_of_attraction` function found three fixed points: the two stable nodes of the
system (labelled A and B) and the saddle point at the origin. The saddle is an unstable
equilibrium and typically will not be found by `basins_of_attraction`. Coincidentally here we initialized an initial condition exactly on the saddle, and hence it was found.
We can always find saddles with the [`edgetracking`](@ref) function. For illustration, let us initialize the algorithm from
two initial conditions `init1` and `init2` (which must belong to different basins
of attraction, see figure below).
```@example MAIN
attractors_AB = Dict(1 => attractors[1], 2 => attractors[2])
init1, init2 = [-1.0, -1.0], [-1.0, 0.2]
```
Now, we run the edge tracking algorithm:
```@example MAIN
et = edgetracking(ds, attractors_AB; u1=init1, u2=init2,
bisect_thresh = 1e-3, diverge_thresh = 2e-3, Δt = 1e-5, abstol = 1e-3
)
et.edge[end]
```
The algorithm has converged to the origin (up to the specified accuracy) where the saddle
is located. The figure below shows how the algorithm has iteratively tracked along the basin
boundary from the two initial conditions (red points) to the saddle (green square). Points
of the edge track (orange) at which a re-bisection occured are marked with a white border.
The figure also depicts two trajectories (blue) intialized on either side of the basin
boundary at the first bisection point. We see that these trajectories follow the basin
boundary for a while but then relax to either attractor before reaching the saddle. By
counteracting the instability of the saddle, the edge tracking algorithm instead allows to
track the basin boundary all the way to the saddle, or edge state.
```@example MAIN
traj1 = trajectory(ds, 2, et.track1[et.bisect_idx[1]], Δt=1e-5)
traj2 = trajectory(ds, 2, et.track2[et.bisect_idx[1]], Δt=1e-5)
fig = Figure()
ax = Axis(fig[1,1], xlabel="x", ylabel="y")
heatmap_basins_attractors!(ax, grid, basins, attractors, add_legend=false, labels=Dict(1=>"Attractor A", 2=>"Attractor B", 3=>"Saddle"))
lines!(ax, traj1[1][:,1], traj1[1][:,2], color=:dodgerblue, linewidth=2, label="Trajectories")
lines!(ax, traj2[1][:,1], traj2[1][:,2], color=:dodgerblue, linewidth=2)
lines!(ax, et.edge[:,1], et.edge[:,2], color=:orange, linestyle=:dash)
scatter!(ax, et.edge[et.bisect_idx,1], et.edge[et.bisect_idx,2], color=:white, markersize=15, marker=:circle)
scatter!(ax, et.edge[:,1], et.edge[:,2], color=:orange, markersize=11, marker=:circle, label="Edge track")
scatter!(ax, [-1.0,-1.0], [-1.0, 0.2], color=:red, markersize=15, label="Initial conditions")
xlims!(ax, -1.2, 1.1); ylims!(ax, -1.3, 0.8)
axislegend(ax, position=:rb)
fig
```
In this simple two-dimensional model, we could of course have found the saddle directly by
computing the zeroes of the ODE system. However, the edge tracking algorithm allows finding
edge states also in high-dimensional and chaotic systems where a simple computation of
unstable equilibria becomes infeasible.
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 485 | # Attractors.jl
```@docs
Attractors
```
```@setup MAIN
using CairoMakie, Attractors
```
## Latest news
- Global continuation can now be performed across any arbitrary curve
in parameter space.
- See the CHANGELOG.md (at the GitHub repo) for more!
## Getting started
Start by having a look at the [tutorial](@ref tutorial), after which you can
consult individual library functions in [API](@ref). Many more examples can be found
in the dedicated [examples](@ref examples) page.
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 7748 | # [Animation illustrating `AttractorsViaRecurrences`](@id recurrences_animation)
The following Julia script inputs a 2D continuous time dynamical system and animates its time evolution while illustrating how [`AttractorsViaRecurrences`](@ref) works.
```julia
using Attractors, CairoMakie
using PredefinedDynamicalSystems
using OrdinaryDiffEq
# Set up dynamical system: bi-stable predator pray
function predator_prey_rule(u, p, t)
r, c, μ, ν, α, β, χ, δ = p
N, P = u
common = α*N*P/(β+N)
dN = r*N*(1 - (c/r)*N)*((N-μ)/(N+ν)) - common
dP = χ*common - δ*P
return SVector(dN, dP)
end
u0 = SVector(8.0, 0.01)
r = 2.0
# r, c, μ, ν, α, β, χ, δ = p
p = [r, 0.19, 0.03, 0.003, 800, 1.5, 0.004, 2.2]
diffeq = (alg = Rodas5P(), abstol = 1e-9, rtol = 1e-9)
ds = CoupledODEs(predator_prey_rule, u0, p; diffeq)
u0s = [ # animation will start from these initial conditions
[10, 0.012],
[15, 0.02],
[12, 0.01],
[13, 0.015],
[5, 0.02],
]
density = 31
xg = range(-0.1, 20; length = density)
yg = range(-0.001, 0.03; length = density)
Δt = 0.1
grid = (xg, yg)
mapper = AttractorsViaRecurrences(ds, grid;
Δt, consecutive_attractor_steps = 10, consecutive_basin_steps = 10, sparse = false,
consecutive_recurrences = 100, attractor_locate_steps = 100,
)
##########################################################################
function animate_attractors_via_recurrences(
mapper::AttractorsViaRecurrences, u0s;
colors = ["#FFFFFF", "#7143E0","#0A9A84","#AF9327","#791457", "#6C768C", "#4287f5",],
filename = "recurrence_algorithm.mp4",
)
grid_nfo = mapper.bsn_nfo.grid_nfo
fig = Figure()
ax = Axis(fig[1,1])
# Populate the grid with poly! rectangle plots. However! The rectangles
# correspond to the same "cells" of the grid. Additionally, all
# rectangles are colored with an _observable_, that can be accessed
# later using the `basin_cell_index` function. The observable
# holds the face color of the rectangle!
# Only 6 colors; need 3 for base, and extra 2 for each attractor.
# will choose initial conditions that are only in the first 2 attractors
COLORS = map(c -> Makie.RGBA(Makie.RGB(to_color(c)), 0.9), colors)
function initialize_cells2!(ax, grid; kwargs...)
# These are all possible outputs of the `basin_cell_index` function
idxs = all_cartesian_idxs(grid)
color_obs = Matrix{Any}(undef, size(idxs)...)
# We now need to reverse-engineer
for i in idxs
rect = cell_index_to_rect(i, grid)
color = Observable(COLORS[1])
color_obs[i] = color
poly!(ax, rect; color = color, strokecolor = :black, strokewidth = 0.5)
end
# Set the axis limits better
mini, maxi = Attractors.minmax_grid_extent(grid)
xlims!(ax, mini[1], maxi[1])
ylims!(ax, mini[2], maxi[2])
return color_obs
end
all_cartesian_idxs(grid::Attractors.RegularGrid) = CartesianIndices(length.(grid.grid))
# Given a cartesian index, the output of `basin_cell_index`, create
# a `Rect` object that corresponds to that grid cell!
function cell_index_to_rect(n::CartesianIndex, grid::Attractors.RegularGrid)
x = grid.grid[1][n[1]]
y = grid.grid[2][n[2]]
dx = grid.grid_steps[1]
dy = grid.grid_steps[2]
rect = Rect(x - dx/2, y - dy/2, dx, dy)
return rect
end
color_obs = initialize_cells2!(ax, grid_nfo)
# plot the trajectory
state2marker = Dict(
:att_search => :circle,
:att_found => :dtriangle,
:att_hit => :rect,
:lost => :star5,
:bas_hit => :xcross,
)
# This function gives correct color to search, recurrence, and
# the individual attractors. Ignores the lost state.
function update_current_cell_color!(cellcolor, bsn_nfo)
# We only alter the cell color at specific situations
state = bsn_nfo.state
if state == :att_search
if cellcolor[] == COLORS[1] # empty
cellcolor[] = COLORS[2] # visited
elseif cellcolor[] == COLORS[2] # visited
cellcolor[] = COLORS[3] # recurrence
end
elseif state == :att_found
attidx = (bsn_nfo.current_att_label ÷ 2)
attlabel = (attidx - 1)*2 + 1
cellcolor[] = COLORS[3+attlabel]
end
return
end
# Iteration and labelling
ds = mapper.ds
bsn_nfo = mapper.bsn_nfo
u0 = current_state(ds)
traj = Observable(SVector{2, Float64}[u0])
point = Observable([u0])
marker = Observable(:circle)
lines!(ax, traj; color = :black, linewidth = 1)
scatter!(ax, point; color = (:black, 0.5), markersize = 20, marker, strokewidth = 1.0, strokecolor = :black)
stateobs = Observable(:att_search)
consecutiveobs = Observable(0)
labeltext = @lift("state: $($(stateobs))\nconsecutive: $($(consecutiveobs))")
Label(fig[0, 1][1,1], labeltext; justification = :left, halign = :left, tellwidth = false)
# add text with options
kwargstext = prod("$(p[1])=$(p[2])\n" for p in mapper.kwargs)
Label(fig[0, 1][1, 2], kwargstext; justification = :right, halign = :right, tellwidth = false)
# make legend
entries = [PolyElement(color = c) for c in COLORS[2:end]]
labels = ["visited", "recurrence", "attr. 1", "basin 1", "attr. 2", "basin 2"]
Legend(fig[:, 2][1, 1], entries, labels)
# %% loop
# The following code is similar to the source code of `recurrences_map_to_label!`
cell_label = 0
record(fig, filename) do io
for u0 in u0s
reinit!(ds, copy(u0))
traj[] = [copy(u0)]
while cell_label == 0
step!(ds, bsn_nfo.Δt)
u = current_state(ds)
# update FSM
n = Attractors.basin_cell_index(u, bsn_nfo.grid_nfo)
cell_label = Attractors.finite_state_machine!(bsn_nfo, n, u; mapper.kwargs...)
state = bsn_nfo.state
if cell_label ≠ 0 # FSM terminated; we assume no lost/divergence in the system
stateobs[] = :terminated
# color-code initial condition if we converged to attractor
# or to basin (even or odd cell label)
u0n = Attractors.basin_cell_index(u0, bsn_nfo.grid_nfo)
basidx = (cell_label - 1)
color_obs[u0n][] = COLORS[3+basidx]
# Clean up: all "visited" cells become white again
visited_idxs = findall(v -> (v[] == COLORS[2] || v[] == COLORS[3]), color_obs)
for n in visited_idxs
color_obs[n][] = COLORS[1] # empty
end
# clean up trajectory line
traj[] = []
for i in 1:15; recordframe!(io); end
cell_label = 0
break
end
# update visuals:
point[] = [u]
push!(traj[], u)
notify(traj)
marker[] = state2marker[state]
stateobs[] = state
consecutiveobs[] = bsn_nfo.consecutive_match
update_current_cell_color!(color_obs[n], bsn_nfo)
recordframe!(io)
end
end
end
end
animate_attractors_via_recurrences(mapper, u0s)
```
```@raw html
<video width="75%" height="auto" controls autoplay loop>
<source src="https://raw.githubusercontent.com/JuliaDynamics/JuliaDynamics/master/videos/attractors/recurrence_algorithm.mp4?raw=true" type="video/mp4">
</video>
```
| Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 1.20.0 | 47c6ed345dbabf0de47873514cb6d67369127733 | docs | 34 | # References
```@bibliography
``` | Attractors | https://github.com/JuliaDynamics/Attractors.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 471 | using Documenter, SpatialIndexing
makedocs(
source = "source",
format = Documenter.HTML(prettyurls=false),
sitename = "SpatialIndexing.jl",
modules = [SpatialIndexing],
pages = [
"Introduction" => "index.md",
"API" => [
"regions.md",
"abstract.md",
"rtree.md",
"simple.md",
"query.md"
],
],
)
deploydocs(
repo = "github.com/alyst/SpatialIndexing.jl.git",
)
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 2058 | # scripts for converting R-tree into `DataFrame`
using DataFrames
# appends node/element information into the `dfcols`
function append_node_info!(dfcols::NamedTuple, node::Any,
parent::Union{SI.Node, Missing},
ix::Union{Integer, Missing})
push!(dfcols.type, string(typeof(node).name.name))
push!(dfcols.level, isa(node, SI.Node) ? SI.level(node) : missing)
push!(dfcols.ix, ix)
push!(dfcols.id, isa(node, SI.Node) ? string(Int(pointer_from_objref(node)), base=16) :
(SI.idtrait(typeof(node)) !== SI.HasNoID ? repr(SI.id(node)) : missing))
push!(dfcols.parent, !ismissing(parent) ? string(Int(pointer_from_objref(parent)), base=16) : missing)
push!(dfcols.area, SI.area(SI.mbr(node)))
push!(dfcols.xmin, SI.mbr(node).low[1])
push!(dfcols.xmax, SI.mbr(node).high[1])
push!(dfcols.ymin, SI.mbr(node).low[2])
push!(dfcols.ymax, SI.mbr(node).high[2])
return dfcols
end
# appends information about all the nodes in the `node` subtree
# into the `dfcols`
function append_subtree_info!(dfcols::NamedTuple, node::Any,
parent::Union{SI.Node, Missing},
ix::Union{Integer, Missing})
append_node_info!(dfcols, node, parent, ix)
if node isa SI.Node
for (i, child) in enumerate(SI.children(node))
append_subtree_info!(dfcols, child, node, i)
end
end
return node
end
# convert `RTree` into `DataFrame`
function Base.convert(::Type{DataFrame}, tree::RTree)
dfcols = (type = Vector{String}(), level = Vector{Union{Int, Missing}}(),
id = Vector{Union{String, Missing}}(),
ix = Vector{Union{Int, Missing}}(),
parent = Vector{Union{String, Missing}}(),
area =Vector{Float64}(),
xmin = Vector{Float64}(), ymin = Vector{Float64}(),
xmax = Vector{Float64}(), ymax = Vector{Float64}())
append_subtree_info!(dfcols, tree.root, missing, missing)
return DataFrame(dfcols)
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 2164 | using Random, DataFrames, PlotlyJS, SpatialIndexing, StableRNGs
using Printf: @sprintf
const SI = SpatialIndexing
rng = StableRNG(1)
pts = Vector{SI.Point{Float64,3}}()
for i in 1:100000
r = 1 - 1 / (1 + abs(randn(rng)))
a = rand(rng) * pi / 2
b = rand(rng) * pi / 2
x = (sin(a) * cos(b))^3 * r
y = (cos(a) * cos(b))^3 * r
z = (sin(b))^3 * r
push!(pts, SI.Point((x, y, z)))
end
seq_tree = RTree{Float64,3}(Int, String, leaf_capacity=20, branch_capacity=20)
for (i, pt) in enumerate(pts)
insert!(seq_tree, pt, i, string(i))
end
SI.check(seq_tree)
#=
rect = SI.Rect((-1.0, -2.0, -3.0), (2.0, -0.5, 1.0))
n_in_rect = sum(br -> in(br, rect), mbrs)
SI.subtract!(seq_tree, rect);
SI.check(seq_tree)
@show seq_tree.nelems seq_tree.nelem_deletions seq_tree.nnode_reinsertions seq_tree.nnode_splits
=#
# insert a point `pt` into pareto frontier
# (i.e. only if `tree` does not contain points that dominate it)
# remove all points that are dominated by `pt`
# return true if `pt` was inserted
function pareto_insert!(tree::RTree{T,N}, pt::SI.Point{T,N}, key, val) where {T,N}
betterbr = SI.Rect(pt.coord, ntuple(_ -> typemax(T), N))
# check if there are points that dominate pt
isempty(tree, betterbr) || return false
# remove the dominated points
worsebr = SI.Rect(ntuple(_ -> typemin(T), N), pt.coord)
SI.subtract!(tree, worsebr)
# insert pt
insert!(tree, pt, key, val)
end
pareto_tree = RTree{Float64,3}(Int, String, leaf_capacity=8, branch_capacity=8)
for (i, pt) in enumerate(pts)
pareto_insert!(pareto_tree, pt, i, string(i))
end
SI.check(pareto_tree)
include(joinpath(@__DIR__, "plot_utils.jl"))
pareto_tree_plot = plot(pareto_tree);
savefig(pareto_tree_plot, joinpath(@__DIR__, "pareto3d_rtree_seq.html"))
bulk_pareto_tree = RTree{Float64,3}(Int, String, leaf_capacity=8, branch_capacity=8)
SI.load!(bulk_pareto_tree, pareto_tree)
SI.check(bulk_pareto_tree)
bulk_pareto_tree_plot = plot(bulk_pareto_tree);
savefig(bulk_pareto_tree_plot, joinpath(@__DIR__, "pareto3d_rtree_bulk.html"))
savefig(bulk_pareto_tree_plot, joinpath(@__DIR__, "pareto3d_rtree_bulk.png"), width=900, height=1000)
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 4801 | # scripts for displaying R-trees using PlotlyJS
using PlotlyJS
using Printf: @sprintf
# webcolor palette for R-tree levels
const LevelsPalette = Dict(
1 => "#228B22", # Forest Green
2 => "#DAA520", # Goldenrod
3 => "#FF6347", # Tomato
4 => "#B22222", # Firebrick
5 => "#800080", # Purple
6 => "#4169E1", # Royal blue
7 => "#008080",) # Teal
# create plotly trace for a single R-tree `node` (rectangle edges)
function node_trace(node::SI.Node{<:Any,2}, ix::Union{Integer, Nothing};
showlegend::Bool)
nbr = SI.mbr(node)
res = scatter(x = [nbr.low[1], nbr.high[1], nbr.high[1], nbr.low[1], nbr.low[1]],
y = [nbr.low[2], nbr.low[2], nbr.high[2], nbr.high[2], nbr.low[2]],
mode=:lines, line_color=get(LevelsPalette, SI.level(node), "#708090"),
line_width=SI.level(node),
hoverinfo=:text, hoveron=:points,
text="lev=$(SI.level(node)) ix=$(ix !== nothing ? ix : "none")<br>nchildren=$(length(node)) nelems=$(SI.nelements(node)) area=$(@sprintf("%.2f", SI.area(SI.mbr(node))))",
name="level $(SI.level(node))",
legendgroup="level $(SI.level(node))", showlegend=showlegend)
return res
end
# create plotly trace for a single R-tree `node` (cube edges)
function node_trace(node::SI.Node, ix::Union{Integer, Nothing};
showlegend::Bool)
nbr = SI.mbr(node)
res = scatter3d(x = [nbr.low[1], nbr.high[1], nbr.high[1], nbr.low[1], nbr.low[1],
nbr.low[1], nbr.high[1], nbr.high[1], nbr.low[1], nbr.low[1],
NaN, nbr.low[1], nbr.low[1],
NaN, nbr.high[1], nbr.high[1],
NaN, nbr.high[1], nbr.high[1]],
y = [nbr.low[2], nbr.low[2], nbr.high[2], nbr.high[2], nbr.low[2],
nbr.low[2], nbr.low[2], nbr.high[2], nbr.high[2], nbr.low[2],
NaN, nbr.high[2], nbr.high[2],
NaN, nbr.high[2], nbr.high[2],
NaN, nbr.low[2], nbr.low[2]],
z = [nbr.low[3], nbr.low[3], nbr.low[3], nbr.low[3], nbr.low[3],
nbr.high[3], nbr.high[3], nbr.high[3], nbr.high[3], nbr.high[3],
NaN, nbr.low[3], nbr.high[3],
NaN, nbr.low[3], nbr.high[3],
NaN, nbr.low[3], nbr.high[3]],
mode=:lines, line_color=get(LevelsPalette, SI.level(node), "#708090"),
line_width=SI.level(node),
hoverinfo=:text, hoveron=:points,
text="lev=$(SI.level(node)) ix=$(ix !== nothing ? ix : "none")<br>nchildren=$(length(node)) nelems=$(SI.nelements(node)) area=$(@sprintf("%.2f", SI.area(SI.mbr(node))))",
name="level $(SI.level(node))",
legendgroup="level $(SI.level(node))", showlegend=showlegend)
return res
end
# create plotly traces for the nodes in a subtree with the `node` root
# and append them to `node_traces`
function append_subtree_traces!(node_traces::Vector{PlotlyBase.AbstractTrace},
node::SI.Node, ix::Union{Integer, Nothing},
levels::Set{Int})
push!(node_traces, node_trace(node, ix, showlegend = SI.level(node) ∉ levels))
push!(levels, SI.level(node)) # show each level once in legend
if node isa SI.Branch
for (i, child) in enumerate(SI.children(node))
append_subtree_traces!(node_traces, child, i, levels)
end
end
return nothing
end
data_trace(tree::RTree{<:Any, 2}) =
scatter(mode=:markers, name=:data, marker_color = "#333333", marker_size = 2,
x=[SI.center(SI.mbr(x)).coord[1] for x in tree],
y=[SI.center(SI.mbr(x)).coord[2] for x in tree],
text=["id=$(SI.id(x))" for x in tree], hoverinfo=:text)
data_trace(tree::RTree) =
scatter3d(mode=:markers, name=:data, marker_color = "#333333", marker_size = 2,
x=[SI.center(SI.mbr(x)).coord[1] for x in tree],
y=[SI.center(SI.mbr(x)).coord[2] for x in tree],
z=[SI.center(SI.mbr(x)).coord[3] for x in tree],
text=["id=$(SI.id(x))" for x in tree], hoverinfo=:text)
# create Plotly plot of the given tree
function PlotlyJS.plot(tree::RTree)
ndims(tree) == 1 && throw(ArgumentError("1-D R-trees not supported"))
ndims(tree) > 3 && @warn("Only 1st-3rd dimensions would be shown for $(ndims(tree))-D trees")
node_traces = Vector{PlotlyBase.AbstractTrace}()
append_subtree_traces!(node_traces, tree.root, nothing, Set{Int}())
PlotlyJS.plot([node_traces; [data_trace(tree)]], Layout(hovermode=:closest))
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 1163 | using Random, SpatialIndexing, StableRNGs
const SI = SpatialIndexing
rng = StableRNG(1)
seq_tree = RTree{Float64,2}(Int, String, leaf_capacity=20, branch_capacity=20)
bulk_tree = RTree{Float64,2}(Int, String, leaf_capacity=10, branch_capacity=10)
mbrs = Vector{SI.mbrtype(seq_tree)}()
for i in 1:10000
t = 10 * rand(rng)
u, v = (0.1 * t)^0.25 * randn(2)
x = t^1.5 * sin(2 * t) + u
y = t^1.5 * cos(2 * t) + v
rmbr = SI.Rect((x, y), (x, y))
push!(mbrs, rmbr)
end
for (i, br) in enumerate(mbrs)
insert!(seq_tree, br, i, string(i))
end
SI.check(seq_tree)
SI.load!(bulk_tree, enumerate(mbrs), convertel=x -> eltype(bulk_tree)(x[2], x[1], string(x[1])))
SI.check(bulk_tree)
include(joinpath(@__DIR__, "dataframe_utils.jl"))
seq_tree_df = convert(DataFrame, seq_tree)
include(joinpath(@__DIR__, "plot_utils.jl"))
seq_tree_plot = plot(seq_tree);
PlotlyJS.savefig(seq_tree_plot, joinpath(@__DIR__, "spiral_rtree_seq.html"))
PlotlyJS.savefig(seq_tree_plot, joinpath(@__DIR__, "spiral_rtree_seq.png"), width=1000, height=800)
bulk_tree_plot = plot(bulk_tree);
PlotlyJS.savefig(bulk_tree_plot, joinpath(@__DIR__, "spiral_rtree_bulk.html")) | SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 575 | module SpatialIndexing
export SpatialIndex, SpatialIndexException, SpatialElem,
RTree, SimpleSpatialIndex,
contained_in, intersects_with
include("regions.jl")
include("pool.jl")
include("abstract.jl")
## Spatial Indices
# SimpleSpatialIndex
include("simple/simpleindex.jl")
# R-tree
include("rtree/node.jl")
include("rtree/rtree.jl")
include("rtree/check.jl")
include("rtree/show.jl")
include("rtree/query.jl")
include("rtree/split.jl")
include("rtree/insert.jl")
include("rtree/adjust.jl")
include("rtree/delete.jl")
include("rtree/bulk.jl")
end # module
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 4887 | """
`SpatialIndex`-related exception raised within Julia
"""
struct SpatialIndexException <: Exception
msg::AbstractString # error message
end
function Base.showerror(io::IO, err::SpatialIndexException)
print(io, "SpatialIndexException: ")
print(io, err.msg)
end
# throws KeyError with or without id (depending on eltype HasID trait)
__spatial_keyerror(eltype::Type, br::Region, id::Any = nothing) =
idtrait(eltype) === HasNoID ? throw(KeyError(br)) : throw(KeyError((br, id)))
"""
Base abstract class for spatial indexing of elements of type `V`
in `N`-dimensional space with dimensions of type `T`.
"""
abstract type SpatialIndex{T<:Number, N, V} end
# basic SpatialIndex API
Base.eltype(::Type{<:SpatialIndex{<:Any, <:Any, V}}) where V = V
Base.eltype(si::SpatialIndex) = eltype(typeof(si))
idtype(::Type{T}) where T<:SpatialIndex = idtype(idtrait(eltype(T)))
idtype(si::SpatialIndex) = idtype(typeof(si))
dimtype(::Type{<:SpatialIndex{T}}) where T = T
dimtype(si::SpatialIndex) = dimtype(typeof(si))
Base.ndims(::Type{<:SpatialIndex{<:Any, N}}) where N = N
Base.ndims(si::SpatialIndex) = ndims(typeof(si))
regiontype(::Type{<:SpatialIndex{T,N}}) where {T,N} = Region{T,N} # default unless overridden
regiontype(si::SpatialIndex) = regiontype(typeof(si))
Base.length(si::SpatialIndex) = si.nelems
Base.isempty(si::SpatialIndex) = length(si) == 0
# SpatialIndex data element iteration support
Base.IteratorEltype(::Type{<:SpatialIndex}) = Base.HasEltype()
Base.IteratorSize(::Type{<:SpatialIndex}) = Base.HasLength()
# concrete SpatialIndex types should implement iterate()
"""
Specifies the kind of spatial data query.
"""
@enum QueryKind QueryContainedIn QueryIntersectsWith # TODO QueryPoint QueryNearestNeighbours
"""
Specifies the result of spatial data query.
"""
@enum QueryMatch::Int QueryNoMatch=0 QueryMatchPartial=1 QueryMatchComplete=2
"""
Base abstract class for implementing spatial queries in `N`-dimensional space.
"""
abstract type SpatialQueryIterator{T<:Number,N,V,Q} end
Base.IteratorEltype(::Type{<:SpatialQueryIterator}) = Base.HasEltype()
Base.IteratorSize(::Type{<:SpatialQueryIterator}) = Base.SizeUnknown()
Base.eltype(::Type{<:SpatialQueryIterator{<:Any,<:Any,V}}) where V = V
Base.eltype(iter::SpatialQueryIterator) = eltype(typeof(iter))
querykind(::Type{<:SpatialQueryIterator{<:Any,<:Any,<:Any,Q}}) where Q = Q
querykind(iter::SpatialQueryIterator) = querykind(typeof(iter))
# arbitrary spatial elements support
"""
Type trait for checking `id()` method support.
If type `V` has this trait (`idtype(V)` returns `HasID{K}`),
then `id(v::V)` should return a unique identifier for `v` of type `K`.
If `V` doesn't have this trait, `idtype(V)` returns `HasNoID`.
If available, `SpatialIndex{T,N,V}` uses unique identifiers of `V`
alongside spatial indexing.
"""
abstract type HasID{K} end
abstract type HasNoID end
idtrait(::Type) = HasNoID
idtype(::Type{HasID{K}}) where K = K
idtype(::Type{HasNoID}) = Union{}
"""
Type trait for checking `mbr()` method support.
If type `V` has this trait (`mbrtype(V)` returns `HasMBR{Rect{T,N}}`),
then `mbr(v::V)` should return a minimal bounding rectangle (MBR) `Rect{T,N}`
that contains `v`.
If `V` doesn't have this trait, `mbrtype(V)` returns `HasNoMBR`.
`SpatialIndex{T,N,V}` *requires* that `V` provides `mbr()` method that
returns `Rect{T,N}`.
"""
abstract type HasMBR{T} end
abstract type HasNoMBR end
mbrtrait(::Type) = HasNoMBR
mbrtype(::Type{HasMBR{T}}) where T = T
mbrtype(::Type{HasNoMBR}) = Union{}
# check whether type V has HasMBR trait and that the returned object
# is `Rect{T,N}`
function check_hasmbr(::Type{Rect{T,N}}, ::Type{V}) where {T, N, V}
R = mbrtrait(V)
R <: HasMBR ||
throw(ArgumentError("Element type $V doesn't have mbr() method"))
mbrtype(R) === Rect{T,N} ||
throw(ArgumentError("Element type $V: MBR type ($(mbrtype(R))) incompatible with ($(Rect{T,N}))"))
return true
end
# check whether type V has HasID trait and that the returned object is `K`
function check_hasid(::Type{K}, ::Type{V}) where {K, V}
R = idtrait(V)
R <: HasID ||
throw(ArgumentError("Element type $V doesn't have id() method"))
idtype(R) === K ||
throw(ArgumentError("Element type $V: ID type ($(idtype(R))) incompatible with ($K)"))
return true
end
"""
Simple `N`-dimensional spatial data element that stores values of type `V`
and could be referenced by the `id` of type `K` (if `K` is not `Nothing`).
Supports `HasMBR{Rect{T,N}}` and `HasID{K}` (if `K` is not `Nothing`) traits.
"""
struct SpatialElem{T,N,K,V}
mbr::Rect{T,N}
id::K
val::V
end
idtrait(::Type{<:SpatialElem{<:Any,<:Any,K}}) where K = HasID{K}
idtrait(::Type{<:SpatialElem{<:Any,<:Any,Nothing}}) = HasNoID
id(el::SpatialElem) = el.id
mbrtrait(::Type{<:SpatialElem{T,N}}) where {T,N} = HasMBR{Rect{T,N}}
mbr(el::SpatialElem) = el.mbr
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 887 | """
Base class for implementating the pool of `T` objects.
The pool allows to reduce the stress on GC by collecting the unneeded objects
(`release!(pool, obj)`) and reusing them later (`acquire!(pool)`).
"""
abstract type AbstractPool{T} end
capacity(pool::AbstractPool) = pool.capacity
Base.eltype(::Type{AbstractPool{T}}) where T = T
Base.eltype(pool::AbstractPool) = eltype(typeof(pool))
Base.length(pool::AbstractPool) = length(pool.objs)
acquire!(pool::AbstractPool) = length(pool) > 0 ? pop!(pool.objs) : newelem(pool)
function release!(pool::AbstractPool{T}, obj::T) where T
if length(pool) >= capacity(pool)
#@warn "Pool capacity exceeded" FIXME add parameter to enable it selectively
else
push!(pool.objs, obj)
end
end
"""
The default `AbstarctPool` implementation.
"""
struct Pool{T} <: AbstractPool{T}
objs::Vector{T}
capacity::Int
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 6072 | """
Base abstract class for implementing regions in `N`-dimensional space with
dimensions of type `T`.
"""
abstract type Region{T,N} end
dimtype(::Type{<:Region{T}}) where T = T
dimtype(r::Region) = dimtype(typeof(r))
Base.ndims(::Type{<:Region{<:Any, N}}) where N = N
Base.ndims(r::Region) = ndims(typeof(r))
"""
`N`-dimensional point.
"""
struct Point{T, N} <: Region{T, N}
coord::NTuple{N, T}
end
"""
empty(::Type{T}) where T<:Region
Generate empty (uninitialized) region of type `T`.
"""
empty(::Type{Point{T,N}}) where {T,N} =
Point{T,N}(ntuple(_ -> convert(T, NaN), N))
empty(::Type{Point{T,N}}) where {T<:Integer,N} =
Point{T,N}(ntuple(_ -> zero(T), N))
"""
area(a::Region)
`N`-dimensional "area" (volume etc) of `a`.
"""
area(a::Point{T}) where T = zero(typeof(zero(T)*zero(T)))
"""
perimeter(a::Region)
The sum of the `a` sides.
"""
perimeter(a::Point{T}) where T = zero(T)
"""
isvalid(a::Region)
Check that the parameters of `a` are valid and it defines a proper region.
"""
isvalid(a::Point) = all(!isnan, a.coord)
"""
Rectangular region constrained by `low[i]`...`high[i]` in each of `N` dimensions.
"""
struct Rect{T, N} <: Region{T, N}
low::NTuple{N, T}
high::NTuple{N, T}
end
Rect(low::NTuple{N, T1}, high::NTuple{N, T2}) where {N, T1<:Number, T2<:Number} =
Rect{Base.promote_type(T1, T2), N}(low, high)
Rect{T,N}(pt::Point{T,N}) where {T,N} = Rect{T,N}(pt.coord, pt.coord)
Rect(pt::Point) = Rect(pt.coord, pt.coord)
# "empty" (uninitialized) rectangles
empty(::Type{Rect{T,N}}) where {T,N} =
Rect{T,N}(ntuple(_ -> convert(T, NaN), N), ntuple(_ -> convert(T, NaN), N))
empty(::Type{Rect{T,N}}) where {T<:Integer,N} =
Rect{T,N}(ntuple(_ -> typemax(T), N), ntuple(_ -> typemax(T), N))
"""
combine(a::Region, b::Region)
MBR that contains both `a` and `b` regions.
"""
combine(a::Rect{T,N}, b::Rect{T,N}) where {T,N} =
@inbounds Rect{T,N}(ntuple(i -> min(a.low[i], b.low[i]), N),
ntuple(i -> max(a.high[i], b.high[i]), N))
# check that coords are not NaN and side lengths not negative.
@generated isvalid(a::Rect{T,N}) where {T,N} =
quote
Base.Cartesian.@nall $N i -> !isnan(a.low[i]) && !isnan(a.high[i]) && a.low[i] <= a.high[i]
end
"""
intersect(a::Region, b::Region)
MBR that is an intersection of `a` and `b` regions.
"""
function intersect(a::Rect{T,N}, b::Rect{T,N}) where {T,N}
res = @inbounds Rect{T,N}(ntuple(i -> max(a.low[i], b.low[i]), N),
ntuple(i -> min(a.high[i], b.high[i]), N))
return isvalid(res) ? res : empty(typeof(a))
end
@generated area(a::Rect{T,N}) where {T,N} =
quote
@inbounds res = a.high[1] - a.low[1]
@inbounds Base.Cartesian.@nexprs $(N-1) i -> res *= (a.high[i+1] - a.low[i+1])
return res
end
@generated perimeter(a::Rect{T,N}) where {T,N} =
quote
@inbounds res = a.high[1] - a.low[1]
@inbounds Base.Cartesian.@nexprs $(N-1) i -> res += (a.high[i+1] - a.low[i+1])
return res*ndims(a)
end
"""
overlap_area(a::Region, b::Region)
The area of MBR for `a` and `b` intersection.
"""
@generated overlap_area(a::Rect{T,N}, b::Rect{T,N}) where {T,N} =
quote
@inbounds res = min(a.high[1], b.high[1]) - max(a.low[1], b.low[1])
res <= 0.0 && return zero(typeof(res))
@inbounds Base.Cartesian.@nexprs $(N-1) i -> begin
width_i = min(a.high[i+1], b.high[i+1]) - max(a.low[i+1], b.low[i+1])
width_i <= zero(typeof(width_i)) && return zero(typeof(res))
res *= width_i
end
return res
end
"""
combined_area(a::Region, b::Region)
The area of MBR for the union of `a` and `b`.
"""
@generated combined_area(a::Rect{T,N}, b::Rect{T,N}) where {T,N} =
quote
@inbounds res = max(a.high[1], b.high[1]) - min(a.low[1], b.low[1])
@inbounds Base.Cartesian.@nexprs $(N-1) i -> res *= max(a.high[i+1], b.high[i+1]) - min(a.low[i+1], b.low[i+1])
return res
end
"""
enlargement(a::Region, b::Region)
How much `a` grows when combined with `b`.
The difference between the MBR area of the `a` and `b` union and the MBR area of `a`.
"""
enlargement(a::Rect{T,N}, b::Rect{T,N}) where {T,N} = combined_area(a, b) - area(a)
"""
center(a::Region)
The center point of `a`.
"""
center(a::Rect{T,N}) where {T,N} =
Point(ntuple(i -> 0.5*(a.low[i] + a.high[i]), N))
@generated sqrdistance(a::Point{T,N}, b::Point{T,N}) where {T,N} =
quote
@inbounds res = abs2(a.coord[1] - b.coord[1])
@inbounds Base.Cartesian.@nexprs $(N-1) i -> res += abs2(a.coord[i+1] - b.coord[i+1])
return res
end
"""
intersects(a::Region, b::Region)
Check whether `a` intersects with `b`.
"""
@generated intersects(a::Rect{T,N}, b::Rect{T,N}) where {T,N} =
quote
@inbounds Base.Cartesian.@nall $N i -> (a.low[i] <= b.low[i] <= a.high[i]) || (b.low[i] <= a.low[i] <= b.high[i])
end
"""
contains(a::Region, b::Region)
Check whether `a` contains `b`.
"""
@generated contains(a::Rect{T,N}, b::Rect{T,N}) where {T,N} =
quote
@inbounds Base.Cartesian.@nall $N i -> (a.low[i] <= b.low[i]) && (a.high[i] >= b.high[i])
end
@generated contains(a::Rect{T,N}, b::Point{T,N}) where {T,N} =
quote
@inbounds Base.Cartesian.@nall $N i -> (a.low[i] <= b.coord[i] <= a.high[i])
end
"""
in(a::Region, b::Region)
Check whether `a` is contained inside `b`.
"""
Base.in(a::Rect, b::Rect) = contains(b, a)
Base.in(a::Point, b::Rect) = contains(b, a)
# point is equal to the MBR if its low and high corners coincides
Base.:(==)(a::Point, b::Rect) = a.coord == b.low == b.high
Base.:(==)(a::Rect, b::Point) = b == a
"""
touches(a::Rect, b::Rect)
Check whether `a` and `b` rectangles touches from the inside
(i.e. any `low` side touches `low` or `high` touches `high`).
"""
@generated touches(a::Rect{T,N}, b::Rect{T,N}) where {T,N} =
quote
@inbounds Base.Cartesian.@nany $N i -> (a.low[i] == b.low[i]) || (a.high[i] == b.high[i])
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 6257 | # condense the tree after the child was removed from the node
# accumulate the nodes that are temporary detached and need to be reinserted in `tmpdetached`
function _condense!(node::Node, tree::RTree, tmpdetached::AbstractVector{<:Node})
min_load = floor(Int, capacity(node, tree) * tree.fill_factor)
@debug "_condense!() lev=$(level(node)) len=$(length(node)) tmpdetached=$(length(tmpdetached)) min_load=$min_load"
if node === tree.root
# eliminate root if it has only one child.
old_root = tree.root
min_root_level = mapreduce(level, max, tmpdetached, init=1)
while (level(node) > min_root_level) && (length(node) == 1)
#@debug "_condense!(): shrinking single-child root (lv=$(level(node)))"
tree.root = node[1]
tree.root.parent = nothing
release(tree, node)
pop!(tree.nnodes_perlevel) # tree became 1 level shorter
node = tree.root
end
if (level(node) >= min_root_level) && isempty(node)
#@debug "_condense!(): resetting empty root (lv=$(level(node)))"
# reset the root to a node of minimal level to accomodate the children of tmpdetached (or leaf)
tree.root = acquire(tree, min_root_level == 1 ? Leaf : Branch, min_root_level)
resize!(tree.nnodes_perlevel, min_root_level)
fill!(tree.nnodes_perlevel, 0)
tree.nnodes_perlevel[end] = 1
elseif node === old_root
# root didn't change, but MBR has to be updated due to data removal.
tree.tight_mbrs && syncmbr!(node)
end
return node
else
# find the entry in the parent, that points to this node
node_ix = pos_in_parent(node)
@assert node_ix !== nothing
if length(node) < min_load
# used space less than the minimum
# 1. eliminate node entry from the parent. deleteEntry will fix the parent's MBR.
_detach!(parent(node), node_ix, tree)
# 2. add this node to the stack in order to reinsert its entries.
push!(tmpdetached, node)
else
# global recalculation necessary since the MBR can only shrink in size,
# due to data removal.
tree.tight_mbrs && syncmbr!(parent(node))
end
return _condense!(parent(node), tree, tmpdetached)
end
end
# reinsert the *children* of the `detached` nodes back to the tree
# the `detached` node themselves are released back to the pool
function _reinsert!(tree::RTree, detached::AbstractVector{<:Node})
@debug "_reinsert!(): reinsert children of $(length(detached)) detached nodes"
isempty(detached) && return tree
con = SubtreeContext(tree)
sort!(detached, by=level, rev=true) # start with the highest nodes
for node in detached
for child in children(node)
_insert!(con, child, level(node))
tree.nnode_reinsertions += 1
end
release(tree, node)
end
empty!(detached)
return tree
end
# update the MBR of node if required due to the child_ix MBR changing from
# child_oldmbr to its current state or if forced,
# propagate the MBR update to the higher tree levels
# return true if MBR was updated
function _updatembr!(node::Branch, child_ix::Integer, child_oldmbr::Rect,
con::SubtreeContext; force::Bool = false)
@debug "_updatembr!() tree_height=$(height(con.tree)) tree_len=$(length(con.tree)) node_lev=$(level(node)) node_len=$(length(node)) force=$(force) child_ix=$(child_ix) oflow=$(isoverflow(con, level(node)))"
child = node[child_ix]
# MBR needs recalculation if either:
# 1. the NEW child MBR is not contained.
# 2. the OLD child MBR is touching.
node_oldmbr = mbr(node)
mbr_dirty = force || !in(mbr(child), node_oldmbr) ||
(con.tree.tight_mbrs && touches(node_oldmbr, child_oldmbr))
mbr_dirty && syncmbr!(node)
if mbr_dirty && hasparent(node)
_updatembr!(parent(node), pos_in_parent(node), node_oldmbr, con, force=force)
end
return mbr_dirty
end
# replace the node (with oldmbr MBR) with the newnode
# return true if node's parent MBR update was necessary
function _replace!(node::Node, newnode::Node, oldmbr::Rect,
con::SubtreeContext)
@debug "_replace!() lev=$(level(node)) len=$(length(node)) newlen=$(length(newnode))"
# find an entry pointing to the old child
@assert level(node) == level(newnode)
par = parent(node)
@assert par !== nothing
node_ix = pos_in_parent(node)
@assert node_ix !== nothing
par[node_ix] = newnode
return _updatembr!(par, node_ix, oldmbr, con)
end
# replace node with n1 and n2
# return true if node's parent MBR update or any other tree
# restructurings were necessary
function _replace!(node::Node, n1::Node, n2::Node,
oldmbr::Rect, con::SubtreeContext)
@debug "_replace!() lev=$(level(node)) len=$(length(node)) newlens=($(length(n1)), $(length(n2)))"
@assert level(node) == level(n1) == level(n2)
# find entry pointing to old node
par = parent(node)
@assert par !== nothing
node_ix = pos_in_parent(node)
@assert node_ix !== nothing
# MBR needs recalculation if either:
# 1. MBRs of n1 and n2 are not contained in parent
# 2. the OLD node MBR is touching parent (FIXME should it be recalced though?)
par_oldmbr = mbr(par)
mbr_dirty = !in(mbr(n1), par_oldmbr) || !in(mbr(n2), par_oldmbr) ||
(con.tree.tight_mbrs && touches(par_oldmbr, oldmbr))
# replace the node with n1
par[node_ix] = n1
mbr_dirty && syncmbr!(par)
con.tree.nnode_splits += 1
con.tree.nnodes_perlevel[level(node)] += 1
# No registering necessary. insert!() will write the node if needed.
#_register!(tree, node)
adjusted = _insert!(par, n2, con)
# if n2 is contained in the node and there was no split or reinsert,
# we need to adjust only if recalculation took place.
# In all other cases insertData above took care of adjustment.
if !adjusted && mbr_dirty && hasparent(par)
_updatembr!(parent(par), pos_in_parent(par), par_oldmbr, con)
end
return adjusted || mbr_dirty
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 6387 | # default branch fill strategy
# returns the tuple:
# the number of 1st dim slices and the number of child nodes in each slice
function omt_branch_fill(tree::RTree; fill_factor::Number=1.0)
@assert 0.0 <= fill_factor <= 1.0
maxlen = ceil(Int, capacity(Branch, tree) * fill_factor)
slicelen = ceil(Int, 0.75*sqrt(maxlen))
nslices = fld1(maxlen, slicelen)
return (nslices, slicelen)
end
"""
load!(tree::RTree{T,N,V}, data::Any;
convertel = identity, method = :OMT,
leaf_fill = capacity(Leaf, tree),
branch_fill::Tuple{Integer, Integer} = omt_branch_fill(tree)) where {T,N,V}
Bulk-load `data` into `tree`.
* `tree`: an *empty* R-tree for storing elements of type `V`
* `data`: iterable container with the elements to put into `tree`
* `convertel`: function to convert elements of `data` to type `V`
* `method`: bulk-loading method
* `leaf_fill`: the average number of elements to store in R-tree leaves (1-level nodes)
* `branch_fill`: the tuple of the number of slices and the number of subtrees per slice
in the R-tree nodes (level ≥ 1).
The supported bulk-loading methods are:
* `:OMT`: *Overlap Minimizing Top-down method* by Taewon Lee and Sukho Lee
"""
function load!(tree::RTree{T,N,V}, data::Any;
convertel = identity,
method::Symbol = :OMT,
leaf_fill::Integer = capacity(Leaf, tree),
branch_fill::Tuple{Integer, Integer} = omt_branch_fill(tree)) where {T, N, V}
# load from arbitrary data into Elem-backed R-tree
isempty(tree) || throw(ArgumentError("Cannot bulk-load into non-empty tree"))
if isempty(data)
@warn "No bulk-load data provided"
return tree
end
0 < leaf_fill <= capacity(Leaf, tree) ||
throw(ArgumentError("Leaf fill should be positive and not exceed leaf capacity"))
prod(branch_fill) > 1 || throw(ArgumentError("Branch fill should be > 1"))
if method == :OMT
return load_omt!(tree, V[convertel(x) for x in data],
leaf_fill=leaf_fill, branch_fill=branch_fill)
else
throw(ArgumentError("Unsupported bulk-loading method $method"))
end
end
# See "OMT: Overlap Minimizing Top-down Bulk Loading Algorithm for R-tree"
# by Taewon Lee and Sukho Lee, http://ceur-ws.org/Vol-74/files/FORUM_18.pdf
# Modified to take into account that leaf and branch capacity is different
# and allow branch slices at any tree level (specified by `branch_fill`)
function load_omt!(tree::RTree, elems::AbstractVector;
leaf_fill::Integer = capacity(Leaf, tree),
branch_fill::Tuple{Integer, Integer} = omt_branch_fill(tree))
# calculate the tree properties
nbranch_subtrees = min(branch_fill[1] * branch_fill[2], capacity(Branch, tree))
height = max(ceil(Int, (log(length(elems)) - log(leaf_fill)) / log(nbranch_subtrees)), 0) + 1 # 1 for leaves
if height > 1
maxelems_subtree = leaf_fill*nbranch_subtrees^(height-2) # max elements in each root subtree
nroot_subtrees = fld1(length(elems), maxelems_subtree)
nroot_slices = floor(Int, sqrt(nroot_subtrees))
else # root === single leaf
maxelems_subtree = nroot_subtrees = length(elems)
nroot_slices = 1
end
#@show length(elems) leaf_fill branch_fill height maxelems_subtree nsubtrees nslices
# sort by the center of the first dim
dim = mod1(height, ndims(tree)) # root level dimension
elems_sorted = sort(elems, by = elem -> mbr(elem).low[dim] + mbr(elem).high[dim])
resize!(tree.nnodes_perlevel, height)
fill!(tree.nnodes_perlevel, 0)
tree.root = omt_subtree(elems_sorted, tree, height,
nroot_slices, nroot_subtrees, leaf_fill, branch_fill)
tree.nnodes_perlevel[end] = 1
return tree
end
# put the elems into the subtree of height lev
# the root node of the subtree should have nsubtree children
# organized into nslices slices along the current elems order
# recursively calls itself
function omt_subtree(elems::AbstractVector, tree::RTree,
lev::Integer, nslices::Integer, nsubtrees::Integer,
leaf_fill::Integer, branch_fill::Tuple{Integer, Integer})
@debug "omt_subtree(): lev=$lev nslices=$nslices nsubtrees=$nsubtrees nelems=$(length(elems))"
@assert lev > 0
if length(elems) <= nsubtrees
# if fewer elements than the number of subtrees,
# then all elements should be put into single leaf
if lev == 1 # create a Leaf and attach all elements
node = acquire(tree, Leaf, lev)
for elem in elems
_attach!(node, elem, tree)
end
tree.nelems += length(elems)
return node
else # not leaf level yet, create a branch with a single child
child = omt_subtree(elems, tree, lev - 1, nslices, nsubtrees,
leaf_fill, branch_fill)
node = _attach!(acquire(tree, Branch, lev), child, tree)
tree.nnodes_perlevel[lev - 1] += 1
return node
end
end
# subtree root
@assert lev > 1
node = acquire(tree, Branch, lev)
# create subtrees
nelems_subtree = fld1(length(elems), nsubtrees) # actual fill of the subtree
nelems_slice = nelems_subtree * fld1(nsubtrees, nslices)
dim = mod1(lev, ndims(tree)) # cycle sorting dimensions through tree levels
for i in 1:nelems_slice:length(elems) # slice using the external elements order (sort-dim of the level above)
# sort the elements of the slice by the current dim
elems_slice = sort(view(elems, i:min(i+nelems_slice-1, length(elems))),
by = elem -> mbr(elem).low[dim] + mbr(elem).high[dim])
# create slice subtrees and attach to the node
for j in 1:nelems_subtree:length(elems_slice)
subtree_elems_range = j:min(j+nelems_subtree-1, length(elems_slice))
child = omt_subtree(view(elems_slice, subtree_elems_range), tree,
lev - 1, branch_fill[1],
min(branch_fill[1] * branch_fill[2], capacity(Branch, tree)),
leaf_fill, branch_fill)
_attach!(node, child, tree)
tree.nnodes_perlevel[lev - 1] += 1
end
end
return node
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 3123 | nelements(node::Leaf) = length(node)
nelements(node::Branch) = mapreduce(nelements, +, children(node), init=0)
# check the R-tree node (branch or leaf):
# * the parent
# * the level
# * the number of attached elements
# * element id uniqueness
# * the MBR (should fit the MBR of children)
function check(node::Node{T,N,V}, tree::RTree{T,N,V},
nnodes_perlevel::AbstractVector{Int}, ids::Union{Set, Nothing}) where {T,N,V}
nnodes_perlevel[level(node)] += 1
for (i, child) in enumerate(children(node))
if node isa Branch
child.parent === node ||
throw(SpatialIndexException("Node (lev=$(level(node)) len=$(length(node))): child #$i references different parent"))
level(child) + 1 == level(node) ||
throw(SpatialIndexException("Node (lev=$(level(node)) len=$(length(node))): child #$i level ($(level(child))) doesn't match parent's ($(level(node)))"))
check(child, tree, nnodes_perlevel, ids)
elseif idtrait(typeof(child)) !== HasNoID
cid = id(child)
(cid ∈ ids) && throw(SpatialIndexException("Duplicate data id=$cid"))
push!(ids, cid)
end
end
br = !isempty(node) ? mapreduce(mbr, combine, node.children) : empty(Rect{T,N})
if isempty(node)
isequal(br, mbr(node)) ||
throw(SpatialIndexException("Node (lev=$(level(node)) len=$(length(node))) MBR ($(mbr(node))) should be empty"))
elseif tree.tight_mbrs && br != mbr(node) || !in(br, mbr(node))
throw(SpatialIndexException("Node (lev=$(level(node)) len=$(length(node))) MBR ($(mbr(node))) doesn't match its children MBR ($(br))"))
end
return true
end
# check the tree:
# * the root
# * the height
# * the number of elements
# * the number of nodes per level
# * element id uniqueness
# * MBRs of the nodes
function check(tree::RTree)
tree.root.parent === nothing ||
throw(SpatialIndexException("RTree: root has a parent"))
level(tree.root) == height(tree) ||
throw(SpatialIndexException("RTree: root level ($(level(tree.root))) doesn't match tree height ($(height(tree)))"))
length(tree.nnodes_perlevel) == height(tree) ||
throw(SpatialIndexException("RTree: nnodes_perlevel length ($(length(tree.nnodes_perlevel))) doesn't match tree height ($(height(tree)))"))
ids = idtype(tree) !== Union{} ? Set{idtype(tree)}() : nothing
nnodes_perlevel = zeros(Int, height(tree))
check(tree.root, tree, nnodes_perlevel, ids)
nelms = nelements(tree.root)
length(tree) == nelms ||
throw(SpatialIndexException("RTree: actual ($(nelms)) and reported ($(length(tree))) number of elements do not match"))
ids === nothing || length(tree) == length(ids) ||
throw(SpatialIndexException("RTree: the number of ids ($(length(ids))) doesn't match the reported number of elements ($(length(tree)))"))
tree.nnodes_perlevel == nnodes_perlevel ||
throw(SpatialIndexException("RTree: actual ($(nnodes_perlevel)) and reported ($(tree.nnodes_perlevel)) number of nodes per level do not match"))
return true
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 5047 | """
delete!(tree::RTree, pt::Point, [id])
delete!(tree::RTree, br::Rect, [id])
Deletes the value identified by `br` bounding box (or point `pt`) and
the `id` (if tree elements support `HasID` trait) from the `tree`.
"""
function Base.delete!(tree::RTree{T,N}, br::Rect{T,N}, id::Any = nothing) where {T,N}
leafx = findfirst(tree, br, id)
leafx === nothing && __spatial_keyerror(eltype(tree), br, id)
_detach!(leafx[1], leafx[2], tree)
tmpdetached = Vector{nodetype(tree)}() # FIXME use pool, Union{Leaf,Branch} ?
_condense!(leafx[1], tree, tmpdetached)
_reinsert!(tree, tmpdetached)
tree.nelems -= 1
tree.nelem_deletions += 1
return tree
end
Base.delete!(tree::RTree{T,N}, pt::Point{T,N}, id::Any = nothing) where {T,N} =
delete!(tree, Rect(pt), id)
# deletes the subtree with the `node` root from the `tree`
# (does not update the parent MBR)
function delete_subtree!(tree::RTree, node::Node)
#@debug "delete_subtree(): lev=$(level(node))"
_release_descendants!(tree, node)
if hasparent(node) # remove the node from the parent
tree.nnodes_perlevel[level(node)] -= 1 # don't count this node anymore
_detach!(parent(node), pos_in_parent(node), tree)
release(tree, node)
# FIXME propagate parent mbr updates (if required)
else # root node just stays empty
node.mbr = empty(mbrtype(node))
empty!(node.children)
end
end
# recursively release all `node` descendants to the pool
function _release_descendants!(tree::RTree, node::Node)
if node isa Branch
for child in children(node)
_release_descendants!(tree, child)
release(tree, child)
end
# update nodes counts
tree.nnodes_perlevel[level(node)-1] -= length(node)
elseif node isa Leaf
tree.nelems -= length(node)
tree.nelem_deletions += length(node)
end
#@debug "_release_descendants(): done node lev=$(level(node)) parent=$(hasparent(node))"
end
# FIXME replace `region` with a more generic `filter`
"""
subtract!(tree::RTree, reg::Region)
Subtracts the `region` from the `tree`, i.e. removes all elements within
`region`.
"""
function subtract!(tree::RTree{T,N}, reg::Region{T,N}) where {T,N}
#@debug "subtract!(): region=$(reg)"
isempty(tree) && return tree
tmpdetached = Vector{nodetype(tree)}()
status = _subtract!(tree.root, 0, reg, tree, tmpdetached)
#@debug "subtract!(): status=$(status) tmpdetached=$(length(tmpdetached))"
if status > 0 # tree changed
_condense!(tree.root, tree, tmpdetached) # try to condense the root
end
_reinsert!(tree, tmpdetached)
return tree
end
function _subtract!(node::Node, node_ix::Int, reg::Region, tree::RTree,
tmpdetached::AbstractVector{<:Node})
nodembr = mbr(node)
#@debug "_subtract!(): lev=$(level(node)) i=$node_ix len=$(length(node))"
# TODO juxtaposition() method that combines in() and intersects()?
if in(nodembr, reg)
#@debug "_subtract!(): delete subtree lev=$(level(node)) i=$node_ix len=$(length(node))"
delete_subtree!(tree, node)
return 2 # node removed
elseif intersects(nodembr, reg)
mbr_dirty = false
i = 1
while i <= length(node)
#@debug "1: lev=$(level(node)) i=$i len=$(length(node))"
child = node[i]
oldmbr = mbr(child)
if node isa Branch
child_res = _subtract!(child, i, reg, tree, tmpdetached)
else
@assert node isa Leaf
if in(oldmbr, reg)
#@debug "_subtract!(): detach elem lev=$(level(node)) i=$i len=$(length(node))"
_detach!(node, i, tree, updatembr = false) # don't update MBR, we do it later
tree.nelems -= 1
tree.nelem_deletions += 1
child_res = 2
# FIXME intersect is not considered (would be important if elem mbr is not a point), should be handled by `filter`
else
child_res = 0
end
end
if !mbr_dirty && (child_res != 0) && tree.tight_mbrs
mbr_dirty = touches(nodembr, oldmbr)
end
if child_res != 2 # don't increment if i-th node removed
i += 1
end
end
if hasparent(node) && length(node) < floor(Int, tree.reinsert_factor * capacity(node, tree))
_detach!(parent(node), node_ix, tree)
tree.nnodes_perlevel[level(node)] -= 1
if isempty(node)
#@debug "Releasing empty node (lv=$(level(node)))"
release(tree, node)
else
push!(tmpdetached, node)
end
return 2 # node removed
elseif mbr_dirty
syncmbr!(node)
return 1 # mbr changed
else
return 0 # no mbr change
end
else
return 0 # no change
end
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 9197 | """
insert!(tree::RTree, pt::Point, [id], val)
insert!(tree::RTree, br::Rect, [id], val)
insert!(tree::RTree, elem::SpatialElem)
Inserts `val` value identified by `br` bounding box (or point `pt`) and
`id` (if tree elememnts support `HasID` trait) into the `tree`.
"""
function Base.insert!(tree::RTree, el::Any)
check_eltype_rtree(el, tree)
_insert!(tree, el, 1)
tree.nelems += 1
tree.nelem_insertions += 1
return tree
end
Base.insert!(tree::RTree{T,N,SpatialElem{T,N,K,V}}, br::Rect{T,N}, id::Any, val::Any) where {T,N,K,V} =
insert!(tree, SpatialElem{T,N,K,V}(br, id, val))
Base.insert!(tree::RTree{T,N,SpatialElem{T,N,K,V}},
pt::Point{T,N}, id::Any, val::Any) where {T,N,K,V} =
insert!(tree, SpatialElem{T,N,K,V}(Rect(pt), id, val))
Base.insert!(tree::RTree{T,N,SpatialElem{T,N,Nothing,V}},
br::Union{Rect{T,N}, Point{T,N}}, val::Any) where {T,N,V} =
insert!(tree, br, nothing, val)
# inserts the child into the node rebalancing R-tree as needed
# returns true if MBR was changed and upstream R-tree readjustments are required
function _insert!(node::Node, child::Any, con::SubtreeContext)
if length(node) < capacity(node, con.tree) # underfull node
oldmbr = mbr(node) # this has to happen before _attach!() modifies node's MBR
_attach!(node, child, con.tree)
if !in(mbr(child), oldmbr) && hasparent(node)
#@debug "_insert!(): mbr change"
_updatembr!(parent(node), pos_in_parent(node), oldmbr, con)
return true
else
return false
end
elseif variant(con.tree) == RTreeStar && (node !== con.tree.root) && !isoverflow(con, level(node))
return _insert!_fullnode_rstar(node, child, con)
else
return _insert!_fullnode(node, child, con)
end
end
function _insert!(con::SubtreeContext, node::Any, lev::Integer)
#@debug "_insert!(con): len=$(length(con.tree)) node_lev=$(node isa Node ? level(node) : 0) node_len=$(node isa Node ? length(node) : 0)"
par = choose_subtree(con.tree.root, lev, mbr(node), con.tree)
@assert level(par) == lev
_insert!(par, node, con)
end
_insert!(tree::RTree, node::Any, lev::Int) =
_insert!(SubtreeContext(tree), node, lev)
# index of the child that would have the least MBR enlargement by br
function find_least_enlargement(node::Node, br::Rect)
min_enl = Inf
best_ix = 0
best_area = Inf
for i in eachindex(children(node))
child_mbr = mbr(@inbounds node[i])
child_area = area(child_mbr)
enl = combined_area(child_mbr, br) - child_area
if enl < min_enl || (min_enl == enl && child_area < best_area)
min_enl = enl
best_area = child_area
best_ix = i
end
end
return best_ix
end
# index of the child that would have the least MBR overlap with br
function find_least_overlap(node::Node, br::Rect, tree::RTree)
min_enl = Inf
best_area = Inf
best_ix = 0
enls = Vector{Float64}(undef, length(node)) # FIXME use pool?
# find combined region and enlargement of every entry and store it.
for (i, child) in enumerate(children(node))
child_area = area(mbr(child))
enls[i] = enl = combined_area(br, mbr(child)) - child_area
if enl < min_enl || (enl == min_enl && child_area < best_area)
min_enl = enl
best_area = child_area
best_ix = i
end
end
abs(min_enl) <= eps(min_enl) && return best_ix # no enlargement
if length(node) > tree.nearmin_overlap
# sort entries in increasing order of enlargement
enl_order = sortperm(enls) # FIXME reuse from pool
@assert min_enl == enls[enl_order[1]] <= enls[enl_order[end]]
niter = tree.nearmin_overlap
else
niter = length(node)
enl_order = collect(1:niter) # FIXME reuse from pool
end
# calculate overlap of most important original entries (near minimum overlap cost).
min_delta_olap = Inf
best_ix = 0
best_area = Inf
best_enl = Inf
for i in 1:niter
node_ix = enl_order[i]
node_mbr = mbr(node[node_ix])
comb_mbr = combine(node_mbr, br)
delta_olap = 0.0
for (j, child) in enumerate(children(node))
if node_ix != j
olap = overlap_area(comb_mbr, mbr(child))
if olap > 0.0
delta_olap += olap - overlap_area(node_mbr, mbr(child))
end
end
end
node_area = area(node_mbr)
# keep the one with the least, in the order:
# delta overlap, enlargement, area
if (delta_olap < min_delta_olap) || (delta_olap == min_delta_olap &&
(enls[node_ix] < best_enl || (enls[node_ix] == best_enl &&
node_area < best_area)))
min_delta_olap = delta_olap
best_ix = node_ix
best_area = node_area
best_enl = enls[node_ix]
end
end
return best_ix
end
# choose the node (for inserting the given mbr at specified level)
function choose_subtree(node::Node, lev::Int, br::Rect, tree::RTree)
while level(node) > lev
if variant(tree) == RTreeLinear || variant(tree) == RTreeQuadratic
child_ix = find_least_enlargement(node, br)
elseif variant(tree) == RTreeStar
child_ix = level(node) == 1 ?
find_least_overlap(node, br, tree) : # for the node pointing to leaves
find_least_enlargement(node, br)
else
throw(SpatialIndexException("RTree variant not supported"))
end
node = node[child_ix]
end
level(node) == lev ||
throw(SpatialIndexException("Couldn't find the node of level $lev in RTree of height $(height(tree))"))
return node
end
# R*-tree-specific insertion into the full node
# splits the node and rebalances the R-tree
function _insert!_fullnode_rstar(node::Node, child::Any, con::SubtreeContext)
#@debug "_insert!_fullnode_rstar(): lev=$(level(node)) len=$(length(node))"
@assert isa(con.level_overflow, BitVector)
@assert hasparent(node)
setoverflow!(con, level(node)) # the R* insert could only be done once per level
oldmbr = mbr(node)
_attach!(node, child, con.tree, force=true) # force-push the child exceeding the capacity
node_center = center(mbr(node))
# calculate relative distance of every entry from the node MBR (ignore square root.)
children_dist = sqrdistance.(Ref(node_center), center.(mbr.(children(node)))) # FIXME reuse array?
# return the indices sorted by the increasing order of distances.
# Since children_dist is sorted in ascending order
# it would match the reinsertion order suggested in the paper.
children_order = sortperm(children_dist) # FIXME reuse array?
nkeep = length(node) - floor(Int, length(node) * con.tree.reinsert_factor)
newnode = acquire(con.tree, typeof(node), level(node)) # the replacement node
for i in 1:nkeep
_attach!(newnode, node[children_order[i]], con.tree)
end
# Divertion from R*-Tree algorithm proposed in libspatialindex:
# First update the path to the root, then start reinserts, to avoid complicated handling
# of changes to the same node from multiple insertions.
#@debug "_insert!_fullnode_rstar(): replace the node"
_replace!(node, newnode, oldmbr, con) # replace the node (so (nkeep+1):... children are detached from the tree)
#@debug "_insert!_fullnode_rstar(): reinsert $(length((nkeep+1):length(children_order))) children of lev=$(level(node)) node"
# don't use par during/after reinsertion, it might have changed
for i in (nkeep+1):length(children_order)
child = node[children_order[i]]
#@debug "_insert!_fullnode_rstar(): reinsert #$i child (type=$(typeof(child)) lev=$(child isa Node ? level(child) : "data") parent=$(isa(child, Node) && hasparent(child)))"
_insert!(con, child, level(node))
con.tree.nnode_reinsertions += 1
end
release(con.tree, node) # return node to the pool
return true
end
# R-tree-specific insertion into the full node
# splits the node and rebalances the R-tree
function _insert!_fullnode(node::Node, child::Any, con::SubtreeContext)
#@debug "_insert!_fullnode(): lev=$(level(node)) len=$(length(node)) parent=$(hasparent(node))"
oldmbr = mbr(node)
_attach!(node, child, con.tree, force=true) # temporary overflow the node capacity
n1, n2 = _split!(node, con.tree)
if node === con.tree.root
#@debug "_insert!_fullnode(): newroot tree_height=$(height(con.tree)) tree_len=$(length(con.tree))"
# the node must be the root, make the new root and attach n1, n2 to it
newroot = acquire(con.tree, Branch, level(node) + 1)
_attach!(newroot, n1, con.tree)
_attach!(newroot, n2, con.tree)
# tree grows
con.tree.root = newroot
con.tree.nnodes_perlevel[level(node)] = 2
push!(con.tree.nnodes_perlevel, 1)
else # non-root, n1 and n2 replace the node in its parent
_replace!(node, n1, n2, oldmbr, con)
end
return true
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 3304 | """
Base class for `RTree` node (`Branch` or `Leaf`).
"""
abstract type Node{T,N,V} end
dimtype(::Type{<:Node{T}}) where T = T
dimtype(node::Node) = dimtype(typeof(node))
Base.ndims(::Type{<:Node{<:Any, N}}) where N = N
Base.ndims(node::Node) = ndims(typeof(node))
mbrtype(::Type{<:Node{T,N}}) where {T,N} = Rect{T,N}
mbrtype(node::Node) = mbrtype(typeof(node))
mbr(node::Node) = node.mbr
parent(node::Node) = node.parent
hasparent(node::Node) = node.parent !== nothing
children(node::Node) = node.children
@inline Base.isempty(node::Node) = isempty(children(node))
@inline Base.length(node::Node) = length(children(node))
@inline Base.getindex(node::Node, i::Integer) = getindex(children(node), i)
Base.keys(node::Node) = keys(children(node)) # for eachindex()
# `node` position among its siblings in `children` vector of the parent or nothing
pos_in_parent(node::Node) =
hasparent(node) ? findfirst(c -> c === node, children(parent(node))) : nothing
# update mbr to match the combined MBR of its children
syncmbr!(node::Node) =
node.mbr = !isempty(node) ? mapreduce(mbr, combine, node.children) : empty(mbrtype(node))
# check whether type E could be used as the data element type in R-tree
# FIXME also need to check whether E could be converted to V of Node
check_eltype_rtree(::Type{E}, ::Type{N}) where {N<:Node, E} =
check_hasmbr(mbrtype(N), E)
check_eltype_rtree(el::Any, node::Node) =
check_eltype_rtree(typeof(el), typeof(node))
# equality check for R-tree elements (by MBR and, optionally, ID)
isequal_rtree(el::Any, reg::Region, id::Any = nothing) =
isequal_rtree(idtrait(typeof(el)), el, reg, id)
isequal_rtree(::Type{<:HasID}, el::Any, reg::Region, key::Any) =
isequal(id(el), convert(idtype(idtrait(typeof(el))), key)) && (mbr(el) == reg)
# if the tree has IDs but `nothing` supplied, skip ID check
isequal_rtree(::Type{<:HasID}, el::Any, reg::Region, ::Nothing = nothing) =
(mbr(el) == reg)
isequal_rtree(::Type{HasNoID}, el::Any, reg::Region, ::Nothing = nothing) =
(mbr(el) == reg)
"""
R-Tree leaf (level 1 node).
Its children are data elements of type `V`.
"""
mutable struct Leaf{T,N,V} <: Node{T,N,V}
parent::Union{Node{T,N,V}, Nothing} # actually Branch{T,N,V}, but cannot do without forward decl
mbr::Rect{T,N}
children::Vector{V}
function Leaf{T,N,V}(parent::Union{Nothing, Node{T,N,V}},
::Type{V}) where {T,N,V}
new{T,N,V}(parent, empty(Rect{T,N}), Vector{V}())
end
end
level(node::Leaf) = 1 # always
"""
R-Tree node for levels above 1 (non-`Leaf`).
"""
mutable struct Branch{T,N,V} <: Node{T,N,V}
parent::Union{Branch{T,N,V}, Nothing}
level::Int # level (thickness) in the R-tree (0=leaves)
mbr::Rect{T,N}
children::Union{Vector{Branch{T,N,V}},Vector{Leaf{T,N,V}}}
function Branch{T,N,V}(parent::Union{Nothing, Branch{T,N,V}}, ::Type{C}) where {T,N,V, C<:Node{T,N,V}}
new{T,N,V}(parent, 0, empty(Rect{T,N}), Vector{C}())
end
end
level(node::Branch) = node.level
function Base.setindex!(node::Branch, child::Node, i::Integer)
(level(node) == level(child) + 1) ||
throw(SpatialIndexException("Parent ($(level(node)) and child ($(level(child))) levels don't match"))
setindex!(children(node), child, i)
child.parent = node
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 9305 | function Base.findfirst(node::Leaf{T,N}, reg::Region{T,N}, id::Any) where {T,N}
for (i, el) in enumerate(children(node))
if isequal_rtree(el, reg, id)
return (node, i)
end
end
return nothing
end
function Base.findfirst(node::Branch{T,N,V}, reg::Region{T,N}, id::Any) where {T,N,V}
for child in children(node)
if contains(mbr(child), reg)
res = findfirst(child, reg, id)
if res !== nothing
return res::Tuple{Leaf{T,N,V}, Int}
end
end
end
return nothing
end
"""
findfirst(tree::RTree{T,N}, reg::Region{T,N}, [id]) where {T,N}
Find the element in the `tree` by its region (`reg`) and, optionally, its `id`.
The region (MBR) of the element and `reg` should match exactly.
Returns the tuple of `Leaf` and position of the element or `nothing`.
"""
Base.findfirst(tree::RTree{T,N}, reg::Region{T,N}, id::Any = nothing) where {T,N} =
findfirst(tree.root, reg, id)
# FIXME: currently isempty() doesn't allow specifying how
# to treat overlapping elements (inside or not), currently treated as outside
"""
isempty(tree::RTree, region::Region)
Check if there are `tree` elements inside `region`.
"""
Base.isempty(tree::RTree{T,N}, region::Region{T,N}) where {T,N} =
_isempty(tree.root, region)
function _isempty(node::Node, region::Region)
isempty(node) && return true
nodebr = mbr(node)
if in(nodebr, region) # there are elements inside rect
return false
elseif intersects(nodebr, region) # there could be node elements inside region
for child in children(node)
if node isa Branch # should be optimized out at compile time
_isempty(child, region) || return false
elseif node isa Leaf
in(mbr(child), region) && return false
end
end
end
return true
end
# the RTreeIterator state
struct RTreeIteratorState{T,N,V}
leaf::Leaf{T,N,V} # current leaf node
indices::Vector{Int} # indices of the nodes (in their parents) in the current subtree
end
# get the current data element pointed by `RTreeIteratorState`
Base.get(state::RTreeIteratorState) = @inbounds(state.leaf[state.indices[1]])
# iterate all R-tree data elements
function Base.iterate(tree::RTree)
isempty(tree) && return nothing
node = tree.root
indices = fill(1, height(tree))
# get the first leaf
while level(node) > 1
node = node[1]
end
state = RTreeIteratorState(node, indices)
return get(state), state # first element of the first leaf
end
function Base.iterate(tree::RTree, state::RTreeIteratorState)
@inbounds if state.indices[1] < length(state.leaf) # fast branch: next data element in the same leaf
state.indices[1] += 1
return get(state), state
end
# leaf iterations is done, go up until the first non-visited branch
node = state.leaf
while state.indices[level(node)] >= length(node)
hasparent(node) || return nothing # returned to root, iteration finished
node = parent(node)
end
# go down into the first leaf of the new subtree
ix = state.indices[level(node)] += 1
node = node[ix]
@inbounds while true
state.indices[level(node)] = 1
level(node) == 1 && break
node = node[1]
end
new_state = RTreeIteratorState(node, state.indices)
return get(new_state), new_state
end
# iterates R-tree data elements matching `Q` query w.r.t `region`
struct RTreeRegionQueryIterator{T,N,V,Q,TT,R} <: SpatialQueryIterator{T,N,V,Q}
tree::TT
region::R
function RTreeRegionQueryIterator{T,N}(kind::QueryKind, tree::TT, region::R) where
{T, N, V, TT <: RTree{T,N,V}, R <: Region{T,N}}
new{T,N,V,kind,TT,R}(tree, region)
end
end
# the RTreeRegionQueryIterator state
struct RTreeQueryIteratorState{T,N,V}
leaf::Leaf{T,N,V} # current leaf node
indices::Vector{Int} # indices of the nodes (in their parents) in the current subtree
needtests::BitVector # whether children MBRs should be tested or not (because they automatically satisfy query)
end
# get the current data element pointed by `RTreeIteratorState`
Base.get(state::RTreeQueryIteratorState) = @inbounds(state.leaf[state.indices[1]])
function Base.iterate(iter::RTreeRegionQueryIterator)
isempty(iter.tree) && return nothing
# no data or doesn't intersect at all
root_match = should_visit(iter.tree.root, iter)
root_match == QueryNoMatch && return nothing
return _iterate(iter, iter.tree.root, fill(1, height(iter.tree)),
root_match == QueryMatchComplete ? falses(height(iter.tree)) : trues(height(iter.tree)))
end
function Base.iterate(iter::RTreeRegionQueryIterator,
state::RTreeQueryIteratorState)
@inbounds ix = state.indices[1] = _nextchild(state.leaf, state.indices[1] + 1, state.needtests[1], iter)[1]
if ix <= length(state.leaf) # fast branch: next data element in the same leaf
return get(state), state
else
return _iterate(iter, state.leaf, state.indices, state.needtests)
end
end
"""
contained_in(index::SpatialIndex, region::Region)
Get iterator for `index` elements contained in `region`.
"""
contained_in(tree::RTree{T,N}, region::Region{T,N}) where {T,N} =
RTreeRegionQueryIterator{T,N}(QueryContainedIn, tree, region)
"""
intersects_with(index::SpatialIndex, region::Region)
Get iterator for `index` elements intersecting with `region`.
"""
intersects_with(tree::RTree{T,N}, region::Region{T,N}) where {T,N} =
RTreeRegionQueryIterator{T,N}(QueryIntersectsWith, tree, region)
# whether the R-tree node/data element should be visited (i.e. its children examined)
# by the region iterator
function should_visit(node::Node, iter::RTreeRegionQueryIterator)
kind = querykind(iter)
if kind == QueryContainedIn || kind == QueryIntersectsWith
contains(iter.region, mbr(node)) && return QueryMatchComplete # node (and all its children) fully contained in query region
intersects(iter.region, mbr(node)) && return QueryMatchPartial # node (and maybe its children) intersects query region
return QueryNoMatch
else
throw(ArgumentError("Unknown spatial query kind: $kind"))
end
end
should_visit(el::Any, iter::RTreeRegionQueryIterator) =
((querykind(iter) == QueryContainedIn) && contains(iter.region, mbr(el))) ||
((querykind(iter) == QueryIntersectsWith) && intersects(iter.region, mbr(el))) ?
QueryMatchComplete : QueryNoMatch
# FIXME update for NotContainedIn etc
# get the index of the first child of `node` starting from `pos` (including)
# that satifies `iter` query (or length(node) + 1 if not found)
@inline function _nextchild(node::Node, pos::Integer, needtests::Bool, iter::RTreeRegionQueryIterator)
res = needtests ? QueryNoMatch : QueryMatchComplete # if tests not needed, all node subtrees are considered fully matching
while pos <= length(node) && needtests &&
((res = should_visit(@inbounds(node[pos]), iter)) == QueryNoMatch)
pos += 1
end
return pos, res
end
# do depth-first search starting from the `node` subtree and return the
# `RTreeIteratorState` for the first leaf that satisfies `iter` query or
# `nothing` if no such leaf in the R-tree.
# The method modifies `indicies` array and uses it for the returned iteration state
function _iterate(iter::RTreeRegionQueryIterator, node::Node,
indices::AbstractVector{Int}, needtests::AbstractVector{Bool})
#@debug"_iterate(): enter lev=$(level(node)) indices=$indices"
@assert length(indices) == height(iter.tree)
ix = @inbounds(indices[level(node)])
while true
ix_new, queryres = _nextchild(node, ix, needtests[level(node)], iter)
#@debug "node=$(Int(Base.pointer_from_objref(node))) lev=$(level(node)) ix_new=$ix_new"
if ix_new > length(node) # all node subtrees visited, go up one level
while ix_new > length(node)
if !hasparent(node)
#@debug "_iterate(): finished lev=$(level(node)) indices=$indices ix_new=$ix_new"
return nothing # returned to root, iteration finished
end
#@debug "_iterate(): up lev=$(level(node)) indices=$indices ix_new=$ix_new"
node = parent(node)
@inbounds ix_new = indices[level(node)] += 1 # next subtree
end
ix = ix_new
#@debug "_iterate(): next subtree lev=$(level(node)) indices=$indices ix_new=$ix_new"
else # subtree found
ix_new > ix && @inbounds(indices[level(node)] = ix_new)
if node isa Branch
# go down into the first child
node = node[ix_new]
indices[level(node)] = ix = 1
needtests[level(node)] = queryres != QueryMatchComplete
#@debug "_iterate(): down lev=$(level(node)) indices=$indices"
else # Leaf
#@debug "_iterate(): return lev=$(level(node)) indices=$indices"
state = RTreeQueryIteratorState(node, indices, needtests)
return get(state), state
end
end
end
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 11207 | """
R-Tree variants.
"""
@enum RTreeVariant::Int RTreeLinear = 0 RTreeQuadratic = 1 RTreeStar = 2
"""
Pool of the `T1` R-tree nodes (`Leaf` or `Branch`) with `T2` children
(`Branch`, `Leaf` or `Elem`).
It allows reusing the deleted nodes and reduce the stress on GC.
"""
mutable struct NodePool{T1<:Node, T2} <: AbstractPool{T1}
objs::Vector{T1}
capacity::Int # pool capacity
node_capacity::Int # node capacity (max number of children)
NodePool{T1,T2}(pool_capacity::Integer, node_capacity::Integer) where {T1<:Node, T2} =
new{T1,T2}(sizehint!(Vector{T1}(), pool_capacity), pool_capacity, node_capacity)
end
const BranchPool{T,N,V} = NodePool{Branch{T,N,V}, Branch{T,N,V}}
const TwigPool{T,N,V} = NodePool{Branch{T,N,V}, Leaf{T,N,V}}
const LeafPool{T,N,V} = NodePool{Leaf{T,N,V}, V}
node_capacity(pool::NodePool) = pool.node_capacity
newelem(pool::NodePool{T1,T2}) where {T1, T2} = T1(nothing, T2)
"""
R-Tree: `N`-dimensional spatial data index [guttman84].
R-tree groups data elements (`V`) into leaves (`Leaf`) and leaves into branches (`Branch`).
It uses various heuristics to ensure that the minimal bounding rectangles (MBRs)
of the nodes (`Rect{T,N}` rectangles that encompass the data elements attached to these nodes)
stay compact and that the MBRs of the nodes that are on the same level of
R-tree hierarchy have minimal overlap with each other.
This property makes R-trees efficient for spatial queries.
To facilitate spatial indexing, the `V` data elements need to support `HasMBR`
trait (i.e. define `mbrtype(V)` and `mbr(v::V)` methods) and, optionally,
`HasID` trait (via `idtype(V)` and `id(v::V)` methods). `mbr(v::V)` should
return minimal bounding rectangle (MBR) of type `Rect{T,N}` that contains `v`.
`SpatialElem{T,N,D}` type provides generic implementation of spatial data element
that explicitly stores `id`, `mbr` and data object of type `D` and implements
`HasMBR` and `HasID` traits.
# Parameters
The behaviour of `RTree` is defined by the parameters supplied at its creation:
* `T`: the numeric type for the spatial coordinate
* `N`: the number of spatial dimensions
* `variant`: one of `RTreeLinear`, `RTreeQuadratic`, or `RTreeStar` (default)
* `tight_mbrs`: recalculate node MBR when the child is removed (default is `true`)
* `branch_capacity`: capacity of branch nodes (default is `100`)
* `leaf_capacity`: capacity of leaf nodes (default is `100`)
* `leafpool_capacity`: How many detached 1st level nodes (leaves) should be kept for reuse (default is `100`)
* `twigpool_capacity`: How many detached 2nd level nodes should be kept for reuse (default is `100`)
* `branchpool_capacity`: How many other (level > 2) detached branch nodes should be kept for reuse (default is `100`)
* `nearmin_overlap`: How many candidates to consider when identifying the node with minimal overlap (default is `32`)
* `fill_factor`: How much should the node be filled (fraction of its capacity) after splitting (default is `0.7`)
* `split_factor`: How much can the sizes of the two nodes differ after splitting (default is `0.4`)
* `reinsert_factor`: How much should the node be underfilled (fraction of its capacity)
to consider removing it and redistributing its children to other nodes (default is `0.3`)
# Performance
The nodes in R-tree have limited capacity (maximual number of children)
specified at `RTree` creation (`leaf_capacity` and `branch_capacity`).
Larger capacities results in shorter trees, but they time required to locate
the specific spatial region grows linearly with the capacity.
# References
[guttman84] “R-Trees: A Dynamic Index Structure for Spatial Searching”
A. Guttman, Proc. 1984 ACM-SIGMOD Conference on Management of
Data (1985), 47-57.
[beckmann90] "The R*-tree: an efficient and robust access method for points and rectangles"
N. Beckmann, H.P. Kriegel, R. Schneider, B. Seeger, Proc. 1990 ACM SIGMOD
international conference on Management of data (1990), p.322
"""
mutable struct RTree{T,N,V} <: SpatialIndex{T,N,V}
# R-tree insert/update policy
variant::RTreeVariant
tight_mbrs::Bool # whether MBR are always updated upon child change/removal
nearmin_overlap::Int
fill_factor::Float64
split_factor::Float64
reinsert_factor::Float64
root::Node{T,N} # root node
nelems::Int # number of data elements in a tree (`length()`)
nnodes_perlevel::Vector{Int} # number of nodes (branches and leaves) at each tree level
nelem_insertions::Int # number of elements insertions
nelem_deletions::Int # number of elements deletions
nnode_splits::Int # number of node splits
nnode_reinsertions::Int # number of node reinsertions
branchpool::BranchPool{T,N,V}
twigpool::TwigPool{T,N,V}
leafpool::LeafPool{T,N,V}
function RTree{T,N,V}(;
variant::RTreeVariant = RTreeStar,
tight_mbrs::Bool = true,
branch_capacity::Integer = 100,
leaf_capacity::Integer = 100,
leafpool_capacity::Integer = 100,
branchpool_capacity::Integer = 100,
nearmin_overlap::Integer = floor(Int, 0.32 * leaf_capacity),
fill_factor::Real = 0.7,
split_factor::Real = 0.4,
reinsert_factor::Real = 0.3
) where {T<:Number,N,V}
check_eltype_rtree(V, Leaf{T,N,V})
leafpool = LeafPool{T,N,V}(leafpool_capacity, leaf_capacity)
new{T,N,V}(variant, tight_mbrs,
nearmin_overlap, fill_factor,
split_factor, reinsert_factor,
acquire!(leafpool),
0, [1], # init with 1 leaf == parent
0, 0, 0, 0,
BranchPool{T,N,V}(branchpool_capacity, branch_capacity),
TwigPool{T,N,V}(branchpool_capacity, branch_capacity),
leafpool)
end
end
"""
RTree{T,N}([K], V; kwargs...) where {T,N,V}
Construct `N`-dimensional [`RTree`](@ref) object that stores
[`SpatialElem{T,N,K,V}`](@ref `SpatialElem`) elements.
If `K` (the type of spatial element identifier) if not specified,
the stored elements will not have ids.
"""
RTree{T,N}(::Type{V}; kwargs...) where {T,N,V} =
RTree{T,N,SpatialElem{T,N,Nothing,V}}(; kwargs...)
RTree{T,N}(::Type{K}, ::Type{V}; kwargs...) where {T,N,K,V} =
RTree{T,N,SpatialElem{T,N,K,V}}(; kwargs...)
# create an empty R-tree of the same type and with the same settings as `tree`
Base.similar(tree::RTree) =
typeof(tree)(variant=tree.variant,
tight_mbrs=tree.tight_mbrs,
branch_capacity=capacity(Branch, tree),
leaf_capacity=capacity(Leaf, tree),
leafpool_capacity=capacity(tree.leafpool),
branchpool_capacity=capacity(tree.branchpool),
nearmin_overlap=tree.nearmin_overlap,
fill_factor=tree.fill_factor,
split_factor=tree.split_factor,
reinsert_factor=tree.reinsert_factor)
mbrtype(::Type{<:RTree{T,N}}) where {T,N} = Rect{T,N}
mbrtype(tree::RTree) = mbrtype(typeof(tree))
regiontype(R::Type{<:RTree}) = mbrtype(R)
leaftype(::Type{RTree{T,N,V}}) where {T,N,V} = Leaf{T,N,V}
leaftype(tree::RTree) = leaftype(typeof(tree))
branchtype(::Type{RTree{T,N,V}}) where {T,N,V} = Branch{T,N,V}
branchtype(tree::RTree) = branchtype(typeof(tree))
nodetype(::Type{RTree{T,N,V}}) where {T,N,V} = Node{T,N,V} # not a concrete type
nodetype(tree::RTree) = nodetype(typeof(tree))
check_eltype_rtree(el::Any, tree::RTree) =
check_eltype_rtree(typeof(el), leaftype(tree))
height(tree::RTree) = level(tree.root)
variant(tree::RTree) = tree.variant
mbr(tree::RTree) = mbr(tree.root)
capacity(::T, tree::RTree) where T<:Node = capacity(T, tree)
capacity(::Type{<:Leaf}, tree::RTree) = node_capacity(tree.leafpool)
capacity(::Type{<:Branch}, tree::RTree) = node_capacity(tree.branchpool)
# acquire Leaf/Branch from the corresponding node pool
function acquire(tree::RTree, ::Type{<:Leaf}, lev::Int = 1, br::Rect = empty(mbrtype(tree)))
@assert lev == 1
leaf = acquire!(tree.leafpool)
@assert isempty(leaf)
leaf.mbr = br
return leaf
end
function acquire(tree::RTree, ::Type{<:Branch}, lev::Int, br::Rect = empty(mbrtype(tree)))
@assert lev > 1
node = acquire!(lev == 2 ? tree.twigpool : tree.branchpool)
@assert isempty(node)
node.mbr = br
node.level = lev
return node
end
# detach the Leaf/Branch from the tree and release it to the corresponding node pool
# it's up to the calling context to take care of the R-tree integrity (parent and children nodes)
function release(tree::RTree, node::Node)
node.parent = nothing # don't refer to the parent (so it could be GCed)
empty!(node.children) # don't refer to the children (so they could be GCed)
if node isa Leaf
release!(tree.leafpool, node)
else
release!(eltype(node.children) <: Leaf ? tree.twigpool : tree.branchpool, node)
end
end
# low-level insertion of a child into the back of the list of the node children
# `child` parent is set to `node`, MBR of `node` is extended with child MBR
# no subtree balancing or anything like that
function _attach!(node::Node, child::Any, tree::RTree; force::Bool = false)
force || (length(node) < capacity(node, tree)) ||
throw(SpatialIndexException("Node is full ($(capacity(node, tree)) items)"))
if child isa Node
(level(node) == level(child) + 1) ||
throw(SpatialIndexException("Parent ($(level(node)) and child ($(level(child))) levels don't match"))
child.parent = node
end
push!(node.children, child)
node.mbr = length(node) > 1 ? combine(node.mbr, mbr(child)) : mbr(child)
return node
end
# low-level removal of a child node from the specified position, no subtree balancing
# return true if node MBR was updated
function _detach!(node::Node, pos::Integer, tree::RTree; updatembr = tree.tight_mbrs)
if length(node) > 1
delmbr = mbr(node[pos]) # cache it, since its required for "touches" later
# copy the last child into i-th position and pop it
# this should be more efficient that deleting the i-th node
if pos < length(node)
node.children[pos] = pop!(node.children)
else
pop!(node.children)
end
if updatembr && touches(mbr(node), delmbr)
syncmbr!(node)
return true
end
else # node becomes empty
@assert pos == 1
pop!(node.children)
node.mbr = empty(mbrtype(node)) # reset br
return true
end
return false
end
# The context for R-tree node insertion/balancing.
struct SubtreeContext{T,N,V,O}
tree::RTree{T,N,V}
level_overflow::O # nothing or an indicator of the R-tree level overflow
function SubtreeContext(tree::RTree{T,N,V}) where {T,N,V}
O = variant(tree) == RTreeStar ? BitVector : Nothing
new{T,N,V,O}(tree, O == BitVector ? falses(height(tree)) : nothing)
end
end
isoverflow(con::SubtreeContext, lev::Int) = con.level_overflow[lev]
setoverflow!(con::SubtreeContext, lev::Int) = con.level_overflow[lev] = true
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 1733 | function Base.show(io::IO, tree::RTree; recurse::Bool=false)
print(io, typeof(tree))
print(io, "(variant="); print(io, tree.variant)
print(io, ", tight_mbrs="); print(io, tree.tight_mbrs)
print(io, ", nearmin_overlap="); print(io, tree.nearmin_overlap)
print(io, ", fill_factor="); print(io, tree.fill_factor)
print(io, ", split_factor="); print(io, tree.split_factor)
print(io, ", reinsert_factor="); print(io, tree.reinsert_factor)
print(io, ", leaf_capacity="); print(io, capacity(Leaf, tree))
print(io, ", branch_capacity="); print(io, capacity(Branch, tree)); println(io, ")")
print(io, length(tree)); print(io, " element(s) in "); print(io, height(tree));
print(io, " level(s) ("); print(io, join(reverse(tree.nnodes_perlevel), ", ")); println(io, " node(s) per level):")
_show(io, tree.root, recurse=recurse, indent=1)
end
function _show(io::IO, node::Node; recurse::Bool=false, indent::Int=0)
for _ in 1:indent; print(io, ' '); end
print(io, "level="); print(io, level(node));
print(io, " nchildren="); print(io, length(node));
print(io, " mbr=("); print(io, mbr(node).low); print(io, ", "); print(io, mbr(node).high); print(io, ")")
if recurse && !isempty(node)
print(io, ':')
if node isa Leaf
for child in children(node)
println(io)
for _ in 1:(indent+1); print(io, ' '); end
show(io, child)
end
else
for child in children(node)
println(io)
_show(io, child, recurse=true, indent=indent+1)
end
end
end
end
function Base.print(io::IO, tree::RTree;)
show(io, tree; recurse=true)
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 8759 | # select the two seeds maximizing separation, O(N)
function _splitseeds_linear(node::Node)
@assert length(node) > 1
seed1 = seed2 = 0
max_separation = -Inf
for n in 1:ndims(node)
argmax_low = argmin_high = 1
min_low = max_low = mbr(node[1]).low[n]
min_high = max_high = mbr(node[1]).high[n]
for i in 2:length(node)
@inbounds lowi = mbr(node[i]).low[n]
@inbounds highi = mbr(node[i]).high[n]
if lowi > max_low
max_low = lowi
argmax_low = i
elseif lowi < min_low
min_low = lowi
end
if highi < min_high
min_high = highi
argmin_high = i
elseif highi > max_high
max_high = highi
end
end
sepn = max_low - min_high
if max_high > min_low
sepn /= (max_high - min_low)
end
if sepn > max_separation
max_separation = sepn
seed1 = argmin_high
seed2 = argmax_low
end
end
@assert seed1 > 0 && seed2 > 0
if seed1 == seed2 # avoid collisions
if seed2 == 1
seed2 += 1
else
seed2 -= 1
end
end
return seed1, seed2
end
# select the two seeds maximizing inefficiency, O(N²)
function _splitseeds_quadratic(node::Node)
@assert length(node) > 1
seed1 = 0
seed2 = 0
inefficiency = -Inf
# for each pair of Regions (account for overflow Region too!)
for i in eachindex(node)
@inbounds mbri = mbr(node[i])
areai = area(mbri)
for j in (i+1):length(node)
# get the combined MBR of those two entries.
@inbounds mbrj = mbr(node[j])
@inbounds r = combine(mbri, mbrj)
# find the inefficiency of grouping these entries together.
d = area(r) - areai - area(mbrj)
if d > inefficiency
inefficiency = d;
seed1 = i
seed2 = j
end
end
end
return seed1, seed2
end
# pick the two seeds (children indices) for splitting the node into two
function _splitseeds(node::Node, tree::RTree)
length(node) > 1 ||
throw(SpatialIndexException("Cannot split the node with less than 2 children"))
if variant(tree) == RTreeLinear || variant(tree) == RTreeStar
return _splitseeds_linear(node)
elseif variant(tree) == RTreeQuadratic
return _splitseeds_quadratic(node)
else
throw(SpatialIndexException("RTree variant not supported"))
end
end
# R-tree split node (select the node by minimal enlargment and area)
function _split!_rtree(node::Node, tree::RTree)
nnodes_min = floor(Int, capacity(node, tree) * tree.fill_factor)
#@debug "_split!_rtree(): lev=$(level(node)) len=$(length(node)) nmin=$nnodes_min"
# initialize each group with the seed entries.
seed1, seed2 = _splitseeds(node, tree)
n1 = _attach!(acquire(tree, typeof(node), level(node)), node[seed1], tree)
n2 = _attach!(acquire(tree, typeof(node), level(node)), node[seed2], tree)
# use this mask for marking visited entries.
available = trues(length(node))
available[seed1] = available[seed2] = false
navail = length(node) - 2
while navail > 0
if length(n1) + navail == nnodes_min || length(n2) + navail == nnodes_min
# all remaining entries must be assigned to n1 or n2 to comply with minimum load requirement.
sink = length(n1) + navail == nnodes_min ? n1 : n2
i = findfirst(available)
while i !== nothing
_attach!(sink, node[i], tree)
available[i] = false
i = findnext(available, i+1)
end
navail = 0
else
# For all remaining entries compute the difference of the cost of grouping an
# entry in either group. When done, choose the entry that yielded the maximum
# difference. In case of linear split, select any entry (e.g. the first one.)
area1 = area(mbr(n1))
area2 = area(mbr(n2))
max_enl_diff = -Inf
sel_enl1 = sel_enl2 = NaN
sel_child_ix = 0
i = findfirst(available)
while i !== nothing
child_mbr = mbr(node[i])
enl1 = area(combine(mbr(n1), child_mbr)) - area1
enl2 = area(combine(mbr(n2), child_mbr)) - area2
enl_diff = abs(enl1 - enl2)
if enl_diff > max_enl_diff
max_enl_diff = enl_diff
sel_enl1 = enl1
sel_enl2 = enl2
sel_child_ix = i
(variant(tree) != RTreeQuadratic) && break
end
i = findnext(available, i+1)
end
# select the node where we should add the new entry.
sink = sel_enl1 < sel_enl2 || (sel_enl1 == sel_enl2 &&
(area1 < area2 || (area1 == area2 &&
length(n1) <= length(n2)))) ? n1 : n2
available[sel_child_ix] = false
navail -= 1
_attach!(sink, node[sel_child_ix], tree)
end
end
@assert !any(available)
return n1, n2
end
# get low/high of a specific MBR dimension
# accessor functions to speedup sortperm!()
_mbr_low(node, dim::Integer) = @inbounds mbr(node).low[dim]
_mbr_high(node, dim::Integer) = @inbounds mbr(node).high[dim]
# R*-star node split
function _split!_rstar(node::Node, tree::RTree)
nsplit = floor(Int, length(node) * tree.split_factor)
nsplit_distr = length(node) - 2 * nsplit + 1
@assert nsplit_distr > 0
#@debug "_split!_rstar(): lev=$(level(node)) len=$(length(node)) nsplit=$nsplit nsplit_distr=$nsplit_distr"
# find split_dim that minimizes the perimeter in all splits
min_perim = Inf
split_dim = 0
loworder = zeros(Int, length(node))
highorder = similar(loworder)
use_low = false
for dim in 1:ndims(node)
sortperm!(loworder, children(node), by=Base.Fix2(_mbr_low, dim))
sortperm!(highorder, children(node), by=Base.Fix2(_mbr_high, dim))
# calculate the sum of perimiters for all splits
low_perim = 0.0
high_perim = 0.0
for i in nsplit:(nsplit + nsplit_distr)
@inbounds br_low1 = mapreduce(j -> @inbounds(mbr(node[j])), combine, view(loworder, 1:i))
@inbounds br_high1 = mapreduce(j -> @inbounds(mbr(node[j])), combine, view(highorder, 1:i))
@inbounds br_low2 = mapreduce(j -> @inbounds(mbr(node[j])), combine, view(loworder, (i+1):length(node)))
@inbounds br_high2 = mapreduce(j -> @inbounds(mbr(node[j])), combine, view(highorder, (i+1):length(node)))
low_perim += perimeter(br_low1) + perimeter(br_low2)
high_perim += perimeter(br_high1) + perimeter(br_high2)
end
perim = min(low_perim, high_perim)
if perim < min_perim
min_perim = perim
split_dim = dim
use_low = low_perim < high_perim
end
end
# final sorting
selorder = use_low ?
sortperm!(loworder, children(node), by=Base.Fix2(_mbr_low, split_dim)) :
sortperm!(highorder, children(node), by=Base.Fix2(_mbr_high, split_dim))
# find the best split point (minimizes split overlap and area)
min_overlap = Inf
best_area_sum = Inf
split_ix = 0
for i in nsplit:(nsplit + nsplit_distr)
@inbounds br1 = mapreduce(i -> mbr(node[selorder[i]]), combine, 1:i)
@inbounds br2 = mapreduce(i -> mbr(node[selorder[i]]), combine, (i+1):length(node))
overlap = overlap_area(br1, br2)
area_sum = area(br1) + area(br2)
if overlap < min_overlap || (overlap == min_overlap &&
area_sum < best_area_sum)
split_ix = i
min_overlap = overlap
best_area_sum = area_sum
end
end
n1 = acquire(tree, typeof(node), level(node))
for i in 1:split_ix
_attach!(n1, node[selorder[i]], tree)
end
n2 = acquire(tree, typeof(node), level(node))
for i in (split_ix+1):length(selorder)
_attach!(n2, node[selorder[i]], tree)
end
return n1, n2
end
# split the node into two
function _split!(node::Node, tree::RTree)
#@debug "_split!(): lev=$(level(node)) len=$(length(node))"
if variant(tree) == RTreeLinear || variant(tree) == RTreeQuadratic
return _split!_rtree(node, tree)
elseif variant(tree) == RTreeStar
return _split!_rstar(node, tree)
else
throw(SpatialIndexException("RTree variant not supported"))
end
end
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 428 | # TODO
"""
Vector-based `SpatialIndex`.
While insertion is `O(1)`, the search is `O(N)`.
Generally should not be used, except for performance comparisons
or when the number of stored elements is expected to be very small (<100).
"""
struct SimpleSpatialIndex{T,N,V} <: SpatialIndex{T,N,V}
elems::Vector{V}
end
Base.length(si::SimpleSpatialIndex) = length(si.elems)
Base.isempty(si::SimpleSpatialIndex) = isempty(si.elems)
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 4153 | @testset "Regions" begin
@testset "Point" begin
@test SI.Point((1, 2)) isa SI.Point{Int,2}
@test SI.Point((1.0, 2.0, 3.0)) isa SI.Point{Float64,3}
@test SI.Point{Float64,3}((1, 2, 3)) isa SI.Point{Float64,3}
@test isequal(SI.empty(SI.Point{Float64,2}).coord, (NaN, NaN))
@test isequal(SI.empty(SI.Point{Int,1}).coord, (0,))
@test SI.isvalid(SI.Point((1, 2)))
@test SI.isvalid(SI.Point((1.0, 2.0, 3.0)))
@test !SI.isvalid(SI.Point((NaN, 1.0)))
@test_throws MethodError SI.Point((1.0, 2, 3.0))
@test_throws InexactError SI.Point{Int,2}((1.5, 3.0))
@test_throws MethodError SI.Point{Int,3}((1, 3))
@test SI.area(SI.Point((1, 2))) === 0
@test SI.area(SI.Point((1.0, 2.0))) === 0.0
@test SI.perimeter(SI.Point((1, 2))) === 0
@test SI.perimeter(SI.Point((1.0, 2.0))) === 0.0
@test SI.sqrdistance(SI.Point((1,)), SI.Point((3,))) === 4
@test SI.sqrdistance(SI.Point((1, 0)), SI.Point((3, -3))) === 13
end
@testset "Rect" begin
@test SI.Rect((1, 2), (2, 3)) isa SI.Rect{Int,2}
@test SI.Rect((1.0, 2.0, 3.0), (2, 3, 4)) isa SI.Rect{Float64,3}
@test SI.Rect{Float64,3}((1, 2, 3), (2, 3, 4)) isa SI.Rect{Float64,3}
@test isequal(SI.empty(SI.Rect{Float64,2}), SI.Rect((NaN, NaN), (NaN, NaN)))
@test isequal(SI.empty(SI.Rect{Int,1}), SI.Rect((typemax(Int),), (typemax(Int),)))
@test SI.isvalid(SI.Rect((1, 2), (2, 3)))
@test SI.isvalid(SI.Rect((1.0, 2.0), (2.0, 3.0)))
@test SI.isvalid(SI.Rect((1.0, 2.0), (Inf, Inf)))
@test SI.isvalid(SI.Rect((-Inf, -Inf), (2.0, 3.0)))
@test !SI.isvalid(SI.Rect((NaN, 2.0), (2.0, 3.0)))
@test !SI.isvalid(SI.Rect((1.0, 2.0), (2.0, NaN)))
@test !SI.isvalid(SI.Rect((2.5, 2.0), (2.0, 3.0)))
@test !SI.isvalid(SI.Rect((1.0, 2.0), (2.0, -3.0)))
@test !SI.isvalid(SI.Rect((1.0, Inf), (2.0, 3.0)))
@test_throws MethodError SI.Rect((1.0, 2, 3.0), (2, 3.0, 4))
@test_throws MethodError SI.Rect((1.0, 3.0), (2, 3.0, 4))
@test_throws InexactError SI.Rect{Int,2}((1.0, 3.0), (1.5, 2.0))
@test SI.area(SI.Rect((1.0,), (2.0,))) === 1.0
@test SI.area(SI.Rect((1,), (0,))) === -1
@test SI.area(SI.Rect((1.0, 2.0), (2.5, 4.0))) === 3.0
@test SI.perimeter(SI.Rect((1.0,), (2.0,))) === 1.0
@test SI.perimeter(SI.Rect((1,), (0,))) === -1
@test SI.perimeter(SI.Rect((1.0, 2.0), (2.5, 4.0))) === 7.0
@test SI.center(SI.Rect((1.0,), (2.0,))) == SI.Point((1.5,))
@test SI.center(SI.Rect((1.0, 2.0), (2.5, 4.0))) == SI.Point((1.75, 3.0))
ai = SI.Rect((0, 0), (1, 1))
bi = SI.Rect((1, 1), (2, 2))
ci = SI.Rect((2, 2), (3, 3))
@test SI.intersect(ai, bi) == SI.Rect((1, 1), (1, 1))
@test SI.intersect(ai, ci) === SI.empty(SI.Rect{Int,2})
@test SI.combine(ai, bi) == SI.Rect((0, 0), (2, 2))
@test SI.center(SI.Rect((2, 2), (3, 4))) == SI.Point((2.5, 3.0))
@test SI.center(SI.Rect((1, 2), (3, 4))) == SI.Point((2.0, 3.0))
a = SI.Rect{Float64,2}((0, 0), (1, 1))
b = SI.Rect{Float64,2}((1, 1), (2, 2))
c = SI.Rect{Float64,2}((2, 2), (3, 3))
@test SI.intersect(a, b) == SI.Rect((1.0, 1.0), (1.0, 1.0))
@test SI.intersect(a, c) === SI.empty(typeof(a))
@test SI.combine(a, b) == SI.Rect((0.0, 0.0), (2.0, 2.0))
@test SI.combined_area(a, b) == 4
@test SI.combined_area(a, c) == 9
@test SI.overlap_area(a, b) == 0
@test SI.overlap_area(a, c) == 0
@test SI.overlap_area(SI.combine(a, b), SI.combine(b, c)) == 1
@test SI.touches(a, SI.combine(a, b))
@test SI.touches(SI.combine(a, b), a)
@test SI.touches(b, SI.combine(a, b))
@test !SI.touches(SI.combine(a, b), c)
@test SI.touches(SI.combine(a, c), a)
@test SI.touches(SI.combine(a, c), c)
@test !SI.touches(SI.combine(a, c), b)
@test SI.touches(SI.combine(a, b), SI.Rect((1.0, 0.0), (2.0, 1.0)))
@test SI.touches(SI.combine(a, b), SI.Rect((-1.0, 0.0), (0.0, 1.0))) #outside
@test SI.touches(SI.combine(a, b), SI.Rect((0.0, -1.0), (1.0, 0.0))) # outside
@test SI.touches(SI.combine(a, b), SI.Rect((2.0, 0.0), (3.0, 1.0))) # outside
@test SI.touches(SI.combine(a, b), SI.Rect((0.0, 2.0), (1.0, 3.0))) # outside
end
end | SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 17387 | @testset "SpatialElem" begin
@test SI.check_hasmbr(SI.Rect{Float64,2}, SpatialElem{Float64,2,Int,Int})
@test_throws ArgumentError SI.check_hasmbr(SI.Rect{Float64,2}, Int)
@test_throws ArgumentError SI.check_hasmbr(SI.Rect{Float64,3}, SpatialElem{Float64,2,Int,Int})
@test_throws ArgumentError SI.check_hasmbr(SI.Rect{Float64,3}, SpatialElem{Int,2,Int,Int})
@test SI.check_hasid(Int, SpatialElem{Float64,2,Int,Int})
@test_throws ArgumentError SI.check_hasid(String, SpatialElem{Float64,2,Int,Int})
@test_throws ArgumentError SI.check_hasid(Int, SpatialElem{Float64,2,Nothing,Int})
end
@testset "RTree" begin
tree_vars = [SI.RTreeStar, SI.RTreeLinear, SI.RTreeQuadratic]
@testset "Basic Operations" begin
@testset "RTree{Float,2,Int32,Int}(variant=$tree_var)" for tree_var in tree_vars
ambr = SI.Rect((0.0, 0.0), (0.0, 0.0))
bmbr = SI.Rect((0.0, 1.0), (0.0, 1.0))
cmbr = SI.Rect((0.5, 0.5), (0.5, 0.6))
tree = RTree{Float64,2}(Int32, Int, variant=tree_var)
@test tree isa RTree{Float64,2,SpatialElem{Float64,2,Int32,Int}}
@test SI.variant(tree) === tree_var
@test eltype(tree) === SpatialElem{Float64,2,Int32,Int}
@test SI.regiontype(tree) === SI.Rect{Float64,2}
@test SI.dimtype(tree) === Float64
@test ndims(tree) === 2
@test length(tree) == 0
@test SI.height(tree) == 1
@test isempty(tree)
@test isempty(tree, ambr)
@test isequal(SI.mbr(tree.root), SI.empty(SI.regiontype(tree)))
@test SI.check(tree)
@test_throws KeyError delete!(tree, SI.empty(SI.regiontype(tree)), 1)
@test SI.check(tree)
@test iterate(tree) === nothing
@test iterate(contained_in(tree, SI.empty(SI.mbrtype(tree)))) === nothing
@test iterate(intersects_with(tree, SI.empty(SI.mbrtype(tree)))) === nothing
@test iterate(contained_in(tree, cmbr)) === nothing
@test iterate(intersects_with(tree, cmbr)) === nothing
@test collect(tree) == eltype(tree)[]
@test collect(contained_in(tree, cmbr)) == eltype(tree)[]
@test collect(intersects_with(tree, cmbr)) == eltype(tree)[]
@test typeof(collect(tree)) === Vector{eltype(tree)}
@test insert!(tree, ambr, 1, 2) === tree
@test length(tree) == 1
@test !isempty(tree)
@test !isempty(tree, ambr)
@test SI.height(tree) == 1
@test isequal(SI.mbr(tree.root), ambr)
@test SI.check(tree)
@test_throws KeyError delete!(tree, bmbr, 1)
@test_throws KeyError delete!(tree, ambr, 2)
@test SI.check(tree)
@test collect(tree) == [SpatialElem(ambr, Int32(1), 2)]
@test insert!(tree, bmbr, 2, 2) === tree
@test length(tree) == 2
@test SI.height(tree) == 1
@test isequal(SI.mbr(tree.root), SI.combine(ambr, bmbr))
@test SI.check(tree)
@test length(collect(tree)) == 2
@test_throws KeyError delete!(tree, bmbr, 1)
@test_throws KeyError delete!(tree, ambr, 2)
@test_throws KeyError delete!(tree, SI.empty(SI.regiontype(tree)), 1)
@test delete!(tree, ambr, 1) === tree
@test length(tree) == 1
@test SI.check(tree)
insert!(tree, ambr, 1, 2)
insert!(tree, cmbr, 2, 3)
@test length(tree) == 3
@test_throws SpatialIndexException SI.check(tree) # duplicate ID=2 (b and c)
@test delete!(tree, cmbr, 2) === tree
@test length(tree) == 2
# prepare tree with a(id=1), b(id=2), c(id=3)
@test insert!(tree, cmbr, 3, 3) === tree
@test length(tree) == 3
@test SI.check(tree)
a = (0.0, 0.0)
b = (0.55, 0.55)
c = (0.6, 0.6)
d = (1.0, 1.0)
@test length(collect(contained_in(tree, SI.Rect(a, d)))) == 3
@test length(collect(intersects_with(tree, SI.Rect(a, d)))) == 3
@test length(collect(contained_in(tree, SI.Rect(a, c)))) == 2
@test length(collect(intersects_with(tree, SI.Rect(a, c)))) == 2
@test length(collect(contained_in(tree, SI.Rect(a, b)))) == 1 # a only
@test length(collect(intersects_with(tree, SI.Rect(a, b)))) == 2 # a and c
tree2 = similar(tree)
@test typeof(tree2) === typeof(tree)
@test tree2 !== tree
@test isempty(tree2)
@testset "findfirst()" begin
@test findfirst(tree, ambr, 2) === nothing
@test_throws MethodError findfirst(tree, ambr, "1") # wrong key type
@test_throws MethodError findfirst(tree, SI.empty(SI.Rect{Int,2}()))
@test findfirst(tree, ambr, 1) == (tree.root, 2)
@test findfirst(tree, ambr) == (tree.root, 2) # search without id ignores it
@test findfirst(tree, bmbr, 1) === nothing
@test findfirst(tree, bmbr, 2) == (tree.root, 1)
@test findfirst(tree, bmbr) == (tree.root, 1)
@test findfirst(tree, cmbr, 2) === nothing
@test findfirst(tree, cmbr, 3) == (tree.root, 3)
@test findfirst(tree, cmbr) == (tree.root, 3)
@test findfirst(tree, SI.combine(ambr, cmbr)) === nothing
@test findfirst(tree, SI.empty(SI.mbrtype(tree))) === nothing
end
end
@testset "RTree{Int,3,String,Nothing}(variant=$tree_var) (no id)" for tree_var in tree_vars
ambr = SI.Rect((0, 0, 0), (0, 0, 0))
bmbr = SI.Rect((0, 1, 1), (0, 1, 1))
tree = RTree{Int,3}(String, variant=tree_var)
@test tree isa RTree{Int,3,SpatialElem{Int,3,Nothing,String}}
@test SI.variant(tree) === tree_var
@test eltype(tree) === SpatialElem{Int,3,Nothing,String}
@test SI.regiontype(tree) === SI.Rect{Int,3}
@test SI.dimtype(tree) === Int
@test ndims(tree) === 3
@test length(tree) == 0
@test SI.height(tree) == 1
@test isempty(tree)
@test isempty(tree, ambr)
@test isequal(SI.mbr(tree.root), SI.empty(SI.regiontype(tree)))
@test SI.check(tree)
@test_throws KeyError delete!(tree, SI.empty(SI.regiontype(tree)), 1)
@test_throws KeyError delete!(tree, SI.empty(SI.regiontype(tree)))
@test SI.check(tree)
@test_throws Exception insert!(tree, ambr, 1, "2")
@test insert!(tree, ambr, "2") === tree
@test length(tree) == 1
@test !isempty(tree)
@test !isempty(tree, ambr)
@test SI.height(tree) == 1
@test isequal(SI.mbr(tree.root), ambr)
@test SI.check(tree)
@test_throws MethodError delete!(tree, bmbr, 1)
@test_throws KeyError delete!(tree, bmbr)
@test SI.check(tree)
@test insert!(tree, bmbr, "3") === tree
@test length(tree) == 2
@test SI.height(tree) == 1
@test isequal(SI.mbr(tree.root), SI.combine(ambr, bmbr))
@test SI.check(tree)
@test_throws MethodError delete!(tree, bmbr, 1)
@test_throws MethodError delete!(tree, SI.empty(SI.Rect{Int,2}))
@test_throws MethodError delete!(tree, SI.empty(SI.Rect{Float64,3}))
@test_throws KeyError delete!(tree, SI.empty(SI.regiontype(tree)))
@test delete!(tree, bmbr) === tree
@test length(tree) == 1
@test SI.check(tree)
@test insert!(tree, bmbr, "4") === tree
@test length(tree) == 2
@test SI.check(tree)
@testset "findfirst()" begin
@test_throws MethodError findfirst(tree, ambr, 2) # no key
@test_throws MethodError findfirst(tree, ambr, "1")
@test_throws MethodError findfirst(tree, SI.empty(SI.Rect{Int,2}()))
@test_throws MethodError findfirst(tree, SI.empty(SI.Rect{Float64,3}()))
@test findfirst(tree, ambr) == (tree.root, 1)
@test findfirst(tree, bmbr) == (tree.root, 2)
@test findfirst(tree, SI.combine(ambr, bmbr)) === nothing
@test findfirst(tree, SI.empty(SI.mbrtype(tree))) === nothing
end
end
end
@testset "add 1000 vertices" begin
# generate random point cloud
Random.seed!(32123)
mbrs = Vector{SI.Rect{Float64,3}}()
for i in 1:1000
w, h, d = 5 .* rand(3)
x, y, z = 50 .* randn(3)
rmbr = SI.Rect((x - w, y - h, z - d), (x + w, y + h, z + d))
push!(mbrs, rmbr)
end
@testset "sequential inserts into RTree(variant=$tree_var)" for tree_var in tree_vars
tree = RTree{SI.dimtype(eltype(mbrs)),ndims(eltype(mbrs))}(Int, String, leaf_capacity=20, branch_capacity=20, variant=tree_var)
@test tree isa RTree{Float64,3,SpatialElem{Float64,3,Int,String}}
for (i, rmbr) in enumerate(mbrs)
insert!(tree, rmbr, i, string(i))
@test length(tree) == i
@test tree.nelem_insertions == i
@test SI.check(tree)
#@debug "$i: len=$(length(tree)) height=$(SI.height(tree))"
end
#@show SI.height(tree)
#@show tree.nnodes_perlevel
@testset "findfirst()" begin
# check that the elements can be found
for i in 1:length(tree)
node_ix = findfirst(tree.root, mbrs[i], i)
@test node_ix !== nothing
if node_ix !== nothing
node, ix = node_ix
elem = node[ix]
@test SI.id(elem) == i
@test elem.val == string(i)
end
end
end
@testset "iterate" begin
all_elems = collect(tree)
@test length(all_elems) == length(tree)
@test eltype(all_elems) === eltype(tree)
bound_mbr = SI.Rect((-40.0, -20.0, -20.0), (30.0, 50.0, 40.0))
in_elems = collect(contained_in(tree, bound_mbr))
@test eltype(in_elems) === eltype(tree)
@test length(in_elems) == sum(br -> in(br, bound_mbr), mbrs)
isect_elems = collect(intersects_with(tree, bound_mbr))
@test eltype(isect_elems) === eltype(tree)
@test length(isect_elems) == sum(br -> SI.intersects(br, bound_mbr), mbrs)
end
end
@testset "load!(RTree(variant=$tree_var)) (OMT bulk load)" for tree_var in tree_vars
tree = RTree{SI.dimtype(eltype(mbrs)),ndims(eltype(mbrs))}(Int, String,
leaf_capacity=20, branch_capacity=20, variant=tree_var)
@test tree === SI.load!(tree, enumerate(mbrs), method=:OMT,
convertel=x -> eltype(tree)(x[2], x[1], string(x[1])))
@test SI.check(tree)
@test length(tree) == length(mbrs)
#@show SI.height(tree)
#@show tree.nnodes_perlevel
# cannot bulk-load into non-empty tree
@test_throws ArgumentError SI.load!(tree, enumerate(mbrs), method=:OMT,
convertel=x -> eltype(tree)(x[2], x[1], string(x[1])))
tree2 = similar(tree)
# can load from tree into another tree
@test SI.load!(tree2, tree) == tree2
@test length(tree2) == length(tree)
@testset "findfirst()" begin
# check that the elements can be found
for i in 1:length(tree)
node_ix = findfirst(tree.root, mbrs[i], i)
@test node_ix !== nothing
if node_ix !== nothing
node, ix = node_ix
elem = node[ix]
@test SI.id(elem) == i
@test elem.val == string(i)
end
end
end
end
end
@testset "subtract!(RTree(variant=$tree_var))" for tree_var in tree_vars
@testset "simple" begin
tree = RTree{Int,2}(Int, String, leaf_capacity=5, branch_capacity=5, variant=tree_var)
pts = [(0, 0), (1, 0), (2, 2), (2, 0), (0, 1), (1, 1), (-1, -1)]
SI.load!(tree, enumerate(pts),
convertel=x -> eltype(tree)(SI.Rect(x[2], x[2]), x[1], string(x[1])))
@test length(tree) == length(pts)
@test SI.check(tree)
rect = SI.Rect((0, 0), (1, 1))
@test !isempty(tree, rect)
@test isempty(tree, SI.Rect((-2, 0), (-1, 1)))
SI.subtract!(tree, rect)
@test SI.check(tree)
@test length(tree) == 3
@test tree.nelem_deletions == 4
for i in [3, 4, 7] # check that the correct points stayed in the tree
@test findfirst(tree.root, SI.Rect(pts[i], pts[i]), i) !== nothing
end
end
@testset "from 1000 points" begin
# generate random point cloud
Random.seed!(32123)
pts = [ntuple(_ -> 5.0 * randn(), 3) for _ in 1:1000]
tree = RTree{Float64,3}(Int, String, leaf_capacity=10, branch_capacity=10, variant=tree_var)
SI.load!(tree, enumerate(pts),
convertel=x -> eltype(tree)(SI.Rect(x[2], x[2]), x[1], string(x[1])))
@test length(tree) == length(pts)
#@show tree.nelems tree.nnodes_perlevel
rect = SI.Rect((-3.0, -4.0, -5.0), (5.0, 8.0, 3.0))
n_in_rect = sum(pt -> in(SI.Point(pt), rect), pts)
SI.subtract!(tree, rect)
@test SI.check(tree)
@test tree.nelem_deletions == n_in_rect
#@show tree.nelems tree.nnodes_perlevel tree.nelem_deletions tree.nelem_insertions
end
# test how well the R-tree can stand the deletion of all but a single element for various tree sizes
@testset "subtract!() removing all but single point" begin
Random.seed!(32123)
pts = [ntuple(_ -> rand(), 2) for _ in 1:200]
reftree = RTree{Float64,2}(Int, String, leaf_capacity=5, branch_capacity=5, variant=tree_var)
loner = eltype(reftree)(SI.Rect((5.0, 5.0), (5.0, 5.0)), 0, "loner")
@testset "removing $n points" for (n, pt) in enumerate(pts)
insert!(reftree, eltype(reftree)(SI.Rect(pt, pt), n, string(n)))
tree = deepcopy(reftree)
insert!(tree, loner)
@test length(tree) == n + 1
SI.subtract!(tree, SI.Rect((0.0, 0.0), (1.0, 1.0)))
@test length(tree) == 1
@test SI.check(tree)
@test SI.id(first(tree)) == 0
end
end
@testset "subtract!() removing n<=N central nodes" begin
Random.seed!(32123)
pts = [ntuple(_ -> 2rand() - 1, 3) for _ in 1:200]
# the test implies that all pts have different distances to the origin
sort!(pts, by=pt -> maximum(abs, pt))
reftree = RTree{Float64,3}(Int, String, leaf_capacity=5, branch_capacity=5, variant=tree_var)
SI.load!(reftree, enumerate(pts),
convertel=x -> eltype(reftree)(SI.Rect(x[2], x[2]), x[1], string(x[1])))
corembr = SI.Rect((0.0, 0.0, 0.0), (0.0, 0.0, 0.0))
tree1 = deepcopy(reftree)
@test length(tree1) == length(reftree)
@testset "removing $n points" for (n, pt) in enumerate(pts)
corembr = SI.combine(corembr, SI.Rect(pt, pt))
# subtracting centrermbr from tree1 removes just 1 point
@test length(tree1) == length(reftree) - n + 1
tree1_to_remove = collect(contained_in(tree1, corembr))
@test length(tree1_to_remove) == 1
@test SI.id(first(tree1_to_remove)) == n
SI.subtract!(tree1, corembr)
@test length(tree1) == length(reftree) - n
@test SI.check(tree1)
# subtracting centrermbr from tree2 removes n points
tree2 = deepcopy(reftree)
SI.subtract!(tree2, corembr)
@test length(tree2) == length(reftree) - n
@test SI.check(tree2)
end
end
end
@testset "show() and print()" begin
mbrs = Vector{SI.Rect{Float64,2}}(
[
SI.Rect((0.0, 0.0), (2.0, 2.0)),
SI.Rect((-1.0, -1.0), (1.0, 1.0)),
SI.Rect((-1.0, 0.0), (1.0, 1.0)),
SI.Rect((0.0, -1.0), (1.0, 1.0)),
SI.Rect((1.0, 1.0), (2.0, 2.0)),
]
)
tree = RTree{SI.dimtype(eltype(mbrs)),ndims(eltype(mbrs))}(Int, String, leaf_capacity=4, branch_capacity=4)
for (i, rmbr) in enumerate(mbrs)
insert!(tree, rmbr, i, string(i))
end
eltyp = eltype(tree)
rectyp = eltype(mbrs)
test_show_string = "$(typeof(tree))(variant=RTreeStar, tight_mbrs=true, nearmin_overlap=1, fill_factor=0.7, split_factor=0.4, reinsert_factor=0.3, leaf_capacity=4, branch_capacity=4)
5 element(s) in 2 level(s) (1, 2 node(s) per level):
level=2 nchildren=2 mbr=((-1.0, -1.0), (2.0, 2.0))"
test_print_string = "$(typeof(tree))(variant=RTreeStar, tight_mbrs=true, nearmin_overlap=1, fill_factor=0.7, split_factor=0.4, reinsert_factor=0.3, leaf_capacity=4, branch_capacity=4)
5 element(s) in 2 level(s) (1, 2 node(s) per level):
level=2 nchildren=2 mbr=((-1.0, -1.0), (2.0, 2.0)):
level=1 nchildren=3 mbr=((-1.0, -1.0), (1.0, 1.0)):
$eltyp($rectyp((-1.0, -1.0), (1.0, 1.0)), 2, \"2\")
$eltyp($rectyp((-1.0, 0.0), (1.0, 1.0)), 3, \"3\")
$eltyp($rectyp((0.0, -1.0), (1.0, 1.0)), 4, \"4\")
level=1 nchildren=2 mbr=((0.0, 0.0), (2.0, 2.0)):
$eltyp($rectyp((0.0, 0.0), (2.0, 2.0)), 1, \"1\")
$eltyp($rectyp((1.0, 1.0), (2.0, 2.0)), 5, \"5\")"
io = IOBuffer()
show(io, tree)
@test String(take!(io)) == test_show_string
print(io, tree)
@test String(take!(io)) == test_print_string
show(io, tree; recurse=false)
@test String(take!(io)) == test_show_string
show(io, tree; recurse=true)
@test String(take!(io)) == test_print_string
end
end | SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | code | 111 | using SpatialIndexing
using Test, Random
const SI = SpatialIndexing
include("regions.jl")
include("rtree.jl") | SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 3667 | SpatialIndexing.jl
==============
[](https://github.com/alyst/SpatialIndexing.jl/actions?query=worflow%3ACI+branch%3Amaster)
[](https://codecov.io/gh/alyst/SpatialIndexing.jl)
**Documentation**: [![][docs-stable-img]][docs-stable-url] [![][docs-latest-img]][docs-latest-url]
`SpatialIndexing` package provides the tools for efficient in-memory indexing of
spatial data in [Julia](https://julialang.org/).
# Installation
```julia
using Pkg; Pkg.add("SpatialIndexing")
```
from Julia REPL.
# Features
## R-tree
[R-tree](https://en.wikipedia.org/wiki/R-tree) organizes data into
hierarchical structure and ensures that:
* minimal bounding rectangles (MBRs) of the nodes (rectangles that
encompass all data elements in the subtree) stay compact,
* MBRs of the nodes from the same R-tree level have minimal overlap
with each other.
The key benefit of R-tree is its ability to rebalance itself
and maintain efficient structure while handling dynamic data (massive insertions
and deletions).
`SpatialIndexing` provides `RTree` type that supports:
* different R-tree variants (classic [R-tree](https://en.wikipedia.org/wiki/R-tree),
[R*-tree](https://en.wikipedia.org/wiki/R*_tree), linear and quadratic node splits)
* `insert!(tree, item)`, `delete!(tree, item)` for element-wise insertion and deletion
* bulk-loading of data using Overlap-minimizing Top-down (OMT) approach (`load!(tree, data)`)
* `subtract!(tree, reg)` for removing data within specified region `reg`
* `findfirst(tree, reg, [id])`, `contained_in(tree, reg)` and `intersects_with(tree, reg)` spatial queries
## Simple Spatial Index
`SimpleSpatialIndex` stores all data elements in a vector. So, while insertion
of new data takes constant time, the time of spatial searches grows linearly
with the number of elements. This spatial index is intended as a reference
implementation for benchmarking and not recommended for production usage.
**TODO**
# Usage
**TODO**
`examples` folder contains `spiral.jl` and `pareto.jl` examples of using R-tree
for storing spatial data.


# See also
Other Julia packages for spatial data:
* [LibSpatialIndex.jl](https://github.com/yeesian/LibSpatialIndex.jl)
([libspatialindex](https://github.com/libspatialindex/libspatialindex) wrapper)
* [NearestNeighbors.jl](https://github.com/KristofferC/NearestNeighbors.jl)
* [RegionTrees.jl](https://github.com/rdeits/RegionTrees.jl)
* [LSH.jl](https://github.com/Keno/LSH.jl)
# References
* A.Guttman, _“R-Trees: A Dynamic Index Structure for Spatial Searching”_
Proc. 1984 ACM-SIGMOD Conference on Management of Data (1985), pp.47-57.
* N. Beckmann, H.P. Kriegel, R. Schneider, B. Seeger,
_"The R*-tree: an efficient and robust access method for points and rectangles"_
Proc. 1990 ACM SIGMOD international conference on Management of data (1990), p.322
* T. Lee and S. Lee, _"OMT: Overlap Minimizing Top-down Bulk Loading Algorithm for R-tree"_,
CAiSE Short Paper Proceedings (2003) [paper](http://ceur-ws.org/Vol-74/files/FORUM_18.pdf)
[docs-latest-img]: https://img.shields.io/badge/docs-latest-blue.svg
[docs-latest-url]: http://alyst.github.io/SpatialIndexing.jl/dev/
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: http://alyst.github.io/SpatialIndexing.jl/stable/
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 193 | # [Basic Spatial Types](@id abstract)
```@docs
SpatialIndex
SpatialElem
SpatialIndexing.HasMBR
SpatialIndexing.HasID
SpatialIndexException
SpatialIndexing.subtract!
SpatialIndexing.load!
```
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 1426 | # SpatialIndexing.jl package
`SpatialIndexing` package provides the tools for efficient in-memory storage and retrieval of
spatial data in [Julia](https://julialang.org/).
## Installation
```julia
using Pkg; Pkg.add("SpatialIndexing")
```
from Julia REPL.
## Spatial Indices
* [spatial primitives](@ref regions)
* [basic types](@ref abstract)
* [R-tree, R*-tree](@ref rtree)
* [simple index](@ref simple_index)
* [spatial queries](@ref query)
## See also
Other Julia packages for spatial data:
* [LibSpatialIndex.jl](https://github.com/yeesian/LibSpatialIndex.jl)
([libspatialindex](https://github.com/libspatialindex/libspatialindex) wrapper)
* [NearestNeighbors.jl](https://github.com/KristofferC/NearestNeighbors.jl)
* [RegionTrees.jl](https://github.com/rdeits/RegionTrees.jl)
* [LSH.jl](https://github.com/Keno/LSH.jl)
## References
* A.Guttman, _“R-Trees: A Dynamic Index Structure for Spatial Searching”_
Proc. 1984 ACM-SIGMOD Conference on Management of Data (1985), pp.47-57.
* N. Beckmann, H.P. Kriegel, R. Schneider, B. Seeger,
_"The R*-tree: an efficient and robust access method for points and rectangles"_
Proc. 1990 ACM SIGMOD international conference on Management of data (1990), p.322
* T. Lee and S. Lee, _"OMT: Overlap Minimizing Top-down Bulk Loading Algorithm for R-tree"_,
CAiSE Short Paper Proceedings (2003) [paper](http://ceur-ws.org/Vol-74/files/FORUM_18.pdf)
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 220 | # [Spatial Queries](@id query)
```@docs
SpatialIndexing.SpatialQueryIterator
SpatialIndexing.QueryKind
SpatialIndexing.QueryMatch
```
```@docs
Base.findfirst
Base.isempty
```
```@docs
contained_in
intersects_with
```
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 456 | # [Spatial Primitives](@id regions)
```@docs
SpatialIndexing.Region
SpatialIndexing.Point
SpatialIndexing.Rect
SpatialIndexing.empty
SpatialIndexing.isvalid
SpatialIndexing.center
SpatialIndexing.area
SpatialIndexing.perimeter
SpatialIndexing.intersects
SpatialIndexing.contains
SpatialIndexing.touches
Base.in
SpatialIndexing.overlap_area
SpatialIndexing.combined_area
SpatialIndexing.enlargement
SpatialIndexing.combine
SpatialIndexing.intersect
``` | SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 1187 | # [R-tree](@id rtree)
[R-tree](https://en.wikipedia.org/wiki/R-tree) organizes data into
hierarchical structure and ensures that:
* minimal bounding rectangles (MBRs) of the nodes (rectangles that
encompass all data elements in the subtree) stay compact,
* MBRs of the nodes from the same R-tree level have minimal overlap
with each other.
The key benefit of R-tree is its ability to rebalance itself
and maintain efficient structure while handling dynamic data (massive insertions
and deletions).
`SpatialIndexing` provides `RTree` type that supports:
* different R-tree variants (classic [R-tree](https://en.wikipedia.org/wiki/R-tree),
[R*-tree](https://en.wikipedia.org/wiki/R*_tree), linear and quadratic node splits)
* `insert!(tree, item)`, `delete!(tree, item)` for element-wise insertion and deletion
* bulk-loading of data using Overlap-minimizing Top-down (OMT) approach (`load!(tree, data)`)
* `subtract!(tree, reg)` for removing data within specified region `reg`
* `findfirst(tree, reg, [id])`, `contained_in(tree, reg)` and `intersects_with(tree, reg)` spatial queries
```@docs
RTree
SpatialIndexing.RTreeVariant
Base.insert!
Base.delete!
```
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 0.1.6 | 84efe17c77e1f2156a7a0d8a7c163c1e1c7bdaed | docs | 382 | # [Simple Spatial Index](@id simple_index)
`SimpleSpatialIndex` stores all data elements in a vector. So, while insertion
of new data takes constant time, the time of spatial searches grows linearly
with the number of elements. This spatial index is intended as a reference
implementation for benchmarking and not recommended for production usage.
```@docs
SimpleSpatialIndex
```
| SpatialIndexing | https://github.com/alyst/SpatialIndexing.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 909 | using Documenter, TableTransforms
using DocumenterTools: Themes
using TransformsBase
DocMeta.setdocmeta!(TableTransforms, :DocTestSetup, :(using TableTransforms); recursive=true)
makedocs(;
warnonly=[:missing_docs],
modules=[TableTransforms, TransformsBase],
authors="Júlio Hoffimann <[email protected]> and contributors",
repo="https://github.com/JuliaML/TableTransforms.jl/blob/{commit}{path}#{line}",
sitename="TableTransforms.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://JuliaML.github.io/TableTransforms.jl",
repolink="https://github.com/JuliaML/TableTransforms.jl"
),
pages=[
"Home" => "index.md",
"Transforms" => "transforms.md",
"Developer guide" => "devguide.md",
"Related" => "related.md"
]
)
deploydocs(; repo="github.com/JuliaML/TableTransforms.jl", devbranch="master", push_preview=true)
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 1979 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENSE in the project root.
# ------------------------------------------------------------------
module TableTransforms
using Tables
using Unitful
using Statistics
using PrettyTables
using AbstractTrees
using LinearAlgebra
using DataScienceTraits
using CategoricalArrays
using Random
using CoDa
using TransformsBase: Transform, Identity, →
using ColumnSelectors: ColumnSelector, SingleColumnSelector
using ColumnSelectors: AllSelector, Column, selector, selectsingle
using DataScienceTraits: SciType, Continuous, Categorical, coerce
using Unitful: AbstractQuantity, AffineQuantity, AffineUnits, Units
using Distributions: ContinuousUnivariateDistribution, Normal
using InverseFunctions: NoInverse, inverse as invfun
using StatsBase: AbstractWeights, Weights, sample
using Distributed: CachingPool, pmap, workers
using NelderMead: optimise
import Distributions: quantile, cdf
import TransformsBase: assertions, parameters, isrevertible, isinvertible
import TransformsBase: apply, revert, reapply, preprocess, inverse
include("tabletraits.jl")
include("distributions.jl")
include("tableselection.jl")
include("tablerows.jl")
include("transforms.jl")
export
# abstract types
TableTransform,
FeatureTransform,
# interface
isrevertible,
isinvertible,
apply,
revert,
reapply,
inverse,
# built-in
Assert,
Select,
Reject,
Satisfies,
Only,
Except,
DropConstant,
Rename,
StdNames,
StdFeats,
Sort,
Sample,
Filter,
DropMissing,
DropNaN,
DropExtrema,
DropUnits,
AbsoluteUnits,
Unitify,
Unit,
Map,
Replace,
Coalesce,
Coerce,
Levels,
Indicator,
OneHot,
Identity,
Center,
LowHigh,
MinMax,
Interquartile,
ZScore,
Quantile,
Functional,
EigenAnalysis,
PCA,
DRS,
SDS,
ProjectionPursuit,
Closure,
Remainder,
Compose,
ALR,
CLR,
ILR,
RowTable,
ColTable,
→,
⊔
end
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 1161 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENSE in the project root.
# ------------------------------------------------------------------
"""
EmpiricalDistribution(values)
An empirical distribution holding continuous values.
"""
struct EmpiricalDistribution{T} <: ContinuousUnivariateDistribution
values::Vector{T}
function EmpiricalDistribution{T}(values) where {T}
_assert(!isempty(values), "values must be provided")
new(sort(values))
end
end
EmpiricalDistribution(values) = EmpiricalDistribution{eltype(values)}(values)
quantile(d::EmpiricalDistribution, p::Real) = quantile(d.values, p, sorted=true)
function cdf(d::EmpiricalDistribution, x)
v = d.values
n = length(v)
head, mid, tail = 1, 1, n
while tail - head > 1
mid = (head + tail) ÷ 2
if x < v[mid]
tail = mid
else
head = mid
end
end
l, u = v[head], v[tail]
if x < l
return 0.0
elseif x > u
return 1.0
else
if l == u
return tail / n
else
pl, pu = head / n, tail / n
return (pu - pl) * (x - l) / (u - l) + pl
end
end
end
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 3138 | """
tablerows(table)
Returns an appropriate iterator for table rows.
The rows are iterable, implement the `Tables.AbstractRow` interface
and the following ways of column access:
```julia
row.colname
row."colname"
row[colindex]
row[:colname]
row["colname"]
```
"""
function tablerows(table)
if !Tables.istable(table)
throw(ArgumentError("the argument is not a table"))
end
if Tables.rowaccess(table)
RTableRows(table)
else
CTableRows(table)
end
end
#------------------
# COMMON INTERFACE
#------------------
abstract type TableRow end
# column access
Base.getproperty(row::TableRow, nm::Symbol) = Tables.getcolumn(row, nm)
Base.getproperty(row::TableRow, nm::AbstractString) = Tables.getcolumn(row, Symbol(nm))
Base.getindex(row::TableRow, i::Int) = Tables.getcolumn(row, i)
Base.getindex(row::TableRow, nm::Symbol) = Tables.getcolumn(row, nm)
Base.getindex(row::TableRow, nm::AbstractString) = Tables.getcolumn(row, Symbol(nm))
# iterator interface
Base.length(row::TableRow) = length(Tables.columnnames(row))
Base.iterate(row::TableRow, state=1) = state > length(row) ? nothing : (Tables.getcolumn(row, state), state + 1)
#--------------
# COLUMN TABLE
#--------------
struct CTableRows{T}
cols::T
nrows::Int
function CTableRows(table)
cols = Tables.columns(table)
nrows = _nrows(table)
new{typeof(cols)}(cols, nrows)
end
end
# iterator interface
Base.length(rows::CTableRows) = rows.nrows
Base.iterate(rows::CTableRows, state=1) = state > length(rows) ? nothing : (CTableRow(rows.cols, state), state + 1)
struct CTableRow{T} <: TableRow
cols::T
ind::Int
end
# getters
getcols(row::CTableRow) = getfield(row, :cols)
getind(row::CTableRow) = getfield(row, :ind)
# AbstractRow interface
Tables.columnnames(row::CTableRow) = Tables.columnnames(getcols(row))
Tables.getcolumn(row::CTableRow, i::Int) = Tables.getcolumn(getcols(row), i)[getind(row)]
Tables.getcolumn(row::CTableRow, nm::Symbol) = Tables.getcolumn(getcols(row), nm)[getind(row)]
#-----------
# ROW TABLE
#-----------
struct RTableRows{T}
rows::T
nrows::Int
function RTableRows(table)
rows = Tables.rows(table)
nrows = _nrows(table)
new{typeof(rows)}(rows, nrows)
end
end
# iterator interface
Base.length(rows::RTableRows) = rows.nrows
function Base.iterate(rows::RTableRows, args...)
next = iterate(rows.rows, args...)
if isnothing(next)
nothing
else
row, state = next
(RTableRow(row), state)
end
end
struct RTableRow{T} <: TableRow
row::T
end
# getters
getrow(row::RTableRow) = getfield(row, :row)
# AbstractRow interface
Tables.columnnames(row::RTableRow) = Tables.columnnames(getrow(row))
Tables.getcolumn(row::RTableRow, i::Int) = Tables.getcolumn(getrow(row), i)
Tables.getcolumn(row::RTableRow, nm::Symbol) = Tables.getcolumn(getrow(row), nm)
#-------
# UTILS
#-------
function _nrows(table)
if Tables.rowaccess(table)
rows = Tables.rows(table)
length(rows)
else
cols = Tables.columns(table)
names = Tables.columnnames(cols)
isempty(names) && return 0
column = Tables.getcolumn(cols, first(names))
length(column)
end
end
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 1861 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENSE in the project root.
# ------------------------------------------------------------------
struct TableSelection{T,C}
table::T
cols::C
ncols::Int
names::Vector{Symbol}
onames::Vector{Symbol}
mapnames::Dict{Symbol,Symbol}
function TableSelection(table::T, names, onames) where {T}
cols = Tables.columns(table)
_assert(onames ⊆ Tables.columnnames(cols), "all selected columns must exist in the table")
ncols = length(names)
mapnames = Dict(zip(names, onames))
new{T,typeof(cols)}(table, cols, ncols, names, onames, mapnames)
end
end
function Base.:(==)(a::TableSelection, b::TableSelection)
a.names != b.names && return false
a.onames != b.onames && return false
all(nm -> Tables.getcolumn(a, nm) == Tables.getcolumn(b, nm), a.names)
end
function Base.show(io::IO, t::TableSelection)
println(io, "TableSelection")
pretty_table(io, t, vcrop_mode=:middle, newline_at_end=false)
end
# Tables.jl interface
Tables.istable(::Type{<:TableSelection}) = true
Tables.columnaccess(::Type{<:TableSelection}) = true
Tables.columns(t::TableSelection) = t
Tables.columnnames(t::TableSelection) = t.names
function Tables.getcolumn(t::TableSelection, i::Int)
1 ≤ i ≤ t.ncols || error("Table has no column with index $i.")
Tables.getcolumn(t.cols, t.mapnames[t.names[i]])
end
function Tables.getcolumn(t::TableSelection, nm::Symbol)
nm ∉ t.names && error("Table has no column $nm.")
Tables.getcolumn(t.cols, t.mapnames[nm])
end
Tables.materializer(t::TableSelection) = Tables.materializer(t.table)
function Tables.schema(t::TableSelection)
schema = Tables.schema(t.cols)
names = schema.names
types = schema.types
inds = indexin(t.onames, collect(names))
Tables.Schema(t.names, types[inds])
end
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 558 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENSE in the project root.
# ------------------------------------------------------------------
"""
features, metadata = divide(table)
Divide the `table` into a table with `features` and
a `metadata` object, e.g. geospatial domain.
"""
divide(table) = table, nothing
"""
table = attach(features, metadata)
Combine a table with `features` and a `metadata`
object into a special type of `table`.
"""
attach(features, ::Nothing) = features
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
|
[
"MIT"
] | 1.33.5 | 9635db5d125f39b6407e60ee895349a028c61aa6 | code | 8176 | # ------------------------------------------------------------------
# Licensed under the MIT License. See LICENSE in the project root.
# ------------------------------------------------------------------
"""
TableTransform
A transform that takes a table as input and produces a new table.
Any transform implementing the `TableTransform` trait should implement the
[`apply`](@ref) function. If the transform [`isrevertible`](@ref),
then it should also implement the [`revert`](@ref) function.
A functor interface is automatically generated from the functions
above, which means that any transform implementing the `TableTransform`
trait can be evaluated directly at any table implementing the
[Tables.jl](https://github.com/JuliaData/Tables.jl) interface.
"""
abstract type TableTransform <: Transform end
"""
FeatureTransform
A transform that operates on the columns of the table containing
features, i.e., simple attributes such as numbers, strings, etc.
"""
abstract type FeatureTransform <: TableTransform end
"""
newfeat, fcache = applyfeat(transform, feat, prep)
Implementation of [`apply`](@ref) without treatment of metadata.
This function is intended for developers of new types.
"""
function applyfeat end
"""
newmeta, mcache = applymeta(transform, meta, prep)
Implementation of [`apply`](@ref) for metadata.
This function is intended for developers of new types.
"""
function applymeta end
"""
feat = revertfeat(transform, newfeat, fcache)
Implementation of [`revert`](@ref) without treatment of metadata.
This function is intended for developers of new types.
"""
function revertfeat end
"""
meta = revertmeta(transform, newmeta, mcache)
Implementation of [`revert`](@ref) for metadata.
This function is intended for developers of new types.
"""
function revertmeta end
"""
StatelessFeatureTransform
This trait is useful to signal that we can [`reapply`](@ref) a transform
"fitted" with training data to "test" data without relying on the `cache`.
"""
abstract type StatelessFeatureTransform <: FeatureTransform end
"""
newfeat = reapplyfeat(transform, feat, fcache)
Implementation of [`reapply`](@ref) without treatment of metadata.
This function is intended for developers of new types.
"""
function reapplyfeat end
"""
newmeta = reapplymeta(transform, meta, mcache)
Implementation of [`reapply`](@ref) for metadata.
This function is intended for developers of new types.
"""
function reapplymeta end
"""
ColwiseFeatureTransform
A feature transform that is applied column-by-column. In this case, the
new type only needs to implement [`colapply`](@ref), [`colrevert`](@ref)
and [`colcache`](@ref). Efficient fallbacks are provided that execute
these functions in parallel for all columns with multiple threads.
## Notes
* `ColwiseFeatureTransform` subtypes must have a `selector` field.
"""
abstract type ColwiseFeatureTransform <: FeatureTransform end
"""
y = colapply(transform, x, c)
Apply `transform` to column `x` with cache `c` and return new column `y`.
"""
function colapply end
"""
x = colrevert(transform, y, c)
Revert `transform` starting from column `y` with cache `c` and return
original column `x`. Only defined when the `transform` [`isrevertible`](@ref).
"""
function colrevert end
"""
c = colcache(transform, x)
Produce cache `c` necessary to [`colapply`](@ref) the `transform` on `x`.
If the `transform` [`isrevertible`](@ref) then the cache `c` can also be
used in [`colrevert`](@ref).
"""
function colcache end
# --------------------
# TRANSFORM FALLBACKS
# --------------------
function apply(transform::FeatureTransform, table)
feat, meta = divide(table)
for assertion in assertions(transform)
assertion(feat)
end
prep = preprocess(transform, feat)
newfeat, fcache = applyfeat(transform, feat, prep)
newmeta, mcache = applymeta(transform, meta, prep)
attach(newfeat, newmeta), (fcache, mcache)
end
function revert(transform::FeatureTransform, newtable, cache)
_assert(isrevertible(transform), "Transform is not revertible")
newfeat, newmeta = divide(newtable)
fcache, mcache = cache
feat = revertfeat(transform, newfeat, fcache)
meta = revertmeta(transform, newmeta, mcache)
attach(feat, meta)
end
function reapply(transform::FeatureTransform, table, cache)
feat, meta = divide(table)
fcache, mcache = cache
for assertion in assertions(transform)
assertion(feat)
end
newfeat = reapplyfeat(transform, feat, fcache)
newmeta = reapplymeta(transform, meta, mcache)
attach(newfeat, newmeta)
end
applymeta(::FeatureTransform, meta, prep) = meta, nothing
revertmeta(::FeatureTransform, newmeta, mcache) = newmeta
reapplymeta(::FeatureTransform, meta, mcache) = meta
# --------------------
# STATELESS FALLBACKS
# --------------------
reapply(transform::StatelessFeatureTransform, table, cache) = apply(transform, table) |> first
# ------------------
# COLWISE FALLBACKS
# ------------------
function applyfeat(transform::ColwiseFeatureTransform, feat, prep)
# retrieve column names and values
cols = Tables.columns(feat)
names = Tables.columnnames(cols)
snames = transform.selector(names)
# transform each column in parallel
pool = CachingPool(workers())
vals = pmap(pool, names) do n
x = Tables.getcolumn(cols, n)
if n ∈ snames
c = colcache(transform, x)
y = colapply(transform, x, c)
else
c = nothing
y = x
end
(n => y), c
end
# new table with transformed columns
𝒯 = (; first.(vals)...)
newfeat = 𝒯 |> Tables.materializer(feat)
# cache values for each column
caches = last.(vals)
# return new table and cache
newfeat, (caches, snames)
end
function revertfeat(transform::ColwiseFeatureTransform, newfeat, fcache)
# transformed columns
cols = Tables.columns(newfeat)
names = Tables.columnnames(cols)
caches, snames = fcache
# revert each column in parallel
pool = CachingPool(workers())
vals = pmap(pool, names, caches) do n, c
y = Tables.getcolumn(cols, n)
x = n ∈ snames ? colrevert(transform, y, c) : y
n => x
end
# new table with transformed columns
(; vals...) |> Tables.materializer(newfeat)
end
function reapplyfeat(transform::ColwiseFeatureTransform, feat, fcache)
# retrieve column names and values
cols = Tables.columns(feat)
names = Tables.columnnames(cols)
caches, snames = fcache
# check that cache is valid
_assert(length(names) == length(caches), "invalid caches for feat")
# transform each column in parallel
pool = CachingPool(workers())
vals = pmap(pool, names, caches) do n, c
x = Tables.getcolumn(cols, n)
y = n ∈ snames ? colapply(transform, x, c) : x
n => y
end
# new table with transformed columns
(; vals...) |> Tables.materializer(feat)
end
# ----------------
# IMPLEMENTATIONS
# ----------------
include("transforms/utils.jl")
include("transforms/assert.jl")
include("transforms/select.jl")
include("transforms/satisfies.jl")
include("transforms/rename.jl")
include("transforms/stdnames.jl")
include("transforms/stdfeats.jl")
include("transforms/sort.jl")
include("transforms/sample.jl")
include("transforms/filter.jl")
include("transforms/dropmissing.jl")
include("transforms/dropnan.jl")
include("transforms/dropextrema.jl")
include("transforms/dropunits.jl")
include("transforms/dropconstant.jl")
include("transforms/absoluteunits.jl")
include("transforms/unitify.jl")
include("transforms/unit.jl")
include("transforms/map.jl")
include("transforms/replace.jl")
include("transforms/coalesce.jl")
include("transforms/coerce.jl")
include("transforms/levels.jl")
include("transforms/indicator.jl")
include("transforms/onehot.jl")
include("transforms/center.jl")
include("transforms/lowhigh.jl")
include("transforms/zscore.jl")
include("transforms/quantile.jl")
include("transforms/functional.jl")
include("transforms/eigenanalysis.jl")
include("transforms/projectionpursuit.jl")
include("transforms/closure.jl")
include("transforms/remainder.jl")
include("transforms/compose.jl")
include("transforms/logratio.jl")
include("transforms/rowtable.jl")
include("transforms/coltable.jl")
include("transforms/parallel.jl")
| TableTransforms | https://github.com/JuliaML/TableTransforms.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.