licenses
listlengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
]
| 1.2.1 | d0675b5245d2b15fa971ef0dc03c7dfe2cf6ffe3 | code | 6279 | # High-level tests
makearray(D, val) = fill(val, ntuple(d -> 1, D))
if comm_rank == 0
const dirname2 = Filesystem.mktempdir()
const filename2 = "$dirname2/test.bp"
@testset "High-level write tests " begin
file = adios_open_serial(filename2, mode_write)
etype = type(file.engine)
@test etype in ("BP4Writer", "BP5Writer")
adios_define_attribute(file, "a1", float(π))
adios_define_attribute(file, "a2", [float(π)])
adios_define_attribute(file, "a3", [float(π), 0])
adios_put!(file, "v1", float(ℯ))
adios_put!(file, "v3", makearray(1, float(ℯ)))
adios_put!(file, "v4", makearray(2, float(ℯ)))
adios_put!(file, "v5", makearray(3, float(ℯ)))
adios_put!(file, "g1/v6", makearray(4, float(ℯ)))
adios_put!(file, "g1/g2/v7", makearray(5, float(ℯ)))
@test shapeid(inquire_variable(file.io, "v1")) == shapeid_local_value
@test shapeid(inquire_variable(file.io, "v3")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "v4")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "v5")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "g1/v6")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "g1/g2/v7")) ==
shapeid_local_array
adios_define_attribute(file, "v4/a4", float(π))
adios_define_attribute(file, "v5", "a5", [float(π)])
adios_define_attribute(file, "g1/v6", "a6", [float(π), 0])
adios_perform_puts!(file)
close(file)
end
@testset "High-level read tests " begin
if ADIOS2_VERSION < v"2.9.0"
# We need to use `mode_read` for ADIOS2 <2.9, and `mode_readRandomAccess` for ADIOS2 ≥2.9
file = adios_open_serial(filename2, mode_read)
else
file = adios_open_serial(filename2, mode_readRandomAccess)
end
etype = type(file.engine)
@test etype in ("BP4Reader", "BP5Reader")
@test Set(adios_subgroup_names(file, "")) == Set(["g1"])
@test_broken Set(adios_subgroup_names(file, "g1")) == Set(["g2"])
@test Set(adios_subgroup_names(file, "g1")) == Set(["/g2"]) # don't want this
@test Set(adios_all_attribute_names(file)) ==
Set(["a1", "a2", "a3", "v4/a4", "v5/a5", "g1/v6/a6"])
@test Set(adios_group_attribute_names(file, "g1")) == Set()
@test Set(adios_group_attribute_names(file, "g1/v6")) ==
Set(["g1/v6/a6"])
@test adios_attribute_data(file, "a1") == float(π)
if etype == "BP4Reader"
@test adios_attribute_data(file, "a2") == float(π)
else
@test adios_attribute_data(file, "a2") == [float(π)]
end
@test adios_attribute_data(file, "a3") == [float(π), 0]
@test adios_attribute_data(file, "v4", "a4") == float(π)
if etype == "BP4Reader"
@test adios_attribute_data(file, "v5/a5") == float(π)
else
@test adios_attribute_data(file, "v5/a5") == [float(π)]
end
@test adios_attribute_data(file, "g1/v6", "a6") == [float(π), 0]
@test Set(adios_all_variable_names(file)) ==
Set(["v1", "v3", "v4", "v5", "g1/v6", "g1/g2/v7"])
@test Set(adios_group_variable_names(file, "g1")) == Set(["g1/v6"])
@test Set(adios_group_variable_names(file, "g1/g2")) ==
Set(["g1/g2/v7"])
# Local values are converted to global arrays
@test shapeid(inquire_variable(file.io, "v1")) == shapeid_global_array
@test shapeid(inquire_variable(file.io, "v3")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "v4")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "v5")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "g1/v6")) == shapeid_local_array
@test shapeid(inquire_variable(file.io, "g1/g2/v7")) ==
shapeid_local_array
@test ndims(inquire_variable(file.io, "v1")) == 1
@test ndims(inquire_variable(file.io, "v3")) == 1
@test ndims(inquire_variable(file.io, "v4")) == 2
@test ndims(inquire_variable(file.io, "v5")) == 3
@test ndims(inquire_variable(file.io, "g1/v6")) == 4
@test ndims(inquire_variable(file.io, "g1/g2/v7")) == 5
@test shape(inquire_variable(file.io, "v1")) == (1,)
@test shape(inquire_variable(file.io, "v3")) ≡ nothing
@test shape(inquire_variable(file.io, "v4")) ≡ nothing
@test shape(inquire_variable(file.io, "v5")) ≡ nothing
@test shape(inquire_variable(file.io, "g1/v6")) ≡ nothing
@test shape(inquire_variable(file.io, "g1/g2/v7")) ≡ nothing
@test start(inquire_variable(file.io, "v1")) == (0,)
@test start(inquire_variable(file.io, "v3")) ≡ nothing
@test start(inquire_variable(file.io, "v4")) ≡ nothing
@test start(inquire_variable(file.io, "v5")) ≡ nothing
@test start(inquire_variable(file.io, "g1/v6")) ≡ nothing
@test start(inquire_variable(file.io, "g1/g2/v7")) ≡ nothing
@test count(inquire_variable(file.io, "v1")) == (1,)
@test count(inquire_variable(file.io, "v3")) == (1,)
@test count(inquire_variable(file.io, "v4")) == (1, 1)
@test count(inquire_variable(file.io, "v5")) == (1, 1, 1)
@test count(inquire_variable(file.io, "g1/v6")) == (1, 1, 1, 1)
@test count(inquire_variable(file.io, "g1/g2/v7")) == (1, 1, 1, 1, 1)
v1 = adios_get(file, "v1")
@test !isready(v1)
@test fetch(v1) == fill(float(ℯ), 1)
@test isready(v1)
v3 = adios_get(file, "v3")
v4 = adios_get(file, "v4")
@test !isready(v3)
@test fetch(v3) == makearray(1, float(ℯ))
@test fetch(v4) == makearray(2, float(ℯ))
@test isready(v3)
v5 = adios_get(file, "v5")
v6 = adios_get(file, "g1/v6")
v7 = adios_get(file, "g1/g2/v7")
@test !isready(v5)
adios_perform_gets(file)
@test isready(v5)
@test fetch(v5) == makearray(3, float(ℯ))
@test fetch(v6) == makearray(4, float(ℯ))
@test fetch(v7) == makearray(5, float(ℯ))
close(file)
end
end
| ADIOS2 | https://github.com/eschnett/ADIOS2.jl.git |
|
[
"MIT"
]
| 1.2.1 | d0675b5245d2b15fa971ef0dc03c7dfe2cf6ffe3 | code | 274 | # Test internals
@testset "Internal tests" begin
for jtype in ADIOS2.julia_types
@test ADIOS2.julia_type(ADIOS2.adios_type(jtype)) ≡ jtype
end
for atype in ADIOS2.adios_types
@test ADIOS2.adios_type(ADIOS2.julia_type(atype)) ≡ atype
end
end
| ADIOS2 | https://github.com/eschnett/ADIOS2.jl.git |
|
[
"MIT"
]
| 1.2.1 | d0675b5245d2b15fa971ef0dc03c7dfe2cf6ffe3 | code | 1616 | using ADIOS2
using Base.Filesystem
using MPI
using Printf
using Test
################################################################################
# Find ADIOS2 version
# There is no official way to find the ADIOS2 library version. Instead
# we check the default engine type after opening a file.
const ADIOS2_VERSION = let
adios = adios_init_serial()
io = declare_io(adios, "IO")
filename = tempname()
engine = open(io, filename, mode_write)
etype = type(engine)
close(engine)
if etype == "BP4Writer"
v"2.8.0"
elseif etype == "BP5Writer"
v"2.9.0"
else
@assert false
end
end
################################################################################
# Initialize MPI
const mpi_initialized = MPI.Initialized()
if !mpi_initialized
MPI.Init()
end
const comm = MPI.COMM_WORLD
const comm_rank = MPI.Comm_rank(comm)
const comm_size = MPI.Comm_size(comm)
const comm_root = 0
const use_mpi = comm_size > 1
################################################################################
"""
Convert an object to a string as the REPL would
"""
function showmime(obj)
buf = IOBuffer()
show(buf, MIME"text/plain"(), obj)
return String(take!(buf))
end
################################################################################
include("internal.jl")
include("basic.jl")
include("highlevel.jl")
include("write_read_selection.jl")
################################################################################
# Finalize MPI
const mpi_finalized = MPI.Finalized()
if mpi_initialized && !mpi_finalized
MPI.Finalize()
end
| ADIOS2 | https://github.com/eschnett/ADIOS2.jl.git |
|
[
"MIT"
]
| 1.2.1 | d0675b5245d2b15fa971ef0dc03c7dfe2cf6ffe3 | code | 3902 | # Test basic write and read using selections
if use_mpi
if comm_rank == comm_root
MPI.bcast(dirname, comm_root, comm)
else
const dirname = MPI.bcast(nothing, comm_root, comm)
end
end
const filename_sel = "$dirname/test_nd_sel_2D.bp"
function _set_data_2D(T, comm_rank, step)
data = ones(T, 10, 10)
for j in 2:4
for i in 2:4
data[i, j] = comm_rank + step
end
end
return data
end
@testset "File write nd global arrays" begin
# Set up ADIOS
if use_mpi
adios = adios_init_mpi(comm)
else
adios = adios_init_serial()
end
@test adios isa Adios
io = declare_io(adios, "io_writer")
@test io isa AIO
count = (10, 10)
start = (0, comm_rank * 10)
shape = (10, comm_size * 10)
# open engine
writer = open(io, filename_sel, mode_write)
for step in 1:3
begin_step(writer)
for T in
Type[Float32, Float64, Complex{Float32}, Complex{Float64}, Int8,
Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64]
# define some nd array variables, 10x10 per MPI process
var_T = step == 1 ?
define_variable(io, string(T), T, shape, start, count) :
inquire_variable(io, string(T))
data_2D = _set_data_2D(T, comm_rank, step)
put!(writer, var_T, data_2D) # deferred mode
end
end_step(writer)
end
close(writer)
finalize(adios)
end
@testset "File read selection nd global arrays" begin
# Set up ADIOS
if use_mpi
adios = adios_init_mpi(comm)
else
adios = adios_init_serial()
end
@test adios isa Adios
io = declare_io(adios, "io_reader")
@test io isa AIO
sel_start = (2, comm_rank * 10 + 2)
sel_count = (2, 2)
# open engine
reader = open(io, filename_sel, mode_read)
for step in 1:3
begin_step(reader)
for T in
Type[Float32, Float64, Complex{Float32}, Complex{Float64}, Int8,
Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64]
var_T = inquire_variable(io, string(T))
@test var_T isa Variable
set_selection(var_T, sel_start, sel_count)
data_in = Array{T,2}(undef, 2, 2)
get(reader, var_T, data_in, mode_sync)
@test first(data_in) == comm_rank + step
allsame(x) = all(y -> y == first(x), x)
@test allsame(data_in)
end
end_step(reader)
end
close(reader)
finalize(adios)
end
@testset "File read step selection nd global arrays" begin
# Set up ADIOS
if use_mpi
adios = adios_init_mpi(comm)
else
adios = adios_init_serial()
end
io = declare_io(adios, "io_reader_set_step")
sel_start = (2, comm_rank * 10 + 2)
sel_count = (2, 2)
# open engine
if ADIOS2_VERSION < v"2.9.0"
# We need to use `mode_read` for ADIOS2 <2.9, and `mode_readRandomAccess` for ADIOS2 ≥2.9
reader = open(io, filename_sel, mode_read)
else
reader = open(io, filename_sel, mode_readRandomAccess)
end
for T in
Type[Float32, Float64, Complex{Float32}, Complex{Float64}, Int8, Int16,
Int32, Int64, UInt8, UInt16, UInt32, UInt64]
var_T = inquire_variable(io, string(T))
@test var_T isa Variable
set_selection(var_T, sel_start, sel_count)
for step in 1:3
# step start = step-1 (adios is zero based) and 1 step count
set_step_selection(var_T, step - 1, 1)
data_in = Array{T,2}(undef, 2, 2)
get(reader, var_T, data_in, mode_sync)
@test first(data_in) == comm_rank + step
allsame(x) = all(y -> y == first(x), x)
@test allsame(data_in)
end
end
close(reader)
finalize(adios)
end
| ADIOS2 | https://github.com/eschnett/ADIOS2.jl.git |
|
[
"MIT"
]
| 1.2.1 | d0675b5245d2b15fa971ef0dc03c7dfe2cf6ffe3 | docs | 2006 | # ADIOS2.jl
A Julia interface to [ADIOS2](https://github.com/ornladios/ADIOS2),
the Adaptable Input Output System version 2.
* [](https://eschnett.github.io/ADIOS2.jl/dev)
* [](https://github.com/eschnett/ADIOS2.jl/actions)
* [](https://codecov.io/gh/eschnett/ADIOS2.jl)
## Examples
It is best to read the ADIOS2 documentation before using this package.
ADIOS2 splits reading/writing variables into three parts:
1. Define the metadata, i.e. the name, type, and shape (if array) of
the variables
2. Schedule the reads/writes, providing pointers to or buffer for the
data
3. Perform the actual reads/writes
This ensures that reads or writes can be performed very efficiently.
### Writing a file
```Julia
# Initialize ADIOS
using ADIOS2
adios = adios_init_serial()
io = declare_io(adios, "IO")
engine = open(io, "example.bp", mode_write)
# Define some variables
scalar = 247.0
svar = define_variable(io, "scalar", scalar)
array = Float64[10i + j for i in 1:2, j in 1:3]
avar = define_variable(io, "array", array)
# Schedule writing the variables
put!(engine, svar, scalar)
put!(engine, avar, array)
# Write the variables
perform_puts!(engine)
close(engine)
```
### Reading a file
```Julia
# Initialize ADIOS
using ADIOS2
adios = adios_init_serial()
io = declare_io(adios, "IO")
engine = open(io, "example.bp", mode_read)
# List all variables
vars = inquire_all_variables(io)
println("Variables:")
for var in vars
println(" ", name(var))
end
svar = inquire_variable(io, "scalar")
avar = inquire_variable(io, "array")
# Schedule reading the variables
scalar = Ref{Float64}()
get(engine, svar, scalar)
array = Array{Float64}(undef, 2, 3)
get(engine, avar, array)
# Read the variables
perform_gets(engine)
println("scalar: $(scalar[])")
println("array: $array")
```
| ADIOS2 | https://github.com/eschnett/ADIOS2.jl.git |
|
[
"MIT"
]
| 1.2.1 | d0675b5245d2b15fa971ef0dc03c7dfe2cf6ffe3 | docs | 2731 | # ADIOS2.jl
[ADIOS2.jl](https://github.com/eschnett/ADIOS2.jl) is a Julia
interface to the [ADIOS2](https://github.com/ornladios/ADIOS2), the
Adaptable Input Output System version 2.
## Installation
```julia
julia>]
pkg> add ADIOS2
```
ADIOS2 binaries are downloaded by default using the `ADIOS2_jll` package
## Using a custom or system provided ADIOS2 library
Set the environment variable `JULIA_ADIOS2_PATH` to the top-level installation directory for ADIOS2,
i.e. the `libadios2_c` and `libadios2_c_mpi` (if using MPI-enabled ADIOS2) libraries should be located
under `$JULIA_ADIOS2_PATH/lib` or `$JULIA_ADIOS2_PATH/lib64`. Then run `import Pkg; Pkg.build("ADIOS2")`.
This is preferred in high-performance computing (HPC) systems for system-wide installations for libraries built against
vendor MPI implementations. It is highly recommended that MPIPreferences points at the system MPI implementation used to build ADIOS2.
Example:
```sh
$ export JULIA_ADIOS2_PATH=/opt/adios2/2.8.3
```
Then in Julia, run:
```julia
pkg> build
```
## Basic API
### Types
```@docs
Error
AdiosType
Mode
StepMode
StepStatus
ShapeId
```
### Adios functions
```@docs
Adios
adios_init_mpi
adios_init_serial
declare_io
adios_finalize
```
### IO functions
```@docs
AIO
define_variable
inquire_variable
inquire_all_variables
inquire_group_variables
define_attribute
define_attribute_array
define_variable_attribute
define_variable_attribute_array
inquire_attribute
inquire_variable_attribute
inquire_all_attributes
inquire_group_attributes
inquire_subgroups
open
engine_type
get_engine
```
### Variable functions
```@docs
Variable
name(variable::Variable)
type(variable::Variable)
shapeid(variable::Variable)
ndims(variable::Variable)
shape(variable::Variable)
start(variable::Variable)
count(variable::Variable)
steps_start(variable::Variable)
steps(variable::Variable)
selection_size(variable::Variable)
minimum(variable::Variable)
maximum(variable::Variable)
```
### Attribute functions
```@docs
Attribute
name(attribute::Attribute)
type(attribute::Attribute)
is_value(attribute::Attribute)
size(attribute::Attribute)
data(attribute::Attribute)
```
### Engine functions
```@docs
Engine
name
type
openmode
begin_step
current_step
steps
put!
perform_puts!
get
perform_gets
end_step
flush(engine::Engine)
close(engine::Engine)
```
## High-Level API
```@docs
AdiosFile
adios_open_serial
adios_open_mpi
flush(file::AdiosFile)
close(file::AdiosFile)
adios_subgroup_names
adios_define_attribute
adios_all_attribute_names
adios_group_attribute_names
adios_attribute_data
adios_put!
adios_perform_puts!
adios_all_variable_names
adios_group_variable_names
IORef
isready(ioref::IORef)
fetch(ioref::IORef)
adios_get
adios_perform_gets
```
| ADIOS2 | https://github.com/eschnett/ADIOS2.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | code | 41432 | module HomotopyOpt
import HomotopyContinuation: @var, evaluate, differentiate, start_parameters!, target_parameters!, track!, solve, real_solutions, solutions, solution, rand_subspace, randn, System, ParameterHomotopy, Expression, Tracker, Variable, track
import LinearAlgebra: norm, transpose, qr, rank, normalize, pinv, eigvals, abs, eigvecs, svd
import Plots: plot, scatter!, Animation, frame
import ForwardDiff: hessian, gradient
import HomotopyContinuation
export ConstraintVariety,
findminima,
watch,
draw,
addSamples!,
setEquationsAtp!,
#INFO: The following package is not maintained by me. Find it here: https://github.com/JuliaHomotopyContinuation/HomotopyContinuation.jl
HomotopyContinuation
#=
Equips a HomotopyContinuation.Tracker with a start Solution that can be changed on the fly
=#
mutable struct TrackerWithStartSolution
tracker
startSolution
#basepoint
function TrackerWithStartSolution(T::Tracker, startSol::Vector)
new(T,startSol)
end
end
function setStartSolution(T::TrackerWithStartSolution, startSol::Vector)
setfield!(T, :startSolution, startSol)
end
#=
An object that describes a constraint variety by giving its generating equations, coordinate variables, its dimension and its jacobian.
Additionally, it contains the system describing the Euclidian Distance Problem and samples from the variety.
=#
mutable struct ConstraintVariety
variables
equations
fullequations
jacobian
ambientdimension
dimensionofvariety
samples
implicitequations
EDTracker
# Given variables and HomotopyContinuation-based equations, sample points from the variety and return the corresponding struct
function ConstraintVariety(varz, eqnz, N::Int, d::Int, numsamples::Int)
dg = differentiate(eqnz, varz)
impliciteq = [p->eqn(varz=>p) for eqn in eqnz]
randL = nothing
randresult = nothing
Ωs = []
if numsamples > 0
randL = rand_subspace(N; codim=d)
randResult = solve(eqnz; target_subspace = randL, variables=varz, show_progress = true)
end
for _ in 1:numsamples
newΩs = solve(
eqnz,
solutions(randResult);
variables = varz,
start_subspace = randL,
target_subspace = rand_subspace(N; codim = d, real = true),
transform_result = (R,p) -> real_solutions(R),
flatten = true,
show_progress = true
)
realsols = real_solutions(newΩs)
push!(Ωs, realsols...)
end
Ωs = filter(t -> norm(t)<1e4,Ωs)
fulleqnz = eqnz
if length(eqnz) + d > N
eqnz = randn(Float64, N-d, length(eqnz))*eqnz
end
@var u[1:N]
@var λ[1:length(eqnz)]
Lagrange = sum((varz-u).^2) + sum(λ.*eqnz)
∇Lagrange = differentiate(Lagrange, vcat(varz,λ))
EDSystem = System(∇Lagrange, variables=vcat(varz,λ), parameters=u)
p0 = randn(Float64, N)
H = ParameterHomotopy(EDSystem, start_parameters = p0, target_parameters = p0)
EDTracker = TrackerWithStartSolution(Tracker(H),[])
new(varz,eqnz,fulleqnz,dg,N,d,Ωs,impliciteq,EDTracker)
end
# Given implicit equations, sample points from the corresponding variety and return the struct
function ConstraintVariety(eqnz::Function, N::Int, d::Int, numsamples::Int)
@var varz[1:N]
algeqnz = eqnz(varz)
if typeof(algeqnz) != Vector{Expression}
algeqnz = [algeqnz]
end
ConstraintVariety(varz, algeqnz, N::Int, d::Int, numsamples::Int)
end
# Implicit Equations, no sampling
function ConstraintVariety(eqnz,N::Int,d::Int)
ConstraintVariety(eqnz::Function, N::Int, d::Int, 0)
end
# HomotopyContinuation-based expressions and variables, no sanples
function ConstraintVariety(varz,eqnz,N::Int,d::Int)
ConstraintVariety(varz, eqnz, N::Int, d::Int, 0)
end
#Let the dimension be determined by the algorithm and calculate samples
function ConstraintVariety(varz,eqnz,p::Vector{Float64},numSamples::Int)
G = ConstraintVariety(varz, eqnz, length(varz), 0,numSamples)
setEquationsAtp!(G,p)
return(G)
end
#Only let the dimension be determined by the algorithm
function ConstraintVariety(varz,eqnz,p::Vector{Float64})
G = ConstraintVariety(varz, eqnz, length(varz), 0)
setEquationsAtp!(G,p)
return(G)
end
end
#=
Add Samples to an already existing ConstraintVariety
=#
function addSamples!(G::ConstraintVariety, newSamples)
setfield!(G, :samples, vcat(newSamples, G.samples))
end
#=
Add Samples to an already existing ConstraintVariety
=#
function setEquationsAtp!(G::ConstraintVariety, p; tol=1e-5)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p); atol=tol)
eqnz = G.fullequations
if length(eqnz) + (G.ambientdimension-jacobianRank) > G.ambientdimension
eqnz = randn(Float64, jacobianRank, length(eqnz))*eqnz
end
setfield!(G, :equations, eqnz)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
@var u[1:G.ambientdimension]
@var λ[1:length(eqnz)]
Lagrange = sum((G.variables-u).^2) + sum(λ.*eqnz)
∇Lagrange = differentiate(Lagrange, vcat(G.variables,λ))
EDSystem = System(∇Lagrange, variables=vcat(G.variables,λ), parameters=u)
H = ParameterHomotopy(EDSystem, start_parameters = p, target_parameters = p)
EDTracker = TrackerWithStartSolution(Tracker(H),[])
setfield!(G, :EDTracker, EDTracker)
end
#=
Compute the system that we need for the onestep and twostep method
=#
function computesystem(p, G::ConstraintVariety,
evaluateobjectivefunctiongradient::Function)
dgp = evaluate.(G.jacobian, G.variables => p)
Up,_ = qr( transpose(dgp) )
Np = Up[:, 1:(G.ambientdimension - G.dimensionofvariety)] # gives ONB for N_p(G) normal space
# we evaluate the gradient of the obj fcn at the point `p`
∇Qp = evaluateobjectivefunctiongradient(p)[2]
w = -∇Qp # direction of decreasing energy function
v = w - Np * (Np' * w) # projected gradient -∇Q(p) onto the tangent space, subtract the normal components
g = G.equations
if G.dimensionofvariety > 1 # Need more linear equations when tangent space has dim > 1
A,_ = qr( hcat(v, Np) )
A = A[:, (G.ambientdimension - G.dimensionofvariety + 1):end] # basis of the orthogonal complement of v inside T_p(G)
L = A' * G.variables - A' * p # affine linear equations through p, containing v, give curve in variety along v
u = v / norm(v)
S = u' * G.variables - u' * (p + Variable(:ε)*u) # create and use the variable ε here.
F = System( vcat(g,L,S); variables=G.variables, parameters=[Variable(:ε)])
return F
else
u = normalize(v)
S = u' * G.variables - u' * (p + Variable(:ε)*u) # create and use the variable ε here.
F = System( vcat(g,S); variables=G.variables, parameters=[Variable(:ε)])
return F
end
end
#=
If we are at a point of slow progression / singularity we blow the point up to a sphere and check the intersections (witness sets) with nearby components
for the sample with lowest energy
=#
function resolveSingularity(p, G::ConstraintVariety, Q::Function, evaluateobjectivefunctiongradient, whichstep; initialtime = Base.time(), maxseconds = 50)
if length(p)>8
q = gaussnewtonstep(G, p, 1e-3, -evaluateobjectivefunctiongradient(p)[2]; initialtime=initialtime, maxseconds=maxseconds)[1]
( Q(q) < Q(p) && return(q, true) ) || return(q, false)
end
eqn = G.fullequations
var = G.variables
d = G.dimensionofvariety
sphereAtPoint = sum((var.-p).^2)-0.0001
samples = []
try
F = System(vcat(eqn,[sphereAtPoint]))
rel = solve(F; show_progress=false)
samples = real_solutions(rel)
catch e
println("dimension -1: ", e)
end
for j in 1:d-1
try
a = rand(Float64, length(var), j)
L = a'*var-a'*p
F = System( vcat(eqn,[sphereAtPoint],L) )
append!(samples, real_solutions(solve(F; show_progress=false)))
catch e
println("dimension -$(j+1): ", e)
end
end
#TODO Alternative for too large to sample varieties.
#Random directions? Sampling via Gaussnewton? Gaussnewtonstep altogether?
minimumvalue = Q(p)
q = Base.copy(p)
for sol in samples
if Q(sol)<minimumvalue
minimumvalue = Q(sol)
q = sol
end
end
if q==p && !isempty(samples)
#In this case, the singularity is optimal in a sense
return(p,false)
else
return(q,true)
end
end
#=
We predict in the projected gradient direction and correct by using the Gauss-Newton method
=#
function gaussnewtonstep(G::ConstraintVariety, p, stepsize, v; tol=1e-8, initialtime, maxseconds)
global q = p+stepsize*v
global damping = 0.5
global qnew = q
jac = hcat([differentiate(eq, G.variables) for eq in G.fullequations]...)
while(norm(evaluate.(G.fullequations, G.variables=>q)) > tol)
J = Matrix{Float64}(evaluate.(jac, G.variables=>q))
global qnew = q .- damping*pinv(J)'*evaluate.(G.fullequations, G.variables=>q)
if norm(evaluate.(G.fullequations, G.variables=>qnew)) <= norm(evaluate.(G.fullequations, G.variables=>q))
global damping = damping*1.2
else
global damping = damping/2
end
q = qnew
if time()-initialtime > maxseconds
return p, false
end
end
return q, true
end
#=
We predict in the projected gradient direction and correct by solving a Euclidian Distance Problem
=#
function EDStep(ConstraintVariety, p, stepsize, v; homotopyMethod, tol=1e-8)
q = p+stepsize*v
if homotopyMethod=="HomotopyContinuation"
target_parameters!(ConstraintVariety.EDTracker.tracker, q)
tracker = track(ConstraintVariety.EDTracker.tracker, ConstraintVariety.EDTracker.startSolution)
result = solution(tracker)
if all(point->Base.abs(point.im)<1e-4, result)
return [point.re for point in result[1:length(p)]], true
else
return p, false
end
elseif homotopyMethod=="Newton"
currentSolution = vcat(q, ConstraintVariety.EDTracker.startSolution[length(q)+1:end])
variables = ConstraintVariety.EDTracker.tracker.homotopy.F.interpreted.system.variables
equations = evaluate(ConstraintVariety.EDTracker.tracker.homotopy.F.interpreted.system.expressions, ConstraintVariety.EDTracker.tracker.homotopy.F.interpreted.system.parameters => q)
jac = hcat([differentiate(eq, variables) for eq in equations]...)
while(norm(evaluate.(equations, variables=>currentSolution)) > tol)
J = evaluate.(jac, variables=>currentSolution)
currentSolution = currentSolution .- J \ evaluate.(equations, variables=>currentSolution)
end
return currentSolution[1:length(q)], true
else
throw(error("Homotopy Method not supported!"))
end
end
#=
Move a line along the projected gradient direction for the length stepsize and calculate the resulting point of intersection with the variety
=#
function onestep(F, p, stepsize)
solveresult = solve(F, [p]; start_parameters=[0.0], target_parameters=[stepsize],
show_progress=false)
sol = real_solutions(solveresult)
success = false
if length(sol) > 0
q = sol[1] # only tracked one solution path, thus there should only be one solution
success = true
else
q = p
end
return q, success
end
#=
Similar to onestep. However, we take an intermediate, complex step to avoid singularities
=#
function twostep(F, p, stepsize)
# we want parameter homotopy from 0.0 to stepsize, so we take two steps
# first from 0.0 to a complex number parameter, then from that parameter to stepsize.
midparam = stepsize/2 + stepsize/2*1.0im # complex number *midway* between 0 and stepsize, but off real line
solveresult = solve(F, [p]; start_parameters=[0.0 + 0.0im], target_parameters=[midparam], show_progress=false)
midsols = solutions(solveresult)
success = false
if length(midsols) > 0
midsolution = midsols[1] # only tracked one solution path, thus there should only be one solution
solveresult = solve(F, [midsolution]; start_parameters=[midparam],
target_parameters=[stepsize + 0.0im],
show_progress=false)
realsols = real_solutions(solveresult)
if length(realsols) > 0
q = realsols[1] # only tracked one solution path, thus there should only be one solution
success = true
else
q = p
end
else
q = p
end
return q, success
end
#=
Checks, whether p is a local minimum of the objective function Q w.r.t. the tangent space Tp
=#
function isMinimum(G::ConstraintVariety, Q::Function, evaluateobjectivefunctiongradient, Tp, v, p::Vector; tol=1e-4, criticaltol=1e-3)
H = hessian(Q, p)
HConstraints = [evaluate.(differentiate(differentiate(eq, G.variables), G.variables), G.variables=>p) for eq in G.fullequations]
Qalg = Q(p)+(G.variables-p)'*gradient(Q,p)+0.5*(G.variables-p)'*H*(G.variables-p) # Taylor Approximation of x, since only the Hessian is of interest anyway
@var λ[1:length(G.fullequations)]
L = Qalg+λ'*G.fullequations
∇L = differentiate(L, vcat(G.variables, λ))
gL = Matrix{Float64}(evaluate(differentiate(∇L, λ), G.variables=>p))
bL = -evaluate.(evaluate(∇L,G.variables=>p), λ=>[0 for _ in 1:length(λ)])
λ0 = map( t-> (t==NaN || t==Inf) ? 1 : t, gL\bL)
Htotal = H+λ0'*HConstraints
projH = Matrix{Float64}(Tp'*Htotal*Tp)
projEigvals = real(eigvals(projH)) #projH symmetric => all real eigenvalues
println("Eigenvalues of the projected Hessian: ", round.(1000 .* projEigvals, sigdigits=3) ./ 1000)
indices = filter(i->abs(projEigvals[i])<=tol, 1:length(projEigvals))
projEigvecs = real(eigvecs(projH))[:, indices]
projEigvecs = Tp*projEigvecs
if all(q-> q>=tol, projEigvals) && norm(v) <= criticaltol
return true
elseif any(q-> q<=-tol, projEigvals) || norm(v) > criticaltol
return false
#TODO Third derivative at x_0 at proj hessian sing. vectors not 0?!
# Else take a small step in gradient descent direction and see if the energy decreases
else
q = gaussnewtonstep(G, p, 1e-2, -evaluateobjectivefunctiongradient(p)[2]; initialtime=Base.time(), maxseconds=10)[1]
return Q(q)<Q(p)
end
end
#=
Determines, which optimization algorithm to use
=#
function stepchoice(F, ConstraintVariety, whichstep, stepsize, p, v; initialtime, maxseconds, homotopyMethod)
if(whichstep=="twostep")
return(twostep(F, p, stepsize))
elseif whichstep=="onestep"
return(onestep(F, p, stepsize))
elseif whichstep=="gaussnewtonstep"
return(gaussnewtonstep(ConstraintVariety, p, stepsize, v; initialtime, maxseconds))
elseif whichstep=="EDStep"
return(EDStep(ConstraintVariety, p, stepsize, v; homotopyMethod))
else
throw(error("A step method needs to be provided!"))
end
end
# WARNING This one is worse than backtracking_linesearch
function alternative_backtracking_linesearch(Q::Function, F::System, G::ConstraintVariety, evaluateobjectivefunctiongradient::Function, p0::Vector, stepsize::Float64; maxstepsize=100.0, r=1e-4, τ=0.7, whichstep="EDStep", initialtime, maxseconds, homotopyMethod)
α=Base.copy(stepsize)
p=Base.copy(p0)
Basenormal, _, basegradient, _ = get_NTv(p0, G, evaluateobjectivefunctiongradient)
if whichstep=="EDStep" || homotopyMethod=="Newton"
q0 = p+1e-3*Basenormal[:,1]
start_parameters!(G.EDTracker.tracker, q0)
A = evaluate.(differentiate(G.EDTracker.tracker.homotopy.F.interpreted.system.expressions, G.EDTracker.tracker.homotopy.F.interpreted.system.variables[length(p)+1:end]), G.variables => p)
λ0 = A\(-evaluate.(evaluate.(evaluate.(G.EDTracker.tracker.homotopy.F.interpreted.system.expressions, G.EDTracker.tracker.homotopy.F.interpreted.system.variables[length(p)+1:end] => [0 for _ in length(p)+1:length(G.EDTracker.tracker.homotopy.F.interpreted.system.variables)]), G.variables => p), G.EDTracker.tracker.homotopy.F.interpreted.system.parameters=>q0))
setStartSolution(G.EDTracker, vcat(p,λ0))
end
while(true)
q, success = stepchoice(F, G, whichstep, α, p0, basegradient; initialtime, maxseconds, homotopyMethod)
success ? p=q : nothing
_, Tq, vq1, vq2 = get_NTv(p, G, evaluateobjectivefunctiongradient)
# Proceed until the Wolfe condition is satisfied or the stepsize becomes too small. First we quickly find a lower bound, then we gradually increase this lower-bound
if (Q(p0)-Q(p) >= r*α*Base.abs(basegradient'*evaluateobjectivefunctiongradient(p0)[1]) && vq2'*basegradient >= 0 && success)
return q, Tq, vq1, vq2, success, α
elseif α<1e-6
return(q, Tq, vq1, vq2, false, stepsize)
else
α=τ*α
end
end
end
#=
Use line search with the strong Wolfe condition to find the optimal step length.
This particular method can be found in Nocedal & Wright: Numerical Optimization
=#
function backtracking_linesearch(Q::Function, F::System, G::ConstraintVariety, evaluateobjectivefunctiongradient::Function, p0::Vector, stepsize::Float64; whichstep="EDStep", maxstepsize=100.0, initialtime, maxseconds, homotopyMethod="HomotopyContinuation", r=1e-3, s=0.8)
Basenormal, _, basegradient, _ = get_NTv(p0, G, evaluateobjectivefunctiongradient)
α = [0, stepsize]
p = Base.copy(p0)
if whichstep=="EDStep" || homotopyMethod=="Newton"
q0 = p+1e-4*Basenormal[:,1]
start_parameters!(G.EDTracker.tracker, q0)
A = evaluate.(differentiate(G.EDTracker.tracker.homotopy.F.interpreted.system.expressions, G.EDTracker.tracker.homotopy.F.interpreted.system.variables[length(p)+1:end]), G.variables => p)
λ0 = A\-evaluate(G.EDTracker.tracker.homotopy.F.interpreted.system.expressions, vcat(G.EDTracker.tracker.homotopy.F.interpreted.system.variables, G.EDTracker.tracker.homotopy.F.interpreted.system.parameters) => vcat(p, [0 for _ in length(p)+1:length(G.EDTracker.tracker.homotopy.F.interpreted.system.variables)], q0))
setStartSolution(G.EDTracker, vcat(p, λ0))
end
print("α: ")
while true
print(round(α[end], digits=3), ", ")
q, success = stepchoice(F, G, whichstep, α[end], p0, basegradient; initialtime, maxseconds, homotopyMethod)
if time()-initialtime > maxseconds
_, Tq, vq1, vq2 = get_NTv(q, G, evaluateobjectivefunctiongradient)
return q, Tq, vq1, vq2, success, α[end]
end
_, Tq, vq1, vq2 = get_NTv(q, G, evaluateobjectivefunctiongradient)
if ( ( Q(q) > Q(p0) + r*α[end]*basegradient'*basegradient || (Q(q) > Q(p0) && q!=p0) ) && success)
helper = zoom(α[end-1], α[end], Q, evaluateobjectivefunctiongradient, F, G, whichstep, p0, basegradient, r, s; initialtime, maxseconds, homotopyMethod)
_, Tq, vq1, vq2 = get_NTv(helper[1], G, evaluateobjectivefunctiongradient)
return helper[1], Tq, vq1, vq2, helper[2], helper[end]
end
if ( abs(basegradient'*vq2) <= s*abs(basegradient'*basegradient) ) && success
return q, Tq, vq1, vq2, success, α[end]
end
if basegradient'*vq2 <= 0 && success
helper = zoom(α[end], α[end-1], Q, evaluateobjectivefunctiongradient, F, G, whichstep, p0, basegradient, r, s; initialtime, maxseconds, homotopyMethod)
_, Tq, vq1, vq2 = get_NTv(helper[1], G, evaluateobjectivefunctiongradient)
return helper[1], Tq, vq1, vq2, helper[2], helper[end]
end
if (success)
push!(α, 2*α[end])
p = q
else
_, Tp, vp1, vp2 = get_NTv(p, G, evaluateobjectivefunctiongradient)
return p, Tp, vp1, vp2, success, α[end]
end
deleteat!(α, 1)
if α[end] > maxstepsize
return q, Tq, vq1, vq2, success, maxstepsize
end
end
end
#=
Zoom in on the step lengths between αlo and αhi to find the optimal step size here. This is part of the backtracking line search
=#
function zoom(αlo, αhi, Q, evaluateobjectivefunctiongradient, F, G, whichstep, p0, basegradient, r, s; initialtime, maxseconds, homotopyMethod)
qlo, suclo = stepchoice(F, G, whichstep, αlo, p0, basegradient; initialtime, maxseconds, homotopyMethod)
# To not get stuck in the iteration, we use a for loop instead of a while loop
# TODO Add a more meaningful stopping criterion
for _ in 1:8
global α = 0.5*(αlo+αhi)
print(round(α, digits=3), ", ")
#println("α: ", α)
global q, success = stepchoice(F, G, whichstep, α, p0, basegradient; initialtime, maxseconds, homotopyMethod)
_, _, _, vq2 = get_NTv(q, G, evaluateobjectivefunctiongradient)
if !success || time()-initialtime > maxseconds
return q, success, α
end
if Q(q) > Q(p0) + r*α*basegradient'*basegradient || Q(q) >= Q(qlo)
αhi = α
else
if Base.abs(basegradient'*vq2) <= Base.abs(basegradient'*basegradient)*s
return q, success, α
end
if basegradient'*vq2*(αhi-αlo) >= 0
αhi = αlo
end
αlo = α
qlo, suclo = q, success
end
end
return q, success, α
end
#=
Get the tangent and normal space of a ConstraintVariety at a point q
=#
function get_NTv(q, G::ConstraintVariety,
evaluateobjectivefunctiongradient::Function)
dgq = evaluate.(G.jacobian, G.variables => q)
Qq,_ = qr(Matrix{Float64}(transpose(dgq)))
#index = count(p->p>1e-8, S)
Nq = Qq[:, 1:(G.ambientdimension - G.dimensionofvariety)] # O.N.B. for the normal space at q
Tq = Qq[:, (G.ambientdimension - G.dimensionofvariety + 1):end] # O.N.B. for tangent space at q
# we evaluate the gradient of the obj fcn at the point `q`
∇Qq1, ∇Qq2 = evaluateobjectivefunctiongradient(q)
w1, w2 = -∇Qq1, -∇Qq2 # direction of decreasing energy function
vq1 = w1 - Nq * (Nq' * w1) # projected gradient -∇Q(p) onto the tangent space, subtract the normal components
vq2 = w2 - Nq * (Nq' * w2)
return Nq, Tq, vq1, vq2
end
#=
Parallel transport the vector vj from the tangent space Tj to the tangent space Ti
=#
function paralleltransport(vj, Tj, Ti)
# transport vj ∈ Tj to become a vector ϕvj ∈ Ti
# cols(Tj) give ONB for home tangent space, cols(Ti) give ONB for target tangent space
U,_,Vt = svd( Ti' * Tj )
Oij = U * Vt # closest orthogonal matrix to the matrix (Ti' * Tj) comes from svd, remove \Sigma
ϕvj = Ti * Oij * (Tj' * vj)
return ϕvj
end
#=
An object that contains the iteration's information like norms of the projected gradient, step sizes and search directions
=#
struct LocalStepsResult
initialpoint
initialstepsize
allcomputedpoints
allcomputedprojectedgradientvectors
allcomputedprojectedgradientvectornorms
newsuggestedstartpoint
newsuggestedstepsize
converged
timesturned
valleysfound
function LocalStepsResult(p,ε0,qs,vs,ns,newp,newε0,converged,timesturned,valleysfound)
new(p,ε0,qs,vs,ns,newp,newε0,converged,timesturned,valleysfound)
end
end
#= Take `maxsteps` steps to try and converge to an optimum. In each step, we use backtracking linesearch
to determine the optimal step size to go along the search direction
WARNING This is redundant and can be merged with findminima
=#
function takelocalsteps(p, ε0, tolerance, G::ConstraintVariety,
objectiveFunction::Function,
evaluateobjectivefunctiongradient::Function;
maxsteps, maxstepsize=2, decreasefactor=2.2, initialtime, maxseconds, whichstep="EDStep", homotopyMethod="HomotopyContinuation")
timesturned, valleysfound, F = 0, 0, System([G.variables[1]])
_, Tp, vp1, vp2 = get_NTv(p, G, evaluateobjectivefunctiongradient)
Ts = [Tp] # normal spaces and tangent spaces, columns of Np and Tp are orthonormal bases
qs, vs, ns = [p], [vp2], [norm(vp1)] # qs=new points on G, vs=projected gradients, ns=norms of projected gradients
stepsize = Base.copy(ε0)
for _ in 1:maxsteps
if Base.time() - initialtime > maxseconds
break;
end
if whichstep=="onestep" || whichstep=="twostep"
F = computesystem(qs[end], G, evaluateobjectivefunctiongradient)
end
q, Tq, vq1, vq2, success, stepsize = backtracking_linesearch(objectiveFunction, F, G, evaluateobjectivefunctiongradient, qs[end], Float64(stepsize); whichstep, maxstepsize, initialtime, maxseconds, homotopyMethod)
print("\n")
push!(qs, q)
push!(Ts, Tq)
length(Ts)>3 ? deleteat!(Ts, 1) : nothing
push!(ns, norm(vq1))
println("ns: ", ns[end])
push!(vs, vq2)
length(vs)>3 ? deleteat!(vs, 1) : nothing
if ns[end] < tolerance
return LocalStepsResult(p,ε0,qs,vs,ns,q,stepsize,true,timesturned,valleysfound)
elseif ((ns[end] - ns[end-1]) > 0.0)
if length(ns) > 2 && ((ns[end-1] - ns[end-2]) < 0.0)
# projected norms were decreasing, but started increasing!
# check parallel transport dot product to see if we should slow down
valleysfound += 1
ϕvj = paralleltransport(vs[end], Ts[end], Ts[end-2])
if ((vs[end-2]' * ϕvj) < 0.0)
# we think there is a critical point we skipped past! slow down!
return LocalStepsResult(p,ε0,qs,vs,ns,qs[end-2],stepsize/decreasefactor,false,timesturned+1,valleysfound)
end
end
end
# The next (initial) stepsize is determined by the previous step and how much the energy function changed - in accordance with RieOpt.
stepsize = Base.minimum([ Base.maximum([ success ? stepsize*vs[end-1]'*evaluateobjectivefunctiongradient(qs[end-1])[2]/(vs[end]'*evaluateobjectivefunctiongradient(qs[end])[2]) : 0.1*stepsize, 1e-4]), maxstepsize])
end
return LocalStepsResult(p,ε0,qs,vs,ns,qs[end],stepsize,false,timesturned,valleysfound)
end
#=
Output object of the method `findminima`
=#
struct OptimizationResult
computedpoints
initialpoint
initialstepsize
tolerance
converged
lastlocalstepsresult
constraintvariety
objectivefunction
lastpointisminimum
function OptimizationResult(ps,p0,ε0,tolerance,converged,lastLSResult,G,Q,lastpointisminimum)
new(ps,p0,ε0,tolerance,converged,lastLSResult,G,Q,lastpointisminimum)
end
end
#=
The main function of this package. Given an initial point, a tolerance, an objective function and a constraint variety,
we try to find the objective function's closest local minimum to the initial guess.
=#
function findminima(p0, tolerance,
G::ConstraintVariety,
objectiveFunction::Function;
maxseconds=100, maxlocalsteps=1, initialstepsize=1.0, whichstep="EDStep", initialtime = Base.time(), stepdirection = "gradientdescent", homotopyMethod = "HomotopyContinuation")
#TODO Rework minimality: We are not necessarily at a minimality, if resolveSingularity does not find any better point. => first setequations, then ismin
#setEquationsAtp!(G,p0)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p0); atol=tolerance^1.5)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
p = copy(p0) # initialize before updating `p` below
ps = [p0] # record the *main steps* from p0, newp, newp, ... until converged
jacobianG = evaluate.(differentiate(G.fullequations, G.variables), G.variables=>p0)
jacRank = rank(jacobianG; atol=tolerance^1.5)
evaluateobjectivefunctiongradient = x -> (gradient(objectiveFunction, x), gradient(objectiveFunction, x))
if stepdirection == "newtonstep"
evaluateobjectivefunctiongradient = x -> (gradient(objectiveFunction, x), hessian(objectiveFunction, x) \ gradient(objectiveFunction, x))
end
if jacRank==0
p, optimality = resolveSingularity(ps[end], G, objectiveFunction, evaluateobjectivefunctiongradient, whichstep; initialtime=initialtime, maxseconds=maxseconds)
setEquationsAtp!(G, p; tol=tolerance^2)
jacobianG = evaluate(differentiate(G.fullequations, G.variables), G.variables=>p0)
jacRank = rank(jacobianG; atol=tolerance^1.5)
end
_, Tq, v1, v2 = get_NTv(p, G, evaluateobjectivefunctiongradient) # Get the projected gradient at the first point
# initialize stepsize. Different to RieOpt! Logic: large projected gradient=>far away, large stepsize is admissible.
ε0 = 2*initialstepsize
lastLSR = LocalStepsResult(p,ε0,[],[],[],p,ε0,false,0,0)
while (Base.time() - initialtime) <= maxseconds
# update LSR, only store the *last local run*
lastLSR = takelocalsteps(p, ε0, tolerance, G, objectiveFunction, evaluateobjectivefunctiongradient; maxsteps=maxlocalsteps, maxstepsize=100., initialtime=initialtime, maxseconds=maxseconds, whichstep=whichstep, homotopyMethod=homotopyMethod)
push!(ps, lastLSR.allcomputedpoints[end])
jacobian = evaluate.(differentiate(G.fullequations, G.variables), G.variables=>lastLSR.newsuggestedstartpoint)
jR = rank(jacobian; atol=tolerance^2)
if lastLSR.converged
# if we are in a singularity do a few steps again - if we revert back to the singularity, it is optiomal
if jR != jacRank || norm(ps[end-1]-ps[end]) < tolerance^2
#setEquationsAtp!(G, ps[end]; tol=tolerance^1.5)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p); atol=tolerance^2)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
_, Tq, v1, _ = get_NTv(ps[end], G, evaluateobjectivefunctiongradient)
optimality = isMinimum(G, objectiveFunction, evaluateobjectivefunctiongradient, Tq, v1, ps[end]; criticaltol=tolerance)
if optimality
return OptimizationResult(ps,p0,initialstepsize,tolerance,true,lastLSR,G,evaluateobjectivefunctiongradient,optimality)
end
println("Resolving")
p, foundsomething = resolveSingularity(lastLSR.allcomputedpoints[end], G, objectiveFunction, evaluateobjectivefunctiongradient, whichstep; initialtime=initialtime, maxseconds=maxseconds)
#setEquationsAtp!(G, p; tol=tolerance^1.5)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p); atol=tolerance^2)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
if foundsomething
optRes = findminima(p, tolerance, G, objectiveFunction; maxseconds = maxseconds, maxlocalsteps=maxlocalsteps, initialstepsize=initialstepsize, whichstep=whichstep, initialtime=initialtime, homotopyMethod=homotopyMethod)
return OptimizationResult(vcat(ps, optRes.computedpoints),p0,lastLSR.newsuggestedstepsize,tolerance,optRes.lastlocalstepsresult.converged,optRes.lastlocalstepsresult,G,evaluateobjectivefunctiongradient,optRes.lastpointisminimum)
end
return OptimizationResult(ps,p0,initialstepsize,tolerance,true,lastLSR,G,evaluateobjectivefunctiongradient,optimality)
else
#setEquationsAtp!(G, ps[end]; tol=tolerance^1.5)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p); atol=tolerance^2)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
_, Tq, v1, _ = get_NTv(ps[end], G, evaluateobjectivefunctiongradient)
optimality = isMinimum(G, objectiveFunction, evaluateobjectivefunctiongradient, Tq, v1, ps[end]; criticaltol=tolerance)
if !optimality
optRes = findminima(ps[end], tolerance, G, objectiveFunction; maxseconds = maxseconds, maxlocalsteps=maxlocalsteps, initialstepsize=initialstepsize, whichstep=whichstep, initialtime=initialtime)
return OptimizationResult(vcat(ps, optRes.computedpoints), p0,lastLSR.newsuggestedstepsize,tolerance,optRes.lastlocalstepsresult.converged,optRes.lastlocalstepsresult,G,evaluateobjectivefunctiongradient,optRes.lastpointisminimum)
end
return OptimizationResult(ps,p0,initialstepsize,tolerance,true,lastLSR,G,evaluateobjectivefunctiongradient,optimality)
end
else
# If we are in a point of slow progress or jacobian rank change, we search the neighborhood
if jR != jacRank || norm(ps[end-1]-ps[end]) < tolerance^2
#setEquationsAtp!(G, ps[end]; tol=tolerance^1.5)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p); atol=tolerance^2)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
_, Tq, v, _ = get_NTv(ps[end], G, evaluateobjectivefunctiongradient)
optimality = isMinimum(G, objectiveFunction, evaluateobjectivefunctiongradient, Tq, v1, ps[end]; criticaltol=tolerance)
if optimality
return OptimizationResult(ps,p0,initialstepsize,tolerance,true,lastLSR,G,evaluateobjectivefunctiongradient,optimality)
end
println("Resolving")
p, foundsomething = resolveSingularity(lastLSR.allcomputedpoints[end], G, objectiveFunction, evaluateobjectivefunctiongradient, whichstep; initialtime=initialtime, maxseconds=maxseconds)
display(norm(p-ps[end]))
#setEquationsAtp!(G, p; tol=tolerance^1.5)
jacobianRank = rank(evaluate.(G.jacobian, G.variables=>p); atol=tolerance^2)
setfield!(G, :dimensionofvariety, (G.ambientdimension-jacobianRank))
if foundsomething
maxseconds = maxseconds
optRes = findminima(p, tolerance, G, objectiveFunction; maxseconds = maxseconds, maxlocalsteps=maxlocalsteps, initialstepsize=initialstepsize, whichstep=whichstep, initialtime=initialtime, homotopyMethod=homotopyMethod)
return OptimizationResult(vcat(ps, optRes.computedpoints),p0,lastLSR.newsuggestedstepsize,tolerance,optRes.lastlocalstepsresult.converged,optRes.lastlocalstepsresult,G,evaluateobjectivefunctiongradient,optRes.lastpointisminimum)
end
else
p = lastLSR.newsuggestedstartpoint
end
jacobian = evaluate.(differentiate(G.equations, G.variables), G.variables=>p)
jacRank = rank(jacobian; atol=tolerance^1.5)
ε0 = lastLSR.newsuggestedstepsize # update and try again!
end
end
display("We ran out of time... Try setting `maxseconds` to a larger value than $(maxseconds)")
p, optimality = resolveSingularity(ps[end], G, objectiveFunction, evaluateobjectivefunctiongradient, whichstep; initialtime=initialtime, maxseconds=maxseconds)
return OptimizationResult(ps,p0,ε0,tolerance,lastLSR.converged,lastLSR,G,evaluateobjectivefunctiongradient,optimality)
end
# Below are functions `watch` and `draw`
# to visualize low-dimensional examples
function watch(result::OptimizationResult; totalseconds=5.0, fullx = [-1.5,1.5], fully = [-1.5,1.5], fullz = [-1.5,1.5], kwargs...)
ps = result.computedpoints
samples = result.constraintvariety.samples
if !isempty(samples)
mediannorm = (sort([norm(p) for p in samples]))[Int(floor(samples/2))]
samples = filter(x -> norm(x) < 2*mediannorm+0.5, samples)
end
initplt = plot() # initialize
M = length(ps)
framespersecond = M / totalseconds
if framespersecond > 45
framespersecond = 45
end
startingtime = Base.time()
dim = length(ps[1])
anim = Animation()
if dim == 2
if !isempty(samples)
fullx = [minimum([q[1] for q in vcat(samples, ps)]) - 0.05, maximum([q[1] for q in vcat(samples, ps)]) + 0.05]
fully = [minimum([q[2] for q in vcat(samples, ps)]) - 0.05, maximum([q[2] for q in vcat(samples, ps)]) + 0.05]
end
g1 = result.constraintvariety.equations[1] # should only be a curve in ambient R^2
initplt = implicit_plot(g1, xlims=fullx, ylims=fully, legend=false)
initplt = scatter!(initplt, [ps[end][1]], [ps[end][2]], legend=false, markersize=5, color=:red, xlims=fullx, ylims=fully)
frame(anim)
for p in ps
# BELOW: only plot next point, delete older points during animation
# plt = scatter!(initplt, [p[1]], [p[2]], legend=false, color=:black, xlims=fullx, ylims=fully)
# BELOW: keep old points during animation.
initplt = scatter!(initplt, [p[1]], [p[2]], legend=false, markersize=3.5, color=:black, xlims=fullx, ylims=fully)
frame(anim)
end
return gif(anim, "watch$startingtime.gif", fps=framespersecond)
elseif dim == 3
if !isempty(samples)
fullx = [minimum([q[1] for q in vcat(samples, ps)]) - 0.05, maximum([q[1] for q in vcat(samples, ps)]) + 0.05]
fully = [minimum([q[2] for q in vcat(samples, ps)]) - 0.05, maximum([q[2] for q in vcat(samples, ps)]) + 0.05]
fullz = [minimum([q[3] for q in vcat(samples, ps)]) - 0.05, maximum([q[3] for q in vcat(samples, ps)]) + 0.05]
end
g1 = result.constraintvariety.implicitequations[1]
#=
if(length(result.constraintvariety.implicitequations)>1)
# should be space curve
g2 = result.constraintvariety.implicitequations[2]
initplt = plot_implicit_curve(g1,g2; xlims = (fullx[1], fullx[2]), ylims = (fully[1], fully[2]), zlims = (fullz[1], fullz[2]), kwargs...)
else
#should be surface
initplt = plot_implicit_surface(g1; xlims = (fullx[1], fullx[2]), ylims = (fully[1], fully[2]), zlims = (fullz[1], fullz[2]), kwargs...)
end
pointsys=[GLMakiePlottingLibrary.Point3f0(p) for p in ps]
GLMakiePlottingLibrary.scatter!(initplt, pointsys[end];
color=:red, markersize=40.0)
GLMakiePlottingLibrary.record(initplt, "watch$startingtime.gif", 1:length(pointsys); framerate = Int64(round(framespersecond))) do i
GLMakiePlottingLibrary.scatter!(initplt, pointsys[i];
color=:black, markersize=30.0)
end
=#
return(initplt)
end
end
function draw(result::OptimizationResult; kwargs...)
dim = length(result.computedpoints[1]) # dimension of the ambient space
ps = result.computedpoints
samples = result.constraintvariety.samples
mediannorm = Statistics.median([LinearAlgebra.norm(p) for p in samples])
# TODO centroid approach rather than mediannorm and then difference from centroid.
samples = filter(x -> LinearAlgebra.norm(x) < 2*mediannorm+0.5, samples)
if dim == 2
fullx = [minimum([q[1] for q in vcat(samples, ps)]) - 0.05, maximum([q[1] for q in vcat(samples, ps)]) + 0.05]
fully = [minimum([q[2] for q in vcat(samples, ps)]) - 0.05, maximum([q[2] for q in vcat(samples, ps)]) + 0.05]
g1 = result.constraintvariety.equations[1] # should only be a curve in ambient R^2
plt1 = plot() #implicit_plot(g1, xlims=fullx, ylims=fully, legend=false)
#f(x,y) = (x^4 + y^4 - 1) * (x^2 + y^2 - 2) + x^5 * y # replace this with `curve`
#plt1 = implicit_plot(curve; xlims=(-2,2), ylims=(-2,2), legend=false)
#plt2 = implicit_plot(curve; xlims=(-2,2), ylims=(-2,2), legend=false)
localqs = result.lastlocalstepsresult.allcomputedpoints
zoomx = [minimum([q[1] for q in localqs]) - 0.05, maximum([q[1] for q in localqs]) + 0.05]
zoomy = [minimum([q[2] for q in localqs]) - 0.05, maximum([q[2] for q in localqs]) + 0.05]
plt2 = plot()#implicit_plot(g1, xlims=zoomx, ylims=zoomy, legend=false)
for q in ps
plt1 = scatter!(plt1, [q[1]], [q[2]], legend=false, color=:black, xlims=fullx, ylims=fully)
end
for q in localqs
plt2 = scatter!(plt2, [q[1]], [q[2]], legend=false, color=:blue, xlims=zoomx, ylims=zoomy)
end
vnorms = result.lastlocalstepsresult.allcomputedprojectedgradientvectornorms
pltvnorms = plot(vnorms, legend=false, title="norm(v) for last local steps")
plt = plot(plt1,plt2,pltvnorms, layout=(1,3), size=(900,300) )
return plt
elseif dim == 3
fullx = [minimum([q[1] for q in vcat(samples, ps)]) - 0.05, maximum([q[1] for q in vcat(samples, ps)]) + 0.05]
fully = [minimum([q[2] for q in vcat(samples, ps)]) - 0.05, maximum([q[2] for q in vcat(samples, ps)]) + 0.05]
fullz = [minimum([q[3] for q in vcat(samples, ps)]) - 0.05, maximum([q[3] for q in vcat(samples, ps)]) + 0.05]
localqs = result.lastlocalstepsresult.allcomputedpoints
zoomx = [minimum([q[1] for q in ps]) - 0.05, maximum([q[1] for q in ps]) + 0.05]
zoomy = [minimum([q[2] for q in ps]) - 0.05, maximum([q[2] for q in ps]) + 0.05]
zoomz = [minimum([q[3] for q in ps]) - 0.05, maximum([q[3] for q in ps]) + 0.05]
#=
fig = GLMakiePlottingLibrary.Figure(resolution = (1450, 550))
ax1 = fig[1, 1] = GLMakiePlottingLibrary.AbstractPlotting.MakieLayout.LScene(fig, width=500, height=500, camera = GLMakiePlottingLibrary.cam3d!, raw = false, limits=GLMakiePlottingLibrary.FRect((fullx[1], fully[1], fullz[1]), (fullx[2]-fullx[1], fully[2]-fully[1], fullz[2]-fullz[1])))
ax2 = fig[1, 2] = GLMakiePlottingLibrary.AbstractPlotting.MakieLayout.LScene(fig, width=500, height=500, camera = GLMakiePlottingLibrary.cam3d!, raw = false, limits=GLMakiePlottingLibrary.FRect((zoomx[1], zoomy[1], zoomz[1]), (zoomx[2]-zoomx[1], zoomy[2]-zoomy[1], zoomz[2]-zoomz[1])))
ax3 = fig[1, 3] = GLMakiePlottingLibrary.AbstractPlotting.MakieLayout.Axis(fig, width=300, height=450, title="norm(v) for last local steps")
g1 = result.constraintvariety.implicitequations[1]
if(length(result.constraintvariety.implicitequations)>1)
# should be space curve
g2 = result.constraintvariety.implicitequations[2]
plot_implicit_curve!(ax1,g1,g2; xlims=(fullx[1],fullx[2]), ylims=(fully[1],fully[2]), zlims=(fullz[1],fullz[2]), kwargs...)
plot_implicit_curve!(ax2,g1,g2; xlims=(zoomx[1],zoomx[2]), ylims=(zoomy[1],zoomy[2]), zlims=(zoomz[1],zoomz[2]), kwargs...)
else
plot_implicit_surface!(ax1,g1; xlims=(fullx[1],fullx[2]), ylims=(fully[1],fully[2]), zlims=(fullz[1],fullz[2]), kwargs...)
plot_implicit_surface!(ax2,g1; xlims=(zoomx[1],zoomx[2]), ylims=(zoomy[1],zoomy[2]), zlims=(zoomz[1],zoomz[2]), kwargs...)
end
for q in ps
GLMakiePlottingLibrary.scatter!(ax1, GLMakiePlottingLibrary.Point3f0(q);
legend=false, color=:black, markersize=15)
GLMakiePlottingLibrary.scatter!(ax2, GLMakiePlottingLibrary.Point3f0(q);
legend=false, color=:black)
end
vnorms = result.lastlocalstepsresult.allcomputedprojectedgradientvectornorms
GLMakiePlottingLibrary.plot!(ax3,vnorms; legend=false)
return fig
=#
end
end
end
| HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | code | 996 | using HomotopyContinuation
@testset "sextic Test" begin
@var x y
V = HomotopyOpt.ConstraintVariety([x,y], [(x^4 + y^4 - 1) * (x^2 + y^2 - 2) + x^5 * y], 2, 1, 100);
p0 = V.samples[1]
objective(x) = sin(x[1])+cos(x[2])+1
println("gaussnewtonstep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=100, whichstep="gaussnewtonstep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
println("EDStep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=100, whichstep="EDStep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
println("twostep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=100, whichstep="twostep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
end
| HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | code | 1934 | using HomotopyContinuation
@testset "whitney umbrella" begin
@var x y z
V = HomotopyOpt.ConstraintVariety([x,y,z], [x^2-y^2*z], 3, 2, 100);
p0 = V.samples[1]
objective(x) = sin(x[1])+cos(x[2])+cos(sin(x[3]))
println("gaussnewtonstep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=120, whichstep="gaussnewtonstep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
println("EDStep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=120, whichstep="EDStep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
println("twostep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=120, whichstep="twostep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
end
@testset "space circle Test" begin
@var x y z
V = HomotopyOpt.ConstraintVariety([x,y,z], [x^2+y^2+z^2-1, z], 3, 1, 100);
p0 = V.samples[1]
objective(x) = exp(x[1]+x[2]+x[3])
println("gaussnewtonstep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=120, whichstep="gaussnewtonstep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
println("EDStep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=120, whichstep="EDStep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
println("twostep")
@time resultminimum = HomotopyOpt.findminima(p0, 1e-4, V, objective; maxseconds=120, whichstep="twostep", initialstepsize=0.5);
@test(resultminimum.converged==true)
@test(resultminimum.lastpointisminimum==true)
end
| HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | code | 5407 | include("./HomotopyOpt.jl/src/HomotopyOpt.jl")
using HomotopyContinuation
println("Twisted Cubic Test")
@var y[1:3] l[1:2]
L = y[1]^2+(y[2]+1)^2+(y[3]-1)^2 + l'*[y[1]^2-y[2], y[1]^3-y[3]]
dL = HomotopyContinuation.differentiate(L, vcat(y,l))
sols=HomotopyContinuation.real_solutions(HomotopyContinuation.solve(dL))
display(sols)
f1 = x->[x[1]^2-x[2], x[1]^3-x[3]]
G = HomotopyOpt.ConstraintVariety(f1,3,1,100)
norm = t->sqrt(t[1]^2+t[2]^2+t[3]^2)
G.samples = filter(t->norm(t)<1000, G.samples)
objective = x->x[1]^2+(x[2]+1)^2+(x[3]-1)^2
abc = HomotopyOpt.findminima([1.,-1,1], 1e-3, G, objective; homotopyMethod = "Newton")
#HomotopyOpt.findminima([1.,-1,1], 1e-3, G, objective; homotopyMethod = "HomotopyContinuation")
global convergedPaths = 0
global localSteps = 0
time1 = Base.time()
for pt in G.samples
res = HomotopyOpt.findminima(pt, 1e-3, G, objective; maxseconds=10, maxlocalsteps=1, homotopyMethod = "Newton")
global convergedPaths = res.converged ? convergedPaths+1 : convergedPaths
global localSteps = localSteps + length(res.computedpoints)
end
println("Newton... ", "Average time: ",(Base.time()-time1)/length(G.samples), "s, ", "% converged: ", 100*convergedPaths/length(G.samples), ", Average local steps: ", localSteps/length(G.samples))
global convergedPaths = 0
global localSteps = 0
time2 = Base.time()
for pt in G.samples
res = HomotopyOpt.findminima(pt, 1e-3, G, objective; maxseconds=10, maxlocalsteps=1, homotopyMethod = "HomotopyContinuation")
global convergedPaths = res.converged ? convergedPaths+1 : convergedPaths
global localSteps = localSteps + length(res.computedpoints)
end
println("HomotopyContinuation... ", "Average time: ",(Base.time()-time2)/length(G.samples), "s, ", "% converged: ", 100*convergedPaths/length(G.samples), ", Average local steps: ", localSteps/length(G.samples))
println(" ")
println("Planar Sextic Test")
@var y[1:2] l
L = (y[1]-0.5)^2+(y[2]-2)^2 + l*((y[1]^4+y[2]^4-1)*(y[1]^2+y[2]^2-2)+y[1]^5*y[2])
dL = HomotopyContinuation.differentiate(L, vcat(y,l))
sols=HomotopyContinuation.real_solutions(HomotopyContinuation.solve(dL))
#display(sols)
f1 = x->[((x[1]^4+x[2]^4-1)*(x[1]^2+x[2]^2-2)+x[1]^5*x[2])]
G = HomotopyOpt.ConstraintVariety(f1,2,1,100)
norm = t->sqrt(t[1]^2+t[2]^2)
G.samples = filter(t->norm(t)<1000, G.samples)
objective = x->(x[1]-0.5)^2+(x[2]-2)^2
abc = HomotopyOpt.findminima([0.,1], 1e-3, G, objective; homotopyMethod = "Newton")
#HomotopyOpt.findminima([1.,-1,1], 1e-3, G, objective; homotopyMethod = "HomotopyContinuation")
global convergedPaths = 0
global localSteps = 0
time1 = Base.time()
for pt in G.samples
res = HomotopyOpt.findminima(pt, 1e-3, G, objective; maxseconds=10, maxlocalsteps=1, homotopyMethod = "Newton")
global convergedPaths = res.converged ? convergedPaths+1 : convergedPaths
global localSteps = localSteps + length(res.computedpoints)
end
println("Newton... ", "Average time: ",(Base.time()-time1)/length(G.samples), "s, ", "% converged: ", 100*convergedPaths/length(G.samples), ", Average local steps: ", localSteps/length(G.samples))
global convergedPaths = 0
global localSteps = 0
time2 = Base.time()
for pt in G.samples
res = HomotopyOpt.findminima(pt, 1e-3, G, objective; maxseconds=10, maxlocalsteps=1, homotopyMethod = "HomotopyContinuation")
global convergedPaths = res.converged ? convergedPaths+1 : convergedPaths
global localSteps = localSteps + length(res.computedpoints)
end
println("HomotopyContinuation... ", "Average time: ",(Base.time()-time2)/length(G.samples), "s, ", "% converged: ", 100*convergedPaths/length(G.samples), ", Average local steps: ", localSteps/length(G.samples))
println(" ")
println("Torus Test")
@var y[1:3] l
R1,R2=2,1
L = (y[1]-2)^2+y[2]^2+(y[3]-2)^2 + l*((y[1]^2+y[2]^2+y[3]^2-R1^2-R2^2)^2/(4*R1^2)+y[3]^2-R2^2)
dL = HomotopyContinuation.differentiate(L, vcat(y,l))
sols=HomotopyContinuation.real_solutions(HomotopyContinuation.solve(dL))
f1 = x->[(x[1]^2+x[2]^2+x[3]^2-R1^2-R2^2)^2/(4*R1^2)+x[3]^2-R2^2]
G = HomotopyOpt.ConstraintVariety(f1,3,2,100)
norm = t->sqrt(t[1]^2+t[2]^2+t[3]^2)
G.samples = filter(t->norm(t)<1000, G.samples)
objective = x->(x[1]-2)^2+x[2]^2+(x[3]-2)^2
abc = HomotopyOpt.findminima([-2.,0,1], 1e-3, G, objective; homotopyMethod = "Newton")
global convergedPaths = 0
global localSteps = 0
time1 = Base.time()
for pt in G.samples
res = HomotopyOpt.findminima(pt, 1e-3, G, objective; maxseconds=10, maxlocalsteps=1, homotopyMethod = "Newton")
global convergedPaths = res.converged ? convergedPaths+1 : convergedPaths
global localSteps = localSteps + length(res.computedpoints)
end
println("Newton... ", "Average time: ",(Base.time()-time1)/length(G.samples), "s, ", "% converged: ", 100*convergedPaths/length(G.samples), ", Average local steps: ", localSteps/length(G.samples))
global convergedPaths = 0
global localSteps = 0
time2 = Base.time()
for pt in G.samples
res = HomotopyOpt.findminima(pt, 1e-3, G, objective; maxseconds=10, maxlocalsteps=1, homotopyMethod = "HomotopyContinuation")
global convergedPaths = res.converged ? convergedPaths+1 : convergedPaths
global localSteps = localSteps + length(res.computedpoints)
end
println("HomotopyContinuation... ", "Average time: ",(Base.time()-time2)/length(G.samples), "s, ", "% converged: ", 100*convergedPaths/length(G.samples), ", Average local steps: ", localSteps/length(G.samples))
println(" ")
| HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | code | 110 | using HomotopyOpt, Test
@testset "HomotopyOpt" begin
include("2DTests.jl")
include("3DTests.jl")
end
| HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | docs | 2358 | # HomotopyOpt.jl
This package solves a constrained optimization problem which minimizes an objective function restricted to an algebraic variety.
There are two main ideas. First, we use parameter homotopy (using `HomotopyContinuation.jl`) to attempt a line search in the direction of the projected gradient vector.
Because we use parameter homotopy, this *line search* is really a *curve search* along a curve that stays on the constraint variety.
Second, we use *parallel transport* to decide when to slow down and search more carefully. Whenever we observe that the norm of the projected
gradient has been decreasing and then starts to increase, we parallel transport a projected gradient from one tangent space to the other,
compute their dot product, and if it's negative, that means the projected gradient has *reversed direction*, so that we skipped past a critical point.
If this happens, we go back a bit, and slow down our search, looking more carefully in that neighborhood.
The end result is that we slow down in the correct places to find critical points where the projected gradient vector is essentially the zero vector.
## Installation
```
julia> ]
(@v1.9) pkg> add HomotopyOpt
```
## Usage
```julia
using HomotopyOpt
sexticcurve(x) = [(x[1]^4 + x[2]^4 - 1) * (x[1]^2 + x[2]^2 - 2) + x[1]^5 * x[2]] # sextic curve
N,d = 2,1 # ambient dimension, variety dimension
numsamples = 100 # we want to compute some random starting points for our optimization problem
G = ConstraintVariety(sexticcurve, N, d, numsamples); # if you dont ask for samples, it will not compute them.
```
Above we created a `ConstraintVariety`, and now we need to create a function that evaluates the gradient of the objective function.
For the objective function, we choose the squared distance from the point $(2,2)$ in the plane, for visualization purposes in this example.
```julia
Q = x->(x[1]-2)^2+(x[2]-2)^2
```
The main function is `findminima` which actually implements our algorithm. It takes inputs as follows:
```julia
p0 = rand(G.samples) # choose a random starting point on the curve
tolerance = 1e-3
result = findminima(p0, tolerance, G, Q);
```
Now we can `watch` our result.
```julia
watch(result)
```
which produces the following output:

| HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.2.0 | 4e4cece45142daa92d0be1483c3a6a5728371296 | docs | 570 | # Tests for HomotopyOpt.jl
To run tests, navigate to the projects folder and activate the project's local environment. Afterwards, simply run the command `test`.
```
julia> cd("<your_julia_home_folder>\\HomotopyOpt.jl")
julia> pwd() # Print the cursor's current location
"<your_julia_home_folder>\\HomotopyOpt.jl"
julia> ] # Pressing ] let's us enter Julia's package manager
(@v1.6) pkg> activate .
(HomotopyOpt) pkg> test
```
At the moment, this runs tests in 2D and in 3D for each of the optimization methods `gaussnewtonstep`, `EDStep` and `twostep`. | HomotopyOpt | https://github.com/matthiashimmelmann/HomotopyOpt.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 646 | using Reinforce
using Reinforce.MountainCarEnv: MountainCar
using Plots
gr()
# Deterministic policy that is solving the problem
mutable struct BasicCarPolicy <: Reinforce.AbstractPolicy end
Reinforce.action(policy::BasicCarPolicy, r, s, A) = s.velocity < 0 ? 1 : 3
# Environment setup
env = MountainCar()
function episode!(env, π = RandomPolicy())
ep = Episode(env, π)
for (s, a, r, s′) in ep
gui(plot(env))
end
ep.total_reward, ep.niter
end
# Main part
R, n = episode!(env, BasicCarPolicy())
println("reward: $R, iter: $n")
# This one can be really long...
R, n = episode!(env, RandomPolicy())
println("reward: $R, iter: $n")
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 4125 | module Reinforce
using Reexport
@reexport using StatsBase
using Distributions
using RecipesBase
@reexport using LearnBase
using LearnBase: DiscreteSet
import LearnBase: learn!, transform!, grad!, grad
using LearningStrategies
import LearningStrategies: setup!, hook, finished, cleanup!
export
AbstractEnvironment,
reset!,
step!,
reward,
state,
finished,
actions,
ismdp,
maxsteps,
AbstractPolicy,
RandomPolicy,
OnlineGAE,
OnlineActorCritic,
EpisodicActorCritic,
action,
AbstractState,
StateVector,
History,
state!,
Episode,
Episodes,
run_episode
# ----------------------------------------------------------------
# Implement this interface for a new environment
abstract type AbstractEnvironment end
"""
reset!(env) -> env
Reset an environment.
"""
function reset! end
"""
r, s′ = step!(env, s, a)
Move the simulation forward, collecting a reward and getting the next state.
"""
function step! end
# note for developers: you should also implement Base.done(env) for episodic environments
finished(env::AbstractEnvironment, s′) = false
"""
A = actions(env, s)
Return a list/set/description of valid actions from state `s`.
"""
function actions end
# note for developers: you don't need to implement these if you have state/reward fields
"""
s = state(env)
Return the current state of the environment.
"""
state(env::AbstractEnvironment) = env.state
"""
r = reward(env)
Return the current reward of the environment.
"""
reward(env::AbstractEnvironment) = env.reward
"""
ismdp(env)::Bool
An environment may be fully observable (MDP) or partially observable (POMDP).
In the case of a partially observable environment,
the state `s` is really an observation `o`.
To maintain consistency, we call everything a state, and assume that an
environment is free to maintain additional (unobserved) internal state.
The `ismdp` query returns true when the environment is MDP, and false otherwise.
"""
ismdp(env::AbstractEnvironment) = false
"""
maxsteps(env)::Int
Return the max steps in single episode.
Default is `0` (unlimited).
"""
maxsteps(env::AbstractEnvironment) = 0
# ----------------------------------------------------------------
# Implement this interface for a new policy
abstract type AbstractPolicy end
"""
a = action(policy, r, s, A)
Take in the last reward `r`, current state `s`,
and set of valid actions `A = actions(env, s)`,
then return the next action `a`.
Note that a policy could do a 'sarsa-style' update simply by saving the last state and action `(s,a)`.
"""
function action end
# ----------------------------------------------------------------
# concrete implementations
# include("episodes.jl")
include("episodes/iterators.jl")
include("states.jl")
include("policies/policies.jl")
include("solvers.jl")
include("envs/cartpole.jl")
include("envs/pendulum.jl")
include("envs/mountain_car.jl")
include("envs/multi-armed-bandit.jl")
@reexport using .MultiArmedBanditEnv
# ----------------------------------------------------------------
# a keyboard action space
struct KeyboardAction
key
end
mutable struct KeyboardActionSet{T} <: AbstractSet{T}
keys::Vector
end
LearnBase.randtype(s::KeyboardActionSet) = KeyboardAction
Base.rand(s::KeyboardActionSet) = KeyboardAction(rand(s.keys))
Base.in(a::KeyboardAction, s::KeyboardActionSet) = a.key in s.keys
Base.length(s::KeyboardActionSet) = 1
# ----------------------------------------------------------------
# a mouse/pointer action space
struct MouseAction
x::Int
y::Int
button::Int
end
mutable struct MouseActionSet{T} <: AbstractSet{T}
screen_width::Int
screen_height::Int
button::DiscreteSet{Vector{Int}}
end
LearnBase.randtype(s::MouseActionSet) = MouseAction
Base.rand(s::MouseActionSet) =
MouseAction(rand(1:s.screen_width), rand(1:s.screen_height), rand(s.button))
Base.in(a::MouseAction, s::MouseActionSet) =
a.x in 1:s.screen_width && a.y in 1:s.screen_height && a.button in s.button
Base.length(s::MouseActionSet) = 1
# ----------------------------------------------------------------
end # module Reinforce
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 27 |
include("solvers/cem.jl")
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 1317 |
abstract type AbstractState end
# ----------------------------------------------------------------
"A StateVector holds both the functions which will populate the state, and the most recent state."
mutable struct StateVector{S} <: AbstractState
queries::Vector{Function}
state::Vector{S}
names::Vector{String}
end
function StateVector(queries::AbstractVector{Function}; names=fill("",length(queries)))
StateVector(queries, zeros(length(queries)), names)
end
function StateVector(queries::Function...; names=fill("",length(queries)))
StateVector(Function[f for f in queries], names=names)
end
Base.length(sv::StateVector) = length(sv.queries)
"retreive the most recently calculated state"
state(sv::StateVector) = sv.state
"update the state, then return it"
function state!(sv::StateVector)
for (i,f) in enumerate(sv.queries)
sv.state[i] = f()
end
sv.state
end
# ----------------------------------------------------------------
mutable struct History{T}
sv::StateVector{T}
states::Matrix{T}
end
History(sv::StateVector{T}) where {T} = History(sv, Matrix{T}(length(sv),0))
function state!(hist::History)
s = state!(hist.sv)
hist.states = hcat(hist.states, s)
s
end
StatsBase.nobs(hist::History) = size(hist.states, 2)
# ----------------------------------------------------------------
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 2707 | module CartPoleEnv
# Ported from: https://github.com/openai/gym/blob/996e5115621bf57b34b9b79941e629a36a709ea1/gym/envs/classic_control/cartpole.py
# which has header:
# Classic cart-pole system implemented by Rich Sutton et al.
# Copied from https://webdocs.cs.ualberta.ca/~sutton/book/code/pole.c
using Reinforce: AbstractEnvironment
using LearnBase: DiscreteSet
using RecipesBase
using Random: seed!
import Reinforce: reset!, actions, finished, step!, state
export
CartPole,
reset!,
step!,
actions,
finished
const gravity = 9.8
const mass_cart = 1.0
const mass_pole = 0.1
const total_mass = mass_cart + mass_pole
const pole_length = 0.5 # actually half the pole's length
const mass_pole_length = mass_pole * pole_length
const force_mag = 10.0
const τ = 0.02 # seconds between state updates
# angle at which to fail the episode
const θ_threshold = 24π / 360
const x_threshold = 2.4
mutable struct CartPole <: AbstractEnvironment
state::Vector{Float64}
reward::Float64
maxsteps::Int # max step in each episode
end
CartPole(; maxsteps = 0) = CartPole(0.1rand(4) .- 0.05, 0.0, maxsteps)
# see https://github.com/FluxML/model-zoo/pull/23#issuecomment-366030179
CartPoleV0() = CartPole(maxsteps = 200)
CartPoleV1() = CartPole(maxsteps = 500)
reset!(env::CartPole) = (env.state = 0.1rand(4) .- 0.05; env.reward = 0.0; env)
actions(env::CartPole, s) = DiscreteSet(1:2)
maxsteps(env::CartPole) = env.maxsteps
function step!(env::CartPole, s, a)
s = state(env)
x, xvel, θ, θvel = s
force = (a == 1 ? -1 : 1) * force_mag
tmp = (force + mass_pole_length * sin(θ) * (θvel^2)) / total_mass
θacc = (gravity * sin(θ) - tmp * cos(θ)) /
(pole_length * (4/3 - mass_pole * (cos(θ)^2) / total_mass))
xacc = tmp - mass_pole_length * θacc * cos(θ) / total_mass
# update state
s[1] = x += τ * xvel
s[2] = xvel += τ * xacc
s[3] = θ += τ * θvel
s[4] = θvel += τ * θacc
env.reward = finished(env, s) ? 0.0 : 1.0
env.reward, s
end
function finished(env::CartPole, s′)
x, xvel, θ, θvel = s′
!(-x_threshold <= x <= x_threshold &&
-θ_threshold <= θ <= θ_threshold)
end
# ------------------------------------------------------------------------
@recipe function f(env::CartPole)
x, xvel, θ, θvel = state(env)
legend := false
xlims := (-x_threshold, x_threshold)
ylims := (-Inf, 2pole_length)
grid := false
ticks := nothing
# pole
@series begin
linecolor := :red
linewidth := 10
[x, x + 2pole_length * sin(θ)], [0.0, 2pole_length * cos(θ)]
end
# cart
@series begin
seriescolor := :black
seriestype := :shape
hw = 0.5
l, r = x-hw, x+hw
t, b = 0.0, -0.1
[l, r, r, l], [t, t, b, b]
end
end
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 2988 | # Ported from https://github.com/openai/gym/blob/996e5115621bf57b34b9b79941e629a36a709ea1/gym/envs/classic_control/mountain_car.py
# which has header
# https://webdocs.cs.ualberta.ca/~sutton/MountainCar/MountainCar1.cp
module MountainCarEnv
using Reinforce: AbstractEnvironment
using LearnBase: DiscreteSet
using RecipesBase
using Distributions
using Random: seed!
import Reinforce: reset!, actions, finished, step!
export
MountainCar,
reset!,
step!,
actions,
finished
const min_position = -1.2
const max_position = 0.6
const max_speed = 0.07
const goal_position = 0.5
const min_start = -0.6
const max_start = 0.4
const car_width = 0.05
const car_height = car_width/2.0
const clearance = 0.2*car_height
const flag_height = 0.05
mutable struct MountainCarState
position::Float64
velocity::Float64
end
mutable struct MountainCar <: AbstractEnvironment
state::MountainCarState
reward::Float64
seed::Int
end
MountainCar(seed=-1) = MountainCar(MountainCarState(0.0, 0.0), 0.0, seed)
function reset!(env::MountainCar)
if env.seed >= 0
seed!(env.seed)
env.seed = -1
end
env.state.position = rand(Uniform(min_start, max_start))
env.state.velocity = 0.0
env
end
actions(env::MountainCar, s) = DiscreteSet(1:3)
finished(env::MountainCar, s′) = env.state.position >= goal_position
function step!(env::MountainCar, s::MountainCarState, a::Int)
position = env.state.position
velocity = env.state.velocity
velocity += (a - 2)*0.001 + cos(3*position)*(-0.0025)
velocity = clamp(velocity, -max_speed, max_speed)
position += velocity
if position <= min_position && velocity < 0
velocity = 0
end
position = clamp(position, min_position, max_position)
env.state = MountainCarState(position, velocity)
env.reward = -1
return env.reward, env.state
end
# ------------------------------------------------------------------------
height(xs) = sin(3 * xs)*0.45 + 0.55
rotate(xs::Array{Float64}, ys::Array{Float64}, Θ::Float64) =
xs.*cos(Θ) .- ys.*sin(Θ), ys.*cos(Θ) .+ xs.*sin(Θ)
translate(xs::Array{Float64}, ys::Array{Float64}, t::Array{Float64}) =
xs .+ t[1], ys .+ t[2]
@recipe function f(env::MountainCar)
legend := false
xlims := (min_position, max_position)
ylims := (0, 1.1)
grid := false
ticks := nothing
# Mountain
@series begin
xs = range(min_position, stop = max_position, length = 100)
ys = height.(xs)
seriestype := :path
linecolor --> :blue
xs, ys
end
# Car
@series begin
fillcolor --> :black
seriestype := :shape
θ = cos(3 * env.state.position)
xs = [-car_width/2, -car_width/2, car_width/2, car_width/2]
ys = [0, car_height, car_height, 0] .+ clearance
xs, ys = rotate(xs, ys, θ)
translate(xs, ys, [env.state.position, height(env.state.position)])
end
# Flag
@series begin
linecolor --> :red
seriestype := :path
[goal_position, goal_position], [height(goal_position), height(goal_position) + flag_height]
end
end
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 1497 | module MultiArmedBanditEnv
using ..Reinforce
using Distributions
export MultiArmedBandit
"""
The multi-armed bandit environment.
MultiArmedBandit(k, n = 100; σ = 1)
- `k` is the number of available arms.
The reward distribution for each arms is a Normal distribution centered
at the range of [-1, 1] and the standard deviation is 1.
- `n` is the max steps for each episode.
- `σ` controls the the standard deviation for all Normal distribution.
MultiArmedBandit(x::Vector{<:Distribution}...)
In case that you want to other distributions as the reward distribution.
"""
mutable struct MultiArmedBandit{K,D<:Vector} <: AbstractEnvironment
arms::D
n::Int # max steps
r::Float64
end
function MultiArmedBandit(k::Int, n::Int = 1000; σ::Real = 1)
k ≤ 0 && throw(ArgumentError("k must > 0"))
arms = map(i -> Normal(rand(Uniform(-1, 1)), σ), 1:k)
MultiArmedBandit{k,typeof(arms)}(arms, n, 0)
end
function MultiArmedBandit(x::Vararg{Distribution,N}) where {N}
y = collect(x)
MultiArmedBandit{N,typeof(y)}(y, N, 0)
end
Reinforce.state(::MultiArmedBandit) = nothing
Reinforce.reward(env::MultiArmedBandit) = env.r
Reinforce.reset!(env::MultiArmedBandit) = (env.r = 0; env)
Reinforce.actions(::MultiArmedBandit{K}, s) where {K} = Base.OneTo(K)
Reinforce.step!(env::MultiArmedBandit, s, a::Int) = (env.r = rand(env.arms[a]); (env.r, nothing))
Reinforce.maxsteps(env::MultiArmedBandit) = env.n
Reinforce.ismdp(::MultiArmedBandit) = true
end # module MultiArmedBanditEnv
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 2676 | module PendulumEnv
# Ported from: https://github.com/openai/gym/blob/996e5115621bf57b34b9b79941e629a36a709ea1/gym/envs/classic_control/pendulum.py
# https://github.com/openai/gym/wiki/Pendulum-v0
using Reinforce: AbstractEnvironment
using LearnBase: IntervalSet
using RecipesBase
using Distributions
using Random: seed!
import Reinforce: reset!, actions, finished, step!, state
export
Pendulum,
reset!,
step!,
actions,
finished,
state
const max_speed = 8.0
const max_torque = 2.0
angle_normalize(x) = ((x+π) % (2π)) - π
mutable struct PendulumState{T<:AbstractFloat} <: AbstractVector{T}
θ::T
θvel::T
end
PendulumState() = PendulumState(0., 0.)
Base.size(::PendulumState) = (2,)
function Base.getindex(s::PendulumState, i::Int)
(i > length(s)) && throw(BoundsError(s, i))
ifelse(i == 1, s.θ, s.θvel)
end
function Base.setindex!(s::PendulumState, x, i::Int)
(i > length(s)) && throw(BoundsError(s, i))
setproperty!(s, ifelse(i == 1, :θ, :θvel), x)
end
mutable struct Pendulum{V<:AbstractVector} <: AbstractEnvironment
state::V
reward::Float64
a::Float64 # last action for rendering
steps::Int
maxsteps::Int
end
Pendulum(maxsteps = 500) = Pendulum(PendulumState(),0., 0., 0, maxsteps)
function reset!(env::Pendulum)
env.state = PendulumState(rand(Uniform(-π, π)), rand(Uniform(-1., 1.)))
env.reward = 0.0
env.a = 0.0
env.steps = 0
env
end
actions(env::Pendulum, s) = IntervalSet(-max_torque, max_torque)
function step!(env::Pendulum, s, a)
θ, θvel = env.state
g = 10.0
m = 1.0
l = 1.0
dt = 0.05
env.a = a
a = clamp(a, -max_torque, max_torque)
env.reward = -(angle_normalize(θ)^2 + 0.1θvel^2 + 0.001a^2)
# update state
newθvel = θvel + (-1.5g/l * sin(θ+π) + 3/(m*l^2)*a) * dt
newθ = θ + newθvel * dt
newθvel = clamp(newθvel, -max_speed, max_speed)
env.state = PendulumState(newθ, newθvel)
env.steps += 1
env.reward, env.state
end
function state(env::Pendulum)
θ, θvel = env.state
Float64[cos(θ), sin(θ), θvel]
end
finished(env::Pendulum, s′) = env.steps >= env.maxsteps
# ------------------------------------------------------------------------
@recipe function f(env::Pendulum)
legend := false
xlims := (-1,1)
ylims := (-1,1)
grid := false
ticks := nothing
# pole
@series begin
w = 0.2
x = [-w,w,w,-w]
y = [-.1,-.1,1,1]
θ = env.state.θ
fillcolor := :red
seriestype := :shape
x*cos(θ) - y*sin(θ), y*cos(θ) + x*sin(θ)
end
# center
@series begin
seriestype := :scatter
markersize := 10
markercolor := :black
annotations := [(0, -0.2, "a: $(round(env.a, digits = 4))", :top)]
[0],[0]
end
end
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 5379 |
mutable struct Episode{E<:AbstractEnvironment,P<:AbstractPolicy,F<:AbstractFloat}
env::E
policy::P
total_reward::F # total reward of the episode
last_reward::F
niter::Int # current step in this episode
freq::Int # number of steps between choosing actions
maxn::Int # max steps in an episode - should be constant during an episode
end
Episode(env::AbstractEnvironment, π::AbstractPolicy; freq = 1, maxn = maxsteps(env)) =
Episode(env, π, 0.0, 0.0, 1, freq, maxn)
function _start!(ep::Episode{E,P,F}) where {E,P,F}
reset!(ep.env)
reset!(ep.policy)
ep.total_reward = zero(F)
ep.niter = 1
end
_done(ep::Episode, i) =
(ep.maxn != 0 && ep.niter >= ep.maxn) || finished(ep.env, state(ep.env))
# take one step in the enviroment after querying the policy for an action
function Base.iterate(ep::Episode, i = _start!(ep))
_done(ep::Episode, i) && return nothing
env = ep.env
π = ep.policy
s = state(env)
A = actions(env, s) # action space
r = reward(env)
a = action(π, r, s, A)
@assert(a ∈ A, "action $a is not in $A")
# take freq steps using action a
last_reward = 0.0
s′ = s
for _ ∈ 1:ep.freq
r, s′ = step!(env, s′, a)
last_reward += r
_done(ep, ep.niter) && break
end
ep.total_reward += last_reward
ep.last_reward = last_reward
ep.niter = i
(s, a, r, s′), i + 1
end
"""
run_episode(f, env, policy)
run_episode(env, policy) do (s, a, r, s′)
# render or something else
end
Helper function for running an episode,
and return the total reward gained in this episode.
"""
function run_episode(f::Base.Callable, env::AbstractEnvironment, π::AbstractPolicy)
ep = Episode(env, π)
for sars in ep
f(sars)
end
ep.total_reward
end
# ---------------------------------------------------------------------
# iterate through many episodes
mutable struct Episodes
env
kw
# note: we have different groups of strategies depending on when they should be applied
episode_strats # learning strategies for each episode
epoch_strats # learning strategies for each complete episode
iter_strats # learning strategies applied at every iteration
end
function Episodes(env;
episode_strats = [],
epoch_strats = [],
iter_strats = [],
kw...)
Episodes(
env,
kw,
MetaLearner(episode_strats...),
MetaLearner(epoch_strats...),
MetaLearner(iter_strats...)
)
end
length_state(eps::Episodes) = length(state(eps.env)) + length(eps.last_action)
# the main function... run episodes until stopped by one of the epoch/iter strats
function learn!(policy, eps::Episodes)
# setup
setup!(eps.epoch_strats, policy)
setup!(eps.iter_strats, policy)
# loop over epochs until done
done = false
epoch = 1
iter = 1
while !done
# one episode
setup!(eps.episode_strats, policy)
ep = Episode(eps.env, policy; eps.kw...)
for sars′ in ep
learn!(policy, sars′...)
# learn steps
for metalearner in (eps.episode_strats, eps.epoch_strats, eps.iter_strats)
for strat in metalearner.managers
learn!(policy, strat, sars′)
end
end
# iter steps
timestep = ep.niter
hook(eps.episode_strats, ep, timestep)
hook(eps.epoch_strats, ep, epoch)
hook(eps.iter_strats, ep, iter)
# finish the timestep with checks
if finished(eps.episode_strats, policy, timestep)
break
end
if finished(eps.epoch_strats, policy, epoch) || finished(eps.iter_strats, policy, iter)
done = true
break
end
iter += 1
end
info("Finished episode $epoch after $(ep.niter) steps. Reward: $(ep.total_reward) mean(Reward): $(ep.total_reward/max(ep.niter,1))")
cleanup!(eps.episode_strats, policy)
epoch += 1
end
# tear down
cleanup!(eps.epoch_strats, policy)
cleanup!(eps.iter_strats, policy)
return
end
# function hook(policy, ep::Episodes, i)
# if ep.should_reset
# reset!(ep.env)
# reset!(policy)
# ep.should_reset = false
# ep.total_reward = 0.0
# ep.nsteps = 0
# for learner in ep.learners
# setup!(learner, policy)
# end
# end
#
# # take one step in the enviroment after querying the policy for an action
# env = ep.env
# s = state(env)
# A = actions(env, s)
# r = reward(env)
# a = action(policy, r, s, A)
# if !(a in A)
# warn("action $a is not in $A")
# # a = rand(A)
# end
# @assert a in A
# r, s′ = step!(env, s, a)
# ep.total_reward += r
#
# # "sars" learn step for the policy...
# # note: ensures that the final reward is included in the learning
# learn!(policy, s, a, r, s′)
#
# ep.nsteps += 1
# for learner in ep.learners
# learn!(policy, learner, ep.nsteps)
# hook(learner, policy, ep.nsteps)
# end
#
# # if this episode is done, just flag it so we reset next time
# if finished(env, s′) || any(learner -> finished(learner, policy, ep.nsteps), ep.learners)
# ep.should_reset = true
# ep.nepisode += 1
# for learner in ep.learners
# cleanup!(learner, policy)
# end
# info("Finished episode $(ep.nepisode) after $(ep.nsteps) steps. Reward: $(ep.total_reward)")
# end
# return
# end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 10196 |
# WARNING: This should not be used as-is. It's unfinished experimentation.
using Transformations
using StochasticOptimization
using PenaltyFunctions
import OnlineStats: Mean, Variances, Weight, BoundedEqualWeight
mutable struct Actor{PHI<:Learnable, DIST<:MvNormalTransformation} <: AbstractPolicy
ϕ::PHI # map states to dist inputs. ∇logπ is grad(ϕ)
D::DIST # the N(ϕ) = N(μ,σ) from which we sample actions
prep::PreprocessStep
last_action
testing::Bool
end
Actor(ϕ,D,prep=NoPreprocessing()) = Actor(ϕ, D, prep, zeros(D.n), false)
# TODO: specialize this on the distribution type
function Reinforce.action(actor::Actor, r, s′, A′)
z = transform!(actor, s′)
# @show map(extrema, (s′, z, params(actor), grad(actor)))
# TODO: make this a general utility method... project_to_actions?
# project our squashed sample onto into the action space to get our actions
# a = (â --> [lo,hi])
a = A′.lo .+ logistic.(z) .* (A′.hi .- A′.lo)
if !(a in A′)
warn("a=$a not in A=$(A′)")
dump(actor)
error()
a = rand(A′)
end
copy!(actor.last_action, a)
a
end
@with actor function grad!(actor::Actor)
grad!(D)
grad!(ϕ, input_grad(D))
end
@with actor function transform!(actor::Actor, xs::AbstractVector)
x = if isa(prep, NoPreprocessing)
xs
else
learn!(prep, xs)
transform!(prep, xs)
end
phi = transform!(ϕ, x)
if testing
# if we're testing, return the mean exactly
phi[1:D.n]
else
transform!(D, phi)
end
end
params(actor::Actor) = params(actor.ϕ)
grad(actor::Actor) = grad(actor.ϕ)
#=
This is an implementation of the "AC" algorithm (Actor-critic Algorithm) from:
Degris et al, "Model-Free Reinforcement Learning with Continuous Action in Practice"
=#
mutable struct OnlineActorCritic{ALGO, T, WGT<:Weight, PEN<:Penalty, ACTOR} <: AbstractPolicy
δ::T # last TD δ
# r̄::T # estimate of average return
r̄::Mean{WGT}
# svar::Variances{WGT} # feaure whitener TODO: do actual whitening!
penalty::PEN
ns::Int # number of inputs
nv::Int # 2ns+na because we do: vcat(s′, s′-s, a)
na::Int # the number of actions
nu::Int # the number of policy params (2na, since ϕ = vcat(μ,σ))
x::Function # a "feature mapping" function x(s)
v::Vector{T} # critic params
eᵛ::Vector{T} # eligibility trace for updating v (critic params)
# ϕ::PHI # u from the paper is really params(ϕ), ∇logπ is grad(ϕ)
# D::DIST # the N(ϕ) = N(μ,σ) from which we sample actions
actor::ACTOR
w::Vector{T} # for INAC algos
eᵘ::Vector{T} # eligibility trace for updating u (actor params)
γ::T # δ decay
λ::T # e decay
# αʳ::T # learning rate for r̄
# αᵛ::T # learning rate for v
# αᵘ::T # learning rate for u
gaᵛ
gaᵘ
# gaʷ
# last_sars′
xs
end
function OnlineActorCritic(s::AbstractVector, na::Int;
T::DataType = eltype(s),
algo::Symbol = :AC,
wgt_lookback::Int = 20000,
prep::PreprocessStep = Whiten(T,2length(s)+na,2length(s)+na,lookback=wgt_lookback),
penalty::Penalty = L2Penalty(1e-5),
ϕ::Learnable = nnet(2length(s)+na, 2na, [], :relu),
D::MvNormalTransformation = MvNormalTransformation(zeros(T,na),zeros(T,na)),
x::Function = identity,
γ::Number = 1.0,
λ::Number = 0.5,
# αʳ::Number = 0.01,
αᵛ::Number = 0.01,
αᵘ::Number = 0.01,
αʷ::Number = 0.01,
gaᵛ = OnlineGradAvg(100, lr=αᵛ),
gaᵘ = OnlineGradAvg(100, lr=αᵘ)
# gaʷ = OnlineGradAvg(100, lr=αʷ)
)
@assert algo in (:AC, :INAC)
T = eltype(s)
ns = length(x(s))
nv = 2ns+na
nu = length(params(ϕ))
wgt = BoundedEqualWeight(wgt_lookback)
r̄ = Mean(wgt)
# svar = Variances(nv, wgt)
actor = Actor(ϕ,D,prep)
link_nodes!(ϕ, D)
setup!(gaᵛ, zeros(nv))
setup!(gaᵘ, ϕ)
# setup!(gaʷ, ϕ)
OnlineActorCritic{algo,T,typeof(wgt),typeof(penalty),typeof(actor)}(
zero(T),
# zero(T),
r̄,
# svar,
penalty,
ns,
nv,
na,
nu,
x,
zeros(T,nv),
zeros(T,nv),
# ϕ,
# D,
actor,
zeros(T,nu),
zeros(T,nu),
γ,
λ,
# αʳ,
# αᵛ,
# αᵘ
gaᵛ,
gaᵘ,
# gaʷ,
# (s, zeros(na), 0.0, s)
vcat(s, zeros(T,ns+na))
)
end
function Reinforce.reset!(ac::OnlineActorCritic{A,T}) where {A,T}
# reset!(ac.actor)
fill!(ac.eᵛ, zero(T))
fill!(ac.eᵘ, zero(T))
end
@with ac function Reinforce.action(ac::OnlineActorCritic, r, s′, A′)
# ignore s′ and use latest xs (which should include s′)
for i=1:ns
xs[i+ns] = s′[i] - xs[i]
xs[i] = s′[i]
end
xs[2ns+1:end] = actor.last_action
a = action(actor, r, xs, A′)
# if !isa(actor.prep, NoPreprocessing)
# xs[:] = output_value(actor.prep)
# end
a
# # for i=1:ns
# # xs[i+ns] = s′[i] - xs[i]
# # xs[i] = s′[i]
# # end
# # xs[ns+1:2ns] = s′ -
# # s′ = vcat(s′, s′-last_sars′[1], last_sars′[2])
# # transform!(ϕ, xs)
# # z = transform!(D)
# z = transform!(actor)
#
# # TODO: make this a general utility method... project_to_actions?
# # project our squashed sample onto into the action space to get our actions
# # a = (â --> [lo,hi])
# a = A′.lo .+ logistic.(z) .* (A′.hi .- A′.lo)
# if !(a in A′)
# warn("a=$a not in A=$(A′)")
# dump(ac)
# error()
# a = rand(A′)
# end
# # xs[2ns+1:end] = a
# a
end
#= Notes:
- we can replace αᵛ/αᵘ with a GradientLearner and call update! instead
- the @with macro (in StochasticOptimization) replaces variables with the
dot versions if that object has a field of that name
=#
# function whiten(x::AbstractArray, vars::Variances)
# return x
# σ = vars.value
# μ = vars.μ
# @assert length(x) == length(σ)
# out = zeros(x)
# @inbounds for (i,j) in enumerate(eachindex(x))
# out[j] = (x[j] - μ[i])
# if σ[i] > 0
# out[j] /= sqrt(σ[i])
# end
# end
# out
# end
# This is similar to replacing traces for continuous values.
# If we're reversing the trace then we simply add, if we're increasing
# the magnitude then we take the larger of ei/xi.
# This should help with the stability of traces.
# Note: invented by @tbreloff, but I'm sure it exists somewhere already.
function update_eligibilty!(e::AbstractArray{T}, x::AbstractArray{T},
γλ::Number; clip::Number = 1e2) where T
@assert length(e) == length(x)
@inbounds for i=1:length(e)
ei = γλ * e[i]
xi = clamp(x[i], -clip, clip)
e[i] = if ei < zero(T)
xi < zero(T) ? min(ei, xi) : ei+xi
else
xi > zero(T) ? max(ei, xi) : ei+xi
end
end
end
@with ac function learn!(ac::OnlineActorCritic, s, a, r, s′)
actor.testing && return
# xs = whiten(x(s), svar)
# xs′ = whiten(x(s′), svar)
#
# # update our input whitener
# fit!(svar, x(s′))
# xs = vcat(s, s-last_sars′[1], last_sars′[2])
xs′ = vcat(s′, s′-s, a)
prepped_xs = transform!(actor.prep, xs)
prepped_xs′ = transform!(actor.prep, xs′)
# compute TD delta
δ = r - mean(r̄) + γ * dot(v, prepped_xs′) - dot(v, prepped_xs)
# update average reward
# r̄ += αʳ * δ
# r̄ = αʳ * r + (one(αʳ) - αʳ) * r̄
fit!(r̄, r)
# update critic
γλ = γ * λ
update_eligibilty!(eᵛ, prepped_xs, γλ)
chg = zeros(v)
for i=1:nv
# eᵛ[i] = γλ * eᵛ[i] + xs[i]
chg[i] = -δ * eᵛ[i] + deriv(penalty, v[i])
# v[i] += αᵛ * chg #+ (one(αᵛ) - αᵛ) * v[i]
end
learn!(v, gaᵛ, chg)
# compute ∇logπ
# TODO: add penalty?
# grad!(D)
# grad!(ϕ)
# update actor eligibility trace
grad!(actor)
∇logπ = grad(actor)
# @show extrema(∇logπ), extrema(eᵘ)
update_eligibilty!(eᵘ, ∇logπ, γλ)
# for i=1:nu
# eᵘ[i] = γλ * eᵘ[i] + ∇logπ[i]
# end
# update the actor (different by algo)
update_actor!(ac, params(actor), ∇logπ)
return
end
@with ac function update_actor!(ac::OnlineActorCritic{:AC}, u, ∇logπ)
# σ² = D.dist.Σ.diag
chg = zeros(u)
for i=1:nu
# note: we multiply by σ² to reduce instabilities
chg[i] = -δ * eᵘ[i] + deriv(penalty, u[i])
if isnan(chg[i])
@show i, δ, eᵘ[i], u[i]
end
# chg = δ * eᵘ[i] * σ²[mod1(i,na)] - deriv(penalty, u[i])
# u[i] += αᵘ * chg
end
learn!(u, gaᵘ, chg)
end
# # BROKEN:
# @with ac function update_actor!{T}(ac::OnlineActorCritic{:INAC,T}, u, ∇logπ)
# ∇ᵀw = dot(∇logπ, w)
#
# # update w
# chg = zeros(u)
# for i=1:nu
# chg[i] = -δ * eᵘ[i] + ∇logπ[i] * ∇ᵀw
# end
# learn!(w, gaʷ, chg)
#
# # update u
# for i=1:nu
# chg[i] = w[i] - deriv(penalty, u[i])
# end
# learn!(u, gaᵘ, chg)
# end
# # BROKEN:
# @with ac function update_actor!{T}(ac::OnlineActorCritic{:INAC,T}, u, ∇logπ)
# ∇ᵀw = dot(∇logπ, w)
# # @show extrema(∇logπ), ∇ᵀw
# chg = zeros(u)
# for i=1:nu
# w[i] += αᵘ * (δ * eᵘ[i] - ∇logπ[i] * ∇ᵀw) #+ (one(αᵘ) - αᵘ) * w[i]
# if !isfinite(w[i])
# @show w δ eᵘ ∇logπ ∇ᵀw
# @show map(extrema, (w, δ, eᵘ, ∇logπ, ∇ᵀw))
# error()
# end
# chg[i] = w[i] - deriv(penalty, u[i])
# # u[i] += αᵘ * chg
# end
# learn!(u, gaᵘ, chg)
# end
# ----------------------------------------------------------------------
# ----------------------------------------------------------------------
mutable struct EpisodicActorCritic
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 7296 |
# WARNING: This should not be used as-is. It's unfinished experimentation.
using Transformations
using StochasticOptimization
using PenaltyFunctions
# ------------------------------------------------------------------
#=
See http://www.breloff.com/DeepRL-OnlineGAE/ for details/explanation of OnlineGAE
Samples from a distribution D(ϕ), where ϕ contains all sufficient statistics.
In the case of a MultivariateNormal N(μ, Σ):
Σ = U'U (we output U to ensure Σ is positive definite)
ϕ := vcat(μ, vec(U))
ϕ(s,θ) is a learnable transformation from states to sufficient statistics
We then sample from our multivariate distribution:
z ~ D(ϕ)
and (deterministically) map that sample to actions (i.e. project squashed samples `z` into the action space `A`):
a = π(z) or a ~ π(s,θ)
---
Notes:
The gradient wrt transformation params θ can be broken into the components of ϕ which map to μ/U.
Assuming the first and last steps are deterministic:
P(a|z,s,θ) = P(a|z) * P(z|ϕ) * P(ϕ|s,θ)
= 1 * P(z|ϕ) * 1
= P(z|ϕ)
So:
∇log P(a|z,s,θ) = ∇log P(z|ϕ)
=#
"""
Maps state to value: V(s)
We update the learnable parameters using gradient vector δ
"""
mutable struct ValueCritic{T,TRANS<:Learnable} <: Learnable
trans::TRANS # nS --> 1 transformation which outputs a value V(s) for state s
γ::T # discount
lastv::T # V(s)
δ::T # TD(0) delta: δ = r + γV(s′) - V(s)
# lastδ::T
end
function ValueCritic(::Type{T}, trans::Learnable, γ::T) where T
ValueCritic{T,typeof(trans)}(trans, γ, zero(T), zero(T))
end
# function transform!(critic::ValueCritic, s::AbstractArray)
# # critic.lastv = output_value(critic.trans)[1]
# transform!(critic.trans, s)
# end
# give reward r, compute output grad: δ = r + γV(s′) - V(s)
# then backprop to get ∇θ
function grad!(critic::ValueCritic{T}, r::Number) where T
Vs′ = output_value(critic.trans)[1]
Vs = critic.lastv
# critic.lastδ = critic.δ
# the loss function is L2 loss with "truth" (r+λVₛ′) and "estimate" Vₛ
# the output gradient is:
# ∂(δ²/2)/∂Vₛ′
# this is the discounted return δ:
critic.δ = r + critic.γ * Vs′ - Vs
output_grad(critic.trans)[1] = -critic.δ
# output_grad(critic.trans)[1] = -critic.γ * critic.δ
# # this tries to solve for the average future reward
# critic.δ = critic.γ * r + (one(T) - critic.γ) * Vs′ - Vs
# output_grad(critic.trans)[1] = -critic.γ * critic.δ
# critic.lastv = Vs′
grad!(critic.trans)
end
"""
Online Generalized Advantage Estimation for Actor-Critic Reinforcement Learning
Transforms states (input) to actions (output) using learnable parameters θ
We assume the general form of mapping states (s) to actions (a):
s --> ϕ(s,θ) --> D(ϕ) --> a
ϕ is:
- a learnable transformation with learnable parameters θ
- the sufficient statistics of distribution D
- some concatenated combination of μ/U/σ for multivariate normals
"""
mutable struct OnlineGAE{T <: Number,
ASET <: AbstractSet,
PHI <: Learnable,
DIST <: MvNormalTransformation,
CRITIC <: ValueCritic,
# P <: Params,
PEN <: Penalty,
AL <: LearningStrategy,
CL <: LearningStrategy
} <: Learnable
A::ASET # the action space
ϕ::PHI # learnable transformation to output sufficient statistics of D
D::DIST # generative transformation for sampling inputs to a
critic::CRITIC # the critic... wraps a learnable estimating value function V(s)
γ::T # the discount for the critic
λ::T # the extra discount for the actor
ϵ::Vector{T} # eligibility traces for the learnable params θ in transformation ϕ
# a::Vector{T} # the action
# t::Int # current timestep
# ∇logP::Vector{T} # policy gradient: ∇log P(a | s) == ∇log P(z | ϕ)
# lastr::T # most recent return
# params::P # the combined parameters from the actor transformation ϕ and the critic transformation
penalty::PEN # a penalty to add to param gradients
actor_learner::AL
critic_learner::CL
end
function OnlineGAE(A::AbstractSet,
ϕ::Learnable,
D::MvNormalTransformation,
critic_trans::Learnable,
γ::T,
λ::T,
actor_learner::LearningStrategy,
critic_learner::LearningStrategy;
penalty::Penalty = NoPenalty()) where T
# connect transformations, init the critic
link_nodes!(ϕ, D)
critic = ValueCritic(T, critic_trans, γ)
np = params_length(ϕ)
ϵ = zeros(T, np)
# ∇logP = zeros(T, np)
# params = consolidate_params(T, ϕ, critic_trans)
setup!(actor_learner, ϕ)
setup!(critic_learner, critic.trans)
OnlineGAE(A, ϕ, D, critic, γ, λ, ϵ, penalty, actor_learner, critic_learner)
end
# don't do anything here... we'll update later
LearnBase.update!(π::OnlineGAE, ::Void) = return
function Reinforce.reset!(π::OnlineGAE{T}) where T
fill!(π.ϵ, zero(T))
# π.critic.lastv = 0
# setup!(π.actor_learner, π.ϕ)
# setup!(π.critic_learner, π.critic.trans)
end
function Reinforce.action(π::OnlineGAE, r, s′, A′)
# sample z ~ N(μ,Σ) which is determined by ϕ
transform!(π.ϕ, s′)
z = transform!(π.D)
# project our squashed sample onto into the action space to get our actions
# a = (â --> [lo,hi])
a = A′.lo .+ logistic.(z) .* (A′.hi .- A′.lo)
if !(a in A′)
warn("a=$a not in A=$(A′)")
a = rand(A′)
end
a
end
function learn!(π::OnlineGAE, s, a, r, s′)
# update the critic. we use the current model to get the lastv == Vₛ
# as well as the current == Vₛ′
π.critic.lastv = transform!(π.critic.trans, s)[1]
transform!(π.critic.trans, s′)
grad!(π.critic, r)
# π.lastr = r
t = π.critic.trans
addgrad!(grad(t), π.penalty, params(t))
learn!(t, π.critic_learner, nothing)
#=
update the actor using the OnlineGAE formulas:
ϵₜ = (γλ)ϵₜ₋₁ + ∇
ĝₜ = δₜϵₜ
note: we use the grad-log-prob from the last timestep, since we
can't update until we compute the critic's δ, which depends
on the next timestep
=#
# update the grad-log-prob of distribution D, and store that for the next timestep
# NOTE: grad(π.ϕ) now contains the grad-log-prob of this timestep... but we don't use this
# until the next timestep
grad!(π.D)
grad!(π.ϕ)
# we use last timestep's ∇logP to update the eligibility trace of the last timestep ϵ
γλ = π.γ * π.λ
ϵ = π.ϵ
∇ = grad(π.ϕ)
addgrad!(∇, π.penalty, params(π.ϕ))
for i=1:length(ϵ)
ϵ[i] = γλ * ϵ[i] + ∇[i]
end
# copy!(π.∇logP, grad(π.ϕ))
# overwrite the gradient estimate: ĝ = δϵ
δ = π.critic.δ
for i=1:length(ϵ)
∇[i] = -δ * ϵ[i]
end
# # add the penalty to the gradient
# addgrad!(∇, π.penalty, params(π.ϕ))
# learn the actor
learn!(π.ϕ, π.actor_learner, nothing)
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 206 |
# default reset
reset!(π::AbstractPolicy) = π
mutable struct RandomPolicy <: AbstractPolicy end
action(policy::RandomPolicy, r, s′, A′) = rand(A′)
# include("online_gae.jl")
# include("actor_critic.jl")
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 3607 |
export
CrossEntropyMethod
# ----------------------------------------------------------------------------
# TODO: add this to MLPlots??
# export
# AnimationStrategy
# # add this to your MasterLearner to save Plots animations of your learning process
# type AnimationStrategy <: LearningStrategy
# anim::Animation
# f::Function
# end
# AnimationStrategy(f::Function) = AnimationStrategy(Animation(), f)
# hook(strat::AnimationStrategy, policy, i) = (strat.f(policy, i); frame(strat.anim))
# cleanup!(strat::AnimationStrategy, policy) = gif(strat.anim)
# ----------------------------------------------------------------------------
# ----------------------------------------------------------------------------
# TODO: this is a strategy and policy combined... they should really be split into a Learnable and a LearningStrategy
mutable struct CrossEntropyMethod <: LearningStrategy
noise_func::Function # additional deviation at each timestep
maxsteps::Int # max num steps in one episode
cem_batchsize::Int
cem_elitefrac::Float64
stopping_norm::Float64
t::Int
n::Int
μ::Vector{Float64}
last_μ::Vector{Float64}
σ::Vector{Float64}
Z::Vector{Float64} # extra variance
CrossEntropyMethod(nf, iter, bs, ef, sn) = new(nf, iter, bs, ef, sn, 0)
end
function CrossEntropyMethod(; #f::Function;
noise_func = t->0.0,
maxsteps::Int = 100,
cem_batchsize::Int = 20,
cem_elitefrac::Float64 = 0.2,
stopping_norm::Float64 = 1e-2)
CrossEntropyMethod(noise_func, maxsteps, cem_batchsize, cem_elitefrac, stopping_norm)
end
function setup!(strat::CrossEntropyMethod, policy)
n = length(params(policy))
strat.n = n
strat.μ = zeros(n)
strat.last_μ = zeros(n)
strat.σ = ones(n)
strat.Z = zeros(n)
return
end
# # the core loop, act/step in a simulation, update the env state, get a reward, update a policy, etc
function learn!(policy::AbstractPolicy, strat::CrossEntropyMethod, env::AbstractEnvironment)
strat.last_μ = copy(strat.μ)
strat.t += 1
# sample thetas from a multivariate normal distribution
N = MultivariateNormal(strat.μ, strat.σ)
θs = [rand(N) for k=1:strat.cem_batchsize]
# overwrite the parameters of the policy and run an episode for each θ
Rs = map(θ -> begin
params(policy)[:] = θ
R = 0
for (i,sars) in enumerate(Episode(env,policy))
R += sars[3]
i < strat.maxsteps || break
end
# R, T = episode!(env, policy; maxsteps = strat.maxsteps)
R
end, θs)
# pick out the elite set
n_elite = round(Int, strat.cem_batchsize * strat.cem_elitefrac)
elite_indices = sortperm(Rs, rev=true)[1:n_elite]
elite_θs = θs[elite_indices]
info("Iteration $(strat.t). mean(R): $(mean(Rs)) max(R): $(maximum(Rs)) ‖μ‖²: $(norm(strat.μ)) ‖σ‖²: $(norm(strat.σ))")
# update the policy from the empirical statistics of the elite set
for j=1:length(strat.μ)
θj = [θ[j] for θ in elite_θs]
strat.μ[j] = mean(θj)
strat.Z[j] = strat.noise_func(strat.t)
strat.σ[j] = sqrt(var(θj) + strat.Z[j])
end
# @show strat.μ strat.σ strat.Z
end
# are we done iterating? check for convergence, etc
function finished(strat::CrossEntropyMethod, policy::AbstractPolicy, i::Int)
strat.t > 0 || return false
normdiff = norm(strat.μ - strat.last_μ)
if normdiff < strat.stopping_norm
info("Converged after $(strat.t * strat.cem_batchsize) episodes.")
return true
end
false
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 2877 | module pgrad
using Reinforce
using OpenAIGym
using Transformations
using StochasticOptimization
using PenaltyFunctions
using MLPlots; gr(size=(1400,1400), leg=false)
# ----------------------------------------------------------------
# initialize a policy, do the learning, then return the policy
function doit(env = GymEnv("BipedalWalker-v2"))
s = state(env)
ns = length(s)
A = actions(env,s)
nA = length(A)
@show s ns
policy = OnlineActorCritic(s, nA,
# ϕ = nnet(2ns+nA, 2nA, [100], :softplus, lookback=10000),
ϕ = resnet(2ns+nA, 2nA, 1, nh=[100], inner_activation=:softplus, lookback=10000),
penalty = L2Penalty(1e-5),
γ = 0.995,
λ = 0.95,
# αʳ = 0.0001,
# αᵛ = 0.01,
# αᵘ = 0.01,
gaᵛ = OnlineGradAvg(50, lr=0.1, pu=RMSProp()),
gaᵘ = OnlineGradAvg(50, lr=0.01, pu=RMSProp()),
# gaʷ = OnlineGradAvg(50, lr=0.5, pu=Adamax())
)
# --------------------------------
# set up the custom visualizations
# chainplots... put one for each of ϕ/C side-by-side
ϕ = policy.actor.ϕ
D = policy.actor.D
cp_ϕ = ChainPlot(ϕ)
tpplt = plot(layout=grid(4,2))
tp_δ = TracePlot(1, sp=tpplt[1], title="delta")
tp_r̄ = TracePlot(1, sp=tpplt[2], title="r")
tp_eᵛ = TracePlot(ns, sp=tpplt[3], title="ev")
tp_v = TracePlot(ns, sp=tpplt[4], title="v")
tp_eμ = TracePlot(nA, sp=tpplt[5], title="e_mu")
tp_μ = TracePlot(nA, sp=tpplt[6], title="mu")
tp_eσ = TracePlot(nA, sp=tpplt[7], title="e_sigma")
tp_σ = TracePlot(nA, sp=tpplt[8], title="sigma")
plt = plot(cp_ϕ.plt, tpplt, layout=grid(2,1,heights=[0.3,0.7]))
# this will be called on every timestep of every episode
function eachiteration(ep,i)
@show i, ep.total_reward
# i<5000 && return
policy.gaᵛ.lr *= 0.999
policy.gaᵘ.lr *= 0.999
# i>=2000 && (policy.αᵘ = 0.0005)
update!(cp_ϕ)
for (tp,var) in [(tp_δ, policy.δ), (tp_r̄, mean(policy.r̄)),
(tp_eᵛ, policy.eᵛ), (tp_v, policy.v),
(tp_eμ, policy.eᵘ[1:nA]), (tp_μ, output_value(ϕ)[1:nA]),
(tp_eσ, policy.eᵘ[nA+1:end]), (tp_σ, output_value(ϕ)[nA+1:end]),
]
push!(tp, i, var)
end
gui()
end
function renderfunc(ep,i)
policy.actor.testing = true
if mod1(ep.niter, 1) == 1
OpenAIGym.render(env, ep.niter, nothing)
end
policy.actor.testing = false
end
learn!(policy, Episodes(
env,
freq = 1,
episode_strats = [MaxIter(1000)],
epoch_strats = [MaxIter(10000), IterFunction(renderfunc, every=5)],
iter_strats = [IterFunction(eachiteration, every=1000)]
# append_action = true
))
env, policy
end
end #module
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 2756 | module cemgym
# this is a port of the example found at
# http://rl-gym-doc.s3-website-us-west-2.amazonaws.com/mlss/lab1.html#starter
using Reinforce
# using OpenAIGym
# using Distributions
using Transformations
using StochasticOptimization
using LearningStrategies
using Plots; gr(size=(500,200))
# ----------------------------------------------------------------
"""
Wraps a LearnBase.Transformation which converts an input vector to action values.
For discrete actions, it chooses the action which produces the highest value.
For continuous (interval) actions, it squashes actions to [0,1].
"""
struct TransformPolicy{T} <: AbstractPolicy
trans::T
end
Transformations.params(tp::TransformPolicy) = params(tp.trans)
Reinforce.action(π::TransformPolicy, r, s, A::DiscreteSet) = A[indmax(transform!(π.trans, s))]
# # continuous: return the transform value, squashed to [0,1]
# # TODO: remove the squashing when a "Affine + Sigmoid" transformation is available
# function Reinforce.action(π::TransformPolicy, r, s, A::IntervalSet)
# Transformations.sigmoid(transform(π.trans, s)[1]) * (A.amax-A.amin) + A.amin
# end
# ----------------------------------------------------------------
# initialize a policy, do the learning, then return the policy
function do_cem_test(sublearners...; env = GymEnv("CartPole-v0"),
maxsteps = 200, # max number of steps in one episode
maxiter = 1000, # max learning iterations
# noise_max = 1.0,
# noise_steps = 20,
# noise_func = t -> max(noise_max - t/noise_steps, 0.0),
kw...)
# generic query of state and action size
s = state(env)
A = actions(env,s)
@assert isa(A, DiscreteSet) # this is the only kind that will work right now
nS, nA = map(length, (s, A))
# create a simple policy: action = argmax(wx+b)
policy = TransformPolicy(Affine(nS, nA))
# initialize the CEM, which will learn Θ = {w,b}
strat = CrossEntropyMethod(;maxsteps=maxsteps, kw...)
# keep a vector of test episode returns. after each iteration, run (and plot)
# an episode using the current CEM μ
Rs = zeros(0)
theme(:dark)
function iterfunc(model, i)
copy!(params(policy), strat.μ)
R = run_episode(env, policy, maxsteps=maxsteps) do
plot(plot(env), plot(Rs, label="Test Reward")) |> display
end
push!(Rs, R)
end
# create a MetaLearner driven by the CEM strategy
learner = strategy(strat, sublearners...;
maxiter=maxiter,
oniter=iterfunc,
kw...)
# do the learning. our iterator just repeatedly gives us the environment
learn!(policy, learner, repeated(env))
@show policy strat
policy, strat
end
end #module
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 3511 | module cemgym
# this is a port of the example found at
# http://rl-gym-doc.s3-website-us-west-2.amazonaws.com/mlss/lab1.html#starter
using Reinforce
using OpenAIGym
# using Distributions
using Transformations
using StochasticOptimization
using LearningStrategies
using MLPlots; gr(size=(500,500))
# ----------------------------------------------------------------
"""
Wraps a LearnBase.Transformation which converts an input vector to action values.
For discrete actions, it chooses the action which produces the highest value.
For continuous (interval) actions, it squashes actions to [0,1].
"""
struct TransformPolicy{T} <: AbstractPolicy
trans::T
end
Transformations.params(tp::TransformPolicy) = params(tp.trans)
get_action(A::DiscreteSet, ŷ::AbstractVector) = A[indmax(ŷ)]
function get_action(A::IntervalSet, ŷ)
val = 0.5 * (1.0 + clamp(first(ŷ), -1.0, 1.0))
val * (A.hi - A.lo) + A.lo
end
# # discrete: our action is the action which maximizes the affine transform
# function Reinforce.action(π::TransformPolicy, r, s, A::DiscreteSet)
# A[indmax(transform!(π.trans, s))]
# end
# most actionsets pass through to get_action
Reinforce.action(π::TransformPolicy, r, s, A) = get_action(A)
# get an action where each part of the TupleSet is associated with part of the
# transformation output
function Reinforce.action(π::TransformPolicy, r, s, A::TupleSet)
ŷ = transform!(π.trans, s)
a = []
i = 0
for Aᵢ in A
nᵢ = length(Aᵢ)
push!(a, get_action(Aᵢ, view(ŷ, i+1:i+nᵢ)))
i += nᵢ
end
# @show a
a
end
# # continuous: return the transform value, squashed to [0,1]
# # TODO: remove the squashing when a "Affine + Sigmoid" transformation is available
# function Reinforce.action(π::TransformPolicy, r, s, A::IntervalSet)
# Transformations.sigmoid(transform(π.trans, s)[1]) * (A.amax-A.amin) + A.amin
# end
# ----------------------------------------------------------------
# function myplot(t, hist_min, hist_mean, hist_max, anim=nothing)
# (env,i,sars) -> if mod1(t,3)==1 && mod1(i,10)==1
# plot(
# plot(hist_mean, c=:black, fill=((hist_min,hist_max), 0.2), title="Progress", leg=false),
# plot(env, title = "Episode: $t Iter: $i")
# )
# if anim == nothing
# gui()
# else
# frame(anim)
# end
# else
# return
# end
# end
# ----------------------------------------------------------------
# initialize a policy, do the learning, then return the policy
function do_cem_test(sublearners...; env = GymEnv("SoccerEmptyGoal-v0"),
maxsteps = 200, # max number of steps in one episode
maxiter = 1000, # max learning iterations
# noise_max = 1.0,
# noise_steps = 20,
# noise_func = t -> max(noise_max - t/noise_steps, 0.0),
kw...)
s = state(env)
A = actions(env,s)
nin = length(s)
nout = length(A)
@show nin, nout
t = nnet(nin, nout, [2], :softplus)
@show t
policy = TransformPolicy(t)
cem = CrossEntropyMethod(;maxsteps=maxsteps, kw...)
tp = TracePlot(2, layout=@layout([a;b{0.2h}]))
tracer = IterFunction((policy,i) -> begin
mod1(i,10)==1 || return
#run one episode
R,N = episode!(env, policy, stepfunc = OpenAIGym.render)
@show R, N
push!(tp, i, [R,N])
gui(tp.plt)
end)
learner = strategy(cem, tracer, sublearners...; maxiter=maxiter, kw...)
learn!(policy, learner, repeated(env))
@show policy cem
end
end #module
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 1861 | module DDPG
using OpenAIGym
using DataStructures
# NOTE: to find other valid environment names, look at the universe code that registers them:
# https://github.com/openai/universe/blob/master/universe/__init__.py
env = gym("flashgames.DuskDrive-v0")
# env = gym("Pong-v3")
# env = gym("wob.mini.CircleCenter-v0")
# env = gym("Breakout-v0")
@show actions(env, state(env))
# error()
# agent/policy
policy = RandomPolicy()
# -----------------------------------
# quick AR process for arbitrary vectors
# used for exploration policy of DDPG
using Distributions
mutable struct ARProcess{T}
prev::T
reversion
noise
end
function Base.get(ar::ARProcess)
ar.prev .= ar.reversion .* ar.prev .+ rand(noise)
end
# -----------------------------------
mutable struct DdpgPolicy
ns; na; nϕ
features
actor
actor_target
critic
critic_target
experience
end
function build_actor_critic(env)
ns = length(state(env))
na = length(actions(env))
# shared feature map: ϕ(s,a)
nϕ = 10
features = nnet(ns, nϕ, [10], :relu)
# actor: μ(s | Θμ)
actor = Chain(features, Affine(nϕ, na))
actor_target = copy(actor)
# critic: Q(s,a | ΘQ)
critic = Chain(features, Concat(nϕ+na), Affine(nϕ+na, 1))
critic_target = copy(critic)
# experience replay buffer
experience = CircularBuffer{Tuple}(100)
DdpgPolicy(ns, na, nϕ, features, actor, actor_target, critic, critic_target, experience)
end
# main loop... run one episode, getting a tuple: (s, a, r, s′)
for sars in Episode(env, policy)
# @show sars
s,a,r,s′ = sars
# @show a,r
# push!(experience, sars)
OpenAIGym.render(env)
#= TODO
- actor/critic share "feature transformation" ϕ(s,a)
- update policy (agent) by sampling from the experience replay
=#
end
# @show length(experience)
end # module
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 801 | import Reinforce: action, actions, finished, ismdp, maxsteps, reset!, reward, state, step!
###############################################################################
# Example Usage
###############################################################################
mutable struct FooEnv <: AbstractEnvironment
s::Int # state
r::Int # reward
FooEnv() = new(1, 0)
end
state(env::FooEnv) = env.s
reward(env::FooEnv) = env.r
reset!(env::FooEnv) = (env.s = 1; env.r = 0; env)
step!(env::FooEnv, s, a) = (env.s += 1; env.r = -1; (env.r, env.s))
maxsteps(env::FooEnv) = 3
actions(env::FooEnv, s′) = [1, 2, 3]
struct FooPolicy <: AbstractPolicy
end
action(π::FooPolicy, r, s, A) = rand(A)
# Iterating a Episode:
#
# ep = Episode(FooEnv(), FooPolicy())
# for (s, a, r, s′) ∈ ep
# ...
# end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 1352 | import Reinforce: action, actions, finished, ismdp, maxsteps, reset!, reward, state, step!
function test_ep_iteration()
@info "interface::iteration::maxsteps"
env = FooEnv()
π = FooPolicy()
ep = Episode(env, π)
# given the default of `finished` is `false`, iteration should hit `maxsteps`
for (i, (s, a, r, s′)) ∈ enumerate(ep)
@test s == i
@test r == -1
@test a ∈ [1, 2, 3]
@test s′ == i + 1
end
@test ep.niter == 3
@test ep.total_reward == -3
end # function test_ep_iteration
function test_ep_finished()
@info "interface::iteration::finished"
env = FooEnv()
π = FooPolicy()
ep = Episode(env, π)
for (s, a, r, s′) ∈ ep
nothing
end
# @eval finished(::FooEnv, s′) = false
@test ep.niter == 1
@test ep.total_reward == -1
end # function test_ep_iteration
function test_run_episode()
@info "interface::run_episode"
env = FooEnv()
π = FooPolicy()
run_episode(env, π) do sars
s, a, r, s′ = sars
@test a ∈ [1, 2, 3]
@test r == -1
@test s + 1 == s′
end
end # function test_run_episode
@testset "interface" begin
@info "interface::iteration"
test_ep_iteration()
begin
@eval finished(::FooEnv, s′) = (s′ == 2)
test_ep_finished()
@eval finished(::FooEnv, s′) = false # reset to default
end
test_run_episode()
end # @testset "env interface"
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 4961 | module pgrad
# this is a port of the example found at
# http://rl-gym-doc.s3-website-us-west-2.amazonaws.com/mlss/lab1.html#starter
using Reinforce
using OpenAIGym
# using Distributions
using Learn
using MLPlots; gr(size=(1400,1400))
# ----------------------------------------------------------------
# """
# Wraps a LearnBase.Transformation which converts an input vector to action values.
# For discrete actions, it chooses the action which produces the highest value.
# For continuous (interval) actions, it squashes actions to [0,1].
# """
# immutable TransformPolicy{T} <: AbstractPolicy
# trans::T
# end
#
# Transformations.params(tp::TransformPolicy) = params(tp.trans)
#
# get_action(A::DiscreteSet, ŷ::AbstractVector) = A[indmax(ŷ)]
# function get_action(A::IntervalSet, ŷ)
# val = 0.5 * (1.0 + clamp(first(ŷ), -1.0, 1.0))
# val * (A.hi - A.lo) + A.lo
# end
#
# # # discrete: our action is the action which maximizes the affine transform
# # function Reinforce.action(π::TransformPolicy, r, s, A::DiscreteSet)
# # A[indmax(transform!(π.trans, s))]
# # end
#
# # most actionsets pass through to get_action
# Reinforce.action(π::TransformPolicy, r, s, A) = get_action(A)
#
# # get an action where each part of the TupleSet is associated with part of the
# # transformation output
# function Reinforce.action(π::TransformPolicy, r, s, A::TupleSet)
# ŷ = transform!(π.trans, s)
# a = []
# i = 0
# for Aᵢ in A
# nᵢ = length(Aᵢ)
# push!(a, get_action(Aᵢ, view(ŷ, i+1:i+nᵢ)))
# i += nᵢ
# end
# # @show a
# a
# end
#
# # # continuous: return the transform value, squashed to [0,1]
# # # TODO: remove the squashing when a "Affine + Sigmoid" transformation is available
# # function Reinforce.action(π::TransformPolicy, r, s, A::IntervalSet)
# # Transformations.sigmoid(transform(π.trans, s)[1]) * (A.amax-A.amin) + A.amin
# # end
# type Critic
# return_func::Function
# baseline_func::Function
# ----------------------------------------------------------------
# initialize a policy, do the learning, then return the policy
function doit(sublearners...; env = GymEnv("BipedalWalker-v2"),
maxsteps = 500, # max number of steps in one episode
maxiter = 1000, # max learning iterations
kw...)
s = state(env)
ns = length(s)
A = actions(env,s)
nA = length(A)
@show s ns
# create a stochastic policy which can sample actions from a multivariate normal dist
# create a multivariate normal transformation with underlying params μ/σ
μ = zeros(nA)
# diagonal
σ = zeros(nA)
D = MvNormalTransformation(μ, σ)
nϕ = 2nA
# # upper-triangular
# U = eye(nA,nA)
# D = MvNormalTransformation(μ, U)
# nϕ = nA*(nA+1)
@show D
# create a neural net mapping: s --> ϕ = vec(μ,U) of the MvNormal
nh = Int[30,20]
ϕ = nnet(ns, nϕ, nh, :relu, :identity)
@show ϕ
# the critic's value function... mapping state to value
C = nnet(ns, 1, nh, :relu, :identity)
@show C
# our discount rates # TODO: can we learn these too??
γ = 0.9
λ = 0.6
# this is a stochastic policy which follows http://www.breloff.com/DeepRL-OnlineGAE/
policy = OnlineGAE(A, ϕ, D, C, γ, λ,
OnlineGradAvg(400, lr=0.1, pu=Adadelta()),
OnlineGradAvg(200, lr=0.1, pu=Adadelta()),
# penalty = ElasticNetPenalty(1e-1,0.5)
penalty = L2Penalty(1e-4)
)
# --------------------------------
# set up the custom visualizations
# chainplots... put one for each of ϕ/C side-by-side
cp_ϕ = ChainPlot(ϕ)
cp_C = ChainPlot(C)
# this will be called on every timestep of every episode
function eachiteration(ep,i)
@show i, ep.total_reward
update!(cp_ϕ)
update!(cp_C)
hm1 = heatmap(reshape(D.dist.μ,nA,1), yflip=true,
title=string(maximum(D.dist.μ)),
xguide=string(minimum(D.dist.μ)),
left_margin=150px)
# Σ = UpperTriangular(D.dist.Σ.chol.factors)
# Σ = Diagonal(D.dist.Σ.diag)
Σ = Diagonal(abs.(output_value(ϕ)[nA+1:end]))
hm2 = heatmap(Σ, yflip=true,
title=string(maximum(Σ)),
xguide=string(minimum(Σ)))
plot(cp_ϕ.plt, cp_C.plt, hm1, hm2, layout = @layout([ϕ; C; hm1{0.2w,0.2h} hm2]))
# i%2000==0 && gui()
gui()
end
function renderfunc(ep,i)
if mod1(ep.niter, 10) == 1
OpenAIGym.render(env, ep.niter, nothing)
end
end
learn!(policy, Episodes(
env,
freq = 5,
episode_strats = [MaxIter(1000)],
epoch_strats = [MaxIter(5000), IterFunction(renderfunc, every=5)],
iter_strats = [IterFunction(eachiteration, every=1000)]
))
env, policy
end
end #module
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 211 | using Reinforce
using Test
@testset "Reinforce" begin
include("foo.jl")
include("interface.jl")
@testset "env" begin
include("env/mountain_car.jl")
include("env/multi-armed-bandit.jl")
end
end
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 231 | using Reinforce.MountainCarEnv
@testset "MountainCarEnv" begin
@info "Reinforce.MountainCarEnv"
env = MountainCar()
i = 0
for sars in Episode(env, RandomPolicy())
i += 1
end
@test i > 0
end # @testset "MountainCarEnv"
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | code | 1056 | using Distributions
using Reinforce
using Test
struct TestEpisodePolicy <: AbstractPolicy end
action(::TestEpisodePolicy, r, s, A) = 2
@testset "MultiArmedBanditEnv" begin
@info "Reinforce.MultiArmedBandit"
@testset "constructor" begin
let
σ = 5
env = MultiArmedBandit(10, 42; σ = σ)
@test iszero(reward(env))
@test maxsteps(env) == 42
@test actions(env, nothing) == 1:10
@test length(env.arms) == 10
for arm ∈ env.arms
@test arm.σ == σ
end
end
let
d₁ = Uniform(1, 42)
d₂ = Gamma()
env = MultiArmedBandit(d₁, d₂)
@test iszero(reward(env))
@test actions(env, nothing) == 1:2
@test length(env.arms) == 2
@test env.arms[1] == d₁
@test env.arms[2] == d₂
end
end # @testset "constructor"
@testset "episode iterator" begin
let
env = MultiArmedBandit(10, 5)
π = TestEpisodePolicy()
@test iszero(reward(env))
for (s, a, r, s′) ∈ Episode(env, π)
@test a == 2
end
@test !iszero(reward(env))
end
end
end # @testset "MultiArmedBanditEnv"
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | docs | 837 | # v0.1.0
- Drop Julia 0.5 support. (#15)
- New interface for controlling episode termination `maxsteps(env)::Int` ([#17]).
The condition of termination is `finished(...) || maxsteps(...)` now.
- New field for `CartPole` environment: `maxsteps`.
An keyword of constructor is added: `CartPole(; maxsteps = 42)` ([#16], [#17]).
Also, there are helper functions of CartPole v0 and v1:
- `CartPoleV0()`: this is equal to `CartPole(maxsteps = 200)`
- `CartPoleV1()`: this is equal to `CartPole(maxsteps = 500)`
- Keyword `maxsteps` of `run_episode` is deprecated,
please overload `maxsteps`. ([#19])
[#15]: https://github.com/JuliaML/Reinforce.jl/pull/15
[#16]: https://github.com/JuliaML/Reinforce.jl/pull/16
[#17]: https://github.com/JuliaML/Reinforce.jl/pull/17
[#19]: https://github.com/JuliaML/Reinforce.jl/pull/19
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.4.0 | a06ac71d93cb5d39feabbd1455129cd8540e4621 | docs | 3019 | # Reinforce
[](https://travis-ci.org/JuliaML/Reinforce.jl)
[](https://gitter.im/reinforcejl/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge)
Reinforce.jl is an interface for Reinforcement Learning. It is intended to connect modular environments, policies, and solvers with a simple interface.


---
Packages which build on Reinforce:
- [AtariAlgos](https://github.com/JuliaML/AtariAlgos.jl): Environment which wraps Atari games using [ArcadeLearningEnvironment](https://github.com/nowozin/ArcadeLearningEnvironment.jl)
- [OpenAIGym](https://github.com/JuliaML/OpenAIGym.jl): Wrapper for OpenAI's python package: gym
## Environment Interface
New environments are created by subtyping `AbstractEnvironment` and implementing
a few methods:
- `reset!(env) -> env`
- `actions(env, s) -> A`
- `step!(env, s, a) -> (r, s′)`
- `finished(env, s′) -> Bool`
and optional overrides:
- `state(env) -> s`
- `reward(env) -> r`
which map to `env.state` and `env.reward` respectively when unset.
- `ismdp(env) -> Bool`
An environment may be fully observable (MDP) or partially observable (POMDP).
In the case of a partially observable environment, the state `s` is really
an observation `o`. To maintain consistency, we call everything a state,
and assume that an environment is free to maintain additional (unobserved)
internal state. The `ismdp` query returns true when the environment is MDP,
and false otherwise.
- `maxsteps(env) -> Int`
The terminating condition of an episode is control by
`maxsteps() || finished()`.
It's default value is `0`, indicates unlimited.
---
An minimal example for testing purpose is `test/foo.jl`.
TODO: more details and examples
## Policy Interface
Agents/policies are created by subtyping `AbstractPolicy` and implementing `action`.
The built-in random policy is a short example:
```julia
struct RandomPolicy <: AbstractPolicy end
action(π::RandomPolicy, r, s, A) = rand(A)
```
Where `A` is the action space.
The `action` method maps the last reward and current state to the next chosen action:
`(r, s) -> a`.
- `reset!(π::AbstractPolicy) -> π`
## Episode Iterator
Iterate through episodes using the `Episode` iterator.
A 4-tuple `(s,a,r,s′)` is returned from each step of the episode:
```julia
ep = Episode(env, π)
for (s, a, r, s′) in ep
# do some custom processing of the sars-tuple
end
R = ep.total_reward
T = ep.niter
```
There is also a convenience method `run_episode`.
The following is an equivalent method to the last example:
```julia
R = run_episode(env, π) do
# anything you want... this section is called after each step
end
```
---
## Author: [Tom Breloff](https://github.com/tbreloff)
| Reinforce | https://github.com/JuliaML/Reinforce.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | code | 477 | module DataDrivenAcoustics
using UnderwaterAcoustics
using DocStringExtensions
using DSP: amp2db, db2amp, pow2db, db2pow
include("pm_RBNN.jl")
include("pm_GPR.jl")
include("pm_core.jl")
include("pm_utility.jl")
function __init__()
UnderwaterAcoustics.addmodel!(RayBasis2D)
UnderwaterAcoustics.addmodel!(RayBasis2DCurv)
UnderwaterAcoustics.addmodel!(RayBasis3D)
UnderwaterAcoustics.addmodel!(RayBasis3DRCNN)
UnderwaterAcoustics.addmodel!(GPR)
end
end | DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | code | 1253 |
using GaussianProcesses
export GPR, GPRCal
"""
$(TYPEDEF)
A Gaussian process regression model to model acoustic propagation.
"""
Base.@kwdef struct GPR{T1, T2, T3, T4, T5} <: DataDrivenPropagationModel{T1}
env::T1
kern::T2
mZero::T3
logObsNoise::Real
GPmodel::T4
calculatefield::T5
twoDimension::Bool
function GPR(env, kern; mZero= MeanZero(), logObsNoise = -2.0, ratioₜ = 1.0, seed = false, calculatefield = GPRCal)
rₜ, pₜ, _, _ = SplitData(env.locations, env.measurements, ratioₜ, seed)
size(env.locations)[1] == 2 ? (twoDimension = true) : (twoDimension = false)
GPmodel = GP(rₜ, vec(pₜ), mZero, kern, logObsNoise)
optimize!(GPmodel)
new{typeof(env), typeof(kern), typeof(mZero),typeof(GPmodel), typeof(calculatefield)}(env, kern, mZero,logObsNoise, GPmodel, calculatefield, twoDimension)
end
end
"""
$(SIGNATURES)
Generate mean or standard deviation of Gaussian process regression prediction at location `xyz` using GPR model. Set `std` to true for mean predictions.
"""
function GPRCal(r::GPR, xyz::AbstractArray; std = false)
if std == false
return predict_y(r.GPmodel, xyz)[1]
else
return predict_y(r.GPmodel, xyz)[2]
end
end
| DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | code | 19882 | using Flux
using Random
using BangBang
using Zygote
export RayBasis2D, RayBasis2DCal, RayBasis2DCurv, RayBasis2DCurvCal, RayBasis3D, RayBasis3DCal, RayBasis3DRCNN, RayBasis3DRCNNCal
abstract type DataDrivenUnderwaterEnvironment end
abstract type DataDrivenPropagationModel{T<:DataDrivenUnderwaterEnvironment} end
"""
$(TYPEDEF)
A 2D plane wave RBNN formualtion.
- `env`: data driven underwater environment
- `calculatefield`: function to estimate acoustic field (default: `RayBasis2DCal`)
- `nrays`: number of rays (default: 60)
- `θ`: azimuthal angle of arrival rays in radian (default: missing)
- `A`: amplitude of arrival rays (default: missing)
- `ϕ`: phase of a rays in radian (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
- `ini_lr`: initial learning rate (default: 0.001)
- `trainloss`: loss function used in training and model update (default: `rmseloss`)
- `dataloss`: data loss function to calculate benchmarking validation error for early stopping (default: `rmseloss`)
- `ratioₜ`: data split ratio = number of training data/(number of training data + number of validation data) (default: 0.7)
- set `seed` to `true` to seed random data selection order (default: `false`)
- `maxepoch`: maximum number of training epoches allowed (default: 10000000)
- `ncount`: maximum number of tries before reducing learning rate (default: 5000)
- model training ends once learning rate is smaller than `minlearnrate` (default: 1e-6)
- learning rate is reduced by `reducedlearnrate` once `ncount` is reached (default: 10)
- set `showloss` to true to display training and validation errors during the model training process, if the validation error is historically the best. (default: `false`)
"""
Base.@kwdef struct RayBasis2D{T1, T2, T3<:AbstractVector, T4, T5} <: DataDrivenPropagationModel{T1}
env::T1
calculatefield::T2
nrays::Int
θ::T3
A::T3
ϕ::T3
k::T4
trainable::T5
function RayBasis2D(env; calculatefield = RayBasis2DCal, nrays = 60, θ = Vector{Missing}(undef, nrays), A = Vector{Missing}(undef, nrays),
ϕ = Vector{Missing}(undef, nrays), k = missing, inilearnrate::Real = 0.001, trainloss = rmseloss, dataloss = rmseloss, ratioₜ::Real = 0.7,
seed = false, maxepoch::Int = 10000000, ncount::Int = 5000, minlearnrate::Real = 1e-6 , reducedlearnrate::Real = 10.0, showloss::Bool = false)
trainable = ()
size(env.locations)[1] == 2 || throw(ArgumentError("RayBasis2D only supports 2D environment"))
ratioₜ <= 1.0 || throw(ArgumentError("Training data split ratio can not exceed 1"))
ratioₜ > 0.0 || throw(ArgumentError("Training data split ratio should be larger than 0"))
seed == true && Random.seed!(6)
if sum(ismissing.(θ)) > 0
θ = rand(nrays) .* π
trainable = push!!(trainable, θ)
end
if sum(ismissing.(A)) > 0
A = rand(nrays)
trainable = push!!(trainable, A)
end
if sum(ismissing.(ϕ)) > 0
ϕ = rand(nrays) .* π
trainable = push!!(trainable, ϕ)
end
if k === missing
if env.soundspeed !== missing && env.frequency !== missing
k = 2.0f0 * π * env.frequency / env.soundspeed
else
k = 2.0f0 * π * 2000.0f0 / 1500.0f0
trainable = push!!(trainable, k)
end
end
x = new{typeof(env), typeof(calculatefield), typeof(θ), typeof(k), typeof(trainable)}(env, calculatefield, nrays, θ, A, ϕ, k, trainable)
ModelFit!(x, inilearnrate, trainloss, dataloss, ratioₜ, seed, maxepoch, ncount, minlearnrate, reducedlearnrate, showloss)
return x
end
end
"""
$(SIGNATURES)
Predict acoustic field at location `xyz` using `RayBasis2D` model. Set `showarrivals` to `true` to return an array of individual complex arrivals.
"""
function RayBasis2DCal(r::RayBasis2D, xy::AbstractArray; showarrivals = false)
x = @view xy[1:1,:]
y = - @view xy[end:end,:]
kx = r.k * (x .* cos.(r.θ) + y .* sin.(r.θ)) .+ r.ϕ
showarrivals == false ? (return sum(r.A .* cis.(kx), dims = 1)) : (return r.A .* cis.(kx))
end
Flux.@functor RayBasis2D
Flux.trainable(r::RayBasis2D) = r.trainable
"""
$(TYPEDEF)
A 2D plane wave RBNN formualtion by modeling curvature of wavefornt.
- `env`: data driven underwater environment
- `calculatefield`: function to estimate acoustic field (default: `RayBasis2DCurvCal`)
- `nrays`: number of rays (default: 60)
- `θ`: azimuthal angle of arrival ray in radian (default: missing)
- `A`: amplitude of arrival rays (default: missing)
- `ϕ`: phase of a rays in radian (default: missing)
- `d`: distance in meters to help in modeling curvature of wavefornt (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
- `ini_lr`: initial learning rate (default: 0.001)
- `trainloss`: loss function used in training and model update (default: `rmseloss`)
- `dataloss`: data loss function to calculate benchmarking validation error for early stopping (default: `rmseloss`)
- `ratioₜ`: data split ratio = number of training data/(number of training data + number of validation data) (default: 0.7)
- set `seed` to `true` to seed random data selection order (default: `false`)
- `maxepoch`: maximum number of training epoches allowed (default: 10000000)
- `ncount`: maximum number of tries before reducing learning rate (default: 5000)
- model training ends once learning rate is smaller than `minlearnrate` (default: 1e-6)
- learning rate is reduced by `reducedlearnrate` once `ncount` is reached (default: 10)
- set `showloss` to true to display training and validation errors during the model training process, if the validation error is historically the best. (default: `false`)
"""
Base.@kwdef struct RayBasis2DCurv{T1, T2, T3<:AbstractVector, T4, T5} <: DataDrivenPropagationModel{T1}
env::T1
calculatefield::T2
nrays::Int
θ::T3
A::T3
ϕ::T3
d::T3
k::T4
trainable::T5
function RayBasis2DCurv(env; calculatefield = RayBasis2DCurvCal, nrays = 60, θ = Vector{Missing}(undef, nrays),
A = Vector{Missing}(undef, nrays), ϕ= Vector{Missing}(undef, nrays), d = Vector{Missing}(undef, nrays), k = missing,
inilearnrate::Real = 0.001, trainloss = rmseloss, dataloss = rmseloss, ratioₜ::Real = 0.7, seed = false, maxepoch::Int = 10000000,
ncount::Int = 5000, minlearnrate::Real = 1e-6 , reducedlearnrate::Real = 10.0, showloss::Bool = false)
size(env.locations)[1] == 2 || throw(ArgumentError("RayBasis2DCurv only supports 2D environment"))
trainable = ()
seed == true && Random.seed!(6)
if sum(ismissing.(θ)) > 0
θ = rand(nrays) .* π
trainable = push!!(trainable, θ)
end
if sum(ismissing.(A)) > 0
A = rand(nrays)
trainable = push!!(trainable, A)
end
if sum(ismissing.(ϕ)) > 0
ϕ = rand(nrays) .* π
trainable = push!!(trainable, ϕ)
end
if sum(ismissing.(d)) > 0
d = rand(nrays)
trainable = push!!(trainable, d)
end
if k === missing
if env.soundspeed !== missing && env.frequency !== missing
k = 2.0f0 * π * env.frequency / env.soundspeed
else
k = 2.0f0 * π * 2000.0f0 / 1500.0f0
trainable = push!!(trainable, k)
end
end
x = new{typeof(env), typeof(calculatefield), typeof(θ), typeof(k), typeof(trainable)}(env, calculatefield, nrays, θ, A, ϕ, d, k, trainable)
ModelFit!(x, inilearnrate,trainloss, dataloss, ratioₜ, seed, maxepoch, ncount, minlearnrate, reducedlearnrate, showloss)
return x
end
end
"""
$(SIGNATURES)
Predict acoustic field at location `xyz` using `RayBasis2DCurv` model. Set `showarrivals` to `true` to return an array of individual complex arrivals.
`xₒ` is the reference location and can be an arbitrary location.
"""
function RayBasis2DCurvCal(r::RayBasis2DCurv, xy::AbstractArray; showarrivals = false, xₒ = [0.0, 0.0])
x = @view xy[1:1,:]
y = - @view xy[end:end,:]
xx = x .- (xₒ[1] .- r.d .* cos.(r.θ))
yy = y .- (xₒ[2] .- r.d .* sin.(r.θ))
l = sqrt.(xx.^2 + yy.^2)
kx = r.k .* l .+ r.ϕ
showarrivals == false ? (return sum(r.A ./ l .* cis.(kx), dims = 1)) : (return r.A ./ l.* cis.(kx))
end
Flux.@functor RayBasis2DCurv
Flux.trainable(r::RayBasis2DCurv) = r.trainable
"""
$(TYPEDEF)
A 3D spherical wave RBNN formualtion.
- `env`: data driven underwater environment
- `calculatefield`: function to estimate acoustic field (default: `RayBasis3DCal`)
- `nrays`: number of rays (default: 60)
- `θ`: nominal azimuthal angle of arrival rays in radian (default: missing)
- `ψ`: nominal elevation angle of arrival rays in radian (default: missing)
- `d`: nominal propagation distance of arrival rays in meters (default: missing)
- `eθ`: error to nominal azimuthal angle of arrival rays in radian (default: missing)
- `eψ`: error to nominal elevation angle of arrival rays in radian (default: missing)
- `ed`: error to nominal propagation distance of arrival rays in meters (default: missing)
- `A`: amplitude of arrival rays (default: missing)
- `ϕ`: phase of a rays in radian (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
- `ini_lr`: initial learning rate (default: 0.001)
- `trainloss`: loss function used in training and model update (default: `rmseloss`)
- `dataloss`: data loss function to calculate benchmarking validation error for early stopping (default: `rmseloss`)
- `ratioₜ`: data split ratio = number of training data/(number of training data + number of validation data) (default: 0.7)
- set `seed` to `true` to seed random data selection order (default: `false`)
- `maxepoch`: maximum number of training epoches allowed (default: 10000000)
- `ncount`: maximum number of tries before reducing learning rate (default: 5000)
- model training ends once learning rate is smaller than `minlearnrate` (default: 1e-6)
- learning rate is reduced by `reducedlearnrate` once `ncount` is reached (default: 10)
- set `showloss` to true to display training and validation errors during the model training process, if the validation error is historically the best. (default: `false`)
"""
Base.@kwdef struct RayBasis3D{T1, T2, T3<:AbstractVector, T4, T5} <: DataDrivenPropagationModel{T1}
env::T1
calculatefield::T2
nrays::Int
θ::T3
ψ::T3
d::T3
eθ::T3
eψ::T3
ed::T3
A::T3
ϕ::T3
k::T4
trainable::T5
function RayBasis3D(env; calculatefield = RayBasis3DCal, nrays = 60, θ = Vector{Missing}(undef, nrays), ψ = Vector{Missing}(undef, nrays),
d = Vector{Missing}(undef, nrays), eθ = Vector{Missing}(undef, nrays), eψ = Vector{Missing}(undef, nrays), ed = Vector{Missing}(undef, nrays),
A = Vector{Missing}(undef, nrays), ϕ = Vector{Missing}(undef, nrays), k = missing, inilearnrate::Real = 0.001, trainloss = rmseloss,
dataloss = rmseloss, ratioₜ::Real = 0.7, seed = false, maxepoch::Int = 10000000, ncount::Int = 5000, minlearnrate::Real = 1e-6 ,
reducedlearnrate::Real = 10.0, showloss::Bool = false)
trainable = ()
seed == true && Random.seed!(6)
size(env.locations)[1] == 3 || throw(ArgumentError("RayBasis3D only supports 3D environment."))
if sum(ismissing.(θ)) > 0
θ = rand(nrays) .* π
trainable = push!!(trainable, θ)
eθ = zeros(nrays) .* π
end
if sum(ismissing.(ψ)) > 0
ψ = rand(nrays) .* π
trainable = push!!(trainable, ψ)
eψ = zeros(nrays) .* π
end
if sum(ismissing.(d)) > 0
d = rand(nrays) .* π
trainable = push!!(trainable, d)
ed = zeros(nrays) .* π
end
if sum(ismissing.(eθ)) > 0
eθ = zeros(nrays) .* π
trainable = push!!(trainable, eθ)
end
if sum(ismissing.(eψ)) > 0
eψ = zeros(nrays) .* π
trainable = push!!(trainable, eψ)
end
if sum(ismissing.(ed)) > 0
ed = zeros(nrays) .* π
trainable = push!!(trainable, ed)
end
if sum(ismissing.(A)) > 0
A = rand(nrays)
trainable = push!!(trainable, A)
end
if sum(ismissing.(ϕ)) > 0
ϕ = rand(nrays) .* π
trainable = push!!(trainable, ϕ)
end
if k === missing
if env.soundspeed !== missing && env.frequency !== missing
k = 2.0f0 * π * env.frequency / env.soundspeed
else
k = 2.0f0 * π * 2000.0f0 / 1500.0f0
trainable = push!!(trainable, k)
end
end
x = new{typeof(env), typeof(calculatefield), typeof(θ), typeof(k), typeof(trainable)}(env, calculatefield, nrays, θ, ψ, d, eθ, eψ, ed, A, ϕ, k, trainable)
ModelFit!(x, inilearnrate,trainloss, dataloss, ratioₜ, seed, maxepoch, ncount, minlearnrate, reducedlearnrate, showloss)
return x
end
end
"""
$(SIGNATURES)
Predict acoustic field at location `xyz` using `RayBasis3D` model. Set `showarrivals` to `true` to return an array of individual complex arrivals.
`xₒ` is the reference location and can be an arbitrary location.
"""
function RayBasis3DCal(r::RayBasis3D, xyz::AbstractArray; showarrivals = false, xₒ = [0.0, 0.0, 0.0])
x = @view xyz[1:1,:]
y = @view xyz[2:2,:]
z = - @view xyz[3:3,:]
xx = x .- (xₒ[1] .- (r.ed .+ r.d) .* cos.(r.eθ .+ r.θ) .* sin.(r.eψ .+ r.ψ))
yy = y .- (xₒ[2] .- (r.ed .+ r.d) .* sin.(r.eθ .+ r.θ) .* sin.(r.eψ .+ r.ψ))
zz = z .- (xₒ[3] .- (r.ed .+ r.d) .* cos.(r.eψ .+ r.ψ))
l = sqrt.(xx.^2.0f0 + yy.^2.0f0 + zz.^2.0f0)
kx = r.k .* l .+ r.ϕ
showarrivals == false ? (return sum(r.A ./ l .* cis.(kx), dims = 1)) : (return r.A ./ l .* cis.(kx))
end
Flux.@functor RayBasis3D
Flux.trainable(r::RayBasis3D) = r.trainable
"""
$(TYPEDEF)
A 3D spherical wave RBNN formualtion with reflection coefficient neural network (RCNN) as part of the model.
- `env`: data driven underwater environment
- `RCNN`: neural network to model seabed reflection coefficient
- `calculatefield`: function to estimate acoustic field (default: `RayBasis3DRCNNCal`)
- `nrays`: number of rays (default: 60)
- `eθ`: error to nominal azimuthal angle of arrival rays in radian (default: missing)
- `eψ`: error to nominal elevation angle of arrival rays in radian (default: missing)
- `ed`: error to nominal propagation distance of arrival rays in meters (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
- `ini_lr`: initial learning rate (default: 0.001)
- `trainloss`: loss function used in training and model update (default: `rmseloss`)
- `dataloss`: data loss function to calculate benchmarking validation error for early stopping (default: `rmseloss`)
- `ratioₜ`: data split ratio = number of training data/(number of training data + number of validation data) (default: 0.7)
- set `seed` to `true` to seed random data selection order (default: `false`)
- `maxepoch`: maximum number of training epoches allowed (default: 10000000)
- `ncount`: maximum number of tries before reducing learning rate (default: 5000)
- model training ends once learning rate is smaller than `minlearnrate` (default: 1e-6)
- learning rate is reduced by `reducedlearnrate` once `ncount` is reached (default: 10)
- set `showloss` to true to display training and validation errors during the model training process, if the validation error is historically the best. (default: `false`)
"""
Base.@kwdef struct RayBasis3DRCNN{T1, T2, T3, T4<:AbstractVector, T5, T6} <: DataDrivenPropagationModel{T1}
env::T1
RCNN::T2
calculatefield::T3
nrays::Int
θ::T4
ψ::T4
d::T4
k::T5
trainable::T6
function RayBasis3DRCNN(env, RCNN; calculatefield = RayBasis3DRCNNCal, nrays = 60, θ = Vector{Missing}(undef, nrays), ψ = Vector{Missing}(undef, nrays),
d = Vector{Missing}(undef, nrays), k = missing, inilearnrate::Real = 0.001, trainloss = rmseloss, dataloss = rmseloss, ratioₜ::Real = 0.7,
seed = false, maxepoch::Int = 10000000, ncount::Int = 5000, minlearnrate::Real = 1e-6 , reducedlearnrate::Real = 10.0, showloss::Bool = false)
trainable = ()
seed == true && Random.seed!(6)
size(env.locations)[1] == 3 || throw(ArgumentError("RayBasis3DRCNN only supports 3D environment."))
trainable = push!!(trainable, RCNN)
env.tx !== missing || throw(ArgumentError("Source location must be provided."))
length(location(env.tx)) == 3 || throw(ArgumentError("Source location must be 3 dimensional."))
env.waterdepth !== missing || throw(ArgumentError("Water depth needs to be provided"))
θ, ψ, d = cartesian2spherical([0.0, 0.0, 0.0].- find_image_src(env.locations[:,1], location(env.tx), nrays, env.waterdepth))
if k === missing
if env.soundspeed !== missing && env.frequency !== missing
k = 2.0f0 * π * env.frequency / env.soundspeed
else
k = 2.0f0 * π * 2000.0f0 / 1500.0f0
trainable = push!!(trainable, k)
end
end
x = new{typeof(env), typeof(RCNN), typeof(calculatefield), typeof(θ), typeof(k), typeof(trainable)}(env, RCNN, calculatefield, nrays, θ, ψ, d, k, trainable)
ModelFit!(x, inilearnrate,trainloss, dataloss, ratioₜ, seed, maxepoch, ncount, minlearnrate, reducedlearnrate, showloss)
return x
end
end
"""
$(SIGNATURES)
Predict acoustic field at location `xyz` using `RayBasis3DRCNN` model. Set `showarrivals` to `true` to return an array of individual complex arrivals.
`xₒ` is the reference location and can be an arbitrary location.
"""
function RayBasis3DRCNNCal(r::RayBasis3DRCNN, xyz::AbstractArray; showarrivals = false, xₒ = [0.0, 0.0, 0.0])
x = @view xyz[1:1,:]
y = @view xyz[2:2,:]
z = - @view xyz[3:3,:]
xx = x .- (xₒ[1] .- r.d .* cos.(r.θ) .* sin.(r.ψ))
yy = y .- (xₒ[2] .- r.d .* sin.(r.θ) .* sin.(r.ψ))
zz = z .- (xₒ[3] .- r.d .* cos.(r.ψ))
l = sqrt.(xx.^2.0f0 + yy.^2.0f0 + zz.^2.0f0)
j = collect(1: 1: r.nrays)
R = (abs2.(location(r.env.tx)[1] .- x) .+ abs2.(location(r.env.tx)[2] .- y)).^ 0.5f0
upward = iseven.(j)
s1 = 2.0f0 .* upward .- 1.0f0
n = div.(j, 2)
s = div.(n .+ upward, 2.0f0)
b = div.(n .+ (1 .- upward), 2.0f0)
s2 = 2.0f0 .* iseven.(n) .- 1.0f0
dz = 2.0f0 .* b .* r.env.waterdepth .+ s1 .*location(r.env.tx)[3] .- s1 .* s2 .* z
incidentangle = Float32.(abs.(atan.(R ./ dz)))
surfaceloss = reflectioncoef(r.env.seasurface, r.env.frequency, incidentangle).^s
RC = Matrix{Float32}(undef, r.nrays,size(zz)[2])
phase = Matrix{Float32}(undef, r.nrays, size(zz)[2])
bufRCNN = Zygote.Buffer(RC, 2, size(zz)[2])
bufphase = Zygote.Buffer(phase, size(phase))
bufRC = Zygote.Buffer(RC, size(RC))
for i in 1 : r.nrays
bufRCNN = r.RCNN(incidentangle[i:i,:])
bufRC[i:i,:] = abs.(bufRCNN[1:1,:])
bufphase[i:i,:] = bufRCNN[2:2,:]
end
totalphase = r.k * l .+ copy(bufphase) .* b
amp = 1.0f0 ./ l .* surfaceloss .* copy(bufRC).^ b .* absorption.(r.env.frequency, l, r.env.salinity)
showarrivals == false ? (return sum(amp.* cis.(totalphase); dims=1)) : (return amp.* cis.(totalphase))
end
Flux.@functor RayBasis3DRCNN
Flux.trainable(r::RayBasis3DRCNN) = r.trainable
| DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | code | 13661 | using RecipesBase
using Printf
export DataDrivenUnderwaterEnvironment, ModelFit!, transfercoef, transmissionloss, check, plot, rays, eigenrays, arrivals
"""
$(TYPEDEF)
Create an underwater environment for data-driven physics-based propagation models by providing locations, acoustic measnreuments and other known environmental and channel geomtry knowledge.
- `locations`: location measurements (in the form of matrix with dimension [dimension of a single location data x number of data points])
- `measurements`: acoustic field measurements (in the form of matrix with dimension [1 x number of data points])
- `soundspeed`: medium sound speed (default: missing)
- `frequency`: source frequency (default: missing)
- `waterdepth`: water depth (default: missing)
- `salinity`: water salinity (default: 35)
- `seasurface`: surface property (dafault: Vacuum)
- `seabed`: seabed property (default: SandySilt)
- `tx`: source location (default: missing)
- set `dB` to `false` if `measurements` are not in dB scale (default: `true`)
"""
Base.@kwdef struct BasicDataDrivenUnderwaterEnvironment{T1<:Matrix, T2, T3, T4, T5<:ReflectionModel, T6<:ReflectionModel, T7} <: DataDrivenUnderwaterEnvironment
locations::T1
measurements::T1
soundspeed::T2
frequency::T3
waterdepth::T4
salinity::Real
seasurface::T5
seabed::T6
tx::T7
dB::Bool
function BasicDataDrivenUnderwaterEnvironment(locations, measurements; soundspeed = missing, frequency = missing, waterdepth = missing, salinity = 35.0, seasurface = Vacuum, seabed = SandySilt, tx = missing, dB = true)
if tx !== missing
length(location(tx)) == size(locations)[1] || throw(ArgumentError("Dimension of source location and measurement locations do not match"))
end
size(locations)[2] == size(measurements)[2] || throw(ArgumentError("Number of locations and fields measurements do not match"))
size(locations)[1] < 4 || throw(ArgumentError("Dimension of location data should not be larger than 3"))
size(measurements)[1] == 1 || throw(ArgumentError("size of acoustic measurements should be 1 × n"))
new{typeof(locations), typeof(soundspeed), typeof(frequency), typeof(waterdepth), typeof(seasurface), typeof(seabed), typeof(tx)}(locations, measurements, soundspeed, frequency, waterdepth, salinity, seasurface, seabed, tx, dB)
end
end
DataDrivenUnderwaterEnvironment(locations, measurements; kwargs...) = BasicDataDrivenUnderwaterEnvironment(locations, measurements; kwargs...)
"""
$(SIGNATURES)
Train data-driven physics-based propagation model.
- `ini_lr`: initial learning rate
- `trainloss`: loss function used in training and model update
- `dataloss`: data loss function to calculate benchmarking validation error for early stopping
- `ratioₜ`: data split ratio = number of training data/(number of training data + number of validation data)
- set `seed` to `true` to seed random data selection order
- `maxepoch`: maximum number of training epoches allowed
- `ncount`: maximum number of tries before reducing learning rate
- model training ends once learning rate is smaller than `minlearnrate`
- learning rate is reduced by `reducedlearnrate` once `ncount` is reached
- set `showloss` to true to display training and validation errors during the model training process, if the validation error is historically the best
"""
function ModelFit!(r::DataDrivenPropagationModel, inilearnrate, trainloss, dataloss, ratioₜ, seed, maxepoch, ncount, minlearnrate, reducedlearnrate, showloss)
rₜ, pₜ, rᵥ, pᵥ = SplitData(r.env.locations, r.env.measurements, ratioₜ, seed)
bestmodel = deepcopy(Flux.params(r))
count = 0
opt = Adam(inilearnrate)
epoch = 0
bestloss = dataloss(rᵥ, pᵥ, r)
while true
Flux.train!((x,y) -> trainloss(x, y, r), Flux.params(r), [(rₜ, pₜ)], opt)
tmploss = dataloss(rᵥ, pᵥ, r)
epoch += 1
if tmploss < bestloss
bestloss = tmploss
# bestmodel = deepcopy(Flux.params(r))
bestmodel = r
count = 0
showloss && (@show epoch, dataloss(rₜ, pₜ, r), dataloss(rᵥ, pᵥ, r))
else
count += 1
end
epoch > maxepoch && break
if count > ncount
count = 0
# Flux.loadparams!(r, bestmodel)
Flux.loadmodel!(r, bestmodel)
opt.eta /= reducedlearnrate
opt.eta < minlearnrate && break
showloss && println("********* reduced learning rate: ",opt.eta, " *********" )
end
end
r
end
"""
$(SIGNATURES)
Calculate transmission coefficient at location `rx` using a data-driven physics-based propagation model.
- `model`: data-driven physics-based propagation model
- `tx`: acoustic source. This is optional. Use `missing` or `nothing` for unknown source.
- `rx`: acoustic receiver location(s)
"""
function UnderwaterAcoustics.transfercoef(model::DataDrivenPropagationModel, tx::Union{Missing, Nothing, AcousticSource}, rx::AcousticReceiver; mode=:coherent) where {T1}
mode === :coherent || throw(ArgumentError("Unsupported mode :" * string(mode)))
if tx !== nothing && tx !== missing
model.env.frequency == nominalfrequency(tx) || throw(ArgumentError("Mismatched frequencies in acoustic source and data driven environment"))
if model.env.tx !== missing
location(model.env.tx) == location(tx) || throw(ArgumentError("Mismatched location in acoustic source and data driven environment"))
else
@warn "Source location is ignored in field calculation"
end
end
if model isa GPR
if model.twoDimension == true
p = model.calculatefield(model, hcat([location(rx)[1], location(rx)[end]]))[1]
else
p = model.calculatefield(model, hcat([location(rx)[1], location(rx)[2], location(rx)[end]]))[1]
end
model.env.dB == true ? (return db2amp.(-p)) : (return p)
else
p = model.calculatefield(model, collect(location(rx)))[1]
end
return p
end
function UnderwaterAcoustics.transfercoef(model::DataDrivenPropagationModel, tx::Union{Missing, Nothing, AcousticSource}, rx::AcousticReceiverGrid2D; mode=:coherent) where {T1}
mode === :coherent || throw(ArgumentError("Unsupported mode :" * string(mode)))
if tx !== nothing && tx !== missing
model.env.frequency == nominalfrequency(tx) || throw(ArgumentError("Mismatched frequencies in acoustic source and data driven environment"))
if model.env.tx !== missing
location(model.env.tx) == location(tx) || throw(ArgumentError("Mismatched location in acoustic source and data driven environment"))
else
@warn "Source location is ignored in field calculation"
end
end
(xlen, ylen) = size(rx)
x = vec(location.(rx))
p = reshape(model.calculatefield(model, hcat(first.(x), last.(x))'), xlen, ylen)
if model isa GPR
model.env.dB == true ? (return db2amp.(-p)) : (return p)
else
return p
end
end
function UnderwaterAcoustics.transfercoef(model::DataDrivenPropagationModel, tx::Union{Missing, Nothing, AcousticSource}, rx::AcousticReceiverGrid3D; mode=:coherent) where {T1}
mode === :coherent || throw(ArgumentError("Unsupported mode :" * string(mode)))
if tx !== nothing && tx !== missing
model.env.frequency == nominalfrequency(tx) || throw(ArgumentError("Mismatched frequencies in acoustic source and data driven environment"))
if model.env.tx !== missing
location(model.env.tx) == location(tx) || throw(ArgumentError("Mismatched location in acoustic source and data driven environment"))
else
@warn "Source location is ignored in field calculation"
end
end
(xlen, ylen, zlen) = size(rx)
x = vec(location.(rx))
if ylen == 1
p = reshape(model.calculatefield(model, hcat(first.(x), getfield.(x, 2), last.(x))'), xlen, zlen)
else
p = reshape(model.calculatefield(model, hcat(first.(x), getfield.(x, 2), last.(x))'), xlen, ylen, zlen)
end
if model isa GPR
model.env.dB == true ? (return db2amp.(-p)) : (return p)
else
return p
end
end
UnderwaterAcoustics.transfercoef(model::DataDrivenPropagationModel, tx::Union{Missing, Nothing, AcousticSource}, rx::AbstractArray{<:AcousticReceiver}) = UnderwaterAcoustics.tmap(rx1 -> transfercoef(model, tx, rx1), rx)
UnderwaterAcoustics.transfercoef(model::DataDrivenPropagationModel, rx::Union{AbstractVector, AbstractMatrix}) = model.calculatefield(model, rx)
UnderwaterAcoustics.transmissionloss(model::DataDrivenPropagationModel, rx::Union{AbstractVector, AbstractMatrix}) = -amp2db.(abs.(transfercoef(model, rx)))
UnderwaterAcoustics.transmissionloss(model::DataDrivenPropagationModel, tx::Union{Missing, Nothing, AcousticSource}, rx::Union{AbstractVector, AbstractMatrix}) = -amp2db.(abs.(transfercoef(model, tx, rx)))
UnderwaterAcoustics.rays(model::DataDrivenPropagationModel, tx, rx) = throw(ArgumentError("This function is not yet supported"))
UnderwaterAcoustics.eigenrays(model::DataDrivenPropagationModel, tx, rx) = throw(ArgumentError("This function is not yet supported"))
abstract type Arrival end
function Base.show(io::IO, a::Arrival)
if a.time === missing
@printf(io, " | | %5.1f dB ϕ%6.1f°", amp2db(abs(a.phasor)), rad2deg(angle(a.phasor)))
else
@printf(io, " | %6.2f ms | %5.1f dB ϕ%6.1f°", 1000*a.time, amp2db(abs(a.phasor)), rad2deg(angle(a.phasor)))
end
end
struct RayArrival{T1,T2} <: Arrival
time::T1
phasor::T2
surface::Missing
bottom::Missing
launchangle::Missing
arrivalangle::Missing
raypath::Missing
end
"""
$(SIGNATURES)
Show arrival rays at a location `rx` using a data-driven physics-based propagation model.
- `model`: data-driven physics-based propagation model
- `tx`: acoustic source. This is optional. Use `missing` or `nothing` for unknown source.
- `rx`: an acoustic receiver
"""
function UnderwaterAcoustics.arrivals(model::DataDrivenPropagationModel, tx::Union{Missing, Nothing, AcousticSource}, rx::Union{AbstractVector, AcousticReceiver}; threshold = 30)
model isa GPR && throw(ArgumentError("GPR model does not support this function"))
arrival = model.calculatefield(model, collect(location(rx)); showarrivals = true)
amp = amp2db.(abs.(arrival))
idx = findall(amp .> (maximum(amp) - threshold))
signficantarrival = arrival[idx]
idx = sortperm(abs.(signficantarrival), rev = true)
if model isa RayBasis2D || model isa RayBasis2DCurv
rays = [RayArrival(missing, signficantarrival[idx[i]], missing, missing, missing, missing, missing) for i in 1 : length(idx)]
elseif model isa RayBasis3DRCNN
rays =[RayArrival(model.d[idx[i]] ./ model.env.soundspeed, signficantarrival[idx[i]], missing, missing, missing, missing, missing) for i in 1 : length(idx)]
else
rays =[RayArrival((model.d[idx[i]] .+ model.ed[idx[i]]) ./ model.env.soundspeed, signficantarrival[idx[i]], missing, missing, missing, missing, missing) for i in 1 : length(idx)]
end
return rays
end
UnderwaterAcoustics.arrivals(model::DataDrivenPropagationModel, rx::Union{AbstractVector, AcousticReceiver}) = UnderwaterAcoustics.arrivals(model, nothing, rx)
@recipe function plot(env::DataDrivenUnderwaterEnvironment; receivers = [], transmissionloss = [], dynamicrange = 42.0)
size(transmissionloss) == size(receivers) || throw(ArgumentError("Mismatched receivers and transmissionloss"))
receivers isa AcousticReceiverGrid2D || throw(ArgumentError("Receivers must be an instance of AcousticReceiverGrid2D"))
minloss = minimum(transmissionloss)
clims --> (-minloss-dynamicrange, -minloss)
colorbar --> true
cguide --> "dB"
ticks --> :native
legend --> false
xguide --> "x (m)"
yguide --> "z (m) "
@series begin
seriestype := :heatmap
receivers.xrange, receivers.zrange, -transmissionloss'
end
end
function UnderwaterAcoustics.check(::Type{RayBasis2D}, env::Union{<:DataDrivenUnderwaterEnvironment,Missing})
if env !== missing
size(env.locations)[1] == 2 || throw(ArgumentError("RayBasis2D only supports 2D environment"))
end
env
end
function UnderwaterAcoustics.check(::Type{RayBasis2DCurv}, env::Union{<:DataDrivenUnderwaterEnvironment,Missing})
if env !== missing
size(env.locations)[1] == 2 || throw(ArgumentError("RayBasis2DCurv only supports 2D environment"))
end
env
end
function UnderwaterAcoustics.check(::Type{RayBasis3D}, env::Union{<:DataDrivenUnderwaterEnvironment,Missing})
if env !== missing
size(env.locations)[1] == 3 || throw(ArgumentError("RayBasis3D only supports 3D environment"))
end
env
end
function UnderwaterAcoustics.check(::Type{RayBasis3DRCNN}, env::Union{<:DataDrivenUnderwaterEnvironment,Missing})
if env !== missing
env.tx === missing || throw(ArgumentError("RayBasis3DRCNN only supports environments with known source location"))
length(location(env.tx)) == 3 || throw(ArgumentError("RayBasis3DRCNN only supports 3D source"))
size(env.locations)[1] == 3|| throw(ArgumentError("RayBasis3DRCNN only supports 3D environment"))
env.waterdepth !== missing || throw(ArgumentError("RayBasis3DRCNN only supports environments with known water depth"))
end
env
end
function UnderwaterAcoustics.check(::Type{GPR}, env::Union{<:DataDrivenUnderwaterEnvironment,Missing})
env
end
| DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | code | 2760 | using LinearAlgebra
export rmseloss, SplitData
"""
$(SIGNATURES)
Split location and acoustic measurement data into training and validation dataset.
- `location`: measurement locations
- `measurement`: coresponding acoustic measurements
- `ratioₜ`: training data split ratio
- set `seed` to `true` to seed the random order generation in data split
"""
function SplitData(location, measurement, ratioₜ, seed)
dsize = size(location)[2]
seed && Random.seed!(8)
idxsequence = randperm(dsize)
rₜ = location[:,idxsequence[1 : Int(round(dsize * ratioₜ))]]
pₜ = measurement[:,idxsequence[1 : Int(round(dsize * ratioₜ))]]
rᵥ = location[:,idxsequence[Int(round(dsize * ratioₜ)) + 1 : end]]
pᵥ = measurement[:,idxsequence[Int(round(dsize * ratioₜ)) + 1: end]]
return rₜ, pₜ, rᵥ, pᵥ
end
function find_image_src(rx, tx, nrays, waterdepth)
IsTwoD = false
(length(tx) == 3) && (IsTwoD == true)
a = 20.0f0
count = 0
s = 2 * (Int(a) * 2 + 1) # no of image sources for a given "a"
IsTwoD ? (all_image_src = zeros(Float32, 2, s)) : (all_image_src = zeros(Float32, 3, s)) # store all image sources
image_src_amp = zeros(Float32, s) # amplitude of arrival rays
ref = zeros(Float32, 2, s) # number of reflection on surface and bottom.
for w = 0.0f0 : 1.0f0 # for all 8 possible combinations of +- (eqn(11)), they can only take values 0 or 1
for n = -a : a # "a" can be any positive number
count += 1
IsTwoD ? (image_src = [tx[1], (1.0f0 - 2.0f0 * w) * tx[2] + 2.0f0 * n * L]) : (image_src = [tx[1], tx[2], (1.0f0 - 2.0f0 * w) * tx[3] + 2.0f0 * n * waterdepth])
d = norm(image_src .- rx)
image_src_amp[count]= 0.2f0^(abs(n)) * (0.99f0)^ (abs(n - w)) / d
all_image_src[:, count] = image_src
ref[:, count] = [abs(n-w), abs(n)]
end
end
idx = sortperm(abs.(image_src_amp), rev = true)[1 : nrays] # sort based on received amplitude to select n_rays image sources
return all_image_src[:, idx]
end
function cartesian2spherical(pos)
x = @view pos[1,:]
y = @view pos[2,:]
z = @view pos[3,:]
d = norm.(eachcol(pos))
θ = atan.(y, x)
ψ = atan.(norm.(eachcol(pos[1:2,:])), z)
return θ, ψ, d
end
"""
$(SIGNATURES)
Root mean sqaure error between ground truth acoustic fields `tl` at locations `rx` and predicted field by data-driven `model`.
"""
function rmseloss(rx, tl, model)
if model.env.dB == true
Flux.mse(transmissionloss(model, rx), tl)^0.5f0
else
Flux.mse(transfercoef(model, rx), tl)^0.5f0
end
end | DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | code | 6366 | using DataDrivenAcoustics
using UnderwaterAcoustics
using Test
using Random
using DSP
using GaussianProcesses
using Flux
function test2d(datapm)
x1 = transfercoef(datapm, nothing, AcousticReceiver(50.0, -5.0))
x2 = transfercoef(datapm, nothing, AcousticReceiver(50.0, -10.0))
x3 = transfercoef(datapm, nothing, AcousticReceiver(50.0, -15.0))
x = transfercoef(datapm, nothing, [AcousticReceiver(50.0, -d) for d ∈ 5.0:5.0:15.0])
@test x isa AbstractVector
@test all(isapprox.([x1, x2, x3], x, atol= 0.000001))
x = transfercoef(datapm, nothing, AcousticReceiverGrid2D(50.0, 0.0, 1, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (1, 3)
@test all(isapprox.([x1 x2 x3], x, atol= 0.000001))
x = transfercoef(datapm, nothing, AcousticReceiverGrid2D(50.0, 10.0, 3, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (3, 3)
@test all(isapprox.([x1 x2 x3], x[1:1, :], atol= 0.000001))
x1 = transmissionloss(datapm, nothing, AcousticReceiver(50.0, -5.0))
x2 = transmissionloss(datapm, nothing, AcousticReceiver(50.0, -10.0))
x3 = transmissionloss(datapm, nothing, AcousticReceiver(50.0, -15.0))
x = transmissionloss(datapm, nothing, [AcousticReceiver(50.0, -d) for d ∈ 5.0:5.0:15.0])
@test x isa AbstractVector
@test all(isapprox.([x1, x2, x3], x, atol= 0.000001))
x = transmissionloss(datapm, nothing, AcousticReceiverGrid2D(50.0, 0.0, 1, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (1, 3)
@test all(isapprox.([x1 x2 x3], x, atol= 0.000001))
x = transmissionloss(datapm, nothing, AcousticReceiverGrid2D(50.0, 10.0, 3, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (3, 3)
@test all(isapprox.([x1 x2 x3], x[1:1,:], atol= 0.000001))
end
function test3d(datapm)
x1 = transfercoef(datapm, nothing, AcousticReceiver(50.0, 0.0, -5.0))
x2 = transfercoef(datapm, nothing, AcousticReceiver(50.0,0.0, -10.0))
x3 = transfercoef(datapm, nothing, AcousticReceiver(50.0, 0.0, -15.0))
x = transfercoef(datapm, nothing, [AcousticReceiver(50.0, 0.0, -d) for d ∈ 5.0:5.0:15.0])
@test x isa AbstractVector
@test all(isapprox.([x1, x2, x3], x, atol= 0.000001))
x = transfercoef(datapm, nothing, AcousticReceiverGrid3D(50.0, 0.0, 1, 0.0, 1.0, 1, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (1, 3)
@test all(isapprox.([x1 x2 x3], x, atol= 0.000001))
x = transfercoef(datapm, nothing, AcousticReceiverGrid3D(50.0, 10.0, 3, 0.0, 1.0, 2, -5.0, -5.0, 3))
@test x isa AbstractArray
@test size(x) == (3, 2, 3)
@test all(isapprox.([x1, x2, x3], x[1, 1,:], atol= 0.000001))
x1 = transmissionloss(datapm, nothing, AcousticReceiver(50.0, 0.0, -5.0))
x2 = transmissionloss(datapm, nothing, AcousticReceiver(50.0, 0.0, -10.0))
x3 = transmissionloss(datapm, nothing, AcousticReceiver(50.0, 0.0, -15.0))
x = transmissionloss(datapm, nothing, [AcousticReceiver(50.0, 0.0, -d) for d ∈ 5.0:5.0:15.0])
@test x isa AbstractVector
@test all(isapprox.([x1, x2, x3], x, atol= 0.000001))
x = transmissionloss(datapm, nothing, AcousticReceiverGrid3D(50.0, 0.0, 1, 0.0, 1.0, 1, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (1, 3)
@test all(isapprox.([x1 x2 x3], x, atol= 0.000001))
x = transmissionloss(datapm, nothing, AcousticReceiverGrid3D(50.0, 10.0, 3, 0.0, 1.0, 2, -5.0, -5.0, 3))
@test x isa AbstractArray
@test size(x) == (3, 2, 3)
@test all(isapprox.([x1, x2, x3], x[1, 1,:], atol= 0.000001))
end
@test RayBasis2D in models()
@test RayBasis2DCurv in models()
@test RayBasis3D in models()
@test RayBasis3DRCNN in models()
@test GPR in models()
env = UnderwaterEnvironment()
pm = PekerisRayModel(env, 7)
Random.seed!(1)
txpos = [0.0, -5.0]
rxpos = rand(2, 500) .* [80.0, -20.0] .+ [1.0, 0.0]
tloss = Array{Float32}(undef, 1, size(rxpos)[2])
for i in 1 : 1 : size(rxpos)[2]
tloss[1, i] = Float32(transmissionloss(pm, AcousticSource(txpos[1], txpos[2], 1000.0), AcousticReceiver(rxpos[1,i], rxpos[2,i]); mode=:coherent))
end
dataenv = DataDrivenUnderwaterEnvironment(rxpos, tloss; frequency = 1000.0, soundspeed = 1540.0);
datapm = RayBasis2D(dataenv; inilearnrate = 0.005, seed = true)
@test datapm isa RayBasis2D
test2d(datapm)
arr = arrivals(datapm, nothing, AcousticReceiver(50.0, -10.0))
@test arr isa AbstractVector{<:DataDrivenAcoustics.RayArrival}
datapm = RayBasis2DCurv(dataenv; inilearnrate = 0.005, seed = true)
@test datapm isa RayBasis2DCurv
test2d(datapm)
arr = arrivals(datapm, nothing, AcousticReceiver(50.0, -10.0))
@test arr isa AbstractVector{<:DataDrivenAcoustics.RayArrival}
kern = Matern(1/2, 0.0, 0.0)
datapm = GPR(dataenv, kern; logObsNoise = -5.0, seed = true, ratioₜ = 1.0)
@test datapm isa GPR
test2d(datapm)
Random.seed!(1)
txpos = [0.0, 0.0, -5.0]
rxpos = rand(3, 500) .* [100.0, 0.0, -20.0] .+ [1.0, 0.0, 0.0];
tloss = Array{Float32}(undef, 1, size(rxpos)[2])
for i in 1 : 1 : size(rxpos)[2]
tloss[1, i] = Float32(transmissionloss(pm, AcousticSource(txpos[1], txpos[2], txpos[3], 1000.0), AcousticReceiver(rxpos[1,i], rxpos[2,i], rxpos[3,i]); mode=:coherent))
end
dataenv = DataDrivenUnderwaterEnvironment(rxpos, tloss; frequency = 1000.0, soundspeed = 1540.0, waterdepth = 20.0, tx = AcousticSource(0.0, 0.0, -5.0, 1000.0))
datapm = RayBasis3D(dataenv; inilearnrate = 0.005, seed = true)
@test datapm isa RayBasis3D
test3d(datapm)
arr = arrivals(datapm, nothing, AcousticReceiver(50.0, 0.0, -10.0))
@test arr isa AbstractVector{<:DataDrivenAcoustics.RayArrival}
Random.seed!(1)
RCNN = Chain(
x -> (x ./ 0.5f0 .* π .- 0.5f0) .* 2.0f0, #normalization of incident angle
Dense(1, 30, sigmoid),
Dense(30, 50, sigmoid),
Dense(50, 2),
)
dataenv = DataDrivenUnderwaterEnvironment(rxpos, tloss; frequency = 1000.0, soundspeed = 1540.0, waterdepth = 20.0, tx = AcousticSource(0.0, 0.0, -5.0, 1000.0))
datapm = RayBasis3DRCNN(dataenv, RCNN; seed = true, inilearnrate = 0.05, ncount = 500)
@test datapm isa RayBasis3DRCNN
test3d(datapm)
arr = arrivals(datapm, nothing, AcousticReceiver(50.0, 0.0, -10.0))
@test arr isa AbstractVector{<:DataDrivenAcoustics.RayArrival}
kern = Matern(1/2, [0.0, 0.0, 0.0], 0.0)
datapm = GPR(dataenv, kern; logObsNoise = -5.0, seed = true, ratioₜ = 1.0)
@test datapm isa GPR
test3d(datapm)
| DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.2.1 | 93d62c1c85cd8d0470633dc50950cc9cdf88bf27 | docs | 15718 | # DataDrivenAcoustics.jl
This package is built upon the ideas discussed in our journal paper "Data-Aided Underwater Acoustic Ray Propagation Modeling" published on IEEE Journal of Oceanic Engineering (available online: https://ieeexplore.ieee.org/abstract/document/10224658).
Conventional acoustic propagation models require accurate environmental knowledge to be available beforehand. While data-driven techniques might allow us to model acoustic propagation without the need for extensive prior environmental knowledge, such techniques tend to be data-hungry. We propose a physics-based data-driven acoustic propagation modeling approach that enables us to train models with only a small amount of data. The proposed modeling framework is not only data-efficient, but also offers flexibility to incorporate varying degrees of environmental knowledge, and generalizes well to permit extrapolation beyond the area where data were collected.
## Installation
```julia
julia> # press ]
pkg> add UnderwaterAcoustics
pkg> add DataDrivenAcoustics
pkg> # press BACKSPACE
julia> using UnderwaterAcoustics
julia> using DataDrivenAcoustics
julia> models()
6-element Vector{Any}:
PekerisRayModel
RayBasis2D
RayBasis2DCurv
RayBasis3D
RayBasis3DRCNN
GPR
```
## Available models
There are five data-driven models provided in current package:
| Model | Description | Calculation function |
|:-----|:---------|:---------|
| `RayBasis2D` | 2D plane wave formulation. | `RayBasis2DCal` |
| `RayBasis2DCurv` | 2D plane wave formulation by modeling curvature of wavefront.| `RayBasis2DCurvCal`|
| `RayBasis3D` | 3D spherical wave formulation. | `RayBasis3DCal` |
| `RayBasis3DRCNN` | 3D spherical wave formulation with reflection coefficient neural network (RCNN) as part of the model. | `RayBasis3DRCNNCal` |
| `GPR` | Gaussian process regression model (2D & 3D) | `GPRCal` |
## Usage
`DataDrivenUnderwaterEnvironment` creates a data-driven environment.
- `locations`: location measurements (in the form of matrix with dimension [dimension of a single location data x number of data points])
- `measurements`: acoustic field measurements (in the form of matrix with dimension [1 x number of data points])
- `soundspeed`: medium sound speed (default: missing)
- `frequency`: source frequency (default: missing)
- `waterdepth`: water depth (default: missing)
- `salinity`: water salinity (default: 35.0)
- `seasurface`: surface property (default: Vacuum)
- `seabed`: seabed property (default: SandySilt)
- `tx`: source location (default: missing)
- set `dB` to `false` if `measurements` are not in dB scale (default: `true`)
`RayBasis2D`: 2D plane wave formulation. This formulation does not require knowledge of channel geometry.
- `env`: data-driven underwater environment
- `calculatefield`: function to estimate acoustic field (default: `RayBasis2DCal`)
- `nrays`: number of rays (default: 60)
- `θ`: azimuthal angle of arrival rays in radian (default: missing)
- `A`: amplitude of arrival rays (default: missing)
- `ϕ`: phase of a rays in radian (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
`RayBasis2DCurv`: 2D formulation by modeling curvature of wavefront. This formulation does not require knowledge of channel geometry.
- `env`: data-driven underwater environment
- `calculatefield`: function to estimate acoustic field (default: `RayBasis2DCurvCal`)
- `nrays`: number of rays (default: 60)
- `θ`: azimuthal angle of arrival ray in radian (default: missing)
- `A`: amplitude of arrival rays (default: missing)
- `ϕ`: phase of a rays in radian (default: missing)
- `d`: distance in meters to help in modeling curvature of wavefront (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
`RayBasis3D`: 3D spherical wave formulation. This formulation allow user to incorporate known channel geometry knowledge by inputting pre-calculated `θ`, `ψ` and `d`. To exclude the error terms from the trainable parameters, set `eθ`, `eψ`, and `ed` to zero if the input values of `θ`, `ψ`, and `d` are accurate.
- `env`: data-driven underwater environment
- `calculatefield`: function to estimate acoustic field (default: `RayBasis3DCal`)
- `nrays`: number of rays (default: 60)
- `θ`: nominal azimuthal angle of arrival rays in radian (default: missing)
- `ψ`: nominal elevation angle of arrival rays in radian (default: missing)
- `d`: nominal propagation distance of arrival rays in meters (default: missing)
- `eθ`: error to nominal azimuthal angle of arrival rays in radian (default: missing)
- `eψ`: error to nominal elevation angle of arrival rays in radian (default: missing)
- `ed`: error to nominal propagation distance of arrival rays in meters (default: missing)
- `A`: amplitude of arrival rays (default: missing)
- `ϕ`: phase of a rays in radian (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
`RayBasis3DRCNN`: 3D spherical wave formulation with reflection coefficient neural network (RCNN) as part of the model. This formulation requires knowledge of channel geometry (water depth and source location) to pre-calculate nominal ray arrival directions, propagation distances and incident angles. This formulation currently only supports flat bathymetry.
- `env`: data-driven underwater environment
- `RCNN`: neural network to model seabed reflections
- `calculatefield`: function to estimate acoustic field (default: `RayBasis3DRCNNCal`)
- `nrays`: number of rays (default: 60)
- `eθ`: error to nominal azimuthal angle of arrival rays in radian (default: missing)
- `eψ`: error to nominal elevation angle of arrival rays in radian (default: missing)
- `ed`: error to nominal propagation distance of arrival rays in meters (default: missing)
- `k`: angular wavenumber in rad/m (default: missing)
- `trainable`: trainable parameters (default: empty)
These four physics-based data-driven propagation models have optional arguments pertaining to model training setups, in addition to the previously explained model parameters.
- `ini_lr`: initial learning rate (default: 0.001)
- `trainloss`: loss function used in model training (default: `rmseloss`)
- `dataloss`: data loss function to calculate benchmarking validation error for early stopping (default: `rmseloss`)
- `ratioₜ`: data split ratio = $\frac{\text{number of training data}}{\text{number of training data + number of validation data}}$ (default: 0.7)
- set `seed` to `true` to seed random data selection order (default: `false`)
- `maxepoch`: maximum number of training epochs allowed (default: 10000000)
- `ncount`: maximum number of attempts without data loss improvement before reducing the learning rate (default: 5000)
- model training ends once learning rate is smaller than `minlearnrate` (default: 1e-6)
- learning rate is reduced by `reducedlearnrate` once `ncount` is reached (default: 10)
- set `showloss` to true to display training and validation errors during the model training process, if the validation error is historically the best. (default: `false`)
`GPR`: Gaussian process regression model that is capable of handling 2D and 3D regression problems.
- `env`: data-driven underwater environment
- `kern`: kernel function
- `mZero`: zero mean function (default: `MeanZero()`)
- `logObsNoise`: log standard deviation of observation noise (default: -2.0)
- `ratioₜ`: training data split ratio (default: 1.0)
- set `seed` to `true` to seed random data selection order (default: `false`)
- `calculatefield`: function to estimate acoustic field (default: `GPRCal`)
**Example:**
If you have a set of measured pressure amplitudes and their corresponding measurement locations as training and validation data, you can load them directly. The location data should be a matrix with dimension [dimension of a single location data x number of data points]. The field data should be a matrix with dimension [1 x number of data points].
Alternatively, you can use the propagation models available in `Undertwateracoustic.jl`, `AcousticRayTracers.jl` or `AcousticsToolbox.jl` to generate synthetic acoustic data.
Here, we use a 7-rays `PekerisRayModel` to generate synthetic acoustic measurements and ground truth fields within an area of interest and an extended region:
```julia
julia> using UnderwaterAcoustics
julia> using DataDrivenAcoustics
julia> env = UnderwaterEnvironment();
julia> pm = PekerisRayModel(env,7);
```
We assume an omnidirectional 1 kHz transmitter `tx` at a depth of 5 m at the origin. We sample modeled acoustic measurements `tloss` from `pm` at 500 random locations `rxpos` covering an 80 m x 20 m area of interest. Those 500 measurements are used to train our physics-based data-driven propagation model. We seed the random generator to allow reader replicate the following results[^1].
[^1]: The presented results are obtained using Apple M2 chip with Julia version 1.7.3.
```julia
julia> using Random
julia> Random.seed!(1);
julia> txpos = [0.0, -5.0]; #source location
julia> f = 1000.0; #frequency at 1kHz
julia> tx = AcousticSource(txpos[1], txpos[2], f); #define a source in UnderwaterAcoustics.jl
julia> rxpos = rand(2, 500) .* [80.0, -20.0] .+ [1.0, 0.0]; #random receiver locations in area of interest
julia> tloss = Array{Float32}(undef, 1, size(rxpos)[2]);
julia> for i in 1 : 1 : size(rxpos)[2]
tloss[1, i] = Float32(transmissionloss(pm, tx, AcousticReceiver(rxpos[1,i], rxpos[2,i]); mode=:coherent))
end
```
We plot measurement locations on top of ground truth field pattern. Note that the region from a range of 80 m to 100 m is the extended region where no measurement data are taken.
```julia
julia> using Plots
julia> rx = AcousticReceiverGrid2D(1.0, 0.1, 1000, -20.0, 0.1, 200);
julia> let x = transmissionloss(pm, tx, rx)
plot(env; receivers = rx, transmissionloss = x, title = "Ground truth", clim = (-40,0))
scatter!(rxpos[1,:], rxpos[2,:]; markersize = 1.5, markercolor =:green, markerstrokewidth = 0)
xlims!(0, 100)
ylims!(-20, 0)
end
```

We plot the measurement locations with scaled size and color for better visualization:
```julia
julia> let s = clamp.(vec(-tloss) ./ 40 .+ 1, 0.0, 1.0) .* 4 .+ 1
plot(rxpos[1,:], rxpos[2,:]; zcolor = vec(-tloss), seriestype=:scatter, clim = (-40, 0), markersize = s, markerstrokewidth = 0, label = nothing, title = "Data", xlabel = "x (m)", ylabel = "z (m)")
xlims!(0, 100)
ylims!(-20, 0)
end
```

Now you can define a data-driven underwater environment by providing locations, measurements and any known environmental or geometric parameters as inputs:
```julia
julia> dataenv = DataDrivenUnderwaterEnvironment(rxpos, tloss; frequency = f, soundspeed = 1540.0);
```
You need to formulate a ray basis neural network (RBNN) model that best suits the given scenario. Currently, this package offers four predefined RBNN formulations, as mentioned earlier. There are three data-driven models capable of handing this specific environment `dataenv`:
```julia
julia> models(dataenv)
3-element Vector{Any}:
RayBasis2D
RayBasis2DCurv
GPR
```
Users have the flexibility to define their own RBNN formulations tailored to the specific environment. As an illustrative example, we utilize the RayBasis2DCurv formulation.
```julia
julia> datapm = RayBasis2DCurv(dataenv; inilearnrate = 0.005, seed = true);
```
This line of code automates the search and random initialization for trainable parameters of the defined RBNN model, allowing the model to learn from data and return a model with optimized trainable parameters.
To query field at an unvisited location, simply call the `transmissionloss` with trained RBNN model `datapm` and a location coordinate:
```julia
julia> transmissionloss(datapm, nothing, AcousticReceiver(50.0, -10.0))
30.47255541988299
```
Note that source location is optional in transmission loss calculation for data-driven propagation models.
You can plot the estimated field patterns within the area of interest and the extended region:
```julia
julia> let x = transmissionloss(datapm, nothing, rx)
plot(env; receivers = rx, transmissionloss = x, title = "RBNN", clim = (-40,0))
xlims!(0, 100)
ylims!(-20, 0)
end
```

Our proposed physics-based data-driven propagation modeling technique has the capability not only to interpolate but also to extrapolate.
You can ask for the significant arrivals[^2]:
```julia
julia> arrivals(datapm, nothing, AcousticReceiver(50, -10))
56-element Vector{DataDrivenAcoustics.RayArrival{Missing, ComplexF64}}:
| | -33.9 dB ϕ -68.6°
| | -34.3 dB ϕ-146.7°
| | -36.0 dB ϕ 155.4°
| | -36.4 dB ϕ -51.1°
| | -36.9 dB ϕ -29.0°
| | -37.0 dB ϕ -88.1°
⋮
| | -60.6 dB ϕ 152.6°
| | -62.5 dB ϕ -88.7°
| | -62.5 dB ϕ 55.4°
| | -62.6 dB ϕ -57.2°
| | -62.7 dB ϕ-169.1°
```
The empty columns represent information that is not provided by data-driven models.
[^2]: Significant arrivals refer to arrivals with amplitudes no smaller than maximum arrival amplitude minus `threshold`. `threshold` is a optional argument in `arrivals` and its default value is set to 30 dB.
For benchmarking, we construct a Gaussian process regression model using `GPR` given a kernel. To take advantage of the kernels available in the `GaussianProcesses.jl` package, please ensure that you have installed it.
```julia
julia> using GaussianProcesses;
julia> kern = Matern(1/2, 0.0, 0.0);
julia> gp = GPR(dataenv, kern; logObsNoise = -5.0, seed = true, ratioₜ = 1.0);
julia> let x = transmissionloss(gp, nothing, rx)
plot(dataenv; receivers = rx, transmissionloss = x, clims=(-40,0), title = "Gaussian Processes")
xlims!(0, 100)
ylims!(-20, 0)
end
```

The Gaussian process model can recover key strcuture in field pattern with low fidelity, but fails to extrapolate beyond the measurement region.
Note that we use 100% of the data (500 measurements) as training data to train the GPR model, as the ratioₜ in GPR is set to 1.0 by default. Our RBNN model, on the other hand, is trained using 350 measurements, while the remaining 150 measurements are used as validation data for early stopping. The provided kernel and hyperparameters yield the best estimated field pattern (determined through visual inspection, as we know the ground truth field pattern) among the various kernels and hyperparameters we experimented with for this specific example. If users lack prior information about the ground truth field pattern, they should allocate some validation data for hyperparameter tuning of the GPR model.
## Publications
### Primary paper
- K. Li and M. Chitre, “Data-aided underwater acoustic ray propagation modeling,” 2023. [Online]. Available: https://ieeexplore.ieee.org/abstract/document/10224658
### Other useful papers
- K. Li and M. Chitre, “Ocean acoustic propagation modeling using scientific machine learning,” in OCEANS: San Diego–Porto. IEEE, 2021, pp. 1–5.
- K. Li and M. Chitre, “Physics-aided data-driven modal ocean acoustic propagation modeling,” in International Congress of Acoustics, 2022.
| DataDrivenAcoustics | https://github.com/org-arl/DataDrivenAcoustics.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 904 | using FieldDistributionNonuniformMedium
using Documenter
DocMeta.setdocmeta!(FieldDistributionNonuniformMedium, :DocTestSetup, :(using FieldDistributionNonuniformMedium); recursive=true)
makedocs(;
modules=[FieldDistributionNonuniformMedium],
authors="JingYu Ning <[email protected]> and contributors",
repo="https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl/blob/{commit}{path}#{line}",
sitename="FieldDistributionNonuniformMedium.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://foldfelis.github.io/FieldDistributionNonuniformMedium.jl",
assets=String[],
),
pages=[
"Home" => "index.md",
"Simulation" => "simulation.md",
"APIs" => "api.md",
],
)
deploydocs(;
repo="github.com/foldfelis/FieldDistributionNonuniformMedium.jl",
devbranch="master",
)
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 112 | module FieldDistributionNonuniformMedium
using ProgressMeter
include("simulation.jl")
include("plot.jl")
end
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 841 | using Plots.PlotMeasures
using Plots
export
plot_ϵ,
plot_e_field
function plot_ϵ(s::Simulator; figsize=(600, 750), left_margin=-100px)
ϵ = s.permittivity.ϵ
return heatmap(
axes(s.grid, 1), axes(s.grid, 2), ϵ',
color=:algae,
size=figsize, left_margin=left_margin, aspect_ratio=:equal
)
end
function plot_e_field(s::Simulator; figsize=(600, 750), left_margin=-100px)
ez = s.ez
ϵ = s.permittivity.ϵ
lim = maximum(abs.(ez))
lim_ϵ = maximum(abs.(ϵ))
p = plot(
clim=(-lim, lim), colorbar=false,
size=figsize, left_margin=left_margin, aspect_ratio=:equal
)
p = heatmap!(
p,
axes(s.grid, 1), axes(s.grid, 2), ez',
color=:coolwarm
)
p = contour!(
p,
axes(s.grid, 1), axes(s.grid, 2), lim .* ϵ' ./ lim_ϵ,
color=:algae
)
return p
end
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 7590 | export
Grid,
build,
boundary,
Light,
Permittivity,
implant!,
Permeability,
Simulator,
next!,
simulate!
const C = 299792458
struct Grid{T<:Real}
nx::Int
ny::Int
nt::Int
Δx::T
Δy::T
Δt::T
max_x::T
max_y::T
max_t::T
end
"""
Grid(max_x, max_y, max_t, nx, ny)
Construct a discretization grid for computational domain.
## Arguments
* `max_x`: Linear sizes of first computational domain in meters.
* `max_y`: Linear sizes of second computational domain in meters.
* `max_t`: Maximum computational time in seconds.
* `nx`: Number of discretization grid for first computational domain.
* `ny`: Number of discretization grid for second computational domain.
## Example
```jldoctest
julia> Grid(3e-6, 10e-6, 1e-12, 60, 200);
```
"""
function Grid(max_x, max_y, max_t, nx, ny)
Δx = max_x / nx
Δy = max_y / ny
Δt = 1 / C / √(1/Δx^2 + 1/Δy^2)
nt = round(Int, max_t/Δt)
return Grid(nx, ny, nt, Δx, Δy, Δt, max_x, max_y, max_t)
end
Base.size(grid::Grid) = (grid.nx, grid.ny)
Base.size(grid::Grid, d) = d::Integer <= 2 ? size(grid)[d] : 1
function Base.axes(grid::Grid)
axes_x = grid.Δx * (Base.OneTo(grid.nx) .- grid.nx/2)
axes_y = grid.Δy * (Base.OneTo(grid.ny) .- grid.Δy/2)
return (axes_x, axes_y)
end
Base.axes(grid::Grid, d) = d::Integer <= 2 ? axes(grid)[d] : 1
boundary(grid::Grid) = (grid.max_x, grid.max_y)
boundary(grid::Grid, d) = d::Integer <= 2 ? boundary(grid)[d] : 1
function build(grid::Grid)
return cat(
repeat(axes(grid, 1), 1, size(grid, 2), 1),
repeat(axes(grid, 2)', size(grid, 1), 1, 1),
dims=3
)
end
struct Light{T<:Real}
λ::T
k::T
end
"""
Light(λ)
Construct a light to propagate.
## Arguments
* `λ`: Wavelength of the light in meters.
## Example
```jldoctest
julia> Light(2.04e-6);
```
"""
function Light(λ)
return Light(λ, 2π/λ)
end
struct Permittivity{T<:AbstractMatrix}
ϵ::T
ϵx::T
ϵy::T
end
"""
Permittivity(ϵ_const::Real, grid::Grid)
Construct a uniform permittivity for the medium.
## Arguments
* `ϵ_const`: Permittivity of the medium in F/m.
* `grid`: Discretization grid.
## Example
```jldoctest
julia> grid = Grid(3e-6, 10e-6, 1e-12, 60, 200);
julia> Permittivity(9., grid);
```
"""
function Permittivity(ϵ_const::Real, grid::Grid)
ϵ = ϵ_const * ones(size(grid))
ϵx = C * grid.Δt/grid.Δx ./ ϵ
ϵy = C * grid.Δt/grid.Δy ./ ϵ
return Permittivity(ϵ, ϵx, ϵy)
end
"""
implant!(
permittivity::Permittivity, ϵ_const::Real,
xs::AbstractVector, ys::AbstractVector, rs::AbstractVector,
grid::Grid
)
Implant some bubble defect into the medium.
## Arguments
* `permittivity`: Permittivity object.
* `ϵ_const`: Permittivity of the defect in F/m.
* `xs`: Position of defect of first computational domain in meters.
* `ys`: Position of defect of second computational domain in meters.
* `rs`: Radius of defect in meters.
* `grid`: Discretization grid.
## Example
```jldoctest
julia> grid = Grid(3e-6, 10e-6, 1e-12, 60, 200);
julia> permittivity = Permittivity(9., grid);
julia> ϵ_defect = 1.;
julia> xs_defect = [0, 1e-6, -1e-6];
julia> ys_defect = [1e-6, 2e-6, 3e-6];
julia> rs_defect = [0.5e-6, 0.1e-6, 0.2e-6];
julia> implant!(
permittivity, ϵ_defect,
xs_defect, ys_defect, rs_defect,
grid
);
```
"""
function implant!(
permittivity::Permittivity, ϵ_const::Real,
xs::AbstractVector, ys::AbstractVector, rs::AbstractVector,
grid::Grid
)
length(xs) == length(ys) == length(rs) || throw(DimensionMismatch("xs, ys, rs must have same length"))
in_circle(i, j) = true in [
√(
(axes(grid, 1)[i] - xs[c])^2 +
(axes(grid, 2)[j] - ys[c])^2
) < rs[c]
for c in 1:length(xs)
]
for i in 1:size(grid, 1), j in 1:size(grid, 2)
in_circle(i, j) && (permittivity.ϵ[i, j] = ϵ_const)
end
permittivity.ϵx .= C * grid.Δt/grid.Δx ./ permittivity.ϵ
permittivity.ϵy .= C * grid.Δt/grid.Δy ./ permittivity.ϵ
return permittivity
end
struct Permeability{T<:AbstractMatrix}
μ::T
μx::T
μy::T
end
"""
Permeability(μ_const::Real, grid::Grid)
Construct a uniform permeability for the medium.
## Arguments
* `μ_const`: Permeability of the medium in N/A².
* `grid`: Discretization grid.
## Example
```jldoctest
julia> grid = Grid(3e-6, 10e-6, 1e-12, 60, 200);
julia> Permeability(1., grid);
```
"""
function Permeability(μ_const::Real, grid::Grid)
μ = μ_const * ones(size(grid))
μx = C * grid.Δt/grid.Δx ./ μ
μy = C * grid.Δt/grid.Δy ./ μ
return Permeability(μ, μx, μy)
end
mutable struct Simulator{T<:AbstractArray}
grid::Grid
light::Light
permittivity::Permittivity
permeability::Permeability
ez::T
hx::T
hy::T
t::Int
end
function get_default_e_field(light::Light, grid::Grid; t=1)
Δt = grid.Δt
k = light.k
return 0.1 * exp.(
-axes(grid, 1)[2:end].^2 ./
(boundary(grid, 1)/4)^2
) * sin(k * C*Δt*t)
end
"""
Simulator(grid::Grid, light::Light, permittivity::Permittivity, permeability::Permeability)
## Arguments
* `grid`: Discretization grid for computational domain.
* `light`: Light to propagate.
* `permittivity`: Permittivity for the medium.
* `permeability`: Permeability for the medium.
## Example
```jldoctest
julia> grid = Grid(3e-6, 10e-6, 1e-12, 60, 200);
julia> light = Light(2.04e-6);
julia> permittivity = Permittivity(9., grid);
julia> permeability = Permeability(1., grid);
julia> Simulator(grid, light, permittivity, permeability);
"""
function Simulator(grid::Grid, light::Light, permittivity::Permittivity, permeability::Permeability)
ez = zeros(Float64, size(grid))
ez[2:end, 1] .= get_default_e_field(light, grid)
return Simulator(
grid,
light,
permittivity,
permeability,
ez,
zeros(Float64, size(grid)),
zeros(Float64, size(grid)),
1
)
end
function Simulator(;
max_x=3e-6, max_y=10e-6, max_t=0.1e-12,
nx=300, ny=1000,
λ=2.04e-6,
ϵ = 9., μ = 1.
)
grid = Grid(max_x, max_y, max_t, nx, ny)
light = Light(λ)
permittivity = Permittivity(ϵ, grid)
permeability = Permeability(μ, grid)
return Simulator(grid, light, permittivity, permeability)
end
function next!(s::Simulator)
s.t += 1
ϵx, ϵy = s.permittivity.ϵx, s.permittivity.ϵy
μx, μy = s.permeability.μx, s.permeability.μy
s.ez[2:end, 1] .+= get_default_e_field(s.light, s.grid, t=s.t)
s.hx[2:end-1, 2:end-1] .+= -μx[2:end-1, 2:end-1].*(s.ez[2:end-1, 2:end-1] - s.ez[2:end-1, 1:end-2])
s.hy[2:end-1, 2:end-1] .+= +μy[2:end-1, 2:end-1].*(s.ez[2:end-1, 2:end-1] - s.ez[1:end-2, 2:end-1])
s.ez[2:end-1, 2:end-1] .+=
ϵx[2:end-1, 2:end-1].*(s.hy[3:end, 2:end-1] - s.hy[2:end-1, 2:end-1]) -
ϵy[2:end-1, 2:end-1].*(s.hx[2:end-1, 3:end] - s.hx[2:end-1, 2:end-1])
return s
end
"""
simulate!(s::Simulator)
Run simulation from current `t` to `max_t`
## Arguments
* `s`: Simulator.
## Example
```julia
julia> grid = Grid(3e-6, 10e-6, 1e-12, 60, 200);
julia> light = Light(2.04e-6);
julia> permittivity = Permittivity(9., grid);
julia> permeability = Permeability(1., grid);
julia> s = Simulator(grid, light, permittivity, permeability);
julia> simulate!(s);
```
"""
function simulate!(s::Simulator)
nt = s.grid.nt
p = Progress(nt)
for _ in (s.t+1):nt
next!(s)
ProgressMeter.next!(p)
end
return s
end
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 957 | using VisualRegressionTests
using Plots
@testset "utils" begin
gr()
# ##########
# # const. #
# ##########
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
nx = 60
ny = 200
λ = 2.04e-6
ϵ = 9.
μ = 1.
ϵ_defect = 1.
xs_defect = [0, 1e-6, -1e-6]
ys_defect = [1e-6, 2e-6, 3e-6]
rs_defect = [0.5e-6, 0.1e-6, 0.2e-6]
# ##############
# # components #
# ##############
grid = Grid(max_x, max_y, max_t, nx, ny)
light = Light(λ)
permittivity = Permittivity(ϵ, grid)
permeability = Permeability(μ, grid)
implant!(permittivity, ϵ_defect, xs_defect, ys_defect, rs_defect, grid)
# #############
# # simulator #
# #############
s = Simulator(grid, light, permittivity, permeability)
simulate!(s)
@plottest begin
plot_ϵ(s)
end "assets/permittivity.png"
@plottest begin
plot_e_field(s)
end "assets/e_field.png"
end
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 236 | using FieldDistributionNonuniformMedium
using Test
const C = 299792458
all_eq(x::AbstractArray) = all(xᵢ -> xᵢ == x[1], x)
@testset "FieldDistributionNonuniformMedium.jl" begin
include("simulation.jl")
include("plot.jl")
end
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | code | 3111 | @testset "grid" begin
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
nx = 60
ny = 200
Δx = max_x / nx
Δy = max_y / ny
Δt = 1 / C / √(1/Δx^2 + 1/Δy^2)
nt = round(Int, max_t/Δt)
axes_x = Δx * (Base.OneTo(nx) .- nx/2)
axes_y = Δy * (Base.OneTo(ny) .- Δy/2)
grid = Grid(max_x, max_y, max_t, nx, ny)
@test grid.Δx == Δx
@test grid.Δy == Δy
@test grid.Δt == Δt
@test grid.nt == nt
@test size(grid) == (nx, ny)
@test size(grid, 1) == nx
@test size(grid, 2) == ny
@test axes(grid) == (axes_x, axes_y)
@test axes(grid, 1) == axes_x
@test axes(grid, 2) == axes_y
@test boundary(grid) == (max_x, max_y)
@test boundary(grid, 1) == max_x
@test boundary(grid, 2) == max_y
@test build(grid) == cat(
repeat(axes_x, 1, ny, 1),
repeat(axes_y', nx, 1, 1),
dims=3
)
end
@testset "Light" begin
λ = 2.04e-6
light = Light(λ)
@test light.λ == λ
@test light.k == 2π/λ
end
@testset "permittivity" begin
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
nx = 60
ny = 200
ϵ = 9.
grid = Grid(max_x, max_y, max_t, nx, ny)
permittivity = Permittivity(ϵ, grid)
@test permittivity.ϵ[1] == ϵ
@test permittivity.ϵx[1] == C * grid.Δt/grid.Δx / ϵ
@test permittivity.ϵy[1] == C * grid.Δt/grid.Δy / ϵ
@test all_eq(permittivity.ϵ)
@test all_eq(permittivity.ϵx)
@test all_eq(permittivity.ϵy)
ϵ_defect = 1.
xs_defect = [0, 1e-6, -1e-6]
ys_defect = [1e-6, 2e-6, 3e-6]
rs_defect = [0.5e-6, 0.1e-6, 0.2e-6]
implant!(permittivity, ϵ_defect, xs_defect, ys_defect, rs_defect, grid)
in_circle(i, j) = true in [
√(
(axes(grid, 1)[i] - xs_defect[c])^2 +
(axes(grid, 2)[j] - ys_defect[c])^2
) < rs_defect[c]
for c in 1:length(rs_defect)
]
@test all(
in_circle(i, j) ? permittivity.ϵ[i, j] == ϵ_defect : permittivity.ϵ[i, j] == ϵ
for i in 1:size(grid, 1), j in 1:size(grid, 2)
)
end
@testset "permeability" begin
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
nx = 60
ny = 200
μ = 1.
grid = Grid(max_x, max_y, max_t, nx, ny)
permeability = Permeability(μ, grid)
@test permeability.μ[1] == μ
@test permeability.μx[1] == C * grid.Δt/grid.Δx / μ
@test permeability.μy[1] == C * grid.Δt/grid.Δy / μ
@test all_eq(permeability.μ)
@test all_eq(permeability.μx)
@test all_eq(permeability.μy)
end
@testset "simulation" begin
# ##########
# # const. #
# ##########
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
nx = 60
ny = 200
λ = 2.04e-6
ϵ = 9.
μ = 1.
# ##############
# # components #
# ##############
grid = Grid(max_x, max_y, max_t, nx, ny)
light = Light(λ)
permittivity = Permittivity(ϵ, grid)
permeability = Permeability(μ, grid)
# #############
# # simulator #
# #############
s = Simulator(nx=nx, ny=ny)
simulate!(s)
s = Simulator(grid, light, permittivity, permeability)
simulate!(s)
end
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | docs | 1113 | # FieldDistributionNonuniformMedium
[](https://foldfelis.github.io/FieldDistributionNonuniformMedium.jl/stable)
[](https://foldfelis.github.io/FieldDistributionNonuniformMedium.jl/dev)
[](https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl/actions/workflows/CI.yml?query=branch%3Amaster)
[](https://codecov.io/gh/foldfelis/FieldDistributionNonuniformMedium.jl)
## Installation
The package can be installed with the Julia package manager.
From the Julia REPL, type `]` to enter the Pkg REPL mode and run:
```julia
pkg> add FieldDistributionNonuniformMedium
```
## Quick start
```julia
julia> using FieldDistributionNonuniformMedium
julia> s = Simulator();
julia> simulate!(s);
julia> plot_e_field(s)
```

| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | docs | 97 | ## Index
```@index
```
## APIs
```@autodocs
Modules = [FieldDistributionNonuniformMedium]
```
| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | docs | 637 | ```@meta
CurrentModule = FieldDistributionNonuniformMedium
```
# FieldDistributionNonuniformMedium
Documentation for [FieldDistributionNonuniformMedium](https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl).
## Installation
The package can be installed with the Julia package manager.
From the Julia REPL, type `]` to enter the Pkg REPL mode and run:
```julia-REPL
pkg> add https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl
```
## Quick start
```julia-REPL
julia> using FieldDistributionNonuniformMedium
julia> s = Simulator();
julia> simulate!(s);
julia> plot_e_field(s)
```

| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.1.0 | 493a787e99086b5af9067488f52509002b2b4dc0 | docs | 2269 | ## Simulation
There are two way to construct a `Simulator` with **uniform** permittivity.
### Construct simulator by parameter
```julia
s = Simulator(
max_x=3e-6, max_y=10e-6, max_t=0.1e-12, # calculation boundaries
nx=300, ny=1000, # discretization
λ=2.04e-6, # wavelength of light
ϵ = 9., μ = 1. # permittivity and permeability
)
```
### Construct simulator by components
#### Declare constants
```julia
# calculation boundaries
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
# discretization
nx = 300
ny = 1000
# wavelength of light
λ = 2.04e-6
# permittivity and permeability
ϵ = 9.
μ = 1.
```
#### Construct components
```julia
grid = Grid(max_x, max_y, max_t, nx, ny)
light = Light(λ)
permittivity = Permittivity(ϵ, grid)
permeability = Permeability(μ, grid)
```
#### Construct simulator
```julia
s = Simulator(grid, light, permittivity, permeability)
```
## Implant defect to modify permittivity
```julia
# ##########
# # const. #
# ##########
# calculation boundaries
max_x = 3e-6
max_y = 10e-6
max_t = 0.1e-12
# discretization
nx = 300
ny = 1000
# wavelength of light
λ = 2.04e-6
# permittivity and permeability
ϵ = 9.
μ = 1.
# defect
ϵ_defect = 1.
xs_defect = [0, 1e-6, -1e-6]
ys_defect = [1e-6, 2e-6, 3e-6]
rs_defect = [0.5e-6, 0.1e-6, 0.2e-6]
# ##############
# # components #
# ##############
grid = Grid(max_x, max_y, max_t, nx, ny)
light = Light(λ)
permittivity = Permittivity(ϵ, grid)
permeability = Permeability(μ, grid)
implant!(permittivity, ϵ_defect, xs_defect, ys_defect, rs_defect, grid)
# #############
# # simulator #
# #############
s = Simulator(grid, light, permittivity, permeability)
```
Or
```julia
ϵ_defect = 1.
xs_defect = [0, 1e-6, -1e-6]
ys_defect = [1e-6, 2e-6, 3e-6]
rs_defect = [0.5e-6, 0.1e-6, 0.2e-6]
s = Simulator(
max_x=3e-6, max_y=10e-6, max_t=0.1e-12, # calculation boundaries
nx=300, ny=1000, # discretization
λ=2.04e-6, # wavelength of light
ϵ = 9., μ = 1. # permittivity and permeability
)
implant!(s.permittivity, ϵ_defect, xs_defect, ys_defect, rs_defect, s.grid)
```
## Run simulation
```julia
simulate!(s)
```
To see permittivity:
```julia
plot_ϵ(s)
```

To sea the result:
```julia
plot_e_field(s)
```

| FieldDistributionNonuniformMedium | https://github.com/foldfelis/FieldDistributionNonuniformMedium.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 2111 |
using Revise, StringDistances, Random
Random.seed!(2)
x = map(Random.randstring, rand(5:25,500_000))
y = map(Random.randstring, rand(5:25,500_000))
function f(t, x, y; min_score = 0.0)
[compare(x[i], y[i], t; min_score = min_score) for i in 1:length(x)]
end
function g(dist, x, y)
[dist(x[i], y[i]) for i in 1:length(x)]
end
@time f(Hamming(), x, y);
#0.05s
@time f(Jaro(), x, y);
#0.3s
@time f(Levenshtein(), x, y);
# 0.33s
@time f(Levenshtein(), x, y, min_score = 0.8);
# 0.11
@time f(OptimalStringAlignment(), x, y);
# 0.44s.
@time f(OptimalStringAlignment(), x, y, min_score = 0.8);
# 0.08
@time f(DamerauLevenshtein(), x, y);
# 0.8s
@time f(RatcliffObershelp(), x, y);
# 0.65s
@time findnearest(x[1], y, Levenshtein());
# 0.1
@time findnearest(x[1], y, OptimalStringAlignment());
# 0.1
@time findnearest(x[1], y, QGram(2));
# 0.75
@time findall(x[1], y, Levenshtein());
# 0.05
@time findall(x[1], y, OptimalStringAlignment());
# 0.05
@time findall(x[1], y, Partial(OptimalStringAlignment()));
# 0.96
@time findall(x[1], y, QGram(2));
# 0.81
@time findall(x[1], y, TokenSort(OptimalStringAlignment()));
# 0.27 (now 0.32)
@time findall(x[1], y, TokenSet(OptimalStringAlignment()));
# 0.55
@time findall(x[1], y, TokenMax(OptimalStringAlignment()));
# 2.25 (now 3.6)
x = map(Random.randstring, rand(5:25,1000))
y = map(Random.randstring, rand(5:25,1000))
@time pairwise(Levenshtein(), x, y)
# 0.25 seconds
@time pairwise(QGram(2), x, y, preprocess = false)
# 2.126829
@time pairwise(QGram(2), x, y, preprocess = true)
# 0.12
#= Rcode
library(stringdist)
x <- sapply(sample(5:25,5 * 1e5,replace=TRUE), function(n) paste(sample(letters,n,replace=TRUE),collapse=""))
y <- sapply(sample(5:25,5 * 1e5,replace=TRUE), function(n) paste(sample(letters,n,replace=TRUE),collapse=""))
system.time(stringdist(x,y,method='lv', nthread = 1))
system.time(stringdist(x,y,method='dl', nthread = 1))
# 0.472
system.time(stringdist(x,y,method='jaccard', nthread = 1))
# 0.739
system.time(stringdist(x,y,method='cosine', nthread = 1))
system.time(stringdist(x,y,method='qgram', nthread = 1))
=#
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 1547 | using StringDistances, Random
using BenchmarkTools
N = if length(ARGS) > 0
try
parse(Int, ARGS[1])
catch _
100
end
else
100 # default value
end
Maxlength = if length(ARGS) > 1
try
parse(Int, ARGS[2])
catch _
100
end
else
100 # default value
end
# If there are strings already cached to disk we start with them and only
# add new ones if needed.
using Serialization
const CacheFile = joinpath(@__DIR__(), "perfteststrings_$(Maxlength).juliabin")
SaveCache = false
S = if isfile(CacheFile)
try
res = deserialize(CacheFile)
println("Read $(length(res)) strings from cache file: $CacheFile")
res
catch err
String[]
end
else
println("Creating $N random strings.")
SaveCache = true
String[randstring(rand(3:Maxlength)) for _ in 1:N]
end
if length(S) < N
for i in (length(S)+1):N
push!(S, randstring(rand(3:Maxlength)))
end
SaveCache = true
end
if SaveCache
println("Saving cache file with $(length(S)) strings: $CacheFile")
serialize(CacheFile, S)
end
println("For ", Threads.nthreads(), " threads and ", N, " strings of max length ", Maxlength, ":")
dist = Cosine(2)
t1 = @belapsed dm1 = pairwise(dist, S; preprocess = false)
t2 = @belapsed dm2 = pairwise(dist, S; preprocess = true)
println(" - time WITHOUT pre-calculation: ", round(t1, digits = 3))
println(" - time WITH pre-calculation: ", round(t2, digits = 3))
println(" - speedup with pre-calculation: ", round(t1/t2, digits = 1))
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 1465 | module StringDistances
using Distances: Distances, SemiMetric, Metric, evaluate, result_type
using StatsAPI: StatsAPI, pairwise, pairwise!
# Distances API
abstract type StringSemiMetric <: SemiMetric end
abstract type StringMetric <: Metric end
const StringDistance = Union{StringSemiMetric, StringMetric}
function Distances.result_type(dist::Union{StringSemiMetric, StringMetric}, s1::Type, s2::Type)
T = typeof(dist("", ""))
if (Missing <: s1) | (Missing <: s2)
T = Union{T, Missing}
end
return T
end
(dist::Union{StringSemiMetric, StringMetric})(s1, s2; max_dist = nothing) = dist(s1, s2)
include("utils.jl")
include("distances/edit.jl")
include("distances/qgram.jl")
include("pairwise.jl")
include("normalize.jl")
include("find.jl")
include("fuzzywuzzy.jl")
##############################################################################
##
## Export
##
##############################################################################
export
StringDistance,
StringSemiMetric,
StringMetric,
# edit distances
Hamming,
Jaro,
JaroWinkler,
Levenshtein,
OptimalStringAlignment,
DamerauLevenshtein,
RatcliffObershelp,
# Qgram distances
AbstractQGramDistance,
QGramDict,
QGramSortedVector,
QGram,
Cosine,
Jaccard,
SorensenDice,
Overlap,
MorisitaOverlap,
NMD,
qgrams,
# normalize
compare,
# fuzzywuzzy
Partial,
TokenSort,
TokenSet,
TokenMax,
# find
findnearest,
# re-rexport from Distances.jl
evaluate,
result_type,
pairwise,
pairwise!
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 4336 | """
compare(s1, s2, dist)
return a similarity score between 0 and 1 for the strings `s1` and
`s2` based on the distance `dist`.
### Examples
```julia-repl
julia> compare("martha", "marhta", Levenshtein())
0.6666666666666667
```
"""
function compare(s1, s2, dist::Union{StringSemiMetric, StringMetric}; min_score = 0.0)
1 - Normalized(dist)(s1, s2; max_dist = 1 - min_score)
end
"""
findnearest(s, itr, dist::Union{StringMetric, StringSemiMetric}) -> (x, index)
`findnearest` returns the value and index of the element of `itr` that has the
lowest distance with `s` according to the distance `dist`.
It is particularly optimized for [`Levenshtein`](@ref) and [`DamerauLevenshtein`](@ref) distances
(as well as their modifications via [`Partial`](@ref), [`TokenSort`](@ref), [`TokenSet`](@ref), or [`TokenMax`](@ref)).
### Examples
```julia-repl
julia> using StringDistances
julia> s = "Newark"
julia> iter = ["New York", "Princeton", "San Francisco"]
julia> findnearest(s, iter, Levenshtein())
("NewYork", 1)
julia> findnearest(s, iter, Levenshtein(); min_score = 0.9)
(nothing, nothing)
```
"""
function findnearest(s, itr, dist::Union{StringSemiMetric, StringMetric}; min_score = 0.0)
_citr = collect(itr)
isempty(_citr) && return (nothing, nothing)
_preprocessed_s = _preprocess(dist, s)
min_score_atomic = Threads.Atomic{Float64}(min_score)
chunk_size = max(1, length(_citr) ÷ (2 * Threads.nthreads()))
data_chunks = Iterators.partition(_citr, chunk_size)
chunk_score_tasks = map(data_chunks) do chunk
Threads.@spawn begin
map(chunk) do x
score = compare(_preprocessed_s, _preprocess(dist, x), dist; min_score = min_score)
Threads.atomic_max!(min_score_atomic, score)
score
end
end
end
# retrieve return type of `compare` for type stability in task
_self_cmp = compare(_preprocessed_s, _preprocessed_s, dist; min_score = min_score)
chunk_scores = fetch.(chunk_score_tasks)::Vector{Vector{typeof(_self_cmp)}}
scores = reduce(vcat, fetch.(chunk_scores))
imax = argmax(scores)
iszero(scores) ? (nothing, nothing) : (_citr[imax], imax)
end
_preprocess(dist::AbstractQGramDistance, ::Missing) = missing
_preprocess(dist::AbstractQGramDistance, s) = QGramSortedVector(s, dist.q)
_preprocess(dist::Union{StringSemiMetric, StringMetric}, s) = s
function Base.findmax(s, itr, dist::Union{StringSemiMetric, StringMetric}; min_score = 0.0)
@warn "findmax(s, itr, dist; min_score) is deprecated. Use findnearest(s, itr, dist; min_score)"
findnearest(s, itr, dist; min_score = min_score)
end
"""
findall(s, itr , dist::StringDistance; min_score = 0.8)
`findall` returns the vector of indices for elements of `itr` that have a
similarity score higher or equal than `min_score` according to the distance `dist`.
If there are no such elements, return an empty array.
It is particularly optimized for [`Levenshtein`](@ref) and [`DamerauLevenshtein`](@ref) distances
(as well as their modifications via `Partial`, `TokenSort`, `TokenSet`, or `TokenMax`).
### Examples
```julia-repl
julia> using StringDistances
julia> s = "Newark"
julia> iter = ["Newwark", "Princeton", "San Francisco"]
julia> findall(s, iter, Levenshtein())
1-element Array{Int64,1}:
1
julia> findall(s, iter, Levenshtein(); min_score = 0.9)
0-element Array{Int64,1}
```
"""
function Base.findall(s, itr, dist::Union{StringSemiMetric, StringMetric}; min_score = 0.8)
_citr = collect(itr)
_preprocessed_s = _preprocess(dist, s)
chunk_size = max(1, length(_citr) ÷ (2 * Threads.nthreads()))
data_chunks = Iterators.partition(itr, chunk_size)
isempty(data_chunks) && return empty(eachindex(_citr))
chunk_score_tasks = map(data_chunks) do chunk
Threads.@spawn begin
map(chunk) do x
compare(_preprocessed_s, _preprocess(dist, x), dist; min_score = min_score)
end
end
end
# retrieve return type of `compare` for type stability in task
_self_cmp = compare(_preprocessed_s, _preprocessed_s, dist; min_score = min_score)
chunk_scores::Vector{Vector{typeof(_self_cmp)}} = fetch.(chunk_score_tasks)
scores = reduce(vcat, fetch.(chunk_scores))
return findall(>=(min_score), scores)
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 6665 | """
Partial(dist)
Creates the `Partial{dist}` distance.
`Partial{dist}` returns the minimum distance between the shorter string and substrings of the longer string that have a length equal to the shorter string.
See http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/
### Examples
```julia-repl
julia> s1 = "New York Mets vs Atlanta Braves"
julia> s2 = "Atlanta Braves vs New York Mets"
julia> Partial(RatcliffObershelp())(s1, s2)
0.5483870967741935
```
"""
struct Partial{S <: Union{StringSemiMetric, StringMetric}} <: StringSemiMetric
dist::S
end
function (dist::Partial)(s1, s2; max_dist = nothing)
(s1 === missing) | (s2 === missing) && return missing
s1, s2 = reorder(s1, s2)
len1, len2 = length(s1), length(s2)
out = dist.dist(s1, s2; max_dist = max_dist)
max_dist0 = (max_dist !== nothing) ? min(max_dist, out) : out
((len1 == 0) | (len1 == len2)) && return out
for x in qgrams(s2, len1)
curr = dist.dist(s1, x; max_dist = max_dist0)
out = min(out, curr)
max_dist0 = min(max_dist0, curr)
end
return out
end
# specialized (faster) version for RatcliffObershelp
function (dist::Partial{<: Union{RatcliffObershelp, Normalized{RatcliffObershelp}}})(s1, s2; max_dist = nothing)
(s1 === missing) | (s2 === missing) && return missing
s1, s2 = reorder(s1, s2)
len1, len2 = length(s1), length(s2)
len1 == len2 && return dist.dist(s1, s2)
out = 1.0
for s2_start in matching_blocks(s1, s2, 1, 1, len1, len2)
# Make sure the substring of s2 has length len1
if s2_start < 1
s2_start = 1
elseif s2_start + len1 - 1 > len2
s2_start += len2 - (s2_start + len1 - 1)
end
n_matched = length_matching_blocks(s1, s2, 1, s2_start, len1, s2_start + len1 - 1)
curr = 1 - 2 * n_matched / (len1 + len1)
out = min(out, curr)
end
return out
end
function matching_blocks(s1, s2, start1::Integer, start2::Integer, end1::Integer, end2::Integer)
x = Set{Int}()
p = zeros(Int, max(end1 - start1, end2 - start2) + 1)
matching_blocks!(x, p, s1, s2, start1, start2, end1, end2)
end
function matching_blocks!(x::Set{Int}, p::Vector{Int}, s1, s2, start1::Integer, start2::Integer, end1::Integer, end2::Integer)
j1, j2, len = longest_common_pattern!(p, s1, s2, start1, start2, end1, end2)
len == 0 && return x
push!(x, j2 - j1 + 1)
matching_blocks!(x, p, s1, s2, start1, start2, j1 - 1, j2 - 1)
matching_blocks!(x, p, s1, s2, j1 + len, j2 + len, end1, end2)
return x
end
Normalized(dist::Partial) = Normalized{typeof(Partial(Normalized(dist.dist)))}(Partial(Normalized(dist.dist)))
"""
TokenSort(dist)
Creates the `TokenSort{dist}` distance.
`TokenSort{dist}` returns the distance between strings after reording words alphabetically.
See http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/
It is only defined on AbstractStrings.
### Examples
```julia-repl
julia> s1 = "New York Mets vs Atlanta Braves"
julia> s1 = "New York Mets vs Atlanta Braves"
julia> s2 = "Atlanta Braves vs New York Mets"
julia> TokenSort(RatcliffObershelp())(s1, s2)
0.0
```
"""
struct TokenSort{S <: Union{StringSemiMetric, StringMetric}} <: StringSemiMetric
dist::S
end
function (dist::TokenSort)(s1::Union{AbstractString, Missing}, s2::Union{AbstractString, Missing}; max_dist = nothing)
(s1 === missing) | (s2 === missing) && return missing
f = s -> join(sort!(split(s)), " ")
dist.dist(f(s1), f(s2); max_dist = max_dist)
end
Normalized(dist::TokenSort) = Normalized{typeof(TokenSort(Normalized(dist.dist)))}(TokenSort(Normalized(dist.dist)))
"""
TokenSet(dist)
Creates the `TokenSet{dist}` distance, which is only defined on AbstractStrings.
`TokenSet{dist}` returns the minimum the distances between:
[SORTED_INTERSECTION]
[SORTED_INTERSECTION] + [SORTED_REST_OF_STRING1]
[SORTED_INTERSECTION] + [SORTED_REST_OF_STRING2]
See: http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/
### Examples
```julia-repl
julia> s1 = "New York Mets vs Atlanta"
julia> s2 = "Atlanta Braves vs New York Mets"
julia> TokenSet(RatcliffObershelp())(s1, s2)
0.0
```
"""
struct TokenSet{S <: Union{StringSemiMetric, StringMetric}} <: StringSemiMetric
dist::S
end
function (dist::TokenSet)(s1::Union{AbstractString, Missing}, s2::Union{AbstractString, Missing}; max_dist = nothing)
(s1 === missing) | (s2 === missing) && return missing
v1 = unique!(sort!(split(s1)))
v2 = unique!(sort!(split(s2)))
v0 = intersect(v1, v2)
s0 = join(v0, " ")
s1 = join(v1, " ")
s2 = join(v2, " ")
isempty(s0) && return dist.dist(s1, s2; max_dist = max_dist)
min(dist.dist(s0, s1; max_dist = max_dist),
dist.dist(s0, s2; max_dist = max_dist),
dist.dist(s1, s2; max_dist = max_dist))
end
Normalized(dist::TokenSet) = Normalized{typeof(TokenSet(Normalized(dist.dist)))}(TokenSet(Normalized(dist.dist)))
"""
TokenMax(dist)
Creates the `TokenMax{dist}` distance, which is only defined on AbstractStrings.
`TokenMax{dist}` normalizes the distance `dist` and returns the minimum of the distance,
its [`Partial`](@ref) modifier, its [`TokenSort`](@ref) modifier, and its
[`TokenSet`](@ref) modifier, with penalty terms depending on the strings lengths.
### Examples
```julia-repl
julia> s1 = "New York Mets vs Atlanta"
julia> s2 = "Atlanta Braves vs New York Mets"
julia> evaluate(TokenMax(RatcliffObershelp()), s1, s2)
0.05
```
"""
struct TokenMax{S <: Normalized} <: StringSemiMetric
dist::S
end
TokenMax(dist::Union{StringSemiMetric, StringMetric}) = TokenMax(Normalized(dist))
function (dist::TokenMax)(s1::Union{AbstractString, Missing}, s2::Union{AbstractString, Missing}; max_dist = 1.0)
(s1 === missing) | (s2 === missing) && return missing
s1, s2 = reorder(s1, s2)
len1, len2 = length(s1), length(s2)
dist0 = dist.dist
out = dist0(s1, s2; max_dist = max_dist)
max_dist = min(max_dist, out)
scale = 0.95
# if one string is much shorter than the other, use partial
if len2 >= 1.5 * len1
dist0 = Partial(dist0)
pscale = 0.9
pout = 1 - pscale * (1 - dist0(s1, s2; max_dist = 1 - (1 - max_dist) / pscale))
out = min(out, pout)
max_dist = min(max_dist, pout)
scale *= pscale
end
out_sort = 1 - scale * (1 - TokenSort(dist0)(s1, s2; max_dist = 1 - (1 - max_dist) / scale))
max_dist = min(max_dist, out_sort)
out_set = 1 - scale * (1 - TokenSet(dist0)(s1, s2; max_dist = 1 - (1 - max_dist) / scale))
out = min(out, out_sort, out_set)
out > max_dist ? 1.0 : out
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 2383 | # Normalized is basically wrapper like Symmetric
"""
Normalized(dist::Union{StringSemiMetric, StringMetric})
Creates a normalized distance. The normalized distance always return a Float64 between 0.0 and 1.0 (or a missing if one of the argument is missing).
A Normalized Distance has a keyword argument `max_dist` that defaults to 1.0. It returns 1.0 if the true distance is higher than `max_dist`.
### Examples
```julia-repl
julia> s1 = "New York Mets vs Atlanta"
julia> s2 = "Atlanta Braves vs New York Mets"
julia> Levenshtein()(s1, s2)
25
julia> StringDistances.Normalized(Levenshtein())(s1, s2)
0.8064
```
"""
struct Normalized{T <: Union{StringSemiMetric, StringMetric}} <: StringSemiMetric
dist::T
end
Normalized(dist::Normalized) = dist
# Consider all distances to be normalized by default
function (dist::Normalized)(s1, s2; max_dist = 1.0)
out = dist.dist(s1, s2; max_dist = max_dist)
max_dist !== nothing && out > max_dist && return 1.0
return out
end
function (dist::Normalized{<:Union{Hamming, DamerauLevenshtein}})(s1, s2; max_dist = 1.0)
(s1 === missing) | (s2 === missing) && return missing
s1, s2 = reorder(s1, s2)
len1, len2 = length(s1), length(s2)
len2 == 0 && return 0.0
out = dist.dist(s1, s2) / len2
max_dist !== nothing && out > max_dist && return 1.0
return out
end
function (dist::Normalized{<:Union{Levenshtein, OptimalStringAlignment}})(s1, s2; max_dist = 1.0)
(s1 === missing) | (s2 === missing) && return missing
s1, s2 = reorder(s1, s2)
len1, len2 = length(s1), length(s2)
len2 == 0 && return 0.0
if max_dist == 1.0
d = dist.dist(s1, s2)
else
d = dist.dist(s1, s2; max_dist = ceil(Int, len2 * max_dist))
end
out = d / len2
max_dist !== nothing && out > max_dist && return 1.0
return out
end
function (dist::Normalized{<:AbstractQGramDistance})(s1, s2; max_dist = 1.0)
(s1 === missing) | (s2 === missing) && return missing
# When string length < q for qgram distance, returns s1 == s2
s1, s2 = reorder(s1, s2)
len1, len2 = length(s1), length(s2)
len1 <= dist.dist.q - 1 && return Float64(s1 != s2)
if dist.dist isa QGram
out = dist.dist(s1, s2) / (len1 + len2 - 2 * dist.dist.q + 2)
else
out = dist.dist(s1, s2)
end
max_dist !== nothing && out > max_dist && return 1.0
return out
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 3088 | """
pairwise(dist::StringDistance, xs::AbstractVector, ys::AbstractVector = xs; preprocess = true)
Compute distances between all pairs of elements in `xs` and `ys` according to the
`StringDistance` `dist`. Returns a matrix R such that `R[i, j]` corrresponds to the distance between `xs[i]` and `ys[j]`.
Set `preprocess` to false if no preprocessing should be used.
Both symmetric and asymmetric versions are available.
### Examples
```julia-repl
julia> using StringDistances
julia> iter = ["New York", "Princeton"]
julia> pairwise(Levenshtein(), iter)
2×2 Array{Float64,2}:
0.0 9.0
9.0 0.0
julia> iter2 = ["San Francisco"]
julia> pairwise(Levenshtein(), iter, iter2)
2×1 Array{Float64,2}:
12.0
10.0
```
"""
function StatsAPI.pairwise(dist::Union{StringSemiMetric, StringMetric}, xs::AbstractVector, ys::AbstractVector = xs; preprocess = true)
T = result_type(dist, eltype(xs), eltype(ys))
R = Matrix{T}(undef, length(xs), length(ys))
pairwise!(R, dist, xs, ys; preprocess = preprocess)
end
"""
pairwise!(R::AbstractMatrix, dist::Union{StringSemiMetric, StringMetric}, xs::AbstractVector, ys::AbstractVector = xs; preprocess = true)
Compute distances between all pairs of elements in `xs` and `ys` according to the
`Union{StringSemiMetric, StringMetric}` `dist` and write the result in `R`. `R[i, j]` corresponds to the distance between `xs[i]` and `ys[j]`.
Set `preprocess` to false if no preprocessing should be used.
"""
function StatsAPI.pairwise!(R::AbstractMatrix, dist::Union{StringSemiMetric, StringMetric}, xs::AbstractVector, ys::AbstractVector = xs; preprocess = true)
length(xs) == size(R, 1) || throw(DimensionMismatch("inconsistent length"))
length(ys) == size(R, 2) || throw(DimensionMismatch("inconsistent length"))
(xs === ys) ?
_symmetric_pairwise!(R, dist, xs; preprocess = preprocess) :
_asymmetric_pairwise!(R, dist, xs, ys; preprocess = preprocess)
end
function _symmetric_pairwise!(R::AbstractMatrix, dist::Union{StringSemiMetric, StringMetric}, xs::AbstractVector; preprocess = true)
if preprocess
xs = _preprocess_list(dist, xs)
end
for i in 1:length(xs)
# handle missing
R[i, i] = xs[i] != xs[i]
Threads.@threads for j in (i+1):length(xs)
R[i, j] = R[j, i] = evaluate(dist, xs[i], xs[j])
end
end
return R
end
function _asymmetric_pairwise!(R::AbstractMatrix, dist::Union{StringSemiMetric, StringMetric}, xs::AbstractVector, ys::AbstractVector; preprocess = true)
if preprocess
objxs = _preprocess_list(dist, xs)
objys = xs === ys ? objxs : _preprocess_list(dist, ys)
else
objxs = xs
objys = ys
end
for i in 1:length(objxs)
Threads.@threads for j in 1:length(objys)
R[i, j] = evaluate(dist, objxs[i], objys[j])
end
end
return R
end
_preprocess_list(dist::Union{StringSemiMetric, StringMetric}, xs) = xs
_preprocess_list(dist::AbstractQGramDistance, xs) = fetch.(map(x -> (Threads.@spawn x === missing ? x : QGramSortedVector(x, dist.q)), xs)) | StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 1900 |
##############################################################################
##
## Some things about Strings
# length: number of characters
# ncodeunits: Return the number of code units in a string (aking to index of vector).
# Not all such indices are valid – they may not be the start of a character,.
# sizeof: Size, in bytes, of the string str. Equal to the number of code units in str
# multiplied by the size, in bytes, of one code unit in str.
# lastindex: Return the last index of a collection
# nextinds(s, i): return the index of the start of the character whose encoding starts after index i
# nextind(s, 0, N): return the index of the Nth character of s (or, if there are
# less than N characters, return ncodeunits(str) + (N - length(s))
##############################################################################
# This type allows to compute length once and for all
struct StringWithLength{T <: AbstractString} <: AbstractString
s::T
l::Int
end
string_with_length(s::AbstractString) = StringWithLength(s, length(s))
# Not really needed but avoid multi-encapsulation
string_with_length(s::StringWithLength) = s
Base.length(s::StringWithLength) = s.l
Base.iterate(s::StringWithLength) = iterate(s.s)
Base.iterate(s::StringWithLength, i::Integer) = iterate(s.s, i)
Base.nextind(s::StringWithLength, i::Int, n::Int = 1) = nextind(s.s, i, n)
Base.ncodeunits(s::StringWithLength) = ncodeunits(s.s)
Base.isvalid(s::StringWithLength, i::Int) = isvalid(s.s, i)
function reorder(s1::AbstractString, s2::AbstractString)
s1 = string_with_length(s1)
s2 = string_with_length(s2)
(length(s1) <= length(s2)) ? (s1, s2) : (s2, s1)
end
function reorder(s1, s2)
(length(s1) <= length(s2)) ? (s1, s2) : (s2, s1)
end
function common_prefix(s1, s2)
l = 0
for (ch1, ch2) in zip(s1, s2)
ch1 != ch2 && break
l += 1
end
return l
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 13655 | """
Hamming()
Creates the Hamming distance
The Hamming distance is defined as the number of characters that do not match
"""
struct Hamming <: StringMetric end
function (dist::Hamming)(s1, s2; max_dist::Union{Integer, Nothing} = nothing)
(s1 === missing) | (s2 === missing) && return missing
out = abs(length(s2) - length(s1))
for (ch1, ch2) in zip(s1, s2)
out += ch1 != ch2
if max_dist !== nothing
out > max_dist && return Int(max_dist + 1)
end
end
return out
end
"""
Jaro()
Creates the Jaro distance
The Jaro distance is defined as
``1 - (m / |s1| + m / |s2| + (m - t) / m) / 3``
where ``m`` is the number of matching characters and
``t`` is half the number of transpositions.
"""
struct Jaro <: StringSemiMetric end
## http://alias-i.com/lingpipe/docs/api/com/aliasi/spell/JaroWinklerDistance.html
function (dist::Jaro)(s1, s2)
(s1 === missing) | (s2 === missing) && return missing
len1, len2 = length(s1), length(s2)
if len1 > len2
s1, s2 = s2, s1
len1, len2 = len2, len1
end
# If both iterators empty, formula in Wikipedia gives 1, but it makes more sense to set it to s1 == s2
len2 > 0 || return Float64(s1 == s2)
d = max(0, div(len2, 2) - 1)
flag = fill(false, len2)
ch1_match = Vector{eltype(s1)}()
for (i1, ch1) in enumerate(s1)
for (i2, ch2) in enumerate(s2)
# for each character in s1, greedy search of matching character in s2 within a distance d
i2 >= i1 - d || continue
i2 <= i1 + d || break
if ch1 == ch2 && !flag[i2]
flag[i2] = true
push!(ch1_match, ch1)
break
end
end
end
if isempty(ch1_match)
return 1.0
else
# m counts number matching characters
m = length(ch1_match)
# t/2 counts number transpositions
t = 0
i1 = 0
for (i2, ch2) in enumerate(s2)
if flag[i2]
i1 += 1
@inbounds t += ch2 != ch1_match[i1]
end
end
return 1 - (m / len1 + m / len2 + (m - 0.5 * t) / m) / 3
end
end
"""
JaroWinkler(;p = 0.1, threshold = 0.3, maxlength = 4)
Creates the JaroWinkler distance
The JaroWinkler distance is defined as the Jaro distance, which is multiplied by
``(1-min(l, maxlength) * p)`` as long as it is lower than `threshold`, and where `l` denotes the length of the common prefix.
"""
struct JaroWinkler <: StringSemiMetric
p::Float64 # scaling factor. Default to 0.1
threshold::Float64 # boost limit. Default to 0.3
maxlength::Integer # max length of common prefix. Default to 4
end
JaroWinkler(; p = 0.1, threshold = 0.3, maxlength = 4) = JaroWinkler(p, threshold, maxlength)
## http://alias-i.com/lingpipe/docs/api/com/aliasi/spell/JaroWinklerDistance.html
function (dist::JaroWinkler)(s1, s2)
(s1 === missing) | (s2 === missing) && return missing
out = Jaro()(s1, s2)
if out <= dist.threshold
l = common_prefix(s1, s2)[1]
out = (1 - min(l, dist.maxlength) * dist.p) * out
end
return out
end
"""
Levenshtein()
Creates the Levenshtein distance
The Levenshtein distance is the minimum number of operations (consisting of insertions, deletions,
substitutions of a single character) required to change one string into the other.
"""
struct Levenshtein <: StringMetric end
## Source: http://blog.softwx.net/2014/12/optimizing-levenshtein-algorithm-in-c.html
# Return max_dist + 1 if distance higher than max_dist
# to differentiate distance equal to max_dist or not, which is important for find fctions.
function (dist::Levenshtein)(s1, s2; max_dist::Union{Integer, Nothing} = nothing)
(s1 === missing) | (s2 === missing) && return missing
len1, len2 = length(s1), length(s2)
if len1 > len2
s1, s2 = s2, s1
len1, len2 = len2, len1
end
if max_dist !== nothing
len2 - len1 > max_dist && return Int(max_dist + 1)
end
# prefix common to both strings can be ignored
k = common_prefix(s1, s2)
k == len1 && return len2 - k
# first row of matrix set to distance between "" and s2[1:i]
v = collect(1:(len2-k))
current = 0
for (i1, ch1) in enumerate(s1)
i1 > k || continue
left = current = i1 - k - 1
if max_dist !== nothing
value_lb = left - 1
end
for (i2, ch2) in enumerate(s2)
i2 > k || continue
above = current
# cost on diagonal (substitution)
current = left
@inbounds left = v[i2 - k]
if ch1 != ch2
# minimum between substitution, deletion and insertion
current = min(current + 1, above + 1, left + 1)
end
if max_dist !== nothing
value_lb = min(value_lb, left)
end
@inbounds v[i2 - k] = current
end
if max_dist !== nothing
value_lb > max_dist && return Int(max_dist + 1)
end
end
if max_dist !== nothing
current > max_dist && return Int(max_dist + 1 )
end
return current
end
"""
OptimalStringAlignment()
Creates the OptimalStringAlignment distance (also known as the restricted DamerauLevenshtein distance).
It is the minimum number of operations (consisting of insertions,
deletions or substitutions of a single character, or transposition of two adjacent characters)
required to change one string into the other.
The distance differs slightly from the DamerauLevenshtein distance by imposing
the restriction that no substring is edited more than once. So for example, "CA" to "ABC" has a distance
of 3 by the OptimalStringAlignment distance but a distance of 2 by the DamerauLevenshtein distance.
In contrast to the DamerauLevenshtein distance, the OptimalStringAlignment distance
does not satisfy the triangle inequality.
"""
struct OptimalStringAlignment <: StringSemiMetric end
## http://blog.softwx.net/2015/01/optimizing-damerau-levenshtein_15.html
# Return max_dist + 1 if distance higher than max_dist
function (dist::OptimalStringAlignment)(s1, s2; max_dist::Union{Integer, Nothing} = nothing)
(s1 === missing) | (s2 === missing) && return missing
len1, len2 = length(s1), length(s2)
if len1 > len2
s1, s2 = s2, s1
len1, len2 = len2, len1
end
if max_dist !== nothing
len2 - len1 > max_dist && return Int(max_dist + 1)
end
k = common_prefix(s1, s2)
k == len1 && return len2 - k
v = collect(1:(len2 - k))
w = similar(v)
prevch1, prevch2 = first(s1), first(s2)
if max_dist !== nothing
i2_start = 0
i2_end = max_dist
end
current = 0
for (i1, ch1) in enumerate(s1)
i1 > k || (prevch1 = ch1 ; continue)
left = i1 - k - 1
current = i1 - k
nextTransCost = 0
if max_dist !== nothing
i2_start += i1 - k - 1 + len2 - len1 > max_dist
i2_end += i2_end < len2
end
for (i2, ch2) in enumerate(s2)
i2 > k || (prevch2 = ch2 ; continue)
# no need to look beyond window of lower right diagonal - max distance cells
# lower right diag is i1 - (len2 - len1)) and the upper left diagonal + max_dist cells (upper left is i1)
if max_dist !== nothing
(k + i2_start < i2 < 1 + k + i2_end) || (prevch2 = ch2 ; continue)
end
above = current
thisTransCost = nextTransCost
@inbounds nextTransCost = w[i2 - k]
@inbounds w[i2 - k] = current = left
@inbounds left = v[i2 - k]
if ch1 != ch2
# minimum between substitution, deletion and insertion
current = min(current + 1, above + 1, left + 1)
if i1 > k + 1 && i2 > k + 1 && ch1 == prevch2 && prevch1 == ch2
thisTransCost += 1
current = min(current, thisTransCost)
end
end
@inbounds v[i2 - k] = current
prevch2 = ch2
end
if max_dist !== nothing
v[i1 - k + len2 - len1] > max_dist && return Int(max_dist + 1)
end
prevch1 = ch1
end
if max_dist !== nothing
current > max_dist && return Int(max_dist + 1)
end
return Int(current)
end
Base.@deprecate_binding OptimalStringAlignement OptimalStringAlignment
"""
DamerauLevenshtein()
Creates the DamerauLevenshtein distance
The DamerauLevenshtein distance is the minimum number of operations (consisting of insertions,
deletions or substitutions of a single character, or transposition of two adjacent characters)
required to change one string into the other.
"""
struct DamerauLevenshtein <: StringMetric end
# https://en.wikipedia.org/wiki/Damerau–Levenshtein_distance
# https://www.lemoda.net/text-fuzzy/damerau-levenshtein/
# Compared to Levenshtein & Restricted distance, cannot get by with only two vectors since transposition can be global
function (dist::DamerauLevenshtein)(s1, s2)
(s1 === missing) | (s2 === missing) && return missing
len1, len2 = length(s1), length(s2)
if len1 > len2
s1, s2 = s2, s1
len1, len2 = len2, len1
end
k = common_prefix(s1, s2)
k == len1 && return len2 - k
# da[ch1] will store last spotted position of ch1 in s1
da = Dict{eltype(s1), UInt32}()
sizehint!(da, len1 - k)
# distm[i1+1, i2+1] will store the distance between first i1 elements of s1 and first i2 elements of s2
distm = zeros(UInt32, len1 + 1 - k, len2 + 1 - k)
distm[:, 1] = 0:(len1-k)
distm[1, :] = 0:(len2-k)
for (i1, ch1) in enumerate(s1)
i1 > k || continue
# j2 is last spotted position of ch1 in s2
# j1 will be last spotted position of ch2 in s1
j2 = 0
for (i2, ch2) in enumerate(s2)
i2 > k || continue
if ch1 == ch2
@inbounds distm[i1 + 1 - k, i2 + 1 - k] = distm[i1 - k, i2 - k]
j2 = i2
else
# minimum between substitution, deletion and insertion
@inbounds pre = min(distm[i1 - k, i2 - k] + one(UInt32),
distm[i1 + 1 - k, i2 - k] + one(UInt32),
distm[i1 - k, i2 + 1 - k] + one(UInt32))
# minimum wrt transposition --- avoid lookup if we know transposition won't be chosen
# either because we're treating first character of s1 or because ch1 has not been spotted in s2 yet
j1 = (i1 == k + 1 || j2 == 0) ? 0 : get(da, ch2, 0)
if j1 > 0
@inbounds pre = min(pre, distm[j1 - k, j2 - k] + (i1 - j1 - 1) + 1 + (i2 - j2 - 1))
end
@inbounds distm[i1 + 1 - k, i2 + 1 - k] = pre
end
end
da[ch1] = i1
end
return Int(distm[end, end])
end
"""
RatcliffObershelp()
Creates the RatcliffObershelp distance
The distance between two strings is defined as one minus the number of matching characters
divided by the total number of characters in the two strings. Matching characters are those
in the longest common subsequence plus, recursively, matching characters in the unmatched
region on either side of the longest common subsequence.
"""
struct RatcliffObershelp <: StringSemiMetric end
function (dist::RatcliffObershelp)(s1, s2)
(s1 === missing) | (s2 === missing) && return missing
len1, len2 = length(s1), length(s2)
n_matched = length_matching_blocks(s1, s2, 1, 1, len1, len2)
len1 + len2 == 0 ? 0.0 : 1 - 2 * n_matched / (len1 + len2)
end
function length_matching_blocks(s1, s2, start1::Integer, start2::Integer, end1::Integer, end2::Integer)
# p is just a storage vector which will be reused
p = zeros(Int, max(end1 - start1, end2 - start2) + 1)
length_matching_blocks!(p, s1, s2, start1, start2, end1, end2)
end
function length_matching_blocks!(p::Vector{Int}, s1, s2, start1::Integer, start2::Integer, end1::Integer, end2::Integer)
end1 >= start1 || return 0
end2 >= start2 || return 0
j1, j2, len = longest_common_pattern!(p, s1, s2, start1, start2, end1, end2)
# exit if there is no common substring
len == 0 && return 0
return len +
length_matching_blocks!(p, s1, s2, start1, start2, j1 - 1, j2 - 1) +
length_matching_blocks!(p, s1, s2, j1 + len, j2 + len, end1, end2)
end
function longest_common_pattern!(p, s1, s2, start1, start2, end1, end2)
if end1 - start1 > end2 - start2
j2, j1, len = longest_common_pattern!(p, s2, s1, start2, start1, end2, end1)
else
j1, j2, len = 0, 0, 0
fill!(p, 0)
# p[i2-start2+1] stores the startingindex of the longest
# common pattern up to i2 with prevch1 as last matching character
for (i1, ch1) in enumerate(s1)
i1 >= start1 || continue
i1 <= end1 || break
oldj2 = 0
for (i2, ch2) in enumerate(s2)
i2 >= start2 || continue
i2 <= end2 || break
if ch1 != ch2
newj2 = 0
else
newj2 = oldj2 > 0 ? oldj2 : i2
newlen = i2 - newj2 + 1
if newlen > len
j1, j2, len = i1 - newlen + 1, newj2, newlen
end
end
p[i2 - start2 + 1], oldj2 = newj2, p[i2 - start2 + 1]
end
end
end
return j1, j2, len
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 12448 | abstract type AbstractQGramDistance <: StringSemiMetric end
"""
QGram(q::Int)
Creates a QGram distance.
The distance corresponds to
``||v(s1, q) - v(s2, q)||``
where ``v(s, q)`` denotes the vector on the space of q-grams of length q,
that contains the number of times a q-gram appears for the string s
"""
struct QGram <: AbstractQGramDistance
q::Int
end
eval_start(::QGram) = 0
@inline function eval_op(::QGram, c::Integer, n1::Integer, n2::Integer)
c + abs(n1 - n2)
end
eval_end(::QGram, c::Integer) = c
"""
Cosine(q::Int)
Creates a Cosine distance.
The distance corresponds to
`` 1 - v(s1, q).v(s2, q) / ||v(s1, q)|| * ||v(s2, q)||``
where ``v(s, q)`` denotes the vector on the space of q-grams of length q,
that contains the number of times a q-gram appears for the string s
"""
struct Cosine <: AbstractQGramDistance
q::Int
end
eval_start(::Cosine) = (0, 0, 0)
@inline function eval_op(::Cosine, c::NTuple{3, <:Integer}, n1::Integer, n2::Integer)
(c[1] + n1^2, c[2] + n2^2, c[3] + n1 * n2)
end
eval_end(::Cosine, c::NTuple{3, <:Integer}) = 1 - c[3] / sqrt(c[1] * c[2])
"""
Jaccard(q::Int)
Creates a Jaccard distance.
The distance corresponds to
``1 - |Q(s1, q) ∩ Q(s2, q)| / |Q(s1, q) ∪ Q(s2, q))|``
where ``Q(s, q)`` denotes the set of q-grams of length n for the string s
"""
struct Jaccard <: AbstractQGramDistance
q::Int
end
eval_start(::Jaccard) = (0, 0, 0)
@inline function eval_op(::Jaccard, c::NTuple{3, <:Integer}, n1::Integer, n2::Integer)
(c[1] + (n1 > 0), c[2] + (n2 > 0), c[3] + (n1 > 0) * (n2 > 0))
end
eval_end(::Jaccard, c::NTuple{3, <:Integer}) = 1 - c[3] / (c[1] + c[2] - c[3])
"""
SorensenDice(q::Int)
Creates a SorensenDice distance.
The distance corresponds to
``1 - 2 * |Q(s1, q) ∩ Q(s2, q)| / (|Q(s1, q)| + |Q(s2, q))|)``
where ``Q(s, q)`` denotes the set of q-grams of length n for the string s
"""
struct SorensenDice <: AbstractQGramDistance
q::Int
end
eval_start(::SorensenDice) = (0, 0, 0)
@inline function eval_op(::SorensenDice, c::NTuple{3, <:Integer}, n1::Integer, n2::Integer)
(c[1] + (n1 > 0), c[2] + (n2 > 0), c[3] + (n1 > 0) * (n2 > 0))
end
eval_end(::SorensenDice, c::NTuple{3, <:Integer}) = 1 - 2 * c[3] / (c[1] + c[2])
"""
Overlap(q::Int)
Creates a Overlap distance.
The distance corresponds to
``1 - |Q(s1, q) ∩ Q(s2, q)| / min(|Q(s1, q)|, |Q(s2, q)|)``
where ``Q(s, q)`` denotes the set of q-grams of length n for the string s
"""
struct Overlap <: AbstractQGramDistance
q::Int
end
eval_start(::Overlap) = (0, 0, 0)
@inline function eval_op(::Overlap, c::NTuple{3, <:Integer}, n1::Integer, n2::Integer)
(c[1] + (n1 > 0), c[2] + (n2 > 0), c[3] + (n1 > 0) * (n2 > 0))
end
eval_end(::Overlap, c::NTuple{3, <:Integer}) = 1 - c[3] / min(c[1], c[2])
"""
NMD(q::Int)
NMD(q::Int)
Creates a NMD (Normalized Multiset Distance) as introduced by Besiris and
Zigouris 2013. The goal with this distance is to behave similarly to a normalized
compression distance without having to do any actual compression (and thus being
faster to compute).
The distance corresponds to
``(sum(max.(m(s1), m(s2)) - min(M(s1), M(s2))) / max(M(s1), M(s2))``
where ``m(s)`` is the vector of q-gram counts for string ``s`` and ``M(s)`` is the
sum of those counts.
For details see:
https://www.sciencedirect.com/science/article/pii/S1047320313001417
"""
struct NMD <: AbstractQGramDistance
q::Int
end
eval_start(::NMD) = (0, 0, 0)
@inline function eval_op(::NMD, c::NTuple{3, <:Integer}, n1::Integer, n2::Integer)
(c[1] + n1, c[2] + n2, c[3] + max(n1, n2))
end
eval_end(::NMD, c::NTuple{3, <:Integer}) = (c[3] - min(c[1], c[2])) / max(c[1], c[2])
"""
MorisitaOverlap(q::Int)
Creates a MorisitaOverlap distance, a general, statistical measure of
dispersion which can also be used on dictionaries such as created
from q-grams. See https://en.wikipedia.org/wiki/Morisita%27s_overlap_index
This is more fine-grained than many of the other QGramDistances since
it is based on the counts per q-gram rather than only which q-grams are
in the strings.
The distance corresponds to
``(2 * sum(m(s1) .* m(s2)) / (sum(m(s1).^2)*M(s2)/M(s1) + sum(m(s2).^2)*M(s1)/M(s2))``
where ``m(s)`` is the vector of q-gram counts for string ``s`` and ``M(s)`` is the
sum of those counts.
"""
struct MorisitaOverlap <: AbstractQGramDistance
q::Int
end
eval_start(::MorisitaOverlap) = (0, 0, 0, 0, 0)
@inline function eval_op(::MorisitaOverlap, c::NTuple{5, <:Integer}, n1::Integer, n2::Integer)
(c[1] + n1, c[2] + n2, c[3] + n1^2, c[4] + n2^2, c[5] + n1 * n2)
end
eval_end(::MorisitaOverlap, c::NTuple{5, <:Integer}) = 1 - 2 * c[5] / (c[3] * c[2] / c[1] + c[4] * c[1] / c[2])
#==========================================================================
QGramIterator
==========================================================================#
@doc """
Return an iterator corresponding to the the q-gram of an iterator.
When the iterator is a String, qgrams are SubStrings.
### Arguments
* `s` iterator
* `q::Integer`: length of q-gram
## Examples
```julia
for x in qgrams("hello", 2)
println(x)
end
```
"""
qgrams
struct QGramIterator{S <: Union{AbstractString, AbstractVector}}
s::S # Collection
q::Int # Length of Qgram
function QGramIterator{S}(s, q) where {S <: Union{AbstractString, AbstractVector}}
q > 0 || throw(ArgumentError("The qgram length must be higher than zero"))
new(s, q)
end
end
function QGramIterator(s::Union{AbstractString, AbstractVector}, q::Integer)
QGramIterator{typeof(s)}(s, q)
end
Base.length(qgram::QGramIterator) = max(length(qgram.s) - qgram.q + 1, 0)
# q-grams of AbstractString
function Base.iterate(qgram::QGramIterator{<: AbstractString},
state = (1, nextind(qgram.s, 0, qgram.q)))
istart, iend = state
iend > ncodeunits(qgram.s) && return nothing
element = SubString(qgram.s, istart, iend)
nextstate = nextind(qgram.s, istart), nextind(qgram.s, iend)
element, nextstate
end
Base.eltype(qgram::QGramIterator{SubString{S}}) where {S} = SubString{S}
Base.eltype(qgram::QGramIterator{S}) where {S <: AbstractString} = SubString{S}
qgrams(s::AbstractString, q::Integer) = QGramIterator(s, q)
# q-grams of General Iterators
function Base.iterate(qgram::QGramIterator{<: AbstractVector}, state = firstindex(qgram.s))
state + qgram.q - 1 > lastindex(qgram.s) && return nothing
view(qgram.s, state:(state + qgram.q - 1)), state + 1
end
Base.eltype(qgram::QGramIterator{<: AbstractVector}) = typeof(first(qgram))
qgrams(s::AbstractVector, q::Integer) = QGramIterator(s, q)
qgrams(s, q::Integer) = QGramIterator(collect(s), q)
#==========================================================================
Compute QGramDistances on general iterators
==========================================================================#
# For two iterators s1 and s2, that define a length and eltype method,
# this returns an iterator that,
# for each element in s1 ∪ s2, returns (numbers of times it appears in s1, numbers of times it appears in s2)
function _count(qgrams1, qgrams2)
K = promote_type(eltype(qgrams1), eltype(qgrams2))
d = Dict{K, Tuple{Int, Int}}()
sizehint!(d, length(qgrams1) + length(qgrams2))
# I use a faster way to change a dictionary key
# see setindex! in https://github.com/JuliaLang/julia/blob/master/base/dict.jl#L380
for x1 in qgrams1
index = Base.ht_keyindex2!(d, x1)
if index > 0
d.age += 1
@inbounds d.keys[index] = x1
@inbounds d.vals[index] = (d.vals[index][1] + 1, 0)
else
@inbounds Base._setindex!(d, (1, 0), x1, -index)
end
end
for x2 in qgrams2
index = Base.ht_keyindex2!(d, x2)
if index > 0
d.age += 1
@inbounds d.keys[index] = x2
@inbounds d.vals[index] = (d.vals[index][1], d.vals[index][2] + 1)
else
@inbounds Base._setindex!(d, (0, 1), x2, -index)
end
end
return values(d)
end
function (dist::AbstractQGramDistance)(s1, s2)
(s1 === missing) | (s2 === missing) && return missing
c = eval_start(dist)
for (n1, n2) in _count(qgrams(s1, dist.q), qgrams(s2, dist.q))
c = eval_op(dist, c, n1, n2)
end
eval_end(dist, c)
end
#==========================================================================
Compute QGramDistances on QGramDicts, iterators that store a dictionary associating qgrams to the number of their occurences
==========================================================================#
"""
QGramDict(s, q::Integer = 2)
An iterator with a pre-computed dictionary of its qgrams. This enables faster calculation of QGram
distances.
Note that the qgram length must correspond with the q length used
in the distance.
## Examples
```julia
str1, str2 = "my string", "another string"
qd1 = QGramDict(str1, 2)
qd2 = QGramDict(str2, 2)
evaluate(Overlap(2), qd1, qd2)
```
"""
struct QGramDict{S, K}
s::S
q::Int
counts::Dict{K, Int}
end
Base.length(s::QGramDict) = length(s.s)
Base.iterate(s::QGramDict, args...) = iterate(s.s, args...)
function QGramDict(s, q::Integer = 2)
(s isa QGramDict) && (s.q == q) && return s
qgs = qgrams(s, q)
countpairs = countdict(qgs)
QGramDict{typeof(s), eltype(qgs)}(s, q, countpairs)
end
# Turn a sequence of qgrams to a count dict for them, i.e. map each
# qgram to the number of times it has been seen.
function countdict(qgrams)
d = Dict{eltype(qgrams), Int}()
for qg in qgrams
index = Base.ht_keyindex2!(d, qg)
if index > 0
d.age += 1
@inbounds d.keys[index] = qg
@inbounds d.vals[index] = d.vals[index][1] + 1
else
@inbounds Base._setindex!(d, 1, qg, -index)
end
end
return d
end
function (dist::AbstractQGramDistance)(qc1::QGramDict, qc2::QGramDict)
dist.q == qc1.q == qc2.q || throw(ArgumentError("The distance and the QGramDict must have the same qgram length"))
d1, d2 = qc1.counts, qc2.counts
c = eval_start(dist)
for (s1, n1) in d1
index = Base.ht_keyindex2!(d2, s1)
if index <= 0
c = eval_op(dist, c, n1, 0)
else
c = eval_op(dist, c, n1, d2.vals[index])
end
end
for (s2, n2) in d2
index = Base.ht_keyindex2!(d1, s2)
if index <= 0
c = eval_op(dist, c, 0, n2)
end
end
eval_end(dist, c)
end
#==========================================================================
Compute QGramDistances on QGramSortedVectors, iterators that store a sorted vector associating qgrams to the number of their occurences
Note that QGramSortedVectors require qgrams to have a natural order
==========================================================================#
"""
QGramSortedVector(s, q::Integer = 2)
An iterator with a pre-computed sorted vector of its qgrams. This enables faster calculation of QGram
distances.
Since qgrams are sorted in lexicographic order QGram distances can be
calculated even faster than when using a QGramDict. However, the
sorting means that updating the counts after creation is less
efficient. However, for most use cases QGramSortedVector is preferred
over a QgramDict.
Note that the qgram length must correspond with the q length used
in the distance.
## Examples
```julia
str1, str2 = "my string", "another string"
qs1 = QGramSortedVector(str1, 2)
qs2 = QGramSortedVector(str2, 2)
evaluate(Jaccard(2), qs1, qs2)
```
"""
struct QGramSortedVector{S, K}
s::S
q::Int
counts::Vector{Pair{K, Int}}
end
Base.length(s::QGramSortedVector) = length(s.s)
Base.iterate(s::QGramSortedVector, args...) = iterate(s.s, args...)
function QGramSortedVector(s, q::Integer = 2)
(s isa QGramSortedVector) && (s.q == q) && return s
qgs = qgrams(s, q)
# todo: maybe more efficient to create sorteddict directly
countpairs = collect(countdict(qgs))
sort!(countpairs, by = first)
QGramSortedVector{typeof(s), eltype(qgs)}(s, q, countpairs)
end
function (dist::AbstractQGramDistance)(qc1::QGramSortedVector, qc2::QGramSortedVector)
dist.q == qc1.q == qc2.q || throw(ArgumentError("The distance and the QGramSortedVectors must have the same qgram length"))
d1, d2 = qc1.counts, qc2.counts
c = eval_start(dist)
i1 = i2 = 1
while true
# length can be zero
if i2 > length(d2)
for i in i1:length(d1)
@inbounds c = eval_op(dist, c, d1[i][2], 0)
end
break
elseif i1 > length(d1)
for i in i2:length(d2)
@inbounds c = eval_op(dist, c, 0, d2[i][2])
end
break
end
@inbounds s1, n1 = d1[i1]
@inbounds s2, n2 = d2[i2]
cmpval = Base.cmp(s1, s2)
if cmpval == -1 # s1 < s2
c = eval_op(dist, c, n1, 0)
i1 += 1
elseif cmpval == 1 # s1 > s2
c = eval_op(dist, c, 0, n2)
i2 += 1
else # s1 == s2
c = eval_op(dist, c, n1, n2)
i1 += 1
i2 += 1
end
end
eval_end(dist, c)
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 16093 | using StringDistances, Unicode, Test, Random
@testset "Distances" begin
@testset "Hamming" begin
@test Hamming()("martha", "marhta") ≈ 2
@test Hamming()("es an ", " vs an") ≈ 6
@test Hamming()([1, 2, 3], [1,2, 4]) ≈ 1
@inferred Hamming()("", "")
@test ismissing(Hamming()("", missing))
end
@testset "Jaro" begin
@test Jaro()("martha", "marhta") ≈ 0.05555555555555547
@test Jaro()("es an ", " vs an") ≈ 0.2777777777777777
@test Jaro()(" vs an", "es an ") ≈ 0.2777777777777777
@test Jaro()([1, 2, 3], [1,2, 4]) ≈ 0.2222222222222222
@test Jaro()(graphemes("alborgów"), graphemes("amoniak")) == Jaro()("alborgów", "amoniak")
@test Jaro()(" vs an", "es an ") ≈ 0.2777777777777777
@test result_type(Jaro(), "hello", "world") == typeof(float(1))
@inferred Jaro()("", "")
@test ismissing(Jaro()("", missing))
end
@testset "Levenshtein" begin
@test Levenshtein()("", "") == 0
@test Levenshtein()("abc", "") == 3
@test Levenshtein()("", "abc") == 3
@test Levenshtein()("bc", "abc") == 1
@test Levenshtein()("kitten", "sitting") == 3
@test Levenshtein()("saturday", "sunday") == 3
@test Levenshtein()("hi, my name is", "my name is") == 4
@test Levenshtein()("a cat", "an act") == 3
@test Levenshtein()("alborgów", "amoniak") == 6
prefix = "my_prefix"
@test Levenshtein()(prefix * "alborgów", prefix * "amoniak") == Levenshtein()("alborgów", "amoniak")
@test Levenshtein()([1, 2, 3], [1, 2, 4]) == 1
@test Levenshtein()(graphemes("alborgów"), graphemes("amoniak")) == Levenshtein()("alborgów", "amoniak")
@test Levenshtein()("", "abc") == 3
@test result_type(Levenshtein(), "hello", "world") == Int
@inferred Levenshtein()("", "")
@test ismissing(Levenshtein()("", missing))
end
@testset "OptimalStringAlignment" begin
@test OptimalStringAlignment()("", "") == 0
@test OptimalStringAlignment()("abc", "") == 3
@test OptimalStringAlignment()("bc", "abc") == 1
@test OptimalStringAlignment()("fuor", "four") == 1
@test OptimalStringAlignment()("abcd", "acb") == 2
@test OptimalStringAlignment()("cape sand recycling ", "edith ann graham") == 17
@test OptimalStringAlignment()("jellyifhs", "jellyfish") == 2
@test OptimalStringAlignment()("ifhs", "fish") == 2
@test OptimalStringAlignment()("a cat", "an act") == 2
@test OptimalStringAlignment()("a cat", "an abct") == 4
@test OptimalStringAlignment()("a cat", "a tc") == 3
@test OptimalStringAlignment()("abcdef", "abcxyf") == 2
@test OptimalStringAlignment()("abcdef", "abcxyf"; max_dist = 2) == 2
prefix = "my_prefix"
@test OptimalStringAlignment()(prefix * "alborgów", prefix * "amoniak") == OptimalStringAlignment()("alborgów", "amoniak")
@test OptimalStringAlignment()([1, 2, 3], [1,2, 4]) == 1
@test OptimalStringAlignment()(graphemes("alborgów"), graphemes("amoniak")) == OptimalStringAlignment()("alborgów", "amoniak")
@test OptimalStringAlignment()("bc", "abc") == 1
@test result_type(OptimalStringAlignment(), "hello", "world") == Int
@inferred OptimalStringAlignment()("", "")
@test ismissing(OptimalStringAlignment()("", missing))
end
@testset "DamerauLevenshtein" begin
@test DamerauLevenshtein()("", "") == 0
@test DamerauLevenshtein()("CA", "ABC") == 2
@test DamerauLevenshtein()("ABCDEF", "ABDCEF") == 1
@test DamerauLevenshtein()("ABCDEF", "BACDFE") == 2
@test DamerauLevenshtein()("ABCDEF", "ABCDE") == 1
@test DamerauLevenshtein()("a cat", "an act") == 2
@test DamerauLevenshtein()("a cat", "an abct") == 3
@test DamerauLevenshtein()("a cat", "a tc") == 2
prefix = "my_prefix"
@test DamerauLevenshtein()(prefix * "alborgów", prefix * "amoniak") == DamerauLevenshtein()("alborgów", "amoniak")
@test result_type(DamerauLevenshtein(), "hello", "world") == Int
@inferred DamerauLevenshtein()("", "")
@test ismissing(DamerauLevenshtein()("", missing))
end
@testset "RatcliffObershelp" begin
@test RatcliffObershelp()("dixon", "dicksonx") ≈ 1 - 0.6153846153846154
@test RatcliffObershelp()("alexandre", "aleksander") ≈ 1 - 0.7368421052631579
@test RatcliffObershelp()("pennsylvania", "pencilvaneya") ≈ 1 - 0.6666666666666
@test RatcliffObershelp()("", "pencilvaneya") ≈ 1.0
@test RatcliffObershelp()("NEW YORK METS", "NEW YORK MEATS") ≈ 1 - 0.962962962963
@test RatcliffObershelp()("Yankees", "New York Yankees") ≈ 0.3913043478260869
@test RatcliffObershelp()("New York Mets", "New York Yankees") ≈ 0.24137931034482762
@test RatcliffObershelp()([1, 2, 3], [1,2, 4]) ≈ 1/3
@test RatcliffObershelp()(graphemes("alborgów"), graphemes("amoniak")) == RatcliffObershelp()("alborgów", "amoniak")
@test RatcliffObershelp()("pennsylvania", "pencilvaneya") ≈ 1 - 0.6666666666666
@test result_type(RatcliffObershelp(), "hello", "world") == typeof(float(1))
@inferred RatcliffObershelp()("", "")
@test ismissing(RatcliffObershelp()("", missing))
end
@testset "QGram" begin
@test QGram(1)("abc", "abc") == 0
@test QGram(1)("", "abc") == 3
@test QGram(1)("abc", "cba") == 0
@test QGram(1)("abc", "ccc") == 4
@test QGram(4)("aü☃", "aüaüafs") == 4
@test QGram(2)(SubString("aü☃", 1, 4), SubString("aüaüafs", 1, 4)) == 2
@test QGram(2)(graphemes("alborgów"), graphemes("amoniak")) ≈ QGram(2)("alborgów", "amoniak")
@test QGram(1)("abc", "cba") == 0
@test result_type(QGram(1), "hello", "world") == Int
@test ismissing(QGram(1)("", missing))
@inferred QGram(1)("", "")
end
@testset "Cosine" begin
@test isnan(Cosine(2)("", "abc"))
@test Cosine(2)("abc", "ccc") ≈ 1 atol = 1e-4
@test Cosine(2)("leia", "leela") ≈ 0.7113249 atol = 1e-4
@test Cosine(2)([1, 2, 3], [1, 2, 4]) ≈ 0.5
@test Cosine(2)(graphemes("alborgów"), graphemes("amoniak")) ≈ Cosine(2)("alborgów", "amoniak")
@test Cosine(2)("leia", "leela") ≈ 0.7113249 atol = 1e-4
@test result_type(Cosine(2), "hello", "world") == typeof(float(1))
@inferred Cosine(2)("", "")
@test ismissing(Cosine(2)("", missing))
end
@testset "Jaccard" begin
@test Jaccard(1)("", "abc") ≈ 1.0
@test Jaccard(1)("abc", "ccc") ≈ 2/3 atol = 1e-4
@test Jaccard(2)("leia", "leela") ≈ 0.83333 atol = 1e-4
@test Jaccard(2)([1, 2, 3], [1, 2, 4]) ≈ 2/3 atol = 1e-4
@test Jaccard(2)(graphemes("alborgów"), graphemes("amoniak")) ≈ Jaccard(2)("alborgów", "amoniak")
@test Jaccard(2)("leia", "leela") ≈ 0.83333 atol = 1e-4
@test result_type(Jaccard(1), "hello", "world") == typeof(float(1))
@inferred Jaccard(1)("", "")
@test ismissing(Jaccard(1)("", missing))
end
@testset "SorensenDice" begin
@test SorensenDice(1)("night", "nacht") ≈ 0.4 atol = 1e-4
@test SorensenDice(2)("night", "nacht") ≈ 0.75 atol = 1e-4
@test SorensenDice(2)(graphemes("alborgów"), graphemes("amoniak")) ≈ SorensenDice(2)("alborgów", "amoniak")
@test SorensenDice(2)("night", "nacht") ≈ 0.75 atol = 1e-4
@test result_type(SorensenDice(1), "hello", "world") == typeof(float(1))
@inferred SorensenDice(1)("", "")
@test ismissing(SorensenDice(1)("", missing))
end
@testset "Overlap" begin
@test Overlap(1)("night", "nacht") ≈ 0.4 atol = 1e-4
@test Overlap(1)("context", "contact") ≈ .2 atol = 1e-4
@test Overlap(1)("context", "contact") ≈ .2 atol = 1e-4
@test result_type(Overlap(1), "hello", "world") == typeof(float(1))
@inferred Overlap(1)("", "")
@test ismissing(Overlap(1)("", missing))
end
@testset "MorisitaOverlap" begin
# overlap for 'n', 'h', and 't' and 5 q-grams per string:
@test MorisitaOverlap(1)("night", "nacht") == 0.4 # 1.0-((2*3)/(5*5/5 + 5*5/5))
# overlap for 'o', 'n', 2-overlap for 'c' and 't' and 7 unique q-grams in total so multiplicity vectors
# ms1 = [1, 1, 1, 2, 1, 1, 0]
# ms2 = [2, 1, 1, 2, 0, 0, 1]
# sum(ms1 .* ms2) = 8, sum(ms1 .^ 2) = 9, sum(ms2 .^ 2) = 11, sum(ms1) = 7, sum(ms2) = 7
@test MorisitaOverlap(1)("context", "contact") ≈ .2 atol = 1e-4 # 1.0-((2*8)/(9*7/7 + 11*7/7)) = 16/20
@test MorisitaOverlap(1)("context", "contact") ≈ .2 atol = 1e-4
# Multiplicity vectors for 2-grams "co", "on", "nt", "te", "ex", "xt", "ta", "ac", "ct"
# ms1 = [1, 1, 1, 1, 1, 1, 0, 0, 0]
# ms2 = [1, 1, 1, 0, 0, 0, 1, 1, 1]
# sum(ms1 .* ms2) = 3, sum(ms1 .^ 2) = 6, sum(ms2 .^ 2) = 6, sum(ms1) = 6, sum(ms2) = 6
@test MorisitaOverlap(2)("context", "contact") == 0.5 # 1.0-((2*3)/(6*6/6 + 6*6/6))
@test result_type(MorisitaOverlap(1), "hello", "world") == typeof(float(1))
@inferred MorisitaOverlap(1)("", "")
@test ismissing(MorisitaOverlap(1)("", missing))
end
@testset "NMD" begin
# m(s1) = [1, 1, 1, 1, 1, 0, 0], m(s2) = [1, 0, 0, 1, 1, 1, 1]
@test NMD(1)("night", "nacht") == 0.4 # (7-5)/5
# ms1 = [1, 1, 1, 2, 1, 1, 0]
# ms2 = [2, 1, 1, 2, 0, 0, 1]
@test NMD(1)("context", "contact") ≈ 0.2857 atol = 1e-4 # ((2+1+1+2+1+1+1)-7)/(7)
@test NMD(1)("context", "contact") ≈ 0.2857 atol = 1e-4
# ms1 = [1, 1, 1, 1, 1, 1, 0, 0, 0]
# ms2 = [1, 1, 1, 0, 0, 0, 1, 1, 1]
@test NMD(2)("context", "contact") == 0.5 # ((1+1+1+1+1+1+1+1+1)-6)/6
@test result_type(NMD(1), "hello", "world") == typeof(float(1))
@inferred NMD(1)("", "")
@test ismissing(NMD(1)("", missing))
end
@testset "QGramDict and QGramSortedVector counts qgrams" begin
# To get something we can more easily compare to:
stringify(p::Pair{<:AbstractString, <:Integer}) = (string(first(p)), last(p))
stringify(p::Pair{V, <:Integer}) where {S<:AbstractString,V<:AbstractVector{S}} = (map(string, first(p)), last(p))
sortedcounts(qc) = sort(collect(qc.counts), by = first)
totuples(qc) = map(stringify, sortedcounts(qc))
s1, s2 = "arnearne", "arnebeda"
qd1, qd2 = QGramDict(s1, 2), QGramDict(s2, 2)
@test totuples(qd1) == [("ar", 2), ("ea", 1), ("ne", 2), ("rn", 2)]
@test totuples(qd2) == [("ar", 1), ("be", 1), ("da", 1), ("eb", 1), ("ed", 1), ("ne", 1), ("rn", 1)]
qc1, qc2 = QGramSortedVector(s1, 2), QGramSortedVector(s2, 2)
@test totuples(qc1) == [("ar", 2), ("ea", 1), ("ne", 2), ("rn", 2)]
@test totuples(qc2) == [("ar", 1), ("be", 1), ("da", 1), ("eb", 1), ("ed", 1), ("ne", 1), ("rn", 1)]
s3 = "rgówów"
qd3a = QGramDict(s3, 2)
@test totuples(qd3a) == [("gó", 1), ("rg", 1), ("wó", 1), ("ów", 2)]
qd3b = QGramDict(graphemes(s3), 2)
@test totuples(qd3b) == [(["g", "ó"], 1), (["r", "g"], 1), (["w", "ó"], 1), (["ó", "w"], 2)]
qc3a = QGramSortedVector(s3, 2)
@test totuples(qc3a) == [("gó", 1), ("rg", 1), ("wó", 1), ("ów", 2)]
qd3b = QGramDict(graphemes(s3), 2)
@test totuples(qd3b) == [(["g", "ó"], 1), (["r", "g"], 1), (["w", "ó"], 1), (["ó", "w"], 2)]
end
function partlyoverlappingstrings(sizerange, chars = nothing)
l = rand(sizerange)
str1 = isnothing(chars) ? randstring(l) : randstring(chars, l)
ci1 = thisind(str1, rand(1:l))
ci2 = thisind(str1, rand(ci1:l))
copied = join(str1[ci1:ci2])
prefix = isnothing(chars) ? randstring(ci1-1) : randstring(chars, ci1-1)
slen = l - length(copied) - length(prefix)
suffix = isnothing(chars) ? randstring(slen) : randstring(chars, slen)
return str1, (prefix * copied * suffix)
end
@testset "Precalculation on unicode strings" begin
Chars = vcat(map(collect, ["δσμΣèìòâôîêûÊÂÛ", 'a':'z', '0':'9'])...)
for _ in 1:100
qlen = rand(2:5)
str1, str2 = partlyoverlappingstrings(6:100, Chars)
dist = Jaccard(qlen)
qd1 = QGramDict(str1, qlen)
qd2 = QGramDict(str2, qlen)
@test dist(str1, str2) == dist(qd1, qd2)
qd1b = QGramDict(graphemes(str1), qlen)
qd2b = QGramDict(graphemes(str2), qlen)
@test dist(str1, str2) == dist(qd1b, qd2b)
qc1 = QGramSortedVector(str1, qlen)
qc2 = QGramSortedVector(str2, qlen)
@test dist(str1, str2) == dist(qc1, qc2)
qc1b = QGramSortedVector(graphemes(str1), qlen)
qc2b = QGramSortedVector(graphemes(str2), qlen)
@test dist(str1, str2) == dist(qc1b, qc2b)
end
end
@testset "QGram distance on short strings" begin
@test isnan(Overlap(2)( "1", "2"))
@test isnan(Jaccard(3)("s1", "s2"))
@test isnan(Cosine(5)( "s1", "s2"))
@test !isnan(Overlap(2)( "s1", "s2"))
@test !isnan(Jaccard(3)("st1", "st2"))
@test !isnan(Cosine(5)( "stri1", "stri2"))
@test !isnan(Jaccard(3)("st1", "str2"))
@test !isnan(Jaccard(3)("str1", "st2"))
end
@testset "Differential testing of String, QGramDict, and QGramSortedVector" begin
for D in [QGram, Cosine, Jaccard, SorensenDice, Overlap, MorisitaOverlap, NMD]
for _ in 1:100
qlen = rand(2:9)
dist = D(qlen)
str1, str2 = partlyoverlappingstrings(10:10000)
# QGramDict gets same result as for standard string
qd1 = QGramDict(str1, qlen)
qd2 = QGramDict(str2, qlen)
expected = dist(str1, str2)
@test expected == dist(qd1, qd2)
# QGramSortedVector gets same result as for standard string
qc1 = QGramSortedVector(str1, qlen)
qc2 = QGramSortedVector(str2, qlen)
@test expected == dist(qc1, qc2)
end
end
end
strings = [
("martha", "marhta"),
("dwayne", "duane") ,
("dixon", "dicksonx"),
("william", "williams"),
("", "foo"),
("a", "a"),
("abc", "xyz"),
("abc", "ccc"),
("kitten", "sitting"),
("saturday", "sunday"),
("hi, my name is", "my name is"),
("alborgów", "amoniak"),
("cape sand recycling ", "edith ann graham"),
( "jellyifhs", "jellyfish"),
("ifhs", "fish"),
("leia", "leela"),
]
solutions = ((Levenshtein(), [2 2 4 1 3 0 3 2 3 3 4 6 17 3 3 2]),
(OptimalStringAlignment(), [1 2 4 1 3 0 3 2 3 3 4 6 17 2 2 2]),
(Jaro(), [0.05555556 0.17777778 0.23333333 0.04166667 1.00000000 0.00000000 1.00000000 0.44444444 0.25396825 0.2805556 0.2285714 0.48809524 0.3916667 0.07407407 0.16666667 0.21666667]),
(QGram(1), [0 3 3 1 3 0 6 4 5 4 4 11 14 0 0 3]),
(QGram(2), [ 6 7 7 1 2 0 4 4 7 8 4 13 32 8 6 5]),
(Jaccard(1), [0.0 0.4285714 0.3750000 0.1666667 1.0 0.0 1.0000000 0.6666667 0.5714286 0.3750000 0.2000000 0.8333333 0.5000000 0.0 0.0 0.2500000]),
(Jaccard(2), [ 0.7500000 0.8750000 0.7777778 0.1428571 1.0 NaN 1.0000000 1.0000000 0.7777778 0.8000000 0.3076923 1.0000000 0.9696970 0.6666667 1.0000000 0.8333333]),
(Cosine(2), [0.6000000 0.7763932 0.6220355 0.0741799 NaN NaN 1.0000000 1.0000000 0.6348516 0.6619383 0.1679497 1.0000000 0.9407651 0.5000000 1.0000000 0.7113249]))
# Test with R package StringDist
for x in solutions
dist, solution = x
for i in eachindex(solution)
if isnan(dist(strings[i]...))
@test isnan(solution[i])
else
@test dist(strings[i]...) ≈ solution[i] atol = 1e-4
end
end
end
# test RatcliffObershelp
solution = [83, 73, 62, 93, 0, 100, 0, 33, 62, 71, 83, 27, 33, 78, 50, 67]
for i in eachindex(strings)
@test round(Int, (1 - RatcliffObershelp()(strings[i]...)) * 100) ≈ solution[i] atol = 1e-4
end
# test max_dist
for i in eachindex(strings)
d = Levenshtein()(strings[i]...)
@test Levenshtein()(strings[i]...; max_dist = d) == d
d = OptimalStringAlignment()(strings[i]...)
@test OptimalStringAlignment()(strings[i]...; max_dist = d) == d
end
end
#= R test
library(stringdist)
strings = matrix(data = c(
"martha", "marhta",
"dwayne", "duane",
"dixon", "dicksonx",
"william", "williams",
"", "foo",
"a", "a",
"abc", "xyz",
"abc", "ccc",
"kitten", "sitting",
"saturday", "sunday",
"hi, my name is", "my name is",
"alborgów", "amoniak",
"cape sand recycling ", "edith ann graham",
"jellyifhs", "jellyfish",
"ifhs", "fish",
"leia", "leela"),
nrow = 2
)
stringdist(strings[1,], strings[2,], method = "jw", p = 0)
stringdist(strings[1,], strings[2,], method = "jw", p = 0.1)
stringdist(strings[1,], strings[2,], method = "qgram", q = 1)
=#
#= Fuzzywuzzy usesRatcliffObershelp if python-Levenshtein not installed, fuzzywuzzy uses RatcliffObershelp)
from fuzzywuzzy import fuzz
strings = [
("martha", "marhta"),
("dwayne", "duane") ,
("dixon", "dicksonx"),
("william", "williams"),
("", "foo"),
("a", "a"),
("abc", "xyz"),
("abc", "ccc"),
("kitten", "sitting"),
("saturday", "sunday"),
("hi, my name is", "my name is"),
("alborgów", "amoniak"),
("cape sand recycling ", "edith ann graham"),
( "jellyifhs", "jellyfish"),
("ifhs", "fish"),
("leia", "leela"),
]
for x in strings:
print(fuzz.ratio(x[0], x[1]))
=#
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 9167 |
using StringDistances, Unicode, Random, Test
@testset "Modifiers" begin
# Partial
@test Partial(QGram(2))("martha", "marhta") == 6
@test Partial(QGram(2))("martha", missing) === missing
@test Partial(Levenshtein())("martha", "marhta") == 2
@test Partial(RatcliffObershelp())("martha", "marhta") ≈ 0.16666666 atol = 1e-5
@test Partial(RatcliffObershelp())("martha", "marhtaXXX") ≈ 0.16666666 atol = 1e-5
@test Partial(RatcliffObershelp())("martha", missing) === missing
# TokenSort
@test TokenSort(QGram(2))("martha", "marhta") == 6
@test TokenSort(QGram(2))("martha", missing) === missing
@test TokenSort(Levenshtein())("martha", "marhta") == 2
@test TokenSort(RatcliffObershelp())("martha", "marhta") ≈ 0.16666666 atol = 1e-5
# TokenSet
@test TokenSet(QGram(2))("martha", "marhta") == 6
@test TokenSet(QGram(2))("martha", missing) === missing
@test TokenSet(Levenshtein())("martha", "marhta") == 2
@test TokenSet(RatcliffObershelp())("martha", "marhta") ≈ 0.16666666 atol = 1e-5
# TokenMax
@test TokenMax(QGram(2))("martha", "marhta") ≈ 0.6
@test TokenMax(QGram(2))("martha", missing) === missing
@test TokenMax(Levenshtein())("martha", "marhta") ≈ 1/3
@test TokenMax(RatcliffObershelp())("martha", "marhta") ≈ 0.16666666 atol = 1e-5
end
@testset "Compare" begin
# Qgram
@test compare("", "abc", QGram(1)) ≈ 0.0 atol = 1e-4
@test compare("abc", "cba", QGram(1)) ≈ 1.0 atol = 1e-4
@test compare("abc", "ccc", QGram(1)) ≈ 1/3 atol = 1e-4
compare("aüa", "aua", TokenMax(QGram(2)))
@test compare("", "abc", Jaccard(2)) ≈ 0.0 atol = 1e-4
@test compare("martha", "martha", Jaccard(2)) ≈ 1.0 atol = 1e-4
@test compare("martha", "martha", Jaccard(2)) ≈ 1.0 atol = 1e-4
@test compare("aa", "aa ", Partial(Jaccard(2))) ≈ 1.0
@test compare("martha", "martha", Cosine(2)) ≈ 1.0 atol = 1e-4
@test compare("martha", "martha", Overlap(2)) ≈ 1.0 atol = 1e-4
@test compare("martha", "martha", SorensenDice(2)) ≈ 1.0 atol = 1e-4
# Jaro
@test compare("aüa", "aua", Hamming()) ≈ 2/3
@test compare("aüa", "aua", Jaro()) ≈ 0.77777777 atol = 1e-4
@test compare("New York Yankees", "", Partial(Jaro())) ≈ 0.0
# JaroWinkler
@test compare("martha", "marhta", JaroWinkler()) ≈ 0.9611 atol = 1e-4
@test compare("dwayne", "duane", JaroWinkler()) ≈ 0.84 atol = 1e-4
@test compare("dixon", "dicksonx", JaroWinkler()) ≈ 0.81333 atol = 1e-4
@test compare("william", "williams", JaroWinkler()) ≈ 0.975 atol = 1e-4
@test compare("", "foo", JaroWinkler()) ≈ 0.0 atol = 1e-4
@test compare("a", "a", JaroWinkler()) ≈ 1.0 atol = 1e-4
@test compare("abc", "xyz", JaroWinkler()) ≈ 0.0 atol = 1e-4
#Levenshtein
compare("aüa", "aua", Levenshtein())
@test compare("ok", missing, Levenshtein()) === missing
compare("aüa", "aua", OptimalStringAlignment())
@test StringDistances.Normalized(Partial(OptimalStringAlignment()))("ab", "cde") == 1.0
@test compare("ab", "de", Partial(OptimalStringAlignment())) == 0
# RatcliffObershelp
@test compare("New York Mets vs Atlanta Braves", "", RatcliffObershelp()) ≈ 0.0
@test round(Int, 100 * compare("为人子女者要堂堂正正做人,千万不可作奸犯科,致使父母蒙羞", "此前稍早些时候中国商务部发布消息称,中美经贸高级别磋商双方牵头人通话,中方就美拟9月1日加征关税进行了严正交涉。", RatcliffObershelp())) == 5
compare("aüa", "aua", TokenMax(RatcliffObershelp()))
@test compare("New York Yankees", "Yankees", Partial(RatcliffObershelp())) ≈ 1.0
@test compare("New York Yankees", "", Partial(RatcliffObershelp())) ≈ 0.0
#@test compare("mariners vs angels", "los angeles angels at seattle mariners", Partial(RatcliffObershelp())) ≈ 0.444444444444
@test compare("HSINCHUANG", "SINJHUAN", Partial(RatcliffObershelp())) ≈ 0.875
@test compare("HSINCHUANG", "LSINJHUANG DISTRIC", Partial(RatcliffObershelp())) ≈ 0.8
@test compare("HSINCHUANG", "SINJHUANG DISTRICT", Partial(RatcliffObershelp())) ≈ 0.8
@test compare("HSINCHUANG", "SINJHUANG", Partial(RatcliffObershelp())) ≈ 0.8888888888888
@test compare("New York Mets vs Atlanta Braves", "Atlanta Braves vs New York Mets", TokenSort(RatcliffObershelp())) ≈ 1.0
@test compare(graphemes("New York Mets vs Atlanta Braves"), graphemes("Atlanta Braves vs New York Mets"), Partial(RatcliffObershelp())) ≈ compare("New York Mets vs Atlanta Braves", "Atlanta Braves vs New York Mets", Partial(RatcliffObershelp()))
@test compare("mariners vs angels", "los angeles angels of anaheim at seattle mariners", TokenSet(RatcliffObershelp())) ≈ 1.0 - 0.09090909090909094
@test compare("New York Mets vs Atlanta Braves", "", TokenSort(RatcliffObershelp())) ≈ 0.0
@test compare("mariners vs angels", "", TokenSet(RatcliffObershelp())) ≈ 0.0
@test compare("mariners vs angels", "los angeles angels at seattle mariners", TokenSet(Partial(RatcliffObershelp()))) ≈ 1.0
@test compare("mariners", "mariner", TokenMax(RatcliffObershelp())) ≈ 0.933333333333333
@test compare("为人子女者要堂堂正正做人,千万不可作奸犯科,致使父母蒙羞", "此前稍早些时候中国商务部发布消息称,中美经贸高级别磋商双方牵头人通话,中方就美拟9月1日加征关税进行了严正交涉。", RatcliffObershelp()) ≈ 5 / 100 atol = 1e-2
@test compare("为人子女者要堂堂正正做人,千万不可作奸犯科,致使父母蒙羞", "此前稍早些时候中国商务部发布消息称,中美经贸高级别磋商双方牵头人通话,中方就美拟9月1日加征关税进行了严正交涉。", Partial(RatcliffObershelp())) ≈ 7 / 100 atol = 1e-2
@test compare("mariners", "mariner are playing tomorrow", TokenMax(RatcliffObershelp())) ≈ 79 / 100 atol = 1e-2
@test compare("mariners", "mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow", Partial(RatcliffObershelp())) ≈ 88 / 100 atol = 1e-2
@test compare("mariners", "mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow", TokenSort(RatcliffObershelp())) ≈ 11 / 100 atol = 1e-2
@test compare("mariners", "are mariner playing tomorrow", RatcliffObershelp()) ≈ 39 / 100 atol = 1e-2
@test compare("mariners", "are mariner playing tomorrow", Partial(RatcliffObershelp())) ≈ 88 / 100 atol = 1e-2
@test compare("mariners", "mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow", TokenSet(RatcliffObershelp())) ≈ 39 / 100 atol = 1e-2
@test compare("mariners", "mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow", TokenSet(Partial(RatcliffObershelp()))) ≈ 88 / 100 atol = 1e-2
# not exactly the same because tokenmax has uses the max of rounded tokenset etc
@test compare("mariners", "mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow mariner are playing tomorrow", TokenMax(RatcliffObershelp())) ≈ 78.75 / 100 atol = 1e-2
# check min
strings = [
("martha", "marhta"),
("dwayne", "duane") ,
("dixon", "dicksonx"),
("william", "williams"),
("", "foo"),
("a", "a"),
("abc", "xyz"),
("abc", "ccc"),
("kitten", "sitting"),
("saturday", "sunday"),
("hi, my name is", "my name is"),
("alborgów", "amoniak"),
("cape sand recycling ", "edith ann graham"),
( "jellyifhs", "jellyfish"),
("ifhs", "fish"),
("leia", "leela"),
]
for dist in (Levenshtein, OptimalStringAlignment)
for i in eachindex(strings)
if compare(strings[i]..., dist()) < 1 / 3
@test compare(strings[i]..., dist() ; min_score = 1/ 3) ≈ 0.0
else
@test compare(strings[i]..., dist() ; min_score = 1/ 3) ≈ compare(strings[i]..., dist())
end
end
end
end
@testset "Find*" begin
# findnearest
@test findnearest("New York", ["NewYork", "Newark", "San Francisco"], Levenshtein()) == ("NewYork", 1)
@test findnearest("New York", ["San Francisco", "NewYork", "Newark"], Levenshtein()) == ("NewYork", 2)
@test findnearest("New York", ["Newark", "San Francisco", "NewYork"], Levenshtein()) == ("NewYork", 3)
@test findnearest("New York", ["NewYork", "Newark", "San Francisco"], Jaro()) == ("NewYork", 1)
@test findnearest("New York", ["NewYork", "Newark", "San Francisco"], QGram(2)) == ("NewYork", 1)
@test findnearest("New York", ["Newark", "San Francisco", "NewYork"], QGram(2)) == ("NewYork", 3)
# findall
@test findall("New York", ["NewYork", "Newark", "San Francisco"], Levenshtein()) == [1]
@test findall("New York", ["NewYork", "Newark", "San Francisco"], Jaro()) == [1, 2]
@test findall("New York", ["NewYork", "Newark", "San Francisco"], Jaro(); min_score = 0.99) == Int[]
@test findall("New York", ["NewYork", "Newark", "San Francisco"], QGram(2); min_score = 0.99) == Int[]
if VERSION >= v"1.2.0"
@test findnearest("New York", skipmissing(["NewYork", "Newark", missing]), Levenshtein()) == ("NewYork", 1)
@test findnearest("New York", skipmissing(Union{AbstractString, Missing}[missing, missing]), Levenshtein()) == (nothing, nothing)
@test findall("New York", skipmissing(["NewYork", "Newark", missing]), Levenshtein()) == [1]
@test findall("New York", skipmissing(Union{AbstractString, Missing}[missing, missing]), Levenshtein()) == []
end
Random.seed!(2)
y = map(Random.randstring, rand(5:25,1_000))
x = Random.randstring(10)
for dist in (Levenshtein(), OptimalStringAlignment(), QGram(2), Partial(OptimalStringAlignment()), TokenMax(OptimalStringAlignment()))
result = [compare(x, y, dist) for y in y]
@test findnearest(x, y, dist)[2] == findmax(result)[2]
@test findall(x, y, dist; min_score = 0.4) == findall(result .>= 0.4)
end
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 2560 | using StringDistances, Unicode, Test, Random
@testset "Pairwise" begin
TestStrings1 = ["", "abc", "bc", "kitten"]
TestStrings2 = ["mew", "ab"]
TestStrings1missing = ["", "abc", "bc", missing]
TestStrings2missing = ["mew", missing]
for d in [Jaro(), Levenshtein(), OptimalStringAlignment(), RatcliffObershelp(),
QGram(2), Cosine(2), Jaccard(2), SorensenDice(2), Overlap(2)]
R = pairwise(d, TestStrings1)
@test size(R) == (4, 4)
# No distance on the diagonal, since comparing strings to themselves
@test R[1, 1] == 0.0
@test R[2, 2] == 0.0
@test R[3, 3] == 0.0
@test R[4, 4] == 0.0
# Since the distance might be NaN:
equalorNaN(x, y) = (x == y) || (isnan(x) && isnan(y))
# First row is comparing "" to the other strings, so:
@test equalorNaN(R[1, 2], evaluate(d, "", "abc"))
@test equalorNaN(R[1, 3], evaluate(d, "", "bc"))
@test equalorNaN(R[1, 4], evaluate(d, "", "kitten"))
# Second row is comparing "abc" to the other strings, so:
@test equalorNaN(R[2, 3], evaluate(d, "abc", "bc"))
@test equalorNaN(R[2, 4], evaluate(d, "abc", "kitten"))
# Third row row is comparing "bc" to the other strings, so:
@test equalorNaN(R[3, 4], evaluate(d, "bc", "kitten"))
# Matrix is symmetric
for i in 1:4
for j in (i+1):4
@test equalorNaN(R[i, j], R[j, i])
end
end
# Test also the assymetric version
R2 = pairwise(d, TestStrings1, TestStrings2)
@test size(R2) == (4, 2)
@test equalorNaN(R2[1, 1], evaluate(d, "", "mew"))
@test equalorNaN(R2[1, 2], evaluate(d, "", "ab"))
@test equalorNaN(R2[2, 1], evaluate(d, "abc", "mew"))
@test equalorNaN(R2[2, 2], evaluate(d, "abc", "ab"))
@test equalorNaN(R2[3, 1], evaluate(d, "bc", "mew"))
@test equalorNaN(R2[3, 2], evaluate(d, "bc", "ab"))
@test equalorNaN(R2[4, 1], evaluate(d, "kitten", "mew"))
@test equalorNaN(R2[4, 2], evaluate(d, "kitten", "ab"))
R3 = pairwise(d, TestStrings2, TestStrings1)
@test size(R3) == (2, 4)
for i in 1:length(TestStrings1)
for j in 1:length(TestStrings2)
@test equalorNaN(R2[i, j], R3[j, i])
end
end
# Ensure same result if preprocessing for QGramDistances
if d isa AbstractQGramDistance
R4 = pairwise(d, TestStrings1; preprocess = true)
@test typeof(R4) == typeof(R)
@test size(R4) == size(R)
for i in 1:size(R4, 1)
for j in 1:size(R4, 2)
@test equalorNaN(R4[i, j], R[i, j])
end
end
end
# ensures missing
R5 = pairwise(d, TestStrings1missing; preprocess = true)
@test eltype(R5) == Union{result_type(d, String, String), Missing}
end
end
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | code | 105 | using StringDistances
using Test
include("distances.jl")
include("pairwise.jl")
include("modifiers.jl")
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.11.3 | 5b2ca70b099f91e54d98064d5caf5cc9b541ad06 | docs | 5874 | [](https://github.com/matthieugomez/StringDistances.jl/actions)
## Installation
The package is registered in the [`General`](https://github.com/JuliaRegistries/General) registry and so can be installed at the REPL with `] add StringDistances`.
## Supported Distances
String distances act over any pair of iterators that define `length` (e.g. `AbstractStrings`, `GraphemeIterators`, or `AbstractVectors`)
The available distances are:
- Edit Distances
- Hamming Distance `Hamming() <: SemiMetric`
- [Jaro and Jaro-Winkler Distance](https://en.wikipedia.org/wiki/Jaro%E2%80%93Winkler_distance) `Jaro()` `JaroWinkler() <: SemiMetric`
- [Levenshtein Distance](https://en.wikipedia.org/wiki/Levenshtein_distance) `Levenshtein() <: Metric`
- [Optimal String Alignment Distance](https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance#Optimal_string_alignment_distance) (a.k.a. restricted Damerau-Levenshtein) `OptimalStringAlignment() <: SemiMetric`
- [Damerau-Levenshtein Distance](https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance#Distance_with_adjacent_transpositions) `DamerauLevenshtein() <: Metric`
- [RatcliffObershelp Distance](https://xlinux.nist.gov/dads/HTML/ratcliffObershelp.html) `RatcliffObershelp() <: SemiMetric`
- Q-gram distances (which compare the set of all substrings of length `q` in each string)
- QGram Distance `QGram(q::Int) <: SemiMetric`
- [Cosine Distance](https://en.wikipedia.org/wiki/Cosine_similarity) `Cosine(q::Int) <: SemiMetric`
- [Jaccard Distance](https://en.wikipedia.org/wiki/Jaccard_index) `Jaccard(q::Int) <: SemiMetric`
- [Overlap Distance](https://en.wikipedia.org/wiki/Overlap_coefficient) `Overlap(q::Int) <: SemiMetric`
- [Sorensen-Dice Distance](https://en.wikipedia.org/wiki/S%C3%B8rensen%E2%80%93Dice_coefficient) `SorensenDice(q::Int) <: SemiMetric`
- [MorisitaOverlap Distance](https://en.wikipedia.org/wiki/Morisita%27s_overlap_index) `MorisitaOverlap(q::Int) <: SemiMetric`
- [Normalized Multiset Distance](https://www.sciencedirect.com/science/article/pii/S1047320313001417) `NMD(q::Int) <: SemiMetric`
## Syntax
Following the `Distances.jl` package, string distances can inherit from two abstract types: `StringSemiMetric <: SemiMetric` or `StringMetric <: Metric`.
## Computing the distance between two strings (or iterators)
You can always compute a certain distance between two strings using the following syntax
```julia
r = evaluate(dist, x, y)
r = dist(x, y)
```
Here, `dist` is an instance of a distance type: for example, the type for the Levenshtein distance is `Levenshtein`. You can compute the Levenshtein distance between `x` and `y` as
```julia
r = evaluate(Levenshtein(), x, y)
r = Levenshtein()(x, y)
```
The function `compare` returns the similarity score, defined as 1 minus the normalized distance between two strings. It always returns an element of type `Float64`. A value of 0.0 means completely different and a value of 1.0 means completely similar.
```julia
Levenshtein()("martha", "martha")
#> 0
compare("martha", "martha", Levenshtein())
#> 1.0
```
## Computing the distance between two AbstractVectors of strings (or iterators)
Consider `X` and `Y` two `AbstractVectors` of iterators. You can compute the matrix of distances across elements, `dist(X[i], Y[j])`, as follows:
```julia
pairwise(dist, X, Y)
```
For instance,
```julia
pairwise(Jaccard(3), ["martha", "kitten"], ["marhta", "sitting"])
```
`pairwise` is optimized in various ways (e.g., for the case of QGram-distances, dictionary of qgrams are pre-computed)
## Find closest string
The package also adds convenience functions to find elements in a iterator of strings closest to a given string
- `findnearest` returns the value and index of the element in `itr` with the highest similarity score with `s`. Its syntax is:
```julia
findnearest(s, itr, dist)
```
- `findall` returns the indices of all elements in `itr` with a similarity score with `s` higher than a minimum score. Its syntax is:
```julia
findall(s, itr, dist; min_score = 0.8)
```
The functions `findnearest` and `findall` are particularly optimized for the `Levenshtein` and `OptimalStringAlignment` distances, as these algorithm can stop early if the distance becomes higher than a certain threshold.
### fuzzywuzzy
The package also defines Distance "modifiers" that are inspired by the Python package - [fuzzywuzzy](http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/). These modifiers are particularly helpful to match strings composed of multiple words (e.g. addresses, company names).
- [Partial](http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/) returns the minimum of the distance between the shorter string and substrings of the longer string.
- [TokenSort](http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/) adjusts for differences in word orders by returning the distance of the two strings, after re-ordering words alphabetically.
- [TokenSet](http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/) adjusts for differences in word orders and word numbers by returning the distance between the intersection of two strings with each string.
- [TokenMax](http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/) normalizes the distance, and combine the `Partial`, `TokenSort` and `TokenSet` modifiers, with penalty terms depending on string. `TokenMax(Levenshtein())` corresponds to the distance defined in [fuzzywuzzy](http://chairnerd.seatgeek.com/fuzzywuzzy-fuzzy-string-matching-in-python/)
```julia
Levenshtein()("this string", "this string is longer") = 10
Partial(Levenshtein())("this string", "this string is longer") = 0
```
## Notes
- All string distances are case sensitive.
| StringDistances | https://github.com/matthieugomez/StringDistances.jl.git |
|
[
"MIT"
]
| 0.2.1 | 05326e2bbca7e6957e8bc15fc1ab5b8942abe1de | code | 946 | module MCMCDebugging
using UnPack, ProgressMeter, RecipesBase, Statistics, LabelledArrays,
Distributions, HypothesisTests, DynamicPPL
abstract type AbstractMCMCTest end
abstract type AbstractMCMCResult end
include("mmd.jl")
export mmd_of
include("geweke.jl")
export GewekeTest
include("clt.jl")
export CLTTest
### DynamicPPL integration
function perform(cfg::GewekeTest, modelgen::Function, rand_θ_given::Function; kwargs...)
model = modelgen()
rand_marginal() = model()
function rand_x_given(θ)
_, x = modelgen(θ)()
return x
end
return perform(cfg, rand_marginal, rand_x_given, rand_θ_given; kwargs...)
end
@recipe function f(res::GewekeTestResult, model::Model)
vi = VarInfo(model)
spl = SampleFromPrior()
function _logjoint(θ, x)
vi[spl] = cat(θ, x; dims=1)
return logjoint(model, vi)
end
res, _logjoint
end
export perform, compute_statistic!
end # module
| MCMCDebugging | https://github.com/TuringLang/MCMCDebugging.jl.git |
|
[
"MIT"
]
| 0.2.1 | 05326e2bbca7e6957e8bc15fc1ab5b8942abe1de | code | 122 | struct CLTTest <: AbstractMCMCTest
n_chains::Int
end
struct CLTTestResult{T} <: AbstractMCMCResult
chains::T
end
| MCMCDebugging | https://github.com/TuringLang/MCMCDebugging.jl.git |
|
[
"MIT"
]
| 0.2.1 | 05326e2bbca7e6957e8bc15fc1ab5b8942abe1de | code | 5472 | struct GewekeTest <: AbstractMCMCTest
n_samples::Int
end
mutable struct GewekeTestResult{T} <: AbstractMCMCResult
samples_fwd::T
samples_bwd::T
statistic
pval
qerror
end
function Base.show(io::IO, res::GewekeTestResult)
println(io, "Geweke (Joint Distribution) Test")
println(io, "--------------------------------")
println(io, "Results:")
println(io, " Number of samples: $(size(res.samples_fwd, 2))")
println(io, " Parameter dimension: $(size(res.samples_fwd.θ, 1))")
println(io, " Data dimension: $(size(res.samples_fwd.x, 1))")
println(io, " Statistic: $(res.statistic)")
println(io, " P-value: $(res.pval)")
if ismissing(res.statistic)
println(io, "")
println(
io,
"""
Test statistic is missing. Please use `compute_statistic!(res, g)`
if you want compute statistic without rerun the simulation.
"""
)
end
if !ismissing(res.qerror)
println(io, " Quantile error: $(res.qerror)")
end
end
"""
perform(cfg::GewekeTest, rand_θ::Function, rand_x_given::Function, rand_θ_given::Function, g=nothing)
Run Geweke (joint distribution) test and compute the test statistic
using `g` as the test function as in Equation (6) of (Geweke, 2014).
"""
function perform(cfg::GewekeTest, rand_marginal::Function, rand_x_given::Function, rand_θ_given::Function; g=nothing, progress=true)
@unpack n_samples = cfg
# Generate samples
local dim_θ, dim_x, samples_fwd, samples_bwd, θ_bwd
pm = Progress(n_samples)
for i in 1:n_samples
# Marginal-cnditional simulator
θ_fwd, x_fwd = rand_marginal()
if i == 1
dim_θ = length(θ_fwd)
dim_x = length(x_fwd)
dim = dim_θ + dim_x
T = eltype(θ_fwd)
samples_fwd = Matrix{T}(undef, dim, n_samples)
samples_bwd = Matrix{T}(undef, dim, n_samples)
end
samples_fwd[:,i] = cat(θ_fwd, x_fwd; dims=1)
# Successive-conditional simulator
if i == 1
θ_bwd, x_bwd = rand_marginal()
else
x_bwd = rand_x_given(θ_bwd)
θ_bwd = rand_θ_given(x_bwd)
end
samples_bwd[:,i] = cat(θ_bwd, x_bwd; dims=1)
# Progress meter
progress && next!(pm)
end
samples_fwd = @LArray samples_fwd (θ=(1:dim_θ,:), x=(dim_θ+1:dim_θ+dim_x,:))
samples_bwd = @LArray samples_bwd (θ=(1:dim_θ,:), x=(dim_θ+1:dim_θ+dim_x,:))
# Compute statistics
if g isa Nothing
@warn "Test function `g` is not provided. Statistic is not computed."
statistic, pval = missing, missing
else
statistic, pval = _compute_statistic(samples_fwd, samples_bwd, g)
end
return GewekeTestResult(samples_fwd, samples_bwd, statistic, pval, missing)
end
function _compute_statistic(samples_fwd, samples_bwd, g)
g_fwd = map(i -> g(samples_fwd.θ[:,i], samples_fwd.x[:,i]), 1:size(samples_fwd, 2))
g_bwd = map(i -> g(samples_bwd.θ[:,i], samples_bwd.x[:,i]), 1:size(samples_bwd, 2))
m_fwd = mean(g_fwd)
v_fwd = mean(x -> x.^2, g_fwd) - m_fwd.^2
m_bwd = mean(g_bwd)
v_bwd = mean(x -> x.^2, g_bwd) - m_bwd.^2
M₁, M₂ = length(g_fwd), length(g_bwd)
statistic = (m_fwd - m_bwd) ./ sqrt.(v_fwd / M₁ + v_bwd / M₂)
pval = pvalue.(Ref(Normal(0, 1)), statistic)
return statistic, pval
end
function compute_statistic!(res::GewekeTestResult, g)
@unpack samples_fwd, samples_bwd = res
res.statistic, res.pval = _compute_statistic(samples_fwd, samples_bwd, g)
return res
end
function mmd_of(res::MCMCDebugging.GewekeTestResult; force=false, kwargs...)
n_samples = size(res.samples_bwd, 2)
if force || n_samples <= 5_000
return mmd_of(res.samples_fwd, res.samples_bwd; kwargs...)
else
@warn "The number of samples ($n_samples) is large and MMD computation would be slow. Please use `mmd_of(res; force=true)` if you still want to compute MMD."
end
end
@recipe function f(res::GewekeTestResult, logjoint::Function; n_grids=100, verbose=true)
@unpack samples_fwd, samples_bwd = res
logjoint_fwd = map(i -> logjoint(samples_fwd.θ[:,i], samples_fwd.x[:,i]), 1:size(samples_fwd, 2))
logjoint_bwd = map(i -> logjoint(samples_bwd.θ[:,i], samples_bwd.x[:,i]), 1:size(samples_bwd, 2))
joint_fwd, joint_bwd = exp.(logjoint_fwd), exp.(logjoint_bwd)
# Compute CDFs
mins, maxs = extrema.([joint_fwd, joint_bwd])
percent_fwd = Vector{Float64}(undef, n_grids)
percent_bwd = Vector{Float64}(undef, n_grids)
for (i, v) in enumerate(range(minimum(mins), maximum(maxs); length=n_grids))
percent_fwd[i] = sum(joint_fwd .< v) / length(joint_fwd)
percent_bwd[i] = sum(joint_bwd .< v) / length(joint_bwd)
end
# Compute the absolute error
res.qerror = mean(abs.(percent_fwd .- percent_bwd))
verbose && println("Quantile error: $(res.qerror)")
# Recipe
legend --> :topleft
@series begin
linecolor := 2
label := "Sampler"
percent_fwd, percent_bwd
end
@series begin
linecolor := nothing
label := "Error"
fillrange := percent_fwd
fillalpha := 0.5
fillcolor := :lightgray
percent_fwd, percent_bwd
end
@series begin
linecolor := :gray
linestyle := :dash
label := "Perfect"
[0, 1], [0, 1]
end
end
| MCMCDebugging | https://github.com/TuringLang/MCMCDebugging.jl.git |
|
[
"MIT"
]
| 0.2.1 | 05326e2bbca7e6957e8bc15fc1ab5b8942abe1de | code | 1113 | function euclidsq(X::T, Y::T) where {T<:AbstractMatrix}
XiXj = transpose(X) * Y
x² = sum(X .^ 2; dims=1)
y² = sum(Y .^ 2; dims=1)
transpose(x²) .+ y² - 2XiXj
end
function euclidsq(X::T) where {T<:AbstractMatrix}
XiXj = transpose(X) * X
x² = sum(X .^ 2; dims=1)
transpose(x²) .+ x² - 2XiXj
end
gaussian_gramian(esq, σ::AbstractFloat) = exp.(-esq ./ 2σ^2)
"""
mmd_of(x_nu, x_de; σ=nothing)
Compute the maximum mean discrepency give two set of samples `x_nu` and `x_de`.
If `σ` is not provided, it will be taken as "median / log(n)" where `median` is
the median of pair-wise Ecludean distances and `n` is the number of samples in `x_de`.
"""
function mmd_of(x_nu, x_de; σ=nothing)
d²_dede, d²_denu, d²_nunu = euclidsq(x_de), euclidsq(x_de, x_nu), euclidsq(x_nu)
# Heuristic: take `σ²` as "median / log(n)"
if σ isa Nothing
h = median(vcat(vec.([d²_dede, d²_denu, d²_nunu]))) / log(size(d²_dede, 1))
σ = sqrt(h)
end
Kdede, Kdenu, Knunu = gaussian_gramian.((d²_dede, d²_denu, d²_nunu), σ)
return mean(Kdede) - 2mean(Kdenu) + mean(Knunu)
end
| MCMCDebugging | https://github.com/TuringLang/MCMCDebugging.jl.git |
|
[
"MIT"
]
| 0.2.1 | 05326e2bbca7e6957e8bc15fc1ab5b8942abe1de | code | 956 | using Distributions, DynamicPPL
# The marginal-conditional simulator defined by DynamicPPL
# See README.md for the expected form of the model definition.
@model function BetaBinomial(θ=missing, x=missing)
θ ~ Beta(2, 3)
x ~ Binomial(3, θ)
return θ, x
end
# The successive-conditional simulator
# 1. Bug-free posterior sampler
# Beta(α + x, β + n - x) is the true posterior.
rand_θ_given(x) = rand(Beta(2 + x, 3 + 3 - x))
# 2. Buggy posterior sampler
rand_θ_given_buggy(x) = rand_θ_given(min(3, x + 1))
# Test function
g(θ, x) = cat(θ, x; dims=1)
using MCMCDebugging
res = perform(GewekeTest(5_000), BetaBinomial, rand_θ_given; g=g)
using Plots
plot(res, BetaBinomial(); size=(300, 300), title="Bug-free sampler")
res_buggy = perform(GewekeTest(5_000), BetaBinomial, rand_θ_given_buggy)
compute_statistic!(res_buggy, g)
plot(res_buggy, BetaBinomial(); size=(300, 300), title="Buggy sampler")
@info "MMD" mmd_of(res) mmd_of(res_buggy)
| MCMCDebugging | https://github.com/TuringLang/MCMCDebugging.jl.git |
|
[
"MIT"
]
| 0.2.1 | 05326e2bbca7e6957e8bc15fc1ab5b8942abe1de | docs | 3013 | # MCMCDebugging.jl: debugging utilities for MCMC samplers
This package implements a few utilities for debugging MCMC samplers, which includes
- [x] Geweke test
- See the references [1,2] or [this blog](https://lips.cs.princeton.edu/testing-mcmc-code-part-2-integration-tests/) for details
- [ ] Central limit theorem test
See the [notebook](https://nbviewer.jupyter.org/github/xukai92/MCMCDebugging.jl/blob/master/docs/example.ipynb) for an example.
## Usage
The example [notebook](https://nbviewer.jupyter.org/github/xukai92/MCMCDebugging.jl/blob/master/docs/example.ipynb) covers most of the usages.
Some details on the model definition via DynamicPPL is explained below.
### Defining test models via DynamicPPL.jl
MCMCDebugging.jl allows using DynamicPPL.jl to define test models.
In the example [notebook](https://nbviewer.jupyter.org/github/xukai92/MCMCDebugging.jl/blob/master/docs/example.ipynb), the test model is defined as
```julia
@model function BetaBinomial(θ=missing, x=missing)
θ ~ Beta(2, 3)
x ~ Binomial(3, θ)
return θ, x
end
```
There are a few requirements from MCMCDebugging.jl to use the defined model.
1. The model should take `θ` and `x` as inputs (in order) and optionally being `missing`.
- So that the model can be used to generate the marginal sampler as e.g. `BetaBinomial()` and conditional sampler as e.g. `BetaBinomial(θ)`
2. The model should return the parameter `θ` and the data `x` as a tuple.
With these two points, MCMCDebugging.jl can generate several functions used by lower-level APIs.
1. `rand_marginal()`: drawing `θ` and `x` as a tuple
2. `rand_x_given(θ)`: drawing `x` conditioned on `θ`
3. `logjoint(θ, x)`: computing the log-joint probability of `θ` and `x`
1 and 2 are used to perform the Geweke test and 3 is used to make the Q-Q plot.
## Lower-level APIs
### Geweke test
Defining the Geweke test
```julia
cfg = GewekeTest(n_samples::Int)
```
where `n_samples` is the number of samples used for testing.
Performing the Geweke test
```julia
res = perform(cfg::GewekeTest, rand_marginal, rand_x_given, rand_θ_given; g=nothing, progress=true)
```
where
- `rand_marginal()` draws `θ` and `x` as a tuple
- `rand_x_given(θ)` draws `x` conditioned on `θ`
- `rand_θ_given(x)` draws `θ` conditioned on `x`
- `g(θ, x)` is the test function
Making the Q-Q plot
```julia
plot(res::GewekeTestResult, logjoint)
```
where
- `logjoint(θ, x)` computes the log-joint probability of `θ` and `x`
In case models are defined by DynamicPPL.jl, you can use
```julia
plot(res::GewekeTestResult, model)
```
For example, `plot(res, BetaBinomial())`. Note we have to pass an instantiated model (i.e. BetaBinomial()) here, for now, to make Julia correctly dispatch the plot recipe.
## References
[1] Geweke J. Getting it right: Joint distribution tests of posterior simulators. Journal of the American Statistical Association. 2004 Sep 1;99(467):799-804.
[2] Grosse RB, Duvenaud DK. Testing mcmc code. arXiv preprint arXiv:1412.5218. 2014 Dec 16.
| MCMCDebugging | https://github.com/TuringLang/MCMCDebugging.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 943 | using Documenter, DiffEqSensitivity
# Make sure that plots don't throw a bunch of warnings / errors!
ENV["GKSwstype"] = "100"
using Plots
include("pages.jl")
makedocs(
sitename = "DiffEqSensitivity.jl",
authors="Chris Rackauckas et al.",
clean = true,
doctest = false,
modules = [DiffEqSensitivity],
strict = [
:doctest,
:linkcheck,
:parse_error,
:example_block,
# Other available options are
# :autodocs_block, :cross_references, :docs_block, :eval_block, :example_block, :footnote, :meta_block, :missing_docs, :setup_block
],
format = Documenter.HTML(#analytics = "",
assets = ["assets/favicon.ico"],
canonical="https://sensitivity.sciml.ai/stable/"),
pages=pages
)
deploydocs(
repo = "github.com/SciML/DiffEqSensitivity.jl.git";
push_preview = true
)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 3128 | pages = [
"DiffEqSensitivity.jl: Automatic Differentiation and Adjoints for (Differential) Equation Solvers" => "index.md",
"Tutorials" => Any[
"Differentiating Ordinary Differential Equations (ODE) Tutorials" => Any[
"ad_examples/differentiating_ode.md",
"ad_examples/direct_sensitivity.md",
"ad_examples/adjoint_continuous_functional.md",
"ad_examples/chaotic_ode.md",
],
"Fitting Ordinary Differential Equation (ODE) Tutorials" => Any[
"ode_fitting/optimization_ode.md",
"ode_fitting/stiff_ode_fit.md",
"ode_fitting/exogenous_input.md",
"ode_fitting/data_parallel.md",
"ode_fitting/prediction_error_method.md",
"ode_fitting/second_order_adjoints.md",
"ode_fitting/second_order_neural.md",
],
"Training Techniques and Tips" => Any[
"training_tips/local_minima.md",
"training_tips/divergence.md",
"training_tips/multiple_nn.md",
],
"Neural Ordinary Differential Equation (Neural ODE) Tutorials" => Any[
"neural_ode/neural_ode_flux.md",
"neural_ode/mnist_neural_ode.md",
"neural_ode/mnist_conv_neural_ode.md",
"neural_ode/GPUs.md",
"neural_ode/neural_gde.md",
"neural_ode/minibatch.md",
],
"Stochastic Differential Equation (SDE) Tutorials" => Any[
"sde_fitting/optimization_sde.md",
"sde_fitting/neural_sde.md",
],
"Delay Differential Equation (DDE) Tutorials" => Any[
"dde_fitting/delay_diffeq.md",
],
"Differential-Algebraic Equation (DAE) Tutorials" => Any[
"dae_fitting/physical_constraints.md",
],
"Partial Differential Equation (PDE) Tutorials" => Any[
"pde_fitting/pde_constrained.md",
],
"Hybrid and Jump Equation Tutorials" => Any[
"hybrid_jump_fitting/hybrid_diffeq.md",
"hybrid_jump_fitting/bouncing_ball.md",
],
"Bayesian Estimation Tutorials" => Any[
"bayesian/turing_bayesian.md",
"bayesian/BayesianNODE_NUTS.md",
"bayesian/BayesianNODE_SGLD.md",
],
"Optimal and Model Predictive Control Tutorials" => Any[
"optimal_control/optimal_control.md",
"optimal_control/feedback_control.md",
"optimal_control/SDE_control.md",
],
],
"Manual and APIs" => Any[
"manual/differential_equation_sensitivities.md",
"manual/nonlinear_solve_sensitivities.md",
"manual/direct_forward_sensitivity.md",
"manual/direct_adjoint_sensitivities.md",
],
"Benchmarks" => "Benchmark.md",
"Sensitivity Math Details" => "sensitivity_math.md",
] | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2234 | module DiffEqSensitivity
using DiffEqBase, ForwardDiff, Tracker, FiniteDiff, Statistics
using DiffEqCallbacks, QuadGK, RecursiveArrayTools, LinearAlgebra
using DiffEqOperators
using Adapt
using LinearSolve
using Parameters: @unpack
using StochasticDiffEq
import DiffEqNoiseProcess
import RandomNumbers: Xorshifts
using Random
import ZygoteRules, Zygote, ReverseDiff
import ArrayInterfaceCore, ArrayInterfaceTracker
import Enzyme
import GPUArrays
using Cassette, DiffRules
using Core: CodeInfo, SlotNumber, SSAValue, ReturnNode, GotoIfNot
using EllipsisNotation
using Markdown
using Reexport
import ChainRulesCore: unthunk, @thunk, NoTangent, @not_implemented
abstract type SensitivityFunction end
abstract type TransformedFunction end
include("hasbranching.jl")
include("sensitivity_algorithms.jl")
include("derivative_wrappers.jl")
include("sensitivity_interface.jl")
include("forward_sensitivity.jl")
include("adjoint_common.jl")
include("lss.jl")
include("nilss.jl")
include("nilsas.jl")
include("backsolve_adjoint.jl")
include("interpolating_adjoint.jl")
include("quadrature_adjoint.jl")
include("callback_tracking.jl")
include("concrete_solve.jl")
include("second_order.jl")
include("steadystate_adjoint.jl")
include("sde_tools.jl")
# AD Extensions
include("reversediff.jl")
include("tracker.jl")
include("zygote.jl")
export extract_local_sensitivities
export ODEForwardSensitivityFunction, ODEForwardSensitivityProblem, SensitivityFunction,
ODEAdjointSensitivityProblem, ODEAdjointProblem, AdjointSensitivityIntegrand,
SDEAdjointProblem, RODEAdjointProblem, SensitivityAlg,
adjoint_sensitivities, adjoint_sensitivities_u0,
ForwardLSSProblem, AdjointLSSProblem,
NILSSProblem, NILSASProblem,
shadow_forward, shadow_adjoint
export BacksolveAdjoint, QuadratureAdjoint, InterpolatingAdjoint,
TrackerAdjoint, ZygoteAdjoint, ReverseDiffAdjoint,
ForwardSensitivity, ForwardDiffSensitivity,
ForwardDiffOverAdjoint,
SteadyStateAdjoint,
ForwardLSS, AdjointLSS, NILSS, NILSAS
export second_order_sensitivities, second_order_sensitivity_product
export TrackerVJP, ZygoteVJP, EnzymeVJP, ReverseDiffVJP
export StochasticTransformedFunction
end # module
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 15343 | struct AdjointDiffCache{UF,PF,G,TJ,PJT,uType,JC,GC,PJC,JNC,PJNC,rateType,DG,DI,AI,FM}
uf::UF
pf::PF
g::G
J::TJ
pJ::PJT
dg_val::uType
jac_config::JC
g_grad_config::GC
paramjac_config::PJC
jac_noise_config::JNC
paramjac_noise_config::PJNC
f_cache::rateType
dg::DG
diffvar_idxs::DI
algevar_idxs::AI
factorized_mass_matrix::FM
issemiexplicitdae::Bool
end
"""
adjointdiffcache(g,sensealg,discrete,sol,dg;quad=false)
return (AdjointDiffCache, y)
"""
function adjointdiffcache(g::G,sensealg,discrete,sol,dg::DG,f;quad=false,noiseterm=false,needs_jac=false) where {G,DG}
prob = sol.prob
if prob isa DiffEqBase.SteadyStateProblem
@unpack u0, p = prob
tspan = (nothing, nothing)
#elseif prob isa SDEProblem
# @unpack tspan, u0, p = prob
else
@unpack u0, p, tspan = prob
end
numparams = p === nothing || p === DiffEqBase.NullParameters() ? 0 : length(p)
numindvar = length(u0)
isautojacvec = get_jacvec(sensealg)
issemiexplicitdae = false
mass_matrix = sol.prob.f.mass_matrix
if mass_matrix isa UniformScaling
factorized_mass_matrix = mass_matrix'
elseif mass_matrix isa Tuple{UniformScaling,UniformScaling}
factorized_mass_matrix = (I',I')
else
mass_matrix = mass_matrix'
diffvar_idxs = findall(x->any(!iszero, @view(mass_matrix[:, x])), axes(mass_matrix, 2))
algevar_idxs = setdiff(eachindex(u0), diffvar_idxs)
# TODO: operator
M̃ = @view mass_matrix[diffvar_idxs, diffvar_idxs]
factorized_mass_matrix = lu(M̃, check=false)
issuccess(factorized_mass_matrix) || error("The submatrix corresponding to the differential variables of the mass matrix must be nonsingular!")
isempty(algevar_idxs) || (issemiexplicitdae = true)
end
if !issemiexplicitdae
diffvar_idxs = eachindex(u0)
algevar_idxs = 1:0
end
if !needs_jac
J = (issemiexplicitdae || !isautojacvec) ? similar(u0, numindvar, numindvar) : nothing
else
# Force construction of the Jacobian
J = similar(u0, numindvar, numindvar)
end
if !discrete
if dg !== nothing
pg = nothing
pg_config = nothing
if dg isa Tuple && length(dg) == 2
dg_val = (similar(u0, numindvar),similar(u0, numparams))
dg_val[1] .= false
dg_val[2] .= false
else
dg_val = similar(u0, numindvar) # number of funcs size
dg_val .= false
end
else
if !(prob isa RODEProblem)
pg = UGradientWrapper(g,tspan[2],p)
else
pg = RODEUGradientWrapper(g,tspan[2],p,last(sol.W))
end
pg_config = build_grad_config(sensealg,pg,u0,p)
dg_val = similar(u0, numindvar) # number of funcs size
dg_val .= false
end
else
dg_val = nothing
pg = nothing
pg_config = nothing
end
if DiffEqBase.has_jac(f) || (J === nothing)
jac_config = nothing
uf = nothing
else
if DiffEqBase.isinplace(prob)
if !(prob isa RODEProblem)
uf = DiffEqBase.UJacobianWrapper(f,tspan[2],p)
else
uf = RODEUJacobianWrapper(f,tspan[2],p,last(sol.W))
end
jac_config = build_jac_config(sensealg,uf,u0)
else
if !(prob isa RODEProblem)
uf = DiffEqBase.UDerivativeWrapper(f,tspan[2],p)
else
uf = RODEUDerivativeWrapper(f,tspan[2],p,last(sol.W))
end
jac_config = nothing
end
end
if prob isa DiffEqBase.SteadyStateProblem
y = copy(sol.u)
else
y = copy(sol.u[end])
end
if typeof(prob.p) <: DiffEqBase.NullParameters
_p = similar(y,(0,))
else
_p = prob.p
end
@assert sensealg.autojacvec !== nothing
if sensealg.autojacvec isa ReverseDiffVJP
if prob isa DiffEqBase.SteadyStateProblem
if DiffEqBase.isinplace(prob)
tape = ReverseDiff.GradientTape((y, _p)) do u,p
du1 = p !== nothing && p !== DiffEqBase.NullParameters() ? similar(p, size(u)) : similar(u)
f(du1,u,p,nothing)
return vec(du1)
end
else
tape = ReverseDiff.GradientTape((y, _p)) do u,p
vec(f(u,p,nothing))
end
end
elseif noiseterm && (!StochasticDiffEq.is_diagonal_noise(prob) || isnoisemixing(sensealg))
tape = nothing
else
if DiffEqBase.isinplace(prob)
if !(prob isa RODEProblem)
tape = ReverseDiff.GradientTape((y, _p, [tspan[2]])) do u,p,t
du1 = (p !== nothing && p !== DiffEqBase.NullParameters()) ? similar(p, size(u)) : similar(u)
f(du1,u,p,first(t))
return vec(du1)
end
else
tape = ReverseDiff.GradientTape((y, _p, [tspan[2]],last(sol.W))) do u,p,t,W
du1 = p !== nothing && p !== DiffEqBase.NullParameters() ? similar(p, size(u)) : similar(u)
f(du1,u,p,first(t),W)
return vec(du1)
end
end
else
if !(prob isa RODEProblem)
tape = ReverseDiff.GradientTape((y, _p, [tspan[2]])) do u,p,t
vec(f(u,p,first(t)))
end
else
tape = ReverseDiff.GradientTape((y, _p, [tspan[2]],last(sol.W))) do u,p,t,W
return f(u,p,first(t),W)
end
end
end
end
if compile_tape(sensealg.autojacvec)
paramjac_config = ReverseDiff.compile(tape)
else
paramjac_config = tape
end
pf = nothing
elseif sensealg.autojacvec isa EnzymeVJP
if typeof(prob.p) <: DiffEqBase.NullParameters
paramjac_config = zero(y),prob.p,zero(y),zero(y)
else
paramjac_config = zero(y),zero(_p),zero(y),zero(y)
end
pf = let f = f.f
if DiffEqBase.isinplace(prob) && prob isa RODEProblem
function (out,u,_p,t,W)
f(out, u, _p, t, W)
nothing
end
elseif DiffEqBase.isinplace(prob)
function (out,u,_p,t)
f(out, u, _p, t)
nothing
end
elseif !DiffEqBase.isinplace(prob) && prob isa RODEProblem
function (out,u,_p,t,W)
out .= f(u, _p, t, W)
nothing
end
else !DiffEqBase.isinplace(prob)
function (out,u,_p,t)
out .= f(u, _p, t)
nothing
end
end
end
elseif DiffEqBase.has_paramjac(f) || isautojacvec || quad || sensealg.autojacvec isa EnzymeVJP
paramjac_config = nothing
pf = nothing
else
if DiffEqBase.isinplace(prob)
if !(prob isa RODEProblem)
pf = DiffEqBase.ParamJacobianWrapper(f,tspan[1],y)
else
pf = RODEParamJacobianWrapper(f,tspan[1],y,last(sol.W))
end
paramjac_config = build_param_jac_config(sensealg,pf,y,p)
else
if !(prob isa RODEProblem)
pf = ParamGradientWrapper(f,tspan[2],y)
else
pf = RODEParamGradientWrapper(f,tspan[2],y,last(sol.W))
end
paramjac_config = nothing
end
end
pJ = (quad || isautojacvec) ? nothing : similar(u0, numindvar, numparams)
f_cache = DiffEqBase.isinplace(prob) ? deepcopy(u0) : nothing
if noiseterm
if sensealg.autojacvec isa ReverseDiffVJP
jac_noise_config = nothing
paramjac_noise_config = []
if DiffEqBase.isinplace(prob)
for i in 1:numindvar
function noisetape(indx)
if StochasticDiffEq.is_diagonal_noise(prob)
ReverseDiff.GradientTape((y, _p, [tspan[2]])) do u,p,t
du1 = p !== nothing && p !== DiffEqBase.NullParameters() ? similar(p, size(u)) : similar(u)
f(du1,u,p,first(t))
return du1[indx]
end
else
ReverseDiff.GradientTape((y, _p, [tspan[2]])) do u,p,t
du1 = similar(p, size(prob.noise_rate_prototype))
du1 .= false
f(du1,u,p,first(t))
return du1[:,indx]
end
end
end
tapei = noisetape(i)
if compile_tape(sensealg.autojacvec)
push!(paramjac_noise_config, ReverseDiff.compile(tapei))
else
push!(paramjac_noise_config, tapei)
end
end
else
for i in 1:numindvar
function noisetapeoop(indx)
if StochasticDiffEq.is_diagonal_noise(prob)
ReverseDiff.GradientTape((y, _p, [tspan[2]])) do u,p,t
f(u,p,first(t))[indx]
end
else
ReverseDiff.GradientTape((y, _p, [tspan[2]])) do u,p,t
f(u,p,first(t))[:,indx]
end
end
end
tapei = noisetapeoop(i)
if compile_tape(sensealg.autojacvec)
push!(paramjac_noise_config, ReverseDiff.compile(tapei))
else
push!(paramjac_noise_config, tapei)
end
end
end
elseif sensealg.autojacvec isa Bool
if DiffEqBase.isinplace(prob)
if StochasticDiffEq.is_diagonal_noise(prob)
pf = DiffEqBase.ParamJacobianWrapper(f,tspan[1],y)
if isnoisemixing(sensealg)
uf = DiffEqBase.UJacobianWrapper(f,tspan[2],p)
jac_noise_config = build_jac_config(sensealg,uf,u0)
else
jac_noise_config = nothing
end
else
pf = ParamNonDiagNoiseJacobianWrapper(f,tspan[1],y,prob.noise_rate_prototype)
uf = UNonDiagNoiseJacobianWrapper(f,tspan[2],p,prob.noise_rate_prototype)
jac_noise_config = build_jac_config(sensealg,uf,u0)
end
paramjac_noise_config = build_param_jac_config(sensealg,pf,y,p)
else
if StochasticDiffEq.is_diagonal_noise(prob)
pf = ParamGradientWrapper(f,tspan[2],y)
if isnoisemixing(sensealg)
uf = DiffEqBase.UDerivativeWrapper(f,tspan[2],p)
end
else
pf = ParamNonDiagNoiseGradientWrapper(f,tspan[1],y)
uf = UNonDiagNoiseGradientWrapper(f,tspan[2],p)
end
paramjac_noise_config = nothing
jac_noise_config = nothing
end
if StochasticDiffEq.is_diagonal_noise(prob)
pJ = similar(u0, numindvar, numparams)
if isnoisemixing(sensealg)
J = similar(u0, numindvar, numindvar)
end
else
pJ = similar(u0, numindvar*numindvar, numparams)
J = similar(u0, numindvar*numindvar, numindvar)
end
else
paramjac_noise_config = nothing
jac_noise_config = nothing
end
else
paramjac_noise_config = nothing
jac_noise_config = nothing
end
adjoint_cache = AdjointDiffCache(uf,pf,pg,J,pJ,dg_val,
jac_config,pg_config,paramjac_config,
jac_noise_config,paramjac_noise_config,
f_cache,dg,diffvar_idxs,algevar_idxs,
factorized_mass_matrix,issemiexplicitdae)
return adjoint_cache, y
end
getprob(S::SensitivityFunction) = (S isa ODEBacksolveSensitivityFunction) ? S.prob : S.sol.prob
inplace_sensitivity(S::SensitivityFunction) = isinplace(getprob(S))
struct ReverseLossCallback{λType,timeType,yType,RefType,FMType,AlgType,gType,cacheType}
isq::Bool
λ::λType
t::timeType
y::yType
cur_time::RefType
idx::Int
F::FMType
sensealg::AlgType
g::gType
diffcache::cacheType
end
function ReverseLossCallback(sensefun, λ, t, g, cur_time)
@unpack sensealg, y = sensefun
isq = (sensealg isa QuadratureAdjoint)
@unpack factorized_mass_matrix = sensefun.diffcache
prob = getprob(sensefun)
idx = length(prob.u0)
return ReverseLossCallback(isq, λ, t, y, cur_time, idx, factorized_mass_matrix, sensealg, g, sensefun.diffcache)
end
function (f::ReverseLossCallback)(integrator)
@unpack isq, λ, t, y, cur_time, idx, F, sensealg, g = f
@unpack diffvar_idxs, algevar_idxs, issemiexplicitdae, J, uf, f_cache, jac_config = f.diffcache
p, u = integrator.p, integrator.u
if sensealg isa BacksolveAdjoint
copyto!(y,integrator.u[end-idx+1:end])
end
# Warning: alias here! Be careful with λ
gᵤ = isq ? λ : @view(λ[1:idx])
g(gᵤ,y,p,t[cur_time[]],cur_time[])
if issemiexplicitdae
jacobian!(J, uf, y, f_cache, sensealg, jac_config)
dhdd = J[algevar_idxs, diffvar_idxs]
dhda = J[algevar_idxs, algevar_idxs]
# TODO: maybe need a `conj`
Δλa = -dhda'\gᵤ[algevar_idxs]
Δλd = dhdd'Δλa + gᵤ[diffvar_idxs]
else
Δλd = gᵤ
end
if F !== nothing
F !== I && F !== (I,I) && ldiv!(F, Δλd)
end
u[diffvar_idxs] .+= Δλd
u_modified!(integrator,true)
cur_time[] -= 1
return nothing
end
function generate_callbacks(sensefun, g, λ, t, t0, callback, init_cb,terminated=false)
if sensefun isa NILSASSensitivityFunction
@unpack sensealg = sensefun.S
else
@unpack sensealg = sensefun
end
if !sensefun.discrete
cur_time = Ref(1)
else
cur_time = Ref(length(t))
end
reverse_cbs = setup_reverse_callbacks(callback,sensealg,g,cur_time,terminated)
sensefun.discrete || return reverse_cbs, nothing
# callbacks can lead to non-unique time points
_t, duplicate_iterator_times = separate_nonunique(t)
rlcb = ReverseLossCallback(sensefun, λ, t, g, cur_time)
if eltype(_t) !== typeof(t0)
_t = convert.(typeof(t0),_t)
end
cb = PresetTimeCallback(_t,rlcb)
# handle duplicates (currently only for double occurances)
if duplicate_iterator_times!==nothing
# use same ref for cur_time to cope with concrete_solve
cbrev_dupl_affect = ReverseLossCallback(sensefun, λ, t, g, cur_time)
cb_dupl = PresetTimeCallback(duplicate_iterator_times[1],cbrev_dupl_affect)
return CallbackSet(cb,reverse_cbs,cb_dupl), duplicate_iterator_times
else
return CallbackSet(cb,reverse_cbs), duplicate_iterator_times
end
end
function separate_nonunique(t)
# t is already sorted
_t = unique(t)
ts_with_occurances = [(i, count(==(i), t)) for i in _t]
# duplicates (only those values which occur > 1 times)
dupl = filter(x->last(x)>1, ts_with_occurances)
ts = first.(dupl)
occurances = last.(dupl)
if isempty(occurances)
itrs = nothing
else
maxoc = maximum(occurances)
maxoc > 2 && error("More than two occurances of the same time point. Please report this.")
# handle also more than two occurances
itrs = [ts[occurances .>= i] for i=2:maxoc]
end
return _t, itrs
end
function out_and_ts(_ts, duplicate_iterator_times, sol)
if duplicate_iterator_times === nothing
ts = _ts
out = sol(ts)
else
# if callbacks are tracked, there is potentially an event_time that must be considered
# in the loss function but doesn't occur in saveat/t. So we need to add it.
# Note that if it doens't occur in saveat/t we even need to add it twice
# However if the callbacks are not saving in the forward, we don't want to compute a loss
# value for them. This information is given by sol.t/checkpoints.
# Additionally we need to store the left and the right limit, respectively.
duplicate_times = duplicate_iterator_times[1] # just treat two occurances at the moment (see separate_nonunique above)
_ts = Array(_ts)
for d in duplicate_times
(d ∉ _ts) && push!(_ts, d)
end
u1 = sol(_ts).u
u2 = sol(duplicate_times,continuity=:right).u
saveat = vcat(_ts, duplicate_times...)
perm = sortperm(saveat)
ts = saveat[perm]
u = vcat(u1, u2)[perm]
out = DiffEqArray(u,ts)
end
return out, ts
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 13220 | struct ODEBacksolveSensitivityFunction{C<:AdjointDiffCache,Alg<:BacksolveAdjoint,uType,pType,fType<:DiffEqBase.AbstractDiffEqFunction} <: SensitivityFunction
diffcache::C
sensealg::Alg
discrete::Bool
y::uType
prob::pType
f::fType
noiseterm::Bool
end
function ODEBacksolveSensitivityFunction(g,sensealg,discrete,sol,dg,f;noiseterm=false)
diffcache, y = adjointdiffcache(g,sensealg,discrete,sol,dg,f;quad=false,noiseterm=noiseterm)
return ODEBacksolveSensitivityFunction(diffcache,sensealg,discrete,
y,sol.prob,f,noiseterm)
end
function (S::ODEBacksolveSensitivityFunction)(du,u,p,t)
@unpack y, prob, discrete = S
λ,grad,_y,dλ,dgrad,dy = split_states(du,u,t,S)
if eltype(_y) <: ForwardDiff.Dual # handle implicit solvers
copyto!(vec(y), ForwardDiff.value.(_y))
else
copyto!(vec(y), _y)
end
if S.noiseterm
if length(u) == length(du)
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad, dy=dy)
elseif length(u) != length(du) && StochasticDiffEq.is_diagonal_noise(prob) && !isnoisemixing(S.sensealg)
vecjacobian!(dλ, y, λ, p, t, S, dy=dy)
jacNoise!(λ, y, p, t, S, dgrad=dgrad)
else
jacNoise!(λ, y, p, t, S, dgrad=dgrad, dλ=dλ, dy=dy)
end
else
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad, dy=dy)
end
dλ .*= -1
discrete || accumulate_cost!(dλ, y, p, t, S, dgrad)
return nothing
end
# u = λ' # for the RODE case
function (S::ODEBacksolveSensitivityFunction)(du,u,p,t,W)
@unpack y, prob, discrete = S
λ,grad,_y,dλ,dgrad,dy = split_states(du,u,t,S)
copyto!(vec(y), _y)
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad, dy=dy,W=W)
dλ .*= -one(eltype(λ))
discrete || accumulate_cost!(dλ, y, p, t, S, dgrad)
return nothing
end
function split_states(du,u,t,S::ODEBacksolveSensitivityFunction;update=true)
@unpack y, prob = S
idx = length(y)
λ = @view u[1:idx]
grad = @view u[idx+1:end-idx]
_y = @view u[end-idx+1:end]
if length(u) == length(du)
# ODE/Drift term and scalar noise
dλ = @view du[1:idx]
dgrad = @view du[idx+1:end-idx]
dy = @view du[end-idx+1:end]
elseif length(u) != length(du) && StochasticDiffEq.is_diagonal_noise(prob) && !isnoisemixing(S.sensealg)
# Diffusion term, diagonal noise, length(du) = u*m
idx1 = [length(u)*(i-1)+i for i in 1:idx] # for diagonal indices of [1:idx,1:idx]
idx2 = [(length(u)+1)*i-idx for i in 1:idx] # for diagonal indices of [end-idx+1:end,1:idx]
dλ = @view du[idx1]
dgrad = @view du[idx+1:end-idx,1:idx]
dy = @view du[idx2]
elseif length(u) != length(du) && StochasticDiffEq.is_diagonal_noise(prob) && isnoisemixing(S.sensealg)
# Diffusion term, diagonal noise, (as above but can handle mixing noise terms)
idx2 = [(length(u)+1)*i-idx for i in 1:idx] # for diagonal indices of [end-idx+1:end,1:idx]
dλ = @view du[1:idx,1:idx]
dgrad = @view du[idx+1:end-idx,1:idx]
dy = @view du[idx2]
elseif typeof(du) <: AbstractMatrix
# non-diagonal noise
dλ = @view du[1:idx, 1:idx]
dgrad = @view du[idx+1:end-idx,1:idx]
dy = @view du[end-idx+1:end, 1:idx]
end
λ,grad,_y,dλ,dgrad,dy
end
# g is either g(t,u,p) or discrete g(t,u,i)
@noinline function ODEAdjointProblem(sol,sensealg::BacksolveAdjoint,
g,t=nothing,dg=nothing;
checkpoints=sol.t,
callback=CallbackSet(),
z0=nothing,
M=nothing,
nilss=nothing,
tspan=sol.prob.tspan,
kwargs...)
# add homogenous adjoint for NILSAS by explicitly passing a z0 and nilss::NILSSSensitivityFunction
@unpack f, p, u0 = sol.prob
# check if solution was terminated, then use reduced time span
terminated = false
if hasfield(typeof(sol),:retcode)
if sol.retcode == :Terminated
tspan = (tspan[1], sol.t[end])
terminated = true
end
end
tspan = reverse(tspan)
discrete = t !== nothing
numstates = length(u0)
numparams = p === nothing || p === DiffEqBase.NullParameters() ? 0 : length(p)
len = length(u0)+numparams
if z0===nothing
λ = p === nothing || p === DiffEqBase.NullParameters() ? similar(u0) : one(eltype(u0)) .* similar(p, len)
λ .= false
else
λ = nothing
end
sense = ODEBacksolveSensitivityFunction(g,sensealg,discrete,sol,dg,f)
if z0!==nothing
sense = NILSASSensitivityFunction{isinplace(f),typeof(nilss),typeof(sense),typeof(M)}(nilss,sense,M,discrete)
end
init_cb = t !== nothing && tspan[1] == t[end]
cb, duplicate_iterator_times = generate_callbacks(sense, g, λ, t, tspan[2], callback, init_cb,terminated)
checkpoints = ischeckpointing(sensealg, sol) ? checkpoints : nothing
if checkpoints !== nothing
cb = backsolve_checkpoint_callbacks(sense, sol, checkpoints, cb, duplicate_iterator_times)
end
if z0===nothing
z0 = [vec(zero(λ)); vec(sense.y)]
end
original_mm = sol.prob.f.mass_matrix
zzz(A, m, n) = fill!(similar(A, m, n), zero(eltype(original_mm)))
if original_mm === I || original_mm === (I,I)
mm = I
else
sense.diffcache.issemiexplicitdae && @warn "`BacksolveAdjoint` is likely to fail on semi-explicit DAEs, if memory is a concern, please consider using InterpolatingAdjoint(checkpoint=true) instead."
II = Diagonal(I, numparams)
Z1 = zzz(original_mm, numstates, numstates+numparams)
Z2 = zzz(original_mm, numparams, numstates)
mm = [copy(original_mm') Z1
Z2 II Z2
Z1 original_mm]
end
jac_prototype = sol.prob.f.jac_prototype
if !sense.discrete || jac_prototype === nothing
adjoint_jac_prototype = nothing
else
J = jac_prototype
Ja = copy(J')
II = Diagonal(I, numparams)
Z1 = zzz(J, numstates, numstates+numparams)
Z2 = zzz(J, numparams, numstates)
adjoint_jac_prototype = [Ja Z1
Z2 II Z2
Z1 J]
end
odefun = ODEFunction(sense, mass_matrix=mm, jac_prototype=adjoint_jac_prototype)
return ODEProblem(odefun,z0,tspan,p,callback=cb)
end
@noinline function SDEAdjointProblem(sol,sensealg::BacksolveAdjoint,
g,t=nothing,dg=nothing;
checkpoints=sol.t,
callback=CallbackSet(),
corfunc_analytical=nothing,diffusion_jac=nothing, diffusion_paramjac=nothing,
kwargs...)
@unpack f, p, u0, tspan = sol.prob
# check if solution was terminated, then use reduced time span
terminated = false
if hasfield(typeof(sol),:retcode)
if sol.retcode == :Terminated
tspan = (tspan[1], sol.t[end])
terminated = true
end
end
tspan = reverse(tspan)
discrete = t !== nothing
p === DiffEqBase.NullParameters() && error("Your model does not have parameters, and thus it is impossible to calculate the derivative of the solution with respect to the parameters. Your model must have parameters to use parameter sensitivity calculations!")
numstates = length(u0)
numparams = length(p)
len = length(u0)+numparams
λ = one(eltype(u0)) .* similar(p, len)
if StochasticDiffEq.alg_interpretation(sol.alg) == :Stratonovich
sense_drift = ODEBacksolveSensitivityFunction(g,sensealg,discrete,sol,dg,sol.prob.f)
else
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,corfunc_analytical)
drift_function = ODEFunction(transformed_function)
sense_drift = ODEBacksolveSensitivityFunction(g,sensealg,discrete,sol,dg,drift_function)
end
diffusion_function = ODEFunction(sol.prob.g, jac=diffusion_jac, paramjac=diffusion_paramjac)
sense_diffusion = ODEBacksolveSensitivityFunction(g,sensealg,discrete,sol,dg,diffusion_function;noiseterm=true)
init_cb = t !== nothing && tspan[1] == t[end]
cb, duplicate_iterator_times = generate_callbacks(sense_drift, g, λ, t, tspan[2], callback, init_cb,terminated)
checkpoints = ischeckpointing(sensealg, sol) ? checkpoints : nothing
if checkpoints !== nothing
cb = backsolve_checkpoint_callbacks(sense_drift, sol, checkpoints, cb, duplicate_iterator_times)
end
z0 = [vec(zero(λ)); vec(sense_drift.y)]
original_mm = sol.prob.f.mass_matrix
if original_mm === I
mm = I
else
sense_drift.diffcache.issemiexplicitdae && @warn "`BacksolveAdjoint` is likely to fail on semi-explicit DAEs, if memory is a concern, please consider using InterpolatingAdjoint(checkpoint=true) instead."
len2 = length(z0)
mm = zeros(len2, len2)
idx = 1:numstates
copyto!(@view(mm[idx, idx]), sol.prob.f.mass_matrix')
idx = numstates+1:numstates+1+numparams
copyto!(@view(mm[idx, idx]), I)
idx = len+1:len2
copyto!(@view(mm[idx, idx]), sol.prob.f.mass_matrix)
end
sdefun = SDEFunction(sense_drift,sense_diffusion,mass_matrix=mm)
# replicated noise
_sol = deepcopy(sol)
backwardnoise = reverse(_sol.W)
if StochasticDiffEq.is_diagonal_noise(sol.prob) && typeof(sol.W[end])<:Number
# scalar noise case
noise_matrix = nothing
else
noise_matrix = similar(z0,length(z0),numstates)
noise_matrix .= false
end
return SDEProblem(sdefun,sense_diffusion,z0,tspan,p,
callback=cb,
noise=backwardnoise,
noise_rate_prototype = noise_matrix
)
end
@noinline function RODEAdjointProblem(sol,sensealg::BacksolveAdjoint,
g,t=nothing,dg=nothing;
checkpoints=sol.t,
callback=CallbackSet(),
kwargs...)
@unpack f, p, u0, tspan = sol.prob
# check if solution was terminated, then use reduced time span
terminated = false
if hasfield(typeof(sol),:retcode)
if sol.retcode == :Terminated
tspan = (tspan[1], sol.t[end])
terminated = true
end
end
tspan = reverse(tspan)
discrete = t !== nothing
p === DiffEqBase.NullParameters() && error("Your model does not have parameters, and thus it is impossible to calculate the derivative of the solution with respect to the parameters. Your model must have parameters to use parameter sensitivity calculations!")
numstates = length(u0)
numparams = length(p)
len = length(u0)+numparams
λ = one(eltype(u0)) .* similar(p, len)
sense = ODEBacksolveSensitivityFunction(g,sensealg,discrete,sol,dg,f;noiseterm=false)
init_cb = t !== nothing && tspan[1] == t[end]
cb, duplicate_iterator_times = generate_callbacks(sense, g, λ, t, tspan[2], callback, init_cb,terminated)
checkpoints = ischeckpointing(sensealg, sol) ? checkpoints : nothing
if checkpoints !== nothing
cb = backsolve_checkpoint_callbacks(sense, sol, checkpoints, cb, duplicate_iterator_times)
end
z0 = [vec(zero(λ)); vec(sense.y)]
original_mm = sol.prob.f.mass_matrix
if original_mm === I
mm = I
else
sense.diffcache.issemiexplicitdae && @warn "`BacksolveAdjoint` is likely to fail on semi-explicit DAEs, if memory is a concern, please consider using InterpolatingAdjoint(checkpoint=true) instead."
len2 = length(z0)
mm = zeros(len2, len2)
idx = 1:numstates
copyto!(@view(mm[idx, idx]), sol.prob.f.mass_matrix')
idx = numstates+1:numstates+1+numparams
copyto!(@view(mm[idx, idx]), I)
idx = len+1:len2
copyto!(@view(mm[idx, idx]), sol.prob.f.mass_matrix)
end
rodefun = RODEFunction(sense,mass_matrix=mm)
# replicated noise
_sol = deepcopy(sol)
backwardnoise = reverse(_sol.W)
return RODEProblem(rodefun,z0,tspan,p,
callback=cb,
noise=backwardnoise
)
end
function backsolve_checkpoint_callbacks(sensefun, sol, checkpoints, callback, duplicate_iterator_times=nothing)
prob = sol.prob
if duplicate_iterator_times !== nothing
_checkpoints = filter(x->x ∉ duplicate_iterator_times[1], checkpoints)
else
_checkpoints = checkpoints
end
cur_time = Ref(length(_checkpoints))
affect! = let sol=sol, cur_time=cur_time, idx=length(prob.u0)
function (integrator)
_y = reshape(@view(integrator.u[end-idx+1:end]), axes(prob.u0))
sol(_y, integrator.t)
u_modified!(integrator,true)
cur_time[] -= 1
return nothing
end
end
cb = PresetTimeCallback(_checkpoints,affect!)
return CallbackSet(cb,callback)
end
function backsolve_checkpoint_callbacks(sensefun::NILSASSensitivityFunction, sol, checkpoints, callback, duplicate_iterator_times=nothing)
prob = sol.prob
if duplicate_iterator_times !== nothing
_checkpoints = filter(x->x ∉ duplicate_iterator_times[1], checkpoints)
else
_checkpoints = checkpoints
end
cur_time = Ref(length(_checkpoints))
affect! = let sol=sol, cur_time=cur_time
function (integrator)
_y = integrator.u.x[3]
sol(_y, integrator.t)
u_modified!(integrator,true)
cur_time[] -= 1
return nothing
end
end
cb = PresetTimeCallback(_checkpoints,affect!)
return CallbackSet(cb,callback)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 18805 | """
Appends a tracking process to determine the time of the callback to be used in
the reverse pass. The rationale is explain in:
https://github.com/SciML/DiffEqSensitivity.jl/issues/4
"""
track_callbacks(cb,t,u,p,sensealg) = track_callbacks(CallbackSet(cb),t,u,p,sensealg)
track_callbacks(cb::CallbackSet,t,u,p,sensealg) = CallbackSet(
map(cb->_track_callback(cb,t,u,p,sensealg), cb.continuous_callbacks),
map(cb->_track_callback(cb,t,u,p,sensealg), cb.discrete_callbacks))
mutable struct ImplicitCorrection{T1,T2,T3,T4,T5,T6,T7,T8,T9,T10,T11,RefType}
gt_val::T1
gu_val::T2
gt::T3
gu::T4
gt_conf::T5
gu_conf::T6
condition::T7
Lu_left::T8
Lu_right::T9
dy_left::T10
dy_right::T11
cur_time::RefType # initialized as "dummy" Ref that gets overwritten by Ref of loss
terminated::Bool
end
ImplicitCorrection(cb::DiscreteCallback,t,u,p,sensealg) = nothing
function ImplicitCorrection(cb,t,u,p,sensealg)
condition = cb.condition
gt_val = similar(u,1)
gu_val = similar(u)
fakeinteg = FakeIntegrator(u,p,t,t)
gt, gu = build_condition_wrappers(cb,condition,u,t,fakeinteg)
gt_conf = build_deriv_config(sensealg,gt,gt_val,t)
gu_conf = build_grad_config(sensealg,gu,u,p)
dy_left = similar(u)
dy_right = similar(u)
Lu_left = similar(u)
Lu_right = similar(u)
cur_time = Ref(1) # initialize the Ref, set to Ref of loss below
terminated = false
ImplicitCorrection(gt_val,gu_val,gt,gu,gt_conf,gu_conf,condition,Lu_left,Lu_right,dy_left,dy_right,cur_time,terminated)
end
struct TrackedAffect{T,T2,T3,T4,T5,T6}
event_times::Vector{T}
tprev::Vector{T}
uleft::Vector{T2}
pleft::Vector{T3}
affect!::T4
correction::T5
event_idx::Vector{T6}
end
TrackedAffect(t::Number,u,p,affect!::Nothing,correction) = nothing
TrackedAffect(t::Number,u,p,affect!,correction) = TrackedAffect(Vector{typeof(t)}(undef,0),Vector{typeof(t)}(undef,0),
Vector{typeof(u)}(undef,0),Vector{typeof(p)}(undef,0),affect!,correction,
Vector{Int}(undef,0))
function (f::TrackedAffect)(integrator,event_idx=nothing)
uleft = deepcopy(integrator.u)
pleft = deepcopy(integrator.p)
if event_idx===nothing
f.affect!(integrator)
else
f.affect!(integrator,event_idx)
end
if integrator.u_modified
if isempty(f.event_times)
push!(f.event_times,integrator.t)
push!(f.tprev,integrator.tprev)
push!(f.uleft,uleft)
push!(f.pleft,pleft)
if event_idx !== nothing
push!(f.event_idx,event_idx)
end
else
if !maximum(.≈(integrator.t, f.event_times, rtol=0.0, atol=1e-14))
push!(f.event_times,integrator.t)
push!(f.tprev,integrator.tprev)
push!(f.uleft,uleft)
push!(f.pleft,pleft)
if event_idx !== nothing
push!(f.event_idx, event_idx)
end
end
end
end
end
function _track_callback(cb::DiscreteCallback,t,u,p,sensealg)
correction = ImplicitCorrection(cb,t,u,p,sensealg)
DiscreteCallback(cb.condition,
TrackedAffect(t,u,p,cb.affect!,correction),
cb.initialize,
cb.finalize,
cb.save_positions)
end
function _track_callback(cb::ContinuousCallback,t,u,p,sensealg)
correction = ImplicitCorrection(cb,t,u,p,sensealg)
ContinuousCallback(
cb.condition,
TrackedAffect(t,u,p,cb.affect!,correction),
TrackedAffect(t,u,p,cb.affect_neg!,correction),
cb.initialize,
cb.finalize,
cb.idxs,
cb.rootfind,cb.interp_points,
cb.save_positions,
cb.dtrelax,cb.abstol,cb.reltol,cb.repeat_nudge)
end
function _track_callback(cb::VectorContinuousCallback,t,u,p,sensealg)
correction = ImplicitCorrection(cb,t,u,p,sensealg)
VectorContinuousCallback(
cb.condition,
TrackedAffect(t,u,p,cb.affect!,correction),
TrackedAffect(t,u,p,cb.affect_neg!,correction),
cb.len,cb.initialize,cb.finalize,cb.idxs,
cb.rootfind,cb.interp_points,
collect(cb.save_positions),
cb.dtrelax,cb.abstol,cb.reltol,cb.repeat_nudge)
end
struct FakeIntegrator{uType,P,tType,tprevType}
u::uType
p::P
t::tType
tprev::tprevType
end
struct CallbackSensitivityFunction{fType,Alg<:DiffEqBase.AbstractSensitivityAlgorithm,C<:AdjointDiffCache,pType} <: SensitivityFunction
f::fType
sensealg::Alg
diffcache::C
prob::pType
end
getprob(S::CallbackSensitivityFunction) = S.prob
inplace_sensitivity(S::CallbackSensitivityFunction) = true
"""
Sets up callbacks for the adjoint pass. This is a version that has an effect
at each event of the forward pass and defines the reverse pass values via the
vjps as described in https://arxiv.org/pdf/1905.10403.pdf Equation 13.
For more information, see https://github.com/SciML/DiffEqSensitivity.jl/issues/4
"""
setup_reverse_callbacks(cb,sensealg,g,cur_time,terminated) = setup_reverse_callbacks(CallbackSet(cb),sensealg,g,cur_time,terminated)
function setup_reverse_callbacks(cb::CallbackSet,sensealg,g,cur_time,terminated)
cb = CallbackSet(_setup_reverse_callbacks.(cb.continuous_callbacks,(sensealg,),(g,),(cur_time,),(terminated,))...,
reverse(_setup_reverse_callbacks.(cb.discrete_callbacks,(sensealg,),(g,),(cur_time,),(terminated,)))...)
return cb
end
function _setup_reverse_callbacks(cb::Union{ContinuousCallback,DiscreteCallback,VectorContinuousCallback},sensealg,g,loss_ref,terminated)
if cb isa Union{ContinuousCallback,VectorContinuousCallback} && cb.affect! !== nothing
cb.affect!.correction.cur_time = loss_ref # set cur_time
cb.affect!.correction.terminated = terminated # flag if time evolution was terminated by callback
end
# ReverseLossCallback adds gradients before and after the callback if save_positions is (true, true).
# This, however, means that we must check the save_positions setting within the callback.
# if save_positions = [1,1] is true the loss gradient is accumulated correctly before and after callback.
# if save_positions = [0,0] no extra gradient is added.
# if save_positions = [0,1] the gradient contribution is added before the callback but no additional gradient is added afterwards.
# if save_positions = [1,0] the gradient contribution is added before, and in principle we would need to correct the adjoint state again. Thefore,
cb.save_positions == [1,0] && error("save_positions=[1,0] is currently not supported.")
function affect!(integrator)
indx, pos_neg = get_indx(cb,integrator.t)
tprev = get_tprev(cb,indx,pos_neg)
event_idx = cb isa VectorContinuousCallback ? get_event_idx(cb,indx,pos_neg) : nothing
w = let tprev=tprev, pos_neg=pos_neg, event_idx=event_idx
function (du,u,p,t)
_affect! = get_affect!(cb,pos_neg)
fakeinteg = FakeIntegrator([x for x in u],[x for x in p],t,tprev)
if cb isa VectorContinuousCallback
_affect!(fakeinteg,event_idx)
else
_affect!(fakeinteg)
end
du .= fakeinteg.u
end
end
S = integrator.f.f # get the sensitivity function
# Create a fake sensitivity function to do the vjps
fakeS = CallbackSensitivityFunction(w,sensealg,S.diffcache,integrator.sol.prob)
du = first(get_tmp_cache(integrator))
λ,grad,y,dλ,dgrad,dy = split_states(du,integrator.u,integrator.t,S)
# if save_positions[2] = false, then the right limit is not saved. Thus, for
# the QuadratureAdjoint we would need to lift y from the left to the right limit.
# However, one also needs to update dgrad later on.
if (sensealg isa QuadratureAdjoint && !cb.save_positions[2]) # || (sensealg isa InterpolatingAdjoint && ischeckpointing(sensealg))
# lifting for InterpolatingAdjoint is not needed anymore. Callback is already applied.
w(y,y,integrator.p,integrator.t)
end
if cb isa Union{ContinuousCallback,VectorContinuousCallback}
# correction of the loss function sensitivity for continuous callbacks
# wrt dependence of event time t on parameters and initial state.
# Must be handled here because otherwise it is unclear if continuous or
# discrete callback was triggered.
@unpack correction = cb.affect!
@unpack dy_right, Lu_right = correction
# compute #f(xτ_right,p_right,τ(x₀,p))
compute_f!(dy_right,S,y,integrator)
# if callback did not terminate the time evolution, we have to compute one more correction term.
if cb.save_positions[2] && !correction.terminated
loss_indx = correction.cur_time[] + 1
loss_correction!(Lu_right,y,integrator,g,loss_indx)
else
Lu_right .*= false
end
end
update_p = copy_to_integrator!(cb,y,integrator.p,integrator.t,indx,pos_neg)
# reshape u and du (y and dy) to match forward pass (e.g., for matrices as initial conditions). Only needed for BacksolveAdjoint
if sensealg isa BacksolveAdjoint
_size = pos_neg ? size(cb.affect!.uleft[indx]) : size(cb.affect_neg!.uleft[indx])
y = reshape(y, _size)
dy = reshape(dy, _size)
end
if cb isa Union{ContinuousCallback,VectorContinuousCallback}
# compute the correction of the right limit (with left state limit inserted into dgdt)
@unpack dy_left, cur_time = correction
compute_f!(dy_left,S,y,integrator)
dgdt(dy_left,correction,sensealg,y,integrator,tprev,event_idx)
if !correction.terminated
implicit_correction!(Lu_right,dλ,λ,dy_right,correction)
correction.terminated = false # additional callbacks might have happened which didn't terminate the time evolution
end
end
if update_p
# changes in parameters
if !(sensealg isa QuadratureAdjoint)
wp = let tprev=tprev, pos_neg=pos_neg, event_idx=event_idx
function (dp,p,u,t)
_affect! = get_affect!(cb,pos_neg)
fakeinteg = FakeIntegrator([x for x in u],[x for x in p],t,tprev)
if cb isa VectorContinuousCallback
_affect!(fakeinteg, event_idx)
else
_affect!(fakeinteg)
end
dp .= fakeinteg.p
end
end
fakeSp = CallbackSensitivityFunction(wp,sensealg,S.diffcache,integrator.sol.prob)
#vjp with Jacobin given by dw/dp before event and vector given by grad
vecjacobian!(dgrad, integrator.p, grad, y, integrator.t, fakeSp;
dgrad=nothing, dy=nothing)
grad .= dgrad
end
end
vecjacobian!(dλ, y, λ, integrator.p, integrator.t, fakeS;
dgrad=dgrad, dy=dy)
if cb isa Union{ContinuousCallback,VectorContinuousCallback}
# second correction to correct for left limit
@unpack Lu_left = correction
implicit_correction!(Lu_left,dλ,dy_left,correction)
dλ .+= Lu_left - Lu_right
if cb.save_positions[1] == true
# if the callback saved the first position, we need to implicitly correct this value as well
loss_indx = correction.cur_time[]
implicit_correction!(Lu_left,dy_left,correction,y,integrator,g,loss_indx)
dλ .+= Lu_left
end
end
λ .= dλ
if !(sensealg isa QuadratureAdjoint)
grad .-= dgrad
end
end
times = if typeof(cb) <: DiscreteCallback
cb.affect!.event_times
else
[cb.affect!.event_times;cb.affect_neg!.event_times]
end
PresetTimeCallback(times,
affect!,
save_positions = (false,false))
end
get_indx(cb::DiscreteCallback,t) = (searchsortedfirst(cb.affect!.event_times,t), true)
function get_indx(cb::Union{ContinuousCallback,VectorContinuousCallback}, t)
if !isempty(cb.affect!.event_times) || !isempty(cb.affect_neg!.event_times)
indx = searchsortedfirst(cb.affect!.event_times,t)
indx_neg = searchsortedfirst(cb.affect_neg!.event_times,t)
if !isempty(cb.affect!.event_times) && cb.affect!.event_times[min(indx,length(cb.affect!.event_times))]==t
return indx, true
elseif !isempty(cb.affect_neg!.event_times) && cb.affect_neg!.event_times[min(indx_neg,length(cb.affect_neg!.event_times))]==t
return indx_neg, false
else
error("Event was triggered but no corresponding event in ContinuousCallback was found. Please report this error.")
end
else
error("No event was recorded. Please report this error.")
end
end
get_tprev(cb::DiscreteCallback,indx,bool) = cb.affect!.tprev[indx]
function get_tprev(cb::Union{ContinuousCallback,VectorContinuousCallback}, indx, bool)
if bool
return cb.affect!.tprev[indx]
else
return cb.affect_neg!.tprev[indx]
end
end
function get_event_idx(cb::VectorContinuousCallback, indx, bool)
if bool
return cb.affect!.event_idx[indx]
else
return cb.affect_neg!.event_idx[indx]
end
end
function copy_to_integrator!(cb::DiscreteCallback, y, p, t, indx, bool)
copyto!(y, cb.affect!.uleft[indx])
update_p = (p != cb.affect!.pleft[indx])
update_p && copyto!(p, cb.affect!.pleft[indx])
update_p
end
function copy_to_integrator!(cb::Union{ContinuousCallback,VectorContinuousCallback}, y, p, t, indx, bool)
if bool
copyto!(y, cb.affect!.uleft[indx])
update_p = (p != cb.affect!.pleft[indx])
update_p && copyto!(p, cb.affect!.pleft[indx])
else
copyto!(y, cb.affect_neg!.uleft[indx])
update_p = (p != cb.affect_neg!.pleft[indx])
update_p && copyto!(p, cb.affect_neg!.pleft[indx])
end
update_p
end
function compute_f!(dy,S,y,integrator)
p, t = integrator.p, integrator.t
if inplace_sensitivity(S)
S.f(dy,y,p,t)
else
dy[:] .= S.f(y,p,t)
end
return nothing
end
function dgdt(dy,correction,sensealg,y,integrator,tprev,event_idx)
# dy refers to f evaluated on left limit
@unpack gt_val, gu_val, gt, gu, gt_conf, gu_conf, condition = correction
p, t = integrator.p, integrator.t
fakeinteg = FakeIntegrator([x for x in y],p,t,tprev)
# derivative and gradient of condition with respect to time and state, respectively
gt.u = y
gt.integrator = fakeinteg
gu.t = t
gu.integrator = fakeinteg
# for VectorContinuousCallback we also need to set the event_idx.
if gt isa VectorConditionTimeWrapper
gt.event_idx = event_idx
gu.event_idx = event_idx
# safety check: evaluate condition to check if several conditions were true.
# This is currently not supported
condition(gt.out_cache,y,t,integrator)
gt.out_cache .= abs.(gt.out_cache) .< 1000*eps(eltype(gt.out_cache))
(sum(gt.out_cache)!=1 || gt.out_cache[event_idx]!=1) && error("Either several events were triggered or `event_idx` was falsely identified. Output of conditions $(gt.out_cache)")
end
derivative!(gt_val, gt, t, sensealg, gt_conf)
gradient!(gu_val, gu, y, sensealg, gu_conf)
gt_val .+= dot(gu_val,dy)
@. gt_val = inv(gt_val) # allocates?
@. gu_val *= -gt_val
return nothing
end
function loss_correction!(Lu,y,integrator,g,indx)
# ∂L∂t correction should be added if L depends explicitly on time.
p, t = integrator.p, integrator.t
g(Lu,y,p,t,indx)
return nothing
end
function implicit_correction!(Lu,dλ,λ,dy,correction)
@unpack gu_val = correction
# remove gradients from adjoint state to compute correction factor
@. dλ = λ - Lu
Lu .= dot(dλ,dy)*gu_val
return nothing
end
function implicit_correction!(Lu,λ,dy,correction)
@unpack gu_val = correction
Lu .= dot(λ,dy)*gu_val
return nothing
end
function implicit_correction!(Lu,dy,correction,y,integrator,g,indx)
@unpack gu_val = correction
p, t = integrator.p, integrator.t
# loss function gradient (not condition!)
# ∂L∂t correction should be added, also ∂L∂p is missing.
# correct adjoint
g(Lu,y,p,t,indx)
Lu .= dot(Lu,dy)*gu_val
# note that we don't add the gradient Lu here again to the correction because it will be added by the ReverseLossCallback.
return nothing
end
# ConditionTimeWrapper: Wrapper for implicit correction for ContinuousCallback
# VectorConditionTimeWrapper: Wrapper for implicit correction for VectorContinuousCallback
function build_condition_wrappers(cb::ContinuousCallback,condition,u,t,fakeinteg)
gt = ConditionTimeWrapper(condition,u,fakeinteg)
gu = ConditionUWrapper(condition,t,fakeinteg)
return gt, gu
end
function build_condition_wrappers(cb::VectorContinuousCallback,condition,u,t,fakeinteg)
out = similar(u, cb.len) # create a cache for condition function (out,u,t,integrator)
gt = VectorConditionTimeWrapper(condition,u,fakeinteg,1,out)
gu = VectorConditionUWrapper(condition,t,fakeinteg,1,out)
return gt, gu
end
mutable struct ConditionTimeWrapper{F,uType,Integrator} <: Function
f::F
u::uType
integrator::Integrator
end
(ff::ConditionTimeWrapper)(t) = [ff.f(ff.u,t,ff.integrator)]
mutable struct ConditionUWrapper{F,tType,Integrator} <: Function
f::F
t::tType
integrator::Integrator
end
(ff::ConditionUWrapper)(u) = ff.f(u,ff.t,ff.integrator)
mutable struct VectorConditionTimeWrapper{F,uType,Integrator,outType} <: Function
f::F
u::uType
integrator::Integrator
event_idx::Int
out_cache::outType
end
(ff::VectorConditionTimeWrapper)(t) = (ff.f(ff.out_cache,ff.u,t,ff.integrator); [ff.out_cache[ff.event_idx]])
mutable struct VectorConditionUWrapper{F,tType,Integrator,outType} <: Function
f::F
t::tType
integrator::Integrator
event_idx::Int
out_cache::outType
end
(ff::VectorConditionUWrapper)(u) = (out = similar(u,length(ff.out_cache)); ff.f(out,u,ff.t,ff.integrator); out[ff.event_idx])
DiffEqBase.terminate!(i::FakeIntegrator) = nothing
# get the affect function of the callback. For example, allows us to get the `f` in PeriodicCallback without the integrator.tstops handling.
get_affect!(cb::DiscreteCallback,bool) = get_affect!(cb.affect!)
get_affect!(cb::Union{ContinuousCallback,VectorContinuousCallback},bool) = bool ? get_affect!(cb.affect!) : get_affect!(cb.affect_neg!)
get_affect!(affect!::TrackedAffect) = get_affect!(affect!.affect!)
get_affect!(affect!) = affect!
get_affect!(affect!::DiffEqCallbacks.PeriodicCallbackAffect) = affect!.affect!
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 38310 | ## High level
# Here is where we can add a default algorithm for computing sensitivities
# Based on problem information!
function inplace_vjp(prob,u0,p,verbose)
du = copy(u0)
ez = try
Enzyme.autodiff(Enzyme.Duplicated(du, du),
copy(u0),copy(p),prob.tspan[1]) do out,u,_p,t
prob.f(out, u, _p, t)
nothing
end
true
catch
false
end
if ez
return EnzymeVJP()
end
# Determine if we can compile ReverseDiff
compile = try
if DiffEqBase.isinplace(prob)
!hasbranching(prob.f,copy(u0),u0,p,prob.tspan[1])
else
!hasbranching(prob.f,u0,p,prob.tspan[1])
end
catch
false
end
vjp = try
ReverseDiff.GradientTape((copy(u0), p, [prob.tspan[1]])) do u,p,t
du1 = similar(u, size(u))
prob.f(du1,u,p,first(t))
return vec(du1)
end
ReverseDiffVJP(compile)
catch
false
end
return vjp
end
function automatic_sensealg_choice(prob::Union{ODEProblem,SDEProblem},u0,p,verbose)
default_sensealg = if p !== DiffEqBase.NullParameters() &&
!(eltype(u0) <: ForwardDiff.Dual) &&
!(eltype(p) <: ForwardDiff.Dual) &&
!(eltype(u0) <: Complex) &&
!(eltype(p) <: Complex) &&
length(u0) + length(p) <= 100
ForwardDiffSensitivity()
elseif u0 isa GPUArrays.AbstractGPUArray || !DiffEqBase.isinplace(prob)
# only Zygote is GPU compatible and fast
# so if out-of-place, try Zygote
if p === nothing || p === DiffEqBase.NullParameters()
# QuadratureAdjoint skips all p calculations until the end
# So it's the fastest when there are no parameters
QuadratureAdjoint(autojacvec=ZygoteVJP())
else
InterpolatingAdjoint(autojacvec=ZygoteVJP())
end
else
vjp = inplace_vjp(prob,u0,p,verbose)
if p === nothing || p === DiffEqBase.NullParameters()
QuadratureAdjoint(autojacvec=vjp)
else
InterpolatingAdjoint(autojacvec=vjp)
end
end
return default_sensealg
end
function automatic_sensealg_choice(prob::Union{NonlinearProblem,SteadyStateProblem}, u0, p, verbose)
default_sensealg = if u0 isa GPUArrays.AbstractGPUArray || !DiffEqBase.isinplace(prob)
# autodiff = false because forwarddiff fails on many GPU kernels
# this only effects the Jacobian calculation and is same computation order
SteadyStateAdjoint(autodiff=false, autojacvec=ZygoteVJP())
else
vjp = inplace_vjp(prob,u0,p,verbose)
SteadyStateAdjoint(autojacvec=vjp)
end
return default_sensealg
end
function DiffEqBase._concrete_solve_adjoint(prob::Union{ODEProblem,SDEProblem},
alg,sensealg::Nothing,u0,p,originator::SciMLBase.ADOriginator,args...;
verbose=true,kwargs...)
if haskey(kwargs,:callback)
has_cb = kwargs[:callback]!==nothing
else
has_cb = false
end
default_sensealg = automatic_sensealg_choice(prob,u0,p,verbose)
if has_cb
default_sensealg = setvjp(default_sensealg, ReverseDiffVJP())
end
DiffEqBase._concrete_solve_adjoint(prob,alg,default_sensealg,u0,p,originator::SciMLBase.ADOriginator,args...;verbose,kwargs...)
end
function DiffEqBase._concrete_solve_adjoint(prob::Union{NonlinearProblem,SteadyStateProblem},alg,
sensealg::Nothing,u0,p,originator::SciMLBase.ADOriginator,args...;
verbose=true,kwargs...)
default_sensealg = automatic_sensealg_choice(prob, u0, p, verbose)
DiffEqBase._concrete_solve_adjoint(prob,alg,default_sensealg,u0,p,originator::SciMLBase.ADOriginator,args...;verbose,kwargs...)
end
function DiffEqBase._concrete_solve_adjoint(prob::Union{DiscreteProblem,DDEProblem,
SDDEProblem,DAEProblem},
alg,sensealg::Nothing,
u0,p,originator::SciMLBase.ADOriginator,args...;kwargs...)
if length(u0) + length(p) > 100
default_sensealg = ReverseDiffAdjoint()
else
default_sensealg = ForwardDiffSensitivity()
end
DiffEqBase._concrete_solve_adjoint(prob,alg,default_sensealg,u0,p,originator::SciMLBase.ADOriginator,args...;kwargs...)
end
function DiffEqBase._concrete_solve_adjoint(prob,alg,
sensealg::AbstractAdjointSensitivityAlgorithm,
u0,p,originator::SciMLBase.ADOriginator,args...;save_start=true,save_end=true,
saveat = eltype(prob.tspan)[],
save_idxs = nothing,
kwargs...)
if !(typeof(p) <: Union{Nothing,SciMLBase.NullParameters,AbstractArray}) || (p isa AbstractArray && !Base.isconcretetype(eltype(p)))
throw(AdjointSensitivityParameterCompatibilityError())
end
# Remove saveat, etc. from kwargs since it's handled separately
# and letting it jump back in there can break the adjoint
kwargs_prob = NamedTuple(filter(x->x[1] != :saveat && x[1] != :save_start && x[1] != :save_end && x[1] != :save_idxs,prob.kwargs))
if haskey(kwargs, :callback)
cb = track_callbacks(CallbackSet(kwargs[:callback]),prob.tspan[1],prob.u0,prob.p,sensealg)
_prob = remake(prob;u0=u0,p=p,kwargs = merge(kwargs_prob,(;callback=cb)))
else
cb = nothing
_prob = remake(prob;u0=u0,p=p,kwargs = kwargs_prob)
end
# Remove callbacks, saveat, etc. from kwargs since it's handled separately
kwargs_fwd = NamedTuple{Base.diff_names(Base._nt_names(
values(kwargs)), (:callback,))}(values(kwargs))
# Capture the callback_adj for the reverse pass and remove both callbacks
kwargs_adj = NamedTuple{Base.diff_names(Base._nt_names(values(kwargs)), (:callback_adj,:callback))}(values(kwargs))
isq = sensealg isa QuadratureAdjoint
if typeof(sensealg) <: BacksolveAdjoint
sol = solve(_prob,alg,args...;save_noise=true,
save_start=save_start,save_end=save_end,
saveat=saveat,kwargs_fwd...)
elseif ischeckpointing(sensealg)
sol = solve(_prob,alg,args...;save_noise=true,
save_start=true,save_end=true,
saveat=saveat,kwargs_fwd...)
else
sol = solve(_prob,alg,args...;save_noise=true,save_start=true,
save_end=true,kwargs_fwd...)
end
# Force `save_start` and `save_end` in the forward pass This forces the
# solver to do the backsolve all the way back to `u0` Since the start aliases
# `_prob.u0`, this doesn't actually use more memory But it cleans up the
# implementation and makes `save_start` and `save_end` arg safe.
if typeof(sensealg) <: BacksolveAdjoint
# Saving behavior unchanged
ts = sol.t
only_end = length(ts) == 1 && ts[1] == _prob.tspan[2]
out = DiffEqBase.sensitivity_solution(sol,sol.u,ts)
elseif saveat isa Number
if _prob.tspan[2] > _prob.tspan[1]
ts = _prob.tspan[1]:convert(typeof(_prob.tspan[2]),abs(saveat)):_prob.tspan[2]
else
ts = _prob.tspan[2]:convert(typeof(_prob.tspan[2]),abs(saveat)):_prob.tspan[1]
end
# if _prob.tspan[2]-_prob.tspan[1] is not a multiple of saveat, one looses the last ts value
sol.t[end] !== ts[end] && (ts = fix_endpoints(sensealg,sol,ts))
if cb === nothing
_out = sol(ts)
else
_, duplicate_iterator_times = separate_nonunique(sol.t)
_out, ts = out_and_ts(ts, duplicate_iterator_times, sol)
end
out = if save_idxs === nothing
out = DiffEqBase.sensitivity_solution(sol,_out.u,ts)
else
out = DiffEqBase.sensitivity_solution(sol,[_out[i][save_idxs] for i in 1:length(_out)],ts)
end
only_end = length(ts) == 1 && ts[1] == _prob.tspan[2]
elseif isempty(saveat)
no_start = !save_start
no_end = !save_end
sol_idxs = 1:length(sol)
no_start && (sol_idxs = sol_idxs[2:end])
no_end && (sol_idxs = sol_idxs[1:end-1])
only_end = length(sol_idxs) <= 1
_u = sol.u[sol_idxs]
u = save_idxs === nothing ? _u : [x[save_idxs] for x in _u]
ts = sol.t[sol_idxs]
out = DiffEqBase.sensitivity_solution(sol,u,ts)
else
_saveat = saveat isa Array ? sort(saveat) : saveat # for minibatching
if cb === nothing
_saveat = eltype(_saveat) <: typeof(prob.tspan[2]) ? convert.(typeof(_prob.tspan[2]),_saveat) : _saveat
ts = _saveat
_out = sol(ts)
else
_ts, duplicate_iterator_times = separate_nonunique(sol.t)
_out, ts = out_and_ts(_saveat, duplicate_iterator_times, sol)
end
out = if save_idxs === nothing
out = DiffEqBase.sensitivity_solution(sol,_out.u,ts)
else
out = DiffEqBase.sensitivity_solution(sol,[_out[i][save_idxs] for i in 1:length(_out)],ts)
end
only_end = length(ts) == 1 && ts[1] == _prob.tspan[2]
end
_save_idxs = save_idxs === nothing ? Colon() : save_idxs
function adjoint_sensitivity_backpass(Δ)
function df(_out, u, p, t, i)
outtype = typeof(_out) <: SubArray ? DiffEqBase.parameterless_type(_out.parent) : DiffEqBase.parameterless_type(_out)
if only_end
eltype(Δ) <: NoTangent && return
if typeof(Δ) <: AbstractArray{<:AbstractArray} && length(Δ) == 1 && i == 1
# user did sol[end] on only_end
if typeof(_save_idxs) <: Number
x = vec(Δ[1])
_out[_save_idxs] .= .-adapt(outtype,@view(x[_save_idxs]))
elseif _save_idxs isa Colon
vec(_out) .= .-adapt(outtype,vec(Δ[1]))
else
vec(@view(_out[_save_idxs])) .= .-adapt(outtype,vec(Δ[1])[_save_idxs])
end
else
Δ isa NoTangent && return
if typeof(_save_idxs) <: Number
x = vec(Δ)
_out[_save_idxs] .= .-adapt(outtype,@view(x[_save_idxs]))
elseif _save_idxs isa Colon
vec(_out) .= .-adapt(outtype,vec(Δ))
else
x = vec(Δ)
vec(@view(_out[_save_idxs])) .= .-adapt(outtype,@view(x[_save_idxs]))
end
end
else
!Base.isconcretetype(eltype(Δ)) && (Δ[i] isa NoTangent || eltype(Δ) <: NoTangent) && return
if typeof(Δ) <: AbstractArray{<:AbstractArray} || typeof(Δ) <: DESolution
x = Δ[i]
if typeof(_save_idxs) <: Number
_out[_save_idxs] = .-@view(x[_save_idxs])
elseif _save_idxs isa Colon
vec(_out) .= .-vec(x)
else
vec(@view(_out[_save_idxs])) .= .-vec(@view(x[_save_idxs]))
end
else
if typeof(_save_idxs) <: Number
_out[_save_idxs] = .-adapt(outtype,reshape(Δ, prod(size(Δ)[1:end-1]), size(Δ)[end])[_save_idxs, i])
elseif _save_idxs isa Colon
vec(_out) .= .-vec(adapt(outtype,reshape(Δ, prod(size(Δ)[1:end-1]), size(Δ)[end])[:, i]))
else
vec(@view(_out[_save_idxs])) .= .-vec(adapt(outtype,reshape(Δ, prod(size(Δ)[1:end-1]), size(Δ)[end])[:, i]))
end
end
end
end
if haskey(kwargs_adj, :callback_adj)
cb2 = CallbackSet(cb,kwargs[:callback_adj])
else
cb2 = cb
end
du0, dp = adjoint_sensitivities(sol,alg,args...,df,ts; sensealg=sensealg,
callback = cb2,
kwargs_adj...)
du0 = reshape(du0,size(u0))
dp = p === nothing || p === DiffEqBase.NullParameters() ? nothing : reshape(dp',size(p))
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(),NoTangent(),du0,dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
else
(NoTangent(),NoTangent(),NoTangent(),du0,dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
end
end
out, adjoint_sensitivity_backpass
end
# Prefer this route since it works better with callback AD
function DiffEqBase._concrete_solve_adjoint(prob, alg, sensealg::AbstractForwardSensitivityAlgorithm,
u0, p, originator::SciMLBase.ADOriginator, args...;
save_idxs=nothing,
kwargs...)
if !(typeof(p) <: Union{Nothing,SciMLBase.NullParameters,AbstractArray}) || (p isa AbstractArray && !Base.isconcretetype(eltype(p)))
throw(ForwardSensitivityParameterCompatibilityError())
end
if p isa AbstractArray && eltype(p) <: ForwardDiff.Dual && !(eltype(u0) <: ForwardDiff.Dual)
# Handle double differentiation case
u0 = eltype(p).(u0)
end
_prob = ODEForwardSensitivityProblem(prob.f, u0, prob.tspan, p, sensealg)
sol = solve(_prob, alg, args...; kwargs...)
_, du = extract_local_sensitivities(sol, sensealg, Val(true))
u = if save_idxs === nothing
[reshape(sol[i][1:length(u0)], size(u0)) for i in 1:length(sol)]
else
[sol[i][_save_idxs] for i in 1:length(sol)]
end
out = DiffEqBase.sensitivity_solution(sol, u, sol.t)
function forward_sensitivity_backpass(Δ)
adj = sum(eachindex(du)) do i
J = du[i]
if Δ isa AbstractVector || Δ isa DESolution || Δ isa AbstractVectorOfArray
v = Δ[i]
elseif Δ isa AbstractMatrix
v = @view Δ[:, i]
else
v = @view Δ[.., i]
end
J'vec(v)
end
du0 = @not_implemented(
"ForwardSensitivity does not differentiate with respect to u0. Change your sensealg."
)
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(), NoTangent(), du0, adj, NoTangent(), ntuple(_ -> NoTangent(), length(args))...)
else
(NoTangent(), NoTangent(), NoTangent(), du0, adj, NoTangent(), ntuple(_ -> NoTangent(), length(args))...)
end
end
out, forward_sensitivity_backpass
end
function DiffEqBase._concrete_solve_forward(prob,alg,
sensealg::AbstractForwardSensitivityAlgorithm,
u0,p,originator::SciMLBase.ADOriginator,args...;save_idxs = nothing,
kwargs...)
_prob = ODEForwardSensitivityProblem(prob.f,u0,prob.tspan,p,sensealg)
sol = solve(_prob,args...;kwargs...)
u,du = extract_local_sensitivities(sol,Val(true))
_save_idxs = save_idxs === nothing ? (1:length(u0)) : save_idxs
out = DiffEqBase.sensitivity_solution(sol,[ForwardDiff.value.(sol[i][_save_idxs]) for i in 1:length(sol)],sol.t)
function _concrete_solve_pushforward(Δself, ::Nothing, ::Nothing, x3, Δp, args...)
x3 !== nothing && error("Pushforward currently requires no u0 derivatives")
du * Δp
end
out,_concrete_solve_pushforward
end
const FORWARDDIFF_SENSITIVITY_PARAMETER_COMPATABILITY_MESSAGE =
"""
ForwardDiffSensitivity assumes the `AbstractArray` interface for `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with ForwardDiffSensitivity requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during ForwardDiffSensitivity
construction. To work around this issue for complicated cases like nested structs,
look into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl.
"""
struct ForwardDiffSensitivityParameterCompatibilityError <: Exception end
function Base.showerror(io::IO, e::ForwardDiffSensitivityParameterCompatibilityError)
print(io, FORWARDDIFF_SENSITIVITY_PARAMETER_COMPATABILITY_MESSAGE)
end
# Generic Fallback for ForwardDiff
function DiffEqBase._concrete_solve_adjoint(prob,alg,
sensealg::ForwardDiffSensitivity{CS,CTS},
u0,p,originator::SciMLBase.ADOriginator,args...;saveat=eltype(prob.tspan)[],
kwargs...) where {CS,CTS}
if !(typeof(p) <: Union{Nothing,SciMLBase.NullParameters,AbstractArray}) || (p isa AbstractArray && !Base.isconcretetype(eltype(p)))
throw(ForwardDiffSensitivityParameterCompatibilityError())
end
if saveat isa Number
_saveat = prob.tspan[1]:saveat:prob.tspan[2]
else
_saveat = saveat
end
sol = solve(remake(prob,p=p,u0=u0),alg,args...;saveat=_saveat, kwargs...)
# saveat values
# seems overcomplicated, but see the PR
if length(sol.t) == 1
ts = sol.t
else
ts = eltype(sol.t)[]
if sol.t[2] != sol.t[1]
push!(ts,sol.t[1])
end
for i in 2:length(sol.t)-1
if sol.t[i] != sol.t[i+1] && sol.t[i] != sol.t[i-1]
push!(ts,sol.t[i])
end
end
if sol.t[end] != sol.t[end-1]
push!(ts,sol.t[end])
end
end
function forward_sensitivity_backpass(Δ)
dp = @thunk begin
chunk_size = if CS === 0 && length(p) < 12
length(p)
elseif CS !== 0
CS
else
12
end
num_chunks = length(p) ÷ chunk_size
num_chunks * chunk_size != length(p) && (num_chunks += 1)
pparts = typeof(p[1:1])[]
for j in 0:(num_chunks-1)
local chunk
if ((j+1)*chunk_size) <= length(p)
chunk = ((j*chunk_size+1) : ((j+1)*chunk_size))
pchunk = vec(p)[chunk]
pdualpart = seed_duals(pchunk,prob.f,ForwardDiff.Chunk{chunk_size}())
else
chunk = ((j*chunk_size+1) : length(p))
pchunk = vec(p)[chunk]
pdualpart = seed_duals(pchunk,prob.f,ForwardDiff.Chunk{length(chunk)}())
end
pdualvec = if j == 0
vcat(pdualpart,p[(j+1)*chunk_size+1 : end])
elseif j == num_chunks-1
vcat(p[1:j*chunk_size],pdualpart)
else
vcat(p[1:j*chunk_size],pdualpart,p[((j+1)*chunk_size)+1 : end])
end
pdual = ArrayInterfaceCore.restructure(p,pdualvec)
u0dual = convert.(eltype(pdualvec),u0)
if (convert_tspan(sensealg) === nothing && (
(haskey(kwargs,:callback) && has_continuous_callback(kwargs[:callback])))) ||
(convert_tspan(sensealg) !== nothing && convert_tspan(sensealg))
tspandual = convert.(eltype(pdual),prob.tspan)
else
tspandual = prob.tspan
end
if typeof(prob.f) <: ODEFunction && prob.f.jac_prototype !== nothing
_f = ODEFunction{SciMLBase.isinplace(prob.f),true}(prob.f,jac_prototype = convert.(eltype(u0dual),prob.f.jac_prototype))
elseif typeof(prob.f) <: SDEFunction && prob.f.jac_prototype !== nothing
_f = SDEFunction{SciMLBase.isinplace(prob.f),true}(prob.f,jac_prototype = convert.(eltype(u0dual),prob.f.jac_prototype))
else
_f = prob.f
end
_prob = remake(prob,f=_f,u0=u0dual,p=pdual,tspan=tspandual)
if _prob isa SDEProblem
_prob.noise_rate_prototype!==nothing && (_prob = remake(_prob, noise_rate_prototype = convert.(eltype(pdual), _prob.noise_rate_prototype)))
end
if saveat isa Number
_saveat = prob.tspan[1]:saveat:prob.tspan[2]
else
_saveat = saveat
end
_sol = solve(_prob,alg,args...;saveat=ts, kwargs...)
_,du = extract_local_sensitivities(_sol, sensealg, Val(true))
_dp = sum(eachindex(du)) do i
J = du[i]
if Δ isa AbstractVector || Δ isa DESolution || Δ isa AbstractVectorOfArray
v = Δ[i]
elseif Δ isa AbstractMatrix
v = @view Δ[:, i]
else
v = @view Δ[.., i]
end
if !(Δ isa NoTangent)
ForwardDiff.value.(J'vec(v))
else
zero(p)
end
end
push!(pparts,vec(_dp))
end
ArrayInterfaceCore.restructure(p,reduce(vcat,pparts))
end
du0 = @thunk begin
chunk_size = if CS === 0 && length(u0) < 12
length(u0)
elseif CS !== 0
CS
else
12
end
num_chunks = length(u0) ÷ chunk_size
num_chunks * chunk_size != length(u0) && (num_chunks += 1)
du0parts = typeof(u0[1:1])[]
for j in 0:(num_chunks-1)
local chunk
if ((j+1)*chunk_size) <= length(u0)
chunk = ((j*chunk_size+1) : ((j+1)*chunk_size))
u0chunk = vec(u0)[chunk]
u0dualpart = seed_duals(u0chunk,prob.f,ForwardDiff.Chunk{chunk_size}())
else
chunk = ((j*chunk_size+1) : length(u0))
u0chunk = vec(u0)[chunk]
u0dualpart = seed_duals(u0chunk,prob.f,ForwardDiff.Chunk{length(chunk)}())
end
u0dualvec = if j == 0
vcat(u0dualpart,u0[(j+1)*chunk_size+1 : end])
elseif j == num_chunks-1
vcat(u0[1:j*chunk_size],u0dualpart)
else
vcat(u0[1:j*chunk_size],u0dualpart,u0[((j+1)*chunk_size)+1 : end])
end
u0dual = ArrayInterfaceCore.restructure(u0,u0dualvec)
pdual = convert.(eltype(u0dual),p)
if (convert_tspan(sensealg) === nothing && (
(haskey(kwargs,:callback) && has_continuous_callback(kwargs[:callback])))) ||
(convert_tspan(sensealg) !== nothing && convert_tspan(sensealg))
tspandual = convert.(eltype(pdual),prob.tspan)
else
tspandual = prob.tspan
end
if typeof(prob.f) <: ODEFunction && prob.f.jac_prototype !== nothing
_f = ODEFunction{SciMLBase.isinplace(prob.f),true}(prob.f,jac_prototype = convert.(eltype(pdual),prob.f.jac_prototype))
elseif typeof(prob.f) <: SDEFunction && prob.f.jac_prototype !== nothing
_f = SDEFunction{SciMLBase.isinplace(prob.f),true}(prob.f,jac_prototype = convert.(eltype(pdual),prob.f.jac_prototype))
else
_f = prob.f
end
_prob = remake(prob,f=_f,u0=u0dual,p=pdual,tspan=tspandual)
if _prob isa SDEProblem
_prob.noise_rate_prototype!==nothing && (_prob = remake(_prob, noise_rate_prototype = convert.(eltype(pdual), _prob.noise_rate_prototype)))
end
if saveat isa Number
_saveat = prob.tspan[1]:saveat:prob.tspan[2]
else
_saveat = saveat
end
_sol = solve(_prob,alg,args...;saveat=ts, kwargs...)
_,du = extract_local_sensitivities(_sol, sensealg, Val(true))
_du0 = sum(eachindex(du)) do i
J = du[i]
if Δ isa AbstractVector || Δ isa DESolution || Δ isa AbstractVectorOfArray
v = Δ[i]
elseif Δ isa AbstractMatrix
v = @view Δ[:, i]
else
v = @view Δ[.., i]
end
if !(Δ isa NoTangent)
ForwardDiff.value.(J'vec(v))
else
zero(u0)
end
end
push!(du0parts,vec(_du0))
end
ArrayInterfaceCore.restructure(u0,reduce(vcat,du0parts))
end
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(),NoTangent(),unthunk(du0),unthunk(dp),NoTangent(),ntuple(_->NoTangent(), length(args))...)
else
(NoTangent(),NoTangent(),NoTangent(),du0,dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
end
end
sol,forward_sensitivity_backpass
end
function DiffEqBase._concrete_solve_adjoint(prob,alg,sensealg::ZygoteAdjoint,
u0,p,originator::SciMLBase.ADOriginator,args...;kwargs...)
Zygote.pullback((u0,p)->solve(prob,alg,args...;u0=u0,p=p,
sensealg = SensitivityADPassThrough(),kwargs...),u0,p)
end
function DiffEqBase._concrete_solve_adjoint(prob,alg,sensealg::TrackerAdjoint,
u0,p,originator::SciMLBase.ADOriginator,args...;
kwargs...)
local sol
function tracker_adjoint_forwardpass(_u0,_p)
if (convert_tspan(sensealg) === nothing && (
(haskey(kwargs,:callback) && has_continuous_callback(kwargs[:callback])))) ||
(convert_tspan(sensealg) !== nothing && convert_tspan(sensealg))
_tspan = convert.(eltype(_p),prob.tspan)
else
_tspan = prob.tspan
end
if DiffEqBase.isinplace(prob)
# use Array{TrackedReal} for mutation to work
# Recurse to all Array{TrackedArray}
_prob = remake(prob,u0=map(identity,_u0),p=_p,tspan=_tspan)
else
# use TrackedArray for efficiency of the tape
if typeof(prob) <: Union{SciMLBase.AbstractDDEProblem,SciMLBase.AbstractDAEProblem,SciMLBase.AbstractSDDEProblem}
_f = function (u,p,h,t) # For DDE, but also works for (du,u,p,t) DAE
out = prob.f(u,p,h,t)
if out isa TrackedArray
return out
else
Tracker.collect(out)
end
end
# Only define `g` for the stochastic ones
if typeof(prob) <: SciMLBase.AbstractSDEProblem
_g = function (u,p,h,t)
out = prob.g(u,p,h,t)
if out isa TrackedArray
return out
else
Tracker.collect(out)
end
end
_prob = remake(prob,f=DiffEqBase.parameterless_type(prob.f){false,true}(_f,_g),u0=_u0,p=_p,tspan=_tspan)
else
_prob = remake(prob,f=DiffEqBase.parameterless_type(prob.f){false,true}(_f),u0=_u0,p=_p,tspan=_tspan)
end
elseif typeof(prob) <: Union{SciMLBase.AbstractODEProblem,SciMLBase.AbstractSDEProblem}
_f = function (u,p,t)
out = prob.f(u,p,t)
if out isa TrackedArray
return out
else
Tracker.collect(out)
end
end
if typeof(prob) <: SciMLBase.AbstractSDEProblem
_g = function (u,p,t)
out = prob.g(u,p,t)
if out isa TrackedArray
return out
else
Tracker.collect(out)
end
end
_prob = remake(prob,f=DiffEqBase.parameterless_type(prob.f){false,true}(_f,_g),u0=_u0,p=_p,tspan=_tspan)
else
_prob = remake(prob,f=DiffEqBase.parameterless_type(prob.f){false,true}(_f),u0=_u0,p=_p,tspan=_tspan)
end
else
error("TrackerAdjont does not currently support the specified problem type. Please open an issue.")
end
end
sol = solve(_prob,alg,args...;sensealg=DiffEqBase.SensitivityADPassThrough(),kwargs...)
if typeof(sol.u[1]) <: Array
return Array(sol)
else
tmp = vec(sol.u[1])
for i in 2:length(sol.u)
tmp = hcat(tmp,vec(sol.u[i]))
end
return reshape(tmp,size(sol.u[1])...,length(sol.u))
end
#adapt(typeof(u0),arr)
sol
end
out,pullback = Tracker.forward(tracker_adjoint_forwardpass,u0,p)
function tracker_adjoint_backpass(ybar)
tmp = if eltype(ybar) <: Number && typeof(u0) <: Array
Array(ybar)
elseif eltype(ybar) <: Number # CuArray{Floats}
ybar
elseif typeof(ybar[1]) <: Array
return Array(ybar)
else
tmp = vec(ybar.u[1])
for i in 2:length(ybar.u)
tmp = hcat(tmp,vec(ybar.u[i]))
end
return reshape(tmp,size(ybar.u[1])...,length(ybar.u))
end
u0bar, pbar = pullback(tmp)
_u0bar = u0bar isa Tracker.TrackedArray ? Tracker.data(u0bar) : Tracker.data.(u0bar)
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(),NoTangent(),_u0bar,Tracker.data(pbar),NoTangent(),ntuple(_->NoTangent(), length(args))...)
else
(NoTangent(),NoTangent(),NoTangent(),_u0bar,Tracker.data(pbar),NoTangent(),ntuple(_->NoTangent(), length(args))...)
end
end
u = u0 isa Tracker.TrackedArray ? Tracker.data.(sol.u) : Tracker.data.(Tracker.data.(sol.u))
DiffEqBase.sensitivity_solution(sol,u,Tracker.data.(sol.t)),tracker_adjoint_backpass
end
const REVERSEDIFF_ADJOINT_GPU_COMPATABILITY_MESSAGE =
"""
ReverseDiffAdjoint is not compatible GPU-based array types. Use a different
sensitivity analysis method, like InterpolatingAdjoint or TrackerAdjoint,
in order to combine with GPUs.
"""
struct ReverseDiffGPUStateCompatibilityError <: Exception end
function Base.showerror(io::IO, e::ReverseDiffGPUStateCompatibilityError)
print(io, FORWARDDIFF_SENSITIVITY_PARAMETER_COMPATABILITY_MESSAGE)
end
function DiffEqBase._concrete_solve_adjoint(prob,alg,sensealg::ReverseDiffAdjoint,
u0,p,originator::SciMLBase.ADOriginator,args...;kwargs...)
if typeof(u0) isa GPUArrays.AbstractGPUArray
throw(ReverseDiffGPUStateCompatibilityError())
end
t = eltype(prob.tspan)[]
u = typeof(u0)[]
local sol
function reversediff_adjoint_forwardpass(_u0,_p)
if (convert_tspan(sensealg) === nothing && (
(haskey(kwargs,:callback) && has_continuous_callback(kwargs[:callback])))) ||
(convert_tspan(sensealg) !== nothing && convert_tspan(sensealg))
_tspan = convert.(eltype(_p),prob.tspan)
else
_tspan = prob.tspan
end
if DiffEqBase.isinplace(prob)
# use Array{TrackedReal} for mutation to work
# Recurse to all Array{TrackedArray}
_prob = remake(prob,u0=reshape([x for x in _u0],size(_u0)),p=_p,tspan=_tspan)
else
# use TrackedArray for efficiency of the tape
_f(args...) = reduce(vcat,prob.f(args...))
if prob isa SDEProblem
_g(args...) = reduce(vcat,prob.g(args...))
_prob = remake(prob,f=DiffEqBase.parameterless_type(prob.f){SciMLBase.isinplace(prob),true}(_f,_g),u0=_u0,p=_p,tspan=_tspan)
else
_prob = remake(prob,f=DiffEqBase.parameterless_type(prob.f){SciMLBase.isinplace(prob),true}(_f),u0=_u0,p=_p,tspan=_tspan)
end
end
sol = solve(_prob,alg,args...;sensealg=DiffEqBase.SensitivityADPassThrough(),kwargs...)
t = sol.t
if DiffEqBase.isinplace(prob)
u = map.(ReverseDiff.value,sol.u)
else
u = map(ReverseDiff.value,sol.u)
end
Array(sol)
end
tape = ReverseDiff.GradientTape(reversediff_adjoint_forwardpass,(u0, p))
tu, tp = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.value!(tu, u0)
typeof(p) <: DiffEqBase.NullParameters || ReverseDiff.value!(tp, p)
ReverseDiff.forward_pass!(tape)
function reversediff_adjoint_backpass(ybar)
_ybar = if ybar isa VectorOfArray
Array(ybar)
elseif eltype(ybar) <: AbstractArray
Array(VectorOfArray(ybar))
else
ybar
end
ReverseDiff.increment_deriv!(output, _ybar)
ReverseDiff.reverse_pass!(tape)
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(),NoTangent(),ReverseDiff.deriv(tu),ReverseDiff.deriv(tp),NoTangent(),ntuple(_->NoTangent(), length(args))...)
else
(NoTangent(),NoTangent(),NoTangent(),ReverseDiff.deriv(tu),ReverseDiff.deriv(tp),NoTangent(),ntuple(_->NoTangent(), length(args))...)
end
end
Array(VectorOfArray(u)),reversediff_adjoint_backpass
end
function DiffEqBase._concrete_solve_adjoint(prob,alg,
sensealg::AbstractShadowingSensitivityAlgorithm,
u0,p,originator::SciMLBase.ADOriginator,args...;save_start=true,save_end=true,
saveat = eltype(prob.tspan)[],
save_idxs = nothing,
kwargs...)
if haskey(kwargs, :callback)
error("Sensitivity analysis based on Least Squares Shadowing is not compatible with callbacks. Please select another `sensealg`.")
else
_prob = remake(prob,u0=u0,p=p)
end
sol = solve(_prob,alg,args...;save_start=save_start,save_end=save_end,saveat=saveat,kwargs...)
if saveat isa Number
if _prob.tspan[2] > _prob.tspan[1]
ts = _prob.tspan[1]:convert(typeof(_prob.tspan[2]),abs(saveat)):_prob.tspan[2]
else
ts = _prob.tspan[2]:convert(typeof(_prob.tspan[2]),abs(saveat)):_prob.tspan[1]
end
_out = sol(ts)
out = if save_idxs === nothing
out = DiffEqBase.sensitivity_solution(sol,_out.u,sol.t)
else
out = DiffEqBase.sensitivity_solution(sol,[_out[i][save_idxs] for i in 1:length(_out)],ts)
end
# only_end
(length(ts) == 1 && ts[1] == _prob.tspan[2]) && error("Sensitivity analysis based on Least Squares Shadowing requires a long-time averaged quantity.")
elseif isempty(saveat)
no_start = !save_start
no_end = !save_end
sol_idxs = 1:length(sol)
no_start && (sol_idxs = sol_idxs[2:end])
no_end && (sol_idxs = sol_idxs[1:end-1])
only_end = length(sol_idxs) <= 1
_u = sol.u[sol_idxs]
u = save_idxs === nothing ? _u : [x[save_idxs] for x in _u]
ts = sol.t[sol_idxs]
out = DiffEqBase.sensitivity_solution(sol,u,ts)
else
_saveat = saveat isa Array ? sort(saveat) : saveat # for minibatching
ts = _saveat
_out = sol(ts)
out = if save_idxs === nothing
out = DiffEqBase.sensitivity_solution(sol,_out.u,ts)
else
out = DiffEqBase.sensitivity_solution(sol,[_out[i][save_idxs] for i in 1:length(_out)],ts)
end
# only_end
(length(ts) == 1 && ts[1] == _prob.tspan[2]) && error("Sensitivity analysis based on Least Squares Shadowing requires a long-time averaged quantity.")
end
_save_idxs = save_idxs === nothing ? Colon() : save_idxs
function adjoint_sensitivity_backpass(Δ)
function df(_out, u, p, t, i)
if typeof(Δ) <: AbstractArray{<:AbstractArray} || typeof(Δ) <: DESolution
if typeof(_save_idxs) <: Number
_out[_save_idxs] = -Δ[i][_save_idxs]
elseif _save_idxs isa Colon
vec(_out) .= -vec(Δ[i])
else
vec(@view(_out[_save_idxs])) .= -vec(Δ[i][_save_idxs])
end
else
if typeof(_save_idxs) <: Number
_out[_save_idxs] = -adapt(DiffEqBase.parameterless_type(u0),reshape(Δ, prod(size(Δ)[1:end-1]), size(Δ)[end])[_save_idxs, i])
elseif _save_idxs isa Colon
vec(_out) .= -vec(adapt(DiffEqBase.parameterless_type(u0),reshape(Δ, prod(size(Δ)[1:end-1]), size(Δ)[end])[:, i]))
else
vec(@view(_out[_save_idxs])) .= -vec(adapt(DiffEqBase.parameterless_type(u0),reshape(Δ, prod(size(Δ)[1:end-1]), size(Δ)[end])[:, i]))
end
end
end
if sensealg isa ForwardLSS
lss_problem = ForwardLSSProblem(sol, sensealg, ts, df)
dp = shadow_forward(lss_problem)
elseif sensealg isa AdjointLSS
adjointlss_problem = AdjointLSSProblem(sol, sensealg, ts, df)
dp = shadow_adjoint(adjointlss_problem)
elseif sensealg isa NILSS
nilss_prob = NILSSProblem(_prob, sensealg, ts, df)
dp = shadow_forward(nilss_prob,alg)
elseif sensealg isa NILSAS
nilsas_prob = NILSASProblem(_prob, sensealg, ts, df)
dp = shadow_adjoint(nilsas_prob,alg)
else
error("No concrete_solve implementation found for sensealg `$sensealg`. Did you spell the sensitivity algorithm correctly? Please report this error.")
end
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(),NoTangent(),NoTangent(),dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
else
(NoTangent(),NoTangent(),NoTangent(),NoTangent(),dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
end
end
out, adjoint_sensitivity_backpass
end
function DiffEqBase._concrete_solve_adjoint(prob::Union{NonlinearProblem,SteadyStateProblem},
alg,sensealg::SteadyStateAdjoint,
u0,p,originator::SciMLBase.ADOriginator,args...;save_idxs = nothing, kwargs...)
_prob = remake(prob,u0=u0,p=p)
sol = solve(_prob,alg,args...;kwargs...)
_save_idxs = save_idxs === nothing ? Colon() : save_idxs
if save_idxs === nothing
out = sol
else
out = DiffEqBase.sensitivity_solution(sol,sol[_save_idxs])
end
function steadystatebackpass(Δ)
# Δ = dg/dx or diffcache.dg_val
# del g/del p = 0
dp = adjoint_sensitivities(sol,alg;sensealg=sensealg,g=nothing,dg=Δ,save_idxs=save_idxs)
if originator isa SciMLBase.TrackerOriginator || originator isa SciMLBase.ReverseDiffOriginator
(NoTangent(),NoTangent(),NoTangent(),dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
else
(NoTangent(),NoTangent(),NoTangent(),NoTangent(),dp,NoTangent(),ntuple(_->NoTangent(), length(args))...)
end
end
out, steadystatebackpass
end
function fix_endpoints(sensealg,sol,ts)
@warn "Endpoints do not match. Return code: $(sol.retcode). Likely your time range is not a multiple of `saveat`. sol.t[end]: $(sol.t[end]), ts[end]: $(ts[end])"
ts = collect(ts)
push!(ts, sol.t[end])
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 22061 | # Not in FiniteDiff because `u` -> scalar isn't used anywhere else,
# but could be upstreamed.
mutable struct UGradientWrapper{fType,tType,P} <: Function
f::fType
t::tType
p::P
end
(ff::UGradientWrapper)(uprev) = ff.f(uprev,ff.p,ff.t)
mutable struct ParamGradientWrapper{fType,tType,uType} <: Function
f::fType
t::tType
u::uType
end
(ff::ParamGradientWrapper)(p) = ff.f(ff.u,p,ff.t)
# the next four definitions are only needed in case of non-diagonal SDEs
mutable struct ParamNonDiagNoiseGradientWrapper{fType,tType,uType} <: Function
f::fType
t::tType
u::uType
end
(ff::ParamNonDiagNoiseGradientWrapper)(p) = vec(ff.f(ff.u,p,ff.t))
mutable struct ParamNonDiagNoiseJacobianWrapper{fType,tType,uType,duType} <: Function
f::fType
t::tType
u::uType
du::duType
end
function (ff::ParamNonDiagNoiseJacobianWrapper)(p)
du1 = similar(p, size(ff.du))
ff.f(du1,ff.u,p,ff.t)
return vec(du1)
end
function (ff::ParamNonDiagNoiseJacobianWrapper)(du1,p)
ff.f(du1,ff.u,p,ff.t)
return vec(du1)
end
mutable struct UNonDiagNoiseGradientWrapper{fType,tType,P} <: Function
f::fType
t::tType
p::P
end
(ff::UNonDiagNoiseGradientWrapper)(uprev) = vec(ff.f(uprev,ff.p,ff.t))
mutable struct UNonDiagNoiseJacobianWrapper{fType,tType,P,duType} <: Function
f::fType
t::tType
p::P
du::duType
end
(ff::UNonDiagNoiseJacobianWrapper)(uprev) = (du1 = similar(ff.du); ff.f(du1,uprev,ff.p,ff.t); vec(du1))
function (ff::UNonDiagNoiseJacobianWrapper)(du1,uprev)
ff.f(du1,uprev,ff.p,ff.t)
return vec(du1)
end
# RODE wrappers
mutable struct RODEUJacobianWrapper{fType,tType,P,WType} <: Function
f::fType
t::tType
p::P
W::WType
end
(ff::RODEUJacobianWrapper)(du1,uprev) = ff.f(du1,uprev,ff.p,ff.t,ff.W)
(ff::RODEUJacobianWrapper)(uprev) = (du1 = similar(uprev); ff.f(du1,uprev,ff.p,ff.t,ff.W); du1)
mutable struct RODEUDerivativeWrapper{F,tType,P,WType} <: Function
f::F
t::tType
p::P
W::WType
end
(ff::RODEUDerivativeWrapper)(u) = ff.f(u,ff.p,ff.t,ff.W)
mutable struct RODEUGradientWrapper{fType,tType,P,WType} <: Function
f::fType
t::tType
p::P
W::WType
end
(ff::RODEUGradientWrapper)(uprev) = ff.f(uprev,ff.p,ff.t,ff.W)
mutable struct RODEParamGradientWrapper{fType,tType,uType,WType} <: Function
f::fType
t::tType
u::uType
W::WType
end
(ff::RODEParamGradientWrapper)(p) = ff.f(ff.u,p,ff.t,ff.W)
mutable struct RODEParamJacobianWrapper{fType,tType,uType,WType} <: Function
f::fType
t::tType
u::uType
W::WType
end
(ff::RODEParamJacobianWrapper)(du1,p) = ff.f(du1,ff.u,p,ff.t,ff.W)
function (ff::RODEParamJacobianWrapper)(p)
du1 = similar(p, size(ff.u))
ff.f(du1,ff.u,p,ff.t,ff.W)
return du1
end
Base.@pure function determine_chunksize(u,alg::DiffEqBase.AbstractSensitivityAlgorithm)
determine_chunksize(u,get_chunksize(alg))
end
Base.@pure function determine_chunksize(u,CS)
if CS != 0
return CS
else
return ForwardDiff.pickchunksize(length(u))
end
end
function jacobian(f, x::AbstractArray{<:Number}, alg::DiffEqBase.AbstractSensitivityAlgorithm)
if alg_autodiff(alg)
J = ForwardDiff.jacobian(f, x)
else
J = FiniteDiff.finite_difference_jacobian(f, x)
end
return J
end
function jacobian!(J::AbstractMatrix{<:Number}, f, x::AbstractArray{<:Number},
fx::Union{Nothing,AbstractArray{<:Number}}, alg::DiffEqBase.AbstractSensitivityAlgorithm, jac_config)
if alg_autodiff(alg)
if fx === nothing
ForwardDiff.jacobian!(J, f, x)
else
ForwardDiff.jacobian!(J, f, fx, x, jac_config)
end
else
FiniteDiff.finite_difference_jacobian!(J, f, x, jac_config)
end
nothing
end
function derivative!(df::AbstractArray{<:Number}, f,
x::Number,
alg::DiffEqBase.AbstractSensitivityAlgorithm, der_config)
if alg_autodiff(alg)
ForwardDiff.derivative!(df, f, x, ) # der_config doesn't work
else
FiniteDiff.finite_difference_derivative!(df, f, x, der_config)
end
nothing
end
function gradient!(df::AbstractArray{<:Number}, f,
x::Union{Number,AbstractArray{<:Number}},
alg::DiffEqBase.AbstractSensitivityAlgorithm, grad_config)
if alg_autodiff(alg)
ForwardDiff.gradient!(df, f, x, grad_config)
else
FiniteDiff.finite_difference_gradient!(df, f, x, grad_config)
end
nothing
end
"""
jacobianvec!(Jv, f, x, v, alg, (buffer, seed)) -> nothing
``Jv <- J(f(x))v``
"""
function jacobianvec!(Jv::AbstractArray{<:Number}, f, x::AbstractArray{<:Number},
v, alg::DiffEqBase.AbstractSensitivityAlgorithm, config)
if alg_autodiff(alg)
buffer, seed = config
TD = typeof(first(seed))
T = typeof(first(seed).partials)
DiffEqBase.@.. seed = TD(x, T(tuple(v)))
f(buffer, seed)
Jv .= ForwardDiff.partials.(buffer, 1)
else
buffer1, buffer2 = config
f(buffer1,x)
T = eltype(x)
# Should it be min? max? mean?
ϵ = sqrt(eps(real(T))) * max(one(real(T)), abs(norm(x)))
@. x += ϵ*v
f(buffer2,x)
@. x -= ϵ*v
@. Jv = (buffer2 - buffer1)/ϵ
end
nothing
end
function jacobianmat!(JM::AbstractMatrix{<:Number}, f, x::AbstractArray{<:Number},
M, alg::DiffEqBase.AbstractSensitivityAlgorithm, config)
buffer, seed = config
T = eltype(seed)
numparams = length(ForwardDiff.partials(seed[1]))
for i in eachindex(seed)
seed[i] = T(x[i],ForwardDiff.Partials(ntuple(j -> M[i,j], numparams)))
end
f(buffer,seed)
for (j,dual) in enumerate(buffer)
for (i,partial) in enumerate(ForwardDiff.partials(dual))
JM[j,i] = partial
end
end
return nothing
end
function vecjacobian!(dλ, y, λ, p, t, S::TS;
dgrad=nothing, dy=nothing, W=nothing) where TS<:SensitivityFunction
_vecjacobian!(dλ, y, λ, p, t, S, S.sensealg.autojacvec, dgrad, dy, W)
return
end
function _vecjacobian!(dλ, y, λ, p, t, S::TS, isautojacvec::Bool, dgrad, dy, W) where TS<:SensitivityFunction
@unpack sensealg, f = S
prob = getprob(S)
@unpack J, uf, f_cache, jac_config = S.diffcache
if !(prob isa DiffEqBase.SteadyStateProblem)
if W===nothing
if DiffEqBase.has_jac(f)
f.jac(J,y,p,t) # Calculate the Jacobian into J
else
uf.t = t
uf.p = p
jacobian!(J, uf, y, f_cache, sensealg, jac_config)
end
else
if DiffEqBase.has_jac(f)
f.jac(J,y,p,t,W) # Calculate the Jacobian into J
else
uf.t = t
uf.p = p
uf.W = W
jacobian!(J, uf, y, f_cache, sensealg, jac_config)
end
end
mul!(dλ',λ',J)
end
if dgrad !== nothing
@unpack pJ, pf, paramjac_config = S.diffcache
if W===nothing
if DiffEqBase.has_paramjac(f)
# Calculate the parameter Jacobian into pJ
f.paramjac(pJ,y,p,t)
else
pf.t = t
pf.u = y
if inplace_sensitivity(S)
jacobian!(pJ, pf, p, f_cache, sensealg, paramjac_config)
else
temp = jacobian(pf, p, sensealg)
pJ .= temp
end
end
else
if DiffEqBase.has_paramjac(f)
# Calculate the parameter Jacobian into pJ
f.paramjac(pJ,y,p,t,W)
else
pf.t = t
pf.u = y
pf.W = W
if inplace_sensitivity(S)
jacobian!(pJ, pf, p, f_cache, sensealg, paramjac_config)
else
temp = jacobian(pf, p, sensealg)
pJ .= temp
end
end
end
mul!(dgrad',λ',pJ)
end
if dy !== nothing
if W===nothing
if inplace_sensitivity(S)
f(dy, y, p, t)
else
dy[:] .= vec(f(y, p, t))
end
else
if inplace_sensitivity(S)
f(dy, y, p, t, W)
else
dy[:] .= vec(f(y, p, t, W))
end
end
end
return
end
function _vecjacobian!(dλ, y, λ, p, t, S::TS, isautojacvec::TrackerVJP, dgrad, dy, W) where TS<:SensitivityFunction
@unpack sensealg, f = S
isautojacvec = get_jacvec(sensealg)
if inplace_sensitivity(S)
if W===nothing
_dy, back = Tracker.forward(y, p) do u, p
out_ = map(zero, u)
f(out_, u, p, t)
Tracker.collect(out_)
end
else
_dy, back = Tracker.forward(y, p) do u, p
out_ = map(zero, u)
f(out_, u, p, t, W)
Tracker.collect(out_)
end
end
tmp1, tmp2 = Tracker.data.(back(λ))
dλ[:] .= vec(tmp1)
dgrad !== nothing && (dgrad[:] .= vec(tmp2))
dy !== nothing && (dy[:] .= vec(Tracker.data(_dy)))
else
if W===nothing
_dy, back = Tracker.forward(y, p) do u, p
Tracker.collect(f(u, p, t))
end
else
_dy, back = Tracker.forward(y, p) do u, p
Tracker.collect(f(u, p, t, W))
end
end
tmp1, tmp2 = Tracker.data.(back(λ))
dλ[:] .= vec(tmp1)
dgrad !== nothing && (dgrad[:] .= vec(tmp2))
dy !== nothing && (dy[:] .= vec(Tracker.data(_dy)))
end
return
end
function _vecjacobian!(dλ, y, λ, p, t, S::TS, isautojacvec::ReverseDiffVJP, dgrad, dy, W) where TS<:SensitivityFunction
@unpack sensealg, f = S
prob = getprob(S)
isautojacvec = get_jacvec(sensealg)
if typeof(p) <: DiffEqBase.NullParameters
_p = similar(y,(0,))
else
_p = p
end
if typeof(prob) <: SteadyStateProblem || (eltype(λ) <: eltype(prob.u0) && typeof(t) <: eltype(prob.u0) && compile_tape(sensealg.autojacvec))
tape = S.diffcache.paramjac_config
## These other cases happen due to autodiff in stiff ODE solvers
elseif inplace_sensitivity(S)
_y = eltype(y) === eltype(λ) ? y : convert.(promote_type(eltype(y),eltype(λ)),y)
if W===nothing
tape = ReverseDiff.GradientTape((_y, _p, [t])) do u,p,t
du1 = similar(u, size(u))
f(du1,u,p,first(t))
return vec(du1)
end
else
_W = eltype(W) === eltype(λ) ? W : convert.(promote_type(eltype(W),eltype(λ)),W)
tape = ReverseDiff.GradientTape((_y, _p, [t], _W)) do u,p,t,Wloc
du1 = p !== nothing && p !== DiffEqBase.NullParameters() ? similar(p, size(u)) : similar(u)
f(du1,u,p,first(t),Wloc)
return vec(du1)
end
end
else
_y = eltype(y) === eltype(λ) ? y : convert.(promote_type(eltype(y),eltype(λ)),y)
if W===nothing
tape = ReverseDiff.GradientTape((_y, _p, [t])) do u,p,t
vec(f(u,p,first(t)))
end
else
_W = eltype(W) === eltype(λ) ? W : convert.(promote_type(eltype(W),eltype(λ)),W)
tape = ReverseDiff.GradientTape((_y, _p, [t], _W)) do u,p,t,Wloc
vec(f(u,p,first(t),Wloc))
end
end
end
if prob isa DiffEqBase.SteadyStateProblem
tu, tp = ReverseDiff.input_hook(tape)
else
if W===nothing
tu, tp, tt = ReverseDiff.input_hook(tape)
else
tu, tp, tt, tW = ReverseDiff.input_hook(tape)
end
end
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
if !(prob isa DiffEqBase.SteadyStateProblem)
ReverseDiff.unseed!(tt)
end
W !== nothing && ReverseDiff.unseed!(tW)
ReverseDiff.value!(tu, y)
typeof(p) <: DiffEqBase.NullParameters || ReverseDiff.value!(tp, p)
if !(prob isa DiffEqBase.SteadyStateProblem)
ReverseDiff.value!(tt, [t])
end
W !== nothing && ReverseDiff.value!(tW, W)
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
copyto!(vec(dλ), ReverseDiff.deriv(tu))
dgrad !== nothing && copyto!(vec(dgrad), ReverseDiff.deriv(tp))
ReverseDiff.pull_value!(output)
dy !== nothing && copyto!(vec(dy), ReverseDiff.value(output))
return
end
function _vecjacobian!(dλ, y, λ, p, t, S::TS, isautojacvec::ZygoteVJP, dgrad, dy, W) where TS<:SensitivityFunction
@unpack sensealg, f = S
prob = getprob(S)
isautojacvec = get_jacvec(sensealg)
if inplace_sensitivity(S)
if W===nothing
_dy, back = Zygote.pullback(y, p) do u, p
out_ = Zygote.Buffer(similar(u))
f(out_, u, p, t)
vec(copy(out_))
end
else
_dy, back = Zygote.pullback(y, p) do u, p
out_ = Zygote.Buffer(similar(u))
f(out_, u, p, t, W)
vec(copy(out_))
end
end
tmp1,tmp2 = back(λ)
dλ[:] .= vec(tmp1)
dgrad !== nothing && tmp2 !== nothing && (dgrad[:] .= vec(tmp2))
dy !== nothing && (dy[:] .= vec(_dy))
else
if W===nothing
_dy, back = Zygote.pullback(y, p) do u, p
vec(f(u, p, t))
end
else
_dy, back = Zygote.pullback(y, p) do u, p
vec(f(u, p, t, W))
end
end
tmp1, tmp2 = back(λ)
tmp1 !== nothing && (dλ[:] .= vec(tmp1))
dy !== nothing && (dy[:] .= vec(_dy))
dgrad !== nothing && tmp2 !== nothing && (dgrad[:] .= vec(tmp2))
end
return
end
function _vecjacobian!(dλ, y, λ, p, t, S::TS, isautojacvec::EnzymeVJP, dgrad, dy, W) where TS<:SensitivityFunction
@unpack sensealg = S
f = S.f.f
prob = getprob(S)
tmp1,tmp2,tmp3,tmp4 = S.diffcache.paramjac_config
tmp1 .= 0 # should be removed for dλ
#if dgrad !== nothing
# tmp2 = dgrad
#else
dup = if !(typeof(tmp2) <: DiffEqBase.NullParameters)
tmp2 .= 0
Enzyme.Duplicated(p, tmp2)
else
p
end
#end
#if dy !== nothing
# tmp3 = dy
#else
tmp3 .= 0
#end
vec(tmp4) .= vec(λ)
isautojacvec = get_jacvec(sensealg)
if inplace_sensitivity(S)
if W===nothing
Enzyme.autodiff(S.diffcache.pf,Enzyme.Duplicated(tmp3, tmp4),
Enzyme.Duplicated(y, tmp1),
dup,
t)
else
Enzyme.autodiff(S.diffcache.pf,Enzyme.Duplicated(tmp3, tmp4),
Enzyme.Duplicated(y, tmp1),
dup,
t,W)
end
dλ .= tmp1
dgrad !== nothing && (dgrad[:] .= vec(tmp2))
dy !== nothing && (dy .= tmp3)
else
if W===nothing
Enzyme.autodiff(S.diffcache.pf,Enzyme.Duplicated(tmp3, tmp4),
Enzyme.Duplicated(y, tmp1),
dup,t)
else
Enzyme.autodiff(S.diffcache.pf,Enzyme.Duplicated(tmp3, tmp4),
Enzyme.Duplicated(y, tmp1),
dup,t,W)
end
if dy !== nothing
out_ = if W===nothing
f(y, p, t)
else
f(y, p, t, W)
end
dy[:] .= vec(out_)
end
dλ .= tmp1
dgrad !== nothing && !(typeof(tmp2) <: DiffEqBase.NullParameters) && (dgrad[:] .= vec(tmp2))
dy !== nothing && (dy .= tmp3)
end
return
end
function jacNoise!(λ, y, p, t, S::SensitivityFunction;
dgrad=nothing, dλ=nothing, dy=nothing)
_jacNoise!(λ, y, p, t, S, S.sensealg.autojacvec, dgrad, dλ, dy)
return
end
function _jacNoise!(λ, y, p, t, S::TS, isnoise::Bool, dgrad, dλ, dy) where TS<:SensitivityFunction
@unpack sensealg, f = S
prob = getprob(S)
if dgrad !== nothing
@unpack pJ, pf, f_cache, paramjac_noise_config = S.diffcache
if DiffEqBase.has_paramjac(f)
# Calculate the parameter Jacobian into pJ
f.paramjac(pJ,y,p,t)
else
pf.t = t
pf.u = y
if inplace_sensitivity(S)
jacobian!(pJ, pf, p, nothing, sensealg, nothing)
#jacobian!(pJ, pf, p, f_cache, sensealg, paramjac_noise_config)
else
temp = jacobian(pf, p, sensealg)
pJ .= temp
end
end
if StochasticDiffEq.is_diagonal_noise(prob)
pJt = transpose(λ).*transpose(pJ)
dgrad[:] .= vec(pJt)
else
m = size(prob.noise_rate_prototype)[2]
for i in 1:m
tmp = λ'*pJ[(i-1)*m+1:i*m,:]
dgrad[:,i] .= vec(tmp)
end
end
end
if dλ !== nothing && (isnoisemixing(sensealg) || !StochasticDiffEq.is_diagonal_noise(prob))
@unpack J, uf, f_cache, jac_noise_config = S.diffcache
if dy!== nothing
if inplace_sensitivity(S)
f(dy, y, p, t)
else
dy .= f(y, p, t)
end
end
if DiffEqBase.has_jac(f)
f.jac(J,y,p,t) # Calculate the Jacobian into J
else
if inplace_sensitivity(S)
if dy !== nothing
ForwardDiff.jacobian!(J,uf,dy,y)
else
if StochasticDiffEq.is_diagonal_noise(prob)
dy = similar(y)
else
dy = similar(prob.noise_rate_prototype)
f(dy, y, p, t)
ForwardDiff.jacobian!(J,uf,dy,y)
end
f(dy, y, p, t)
ForwardDiff.jacobian!(J,uf,dy,y)
end
else
tmp = ForwardDiff.jacobian(uf,y)
J .= tmp
end
# uf.t = t
# uf.p = p
# jacobian!(J, uf, y, nothing, sensealg, nothing)
end
if StochasticDiffEq.is_diagonal_noise(prob)
Jt = transpose(λ).*transpose(J)
dλ[:] .= vec(Jt)
else
for i in 1:m
tmp = λ'*J[(i-1)*m+1:i*m,:]
dλ[:,i] .= vec(tmp)
end
end
end
return
end
function _jacNoise!(λ, y, p, t, S::TS, isnoise::ReverseDiffVJP, dgrad, dλ, dy) where TS<:SensitivityFunction
@unpack sensealg, f = S
prob = getprob(S)
for (i, λi) in enumerate(λ)
tapei = S.diffcache.paramjac_noise_config[i]
tu, tp, tt = ReverseDiff.input_hook(tapei)
output = ReverseDiff.output_hook(tapei)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, y)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tapei)
if StochasticDiffEq.is_diagonal_noise(prob)
ReverseDiff.increment_deriv!(output, λi)
else
ReverseDiff.increment_deriv!(output, λ)
end
ReverseDiff.reverse_pass!(tapei)
deriv = ReverseDiff.deriv(tp)
dgrad[:,i] .= vec(deriv)
ReverseDiff.pull_value!(output)
if StochasticDiffEq.is_diagonal_noise(prob)
dλ !== nothing && (dλ[:,i] .= vec(ReverseDiff.deriv(tu)))
dy !== nothing && (dy[i] = ReverseDiff.value(output))
else
dλ !== nothing && (dλ[:,i] .= vec(ReverseDiff.deriv(tu)))
dy !== nothing && (dy[:,i] .= vec(ReverseDiff.value(output)))
end
end
return
end
function _jacNoise!(λ, y, p, t, S::TS, isnoise::ZygoteVJP, dgrad, dλ, dy) where TS<:SensitivityFunction
@unpack sensealg, f = S
prob = getprob(S)
if StochasticDiffEq.is_diagonal_noise(prob)
if inplace_sensitivity(S)
for (i, λi) in enumerate(λ)
_dy, back = Zygote.pullback(y, p) do u, p
out_ = Zygote.Buffer(similar(u))
f(out_, u, p, t)
copy(out_[i])
end
tmp1,tmp2 = back(λi) #issue: tmp2 = zeros(p)
dgrad[:,i] .= vec(tmp2)
dλ !== nothing && (dλ[:,i] .= vec(tmp1))
dy !== nothing && (dy[i] = _dy)
end
else
for (i, λi) in enumerate(λ)
_dy, back = Zygote.pullback(y, p) do u, p
f(u, p, t)[i]
end
tmp1,tmp2 = back(λi)
dgrad[:,i] .= vec(tmp2)
dλ !== nothing && (dλ[:,i] .= vec(tmp1))
dy !== nothing && (dy[i] = _dy)
end
end
else
if inplace_sensitivity(S)
for (i, λi) in enumerate(λ)
_dy, back = Zygote.pullback(y, p) do u, p
out_ = Zygote.Buffer(similar(prob.noise_rate_prototype))
f(out_, u, p, t)
copy(out_[:,i])
end
tmp1,tmp2 = back(λ)#issue with Zygote.Buffer
dgrad[:,i] .= vec(tmp2)
dλ !== nothing && (dλ[:,i] .= vec(tmp1))
dy !== nothing && (dy[:,i] .= vec(_dy))
end
else
for (i, λi) in enumerate(λ)
_dy, back = Zygote.pullback(y, p) do u, p
f(u, p, t)[:,i]
end
tmp1,tmp2 = back(λ)
dgrad[:,i] .= vec(tmp2)
if tmp1 === nothing
# if a column of the noise matrix is zero, Zygote returns nothing.
dλ !== nothing && (dλ[:,i] .= false)
else
dλ !== nothing && (dλ[:,i] .= vec(tmp1))
end
dy !== nothing && (dy[:,i] .= vec(_dy))
end
end
end
return
end
function accumulate_cost!(dλ, y, p, t, S::TS, dgrad=nothing) where TS<:SensitivityFunction
@unpack dg, dg_val, g, g_grad_config = S.diffcache
if dg !== nothing
if !(dg isa Tuple)
dg(dg_val,y,p,t)
dλ .+= vec(dg_val)
else
dg[1](dg_val[1],y,p,t)
dλ .+= vec(dg_val[1])
if dgrad !== nothing
dg[2](dg_val[2],y,p,t)
dgrad .-= vec(dg_val[2])
end
end
else
g.t = t
gradient!(dg_val, g, y, S.sensealg, g_grad_config)
dλ .+= vec(dg_val)
end
return nothing
end
function build_jac_config(alg,uf,u)
if alg_autodiff(alg)
jac_config = ForwardDiff.JacobianConfig(uf,u,u,
ForwardDiff.Chunk{determine_chunksize(u,alg)}())
else
if diff_type(alg) != Val{:complex}
jac_config = FiniteDiff.JacobianCache(similar(u),similar(u),
similar(u),diff_type(alg))
else
tmp = Complex{eltype(u)}.(u)
du1 = Complex{eltype(u)}.(du1)
jac_config = FiniteDiff.JacobianCache(tmp,du1,nothing,diff_type(alg))
end
end
jac_config
end
function build_param_jac_config(alg,pf,u,p)
if alg_autodiff(alg)
jac_config = ForwardDiff.JacobianConfig(pf,u,p,
ForwardDiff.Chunk{determine_chunksize(p,alg)}())
else
if diff_type(alg) != Val{:complex}
jac_config = FiniteDiff.JacobianCache(similar(p),similar(u),
similar(u),diff_type(alg))
else
tmp = Complex{eltype(p)}.(p)
du1 = Complex{eltype(u)}.(u)
jac_config = FiniteDiff.JacobianCache(tmp,du1,nothing,diff_type(alg))
end
end
jac_config
end
function build_grad_config(alg,tf,du1,t)
if alg_autodiff(alg)
grad_config = ForwardDiff.GradientConfig(tf,du1,
ForwardDiff.Chunk{determine_chunksize(du1,alg)}())
else
grad_config = FiniteDiff.GradientCache(du1,t,diff_type(alg))
end
grad_config
end
function build_deriv_config(alg,tf,du1,t)
if alg_autodiff(alg)
grad_config = ForwardDiff.DerivativeConfig(tf,du1,t)
else
grad_config = FiniteDiff.DerivativeCache(du1,t,diff_type(alg))
end
grad_config
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 23187 | """
ODEForwardSensitivityFunction{iip,F,A,Tt,OJ,J,JP,S,PJ,TW,TWt,UF,PF,JC,PJC,Alg,fc,JM,pJM,MM,CV} <: DiffEqBase.AbstractODEFunction{iip}
ODEForwardSensitivityFunction is an internal to the ODEForwardSensitivityProblem which extends the AbstractODEFunction
to be used in an ODEProblem, but defines the tools requires for calculating the extra differential equations associated
with the derivative terms.
ODEForwardSensitivityFunction is not intended to be part of the public API.
"""
struct ODEForwardSensitivityFunction{iip,F,A,Tt,OJ,J,JP,S,PJ,TW,TWt,UF,PF,JC,PJC,Alg,fc,JM,pJM,MM,CV} <: DiffEqBase.AbstractODEFunction{iip}
f::F
analytic::A
tgrad::Tt
original_jac::OJ
jac::J
jac_prototype::JP
sparsity::S
paramjac::PJ
Wfact::TW
Wfact_t::TWt
uf::UF
pf::PF
J::JM
pJ::pJM
jac_config::JC
paramjac_config::PJC
alg::Alg
numparams::Int
numindvar::Int
f_cache::fc
mass_matrix::MM
isautojacvec::Bool
isautojacmat::Bool
colorvec::CV
end
has_original_jac(S) = isdefined(S, :original_jac) && S.jac !== nothing
struct NILSSForwardSensitivityFunction{iip,sensefunType,senseType,MM} <: DiffEqBase.AbstractODEFunction{iip}
S::sensefunType
sensealg::senseType
nus::Int
mass_matrix::MM
end
function ODEForwardSensitivityFunction(f,analytic,tgrad,original_jac,jac,jac_prototype,sparsity,paramjac,Wfact,Wfact_t,uf,pf,u0,
jac_config,paramjac_config,alg,p,f_cache,mm,
isautojacvec,isautojacmat,colorvec,nus)
numparams = length(p)
numindvar = length(u0)
J = isautojacvec ? nothing : Matrix{eltype(u0)}(undef,numindvar,numindvar)
pJ = Matrix{eltype(u0)}(undef,numindvar,numparams) # number of funcs size
sensefun = ODEForwardSensitivityFunction{isinplace(f),typeof(f),typeof(analytic),
typeof(tgrad),typeof(original_jac),
typeof(jac),typeof(jac_prototype),typeof(sparsity),
typeof(paramjac),
typeof(Wfact),typeof(Wfact_t),typeof(uf),
typeof(pf),typeof(jac_config),
typeof(paramjac_config),typeof(alg),
typeof(f_cache),
typeof(J),typeof(pJ),typeof(mm),typeof(f.colorvec)}(
f,analytic,tgrad,original_jac,jac,jac_prototype,
sparsity,paramjac,Wfact,Wfact_t,uf,pf,J,pJ,
jac_config,paramjac_config,alg,
numparams,numindvar,f_cache,mm,isautojacvec,isautojacmat,colorvec,
)
if nus!==nothing
sensefun = NILSSForwardSensitivityFunction{isinplace(f), typeof(sensefun),
typeof(alg),typeof(mm)}(sensefun,alg,nus,mm)
end
return sensefun
end
function (S::ODEForwardSensitivityFunction)(du,u,p,t)
y = @view u[1:S.numindvar] # These are the independent variables
dy = @view du[1:S.numindvar]
S.f(dy,y,p,t) # Make the first part be the ODE
# Now do sensitivities
# Compute the Jacobian
if !S.isautojacvec && !S.isautojacmat
if has_original_jac(S)
S.original_jac(S.J,y,p,t) # Calculate the Jacobian into J
else
S.uf.t = t
jacobian!(S.J, S.uf, y, S.f_cache, S.alg, S.jac_config)
end
end
if DiffEqBase.has_paramjac(S.f)
S.paramjac(S.pJ,y,p,t) # Calculate the parameter Jacobian into pJ
else
S.pf.t = t
copyto!(S.pf.u,y)
jacobian!(S.pJ, S.pf, p, S.f_cache, S.alg, S.paramjac_config)
end
# Compute the parameter derivatives
if !S.isautojacvec && !S.isautojacmat
dp = @view du[reshape(S.numindvar+1:(length(p)+1)*S.numindvar,S.numindvar,length(p))]
Sj = @view u[reshape(S.numindvar+1:(length(p)+1)*S.numindvar,S.numindvar,length(p))]
mul!(dp,S.J,Sj)
DiffEqBase.@.. dp += S.pJ
elseif S.isautojacmat
S.uf.t = t
Sj = @view u[reshape(S.numindvar+1:end,S.numindvar,S.numparams)]
dp = @view du[reshape(S.numindvar+1:end,S.numindvar,S.numparams)]
jacobianmat!(dp, S.uf, y, Sj, S.alg, S.jac_config)
DiffEqBase.@.. dp += S.pJ
else
S.uf.t = t
for i in eachindex(p)
Sj = @view u[i*S.numindvar+1:(i+1)*S.numindvar]
dp = @view du[i*S.numindvar+1:(i+1)*S.numindvar]
jacobianvec!(dp, S.uf, y, Sj, S.alg, S.jac_config)
dp .+= @view S.pJ[:,i]
end
end
return nothing
end
@deprecate ODELocalSensitivityProblem(args...;kwargs...) ODEForwardSensitivityProblem(args...;kwargs...)
struct ODEForwardSensitivityProblem{iip,A}
sensealg::A
end
function ODEForwardSensitivityProblem(f::F,args...;kwargs...) where F
ODEForwardSensitivityProblem(ODEFunction(f),args...;kwargs...)
end
function ODEForwardSensitivityProblem(prob::ODEProblem,alg;kwargs...)
ODEForwardSensitivityProblem(prob.f,prob.u0,prob.tspan,prob.p,alg;kwargs...)
end
const FORWARD_SENSITIVITY_PARAMETER_COMPATABILITY_MESSAGE =
"""
ODEForwardSensitivityProblem requires being able to solve
a differential equation defined by the parameter struct `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with ODEForwardSensitivityProblem requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during ODEForwardSensitivityProblem
construction. To work around this issue for complicated cases like nested structs,
look into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl.
"""
struct ForwardSensitivityParameterCompatibilityError <: Exception end
function Base.showerror(io::IO, e::ForwardSensitivityParameterCompatibilityError)
print(io, FORWARD_SENSITIVITY_PARAMETER_COMPATABILITY_MESSAGE)
end
const FORWARD_SENSITIVITY_OUT_OF_PLACE_MESSAGE =
"""
ODEForwardSensitivityProblem is not compatible with out of place ODE definitions,
i.e. `du=f(u,p,t)` definitions. It requires an in-place mutating function
`f(du,u,p,t)`. For more information on in-place vs out-of-place ODE definitions,
see the ODEProblem or ODEFunction documentation.
"""
struct ForwardSensitivityOutOfPlaceError <: Exception end
function Base.showerror(io::IO, e::ForwardSensitivityOutOfPlaceError)
print(io, FORWARD_SENSITIVITY_OUT_OF_PLACE_MESSAGE)
end
@doc doc"""
function ODEForwardSensitivityProblem(f::Union{Function,DiffEqBase.AbstractODEFunction},
u0,tspan,p=nothing,
alg::AbstractForwardSensitivityAlgorithm = ForwardSensitivity();
kwargs...)
Local forward sensitivity analysis gives a solution along with a timeseries of
the sensitivities. Thus if one wishes to have a derivative at every possible
time point, directly using the `ODEForwardSensitivityProblem` can be the most
efficient method.
!!! warning
ODEForwardSensitivityProblem requires being able to solve
a differential equation defined by the parameter struct `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with ODEForwardSensitivityProblem requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during ODEForwardSensitivityProblem
construction. To work around this issue for complicated cases like nested structs,
look into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl.
### ODEForwardSensitivityProblem Syntax
`ODEForwardSensitivityProblem` is similar to an `ODEProblem`, but takes an
`AbstractForwardSensitivityAlgorithm` that describes how to append the forward sensitivity
equation calculation to the time evolution to simultaneously compute the derivative
of the solution with respect to parameters.
```julia
ODEForwardSensitivityProblem(f::SciMLBase.AbstractODEFunction,u0,
tspan,p=nothing,
sensealg::AbstractForwardSensitivityAlgorithm = ForwardSensitivity();
kwargs...)
```
Once constructed, this problem can be used in `solve` just like any other ODEProblem.
The solution can be deconstructed into the ODE solution and sensitivities parts using the
`extract_local_sensitivities` function, with the following dispatches:
```julia
extract_local_sensitivities(sol, asmatrix::Val=Val(false)) # Decompose the entire time series
extract_local_sensitivities(sol, i::Integer, asmatrix::Val=Val(false)) # Decompose sol[i]
extract_local_sensitivities(sol, t::Union{Number,AbstractVector}, asmatrix::Val=Val(false)) # Decompose sol(t)
```
For information on the mathematics behind these calculations, consult
[the sensitivity math page](@ref sensitivity_math)
### Example using an ODEForwardSensitivityProblem
To define a sensitivity problem, simply use the `ODEForwardSensitivityProblem` type
instead of an ODE type. For example, we generate an ODE with the sensitivity
equations attached for the Lotka-Volterra equations by:
```julia
function f(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + u[1]*u[2]
end
p = [1.5,1.0,3.0]
prob = ODEForwardSensitivityProblem(f,[1.0;1.0],(0.0,10.0),p)
```
This generates a problem which the ODE solvers can solve:
```julia
sol = solve(prob,DP8())
```
Note that the solution is the standard ODE system and the sensitivity system combined.
We can use the following helper functions to extract the sensitivity information:
```julia
x,dp = extract_local_sensitivities(sol)
x,dp = extract_local_sensitivities(sol,i)
x,dp = extract_local_sensitivities(sol,t)
```
In each case, `x` is the ODE values and `dp` is the matrix of sensitivities
The first gives the full timeseries of values and `dp[i]` contains the time series of the
sensitivities of all components of the ODE with respect to `i`th parameter.
The second returns the `i`th time step, while the third
interpolates to calculate the sensitivities at time `t`. For example, if we do:
```julia
x,dp = extract_local_sensitivities(sol)
da = dp[1]
```
then `da` is the timeseries for ``\frac{\partial u(t)}{\partial p}``. We can
plot this
```julia
plot(sol.t,da',lw=3)
```
transposing so that the rows (the timeseries) is plotted.
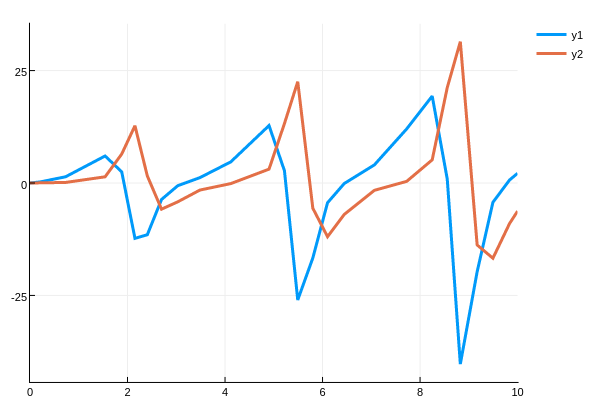
Here we see that there is a periodicity to the sensitivity which matches
the periodicity of the Lotka-Volterra solutions. However, as time goes on the
sensitivity increases. This matches the analysis of Wilkins in Sensitivity
Analysis for Oscillating Dynamical Systems.
We can also quickly see that these values are equivalent to those given by
automatic differentiation and numerical differentiation through the ODE solver:
```julia
using ForwardDiff, Calculus
function test_f(p)
prob = ODEProblem(f,eltype(p).([1.0,1.0]),eltype(p).((0.0,10.0)),p)
solve(prob,Vern9(),abstol=1e-14,reltol=1e-14,save_everystep=false)[end]
end
p = [1.5,1.0,3.0]
fd_res = ForwardDiff.jacobian(test_f,p)
calc_res = Calculus.finite_difference_jacobian(test_f,p)
```
Here we just checked the derivative at the end point.
### Internal representation of the Solution
For completeness, we detail the internal representation. When using
ForwardDiffSensitivity, the representation is with `Dual` numbers under the
standard interpretation. The values for the ODE's solution at time `i` are the
`ForwardDiff.value.(sol[i])` portions, and the derivative with respect to
parameter `j` is given by `ForwardDiff.partials.(sol[i])[j]`.
When using ForwardSensitivity, the solution to the ODE are the first `n`
components of the solution. This means we can grab the matrix of solution
values like:
```julia
x = sol[1:sol.prob.indvars,:]
```
Since each sensitivity is a vector of derivatives for each function, the sensitivities
are each of size `sol.prob.indvars`. We can pull out the parameter sensitivities from
the solution as follows:
```julia
da = sol[sol.prob.indvars+1:sol.prob.indvars*2,:]
db = sol[sol.prob.indvars*2+1:sol.prob.indvars*3,:]
dc = sol[sol.prob.indvars*3+1:sol.prob.indvars*4,:]
```
This means that `da[1,i]` is the derivative of the `x(t)` by the parameter `a`
at time `sol.t[i]`. Note that all of the functionality available to ODE solutions
is available in this case, including interpolations and plot recipes (the recipes
will plot the expanded system).
"""
function ODEForwardSensitivityProblem(f::F,u0,
tspan,p=nothing,
alg::ForwardSensitivity = ForwardSensitivity();
nus=nothing, # determine if Nilss is used
w0=nothing,
v0=nothing,
kwargs...) where F<:DiffEqBase.AbstractODEFunction
isinplace = SciMLBase.isinplace(f)
# if there is an analytical Jacobian provided, we are not going to do automatic `jac*vec`
isautojacmat = get_jacmat(alg)
isautojacvec = get_jacvec(alg)
p === nothing && error("You must have parameters to use parameter sensitivity calculations!")
if !(typeof(p) <: Union{Nothing,SciMLBase.NullParameters,AbstractArray}) || (p isa AbstractArray && !Base.isconcretetype(eltype(p)))
throw(ForwardSensitivityParameterCompatibilityError())
end
uf = DiffEqBase.UJacobianWrapper(f,tspan[1],p)
pf = DiffEqBase.ParamJacobianWrapper(f,tspan[1],copy(u0))
if isautojacmat
if alg_autodiff(alg)
jac_config_seed = ForwardDiff.Dual{typeof(uf)}.(u0,[ntuple(x -> zero(eltype(u0)), length(p)) for i in eachindex(u0)])
jac_config_buffer = similar(jac_config_seed)
jac_config = jac_config_seed, jac_config_buffer
else
error("Jacobian matrix products only work with automatic differentiation.")
end
elseif isautojacvec
if alg_autodiff(alg)
# if we are using automatic `jac*vec`, then we need to use a `jac_config`
# that is a tuple in the form of `(seed, buffer)`
jac_config_seed = ForwardDiff.Dual{typeof(jacobianvec!)}.(u0,u0)
jac_config_buffer = similar(jac_config_seed)
jac_config = jac_config_seed, jac_config_buffer
else
jac_config = (similar(u0),similar(u0))
end
elseif DiffEqBase.has_jac(f)
jac_config = nothing
else
jac_config = build_jac_config(alg,uf,u0)
end
if DiffEqBase.has_paramjac(f)
paramjac_config = nothing
else
paramjac_config = build_param_jac_config(alg,pf,u0,p)
end
# TODO: make it better
if f.mass_matrix isa UniformScaling
mm = f.mass_matrix
else
nn = size(f.mass_matrix, 1)
mm = zeros(eltype(f.mass_matrix), (length(p)+1)*nn, (length(p)+1)*nn)
mm[1:nn, 1:nn] = f.mass_matrix
for i = 1:length(p)
mm[i*nn+1:(i+1)nn, i*nn+1:(i+1)nn] = f.mass_matrix
end
end
# TODO: Use user tgrad. iW can be safely ignored here.
sense = ODEForwardSensitivityFunction(f,f.analytic,nothing,f.jac,nothing,
nothing,nothing,f.paramjac,
nothing,nothing,
uf,pf,u0,jac_config,
paramjac_config,alg,
p,similar(u0),mm,
isautojacvec,isautojacmat,f.colorvec,nus)
if !SciMLBase.isinplace(sense)
throw(ForwardSensitivityOutOfPlaceError())
end
if nus===nothing
sense_u0 = [u0;zeros(eltype(u0),sense.numindvar*sense.numparams)]
else
if w0===nothing && v0===nothing
sense_u0 = [u0;zeros(eltype(u0),(nus+1)*sense.S.numindvar*sense.S.numparams)]
else
sense_u0 = [u0;w0;v0]
end
end
ODEProblem(sense,sense_u0,tspan,p,
ODEForwardSensitivityProblem{DiffEqBase.isinplace(f),
typeof(alg)}(alg);
kwargs...)
end
function seed_duals(x::AbstractArray{V},f,
::ForwardDiff.Chunk{N} = ForwardDiff.Chunk(x,typemax(Int64)),
) where {V,T,N}
seeds = ForwardDiff.construct_seeds(ForwardDiff.Partials{N,V})
duals = ForwardDiff.Dual{typeof(ForwardDiff.Tag(f,eltype(vec(x))))}.(vec(x),seeds)
end
has_continuous_callback(cb::DiscreteCallback) = false
has_continuous_callback(cb::ContinuousCallback) = true
has_continuous_callback(cb::CallbackSet) = !isempty(cb.continuous_callbacks)
function ODEForwardSensitivityProblem(f::DiffEqBase.AbstractODEFunction,u0,
tspan,p,alg::ForwardDiffSensitivity;
du0=zeros(eltype(u0),length(u0),length(p)), # perturbations of initial condition
dp=I(length(p)), # perturbations of parameters
kwargs...)
num_sen_par = size(du0,2)
if num_sen_par != size(dp,2)
error("Same number of perturbations of initial conditions and parameters required")
end
if size(du0,1) != length(u0)
error("Perturbations for all initial conditions required")
end
if size(dp,1) != length(p)
error("Perturbations for all parameters required")
end
pdual = ForwardDiff.Dual{typeof(ForwardDiff.Tag(f,eltype(vec(p))))}.(p, [ntuple(j -> dp[i,j], num_sen_par) for i in eachindex(p)])
u0dual = ForwardDiff.Dual{typeof(ForwardDiff.Tag(f,eltype(vec(u0))))}.(u0, [ntuple(j -> du0[i,j], num_sen_par) for i in eachindex(u0)])
if (convert_tspan(alg) === nothing &&
haskey(kwargs,:callback) && has_continuous_callback(kwargs.callback)
) || (convert_tspan(alg) !== nothing && convert_tspan(alg))
tspandual = convert.(eltype(pdual),tspan)
else
tspandual = tspan
end
prob_dual = ODEProblem(f,u0dual,tspan,pdual,
ODEForwardSensitivityProblem{DiffEqBase.isinplace(f),
typeof(alg)}(alg);
kwargs...)
end
"""
extract_local_sensitivities
Extracts the time series for the local sensitivities from the ODE solution. This requires
that the ODE was defined via `ODEForwardSensitivityProblem`.
```julia
extract_local_sensitivities(sol, asmatrix::Val=Val(false)) # Decompose the entire time series
extract_local_sensitivities(sol, i::Integer, asmatrix::Val=Val(false)) # Decompose sol[i]
extract_local_sensitivities(sol, t::Union{Number,AbstractVector}, asmatrix::Val=Val(false)) # Decompose sol(t)
```
"""
extract_local_sensitivities(sol, asmatrix::Val=Val(false)) = extract_local_sensitivities(sol,sol.prob.problem_type.sensealg, asmatrix)
extract_local_sensitivities(sol, asmatrix::Bool) = extract_local_sensitivities(sol, Val{asmatrix}())
extract_local_sensitivities(sol, i::Integer, asmatrix::Val=Val(false)) = _extract(sol, sol.prob.problem_type.sensealg, sol[i], asmatrix)
extract_local_sensitivities(sol, i::Integer, asmatrix::Bool) = extract_local_sensitivities(sol, i, Val{asmatrix}())
extract_local_sensitivities(sol, t::Union{Number,AbstractVector}, asmatrix::Val=Val(false)) = _extract(sol, sol.prob.problem_type.sensealg, sol(t), asmatrix)
extract_local_sensitivities(sol, t, asmatrix::Bool) = extract_local_sensitivities(sol, t, Val{asmatrix}())
extract_local_sensitivities(tmp, sol, t::Union{Number,AbstractVector}, asmatrix::Val=Val(false)) = _extract(sol, sol.prob.problem_type.sensealg, sol(tmp, t), asmatrix)
extract_local_sensitivities(tmp, sol, t, asmatrix::Bool) = extract_local_sensitivities(tmp, sol, t, Val{asmatrix}())
# Get ODE u vector and sensitivity values from all time points
function extract_local_sensitivities(sol,::ForwardSensitivity, ::Val{false})
ni = sol.prob.f.numindvar
u = sol[1:ni, :]
du = [sol[ni*j+1:ni*(j+1),:] for j in 1:sol.prob.f.numparams]
return u, du
end
function extract_local_sensitivities(sol,::ForwardDiffSensitivity, ::Val{false})
u = ForwardDiff.value.(sol)
du_full = ForwardDiff.partials.(sol)
firststate = first(du_full)
firstparam = first(firststate)
Js = map(1:length(firstparam)) do j
map(CartesianIndices(du_full)) do II
du_full[II][j]
end
end
return u, Js
end
function extract_local_sensitivities(sol,::ForwardSensitivity, ::Val{true})
prob = sol.prob
ni = prob.f.numindvar
pn = prob.f.numparams
jsize = (ni, pn)
sol[1:ni, :], map(sol.u) do u
collect(reshape((@view u[ni+1:end]), jsize))
end
end
function extract_local_sensitivities(sol,::ForwardDiffSensitivity, ::Val{true})
retu = ForwardDiff.value.(sol)
jsize = length(sol.u[1]), ForwardDiff.npartials(sol.u[1][1])
du = map(sol.u) do u
du_i = similar(retu, jsize)
for i in eachindex(u)
du_i[i, :] = ForwardDiff.partials(u[i])
end
du_i
end
retu, du
end
# Get ODE u vector and sensitivity values from sensitivity problem u vector
function _extract(sol, sensealg::ForwardSensitivity, su::AbstractVector, asmatrix::Val = Val(false))
u = view(su, 1:sol.prob.f.numindvar)
du = _extract_du(sol, sensealg, su, asmatrix)
return u, du
end
function _extract(sol, sensealg::ForwardDiffSensitivity, su::AbstractVector, asmatrix::Val = Val(false))
u = ForwardDiff.value.(su)
du = _extract_du(sol, sensealg, su, asmatrix)
return u, du
end
# Get sensitivity values from sensitivity problem u vector (nested form)
function _extract_du(sol, ::ForwardSensitivity, su::Vector, ::Val{false})
ni = sol.prob.f.numindvar
return [view(su, ni*j+1:ni*(j+1)) for j in 1:sol.prob.f.numparams]
end
function _extract_du(sol, ::ForwardDiffSensitivity, su::Vector, ::Val{false})
du_full = ForwardDiff.partials.(su)
return [[du_full[i][j] for i in 1:size(du_full,1)] for j in 1:length(du_full[1])]
end
# Get sensitivity values from sensitivity problem u vector (matrix form)
function _extract_du(sol, ::ForwardSensitivity, su::Vector, ::Val{true})
ni = sol.prob.f.numindvar
np = sol.prob.f.numparams
return view(reshape(su, ni, np+1), :, 2:np+1)
end
function _extract_du(sol, ::ForwardDiffSensitivity, su::Vector, ::Val{true})
du_full = ForwardDiff.partials.(su)
return [du_full[i][j] for i in 1:size(du_full,1), j in 1:length(du_full[1])]
end
### Bonus Pieces
function SciMLBase.remake(prob::ODEProblem{uType,tType,isinplace,P,F,K,<:ODEForwardSensitivityProblem};
f=nothing,tspan=nothing,u0=nothing,p=nothing,kwargs...) where
{uType,tType,isinplace,P,F,K}
_p = p === nothing ? prob.p : p
_f = f === nothing ? prob.f.f : f
_u0 = u0 === nothing ? prob.u0[1:prob.f.numindvar] : u0[1:prob.f.numindvar]
_tspan = tspan === nothing ? prob.tspan : tspan
ODEForwardSensitivityProblem(_f,_u0,
_tspan,_p,prob.problem_type.sensealg;
prob.kwargs...,kwargs...)
end
SciMLBase.ODEFunction(f::ODEForwardSensitivityFunction; kwargs...) = f
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2625 | const printbranch = false
Cassette.@context HasBranchingCtx
function Cassette.overdub(ctx::HasBranchingCtx, f, args...)
if Cassette.canrecurse(ctx, f, args...)
return Cassette.recurse(ctx, f, args...)
else
return Cassette.fallback(ctx, f, args...)
end
end
for (mod, f, n) in DiffRules.diffrules()
isdefined(@__MODULE__, mod) || continue
@eval Cassette.overdub(::HasBranchingCtx, f::Core.Typeof($mod.$f), x::Vararg{Any, $n}) = f(x...)
end
function _pass(::Type{<:HasBranchingCtx}, reflection::Cassette.Reflection)
ir = reflection.code_info
if any(x -> isa(x, GotoIfNot), ir.code)
printbranch && println("GotoIfNot detected in $(reflection.method)\nir = $ir\n")
Cassette.insert_statements!(
ir.code, ir.codelocs,
(stmt, i) -> i == 1 ? 3 : nothing,
(stmt, i) -> Any[
Expr(:call, Expr(:nooverdub, GlobalRef(Base, :getfield)), Expr(:contextslot), QuoteNode(:metadata)),
Expr(:call, Expr(:nooverdub, GlobalRef(Base, :setindex!)), SSAValue(1), true, QuoteNode(:has_branching)),
stmt,
],
)
Cassette.insert_statements!(
ir.code, ir.codelocs,
(stmt, i) -> i > 2 && isa(stmt, Expr) ? 1 : nothing,
(stmt, i) -> begin
callstmt = Meta.isexpr(stmt, :(=)) ? stmt.args[2] : stmt
Meta.isexpr(stmt, :call) || Meta.isexpr(stmt, :invoke) || return Any[stmt]
callstmt = Expr(callstmt.head, Expr(:nooverdub, callstmt.args[1]), callstmt.args[2:end]...)
return Any[
Meta.isexpr(stmt, :(=)) ? Expr(:(=), stmt.args[1], callstmt) : callstmt,
]
end,
)
end
return ir
end
const pass = Cassette.@pass _pass
function hasbranching(f, x...)
metadata = Dict(:has_branching => false)
Cassette.overdub(Cassette.disablehooks(HasBranchingCtx(; pass, metadata)), f, x...)
return metadata[:has_branching]
end
Cassette.overdub(::HasBranchingCtx, ::typeof(+), x...) = +(x...)
Cassette.overdub(::HasBranchingCtx, ::typeof(*), x...) = *(x...)
Cassette.overdub(::HasBranchingCtx, ::typeof(Base.materialize), x...) = Base.materialize(x...)
Cassette.overdub(::HasBranchingCtx, ::typeof(Base.literal_pow), x...) = Base.literal_pow(x...)
Cassette.overdub(::HasBranchingCtx, ::typeof(Base.getindex), x...) = Base.getindex(x...)
Cassette.overdub(::HasBranchingCtx, ::typeof(Core.Typeof), x...) = Core.Typeof(x...)
Cassette.overdub(::HasBranchingCtx, ::Type{Base.OneTo{T}}, stop) where {T <: Integer} = Base.OneTo{T}(stop)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 19732 | struct ODEInterpolatingAdjointSensitivityFunction{C<:AdjointDiffCache,Alg<:InterpolatingAdjoint,
uType,SType,CPS,pType,fType<:DiffEqBase.AbstractDiffEqFunction} <: SensitivityFunction
diffcache::C
sensealg::Alg
discrete::Bool
y::uType
sol::SType
checkpoint_sol::CPS
prob::pType
f::fType
noiseterm::Bool
end
mutable struct CheckpointSolution{S,I,T,T2}
cpsol::S # solution in a checkpoint interval
intervals::I # checkpoint intervals
cursor::Int # sol.prob.tspan = intervals[cursor]
tols::T
tstops::T2 # for callbacks
end
function ODEInterpolatingAdjointSensitivityFunction(g,sensealg,discrete,sol,dg,f,checkpoints,tols,tstops=nothing;noiseterm=false)
tspan = reverse(sol.prob.tspan)
checkpointing = ischeckpointing(sensealg, sol)
(checkpointing && checkpoints === nothing) && error("checkpoints must be passed when checkpointing is enabled.")
checkpoint_sol = if checkpointing
intervals = map(tuple, @view(checkpoints[1:end-1]), @view(checkpoints[2:end]))
interval_end = intervals[end][end]
tspan[1] > interval_end && push!(intervals, (interval_end, tspan[1]))
cursor = lastindex(intervals)
interval = intervals[cursor]
if typeof(sol.prob) <: Union{SDEProblem,RODEProblem}
# replicated noise
_sol = deepcopy(sol)
idx1 = searchsortedfirst(_sol.W.t, interval[1]-1000eps(interval[1]))
if typeof(sol.W) <: DiffEqNoiseProcess.NoiseProcess
sol.W.save_everystep = false
_sol.W.save_everystep = false
forwardnoise = DiffEqNoiseProcess.NoiseWrapper(_sol.W, indx=idx1)
elseif typeof(sol.W) <: DiffEqNoiseProcess.NoiseGrid
#idx2 = searchsortedfirst(_sol.W.t, interval[2]+1000eps(interval[1]))
forwardnoise = DiffEqNoiseProcess.NoiseGrid(_sol.W.t[idx1:end], _sol.W.W[idx1:end])
else
error("NoiseProcess type not implemented.")
end
dt = choose_dt((_sol.W.t[idx1]-_sol.W.t[idx1+1]), _sol.W.t, interval)
cpsol = solve(remake(sol.prob, tspan=interval, u0=sol(interval[1]), noise=forwardnoise),
sol.alg, save_noise=false; dt=dt, tstops=_sol.t[idx1:end] ,tols...)
else
if tstops === nothing
cpsol = solve(remake(sol.prob, tspan=interval, u0=sol(interval[1])),sol.alg; tols...)
else
if maximum(interval[1] .< tstops .< interval[2])
# callback might have changed p
_p = reset_p(sol.prob.kwargs[:callback], interval)
cpsol = solve(remake(sol.prob, tspan=interval, u0=sol(interval[1])),tstops=tstops,
p=_p, sol.alg; tols...)
else
cpsol = solve(remake(sol.prob, tspan=interval, u0=sol(interval[1])),tstops=tstops, sol.alg; tols...)
end
end
end
CheckpointSolution(cpsol, intervals, cursor, tols, tstops)
else
nothing
end
diffcache, y = adjointdiffcache(g,sensealg,discrete,sol,dg,f;quad=false,noiseterm=noiseterm)
return ODEInterpolatingAdjointSensitivityFunction(diffcache,sensealg,
discrete,y,sol,
checkpoint_sol,sol.prob,f,noiseterm)
end
function findcursor(intervals, t)
# equivalent with `findfirst(x->x[1] <= t <= x[2], intervals)`
lt(x, t) = <(x[2], t)
return searchsortedfirst(intervals, t, lt=lt)
end
function choose_dt(dt, ts, interval)
if dt < 1000eps(interval[2])
if length(ts) > 2
dt = ts[end-1]-ts[end-2]
if dt < 1000eps(interval[2])
dt = interval[2] - interval[1]
end
else
dt = interval[2] - interval[1]
end
end
return dt
end
# u = λ'
# add tstop on all the checkpoints
function (S::ODEInterpolatingAdjointSensitivityFunction)(du,u,p,t)
@unpack sol,checkpoint_sol, discrete, prob, f = S
λ,grad,y,dλ,dgrad,dy = split_states(du,u,t,S)
if S.noiseterm
if length(u) == length(du)
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad)
elseif length(u) != length(du) && StochasticDiffEq.is_diagonal_noise(prob) && !isnoisemixing(S.sensealg)
vecjacobian!(dλ, y, λ, p, t, S)
jacNoise!(λ, y, p, t, S, dgrad=dgrad)
else
jacNoise!(λ, y, p, t, S, dgrad=dgrad, dλ=dλ)
end
else
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad)
end
dλ .*= -one(eltype(λ))
discrete || accumulate_cost!(dλ, y, p, t, S, dgrad)
return nothing
end
function (S::ODEInterpolatingAdjointSensitivityFunction)(du,u,p,t,W)
@unpack sol,checkpoint_sol, discrete, prob, f = S
λ,grad,y,dλ,dgrad,dy = split_states(du,u,t,S)
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad, W=W)
dλ .*= -one(eltype(λ))
discrete || accumulate_cost!(dλ, y, p, t, S, dgrad)
return nothing
end
function split_states(du,u,t,S::TS;update=true) where TS<:ODEInterpolatingAdjointSensitivityFunction
@unpack sol, y, checkpoint_sol, discrete, prob, f = S
idx = length(y)
if update
if checkpoint_sol === nothing
if typeof(t) <: ForwardDiff.Dual && eltype(S.y) <: AbstractFloat
y = sol(t, continuity=:right)
else
sol(y,t, continuity=:right)
end
else
intervals = checkpoint_sol.intervals
interval = intervals[checkpoint_sol.cursor]
if !(interval[1] <= t <= interval[2])
cursor′ = findcursor(intervals, t)
interval = intervals[cursor′]
cpsol_t = checkpoint_sol.cpsol.t
if typeof(t) <: ForwardDiff.Dual && eltype(S.y) <: AbstractFloat
y = sol(interval[1])
else
sol(y, interval[1])
end
if typeof(sol.prob) <: Union{SDEProblem,RODEProblem}
#idx1 = searchsortedfirst(sol.t, interval[1])
_sol = deepcopy(sol)
idx1 = searchsortedfirst(_sol.t, interval[1]-100eps(interval[1]))
idx2 = searchsortedfirst(_sol.t, interval[2]+100eps(interval[2]))
idx_noise = searchsortedfirst(_sol.W.t, interval[1]-100eps(interval[1]))
if typeof(sol.W) <: DiffEqNoiseProcess.NoiseProcess
_sol.W.save_everystep = false
forwardnoise = DiffEqNoiseProcess.NoiseWrapper(_sol.W, indx=idx_noise)
elseif typeof(sol.W) <: DiffEqNoiseProcess.NoiseGrid
forwardnoise = DiffEqNoiseProcess.NoiseGrid(_sol.W.t[idx_noise:end], _sol.W.W[idx_noise:end])
else
error("NoiseProcess type not implemented.")
end
prob′ = remake(prob, tspan=intervals[cursor′], u0=y, noise=forwardnoise)
dt = choose_dt(abs(cpsol_t[1]-cpsol_t[2]), cpsol_t, interval)
cpsol′ = solve(prob′, sol.alg, save_noise=false; dt=dt, tstops=_sol.t[idx1:idx2], checkpoint_sol.tols...)
else
if checkpoint_sol.tstops===nothing
prob′ = remake(prob, tspan=intervals[cursor′], u0=y)
cpsol′ = solve(prob′, sol.alg; dt=abs(cpsol_t[end] - cpsol_t[end-1]), checkpoint_sol.tols...)
else
if maximum(interval[1] .< checkpoint_sol.tstops .< interval[2])
# callback might have changed p
_p = reset_p(prob.kwargs[:callback], interval)
prob′ = remake(prob, tspan=intervals[cursor′], u0=y, p=_p)
cpsol′ = solve(prob′, sol.alg; dt=abs(cpsol_t[end] - cpsol_t[end-1]), tstops=checkpoint_sol.tstops, checkpoint_sol.tols...)
else
prob′ = remake(prob, tspan=intervals[cursor′], u0=y)
cpsol′ = solve(prob′, sol.alg; dt=abs(cpsol_t[end] - cpsol_t[end-1]), tstops=checkpoint_sol.tstops, checkpoint_sol.tols...)
end
end
end
checkpoint_sol.cpsol = cpsol′
checkpoint_sol.cursor = cursor′
end
checkpoint_sol.cpsol(y, t, continuity=:right)
end
end
λ = @view u[1:idx]
grad = @view u[idx+1:end]
if length(u) == length(du)
dλ = @view du[1:idx]
dgrad = @view du[idx+1:end]
elseif length(u) != length(du) && StochasticDiffEq.is_diagonal_noise(prob) && !isnoisemixing(S.sensealg)
idx1 = [length(u)*(i-1)+i for i in 1:idx] # for diagonal indices of [1:idx,1:idx]
dλ = @view du[idx1]
dgrad = @view du[idx+1:end,1:idx]
elseif typeof(du) <: AbstractMatrix
# non-diagonal noise and noise mixing case
dλ = @view du[1:idx,1:idx]
dgrad = @view du[idx+1:end,1:idx]
end
λ,grad,y,dλ,dgrad,nothing
end
# g is either g(t,u,p) or discrete g(t,u,i)
@noinline function ODEAdjointProblem(sol,sensealg::InterpolatingAdjoint,
g::G,t=nothing,dg::DG=nothing;
checkpoints=sol.t,
callback=CallbackSet(),
reltol=nothing, abstol=nothing,
kwargs...) where {G,DG}
@unpack f, p, u0, tspan = sol.prob
tspan = reverse(tspan)
discrete = t !== nothing
# remove duplicates from checkpoints
if ischeckpointing(sensealg, sol) && (length(unique(checkpoints)) != length(checkpoints))
_checkpoints, duplicate_iterator_times = separate_nonunique(checkpoints)
tstops = duplicate_iterator_times[1]
checkpoints = filter(x -> x ∉ tstops, _checkpoints)
# check if start is in checkpoints. Otherwise first interval is missed.
if checkpoints[1] != tspan[2]
pushfirst!(checkpoints, tspan[2])
end
if haskey(kwargs, :tstops)
(tstops !== kwargs[:tstops]) && unique!(push!(tstops, kwargs[:tstops]...))
end
else
tstops = nothing
end
numstates = length(u0)
numparams = p === nothing || p === DiffEqBase.NullParameters() ? 0 : length(p)
len = numstates+numparams
λ = p === nothing || p === DiffEqBase.NullParameters() ? similar(u0) : one(eltype(u0)) .* similar(p, len)
λ .= false
sense = ODEInterpolatingAdjointSensitivityFunction(g,sensealg,discrete,sol,dg,f,
checkpoints,
(reltol=reltol,abstol=abstol),
tstops)
init_cb = t !== nothing && tspan[1] == t[end]
cb, duplicate_iterator_times = generate_callbacks(sense, g, λ, t, tspan[2], callback, init_cb)
z0 = vec(zero(λ))
original_mm = sol.prob.f.mass_matrix
if original_mm === I || original_mm === (I,I)
mm = I
else
adjmm = copy(sol.prob.f.mass_matrix')
zzz = similar(adjmm, numstates, numparams)
fill!(zzz, zero(eltype(zzz)))
# using concrate I is slightly more efficient
II = Diagonal(I, numparams)
mm = [adjmm zzz
copy(zzz') II]
end
jac_prototype = sol.prob.f.jac_prototype
if !sense.discrete || jac_prototype === nothing
adjoint_jac_prototype = nothing
else
_adjoint_jac_prototype = copy(jac_prototype')
zzz = similar(_adjoint_jac_prototype, numstates, numparams)
fill!(zzz, zero(eltype(zzz)))
II = Diagonal(I, numparams)
adjoint_jac_prototype = [_adjoint_jac_prototype zzz
copy(zzz') II]
end
odefun = ODEFunction(sense, mass_matrix=mm, jac_prototype=adjoint_jac_prototype)
return ODEProblem(odefun,z0,tspan,p,callback=cb)
end
@noinline function SDEAdjointProblem(sol,sensealg::InterpolatingAdjoint,
g,t=nothing,dg=nothing;
checkpoints=sol.t,
callback=CallbackSet(),
reltol=nothing, abstol=nothing,
diffusion_jac=nothing, diffusion_paramjac=nothing,
kwargs...)
@unpack f, p, u0, tspan = sol.prob
tspan = reverse(tspan)
discrete = t !== nothing
# remove duplicates from checkpoints
if ischeckpointing(sensealg,sol) && (length(unique(checkpoints)) != length(checkpoints))
_checkpoints, duplicate_iterator_times = separate_nonunique(checkpoints)
tstops = duplicate_iterator_times[1]
checkpoints = filter(x->x ∉ tstops, _checkpoints)
# check if start is in checkpoints. Otherwise first interval is missed.
if checkpoints[1] != tspan[2]
pushfirst!(checkpoints,tspan[2])
end
else
tstops = nothing
end
numstates = length(u0)
numparams = p === nothing || p === DiffEqBase.NullParameters() ? 0 : length(p)
len = numstates+numparams
λ = one(eltype(u0)) .* similar(p, len)
λ .= false
sense_drift = ODEInterpolatingAdjointSensitivityFunction(g,sensealg,discrete,sol,dg,sol.prob.f,
checkpoints,(reltol=reltol,abstol=abstol))
diffusion_function = ODEFunction(sol.prob.g, jac=diffusion_jac, paramjac=diffusion_paramjac)
sense_diffusion = ODEInterpolatingAdjointSensitivityFunction(g,sensealg,discrete,sol,dg,diffusion_function,
checkpoints,(reltol=reltol,abstol=abstol);noiseterm=true)
init_cb = t !== nothing && tspan[1] == t[end]
cb, duplicate_iterator_times = generate_callbacks(sense_drift, g, λ, t, tspan[2], callback, init_cb)
z0 = vec(zero(λ))
original_mm = sol.prob.f.mass_matrix
if original_mm === I || original_mm === (I,I)
mm = I
else
adjmm = copy(sol.prob.f.mass_matrix')
zzz = similar(adjmm, numstates, numparams)
fill!(zzz, zero(eltype(zzz)))
# using concrate I is slightly more efficient
II = Diagonal(I, numparams)
mm = [adjmm zzz
copy(zzz') II]
end
jac_prototype = sol.prob.f.jac_prototype
if !sense_drift.discrete || jac_prototype === nothing
adjoint_jac_prototype = nothing
else
_adjoint_jac_prototype = copy(jac_prototype')
zzz = similar(_adjoint_jac_prototype, numstates, numparams)
fill!(zzz, zero(eltype(zzz)))
II = Diagonal(I, numparams)
adjoint_jac_prototype = [_adjoint_jac_prototype zzz
copy(zzz') II]
end
sdefun = SDEFunction(sense_drift,sense_diffusion,mass_matrix=mm,jac_prototype=adjoint_jac_prototype)
# replicated noise
_sol = deepcopy(sol)
backwardnoise = reverse(_sol.W)
if StochasticDiffEq.is_diagonal_noise(sol.prob) && typeof(sol.W[end])<:Number
# scalar noise case
noise_matrix = nothing
else
noise_matrix = similar(z0,length(z0),numstates)
noise_matrix .= false
end
return SDEProblem(sdefun,sense_diffusion,z0,tspan,p,
callback=cb,
noise=backwardnoise,
noise_rate_prototype = noise_matrix
)
end
@noinline function RODEAdjointProblem(sol,sensealg::InterpolatingAdjoint,
g,t=nothing,dg=nothing;
checkpoints=sol.t,
callback=CallbackSet(),
reltol=nothing, abstol=nothing,
kwargs...)
@unpack f, p, u0, tspan = sol.prob
tspan = reverse(tspan)
discrete = t !== nothing
# remove duplicates from checkpoints
if ischeckpointing(sensealg,sol) && (length(unique(checkpoints)) != length(checkpoints))
_checkpoints, duplicate_iterator_times = separate_nonunique(checkpoints)
tstops = duplicate_iterator_times[1]
checkpoints = filter(x->x ∉ tstops, _checkpoints)
# check if start is in checkpoints. Otherwise first interval is missed.
if checkpoints[1] != tspan[2]
pushfirst!(checkpoints,tspan[2])
end
else
tstops = nothing
end
numstates = length(u0)
numparams = p === nothing || p === DiffEqBase.NullParameters() ? 0 : length(p)
len = numstates+numparams
λ = p === nothing || p === DiffEqBase.NullParameters() ? similar(u0) : one(eltype(u0)) .* similar(p, len)
λ .= false
sense = ODEInterpolatingAdjointSensitivityFunction(g,sensealg,discrete,sol,dg,f,
checkpoints,
(reltol=reltol,abstol=abstol),
tstops)
init_cb = t !== nothing && tspan[1] == t[end]
cb, duplicate_iterator_times = generate_callbacks(sense, g, λ, t, tspan[2], callback, init_cb)
z0 = vec(zero(λ))
original_mm = sol.prob.f.mass_matrix
if original_mm === I || original_mm === (I,I)
mm = I
else
adjmm = copy(sol.prob.f.mass_matrix')
zzz = similar(adjmm, numstates, numparams)
fill!(zzz, zero(eltype(zzz)))
# using concrate I is slightly more efficient
II = Diagonal(I, numparams)
mm = [adjmm zzz
copy(zzz') II]
end
jac_prototype = sol.prob.f.jac_prototype
if !sense.discrete || jac_prototype === nothing
adjoint_jac_prototype = nothing
else
_adjoint_jac_prototype = copy(jac_prototype')
zzz = similar(_adjoint_jac_prototype, numstates, numparams)
fill!(zzz, zero(eltype(zzz)))
II = Diagonal(I, numparams)
adjoint_jac_prototype = [_adjoint_jac_prototype zzz
copy(zzz') II]
end
rodefun = RODEFunction(sense, mass_matrix=mm, jac_prototype=adjoint_jac_prototype)
# replicated noise
_sol = deepcopy(sol)
backwardnoise = reverse(_sol.W)
# make sure noise grid starts at correct time values, e.g., if sol.W.t is longer than sol.t
tspan[1]!=backwardnoise.t[1] && reinit!(backwardnoise,backwardnoise.t[2]-backwardnoise.t[1],t0=tspan[1])
return RODEProblem(rodefun,z0,tspan,p,callback=cb,
noise=backwardnoise)
end
function reset_p(CBS, interval)
# check which events are close to tspan[1]
if !isempty(CBS.discrete_callbacks)
ts = map(CBS.discrete_callbacks) do cb
indx = searchsortedfirst(cb.affect!.event_times, interval[1])
(indx, cb.affect!.event_times[indx])
end
perm = minimum(sortperm([t for t in getindex.(ts,2)]))
end
if !isempty(CBS.continuous_callbacks)
ts2 = map(CBS.continuous_callbacks) do cb
if !isempty(cb.affect!.event_times) && isempty(cb.affect_neg!.event_times)
indx = searchsortedfirst(cb.affect!.event_times, interval[1])
return (indx, cb.affect!.event_times[indx],0) # zero for affect!
elseif isempty(cb.affect!.event_times) && !isempty(cb.affect_neg!.event_times)
indx = searchsortedfirst(cb.affect_neg!.event_times, interval[1])
return (indx, cb.affect_neg!.event_times[indx],1) # one for affect_neg!
elseif !isempty(cb.affect!.event_times) && !isempty(cb.affect_neg!.event_times)
indx1 = searchsortedfirst(cb.affect!.event_times, interval[1])
indx2 = searchsortedfirst(cb.affect_neg!.event_times, interval[1])
if cb.affect!.event_times[indx1] < cb.affect_neg!.event_times[indx2]
return (indx1, cb.affect!.event_times[indx1],0)
else
return (indx2, cb.affect_neg!.event_times[indx2],1)
end
else
error("Expected event but reset_p couldn't find event time. Please report this error.")
end
end
perm2 = minimum(sortperm([t for t in getindex.(ts2,2)]))
# check if continuous or discrete callback was applied first if both occur in interval
if isempty(CBS.discrete_callbacks)
if ts2[perm2][3] == 0
p = deepcopy(CBS.continuous_callbacks[perm2].affect!.pleft[getindex.(ts2,1)[perm2]])
else
p = deepcopy(CBS.continuous_callbacks[perm2].affect_neg!.pleft[getindex.(ts2,1)[perm2]])
end
else
if ts[perm][2] < ts2[perm2][2]
p = deepcopy(CBS.discrete_callbacks[perm].affect!.pleft[getindex.(ts,1)[perm]])
else
if ts2[perm2][3] == 0
p = deepcopy(CBS.continuous_callbacks[perm2].affect!.pleft[getindex.(ts2,1)[perm2]])
else
p = deepcopy(CBS.continuous_callbacks[perm2].affect_neg!.pleft[getindex.(ts2,1)[perm2]])
end
end
end
else
p = deepcopy(CBS.discrete_callbacks[perm].affect!.pleft[getindex.(ts,1)[perm]])
end
return p
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 17937 | struct LSSSchur{wBType,wEType,BType,EType}
wBinv::wBType
wEinv::wEType
B::BType
E::EType
end
struct LSSSensitivityFunction{iip,F,A,J,JP,S,PJ,UF,PF,JC,PJC,Alg,fc,JM,pJM,MM,CV,
PGPU,PGPP,CONFU,CONGP,DG} <: DiffEqBase.AbstractODEFunction{iip}
f::F
analytic::A
jac::J
jac_prototype::JP
sparsity::S
paramjac::PJ
uf::UF
pf::PF
J::JM
pJ::pJM
jac_config::JC
paramjac_config::PJC
alg::Alg
numparams::Int
numindvar::Int
f_cache::fc
mass_matrix::MM
colorvec::CV
pgpu::PGPU
pgpp::PGPP
pgpu_config::CONFU
pgpp_config::CONGP
dg_val::DG
end
function LSSSensitivityFunction(sensealg,f,analytic,jac,jac_prototype,sparsity,paramjac,u0,
alg,p,f_cache,mm,
colorvec,tspan,g,dg)
uf = DiffEqBase.UJacobianWrapper(f,tspan[1],p)
pf = DiffEqBase.ParamJacobianWrapper(f,tspan[1],copy(u0))
if DiffEqBase.has_jac(f)
jac_config = nothing
else
jac_config = build_jac_config(sensealg,uf,u0)
end
if DiffEqBase.has_paramjac(f)
paramjac_config = nothing
else
paramjac_config = build_param_jac_config(sensealg,pf,u0,p)
end
numparams = length(p)
numindvar = length(u0)
J = Matrix{eltype(u0)}(undef,numindvar,numindvar)
pJ = Matrix{eltype(u0)}(undef,numindvar,numparams) # number of funcs size
# compute gradients of objective
if dg !== nothing
pgpu = nothing
pgpp = nothing
pgpu_config = nothing
pgpp_config = nothing
if dg isa Tuple && length(dg) == 2
dg_val = (similar(u0, numindvar),similar(u0, numparams))
dg_val[1] .= false
dg_val[2] .= false
else
dg_val = similar(u0, numindvar) # number of funcs size
dg_val .= false
end
else
pgpu = UGradientWrapper(g,tspan[1],p) # ∂g∂u
pgpp = ParamGradientWrapper(g,tspan[1],u0) #∂g∂p
pgpu_config = build_grad_config(sensealg,pgpu,u0,tspan[1])
pgpp_config = build_grad_config(sensealg,pgpp,p,tspan[1])
dg_val = (similar(u0, numindvar),similar(u0, numparams))
dg_val[1] .= false
dg_val[2] .= false
end
LSSSensitivityFunction{isinplace(f),typeof(f),typeof(analytic),
typeof(jac),typeof(jac_prototype),typeof(sparsity),
typeof(paramjac),
typeof(uf),
typeof(pf),typeof(jac_config),
typeof(paramjac_config),typeof(alg),
typeof(f_cache),
typeof(J),typeof(pJ),typeof(mm),typeof(f.colorvec),
typeof(pgpu),typeof(pgpp),typeof(pgpu_config),typeof(pgpp_config),typeof(dg_val)}(
f,analytic,jac,jac_prototype,sparsity,paramjac,uf,pf,J,pJ,
jac_config,paramjac_config,alg,
numparams,numindvar,f_cache,mm,colorvec,
pgpu,pgpp,pgpu_config,pgpp_config,dg_val)
end
struct ForwardLSSProblem{A,C,solType,dtType,umidType,dudtType,SType,Ftype,bType,ηType,wType,vType,windowType,
ΔtType,G0,G,DG,resType}
sensealg::A
diffcache::C
sol::solType
dt::dtType
umid::umidType
dudt::dudtType
S::SType
F::Ftype
b::bType
η::ηType
w::wType
v::vType
window::windowType
Δt::ΔtType
Nt::Int
g0::G0
g::G
dg::DG
res::resType
end
function ForwardLSSProblem(sol, sensealg::ForwardLSS, t=nothing, dg = nothing;
kwargs...)
@unpack f, p, u0, tspan = sol.prob
@unpack g = sensealg
isinplace = DiffEqBase.isinplace(f)
# some shadowing sensealgs require knowledge of g
check_for_g(sensealg,g)
p === nothing && error("You must have parameters to use parameter sensitivity calculations!")
!(sol.u isa AbstractVector) && error("`u` has to be an AbstractVector.")
sense = LSSSensitivityFunction(sensealg,f,f.analytic,f.jac,
f.jac_prototype,f.sparsity,f.paramjac,
u0,sensealg,
p,similar(u0),f.mass_matrix,
f.colorvec,
tspan,g,dg)
@unpack numparams, numindvar = sense
Nt = length(sol.t)
Ndt = Nt-one(Nt)
# pre-allocate variables
dt = similar(sol.t, Ndt)
umid = Matrix{eltype(u0)}(undef,numindvar,Ndt)
dudt = Matrix{eltype(u0)}(undef,numindvar,Ndt)
# compute their values
discretize_ref_trajectory!(dt, umid, dudt, sol, Ndt)
# assert that all ts are hit if concrete solve interface/discrete costs are used
if t !== nothing
@assert sol.t == t
end
S = LSSSchur(dt,u0,numindvar,Nt,Ndt,sensealg.LSSregularizer)
if sensealg.LSSregularizer isa TimeDilation
η = similar(dt,Ndt)
window = nothing
g0 = g(u0,p,tspan[1])
else
η = nothing
window = similar(dt,Nt)
g0 = nothing
end
b = Matrix{eltype(u0)}(undef,numindvar*Ndt,numparams)
w = similar(dt,numindvar*Ndt)
v = similar(dt,numindvar*Nt)
Δt = tspan[2] - tspan[1]
wB!(S,Δt,Nt,numindvar,dt)
wE!(S,Δt,dt,sensealg.LSSregularizer)
B!(S,dt,umid,sense,sensealg)
E!(S,dudt,sensealg.LSSregularizer)
F = SchurLU(S)
res = similar(u0, numparams)
ForwardLSSProblem{typeof(sensealg),typeof(sense),typeof(sol),typeof(dt),
typeof(umid),typeof(dudt),
typeof(S),typeof(F),typeof(b),typeof(η),typeof(w),typeof(v),typeof(window),typeof(Δt),
typeof(g0),typeof(g),typeof(dg),typeof(res)}(sensealg,sense,sol,dt,umid,dudt,S,F,b,η,w,v,
window,Δt,Nt,g0,g,dg,res)
end
function LSSSchur(dt,u0,numindvar,Nt,Ndt,LSSregularizer::TimeDilation)
wBinv = similar(dt,numindvar*Nt)
wEinv = similar(dt,Ndt)
E = Matrix{eltype(u0)}(undef,numindvar*Ndt,Ndt)
B = Matrix{eltype(u0)}(undef,numindvar*Ndt,numindvar*Nt)
LSSSchur(wBinv,wEinv,B,E)
end
function LSSSchur(dt,u0,numindvar,Nt,Ndt,LSSregularizer::AbstractCosWindowing)
wBinv = similar(dt,numindvar*Nt)
wEinv = nothing
E = nothing
B = Matrix{eltype(u0)}(undef,numindvar*Ndt,numindvar*Nt)
LSSSchur(wBinv,wEinv,B,E)
end
# compute discretized reference trajectory
function discretize_ref_trajectory!(dt, umid, dudt, sol, Ndt)
for i=1:Ndt
tr = sol.t[i+1]
tl = sol.t[i]
ur = sol.u[i+1]
ul = sol.u[i]
dt[i] = tr-tl
copyto!((@view umid[:,i]), (ur + ul)/2)
copyto!((@view dudt[:,i]), (ur - ul)/dt[i])
end
return nothing
end
function wB!(S::LSSSchur,Δt,Nt,numindvar,dt)
@unpack wBinv = S
fill!(wBinv, one(Δt))
dim = numindvar * Nt
tmp = @view wBinv[1:numindvar]
tmp ./= dt[1]
tmp = @view wBinv[dim-2:end]
tmp ./= dt[end]
for indx = 2:Nt-1
tmp = @view wBinv[(indx-1)*numindvar+1:indx*numindvar]
tmp ./= (dt[indx]+dt[indx-1])
end
wBinv .*= 2*Δt
return nothing
end
wE!(S::LSSSchur,Δt,dt,LSSregularizer::AbstractCosWindowing) = nothing
function wE!(S::LSSSchur,Δt,dt,LSSregularizer::TimeDilation)
@unpack wEinv = S
@unpack alpha = LSSregularizer
@. wEinv = Δt/(alpha^2*dt)
return nothing
end
function B!(S::LSSSchur,dt,umid,sense,sensealg)
@unpack B = S
@unpack f,J,uf,numindvar,f_cache,jac_config = sense
fill!(B, zero(eltype(J)))
for (i,u) in enumerate(eachcol(umid))
if DiffEqBase.has_jac(f)
f.jac(J,u,uf.p,uf.t) # Calculate the Jacobian into J
else
jacobian!(J, uf, u, f_cache, sensealg, jac_config)
end
B0 = @view B[(i-1)*numindvar+1:i*numindvar,i*numindvar+1:(i+1)*numindvar]
B1 = @view B[(i-1)*numindvar+1:i*numindvar,(i-1)*numindvar+1:i*numindvar]
B0 .+= I/dt[i] - J/2
B1 .+= -I/dt[i] -J/2
end
return nothing
end
E!(S::LSSSchur,dudt,LSSregularizer::AbstractCosWindowing) = nothing
function E!(S::LSSSchur,dudt,LSSregularizer::TimeDilation)
@unpack E = S
numindvar, Ndt = size(dudt)
for i=1:Ndt
tmp = @view E[(i-1)*numindvar+1:i*numindvar,i]
copyto!(tmp, (@view dudt[:,i]))
end
return nothing
end
# compute Schur
function SchurLU(S::LSSSchur)
@unpack B, E, wBinv, wEinv = S
Smat = B*Diagonal(wBinv)*B'
(wEinv !== nothing) && (Smat .+= E*Diagonal(wEinv)*E')
F = lu!(Smat)
return F
end
function b!(b, prob::ForwardLSSProblem)
@unpack diffcache, umid, sensealg = prob
@unpack f, f_cache, pJ, pf, paramjac_config, uf, numindvar = diffcache
for (i,u) in enumerate(eachcol(umid))
if DiffEqBase.has_paramjac(f)
f.paramjac(pJ, u, uf.p, pf.t)
else
pf.u = u
jacobian!(pJ, pf, uf.p, f_cache, sensealg, paramjac_config)
end
tmp = @view b[(i-1)*numindvar+1:i*numindvar,:]
copyto!(tmp, pJ)
end
return nothing
end
function shadow_forward(prob::ForwardLSSProblem; sensealg=prob.sensealg)
shadow_forward(prob,sensealg,sensealg.LSSregularizer)
end
function shadow_forward(prob::ForwardLSSProblem,sensealg::ForwardLSS,LSSregularizer::TimeDilation)
@unpack sol, S, F, window, Δt, diffcache, b, w, v, η, res, g, g0, dg, umid = prob
@unpack wBinv, wEinv, B, E = S
@unpack dg_val, numparams, numindvar, uf = diffcache
@unpack t0skip, t1skip = LSSregularizer
n0 = searchsortedfirst(sol.t, sol.t[1]+t0skip)
n1 = searchsortedfirst(sol.t, sol.t[end]-t1skip)
b!(b,prob)
ures = @view sol.u[n0:n1]
umidres = @view umid[:,n0:n1-1]
# reset
res .*=false
for i=1:numparams
#running average
g0 *= false
bpar = @view b[:,i]
w .= F\bpar
v .= Diagonal(wBinv)*(B'*w)
η .= Diagonal(wEinv)*(E'*w)
ηres = @view η[n0:n1-1]
for (j, u) in enumerate(ures)
vtmp = @view v[(n0+j-2)*numindvar+1:(n0+j-1)*numindvar]
# final gradient result for ith parameter
accumulate_cost!(dg, u, uf.p, uf.t, sensealg, diffcache, n0+j-1)
if dg_val isa Tuple
res[i] += dot(dg_val[1], vtmp)
res[i] += dg_val[2][i]
else
res[i] += dot(dg_val, vtmp)
end
end
# mean value
res[i] = res[i]/(n1-n0+1)
for (j,u) in enumerate(eachcol(umidres))
# compute objective
gtmp = g(u,uf.p,nothing)
g0 += gtmp
res[i] -= ηres[j]*gtmp/(n1-n0)
end
res[i] = res[i] + sum(ηres)*g0/(n1-n0)^2
end
return res
end
function shadow_forward(prob::ForwardLSSProblem,sensealg::ForwardLSS,LSSregularizer::CosWindowing)
@unpack sol, S, F, window, Δt, diffcache, b, w, v, dg, res = prob
@unpack wBinv, B = S
@unpack dg_val, numparams, numindvar, uf = diffcache
b!(b,prob)
# windowing (cos)
@. window = (sol.t-sol.t[1])*convert(eltype(Δt),2*pi/Δt)
@. window = one(eltype(window)) - cos(window)
window ./= sum(window)
res .*= false
for i=1:numparams
bpar = @view b[:,i]
w .= F\bpar
v .= Diagonal(wBinv)*(B'*w)
for (j,u) in enumerate(sol.u)
vtmp = @view v[(j-1)*numindvar+1:j*numindvar]
# final gradient result for ith parameter
accumulate_cost!(dg, u, uf.p, uf.t, sensealg, diffcache, j)
if dg_val isa Tuple
res[i] += dot(dg_val[1], vtmp) * window[j]
res[i] += dg_val[2][i] * window[j]
else
res[i] += dot(dg_val, vtmp) * window[j]
end
end
end
return res
end
function shadow_forward(prob::ForwardLSSProblem,sensealg::ForwardLSS,LSSregularizer::Cos2Windowing)
@unpack sol, S, F, window, Δt, diffcache, b, w, v, dg, res = prob
@unpack wBinv, B = S
@unpack dg_val, numparams, numindvar, uf = diffcache
b!(b,prob)
res .*= false
# windowing cos2
@. window = (sol.t-sol.t[1])*convert(eltype(Δt),2*pi/Δt)
@. window = (one(eltype(window)) - cos(window))^2
window ./= sum(window)
for i=1:numparams
bpar = @view b[:,i]
w .= F\bpar
v .= Diagonal(wBinv)*(B'*w)
for (j, u) in enumerate(sol.u)
vtmp = @view v[(j-1)*numindvar+1:j*numindvar]
# final gradient result for ith parameter
accumulate_cost!(dg, u, uf.p, uf.t, sensealg, diffcache, j)
if dg_val isa Tuple
res[i] += dot(dg_val[1], vtmp) * window[j]
res[i] += dg_val[2][i] * window[j]
else
res[i] += dot(dg_val, vtmp) * window[j]
end
end
end
return res
end
function accumulate_cost!(dg, u, p, t, sensealg::ForwardLSS, diffcache, indx)
@unpack dg_val, pgpu, pgpu_config, pgpp, pgpp_config, uf = diffcache
if dg === nothing
if dg_val isa Tuple
DiffEqSensitivity.gradient!(dg_val[1], pgpu, u, sensealg, pgpu_config)
DiffEqSensitivity.gradient!(dg_val[2], pgpp, p, sensealg, pgpp_config)
else
DiffEqSensitivity.gradient!(dg_val, pgpu, u, sensealg, pgpu_config)
end
else
if dg_val isa Tuple
dg[1](dg_val[1], u, p, nothing, indx) # indx = n0 + j - 1 for LSSregularizer and j for windowing
dg[2](dg_val[2], u, p, nothing, indx)
dg_val[1] .*= -1 # flipped concrete_solve sign
dg_val[2] .*= -1
else
dg(dg_val, u, p, nothing, indx)
dg_val .*= -1
end
end
return nothing
end
struct AdjointLSSProblem{A,C,solType,dtType,umidType,dudtType,SType,FType,hType,bType,wType,
ΔtType,G0,G,DG,resType}
sensealg::A
diffcache::C
sol::solType
dt::dtType
umid::umidType
dudt::dudtType
S::SType
F::FType
h::hType
b::bType
wa::wType
Δt::ΔtType
Nt::Int
g0::G0
g::G
dg::DG
res::resType
end
function AdjointLSSProblem(sol, sensealg::AdjointLSS, t=nothing, dg = nothing;
kwargs...)
@unpack f, p, u0, tspan = sol.prob
@unpack g = sensealg
isinplace = DiffEqBase.isinplace(f)
# some shadowing sensealgs require knowledge of g
check_for_g(sensealg,g)
p === nothing && error("You must have parameters to use parameter sensitivity calculations!")
!(sol.u isa AbstractVector) && error("`u` has to be an AbstractVector.")
# assert that all ts are hit if concrete solve interface/discrete costs are used
if t !== nothing
@assert sol.t == t
end
sense = LSSSensitivityFunction(sensealg,f,f.analytic,f.jac,
f.jac_prototype,f.sparsity,f.paramjac,
u0,sensealg,
p,similar(u0),f.mass_matrix,
f.colorvec,
tspan,g,dg)
@unpack numparams, numindvar = sense
Nt = length(sol.t)
Ndt = Nt-one(Nt)
# pre-allocate variables
dt = similar(sol.t, Ndt)
umid = Matrix{eltype(u0)}(undef,numindvar,Ndt)
dudt = Matrix{eltype(u0)}(undef,numindvar,Ndt)
# compute their values
discretize_ref_trajectory!(dt, umid, dudt, sol, Ndt)
S = LSSSchur(dt,u0,numindvar,Nt,Ndt,sensealg.LSSregularizer)
if sensealg.LSSregularizer isa TimeDilation
g0 = g(u0,p,tspan[1])
else
g0 = nothing
end
b = Vector{eltype(u0)}(undef,numindvar*Ndt)
h = Vector{eltype(u0)}(undef,Ndt)
wa = similar(dt,numindvar*Ndt)
Δt = tspan[2] - tspan[1]
wB!(S,Δt,Nt,numindvar,dt)
wE!(S,Δt,dt,sensealg.LSSregularizer)
B!(S,dt,umid,sense,sensealg)
E!(S,dudt,sensealg.LSSregularizer)
F = SchurLU(S)
wBcorrect!(S,sol,g,Nt,sense,sensealg,dg)
h!(h,g0,g,umid,p,S.wEinv)
res = similar(u0, numparams)
AdjointLSSProblem{typeof(sensealg),typeof(sense),typeof(sol),typeof(dt),
typeof(umid),typeof(dudt),
typeof(S),typeof(F),typeof(h),typeof(b),typeof(wa),typeof(Δt),
typeof(g0),typeof(g),typeof(dg),typeof(res)}(sensealg,sense,sol,dt,umid,dudt,S,F,h,b,wa,
Δt,Nt,g0,g,dg,res)
end
function h!(h,g0,g,u,p,wEinv)
for (j,uj) in enumerate(eachcol(u))
# compute objective
h[j] = g(uj,p,nothing)
end
h .= -(h .- mean(h)) / (size(u)[2])
@. h = wEinv*h
return nothing
end
function wBcorrect!(S,sol,g,Nt,sense,sensealg,dg)
@unpack dg_val, pgpu, pgpu_config, numparams, numindvar, uf = sense
@unpack wBinv = S
for (i,u) in enumerate(sol.u)
_wBinv = @view wBinv[(i-1)*numindvar+1:i*numindvar]
if dg === nothing
if dg_val isa Tuple
DiffEqSensitivity.gradient!(dg_val[1], pgpu, u, sensealg, pgpu_config)
@. _wBinv = _wBinv*dg_val[1]/Nt
else
DiffEqSensitivity.gradient!(dg_val, pgpu, u, sensealg, pgpu_config)
@. _wBinv = _wBinv*dg_val/Nt
end
else
if dg_val isa Tuple
dg[1](dg_val[1],u,uf.p,nothing,i)
@. _wBinv = -_wBinv*dg_val[1]/Nt
else
dg(dg_val,u,uf.p,nothing,i)
@. _wBinv = -_wBinv*dg_val/Nt
end
end
end
return nothing
end
function shadow_adjoint(prob::AdjointLSSProblem; sensealg=prob.sensealg)
shadow_adjoint(prob,sensealg,sensealg.LSSregularizer)
end
function shadow_adjoint(prob::AdjointLSSProblem,sensealg::AdjointLSS,LSSregularizer::TimeDilation)
@unpack sol, S, F, Δt, diffcache, h, b, wa, res, g, g0, dg, umid = prob
@unpack wBinv, B, E = S
@unpack dg_val, pgpp, pgpp_config, numparams, numindvar, uf, f, f_cache, pJ, pf, paramjac_config = diffcache
@unpack t0skip, t1skip = LSSregularizer
b .= E*h + B*wBinv
wa .= F\b
n0 = searchsortedfirst(sol.t, sol.t[1]+t0skip)
n1 = searchsortedfirst(sol.t, sol.t[end]-t1skip)
umidres = @view umid[:,n0:n1-1]
wares = @view wa[(n0-1)*numindvar+1:(n1-1)*numindvar]
# reset
res .*= false
if dg_val isa Tuple
for (j,u) in enumerate(eachcol(umidres))
if dg === nothing
DiffEqSensitivity.gradient!(dg_val[2], pgpp, uf.p, sensealg, pgpp_config)
@. res += dg_val[2]
else
dg[2](dg_val[2],u,uf.p,nothing,n0+j-1)
@. res -= dg_val[2]
end
end
res ./= (size(umidres)[2])
end
for (j,u) in enumerate(eachcol(umidres))
_wares = @view wares[(j-1)*numindvar+1:j*numindvar]
if DiffEqBase.has_paramjac(f)
f.paramjac(pJ, u, uf.p, pf.t)
else
pf.u = u
jacobian!(pJ, pf, uf.p, f_cache, sensealg, paramjac_config)
end
res .+= pJ'*_wares
end
return res
end
check_for_g(sensealg::Union{ForwardLSS,AdjointLSS},g)=((sensealg.LSSregularizer isa TimeDilation && g===nothing) && error("Time dilation needs explicit knowledge of g. Either pass `g` as a kwarg to `ForwardLSS(g=g)` or `AdjointLSS(g=g)` or use ForwardLSS/AdjointLSS with windowing."))
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 11339 | struct NILSASSensitivityFunction{iip,NILSS,ASF,Mtype} <: DiffEqBase.AbstractODEFunction{iip}
nilss::NILSS
S::ASF # Adjoint sensitivity function
M::Mtype
discrete::Bool
end
struct QuadratureCache{A1,A2,A3,A4,A5}
dwv::A1
dwf::A1
dwfs::A2
dvf::A3
dvfs::A4
dJs::A4
C::A5
R::A5
b::A1
end
function QuadratureCache(u0, M, nseg, numparams)
dwv = Array{eltype(u0)}(undef, M, nseg)
dwf = Array{eltype(u0)}(undef, M, nseg)
dwfs = Array{eltype(u0)}(undef, numparams*M, nseg)
dvf = Array{eltype(u0)}(undef, 1, nseg)
dvfs = Array{eltype(u0)}(undef, numparams, nseg)
dJs = Array{eltype(u0)}(undef, numparams, nseg)
C = Array{eltype(u0)}(undef, M, M, nseg)
R = Array{eltype(u0)}(undef, M, M, nseg)
b = Array{eltype(u0)}(undef, M, nseg)
QuadratureCache{typeof(dwv),typeof(dwfs),typeof(dvf),typeof(dvfs),typeof(C)}(dwv,dwf,dwfs,dvf,dvfs,dJs,C,R,b)
end
struct NILSASProblem{A,NILSS,Aprob,Qcache,solType,z0Type,G,DG,T}
sensealg::A
nilss::NILSS # diffcache
adjoint_prob::Aprob
quadcache::Qcache
sol::solType
z0::z0Type
g::G
dg::DG
T_seg::T
dtsave::T
end
function NILSASProblem(sol, sensealg::NILSAS, t=nothing, dg = nothing; kwargs...)
@unpack f, p, u0, tspan = sol.prob
@unpack nseg, nstep, rng, adjoint_sensealg, M, g = sensealg #number of segments on time interval, number of steps saved on each segment
numindvar = length(u0)
numparams = length(p)
# some shadowing sensealgs require knowledge of g
check_for_g(sensealg,g)
# sensealg choice
adjoint_sensealg === nothing && (adjoint_sensealg = automatic_sensealg_choice(sol.prob,u0,p,false))
p === nothing && error("You must have parameters to use parameter sensitivity calculations!")
!(u0 isa AbstractVector) && error("`u` has to be an AbstractVector.")
nstep <= 1 && error("At least the start and the end point of each segment must be stored. Please use `nstep >=2`.")
!(u0 isa AbstractVector) && error("`u` has to be an AbstractVector.")
# segmentation: determine length of segmentation and spacing between saved points
T_seg = (tspan[2]-tspan[1])/nseg # length of each segment
dtsave = T_seg/(nstep-1)
# homogenous + inhomogenous adjoint sensitivity problem
# assign initial values to y, vstar, w
y = copy(sol.u[end])
z0 = terminate_conditions(adjoint_sensealg,rng,f,y,p,tspan[2],numindvar,numparams,M)
nilss = NILSSSensitivityFunction(sensealg,f,u0,p,tspan,g,dg)
tspan = (tspan[2] - T_seg, tspan[2])
checkpoints = tspan[1]:dtsave:tspan[2]
adjoint_prob = ODEAdjointProblem(sol,adjoint_sensealg,g,t,dg; checkpoints=checkpoints, z0=z0, M=M, nilss=nilss, tspan=tspan, kwargs...)
# pre-allocate variables for integration Eq.(23) in NILSAS paper.
quadcache = QuadratureCache(u0, M, nseg, numparams)
NILSASProblem{typeof(sensealg),typeof(nilss),typeof(adjoint_prob),typeof(quadcache),
typeof(sol),typeof(z0),typeof(g),typeof(dg),typeof(T_seg)}(sensealg,nilss,
adjoint_prob,quadcache,sol,deepcopy(z0),g,dg,T_seg,dtsave)
end
function terminate_conditions(alg::BacksolveAdjoint,rng,f,y,p,t,numindvar,numparams,M)
if isinplace(f)
f_unit = zero(y)
f(f_unit,y,p,t)
normalize!(f_unit)
else
f_unit = f(y,p,t)
normalize!(f_unit)
end
if M>1
W = rand(rng,numindvar,M-1)
W .-= (f_unit'*W) .* f_unit
w, _ = qr(W)
_w = @view w[:,1:M-1]
W = hcat(_w, f_unit)
else
W = f_unit
end
vst = zeros(numindvar)
# quadratures
C = zeros(M,M)
dwv = zeros(M)
dwf = zeros(M)
dvf = zeros(1)
dJs = zeros(numparams)
return ArrayPartition([vst;vec(W)],zeros(numparams*(M+1)),y,C,dwv,dwf,dvf,dJs)
end
function split_states(du,u,t,NS::NILSASSensitivityFunction,j;update=true)
@unpack nilss, S = NS
@unpack numindvar,numparams = nilss
indx1 = (j-1)*(numindvar) + 1
indx2 = indx1 + (numindvar-1)
indx3 = (j-1)*(numparams) + 1
indx4 = indx3 + (numparams-1)
λ = @view u.x[1][indx1:indx2]
grad = @view u.x[2][indx3:indx4]
_y = u.x[3]
# like ODE/Drift term and scalar noise
dλ = @view du.x[1][indx1:indx2]
dgrad = @view du.x[2][indx3:indx4]
dy = du.x[3]
λ,grad,_y,dλ,dgrad,dy
end
function split_quadratures(du,u,t,NS::NILSASSensitivityFunction;update=true)
@unpack nilss, S = NS
@unpack numindvar,numparams = nilss
C = u.x[4]
dwv = u.x[5]
dwf = u.x[6]
dvf = u.x[7]
dJs = u.x[8]
dC = du.x[4]
ddwv = du.x[5]
ddwf = du.x[6]
ddvf = du.x[7]
ddJs = du.x[8]
dC,ddwv,ddwf,ddvf,ddJs, C,dwv,dwf,dvf,dJs
end
function (NS::NILSASSensitivityFunction)(du,u,p,t)
@unpack nilss, S, M = NS
@unpack f, dg, dg_val, pgpu, pgpu_config, pgpp, pgpp_config, numparams, numindvar, alg = nilss
@unpack y, discrete = S
λ,_,_y,dλ,dgrad,dy = split_states(du,u,t,NS,1)
copyto!(vec(y), _y)
# compute gradient of objective wrt. state
if !discrete
accumulate_cost!(dg, y, p, t, nilss)
end
# loop over all adjoint states
for j=1:M+1
λ,_,_,dλ,dgrad,dy = split_states(du,u,t,NS,j)
vecjacobian!(dλ, y, λ, p, t, S, dgrad=dgrad, dy=dy)
dλ .*= -1
if j==1
# j = 1 is the inhomogenous adjoint solution
if !discrete
if dg_val isa Tuple
dλ .-= vec(dg_val[1])
else
dλ .-= vec(dg_val)
end
end
end
end
# quadratures
dC,ddwv,ddwf,ddvf,ddJs, _,_,_,_,_ = split_quadratures(du,u,t,NS)
# j = 1 is the inhomogenous adjoint solution
λv,_,_,_,_,dy = split_states(du,u,t,NS,1)
ddvf .= -dot(λv,dy)
for j=1:M
λ,_,_,_,_,_ = split_states(du,u,t,NS,j+1)
ddwf[j] = -dot(λ,dy)
ddwv[j] = -dot(λ,λv)
for i=j+1:M
λ2,_,_,_,_,_ = split_states(du,u,t,NS,i+1)
dC[j,i] = -dot(λ,λ2)
dC[i,j] = dC[j,i]
end
dC[j,j] = -dot(λ,λ)
end
if dg_val isa Tuple && !discrete
ddJs = -vec(dg_val[2])
end
return nothing
end
function accumulate_cost!(dg, y, p, t, nilss::NILSSSensitivityFunction)
@unpack dg_val, pgpu, pgpu_config, pgpp, pgpp_config, alg = nilss
if dg===nothing
if dg_val isa Tuple
DiffEqSensitivity.gradient!(dg_val[1],pgpu,y,alg,pgpu_config)
DiffEqSensitivity.gradient!(dg_val[2],pgpp,y,alg,pgpp_config)
dg_val[1] .*= -1
dg_val[2] .*= -1
else
DiffEqSensitivity.gradient!(dg_val,pgpu,y,alg,pgpu_config)
dg_val .*= -1
end
else
if dg_val isa Tuple
dg[1](dg_val[1],y,p,t)
dg[2](dg_val[2],y,p,t)
else
dg(dg_val,y,p,t)
end
end
return nothing
end
function adjoint_sense(prob::NILSASProblem,nilsas::NILSAS,alg; kwargs...)
@unpack M, nseg, nstep, adjoint_sensealg = nilsas
@unpack sol, nilss, z0, g, dg, T_seg, dtsave, adjoint_prob = prob
@unpack u0, tspan = adjoint_prob
copyto!(z0,u0)
@assert haskey(adjoint_prob.kwargs, :callback)
# get loss callback
cb = adjoint_prob.kwargs[:callback]
# adjoint sensitivities on segments
for iseg=nseg:-1:1
t1 = tspan[1]-(nseg-iseg+1)*T_seg
t2 = tspan[1]-(nseg-iseg)*T_seg
checkpoints=t1:dtsave:t2
_prob = ODEAdjointProblem(sol,adjoint_sensealg,g,nothing,dg;
checkpoints=checkpoints,z0=z0,M=M,nilss=nilss,tspan=(t1,t2),kwargs...)
_sol = solve(_prob,alg; save_everystep=false,save_start=false,saveat=eltype(sol[1])[],
dt = dtsave,
tstops=checkpoints,
callback = cb,
kwargs...)
# renormalize at interfaces and store quadratures
# update sense problem
renormalize!(prob, _sol, z0, iseg)
end
return nothing
end
function renormalize!(prob::NILSASProblem, sol, z0, iseg)
@unpack quadcache, nilss, sensealg = prob
@unpack M = sensealg
@unpack numparams, numindvar = nilss
@unpack R,b = quadcache
x = sol.u[end].x
# vstar_right (inhomogenous adjoint on the rhs of the interface)
vstar = @view x[1][1:numindvar]
# homogenous adjoint on the rhs of the interface
W = @view x[1][numindvar+1:end]
W = reshape(W, numindvar, M)
Q_, R_ = qr(W)
Q = @view Q_[:,1:M]
b_ = (Q'*vstar)
# store R and b to solve NILSAS problem
copyto!( (@view R[:,:,iseg]), R_)
copyto!( (@view b[:,iseg]), b_)
# store quadrature values
store_quad(quadcache, x, numparams, iseg)
# reset z0
reset!(z0, numindvar, vstar, b_, Q)
return nothing
end
function store_quad(quadcache, x, numparams, iseg)
@unpack dwv,dwf,dwfs,dvf,dvfs,dJs,C = quadcache
grad_vfs = @view x[2][1:numparams]
copyto!( (@view dvfs[:,iseg]), grad_vfs)
grad_wfs = @view x[2][numparams+1:end]
copyto!( (@view dwfs[:,iseg]), grad_wfs)
# C_i = x[4]
copyto!( (@view C[:,:,iseg]), x[4])
# dwv_i = x[5]
copyto!( (@view dwv[:,iseg]), x[5])
# dwf_i = x[6]
copyto!( (@view dwf[:,iseg]), x[6])
# dvf_i = x[7]
copyto!( (@view dvf[:,iseg]), x[7])
# dJs_i = x[8]
copyto!( (@view dJs[:,iseg]), x[8])
return nothing
end
function reset!(z0, numindvar, vstar, b, Q)
# modify z0
x0 = z0.x
# vstar_left
v = @view x0[1][1:numindvar]
v .= vstar - vec(b'*Q')
# W_left (homogenous adjoint on lhs of the interface)
w = @view x0[1][numindvar+1:end]
w .= vec(Q)
# reset all other values t0 zero
x0[2] .*= false
x0[4] .*= false
x0[5] .*= false
x0[6] .*= false
x0[7] .*= false
x0[8] .*= false
return nothing
end
function nilsas_min(cache::QuadratureCache)
@unpack dwv,dwf,dvf,C,R,b = cache
# Construct Schur complement of the Lagrange multiplier method of the NILSAS problem.
# see description in Appendix A of Nilsas paper.
# M= # unstable CLVs, K = # segments
M, K = size(dwv)
# construct Cinv
# Cinv is a block diagonal matrix
Cinv = zeros(eltype(C), M*K, M*K)
for i=1:K
Ci = @view C[:, :, i]
_Cinv = @view Cinv[(i-1)*M+1:i*M, (i-1)*M+1:i*M]
Ciinv = inv(Ci)
copyto!(_Cinv,Ciinv)
end
# construct B, also very sparse if K >> M
B = zeros(eltype(C), M*K-M+1, M*K)
for i=1:K
if i<K
# off diagonal Rs
_B = @view B[(i-1)*M+1:i*M, i*M+1:(i+1)*M]
_R = @view R[:,:,i+1]
copyto!(_B, _R)
_B .*= -1
# diagonal ones
for j=1:M
B[(i-1)*M+j, (i-1)*M+j] = one(eltype(R))
end
end
# last row
dwfi = dwf[:,i]
_B = @view B[end, (i-1)*M+1:i*M]
copyto!(_B, dwfi)
end
# construct d
d = vec(dwv)
# construct b
_b = [b[M+1:end]; -sum(dvf)]
# compute Lagrange multiplier
λ = (-B*Cinv*B') \ (B*Cinv*d + _b)
# return a
return reshape(-Cinv*(B'*λ + d), M, K)
end
function shadow_adjoint(prob::NILSASProblem,alg; sensealg=prob.sensealg, kwargs...)
shadow_adjoint(prob,sensealg,alg; kwargs...)
end
function shadow_adjoint(prob::NILSASProblem,sensealg::NILSAS,alg; kwargs...)
# compute adjoint sensitivities
adjoint_sense(prob,sensealg,alg; kwargs...)
# compute NILSAS problem on multiple segments
a = nilsas_min(prob.quadcache)
# compute gradient, Eq. (28) -- second part to avoid explicit construction of vbar
@unpack M, nseg = sensealg
@unpack dvfs, dJs, dwfs = prob.quadcache
res = vec(sum(dvfs,dims=2)) + vec(sum(dJs,dims=2))
NP = length(res) # number of parameters
# loop over segments
for (i,ai) in enumerate(eachcol(a))
dwfsi = @view dwfs[:,i]
dwfsi = reshape(dwfsi,NP,M)
res .+= dwfsi*ai
end
return res/(nseg*prob.T_seg)
end
check_for_g(sensealg::NILSAS,g) = (g===nothing && error("To use NILSAS, g must be passed as a kwarg to `NILSAS(g=g)`."))
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 16389 | struct NILSSSensitivityFunction{iip,F,Alg,
PGPU,PGPP,CONFU,CONGP,DGVAL,DG,jType,RefType} <: DiffEqBase.AbstractODEFunction{iip}
f::F
alg::Alg
numparams::Int
numindvar::Int
pgpu::PGPU
pgpp::PGPP
pgpu_config::CONFU
pgpp_config::CONGP
dg_val::DGVAL
dg::DG
jevery::jType # if concrete_solve interface for discrete cost functions is used
cur_time::RefType
end
function NILSSSensitivityFunction(sensealg,f,u0,p,tspan,g,dg,jevery=nothing,cur_time=nothing)
numparams = length(p)
numindvar = length(u0)
# compute gradients of objective
if dg !== nothing
pgpu = nothing
pgpp = nothing
pgpu_config = nothing
pgpp_config = nothing
if dg isa Tuple && length(dg) == 2
dg_val = (similar(u0, numindvar),similar(u0, numparams))
dg_val[1] .= false
dg_val[2] .= false
else
dg_val = similar(u0, numindvar) # number of funcs size
dg_val .= false
end
else
pgpu = UGradientWrapper(g,tspan[1],p) # ∂g∂u
pgpp = ParamGradientWrapper(g,tspan[1],u0) #∂g∂p
pgpu_config = build_grad_config(sensealg,pgpu,u0,tspan[1])
pgpp_config = build_grad_config(sensealg,pgpp,u0,tspan[1])
dg_val = (similar(u0, numindvar),similar(u0, numparams))
dg_val[1] .= false
dg_val[2] .= false
end
NILSSSensitivityFunction{isinplace(f),typeof(f),typeof(sensealg),
typeof(pgpu),typeof(pgpp),typeof(pgpu_config),typeof(pgpp_config),typeof(dg_val),typeof(dg),typeof(jevery),typeof(cur_time)}(
f,sensealg,numparams,numindvar,pgpu,pgpp,pgpu_config,pgpp_config,dg_val,dg,jevery,cur_time)
end
struct NILSSProblem{A,CacheType,FSprob,probType,u0Type,vstar0Type,w0Type,
TType,dtType,gType,yType,vstarType,
wType,RType,bType,weightType,CType,dType,BType,aType,vType,xiType,
G,DG,resType}
sensealg::A
diffcache::CacheType
forward_prob::FSprob
prob::probType
u0::u0Type
vstar0::vstar0Type
w0::w0Type
nus::Int
T_seg::TType
dtsave::dtType
gsave::gType
y::yType
dudt::yType
dgdu::yType
vstar::vstarType
vstar_perp::vstarType
w::wType
w_perp::wType
R::RType
b::bType
weight::weightType
Cinv::CType
d::dType
B::BType
a::aType
v::vType
v_perp::vType
ξ::xiType
g::G
dg::DG
res::resType
end
function NILSSProblem(prob, sensealg::NILSS, t=nothing, dg = nothing;
kwargs...)
@unpack f, p, u0, tspan = prob
@unpack nseg, nstep, nus, rng, g = sensealg #number of segments on time interval, number of steps saved on each segment
numindvar = length(u0)
numparams = length(p)
# some shadowing sensealgs require knowledge of g
check_for_g(sensealg,g)
# integer dimension of the unstable subspace
if nus === nothing
nus = numindvar - one(numindvar)
end
(nus >= numindvar) && error("`nus` must be smaller than `numindvar`.")
isinplace = DiffEqBase.isinplace(f)
p === nothing && error("You must have parameters to use parameter sensitivity calculations!")
!(u0 isa AbstractVector) && error("`u` has to be an AbstractVector.")
# segmentation: determine length of segmentation and spacing between saved points
T_seg = (tspan[2]-tspan[1])/nseg # length of each segment
dtsave = T_seg/(nstep-1)
# assert that dtsave is chosen such that all ts are hit if concrete solve interface/discrete costs are used
if t!==nothing
@assert t isa StepRangeLen
dt_ts = step(t)
@assert dt_ts >= dtsave
@assert T_seg >= dt_ts
jevery = Int(dt_ts/dtsave) # will throw an inexact error if dt_ts is not a multiple of dtsave. (could be more sophisticated)
cur_time = Ref(1)
else
jevery = nothing
cur_time = nothing
end
# inhomogenous forward sensitivity problem
chunk_size = determine_chunksize(numparams,sensealg)
autodiff = alg_autodiff(sensealg)
difftype = diff_type(sensealg)
autojacvec = sensealg.autojacvec
# homogenous + inhomogenous forward sensitivity problems
forward_prob = ODEForwardSensitivityProblem(f,u0,tspan,p,ForwardSensitivity(chunk_size=chunk_size,autodiff=autodiff,
diff_type=difftype,autojacvec=autojacvec);nus=nus, kwargs...)
sense = NILSSSensitivityFunction(sensealg,f,u0,p,tspan,g,dg,jevery,cur_time)
# pre-allocate variables
gsave = Matrix{eltype(u0)}(undef, nstep, nseg)
y = Array{eltype(u0)}(undef, numindvar, nstep, nseg)
dudt = similar(y)
dgdu = similar(y)
vstar = Array{eltype(u0)}(undef, numparams, numindvar, nstep, nseg) # generalization for several parameters numindvar*numparams
vstar_perp = similar(vstar)
w = Array{eltype(u0)}(undef, numindvar, nstep, nseg, nus)
w_perp = similar(w)
# assign initial values to y, v*, w
y[:,1,1] .= u0
for i=1:numparams
_vstar = @view vstar[i,:,1,1]
copyto!(_vstar, zero(u0))
end
for ius=1:nus
_w = @view w[:,1,1,ius]
rand!(rng,_w)
normalize!(_w)
end
vstar0 = zeros(eltype(u0), numindvar*numparams)
w0 = vec(w[:,1,1,:])
R = Array{eltype(u0)}(undef, numparams, nseg-1, nus, nus)
b = Array{eltype(u0)}(undef, numparams, (nseg-1)*nus)
# a weight matrix for integration, 0.5 at interfaces
weight = ones(1,nstep)
weight[1] /= 2
weight[end] /= 2
# Construct Schur complement of the Lagrange multiplier method of the NILSS problem.
# See the paper on FD-NILSS
# find C^-1
Cinv = Matrix{eltype(u0)}(undef, nseg*nus, nseg*nus)
Cinv .*= false
d = Vector{eltype(u0)}(undef, nseg*nus)
B = Matrix{eltype(u0)}(undef, (nseg-1)*nus, nseg*nus)
B .*= false
a = Vector{eltype(u0)}(undef, nseg*nus)
v = Array{eltype(u0)}(undef, numindvar, nstep, nseg)
v_perp = similar(v)
# only need to use last step in each segment
ξ = Matrix{eltype(u0)}(undef, nseg, 2)
res = similar(u0, numparams)
NILSSProblem{typeof(sensealg),typeof(sense),typeof(forward_prob),typeof(prob),
typeof(u0), typeof(vstar0), typeof(w0),
typeof(T_seg),typeof(dtsave),typeof(gsave),typeof(y),typeof(vstar),typeof(w),typeof(R),
typeof(b),typeof(weight),typeof(Cinv),typeof(d),typeof(B),typeof(a),typeof(v),typeof(ξ),
typeof(g),typeof(dg),typeof(res)}(sensealg,sense,forward_prob,prob,u0,vstar0,w0,
nus,T_seg,dtsave,gsave,y,dudt,dgdu,vstar,vstar_perp,w,w_perp,R,b,weight,Cinv,d,
B,a,v,v_perp,ξ,g,dg,res)
end
function (NS::NILSSForwardSensitivityFunction)(du,u,p,t)
@unpack S, nus = NS
y = @view u[1:S.numindvar] # These are the independent variables
dy = @view du[1:S.numindvar]
S.f(dy,y,p,t) # Make the first part be the ODE
# Now do sensitivities
# Compute the Jacobian
if !S.isautojacvec
if has_original_jac(S.f)
S.original_jac(S.J,y,p,t) # Calculate the Jacobian into J
else
S.uf.t = t
jacobian!(S.J, S.uf, y, S.f_cache, S.alg, S.jac_config)
end
end
if DiffEqBase.has_paramjac(S.f)
S.paramjac(S.pJ,y,p,t) # Calculate the parameter Jacobian into pJ
else
S.pf.t = t
S.pf.u .= y
jacobian!(S.pJ, S.pf, p, S.f_cache, S.alg, S.paramjac_config)
end
# Compute the parameter derivatives
for j=1:nus+1
for i in eachindex(p)
indx1 = (j-1)*S.numindvar*1 + i*S.numindvar+1
indx2 = (j-1)*S.numindvar*1 + (i+1)*S.numindvar
Sj = @view u[indx1:indx2]
dp = @view du[indx1:indx2]
if !S.isautojacvec
mul!(dp,S.J,Sj)
else
jacobianvec!(dp, S.uf, y, Sj, S.alg, S.jac_config)
end
if j == nus+1
# inhomogenous (otherwise homogenous tangent solution)
dp .+= @view S.pJ[:,i]
end
end
end
return nothing
end
function forward_sense(prob::NILSSProblem,nilss::NILSS,alg)
#TODO determine a good dtsave (ΔT in paper, see Sec.4.2)
@unpack nus, T_seg, dtsave, vstar, vstar_perp, w, w_perp, R, b, y, dudt, gsave, dgdu, forward_prob, u0, vstar0, w0 = prob
@unpack p, f = forward_prob
@unpack S, sensealg = f
@unpack nseg, nstep = nilss
@unpack numindvar, numparams = S
# push forward
t1 = forward_prob.tspan[1]
t2 = forward_prob.tspan[1]+T_seg
_prob = ODEForwardSensitivityProblem(S.f,u0,(t1,t2),p,sensealg;nus=nus,w0=w0,v0=vstar0)
for iseg=1:nseg
# compute y, w, vstar
# _sol is a numindvar*(1+nus+1) x nstep matrix
dt = (t2 - t1) / (nstep-1)
_sol = Array(solve(_prob, alg, saveat=t1:dt:t2))
store_y_w_vstar!(y, w, vstar, _sol, nus, numindvar, numparams, iseg)
# store dudt, objective g (gsave), and its derivative wrt. to u (dgdu)
dudt_g_dgdu!(dudt, gsave, dgdu, prob, y, forward_prob.p, iseg)
# calculate w_perp, vstar_perp
perp!(w_perp, vstar_perp, w, vstar, dudt, iseg, numparams, nstep, nus)
# update sense problem
if iseg < nseg
# renormalize at interfaces
renormalize!(R,b,w_perp,vstar_perp,y,vstar,w,iseg,numparams,nus)
t1 = forward_prob.tspan[1]+iseg*T_seg
t2 = forward_prob.tspan[1]+(iseg+1)*T_seg
_prob = ODEForwardSensitivityProblem(S.f,y[:,1,iseg+1],(t1,t2),p,sensealg; nus=nus,
w0=vec(w[:,1,iseg+1,:]),v0=vec(vstar[:,:,1,iseg+1]))
end
end
end
function store_y_w_vstar!(y, w, vstar, sol, nus, numindvar, numparams, iseg)
# fill y
_y = @view y[:,:,iseg]
copyto!(_y, (@view sol[1:numindvar,:]))
# fill w
# only calculate w one time, w can be reused for each parameter
for j=1:nus
indx1 = (j-1)*numindvar*1 + numindvar+1
indx2 = (j-1)*numindvar*1 + 2*numindvar
_w = @view w[:,:,iseg, j]
copyto!(_w, (@view sol[indx1:indx2,:]))
end
# fill vstar
for i=1:numparams
indx1 = nus*numindvar*1 + i*numindvar+1
indx2 = nus*numindvar*1 + (i+1)*numindvar
_vstar = @view vstar[i,:,:,iseg]
copyto!(_vstar, (@view sol[indx1:indx2,:]))
end
return nothing
end
function dudt_g_dgdu!(dudt, gsave, dgdu, nilssprob::NILSSProblem, y, p, iseg)
@unpack sensealg, diffcache, dg, g, prob = nilssprob
@unpack prob = nilssprob
@unpack jevery, cur_time = diffcache # akin to ``discrete"
_y = @view y[:,:,iseg]
for (j,u) in enumerate(eachcol(_y))
_dgdu = @view dgdu[:,j,iseg]
_dudt = @view dudt[:,j,iseg]
# compute dudt
if isinplace(prob)
prob.f(_dudt,u,p,nothing)
else
copyto!(_dudt,prob.f(u,p,nothing))
end
# compute objective
gsave[j,iseg] = g(u,p,nothing)
# compute gradient of objective wrt. state
if jevery!==nothing
# only bump on every jevery entry
# corresponds to (iseg-1)* value of dg
if (j-1) % jevery == 0
accumulate_cost!(_dgdu, dg, u, p, nothing, sensealg, diffcache, cur_time[])
cur_time[] += one(jevery)
end
else
# continuous cost function
accumulate_cost!(_dgdu, dg, u, p, nothing, sensealg, diffcache, j)
end
end
jevery !== nothing && (cur_time[] -= one(jevery)) # interface between segments gets two bumps
return nothing
end
function perp!(w_perp, vstar_perp, w, vstar, dudt, iseg, numparams, nsteps, nus)
for indx_steps=1:nsteps
_dudt = @view dudt[:,indx_steps,iseg]
for indx_nus=1:nus
_w_perp = @view w_perp[:,indx_steps,iseg,indx_nus]
_w = @view w[:,indx_steps,iseg,indx_nus]
perp!(_w_perp, _w, _dudt)
end
for indx_params=1:numparams
_vstar_perp = @view vstar_perp[indx_params,:,indx_steps,iseg]
_vstar = @view vstar[indx_params,:,indx_steps,iseg]
perp!(_vstar_perp, _vstar, _dudt)
end
end
return nothing
end
function perp!(v1, v2, v3)
v1 .= v2 - dot(v2, v3)/dot(v3, v3) * v3
end
function renormalize!(R,b,w_perp,vstar_perp,y,vstar,w,iseg,numparams,nus)
for i=1:numparams
_b = @view b[i,(iseg-1)*nus+1:iseg*nus]
_R = @view R[i,iseg,:,:]
_w_perp = @view w_perp[:,end,iseg,:]
_vstar_perp = @view vstar_perp[i,:,end,iseg]
_w = @view w[:,1,iseg+1,:]
_vstar = @view vstar[i,:,1,iseg+1]
Q_temp, R_temp = qr(_w_perp)
b_tmp = @view (Q_temp'*_vstar_perp)[1:nus]
copyto!(_b, b_tmp)
copyto!(_R, R_temp)
# set new initial values
copyto!(_w, (@view Q_temp[:,1:nus]))
copyto!(_vstar, _vstar_perp - Q_temp*b_tmp)
end
_yend = @view y[:,end,iseg]
_ystart = @view y[:,1,iseg+1]
copyto!(_ystart, _yend)
return nothing
end
function compute_Cinv!(Cinv,w_perp,weight,nseg,nus,indxp)
# construct Schur complement of Lagrange multiplier
_weight = @view weight[1,:]
for iseg=1:nseg
_C = @view Cinv[(iseg-1)*nus+1:iseg*nus, (iseg-1)*nus+1:iseg*nus]
for i=1:nus
wi = @view w_perp[:,:,iseg,i]
for j =1:nus
wj = @view w_perp[:,:,iseg,j]
_C[i,j] = sum(wi .* wj * _weight)
end
end
invC = inv(_C)
copyto!(_C, invC)
end
return nothing
end
function compute_d!(d,w_perp,vstar_perp,weight,nseg,nus,indxp)
# construct d
_weight = @view weight[1,:]
for iseg=1:nseg
_d = @view d[(iseg-1)*nus+1:iseg*nus]
vi = @view vstar_perp[indxp,:,:,iseg]
for i=1:nus
wi = @view w_perp[:,:,iseg,i]
_d[i] = sum(wi .* vi * _weight)
end
end
return nothing
end
function compute_B!(B,R,nseg,nus,indxp)
for iseg=1:nseg-1
_B = @view B[(iseg-1)*nus+1:iseg*nus, (iseg-1)*nus+1:iseg*nus]
_R = @view R[indxp,iseg,:,:]
copyto!(_B, -_R)
# off diagonal one
for i=1:nus
B[(iseg-1)*nus+i, iseg*nus+i] = one(eltype(R))
end
end
return nothing
end
function compute_a!(a,B,Cinv,b,d,indxp)
_b = @view b[indxp,:]
lbd = (-B*Cinv*B') \ (B*Cinv*d + _b)
a .= -Cinv*(B'*lbd + d)
return nothing
end
function compute_v!(v,v_perp,vstar,vstar_perp,w,w_perp,a,nseg,nus,indxp)
_vstar = @view vstar[indxp,:,:,:]
_vstar_perp = @view vstar_perp[indxp,:,:,:]
copyto!(v, _vstar)
copyto!(v_perp, _vstar_perp)
for iseg=1:nseg
vi = @view v[:,:,iseg]
vpi = @view v_perp[:,:,iseg]
for i=1:nus
wi = @view w[:,:,iseg,i]
wpi = @view w_perp[:,:,iseg,i]
vi .+= a[(iseg-1)*nus+i]*wi
vpi .+= a[(iseg-1)*nus+i]*wpi
end
end
return nothing
end
function compute_xi(ξ,v,dudt,nseg)
for iseg=1:nseg
_v = @view v[:,1,iseg]
_dudt = @view dudt[:,1,iseg]
ξ[iseg,1] = dot(_v,_dudt)/dot(_dudt,_dudt)
_v = @view v[:,end,iseg]
_dudt = @view dudt[:,end,iseg]
ξ[iseg,2] = dot(_v,_dudt)/dot(_dudt,_dudt)
end
# check if segmentation is chosen correctly
_ξ = ξ[:,1]
all(_ξ.<1e-4) || @warn "Detected a large value of ξ at the beginning of a segment."
return nothing
end
function accumulate_cost!(_dgdu, dg, u, p, t, sensealg::NILSS, diffcache::NILSSSensitivityFunction, j)
@unpack dg_val, pgpu, pgpu_config, pgpp, pgpp_config = diffcache
if dg===nothing
if dg_val isa Tuple
DiffEqSensitivity.gradient!(dg_val[1], pgpu, u, sensealg, pgpu_config)
copyto!(_dgdu, dg_val[1])
else
DiffEqSensitivity.gradient!(dg_val, pgpu, u, sensealg, pgpu_config)
copyto!(_dgdu, dg_val)
end
else
if dg_val isa Tuple
dg[1](dg_val[1],u,p,nothing,j)
@. _dgdu = -dg_val[1]
else
dg(dg_val,u,p,nothing,j)
@. _dgdu = -dg_val
end
end
return nothing
end
function shadow_forward(prob::NILSSProblem,alg; sensealg=prob.sensealg)
shadow_forward(prob,sensealg,alg)
end
function shadow_forward(prob::NILSSProblem,sensealg::NILSS,alg)
@unpack nseg, nstep = sensealg
@unpack res, nus, dtsave, vstar, vstar_perp, w, w_perp, R, b, dudt,
gsave, dgdu, forward_prob, weight, Cinv, d, B, a, v, v_perp, ξ = prob
@unpack numindvar, numparams = forward_prob.f.S
# reset dg pointer
@unpack jevery, cur_time = prob.diffcache
jevery !== nothing && (cur_time[] = one(jevery))
# compute vstar, w
forward_sense(prob,sensealg,alg)
# compute avg objective
gavg = sum(prob.weight*gsave)/((nstep-1)*nseg)
# reset gradient
res .*= false
# loop over parameters
for i=1:numparams
compute_Cinv!(Cinv,w_perp,weight,nseg,nus,i)
compute_d!(d,w_perp,vstar_perp,weight,nseg,nus,i)
compute_B!(B,R,nseg,nus,i)
compute_a!(a,B,Cinv,b,d,i)
compute_v!(v,v_perp,vstar,vstar_perp,w,w_perp,a,nseg,nus,i)
compute_xi(ξ,v,dudt,nseg)
_weight = @view weight[1,:]
for iseg=1:nseg
_dgdu = @view dgdu[:,:,iseg]
_v = @view v[:,:,iseg]
res[i] += sum((_v.*_dgdu)*_weight)/((nstep-1)*nseg)
res[i] += ξ[iseg,end]*(gavg-gsave[end,iseg])/(dtsave*(nstep-1)*nseg)
end
end
return res
end
check_for_g(sensealg::NILSS,g) = (g===nothing && error("To use NILSS, g must be passed as a kwarg to `NILSS(g=g)`."))
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 10542 | struct ODEQuadratureAdjointSensitivityFunction{C<:AdjointDiffCache,Alg<:QuadratureAdjoint,
uType,SType,fType<:DiffEqBase.AbstractDiffEqFunction} <: SensitivityFunction
diffcache::C
sensealg::Alg
discrete::Bool
y::uType
sol::SType
f::fType
end
function ODEQuadratureAdjointSensitivityFunction(g,sensealg,discrete,sol,dg)
diffcache, y = adjointdiffcache(g,sensealg,discrete,sol,dg,sol.prob.f;quad=true)
return ODEQuadratureAdjointSensitivityFunction(diffcache,sensealg,discrete,
y,sol,sol.prob.f)
end
# u = λ'
function (S::ODEQuadratureAdjointSensitivityFunction)(du,u,p,t)
@unpack sol, discrete = S
f = sol.prob.f
λ,grad,y,dλ,dgrad,dy = split_states(du,u,t,S)
vecjacobian!(dλ, y, λ, p, t, S)
dλ .*= -one(eltype(λ))
discrete || accumulate_cost!(dλ, y, p, t, S)
return nothing
end
function split_states(du,u,t,S::ODEQuadratureAdjointSensitivityFunction;update=true)
@unpack y, sol = S
if update
if typeof(t) <: ForwardDiff.Dual && eltype(y) <: AbstractFloat
y = sol(t, continuity=:right)
else
sol(y,t, continuity=:right)
end
end
λ = u
dλ = du
λ,nothing,y,dλ,nothing,nothing
end
# g is either g(t,u,p) or discrete g(t,u,i)
@noinline function ODEAdjointProblem(sol,sensealg::QuadratureAdjoint,g,
t=nothing,dg=nothing,
callback=CallbackSet())
@unpack f, p, u0, tspan = sol.prob
terminated = false
if hasfield(typeof(sol),:retcode)
if sol.retcode == :Terminated
tspan = (tspan[1], sol.t[end])
terminated = true
end
end
tspan = reverse(tspan)
discrete = t !== nothing
len = length(u0)
λ = similar(u0, len)
λ .= false
sense = ODEQuadratureAdjointSensitivityFunction(g,sensealg,discrete,sol,dg)
init_cb = t !== nothing && tspan[1] == t[end]
z0 = vec(zero(λ))
cb, duplicate_iterator_times = generate_callbacks(sense, g, λ, t, tspan[2], callback, init_cb, terminated)
jac_prototype = sol.prob.f.jac_prototype
adjoint_jac_prototype = !sense.discrete || jac_prototype === nothing ? nothing : copy(jac_prototype')
original_mm = sol.prob.f.mass_matrix
if original_mm === I || original_mm === (I,I)
odefun = ODEFunction(sense, jac_prototype=adjoint_jac_prototype)
else
odefun = ODEFunction(sense, mass_matrix=sol.prob.f.mass_matrix', jac_prototype=adjoint_jac_prototype)
end
return ODEProblem(odefun,z0,tspan,p,callback=cb)
end
struct AdjointSensitivityIntegrand{pType,uType,lType,rateType,S,AS,PF,PJC,PJT,DGP,G}
sol::S
adj_sol::AS
p::pType
y::uType
λ::lType
pf::PF
f_cache::rateType
pJ::PJT
paramjac_config::PJC
sensealg::QuadratureAdjoint
dgdp_cache::DGP
dgdp::G
end
function AdjointSensitivityIntegrand(sol,adj_sol,sensealg,dgdp=nothing)
prob = sol.prob
@unpack f, p, tspan, u0 = prob
numparams = length(p)
y = zero(sol.prob.u0)
λ = zero(adj_sol.prob.u0)
# we need to alias `y`
f_cache = zero(y)
f_cache .= false
isautojacvec = get_jacvec(sensealg)
dgdp_cache = dgdp === nothing ? nothing : zero(p)
if sensealg.autojacvec isa ReverseDiffVJP
tape = if DiffEqBase.isinplace(prob)
ReverseDiff.GradientTape((y, prob.p, [tspan[2]])) do u,p,t
du1 = similar(p, size(u))
du1 .= false
f(du1,u,p,first(t))
return vec(du1)
end
else
ReverseDiff.GradientTape((y, prob.p, [tspan[2]])) do u,p,t
vec(f(u,p,first(t)))
end
end
if compile_tape(sensealg.autojacvec)
paramjac_config = ReverseDiff.compile(tape)
else
paramjac_config = tape
end
pf = nothing
pJ = nothing
elseif sensealg.autojacvec isa EnzymeVJP
paramjac_config = zero(y),zero(y)
pf = let f = f.f
if DiffEqBase.isinplace(prob) && prob isa RODEProblem
function (out,u,_p,t,W)
f(out, u, _p, t, W)
nothing
end
elseif DiffEqBase.isinplace(prob)
function (out,u,_p,t)
f(out, u, _p, t)
nothing
end
elseif !DiffEqBase.isinplace(prob) && prob isa RODEProblem
function (out,u,_p,t,W)
out .= f(u, _p, t, W)
nothing
end
else !DiffEqBase.isinplace(prob)
function (out,u,_p,t)
out .= f(u, _p, t)
nothing
end
end
end
pJ = nothing
elseif isautojacvec # Zygote
paramjac_config = nothing
pf = nothing
pJ = nothing
else
pf = DiffEqBase.ParamJacobianWrapper(f,tspan[1],y)
pJ = similar(u0,length(u0),numparams)
paramjac_config = build_param_jac_config(sensealg,pf,y,p)
end
AdjointSensitivityIntegrand(sol,adj_sol,p,y,λ,pf,f_cache,pJ,paramjac_config,sensealg,dgdp_cache,dgdp)
end
function (S::AdjointSensitivityIntegrand)(out,t)
@unpack y, λ, pJ, pf, p, f_cache, dgdp_cache, paramjac_config, sensealg, sol, adj_sol = S
f = sol.prob.f
sol(y,t)
adj_sol(λ,t)
λ .*= -one(eltype(λ))
isautojacvec = get_jacvec(sensealg)
# y is aliased
if !isautojacvec
if DiffEqBase.has_paramjac(f)
f.paramjac(pJ,y,p,t) # Calculate the parameter Jacobian into pJ
else
pf.t = t
jacobian!(pJ, pf, p, f_cache, sensealg, paramjac_config)
end
mul!(out',λ',pJ)
elseif sensealg.autojacvec isa ReverseDiffVJP
tape = paramjac_config
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, y)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
copyto!(vec(out), ReverseDiff.deriv(tp))
elseif sensealg.autojacvec isa ZygoteVJP
_dy, back = Zygote.pullback(p) do p
vec(f(y, p, t))
end
tmp = back(λ)
out[:] .= vec(tmp[1])
elseif sensealg.autojacvec isa EnzymeVJP
tmp3,tmp4 = paramjac_config
tmp4 .= λ
out .= 0
Enzyme.autodiff(pf,Enzyme.Duplicated(tmp3,tmp4),
y,Enzyme.Duplicated(p, out),t)
end
# TODO: Add tracker?
if S.dgdp !== nothing
S.dgdp(dgdp_cache, y, p, t)
out .+= dgdp_cache
end
out'
end
function (S::AdjointSensitivityIntegrand)(t)
out = similar(S.p)
S(out,t)
end
function _adjoint_sensitivities(sol,sensealg::QuadratureAdjoint,alg,g,
t=nothing,dg=nothing;
abstol=sensealg.abstol,reltol=sensealg.reltol,
callback = nothing,
kwargs...)
dgdu, dgdp = dg isa Tuple ? dg : (dg, nothing)
adj_prob = ODEAdjointProblem(sol,sensealg,g,t,dgdu,callback)
adj_sol = solve(adj_prob,alg;abstol=abstol,reltol=reltol,
save_everystep=true,save_start=true,kwargs...)
p = sol.prob.p
if p === nothing || p === DiffEqBase.NullParameters()
return -adj_sol[end],nothing
else
integrand = AdjointSensitivityIntegrand(sol,adj_sol,sensealg,dgdp)
if t === nothing
res,err = quadgk(integrand,sol.prob.tspan[1],sol.prob.tspan[2],
atol=abstol,rtol=reltol)
else
res = zero(integrand.p)'
if callback!==nothing
cur_time = length(t)
dλ = similar(integrand.λ)
dλ .*= false
dgrad = similar(res)
dgrad .*= false
end
for i in length(t)-1:-1:1
res .+= quadgk(integrand,t[i],t[i+1],
atol=abstol,rtol=reltol)[1]
if t[i]==t[i+1]
for cb in callback.discrete_callbacks
if t[i] ∈ cb.affect!.event_times
integrand = update_integrand_and_dgrad(res,sensealg,cb,integrand,adj_prob,sol,dgdu,g,dλ,dgrad,t[i],cur_time)
end
end
for cb in callback.continuous_callbacks
if t[i] ∈ cb.affect!.event_times || t[i] ∈ cb.affect_neg!.event_times
integrand = update_integrand_and_dgrad(res,sensealg,cb,integrand,adj_prob,sol,dgdu,g,dλ,dgrad,t[i],cur_time)
end
end
end
callback!==nothing && (cur_time -= one(cur_time))
end
if t[1] != sol.prob.tspan[1]
res .+= quadgk(integrand,sol.prob.tspan[1],t[1],
atol=abstol,rtol=reltol)[1]
end
end
return -adj_sol[end], res
end
end
function update_p_integrand(integrand::AdjointSensitivityIntegrand,p)
@unpack sol, adj_sol, y, λ, pf, f_cache, pJ, paramjac_config, sensealg, dgdp_cache, dgdp = integrand
AdjointSensitivityIntegrand(sol,adj_sol,p,y,λ,pf,f_cache,pJ,paramjac_config,sensealg,dgdp_cache,dgdp)
end
function update_integrand_and_dgrad(res,sensealg::QuadratureAdjoint,cb,integrand,adj_prob,sol,dgdu,g,dλ,dgrad,t,cur_time)
indx, pos_neg = get_indx(cb, t)
tprev = get_tprev(cb,indx,pos_neg)
wp = let tprev=tprev, pos_neg=pos_neg
function (dp,p,u,t)
_affect! = get_affect!(cb,pos_neg)
fakeinteg = FakeIntegrator([x for x in u],[x for x in p],t,tprev)
_affect!(fakeinteg)
dp .= fakeinteg.p
end
end
_p = similar(integrand.p, size(integrand.p))
wp(_p,integrand.p,integrand.y,t)
if _p != integrand.p
fakeSp = CallbackSensitivityFunction(wp,sensealg,adj_prob.f.f.diffcache,sol.prob)
#vjp with Jacobin given by dw/dp before event and vector given by grad
vecjacobian!(res, integrand.p, res, integrand.y, t, fakeSp;
dgrad=nothing, dy=nothing)
integrand = update_p_integrand(integrand,_p)
end
w = let tprev=tprev, pos_neg=pos_neg
function (du,u,p,t)
_affect! = get_affect!(cb,pos_neg)
fakeinteg = FakeIntegrator([x for x in u],[x for x in p],t,tprev)
_affect!(fakeinteg)
du .= vec(fakeinteg.u)
end
end
# Create a fake sensitivity function to do the vjps needs to be done
# to account for parameter dependence of affect function
fakeS = CallbackSensitivityFunction(w,sensealg,adj_prob.f.f.diffcache,sol.prob)
if dgdu === nothing
g(dλ,integrand.y,integrand.p,t,cur_time)
else
dgdu(dλ,integrand.y,integrand.p,t,cur_time)
end
# account for implicit events
dλ .= dλ-integrand.λ
vecjacobian!(dλ, integrand.y, dλ, integrand.p, t, fakeS; dgrad=dgrad)
res .-= dgrad
return integrand
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 4180 | # Piracy that used to be requires, allowing ReverseDiff.jl to be specialized for SciML
DiffEqBase.value(x::ReverseDiff.TrackedReal) = x.value
DiffEqBase.value(x::ReverseDiff.TrackedArray) = x.value
DiffEqBase.promote_u0(u0::ReverseDiff.TrackedArray, p::ReverseDiff.TrackedArray, t0) = u0
DiffEqBase.promote_u0(u0::AbstractArray{<:ReverseDiff.TrackedReal}, p::ReverseDiff.TrackedArray, t0) = u0
DiffEqBase.promote_u0(u0::ReverseDiff.TrackedArray, p::AbstractArray{<:ReverseDiff.TrackedReal}, t0) = u0
DiffEqBase.promote_u0(u0::AbstractArray{<:ReverseDiff.TrackedReal}, p::AbstractArray{<:ReverseDiff.TrackedReal}, t0) = u0
DiffEqBase.promote_u0(u0, p::ReverseDiff.TrackedArray, t0) = ReverseDiff.track(u0)
DiffEqBase.promote_u0(u0, p::AbstractArray{<:ReverseDiff.TrackedReal}, t0) = eltype(p).(u0)
# Support adaptive with non-tracked time
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::ReverseDiff.TrackedArray, t) where {N}
sqrt(sum(abs2, DiffEqBase.value(u)) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::AbstractArray{<:ReverseDiff.TrackedReal,N}, t) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip((DiffEqBase.value(x) for x in u), Iterators.repeated(t))) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::Array{<:ReverseDiff.TrackedReal,N}, t) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip((DiffEqBase.value(x) for x in u), Iterators.repeated(t))) / length(u))
end
@inline DiffEqBase.ODE_DEFAULT_NORM(u::ReverseDiff.TrackedReal, t) = abs(DiffEqBase.value(u))
# Support TrackedReal time, don't drop tracking on the adaptivity there
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::ReverseDiff.TrackedArray, t::ReverseDiff.TrackedReal) where {N}
sqrt(sum(abs2, u) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::AbstractArray{<:ReverseDiff.TrackedReal,N}, t::ReverseDiff.TrackedReal) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip(u, Iterators.repeated(t))) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::Array{<:ReverseDiff.TrackedReal,N}, t::ReverseDiff.TrackedReal) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip(u, Iterators.repeated(t))) / length(u))
end
@inline DiffEqBase.ODE_DEFAULT_NORM(u::ReverseDiff.TrackedReal, t::ReverseDiff.TrackedReal) = abs(u)
function DiffEqBase.solve_up(prob::DiffEqBase.DEProblem, sensealg::Union{DiffEqBase.AbstractSensitivityAlgorithm,Nothing}, u0::ReverseDiff.TrackedArray, p::ReverseDiff.TrackedArray, args...; kwargs...)
ReverseDiff.track(DiffEqBase.solve_up, prob, sensealg, u0, p, args...; kwargs...)
end
function DiffEqBase.solve_up(prob::DiffEqBase.DEProblem, sensealg::Union{DiffEqBase.AbstractSensitivityAlgorithm,Nothing}, u0, p::ReverseDiff.TrackedArray, args...; kwargs...)
ReverseDiff.track(DiffEqBase.solve_up, prob, sensealg, u0, p, args...; kwargs...)
end
function DiffEqBase.solve_up(prob::DiffEqBase.DEProblem, sensealg::Union{DiffEqBase.AbstractSensitivityAlgorithm,Nothing}, u0::ReverseDiff.TrackedArray, p, args...; kwargs...)
ReverseDiff.track(DiffEqBase.solve_up, prob, sensealg, u0, p, args...; kwargs...)
end
@inline function DiffEqNoiseProcess.wiener_randn(rng::Random.AbstractRNG, proto::ReverseDiff.TrackedArray)
ReverseDiff.track(convert.(eltype(proto.value), randn(rng, size(proto))))
end
@inline function DiffEqNoiseProcess.wiener_randn!(rng::AbstractRNG, rand_vec::Array{<:ReverseDiff.TrackedReal})
rand_vec .= ReverseDiff.track.(randn.((rng,), typeof.(DiffEqBase.value.(rand_vec))))
end
@inline function DiffEqNoiseProcess.wiener_randn!(rng::AbstractRNG, rand_vec::AbstractArray{<:ReverseDiff.TrackedReal})
rand_vec .= ReverseDiff.track.(randn.((rng,), typeof.(DiffEqBase.value.(rand_vec))))
end
# Required becase ReverseDiff.@grad function DiffEqBase.solve_up is not supported!
import DiffEqBase: solve_up
ReverseDiff.@grad function solve_up(prob,sensealg,u0,p,args...;kwargs...)
out = DiffEqBase._solve_adjoint(prob,sensealg,ReverseDiff.value(u0),ReverseDiff.value(p),
SciMLBase.ReverseDiffOriginator(),args...;kwargs...)
Array(out[1]),out[2]
end | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2048 | # for Ito / Stratonovich conversion
struct StochasticTransformedFunction{pType,fType<:DiffEqBase.AbstractDiffEqFunction,gType,noiseType,cfType} <: TransformedFunction
prob::pType
f::fType
g::gType
gtmp::noiseType
inplace::Bool
corfunc_analytical::cfType
end
function StochasticTransformedFunction(sol,f,g, corfunc_analytical=nothing)
@unpack prob = sol
if StochasticDiffEq.is_diagonal_noise(prob)
gtmp = copy(sol.u[end])
else
gtmp = similar(prob.p, size(prob.noise_rate_prototype))
end
return StochasticTransformedFunction(prob,f,g,gtmp,DiffEqBase.isinplace(prob),corfunc_analytical)
end
function (Tfunc::StochasticTransformedFunction)(du,u,p,t)
@unpack gtmp, f, g, corfunc_analytical = Tfunc
ducor = similar(u, size(u))
if corfunc_analytical !== nothing
corfunc_analytical(ducor,u,p,t)
else
tape = ReverseDiff.GradientTape((u, p, [t])) do uloc,ploc,tloc
du1 = similar(uloc, size(gtmp))
g(du1,uloc,ploc,first(tloc))
return vec(du1)
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, vec(ReverseDiff.value(output)))
ReverseDiff.reverse_pass!(tape)
ReverseDiff.deriv(tu)
ReverseDiff.pull_value!(output)
copyto!(vec(ducor), ReverseDiff.deriv(tu))
end
f(du,u,p,t)
@. du = du - ducor
return nothing
end
function (Tfunc::StochasticTransformedFunction)(u,p,t)
@unpack f, g, corfunc_analytical = Tfunc
#ducor = vecjacobian(u, p, t, Tfunc)
if corfunc_analytical !== nothing
ducor = corfunc_analytical(u,p,t)
else
_dy, back = Zygote.pullback(u, p) do uloc, ploc
vec(g(uloc, ploc, t))
end
ducor, _ = back(_dy)
end
du = f(u,p,t)
du = @. du - ducor
return du
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 688 | function _second_order_sensitivities(loss,prob,alg,sensealg::ForwardDiffOverAdjoint,
args...;kwargs...)
ForwardDiff.jacobian(prob.p) do p
x = Zygote.gradient(p) do _p
loss(solve(prob,alg,args...;p=_p,sensealg=sensealg.adjalg,kwargs...))
end
first(x)
end
end
function _second_order_sensitivity_product(loss,v,prob,alg,sensealg::ForwardDiffOverAdjoint,
args...;kwargs...)
θ = ForwardDiff.Dual.(prob.p,v)
_loss = p -> loss(solve(prob,alg,args...;p=p,sensealg=sensealg.adjalg,kwargs...))
getindex.(ForwardDiff.partials.(Zygote.gradient(_loss,θ)[1]),1)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 47433 | SensitivityAlg(args...;kwargs...) = @error("The SensitivtyAlg choice mechanism was completely overhauled. Please consult the local sensitivity documentation for more information")
abstract type AbstractForwardSensitivityAlgorithm{CS,AD,FDT} <: DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT} end
abstract type AbstractAdjointSensitivityAlgorithm{CS,AD,FDT} <: DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT} end
abstract type AbstractSecondOrderSensitivityAlgorithm{CS,AD,FDT} <: DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT} end
abstract type AbstractShadowingSensitivityAlgorithm{CS,AD,FDT} <: DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT} end
"""
ForwardSensitivity{CS,AD,FDT} <: AbstractForwardSensitivityAlgorithm{CS,AD,FDT}
An implementation of continuous forward sensitivity analysis for propagating
derivatives by solving the extended ODE. When used within adjoint differentiation
(i.e. via Zygote), this will cause forward differentiation of the `solve` call
within the reverse-mode automatic differentiation environment.
## Constructor
```julia
function ForwardSensitivity(;
chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=autodiff,
autojacmat=false)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation in the internal sensitivity algorithm
computations. Default is `true`.
* `chunk_size`: Chunk size for forward mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `autojacvec`: Calculate the Jacobian-vector product via automatic
differentiation with special seeding.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
Further details:
- If `autodiff=true` and `autojacvec=true`, then the one chunk `J*v` forward-mode
directional derivative calculation trick is used to compute the product without
constructing the Jacobian (via ForwardDiff.jl).
- If `autodiff=false` and `autojacvec=true`, then the numerical direction derivative
trick `(f(x+epsilon*v)-f(x))/epsilon` is used to compute `J*v` without constructing
the Jacobian.
- If `autodiff=true` and `autojacvec=false`, then the Jacobian is constructed via
chunked forward-mode automatic differentiation (via ForwardDiff.jl).
- If `autodiff=false` and `autojacvec=false`, then the Jacobian is constructed via
finite differences via FiniteDiff.jl.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s without callbacks (events).
"""
struct ForwardSensitivity{CS,AD,FDT} <: AbstractForwardSensitivityAlgorithm{CS,AD,FDT}
autojacvec::Bool
autojacmat::Bool
end
Base.@pure function ForwardSensitivity(;
chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=autodiff,
autojacmat=false)
autojacvec && autojacmat && error("Choose either Jacobian matrix products or Jacobian vector products,
autojacmat and autojacvec cannot both be true")
ForwardSensitivity{chunk_size,autodiff,diff_type}(autojacvec,autojacmat)
end
"""
ForwardDiffSensitivity{CS,CTS} <: AbstractForwardSensitivityAlgorithm{CS,Nothing,Nothing}
An implementation of discrete forward sensitivity analysis through ForwardDiff.jl.
When used within adjoint differentiation (i.e. via Zygote), this will cause forward
differentiation of the `solve` call within the reverse-mode automatic differentiation
environment.
## Constructor
```julia
ForwardDiffSensitivity(;chunk_size=0,convert_tspan=nothing)
```
## Keyword Arguments
* `chunk_size`: the chunk size used by ForwardDiff for computing the Jacobian, i.e. the
number of simultaneous columns computed.
* `convert_tspan`: whether to convert time to also be `Dual` valued. By default this is
`nothing` which will only convert if callbacks are found. Conversion is required in order
to accurately differentiate callbacks (hybrid equations).
## SciMLProblem Support
This `sensealg` supports any `SciMLProblem`s, provided that the solver algorithms is
`SciMLBase.isautodifferentiable`. Note that `ForwardDiffSensitivity` can
accurately differentiate code with callbacks only when `convert_tspan=true`.
"""
struct ForwardDiffSensitivity{CS,CTS} <: AbstractForwardSensitivityAlgorithm{CS,Nothing,Nothing}
end
Base.@pure function ForwardDiffSensitivity(;chunk_size=0,convert_tspan=nothing)
ForwardDiffSensitivity{chunk_size,convert_tspan}()
end
"""
BacksolveAdjoint{CS,AD,FDT,VJP} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
An implementation of adjoint sensitivity analysis using a backwards solution of the ODE.
By default this algorithm will use the values from the forward pass to perturb the
backwards solution to the correct spot, allowing reduced memory (O(1) memory). Checkpointing
stabilization is included for additional numerical stability over the naive implementation.
## Constructor
```julia
BacksolveAdjoint(;chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=nothing,
checkpointing=true, noisemixing=false)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `autojacvec`: Calculate the vector-Jacobian product (`J'*v`) via automatic
differentiation with special seeding. The default is `true`. The total set
of choices are:
- `false`: the Jacobian is constructed via FiniteDiff.jl
- `true`: the Jacobian is constructed via ForwardDiff.jl
- `TrackerVJP`: Uses Tracker.jl for the vjp.
- `ZygoteVJP`: Uses Zygote.jl for the vjp.
- `EnzymeVJP`: Uses Enzyme.jl for the vjp.
- `ReverseDiffVJP(compile=false)`: Uses ReverseDiff.jl for the vjp. `compile`
is a boolean for whether to precompile the tape, which should only be done
if there are no branches (`if` or `while` statements) in the `f` function.
* `checkpointing`: whether checkpointing is enabled for the reverse pass. Defaults
to `true`.
* `noisemixing`: Handle noise processes that are not of the form `du[i] = f(u[i])`.
For example, to compute the sensitivities of an SDE with diagonal diffusion
```julia
function g_mixing!(du,u,p,t)
du[1] = p[3]*u[1] + p[4]*u[2]
du[2] = p[3]*u[1] + p[4]*u[2]
nothing
end
```
correctly, `noisemixing=true` must be enabled. The default is `false`.
For more details on the vjp choices, please consult the sensitivity algorithms
documentation page or the docstrings of the vjp types.
## Applicability of Backsolve and Caution
When `BacksolveAdjoint` is applicable, it is a fast method and requires the least memory.
However, one must be cautious because not all ODEs are stable under backwards integration
by the majority of ODE solvers. An example of such an equation is the Lorenz equation.
Notice that if one solves the Lorenz equation forward and then in reverse with any
adaptive time step and non-reversible integrator, then the backwards solution diverges
from the forward solution. As a quick demonstration:
```julia
using Sundials
function lorenz(du,u,p,t)
du[1] = 10.0*(u[2]-u[1])
du[2] = u[1]*(28.0-u[3]) - u[2]
du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,Tsit5(),reltol=1e-12,abstol=1e-12)
prob2 = ODEProblem(lorenz,sol[end],(100.0,0.0))
sol = solve(prob,Tsit5(),reltol=1e-12,abstol=1e-12)
@show sol[end]-u0 #[-3.22091, -1.49394, 21.3435]
```
Thus one should check the stability of the backsolve on their type of problem before
enabling this method. Additionally, using checkpointing with backsolve can be a
low memory way to stabilize it.
For more details on this topic, see
[Stiff Neural Ordinary Differential Equations](https://aip.scitation.org/doi/10.1063/5.0060697).
## Checkpointing
To improve the numerical stability of the reverse pass, `BacksolveAdjoint` includes a checkpointing
feature. If `sol.u` is a time series, then whenever a time `sol.t` is hit while reversing, a callback
will replace the reversing ODE portion with `sol.u[i]`. This nudges the solution back onto the appropriate
trajectory and reduces the numerical caused by drift.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s, `SDEProblem`s, and `RODEProblem`s. This `sensealg` supports
callback functions (events).
## References
ODE:
Rackauckas, C. and Ma, Y. and Martensen, J. and Warner, C. and Zubov, K. and Supekar,
R. and Skinner, D. and Ramadhana, A. and Edelman, A., Universal Differential Equations
for Scientific Machine Learning, arXiv:2001.04385
Hindmarsh, A. C. and Brown, P. N. and Grant, K. E. and Lee, S. L. and Serban, R.
and Shumaker, D. E. and Woodward, C. S., SUNDIALS: Suite of nonlinear and
differential/algebraic equation solvers, ACM Transactions on Mathematical
Software (TOMS), 31, pp:363–396 (2005)
Chen, R.T.Q. and Rubanova, Y. and Bettencourt, J. and Duvenaud, D. K.,
Neural ordinary differential equations. In Advances in neural information processing
systems, pp. 6571–6583 (2018)
Pontryagin, L. S. and Mishchenko, E.F. and Boltyanskii, V.G. and Gamkrelidze, R.V.
The mathematical theory of optimal processes. Routledge, (1962)
Rackauckas, C. and Ma, Y. and Dixit, V. and Guo, X. and Innes, M. and Revels, J.
and Nyberg, J. and Ivaturi, V., A comparison of automatic differentiation and
continuous sensitivity analysis for derivatives of differential equation solutions,
arXiv:1812.01892
DAE:
Cao, Y. and Li, S. and Petzold, L. and Serban, R., Adjoint sensitivity analysis
for differential-algebraic equations: The adjoint DAE system and its numerical
solution, SIAM journal on scientific computing 24 pp: 1076-1089 (2003)
SDE:
Gobet, E. and Munos, R., Sensitivity Analysis Using Ito-Malliavin Calculus and
Martingales, and Application to Stochastic Optimal Control,
SIAM Journal on control and optimization, 43, pp. 1676-1713 (2005)
Li, X. and Wong, T.-K. L.and Chen, R. T. Q. and Duvenaud, D.,
Scalable Gradients for Stochastic Differential Equations,
PMLR 108, pp. 3870-3882 (2020), http://proceedings.mlr.press/v108/li20i.html
"""
struct BacksolveAdjoint{CS,AD,FDT,VJP} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
autojacvec::VJP
checkpointing::Bool
noisemixing::Bool
end
Base.@pure function BacksolveAdjoint(;chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=nothing,
checkpointing=true, noisemixing=false)
BacksolveAdjoint{chunk_size,autodiff,diff_type,typeof(autojacvec)}(autojacvec,checkpointing,noisemixing)
end
setvjp(sensealg::BacksolveAdjoint{CS,AD,FDT,Nothing}, vjp) where {CS,AD,FDT} =
BacksolveAdjoint{CS,AD,FDT,typeof(vjp)}(vjp,sensealg.checkpointing,
sensealg.noisemixing)
"""
InterpolatingAdjoint{CS,AD,FDT,VJP} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
An implementation of adjoint sensitivity analysis which uses the interpolation of
the forward solution for the reverse solve vector-Jacobian products. By
default it requires a dense solution of the forward pass and will internally
ignore saving arguments during the gradient calculation. When checkpointing is
enabled it will only require the memory to interpolate between checkpoints.
## Constructor
```julia
function InterpolatingAdjoint(;chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=nothing,
checkpointing=false, noisemixing=false)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `autojacvec`: Calculate the vector-Jacobian product (`J'*v`) via automatic
differentiation with special seeding. The default is `true`. The total set
of choices are:
- `false`: the Jacobian is constructed via FiniteDiff.jl
- `true`: the Jacobian is constructed via ForwardDiff.jl
- `TrackerVJP`: Uses Tracker.jl for the vjp.
- `ZygoteVJP`: Uses Zygote.jl for the vjp.
- `EnzymeVJP`: Uses Enzyme.jl for the vjp.
- `ReverseDiffVJP(compile=false)`: Uses ReverseDiff.jl for the vjp. `compile`
is a boolean for whether to precompile the tape, which should only be done
if there are no branches (`if` or `while` statements) in the `f` function.
* `checkpointing`: whether checkpointing is enabled for the reverse pass. Defaults
to `true`.
* `noisemixing`: Handle noise processes that are not of the form `du[i] = f(u[i])`.
For example, to compute the sensitivities of an SDE with diagonal diffusion
```julia
function g_mixing!(du,u,p,t)
du[1] = p[3]*u[1] + p[4]*u[2]
du[2] = p[3]*u[1] + p[4]*u[2]
nothing
end
```
correctly, `noisemixing=true` must be enabled. The default is `false`.
For more details on the vjp choices, please consult the sensitivity algorithms
documentation page or the docstrings of the vjp types.
## Checkpointing
To reduce the memory usage of the reverse pass, `InterpolatingAdjoint` includes a checkpointing
feature. If `sol` is `dense`, checkpointing is ignored and the continuous solution is used for
calculating `u(t)` at arbitrary time points. If `checkpointing=true` and `sol` is not `dense`,
then dense intervals between `sol.t[i]` and `sol.t[i+1]` are reconstructed on-demand for calculating
`u(t)` at arbitrary time points. This reduces the total memory requirement to only the cost of
holding the dense solution over the largest time interval (in terms of number of required steps).
The total compute cost is no more than double the original forward compute cost.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s, `SDEProblem`s, and `RODEProblem`s. This `sensealg`
supports callbacks (events).
## References
Rackauckas, C. and Ma, Y. and Martensen, J. and Warner, C. and Zubov, K. and Supekar,
R. and Skinner, D. and Ramadhana, A. and Edelman, A., Universal Differential Equations
for Scientific Machine Learning, arXiv:2001.04385
Hindmarsh, A. C. and Brown, P. N. and Grant, K. E. and Lee, S. L. and Serban, R.
and Shumaker, D. E. and Woodward, C. S., SUNDIALS: Suite of nonlinear and
differential/algebraic equation solvers, ACM Transactions on Mathematical
Software (TOMS), 31, pp:363–396 (2005)
Rackauckas, C. and Ma, Y. and Dixit, V. and Guo, X. and Innes, M. and Revels, J.
and Nyberg, J. and Ivaturi, V., A comparison of automatic differentiation and
continuous sensitivity analysis for derivatives of differential equation solutions,
arXiv:1812.01892
"""
struct InterpolatingAdjoint{CS,AD,FDT,VJP} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
autojacvec::VJP
checkpointing::Bool
noisemixing::Bool
end
Base.@pure function InterpolatingAdjoint(;chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=nothing,
checkpointing=false,noisemixing=false)
InterpolatingAdjoint{chunk_size,autodiff,diff_type,typeof(autojacvec)}(autojacvec,checkpointing,noisemixing)
end
setvjp(sensealg::InterpolatingAdjoint{CS,AD,FDT,Nothing},vjp) where {CS,AD,FDT} =
InterpolatingAdjoint{CS,AD,FDT,typeof(vjp)}(vjp,sensealg.checkpointing,
sensealg.noisemixing)
"""
QuadratureAdjoint{CS,AD,FDT,VJP} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
An implementation of adjoint sensitivity analysis which develops a full
continuous solution of the reverse solve in order to perform a post-ODE
quadrature. This method requires the the dense solution and will ignore
saving arguments during the gradient calculation. The tolerances in the
constructor control the inner quadrature. The inner quadrature uses a
ReverseDiff vjp if autojacvec, and `compile=false` by default but can
compile the tape under the same circumstances as `ReverseDiffVJP`.
This method is O(n^3 + p) for stiff / implicit equations (as opposed to the
O((n+p)^3) scaling of BacksolveAdjoint and InterpolatingAdjoint), and thus
is much more compute efficient. However, it requires holding a dense reverse
pass and is thus memory intensive.
## Constructor
```julia
function QuadratureAdjoint(;chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=nothing,abstol=1e-6,
reltol=1e-3,compile=false)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `autojacvec`: Calculate the vector-Jacobian product (`J'*v`) via automatic
differentiation with special seeding. The default is `true`. The total set
of choices are:
- `false`: the Jacobian is constructed via FiniteDiff.jl
- `true`: the Jacobian is constructed via ForwardDiff.jl
- `TrackerVJP`: Uses Tracker.jl for the vjp.
- `ZygoteVJP`: Uses Zygote.jl for the vjp.
- `EnzymeVJP`: Uses Enzyme.jl for the vjp.
- `ReverseDiffVJP(compile=false)`: Uses ReverseDiff.jl for the vjp. `compile`
is a boolean for whether to precompile the tape, which should only be done
if there are no branches (`if` or `while` statements) in the `f` function.
* `abstol`: absolute tolerance for the quadrature calculation
* `reltol`: relative tolerance for the quadrature calculation
* `compile`: whether to compile the vjp calculation for the integrand calculation.
See `ReverseDiffVJP` for more details.
For more details on the vjp choices, please consult the sensitivity algorithms
documentation page or the docstrings of the vjp types.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s. This `sensealg` supports events (callbacks).
## References
Rackauckas, C. and Ma, Y. and Martensen, J. and Warner, C. and Zubov, K. and Supekar,
R. and Skinner, D. and Ramadhana, A. and Edelman, A., Universal Differential Equations
for Scientific Machine Learning, arXiv:2001.04385
Hindmarsh, A. C. and Brown, P. N. and Grant, K. E. and Lee, S. L. and Serban, R.
and Shumaker, D. E. and Woodward, C. S., SUNDIALS: Suite of nonlinear and
differential/algebraic equation solvers, ACM Transactions on Mathematical
Software (TOMS), 31, pp:363–396 (2005)
Rackauckas, C. and Ma, Y. and Dixit, V. and Guo, X. and Innes, M. and Revels, J.
and Nyberg, J. and Ivaturi, V., A comparison of automatic differentiation and
continuous sensitivity analysis for derivatives of differential equation solutions,
arXiv:1812.01892
Kim, S., Ji, W., Deng, S., Ma, Y., & Rackauckas, C. (2021). Stiff neural ordinary
differential equations. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31(9), 093122.
"""
struct QuadratureAdjoint{CS,AD,FDT,VJP} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
autojacvec::VJP
abstol::Float64
reltol::Float64
end
Base.@pure function QuadratureAdjoint(;chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=nothing,abstol=1e-6,
reltol=1e-3)
QuadratureAdjoint{chunk_size,autodiff,diff_type,typeof(autojacvec)}(autojacvec,abstol,reltol)
end
setvjp(sensealg::QuadratureAdjoint{CS,AD,FDT,Nothing},vjp) where {CS,AD,FDT} =
QuadratureAdjoint{CS,AD,FDT,typeof(vjp)}(vjp,sensealg.abstol,
sensealg.reltol)
"""
TrackerAdjoint <: AbstractAdjointSensitivityAlgorithm{nothing,true,nothing}
An implementation of discrete adjoint sensitivity analysis
using the Tracker.jl tracing-based AD. Supports in-place functions through
an Array of Structs formulation, and supports out of place through struct of
arrays.
## Constructor
```julia
TrackerAdjoint()
```
## SciMLProblem Support
This `sensealg` supports any `DEProblem` if the algorithm is `SciMLBase.isautodifferentiable`
Compatible with a limited subset of `AbstractArray` types for `u0`, including `CuArrays`.
!!! warn
TrackerAdjoint is incompatible with Stiff ODE solvers using forward-mode automatic
differentiation for the Jacobians. Thus for example, `TRBDF2()` will error. Instead,
use `autodiff=false`, i.e. `TRBDF2(autodiff=false)`. This will only remove the
forward-mode automatic differentiation of the Jacobian construction, not the reverse-mode
AD usage, and thus performance will still be nearly the same, though Jacobian accuracy
may suffer which could cause more steps to be required.
"""
struct TrackerAdjoint <: AbstractAdjointSensitivityAlgorithm{nothing,true,nothing} end
"""
ReverseDiffAdjoint <: AbstractAdjointSensitivityAlgorithm{nothing,true,nothing}
An implementation of discrete adjoint sensitivity analysis using the ReverseDiff.jl
tracing-based AD. Supports in-place functions through an Array of Structs formulation,
and supports out of place through struct of arrays.
## Constructor
```julia
ReverseDiffAdjoint()
```
## SciMLProblem Support
This `sensealg` supports any `DEProblem` if the algorithm is `SciMLBase.isautodifferentiable`.
Requires that the state variables are CPU-based `Array` types.
"""
struct ReverseDiffAdjoint <: AbstractAdjointSensitivityAlgorithm{nothing,true,nothing} end
"""
ZygoteAdjoint <: AbstractAdjointSensitivityAlgorithm{nothing,true,nothing}
An implementation of discrete adjoint sensitivity analysis
using the Zygote.jl source-to-source AD directly on the differential equation
solver.
## Constructor
```julia
ZygoteAdjoint()
```
## SciMLProblem Support
Currently fails on almost every solver.
"""
struct ZygoteAdjoint <: AbstractAdjointSensitivityAlgorithm{nothing,true,nothing} end
"""
ForwardLSS{CS,AD,FDT,RType,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
An implementation of the discrete, forward-mode
[least squares shadowing](https://arxiv.org/abs/1204.0159) (LSS) method. LSS replaces
the ill-conditioned initial value probem (`ODEProblem`) for chaotic systems by a
well-conditioned least-squares problem. This allows for computing sensitivities of
long-time averaged quantities with respect to the parameters of the `ODEProblem`. The
computational cost of LSS scales as (number of states x number of time steps). Converges
to the correct sensitivity at a rate of `T^(-1/2)`, where `T` is the time of the trajectory.
See `NILSS()` and `NILSAS()` for a more efficient non-intrusive formulation.
## Constructor
```julia
ForwardLSS(;
chunk_size=0,autodiff=true,
diff_type=Val{:central},
LSSregularizer=TimeDilation(10.0,0.0,0.0),
g=nothing)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `LSSregularizer`: Using `LSSregularizer`, one can choose between three different
regularization routines. The default choice is `TimeDilation(10.0,0.0,0.0)`.
- `CosWindowing()`: cos windowing of the time grid, i.e. the time grid (saved
time steps) is transformed using a cosine.
- `Cos2Windowing()`: cos^2 windowing of the time grid.
- `TimeDilation(alpha::Number,t0skip::Number,t1skip::Number)`: Corresponds to
a time dilation. `alpha` controls the weight. `t0skip` and `t1skip` indicate
the times truncated at the beginnning and end of the trajectory, respectively.
* `g`: instantaneous objective function of the long-time averaged objective.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s. This `sensealg` does not support
events (callbacks). This `sensealg` assumes that the objective is a long-time averaged
quantity and ergodic, i.e. the time evolution of the system behaves qualitatively the
same over infinite time independent of the specified initial conditions, such that only
the sensitivity with respect to the parameters is of interest.
## References
Wang, Q., Hu, R., and Blonigan, P. Least squares shadowing sensitivity analysis of
chaotic limit cycle oscillations. Journal of Computational Physics, 267, 210-224 (2014).
Wang, Q., Convergence of the Least Squares Shadowing Method for Computing Derivative of Ergodic
Averages, SIAM Journal on Numerical Analysis, 52, 156–170 (2014).
Blonigan, P., Gomez, S., Wang, Q., Least Squares Shadowing for sensitivity analysis of turbulent
fluid flows, in: 52nd Aerospace Sciences Meeting, 1–24 (2014).
"""
struct ForwardLSS{CS,AD,FDT,RType,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
LSSregularizer::RType
g::gType
end
Base.@pure function ForwardLSS(;
chunk_size=0, autodiff=true,
diff_type=Val{:central},
LSSregularizer=TimeDilation(10.0,0.0,0.0),
g=nothing)
ForwardLSS{chunk_size,autodiff,diff_type,typeof(LSSregularizer),typeof(g)}(LSSregularizer, g)
end
"""
AdjointLSS{CS,AD,FDT,RType,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
An implementation of the discrete, adjoint-mode
[least square shadowing](https://arxiv.org/abs/1204.0159) method. LSS replaces
the ill-conditioned initial value probem (`ODEProblem`) for chaotic systems by a
well-conditioned least-squares problem. This allows for computing sensitivities of
long-time averaged quantities with respect to the parameters of the `ODEProblem`. The
computational cost of LSS scales as (number of states x number of time steps). Converges
to the correct sensitivity at a rate of `T^(-1/2)`, where `T` is the time of the trajectory.
See `NILSS()` and `NILSAS()` for a more efficient non-intrusive formulation.
## Constructor
```julia
AdjointLSS(;
chunk_size=0,autodiff=true,
diff_type=Val{:central},
LSSRegularizer=CosWindowing(),
g=nothing)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `LSSregularizer`: Using `LSSregularizer`, one can choose between different
regularization routines. The default choice is `TimeDilation(10.0,0.0,0.0)`.
- `TimeDilation(alpha::Number,t0skip::Number,t1skip::Number)`: Corresponds to
a time dilation. `alpha` controls the weight. `t0skip` and `t1skip` indicate
the times truncated at the beginnning and end of the trajectory, respectively.
The default value for `t0skip` and `t1skip` is `zero(alpha)`.
* `g`: instantaneous objective function of the long-time averaged objective.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s. This `sensealg` does not support
events (callbacks). This `sensealg` assumes that the objective is a long-time averaged
quantity and ergodic, i.e. the time evolution of the system behaves qualitatively the
same over infinite time independent of the specified initial conditions, such that only
the sensitivity with respect to the parameters is of interest.
## References
Wang, Q., Hu, R., and Blonigan, P. Least squares shadowing sensitivity analysis of
chaotic limit cycle oscillations. Journal of Computational Physics, 267, 210-224 (2014).
"""
struct AdjointLSS{CS,AD,FDT,RType,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
LSSregularizer::RType
g::gType
end
Base.@pure function AdjointLSS(;
chunk_size=0, autodiff=true,
diff_type=Val{:central},
LSSregularizer=TimeDilation(10.0, 0.0, 0.0),
g=nothing)
AdjointLSS{chunk_size,autodiff,diff_type,typeof(LSSregularizer),typeof(g)}(LSSregularizer, g)
end
abstract type AbstractLSSregularizer end
abstract type AbstractCosWindowing <: AbstractLSSregularizer end
struct CosWindowing <: AbstractCosWindowing end
struct Cos2Windowing <: AbstractCosWindowing end
"""
TimeDilation{T1<:Number} <: AbstractLSSregularizer
A regularization method for `LSS`. See `?LSS` for
additional information and other methods.
## Constructor
```julia
TimeDilation(alpha;
t0skip=zero(alpha),
t1skip=zero(alpha))
```
"""
struct TimeDilation{T1<:Number} <: AbstractLSSregularizer
alpha::T1 # alpha: weight of the time dilation term in LSS.
t0skip::T1
t1skip::T1
end
function TimeDilation(alpha,t0skip=zero(alpha),t1skip=zero(alpha))
TimeDilation{typeof(alpha)}(alpha,t0skip,t1skip)
end
"""
struct NILSS{CS,AD,FDT,RNG,nType,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
An implementation of the forward-mode, continuous
[non-intrusive least squares shadowing](https://arxiv.org/abs/1611.00880) method. `NILSS`
allows for computing sensitivities of long-time averaged quantities with respect to the
parameters of an `ODEProblem` by constraining the computation to the unstable subspace.
`NILSS` employs the continuous-time `ForwardSensitivity` method as tangent solver. To
avoid an exponential blow-up of the (homogenous and inhomogenous) tangent solutions,
the trajectory should be divided into sufficiently small segments, where the tangent solutions
are rescaled on the interfaces. The computational and memory cost of NILSS scale with
the number of unstable (positive) Lyapunov exponents (instead of the number of states as
in the LSS method). `NILSS` avoids the explicit construction of the Jacobian at each time
step and thus should generally be preferred (for large system sizes) over `ForwardLSS`.
## Constructor
```julia
NILSS(nseg, nstep; nus = nothing,
rng = Xorshifts.Xoroshiro128Plus(rand(UInt64)),
chunk_size=0,autodiff=true,
diff_type=Val{:central},
autojacvec=autodiff,
g=nothing)
```
## Arguments
* `nseg`: Number of segments on full time interval on the attractor.
* `nstep`: number of steps on each segment.
## Keyword Arguments
* `nus`: Dimension of the unstable subspace. Default is `nothing`. `nus` must be
smaller or equal to the state dimension (`length(u0)`). With the default choice,
`nus = length(u0) - 1` will be set at compile time.
* `rng`: (Pseudo) random number generator. Used for initializing the homogenous
tangent states (`w`). Default is `Xorshifts.Xoroshiro128Plus(rand(UInt64))`.
* `autodiff`: Use automatic differentiation in the internal sensitivity algorithm
computations. Default is `true`.
* `chunk_size`: Chunk size for forward mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `autojacvec`: Calculate the Jacobian-vector product via automatic
differentiation with special seeding.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `g`: instantaneous objective function of the long-time averaged objective.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s. This `sensealg` does not support
events (callbacks). This `sensealg` assumes that the objective is a long-time averaged
quantity and ergodic, i.e. the time evolution of the system behaves qualitatively the
same over infinite time independent of the specified initial conditions, such that only
the sensitivity with respect to the parameters is of interest.
## References
Ni, A., Blonigan, P. J., Chater, M., Wang, Q., Zhang, Z., Sensitivity analy-
sis on chaotic dynamical system by Non-Intrusive Least Square Shadowing
(NI-LSS), in: 46th AIAA Fluid Dynamics Conference, AIAA AVIATION Forum (AIAA 2016-4399),
American Institute of Aeronautics and Astronautics, 1–16 (2016).
Ni, A., and Wang, Q. Sensitivity analysis on chaotic dynamical systems by Non-Intrusive
Least Squares Shadowing (NILSS). Journal of Computational Physics 347, 56-77 (2017).
"""
struct NILSS{CS,AD,FDT,RNG,nType,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
rng::RNG
nseg::Int
nstep::Int
nus::nType
autojacvec::Bool
g::gType
end
Base.@pure function NILSS(nseg, nstep; nus=nothing, rng=Xorshifts.Xoroshiro128Plus(rand(UInt64)),
chunk_size=0, autodiff=true,
diff_type=Val{:central},
autojacvec=autodiff,
g=nothing
)
NILSS{chunk_size,autodiff,diff_type,typeof(rng),typeof(nus),typeof(g)}(rng,nseg,nstep,nus,autojacvec,g)
end
"""
NILSAS{CS,AD,FDT,RNG,SENSE,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
An implementation of the adjoint-mode, continuous
[non-intrusive adjoint least squares shadowing](https://arxiv.org/abs/1801.08674) method.
`NILSAS` allows for computing sensitivities of long-time averaged quantities with respect
to the parameters of an `ODEProblem` by constraining the computation to the unstable subspace.
`NILSAS` employs SciMLSensitivity.jl's continuous adjoint sensitivity methods on each segment
to compute (homogenous and inhomogenous) adjoint solutions. To avoid an exponential blow-up
of the adjoint solutions, the trajectory should be divided into sufficiently small segments,
where the adjoint solutions are rescaled on the interfaces. The computational and memory cost
of NILSAS scale with the number of unstable, adjoint Lyapunov exponents (instead of the number
of states as in the LSS method). `NILSAS` avoids the explicit construction of the Jacobian at
each time step and thus should generally be preferred (for large system sizes) over `AdjointLSS`.
`NILSAS` is favourable over `NILSS` for many parameters because NILSAS computes the gradient
with respect to multiple parameters with negligible additional cost.
## Constructor
```julia
NILSAS(nseg, nstep, M=nothing; rng = Xorshifts.Xoroshiro128Plus(rand(UInt64)),
adjoint_sensealg = BacksolveAdjoint(autojacvec=ReverseDiffVJP()),
chunk_size=0,autodiff=true,
diff_type=Val{:central},
g=nothing
)
```
## Arguments
* `nseg`: Number of segments on full time interval on the attractor.
* `nstep`: number of steps on each segment.
* `M`: number of homogenous adjoint solutions. This number must be bigger or equal
than the number of (positive, adjoint) Lyapunov exponents. Default is `nothing`.
## Keyword Arguments
* `rng`: (Pseudo) random number generator. Used for initializing the terminate
conditions of the homogenous adjoint states (`w`). Default is `Xorshifts.Xoroshiro128Plus(rand(UInt64))`.
* `adjoint_sensealg`: Continuous adjoint sensitivity method to compute homogenous
and inhomogenous adjoint solutions on each segment. Default is `BacksolveAdjoint(autojacvec=ReverseDiffVJP())`.
* `autojacvec`: Calculate the vector-Jacobian product (`J'*v`) via automatic
differentiation with special seeding. The default is `true`. The total set
of choices are:
- `false`: the Jacobian is constructed via FiniteDiff.jl
- `true`: the Jacobian is constructed via ForwardDiff.jl
- `TrackerVJP`: Uses Tracker.jl for the vjp.
- `ZygoteVJP`: Uses Zygote.jl for the vjp.
- `EnzymeVJP`: Uses Enzyme.jl for the vjp.
- `ReverseDiffVJP(compile=false)`: Uses ReverseDiff.jl for the vjp. `compile`
is a boolean for whether to precompile the tape, which should only be done
if there are no branches (`if` or `while` statements) in the `f` function.
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `g`: instantaneous objective function of the long-time averaged objective.
## SciMLProblem Support
This `sensealg` only supports `ODEProblem`s. This `sensealg` does not support
events (callbacks). This `sensealg` assumes that the objective is a long-time averaged
quantity and ergodic, i.e. the time evolution of the system behaves qualitatively the
same over infinite time independent of the specified initial conditions, such that only
the sensitivity with respect to the parameters is of interest.
## References
Ni, A., and Talnikar, C., Adjoint sensitivity analysis on chaotic dynamical systems
by Non-Intrusive Least Squares Adjoint Shadowing (NILSAS). Journal of Computational
Physics 395, 690-709 (2019).
"""
struct NILSAS{CS,AD,FDT,RNG,SENSE,gType} <: AbstractShadowingSensitivityAlgorithm{CS,AD,FDT}
rng::RNG
adjoint_sensealg::SENSE
M::Int
nseg::Int
nstep::Int
g::gType
end
Base.@pure function NILSAS(nseg, nstep, M=nothing; rng=Xorshifts.Xoroshiro128Plus(rand(UInt64)),
adjoint_sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()),
chunk_size=0, autodiff=true,
diff_type=Val{:central},
g=nothing
)
# integer dimension of the unstable subspace
M === nothing && error("Please provide an `M` with `M >= nus + 1`, where nus is the number of unstable covariant Lyapunov vectors.")
NILSAS{chunk_size,autodiff,diff_type,typeof(rng),typeof(adjoint_sensealg),typeof(g)}(rng, adjoint_sensealg, M,
nseg, nstep, g)
end
"""
SteadyStateAdjoint{CS,AD,FDT,VJP,LS} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
An implementation of the adjoint differentiation of a nonlinear solve. Uses the
implicit function theorem to directly compute the derivative of the solution to
``f(u,p) = 0`` with respect to `p`.
## Constructor
```julia
SteadyStateAdjoint(;chunk_size = 0, autodiff = true,
diff_type = Val{:central},
autojacvec = autodiff, linsolve = nothing)
```
## Keyword Arguments
* `autodiff`: Use automatic differentiation for constructing the Jacobian
if the Jacobian needs to be constructed. Defaults to `true`.
* `chunk_size`: Chunk size for forward-mode differentiation if full Jacobians are
built (`autojacvec=false` and `autodiff=true`). Default is `0` for automatic
choice of chunk size.
* `diff_type`: The method used by FiniteDiff.jl for constructing the Jacobian
if the full Jacobian is required with `autodiff=false`.
* `autojacvec`: Calculate the vector-Jacobian product (`J'*v`) via automatic
differentiation with special seeding. The default is `nothing`. The total set
of choices are:
- `false`: the Jacobian is constructed via FiniteDiff.jl
- `true`: the Jacobian is constructed via ForwardDiff.jl
- `TrackerVJP`: Uses Tracker.jl for the vjp.
- `ZygoteVJP`: Uses Zygote.jl for the vjp.
- `EnzymeVJP`: Uses Enzyme.jl for the vjp.
- `ReverseDiffVJP(compile=false)`: Uses ReverseDiff.jl for the vjp. `compile`
is a boolean for whether to precompile the tape, which should only be done
if there are no branches (`if` or `while` statements) in the `f` function.
* `linsolve`: the linear solver used in the adjoint solve. Defaults to `nothing`,
which uses a polyalgorithm to attempt to automatically choose an efficient
algorithm.
For more details on the vjp choices, please consult the sensitivity algorithms
documentation page or the docstrings of the vjp types.
## References
Johnson, S. G., Notes on Adjoint Methods for 18.336, Online at
http://math.mit.edu/stevenj/18.336/adjoint.pdf (2007)
"""
struct SteadyStateAdjoint{CS,AD,FDT,VJP,LS} <: AbstractAdjointSensitivityAlgorithm{CS,AD,FDT}
autojacvec::VJP
linsolve::LS
end
Base.@pure function SteadyStateAdjoint(;chunk_size = 0, autodiff = true, diff_type = Val{:central},
autojacvec = nothing, linsolve = nothing)
SteadyStateAdjoint{chunk_size,autodiff,diff_type,typeof(autojacvec),typeof(linsolve)}(autojacvec,linsolve)
end
setvjp(sensealg::SteadyStateAdjoint{CS,AD,FDT,LS},vjp) where {CS,AD,FDT,LS} =
SteadyStateAdjoint{CS,AD,FDT,typeof(vjp),LS}(vjp,sensealg.linsolve)
abstract type VJPChoice end
"""
ZygoteVJP <: VJPChoice
Uses Zygote.jl to compute vector-Jacobian products. Tends to be the fastest VJP method if the
ODE/DAE/SDE/DDE is written with mostly vectorized functions (like neural networks and other
layers from Flux.jl) and the `f` functions is given out-of-place. If the `f` function is
in-place, then `Zygote.Buffer` arrays are used internally which can greatly reduce the
performance of the VJP method.
## Constructor
```julia
ZygoteVJP(compile=false)
```
"""
struct ZygoteVJP <: VJPChoice end
"""
EnzymeVJP <: VJPChoice
Uses Enzyme.jl to compute vector-Jacobian products. Is the fastest VJP whenever applicable,
though Enzyme.jl currently has low coverage over the Julia programming language, for example
restricting the user's defined `f` function to not do things like require garbage collection
or calls to BLAS/LAPACK. However, mutation is supported, meaning that in-place `f` with
fully mutating non-allocating code will work with Enzyme (provided no high level calls to C
like BLAS/LAPACK are used) and this will be the most efficient adjoint implementation.
## Constructor
```julia
EnzymeVJP(compile=false)
```
"""
struct EnzymeVJP <: VJPChoice end
"""
TrackerVJP <: VJPChoice
Uses Tracker.jl to compute the vector-Jacobian products. If `f` is in-place,
then it uses a array of structs formulation to do scalarized reverse mode,
while if `f` is out-of-place then it uses an array-based reverse mode.
Not as efficient as `ReverseDiffVJP`, but supports GPUs when doing array-based
reverse mode.
## Constructor
```julia
TrackerVJP(compile=false)
```
"""
struct TrackerVJP <: VJPChoice end
"""
ReverseDiffVJP{compile} <: VJPChoice
Uses ReverseDiff.jl to compute the vector-Jacobian products. If `f` is in-place,
then it uses a array of structs formulation to do scalarized reverse mode,
while if `f` is out-of-place then it uses an array-based reverse mode.
Usually the fastest when scalarized operations exist in the f function
(like in scientific machine learning applications like Universal Differential Equations)
and the boolean compilation is enabled (i.e. ReverseDiffVJP(true)), if EnzymeVJP fails on
a given choice of `f`.
Does not support GPUs (CuArrays).
## Constructor
```julia
ReverseDiffVJP(compile=false)
```
## Keyword Arguments
* `compile`: Whether to cache the compilation of the reverse tape. This heavily increases
the performance of the method but requires that the `f` function of the ODE/DAE/SDE/DDE
has no branching.
"""
struct ReverseDiffVJP{compile} <: VJPChoice
ReverseDiffVJP(compile=false) = new{compile}()
end
@inline convert_tspan(::ForwardDiffSensitivity{CS,CTS}) where {CS,CTS} = CTS
@inline convert_tspan(::Any) = nothing
@inline alg_autodiff(alg::DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT}) where {CS,AD,FDT} = AD
@inline get_chunksize(alg::DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT}) where {CS,AD,FDT} = CS
@inline diff_type(alg::DiffEqBase.AbstractSensitivityAlgorithm{CS,AD,FDT}) where {CS,AD,FDT} = FDT
@inline function get_jacvec(alg::DiffEqBase.AbstractSensitivityAlgorithm)
alg.autojacvec isa Bool ? alg.autojacvec : true
end
@inline function get_jacmat(alg::DiffEqBase.AbstractSensitivityAlgorithm)
alg.autojacmat isa Bool ? alg.autojacmat : true
end
@inline ischeckpointing(alg::DiffEqBase.AbstractSensitivityAlgorithm, sol=nothing) = false
@inline ischeckpointing(alg::InterpolatingAdjoint) = alg.checkpointing
@inline ischeckpointing(alg::InterpolatingAdjoint, sol) = alg.checkpointing || !sol.dense
@inline ischeckpointing(alg::BacksolveAdjoint, sol=nothing) = alg.checkpointing
@inline isnoisemixing(alg::DiffEqBase.AbstractSensitivityAlgorithm) = false
@inline isnoisemixing(alg::InterpolatingAdjoint) = alg.noisemixing
@inline isnoisemixing(alg::BacksolveAdjoint) = alg.noisemixing
@inline compile_tape(vjp::ReverseDiffVJP{compile}) where compile = compile
@inline compile_tape(autojacvec::Bool) = false
"""
ForwardDiffOverAdjoint{A} <: AbstractSecondOrderSensitivityAlgorithm{nothing,true,nothing}
ForwardDiff.jl over a choice of `sensealg` method for the adjoint.
## Constructor
```julia
ForwardDiffOverAdjoint(sensealg)
```
## SciMLProblem Support
This supports any SciMLProblem that the `sensealg` choice supports, provided the solver algorithm
is `SciMLBase.isautodifferentiable`.
## References
Hindmarsh, A. C. and Brown, P. N. and Grant, K. E. and Lee, S. L. and Serban, R.
and Shumaker, D. E. and Woodward, C. S., SUNDIALS: Suite of nonlinear and
differential/algebraic equation solvers, ACM Transactions on Mathematical
Software (TOMS), 31, pp:363–396 (2005)
"""
struct ForwardDiffOverAdjoint{A} <: AbstractSecondOrderSensitivityAlgorithm{nothing,true,nothing}
adjalg::A
end | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 18058 | ## Direct calls
const ADJOINT_PARAMETER_COMPATABILITY_MESSAGE =
"""
Adjoint sensitivity analysis functionality requires being able to solve
a differential equation defined by the parameter struct `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with adjoint sensitivity analysis requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during adjoint differentiation.
To work around this issue for complicated cases like nested structs, look
into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl so that `p` is an `AbstractArray` with a concrete element type.
"""
struct AdjointSensitivityParameterCompatibilityError <: Exception end
function Base.showerror(io::IO, e::AdjointSensitivityParameterCompatibilityError)
print(io, ADJOINT_PARAMETER_COMPATABILITY_MESSAGE)
end
@doc doc"""
adjoint_sensitivities(sol,alg,g,t=nothing,dg=nothing;
abstol=1e-6,reltol=1e-3,
checkpoints=sol.t,
corfunc_analytical=nothing,
callback = nothing,
sensealg=InterpolatingAdjoint(),
kwargs...)
Adjoint sensitivity analysis is used to find the gradient of the solution
with respect to some functional of the solution. In many cases this is used
in an optimization problem to return the gradient with respect to some cost
function. It is equivalent to "backpropagation" or reverse-mode automatic
differentiation of a differential equation.
Using `adjoint_sensitivities` directly let's you do three things. One it can
allow you to be more efficient, since the sensitivity calculation can be done
directly on a cost function, avoiding the overhead of building the derivative
of the full concretized solution. It can also allow you to be more efficient
by directly controlling the forward solve that is then reversed over. Lastly,
it allows one to define a continuous cost function on the continuous solution,
instead of just at discrete data points.
!!! warning
Adjoint sensitivity analysis functionality requires being able to solve
a differential equation defined by the parameter struct `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with adjoint sensitivity analysis requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during adjoint differentiation.
To work around this issue for complicated cases like nested structs, look
into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl so that `p` is an `AbstractArray` with a concrete element type.
!!! warning
Non-checkpointed InterpolatingAdjoint and QuadratureAdjoint sensealgs
require that the forward solution `sol(t)` has an accurate dense
solution unless checkpointing is used. This means that you should
not use `solve(prob,alg,saveat=ts)` unless checkpointing. If specific
saving is required, one should solve dense `solve(prob,alg)`, use the
solution in the adjoint, and then `sol(ts)` interpolate.
### Syntax
There are two forms. For discrete adjoints, the form is:
```julia
du0,dp = adjoint_sensitivities(sol,alg,dg,ts;sensealg=InterpolatingAdjoint(),
checkpoints=sol.t,kwargs...)
```
where `alg` is the ODE algorithm to solve the adjoint problem, `dg` is the jump
function, `sensealg` is the sensitivity algorithm, and `ts` is the time points
for data. `dg` is given by:
```julia
dg(out,u,p,t,i)
```
which is the in-place gradient of the cost functional `g` at time point `ts[i]`
with `u=u(t)`.
For continuous functionals, the form is:
```julia
du0,dp = adjoint_sensitivities(sol,alg,g,nothing,(dgdu,dgdp);sensealg=InterpolatingAdjoint(),
checkpoints=sol.t,,kwargs...)
```
for the cost functional
```julia
g(u,p,t)
```
with in-place gradient
```julia
dgdu(out,u,p,t)
dgdp(out,u,p,t)
```
If the gradient is omitted, i.e.
```julia
du0,dp = adjoint_sensitivities(sol,alg,g,nothing;kwargs...)
```
then we assume `dgdp` is zero and `dgdu` will be computed automatically using ForwardDiff or finite
differencing, depending on the `autodiff` setting in the `AbstractSensitivityAlgorithm`.
Note that the keyword arguments are passed to the internal ODE solver for
solving the adjoint problem.
### Example discrete adjoints on a cost function
In this example we will show solving for the adjoint sensitivities of a discrete
cost functional. First let's solve the ODE and get a high quality continuous
solution:
```julia
function f(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + u[1]*u[2]
end
p = [1.5,1.0,3.0]
prob = ODEProblem(f,[1.0;1.0],(0.0,10.0),p)
sol = solve(prob,Vern9(),abstol=1e-10,reltol=1e-10)
```
Now let's calculate the sensitivity of the ``\ell_2`` error against 1 at evenly spaced
points in time, that is:
```math
L(u,p,t)=\sum_{i=1}^{n}\frac{\Vert1-u(t_{i},p)\Vert^{2}}{2}
```
for ``t_i = 0.5i``. This is the assumption that the data is `data[i]=1.0`.
For this function, notice we have that:
```math
\begin{aligned}
dg_{1}&=1-u_{1} \\
dg_{2}&=1-u_{2} \\
& \quad \vdots
\end{aligned}
```
and thus:
```julia
dg(out,u,p,t,i) = (out.=1.0.-u)
```
Also, we can omit `dgdp`, because the cost function doesn't dependent on `p`. If we had data, we'd just replace `1.0` with `data[i]`. To get the adjoint
sensitivities, call:
```julia
ts = 0:0.5:10
res = adjoint_sensitivities(sol,Vern9(),dg,ts,abstol=1e-14,
reltol=1e-14)
```
This is super high accuracy. As always, there's a tradeoff between accuracy
and computation time. We can check this almost exactly matches the
autodifferentiation and numerical differentiation results:
```julia
using ForwardDiff,Calculus,Tracker
function G(p)
tmp_prob = remake(prob,u0=convert.(eltype(p),prob.u0),p=p)
sol = solve(tmp_prob,Vern9(),abstol=1e-14,reltol=1e-14,saveat=ts,
sensealg=SensitivityADPassThrough())
A = convert(Array,sol)
sum(((1 .- A).^2)./2)
end
G([1.5,1.0,3.0])
res2 = ForwardDiff.gradient(G,[1.5,1.0,3.0])
res3 = Calculus.gradient(G,[1.5,1.0,3.0])
res4 = Tracker.gradient(G,[1.5,1.0,3.0])
res5 = ReverseDiff.gradient(G,[1.5,1.0,3.0])
```
and see this gives the same values.
### Example controlling adjoint method choices and checkpointing
In the previous examples, all calculations were done using the interpolating
method. This maximizes speed but at a cost of requiring a dense `sol`. If it
is not possible to hold a dense forward solution in memory, then one can use
checkpointing. For example:
```julia
ts = [0.0,0.2,0.5,0.7]
sol = solve(prob,Vern9(),saveat=ts)
```
Creates a non-dense solution with checkpoints at `[0.0,0.2,0.5,0.7]`. Now we
can do:
```julia
res = adjoint_sensitivities(sol,Vern9(),dg,ts,
sensealg=InterpolatingAdjoint(checkpointing=true))
```
When grabbing a Jacobian value during the backwards solution, it will no longer
interpolate to get the value. Instead, it will start a forward solution at the
nearest checkpoint to build local interpolants in a way that conserves memory.
By default the checkpoints are at `sol.t`, but we can override this:
```julia
res = adjoint_sensitivities(sol,Vern9(),dg,ts,
sensealg=InterpolatingAdjoint(checkpointing=true),
checkpoints = [0.0,0.5])
```
### Example continuous adjoints on an energy functional
In this case we'd like to calculate the adjoint sensitivity of the scalar energy
functional:
```math
G(u,p)=\int_{0}^{T}\frac{\sum_{i=1}^{n}u_{i}^{2}(t)}{2}dt
```
which is:
```julia
g(u,p,t) = (sum(u).^2) ./ 2
```
Notice that the gradient of this function with respect to the state `u` is:
```julia
function dg(out,u,p,t)
out[1]= u[1] + u[2]
out[2]= u[1] + u[2]
end
```
To get the adjoint sensitivities, we call:
```julia
res = adjoint_sensitivities(sol,Vern9(),g,nothing,dg,abstol=1e-8,
reltol=1e-8,iabstol=1e-8,ireltol=1e-8)
```
Notice that we can check this against autodifferentiation and numerical
differentiation as follows:
```julia
using QuadGK
function G(p)
tmp_prob = remake(prob,p=p)
sol = solve(tmp_prob,Vern9(),abstol=1e-14,reltol=1e-14)
res,err = quadgk((t)-> (sum(sol(t)).^2)./2,0.0,10.0,atol=1e-14,rtol=1e-10)
res
end
res2 = ForwardDiff.gradient(G,[1.5,1.0,3.0])
res3 = Calculus.gradient(G,[1.5,1.0,3.0])
```
"""
function adjoint_sensitivities(sol,args...;
sensealg=InterpolatingAdjoint(),
verbose=true,kwargs...)
if hasfield(typeof(sensealg),:autojacvec) && sensealg.autojacvec === nothing
if haskey(kwargs, :callback)
has_cb = kwargs[:callback] !== nothing
else
has_cb = false
end
if !has_cb
_sensealg = if isinplace(sol.prob)
setvjp(sensealg,inplace_vjp(sol.prob,sol.prob.u0,sol.prob.p,verbose))
else
setvjp(sensealg,ZygoteVJP())
end
else
_sensealg = setvjp(sensealg, ReverseDiffVJP())
end
return try
_adjoint_sensitivities(sol,_sensealg,args...;verbose,kwargs...)
catch e
verbose && @warn "Automatic AD choice of autojacvec failed in ODE adjoint, failing back to ODE adjoint + numerical vjp"
_adjoint_sensitivities(sol,setvjp(sensealg,false),args...;verbose,kwargs...)
end
else
return _adjoint_sensitivities(sol,sensealg,args...;verbose,kwargs...)
end
end
function _adjoint_sensitivities(sol,sensealg,alg,g,t=nothing,dg=nothing;
abstol=1e-6,reltol=1e-3,
checkpoints=sol.t,
corfunc_analytical=nothing,
callback = nothing,
kwargs...)
if !(typeof(sol.prob.p) <: Union{Nothing,SciMLBase.NullParameters,AbstractArray}) || (sol.prob.p isa AbstractArray && !Base.isconcretetype(eltype(sol.prob.p)))
throw(AdjointSensitivityParameterCompatibilityError())
end
if sol.prob isa ODEProblem
adj_prob = ODEAdjointProblem(sol,sensealg,g,t,dg; checkpoints=checkpoints,
callback = callback,
abstol=abstol,reltol=reltol, kwargs...)
elseif sol.prob isa SDEProblem
adj_prob = SDEAdjointProblem(sol,sensealg,g,t,dg,checkpoints=checkpoints,
callback = callback,
abstol=abstol,reltol=reltol,
corfunc_analytical=corfunc_analytical)
elseif sol.prob isa RODEProblem
adj_prob = RODEAdjointProblem(sol,sensealg,g,t,dg,checkpoints=checkpoints,
callback = callback,
abstol=abstol,reltol=reltol,
corfunc_analytical=corfunc_analytical)
else
error("Continuous adjoint sensitivities are only supported for ODE/SDE/RODE problems.")
end
tstops = ischeckpointing(sensealg, sol) ? checkpoints : similar(sol.t, 0)
adj_sol = solve(adj_prob,alg;
save_everystep=false,save_start=false,saveat=eltype(sol[1])[],
tstops=tstops,abstol=abstol,reltol=reltol,kwargs...)
p = sol.prob.p
l = p === nothing || p === DiffEqBase.NullParameters() ? 0 : length(sol.prob.p)
du0 = -adj_sol[end][1:length(sol.prob.u0)]
if eltype(sol.prob.p) <: real(eltype(adj_sol[end]))
dp = real.(adj_sol[end][(1:l) .+ length(sol.prob.u0)])'
elseif p === nothing || p === DiffEqBase.NullParameters()
dp = nothing
else
dp = adj_sol[end][(1:l) .+ length(sol.prob.u0)]'
end
du0,dp
end
function _adjoint_sensitivities(sol,sensealg::SteadyStateAdjoint,alg,g,dg=nothing;
abstol=1e-6,reltol=1e-3,
kwargs...)
SteadyStateAdjointProblem(sol,sensealg,g,dg;kwargs...)
end
function _adjoint_sensitivities(sol,sensealg::SteadyStateAdjoint,alg;
g=nothing,dg=nothing,
abstol=1e-6,reltol=1e-3,
kwargs...)
SteadyStateAdjointProblem(sol,sensealg,g,dg;kwargs...)
end
@doc doc"""
H = second_order_sensitivities(loss,prob,alg,args...;
sensealg=ForwardDiffOverAdjoint(InterpolatingAdjoint(autojacvec=ReverseDiffVJP())),
kwargs...)
Second order sensitivity analysis is used for the fast calculation of Hessian
matrices.
!!! warning
Adjoint sensitivity analysis functionality requires being able to solve
a differential equation defined by the parameter struct `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with adjoint sensitivity analysis requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during adjoint differentiation.
To work around this issue for complicated cases like nested structs, look
into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl so that `p` is an `AbstractArray` with a concrete element type.
### Example second order sensitivity analysis calculation
```julia
using DiffEqSensitivity, OrdinaryDiffEq, ForwardDiff
using Test
function lotka!(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(lotka!,u0,(0.0,10.0),p)
loss(sol) = sum(sol)
v = ones(4)
H = second_order_sensitivities(loss,prob,Vern9(),saveat=0.1,abstol=1e-12,reltol=1e-12)
```
## Arguments
The arguments for this function match `adjoint_sensitivities`. The only notable difference
is `sensealg` which requires a second order sensitivity algorithm, of which currently the
only choice is `ForwardDiffOverAdjoint` which uses forward-over-reverse to mix a forward-mode
sensitivity analysis with an adjoint sensitivity analysis for a faster computation than either
double forward or double reverse. `ForwardDiffOverAdjoint`'s positional argument just accepts
a first order sensitivity algorithm.
"""
function second_order_sensitivities(loss,prob,alg,args...;
sensealg=ForwardDiffOverAdjoint(InterpolatingAdjoint(autojacvec=ReverseDiffVJP())),
kwargs...)
_second_order_sensitivities(loss,prob,alg,sensealg,args...;kwargs...)
end
@doc doc"""
Hv = second_order_sensitivity_product(loss,v,prob,alg,args...;
sensealg=ForwardDiffOverAdjoint(InterpolatingAdjoint(autojacvec=ReverseDiffVJP())),
kwargs...)
Second order sensitivity analysis product is used for the fast calculation of
Hessian-vector products ``Hv`` without requiring the construction of the Hessian
matrix.
!!! warning
Adjoint sensitivity analysis functionality requires being able to solve
a differential equation defined by the parameter struct `p`. Thus while
DifferentialEquations.jl can support any parameter struct type, usage
with adjoint sensitivity analysis requires that `p` could be a valid
type for being the initial condition `u0` of an array. This means that
many simple types, such as `Tuple`s and `NamedTuple`s, will work as
parameters in normal contexts but will fail during adjoint differentiation.
To work around this issue for complicated cases like nested structs, look
into defining `p` using `AbstractArray` libraries such as RecursiveArrayTools.jl
or ComponentArrays.jl so that `p` is an `AbstractArray` with a concrete element type.
### Example second order sensitivity analysis calculation
```julia
using DiffEqSensitivity, OrdinaryDiffEq, ForwardDiff
using Test
function lotka!(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(lotka!,u0,(0.0,10.0),p)
loss(sol) = sum(sol)
v = ones(4)
Hv = second_order_sensitivity_product(loss,v,prob,Vern9(),saveat=0.1,abstol=1e-12,reltol=1e-12)
```
## Arguments
The arguments for this function match `adjoint_sensitivities`. The only notable difference
is `sensealg` which requires a second order sensitivity algorithm, of which currently the
only choice is `ForwardDiffOverAdjoint` which uses forward-over-reverse to mix a forward-mode
sensitivity analysis with an adjoint sensitivity analysis for a faster computation than either
double forward or double reverse. `ForwardDiffOverAdjoint`'s positional argument just accepts
a first order sensitivity algorithm.
"""
function second_order_sensitivity_product(loss,v,prob,alg,args...;
sensealg=ForwardDiffOverAdjoint(InterpolatingAdjoint(autojacvec=ReverseDiffVJP())),
kwargs...)
_second_order_sensitivity_product(loss,v,prob,alg,sensealg,args...;kwargs...)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 4736 | struct SteadyStateAdjointSensitivityFunction{
C<:AdjointDiffCache,
Alg<:SteadyStateAdjoint,
uType,
SType,
fType<:ODEFunction,
CV,
λType,
VJPType,
LS,
} <: SensitivityFunction
diffcache::C
sensealg::Alg
discrete::Bool
y::uType
sol::SType
f::fType
colorvec::CV
λ::λType
vjp::VJPType
linsolve::LS
end
function SteadyStateAdjointSensitivityFunction(
g,
sensealg,
discrete,
sol,
dg,
colorvec,
needs_jac,
)
@unpack f, p, u0 = sol.prob
diffcache, y = adjointdiffcache(
g,
sensealg,
discrete,
sol,
dg,
f;
quad = false,
needs_jac = needs_jac,
)
λ = zero(y)
linsolve = needs_jac ? nothing : sensealg.linsolve
vjp = similar(λ, length(p))
SteadyStateAdjointSensitivityFunction(
diffcache,
sensealg,
discrete,
y,
sol,
f,
colorvec,
λ,
vjp,
linsolve,
)
end
@noinline function SteadyStateAdjointProblem(
sol,
sensealg::SteadyStateAdjoint,
g,
dg;
save_idxs = nothing,
kwargs...
)
@unpack f, p, u0 = sol.prob
discrete = false
# TODO: What is the correct heuristic? Can we afford to compute Jacobian for
# cases where the length(u0) > 50 and if yes till what threshold
needs_jac = (sensealg.linsolve === nothing && length(u0) <= 50) || LinearSolve.needs_concrete_A(sensealg.linsolve)
p === DiffEqBase.NullParameters() && error(
"Your model does not have parameters, and thus it is impossible to calculate the derivative of the solution with respect to the parameters. Your model must have parameters to use parameter sensitivity calculations!",
)
sense = SteadyStateAdjointSensitivityFunction(
g,
sensealg,
discrete,
sol,
dg,
f.colorvec,
needs_jac,
)
@unpack diffcache, y, sol, λ, vjp, linsolve = sense
if needs_jac
if DiffEqBase.has_jac(f)
f.jac(diffcache.J, y, p, nothing)
else
if DiffEqBase.isinplace(sol.prob)
jacobian!(
diffcache.J,
diffcache.uf,
y,
diffcache.f_cache,
sensealg,
diffcache.jac_config,
)
else
temp = jacobian(diffcache.uf, y, sensealg)
@. diffcache.J = temp
end
end
end
_save_idxs = save_idxs === nothing ? Colon() : save_idxs
if dg !== nothing
if g !== nothing
dg(vec(diffcache.dg_val), y, p, nothing, nothing)
else
if typeof(_save_idxs) <: Number
diffcache.dg_val[_save_idxs] = dg[_save_idxs]
elseif typeof(dg) <: Number
@. diffcache.dg_val[_save_idxs] = dg
else
@. diffcache.dg_val[_save_idxs] = dg[_save_idxs]
end
end
else
if g !== nothing
gradient!(
vec(diffcache.dg_val),
diffcache.g,
y,
sensealg,
diffcache.g_grad_config,
)
end
end
if !needs_jac
# NOTE: Zygote doesn't support inplace
linear_problem = LinearProblem(VecJacOperator(f, y, p; autodiff = !DiffEqBase.isinplace(sol.prob)),
vec(diffcache.dg_val),
u0 = vec(λ))
else
linear_problem = LinearProblem(diffcache.J',vec(diffcache.dg_val'),u0 = vec(λ))
end
solve(linear_problem, linsolve) # u is vec(λ)
try
vecjacobian!(
vec(diffcache.dg_val),
y,
λ,
p,
nothing,
sense,
dgrad = vjp,
dy = nothing
)
catch e
if sense.sensealg.autojacvec === nothing
@warn "Automatic AD choice of autojacvec failed in nonlinear solve adjoint, failing back to ODE adjoint + numerical vjp"
vecjacobian!(vec(diffcache.dg_val),y,λ,p,nothing,false,dgrad = vjp,dy = nothing)
else
@warn "AD choice of autojacvec failed in nonlinear solve adjoint"
throw(e)
end
end
if g !== nothing
# compute del g/del p
dg_dp_val = zero(p)
dg_dp = ParamGradientWrapper(g, nothing, y)
dg_dp_config = build_grad_config(sensealg, dg_dp, p, p)
gradient!(dg_dp_val, dg_dp, p, sensealg, dg_dp_config)
@. dg_dp_val = dg_dp_val - vjp
return dg_dp_val
else
return -vjp
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 3894 | # Piracy that used to be requires, allowing Tracker.jl to be specialized for SciML
function RecursiveArrayTools.recursivecopy!(b::AbstractArray{T,N}, a::AbstractArray{T2,N}) where {T<:Tracker.TrackedArray,T2<:Tracker.TrackedArray,N}
@inbounds for i in eachindex(a)
b[i] = copy(a[i])
end
end
DiffEqBase.value(x::Type{Tracker.TrackedReal{T}}) where {T} = T
DiffEqBase.value(x::Type{Tracker.TrackedArray{T,N,A}}) where {T,N,A} = Array{T,N}
DiffEqBase.value(x::Tracker.TrackedReal) = x.data
DiffEqBase.value(x::Tracker.TrackedArray) = x.data
DiffEqBase.promote_u0(u0::Tracker.TrackedArray, p::Tracker.TrackedArray, t0) = u0
DiffEqBase.promote_u0(u0::AbstractArray{<:Tracker.TrackedReal}, p::Tracker.TrackedArray, t0) = u0
DiffEqBase.promote_u0(u0::Tracker.TrackedArray, p::AbstractArray{<:Tracker.TrackedReal}, t0) = u0
DiffEqBase.promote_u0(u0::AbstractArray{<:Tracker.TrackedReal}, p::AbstractArray{<:Tracker.TrackedReal}, t0) = u0
DiffEqBase.promote_u0(u0, p::Tracker.TrackedArray, t0) = Tracker.track(u0)
DiffEqBase.promote_u0(u0, p::AbstractArray{<:Tracker.TrackedReal}, t0) = eltype(p).(u0)
@inline DiffEqBase.fastpow(x::Tracker.TrackedReal, y::Tracker.TrackedReal) = x^y
@inline Base.any(f::Function, x::Tracker.TrackedArray) = any(f, Tracker.data(x))
# Support adaptive with non-tracked time
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::Tracker.TrackedArray, t) where {N}
sqrt(sum(abs2, DiffEqBase.value(u)) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::AbstractArray{<:Tracker.TrackedReal,N}, t) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip((DiffEqBase.value(x) for x in u), Iterators.repeated(t))) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::Array{<:Tracker.TrackedReal,N}, t) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip((DiffEqBase.value(x) for x in u), Iterators.repeated(t))) / length(u))
end
@inline DiffEqBase.ODE_DEFAULT_NORM(u::Tracker.TrackedReal, t) = abs(DiffEqBase.value(u))
# Support TrackedReal time, don't drop tracking on the adaptivity there
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::Tracker.TrackedArray, t::Tracker.TrackedReal) where {N}
sqrt(sum(abs2, u) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::AbstractArray{<:Tracker.TrackedReal,N}, t::Tracker.TrackedReal) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip(u, Iterators.repeated(t))) / length(u))
end
@inline function DiffEqBase.ODE_DEFAULT_NORM(u::Array{<:Tracker.TrackedReal,N}, t::Tracker.TrackedReal) where {N}
sqrt(sum(x -> DiffEqBase.ODE_DEFAULT_NORM(x[1], x[2]), zip(u, Iterators.repeated(t))) / length(u))
end
@inline DiffEqBase.ODE_DEFAULT_NORM(u::Tracker.TrackedReal, t::Tracker.TrackedReal) = abs(u)
function DiffEqBase.solve_up(prob::DiffEqBase.DEProblem, sensealg::Union{DiffEqBase.AbstractSensitivityAlgorithm,Nothing}, u0::Tracker.TrackedArray, p::Tracker.TrackedArray, args...; kwargs...)
Tracker.track(DiffEqBase.solve_up, prob, sensealg, u0, p, args...; kwargs...)
end
function DiffEqBase.solve_up(prob::DiffEqBase.DEProblem, sensealg::Union{DiffEqBase.AbstractSensitivityAlgorithm,Nothing}, u0::Tracker.TrackedArray, p, args...; kwargs...)
Tracker.track(DiffEqBase.solve_up, prob, sensealg, u0, p, args...; kwargs...)
end
function DiffEqBase.solve_up(prob::DiffEqBase.DEProblem, sensealg::Union{DiffEqBase.AbstractSensitivityAlgorithm,Nothing}, u0, p::Tracker.TrackedArray, args...; kwargs...)
Tracker.track(DiffEqBase.solve_up, prob, sensealg, u0, p, args...; kwargs...)
end
Tracker.@grad function DiffEqBase.solve_up(prob, sensealg::Union{Nothing,DiffEqBase.AbstractSensitivityAlgorithm},
u0, p, args...;
kwargs...)
DiffEqBase._solve_adjoint(prob, sensealg, Tracker.data(u0), Tracker.data(p),
SciMLBase.TrackerOriginator(), args...; kwargs...)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
]
| 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1711 | # Piracy that used to be requires, allowing Zyogote.jl to be specialized for SciML
function ∇tmap(cx, f, args...)
ys_and_backs = SciMLBase.tmap((args...) -> Zygote._pullback(cx, f, args...), args...)
if isempty(ys_and_backs)
ys_and_backs, _ -> (NoTangent(), NoTangent())
else
ys, backs = Zygote.unzip(ys_and_backs)
function ∇tmap_internal(Δ)
Δf_and_args_zipped = SciMLBase.tmap((f, δ) -> f(δ), backs, Δ)
Δf_and_args = Zygote.unzip(Δf_and_args_zipped)
Δf = reduce(Zygote.accum, Δf_and_args[1])
(Δf, Δf_and_args[2:end]...)
end
ys, ∇tmap_internal
end
end
function ∇responsible_map(cx, f, args...)
ys_and_backs = SciMLBase.responsible_map((args...) -> Zygote._pullback(cx, f, args...), args...)
if isempty(ys_and_backs)
ys_and_backs, _ -> (NoTangent(), NoTangent())
else
ys, backs = Zygote.unzip(ys_and_backs)
ys, function ∇responsible_map_internal(Δ)
# Apply pullbacks in reverse order. Needed for correctness if `f` is stateful.
Δf_and_args_zipped = SciMLBase.responsible_map((f, δ) -> f(δ), Zygote._tryreverse(SciMLBase.responsible_map, backs, Δ)...)
Δf_and_args = Zygote.unzip(Zygote._tryreverse(SciMLBase.responsible_map, Δf_and_args_zipped))
Δf = reduce(Zygote.accum, Δf_and_args[1])
(Δf, Δf_and_args[2:end]...)
end
end
end
ZygoteRules.@adjoint function SciMLBase.tmap(f, args::Union{AbstractArray,Tuple}...)
∇tmap(__context__, f, args...)
end
ZygoteRules.@adjoint function SciMLBase.responsible_map(f, args::Union{AbstractArray,Tuple}...)
∇responsible_map(__context__, f, args...)
end | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.