licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 6551 | using DiffEqSensitivity, OrdinaryDiffEq, DiffEqCallbacks, Flux
using Random, Test
using Zygote
function test_hybridNODE(sensealg)
Random.seed!(12345)
datalength = 100
tspan = (0.0,100.0)
t = range(tspan[1],tspan[2],length=datalength)
target = 3.0*(1:datalength)./datalength # some dummy data to fit to
cbinput = rand(1, datalength) #some external ODE contribution
pmodel = Chain(
Dense(2, 10, init=zeros),
Dense(10, 2, init=zeros))
p, re = Flux.destructure(pmodel)
dudt(u,p,t) = re(p)(u)
# callback changes the first component of the solution every time
# t is an integer
function affect!(integrator, cbinput)
event_index = round(Int,integrator.t)
integrator.u[1] += 0.2*cbinput[event_index]
end
callback = PresetTimeCallback(collect(1:datalength),(int)->affect!(int, cbinput))
# ODE with Callback
prob = ODEProblem(dudt,[0.0, 1.0],tspan,p)
function predict_n_ode(p)
arr = Array(solve(prob, Tsit5(),
p=p, sensealg=sensealg, saveat=2.0, callback=callback))[1,2:2:end]
return arr[1:datalength]
end
function loss_n_ode()
pred = predict_n_ode(p)
loss = sum(abs2,target .- pred)./datalength
end
cb = function () #callback function to observe training
pred = predict_n_ode(p)
display(loss_n_ode())
end
@show sensealg
Flux.train!(loss_n_ode, Flux.params(p), Iterators.repeated((), 20), ADAM(0.005), cb = cb)
@test loss_n_ode() < 0.5
println(" ")
end
function test_hybridNODE2(sensealg)
Random.seed!(12345)
u0 = Float32[2.; 0.; 0.; 0.]
tspan = (0f0,1f0)
## Get goal data
function trueaffect!(integrator)
integrator.u[3:4] = -3*integrator.u[1:2]
end
function trueODEfunc(dx,x,p,t)
@views dx[1:2] .= x[1:2] + x[3:4]
dx[1] += x[2]
dx[2] += x[1]
dx[3:4] .= 0f0
end
cb_ = PeriodicCallback(trueaffect!,0.1f0,save_positions=(true,true),initial_affect=true)
prob = ODEProblem(trueODEfunc,u0,tspan)
sol = solve(prob,Tsit5(),callback=cb_,save_everystep=false,save_start=true)
ode_data = Array(sol)[1:2,1:end]'
## Make model
dudt2 = Chain(Dense(4,50,tanh),
Dense(50,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
function affect!(integrator)
integrator.u[3:4] = -3*integrator.u[1:2]
end
function ODEfunc(dx,x,p,t)
dx[1:2] .= re(p)(x)
dx[3:4] .= 0f0
end
z0 = u0
prob = ODEProblem(ODEfunc,z0,tspan)
cb = PeriodicCallback(affect!,0.1f0,save_positions=(true,true),initial_affect=true)
## Initialize learning functions
function predict_n_ode()
_prob = remake(prob,p=p)
Array(solve(_prob,Tsit5(),u0=z0,p=p,callback=cb,save_everystep=false,save_start=true,sensealg=sensealg))[1:2,:]
end
function loss_n_ode()
pred = predict_n_ode()[1:2,1:end]'
loss = sum(abs2,ode_data .- pred)
loss
end
loss_n_ode() # n_ode.p stores the initial parameters of the neural ODE
cba = function () #callback function to observe training
pred = predict_n_ode()[1:2,1:end]'
display(sum(abs2,ode_data .- pred))
return false
end
cba()
## Learn
ps = Flux.params(p)
data = Iterators.repeated((), 25)
@show sensealg
Flux.train!(loss_n_ode, ps, data, ADAM(0.0025), cb = cba)
@test loss_n_ode() < 0.5
println(" ")
end
mutable struct Affect{T}
callback_data::T
end
compute_index(t) = round(Int,t)+1
function (cb::Affect)(integrator)
indx = compute_index(integrator.t)
integrator.u .= integrator.u .+ @view(cb.callback_data[:, indx, 1]) * (integrator.t - integrator.tprev)
end
function test_hybridNODE3(sensealg)
u0 = Float32[2.; 0.]
datasize = 101
tspan = (0.0f0,10.0f0)
function trueODEfunc(du,u,p,t)
du .= -u
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))
true_data = reshape(ode_data,(2,length(t),1))
true_data = convert.(Float32,true_data)
callback_data = true_data * 1f-3
train_dataloader = Flux.Data.DataLoader((true_data = true_data,callback_data = callback_data),batchsize=1)
dudt2 = Chain(Dense(2,50,tanh),
Dense(50,2))
p,re = Flux.destructure(dudt2)
function dudt(du,u,p,t)
du .= re(p)(u)
end
z0 = Float32[2.; 0.]
prob = ODEProblem(dudt,z0,tspan)
function callback_(callback_data)
affect! = Affect(callback_data)
condition(u,t,integrator) = integrator.t > 0
DiscreteCallback(condition,affect!,save_positions=(false,false))
end
function predict_n_ode(true_data_0,callback_data, sense)
_prob = remake(prob,p=p,u0=true_data_0)
solve(_prob,Tsit5(),callback=callback_(callback_data),saveat=t,sensealg=sense)
end
function loss_n_ode(true_data,callback_data)
sol = predict_n_ode((vec(true_data[:,1,:])),callback_data,sensealg)
pred = Array(sol)
loss = Flux.mse((true_data[:,:,1]),pred)
loss
end
ps = Flux.params(p)
opt = ADAM(0.1)
epochs = 10
function cb1(true_data,callback_data)
display(loss_n_ode(true_data,callback_data))
return false
end
function train!(loss, ps, data, opt, cb)
ps = Params(ps)
for (true_data,callback_data) in data
gs = gradient(ps) do
loss(true_data,callback_data)
end
Flux.update!(opt, ps, gs)
cb(true_data,callback_data)
end
return nothing
end
@Flux.epochs epochs train!(loss_n_ode, Params(ps),train_dataloader, opt, cb1)
loss = loss_n_ode(true_data[:,:,1],callback_data)
@info loss
@test loss < 0.5
end
@testset "PresetTimeCallback" begin
test_hybridNODE(ForwardDiffSensitivity())
test_hybridNODE(BacksolveAdjoint())
test_hybridNODE(InterpolatingAdjoint())
test_hybridNODE(QuadratureAdjoint())
end
@testset "PeriodicCallback" begin
test_hybridNODE2(ReverseDiffAdjoint())
test_hybridNODE2(BacksolveAdjoint())
test_hybridNODE2(InterpolatingAdjoint())
test_hybridNODE2(QuadratureAdjoint())
end
@testset "tprevCallback" begin
test_hybridNODE3(ReverseDiffAdjoint())
test_hybridNODE3(BacksolveAdjoint())
test_hybridNODE3(InterpolatingAdjoint())
test_hybridNODE3(QuadratureAdjoint())
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 34224 | using DiffEqSensitivity, OrdinaryDiffEq, RecursiveArrayTools, DiffEqBase,
ForwardDiff, Calculus, QuadGK, LinearAlgebra, Zygote
using Test
function fb(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]*t
du[2] = dy = -p[3]*u[2] + t*p[4]*u[1]*u[2]
end
function foop(u,p,t)
dx = p[1]*u[1] - p[2]*u[1]*u[2]*t
dy = -p[3]*u[2] + t*p[4]*u[1]*u[2]
[dx,dy]
end
function jac(J,u,p,t)
(x, y, a, b, c, d) = (u[1], u[2], p[1], p[2], p[3], p[4])
J[1,1] = a + y * b * -1 * t
J[2,1] = t * y * d
J[1,2] = b * x * -1 * t
J[2,2] = c * -1 + t * x * d
end
f = ODEFunction(fb,jac=jac)
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(f,u0,(0.0,10.0),p)
sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
probb = ODEProblem(fb,u0,(0.0,10.0),p)
proboop = ODEProblem(foop,u0,(0.0,10.0),p)
solb = solve(probb,Tsit5(),abstol=1e-14,reltol=1e-14)
sol_end = solve(probb,Tsit5(),abstol=1e-14,reltol=1e-14,
save_everystep=false,save_start=false)
sol_nodense = solve(probb,Tsit5(),abstol=1e-14,reltol=1e-14,dense=false)
soloop = solve(proboop,Tsit5(),abstol=1e-14,reltol=1e-14)
soloop_nodense = solve(proboop,Tsit5(),abstol=1e-14,reltol=1e-14,dense=false)
# Do a discrete adjoint problem
println("Calculate discrete adjoint sensitivities")
t = 0.0:0.5:10.0
# g(t,u,i) = (1-u)^2/2, L2 away from 1
function dg(out,u,p,t,i)
(out.=2.0.-u)
end
_,easy_res = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14)
_,easy_res2 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14))
_,easy_res22 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(autojacvec=false,abstol=1e-14,reltol=1e-14))
_,easy_res23 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=ReverseDiffVJP(true)))
_,easy_res3 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint())
_,easy_res32 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=false))
_,easy_res4 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint())
_,easy_res42 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false))
_,easy_res43 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false,checkpointing=false))
_,easy_res5 = adjoint_sensitivities(sol,Kvaerno5(nlsolve=NLAnderson(), smooth_est=false),
dg,t,abstol=1e-12,
reltol=1e-10,
sensealg=BacksolveAdjoint())
_,easy_res6 = adjoint_sensitivities(sol_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true),
checkpoints=sol.t[1:500:end])
_,easy_res62 = adjoint_sensitivities(sol_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false),
checkpoints=sol.t[1:500:end])
# It should automatically be checkpointing since the solution isn't dense
_,easy_res7 = adjoint_sensitivities(sol_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(),
checkpoints=sol.t[1:500:end])
_,easy_res8 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.TrackerVJP()))
_,easy_res9 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.ZygoteVJP()))
_,easy_res10 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.ReverseDiffVJP())
)
_,easy_res11 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.ReverseDiffVJP(true))
)
_,easy_res12 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.EnzymeVJP())
)
_,easy_res13 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(autojacvec=DiffEqSensitivity.EnzymeVJP())
)
adj_prob = ODEAdjointProblem(sol,QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=DiffEqSensitivity.ReverseDiffVJP()),dg,t)
adj_sol = solve(adj_prob,Tsit5(),abstol=1e-14,reltol=1e-14)
integrand = AdjointSensitivityIntegrand(sol,adj_sol,QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=DiffEqSensitivity.ReverseDiffVJP()))
res,err = quadgk(integrand,0.0,10.0,atol=1e-14,rtol=1e-12)
@test isapprox(res, easy_res, rtol = 1e-10)
@test isapprox(res, easy_res2, rtol = 1e-10)
@test isapprox(res, easy_res22, rtol = 1e-10)
@test isapprox(res, easy_res23, rtol = 1e-10)
@test isapprox(res, easy_res3, rtol = 1e-10)
@test isapprox(res, easy_res32, rtol = 1e-10)
@test isapprox(res, easy_res4, rtol = 1e-10)
@test isapprox(res, easy_res42, rtol = 1e-10)
@test isapprox(res, easy_res43, rtol = 1e-10)
@test isapprox(res, easy_res5, rtol = 1e-7)
@test isapprox(res, easy_res6, rtol = 1e-9)
@test isapprox(res, easy_res62, rtol = 1e-9)
@test all(easy_res6 .== easy_res7) # should be the same!
@test isapprox(res, easy_res8, rtol = 1e-9)
@test isapprox(res, easy_res9, rtol = 1e-9)
@test isapprox(res, easy_res10, rtol = 1e-9)
@test isapprox(res, easy_res11, rtol = 1e-9)
@test isapprox(res, easy_res12, rtol = 1e-9)
@test isapprox(res, easy_res13, rtol = 1e-9)
println("OOP adjoint sensitivities ")
_,easy_res = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14)
_,easy_res2 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14))
@test_broken easy_res22 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(autojacvec=false,abstol=1e-14,reltol=1e-14))[1] isa AbstractArray
_,easy_res2 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=ReverseDiffVJP(true)))
_,easy_res3 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint())
@test easy_res32 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=false))[1] isa AbstractArray
_,easy_res4 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint())
@test easy_res42 = adjoint_sensitivities(soloop,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false))[1] isa AbstractArray
_,easy_res5 = adjoint_sensitivities(soloop,Kvaerno5(nlsolve=NLAnderson(), smooth_est=false),
dg,t,abstol=1e-12,
reltol=1e-10,
sensealg=BacksolveAdjoint())
_,easy_res6 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true),
checkpoints=soloop_nodense.t[1:5:end])
@test_broken easy_res62 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false),
checkpoints=soloop_nodense.t[1:5:end])
_,easy_res8 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.TrackerVJP()))
_,easy_res9 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.ZygoteVJP()))
_,easy_res10 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.ReverseDiffVJP())
)
_,easy_res11 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.ReverseDiffVJP(true))
)
#@test_broken _,easy_res12 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
# reltol=1e-14,
# sensealg=InterpolatingAdjoint(autojacvec=DiffEqSensitivity.EnzymeVJP())
# ) isa Tuple
#@test_broken _,easy_res13 = adjoint_sensitivities(soloop_nodense,Tsit5(),dg,t,abstol=1e-14,
# reltol=1e-14,
# sensealg=QuadratureAdjoint(autojacvec=DiffEqSensitivity.EnzymeVJP())
# ) isa Tuple
@test isapprox(res, easy_res, rtol = 1e-10)
@test isapprox(res, easy_res2, rtol = 1e-10)
@test isapprox(res, easy_res22, rtol = 1e-10)
@test isapprox(res, easy_res23, rtol = 1e-10)
@test isapprox(res, easy_res3, rtol = 1e-10)
@test isapprox(res, easy_res32, rtol = 1e-10)
@test isapprox(res, easy_res4, rtol = 1e-10)
@test isapprox(res, easy_res42, rtol = 1e-10)
@test isapprox(res, easy_res5, rtol = 1e-9)
@test isapprox(res, easy_res6, rtol = 1e-10)
@test isapprox(res, easy_res62, rtol = 1e-9)
@test isapprox(res, easy_res8, rtol = 1e-9)
@test isapprox(res, easy_res9, rtol = 1e-9)
@test isapprox(res, easy_res10, rtol = 1e-9)
@test isapprox(res, easy_res11, rtol = 1e-9)
#@test isapprox(res, easy_res12, rtol = 1e-9)
#@test isapprox(res, easy_res13, rtol = 1e-9)
println("Calculate adjoint sensitivities ")
_,easy_res8 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
save_everystep=false,save_start=false,
sensealg=BacksolveAdjoint())
_,easy_res82 = adjoint_sensitivities(solb,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
save_everystep=false,save_start=false,
sensealg=BacksolveAdjoint(checkpointing=false))
@test isapprox(res, easy_res8, rtol = 1e-9)
@test isapprox(res, easy_res82, rtol = 1e-9)
_,end_only_res = adjoint_sensitivities(sol_end,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14,
save_everystep=false,save_start=false,
sensealg=BacksolveAdjoint())
@test isapprox(res, end_only_res, rtol = 1e-9)
println("Calculate adjoint sensitivities from autodiff & numerical diff")
function G(p)
tmp_prob = remake(prob,u0=convert.(eltype(p),prob.u0),p=p)
sol = solve(tmp_prob,Tsit5(),abstol=1e-14,reltol=1e-14,sensealg=DiffEqBase.SensitivityADPassThrough(),saveat=t)
A = Array(sol)
sum(((2 .- A).^2)./2)
end
G([1.5,1.0,3.0,1.0])
res2 = ForwardDiff.gradient(G,[1.5,1.0,3.0,1.0])
res3 = Calculus.gradient(G,[1.5,1.0,3.0,1.0])
@test norm(res' .- res2) < 1e-7
@test norm(res' .- res3) < 1e-5
# check other t handling
t2 = [0.5, 1.0]
t3 = [0.0, 0.5, 1.0]
t4 = [0.5, 1.0, 10.0]
_,easy_res2 = adjoint_sensitivities(sol,Tsit5(),dg,t2,abstol=1e-14,
reltol=1e-14)
_,easy_res3 = adjoint_sensitivities(sol,Tsit5(),dg,t3,abstol=1e-14,
reltol=1e-14)
_,easy_res4 = adjoint_sensitivities(sol,Tsit5(),dg,t4,abstol=1e-14,
reltol=1e-14)
function G(p,ts)
tmp_prob = remake(prob,u0=convert.(eltype(p),prob.u0),p=p)
sol = solve(tmp_prob,Tsit5(),abstol=1e-10,reltol=1e-10,sensealg=DiffEqBase.SensitivityADPassThrough(),saveat=ts)
A = convert(Array,sol)
sum(((2 .- A).^2)./2)
end
res2 = ForwardDiff.gradient(p->G(p,t2),[1.5,1.0,3.0,1.0])
res3 = ForwardDiff.gradient(p->G(p,t3),[1.5,1.0,3.0,1.0])
res4 = ForwardDiff.gradient(p->G(p,t4),[1.5,1.0,3.0,1.0])
@test easy_res2' ≈ res2
@test easy_res3' ≈ res3
@test easy_res4' ≈ res4
println("Adjoints of u0")
function dg(out,u,p,t,i)
out .= 1 .- u
end
ū0,adj = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14)
_,adjnou0 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14)
ū02,adj2 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=BacksolveAdjoint(),
reltol=1e-14)
ū022,adj22 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false),
reltol=1e-14)
ū023,adj23 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false,checkpointing=false),
reltol=1e-14)
ū03,adj3 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=InterpolatingAdjoint(),
reltol=1e-14)
ū032,adj32 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=false),
reltol=1e-14)
ū04,adj4 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true),
checkpoints=sol.t[1:500:end],
reltol=1e-14)
@test_nowarn adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true),
checkpoints=sol.t[1:5:end],
reltol=1e-14)
ū042,adj42 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false),
checkpoints=sol.t[1:500:end],
reltol=1e-14)
ū05,adj5 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14),
reltol=1e-14)
ū052,adj52 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=QuadratureAdjoint(autojacvec=false,abstol=1e-14,reltol=1e-14),
reltol=1e-14)
ū05,adj53 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=ReverseDiffVJP(true)),
reltol=1e-14)
ū0args,adjargs = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
save_everystep=false, save_start=false,
sensealg=BacksolveAdjoint(),
reltol=1e-14)
ū0args2,adjargs2 = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
save_everystep=false, save_start=false,
sensealg=InterpolatingAdjoint(),
reltol=1e-14)
res = ForwardDiff.gradient(prob.u0) do u0
tmp_prob = remake(prob,u0=u0)
sol = solve(tmp_prob,Tsit5(),abstol=1e-14,reltol=1e-14,saveat=t)
A = convert(Array,sol)
sum(((1 .- A).^2)./2)
end
@test ū0 ≈ res rtol = 1e-10
@test ū02 ≈ res rtol = 1e-10
@test ū022 ≈ res rtol = 1e-10
@test ū023 ≈ res rtol = 1e-10
@test ū03 ≈ res rtol = 1e-10
@test ū032 ≈ res rtol = 1e-10
@test ū04 ≈ res rtol = 1e-10
@test ū042 ≈ res rtol = 1e-10
@test ū05 ≈ res rtol = 1e-10
@test ū052 ≈ res rtol = 1e-10
@test adj ≈ adjnou0 rtol = 1e-10
@test adj ≈ adj2 rtol = 1e-10
@test adj ≈ adj22 rtol = 1e-10
@test adj ≈ adj23 rtol = 1e-10
@test adj ≈ adj3 rtol = 1e-10
@test adj ≈ adj32 rtol = 1e-10
@test adj ≈ adj4 rtol = 1e-10
@test adj ≈ adj42 rtol = 1e-10
@test adj ≈ adj5 rtol = 1e-10
@test adj ≈ adj52 rtol = 1e-10
@test adj ≈ adj53 rtol = 1e-10
@test ū0args ≈ res rtol = 1e-10
@test adjargs ≈ adj rtol = 1e-10
@test ū0args2 ≈ res rtol = 1e-10
@test adjargs2 ≈ adj rtol = 1e-10
println("Do a continuous adjoint problem")
# Energy calculation
g(u,p,t) = (sum(u).^2) ./ 2
# Gradient of (u1 + u2)^2 / 2
function dg(out,u,p,t)
out[1]= u[1] + u[2]
out[2]= u[1] + u[2]
end
adj_prob = ODEAdjointProblem(sol,QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=DiffEqSensitivity.ReverseDiffVJP()),g,nothing,dg)
adj_sol = solve(adj_prob,Tsit5(),abstol=1e-14,reltol=1e-10)
integrand = AdjointSensitivityIntegrand(sol,adj_sol,QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=DiffEqSensitivity.ReverseDiffVJP()))
res,err = quadgk(integrand,0.0,10.0,atol=1e-14,rtol=1e-10)
println("Test the `adjoint_sensitivities` utility function")
_,easy_res = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14)
println("2")
_,easy_res2 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint())
_,easy_res22 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=false))
println("23")
_,easy_res23 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14))
_,easy_res232 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14,autojacvec=ReverseDiffVJP(false)))
_,easy_res24 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(autojacvec=false,abstol=1e-14,reltol=1e-14))
println("25")
_,easy_res25 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint())
_,easy_res26 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false))
_,easy_res262 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false,checkpointing=false))
println("27")
_,easy_res27 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
checkpoints=sol.t[1:500:end],
sensealg=InterpolatingAdjoint(checkpointing=true))
_,easy_res28 = adjoint_sensitivities(sol,Tsit5(),g,nothing,dg,abstol=1e-14,
reltol=1e-14,
checkpoints=sol.t[1:500:end],
sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false))
println("3")
_,easy_res3 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint())
_,easy_res32 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
sensealg=InterpolatingAdjoint(autojacvec=false))
println("33")
_,easy_res33 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(abstol=1e-14,reltol=1e-14))
_,easy_res34 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
sensealg=QuadratureAdjoint(autojacvec=false,abstol=1e-14,reltol=1e-14))
println("35")
_,easy_res35 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint())
_,easy_res36 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
sensealg=BacksolveAdjoint(autojacvec=false))
println("37")
_,easy_res37 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
checkpoints=sol.t[1:500:end],
sensealg=InterpolatingAdjoint(checkpointing=true))
_,easy_res38 = adjoint_sensitivities(sol,Tsit5(),g,nothing,abstol=1e-14,
reltol=1e-14,
checkpoints=sol.t[1:500:end],
sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false))
@test norm(easy_res .- res) < 1e-8
@test norm(easy_res2 .- res) < 1e-8
@test norm(easy_res22 .- res) < 1e-8
@test norm(easy_res23 .- res) < 1e-8
@test norm(easy_res232 .- res) < 1e-8
@test norm(easy_res24 .- res) < 1e-8
@test norm(easy_res25 .- res) < 1e-8
@test norm(easy_res26 .- res) < 1e-8
@test norm(easy_res262 .- res) < 1e-8
@test norm(easy_res27 .- res) < 1e-8
@test norm(easy_res28 .- res) < 1e-8
@test norm(easy_res3 .- res) < 1e-8
@test norm(easy_res32 .- res) < 1e-8
@test norm(easy_res33 .- res) < 1e-8
@test norm(easy_res34 .- res) < 1e-8
@test norm(easy_res35 .- res) < 1e-8
@test norm(easy_res36 .- res) < 1e-8
@test norm(easy_res37 .- res) < 1e-8
@test norm(easy_res38 .- res) < 1e-8
println("Calculate adjoint sensitivities from autodiff & numerical diff")
function G(p)
tmp_prob = remake(prob,u0=eltype(p).(prob.u0),p=p,
tspan=eltype(p).(prob.tspan))
sol = solve(tmp_prob,Tsit5(),abstol=1e-14,reltol=1e-14)
res,err = quadgk((t)-> (sum(sol(t)).^2)./2,0.0,10.0,atol=1e-14,rtol=1e-10)
res
end
res2 = ForwardDiff.gradient(G,[1.5,1.0,3.0,1.0])
res3 = Calculus.gradient(G,[1.5,1.0,3.0,1.0])
@test norm(res' .- res2) < 1e-8
@test norm(res' .- res3) < 1e-6
# Buffer length test
f = (du, u, p, t) -> du .= 0
p = zeros(3); u = zeros(50)
prob = ODEProblem(f,u,(0.0,10.0),p)
sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
@test_nowarn _,res = adjoint_sensitivities(sol,Tsit5(),dg,t,abstol=1e-14,
reltol=1e-14)
@testset "Checkpointed backsolve" begin
using DiffEqSensitivity, OrdinaryDiffEq
tf = 10.0
function lorenz(du,u,p,t)
σ, ρ, β = p
du[1] = σ*(u[2]-u[1])
du[2] = u[1]*(ρ-u[3]) - u[2]
du[3] = u[1]*u[2] - β*u[3]
return nothing
end
prob_lorenz = ODEProblem(lorenz, [1.0, 0.0, 0.0], (0, tf), [10, 28, 8/3])
sol_lorenz = solve(prob_lorenz,Tsit5(),reltol=1e-6,abstol=1e-9)
function dg(out,u,p,t,i)
(out.=2.0.-u)
end
t = 0:0.1:tf
_,easy_res1 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint())
_,easy_res2 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=InterpolatingAdjoint())
_,easy_res3 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint(),
checkpoints=sol_lorenz.t[1:10:end])
_,easy_res4 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint(),
checkpoints=sol_lorenz.t[1:20:end])
# cannot finish in a reasonable amount of time
@test_skip adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint(checkpointing=false))
@test easy_res2 ≈ easy_res1 rtol=1e-5
@test easy_res2 ≈ easy_res3 rtol=1e-5
@test easy_res2 ≈ easy_res4 rtol=1e-4
ū1,adj1 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint())
ū2,adj2 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=InterpolatingAdjoint())
ū3,adj3 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint(),
checkpoints=sol_lorenz.t[1:10:end])
ū4,adj4 = adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint(),
checkpoints=sol_lorenz.t[1:20:end])
# cannot finish in a reasonable amount of time
@test_skip adjoint_sensitivities(sol_lorenz,Tsit5(),dg,t,abstol=1e-6,
reltol=1e-9,
sensealg=BacksolveAdjoint(checkpointing=false))
@test ū2 ≈ ū1 rtol=1e-5
@test adj2 ≈ adj1 rtol=1e-5
@test ū2 ≈ ū3 rtol=1e-5
@test adj2 ≈ adj3 rtol=1e-5
@test ū2 ≈ ū4 rtol=1e-4
@test adj2 ≈ adj4 rtol=1e-4
# LQR Tests from issue https://github.com/SciML/DiffEqSensitivity.jl/issues/300
x_dim = 2
T = 40.0
cost = (x, u) -> x'*x
params = [-0.4142135623730951, 0.0, -0.0, -0.4142135623730951, 0.0, 0.0]
function dynamics!(du,u,p,t)
du[1] = -u[1] + tanh(p[1]*u[1]+p[2]*u[2])
du[2] = -u[2] + tanh(p[3]*u[1]+p[4]*u[2])
end
function backsolve_grad(sol, lqr_params, checkpointing)
bwd_sol = solve(
ODEAdjointProblem(
sol,
BacksolveAdjoint(autojacvec=EnzymeVJP(),checkpointing = checkpointing),
(x, lqr_params, t) -> cost(x,lqr_params),
),
Tsit5(),
dense = false,
save_everystep = false,
)
bwd_sol.u[end][1:end-x_dim]
#fwd_sol, bwd_sol
end
x0 = ones(x_dim)
fwd_sol = solve(
ODEProblem(dynamics!, x0, (0, T), params),
Tsit5(),abstol=1e-9, reltol=1e-9,
u0 = x0,
p = params,
dense = false,
save_everystep = true
)
backsolve_results = backsolve_grad(fwd_sol, params, false)
backsolve_checkpointing_results = backsolve_grad(fwd_sol, params, true)
@test backsolve_results != backsolve_checkpointing_results
int_u0, int_p = adjoint_sensitivities(fwd_sol,Tsit5(),(x, params, t)->cost(x,params), nothing, sensealg=InterpolatingAdjoint())
@test isapprox(-backsolve_checkpointing_results[1:length(x0)], int_u0, rtol=1e-10)
@test isapprox(backsolve_checkpointing_results[(1:length(params)) .+ length(x0)], int_p', rtol=1e-10)
end
using Test
using LinearAlgebra, DiffEqSensitivity, OrdinaryDiffEq, ForwardDiff, QuadGK
@testset "Adjoint of differential algebric equations with mass matrix" begin
function G(p, prob, ts, cost)
tmp_prob_mm = remake(prob,u0=convert.(eltype(p),prob.u0),p=p)
sol = solve(tmp_prob_mm,Rodas5(autodiff=false),abstol=1e-14,reltol=1e-14,saveat=ts)
cost(sol)
end
alg = Rodas5(autodiff=false)
@testset "Fully ranked mass matrix" begin
@info "discrete cost"
A = [1 2 3; 4 5 6; 7 8 9]
function foo(du, u, p, t)
mul!(du, A, u)
du .= du .+ p
du[2] += sum(p)
return nothing
end
mm = -[1 2 4; 2 3 7; 1 3 41]
u0 = [1, 2.0, 3]
p = [1.0, 2.0, 3]
prob_mm = ODEProblem(ODEFunction(foo, mass_matrix=mm), u0, (0, 1.0), p)
sol_mm = solve(prob_mm, Rodas5(), reltol=1e-14, abstol=1e-14)
ts = 0:0.01:1
dg(out,u,p,t,i) = out .= -1
_, res = adjoint_sensitivities(sol_mm,alg,dg,ts,abstol=1e-14,reltol=1e-14,sensealg=QuadratureAdjoint())
reference_sol = ForwardDiff.gradient(p->G(p, prob_mm, ts, sum),vec(p))
@test res' ≈ reference_sol rtol=1e-11
_, res_interp = adjoint_sensitivities(sol_mm,alg,dg,ts,abstol=1e-14,reltol=1e-14,sensealg=InterpolatingAdjoint())
@test res_interp ≈ res rtol = 1e-11
_, res_interp2 = adjoint_sensitivities(sol_mm,alg,dg,ts,abstol=1e-14,reltol=1e-14,sensealg=InterpolatingAdjoint(checkpointing=true),checkpoints=sol_mm.t[1:10:end])
@test res_interp2 ≈ res rtol = 1e-11
_, res_bs = adjoint_sensitivities(sol_mm,alg,dg,ts,abstol=1e-14,reltol=1e-14,sensealg=BacksolveAdjoint(checkpointing=false))
@test res_bs ≈ res rtol = 1e-11
_, res_bs2 = adjoint_sensitivities(sol_mm,alg,dg,ts,abstol=1e-14,reltol=1e-14,sensealg=BacksolveAdjoint(checkpointing=true),checkpoints=sol_mm.t)
@test res_bs2 ≈ res rtol = 1e-11
@info "continuous cost"
g_cont(u,p,t) = (sum(u).^2) ./ 2
dg_cont(out,u,p,t) = out .= sum(u)
_,easy_res_cont = adjoint_sensitivities(sol_mm,alg,g_cont,nothing,
dg_cont,abstol=1e-10,reltol=1e-10,
sensealg=QuadratureAdjoint())
function G_cont(p)
tmp_prob_mm = remake(prob_mm,u0=eltype(p).(prob_mm.u0),p=p,
tspan=eltype(p).(prob_mm.tspan))
sol = solve(tmp_prob_mm,Rodas5(autodiff=false),abstol=1e-14,reltol=1e-14)
res,err = quadgk((t)-> (sum(sol(t)).^2)./2,prob_mm.tspan...,atol=1e-14,rtol=1e-10)
res
end
reference_sol_cont = ForwardDiff.gradient(G_cont, p)
@test easy_res_cont' ≈ reference_sol_cont rtol=1e-3
end
@testset "Singular mass matrix" begin
function rober(du,u,p,t)
y₁,y₂,y₃ = u
k₁,k₂,k₃ = p
du[1] = -k₁*y₁+k₃*y₂*y₃
du[2] = k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
du[3] = y₁ + y₂ + y₃ - 1
nothing
end
function rober(u,p,t)
y₁,y₂,y₃ = u
k₁,k₂,k₃ = p
return [-k₁*y₁+k₃*y₂*y₃,
k₁*y₁-k₂*y₂^2-k₃*y₂*y₃,
y₁ + y₂ + y₃ - 1]
end
M = [1. 0 0
0 1. 0
0 0 0]
for iip in [true, false]
f = ODEFunction{iip}(rober,mass_matrix=M)
p = [0.04,3e7,1e4]
prob_singular_mm = ODEProblem(f,[1.0,0.0,0.0],(0.0,100),p)
sol_singular_mm = solve(prob_singular_mm,Rodas5(autodiff=false),reltol=1e-12,abstol=1e-12)
ts = [50, sol_singular_mm.t[end]]
dg_singular(out,u,p,t,i) = (fill!(out, 0); out[end] = -1)
_, res = adjoint_sensitivities(sol_singular_mm,alg,dg_singular,ts,abstol=1e-8,reltol=1e-8,sensealg=QuadratureAdjoint(),maxiters=Int(1e6))
reference_sol = ForwardDiff.gradient(p->G(p, prob_singular_mm, ts, sol->sum(last, sol.u)), vec(p))
@test res' ≈ reference_sol rtol = 1e-5
_, res_interp = adjoint_sensitivities(sol_singular_mm,alg,dg_singular,ts,abstol=1e-8,reltol=1e-8,sensealg=InterpolatingAdjoint(),maxiters=Int(1e6))
@test res_interp ≈ res rtol = 1e-5
_, res_interp2 = adjoint_sensitivities(sol_singular_mm,alg,dg_singular,ts,abstol=1e-8,reltol=1e-8,sensealg=InterpolatingAdjoint(checkpointing=true),checkpoints=sol_singular_mm.t[1:10:end])
@test res_interp2 ≈ res rtol = 1e-5
# backsolve doesn't work
_, res_bs = adjoint_sensitivities(sol_singular_mm,alg,dg_singular,ts,abstol=1e-8,reltol=1e-8,sensealg=BacksolveAdjoint(checkpointing=false))
@test_broken res_bs ≈ res rtol = 1e-5
_, res_bs2 = adjoint_sensitivities(sol_singular_mm,alg,dg_singular,ts,abstol=1e-8,reltol=1e-8,sensealg=BacksolveAdjoint(checkpointing=true),checkpoints=sol_singular_mm.t)
@test_broken res_bs2 ≈ res rtol = 1e-5
end
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 3171 | using Test
using OrdinaryDiffEq
using DiffEqSensitivity
using DiffEqBase
using ForwardDiff
using QuadGK
using Zygote
function pendulum_eom(dx, x, p, t)
dx[1] = p[1] * x[2]
dx[2] = -sin(x[1]) + (-p[1]*sin(x[1]) + p[2]*x[2]) # Second term is a simple controller that stabilizes π
end
x0 = [0.1, 0.0]
tspan = (0.0, 10.0)
p = [1.0, -24.05, -19.137]
prob = ODEProblem(pendulum_eom, x0, tspan, p)
sol = solve(prob, Vern9(), abstol=1e-8, reltol=1e-8)
g(x, p, t) = 1.0*(x[1] - π)^2 + 1.0*x[2]^2 + 5.0*(-p[1]*sin(x[1]) + p[2]*x[2])^2
dgdu(out, y, p, t) = ForwardDiff.gradient!(out, y -> g(y, p, t), y)
dgdp(out, y, p, t) = ForwardDiff.gradient!(out, p -> g(y, p, t), p)
res_interp = adjoint_sensitivities(sol,Vern9(),g,nothing,(dgdu, dgdp),abstol=1e-8,
reltol=1e-8,iabstol=1e-8,ireltol=1e-8, sensealg=InterpolatingAdjoint())
res_quad = adjoint_sensitivities(sol,Vern9(),g,nothing,(dgdu, dgdp),abstol=1e-8,
reltol=1e-8,iabstol=1e-8,ireltol=1e-8, sensealg=QuadratureAdjoint())
#res_back = adjoint_sensitivities(sol,Vern9(),g,nothing,(dgdu, dgdp),abstol=1e-8,
# reltol=1e-8,iabstol=1e-8,ireltol=1e-8, sensealg=BacksolveAdjoint(checkpointing=true), sol=sol.t) # it's blowing up
function G(p)
tmp_prob = remake(prob,p=p,u0=convert.(eltype(p), prob.u0))
sol = solve(tmp_prob,Vern9(),abstol=1e-8,reltol=1e-8)
res,err = quadgk((t)-> g(sol(t), p, t), 0.0,10.0,atol=1e-8,rtol=1e-8)
res
end
res2 = ForwardDiff.gradient(G,p)
@test res_interp[2]' ≈ res2 atol=1e-5
@test res_quad[2]' ≈ res2 atol=1e-5
p = [2.0,3.0]
u0 = [2.0]
function f(du,u,p,t)
du[1] = -u[1]*p[1]-p[2]
end
prob = ODEProblem(f,u0,(0.0,1.0),p)
sol = solve(prob,Tsit5(),abstol=1e-10,reltol=1e-10);
g(u,p,t) = -u[1]*p[1]-p[2]
dgdu(out, y, p, t) = ForwardDiff.gradient!(out, y -> g(y, p, t), y)
dgdp(out, y, p, t) = ForwardDiff.gradient!(out, p -> g(y, p, t), p)
du0,dp = adjoint_sensitivities(sol,Vern9(),g,nothing,(dgdu,dgdp);abstol=1e-10,reltol=1e-10)
function G(p)
tmp_prob = remake(prob,p=p,u0=convert.(eltype(p), prob.u0))
sol = solve(tmp_prob,Vern9(),abstol=1e-8,reltol=1e-8)
res,err = quadgk((t)-> g(sol(t), p, t), 0.0,10.0,atol=1e-8,rtol=1e-8)
res
end
res2 = ForwardDiff.gradient(G,p)
@test dp' ≈ res2 atol=1e-5
function model(p)
N_oscillators = 30
u0 = repeat([0.0; 1.0], 1, N_oscillators) # size(u0) = (2, 30)
function du!(du, u, p, t)
W, b = p # Parameters
dy = @view du[1,:] # 30 elements
dy′ = @view du[2,:]
y = @view u[1,:]
y′= @view u[2,:]
@. dy′ = -y * W
@. dy = y′ * b
end
output = solve(
ODEProblem(
du!,
u0,
(0.0, 10.0),
p,
jac = true,
abstol = 1e-12,
reltol = 1e-12),
Tsit5(),
jac = true,
saveat = collect(0:0.1:7),
sensealg = QuadratureAdjoint(),
)
return Array(output[1, :, :]) # only return y, not y′
end
p=[1.5, 0.1]
y = model(p)
loss(p) = sum(model(p))
dp1 = Zygote.gradient(loss,p)[1]
dp2 = ForwardDiff.gradient(loss,p)
@test dp1 ≈ dp2
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1354 | using OrdinaryDiffEq, DiffEqSensitivity, Zygote
tspan = (0., 1.)
X = randn(3, 4)
p = randn(3, 4)
f(u,p,t) = u .* p
f(du,u,p,t) = (du .= u .* p)
prob_ube = ODEProblem{false}(f, X, tspan, p)
Zygote.gradient(p->sum(solve(prob_ube, Midpoint(), u0 = X, p = p)),p)
prob_ube = ODEProblem{true}(f, X, tspan, p)
Zygote.gradient(p->sum(solve(prob_ube, Midpoint(), u0 = X, p = p)),p)
function aug_dynamics!(dz, z, K, t)
x = @view z[2:end]
u = -K * x
dz[1] = x' * x + u' * u
dz[2:end] = x + u
end
policy_params = ones(2, 2)
z0 = zeros(3)
fwd_sol = solve(
ODEProblem(aug_dynamics!, z0, (0.0, 1.0), policy_params),
Tsit5(),
u0 = z0,
p = policy_params)
solve(
ODEAdjointProblem(
fwd_sol,
InterpolatingAdjoint(),
(out, x, p, t, i) -> (out .= 1),
[1.0],
),Tsit5()
)
A = ones(2, 2)
B = ones(2, 2)
Q = ones(2, 2)
R = ones(2, 2)
function aug_dynamics!(dz, z, K, t)
x = @view z[2:end]
u = -K * x
dz[1] = x' * Q * x + u' * R * u
dz[2:end] = A * x + B * u # or just `x + u`
end
policy_params = ones(2, 2)
z0 = zeros(3)
fwd_sol = solve(
ODEProblem(aug_dynamics!, z0, (0.0, 1.0), policy_params),
u0 = z0,
p = policy_params,
)
solve(
ODEAdjointProblem(
fwd_sol,
InterpolatingAdjoint(),
(out, x, p, t, i) -> (out .= 1),
[1.0],
),
)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 4858 | using OrdinaryDiffEq, DiffEqSensitivity, ForwardDiff, Zygote, ReverseDiff, Tracker
using Test
prob = ODEProblem((u,p,t)->u .* p,[2.0],(0.0,1.0),[3.0])
struct senseloss; sense end
(f::senseloss)(u0p) = sum(solve(prob,Tsit5(),u0=u0p[1:1],p=u0p[2:2],abstol=1e-12,
reltol=1e-12,saveat=0.1,sensealg=f.sense))
loss(u0p) = sum(solve(prob,Tsit5(),u0=u0p[1:1],p=u0p[2:2],abstol=1e-12,reltol=1e-12,saveat=0.1))
u0p = [2.0,3.0]
dup = Zygote.gradient(senseloss(InterpolatingAdjoint()),u0p)[1]
@test ReverseDiff.gradient(senseloss(InterpolatingAdjoint()),u0p) ≈ dup
@test_broken ReverseDiff.gradient(senseloss(ReverseDiffAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss(TrackerAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss(ForwardDiffSensitivity()),u0p) ≈ dup
@test_throws DiffEqSensitivity.ForwardSensitivityOutOfPlaceError ReverseDiff.gradient(senseloss(ForwardSensitivity()),u0p) ≈ dup
@test Tracker.gradient(senseloss(InterpolatingAdjoint()),u0p)[1] ≈ dup
@test_broken Tracker.gradient(senseloss(ReverseDiffAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss(TrackerAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss(ForwardDiffSensitivity()),u0p)[1] ≈ dup
@test_throws DiffEqSensitivity.ForwardSensitivityOutOfPlaceError Tracker.gradient(senseloss(ForwardSensitivity()),u0p)[1] ≈ dup
@test ForwardDiff.gradient(senseloss(InterpolatingAdjoint()),u0p) ≈ dup
struct senseloss2; sense end
prob2 = ODEProblem((du,u,p,t)->du .= u .* p,[2.0],(0.0,1.0),[3.0])
(f::senseloss2)(u0p) = sum(solve(prob2,Tsit5(),u0=u0p[1:1],p=u0p[2:2],abstol=1e-12,
reltol=1e-12,saveat=0.1,sensealg=f.sense))
u0p = [2.0,3.0]
dup = Zygote.gradient(senseloss2(InterpolatingAdjoint()),u0p)[1]
@test ReverseDiff.gradient(senseloss2(InterpolatingAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss2(ReverseDiffAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss2(TrackerAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss2(ForwardDiffSensitivity()),u0p) ≈ dup
@test_broken ReverseDiff.gradient(senseloss2(ForwardSensitivity()),u0p) ≈ dup
@test Tracker.gradient(senseloss2(InterpolatingAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss2(ReverseDiffAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss2(TrackerAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss2(ForwardDiffSensitivity()),u0p)[1] ≈ dup
@test_broken Tracker.gradient(senseloss2(ForwardSensitivity()),u0p)[1] ≈ dup
@test ForwardDiff.gradient(senseloss2(InterpolatingAdjoint()),u0p) ≈ dup
struct senseloss3; sense end
(f::senseloss3)(u0p) = sum(solve(prob2,Tsit5(),p=u0p,abstol=1e-12,
reltol=1e-12,saveat=0.1,sensealg=f.sense))
u0p = [3.0]
dup = Zygote.gradient(senseloss3(InterpolatingAdjoint()),u0p)[1]
@test ReverseDiff.gradient(senseloss3(InterpolatingAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss3(ReverseDiffAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss3(TrackerAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss3(ForwardDiffSensitivity()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss3(ForwardSensitivity()),u0p) ≈ dup
@test Tracker.gradient(senseloss3(InterpolatingAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss3(ReverseDiffAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss3(TrackerAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss3(ForwardDiffSensitivity()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss3(ForwardSensitivity()),u0p)[1] ≈ dup
@test ForwardDiff.gradient(senseloss3(InterpolatingAdjoint()),u0p) ≈ dup
struct senseloss4; sense end
(f::senseloss4)(u0p) = sum(solve(prob,Tsit5(),p=u0p,abstol=1e-12,
reltol=1e-12,saveat=0.1,sensealg=f.sense))
u0p = [3.0]
dup = Zygote.gradient(senseloss4(InterpolatingAdjoint()),u0p)[1]
@test ReverseDiff.gradient(senseloss4(InterpolatingAdjoint()),u0p) ≈ dup
@test_broken ReverseDiff.gradient(senseloss4(ReverseDiffAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss4(TrackerAdjoint()),u0p) ≈ dup
@test ReverseDiff.gradient(senseloss4(ForwardDiffSensitivity()),u0p) ≈ dup
@test_throws DiffEqSensitivity.ForwardSensitivityOutOfPlaceError ReverseDiff.gradient(senseloss4(ForwardSensitivity()),u0p) ≈ dup
@test Tracker.gradient(senseloss4(InterpolatingAdjoint()),u0p)[1] ≈ dup
@test_broken Tracker.gradient(senseloss4(ReverseDiffAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss4(TrackerAdjoint()),u0p)[1] ≈ dup
@test Tracker.gradient(senseloss4(ForwardDiffSensitivity()),u0p)[1] ≈ dup
@test_throws DiffEqSensitivity.ForwardSensitivityOutOfPlaceError Tracker.gradient(senseloss4(ForwardSensitivity()),u0p)[1] ≈ dup
@test ForwardDiff.gradient(senseloss4(InterpolatingAdjoint()),u0p) ≈ dup | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2264 | import OrdinaryDiffEq
import DiffEqBase: DynamicalODEProblem
import DiffEqSensitivity:
solve,
ODEProblem,
ODEAdjointProblem,
InterpolatingAdjoint,
ZygoteVJP,
ReverseDiffVJP
import RecursiveArrayTools: ArrayPartition
sol = solve(
DynamicalODEProblem(
(v, x, p, t) -> [0.0, 0.0],
# ERROR: LoadError: type Nothing has no field x
# (v, x, p, t) -> [0.0, 0.0],
# ERROR: LoadError: MethodError: no method matching ndims(::Type{Nothing})
(v, x, p, t) -> v,
[0.0, 0.0],
[0.0, 0.0],
(0.0, 1.0),
),OrdinaryDiffEq.Tsit5()
)
solve(
ODEAdjointProblem(
sol,
InterpolatingAdjoint(autojacvec=ZygoteVJP()),
(out, x, p, t, i) -> (out .= 0),
[sol.t[end]],
),OrdinaryDiffEq.Tsit5()
)
dyn_v(v_ap, x_ap, p, t) = ArrayPartition(zeros(), [0.0])
# Originally, I imagined that this may be a bug in Zygote, and it still may be, but I tried doing a pullback on this
# function on its own and didn't have any trouble with that. So I'm led to believe that it has something to do with
# how DiffEqSensitivity is invoking Zygote. At least this was as far as I was able to simplify the reproduction.
dyn_x(v_ap, x_ap, p, t) = begin
# ERROR: LoadError: MethodError: no method matching ndims(::Type{NamedTuple{(:x,),Tuple{Tuple{Nothing,Array{Float64,1}}}}})
v = v_ap.x[2]
# ERROR: LoadError: type Nothing has no field x
# v = [0.0]
ArrayPartition(zeros(), v)
end
v0 = [-1.0]
x0 = [0.75]
sol = solve(
DynamicalODEProblem(
dyn_v,
dyn_x,
ArrayPartition(zeros(), v0),
ArrayPartition(zeros(), x0),
(0.0, 1.0),
zeros()
),OrdinaryDiffEq.Tsit5(),
# Without setting parameters, we end up with https://github.com/SciML/DifferentialEquations.jl/issues/679 again.
p = zeros()
)
g = ArrayPartition(ArrayPartition(zeros(), zero(v0)), ArrayPartition(zeros(), zero(x0)))
bwd_sol = solve(
ODEAdjointProblem(
sol,
InterpolatingAdjoint(autojacvec=ZygoteVJP()),
# Also fails, but due to a different bug:
# InterpolatingAdjoint(autojacvec=ReverseDiffVJP()),
(out, x, p, t, i) -> (out[:] = g),
[sol.t[end]],
),OrdinaryDiffEq.Tsit5()
)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1907 | using DiffEqSensitivity
using OrdinaryDiffEq, Calculus, Test
using Zygote
function f(du,u,p,t)
du[1] = u[2]
du[2] = -p[1]
end
function condition(u,t,integrator) # Event when event_f(u,t) == 0
u[1]
end
function affect!(integrator)
@show integrator.t
println("bounced.")
integrator.u[2] = -integrator.p[2]*integrator.u[2]
end
cb = ContinuousCallback(condition, affect!)
p = [9.8, 0.8]
prob = ODEProblem(f,eltype(p).([1.0,0.0]),eltype(p).((0.0,1.0)),copy(p))
function test_f(p)
_prob = remake(prob, p=p)
solve(_prob,Tsit5(),abstol=1e-14,reltol=1e-14,callback=cb,save_everystep=false)[end]
end
findiff = Calculus.finite_difference_jacobian(test_f,p)
findiff
using ForwardDiff
ad = ForwardDiff.jacobian(test_f,p)
ad
@test ad ≈ findiff
function test_f2(p, sensealg=ForwardDiffSensitivity(), controller=nothing, alg=Tsit5())
_prob = remake(prob, p=p)
u = solve(_prob,alg,sensealg=sensealg,controller=controller,
abstol=1e-14,reltol=1e-14,callback=cb,save_everystep=false)
u[end][end]
end
@test test_f2(p) == test_f(p)[end]
g1 = Zygote.gradient(θ->test_f2(θ,ForwardDiffSensitivity()), p)
g2 = Zygote.gradient(θ->test_f2(θ,ReverseDiffAdjoint()), p)
g3 = Zygote.gradient(θ->test_f2(θ,ReverseDiffAdjoint(), IController()), p)
g4 = Zygote.gradient(θ->test_f2(θ,ReverseDiffAdjoint(), PIController(7//50, 2//25)), p)
@test_broken g5 = Zygote.gradient(θ->test_f2(θ,ReverseDiffAdjoint(), PIDController(1/18. , 1/9., 1/18.)), p)
g6 = Zygote.gradient(θ->test_f2(θ,ForwardDiffSensitivity(),
OrdinaryDiffEq.PredictiveController(), TRBDF2()), p)
@test_broken g7 = Zygote.gradient(θ->test_f2(θ,ReverseDiffAdjoint(),
OrdinaryDiffEq.PredictiveController(), TRBDF2()), p)
@test g1[1] ≈ findiff[2,1:2]
@test g2[1] ≈ findiff[2,1:2]
@test g3[1] ≈ findiff[2,1:2]
@test g4[1] ≈ findiff[2,1:2]
@test_broken g5[1] ≈ findiff[2,1:2]
@test g6[1] ≈ findiff[2,1:2]
@test_broken g7[1] ≈ findiff[2,1:2]
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1566 | using DiffEqSensitivity, OrdinaryDiffEq, Zygote, Test
function get_param(breakpoints, values, t)
for (i, tᵢ) in enumerate(breakpoints)
if t <= tᵢ
return values[i]
end
end
return values[end]
end
function fiip(du, u, p, t)
a = get_param([1., 2., 3.], p[1:4], t)
du[1] = dx = a * u[1] - u[1] * u[2]
du[2] = dy = -a * u[2] + u[1] * u[2]
end
p = [1., 1., 1., 1.]; u0 = [1.0;1.0]
prob = ODEProblem(fiip, u0, (0.0, 4.0), p);
dp1 = Zygote.gradient(p->sum(solve(prob, Tsit5(), u0=u0, p=p, sensealg = ForwardDiffSensitivity(), saveat = 0.1, abstol=1e-12, reltol=1e-12)), p)
dp2 = Zygote.gradient(p->sum(solve(prob, Tsit5(), u0=u0, p=p, sensealg = ForwardDiffSensitivity(convert_tspan=true), saveat = 0.1, abstol=1e-12, reltol=1e-12)), p)
dp3 = Zygote.gradient(p->sum(solve(prob, Tsit5(), u0=u0, p=p, sensealg = ForwardSensitivity(), saveat = 0.1, abstol=1e-12, reltol=1e-12)), p)
dp4 = Zygote.gradient(p->sum(solve(prob, Tsit5(), u0=u0, p=p, saveat = 0.1, abstol=1e-12, reltol=1e-12)), p)
dp5 = Zygote.gradient(p->sum(solve(prob, Tsit5(), u0=u0, p=p, saveat = 0.1, abstol=1e-12, reltol=1e-12, sensealg = InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))), p)
dp6 = Zygote.gradient(p->sum(solve(prob, Tsit5(), u0=u0, p=p, saveat = 0.1, abstol=1e-12, reltol=1e-12, sensealg = InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true)))), p)
@test dp1[1] ≈ dp2[1]
@test dp1[1] ≈ dp3[1]
@test dp1[1] ≈ dp4[1]
@test dp1[1] ≈ dp5[1]
@test sum(dp5[1]) ≈ sum(dp6[1])
@test all(dp6[1][1:3] .== 0)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1785 | using OrdinaryDiffEq, Flux, DiffEqSensitivity, DiffEqCallbacks, Test
using Random
Random.seed!(1234)
u0 = Float32[2.; 0.]
datasize = 100
tspan = (0.0f0,10.5f0)
dosetimes = [1.0,2.0,4.0,8.0]
function affect!(integrator)
integrator.u = integrator.u.+1
end
cb_ = PresetTimeCallback(dosetimes,affect!,save_positions=(false,false))
function trueODEfunc(du,u,p,t)
du .= -u
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),callback=cb_,saveat=t))
dudt2 = Chain(Dense(2,50,tanh),
Dense(50,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
function dudt(du,u,p,t)
du[1:2] .= -u[1:2]
du[3:end] .= re(p)(u[1:2]) #re(p)(u[3:end])
end
z0 = Float32[u0;u0]
prob = ODEProblem(dudt,z0,tspan)
affect!(integrator) = integrator.u[1:2] .= integrator.u[3:end]
cb = PresetTimeCallback(dosetimes,affect!,save_positions=(false,false))
function predict_n_ode()
_prob = remake(prob,p=p)
Array(solve(_prob,Tsit5(),u0=z0,p=p,callback=cb,saveat=t,sensealg=ReverseDiffAdjoint()))[1:2,:]
#Array(solve(prob,Tsit5(),u0=z0,p=p,saveat=t))[1:2,:]
end
function loss_n_ode()
pred = predict_n_ode()
loss = sum(abs2,ode_data .- pred)
loss
end
loss_n_ode() # n_ode.p stores the initial parameters of the neural ODE
cba = function (;doplot=false) #callback function to observe training
pred = predict_n_ode()
display(sum(abs2,ode_data .- pred))
# plot current prediction against data
#pl = scatter(t,ode_data[1,:],label="data")
#scatter!(pl,t,pred[1,:],label="prediction")
#display(plot(pl))
return false
end
cba()
ps = Flux.params(p)
data = Iterators.repeated((), 200)
Flux.train!(loss_n_ode, ps, data, ADAM(0.05), cb = cba)
@test loss_n_ode() < 0.4
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2048 | using DiffEqSensitivity, OrdinaryDiffEq, Zygote, LinearAlgebra, FiniteDiff, Test
A = [1.0*im 2.0; 3.0 4.0]
u0 = [1.0 0.0*im; 0.0 1.0]
tspan = (0.0, 1.0)
function f(u,p,t)
(A*u)*(p[1]*t + p[2]*t^2 + p[3]*t^3 + p[4]*t^4)
end
p = [1.5 + im, 1.0, 3.0, 1.0]
prob = ODEProblem{false}(f,u0,tspan,p)
utarget = [0.0*im 1.0; 1.0 0.0]
function loss_adjoint(p)
ufinal = last(solve(prob, Tsit5(), p=p, abstol=1e-12, reltol=1e-12, sensealg = InterpolatingAdjoint()))
loss = 1 - abs(tr(ufinal*utarget')/2)^2
return loss
end
grad1 = Zygote.gradient(loss_adjoint,Complex{Float64}[1.5, 1.0, 3.0, 1.0])[1]
grad2 = FiniteDiff.finite_difference_gradient(loss_adjoint,Complex{Float64}[1.5, 1.0, 3.0, 1.0])
@test grad1 ≈ grad2
function rhs(u, p, t)
p .* u
end
function loss_fun(sol)
final_u = sol[:, end]
err = sum(abs.(final_u))
return err
end
function inner_loop(prob, p, loss_fun; sensealg = InterpolatingAdjoint())
sol = solve(prob, Tsit5(), p=p, saveat=0.1; sensealg)
err = loss_fun(sol)
return err
end
tspan = (0.0, 1.0)
p = [1.0]
u0=[1.0, 2.0]
prob = ODEProblem(rhs, u0, tspan, p)
grads = Zygote.gradient((p)->inner_loop(prob, p, loss_fun), p)[1]
u0=[1.0 + 2.0*im, 2.0 + 1.0*im]
prob = ODEProblem(rhs, u0, tspan, p)
dp1 = Zygote.gradient((p)->inner_loop(prob, p, loss_fun), p)[1]
dp2 = Zygote.gradient((p)->inner_loop(prob, p, loss_fun; sensealg = QuadratureAdjoint()), p)[1]
dp3 = Zygote.gradient((p)->inner_loop(prob, p, loss_fun; sensealg = BacksolveAdjoint()), p)[1]
@test dp1 ≈ dp2 ≈ dp3
@test eltype(dp1) <: Float64
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0; 1.0]
prob = ODEProblem(fiip,complex(u0),(0.0,10.0),complex(p))
function sum_of_solution(u0, p)
_prob = remake(prob,u0=u0,p=p)
real(sum(solve(_prob,Tsit5(),reltol=1e-6,abstol=1e-6,saveat=0.1)))
end
dx = Zygote.gradient(sum_of_solution, complex(u0), complex(p))
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 673 | using OrdinaryDiffEq, DiffEqSensitivity, LinearAlgebra, Optimization, OptimizationFlux, Flux
nn = Chain(Dense(1,16),Dense(16,16,tanh),Dense(16,2))
initial,re = Flux.destructure(nn)
function ode2!(u, p, t)
f1, f2 = re(p)([t])
[-f1^2; f2]
end
tspan = (0.0, 10.0)
prob = ODEProblem(ode2!, Complex{Float64}[0;0], tspan, initial)
function loss(p)
sol = last(solve(prob, Tsit5(), p=p, sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP())))
return norm(sol)
end
optf = Optimization.OptimizationFunction((x,p) -> loss(x), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, initial)
res = Optimization.solve(optprob, ADAM(0.1), maxiters = 100)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 13232 | using DiffEqSensitivity, OrdinaryDiffEq, Zygote
using Test, ForwardDiff
import Tracker, ReverseDiff, ChainRulesCore
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
function foop(u,p,t)
dx = p[1]*u[1] - p[2]*u[1]*u[2]
dy = -p[3]*u[2] + p[4]*u[1]*u[2]
[dx,dy]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(fiip,u0,(0.0,10.0),p)
proboop = ODEProblem(foop,u0,(0.0,10.0),p)
sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
@test sol isa ODESolution
sumsol = sum(sol)
@test sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14)) == sumsol
@test sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,sensealg=ForwardDiffSensitivity())) == sumsol
@test sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,sensealg=BacksolveAdjoint())) == sumsol
###
### adjoint
###
_sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
ū0,adj = adjoint_sensitivities(_sol,Tsit5(),((out,u,p,t,i) -> out .= -1),0.0:0.1:10,abstol=1e-14,reltol=1e-14)
du01,dp1 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=QuadratureAdjoint())),u0,p)
du02,dp2 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint())),u0,p)
du03,dp3 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=BacksolveAdjoint())),u0,p)
du04,dp4 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=TrackerAdjoint())),u0,p)
@test_broken Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ZygoteAdjoint())),u0,p) isa Tuple
du06,dp6 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ReverseDiffAdjoint())),u0,p)
du07,dp7 = Zygote.gradient((u0,p)->sum(concrete_solve(prob,Tsit5(),u0,p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=BacksolveAdjoint())),u0,p)
csol = concrete_solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
@test ū0 ≈ du01 rtol=1e-12
@test ū0 == du02
@test ū0 ≈ du03 rtol=1e-12
@test ū0 ≈ du04 rtol=1e-12
#@test ū0 ≈ du05 rtol=1e-12
@test ū0 ≈ du06 rtol=1e-12
@test ū0 ≈ du07 rtol=1e-12
@test adj ≈ dp1' rtol=1e-12
@test adj == dp2'
@test adj ≈ dp3' rtol=1e-12
@test adj ≈ dp4' rtol=1e-12
#@test adj ≈ dp5' rtol=1e-12
@test adj ≈ dp6' rtol=1e-12
@test adj ≈ dp7' rtol=1e-12
###
### Direct from prob
###
du01,dp1 = Zygote.gradient(u0,p) do u0,p
sum(solve(remake(prob,u0=u0,p=p),Tsit5(),abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=QuadratureAdjoint()))
end
@test ū0 ≈ du01 rtol=1e-12
@test adj ≈ dp1' rtol=1e-12
###
### forward
###
du06,dp6 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardSensitivity())),u0,p)
du07,dp7 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity())),u0,p)
@test_broken du08,dp8 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs = 1:1,sensealg=ForwardSensitivity())),u0,p)
du09,dp9 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs = 1:1,sensealg=ForwardDiffSensitivity())),u0,p)
@test du06 isa Nothing
@test ū0 ≈ du07 rtol=1e-12
@test adj ≈ dp6' rtol=1e-12
@test adj ≈ dp7' rtol=1e-12
ū02,adj2 = Zygote.gradient((u0,p)->sum(Array(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint()))[1,:]),u0,p)
du05,dp5 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=InterpolatingAdjoint())),u0,p)
du06,dp6 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.0:0.1:10.0,save_idxs=1:1,sensealg=QuadratureAdjoint())),u0,p)
du07,dp7 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1,sensealg=InterpolatingAdjoint())),u0,p)
du08,dp8 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=InterpolatingAdjoint())),u0,p)
du09,dp9 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1,sensealg=ReverseDiffAdjoint())),u0,p)
du010,dp10 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=TrackerAdjoint())),u0,p)
@test_broken du011,dp11 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=ForwardSensitivity())),u0,p)
du012,dp12 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=ForwardDiffSensitivity())),u0,p)
@test ū02 ≈ du05 rtol=1e-12
@test ū02 ≈ du06 rtol=1e-12
@test ū02 ≈ du07 rtol=1e-12
@test ū02 ≈ du08 rtol=1e-12
@test ū02 ≈ du09 rtol=1e-12
@test ū02 ≈ du010 rtol=1e-12
#@test ū02 ≈ du011 rtol=1e-12
@test ū02 ≈ du012 rtol=1e-12
@test adj2 ≈ dp5 rtol=1e-12
@test adj2 ≈ dp6 rtol=1e-12
@test adj2 ≈ dp7 rtol=1e-12
@test adj2 ≈ dp8 rtol=1e-12
@test adj2 ≈ dp9 rtol=1e-12
@test adj2 ≈ dp10 rtol=1e-12
#@test adj2 ≈ dp11 rtol=1e-12
@test adj2 ≈ dp12 rtol=1e-12
###
### Only End
###
ū0,adj = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,save_everystep=false,save_start=false,sensealg=InterpolatingAdjoint())),u0,p)
du03,dp3 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,save_everystep=false,save_start=false,sensealg=ReverseDiffAdjoint())),u0,p)
du04,dp4 = Zygote.gradient((u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,save_everystep=false,save_start=false,sensealg=InterpolatingAdjoint())[end]),u0,p)
@test ū0 ≈ du03 rtol=1e-11
@test ū0 ≈ du04 rtol=1e-12
@test adj ≈ dp3 rtol=1e-12
@test adj ≈ dp4 rtol=1e-12
###
### OOPs
###
_sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
ū0,adj = adjoint_sensitivities(_sol,Tsit5(),((out,u,p,t,i) -> out .= -1),0.0:0.1:10,abstol=1e-14,reltol=1e-14)
###
### adjoint
###
du01,dp1 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=QuadratureAdjoint())),u0,p)
du02,dp2 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint())),u0,p)
du03,dp3 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=BacksolveAdjoint())),u0,p)
du04,dp4 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=TrackerAdjoint())),u0,p)
@test_broken du05,dp5 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ZygoteAdjoint())),u0,p) isa Tuple
du06,dp6 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ReverseDiffAdjoint())),u0,p)
@test ū0 ≈ du01 rtol=1e-12
@test ū0 ≈ du02 rtol=1e-12
@test ū0 ≈ du03 rtol=1e-12
@test ū0 ≈ du04 rtol=1e-12
#@test ū0 ≈ du05 rtol=1e-12
@test ū0 ≈ du06 rtol=1e-12
@test adj ≈ dp1' rtol=1e-12
@test adj ≈ dp2' rtol=1e-12
@test adj ≈ dp3' rtol=1e-12
@test adj ≈ dp4' rtol=1e-12
#@test adj ≈ dp5' rtol=1e-12
@test adj ≈ dp6' rtol=1e-12
###
### forward
###
@test_broken Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardSensitivity())),u0,p) isa Tuple
du07,dp7 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity())),u0,p)
#@test du06 === nothing
@test du07 ≈ ū0 rtol=1e-12
#@test adj ≈ dp6' rtol=1e-12
@test adj ≈ dp7' rtol=1e-12
ū02,adj2 = Zygote.gradient((u0,p)->sum(Array(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint()))[1,:]),u0,p)
du05,dp5 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=InterpolatingAdjoint())),u0,p)
du06,dp6 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.0:0.1:10.0,save_idxs=1:1,sensealg=QuadratureAdjoint())),u0,p)
du07,dp7 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1,sensealg=InterpolatingAdjoint())),u0,p)
du08,dp8 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=InterpolatingAdjoint())),u0,p)
du09,dp9 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1,sensealg=ReverseDiffAdjoint())),u0,p)
du010,dp10 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=TrackerAdjoint())),u0,p)
@test_broken du011,dp11 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=ForwardSensitivity())),u0,p)
du012,dp12 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=ForwardDiffSensitivity())),u0,p)
# Redundent to test aliasing
du013,dp13 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,save_idxs=1:1,sensealg=InterpolatingAdjoint())),u0,p)
du014,dp14 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,save_idxs=1,saveat=0.1,sensealg=InterpolatingAdjoint())),u0,p)
@test ū02 ≈ du05 rtol=1e-12
@test ū02 ≈ du06 rtol=1e-12
@test ū02 ≈ du07 rtol=1e-12
@test ū02 ≈ du08 rtol=1e-12
@test ū02 ≈ du09 rtol=1e-12
@test ū02 ≈ du010 rtol=1e-12
#@test ū02 ≈ du011 rtol=1e-12
@test ū02 ≈ du012 rtol=1e-12
@test ū02 ≈ du013 rtol=1e-12
@test ū02 ≈ du014 rtol=1e-12
@test adj2 ≈ dp5 rtol=1e-12
@test adj2 ≈ dp6 rtol=1e-12
@test adj2 ≈ dp7 rtol=1e-12
@test adj2 ≈ dp8 rtol=1e-12
@test adj2 ≈ dp9 rtol=1e-12
@test adj2 ≈ dp10 rtol=1e-12
#@test adj2 ≈ dp11 rtol=1e-12
@test adj2 ≈ dp12 rtol=1e-12
@test adj2 ≈ dp13 rtol=1e-12
@test adj2 ≈ dp14 rtol=1e-12
# Handle VecOfArray Derivatives
dp1 = Zygote.gradient((p)->sum(last(solve(prob,Tsit5(),p=p,saveat=10.0,abstol=1e-14,reltol=1e-14))),p)[1]
dp2 = ForwardDiff.gradient((p)->sum(last(solve(prob,Tsit5(),p=p,saveat=10.0,abstol=1e-14,reltol=1e-14))),p)
@test dp1 ≈ dp2
dp1 = Zygote.gradient((p)->sum(last(solve(proboop,Tsit5(),u0=u0,p=p,saveat=10.0,abstol=1e-14,reltol=1e-14))),p)[1]
dp2 = ForwardDiff.gradient((p)->sum(last(solve(proboop,Tsit5(),u0=u0,p=p,saveat=10.0,abstol=1e-14,reltol=1e-14))),p)
@test dp1 ≈ dp2
# tspan[2]-tspan[1] not a multiple of saveat tests
du0,dp = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=2.3,sensealg=ReverseDiffAdjoint())),u0,p)
du01,dp1 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=2.3,sensealg=QuadratureAdjoint())),u0,p)
du02,dp2 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=2.3,sensealg=InterpolatingAdjoint())),u0,p)
du03,dp3 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=2.3,sensealg=BacksolveAdjoint())),u0,p)
du04,dp4 = Zygote.gradient((u0,p)->sum(solve(proboop,Tsit5(),save_end=true,u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=2.3,sensealg=ForwardDiffSensitivity())),u0,p)
@test du0 ≈ du01 rtol=1e-12
@test du0 ≈ du02 rtol=1e-12
@test du0 ≈ du03 rtol=1e-12
@test du0 ≈ du04 rtol=1e-12
@test dp ≈ dp1 rtol=1e-12
@test dp ≈ dp2 rtol=1e-12
@test dp ≈ dp3 rtol=1e-12
@test dp ≈ dp4 rtol=1e-12
###
### SDE
###
using StochasticDiffEq
using Random
seed = 100
function σiip(du,u,p,t)
du[1] = p[5]*u[1]
du[2] = p[6]*u[2]
end
function σoop(u,p,t)
dx = p[5]*u[1]
dy = p[6]*u[2]
[dx,dy]
end
function σoop(u::Tracker.TrackedArray,p,t)
dx = p[5]*u[1]
dy = p[6]*u[2]
Tracker.collect([dx,dy])
end
p = [1.5,1.0,3.0,1.0,0.1,0.1]
u0 = [1.0;1.0]
tarray = collect(0.0:0.01:1)
prob = SDEProblem(fiip,σiip,u0,(0.0,1.0),p)
proboop = SDEProblem(foop,σoop,u0,(0.0,1.0),p)
###
### OOPs
###
_sol = solve(proboop,EulerHeun(),dt=1e-2,adaptive=false,save_noise=true,seed=seed)
ū0,adj = adjoint_sensitivities(_sol,EulerHeun(),((out,u,p,t,i) -> out .= -1),tarray, sensealg=BacksolveAdjoint())
du01,dp1 = Zygote.gradient((u0,p)->sum(solve(proboop,EulerHeun(),
u0=u0,p=p,dt=1e-2,saveat=0.01,sensealg=BacksolveAdjoint(),seed=seed)),u0,p)
du02,dp2 = Zygote.gradient(
(u0,p)->sum(solve(proboop,EulerHeun(),u0=u0,p=p,dt=1e-2,saveat=0.01,sensealg=ForwardDiffSensitivity(),seed=seed)),u0,p)
@test isapprox(ū0, du01, rtol = 1e-4)
@test isapprox(adj, dp1', rtol = 1e-4)
@test isapprox(adj, dp2', rtol = 1e-4)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 882 | using OrdinaryDiffEq, DiffEqSensitivity, ForwardDiff, Zygote, Test
A = [0. 1.; 1. 0.; 0 0; 0 0];
B = [1. 0.; 0. 1.; 0 0; 0 0];
utarget = A;
const T = 10.0;
function f(u, p, t)
return -p[1]*u # just a silly example to demonstrate the issue
end
u0 = [1.0 0.0; 0.0 1.0; 0.0 0.0; 0.0 0.0];
tspan = (0.0, T)
tsteps = 0.0:T/100.0:T
p = [1.7, 1.0, 3.0, 1.0]
prob_ode = ODEProblem(f, u0, tspan, p);
fd_ode = ForwardDiff.gradient(p) do p
sum(last(solve(prob_ode, Tsit5(),p=p,abstol=1e-12,reltol=1e-12)))
end
grad_ode = Zygote.gradient(p) do p
sum(last(solve(prob_ode, Tsit5(),p=p,abstol=1e-12,reltol=1e-12)))
end[1]
@test fd_ode ≈ grad_ode rtol=1e-6
grad_ode = Zygote.gradient(p) do p
sum(last(solve(prob_ode, Tsit5(),p=p,abstol=1e-12,reltol=1e-12, sensealg = InterpolatingAdjoint())))
end[1]
@test fd_ode ≈ grad_ode rtol=1e-6
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 575 | using OrdinaryDiffEq, DiffEqSensitivity, Zygote, Test
function loss1(p;sensealg=nothing)
f(x,p,t) = [p[1]]
prob = DiscreteProblem(f, [0.0], (1,10), p)
sol = solve(prob, FunctionMap(scale_by_time = true), saveat=[1,2,3])
return sum(sol)
end
dp1 = Zygote.gradient(loss1,[1.0])[1]
dp2 = Zygote.gradient(x->loss1(x,sensealg=TrackerAdjoint()),[1.0])[1]
dp3 = Zygote.gradient(x->loss1(x,sensealg=ReverseDiffAdjoint()),[1.0])[1]
dp4 = Zygote.gradient(x->loss1(x,sensealg=ForwardDiffSensitivity()),[1.0])[1]
@test dp1 == dp2
@test dp1 == dp3
@test dp1 == dp4
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 831 | using Distributed, Flux
addprocs(2)
@everywhere begin
using DiffEqSensitivity, OrdinaryDiffEq, Test
pa = [1.0]
u0 = [3.0]
end
function model4()
prob = ODEProblem((u, p, t) -> 1.01u .* p, u0, (0.0, 1.0), pa)
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), EnsembleDistributed(), saveat = 0.1, trajectories = 100)
end
# loss function
loss() = sum(abs2,1.0.-Array(model4()))
data = Iterators.repeated((), 10)
cb = function () # callback function to observe training
@show loss()
end
pa = [1.0]
u0 = [3.0]
opt = Flux.ADAM(0.1)
println("Starting to train")
l1 = loss()
Flux.@epochs 10 Flux.train!(loss, Flux.params([pa,u0]), data, opt; cb = cb)
l2 = loss()
@test 10l2 < l1
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1984 | using Flux, OrdinaryDiffEq, Test
pa = [1.0]
u0 = [3.0]
function model1()
prob = ODEProblem((u, p, t) -> 1.01u .* p, u0, (0.0, 1.0), pa)
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), EnsembleSerial(), saveat = 0.1, trajectories = 100)
end
# loss function
loss() = sum(abs2,1.0.-Array(model1()))
data = Iterators.repeated((), 10)
cb = function () # callback function to observe training
@show loss()
end
opt = ADAM(0.1)
println("Starting to train")
l1 = loss()
Flux.@epochs 10 Flux.train!(loss, Flux.params([pa,u0]), data, opt; cb = cb)
l2 = loss()
@test 10l2 < l1
function model2()
prob = ODEProblem((u, p, t) -> 1.01u .* p, u0, (0.0, 1.0), pa)
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), EnsembleSerial(), saveat = 0.1, trajectories = 100).u
end
loss() = sum(abs2,[sum(abs2,1.0.-u) for u in model2()])
pa = [1.0]
u0 = [3.0]
opt = ADAM(0.1)
println("Starting to train")
l1 = loss()
Flux.@epochs 10 Flux.train!(loss, Flux.params([pa,u0]), data, opt; cb = cb)
l2 = loss()
@test 10l2 < l1
function model3()
prob = ODEProblem((u, p, t) -> 1.01u .* p, u0, (0.0, 1.0), pa)
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), EnsembleThreads(), saveat = 0.1, trajectories = 100)
end
# loss function
loss() = sum(abs2,1.0.-Array(model3()))
data = Iterators.repeated((), 10)
cb = function () # callback function to observe training
@show loss()
end
pa = [1.0]
u0 = [3.0]
opt = ADAM(0.1)
println("Starting to train")
l1 = loss()
Flux.@epochs 10 Flux.train!(loss, Flux.params([pa,u0]), data, opt; cb = cb)
l2 = loss()
@test 10l2 < l1
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 8183 | using DiffEqSensitivity, OrdinaryDiffEq, ForwardDiff, Calculus
using Test
function fb(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -t*p[3]*u[2] + t*u[1]*u[2]
end
function jac(J,u,p,t)
(x, y, a, b, c) = (u[1], u[2], p[1], p[2], p[3])
J[1,1] = a + y * b * -1
J[2,1] = t * y
J[1,2] = b * x * -1
J[2,2] = t * c * -1 + t * x
end
function paramjac(pJ,u,p,t)
(x, y, a, b, c) = (u[1], u[2], p[1], p[2], p[3])
pJ[1,1] = x
pJ[2,1] = 0.0
pJ[1,2] = - x * y
pJ[2,2] = 0.0
pJ[1,3] = 0.0
pJ[2,3] = - t * y
end
f = ODEFunction(fb,jac=jac,paramjac=paramjac)
p = [1.5,1.0,3.0]
prob = ODEForwardSensitivityProblem(f,[1.0;1.0],(0.0,10.0),p)
probInpl = ODEForwardSensitivityProblem(fb,[1.0;1.0],(0.0,10.0),p)
probnoad = ODEForwardSensitivityProblem(fb,[1.0;1.0],(0.0,10.0),p,
ForwardSensitivity(autodiff=false))
probnoadjacvec = ODEForwardSensitivityProblem(fb,[1.0;1.0],(0.0,10.0),p,
ForwardSensitivity(autodiff=false,autojacvec=true))
probnoad2 = ODEForwardSensitivityProblem(f,[1.0;1.0],(0.0,10.0),p,
ForwardSensitivity(autodiff=false))
probvecmat = ODEForwardSensitivityProblem(fb,[1.0;1.0],(0.0,10.0),p,
ForwardSensitivity(autojacvec=false,autojacmat=true))
sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14)
@test_broken solve(probInpl,KenCarp4(),abstol=1e-14,reltol=1e-14).retcode == :Success
solInpl = solve(probInpl,KenCarp4(autodiff=false),abstol=1e-14,reltol=1e-14)
solInpl2 = solve(probInpl,Rodas4(autodiff=false),abstol=1e-10,reltol=1e-10)
solnoad = solve(probnoad,KenCarp4(autodiff=false),abstol=1e-14,reltol=1e-14)
solnoadjacvec = solve(probnoadjacvec,KenCarp4(autodiff=false),abstol=1e-14,reltol=1e-14)
solnoad2 = solve(probnoad,KenCarp4(autodiff=false),abstol=1e-14,reltol=1e-14)
solvecmat = solve(probvecmat,Tsit5(),abstol=1e-14,reltol=1e-14)
x = sol[1:sol.prob.f.numindvar,:]
@test sol(5.0) ≈ solnoad(5.0)
@test sol(5.0) ≈ solnoad2(5.0)
@test sol(5.0) ≈ solnoadjacvec(5.0) atol=1e-6 rtol=1e-6
@test sol(5.0) ≈ solInpl(5.0)
@test isapprox(solInpl(5.0), solInpl2(5.0),rtol=1e-5)
@test sol(5.0) ≈ solvecmat(5.0)
# Get the sensitivities
da = sol[sol.prob.f.numindvar+1:sol.prob.f.numindvar*2,:]
db = sol[sol.prob.f.numindvar*2+1:sol.prob.f.numindvar*3,:]
dc = sol[sol.prob.f.numindvar*3+1:sol.prob.f.numindvar*4,:]
sense_res1 = [da[:,end] db[:,end] dc[:,end]]
prob = ODEForwardSensitivityProblem(f.f,[1.0;1.0],(0.0,10.0),p,
ForwardSensitivity(autojacvec=true))
sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14,saveat=0.01)
x = sol[1:sol.prob.f.numindvar,:]
# Get the sensitivities
res = sol[1:sol.prob.f.numindvar,:]
da = sol[sol.prob.f.numindvar+1:sol.prob.f.numindvar*2,:]
db = sol[sol.prob.f.numindvar*2+1:sol.prob.f.numindvar*3,:]
dc = sol[sol.prob.f.numindvar*3+1:sol.prob.f.numindvar*4,:]
sense_res2 = [da[:,end] db[:,end] dc[:,end]]
function test_f(p)
prob = ODEProblem(f,eltype(p).([1.0,1.0]),(0.0,10.0),p)
solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14,save_everystep=false)[end]
end
p = [1.5,1.0,3.0]
fd_res = ForwardDiff.jacobian(test_f,p)
calc_res = Calculus.finite_difference_jacobian(test_f,p)
@test sense_res1 ≈ sense_res2 ≈ fd_res
@test sense_res1 ≈ sense_res2 ≈ calc_res
## Check extraction
xall, dpall = extract_local_sensitivities(sol)
@test xall == res
@test dpall[1] == da
_,dpall_matrix = extract_local_sensitivities(sol,Val(true))
@test mapreduce(x->x[:, 2], hcat, dpall) == dpall_matrix[2]
x, dp = extract_local_sensitivities(sol,length(sol.t))
sense_res2 = reduce(hcat,dp)
@test sense_res1 == sense_res2
@test extract_local_sensitivities(sol,sol.t[3]) == extract_local_sensitivities(sol,3)
tmp = similar(sol[1])
@test extract_local_sensitivities(tmp,sol,sol.t[3]) == extract_local_sensitivities(sol,3)
# asmatrix=true
@test extract_local_sensitivities(sol, length(sol), true) == (x, sense_res2)
@test extract_local_sensitivities(sol, sol.t[end], true) == (x, sense_res2)
@test extract_local_sensitivities(tmp, sol, sol.t[end], true) == (x, sense_res2)
# Return type inferred
@inferred extract_local_sensitivities(sol, 1)
@inferred extract_local_sensitivities(sol, 1, Val(true))
@inferred extract_local_sensitivities(sol, sol.t[3])
@inferred extract_local_sensitivities(sol, sol.t[3], Val(true))
@inferred extract_local_sensitivities(tmp, sol, sol.t[3])
@inferred extract_local_sensitivities(tmp, sol, sol.t[3], Val(true))
### ForwardDiff version
prob = ODEForwardSensitivityProblem(f.f,[1.0;1.0],(0.0,10.0),p,
ForwardDiffSensitivity())
sol = solve(prob,Tsit5(),abstol=1e-14,reltol=1e-14,saveat=0.01)
xall, dpall = extract_local_sensitivities(sol)
@test xall ≈ res
@test dpall[1] ≈ da atol=1e-9
_,dpall_matrix = extract_local_sensitivities(sol,Val(true))
@test mapreduce(x->x[:, 2], hcat, dpall) == dpall_matrix[2]
x, dp = extract_local_sensitivities(sol,length(sol.t))
sense_res2 = reduce(hcat,dp)
@test fd_res == sense_res2
@test extract_local_sensitivities(sol,sol.t[3]) == extract_local_sensitivities(sol,3)
tmp = similar(sol[1])
@test extract_local_sensitivities(tmp,sol,sol.t[3]) == extract_local_sensitivities(sol,3)
# asmatrix=true
@test extract_local_sensitivities(sol, length(sol), true) == (x, sense_res2)
@test extract_local_sensitivities(sol, sol.t[end], true) == (x, sense_res2)
@test extract_local_sensitivities(tmp, sol, sol.t[end], true) == (x, sense_res2)
# Return type inferred
@inferred extract_local_sensitivities(sol, 1)
@inferred extract_local_sensitivities(sol, 1, Val(true))
@inferred extract_local_sensitivities(sol, sol.t[3])
@inferred extract_local_sensitivities(sol, sol.t[3], Val(true))
@inferred extract_local_sensitivities(tmp, sol, sol.t[3])
@inferred extract_local_sensitivities(tmp, sol, sol.t[3], Val(true))
# Test mass matrix
function rober_MM(du, u, p, t)
y₁, y₂, y₃ = u
k₁, k₂, k₃ = p
du[1] = -k₁ * y₁ + k₃ * y₂ * y₃
du[2] = k₁ * y₁ - k₂ * y₂^2 - k₃ * y₂ * y₃
du[3] = y₁ + y₂ + y₃ - 1
nothing
end
function rober_no_MM(du, u, p, t)
y₁, y₂, y₃ = u
k₁, k₂, k₃ = p
du[1] = -k₁ * y₁ + k₃ * y₂ * y₃
du[2] = k₁ * y₁ - k₂ * y₂^2 - k₃ * y₂ * y₃
du[3] = k₂*y₂^2
nothing
end
M = [1.0 0 0; 0 1.0 0; 0 0 0]
p = [0.04, 3e7, 1e4]
u0 = [1.0, 0.0, 0.0]
tspan = (0.0, 12.0)
f_MM= ODEFunction(rober_MM, mass_matrix = M)
f_no_MM= ODEFunction(rober_no_MM)
prob_MM_ForwardSensitivity = ODEForwardSensitivityProblem(f_MM, u0, tspan, p, ForwardSensitivity())
sol_MM_ForwardSensitivity = solve(prob_MM_ForwardSensitivity , Rodas4(autodiff = false), reltol = 1e-14, abstol = 1e-14)
prob_MM_ForwardDiffSensitivity = ODEForwardSensitivityProblem(f_MM, u0, tspan, p, ForwardDiffSensitivity())
sol_MM_ForwardDiffSensitivity = solve(prob_MM_ForwardDiffSensitivity, Rodas4(autodiff = false), reltol = 1e-14, abstol = 1e-14)
prob_no_MM = ODEForwardSensitivityProblem(f_no_MM, u0, tspan, p, ForwardSensitivity())
sol_no_MM= solve(prob_no_MM, Rodas4(autodiff = false), reltol = 1e-14, abstol = 1e-14)
sen_MM_ForwardSensitivity = extract_local_sensitivities(sol_MM_ForwardSensitivity,10.0,true)
sen_MM_ForwardDiffSensitivity = extract_local_sensitivities(sol_MM_ForwardDiffSensitivity,10.0,true)
sen_no_MM = extract_local_sensitivities(sol_no_MM,10.0,true)
@test sen_MM_ForwardSensitivity[2] ≈ sen_MM_ForwardDiffSensitivity[2] atol=1e-10 rtol=1e-10
@test sen_MM_ForwardSensitivity[2] ≈ sen_no_MM[2] atol=1e-10 rtol=1e-10
# Test Float32
function f32(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + u[1]*u[2]
end
p = [1.5f0,1.0f0,3.0f0]
prob = ODEForwardSensitivityProblem(f32,[1.0f0;1.0f0],(0.0f0,10.0f0),p)
sol = solve(prob,Tsit5())
# Out Of Place Error
function lotka_volterra_oop(u, p, t)
du = zeros(2)
du[1] = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = -p[3]*u[2] + p[4]*u[1]*u[2]
return du
end
u0 = [1.0, 1.0]
p = [1.5, 1.0, 3.0, 1.0]
@test_throws DiffEqSensitivity.ForwardSensitivityOutOfPlaceError ODEForwardSensitivityProblem(lotka_volterra_oop, u0, (0.0, 10.0), p) | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 4061 | using DiffEqSensitivity, OrdinaryDiffEq, Zygote, Test, ForwardDiff
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*p[51]*p[75]*u[1]*u[2]
du[2] = dy = -p[3]*p[81]*p[25]*u[2] + (sum(@view(p[4:end]))/100)*u[1]*u[2]
end
function foop(u,p,t)
dx = p[1]*u[1] - p[2]*p[51]*p[75]*u[1]*u[2]
dy = -p[3]*p[81]*p[25]*u[2] + (sum(@view(p[4:end]))/100)*p[4]*u[1]*u[2]
[dx,dy]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
p = reshape(vcat(p,ones(100)),4,26)
prob = ODEProblem(fiip,u0,(0.0,10.0),p)
proboop = ODEProblem(foop,u0,(0.0,10.0),p)
loss = (u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity()))
@time du01,dp1 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint()))
@time du02,dp2 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity(chunk_size=104)))
@time du03,dp3 = Zygote.gradient(loss,u0,p)
dp = ForwardDiff.gradient(p->loss(u0,p),p)
du0 = ForwardDiff.gradient(u0->loss(u0,p),u0)
@test du01 ≈ du0 rtol=1e-12
@test du01 ≈ du02 rtol=1e-12
@test du01 ≈ du03 rtol=1e-12
@test dp1 ≈ dp rtol=1e-12
@test dp1 ≈ dp2 rtol=1e-12
@test dp1 ≈ dp3 rtol=1e-12
loss = (u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity()))
@time du01,dp1 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint()))
@time du02,dp2 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity(chunk_size=104)))
@time du03,dp3 = Zygote.gradient(loss,u0,p)
dp = ForwardDiff.gradient(p->loss(u0,p),p)
du0 = ForwardDiff.gradient(u0->loss(u0,p),u0)
@test du01 ≈ du0 rtol=1e-12
@test du01 ≈ du02 rtol=1e-12
@test du01 ≈ du03 rtol=1e-12
@test dp1 ≈ dp rtol=1e-12
@test dp1 ≈ dp2 rtol=1e-12
@test dp1 ≈ dp3 rtol=1e-12
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
du[3:end] .= p[4]
end
function foop(u,p,t)
dx = p[1]*u[1] - p[2]*u[1]*u[2]
dy = -p[3]*u[2] + p[4]*u[1]*u[2]
reshape(vcat(dx,dy,repeat([p[4]],100)),2,51)
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
u0 = reshape(vcat(u0,ones(100)),2,51)
prob = ODEProblem(fiip,u0,(0.0,10.0),p)
proboop = ODEProblem(foop,u0,(0.0,10.0),p)
loss = (u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity()))
@time du01,dp1 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint()))
@time du02,dp2 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(prob,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity(chunk_size=102)))
@time du03,dp3 = Zygote.gradient(loss,u0,p)
dp = ForwardDiff.gradient(p->loss(u0,p),p)
du0 = ForwardDiff.gradient(u0->loss(u0,p),u0)
@test du01 ≈ du0 rtol=1e-12
@test du01 ≈ du02 rtol=1e-12
@test du01 ≈ du03 rtol=1e-12
@test dp1 ≈ dp rtol=1e-12
@test dp1 ≈ dp2 rtol=1e-12
@test dp1 ≈ dp3 rtol=1e-12
loss = (u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity()))
@time du01,dp1 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=InterpolatingAdjoint()))
@time du02,dp2 = Zygote.gradient(loss,u0,p)
loss = (u0,p)->sum(solve(proboop,Tsit5(),u0=u0,p=p,abstol=1e-14,reltol=1e-14,saveat=0.1,sensealg=ForwardDiffSensitivity(chunk_size=102)))
@time du03,dp3 = Zygote.gradient(loss,u0,p)
dp = ForwardDiff.gradient(p->loss(u0,p),p)
du0 = ForwardDiff.gradient(u0->loss(u0,p),u0)
@test du01 ≈ du0 rtol=1e-12
@test du01 ≈ du02 rtol=1e-12
@test du01 ≈ du03 rtol=1e-12
@test dp1 ≈ dp rtol=1e-12
@test dp1 ≈ dp2 rtol=1e-12
@test dp1 ≈ dp3 rtol=1e-12
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 993 | using DiffEqSensitivity
using OrdinaryDiffEq
using FiniteDiff
using Zygote
using ForwardDiff
u0 = [1.0,1.0]
p = [1.5,1.0,3.0,1.0]
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
prob = ODEProblem(fiip,u0,(0.0,10.0),[1.5,1.0,3.0,1.0],reltol = 1e-14,abstol=1e-14)
function cost(p1)
_prob = remake(prob,p=vcat(p1,p[2:end]))
sol = solve(_prob,Tsit5(),sensealg=ForwardDiffSensitivity(),saveat=0.1)
sum(sol)
end
res = FiniteDiff.finite_difference_derivative(cost,p[1]) # 8.305557728239275
res2 = ForwardDiff.derivative(cost,p[1]) # 8.305305252400714 # only 1 dual number
res3 = Zygote.gradient(cost,p[1])[1] # (8.305266428305409,) # 4 dual numbers
function cost(p1)
_prob = remake(prob,p=vcat(p1,p[2:end]))
sol = solve(_prob,Tsit5(),sensealg=ForwardSensitivity(),saveat=0.1)
sum(sol)
end
res4 = Zygote.gradient(cost,p[1])[1] # (7.720368430265481,)
@test res ≈ res2
@test res ≈ res3
@test res ≈ res4
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1220 | using DiffEqSensitivity, ForwardDiff, Distributions, OrdinaryDiffEq,
LinearAlgebra, Test
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
function g(sol)
J = extract_local_sensitivities(sol,true)[2]
det(J'*J)
end
u0 = [1.0,1.0]
p = [1.5,1.0,3.0,1.0]
prob = ODEForwardSensitivityProblem(fiip,u0,(0.0,10.0),p,saveat=0:10)
sol = solve(prob, Tsit5())
u0_dist = [Uniform(0.9,1.1), 1.0]
p_dist = [1.5, truncated(Normal(1.5,.1),1.1, 1.9),3.0,1.0]
u0_dist_extended = vcat(u0_dist,zeros(length(p)*length(u0)))
function fiip_expe_SciML_forw_sen_SciML()
prob = ODEForwardSensitivityProblem(fiip,u0,(0.0,10.0),p,saveat=0:10)
prob_func = function (prob, i, repeat)
_prob = remake(prob, u0=[isa(ui,Distribution) ? rand(ui) : ui for ui in u0_dist], p=[isa(pj,Distribution) ? rand(pj) : pj for pj in p_dist])
_prob
end
output_func = function (sol, i)
(g(sol), false)
end
monte_prob = EnsembleProblem(prob;output_func=output_func,prob_func=prob_func)
sol = solve(monte_prob,Tsit5(),EnsembleSerial(),trajectories=100_000)
mean(sol.u)
end
@test fiip_expe_SciML_forw_sen_SciML() ≈ 3.56e6 rtol=4e-2
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1082 | using OrdinaryDiffEq, DiffEqSensitivity, Flux
using ComponentArrays, LinearAlgebra, Optimization, Test
const nknots = 10
const h = 1.0/(nknots+1)
x = range(0, step=h, length=nknots)
u0 = sin.(π*x)
@inline function f(du,u,p,t)
du .= zero(eltype(u))
u₃ = @view u[3:end]
u₂ = @view u[2:end-1]
u₁ = @view u[1:end-2]
@. du[2:end-1] = p.k*((u₃ - 2*u₂ + u₁)/(h^2.0))
nothing
end
p_true = ComponentArray(k=0.42)
jac_proto = Tridiagonal(similar(u0,nknots-1), similar(u0), similar(u0, nknots-1))
prob = ODEProblem(ODEFunction(f,jac_prototype=jac_proto), u0, (0.0,1.0), p_true)
@time sol_true = solve(prob, Rodas4P(), saveat=0.1)
function loss(p)
_prob = remake(prob, p=p)
sol = solve(_prob, Rodas4P(autodiff=false), saveat=0.1, sensealg=ForwardDiffSensitivity())
sum((sol .- sol_true).^2)
end
p0 = ComponentArray(k=1.0)
optf = Optimization.OptimizationFunction((x,p) -> loss(x), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, p0)
res = Optimization.solve(optprob, ADAM(0.01), maxiters = 100)
@test res.u.k ≈ 0.42461977305259074 rtol=1e-1
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 3410 | using DiffEqSensitivity, Flux, OrdinaryDiffEq, LinearAlgebra, Test
GDP = [11394358246872.6, 11886411296037.9, 12547852149499.6, 13201781525927, 14081902622923.3, 14866223429278.3, 15728198883149.2, 16421593575529.9, 17437921118338, 18504710349537.1, 19191754995907.1, 20025063402734.2, 21171619915190.4, 22549236163304.4, 22999815176366.2, 23138798276196.2, 24359046058098.6, 25317009721600.9, 26301669369287.8, 27386035164588.8, 27907493159394.4, 28445139283067.1, 28565588996657.6, 29255060755937.6, 30574152048605.8, 31710451102539.4, 32786657119472.8, 34001004119223.5, 35570841010027.7, 36878317437617.5, 37952345258555.4, 38490918890678.7, 39171116855465.5, 39772082901255.8, 40969517920094.4, 42210614326789.4, 43638265675924.6, 45254805649669.6, 46411399944618.2, 47929948653387.3, 50036361141742.2, 51009550274808.6, 52127765360545.5, 53644090247696.9, 55995239099025.6, 58161311618934.2, 60681422072544.7, 63240595965946.1, 64413060738139.7, 63326658023605.9, 66036918504601.7, 68100669928597.9, 69811348331640.1, 71662400667935.7, 73698404958519.1, 75802901433146, 77752106717302.4, 80209237761564.8, 82643194654568.3]
function monomial(cGDP, parameters, t)
α1, β1, nu1, nu2, δ, δ2 = parameters
[α1 * ((cGDP[1]))^β1]
end
GDP0 = GDP[1]
tspan = (1.0, 59.0)
p = [474.8501513113645, 0.7036417845990167, 0.0, 1e-10, 1e-10, 1e-10]
u0 = [GDP0]
if false
prob = ODEProblem(monomial,[GDP0],tspan,p)
else ## false crashes. that is when i am tracking the initial conditions
prob = ODEProblem(monomial,u0,tspan,p)
end
function predict_rd() # Our 1-layer neural network
Array(solve(prob,Tsit5(),p=p,saveat=1.0:1.0:59.0,reltol=1e-4,sensealg=TrackerAdjoint()))
end
function loss_rd() ##L2 norm biases the newer times unfairly
##Graph looks better if we minimize relative error squared
c = 0.0
a = predict_rd()
d = 0.0
for i=1:59
c += (a[i][1]/GDP[i]-1)^2 ## L2 of relative error
end
c + 3 * d
end
data = Iterators.repeated((), 100)
opt = ADAM(0.01)
peek = function () #callback function to observe training
#reduces training speed by a lot
println("Loss: ",loss_rd())
end
peek()
Flux.train!(loss_rd, Flux.params(p,u0), data, opt, cb=peek)
peek()
@test loss_rd() < 0.2
function monomial(dcGDP, cGDP, parameters, t)
α1, β1, nu1, nu2, δ, δ2 = parameters
dcGDP[1] = α1 * ((cGDP[1]))^β1
end
GDP0 = GDP[1]
tspan = (1.0, 59.0)
p = [474.8501513113645, 0.7036417845990167, 0.0, 1e-10, 1e-10, 1e-10]
u0 = [GDP0]
if false
prob = ODEProblem(monomial,[GDP0],tspan,p)
else ## false crashes. that is when i am tracking the initial conditions
prob = ODEProblem(monomial,u0,tspan,p)
end
function predict_adjoint() # Our 1-layer neural network
Array(solve(prob,Tsit5(),p=p,saveat=1.0,reltol=1e-4,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true))))
end
function loss_adjoint() ##L2 norm biases the newer times unfairly
##Graph looks better if we minimize relative error squared
c = 0.0
a = predict_adjoint()
d = 0.0
for i=1:59
c += (a[i][1]/GDP[i]-1)^2 ## L2 of relative error
end
c + 3 * d
end
data = Iterators.repeated((), 100)
opt = ADAM(0.01)
peek = function () #callback function to observe training
#reduces training speed by a lot
println("Loss: ",loss_adjoint())
end
peek()
Flux.train!(loss_adjoint, Flux.params(p,u0), data, opt, cb=peek)
peek()
@test loss_adjoint() < 0.2
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 205 | using DiffEqSensitivity, Test
@test DiffEqSensitivity.hasbranching(1, 2) do x, y
(x < 0 ? -x : x) + exp(y)
end
@test !DiffEqSensitivity.hasbranching(1, 2) do x, y
ifelse(x < 0, -x, x) + exp(y)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1760 | using Flux, DiffEqSensitivity, DiffEqCallbacks, OrdinaryDiffEq, Test # , Plots
u0 = Float32[2.; 0.]
datasize = 100
tspan = (0.0f0,10.5f0)
dosetimes = [1.0,2.0,4.0,8.0]
function affect!(integrator)
integrator.u = integrator.u.+1
end
cb_ = PresetTimeCallback(dosetimes,affect!,save_positions=(false,false))
function trueODEfunc(du,u,p,t)
du .= -u
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),callback=cb_,saveat=t))
dudt2 = Chain(Dense(2,50,tanh),
Dense(50,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
function dudt(du,u,p,t)
du[1:2] .= -u[1:2]
du[3:end] .= re(p)(u[1:2]) #re(p)(u[3:end])
end
z0 = Float32[u0;u0]
prob = ODEProblem(dudt,z0,tspan)
affect!(integrator) = integrator.u[1:2] .= integrator.u[3:end]
cb = PresetTimeCallback(dosetimes,affect!,save_positions=(false,false))
function predict_n_ode()
_prob = remake(prob,p=p)
Array(solve(_prob,Tsit5(),u0=z0,p=p,callback=cb,saveat=t,sensealg=ReverseDiffAdjoint()))[1:2,:]
# Array(solve(prob,Tsit5(),u0=z0,p=p,saveat=t))[1:2,:]
end
function loss_n_ode()
pred = predict_n_ode()
loss = sum(abs2,ode_data .- pred)
loss
end
loss_n_ode() # n_ode.p stores the initial parameters of the neural ODE
cba = function (;doplot=false) #callback function to observe training
pred = predict_n_ode()
display(sum(abs2,ode_data .- pred))
# plot current prediction against data
# pl = scatter(t,ode_data[1,:],label="data")
# scatter!(pl,t,pred[1,:],label="prediction")
# display(plot(pl))
return false
end
cba()
ps = Flux.params(p)
data = Iterators.repeated((), 200)
Flux.train!(loss_n_ode, ps, data, ADAM(0.05), cb = cba)
loss_n_ode() < 1.0
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2241 | using DiffEqSensitivity, Flux, Zygote, OrdinaryDiffEq, Test # , Plots
function lotka_volterra(du,u,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = (α - β*y)x
du[2] = dy = (δ*x - γ)y
end
p = [2.2, 1.0, 2.0, 0.4]
u0 = [1.0,1.0]
prob = ODEProblem(lotka_volterra,u0,(0.0,10.0),p)
# Reverse-mode
function predict_rd(p)
Array(solve(prob,Tsit5(),p=p,saveat=0.1,reltol=1e-4,sensealg=TrackerAdjoint()))
end
loss_rd(p) = sum(abs2,x-1 for x in predict_rd(p))
loss_rd() = sum(abs2,x-1 for x in predict_rd(p))
loss_rd()
grads = Zygote.gradient(loss_rd, p)
@test !iszero(grads[1])
opt = ADAM(0.1)
cb = function ()
display(loss_rd())
# display(plot(solve(remake(prob,p=p),Tsit5(),saveat=0.1),ylim=(0,6)))
end
# Display the ODE with the current parameter values.
loss1 = loss_rd()
Flux.train!(loss_rd, Flux.params(p), Iterators.repeated((), 100), opt, cb = cb)
loss2 = loss_rd()
@test 10loss2 < loss1
# Forward-mode, R^n -> R^m layer
p = [2.2, 1.0, 2.0, 0.4]
function predict_fd()
vec(Array(solve(prob,Tsit5(),p=p,saveat=0.0:0.1:1.0,reltol=1e-4,sensealg=ForwardDiffSensitivity())))
end
loss_fd() = sum(abs2,x-1 for x in predict_fd())
loss_fd()
ps = Flux.params(p)
grads = Zygote.gradient(loss_fd, ps)
@test !iszero(grads[p])
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
display(loss_fd())
# display(plot(solve(remake(prob,p=p),Tsit5(),saveat=0.1),ylim=(0,6)))
end
# Display the ODE with the current parameter values.
loss1 = loss_fd()
Flux.train!(loss_fd, ps, data, opt, cb = cb)
loss2 = loss_fd()
@test 10loss2 < loss1
# Adjoint sensitivity
p = [2.2, 1.0, 2.0, 0.4]
ps = Flux.params(p)
function predict_adjoint()
solve(remake(prob,p=p),Tsit5(),saveat=0.1,reltol=1e-4)
end
loss_reduction(sol) = sum(abs2,x-1 for x in vec(sol))
loss_adjoint() = loss_reduction(predict_adjoint())
loss_adjoint()
grads = Zygote.gradient(loss_adjoint, ps)
@test !iszero(grads[p])
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
display(loss_adjoint())
# display(plot(solve(remake(prob,p=p),Tsit5(),saveat=0.1),ylim=(0,6)))
end
# Display the ODE with the current parameter values.
loss1 = loss_adjoint()
Flux.train!(loss_adjoint, ps, data, opt, cb = cb)
loss2 = loss_adjoint()
@test 10loss2 < loss1
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 959 | using DiffEqSensitivity, Flux, Zygote, DelayDiffEq, Test
## Setup DDE to optimize
function delay_lotka_volterra(du,u,h,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
prob = DDEProblem(delay_lotka_volterra,[1.0,1.0],h,(0.0,10.0),constant_lags=[0.1])
p = [2.2, 1.0, 2.0, 0.4]
function predict_fd_dde(p)
solve(prob,MethodOfSteps(Tsit5()),p=p,saveat=0.0:0.1:10.0,reltol=1e-4,sensealg=ForwardDiffSensitivity())[1,:]
end
loss_fd_dde(p) = sum(abs2,x-1 for x in predict_fd_dde(p))
loss_fd_dde(p)
@test !iszero(Zygote.gradient(loss_fd_dde,p)[1])
function predict_rd_dde(p)
solve(prob,MethodOfSteps(Tsit5()),p=p,saveat=0.1,reltol=1e-4,sensealg=TrackerAdjoint())[1,:]
end
loss_rd_dde(p) = sum(abs2,x-1 for x in predict_rd_dde(p))
loss_rd_dde(p)
@test !iszero(Zygote.gradient(loss_rd_dde,p)[1])
@test Zygote.gradient(loss_fd_dde,p)[1] ≈ Zygote.gradient(loss_rd_dde,p)[1] rtol=1e-2
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1664 | using DiffEqSensitivity, Flux, Zygote, StochasticDiffEq, Test
function lotka_volterra(du,u,p,t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
function lotka_volterra(u,p,t)
x, y = u
α, β, δ, γ = p
dx = α*x - β*x*y
dy = -δ*y + γ*x*y
[dx,dy]
end
function lotka_volterra_noise(du,u,p,t)
du[1] = 0.01u[1]
du[2] = 0.01u[2]
end
function lotka_volterra_noise(u,p,t)
[0.01u[1],0.01u[2]]
end
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))
p = [2.2, 1.0, 2.0, 0.4]
function predict_fd_sde(p)
solve(prob,SOSRI(),p=p,saveat=0.0:0.1:0.5,sensealg=ForwardDiffSensitivity())[1,:]
end
loss_fd_sde(p) = sum(abs2,x-1 for x in predict_fd_sde(p))
loss_fd_sde(p)
prob = SDEProblem{false}(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))
p = [2.2, 1.0, 2.0, 0.4]
function predict_fd_sde(p)
solve(prob,SOSRI(),p=p,saveat=0.0:0.1:0.5,sensealg=ForwardDiffSensitivity())[1,:]
end
loss_fd_sde(p) = sum(abs2,x-1 for x in predict_fd_sde(p))
loss_fd_sde(p)
@test !iszero(Zygote.gradient(loss_fd_sde,p)[1])
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,0.5))
function predict_rd_sde(p)
solve(prob,SOSRI(),p=p,saveat=0.0:0.1:0.5,sensealg=TrackerAdjoint())[1,:]
end
loss_rd_sde(p) = sum(abs2,x-1 for x in predict_rd_sde(p))
@test !iszero(Zygote.gradient(loss_rd_sde,p)[1])
prob = SDEProblem{false}(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,0.5))
function predict_rd_sde(p)
solve(prob,SOSRI(),p=p,saveat=0.0:0.1:0.5,sensealg=TrackerAdjoint())[1,:]
end
loss_rd_sde(p) = sum(abs2,x-1 for x in predict_rd_sde(p))
@test !iszero(Zygote.gradient(loss_rd_sde,p)[1])
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 545 | using DiffEqSensitivity, OrdinaryDiffEq, Zygote, Test
function lv!(du, u, p, t)
x,y = u
a, b, c, d = p
du[1] = a*x - b*x*y
du[2] = -c*y + d*x*y
end
function test(u0,p)
tspan = [0.,1.]
prob = ODEProblem(lv!, u0, tspan, p)
sol = solve(prob,Tsit5())
return sol.u[end][1]
end
function test2(u0,p)
tspan = [0.,1.]
prob = ODEProblem(lv!, u0, tspan, p)
sol = solve(prob,Tsit5())
return Array(sol)[1,end]
end
u0 = [1.,1.]
p = [1.,1.,1.,1.]
@test Zygote.gradient(test,u0,p) == Zygote.gradient(test2,u0,p)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 3720 | import OrdinaryDiffEq: ODEProblem, solve, Tsit5
import Zygote
using DiffEqSensitivity, Test
dynamics = (x, _p, _t) -> x
function loss(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0), params)
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = InterpolatingAdjoint(autojacvec=ZygoteVJP()))
sum(Array(rollout)[:, end])
end
function loss2(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0), params)
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
sum(Array(rollout)[:, end])
end
function loss3(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0), params)
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = InterpolatingAdjoint(autojacvec=TrackerVJP()))
sum(Array(rollout)[:, end])
end
function loss4(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = InterpolatingAdjoint(autojacvec=ZygoteVJP()))
sum(Array(rollout)[:, end])
end
function loss5(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = InterpolatingAdjoint(autojacvec=EnzymeVJP()))
sum(Array(rollout)[:, end])
end
function loss6(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = BacksolveAdjoint(autojacvec=ZygoteVJP()))
sum(Array(rollout)[:, end])
end
function loss7(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = QuadratureAdjoint(autojacvec=ZygoteVJP()))
sum(Array(rollout)[:, end])
end
function loss8(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = QuadratureAdjoint(autojacvec=ReverseDiffVJP()))
sum(Array(rollout)[:, end])
end
function loss9(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params, sensealg = QuadratureAdjoint(autojacvec=EnzymeVJP()))
sum(Array(rollout)[:, end])
end
function loss10(params)
u0 = zeros(2)
problem = ODEProblem(dynamics, u0, (0.0, 1.0))
rollout = solve(problem, Tsit5(), u0 = u0, p = params)
sum(Array(rollout)[:, end])
end
@test Zygote.gradient(dynamics, 0.0, nothing, nothing) == (1.0,nothing,nothing)
@test Zygote.gradient(loss, nothing)[1] === nothing
@test_broken Zygote.gradient(loss2, nothing)
@test_broken Zygote.gradient(loss3, nothing)
@test Zygote.gradient(loss4, nothing)[1] === nothing
@test Zygote.gradient(loss5, nothing)[1] === nothing
@test Zygote.gradient(loss6, nothing)[1] === nothing
@test Zygote.gradient(loss7, nothing)[1] === nothing
@test Zygote.gradient(loss8, nothing)[1] === nothing
@test Zygote.gradient(loss9, nothing)[1] === nothing
@test Zygote.gradient(loss10, nothing)[1] === nothing
@test Zygote.gradient(loss, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss2, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss3, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss4, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss5, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss6, zeros(123))[1] == zeros(123)
@test_broken Zygote.gradient(loss7, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss8, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss9, zeros(123))[1] == zeros(123)
@test Zygote.gradient(loss10, zeros(123))[1] == zeros(123)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1272 | using OrdinaryDiffEq, DiffEqSensitivity, Zygote, Test
function f!(du,u,p,t)
du[1] = -p[1]'*u
du[2] = (p[2].a + p[2].b)u[2]
du[3] = p[3](u,t)
return nothing
end
struct mystruct
a
b
end
function control(u,t)
return -exp(-t)*u[3]
end
u0 = [10,15,20]
p = [[1;2;3], mystruct(-1,-2), control]
tspan = (0.0,10.0)
prob = ODEProblem(f!,u0, tspan, p)
sol = solve(prob, Tsit5()) # Solves without errors
function loss(p1)
sol = solve(prob, Tsit5(), p=[p1, mystruct(-1,-2), control])
return sum(abs2, sol)
end
grad(p) = Zygote.gradient(loss, p)
p2 = [4;5;6]
@test_throws DiffEqSensitivity.ForwardDiffSensitivityParameterCompatibilityError grad(p2)
function loss(p1)
sol = solve(prob, Tsit5(), p=[p1, mystruct(-1,-2), control], sensealg = InterpolatingAdjoint())
return sum(abs2, sol)
end
@test_throws DiffEqSensitivity.AdjointSensitivityParameterCompatibilityError grad(p2)
function loss(p1)
sol = solve(prob, Tsit5(), p=[p1, mystruct(-1,-2), control], sensealg = ForwardSensitivity())
return sum(abs2, sol)
end
@test_throws DiffEqSensitivity.ForwardSensitivityParameterCompatibilityError grad(p2)
@test_throws DiffEqSensitivity.ForwardSensitivityParameterCompatibilityError ODEForwardSensitivityProblem(f!,u0, tspan, p) | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2320 | using DiffEqSensitivity, Flux, Optimization, OptimizationFlux, OptimizationOptimJL, OrdinaryDiffEq, Test
x = Float32[0.8; 0.8]
tspan = (0.0f0,10.0f0)
ann = Chain(Dense(2,10,tanh), Dense(10,1))
p = Float32[-2.0,1.1]
p2,re = Flux.destructure(ann)
_p = [p;p2]
θ = [x;_p]
function dudt2_(u,p,t)
x, y = u
[(re(p[3:end])(u)[1]),p[1]*y + p[2]*x]
end
prob = ODEProblem(dudt2_,x,tspan,_p)
solve(prob,Tsit5())
function predict_rd(θ)
Array(solve(prob,Tsit5(),u0=θ[1:2],p=θ[3:end],abstol=1e-7,reltol=1e-5,sensealg=TrackerAdjoint()))
end
loss_rd(p) = sum(abs2,x-1 for x in predict_rd(p))
l = loss_rd(θ)
cb = function (θ,l)
@show l
# display(plot(solve(remake(prob,u0=Flux.data(_x),p=Flux.data(p)),Tsit5(),saveat=0.1),ylim=(0,6)))
false
end
# Display the ODE with the current parameter values.
cb(θ,l)
loss1 = loss_rd(θ)
optfunc = Optimization.OptimizationFunction((x, p) -> loss_rd(x), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optfunc, θ)
res = Optimization.solve(optprob, BFGS(initial_stepnorm = 0.01), callback = cb)
loss2 = res.minimum
@test 2loss2 < loss1
## Partial Neural Adjoint
u0 = Float32[0.8; 0.8]
tspan = (0.0f0,25.0f0)
ann = Chain(Dense(2,10,tanh), Dense(10,1))
p1,re = Flux.destructure(ann)
p2 = Float32[-2.0,1.1]
p3 = [p1;p2]
θ = [u0;p3]
function dudt_(du,u,p,t)
x, y = u
du[1] = re(p[1:41])(u)[1]
du[2] = p[end-1]*y + p[end]*x
end
prob = ODEProblem(dudt_,u0,tspan,p3)
solve(prob,Tsit5(),abstol=1e-8,reltol=1e-6)
function predict_adjoint(θ)
Array(solve(prob,Tsit5(),u0=θ[1:2],p=θ[3:end],saveat=0.0:1:25.0))
end
loss_adjoint(θ) = sum(abs2,x-1 for x in predict_adjoint(θ))
l = loss_adjoint(θ)
cb = function (θ,l)
@show l
# display(plot(solve(remake(prob,p=Flux.data(p3),u0=Flux.data(u0)),Tsit5(),saveat=0.1),ylim=(0,6)))
false
end
# Display the ODE with the current parameter values.
cb(θ,l)
loss1 = loss_adjoint(θ)
optfunc = Optimization.OptimizationFunction((x, p) -> loss_adjoint(x), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optfunc, θ)
res1 = Optimization.solve(optprob, ADAM(0.01), callback = cb, maxiters = 100)
optprob = Optimization.OptimizationProblem(optfunc, res1.minimizer)
res = Optimization.solve(optprob, BFGS(initial_stepnorm = 0.01), callback = cb)
loss2 = res.minimum
@test 2loss2 < loss1
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 907 | using OrdinaryDiffEq, DiffEqSensitivity
function growth(du, u, p, t)
@. du = p * u * (1 - u)
end
u0 = [0.1]
tspan = (0.0, 2.0)
prob = ODEProblem(growth, u0, tspan, [1.0])
sol = solve(prob, Tsit5(), reltol = 1e-8, abstol = 1e-8)
savetimes = [0.0, 1.0, 1.9]
function f(a)
_prob = remake(prob,p=[a[1]],saveat=savetimes)
predicted = solve(_prob, Tsit5(), sensealg=InterpolatingAdjoint(), abstol=1e-12, reltol=1e-12)
sum(predicted[end])
end
function f2(a)
_prob = remake(prob,p=[a[1]],saveat=savetimes)
predicted = solve(_prob, Tsit5(), sensealg=ForwardDiffSensitivity(), abstol=1e-12, reltol=1e-12)
sum(predicted[end])
end
using Zygote
a = ones(3)
@test Zygote.gradient(f,a)[1][1] ≈ Zygote.gradient(f2,a)[1][1]
@test Zygote.gradient(f,a)[1][2] == Zygote.gradient(f2,a)[1][2] == 0
@test Zygote.gradient(f,a)[1][3] == Zygote.gradient(f2,a)[1][3] == 0
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 15678 | using StochasticDiffEq
using DiffEqSensitivity
using DiffEqNoiseProcess
using LinearAlgebra, Statistics, Random
using Zygote, ReverseDiff, ForwardDiff
using Test
#using DifferentialEquations
seed = 12345
Random.seed!(seed)
function g(u,p,t)
sum(u.^2.0/2.0)
end
function dg!(out,u,p,t,i)
(out.=-u)
end
@testset "noise iip tests" begin
function f(du,u,p,t,W)
du[1] = p[1]*u[1]*sin(W[1] - W[2])
du[2] = p[2]*u[2]*cos(W[1] + W[2])
return nothing
end
dt = 1e-4
u0 = [1.00;1.00]
tspan = (0.0,5.0)
t = tspan[1]:0.1:tspan[2]
p = [2.0,-2.0]
prob = RODEProblem(f,u0,tspan,p)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true)
# check reversion with usage of Noise Grid
_sol = deepcopy(sol)
noise_reverse = NoiseGrid(reverse(_sol.t),reverse(_sol.W.W))
prob_reverse = RODEProblem(f,_sol[end],reverse(tspan),p,noise=noise_reverse)
sol_reverse = solve(prob_reverse,RandomEM(),dt=dt)
@test sol.u ≈ reverse(sol_reverse.u) rtol=1e-3
@show minimum(sol.u)
# Test if Forward and ReverseMode AD agree.
Random.seed!(seed)
du0ReverseDiff,dpReverseDiff = Zygote.gradient((u0,p)->sum(
Array(solve(prob,RandomEM(),dt=dt,u0=u0,p=p,saveat=t,sensealg=ReverseDiffAdjoint())).^2/2)
,u0,p)
Random.seed!(seed)
dForward = ForwardDiff.gradient((θ)->sum(
Array(solve(prob,RandomEM(),dt=dt,u0=θ[1:2],p=θ[3:4],saveat=t)).^2/2)
,[u0;p])
@info dForward
@test du0ReverseDiff ≈ dForward[1:2]
@test dpReverseDiff ≈ dForward[3:4]
# test gradients
Random.seed!(seed)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true, saveat=t)
###
## BacksolveAdjoint
###
# ReverseDiff
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint())
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
@info du0, dp'
# ReverseDiff with compiled tape
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP(true)))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Tracker
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=TrackerVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false and with jac and paramjac
function jac(J,u,p,t,W)
J[1,1] = p[1]*sin(W[1] - W[2])
J[2,1] = zero(u[1])
J[1,2] = zero(u[1])
J[2,2] = p[2]*cos(W[1] + W[2])
end
function paramjac(J,u,p,t,W)
J[1,1] = u[1]*sin(W[1] - W[2])
J[2,1] = zero(u[1])
J[1,2] = zero(u[1])
J[2,2] = u[2]*cos(W[1] + W[2])
end
Random.seed!(seed)
faug = RODEFunction(f,jac=jac,paramjac=paramjac)
prob_aug = RODEProblem{true}(faug,u0,tspan,p)
sol = solve(prob_aug,RandomEM(),dt=dt, save_noise=true, saveat=t)
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
###
## InterpolatingAdjoint
###
# test gradients with dense solution and no checkpointing
Random.seed!(seed)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true, dense=true)
# ReverseDiff
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# ReverseDiff with compiled tape
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true)))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Zygote
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Tracker
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=TrackerVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false and with jac and paramjac
Random.seed!(seed)
faug = RODEFunction(f,jac=jac,paramjac=paramjac)
prob_aug = RODEProblem{true}(faug,u0,tspan,p)
sol = solve(prob_aug,RandomEM(),dt=dt, save_noise=true, dense=true)
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# test gradients with saveat solution and checkpointing
# need to simulate for dt beyond last tspan to avoid errors in NoiseGrid
Random.seed!(seed)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true, dense=true)
Random.seed!(seed)
sol_long = solve(remake(prob, tspan=(tspan[1],tspan[2]+10dt)),RandomEM(),dt=dt, save_noise=true, dense=true)
@test sol_long(t) ≈ sol(t) rtol=1e-12
@test sol_long.W.W[1:end-10] ≈ sol.W.W[1:end] rtol=1e-12
# test gradients with saveat solution and checkpointing
noise = NoiseGrid(sol_long.W.t,sol_long.W.W)
sol2 = solve(remake(prob,noise=noise,tspan=(tspan[1],tspan[2])),RandomEM(),dt=dt, saveat=t)
@test sol_long(t) ≈ sol2(t) rtol=1e-12
@test sol_long.W.W ≈ sol2.W.W rtol=1e-12
# ReverseDiff
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=ReverseDiffVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# ReverseDiff with compiled tape
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=ReverseDiffVJP(true)))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Zygote
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=ZygoteVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Tracker
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=TrackerVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false and with jac and paramjac
Random.seed!(seed)
faug = RODEFunction(f,jac=jac,paramjac=paramjac)
prob_aug = RODEProblem{true}(faug,u0,tspan,p, noise=noise)
sol = solve(prob_aug,RandomEM(),dt=dt, save_noise=false, dense=false, saveat=t)
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
end
@testset "noise oop tests" begin
function f(u,p,t,W)
dx = p[1]*u[1]*sin(W[1] - W[2])
dy = p[2]*u[2]*cos(W[1] + W[2])
return [dx,dy]
end
dt = 1e-4
u0 = [1.00;1.00]
tspan = (0.0,5.0)
t = tspan[1]:0.1:tspan[2]
p = [2.0,-2.0]
prob = RODEProblem{false}(f,u0,tspan,p)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true)
# check reversion with usage of Noise Grid
_sol = deepcopy(sol)
noise_reverse = NoiseGrid(reverse(_sol.t),reverse(_sol.W.W))
prob_reverse = RODEProblem(f,_sol[end],reverse(tspan),p,noise=noise_reverse)
sol_reverse = solve(prob_reverse,RandomEM(),dt=dt)
@test sol.u ≈ reverse(sol_reverse.u) rtol=1e-3
@show minimum(sol.u)
# Test if Forward and ReverseMode AD agree.
Random.seed!(seed)
du0ReverseDiff,dpReverseDiff = Zygote.gradient((u0,p)->sum(
Array(solve(prob,RandomEM(),dt=dt,u0=u0,p=p,saveat=t,sensealg=ReverseDiffAdjoint())).^2/2)
,u0,p)
Random.seed!(seed)
dForward = ForwardDiff.gradient((θ)->sum(
Array(solve(prob,RandomEM(),dt=dt,u0=θ[1:2],p=θ[3:4],saveat=t)).^2/2)
,[u0;p])
@info dForward
@test du0ReverseDiff ≈ dForward[1:2]
@test dpReverseDiff ≈ dForward[3:4]
# test gradients
Random.seed!(seed)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true, saveat=t)
###
## BacksolveAdjoint
###
# ReverseDiff
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
@info du0, dp'
# ReverseDiff with compiled tape
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP(true)))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Zygote
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Tracker
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=TrackerVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false and with jac and paramjac
function jac(J,u,p,t,W)
J[1,1] = p[1]*sin(W[1] - W[2])
J[2,1] = zero(u[1])
J[1,2] = zero(u[1])
J[2,2] = p[2]*cos(W[1] + W[2])
end
function paramjac(J,u,p,t,W)
J[1,1] = u[1]*sin(W[1] - W[2])
J[2,1] = zero(u[1])
J[1,2] = zero(u[1])
J[2,2] = u[2]*cos(W[1] + W[2])
end
Random.seed!(seed)
faug = RODEFunction(f,jac=jac,paramjac=paramjac)
prob_aug = RODEProblem{false}(faug,u0,tspan,p)
sol = solve(prob_aug,RandomEM(),dt=dt, save_noise=true, saveat=t)
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
###
## InterpolatingAdjoint
###
# test gradients with dense solution and no checkpointing
Random.seed!(seed)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true, dense=true)
# ReverseDiff
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# ReverseDiff with compiled tape
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true)))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Zygote
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Tracker
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=TrackerVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false and with jac and paramjac
Random.seed!(seed)
faug = RODEFunction(f,jac=jac,paramjac=paramjac)
prob_aug = RODEProblem{false}(faug,u0,tspan,p)
sol = solve(prob_aug,RandomEM(),dt=dt, save_noise=true, dense=true)
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# test gradients with saveat solution and checkpointing
# need to simulate for dt beyond last tspan to avoid errors in NoiseGrid
Random.seed!(seed)
sol = solve(prob,RandomEM(),dt=dt, save_noise=true, dense=true)
Random.seed!(seed)
sol_long = solve(remake(prob, tspan=(tspan[1],tspan[2]+10dt)),RandomEM(),dt=dt, save_noise=true, dense=true)
@test sol_long(t) ≈ sol(t) rtol=1e-12
@test sol_long.W.W[1:end-10] ≈ sol.W.W[1:end] rtol=1e-12
# test gradients with saveat solution and checkpointing
noise = NoiseGrid(sol_long.W.t,sol_long.W.W)
sol2 = solve(remake(prob,noise=noise,tspan=(tspan[1],tspan[2])),RandomEM(),dt=dt, saveat=t)
@test sol_long(t) ≈ sol2(t) rtol=1e-12
@test sol_long.W.W ≈ sol2.W.W rtol=1e-12
# ReverseDiff
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=ReverseDiffVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# ReverseDiff with compiled tape
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=ReverseDiffVJP(true)))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Zygote
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=ZygoteVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# Tracker
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=TrackerVJP()))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false
du0, dp = adjoint_sensitivities(sol2,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
# isautojacvec = false and with jac and paramjac
Random.seed!(seed)
faug = RODEFunction(f,jac=jac,paramjac=paramjac)
prob_aug = RODEProblem{false}(faug,u0,tspan,p,noise=noise)
sol = solve(prob_aug,RandomEM(),dt=dt, save_noise=false, saveat=t, dense=false)
du0, dp = adjoint_sensitivities(sol,RandomEM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=InterpolatingAdjoint(checkpointing=true,autojacvec=false))
@test du0ReverseDiff ≈ du0 rtol=1e-2
@test dpReverseDiff ≈ dp' rtol=1e-2
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 5792 | using DiffEqSensitivity, SafeTestsets
using Test, Pkg
const GROUP = get(ENV, "GROUP", "All")
function activate_gpu_env()
Pkg.activate("gpu")
Pkg.develop(PackageSpec(path=dirname(@__DIR__)))
Pkg.instantiate()
end
@time begin
if GROUP == "All" || GROUP == "Core1" || GROUP == "Downstream"
@time @safetestset "Forward Sensitivity" begin include("forward.jl") end
@time @safetestset "Sparse Adjoint Sensitivity" begin include("sparse_adjoint.jl") end
@time @safetestset "Second Order Sensitivity" begin include("second_order.jl") end
@time @safetestset "Concrete Solve Derivatives" begin include("concrete_solve_derivatives.jl") end
@time @safetestset "Branching Derivatives" begin include("branching_derivatives.jl") end
@time @safetestset "Derivative Shapes" begin include("derivative_shapes.jl") end
@time @safetestset "save_idxs" begin include("save_idxs.jl") end
@time @safetestset "ArrayPartitions" begin include("array_partitions.jl") end
@time @safetestset "Complex Adjoints" begin include("complex_adjoints.jl") end
@time @safetestset "Forward Remake" begin include("forward_remake.jl") end
@time @safetestset "Prob Kwargs" begin include("prob_kwargs.jl") end
@time @safetestset "DiscreteProblem Adjoints" begin include("discrete.jl") end
@time @safetestset "Time Type Mixing Adjoints" begin include("time_type_mixing.jl") end
end
if GROUP == "All" || GROUP == "Core2"
@time @safetestset "hasbranching" begin include("hasbranching.jl") end
@time @safetestset "Literal Adjoint" begin include("literal_adjoint.jl") end
@time @safetestset "ForwardDiff Chunking Adjoints" begin include("forward_chunking.jl") end
@time @safetestset "Stiff Adjoints" begin include("stiff_adjoints.jl") end
@time @safetestset "Autodiff Events" begin include("autodiff_events.jl") end
@time @safetestset "Null Parameters" begin include("null_parameters.jl") end
@time @safetestset "Forward Mode Prob Kwargs" begin include("forward_prob_kwargs.jl") end
@time @safetestset "Steady State Adjoint" begin include("steady_state.jl") end
@time @safetestset "Concrete Solve Derivatives of Second Order ODEs" begin include("second_order_odes.jl") end
@time @safetestset "Parameter Compatibility Errors" begin include("parameter_compatibility_errors.jl") end
end
if GROUP == "All" || GROUP == "Core3" || GROUP == "Downstream"
@time @safetestset "Adjoint Sensitivity" begin include("adjoint.jl") end
end
if GROUP == "All" || GROUP == "Core4"
@time @safetestset "Ensemble Tests" begin include("ensembles.jl") end
@time @safetestset "GDP Regression Tests" begin include("gdp_regression_test.jl") end
@time @safetestset "Layers Tests" begin include("layers.jl") end
@time @safetestset "Layers SDE" begin include("layers_sde.jl") end
@time @safetestset "Layers DDE" begin include("layers_dde.jl") end
@time @safetestset "SDE - Neural" begin include("sde_neural.jl") end
# No `@safetestset` since it requires running in Main
@time @testset "Distributed" begin include("distributed.jl") end
end
if GROUP == "All" || GROUP == "Core5"
@time @safetestset "Partial Neural Tests" begin include("partial_neural.jl") end
@time @safetestset "Size Handling in Adjoint Tests" begin include("size_handling_adjoint.jl") end
@time @safetestset "Callback - ReverseDiff" begin include("callback_reversediff.jl") end
@time @safetestset "Alternative AD Frontend" begin include("alternative_ad_frontend.jl") end
@time @safetestset "Hybrid DE" begin include("hybrid_de.jl") end
@time @safetestset "HybridNODE" begin include("HybridNODE.jl") end
@time @safetestset "ForwardDiff Sparsity Components" begin include("forwarddiffsensitivity_sparsity_components.jl") end
@time @safetestset "Complex No u" begin include("complex_no_u.jl") end
end
if GROUP == "All" || GROUP == "SDE1"
@time @safetestset "SDE Adjoint" begin include("sde_stratonovich.jl") end
@time @safetestset "SDE Scalar Noise" begin include("sde_scalar_stratonovich.jl") end
@time @safetestset "SDE Checkpointing" begin include("sde_checkpointing.jl") end
end
if GROUP == "All" || GROUP == "SDE2"
@time @safetestset "SDE Non-Diagonal Noise" begin include("sde_nondiag_stratonovich.jl") end
end
if GROUP == "All" || GROUP == "SDE3"
@time @safetestset "RODE Tests" begin include("rode.jl") end
@time @safetestset "SDE Ito Conversion Tests" begin include("sde_transformation_test.jl") end
@time @safetestset "SDE Ito Scalar Noise" begin include("sde_scalar_ito.jl") end
end
if GROUP == "Callbacks1"
@time @safetestset "Discrete Callbacks with ForwardDiffSensitivity" begin include("callbacks/forward_sensitivity_callback.jl") end
@time @safetestset "Discrete Callbacks with Adjoints" begin include("callbacks/discrete_callbacks.jl") end
@time @safetestset "SDE Callbacks" begin include("callbacks/SDE_callbacks.jl") end
end
if GROUP == "Callbacks2"
@time @safetestset "Continuous vs. discrete Callbacks" begin include("callbacks/continuous_vs_discrete.jl") end
@time @safetestset "Continuous Callbacks with Adjoints" begin include("callbacks/continuous_callbacks.jl") end
@time @safetestset "VectorContinuousCallbacks with Adjoints" begin include("callbacks/vector_continuous_callbacks.jl") end
end
if GROUP == "Shadowing"
@time @safetestset "Shadowing Tests" begin include("shadowing.jl") end
end
if GROUP == "GPU"
activate_gpu_env()
@time @safetestset "Standard DiffEqFlux GPU" begin include("gpu/diffeqflux_standard_gpu.jl") end
@time @safetestset "Mixed GPU/CPU" begin include("gpu/mixed_gpu_cpu_adjoint.jl") end
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 754 | using OrdinaryDiffEq, DiffEqSensitivity, Zygote, ForwardDiff, Test
function lotka_volterra!(du, u, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
# Initial condition
u0 = [1.0, 1.0]
# Simulation interval and intermediary points
tspan = (0.0, 10.0)
tsteps = 0.0:0.1:10.0
# LV equation parameter. p = [α, β, δ, γ]
p = [1.5, 1.0, 3.0, 1.0]
# Setup the ODE problem, then solve
prob = ODEProblem(lotka_volterra!, u0, tspan, p)
function loss(p)
sol = solve(prob, Tsit5(), p=p, save_idxs=[2], saveat = tsteps, abstol=1e-14, reltol=1e-14)
loss = sum(abs2, sol.-1)
return loss
end
grad1 = Zygote.gradient(loss,p)[1]
grad2 = ForwardDiff.gradient(loss,p)
@test grad1 ≈ grad2
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 2549 | using Test, LinearAlgebra
using DiffEqSensitivity, StochasticDiffEq
using Random
@info "SDE Checkpointing"
seed = 100
Random.seed!(seed)
u₀ = [0.5]
tstart = 0.0
tend = 0.1
dt = 0.005
trange = (tstart, tend)
t = tstart:dt:tend
tarray = collect(t)
function g(u,p,t)
sum(u.^2.0/2.0)
end
function dg!(out,u,p,t,i)
(out.=-u)
end
p2 = [1.01,0.87]
f_oop_linear(u,p,t) = p[1]*u
σ_oop_linear(u,p,t) = p[2]*u
dt1 = tend/1e3
Random.seed!(seed)
prob_oop = SDEProblem(f_oop_linear,σ_oop_linear,u₀,trange,p2)
sol_oop = solve(prob_oop,EulerHeun(),dt=dt1,adaptive=false,save_noise=true)
@show length(sol_oop)
res_u0, res_p = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
res_u0a, res_pa = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()),
checkpoints=sol_oop.t[1:2:end])
@test isapprox(res_u0, res_u0a, rtol = 1e-5)
@test isapprox(res_p, res_pa, rtol = 1e-2)
res_u0a, res_pa = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()),
checkpoints=sol_oop.t[1:10:end])
@test isapprox(res_u0, res_u0a, rtol = 1e-5)
@test isapprox(res_p, res_pa, rtol = 1e-1)
dt1 = tend/1e4
Random.seed!(seed)
prob_oop = SDEProblem(f_oop_linear,σ_oop_linear,u₀,trange,p2)
sol_oop = solve(prob_oop,EulerHeun(),dt=dt1,adaptive=false,save_noise=true)
@show length(sol_oop)
res_u0, res_p = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,
sensealg = InterpolatingAdjoint(autojacvec=ZygoteVJP()))
res_u0a, res_pa = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()),
checkpoints=sol_oop.t[1:2:end])
@test isapprox(res_u0, res_u0a, rtol = 1e-6)
@test isapprox(res_p, res_pa, rtol = 1e-3)
res_u0a, res_pa = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()),
checkpoints=sol_oop.t[1:10:end])
@test isapprox(res_u0, res_u0a, rtol = 1e-6)
@test isapprox(res_p, res_pa, rtol = 1e-2)
res_u0a, res_pa = adjoint_sensitivities(sol_oop,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()),
checkpoints=sol_oop.t[1:500:end])
@test isapprox(res_u0, res_u0a, rtol = 1e-3)
@test isapprox(res_p, res_pa, rtol = 1e-2)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 7243 | using DiffEqSensitivity, Flux, LinearAlgebra
using DiffEqNoiseProcess
using StochasticDiffEq
using Statistics
using DiffEqSensitivity
using DiffEqBase.EnsembleAnalysis
using Zygote
using Optimization, OptimizationFlux
using Random
Random.seed!(238248735)
@testset "Neural SDE" begin
function sys!(du, u, p, t)
r, e, μ, h, ph, z, i = p
du[1] = e * 0.5 * (5μ - u[1]) # nutrient input time series
du[2] = e * 0.05 * (10μ - u[2]) # grazer density time series
du[3] = 0.2 * exp(u[1]) - 0.05 * u[3] - r * u[3] / (h + u[3]) * u[4] # nutrient concentration
du[4] =
r * u[3] / (h + u[3]) * u[4] - 0.1 * u[4] -
0.02 * u[4]^z / (ph^z + u[4]^z) * exp(u[2] / 2.0) + i #Algae density
end
function noise!(du, u, p, t)
du[1] = p[end] # n
du[2] = p[end] # n
du[3] = 0.0
du[4] = 0.0
end
datasize = 10
tspan = (0.0f0, 3.0f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
u0 = [1.0, 1.0, 1.0, 1.0]
p_ = [1.1, 1.0, 0.0, 2.0, 1.0, 1.0, 1e-6, 1.0]
prob = SDEProblem(sys!, noise!, u0, tspan, p_)
ensembleprob = EnsembleProblem(prob)
solution = solve(
ensembleprob,
SOSRI(),
EnsembleThreads();
trajectories = 1000,
abstol = 1e-5,
reltol = 1e-5,
maxiters = 1e8,
saveat = tsteps,
)
(truemean, truevar) = Array.(timeseries_steps_meanvar(solution))
ann = Chain(Dense(4, 32, tanh), Dense(32, 32, tanh), Dense(32, 2))
α,re = Flux.destructure(ann)
α = Float64.(α)
function dudt_(du, u, p, t)
r, e, μ, h, ph, z, i = p_
MM = re(p)(u)
du[1] = e * 0.5 * (5μ - u[1]) # nutrient input time series
du[2] = e * 0.05 * (10μ - u[2]) # grazer density time series
du[3] = 0.2 * exp(u[1]) - 0.05 * u[3] - MM[1] # nutrient concentration
du[4] = MM[2] - 0.1 * u[4] - 0.02 * u[4]^z / (ph^z + u[4]^z) * exp(u[2] / 2.0) + i #Algae density
return nothing
end
function dudt_op(u, p, t)
r, e, μ, h, ph, z, i = p_
MM = re(p)(u)
[e * 0.5 * (5μ - u[1]), # nutrient input time series
e * 0.05 * (10μ - u[2]), # grazer density time series
0.2 * exp(u[1]) - 0.05 * u[3] - MM[1], # nutrient concentration
MM[2] - 0.1 * u[4] - 0.02 * u[4]^z / (ph^z + u[4]^z) * exp(u[2] / 2.0) + i] #Algae density
end
function noise_(du, u, p, t)
du[1] = p_[end]
du[2] = p_[end]
du[3] = 0.0
du[4] = 0.0
return nothing
end
function noise_op(u, p, t)
[p_[end],
p_[end],
0.0,
0.0]
end
prob_nn = SDEProblem(dudt_, noise_, u0, tspan, p = nothing)
prob_nn_op = SDEProblem(dudt_op, noise_op, u0, tspan, p = nothing)
function loss(θ)
tmp_prob = remake(prob_nn, p = θ)
ensembleprob = EnsembleProblem(tmp_prob)
tmp_sol = Array(solve(
ensembleprob,
EM();
dt = tsteps.step,
trajectories = 100,
sensealg = ReverseDiffAdjoint(),
))
tmp_mean = mean(tmp_sol,dims=3)[:,:]
tmp_var = var(tmp_sol,dims=3)[:,:]
sum(abs2, truemean - tmp_mean) + 0.1 * sum(abs2, truevar - tmp_var), tmp_mean
end
function loss_op(θ)
tmp_prob = remake(prob_nn_op, p = θ)
ensembleprob = EnsembleProblem(tmp_prob)
tmp_sol = Array(solve(
ensembleprob,
EM();
dt = tsteps.step,
trajectories = 100,
sensealg = ReverseDiffAdjoint(),
))
tmp_mean = mean(tmp_sol,dims=3)[:,:]
tmp_var = var(tmp_sol,dims=3)[:,:]
sum(abs2, truemean - tmp_mean) + 0.1 * sum(abs2, truevar - tmp_var), tmp_mean
end
losses = []
callback(θ, l, pred) = begin
push!(losses, l)
if length(losses)%50 == 0
println("Current loss after $(length(losses)) iterations: $(losses[end])")
end
false
end
println("Test mutating form")
optf = Optimization.OptimizationFunction((x,p) -> loss(x), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, α)
res1 = Optimization.solve(optprob, ADAM(0.001), callback = callback, maxiters = 200)
println("Test non-mutating form")
optf = Optimization.OptimizationFunction((x,p) -> loss_op(x), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, α)
res2 = Optimization.solve(optprob, ADAM(0.001), callback = callback, maxiters = 200)
end
@testset "Adaptive neural SDE" begin
x_size = 2 # Size of the spatial dimensions in the SDE
v_size = 2 # Output size of the control
# Define Neural Network for the control input
input_size = x_size + 1 # size of the spatial dimensions PLUS one time dimensions
nn_initial = Chain(Dense(input_size,v_size)) # The actual neural network
p_nn, model = Flux.destructure(nn_initial)
nn(x,p) = model(p)(x)
# Define the right hand side of the SDE
const_mat = zeros(Float64, (x_size, v_size))
for i = 1:max(x_size,v_size)
const_mat[i,i] = 1
end
function f!(du,u,p,t)
MM = nn([u;t],p)
du .= u + const_mat*MM
end
function g!(du,u,p,t)
du .= false*u .+ sqrt(2*0.001)
end
# Define SDE problem
u0 = vec(rand(Float64, (x_size,1)))
tspan = (0.0, 1.0)
ts = collect(0:0.1:1)
prob = SDEProblem{true}(f!, g!, u0, tspan, p_nn)
W = WienerProcess(0.0,0.0,0.0)
probscalar = SDEProblem{true}(f!, g!, u0, tspan, p_nn, noise=W)
# Defining the loss function
function loss(pars, prob, alg)
function prob_func(prob, i, repeat)
# Prepare new initial state and remake the problem
u0tmp = vec(rand(Float64,(x_size,1)))
remake(prob, p = pars, u0 = u0tmp)
end
ensembleprob = EnsembleProblem(prob, prob_func = prob_func)
_sol = solve(ensembleprob, alg, EnsembleThreads(), sensealg = BacksolveAdjoint(), saveat = ts, trajectories = 10,
abstol=1e-1, reltol=1e-1)
A = convert(Array, _sol)
sum(abs2, A .- 1), mean(A)
end
# Actually training/fitting the model
losses = []
callback(θ, l, pred) = begin
push!(losses, l)
if length(losses)%1 == 0
println("Current loss after $(length(losses)) iterations: $(losses[end])")
end
false
end
optf = Optimization.OptimizationFunction((p,_) -> loss(p,probscalar, LambaEM()), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, p_nn)
res1 = Optimization.solve(optprob, ADAM(0.1), callback = callback, maxiters = 5)
optf = Optimization.OptimizationFunction((p,_) -> loss(p,probscalar, SOSRI()), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, p_nn)
res2 = Optimization.solve(optprob, ADAM(0.1), callback = callback, maxiters = 5)
optf = Optimization.OptimizationFunction((p,_) -> loss(p,prob, LambaEM()), Optimization.AutoZygote())
optprob = Optimization.OptimizationProblem(optf, p_nn)
res1 = Optimization.solve(optprob, ADAM(0.1), callback = callback, maxiters = 5)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 18206 | using Test, LinearAlgebra
using DiffEqSensitivity, StochasticDiffEq
using ForwardDiff, Zygote
using Random
@info "SDE Non-Diagonal Noise Adjoints"
seed = 100
Random.seed!(seed)
tstart = 0.0
tend = 0.1
dt = 0.005
trange = (tstart, tend)
t = tstart:dt:tend
tarray = collect(t)
function g(u,p,t)
sum(u.^2.0/2.0)
end
function dg!(out,u,p,t,i)
(out.=-u)
end
# non-diagonal noise
@testset "Non-diagonal noise tests" begin
Random.seed!(seed)
u₀ = [0.75,0.5]
p = [-1.5,0.05,0.2, 0.01]
dtnd = tend/1e3
# Example from Roessler, SIAM J. NUMER. ANAL, 48, 922–952 with d = 2; m = 2
function f_nondiag!(du,u,p,t)
du[1] = p[1]*u[1] + p[2]*u[2]
du[2] = p[2]*u[1] + p[1]*u[2]
nothing
end
function g_nondiag!(du,u,p,t)
du[1,1] = p[3]*u[1] + p[4]*u[2]
du[1,2] = p[3]*u[1] + p[4]*u[2]
du[2,1] = p[4]*u[1] + p[3]*u[2]
du[2,2] = p[4]*u[1] + p[3]*u[2]
nothing
end
function f_nondiag(u,p,t)
dx = p[1]*u[1] + p[2]*u[2]
dy = p[2]*u[1] + p[1]*u[2]
[dx,dy]
end
function g_nondiag(u,p,t)
du11 = p[3]*u[1] + p[4]*u[2]
du12 = p[3]*u[1] + p[4]*u[2]
du21 = p[4]*u[1] + p[3]*u[2]
du22 = p[4]*u[1] + p[3]*u[2]
[du11 du12
du21 du22]
end
function f_nondiag_analytic(u0,p,t,W)
A = [[p[1], p[2]] [p[2], p[1]]]
B = [[p[3], p[4]] [p[4], p[3]]]
tmp = A*t + B*W[1] + B*W[2]
exp(tmp)*u0
end
noise_matrix = similar(p,2,2)
noise_matrix .= false
Random.seed!(seed)
prob = SDEProblem(f_nondiag!,g_nondiag!,u₀,trange,p,noise_rate_prototype=noise_matrix)
sol = solve(prob, EulerHeun(), dt=dtnd, save_noise=true)
noise_matrix = similar(p,2,2)
noise_matrix .= false
Random.seed!(seed)
proboop = SDEProblem(f_nondiag,g_nondiag,u₀,trange,p,noise_rate_prototype=noise_matrix)
soloop = solve(proboop,EulerHeun(), dt=dtnd, save_noise=true)
res_sde_u0, res_sde_p = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=BacksolveAdjoint())
@info res_sde_p
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-4)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-4)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-4)
@info res_sde_pa
@test_broken res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=BacksolveAdjoint())
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
@test_broken res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-4)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-4)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtnd,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-4)
@info res_sde_pa
function compute_grads_nd(sol)
xdis = sol(tarray)
mat1 = Matrix{Int}(I, 2, 2)
mat2 = ones(2,2)-mat1
tmp1 = similar(p)
tmp1 *= false
tmp2 = similar(xdis.u[1])
tmp2 *= false
for (i, u) in enumerate(xdis)
tmp1[1]+=xdis.t[i]*u'*mat1*u
tmp1[2]+=xdis.t[i]*u'*mat2*u
tmp1[3]+=sum(sol.W(xdis.t[i])[1])*u'*mat1*u
tmp1[4]+=sum(sol.W(xdis.t[i])[1])*u'*mat2*u
tmp2 += u.^2
end
return tmp2 ./ xdis.u[1], tmp1
end
res1, res2 = compute_grads_nd(soloop)
@test isapprox(res1, res_sde_u0, rtol=1e-4)
@test isapprox(res2, res_sde_p', rtol=1e-4)
end
@testset "diagonal but mixing noise tests" begin
Random.seed!(seed)
u₀ = [0.75,0.5]
p = [-1.5,0.05,0.2, 0.01]
dtmix = tend/1e3
# Example from Roessler, SIAM J. NUMER. ANAL, 48, 922–952 with d = 2; m = 2
function f_mixing!(du,u,p,t)
du[1] = p[1]*u[1] + p[2]*u[2]
du[2] = p[2]*u[1] + p[1]*u[2]
nothing
end
function g_mixing!(du,u,p,t)
du[1] = p[3]*u[1] + p[4]*u[2]
du[2] = p[3]*u[1] + p[4]*u[2]
nothing
end
function f_mixing(u,p,t)
dx = p[1]*u[1] + p[2]*u[2]
dy = p[2]*u[1] + p[1]*u[2]
[dx,dy]
end
function g_mixing(u,p,t)
dx = p[3]*u[1] + p[4]*u[2]
dy = p[3]*u[1] + p[4]*u[2]
[dx,dy]
end
Random.seed!(seed)
prob = SDEProblem(f_mixing!,g_mixing!,u₀,trange,p)
soltsave = collect(trange[1]:dtmix:trange[2])
sol = solve(prob, EulerHeun(), dt=dtmix, save_noise=true, saveat=soltsave)
Random.seed!(seed)
proboop = SDEProblem(f_mixing,g_mixing,u₀,trange,p)
soloop = solve(proboop,EulerHeun(), dt=dtmix, save_noise=true, saveat=soltsave)
#oop
res_sde_u0, res_sde_p = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(noisemixing=true))
@info res_sde_p
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP(), noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false,noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,Array(t)
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP(), noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(noisemixing=true, autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false, noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
@test_broken res_sde_u0, res_sde_p = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_p
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP(), noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false,noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP(), noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-6)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-6)
@info res_sde_pa
@test_broken res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5) # would pass with 1e-4 but last noise value is off
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(noisemixing=true, autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false, noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true))
@test isapprox(res_sde_u0a, res_sde_u0, rtol=1e-5)
@test isapprox(res_sde_pa, res_sde_p, rtol=1e-5)
@info res_sde_pa
function GSDE(p)
Random.seed!(seed)
tmp_prob = remake(prob,u0=eltype(p).(prob.u0),p=p,
tspan=eltype(p).(prob.tspan))
_sol = solve(tmp_prob,EulerHeun(),dt=dtmix,adaptive=false,saveat=Array(t))
A = convert(Array,_sol)
res = g(A,p,nothing)
end
res_sde_forward = ForwardDiff.gradient(GSDE,p)
@test isapprox(res_sde_p', res_sde_forward, rtol=1e-5)
function GSDE2(u0)
Random.seed!(seed)
tmp_prob = remake(prob,u0=u0,p=eltype(p).(prob.p),
tspan=eltype(p).(prob.tspan))
_sol = solve(tmp_prob,EulerHeun(),dt=dtmix,adaptive=false,saveat=Array(t))
A = convert(Array,_sol)
res = g(A,p,nothing)
end
res_sde_forward = ForwardDiff.gradient(GSDE2,u₀)
@test isapprox(res_sde_forward, res_sde_u0, rtol=1e-5)
end
@testset "mixing noise inplace/oop tests" begin
Random.seed!(seed)
u₀ = [0.75,0.5]
p = [-1.5,0.05,0.2, 0.01]
dtmix = tend/1e3
# Example from Roessler, SIAM J. NUMER. ANAL, 48, 922–952 with d = 2; m = 2
function f_mixing!(du,u,p,t)
du[1] = p[1]*u[1] + p[2]*u[2]
du[2] = p[2]*u[1] + p[1]*u[2]
nothing
end
function g_mixing!(du,u,p,t)
du[1] = p[3]*u[1] + p[4]*u[2]
du[2] = p[3]*u[1] + p[4]*u[2]
nothing
end
function f_mixing(u,p,t)
dx = p[1]*u[1] + p[2]*u[2]
dy = p[2]*u[1] + p[1]*u[2]
[dx,dy]
end
function g_mixing(u,p,t)
dx = p[3]*u[1] + p[4]*u[2]
dy = p[3]*u[1] + p[4]*u[2]
[dx,dy]
end
Random.seed!(seed)
prob = SDEProblem(f_mixing!,g_mixing!,u₀,trange,p)
soltsave = collect(trange[1]:dtmix:trange[2])
sol = solve(prob, EulerHeun(), dt=dtmix, save_noise=true, saveat=soltsave)
Random.seed!(seed)
proboop = SDEProblem(f_mixing,g_mixing,u₀,trange,p)
soloop = solve(proboop,EulerHeun(), dt=dtmix, save_noise=true, saveat=soltsave)
@test sol.u ≈ soloop.u atol = 1e-14
# BacksolveAdjoint
res_sde_u0, res_sde_p = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(noisemixing=true))
@test_broken res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=BacksolveAdjoint(noisemixing=true))
@test_broken res_sde_u0 ≈ res_sde_u02 atol = 1e-14
@test_broken res_sde_p ≈ res_sde_p2 atol = 1e-14
@show res_sde_u0
adjproboop = SDEAdjointProblem(soloop,BacksolveAdjoint(autojacvec=ZygoteVJP(),noisemixing=true),dg!,tarray, nothing)
adj_soloop = solve(adjproboop,EulerHeun(); dt=dtmix, tstops=soloop.t, adaptive=false)
@test adj_soloop[end][length(p)+length(u₀)+1:end] == soloop.u[1]
@test - adj_soloop[end][1:length(u₀)] == res_sde_u0
@test adj_soloop[end][length(u₀)+1:end-length(u₀)] == res_sde_p'
adjprob = SDEAdjointProblem(sol,BacksolveAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true,checkpointing=true),dg!,tarray, nothing)
adj_sol = solve(adjprob,EulerHeun(); dt=dtmix, adaptive=false,tstops=soloop.t)
@test adj_soloop[end] ≈ adj_sol[end] rtol=1e-15
adjprob = SDEAdjointProblem(sol,BacksolveAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true,checkpointing=false),dg!,tarray, nothing)
adj_sol = solve(adjprob,EulerHeun(); dt=dtmix, adaptive=false,tstops=soloop.t)
@test adj_soloop[end] ≈ adj_sol[end] rtol=1e-8
# InterpolatingAdjoint
res_sde_u0, res_sde_p = adjoint_sensitivities(soloop,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(noisemixing=true))
@test_broken res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,tarray
,dt=dtmix,adaptive=false,sensealg=InterpolatingAdjoint(noisemixing=true))
@test_broken res_sde_u0 ≈ res_sde_u02 atol = 1e-8
@test_broken res_sde_p ≈ res_sde_p2 atol = 5e-8
@show res_sde_u0
adjproboop = SDEAdjointProblem(soloop,InterpolatingAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true),dg!,tarray, nothing)
adj_soloop = solve(adjproboop,EulerHeun(); dt=dtmix, tstops=soloop.t, adaptive=false)
@test - adj_soloop[end][1:length(u₀)] ≈ res_sde_u0 atol = 1e-14
@test adj_soloop[end][length(u₀)+1:end] ≈ res_sde_p' atol = 1e-14
adjprob = SDEAdjointProblem(sol,InterpolatingAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true,checkpointing=true),dg!,tarray, nothing)
adj_sol = solve(adjprob,EulerHeun(); dt=dtmix, adaptive=false,tstops=soloop.t)
@test adj_soloop[end] ≈ adj_sol[end] rtol=1e-8
adjprob = SDEAdjointProblem(sol,InterpolatingAdjoint(autojacvec=ReverseDiffVJP(),noisemixing=true,checkpointing=false),dg!,tarray, nothing)
adj_sol = solve(adjprob,EulerHeun(); dt=dtmix, adaptive=false,tstops=soloop.t)
@test adj_soloop[end] ≈ adj_sol[end] rtol=1e-8
end
@testset "mutating non-diagonal noise" begin
a!(du,u,_p,t) = (du .= -u)
a(u,_p,t) = -u
function b!(du,u,_p,t)
KR, KI = _p[1:2]
du[1,1] = KR
du[2,1] = KI
end
function b(u,_p,t)
KR, KI = _p[1:2]
[ KR zero(KR)
KI zero(KR) ]
end
p = [1.,0.]
prob! = SDEProblem{true}(a!,b!,[0.,0.],(0.0,0.1),p,noise_rate_prototype=eltype(p).(zeros(2,2)))
prob = SDEProblem{false}(a,b,[0.,0.],(0.0,0.1),p,noise_rate_prototype=eltype(p).(zeros(2,2)))
function loss(p;SDEprob=prob,sensealg=BacksolveAdjoint())
_prob = remake(SDEprob,p=p)
sol = solve(_prob, EulerHeun(), dt=1e-5, sensealg=sensealg)
return sum(Array(sol))
end
function compute_dp(p, SDEprob, sensealg)
Random.seed!(seed)
Zygote.gradient(p->loss(p,SDEprob=SDEprob,sensealg=sensealg), p)[1]
end
# test mutating against non-mutating
# non-mutating
dp1 = compute_dp(p, prob, ForwardDiffSensitivity())
dp2 = compute_dp(p, prob, BacksolveAdjoint())
dp3 = compute_dp(p, prob, InterpolatingAdjoint())
@show dp1 dp2 dp3
# different vjp choice
_dp2 = compute_dp(p, prob, BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test dp2 ≈ _dp2 rtol=1e-8
_dp3 = compute_dp(p, prob, InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test dp3 ≈ _dp3 rtol=1e-8
# mutating
_dp1 = compute_dp(p, prob!, ForwardDiffSensitivity())
_dp2 = compute_dp(p, prob!, BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
_dp3 = compute_dp(p, prob!, InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test_broken _dp4 = compute_dp(p, prob!, InterpolatingAdjoint())
@test dp1 ≈ _dp1 rtol=1e-8
@test dp2 ≈ _dp2 rtol=1e-8
@test dp3 ≈ _dp3 rtol=1e-8
@test_broken dp3 ≈ _dp4 rtol=1e-8
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 5314 | using Test, LinearAlgebra
using DiffEqSensitivity, StochasticDiffEq
using Random
using DiffEqNoiseProcess
using ForwardDiff
using ReverseDiff
@info "SDE scalar Adjoints"
seed = 100
Random.seed!(seed)
tstart = 0.0
tend = 0.1
trange = (tstart, tend)
t = tstart:0.01:tend
tarray = collect(t)
function g(u,p,t)
sum(u.^2.0/2.0)
end
function dg!(out,u,p,t,i)
(out.=-u)
end
dt = tend/1e4
# non-exploding initialization.
α = 1/(exp(-randn())+1)
β = -α^2 - 1/(exp(-randn())+1)
p = [α,β]
fIto(u,p,t) = p[1]*u #p[1]*u.+p[2]^2/2*u
fStrat(u,p,t) = p[1]*u.-p[2]^2/2*u #p[1]*u
σ(u,p,t) = p[2]*u
# Ito sense (Strat sense for commented version)
linear_analytic(u0,p,t,W) = @.(u0*exp(p[1]*t+p[2]*W))
corfunc(u,p,t) = p[2]^2*u
"""
1D oop
"""
# generate noise values
# Z = randn(length(tstart:dt:tend))
# Z1 = cumsum([0;sqrt(dt)*Z[1:end]])
# NG = NoiseGrid(Array(tstart:dt:(tend+dt)),[Z for Z in Z1])
# set initial state
u0 = [1/6]
# define problem in Ito sense
Random.seed!(seed)
probIto = SDEProblem(fIto,
σ,u0,trange,p,
#noise=NG
)
# solve Ito sense
solIto = solve(probIto, EM(), dt=dt, adaptive=false, save_noise=true, saveat=dt)
# define problem in Stratonovich sense
Random.seed!(seed)
probStrat = SDEProblem(SDEFunction(fStrat,σ,),
σ,u0,trange,p,
#noise=NG
)
# solve Strat sense
solStrat = solve(probStrat,RKMil(interpretation=:Stratonovich), dt=dt,
adaptive=false, save_noise=true, saveat=dt)
# check that forward solution agrees
@test isapprox(solIto.u, solStrat.u, rtol=1e-3)
@test isapprox(solIto.u, solStrat.u, atol=1e-2)
#@test isapprox(solIto.u, solIto.u_analytic, rtol=1e-3)
"""
solve with continuous adjoint sensitivity tools
"""
# for Ito sense
gs_u0, gs_p = adjoint_sensitivities(solIto,EM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(),corfunc_analytical=corfunc)
@info gs_u0, gs_p
gs_u0a, gs_pa = adjoint_sensitivities(solIto,EM(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=DiffEqSensitivity.ReverseDiffVJP()))
@info gs_u0a, gs_pa
@test isapprox(gs_u0, gs_u0a, rtol=1e-8)
@test isapprox(gs_p, gs_pa, rtol=1e-8)
# for Strat sense
res_u0, res_p = adjoint_sensitivities(solStrat,EulerHeun(),dg!,Array(t)
,dt=dt,adaptive=false,sensealg=BacksolveAdjoint())
@info res_u0, res_p
"""
Tests with respect to analytical result, forward and reverse mode AD
"""
# tests for parameter gradients
function Gp(p; sensealg = ReverseDiffAdjoint())
Random.seed!(seed)
tmp_prob = remake(probStrat,p=p)
_sol = solve(tmp_prob,EulerHeun(),dt=dt,adaptive=false,saveat=Array(t),sensealg=sensealg)
A = convert(Array,_sol)
res = g(A,p,nothing)
end
res_forward = ForwardDiff.gradient(p -> Gp(p,sensealg=ForwardDiffSensitivity()), p)
@info res_forward
Wfix = [solStrat.W(t)[1][1] for t in tarray]
resp1 = sum(@. tarray*u0^2*exp(2*(p[1]-p[2]^2/2)*tarray+2*p[2]*Wfix))
resp2 = sum(@. (Wfix-p[2]*tarray)*u0^2*exp(2*(p[1]-p[2]^2/2)*tarray+2*p[2]*Wfix))
resp = [resp1, resp2]
@show resp
@test isapprox(resp, gs_p', atol=3e-2) # exact vs ito adjoint
@test isapprox(res_p, gs_p, atol=3e-2) # strat vs ito adjoint
@test isapprox(gs_p', res_forward, atol=3e-2) # ito adjoint vs forward
@test isapprox(resp, res_p', rtol=2e-5) # exact vs strat adjoint
@test isapprox(resp, res_forward, rtol=2e-5) # exact vs forward
# tests for initial state gradients
function Gu0(u0; sensealg = ReverseDiffAdjoint())
Random.seed!(seed)
tmp_prob = remake(probStrat,u0=u0)
_sol = solve(tmp_prob,EulerHeun(),dt=dt,adaptive=false,saveat=Array(t),sensealg=sensealg)
A = convert(Array,_sol)
res = g(A,p,nothing)
end
res_forward = ForwardDiff.gradient(u0 -> Gu0(u0,sensealg=ForwardDiffSensitivity()), u0)
resu0 = sum(@. u0*exp(2*(p[1]-p[2]^2/2)*tarray+2*p[2]*Wfix))
@show resu0
@test isapprox(resu0, gs_u0[1], rtol=5e-2) # exact vs ito adjoint
@test isapprox(res_u0, gs_u0, rtol=5e-2) # strat vs ito adjoint
@test isapprox(gs_u0, res_forward, rtol=5e-2) # ito adjoint vs forward
@test isapprox(resu0, res_u0[1], rtol=1e-3) # exact vs strat adjoint
@test isapprox(res_u0, res_forward, rtol=1e-3) # strat adjoint vs forward
@test isapprox(resu0, res_forward[1], rtol=1e-3) # exact vs forward
adj_probStrat = SDEAdjointProblem(solStrat,BacksolveAdjoint(autojacvec=ZygoteVJP()),dg!,t,nothing)
adj_solStrat = solve(adj_probStrat,EulerHeun(), dt=dt)
#@show adj_solStrat[end]
adj_probIto = SDEAdjointProblem(solIto,BacksolveAdjoint(autojacvec=ZygoteVJP()),dg!,t,nothing,
corfunc_analytical=corfunc)
adj_solIto = solve(adj_probIto,EM(), dt=dt)
@test isapprox(adj_solStrat[4,:], adj_solIto[4,:], rtol=1e-3)
# using Plots
# pl1 = plot(solStrat, label="Strat forward")
# plot!(pl1,solIto, label="Ito forward")
#
# pl1 = plot(adj_solStrat.t, adj_solStrat[4,:], label="Strat reverse")
# plot!(pl1,adj_solIto.t, adj_solIto[4,:], label="Ito reverse")
#
# pl2 = plot(adj_solStrat.t, adj_solStrat[1,:], label="Strat reverse")
# plot!(pl2, adj_solIto.t, adj_solIto[1,:], label="Ito reverse", legend=:bottomright)
#
# pl3 = plot(adj_solStrat.t, adj_solStrat[2,:], label="Strat reverse")
# plot!(pl3, adj_solIto.t, adj_solIto[2,:], label="Ito reverse")
#
# pl4 = plot(adj_solStrat.t, adj_solStrat[3,:], label="Strat reverse")
# plot!(pl4, adj_solIto.t, adj_solIto[3,:], label="Ito reverse")
#
# pl = plot(pl1,pl2,pl3,pl4)
#
# savefig(pl, "plot.png")
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 6184 | using Test, LinearAlgebra
using DiffEqSensitivity, StochasticDiffEq
using Random
@info "SDE Adjoints"
seed = 100
Random.seed!(seed)
tstart = 0.0
tend = 0.1
dt = 0.005
trange = (tstart, tend)
t = tstart:dt:tend
tarray = collect(t)
function g(u,p,t)
sum(u.^2.0/2.0)
end
function dg!(out,u,p,t,i)
(out.=-u)
end
p2 = [1.01,0.87]
# scalar noise
@testset "SDE inplace scalar noise tests" begin
using DiffEqNoiseProcess
dtscalar = tend/1e3
f!(du,u,p,t) = (du .= p[1]*u)
σ!(du,u,p,t) = (du .= p[2]*u)
@info "scalar SDE"
Random.seed!(seed)
W = WienerProcess(0.0,0.0,0.0)
u0 = rand(2)
linear_analytic_strat(u0,p,t,W) = @.(u0*exp(p[1]*t+p[2]*W))
prob = SDEProblem(SDEFunction(f!,σ!,analytic=linear_analytic_strat),σ!,u0,trange,p2,
noise=W
)
sol = solve(prob,EulerHeun(), dt=dtscalar, save_noise=true)
@test isapprox(sol.u_analytic,sol.u, atol=1e-4)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=BacksolveAdjoint())
@show res_sde_u0, res_sde_p
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_u0, res_sde_u02, atol=1e-8)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-8)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u0, res_sde_u02, atol=1e-8)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-8)
@show res_sde_u02, res_sde_p2
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=tend/1e2,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, rtol=1e-4)
@show res_sde_u02, res_sde_p2
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, rtol=1e-4)
@show res_sde_u02, res_sde_p2
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, rtol=1e-4)
@show res_sde_u02, res_sde_p2
function compute_grads(sol, scale=1.0)
_sol = deepcopy(sol)
_sol.W.save_everystep = false
xdis = _sol(tarray)
helpu1 = [u[1] for u in xdis.u]
tmp1 = sum((@. xdis.t*helpu1*helpu1))
Wtmp = [_sol.W(t)[1][1] for t in tarray]
tmp2 = sum((@. Wtmp*helpu1*helpu1))
tmp3 = sum((@. helpu1*helpu1))/helpu1[1]
return [tmp3, scale*tmp3], [tmp1*(1.0+scale^2), tmp2*(1.0+scale^2)]
end
true_grads = compute_grads(sol, u0[2]/u0[1])
@show true_grads
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, rtol=1e-4)
@test isapprox(true_grads[2], res_sde_p', atol=1e-4)
@test isapprox(true_grads[1], res_sde_u0, rtol=1e-4)
@test isapprox(true_grads[2], res_sde_p2', atol=1e-4)
@test isapprox(true_grads[1], res_sde_u02, rtol=1e-4)
end
@testset "SDE oop scalar noise tests" begin
using DiffEqNoiseProcess
dtscalar = tend/1e3
f(u,p,t) = p[1]*u
σ(u,p,t) = p[2]*u
Random.seed!(seed)
W = WienerProcess(0.0,0.0,0.0)
u0 = rand(2)
linear_analytic_strat(u0,p,t,W) = @.(u0*exp(p[1]*t+p[2]*W))
prob = SDEProblem(SDEFunction(f,σ,analytic=linear_analytic_strat),σ,u0,trange,p2,
noise=W
)
sol = solve(prob,EulerHeun(), dt=dtscalar, save_noise=true)
@test isapprox(sol.u_analytic,sol.u, atol=1e-4)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=BacksolveAdjoint())
@show res_sde_u0, res_sde_p
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_u0, res_sde_u02, atol=1e-8)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-8)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u0, res_sde_u02, atol=1e-8)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-8)
@show res_sde_u02, res_sde_p2
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=tend/1e2,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-4)
@show res_sde_u02, res_sde_p2
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-4)
@show res_sde_u02, res_sde_p2
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol,EulerHeun(),dg!,Array(t)
,dt=dtscalar,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u0, res_sde_u02, rtol=1e-4)
@test isapprox(res_sde_p, res_sde_p2, atol=1e-4)
@show res_sde_u02, res_sde_p2
function compute_grads(sol, scale=1.0)
_sol = deepcopy(sol)
_sol.W.save_everystep = false
xdis = _sol(tarray)
helpu1 = [u[1] for u in xdis.u]
tmp1 = sum((@. xdis.t*helpu1*helpu1))
Wtmp = [_sol.W(t)[1][1] for t in tarray]
tmp2 = sum((@. Wtmp*helpu1*helpu1))
tmp3 = sum((@. helpu1*helpu1))/helpu1[1]
return [tmp3, scale*tmp3], [tmp1*(1.0+scale^2), tmp2*(1.0+scale^2)]
end
true_grads = compute_grads(sol, u0[2]/u0[1])
@show true_grads
@test isapprox(true_grads[2], res_sde_p', atol=1e-4)
@test isapprox(true_grads[1], res_sde_u0, rtol=1e-4)
@test isapprox(true_grads[2], res_sde_p2', atol=1e-4)
@test isapprox(true_grads[1], res_sde_u02, rtol=1e-4)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 16760 | using Test, LinearAlgebra
using OrdinaryDiffEq
using DiffEqSensitivity, StochasticDiffEq, DiffEqBase
using ForwardDiff, ReverseDiff
using Random
import Tracker, Zygote
@info "SDE Adjoints"
seed = 100
Random.seed!(seed)
abstol = 1e-4
reltol = 1e-4
u₀ = [0.5]
tstart = 0.0
tend = 0.1
dt = 0.005
trange = (tstart, tend)
t = tstart:dt:tend
tarray = collect(t)
function g(u,p,t)
sum(u.^2.0/2.0)
end
function dg!(out,u,p,t,i)
(out.=-u)
end
p2 = [1.01,0.87]
@testset "SDE oop Tests (no noise)" begin
f_oop_linear(u,p,t) = p[1]*u
σ_oop_linear(u,p,t) = p[2]*u
p = [1.01,0.0]
# generate ODE adjoint results
prob_oop_ode = ODEProblem(f_oop_linear,u₀,(tstart,tend),p)
sol_oop_ode = solve(prob_oop_ode,Tsit5(),saveat=t,abstol=abstol,reltol=reltol)
res_ode_u0, res_ode_p = adjoint_sensitivities(sol_oop_ode,Tsit5(),dg!,t
,abstol=abstol,reltol=reltol,sensealg=BacksolveAdjoint())
function G(p)
tmp_prob = remake(prob_oop_ode,u0=eltype(p).(prob_oop_ode.u0),p=p,
tspan=eltype(p).(prob_oop_ode.tspan),abstol=abstol, reltol=reltol)
sol = solve(tmp_prob,Tsit5(),saveat=tarray,abstol=abstol, reltol=reltol)
res = g(sol,p,nothing)
end
res_ode_forward = ForwardDiff.gradient(G,p)
@test isapprox(res_ode_forward[1], sum(@. u₀^2*exp(2*p[1]*t)*t), rtol = 1e-4)
#@test isapprox(res_ode_reverse[1], sum(@. u₀^2*exp(2*p[1]*t)*t), rtol = 1e-4)
@test isapprox(res_ode_p'[1], sum(@. u₀^2*exp(2*p[1]*t)*t), rtol = 1e-4)
#@test isapprox(res_ode_p', res_ode_trackerp, rtol = 1e-4)
# SDE adjoint results (with noise == 0, so should agree with above)
Random.seed!(seed)
prob_oop_sde = SDEProblem(f_oop_linear,σ_oop_linear,u₀,trange,p)
sol_oop_sde = solve(prob_oop_sde,EulerHeun(),dt=1e-4,adaptive=false,save_noise=true)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_oop_sde,
EulerHeun(),dg!,t,dt=1e-2,sensealg=BacksolveAdjoint())
@info res_sde_p
res_sde_u0a, res_sde_pa = adjoint_sensitivities(sol_oop_sde,
EulerHeun(),dg!,t,dt=1e-2,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_u0, res_sde_u0a, rtol = 1e-6)
@test isapprox(res_sde_p, res_sde_pa, rtol = 1e-6)
function GSDE1(p)
Random.seed!(seed)
tmp_prob = remake(prob_oop_sde,u0=eltype(p).(prob_oop_sde.u0),p=p,
tspan=eltype(p).(prob_oop_sde.tspan))
sol = solve(tmp_prob,RKMil(interpretation=:Stratonovich),dt=tend/10000,adaptive=false,sensealg=DiffEqBase.SensitivityADPassThrough(),saveat=tarray)
A = convert(Array,sol)
res = g(A,p,nothing)
end
res_sde_forward = ForwardDiff.gradient(GSDE1,p)
noise = vec((@. sol_oop_sde.W(tarray)))
Wfix = [W[1][1] for W in noise]
@test isapprox(res_sde_forward[1], sum(@. u₀^2*exp(2*p[1]*t)*t), rtol = 1e-4)
@test isapprox(res_sde_p'[1], sum(@. u₀^2*exp(2*p[1]*t)*t), rtol = 1e-4)
@test isapprox(res_sde_p'[2], sum(@. (Wfix)*u₀^2*exp(2*(p[1])*tarray+2*p[2]*Wfix)), rtol = 1e-4)
end
@testset "SDE oop Tests (with noise)" begin
f_oop_linear(u,p,t) = p[1]*u
σ_oop_linear(u,p,t) = p[2]*u
# SDE adjoint results (with noise != 0)
dt1 = tend/1e3
Random.seed!(seed)
prob_oop_sde2 = SDEProblem(f_oop_linear,σ_oop_linear,u₀,trange,p2)
sol_oop_sde2 = solve(prob_oop_sde2,RKMil(interpretation=:Stratonovich),dt=dt1,adaptive=false,save_noise=true)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint())
@info res_sde_p2
# test consitency for different switches for the noise Jacobian
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-6)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-6)
@info res_sde_p2a
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-6)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-6)
@info res_sde_p2a
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=tend/dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-6)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-6)
@info res_sde_p2a
function GSDE2(p)
Random.seed!(seed)
tmp_prob = remake(prob_oop_sde2,u0=eltype(p).(prob_oop_sde2.u0),p=p,
tspan=eltype(p).(prob_oop_sde2.tspan)
#,abstol=abstol, reltol=reltol
)
sol = solve(tmp_prob,RKMil(interpretation=:Stratonovich),dt=dt1,adaptive=false,sensealg=DiffEqBase.SensitivityADPassThrough(),saveat=tarray)
A = convert(Array,sol)
res = g(A,p,nothing)
end
res_sde_forward2 = ForwardDiff.gradient(GSDE2,p2)
Wfix = [sol_oop_sde2.W(t)[1][1] for t in tarray]
resp1 = sum(@. tarray*u₀^2*exp(2*(p2[1])*tarray+2*p2[2]*Wfix))
resp2 = sum(@. (Wfix)*u₀^2*exp(2*(p2[1])*tarray+2*p2[2]*Wfix))
resp = [resp1, resp2]
@test isapprox(res_sde_forward2, resp, rtol = 8e-4)
@test isapprox(res_sde_p2', res_sde_forward2, rtol = 1e-3)
@test isapprox(res_sde_p2', resp, rtol = 1e-3)
@info "ForwardDiff" res_sde_forward2
@info "Exact" resp
@info "BacksolveAdjoint SDE" res_sde_p2
# InterpolatingAdjoint
@info "InterpolatingAdjoint SDE"
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-4)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-3)
@info res_sde_p2a
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-6)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-6)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-6)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-6)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-6)
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-6)
# Free memory to help Travis
Wfix = nothing
res_sde_forward2 = nothing
res_sde_reverse2 = nothing
resp = nothing
res_sde_trackerp2 = nothing
res_sde_u02 = nothing
sol_oop_sde2 = nothing
res_sde_u02a = nothing
res_sde_p2a = nothing
res_sde_p2 = nothing
sol_oop_sde = nothing
GC.gc()
# SDE adjoint results with diagonal noise
Random.seed!(seed)
prob_oop_sde2 = SDEProblem(f_oop_linear,σ_oop_linear,[u₀;u₀;u₀],trange,p2)
sol_oop_sde2 = solve(prob_oop_sde2,EulerHeun(),dt=dt1,adaptive=false,save_noise=true)
@info "Diagonal Adjoint"
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint())
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 5e-4)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 2e-5)
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 5e-4)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 2e-5)
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 5e-4)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 2e-5)
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 5e-4)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 2e-5)
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-7)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-7)
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-7)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-7)
res_sde_u02a, res_sde_p2a = adjoint_sensitivities(sol_oop_sde2,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_p2, res_sde_p2a, rtol = 1e-7)
@test isapprox(res_sde_u02, res_sde_u02a, rtol = 1e-7)
@info res_sde_p2
sol_oop_sde2 = nothing
GC.gc()
@info "Diagonal ForwardDiff"
res_sde_forward2 = ForwardDiff.gradient(GSDE2,p2)
#@test isapprox(res_sde_forward2, res_sde_reverse2, rtol = 1e-6)
@test isapprox(res_sde_p2', res_sde_forward2, rtol = 1e-3)
#@test isapprox(res_sde_p2', res_sde_reverse2, rtol = 1e-3)
# u0
function GSDE3(u)
Random.seed!(seed)
tmp_prob = remake(prob_oop_sde2,u0=u)
sol = solve(tmp_prob,RKMil(interpretation=:Stratonovich),dt=dt1,adaptive=false,saveat=tarray)
A = convert(Array,sol)
res = g(A,nothing,nothing)
end
@info "ForwardDiff u0"
res_sde_forward2 = ForwardDiff.gradient(GSDE3,[u₀;u₀;u₀])
@test isapprox(res_sde_u02, res_sde_forward2, rtol = 1e-4)
end
##
## Inplace
##
@testset "SDE inplace Tests" begin
f!(du,u,p,t) = du.=p[1]*u
σ!(du,u,p,t) = du.=p[2]*u
dt1 = tend/1e3
Random.seed!(seed)
prob_sde = SDEProblem(f!,σ!,u₀,trange,p2)
sol_sde = solve(prob_sde,EulerHeun(),dt=dt1,adaptive=false, save_noise=true)
function GSDE(p)
Random.seed!(seed)
tmp_prob = remake(prob_sde,u0=eltype(p).(prob_sde.u0),p=p,
tspan=eltype(p).(prob_sde.tspan))
sol = solve(tmp_prob,EulerHeun(),dt=dt1,adaptive=false,saveat=tarray)
A = convert(Array,sol)
res = g(A,p,nothing)
end
res_sde_forward = ForwardDiff.gradient(GSDE,p2)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint())
@test isapprox(res_sde_p', res_sde_forward, rtol = 1e-4)
@info res_sde_p
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@info res_sde_p2
@test isapprox(res_sde_p, res_sde_p2, rtol = 1e-5)
@test isapprox(res_sde_u0, res_sde_u02, rtol = 1e-5)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@info res_sde_p2
@test isapprox(res_sde_p, res_sde_p2, rtol = 1e-5) # not broken here because it just uses the vjps
@test isapprox(res_sde_u0 ,res_sde_u02, rtol = 1e-5)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@info res_sde_p2
@test isapprox(res_sde_p, res_sde_p2, rtol = 1e-10)
@test isapprox(res_sde_u0 ,res_sde_u02, rtol = 1e-10)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_p, res_sde_p2, rtol = 2e-4)
@test isapprox(res_sde_u0 ,res_sde_u02, rtol = 1e-4)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_p, res_sde_p2, rtol = 1e-7)
@test isapprox(res_sde_u0 ,res_sde_u02, rtol = 1e-7)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_p, res_sde_p2, rtol = 1e-7)
@test isapprox(res_sde_u0 ,res_sde_u02, rtol = 1e-7)
res_sde_u02, res_sde_p2 = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_p, res_sde_p2, rtol = 1e-7)
@test isapprox(res_sde_u0 ,res_sde_u02, rtol = 1e-7)
# diagonal noise
#compare with oop version
f_oop_linear(u,p,t) = p[1]*u
σ_oop_linear(u,p,t) = p[2]*u
Random.seed!(seed)
prob_oop_sde = SDEProblem(f_oop_linear,σ_oop_linear,[u₀;u₀;u₀],trange,p2)
sol_oop_sde = solve(prob_oop_sde,EulerHeun(),dt=dt1,adaptive=false,save_noise=true)
res_oop_u0, res_oop_p = adjoint_sensitivities(sol_oop_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint())
@info res_oop_p
Random.seed!(seed)
prob_sde = SDEProblem(f!,σ!,[u₀;u₀;u₀],trange,p2)
sol_sde = solve(prob_sde,EulerHeun(),dt=dt1,adaptive=false,save_noise=true)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint())
isapprox(res_sde_p, res_oop_p, rtol = 1e-6)
isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-6)
@info res_sde_p
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=false))
@test isapprox(res_sde_p, res_oop_p, rtol = 1e-6)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-6)
@info res_sde_p
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
@test isapprox(res_sde_p, res_oop_p, rtol = 1e-6)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-6)
@info res_sde_p
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_p, res_oop_p, rtol = 1e-6)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-6)
@info res_sde_p
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP()))
@test isapprox(res_sde_p, res_oop_p, rtol = 5e-4)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-4)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint())
@test isapprox(res_sde_p, res_oop_p, rtol = 5e-4)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-4)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=false))
@test isapprox(res_sde_p, res_oop_p, rtol = 5e-4)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-4)
res_sde_u0, res_sde_p = adjoint_sensitivities(sol_sde,EulerHeun(),dg!,tarray
,dt=dt1,adaptive=false,sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
@test_broken isapprox(res_sde_p, res_oop_p, rtol = 1e-4)
@test isapprox(res_sde_u0 ,res_oop_u0, rtol = 1e-4)
end
@testset "SDE oop Tests (Tracker)" begin
f_oop_linear(u,p,t) = p[1]*u
σ_oop_linear(u,p,t) = p[2]*u
function f_oop_linear(u::Tracker.TrackedArray,p,t)
p[1].*u
end
function σ_oop_linear(u::Tracker.TrackedArray,p,t)
p[2].*u
end
Random.seed!(seed)
prob_oop_sde = SDEProblem(f_oop_linear,σ_oop_linear,u₀,trange,p2)
function GSDE1(p)
Random.seed!(seed)
tmp_prob = remake(prob_oop_sde,u0=eltype(p).(prob_oop_sde.u0),p=p,
tspan=eltype(p).(prob_oop_sde.tspan))
sol = solve(tmp_prob,RKMil(interpretation=:Stratonovich),dt=5e-4,adaptive=false,sensealg=DiffEqBase.SensitivityADPassThrough(),saveat=tarray)
A = convert(Array,sol)
res = g(A,p,nothing)
end
res_sde_forward = ForwardDiff.gradient(GSDE1,p2)
Random.seed!(seed)
res_sde_trackeru0, res_sde_trackerp = Zygote.gradient((u0,p)->sum(Array(solve(prob_oop_sde,
RKMil(interpretation=:Stratonovich),dt=5e-4,adaptive=false,u0=u0,p=p,saveat=tarray,
sensealg=TrackerAdjoint())).^2.0/2.0),u₀,p2)
@test isapprox(res_sde_forward, res_sde_trackerp, rtol = 1e-5)
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 14631 | using Test, LinearAlgebra
using DiffEqSensitivity, StochasticDiffEq
using Random
@info "Test SDE Transformation"
seed = 100
tspan = (0.0, 0.1)
p = [1.01,0.87]
# scalar
f(u,p,t) = p[1]*u
σ(u,p,t) = p[2]*u
Random.seed!(seed)
u0 = rand(1)
linear_analytic(u0,p,t,W) = @.(u0*exp((p[1]-p[2]^2/2)*t+p[2]*W))
prob = SDEProblem(SDEFunction(f,σ,analytic=linear_analytic),σ,u0,tspan,p)
sol = solve(prob,SOSRI(),adaptive=false, dt=0.001, save_noise=true)
@test isapprox(sol.u_analytic,sol.u, atol=1e-4)
du = zeros(size(u0))
u = sol.u[end]
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
#transformed_function(du,u,p,tspan[2])
du2 = transformed_function(u,p,tspan[2])
#@test du[1] == (p[1]*u[1]-p[2]^2*u[1])
@test isapprox(du2[1], (p[1]*u[1]-p[2]^2*u[1]), atol=1e-15)
#@test du2 == du
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(u,p,t)->p[2]^2*u)
du2 = transformed_function(u,p,tspan[2])
@test isapprox(du2[1], (p[1]*u[1]-p[2]^2*u[1]), atol=1e-15)
linear_analytic_strat(u0,p,t,W) = @.(u0*exp((p[1])*t+p[2]*W))
prob_strat = SDEProblem{false}(SDEFunction((u,p,t)->p[1]*u-1//2*p[2]^2*u,σ,analytic=linear_analytic_strat),σ,u0,tspan,p)
Random.seed!(seed)
sol_strat = solve(prob_strat,RKMil(interpretation=:Stratonovich),adaptive=false, dt=0.0001, save_noise=true)
prob_strat1 = SDEProblem{false}(SDEFunction((u,p,t)->transformed_function(u,p,t).+1//2*p[2]^2*u[1],σ,analytic=linear_analytic),σ,u0,tspan,p)
Random.seed!(seed)
sol_strat1 = solve(prob_strat1,RKMil(interpretation=:Stratonovich),adaptive=false, dt=0.0001, save_noise=true)
# Test if we recover Ito solution in Stratonovich sense
@test isapprox(sol_strat.u, sol_strat1.u, atol=1e-4) # own transformation and custom function agree
@test !isapprox(sol_strat.u_analytic,sol_strat.u, atol=1e-4) # we don't get the stratonovich solution for the linear SDE
@test isapprox(sol_strat1.u_analytic,sol_strat.u, atol=1e-3) # we do recover the analytic solution from the Ito sense
# inplace
f!(du,u,p,t) = @.(du = p[1]*u)
σ!(du,u,p,t) = @.(du = p[2]*u)
prob = SDEProblem(SDEFunction(f!,σ!,analytic=linear_analytic),σ!,u0,tspan,p)
sol = solve(prob,SOSRI(),adaptive=false, dt=0.001, save_noise=true)
@test isapprox(sol.u_analytic,sol.u, atol=1e-4)
du = zeros(size(u0))
u = sol.u[end]
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
transformed_function(du,u,p,tspan[2])
@test isapprox(du[1], (p[1]*u[1]-p[2]^2*u[1]), atol=1e-15)
# @test isapprox(du2[1], (p[1]*u[1]-p[2]^2*u[1]), atol=1e-15)
# @test isapprox(du2, du, atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(du,u,p,t)-> (du.=p[2]^2*u))
transformed_function(du,u,p,tspan[2])
@test du[1] == (p[1]*u[1]-p[2]^2*u[1])
# diagonal noise
u0 = rand(3)
prob = SDEProblem(SDEFunction(f,σ,analytic=linear_analytic),σ,u0,tspan,p)
sol = solve(prob,SOSRI(),adaptive=false, dt=0.001, save_noise=true)
u = sol.u[end]
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
du2 = transformed_function(u,p,tspan[2])
@test isapprox(du2,(p[1]*u-p[2]^2*u), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(u,p,t)->p[2]^2*u)
du2 = transformed_function(u,p,tspan[2])
@test du2[1] == (p[1]*u[1]-p[2]^2*u[1])
prob = SDEProblem(SDEFunction(f!,σ!,analytic=linear_analytic),σ!,u0,tspan,p)
sol = solve(prob,SOSRI(),adaptive=false, dt=0.001, save_noise=true)
du = zeros(size(u0))
u = sol.u[end]
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
transformed_function(du,u,p,tspan[2])
@test isapprox(du,(p[1]*u-p[2]^2*u), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(du,u,p,t)-> (du.=p[2]^2*u))
transformed_function(du,u,p,tspan[2])
@test isapprox(du,(p[1]*u-p[2]^2*u), atol=1e-15)
# non-diagonal noise torus
u0 = rand(2)
p = rand(1)
fnd(u,p,t) = 0*u
function σnd(u,p,t)
du = [cos(p[1])*sin(u[1]) cos(p[1])*cos(u[1]) -sin(p[1])*sin(u[2]) -sin(p[1])*cos(u[2])
sin(p[1])*sin(u[1]) sin(p[1])*cos(u[1]) cos(p[1])*sin(u[2]) cos(p[1])*cos(u[2]) ]
return du
end
prob = SDEProblem(fnd,σnd,u0,tspan,p,noise_rate_prototype=zeros(2,4))
sol = solve(prob,EM(),adaptive=false, dt=0.001, save_noise=true)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
du2 = transformed_function(u0,p,tspan[2])
@test isapprox(du2,zeros(2), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(u,p,t)->false*u)
du2 = transformed_function(u0,p,tspan[2])
@test isapprox(du2,zeros(2), atol=1e-15)
fnd!(du,u,p,t) = du .= false
function σnd!(du,u,p,t)
du[1,1] = cos(p[1])*sin(u[1])
du[1,2] = cos(p[1])*cos(u[1])
du[1,3] = -sin(p[1])*sin(u[2])
du[1,4] = -sin(p[1])*cos(u[2])
du[2,1] = sin(p[1])*sin(u[1])
du[2,2] = sin(p[1])*cos(u[1])
du[2,3] = cos(p[1])*sin(u[2])
du[2,4] = cos(p[1])*cos(u[2])
return nothing
end
prob = SDEProblem(fnd!,σnd!,u0,tspan,p,noise_rate_prototype=zeros(2,4))
sol = solve(prob,EM(),adaptive=false, dt=0.001, save_noise=true)
du = zeros(size(u0))
u = sol.u[end]
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
transformed_function(du,u,p,tspan[2])
@test isapprox(du,zeros(2), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(du,u,p,t)-> (du.=false*u))
transformed_function(du,u,p,tspan[2])
@test isapprox(du,zeros(2), atol=1e-15)
t = sol.t[end]
"""
Check compatibility of StochasticTransformedFunction with vjp for adjoints
"""
###
# Check general compatibility of StochasticTransformedFunction() with Zygote
###
using Zygote
# scalar case
Random.seed!(seed)
u0 = rand(1)
p = rand(2)
λ = rand(1)
_dy, back = Zygote.pullback(u0, p) do u, p
vec(f(u, p, t)-p[2]^2*u)
end
∇1,∇2 = back(λ)
@test isapprox(∇1, (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(∇2, (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
prob = SDEProblem(f,σ,u0,tspan,p)
sol = solve(prob,SOSRI(),adaptive=false, dt=0.001, save_noise=true)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
# Zygote doesn't allow nesting
_dy, back = Zygote.pullback(u0, p) do u, p
vec(transformed_function(u, p, t))
end
@test_broken back(λ)
# @test isapprox(∇1, (p[1]-p[2]^2)*λ, atol=1e-15)
# @test isapprox(∇2, (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g, (u,p,t)->p[2]^2*u)
_dy, back = Zygote.pullback(u0, p) do u, p
vec(transformed_function(u, p, t))
end
∇1,∇2 = back(λ)
@test isapprox(∇1, (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(∇2, (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
###
# Check general compatibility of StochasticTransformedFunction() with ReverseDiff
###
using ReverseDiff
# scalar
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
vec(f(u, p, t)-p[2]^2*u)
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, prob.p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
_dy, back = Zygote.pullback(u, p) do u, p
vec(σ(u, p, t))
end
tmp1,tmp2 = back(_dy)
return f(u, p, t) - vec(tmp1)
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, prob.p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
vec(transformed_function(u, p, first(t)))
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, prob.p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
# diagonal
Random.seed!(seed)
u0 = rand(3)
λ = rand(3)
_dy, back = Zygote.pullback(u0, p) do u, p
vec(f(u, p, t)-p[2]^2*u)
end
∇1,∇2 = back(λ)
@test isapprox(∇1, (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(∇2[1], dot(u0,λ), atol=1e-15)
@test isapprox(∇2[2], -2*p[2]*dot(u0,λ), atol=1e-15)
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
vec(transformed_function(u, p, first(t)))
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
tmptp = ReverseDiff.deriv(tp)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(tmptp[1], dot(u0,λ), atol=1e-15)
@test isapprox(tmptp[2], -2*p[2]*dot(u0,λ), atol=1e-15)
# non-diagonal
Random.seed!(seed)
u0 = rand(2)
p = rand(1)
λ = rand(2)
_dy, back = Zygote.pullback(u0, p) do u, p
vec(fnd(u, p, t))
end
∇1,∇2 = back(λ)
@test isapprox(∇1, zero(∇1), atol=1e-15)
prob = SDEProblem(fnd,σnd,u0,tspan,p,noise_rate_prototype=zeros(2,4))
sol = solve(prob,EM(),adaptive=false, dt=0.001, save_noise=true)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
vec(transformed_function(u, p, first(t)))
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), zero(u0), atol=1e-15)
@test isapprox(ReverseDiff.deriv(tp), zero(p), atol=1e-15)
###
# Check Mutating functions
###
# scalar
Random.seed!(seed)
u0 = rand(1)
p = rand(2)
λ = rand(1)
prob = SDEProblem(SDEFunction(f!,σ!,analytic=linear_analytic),σ!,u0,tspan,p)
sol = solve(prob,SOSRI(),adaptive=false, dt=0.001, save_noise=true)
du = zeros(size(u0))
u = sol.u[end]
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g)
function inplacefunc!(du,u,p,t)
du .= p[2]^2*u
return nothing
end
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
du1 = similar(u, size(u))
du2 = similar(u, size(u))
f!(du1, u, p, first(t))
inplacefunc!(du2, u, p, first(t))
return vec(du1-du2)
end
tu, tp, tt = ReverseDiff.input_hook(tape) # u0
output = ReverseDiff.output_hook(tape) # p[1]*u0 -p[2]^2*u0
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15) # -0.016562475307537294
@test isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15) #[0.017478629739736098, -0.023103635221731166]
tape = ReverseDiff.GradientTape((u0, p, [t])) do u,p,t
_dy, back = Zygote.pullback(u, p) do u, p
out_ = Zygote.Buffer(similar(u))
σ!(out_, u, p, t)
vec(copy(out_))
end
tmp1,tmp2 = back(λ)
du1 = similar(u, size(u))
f!(du1, u, p, first(t))
return vec(du1-tmp1)
end
tu, tp, tt = ReverseDiff.input_hook(tape)
output = ReverseDiff.output_hook(tape)
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test_broken isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test_broken isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
tape = ReverseDiff.GradientTape((u0, p, [t])) do u1,p1,t1
du1 = similar(u1, size(u1))
transformed_function(du1, u1, p1, first(t1))
return vec(du1)
end
tu, tp, tt = ReverseDiff.input_hook(tape) # p[1]*u0
output = ReverseDiff.output_hook(tape) # p[1]*u0 -p[2]^2*u0
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
transformed_function = StochasticTransformedFunction(sol,sol.prob.f,sol.prob.g,(du,u,p,t)-> (du.=p[2]^2*u))
tape = ReverseDiff.GradientTape((u0, p, [t])) do u1,p1,t1
du1 = similar(u1, size(u1))
transformed_function(du1, u1, p1, first(t1))
return vec(du1)
end
tu, tp, tt = ReverseDiff.input_hook(tape) # p[1]*u0
output = ReverseDiff.output_hook(tape) # p[1]*u0 -p[2]^2*u0
ReverseDiff.unseed!(tu) # clear any "leftover" derivatives from previous calls
ReverseDiff.unseed!(tp)
ReverseDiff.unseed!(tt)
ReverseDiff.value!(tu, u0)
ReverseDiff.value!(tp, p)
ReverseDiff.value!(tt, [t])
ReverseDiff.forward_pass!(tape)
ReverseDiff.increment_deriv!(output, λ)
ReverseDiff.reverse_pass!(tape)
@test isapprox(ReverseDiff.deriv(tu), (p[1]-p[2]^2)*λ, atol=1e-15)
@test isapprox(ReverseDiff.deriv(tp), (@. [1,-2*p[2]]*u0*λ[1]), atol=1e-15)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 860 | using DiffEqSensitivity, OrdinaryDiffEq, DiffEqBase, ForwardDiff
using Test
function fb(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
function jac(J,u,p,t)
(x, y, a, b, c) = (u[1], u[2], p[1], p[2], p[3])
J[1,1] = a + y * b * -1
J[2,1] = y
J[1,2] = b * x * -1
J[2,2] = c * -1 + x
end
f = ODEFunction(fb,jac=jac)
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(f,u0,(0.0,10.0),p)
loss(sol) = sum(sol)
v = ones(4)
H = second_order_sensitivities(loss,prob,Vern9(),saveat=0.1,abstol=1e-12,reltol=1e-12)
Hv = second_order_sensitivity_product(loss,v,prob,Vern9(),saveat=0.1,abstol=1e-12,reltol=1e-12)
_loss(p) = loss(solve(prob,Vern9();u0=u0,p=p,saveat=0.1,abstol=1e-12,reltol=1e-12))
H2 = ForwardDiff.hessian(_loss,p)
H2v = H*v
@test H ≈ H2
@test Hv ≈ H2v
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1198 | using OrdinaryDiffEq, DiffEqSensitivity, Zygote, RecursiveArrayTools, Test
u0 = Float32[1.; 2.]
du0 = Float32[0.; 2.]
tspan = (0.0f0, 1.0f0)
t = range(tspan[1], tspan[2], length=20)
p = Float32[1.01,0.9]
ff(du,u,p,t) = -p.*u
prob = SecondOrderODEProblem{false}(ff, du0, u0, tspan, p)
ddu01, du01, dp1 = Zygote.gradient((du0,u0,p)->sum(Array(solve(prob, Tsit5(), u0=ArrayPartition(du0,u0), p=p, saveat=t, sensealg = InterpolatingAdjoint(autojacvec=ZygoteVJP())))),du0,u0,p)
ddu02, du02, dp2 = Zygote.gradient((du0,u0,p)->sum(Array(solve(prob, Tsit5(), u0=ArrayPartition(du0,u0), p=p, saveat=t, sensealg = BacksolveAdjoint(autojacvec=ZygoteVJP())))),du0,u0,p)
ddu03, du03, dp3 = Zygote.gradient((du0,u0,p)->sum(Array(solve(prob, Tsit5(), u0=ArrayPartition(du0,u0), p=p, saveat=t, sensealg = QuadratureAdjoint(autojacvec=ZygoteVJP())))),du0,u0,p)
ddu04, du04, dp4 = Zygote.gradient((du0,u0,p)->sum(Array(solve(prob, Tsit5(), u0=ArrayPartition(du0,u0), p=p, saveat=t, sensealg = ForwardDiffSensitivity()))),du0,u0,p)
@test ddu01 ≈ ddu02
@test ddu01 ≈ ddu03
@test ddu01 ≈ ddu04
@test du01 ≈ du02
@test du01 ≈ du03
@test du01 ≈ du04
@test dp1 ≈ dp2
@test dp1 ≈ dp3
@test dp1 ≈ dp4
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 17693 | using Random; Random.seed!(1238)
using OrdinaryDiffEq
using Statistics
using DiffEqSensitivity
using Test
using Zygote
@testset "LSS" begin
@info "LSS"
@testset "Lorenz single parameter" begin
function lorenz!(du,u,p,t)
du[1] = 10*(u[2]-u[1])
du[2] = u[1]*(p[1]-u[3]) - u[2]
du[3] = u[1]*u[2] - (8//3)*u[3]
end
p = [28.0]
tspan_init = (0.0,30.0)
tspan_attractor = (30.0,50.0)
u0 = rand(3)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14)
g(u,p,t) = u[end]
function dg(out,u,p,t,i)
fill!(out, zero(eltype(u)))
out[end] = -one(eltype(u))
end
lss_problem1 = ForwardLSSProblem(sol_attractor, ForwardLSS(g=g))
lss_problem1a = ForwardLSSProblem(sol_attractor, ForwardLSS(g=g), nothing, dg)
lss_problem2 = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.Cos2Windowing(),g=g))
lss_problem2a = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.Cos2Windowing()), nothing, dg)
lss_problem3 = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
lss_problem3a = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, dg) #ForwardLSS with time dilation requires knowledge of g
adjointlss_problem = AdjointLSSProblem(sol_attractor, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
adjointlss_problem_a = AdjointLSSProblem(sol_attractor, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, dg)
res1 = shadow_forward(lss_problem1)
res1a = shadow_forward(lss_problem1a)
res2 = shadow_forward(lss_problem2)
res2a = shadow_forward(lss_problem2a)
res3 = shadow_forward(lss_problem3)
res3a = shadow_forward(lss_problem3a)
res4 = shadow_adjoint(adjointlss_problem)
res4a = shadow_adjoint(adjointlss_problem_a)
@test res1[1] ≈ 1 atol=1e-1
@test res2[1] ≈ 1 atol=1e-1
@test res3[1] ≈ 1 atol=5e-2
@test res1 ≈ res1a atol=1e-10
@test res2 ≈ res2a atol=1e-10
@test res3 ≈ res3a atol=1e-10
@test res3 ≈ res4 atol=1e-10
@test res3 ≈ res4a atol=1e-10
# fixed saveat to compare with concrete solve
sol_attractor2 = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14, saveat=0.01)
lss_problem1 = ForwardLSSProblem(sol_attractor2, ForwardLSS(g=g))
lss_problem1a = ForwardLSSProblem(sol_attractor2, ForwardLSS(g=g), nothing, dg)
lss_problem2 = ForwardLSSProblem(sol_attractor2, ForwardLSS(LSSregularizer=DiffEqSensitivity.Cos2Windowing(),g=g))
lss_problem2a = ForwardLSSProblem(sol_attractor2, ForwardLSS(LSSregularizer=DiffEqSensitivity.Cos2Windowing()), nothing, dg)
lss_problem3 = ForwardLSSProblem(sol_attractor2, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
lss_problem3a = ForwardLSSProblem(sol_attractor2, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, dg) #ForwardLSS with time dilation requires knowledge of g
adjointlss_problem = AdjointLSSProblem(sol_attractor2, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
adjointlss_problem_a = AdjointLSSProblem(sol_attractor2, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, dg)
res1 = shadow_forward(lss_problem1)
res1a = shadow_forward(lss_problem1a)
res2 = shadow_forward(lss_problem2)
res2a = shadow_forward(lss_problem2a)
res3 = shadow_forward(lss_problem3)
res3a = shadow_forward(lss_problem3a)
res4 = shadow_adjoint(adjointlss_problem)
res4a = shadow_adjoint(adjointlss_problem_a)
@test res1[1] ≈ 1 atol=5e-2
@test res2[1] ≈ 1 atol=5e-2
@test res3[1] ≈ 1 atol=5e-2
@test res1 ≈ res1a atol=1e-10
@test res2 ≈ res2a atol=1e-10
@test res3 ≈ res3a atol=1e-10
@test res3 ≈ res4 atol=1e-10
@test res3 ≈ res4a atol=1e-10
function G(p; sensealg=ForwardLSS(g=g), dt=0.01)
_prob = remake(prob_attractor,p=p)
_sol = solve(_prob,Vern9(),abstol=1e-14,reltol=1e-14,saveat=dt,sensealg=sensealg)
sum(getindex.(_sol.u,3))
end
dp1 = Zygote.gradient((p)->G(p),p)
@test res1 ≈ dp1[1] atol=1e-10
dp1 = Zygote.gradient((p)->G(p, sensealg=ForwardLSS(LSSregularizer=DiffEqSensitivity.Cos2Windowing())),p)
@test res2 ≈ dp1[1] atol=1e-10
dp1 = Zygote.gradient((p)->G(p, sensealg=ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g)),p)
@test res3 ≈ dp1[1] atol=1e-10
dp1 = Zygote.gradient((p)->G(p, sensealg=AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g)),p)
@test res4 ≈ dp1[1] atol=1e-10
@show res1[1] res2[1] res3[1]
end
@testset "Lorenz" begin
function lorenz!(du,u,p,t)
du[1] = p[1]*(u[2]-u[1])
du[2] = u[1]*(p[2]-u[3]) - u[2]
du[3] = u[1]*u[2] - p[3]*u[3]
end
p = [10.0, 28.0, 8/3]
tspan_init = (0.0,30.0)
tspan_attractor = (30.0,50.0)
u0 = rand(3)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14)
g(u,p,t) = u[end] + sum(p)
function dgu(out,u,p,t,i)
fill!(out, zero(eltype(u)))
out[end] = -one(eltype(u))
end
function dgp(out,u,p,t,i)
fill!(out, -one(eltype(p)))
end
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
lss_problem_a = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, (dgu,dgp))
adjointlss_problem = AdjointLSSProblem(sol_attractor, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
adjointlss_problem_a = AdjointLSSProblem(sol_attractor, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, (dgu,dgp))
resfw = shadow_forward(lss_problem)
resfw_a = shadow_forward(lss_problem_a)
resadj = shadow_adjoint(adjointlss_problem)
resadj_a = shadow_adjoint(adjointlss_problem_a)
@test resfw ≈ resadj rtol=1e-10
@test resfw ≈ resfw_a rtol=1e-10
@test resfw ≈ resadj_a rtol=1e-10
sol_attractor2 = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14, saveat=0.01)
lss_problem = ForwardLSSProblem(sol_attractor2, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
resfw = shadow_forward(lss_problem)
function G(p; sensealg=ForwardLSS(), dt=0.01)
_prob = remake(prob_attractor,p=p)
_sol = solve(_prob,Vern9(),abstol=1e-14,reltol=1e-14,saveat=dt,sensealg=sensealg)
sum(getindex.(_sol.u,3)) + sum(p)
end
dp1 = Zygote.gradient((p)->G(p, sensealg=ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g)),p)
@test resfw ≈ dp1[1] atol=1e-10
dp1 = Zygote.gradient((p)->G(p, sensealg=AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g)),p)
@test resfw ≈ dp1[1] atol=1e-10
@show resfw
end
@testset "T0skip and T1skip" begin
function lorenz!(du,u,p,t)
du[1] = p[1]*(u[2]-u[1])
du[2] = u[1]*(p[2]-u[3]) - u[2]
du[3] = u[1]*u[2] - p[3]*u[3]
end
p = [10.0, 28.0, 8/3]
tspan_init = (0.0,30.0)
tspan_attractor = (30.0,50.0)
u0 = rand(3)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14, saveat=0.01)
g(u,p,t) = u[end]^2/2 + sum(p)
function dgu(out,u,p,t,i)
fill!(out, zero(eltype(u)))
out[end] = -u[end]
end
function dgp(out,u,p,t,i)
fill!(out, -one(eltype(p)))
end
function G(p; sensealg=ForwardLSS(g=g), dt=0.01)
_prob = remake(prob_attractor,p=p)
_sol = solve(_prob,Vern9(),abstol=1e-14,reltol=1e-14,saveat=dt,sensealg=sensealg)
sum(getindex.(_sol.u,3).^2)/2 + sum(p)
end
## ForwardLSS
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0), g=g))
resfw = shadow_forward(lss_problem)
res = deepcopy(resfw)
dp1 = Zygote.gradient((p)->G(p, sensealg=ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g)),p)
@test res ≈ dp1[1] atol=1e-10
resfw = shadow_forward(lss_problem, sensealg = ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0,10.0,5.0), g=g))
resskip = deepcopy(resfw)
dp1 = Zygote.gradient((p)->G(p, sensealg=ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0,10.0,5.0), g=g)),p)
@test resskip ≈ dp1[1] atol=1e-10
@show res resskip
## ForwardLSS with dgdu and dgdp
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g), nothing, (dgu,dgp))
res2 = shadow_forward(lss_problem)
@test res ≈ res2 atol=1e-10
res2 = shadow_forward(lss_problem, sensealg = ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0,10.0,5.0), g=g))
@test resskip ≈ res2 atol=1e-10
## AdjointLSS
lss_problem = AdjointLSSProblem(sol_attractor, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
res2 = shadow_adjoint(lss_problem)
@test res ≈ res2 atol=1e-10
res2 = shadow_adjoint(lss_problem, sensealg = AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0,10.0,5.0), g=g))
@test_broken resskip ≈ res2 atol=1e-10
dp1 = Zygote.gradient((p)->G(p, sensealg=AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g)),p)
@test res ≈ dp1[1] atol=1e-10
dp1 = Zygote.gradient((p)->G(p, sensealg=AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0,10.0,5.0), g=g)),p)
@test res2 ≈ dp1[1] atol=1e-10
## AdjointLSS with dgdu and dgd
lss_problem = AdjointLSSProblem(sol_attractor, AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0), g=g), nothing, (dgu,dgp))
res2 = shadow_adjoint(lss_problem)
@test res ≈ res2 atol=1e-10
res2 = shadow_adjoint(lss_problem, sensealg = AdjointLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0,10.0,5.0), g=g))
@test_broken resskip ≈ res2 atol=1e-10
end
end
@testset "NILSS" begin
@info "NILSS"
@testset "Lorenz single parameter" begin
function lorenz!(du,u,p,t)
du[1] = 10*(u[2]-u[1])
du[2] = u[1]*(p[1]-u[3]) - u[2]
du[3] = u[1]*u[2] - (8//3)*u[3]
end
p = [28.0]
tspan_init = (0.0,100.0)
tspan_attractor = (100.0,120.0)
u0 = rand(3)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
g(u,p,t) = u[end]
function dg(out,u,p,t,i)
fill!(out, zero(eltype(u)))
out[end] = -one(eltype(u))
end
nseg = 50 # number of segments on time interval
nstep = 2001 # number of steps on each segment
# fix seed here for res1==res2 check, otherwise hom. tangent
# are initialized randomly
Random.seed!(1234)
nilss_prob1 = NILSSProblem(prob_attractor, NILSS(nseg, nstep, g=g))
res1 = DiffEqSensitivity.shadow_forward(nilss_prob1,Tsit5())
Random.seed!(1234)
nilss_prob2 = NILSSProblem(prob_attractor, NILSS(nseg, nstep, g=g), nothing, dg)
res2 = DiffEqSensitivity.shadow_forward(nilss_prob2,Tsit5())
@test res1[1] ≈ 1 atol=5e-2
@test res2[1] ≈ 1 atol=5e-2
@test res1 ≈ res2 atol=1e-10
function G(p; dt=nilss_prob1.dtsave)
_prob = remake(prob_attractor,p=p)
_sol = solve(_prob,Tsit5(),saveat=dt,sensealg=NILSS(nseg, nstep, g=g))
sum(getindex.(_sol.u,3))
end
Random.seed!(1234)
dp1 = Zygote.gradient((p)->G(p),p)
@test res1 ≈ dp1[1] atol=1e-10
end
@testset "Lorenz" begin
# Here we test LSS output to NILSS output w/ multiple params
function lorenz!(du,u,p,t)
du[1] = p[1]*(u[2]-u[1])
du[2] = u[1]*(p[2]-u[3]) - u[2]
du[3] = u[1]*u[2] - p[3]*u[3]
end
p = [10.0, 28.0, 8/3]
u0 = rand(3)
# Relatively short tspan_attractor since increasing more infeasible w/
# computational cost of LSS
tspan_init = (0.0,100.0)
tspan_attractor = (100.0,120.0)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14)
g(u,p,t) = u[end]
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0),g=g))
resfw = shadow_forward(lss_problem)
# NILSS can handle w/ longer timespan and get lower noise in sensitivity estimate
tspan_init = (0.0,100.0)
tspan_attractor = (100.0,150.0)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14)
nseg = 50 # number of segments on time interval
nstep = 2001 # number of steps on each segment
nilss_prob = NILSSProblem(prob_attractor, NILSS(nseg, nstep; g));
res = shadow_forward(nilss_prob, Tsit5())
# There is larger noise in LSS estimate of parameter 3 due to shorter timespan considered,
# so test tolerance for parameter 3 is larger.
@test resfw[1] ≈ res[1] atol=5e-2
@test resfw[2] ≈ res[2] atol=5e-2
@test resfw[3] ≈ res[3] atol=5e-1
end
end
@testset "NILSAS" begin
@info "NILSAS"
@testset "nilsas_min function" begin
u0 = rand(3)
M = 2
nseg = 2
numparams = 1
quadcache = DiffEqSensitivity.QuadratureCache(u0, M, nseg, numparams)
C = quadcache.C
C[:,:,1] .= [
1. 0.
0. 1.]
C[:,:,2] .= [
4. 0.
0. 1.]
dwv = quadcache.dwv
dwv[:,1] .= [1., 0.]
dwv[:,2] .= [1., 4.]
dwf = quadcache.dwf
dwf[:,1] .= [1., 1.]
dwf[:,2] .= [3., 1.]
dvf = quadcache.dvf
dvf[1] = 1.
dvf[2] = 2.
R = quadcache.R
R[:,:,1] .= [
Inf Inf
Inf Inf]
R[:,:,2] .= [
1. 1.
0. 2.]
b = quadcache.b
b[:,1] = [Inf, Inf]
b[:,2] = [0., 1.]
@test DiffEqSensitivity.nilsas_min(quadcache) ≈ [-1. 0.
-1. -1.]
end
@testset "Lorenz" begin
function lorenz!(du,u,p,t)
du[1] = p[1]*(u[2]-u[1])
du[2] = u[1]*(p[2]-u[3]) - u[2]
du[3] = u[1]*u[2] - p[3]*u[3]
return nothing
end
u0_trans = rand(3)
p = [10.0, 28.0, 8/3]
# parameter passing to NILSAS
M = 2
nseg = 40
nstep = 101
tspan_transient = (0.0,30.0)
prob_transient = ODEProblem(lorenz!,u0_trans,tspan_transient,p)
sol_transient = solve(prob_transient, Tsit5())
u0 = sol_transient.u[end]
tspan_attractor = (0.0,40.0)
prob_attractor = ODEProblem(lorenz!,u0,tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14,saveat=0.01)
g(u,p,t) = u[end]
function dg(out,u,p,t,i=nothing)
fill!(out, zero(eltype(u)))
out[end] = -one(eltype(u))
end
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0), g=g), nothing, dg)
resfw = shadow_forward(lss_problem)
@info resfw
nilsas_prob = NILSASProblem(sol_attractor, NILSAS(nseg,nstep,M, g=g))
res = shadow_adjoint(nilsas_prob, Tsit5())
@info res
@test resfw ≈ res atol=1e-1
nilsas_prob = NILSASProblem(sol_attractor, NILSAS(nseg,nstep,M, g=g), nothing, dg)
res = shadow_adjoint(nilsas_prob, Tsit5())
@info res
@test resfw ≈ res atol=1e-1
end
@testset "Lorenz parameter-dependent loss function" begin
function lorenz!(du,u,p,t)
du[1] = p[1]*(u[2]-u[1])
du[2] = u[1]*(p[2]-u[3]) - u[2]
du[3] = u[1]*u[2] - p[3]*u[3]
return nothing
end
u0_trans = rand(3)
p = [10.0, 28.0, 8/3]
# parameter passing to NILSAS
M = 2
nseg = 100
nstep = 101
tspan_transient = (0.0,100.0)
prob_transient = ODEProblem(lorenz!,u0_trans,tspan_transient,p)
sol_transient = solve(prob_transient, Tsit5())
u0 = sol_transient.u[end]
tspan_attractor = (0.0,50.0)
prob_attractor = ODEProblem(lorenz!,u0,tspan_attractor,p)
sol_attractor = solve(prob_attractor,Vern9(),abstol=1e-14,reltol=1e-14,saveat=0.01)
g(u,p,t) = u[end]^2/2 + sum(p)
function dgu(out,u,p,t,i=nothing)
fill!(out, zero(eltype(u)))
out[end] = -u[end]
end
function dgp(out,u,p,t,i=nothing)
fill!(out, -one(eltype(p)))
end
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(LSSregularizer=DiffEqSensitivity.TimeDilation(10.0), g=g), nothing, (dgu,dgp))
resfw = shadow_forward(lss_problem)
@info resfw
nilsas_prob = NILSASProblem(sol_attractor, NILSAS(nseg,nstep,M, g=g))
res = shadow_adjoint(nilsas_prob, Tsit5())
@info res
@test resfw ≈ res rtol=1e-1
nilsas_prob = NILSASProblem(sol_attractor, NILSAS(nseg,nstep,M, g=g), nothing, (dgu,dgp))
res = shadow_adjoint(nilsas_prob, Tsit5())
@info res
@test resfw ≈ res rtol=1e-1
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 868 | using DiffEqSensitivity, Flux, OrdinaryDiffEq, Test # , Plots
p = [1.5 1.0;3.0 1.0]
function lotka_volterra(du,u,p,t)
du[1] = p[1,1]*u[1] - p[1,2]*u[1]*u[2]
du[2] = -p[2,1]*u[2] + p[2,2]*u[1]*u[2]
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5())
# plot(sol)
p = [2.2 1.0;2.0 0.4] # Tweaked Initial Parameter Array
ps = Flux.params(p)
function predict_adjoint() # Our 1-layer neural network
Array(solve(prob,Tsit5(),p=p,saveat=0.0:0.1:10.0))
end
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())
data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () #callback function to observe training
display(loss_adjoint())
end
predict_adjoint()
# Display the ODE with the initial parameter values.
cb()
Flux.train!(loss_adjoint, ps, data, opt, cb = cb)
@test loss_adjoint() < 1
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1920 | using DiffEqSensitivity, OrdinaryDiffEq, LinearAlgebra, SparseArrays, Zygote, LinearSolve
using AlgebraicMultigrid: AlgebraicMultigrid
using Test
foop(u, p, t) = jac(u, p, t) * u
jac(u, p, t) = spdiagm(0=>p)
paramjac(u, p, t) = SparseArrays.spdiagm(0=>u)
@Zygote.adjoint foop(u, p, t) = foop(u, p, t), delta->(jac(u, p, t)' * delta, paramjac(u, p, t)' * delta, zeros(length(u)))
n = 2
p = collect(1.0:n)
u0 = ones(n)
tspan = [0.0, 1]
odef = ODEFunction(foop; jac=jac, jac_prototype=jac(u0, p, 0.0), paramjac=paramjac)
function g_helper(p; alg=Rosenbrock23(linsolve=LUFactorization()))
prob = ODEProblem(odef, u0, tspan, p)
soln = Array(solve(prob, alg; u0=prob.u0, p=prob.p, abstol=1e-4, reltol=1e-4, sensealg=InterpolatingAdjoint()))[:, end]
return soln
end
function g(p; kwargs...)
soln = g_helper(p; kwargs...)
return sum(soln)
end
@test isapprox(exp.(p), g_helper(p); atol=1e-3, rtol=1e-3)
@test isapprox(exp.(p), Zygote.gradient(g, p)[1]; atol=1e-3, rtol=1e-3)
@test isapprox(exp.(p), g_helper(p; alg=Rosenbrock23(linsolve=KLUFactorization())); atol=1e-3, rtol=1e-3)
@test isapprox(exp.(p), Zygote.gradient(p->g(p; alg=Rosenbrock23(linsolve=KLUFactorization())), p)[1]; atol=1e-3, rtol=1e-3)
@test isapprox(exp.(p), g_helper(p; alg=ImplicitEuler(linsolve=LUFactorization())); atol=1e-1, rtol=1e-1)
@test isapprox(exp.(p), Zygote.gradient(p->g(p; alg=ImplicitEuler(linsolve=LUFactorization())), p)[1]; atol=1e-1, rtol=1e-1)
@test isapprox(exp.(p), g_helper(p; alg=ImplicitEuler(linsolve=UMFPACKFactorization())); atol=1e-1, rtol=1e-1)
@test isapprox(exp.(p), Zygote.gradient(p->g(p; alg=ImplicitEuler(linsolve=UMFPACKFactorization())), p)[1]; atol=1e-1, rtol=1e-1)
@test isapprox(exp.(p), g_helper(p; alg=ImplicitEuler(linsolve=KrylovJL_GMRES())); atol=1e-1, rtol=1e-1)
@test isapprox(exp.(p), Zygote.gradient(p->g(p; alg=ImplicitEuler(linsolve=KrylovJL_GMRES())), p)[1]; atol=1e-1, rtol=1e-1)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 12345 | using Test, LinearAlgebra
using DiffEqSensitivity, SteadyStateDiffEq, DiffEqBase, NLsolve
using OrdinaryDiffEq
using ForwardDiff, Calculus
using Random
Random.seed!(12345)
@testset "Adjoint sensitivities of steady state solver" begin
function f!(du,u,p,t)
du[1] = p[1] + p[2]*u[1]
du[2] = p[3]*u[1] + p[4]*u[2]
end
function jac!(J,u,p,t) #df/dx
J[1,1] = p[2]
J[2,1] = p[3]
J[1,2] = 0
J[2,2] = p[4]
nothing
end
function paramjac!(fp,u,p,t) #df/dp
fp[1,1] = 1
fp[2,1] = 0
fp[1,2] = u[1]
fp[2,2] = 0
fp[1,3] = 0
fp[2,3] = u[1]
fp[1,4] = 0
fp[2,4] = u[2]
nothing
end
function dg!(out,u,p,t,i)
(out.=-2.0.+u)
end
function g(u,p,t)
sum((2.0.-u).^2)/2 + sum(p.^2)/2
end
u0 = zeros(2)
p = [2.0,-2.0,1.0,-4.0]
prob = SteadyStateProblem(f!,u0,p)
abstol = 1e-10
@testset "for p" begin
println("Calculate adjoint sensitivities from Jacobians")
sol_analytical = [-p[1]/p[2], p[1]*p[3]/(p[2]*p[4])]
J = zeros(2,2)
fp = zeros(2,4)
gp = zeros(4)
gx = zeros(1,2)
delg_delp = copy(p)
jac!(J,sol_analytical,p,nothing)
dg!(vec(gx),sol_analytical,p,nothing,nothing)
paramjac!(fp,sol_analytical,p,nothing)
lambda = J' \ gx'
res_analytical = delg_delp' - lambda' * fp # = -gx*inv(J)*fp
@info "Expected result" sol_analytical, res_analytical, delg_delp'-gx*inv(J)*fp
@info "Calculate adjoint sensitivities from autodiff & numerical diff"
function G(p)
tmp_prob = remake(prob,u0=convert.(eltype(p),prob.u0),p=p)
sol = solve(tmp_prob,
SSRootfind(nlsolve = (f!,u0,abstol) -> (res=NLsolve.nlsolve(f!,u0,autodiff=:forward,method=:newton,iterations=Int(1e6),ftol=1e-14);res.zero))
)
A = convert(Array,sol)
g(A,p,nothing)
end
res1 = ForwardDiff.gradient(G,p)
res2 = Calculus.gradient(G,p)
#@info res1, res2, res_analytical
@test res1 ≈ res_analytical' rtol = 1e-7
@test res2 ≈ res_analytical' rtol = 1e-7
@test res1 ≈ res2 rtol = 1e-7
@info "Adjoint sensitivities"
# with jac, param_jac
f1 = ODEFunction(f!;jac=jac!, paramjac=paramjac!)
prob1 = SteadyStateProblem(f1,u0,p)
sol1 = solve(prob1,DynamicSS(Rodas5(),reltol=1e-14,abstol=1e-14),reltol=1e-14,abstol=1e-14)
res1a = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,dg!)
res1b = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,nothing)
res1c = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false),g,nothing)
res1d = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=TrackerVJP()),g,nothing)
res1e = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ReverseDiffVJP()),g,nothing)
res1f = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ZygoteVJP()),g,nothing)
res1g = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false,autojacvec=false),g,nothing)
res1h = adjoint_sensitivities(sol1,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=EnzymeVJP()),g,nothing)
# with jac, without param_jac
f2 = ODEFunction(f!;jac=jac!)
prob2 = SteadyStateProblem(f2,u0,p)
sol2 = solve(prob2,DynamicSS(Rodas5(),reltol=1e-14,abstol=1e-14),reltol=1e-14,abstol=1e-14)
res2a = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,dg!)
res2b = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,nothing)
res2c = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false),g,nothing)
res2d = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=TrackerVJP()),g,nothing)
res2e = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ReverseDiffVJP()),g,nothing)
res2f = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ZygoteVJP()),g,nothing)
res2g = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false,autojacvec=false),g,nothing)
res2h = adjoint_sensitivities(sol2,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=EnzymeVJP()),g,nothing)
# without jac, without param_jac
f3 = ODEFunction(f!)
prob3 = SteadyStateProblem(f3,u0,p)
sol3 = solve(prob3,DynamicSS(Rodas5(),reltol=1e-14,abstol=1e-14),reltol=1e-14,abstol=1e-14)
res3a = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,dg!)
res3b = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,nothing)
res3c = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false),g,nothing)
res3d = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=TrackerVJP()),g,nothing)
res3e = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ReverseDiffVJP()),g,nothing)
res3f = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ZygoteVJP()),g,nothing)
res3g = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false,autojacvec=false),g,nothing)
res3h = adjoint_sensitivities(sol3,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=EnzymeVJP()),g,nothing)
@test norm(res_analytical' .- res1a) < 1e-7
@test norm(res_analytical' .- res1b) < 1e-7
@test norm(res_analytical' .- res1c) < 1e-7
@test norm(res_analytical' .- res1d) < 1e-7
@test norm(res_analytical' .- res1e) < 1e-7
@test norm(res_analytical' .- res1f) < 1e-7
@test norm(res_analytical' .- res1g) < 1e-7
@test norm(res_analytical' .- res1h) < 1e-7
@test norm(res_analytical' .- res2a) < 1e-7
@test norm(res_analytical' .- res2b) < 1e-7
@test norm(res_analytical' .- res2c) < 1e-7
@test norm(res_analytical' .- res2d) < 1e-7
@test norm(res_analytical' .- res2e) < 1e-7
@test norm(res_analytical' .- res2f) < 1e-7
@test norm(res_analytical' .- res2g) < 1e-7
@test norm(res_analytical' .- res2h) < 1e-7
@test norm(res_analytical' .- res3a) < 1e-7
@test norm(res_analytical' .- res3b) < 1e-7
@test norm(res_analytical' .- res3c) < 1e-7
@test norm(res_analytical' .- res3d) < 1e-7
@test norm(res_analytical' .- res3e) < 1e-7
@test norm(res_analytical' .- res3f) < 1e-7
@test norm(res_analytical' .- res3g) < 1e-7
@test norm(res_analytical' .- res3h) < 1e-7
@info "oop checks"
function foop(u,p,t)
dx = p[1] + p[2]*u[1]
dy = p[3]*u[1] + p[4]*u[2]
[dx,dy]
end
proboop = SteadyStateProblem(foop,u0,p)
soloop = solve(proboop,DynamicSS(Rodas5(),reltol=1e-14,abstol=1e-14),reltol=1e-14,abstol=1e-14)
res4a = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,dg!)
res4b = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g,nothing)
res4c = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false),g,nothing)
res4d = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=TrackerVJP()),g,nothing)
res4e = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ReverseDiffVJP()),g,nothing)
res4f = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autojacvec=ZygoteVJP()),g,nothing)
res4g = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=false,autojacvec=false),g,nothing)
res4h = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(autodiff=true,autojacvec=false),g,nothing)
@test norm(res_analytical' .- res4a) < 1e-7
@test norm(res_analytical' .- res4b) < 1e-7
@test norm(res_analytical' .- res4c) < 1e-7
@test norm(res_analytical' .- res4d) < 1e-7
@test norm(res_analytical' .- res4e) < 1e-7
@test norm(res_analytical' .- res4f) < 1e-7
@test norm(res_analytical' .- res4g) < 1e-7
@test norm(res_analytical' .- res4h) < 1e-7
end
@testset "for u0: (should be zero, steady state does not depend on initial condition)" begin
res5 = ForwardDiff.gradient(prob.u0) do u0
tmp_prob = remake(prob,u0=u0)
sol = solve(tmp_prob,
SSRootfind(nlsolve = (f!,u0,abstol) -> (res=NLsolve.nlsolve(f!,u0,autodiff=:forward,method=:newton,iterations=Int(1e6),ftol=1e-14);res.zero) )
)
A = convert(Array,sol)
g(A,p,nothing)
end
@test abs(dot(res5,res5)) < 1e-7
end
end
using Zygote
@testset "concrete_solve derivatives steady state solver" begin
function g1(u,p,t)
sum(u)
end
function g2(u,p,t)
sum((2.0.-u).^2)/2
end
u0 = zeros(2)
p = [2.0,-2.0,1.0,-4.0]
@testset "iip" begin
function f!(du,u,p,t)
du[1] = p[1] + p[2]*u[1]
du[2] = p[3]*u[1] + p[4]*u[2]
end
prob = SteadyStateProblem(f!,u0,p)
sol = solve(prob,DynamicSS(Rodas5()))
res1 = adjoint_sensitivities(sol,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g1,nothing)
res2 = adjoint_sensitivities(sol,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g2,nothing)
dp1 = Zygote.gradient(p->sum(solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,sensealg=SteadyStateAdjoint())),p)
dp2 = Zygote.gradient(p->sum((2.0.-solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,sensealg=SteadyStateAdjoint())).^2)/2.0,p)
dp1d = Zygote.gradient(p->sum(solve(prob,DynamicSS(Rodas5()),u0=u0,p=p)),p)
dp2d = Zygote.gradient(p->sum((2.0.-solve(prob,DynamicSS(Rodas5()),u0=u0,p=p)).^2)/2.0,p)
@test res1 ≈ dp1[1] rtol=1e-12
@test res2 ≈ dp2[1] rtol=1e-12
@test res1 ≈ dp1d[1] rtol=1e-12
@test res2 ≈ dp2d[1] rtol=1e-12
res1 = Zygote.gradient(p->sum(Array(solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,sensealg=SteadyStateAdjoint()))[1]),p)
dp1 = Zygote.gradient(p->sum(solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1:1,sensealg=SteadyStateAdjoint())),p)
dp2 = Zygote.gradient(p->solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1,sensealg=SteadyStateAdjoint())[1],p)
dp1d = Zygote.gradient(p->sum(solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1:1)),p)
dp2d = Zygote.gradient(p->solve(prob,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1)[1],p)
@test res1[1] ≈ dp1[1] rtol=1e-10
@test res1[1] ≈ dp2[1] rtol=1e-10
@test res1[1] ≈ dp1d[1] rtol=1e-10
@test res1[1] ≈ dp2d[1] rtol=1e-10
end
@testset "oop" begin
function f(u,p,t)
dx = p[1] + p[2]*u[1]
dy = p[3]*u[1] + p[4]*u[2]
[dx,dy]
end
proboop = SteadyStateProblem(f,u0,p)
soloop = solve(proboop,DynamicSS(Rodas5()))
res1oop = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g1,nothing)
res2oop = adjoint_sensitivities(soloop,DynamicSS(Rodas5()),sensealg=SteadyStateAdjoint(),g2,nothing)
dp1oop = Zygote.gradient(p->sum(solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,sensealg=SteadyStateAdjoint())),p)
dp2oop = Zygote.gradient(p->sum((2.0.-solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,sensealg=SteadyStateAdjoint())).^2)/2.0,p)
dp1oopd = Zygote.gradient(p->sum(solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p)),p)
dp2oopd = Zygote.gradient(p->sum((2.0.-solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p)).^2)/2.0,p)
@test res1oop ≈ dp1oop[1] rtol=1e-12
@test res2oop ≈ dp2oop[1] rtol=1e-12
@test res1oop ≈ dp1oopd[1] rtol=1e-8
@test res2oop ≈ dp2oopd[1] rtol=1e-8
res1oop = Zygote.gradient(p->sum(Array(solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,sensealg=SteadyStateAdjoint()))[1]),p)
dp1oop = Zygote.gradient(p->sum(solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1:1,sensealg=SteadyStateAdjoint())),p)
dp2oop = Zygote.gradient(p->solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1,sensealg=SteadyStateAdjoint())[1],p)
dp1oopd = Zygote.gradient(p->sum(solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1:1)),p)
dp2oopd = Zygote.gradient(p->solve(proboop,DynamicSS(Rodas5()),u0=u0,p=p,save_idxs=1)[1],p)
@test res1oop[1] ≈ dp1oop[1] rtol=1e-10
@test res1oop[1] ≈ dp2oop[1] rtol=1e-10
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 5889 | using Zygote, DiffEqSensitivity
println("Starting tests")
using OrdinaryDiffEq, ForwardDiff, Test
function lotka_volterra(u, p, t)
x, y = u
α, β, δ, γ = p
[α * x - β * x * y,-δ * y + γ * x * y]
end
function lotka_volterra(du, u, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α * x - β * x * y
du[2] = dy = -δ * y + γ * x * y
end
u0 = [1.0,1.0];
tspan = (0.0,10.0);
p0 = [1.5,1.0,3.0,1.0];
prob0 = ODEProblem(lotka_volterra,u0,tspan,p0);
# Solve the ODE and collect solutions at fixed intervals
target_data = solve(prob0,RadauIIA5(), saveat = 0:0.5:10.0);
loss_function = function(p)
prob = remake(prob0;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, RadauIIA5(); saveat = 0.0:0.5:10.0,abstol=1e-10,reltol=1e-10)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
p=[1.5,1.2,1.4,1.6];
fdgrad = ForwardDiff.gradient(loss_function,p)
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-5
loss_function = function(p)
prob = remake(prob0;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, TRBDF2(); saveat = 0.0:0.5:10.0,abstol=1e-10,reltol=1e-10)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-3
loss_function = function(p)
prob = remake(prob0;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, Rosenbrock23(); saveat = 0.0:0.5:10.0,abstol=1e-8,reltol=1e-8)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-3
loss_function = function(p)
prob = remake(prob0;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, Rodas5(); saveat = 0.0:0.5:10.0,abstol=1e-8,reltol=1e-8)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-3
### OOP
prob0_oop = ODEProblem{false}(lotka_volterra,u0,tspan,p0);
# Solve the ODE and collect solutions at fixed intervals
target_data = solve(prob0,RadauIIA5(), saveat = 0:0.5:10.0);
loss_function = function(p)
prob = remake(prob0_oop;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, RadauIIA5(); saveat = 0.0:0.5:10.0,abstol=1e-10,reltol=1e-10)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
p=[1.5,1.2,1.4,1.6];
fdgrad = ForwardDiff.gradient(loss_function,p)
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-4
loss_function = function(p)
prob = remake(prob0_oop;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, TRBDF2(); saveat = 0.0:0.5:10.0,abstol=1e-10,reltol=1e-10)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-3
loss_function = function(p)
prob = remake(prob0_oop;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, Rosenbrock23(); saveat = 0.0:0.5:10.0,abstol=1e-8,reltol=1e-8)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-4
loss_function = function(p)
prob = remake(prob0_oop;u0=convert.(eltype(p),prob0.u0),p=p)
prediction = solve(prob, Rodas5(); saveat = 0.0:0.5:10.0,abstol=1e-12,reltol=1e-12)
tmpdata=prediction[[1,2],:];
tdata=target_data[[1,2],:];
# Calculate squared error
return sum(abs2,tmpdata-tdata)
end
rdgrad = Zygote.gradient(loss_function,p)[1]
@test fdgrad ≈ rdgrad rtol=1e-3
# all implicit solvers
solvers = [
# SDIRK Methods (ok)
ImplicitEuler(),
TRBDF2(),
KenCarp4(),
# Fully-Implicit Runge-Kutta Methods (FIRK)
RadauIIA5(),
# Fully-Implicit Runge-Kutta Methods (FIRK)
#PDIRK44(),
# Rosenbrock Methods
Rodas3(),
Rodas4(),
Rodas5(),
# Rosenbrock-W Methods
Rosenbrock23(),
ROS34PW3(),
# Stabilized Explicit Methods (ok)
ROCK2(),
ROCK4(),
RKC(),
# SERK2v2(), not defined?
ESERK5()];
p = rand(3)
function dudt(u,p,t)
u .* p
end
for solver in solvers
function loss(p)
prob = ODEProblem(dudt, [3.0, 2.0, 1.0], (0.0, 1.0), p)
sol = solve(prob, solver, dt=0.01, saveat=0.1, abstol=1e-5, reltol=1e-5)
sum(abs2, Array(sol))
end
println(DiffEqBase.parameterless_type(solver))
loss(p)
dp = Zygote.gradient(loss, p)[1]
function loss(p, sensealg)
prob = ODEProblem(dudt, [3.0, 2.0, 1.0], (0.0, 1.0), p)
sol = solve(prob, solver, dt=0.01, saveat=0.1, sensealg=sensealg, abstol=1e-5, reltol=1e-5)
sum(abs2, Array(sol))
end
dp1 = Zygote.gradient(p -> loss(p, InterpolatingAdjoint()), p)[1]
@test dp ≈ dp1 rtol = 1e-2
dp1 = Zygote.gradient(p -> loss(p, BacksolveAdjoint()), p)[1]
@test dp ≈ dp1 rtol = 1e-2
dp1 = Zygote.gradient(p -> loss(p, QuadratureAdjoint()), p)[1]
@test dp ≈ dp1 rtol = 1e-2
dp1 = Zygote.gradient(p -> loss(p, ForwardDiffSensitivity()), p)[1]
@test dp ≈ dp1 rtol = 1e-2
dp1 = @test_broken Zygote.gradient(p -> loss(p, ReverseDiffAdjoint()), p)[1]
@test_broken dp ≈ dp1 rtol = 1e-2
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1087 | using OrdinaryDiffEq, Zygote, DiffEqSensitivity, Test
p_model = [1f0]
u0 = Float32.([0.0])
function dudt(du, u, p, t)
du[1] = p[1]
end
prob = ODEProblem(dudt,u0,(0f0,99.9f0))
function predict_neuralode(p)
_prob = remake(prob,p=p)
Array(solve(_prob,Tsit5(), saveat=0.1))
end
loss(p) = sum(abs2,predict_neuralode(p))/length(p)
p_model_ini = copy(p_model)
@test !iszero(Zygote.gradient(loss,p_model_ini)[1])
## https://github.com/SciML/DiffEqSensitivity.jl/issues/675
u0 = Float32[2.0; 0.0] # Initial condition
p = [-0.1 2.0; -2.0 -0.1]
datasize = 30 # Number of data points
tspan = (0.0f0, 1.5f0) # Time range
# tsteps = range(tspan[1], tspan[2], length = datasize) # Split time range into equal steps for each data point
tsteps = (rand(datasize) .* (tspan[2] - tspan[1]) .+ tspan[1]) |> sort
function f(du,u,p,t)
du .= p*u
end
function loss(p)
prob = ODEProblem(f,u0,tspan,p)
sol = solve(prob,Tsit5(),saveat=tsteps,sensealg=InterpolatingAdjoint())
sum(sol)
end
Zygote.gradient(loss, p)[1]
@test !(Zygote.gradient(loss, p)[1] .|> iszero |> all)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1079 | using StochasticDiffEq, Zygote
using DiffEqSensitivity, Test, ForwardDiff
abstol = 1e-12
reltol = 1e-12
savingtimes = 0.5
function test_SDE_callbacks()
function dt!(du, u, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α * x - β * x * y
du[2] = dy = -δ * y + γ * x * y
end
function dW!(du, u, p, t)
du[1] = 0.1u[1]
du[2] = 0.1u[2]
end
u0 = [1.0, 1.0]
tspan = (0.0, 10.0)
p = [2.2, 1.0, 2.0, 0.4]
prob_sde = SDEProblem(dt!, dW!, u0, tspan, p)
condition(u, t, integrator) = integrator.t > 9.0 #some condition
function affect!(integrator)
#println("Callback") #some callback
end
cb = DiscreteCallback(condition, affect!, save_positions=(false, false))
function predict_sde(p)
return Array(solve(prob_sde, EM(), p=p, saveat=savingtimes, sensealg=ForwardDiffSensitivity(), dt=0.001, callback=cb))
end
loss_sde(p) = sum(abs2, x - 1 for x in predict_sde(p))
loss_sde(p)
@time dp = gradient(p) do p
loss_sde(p)
end
@test !iszero(dp[1])
end
@testset "SDEs" begin
println("SDEs")
test_SDE_callbacks()
end | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 8155 | using OrdinaryDiffEq, Zygote
using DiffEqSensitivity, Test, ForwardDiff
abstol = 1e-12
reltol = 1e-12
savingtimes = 0.5
function test_continuous_callback(cb, g, dg!; only_backsolve=false)
function fiip(du, u, p, t)
du[1] = u[2]
du[2] = -p[1]
end
function foop(u, p, t)
dx = u[2]
dy = -p[1]
[dx, dy]
end
u0 = [5.0, 0.0]
tspan = (0.0, 2.5)
p = [9.8, 0.8]
prob = ODEProblem(fiip, u0, tspan, p)
proboop = ODEProblem(fiip, u0, tspan, p)
sol1 = solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes)
sol2 = solve(prob, Tsit5(), u0=u0, p=p, abstol=abstol, reltol=reltol, saveat=savingtimes)
if cb.save_positions == [1, 1]
@test length(sol1.t) != length(sol2.t)
else
@test length(sol1.t) == length(sol2.t)
end
du01, dp1 = @time Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint())),
u0, p)
du01b, dp1b = Zygote.gradient(
(u0, p) -> g(solve(proboop, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint())),
u0, p)
du01c, dp1c = Zygote.gradient(
(u0, p) -> g(solve(proboop, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint(checkpointing=false))),
u0, p)
if !only_backsolve
@test_broken du02, dp2 = @time Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=ReverseDiffAdjoint())), u0, p)
du03, dp3 = @time Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=InterpolatingAdjoint(checkpointing=true))),
u0, p)
du03c, dp3c = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=InterpolatingAdjoint(checkpointing=false))),
u0, p)
du04, dp4 = @time Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=QuadratureAdjoint())),
u0, p)
end
dstuff = @time ForwardDiff.gradient(
(θ) -> g(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4], callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes)),
[u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
@test du01b ≈ dstuff[1:2]
@test dp1b ≈ dstuff[3:4]
@test du01c ≈ dstuff[1:2]
@test dp1c ≈ dstuff[3:4]
if !only_backsolve
@test_broken du01 ≈ du02
@test du01 ≈ du03 rtol = 1e-7
@test du01 ≈ du03c rtol = 1e-7
@test du03 ≈ du03c
@test du01 ≈ du04
@test_broken dp1 ≈ dp2
@test dp1 ≈ dp3
@test dp1 ≈ dp3c
@test dp3 ≈ dp3c
@test dp1 ≈ dp4 rtol = 1e-7
@test_broken du02 ≈ dstuff[1:2]
@test_broken dp2 ≈ dstuff[3:4]
end
cb2 = DiffEqSensitivity.track_callbacks(CallbackSet(cb), prob.tspan[1], prob.u0, prob.p, BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
sol_track = solve(prob, Tsit5(), u0=u0, p=p, callback=cb2, abstol=abstol, reltol=reltol, saveat=savingtimes)
adj_prob = ODEAdjointProblem(sol_track, BacksolveAdjoint(autojacvec=ReverseDiffVJP()), dg!, sol_track.t, nothing,
callback=cb2,
abstol=abstol, reltol=reltol)
adj_sol = solve(adj_prob, Tsit5(), abstol=abstol, reltol=reltol)
@test du01 ≈ -adj_sol[1:2, end]
@test dp1 ≈ adj_sol[3:4, end]
# adj_prob = ODEAdjointProblem(sol_track,InterpolatingAdjoint(),dg!,sol_track.t,nothing,
# callback = cb2,
# abstol=abstol,reltol=reltol)
# adj_sol = solve(adj_prob, Tsit5(), abstol=abstol,reltol=reltol)
#
# @test du01 ≈ -adj_sol[1:2,end]
# @test dp1 ≈ adj_sol[3:6,end]
end
println("Continuous Callbacks")
@testset "Continuous callbacks" begin
@testset "simple loss function bouncing ball" begin
g(sol) = sum(sol)
function dg!(out, u, p, t, i)
(out .= -1)
end
@testset "callbacks with no effect" begin
condition(u, t, integrator) = u[1] # Event when event_f(u,t) == 0
affect!(integrator) = (integrator.u[2] += 0)
cb = ContinuousCallback(condition, affect!, save_positions=(false, false))
test_continuous_callback(cb, g, dg!)
end
@testset "callbacks with no effect except saving the state" begin
condition(u, t, integrator) = u[1]
affect!(integrator) = (integrator.u[2] += 0)
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!)
end
@testset "+= callback" begin
condition(u, t, integrator) = u[1]
affect!(integrator) = (integrator.u[2] += 50.0)
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!)
end
@testset "= callback with parameter dependence and save" begin
condition(u, t, integrator) = u[1]
affect!(integrator) = (integrator.u[2] = -integrator.p[2] * integrator.u[2])
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!)
end
@testset "= callback with parameter dependence but without save" begin
condition(u, t, integrator) = u[1]
affect!(integrator) = (integrator.u[2] = -integrator.p[2] * integrator.u[2])
cb = ContinuousCallback(condition, affect!, save_positions=(false, false))
test_continuous_callback(cb, g, dg!; only_backsolve=true)
end
@testset "= callback with non-linear affect" begin
condition(u, t, integrator) = u[1]
affect!(integrator) = (integrator.u[2] = integrator.u[2]^2)
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!)
end
@testset "= callback with terminate" begin
condition(u, t, integrator) = u[1]
affect!(integrator) = (integrator.u[2] = -integrator.p[2] * integrator.u[2]; terminate!(integrator))
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!; only_backsolve=true)
end
end
@testset "MSE loss function bouncing-ball like" begin
g(u) = sum((1.0 .- u) .^ 2) ./ 2
dg!(out, u, p, t, i) = (out .= 1.0 .- u)
condition(u, t, integrator) = u[1]
@testset "callback with non-linear affect" begin
function affect!(integrator)
integrator.u[1] += 3.0
integrator.u[2] = integrator.u[2]^2
end
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!)
end
@testset "callback with non-linear affect and terminate" begin
function affect!(integrator)
integrator.u[1] += 3.0
integrator.u[2] = integrator.u[2]^2
terminate!(integrator)
end
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
test_continuous_callback(cb, g, dg!; only_backsolve=true)
end
end
@testset "MSE loss function free particle" begin
g(u) = sum((1.0 .- u) .^ 2) ./ 2
dg!(out, u, p, t, i) = (out .= 1.0 .- u)
function fiip(du, u, p, t)
du[1] = u[2]
du[2] = 0
end
function foop(u, p, t)
dx = u[2]
dy = 0
[dx, dy]
end
u0 = [5.0, -1.0]
p = [0.0, 0.0]
tspan = (0.0, 2.0)
prob = ODEProblem(fiip, u0, tspan, p)
proboop = ODEProblem(fiip, u0, tspan, p)
condition(u, t, integrator) = u[1] # Event when event_f(u,t) == 0
affect!(integrator) = (integrator.u[2] = -integrator.u[2])
cb = ContinuousCallback(condition, affect!)
du01, dp1 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint())),
u0, p)
dstuff = @time ForwardDiff.gradient(
(θ) -> g(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4], callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes)),
[u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 4961 | using OrdinaryDiffEq, Zygote
using DiffEqSensitivity, Test, ForwardDiff
abstol = 1e-12
reltol = 1e-12
savingtimes = 0.5
function test_continuous_wrt_discrete_callback()
# test the continuous callbacks wrt to the equivalent discrete callback
function f(du, u, p, t)
#Bouncing Ball
du[1] = u[2]
du[2] = -p[1]
end
# no saving in Callbacks; prescribed vafter and vbefore; loss on the endpoint
tstop = 3.1943828249997
vbefore = -31.30495168499705
vafter = 25.04396134799764
u0 = [50.0, 0.0]
tspan = (0.0, 5.0)
p = [9.8, 0.8]
prob = ODEProblem(f, u0, tspan, p)
function condition(u, t, integrator) # Event when event_f(u,t) == 0
t - tstop
end
function affect!(integrator)
integrator.u[2] += vafter - vbefore
end
cb = ContinuousCallback(condition, affect!, save_positions=(false, false))
condition2(u, t, integrator) = t == tstop
cb2 = DiscreteCallback(condition2, affect!, save_positions=(false, false))
du01, dp1 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb2, tstops=[tstop],
sensealg=BacksolveAdjoint(),
saveat=tspan[2], save_start=false)), u0, p)
du02, dp2 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb,
sensealg=BacksolveAdjoint(),
saveat=tspan[2], save_start=false)), u0, p)
dstuff = ForwardDiff.gradient((θ) -> sum(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4],
callback=cb, saveat=tspan[2], save_start=false)), [u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
@test du02 ≈ dstuff[1:2]
@test dp2 ≈ dstuff[3:4]
# no saving in Callbacks; prescribed vafter and vbefore; loss on the endpoint by slicing
du01, dp1 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb2, tstops=[tstop],
sensealg=BacksolveAdjoint())[end]), u0, p)
du02, dp2 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb,
sensealg=BacksolveAdjoint())[end]), u0, p)
dstuff = ForwardDiff.gradient((θ) -> sum(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4],
callback=cb)[end]), [u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
@test du02 ≈ dstuff[1:2]
@test dp2 ≈ dstuff[3:4]
# with saving in Callbacks; prescribed vafter and vbefore; loss on the endpoint
cb = ContinuousCallback(condition, affect!, save_positions=(true, true))
cb2 = DiscreteCallback(condition2, affect!, save_positions=(true, true))
du01, dp1 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb2, tstops=[tstop],
sensealg=BacksolveAdjoint(),
saveat=tspan[2], save_start=false)), u0, p)
du02, dp2 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb,
sensealg=BacksolveAdjoint(),
saveat=tspan[2], save_start=false)), u0, p)
dstuff = ForwardDiff.gradient((θ) -> sum(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4],
callback=cb, saveat=tspan[2], save_start=false)), [u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
@test du02 ≈ dstuff[1:2]
@test dp2 ≈ dstuff[3:4]
# with saving in Callbacks; prescribed vafter and vbefore; loss on the endpoint by slicing
du01, dp1 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb2, tstops=[tstop],
sensealg=BacksolveAdjoint())[end]), u0, p)
du02, dp2 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb,
sensealg=BacksolveAdjoint())[end]), u0, p)
dstuff = ForwardDiff.gradient((θ) -> sum(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4],
callback=cb)[end]), [u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
@test du02 ≈ dstuff[1:2]
@test dp2 ≈ dstuff[3:4]
# with saving in Callbacks; different affect function
function affect2!(integrator)
integrator.u[2] = -integrator.p[2] * integrator.u[2]
end
cb = ContinuousCallback(condition, affect2!, save_positions=(true, true))
cb2 = DiscreteCallback(condition2, affect2!, save_positions=(true, true))
du01, dp1 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb2, tstops=[tstop],
sensealg=BacksolveAdjoint(),
saveat=tspan[2], save_start=false)), u0, p)
du02, dp2 = Zygote.gradient(
(u0, p) -> sum(solve(prob, Tsit5(), u0=u0, p=p,
callback=cb,
sensealg=BacksolveAdjoint(),
saveat=tspan[2], save_start=false)), u0, p)
dstuff = ForwardDiff.gradient((θ) -> sum(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:4],
callback=cb, saveat=tspan[2], save_start=false)), [u0; p])
@info dstuff
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:4]
@test du02 ≈ dstuff[1:2]
@test dp2 ≈ dstuff[3:4]
@test du01 ≈ du02
@test dp1 ≈ dp2
end
@testset "Compare continuous with discrete callbacks" begin
test_continuous_wrt_discrete_callback()
end | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 10481 | using OrdinaryDiffEq, Zygote
using DiffEqSensitivity, Test, ForwardDiff
abstol = 1e-12
reltol = 1e-12
savingtimes = 0.5
function test_discrete_callback(cb, tstops, g, dg!, cboop=nothing, tprev=false)
function fiip(du, u, p, t)
du[1] = dx = p[1] * u[1] - p[2] * u[1] * u[2]
du[2] = dy = -p[3] * u[2] + p[4] * u[1] * u[2]
end
function foop(u, p, t)
dx = p[1] * u[1] - p[2] * u[1] * u[2]
dy = -p[3] * u[2] + p[4] * u[1] * u[2]
[dx, dy]
end
p = [1.5, 1.0, 3.0, 1.0]
u0 = [1.0; 1.0]
prob = ODEProblem(fiip, u0, (0.0, 10.0), p)
proboop = ODEProblem(foop, u0, (0.0, 10.0), p)
sol1 = solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes)
sol2 = solve(prob, Tsit5(), u0=u0, p=p, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes)
if cb.save_positions == [1, 1]
@test length(sol1.t) != length(sol2.t)
else
@test length(sol1.t) == length(sol2.t)
end
du01, dp1 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint())),
u0, p)
du01b, dp1b = Zygote.gradient(
(u0, p) -> g(solve(proboop, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint())),
u0, p)
du01c, dp1c = Zygote.gradient(
(u0, p) -> g(solve(proboop, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint(checkpointing=false))),
u0, p)
if cboop === nothing
du02, dp2 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=ReverseDiffAdjoint())), u0, p)
else
du02, dp2 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cboop, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=ReverseDiffAdjoint())), u0, p)
end
du03, dp3 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=InterpolatingAdjoint(checkpointing=true))),
u0, p)
du03c, dp3c = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=InterpolatingAdjoint(checkpointing=false))),
u0, p)
du04, dp4 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=QuadratureAdjoint())),
u0, p)
dstuff = ForwardDiff.gradient(
(θ) -> g(solve(prob, Tsit5(), u0=θ[1:2], p=θ[3:6], callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes)),
[u0; p])
@info dstuff
# tests wrt discrete sensitivities
if tprev
# tprev depends on stepping behaviour of integrator. Thus sensitivities are necessarily (slightly) different.
@test du02 ≈ dstuff[1:2] rtol = 1e-3
@test dp2 ≈ dstuff[3:6] rtol = 1e-3
@test du01 ≈ dstuff[1:2] rtol = 1e-3
@test dp1 ≈ dstuff[3:6] rtol = 1e-3
@test du01 ≈ du02 rtol = 1e-3
@test dp1 ≈ dp2 rtol = 1e-3
else
@test du02 ≈ dstuff[1:2]
@test dp2 ≈ dstuff[3:6]
@test du01 ≈ dstuff[1:2]
@test dp1 ≈ dstuff[3:6]
@test du01 ≈ du02
@test dp1 ≈ dp2
end
# tests wrt continuous sensitivities
@test du01b ≈ du01
@test dp1b ≈ dp1
@test du01c ≈ du01
@test dp1c ≈ dp1
@test du01 ≈ du03 rtol = 1e-7
@test du01 ≈ du03c rtol = 1e-7
@test du03 ≈ du03c
@test du01 ≈ du04
@test dp1 ≈ dp3
@test dp1 ≈ dp3c
@test dp1 ≈ dp4 rtol = 1e-7
cb2 = DiffEqSensitivity.track_callbacks(CallbackSet(cb), prob.tspan[1], prob.u0, prob.p, BacksolveAdjoint(autojacvec=ReverseDiffVJP()))
sol_track = solve(prob, Tsit5(), u0=u0, p=p, callback=cb2, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes)
#cb_adj = DiffEqSensitivity.setup_reverse_callbacks(cb2,BacksolveAdjoint())
adj_prob = ODEAdjointProblem(sol_track, BacksolveAdjoint(autojacvec=ReverseDiffVJP()), dg!, sol_track.t, nothing,
callback=cb2,
abstol=abstol, reltol=reltol)
adj_sol = solve(adj_prob, Tsit5(), abstol=abstol, reltol=reltol)
@test du01 ≈ -adj_sol[1:2, end]
@test dp1 ≈ adj_sol[3:6, end]
# adj_prob = ODEAdjointProblem(sol_track,InterpolatingAdjoint(),dg!,sol_track.t,nothing,
# callback = cb2,
# abstol=abstol,reltol=reltol)
# adj_sol = solve(adj_prob, Tsit5(), abstol=abstol,reltol=reltol)
#
# @test du01 ≈ -adj_sol[1:2,end]
# @test dp1 ≈ adj_sol[3:6,end]
end
@testset "Discrete callbacks" begin
@testset "ODEs" begin
println("ODEs")
@testset "simple loss function" begin
g(sol) = sum(sol)
function dg!(out, u, p, t, i)
(out .= -1)
end
@testset "callbacks with no effect" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = integrator.u[1] += 0.0
cb = DiscreteCallback(condition, affect!, save_positions=(false, false))
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "callbacks with no effect except saving the state" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = integrator.u[1] += 0.0
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "callback at single time point" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = integrator.u[1] += 2.0
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "callback at multiple time points" begin
affecttimes = [2.03, 4.0, 8.0]
condition(u, t, integrator) = t ∈ affecttimes
affect!(integrator) = integrator.u[1] += 2.0
cb = DiscreteCallback(condition, affect!)
test_discrete_callback(cb, affecttimes, g, dg!)
end
@testset "state-dependent += callback at single time point" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = (integrator.u .+= integrator.p[2] / 8 * sin.(integrator.u))
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "other callback at single time point" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = (integrator.u[1] = 2.0; @show "triggered!")
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "parameter changing callback at single time point" begin
condition(u, t, integrator) = t == 5.1
affect!(integrator) = (integrator.p .= 2 * integrator.p .- 0.5)
affect(integrator) = (integrator.p = 2 * integrator.p .- 0.5)
cb = DiscreteCallback(condition, affect!)
cboop = DiscreteCallback(condition, affect)
cb = DiscreteCallback(condition, affect!)
tstops = [5.1]
test_discrete_callback(cb, tstops, g, dg!, cboop)
end
@testset "tprev dependent callback" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = (@show integrator.tprev; integrator.u[1] += integrator.t - integrator.tprev)
cb = DiscreteCallback(condition, affect!)
tstops = [4.999, 5.0]
test_discrete_callback(cb, tstops, g, dg!, nothing, true)
end
end
@testset "MSE loss function" begin
g(u) = sum((1.0 .- u) .^ 2) ./ 2
dg!(out, u, p, t, i) = (out .= 1.0 .- u)
@testset "callbacks with no effect" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = integrator.u[1] += 0.0
cb = DiscreteCallback(condition, affect!, save_positions=(false, false))
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "callbacks with no effect except saving the state" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = integrator.u[1] += 0.0
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "callback at single time point" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = integrator.u[1] += 2.0
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "callback at multiple time points" begin
affecttimes = [2.03, 4.0, 8.0]
condition(u, t, integrator) = t ∈ affecttimes
affect!(integrator) = integrator.u[1] += 2.0
cb = DiscreteCallback(condition, affect!)
test_discrete_callback(cb, affecttimes, g, dg!)
end
@testset "state-dependent += callback at single time point" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = (integrator.u .+= integrator.p[2] / 8 * sin.(integrator.u))
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "other callback at single time point" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = (integrator.u[1] = 2.0; @show "triggered!")
cb = DiscreteCallback(condition, affect!)
tstops = [5.0]
test_discrete_callback(cb, tstops, g, dg!)
end
@testset "parameter changing callback at single time point" begin
condition(u, t, integrator) = t == 5.1
affect!(integrator) = (integrator.p .= 2 * integrator.p .- 0.5)
affect(integrator) = (integrator.p = 2 * integrator.p .- 0.5)
cb = DiscreteCallback(condition, affect!)
cboop = DiscreteCallback(condition, affect)
tstops = [5.1]
test_discrete_callback(cb, tstops, g, dg!, cboop)
end
@testset "tprev dependent callback" begin
condition(u, t, integrator) = t == 5
affect!(integrator) = (@show integrator.tprev; integrator.u[1] += integrator.t - integrator.tprev)
cb = DiscreteCallback(condition, affect!)
tstops = [4.999, 5.0]
test_discrete_callback(cb, tstops, g, dg!, nothing, true)
end
end
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1740 | using OrdinaryDiffEq, DiffEqCallbacks
using DiffEqSensitivity, Zygote, Test
import ForwardDiff
import FiniteDiff
abstol = 1e-6
reltol = 1e-6
savingtimes = 0.1
function test_discrete_callback(cb, tstops, g)
function fiip(du, u, p, t)
#du[1] = dx = p[1]*u[1]
du[:] .= p[1]*u
end
p = Float64[0.8123198]
u0 = Float64[1.0]
prob = ODEProblem(fiip, u0, (0.0, 1.0), p)
@show g(solve(prob, Tsit5(), callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes))
du01, dp1 = Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes,
sensealg=ForwardDiffSensitivity(;convert_tspan=true))),
u0, p)
dstuff1 = ForwardDiff.gradient(
(θ) -> g(solve(prob, Tsit5(), u0=θ[1:1], p=θ[2:2], callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes)),
[u0; p])
dstuff2 = FiniteDiff.finite_difference_gradient(
(θ) -> g(solve(prob, Tsit5(), u0=θ[1:1], p=θ[2:2], callback=cb, tstops=tstops, abstol=abstol, reltol=reltol, saveat=savingtimes)),
[u0; p])
@show du01 dp1 dstuff1 dstuff2
@test du01 ≈ dstuff1[1:1] atol=1e-6
@test dp1 ≈ dstuff1[2:2] atol=1e-6
@test du01 ≈ dstuff2[1:1] atol=1e-6
@test dp1 ≈ dstuff2[2:2] atol=1e-6
end
@testset "ForwardDiffSensitivity: Discrete callbacks" begin
g(u) = sum(u.^2)
@testset "reset to initial condition" begin
affecttimes = range(0.0, 1.0, length=6)[2:end]
u0 = [1.0]
condition(u, t, integrator) = t ∈ affecttimes
affect!(integrator) = (integrator.u .= u0; @show "triggered!")
cb = DiscreteCallback(condition, affect!, save_positions=(false,false))
test_discrete_callback(cb, affecttimes, g)
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1667 | using OrdinaryDiffEq, Zygote
using DiffEqSensitivity, Test, ForwardDiff
abstol = 1e-12
reltol = 1e-12
savingtimes = 0.5
# see https://diffeq.sciml.ai/stable/features/callback_functions/#VectorContinuousCallback-Example
function test_vector_continuous_callback(cb,g)
function f(du, u, p, t)
du[1] = u[2]
du[2] = -p[1]
du[3] = u[4]
du[4] = 0.0
end
u0 = [50.0, 0.0, 0.0, 2.0]
tspan = (0.0, 10.0)
p = [9.8, 0.9]
prob = ODEProblem(f,u0,tspan,p)
sol = solve(prob, Tsit5(), callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes)
du01, dp1 = @time Zygote.gradient(
(u0, p) -> g(solve(prob, Tsit5(), u0=u0, p=p, callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes, sensealg=BacksolveAdjoint())),
u0, p)
dstuff = @time ForwardDiff.gradient(
(θ) -> g(solve(prob, Tsit5(), u0=θ[1:4], p=θ[5:6], callback=cb, abstol=abstol, reltol=reltol, saveat=savingtimes)),
[u0; p])
@test du01 ≈ dstuff[1:4]
@test dp1 ≈ dstuff[5:6]
end
@testset "VectorContinuous callbacks" begin
@testset "MSE loss function bouncing-ball like" begin
g(u) = sum((1.0.-u).^2)./2
function condition(out, u, t, integrator) # Event when event_f(u,t) == 0
out[1] = u[1]
out[2] = (u[3]-10.0)u[3]
end
@testset "callback with linear affect" begin
function affect!(integrator, idx)
if idx == 1
integrator.u[2] = -integrator.p[2]*integrator.u[2]
elseif idx == 2
integrator.u[4] = -integrator.p[2]*integrator.u[4]
end
end
cb = VectorContinuousCallback(condition, affect!, 2)
test_vector_continuous_callback(cb, g)
end
end
end
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1104 | using DiffEqSensitivity, OrdinaryDiffEq, Flux, DiffEqFlux, CUDA, Zygote
CUDA.allowscalar(false) # Makes sure no slow operations are occuring
# Generate Data
u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 1.5f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
# Make the data into a GPU-based array if the user has a GPU
ode_data = gpu(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = Chain(x -> x.^3,
Dense(2, 50, tanh),
Dense(50, 2)) |> gpu
u0 = Float32[2.0; 0.0] |> gpu
_p,re = Flux.destructure(dudt2)
p = gpu(_p)
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
function predict_neuralode(p)
gpu(prob_neuralode(u0,p))
end
function loss_neuralode(p)
pred = predict_neuralode(p)
loss = sum(abs2, ode_data .- pred)
return loss
end
# Callback function to observe training
list_plots = []
iter = 0
Zygote.gradient(loss_neuralode, p) | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | code | 1456 | using DiffEqSensitivity, OrdinaryDiffEq
using Flux, CUDA, Test, Zygote, Random, LinearAlgebra
CUDA.allowscalar(false)
H = CuArray(rand(Float32, 2, 2))
ann = Chain(Dense(1, 4, tanh))
p,re = Flux.destructure(ann)
function func(x, p, t)
(re(p)([t])[1]*H)*x
end
x0 = CuArray(rand(Float32, 2))
x1 = CuArray(rand(Float32, 2))
prob = ODEProblem(func, x0, (0.0f0, 1.0f0))
function evolve(p)
solve(prob, Tsit5(), p=p, save_start=false,
save_everystep=false, abstol=1e-4, reltol=1e-4,
sensealg=QuadratureAdjoint(autojacvec=ZygoteVJP())).u[1]
end
function cost(p)
x = evolve(p)
c = sum(abs,x - x1)
#println(c)
c
end
grad = Zygote.gradient(cost,p)[1]
@test !iszero(grad[1])
@test iszero(grad[2:4])
@test !iszero(grad[5])
@test iszero(grad[6:end])
###
# https://github.com/SciML/DiffEqSensitivity.jl/issues/632
###
rng = MersenneTwister(1234)
m = 32
n = 16
Z = randn(rng, Float32, (n,m)) |> gpu
𝒯 = 2.0
Δτ = 0.1
ca_init = [zeros(1) ; ones(m)] |> gpu
function f(ca, Z, t)
a = ca[2:end]
a_unit = a / sum(a)
w_unit = Z*a_unit
Ka_unit = Z'*w_unit
z_unit = dot(abs.(Ka_unit), a_unit)
aKa_over_z = a .* Ka_unit / z_unit
[sum(aKa_over_z) / m; -abs.(aKa_over_z)] |> gpu
end
function c(Z)
prob = ODEProblem(f, ca_init, (0.,𝒯), Z, saveat=Δτ)
sol = solve(prob, Tsit5(), sensealg=BacksolveAdjoint(), saveat=Δτ)
sum(last(sol.u))
end
println("forward:", c(Z))
println("backward: ", Zygote.gradient(c, Z))
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 1704 | # DiffEqSensitivity.jl
[](https://gitter.im/JuliaDiffEq/Lobby?utm_source=badge&utm_medium=badge&utm_campaign=pr-badge&utm_content=badge)
[](https://github.com/SciML/DiffEqSensitivity.jl/actions?query=workflow%3ACI)
[](https://buildkite.com/julialang/diffeqsensitivity-dot-jl)
[](http://sensitivity.sciml.ai/stable/)
[](http://sensitivity.sciml.ai/dev/)
[](https://github.com/SciML/ColPrac)
[](https://github.com/SciML/SciMLStyle)
DiffEqSensitivity.jl is a component package in the [SciML Scientific Machine Learning ecosystem](https://sciml.ai/).
It holds the sensitivity analysis utilities. Users interested in using this
functionality should check out [DifferentialEquations.jl](https://github.com/JuliaDiffEq/DifferentialEquations.jl).
## Tutorials and Documentation
For information on using the package,
[see the stable documentation](https://sensitivity.sciml.ai/stable/). Use the
[in-development documentation](https://sensitivity.sciml.ai/dev/) for the version of
the documentation, which contains the unreleased features. | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 5085 | # Benchmarks
## Vs Torchdiffeq 1 million and less ODEs
A raw ODE solver benchmark showcases [>30x performance advantage for DifferentialEquations.jl](https://gist.github.com/ChrisRackauckas/cc6ac746e2dfd285c28e0584a2bfd320)
for ODEs ranging in size from 3 to nearly 1 million.
## Vs Torchdiffeq on neural ODE training
A training benchmark using the spiral ODE from the original neural ODE paper
[demonstrates a 100x performance advantage for DiffEqFlux in training neural ODEs](https://gist.github.com/ChrisRackauckas/4a4d526c15cc4170ce37da837bfc32c4).
## Vs torchsde on small SDEs
Using the code from torchsde's README we demonstrated a [>70,000x performance
advantage over torchsde](https://gist.github.com/ChrisRackauckas/6a03e7b151c86b32d74b41af54d495c6).
Further benchmarking is planned but was found to be computationally infeasible
for the time being.
## A bunch of adjoint choices on neural ODEs
Quick summary:
- `BacksolveAdjoint` can be the fastest (but use with caution!); about 25% faster
- Using `ZygoteVJP` is faster than other vjp choices with FastDense due to the overloads
```julia
using DiffEqFlux, OrdinaryDiffEq, Flux, Optim, Plots, DiffEqSensitivity,
Zygote, BenchmarkTools, Random
u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 1.5f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = FastChain((x, p) -> x.^3,
FastDense(2, 50, tanh),
FastDense(50, 2))
Random.seed!(100)
p = initial_params(dudt2)
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
function loss_neuralode(p)
pred = Array(prob_neuralode(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode,p)
# 2.709 ms (56506 allocations: 6.62 MiB)
prob_neuralode_interpolating = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true)))
function loss_neuralode_interpolating(p)
pred = Array(prob_neuralode_interpolating(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_interpolating,p)
# 5.501 ms (103835 allocations: 2.57 MiB)
prob_neuralode_interpolating_zygote = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=InterpolatingAdjoint(autojacvec=ZygoteVJP()))
function loss_neuralode_interpolating_zygote(p)
pred = Array(prob_neuralode_interpolating_zygote(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_interpolating_zygote,p)
# 2.899 ms (56150 allocations: 6.61 MiB)
prob_neuralode_backsolve = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP(true)))
function loss_neuralode_backsolve(p)
pred = Array(prob_neuralode_backsolve(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_backsolve,p)
# 4.871 ms (85855 allocations: 2.20 MiB)
prob_neuralode_quad = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=QuadratureAdjoint(autojacvec=ReverseDiffVJP(true)))
function loss_neuralode_quad(p)
pred = Array(prob_neuralode_quad(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_quad,p)
# 11.748 ms (79549 allocations: 3.87 MiB)
prob_neuralode_backsolve_tracker = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=BacksolveAdjoint(autojacvec=TrackerVJP()))
function loss_neuralode_backsolve_tracker(p)
pred = Array(prob_neuralode_backsolve_tracker(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_backsolve_tracker,p)
# 27.604 ms (186143 allocations: 12.22 MiB)
prob_neuralode_backsolve_zygote = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=BacksolveAdjoint(autojacvec=ZygoteVJP()))
function loss_neuralode_backsolve_zygote(p)
pred = Array(prob_neuralode_backsolve_zygote(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_backsolve_zygote,p)
# 2.091 ms (49883 allocations: 6.28 MiB)
prob_neuralode_backsolve_false = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=BacksolveAdjoint(autojacvec=ReverseDiffVJP(false)))
function loss_neuralode_backsolve_false(p)
pred = Array(prob_neuralode_backsolve_false(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_backsolve_false,p)
# 4.822 ms (9956 allocations: 1.03 MiB)
prob_neuralode_tracker = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps, sensealg=TrackerAdjoint())
function loss_neuralode_tracker(p)
pred = Array(prob_neuralode_tracker(u0, p))
loss = sum(abs2, ode_data .- pred)
return loss
end
@btime Zygote.gradient(loss_neuralode_tracker,p)
# 12.614 ms (76346 allocations: 3.12 MiB)
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 11441 | # DiffEqSensitivity: Automatic Differentiation and Adjoints for (Differential) Equation Solvers
DiffEqSensitivity.jl is the automatic differentiation and adjoints system for the SciML
ecosystem. Also known as local sensitivity analysis, these methods allow for calculation
of fast derivatives of SciML problem types which are commonly used to analyze model
sensitivities, callibrate models to data, train neural ODEs, perform automated model
discovery via universal differential equations, and more. SciMLSensitivity.jl is
a high level interface that pulls together all of the tools with heuristics
and helper functions to make solving inverse problems and inferring models
as easy as possible without losing efficiency.
Thus, what DiffEqSensitivity.jl provides is:
- Automatic differentiation overloads for improving the performance and flexibility
of AD calls over `solve`.
- A bunch of tutorials, documentation, and test cases for this combination
with parameter estimation (data fitting / model calibration), neural network
libraries and GPUs.
!!! note
This documentation assumes familiarity with the solver packages for the respective problem
types. If one is not familiar with the solver packages, please consult the documentation
for pieces like [DifferentialEquations.jl](https://diffeq.sciml.ai/stable/),
[NonlinearSolve.jl](https://nonlinearsolve.sciml.ai/dev/),
[LinearSolve.jl](http://linearsolve.sciml.ai/dev/), etc. first.
## High Level Interface: `sensealg`
The highest level interface is provided by the function `solve`:
```julia
solve(prob,args...;sensealg=InterpolatingAdjoint(),
checkpoints=sol.t,kwargs...)
```
`solve` is fully compatible with automatic differentiation libraries
like:
- [Zygote.jl](https://github.com/FluxML/Zygote.jl)
- [ReverseDiff.jl](https://github.com/JuliaDiff/ReverseDiff.jl)
- [Tracker.jl](https://github.com/FluxML/Tracker.jl)
- [ForwardDiff.jl](https://github.com/JuliaDiff/ForwardDiff.jl)
and will automatically replace any calculations of the solution's derivative
with a fast method. The keyword argument `sensealg` controls the dispatch to the
`AbstractSensitivityAlgorithm` used for the sensitivity calculation.
Note that `solve` in an AD context does not allow higher order
interpolations unless `sensealg=DiffEqBase.SensitivityADPassThrough()`
is used, i.e. going back to the AD mechanism.
!!! note
The behavior of ForwardDiff.jl is different from the other automatic differentiation libraries mentioned above.
The `sensealg` keyword is ignored. Instead, the differential equations are solved using `Dual` numbers for `u0` and `p`.
If only `p` is perturbed in the sensitivity analysis, but not `u0`, the state is still implemented as a `Dual` number.
ForwardDiff.jl will thus not dispatch into continuous forward nor adjoint sensitivity analysis even if a `sensealg` is provided.
## Equation Scope
SciMLSensitivity.jl supports all of the equation types of the
[SciML Common Interface](https://scimlbase.sciml.ai/dev/), extending the problem
types by adding overloads for automatic differentiation to improve the performance
and flexibility of the differentiation system. This includes:
- Linear systems (`LinearProblem`)
- Direct methods for dense and sparse
- Iterative solvers with preconditioning
- Nonlinear Systems (`NonlinearProblem`)
- Systems of nonlinear equations
- Scalar bracketing systems
- Integrals (quadrature) (`QuadratureProblem`)
- Differential Equations
- Discrete equations (function maps, discrete stochastic (Gillespie/Markov)
simulations) (`DiscreteProblem`)
- Ordinary differential equations (ODEs) (`ODEProblem`)
- Split and Partitioned ODEs (Symplectic integrators, IMEX Methods) (`SplitODEProblem`)
- Stochastic ordinary differential equations (SODEs or SDEs) (`SDEProblem`)
- Stochastic differential-algebraic equations (SDAEs) (`SDEProblem` with mass matrices)
- Random differential equations (RODEs or RDEs) (`RODEProblem`)
- Differential algebraic equations (DAEs) (`DAEProblem` and `ODEProblem` with mass matrices)
- Delay differential equations (DDEs) (`DDEProblem`)
- Neutral, retarded, and algebraic delay differential equations (NDDEs, RDDEs, and DDAEs)
- Stochastic delay differential equations (SDDEs) (`SDDEProblem`)
- Experimental support for stochastic neutral, retarded, and algebraic delay differential equations (SNDDEs, SRDDEs, and SDDAEs)
- Mixed discrete and continuous equations (Hybrid Equations, Jump Diffusions) (`DEProblem`s with callbacks)
- Optimization (`OptimizationProblem`)
- Nonlinear (constrained) optimization
- (Stochastic/Delay/Differential-Algebraic) Partial Differential Equations (`PDESystem`)
- Finite difference and finite volume methods
- Interfaces to finite element methods
- Physics-Informed Neural Networks (PINNs)
- Integro-Differential Equations
- Fractional Differential Equations
## SciMLSensitivity and Universal Differential Equations
SciMLSensitivity is for universal differential equations, where these can include
delays, physical constraints, stochasticity, events, and all other kinds of
interesting behavior that shows up in scientific simulations. Neural networks can
be all or part of the model. They can be around the differential equation,
in the cost function, or inside of the differential equation. Neural networks
representing unknown portions of the model or functions can go anywhere you
have uncertainty in the form of the scientific simulator. Forward sensitivity
and adjoint equations are automatically generated with checkpointing and
stabilization to ensure it works for large stiff equations, while specializations
on static objects allows for high efficiency on small equations. For an overview
of the topic with applications, consult the paper
[Universal Differential Equations for Scientific Machine
Learning](https://arxiv.org/abs/2001.04385).
You can efficiently use the package for:
- Parameter estimation of scientific models (ODEs, SDEs, DDEs, DAEs, etc.)
- Neural ODEs, Neural SDE, Neural DAEs, Neural DDEs, etc.
- Nonlinear optimal control, including training neural controllers
- (Stiff) universal ordinary differential equations (universal ODEs)
- Universal stochastic differential equations (universal SDEs)
- Universal delay differential equations (universal DDEs)
- Universal partial differential equations (universal PDEs)
- Universal jump stochastic differential equations (universal jump diffusions)
- Hybrid universal differential equations (universal DEs with event handling)
with high order, adaptive, implicit, GPU-accelerated, Newton-Krylov, etc.
methods. For examples, please refer to [the DiffEqFlux release blog
post](https://julialang.org/blog/2019/01/fluxdiffeq) (which we try to keep
updated for changes to the libraries). Additional demonstrations, like neural
PDEs and neural jump SDEs, can be found [at this blog
post](http://www.stochasticlifestyle.com/neural-jump-sdes-jump-diffusions-and-neural-pdes/)
(among many others!). All of these features are only part of the advantage, as this library
[routinely benchmarks orders of magnitude faster than competing libraries like torchdiffeq](@ref Benchmarks).
Use with GPUs is highly optimized by
[recompiling the solvers to GPUs to remove all CPU-GPU data transfers](https://www.stochasticlifestyle.com/solving-systems-stochastic-pdes-using-gpus-julia/),
while use with CPUs uses specialized kernels for accelerating differential equation solves.
Many different training techniques are supported by this package, including:
- Optimize-then-discretize (backsolve adjoints, checkpointed adjoints, quadrature adjoints)
- Discretize-then-optimize (forward and reverse mode discrete sensitivity analysis)
- This is a generalization of [ANODE](https://arxiv.org/pdf/1902.10298.pdf) and
[ANODEv2](https://arxiv.org/pdf/1906.04596.pdf) to all
[DifferentialEquations.jl ODE solvers](https://diffeq.sciml.ai/latest/solvers/ode_solve/)
- Hybrid approaches (adaptive time stepping + AD for adaptive discretize-then-optimize)
- O(1) memory backprop of ODEs via BacksolveAdjoint, and Virtual Brownian Trees for O(1) backprop of SDEs
- [Continuous adjoints for integral loss functions](@ref continuous_loss)
- Probabilistic programming and variational inference on ODEs/SDEs/DAEs/DDEs/hybrid
equations etc. is provided by integration with [Turing.jl](https://turing.ml/dev/)
and [Gen.jl](https://github.com/probcomp/Gen.jl). Reproduce
[variational loss functions](https://arxiv.org/abs/2001.01328) by plugging
[composible libraries together](https://turing.ml/dev/tutorials/9-variationalinference/).
all while mixing forward mode and reverse mode approaches as appropriate for the
most speed. For more details on the adjoint sensitivity analysis methods for
computing fast gradients, see the [adjoints details page](@ref sensitivity_diffeq).
With this package, you can explore various ways to integrate the two methodologies:
- Neural networks can be defined where the “activations” are nonlinear functions
described by differential equations
- Neural networks can be defined where some layers are ODE solves
- ODEs can be defined where some terms are neural networks
- Cost functions on ODEs can define neural networks
## Note on Modularity and Composability with Solvers
Note that DiffEqSensitivity.jl purely built on composable and modular infrastructure.
DiffEqSensitivity provides high level helper functions and documentation for the user, but the
code generation stack is modular and composes in many different ways. For example, one can
use and swap out the ODE solver between any common interface compatible library, like:
- Sundials.jl
- OrdinaryDiffEq.jl
- LSODA.jl
- [IRKGaussLegendre.jl](https://github.com/mikelehu/IRKGaussLegendre.jl)
- [SciPyDiffEq.jl](https://github.com/SciML/SciPyDiffEq.jl)
- [... etc. many other choices!](https://diffeq.sciml.ai/stable/solvers/ode_solve/)
In addition, due to the composability of the system, none of the components are directly
tied to the Flux.jl machine learning framework. For example, you can [use DiffEqSensitivity.jl
to generate TensorFlow graphs and train the neural network with TensorFlow.jl](https://youtu.be/n2MwJ1guGVQ?t=284),
[use PyTorch arrays via Torch.jl](https://github.com/FluxML/Torch.jl), and more all with
single line code changes by utilizing the underlying code generation. The tutorials shown here
are thus mostly a guide on how to use the ecosystem as a whole, only showing a small snippet
of the possible ways to compose the thousands of differentiable libraries together! Swap out
ODEs for SDEs, DDEs, DAEs, etc., put quadrature libraries or
[Tullio.jl](https://github.com/mcabbott/Tullio.jl) in the loss function, the world is your
oyster!
As a proof of composability, note that the implementation of Bayesian neural ODEs required
zero code changes to the library, and instead just relied on the composability with other
Julia packages.
## Citation
If you use DiffEqSensitivity.jl or are influenced by its ideas, please cite:
```
@article{rackauckas2020universal,
title={Universal differential equations for scientific machine learning},
author={Rackauckas, Christopher and Ma, Yingbo and Martensen, Julius and Warner, Collin and Zubov, Kirill and Supekar, Rohit and Skinner, Dominic and Ramadhan, Ali},
journal={arXiv preprint arXiv:2001.04385},
year={2020}
}
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 4874 | # [Mathematics of Sensitivity Analysis](@id sensitivity_math)
## Forward Sensitivity Analysis
The local sensitivity is computed using the sensitivity ODE:
```math
\frac{d}{dt}\frac{\partial u}{\partial p_{j}}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial p_{j}}+\frac{\partial f}{\partial p_{j}}=J\cdot S_{j}+F_{j}
```
where
```math
J=\left(\begin{array}{cccc}
\frac{\partial f_{1}}{\partial u_{1}} & \frac{\partial f_{1}}{\partial u_{2}} & \cdots & \frac{\partial f_{1}}{\partial u_{k}}\\
\frac{\partial f_{2}}{\partial u_{1}} & \frac{\partial f_{2}}{\partial u_{2}} & \cdots & \frac{\partial f_{2}}{\partial u_{k}}\\
\cdots & \cdots & \cdots & \cdots\\
\frac{\partial f_{k}}{\partial u_{1}} & \frac{\partial f_{k}}{\partial u_{2}} & \cdots & \frac{\partial f_{k}}{\partial u_{k}}
\end{array}\right)
```
is the Jacobian of the system,
```math
F_{j}=\left(\begin{array}{c}
\frac{\partial f_{1}}{\partial p_{j}}\\
\frac{\partial f_{2}}{\partial p_{j}}\\
\vdots\\
\frac{\partial f_{k}}{\partial p_{j}}
\end{array}\right)
```
are the parameter derivatives, and
```math
S_{j}=\left(\begin{array}{c}
\frac{\partial u_{1}}{\partial p_{j}}\\
\frac{\partial u_{2}}{\partial p_{j}}\\
\vdots\\
\frac{\partial u_{k}}{\partial p_{j}}
\end{array}\right)
```
is the vector of sensitivities. Since this ODE is dependent on the values of the
independent variables themselves, this ODE is computed simultaneously with the
actual ODE system.
Note that the Jacobian-vector product
```math
\frac{\partial f}{\partial u}\frac{\partial u}{\partial p_{j}}
```
can be computed without forming the Jacobian. With finite differences, this through using the following
formula for the directional derivative
```math
Jv \approx \frac{f(x+v \epsilon) - f(x)}{\epsilon},
```
or, alternatively and without truncation error,
by using a dual number with a single partial dimension, ``d = x + v \epsilon`` we get that
```math
f(d) = f(x) + Jv \epsilon
```
as a fast way to calcuate ``Jv``. Thus, except when a sufficiently good function for `J` is given
by the user, the Jacobian is never formed. For more details, consult the
[MIT 18.337 lecture notes on forward mode AD](https://mitmath.github.io/18337/lecture8/automatic_differentiation.html).
## Adjoint Sensitivity Analysis
This adjoint requires the definition of some scalar functional ``g(u,p)``
where ``u(t,p)`` is the (numerical) solution to the differential equation
``d/dt u(t,p)=f(t,u,p)`` with ``t\in [0,T]`` and ``u(t_0,p)=u_0``.
Adjoint sensitivity analysis finds the gradient of
```math
G(u,p)=G(u(\cdot,p))=\int_{t_{0}}^{T}g(u(t,p),p)dt
```
some integral of the solution. It does so by solving the adjoint problem
```math
\frac{d\lambda^{\star}}{dt}=g_{u}(u(t,p),p)-\lambda^{\star}(t)f_{u}(t,u(t,p),p),\thinspace\thinspace\thinspace\lambda^{\star}(T)=0
```
where ``f_u`` is the Jacobian of the system with respect to the state ``u`` while
``f_p`` is the Jacobian with respect to the parameters. The adjoint problem's
solution gives the sensitivities through the integral:
```math
\frac{dG}{dp}=\int_{t_{0}}^{T}\lambda^{\star}(t)f_{p}(t)+g_{p}(t)dt+\lambda^{\star}(t_{0})u_{p}(t_{0})
```
Notice that since the adjoints require the Jacobian of the system at the state,
it requires the ability to evaluate the state at any point in time. Thus it
requires the continuous forward solution in order to solve the adjoint solution,
and the adjoint solution is required to be continuous in order to calculate the
resulting integral.
There is one extra detail to consider. In many cases we would like to calculate
the adjoint sensitivity of some discontinuous functional of the solution. One
canonical function is the L2 loss against some data points, that is:
```math
L(u,p)=\sum_{i=1}^{n}\Vert\tilde{u}(t_{i})-u(t_{i},p)\Vert^{2}
```
In this case, we can reinterpret our summation as the distribution integral:
```math
G(u,p)=\int_{0}^{T}\sum_{i=1}^{n}\Vert\tilde{u}(t_{i})-u(t_{i},p)\Vert^{2}\delta(t_{i}-t)dt
```
where ``δ`` is the Dirac distribution. In this case, the integral is continuous
except at finitely many points. Thus it can be calculated between each ``t_i``.
At a given ``t_i``, given that the ``t_i`` are unique, we have that
```math
g_{u}(t_{i})=2\left(\tilde{u}(t_{i})-u(t_{i},p)\right)
```
Thus the adjoint solution ``\lambda^{\star}(t)`` is given by integrating between the integrals and
applying the jump function ``g_u`` at every data point ``t_i``.
We note that
```math
\lambda^{\star}(t)f_{u}(t)
```
is a vector-transpose Jacobian product, also known as a `vjp`, which can be efficiently computed
using the pullback of backpropogation on the user function `f` with a forward pass at `u` with a
pullback vector ``\lambda^{\star}``. For more information, consult the
[MIT 18.337 lecture notes on reverse mode AD](https://mitmath.github.io/18337/lecture10/estimation_identification)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 3968 | # [Adjoint Sensitivity Analysis of Continuous Functionals](@id continuous_loss)
[The automatic differentiation tutorial](@ref auto_diff) demonstrated
how to use AD packages like ForwardDiff.jl and Zygote.jl to compute derivatives
of differential equation solutions with respect to initial conditions and
parameters. The subsequent [direct sensitivity analysis tutorial](@ref direct_sensitivity)
showed how to directly use the SciMLSensitivity.jl internals to define and solve
the augmented differential equation systems which are used in the automatic
differentiation process.
While these internal functions give more flexibility, the previous demonstration
focused on a case which was possible via automatic differentiation: discrete cost functionals.
What is meant by discrete cost functionals is differentiation of a cost which uses a finite
number of time points. In the automatic differentiation case, these finite time points are
the points returned by `solve`, i.e. those chosen by the `saveat` option in the solve call.
In the direct adjoint sensitivity tooling, these were the time points chosen by the `ts`
vector.
However, there is an expanded set of cost functionals supported by SciMLSensitivity.jl,
continuous cost functionals, which are not possible through automatic differentiation
interfaces. In an abstract sense, a continuous cost functional is a total cost ``G``
defined as the integral of the instantanious cost ``g`` at all time points. In other words,
the total cost is defined as:
```math
G(u,p)=G(u(\cdot,p))=\int_{t_{0}}^{T}g(u(t,p),p)dt
```
Notice that this cost function cannot accurately be computed using only estimates of `u`
at discrete time points. The purpose of this tutorial is to demonstrate how such cost
functionals can be easily evaluated using the direct sensitivity analysis interfaces.
## Example: Continuous Functionals with Forward Sensitivity Analysis via Interpolation
Evaluating continuous cost functionals with forward sensitivity analysis is rather
straightforward since one can simply use the fact that the solution from
`ODEForwardSensitivityProblem` is continuous when `dense=true`. For example,
```@example continuousadjoint
using OrdinaryDiffEq, DiffEqSensitivity
function f(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + u[1]*u[2]
end
p = [1.5,1.0,3.0]
prob = ODEForwardSensitivityProblem(f,[1.0;1.0],(0.0,10.0),p)
sol = solve(prob,DP8())
```
gives a continuous solution `sol(t)` with the derivative at each time point. This
can then be used to define a continuous cost function via
[Integrals.jl](https://github.com/SciML/Integrals.jl), though the derivative would
need to be defined by hand using the extra sensitivity terms.
## Example: Continuous Adjoints on an Energy Functional
Continuous adjoints on a continuous functional are more automatic than forward mode.
In this case we'd like to calculate the adjoint sensitivity of the scalar energy
functional:
```math
G(u,p)=\int_{0}^{T}\frac{\sum_{i=1}^{n}u_{i}^{2}(t)}{2}dt
```
which is:
```@example continuousadjoint
g(u,p,t) = (sum(u).^2) ./ 2
```
Notice that the gradient of this function with respect to the state `u` is:
```@example continuousadjoint
function dg(out,u,p,t)
out[1]= u[1] + u[2]
out[2]= u[1] + u[2]
end
```
To get the adjoint sensitivities, we call:
```@example continuousadjoint
prob = ODEProblem(f,[1.0;1.0],(0.0,10.0),p)
sol = solve(prob,DP8())
res = adjoint_sensitivities(sol,Vern9(),g,nothing,dg,abstol=1e-8,reltol=1e-8)
```
Notice that we can check this against autodifferentiation and numerical
differentiation as follows:
```@example continuousadjoint
using QuadGK, ForwardDiff, Calculus
function G(p)
tmp_prob = remake(prob,p=p)
sol = solve(tmp_prob,Vern9(),abstol=1e-14,reltol=1e-14)
res,err = quadgk((t)-> (sum(sol(t)).^2)./2,0.0,10.0,atol=1e-14,rtol=1e-10)
res
end
res2 = ForwardDiff.gradient(G,[1.5,1.0,3.0])
res3 = Calculus.gradient(G,[1.5,1.0,3.0])
``` | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 5811 | # [Sensitivity analysis for chaotic systems (shadowing methods)](@id shadowing_methods)
Let us define the instantaneous objective ``g(u,p)`` which depends on the state `u`
and the parameter `p` of the differential equation. Then, if the objective is a
long-time average quantity
```math
\langle g \rangle_∞ = \lim_{T \rightarrow ∞} \langle g \rangle_T,
```
where
```math
\langle g \rangle_T = \frac{1}{T} \int_0^T g(u,p) \text{d}t,
```
under the assumption of ergodicity, ``\langle g \rangle_∞`` only depends on `p`.
In the case of chaotic systems, the trajectories diverge with ``O(1)`` error]. This
can be seen, for instance, when solving the [Lorenz system](https://en.wikipedia.org/wiki/Lorenz_system) at
`1e-14` tolerances with 9th order integrators and a small machine-epsilon perturbation:
```julia
using OrdinaryDiffEq
function lorenz!(du, u, p, t)
du[1] = 10 * (u[2] - u[1])
du[2] = u[1] * (p[1] - u[3]) - u[2]
du[3] = u[1] * u[2] - (8 // 3) * u[3]
end
p = [28.0]
tspan = (0.0, 100.0)
u0 = [1.0, 0.0, 0.0]
prob = ODEProblem(lorenz!, u0, tspan, p)
sol = solve(prob, Vern9(), abstol = 1e-14, reltol = 1e-14)
sol2 = solve(prob, Vern9(), abstol = 1e-14 + eps(Float64), reltol = 1e-14)
```

More formally, such chaotic behavior can be analyzed using tools from
[uncertainty quantification](@ref uncertainty_quantification).
This effect of diverging trajectories is known as the butterfly effect and can be
formulated as "most (small) perturbations on initial conditions or parameters lead
to new trajectories diverging exponentially fast from the original trajectory".
The latter statement can be roughly translated to the level of sensitivity calculation
as follows: "For most initial conditions, the (homogeneous) tangent solutions grow
exponentially fast."
To compute derivatives of an objective ``\langle g \rangle_∞`` with respect to the
parameters `p` of a chaotic systems, one thus encounters that "traditional" forward
and adjoint sensitivity methods diverge because the tangent space diverges with a
rate given by the Lyapunov exponent. Taking the average of these derivative can then
also fail, i.e., one finds that the average derivative is not the derivative of
the average.
Although numerically computed chaotic trajectories diverge from the true/original
trajectory, the [shadowing theorem](http://mathworld.wolfram.com/ShadowingTheorem.html) guarantees that there exists an errorless trajectory
with a slightly different initial condition that stays near ("shadows") the numerically
computed one, see, e.g, the [blog post](https://frankschae.github.io/post/shadowing/) or the [non-intrusive least squares shadowing paper](https://arxiv.org/abs/1611.00880) for more details.
Essentially, the idea is to replace the ill-conditioned ODE by a well-conditioned
optimization problem. Shadowing methods use the shadowing theorem within a renormalization
procedure to distill the long-time effect from the joint observation of the long-time
and the butterfly effect. This allows us to accurately compute derivatives w.r.t.
the long-time average quantities.
The following `sensealg` choices exist
- `ForwardLSS(;alpha=CosWindowing(),ADKwargs...)`: An implementation of the forward
[least square shadowing](https://arxiv.org/abs/1204.0159) method. For `alpha`,
one can choose between two different windowing options, `CosWindowing` (default)
and `Cos2Windowing`, and `alpha::Number` which corresponds to the weight of the
time dilation term in `ForwardLSS`.
- `AdjointLSS(;alpha=10.0,ADKwargs...)`: An implementation of the adjoint-mode
[least square shadowing](https://arxiv.org/abs/1204.0159) method. `alpha`
controls the weight of the time dilation term in `AdjointLSS`.
- `NILSS(nseg, nstep; rng = Xorshifts.Xoroshiro128Plus(rand(UInt64)), ADKwargs...)`:
An implementation of the [non-intrusive least squares shadowing (NILSS)](https://arxiv.org/abs/1611.00880)
method. `nseg` is the number of segments. `nstep` is the number of steps per
segment.
- `NILSAS(nseg, nstep, M=nothing; rng = Xorshifts.Xoroshiro128Plus(rand(UInt64)), ADKwargs...)`:
An implementation of the [non-intrusive least squares adjoint shadowing (NILSAS)](https://arxiv.org/abs/1801.08674)
method. `nseg` is the number of segments. `nstep` is the number of steps per
segment, `M >= nus + 1` has to be provided, where `nus` is the number of unstable
covariant Lyapunov vectors.
Recommendation: Since the computational and memory costs of `NILSS()` scale with
the number of positive (unstable) Lyapunov, it is typically less expensive than
`ForwardLSS()`. `AdjointLSS()` and `NILSAS()` are favorable for a large number
of system parameters.
As an example, for the Lorenz system with `g(u,p,t) = u[3]`, i.e., the ``z`` coordinate,
as the instantaneous objective, we can use the direct interface by passing `ForwardLSS`
as the `sensealg`:
```julia
function lorenz!(du,u,p,t)
du[1] = p[1]*(u[2]-u[1])
du[2] = u[1]*(p[2]-u[3]) - u[2]
du[3] = u[1]*u[2] - p[3]*u[3]
end
p = [10.0, 28.0, 8/3]
tspan_init = (0.0,30.0)
tspan_attractor = (30.0,50.0)
u0 = rand(3)
prob_init = ODEProblem(lorenz!,u0,tspan_init,p)
sol_init = solve(prob_init,Tsit5())
prob_attractor = ODEProblem(lorenz!,sol_init[end],tspan_attractor,p)
g(u,p,t) = u[end]
function G(p)
_prob = remake(prob_attractor,p=p)
_sol = solve(_prob,Vern9(),abstol=1e-14,reltol=1e-14,saveat=0.01,sensealg=ForwardLSS(alpha=10),g=g)
sum(getindex.(_sol.u,3))
end
dp1 = Zygote.gradient(p->G(p),p)
```
Alternatively, we can define the `ForwardLSSProblem` and solve it
via `shadow_forward` as follows:
```julia
lss_problem = ForwardLSSProblem(sol_attractor, ForwardLSS(alpha=10), g)
resfw = shadow_forward(lss_problem)
@test res ≈ dp1[1] atol=1e-10
``` | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 5434 | # [Differentiating an ODE Solution with Automatic Differentiation](@id auto_diff)
!!! note
This tutorial assumes familiarity with DifferentialEquations.jl
If you are not familiar with DifferentialEquations.jl, please consult
[the DifferentialEquations.jl documentation](https://diffeq.sciml.ai/stable/)
In this tutorial we will introduce how to use local sensitivity analysis via
automatic differentiation. The automatic differentiation interfaces are the
most common ways that local sensitivity analysis is done. It's fairly fast
and flexible, but most notably, it's a very small natural extension to the
normal differential equation solving code and is thus the easiest way to
do most things.
## Setup
Let's first define a differential equation we wish to solve. We will choose the
Lotka-Volterra equation. This is done via DifferentialEquations.jl using:
```@example diffode
using DifferentialEquations
function lotka_volterra!(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(lotka_volterra!,u0,(0.0,10.0),p)
sol = solve(prob,Tsit5(),reltol=1e-6,abstol=1e-6)
```
Now let's differentiate the solution to this ODE using a few different automatic
differentiation methods.
## Forward-Mode Automatic Differentiation with ForwardDiff.jl
Let's say we need the derivative of the solution with respect to the initial condition
`u0` and its parameters `p`. One of the simplest ways to do this is via ForwardDiff.jl.
To do this, all that one needs to do is use
[the ForwardDiff.jl library](https://github.com/JuliaDiff/ForwardDiff.jl) to differentiate
some function `f` which uses a differential equation `solve` inside of it. For example,
let's say we want the derivative of the first component of ODE solution with respect to
these quantities at evenly spaced time points of `dt = 1`. We can compute this via:
```@example diffode
using ForwardDiff
function f(x)
_prob = remake(prob,u0=x[1:2],p=x[3:end])
solve(_prob,Tsit5(),reltol=1e-6,abstol=1e-6,saveat=1)[1,:]
end
x = [u0;p]
dx = ForwardDiff.jacobian(f,x)
```
Let's dig into what this is saying a bit. `x` is a vector which concatenates the initial condition
and parameters, meaning that the first 2 values are the initial conditions and the last 4 are the
parameters. We use the `remake` function to build a function `f(x)` which uses these new initial
conditions and parameters to solve the differential equation and return the time series of the first
component.
Then `ForwardDiff.jacobian(f,x)` computes the Jacobian of `f` with respect to `x`. The
output `dx[i,j]` corresponds to the derivative of the solution of the first component at time `t=j-1`
with respect to `x[i]`. For example, `dx[3,2]` is the derivative of the first component of the
solution at time `t=1` with respect to `p[1]`.
!!! note
Since [the global error is 1-2 orders of magnitude higher than the local error](https://diffeq.sciml.ai/stable/basics/faq/#What-does-tolerance-mean-and-how-much-error-should-I-expect), we use accuracies of 1e-6 (instead of the default 1e-3) to get reasonable sensitivities
## Reverse-Mode Automatic Differentiation
[The `solve` function is automatically compatible with AD systems like Zygote.jl](https://diffeq.sciml.ai/latest/analysis/sensitivity/)
and thus there is no machinery that is necessary to use other than to put `solve` inside of
a function that is differentiated by Zygote. For example, the following computes the solution
to an ODE and computes the gradient of a loss function (the sum of the ODE's output at each
timepoint with dt=0.1) via the adjoint method:
```@example diffode
using Zygote, DiffEqSensitivity
function sum_of_solution(u0,p)
_prob = remake(prob,u0=u0,p=p)
sum(solve(_prob,Tsit5(),reltol=1e-6,abstol=1e-6,saveat=0.1))
end
du01,dp1 = Zygote.gradient(sum_of_solution,u0,p)
```
Zygote.jl's automatic differentiation system is overloaded to allow SciMLSensitivity.jl
to redefine the way the derivatives are computed, allowing trade-offs between numerical
stability, memory, and compute performance, similar to how ODE solver algorithms are
chosen. The algorithms for differentiation calculation are called `AbstractSensitivityAlgorithms`,
or `sensealg`s for short. These are choosen by passing the `sensealg` keyword argument into solve.
Let's demonstrate this by choosing the `QuadratureAdjoint` `sensealg` for the differentiation of
this system:
```@example diffode
function sum_of_solution(u0,p)
_prob = remake(prob,u0=u0,p=p)
sum(solve(_prob,Tsit5(),reltol=1e-6,abstol=1e-6,saveat=0.1,sensealg=QuadratureAdjoint()))
end
du01,dp1 = Zygote.gradient(sum_of_solution,u0,p)
```
Here this computes the derivative of the output with respect to the initial
condition and the the derivative with respect to the parameters respectively
using the `QuadratureAdjoint()`. For more information on the choices of sensitivity
algorithms, see the [reference documentation in choosing sensitivity algorithms](@ref sensitivity_diffeq)
## When Should You Use Forward or Reverse Mode?
Good question! The simple answer is, if you are differentiating a system of
100 equations or less, use forward-mode, otherwise reverse-mode. But it can
be a lot more complicated than that! For more information, see the
[reference documentation in choosing sensitivity algorithms](@ref sensitivity_diffeq) | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 4366 | # [Direct Sensitivity Analysis Functionality](@id direct_sensitivity)
While sensitivity analysis tooling can be used implicitly via integration with
automatic differentiation libraries, one can often times obtain more speed
and flexibility with the direct sensitivity analysis interfaces. This tutorial
demonstrates some of those functions.
## Example using an ODEForwardSensitivityProblem
Forward sensitivity analysis is performed by defining and solving an augmented
ODE. To define this augmented ODE, use the `ODEForwardSensitivityProblem` type
instead of an ODE type. For example, we generate an ODE with the sensitivity
equations attached for the Lotka-Volterra equations by:
```@example directsense
using OrdinaryDiffEq, DiffEqSensitivity
function f(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + u[1]*u[2]
end
p = [1.5,1.0,3.0]
prob = ODEForwardSensitivityProblem(f,[1.0;1.0],(0.0,10.0),p)
```
This generates a problem which the ODE solvers can solve:
```@example directsense
sol = solve(prob,DP8())
```
Note that the solution is the standard ODE system and the sensitivity system combined.
We can use the following helper functions to extract the sensitivity information:
```julia
x,dp = extract_local_sensitivities(sol)
x,dp = extract_local_sensitivities(sol,i)
x,dp = extract_local_sensitivities(sol,t)
```
In each case, `x` is the ODE values and `dp` is the matrix of sensitivities
The first gives the full timeseries of values and `dp[i]` contains the time series of the
sensitivities of all components of the ODE with respect to `i`th parameter.
The second returns the `i`th time step, while the third
interpolates to calculate the sensitivities at time `t`. For example, if we do:
```@example directsense
x,dp = extract_local_sensitivities(sol)
da = dp[1]
```
then `da` is the timeseries for ``\frac{\partial u(t)}{\partial p}``. We can
plot this
```@example directsense
using Plots
plot(sol.t,da',lw=3)
```
transposing so that the rows (the timeseries) is plotted.
For more information on the internal representation of the `ODEForwardSensitivityProblem`
solution, see the [direct forward sensitivity analysis manual page](@ref forward_sense).
## Example using `adjoint_sensitivities` for discrete adjoints
In this example we will show solving for the adjoint sensitivities of a discrete
cost functional. First let's solve the ODE and get a high quality continuous
solution:
```@example directsense
function f(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + u[1]*u[2]
end
p = [1.5,1.0,3.0]
prob = ODEProblem(f,[1.0;1.0],(0.0,10.0),p)
sol = solve(prob,Vern9(),abstol=1e-10,reltol=1e-10)
```
Now let's calculate the sensitivity of the ``\ell_2`` error against 1 at evenly spaced
points in time, that is:
```math
L(u,p,t)=\sum_{i=1}^{n}\frac{\Vert1-u(t_{i},p)\Vert^{2}}{2}
```
for ``t_i = 0.5i``. This is the assumption that the data is `data[i]=1.0`.
For this function, notice we have that:
```math
\begin{aligned}
dg_{1}&=1-u_{1} \\
dg_{2}&=1-u_{2} \\
& \quad \vdots
\end{aligned}
```
and thus:
```@example directsense
dg(out,u,p,t,i) = (out.=1.0.-u)
```
Also, we can omit `dgdp`, because the cost function doesn't dependent on `p`.
If we had data, we'd just replace `1.0` with `data[i]`. To get the adjoint
sensitivities, call:
```@example directsense
ts = 0:0.5:10
res = adjoint_sensitivities(sol,Vern9(),dg,ts,abstol=1e-14,
reltol=1e-14)
```
This is super high accuracy. As always, there's a tradeoff between accuracy
and computation time. We can check this almost exactly matches the
autodifferentiation and numerical differentiation results:
```@example directsense
using ForwardDiff,Calculus,ReverseDiff,Tracker
function G(p)
tmp_prob = remake(prob,u0=convert.(eltype(p),prob.u0),p=p)
sol = solve(tmp_prob,Vern9(),abstol=1e-14,reltol=1e-14,saveat=ts,
sensealg=SensitivityADPassThrough())
A = convert(Array,sol)
sum(((1 .- A).^2)./2)
end
G([1.5,1.0,3.0])
res2 = ForwardDiff.gradient(G,[1.5,1.0,3.0])
res3 = Calculus.gradient(G,[1.5,1.0,3.0])
res4 = Tracker.gradient(G,[1.5,1.0,3.0])
res5 = ReverseDiff.gradient(G,[1.5,1.0,3.0])
```
and see this gives the same values. | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 8843 | # Bayesian Neural ODEs: NUTS
In this tutorial, we show how the DiffEqFlux.jl library in Julia can be seamlessly combined with Bayesian estimation libraries like AdvancedHMC.jl and Turing.jl. This enables converting Neural ODEs to Bayesian Neural ODEs, which enables us to estimate the error in the Neural ODE estimation and forecasting.
In this tutorial, a working example of the Bayesian Neural ODE: NUTS sampler is shown.
For more details, please refer to [Bayesian Neural Ordinary Differential Equations](https://arxiv.org/abs/2012.07244).
## Copy-Pasteable Code
Before getting to the explanation, here's some code to start with. We will follow
wil a full explanation of the definition and training process:
```julia
using DiffEqFlux, DifferentialEquations, Plots, AdvancedHMC, MCMCChains
using JLD, StatsPlots
u0 = [2.0; 0.0]
datasize = 40
tspan = (0.0, 1)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = FastChain((x, p) -> x.^3,
FastDense(2, 50, tanh),
FastDense(50, 2))
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
function predict_neuralode(p)
Array(prob_neuralode(u0, p))
end
function loss_neuralode(p)
pred = predict_neuralode(p)
loss = sum(abs2, ode_data .- pred)
return loss, pred
end
l(θ) = -sum(abs2, ode_data .- predict_neuralode(θ)) - sum(θ .* θ)
function dldθ(θ)
x,lambda = Flux.Zygote.pullback(l,θ)
grad = first(lambda(1))
return x, grad
end
metric = DiagEuclideanMetric(length(prob_neuralode.p))
h = Hamiltonian(metric, l, dldθ)
integrator = Leapfrog(find_good_stepsize(h, Float64.(prob_neuralode.p)))
prop = AdvancedHMC.NUTS{MultinomialTS, GeneralisedNoUTurn}(integrator)
adaptor = StanHMCAdaptor(MassMatrixAdaptor(metric), StepSizeAdaptor(0.45, integrator))
samples, stats = sample(h, prop, Float64.(prob_neuralode.p), 500, adaptor, 500; progress=true)
losses = map(x-> x[1],[loss_neuralode(samples[i]) for i in 1:length(samples)])
##################### PLOTS: LOSSES ###############
scatter(losses, ylabel = "Loss", yscale= :log, label = "Architecture1: 500 warmup, 500 sample")
################### RETRODICTED PLOTS: TIME SERIES #################
pl = scatter(tsteps, ode_data[1,:], color = :red, label = "Data: Var1", xlabel = "t", title = "Spiral Neural ODE")
scatter!(tsteps, ode_data[2,:], color = :blue, label = "Data: Var2")
for k in 1:300
resol = predict_neuralode(samples[100:end][rand(1:400)])
plot!(tsteps,resol[1,:], alpha=0.04, color = :red, label = "")
plot!(tsteps,resol[2,:], alpha=0.04, color = :blue, label = "")
end
idx = findmin(losses)[2]
prediction = predict_neuralode(samples[idx])
plot!(tsteps,prediction[1,:], color = :black, w = 2, label = "")
plot!(tsteps,prediction[2,:], color = :black, w = 2, label = "Best fit prediction", ylims = (-2.5, 3.5))
#################### RETRODICTED PLOTS - CONTOUR ####################
pl = scatter(ode_data[1,:], ode_data[2,:], color = :red, label = "Data", xlabel = "Var1", ylabel = "Var2", title = "Spiral Neural ODE")
for k in 1:300
resol = predict_neuralode(samples[100:end][rand(1:400)])
plot!(resol[1,:],resol[2,:], alpha=0.04, color = :red, label = "")
end
plot!(prediction[1,:], prediction[2,:], color = :black, w = 2, label = "Best fit prediction", ylims = (-2.5, 3))
```
Time Series Plots:
Contour Plots:
```julia
######################## CHAIN DIAGNOSIS PLOTS#########################
samples = hcat(samples...)
samples_reduced = samples[1:5, :]
samples_reshape = reshape(samples_reduced, (500, 5, 1))
Chain_Spiral = Chains(samples_reshape)
plot(Chain_Spiral)
autocorplot(Chain_Spiral)
```
Chain Mixing Plot:
Auto-Correlation Plot:
## Explanation
#### Step 1: Get the data from the Spiral ODE example
```julia
u0 = [2.0; 0.0]
datasize = 40
tspan = (0.0, 1)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
```
#### Step 2: Define the Neural ODE architecture.
Note that this step potentially offers a lot of flexibility in the number of layers/ number of units in each layer. It may not necessarily be true that a 100 units
architecture is better at prediction/forecasting than a 50 unit architecture. On the other hand, a complicated architecture can take a huge computational time without increasing performance.
```julia
dudt2 = FastChain((x, p) -> x.^3,
FastDense(2, 50, tanh),
FastDense(50, 2))
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
```
#### Step 3: Define the loss function for the Neural ODE.
```julia
function predict_neuralode(p)
Array(prob_neuralode(u0, p))
end
function loss_neuralode(p)
pred = predict_neuralode(p)
loss = sum(abs2, ode_data .- pred)
return loss, pred
end
```
#### Step 4: Now we start integrating the Bayesian estimation workflow as prescribed by the AdvancedHMC interface with the NeuralODE defined above.
The Advanced HMC interface requires us to specify: (a) the hamiltonian log density and its gradient , (b) the sampler and (c) the step size
adaptor function.
For the hamiltonian log density, we use the loss function. The θ*θ term denotes the use of
Gaussian priors.
The user can make several modifications to Step 4. The user can try different acceptance ratios, warmup samples and posterior samples. One can also use the Variational Inference (ADVI) framework, which doesn't work quite as well as NUTS. The SGLD (Stochastic Langevin Gradient Descent) sampler is seen to have a better performance than NUTS. Have a look at https://sebastiancallh.github.io/post/langevin/ for a quick introduction to SGLD.
```julia
l(θ) = -sum(abs2, ode_data .- predict_neuralode(θ)) - sum(θ .* θ)
function dldθ(θ)
x,lambda = Flux.Zygote.pullback(l,θ)
grad = first(lambda(1))
return x, grad
end
metric = DiagEuclideanMetric(length(prob_neuralode.p))
h = Hamiltonian(metric, l, dldθ)
```
We use the NUTS sampler with a acceptance ratio of δ= 0.45 in this example.
In addition, we use Nesterov Dual Averaging for the Step Size adaptation.
We sample using 500 warmup samples and 500 posterior samples.
```julia
integrator = Leapfrog(find_good_stepsize(h, Float64.(prob_neuralode.p)))
prop = AdvancedHMC.NUTS{MultinomialTS, GeneralisedNoUTurn}(integrator)
adaptor = StanHMCAdaptor(MassMatrixAdaptor(metric), StepSizeAdaptor(0.45, integrator))
samples, stats = sample(h, prop, Float64.(prob_neuralode.p), 500, adaptor, 500; progress=true)
```
#### Step 5: Plot diagnostics.
A: Plot chain object and auto-correlation plot of the first 5 parameters.
```julia
samples = hcat(samples...)
samples_reduced = samples[1:5, :]
samples_reshape = reshape(samples_reduced, (500, 5, 1))
Chain_Spiral = Chains(samples_reshape)
plot(Chain_Spiral)
autocorplot(Chain_Spiral)
```
B: Plot retrodicted data.
```julia
####################TIME SERIES PLOTS###################
pl = scatter(tsteps, ode_data[1,:], color = :red, label = "Data: Var1", xlabel = "t", title = "Spiral Neural ODE")
scatter!(tsteps, ode_data[2,:], color = :blue, label = "Data: Var2")
for k in 1:300
resol = predict_neuralode(samples[100:end][rand(1:400)])
plot!(tsteps,resol[1,:], alpha=0.04, color = :red, label = "")
plot!(tsteps,resol[2,:], alpha=0.04, color = :blue, label = "")
end
idx = findmin(losses)[2]
prediction = predict_neuralode(samples[idx])
plot!(tsteps,prediction[1,:], color = :black, w = 2, label = "")
plot!(tsteps,prediction[2,:], color = :black, w = 2, label = "Best fit prediction", ylims = (-2.5, 3.5))
####################CONTOUR PLOTS#########################3
pl = scatter(ode_data[1,:], ode_data[2,:], color = :red, label = "Data", xlabel = "Var1", ylabel = "Var2", title = "Spiral Neural ODE")
for k in 1:300
resol = predict_neuralode(samples[100:end][rand(1:400)])
plot!(resol[1,:],resol[2,:], alpha=0.04, color = :red, label = "")
end
plot!(prediction[1,:], prediction[2,:], color = :black, w = 2, label = "Best fit prediction", ylims = (-2.5, 3))
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 8493 | # Bayesian Neural ODEs: SGLD
Recently, Neural Ordinary Differential Equations has emerged as a powerful framework for modeling physical simulations without explicitly defining the ODEs governing the system, but learning them via machine learning.
However, the question: Can Bayesian learning frameworks be integrated with Neural ODEs to robustly quantify the uncertainty in the weights of a Neural ODE? remains unanswered.
In this tutorial, a working example of the Bayesian Neural ODE: SGLD sampler is shown. SGLD stands for Stochastic Langevin Gradient Descent.
For an introduction to SGLD, please refer to [Introduction to SGLD in Julia](https://sebastiancallh.github.io/post/langevin/)
For more details regarding Bayesian Neural ODEs, please refer to [Bayesian Neural Ordinary Differential Equations](https://arxiv.org/abs/2012.07244).
## Copy-Pasteable Code
Before getting to the explanation, here's some code to start with. We will follow
with a full explanation of the definition and training process:
```julia
using DiffEqFlux, DifferentialEquations, Flux
using Plots, StatsPlots
u0 = Float32[1., 1.]
p = [1.5, 1., 3., 1.]
datasize = 45
tspan = (0.0f0, 14.f0)
tsteps = tspan[1]:0.1:tspan[2]
function lv(u, p, t)
x, y = u
α, β, γ, δ = p
dx = α*x - β*x*y
dy = δ*x*y - γ*y
du = [dx, dy]
end
trueodeprob = ODEProblem(lv, u0, tspan, p)
ode_data = Array(solve(trueodeprob, Tsit5(), saveat = tsteps))
y_train = ode_data[:, 1:35]
dudt = FastChain(FastDense(2, 50, tanh), FastDense(50, 2))
prob_node = NeuralODE(dudt, (0., 14.), Tsit5(), saveat = tsteps)
train_prob = NeuralODE(dudt, (0., 3.5), Tsit5(), saveat = tsteps[1:35])
function predict(p)
Array(train_prob(u0, p))
end
function loss(p)
sum(abs2, y_train .- predict(p))
end
sgld(∇L, θᵢ, t, a = 2.5e-3, b = 0.05, γ = 0.35) = begin
ϵ = a*(b + t)^-γ
η = ϵ.*randn(size(θᵢ))
Δθᵢ = .5ϵ*∇L + η
θᵢ .-= Δθᵢ
end
parameters = []
losses = Float64[]
grad_norm = Float64[]
θ = deepcopy(prob_node.p)
@time for t in 1:45000
grad = gradient(loss, θ)[1]
sgld(grad, θ, t)
tmp = deepcopy(θ)
append!(losses, loss(θ))
append!(grad_norm, sum(abs2, grad))
append!(parameters, [tmp])
println(loss(θ))
end
plot(losses, yscale = :log10)
plot(grad_norm, yscale =:log10)
using StatsPlots
sampled_par = parameters[43000: 45000]
##################### PLOTS: LOSSES ###############
sampled_loss = [loss(p) for p in sampled_par]
density(sampled_loss)
#################### RETRODICTED PLOTS - TIME SERIES AND CONTOUR PLOTS ####################
_, i_min = findmin(sampled_loss)
plt = scatter(tsteps,ode_data[1,:], colour = :blue, label = "Data: u1", ylim = (-.5, 10.))
scatter!(plt, tsteps, ode_data[2,:], colour = :red, label = "Data: u2")
phase_plt = scatter(ode_data[1,:], ode_data[2,:], colour = :red, label = "Data", xlim = (-.25, 7.), ylim = (-2., 6.5))
for p in sampled_par
s = prob_node(u0, p)
plot!(plt, tsteps[1:35], s[1,1:35], colour = :blue, lalpha = 0.04, label =:none)
plot!(plt, tsteps[35:end], s[1, 35:end], colour =:purple, lalpha = 0.04, label =:none)
plot!(plt, tsteps[1:35], s[2,1:35], colour = :red, lalpha = 0.04, label=:none)
plot!(plt, tsteps[35:end], s[2,35:end], colour = :purple, lalpha = 0.04, label=:none)
plot!(phase_plt, s[1,1:35], s[2,1:35], colour =:red, lalpha = 0.04, label=:none)
plot!(phase_plt, s[1,35:end], s[2, 35:end], colour = :purple, lalpha = 0.04, label=:none)
end
plt
phase_plt
plot!(plt, [3.5], seriestype =:vline, colour = :green, linestyle =:dash,label = "Training Data End")
bestfit = prob_node(u0, sampled_par[i_min])
plot(bestfit)
plot!(plt, tsteps[1:35], bestfit[2, 1:35], colour =:black, label = "Training: Best fit prediction")
plot!(plt, tsteps[35:end], bestfit[2, 35:end], colour =:purple, label = "Forecasting: Best fit prediction")
plot!(plt, tsteps[1:35], bestfit[1, 1:35], colour =:black, label = :none)
plot!(plt, tsteps[35:end], bestfit[1, 35:end], colour =:purple, label = :none)
plot!(phase_plt,bestfit[1,1:40], bestfit[2, 1:40], colour = :black, label = "Training: Best fit prediction")
plot!(phase_plt,bestfit[1, 40:end], bestfit[2, 40:end], colour = :purple, label = "Forecasting: Best fit prediction")
savefig(plt, "C:/Users/16174/Desktop/Julia Lab/MSML2021/BayesianNODE_SGLD_Plot1.png")
savefig(phase_plt, "C:/Users/16174/Desktop/Julia Lab/MSML2021/BayesianNODE_SGLD_Plot2.png")
```
Time Series Plots:
Contour Plots:
## Explanation
#### Step1: Get the data from the Lotka Volterra ODE example
```julia
u0 = Float32[1., 1.]
p = [1.5, 1., 3., 1.]
datasize = 45
tspan = (0.0f0, 14.f0)
tsteps = tspan[1]:0.1:tspan[2]
function lv(u, p, t)
x, y = u
α, β, γ, δ = p
dx = α*x - β*x*y
dy = δ*x*y - γ*y
du = [dx, dy]
end
trueodeprob = ODEProblem(lv, u0, tspan, p)
ode_data = Array(solve(trueodeprob, Tsit5(), saveat = tsteps))
y_train = ode_data[:, 1:35]
```
#### Step2: Define the Neural ODE architecture. Note that this step potentially offers a lot of flexibility in the number of layers/ number of units in each layer.
```julia
dudt = FastChain(FastDense(2, 50, tanh), FastDense(50, 2))
prob_node = NeuralODE(dudt, (0., 14.), Tsit5(), saveat = tsteps)
train_prob = NeuralODE(dudt, (0., 3.5), Tsit5(), saveat = tsteps[1:35])
```
#### Step3: Define the loss function for the Neural ODE.
```julia
function predict(p)
Array(train_prob(u0, p))
end
function loss(p)
sum(abs2, y_train .- predict(p))
end
```
#### Step4: Now we start integrating the Stochastic Langevin Gradient Descent(SGLD) framework.
The SGLD (Stochastic Langevin Gradient Descent) sampler is seen to have a better performance than NUTS whose tutorial is also shown in a separate document.
Have a look at https://sebastiancallh.github.io/post/langevin/ for a quick introduction to SGLD.
Note that we sample from the last 2000 iterations.
```julia
sgld(∇L, θᵢ, t, a = 2.5e-3, b = 0.05, γ = 0.35) = begin
ϵ = a*(b + t)^-γ
η = ϵ.*randn(size(θᵢ))
Δθᵢ = .5ϵ*∇L + η
θᵢ .-= Δθᵢ
end
parameters = []
losses = Float64[]
grad_norm = Float64[]
θ = deepcopy(prob_node.p)
@time for t in 1:45000
grad = gradient(loss, θ)[1]
sgld(grad, θ, t)
tmp = deepcopy(θ)
append!(losses, loss(θ))
append!(grad_norm, sum(abs2, grad))
append!(parameters, [tmp])
println(loss(θ))
end
plot(losses, yscale = :log10)
plot(grad_norm, yscale =:log10)
using StatsPlots
sampled_par = parameters[43000: 45000]
```
#### Step5: Plot Retrodicted Plots (Estimation and Forecasting).
```julia
################### RETRODICTED PLOTS - TIME SERIES AND CONTOUR PLOTS ####################
_, i_min = findmin(sampled_loss)
plt = scatter(tsteps,ode_data[1,:], colour = :blue, label = "Data: u1", ylim = (-.5, 10.))
scatter!(plt, tsteps, ode_data[2,:], colour = :red, label = "Data: u2")
phase_plt = scatter(ode_data[1,:], ode_data[2,:], colour = :red, label = "Data", xlim = (-.25, 7.), ylim = (-2., 6.5))
for p in sampled_par
s = prob_node(u0, p)
plot!(plt, tsteps[1:35], s[1,1:35], colour = :blue, lalpha = 0.04, label =:none)
plot!(plt, tsteps[35:end], s[1, 35:end], colour =:purple, lalpha = 0.04, label =:none)
plot!(plt, tsteps[1:35], s[2,1:35], colour = :red, lalpha = 0.04, label=:none)
plot!(plt, tsteps[35:end], s[2,35:end], colour = :purple, lalpha = 0.04, label=:none)
plot!(phase_plt, s[1,1:35], s[2,1:35], colour =:red, lalpha = 0.04, label=:none)
plot!(phase_plt, s[1,35:end], s[2, 35:end], colour = :purple, lalpha = 0.04, label=:none)
end
plt
phase_plt
plot!(plt, [3.5], seriestype =:vline, colour = :green, linestyle =:dash,label = "Training Data End")
bestfit = prob_node(u0, sampled_par[i_min])
plot(bestfit)
plot!(plt, tsteps[1:35], bestfit[2, 1:35], colour =:black, label = "Training: Best fit prediction")
plot!(plt, tsteps[35:end], bestfit[2, 35:end], colour =:purple, label = "Forecasting: Best fit prediction")
plot!(plt, tsteps[1:35], bestfit[1, 1:35], colour =:black, label = :none)
plot!(plt, tsteps[35:end], bestfit[1, 35:end], colour =:purple, label = :none)
plot!(phase_plt,bestfit[1,1:40], bestfit[2, 1:40], colour = :black, label = "Training: Best fit prediction")
plot!(phase_plt,bestfit[1, 40:end], bestfit[2, 40:end], colour = :purple, label = "Forecasting: Best fit prediction")
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 326 | # Bayesian Estimation of Differential Equations with Probabilistic Programming
For a good overview of how to use the tools of SciML in conjunction with the
Turing.jl probabilistic programming language, see the
[Bayesian Differential Equation Tutorial](https://turing.ml/stable/tutorials/10-bayesian-differential-equations/).
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 5917 | # Enforcing Physical Constraints via Universal Differential-Algebraic Equations
As shown in the [stiff ODE tutorial](https://docs.juliadiffeq.org/latest/tutorials/advanced_ode_example/#Handling-Mass-Matrices-1),
differential-algebraic equations (DAEs) can be used to impose physical
constraints. One way to define a DAE is through an ODE with a singular mass
matrix. For example, if we make `Mu' = f(u)` where the last row of `M` is all
zeros, then we have a constraint defined by the right hand side. Using
`NeuralODEMM`, we can use this to define a neural ODE where the sum of all 3
terms must add to one. An example of this is as follows:
```julia
using Lux, DiffEqFlux, Optimization, OptimizationOptimJL, DifferentialEquations, Plots
using Random
rng = Random.default_rng()
function f!(du, u, p, t)
y₁, y₂, y₃ = u
k₁, k₂, k₃ = p
du[1] = -k₁*y₁ + k₃*y₂*y₃
du[2] = k₁*y₁ - k₃*y₂*y₃ - k₂*y₂^2
du[3] = y₁ + y₂ + y₃ - 1
return nothing
end
u₀ = [1.0, 0, 0]
M = [1. 0 0
0 1. 0
0 0 0]
tspan = (0.0,1.0)
p = [0.04, 3e7, 1e4]
stiff_func = ODEFunction(f!, mass_matrix = M)
prob_stiff = ODEProblem(stiff_func, u₀, tspan, p)
sol_stiff = solve(prob_stiff, Rodas5(), saveat = 0.1)
nn_dudt2 = Lux.Chain(Lux.Dense(3, 64, tanh),
Lux.Dense(64, 2))
pinit, st = Lux.setup(rng, nn_dudt2)
model_stiff_ndae = NeuralODEMM(nn_dudt2, (u, p, t) -> [u[1] + u[2] + u[3] - 1],
tspan, M, Rodas5(autodiff=false), saveat = 0.1)
model_stiff_ndae(u₀, Lux.ComponentArray(pinit), st)
function predict_stiff_ndae(p)
return model_stiff_ndae(u₀, p, st)[1]
end
function loss_stiff_ndae(p)
pred = predict_stiff_ndae(p)
loss = sum(abs2, Array(sol_stiff) .- pred)
return loss, pred
end
# callback = function (p, l, pred) #callback function to observe training
# display(l)
# return false
# end
l1 = first(loss_stiff_ndae(Lux.ComponentArray(pinit)))
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss_stiff_ndae(x), adtype)
optprob = Optimization.OptimizationProblem(optf, Lux.ComponentArray(pinit))
result_stiff = Optimization.solve(optprob, BFGS(), maxiters=100)
```
## Step-by-Step Description
### Load Packages
```julia
using Lux, DiffEqFlux, Optimization, OptimizationOptimJL, DifferentialEquations, Plots
using Random
rng = Random.default_rng()
```
### Differential Equation
First, we define our differential equations as a highly stiff problem which makes the
fitting difficult.
```Julia
function f!(du, u, p, t)
y₁, y₂, y₃ = u
k₁, k₂, k₃ = p
du[1] = -k₁*y₁ + k₃*y₂*y₃
du[2] = k₁*y₁ - k₃*y₂*y₃ - k₂*y₂^2
du[3] = y₁ + y₂ + y₃ - 1
return nothing
end
```
### Parameters
```Julia
u₀ = [1.0, 0, 0]
M = [1. 0 0
0 1. 0
0 0 0]
tspan = (0.0,1.0)
p = [0.04, 3e7, 1e4]
```
- `u₀` = Initial Conditions
- `M` = Semi-explicit Mass Matrix (last row is the constraint equation and are therefore
all zeros)
- `tspan` = Time span over which to evaluate
- `p` = parameters `k1`, `k2` and `k3` of the differential equation above
### ODE Function, Problem and Solution
We define and solve our ODE problem to generate the "labeled" data which will be used to
train our Neural Network.
```Julia
stiff_func = ODEFunction(f!, mass_matrix = M)
prob_stiff = ODEProblem(stiff_func, u₀, tspan, p)
sol_stiff = solve(prob_stiff, Rodas5(), saveat = 0.1)
```
Because this is a DAE we need to make sure to use a **compatible solver**.
`Rodas5` works well for this example.
### Neural Network Layers
Next, we create our layers using `Lux.Chain`. We use this instead of `Flux.Chain` because it
is more suited to SciML applications (similarly for
`Lux.Dense`). The input to our network will be the initial conditions fed in as `u₀`.
```Julia
nn_dudt2 = Lux.Chain(Lux.Dense(3, 64, tanh),
Lux.Dense(64, 2))
pinit, st = Lux.setup(rng, nn_dudt2)
model_stiff_ndae = NeuralODEMM(nn_dudt2, (u, p, t) -> [u[1] + u[2] + u[3] - 1],
tspan, M, Rodas5(autodiff=false), saveat = 0.1)
model_stiff_ndae(u₀, Lux.ComponentArray(pinit), st)
```
Because this is a stiff problem, we have manually imposed that sum constraint via
`(u,p,t) -> [u[1] + u[2] + u[3] - 1]`, making the fitting easier.
### Prediction Function
For simplicity, we define a wrapper function that only takes in the model's parameters
to make predictions.
```Julia
function predict_stiff_ndae(p)
return model_stiff_ndae(u₀, p, st)[1]
end
```
### Train Parameters
Training our network requires a **loss function**, an **optimizer** and a
**callback function** to display the progress.
#### Loss
We first make our predictions based on the current parameters, then calculate the loss
from these predictions. In this case, we use **least squares** as our loss.
```Julia
function loss_stiff_ndae(p)
pred = predict_stiff_ndae(p)
loss = sum(abs2, sol_stiff .- pred)
return loss, pred
end
l1 = first(loss_stiff_ndae(Lux.ComponentArray(pinit)))
```
Notice that we are feeding the **parameters** of `model_stiff_ndae` to the `loss_stiff_ndae`
function. `model_stiff_node.p` are the weights of our NN and is of size *386*
(4 * 64 + 65 * 2) including the biases.
#### Optimizer
The optimizer is `BFGS`(see below).
#### Callback
The callback function displays the loss during training.
```Julia
callback = function (p, l, pred) #callback function to observe training
display(l)
return false
end
```
### Train
Finally, training with `Optimization.solve` by passing: *loss function*, *model parameters*,
*optimizer*, *callback* and *maximum iteration*.
```Julia
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss_stiff_ndae(x), adtype)
optprob = Optimization.OptimizationProblem(optf, Lux.ComponentArray(pinit))
result_stiff = Optimization.solve(optprob, BFGS(), maxiters=100)
```
### Expected Output
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2343 | # Delay Differential Equations
Other differential equation problem types from DifferentialEquations.jl are
supported. For example, we can build a layer with a delay differential equation
like:
```julia
using DifferentialEquations, Optimization, OptimizationPolyalgorithms
# Define the same LV equation, but including a delay parameter
function delay_lotka_volterra!(du, u, h, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = (α - β*y) * h(p, t-0.1)[1]
du[2] = dy = (δ*x - γ) * y
end
# Initial parameters
p = [2.2, 1.0, 2.0, 0.4]
# Define a vector containing delays for each variable (although only the first
# one is used)
h(p, t) = ones(eltype(p), 2)
# Initial conditions
u0 = [1.0, 1.0]
# Define the problem as a delay differential equation
prob_dde = DDEProblem(delay_lotka_volterra!, u0, h, (0.0, 10.0),
constant_lags = [0.1])
function predict_dde(p)
return Array(solve(prob_dde, MethodOfSteps(Tsit5()),
u0=u0, p=p, saveat = 0.1,
sensealg = ReverseDiffAdjoint()))
end
loss_dde(p) = sum(abs2, x-1 for x in predict_dde(p))
#using Plots
callback = function (p,l...)
display(loss_dde(p))
#display(plot(solve(remake(prob_dde,p=p),MethodOfSteps(Tsit5()),saveat=0.1),ylim=(0,6)))
return false
end
callback(p,loss_dde(p))
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_dde(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
result_dde = Optimization.solve(optprob, PolyOpt(), p, callback=callback)
```
Notice that we chose `sensealg = ReverseDiffAdjoint()` to utilize the ReverseDiff.jl
reverse-mode to handle the delay differential equation.
We define a callback to display the solution at the current parameters for each step of the training:
```julia
#using Plots
callback = function (p,l...)
display(loss_dde(p))
#display(plot(solve(remake(prob_dde,p=p),MethodOfSteps(Tsit5()),saveat=0.1),ylim=(0,6)))
return false
end
callback(p,loss_dde(p))
```
We use `Optimization.solve` to optimize the parameters for our loss function:
```julia
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_dde(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
result_dde = Optimization.solve(optprob, PolyOpt(), p, callback=callback)
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2476 | # Bouncing Ball Hybrid ODE Optimization
The bouncing ball is a classic hybrid ODE which can be represented in
the [DifferentialEquations.jl event handling system](https://diffeq.sciml.ai/stable/features/callback_functions/). This can be applied to ODEs, SDEs, DAEs, DDEs,
and more. Let's now add the DiffEqFlux machinery to this
problem in order to optimize the friction that's required to match
data. Assume we have data for the ball's height after 15 seconds. Let's
first start by implementing the ODE:
```julia
using Optimization, OptimizationPolyalgorithms, DifferentialEquations
function f(du,u,p,t)
du[1] = u[2]
du[2] = -p[1]
end
function condition(u,t,integrator) # Event when event_f(u,t) == 0
u[1]
end
function affect!(integrator)
integrator.u[2] = -integrator.p[2]*integrator.u[2]
end
callback = ContinuousCallback(condition,affect!)
u0 = [50.0,0.0]
tspan = (0.0,15.0)
p = [9.8, 0.8]
prob = ODEProblem(f,u0,tspan,p)
sol = solve(prob,Tsit5(),callback=callback)
```
Here we have a friction coefficient of `0.8`. We want to refine this
coefficient to find the value so that the predicted height of the ball
at the endpoint is 20. We do this by minimizing a loss function against
the value 20:
```julia
function loss(θ)
sol = solve(prob,Tsit5(),p=[9.8,θ[1]],callback=callback)
target = 20.0
abs2(sol[end][1] - target)
end
loss([0.8])
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, [0.8])
@time res = Optimization.solve(optprob, PolyOpt(), [0.8])
@show res.u # [0.866554105436901]
```
This runs in about `0.091215 seconds (533.45 k allocations: 80.717 MiB)` and finds
an optimal drag coefficient.
## Note on Sensitivity Methods
The continuous adjoint sensitivities `BacksolveAdjoint`, `InterpolatingAdjoint`,
and `QuadratureAdjoint` are compatible with events for ODEs. `BacksolveAdjoint` and
`InterpolatingAdjoint` can also handle events for SDEs. Use `BacksolveAdjoint` if
the event terminates the time evolution and several states are saved. Currently,
the continuous adjoint sensitivities do not support multiple events per time point.
All methods based on discrete sensitivity analysis via automatic differentiation,
like `ReverseDiffAdjoint`, `TrackerAdjoint`, or `ForwardDiffSensitivity` are the methods
to use (and `ReverseDiffAdjoint` is demonstrated above), are compatible with events.
This applies to SDEs, DAEs, and DDEs as well.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 3070 | # Training Neural Networks in Hybrid Differential Equations
Hybrid differential equations are differential equations with implicit or
explicit discontinuities as specified by [callbacks](https://diffeq.sciml.ai/stable/features/callback_functions/).
In the following example, explicit dosing times are given for a pharmacometric
model and the universal differential equation is trained to uncover the missing
dynamical equations.
```julia
using DiffEqFlux, DifferentialEquations, Plots
u0 = Float32[2.; 0.]
datasize = 100
tspan = (0.0f0,10.5f0)
dosetimes = [1.0,2.0,4.0,8.0]
function affect!(integrator)
integrator.u = integrator.u.+1
end
cb_ = PresetTimeCallback(dosetimes,affect!,save_positions=(false,false))
function trueODEfunc(du,u,p,t)
du .= -u
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),callback=cb_,saveat=t))
dudt2 = Flux.Chain(Flux.Dense(2,50,tanh),
Flux.Dense(50,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
function dudt(du,u,p,t)
du[1:2] .= -u[1:2]
du[3:end] .= re(p)(u[1:2]) #re(p)(u[3:end])
end
z0 = Float32[u0;u0]
prob = ODEProblem(dudt,z0,tspan)
affect!(integrator) = integrator.u[1:2] .= integrator.u[3:end]
callback = PresetTimeCallback(dosetimes,affect!,save_positions=(false,false))
function predict_n_ode()
_prob = remake(prob,p=p)
Array(solve(_prob,Tsit5(),u0=z0,p=p,callback=callback,saveat=t,sensealg=ReverseDiffAdjoint()))[1:2,:]
#Array(solve(prob,Tsit5(),u0=z0,p=p,saveat=t))[1:2,:]
end
function loss_n_ode()
pred = predict_n_ode()
loss = sum(abs2,ode_data .- pred)
loss
end
loss_n_ode() # n_ode.p stores the initial parameters of the neural ODE
cba = function (;doplot=false) #callback function to observe training
pred = predict_n_ode()
display(sum(abs2,ode_data .- pred))
# plot current prediction against data
pl = scatter(t,ode_data[1,:],label="data")
scatter!(pl,t,pred[1,:],label="prediction")
display(plot(pl))
return false
end
cba()
ps = Flux.params(p)
data = Iterators.repeated((), 200)
Flux.train!(loss_n_ode, ps, data, ADAM(0.05), callback = cba)
```
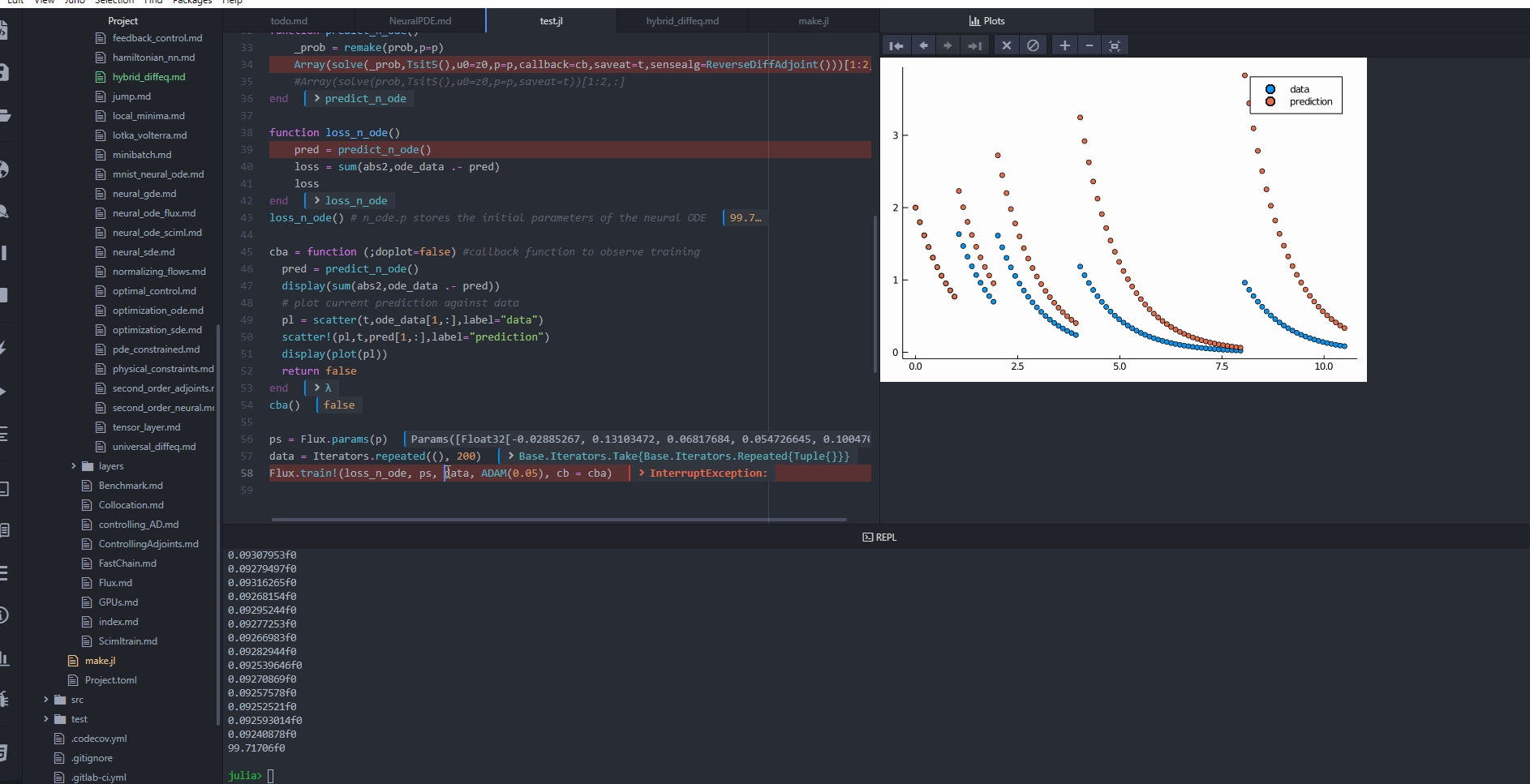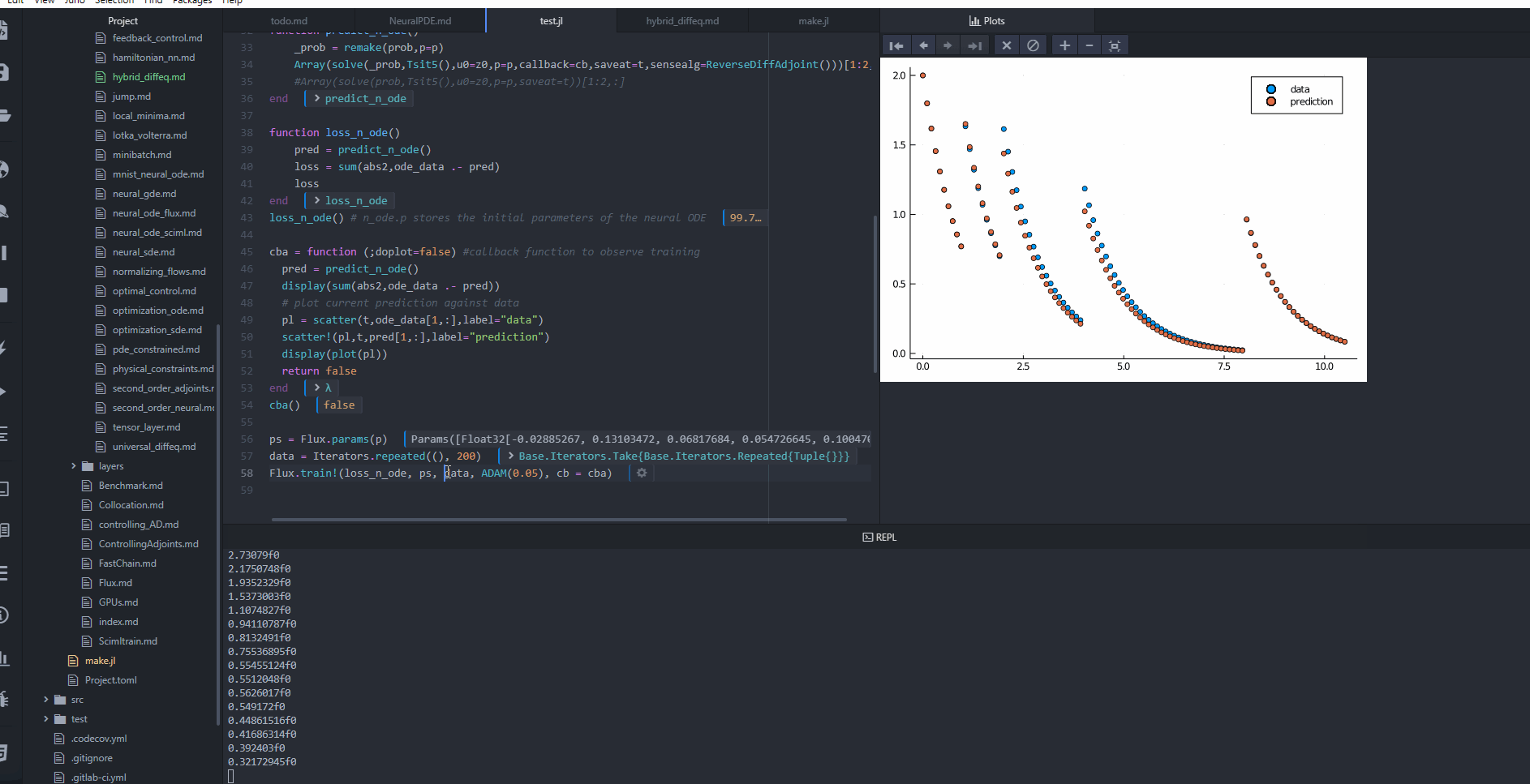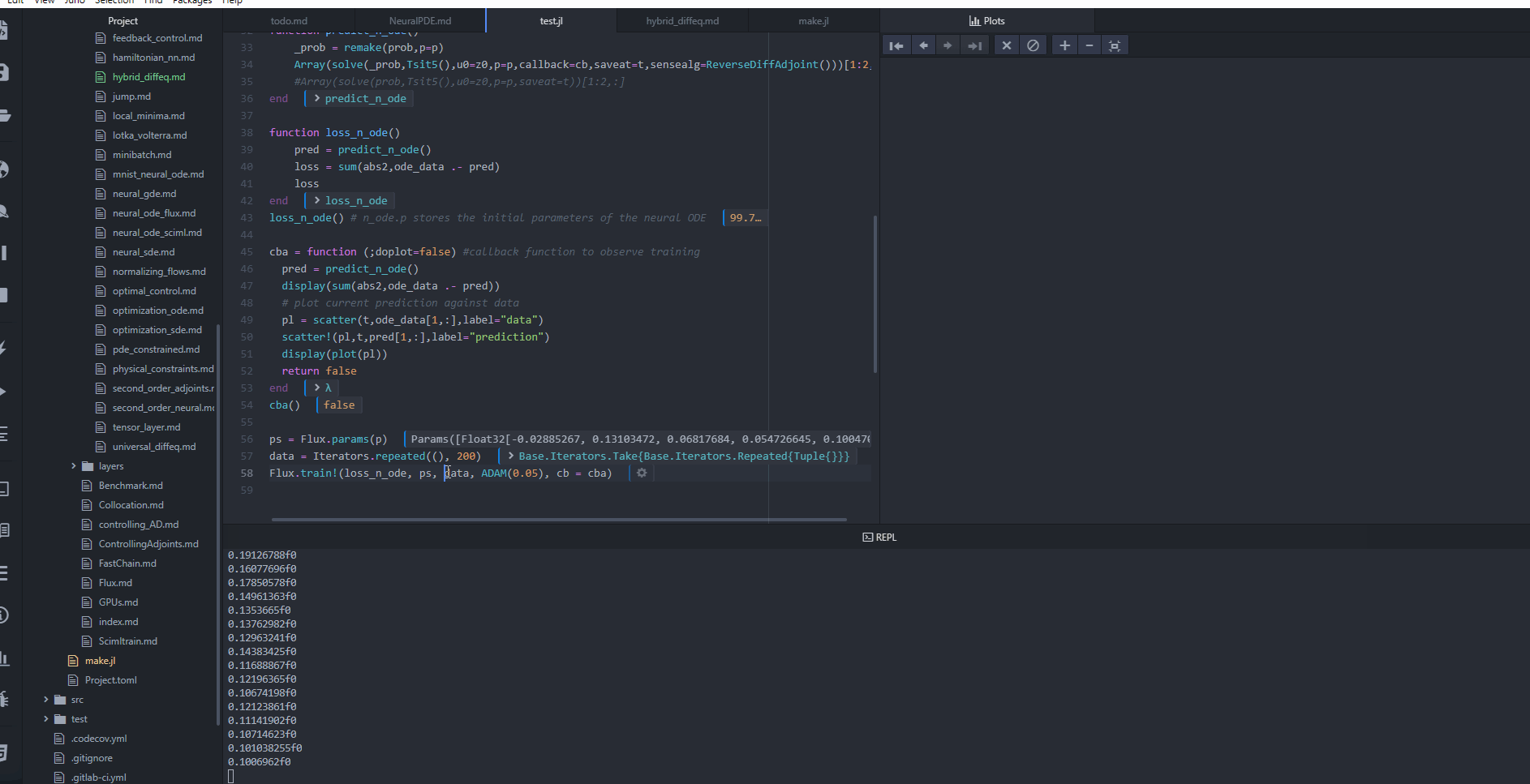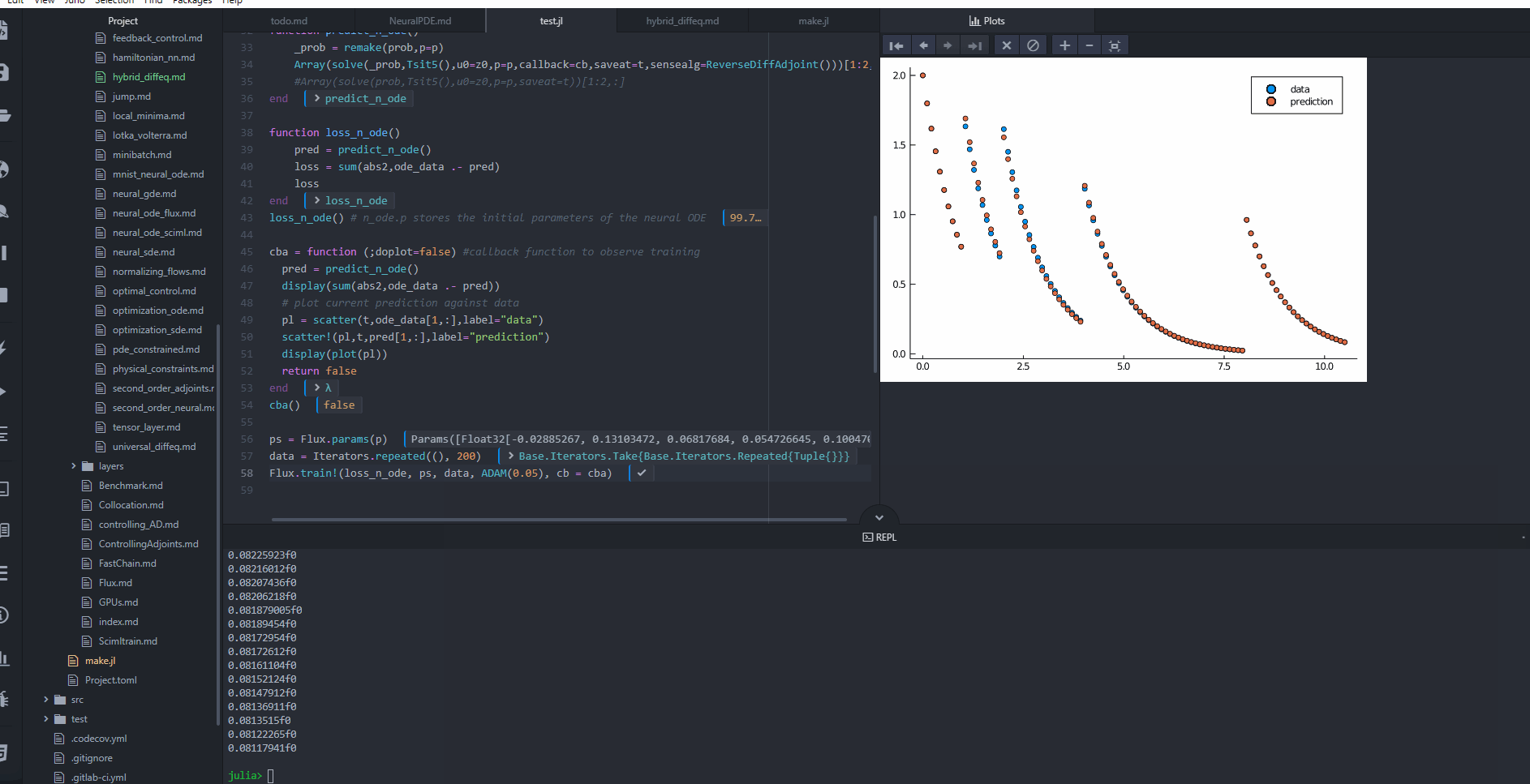
## Note on Sensitivity Methods
The continuous adjoint sensitivities `BacksolveAdjoint`, `InterpolatingAdjoint`,
and `QuadratureAdjoint` are compatible with events for ODEs. `BacksolveAdjoint` and
`InterpolatingAdjoint` can also handle events for SDEs. Use `BacksolveAdjoint` if
the event terminates the time evolution and several states are saved. Currently,
the continuous adjoint sensitivities do not support multiple events per time point.
All methods based on discrete sensitivity analysis via automatic differentiation,
like `ReverseDiffAdjoint`, `TrackerAdjoint`, or `ForwardDiffSensitivity` are the methods
to use (and `ReverseDiffAdjoint` is demonstrated above), are compatible with events.
This applies to SDEs, DAEs, and DDEs as well.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 14589 | # [Sensitivity Algorithms for Differential Equations with Automatic Differentiation (AD)](@id sensitivity_diffeq)
DiffEqSensitivity.jl's high level interface allows for specifying a
sensitivity algorithm (`sensealg`) to control the method by which
`solve` is differentiated in an automatic differentiation (AD)
context by a compatible AD library. The underlying algorithms then
use the direct interface methods, like `ODEForwardSensitivityProblem`
and `adjoint_sensitivities`, to compute the derivatives without
requiring the user to do any of the setup.
Current AD libraries whose calls are captured by the sensitivity
system are:
- [Zygote.jl](https://github.com/FluxML/Zygote.jl)
- [Diffractor.jl](https://github.com/JuliaDiff/Diffractor.jl)
## Using and Controlling Sensitivity Algorithms within AD
Take for example this simple differential equation solve on Lotka-Volterra:
```julia
using DiffEqSensitivity, OrdinaryDiffEq, Zygote
function fiip(du,u,p,t)
du[1] = dx = p[1]*u[1] - p[2]*u[1]*u[2]
du[2] = dy = -p[3]*u[2] + p[4]*u[1]*u[2]
end
p = [1.5,1.0,3.0,1.0]; u0 = [1.0;1.0]
prob = ODEProblem(fiip,u0,(0.0,10.0),p)
sol = solve(prob,Tsit5())
loss(u0,p) = sum(solve(prob,Tsit5(),u0=u0,p=p,saveat=0.1))
du0,dp = Zygote.gradient(loss,u0,p)
```
This will compute the gradient of the loss function "sum of the values of the
solution to the ODE at timepoints dt=0.1" using an adjoint method, where `du0`
is the derivative of the loss function with respect to the initial condition
and `dp` is the derivative of the loss function with respect to the parameters.
Because the gradient is calculated by `Zygote.gradient` and Zygote.jl is one of
the compatible AD libraries, this derivative calculation will be captured
by the `sensealg` system, and one of DiffEqSensitivity.jl's adjoint overloads
will be used to compute the derivative. By default, if the `sensealg` keyword
argument is not defined, then a smart polyalgorithm is used to automatically
determine the most appropriate method for a given equation.
Likewise, the `sensealg` argument can be given to directly control the method
by which the derivative is computed. For example:
```julia
loss(u0,p) = sum(solve(prob,Tsit5(),u0=u0,p=p,saveat=0.1))
du0,dp = Zygote.gradient(loss,u0,p)
```
## Choosing a Sensitivity Algorithm
There are two classes of algorithms: the continuous sensitivity analysis
methods, and the discrete sensitivity analysis methods (direct automatic
differentiation). Generally:
- [Continuous sensitivity analysis are more efficient while the discrete
sensitivity analysis is more stable](https://arxiv.org/abs/2001.04385)
(full discussion is in the appendix of that paper)
- Continuous sensitivity analysis methods only support a subset of
equations, which currently includes:
- ODEProblem (with mass matrices for differential-algebraic equations (DAEs)
- SDEProblem
- SteadyStateProblem / NonlinearProblem
- Discrete sensitivity analysis methods only support a subset of algorithms,
namely, the pure Julia solvers which are written generically.
For an analysis of which methods will be most efficient for computing the
solution derivatives for a given problem, consult our analysis
[in this arxiv paper](https://arxiv.org/abs/1812.01892). A general rule of thumb
is:
- `ForwardDiffSensitivity` is the fastest for differential equations with small
numbers of parameters (<100) and can be used on any differential equation
solver that is native Julia. If the chosen ODE solver is not compatible
with direct automatic differentiation, `ForwardSensitivty` may be used instead.
- Adjoint senstivity analysis is the fastest when the number of parameters is
sufficiently large. There are three configurations of note. Using
`QuadratureAdjoint` is the fastest but uses the most memory, `BacksolveAdjoint`
uses the least memory but on very stiff problems it may be unstable and
require a lot of checkpoints, while `InterpolatingAdjoint` is in the middle,
allowing checkpointing to control total memory use.
- The methods which use direct automatic differentiation (`ReverseDiffAdjoint`,
`TrackerAdjoint`, `ForwardDiffSensitivity`, and `ZygoteAdjoint`) support
the full range of DifferentialEquations.jl features (SDEs, DDEs, events, etc.),
but only work on native Julia solvers.
- For non-ODEs with large numbers of parameters, `TrackerAdjoint` in out-of-place
form may be the best performer on GPUs, and `ReverseDiffAdjoint`
- `TrackerAdjoint` is able to use a `TrackedArray` form with out-of-place
functions `du = f(u,p,t)` but requires an `Array{TrackedReal}` form for
`f(du,u,p,t)` mutating `du`. The latter has much more overhead, and should be
avoided if possible. Thus if solving non-ODEs with lots of parameters, using
`TrackerAdjoint` with an out-of-place definition may be the current best
option.
!!! note
Compatibility with direct automatic differentiation algorithms (`ForwardDiffSensitivity`,
`ReverseDiffAdjoint`, etc.) can be queried using the
`SciMLBase.isautodifferentiable(::SciMLAlgorithm)` trait function.
If the chosen algorithm is a continuous sensitivity analysis algorithm, then an `autojacvec`
argument can be given for choosing how the Jacobian-vector product (`J*v`) or vector-Jacobian
product (`J'*v`) calculation is computed. For the forward sensitivity methods, `autojacvec=true`
is the most efficient, though `autojacvec=false` is slightly less accurate but very close in
efficiency. For adjoint methods it's more complicated and dependent on the way that the user's
`f` function is implemented:
- `EnzymeVJP()` is the most efficient if it's applicable on your equation.
- If your function has no branching (no if statements) but uses mutation, `ReverseDiffVJP(true)`
will be the most efficient after Enzyme. Otherwise `ReverseDiffVJP()`, but you may wish to
proceed with eliminating mutation as without compilation enabled this can be slow.
- If your on the CPU or GPU and your function is very vectorized and has no mutation, choose `ZygoteVJP()`.
- Else fallback to `TrackerVJP()` if Zygote does not support the function.
## Special Notes on Non-ODE Differential Equation Problems
While all of the choices are compatible with ordinary differential
equations, specific notices apply to other forms:
### Differential-Algebraic Equations
We note that while all 3 are compatible with index-1 DAEs via the
[derivation in the universal differential equations paper](https://arxiv.org/abs/2001.04385)
(note the reinitialization), we do not recommend `BacksolveAdjoint`
one DAEs because the stiffness inherent in these problems tends to
cause major difficulties with the accuracy of the backwards solution
due to reinitialization of the algebraic variables.
### Stochastic Differential Equations
We note that all of the adjoints except `QuadratureAdjoint` are applicable
to stochastic differential equations.
### Delay Differential Equations
We note that only the discretize-then-optimize methods are applicable
to delay differential equations. Constant lag and variable lag
delay differential equation parameters can be estimated, but the lag
times themselves are unable to be estimated through these automatic
differentiation techniques.
### Hybrid Equations (Equations with events/callbacks) and Jump Equations
`ForwardDiffSensitivity` can differentiate code with callbacks when `convert_tspan=true`.
`ForwardSensitivity` is not compatible with hybrid equations. The shadowing methods are
not compatible with callbacks. All methods based on discrete adjoint sensitivity analysis
via automatic differentiation, like `ReverseDiffAdjoint`, `TrackerAdjoint`, or
`QuadratureAdjoint` are fully compatible with events. This applies to ODEs, SDEs, DAEs,
and DDEs. The continuous adjoint sensitivities `BacksolveAdjoint`, `InterpolatingAdjoint`,
and `QuadratureAdjoint` are compatible with events for ODEs. `BacksolveAdjoint` and
`InterpolatingAdjoint` can also handle events for SDEs. Use `BacksolveAdjoint` if
the event terminates the time evolution and several states are saved. Currently,
the continuous adjoint sensitivities do not support multiple events per time point.
## Manual VJPs
Note that when defining your differential equation the vjp can be
manually overwritten by providing the `AbstractSciMLFunction` definition
with a `vjp(u,p,t)` that returns a tuple `f(u,p,t),v->J*v` in the form of
[ChainRules.jl](https://www.juliadiff.org/ChainRulesCore.jl/stable/).
When this is done, the choice of `ZygoteVJP` will utilize your VJP
function during the internal steps of the adjoint. This is useful for
models where automatic differentiation may have trouble producing
optimal code. This can be paired with
[ModelingToolkit.jl](https://github.com/SciML/ModelingToolkit.jl)
for producing hyper-optimized, sparse, and parallel VJP functions utilizing
the automated symbolic conversions.
## Sensitivity Algorithms
The following algorithm choices exist for `sensealg`. See
[the sensitivity mathematics page](@ref sensitivity_math) for more details on
the definition of the methods.
```@docs
ForwardSensitivity
ForwardDiffSensitivity
BacksolveAdjoint
InterpolatingAdjoint
QuadratureAdjoint
ReverseDiffAdjoint
TrackerAdjoint
ZygoteAdjoint
ForwardLSS
AdjointLSS
NILSS
NILSAS
```
## Vector-Jacobian Product (VJP) Choices
```@docs
ZygoteVJP
EnzymeVJP
TrackerVJP
ReverseDiffVJP
```
## More Details on Sensitivity Algorithm Choices
The following section describes a bit more details to consider when choosing
a sensitivity algorithm.
### Optimize-then-Discretize
[The original neural ODE paper](https://arxiv.org/abs/1806.07366)
popularized optimize-then-discretize with O(1) adjoints via backsolve.
This is the methodology `BacksolveAdjoint`
When training non-stiff neural ODEs, `BacksolveAdjoint` with `ZygoteVJP`
is generally the fastest method. Additionally, this method does not
require storing the values of any intermediate points and is thus the
most memory efficient. However, `BacksolveAdjoint` is prone
to instabilities whenever the Lipschitz constant is sufficiently large,
like in stiff equations, PDE discretizations, and many other contexts,
so it is not used by default. When training a neural ODE for machine
learning applications, the user should try `BacksolveAdjoint` and see
if it is sufficiently accurate on their problem. More details on this
topic can be found in
[Stiff Neural Ordinary Differential Equations](https://aip.scitation.org/doi/10.1063/5.0060697)
Note that DiffEqFlux's implementation of `BacksolveAdjoint` includes
an extra feature `BacksolveAdjoint(checkpointing=true)` which mixes
checkpointing with `BacksolveAdjoint`. What this method does is that,
at `saveat` points, values from the forward pass are saved. Since the
reverse solve should numerically be the same as the forward pass, issues
with divergence of the reverse pass are mitigated by restarting the
reverse pass at the `saveat` value from the forward pass. This reduces
the divergence and can lead to better gradients at the cost of higher
memory usage due to having to save some values of the forward pass.
This can stabilize the adjoint in some applications, but for highly
stiff applications the divergence can be too fast for this to work in
practice.
To avoid the issues of backwards solving the ODE, `InterpolatingAdjoint`
and `QuadratureAdjoint` utilize information from the forward pass.
By default these methods utilize the [continuous solution](https://diffeq.sciml.ai/latest/basics/solution/#Interpolations-1)
provided by DifferentialEquations.jl in the calculations of the
adjoint pass. `QuadratureAdjoint` uses this to build a continuous
function for the solution of adjoint equation and then performs an
adaptive quadrature via [Quadrature.jl](https://github.com/SciML/Quadrature.jl),
while `InterpolatingAdjoint` appends the integrand to the ODE so it's
computed simultaneously to the Lagrange multiplier. When memory is
not an issue, we find that the `QuadratureAdjoint` approach tends to
be the most efficient as it has a significantly smaller adjoint
differential equation and the quadrature converges very fast, but this
form requires holding the full continuous solution of the adjoint which
can be a significant burden for large parameter problems. The
`InterpolatingAdjoint` is thus a compromise between memory efficiency
and compute efficiency, and is in the same spirit as [CVODES](https://computing.llnl.gov/projects/sundials).
However, if the memory cost of the `InterpolatingAdjoint` is too high,
checkpointing can be used via `InterpolatingAdjoint(checkpointing=true)`.
When this is used, the checkpoints default to `sol.t` of the forward
pass (i.e. the saved timepoints usually set by `saveat`). Then in the
adjoint, intervals of `sol.t[i-1]` to `sol.t[i]` are re-solved in order
to obtain a short interpolation which can be utilized in the adjoints.
This at most results in two full solves of the forward pass, but
dramatically reduces the computational cost while being a low-memory
format. This is the preferred method for highly stiff equations
when memory is an issue, i.e. stiff PDEs or large neural DAEs.
For forward-mode, the `ForwardSensitivty` is the version that performs
the optimize-then-discretize approach. In this case, `autojacvec` corresponds
to the method for computing `J*v` within the forward sensitivity equations,
which is either `true` or `false` for whether to use Jacobian-free
forward-mode AD (via ForwardDiff.jl) or Jacobian-free numerical
differentiation.
### Discretize-then-Optimize
In this approach the discretization is done first and then optimization
is done on the discretized system. While traditionally this can be
done discrete sensitivity analysis, this is can be equivalently done
by automatic differentiation on the solver itself. `ReverseDiffAdjoint`
performs reverse-mode automatic differentiation on the solver via
[ReverseDiff.jl](https://github.com/JuliaDiff/ReverseDiff.jl),
`ZygoteAdjoint` performs reverse-mode automatic
differentiation on the solver via
[Zygote.jl](https://github.com/FluxML/Zygote.jl), and `TrackerAdjoint`
performs reverse-mode automatic differentiation on the solver via
[Tracker.jl](https://github.com/FluxML/Tracker.jl). In addition,
`ForwardDiffSensitivty` performs forward-mode automatic differentiation
on the solver via [ForwardDiff.jl](https://github.com/JuliaDiff/ForwardDiff.jl).
We note that many studies have suggested that [this approach produces
more accurate gradients than the optimize-than-discretize approach](https://arxiv.org/abs/2005.13420)
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 264 | # [Direct Adjoint Sensitivities of Differential Equations](@id adjoint_sense)
## First Order Adjoint Sensitivities
```@docs
adjoint_sensitivities
```
## Second Order Adjoint Sensitivities
```@docs
second_order_sensitivities
second_order_sensitivity_product
``` | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 137 | # [Direct Forward Sensitivity Analysis of ODEs](@id forward_sense)
```@docs
ODEForwardSensitivityProblem
extract_local_sensitivities
``` | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 145 | # [Sensitivity Algorithms for Nonlinear Problems with Automatic Differentiation (AD)](@id sensitivity_nonlinear)
```@docs
SteadyStateAdjoint
``` | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 3790 | # Neural ODEs on GPUs
Note that the differential equation solvers will run on the GPU if the initial
condition is a GPU array. Thus, for example, we can define a neural ODE by hand
that runs on the GPU (if no GPU is available, the calculation defaults back to the CPU):
```julia
using DifferentialEquations, Lux, Optim, DiffEqFlux, DiffEqSensitivity
using Random
rng = Random.default_rng()
model_gpu = Lux.Chain(Lux.Dense(2, 50, tanh), Lux.Dense(50, 2)) |> gpu
p, st = Lux.setup(rng, model_gpu)
dudt!(u, p, t) = model_gpu(u, p, st)[1]
# Simulation interval and intermediary points
tspan = (0.0, 10.0)
tsteps = 0.0:0.1:10.0
u0 = Float32[2.0; 0.0] |> gpu
prob_gpu = ODEProblem(dudt!, u0, tspan, p)
# Runs on a GPU
sol_gpu = solve(prob_gpu, Tsit5(), saveat = tsteps)
```
Or we could directly use the neural ODE layer function, like:
```julia
prob_neuralode_gpu = NeuralODE(gpu(dudt2), tspan, Tsit5(), saveat = tsteps)
```
If one is using `Lux.Chain`, then the computation takes place on the GPU with
`f(x,p,st)` if `x`, `p` and `st` are on the GPU. This commonly looks like:
```julia
dudt2 = Lux.Chain(ActivationFunction(x -> x.^3),
Lux.Dense(2,50,tanh),
Lux.Dense(50,2))
u0 = Float32[2.; 0.] |> gpu
p, st = Lux.setup(rng, dudt2) |> gpu
dudt2_(u, p, t) = dudt2(u,p,st)[1]
# Simulation interval and intermediary points
tspan = (0.0, 10.0)
tsteps = 0.0:0.1:10.0
prob_gpu = ODEProblem(dudt2_, u0, tspan, p)
# Runs on a GPU
sol_gpu = solve(prob_gpu, Tsit5(), saveat = tsteps)
```
or via the NeuralODE struct:
```julia
prob_neuralode_gpu = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
prob_neuralode_gpu(u0,p,st)
```
## Neural ODE Example
Here is the full neural ODE example. Note that we use the `gpu` function so that the
same code works on CPUs and GPUs, dependent on `using CUDA`.
```julia
using Lux, DiffEqFlux, Optimization, OptimizationOptimJL, OrdinaryDiffEq, Optim, Plots, CUDA, DiffEqSensitivity, Random
CUDA.allowscalar(false) # Makes sure no slow operations are occuring
#rng for Lux.setup
rng = Random.default_rng()
# Generate Data
u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 1.5f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
# Make the data into a GPU-based array if the user has a GPU
ode_data = gpu(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = Lux.Chain(ActivationFunction(x -> x.^3),
Lux.Dense(2, 50, tanh),
Lux.Dense(50, 2))
u0 = Float32[2.0; 0.0] |> gpu
p,st = Lux.setup(rng, dudt2) |> gpu
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
function predict_neuralode(p)
gpu(prob_neuralode(u0,p,st)[1])
end
function loss_neuralode(p)
pred = predict_neuralode(p)
loss = sum(abs2, ode_data .- pred)
return loss, pred
end
# Callback function to observe training
list_plots = []
iter = 0
callback = function (p, l, pred; doplot = false)
global list_plots, iter
if iter == 0
list_plots = []
end
iter += 1
display(l)
# plot current prediction against data
plt = scatter(tsteps, Array(ode_data[1,:]), label = "data")
scatter!(plt, tsteps, Array(pred[1,:]), label = "prediction")
push!(list_plots, plt)
if doplot
display(plot(plt))
end
return false
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_neuralode(x), adtype)
optprob = Optimization.OptimizationProblem(optf, Lux.ComponentArray(p))
result_neuralode = Optimization.solve(optfunc,
ADAM(0.05),
callback = callback,
maxiters = 300)
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 7943 | # Training a Neural Ordinary Differential Equation with Mini-Batching
```julia
using DifferentialEquations, DiffEqFlux, Lux, Random, Plots
using IterTools: ncycle
rng = Random.default_rng()
function newtons_cooling(du, u, p, t)
temp = u[1]
k, temp_m = p
du[1] = dT = -k*(temp-temp_m)
end
function true_sol(du, u, p, t)
true_p = [log(2)/8.0, 100.0]
newtons_cooling(du, u, true_p, t)
end
ann = Lux.Chain(Lux.Dense(1,8,tanh), Lux.Dense(8,1,tanh))
θ, st = Lux.setup(rng, ann)
function dudt_(u,p,t)
ann(u, p, st)[1].* u
end
function predict_adjoint(time_batch)
_prob = remake(prob,u0=u0,p=θ)
Array(solve(_prob, Tsit5(), saveat = time_batch))
end
function loss_adjoint(batch, time_batch)
pred = predict_adjoint(time_batch)
sum(abs2, batch - pred)#, pred
end
u0 = Float32[200.0]
datasize = 30
tspan = (0.0f0, 3.0f0)
t = range(tspan[1], tspan[2], length=datasize)
true_prob = ODEProblem(true_sol, u0, tspan)
ode_data = Array(solve(true_prob, Tsit5(), saveat=t))
prob = ODEProblem{false}(dudt_, u0, tspan, θ)
k = 10
train_loader = Flux.Data.DataLoader((ode_data, t), batchsize = k)
for (x, y) in train_loader
@show x
@show y
end
numEpochs = 300
losses=[]
callback() = begin
l=loss_adjoint(ode_data, t)
push!(losses, l)
@show l
pred=predict_adjoint(t)
pl = scatter(t,ode_data[1,:],label="data", color=:black, ylim=(150,200))
scatter!(pl,t,pred[1,:],label="prediction", color=:darkgreen)
display(plot(pl))
false
end
opt=ADAM(0.05)
Flux.train!(loss_adjoint, Flux.params(θ), ncycle(train_loader,numEpochs), opt, callback=Flux.throttle(callback, 10))
#Now lets see how well it generalizes to new initial conditions
starting_temp=collect(10:30:250)
true_prob_func(u0)=ODEProblem(true_sol, [u0], tspan)
color_cycle=palette(:tab10)
pl=plot()
for (j,temp) in enumerate(starting_temp)
ode_test_sol = solve(ODEProblem(true_sol, [temp], (0.0f0,10.0f0)), Tsit5(), saveat=0.0:0.5:10.0)
ode_nn_sol = solve(ODEProblem{false}(dudt_, [temp], (0.0f0,10.0f0), θ))
scatter!(pl, ode_test_sol, var=(0,1), label="", color=color_cycle[j])
plot!(pl, ode_nn_sol, var=(0,1), label="", color=color_cycle[j], lw=2.0)
end
display(pl)
title!("Neural ODE for Newton's Law of Cooling: Test Data")
xlabel!("Time")
ylabel!("Temp")
# How to use MLDataUtils
using MLDataUtils
train_loader, _, _ = kfolds((ode_data, t))
@info "Now training using the MLDataUtils format"
Flux.train!(loss_adjoint, Flux.params(θ), ncycle(eachbatch(train_loader[1], k), numEpochs), opt, callback=Flux.throttle(callback, 10))
```
When training a neural network we need to find the gradient with respect to our data set. There are three main ways to partition our data when using a training algorithm like gradient descent: stochastic, batching and mini-batching. Stochastic gradient descent trains on a single random data point each epoch. This allows for the neural network to better converge to the global minimum even on noisy data but is computationally inefficient. Batch gradient descent trains on the whole data set each epoch and while computationally efficient is prone to converging to local minima. Mini-batching combines both of these advantages and by training on a small random "mini-batch" of the data each epoch can converge to the global minimum while remaining more computationally efficient than stochastic descent. Typically we do this by randomly selecting subsets of the data each epoch and use this subset to train on. We can also pre-batch the data by creating an iterator holding these randomly selected batches before beginning to train. The proper size for the batch can be determined experimentally. Let us see how to do this with Julia.
For this example we will use a very simple ordinary differential equation, newtons law of cooling. We can represent this in Julia like so.
```julia
using DifferentialEquations, DiffEqFlux, Lux, Random, Plots
using IterTools: ncycle
rng = Random.default_rng()
function newtons_cooling(du, u, p, t)
temp = u[1]
k, temp_m = p
du[1] = dT = -k*(temp-temp_m)
end
function true_sol(du, u, p, t)
true_p = [log(2)/8.0, 100.0]
newtons_cooling(du, u, true_p, t)
end
```
Now we define a neural-network using a linear approximation with 1 hidden layer of 8 neurons.
```julia
ann = Lux.Chain(Lux.Dense(1,8,tanh), Lux.Dense(8,1,tanh))
θ, st = Lux.setup(rng, ann)
function dudt_(u,p,t)
ann(u, p, st)[1].* u
end
```
From here we build a loss function around it.
```julia
function predict_adjoint(time_batch)
_prob = remake(prob, u0=u0, p=θ)
Array(solve(_prob, Tsit5(), saveat = time_batch))
end
function loss_adjoint(batch, time_batch)
pred = predict_adjoint(time_batch)
sum(abs2, batch - pred)#, pred
end
```
To add support for batches of size `k` we use `Flux.Data.DataLoader`. To use this we pass in the `ode_data` and `t` as the 'x' and 'y' data to batch respectively. The parameter `batchsize` controls the size of our batches. We check our implementation by iterating over the batched data.
```julia
u0 = Float32[200.0]
datasize = 30
tspan = (0.0f0, 3.0f0)
t = range(tspan[1], tspan[2], length=datasize)
true_prob = ODEProblem(true_sol, u0, tspan)
ode_data = Array(solve(true_prob, Tsit5(), saveat=t))
prob = ODEProblem{false}(dudt_, u0, tspan, θ)
k = 10
train_loader = Flux.Data.DataLoader((ode_data, t), batchsize = k)
for (x, y) in train_loader
@show x
@show y
end
#x = Float32[200.0 199.55284 199.1077 198.66454 198.22334 197.78413 197.3469 196.9116 196.47826 196.04686]
#y = Float32[0.0, 0.05172414, 0.10344828, 0.15517241, 0.20689656, 0.25862068, 0.31034482, 0.36206895, 0.41379312, 0.46551725]
#x = Float32[195.61739 195.18983 194.76418 194.34044 193.9186 193.49864 193.08057 192.66435 192.25 191.8375]
#y = Float32[0.51724136, 0.5689655, 0.62068963, 0.67241377, 0.7241379, 0.7758621, 0.82758623, 0.87931037, 0.9310345, 0.98275864]
#x = Float32[191.42683 191.01802 190.61102 190.20586 189.8025 189.40094 189.00119 188.60321 188.20702 187.8126]
#y = Float32[1.0344827, 1.0862069, 1.137931, 1.1896552, 1.2413793, 1.2931035, 1.3448275, 1.3965517, 1.4482758, 1.5]
```
Now we train the neural network with a user defined call back function to display loss and the graphs with a maximum of 300 epochs.
```julia
numEpochs = 300
losses=[]
callback() = begin
l=loss_adjoint(ode_data, t)
push!(losses, l)
@show l
pred=predict_adjoint(t)
pl = scatter(t,ode_data[1,:],label="data", color=:black, ylim=(150,200))
scatter!(pl,t,pred[1,:],label="prediction", color=:darkgreen)
display(plot(pl))
false
end
opt=ADAM(0.05)
Flux.train!(loss_adjoint, Flux.params(θ), ncycle(train_loader,numEpochs), opt, callback=Flux.throttle(callback, 10))
```
Finally we can see how well our trained network will generalize to new initial conditions.
```julia
starting_temp=collect(10:30:250)
true_prob_func(u0)=ODEProblem(true_sol, [u0], tspan)
color_cycle=palette(:tab10)
pl=plot()
for (j,temp) in enumerate(starting_temp)
ode_test_sol = solve(ODEProblem(true_sol, [temp], (0.0f0,10.0f0)), Tsit5(), saveat=0.0:0.5:10.0)
ode_nn_sol = solve(ODEProblem{false}(dudt_, [temp], (0.0f0,10.0f0), θ))
scatter!(pl, ode_test_sol, var=(0,1), label="", color=color_cycle[j])
plot!(pl, ode_nn_sol, var=(0,1), label="", color=color_cycle[j], lw=2.0)
end
display(pl)
title!("Neural ODE for Newton's Law of Cooling: Test Data")
xlabel!("Time")
ylabel!("Temp")
```
We can also minibatch using tools from `MLDataUtils`. To do this we need to slightly change our implementation and is shown below again with a batch size of k and the same number of epochs.
```julia
using MLDataUtils
train_loader, _, _ = kfolds((ode_data, t))
@info "Now training using the MLDataUtils format"
Flux.train!(loss_adjoint, Flux.params(θ), ncycle(eachbatch(train_loader[1], k), numEpochs), opt, callback=Flux.throttle(callback, 10))
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 15180 | # Convolutional Neural ODE MNIST Classifier on GPU
Training a Convolutional Neural Net Classifier for **MNIST** using a neural
ordinary differential equation **NN-ODE** on **GPUs** with **Minibatching**.
(Step-by-step description below)
```julia
using DiffEqFlux, DifferentialEquations, Printf
using Flux.Losses: logitcrossentropy
using Flux.Data: DataLoader
using MLDatasets
using MLDataUtils: LabelEnc, convertlabel, stratifiedobs
using CUDA
CUDA.allowscalar(false)
function loadmnist(batchsize = bs, train_split = 0.9)
# Use MLDataUtils LabelEnc for natural onehot conversion
onehot(labels_raw) = convertlabel(LabelEnc.OneOfK, labels_raw,
LabelEnc.NativeLabels(collect(0:9)))
# Load MNIST
imgs, labels_raw = MNIST.traindata();
# Process images into (H,W,C,BS) batches
x_data = Float32.(reshape(imgs, size(imgs,1), size(imgs,2), 1, size(imgs,3)))
y_data = onehot(labels_raw)
(x_train, y_train), (x_test, y_test) = stratifiedobs((x_data, y_data),
p = train_split)
return (
# Use Flux's DataLoader to automatically minibatch and shuffle the data
DataLoader(gpu.(collect.((x_train, y_train))); batchsize = batchsize,
shuffle = true),
# Don't shuffle the test data
DataLoader(gpu.(collect.((x_test, y_test))); batchsize = batchsize,
shuffle = false)
)
end
# Main
const bs = 128
const train_split = 0.9
train_dataloader, test_dataloader = loadmnist(bs, train_split);
down = Flux.Chain(Flux.Conv((3, 3), 1=>64, relu, stride = 1), Flux.GroupNorm(64, 64),
Flux.Conv((4, 4), 64=>64, relu, stride = 2, pad=1), Flux.GroupNorm(64, 64),
Flux.Conv((4, 4), 64=>64, stride = 2, pad = 1)) |>gpu
dudt = Flux.Chain(Flux.Conv((3, 3), 64=>64, tanh, stride=1, pad=1),
Flux.Conv((3, 3), 64=>64, tanh, stride=1, pad=1)) |>gpu
fc = Flux.Chain(Flux.GroupNorm(64, 64), x -> relu.(x), Flux.MeanPool((6, 6)),
x -> reshape(x, (64, :)), Flux.Dense(64,10)) |> gpu
nn_ode = NeuralODE(dudt, (0.f0, 1.f0), Tsit5(),
save_everystep = false,
reltol = 1e-3, abstol = 1e-3,
save_start = false) |> gpu
function DiffEqArray_to_Array(x)
xarr = gpu(x)
return xarr[:,:,:,:,1]
end
# Build our over-all model topology
model = Flux.Chain(down, # (28, 28, 1, BS) -> (6, 6, 64, BS)
nn_ode, # (6, 6, 64, BS) -> (6, 6, 64, BS, 1)
DiffEqArray_to_Array, # (6, 6, 64, BS, 1) -> (6, 6, 64, BS)
fc) # (6, 6, 64, BS) -> (10, BS)
# To understand the intermediate NN-ODE layer, we can examine it's dimensionality
img, lab = train_dataloader.data[1][:, :, :, 1:1], train_dataloader.data[2][:, 1:1]
x_d = down(img)
# We can see that we can compute the forward pass through the NN topology
# featuring an NNODE layer.
x_m = model(img)
classify(x) = argmax.(eachcol(x))
function accuracy(model, data; n_batches = 100)
total_correct = 0
total = 0
for (i, (x, y)) in enumerate(data)
# Only evaluate accuracy for n_batches
i > n_batches && break
target_class = classify(cpu(y))
predicted_class = classify(cpu(model(x)))
total_correct += sum(target_class .== predicted_class)
total += length(target_class)
end
return total_correct / total
end
# burn in accuracy
accuracy(model, train_dataloader)
loss(x, y) = logitcrossentropy(model(x), y)
# burn in loss
loss(img, lab)
opt = ADAM(0.05)
iter = 0
callback() = begin
global iter += 1
# Monitor that the weights do infact update
# Every 10 training iterations show accuracy
if iter % 10 == 1
train_accuracy = accuracy(model, train_dataloader) * 100
test_accuracy = accuracy(model, test_dataloader;
n_batches = length(test_dataloader)) * 100
@printf("Iter: %3d || Train Accuracy: %2.3f || Test Accuracy: %2.3f\n",
iter, train_accuracy, test_accuracy)
end
end
Flux.train!(loss, Flux.params(down, nn_ode.p, fc), train_dataloader, opt, callback = callback)
```
## Step-by-Step Description
### Load Packages
```julia
using DiffEqFlux, DifferentialEquations, Printf
using Flux.Losses: logitcrossentropy
using Flux.Data: DataLoader
using MLDatasets
using MLDataUtils: LabelEnc, convertlabel, stratifiedobs
```
### GPU
A good trick used here:
```julia
using CUDA
CUDA.allowscalar(false)
```
Ensures that only optimized kernels are called when using the GPU.
Additionally, the `gpu` function is shown as a way to translate models and data over to the GPU.
Note that this function is CPU-safe, so if the GPU is disabled or unavailable, this
code will fallback to the CPU.
### Load MNIST Dataset into Minibatches
The preprocessing is done in `loadmnist` where the raw MNIST data is split into features `x_train`
and labels `y_train` by specifying batchsize `bs`. The function `convertlabel` will then transform
the current labels (`labels_raw`) from numbers 0 to 9 (`LabelEnc.NativeLabels(collect(0:9))`) into
one hot encoding (`LabelEnc.OneOfK`).
Features are reshaped into format **[Height, Width, Color, BatchSize]** or in this case **[28, 28, 1, 128]**
meaning that every minibatch will contain 128 images with a single color channel of 28x28 pixels.
The entire dataset of 60,000 images is split into the train and test dataset, ensuring a balanced ratio
of labels. These splits are then passed to Flux's DataLoader. This automatically minibatches both the images and
labels. Additionally, it allows us to shuffle the train dataset in each epoch while keeping the order of the
test data the same.
```julia
function loadmnist(batchsize = bs, train_split = 0.9)
# Use MLDataUtils LabelEnc for natural onehot conversion
onehot(labels_raw) = convertlabel(LabelEnc.OneOfK, labels_raw,
LabelEnc.NativeLabels(collect(0:9)))
# Load MNIST
imgs, labels_raw = MNIST.traindata();
# Process images into (H,W,C,BS) batches
x_data = Float32.(reshape(imgs, size(imgs,1), size(imgs,2), 1, size(imgs,3)))
y_data = onehot(labels_raw)
(x_train, y_train), (x_test, y_test) = stratifiedobs((x_data, y_data),
p = train_split)
return (
# Use Flux's DataLoader to automatically minibatch and shuffle the data
DataLoader(gpu.(collect.((x_train, y_train))); batchsize = batchsize,
shuffle = true),
# Don't shuffle the test data
DataLoader(gpu.(collect.((x_test, y_test))); batchsize = batchsize,
shuffle = false)
)
end
```
and then loaded from main:
```julia
# Main
const bs = 128
const train_split = 0.9
train_dataloader, test_dataloader = loadmnist(bs, train_split)
```
### Layers
The Neural Network requires passing inputs sequentially through multiple layers. We use
`Chain` which allows inputs to functions to come from previous layer and sends the outputs
to the next. Four different sets of layers are used here:
```julia
down = Flux.Chain(Flux.Conv((3, 3), 1=>64, relu, stride = 1), Flux.GroupNorm(64, 64),
Flux.Conv((4, 4), 64=>64, relu, stride = 2, pad=1), Flux.GroupNorm(64, 64),
Flux.Conv((4, 4), 64=>64, stride = 2, pad = 1)) |>gpu
dudt = Flux.Chain(Flux.Conv((3, 3), 64=>64, tanh, stride=1, pad=1),
Flux.Conv((3, 3), 64=>64, tanh, stride=1, pad=1)) |>gpu
fc = Flux.Chain(Flux.GroupNorm(64, 64), x -> relu.(x), Flux.MeanPool((6, 6)),
x -> reshape(x, (64, :)), Flux.Dense(64,10)) |> gpu
nn_ode = NeuralODE(dudt, (0.f0, 1.f0), Tsit5(),
save_everystep = false,
reltol = 1e-3, abstol = 1e-3,
save_start = false) |> gpu
```
`down`: This layer downsamples our images into `6 x 6 x 64` dimensional features.
It takes a 28 x 28 image, and passes it through a convolutional neural network
layer with `relu` activation
`nn`: A 2 layer Convolutional Neural Network Chain with `tanh` activation which is used to model
our differential equation
`nn_ode`: ODE solver layer
`fc`: The final fully connected layer which maps our learned features to the probability of
the feature vector of belonging to a particular class
`gpu`: A utility function which transfers our model to GPU, if one is available
### Array Conversion
When using `NeuralODE`, we can use the following function as a cheap conversion of `DiffEqArray`
from the ODE solver into a Matrix that can be used in the following layer:
```julia
function DiffEqArray_to_Array(x)
xarr = gpu(x)
return xarr[:,:,:,:,1]
end
```
For CPU: If this function does not automatically fallback to CPU when no GPU is present, we can
change `gpu(x)` with `Array(x)`.
### Build Topology
Next we connect all layers together in a single chain:
```julia
# Build our over-all model topology
model = Flux.Chain(down, # (28, 28, 1, BS) -> (6, 6, 64, BS)
nn_ode, # (6, 6, 64, BS) -> (6, 6, 64, BS, 1)
DiffEqArray_to_Array, # (6, 6, 64, BS, 1) -> (6, 6, 64, BS)
fc) # (6, 6, 64, BS) -> (10, BS)
```
There are a few things we can do to examine the inner workings of our neural network:
```julia
img, lab = train_dataloader.data[1][:, :, :, 1:1], train_dataloader.data[2][:, 1:1]
# To understand the intermediate NN-ODE layer, we can examine it's dimensionality
x_d = down(img)
# We can see that we can compute the forward pass through the NN topology
# featuring an NNODE layer.
x_m = model(img)
```
This can also be built without the NN-ODE by replacing `nn-ode` with a simple `nn`:
```julia
# We can also build the model topology without a NN-ODE
m_no_ode = Flux.Chain(down, nn, fc) |> gpu
x_m = m_no_ode(img)
```
### Prediction
To convert the classification back into readable numbers, we use `classify` which returns the
prediction by taking the arg max of the output for each column of the minibatch:
```julia
classify(x) = argmax.(eachcol(x))
```
### Accuracy
We then evaluate the accuracy on `n_batches` at a time through the entire network:
```julia
function accuracy(model, data; n_batches = 100)
total_correct = 0
total = 0
for (i, (x, y)) in enumerate(data)
# Only evaluate accuracy for n_batches
i > n_batches && break
target_class = classify(cpu(y))
predicted_class = classify(cpu(model(x)))
total_correct += sum(target_class .== predicted_class)
total += length(target_class)
end
return total_correct / total
end
# burn in accuracy
accuracy(model, train_dataloader)
```
### Training Parameters
Once we have our model, we can train our neural network by backpropagation using `Flux.train!`.
This function requires **Loss**, **Optimizer** and **Callback** functions.
#### Loss
**Cross Entropy** is the loss function computed here which applies a **Softmax** operation on the
final output of our model. `logitcrossentropy` takes in the prediction from our
model `model(x)` and compares it to actual output `y`:
```julia
loss(x, y) = logitcrossentropy(model(x), y)
# burn in loss
loss(img, lab)
```
#### Optimizer
`ADAM` is specified here as our optimizer with a **learning rate of 0.05**:
```julia
opt = ADAM(0.05)
```
#### CallBack
This callback function is used to print both the training and testing accuracy after
10 training iterations:
```julia
callback() = begin
global iter += 1
# Monitor that the weights update
# Every 10 training iterations show accuracy
if iter % 10 == 1
train_accuracy = accuracy(model, train_dataloader) * 100
test_accuracy = accuracy(model, test_dataloader;
n_batches = length(test_dataloader)) * 100
@printf("Iter: %3d || Train Accuracy: %2.3f || Test Accuracy: %2.3f\n",
iter, train_accuracy, test_accuracy)
end
end
```
### Train
To train our model, we select the appropriate trainable parameters of our network with `params`.
In our case, backpropagation is required for `down`, `nn_ode` and `fc`. Notice that the parameters
for Neural ODE is given by `nn_ode.p`:
```julia
# Train the NN-ODE and monitor the loss and weights.
Flux.train!(loss, Flux.params(down, nn_ode.p, fc), train_dataloader, opt, callback = callback)
```
### Expected Output
```julia
Iter: 1 || Train Accuracy: 8.453 || Test Accuracy: 8.883
Iter: 11 || Train Accuracy: 14.773 || Test Accuracy: 14.967
Iter: 21 || Train Accuracy: 24.383 || Test Accuracy: 24.433
Iter: 31 || Train Accuracy: 38.820 || Test Accuracy: 38.000
Iter: 41 || Train Accuracy: 30.852 || Test Accuracy: 31.350
Iter: 51 || Train Accuracy: 29.852 || Test Accuracy: 29.433
Iter: 61 || Train Accuracy: 45.195 || Test Accuracy: 45.217
Iter: 71 || Train Accuracy: 70.336 || Test Accuracy: 68.850
Iter: 81 || Train Accuracy: 76.250 || Test Accuracy: 75.783
Iter: 91 || Train Accuracy: 80.867 || Test Accuracy: 81.017
Iter: 101 || Train Accuracy: 86.398 || Test Accuracy: 85.317
Iter: 111 || Train Accuracy: 90.852 || Test Accuracy: 90.650
Iter: 121 || Train Accuracy: 93.477 || Test Accuracy: 92.550
Iter: 131 || Train Accuracy: 93.320 || Test Accuracy: 92.483
Iter: 141 || Train Accuracy: 94.273 || Test Accuracy: 93.567
Iter: 151 || Train Accuracy: 94.531 || Test Accuracy: 93.583
Iter: 161 || Train Accuracy: 94.992 || Test Accuracy: 94.067
Iter: 171 || Train Accuracy: 95.398 || Test Accuracy: 94.883
Iter: 181 || Train Accuracy: 96.945 || Test Accuracy: 95.633
Iter: 191 || Train Accuracy: 96.430 || Test Accuracy: 95.750
Iter: 201 || Train Accuracy: 96.859 || Test Accuracy: 95.983
Iter: 211 || Train Accuracy: 97.359 || Test Accuracy: 96.500
Iter: 221 || Train Accuracy: 96.586 || Test Accuracy: 96.133
Iter: 231 || Train Accuracy: 96.992 || Test Accuracy: 95.833
Iter: 241 || Train Accuracy: 97.148 || Test Accuracy: 95.950
Iter: 251 || Train Accuracy: 96.422 || Test Accuracy: 95.950
Iter: 261 || Train Accuracy: 96.094 || Test Accuracy: 95.633
Iter: 271 || Train Accuracy: 96.719 || Test Accuracy: 95.767
Iter: 281 || Train Accuracy: 96.719 || Test Accuracy: 96.000
Iter: 291 || Train Accuracy: 96.609 || Test Accuracy: 95.817
Iter: 301 || Train Accuracy: 96.656 || Test Accuracy: 96.033
Iter: 311 || Train Accuracy: 97.594 || Test Accuracy: 96.500
Iter: 321 || Train Accuracy: 97.633 || Test Accuracy: 97.083
Iter: 331 || Train Accuracy: 98.008 || Test Accuracy: 97.067
Iter: 341 || Train Accuracy: 98.070 || Test Accuracy: 97.150
Iter: 351 || Train Accuracy: 97.875 || Test Accuracy: 97.050
Iter: 361 || Train Accuracy: 96.922 || Test Accuracy: 96.500
Iter: 371 || Train Accuracy: 97.188 || Test Accuracy: 96.650
Iter: 381 || Train Accuracy: 97.820 || Test Accuracy: 96.783
Iter: 391 || Train Accuracy: 98.156 || Test Accuracy: 97.567
Iter: 401 || Train Accuracy: 98.250 || Test Accuracy: 97.367
Iter: 411 || Train Accuracy: 97.969 || Test Accuracy: 97.267
Iter: 421 || Train Accuracy: 96.555 || Test Accuracy: 95.667
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 14261 | # [GPU-based MNIST Neural ODE Classifier](@id mnist)
Training a classifier for **MNIST** using a neural ordinary differential equation **NN-ODE**
on **GPUs** with **Minibatching**.
(Step-by-step description below)
```julia
using DiffEqFlux, DifferentialEquations, NNlib, MLDataUtils, Printf
using Flux.Losses: logitcrossentropy
using Flux.Data: DataLoader
using MLDatasets
using CUDA
CUDA.allowscalar(false)
function loadmnist(batchsize = bs, train_split = 0.9)
# Use MLDataUtils LabelEnc for natural onehot conversion
onehot(labels_raw) = convertlabel(LabelEnc.OneOfK, labels_raw,
LabelEnc.NativeLabels(collect(0:9)))
# Load MNIST
imgs, labels_raw = MNIST.traindata();
# Process images into (H,W,C,BS) batches
x_data = Float32.(reshape(imgs, size(imgs,1), size(imgs,2), 1, size(imgs,3)))
y_data = onehot(labels_raw)
(x_train, y_train), (x_test, y_test) = stratifiedobs((x_data, y_data),
p = train_split)
return (
# Use Flux's DataLoader to automatically minibatch and shuffle the data
DataLoader(gpu.(collect.((x_train, y_train))); batchsize = batchsize,
shuffle = true),
# Don't shuffle the test data
DataLoader(gpu.(collect.((x_test, y_test))); batchsize = batchsize,
shuffle = false)
)
end
# Main
const bs = 128
const train_split = 0.9
train_dataloader, test_dataloader = loadmnist(bs, train_split)
down = Flux.Chain(Flux.flatten, Flux.Dense(784, 20, tanh)) |> gpu
nn = Flux.Chain(Flux.Dense(20, 10, tanh),
Flux.Dense(10, 10, tanh),
Flux.Dense(10, 20, tanh)) |> gpu
nn_ode = NeuralODE(nn, (0.f0, 1.f0), Tsit5(),
save_everystep = false,
reltol = 1e-3, abstol = 1e-3,
save_start = false) |> gpu
fc = Flux.Chain(Flux.Dense(20, 10)) |> gpu
function DiffEqArray_to_Array(x)
xarr = gpu(x)
return reshape(xarr, size(xarr)[1:2])
end
# Build our overall model topology
model = Flux.Chain(down,
nn_ode,
DiffEqArray_to_Array,
fc) |> gpu;
# To understand the intermediate NN-ODE layer, we can examine it's dimensionality
img, lab = train_dataloader.data[1][:, :, :, 1:1], train_dataloader.data[2][:, 1:1]
x_d = down(img)
# We can see that we can compute the forward pass through the NN topology
# featuring an NNODE layer.
x_m = model(img)
classify(x) = argmax.(eachcol(x))
function accuracy(model, data; n_batches = 100)
total_correct = 0
total = 0
for (i, (x, y)) in enumerate(collect(data))
# Only evaluate accuracy for n_batches
i > n_batches && break
target_class = classify(cpu(y))
predicted_class = classify(cpu(model(x)))
total_correct += sum(target_class .== predicted_class)
total += length(target_class)
end
return total_correct / total
end
# burn in accuracy
accuracy(model, train_dataloader)
loss(x, y) = logitcrossentropy(model(x), y)
# burn in loss
loss(img, lab)
opt = ADAM(0.05)
iter = 0
callback() = begin
global iter += 1
# Monitor that the weights do infact update
# Every 10 training iterations show accuracy
if iter % 10 == 1
train_accuracy = accuracy(model, train_dataloader) * 100
test_accuracy = accuracy(model, test_dataloader;
n_batches = length(test_dataloader)) * 100
@printf("Iter: %3d || Train Accuracy: %2.3f || Test Accuracy: %2.3f\n",
iter, train_accuracy, test_accuracy)
end
end
# Train the NN-ODE and monitor the loss and weights.
Flux.train!(loss, Flux.params(down, nn_ode.p, fc), train_dataloader, opt, callback = callback)
```
## Step-by-Step Description
### Load Packages
```julia
using DiffEqFlux, DifferentialEquations, NNlib, MLDataUtils, Printf
using Flux.Losses: logitcrossentropy
using Flux.Data: DataLoader
using MLDatasets
```
### GPU
A good trick used here:
```julia
using CUDA
CUDA.allowscalar(false)
```
ensures that only optimized kernels are called when using the GPU.
Additionally, the `gpu` function is shown as a way to translate models and data over to the GPU.
Note that this function is CPU-safe, so if the GPU is disabled or unavailable, this
code will fallback to the CPU.
### Load MNIST Dataset into Minibatches
The preprocessing is done in `loadmnist` where the raw MNIST data is split into features `x_train`
and labels `y_train` by specifying batchsize `bs`. The function `convertlabel` will then transform
the current labels (`labels_raw`) from numbers 0 to 9 (`LabelEnc.NativeLabels(collect(0:9))`) into
one hot encoding (`LabelEnc.OneOfK`).
Features are reshaped into format **[Height, Width, Color, BatchSize]** or in this case **[28, 28, 1, 128]**
meaning that every minibatch will contain 128 images with a single color channel of 28x28 pixels.
The entire dataset of 60,000 images is split into the train and test dataset, ensuring a balanced ratio
of labels. These splits are then passed to Flux's DataLoader. This automatically minibatches both the images and
labels. Additionally, it allows us to shuffle the train dataset in each epoch while keeping the order of the
test data the same.
```julia
function loadmnist(batchsize = bs, train_split = 0.9)
# Use MLDataUtils LabelEnc for natural onehot conversion
onehot(labels_raw) = convertlabel(LabelEnc.OneOfK, labels_raw,
LabelEnc.NativeLabels(collect(0:9)))
# Load MNIST
imgs, labels_raw = MNIST.traindata();
# Process images into (H,W,C,BS) batches
x_data = Float32.(reshape(imgs, size(imgs,1), size(imgs,2), 1, size(imgs,3)))
y_data = onehot(labels_raw)
(x_train, y_train), (x_test, y_test) = stratifiedobs((x_data, y_data),
p = train_split)
return (
# Use Flux's DataLoader to automatically minibatch and shuffle the data
DataLoader(gpu.(collect.((x_train, y_train))); batchsize = batchsize,
shuffle = true),
# Don't shuffle the test data
DataLoader(gpu.(collect.((x_test, y_test))); batchsize = batchsize,
shuffle = false)
)
end
```
and then loaded from main:
```
# Main
const bs = 128
const train_split = 0.9
train_dataloader, test_dataloader = loadmnist(bs, train_split)
```
### Layers
The Neural Network requires passing inputs sequentially through multiple layers. We use
`Chain` which allows inputs to functions to come from previous layer and sends the outputs
to the next. Four different sets of layers are used here:
```julia
down = Flux.Chain(Flux.flatten, Flux.Dense(784, 20, tanh)) |> gpu
nn = Flux.Chain(Flux.Dense(20, 10, tanh),
Flux.Dense(10, 10, tanh),
Flux.Dense(10, 20, tanh)) |> gpu
nn_ode = NeuralODE(nn, (0.f0, 1.f0), Tsit5(),
save_everystep = false,
reltol = 1e-3, abstol = 1e-3,
save_start = false) |> gpu
fc = Flux.Chain(Flux.Dense(20, 10)) |> gpu
```
`down`: This layer downsamples our images into a 20 dimensional feature vector.
It takes a 28 x 28 image, flattens it, and then passes it through a fully connected
layer with `tanh` activation
`nn`: A 3 layers Deep Neural Network Chain with `tanh` activation which is used to model
our differential equation
`nn_ode`: ODE solver layer
`fc`: The final fully connected layer which maps our learned feature vector to the probability of
the feature vector of belonging to a particular class
`|> gpu`: An utility function which transfers our model to GPU, if it is available
### Array Conversion
When using `NeuralODE`, this function converts the ODESolution's `DiffEqArray` to
a Matrix (CuArray), and reduces the matrix from 3 to 2 dimensions for use in the next layer.
```julia
function DiffEqArray_to_Array(x)
xarr = gpu(x)
return reshape(xarr, size(xarr)[1:2])
end
```
For CPU: If this function does not automatically fallback to CPU when no GPU is present, we can
change `gpu(x)` to `Array(x)`.
### Build Topology
Next we connect all layers together in a single chain:
```julia
# Build our overall model topology
model = Flux.Chain(down,
nn_ode,
DiffEqArray_to_Array,
fc) |> gpu;
```
There are a few things we can do to examine the inner workings of our neural network:
```julia
img, lab = train_dataloader.data[1][:, :, :, 1:1], train_dataloader.data[2][:, 1:1]
# To understand the intermediate NN-ODE layer, we can examine it's dimensionality
x_d = down(img)
# We can see that we can compute the forward pass through the NN topology
# featuring an NNODE layer.
x_m = model(img)
```
This can also be built without the NN-ODE by replacing `nn-ode` with a simple `nn`:
```julia
# We can also build the model topology without a NN-ODE
m_no_ode = Flux.Chain(down,
nn,
fc) |> gpu
x_m = m_no_ode(img)
```
### Prediction
To convert the classification back into readable numbers, we use `classify` which returns the
prediction by taking the arg max of the output for each column of the minibatch:
```julia
classify(x) = argmax.(eachcol(x))
```
### Accuracy
We then evaluate the accuracy on `n_batches` at a time through the entire network:
```julia
function accuracy(model, data; n_batches = 100)
total_correct = 0
total = 0
for (i, (x, y)) in enumerate(collect(data))
# Only evaluate accuracy for n_batches
i > n_batches && break
target_class = classify(cpu(y))
predicted_class = classify(cpu(model(x)))
total_correct += sum(target_class .== predicted_class)
total += length(target_class)
end
return total_correct / total
end
# burn in accuracy
accuracy(m, train_dataloader)
```
### Training Parameters
Once we have our model, we can train our neural network by backpropagation using `Flux.train!`.
This function requires **Loss**, **Optimizer** and **Callback** functions.
#### Loss
**Cross Entropy** is the loss function computed here which applies a **Softmax** operation on the
final output of our model. `logitcrossentropy` takes in the prediction from our
model `model(x)` and compares it to actual output `y`:
```julia
loss(x, y) = logitcrossentropy(model(x), y)
# burn in loss
loss(img, lab)
```
#### Optimizer
`ADAM` is specified here as our optimizer with a **learning rate of 0.05**:
```julia
opt = ADAM(0.05)
```
#### CallBack
This callback function is used to print both the training and testing accuracy after
10 training iterations:
```julia
callback() = begin
global iter += 1
# Monitor that the weights update
# Every 10 training iterations show accuracy
if iter % 10 == 1
train_accuracy = accuracy(model, train_dataloader) * 100
test_accuracy = accuracy(model, test_dataloader;
n_batches = length(test_dataloader)) * 100
@printf("Iter: %3d || Train Accuracy: %2.3f || Test Accuracy: %2.3f\n",
iter, train_accuracy, test_accuracy)
end
end
```
### Train
To train our model, we select the appropriate trainable parameters of our network with `params`.
In our case, backpropagation is required for `down`, `nn_ode` and `fc`. Notice that the parameters
for Neural ODE is given by `nn_ode.p`:
```julia
# Train the NN-ODE and monitor the loss and weights.
Flux.train!(loss, Flux.params( down, nn_ode.p, fc), zip( x_train, y_train ), opt, callback = callback)
```
### Expected Output
```julia
Iter: 1 || Train Accuracy: 16.203 || Test Accuracy: 16.933
Iter: 11 || Train Accuracy: 64.406 || Test Accuracy: 64.900
Iter: 21 || Train Accuracy: 76.656 || Test Accuracy: 76.667
Iter: 31 || Train Accuracy: 81.758 || Test Accuracy: 81.683
Iter: 41 || Train Accuracy: 81.078 || Test Accuracy: 81.967
Iter: 51 || Train Accuracy: 83.953 || Test Accuracy: 84.417
Iter: 61 || Train Accuracy: 85.266 || Test Accuracy: 85.017
Iter: 71 || Train Accuracy: 85.938 || Test Accuracy: 86.400
Iter: 81 || Train Accuracy: 84.836 || Test Accuracy: 85.533
Iter: 91 || Train Accuracy: 86.148 || Test Accuracy: 86.583
Iter: 101 || Train Accuracy: 83.859 || Test Accuracy: 84.500
Iter: 111 || Train Accuracy: 86.227 || Test Accuracy: 86.617
Iter: 121 || Train Accuracy: 87.508 || Test Accuracy: 87.200
Iter: 131 || Train Accuracy: 86.227 || Test Accuracy: 85.917
Iter: 141 || Train Accuracy: 84.453 || Test Accuracy: 84.850
Iter: 151 || Train Accuracy: 86.063 || Test Accuracy: 85.650
Iter: 161 || Train Accuracy: 88.375 || Test Accuracy: 88.033
Iter: 171 || Train Accuracy: 87.398 || Test Accuracy: 87.683
Iter: 181 || Train Accuracy: 88.070 || Test Accuracy: 88.350
Iter: 191 || Train Accuracy: 86.836 || Test Accuracy: 87.150
Iter: 201 || Train Accuracy: 89.266 || Test Accuracy: 88.583
Iter: 211 || Train Accuracy: 86.633 || Test Accuracy: 85.550
Iter: 221 || Train Accuracy: 89.313 || Test Accuracy: 88.217
Iter: 231 || Train Accuracy: 88.641 || Test Accuracy: 89.417
Iter: 241 || Train Accuracy: 88.617 || Test Accuracy: 88.550
Iter: 251 || Train Accuracy: 88.211 || Test Accuracy: 87.950
Iter: 261 || Train Accuracy: 87.742 || Test Accuracy: 87.317
Iter: 271 || Train Accuracy: 89.070 || Test Accuracy: 89.217
Iter: 281 || Train Accuracy: 89.703 || Test Accuracy: 89.067
Iter: 291 || Train Accuracy: 88.484 || Test Accuracy: 88.250
Iter: 301 || Train Accuracy: 87.898 || Test Accuracy: 88.367
Iter: 311 || Train Accuracy: 88.438 || Test Accuracy: 88.633
Iter: 321 || Train Accuracy: 88.664 || Test Accuracy: 88.567
Iter: 331 || Train Accuracy: 89.906 || Test Accuracy: 89.883
Iter: 341 || Train Accuracy: 88.883 || Test Accuracy: 88.667
Iter: 351 || Train Accuracy: 89.609 || Test Accuracy: 89.283
Iter: 361 || Train Accuracy: 89.516 || Test Accuracy: 89.117
Iter: 371 || Train Accuracy: 89.898 || Test Accuracy: 89.633
Iter: 381 || Train Accuracy: 89.055 || Test Accuracy: 89.017
Iter: 391 || Train Accuracy: 89.445 || Test Accuracy: 89.467
Iter: 401 || Train Accuracy: 89.156 || Test Accuracy: 88.250
Iter: 411 || Train Accuracy: 88.977 || Test Accuracy: 89.083
Iter: 421 || Train Accuracy: 90.109 || Test Accuracy: 89.417
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 8290 | # Neural Graph Differential Equations
This tutorial has been adapted from [here](https://github.com/yuehhua/GeometricFlux.jl/blob/master/examples/gcn.jl).
In this tutorial we will use Graph Differential Equations (GDEs) to perform classification on the [CORA Dataset](https://relational.fit.cvut.cz/dataset/CORA). We shall be using the Graph Neural Networks primitives from the package [GeometricFlux](https://github.com/yuehhua/GeometricFlux.jl).
```julia
# Load the packages
using GeometricFlux, JLD2, SparseArrays, DiffEqFlux, DifferentialEquations
using Flux: onehotbatch, onecold, throttle
using Flux.Losses: logitcrossentropy
using Statistics: mean
using LightGraphs: adjacency_matrix
# Download the dataset
download("https://rawcdn.githack.com/yuehhua/GeometricFlux.jl/a94ca7ce2ad01a12b23d68eb6cd991ee08569303/data/cora_features.jld2", "cora_features.jld2")
download("https://rawcdn.githack.com/yuehhua/GeometricFlux.jl/a94ca7ce2ad01a12b23d68eb6cd991ee08569303/data/cora_graph.jld2", "cora_graph.jld2")
download("https://rawcdn.githack.com/yuehhua/GeometricFlux.jl/a94ca7ce2ad01a12b23d68eb6cd991ee08569303/data/cora_labels.jld2", "cora_labels.jld2")
# Load the dataset
@load "./cora_features.jld2" features
@load "./cora_labels.jld2" labels
@load "./cora_graph.jld2" g
# Model and Data Configuration
num_nodes = 2708
num_features = 1433
hidden = 16
target_catg = 7
epochs = 40
# Preprocess the data and compute adjacency matrix
train_X = Float32.(features) # dim: num_features * num_nodes
train_y = Float32.(labels) # dim: target_catg * num_nodes
adj_mat = FeaturedGraph(Matrix{Float32}(adjacency_matrix(g)))
# Define the Neural GDE
diffeqarray_to_array(x) = reshape(cpu(x), size(x)[1:2])
node = NeuralODE(
GCNConv(adj_mat, hidden=>hidden),
(0.f0, 1.f0), Tsit5(), save_everystep = false,
reltol = 1e-3, abstol = 1e-3, save_start = false
)
model = Flux.Chain(GCNConv(adj_mat, num_features=>hidden, relu),
Flux.Dropout(0.5),
node,
diffeqarray_to_array,
GCNConv(adj_mat, hidden=>target_catg))
# Loss
loss(x, y) = logitcrossentropy(model(x), y)
accuracy(x, y) = mean(onecold(model(x)) .== onecold(y))
# Training
## Model Parameters
ps = Flux.params(model, node.p);
## Training Data
train_data = [(train_X, train_y)]
## Optimizer
opt = ADAM(0.01)
## Callback Function for printing accuracies
evalcb() = @show(accuracy(train_X, train_y))
## Training Loop
for i = 1:epochs
Flux.train!(loss, ps, train_data, opt, callback=throttle(evalcb, 10))
end
```
# Step by Step Explanation
## Load the Required Packages
```julia
# Load the packages
using GeometricFlux, JLD2, SparseArrays, DiffEqFlux, DifferentialEquations
using Flux: onehotbatch, onecold, throttle
using Flux.Losses: crossentropy
using Statistics: mean
using LightGraphs: adjacency_matrix
```
## Load the Dataset
The dataset is available in the desired format in the GeometricFlux repository. We shall download the dataset from there, and use the JLD2 package to load the data.
```julia
download("https://rawcdn.githack.com/yuehhua/GeometricFlux.jl/a94ca7ce2ad01a12b23d68eb6cd991ee08569303/data/cora_features.jld2", "cora_features.jld2")
download("https://rawcdn.githack.com/yuehhua/GeometricFlux.jl/a94ca7ce2ad01a12b23d68eb6cd991ee08569303/data/cora_graph.jld2", "cora_graph.jld2")
download("https://rawcdn.githack.com/yuehhua/GeometricFlux.jl/a94ca7ce2ad01a12b23d68eb6cd991ee08569303/data/cora_labels.jld2", "cora_labels.jld2")
@load "./cora_features.jld2" features
@load "./cora_labels.jld2" labels
@load "./cora_graph.jld2" g
```
## Model and Data Configuration
The `num_nodes`, `target_catg` and `num_features` are defined by the data itself. We shall use a shallow GNN with only 16 hidden state dimension.
```julia
num_nodes = 2708
num_features = 1433
hidden = 16
target_catg = 7
epochs = 40
```
## Preprocessing the Data
Convert the data to float32 and use `LightGraphs` to get the adjacency matrix from the graph `g`.
```julia
train_X = Float32.(features) # dim: num_features * num_nodes
train_y = Float32.(labels) # dim: target_catg * num_nodes
adj_mat = Matrix{Float32}(adjacency_matrix(g))
```
## Neural Graph Ordinary Differential Equations
Let us now define the final model. We will use a single layer GNN for approximating the gradients for the neural ODE. We use two additional `GCNConv` layers, one to project the data to a latent space and the other to project it from the latent space to the predictions. Finally a softmax layer gives us the probability of the input belonging to each target category.
```julia
diffeqarray_to_array(x) = reshape(cpu(x), size(x)[1:2])
node = NeuralODE(
GCNConv(adj_mat, hidden=>hidden),
(0.f0, 1.f0), Tsit5(), save_everystep = false,
reltol = 1e-3, abstol = 1e-3, save_start = false
)
model = Flux.Chain(GCNConv(adj_mat, num_features=>hidden, relu),
Flux.Dropout(0.5),
node,
diffeqarray_to_array,
GCNConv(adj_mat, hidden=>target_catg))
```
## Training Configuration
### Loss Function and Accuracy
We shall be using the standard categorical crossentropy loss function which is used for multiclass classification tasks.
```julia
loss(x, y) = logitcrossentropy(model(x), y)
accuracy(x, y) = mean(onecold(model(x)) .== onecold(y))
```
### Model Parameters
Now we extract the model parameters which we want to learn.
```julia
ps = Flux.params(model, node.p);
```
### Training Data
GNNs operate on an entire graph, so we can't do any sort of minibatching here. We need to pass the entire data in a single pass. So our dataset is an array with a single tuple.
```julia
train_data = [(train_X, train_y)]
```
### Optimizer
For this task we will be using the `ADAM` optimizer with a learning rate of `0.01`.
```julia
opt = ADAM(0.01)
```
### Callback Function
We also define a utility function for printing the accuracy of the model over time.
```julia
evalcb() = @show(accuracy(train_X, train_y))
```
## Training Loop
Finally, with the configuration ready and all the utilities defined we can use the `Flux.train!` function to learn the parameters `ps`. We run the training loop for `epochs` number of iterations.
```julia
for i = 1:epochs
Flux.train!(loss, ps, train_data, opt, callback=throttle(evalcb, 10))
end
```
## Expected Output
```julia
accuracy(train_X, train_y) = 0.12370753323485968
accuracy(train_X, train_y) = 0.11632200886262925
accuracy(train_X, train_y) = 0.1189069423929099
accuracy(train_X, train_y) = 0.13404726735598227
accuracy(train_X, train_y) = 0.15620384047267355
accuracy(train_X, train_y) = 0.1776218611521418
accuracy(train_X, train_y) = 0.19793205317577547
accuracy(train_X, train_y) = 0.21122599704579026
accuracy(train_X, train_y) = 0.22673559822747416
accuracy(train_X, train_y) = 0.2429837518463811
accuracy(train_X, train_y) = 0.25406203840472674
accuracy(train_X, train_y) = 0.26809453471196454
accuracy(train_X, train_y) = 0.2869276218611521
accuracy(train_X, train_y) = 0.2961595273264402
accuracy(train_X, train_y) = 0.30797636632200887
accuracy(train_X, train_y) = 0.31831610044313147
accuracy(train_X, train_y) = 0.3257016248153619
accuracy(train_X, train_y) = 0.3378877400295421
accuracy(train_X, train_y) = 0.3500738552437223
accuracy(train_X, train_y) = 0.3629985228951256
accuracy(train_X, train_y) = 0.37259970457902514
accuracy(train_X, train_y) = 0.3777695716395864
accuracy(train_X, train_y) = 0.3895864106351551
accuracy(train_X, train_y) = 0.396602658788774
accuracy(train_X, train_y) = 0.4010339734121123
accuracy(train_X, train_y) = 0.40472673559822747
accuracy(train_X, train_y) = 0.41285081240768096
accuracy(train_X, train_y) = 0.422821270310192
accuracy(train_X, train_y) = 0.43057607090103395
accuracy(train_X, train_y) = 0.43833087149187594
accuracy(train_X, train_y) = 0.44645494830132937
accuracy(train_X, train_y) = 0.4538404726735598
accuracy(train_X, train_y) = 0.45901033973412114
accuracy(train_X, train_y) = 0.4630723781388479
accuracy(train_X, train_y) = 0.46971935007385524
accuracy(train_X, train_y) = 0.474519940915805
accuracy(train_X, train_y) = 0.47858197932053176
accuracy(train_X, train_y) = 0.4815361890694239
accuracy(train_X, train_y) = 0.4804283604135894
accuracy(train_X, train_y) = 0.4848596750369276
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 4964 | # Neural Ordinary Differential Equations with Flux
All of the tools of DiffEqSensitivity.jl can be used with Flux.jl. A lot of the examples
have been written to use `FastChain` and `sciml_train`, but in all cases this
can be changed to the `Chain` and `Flux.train!` workflow.
## Using Flux `Chain` neural networks with Flux.train!
This should work almost automatically by using `solve`. Here is an
example of optimizing `u0` and `p`.
```@example neuralode1
using OrdinaryDiffEq, DiffEqSensitivity, Flux, Plots
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)
function trueODEfunc(du,u,p,t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))
dudt2 = Flux.Chain(x -> x.^3,
Flux.Dense(2,50,tanh),
Flux.Dense(50,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
dudt(u,p,t) = re(p)(u) # need to restrcture for backprop!
prob = ODEProblem(dudt,u0,tspan)
function predict_n_ode()
Array(solve(prob,Tsit5(),u0=u0,p=p,saveat=t))
end
function loss_n_ode()
pred = predict_n_ode()
loss = sum(abs2,ode_data .- pred)
loss
end
loss_n_ode() # n_ode.p stores the initial parameters of the neural ODE
callback = function (;doplot=false) #callback function to observe training
pred = predict_n_ode()
display(sum(abs2,ode_data .- pred))
# plot current prediction against data
pl = scatter(t,ode_data[1,:],label="data")
scatter!(pl,t,pred[1,:],label="prediction")
display(plot(pl))
return false
end
# Display the ODE with the initial parameter values.
callback()
data = Iterators.repeated((), 1000)
res1 = Flux.train!(loss_n_ode, Flux.params(u0,p), data, ADAM(0.05), cb = callback)
callback()
```
## Using Flux `Chain` neural networks with GalacticOptim
Flux neural networks can be used with Optimization.jl by using
the `Flux.destructure` function. In this case, if `dudt` is a Flux
chain, then:
```julia
p,re = Flux.destructure(chain)
```
returns `p` which is the vector of parameters for the chain and `re` which is
a function `re(p)` that reconstructs the neural network with new parameters
`p`. Using this function we can thus build our neural differential equations in
an explicit parameter style.
Let's use this to build and train a neural ODE from scratch. In this example we will
optimize both the neural network parameters `p` and the input initial condition `u0`.
Notice that Optimization.jl works on a vector input, so we have to concatenate `u0`
and `p` and then in the loss function split to the pieces.
```@example neuralode2
using Flux, OrdinaryDiffEq, DiffEqSensitivity, Optimization, OptimizationOptimisers, OptimizationOptimJL, Plots
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)
function trueODEfunc(du,u,p,t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))
dudt2 = Flux.Chain(x -> x.^3,
Flux.Dense(2,50,tanh),
Flux.Dense(50,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
dudt(u,p,t) = re(p)(u) # need to restrcture for backprop!
prob = ODEProblem(dudt,u0,tspan)
θ = [u0;p] # the parameter vector to optimize
function predict_n_ode(θ)
Array(solve(prob,Tsit5(),u0=θ[1:2],p=θ[3:end],saveat=t))
end
function loss_n_ode(θ)
pred = predict_n_ode(θ)
loss = sum(abs2,ode_data .- pred)
loss,pred
end
loss_n_ode(θ)
callback = function (θ,l,pred;doplot=false) #callback function to observe training
display(l)
# plot current prediction against data
pl = scatter(t,ode_data[1,:],label="data")
scatter!(pl,t,pred[1,:],label="prediction")
display(plot(pl))
return false
end
# Display the ODE with the initial parameter values.
callback(θ,loss_n_ode(θ)...)
# use Optimization.jl to solve the problem
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((p,_)->loss_n_ode(p), adtype)
optprob = Optimization.OptimizationProblem(optf, θ)
result_neuralode = Optimization.solve(optprob,
OptimizationOptimisers.Adam(0.05),
callback = callback,
maxiters = 300)
optprob2 = remake(optprob,u0 = result_neuralode.u)
result_neuralode2 = Optimization.solve(optprob2,
LBFGS(),
callback = callback,
allow_f_increases = false)
```
Notice that the advantage of this format is that we can use Optim's optimizers, like
`LBFGS` with a full `Chain` object for all of Flux's neural networks, like
convolutional neural networks.
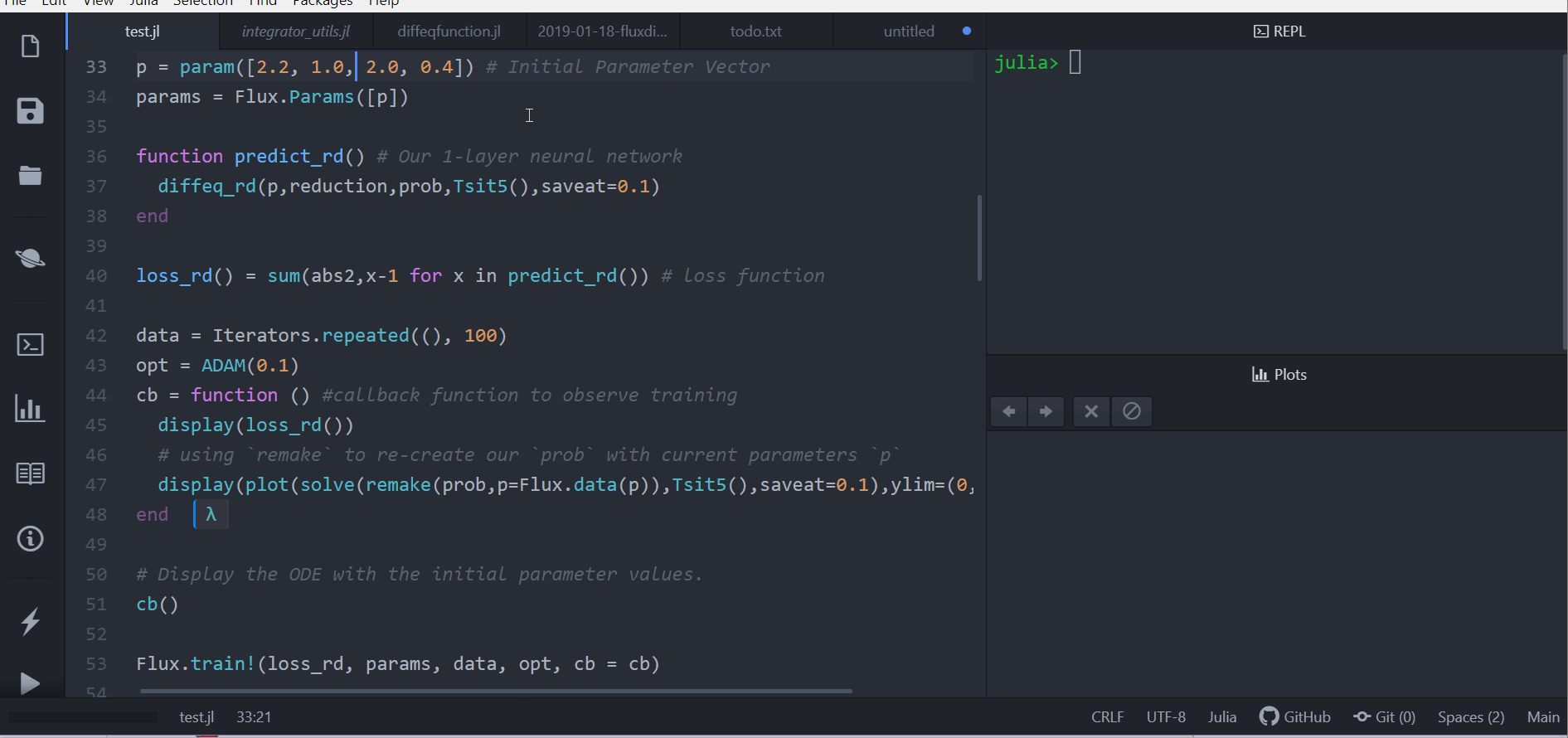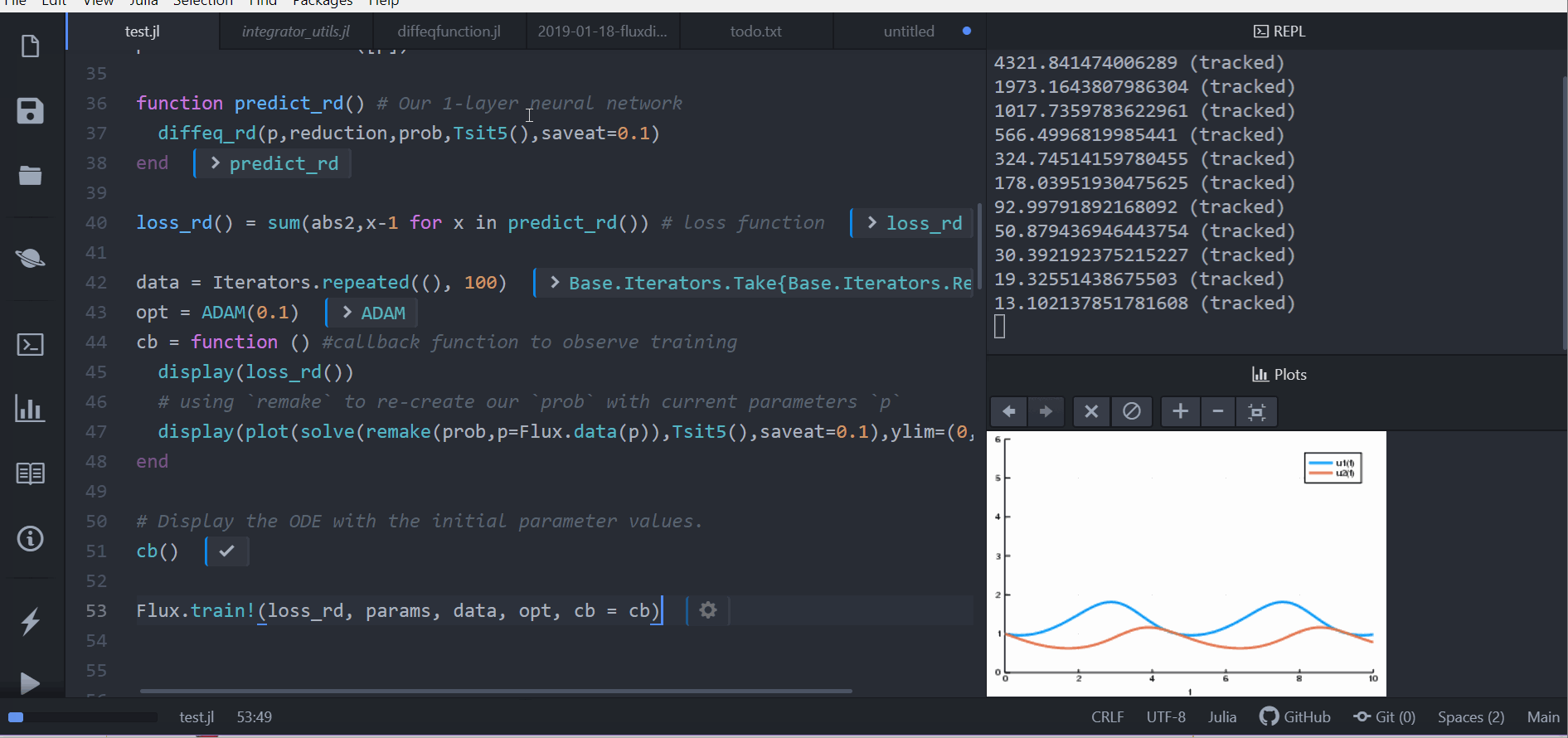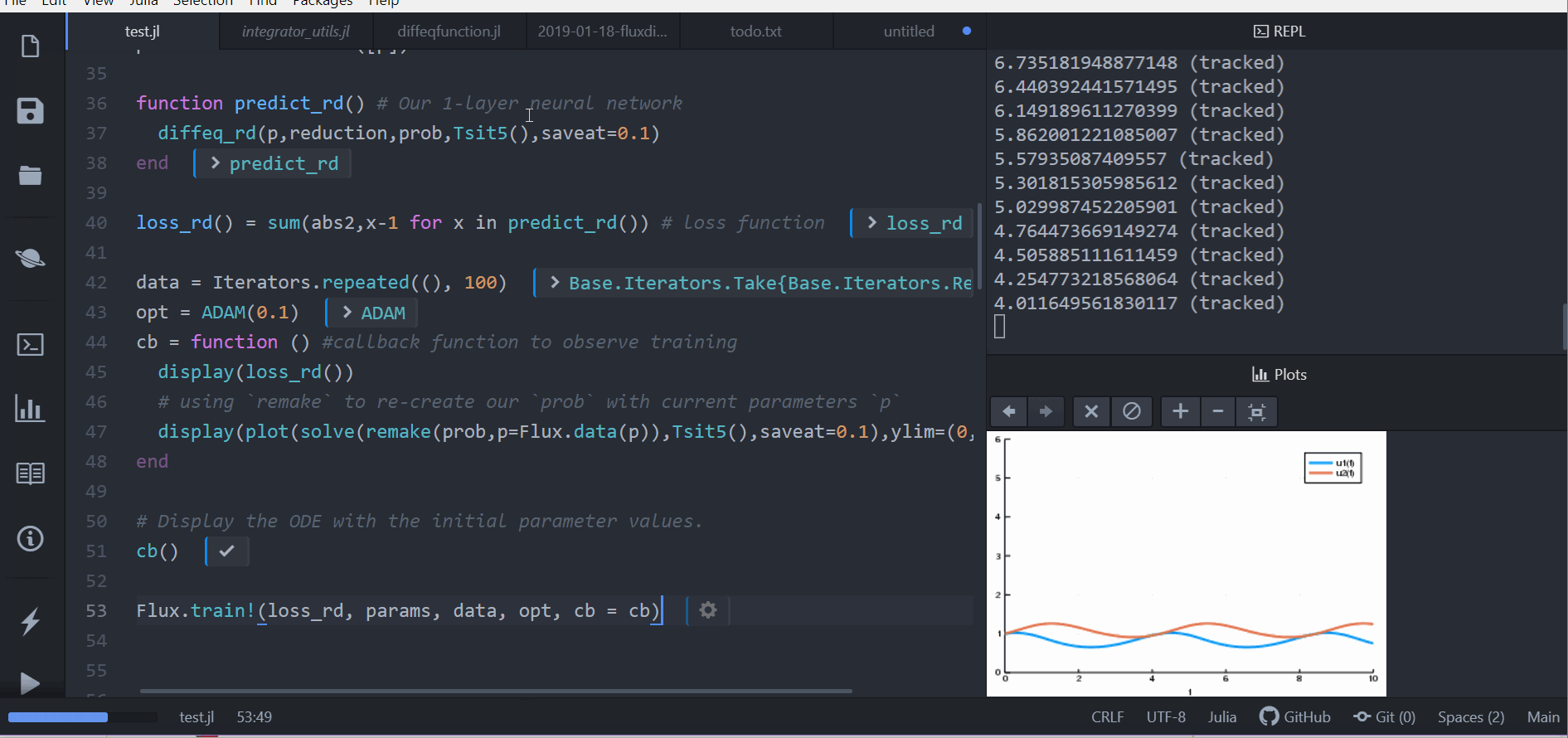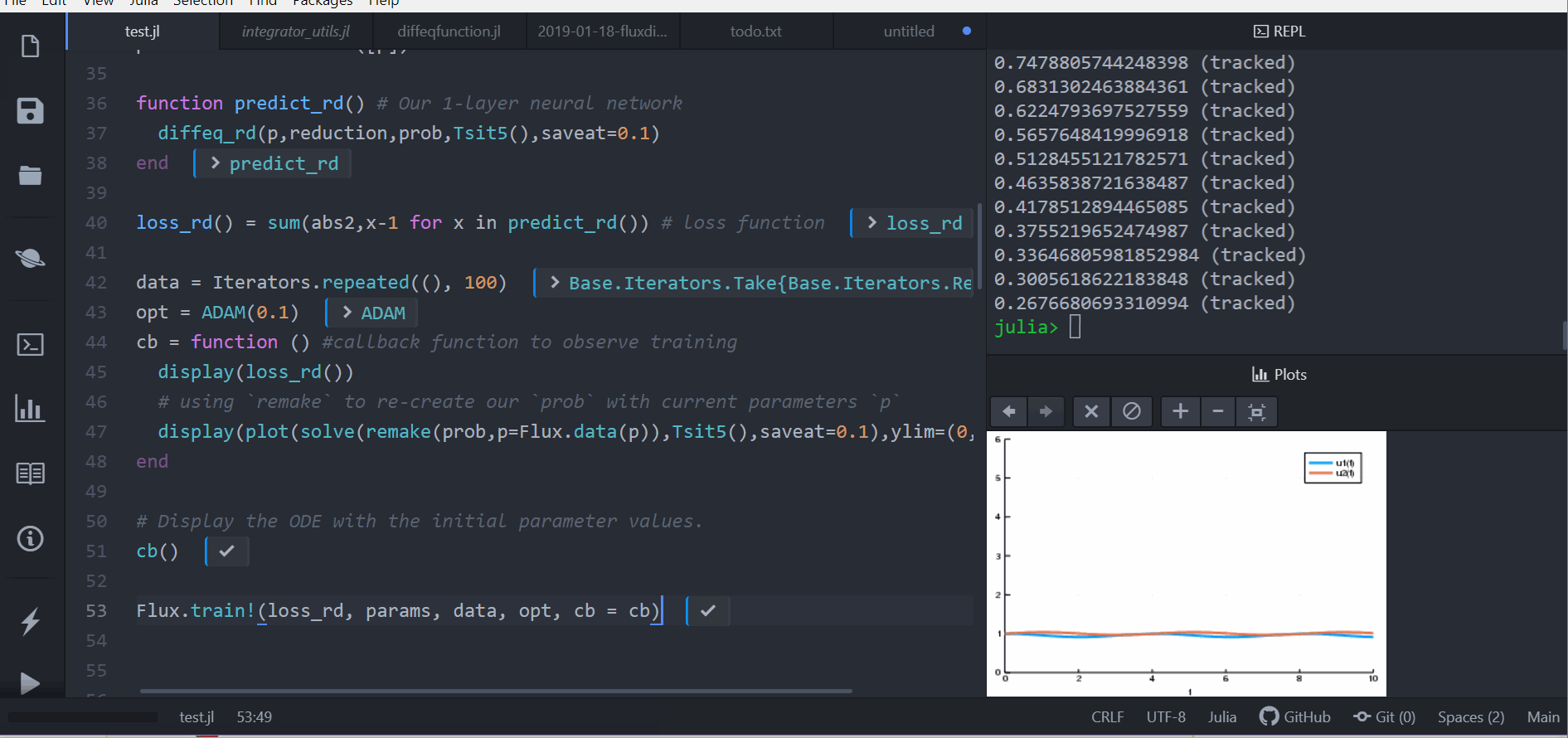
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 9994 | # Data-Parallel Multithreaded, Distributed, and Multi-GPU Batching
DiffEqFlux.jl allows for data-parallel batching optimally on one
computer, across an entire compute cluster, and batching along GPUs.
This can be done by parallelizing within an ODE solve or between the
ODE solves. The automatic differentiation tooling is compatible with
the parallelism. The following examples demonstrate training over a few
different modes of parallelism. These examples are not exhaustive.
## Within-ODE Multithreaded and GPU Batching
We end by noting that there is an alternative way of batching which
can be more efficient in some cases like neural ODEs. With a neural
networks, columns are treated independently (by the properties of
matrix multiplication). Thus for example, with `Chain` we can
define an ODE:
```@example dataparallel
using Lux, DiffEqFlux, DifferentialEquations, Random
rng = Random.default_rng()
dudt = Lux.Chain(Lux.Dense(2,50,tanh),Lux.Dense(50,2))
p,st = Lux.setup(rng, dudt)
f(u,p,t) = dudt(u,p,st)[1]
```
and we can solve this ODE where the initial condition is a vector:
```@example dataparallel
u0 = Float32[2.; 0.]
prob = ODEProblem(f,u0,(0f0,1f0),p)
solve(prob,Tsit5())
```
or we can solve this ODE where the initial condition is a matrix, where
each column is an independent system:
```@example dataparallel
u0 = Float32.([0 1 2
0 0 0])
prob = ODEProblem(f,u0,(0f0,1f0),p)
solve(prob,Tsit5())
```
On the CPU this will multithread across the system (due to BLAS) and
on GPUs this will parallelize the operations across the GPU. To GPU
this, you'd simply move the parameters and the initial condition to the
GPU:
```julia
xs = Float32.([0 1 2
0 0 0])
prob = ODEProblem(f,gpu(u0),(0f0,1f0),gpu(p))
solve(prob,Tsit5())
```
This method of parallelism is optimal if all of the operations are
linear algebra operations such as a neural ODE. Thus this method of
parallelism is demonstrated in the [MNIST tutorial](@ref mnist).
However, this method of parallelism has many limitations. First of all,
the ODE function is required to be written in a way that is independent
across the columns. Not all ODEs are written like this, so one needs to
be careful. But additionally, this method is ineffective if the ODE
function has many serial operations, like `u[1]*u[2] - u[3]`. In such
a case, this indexing behavior will dominate the runtime and cause the
parallelism to sometimes even be detrimental.
# Out of ODE Parallelism
Instead of parallelizing within an ODE solve, one can parallelize the
solves to the ODE itself. While this will be less effective on very
large ODEs, like big neural ODE image classifiers, this method be effective
even if the ODE is small or the `f` function is not well-parallelized.
This kind of parallelism is done via the [DifferentialEquations.jl ensemble interface](https://diffeq.sciml.ai/stable/features/ensemble/). The following examples
showcase multithreaded, cluster, and (multi)GPU parallelism through this
interface.
## Multithreaded Batching At a Glance
The following is a full copy-paste example for the multithreading.
Distributed and GPU minibatching are described below.
```@example dataparallel2
using DifferentialEquations, Optimization, OptimizationOptimJL, OptimizationFlux
pa = [1.0]
u0 = [3.0]
θ = [u0;pa]
function model1(θ,ensemble)
prob = ODEProblem((u, p, t) -> 1.01u .* p, [θ[1]], (0.0, 1.0), [θ[2]])
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), ensemble, saveat = 0.1, trajectories = 100)
end
# loss function
loss_serial(θ) = sum(abs2,1.0.-Array(model1(θ,EnsembleSerial())))
loss_threaded(θ) = sum(abs2,1.0.-Array(model1(θ,EnsembleThreads())))
callback = function (θ,l) # callback function to observe training
@show l
false
end
opt = ADAM(0.1)
l1 = loss_serial(θ)
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_serial(x), adtype)
optprob = Optimization.OptimizationProblem(optf, θ)
res_serial = Optimization.solve(optprob, opt; callback = callback, maxiters=100)
optf2 = Optimization.OptimizationFunction((x,p)->loss_threaded(x), adtype)
optprob2 = Optimization.OptimizationProblem(optf2, θ)
res_threads = Optimization.solve(optprob2, opt; callback = callback, maxiters=100)
```
## Multithreaded Batching In-Depth
In order to make use of the ensemble interface, we need to build an
`EnsembleProblem`. The `prob_func` is the function for determining
the different `DEProblem`s to solve. This is the place where we can
randomly sample initial conditions or pull initial conditions from
an array of batches in order to perform our study. To do this, we
first define a prototype `DEProblem`. Here we use the following
`ODEProblem` as our base:
```julia
prob = ODEProblem((u, p, t) -> 1.01u .* p, [θ[1]], (0.0, 1.0), [θ[2]])
```
In the `prob_func` we define how to build a new problem based on the
base problem. In this case, we want to change `u0` by a constant, i.e.
`0.5 .+ i/100 .* prob.u0` for different trajectories labelled by `i`.
Thus we use the [remake function from the problem interface](https://diffeq.sciml.ai/stable/basics/problem/#Modification-of-problem-types) to do so:
```julia
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
```
We now build the `EnsembleProblem` with this basis:
```julia
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
```
Now to solve an ensemble problem, we need to choose an ensembling
algorithm and choose the number of trajectories to solve. Here let's
solve this in serial with 100 trajectories. Note that `i` will thus run
from `1:100`.
```julia
sim = solve(ensemble_prob, Tsit5(), EnsembleSerial(), saveat = 0.1, trajectories = 100)
```
and thus running in multithreading would be:
```julia
sim = solve(ensemble_prob, Tsit5(), EnsembleThreads(), saveat = 0.1, trajectories = 100)
```
This whole mechanism is differentiable, so we then put it in a training
loop and it soars. Note that you need to make sure that [Julia's multithreading](https://docs.julialang.org/en/v1/manual/multi-threading/)
is enabled, which you can do via:
```julia
Threads.nthreads()
```
## Distributed Batching Across a Cluster
Changing to distributed computing is very simple as well. The setup is
all the same, except you utilize `EnsembleDistributed` as the ensembler:
```julia
sim = solve(ensemble_prob, Tsit5(), EnsembleDistributed(), saveat = 0.1, trajectories = 100)
```
Note that for this to work you need to ensure that your processes are
already started. For more information on setting up processes and utilizing
a compute cluster, see [the official distributed documentation](https://docs.julialang.org/en/v1/manual/distributed-computing/). The key feature to recognize is that, due to
the message passing required for cluster compute, one needs to ensure
that all of the required functions are defined on the worker processes.
The following is a full example of a distributed batching setup:
```julia
using Distributed
addprocs(4)
@everywhere begin
using DifferentialEquations, Optimization, OptimizationOptimJL
function f(u,p,t)
1.01u .* p
end
end
pa = [1.0]
u0 = [3.0]
θ = [u0;pa]
function model1(θ,ensemble)
prob = ODEProblem(f, [θ[1]], (0.0, 1.0), [θ[2]])
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), ensemble, saveat = 0.1, trajectories = 100)
end
callback = function (θ,l) # callback function to observe training
@show l
false
end
opt = ADAM(0.1)
loss_distributed(θ) = sum(abs2,1.0.-Array(model1(θ,EnsembleDistributed())))
l1 = loss_distributed(θ)
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_distributed(x), adtype)
optprob = Optimization.OptimizationProblem(optf, θ)
res_distributed = Optimization.solve(optprob, opt; callback = callback, maxiters = 100)
```
And note that only `addprocs(4)` needs to be changed in order to make
this demo run across a cluster. For more information on adding processes
to a cluster, check out [ClusterManagers.jl](https://github.com/JuliaParallel/ClusterManagers.jl).
## Minibatching Across GPUs with DiffEqGPU
DiffEqGPU.jl allows for generating code parallelizes an ensemble on
generated CUDA kernels. This method is efficient for sufficiently
small (<100 ODE) problems where the significant computational cost
is due to the large number of batch trajectories that need to be
solved. This kernel-building process adds a few restrictions to the
function, such as requiring it has no boundschecking or allocations.
The following is an example of minibatch ensemble parallelism across
a GPU:
```julia
using DifferentialEquations, Optimization, OptimizationOptimJL
function f(du,u,p,t)
@inbounds begin
du[1] = 1.01 * u[1] * p[1] * p[2]
end
end
pa = [1.0]
u0 = [3.0]
θ = [u0;pa]
function model1(θ,ensemble)
prob = ODEProblem(f, [θ[1]], (0.0, 1.0), [θ[2]])
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), ensemble, saveat = 0.1, trajectories = 100)
end
callback = function (θ,l) # callback function to observe training
@show l
false
end
opt = ADAM(0.1)
loss_gpu(θ) = sum(abs2,1.0.-Array(model1(θ,EnsembleGPUArray())))
l1 = loss_gpu(θ)
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_gpu(x), adtype)
optprob = Optimization.OptimizationProblem(optf, θ)
res_gpu = Optimization.solve(optprob, opt; callback = callback, maxiters = 100)
```
## Multi-GPU Batching
DiffEqGPU supports batching across multiple GPUs. See [its README](https://github.com/SciML/DiffEqGPU.jl#setting-up-multi-gpu)
for details on setting it up.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2825 | # Handling Exogenous Input Signals
The key to using exogeneous input signals is the same as in the rest of the
SciML universe: just use the function in the definition of the differential
equation. For example, if it's a standard differential equation, you can
use the form
```julia
I(t) = t^2
function f(du,u,p,t)
du[1] = I(t)
du[2] = u[1]
end
```
so that `I(t)` is an exogenous input signal into `f`. Another form that could be
useful is a closure. For example:
```julia
function f(du,u,p,t,I)
du[1] = I(t)
du[2] = u[1]
end
_f(du,u,p,t) = f(du,u,p,t,x -> x^2)
```
which encloses an extra argument into `f` so that `_f` is now the interface-compliant
differential equation definition.
Note that you can also learn what the exogenous equation is from data. For an
example on how to do this, you can use the [Optimal Control Example](@ref optcontrol)
which shows how to parameterize a `u(t)` by a universal function and learn that
from data.
## Example of a Neural ODE with Exogenous Input
In the following example, a discrete exogenous input signal `ex` is defined and
used as an input into the neural network of a neural ODE system.
```@example exogenous
using DifferentialEquations, Lux, DiffEqFlux, Optimization, OptimizationPolyalgorithms, OptimizationFlux, Plots, Random
rng = Random.default_rng()
tspan = (0.1f0, Float32(10.0))
tsteps = range(tspan[1], tspan[2], length = 100)
t_vec = collect(tsteps)
ex = vec(ones(Float32,length(tsteps), 1))
f(x) = (atan(8.0 * x - 4.0) + atan(4.0)) / (2.0 * atan(4.0))
function hammerstein_system(u)
y= zeros(size(u))
for k in 2:length(u)
y[k] = 0.2 * f(u[k-1]) + 0.8 * y[k-1]
end
return y
end
y = Float32.(hammerstein_system(ex))
plot(collect(tsteps), y, ticks=:native)
nn_model = Lux.Chain(Lux.Dense(2,8, tanh), Lux.Dense(8, 1))
p_model,st = Lux.setup(rng, nn_model)
u0 = Float32.([0.0])
function dudt(u, p, t)
global st
#input_val = u_vals[Int(round(t*10)+1)]
out,st = nn_model(vcat(u[1], ex[Int(round(10*0.1))]), p, st)
return out
end
prob = ODEProblem(dudt,u0,tspan,nothing)
function predict_neuralode(p)
_prob = remake(prob,p=p)
Array(solve(_prob, Tsit5(), saveat=tsteps, abstol = 1e-8, reltol = 1e-6))
end
function loss(p)
sol = predict_neuralode(p)
N = length(sol)
return sum(abs2.(y[1:N] .- sol'))/N
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, Lux.ComponentArray(p_model))
res0 = Optimization.solve(optprob, PolyOpt(),maxiters=100)
sol = predict_neuralode(res0.u)
plot(tsteps,sol')
N = length(sol)
scatter!(tsteps,y[1:N])
savefig("trained.png")
```

| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 4773 | # Optimization of Ordinary Differential Equations
## Copy-Paste Code
If you want to just get things running, try the following! Explanation will
follow.
```@example optode_cp
using DifferentialEquations, Optimization, OptimizationPolyalgorithms, OptimizationOptimJL, Plots
function lotka_volterra!(du, u, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
# Initial condition
u0 = [1.0, 1.0]
# Simulation interval and intermediary points
tspan = (0.0, 10.0)
tsteps = 0.0:0.1:10.0
# LV equation parameter. p = [α, β, δ, γ]
p = [1.5, 1.0, 3.0, 1.0]
# Setup the ODE problem, then solve
prob = ODEProblem(lotka_volterra!, u0, tspan, p)
sol = solve(prob, Tsit5())
# Plot the solution
using Plots
plot(sol)
savefig("LV_ode.png")
function loss(p)
sol = solve(prob, Tsit5(), p=p, saveat = tsteps)
loss = sum(abs2, sol.-1)
return loss, sol
end
callback = function (p, l, pred)
display(l)
plt = plot(pred, ylim = (0, 6))
display(plt)
# Tell Optimization.solve to not halt the optimization. If return true, then
# optimization stops.
return false
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
result_ode = Optimization.solve(optprob, PolyOpt(),
callback = callback,
maxiters = 100)
```
## Explanation
First let's create a Lotka-Volterra ODE using DifferentialEquations.jl. For
more details, [see the DifferentialEquations.jl documentation](http://docs.juliadiffeq.org/dev/). The Lotka-Volterra equations have the form:
```math
\begin{aligned}
\frac{dx}{dt} &= \alpha x - \beta x y \\
\frac{dy}{dt} &= -\delta y + \gamma x y \\
\end{aligned}
```
```@example optode
using DifferentialEquations, Optimization, OptimizationPolyalgorithms, OptimizationOptimJL, Plots
function lotka_volterra!(du, u, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
# Initial condition
u0 = [1.0, 1.0]
# Simulation interval and intermediary points
tspan = (0.0, 10.0)
tsteps = 0.0:0.1:10.0
# LV equation parameter. p = [α, β, δ, γ]
p = [1.5, 1.0, 3.0, 1.0]
# Setup the ODE problem, then solve
prob = ODEProblem(lotka_volterra!, u0, tspan, p)
sol = solve(prob, Tsit5())
# Plot the solution
using Plots
plot(sol)
savefig("LV_ode.png")
```
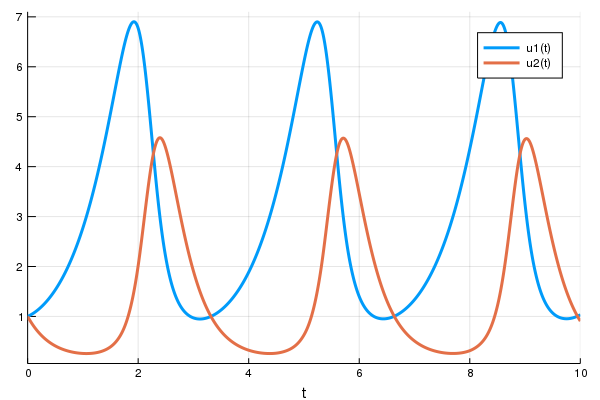
For this first example, we do not yet include a neural network. We take
[AD-compatible `solve`
function](https://docs.juliadiffeq.org/latest/analysis/sensitivity/) function
that takes the parameters and an initial condition and returns the solution of
the differential equation. Next we choose a loss function. Our goal will be to
find parameters that make the Lotka-Volterra solution constant `x(t)=1`, so we
define our loss as the squared distance from 1.
```@example optode
function loss(p)
sol = solve(prob, Tsit5(), p=p, saveat = tsteps)
loss = sum(abs2, sol.-1)
return loss, sol
end
```
Lastly, we use the `Optimization.solve` function to train the parameters using `ADAM` to
arrive at parameters which optimize for our goal. `Optimization.solve` allows defining
a callback that will be called at each step of our training loop. It takes in
the current parameter vector and the returns of the last call to the loss
function. We will display the current loss and make a plot of the current
situation:
```@example optode
callback = function (p, l, pred)
display(l)
plt = plot(pred, ylim = (0, 6))
display(plt)
# Tell Optimization.solve to not halt the optimization. If return true, then
# optimization stops.
return false
end
```
Let's optimize the model.
```@example optode
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
result_ode = Optimization.solve(optprob, PolyOpt(),
callback = callback,
maxiters = 100)
```
In just seconds we found parameters which give a relative loss of `1e-16`! We can
get the final loss with `result_ode.minimum`, and get the optimal parameters
with `result_ode.u`. For example, we can plot the final outcome and show
that we solved the control problem and successfully found parameters to make the
ODE solution constant:
```@example optode
remade_solution = solve(remake(prob, p = result_ode.u), Tsit5(),
saveat = tsteps)
plot(remade_solution, ylim = (0, 6))
```

| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 11476 | # [Prediction error method (PEM)](@id pemethod)
When identifying linear systems from noisy data, the prediction-error method [^Ljung] is close to a gold standard when it comes to the quality of the models it produces, but is also one of the computationally more expensive methods due to its reliance on iterative, gradient-based estimation. When we are identifying nonlinear models, we typically do not have the luxury of closed-form, non-iterative solutions, while PEM is easier to adopt to the nonlinear setting.[^Larsson]
Fundamentally, PEM changes the problem from minimizing a loss based on the simulation performance, to minimizing a loss based on shorter-term predictions. There are several benefits of doing so, and this example will highlight two:
- The loss is often easier to optimize.
- In addition to an accurate simulator, you also obtain a prediction for the system.
- With PEM, it's possible to estimate *disturbance models*.
The last point will not be illustrated in this tutorial, but we will briefly expand upon it here. Gaussian, zero-mean measurement noise is usually not very hard to handle. Disturbances that affect the state of the system may, however, cause all sorts of havoc on the estimate. Consider wind affecting an aircraft, deriving a statistical and dynamical model of the wind may be doable, but unless you measure the exact wind affecting the aircraft, making use of the model during parameter estimation is impossible. The wind is an *unmeasured load disturbance* that affects the state of the system through its own dynamics model. Using the techniques illustrated in this tutorial, it's possible to estimate the influence of the wind during the experiment that generated the data and reduce or eliminate the bias it otherwise causes in the parameter estimates.
We will start by illustrating a common problem with simulation-error minimization. Imagine a pendulum with unknown length that is to be estimated. A small error in the pendulum length causes the frequency of oscillation to change. Over sufficiently large horizon, two sinusoidal signals with different frequencies become close to orthogonal to each other. If some form of squared-error loss is used, the loss landscape will be horribly non-convex in this case, indeed, we will illustrate exactly this below.
Another case that poses a problem for simulation-error estimation is when the system is unstable or chaotic. A small error in either the initial condition or the parameters may cause the simulation error to diverge and its gradient to become meaningless.
In both of these examples, we may make use of measurements we have of the evolution of the system to prevent the simulation error from diverging. For instance, if we have measured the angle of the pendulum, we can make use of this measurement to adjust the angle during the simulation to make sure it stays close to the measured angle. Instead of performing a pure simulation, we instead say that we *predict* the state a while forward in time, given all the measurements up until the current time point. By minimizing this prediction rather than the pure simulation, we can often prevent the model error from diverging even though we have a poor initial guess.
We start by defining a model of the pendulum. The model takes a parameter $L$ corresponding to the length of the pendulum.
```julia
using DifferentialEquations, Optimization, OptimizationOptimJL, OptimizationPolyalgorithms, Plots, Statistics, DataInterpolations, ForwardDiff
tspan = (0.1f0, Float32(20.0))
tsteps = range(tspan[1], tspan[2], length = 1000)
u0 = [0f0, 3f0] # Initial angle and angular velocity
function simulator(du,u,p,t) # Pendulum dynamics
g = 9.82f0 # Gravitational constant
L = p isa Number ? p : p[1] # Length of the pendulum
gL = g/L
θ = u[1]
dθ = u[2]
du[1] = dθ
du[2] = -gL * sin(θ)
end
```
We assume that the true length of the pendulum is $L = 1$, and generate some data from this system.
```julia
prob = ODEProblem(simulator,u0,tspan,1.0) # Simulate with L = 1
sol = solve(prob, Tsit5(), saveat=tsteps, abstol = 1e-8, reltol = 1e-6)
y = sol[1,:] # This is the data we have available for parameter estimation
plot(y, title="Pendulum simulation", label="angle")
```
We also define functions that simulate the system and calculate the loss, given a parameter `p` corresponding to the length.
```julia
function simulate(p)
_prob = remake(prob,p=p)
solve(_prob, Tsit5(), saveat=tsteps, abstol = 1e-8, reltol = 1e-6)[1,:]
end
function simloss(p)
yh = simulate(p)
e2 = yh
e2 .= abs2.(y .- yh)
return mean(e2)
end
```
We now look at the loss landscape as a function of the pendulum length:
```julia
Ls = 0.01:0.01:2
simlosses = simloss.(Ls)
fig_loss = plot(Ls, simlosses, title = "Loss landscape", xlabel="Pendulum length", ylabel = "MSE loss", lab="Simulation loss")
```
This figure is interesting, the loss is of course 0 for the true value $L=1$, but for values $L < 1$, the overall slope actually points in the wrong direction! Moreover, the loss is oscillatory, indicating that this is a terrible function to optimize, and that we would need a very good initial guess for a local search to converge to the true value. Note, this example is chosen to be one-dimensional in order to allow these kinds of visualizations, and one-dimensional problems are typically not hard to solve, but the reasoning extends to higher-dimensional and harder problems.
We will now move on to defining a *predictor* model. Our predictor will be very simple, each time step, we will calculate the error $e$ between the simulated angle $\theta$ and the measured angle $y$. A part of this error will be used to correct the state of the pendulum. The correction we use is linear and looks like $Ke = K(y - \theta)$. We have formed what is commonly referred to as a (linear) *observer*. The [Kalman filter](https://en.wikipedia.org/wiki/Kalman_filter) is a particular kind of linear observer, where $K$ is calculated based on a statistical model of the disturbances that act on the system. We will stay with a simple, fixed-gain observer here for simplicity.
To feed the sampled data into the continuous-time simulation, we make use of an interpolator. We also define new functions, `predictor` that contains the pendulum dynamics with the observer correction, a `prediction` function that performs the rollout (we're not using the word simulation to not confuse with the setting above) and a loss function.
```julia
y_int = LinearInterpolation(y,tsteps)
function predictor(du,u,p,t)
g = 9.82f0
L, K, y = p # pendulum length, observer gain and measurements
gL = g/L
θ = u[1]
dθ = u[2]
yt = y(t)
e = yt - θ
du[1] = dθ + K*e
du[2] = -gL * sin(θ)
end
predprob = ODEProblem(predictor,u0,tspan,nothing)
function prediction(p)
p_full = (p..., y_int)
_prob = remake(predprob,u0=eltype(p_full).(u0),p=p_full)
solve(_prob, Tsit5(), saveat=tsteps, abstol = 1e-8, reltol = 1e-6)[1,:]
end
function predloss(p)
yh = prediction(p)
e2 = yh
e2 .= abs2.(y .- yh)
return mean(e2)
end
predlosses = map(Ls) do L
p = (L, 1) # use K = 1
predloss(p)
end
plot!(Ls, predlosses, lab="Prediction loss")
```
Once gain we look at the loss as a function of the parameter, and this time it looks a lot better. The loss is not convex, but the gradient points in the right direction over a much larger interval. Here, we arbitrarily set the observer gain to $K=1$, we will later let the optimizer learn this parameter.
For completeness, we also perform estimation using both losses. We choose an initial guess we know will be hard for the simulation-error minimization just to drive home the point:
```julia
L0 = [0.7] # Initial guess of pendulum length
adtype = Optimization.AutoForwardDiff()
optf = Optimization.OptimizationFunction((x,p)->simloss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, L0)
ressim = Optimization.solve(optprob, PolyOpt(),
maxiters = 5000)
ysim = simulate(ressim.u)
plot(tsteps, [y ysim], label=["Data" "Simulation model"])
p0 = [0.7, 1.0] # Initial guess of length and observer gain K
optf2 = Optimization.OptimizationFunction((p,_)->predloss(p), adtype)
optfunc2 = Optimization.instantiate_function(optf2, p0, adtype, nothing)
optprob2 = Optimization.OptimizationProblem(optfunc2, p0)
respred = Optimization.solve(optprob2, PolyOpt(),
maxiters = 5000)
ypred = simulate(respred.u)
plot!(tsteps, ypred, label="Prediction model")
```
The estimated parameters $(L, K)$ are
```julia
respred.u
```
Now, we might ask ourselves why we used a correct on the form $Ke$ and didn't instead set the angle in the simulation *equal* to the measurement. The reason is twofold
1. If our prediction of the angle is 100% based on the measurements, the model parameters do not matter for the prediction and we can thus not hope to learn their values.
2. The measurement is usually noisy, and we thus want to *fuse* the predictive power of the model with the information of the measurements. The Kalman filter is an optimal approach to this information fusion under special circumstances (linear model, Gaussian noise).
We thus let the optimization *learn* the best value of the observer gain in order to make the best predictions.
As a last step, we perform the estimation also with some measurement noise to verify that it does something reasonable:
```julia
yn = y .+ 0.1f0 .* randn.(Float32)
y_int = LinearInterpolation(yn,tsteps) # redefine the interpolator to contain noisy measurements
optf = Optimization.OptimizationFunction((x,p)->predloss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p0)
resprednoise = Optimization.solve(optprob, PolyOpt(),
maxiters = 5000)
yprednoise = prediction(resprednoise.u)
plot!(tsteps, yprednoise, label="Prediction model with noisy measurements")
```
```julia
resprednoise.u
```
This example has illustrated basic use of the prediction-error method for parameter estimation. In our example, the measurement we had corresponded directly to one of the states, and coming up with an observer/predictor that worked was not too hard. For more difficult cases, we may opt to use a nonlinear observer, such as an extended Kalman filter (EKF) or design a Kalman filter based on a linearization of the system around some operating point.
As a last note, there are several other methods available to improve the loss landscape and avoid local minima, such as multiple-shooting. The prediction-error method can easily be combined with most of those methods.
References:
[^Ljung]: Ljung, Lennart. "System identification---Theory for the user".
[^Larsson]: Larsson, Roger, et al. "Direct prediction-error identification of unstable nonlinear systems applied to flight test data." | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2860 | # Newton and Hessian-Free Newton-Krylov with Second Order Adjoint Sensitivity Analysis
In many cases it may be more optimal or more stable to fit using second order
Newton-based optimization techniques. Since DiffEqSensitivity.jl provides
second order sensitivity analysis for fast Hessians and Hessian-vector
products (via forward-over-reverse), we can utilize these in our neural/universal
differential equation training processes.
`sciml_train` is setup to automatically use second order sensitivity analysis
methods if a second order optimizer is requested via Optim.jl. Thus `Newton`
and `NewtonTrustRegion` optimizers will use a second order Hessian-based
optimization, while `KrylovTrustRegion` will utilize a Krylov-based method
with Hessian-vector products (never forming the Hessian) for large parameter
optimizations.
```@example secondorderadjoints
using Flux, DiffEqFlux, Optimization, OptimizationFlux, DifferentialEquations, Plots, Random
u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 1.5f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = Flux.Chain(x -> x.^3,
Flux.Dense(2, 50, tanh),
Flux.Dense(50, 2))
prob_neuralode = NeuralODE(dudt2, tspan, Tsit5(), saveat = tsteps)
function predict_neuralode(p)
Array(prob_neuralode(u0, p)[1])
end
function loss_neuralode(p)
pred = predict_neuralode(p)
loss = sum(abs2, ode_data .- pred)
return loss, pred
end
# Callback function to observe training
list_plots = []
iter = 0
callback = function (p, l, pred; doplot = false)
global list_plots, iter
if iter == 0
list_plots = []
end
iter += 1
display(l)
# plot current prediction against data
plt = scatter(tsteps, ode_data[1,:], label = "data")
scatter!(plt, tsteps, pred[1,:], label = "prediction")
push!(list_plots, plt)
if doplot
display(plot(plt))
end
return l < 0.01
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_neuralode(x), adtype)
optprob1 = Optimization.OptimizationProblem(optf, prob_neuralode.p)
pstart = Optimization.solve(optprob1, ADAM(0.01), callback=callback, maxiters = 100).u
optprob2 = Optimization.OptimizationProblem(optf, pstart)
pmin = Optimization.solve(optprob2, NewtonTrustRegion(), callback=callback, maxiters = 200)
pmin = Optimization.solve(optprob2, Optim.KrylovTrustRegion(), callback=callback, maxiters = 200)
```
Note that we do not demonstrate `Newton()` because we have not found a single
case where it is competitive with the other two methods. `KrylovTrustRegion()`
is generally the fastest due to its use of Hessian-vector products.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 1692 | # Neural Second Order Ordinary Differential Equation
The neural ODE focuses and finding a neural network such that:
```math
u^\prime = NN(u)
```
However, in many cases in physics-based modeling, the key object is not the
velocity but the acceleration: knowing the acceleration tells you the force
field and thus the generating process for the dynamical system. Thus what we want
to do is find the force, i.e.:
```math
u^{\prime\prime} = NN(u)
```
(Note that in order to be the acceleration, we should divide the output of the
neural network by the mass!)
An example of training a neural network on a second order ODE is as follows:
```@example secondorderneural
using DifferentialEquations, Flux, Optimization, OptimizationFlux, RecursiveArrayTools, Random
u0 = Float32[0.; 2.]
du0 = Float32[0.; 0.]
tspan = (0.0f0, 1.0f0)
t = range(tspan[1], tspan[2], length=20)
model = Flux.Chain(Flux.Dense(2, 50, tanh), Flux.Dense(50, 2))
p,re = Flux.destructure(model)
ff(du,u,p,t) = re(p)(u)
prob = SecondOrderODEProblem{false}(ff, du0, u0, tspan, p)
function predict(p)
Array(solve(prob, Tsit5(), p=p, saveat=t))
end
correct_pos = Float32.(transpose(hcat(collect(0:0.05:1)[2:end], collect(2:-0.05:1)[2:end])))
function loss_n_ode(p)
pred = predict(p)
sum(abs2, correct_pos .- pred[1:2, :]), pred
end
data = Iterators.repeated((), 1000)
opt = ADAM(0.01)
l1 = loss_n_ode(p)
callback = function (p,l,pred)
println(l)
l < 0.01
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_n_ode(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
res = Optimization.solve(optprob, opt; callback = callback, maxiters=1000)
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 5471 | # Parameter Estimation on Highly Stiff Systems
This tutorial goes into training a model on stiff chemical reaction system data.
## Copy-Pasteable Code
Before getting to the explanation, here's some code to start with. We will
follow a full explanation of the definition and training process:
```julia
using DifferentialEquations, DiffEqFlux, Optimization, OptimizationOptimJL, LinearAlgebra
using ForwardDiff
using DiffEqBase: UJacobianWrapper
using Plots
function rober(du,u,p,t)
y₁,y₂,y₃ = u
k₁,k₂,k₃ = p
du[1] = -k₁*y₁+k₃*y₂*y₃
du[2] = k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
du[3] = k₂*y₂^2
nothing
end
p = [0.04,3e7,1e4]
u0 = [1.0,0.0,0.0]
prob = ODEProblem(rober,u0,(0.0,1e5),p)
sol = solve(prob,Rosenbrock23())
ts = sol.t
Js = map(u->I + 0.1*ForwardDiff.jacobian(UJacobianWrapper(rober, 0.0, p), u), sol.u)
function predict_adjoint(p)
p = exp.(p)
_prob = remake(prob,p=p)
Array(solve(_prob,Rosenbrock23(autodiff=false),saveat=ts,sensealg=QuadratureAdjoint(autojacvec=ReverseDiffVJP(true))))
end
function loss_adjoint(p)
prediction = predict_adjoint(p)
prediction = [prediction[:, i] for i in axes(prediction, 2)]
diff = map((J,u,data) -> J * (abs2.(u .- data)) , Js, prediction, sol.u)
loss = sum(abs, sum(diff)) |> sqrt
loss, prediction
end
callback = function (p,l,pred) #callback function to observe training
println("Loss: $l")
println("Parameters: $(exp.(p))")
# using `remake` to re-create our `prob` with current parameters `p`
plot(solve(remake(prob, p=exp.(p)), Rosenbrock23())) |> display
return false # Tell it to not halt the optimization. If return true, then optimization stops
end
initp = ones(3)
# Display the ODE with the initial parameter values.
callback(initp,loss_adjoint(initp)...)
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_adjoint(x), adtype)
optprob = Optimization.OptimizationProblem(optf, initp)
res = Optimization.solve(optprob, ADAM(0.01), callback = callback, maxiters = 300)
optprob2 = Optimization.OptimizationProblem(optf, res.u)
res2 = Optimization.solve(optprob2, BFGS(), callback = callback, maxiters = 30, allow_f_increases=true)
println("Ground truth: $(p)\nFinal parameters: $(round.(exp.(res2.u), sigdigits=5))\nError: $(round(norm(exp.(res2.u) - p) ./ norm(p) .* 100, sigdigits=3))%")
```
Output:
```
Ground truth: [0.04, 3.0e7, 10000.0]
Final parameters: [0.040002, 3.0507e7, 10084.0]
Error: 1.69%
```
## Explanation
First, let's get a time series array from the Robertson's equation as data.
```julia
using DifferentialEquations, DiffEqFlux, Optimization, OptimizationOptimJL, LinearAlgebra
using ForwardDiff
using DiffEqBase: UJacobianWrapper
using Plots
function rober(du,u,p,t)
y₁,y₂,y₃ = u
k₁,k₂,k₃ = p
du[1] = -k₁*y₁+k₃*y₂*y₃
du[2] = k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
du[3] = k₂*y₂^2
nothing
end
p = [0.04,3e7,1e4]
u0 = [1.0,0.0,0.0]
prob = ODEProblem(rober,u0,(0.0,1e5),p)
sol = solve(prob,Rosenbrock23())
ts = sol.t
Js = map(u->I + 0.1*ForwardDiff.jacobian(UJacobianWrapper(rober, 0.0, p), u), sol.u)
```
Note that we also computed a shifted and scaled Jacobian along with the
solution. We will use this matrix to scale the loss later.
We fit the parameters in log space, so we need to compute `exp.(p)` to get back
the original parameters.
```julia
function predict_adjoint(p)
p = exp.(p)
_prob = remake(prob,p=p)
Array(solve(_prob,Rosenbrock23(autodiff=false),saveat=ts,sensealg=QuadratureAdjoint(autojacvec=ReverseDiffVJP(true))))
end
function loss_adjoint(p)
prediction = predict_adjoint(p)
prediction = [prediction[:, i] for i in axes(prediction, 2)]
diff = map((J,u,data) -> J * (abs2.(u .- data)) , Js, prediction, sol.u)
loss = sum(abs, sum(diff)) |> sqrt
loss, prediction
end
```
The difference between the data and the prediction is weighted by the transformed
Jacobian to do a relative scaling of the loss.
We define a callback function.
```julia
callback = function (p,l,pred) #callback function to observe training
println("Loss: $l")
println("Parameters: $(exp.(p))")
# using `remake` to re-create our `prob` with current parameters `p`
plot(solve(remake(prob, p=exp.(p)), Rosenbrock23())) |> display
return false # Tell it to not halt the optimization. If return true, then optimization stops
end
```
We then use a combination of `ADAM` and `BFGS` to minimize the loss function to
accelerate the optimization. The initial guess of the parameters are chosen to
be `[1, 1, 1.0]`.
```julia
initp = ones(3)
# Display the ODE with the initial parameter values.
callback(initp,loss_adjoint(initp)...)
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_adjoint(x), adtype)
optprob = Optimization.OptimizationProblem(optf, initp)
res = Optimization.solve(optprob, ADAM(0.01), callback = callback, maxiters = 300)
optprob2 = Optimization.OptimizationProblem(optf, res.u)
res2 = Optimization.solve(optprob2, BFGS(), callback = callback, maxiters = 30, allow_f_increases=true)
```
Finally, we can analyze the difference between the fitted parameters and the
ground truth.
```julia
println("Ground truth: $(p)\nFinal parameters: $(round.(exp.(res2.u), sigdigits=5))\nError: $(round(norm(exp.(res2.u) - p) ./ norm(p) .* 100, sigdigits=3))%")
```
It gives the output
```
Ground truth: [0.04, 3.0e7, 10000.0]
Final parameters: [0.040002, 3.0507e7, 10084.0]
Error: 1.69%
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 20141 | # Controlling Stochastic Differential Equations
In this tutorial, we show how to use DiffEqFlux to control the time evolution of a system
described by a stochastic differential equations (SDE). Specifically, we consider a
continuously monitored qubit described by an SDE in the Ito sense with multiplicative
scalar noise (see [1] for a reference):
```math
dψ = b(ψ(t), Ω(t))ψ(t) dt + σ(ψ(t))ψ(t) dW_t .
```
We use a predictive model to map the quantum state of the qubit, ψ(t), at each time
to the control parameter Ω(t) which rotates the quantum state about the `x`-axis of the Bloch sphere
to ultimately prepare and stabilize the qubit in the excited state.
## Copy-Pasteable Code
Before getting to the explanation, here's some code to start with. We will
follow a full explanation of the definition and training process:
```julia
# load packages
using DiffEqFlux
using StochasticDiffEq, DiffEqCallbacks, DiffEqNoiseProcess
using Statistics, LinearAlgebra, Random
using Plots
#################################################
lr = 0.01f0
epochs = 100
numtraj = 16 # number of trajectories in parallel simulations for training
numtrajplot = 32 # .. for plotting
# time range for the solver
dt = 0.0005f0
tinterval = 0.05f0
tstart = 0.0f0
Nintervals = 20 # total number of intervals, total time = t_interval*Nintervals
tspan = (tstart,tinterval*Nintervals)
ts = Array(tstart:dt:(Nintervals*tinterval+dt)) # time array for noise grid
# Hamiltonian parameters
Δ = 20.0f0
Ωmax = 10.0f0 # control parameter (maximum amplitude)
κ = 0.3f0
# loss hyperparameters
C1 = Float32(1.0) # evolution state fidelity
struct Parameters{flType,intType,tType}
lr::flType
epochs::intType
numtraj::intType
numtrajplot::intType
dt::flType
tinterval::flType
tspan::tType
Nintervals::intType
ts::Vector{flType}
Δ::flType
Ωmax::flType
κ::flType
C1::flType
end
myparameters = Parameters{typeof(dt),typeof(numtraj), typeof(tspan)}(
lr, epochs, numtraj, numtrajplot, dt, tinterval, tspan, Nintervals, ts,
Δ, Ωmax, κ, C1)
################################################
# Define Neural Network
# state-aware
nn = FastChain(
FastDense(4, 32, relu),
FastDense(32, 1, tanh))
p_nn = initial_params(nn) # random initial parameters
###############################################
# initial state anywhere on the Bloch sphere
function prepare_initial(dt, n_par)
# shape 4 x n_par
# input number of parallel realizations and dt for type inference
# random position on the Bloch sphere
theta = acos.(2*rand(typeof(dt),n_par).-1) # uniform sampling for cos(theta) between -1 and 1
phi = rand(typeof(dt),n_par)*2*pi # uniform sampling for phi between 0 and 2pi
# real and imaginary parts ceR, cdR, ceI, cdI
u0 = [cos.(theta/2), sin.(theta/2).*cos.(phi), false*theta, sin.(theta/2).*sin.(phi)]
return vcat(transpose.(u0)...) # build matrix
end
# target state
# ψtar = |up>
u0 = prepare_initial(myparameters.dt, myparameters.numtraj)
###############################################
# Define SDE
function qubit_drift!(du,u,p,t)
# expansion coefficients |Ψ> = ce |e> + cd |d>
ceR, cdR, ceI, cdI = u # real and imaginary parts
# Δ: atomic frequency
# Ω: Rabi frequency for field in x direction
# κ: spontaneous emission
Δ, Ωmax, κ = p[end-2:end]
nn_weights = p[1:end-3]
Ω = (nn(u, nn_weights).*Ωmax)[1]
@inbounds begin
du[1] = 1//2*(ceI*Δ-ceR*κ+cdI*Ω)
du[2] = -cdI*Δ/2 + 1*ceR*(cdI*ceI+cdR*ceR)*κ+ceI*Ω/2
du[3] = 1//2*(-ceR*Δ-ceI*κ-cdR*Ω)
du[4] = cdR*Δ/2 + 1*ceI*(cdI*ceI+cdR*ceR)*κ-ceR*Ω/2
end
return nothing
end
function qubit_diffusion!(du,u,p,t)
ceR, cdR, ceI, cdI = u # real and imaginary parts
κ = p[end]
du .= false
@inbounds begin
#du[1] = zero(ceR)
du[2] += sqrt(κ)*ceR
#du[3] = zero(ceR)
du[4] += sqrt(κ)*ceI
end
return nothing
end
# normalization callback
condition(u,t,integrator) = true
function affect!(integrator)
integrator.u=integrator.u/norm(integrator.u)
end
callback = DiscreteCallback(condition,affect!,save_positions=(false,false))
CreateGrid(t,W1) = NoiseGrid(t,W1)
Zygote.@nograd CreateGrid #avoid taking grads of this function
# set scalar random process
W = sqrt(myparameters.dt)*randn(typeof(myparameters.dt),size(myparameters.ts)) #for 1 trajectory
W1 = cumsum([zero(myparameters.dt); W[1:end-1]], dims=1)
NG = CreateGrid(myparameters.ts,W1)
# get control pulses
p_all = [p_nn; myparameters.Δ; myparameters.Ωmax; myparameters.κ]
# define SDE problem
prob = SDEProblem{true}(qubit_drift!, qubit_diffusion!, vec(u0[:,1]), myparameters.tspan, p_all,
callback=callback, noise=NG
)
#########################################
# compute loss
function g(u,p,t)
ceR = @view u[1,:,:]
cdR = @view u[2,:,:]
ceI = @view u[3,:,:]
cdI = @view u[4,:,:]
p[1]*mean((cdR.^2 + cdI.^2) ./ (ceR.^2 + cdR.^2 + ceI.^2 + cdI.^2))
end
function loss(p, u0, prob::SDEProblem, myparameters::Parameters;
alg=EM(), sensealg = BacksolveAdjoint()
)
pars = [p; myparameters.Δ; myparameters.Ωmax; myparameters.κ]
function prob_func(prob, i, repeat)
# prepare initial state and applied control pulse
u0tmp = deepcopy(vec(u0[:,i]))
W = sqrt(myparameters.dt)*randn(typeof(myparameters.dt),size(myparameters.ts)) #for 1 trajectory
W1 = cumsum([zero(myparameters.dt); W[1:end-1]], dims=1)
NG = CreateGrid(myparameters.ts,W1)
remake(prob,
p = pars,
u0 = u0tmp,
callback = callback,
noise=NG)
end
ensembleprob = EnsembleProblem(prob,
prob_func = prob_func,
safetycopy = true
)
_sol = solve(ensembleprob, alg, EnsembleThreads(),
sensealg=sensealg,
saveat=myparameters.tinterval,
dt=myparameters.dt,
adaptive=false,
trajectories=myparameters.numtraj, batch_size=myparameters.numtraj)
A = convert(Array,_sol)
loss = g(A,[myparameters.C1],nothing)
return loss
end
#########################################
# visualization -- run for new batch
function visualize(p, u0, prob::SDEProblem, myparameters::Parameters;
alg=EM(),
)
pars = [p; myparameters.Δ; myparameters.Ωmax; myparameters.κ]
function prob_func(prob, i, repeat)
# prepare initial state and applied control pulse
u0tmp = deepcopy(vec(u0[:,i]))
W = sqrt(myparameters.dt)*randn(typeof(myparameters.dt),size(myparameters.ts)) #for 1 trajectory
W1 = cumsum([zero(myparameters.dt); W[1:end-1]], dims=1)
NG = CreateGrid(myparameters.ts,W1)
remake(prob,
p = pars,
u0 = u0tmp,
callback = callback,
noise=NG)
end
ensembleprob = EnsembleProblem(prob,
prob_func = prob_func,
safetycopy = true
)
u = solve(ensembleprob, alg, EnsembleThreads(),
saveat=myparameters.tinterval,
dt=myparameters.dt,
adaptive=false, #abstol=1e-6, reltol=1e-6,
trajectories=myparameters.numtrajplot, batch_size=myparameters.numtrajplot)
ceR = @view u[1,:,:]
cdR = @view u[2,:,:]
ceI = @view u[3,:,:]
cdI = @view u[4,:,:]
infidelity = @. (cdR^2 + cdI^2) / (ceR^2 + cdR^2 + ceI^2 + cdI^2)
meaninfidelity = mean(infidelity)
loss = myparameters.C1*meaninfidelity
@info "Loss: " loss
fidelity = @. (ceR^2 + ceI^2) / (ceR^2 + cdR^2 + ceI^2 + cdI^2)
mf = mean(fidelity, dims=2)[:]
sf = std(fidelity, dims=2)[:]
pl1 = plot(0:myparameters.Nintervals, mf,
ribbon = sf,
ylim = (0,1), xlim = (0,myparameters.Nintervals),
c=1, lw = 1.5, xlabel = "steps i", ylabel="Fidelity", legend=false)
pl = plot(pl1, legend = false, size=(400,360))
return pl, loss
end
###################################
# training loop
@info "Start Training.."
# optimize the parameters for a few epochs with ADAM on time span Nint
opt = ADAM(myparameters.lr)
list_plots = []
losses = []
for epoch in 1:myparameters.epochs
println("epoch: $epoch / $(myparameters.epochs)")
local u0 = prepare_initial(myparameters.dt, myparameters.numtraj)
_dy, back = @time Zygote.pullback(p -> loss(p, u0, prob, myparameters,
sensealg=BacksolveAdjoint()
), p_nn)
@show _dy
gs = @time back(one(_dy))[1]
# store loss
push!(losses, _dy)
if (epoch % myparameters.epochs == 0) || (epoch == 1)
# plot/store every xth epoch
@info "plotting.."
local u0 = prepare_initial(myparameters.dt, myparameters.numtrajplot)
pl, test_loss = visualize(p_nn, u0, prob, myparameters)
println("Loss (epoch: $epoch): $test_loss")
display(pl)
push!(list_plots, pl)
end
Flux.Optimise.update!(opt, p_nn, gs)
println("")
end
# plot training loss
pl = plot(losses, lw = 1.5, xlabel = "some epochs", ylabel="Loss", legend=false)
savefig(display(list_plots[end], "fidelity.png")
```
Output:
```
[ Info: Start Training..
epoch: 1 / 100
38.519219 seconds (85.38 M allocations: 4.316 GiB, 3.37% gc time)
_dy = 0.63193643f0
26.232970 seconds (122.33 M allocations: 5.899 GiB, 7.26% gc time)
...
[ Info: plotting..
┌ Info: Loss:
└ loss = 0.11777343f0
Loss (epoch: 100): 0.11777343
```
## Step-by-step description
### Load packages
```julia
using DiffEqFlux
using StochasticDiffEq, DiffEqCallbacks, DiffEqNoiseProcess
using Statistics, LinearAlgebra, Random
using Plots
```
### Parameters
We define the parameters of the qubit and hyper-parameters of the training process.
```julia
lr = 0.01f0
epochs = 100
numtraj = 16 # number of trajectories in parallel simulations for training
numtrajplot = 32 # .. for plotting
# time range for the solver
dt = 0.0005f0
tinterval = 0.05f0
tstart = 0.0f0
Nintervals = 20 # total number of intervals, total time = t_interval*Nintervals
tspan = (tstart,tinterval*Nintervals)
ts = Array(tstart:dt:(Nintervals*tinterval+dt)) # time array for noise grid
# Hamiltonian parameters
Δ = 20.0f0
Ωmax = 10.0f0 # control parameter (maximum amplitude)
κ = 0.3f0
# loss hyperparameters
C1 = Float32(1.0) # evolution state fidelity
struct Parameters{flType,intType,tType}
lr::flType
epochs::intType
numtraj::intType
numtrajplot::intType
dt::flType
tinterval::flType
tspan::tType
Nintervals::intType
ts::Vector{flType}
Δ::flType
Ωmax::flType
κ::flType
C1::flType
end
myparameters = Parameters{typeof(dt),typeof(numtraj), typeof(tspan)}(
lr, epochs, numtraj, numtrajplot, dt, tinterval, tspan, Nintervals, ts,
Δ, Ωmax, κ, C1)
```
In plain terms, the quantities that were defined are:
- `lr` = learning rate of the optimizer
- `epochs` = number of epochs in the training process
- `numtraj` = number of simulated trajectories in the training process
- `numtrajplot` = number of simulated trajectories to visualize the performance
- `dt` = time step for solver (initial `dt` if adaptive)
- `tinterval` = time spacing between checkpoints
- `tspan` = time span
- `Nintervals` = number of checkpoints
- `ts` = discretization of the entire time interval, used for `NoiseGrid`
- `Δ` = detuning between the qubit and the laser
- `Ωmax` = maximum frequency of the control laser
- `κ` = decay rate
- `C1` = loss function hyper-parameter
### Controller
We use a neural network to control the parameter Ω(t). Alternatively, one could
also, e.g., use [tensor layers](https://diffeqflux.sciml.ai/dev/layers/TensorLayer/).
```julia
# state-aware
nn = FastChain(
FastDense(4, 32, relu),
FastDense(32, 1, tanh))
p_nn = initial_params(nn) # random initial parameters
```
### Initial state
We prepare `n_par` initial states, uniformly distributed over the Bloch sphere.
To avoid complex numbers in our simulations, we split the state of the qubit
```math
ψ(t) = c_e(t) (1,0) + c_d(t) (0,1)
```
into its real and imaginary part.
```julia
# initial state anywhere on the Bloch sphere
function prepare_initial(dt, n_par)
# shape 4 x n_par
# input number of parallel realizations and dt for type inference
# random position on the Bloch sphere
theta = acos.(2*rand(typeof(dt),n_par).-1) # uniform sampling for cos(theta) between -1 and 1
phi = rand(typeof(dt),n_par)*2*pi # uniform sampling for phi between 0 and 2pi
# real and imaginary parts ceR, cdR, ceI, cdI
u0 = [cos.(theta/2), sin.(theta/2).*cos.(phi), false*theta, sin.(theta/2).*sin.(phi)]
return vcat(transpose.(u0)...) # build matrix
end
# target state
# ψtar = |e>
u0 = prepare_initial(myparameters.dt, myparameters.numtraj)
```
### Defining the SDE
We define the drift and diffusion term of the qubit. The SDE doesn't preserve the
norm of the quantum state. To ensure the normalization of the state, we add a
`DiscreteCallback` after each time step. Further, we use a NoiseGrid
from the [DiffEqNoiseProcess](https://diffeq.sciml.ai/latest/features/noise_process/#Direct-Construction-Example)
package, as one possibility to simulate a 1D Brownian motion. Note that the NN
is placed directly into the drift function, thus the control parameter Ω is
continuously updated.
```julia
# Define SDE
function qubit_drift!(du,u,p,t)
# expansion coefficients |Ψ> = ce |e> + cd |d>
ceR, cdR, ceI, cdI = u # real and imaginary parts
# Δ: atomic frequency
# Ω: Rabi frequency for field in x direction
# κ: spontaneous emission
Δ, Ωmax, κ = p[end-2:end]
nn_weights = p[1:end-3]
Ω = (nn(u, nn_weights).*Ωmax)[1]
@inbounds begin
du[1] = 1//2*(ceI*Δ-ceR*κ+cdI*Ω)
du[2] = -cdI*Δ/2 + 1*ceR*(cdI*ceI+cdR*ceR)*κ+ceI*Ω/2
du[3] = 1//2*(-ceR*Δ-ceI*κ-cdR*Ω)
du[4] = cdR*Δ/2 + 1*ceI*(cdI*ceI+cdR*ceR)*κ-ceR*Ω/2
end
return nothing
end
function qubit_diffusion!(du,u,p,t)
ceR, cdR, ceI, cdI = u # real and imaginary parts
κ = p[end]
du .= false
@inbounds begin
#du[1] = zero(ceR)
du[2] += sqrt(κ)*ceR
#du[3] = zero(ceR)
du[4] += sqrt(κ)*ceI
end
return nothing
end
# normalization callback
condition(u,t,integrator) = true
function affect!(integrator)
integrator.u=integrator.u/norm(integrator.u)
end
callback = DiscreteCallback(condition,affect!,save_positions=(false,false))
CreateGrid(t,W1) = NoiseGrid(t,W1)
Zygote.@nograd CreateGrid #avoid taking grads of this function
# set scalar random process
W = sqrt(myparameters.dt)*randn(typeof(myparameters.dt),size(myparameters.ts)) #for 1 trajectory
W1 = cumsum([zero(myparameters.dt); W[1:end-1]], dims=1)
NG = CreateGrid(myparameters.ts,W1)
# get control pulses
p_all = [p_nn; myparameters.Δ; myparameters.Ωmax; myparameters.κ]
# define SDE problem
prob = SDEProblem{true}(qubit_drift!, qubit_diffusion!, vec(u0[:,1]), myparameters.tspan, p_all,
callback=callback, noise=NG
)
```
### Compute loss function
We'd like to prepare the excited state of the qubit. An appropriate choice for
the loss function is the infidelity of the state ψ(t) with respect to the excited
state. We create a parallelized `EnsembleProblem`, where the `prob_func` creates a
new `NoiseGrid` for every trajectory and loops over the initial states. The number
of parallel trajectories and the used batch size can be tuned by the
kwargs `trajectories=..` and `batchsize=..` in the `solve` call. See also [the
parallel ensemble simulation docs](https://diffeq.sciml.ai/latest/features/ensemble/)
for a description of the available ensemble algorithms. To optimize only the parameters
of the neural network, we use `pars = [p; myparameters.Δ; myparameters.Ωmax; myparameters.κ]`
``` julia
# compute loss
function g(u,p,t)
ceR = @view u[1,:,:]
cdR = @view u[2,:,:]
ceI = @view u[3,:,:]
cdI = @view u[4,:,:]
p[1]*mean((cdR.^2 + cdI.^2) ./ (ceR.^2 + cdR.^2 + ceI.^2 + cdI.^2))
end
function loss(p, u0, prob::SDEProblem, myparameters::Parameters;
alg=EM(), sensealg = BacksolveAdjoint()
)
pars = [p; myparameters.Δ; myparameters.Ωmax; myparameters.κ]
function prob_func(prob, i, repeat)
# prepare initial state and applied control pulse
u0tmp = deepcopy(vec(u0[:,i]))
W = sqrt(myparameters.dt)*randn(typeof(myparameters.dt),size(myparameters.ts)) #for 1 trajectory
W1 = cumsum([zero(myparameters.dt); W[1:end-1]], dims=1)
NG = CreateGrid(myparameters.ts,W1)
remake(prob,
p = pars,
u0 = u0tmp,
callback = callback,
noise=NG)
end
ensembleprob = EnsembleProblem(prob,
prob_func = prob_func,
safetycopy = true
)
_sol = solve(ensembleprob, alg, EnsembleThreads(),
sensealg=sensealg,
saveat=myparameters.tinterval,
dt=myparameters.dt,
adaptive=false,
trajectories=myparameters.numtraj, batch_size=myparameters.numtraj)
A = convert(Array,_sol)
loss = g(A,[myparameters.C1],nothing)
return loss
end
```
### Visualization
To visualize the performance of the controller, we plot the mean value and
standard deviation of the fidelity of a bunch of trajectories (`myparameters.numtrajplot`) as
a function of the time steps at which loss values are computed.
```julia
function visualize(p, u0, prob::SDEProblem, myparameters::Parameters;
alg=EM(),
)
pars = [p; myparameters.Δ; myparameters.Ωmax; myparameters.κ]
function prob_func(prob, i, repeat)
# prepare initial state and applied control pulse
u0tmp = deepcopy(vec(u0[:,i]))
W = sqrt(myparameters.dt)*randn(typeof(myparameters.dt),size(myparameters.ts)) #for 1 trajectory
W1 = cumsum([zero(myparameters.dt); W[1:end-1]], dims=1)
NG = CreateGrid(myparameters.ts,W1)
remake(prob,
p = pars,
u0 = u0tmp,
callback = callback,
noise=NG)
end
ensembleprob = EnsembleProblem(prob,
prob_func = prob_func,
safetycopy = true
)
u = solve(ensembleprob, alg, EnsembleThreads(),
saveat=myparameters.tinterval,
dt=myparameters.dt,
adaptive=false, #abstol=1e-6, reltol=1e-6,
trajectories=myparameters.numtrajplot, batch_size=myparameters.numtrajplot)
ceR = @view u[1,:,:]
cdR = @view u[2,:,:]
ceI = @view u[3,:,:]
cdI = @view u[4,:,:]
infidelity = @. (cdR^2 + cdI^2) / (ceR^2 + cdR^2 + ceI^2 + cdI^2)
meaninfidelity = mean(infidelity)
loss = myparameters.C1*meaninfidelity
@info "Loss: " loss
fidelity = @. (ceR^2 + ceI^2) / (ceR^2 + cdR^2 + ceI^2 + cdI^2)
mf = mean(fidelity, dims=2)[:]
sf = std(fidelity, dims=2)[:]
pl1 = plot(0:myparameters.Nintervals, mf,
ribbon = sf,
ylim = (0,1), xlim = (0,myparameters.Nintervals),
c=1, lw = 1.5, xlabel = "steps i", ylabel="Fidelity", legend=false)
pl = plot(pl1, legend = false, size=(400,360))
return pl, loss
end
```
### Training
We use the `ADAM` optimizer to optimize the parameters of the neural network.
In each epoch, we draw new initial quantum states, compute the forward evolution,
and, subsequently, the gradients of the loss function with respect to the parameters
of the neural network.
`sensealg` allows one to switch between the different [sensitivity modes](https://diffeqflux.sciml.ai/dev/ControllingAdjoints/).
`InterpolatingAdjoint` and `BacksolveAdjoint` are the two possible continuous adjoint
sensitivity methods. The necessary correction between Ito and Stratonovich integrals
is computed under the hood in the DiffEqSensitivity package.
```julia
# optimize the parameters for a few epochs with ADAM on time span Nint
opt = ADAM(myparameters.lr)
list_plots = []
losses = []
for epoch in 1:myparameters.epochs
println("epoch: $epoch / $(myparameters.epochs)")
local u0 = prepare_initial(myparameters.dt, myparameters.numtraj)
_dy, back = @time Zygote.pullback(p -> loss(p, u0, prob, myparameters,
sensealg=BacksolveAdjoint()
), p_nn)
@show _dy
gs = @time back(one(_dy))[1]
# store loss
push!(losses, _dy)
if (epoch % myparameters.epochs == 0) || (epoch == 1)
# plot/store every xth epoch
@info "plotting.."
local u0 = prepare_initial(myparameters.dt, myparameters.numtrajplot)
pl, test_loss = visualize(p_nn, u0, prob, myparameters)
println("Loss (epoch: $epoch): $test_loss")
display(pl)
push!(list_plots, pl)
end
Flux.Optimise.update!(opt, p_nn, gs)
println("")
end
```
## References
[1] Schäfer, Frank, Pavel Sekatski, Martin Koppenhöfer, Christoph Bruder, and Michal Kloc. "Control of stochastic quantum dynamics by differentiable programming." Machine Learning: Science and Technology 2, no. 3 (2021): 035004.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2635 | # Universal Differential Equations for Neural Feedback Control
You can also mix a known differential equation and a neural differential
equation, so that the parameters and the neural network are estimated
simultaneously!
We will assume that we know the dynamics of the second equation
(linear dynamics), and our goal is to find a neural network that is dependent
on the current state of the dynamical system that will control the second
equation to stay close to 1.
```julia
using Lux, Optimization, OptimizationPolyalgorithms, OptimizatonOptimJL, DifferentialEquations, Plots, Random
rng = Random.default_rng()
u0 = 1.1f0
tspan = (0.0f0, 25.0f0)
tsteps = 0.0f0:1.0:25.0f0
model_univ = Lux.Chain(Lux.Dense(2, 16, tanh),
Lux.Dense(16, 16, tanh),
Lux.Dense(16, 1))
# The model weights are destructured into a vector of parameters
p_model, st = Lux.setup(rng, model_univ)
p_model = Lux.ComponentArray(p_model)
n_weights = length(p_model)
# Parameters of the second equation (linear dynamics)
p_system = Float32[0.5, -0.5]
p_all = [p_model; p_system]
θ = Float32[u0; p_all]
function dudt_univ!(du, u, p, t)
# Destructure the parameters
model_weights = p[1:n_weights]
α = p[end - 1]
β = p[end]
# The neural network outputs a control taken by the system
# The system then produces an output
model_control, system_output = u
# Dynamics of the control and system
dmodel_control = (model_univ(u, model_weights, st)[1])[1]
dsystem_output = α*system_output + β*model_control
# Update in place
du[1] = dmodel_control
du[2] = dsystem_output
end
prob_univ = ODEProblem(dudt_univ!, [0f0, u0], tspan, p_all)
sol_univ = solve(prob_univ, Tsit5(),abstol = 1e-8, reltol = 1e-6)
function predict_univ(θ)
return Array(solve(prob_univ, Tsit5(), u0=[0f0, θ[1]], p=θ[2:end],
sensealg = InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true)),
saveat = tsteps))
end
loss_univ(θ) = sum(abs2, predict_univ(θ)[2,:] .- 1)
l = loss_univ(θ)
```
```julia
list_plots = []
iter = 0
callback = function (θ, l)
global list_plots, iter
if iter == 0
list_plots = []
end
iter += 1
println(l)
plt = plot(predict_univ(θ)', ylim = (0, 6))
push!(list_plots, plt)
display(plt)
return false
end
```
```julia
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_univ(x), adtype)
optprob = Optimization.OptimizationProblem(optf, θ)
result_univ = Optimization.solve(optprob, PolyOpt(),
callback = callback)
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 3462 | # [Solving Optimal Control Problems with Universal Differential Equations](@id optcontrol)
Here we will solve a classic optimal control problem with a universal differential
equation. Let
```math
x^{′′} = u^3(t)
```
where we want to optimize our controller `u(t)` such that the following is
minimized:
```math
L(\theta) = \sum_i \Vert 4 - x(t_i) \Vert + 2 \Vert x^\prime(t_i) \Vert + \Vert u(t_i) \Vert
```
where ``i`` is measured on (0,8) at 0.01 intervals. To do this, we rewrite the
ODE in first order form:
```math
\begin{aligned}
x^\prime &= v \\
v^′ &= u^3(t) \\
\end{aligned}
```
and thus
```math
L(\theta) = \sum_i \Vert 4 - x(t_i) \Vert + 2 \Vert v(t_i) \Vert + \Vert u(t_i) \Vert
```
is our loss function on the first order system. We thus choose a neural network
form for ``u`` and optimize the equation with respect to this loss. Note that we
will first reduce control cost (the last term) by 10x in order to bump the network out
of a local minimum. This looks like:
```julia
using Lux, DifferentialEquations, Optimization, OptimizationOptimJL, OptimizationFlux, Plots, Statistics, Random
rng = Random.default_rng()
tspan = (0.0f0,8.0f0)
ann = Lux.Chain(Lux.Dense(1,32,tanh), Lux.Dense(32,32,tanh), Lux.Dense(32,1))
θ, st = Lux.setup(rng, ann)
function dxdt_(dx,x,p,t)
x1, x2 = x
dx[1] = x[2]
dx[2] = (ann([t],p,st)[1])[1]^3
end
x0 = [-4f0,0f0]
ts = Float32.(collect(0.0:0.01:tspan[2]))
prob = ODEProblem(dxdt_,x0,tspan,θ)
solve(prob,Vern9(),abstol=1e-10,reltol=1e-10)
function predict_adjoint(θ)
Array(solve(prob,Vern9(),p=θ,saveat=ts,sensealg=InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true))))
end
function loss_adjoint(θ)
x = predict_adjoint(θ)
mean(abs2,4.0 .- x[1,:]) + 2mean(abs2,x[2,:]) + mean(abs2,[first(ann([t],θ)) for t in ts])/10
end
l = loss_adjoint(θ)
callback = function (θ,l)
println(l)
p = plot(solve(remake(prob,p=θ),Tsit5(),saveat=0.01),ylim=(-6,6),lw=3)
plot!(p,ts,[first(ann([t],θ)) for t in ts],label="u(t)",lw=3)
display(p)
return false
end
# Display the ODE with the current parameter values.
callback(θ,l)
loss1 = loss_adjoint(θ)
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss_adjoint(x), adtype)
optprob = Optimization.OptimizationProblem(optf, θ)
res1 = Optimization.solve(optprob, ADAM(0.005), callback = callback,maxiters=100)
optprob2 = Optimization.OptimizationProblem(optf, res1.u)
res2 = Optimization.solve(optprob2,
BFGS(), maxiters=100,
allow_f_increases = false)
```
Now that the system is in a better behaved part of parameter space, we return to
the original loss function to finish the optimization:
```julia
function loss_adjoint(θ)
x = predict_adjoint(θ)
mean(abs2,4.0 .- x[1,:]) + 2mean(abs2,x[2,:]) + mean(abs2,[first(ann([t],θ)) for t in ts])
end
optf3 = Optimization.OptimizationFunction((x,p)->loss_adjoint(x), adtype)
optprob3 = Optimization.OptimizationProblem(optf3, res2.u)
res3 = Optimization.solve(optprob3,
BFGS(),maxiters=100,
allow_f_increases = false)
l = loss_adjoint(res3.u)
callback(res3.u,l)
p = plot(solve(remake(prob,p=res3.u),Tsit5(),saveat=0.01),ylim=(-6,6),lw=3)
plot!(p,ts,[first(ann([t],res3.u)) for t in ts],label="u(t)",lw=3)
savefig("optimal_control.png")
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 10127 | # Partial Differential Equation (PDE) Constrained Optimization
This example uses a prediction model to optimize the one-dimensional Heat Equation.
(Step-by-step description below)
```julia
using DelimitedFiles,Plots
using DifferentialEquations, Optimization, OptimizationPolyalgorithms, OptimizationOptimJL
# Problem setup parameters:
Lx = 10.0
x = 0.0:0.01:Lx
dx = x[2] - x[1]
Nx = size(x)
u0 = exp.(-(x.-3.0).^2) # I.C
## Problem Parameters
p = [1.0,1.0] # True solution parameters
xtrs = [dx,Nx] # Extra parameters
dt = 0.40*dx^2 # CFL condition
t0, tMax = 0.0 ,1000*dt
tspan = (t0,tMax)
t = t0:dt:tMax;
## Definition of Auxiliary functions
function ddx(u,dx)
"""
2nd order Central difference for 1st degree derivative
"""
return [[zero(eltype(u))] ; (u[3:end] - u[1:end-2]) ./ (2.0*dx) ; [zero(eltype(u))]]
end
function d2dx(u,dx)
"""
2nd order Central difference for 2nd degree derivative
"""
return [[zero(eltype(u))]; (u[3:end] - 2.0.*u[2:end-1] + u[1:end-2]) ./ (dx^2); [zero(eltype(u))]]
end
## ODE description of the Physics:
function heat(u,p,t)
# Model parameters
a0, a1 = p
dx,Nx = xtrs #[1.0,3.0,0.125,100]
return 2.0*a0 .* u + a1 .* d2dx(u, dx)
end
# Testing Solver on linear PDE
prob = ODEProblem(heat,u0,tspan,p)
sol = solve(prob,Tsit5(), dt=dt,saveat=t);
plot(x, sol.u[1], lw=3, label="t0", size=(800,500))
plot!(x, sol.u[end],lw=3, ls=:dash, label="tMax")
ps = [0.1, 0.2]; # Initial guess for model parameters
function predict(θ)
Array(solve(prob,Tsit5(),p=θ,dt=dt,saveat=t))
end
## Defining Loss function
function loss(θ)
pred = predict(θ)
l = predict(θ) - sol
return sum(abs2, l), pred # Mean squared error
end
l,pred = loss(ps)
size(pred), size(sol), size(t) # Checking sizes
LOSS = [] # Loss accumulator
PRED = [] # prediction accumulator
PARS = [] # parameters accumulator
callback = function (θ,l,pred) #callback function to observe training
display(l)
append!(PRED, [pred])
append!(LOSS, l)
append!(PARS, [θ])
false
end
callback(ps,loss(ps)...) # Testing callback function
# Let see prediction vs. Truth
scatter(sol[:,end], label="Truth", size=(800,500))
plot!(PRED[end][:,end], lw=2, label="Prediction")
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, ps)
res = Optimization.solve(optprob, PolyOpt(), callback = callback)
@show res.u # returns [0.999999999613485, 0.9999999991343996]
```
## Step-by-step Description
### Load Packages
```julia
using DelimitedFiles,Plots
using DifferentialEquations, DiffEqFlux
```
### Parameters
First, we setup the 1-dimensional space over which our equations will be evaluated.
`x` spans **from 0.0 to 10.0** in steps of **0.01**; `t` spans **from 0.00 to 0.04** in
steps of **4.0e-5**.
```julia
# Problem setup parameters:
Lx = 10.0
x = 0.0:0.01:Lx
dx = x[2] - x[1]
Nx = size(x)
u0 = exp.(-(x.-3.0).^2) # I.C
## Problem Parameters
p = [1.0,1.0] # True solution parameters
xtrs = [dx,Nx] # Extra parameters
dt = 0.40*dx^2 # CFL condition
t0, tMax = 0.0 ,1000*dt
tspan = (t0,tMax)
t = t0:dt:tMax;
```
In plain terms, the quantities that were defined are:
- `x` (to `Lx`) spans the specified 1D space
- `dx` = distance between two points
- `Nx` = total size of space
- `u0` = initial condition
- `p` = true solution
- `xtrs` = convenient grouping of `dx` and `Nx` into Array
- `dt` = time distance between two points
- `t` (`t0` to `tMax`) spans the specified time frame
- `tspan` = span of `t`
### Auxiliary Functions
We then define two functions to compute the derivatives numerically. The **Central
Difference** is used in both the 1st and 2nd degree derivatives.
```julia
## Definition of Auxiliary functions
function ddx(u,dx)
"""
2nd order Central difference for 1st degree derivative
"""
return [[zero(eltype(u))] ; (u[3:end] - u[1:end-2]) ./ (2.0*dx) ; [zero(eltype(u))]]
end
function d2dx(u,dx)
"""
2nd order Central difference for 2nd degree derivative
"""
return [[zero(eltype(u))]; (u[3:end] - 2.0.*u[2:end-1] + u[1:end-2]) ./ (dx^2); [zero(eltype(u))]]
end
```
### Heat Differential Equation
Next, we setup our desired set of equations in order to define our problem.
```julia
## ODE description of the Physics:
function heat(u,p,t)
# Model parameters
a0, a1 = p
dx,Nx = xtrs #[1.0,3.0,0.125,100]
return 2.0*a0 .* u + a1 .* d2dx(u, dx)
end
```
### Solve and Plot Ground Truth
We then solve and plot our partial differential equation. This is the true solution which we
will compare to further on.
```julia
# Testing Solver on linear PDE
prob = ODEProblem(heat,u0,tspan,p)
sol = solve(prob,Tsit5(), dt=dt,saveat=t);
plot(x, sol.u[1], lw=3, label="t0", size=(800,500))
plot!(x, sol.u[end],lw=3, ls=:dash, label="tMax")
```
### Building the Prediction Model
Now we start building our prediction model to try to obtain the values `p`. We make an
initial guess for the parameters and name it `ps` here. The `predict` function is a
non-linear transformation in one layer using `solve`. If unfamiliar with the concept,
refer to [here](https://julialang.org/blog/2019/01/fluxdiffeq/).
```julia
ps = [0.1, 0.2]; # Initial guess for model parameters
function predict(θ)
Array(solve(prob,Tsit5(),p=θ,dt=dt,saveat=t))
end
```
### Train Parameters
Training our model requires a **loss function**, an **optimizer** and a **callback
function** to display the progress.
#### Loss
We first make our predictions based on the current values of our parameters `ps`, then
take the difference between the predicted solution and the truth above. For the loss, we
use the **Mean squared error**.
```julia
## Defining Loss function
function loss(θ)
pred = predict(θ)
l = predict(θ) - sol
return sum(abs2, l), pred # Mean squared error
end
l,pred = loss(ps)
size(pred), size(sol), size(t) # Checking sizes
```
#### Optimizer
The optimizers `ADAM` with a learning rate of 0.01 and `BFGS` are directly passed in
training (see below)
#### Callback
The callback function displays the loss during training. We also keep a history of the
loss, the previous predictions and the previous parameters with `LOSS`, `PRED` and `PARS`
accumulators.
```julia
LOSS = [] # Loss accumulator
PRED = [] # prediction accumulator
PARS = [] # parameters accumulator
callback = function (θ,l,pred) #callback function to observe training
display(l)
append!(PRED, [pred])
append!(LOSS, l)
append!(PARS, [θ])
false
end
callback(ps,loss(ps)...) # Testing callback function
```
### Plotting Prediction vs Ground Truth
The scatter points plotted here are the ground truth obtained from the actual solution we
solved for above. The solid line represents our prediction. The goal is for both to overlap
almost perfectly when the PDE finishes its training and the loss is close to 0.
```julia
# Let see prediction vs. Truth
scatter(sol[:,end], label="Truth", size=(800,500))
plot!(PRED[end][:,end], lw=2, label="Prediction")
```
### Train
The parameters are trained using `Optimization.solve` and adjoint sensitivities.
The resulting best parameters are stored in `res` and `res.u` returns the
parameters that minimizes the cost function.
```julia
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p)->loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, ps)
res = Optimization.solve(optprob, PolyOpt(), callback = callback)
@show res.u # returns [0.999999999613485, 0.9999999991343996]
```
We successfully predict the final `ps` to be equal to **[0.999999999999975,
1.0000000000000213]** vs the true solution of `p` = **[1.0, 1.0]**
### Expected Output
```julia
153.74716386883014
153.74716386883014
150.31001476832154
146.91327105278128
143.55759898759374
140.24363496931753
136.97198347241257
133.7432151677673
130.55786524987215
127.4164319720337
124.31937540894337
121.26711645161134
118.26003603654628
115.29847461603427
112.3827318609633
109.51306659138356
106.68969692777314
103.9128006498965
101.18251574195561
98.4989411191655
95.8621374998964
93.27212842357801
90.7289013677808
88.23240896985287
85.7825703121191
83.37927225399383
81.02237079935475
78.71169247246975
76.44703568540336
74.22817209335733
72.05484791455291
69.92678520204167
67.84368308185877
65.80521891873633
63.81104944163126
61.860811797059554
59.95412455791812
58.090588663826914
56.26978832428055
54.491291863817686
52.75465253618253
51.05940929392087
49.405087540342564
47.79119984816457
46.217246667009626
44.68271701552145
43.18708916553295
41.729831330086824
40.310402328506555
38.928252289762675
37.58282331100446
36.27355015737786
34.99986094007708
33.76117780641769
32.55691762379305
31.386492661205562
30.249311268822595
29.144778544729924
28.07229699202965
27.031267166855155
26.0210883069299
25.041158938495613
24.09087747422764
23.169642780270983
22.276854715336583
21.411914664407295
20.57422602075309
19.76319467338999
18.978229434706996
18.218742481097735
17.48414972880479
16.773871221320032
16.087331469276343
15.423959781047255
14.78319057598673
14.164463661389682
13.567224508247984
12.990924508800399
12.435021204904853
11.898978515303417
11.382266943971572
10.884363779196345
10.404753276294088
9.942926832732251
9.49838314770057
9.070628379941386
8.659176278010788
8.263548334737965
7.883273889583058
7.517890250788576
7.1669427976429585
6.829985075319055
6.506578881124348
6.19629433688754
5.898709957062298
5.613412692266443
5.339997993203038
5.078069839645422
4.827240754206443
4.587131834698446
4.357372763056912
4.357372763056912
4.137601774726927
1.5254536025963588
0.0023707487489687726
4.933077457357198e-7
8.157805551380282e-14
1.6648677430325974e-16
res.u = [0.999999999999975, 1.0000000000000213]
2-element Array{Float64,1}:
0.999999999999975
1.0000000000000213
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 6651 | # Neural Stochastic Differential Equations
With neural stochastic differential equations, there is once again a helper form
`neural_dmsde` which can be used for the multiplicative noise case (consult the
layers API documentation, or [this full example using the layer
function](https://github.com/MikeInnes/zygote-paper/blob/master/neural_sde/neural_sde.jl)).
However, since there are far too many possible combinations for the API to
support, in many cases you will want to performantly define neural differential
equations for non-ODE systems from scratch. For these systems, it is generally
best to use `TrackerAdjoint` with non-mutating (out-of-place) forms. For
example, the following defines a neural SDE with neural networks for both the
drift and diffusion terms:
```julia
dudt(u, p, t) = model(u)
g(u, p, t) = model2(u)
prob = SDEProblem(dudt, g, x, tspan, nothing)
```
where `model` and `model2` are different neural networks. The same can apply to
a neural delay differential equation. Its out-of-place formulation is
`f(u,h,p,t)`. Thus for example, if we want to define a neural delay differential
equation which uses the history value at `p.tau` in the past, we can define:
```julia
dudt!(u, h, p, t) = model([u; h(t - p.tau)])
prob = DDEProblem(dudt_, u0, h, tspan, nothing)
```
First let's build training data from the same example as the neural ODE:
```julia
using Plots, Statistics
using Lux, Optimization, OptimizationFlux, DiffEqFlux, StochasticDiffEq, DiffEqBase.EnsembleAnalysis, Random
rng = Random.default_rng()
u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0, 1.0f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
```
```julia
function trueSDEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
mp = Float32[0.2, 0.2]
function true_noise_func(du, u, p, t)
du .= mp.*u
end
prob_truesde = SDEProblem(trueSDEfunc, true_noise_func, u0, tspan)
```
For our dataset we will use DifferentialEquations.jl's [parallel ensemble
interface](http://docs.juliadiffeq.org/dev/features/ensemble.html) to generate
data from the average of 10,000 runs of the SDE:
```julia
# Take a typical sample from the mean
ensemble_prob = EnsembleProblem(prob_truesde)
ensemble_sol = solve(ensemble_prob, SOSRI(), trajectories = 10000)
ensemble_sum = EnsembleSummary(ensemble_sol)
sde_data, sde_data_vars = Array.(timeseries_point_meanvar(ensemble_sol, tsteps))
```
Now we build a neural SDE. For simplicity we will use the `NeuralDSDE`
neural SDE with diagonal noise layer function:
```julia
drift_dudt = Lux.Chain(ActivationFunction(x -> x.^3),
Lux.Dense(2, 50, tanh),
Lux.Dense(50, 2))
p1, st1 = Lux.setup(rng, drift_dudt)
diffusion_dudt = Lux.Chain(Lux.Dense(2, 2))
p2, st2 = Lux.setup(rng, diffusion_dudt)
p1 = Lux.ComponentArray(p1)
p2 = Lux.ComponentArray(p2)
#Component Arrays doesn't provide a name to the first ComponentVector, only subsequent ones get a name for dereferencing
p = [p1, p2]
neuralsde = NeuralDSDE(drift_dudt, diffusion_dudt, tspan, SOSRI(),
saveat = tsteps, reltol = 1e-1, abstol = 1e-1)
```
Let's see what that looks like:
```julia
# Get the prediction using the correct initial condition
prediction0, st1, st2 = neuralsde(u0,p,st1,st2)
drift_(u, p, t) = drift_dudt(u, p[1], st1)[1]
diffusion_(u, p, t) = diffusion_dudt(u, p[2], st2)[1]
prob_neuralsde = SDEProblem(drift_, diffusion_, u0,(0.0f0, 1.2f0), p)
ensemble_nprob = EnsembleProblem(prob_neuralsde)
ensemble_nsol = solve(ensemble_nprob, SOSRI(), trajectories = 100,
saveat = tsteps)
ensemble_nsum = EnsembleSummary(ensemble_nsol)
plt1 = plot(ensemble_nsum, title = "Neural SDE: Before Training")
scatter!(plt1, tsteps, sde_data', lw = 3)
scatter(tsteps, sde_data[1,:], label = "data")
scatter!(tsteps, prediction0[1,:], label = "prediction")
```
Now just as with the neural ODE we define a loss function that calculates the
mean and variance from `n` runs at each time point and uses the distance from
the data values:
```julia
function predict_neuralsde(p, u = u0)
return Array(neuralsde(u, p, st1, st2)[1])
end
function loss_neuralsde(p; n = 100)
u = repeat(reshape(u0, :, 1), 1, n)
samples = predict_neuralsde(p, u)
means = mean(samples, dims = 2)
vars = var(samples, dims = 2, mean = means)[:, 1, :]
means = means[:, 1, :]
loss = sum(abs2, sde_data - means) + sum(abs2, sde_data_vars - vars)
return loss, means, vars
end
```
```julia
list_plots = []
iter = 0
# Callback function to observe training
callback = function (p, loss, means, vars; doplot = false)
global list_plots, iter
if iter == 0
list_plots = []
end
iter += 1
# loss against current data
display(loss)
# plot current prediction against data
plt = Plots.scatter(tsteps, sde_data[1,:], yerror = sde_data_vars[1,:],
ylim = (-4.0, 8.0), label = "data")
Plots.scatter!(plt, tsteps, means[1,:], ribbon = vars[1,:], label = "prediction")
push!(list_plots, plt)
if doplot
display(plt)
end
return false
end
```
Now we train using this loss function. We can pre-train a little bit using a
smaller `n` and then decrease it after it has had some time to adjust towards
the right mean behavior:
```julia
opt = ADAM(0.025)
# First round of training with n = 10
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss_neuralsde(x, n=10), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
result1 = Optimization.solve(optprob, opt,
callback = callback, maxiters = 100)
```
We resume the training with a larger `n`. (WARNING - this step is a couple of
orders of magnitude longer than the previous one).
```julia
optf2 = Optimization.OptimizationFunction((x,p) -> loss_neuralsde(x, n=100), adtype)
optprob2 = Optimization.OptimizationProblem(optf2, result1.u)
result2 = Optimization.solve(optprob2, opt,
callback = callback, maxiters = 100)
```
And now we plot the solution to an ensemble of the trained neural SDE:
```julia
_, means, vars = loss_neuralsde(result2.u, n = 1000)
plt2 = Plots.scatter(tsteps, sde_data', yerror = sde_data_vars',
label = "data", title = "Neural SDE: After Training",
xlabel = "Time")
plot!(plt2, tsteps, means', lw = 8, ribbon = vars', label = "prediction")
plt = plot(plt1, plt2, layout = (2, 1))
savefig(plt, "NN_sde_combined.png"); nothing # sde
```
Try this with GPUs as well!
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 6106 | # Optimization of Stochastic Differential Equations
Here we demonstrate `sensealg = ForwardDiffSensitivity()` (provided by
DiffEqSensitivity.jl) for forward-mode automatic differentiation of a small
stochastic differential equation. For large parameter equations, like neural
stochastic differential equations, you should use reverse-mode automatic
differentiation. However, forward-mode can be more efficient for low numbers
of parameters (<100). (Note: the default is reverse-mode AD which is more suitable
for things like neural SDEs!)
## Example 1: Fitting Data with SDEs via Method of Moments and Parallelism
Let's do the most common scenario: fitting data. Let's say our ecological system
is a stochastic process. Each time we solve this equation we get a different
solution, so we need a sensible data source.
```julia
using DiffEqFlux, DifferentialEquations, Plots
function lotka_volterra!(du,u,p,t)
x,y = u
α,β,γ,δ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = δ*x*y - γ*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
function multiplicative_noise!(du,u,p,t)
x,y = u
du[1] = p[5]*x
du[2] = p[6]*y
end
p = [1.5,1.0,3.0,1.0,0.3,0.3]
prob = SDEProblem(lotka_volterra!,multiplicative_noise!,u0,tspan,p)
sol = solve(prob)
plot(sol)
```
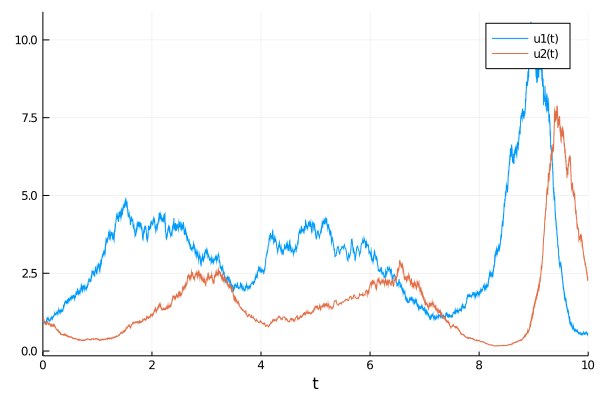
Let's assume that we are observing the seasonal behavior of this system and have
10,000 years of data, corresponding to 10,000 observations of this timeseries.
We can utilize this to get the seasonal means and variances. To simulate that
scenario, we will generate 10,000 trajectories from the SDE to build our dataset:
```julia
using Statistics
ensembleprob = EnsembleProblem(prob)
@time sol = solve(ensembleprob,SOSRI(),saveat=0.1,trajectories=10_000)
truemean = mean(sol,dims=3)[:,:]
truevar = var(sol,dims=3)[:,:]
```
From here, we wish to utilize the method of moments to fit the SDE's parameters.
Thus our loss function will be to solve the SDE a bunch of times and compute
moment equations and use these as our loss against the original series. We
then plot the evolution of the means and variances to verify the fit. For example:
```julia
function loss(p)
tmp_prob = remake(prob,p=p)
ensembleprob = EnsembleProblem(tmp_prob)
tmp_sol = solve(ensembleprob,SOSRI(),saveat=0.1,trajectories=1000)
arrsol = Array(tmp_sol)
sum(abs2,truemean - mean(arrsol,dims=3)) + 0.1sum(abs2,truevar - var(arrsol,dims=3)),arrsol
end
function cb2(p,l,arrsol)
@show p,l
means = mean(arrsol,dims=3)[:,:]
vars = var(arrsol,dims=3)[:,:]
p1 = plot(sol[1].t,means',lw=5)
scatter!(p1,sol[1].t,truemean')
p2 = plot(sol[1].t,vars',lw=5)
scatter!(p2,sol[1].t,truevar')
p = plot(p1,p2,layout = (2,1))
display(p)
false
end
```
We can then use `Optimization.solve` to fit the SDE:
```julia
using Optimization, OptimizationOptimJL
pinit = [1.2,0.8,2.5,0.8,0.1,0.1]
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, pinit)
@time res = Optimization.solve(optprob,ADAM(0.05),callback=cb2,maxiters = 100)
```
The final print out was:
```julia
(p, l) = ([1.5242134195974462, 1.019859938499017, 2.9120928257869227, 0.9840408090733335, 0.29427123791721765, 0.3334393815923646], 1.7046719990657184)
```
Notice that **both the parameters of the deterministic drift equations and the
stochastic portion (the diffusion equation) are fit through this process!**
Also notice that the final fit of the moment equations is close:
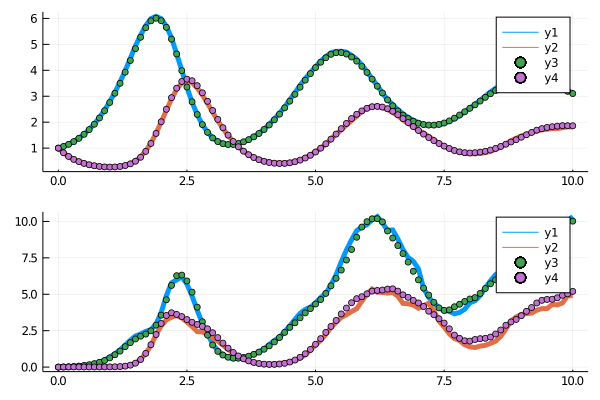
The time for the full fitting process was:
```
250.654845 seconds (4.69 G allocations: 104.868 GiB, 11.87% gc time)
```
approximately 4 minutes.
## Example 2: Fitting SDEs via Bayesian Quasi-Likelihood Approaches
An inference method which can be much more efficient in many cases is the quasi-likelihood approach.
This approach matches the random likelihood of the SDE output with the random sampling of a Bayesian
inference problem to more efficiently directly estimate the posterior distribution. For more information,
please see [the Turing.jl Bayesian Differential Equations tutorial](https://github.com/TuringLang/TuringTutorials/blob/master/10_diffeq.ipynb)
## Example 3: Controlling SDEs to an objective
In this example, we will find the parameters of the SDE that force the
solution to be close to the constant 1.
```julia
using DifferentialEquations, DiffEqFlux, Optimization, OptimizationJL, Plots
function lotka_volterra!(du, u, p, t)
x, y = u
α, β, δ, γ = p
du[1] = dx = α*x - β*x*y
du[2] = dy = -δ*y + γ*x*y
end
function lotka_volterra_noise!(du, u, p, t)
du[1] = 0.1u[1]
du[2] = 0.1u[2]
end
u0 = [1.0,1.0]
tspan = (0.0, 10.0)
p = [2.2, 1.0, 2.0, 0.4]
prob_sde = SDEProblem(lotka_volterra!, lotka_volterra_noise!, u0, tspan)
function predict_sde(p)
return Array(solve(prob_sde, SOSRI(), p=p,
sensealg = ForwardDiffSensitivity(), saveat = 0.1))
end
loss_sde(p) = sum(abs2, x-1 for x in predict_sde(p))
```
For this training process, because the loss function is stochastic, we will use
the `ADAM` optimizer from Flux.jl. The `Optimization.solve` function is the same as
before. However, to speed up the training process, we will use a global counter
so that way we only plot the current results every 10 iterations. This looks
like:
```julia
callback = function (p, l)
display(l)
remade_solution = solve(remake(prob_sde, p = p), SOSRI(), saveat = 0.1)
plt = plot(remade_solution, ylim = (0, 6))
display(plt)
return false
end
```
Let's optimize
```julia
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss_sde(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
result_sde = Optimization.solve(optprob, ADAM(0.1),
callback = callback, maxiters = 100)
```
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2890 | # Handling Divergent and Unstable Trajectories
It is not uncommon for a set of parameters in an ODE model to simply give a
divergent trajectory. If the rate of growth compounds and outpaces the rate
of decay, you will end up at infinity in finite time. This it is not uncommon
to see divergent trajectories in the optimization of parameters, as many times
an optimizer can take an excursion into a parameter regime which simply gives
a model with an infinite solution.
This can be addressed by using the retcode system. In DifferentialEquations.jl,
[RetCodes](https://diffeq.sciml.ai/stable/basics/solution/#retcodes) detail
the status of the returned solution. Thus if the retcode corresponds to a
failure, we can use this to give an infinite loss and effectively discard the
parameters. This is shown in the loss function:
```julia
function loss(p)
tmp_prob = remake(prob, p=p)
tmp_sol = solve(tmp_prob,Tsit5(),saveat=0.1)
if tmp_sol.retcode == :Success
return sum(abs2,Array(tmp_sol) - dataset)
else
return Inf
end
end
```
A full example making use of this trick is:
```julia
using DifferentialEquations, Optimization, OptimizationOptimJL, Plots
function lotka_volterra!(du,u,p,t)
rab, wol = u
α,β,γ,δ=p
du[1] = drab = α*rab - β*rab*wol
du[2] = dwol = γ*rab*wol - δ*wol
nothing
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra!,u0,tspan,p)
sol = solve(prob,saveat=0.1)
plot(sol)
dataset = Array(sol)
scatter!(sol.t,dataset')
tmp_prob = remake(prob, p=[1.2,0.8,2.5,0.8])
tmp_sol = solve(tmp_prob)
plot(tmp_sol)
scatter!(sol.t,dataset')
function loss(p)
tmp_prob = remake(prob, p=p)
tmp_sol = solve(tmp_prob,Tsit5(),saveat=0.1)
if tmp_sol.retcode == :Success
return sum(abs2,Array(tmp_sol) - dataset)
else
return Inf
end
end
pinit = [1.2,0.8,2.5,0.8]
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, pinit)
res = Optimization.solve(optprob,ADAM(), maxiters = 1000)
# res = Optimization.solve(optprob,BFGS(), maxiters = 1000) ### errors!
#try Newton method of optimization
res = Optimization.solve(optprob,Newton(), Optimization.AutoForwardDiff())
```
You might notice that `AutoZygote` (default) fails for the above `Optimization.solve` call with Optim's optimizers which happens because
of Zygote's behaviour for zero gradients in which case it returns `nothing`. To avoid such issue you can just use a different version of the same check which compares the size of the obtained
solution and the data we have, shown below, which is easier to AD.
```julia
function loss(p)
tmp_prob = remake(prob, p=p)
tmp_sol = solve(tmp_prob,Tsit5(),saveat=0.1)
if size(tmp_sol) == size(dataset)
return sum(abs2,Array(tmp_sol) .- dataset)
else
return Inf
end
end
``` | DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 9213 | # Strategies to Avoid Local Minima
Local minima can be an issue with fitting neural differential equations. However,
there are many strategies to avoid local minima:
1. Insert stochasticity into the loss function through minibatching
2. Weigh the loss function to allow for fitting earlier portions first
3. Changing the optimizers to `allow_f_increases`
4. Iteratively grow the fit
5. Training the initial conditions and the parameters to start
## `allow_f_increases=true`
With Optim.jl optimizers, you can set `allow_f_increases=true` in order to let
increases in the loss function not cause an automatic halt of the optimization
process. Using a method like BFGS or NewtonTrustRegion is not guaranteed to
have monotonic convergence and so this can stop early exits which can result
in local minima. This looks like:
```julia
pmin = Optimization.solve(optprob, NewtonTrustRegion(), callback=callback,
maxiters = 200, allow_f_increases = true)
```
## Iterative Growing Of Fits to Reduce Probability of Bad Local Minima
In this example we will show how to use strategy (4) in order to increase the
robustness of the fit. Let's start with the same neural ODE example we've used
before except with one small twist: we wish to find the neural ODE that fits
on `(0,5.0)`. Naively, we use the same training strategy as before:
```julia
using Lux, DiffEqFlux, DifferentialEquations, Optimizaton, OptimizationOptimJL, Plots, Random
rng = Random.default_rng()
u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 5.0f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = Lux.Chain(ActivationFunction(x -> x.^3),
Lux.Dense(2, 16, tanh),
Lux.Dense(16, 2))
pinit, st = Lux.setup(rng, dudt2)
prob_neuralode = NeuralODE(dudt2, tspan, Vern7(), saveat = tsteps, abstol=1e-6, reltol=1e-6)
function predict_neuralode(p)
Array(prob_neuralode(u0, p, st)[1])
end
function loss_neuralode(p)
pred = predict_neuralode(p)
loss = sum(abs2, (ode_data[:,1:size(pred,2)] .- pred))
return loss, pred
end
iter = 0
callback = function (p, l, pred; doplot = true)
global iter
iter += 1
display(l)
if doplot
# plot current prediction against data
plt = scatter(tsteps[1:size(pred,2)], ode_data[1,1:size(pred,2)], label = "data")
scatter!(plt, tsteps[1:size(pred,2)], pred[1,:], label = "prediction")
display(plot(plt))
end
return false
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss_neuralode(x), adtype)
optprob = Optimization.OptimizationProblem(optf, Lux.ComponentArray(pinit))
result_neuralode = Optimization.solve(optprob,
ADAM(0.05), callback = callback,
maxiters = 300)
callback(result_neuralode.u,loss_neuralode(result_neuralode.u)...;doplot=true)
savefig("local_minima.png")
```
However, we've now fallen into a trap of a local minima. If the optimizer changes
the parameters so it dips early, it will increase the loss because there will
be more error in the later parts of the time series. Thus it tends to just stay
flat and never fit perfectly. This thus suggests strategies (2) and (3): do not
allow the later parts of the time series to influence the fit until the later
stages. Strategy (3) seems to be more robust, so this is what will be demonstrated.
Let's start by reducing the timespan to `(0,1.5)`:
```julia
prob_neuralode = NeuralODE(dudt2, (0.0,1.5), Tsit5(), saveat = tsteps[tsteps .<= 1.5])
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss_neuralode(x), adtype)
optprob = Optimization.OptimizationProblem(optf, ComponentArray(pinit))
result_neuralode2 = Optimization.solve(optprob,
ADAM(0.05), callback = callback,
maxiters = 300)
callback(result_neuralode2.u,loss_neuralode(result_neuralode2.u)...;doplot=true)
savefig("shortplot1.png")
```
This fits beautifully. Now let's grow the timespan and utilize the parameters
from our `(0,1.5)` fit as the initial condition to our next fit:
```julia
prob_neuralode = NeuralODE(dudt2, (0.0,3.0), Tsit5(), saveat = tsteps[tsteps .<= 3.0])
optprob = Optimization.OptimizationProblem(optf, result_neuralode.u)
result_neuralode3 = Optimization.solve(optprob,
ADAM(0.05), maxiters = 300,
callback = callback)
callback(result_neuralode3.u,loss_neuralode(result_neuralode3.u)...;doplot=true)
savefig("shortplot2.png")
```
Once again a great fit. Now we utilize these parameters as the initial condition
to the full fit:
```julia
prob_neuralode = NeuralODE(dudt2, (0.0,5.0), Tsit5(), saveat = tsteps)
optprob = Optimization.OptimizationProblem(optf, result_neuralode3.u)
result_neuralode4 = Optimization.solve(optprob,
ADAM(0.01), maxiters = 300,
callback = callback)
callback(result_neuralode4.u,loss_neuralode(result_neuralode4.u)...;doplot=true)
savefig("fullplot.png")
```
## Training both the initial conditions and the parameters to start
In this example we will show how to use strategy (5) in order to accomplish the
same goal, except rather than growing the trajectory iteratively, we can train on
the whole trajectory. We do this by allowing the neural ODE to learn both the
initial conditions and parameters to start, and then reset the initial conditions
back and train only the parameters. Note: this strategy is demonstrated for the (0, 5)
time span and (0, 10), any longer and more iterations will be required. Alternatively,
one could use a mix of (4) and (5), or breaking up the trajectory into chunks and just (5).
```julia
using Flux, Plots, DifferentialEquations
#Starting example with tspan (0, 5)
u0 = Float32[2.0; 0.0]
datasize = 30
tspan = (0.0f0, 5.0f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
function trueODEfunc(du, u, p, t)
true_A = [-0.1 2.0; -2.0 -0.1]
du .= ((u.^3)'true_A)'
end
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
#Using flux here to easily demonstrate the idea, but this can be done with Optimization.solve!
dudt2 = Chain(Dense(2,16, tanh),
Dense(16,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
dudt(u,p,t) = re(p)(u) # need to restrcture for backprop!
prob = ODEProblem(dudt,u0,tspan)
function predict_n_ode()
Array(solve(prob,u0=u0,p=p, saveat=tsteps))
end
function loss_n_ode()
pred = predict_n_ode()
sqnorm(x) = sum(abs2, x)
loss = sum(abs2,ode_data .- pred)
loss
end
function callback(;doplot=false) #callback function to observe training
pred = predict_n_ode()
display(sum(abs2,ode_data .- pred))
if doplot
# plot current prediction against data
pl = plot(tsteps,ode_data[1,:],label="data")
plot!(pl,tsteps,pred[1,:],label="prediction")
display(plot(pl))
end
return false
end
predict_n_ode()
loss_n_ode()
callback(;doplot=true)
data = Iterators.repeated((), 1000)
#Specify to flux to include both the initial conditions (IC) and parameters of the NODE to train
Flux.train!(loss_n_ode, Flux.params(u0, p), data,
Flux.Optimise.ADAM(0.05), callback = callback)
#Here we reset the IC back to the original and train only the NODE parameters
u0 = Float32[2.0; 0.0]
Flux.train!(loss_n_ode, Flux.params(p), data,
Flux.Optimise.ADAM(0.05), callback = callback)
callback(;doplot=true)
#Now use the same technique for a longer tspan (0, 10)
datasize = 30
tspan = (0.0f0, 10.0f0)
tsteps = range(tspan[1], tspan[2], length = datasize)
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
dudt2 = Chain(Dense(2,16, tanh),
Dense(16,2))
p,re = Flux.destructure(dudt2) # use this p as the initial condition!
dudt(u,p,t) = re(p)(u) # need to restrcture for backprop!
prob = ODEProblem(dudt,u0,tspan)
data = Iterators.repeated((), 1500)
Flux.train!(loss_n_ode, Flux.params(u0, p), data,
Flux.Optimise.ADAM(0.05), callback = callback)
u0 = Float32[2.0; 0.0]
Flux.train!(loss_n_ode, Flux.params(p), data,
Flux.Optimise.ADAM(0.05), callback = callback)
callback(;doplot=true)
```
And there we go, a set of robust strategies for fitting an equation that would otherwise
get stuck in a local optima.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 6.79.0 | 87fd2c08bd8749906cdf253a240b21a5c92b7214 | docs | 2961 | # Simultaneous Fitting of Multiple Neural Networks
In many cases users are interested in fitting multiple neural networks
or parameters simultaneously. This tutorial addresses how to perform
this kind of study.
The following is a fully working demo on the Fitzhugh-Nagumo ODE:
```julia
using Lux, DiffEqFlux, Optimizaton, OptimizationOptimJL, DifferentialEquations, Random
rng = Random.default_rng()
function fitz(du,u,p,t)
v,w = u
a,b,τinv,l = p
du[1] = v - v^3/3 -w + l
du[2] = τinv*(v + a - b*w)
end
p_ = Float32[0.7,0.8,1/12.5,0.5]
u0 = [1f0;1f0]
tspan = (0f0,10f0)
prob = ODEProblem(fitz,u0,tspan,p_)
sol = solve(prob, Tsit5(), saveat = 0.5 )
# Ideal data
X = Array(sol)
Xₙ = X + Float32(1e-3)*randn(eltype(X), size(X)) #noisy data
# For xz term
NN_1 = Lux.Chain(Lux.Dense(2, 16, tanh), Lux.Dense(16, 1))
p1,st1 = Lux.setup(rng, NN_1)
# for xy term
NN_2 = Lux.Chain(Lux.Dense(3, 16, tanh), Lux.Dense(16, 1))
p2 = Lux.setup(rng, NN_2)
scaling_factor = 1f0
p1 = Lux.ComponentArray(p1)
p2 = Lux.ComponentArray(p2)
p = Lux.ComponentArray(p1;p1)
p = Lux.ComponentArray(p;p2)
function dudt_(u,p,t)
v,w = u
z1 = NN_1([v,w], p.p1, st1)[1]
z2 = NN_2([v,w,t], p.p2, st2)[1]
[z1[1],scaling_factor*z2[1]]
end
prob_nn = ODEProblem(dudt_,u0, tspan, p)
sol_nn = solve(prob_nn, Tsit5(),saveat = sol.t)
function predict(θ)
Array(solve(prob_nn, Vern7(), p=θ, saveat = sol.t,
abstol=1e-6, reltol=1e-6,
sensealg = InterpolatingAdjoint(autojacvec=ReverseDiffVJP(true))))
end
# No regularisation right now
function loss(θ)
pred = predict(θ)
sum(abs2, Xₙ .- pred), pred
end
loss(p)
const losses = []
callback(θ,l,pred) = begin
push!(losses, l)
if length(losses)%50==0
println(losses[end])
end
false
end
adtype = Optimization.AutoZygote()
optf = Optimization.OptimizationFunction((x,p) -> loss(x), adtype)
optprob = Optimization.OptimizationProblem(optf, p)
res1_uode = Optimization.solve(optprob, ADAM(0.01), callback=callback, maxiters = 500)
optprob2 = Optimization.OptimizationProblem(optf, res1_uode.u)
res2_uode = Optimization.solve(optprob2, BFGS(), maxiters = 10000)
```
The key is that `Optimization.solve` acts on a single parameter vector `p`.
Thus what we do here is concatenate all of the parameters into a single
vector `p = [p1;p2;scaling_factor]` and then train on this parameter
vector. Whenever we need to evaluate the neural networks, we cut the
vector and grab the portion that corresponds to the neural network.
For example, the `p1` portion is `p[1:length(p1)]`, which is why the
first neural network's evolution is written like `NN_1([v,w], p[1:length(p1)])`.
This method is flexible to use with many optimizers and in fairly
optimized ways. The allocations can be reduced by using `@view p[1:length(p1)]`.
We can also see with the `scaling_factor` that we can grab parameters
directly out of the vector and use them as needed.
| DiffEqSensitivity | https://github.com/SciML/DiffEqSensitivity.jl.git |
|
[
"MIT"
] | 0.3.0 | 215ea07f170cd9732aa7d7745c672f69baf3dc02 | code | 6089 | module AllenNeuropixelsBase
using PythonCall
using DataFrames
using CSV
using TimeseriesTools
using Preferences
using AllenSDK
using Downloads
using Scratch
const brain_observatory = PythonCall.pynew()
const stimulusmapping = PythonCall.pynew()
const ecephys_project_cache = PythonCall.pynew()
const ecephys_project_api = PythonCall.pynew()
const ephys_features = PythonCall.pynew()
const brain_observatory_cache = PythonCall.pynew()
const stimulus_info = PythonCall.pynew()
const mouse_connectivity_cache = PythonCall.pynew()
const ontologies_api = PythonCall.pynew()
const reference_space_cache = PythonCall.pynew()
const reference_space = PythonCall.pynew()
const nwb_api = PythonCall.pynew()
const behavior_project_cache = PythonCall.pynew()
const behavior_ecephys_session = PythonCall.pynew()
const _behaviorcache = PythonCall.pynew()
export allensdk, brain_observatory, ecephys, ecephys_project_cache,
mouse_connectivity_cache, ontologies_api, reference_space_cache, reference_space,
behavior_ecephys_session, behavior_project_cache
function setdatadir(datadir::String)
@set_preferences!("datadir"=>datadir)
@info("New default datadir set; restart your Julia session for this change to take effect")
end
const datadir = replace(@load_preference("datadir",
joinpath(get_scratch!("allensdk_manifest"),
"data/")),
"\\" => "/")
const ecephysmanifest = replace(joinpath(datadir, "Ecephys", "manifest.json"), "\\" => "/")
const behaviormanifest = replace(joinpath(datadir, "Behavior"),
"\\" => "/")
const brainobservatorymanifest = replace(joinpath(datadir, "BrainObservatory",
"manifest.json"), "\\" => "/")
const mouseconnectivitymanifest = replace(joinpath(datadir, "MouseConnectivity",
"manifest.json"), "\\" => "/")
const referencespacemanifest = replace(joinpath(datadir, "ReferenceSpace", "manifest.json"),
"\\" => "/")
export setdatadir, datadir, ecephysmanifest, brainobservatorymanifest,
mouseconnectivitymanifest, referencespacemanifest, behaviormanifest
const streamlinepath = abspath(referencespacemanifest, "../laplacian_10.nrrd")
function __init__()
PythonCall.pycopy!(brain_observatory, pyimport("allensdk.brain_observatory"))
PythonCall.pycopy!(stimulus_info, pyimport("allensdk.brain_observatory.stimulus_info"))
PythonCall.pycopy!(stimulusmapping,
pyimport("allensdk.brain_observatory.ecephys.stimulus_analysis.receptive_field_mapping"))
PythonCall.pycopy!(ecephys_project_cache,
pyimport("allensdk.brain_observatory.ecephys.ecephys_project_cache"))
PythonCall.pycopy!(ecephys_project_api,
pyimport("allensdk.brain_observatory.ecephys.ecephys_project_api"))
PythonCall.pycopy!(ephys_features, pyimport("allensdk.ephys.ephys_features"))
PythonCall.pycopy!(brain_observatory_cache,
pyimport("allensdk.core.brain_observatory_cache"))
PythonCall.pycopy!(mouse_connectivity_cache,
pyimport("allensdk.core.mouse_connectivity_cache"))
PythonCall.pycopy!(ontologies_api, pyimport("allensdk.api.queries.ontologies_api"))
PythonCall.pycopy!(reference_space_cache,
pyimport("allensdk.core.reference_space_cache"))
PythonCall.pycopy!(reference_space, pyimport("allensdk.core.reference_space"))
PythonCall.pycopy!(nwb_api, pyimport("allensdk.brain_observatory.nwb.nwb_api"))
PythonCall.pycopy!(behavior_project_cache,
pyimport("allensdk.brain_observatory.behavior.behavior_project_cache"))
PythonCall.pycopy!(behavior_ecephys_session,
pyimport("allensdk.brain_observatory.ecephys.behavior_ecephys_session"))
ecephys_project_cache.EcephysProjectCache.from_warehouse(manifest = ecephysmanifest)
if !isfile(streamlinepath)
mkpath(dirname(streamlinepath))
@info "Downloading streamline data to $streamlinepath, this may take a few minutes"
Downloads.download("https://www.dropbox.com/sh/7me5sdmyt5wcxwu/AACFY9PQ6c79AiTsP8naYZUoa/laplacian_10.nrrd?dl=1",
streamlinepath)
@info "Download streamline data with status $(isfile(streamlinepath))"
end
PythonCall.pycopy!(_behaviorcache, __behaviorcache())
warnings = pyimport("warnings")
warnings.filterwarnings("ignore", message = ".*(Ignoring cached namespace).*")
warnings.filterwarnings("ignore",
message = ".*(Unable to parse cre_line from full_genotype).*")
end
# * Override DimensionalData syntax for newer TimeseriesTools versions. This is local only,
# and we'll aim to replace all these in the near future
"""
loaddataframe(file, dir=datadir)::DataFrame
Load a CSV file into a DataFrame.
Arguments:
- `file`: A string representing the name of the CSV file to be loaded.
- `dir` (optional): A string representing the directory containing the CSV file. Default is `datadir`.
Returns:
A `DataFrame` object containing the contents of the CSV file.
Example:
```julia
using DataFrames
df = loaddataframe("mydata.csv", "/path/to/my/data/")
```
"""
function loaddataframe(file, dir = datadir)::DataFrame
CSV.File(abspath(dir, file)) |> DataFrame
end
export loaddataframe
DimensionalData.@dim Chan ToolsDim "Channel"
DimensionalData.@dim Unit ToolsDim "Unit"
DimensionalData.@dim Depth ToolsDim "Depth"
DimensionalData.@dim Log𝑓 ToolsDim "Log Frequency"
export Chan, Unit, Depth, Log𝑓
include("./EcephysCache.jl")
include("./BrainObservatory.jl")
# include("./HybridSession.jl")
include("./SparseToolsArray.jl")
include("./MouseConnectivityCache.jl")
include("./Ontologies.jl")
include("./ReferenceSpace.jl")
include("./NWBSession.jl")
include("./LFP.jl")
include("./SpikeBand.jl")
include("./Behaviour.jl")
include("./VisualBehavior.jl")
end
| AllenNeuropixelsBase | https://github.com/brendanjohnharris/AllenNeuropixelsBase.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.