code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
# Tutorial 5: Trace - training control and debugging
In this tutorial, we will talk about another important concept in FastEstimator - Trace.
`Trace` is a class contains has 6 event functions below, each event function will be executed on different events of training loop when putting `Trace` inside `Estimator`. If you are a Keras user, you would see that `Trace` is a combination of callbacks and metrics.
* on_begin
* on_epoch_begin
* on_batch_begin
* on_batch_end
* on_epoch_end
* on_end
`Trace` differs from keras's callback in the following places:
1. Trace has full access to the preprocessing data and prediction data
2. Trace can pass data among each other
3. Trace is simpler and has fewer event functions than keras callbacks
`Trace` can be used for anything that involves training loop, such as changing learning rate, calculating metrics, writing checkpoints and so on.
## debugging training loop with Trace
Since `Trace` can have full access to data used in training loop, one natural usage of `Trace` is debugging training loop, for example, printing network prediction for each batch.
Remember in tutorial 3, we customized an operation that scales the prediction score by 10 and write to a new key, let's see whether the operation is working correctly using `Trace`.
```
import tempfile
import numpy as np
import tensorflow as tf
import fastestimator as fe
from fastestimator.architecture import LeNet
from fastestimator.estimator.trace import Accuracy, ModelSaver
from fastestimator.network.loss import SparseCategoricalCrossentropy
from fastestimator.network.model import FEModel, ModelOp
from fastestimator.pipeline.processing import Minmax
from fastestimator.util.op import TensorOp
class Scale(TensorOp):
def forward(self, data, state):
data = data * 10
return data
(x_train, y_train), (x_eval, y_eval) = tf.keras.datasets.mnist.load_data()
train_data = {"x": np.expand_dims(x_train, -1), "y": y_train}
eval_data = {"x": np.expand_dims(x_eval, -1), "y": y_eval}
data = {"train": train_data, "eval": eval_data}
pipeline = fe.Pipeline(batch_size=32, data=data, ops=Minmax(inputs="x", outputs="x"))
# step 2. prepare model
model = FEModel(model_def=LeNet, model_name="lenet", optimizer="adam")
network = fe.Network(
ops=[ModelOp(inputs="x", model=model, outputs="y_pred"),
SparseCategoricalCrossentropy(inputs=("y", "y_pred")),
Scale(inputs="y_pred", outputs="y_pred_scaled")])
```
## define trace
```
from fastestimator.estimator.trace import Trace
class ShowPred(Trace):
def on_batch_end(self, state):
if state["mode"] == "train":
batch_data = state["batch"]
print("step: {}".format(state["batch_idx"]))
print("batch data has following keys: {}".format(list(batch_data.keys())))
print("scaled_prediction is:")
print(batch_data["y_pred_scaled"])
# step 3.prepare estimator
estimator = fe.Estimator(network=network, pipeline=pipeline, epochs=1, traces=ShowPred(), steps_per_epoch=1)
estimator.fit()
```
| github_jupyter |
# Flopy MODFLOW Boundary Conditions
Flopy has a new way to enter boundary conditions for some MODFLOW packages. These changes are substantial. Boundary conditions can now be entered as a list of boundaries, as a numpy recarray, or as a dictionary. These different styles are described in this notebook.
Flopy also now requires zero-based input. This means that **all boundaries are entered in zero-based layer, row, and column indices**. This means that older Flopy scripts will need to be modified to account for this change. If you are familiar with Python, this should be natural, but if not, then it may take some time to get used to zero-based numbering. Flopy users submit all information in zero-based form, and Flopy converts this to the one-based form required by MODFLOW.
The following MODFLOW packages are affected by this change:
* Well
* Drain
* River
* General-Head Boundary
* Time-Variant Constant Head
This notebook explains the different ways to enter these types of boundary conditions.
```
#begin by importing flopy
import os
import sys
import numpy as np
# run installed version of flopy or add local path
try:
import flopy
except:
fpth = os.path.abspath(os.path.join('..', '..'))
sys.path.append(fpth)
import flopy
workspace = os.path.join('data')
#make sure workspace directory exists
if not os.path.exists(workspace):
os.makedirs(workspace)
print(sys.version)
print('numpy version: {}'.format(np.__version__))
print('flopy version: {}'.format(flopy.__version__))
```
## List of Boundaries
Boundary condition information is passed to a package constructor as stress_period_data. In its simplest form, stress_period_data can be a list of individual boundaries, which themselves are lists. The following shows a simple example for a MODFLOW River Package boundary:
```
stress_period_data = [
[2, 3, 4, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 5, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 6, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
]
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
```
If we look at the River Package created here, you see that the layer, row, and column numbers have been increased by one.
```
!head -n 10 'data/test.riv'
```
If this model had more than one stress period, then Flopy will assume that this boundary condition information applies until the end of the simulation
```
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
dis = flopy.modflow.ModflowDis(m, nper=3)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
!head -n 10 'data/test.riv'
```
## Recarray of Boundaries
Numpy allows the use of recarrays, which are numpy arrays in which each column of the array may be given a different type. Boundary conditions can be entered as recarrays. Information on the structure of the recarray for a boundary condition package can be obtained from that particular package. The structure of the recarray is contained in the dtype.
```
riv_dtype = flopy.modflow.ModflowRiv.get_default_dtype()
print(riv_dtype)
```
Now that we know the structure of the recarray that we want to create, we can create a new one as follows.
```
stress_period_data = np.zeros((3), dtype=riv_dtype)
stress_period_data = stress_period_data.view(np.recarray)
print('stress_period_data: ', stress_period_data)
print('type is: ', type(stress_period_data))
```
We can then fill the recarray with our boundary conditions.
```
stress_period_data[0] = (2, 3, 4, 10.7, 5000., -5.7)
stress_period_data[1] = (2, 3, 5, 10.7, 5000., -5.7)
stress_period_data[2] = (2, 3, 6, 10.7, 5000., -5.7)
print(stress_period_data)
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
!head -n 10 'data/test.riv'
```
As before, if we have multiple stress periods, then this recarray will apply to all of them.
```
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
dis = flopy.modflow.ModflowDis(m, nper=3)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
!head -n 10 'data/test.riv'
```
## Dictionary of Boundaries
The power of the new functionality in Flopy3 is the ability to specify a dictionary for stress_period_data. If specified as a dictionary, the key is the stress period number (**as a zero-based number**), and the value is either a nested list, an integer value of 0 or -1, or a recarray for that stress period.
Let's say that we want to use the following schedule for our rivers:
0. No rivers in stress period zero
1. Rivers specified by a list in stress period 1
2. No rivers
3. No rivers
4. No rivers
5. Rivers specified by a recarray
6. Same recarray rivers
7. Same recarray rivers
8. Same recarray rivers
```
sp1 = [
[2, 3, 4, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 5, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 6, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
]
print(sp1)
riv_dtype = flopy.modflow.ModflowRiv.get_default_dtype()
sp5 = np.zeros((3), dtype=riv_dtype)
sp5 = sp5.view(np.recarray)
sp5[0] = (2, 3, 4, 20.7, 5000., -5.7)
sp5[1] = (2, 3, 5, 20.7, 5000., -5.7)
sp5[2] = (2, 3, 6, 20.7, 5000., -5.7)
print(sp5)
sp_dict = {0:0, 1:sp1, 2:0, 5:sp5}
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
dis = flopy.modflow.ModflowDis(m, nper=8)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=sp_dict)
m.write_input()
!head -n 10 'data/test.riv'
```
## MODFLOW Auxiliary Variables
Flopy works with MODFLOW auxiliary variables by allowing the recarray to contain additional columns of information. The auxiliary variables must be specified as package options as shown in the example below.
In this example, we also add a string in the last column of the list in order to name each boundary condition. In this case, however, we do not include boundname as an auxiliary variable as MODFLOW would try to read it as a floating point number.
```
#create an empty array with an iface auxiliary variable at the end
riva_dtype = [('k', '<i8'), ('i', '<i8'), ('j', '<i8'),
('stage', '<f4'), ('cond', '<f4'), ('rbot', '<f4'),
('iface', '<i4'), ('boundname', object)]
riva_dtype = np.dtype(riva_dtype)
stress_period_data = np.zeros((3), dtype=riva_dtype)
stress_period_data = stress_period_data.view(np.recarray)
print('stress_period_data: ', stress_period_data)
print('type is: ', type(stress_period_data))
stress_period_data[0] = (2, 3, 4, 10.7, 5000., -5.7, 1, 'riv1')
stress_period_data[1] = (2, 3, 5, 10.7, 5000., -5.7, 2, 'riv2')
stress_period_data[2] = (2, 3, 6, 10.7, 5000., -5.7, 3, 'riv3')
print(stress_period_data)
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data, dtype=riva_dtype, options=['aux iface'])
m.write_input()
!head -n 10 'data/test.riv'
```
## Working with Unstructured Grids
Flopy can create an unstructured grid boundary condition package for MODFLOW-USG. This can be done by specifying a custom dtype for the recarray. The following shows an example of how that can be done.
```
#create an empty array based on nodenumber instead of layer, row, and column
rivu_dtype = [('nodenumber', '<i8'), ('stage', '<f4'), ('cond', '<f4'), ('rbot', '<f4')]
rivu_dtype = np.dtype(rivu_dtype)
stress_period_data = np.zeros((3), dtype=rivu_dtype)
stress_period_data = stress_period_data.view(np.recarray)
print('stress_period_data: ', stress_period_data)
print('type is: ', type(stress_period_data))
stress_period_data[0] = (77, 10.7, 5000., -5.7)
stress_period_data[1] = (245, 10.7, 5000., -5.7)
stress_period_data[2] = (450034, 10.7, 5000., -5.7)
print(stress_period_data)
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data, dtype=rivu_dtype)
m.write_input()
print(workspace)
!head -n 10 'data/test.riv'
```
## Combining two boundary condition packages
```
ml = flopy.modflow.Modflow(modelname="test",model_ws=workspace)
dis = flopy.modflow.ModflowDis(ml,10,10,10,10)
sp_data1 = {3: [1, 1, 1, 1.0],5:[1,2,4,4.0]}
wel1 = flopy.modflow.ModflowWel(ml, stress_period_data=sp_data1)
ml.write_input()
!head -n 10 'data/test.wel'
sp_data2 = {0: [1, 1, 3, 3.0],8:[9,2,4,4.0]}
wel2 = flopy.modflow.ModflowWel(ml, stress_period_data=sp_data2)
ml.write_input()
!head -n 10 'data/test.wel'
```
Now we create a third wel package, using the ```MfList.append()``` method:
```
wel3 = flopy.modflow.ModflowWel(ml,stress_period_data=\
wel2.stress_period_data.append(
wel1.stress_period_data))
ml.write_input()
!head -n 10 'data/test.wel'
```
| github_jupyter |
<a href="https://colab.research.google.com/github/rvignav/aigents-java-nlp/blob/master/src/test/resources/Baseline_QA/Baseline_QA_ELECTRA.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install --quiet transformers sentence-transformers nltk pyter3
import json
from pathlib import Path
def read_squad(path):
path = Path(path)
with open(path, 'rb') as f:
squad_dict = json.load(f)
contexts = []
questions = []
answers = []
for group in squad_dict['data']:
for passage in group['paragraphs']:
context = passage['context']
for qa in passage['qas']:
question = qa['question']
for answer in qa['answers']:
contexts.append(context)
questions.append(question)
answers.append(answer)
return contexts, questions, answers
train_contexts, train_questions, train_answers = read_squad('/content/drive/MyDrive/squad/train-v2.0.json')
val_contexts, val_questions, val_answers = read_squad('/content/drive/MyDrive/squad/dev-v2.0.json')
def add_end_idx(answers, contexts):
for answer, context in zip(answers, contexts):
gold_text = answer['text']
start_idx = answer['answer_start']
end_idx = start_idx + len(gold_text)
answer['answer_end'] = end_idx
add_end_idx(train_answers, train_contexts)
add_end_idx(val_answers, val_contexts)
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained('deepset/electra-base-squad2')
train_encodings = tokenizer(train_contexts, train_questions, truncation=True, padding=True)
val_encodings = tokenizer(val_contexts, val_questions, truncation=True, padding=True)
def add_token_positions(encodings, answers):
start_positions = []
end_positions = []
for i in range(len(answers)):
start_positions.append(encodings.char_to_token(i, answers[i]['answer_start']))
end_positions.append(encodings.char_to_token(i, answers[i]['answer_end'] - 1))
# if start position is None, the answer passage has been truncated
if start_positions[-1] is None:
start_positions[-1] = tokenizer.model_max_length
if end_positions[-1] is None:
end_positions[-1] = tokenizer.model_max_length
encodings.update({'start_positions': start_positions, 'end_positions': end_positions})
add_token_positions(train_encodings, train_answers)
add_token_positions(val_encodings, val_answers)
import torch
class SquadDataset(torch.utils.data.Dataset):
def __init__(self, encodings):
self.encodings = encodings
def __getitem__(self, idx):
return {key: torch.tensor(val[idx]) for key, val in self.encodings.items()}
def __len__(self):
return len(self.encodings.input_ids)
train_dataset = SquadDataset(train_encodings)
val_dataset = SquadDataset(val_encodings)
from transformers import AutoModelForQuestionAnswering
model = AutoModelForQuestionAnswering.from_pretrained("deepset/electra-base-squad2")
from torch.utils.data import DataLoader
from transformers import AdamW
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
model.to(device)
model.train()
train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True)
optim = AdamW(model.parameters(), lr=5e-5)
for epoch in range(3):
print("Epoch: ", epoch+1)
for batch in train_loader:
optim.zero_grad()
input_ids = batch['input_ids'].to(device)
attention_mask = batch['attention_mask'].to(device)
start_positions = batch['start_positions'].to(device)
end_positions = batch['end_positions'].to(device)
outputs = model(input_ids, attention_mask=attention_mask, start_positions=start_positions, end_positions=end_positions)
loss = outputs[0]
loss.backward()
optim.step()
model.eval()
def wer_score(hyp, ref, print_matrix=False):
import numpy as np
N = len(hyp)
M = len(ref)
L = np.zeros((N,M))
for i in range(0, N):
for j in range(0, M):
if min(i,j) == 0:
L[i,j] = max(i,j)
else:
deletion = L[i-1,j] + 1
insertion = L[i,j-1] + 1
sub = 1 if hyp[i] != ref[j] else 0
substitution = L[i-1,j-1] + sub
L[i,j] = min(deletion, min(insertion, substitution))
if print_matrix:
print("WER matrix ({}x{}): ".format(N, M))
print(L)
return int(L[N-1, M-1])
def metrics(fname):
# BLEU
from nltk.translate.bleu_score import sentence_bleu, corpus_bleu
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = [arr]
for c in candidate:
# print(reference, c, ': ', sentence_bleu(reference, c, weights=(1,0)))
scores.append(sentence_bleu(reference, c, weights=(1,0)))
print("BLEU: " + str(sum(scores)/(1.0*len(scores))))
# Word2Vec Cosine Similarity
import torch
import torch.nn.functional as F
from sentence_transformers import SentenceTransformer
import nltk
nltk.download('punkt')
from nltk import tokenize
def similarity(par1, par2):
transformer = SentenceTransformer('roberta-base-nli-stsb-mean-tokens')
transformer.eval()
par1 = tokenize.sent_tokenize(par1)
vec1 = torch.Tensor(transformer.encode(par1))
vec1 = vec1.mean(0)
par2 = tokenize.sent_tokenize(par2)
vec2 = torch.Tensor(transformer.encode(par2))
vec2 = vec2.mean(0)
cos_sim = F.cosine_similarity(vec1, vec2, dim=0)
return cos_sim.item()
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
if (len(arr) == 1):
continue
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = arr
for c in candidate:
scores.append(similarity(" ".join(reference), " ".join(c)))
print("Word2Vec Cosine Similarity: " + str(sum(scores)/(1.0*len(scores))))
# WER
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
if (len(arr) == 1):
continue
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = arr
for c in candidate:
scores.append(wer_score(c, reference))
print("WER: " + str(sum(scores)/(1.0*len(scores))))
# TER
import pyter
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
if (len(arr) == 1):
continue
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = arr
for c in candidate:
scores.append(pyter.ter(reference, c))
print("TER: " + str(sum(scores)/(1.0*len(scores))))
def run(modelname, model, tokenizer):
# model = AutoModelForQuestionAnswering.from_pretrained(modelname)
# tokenizer = AutoTokenizer.from_pretrained(modelname)
from transformers import pipeline
nlp = pipeline('question-answering', model=model, tokenizer=tokenizer)
rel_and_food = "A mom is a human. A dad is a human. A mom is a parent. A dad is a parent. A son is a child. A daughter is a child. A son is a human. A daughter is a human. A mom likes cake. A daughter likes cake. A son likes sausage. A dad likes sausage. Cake is a food. Sausage is a food. Mom is a human now. Dad is a human now. Mom is a parent now. Dad is a parent now. Son is a child now. Daughter is a child now. Son is a human now. Daughter is a human now. Mom likes cake now. Daughter likes cake now. Son likes sausage now. Dad likes sausage now. Cake is a food now. Sausage is a food now. Mom was a daughter before. Dad was a son before. Mom was not a parent before. Dad was not a parent before. Mom liked cake before. Dad liked sausage before. Cake was a food before. Sausage was a food before."
prof = "Mom is on the board of directors. Dad is on the board of directors. Son is on the board of directors. Daughter is on the board of directors. Mom writes with chalk on the board. Dad writes with chalk on the board. Son writes with chalk on the board. Daughter writes with chalk on the board. Dad wants Mom to be on the board of directors. Mom wants Dad to be on the board of directors. Dad wants his son to be on the board of directors. Mom wants her daughter to be on the board of directors. Mom writes to Dad with chalk on the board. Dad writes to Mom with chalk on the board. Son writes to Dad with chalk on the board. Daughter writes to Mom with chalk on the board."
tools_and_pos = "Mom has a hammer. Mom has a saw. Dad has a hammer. Dad has a saw. Mom has a telescope. Mom has binoculars. Dad has a telescope. Dad has binoculars. Mom saw Dad with a hammer. Mom saw Dad with a saw. Dad saw Mom with a hammer. Dad saw Mom with a saw. Saw is a tool. Hammer is a tool. Binoculars are a tool. A telescope is a tool. Mom sawed the wood with a saw. Dad sawed the wood with a saw. Son sawed the wood with a saw. Daughter sawed the wood with a saw. Mom knocked the wood with a hammer. Dad knocked the wood with a hammer. Son knocked the wood with a hammer. Daughter knocked the wood with a hammer. Mom saw Dad with binoculars. Mom saw Dad with a telescope. Dad saw Mom with binoculars. Dad saw Mom with a telescope."
f = open("/content/drive/MyDrive/squad/poc_english_queries.txt", "r")
f2name = modelname.split("/")[1] + ".txt"
f2 = open(f2name, "w")
for line in f:
parts = line.split(" ")
context = ""
if "relationships" in parts[0]:
context = rel_and_food
elif "tools" in parts[0]:
context = tools_and_pos
else:
context = prof
question = ""
for i in range(len(parts)-1):
question = question + parts[i+1].rstrip() + " "
question = question[0:len(question)-1] + "?"
f2.write(nlp({'question': question, 'context': context })['answer'].replace(".",",") + "\n")
f2.close()
print(f2name)
metrics(f2name)
print('\n')
run('deepset/electra-base-squad2', model, tokenizer)
```
| github_jupyter |
# Machine Translation Inference Pipeline
## Packages
```
import os
import shutil
from typing import Dict
from transformers import T5Tokenizer, T5ForConditionalGeneration
from forte import Pipeline
from forte.data import DataPack
from forte.common import Resources, Config
from forte.processors.base import PackProcessor
from forte.data.readers import PlainTextReader
```
## Background
After a Data Scientist is satisfied with the results of a training model, they will have their notebook over to an MLE who has to convert their model into an inference model.
## Inference Workflow
### Pipeline
We consider `t5-small` as a trained MT model to simplify the example. We should always consider pipeline first when it comes to an inference workflow. As the [glossary](https://asyml-forte.readthedocs.io/en/latest/index_appendices.html#glossary) suggests, it's an inference system that contains a set of processing components.
Therefore, we initialize a `pipeline` below.
```
pipeline: Pipeline = Pipeline[DataPack]()
```
### Reader
After observing the dataset, it's a plain `txt` file. Therefore, we can use `PlainTextReader` directly.
```
pipeline.set_reader(PlainTextReader())
```
However, it's still beneficial to take a deeper look at how to design this class so that users can customize a reader when needed.
### Processor
We already have an inference model, `t5-small`, and we need a component to make an inference. Therefore, besides the model itself, there are several behaviors needed.
1. tokenization that transforms input text into sequences of tokens.
2. since T5 has a better performance given a task prompt, we also want to include the prompt in our data.
In forte, we have a generic class `PackProcessor` that wraps model and inference-related components and behaviors to process `DataPack`. We need to create a class that inherits the generic method and customizes the behaviors.
The generic method to process `DataPack` is `_process(self, input_pack: DataPack)`. It should tokenize the input text, use the model class to make an inference, decode the output token ids, and finally writes the output to a target file.
Given what we discussed, we have a processor class below, and we need to add it to the pipeline after defining it.
```
class MachineTranslationProcessor(PackProcessor):
"""
Translate the input text and output to a file.
"""
def initialize(self, resources: Resources, configs: Config):
super().initialize(resources, configs)
# Initialize the tokenizer and model
model_name: str = self.configs.pretrained_model
self.tokenizer = T5Tokenizer.from_pretrained(model_name)
self.model = T5ForConditionalGeneration.from_pretrained(model_name)
self.task_prefix = "translate English to German: "
self.tokenizer.padding_side = "left"
self.tokenizer.pad_token = self.tokenizer.eos_token
if not os.path.isdir(self.configs.output_folder):
os.mkdir(self.configs.output_folder)
def _process(self, input_pack: DataPack):
file_name: str = os.path.join(
self.configs.output_folder, os.path.basename(input_pack.pack_name)
)
# en2de machine translation
inputs = self.tokenizer([
self.task_prefix + sentence
for sentence in input_pack.text.split('\n')
], return_tensors="pt", padding=True)
output_sequences = self.model.generate(
input_ids=inputs["input_ids"],
attention_mask=inputs["attention_mask"],
do_sample=False,
)
outputs = self.tokenizer.batch_decode(
output_sequences, skip_special_tokens=True
)
# Write output to the specified file
with open(file=file_name, mode='w') as f:
f.write('\n'.join(outputs))
@classmethod
def default_configs(cls) -> Dict:
return {
"pretrained_model": "t5-small",
"output_folder": "mt_test_output"
}
pipeline.add(MachineTranslationProcessor(), config={
"pretrained_model": "t5-small"
})
```
### Examples
We have a working [MT translation pipeline example](https://github.com/asyml/forte/blob/master/docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb).
There are several basic functions of the processor and internal functions defined in this example.
* ``initialize()``: Pipeline will call it at the start of processing. The processor will be initialized with
``configs``, and register global resources into ``resource``. The
implementation should set up the states of the component.
- initialize a pre-trained model
- initialize tokenizer
- initialize model-specific attributes such as task prefix
* ``process()``: using the loaded model to make predictions and write the prediction results out.
- we first tokenize the input text
- then, we use model to generate output sequence ids
- then, we decode output sequence ids into tokens and write the output into a file
After setting up the pipeline's components, we can run the pipeline on the input directory as below.
```
dir_path = os.path.abspath(
os.path.join("data_samples", "machine_translation")
) # notebook should be running from project root folder
pipeline.run(dir_path)
print("Done successfully")
```
One can investigate the machine translation output in folder `mt_test_output` located under the script's directory.
Then we remove the output folder below.
```
shutil.rmtree(MachineTranslationProcessor.default_configs()["output_folder"])
```
| github_jupyter |
# T81-558: Applications of Deep Neural Networks
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
**Module 3 Assignment: Creating Columns in Pandas**
**Student Name: Your Name**
# Assignment Instructions
For this assignment you will use the **reg-30-spring-2018.csv** dataset. This is a dataset that I generated specifically for this semester. You can find the CSV file in the **data** directory of the class GitHub repository here: [reg-30-spring-2018.csv](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/data/reg-30-spring-2018.csv).
For this assignment, load and modify the data set. You will submit this modified dataset to the **submit** function. See [Assignment #1](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/assignments/assignment_yourname_class1.ipynb) for details on how to submit an assignment or check that one was submitted.
Modify the dataset as follows:
* Add a column named *density* that is *weight* divided by *volume*.
* Replace the *region* column with dummy variables.
* Replace the *item* column with an index encoding value (for example 0 for the first class, 1 for the next, etc. see function *encode_text_index*)
* Your submitted dataframe will have these columns: id, distance, height, landings, number, pack, age, usage, weight, item, volume, width, max, power, size, target, density, region-RE-0, region-RE-1, region-RE-10, region-RE-11, region-RE-2, region-RE-3, region-RE-4, region-RE-5, region-RE-6, region-RE-7, region-RE-8, region-RE-9, region-RE-A, region-RE-B, region-RE-C, region-RE-D, region-RE-E, region-RE-F.
# Helpful Functions
You will see these at the top of every module and assignment. These are simply a set of reusable functions that we will make use of. Each of them will be explained as the semester progresses. They are explained in greater detail as the course progresses. Class 4 contains a complete overview of these functions.
```
from sklearn import preprocessing
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shutil
import os
import requests
import base64
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = "{}-{}".format(name, x)
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the original column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df, name, target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x) == str(tv) else 0 for x in l]
name2 = "{}-{}".format(name, tv)
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df, name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df.as_matrix(result).astype(np.float32), dummies.as_matrix().astype(np.float32)
else:
# Regression
return df.as_matrix(result).astype(np.float32), df.as_matrix([target]).astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return "{}:{:>02}:{:>05.2f}".format(h, m, s)
# Regression chart.
def chart_regression(pred,y,sort=True):
t = pd.DataFrame({'pred' : pred, 'y' : y.flatten()})
if sort:
t.sort_values(by=['y'],inplace=True)
a = plt.plot(t['y'].tolist(),label='expected')
b = plt.plot(t['pred'].tolist(),label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name] - df[name].mean()) >= (sd * df[name].std()))]
df.drop(drop_rows, axis=0, inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low=-1, normalized_high=1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text))
```
# Assignment #3 Sample Code
The following code provides a starting point for this assignment.
```
import os
import pandas as pd
from scipy.stats import zscore
# This is your student key that I emailed to you at the beginnning of the semester.
key = "qgABjW9GKV1vvFSQNxZW9akByENTpTAo2T9qOjmh" # This is an example key and will not work.
# You must also identify your source file. (modify for your local setup)
# file='/resources/t81_558_deep_learning/assignment_yourname_class1.ipynb' # IBM Data Science Workbench
# file='C:\\Users\\jeffh\\projects\\t81_558_deep_learning\\t81_558_class1_intro_python.ipynb' # Windows
#file='/Users/jeff/projects/t81_558_deep_learning/assignment_yourname_class1.ipynb' # Mac/Linux
file = '...location of your source file...'
# Begin assignment
path = "./data/"
filename_read = os.path.join(path,"reg-30-spring-2018.csv")
df = pd.read_csv(filename_read)
# Calculate density
# Encode dummies
# Save a copy to examine, if you like
df.to_csv('3.csv',index=False)
# Submit
submit(source_file=file,data=df,key=key,no=3)
```
# Checking Your Submission
You can always double check to make sure your submission actually happened. The following utility code will help with that.
```
import requests
import pandas as pd
import base64
import os
def list_submits(key):
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key': key},
json={})
if r.status_code == 200:
print("Success: \n{}".format(r.text))
else:
print("Failure: {}".format(r.text))
def display_submit(key,no):
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key': key},
json={'assignment':no})
if r.status_code == 200:
print("Success: \n{}".format(r.text))
else:
print("Failure: {}".format(r.text))
# Show a listing of all submitted assignments.
key = "qgABjW9GKV1vvFSQNxZW9akByENTpTAo2T9qOjmh"
list_submits(key)
# Show one assignment, by number.
display_submit(key,3)
```
| github_jupyter |
```
import statistics
import pprint
import pandas as pd
import numpy as np
from random import uniform
from tslearn.utils import to_time_series_dataset
from tslearn.metrics import dtw#, gak
import plotly.express as px
import scipy.stats as st
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import seaborn as sns; sns.set()
#ToDo: Threading
def get_best_distribution(data):
dist_names = ["gamma", "gumbel_l", "cauchy", "dgamma", "beta", "betaprime", "exponweib", "rayleigh", "fisk",
"gausshyper", "invweibull", "pareto", "alpha", "expon", "hypsecant", "mielke", "loggamma",
"rdist", "rice"] ## Agregar más a voluntad
dist_results = []
params = {}
for dist_name in dist_names:
dist = getattr(st, dist_name)
param = dist.fit(data)
params[dist_name] = param
# Applying the Kolmogorov-Smirnov test
D, p = st.kstest(data, dist_name, args=param)
print("p value for "+dist_name+" = "+str(p))
dist_results.append((dist_name, p))
# select the best fitted distribution
best_dist, best_p = (max(dist_results, key=lambda item: item[1]))
# store the name of the best fit and its p value
print("Best fitting distribution: "+str(best_dist))
print("Best p value: "+ str(best_p))
parms = params[best_dist]
#print("Parameters for the best fit: "+ str(parms))
map_parms = {}
dist = getattr(st, best_dist)
try:
counter_wrong_chars = 0 #To solve a bug
for position, shape_parameter in enumerate(dist.shapes):
#print(position, shape_parameter)
if shape_parameter not in [' ', ',']:
map_parms[shape_parameter] = parms[position-counter_wrong_chars]
else:
counter_wrong_chars += 1
except:
pass
finally:
map_parms["loc"] = parms[-2]
map_parms["scale"] = parms[-1]
print("Parameters for the best fit: "+ str(map_parms))
return best_dist, best_p, parms, map_parms
def get_optimal_curves(df_curves, example_curves, ts_example_curves, dict_probability_distrs, prob_distrs,
min_count_generated_curves, a, b, E_min, min_f_load, roof_dtw_distance, min_corr):
I = 5000 #5000
acum_generated_curves = 0
while acum_generated_curves < min_count_generated_curves:
for i in range(1,I+1):
C_i = [None] * 24
h_max = int(round(uniform(19, 21),0))
C_i[h_max] = 1
for h, none in enumerate(C_i):
if h != h_max:
function = dict_probability_distrs[prob_distrs[h][0]]
parms = prob_distrs[h][1]
was_random_number_found = False
while was_random_number_found is False:
E = function.rvs(**parms, size=1)[0]
if (E>=E_min and E<1):
was_random_number_found = True
C_i[h] = E
E_acum = sum(C_i)
if (E_acum>=a and E_acum<=b):
#print(C_i, type(C_i))
f_load = statistics.mean(C_i) / max(C_i)
if f_load >= min_f_load:
ts_C_i = to_time_series_dataset(C_i)[0]
dtw_distances = []
for k, curve in enumerate(ts_example_curves):
dtw_distance = dtw(ts_C_i, curve)
dtw_distances.append(dtw_distance)
average_dtw = statistics.mean(dtw_distances)
if average_dtw < roof_dtw_distance:
corrs = []
for example_curve in example_curves:
corr = np.corrcoef(C_i, example_curve)
corrs.append(corr[0][1])
average_corr = statistics.mean(corrs)
if average_corr>=min_corr:
print(i, f_load, E_acum, average_dtw, average_corr)
df_curves = df_curves.append(
{ '0': C_i[0], '1': C_i[1], '2': C_i[2],
'3': C_i[3], '4': C_i[4], '5': C_i[5],
'6': C_i[6], '7': C_i[7], '8': C_i[8],
'9': C_i[9], '10': C_i[10], '11': C_i[11],
'12': C_i[12], '13': C_i[13], '14': C_i[14],
'15': C_i[15], '16': C_i[16], '17': C_i[17],
'18': C_i[18], '19': C_i[19], '20': C_i[20],
'21': C_i[21], '22': C_i[22], '23': C_i[23],
'FC': f_load, 'Sum': E_acum,
'DTW_avg_distance': average_dtw, 'Avg_correlation': average_corr },
ignore_index=True
)
acum_generated_curves += 1
if acum_generated_curves>=min_count_generated_curves:
return (df_curves)
df_example_curves = pd.read_excel (r'Curvas.xlsx')
df_example_curves.drop(
df_example_curves.columns[
df_example_curves.columns.str.contains('unnamed', case = False, na=False)
],
axis = 1,
inplace = True
)
a = df_example_curves['Sum'].min()
b = df_example_curves['Sum'].max()
df_example_curves = df_example_curves.drop(['FC', 'Sum', 'Comentario'], axis=1)
print("a: ", a, " b: ", b)
print(df_example_curves)
prob_distrs = []
plots = []
for (columnName, columnData) in df_example_curves.iteritems():
## Maximizar el p-value ##
print('Colunm Name : ', columnName)
#print('Column Contents : ', columnData.values, type(columnData.values), columnData.values.shape)
best_dist, best_p, parms, map_parms = get_best_distribution(columnData.values)
prob_distrs.append([best_dist, map_parms])
#if columnName == 12:
# ax = sns.distplot(columnData.values, kde=False)
#ax = sns.distplot(columnData.values, kde=False)
print("prob_distrs: ")
pprint.pprint(prob_distrs)
dict_probability_distrs = { "gamma": st.gamma, "gumbel_l": st.gumbel_l, "cauchy": st.cauchy, "dgamma": st.dgamma,
"beta": st.beta, "betaprime": st.betaprime, "exponweib": st.exponweib, "rayleigh": st.rayleigh,
"fisk": st.fisk, "gausshyper": st.gausshyper, "invweibull": st.invweibull, "pareto": st.pareto,
"alpha": st.alpha, "expon": st.expon, "hypsecant": st.hypsecant, "mielke": st.mielke,
"loggamma": st.loggamma, "rdist": st.rdist, "rice": st.rice }
example_curves = df_example_curves.values.tolist()
ts_example_curves = to_time_series_dataset(example_curves)
#pprint.pprint(ts_example_curves)
df_curves = pd.DataFrame(
columns=[
'0','1','2','3','4','5','6','7','8','9','10','11','12','13','14','15','16','17','18','19','20','21','22','23',
'FC','Sum','DTW_avg_distance','Avg_correlation'
]
)
print(df_curves)
E_min = 0.375
min_f_load = 0.7625
min_count_generated_curves = 25
roof_dtw_distance = 0.25 #0.25
min_corr = 0.95 #0.95
df_curves = get_optimal_curves(df_curves, example_curves, ts_example_curves, dict_probability_distrs, prob_distrs,
min_count_generated_curves, a, b, E_min, min_f_load, roof_dtw_distance, min_corr)
print(df_curves)
for index, row in df_curves.loc[:, "0":"23"].iterrows():
fig = px.line(row, width=600, height=300, xlabel='Hora')
fig.show()
average_optimal_curve = df_curves.loc[:, "0":"23"].mean(axis=0)
print(average_optimal_curve, type(average_optimal_curve))
average_optimal_curve.plot(linewidth=3.0, marker='x', ms=6.5)
plt.axis((None,None,0,1))
plt.grid(b=True, which='major', color='k', linestyle='--')
plt.minorticks_on()
plt.grid(b=True, which='minor', color='grey', linestyle=':')
plt.show()
final_load_factor = average_optimal_curve.mean() / average_optimal_curve.max()
print("final_load_factor: ", final_load_factor)
final_energy_sum = average_optimal_curve.sum()
print("final_energy_sum: ", final_energy_sum)
```
| github_jupyter |
# Reading and writing fields
There are two main file formats to which a `discretisedfield.Field` object can be saved:
- [VTK](https://vtk.org/) for visualisation using e.g., [ParaView](https://www.paraview.org/) or [Mayavi](https://docs.enthought.com/mayavi/mayavi/)
- OOMMF [Vector Field File Format (OVF)](https://math.nist.gov/oommf/doc/userguide12a5/userguide/Vector_Field_File_Format_OV.html) for exchanging fields with micromagnetic simulators.
Let us say we have a nanosphere sample:
$$x^2 + y^2 + z^2 <= r^2$$
with $r=5\,\text{nm}$. The space is discretised into cells with dimensions $(0.5\,\text{nm}, 0.5\,\text{nm}, 0.5\,\text{nm})$. The value of the field at $(x, y, z)$ point is $(-cy, cx, cz)$, with $c=10^{9}$. The norm of the field inside the cylinder is $10^{6}$.
Let us first build that field.
```
import discretisedfield as df
r = 5e-9
cell = (0.5e-9, 0.5e-9, 0.5e-9)
mesh = df.Mesh(p1=(-r, -r, -r), p2=(r, r, r), cell=cell)
def norm_fun(pos):
x, y, z = pos
if x**2 + y**2 + z**2 <= r**2:
return 1e6
else:
return 0
def value_fun(pos):
x, y, z = pos
c = 1e9
return (-c*y, c*x, c*z)
field = df.Field(mesh, dim=3, value=value_fun, norm=norm_fun)
```
Let us have a quick view of the field we created
```
# NBVAL_IGNORE_OUTPUT
field.plane('z').k3d.vector(color_field=field.z)
```
## Writing the field to a file
The main method used for saving field in different files is `discretisedfield.Field.write()`. It takes `filename` as an argument, which is a string with one of the following extensions:
- `'.vtk'` for saving in the VTK format
- `'.ovf'`, `'.omf'`, `'.ohf'` for saving in the OVF format
Let us firstly save the field in the VTK file.
```
vtkfilename = 'my_vtk_file.vtk'
field.write(vtkfilename)
```
We can check if the file was saved in the current directory.
```
import os
os.path.isfile(f'./{vtkfilename}')
```
Now, we can delete the file:
```
os.remove(f'./{vtkfilename}')
```
Next, we can save the field in the OVF format and check whether it was created in the current directory.
```
omffilename = 'my_omf_file.omf'
field.write(omffilename)
os.path.isfile(f'./{omffilename}')
```
There are three different possible representations of an OVF file: one ASCII (`txt`) and two binary (`bin4` or `bin8`). ASCII `txt` representation is a default representation when `discretisedfield.Field.write()` is called. If any different representation is required, it can be passed via `representation` argument.
```
field.write(omffilename, representation='bin8')
os.path.isfile(f'./{omffilename}')
```
## Reading the OVF file
The method for reading OVF files is a class method `discretisedfield.Field.fromfile()`. By passing a `filename` argument, it reads the file and creates a `discretisedfield.Field` object. It is not required to pass the representation of the OVF file to the `discretisedfield.Field.fromfile()` method, because it can retrieve it from the content of the file.
```
read_field = df.Field.fromfile(omffilename)
```
Like previouly, we can quickly visualise the field
```
# NBVAL_IGNORE_OUTPUT
read_field.plane('z').k3d.vector(color_field=read_field.z)
```
Finally, we can delete the OVF file we created.
```
os.remove(f'./{omffilename}')
```
| github_jupyter |
# Sesiones prácticas
## 0
Instalación de Python + ecosistema científico + opencv + opengl
- aula virtual -> página web -> install
- git o unzip master
- anaconda completo o miniconda
- windows: opencv y probar los ejemplos
- linux: primer método más seguro, con paquetes seleccionados
- probar webcam.py stream.py, surface.py, image_gl.py, hog/facelandmarks.py (en ../data get.sh)
- manejo básico de jupyter
Opcional:
- compilación opencv
- probar docker
## 2
Dispositivos de captura
- webcam.py con opencv crudo
- spyder
- umucv (install con --upgrade) (update_umucv.sh)
- PYTHONPATH
- stream.py, opciones de autostream, efecto de teclas, --help, --dev=help
- webcams
- videos
- carpeta de imágenes
- teléfono
- youtube
- urls de tv
- ejemplo de recorte invertido
- grabar video de demo (save_video.py)
## 3
Más utilidades: mouse coords, tracker, roi
- medidor.py
- inrange.py
(**PROVISIONAL**)
## 4
- captura en hilo aparte
- mean shift / camshift
## 5
- hog/hog0.py
- hog/pedestrian.py con
- dlib: hog/facelandmarks.py
- dlib: herramienta imglab, hog/train_detector.py, hog/run_detector.py
## 6
- LK/corners0.py, 1, 2, 3, LK/lk_tracks.py
## 7
En esta sesión vamos a experimentar con el detector de puntos de interés SIFT. (La implementación de opencv está en un repositorio aparte con las contribuciones "non free", pero la patente ha expirado hace unos días. En cualquier caso, la versión de opencv que estamos usando lo incluye.)
Nuestro objetivo es calcular un conjunto de "keypoints", cada uno con su descriptor (vector de características que describe el entorno del punto), que nos permita encontrarlo en imágenes futuras. Esto tiene una aplicación inmediata para reconocer objetos y más adelante en geometría visual.
Empezamos con el ejemplo de código code/SIFT/sift0.py, que simplemente calcula y muestra los puntos de interés. Es interesante observar el efecto de los parámetros del método y el tiempo de cómputo en función del tamaño de la imagen (que puedes cambiar con --size o --resize).
El siguiente ejemplo code/SIFT/sift1.py muestra un primer ataque para establecer correspondencias. Los resultados son bastante pobres.
Finalmente, en code/SIFT/sift.py aplicamos un criterio de selección para eliminar muchas correspondencias erróneas (aunque no todas). Esto es en principio suficiente para el reconocimiento de objetos. (Más adelante veremos una forma mucho mejor de eliminar correspondencias erróneas, necesaria para aplicaciones de geometría.)
El ejercicio obligatorio **SIFT** es una ampliación sencilla de este código. Se trata de almacenar un conjunto de modelos (¡con textura! para que tengan suficientes keypoints) como portadas de libros, discos, videojuegos, etc. y reconocerlos en base a la proporción de coincidencias detectadas.
Una segunda actividad en esta sesión consiste en comentar el ejemplo de código code/server.py. Utiliza el paquete [flask][flask] para crear un sencillo servidor web que devuelve la imagen de la cámara modificada como deseemos. Sirve como punto de partida para el ejercicio opcional **WEB**.
[flask]: https://en.wikipedia.org/wiki/Flask_(web_framework)
## 8
En esta sesión vamos a explorar el reconocimiento de formas mediante descriptores frecuenciales.
Nuestro objetivo es hacer un programa que reconozca la forma de trébol, como se muestra [en este pantallazo](../../images/demos/shapedetect.png). Si no tenéis a mano un juego de cartas podéis usar --dev=dir:../images/card*.png para hacer las pruebas, aunque lo ideal es hacerlo funcionar con una cámara en vivo.
Trabajaremos con los ejemplos de la carpeta `code/shapes` y, como es habitual, iremos añadiendo poco a poco funcionalidad. En cada nuevo paso los comentarios explican los cambios respecto al paso anterior.
Empezamos con el ejemplo shapes/trebol1.py, que simplemente prepara un bucle de captura básico, binariza la imagen y muestra los contornos encontrados. Se muestran varias formas de realizar la binarización y se puede experimentar con ellas, pero en principio el método automático propuesto suele funcionar bien en muchos casos.
El segundo paso en shapes/trebol2.py junta la visualización en una ventana y selecciona los contornos oscuros de tamaño razonable. Esto no es imprescincible para nuestra aplicación, pero es interesante trabajar con el concepto de orientación de un contorno.
En shapes/trebol3.py leemos un modelo de la silueta trébol de una imagen que tenemos en el repositorio y la mostramos en una ventana.
En shapes/trebol3b.py hacemos una utilidad para ver gráficamente las componentes frecuenciales como elipses que componen la figura. Podemos ver las componentes en su tamaño natural, incluyendo la frecuencia principal, [como aquí](../images/demos/full-components.png), o quitando la frecuencia principal y ampliando el tamaño de las siguientes, que son la base del descriptor de forma, [como se ve aquí](../images/demos/shape-components.png). Observa que las configuraciones de elipses son parecidas cuando corresponden a la misma silueta.
En shapes/trebol4.py definimos la función que calcula el descriptor invariante. Se basa esencialmente en calcular los tamaños relativos de estas elipses. En el código se explica cómo se consigue la invarianza a las transformaciones deseadas: posición, tamaño, giros, punto de partida del contorno y ruido de medida.
Finalmente, en shapes/trebol5.py calculamos el descriptor del modelo y en el bucle de captura calculamos los descriptores de los contornos oscuros detectados para marcar las siluetas que tienen un descriptor muy parecido al del trébol.
El ejercicio opcional SILU consiste en ampliar este código para reconocer un conjunto más amplio de siluetas en alguna aplicación que se os parezca interesante. Por ejemplo, en images/shapes tenéis los modelos de caracteres de las placas de matrícula.
## 9
En esta sesión vamos a hacer varias actividades. Necesitamos algunos paquetes. En Linux son:
sudo apt install tesseract-ocr tesseract-ocr-spa libtesseract-dev
pip install tesserocr
sudo apt install libzbar-dev
pip install pyzbar
Usuarios de Mac y Windows: investigad la forma de instalarlo.
1) En primer lugar nos fijamos en el script `code/ocr.png`, cuya misión es poner en marcha el OCR con la cámara en vivo. Usamos el paquete de python `tesserocr`. Vamos a verificar el funcionamiento con una imagen estática, pero lo ideal es probarlo con la cámara en vivo.
python ocr.py python ocr.py --dev=dir:../images/texto/bo0.png
Está pensado para marcar una sola línea de texto, [como se muestra aquí](../images/demos/ocr.png). Este pantallazo se ha hecho con la imagen bo1.png disponible en la misma carpeta, que está desenfocada, pero aún así el OCR funciona bien.
2) El segundo ejemplo es `code/zbardemo.png` que muestra el uso del paquete pyzbar para leer códigos de barras ([ejemplo](../images/demos/barcode.png)) y códigos QR ([ejemplo](../images/demos/qr.png)) con la cámara. En los códigos de barras se detectan puntos de referencia, y en los QR se detectan las 4 esquinas del cuadrado, que pueden ser útiles como referencia en algunas aplicaciones de geometría.
3) A continuación vamos a jugar con un bot de telegram que nos permite comunicarnos cómodamente con nuestro ordenador desde el teléfono móvil, sin necesidad de tener una dirección pública de internet.
Voy a dejar durante esta mañana un bot funcionando para que hagáis pruebas. El bot se llama "BichoBot" y su foto de perfil es una pequeña plataforma con ruedas con un raspberry pi encima. Responde al comando /hello y si le enviáis una foto os la devolverá en blanco y negro e invertida. (Está basado en bot3.py).
Simplemente necesitamos:
pip install python-telegram-bot
El ejemplo `bot/bot0.py` nos envía al teléfono la IP del ordenador (es útil si necesitamos conectarnos por ssh con una máquina que tiene IP dinámica).
El ejemplo `bot/bot1.py` explica la forma de enviar una imagen nuestro teléfono cuando ocurre algo. En este caso se envía cuando se pulsa una tecla, pero lo normal es detectar automáticamente algún evento con las técnicas de visión artificial que estamos estudiando.
El ejemplo `bot/bot2.py` explica la forma de hacer que el bot responda a comandos. El comando /hello nos devuelve el saludo, el comando /stop detiene el programa y el comando /image nos devuelve una captura de nuestra webcam. (Se ha usado la captura en un hilo).
El ejemplo `bot/bot3.py` explica la forma de capturar comandos con argumentos y el procesamiento de una imagen enviada por el usuario.
Esta práctica es completamente opcional, pero es muy útil para enviar cómodamente a nuestros programas de visión artificial una imagen tomada con la cámara sin necesidad de escribir una aplicación específica para el móvil. Algunos ejercicios que estamos haciendo se pueden adaptar fácilmente para probarlos a través de un bot de este tipo.
Para crearos vuestro propio bot tenéis que contactar con el bot de telegram "BotFather", que os guiará paso a paso y os dará el token de acceso. Y luego el "IDBot" os dirá el id numérico de vuestro usuario.
En la carpeta hay otros ejemplos más avanzados.
4) En la dirección
https://github.com/ruvelro/TV-Online-TDT-Spain
se pueden encontrar las url de muchos canales de televisión que están haciendo streaming en directo. Abriendo los ficheros m3u8 encontramos las url que podemos poner en --dev en nuestras aplicaciones (hay distintas resoluciones de imagen). Por ejemplo, la TVE1 está aquí:
http://hlsliveamdgl7-lh.akamaihd.net/i/hlsdvrlive_1@583042/index_0400_av-p.m3u8?sd=10&rebase=on
(Funciona a saltos porque autoStream lee los frames lo más rápido posible. Se puede poner un time.sleep para que vaya a ritmo normal).
Próximamente propondré un ejercicio opcional relacionado con esto.
## 10
Esta sesión está dedicada a poner en marcha una red convolucional sencilla. La tarea que vamos a resolver es el reconocimiento de dígitos manuscritos. Por eso, en primer lugar es conveniente escribir unos cuantos números en una hoja de papel, con un bolígrafo que tenga un trazo no demasiado fino, y sin preocuparnos mucho de que estén bien escritos. Pueden tener distintos tamaños, pero no deben estar muy girados. Para desarrollar el programa y hacer pruebas cómodamente se puede trabajar con una imagen fija, pero la idea es que nuestro programa funcione con la cámara en vivo.
Trabajaremos en la carpeta [code/DL/CNN](../code/DL/CNN), donde tenemos las diferentes etapas de ejercicio y una imagen de prueba.
El primer paso es `digitslive-1.py` que simplemente encuentra las manchas de tinta que pueden ser posibles números.
En `digitslive-2.py` normalizamos el tamaño de las detecciones para poder utilizar la base de datos MNIST.
En `digitslive-3.py` implementamos un clasificador gaussiano con reducción de dimensión mediante PCA y lo ponemos en marcha con la imagen en vivo. (Funciona bastante bien pero, p.ej., en la imagen de prueba comete un error).
Finalmente, en `digitslive-4.py` implementamos la clasificación mediante una red convolucional mediante el paquete **keras**. Usamos unos pesos precalculados. (Esta máquina ya no comete el error anterior.)
Como siempre, en cada fase del ejercicio los comentarios explican el código que se va añadiendo.
Una vez conseguido esto, la sesión práctica tiene una segunda actividad que consiste en **entrenar los pesos** de (por ejemplo) esta misma red convolucional. Para hacerlo en nuestro ordenador sin perder la paciencia necesitamos una GPU con CUDA y libCUDNN. La instalación de todo lo necesario puede no ser trivial.
Una alternativa muy práctica es usar [google colab](https://colab.research.google.com/), que proporciona gratuitamente máquinas virtuales con GPU y un entorno de notebooks jupyter (un poco modificados pero compatibles). Para probarlo, entrad con vuestra cuenta de google y abrid un nuevo notebook. En la opción de menú **Runtime** hay que seleccionar **Change runtime type** y en hardware accelerator ponéis GPU. En una celda del notebook copiáis directamente el contenido del archivo `cnntest.py` que hay en este mismo directorio donde estamos trabajando hoy. Al evaluar la celda se descargará la base de datos y se lanzará un proceso de entrenamiento. Cada epoch tarda unos 4s. Podéis comparar con lo que se consigue con la CPU en vuestro propio ordenador. Se puede lanzar un entrenamiento más completo, guardar los pesos y descargarlos a vuestra máquina.
Como curiosidad, podéis comparar con lo que conseguiría el OCR tesseract, y guardar algunos casos de dígitos que estén bien dibujados pero que la red clasifique mal.
## 11
En esta sesión vamos a poner en marcha los modelos avanzados de deep learning que presentamos ayer.
Los ejemplos de código se han probado sobre LINUX. En Windows o Mac puede ser necesario hacer modificaciones; para no perder mucho tiempo mi recomendación es probarlo primero en una máquina virtual.
Si tenéis una GPU nvidia reciente lo ideal es instalar CUDA y libCUDNN para conseguir una mayor velocidad de proceso. Si no tenéis GPU no hay ningún problema, todos los modelos funcionan con CPU. (Los ejercicios de deep learning que requieren entrenamiento son opcionales.)
Para ejecutar las máquinas inception, YOLO y el reconocimiento de caras necesitamos los siguientes paquetes:
pip install face_recognition tensorflow==1.15.0 keras easydict
La detección de marcadores corporales *openpose* requiere unos pasos de instalación adicionales que explicaremos más adelante.
(La versión 1.15.0 de tensorflow es necesaria para YOLO y openpose. Producirá algunos warnings sin mucha importancia. Si tenemos una versión más reciente de tensorflow podemos hacer `pip install --upgrade tensorflow=1.15.0` o crear un entorno de conda especial para este tema).
1) Para probar el **reconocimiento de caras** nos vamos a la carpeta code/DL/facerec. Debe estar correctamente instalado DLIB.
En el directorio `gente` se guardan los modelos. Como ejemplo tenemos a los miembros de Monty Python:
./facerec.py --dev=dir:../../../images/monty-python*
(Recuerda que las imágenes seleccionadas con --dev=dir: se avanzan pinchando con el ratón en la ventana pequeña de muestra).
Puedes meter fotos tuyas y de tu familia en la carpeta `gente` para probar con la webcam o con otras fotos.
Con pequeñas modificaciones de este programa se puede resolver el ejercicio ANON: selecciona una cara en la imagen en vivo pinchando con el ratón para ocultarla (emborronándola o pixelizándola) cuando se reconozca en las imágenes siguientes.
Esta versión del reconocimiento de caras no tiene aceleración con GPU (tal vez se puede configurar). Si reducimos un poco el tamaño de la imagen funciona con bastante fluidez.
2) Para probar la máquina **inception** nos movemos a la carpeta code/DL/inception.
./inception0.py
(Se descargará el modelo del la red). Se puede probar con las fotos incluidas en la carpeta con `--dev=dir:*.png`. La versión `inception1.py` captura en hilo aparte y muestra en consola las 5 categorías más probables.
Aunque se supone que consigue buenos resultados en las competiciones, sobre imágenes naturales comete bastante errores.
3) El funcionamiento de **YOLO** es mucho mejor. Nos vamos a la carpeta code/DL y ejecutamos lo siguiente para para descargar el código y los datos de esta máquina (y de openpose).
bash get.sh
Nos metemos en code/DL/yolo y ejecutamos:
/.yolo-v3.py
Se puede probar también con las imágenes de prueba incluidas añadiendo `--dev=dir:*.png`.
El artículo de [YOLO V3](https://pjreddie.com/media/files/papers/YOLOv3.pdf) es interesante. En la sección 5 el autor explica que abandonó esta línea de investigación por razones éticas. Os recomiendo que la leáis. Como curiosidad, hace unos días apareció [YOLO V4](https://arxiv.org/abs/2004.10934).
4) Para probar **openpose** nos vamos a code/DL/openpose. Los archivos necesarios ya se han descargado en el paso anterior, pero necesitamos instalar algunos paquetes. El proceso se explica en el README.
En la carpeta `docker` hay un script para ejecutar una imagen docker que tiene instalados todos los paquetes que hemos estamos usando en la asignatura. Es experimental. No perdaís ahora tiempo con esto si no estáis familiarizados con docker.
El tema de deep learning en visión artificial es amplísimo. Para estudiarlo en detalle hace falta (como mínimo) una asignatura avanzada (master). Nuestro objetivo es familizarizarnos un poco con algunas de las máquinas preentrenadas disponibles para hacernos una idea de sus ventajas y limitaciones.
Si estáis interesados en estos temas el paso siguiente es adaptar alguno de estos modelos a un problema propio mediante "transfer learning", que consiste en utilizar las primeras etapas de una red preentrenada para transformar nuestros datos y ajustar un clasificador sencillo. Alternativamente, se puede reajustar los pesos de un modelo preentrenado, fijando las capas iniciales al principio. Para remediar la posible falta de ejemplos se utilizan técnicas de "data augmentation", que generan variantes de los ejemplos de entrenamiento con múltiples transformaciones.
## 12
Hoy vamos a rectificar el plano de la mesa apoyándonos en marcadores artificiales.
En primer lugar trabajaremos con marcadores poligonales. Nuestro objetivo es detectar un marcador como el que aparece en el vídeo `images/rot4.mjpg`. Nos vamos a la carpeta `code/polygon`.
El primer paso (`polygon0.py`) es detectar figuras poligonales con el número de lados correcto a partir de los contornos detectados.
A continuación (`polygon1.py`) nos quedamos con los polígonos que realmente pueden corresponder al marcador. Esto se hace viendo si existe una homografía que relaciona con precisión suficiente el marcador real y su posible imagen.
Finalmente (`polygon2.py`) obtiene el plano rectificado
También se puede añadir información "virtual" a la imagen original, como por ejemplo los ejes de coordenadas definidos por el marcador (`polygon3.py`).
Como segunda actividad, en la carpeta `code/elipses` se muestra la forma de detectar un marcador basado en 4 círculos.
## 13
En esta sesión vamos a extraer la matriz de cámara a partir del marcador utilizado en la sesión anterior, lo que nos permitirá añadir objetos virtuales tridimensionales a la escena y determinar la posición de la cámara en el espacio.
Nos vamos a la carpeta `code/pose`, donde encontraremos los siguientes ejemplos de código:
`pose0.py` incluye el código completo para extraer contornos, detectar el marcador poligonal, extraer la matriz de cámara y dibujar un cubo encima del marcador.
`pose1.py` hace lo mismo con funciones de umucv.
`pose2.py` trata de ocultar el marcador y dibuja un objeto que cambia de tamaño.
`pose3.py` explica la forma de proyectar una imagen en la escena escapando del plano del marcador.
`pose3D.py` es un ejemplo un poco más avanzado que utiliza el paquete pyqtgraph para mostrar en 3D la posición de la cámara en el espacio.
En el ejercicio **RA** puedes intentar que el comportamiento del objeto virtual dependa de acciones del usuario (p. ej. señalando con el ratón un punto del plano) o de objetos que se encuentran en la escena.
| github_jupyter |
```
# Import the SPICE module
import spiceypy
# We want to determine the position of our home planet with respect to the Sun.
# The datetime shall be set as "today" (midnight). SPICE requires the
# Ephemeris Time (ET); thus, we need to convert a UTC datetime string to ET.
import datetime
# get today's date
DATE_TODAY = datetime.datetime.today()
# convert the datetime to a string, replacing the time with midnight
DATE_TODAY = DATE_TODAY.strftime('%Y-%m-%dT00:00:00')
# convert the utc midnight string to the corresponding ET
spiceypy.furnsh('../kernels/lsk/naif0012.tls') #<-- This is needed.
ET_TODAY_MIDNIGHT = spiceypy.utc2et(DATE_TODAY)
# To compute now the position and velocity (so called state) of the Earth
# with respect to the Sun, we use the following function to determine the
# state vector and the so called light time (travel time of the light between
# the Sun and our home planet). Positions are always given in km, velocities
# in km/s and times in seconds
#First we load the kernel for positional information first:
spiceypy.furnsh('../kernels/spk/de432s.bsp')
# targ : Object that shall be pointed at (399 := Earth)
# et : The ET of the computation (Set for today)
# ref : The reference frame. Here, it is ECLIPJ2000 (the ecliptic plane of the Earth)
# obs : The observer respectively the center of our state vector computation (10 := Sun)
EARTH_STATE_WRT_SUN, EARTH_SUN_LT = spiceypy.spkgeo(targ=399, \
et=ET_TODAY_MIDNIGHT, \
ref='ECLIPJ2000', \
obs=10)
#The first 3 values are the x, y, z components in km.
#The last 3 values are the corresponding velocity components in km/s.
print(EARTH_STATE_WRT_SUN)
# Is the one-way light time from the observing body
# to the geometric position of the target body
# in seconds at the specified epoch.
# It should be around 8mins
print(EARTH_SUN_LT/60)
# The (Euclidean) distance should be around 1 AU. Why "around"? Well the Earth
# revolves the Sun in a slightly non-perfect circle (elliptic orbit). First,
# we compute the distance in km.
import math
EARTH_SUN_DISTANCE = math.sqrt(EARTH_STATE_WRT_SUN[0]**2.0 \
+ EARTH_STATE_WRT_SUN[1]**2.0 \
+ EARTH_STATE_WRT_SUN[2]**2.0)
# Convert the distance in astronomical units (1 AU)
# Instead of searching for the "most recent" value, we use the default value
# in SPICE. This way, we can easily compare our results with the results of
# others.
EARTH_SUN_DISTANCE_AU = spiceypy.convrt(EARTH_SUN_DISTANCE, 'km', 'AU')
# Cool, it works!
print('Current distance between the Earth and the Sun in AU:', \
EARTH_SUN_DISTANCE_AU)
#Lets comute the oribital speed of the Earth in km/s
# First, we compute the actual orbital speed of the Earth around the Sun
EARTH_ORB_SPEED_WRT_SUN = math.sqrt(EARTH_STATE_WRT_SUN[3]**2.0 \
+ EARTH_STATE_WRT_SUN[4]**2.0 \
+ EARTH_STATE_WRT_SUN[5]**2.0)
# It's around 30 km/s
print('Current orbital speed of the Earth around the Sun in km/s:', \
EARTH_ORB_SPEED_WRT_SUN)
```
Now we get the theoretical earth orbital speed:
```
# Now let's compute the theoretical expectation. First, we load a pck file
# that contain miscellanoeus information, like the G*M values for different
# objects
# First, load the kernel
spiceypy.furnsh('../kernels/pck/gm_de431.tpc')
_, GM_SUN = spiceypy.bodvcd(bodyid=10, item='GM', maxn=1)
# Now compute the orbital speed
V_ORB_FUNC = lambda gm, r: math.sqrt(gm/r)
EARTH_ORB_SPEED_WRT_SUN_THEORY = V_ORB_FUNC(GM_SUN[0], EARTH_SUN_DISTANCE)
# Print the result
print('Theoretical orbital speed of the Earth around the Sun in km/s:', \
EARTH_ORB_SPEED_WRT_SUN_THEORY)
```
| github_jupyter |
<img align="center" style="max-width: 1000px" src="banner.png">
<img align="right" style="max-width: 200px; height: auto" src="hsg_logo.png">
## Lab 05 - "Convolutional Neural Networks (CNNs)" Assignments
GSERM'21 course "Deep Learning: Fundamentals and Applications", University of St. Gallen
In the last lab we learned how to enhance vanilla Artificial Neural Networks (ANNs) using `PyTorch` to classify even more complex images. Therefore, we used a special type of deep neural network referred to **Convolutional Neural Networks (CNNs)**. CNNs encompass the ability to take advantage of the hierarchical pattern in data and assemble more complex patterns using smaller and simpler patterns. In this lab, we aim to leverage that knowledge by applying it to a set of self-coding assignments. But before we do so let's start with another motivational video by NVIDIA:
```
from IPython.display import YouTubeVideo
# NVIDIA: "Official Intro | GTC 2020 | I AM AI"
YouTubeVideo('e2_hsjpTi4w', width=1000, height=500)
```
As always, pls. don't hesitate to ask all your questions either during the lab, post them in our CANVAS (StudyNet) forum (https://learning.unisg.ch), or send us an email (using the course email).
## 1. Assignment Objectives:
Similar today's lab session, after today's self-coding assignments you should be able to:
> 1. Understand the basic concepts, intuitions and major building blocks of **Convolutional Neural Networks (CNNs)**.
> 2. Know how to **implement and to train a CNN** to learn a model of tiny image data.
> 3. Understand how to apply such a learned model to **classify images** images based on their content into distinct categories.
> 4. Know how to **interpret and visualize** the model's classification results.
## 2. Setup of the Jupyter Notebook Environment
Similar to the previous labs, we need to import a couple of Python libraries that allow for data analysis and data visualization. We will mostly use the `PyTorch`, `Numpy`, `Sklearn`, `Matplotlib`, `Seaborn` and a few utility libraries throughout this lab:
```
# import standard python libraries
import os, urllib, io
from datetime import datetime
import numpy as np
```
Import Python machine / deep learning libraries:
```
# import the PyTorch deep learning library
import torch, torchvision
import torch.nn.functional as F
from torch import nn, optim
from torch.autograd import Variable
```
Import the sklearn classification metrics:
```
# import sklearn classification evaluation library
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
```
Import Python plotting libraries:
```
# import matplotlib, seaborn, and PIL data visualization libary
import matplotlib.pyplot as plt
import seaborn as sns
from PIL import Image
```
Enable notebook matplotlib inline plotting:
```
%matplotlib inline
```
Import Google's GDrive connector and mount your GDrive directories:
```
# import the Google Colab GDrive connector
from google.colab import drive
# mount GDrive inside the Colab notebook
drive.mount('/content/drive')
```
Create a structure of Colab Notebook sub-directories inside of GDrive to store (1) the data as well as (2) the trained neural network models:
```
# create Colab Notebooks directory
notebook_directory = '/content/drive/MyDrive/Colab Notebooks'
if not os.path.exists(notebook_directory): os.makedirs(notebook_directory)
# create data sub-directory inside the Colab Notebooks directory
data_directory = '/content/drive/MyDrive/Colab Notebooks/data'
if not os.path.exists(data_directory): os.makedirs(data_directory)
# create models sub-directory inside the Colab Notebooks directory
models_directory = '/content/drive/MyDrive/Colab Notebooks/models'
if not os.path.exists(models_directory): os.makedirs(models_directory)
```
Set a random `seed` value to obtain reproducable results:
```
# init deterministic seed
seed_value = 1234
np.random.seed(seed_value) # set numpy seed
torch.manual_seed(seed_value) # set pytorch seed CPU
```
Google Colab provides the use of free GPUs for running notebooks. However, if you just execute this notebook as is, it will use your device's CPU. To run the lab on a GPU, got to `Runtime` > `Change runtime type` and set the Runtime type to `GPU` in the drop-down. Running this lab on a CPU is fine, but you will find that GPU computing is faster. *CUDA* indicates that the lab is being run on GPU.
Enable GPU computing by setting the `device` flag and init a `CUDA` seed:
```
# set cpu or gpu enabled device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu').type
# init deterministic GPU seed
torch.cuda.manual_seed(seed_value)
# log type of device enabled
print('[LOG] notebook with {} computation enabled'.format(str(device)))
```
Let's determine if we have access to a GPU provided by e.g. Google's COLab environment:
```
!nvidia-smi
```
## 3. Convolutional Neural Networks (CNNs) Assignments
### 3.1 CIFAR-10 Dataset Download and Data Assessment
The **CIFAR-10 database** (**C**anadian **I**nstitute **F**or **A**dvanced **R**esearch) is a collection of images that are commonly used to train machine learning and computer vision algorithms. The database is widely used to conduct computer vision research using machine learning and deep learning methods:
<img align="center" style="max-width: 500px; height: 500px" src="cifar10.png">
(Source: https://www.kaggle.com/c/cifar-10)
Further details on the dataset can be obtained via: *Krizhevsky, A., 2009. "Learning Multiple Layers of Features from Tiny Images",
( https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf )."*
The CIFAR-10 database contains **60,000 color images** (50,000 training images and 10,000 validation images). The size of each image is 32 by 32 pixels. The collection of images encompasses 10 different classes that represent airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks. Let's define the distinct classs for further analytics:
```
cifar10_classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
```
Thereby the dataset contains 6,000 images for each of the ten classes. The CIFAR-10 is a straightforward dataset that can be used to teach a computer how to recognize objects in images.
Let's download, transform and inspect the training images of the dataset. Therefore, we first will define the directory we aim to store the training data:
```
train_path = data_directory + '/train_cifar10'
```
Now, let's download the training data accordingly:
```
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# download and transform training images
cifar10_train_data = torchvision.datasets.CIFAR10(root=train_path, train=True, transform=transf, download=True)
```
Verify the volume of training images downloaded:
```
# get the length of the training data
len(cifar10_train_data)
```
Let's now decide on where we want to store the evaluation data:
```
eval_path = data_directory + '/eval_cifar10'
```
And download the evaluation data accordingly:
```
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# download and transform validation images
cifar10_eval_data = torchvision.datasets.CIFAR10(root=eval_path, train=False, transform=transf, download=True)
```
Let's also verfify the volume of validation images downloaded:
```
# get the length of the training data
len(cifar10_eval_data)
```
### 3.2 Convolutional Neural Network (CNN) Model Training and Evaluation
<img align="center" style="max-width: 900px" src="classification.png">
We recommend you to try the following exercises as part of the self-coding session:
**Exercise 1: Train the neural network architecture of the lab with increased learning rate.**
> Increase the learning rate of the network training to a value of **0.1** (instead of currently 0.001) and re-run the network training for 10 training epochs. Load and evaluate the model exhibiting the lowest training loss. What kind of behavior in terms of loss convergence and prediction accuracy can be observed?
```
#### Step 1. define and init neural network architecture #############################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 2. define loss, training hyperparameters and dataloader ####################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 3. run model training ######################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 4. run model evaluation ####################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
```
**2. Evaluation of "shallow" vs. "deep" neural network architectures.**
> In addition to the architecture of the lab notebook, evaluate further (more **shallow** as well as more **deep**) neural network architectures by either **removing or adding convolutional layers** to the network. Train a model (using the architectures you selected) for at least **20 training epochs**. Analyze the prediction performance of the trained models in terms of training time and prediction accuracy.
```
#### Step 1. define and init neural network architecture #############################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 2. define loss, training hyperparameters and dataloader ####################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 3. run model training ######################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 4. run model evaluation ####################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
```
| github_jupyter |
# Calibrate mean and integrated intensity of a fluorescence marker versus concentration
## Requirements
- Images with different concentrations of the fluorescent tag with the concentration clearly specified in the image name
Prepare pure solutions of various concentrations of fluorescent tag in imaging media and collect images using parameters that are identical to those used for the experimental data collection (laser power, acquisition time, magnification, etc).
We recommend collecting images for 20-30 different concentrations, with 5-10 images per concentration.
Clearly mark the concentration in the file or subfolder name in nM or uM. See [example_data/calibration](../../example_data/calibration) for examples of image naming.
Note that the example images that we provide are cropped versions of the full images. You should use full images for calibration!
## Config
### The following code imports and declares functions used for the processing:
```
#################################
# Don't modify the code below #
#################################
import intake_io
import os
import re
import numpy as np
import pylab as plt
import seaborn as sns
from skimage import io
import pandas as pd
from tqdm import tqdm
from skimage.measure import regionprops_table
from am_utils.utils import walk_dir, combine_statistics
```
## Data & parameters
`input_dir`: folder with images to be analyzed
`output_dir`: folder to save results
`channel_name`: name of the fluorecent tag (e.g. "GFP")
## Specify data paths and parameters
```
input_dir = "../../example_data/calibration"
output_dir = "../../test_output/calibration"
channel_name = 'GFP'
```
### The following code lists all images in the input directory:
```
#################################
# Don't modify the code below #
#################################
samples = walk_dir(input_dir)
print(f'{len(samples)} images were found:')
print(np.array(samples))
```
### The following code loads a random image:
```
#################################
# Don't modify the code below #
#################################
sample = samples[np.random.randint(len(samples))]
dataset = intake_io.imload(sample)
if 'z' in dataset.dims:
dataset = dataset.max('z')
plt.figure(figsize=(7, 7))
io.imshow(dataset['image'].data)
```
### The following code quantifies all input images:
```
%%time
#################################
# Don't modify the code below #
#################################
def quantify(sample, input_dir, output_dir, channel_name):
dataset = intake_io.imload(sample)
img = np.array(dataset['image'].data)
df = pd.DataFrame(regionprops_table(label_image=np.ones_like(img),
intensity_image=img,
properties=['area', 'mean_intensity']))
df = df.rename(columns={'area': 'image volume pix', 'mean_intensity': rf'{channel_name} mean intensity per image'})
df[rf'{channel_name} integrated intensity per image'] = df[rf'{channel_name} mean intensity per image'] * df['image volume pix']
p_nm = re.compile(rf'([0-9]*\.?[0-9]+)nM')
p_um = re.compile(rf'([0-9]*\.?[0-9]+)uM')
fn = sample[len(input_dir)+1:]
conc_nM = 0
if len(p_nm.findall(fn)) > 0:
conc_nM = float(p_nm.findall(fn)[0])
if len(p_um.findall(fn)) > 0:
conc_nM = float(p_um.findall(fn)[0]) * 1000
df[rf'{channel_name} concentration nM'] = conc_nM
df['Image name'] = fn
fn_out = os.path.join(output_dir, fn.replace('.' + sample.split('.')[-1], '.csv'))
# save the stats
os.makedirs(os.path.dirname(fn_out), exist_ok=True)
df.to_csv(fn_out, index=False)
for sample in tqdm(samples):
quantify(sample, input_dir, output_dir, channel_name)
# combine the cell stats
print('Combining stats...')
combine_statistics(output_dir)
df = pd.read_csv(output_dir.rstrip('/') + '.csv')
df
```
### The following code plots intensity versus concentration for sanity check
```
#################################
# Don't modify the code below #
#################################
for col in [rf'{channel_name} concentration nM', rf'{channel_name} mean intensity per image', rf'{channel_name} integrated intensity per image']:
df['Log ' + col] = np.log10(df[col])
for col in [rf'{channel_name} mean intensity per image', rf'{channel_name} integrated intensity per image']:
plt.figure(figsize=(10, 6))
ax = sns.scatterplot(x = rf'{channel_name} concentration nM', y=col, data=df)
plt.figure(figsize=(10, 6))
ax = sns.scatterplot(x = rf'Log {channel_name} concentration nM', y='Log ' + col, data=df)
```
| github_jupyter |
# Circuit Quantum Electrodynamics
## Contents
1. [Introduction](#intro)
2. [The Schrieffer-Wolff Transformation](#tswt)
3. [Block-diagonalization of the Jaynes-Cummings Hamiltonian](#bdotjch)
4. [Full Transmon](#full-transmon)
5. [Qubit Drive with cQED](#qdwcqed)
6. [The Cross Resonance Entangling Gate](#tcreg)
## 1. Introduction <a id='intro'></a>
By analogy with Cavity Quantum Electrodynamics (CQED), circuit QED (cQED) exploits the fact that a simple model can be used to both describe the interaction of an atom with an optical cavity and a qubit with a microwave resonator. This model includes the number of photons in the cavity/resonator, the state of the atom/qubit, and the electric dipole interaction between the atom/qubit and cavity/resonator. As we saw in the last section, transmons are actually multi-level systems, but restricting ourselves to the ground $|0\rangle = |g\rangle$ and first excited $|1\rangle = |e\rangle$ states is possible because of the anharmonicity of the transmon. Therefore we can describe the transmon as a qubit desicribed by the Pauli spin matrices
$$
\sigma^x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \qquad
\sigma^y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \qquad
\sigma^z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \qquad
$$
that generate rotations the respective axes around the Bloch sphere. In that case, the simplest model to describe this interaction is the Jaynes-Cummings Hamiltonian in the rotating wave approximation,
$$
H_{\rm JC}^{\rm (RWA)}/\hbar = \omega_r a^\dagger a - \frac{1}{2} \omega_q \sigma_z + g(a^\dagger \sigma^- + a \sigma^+).
$$
where $\omega_r$ and $\omega_r$ are the frequencies of the resonator and "qubit", respectively, $a$ ($a^\dagger$) is the resonator photon annihilation (creation) operator, and $g$ is the electric dipole coupling (half the vacuum Rabi splitting). Note that we are now omitting the hats from the operators. Here, the first term corresponds to the number of photons in the resonator, the second term corresponds to the state of the qubit, and the third is the electric dipole interaction, where $\sigma^\pm = (1/2)(\sigma^x \mp i\sigma^y)$ is the qubit raising/lowering operator. (Note that the signs are inverted from those of *spin* raising/lowering operators, as discussed in the previous chapter).
This Hamiltonian can be solved exactly, and the solutions are hybrid qubit/resonator states where an excitation (either a photon in the resonator or excited state of the qubit) swaps between the two at a rate $g$ when they are on-resonance ($\omega_r = \omega_q$). For example, the $a^\dagger \sigma^-$ in the third term creates a photon in the resonator and lowers the qubit from $|1\rangle$ to $|0\rangle$, while the $a\sigma^+$ term destroys a photon in the resonators and excites the qubit from $|0\rangle$ to $|1\rangle$. While interesting, for our quantum computer we want to deal with qubits, and not these hybrid states. This means we want to move to a regimes where the resonator acts as a perturbation to the qubit (and vice-versa), so that their properties merely become "dressed" by the presence of the other. Using a type of perturbation theory, called the Schrieffer-Wolff (S-W) transformation, we can calculate the properties of the qubit and resonator in the regime we wish to operate. Here it should be noted that treating the transmon as a qubit is illustrative for pedagogical reasons, but the same techniques apply when you consider all the levels of the transmon. The higher levels of the transmon have profound effects and must be considered when designing and simulating them.
## 2. The Schrieffer-Wolff Transformation <a id='tswt'></a>
<details>
<summary>Schrödinger's Equation (Click here to expand)</summary>
Problems in quantum mechanics are often that of diagolizing a Hamiltonian eigenvalue equation
$$
H\psi_m = E_m \psi_m \qquad {\rm for} \quad 1 \le m \le n
$$
where the $\psi_m$ are the eigenstates with eigenvalue $E_m$. This consists of finding a unitary matrix $U$, such that $H' = U H U^\dagger$ is diagonal. Then the eigenvalue equation
$$
\hat{H} \psi_m = E_m \psi_m \Longrightarrow U H U^\dagger U \psi_m = E_m U \psi_m \Longrightarrow H' \psi_m' = E_m \psi_m'
$$
where $\psi_m' = U\psi_m$ are the transformed eigenstates and
$$
H' = \begin{pmatrix}
E_1 & 0 & \cdots & 0 \\
0 & E_2 & \cdots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \cdots & E_n \end{pmatrix}
$$
is the diagonalized Hamiltonian.
</details>
With the S-W transformation, instead of diagolizing the Hamiltonian, we seek to *block-diagonalize* it. Suppose we have a Hamiltonian that can be broken up into a diagonal part and perturbation
$$
H \quad = \quad \underbrace{\begin{pmatrix}
\Box & & & & & & \\
& \Box & & & & & \\
& & \Box & & & & \\
& & & \Box & & & \\
& & & & \Box & & \\
& & & & & \Box & \\
& & & & & & \Box \end{pmatrix}}_\text{diagonal} \quad + \quad
\underbrace{\begin{pmatrix}
\times & \times & \times & \times & \cdot & \cdot & \cdot \\
\times & \times & \times & \times & \cdot & \cdot & \cdot \\
\times & \times & \times & \times & \cdot & \cdot & \cdot \\
\times & \times & \times & \times & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot & \times & \times & \times \\
\cdot & \cdot & \cdot & \cdot & \times & \times & \times \\
\cdot & \cdot & \cdot & \cdot & \times & \times & \times \end{pmatrix}}_\text{perturbation}
$$
and then write the perturbation as $H_1 + H_2$ so that $H = H_0 + H_1 + H_2$, with $H_0$ diagonal, $H_1$ block-diagonal, and $H_2$ non-block diagonal, and we have
$$
H \quad = \quad \underbrace{\begin{pmatrix}
\Box & & & & & & \\
& \Box & & & & & \\
& & \Box & & & & \\
& & & \Box & & & \\
& & & & \Box & & \\
& & & & & \Box & \\
& & & & & & \Box \end{pmatrix}}_\text{diagonal}
\quad + \quad
\underbrace{\begin{pmatrix}
\times & \times & \times & \times & & & \\
\times & \times & \times & \times & & & \\
\times & \times & \times & \times & & & \\
\times & \times & \times & \times & & & \\
& & & & \times & \times & \times \\
& & & & \times & \times & \times \\
& & & & \times & \times & \times \end{pmatrix}}_\text{block diagonal}
\quad + \quad
\underbrace{\begin{pmatrix}
& & & & \cdot & \cdot & \cdot \\
& & & & \cdot & \cdot & \cdot \\
& & & & \cdot & \cdot & \cdot \\
& & & & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot & & & \\
\cdot & \cdot & \cdot & \cdot & & & \\
\cdot & \cdot & \cdot & \cdot & & & \end{pmatrix}}_\text{block off-diagonal}
$$
Block-diagonalizing $H$ consists of finding an operator $S$ such that
$$
H_{\rm eff} = e^{iS} H e^{-iS} = \sum_{m=0}^\infty \frac{1}{m!} [H, S]^{(m)} = \sum_{m=0}^\infty \lambda^m H^{(m)},
$$
where $H^{(m)}$ are successive approximations to $H$ (with $H^{(0)} = H_0$) and the generalized commutator is defined resursively as
$$
[H,S]^{(m)} = [[H,S]^{(m-1)},S] \qquad {\rm with} \qquad [H,S]^{(0)} = H.
$$
Here we treat $S$ as a Taylor series with
$$ S = \sum_{m=1}^\infty \lambda^m S^{(m)} $$
to keep track of the order $\lambda$. Then expanding the effective Hamiltonian as a perturbation of $H_1+H_2$ to second order in $\lambda$,
$$
H_{\rm eff} = H_0 + \lambda (H_1+H_2) + \left[H_0 + \lambda(H_1+H_2), \lambda S^{(1)}\right]
+ \frac{1}{2} \left[ \left[ H_0 + \lambda(H_1+H_2), \lambda S^{(1)}\right], \lambda S^{(1)}\right]
+ \left[H_0 + \lambda(H_1+H_2), \lambda^2 S^{(2)}\right] + \ldots \\
\approx H_0 + \lambda \left( H_1 + H_2 + \left[H_0, S^{(1)}\right] \right)
+ \lambda^2 \left( \left[H_1+H_2, S^{(1)}\right] + \frac{1}{2} \left[ \left[H_0, S^{(1)},\right] S^{(1)}\right] + \left[H_0, S^{(2)}\right]\right)
$$
Now we know $S$ must be block off-diagonal and anti-hermitian to force the block off-diagonal elements of $H_{\rm eff}$ to vanish, we must have that
$$
H_{\rm eff}^{\rm off-diag} = \sum_{m=0}^\infty \frac{1}{(2m+1)!} [\underbrace{H_0 + H_1}_\text{block diag}, S]^{(2m+1)} + \sum_{m=0}^\infty \frac{1}{(2m)!} [\underbrace{H_2}_\text{block off-diag}, S]^{(2m)} \equiv 0,
$$
noting that all the terms in the first series are block off-diagonal and all of those in the second series are block diagonal. This is because the commutator of a block diagonal and block off-diagonal matrix is block off-diagonal and the commutator of two block off-diagonal matrices is block diagonal. Expanding this to the generalized commutator, we can see that $[H^0 + H^1, S]^{(n)}$ with odd $n$ must always be block off-diagonal as well as $[H^2, S]^{(n)}$ with even $n$. Now expanding the off-diagonal part of the Hamiltonain to second order yields
$$
H_{\rm eff}^{\rm off-diag} = \left[ H_0 + \lambda H_1, \lambda S^{(1)} \right]+\lambda H_2 + \left[H_0 + \lambda H_1, \lambda^2 S^{(2)}\right]
+ \frac{1}{3!} \left[ H_0+\lambda H_1, \lambda S^{(1)}\right]^{(3)} + \frac{1}{2!} \left[ \lambda H_2, \lambda S^{(1)}\right]^{(2)} \\
= \lambda \left( \left[ H_0, S^{(1)} \right] + H_2 \right) + \lambda^2 \left( \left[H_1, S^{(1)} \right] + \left[H_0, S^{(2)}\right]\right) + \ldots.
$$
Since each order of $\lambda$ must be identically zero, the following equations determine $S^{(m)}$,
$$
[H_0, S^{(1)}] = -H_2 \qquad
[H_0, S^{(2)}] = -[H_1, S^{(1)}] \qquad
[H_0, S^{(3)}] = -[H_1, S^{(2)}] - \frac{1}{3} [[H_2, S^{(1)}], S^{(1)}],
$$
where our ansatz that satisfied these equations is guaranteed unique by Winkler's work. Then our effective Hamiltonian becomes
$$
H_{\rm eff} = H_0+H_1+[H_2,S^{(1)}] + \frac{1}{2} [[H_0, S^{(1)}], S^{(1)}] + \ldots = H_0+H_1+\frac{1}{2}[H_2,S^{(1)}] + \ldots
$$
where the effective Hamiltonian is calculated here to second order and we have taken $\lambda \to 1$.
## 3. Block-diagonalization of the Jaynes-Cummings Hamiltonian <a id='bdotjch'></a>
Using the S-W transformation consists of two problems: 1) finding the correct ansatz, and 2) performing the calculations. In most examples, an ansatz of similar form (i.e. anti-hermitian) to the off-diagonal parts is made and confirmed *a postori*. Recently, the manuscript [A Systematic Method for Schrieffer-Wolff Transformation and Its Generalizations](http://www.arxiv.org/abs/2004.06534) has appeared on the arXiv attesting to systematically providing the ansatz and applying it to numerous systems (including the Jaynes-Cumming Hamiltonian below).
As such, the *generator* $\eta$ is calculated as $\eta = [H_0, H_2]$. In keeping the scalar coefficients of $\eta$ undetermined, then $S^{(1)}$ can be calculated as the specific $\eta$ that satisfies $[H_0, \eta]=H_2$. Note the hermiticity of $H_0$ and $H_2$ guarantee the anti-hermiticity of $\eta$ and thus $S^{(1)}$.
For ease of tedious calculations, we will use the Python package [`sympy`](http://www.sympy.org) for symbolic mathematics.
```
# import SymPy and define symbols
import sympy as sp
sp.init_printing(use_unicode=True)
wr = sp.Symbol('\omega_r') # resonator frequency
wq = sp.Symbol('\omega_q') # qubit frequency
g = sp.Symbol('g', real=True) # vacuum Rabi coupling
Delta = sp.Symbol('Delta', real=True) # wr - wq; defined later
# import operator relations and define them
from sympy.physics.quantum.boson import BosonOp
a = BosonOp('a') # resonator photon annihilation operator
from sympy.physics.quantum import pauli, Dagger, Commutator
from sympy.physics.quantum.operatorordering import normal_ordered_form
# Pauli matrices
sx = pauli.SigmaX()
sy = pauli.SigmaY()
sz = pauli.SigmaZ()
# qubit raising and lowering operators
splus = pauli.SigmaPlus()
sminus = pauli.SigmaMinus()
# define J-C Hamiltonian in terms of diagonal and non-block diagonal terms
H0 = wr*Dagger(a)*a - (1/2)*wq*sz;
H2 = g*(Dagger(a)*sminus + a*splus);
HJC = H0 + H2; HJC # print
# using the above method for finding the ansatz
eta = Commutator(H0, H2); eta
```
As a note about `sympy`, we will need to used the methods `doit()`, `expand`, `normal_ordered_form`, and `qsimplify_pauli` to proceed with actually taking the commutator, expanding it into terms, normal ordering the bosonic modes (creation before annihilation), and simplify the Pauli algebra. Trying this with $\eta$ yields
```
pauli.qsimplify_pauli(normal_ordered_form(eta.doit().expand()))
```
Now take $A$ and $B$ as the coefficients of $a^\dagger \sigma_-$ and $a\sigma_+$, respectively. Then the commutator
```
A = sp.Symbol('A')
B = sp.Symbol('B')
eta = A * Dagger(a) * sminus - B * a * splus;
pauli.qsimplify_pauli(normal_ordered_form(Commutator(H0, eta).doit().expand()))
```
This expression should be equal to $H_2$
```
H2
```
which implies $A = B = g/\Delta$ where $\Delta = \omega_r - \omega_q$ is the frequency detuning between the resonator and qubit. Therefore our $S^{(1)}$ is determined to be
```
S1 = eta.subs(A, g/Delta)
S1 = S1.subs(B, g/Delta); S1.factor()
```
Then we can calculate the effective second order correction to $H_0$
```
Heff = H0 + 0.5*pauli.qsimplify_pauli(normal_ordered_form(Commutator(H2, S1).doit().expand())).simplify(); Heff
```
This is typically written as
$$
H_{\rm eff} = \left(\omega_r + \frac{g^2}{\Delta}\sigma_z\right)a^\dagger a - \frac{1}{2}\left(\omega_q -\frac{g^2}{\Delta}\right) \sigma_z
$$
which shows a state-dependent shift by $\chi \equiv g^2/\Delta$ of the resonator frequency called the *ac Stark shift* and a shift in qubit frequency due to quantum vacuum fluctuations called the *Lamb shift*.
## 4. Full Transmon <a id='full-transmon'></a>
Because we are using *transmons* instead of *qubits*, we need to be careful to take the higher-order energy terms into effect when designing and simulating devices. The full transmon Hamiltonian coupled to the readout resonators is
$$
H^{\rm tr} = \omega_r a^\dagger a + \sum_j \omega_j |j\rangle\langle j| + g\left(a^\dagger c + ac^\dagger \right),
$$
where now $c = \sum_j \sqrt{j+1}|j\rangle\langle j+1|$ is the transmon lowering operator. Similarly, taking the weakly interacting subsets $A$ as the even-numbered transmon modes and $B$ as the odd-numbered transmon modes. Using the ansatz
$$
S^{(1)} = \sum_j \alpha_j a^\dagger \sqrt{j+1}|j\rangle\langle j+1| - \alpha_j^* a \sqrt{j+1}|j+1\rangle\langle j|,
$$
one may proceed along a messier version of the Jaynes-Cummings Hamiltonian. With some effort one can show the second order effective Hamiltonian is
$$
H^{\rm tr}_{\rm eff} = \left( \omega_r + \sum_j \frac{g^2(\omega_r-\omega+\delta)}{(\omega_r-\omega-\delta j)(\omega_r - \omega - \delta(j-1))} |j\rangle\langle j| \right) a^\dagger a + \sum_j
\left[
j\omega + \frac{\delta}{2} (j-1)j + \frac{jg^2}{\omega-\omega_r+(j-1)\delta} \right]|j\rangle\langle j|.
$$
## 5. Qubit Drive with cQED <a id='qdwcqed'></a>
Following that of [Blais *et al* (2004)](https://arxiv.org/abs/cond-mat/0402216), we model the drive Hamiltonian as
$$
H^d(t) = \xi(t)\left( a^\dagger e^{-i\omega_d t} + ae^{i\omega_d t}\right).
$$
Following the treatment in the [Ph.D. dissertation of Lev Bishop](https://arxiv.org/abs/1007.3520), the drive acts on the qubit via the Glauber operator
$$
D(\alpha) = e^{\alpha(t) a^\dagger - \alpha^*(t) a}.
$$
Moving to the Jaynes-Cumming Hamiltonian rotating at the drive frequency,
$$
H = \Delta_r a^\dagger a - \frac{1}{2} \Delta_q \sigma^z + g(a^\dagger \sigma^- + a\sigma^+) + \xi(t)(a^\dagger + a)
$$
with $\Delta_r = \omega_r - \omega_d$ and $\Delta_q = \omega_q - \omega_d$. Applying Hadamard's Lemma to nested commutators,
$$
e^{A}BA^{-A} = B + [A,B] + \frac{1}{2!} [A,[A,B]] + \frac{1}{3!}[A,[A,[A,B]]] + \ldots
$$
we see that
$$
D^\dagger a^{(\dagger)} D = \exp\{-\alpha(t) a^\dagger + \alpha^*(t) a\} a^{(\dagger)}\exp\{\alpha(t) a^\dagger - \alpha^*(t) a\}
= a^{(\dagger)} + \left[-\alpha(t) a^\dagger + \alpha^*(t) a, a^{(\dagger)}\right] + \frac{1}{2!}\left[-\alpha(t) a^\dagger + \alpha^*(t) a, \left[-\alpha(t) a^\dagger + \alpha^*(t) a, a^{(\dagger)}\right]\right] + \ldots
= a^{(\dagger)} + \alpha^{(*)}
$$
and
$$
D^\dagger a^\dagger a D = a^\dagger a + \left[-\alpha(t) a^\dagger + \alpha^*(t) a, a^\dagger a\right] + \frac{1}{2!}\left[-\alpha(t) a^\dagger + \alpha^*(t) a, \left[-\alpha(t) a^\dagger + \alpha^*(t) a, a^\dagger a\right]\right] + \ldots
= a^\dagger a + \alpha(t)a^\dagger + \alpha^*(t)a + |\alpha(t)|^2
$$
So that we can transform the Hamiltonian
$$
\tilde{H} = D^\dagger H D - iD^\dagger \dot{D} = \Delta_r\left(a^\dagger a + \alpha(t)a^\dagger + \alpha^*(t)a + |\alpha(t)|^2\right) - \frac{1}{2} \Delta_q \sigma^z \\ + g\left((a^\dagger + \alpha^*(t))\sigma^- + (a+\alpha(t))\sigma^+\right) + \xi(t)\left(a^\dagger + \alpha^*(t) + a + \alpha(t) \right) - i\left(\dot{\alpha}(t) a^\dagger - \dot{\alpha}^*(t) a\right) \\
= \Delta_r a^\dagger a - \frac{1}{2}\Delta_q \sigma^z + g\left((a^\dagger + \alpha^*(t))\sigma^- + (a+\alpha(t))\sigma^+\right) \\
+\xi(t)\left(a^\dagger + a \right) + \Delta_r\left(\alpha(t)a^\dagger + \alpha^*(t)a\right)- i\left(\dot{\alpha}(t) a^\dagger - \dot{\alpha}^*(t) a\right)
$$
where the non-operator terms have been dropped. The last line can be set to zero if we choose
$$
-i\dot{\alpha}(t) + \Delta_r \alpha(t) + \xi(t) = 0,
$$
and finally introducting the Rabi frequency $\Omega(t) = 2g\alpha(t)$, we arrive at
$$
\tilde{H} = \Delta_r a^\dagger a - \frac{1}{2}\Delta_q \sigma^z + g\left(a^\dagger\sigma^- + a\sigma^+\right)
+\frac{1}{2} \left( \Omega^*(t)\sigma^- + \Omega(t) \sigma^+\right).
$$
Since the drive part of the Hamiltonian is block off-diagonal, we can perform a Schrieffer-Wolff transformation on it (for a real drive $\Omega^*(t) = \Omega(t)$) and add it to the effective Hamiltonian,
$$
[\tilde{H}^d, S^{(1)}] = -\frac{\Omega(t)}{2} \left[ (\sigma^- + \sigma^+),\frac{g}{\Delta}\left( a^\dagger \sigma^- - a\sigma^+\right)\right] = \frac{g\Omega(t)}{2\Delta}(a + a^\dagger)\sigma^z
$$
so the effective Hamiltonian becomes
$$
\tilde{H}_{\rm eff} = \left( \Delta_r + \frac{g^2}{\Delta}\sigma^z\right) a^\dagger a - \frac{1}{2}\left(\Delta_q - \frac{g^2}{\Delta}\right) \sigma^z + \frac{\Omega(t)}{2}\sigma^x
+ \frac{g\Omega(t)}{4\Delta}(a + a^\dagger)\sigma^z.
$$
Note here that to eliminate the $z$ rotations, one should drive at the Lamb-shifted qubit frequency. The additional $\sigma^z$ term is small because $\Delta \gg g$ in the dispersive regime.
## 6. The Cross Resonance Entangling Gate <a id='tcreg'></a>
Driving qubit one at the frequency of qubit two can be written as
$$
H^d(t) = \frac{\Omega(t)}{2} \left( \sigma_1^+ e^{-i\tilde{\omega}_2 t} + \sigma_1^- e^{i\tilde{\omega}_2 t}\right).
$$
Now, we need to apply Schrieffer-Wolff to the drive term to get the effective Hamiltonian, and then do the RWA at frequency $\tilde{\omega}_2$.
$$
[\tilde{H}^d, S^{(1)}] = -\frac{J\Omega(t)}{2\Delta_{12}} \left[ \sigma_1^+ e^{-i\tilde{\omega}_2 t} + \sigma_1^- e^{i\tilde{\omega}_2 t}, \sigma_1^+ \sigma_2^- - \sigma_2^+ \sigma_1^-\right]
=-\frac{J\Omega(t)}{2\Delta_{12}} \left(\sigma_1^z \sigma_2^+ e^{-i\tilde{\omega}_2 t}
+\sigma_1^z \sigma_2^- e^{i\tilde{\omega}_2 t} \right)
$$
Transforming back the the rotating frame at $\omega_2$, we get the effective qubit cross resonance Hamiltonian
$$
\tilde{H}_{\rm eff}^{\rm CR} = - \frac{\tilde{\omega}_1-\tilde{\omega}_2}{2}\sigma_1^z
+ \frac{\Omega(t)}{2} \left(\sigma_2^x - \frac{J}{2\Delta_{12}} \sigma_1^z \sigma_2^x \right).
$$
The first two terms involve the $ZI$ interaction due to a Stark shift on qubit 1 and an unconditional $IX$ rotation on qubit 2, but the final term represents the $ZX$-interaction that produces entanglement. By putting qubit 1 into a an equal superposition of $|0\rangle$ and $|1\rangle$ and applying the cross resonance gate for a duration corresponding to a $\pi/2$ rotation around the $x$-axis, a maximally entangled state is produced. Using Qiskit to characterize the two-qubit cross resonance Hamiltonian for transmons can be done with [this tutorial](https://github.com/Qiskit/qiskit-tutorials/blob/9405254b38312771f8d5c2dd6f451cec35307995/tutorials/noise/1_hamiltonian_and_gate_characterization.ipynb). Further reading on the cross resonance gate is found [here](https://arxiv.org/abs/1106.0553) and [here](https://arxiv.org/abs/1603.04821).
| github_jupyter |
[[source]](../api/alibi.explainers.anchor_tabular.rst)
# Anchors
## Overview
The anchor algorithm is based on the [Anchors: High-Precision Model-Agnostic Explanations](https://homes.cs.washington.edu/~marcotcr/aaai18.pdf) paper by Ribeiro et al. and builds on the open source [code](https://github.com/marcotcr/anchor) from the paper's first author.
The algorithm provides model-agnostic (*black box*) and human interpretable explanations suitable for classification models applied to images, text and tabular data. The idea behind anchors is to explain the behaviour of complex models with high-precision rules called *anchors*. These anchors are locally sufficient conditions to ensure a certain prediction with a high degree of confidence.
Anchors address a key shortcoming of local explanation methods like [LIME](https://arxiv.org/abs/1602.04938) which proxy the local behaviour of the model in a linear way. It is however unclear to what extent the explanation holds up in the region around the instance to be explained, since both the model and data can exhibit non-linear behaviour in the neighborhood of the instance. This approach can easily lead to overconfidence in the explanation and misleading conclusions on unseen but similar instances. The anchor algorithm tackles this issue by incorporating coverage, the region where the explanation applies, into the optimization problem. A simple example from sentiment classification illustrates this (Figure 1). Dependent on the sentence, the occurrence of the word *not* is interpreted as positive or negative for the sentiment by LIME. It is clear that the explanation using *not* is very local. Anchors however aim to maximize the coverage, and require *not* to occur together with *good* or *bad* to ensure respectively negative or positive sentiment.

Ribeiro et al., *Anchors: High-Precision Model-Agnostic Explanations*, 2018
As highlighted by the above example, an anchor explanation consists of *if-then rules*, called the anchors, which sufficiently guarantee the explanation locally and try to maximize the area for which the explanation holds. This means that as long as the anchor holds, the prediction should remain the same regardless of the values of the features not present in the anchor. Going back to the sentiment example: as long as *not good* is present, the sentiment is negative, regardless of the other words in the movie review.
### Text
For text classification, an interpretable anchor consists of the words that need to be present to ensure a prediction, regardless of the other words in the input. The words that are not present in a candidate anchor can be sampled in 3 ways:
* Replace word token by UNK token.
* Replace word token by sampled token from a corpus with the same POS tag and probability proportional to the similarity in the embedding space. By sampling similar words, we keep more context than simply using the UNK token.
* Replace word tokens with sampled tokens according to the masked language model probability distribution. The tokens can be sampled in parallel, independent of one another, or sequentially(autoregressive), conditioned on the previously generated tokens.
### Tabular Data
Anchors are also suitable for tabular data with both categorical and continuous features. The continuous features are discretized into quantiles (e.g. deciles), so they become more interpretable. The features in a candidate anchor are kept constant (same category or bin for discretized features) while we sample the other features from a training set. As a result, anchors for tabular data need access to training data. Let's illustrate this with an example. Say we want to predict whether a person makes less or more than £50,000 per year based on the person's characteristics including age (continuous variable) and marital status (categorical variable). The following would then be a potential anchor: Hugo makes more than £50,000 because he is married and his age is between 35 and 45 years.
### Images
Similar to LIME, images are first segmented into superpixels, maintaining local image structure. The interpretable representation then consists of the presence or absence of each superpixel in the anchor. It is crucial to generate meaningful superpixels in order to arrive at interpretable explanations. The algorithm supports a number of standard image segmentation algorithms ([felzenszwalb, slic and quickshift](https://scikit-image.org/docs/dev/auto_examples/segmentation/plot_segmentations.html#sphx-glr-auto-examples-segmentation-plot-segmentations-py)) and allows the user to provide a custom segmentation function.
The superpixels not present in a candidate anchor can be masked in 2 ways:
* Take the average value of that superpixel.
* Use the pixel values of a superimposed picture over the masked superpixels.

Ribeiro et al., *Anchors: High-Precision Model-Agnostic Explanations*, 2018
### Efficiently Computing Anchors
The anchor needs to return the same prediction as the original instance with a minimal confidence of e.g. 95%. If multiple candidate anchors satisfy this constraint, we go with the anchor that has the largest coverage. Because the number of potential anchors is exponential in the feature space, we need a faster approximate solution.
The anchors are constructed bottom-up in combination with [beam search](https://en.wikipedia.org/wiki/Beam_search). We start with an empty rule or anchor, and incrementally add an *if-then* rule in each iteration until the minimal confidence constraint is satisfied. If multiple valid anchors are found, the one with the largest coverage is returned.
In order to select the best candidate anchors for the beam width efficiently during each iteration, we formulate the problem as a [pure exploration multi-armed bandit](https://www.cse.iitb.ac.in/~shivaram/papers/kk_colt_2013.pdf) problem. This limits the number of model prediction calls which can be a computational bottleneck.
For more details, we refer the reader to the original [paper](https://homes.cs.washington.edu/~marcotcr/aaai18.pdf).
## Usage
While each data type has specific requirements to initialize the explainer and return explanations, the underlying algorithm to construct the anchors is the same.
In order to efficiently generate anchors, the following hyperparameters need to be set to sensible values when calling the `explain` method:
* `threshold`: the previously discussed minimal confidence level. `threshold` defines the minimum fraction of samples for a candidate anchor that need to lead to the same prediction as the original instance. A higher value gives more confidence in the anchor, but also leads to more computation time. The default value is 0.95.
* `tau`: determines when we assume convergence for the multi-armed bandit. A bigger value for `tau` means faster convergence but also looser anchor conditions. By default equal to 0.15.
* `beam_size`: the size of the beam width. A bigger beam width can lead to a better overall anchor at the expense of more computation time.
* `batch_size`: the batch size used for sampling. A bigger batch size gives more confidence in the anchor, again at the expense of computation time since it involves more model prediction calls. The default value is 100.
* `coverage_samples`: number of samples used to compute the coverage of the anchor. By default set to 10000.
### Text
#### Predictor
Since the explainer works on black-box models, only access to a predict function is needed. The model below is a simple logistic regression trained on movie reviews with negative or positive sentiment and pre-processed with a CountVectorizer:
```python
predict_fn = lambda x: clf.predict(vectorizer.transform(x))
```
#### Simple sampling strategies
`AnchorText` provides two simple sampling strategies: `unknown` and `similarity`. Randomly chosen words, except those in queried anchor, are replaced by the `UNK` token for the `unknown` strategy, and by similar words with the same part of speech of tag for the `similarity` strategy.
To perform text tokenization, pos-tagging, compute word similarity, etc., we use spaCy. The spaCy model can be loaded as follows:
```python
import spacy
from alibi.utils import spacy_model
model = 'en_core_web_md'
spacy_model(model=model)
nlp = spacy.load(model)
```
If we choose to replace words with the `UNK` token, we define the explainer as follows:
```python
explainer = AnchorText(predictor=predict_fn, sampling_strategy='unknown', nlp=nlp)
```
Likewise, if we choose to sample similar words from a corpus, we define the explainer as follows:
```python
explainer = AnchorText(predictor=predict_fn, sampling_strategy='similarity', nlp=nlp)
```
#### Language model
`AnchorText` provides the option to define the perturbation distribution through a `language_model` sampling strategy. In this case, randomly chosen words, except those in the queried anchor, are replaced by words sampled according to the language model's predictions. We provide support for three transformer based language models: `DistilbertBaseUncased`, `BertBaseUncased`, and `RobertaBase`.
A language model can be loaded as follows:
```python
language_model = DistilbertBaseUncased()
```
Then we can initialize the explainer as follows:
```python
explainer = AnchorText(predictor=predict_fn, sampling_strategy="language_model",
language_model=language_model)
```
#### Sampling parameters
Parameters specific to each sampling strategy can be passed to the constructor via `kwargs`. For example:
* If `sampling_strategy="unknown"` we can initialize the explainer as follows:
```python
explainer = AnchorText(
predictor=predict_fn,
sampling_strategy='unknown', # replace a word by UNK token
nlp=nlp, # spacy object
sample_proba=0.5, # probability of a word to be replaced by UNK token
)
```
* If `sampling_strategy="similarity"` we can initialize the explainer as follows:
```python
explainer = AnchorText(
predictor=predict_fn,
sampling_strategy='similarity', # replace a word by similar words
nlp=nlp, # spacy object
sample_proba=0.5, # probability of a word to be replaced by as similar word
use_proba=True, # sample according to the similarity distribution
top_n=20, # consider only top 20 most similar words
temperature=0.2 # higher temperature implies more randomness when sampling
)
```
* Or if `sampling_strategy="language_model"`, the explainer can be defined as:
```python
explainer = AnchorText(
predictor=predict_fn,
sampling_strategy="language_model", # use language model to predict the masked words
language_model=language_model, # language model to be used
filling="parallel", # just one pass through the transformer
sample_proba=0.5, # probability of masking and replacing a word according to the LM
frac_mask_templates=0.1, # fraction of masking templates
use_proba=True, # use words distribution when sampling (if false sample uniform)
top_n=50, # consider the fist 50 most likely words
temperature=0.2, # higher temperature implies more randomness when sampling
stopwords=['and', 'a', 'but'], # those words will not be masked/disturbed
punctuation=string.punctuation, # punctuation tokens contained here will not be masked/disturbed
sample_punctuation=False, # if False tokens included in `punctuation` will not be sampled
batch_size_lm=32 # batch size used for the language model
)
```
Words outside of the candidate anchor can be replaced by `UNK` token, similar words, or masked out and replaced by the most likely words according to language model prediction, with a probability equal to `sample_proba`. We can sample the *top n* most similar words or the *top n* most likely language model predictions by setting the `top_n` parameter. We can put more weight on similar or most likely words by decreasing the `temperature` argument. It is also possible to sample words from the corpus proportional to the word similarity with the ground truth word or according to the language model's conditional probability distribution by setting `use_proba` to `True`. Furthermore, we can avoid masking specific words by including them in the `stopwords` list.
Working with transformers can be computationally and memory-wise expensive. For `sampling_strategy="language_model"` we provide two methods to predict the masked words: `filling="parallel"` and `filling="autoregressive"`.
If `filling="parallel"`, we perform a single forward pass through the transformer. After obtaining the probability distribution of the masked words, each word is sampled independently of the others.
If `filling="autoregressive"`, we perform multiple forward passes through the transformer and generate the words one at a time. Thus, the masked words will be conditioned on the previous ones. **Note that this filling method is computationally expensive**.
To further decrease the explanation runtime, for `sampling_strategy="language_model", filling="parallel"`, we provide a secondary functionality through the `frac_mask_templates`. Behind the scenes, the anchor algorithm is constantly requesting samples to query the predictor. Thus, we need to generate what we call *mask templates*, which are sentences containing words outside the candidate anchors replaced by the `<MASK>` token. The `frac_mask_templates` controls the fraction of mask templates to be generated. For example, if we need to generate 100 samples and the `frac_mask_templates=0.1`, we will generate only 10 mask templates. Those 10 templates are then passed to the language model to predict the masked words. Having the distribution of each word in each mask template, we can generate 100 samples as requested. Note that instead of passing 100 masked sentences through the language model (which is expensive), we only pass 10 sentences. Although this can increase the speed considerably, it can also decrease the diversity of the samples. The maximum batch size used in a forward pass through the language model can be specified by setting `batch_size_lm`.
When `sampling_strategy="language_model"`, we can specify the `punctuation` considered by the sampling algorithm. Any token composed only from characters in the `punctuation` string, will not be perturbed (we call those *punctuation tokens*). Furthermore, we can decide whether to sample *punctuation tokens* by setting the `sample_punctuation` parameter. If `sample_punctuation=False`, then *punctuation tokens* will not be sampled.
#### Explanation
Let's define the instance we want to explain and verify that the sentiment prediction on the original instance is positive:
```python
text = 'This is a good book .'
class_names = ['negative', 'positive']
pred = class_names[predict_fn([text])[0]]
```
Now we can explain the instance:
```python
explanation = explainer.explain(text, threshold=0.95)
```
The `explain` method returns an `Explanation` object with the following attributes:
* *anchor*: a list of words in the anchor.
* *precision*: the fraction of times the sampled instances where the anchor holds yields the same prediction as the original instance. The precision will always be $\geq$ `threshold` for a valid anchor.
* *coverage*: the fraction of sampled instances the anchor applies to.
The *raw* attribute is a dictionary which also contains example instances where the anchor holds and the prediction is the same as on the original instance, as well as examples where the anchor holds but the prediction changed to give the user a sense of where the anchor fails. *raw* also stores information on the *anchor*, *precision* and *coverage* of partial anchors. This allows the user to track the improvement in for instance the *precision* as more features (words in the case of text) are added to the anchor.
### Tabular Data
#### Initialization and fit
To initialize the explainer, we provide a predict function, a list with the feature names to make the anchors easy to understand as well as an optional mapping from the encoded categorical features to a description of the category. An example for `categorical_names` would be
```python
category_map = {0: ["married", "divorced"], 3: ["high school diploma", "master's degree"]}
```
Each key in *category_map* refers to the column index in the input for the relevant categorical variable, while the values are lists with the options for each categorical variable. To make it easy, we provide a utility function `gen_category_map` to generate this map automatically from a Pandas dataframe:
```python
from alibi.utils import gen_category_map
category_map = gen_category_map(df)
```
Then initialize the explainer:
```python
predict_fn = lambda x: clf.predict(preprocessor.transform(x))
explainer = AnchorTabular(predict_fn, feature_names, categorical_names=category_map)
```
The implementation supports one-hot encoding representation of the cateforical features by setting `ohe=True`. The `feature_names` and `categorical_names(category_map)` remain unchanged. The prediction function `predict_fn` should expect as input datapoints with one-hot encoded categorical features. To initialize the explainer with the one-hot encoding support:
```python
explainer = AnchorTabular(predict_fn, feature_names, categorical_names=category_map, ohe=True)
```
Tabular data requires a fit step to map the ordinal features into quantiles and therefore needs access to a representative set of the training data. `disc_perc` is a list with percentiles used for binning:
```python
explainer.fit(X_train, disc_perc=[25, 50, 75])
```
Note that if one-hot encoding support is enabled (`ohe=True`), the `fit` calls expect the data to be one-hot encoded.
#### Explanation
Let's check the prediction of the model on the original instance and explain:
```python
class_names = ['<=50K', '>50K']
pred = class_names[explainer.predict_fn(X)[0]]
explanation = explainer.explain(X, threshold=0.95)
```
The returned `Explanation` object contains the same attributes as the text explainer, so you could explain a prediction as follows:
```
Prediction: <=50K
Anchor: Marital Status = Never-Married AND Relationship = Own-child
Precision: 1.00
Coverage: 0.13
```
Note that if one-hot encoding support is enabled (`ohe=True`), the `explain` calls expect the data to be one-hot encode.
### Images
#### Initialization
Besides the predict function, we also need to specify either a built in or custom superpixel segmentation function. The built in methods are [felzenszwalb](https://scikit-image.org/docs/dev/api/skimage.segmentation.html#skimage.segmentation.felzenszwalb), [slic](https://scikit-image.org/docs/dev/api/skimage.segmentation.html#skimage.segmentation.slic) and [quickshift](https://scikit-image.org/docs/dev/api/skimage.segmentation.html#skimage.segmentation.quickshift). It is important to create sensible superpixels in order to speed up convergence and generate interpretable explanations. Tuning the hyperparameters of the segmentation method is recommended.
```python
explainer = AnchorImage(predict_fn, image_shape, segmentation_fn='slic',
segmentation_kwargs={'n_segments': 15, 'compactness': 20, 'sigma': .5},
images_background=None)
```
Example of superpixels generated for the Persian cat picture using the *slic* method:


The following function would be an example of a custom segmentation function dividing the image into rectangles.
```python
def superpixel(image, size=(4, 7)):
segments = np.zeros([image.shape[0], image.shape[1]])
row_idx, col_idx = np.where(segments == 0)
for i, j in zip(row_idx, col_idx):
segments[i, j] = int((image.shape[1]/size[1]) * (i//size[0]) + j//size[1])
return segments
```
The `images_background` parameter allows the user to provide images used to superimpose on the masked superpixels, not present in the candidate anchor, instead of taking the average value of the masked superpixel. The superimposed images need to have the same shape as the explained instance.
#### Explanation
We can then explain the instance in the usual way:
```python
explanation = explainer.explain(image, p_sample=.5)
```
`p_sample` determines the fraction of superpixels that are either changed to the average superpixel value or that are superimposed.
The `Explanation` object again contains information about the anchor's *precision*, *coverage* and examples where the anchor does or does not hold. On top of that, it also contains a masked image with only the anchor superpixels visible under the *anchor* attribute (see image below) as well as the image's superpixels under *segments*.

## Examples
### Image
[Anchor explanations for ImageNet](../examples/anchor_image_imagenet.ipynb)
[Anchor explanations for fashion MNIST](../examples/anchor_image_fashion_mnist.ipynb)
### Tabular Data
[Anchor explanations on the Iris dataset](../examples/anchor_tabular_iris.ipynb)
[Anchor explanations for income prediction](../examples/anchor_tabular_adult.ipynb)
### Text
[Anchor explanations for movie sentiment](../examples/anchor_text_movie.ipynb)
| github_jupyter |
```
import torch
import torch.nn.functional as F
from torch.autograd import Variable
from sklearn.metrics import accuracy_score
import numpy as np
from torch.utils.tensorboard import SummaryWriter
from tqdm.notebook import tqdm
torch.manual_seed(824)
np.random.seed(824)
np.set_printoptions(threshold=np.inf)
# build train set
mul1, sigma1 = [1, 0], [[1, 0.75], [0.75, 1]]
mul2, sigma2 = [0, 1], [[1, 0.75], [0.75, 1]]
train_size = 500
test_size = 250
train1 = np.random.multivariate_normal(mean=mul1, cov=sigma1, size=train_size)
train1_label = np.zeros((train_size, 1))
train2 = np.random.multivariate_normal(mean=mul2, cov=sigma2, size=train_size)
train2_label = np.ones((train_size, 1))
X_train = np.vstack([train1, train2])
y_train = np.vstack([train1_label, train2_label])
print("Train set samples: \n",X_train[:5], X_train[-5:])
print("Train set labels: \n", y_train[:5], y_train[-5:])
test1 = np.random.multivariate_normal(mean=mul1, cov=sigma1, size=test_size)
test1_label = np.zeros((test_size, 1))
test2 = np.random.multivariate_normal(mean=mul2, cov=sigma2, size=test_size)
test2_label = np.ones((test_size, 1))
X_test = np.vstack([test1, test2])
y_test = np.vstack([test1_label, test2_label])
print("Test set samples: \n", X_test[:5], X_test[-5:])
print("Test set labels: \n", y_test[:5], y_test[-5:])
num_epochs = 100000
learning_rates = [1, 0.1, 0.01, 0.001]
class LogisticReg(torch.nn.Module):
def __init__(self):
super(LogisticReg, self).__init__()
self.fc = torch.nn.Linear(2, 1)
def forward(self, x):
x = self.fc(x)
return F.sigmoid(x)
class NormDataset(torch.utils.data.Dataset):
def __init__(self, x, y):
self.len = x.shape[0]
self.device = 'cuda'if torch.cuda.is_available() else 'cpu'
self.x_data = torch.as_tensor(x, device=self.device, dtype=torch.float)
self.y_data = torch.as_tensor(y, device=self.device, dtype=torch.float)
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
loss_func = torch.nn.BCELoss()
train_set, test_set = NormDataset(X_train, y_train), NormDataset(X_test, y_test)
train_loader = torch.utils.data.DataLoader(dataset=train_set, batch_size=32, shuffle=False)
X_test_tsr, y_test_tsr = Variable(torch.from_numpy(X_test).float(), requires_grad=False), Variable(torch.from_numpy(y_test).float(), requires_grad=False)
writer = SummaryWriter()
for lr in learning_rates:
model = LogisticReg()
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
prev_norm, norms, cnt = torch.tensor(0), torch.tensor(0), 0
print("Parameters before training:")
for name, param in model.named_parameters():
if param.requires_grad:
print(name, param.data)
for epoch in tqdm(range(num_epochs)):
early_stop = False
for i, data in enumerate(train_loader):
X_train_tsr, y_train_tsr = data
y_pred = model(X_train_tsr)
loss = loss_func(y_pred, y_train_tsr)
optimizer.zero_grad()
loss.backward()
optimizer.step()
norms = torch.norm(model.fc.weight.grad)+torch.norm(model.fc.bias.grad)
if prev_norm.data==norms.data and cnt<10:
cnt += 1
if cnt==10:
print('Early stopping at {} epoch when norms={}'.format(epoch, norms.data))
break
writer.add_scalar('Loss/lr='+str(lr), loss, epoch)
writer.add_scalar('GradNorm/lr='+str(lr), norms, epoch)
prev_norm = norms
test_pred = model.forward(X_test_tsr).data.numpy()
test_pred = np.where(test_pred>0.5, 1., 0.)
acc = accuracy_score(test_pred, y_test_tsr.data.numpy())
print("\nParameters after training:")
for name, param in model.named_parameters():
if param.requires_grad:
print(name, param.data)
print('\nWhen lr={}, the accuracy is {}'.format(lr, acc))
print('------'*10)
train_set, test_set = NormDataset(X_train, y_train), NormDataset(X_test, y_test)
train_loader = torch.utils.data.DataLoader(dataset=train_set, batch_size=1, shuffle=False)
X_test_tsr, y_test_tsr = Variable(torch.from_numpy(X_test).float(), requires_grad=False), Variable(torch.from_numpy(y_test).float(), requires_grad=False)
writer = SummaryWriter()
for lr in learning_rates:
model = LogisticReg()
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
prev_norm, norms, cnt = torch.tensor(0), torch.tensor(0), 0
print("Parameters before training:")
for name, param in model.named_parameters():
if param.requires_grad:
print(name, param.data)
for epoch in tqdm(range(num_epochs)):
early_stop = False
for i, data in enumerate(train_loader):
X_train_tsr, y_train_tsr = data
y_pred = model(X_train_tsr)
loss = loss_func(y_pred, y_train_tsr)
optimizer.zero_grad()
loss.backward()
optimizer.step()
norms = torch.norm(model.fc.weight.grad)+torch.norm(model.fc.bias.grad)
if prev_norm.data==norms.data and cnt<10:
cnt += 1
if cnt==10:
print('Early stopping at {} epoch when norms={}'.format(epoch, norms.data))
break
writer.add_scalar('Loss/lr='+str(lr), loss, epoch)
writer.add_scalar('GradNorm/lr='+str(lr), norms, epoch)
prev_norm = norms
test_pred = model.forward(X_test_tsr).data.numpy()
test_pred = np.where(test_pred>0.5, 1., 0.)
acc = accuracy_score(test_pred, y_test_tsr.data.numpy())
print("\nParameters after training:")
for name, param in model.named_parameters():
if param.requires_grad:
print(name, param.data)
print('\nWhen lr={}, the accuracy is {}'.format(lr, acc))
print('------'*10)
import matplotlib.pyplot as plt
# Visualizations
def plot_decision_boundary(X, y):
# Set min and max values and give it some padding
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
test_grid = np.c_[xx.ravel(), yy.ravel()]
test_grid_tsr = torch.from_numpy(test_grid).type(torch.FloatTensor)
Z = model(test_grid_tsr)
Z = np.where(Z>0.5, 1., 0.)
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(test1[:, 0], test1[:, 1], label='$\mu_1, \sigma_1$')
plt.scatter(test2[:, 0], test2[:, 1], label='$\mu_2, \sigma_2$')
plt.legend()
plot_decision_boundary(X_test, y_test)
```
| github_jupyter |
# Tutorial sobre Scala
## Declaraciones
### Declaración de variables
Existen dos categorias de variables: inmutables y mutables. Las variables mutables son aquellas en las que es posible modificar el contenido de la variable. Las variables inmutables son aquellas en las que no es posible alterar el contenido de las variables, se recomienda el uso de esta ultima. La declaración del tipo de la variable es opcional, Scala es capaz de inferir el tipo del dato.
```
//Variable inmutable
val a:Int=1
//variable mutable
var b:Int=2
```
### Tipos de datos
Siempre que se infiere un tipo en Scala, el tipo escogido será siempre el mas bajo posible en la jerarquía.
Algunos tipos especiales:
- **Any**: Es la clase de la que heredan todas las clases en Scala. Es la clase mas basica.
- **AnyVal**: Es la clase padre de todas las clases que representan tipos primitivos.
- **AnyRef**: Es la clase padre de todas las clases que no representan tipos primitivos. Todas las subclases de Scala y Java heredan de ella.
- **ScalaObject**: Es la clase de la que heredan todas y solo las clases de Scala.
- **Unit**: Equivale a `void`. Usar cuando una función no debe retornar ningún valor.
- **Nothing**: Es la clase que hereda de todas las clases. Usar solo cuando no acaba la ejecución como en `While(true)`.
### Declaración de funciones
```
def funcion1(a:Int,b:Int):Int={
return a+b
}
def funcion2(a:Int,b:Int)={
a+b
}
def funcion3(a:Int,b:Int)=a+b
```
Al igual que con la declaración de variables no es obligatorio declarar el tipo devuelto por la función. Si no se declara una sentencia `return`, el valor de la ultima instrucción es el devuelto por la función.
### Interpolación de cadenas
La interpolación de cadenas consiste insertar el valor de una variable dentro de una cadena, tambien es posible usar expresiones.
```
val valor=1
val expresion=2
println(s"El valor de la variable ${valor} y la expresion vale ${expresion+1}")
```
## Estructuras de selección
### If/Else
```
//Funciona igual que en Java
val verdad:Boolean=true;
if (verdad){
println("Hola")
}else{
println("Adios")
}
```
En Scala no existe la estructura `switch`, en su lugar existe lo conocido como *pattern matching*
### Match
```
val numero:Int=3
val nombre=numero match{ //Puede ir dentro de la llamada a una funcion
case 1=> "Uno"
case 2=> "Dos"
case 3=> "Tres"
case _=> "Ninguno" //Es obligatorio incluir una clausula con _ que se ejecuta cuando no hay coincidencia
}
println(nombre)
```
## Estructuras de repetición
### Bucle *While*
```
//Igual que en Java
var x=0
while(x<5){
print(x)
x+=1
}
```
### Bucle *Do While*
```
//Igual que en Java
var x=0
do{
print(x)
x+=1
}while(x<5)
```
### Bucle *For*
```
println("For to")
for(i<- 1 to 5){ //Hasta el limite inclusive
print(i)
}
println("\nFor until")
for(i<- 1 until 5){ //Hasta el limite exclusive
print(i)
}
println("\nFor para colecciones")
for(i <- List(1,2,3,4)){ //For para recorrer colecciones
print(i)
}
```
### *foreach*
```
val lista=List(1,2,3,4)
lista.foreach(x=> print(x)) //La funcion no devuelve nada y no modifica el conjunto
```
## Clases
### Indicaciones previas
Se deben declarar entre parentesis todos los atributos que vaya a usar la clase. Se pueden declarar otros constructores mediante la definición de this, pero siempre se debe llamar al constructor por defecto que es el que contiene todos los atributos.
Los parametros de un constructor constituyen los atributos de la clase y son privados por defecto, si se desea que sean públicos, se debe agregar val (o var) en la declaracion del argumento. Tambien es posible declarar atributos dentro de la propia clase. Estos pueden llevar los modificadores de `public`, `private` o `readonly`.
### Constructor por defecto
```
//Declaracion de clases
class Saludo(mensaje: String) { //Estos son los atributos y son accesibles desde cualquier metodo de la clase
def diHola(nombre:String):Unit ={
println(mensaje+" "+nombre);
}
}
val saludo = new Saludo("Hola")
saludo.diHola("Pepe")
```
### Constructor propio
```
class OtroSaludo(m:String,nombre:String){ //Se deben declarar todos los atributos que se vayan a usar
def this()={
this("Hola","Pepe") //Siempre se debe llamar al constructor por defecto
}
def this(mensaje:String){
this("Hola","Jose")
}
def saludar()={
println(this.m+" "+nombre)
}
}
val sal=new OtroSaludo()
sal.saludar()
```
### Herencia
```
class Punto(var x:Int,var y:Int){
def mover(dx:Int,dy:Int):Unit={
this.x=dx
this.y=dy
}
}
class Particula(x:Int,y:Int,masa:Int) extends Punto(x:Int,y:Int){
override def toString():String={ //Para redefinir un metodo de una clase padre agregar override
return s"X:${this.x} Y:${this.y} M:${this.masa}";
}
}
val particula=new Particula(0,0,0);
particula.mover(1,1)
println(particula.toString())
```
### Clases abstractas
```
abstract class Figura(lado:Int){
def getPerimetro():Double; //Metodo sin implementacion
def printLado():Unit= println("El lado mide "+this.lado) //Metodo implementado
}
class Cuadrado(lado:Int,n:Int) extends Figura(lado:Int){
override def getPerimetro():Double={
return lado*lado;
}
}
val figura:Figura=new Cuadrado(4,0)
println("El perimetro es "+figura.getPerimetro())
figura.printLado();
```
## Traits
Son similares a las interfaces de otros lenguajes de programación. Sin embargo cuenta con dos principales diferencias respecto de las interfaces:
- Pueden ser parcialmente implementadas como ocurre en las clases abstractas.
- No pueden tener parametros en el constructor.
```
trait Correo{
def enviar():Unit;
def recibir(mensaje:String):Unit={
println(s"Mensaje recibido: ${mensaje}")
}
}
class CorreoPostal() extends Correo{
override def enviar()={
println("Enviado desde correo postal")
}
}
class CorreoElectronico(usuario:String) extends Correo{
override def enviar()={
println(s"Enviado por ${usuario}")
}
}
val carta:Correo=new CorreoPostal()
val email:Correo=new CorreoElectronico("pepe")
carta.enviar()
carta.recibir("Hola desde carta")
email.enviar()
email.recibir("Hola desde email")
```
## Colecciones
Las colecciones por defecto incluidas son inmutables, no se puede agregar ni eliminar elementos. Las operaciones como *add* y similares lo que hacen es devolver una nueva colección con los nuevos elementos. Al crear la nueva colección se agregan las referencias de los objetos y por tanto casi no tiene penalización en tiempo de ejecución y en consumo de memoria.
```
val lista=List(1,2,3) //Lista inmutable
0::lista //Devuelve una lista con el nuevo elemento insertado al principio
lista.head //Devuelve el primer elemento de la lista
lista.tail //Devuelve toda la lista excepto el primer elemento
lista:::lista //Concatena dos listas y devuelve el resultado
```
### Operaciones y funciones sobre conjuntos (y similares)
```
val conjunto=Set(1,2,3)
val conjunto2=conjunto.map(x => x+3) //Ejecuta la funcion que se le pasa a cada miembro de la coleccion
val conjunto3=List(conjunto,conjunto2).flatten //Crea una nueva coleccion con los elementos de las sub-colecciones
Set(1,4,9).flatMap { x => Set(x,x+1) } //FlatMap
val lista=(List(1,2,3)++List(1,2,3))
lista.distinct //Devuelve una lista con todos los elementos distintos
Set(1,2,3)(1) //Devuelve true si el elemento esta contenido en la coleccion, false en caso contrario
List(4,5,6)(1) //Devuelve el elemento de la posicion indicada
val conjuntoImpares=conjunto.filter(x => x%2!=0) //Devuelve otro conjunto con los elementos que superen el filtro
val escalar:Int=1
//Para conjuntos inmutables
conjunto+escalar //Agrega el elemento al conjunto y devuelve una copia
conjunto++conjunto2 //Union de conjuntos
conjunto-escalar //Extrae del conjunto
conjunto--conjunto2 //Diferencia de conjuntos
conjunto&conjunto2 //Interseccion
//Solo para conjuntos mutables
val conjuntoMutable=scala.collection.mutable.Set(1,2,3)
val conjuntoMutable2=scala.collection.mutable.Set(3,4,5)
conjuntoMutable+= escalar //Agrega el valor al conjunto
conjuntoMutable++=conjuntoMutable2 //Agrega los elementos del segundo conjunto al primero
conjuntoMutable retain { x=> x%2==0} //Se queda solo con los elementos que cumplan la condicion
```
## Mapas
Son estructuras clave/valor similares a los Mapas de Java o los diccionarios de Python.
```
val mapa=Map(1->"Uno",2->"Dos",3->"Tres")
```
| github_jupyter |
# Colab FAQ
For some basic overview and features offered in Colab notebooks, check out: [Overview of Colaboratory Features](https://colab.research.google.com/notebooks/basic_features_overview.ipynb)
You need to use the colab GPU for this assignmentby selecting:
> **Runtime** → **Change runtime type** → **Hardware Accelerator: GPU**
# Setup PyTorch
All files are stored at /content/csc421/a4/ folder
```
######################################################################
# Setup python environment and change the current working directory
######################################################################
!pip install torch torchvision
!pip install imageio
!pip install matplotlib
%mkdir -p /content/csc413/a4/
%cd /content/csc413/a4
```
# Helper code
## Utility functions
```
import os
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.nn import Parameter
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision import transforms
from six.moves.urllib.request import urlretrieve
import tarfile
import imageio
from urllib.error import URLError
from urllib.error import HTTPError
def get_file(fname,
origin,
untar=False,
extract=False,
archive_format='auto',
cache_dir='data'):
datadir = os.path.join(cache_dir)
if not os.path.exists(datadir):
os.makedirs(datadir)
if untar:
untar_fpath = os.path.join(datadir, fname)
fpath = untar_fpath + '.tar.gz'
else:
fpath = os.path.join(datadir, fname)
print(fpath)
if not os.path.exists(fpath):
print('Downloading data from', origin)
error_msg = 'URL fetch failure on {}: {} -- {}'
try:
try:
urlretrieve(origin, fpath)
except URLError as e:
raise Exception(error_msg.format(origin, e.errno, e.reason))
except HTTPError as e:
raise Exception(error_msg.format(origin, e.code, e.msg))
except (Exception, KeyboardInterrupt) as e:
if os.path.exists(fpath):
os.remove(fpath)
raise
if untar:
if not os.path.exists(untar_fpath):
print('Extracting file.')
with tarfile.open(fpath) as archive:
archive.extractall(datadir)
return untar_fpath
return fpath
class AttrDict(dict):
def __init__(self, *args, **kwargs):
super(AttrDict, self).__init__(*args, **kwargs)
self.__dict__ = self
def to_var(tensor, cuda=True):
"""Wraps a Tensor in a Variable, optionally placing it on the GPU.
Arguments:
tensor: A Tensor object.
cuda: A boolean flag indicating whether to use the GPU.
Returns:
A Variable object, on the GPU if cuda==True.
"""
if cuda:
return Variable(tensor.cuda())
else:
return Variable(tensor)
def to_data(x):
"""Converts variable to numpy."""
if torch.cuda.is_available():
x = x.cpu()
return x.data.numpy()
def create_dir(directory):
"""Creates a directory if it doesn't already exist.
"""
if not os.path.exists(directory):
os.makedirs(directory)
def gan_checkpoint(iteration, G, D, opts):
"""Saves the parameters of the generator G and discriminator D.
"""
G_path = os.path.join(opts.checkpoint_dir, 'G.pkl')
D_path = os.path.join(opts.checkpoint_dir, 'D.pkl')
torch.save(G.state_dict(), G_path)
torch.save(D.state_dict(), D_path)
def load_checkpoint(opts):
"""Loads the generator and discriminator models from checkpoints.
"""
G_path = os.path.join(opts.load, 'G.pkl')
D_path = os.path.join(opts.load, 'D_.pkl')
G = DCGenerator(noise_size=opts.noise_size, conv_dim=opts.g_conv_dim, spectral_norm=opts.spectral_norm)
D = DCDiscriminator(conv_dim=opts.d_conv_dim)
G.load_state_dict(torch.load(G_path, map_location=lambda storage, loc: storage))
D.load_state_dict(torch.load(D_path, map_location=lambda storage, loc: storage))
if torch.cuda.is_available():
G.cuda()
D.cuda()
print('Models moved to GPU.')
return G, D
def merge_images(sources, targets, opts):
"""Creates a grid consisting of pairs of columns, where the first column in
each pair contains images source images and the second column in each pair
contains images generated by the CycleGAN from the corresponding images in
the first column.
"""
_, _, h, w = sources.shape
row = int(np.sqrt(opts.batch_size))
merged = np.zeros([3, row * h, row * w * 2])
for (idx, s, t) in (zip(range(row ** 2), sources, targets, )):
i = idx // row
j = idx % row
merged[:, i * h:(i + 1) * h, (j * 2) * h:(j * 2 + 1) * h] = s
merged[:, i * h:(i + 1) * h, (j * 2 + 1) * h:(j * 2 + 2) * h] = t
return merged.transpose(1, 2, 0)
def generate_gif(directory_path, keyword=None):
images = []
for filename in sorted(os.listdir(directory_path)):
if filename.endswith(".png") and (keyword is None or keyword in filename):
img_path = os.path.join(directory_path, filename)
print("adding image {}".format(img_path))
images.append(imageio.imread(img_path))
if keyword:
imageio.mimsave(
os.path.join(directory_path, 'anim_{}.gif'.format(keyword)), images)
else:
imageio.mimsave(os.path.join(directory_path, 'anim.gif'), images)
def create_image_grid(array, ncols=None):
"""
"""
num_images, channels, cell_h, cell_w = array.shape
if not ncols:
ncols = int(np.sqrt(num_images))
nrows = int(np.math.floor(num_images / float(ncols)))
result = np.zeros((cell_h * nrows, cell_w * ncols, channels), dtype=array.dtype)
for i in range(0, nrows):
for j in range(0, ncols):
result[i * cell_h:(i + 1) * cell_h, j * cell_w:(j + 1) * cell_w, :] = array[i * ncols + j].transpose(1, 2,
0)
if channels == 1:
result = result.squeeze()
return result
def gan_save_samples(G, fixed_noise, iteration, opts):
generated_images = G(fixed_noise)
generated_images = to_data(generated_images)
grid = create_image_grid(generated_images)
# merged = merge_images(X, fake_Y, opts)
path = os.path.join(opts.sample_dir, 'sample-{:06d}.png'.format(iteration))
imageio.imwrite(path, grid)
print('Saved {}'.format(path))
```
## Data loader
```
def get_emoji_loader(emoji_type, opts):
"""Creates training and test data loaders.
"""
transform = transforms.Compose([
transforms.Scale(opts.image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
train_path = os.path.join('data/emojis', emoji_type)
test_path = os.path.join('data/emojis', 'Test_{}'.format(emoji_type))
train_dataset = datasets.ImageFolder(train_path, transform)
test_dataset = datasets.ImageFolder(test_path, transform)
train_dloader = DataLoader(dataset=train_dataset, batch_size=opts.batch_size, shuffle=True, num_workers=opts.num_workers)
test_dloader = DataLoader(dataset=test_dataset, batch_size=opts.batch_size, shuffle=False, num_workers=opts.num_workers)
return train_dloader, test_dloader
```
## Training and evaluation code
```
def print_models(G_XtoY, G_YtoX, D_X, D_Y):
"""Prints model information for the generators and discriminators.
"""
print(" G ")
print("---------------------------------------")
print(G_XtoY)
print("---------------------------------------")
print(" D ")
print("---------------------------------------")
print(D_X)
print("---------------------------------------")
def create_model(opts):
"""Builds the generators and discriminators.
"""
### GAN
G = DCGenerator(noise_size=opts.noise_size, conv_dim=opts.g_conv_dim, spectral_norm=opts.spectral_norm)
D = DCDiscriminator(conv_dim=opts.d_conv_dim, spectral_norm=opts.spectral_norm)
print_models(G, None, D, None)
if torch.cuda.is_available():
G.cuda()
D.cuda()
print('Models moved to GPU.')
return G, D
def train(opts):
"""Loads the data, creates checkpoint and sample directories, and starts the training loop.
"""
# Create train and test dataloaders for images from the two domains X and Y
dataloader_X, test_dataloader_X = get_emoji_loader(emoji_type=opts.X, opts=opts)
# Create checkpoint and sample directories
create_dir(opts.checkpoint_dir)
create_dir(opts.sample_dir)
# Start training
if opts.least_squares_gan:
G, D = gan_training_loop_leastsquares(dataloader_X, test_dataloader_X, opts)
else:
G, D = gan_training_loop_regular(dataloader_X, test_dataloader_X, opts)
return G, D
def print_opts(opts):
"""Prints the values of all command-line arguments.
"""
print('=' * 80)
print('Opts'.center(80))
print('-' * 80)
for key in opts.__dict__:
if opts.__dict__[key]:
print('{:>30}: {:<30}'.format(key, opts.__dict__[key]).center(80))
print('=' * 80)
```
# Your code for generators and discriminators
## Helper modules
```
def sample_noise(batch_size, dim):
"""
Generate a PyTorch Tensor of uniform random noise.
Input:
- batch_size: Integer giving the batch size of noise to generate.
- dim: Integer giving the dimension of noise to generate.
Output:
- A PyTorch Tensor of shape (batch_size, dim, 1, 1) containing uniform
random noise in the range (-1, 1).
"""
return to_var(torch.rand(batch_size, dim) * 2 - 1).unsqueeze(2).unsqueeze(3)
def upconv(in_channels, out_channels, kernel_size, stride=2, padding=2, batch_norm=True, spectral_norm=False):
"""Creates a upsample-and-convolution layer, with optional batch normalization.
"""
layers = []
if stride>1:
layers.append(nn.Upsample(scale_factor=stride))
conv_layer = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=1, padding=padding, bias=False)
if spectral_norm:
layers.append(SpectralNorm(conv_layer))
else:
layers.append(conv_layer)
if batch_norm:
layers.append(nn.BatchNorm2d(out_channels))
return nn.Sequential(*layers)
def conv(in_channels, out_channels, kernel_size, stride=2, padding=2, batch_norm=True, init_zero_weights=False, spectral_norm=False):
"""Creates a convolutional layer, with optional batch normalization.
"""
layers = []
conv_layer = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride, padding=padding, bias=False)
if init_zero_weights:
conv_layer.weight.data = torch.randn(out_channels, in_channels, kernel_size, kernel_size) * 0.001
if spectral_norm:
layers.append(SpectralNorm(conv_layer))
else:
layers.append(conv_layer)
if batch_norm:
layers.append(nn.BatchNorm2d(out_channels))
return nn.Sequential(*layers)
class ResnetBlock(nn.Module):
def __init__(self, conv_dim):
super(ResnetBlock, self).__init__()
self.conv_layer = conv(in_channels=conv_dim, out_channels=conv_dim, kernel_size=3, stride=1, padding=1)
def forward(self, x):
out = x + self.conv_layer(x)
return out
```
## DCGAN
### Spectral Norm class
```
def l2normalize(v, eps=1e-12):
return v / (v.norm() + eps)
class SpectralNorm(nn.Module):
def __init__(self, module, name='weight', power_iterations=1):
super(SpectralNorm, self).__init__()
self.module = module
self.name = name
self.power_iterations = power_iterations
if not self._made_params():
self._make_params()
def _update_u_v(self):
u = getattr(self.module, self.name + "_u")
v = getattr(self.module, self.name + "_v")
w = getattr(self.module, self.name + "_bar")
height = w.data.shape[0]
for _ in range(self.power_iterations):
v.data = l2normalize(torch.mv(torch.t(w.view(height,-1).data), u.data))
u.data = l2normalize(torch.mv(w.view(height,-1).data, v.data))
# sigma = torch.dot(u.data, torch.mv(w.view(height,-1).data, v.data))
sigma = u.dot(w.view(height, -1).mv(v))
setattr(self.module, self.name, w / sigma.expand_as(w))
def _made_params(self):
try:
u = getattr(self.module, self.name + "_u")
v = getattr(self.module, self.name + "_v")
w = getattr(self.module, self.name + "_bar")
return True
except AttributeError:
return False
def _make_params(self):
w = getattr(self.module, self.name)
height = w.data.shape[0]
width = w.view(height, -1).data.shape[1]
u = Parameter(w.data.new(height).normal_(0, 1), requires_grad=False)
v = Parameter(w.data.new(width).normal_(0, 1), requires_grad=False)
u.data = l2normalize(u.data)
v.data = l2normalize(v.data)
w_bar = Parameter(w.data)
del self.module._parameters[self.name]
self.module.register_parameter(self.name + "_u", u)
self.module.register_parameter(self.name + "_v", v)
self.module.register_parameter(self.name + "_bar", w_bar)
def forward(self, *args):
self._update_u_v()
return self.module.forward(*args)
```
### **[Your Task]** GAN generator
```
class DCGenerator(nn.Module):
def __init__(self, noise_size, conv_dim, spectral_norm=False):
super(DCGenerator, self).__init__()
self.conv_dim = conv_dim
###########################################
## FILL THIS IN: CREATE ARCHITECTURE ##
###########################################
# self.linear_bn = ...
# self.upconv1 = ...
# self.upconv2 = ...
# self.upconv3 = ...
def forward(self, z):
"""Generates an image given a sample of random noise.
Input
-----
z: BS x noise_size x 1 x 1 --> BSx100x1x1 (during training)
Output
------
out: BS x channels x image_width x image_height --> BSx3x32x32 (during training)
"""
batch_size = z.size(0)
out = F.relu(self.linear_bn(z)).view(-1, self.conv_dim*4, 4, 4) # BS x 128 x 4 x 4
out = F.relu(self.upconv1(out)) # BS x 64 x 8 x 8
out = F.relu(self.upconv2(out)) # BS x 32 x 16 x 16
out = F.tanh(self.upconv3(out)) # BS x 3 x 32 x 32
out_size = out.size()
if out_size != torch.Size([batch_size, 3, 32, 32]):
raise ValueError("expect {} x 3 x 32 x 32, but get {}".format(batch_size, out_size))
return out
```
### GAN discriminator
```
class DCDiscriminator(nn.Module):
"""Defines the architecture of the discriminator network.
Note: Both discriminators D_X and D_Y have the same architecture in this assignment.
"""
def __init__(self, conv_dim=64, spectral_norm=False):
super(DCDiscriminator, self).__init__()
self.conv1 = conv(in_channels=3, out_channels=conv_dim, kernel_size=5, stride=2, spectral_norm=spectral_norm)
self.conv2 = conv(in_channels=conv_dim, out_channels=conv_dim*2, kernel_size=5, stride=2, spectral_norm=spectral_norm)
self.conv3 = conv(in_channels=conv_dim*2, out_channels=conv_dim*4, kernel_size=5, stride=2, spectral_norm=spectral_norm)
self.conv4 = conv(in_channels=conv_dim*4, out_channels=1, kernel_size=5, stride=2, padding=1, batch_norm=False, spectral_norm=spectral_norm)
def forward(self, x):
batch_size = x.size(0)
out = F.relu(self.conv1(x)) # BS x 64 x 16 x 16
out = F.relu(self.conv2(out)) # BS x 64 x 8 x 8
out = F.relu(self.conv3(out)) # BS x 64 x 4 x 4
out = self.conv4(out).squeeze()
out_size = out.size()
if out_size != torch.Size([batch_size,]):
raise ValueError("expect {} x 1, but get {}".format(batch_size, out_size))
return out
```
### **[Your Task]** GAN training loop
* Regular GAN
* Least Squares GAN
```
def gan_training_loop_regular(dataloader, test_dataloader, opts):
"""Runs the training loop.
* Saves checkpoint every opts.checkpoint_every iterations
* Saves generated samples every opts.sample_every iterations
"""
# Create generators and discriminators
G, D = create_model(opts)
g_params = G.parameters() # Get generator parameters
d_params = D.parameters() # Get discriminator parameters
# Create optimizers for the generators and discriminators
g_optimizer = optim.Adam(g_params, opts.lr, [opts.beta1, opts.beta2])
d_optimizer = optim.Adam(d_params, opts.lr * 2., [opts.beta1, opts.beta2])
train_iter = iter(dataloader)
test_iter = iter(test_dataloader)
# Get some fixed data from domains X and Y for sampling. These are images that are held
# constant throughout training, that allow us to inspect the model's performance.
fixed_noise = sample_noise(100, opts.noise_size) # # 100 x noise_size x 1 x 1
iter_per_epoch = len(train_iter)
total_train_iters = opts.train_iters
losses = {"iteration": [], "D_fake_loss": [], "D_real_loss": [], "G_loss": []}
gp_weight = 1
adversarial_loss = torch.nn.BCEWithLogitsLoss() # Use this loss
# [Hint: you may find the folowing code helpful]
# ones = Variable(torch.Tensor(real_images.shape[0]).float().cuda().fill_(1.0), requires_grad=False)
try:
for iteration in range(1, opts.train_iters + 1):
# Reset data_iter for each epoch
if iteration % iter_per_epoch == 0:
train_iter = iter(dataloader)
real_images, real_labels = train_iter.next()
real_images, real_labels = to_var(real_images), to_var(real_labels).long().squeeze()
for d_i in range(opts.d_train_iters):
d_optimizer.zero_grad()
# FILL THIS IN
# 1. Compute the discriminator loss on real images
# D_real_loss = ...
# 2. Sample noise
# noise = ...
# 3. Generate fake images from the noise
# fake_images = ...
# 4. Compute the discriminator loss on the fake images
# D_fake_loss = ...
# ---- Gradient Penalty ----
if opts.gradient_penalty:
alpha = torch.rand(real_images.shape[0], 1, 1, 1)
alpha = alpha.expand_as(real_images).cuda()
interp_images = Variable(alpha * real_images.data + (1 - alpha) * fake_images.data, requires_grad=True).cuda()
D_interp_output = D(interp_images)
gradients = torch.autograd.grad(outputs=D_interp_output, inputs=interp_images,
grad_outputs=torch.ones(D_interp_output.size()).cuda(),
create_graph=True, retain_graph=True)[0]
gradients = gradients.view(real_images.shape[0], -1)
gradients_norm = torch.sqrt(torch.sum(gradients ** 2, dim=1) + 1e-12)
gp = gp_weight * gradients_norm.mean()
else:
gp = 0.0
# --------------------------
# 5. Compute the total discriminator loss
# D_total_loss = ...
D_total_loss.backward()
d_optimizer.step()
###########################################
### TRAIN THE GENERATOR ###
###########################################
g_optimizer.zero_grad()
# FILL THIS IN
# 1. Sample noise
# noise = ...
# 2. Generate fake images from the noise
# fake_images = ...
# 3. Compute the generator loss
# G_loss = ...
G_loss.backward()
g_optimizer.step()
# Print the log info
if iteration % opts.log_step == 0:
losses['iteration'].append(iteration)
losses['D_real_loss'].append(D_real_loss.item())
losses['D_fake_loss'].append(D_fake_loss.item())
losses['G_loss'].append(G_loss.item())
print('Iteration [{:4d}/{:4d}] | D_real_loss: {:6.4f} | D_fake_loss: {:6.4f} | G_loss: {:6.4f}'.format(
iteration, total_train_iters, D_real_loss.item(), D_fake_loss.item(), G_loss.item()))
# Save the generated samples
if iteration % opts.sample_every == 0:
gan_save_samples(G, fixed_noise, iteration, opts)
# Save the model parameters
if iteration % opts.checkpoint_every == 0:
gan_checkpoint(iteration, G, D, opts)
except KeyboardInterrupt:
print('Exiting early from training.')
return G, D
plt.figure()
plt.plot(losses['iteration'], losses['D_real_loss'], label='D_real')
plt.plot(losses['iteration'], losses['D_fake_loss'], label='D_fake')
plt.plot(losses['iteration'], losses['G_loss'], label='G')
plt.legend()
plt.savefig(os.path.join(opts.sample_dir, 'losses.png'))
plt.close()
return G, D
def gan_training_loop_leastsquares(dataloader, test_dataloader, opts):
"""Runs the training loop.
* Saves checkpoint every opts.checkpoint_every iterations
* Saves generated samples every opts.sample_every iterations
"""
# Create generators and discriminators
G, D = create_model(opts)
g_params = G.parameters() # Get generator parameters
d_params = D.parameters() # Get discriminator parameters
# Create optimizers for the generators and discriminators
g_optimizer = optim.Adam(g_params, opts.lr, [opts.beta1, opts.beta2])
d_optimizer = optim.Adam(d_params, opts.lr * 2., [opts.beta1, opts.beta2])
train_iter = iter(dataloader)
test_iter = iter(test_dataloader)
# Get some fixed data from domains X and Y for sampling. These are images that are held
# constant throughout training, that allow us to inspect the model's performance.
fixed_noise = sample_noise(100, opts.noise_size) # # 100 x noise_size x 1 x 1
iter_per_epoch = len(train_iter)
total_train_iters = opts.train_iters
losses = {"iteration": [], "D_fake_loss": [], "D_real_loss": [], "G_loss": []}
#adversarial_loss = torch.nn.BCEWithLogitsLoss()
gp_weight = 1
try:
for iteration in range(1, opts.train_iters + 1):
# Reset data_iter for each epoch
if iteration % iter_per_epoch == 0:
train_iter = iter(dataloader)
real_images, real_labels = train_iter.next()
real_images, real_labels = to_var(real_images), to_var(real_labels).long().squeeze()
for d_i in range(opts.d_train_iters):
d_optimizer.zero_grad()
# FILL THIS IN
# 1. Compute the discriminator loss on real images
# D_real_loss = ...
# 2. Sample noise
# noise = ...
# 3. Generate fake images from the noise
# fake_images = ...
# 4. Compute the discriminator loss on the fake images
# D_fake_loss = ...
# ---- Gradient Penalty ----
if opts.gradient_penalty:
alpha = torch.rand(real_images.shape[0], 1, 1, 1)
alpha = alpha.expand_as(real_images).cuda()
interp_images = Variable(alpha * real_images.data + (1 - alpha) * fake_images.data, requires_grad=True).cuda()
D_interp_output = D(interp_images)
gradients = torch.autograd.grad(outputs=D_interp_output, inputs=interp_images,
grad_outputs=torch.ones(D_interp_output.size()).cuda(),
create_graph=True, retain_graph=True)[0]
gradients = gradients.view(real_images.shape[0], -1)
gradients_norm = torch.sqrt(torch.sum(gradients ** 2, dim=1) + 1e-12)
gp = gp_weight * gradients_norm.mean()
else:
gp = 0.0
# --------------------------
# 5. Compute the total discriminator loss
# D_total_loss = ...
D_total_loss.backward()
d_optimizer.step()
###########################################
### TRAIN THE GENERATOR ###
###########################################
g_optimizer.zero_grad()
# FILL THIS IN
# 1. Sample noise
# noise = ...
# 2. Generate fake images from the noise
# fake_images = ...
# 3. Compute the generator loss
# G_loss = ...
G_loss.backward()
g_optimizer.step()
# Print the log info
if iteration % opts.log_step == 0:
losses['iteration'].append(iteration)
losses['D_real_loss'].append(D_real_loss.item())
losses['D_fake_loss'].append(D_fake_loss.item())
losses['G_loss'].append(G_loss.item())
print('Iteration [{:4d}/{:4d}] | D_real_loss: {:6.4f} | D_fake_loss: {:6.4f} | G_loss: {:6.4f}'.format(
iteration, total_train_iters, D_real_loss.item(), D_fake_loss.item(), G_loss.item()))
# Save the generated samples
if iteration % opts.sample_every == 0:
gan_save_samples(G, fixed_noise, iteration, opts)
# Save the model parameters
if iteration % opts.checkpoint_every == 0:
gan_checkpoint(iteration, G, D, opts)
except KeyboardInterrupt:
print('Exiting early from training.')
return G, D
plt.figure()
plt.plot(losses['iteration'], losses['D_real_loss'], label='D_real')
plt.plot(losses['iteration'], losses['D_fake_loss'], label='D_fake')
plt.plot(losses['iteration'], losses['G_loss'], label='G')
plt.legend()
plt.savefig(os.path.join(opts.sample_dir, 'losses.png'))
plt.close()
return G, D
```
# **[Your Task]** Training
## Download dataset
```
######################################################################
# Download Translation datasets
######################################################################
data_fpath = get_file(fname='emojis',
origin='http://www.cs.toronto.edu/~jba/emojis.tar.gz',
untar=True)
```
## Train DCGAN
```
SEED = 11
# Set the random seed manually for reproducibility.
np.random.seed(SEED)
torch.manual_seed(SEED)
if torch.cuda.is_available():
torch.cuda.manual_seed(SEED)
args = AttrDict()
args_dict = {
'image_size':32,
'g_conv_dim':32,
'd_conv_dim':64,
'noise_size':100,
'num_workers': 0,
'train_iters':20000,
'X':'Apple', # options: 'Windows' / 'Apple'
'Y': None,
'lr':0.00003,
'beta1':0.5,
'beta2':0.999,
'batch_size':32,
'checkpoint_dir': 'results/checkpoints_gan_gp1_lr3e-5',
'sample_dir': 'results/samples_gan_gp1_lr3e-5',
'load': None,
'log_step':200,
'sample_every':200,
'checkpoint_every':1000,
'spectral_norm': False,
'gradient_penalty': True,
'least_squares_gan': False,
'd_train_iters': 1
}
args.update(args_dict)
print_opts(args)
G, D = train(args)
generate_gif("results/samples_gan_gp1_lr3e-5")
```
## Download your output
```
!zip -r /content/csc413/a4/results/samples.zip /content/csc413/a4/results/samples_gan_gp1_lr3e-5
from google.colab import files
files.download("/content/csc413/a4/results/samples.zip")
```
| github_jupyter |
## Initial Setup
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import itertools
import os
import math
import string
import re
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
import helper
import pickle
import keras
from keras.models import Sequential,load_model
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D,Conv1D,MaxPooling1D
layers = keras.layers
```
## Training Parameters
We'll set the hyperparameters for training our model. If you understand what they mean, feel free to play around - otherwise, we recommend keeping the defaults for your first run 🙂
```
# Hyperparams if GPU is available
if tf.test.is_gpu_available():
print('---- We are using GPU now ----')
# GPU
BATCH_SIZE = 512 # Number of examples used in each iteration
EPOCHS = 80 # Number of passes through entire dataset
# Hyperparams for CPU training
else:
print('---- We are using CPU now ----')
# CPU
BATCH_SIZE = 256
EPOCHS = 100
```
## Data
The wine reviews dataset is already attached to your workspace (if you want to attach your own data, [check out our docs](https://docs.floydhub.com/guides/workspace/#attaching-floydhub-datasets)).
Let's take a look at data.
```
data_path = '/floyd/input/gengduoshuju/' # ADD path/to/dataset
Y= pickle.load( open(os.path.join(data_path,'Y.pks'), "rb" ) )
X= pickle.load( open(os.path.join(data_path,'X.pks'), "rb" ) )
X = X.reshape((X.shape[0],X.shape[1],1))
print("Size of X :" + str(X.shape))
print("Size of Y :" + str(Y.shape))
X = X.astype(np.float64)
X = np.nan_to_num(X)
```
## Data Preprocessing
```
X_train, X_test, Y_train_orig,Y_test_orig= helper.divide_data(X,Y)
print(Y.min())
print(Y.max())
num_classes = 332
Y_train = keras.utils.to_categorical(Y_train_orig, num_classes)
Y_test = keras.utils.to_categorical(Y_test_orig, num_classes)
print("number of training examples = " + str(X_train.shape[0]))
print("number of test examples = " + str(X_test.shape[0]))
print("X_train shape: " + str(X_train.shape))
print("Y_train shape: " + str(Y_train.shape))
print("X_test shape: " + str(X_test.shape))
print("Y_test shape: " + str(Y_test.shape))
input_shape = X_train.shape[1:]
print(input_shape)
```
# Model definition
The *Tokens per sentence* plot (see above) is useful for setting the `MAX_LEN` training hyperparameter.
```
# ===================================================================================
# Load the model what has already ben trained
# ===================================================================================
model = load_model(r"floyd_model_xxl_data_ver8.h5")
```
# Model Training
```
opt = keras.optimizers.Adam(lr=0.0001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
model.summary()
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
model.fit(X_train, Y_train,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
validation_data=(X_test, Y_test),
shuffle=True)
model.save(r"floyd_model_xxl_data_ver9.h5")
print('Training is done!')
```
| github_jupyter |
```
import os, json, sys, time, random
import numpy as np
import torch
from easydict import EasyDict
from math import floor
from easydict import EasyDict
from steves_utils.vanilla_train_eval_test_jig import Vanilla_Train_Eval_Test_Jig
from steves_utils.torch_utils import get_dataset_metrics, independent_accuracy_assesment
from steves_models.configurable_vanilla import Configurable_Vanilla
from steves_utils.torch_sequential_builder import build_sequential
from steves_utils.lazy_map import Lazy_Map
from steves_utils.sequence_aggregator import Sequence_Aggregator
from steves_utils.stratified_dataset.traditional_accessor import Traditional_Accessor_Factory
from steves_utils.cnn_do_report import (
get_loss_curve,
get_results_table,
get_parameters_table,
get_domain_accuracies,
)
from steves_utils.torch_utils import (
confusion_by_domain_over_dataloader,
independent_accuracy_assesment
)
from steves_utils.utils_v2 import (
per_domain_accuracy_from_confusion,
get_datasets_base_path
)
# from steves_utils.ptn_do_report import TBD
required_parameters = {
"experiment_name",
"lr",
"device",
"dataset_seed",
"seed",
"labels",
"domains_target",
"domains_source",
"num_examples_per_domain_per_label_source",
"num_examples_per_domain_per_label_target",
"batch_size",
"n_epoch",
"patience",
"criteria_for_best",
"normalize_source",
"normalize_target",
"x_net",
"NUM_LOGS_PER_EPOCH",
"BEST_MODEL_PATH",
"pickle_name_source",
"pickle_name_target",
"torch_default_dtype",
}
from steves_utils.ORACLE.utils_v2 import (
ALL_SERIAL_NUMBERS,
ALL_DISTANCES_FEET_NARROWED,
)
standalone_parameters = {}
standalone_parameters["experiment_name"] = "MANUAL CORES CNN"
standalone_parameters["lr"] = 0.0001
standalone_parameters["device"] = "cuda"
standalone_parameters["dataset_seed"] = 1337
standalone_parameters["seed"] = 1337
standalone_parameters["labels"] = ALL_SERIAL_NUMBERS
standalone_parameters["domains_source"] = [8,32,50]
standalone_parameters["domains_target"] = [14,20,26,38,44,]
standalone_parameters["num_examples_per_domain_per_label_source"]=-1
standalone_parameters["num_examples_per_domain_per_label_target"]=-1
standalone_parameters["pickle_name_source"] = "oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl"
standalone_parameters["pickle_name_target"] = "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"
standalone_parameters["torch_default_dtype"] = "torch.float32"
standalone_parameters["batch_size"]=128
standalone_parameters["n_epoch"] = 3
standalone_parameters["patience"] = 10
standalone_parameters["criteria_for_best"] = "target_accuracy"
standalone_parameters["normalize_source"] = False
standalone_parameters["normalize_target"] = False
standalone_parameters["x_net"] = [
{"class": "nnReshape", "kargs": {"shape":[-1, 1, 2, 256]}},
{"class": "Conv2d", "kargs": { "in_channels":1, "out_channels":256, "kernel_size":(1,7), "bias":False, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":256}},
{"class": "Conv2d", "kargs": { "in_channels":256, "out_channels":80, "kernel_size":(2,7), "bias":True, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 80*256, "out_features": 256}}, # 80 units per IQ pair
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features":256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": len(standalone_parameters["labels"])}},
]
standalone_parameters["NUM_LOGS_PER_EPOCH"] = 10
standalone_parameters["BEST_MODEL_PATH"] = "./best_model.pth"
# Parameters
parameters = {
"experiment_name": "cnn_1:oracle.run1_limited",
"labels": [
"3123D52",
"3123D65",
"3123D79",
"3123D80",
"3123D54",
"3123D70",
"3123D7B",
"3123D89",
"3123D58",
"3123D76",
"3123D7D",
"3123EFE",
"3123D64",
"3123D78",
"3123D7E",
"3124E4A",
],
"domains_source": [8, 32, 50],
"domains_target": [14, 20, 26, 38, 44],
"pickle_name_source": "oracle.Run1_10kExamples_stratified_ds.2022A.pkl",
"pickle_name_target": "oracle.Run1_10kExamples_stratified_ds.2022A.pkl",
"device": "cuda",
"lr": 0.0001,
"batch_size": 128,
"normalize_source": False,
"normalize_target": False,
"num_examples_per_domain_per_label_source": 2000,
"num_examples_per_domain_per_label_target": 2000,
"torch_default_dtype": "torch.float32",
"n_epoch": 50,
"patience": 3,
"criteria_for_best": "target_accuracy",
"x_net": [
{"class": "nnReshape", "kargs": {"shape": [-1, 1, 2, 256]}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 1,
"out_channels": 256,
"kernel_size": [1, 7],
"bias": False,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 256}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 256,
"out_channels": 80,
"kernel_size": [2, 7],
"bias": True,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 20480, "out_features": 256}},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features": 256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 16}},
],
"NUM_LOGS_PER_EPOCH": 10,
"BEST_MODEL_PATH": "./best_model.pth",
"dataset_seed": 7,
"seed": 7,
}
# Set this to True if you want to run this template directly
STANDALONE = False
if STANDALONE:
print("parameters not injected, running with standalone_parameters")
parameters = standalone_parameters
if not 'parameters' in locals() and not 'parameters' in globals():
raise Exception("Parameter injection failed")
#Use an easy dict for all the parameters
p = EasyDict(parameters)
supplied_keys = set(p.keys())
if supplied_keys != required_parameters:
print("Parameters are incorrect")
if len(supplied_keys - required_parameters)>0: print("Shouldn't have:", str(supplied_keys - required_parameters))
if len(required_parameters - supplied_keys)>0: print("Need to have:", str(required_parameters - supplied_keys))
raise RuntimeError("Parameters are incorrect")
###################################
# Set the RNGs and make it all deterministic
###################################
np.random.seed(p.seed)
random.seed(p.seed)
torch.manual_seed(p.seed)
torch.use_deterministic_algorithms(True)
torch.set_default_dtype(eval(p.torch_default_dtype))
###################################
# Build the network(s)
# Note: It's critical to do this AFTER setting the RNG
###################################
x_net = build_sequential(p.x_net)
start_time_secs = time.time()
def wrap_in_dataloader(p, ds):
return torch.utils.data.DataLoader(
ds,
batch_size=p.batch_size,
shuffle=True,
num_workers=1,
persistent_workers=True,
prefetch_factor=50,
pin_memory=True
)
taf_source = Traditional_Accessor_Factory(
labels=p.labels,
domains=p.domains_source,
num_examples_per_domain_per_label=p.num_examples_per_domain_per_label_source,
pickle_path=os.path.join(get_datasets_base_path(), p.pickle_name_source),
seed=p.dataset_seed
)
train_original_source, val_original_source, test_original_source = \
taf_source.get_train(), taf_source.get_val(), taf_source.get_test()
taf_target = Traditional_Accessor_Factory(
labels=p.labels,
domains=p.domains_target,
num_examples_per_domain_per_label=p.num_examples_per_domain_per_label_source,
pickle_path=os.path.join(get_datasets_base_path(), p.pickle_name_target),
seed=p.dataset_seed
)
train_original_target, val_original_target, test_original_target = \
taf_target.get_train(), taf_target.get_val(), taf_target.get_test()
# For CNN We only use X and Y. And we only train on the source.
# Properly form the data using a transform lambda and Lazy_Map. Finally wrap them in a dataloader
transform_lambda = lambda ex: ex[:2] # Strip the tuple to just (x,y)
train_processed_source = wrap_in_dataloader(
p,
Lazy_Map(train_original_source, transform_lambda)
)
val_processed_source = wrap_in_dataloader(
p,
Lazy_Map(val_original_source, transform_lambda)
)
test_processed_source = wrap_in_dataloader(
p,
Lazy_Map(test_original_source, transform_lambda)
)
train_processed_target = wrap_in_dataloader(
p,
Lazy_Map(train_original_target, transform_lambda)
)
val_processed_target = wrap_in_dataloader(
p,
Lazy_Map(val_original_target, transform_lambda)
)
test_processed_target = wrap_in_dataloader(
p,
Lazy_Map(test_original_target, transform_lambda)
)
datasets = EasyDict({
"source": {
"original": {"train":train_original_source, "val":val_original_source, "test":test_original_source},
"processed": {"train":train_processed_source, "val":val_processed_source, "test":test_processed_source}
},
"target": {
"original": {"train":train_original_target, "val":val_original_target, "test":test_original_target},
"processed": {"train":train_processed_target, "val":val_processed_target, "test":test_processed_target}
},
})
ep = next(iter(test_processed_target))
ep[0].dtype
model = Configurable_Vanilla(
x_net=x_net,
label_loss_object=torch.nn.NLLLoss(),
learning_rate=p.lr
)
jig = Vanilla_Train_Eval_Test_Jig(
model=model,
path_to_best_model=p.BEST_MODEL_PATH,
device=p.device,
label_loss_object=torch.nn.NLLLoss(),
)
jig.train(
train_iterable=datasets.source.processed.train,
source_val_iterable=datasets.source.processed.val,
target_val_iterable=datasets.target.processed.val,
patience=p.patience,
num_epochs=p.n_epoch,
num_logs_per_epoch=p.NUM_LOGS_PER_EPOCH,
criteria_for_best=p.criteria_for_best
)
total_experiment_time_secs = time.time() - start_time_secs
source_test_label_accuracy, source_test_label_loss = jig.test(datasets.source.processed.test)
target_test_label_accuracy, target_test_label_loss = jig.test(datasets.target.processed.test)
source_val_label_accuracy, source_val_label_loss = jig.test(datasets.source.processed.val)
target_val_label_accuracy, target_val_label_loss = jig.test(datasets.target.processed.val)
history = jig.get_history()
total_epochs_trained = len(history["epoch_indices"])
val_dl = wrap_in_dataloader(p, Sequence_Aggregator((datasets.source.original.val, datasets.target.original.val)))
confusion = confusion_by_domain_over_dataloader(model, p.device, val_dl, forward_uses_domain=False)
per_domain_accuracy = per_domain_accuracy_from_confusion(confusion)
# Add a key to per_domain_accuracy for if it was a source domain
for domain, accuracy in per_domain_accuracy.items():
per_domain_accuracy[domain] = {
"accuracy": accuracy,
"source?": domain in p.domains_source
}
# Do an independent accuracy assesment JUST TO BE SURE!
# _source_test_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.test, p.device)
# _target_test_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.test, p.device)
# _source_val_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.val, p.device)
# _target_val_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.val, p.device)
# assert(_source_test_label_accuracy == source_test_label_accuracy)
# assert(_target_test_label_accuracy == target_test_label_accuracy)
# assert(_source_val_label_accuracy == source_val_label_accuracy)
# assert(_target_val_label_accuracy == target_val_label_accuracy)
###################################
# Write out the results
###################################
experiment = {
"experiment_name": p.experiment_name,
"parameters": p,
"results": {
"source_test_label_accuracy": source_test_label_accuracy,
"source_test_label_loss": source_test_label_loss,
"target_test_label_accuracy": target_test_label_accuracy,
"target_test_label_loss": target_test_label_loss,
"source_val_label_accuracy": source_val_label_accuracy,
"source_val_label_loss": source_val_label_loss,
"target_val_label_accuracy": target_val_label_accuracy,
"target_val_label_loss": target_val_label_loss,
"total_epochs_trained": total_epochs_trained,
"total_experiment_time_secs": total_experiment_time_secs,
"confusion": confusion,
"per_domain_accuracy": per_domain_accuracy,
},
"history": history,
"dataset_metrics": get_dataset_metrics(datasets, "cnn"),
}
get_loss_curve(experiment)
get_results_table(experiment)
get_domain_accuracies(experiment)
print("Source Test Label Accuracy:", experiment["results"]["source_test_label_accuracy"], "Target Test Label Accuracy:", experiment["results"]["target_test_label_accuracy"])
print("Source Val Label Accuracy:", experiment["results"]["source_val_label_accuracy"], "Target Val Label Accuracy:", experiment["results"]["target_val_label_accuracy"])
json.dumps(experiment)
```
| github_jupyter |
```
import numpy as np
%%html
<style>
.pquote {
text-align: left;
margin: 40px 0 40px auto;
width: 70%;
font-size: 1.5em;
font-style: italic;
display: block;
line-height: 1.3em;
color: #5a75a7;
font-weight: 600;
border-left: 5px solid rgba(90, 117, 167, .1);
padding-left: 6px;
}
.notes {
font-style: italic;
display: block;
margin: 40px 10%;
}
</style>
```
$$
\newcommand\bs[1]{\boldsymbol{#1}}
$$
<span class='notes'>
This content is part of a series following the chapter 2 on linear algebra from the [Deep Learning Book](http://www.deeplearningbook.org/) by Goodfellow, I., Bengio, Y., and Courville, A. (2016). It aims to provide intuitions/drawings/python code on mathematical theories and is constructed as my understanding of these concepts. You can check the syllabus in the [introduction post](https://hadrienj.github.io/posts/Deep-Learning-Book-Series-Introduction/).
</span>
# Introduction
This is the first post/notebook of a series following the syllabus of the [linear algebra chapter from the Deep Learning Book](http://www.deeplearningbook.org/contents/linear_algebra.html) by Goodfellow et al.. This work is a collection of thoughts/details/developements/examples I made while reading this chapter. It is designed to help you go through their introduction to linear algebra. For more details about this series and the syllabus, please see the [introduction post](https://hadrienj.github.io/posts/Deep-Learning-Book-Series-Introduction/).
This first chapter is quite light and concerns the basic elements used in linear algebra and their definitions. It also introduces important functions in Python/Numpy that we will use all along this series. It will explain how to create and use vectors and matrices through examples.
# 2.1 Scalars, Vectors, Matrices and Tensors
Let's start with some basic definitions:
<img src="images/scalar-tensor.png" width="400" alt="scalar-tensor">
- A scalar is a single number
- A vector is an array of numbers.
$$
\bs{x} =\begin{bmatrix}
x_1 \\\\
x_2 \\\\
\cdots \\\\
x_n
\end{bmatrix}
$$
- A matrix is a 2-D array
$$
\bs{A}=
\begin{bmatrix}
A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\\\
A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\\\
\cdots & \cdots & \cdots & \cdots \\\\
A_{m,1} & A_{m,2} & \cdots & A_{m,n}
\end{bmatrix}
$$
- A tensor is a $n$-dimensional array with $n>2$
We will follow the conventions used in the [Deep Learning Book](http://www.deeplearningbook.org/):
- scalars are written in lowercase and italics. For instance: $n$
- vectors are written in lowercase, italics and bold type. For instance: $\bs{x}$
- matrices are written in uppercase, italics and bold. For instance: $\bs{X}$
### Example 1.
#### Create a vector with Python and Numpy
*Coding tip*: Unlike the `matrix()` function which necessarily creates $2$-dimensional matrices, you can create $n$-dimensionnal arrays with the `array()` function. The main advantage to use `matrix()` is the useful methods (conjugate transpose, inverse, matrix operations...). We will use the `array()` function in this series.
We will start by creating a vector. This is just a $1$-dimensional array:
```
x = np.array([1, 2, 3, 4])
x
```
### Example 2.
#### Create a (3x2) matrix with nested brackets
The `array()` function can also create $2$-dimensional arrays with nested brackets:
```
A = np.array([[1, 2], [3, 4], [5, 6]])
A
```
### Shape
The shape of an array (that is to say its dimensions) tells you the number of values for each dimension. For a $2$-dimensional array it will give you the number of rows and the number of columns. Let's find the shape of our preceding $2$-dimensional array `A`. Since `A` is a Numpy array (it was created with the `array()` function) you can access its shape with:
```
A.shape
```
We can see that $\bs{A}$ has 3 rows and 2 columns.
Let's check the shape of our first vector:
```
x.shape
```
As expected, you can see that $\bs{x}$ has only one dimension. The number corresponds to the length of the array:
```
len(x)
```
# Transposition
With transposition you can convert a row vector to a column vector and vice versa:
<img src="images/transposeVector.png" alt="transposeVector" width="200">
The transpose $\bs{A}^{\text{T}}$ of the matrix $\bs{A}$ corresponds to the mirrored axes. If the matrix is a square matrix (same number of columns and rows):
<img src="images/transposeMatrixSquare.png" alt="transposeMatrixSquare" width="300">
If the matrix is not square the idea is the same:
<img src="images/transposeMatrix.png" alt="transposeMatrix" width="300">
The superscript $^\text{T}$ is used for transposed matrices.
$$
\bs{A}=
\begin{bmatrix}
A_{1,1} & A_{1,2} \\\\
A_{2,1} & A_{2,2} \\\\
A_{3,1} & A_{3,2}
\end{bmatrix}
$$
$$
\bs{A}^{\text{T}}=
\begin{bmatrix}
A_{1,1} & A_{2,1} & A_{3,1} \\\\
A_{1,2} & A_{2,2} & A_{3,2}
\end{bmatrix}
$$
The shape ($m \times n$) is inverted and becomes ($n \times m$).
<img src="images/transposeMatrixDim.png" alt="transposeMatrixDim" width="300">
### Example 3.
#### Create a matrix A and transpose it
```
A = np.array([[1, 2], [3, 4], [5, 6]])
A
A_t = A.T
A_t
```
We can check the dimensions of the matrices:
```
A.shape
A_t.shape
```
We can see that the number of columns becomes the number of rows with transposition and vice versa.
# Addition
<img src="images/additionMatrix.png" alt="additionMatrix" width="300">
Matrices can be added if they have the same shape:
$$\bs{A} + \bs{B} = \bs{C}$$
Each cell of $\bs{A}$ is added to the corresponding cell of $\bs{B}$:
$$\bs{A}_{i,j} + \bs{B}_{i,j} = \bs{C}_{i,j}$$
$i$ is the row index and $j$ the column index.
$$
\begin{bmatrix}
A_{1,1} & A_{1,2} \\\\
A_{2,1} & A_{2,2} \\\\
A_{3,1} & A_{3,2}
\end{bmatrix}+
\begin{bmatrix}
B_{1,1} & B_{1,2} \\\\
B_{2,1} & B_{2,2} \\\\
B_{3,1} & B_{3,2}
\end{bmatrix}=
\begin{bmatrix}
A_{1,1} + B_{1,1} & A_{1,2} + B_{1,2} \\\\
A_{2,1} + B_{2,1} & A_{2,2} + B_{2,2} \\\\
A_{3,1} + B_{3,1} & A_{3,2} + B_{3,2}
\end{bmatrix}
$$
The shape of $\bs{A}$, $\bs{B}$ and $\bs{C}$ are identical. Let's check that in an example:
### Example 4.
#### Create two matrices A and B and add them
With Numpy you can add matrices just as you would add vectors or scalars.
```
A = np.array([[1, 2], [3, 4], [5, 6]])
A
B = np.array([[2, 5], [7, 4], [4, 3]])
B
# Add matrices A and B
C = A + B
C
```
It is also possible to add a scalar to a matrix. This means adding this scalar to each cell of the matrix.
$$
\alpha+ \begin{bmatrix}
A_{1,1} & A_{1,2} \\\\
A_{2,1} & A_{2,2} \\\\
A_{3,1} & A_{3,2}
\end{bmatrix}=
\begin{bmatrix}
\alpha + A_{1,1} & \alpha + A_{1,2} \\\\
\alpha + A_{2,1} & \alpha + A_{2,2} \\\\
\alpha + A_{3,1} & \alpha + A_{3,2}
\end{bmatrix}
$$
### Example 5.
#### Add a scalar to a matrix
```
A
# Exemple: Add 4 to the matrix A
C = A+4
C
```
# Broadcasting
Numpy can handle operations on arrays of different shapes. The smaller array will be extended to match the shape of the bigger one. The advantage is that this is done in `C` under the hood (like any vectorized operations in Numpy). Actually, we used broadcasting in the example 5. The scalar was converted in an array of same shape as $\bs{A}$.
Here is another generic example:
$$
\begin{bmatrix}
A_{1,1} & A_{1,2} \\\\
A_{2,1} & A_{2,2} \\\\
A_{3,1} & A_{3,2}
\end{bmatrix}+
\begin{bmatrix}
B_{1,1} \\\\
B_{2,1} \\\\
B_{3,1}
\end{bmatrix}
$$
is equivalent to
$$
\begin{bmatrix}
A_{1,1} & A_{1,2} \\\\
A_{2,1} & A_{2,2} \\\\
A_{3,1} & A_{3,2}
\end{bmatrix}+
\begin{bmatrix}
B_{1,1} & B_{1,1} \\\\
B_{2,1} & B_{2,1} \\\\
B_{3,1} & B_{3,1}
\end{bmatrix}=
\begin{bmatrix}
A_{1,1} + B_{1,1} & A_{1,2} + B_{1,1} \\\\
A_{2,1} + B_{2,1} & A_{2,2} + B_{2,1} \\\\
A_{3,1} + B_{3,1} & A_{3,2} + B_{3,1}
\end{bmatrix}
$$
where the ($3 \times 1$) matrix is converted to the right shape ($3 \times 2$) by copying the first column. Numpy will do that automatically if the shapes can match.
### Example 6.
#### Add two matrices of different shapes
```
A = np.array([[1, 2], [3, 4], [5, 6]])
A
B = np.array([[2], [4], [6]])
B
# Broadcasting
C=A+B
C
```
You can find basics operations on matrices simply explained [here](https://www.mathsisfun.com/algebra/matrix-introduction.html).
<span class='notes'>
Feel free to drop me an email or a comment. The syllabus of this series can be found [in the introduction post](https://hadrienj.github.io/posts/Deep-Learning-Book-Series-Introduction/). All the notebooks can be found on [Github](https://github.com/hadrienj/deepLearningBook-Notes).
</span>
# References
- [Broadcasting in Numpy](https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
- [Discussion on Arrays and matrices](https://stackoverflow.com/questions/4151128/what-are-the-differences-between-numpy-arrays-and-matrices-which-one-should-i-u)
- [Math is fun - Matrix introduction](https://www.mathsisfun.com/algebra/matrix-introduction.html)
| github_jupyter |
```
import openmc
import openmc.deplete
%matplotlib inline
import numpy as np
fuel = openmc.Material(name="uo2")
fuel.add_element("U", 1, percent_type="ao", enrichment=4.25)
fuel.add_element("O", 2)
fuel.set_density("g/cc", 10.4)
clad = openmc.Material(name='clad');
clad.add_element("Zr",1);
clad.set_density('g/cc',6.0);
water = openmc.Material(name='water');
water.add_element('O',1);
water.add_element('H',2)
water.set_density('g/cc',0.712); # high temperature density
water.add_s_alpha_beta('c_H_in_H2O');
materials = openmc.Materials([fuel,clad,water]);
h_core = 300.;
h_fuel = 200.;
r_fuel = 0.42;
r_pin = 0.45;
P_D = 1.6;
pitch = P_D*2*r_pin;
fuel_temp = 900; # K, guess at fuel temperature
mod_temp = 600; # K, moderator temperature
# fuel cylinder:
fuel_cyl = openmc.model.RightCircularCylinder([0.,0.,-h_fuel/2.],
h_fuel, r_fuel);
fuel.volume = np.pi*(r_fuel**2)*h_fuel;
# pin cylinder
pin_cyl = openmc.model.RightCircularCylinder([0.,0.,-(h_fuel+(r_pin-r_fuel))/2.],
h_fuel+(r_pin-r_fuel)*2.,r_pin);
# pin cell container
core_cell = openmc.model.RectangularParallelepiped(-pitch/2.,pitch/2.,
-pitch/2.,pitch/2.,
-h_core/2.,h_core/2.,
boundary_type='reflective');
fuel_cell = openmc.Cell();
fuel_cell.region = -fuel_cyl
fuel_cell.fill = fuel;
fuel_cell.temperature = fuel_temp;
clad_cell = openmc.Cell();
clad_cell.region = +fuel_cyl & -pin_cyl;
clad_cell.fill = clad;
mod_cell = openmc.Cell();
mod_cell.region = +pin_cyl & -core_cell;
mod_cell.fill = water
root_univ = openmc.Universe();
root_univ.add_cells([fuel_cell,clad_cell,mod_cell]);
geometry = openmc.Geometry();
geometry.root_universe = root_univ;
materials.export_to_xml();
geometry.export_to_xml();
settings = openmc.Settings();
settings.run_mode = 'eigenvalue';
settings.particles = 10000;
settings.batches = 100;
settings.inactive = 25
box = openmc.stats.Box(lower_left = (-r_fuel,-r_fuel,-h_fuel/2.),
upper_right = (r_fuel,r_fuel,h_fuel/2.),
only_fissionable=True);
src = openmc.Source(space=box);
settings.source = src;
settings.temperature['method']='interpolation';
settings.export_to_xml();
root_univ.plot(width=(pitch,pitch));
openmc.run();
operator = openmc.deplete.Operator(geometry,settings,"chain_casl_pwr.xml");
power = 1e4;
days = 24*3600;
time_steps = [0.1*days,0.1*days,0.3*days,0.5*days,1.*days,30.*days,30.*days,100.*days, 360.*days, 360.*days, 360.*days,360.*days,720.*days,720.*days];
integrator = openmc.deplete.PredictorIntegrator(operator,time_steps,power=power);
integrator.integrate()
results = openmc.deplete.ResultsList.from_hdf5('./depletion_results.h5')
time,k = results.get_eigenvalue()
time /= (24*60*60);
from matplotlib import pyplot
pyplot.errorbar(time,k[:,0],yerr=k[:,1]);
pyplot.title('Burnup Result for Pincell')
pyplot.xlabel('Time [d]');
pyplot.ylabel('$k_{eff} \pm \sigma$');
pyplot.grid()
```
| github_jupyter |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
print(os.listdir("../input"))
# Any results you write to the current directory are saved as output.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Read the data
data = pd.read_csv('../input/Dataset.csv')
# View first and last 5 observations
print(data.head())
print(data.tail())
# Describe statistical information of data
print(data.describe())
# Below stats show that 75 percentile of obseravtions belong to class 1
# Check column types
print(data.info())
# All comumns are int type, so no change is required
# Plot distribution of classes using Histograms
plt.figure(figsize =(8,8))
plt.hist(data.Result)
# It shows that benign class have about 1000+ observations than malware
# Look for missing values
print(data.isnull().sum())
# No missing values found, so no need to drop or replace any value
# Generate correlation matrix
print(data.corr())
import seaborn as sns
plt.figure(figsize =(8,8))
sns.heatmap(data.corr()) # Generate heatmap (though very less clarity due to large no. of ftrs
print(data.corr()['Result'].sort_values()) # Print correlation with target variable
# Remove features having correlation coeff. between +/- 0.03
data.drop(['Favicon','Iframe','Redirect',
'popUpWidnow','RightClick','Submitting_to_email'],axis=1,inplace=True)
print(len(data.columns))
# Prepare data for models
y = data['Result'].values
X = data.drop(['Result'], axis = 1)
from sklearn.metrics import accuracy_score,roc_curve,auc, confusion_matrix
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
# Split the data as training and testing data - 70% train size, 30% test size
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = None)
#1 Classification using Random Forest Classifier
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc = rfc.fit(X_train,y_train)
prediction = rfc.predict(X_test)
print("Accuracy with RF classifier:",accuracy_score(y_test, prediction))
fpr,tpr,thresh = roc_curve(y_test,prediction)
roc_auc = accuracy_score(y_test,prediction) # Calculate ROC AUC
# Plot ROC curve for Random Forest
plt.plot(fpr,tpr,'g',label = 'Random Forest')
plt.legend("Random Forest", loc='lower right')
plt.legend(loc='lower right')
print("Conf matrix RF classifier:",confusion_matrix(y_test,prediction)) # Generate confusion matrix
#2 Classification using logistic regression
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
logreg = logreg.fit(X_train,y_train)
prediction = logreg.predict(X_test)
print("Accuracy with Log Reg:", accuracy_score(y_test, prediction))
print ("Conf matrix Log Reg:",confusion_matrix(y_test,prediction))
fpr,tpr,thresh = roc_curve(y_test,prediction)
roc_auc = accuracy_score(y_test,prediction)
# Plot ROC curve for Logistic Regression
plt.plot(fpr,tpr,'orange',label = 'Logistic Regression')
plt.legend("Logistic Regression", loc='lower right')
plt.xlabel("False positive rate")
plt.ylabel("True positive rate")
plt.legend(loc='lower right')
#3 Classification using SVM
from sklearn.svm import SVC
svc_l = SVC(kernel = "linear", C = 0.025)
svc_l = svc_l.fit(X_train,y_train)
prediction = svc_l.predict(X_test)
print("Accuracy with SVM-Linear:",accuracy_score(y_test, prediction))
fpr,tpr,thresh = roc_curve(y_test,prediction)
roc_auc = accuracy_score(y_test,prediction)
# Plot ROC curve for SVM-linear
plt.plot(fpr,tpr,'b',label = 'SVM')
plt.legend("SVM", loc ='lower right')
plt.legend(loc ='lower right')
print("Conf matrix SVM-linear:",confusion_matrix(y_test,prediction))
plt.show()
'''
# -------- Apply Recursive Feature Elimination(RFE) and use reduced feature set for prediction ------------------------
# Recursive Feature Elimination(RFE) is a technique that takes entire feature set as input and removes features one at
# a time up to a specified number or until a stopping criteria is met.
'''
from sklearn.feature_selection import RFE
rfe = RFE(rfc,27)
rfe = rfe.fit(X_train, y_train) # Train RF classifier with only 27 features now
pred = rfe.predict(X_test)
# Test accuracy on reduced data
print("Accuracy by RFClassifier after RFE is applied:", accuracy_score(y_test,pred))
rfe = RFE(svc_l,27)
rfe = rfe.fit(X_train, y_train) # Train SVM with only 27 features now
pred = rfe.predict(X_test)
print("Accuracy by SVM-Linear after RFE is applied:", accuracy_score(y_test,pred))
rfe = RFE(logreg,27)
rfe = rfe.fit(X_train, y_train) # Train Logistic-Reg with only 27 features now
pred = rfe.predict(X_test)
print("Accuracy by Logistic Regression after RFE is applied:", accuracy_score(y_test,pred))
```
| github_jupyter |
# Artificial Intelligence Nanodegree
## Voice User Interfaces
## Project: Speech Recognition with Neural Networks
---
In this notebook, some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this project. You will not need to modify the included code beyond what is requested. Sections that begin with **'(IMPLEMENTATION)'** in the header indicate that the following blocks of code will require additional functionality which you must provide. Please be sure to read the instructions carefully!
> **Note**: Once you have completed all of the code implementations, you need to finalize your work by exporting the Jupyter Notebook as an HTML document. Before exporting the notebook to html, all of the code cells need to have been run so that reviewers can see the final implementation and output. You can then export the notebook by using the menu above and navigating to \n",
"**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
>**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. Markdown cells can be edited by double-clicking the cell to enter edit mode.
The rubric contains _optional_ "Stand Out Suggestions" for enhancing the project beyond the minimum requirements. If you decide to pursue the "Stand Out Suggestions", you should include the code in this Jupyter notebook.
---
## Introduction
In this notebook, you will build a deep neural network that functions as part of an end-to-end automatic speech recognition (ASR) pipeline! Your completed pipeline will accept raw audio as input and return a predicted transcription of the spoken language. The full pipeline is summarized in the figure below.
<img src="images/pipeline.png">
- **STEP 1** is a pre-processing step that converts raw audio to one of two feature representations that are commonly used for ASR.
- **STEP 2** is an acoustic model which accepts audio features as input and returns a probability distribution over all potential transcriptions. After learning about the basic types of neural networks that are often used for acoustic modeling, you will engage in your own investigations, to design your own acoustic model!
- **STEP 3** in the pipeline takes the output from the acoustic model and returns a predicted transcription.
Feel free to use the links below to navigate the notebook:
- [The Data](#thedata)
- [**STEP 1**](#step1): Acoustic Features for Speech Recognition
- [**STEP 2**](#step2): Deep Neural Networks for Acoustic Modeling
- [Model 0](#model0): RNN
- [Model 1](#model1): RNN + TimeDistributed Dense
- [Model 2](#model2): CNN + RNN + TimeDistributed Dense
- [Model 3](#model3): Deeper RNN + TimeDistributed Dense
- [Model 4](#model4): Bidirectional RNN + TimeDistributed Dense
- [Models 5+](#model5)
- [Compare the Models](#compare)
- [Final Model](#final)
- [**STEP 3**](#step3): Obtain Predictions
<a id='thedata'></a>
## The Data
We begin by investigating the dataset that will be used to train and evaluate your pipeline. [LibriSpeech](http://www.danielpovey.com/files/2015_icassp_librispeech.pdf) is a large corpus of English-read speech, designed for training and evaluating models for ASR. The dataset contains 1000 hours of speech derived from audiobooks. We will work with a small subset in this project, since larger-scale data would take a long while to train. However, after completing this project, if you are interested in exploring further, you are encouraged to work with more of the data that is provided [online](http://www.openslr.org/12/).
In the code cells below, you will use the `vis_train_features` module to visualize a training example. The supplied argument `index=0` tells the module to extract the first example in the training set. (You are welcome to change `index=0` to point to a different training example, if you like, but please **DO NOT** amend any other code in the cell.) The returned variables are:
- `vis_text` - transcribed text (label) for the training example.
- `vis_raw_audio` - raw audio waveform for the training example.
- `vis_mfcc_feature` - mel-frequency cepstral coefficients (MFCCs) for the training example.
- `vis_spectrogram_feature` - spectrogram for the training example.
- `vis_audio_path` - the file path to the training example.
```
from data_generator import vis_train_features
# extract label and audio features for a single training example
vis_text, vis_raw_audio, vis_mfcc_feature, vis_spectrogram_feature, vis_audio_path = vis_train_features()
```
The following code cell visualizes the audio waveform for your chosen example, along with the corresponding transcript. You also have the option to play the audio in the notebook!
```
from IPython.display import Markdown, display
from data_generator import vis_train_features, plot_raw_audio
from IPython.display import Audio
%matplotlib inline
# plot audio signal
plot_raw_audio(vis_raw_audio)
# print length of audio signal
display(Markdown('**Shape of Audio Signal** : ' + str(vis_raw_audio.shape)))
# print transcript corresponding to audio clip
display(Markdown('**Transcript** : ' + str(vis_text)))
# play the audio file
Audio(vis_audio_path)
```
<a id='step1'></a>
## STEP 1: Acoustic Features for Speech Recognition
For this project, you won't use the raw audio waveform as input to your model. Instead, we provide code that first performs a pre-processing step to convert the raw audio to a feature representation that has historically proven successful for ASR models. Your acoustic model will accept the feature representation as input.
In this project, you will explore two possible feature representations. _After completing the project_, if you'd like to read more about deep learning architectures that can accept raw audio input, you are encouraged to explore this [research paper](https://pdfs.semanticscholar.org/a566/cd4a8623d661a4931814d9dffc72ecbf63c4.pdf).
### Spectrograms
The first option for an audio feature representation is the [spectrogram](https://www.youtube.com/watch?v=_FatxGN3vAM). In order to complete this project, you will **not** need to dig deeply into the details of how a spectrogram is calculated; but, if you are curious, the code for calculating the spectrogram was borrowed from [this repository](https://github.com/baidu-research/ba-dls-deepspeech). The implementation appears in the `utils.py` file in your repository.
The code that we give you returns the spectrogram as a 2D tensor, where the first (_vertical_) dimension indexes time, and the second (_horizontal_) dimension indexes frequency. To speed the convergence of your algorithm, we have also normalized the spectrogram. (You can see this quickly in the visualization below by noting that the mean value hovers around zero, and most entries in the tensor assume values close to zero.)
```
from data_generator import plot_spectrogram_feature
# plot normalized spectrogram
plot_spectrogram_feature(vis_spectrogram_feature)
# print shape of spectrogram
display(Markdown('**Shape of Spectrogram** : ' + str(vis_spectrogram_feature.shape)))
```
### Mel-Frequency Cepstral Coefficients (MFCCs)
The second option for an audio feature representation is [MFCCs](https://en.wikipedia.org/wiki/Mel-frequency_cepstrum). You do **not** need to dig deeply into the details of how MFCCs are calculated, but if you would like more information, you are welcome to peruse the [documentation](https://github.com/jameslyons/python_speech_features) of the `python_speech_features` Python package. Just as with the spectrogram features, the MFCCs are normalized in the supplied code.
The main idea behind MFCC features is the same as spectrogram features: at each time window, the MFCC feature yields a feature vector that characterizes the sound within the window. Note that the MFCC feature is much lower-dimensional than the spectrogram feature, which could help an acoustic model to avoid overfitting to the training dataset.
```
from data_generator import plot_mfcc_feature
# plot normalized MFCC
plot_mfcc_feature(vis_mfcc_feature)
# print shape of MFCC
display(Markdown('**Shape of MFCC** : ' + str(vis_mfcc_feature.shape)))
```
When you construct your pipeline, you will be able to choose to use either spectrogram or MFCC features. If you would like to see different implementations that make use of MFCCs and/or spectrograms, please check out the links below:
- This [repository](https://github.com/baidu-research/ba-dls-deepspeech) uses spectrograms.
- This [repository](https://github.com/mozilla/DeepSpeech) uses MFCCs.
- This [repository](https://github.com/buriburisuri/speech-to-text-wavenet) also uses MFCCs.
- This [repository](https://github.com/pannous/tensorflow-speech-recognition/blob/master/speech_data.py) experiments with raw audio, spectrograms, and MFCCs as features.
<a id='step2'></a>
## STEP 2: Deep Neural Networks for Acoustic Modeling
In this section, you will experiment with various neural network architectures for acoustic modeling.
You will begin by training five relatively simple architectures. **Model 0** is provided for you. You will write code to implement **Models 1**, **2**, **3**, and **4**. If you would like to experiment further, you are welcome to create and train more models under the **Models 5+** heading.
All models will be specified in the `sample_models.py` file. After importing the `sample_models` module, you will train your architectures in the notebook.
After experimenting with the five simple architectures, you will have the opportunity to compare their performance. Based on your findings, you will construct a deeper architecture that is designed to outperform all of the shallow models.
For your convenience, we have designed the notebook so that each model can be specified and trained on separate occasions. That is, say you decide to take a break from the notebook after training **Model 1**. Then, you need not re-execute all prior code cells in the notebook before training **Model 2**. You need only re-execute the code cell below, that is marked with **`RUN THIS CODE CELL IF YOU ARE RESUMING THE NOTEBOOK AFTER A BREAK`**, before transitioning to the code cells corresponding to **Model 2**.
```
#####################################################################
# RUN THIS CODE CELL IF YOU ARE RESUMING THE NOTEBOOK AFTER A BREAK #
#####################################################################
# allocate 50% of GPU memory (if you like, feel free to change this)
from keras.backend.tensorflow_backend import set_session
import tensorflow as tf
config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 0.4
set_session(tf.Session(config=config))
# watch for any changes in the sample_models module, and reload it automatically
%load_ext autoreload
%autoreload 2
# import NN architectures for speech recognition
from sample_models import *
# import function for training acoustic model
from train_utils import train_model
```
<a id='model0'></a>
### Model 0: RNN
Given their effectiveness in modeling sequential data, the first acoustic model you will use is an RNN. As shown in the figure below, the RNN we supply to you will take the time sequence of audio features as input.
<img src="images/simple_rnn.png" width="50%">
At each time step, the speaker pronounces one of 28 possible characters, including each of the 26 letters in the English alphabet, along with a space character (" "), and an apostrophe (').
The output of the RNN at each time step is a vector of probabilities with 29 entries, where the $i$-th entry encodes the probability that the $i$-th character is spoken in the time sequence. (The extra 29th character is an empty "character" used to pad training examples within batches containing uneven lengths.) If you would like to peek under the hood at how characters are mapped to indices in the probability vector, look at the `char_map.py` file in the repository. The figure below shows an equivalent, rolled depiction of the RNN that shows the output layer in greater detail.
<img src="images/simple_rnn_unrolled.png" width="60%">
The model has already been specified for you in Keras. To import it, you need only run the code cell below.
```
model_0 = simple_rnn_model(input_dim=161) # change to 13 if you would like to use MFCC features
```
As explored in the lesson, you will train the acoustic model with the [CTC loss](http://www.cs.toronto.edu/~graves/icml_2006.pdf) criterion. Custom loss functions take a bit of hacking in Keras, and so we have implemented the CTC loss function for you, so that you can focus on trying out as many deep learning architectures as possible :). If you'd like to peek at the implementation details, look at the `add_ctc_loss` function within the `train_utils.py` file in the repository.
To train your architecture, you will use the `train_model` function within the `train_utils` module; it has already been imported in one of the above code cells. The `train_model` function takes three **required** arguments:
- `input_to_softmax` - a Keras model instance.
- `pickle_path` - the name of the pickle file where the loss history will be saved.
- `save_model_path` - the name of the HDF5 file where the model will be saved.
If we have already supplied values for `input_to_softmax`, `pickle_path`, and `save_model_path`, please **DO NOT** modify these values.
There are several **optional** arguments that allow you to have more control over the training process. You are welcome to, but not required to, supply your own values for these arguments.
- `minibatch_size` - the size of the minibatches that are generated while training the model (default: `20`).
- `spectrogram` - Boolean value dictating whether spectrogram (`True`) or MFCC (`False`) features are used for training (default: `True`).
- `mfcc_dim` - the size of the feature dimension to use when generating MFCC features (default: `13`).
- `optimizer` - the Keras optimizer used to train the model (default: `SGD(lr=0.02, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=5)`).
- `epochs` - the number of epochs to use to train the model (default: `20`). If you choose to modify this parameter, make sure that it is *at least* 20.
- `verbose` - controls the verbosity of the training output in the `model.fit_generator` method (default: `1`).
- `sort_by_duration` - Boolean value dictating whether the training and validation sets are sorted by (increasing) duration before the start of the first epoch (default: `False`).
The `train_model` function defaults to using spectrogram features; if you choose to use these features, note that the acoustic model in `simple_rnn_model` should have `input_dim=161`. Otherwise, if you choose to use MFCC features, the acoustic model should have `input_dim=13`.
We have chosen to use `GRU` units in the supplied RNN. If you would like to experiment with `LSTM` or `SimpleRNN` cells, feel free to do so here. If you change the `GRU` units to `SimpleRNN` cells in `simple_rnn_model`, you may notice that the loss quickly becomes undefined (`nan`) - you are strongly encouraged to check this for yourself! This is due to the [exploding gradients problem](http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/). We have already implemented [gradient clipping](https://arxiv.org/pdf/1211.5063.pdf) in your optimizer to help you avoid this issue.
__IMPORTANT NOTE:__ If you notice that your gradient has exploded in any of the models below, feel free to explore more with gradient clipping (the `clipnorm` argument in your optimizer) or swap out any `SimpleRNN` cells for `LSTM` or `GRU` cells. You can also try restarting the kernel to restart the training process.
```
train_model(input_to_softmax=model_0,
pickle_path='model_0.pickle',
save_model_path='model_0.h5',
optimizer=SGD(lr=0.02, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
<a id='model1'></a>
### (IMPLEMENTATION) Model 1: RNN + TimeDistributed Dense
Read about the [TimeDistributed](https://keras.io/layers/wrappers/) wrapper and the [BatchNormalization](https://keras.io/layers/normalization/) layer in the Keras documentation. For your next architecture, you will add [batch normalization](https://arxiv.org/pdf/1510.01378.pdf) to the recurrent layer to reduce training times. The `TimeDistributed` layer will be used to find more complex patterns in the dataset. The unrolled snapshot of the architecture is depicted below.
<img src="images/rnn_model.png" width="60%">
The next figure shows an equivalent, rolled depiction of the RNN that shows the (`TimeDistrbuted`) dense and output layers in greater detail.
<img src="images/rnn_model_unrolled.png" width="60%">
Use your research to complete the `rnn_model` function within the `sample_models.py` file. The function should specify an architecture that satisfies the following requirements:
- The first layer of the neural network should be an RNN (`SimpleRNN`, `LSTM`, or `GRU`) that takes the time sequence of audio features as input. We have added `GRU` units for you, but feel free to change `GRU` to `SimpleRNN` or `LSTM`, if you like!
- Whereas the architecture in `simple_rnn_model` treated the RNN output as the final layer of the model, you will use the output of your RNN as a hidden layer. Use `TimeDistributed` to apply a `Dense` layer to each of the time steps in the RNN output. Ensure that each `Dense` layer has `output_dim` units.
Use the code cell below to load your model into the `model_1` variable. Use a value for `input_dim` that matches your chosen audio features, and feel free to change the values for `units` and `activation` to tweak the behavior of your recurrent layer.
```
model_1 = rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
units=246,
activation='relu',
dropout_rate=0.0)
```
Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_1.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_1.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
```
from keras.optimizers import SGD
train_model(input_to_softmax=model_1,
pickle_path='model_1.pickle',
save_model_path='model_1.h5',
optimizer=SGD(lr=0.07693823225442271, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
<a id='model2'></a>
### (IMPLEMENTATION) Model 2: CNN + RNN + TimeDistributed Dense
The architecture in `cnn_rnn_model` adds an additional level of complexity, by introducing a [1D convolution layer](https://keras.io/layers/convolutional/#conv1d).
<img src="images/cnn_rnn_model.png" width="100%">
This layer incorporates many arguments that can be (optionally) tuned when calling the `cnn_rnn_model` module. We provide sample starting parameters, which you might find useful if you choose to use spectrogram audio features.
If you instead want to use MFCC features, these arguments will have to be tuned. Note that the current architecture only supports values of `'same'` or `'valid'` for the `conv_border_mode` argument.
When tuning the parameters, be careful not to choose settings that make the convolutional layer overly small. If the temporal length of the CNN layer is shorter than the length of the transcribed text label, your code will throw an error.
Before running the code cell below, you must modify the `cnn_rnn_model` function in `sample_models.py`. Please add batch normalization to the recurrent layer, and provide the same `TimeDistributed` layer as before.
```
model_2 = cnn_rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
filters=185,
kernel_size=5,
conv_stride=3,
conv_border_mode='valid',
units=350,
dropout_rate=0.5)
```
Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_2.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_2.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
```
from keras.optimizers import SGD
train_model(input_to_softmax=model_2,
pickle_path='model_2.pickle',
save_model_path='model_2.h5',
optimizer=SGD(lr=0.05, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
<a id='model3'></a>
### (IMPLEMENTATION) Model 3: Deeper RNN + TimeDistributed Dense
Review the code in `rnn_model`, which makes use of a single recurrent layer. Now, specify an architecture in `deep_rnn_model` that utilizes a variable number `recur_layers` of recurrent layers. The figure below shows the architecture that should be returned if `recur_layers=2`. In the figure, the output sequence of the first recurrent layer is used as input for the next recurrent layer.
<img src="images/deep_rnn_model.png" width="80%">
Feel free to change the supplied values of `units` to whatever you think performs best. You can change the value of `recur_layers`, as long as your final value is greater than 1. (As a quick check that you have implemented the additional functionality in `deep_rnn_model` correctly, make sure that the architecture that you specify here is identical to `rnn_model` if `recur_layers=1`.)
```
model_3 = deep_rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
units=290,
recur_layers=3,
dropout_rate=0.3035064397585259)
```
Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_3.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_3.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
```
from keras.optimizers import SGD
train_model(input_to_softmax=model_3,
pickle_path='model_3.pickle',
save_model_path='model_3.h5',
optimizer=SGD(lr=0.0635459438114008, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
<a id='model4'></a>
### (IMPLEMENTATION) Model 4: Bidirectional RNN + TimeDistributed Dense
Read about the [Bidirectional](https://keras.io/layers/wrappers/) wrapper in the Keras documentation. For your next architecture, you will specify an architecture that uses a single bidirectional RNN layer, before a (`TimeDistributed`) dense layer. The added value of a bidirectional RNN is described well in [this paper](http://www.cs.toronto.edu/~hinton/absps/DRNN_speech.pdf).
> One shortcoming of conventional RNNs is that they are only able to make use of previous context. In speech recognition, where whole utterances are transcribed at once, there is no reason not to exploit future context as well. Bidirectional RNNs (BRNNs) do this by processing the data in both directions with two separate hidden layers which are then fed forwards to the same output layer.
<img src="images/bidirectional_rnn_model.png" width="80%">
Before running the code cell below, you must complete the `bidirectional_rnn_model` function in `sample_models.py`. Feel free to use `SimpleRNN`, `LSTM`, or `GRU` units. When specifying the `Bidirectional` wrapper, use `merge_mode='concat'`.
```
model_4 = bidirectional_rnn_model(
input_dim=161, # change to 13 if you would like to use MFCC features
units=250,
dropout_rate=0.1)
```
Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_4.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_4.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
```
train_model(input_to_softmax=model_4,
pickle_path='model_4.pickle',
save_model_path='model_4.h5',
optimizer=SGD(lr=0.06, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
<a id='model5'></a>
### (OPTIONAL IMPLEMENTATION) Models 5+
If you would like to try out more architectures than the ones above, please use the code cell below. Please continue to follow the same convention for saving the models; for the $i$-th sample model, please save the loss at **`model_i.pickle`** and saving the trained model at **`model_i.h5`**.
```
model_5 = cnn2d_rnn_model(
input_dim=161, # change to 13 if you would like to use MFCC features
filters=50,
kernel_size=(11,11),
conv_stride=1,
conv_border_mode='same',
pool_size=(1,5),
units=200,
dropout_rate=0.1)
from keras.optimizers import SGD
train_model(input_to_softmax=model_5,
pickle_path='model_5.pickle',
save_model_path='model_5.h5',
optimizer=SGD(lr=0.06, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
<a id='compare'></a>
### Compare the Models
Execute the code cell below to evaluate the performance of the drafted deep learning models. The training and validation loss are plotted for each model.
```
from glob import glob
import numpy as np
import _pickle as pickle
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
sns.set_style(style='white')
# obtain the paths for the saved model history
all_pickles = sorted(glob("results/*.pickle"))
# extract the name of each model
model_names = [item[8:-7] for item in all_pickles]
# extract the loss history for each model
valid_loss = [pickle.load( open( i, "rb" ) )['val_loss'] for i in all_pickles]
train_loss = [pickle.load( open( i, "rb" ) )['loss'] for i in all_pickles]
# save the number of epochs used to train each model
num_epochs = [len(valid_loss[i]) for i in range(len(valid_loss))]
fig = plt.figure(figsize=(16,5))
# plot the training loss vs. epoch for each model
ax1 = fig.add_subplot(121)
for i in range(len(all_pickles)):
ax1.plot(np.linspace(1, num_epochs[i], num_epochs[i]),
train_loss[i], label=model_names[i])
# clean up the plot
ax1.legend()
ax1.set_xlim([1, max(num_epochs)])
plt.xlabel('Epoch')
plt.ylabel('Training Loss')
# plot the validation loss vs. epoch for each model
ax2 = fig.add_subplot(122)
for i in range(len(all_pickles)):
ax2.plot(np.linspace(1, num_epochs[i], num_epochs[i]),
valid_loss[i], label=model_names[i])
# clean up the plot
ax2.legend()
ax2.set_xlim([1, max(num_epochs)])
plt.xlabel('Epoch')
plt.ylabel('Validation Loss')
plt.show()
```
##### __Question 1:__ Use the plot above to analyze the performance of each of the attempted architectures. Which performs best? Provide an explanation regarding why you think some models perform better than others.
__Answer:__
The following table gives the model performance in ascending order of (best) validation loss.
| Rank | Model | Description | Best Loss |
| -- | -- | -- | -- |
| 1 | 5| 2D CNN + RNN + TimeDistributed Dense | 118.3596 |
| 2 | 3 | Deeper RNN + TimeDistributed Dense | 130.7026 |
| 3 | 2 | CNN + RNN + TimeDistributed Dense | 130.9444 |
| 4 | 1 | RNN + TimeDistributed Dense | 131.8664 |
| 5 | 4 | Bidirectional RNN + TimeDistributed Dense | 138.3626 |
| 6 | 0 | RNN | 721.1129 |
All of the time distributed models perform well, indicating that the time series gives valuable signal (as expected). The models that preprocessed the input with CNNs performed well, but we prone to overfitting. The network with the two-dimensional convolutional layer performed best, indicating that the convolutional layer can produce features beyond what a time series model alone infer. In particular, the frequency dimension has informative patterns that can be mined. Deeper recurrent layers do not seem to add much to performance, as evidenced by the model 3 to model 1 comparison, within the 20-epoch evaluation. Models 3 and 4, with sufficient dropout rates, do seem like they are not prone to overfitting and may perform better with more epochs than the models with convolutional layers. The latter two models both use recurrent layers that are less prone to gradient explosions, possibly why they take longer to train.
The final model combines the best convolutional layer with the bidirectional RNN with time distributed dense layers.
<a id='final'></a>
### (IMPLEMENTATION) Final Model
Now that you've tried out many sample models, use what you've learned to draft your own architecture! While your final acoustic model should not be identical to any of the architectures explored above, you are welcome to merely combine the explored layers above into a deeper architecture. It is **NOT** necessary to include new layer types that were not explored in the notebook.
However, if you would like some ideas for even more layer types, check out these ideas for some additional, optional extensions to your model:
- If you notice your model is overfitting to the training dataset, consider adding **dropout**! To add dropout to [recurrent layers](https://faroit.github.io/keras-docs/1.0.2/layers/recurrent/), pay special attention to the `dropout_W` and `dropout_U` arguments. This [paper](http://arxiv.org/abs/1512.05287) may also provide some interesting theoretical background.
- If you choose to include a convolutional layer in your model, you may get better results by working with **dilated convolutions**. If you choose to use dilated convolutions, make sure that you are able to accurately calculate the length of the acoustic model's output in the `model.output_length` lambda function. You can read more about dilated convolutions in Google's [WaveNet paper](https://arxiv.org/abs/1609.03499). For an example of a speech-to-text system that makes use of dilated convolutions, check out this GitHub [repository](https://github.com/buriburisuri/speech-to-text-wavenet). You can work with dilated convolutions [in Keras](https://keras.io/layers/convolutional/) by paying special attention to the `padding` argument when you specify a convolutional layer.
- If your model makes use of convolutional layers, why not also experiment with adding **max pooling**? Check out [this paper](https://arxiv.org/pdf/1701.02720.pdf) for example architecture that makes use of max pooling in an acoustic model.
- So far, you have experimented with a single bidirectional RNN layer. Consider stacking the bidirectional layers, to produce a [deep bidirectional RNN](https://www.cs.toronto.edu/~graves/asru_2013.pdf)!
All models that you specify in this repository should have `output_length` defined as an attribute. This attribute is a lambda function that maps the (temporal) length of the input acoustic features to the (temporal) length of the output softmax layer. This function is used in the computation of CTC loss; to see this, look at the `add_ctc_loss` function in `train_utils.py`. To see where the `output_length` attribute is defined for the models in the code, take a look at the `sample_models.py` file. You will notice this line of code within most models:
```
model.output_length = lambda x: x
```
The acoustic model that incorporates a convolutional layer (`cnn_rnn_model`) has a line that is a bit different:
```
model.output_length = lambda x: cnn_output_length(
x, kernel_size, conv_border_mode, conv_stride)
```
In the case of models that use purely recurrent layers, the lambda function is the identity function, as the recurrent layers do not modify the (temporal) length of their input tensors. However, convolutional layers are more complicated and require a specialized function (`cnn_output_length` in `sample_models.py`) to determine the temporal length of their output.
You will have to add the `output_length` attribute to your final model before running the code cell below. Feel free to use the `cnn_output_length` function, if it suits your model.
```
# specify the model
model_end = final_model(
input_dim=161,
filters=50,
kernel_size=(11,11),
conv_stride=1,
conv_border_mode='same',
pool_size=(1,5),
units=200,
recur_layers=1,
dropout_rate=0.5)
```
Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_end.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_end.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
```
from keras.optimizers import SGD
train_model(input_to_softmax=model_end,
pickle_path='model_end.pickle',
save_model_path='model_end.h5',
optimizer=SGD(lr=0.05, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=1),
spectrogram=True) # change to False if you would like to use MFCC features
```
__Question 2:__ Describe your final model architecture and your reasoning at each step.
__Answer:__
The final architecture included a two-dimensional convolutional layer followed by a max-pooling layer. The output of the max pooling layer fed into a bi-directional GRU layer, which outputted to a time-distributed dense layer. In total, the network has 2,179,729.
The 2D convolutional and max pooling layers are used to transform the time and frequency matrix into a time and feature matrix input, hopefully producing meaningful distilations of common waveforms. As in the base models in the previous section, the bidirectional GRU allows more flexibility by processing in both directions in time. The latter does not appear to add much improvement over a GRU with comparable parameters.
<a id='step3'></a>
## STEP 3: Obtain Predictions
We have written a function for you to decode the predictions of your acoustic model. To use the function, please execute the code cell below.
```
import numpy as np
from data_generator import AudioGenerator
from keras import backend as K
from utils import int_sequence_to_text
from IPython.display import Audio
def get_predictions(index, partition, input_to_softmax, model_path):
""" Print a model's decoded predictions
Params:
index (int): The example you would like to visualize
partition (str): One of 'train' or 'validation'
input_to_softmax (Model): The acoustic model
model_path (str): Path to saved acoustic model's weights
"""
# load the train and test data
data_gen = AudioGenerator()
data_gen.load_train_data()
data_gen.load_validation_data()
# obtain the true transcription and the audio features
if partition == 'validation':
transcr = data_gen.valid_texts[index]
audio_path = data_gen.valid_audio_paths[index]
data_point = data_gen.normalize(data_gen.featurize(audio_path))
elif partition == 'train':
transcr = data_gen.train_texts[index]
audio_path = data_gen.train_audio_paths[index]
data_point = data_gen.normalize(data_gen.featurize(audio_path))
else:
raise Exception('Invalid partition! Must be "train" or "validation"')
# obtain and decode the acoustic model's predictions
input_to_softmax.load_weights(model_path)
prediction = input_to_softmax.predict(np.expand_dims(data_point, axis=0))
output_length = [input_to_softmax.output_length(data_point.shape[0])]
pred_ints = (K.eval(K.ctc_decode(
prediction, output_length)[0][0])+1).flatten().tolist()
# play the audio file, and display the true and predicted transcriptions
print('-'*80)
Audio(audio_path)
print('True transcription:\n' + '\n' + transcr)
print('-'*80)
print('Predicted transcription:\n' + '\n' + ''.join(int_sequence_to_text(pred_ints)))
print('-'*80)
```
Use the code cell below to obtain the transcription predicted by your final model for the first example in the training dataset.
```
get_predictions(index=0,
partition='train',
input_to_softmax=model_end,
model_path='results/model_end.h5')
```
Use the next code cell to visualize the model's prediction for the first example in the validation dataset.
```
get_predictions(index=0,
partition='validation',
input_to_softmax=model_end,
model_path='results/model_end.h5')
```
One standard way to improve the results of the decoder is to incorporate a language model. We won't pursue this in the notebook, but you are welcome to do so as an _optional extension_.
If you are interested in creating models that provide improved transcriptions, you are encouraged to download [more data](http://www.openslr.org/12/) and train bigger, deeper models. But beware - the model will likely take a long while to train. For instance, training this [state-of-the-art](https://arxiv.org/pdf/1512.02595v1.pdf) model would take 3-6 weeks on a single GPU!
```
!!python -m nbconvert *.ipynb
!!zip submission.zip vui_notebook.ipynb report.html sample_models.py results/*
```
| github_jupyter |
```
# Copyright 2021 NVIDIA Corporation. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================
```
<img src="https://upload.wikimedia.org/wikipedia/en/6/6d/Nvidia_image_logo.svg" style="width: 90px; float: right;">
# QA Inference on BERT using TensorRT
## 1. Overview
Bidirectional Embedding Representations from Transformers (BERT), is a method of pre-training language representations which obtains state-of-the-art results on a wide array of Natural Language Processing (NLP) tasks.
The original paper can be found here: https://arxiv.org/abs/1810.04805.
### 1.a Learning objectives
This notebook demonstrates:
- Inference on Question Answering (QA) task with BERT Base/Large model
- The use fine-tuned NVIDIA BERT models
- Use of BERT model with TRT
## 2. Requirements
Please refer to the ReadMe file
## 3. BERT Inference: Question Answering
We can run inference on a fine-tuned BERT model for tasks like Question Answering.
Here we use a BERT model fine-tuned on a [SQuaD 2.0 Dataset](https://rajpurkar.github.io/SQuAD-explorer/) which contains 100,000+ question-answer pairs on 500+ articles combined with over 50,000 new, unanswerable questions.
### 3.a Paragraph and Queries
The paragraph and the questions can be customized by changing the text below. Note that when using models with small sequence lengths, you should use a shorter paragraph:
#### Paragraph:
```
paragraph_text = "The Apollo program, also known as Project Apollo, was the third United States human spaceflight program carried out by the National Aeronautics and Space Administration (NASA), which accomplished landing the first humans on the Moon from 1969 to 1972. First conceived during Dwight D. Eisenhower's administration as a three-man spacecraft to follow the one-man Project Mercury which put the first Americans in space, Apollo was later dedicated to President John F. Kennedy's national goal of landing a man on the Moon and returning him safely to the Earth by the end of the 1960s, which he proposed in a May 25, 1961, address to Congress. Project Mercury was followed by the two-man Project Gemini. The first manned flight of Apollo was in 1968. Apollo ran from 1961 to 1972, and was supported by the two-man Gemini program which ran concurrently with it from 1962 to 1966. Gemini missions developed some of the space travel techniques that were necessary for the success of the Apollo missions. Apollo used Saturn family rockets as launch vehicles. Apollo/Saturn vehicles were also used for an Apollo Applications Program, which consisted of Skylab, a space station that supported three manned missions in 1973-74, and the Apollo-Soyuz Test Project, a joint Earth orbit mission with the Soviet Union in 1975."
# Short paragraph version for BERT models with max sequence length of 128
short_paragraph_text = "The Apollo program was the third United States human spaceflight program. First conceived as a three-man spacecraft to follow the one-man Project Mercury which put the first Americans in space, Apollo was dedicated to President John F. Kennedy's national goal of landing a man on the Moon. The first manned flight of Apollo was in 1968. Apollo ran from 1961 to 1972 followed by the Apollo-Soyuz Test Project a joint Earth orbit mission with the Soviet Union in 1975."
```
#### Question:
```
question_text = "What project put the first Americans into space?"
#question_text = "What year did the first manned Apollo flight occur?"
#question_text = "What President is credited with the original notion of putting Americans in space?"
#question_text = "Who did the U.S. collaborate with on an Earth orbit mission in 1975?"
```
In this example we ask our BERT model questions related to the following paragraph:
**The Apollo Program**
_"The Apollo program, also known as Project Apollo, was the third United States human spaceflight program carried out by the National Aeronautics and Space Administration (NASA), which accomplished landing the first humans on the Moon from 1969 to 1972. First conceived during Dwight D. Eisenhower's administration as a three-man spacecraft to follow the one-man Project Mercury which put the first Americans in space, Apollo was later dedicated to President John F. Kennedy's national goal of landing a man on the Moon and returning him safely to the Earth by the end of the 1960s, which he proposed in a May 25, 1961, address to Congress. Project Mercury was followed by the two-man Project Gemini. The first manned flight of Apollo was in 1968. Apollo ran from 1961 to 1972, and was supported by the two-man Gemini program which ran concurrently with it from 1962 to 1966. Gemini missions developed some of the space travel techniques that were necessary for the success of the Apollo missions. Apollo used Saturn family rockets as launch vehicles. Apollo/Saturn vehicles were also used for an Apollo Applications Program, which consisted of Skylab, a space station that supported three manned missions in 1973-74, and the Apollo-Soyuz Test Project, a joint Earth orbit mission with the Soviet Union in 1975."_
The questions and relative answers expected are shown below:
- **Q1:** "What project put the first Americans into space?"
- **A1:** "Project Mercury"
- **Q2:** "What program was created to carry out these projects and missions?"
- **A2:** "The Apollo program"
- **Q3:** "What year did the first manned Apollo flight occur?"
- **A3:** "1968"
- **Q4:** "What President is credited with the original notion of putting Americans in space?"
- **A4:** "John F. Kennedy"
- **Q5:** "Who did the U.S. collaborate with on an Earth orbit mission in 1975?"
- **A5:** "Soviet Union"
- **Q6:** "How long did Project Apollo run?"
- **A6:** "1961 to 1972"
- **Q7:** "What program helped develop space travel techniques that Project Apollo used?"
- **A7:** "Gemini Mission"
- **Q8:** "What space station supported three manned missions in 1973-1974?"
- **A8:** "Skylab"
## Data Preprocessing
Let's convert the paragraph and the question to BERT input with the help of the tokenizer:
```
import helpers.data_processing as dp
import helpers.tokenization as tokenization
tokenizer = tokenization.FullTokenizer(vocab_file="/workspace/TensorRT/demo/BERT/models/fine-tuned/bert_tf_ckpt_large_qa_squad2_amp_128_v19.03.1/vocab.txt", do_lower_case=True)
# The maximum number of tokens for the question. Questions longer than this will be truncated to this length.
max_query_length = 64
# When splitting up a long document into chunks, how much stride to take between chunks.
doc_stride = 128
# The maximum total input sequence length after WordPiece tokenization.
# Sequences longer than this will be truncated, and sequences shorter
max_seq_length = 128
# Extract tokens from the paragraph
doc_tokens = dp.convert_doc_tokens(short_paragraph_text)
# Extract features from the paragraph and question
features = dp.convert_example_to_features(doc_tokens, question_text, tokenizer, max_seq_length, doc_stride, max_query_length)
```
## TensorRT Inference
```
import tensorrt as trt
TRT_LOGGER = trt.Logger(trt.Logger.INFO)
import ctypes
import os
ctypes.CDLL("libnvinfer_plugin.so", mode=ctypes.RTLD_GLOBAL)
import pycuda.driver as cuda
import pycuda.autoinit
import collections
import numpy as np
import time
# Load the BERT-Large Engine
with open("/workspace/TensorRT/demo/BERT/engines/bert_large_128.engine", "rb") as f, \
trt.Runtime(TRT_LOGGER) as runtime, \
runtime.deserialize_cuda_engine(f.read()) as engine, \
engine.create_execution_context() as context:
# We always use batch size 1.
input_shape = (1, max_seq_length)
input_nbytes = trt.volume(input_shape) * trt.int32.itemsize
# Allocate device memory for inputs.
d_inputs = [cuda.mem_alloc(input_nbytes) for binding in range(3)]
# Create a stream in which to copy inputs/outputs and run inference.
stream = cuda.Stream()
# Specify input shapes. These must be within the min/max bounds of the active profile (0th profile in this case)
# Note that input shapes can be specified on a per-inference basis, but in this case, we only have a single shape.
for binding in range(3):
context.set_binding_shape(binding, input_shape)
assert context.all_binding_shapes_specified
# Allocate output buffer by querying the size from the context. This may be different for different input shapes.
h_output = cuda.pagelocked_empty(tuple(context.get_binding_shape(3)), dtype=np.float32)
d_output = cuda.mem_alloc(h_output.nbytes)
print("\nRunning Inference...")
_NetworkOutput = collections.namedtuple( # pylint: disable=invalid-name
"NetworkOutput",
["start_logits", "end_logits", "feature_index"])
networkOutputs = []
eval_time_elapsed = 0
for feature_index, feature in enumerate(features):
# Copy inputs
input_ids = cuda.register_host_memory(np.ascontiguousarray(feature.input_ids.ravel()))
segment_ids = cuda.register_host_memory(np.ascontiguousarray(feature.segment_ids.ravel()))
input_mask = cuda.register_host_memory(np.ascontiguousarray(feature.input_mask.ravel()))
eval_start_time = time.time()
cuda.memcpy_htod_async(d_inputs[0], input_ids, stream)
cuda.memcpy_htod_async(d_inputs[1], segment_ids, stream)
cuda.memcpy_htod_async(d_inputs[2], input_mask, stream)
# Run inference
context.execute_async_v2(bindings=[int(d_inp) for d_inp in d_inputs] + [int(d_output)], stream_handle=stream.handle)
# Synchronize the stream
stream.synchronize()
eval_time_elapsed += (time.time() - eval_start_time)
# Transfer predictions back from GPU
cuda.memcpy_dtoh_async(h_output, d_output, stream)
stream.synchronize()
for index, batch in enumerate(h_output):
# Data Post-processing
networkOutputs.append(_NetworkOutput(
start_logits = np.array(batch.squeeze()[:, 0]),
end_logits = np.array(batch.squeeze()[:, 1]),
feature_index = feature_index
))
eval_time_elapsed /= len(features)
print("-----------------------------")
print("Running Inference at {:.3f} Sentences/Sec".format(1.0/eval_time_elapsed))
print("-----------------------------")
```
## Data Post-Processing
Now that we have the inference results let's extract the actual answer to our question
```
# The total number of n-best predictions to generate in the nbest_predictions.json output file
n_best_size = 20
# The maximum length of an answer that can be generated. This is needed
# because the start and end predictions are not conditioned on one another
max_answer_length = 30
prediction, nbest_json, scores_diff_json = dp.get_predictions(doc_tokens, features,
networkOutputs, n_best_size, max_answer_length)
for index, output in enumerate(networkOutputs):
print("Processing output")
print("Answer: '{}'".format(prediction))
print("with prob: {:.3f}%".format(nbest_json[0]['probability'] * 100.0))
```
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# X is the 10 X 10 Hilbert Matrix
X = 1. / (np.arange(1, 11) + np.arange(0,10)[:, np.newaxis])
y = np.ones(10)
print(X.shape)
X
# Compute paths
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
coefs = []
for a in alphas:
ridge = linear_model.Ridge(alpha= a, fit_intercept= False)
# print(ridge)
ridge.fit(X,y)
coefs.append(ridge.coef_)
# Display Results
plt.figure(figsize=(10,8))
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title("Ridge coefficient as a function of the regularization")
plt.axis('tight')
plt.show()
```
# Outliers Impact
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
import pandas as pd
```
## Linear Regression
```
from sklearn.linear_model import LinearRegression
np.random.seed(42)
n_samples = 100
rng = np.random.randn(n_samples) * 10
print("Feeature shape: ", rng.shape)
y_gen = 0.5 * rng + 2 * np.random.randn(n_samples)
print("\nTarget shape: ", y_gen.shape)
lr = LinearRegression()
lr.fit(rng.reshape(-1, 1), y_gen)
model_pred = lr.predict(rng.reshape(-1, 1))
# plotting
plt.figure(figsize= (10, 8));
plt.scatter(rng, y_gen);
plt.plot(rng, model_pred);
print("Coefficient Estimate: ", lr.coef_);
idx= rng.argmax()
y_gen[idx] = 200
plt.figure(figsize=(10, 8));
plt.scatter(rng, y_gen);
o_lr = LinearRegression(normalize= True)
o_lr.fit(rng.reshape(-1, 1), y_gen)
o_model_pred = o_lr.predict(rng.reshape(-1, 1))
plt.scatter(rng, y_gen);
plt.plot(rng, o_model_pred)
print("Coefficient Estimate: ", o_lr.coef_)
```
## Ridge Regression
```
from sklearn.linear_model import Ridge
ridge_mod = Ridge(alpha= 1, normalize= True)
ridge_mod.fit(rng.reshape(-1, 1), y_gen)
ridge_mod_pred = ridge_mod.predict(rng.reshape(-1,1))
plt.figure(figsize=(10,8))
plt.scatter(rng, y_gen);
plt.plot(rng, ridge_mod_pred);
print("Coefficient of Estimation: ", ridge_mod.coef_)
# ridge_mod_pred
```
# Lasso Regression
```
from sklearn.linear_model import Lasso
# define model
lasso_mod = Lasso(alpha= 0.4, normalize= True)
lasso_mod.fit(rng.reshape(-1, 1), y_gen) # (features, target)
lasso_mod_pred = lasso_mod.predict(rng.reshape(-1,1)) # (features)
# plotting
plt.figure(figsize=(10, 8));
plt.scatter(rng, y_gen); # (features, target)
plt.plot(rng, lasso_mod_pred); # (features, prediction)
print("Coefficient Estimation: ", lasso_mod.coef_) # coefficent change by the rate of alpha
```
# Elastic Net Regression
```
from sklearn.linear_model import ElasticNet
# defining model and prediction
elnet_mod = ElasticNet(alpha= 0.02, normalize= True)
elnet_mod.fit(rng.reshape(-1, 1), y_gen)
elnet_pred = elnet_mod.predict(rng.reshape(-1,1))
# plotting
plt.figure(figsize=(10, 8));
plt.scatter(rng, y_gen);
plt.plot(rng, elnet_pred);
print("Coefficent Estimation: ", elnet_mod.coef_)
```
| github_jupyter |

# Add Column using Expression
With Azure ML Data Prep you can add a new column to data with `Dataflow.add_column` by using a Data Prep expression to calculate the value from existing columns. This is similar to using Python to create a [new script column](./custom-python-transforms.ipynb#New-Script-Column) except the Data Prep expressions are more limited and will execute faster. The expressions used are the same as for [filtering rows](./filtering.ipynb#Filtering-rows) and hence have the same functions and operators available.
<p>
Here we add additional columns. First we get input data.
```
import azureml.dataprep as dprep
# loading data
dflow = dprep.auto_read_file('../data/crime-spring.csv')
dflow.head(5)
```
#### `substring(start, length)`
Add a new column "Case Category" using the `substring(start, length)` expression to extract the prefix from the "Case Number" column.
```
case_category = dflow.add_column(new_column_name='Case Category',
prior_column='Case Number',
expression=dflow['Case Number'].substring(0, 2))
case_category.head(5)
```
#### `substring(start)`
Add a new column "Case Id" using the `substring(start)` expression to extract just the number from "Case Number" column and then convert it to numeric.
```
case_id = dflow.add_column(new_column_name='Case Id',
prior_column='Case Number',
expression=dflow['Case Number'].substring(2))
case_id = case_id.to_number('Case Id')
case_id.head(5)
```
#### `length()`
Using the length() expression, add a new numeric column "Length", which contains the length of the string in "Primary Type".
```
dflow_length = dflow.add_column(new_column_name='Length',
prior_column='Primary Type',
expression=dflow['Primary Type'].length())
dflow_length.head(5)
```
#### `to_upper()`
Using the to_upper() expression, add a new numeric column "Upper Case", which contains the string in "Primary Type" in upper case.
```
dflow_to_upper = dflow.add_column(new_column_name='Upper Case',
prior_column='Primary Type',
expression=dflow['Primary Type'].to_upper())
dflow_to_upper.head(5)
```
#### `to_lower()`
Using the to_lower() expression, add a new numeric column "Lower Case", which contains the string in "Primary Type" in lower case.
```
dflow_to_lower = dflow.add_column(new_column_name='Lower Case',
prior_column='Primary Type',
expression=dflow['Primary Type'].to_lower())
dflow_to_lower.head(5)
```
#### `col(column1) + col(column2)`
Add a new column "Total" to show the result of adding the values in the "FBI Code" column to the "Community Area" column.
```
dflow_total = dflow.add_column(new_column_name='Total',
prior_column='FBI Code',
expression=dflow['Community Area']+dflow['FBI Code'])
dflow_total.head(5)
```
#### `col(column1) - col(column2)`
Add a new column "Subtract" to show the result of subtracting the values in the "FBI Code" column from the "Community Area" column.
```
dflow_diff = dflow.add_column(new_column_name='Difference',
prior_column='FBI Code',
expression=dflow['Community Area']-dflow['FBI Code'])
dflow_diff.head(5)
```
#### `col(column1) * col(column2)`
Add a new column "Product" to show the result of multiplying the values in the "FBI Code" column to the "Community Area" column.
```
dflow_prod = dflow.add_column(new_column_name='Product',
prior_column='FBI Code',
expression=dflow['Community Area']*dflow['FBI Code'])
dflow_prod.head(5)
```
#### `col(column1) / col(column2)`
Add a new column "True Quotient" to show the result of true (decimal) division of the values in "Community Area" column by the "FBI Code" column.
```
dflow_true_div = dflow.add_column(new_column_name='True Quotient',
prior_column='FBI Code',
expression=dflow['Community Area']/dflow['FBI Code'])
dflow_true_div.head(5)
```
#### `col(column1) // col(column2)`
Add a new column "Floor Quotient" to show the result of floor (integer) division of the values in "Community Area" column by the "FBI Code" column.
```
dflow_floor_div = dflow.add_column(new_column_name='Floor Quotient',
prior_column='FBI Code',
expression=dflow['Community Area']//dflow['FBI Code'])
dflow_floor_div.head(5)
```
#### `col(column1) % col(column2)`
Add a new column "Mod" to show the result of applying the modulo operation on the "FBI Code" column and the "Community Area" column.
```
dflow_mod = dflow.add_column(new_column_name='Mod',
prior_column='FBI Code',
expression=dflow['Community Area']%dflow['FBI Code'])
dflow_mod.head(5)
```
#### `col(column1) ** col(column2)`
Add a new column "Power" to show the result of applying the exponentiation operation when the base is the "Community Area" column and the exponent is "FBI Code" column.
```
dflow_pow = dflow.add_column(new_column_name='Power',
prior_column='FBI Code',
expression=dflow['Community Area']**dflow['FBI Code'])
dflow_pow.head(5)
```
| github_jupyter |
# Purpose: A basic object identification package for the lab to use
*Step 1: import packages*
```
import os.path as op
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#Sci-kit Image Imports
from skimage import io
from skimage import filters
from skimage.feature import canny
from skimage import measure
from scipy import ndimage as ndi
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
```
*Step 2: User Inputs*
```
file_location = '../../31.2_DG_quant.tif'
plot_name = 'practice2.png'
channel_1_color = 'Blue'
channel_2_color = 'Green'
```
*Step 3: Read the image into the notebook*
```
#Read in the file
im = io.imread(file_location)
#Convert image to numpy array
imarray = np.array(im)
#Checking the image shape
imarray.shape
```
*Step 4: Color Split*
```
channel_1 = im[0, :, :]
channel_2 = im[1, :, :]
```
*Step 5: Visualization Check*
```
fig = plt.figure()
ax1 = fig.add_subplot(2,2,1)
ax1.set_title(channel_1_color)
ax1.imshow(channel_1, cmap='gray')
ax2 = fig.add_subplot(2,2,2)
ax2.set_title(channel_2_color)
ax2.imshow(channel_2, cmap='gray')
fig.set_size_inches(10.5, 10.5, forward=True)
```
*Step 6: Apply a Threshold*
```
threshold_local = filters.threshold_otsu(channel_1)
binary_c1 = channel_1 > threshold_local
threshold_local = filters.threshold_otsu(channel_2)
binary_c2 = channel_2 > threshold_local
fig = plt.figure()
ax1 = fig.add_subplot(2,2,1)
ax1.set_title(str(channel_1_color + ' Threshold'))
ax1.imshow(binary_c1, cmap='gray')
ax2 = fig.add_subplot(2,2,2)
ax2.set_title(str(channel_2_color + ' Threshold'))
ax2.imshow(binary_c2, cmap='gray')
fig.set_size_inches(10.5, 10.5, forward=True)
```
*Step 7: Fill in Objects*
```
filled_c1 = ndi.binary_fill_holes(binary_c1)
filled_c2 = ndi.binary_fill_holes(binary_c2)
```
*Step 8: Visualization Check*
```
fig = plt.figure()
ax1 = fig.add_subplot(2,2,1)
ax1.set_title(str(channel_1_color + ' Filled'))
ax1.imshow(filled_c1, cmap='gray')
ax2 = fig.add_subplot(2,2,2)
ax2.set_title(str(channel_2_color + ' Filled'))
ax2.imshow(filled_c2, cmap='gray')
fig.set_size_inches(10.5, 10.5, forward=True)
```
*Step 9: Labeling Objects*
```
label_objects1, nb_labels1 = ndi.label(filled_c1)
sizes1 = np.bincount(label_objects1.ravel())
mask_sizes1 = sizes1 > 100
mask_sizes1[0] = 0
cells_cleaned_c1 = mask_sizes1[label_objects1]
label_objects2, nb_labels2 = ndi.label(filled_c2)
sizes2 = np.bincount(label_objects2.ravel())
mask_sizes2 = sizes2 > 100
mask_sizes2[0] = 0
cells_cleaned_c2 = mask_sizes2[label_objects2]
labeled_c1, _ = ndi.label(cells_cleaned_c1)
labeled_c2, _ = ndi.label(cells_cleaned_c2)
```
*Step 10: Visualization Check*
```
fig = plt.figure()
ax1 = fig.add_subplot(2,2,1)
ax1.set_title(str(channel_1_color + ' Labeled'))
ax1.imshow(labeled_c1)
ax2 = fig.add_subplot(2,2,2)
ax2.set_title(str(channel_2_color + ' Labeled'))
ax2.imshow(labeled_c2)
fig.set_size_inches(10.5, 10.5, forward=True)
```
*Step 11: Get Region Props*
```
regionprops_c1 = measure.regionprops(labeled_c1)
regionprops_c2 = measure.regionprops(labeled_c2)
df = pd.DataFrame(columns=['centroid x', 'centroid y','equiv_diam'])
k = 1
for props in regionprops_c1:
#Get the properties that I need for areas
#Add them into a pandas dataframe that has the same number of rows as objects detected
#
centroid = props.centroid
centroid_x = centroid[0]
centroid_y = centroid[1]
equiv_diam = props.equivalent_diameter
df.loc[k] = [centroid_x, centroid_y, equiv_diam]
k = k + 1
df2 = pd.DataFrame(columns=['centroid x', 'centroid y','equiv_diam'])
k = 1
for props in regionprops_c2:
#Get the properties that I need for areas
#Add them into a pandas dataframe that has the same number of rows as objects detected
#
centroid = props.centroid
centroid_x = centroid[0]
centroid_y = centroid[1]
equiv_diam = props.equivalent_diameter
df2.loc[k] = [centroid_x, centroid_y, equiv_diam]
k = k + 1
count_c1 = df.shape[0]
print('Count ' + channel_1_color + ': ' + str(count_c1))
count_c2 = df2.shape[0]
print('Count ' + channel_2_color + ': ' + str(count_c2))
```
| github_jupyter |
```
from __future__ import print_function, unicode_literals, absolute_import, division
import sys
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from glob import glob
from tqdm import tqdm
from tifffile import imread
from csbdeep.utils import Path, normalize
from stardist import fill_label_holes, random_label_cmap, calculate_extents, gputools_available
from stardist.models import Config2D, StarDist2D, StarDistData2D
np.random.seed(42)
lbl_cmap = random_label_cmap()
```
# Data
We assume that data has already been downloaded via notebook [1_data.ipynb](1_data.ipynb).
<div class="alert alert-block alert-info">
Training data (for input `X` with associated label masks `Y`) can be provided via lists of numpy arrays, where each image can have a different size. Alternatively, a single numpy array can also be used if all images have the same size.
Input images can either be two-dimensional (single-channel) or three-dimensional (multi-channel) arrays, where the channel axis comes last. Label images need to be integer-valued.
</div>
```
X = sorted(glob('data/dsb2018/train/images/*.tif'))
Y = sorted(glob('data/dsb2018/train/masks/*.tif'))
assert all(Path(x).name==Path(y).name for x,y in zip(X,Y))
X = list(map(imread,X))
Y = list(map(imread,Y))
n_channel = 1 if X[0].ndim == 2 else X[0].shape[-1]
```
Normalize images and fill small label holes.
```
axis_norm = (0,1) # normalize channels independently
# axis_norm = (0,1,2) # normalize channels jointly
if n_channel > 1:
print("Normalizing image channels %s." % ('jointly' if axis_norm is None or 2 in axis_norm else 'independently'))
sys.stdout.flush()
X = [normalize(x,1,99.8,axis=axis_norm) for x in tqdm(X)]
Y = [fill_label_holes(y) for y in tqdm(Y)]
```
Split into train and validation datasets.
```
assert len(X) > 1, "not enough training data"
rng = np.random.RandomState(42)
ind = rng.permutation(len(X))
n_val = max(1, int(round(0.15 * len(ind))))
ind_train, ind_val = ind[:-n_val], ind[-n_val:]
X_val, Y_val = [X[i] for i in ind_val] , [Y[i] for i in ind_val]
X_trn, Y_trn = [X[i] for i in ind_train], [Y[i] for i in ind_train]
print('number of images: %3d' % len(X))
print('- training: %3d' % len(X_trn))
print('- validation: %3d' % len(X_val))
```
Training data consists of pairs of input image and label instances.
```
i = min(9, len(X)-1)
img, lbl = X[i], Y[i]
assert img.ndim in (2,3)
img = img if img.ndim==2 else img[...,:3]
plt.figure(figsize=(16,10))
plt.subplot(121); plt.imshow(img,cmap='gray'); plt.axis('off'); plt.title('Raw image')
plt.subplot(122); plt.imshow(lbl,cmap=lbl_cmap); plt.axis('off'); plt.title('GT labels')
None;
```
# Configuration
A `StarDist2D` model is specified via a `Config2D` object.
```
print(Config2D.__doc__)
# 32 is a good default choice (see 1_data.ipynb)
n_rays = 32
# Use OpenCL-based computations for data generator during training (requires 'gputools')
use_gpu = False and gputools_available()
# Predict on subsampled grid for increased efficiency and larger field of view
grid = (2,2)
conf = Config2D (
n_rays = n_rays,
grid = grid,
use_gpu = use_gpu,
n_channel_in = n_channel,
)
print(conf)
vars(conf)
if use_gpu:
from csbdeep.utils.tf import limit_gpu_memory
# adjust as necessary: limit GPU memory to be used by TensorFlow to leave some to OpenCL-based computations
limit_gpu_memory(0.8)
```
**Note:** The trained `StarDist2D` model will *not* predict completed shapes for partially visible objects at the image boundary if `train_shape_completion=False` (which is the default option).
```
model = StarDist2D(conf, name='stardist', basedir='models')
```
Check if the neural network has a large enough field of view to see up to the boundary of most objects.
```
median_size = calculate_extents(list(Y), np.median)
fov = np.array(model._axes_tile_overlap('YX'))
if any(median_size > fov):
print("WARNING: median object size larger than field of view of the neural network.")
```
# Training
You can define a function/callable that applies augmentation to each batch of the data generator.
```
augmenter = None
# def augmenter(X_batch, Y_batch):
# """Augmentation for data batch.
# X_batch is a list of input images (length at most batch_size)
# Y_batch is the corresponding list of ground-truth label images
# """
# # ...
# return X_batch, Y_batch
```
We recommend to monitor the progress during training with [TensorBoard](https://www.tensorflow.org/programmers_guide/summaries_and_tensorboard). You can start it in the shell from the current working directory like this:
$ tensorboard --logdir=.
Then connect to [http://localhost:6006/](http://localhost:6006/) with your browser.
```
quick_demo = True
if quick_demo:
print (
"NOTE: This is only for a quick demonstration!\n"
" Please set the variable 'quick_demo = False' for proper (long) training.",
file=sys.stderr, flush=True
)
model.train(X_trn, Y_trn, validation_data=(X_val,Y_val), augmenter=augmenter,
epochs=2, steps_per_epoch=10)
print("====> Stopping training and loading previously trained demo model from disk.", file=sys.stderr, flush=True)
model = StarDist2D(None, name='2D_demo', basedir='../../models/examples')
model.basedir = None # to prevent files of the demo model to be overwritten (not needed for your model)
else:
model.train(X_trn, Y_trn, validation_data=(X_val,Y_val), augmenter=augmenter)
None;
```
# Threshold optimization
While the default values for the probability and non-maximum suppression thresholds already yield good results in many cases, we still recommend to adapt the thresholds to your data. The optimized threshold values are saved to disk and will be automatically loaded with the model.
```
model.optimize_thresholds(X_val, Y_val)
```
| github_jupyter |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Datasets/Vectors/landsat_wrs2_grid.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Vectors/landsat_wrs2_grid.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Datasets/Vectors/landsat_wrs2_grid.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Vectors/landsat_wrs2_grid.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
dataset = ee.FeatureCollection('projects/google/wrs2_descending')
empty = ee.Image().byte()
Map.setCenter(-78, 36, 8)
Map.addLayer(empty.paint(dataset, 0, 2), {}, 'Landsat WRS-2 grid')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| github_jupyter |
```
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# set random seed for comparing the two result calculations
tf.set_random_seed(1)
# this is data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
# hyperparameters
lr = 0.001
training_iters = 100000
batch_size = 128
n_inputs = 28 # MNIST data input (img shape: 28*28)
n_steps = 28 # time steps
n_hidden_units = 128 # neurons in hidden layer
n_classes = 10 # MNIST classes (0-9 digits)
num_layers=2
# tf Graph input
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_classes])
# Define weights
weights = {
# (28, 128)
'in': tf.Variable(tf.random_normal([n_inputs, n_hidden_units])),
# (128, 10)
'out': tf.Variable(tf.random_normal([n_hidden_units, n_classes]))
}
biases = {
# (128, )
'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_units, ])),
# (10, )
'out': tf.Variable(tf.constant(0.1, shape=[n_classes, ]))
}
print ("parameters ready")
# tf Graph input
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_classes])
# Define weights
weights = {
# (28, 128)
'in': tf.Variable(tf.random_normal([n_inputs, n_hidden_units])),
# (128, 10)
'out': tf.Variable(tf.random_normal([n_hidden_units, n_classes]))
}
biases = {
# (128, )
'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_units, ])),
# (10, )
'out': tf.Variable(tf.constant(0.1, shape=[n_classes, ]))
}
def RNN(X, weights, biases):
# hidden layer for input to cell
########################################
# transpose the inputs shape from
# X ==> (128 batch * 28 steps, 28 inputs)
X = tf.reshape(X, [-1, n_inputs])
# into hidden
# X_in = (128 batch * 28 steps, 128 hidden)
X_in = tf.matmul(X, weights['in']) + biases['in']
# X_in ==> (128 batch, 28 steps, 128 hidden)
X_in = tf.reshape(X_in, [-1, n_steps, n_hidden_units])
# cell
##########################################
# basic LSTM Cell.
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_units, forget_bias=1.0, state_is_tuple=True)
cell = tf.nn.rnn_cell.DropoutWrapper(cell, output_keep_prob=0.5)
cell = tf.nn.rnn_cell.MultiRNNCell([cell] * num_layers)
else:
cell = tf.contrib.rnn.BasicLSTMCell(n_hidden_units)
cell = tf.contrib.rnn.DropoutWrapper(cell, output_keep_prob=0.5)
cell = tf.contrib.rnn.MultiRNNCell([cell] * num_layers)
# lstm cell is divided into two parts (c_state, h_state)
init_state = cell.zero_state(batch_size, dtype=tf.float32)
# You have 2 options for following step.
# 1: tf.nn.rnn(cell, inputs);
# 2: tf.nn.dynamic_rnn(cell, inputs).
# If use option 1, you have to modified the shape of X_in, go and check out this:
# https://github.com/aymericdamien/TensorFlow-Examples/blob/master/examples/3_NeuralNetworks/recurrent_network.py
# In here, we go for option 2.
# dynamic_rnn receive Tensor (batch, steps, inputs) or (steps, batch, inputs) as X_in.
# Make sure the time_major is changed accordingly.
outputs, final_state = tf.nn.dynamic_rnn(cell, X_in, initial_state=init_state, time_major=False)
# hidden layer for output as the final results
#############################################
# results = tf.matmul(final_state[1], weights['out']) + biases['out']
# # or
# unpack to list [(batch, outputs)..] * steps
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
outputs = tf.unpack(tf.transpose(outputs, [1, 0, 2])) # states is the last outputs
else:
outputs = tf.unstack(tf.transpose(outputs, [1,0,2]))
results = tf.matmul(outputs[-1], weights['out']) + biases['out'] # shape = (128, 10)
return results
pred = RNN(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
train_op = tf.train.AdamOptimizer(lr).minimize(cost)
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
print ("Network ready")
with tf.Session() as sess:
# tf.initialize_all_variables() no long valid from
# 2017-03-02 if using tensorflow >= 0.12
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
init = tf.initialize_all_variables()
else:
init = tf.global_variables_initializer()
sess.run(init)
step = 0
while step * batch_size < training_iters:
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
batch_xs = batch_xs.reshape([batch_size, n_steps, n_inputs])
_, acc, loss=sess.run([train_op,accuracy,cost], feed_dict={
x: batch_xs,
y: batch_ys,
})
if step % 20 == 0:
print ("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
step += 1
```
| github_jupyter |
This notebook shows:
* How to launch the [**StarGANv1**](https://arxiv.org/abs/1711.09020) model for inference
* Example of results for both
* attrubutes **detection**
* new face **generation** with desired attributes
Here I use [**PyTorch** implementation](https://github.com/yunjey/stargan) of the StarGANv1 model.
[StarGANv1](https://arxiv.org/abs/1711.09020) was chosen because:
* It provides an ability to generate images **contitionally**. One can control the "amount" of each desired feature via input vector.
* It can **train (relatively) fast** on (relatively) small resources.
The model is pretty old though and has its own drawbacks:
* It works well only with small resolution images (~128).
* For bigger images the artifacts are inavoidable. They sometimes happen even for 128x128 images.
The obvious improvement is to use newer model, e.g., [StarGANv2](https://arxiv.org/abs/1912.01865) which was released in April 2020. It generates much better images at much higher resolution. But it requires both huge resoruces and lots of time to train.
Prior to running this notebook please download the pretrained models:
```
../scripts/get_models.sh
```
# Imports
Imort necessary libraries
```
import os
import sys
os.environ["KMP_DUPLICATE_LIB_OK"] = "True"
sys.path.extend(["../code/", "../stargan/"])
import torch
import torchvision.transforms as T
from PIL import Image
import matplotlib.pyplot as plt
from config import get_config
from solver import Solver
```
# Load model
Let's first load the config for the model. It is mostly default except for the:
* model checkpoint path
* style classes, their order and number
Note that in the original StarGANv1 model 5 classes are used: `[Black_Hair Blond_Hair Brown_Hair Male Young]`.
I retrained the model **4** times for different **face parts**. Each face part has several classes connected to it (see `DataExploration` notebook):
* **nose**: `[Big_Nose, Pointy_Nose]`
* **mouth**: `[Mouth_Slightly_Open, Smiling]`
* **eyes**: `[Arched_Eyebrows, Bushy_Eyebrows, Bags_Under_Eyes, Eyeglasses, Narrow_Eyes]`
* **hair**: `[Black_Hair, Blond_Hair, Brown_Hair, Gray_Hair, Bald Bangs, Receding_Hairline, Straight_Hair, Wavy_Hair]`
Here I show the examples only for **eyes** class. But all other classes works in the same way and prediction examples are shown in the repo and in other notebooks.
```
config = get_config("""
--model_save_dir ../models/celeba_128_eyes/
--test_iters 200000
--c_dim 5
--selected_attrs Arched_Eyebrows Bushy_Eyebrows Bags_Under_Eyes Eyeglasses Narrow_Eyes
""")
```
Load the model architecture with the provided config.
```
model = Solver(None, None, config)
```
Restore model weights.
```
model.restore_model(model.test_iters)
```
# Prediction example
Let's read a test image.
Note that the **face position and size** should be comparable to what the model has seen in the training data (CelebA). Here I do not use any face detector and crop the faces manually. But in production environment one needs to setup the face detector correspondingly.
```
image = Image.open("../data/test.jpg")
image
```
The input to the network is **3x128x128 image in a range [-1; 1]** (note that the channels is the first dimension).
Thus one need to do preprocessing in advance.
```
transform = []
transform.append(T.Resize(128))
transform.append(T.CenterCrop(128))
transform.append(T.ToTensor())
transform.append(T.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5)))
transform = T.Compose(transform)
```
Create a batch of 1 image
```
x_real = torch.stack([transform(image)])
x_real.shape
```
## Attributes prediction
Let's first predict the attbibutes of the image. To do so I use the **Discriminator** part of the network. In StarGAN architecture it predicts not only the fake/real label but also the classes/attributes/styles of the image.
Here I call this vector **eigen style vector**. Note that due to the possible co-existence of multiple labels and the corresponding training procedure (Sigmoid + BCELoss instead of Softmax + CrossEntropyLoss) I use sigmoid activation function here and treat predicted labels separately (instead of softmax and 1-of-all).
```
with torch.no_grad():
eigen_style_vector = torch.sigmoid(model.D(x_real)[1])
```
Below is the probability of each label. The photo indeed depicts a person with big and little bit arched eyebrows.
```
for proba, tag in zip(eigen_style_vector.numpy()[0], model.selected_attrs):
print(f"{tag:20s}: {proba:.3f}")
```
Now let's look at how well the **Generator** model can recreate the face without altering it using the just computed eigen style vector.
```
with torch.no_grad():
res_eigen = model.G(x_real, eigen_style_vector)
res_eigen.shape
```
Plot the original face and the reconstructed one:
```
plt.figure(figsize=(9, 8))
plt.subplot(121)
_img = model.denorm(x_real).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Original", fontsize=16)
plt.subplot(122)
_img = model.denorm(res_eigen).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Eigen style reconstruction", fontsize=16);
```
Looks good enough.
## Face modification using new attributes
Now let's try to modify the face starting from the eigen style vector.
Let's say, I want to **add eyeglasses**. To do so I am to set the corresponding style vector component to 1.
```
eigen_style_vector_modified_1 = eigen_style_vector.clone()
eigen_style_vector_modified_1[:, 3] = 1
```
Now the style vector looks the following:
```
for proba, tag in zip(eigen_style_vector_modified_1.numpy()[0], model.selected_attrs):
print(f"{tag:20s}: {proba:.3f}")
```
Let's try to generate face with this modified style vector:
```
with torch.no_grad():
res_modified_1 = model.G(x_real, eigen_style_vector_modified_1)
res_modified_1.shape
```
Plot the faces:
```
plt.figure(figsize=(13.5, 8))
plt.subplot(131)
_img = model.denorm(x_real).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Original", fontsize=16)
plt.subplot(132)
_img = model.denorm(res_eigen).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Eigen style reconstruction", fontsize=16);
plt.subplot(133)
_img = model.denorm(res_modified_1).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Eyeglasses", fontsize=16);
```
Now let's try to **change two attributes simultaneously**:
* Make the eyes narrow
* Add archness to the eyebrows
```
eigen_style_vector_modified_2 = eigen_style_vector.clone()
eigen_style_vector_modified_2[:, 0] = 1
eigen_style_vector_modified_2[:, 4] = 1
```
Now the style vector looks the following:
```
for proba, tag in zip(eigen_style_vector_modified_2.numpy()[0], model.selected_attrs):
print(f"{tag:20s}: {proba:.3f}")
```
Let's try to generate face with this modified style vector:
```
with torch.no_grad():
res_modified_2 = model.G(x_real, eigen_style_vector_modified_2)
res_modified_2.shape
```
Plot the faces:
```
plt.figure(figsize=(18, 8))
plt.subplot(141)
_img = model.denorm(x_real).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Original", fontsize=16)
plt.subplot(142)
_img = model.denorm(res_eigen).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Eigen style reconstruction", fontsize=16);
plt.subplot(143)
_img = model.denorm(res_modified_1).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Eyeglasses", fontsize=16);
plt.subplot(144)
_img = model.denorm(res_modified_2).numpy()[0].transpose((1, 2, 0))
plt.imshow(_img)
plt.axis("off")
plt.title("Arched eyebrows + Narrow", fontsize=16);
```
Looks good!
| github_jupyter |
```
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.tree import export_text
```
This example uses the [Universal Bank](https://www.kaggle.com/sriharipramod/bank-loan-classification) data set and some example code of running classification trees from chapter 9 of [Data Mining for Business Analytics](https://www.dataminingbook.com/book/python-edition)
> The data include customer demographic information (age, income, etc.), the customer's relationship with the bank (mortgage, securities account, etc.), and the customer response to the last personal loan campaign (Personal Loan). Among these 5000 customers, only 480 (= 9.6%) accepted the personal loan that was offered to them in the earlier campaign
[Source](https://www.kaggle.com/itsmesunil/campaign-for-selling-personal-loans)
1. Train a decision tree classifier, print the tree and evaluate its accuracy.
2. Prune the tree by changing its hyper parameters, evaluate the accuracy of the new tree.
3. Using [grid search](https://scikit-learn.org/stable/modules/grid_search.html), perform a systematic tuning of the decision tree hyper parameters.
```
data = pd.read_csv('data/UniversalBank.csv')
data.head()
```
```
bank_df = data.drop(columns=['ID', 'ZIP Code'])
X = bank_df.drop(columns=['Personal Loan'])
y = bank_df['Personal Loan']
train_X, valid_X, train_y, valid_y = train_test_split(X, y, test_size=0.4, random_state=1)
dtree = DecisionTreeClassifier()
dtree.fit(train_X, train_y)
print(export_text(dtree, feature_names=list(X.columns)))
print(confusion_matrix(train_y, dtree.predict(train_X)))
print(confusion_matrix(valid_y, dtree.predict(valid_X)))
accuracy_score(train_y, dtree.predict(train_X)), accuracy_score(valid_y, dtree.predict(valid_X))
dtree = DecisionTreeClassifier(max_depth=30, min_samples_split=20, min_impurity_decrease=0.01)
dtree.fit(train_X, train_y)
print(export_text(dtree, feature_names=list(X.columns)))
print(confusion_matrix(train_y, dtree.predict(train_X)))
print(confusion_matrix(valid_y, dtree.predict(valid_X)))
accuracy_score(train_y, dtree.predict(train_X)), accuracy_score(valid_y, dtree.predict(valid_X))
# Start with an initial guess for parameters
param_grid = {
'max_depth': [10, 20, 30, 40],
'min_samples_split': [20, 40, 60, 80, 100],
'min_impurity_decrease': [0, 0.0005, 0.001, 0.005, 0.01],
}
gridSearch = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5, n_jobs=-1)
gridSearch.fit(train_X, train_y)
print('Score: ', gridSearch.best_score_)
print('Parameters: ', gridSearch.best_params_)
dtree = gridSearch.best_estimator_
print(confusion_matrix(train_y, dtree.predict(train_X)))
print(confusion_matrix(valid_y, dtree.predict(valid_X)))
accuracy_score(train_y, dtree.predict(train_X)), accuracy_score(valid_y, dtree.predict(valid_X))
print(export_text(dtree, feature_names=list(X.columns)))
```
| github_jupyter |
# Data Set-up and Cleaning
```
# Standard Library Imports
import pandas as pd
import numpy as np
```
For this section, I will be concatenating all the data sets into one large dataset.
### Load the datasets
```
inpatient = pd.read_csv('./data/Train_Inpatientdata-1542865627584.csv')
outpatient = pd.read_csv('./data/Train_Outpatientdata-1542865627584.csv')
beneficiary = pd.read_csv('./data/Train_Beneficiarydata-1542865627584.csv')
fraud = pd.read_csv('./data/Train-1542865627584.csv')
# Increase the max display options of the columns and rows
pd.set_option('display.max_columns', 100)
```
### Inspect the first 5 rows of the datasets
```
# Inspect the first 5 rows of the inpatient claims
inpatient.head()
# Inspect the first 5 rows of the outpatient claims
outpatient.head()
# Inspect the first 5 rows of the beneficiary dataset
beneficiary.head()
# Inspect the first 5 rows of the fraud column
fraud.head()
```
### Check the number of rows and columns for each dataset
```
inpatient.shape
outpatient.shape
beneficiary.shape
fraud.shape
```
Some columns in the inpatient dataset are not in the outpatient dataset or in the fraud (target) dataset and vice versa. In order to make sense of the data I would have to merge them together.
### Combine the Inpatient, Outpatient, beneficiary and fraud datasets
```
# Map the inpatient and outpatient columns, 1 for outpatient, 0 for inpatient
inpatient["IsOutpatient"] = 0
outpatient["IsOutpatient"] = 1
# Merging the datasets together
patient_df = pd.concat([inpatient, outpatient],axis = 0)
patient_df = patient_df.merge(beneficiary, how = 'left', on = 'BeneID').merge(fraud, how = 'left', on = 'Provider')
print("The shape of the dataset after merging is:", patient_df.shape)
# Inspect the final dataset after merging
patient_df.head()
```
After merging the dataset, we now have a dataframe with the fraud target column.
```
patient_df.describe()
patient_df.dtypes
# Convert columns with Date attributes to Datetime datatype : "ClaimStartDt", "ClaimEndDt", "AdmissionDt", "DischargeDt", "DOB", "DOD"
patient_df[["ClaimStartDt", "ClaimEndDt", "AdmissionDt", "DischargeDt", "DOB", "DOD"]] = patient_df[["ClaimStartDt", "ClaimEndDt", "AdmissionDt", "DischargeDt", "DOB", "DOD"]].apply(pd.to_datetime, format = '%Y-%m-%d', errors = 'coerce')
# Convert the Claims Procedure Code columns to object just as the Claims diagnoses code
patient_df.loc[:, patient_df.columns.str.contains('ClmProcedureCode')] = patient_df.loc[:, patient_df.columns.str.contains('ClmProcedureCode')].astype(object)
# Convert Race, County and State to objects
patient_df[['Race', 'State', 'County' ]] = patient_df[['Race', 'State', 'County']].astype(object)
# Investigate the RenalDiseasIndicator
patient_df['RenalDiseaseIndicator'].value_counts()
# Replace 'Y' with 1 in RenalDiseaseIndicator
patient_df['RenalDiseaseIndicator'] = patient_df['RenalDiseaseIndicator'].replace({'Y': 1})
# Check to see if replacement worked
patient_df['RenalDiseaseIndicator'].value_counts()
```
### Change other binary variables to 0 and 1
```
# Change the Gender column and any column having 'ChronicCond' to binary variables to 0 and 1
chronic = patient_df.columns[patient_df.columns.str.contains("ChronicCond")].tolist()
patient_df[chronic] = patient_df[chronic].apply(lambda x: np.where(x == 2,0,1))
patient_df['Gender'] = patient_df['Gender'].apply(lambda x: np.where(x == 2,0,1))
# Check to see if it changed
patient_df['Gender'].value_counts()
# Checking the change
patient_df['ChronicCond_Alzheimer'].value_counts()
# Check the data types again
patient_df.dtypes
# Save the data as 'patients'
patient_df.to_csv('./data/patients.csv', index=False)
patient_df.to_pickle('./data/patients.pkl')
```
| github_jupyter |
# Understanding the data
In this first part, we load the data and perform some initial exploration on it. The main goal of this step is to acquire some basic knowledge about the data, how the various features are distributed, if there are missing values in it and so on.
```
### imports
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# load hourly data
hourly_data = pd.read_csv('../data/hour.csv')
```
Check data format, number of missing values in the data and general statistics:
```
# print some generic statistics about the data
print(f"Shape of data: {hourly_data.shape}")
print(f"Number of missing values in the data: {hourly_data.isnull().sum().sum()}")
# get statistics on the numerical columns
hourly_data.describe().T
# create a copy of the original data
preprocessed_data = hourly_data.copy()
# tranform seasons
seasons_mapping = {1: 'winter', 2: 'spring', 3: 'summer', 4: 'fall'}
preprocessed_data['season'] = preprocessed_data['season'].apply(lambda x: seasons_mapping[x])
# transform yr
yr_mapping = {0: 2011, 1: 2012}
preprocessed_data['yr'] = preprocessed_data['yr'].apply(lambda x: yr_mapping[x])
# transform weekday
weekday_mapping = {0: 'Sunday', 1: 'Monday', 2: 'Tuesday', 3: 'Wednesday', 4: 'Thursday', 5: 'Friday', 6: 'Saturday'}
preprocessed_data['weekday'] = preprocessed_data['weekday'].apply(lambda x: weekday_mapping[x])
# transform weathersit
weather_mapping = {1: 'clear', 2: 'cloudy', 3: 'light_rain_snow', 4: 'heavy_rain_snow'}
preprocessed_data['weathersit'] = preprocessed_data['weathersit'].apply(lambda x: weather_mapping[x])
# transorm hum and windspeed
preprocessed_data['hum'] = preprocessed_data['hum']*100
preprocessed_data['windspeed'] = preprocessed_data['windspeed']*67
# visualize preprocessed columns
cols = ['season', 'yr', 'weekday', 'weathersit', 'hum', 'windspeed']
preprocessed_data[cols].sample(10, random_state=123)
```
### Registered vs casual use analysis
```
# assert that total numer of rides is equal to the sum of registered and casual ones
assert (preprocessed_data.casual + preprocessed_data.registered == preprocessed_data.cnt).all(), \
'Sum of casual and registered rides not equal to total number of rides'
# plot distributions of registered vs casual rides
sns.distplot(preprocessed_data['registered'], label='registered')
sns.distplot(preprocessed_data['casual'], label='casual')
plt.legend()
plt.xlabel('rides')
plt.ylabel("frequency")
plt.title("Rides distributions")
plt.savefig('figs/rides_distributions.png', format='png')
# plot evolution of rides over time
plot_data = preprocessed_data[['registered', 'casual', 'dteday']]
ax = plot_data.groupby('dteday').sum().plot(figsize=(10,6))
ax.set_xlabel("time");
ax.set_ylabel("number of rides per day");
plt.savefig('figs/rides_daily.png', format='png')
# create new dataframe with necessary for plotting columns, and
# obtain number of rides per day, by grouping over each day
plot_data = preprocessed_data[['registered', 'casual', 'dteday']]
plot_data = plot_data.groupby('dteday').sum()
# define window for computing the rolling mean and standard deviation
window = 7
rolling_means = plot_data.rolling(window).mean()
rolling_deviations = plot_data.rolling(window).std()
# create a plot of the series, where we first plot the series of rolling means,
# then we color the zone between the series of rolling means
# +- 2 rolling standard deviations
ax = rolling_means.plot(figsize=(10,6))
ax.fill_between(rolling_means.index, \
rolling_means['registered'] + 2*rolling_deviations['registered'], \
rolling_means['registered'] - 2*rolling_deviations['registered'], \
alpha = 0.2)
ax.fill_between(rolling_means.index, \
rolling_means['casual'] + 2*rolling_deviations['casual'], \
rolling_means['casual'] - 2*rolling_deviations['casual'], \
alpha = 0.2)
ax.set_xlabel("time");
ax.set_ylabel("number of rides per day");
plt.savefig('figs/rides_aggregated.png', format='png')
# select relevant columns
plot_data = preprocessed_data[['hr', 'weekday', 'registered', 'casual']]
# transform the data into a format, in number of entries are computed as count,
# for each distinct hr, weekday and type (registered or casual)
plot_data = plot_data.melt(id_vars=['hr', 'weekday'], var_name='type', value_name='count')
# create FacetGrid object, in which a grid plot is produced.
# As columns, we have the various days of the week,
# as rows, the different types (registered and casual)
grid = sns.FacetGrid(plot_data, row='weekday', col='type', height=2.5,\
aspect=2.5, row_order=['Monday', 'Tuesday', \
'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday'])
# populate the FacetGrid with the specific plots
grid.map(sns.barplot, 'hr', 'count', alpha=0.5)
grid.savefig('figs/weekday_hour_distributions.png', format='png')
# select subset of the data
plot_data = preprocessed_data[['hr', 'season', 'registered', 'casual']]
# unpivot data from wide to long format
plot_data = plot_data.melt(id_vars=['hr', 'season'], var_name='type', \
value_name='count')
# define FacetGrid
grid = sns.FacetGrid(plot_data, row='season', \
col='type', height=2.5, aspect=2.5, \
row_order=['winter', 'spring', 'summer', 'fall'])
# apply plotting function to each element in the grid
grid.map(sns.barplot, 'hr', 'count', alpha=0.5)
# save figure
grid.savefig('figs/exercise_1_02_a.png', format='png')
plot_data = preprocessed_data[['weekday', 'season', 'registered', 'casual']]
plot_data = plot_data.melt(id_vars=['weekday', 'season'], var_name='type', value_name='count')
grid = sns.FacetGrid(plot_data, row='season', col='type', height=2.5, aspect=2.5,
row_order=['winter', 'spring', 'summer', 'fall'])
grid.map(sns.barplot, 'weekday', 'count', alpha=0.5,
order=['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday'])
# save figure
grid.savefig('figs/exercise_1_02_b.png', format='png')
```
Exercise 1.03: Estimating average registered rides
```
# compute population mean of registered rides
population_mean = preprocessed_data.registered.mean()
# get sample of the data (summer 2011)
sample = preprocessed_data[(preprocessed_data.season == "summer") &\
(preprocessed_data.yr == 2011)].registered
# perform t-test and compute p-value
from scipy.stats import ttest_1samp
test_result = ttest_1samp(sample, population_mean)
print(f"Test statistic: {test_result[0]:.03f}, p-value: {test_result[1]:.03f}")
# get sample as 5% of the full data
import random
random.seed(111)
sample_unbiased = preprocessed_data.registered.sample(frac=0.05)
test_result_unbiased = ttest_1samp(sample_unbiased, population_mean)
print(f"Unbiased test statistic: {test_result_unbiased[0]:.03f}, p-value: {test_result_unbiased[1]:.03f}")
```
| github_jupyter |
# Finetuning of the pretrained Japanese BERT model
Finetune the pretrained model to solve multi-class classification problems.
This notebook requires the following objects:
- trained sentencepiece model (model and vocab files)
- pretraiend Japanese BERT model
Dataset is livedoor ニュースコーパス in https://www.rondhuit.com/download.html.
We make test:dev:train = 2:2:6 datasets.
Results:
- Full training data
- BERT with SentencePiece
```
precision recall f1-score support
dokujo-tsushin 0.98 0.94 0.96 178
it-life-hack 0.96 0.97 0.96 172
kaden-channel 0.99 0.98 0.99 176
livedoor-homme 0.98 0.88 0.93 95
movie-enter 0.96 0.99 0.98 158
peachy 0.94 0.98 0.96 174
smax 0.98 0.99 0.99 167
sports-watch 0.98 1.00 0.99 190
topic-news 0.99 0.98 0.98 163
micro avg 0.97 0.97 0.97 1473
macro avg 0.97 0.97 0.97 1473
weighted avg 0.97 0.97 0.97 1473
```
- sklearn GradientBoostingClassifier with MeCab
```
precision recall f1-score support
dokujo-tsushin 0.89 0.86 0.88 178
it-life-hack 0.91 0.90 0.91 172
kaden-channel 0.90 0.94 0.92 176
livedoor-homme 0.79 0.74 0.76 95
movie-enter 0.93 0.96 0.95 158
peachy 0.87 0.92 0.89 174
smax 0.99 1.00 1.00 167
sports-watch 0.93 0.98 0.96 190
topic-news 0.96 0.86 0.91 163
micro avg 0.92 0.92 0.92 1473
macro avg 0.91 0.91 0.91 1473
weighted avg 0.92 0.92 0.91 1473
```
- Small training data (1/5 of full training data)
- BERT with SentencePiece
```
precision recall f1-score support
dokujo-tsushin 0.97 0.87 0.92 178
it-life-hack 0.86 0.86 0.86 172
kaden-channel 0.95 0.94 0.95 176
livedoor-homme 0.82 0.82 0.82 95
movie-enter 0.97 0.99 0.98 158
peachy 0.89 0.95 0.92 174
smax 0.94 0.96 0.95 167
sports-watch 0.97 0.97 0.97 190
topic-news 0.94 0.94 0.94 163
micro avg 0.93 0.93 0.93 1473
macro avg 0.92 0.92 0.92 1473
weighted avg 0.93 0.93 0.93 1473
```
- sklearn GradientBoostingClassifier with MeCab
```
precision recall f1-score support
dokujo-tsushin 0.82 0.71 0.76 178
it-life-hack 0.86 0.88 0.87 172
kaden-channel 0.91 0.87 0.89 176
livedoor-homme 0.67 0.63 0.65 95
movie-enter 0.87 0.95 0.91 158
peachy 0.70 0.78 0.73 174
smax 1.00 1.00 1.00 167
sports-watch 0.87 0.95 0.91 190
topic-news 0.92 0.82 0.87 163
micro avg 0.85 0.85 0.85 1473
macro avg 0.85 0.84 0.84 1473
weighted avg 0.86 0.85 0.85 1473
```
```
import configparser
import glob
import os
import pandas as pd
import subprocess
import sys
import tarfile
from urllib.request import urlretrieve
CURDIR = os.getcwd()
CONFIGPATH = os.path.join(CURDIR, os.pardir, 'config.ini')
config = configparser.ConfigParser()
config.read(CONFIGPATH)
```
## Data preparing
You need execute the following cells just once.
```
FILEURL = config['FINETUNING-DATA']['FILEURL']
FILEPATH = config['FINETUNING-DATA']['FILEPATH']
EXTRACTDIR = config['FINETUNING-DATA']['TEXTDIR']
```
Download and unzip data.
```
%%time
urlretrieve(FILEURL, FILEPATH)
mode = "r:gz"
tar = tarfile.open(FILEPATH, mode)
tar.extractall(EXTRACTDIR)
tar.close()
```
Data preprocessing.
```
def extract_txt(filename):
with open(filename) as text_file:
# 0: URL, 1: timestamp
text = text_file.readlines()[2:]
text = [sentence.strip() for sentence in text]
text = list(filter(lambda line: line != '', text))
return ''.join(text)
categories = [
name for name
in os.listdir( os.path.join(EXTRACTDIR, "text") )
if os.path.isdir( os.path.join(EXTRACTDIR, "text", name) ) ]
categories = sorted(categories)
categories
table = str.maketrans({
'\n': '',
'\t': ' ',
'\r': '',
})
%%time
all_text = []
all_label = []
for cat in categories:
files = glob.glob(os.path.join(EXTRACTDIR, "text", cat, "{}*.txt".format(cat)))
files = sorted(files)
body = [ extract_txt(elem).translate(table) for elem in files ]
label = [cat] * len(body)
all_text.extend(body)
all_label.extend(label)
df = pd.DataFrame({'text' : all_text, 'label' : all_label})
df.head()
df = df.sample(frac=1, random_state=23).reset_index(drop=True)
df.head()
```
Save data as tsv files.
test:dev:train = 2:2:6. To check the usability of finetuning, we also prepare sampled training data (1/5 of full training data).
```
df[:len(df) // 5].to_csv( os.path.join(EXTRACTDIR, "test.tsv"), sep='\t', index=False)
df[len(df) // 5:len(df)*2 // 5].to_csv( os.path.join(EXTRACTDIR, "dev.tsv"), sep='\t', index=False)
df[len(df)*2 // 5:].to_csv( os.path.join(EXTRACTDIR, "train.tsv"), sep='\t', index=False)
### 1/5 of full training data.
# df[:len(df) // 5].to_csv( os.path.join(EXTRACTDIR, "test.tsv"), sep='\t', index=False)
# df[len(df) // 5:len(df)*2 // 5].to_csv( os.path.join(EXTRACTDIR, "dev.tsv"), sep='\t', index=False)
# df[len(df)*2 // 5:].sample(frac=0.2, random_state=23).to_csv( os.path.join(EXTRACTDIR, "train.tsv"), sep='\t', index=False)
```
## Finetune pre-trained model
It will take a lot of hours to execute the following cells on CPU environment.
You can also use colab to recieve the power of TPU. You need to uplode the created data onto your GCS bucket.
[](https://colab.research.google.com/drive/1zZH2GWe0U-7GjJ2w2duodFfEUptvHjcx)
```
PRETRAINED_MODEL_PATH = '../model/model.ckpt-1400000'
FINETUNE_OUTPUT_DIR = '../model/livedoor_output'
%%time
# It will take many hours on CPU environment.
!python3 ../src/run_classifier.py \
--task_name=livedoor \
--do_train=true \
--do_eval=true \
--data_dir=../data/livedoor \
--model_file=../model/wiki-ja.model \
--vocab_file=../model/wiki-ja.vocab \
--init_checkpoint={PRETRAINED_MODEL_PATH} \
--max_seq_length=512 \
--train_batch_size=4 \
--learning_rate=2e-5 \
--num_train_epochs=10 \
--output_dir={FINETUNE_OUTPUT_DIR}
```
## Predict using the finetuned model
Let's predict test data using the finetuned model.
```
import sys
sys.path.append("../src")
import tokenization_sentencepiece as tokenization
from run_classifier import LivedoorProcessor
from run_classifier import model_fn_builder
from run_classifier import file_based_input_fn_builder
from run_classifier import file_based_convert_examples_to_features
from utils import str_to_value
sys.path.append("../bert")
import modeling
import optimization
import tensorflow as tf
import configparser
import json
import glob
import os
import pandas as pd
import tempfile
bert_config_file = tempfile.NamedTemporaryFile(mode='w+t', encoding='utf-8', suffix='.json')
bert_config_file.write(json.dumps({k:str_to_value(v) for k,v in config['BERT-CONFIG'].items()}))
bert_config_file.seek(0)
bert_config = modeling.BertConfig.from_json_file(bert_config_file.name)
output_ckpts = glob.glob("{}/model.ckpt*data*".format(FINETUNE_OUTPUT_DIR))
latest_ckpt = sorted(output_ckpts)[-1]
FINETUNED_MODEL_PATH = latest_ckpt.split('.data-00000-of-00001')[0]
class FLAGS(object):
'''Parameters.'''
def __init__(self):
self.model_file = "../model/wiki-ja.model"
self.vocab_file = "../model/wiki-ja.vocab"
self.do_lower_case = True
self.use_tpu = False
self.output_dir = "/dummy"
self.data_dir = "../data/livedoor"
self.max_seq_length = 512
self.init_checkpoint = FINETUNED_MODEL_PATH
self.predict_batch_size = 4
# The following parameters are not used in predictions.
# Just use to create RunConfig.
self.master = None
self.save_checkpoints_steps = 1
self.iterations_per_loop = 1
self.num_tpu_cores = 1
self.learning_rate = 0
self.num_warmup_steps = 0
self.num_train_steps = 0
self.train_batch_size = 0
self.eval_batch_size = 0
FLAGS = FLAGS()
processor = LivedoorProcessor()
label_list = processor.get_labels()
tokenizer = tokenization.FullTokenizer(
model_file=FLAGS.model_file, vocab_file=FLAGS.vocab_file,
do_lower_case=FLAGS.do_lower_case)
tpu_cluster_resolver = None
is_per_host = tf.contrib.tpu.InputPipelineConfig.PER_HOST_V2
run_config = tf.contrib.tpu.RunConfig(
cluster=tpu_cluster_resolver,
master=FLAGS.master,
model_dir=FLAGS.output_dir,
save_checkpoints_steps=FLAGS.save_checkpoints_steps,
tpu_config=tf.contrib.tpu.TPUConfig(
iterations_per_loop=FLAGS.iterations_per_loop,
num_shards=FLAGS.num_tpu_cores,
per_host_input_for_training=is_per_host))
model_fn = model_fn_builder(
bert_config=bert_config,
num_labels=len(label_list),
init_checkpoint=FLAGS.init_checkpoint,
learning_rate=FLAGS.learning_rate,
num_train_steps=FLAGS.num_train_steps,
num_warmup_steps=FLAGS.num_warmup_steps,
use_tpu=FLAGS.use_tpu,
use_one_hot_embeddings=FLAGS.use_tpu)
estimator = tf.contrib.tpu.TPUEstimator(
use_tpu=FLAGS.use_tpu,
model_fn=model_fn,
config=run_config,
train_batch_size=FLAGS.train_batch_size,
eval_batch_size=FLAGS.eval_batch_size,
predict_batch_size=FLAGS.predict_batch_size)
predict_examples = processor.get_test_examples(FLAGS.data_dir)
predict_file = tempfile.NamedTemporaryFile(mode='w+t', encoding='utf-8', suffix='.tf_record')
file_based_convert_examples_to_features(predict_examples, label_list,
FLAGS.max_seq_length, tokenizer,
predict_file.name)
predict_drop_remainder = True if FLAGS.use_tpu else False
predict_input_fn = file_based_input_fn_builder(
input_file=predict_file.name,
seq_length=FLAGS.max_seq_length,
is_training=False,
drop_remainder=predict_drop_remainder)
result = estimator.predict(input_fn=predict_input_fn)
%%time
# It will take a few hours on CPU environment.
result = list(result)
result[:2]
```
Read test data set and add prediction results.
```
import pandas as pd
test_df = pd.read_csv("../data/livedoor/test.tsv", sep='\t')
test_df['predict'] = [ label_list[elem['probabilities'].argmax()] for elem in result ]
test_df.head()
sum( test_df['label'] == test_df['predict'] ) / len(test_df)
```
A littel more detailed check using `sklearn.metrics`.
```
!pip install scikit-learn
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
print(classification_report(test_df['label'], test_df['predict']))
print(confusion_matrix(test_df['label'], test_df['predict']))
```
### Simple baseline model.
```
import pandas as pd
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
train_df = pd.read_csv("../data/livedoor/train.tsv", sep='\t')
dev_df = pd.read_csv("../data/livedoor/dev.tsv", sep='\t')
test_df = pd.read_csv("../data/livedoor/test.tsv", sep='\t')
!apt-get install -q -y mecab libmecab-dev mecab-ipadic mecab-ipadic-utf8
!pip install mecab-python3==0.7
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.ensemble import GradientBoostingClassifier
import MeCab
m = MeCab.Tagger("-Owakati")
train_dev_df = pd.concat([train_df, dev_df])
train_dev_xs = train_dev_df['text'].apply(lambda x: m.parse(x))
train_dev_ys = train_dev_df['label']
test_xs = test_df['text'].apply(lambda x: m.parse(x))
test_ys = test_df['label']
vectorizer = TfidfVectorizer(max_features=750)
train_dev_xs_ = vectorizer.fit_transform(train_dev_xs)
test_xs_ = vectorizer.transform(test_xs)
```
The following set up is not exactly identical to that of BERT because inside Classifier it uses `train_test_split` with shuffle.
In addition, parameters are not well tuned, however, we think it's enough to check the power of BERT.
```
%%time
model = GradientBoostingClassifier(n_estimators=200,
validation_fraction=len(train_df)/len(dev_df),
n_iter_no_change=5,
tol=0.01,
random_state=23)
### 1/5 of full training data.
# model = GradientBoostingClassifier(n_estimators=200,
# validation_fraction=len(dev_df)/len(train_df),
# n_iter_no_change=5,
# tol=0.01,
# random_state=23)
model.fit(train_dev_xs_, train_dev_ys)
print(classification_report(test_ys, model.predict(test_xs_)))
print(confusion_matrix(test_ys, model.predict(test_xs_)))
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from PIL import Image
import os
from sklearn.model_selection import train_test_split
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPool2D, Dense, Flatten, Dropout
from sklearn.metrics import accuracy_score
from tensorflow.keras import callbacks
data = []
labels = []
classes = 43
cur_path = os.getcwd()
for i in range(classes):
path = os.path.join(cur_path, 'data/Train', str(i))
# print(path)
images = os.listdir(path)
for a in images:
try:
image = Image.open(path + '\\' + a)
image = image.resize((30, 30))
image = np.array(image)
#sim = Image.fromarray(image)
data.append(image)
labels.append(i)
except:
print("Error loading image")
data = np.array(data)
labels = np.array(labels)
print(data.shape)
print (labels.shape)
X_train, X_test, y_train, y_test = train_test_split(data, labels, test_size=0.2, random_state=42)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
y_train = to_categorical(y_train, 43)
y_test = to_categorical(y_test, 43)
print(y_train[1])
# Build a CNN model
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(5,5), activation='relu', input_shape=X_train.shape[1:]))
model.add(Conv2D(filters=32, kernel_size=(5,5), activation='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(rate=0.25))
model.add(Conv2D(filters=64, kernel_size=(3,3), activation='relu'))
model.add(Conv2D(filters=64, kernel_size=(3,3), activation='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(rate=0.25))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(rate=0.5))
model.add(Dense(43, activation='softmax'))
# Compile the model
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# Train and validate the model
epochs = 15
history = model.fit(X_train, y_train, batch_size=32, epochs=epochs, validation_split=0.2)
# Plot accuracy and loss
plt.figure(0)
plt.plot(history.history['accuracy'], label='training accuracy')
plt.plot(history.history['val_accuracy'], label='val accuracy')
plt.title('Accuracy')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend()
plt.figure(1)
plt.plot(history.history['loss'], label='training loss')
plt.plot(history.history['val_loss'], label='val loss')
plt.title('Loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend()
y_test = pd.read_csv('data/Test.csv')
labels = y_test['ClassId'].values
imgs = y_test['Path'].values
data=[]
for img in imgs:
path = 'data/'+img
image = Image.open(path)
image = image.resize((30, 30))
data.append(np.array(image))
X_test = np.array(data)
# pred = model.predict_classes(X_test) - depricated
pred = np.argmax(model.predict(X_test), axis=-1)
accuracy_score(labels, pred)
model.save('traffic_classifier.h5')
```
| github_jupyter |
```
import json
import math
import numpy as np
import openrtdynamics2.lang as dy
import openrtdynamics2.targets as tg
from vehicle_lib.vehicle_lib import *
# load track data
with open("track_data/simple_track.json", "r") as read_file:
track_data = json.load(read_file)
#
# Demo: a vehicle controlled to follow a given path
#
# Implemented using the code generator openrtdynamics 2 - https://pypi.org/project/openrtdynamics2/ .
# This generates c++ code for Web Assembly to be run within the browser.
#
system = dy.enter_system()
velocity = dy.system_input( dy.DataTypeFloat64(1), name='velocity', default_value=6.0, value_range=[0, 25], title="vehicle velocity")
max_lateral_velocity = dy.system_input( dy.DataTypeFloat64(1), name='max_lateral_velocity', default_value=1.0, value_range=[0, 4.0], title="maximal lateral velocity")
max_lateral_accleration = dy.system_input( dy.DataTypeFloat64(1), name='max_lateral_accleration', default_value=2.0, value_range=[1.0, 4.0], title="maximal lateral acceleration")
# parameters
wheelbase = 3.0
# sampling time
Ts = 0.01
# create storage for the reference path:
path = import_path_data(track_data)
# create placeholders for the plant output signals
x = dy.signal()
y = dy.signal()
psi = dy.signal()
# track the evolution of the closest point on the path to the vehicles position
projection = track_projection_on_path(path, x, y)
d_star = projection['d_star'] # the distance parameter of the path describing the closest point to the vehicle
x_r = projection['x_r'] # (x_r, y_r) the projected vehicle position on the path
y_r = projection['y_r']
psi_rr = projection['psi_r'] # the orientation angle (tangent of the path)
K_r = projection['K_r'] # the curvature of the path
Delta_l = projection['Delta_l'] # the lateral distance between vehicle and path
#
# project the vehicle velocity onto the path yielding v_star
#
# Used formula inside project_velocity_on_path:
# v_star = d d_star / dt = v * cos( Delta_u ) / ( 1 - Delta_l * K(d_star) )
#
Delta_u = dy.signal() # feedback from control
v_star = project_velocity_on_path(velocity, Delta_u, Delta_l, K_r)
dy.append_output(v_star, 'v_star')
#
# compute an enhanced (less noise) signal for the path orientation psi_r by integrating the
# curvature profile and fusing the result with psi_rr to mitigate the integration drift.
#
psi_r, psi_r_dot = compute_path_orientation_from_curvature( Ts, v_star, psi_rr, K_r, L=1.0 )
dy.append_output(psi_rr, 'psi_rr')
dy.append_output(psi_r_dot, 'psi_r_dot')
#
# lateral open-loop control to realize an 'obstacle-avoiding maneuver'
#
# the dynamic model for the lateral distance Delta_l is
#
# d/dt Delta_l = u,
#
# meaning u is the lateral velocity to which is used to control the lateral
# distance to the path.
#
# generate a velocity profile
u_move_left = dy.signal_step( dy.int32(50) ) - dy.signal_step( dy.int32(200) )
u_move_right = dy.signal_step( dy.int32(500) ) - dy.signal_step( dy.int32(350) )
# apply a rate limiter to limit the acceleration
u = dy.rate_limit( max_lateral_velocity * (u_move_left + u_move_right), Ts, dy.float64(-1) * max_lateral_accleration, max_lateral_accleration)
dy.append_output(u, 'u')
# internal lateral model (to verify the lateral dynamics of the simulated vehicle)
Delta_l_mdl = dy.euler_integrator(u, Ts)
dy.append_output(Delta_l_mdl, 'Delta_l_mdl')
#
# path tracking control
#
# Control of the lateral distance to the path can be performed via the augmented control
# variable u.
#
# Herein, a linearization yielding the resulting lateral dynamics u --> Delta_l : 1/s is applied.
#
Delta_u << dy.asin( dy.saturate(u / velocity, -0.99, 0.99) )
delta_star = psi_r - psi
delta = delta_star + Delta_u
delta = dy.unwrap_angle(angle=delta, normalize_around_zero = True)
dy.append_output(Delta_u, 'Delta_u')
dy.append_output(delta_star, 'delta_star')
#
# The model of the vehicle including a disturbance
#
# steering angle limit
delta = dy.saturate(u=delta, lower_limit=-math.pi/2.0, upper_limit=math.pi/2.0)
# the model of the vehicle
x_, y_, psi_, x_dot, y_dot, psi_dot = discrete_time_bicycle_model(delta, velocity, Ts, wheelbase)
# close the feedback loops
x << x_
y << y_
psi << psi_
#
# outputs: these are available for visualization in the html set-up
#
dy.append_output(x, 'x')
dy.append_output(y, 'y')
dy.append_output(psi, 'psi')
dy.append_output(delta, 'steering')
dy.append_output(x_r, 'x_r')
dy.append_output(y_r, 'y_r')
dy.append_output(psi_r, 'psi_r')
dy.append_output(Delta_l, 'Delta_l')
# generate code for Web Assembly (wasm), requires emcc (emscripten) to build
code_gen_results = dy.generate_code(template=tg.TargetCppWASM(), folder="generated/path_following_lateral_dynamics", build=True)
#
dy.clear()
import IPython
IPython.display.IFrame(src='../vehicle_control_tutorial/path_following_lateral_dynamics.html', width='100%', height=1000)
```
| github_jupyter |
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Mixed precision
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/guide/mixed_precision"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/guide/mixed_precision.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/guide/mixed_precision.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/mixed_precision.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Overview
Mixed precision is the use of both 16-bit and 32-bit floating-point types in a model during training to make it run faster and use less memory. By keeping certain parts of the model in the 32-bit types for numeric stability, the model will have a lower step time and train equally as well in terms of the evaluation metrics such as accuracy. This guide describes how to use the experimental Keras mixed precision API to speed up your models. Using this API can improve performance by more than 3 times on modern GPUs and 60% on TPUs.
Note: The Keras mixed precision API is currently experimental and may change.
Today, most models use the float32 dtype, which takes 32 bits of memory. However, there are two lower-precision dtypes, float16 and bfloat16, each which take 16 bits of memory instead. Modern accelerators can run operations faster in the 16-bit dtypes, as they have specialized hardware to run 16-bit computations and 16-bit dtypes can be read from memory faster.
NVIDIA GPUs can run operations in float16 faster than in float32, and TPUs can run operations in bfloat16 faster than float32. Therefore, these lower-precision dtypes should be used whenever possible on those devices. However, variables and a few computations should still be in float32 for numeric reasons so that the model trains to the same quality. The Keras mixed precision API allows you to use a mix of either float16 or bfloat16 with float32, to get the performance benefits from float16/bfloat16 and the numeric stability benefits from float32.
Note: In this guide, the term "numeric stability" refers to how a model's quality is affected by the use of a lower-precision dtype instead of a higher precision dtype. We say an operation is "numerically unstable" in float16 or bfloat16 if running it in one of those dtypes causes the model to have worse evaluation accuracy or other metrics compared to running the operation in float32.
## Setup
The Keras mixed precision API is available in TensorFlow 2.1.
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.mixed_precision import experimental as mixed_precision
```
## Supported hardware
While mixed precision will run on most hardware, it will only speed up models on recent NVIDIA GPUs and Cloud TPUs. NVIDIA GPUs support using a mix of float16 and float32, while TPUs support a mix of bfloat16 and float32.
Among NVIDIA GPUs, those with compute capability 7.0 or higher will see the greatest performance benefit from mixed precision because they have special hardware units, called Tensor Cores, to accelerate float16 matrix multiplications and convolutions. Older GPUs offer no math performance benefit for using mixed precision, however memory and bandwidth savings can enable some speedups. You can look up the compute capability for your GPU at NVIDIA's [CUDA GPU web page](https://developer.nvidia.com/cuda-gpus). Examples of GPUs that will benefit most from mixed precision include RTX GPUs, the Titan V, and the V100.
Note: If running this guide in Google Colab, the GPU runtime typically has a P100 connected. The P100 has compute capability 6.0 and is not expected to show a significant speedup.
You can check your GPU type with the following. The command only exists if the
NVIDIA drivers are installed, so the following will raise an error otherwise.
```
!nvidia-smi -L
```
All Cloud TPUs support bfloat16.
Even on CPUs and older GPUs, where no speedup is expected, mixed precision APIs can still be used for unit testing, debugging, or just to try out the API.
## Setting the dtype policy
To use mixed precision in Keras, you need to create a `tf.keras.mixed_precision.experimental.Policy`, typically referred to as a *dtype policy*. Dtype policies specify the dtypes layers will run in. In this guide, you will construct a policy from the string `'mixed_float16'` and set it as the global policy. This will will cause subsequently created layers to use mixed precision with a mix of float16 and float32.
```
policy = mixed_precision.Policy('mixed_float16')
mixed_precision.set_policy(policy)
```
The policy specifies two important aspects of a layer: the dtype the layer's computations are done in, and the dtype of a layer's variables. Above, you created a `mixed_float16` policy (i.e., a `mixed_precision.Policy` created by passing the string `'mixed_float16'` to its constructor). With this policy, layers use float16 computations and float32 variables. Computations are done in float16 for performance, but variables must be kept in float32 for numeric stability. You can directly query these properties of the policy.
```
print('Compute dtype: %s' % policy.compute_dtype)
print('Variable dtype: %s' % policy.variable_dtype)
```
As mentioned before, the `mixed_float16` policy will most significantly improve performance on NVIDIA GPUs with compute capability of at least 7.0. The policy will run on other GPUs and CPUs but may not improve performance. For TPUs, the `mixed_bfloat16` policy should be used instead.
## Building the model
Next, let's start building a simple model. Very small toy models typically do not benefit from mixed precision, because overhead from the TensorFlow runtime typically dominates the execution time, making any performance improvement on the GPU negligible. Therefore, let's build two large `Dense` layers with 4096 units each if a GPU is used.
```
inputs = keras.Input(shape=(784,), name='digits')
if tf.config.list_physical_devices('GPU'):
print('The model will run with 4096 units on a GPU')
num_units = 4096
else:
# Use fewer units on CPUs so the model finishes in a reasonable amount of time
print('The model will run with 64 units on a CPU')
num_units = 64
dense1 = layers.Dense(num_units, activation='relu', name='dense_1')
x = dense1(inputs)
dense2 = layers.Dense(num_units, activation='relu', name='dense_2')
x = dense2(x)
```
Each layer has a policy and uses the global policy by default. Each of the `Dense` layers therefore have the `mixed_float16` policy because you set the global policy to `mixed_float16` previously. This will cause the dense layers to do float16 computations and have float32 variables. They cast their inputs to float16 in order to do float16 computations, which causes their outputs to be float16 as a result. Their variables are float32 and will be cast to float16 when the layers are called to avoid errors from dtype mismatches.
```
print('x.dtype: %s' % x.dtype.name)
# 'kernel' is dense1's variable
print('dense1.kernel.dtype: %s' % dense1.kernel.dtype.name)
```
Next, create the output predictions. Normally, you can create the output predictions as follows, but this is not always numerically stable with float16.
```
# INCORRECT: softmax and model output will be float16, when it should be float32
outputs = layers.Dense(10, activation='softmax', name='predictions')(x)
print('Outputs dtype: %s' % outputs.dtype.name)
```
A softmax activation at the end of the model should be float32. Because the dtype policy is `mixed_float16`, the softmax activation would normally have a float16 compute dtype and output a float16 tensors.
This can be fixed by separating the Dense and softmax layers, and by passing `dtype='float32'` to the softmax layer
```
# CORRECT: softmax and model output are float32
x = layers.Dense(10, name='dense_logits')(x)
outputs = layers.Activation('softmax', dtype='float32', name='predictions')(x)
print('Outputs dtype: %s' % outputs.dtype.name)
```
Passing `dtype='float32'` to the softmax layer constructor overrides the layer's dtype policy to be the `float32` policy, which does computations and keeps variables in float32. Equivalently, we could have instead passed `dtype=mixed_precision.Policy('float32')`; layers always convert the dtype argument to a policy. Because the `Activation` layer has no variables, the policy's variable dtype is ignored, but the policy's compute dtype of float32 causes softmax and the model output to be float32.
Adding a float16 softmax in the middle of a model is fine, but a softmax at the end of the model should be in float32. The reason is that if the intermediate tensor flowing from the softmax to the loss is float16 or bfloat16, numeric issues may occur.
You can override the dtype of any layer to be float32 by passing `dtype='float32'` if you think it will not be numerically stable with float16 computations. But typically, this is only necessary on the last layer of the model, as most layers have sufficient precision with `mixed_float16` and `mixed_bfloat16`.
Even if the model does not end in a softmax, the outputs should still be float32. While unnecessary for this specific model, the model outputs can be cast to float32 with the following:
```
# The linear activation is an identity function. So this simply casts 'outputs'
# to float32. In this particular case, 'outputs' is already float32 so this is a
# no-op.
outputs = layers.Activation('linear', dtype='float32')(outputs)
```
Next, finish and compile the model, and generate input data.
```
model = keras.Model(inputs=inputs, outputs=outputs)
model.compile(loss='sparse_categorical_crossentropy',
optimizer=keras.optimizers.RMSprop(),
metrics=['accuracy'])
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000, 784).astype('float32') / 255
x_test = x_test.reshape(10000, 784).astype('float32') / 255
```
This example cast the input data from int8 to float32. We don't cast to float16 since the division by 255 is on the CPU, which runs float16 operations slower than float32 operations. In this case, the performance difference in negligible, but in general you should run input processing math in float32 if it runs on the CPU. The first layer of the model will cast the inputs to float16, as each layer casts floating-point inputs to its compute dtype.
The initial weights of the model are retrieved. This will allow training from scratch again by loading the weights.
```
initial_weights = model.get_weights()
```
## Training the model with Model.fit
Next, train the model.
```
history = model.fit(x_train, y_train,
batch_size=8192,
epochs=5,
validation_split=0.2)
test_scores = model.evaluate(x_test, y_test, verbose=2)
print('Test loss:', test_scores[0])
print('Test accuracy:', test_scores[1])
```
Notice the model prints the time per sample in the logs: for example, "4us/sample". The first epoch may be slower as TensorFlow spends some time optimizing the model, but afterwards the time per sample should stabilize.
If you are running this guide in Colab, you can compare the performance of mixed precision with float32. To do so, change the policy from `mixed_float16` to `float32` in the "Setting the dtype policy" section, then rerun all the cells up to this point. On GPUs with at least compute capability 7.0, you should see the time per sample significantly increase, indicating mixed precision sped up the model. For example, with a Titan V GPU, the per-sample time increases from 4us to 12us. Make sure to change the policy back to `mixed_float16` and rerun the cells before continuing with the guide.
For many real-world models, mixed precision also allows you to double the batch size without running out of memory, as float16 tensors take half the memory. This does not apply however to this toy model, as you can likely run the model in any dtype where each batch consists of the entire MNIST dataset of 60,000 images.
If running mixed precision on a TPU, you will not see as much of a performance gain compared to running mixed precision on GPUs. This is because TPUs already do certain ops in bfloat16 under the hood even with the default dtype policy of `float32`. TPU hardware does not support float32 for certain ops which are numerically stable in bfloat16, such as matmul. For such ops the TPU backend will silently use bfloat16 internally instead. As a consequence, passing `dtype='float32'` to layers which use such ops may have no numerical effect, however it is unlikely running such layers with bfloat16 computations will be harmful.
## Loss scaling
Loss scaling is a technique which `tf.keras.Model.fit` automatically performs with the `mixed_float16` policy to avoid numeric underflow. This section describes loss scaling and how to customize its behavior.
### Underflow and Overflow
The float16 data type has a narrow dynamic range compared to float32. This means values above $65504$ will overflow to infinity and values below $6.0 \times 10^{-8}$ will underflow to zero. float32 and bfloat16 have a much higher dynamic range so that overflow and underflow are not a problem.
For example:
```
x = tf.constant(256, dtype='float16')
(x ** 2).numpy() # Overflow
x = tf.constant(1e-5, dtype='float16')
(x ** 2).numpy() # Underflow
```
In practice, overflow with float16 rarely occurs. Additionally, underflow also rarely occurs during the forward pass. However, during the backward pass, gradients can underflow to zero. Loss scaling is a technique to prevent this underflow.
### Loss scaling background
The basic concept of loss scaling is simple: simply multiply the loss by some large number, say $1024$. We call this number the *loss scale*. This will cause the gradients to scale by $1024$ as well, greatly reducing the chance of underflow. Once the final gradients are computed, divide them by $1024$ to bring them back to their correct values.
The pseudocode for this process is:
```
loss_scale = 1024
loss = model(inputs)
loss *= loss_scale
# We assume `grads` are float32. We do not want to divide float16 gradients
grads = compute_gradient(loss, model.trainable_variables)
grads /= loss_scale
```
Choosing a loss scale can be tricky. If the loss scale is too low, gradients may still underflow to zero. If too high, the opposite the problem occurs: the gradients may overflow to infinity.
To solve this, TensorFlow dynamically determines the loss scale so you do not have to choose one manually. If you use `tf.keras.Model.fit`, loss scaling is done for you so you do not have to do any extra work. This is explained further in the next section.
### Choosing the loss scale
Each dtype policy optionally has an associated `tf.mixed_precision.experimental.LossScale` object, which represents a fixed or dynamic loss scale. By default, the loss scale for the `mixed_float16` policy is a `tf.mixed_precision.experimental.DynamicLossScale`, which dynamically determines the loss scale value. Other policies do not have a loss scale by default, as it is only necessary when float16 is used. You can query the loss scale of the policy:
```
loss_scale = policy.loss_scale
print('Loss scale: %s' % loss_scale)
```
The loss scale prints a lot of internal state, but you can ignore it. The most important part is the `current_loss_scale` part, which shows the loss scale's current value.
You can instead use a static loss scale by passing a number when constructing a dtype policy.
```
new_policy = mixed_precision.Policy('mixed_float16', loss_scale=1024)
print(new_policy.loss_scale)
```
The dtype policy constructor always converts the loss scale to a `LossScale` object. In this case, it's converted to a `tf.mixed_precision.experimental.FixedLossScale`, the only other `LossScale` subclass other than `DynamicLossScale`.
Note: *Using anything other than a dynamic loss scale is not recommended*. Choosing a fixed loss scale can be difficult, as making it too low will cause the model to not train as well, and making it too high will cause Infs or NaNs to appear in the gradients. A dynamic loss scale is typically near the optimal loss scale, so you do not have to do any work. Currently, dynamic loss scales are a bit slower than fixed loss scales, but the performance will be improved in the future.
Models, like layers, each have a dtype policy. If present, a model uses its policy's loss scale to apply loss scaling in the `tf.keras.Model.fit` method. This means if `Model.fit` is used, you do not have to worry about loss scaling at all: The `mixed_float16` policy will have a dynamic loss scale by default, and `Model.fit` will apply it.
With custom training loops, the model will ignore the policy's loss scale, and you will have to apply it manually. This is explained in the next section.
## Training the model with a custom training loop
So far, you trained a Keras model with mixed precision using `tf.keras.Model.fit`. Next, you will use mixed precision with a custom training loop. If you do not already know what a custom training loop is, please read [the Custom training guide](../tutorials/customization/custom_training_walkthrough.ipynb) first.
Running a custom training loop with mixed precision requires two changes over running it in float32:
1. Build the model with mixed precision (you already did this)
2. Explicitly use loss scaling if `mixed_float16` is used.
For step (2), you will use the `tf.keras.mixed_precision.experimental.LossScaleOptimizer` class, which wraps an optimizer and applies loss scaling. It takes two arguments: the optimizer and the loss scale. Construct one as follows to use a dynamic loss scale
```
optimizer = keras.optimizers.RMSprop()
optimizer = mixed_precision.LossScaleOptimizer(optimizer, loss_scale='dynamic')
```
Passing `'dynamic'` is equivalent to passing `tf.mixed_precision.experimental.DynamicLossScale()`.
Next, define the loss object and the `tf.data.Dataset`s.
```
loss_object = tf.keras.losses.SparseCategoricalCrossentropy()
train_dataset = (tf.data.Dataset.from_tensor_slices((x_train, y_train))
.shuffle(10000).batch(8192))
test_dataset = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(8192)
```
Next, define the training step function. Two new methods from the loss scale optimizer are used in order to scale the loss and unscale the gradients:
* `get_scaled_loss(loss)`: Multiplies the loss by the loss scale
* `get_unscaled_gradients(gradients)`: Takes in a list of scaled gradients as inputs, and divides each one by the loss scale to unscale them
These functions must be used in order to prevent underflow in the gradients. `LossScaleOptimizer.apply_gradients` will then apply gradients if none of them have Infs or NaNs. It will also update the loss scale, halving it if the gradients had Infs or NaNs and potentially increasing it otherwise.
```
@tf.function
def train_step(x, y):
with tf.GradientTape() as tape:
predictions = model(x)
loss = loss_object(y, predictions)
scaled_loss = optimizer.get_scaled_loss(loss)
scaled_gradients = tape.gradient(scaled_loss, model.trainable_variables)
gradients = optimizer.get_unscaled_gradients(scaled_gradients)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
return loss
```
The `LossScaleOptimizer` will likely skip the first few steps at the start of training. The loss scale starts out high so that the optimal loss scale can quickly be determined. After a few steps, the loss scale will stabilize and very few steps will be skipped. This process happens automatically and does not affect training quality.
Now define the test step.
```
@tf.function
def test_step(x):
return model(x, training=False)
```
Load the initial weights of the model, so you can retrain from scratch.
```
model.set_weights(initial_weights)
```
Finally, run the custom training loop.
```
for epoch in range(5):
epoch_loss_avg = tf.keras.metrics.Mean()
test_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='test_accuracy')
for x, y in train_dataset:
loss = train_step(x, y)
epoch_loss_avg(loss)
for x, y in test_dataset:
predictions = test_step(x)
test_accuracy.update_state(y, predictions)
print('Epoch {}: loss={}, test accuracy={}'.format(epoch, epoch_loss_avg.result(), test_accuracy.result()))
```
## GPU performance tips
Here are some performance tips when using mixed precision on GPUs.
### Increasing your batch size
If it doesn't affect model quality, try running with double the batch size when using mixed precision. As float16 tensors use half the memory, this often allows you to double your batch size without running out of memory. Increasing batch size typically increases training throughput, i.e. the training elements per second your model can run on.
### Ensuring GPU Tensor Cores are used
As mentioned previously, modern NVIDIA GPUs use a special hardware unit called Tensor Cores that can multiply float16 matrices very quickly. However, Tensor Cores requires certain dimensions of tensors to be a multiple of 8. In the examples below, an argument is bold if and only if it needs to be a multiple of 8 for Tensor Cores to be used.
* tf.keras.layers.Dense(**units=64**)
* tf.keras.layers.Conv2d(**filters=48**, kernel_size=7, stride=3)
* And similarly for other convolutional layers, such as tf.keras.layers.Conv3d
* tf.keras.layers.LSTM(**units=64**)
* And similar for other RNNs, such as tf.keras.layers.GRU
* tf.keras.Model.fit(epochs=2, **batch_size=128**)
You should try to use Tensor Cores when possible. If you want to learn more [NVIDIA deep learning performance guide](https://docs.nvidia.com/deeplearning/sdk/dl-performance-guide/index.html) describes the exact requirements for using Tensor Cores as well as other Tensor Core-related performance information.
### XLA
XLA is a compiler that can further increase mixed precision performance, as well as float32 performance to a lesser extent. See the [XLA guide](https://www.tensorflow.org/xla) for details.
## Cloud TPU performance tips
As on GPUs, you should try doubling your batch size, as bfloat16 tensors use half the memory. Doubling batch size may increase training throughput.
TPUs do not require any other mixed precision-specific tuning to get optimal performance. TPUs already require the use of XLA. They benefit from having certain dimensions being multiples of $128$, but this applies equally to float32 as it does for mixed precision. See the [Cloud TPU Performance Guide](https://cloud.google.com/tpu/docs/performance-guide) for general TPU performance tips, which apply to mixed precision as well as float32.
## Summary
* You should use mixed precision if you use TPUs or NVIDIA GPUs with at least compute capability 7.0, as it will improve performance by up to 3x.
* You can use mixed precision with the following lines:
```
# On TPUs, use 'mixed_bfloat16' instead
policy = tf.keras.mixed_precision.experimental.Policy('mixed_float16')
mixed_precision.set_policy(policy)
```
* If your model ends in softmax, make sure it is float32. And regardless of what your model ends in, make sure the output is float32.
* If you use a custom training loop with `mixed_float16`, in addition to the above lines, you need to wrap your optimizer with a `tf.keras.mixed_precision.experimental.LossScaleOptimizer`. Then call `optimizer.get_scaled_loss` to scale the loss, and `optimizer.get_unscaled_gradients` to unscale the gradients.
* Double the training batch size if it does not reduce evaluation accuracy
* On GPUs, ensure most tensor dimensions are a multiple of $8$ to maximize performance
For more examples of mixed precision using the `tf.keras.mixed_precision` API, see the [official models repository](https://github.com/tensorflow/models/tree/master/official). Most official models, such as [ResNet](https://github.com/tensorflow/models/tree/master/official/vision/image_classification) and [Transformer](https://github.com/tensorflow/models/blob/master/official/nlp/transformer) will run using mixed precision by passing `--dtype=fp16`.
| github_jupyter |
# Tabular Datasets
As we have already discovered, Elements are simple wrappers around your data that provide a semantically meaningful representation. HoloViews can work with a wide variety of data types, but many of them can be categorized as either:
* **Tabular:** Tables of flat columns, or
* **Gridded:** Array-like data on 2-dimensional or N-dimensional grids
These two general data types are explained in detail in the [Tabular Data](../user_guide/07-Tabular_Datasets.ipynb) and [Gridded Data](../user_guide/08-Gridded_Datasets.ipynb) user guides, including all the many supported formats (including Python dictionaries of NumPy arrays, pandas ``DataFrames``, dask ``DataFrames``, and xarray ``DataArrays`` and ``Datasets``).
In this Getting-Started guide we provide a quick overview and introduction to two of the most flexible and powerful formats: columnar **pandas** DataFrames (in this section), and gridded **xarray** Datasets (in the next section).
## Tabular
Tabular data (also called columnar data) is one of the most common, general, and versatile data formats, corresponding to how data is laid out in a spreadsheet. There are many different ways to put data into a tabular format, but for interactive analysis having [**tidy data**](http://www.jeannicholashould.com/tidy-data-in-python.html) provides flexibility and simplicity. For tidy data, the **columns** of the table represent **variables** or **dimensions** and the **rows** represent **observations**. The best way to understand this format is to look at such a dataset:
```
import numpy as np
import pandas as pd
import holoviews as hv
hv.extension('bokeh', 'matplotlib')
diseases = pd.read_csv('../assets/diseases.csv.gz')
diseases.head()
```
This particular dataset was the subject of an excellent piece of visual journalism in the [Wall Street Journal](http://graphics.wsj.com/infectious-diseases-and-vaccines/#b02g20t20w15). The WSJ data details the incidence of various diseases over time, and was downloaded from the [University of Pittsburgh's Project Tycho](http://www.tycho.pitt.edu/). We can see we have 5 data columns, which each correspond either to independent variables that specify a particular measurement ('Year', 'Week', 'State'), or observed/dependent variables reporting what was then actually measured (the 'measles' or 'pertussis' incidence).
Knowing the distinction between those two types of variables is crucial for doing visualizations, but unfortunately the tabular format does not declare this information. Plotting 'Week' against 'State' would not be meaningful, whereas 'measles' for each 'State' (averaging or summing across the other dimensions) would be fine, and there's no way to deduce those constraints from the tabular format. Accordingly, we will first make a HoloViews object called a ``Dataset`` that declares the independent variables (called key dimensions or **kdims** in HoloViews) and dependent variables (called value dimensions or **vdims**) that you want to work with:
```
vdims = [('measles', 'Measles Incidence'), ('pertussis', 'Pertussis Incidence')]
ds = hv.Dataset(diseases, ['Year', 'State'], vdims)
```
Here we've used an optional tuple-based syntax **``(name,label)``** to specify a more meaningful description for the ``vdims``, while using the original short descriptions for the ``kdims``. We haven't yet specified what to do with the ``Week`` dimension, but we are only interested in yearly averages, so let's just tell HoloViews to average over all remaining dimensions:
```
ds = ds.aggregate(function=np.mean)
ds
```
(We'll cover aggregations like ``np.mean`` in detail later, but here the important bit is simply that the ``Week`` dimension can now be ignored.)
The ``repr`` shows us both the ``kdims`` (in square brackets) and the ``vdims`` (in parentheses) of the ``Dataset``. Because it can hold arbitrary combinations of dimensions, a ``Dataset`` is *not* immediately visualizable. There's no single clear mapping from these four dimensions onto a two-dimensional page, hence the textual representation shown above.
To make this data visualizable, we'll need to provide a bit more metadata, by selecting one of the large library of Elements that can help answer the questions we want to ask about the data. Perhaps the most obvious representation of this dataset is as a ``Curve`` displaying the incidence for each year, for each state. We could pull out individual columns one by one from the original dataset, but now that we have declared information about the dimensions, the cleanest approach is to map the dimensions of our ``Dataset`` onto the dimensions of an Element using ``.to``:
```
%%opts Curve [width=600 height=250] {+framewise}
(ds.to(hv.Curve, 'Year', 'measles') + ds.to(hv.Curve, 'Year', 'pertussis')).cols(1)
```
Here we specified two ``Curve`` elements showing measles and pertussis incidence respectively (the vdims), per year (the kdim), and laid them out in a vertical column. You'll notice that even though we specified only the short name for the value dimensions, the plot shows the longer names ("Measles Incidence", "Pertussis Incidence") that we declared on the ``Dataset``.
You'll also notice that we automatically received a dropdown menu to select which ``State`` to view. Each ``Curve`` ignores unused value dimensions, because additional measurements don't affect each other, but HoloViews has to do *something* with every key dimension for every such plot. If the ``State`` (or any other key dimension) isn't somehow plotted or aggregated over, then HoloViews has to leave choosing a value for it to the user, hence the selection widget. Other options for what to do with extra dimensions or just extra data ranges are illustrated below.
### Selecting
One of the most common thing we might want to do is to select only a subset of the data. The ``select`` method makes this extremely easy, letting you select a single value, a list of values supplied as a list, or a range of values supplied as a tuple. Here we will use ``select`` to display the measles incidence in four states over one decade. After applying the selection, we use the ``.to`` method as shown earlier, now displaying the data as ``Bars`` indexed by 'Year' and 'State' key dimensions and displaying the 'Measles Incidence' value dimension:
```
%%opts Bars [width=800 height=400 tools=['hover'] group_index=1 legend_position='top_left']
states = ['New York', 'New Jersey', 'California', 'Texas']
ds.select(State=states, Year=(1980, 1990)).to(hv.Bars, ['Year', 'State'], 'measles').sort()
```
### Faceting
Above we already saw what happens to key dimensions that we didn't explicitly assign to the Element using the ``.to`` method: they are grouped over, popping up a set of widgets so the user can select the values to show at any one time. However, using widgets is not always the most effective way to view the data, and a ``Dataset`` lets you specify other alternatives using the ``.overlay``, ``.grid`` and ``.layout`` methods. For instance, we can lay out each state separately using ``.grid``:
```
%%opts Curve [width=200] (color='indianred')
grouped = ds.select(State=states, Year=(1930, 2005)).to(hv.Curve, 'Year', 'measles')
grouped.grid('State')
```
Or we can take the same grouped object and ``.overlay`` the individual curves instead of laying them out in a grid:
```
%%opts Curve [width=600] (color=Cycle(values=['indianred', 'slateblue', 'lightseagreen', 'coral']))
grouped.overlay('State')
```
These faceting methods even compose together, meaning that if we had more key dimensions we could ``.overlay`` one dimension, ``.grid`` another and have a widget for any other remaining key dimensions.
### Aggregating
Instead of selecting a subset of the data, another common operation supported by HoloViews is computing aggregates. When we first loaded this dataset, we aggregated over the 'Week' column to compute the mean incidence for every year, thereby reducing our data significantly. The ``aggregate`` method is therefore very useful to compute statistics from our data.
A simple example using our dataset is to compute the mean and standard deviation of the Measles Incidence by ``'Year'``. We can express this simply by passing the key dimensions to aggregate over (in this case just the 'Year') along with a function and optional ``spreadfn`` to compute the statistics we want. The ``spread_fn`` will append the name of the function to the dimension name so we can reference the computed value separately. Once we have computed the aggregate, we can simply cast it to a ``Curve`` and ``ErrorBars``:
```
%%opts Curve [width=600]
agg = ds.aggregate('Year', function=np.mean, spreadfn=np.std)
(hv.Curve(agg) * hv.ErrorBars(agg,vdims=['measles', 'measles_std'])).redim.range(measles=(0, None))
```
In this way we can summarize a multi-dimensional dataset as something that can be visualized directly, while allowing us to compute arbitrary statistics along a dimension.
## Other data
If you want to know more about working with tabular data, particularly when using datatypes other than pandas, have a look at the [user guide](../user_guide/07-Tabular_Datasets.ipynb). The different interfaces allow you to work with everything from simple NumPy arrays to out-of-core dataframes using dask. Dask dataframes scale to visualizations of billions of rows, when using [datashader](https://anaconda.org/jbednar/holoviews_datashader/notebook) with HoloViews to aggregate the data as needed.
| github_jupyter |
# First steps with xmovie
```
import warnings
import matplotlib.pyplot as plt
import xarray as xr
from shapely.errors import ShapelyDeprecationWarning
from xmovie import Movie
warnings.filterwarnings(
action='ignore',
category=ShapelyDeprecationWarning, # in cartopy
)
warnings.filterwarnings(
action="ignore",
category=UserWarning,
message=r"No `(vmin|vmax)` provided. Data limits are calculated from input. Depending on the input this can take long. Pass `\1` to avoid this step"
)
%matplotlib inline
```
## Basics
```
# Load test dataset
ds = xr.tutorial.open_dataset('air_temperature').isel(time=slice(0, 150))
# Create movie object
mov = Movie(ds.air)
```
### Preview movie frames
```
# Preview 10th frame
mov.preview(10)
plt.savefig("movie_preview.png")
! rm -f frame*.png *.mp4 *.gif
```
### Create movie files
```
mov.save('movie.mp4') # Use to save a high quality mp4 movie
mov.save('movie_gif.gif') # Use to save a gif
```
In many cases it is useful to have both a high quality movie and a lower resolution gif of the same animation. If that is desired, just deactivate the `remove_movie` option and give a filename with `.gif`. xmovie will first render a high quality movie and then convert it to a gif, without removing the movie afterwards.
### Optional frame-generation progress bars
Display a progressbar with `progress=True`, (requires tqdm). This can be helpful for long running animations.
```
mov.save('movie_combo.gif', remove_movie=False, progress=True)
```
Modify the framerate of the output with the keyword arguments `framerate` (for movies) and `gif_framerate` (for gifs).
```
mov.save('movie_fast.gif', remove_movie=False, progress=True, framerate=20, gif_framerate=20)
mov.save('movie_slow.gif', remove_movie=False, progress=True, framerate=5, gif_framerate=5)
```



### Frame dimension selection
By default, the movie passes through the `'time'` dimension of the DataArray, but this can be easily changed with the `framedim` argument:
```
mov = Movie(ds.air, framedim='lon')
mov.save('lon_movie.gif')
```

## Modifying plots
### Rotating globe (preset)
```
from xmovie.presets import rotating_globe
mov = Movie(ds.air, plotfunc=rotating_globe)
mov.save('movie_rotating.gif', progress=True)
```

```
mov = Movie(ds.air, plotfunc=rotating_globe, style='dark')
mov.save('movie_rotating_dark.gif', progress=True)
```

### Specifying xarray plot method to be used
Change the plotting function with the parameter `plotmethod`.
```
mov = Movie(ds.air, rotating_globe, plotmethod='contour')
mov.save('movie_cont.gif')
mov = Movie(ds.air, rotating_globe, plotmethod='contourf')
mov.save('movie_contf.gif')
```


### Changing preset settings
```
import numpy as np
ds = xr.tutorial.open_dataset('rasm', decode_times=False).Tair # 36 times in total
# Interpolate time for smoother animation
ds['time'].values[:] = np.arange(len(ds['time']))
ds = ds.interp(time=np.linspace(0, 10, 60))
# `Movie` accepts keywords for the xarray plotting interface and provides a set of 'own' keywords like
# `coast`, `land` and `style` to facilitate the styling of plots
mov = Movie(ds, rotating_globe,
# Keyword arguments to the xarray plotting interface
cmap='RdYlBu_r',
x='xc',
y='yc',
shading='auto',
# Custom keyword arguments to `rotating_globe
lat_start=45,
lat_rotations=0.05,
lon_rotations=0.2,
land=False,
coastline=True,
style='dark')
mov.save('movie_rasm.gif', progress=True)
```

### User-provided
Besides the presets, xmovie is designed to animate any custom plot which can be wrapped in a function acting on a matplotlib figure. This can contain xarray plotting commands, 'pure' matplotlib or a combination of both. This can come in handy when you want to animate a complex static plot.
```
ds = xr.tutorial.open_dataset('rasm', decode_times=False).Tair
fig = plt.figure(figsize=[10,5])
tt = 30
station = dict(x=100, y=150)
ds_station = ds.sel(**station)
(ax1, ax2) = fig.subplots(ncols=2)
ds.isel(time=tt).plot(ax=ax1)
ax1.plot(station['x'], station['y'], marker='*', color='k' ,markersize=15)
ax1.text(station['x']+4, station['y']+4, 'Station', color='k' )
ax1.set_aspect(1)
ax1.set_facecolor('0.5')
ax1.set_title('');
# Time series
ds_station.isel(time=slice(0,tt+1)).plot.line(ax=ax2, x='time')
ax2.set_xlim(ds.time.min().data, ds.time.max().data)
ax2.set_ylim(ds_station.min(), ds_station.max())
ax2.set_title('Data at station');
fig.subplots_adjust(wspace=0.6)
fig.savefig("static.png")
```
All you need to do is wrap your plotting calls into a functions `func(ds, fig, frame)`, where ds is an xarray dataset you pass to `Movie`, fig is a matplotlib.figure handle and tt is the movie frame.
```
def custom_plotfunc(ds, fig, tt, *args, **kwargs):
# Define station location for timeseries
station = dict(x=100, y=150)
ds_station = ds.sel(**station)
(ax1, ax2) = fig.subplots(ncols=2)
# Map axis
# Colorlimits need to be fixed or your video is going to cause seizures.
# This is the only modification from the code above!
ds.isel(time=tt).plot(ax=ax1, vmin=ds.min(), vmax=ds.max(), cmap='RdBu_r')
ax1.plot(station['x'], station['y'], marker='*', color='k' ,markersize=15)
ax1.text(station['x']+4, station['y']+4, 'Station', color='k' )
ax1.set_aspect(1)
ax1.set_facecolor('0.5')
ax1.set_title('');
# Time series
ds_station.isel(time=slice(0,tt+1)).plot.line(ax=ax2, x='time')
ax2.set_xlim(ds.time.min().data, ds.time.max().data)
ax2.set_ylim(ds_station.min(), ds_station.max())
ax2.set_title('Data at station');
fig.subplots_adjust(wspace=0.6)
return None, None
# ^ This is not strictly necessary, but otherwise a warning will be raised.
mov_custom = Movie(ds, custom_plotfunc)
mov_custom.preview(30)
mov_custom.save('movie_custom.gif', progress=True)
```

| github_jupyter |
# Summarize titers and sequences by date
Create a single histogram on the same scale for number of titer measurements and number of genomic sequences per year to show the relative contribution of each data source.
```
import Bio
import Bio.SeqIO
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
# Configure matplotlib theme.
fontsize = 14
matplotlib_params = {
'axes.labelsize': fontsize,
'font.size': fontsize,
'legend.fontsize': 12,
'xtick.labelsize': fontsize,
'ytick.labelsize': fontsize,
'text.usetex': False,
'figure.figsize': [6, 4],
'savefig.dpi': 300,
'figure.dpi': 300,
'text.usetex': False
}
plt.rcParams.update(matplotlib_params)
# Turn off spines for all plots.
plt.rc("axes.spines", top=False, right=False)
matplotlib.get_configdir()
plt.style.use("huddlej")
plt.style.available
```
## Load sequences
```
ls ../../seasonal-flu/data/*.fasta
# Open FASTA of HA sequences for H3N2.
sequences = Bio.SeqIO.parse("../../seasonal-flu/data/h3n2_ha.fasta", "fasta")
# Get strain names from sequences.
distinct_strains_with_sequences = pd.Series([sequence.name.split("|")[0].replace("-egg", "")
for sequence in sequences]).drop_duplicates()
distinct_strains_with_sequences.shape
# Parse years from distinct strains with titers.
sequence_years = distinct_strains_with_sequences.apply(lambda strain: int(strain.split("/")[-1])).values
# Omit invalid sequence years.
sequence_years = sequence_years[sequence_years < 2019]
sequence_years.shape
```
## Load titers
```
# Read titers into a data frame.
titers = pd.read_table(
"../../seasonal-flu/data/cdc_h3n2_egg_hi_titers.tsv",
header=None,
index_col=False,
names=["test", "reference", "serum", "source", "titer", "assay"]
)
titers.head()
titers["test_year"] = titers["test"].apply(lambda strain: int(strain.replace("-egg", "").split("/")[-1]))
(titers["test_year"] < 2007).sum()
titers["test_year"].value_counts()
titers.shape
titers[titers["test_year"] < 2007]["test"].unique().shape
titers[titers["test_year"] < 2007]["test"].unique()
# Identify distinct viruses represented as test strains in titers.
distinct_strains_with_titers = titers["test"].str.replace("-egg", "").drop_duplicates()
# Parse years from distinct strains with titers.
titer_years = distinct_strains_with_titers.apply(lambda strain: int(strain.split("/")[-1])).values
# Omit invalid titer years.
titer_years = titer_years[titer_years < 2019]
titer_years.shape
```
## Plot sequence and titer strains by year
```
sequence_years.min()
sequence_years.max()
[sequence_years, titer_years]
sequence
fig, ax = plt.subplots(1, 1)
bins = np.arange(1968, 2019)
ax.hist([sequence_years, titer_years], bins, histtype="bar", label=["HA sequence", "HI titer"])
legend = ax.legend(
loc="upper left",
ncol=1,
frameon=False,
handlelength=1,
fancybox=False,
handleheight=1
)
legend.set_title("Virus measurement", prop={"size": 12})
legend._legend_box.align = "left"
ax.set_xlim(1990)
ax.set_xlabel("Year")
ax.set_ylabel("Number of viruses measured")
fig, ax = plt.subplots(1, 1)
bins = np.arange(1968, 2019)
ax.hist([titer_years], bins, histtype="bar", label=["HI titer"])
ax.set_xlim(1990)
ax.set_xlabel("Year")
ax.set_ylabel("Viruses measured by HI")
len(titer_years)
(titer_years < 2010).sum()
```
| github_jupyter |
```
import re
import pprint
import json
import logging
# re.match(pattern, string, flags=0)
print(re.match('www', 'www.qwer.com').span()) # 在起始位置匹配
print(re.match('com', 'www.qwer.com')) # 不在起始位置匹配
line = "Cats are smarter than dogs"
matchObj = re.match(r'(.*) are (.*?) (.*)', line, re.M | re.I)
if matchObj:
print("matchObj.group() : ", matchObj.group())
print("matchObj.group(1) : ", matchObj.group(1))
print("matchObj.group(2) : ", matchObj.group(2))
else:
print("No match!!")
# re.search(pattern, string, flags=0)
print(re.search('www', 'www.1234.com').span()) # 在起始位置匹配
print(re.search('com', 'www.1234.com').span()) # 不在起始位置匹配
line = "Cats are smarter than dogs"
searchObj = re.search(r'(.*) are (.*?) (.*)', line, re.M | re.I)
if searchObj:
print("searchObj.group() : ", searchObj.group())
print("searchObj.group(1) : ", searchObj.group(1))
print("searchObj.group(2) : ", searchObj.group(2))
else:
print("Nothing found!!")
# re.match 只匹配字符串的开始,如果字符串开始不符合正则表达式,则匹配失败,函数返回 None
# re.search 匹配整个字符串,直到找到一个匹配
line = "Cats are smarter than dogs"
matchObj = re.match(r'dogs', line, re.M | re.I)
if matchObj:
print("match --> matchObj.group() : ", matchObj.group())
else:
print("No match!!")
matchObj = re.search(r'dogs', line, re.M | re.I)
if matchObj:
print("search --> matchObj.group() : ", matchObj.group())
else:
print("No match!!")
```
## 参数
| | |
| --------- | ---------------------------------------------------------------------- |
| 参数 | 描述 |
| `pattern` | 匹配的正则表达式 |
| `string` | 要匹配的字符串。 |
| `flags` | 标志位,用于控制正则表达式的匹配方式,如:是否区分大小写,多行匹配等等 |
| | |
| ------ | -------------------------------------------------------------- |
| 修饰符 | 描述 |
| `re.I` | 使匹配对大小写不敏感 |
| `re.L` | 做本地化识别(locale-aware)匹配 |
| `re.M` | 多行匹配,影响 ^ 和 $ |
| `re.S` | 使 . 匹配包括换行在内的所有字符 |
| `re.U` | 根据Unicode字符集解析字符。这个标志影响 `\w`,` \W`, `\b`, `\B` |
| `re.X` | 该标志通过给予你更灵活的格式以便你将正则表达式写得更易于理解。 |
可以使用`group(num)` 或 `groups()` 匹配对象函数来获取匹配表达式。
| | |
| -------------- | --------------------------------------------------------- |
| 匹配对象方法 | 描述 |
| `group(num=0)` | 匹配的整个表达式的字符串,`group()` |
| | 可以一次输入多个组号,在这种情况下它 将返回一个包含那些组所对应值的元组。 |
| `groups()` | 返回一个包含所有小组字符串的元组,从 1 到 所含的小组号。 |
| | |
| --------------------- | -------------------------------------------------------------------------------------------------- |
| `group([group1, …]`) | 获得一个或多个分组匹配的字符串,当要获得整个匹配的子串时,可直接使用 `group()` 或 `group(0)` |
| `start([group])` | 获取分组匹配的子串在整个字符串中的起始位置(子串第一个字符的索引),参数默认值为 0; |
| `end([group])` | 获取分组匹配的子串在整个字符串中的结束位置(子串最后一个字符的索引+1),参数默认值为 0; |
| `span([group])` | 方法返回 `(start(group), end(group))` |
```
# re.sub(pattern, repl, string, count=0, flags=0)
# pattern 正则中的模式字符串。
# repl 替换的字符串,也可为一个函数。
# string 要被查找替换的原始字符串。
# count 模式匹配后替换的最大次数,默认 0 表示替换所有的匹配。
phone = "123-456-789 # 这是一个电话号码"
print(re.sub(r'#.*$', "", phone))
print(re.sub(r'\D', "", phone))
def double(matched):
"""将匹配的数字*2
:param matched: 传入的匹配的参数 value
:return: str 类型的 value*2
"""
value = int(matched.group('value'))
return str(value * 2)
s = 'A1111G4HFD2222'
print(re.sub('(?P<value>\d+)', double, s))
# 编译表达式 re.compile(pattern[, flags])
# pattern 一个字符串形式的正则表达式
# flags 可选,表示匹配模式,比如忽略大小写,多行模式等,具体参数为
# re.I 忽略大小写
# re.L 表示特殊字符集 `\w`, `\W`, `\b`, `\B`, `\s`,`\S` 依赖于当前环境
# re.M 多行模式
# re.S 即为 . 并且包括换行符在内的任意字符(. 不包括换行符)
# re.U 表示特殊字符集 `\w`, `\W`, `\b`, `\B`, `\d`, `\D`, `\s`, `\S` 依赖于 Unicode 字符属性据库
# re.X 为了增加可读性,忽略空格和 # 后面的注释
pattern = re.compile(r'\d+')
math_item = pattern.match('one12twothree34four')
print(1, math_item)
math_item = pattern.match('one12twothree34four', 2, 10)
print(2, math_item)
math_item = pattern.match('one12twothree34four', 3, 10)
print(3, math_item) # 返回一个 Match 对象
# 可省略 0
print(1, math_item.group(0))
print(2, math_item.start(0))
print(3, math_item.end(0))
print(4, math_item.span(0))
pattern = re.compile(r'([a-z]+) ([a-z]+)', re.I)
math_item = pattern.match('Hello World Wide Web')
print(1, math_item) # 匹配成功,返回一个 Match 对象
print(1, math_item.group(0)) # 返回匹配成功的整个子串
print(1, math_item.span(0)) # 返回匹配成功的整个子串的索引
print(2, math_item.group(1)) # 返回第一个分组匹配成功的子串
print(2, math_item.span(1)) # 返回第一个分组匹配成功的子串的索引
print(3, math_item.group(2)) # 返回第二个分组匹配成功的子串
print(3, math_item.span(2)) # 返回第二个分组匹配成功的子串
print(4, math_item.groups()) # 等价于 (m.group(1), m.group(2), ...)
try:
item = math_item.group(3) # 不存在第三个分组
except IndexError as e:
print(e)
# 查找所有 re.findall(string[, pos[, endpos]])
# string 待匹配的字符串。
# pos 可选参数,指定字符串的起始位置,默认为 0。
# endpos 可选参数,指定字符串的结束位置,默认为字符串的长度
pattern = re.compile(r'\d+')
print(1, pattern.findall('qwer 123 google 456'))
print(1, pattern.findall('qwe88rty123456google456', 0, 10))
# 查找所有 `re.finditer` 和 `re.findall` 类似,在字符串中找到正则表达式所匹配的所有子串,并把它们作为一个迭代器返回。
matchs = re.finditer(r"\d+", "12a32bc43jf3")
print(2, matchs)
for item in matchs:
print(3, item.group())
# 分割 re.split(pattern, string[, maxsplit=0, flags=0])
# maxsplit 分隔次数,maxsplit = 1 分隔一次,默认为0,不限制次数
print(1, re.split('\W+', 'runoob, runoob, runoob.'))
print(2, re.split('(\W+)', ' runoob, runoob, runoob.'))
print(3, re.split('\W+', ' runoob, runoob, runoob.', 1))
print(4, re.split('a*', 'hello world')) # 对于一个找不到匹配的字符串而言,split 不会对其作出分割
```
## 其他
```
re.RegexObject
re.compile()
返回
RegexObject
对象。
re.MatchObject
group()
返回被
RE
匹配的字符串。
```
```
dytt_title = ".*\[(.*)\].*"
name_0 = r"罗拉快跑BD国德双语中字[电影天堂www.dy2018.com].mkv"
name_1 = r"[电影天堂www.dy2018.com]罗拉快跑BD国德双语中字.mkv"
print(1, re.findall(dytt_title, name_0))
print(1, re.findall(dytt_title, name_1))
data = "xxxxxxxxxxxentry某某内容for-----------"
result = re.findall(".*entry(.*)for.*", data)
print(3, result)
```
| github_jupyter |
# 1- Class Activation Map with convolutions
In this firt part, we will code class activation map as described in the paper [Learning Deep Features for Discriminative Localization](http://cnnlocalization.csail.mit.edu/)
There is a GitHub repo associated with the paper:
https://github.com/zhoubolei/CAM
And even a demo in PyTorch:
https://github.com/zhoubolei/CAM/blob/master/pytorch_CAM.py
The code below is adapted from this demo but we will not use hooks only convolutions...
```
import io
import requests
from PIL import Image
import torch
import torch.nn as nn
from torchvision import models, transforms
from torch.nn import functional as F
import torch.optim as optim
import numpy as np
import cv2
import pdb
from matplotlib.pyplot import imshow
# input image
LABELS_URL = 'https://s3.amazonaws.com/deep-learning-models/image-models/imagenet_class_index.json'
IMG_URL = 'http://media.mlive.com/news_impact/photo/9933031-large.jpg'
```
As in the demo, we will use the Resnet18 architecture. In order to get CAM, we need to transform this network in a fully convolutional network: at all layers, we need to deal with images, i.e. with a shape $\text{Number of channels} \times W\times H$ . In particular, we are interested in the last images as shown here:

As we deal with a Resnet18 architecture, the image obtained before applying the `AdaptiveAvgPool2d` has size $512\times 7 \times 7$ if the input has size $3\times 224\times 224 $:
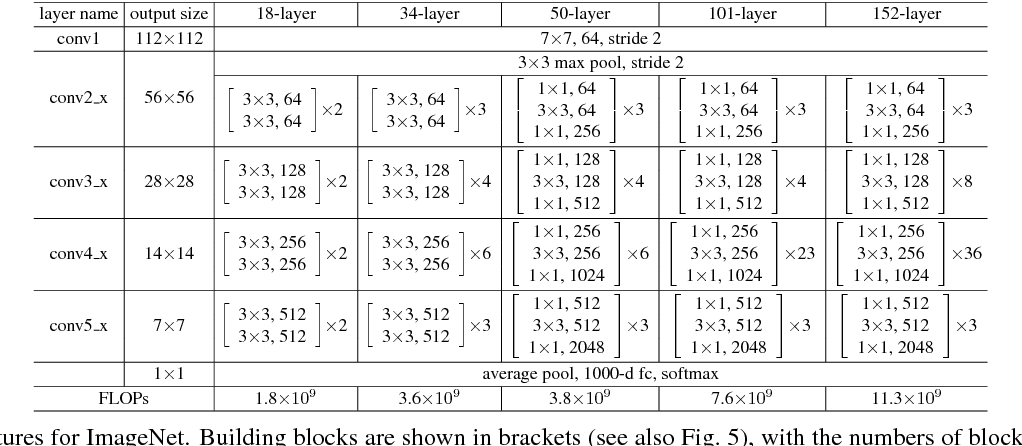
A- The first thing, you will need to do is 'removing' the last layers of the resnet18 model which are called `(avgpool)` and `(fc)`. Check that for an original image of size $3\times 224\times 224 $, you obtain an image of size $512\times 7\times 7$.
B- Then you need to retrieve the weights (and bias) of the `fc` layer, i.e. a matrix of size $1000\times 512$ transforming a vector of size 512 into a vector of size 1000 to make the prediction. Then you need to use these weights and bias to apply it pixelwise in order to transform your $512\times 7\times 7$ image into a $1000\times 7\times 7$ output (Hint: use a convolution). You can interpret this output as follows: `output[i,j,k]` is the logit for 'pixel' `[j,k]` for being of class `i`.
C- From this $1000\times 7\times 7$ output, check that you can retrieve the original output given by the `resnet18` by using an `AdaptiveAvgPool2d`. Can you understand why this is true?
D- In addition, you can construct the Class Activation Map. Draw the activation map for the class mountain bike, for the class lakeside.
## Validation:
1. make sure that when running your notebook, you display both CAM for the class mountain bike and for the class lakeside.
2. for question B above, what convolution did you use? Your answer, i.e. the name of the Pytorch layer with the correct parameters (in_channel,kernel...) here:
<span style="color:red">Replace by your answer</span>
3. your short explanation of why your network gives the same predicition as the original `resnet18`:
<span style="color:red">Replace by your answer</span>
4. Is your network working on an image which is not of size $224\times 224$, i.e. without resizing? and what about `resnet18`? Explain why?
<span style="color:red">Replace by your answer</span>
```
net = models.resnet18(pretrained=True)
net.eval()
x = torch.randn(5, 3, 224, 224)
y = net(x)
y.shape
n_mean = [0.485, 0.456, 0.406]
n_std = [0.229, 0.224, 0.225]
normalize = transforms.Normalize(
mean=n_mean,
std=n_std
)
preprocess = transforms.Compose([
transforms.Resize((224,224)),
transforms.ToTensor(),
normalize
])
# Display the image we will use.
response = requests.get(IMG_URL)
img_pil = Image.open(io.BytesIO(response.content))
imshow(img_pil);
img_tensor = preprocess(img_pil)
net = net.eval()
logit = net(img_tensor.unsqueeze(0))
logit.shape
img_tensor.shape
# download the imagenet category list
classes = {int(key):value for (key, value)
in requests.get(LABELS_URL).json().items()}
def print_preds(logit):
# print the predicitions with their 'probabilities' from the logit
h_x = F.softmax(logit, dim=1).data.squeeze()
probs, idx = h_x.sort(0, True)
probs = probs.numpy()
idx = idx.numpy()
# output the prediction
for i in range(0, 5):
print('{:.3f} -> {}'.format(probs[i], classes[idx[i]]))
return idx
idx = print_preds(logit)
def returnCAM(feature_conv, idx):
# input: tensor feature_conv of dim 1000*W*H and idx between 0 and 999
# output: image W*H with entries rescaled between 0 and 255 for the display
cam = feature_conv[idx].detach().numpy()
cam = cam - np.min(cam)
cam_img = cam / np.max(cam)
cam_img = np.uint8(255 * cam_img)
return cam_img
#some utilities
def pil_2_np(img_pil):
# transform a PIL image in a numpy array
return np.asarray(img_pil)
def display_np(img_np):
imshow(Image.fromarray(np.uint8(img_np)))
def plot_CAM(img_np, CAM):
height, width, _ = img_np.shape
heatmap = cv2.applyColorMap(cv2.resize(CAM,(width, height)), cv2.COLORMAP_JET)
result = heatmap * 0.3 + img_np * 0.5
display_np(result)
# here is a fake example to see how things work
img_np = pil_2_np(img_pil)
diag_CAM = returnCAM(torch.eye(7).unsqueeze(0),0)
plot_CAM(img_np,diag_CAM)
# your code here for your new network
net_conv =
# do not forget:
net_conv = net_conv.eval()
# to test things are right
x = torch.randn(5, 3, 224, 224)
y = net_conv(x)
y.shape
logit_conv = net_conv(img_tensor.unsqueeze(0))
logit_conv.shape
# transfor this to a [1,1000] tensor with AdaptiveAvgPool2d
logit_new =
idx = print_preds(logit_new)
i = #index of lakeside
CAM1 = returnCAM(logit_conv.squeeze(),idx[i])
plot_CAM(img_np,CAM1)
i = #index of mountain bike
CAM2 = returnCAM(logit_conv.squeeze(),idx[i])
plot_CAM(img_np,CAM2)
```
# 2- Adversarial examples
In this second part, we will look at [adversarial examples](https://arxiv.org/abs/1607.02533): "An adversarial example is a sample of input data which has been modified very slightly in a way that is intended to cause a machine learning classifier to misclassify it. In many cases, these modifications can be so subtle that a human observer does not even notice the modification at all, yet the classifier still makes a mistake. Adversarial examples pose security concerns because they could be used to perform an attack on machine learning systems..."
Rules of the game:
- the attacker cannot modify the classifier, i.e. the neural net with the preprocessing done on the image before being fed to the network.
- even if the attacker cannot modifiy the classifier, we assume that the attacker knows the architecture of the classifier. Here, we will still work with `resnet18` and the standard Imagenet normalization.
- the attacker can only modify the physical image fed into the network.
- the attacker should fool the classifier, i.e. the label obtained on the corrupted image should not be the same as the label predicted on the original image.
First, you will implement *Fast gradient sign method (FGSM)* wich is described in Section 2.1 of [Adversarial examples in the physical world](https://arxiv.org/abs/1607.02533). The idea is simple, suppose you have an image $\mathbf{x}$ and when you pass it through the network, you get the 'true' label $y$. You know that your network has been trained by minimizing the loss $J(\mathbf{\theta}, \mathbf{x}, y)$ with respect to the parameters of the network $\theta$. Now, $\theta$ is fixed as you cannot modify the classifier so you need to modify $\mathbf{x}$. In order to do so, you can compute the gradient of the loss with respect to $\mathbf{x}$ i.e. $\nabla_{\mathbf{x}} J(\mathbf{\theta}, \mathbf{x}, y)$ and use it as follows to get the modified image $\tilde{\mathbf{x}}$:
$$
\tilde{\mathbf{x}} = \text{Clamp}\left(\mathbf{x} + \epsilon *
\text{sign}(\nabla_{\mathbf{x}} J(\mathbf{\theta}, \mathbf{x}, y)),0,1\right),
$$
where $\text{Clamp}(\cdot, 0,1)$ ensures that $\tilde{\mathbf{x}}$ is a proper image.
Note that if instead of sign, you take the full gradient, you are now following the gradient i.e. increasing the loss $J(\mathbf{\theta}, \mathbf{x}, y)$ so that $y$ becomes less likely to be the predicited label.
## Validation:
1. Implement this attack. Make sure to display the corrupted image.
2. For what value of epsilon is your attack successful? What is the predicited class then?
<span style="color:red">Replace by your answer</span>
3. plot the sign of the gradient and pass this image through the network. What prediction do you obtain? Compare to [Explaining and Harnessing Adversarial Examples](https://arxiv.org/abs/1412.6572)
<span style="color:red">Replace by your answer</span>
```
# Image under attack!
url_car = 'https://cdn130.picsart.com/263132982003202.jpg?type=webp&to=min&r=640'
response = requests.get(url_car)
img_pil = Image.open(io.BytesIO(response.content))
imshow(img_pil);
# same as above
preprocess = transforms.Compose([
transforms.Resize((224,224)),
transforms.ToTensor(),
normalize
])
for p in net.parameters():
p.requires_grad = False
x = preprocess(img_pil).clone().unsqueeze(0)
logit = net(x)
_ = print_preds(logit)
t_std = torch.from_numpy(np.array(n_std, dtype=np.float32)).view(-1, 1, 1)
t_mean = torch.from_numpy(np.array(n_mean, dtype=np.float32)).view(-1, 1, 1)
def plot_img_tensor(img):
imshow(np.transpose(img.detach().numpy(), [1,2,0]))
def plot_untransform(x_t):
x_np = (x_t * t_std + t_mean).detach().numpy()
x_np = np.transpose(x_np, [1, 2, 0])
imshow(x_np)
# here we display an image given as a tensor
x_img = (x * t_std + t_mean).squeeze(0)
plot_img_tensor(x_img)
# your implementation of the attack
def fgsm_attack(image, epsilon, data_grad):
# Collect the element-wise sign of the data gradient
# Create the perturbed image by adjusting each pixel of the input image
# Adding clipping to maintain [0,1] range
# Return the perturbed image
return perturbed_image
idx = 656 #minivan
criterion = nn.CrossEntropyLoss()
x_img.requires_grad = True
logit = net(normalize(x_img).unsqueeze(0))
target = torch.tensor([idx])
#TODO: compute the loss to backpropagate
_ = print_preds(logit)
# your attack here
epsilon = 0
x_att = fgsm_attack(x_img,epsilon,?)
# the new prediction for the corrupted image
logit = net(normalize(x_att).unsqueeze(0))
_ = print_preds(logit)
# can you see the difference?
plot_img_tensor(x_att)
# do not forget to plot the sign of the gradient
gradient =
plot_img_tensor((1+gradient)/2)
# what is the prediction for the gradient?
logit = net(normalize(gradient).unsqueeze(0))
_ = print_preds(logit)
```
# 3- Transforming a car into a cat
We now implement the *Iterative Target Class Method (ITCM)* as defined by equation (4) in [Adversarial Attacks and Defences Competition](https://arxiv.org/abs/1804.00097)
To test it, we will transform the car (labeled minivan by our `resnet18`) into a [Tabby cat](https://en.wikipedia.org/wiki/Tabby_cat) (classe 281 in Imagenet). But you can try with any other target.
## Validation:
1. Implement the ITCM and make sure to display the resulting image.
```
x = preprocess(img_pil).clone()
xd = preprocess(img_pil).clone()
xd.requires_grad = True
idx = 281 #tabby
optimizer = optim.SGD([xd], lr=0.01)
for i in range(200):
#TODO: your code here
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(loss.item())
_ = print_preds(output)
print(i,'-----------------')
# TODO: break the loop once we are satisfied
if ?:
break
_ = print_preds(output)
# plot the corrupted image
```
# 4- Where is the cat hidden?
Last, we use CAM to understand where the network see a cat in the image.
## Validation:
1. display the CAM for the class tabby
2. display the CAM for the class minivan
3. where is the cat?
| github_jupyter |
```
# linear equations
# SolveLinearSystem.py
# Code to read A and b
# Then solve Ax = b for x by Gaussian elimination with back substitution
# linearsolver with pivoting adapted from
# https://stackoverflow.com/questions/31957096/gaussian-elimination-with-pivoting-in-python/31959226
def linearsolver(A,b):
n = len(A)
M = A
i = 0
for x in M:
x.append(b[i])
i += 1
# row reduction with pivots
for k in range(n):
for i in range(k,n):
if abs(M[i][k]) > abs(M[k][k]):
M[k], M[i] = M[i],M[k]
else:
pass
for j in range(k+1,n):
q = float(M[j][k]) / M[k][k]
for m in range(k, n+1):
M[j][m] -= q * M[k][m]
# allocate space for result
x = [0 for i in range(n)]
# back-substitution
x[n-1] =float(M[n-1][n])/M[n-1][n-1]
for i in range (n-1,-1,-1):
z = 0
for j in range(i+1,n):
z = z + float(M[i][j])*x[j]
x[i] = float(M[i][n] - z)/M[i][i]
# return result
return(x)
#######
#
# Code to read A and b
amatrix = [] # null list to store matrix read
bvector = [] # null list to store vector read
rowNumA = 0
colNumA = 0
rowNumB = 0
afile = open("A.txt","r") # connect and read file for MATRIX A
for line in afile:
amatrix.append([float(n) for n in line.strip().split()])
rowNumA += 1
afile.close() # Disconnect the file
colNumA = len(amatrix[0])
afile = open("B.txt","r") # connect and read file for VECTOR b
for line in afile:
bvector.append(float(line)) # vector read different -- just float the line
rowNumB += 1
afile.close() # Disconnect the file
#
# check the arrays
if rowNumA != rowNumB:
print ("row ranks not same -- aborting now")
quit()
else:
print ("row ranks same -- solve for x in Ax=b \n")
# print all columns each row
cmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
dmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
xvector = [0 for i in range(rowNumA)]
dvector = [0 for i in range(rowNumA)]
# copy amatrix into cmatrix to preserve original structure
cmatrix = [[amatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)]
dmatrix = [[amatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)]
dvector = [bvector[i] for i in range(rowNumA)]
dvector = linearsolver(amatrix,bvector) #Solve the linear system
print ("[A]*[x] = b \n")
for i in range(0,rowNumA,1):
print ( (cmatrix[i][0:colNumA]), "* [","%6.3f"% (dvector[i]),"] = ", "%6.3f"% (bvector[i]))
#print ("-----------------------------")
#for i in range(0,rowNumA,1):
# print ("%6.3f"% (dvector[i]))
#print ("-----------------------------")
```
| github_jupyter |
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
activation(torch.sum(weights*features) + bias)
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
torch.matmul(features,weights.reshape(5,1))+bias
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
activation(torch.matmul(activation(torch.matmul(features,W1) + B1),W2) + B2)
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import wikipedia
import xml.etree.ElementTree as ET
import re
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score
import xgboost as xgb
from sklearn.metrics import r2_score
%matplotlib inline
df = pd.read_csv('2020.1 - sysarmy - Encuesta de remuneración salarial Argentina - Argentina.csv', skiprows=9)
df = df[df['Salario mensual BRUTO (en tu moneda local)'] < 1_000_000]
df = df[df['Años en la empresa actual'] < 40]
df = df[(df['Salario mensual BRUTO (en tu moneda local)'] >= 10_000) & (df['Salario mensual BRUTO (en tu moneda local)'] <= 1_000_000)]
df.head()
df['Bases de datos']
df_databases_cols = df['Bases de datos'].fillna('').apply(lambda pls: pd.Series([v.lower().strip() for v in pls.replace('Microsoft Azure (Tables, CosmosDB, SQL, etc)', 'Microsoft Azure(TablesCosmosDBSQLetc)').split(',') if v.lower().strip() not in ('', 'ninguno')], dtype=str))
count_databases = pd.concat((df_databases_cols[i] for i in range(df_databases_cols.shape[1]))).value_counts()
count_databases
count_databases = count_databases[count_databases > 10]
count_databases
count_databases = count_databases.drop(['proxysql', 'percona xtrabackup'])
def find_categories(database):
database = {
'oracle': 'Oracle Database',
'microsoft azure(tablescosmosdbsqletc)': 'Cosmos DB',
'amazon rds/aurora': 'Amazon Aurora',
'amazon dynamodb': 'Amazon DynamoDB',
'google cloud storage': 'Google Storage',
'ibm db2': 'Db2 Database',
'hana': 'SAP HANA',
'amazon redshift': 'Amazon Redshift',
'apache hive': 'Apache Hive',
'apache hbase': 'Apache HBase',
'percona server': 'Percona Server for MySQL',
'sql server': 'Microsoft SQL Server',
}.get(database, database)
# autosuggest redirects linux to line (why?)
return wikipedia.page(database, auto_suggest=False).categories
database_categories = {p: find_categories(p) for p in count_databases.index}
database_categories
catcount = {}
for categories in database_categories.values():
for cat in categories:
catcount[cat] = catcount.get(cat, 0) + 1
catcount = pd.Series(catcount)
catcount = catcount[catcount > 1]
catcount
df_databases = pd.DataFrame({plat: {cat: cat in cats for cat in catcount.index} for plat, cats in database_categories.items()}).T
df_databases.head()
_, ax = plt.subplots(1, 1, figsize=(10, 10))
df_embedded = PCA(n_components=2).fit_transform(df_databases)
ax.scatter(df_embedded[:, 0], df_embedded[:, 1])
for lang, (x, y) in zip(df_databases.index, df_embedded):
ax.annotate(lang, (x, y))
ax.set_xticks([]);
ax.set_yticks([]);
from sklearn.cluster import SpectralClustering
clustering = SpectralClustering(n_clusters=8, assign_labels="discretize", random_state=0).fit(df_embedded)
_, ax = plt.subplots(1, 1, figsize=(10, 10))
ax.scatter(df_embedded[:, 0], df_embedded[:, 1], c=clustering.labels_, cmap='Accent')
for plat, (x, y) in zip(df_databases.index, df_embedded):
ax.annotate(plat, (x, y))
ax.set_xticks([]);
ax.set_yticks([]);
best = {'colsample_bytree': 0.7000000000000001, 'gamma': 0.8500000000000001, 'learning_rate': 0.025, 'max_depth': 16, 'min_child_weight': 15.0, 'n_estimators': 175, 'subsample': 0.8099576733552297}
regions_map = {
'Ciudad Autónoma de Buenos Aires': 'AMBA',
'GBA': 'AMBA',
'Catamarca': 'NOA',
'Chaco': 'NEA',
'Chubut': 'Patagonia',
'Corrientes': 'NEA',
'Entre Ríos': 'NEA',
'Formosa': 'NEA',
'Jujuy': 'NOA',
'La Pampa': 'Pampa',
'La Rioja': 'NOA',
'Mendoza': 'Cuyo',
'Misiones': 'NEA',
'Neuquén': 'Patagonia',
'Río Negro': 'Patagonia',
'Salta': 'NOA',
'San Juan': 'Cuyo',
'San Luis': 'Cuyo',
'Santa Cruz': 'Patagonia',
'Santa Fe': 'Pampa',
'Santiago del Estero': 'NOA',
'Tucumán': 'NOA',
'Córdoba': 'Pampa',
'Provincia de Buenos Aires': 'Pampa',
'Tierra del Fuego': 'Patagonia',
}
class BaseModel:
def __init__(self, **params):
self.regressor_ = xgb.XGBRegressor(**params)
def get_params(self, deep=True):
return self.regressor_.get_params(deep=deep)
def set_params(self, **params):
return self.regressor_.set_params(**params)
def clean_words(self, field, value):
value = value.replace('Microsoft Azure (Tables, CosmosDB, SQL, etc)', 'Microsoft Azure(TablesCosmosDBSQLetc)')
value = value.replace('Snacks, golosinas, bebidas', 'snacks')
value = value.replace('Descuentos varios (Clarín 365, Club La Nación, etc)', 'descuentos varios')
value = value.replace('Sí, de forma particular', 'de forma particular')
value = value.replace('Sí, los pagó un empleador', 'los pagó un empleador')
value = value.replace('Sí, activa', 'activa')
value = value.replace('Sí, pasiva', 'pasiva')
return [self.clean_word(field, v) for v in value.split(',') if self.clean_word(field, v)]
def clean_word(self, field, word):
val = str(word).lower().strip().replace(".", "")
if val in ('ninguno', 'ninguna', 'no', '0', 'etc)', 'nan'):
return ''
if field == 'Lenguajes de programación' and val == 'Microsoft Azure(TablesCosmosDBSQLetc)':
return 'Microsoft Azure (Tables, CosmosDB, SQL, etc)'
if field == '¿A qué eventos de tecnología asististe en el último año?' and val in ('pycon', 'pyconar'):
return 'pyconar'
if field == '¿A qué eventos de tecnología asististe en el último año?' and val in ('nodeconf', 'nodeconfar'):
return 'nodeconfar'
if field == '¿A qué eventos de tecnología asististe en el último año?' and val in ('meetup', 'meetups'):
return 'meetups'
if field == '¿A qué eventos de tecnología asististe en el último año?':
return val.replace(' ', '')
if field == 'Beneficios extra' and val == 'snacks':
return 'snacks, golosinas, bebidas'
if field == 'Beneficios extra' and val == 'descuentos varios':
return 'descuentos varios (clarín 365, club la nación, etc)'
return val
def row_to_words(self, row):
return [
f'{key}={row.fillna("")[key]}'
for key
in (
'Me identifico',
'Nivel de estudios alcanzado',
'Universidad',
'Estado',
'Carrera',
'¿Contribuís a proyectos open source?',
'¿Programás como hobbie?',
'Trabajo de',
'¿Qué SO usás en tu laptop/PC para trabajar?',
'¿Y en tu celular?',
'Tipo de contrato',
'Orientación sexual',
'Cantidad de empleados',
'Actividad principal',
)
] + [
f'{k}={v}' for k in (
'¿Tenés guardias?',
'Realizaste cursos de especialización',
'¿A qué eventos de tecnología asististe en el último año?',
'Beneficios extra',
'Plataformas',
'Lenguajes de programación',
'Frameworks, herramientas y librerías',
'Bases de datos',
'QA / Testing',
'IDEs',
'Lenguajes de programación'
) for v in self.clean_words(k, row.fillna('')[k])
] + [
f'region={regions_map[row["Dónde estás trabajando"]]}'
]
def encode_row(self, row):
ws = self.row_to_words(row)
return pd.Series([w in ws for w in self.valid_words_] + [
row['¿Gente a cargo?'],
row['Años de experiencia'],
row['Tengo'],
])
def fit(self, X, y, **params):
counts = {}
for i in range(X.shape[0]):
for word in self.row_to_words(X.iloc[i]):
counts[word] = counts.get(word, 0) + 1
self.valid_words_ = [word for word, c in counts.items() if c > 0.01*X.shape[0]]
self.regressor_.fit(X.apply(self.encode_row, axis=1).astype(float), y, **params)
return self
def predict(self, X):
return self.regressor_.predict(X.apply(self.encode_row, axis=1).astype(float))
def score(self, X, y):
return r2_score(y, self.predict(X))
cross_val_score(BaseModel(), df, df['Salario mensual BRUTO (en tu moneda local)'])
database_embeddings = {l: [] for l in clustering.labels_}
for database, label in zip(df_databases.index, clustering.labels_):
database_embeddings[label].append(database)
database_embeddings
class ModelPCA:
def __init__(self, **params):
self.regressor_ = xgb.XGBRegressor(**params)
def get_params(self, deep=True):
return self.regressor_.get_params(deep=deep)
def set_params(self, **params):
return self.regressor_.set_params(**params)
def clean_words(self, field, value):
value = value.replace('Microsoft Azure (Tables, CosmosDB, SQL, etc)', 'Microsoft Azure(TablesCosmosDBSQLetc)')
value = value.replace('Snacks, golosinas, bebidas', 'snacks')
value = value.replace('Descuentos varios (Clarín 365, Club La Nación, etc)', 'descuentos varios')
value = value.replace('Sí, de forma particular', 'de forma particular')
value = value.replace('Sí, los pagó un empleador', 'los pagó un empleador')
value = value.replace('Sí, activa', 'activa')
value = value.replace('Sí, pasiva', 'pasiva')
return [self.clean_word(field, v) for v in value.split(',') if self.clean_word(field, v)]
def clean_word(self, field, word):
val = str(word).lower().strip().replace(".", "")
if val in ('ninguno', 'ninguna', 'no', '0', 'etc)', 'nan'):
return ''
if field == 'Lenguajes de programación' and val == 'Microsoft Azure(TablesCosmosDBSQLetc)':
return 'Microsoft Azure (Tables, CosmosDB, SQL, etc)'
if field == '¿A qué eventos de tecnología asististe en el último año?' and val in ('pycon', 'pyconar'):
return 'pyconar'
if field == '¿A qué eventos de tecnología asististe en el último año?' and val in ('nodeconf', 'nodeconfar'):
return 'nodeconfar'
if field == '¿A qué eventos de tecnología asististe en el último año?' and val in ('meetup', 'meetups'):
return 'meetups'
if field == '¿A qué eventos de tecnología asististe en el último año?':
return val.replace(' ', '')
if field == 'Beneficios extra' and val == 'snacks':
return 'snacks, golosinas, bebidas'
if field == 'Beneficios extra' and val == 'descuentos varios':
return 'descuentos varios (clarín 365, club la nación, etc)'
return val
def contains_database(self, row, databases):
k = 'Bases de datos'
for v in self.clean_words(k, row.fillna('')[k]):
if v in databases:
return True
return False
def row_to_words(self, row):
return [
f'{key}={row.fillna("")[key]}'
for key
in (
'Me identifico',
'Nivel de estudios alcanzado',
'Universidad',
'Estado',
'Carrera',
'¿Contribuís a proyectos open source?',
'¿Programás como hobbie?',
'Trabajo de',
'¿Qué SO usás en tu laptop/PC para trabajar?',
'¿Y en tu celular?',
'Tipo de contrato',
'Orientación sexual',
'Cantidad de empleados',
'Actividad principal',
)
] + [
f'{k}={v}' for k in (
'¿Tenés guardias?',
'Realizaste cursos de especialización',
'¿A qué eventos de tecnología asististe en el último año?',
'Beneficios extra',
'Plataformas',
'Frameworks, herramientas y librerías',
'Bases de datos',
'QA / Testing',
'IDEs',
'Lenguajes de programación'
) for v in self.clean_words(k, row.fillna('')[k])
] + [
f'region={regions_map[row["Dónde estás trabajando"]]}'
] + [
f'database_type={i}'
for i, databases in database_embeddings.items()
if self.contains_database(row, databases)
]
def encode_row(self, row):
ws = self.row_to_words(row)
return pd.Series([w in ws for w in self.valid_words_] + [
row['¿Gente a cargo?'],
row['Años de experiencia'],
row['Tengo'],
])
def fit(self, X, y, **params):
counts = {}
for i in range(X.shape[0]):
for word in self.row_to_words(X.iloc[i]):
counts[word] = counts.get(word, 0) + 1
self.valid_words_ = [word for word, c in counts.items() if c > 0.01*X.shape[0]]
self.regressor_.fit(X.apply(self.encode_row, axis=1).astype(float), y, **params)
return self
def predict(self, X):
return self.regressor_.predict(X.apply(self.encode_row, axis=1).astype(float))
def score(self, X, y):
return r2_score(y, self.predict(X))
cross_val_score(ModelPCA(), df, df['Salario mensual BRUTO (en tu moneda local)'])
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yaml
from pathlib import Path
from collections import defaultdict
from pandas.api.types import CategoricalDtype
EXPERIMENTS_PATH = Path.home() / "ba" / "experiments"
benchmarks_paths = list((EXPERIMENTS_PATH / "C4P4").glob("lb.*/*.benchmarks.yaml"))
benchmarks_paths
DEFAULT_CATEGORY = lambda: "category"
CATEGORIES = defaultdict(DEFAULT_CATEGORY,
forbidden_subgraphs=CategoricalDtype([
"P3", "P4", "P5", "P6", "C4P4", "C5P5", "C6P6", ", C4_C5_2K2", "C4_C5_P5_Bowtie_Necktie"]),
lower_bound_algorithm=CategoricalDtype([
"Trivial", "Greedy", "SortedGreedy", "LocalSearch", "LPRelaxation", "NPS_MWIS_Solver",
"LSSWZ_MWIS_Solver", "fpt-editing-LocalSearch", "GreedyWeightedPacking"]),
dataset=CategoricalDtype([
"barabasi-albert", "bio", "bio-C4P4-subset", "bio-subset-A", "duplication-divergence",
"misc", "powerlaw-cluster", "bio-subset-B", "bio-unweighted"])
)
def load_raw_df(paths):
docs = []
for path in paths:
with path.open() as file:
docs += list(yaml.safe_load_all(file))
return pd.DataFrame(docs)
def load_data_unweighted_fpt_editing(paths):
df = load_raw_df(paths)
df[["dataset", "instance"]] = df["instance"].str.split("/", expand=True)[[1, 2]]
df["lower_bound_algorithm"] = "fpt-editing-LocalSearch"
return df
def load_data_weighted_fpt_editing(paths):
df = load_raw_df(paths)
df["value"] = df["values"].str[0]
df.rename(columns={"lower_bound_name": "lower_bound_algorithm"}, inplace=True)
df[["dataset", "instance"]] = df["instance"].str.split("/", expand=True)[[1, 2]]
return df
def load_data(paths):
columns = ["forbidden_subgraphs", "dataset", "instance", "lower_bound_algorithm", "value"]
df1 = load_data_weighted_fpt_editing([p for p in paths if "fpt-editing" not in p.parent.name])
df2 = load_data_unweighted_fpt_editing([p for p in paths if "fpt-editing" in p.parent.name])
df1 = df1[columns]
df2 = df2[columns]
df = pd.concat([df1, df2], ignore_index=True)
df = df.astype({k: CATEGORIES[k] for k in
["forbidden_subgraphs", "lower_bound_algorithm", "dataset"]})
df.loc[df["value"] < 0, "value"] = np.nan
m = df["lower_bound_algorithm"] == "fpt-editing-LocalSearch"
df.loc[m, "value"] = df.loc[m, "value"] / 100
return df
df = load_data(benchmarks_paths)
df.head()
for lb, df_lb in df.groupby(["lower_bound_algorithm", "dataset"]):
print(lb, len(df_lb))
# df = df[df["dataset"] == "bio"]
def plot_line_scatter(x, y, xlabel, ylabel, path=None):
fig, ax = plt.subplots(figsize=(6, 6))
ax.set_aspect("equal")
ax.scatter(x, y, alpha=0.2)
ax.plot([0, 5e5], [0, 5e5])
ax.set_yscale("log"); ax.set_xscale("log")
ax.set_ylim([1e-1, 5e5]); ax.set_xlim([1e-1, 5e5])
ax.set_ylabel(ylabel); ax.set_xlabel(xlabel)
if path is not None:
plt.savefig(path)
plt.show()
def plot_ratio_scatter(x, y, xlabel, ylabel):
ratio = x / y
ratio[x == y] = 1
fig, ax = plt.subplots(figsize=(6, 4))
ax.scatter(x, ratio, alpha=0.2)
ax.set_xscale("log")
ax.set_xlim((1e0, 5e5))
ax.set_xlabel(xlabel); ax.set_ylabel(f"{xlabel} / {ylabel}")
plt.show()
def plot_ratio(x, y, xlabel, ylabel, path=None):
ratio = x / y
ratio[x == y] = 1
print("-" * 10)
print(f"path: {path}")
print(f"{((x==0) & (y==0)).sum()} or {100*((x==0) & (y==0)).mean():.4}% where x = y = 0")
print(f"{(ratio == 1).sum()} / {ratio.shape[0]} or {100*(ratio == 1).mean():.4}% where ratio = 1")
print(f"{ratio.isnull().sum()} / {ratio.shape[0]} where ratio = NaN")
# TODO: print quantiles
q = np.array([0, 0.05, 0.1, 0.5, 0.9, 0.95, 1])
x = np.quantile(ratio[~ratio.isnull()], q)
# print(f"{x}")
for q_i, x_i in zip(q, x):
print(f"{100*q_i:>6.2f}% {ylabel} / {xlabel} > {100 / x_i:>7.2f}%")
q_line = " & ".join([f"{q_i:.2f}\\%" for q_i in q])
x_line = " & ".join([f"{100 / x_i:.2f}\\%" for x_i in x])
print(f"""\\begin{{table}}[h]
\\begin{{tabular}}{{lllllll}}
{q_line} \\\\ \\hline
{x_line}
\\end{{tabular}}
\\end{{table}}""")
fig, ax = plt.subplots(figsize=(6, 4))
ax.hist(ratio[ratio != 1], bins=np.linspace(min([0, ratio.min()]), max([0, ratio.max()]), 31))
ax.set_xlabel(f"{xlabel} / {ylabel}"); ax.set_ylabel("count")
if path is not None:
plt.savefig(path)
plt.show()
def draw_plots(df, dataset=""):
a = df[(df["lower_bound_algorithm"] == "SortedGreedy")].reset_index()
b = df[(df["lower_bound_algorithm"] == "LPRelaxation")].reset_index()
c = df[(df["lower_bound_algorithm"] == "NPS_MWIS_Solver")].reset_index()
d = df[(df["lower_bound_algorithm"] == "LocalSearch")].reset_index()
e = df[(df["lower_bound_algorithm"] == "fpt-editing-LocalSearch")].reset_index()
b.loc[b["value"] < 0, "value"] = np.nan
# plot_line_scatter(a["value"], b["value"], "SortedGreedy", "LPRelaxation")
# plot_ratio_scatter(a["value"], b["value"], "SortedGreedy", "LPRelaxation")
# plot_ratio_scatter(a["value"], c["value"], "SortedGreedy", "NPS_MWIS_Solver")
# plot_ratio(a["value"], b["value"], "SortedGreedy", "LPRelaxation",
# path=f"ratio-histogram-SortedGreedy-LPRelaxation-{dataset}.pdf")
# plot_ratio(a["value"], c["value"], "SortedGreedy", "NPS_MWIS_Solver",
# path=f"ratio-histogram-SortedGreedy-NPS_MWIS_Solver-{dataset}.pdf")
# plot_ratio(c["value"], b["value"], "NPS_MWIS_Solver", "LPRelaxation",
# path=f"ratio-histogram-NPS_MWIS_Solver-LPRelaxation-{dataset}.pdf")
plot_ratio(d["value"], b["value"], "LocalSearch", "LPRelaxation",
path=f"ratio-histogram-LocalSearch-LPRelaxation-{dataset}.pdf")
plot_ratio(a["value"], d["value"], "SortedGreedy", "LocalSearch",
path=f"ratio-histogram-SortedGreedy-LocalSearch-{dataset}.pdf")
#if len(e) > 0:
# plot_ratio(e["value"], b["value"], "fpt-editing-LocalSearch", "LPRelaxation")
# plot_ratio(d["value"], e["value"], "LocalSearch", "fpt-editing-LocalSearch")
#draw_plots(df[df["dataset"] == "bio"], dataset="bio")
#draw_plots(df[df["dataset"] == "bio-unweighted"], dataset="bio-unweighted")
X_unweighted = [(g[0], df.reset_index()["value"]) for (g, df) in df.groupby(["lower_bound_algorithm", "dataset"]) if g[1] == "bio-unweighted"]
X_weighted = [(g[0], df.reset_index()["value"]) for (g, df) in df.groupby(["lower_bound_algorithm", "dataset"]) if g[1] == "bio"]
def plot_matrix_histogram(X, ignore_zero_lb=False, ignore_equality=False, xmin=0, xmax=None, path=None):
n = len(X)
fig, axes = plt.subplots(nrows=n, ncols=n, figsize=(2*n, 2*n), sharex=True, sharey=True)
for i, (lb_i, x_i) in enumerate(X):
axes[i, 0].set_ylabel(lb_i)
axes[-1, i].set_xlabel(lb_i)
for j, (lb_j, x_j) in enumerate(X):
if i != j:
r = x_i / x_j
if not ignore_zero_lb:
r[(x_i == 0) & (x_j == 0)] == 1
if ignore_equality:
r[r == 1] = np.nan
if xmax is None:
xmax = r.max()
axes[i, j].axvline(1, c="k", ls="--", alpha=0.5)
axes[i, j].hist(r, bins=np.linspace(xmin, xmax, 25))
#axes[i, j].set_title(" ".join([
# f"{100*x:.2f}%" for x in np.quantile(r[~np.isnan(r)], [0.05, 0.5, 0.95])]), fontdict=dict(fontsize=10))
fig.tight_layout()
if path is not None:
plt.savefig(path)
plt.show()
plot_matrix_histogram(X_unweighted, xmax=2, path="lb-ratio-bio-unweighted.pdf")
plot_matrix_histogram(X_weighted, xmax=5, path="lb-ratio-bio.pdf")
plot_matrix_histogram(X_unweighted, xmax=2, ignore_equality=True, ignore_zero_lb=True, path="lb-ratio-bio-unweighted-filtered.pdf")
plot_matrix_histogram(X_weighted, xmax=5, ignore_equality=True, ignore_zero_lb=True, path="lb-ratio-bio-filtered.pdf")
def plot_matrix_scatter(X, ignore_zero_lb=False, ignore_equality=False, xmin=0, xmax=None, path=None):
n = len(X)
fig, axes = plt.subplots(nrows=n, ncols=n, figsize=(2*n, 2*n))
for ax in axes.flatten():
ax.set_aspect("equal")
for i, (lb_i, x_i) in enumerate(X):
axes[i, 0].set_ylabel(lb_i)
axes[-1, i].set_xlabel(lb_i)
for j, (lb_j, x_j) in enumerate(X):
if i != j:
m = ~np.isnan(x_i) & ~np.isnan(x_j)
l, u = min([x_i[m].min(), x_j[m].min()]), max([x_i[m].max(), x_j[m].max()])
axes[i, j].plot([l, u], [l, u], c="k", ls="--", alpha=0.5)
axes[i, j].scatter(x_i, x_j)
#axes[i, j].set_title(" ".join([
# f"{100*x:.2f}%" for x in np.quantile(r[~np.isnan(r)], [0.05, 0.5, 0.95])]), fontdict=dict(fontsize=10))
fig.tight_layout()
if path is not None:
plt.savefig(path)
plt.show()
plot_matrix_scatter(X_weighted)
plt.scatter()
X_weighted[1]
```
| github_jupyter |
```
import pandas as pd
from os import getcwd
import numpy as np
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
getcwd()
infile_01 = 'crypto_data.csv'
df = pd.read_csv(infile_01,index_col=0)
df.head()
# observe values columns
df.describe()
# data types of each column
df.info()
# data best dtypes
df = df.convert_dtypes()
df.info()
# remove unneeded commas,whitespace,and periods
strip_list = []
old_list = df['TotalCoinSupply'].to_list()
for i in range(len(old_list)):
entry=old_list[i].replace('.','').replace(' ','').replace(',','')
strip_list.append(entry)
df['TotalCoinSupply'] = strip_list
# convert strings to int64
df['TotalCoinSupply']=pd.to_numeric(df['TotalCoinSupply'],downcast='float')
df.info()
# duplicated columns
dupes = df.duplicated()
dupes.value_counts()
# null values
for column in df.columns:
print(f"Column - {column} has {df[column].isnull().sum()} null values")
# drop currencies not being traded
df_trading = df.loc[df['IsTrading'] == True]
df_mined = df_trading.loc[df_trading['TotalCoinsMined']>0]
df_clean = df_mined.drop(columns=['IsTrading','CoinName'],axis=1)
# drop all NaN
df_clean = df_clean.dropna(how='any')
# show data loss as percentage
print(f'Rows in initial DF -> {len(df_trading.index)}')
print(f'Rows with No NaN DF -> {len(df_clean.index)}')
print(f'{round((len(df_clean.index)) / (len(df_trading.index)) * 100,2)}% information was NaN')
df_clean
# process the string data into dummy columns for model
X_dummies = pd.get_dummies(data = df_clean, columns = ['Algorithm','ProofType'])
X_dummies.shape
X_dummies
# scale the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_dummies)
X_scaled.shape
# dimensionality reduction using PCA
pca = PCA(n_components=.9)
components = pca.fit_transform(X_scaled)
components.shape
# dimensionality reduction using t-SNE
X_embedded = TSNE(perplexity=30).fit_transform(components)
X_embedded.shape
fig = plt.figure(figsize = (10.20,10.80))
plt.scatter(X_embedded[:,0],X_embedded[:,1])
plt.grid()
plt.show()
inertia = []
k = list(range(1, 11))
# Calculate the inertia for the range of k values
for i in k:
km = KMeans(n_clusters=i, random_state=0)
km.fit(X_embedded)
inertia.append(km.inertia_)
# Create the Elbow Curve using hvPlot
elbow_data = {"k": k, "inertia": inertia}
df_elbow = pd.DataFrame(elbow_data)
df_elbow
# Plot the elbow curve to find the best candidate(s) for k
fig = plt.figure(figsize = (10.20,10.80))
plt.plot(df_elbow['k'], df_elbow['inertia'])
plt.xticks(range(1,11))
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Elbow curve')
plt.grid()
plt.show()
def get_clusters(k, data):
# Initialize the K-Means model
model = KMeans(n_clusters=k, random_state=0)
# Train the model
model.fit(data)
# Predict clusters
predictions = model.predict(data)
# Create return DataFrame with predicted clusters
data["class"] = model.labels_
return data
# transform embedded array into df for clustering purposes
cluster_df = pd.DataFrame(X_embedded, columns=['col_1','col_2'])
# display the cluster df
cluster_df
# after plotting the inertia of the K-means cluster data, 4 clusters was determined to be the best
clusters = get_clusters(4, cluster_df)
# cluster_df with defined classes
clusters
def show_clusters(df):
fig = plt.figure(figsize = (10.20,10.80))
plt.scatter(df['col_1'], df['col_2'], c=df['class'])
plt.xlabel('col_1')
plt.ylabel('col_2')
plt.grid()
plt.show()
show_clusters(clusters)
```
| github_jupyter |
# Circuit visualize
このドキュメントでは scikit-qulacs に用意されている量子回路を可視化します。
scikitqulacsには現在、以下のような量子回路を用意しています。
- create_qcl_ansatz(n_qubit: int, c_depth: int, time_step: float, seed=None): [arXiv:1803.00745](https://arxiv.org/abs/1803.00745)
- create_farhi_neven_ansatz(n_qubit: int, c_depth: int, seed: Optional[int] = None): [arXiv:1802.06002](https://arxiv.org/pdf/1802.06002)
- create_ibm_embedding_circuit(n_qubit: int): [arXiv:1804.11326](https://arxiv.org/abs/1804.11326)
- create_shirai_ansatz(n_qubit: int, c_depth: int = 5, seed: int = 0): [arXiv:2111.02951](http://arxiv.org/abs/2111.02951)
注:微妙に細部が異なる可能性あり
- create_npqcd_ansatz(n_qubit: int, c_depth: int, c: float = 0.1): [arXiv:2108.01039](https://arxiv.org/abs/2108.01039)
- create_yzcx_ansatz(n_qubit: int, c_depth: int = 4, c: float = 0.1, seed: int = 9):[arXiv:2108.01039](https://arxiv.org/abs/2108.01039)
create_qcnn_ansatz(n_qubit: int, seed: int = 0):Creates circuit used in https://www.tensorflow.org/quantum/tutorials/qcnn?hl=en, Section 1.
回路を見やすくするために、パラメータの値を通常より小さくしています。
量子回路の可視化には[qulacs-visualizer](https://github.com/Qulacs-Osaka/qulacs-visualizer)を使用しています。
qulacs-visualizerはpipを使ってインストールできます。
```bash
pip install qulacsvis
```
## qcl_ansatz
create_qcl_ansatz(
n_qubit: int, c_depth: int, time_step: float = 0.5, seed: Optional[int] = None
)
[arXiv:1803.00745](https://arxiv.org/abs/1803.00745)
```
from skqulacs.circuit.pre_defined import create_qcl_ansatz
from qulacsvis import circuit_drawer
n_qubit = 4
c_depth = 2
time_step = 1.
ansatz = create_qcl_ansatz(n_qubit, c_depth, time_step)
circuit_drawer(ansatz._circuit,"latex")
```
## farhi_neven_ansatz
create_farhi_neven_ansatz(
n_qubit: int, c_depth: int, seed: Optional[int] = None
)
[arXiv:1802.06002](https://arxiv.org/abs/1802.06002)
```
from skqulacs.circuit.pre_defined import create_farhi_neven_ansatz
n_qubit = 4
c_depth = 2
ansatz = create_farhi_neven_ansatz(n_qubit, c_depth)
circuit_drawer(ansatz._circuit,"latex")
```
## farhi_neven_watle_ansatz
farhi_neven_ansatzを @WATLE さんが改良したもの
create_farhi_neven_watle_ansatz(
n_qubit: int, c_depth: int, seed: Optional[int] = None
)
```
from skqulacs.circuit.pre_defined import create_farhi_neven_watle_ansatz
n_qubit = 4
c_depth = 2
ansatz = create_farhi_neven_watle_ansatz(n_qubit, c_depth)
circuit_drawer(ansatz._circuit,"latex")
```
## ibm_embedding_circuit
create_ibm_embedding_circuit(n_qubit: int)
[arXiv:1802.06002](https://arxiv.org/abs/1802.06002)
```
from skqulacs.circuit.pre_defined import create_ibm_embedding_circuit
n_qubit = 4
circuit = create_ibm_embedding_circuit(n_qubit)
circuit_drawer(circuit._circuit,"latex")
```
## shirai_ansatz
create_shirai_ansatz(
n_qubit: int, c_depth: int = 5, seed: int = 0
)
[arXiv:2111.02951](https://arxiv.org/abs/2111.02951)
```
from skqulacs.circuit.pre_defined import create_shirai_ansatz
n_qubit = 4
c_depth = 2
ansatz = create_shirai_ansatz(n_qubit, c_depth)
circuit_drawer(ansatz._circuit,"latex")
```
## npqcd_ansatz
create_npqcd_ansatz(
n_qubit: int, c_depth: int, c: float = 0.1
)
[arXiv:2108.01039](https://arxiv.org/abs/2108.01039)
```
from skqulacs.circuit.pre_defined import create_npqc_ansatz
n_qubit = 4
c_depth = 2
ansatz = create_npqc_ansatz(n_qubit, c_depth)
circuit_drawer(ansatz._circuit,"latex")
```
## yzcx_ansatz
create_yzcx_ansatz(
n_qubit: int, c_depth: int = 4, c: float = 0.1, seed: int = 9
)
[arXiv:2108.01039](https://arxiv.org/abs/2108.01039)
```
from skqulacs.circuit.pre_defined import create_yzcx_ansatz
n_qubit = 4
c_depth = 2
ansatz = create_yzcx_ansatz(n_qubit, c_depth)
circuit_drawer(ansatz._circuit,"latex")
```
## qcnn_ansatz
create_qcnn_ansatz(n_qubit: int, seed: int = 0)
Creates circuit used in https://www.tensorflow.org/quantum/tutorials/qcnn?hl=en, Section 1.
```
from skqulacs.circuit.pre_defined import create_qcnn_ansatz
n_qubit = 8
ansatz = create_qcnn_ansatz(n_qubit)
circuit_drawer(ansatz._circuit,"latex")
```
| github_jupyter |
```
import pandas as pd
import numpy as np
```
## **Downloading data from Google Drive**
```
!pip install -U -q PyDrive
import os
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
import zipfile
from google.colab import drive
# 1. Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# choose a local (colab) directory to store the data.
local_download_path = os.path.expanduser('content/data')
try:
os.makedirs(local_download_path)
except: pass
# 2. Auto-iterate using the query syntax
# https://developers.google.com/drive/v2/web/search-parameters
# list of files in Google Drive folder
file_list = drive.ListFile(
{'q': "'1MsgfnmWPV-Nod0s1ZejYfsvbIwRMKZg_' in parents"}).GetList()
# find data in .zip format and save it
for f in file_list:
if f['title'] == "severstal-steel-defect-detection.zip":
fname = os.path.join(local_download_path, f['title'])
f_ = drive.CreateFile({'id': f['id']})
f_.GetContentFile(fname)
# extract files from zip to "extracted/" directory, this directory will be
# used for further data modelling
zip_ref = zipfile.ZipFile(fname, 'r')
zip_ref.extractall(os.path.join(local_download_path, "extracted"))
zip_ref.close()
```
Define working directories
```
working_dir = os.path.join(local_download_path, "extracted")
# defining working folders and labels
train_images_folder = os.path.join(working_dir, "train_images")
train_labels_file = os.path.join(working_dir, "train.csv")
test_images_folder = os.path.join(working_dir, "test_images")
test_labels_file = os.path.join(working_dir, "sample_submission.csv")
train_labels = pd.read_csv(train_labels_file)
test_labels = pd.read_csv(test_labels_file)
```
# **Data preprocessing**
Drop duplicates
```
train_labels.drop_duplicates("ImageId", keep="last", inplace=True)
```
Add to the train dataframe all non-defective images, setting None as value of EncodedPixels column
```
images = os.listdir(train_images_folder)
present_rows = train_labels.ImageId.tolist()
for img in images:
if img not in present_rows:
train_labels = train_labels.append({"ImageId" : img, "ClassId" : 1, "EncodedPixels" : None},
ignore_index=True)
```
Change EncodedPixels column, by setting 1 if images is defected and 0 otherwise
```
for index, row in train_labels.iterrows():
train_labels.at[index, "EncodedPixels"] = int(train_labels.at[index, "EncodedPixels"] is not None)
```
In total we got 12,568 training samples
```
train_labels
```
Create data flow using ImageDataGenerator, see example here: https://medium.com/@vijayabhaskar96/tutorial-on-keras-flow-from-dataframe-1fd4493d237c
```
from keras_preprocessing.image import ImageDataGenerator
def create_datagen():
return ImageDataGenerator(
fill_mode='constant',
cval=0.,
rotation_range=10,
height_shift_range=0.1,
width_shift_range=0.1,
vertical_flip=True,
rescale=1./255,
zoom_range=0.1,
horizontal_flip=True,
validation_split=0.15
)
def create_test_gen():
return ImageDataGenerator(rescale=1/255.).flow_from_dataframe(
dataframe=test_labels,
directory=test_images_folder,
x_col='ImageId',
class_mode=None,
target_size=(256, 512),
batch_size=1,
shuffle=False
)
def create_flow(datagen, subset_name):
return datagen.flow_from_dataframe(
dataframe=train_labels,
directory=train_images_folder,
x_col='ImageId',
y_col='EncodedPixels',
class_mode='other',
target_size=(256, 512),
batch_size=32,
subset=subset_name
)
data_generator = create_datagen()
train_gen = create_flow(data_generator, 'training')
val_gen = create_flow(data_generator, 'validation')
test_gen = create_test_gen()
```
# **Building and fiting model**
```
from keras.applications import InceptionResNetV2
from keras.models import Model
from keras.layers.core import Dense
from keras.layers.pooling import GlobalAveragePooling2D
from keras import optimizers
model = InceptionResNetV2(weights='imagenet', input_shape=(256,512,3), include_top=False)
#model.load_weights('/kaggle/input/inceptionresnetv2/inception_resent_v2_weights_tf_dim_ordering_tf_kernels_notop.h5')
model.trainable=False
x=model.output
x=GlobalAveragePooling2D()(x)
x=Dense(128,activation='relu')(x)
x=Dense(64,activation='relu')(x)
out=Dense(1,activation='sigmoid')(x) #final layer binary classifier
model_binary=Model(inputs=model.input,outputs=out)
model_binary.compile(
loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy']
)
```
Fittting the data
```
STEP_SIZE_TRAIN=train_gen.n//train_gen.batch_size
STEP_SIZE_VALID=val_gen.n//val_gen.batch_size
STEP_SIZE_TEST=test_gen.n//test_gen.batch_size
model_binary.fit_generator(generator=train_gen,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=val_gen,
validation_steps=STEP_SIZE_VALID,
epochs=15
)
```
Predicting test labels
```
test_gen.reset()
pred=model_binary.predict_generator(test_gen,
steps=STEP_SIZE_TEST,
verbose=1)
```
# **Saving results**
Create dataframe with probalities of having defects for each image
```
ids = np.array(test_labels.ImageId)
pred = np.array([p[0] for p in pred])
probabilities_df = pd.DataFrame({'ImageId': ids, 'Probability': pred}, columns=['ImageId', 'Probability'])
probabilities_df
from google.colab import files
df.to_csv('filename.csv')
files.download('filename.csv')
drive.mount('/content/gdrive')
!cp /content/defect_present_probabilities.csv gdrive/My\ Drive
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
class Datafuzzy():
def __init__(self, score, decission):
self.score = score
self.decission = decission
markFollower = [0, 15000, 33000, 51000, 79000, 100000]
markEngagement = [0, 0.6, 1.7, 5, 7, 8, 10]
lingFollower = ['NANO', 'MICRO', 'MEDIUM']
lingEngagement = ['NANO', 'MICRO', 'MEDIUM', 'MEGA']
```
### PLOT FOR FOLLOWER
```
# THE FOLLOWERS'S VALUE AND NAME
plt.plot(markFollower[:3], [1, 1, 0])
plt.suptitle("FOLLOWER - NANO")
plt.show()
plt.plot(markFollower[1:5], [0, 1, 1,0])
plt.suptitle("FOLLOWER - MICRO")
plt.show()
plt.plot(markFollower[3:], [0, 1, 1])
plt.suptitle("FOLLOWER - MEDIUM")
plt.show()
plt.plot(markFollower[:3], [1, 1, 0], label="NANO")
plt.plot(markFollower[1:5], [0, 1, 1,0], label="MICRO")
plt.plot(markFollower[3:], [0, 1, 1], label="MEDIUM")
plt.suptitle("FOLLOWER")
plt.show()
```
### PLOT FOR LINGUSITIC
```
# THE LINGUISTIC'S VALUE AND NAME
markEngagement = [0, 0.6, 1.7, 4.7, 6.9, 8, 10]
plt.plot(markEngagement[:3], [1, 1, 0])
plt.suptitle("ENGAGEMENT - NANO")
plt.show()
plt.plot(markEngagement[1:4], [0, 1, 0])
plt.suptitle("ENGAGEMENT - MICRO")
plt.show()
plt.plot(markEngagement[2:6], [0, 1, 1, 0])
plt.suptitle("ENGAGEMENT - MEDIUM")
plt.show()
plt.plot(markEngagement[4:], [0, 1, 1])
plt.suptitle("ENGAGEMENT - MEGA")
plt.show()
plt.plot(markEngagement[:3], [1, 1, 0], label="NANO")
plt.plot(markEngagement[1:4], [0, 1, 0], label="MICRO")
plt.plot(markEngagement[2:6], [0, 1, 1, 0], label="MEDIUM")
plt.plot(markEngagement[4:], [0, 1, 1], label="MEGA")
plt.suptitle("ENGAGEMENT")
plt.show()
```
## Fuzzification
```
# FOLLOWER=========================================
# membership function
def fuzzyFollower(countFol):
follower = []
# STABLE GRAPH
if (markFollower[0] <= countFol and countFol < markFollower[1]):
scoreFuzzy = 1
follower.append(Datafuzzy(scoreFuzzy, lingFollower[0]))
# GRAPH DOWN
elif (markFollower[1] <= countFol and countFol <= markFollower[2]):
scoreFuzzy = np.absolute((markFollower[2] - countFol) / (markFollower[2] - markFollower[1]))
follower.append(Datafuzzy(scoreFuzzy, lingFollower[0]))
# MICRO
# GRAPH UP
if (markFollower[1] <= countFol and countFol <= markFollower[2]):
scoreFuzzy = 1 - np.absolute((markFollower[2] - countFol) / (markFollower[2] - markFollower[1]))
follower.append(Datafuzzy(scoreFuzzy, lingFollower[1]))
# STABLE GRAPH
elif (markFollower[2] < countFol and countFol < markFollower[3]):
scoreFuzzy = 1
follower.append(Datafuzzy(scoreFuzzy, lingFollower[1]))
# GRAPH DOWN
elif (markFollower[3] <= countFol and countFol <= markFollower[4]):
scoreFuzzy = np.absolute((markFollower[4] - countFol) / (markFollower[4] - markFollower[3]))
follower.append(Datafuzzy(scoreFuzzy, lingFollower[1]))
# MEDIUM
# GRAPH UP
if (markFollower[3] <= countFol and countFol <= markFollower[4]):
scoreFuzzy = 1 - scoreFuzzy
follower.append(Datafuzzy(scoreFuzzy, lingFollower[2]))
# STABLE GRAPH
elif (countFol > markFollower[4]):
scoreFuzzy = 1
follower.append(Datafuzzy(scoreFuzzy, lingFollower[2]))
return follower
# ENGAGEMENT RATE =========================================
# membership function
def fuzzyEngagement(countEng):
engagement = []
# STABLE GRAPH
if (markEngagement[0] < countEng and countEng < markEngagement[1]):
scoreFuzzy = 1
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[0]))
# GRAPH DOWN
elif (markEngagement[1] <= countEng and countEng < markEngagement[2]):
scoreFuzzy = np.absolute((markEngagement[2] - countEng) / (markEngagement[2] - markEngagement[1]))
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[0]))
# MICRO
# THE GRAPH GOES UP
if (markEngagement[1] <= countEng and countEng < markEngagement[2]):
scoreFuzzy = 1 - scoreFuzzy
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[1]))
# GRAPH DOWN
elif (markEngagement[2] <= countEng and countEng < markEngagement[3]):
scoreFuzzy = np.absolute((markEngagement[3] - countEng) / (markEngagement[3] - markEngagement[2]))
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[1]))
#MEDIUM
# THE GRAPH GOES UP
if (markEngagement[2] <= countEng and countEng < markEngagement[3]):
scoreFuzzy = 1 - scoreFuzzy
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[2]))
# STABLE GRAPH
elif (markEngagement[3] <= countEng and countEng < markEngagement[4]):
scoreFuzzy = 1
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[2]))
# GRAPH DOWN
elif (markEngagement[4] <= countEng and countEng < markEngagement[5]):
scoreFuzzy = np.absolute((markEngagement[5] - countEng) / (markEngagement[5] - markEngagement[4]))
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[2]))
# MEGA
# THE GRAPH GOES UP
if (markEngagement[4] <= countEng and countEng < markEngagement[5]):
scoreFuzzy = 1 - scoreFuzzy
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[3]))
# STABLE GRAPH
elif (countEng > markEngagement[5]):
scoreFuzzy = 1
engagement.append(Datafuzzy(scoreFuzzy, lingEngagement[3]))
return engagement
```
## Inference
```
def cekDecission(follower, engagement):
temp_yes = []
temp_no = []
if (follower.decission == "NANO"):
# Get minimal score fuzzy every decision NO or YES
temp_yes.append(min(follower.score,engagement[0].score))
# if get 2 data fuzzy Engagement
if (len(engagement) > 1):
temp_yes.append(min(follower.score,engagement[1].score))
elif (follower.decission == "MICRO"):
if (engagement[0].decission == "NANO"):
temp_no.append(min(follower.score, engagement[0].score))
else:
temp_yes.append(min(follower.score, engagement[0].score))
if (len(engagement) > 1):
if (engagement[1].decission == "NANO"):
temp_no.append(min(follower.score, engagement[1].score))
else:
temp_yes.append(min(follower.score, engagement[1].score))
else:
if (engagement[0].decission == "NANO" or engagement[0].decission == "MICRO"):
temp_no.append(min(follower.score, engagement[0].score))
else:
temp_yes.append(min(follower.score, engagement[0].score))
# if get 2 data fuzzy engagement
if (len(engagement) > 1):
if (engagement[1].decission == "NANO" or engagement[1].decission == "MICRO"):
temp_no.append(min(follower.score, engagement[1].score))
else:
temp_yes.append(min(follower.score, engagement[1].score))
return temp_yes, temp_no
# Fuzzy Rules
def fuzzyRules(follower, engagement):
temp_yes = []
temp_no = []
temp_y = []
temp_n = []
temp_yes, temp_no = cekDecission(follower[0], engagement)
# if get 2 data fuzzy Follower
if (len(follower) > 1):
temp_y, temp_n = cekDecission(follower[1], engagement)
temp_yes += temp_y
temp_no += temp_n
return temp_yes, temp_no
```
### Result
```
# Result
def getResult(resultYes, resultNo):
yes = 0
no = 0
if(resultNo):
no = max(resultNo)
if(resultYes):
yes = max(resultYes)
return yes, no
```
### Defuzzification
```
def finalDecission(yes, no):
mamdani = (((10 + 20 + 30 + 40 + 50 + 60 + 70) * no) + ((80 + 90 + 100) * yes)) / ((7 * no) + (yes * 3))
return mamdani
```
### Main Function
```
def mainFunction(followerCount, engagementRate):
follower = fuzzyFollower(followerCount)
engagement = fuzzyEngagement(engagementRate)
resultYes, resultNo = fuzzyRules(follower, engagement)
yes, no = getResult(resultYes, resultNo)
return finalDecission(yes, no)
data = pd.read_csv('influencers.csv')
data
hasil = []
result = []
idd = []
for i in range (len(data)):
# Insert ID and the score into the list
hasil.append([data.loc[i, 'id'], mainFunction(data.loc[i, 'followerCount'], data.loc[i, 'engagementRate'])])
result.append([data.loc[i, 'id'], (data.loc[i, 'followerCount'] * data.loc[i, 'engagementRate'] / 100)])
# Sorted list of hasil by fuzzy score DECREMENT
hasil.sort(key=lambda x:x[1], reverse=True)
result.sort(key=lambda x:x[1], reverse=True)
result = result[:20]
hasil = hasil[:20]
idd = [row[0] for row in result]
hasil
idd
def cekAkurasi(hasil, result):
count = 0
for i in range(len(hasil)):
if (hasil[i][0] in idd):
count += 1
return count
print("AKURASI : ", cekAkurasi(hasil, result)/20*100, " %")
chosen = pd.DataFrame(hasil[:20], columns=['ID', 'Score'])
chosen
chosen.to_csv('choosen.csv')
```
| github_jupyter |
### Road Following - Live demo (TensorRT) with collision avoidance
### Added collision avoidance ResNet18 TRT
### threshold between free and blocked is the controller - action: just a pause as long the object is in front or by time
### increase in speed_gain requires some small increase in steer_gain (once a slider is blue (mouse click), arrow keys left/right can be used)
### 10/11/2020
# TensorRT
```
import torch
device = torch.device('cuda')
```
Load the TRT optimized models by executing the cell below
```
import torch
from torch2trt import TRTModule
model_trt = TRTModule()
model_trt.load_state_dict(torch.load('best_steering_model_xy_trt.pth')) # well trained road following model
model_trt_collision = TRTModule()
model_trt_collision.load_state_dict(torch.load('best_model_trt.pth')) # anti collision model trained for one object to block and street signals (ground, strips) as free
```
### Creating the Pre-Processing Function
We have now loaded our model, but there's a slight issue. The format that we trained our model doesnt exactly match the format of the camera. To do that, we need to do some preprocessing. This involves the following steps:
1. Convert from HWC layout to CHW layout
2. Normalize using same parameters as we did during training (our camera provides values in [0, 255] range and training loaded images in [0, 1] range so we need to scale by 255.0
3. Transfer the data from CPU memory to GPU memory
4. Add a batch dimension
```
import torchvision.transforms as transforms
import torch.nn.functional as F
import cv2
import PIL.Image
import numpy as np
mean = torch.Tensor([0.485, 0.456, 0.406]).cuda().half()
std = torch.Tensor([0.229, 0.224, 0.225]).cuda().half()
def preprocess(image):
image = PIL.Image.fromarray(image)
image = transforms.functional.to_tensor(image).to(device).half()
image.sub_(mean[:, None, None]).div_(std[:, None, None])
return image[None, ...]
```
Awesome! We've now defined our pre-processing function which can convert images from the camera format to the neural network input format.
Now, let's start and display our camera. You should be pretty familiar with this by now.
```
from IPython.display import display
import ipywidgets
import traitlets
from jetbot import Camera, bgr8_to_jpeg
camera = Camera()
import IPython
image_widget = ipywidgets.Image()
traitlets.dlink((camera, 'value'), (image_widget, 'value'), transform=bgr8_to_jpeg)
```
We'll also create our robot instance which we'll need to drive the motors.
```
from jetbot import Robot
robot = Robot()
```
Now, we will define sliders to control JetBot
> Note: We have initialize the slider values for best known configurations, however these might not work for your dataset, therefore please increase or decrease the sliders according to your setup and environment
1. Speed Control (speed_gain_slider): To start your JetBot increase ``speed_gain_slider``
2. Steering Gain Control (steering_gain_sloder): If you see JetBot is woblling, you need to reduce ``steering_gain_slider`` till it is smooth
3. Steering Bias control (steering_bias_slider): If you see JetBot is biased towards extreme right or extreme left side of the track, you should control this slider till JetBot start following line or track in the center. This accounts for motor biases as well as camera offsets
> Note: You should play around above mentioned sliders with lower speed to get smooth JetBot road following behavior.
```
speed_gain_slider = ipywidgets.FloatSlider(min=0.0, max=1.0, step=0.01, description='speed gain')
steering_gain_slider = ipywidgets.FloatSlider(min=0.0, max=1.0, step=0.01, value=0.10, description='steering gain')
steering_dgain_slider = ipywidgets.FloatSlider(min=0.0, max=0.5, step=0.001, value=0.23, description='steering kd')
steering_bias_slider = ipywidgets.FloatSlider(min=-0.3, max=0.3, step=0.01, value=0.0, description='steering bias')
display(speed_gain_slider, steering_gain_slider, steering_dgain_slider, steering_bias_slider)
#anti collision ---------------------------------------------------------------------------------------------------
blocked_slider = ipywidgets.FloatSlider(description='blocked', min=0.0, max=1.0, orientation='horizontal')
stopduration_slider= ipywidgets.IntSlider(min=1, max=1000, step=1, value=10, description='Manu. time stop') #anti-collision stop time
#set value according the common threshold e.g. 0.8
block_threshold= ipywidgets.FloatSlider(min=0, max=1.2, step=0.01, value=0.8, description='Manu. bl threshold') #anti-collision block probability
display(image_widget)
d2 = IPython.display.display("", display_id=2)
display(ipywidgets.HBox([blocked_slider, block_threshold, stopduration_slider]))
# TIME STOP slider is to select manually time-for-stop when object has been discovered
#x_slider = ipywidgets.FloatSlider(min=-1.0, max=1.0, description='x')
#y_slider = ipywidgets.FloatSlider(min=0, max=1.0, orientation='vertical', description='y')
#steering_slider = ipywidgets.FloatSlider(min=-1.0, max=1.0, description='steering')
#speed_slider = ipywidgets.FloatSlider(min=0, max=1.0, orientation='vertical', description='speed')
#display(ipywidgets.HBox([y_slider, speed_slider,x_slider, steering_slider])) #sliders take time , reduce FPS a couple of frames per second
#observation sliders only
from threading import Thread
def display_class_probability(prob_blocked):
global blocked_slide
blocked_slider.value = prob_blocked
return
def model_new(image_preproc):
global model_trt_collision,angle_last
xy = model_trt(image_preproc).detach().float().cpu().numpy().flatten()
x = xy[0]
y = (0.5 - xy[1]) / 2.0
angle=math.atan2(x, y)
pid =angle * steer_gain + (angle - angle_last) * steer_dgain
steer_val = pid + steer_bias
angle_last = angle
robot.left_motor.value = max(min(speed_value + steer_val, 1.0), 0.0)
robot.right_motor.value = max(min(speed_value - steer_val, 1.0), 0.0)
return
```
Next, we'll create a function that will get called whenever the camera's value changes. This function will do the following steps
1. Pre-process the camera image
2. Execute the neural network
3. Compute the approximate steering value
4. Control the motors using proportional / derivative control (PD)
```
import time
import os
import math
angle = 0.0
angle_last = 0.0
angle_last_block=0
count_stops=0
go_on=1
stop_time=20 #number of frames to remain stopped
x=0.0
y=0.0
speed_value=speed_gain_slider.value
t1=0
road_following=1
speed_value_block=0
def execute(change):
global angle, angle_last, angle_last_block, blocked_slider, robot,count_stops, stop_time,go_on,x,y,block_threshold
global speed_value, steer_gain, steer_dgain, steer_bias,t1,model_trt, model_trt_collision,road_following,speed_value_block
steer_gain=steering_gain_slider.value
steer_dgain=steering_dgain_slider.value
steer_bias=steering_bias_slider.value
image_preproc = preprocess(change['new']).to(device)
#anti_collision model-----
prob_blocked = float(F.softmax(model_trt_collision(image_preproc), dim=1) .flatten()[0])
#blocked_slider.value = prob_blocked
#display of detection probability value for the four classes
t = Thread(target = display_class_probability, args =(prob_blocked,), daemon=False)
t.start()
stop_time=stopduration_slider.value
if go_on==1:
if prob_blocked > block_threshold.value: # threshold should be above 0.5,
#start of collision_avoidance
count_stops +=1
go_on=2
road_following=2
x=0.0 #set steering zero
y=0 #set steering zero
speed_value_block=0 # set speed zero or negative or turn
#anti_collision end-------
else:
#start of road following
go_on=1
count_stops=0
speed_value = speed_gain_slider.value #
t = Thread(target = model_new, args =(image_preproc,), daemon=True)
t.start()
road_following=1
else:
count_stops += 1
if count_stops<stop_time:
go_on=2
else:
go_on=1
count_stops=0
road_following=1
#x_slider.value = x #take time 4 FPS
#y_slider.value = y #y_speed
if road_following>1:
angle_block=math.atan2(x, y)
pid =angle_block * steer_gain + (angle - angle_last) * steer_dgain
steer_val_block = pid + steer_bias
angle_last_block = angle_block
robot.left_motor.value = max(min(speed_value_block + steer_val_block, 1.0), 0.0)
robot.right_motor.value = max(min(speed_value_block - steer_val_block, 1.0), 0.0)
t2 = time.time()
s = f"""{int(1/(t2-t1))} FPS"""
d2.update(IPython.display.HTML(s) )
t1 = time.time()
execute({'new': camera.value})
```
Cool! We've created our neural network execution function, but now we need to attach it to the camera for processing.
We accomplish that with the observe function.
>WARNING: This code will move the robot!! Please make sure your robot has clearance and it is on Lego or Track you have collected data on. The road follower should work, but the neural network is only as good as the data it's trained on!
```
camera.observe(execute, names='value')
```
Awesome! If your robot is plugged in it should now be generating new commands with each new camera frame.
You can now place JetBot on Lego or Track you have collected data on and see whether it can follow track.
If you want to stop this behavior, you can unattach this callback by executing the code below.
```
import time
camera.unobserve(execute, names='value')
time.sleep(0.1) # add a small sleep to make sure frames have finished processing
robot.stop()
camera.stop()
```
### Conclusion
That's it for this live demo! Hopefully you had some fun seeing your JetBot moving smoothly on track follwing the road!!!
If your JetBot wasn't following road very well, try to spot where it fails. The beauty is that we can collect more data for these failure scenarios and the JetBot should get even better :)
| github_jupyter |
```
# %load hovorka.py
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def model(x, t, t_offset=None):
w = 100
ka1 = 0.006 #
ka2 = 0.06 #
ka3 = 0.03 #
kb1 = 0.0034 #
kb2 = 0.056 #
kb3 = 0.024 #
u_b = 0.0555
tmaxI = 55 #
VI = 0.12 * w #
ke = 0.138 #
k12 = 0.066 #
VG = 0.16 * w #
# G = x[0] / VG
F01 = 0.0097 * w #
FR = 0
EGP0 = 0.0161 * w #
AG = 0.8 #
Gmolar = 180.1559
tmaxG = 40 #
sp = 110 * VG / 18
l = (x[14] * x[10] + x[13] * x[11] + x[12] * (-(
- F01 - x[5] * x[0] + k12 * x[1] - FR + EGP0 * (1 - x[7]) + (x[9] * AG * 1000 / Gmolar) * x[8] * np.exp(
-x[8] / tmaxG) / (tmaxG ** 2)))) + u_b - x[2] / tmaxI,
dxdt = [
- F01 - x[5] * x[0] + k12 * x[1] - FR + EGP0 * (1 - x[7]) + (x[9] * AG * 1000 / Gmolar) * x[8] * np.exp(
-x[8] / tmaxG) / (tmaxG ** 2),
x[5] * x[0] - (k12 + x[6]) * x[1],
((x[14] * x[10] + x[13] * x[11] + x[12] * (-(
- F01 - x[5] * x[0] + k12 * x[1] - FR + EGP0 * (1 - x[7]) + (x[9] * AG * 1000 / Gmolar) * x[8] * np.exp(
-x[8] / tmaxG) / (tmaxG ** 2)))) + u_b - x[2] / tmaxI) + u_b - x[2] / tmaxI,
(x[2] - x[3]) / tmaxI,
x[3] / (tmaxI * VI) - ke * x[4],
- ka1 * x[5] + kb1 * x[4],
- ka2 * x[6] + kb2 * x[4],
- ka3 * x[7] + kb3 * x[4],
1,
0,
0 - (- F01 - x[5] * x[0] + k12 * x[1] - FR + EGP0 * (1 - x[7]) + (x[9] * AG * 1000 / Gmolar) * x[8] * np.exp(
-x[8] / tmaxG) / (tmaxG ** 2)),
sp - x[0],
0,
0,
0,
(sp - x[0])**2,
(x[8] + t_offset)**2 * (sp - x[0])**2
]
return dxdt
w=100
VG = 0.16 * w
sp = 110 * VG / 18
# initial condition
Kd = [0, -0.0602, -0.0573, -0.06002, -0.0624]
Ki = [0, -3.53e-07, -3e-07, -1.17e-07, -7.55e-07]
Kp = [0, -6.17e-04, -6.39e-04, -6.76e-04, -5.42e-04]
i=1
dg1 = np.random.normal(40,10)
dg2 = np.random.normal(90,10)
dg3 = np.random.normal(60,10)
# dg1 = 40
# dg2 = 90
# dg3 = 60
x0 = [97.77, 19.08024, 3.0525, 3.0525, 0.033551, 0.01899, 0.03128, 0.02681, 0.0, dg1, 0.0, 0.0, Kd[i], Ki[i], Kp[i], 0, 0];
# time points
t_offset=0
t_sleep = 540
t_meal = 300
t = np.arange(0,t_meal,0.2)
y = odeint(model,x0,t,args=(t_offset,))
ytot = y
ttot = t
ystart = y[-1,:]
ystart[8] = 0
ystart[9] = dg2
y = odeint(model,ystart,t,args=(t_offset,))
ytot = np.vstack([ytot,y])
ttot = np.hstack([ttot,t+ttot[-1]])
ystart = y[-1,:]
ystart[8] = 0
ystart[9] = dg3
t = np.arange(0,t_meal+t_sleep,0.2)
y = odeint(model,ystart,t,args=(t_offset,))
ytot = np.vstack([ytot,y])
ttot = np.hstack([ttot,t+ttot[-1]])
# plot results
plt.fill_between([ttot[0],ttot[-1]], [4,4],[16,16],alpha=0.5)
plt.plot(ttot,ytot[:,0]/VG,'r-',linewidth=2)
plt.axhline(y=sp/VG, color='k', linestyle='-')
plt.xlabel('time')
plt.ylabel('y(t)')
plt.legend()
plt.xlabel('Time (min)')
plt.ylabel('BG (mmol/L)')
plt.show()
ttot,ytot[:,0]/VG
```
| github_jupyter |
# Building a Bayesian Network
---
In this tutorial, we introduce how to build a **Bayesian (belief) network** based on domain knowledge of the problem.
If we build the Bayesian network in different ways, the built network can have different graphs and sizes, which can greatly affect the memory requirement and inference efficience. To represent the size of the Bayesian network, we first introduce the **number of free parameters**.
## Number of Free Parameters <a name="freepara"></a>
---
The size of a Bayesian network includes the size of the graph and the probability tables of each node. Obviously, the probability tables dominate the graph, thus we focus on the size of the probability tables.
For the sake of convenience, we only consider **discrete** variables in the network, and the continuous variables will be discretised. Then, for each variable $X$ in the network, we have the following notations.
- $\Omega(X)$: the domain (set of possible values) of $X$
- $|\Omega(X)|$: the number of possible values of $X$
- $parents(X)$: the parents (direct causes) of $X$ in the network
For each variable $X$, the probability table contains the probabilities for $P(X\ |\ parents(X))$ for all possible $X$ values and $parent(X)$ values. Let's consider the following situations:
1. $X$ does not have any parent. In this case, the table stores $P(X)$. There are $|\Omega(X)|$ probabilities, each for a possible value of $X$. However, due to the [normalisation rule](https://github.com/meiyi1986/tutorials/blob/master/notebooks/reasoning-under-uncertainty-basics.ipynb), all the probabilities add up to 1. Thus, we need to store only $|\Omega(X)|-1$ probabilities, and the last probability can be calculated by ($1-$the sum of the stored probabilities). Therefore, the probability table contains $|\Omega(X)|-1$ rows/probabilities.
2. $X$ has one parent $Y$. In this case, for each condition $y \in \Omega(Y)$, we need to store the conditional probabilities $P(X\ |\ Y = y)$. Again, we need to store $|\Omega(X)|-1$ conditional probabilities for $P(X\ |\ Y = y)$, and can calculate the last conditional probability by the normalisation rule. Therefore, the probability table contains $(|\Omega(X)|-1)*|\Omega(Y)|$ rows/probabilities.
3. $X$ has multiple parents $Y_1, \dots, Y_m$. In this case, there are $|\Omega(Y_1)|*\dots * |\Omega(Y_m)|$ possible conditions $[Y_1 = y_1, \dots, Y_m = y_m]$. For each condition, we need to store $|\Omega(X)|-1$ conditional probabilities for $P(X\ |\ Y_1 = y_1, \dots, Y_m = y_m)$. Therefore, the probability table contains $(|\Omega(X)|-1)*|\Omega(Y_1)|*\dots * |\Omega(Y_m)|$ rows/probabilities.
As shown in the above alarm network, all the variables are binary, i.e. $|\Omega(X)| = 2$. Therefore, $B$ and $E$ have only 1 row in their probability tables, since they have no parent. $A$ has $1 \times 2 \times 2 = 4$ rows in its probability tables, since it has two binary parents $B$ and $E$, leading to four possible conditions.
> **DEFINITION**: The **number of free parameters** of a Bayesian network is the number of probabilities we need to estimate (can NOT be derived/calculated) in the probability tables.
Consider a Bayesian network with the factorisation
$$
\begin{aligned}
& P(X_1, \dots, X_n) \\
& = P(X_1\ |\ parents(X_1)) \dots * P(X_n\ |\ parents(X_n)),
\end{aligned}
$$
the number of free parameters is
$$
\begin{aligned}
P(X_1, \dots, X_n) & = (|\Omega(X_1)|-1)*\prod_{Y \in parents(X_1)}|\Omega(Y)| \\
& + (|\Omega(X_2)|-1)*\prod_{Y \in parents(X_2)}|\Omega(Y)| \\
& + \dots \\
& + (|\Omega(X_n)|-1)*\prod_{Y \in parents(X_n)}|\Omega(Y)|. \\
\end{aligned}
$$
Let's calculate the number of free parameters of the following simple networks, assuming that all the variables are binary.
<img src="img/cause-effect.png" width=550></img>
- **Direct cause**: $P(A)$ has 1 free parameter, $P(B\ |\ A)$ has 2 free parameters. The network has $1+2 = 3$ free parameters.
- **Indirect cause**: $P(A)$ has 1 free parameter, $P(B\ |\ A)$ and $P(C\ |\ B)$ have 2 free parameters. The network has $1+2+2 = 5$ free parameters.
- **Common cause**: $P(A)$ has 1 free parameter, $P(B\ |\ A)$ and $P(C\ |\ A)$ have 2 free parameters. The network has $1+2+2 = 5$ free parameters.
- **Common effect**: $P(A)$ and $P(B)$ have 1 free parameter, $P(C\ |\ A, B)$ has $2\times 2 = 4$ free parameters. The network has $1+1+4 = 6$ free parameters.
> **NOTE**: We can see that the common effect dependency causes the most free parameters required for the network. Therefore, when building a Bayesian network, we should try to reduce the number of such dependencies to reduce the number of free parameters of the network.
## Building Bayesian Network from Domain Knowledge<a name="building"></a>
---
Building a Bayesian network mainly consists of the following three steps:
1. Identify a set of **random variables** that describe the problem, using domain knowledge.
2. Build the **directed acyclic graph**, i.e., the **directed links** between the random variables based on domain knowledge about the causal relationships between the variables.
3. Build the **conditional probability table** for each variable, by estimating the necessary probabilities using domain knowledge or historical data.
Here, we introduce the Pearl's network construction algorithm, which is a way to build the network based on **node ordering**.
```Python
# Step 1: identify variables
Identify the random variables that describe the world of reasoning
# Step 2: build the graph, add the links
Sort the random variables by some order
Set bn = []
for var in sorted_vars:
Find the minimum subset of variables in bn so that P(var | bn) = P(var | subset)
Add var into bn
for bn_var in subset:
Add a direct link [bn_var, var]
# Step 3: estimate the conditional probability table
Estimate the conditional probabilities P(var | subset)
```
In this algorithm, the **node ordering** is critical to determine the number of links between the nodes, and thus the size of the conditional probability tables.
We show how the links are added in to the network under different node orders, using the alarm network as an example.
----------
#### Order 1: $B \rightarrow E \rightarrow A \rightarrow J \rightarrow M$
- **Step 1**: The node $B$ is added into the network. No edge is added, since there is only one node in the network.
- **Step 2**: The node $E$ is added into the network. No edge from $B$ to $E$ is added, since $B$ and $E$ are <span style="color: blue;">independent</span>.
- **Step 3**: The node $A$ is added into the network. Two edges $[B, A]$ and $[E, A]$ are added. This is because $B$ and $E$ are both direct causes of $A$, and thus $A$ is <span style="color: red;">dependent</span> on $B$ and $E$.
- **Step 4**: The node $J$ is added into the network. The minimum subset $A \subseteq \{B, E, A\}$ in the network is found to be the parent of $J$, since $J$ is <span style="color: blue;">conditionally independent</span> from $B$ and $E$ given $A$, i.e., $P(J\ |\ B, E, A) = P(J\ |\ A)$. An edge $[A, J]$ is added into the network.
- **Step 5**: The node $M$ is added into the network. The minimum subset $A \subseteq \{B, E, A, J\}$ in the network is found to be the parent of $M$, since $M$ is <span style="color: blue;">conditionally independent</span> from $B$, $E$ and $J$ given $A$, i.e., $P(M\ |\ B, E, A, J) = P(M\ |\ A)$. An edge $[A, M]$ is added into the network.
The built network is shows as follows. The number of free parameters in this network is $1 + 1 + 4 + 2 + 2 = 10$.
<img src="img/alarm-dag.png" width=150></img>
----------
#### Order 2: $J \rightarrow M \rightarrow A \rightarrow B \rightarrow E$
- **Step 1**: The node $J$ is added into the network. No edge is added, since there is only one node in the network.
- **Step 2**: The node $M$ is added into the network. $M$ and $J$ are <span style="color: red;">dependent</span> (_note that the common cause $A$ has not been given yet at this step_), i.e., $P(M\ |\ J) \neq P(M)$. Therefore, an edge $[J, M]$ is added into the network.
- **Step 3**: The node $A$ is added into the network. Two edges $[J, A]$ and $[M, A]$ are added, since $J$ and $M$ are both <span style="color: red;">dependent</span> on $A$.
- **Step 4**: The node $B$ is added into the network. The minimum subset $A \subseteq \{J, M, A\}$ in the network is found to be the parent of $B$, since $B$ is <span style="color: blue;">conditionally independent</span> from $J$ and $M$ given $A$, i.e., $P(B\ |\ J, M, A) = P(B\ |\ A)$. An edge $[A, B]$ is added into the network.
- **Step 5**: The node $E$ is added into the network. The minimum subset $\{A, B\} \subseteq \{J, M, A, B\}$ in the network is found to be the parent of $E$, since $E$ is <span style="color: blue;">conditionally independent</span> from $J$ and $M$ given $A$ and $E$, i.e., $P(M\ |\ J, M, A, B) = P(M\ |\ A, B)$ (_note that $B$ and $E$ have the common effect $A$, thus when $A$ is given, $B$ and $E$ are <span style="color: red;">conditionally dependent</span>_). Two edges $[A, E]$ and $[B, E]$ are added into the network.
The built network is shows as follows. The number of free parameters in this network is $1 + 2 + 4 + 2 + 4 = 13$.
<img src="img/alarm-dag2.png" width=150></img>
----------
#### Order 3: $J \rightarrow M \rightarrow B \rightarrow E \rightarrow A$
- **Step 1**: The node $J$ is added into the network. No edge is added, since there is only one node in the network.
- **Step 2**: The node $M$ is added into the network. $M$ and $J$ are <span style="color: red;">dependent</span> (note that the common cause $A$ is not given at this step), i.e., $P(M\ |\ J) \neq P(M)$. Therefore, an edge $[J, M]$ is added into the network.
- **Step 3**: The node $B$ is added into the network. Two edges $[J, B]$ and $[M, B]$ are added, since $J$ and $M$ are both <span style="color: red;">dependent</span> on $B$ (through $A$, which has not been added yet).
- **Step 4**: The node $E$ is added into the network. There is NO conditional independence found among $\{J, M, B, E\}$ without giving $A$. Therefore, three edges $[J, E]$, $[M, E]$, $[B, E]$ are added into the network.
- **Step 5**: The node $A$ is added into the network. First, two edges Two edges $[J, A]$ and $[M, A]$ are added, since $J$ and $M$ are both <span style="color: red;">dependent</span> on $A$. Then, another two edges $[B, A]$ and $[E, A]$ are also added, since $B$ and $E$ are both direct causes of $A$.
The built network is shows as follows. The number of free parameters in this network is $1 + 2 + 4 + 8 + 16 = 31$.
<img src="img/alarm-dag3.png" width=200></img>
---------
We can see that different node orders can lead to greatly different graphs and numbers of free parameters. Therefore, we should find the **optimal node order** that leads to the most **compact** network (with the fewest free parameters).
> **QUESTION**: How to find the optimal node order that leads to the most compact Bayesian network?
The node order is mainly determined based on our **domain knowledge** about **cause and effect**. At first, we add the nodes with no cause (i.e., the root causes) into the ordered list. Then, at each step, we find the remaining nodes whose direct causes are all in the current ordered list (i.e., all their direct causes are given) and append them into the end of the ordered list. This way, we only need to add direct links from their direct causes to them.
The pseucode of the node ordering is shown as follows.
```Python
def node_ordering(all_nodes):
Set ordered_nodes = [], remaining_nodes = all_nodes
while remaining_nodes is not empty:
Select the nodes whose direct causes are all in ordered_nodes
Append the selected nodes into ordered_nodes
Remove the selected nodes from remaining_nodes
return ordered_nodes
```
For the alarm network, first we add two nodes $\{B, E\}$ into the ordered list, since they are the root causes, and have no direct cause. Then, we add $A$ into the ordered list, since it has two direct causes $B$ and $E$, both are already in the ordered list. Finally, we add $J$ and $M$ into the list, since their direct cause $A$ is already in the ordered list.
## Building Alarm Network through `pgmpy` <a name="pgmpy"></a>
---
Here, we show how to build the alarm network through the Python [pgmpy](https://pgmpy.org) library. The alarm network is displayed again below.
<img src="img/alarm-bn.png" width=500></img>
First, we install the library using `pip`.
```
pip install pgmpy
```
Then, we import the necessary modules for the Bayesian network as follows.
```
from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
```
Now, we build the alarm Bayesian network as follows.
1. We define the network structure by specifying the four links.
2. We define (estimate) the discrete conditional probability tables, represented as the `TabularCPD` class.
```
# Define the network structure
alarm_model = BayesianNetwork(
[
("Burglary", "Alarm"),
("Earthquake", "Alarm"),
("Alarm", "JohnCall"),
("Alarm", "MaryCall"),
]
)
# Define the probability tables by TabularCPD
cpd_burglary = TabularCPD(
variable="Burglary", variable_card=2, values=[[0.999], [0.001]]
)
cpd_earthquake = TabularCPD(
variable="Earthquake", variable_card=2, values=[[0.998], [0.002]]
)
cpd_alarm = TabularCPD(
variable="Alarm",
variable_card=2,
values=[[0.999, 0.71, 0.06, 0.05], [0.001, 0.29, 0.94, 0.95]],
evidence=["Burglary", "Earthquake"],
evidence_card=[2, 2],
)
cpd_johncall = TabularCPD(
variable="JohnCall",
variable_card=2,
values=[[0.95, 0.1], [0.05, 0.9]],
evidence=["Alarm"],
evidence_card=[2],
)
cpd_marycall = TabularCPD(
variable="MaryCall",
variable_card=2,
values=[[0.99, 0.3], [0.01, 0.7]],
evidence=["Alarm"],
evidence_card=[2],
)
# Associating the probability tables with the model structure
alarm_model.add_cpds(
cpd_burglary, cpd_earthquake, cpd_alarm, cpd_johncall, cpd_marycall
)
```
We can view the nodes of the alarm network.
```
# Viewing nodes of the model
alarm_model.nodes()
```
We can also view the edges of the alarm network.
```
# Viewing edges of the model
alarm_model.edges()
```
We can show the probability tables using the `print()` method.
> **NOTE**: the `pgmpy` library stores ALL the probabilities (including the last probability). This requires a bit more memory, but can save time for calculating the last probability by normalisation rule.
Let's print the probability tables for **Alarm** and **MaryCalls**. For each variable, the value (0) stands for `False`, while the value (1) is `True`.
```
# Print the probability table of the Alarm node
print(cpd_alarm)
# Print the probability table of the MaryCalls node
print(cpd_marycall)
```
We can find all the **(conditional) independencies** between the nodes in the network.
```
alarm_model.get_independencies()
```
We can also find the **local (conditional) independencies of a specific node** in the network as follows.
```
# Checking independcies of a node
alarm_model.local_independencies("JohnCall")
```
---
- More tutorials can be found [here](https://github.com/meiyi1986/tutorials).
- [Yi Mei's homepage](https://meiyi1986.github.io/)
| github_jupyter |
# 1. Introduction
```
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from prml.linear import (
LinearRegression,
RidgeRegression,
BayesianRegression
)
from prml.preprocess.polynomial import PolynomialFeature
```
## 1.1. Example: Polynomial Curve Fitting
```
def create_toy_data(func, sample_size, std):
x = np.linspace(0, 1, sample_size)
t = func(x) + np.random.normal(scale=std, size=x.shape)
return x, t
def func(x):
return np.sin(2 * np.pi * x)
x_train, y_train = create_toy_data(func, 10, 0.25)
x_test = np.linspace(0, 1, 100)
y_test = func(x_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.legend()
plt.show()
for i, degree in enumerate([0, 1, 3, 9]):
plt.subplot(2, 2, i + 1)
feature = PolynomialFeature(degree)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.annotate("M={}".format(degree), xy=(-0.15, 1))
plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.show()
def rmse(a, b):
return np.sqrt(np.mean(np.square(a - b)))
training_errors = []
test_errors = []
for i in range(10):
feature = PolynomialFeature(i)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
training_errors.append(rmse(model.predict(X_train), y_train))
test_errors.append(rmse(model.predict(X_test), y_test + np.random.normal(scale=0.25, size=len(y_test))))
plt.plot(training_errors, 'o-', mfc="none", mec="b", ms=10, c="b", label="Training")
plt.plot(test_errors, 'o-', mfc="none", mec="r", ms=10, c="r", label="Test")
plt.legend()
plt.xlabel("degree")
plt.ylabel("RMSE")
plt.show()
```
#### Regularization
```
feature = PolynomialFeature(9)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = RidgeRegression(alpha=1e-3)
model.fit(X_train, y_train)
y = model.predict(X_test)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.annotate("M=9", xy=(-0.15, 1))
plt.show()
```
### 1.2.6 Bayesian curve fitting
```
model = BayesianRegression(alpha=2e-3, beta=2)
model.fit(X_train, y_train)
y, y_err = model.predict(X_test, return_std=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="mean")
plt.fill_between(x_test, y - y_err, y + y_err, color="pink", label="std.", alpha=0.5)
plt.xlim(-0.1, 1.1)
plt.ylim(-1.5, 1.5)
plt.annotate("M=9", xy=(0.8, 1))
plt.legend(bbox_to_anchor=(1.05, 1.), loc=2, borderaxespad=0.)
plt.show()
```
| github_jupyter |
```
from keras.layers import Input, Dropout, Dense, Flatten, concatenate
from keras.layers.convolutional import MaxPooling3D, Conv3D, Conv3DTranspose
from keras.models import Model
_input = Input(shape=(1, 3, 9600, 3600))
conv1 = Conv3D(32, (1, 2, 2), strides=(1, 2, 2),
activation='relu', padding='same',
data_format='channels_first',
name='block1_conv1')(_input)
pool1 = MaxPooling3D((1, 2, 2), strides=(1, 2, 2),
data_format='channels_first',
name='block1_pool')(conv1)
# Block 2
conv2 = Conv3D(64, (1, 2, 2), strides=(1, 2, 2),
activation='relu', padding='same',
data_format='channels_first',
name='block2_conv1')(pool1)
pool2 = MaxPooling3D((1, 2, 2), strides=(1, 2, 2),
data_format='channels_first',
name='block2_pool')(conv2)
# Block 3
conv3 = Conv3D(128, (3, 2, 2), strides=(3, 2, 2),
activation='relu', padding='same',
data_format='channels_first',
name='block3_conv1')(pool2)
pool3 = MaxPooling3D((1, 2, 2), strides=(1, 2, 2),
data_format='channels_first',
name='block3_pool')(conv3)
# Block 4
conv4 = Conv3D(256, (1, 2, 2), strides=(1, 2, 2),
activation='relu', padding='same',
data_format='channels_first',
name='block4_conv1')(pool3)
pool4 = MaxPooling3D((1, 2, 2), strides=(1, 2, 2), name='block4_pool',
data_format='channels_first')(conv4)
# Block 5
conv5 = Conv3D(512, (1, 2, 2), strides=(1, 2, 2), activation='relu',
padding='same', data_format='channels_first')(pool4)
# Block 6^T
up6 = concatenate([Conv3DTranspose(256, (1, 4, 4),
strides=(1, 4, 4), padding='same',
data_format='channels_first')(conv5),
conv4], axis=1)
conv6 = Conv3D(256, (1, 2, 2), strides=(1, 2, 2), activation='relu',
padding='same', data_format='channels_first')(up6)
# Block 7^T
up7 = concatenate([Conv3DTranspose(128, (1, 4, 4),
strides=(1, 4, 4), padding='same',
data_format='channels_first')(conv6),
conv3], axis=1)
conv7 = Conv3D(128, (1, 2, 2), strides=(1, 2, 2), activation='relu',
padding='same', data_format='channels_first')(up7)
# Block 8^T
up8 = concatenate([Conv3DTranspose(64, (3, 4, 4),
strides=(3, 4, 7), padding='same',
data_format='channels_first')(conv7),
conv2], axis=1)
conv8 = Conv3D(64, (1, 3, 6), activation='relu', padding='same',
data_format='channels_first')(up8)
# Block 9^T
up9 = concatenate([Conv3DTranspose(32, (3, 3, 6),
strides=(3, 3, 6), padding='same',
data_format='channels_first')(up8),
conv1], axis=1)
conv9 = Conv3D(32, (1, 3, 6), activation='relu', padding='same',
data_format='channels_first')(up9)
model = Model(_input, conv9)
model.compile(loss='categorical_crossentropy', optimizer='sgd',
metrics=['accuracy'])
```
| github_jupyter |
**Chapter 10 – Introduction to Artificial Neural Networks**
_This notebook contains all the sample code and solutions to the exercises in chapter 10._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# Perceptrons
```
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(max_iter=100, random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
y_pred
a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]
axes = [0, 5, 0, 2]
x0, x1 = np.meshgrid(
np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)
save_fig("perceptron_iris_plot")
plt.show()
```
# Activation functions
```
def logit(z):
return 1 / (1 + np.exp(-z))
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
z = np.linspace(-5, 5, 200)
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(z, np.sign(z), "r-", linewidth=2, label="Step")
plt.plot(z, logit(z), "g--", linewidth=2, label="Logit")
plt.plot(z, np.tanh(z), "b-", linewidth=2, label="Tanh")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
plt.legend(loc="center right", fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.axis([-5, 5, -1.2, 1.2])
plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=2, label="Step")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(logit, z), "g--", linewidth=2, label="Logit")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=2, label="Tanh")
plt.plot(z, derivative(relu, z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
#plt.legend(loc="center right", fontsize=14)
plt.title("Derivatives", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("activation_functions_plot")
plt.show()
def heaviside(z):
return (z >= 0).astype(z.dtype)
def sigmoid(z):
return 1/(1+np.exp(-z))
def mlp_xor(x1, x2, activation=heaviside):
return activation(-activation(x1 + x2 - 1.5) + activation(x1 + x2 - 0.5) - 0.5)
x1s = np.linspace(-0.2, 1.2, 100)
x2s = np.linspace(-0.2, 1.2, 100)
x1, x2 = np.meshgrid(x1s, x2s)
z1 = mlp_xor(x1, x2, activation=heaviside)
z2 = mlp_xor(x1, x2, activation=sigmoid)
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.contourf(x1, x2, z1)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: heaviside", fontsize=14)
plt.grid(True)
plt.subplot(122)
plt.contourf(x1, x2, z2)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: sigmoid", fontsize=14)
plt.grid(True)
```
# FNN for MNIST
## Using the Estimator API (formerly `tf.contrib.learn`)
```
import tensorflow as tf
```
**Warning**: `tf.examples.tutorials.mnist` is deprecated. We will use `tf.keras.datasets.mnist` instead. Moreover, the `tf.contrib.learn` API was promoted to `tf.estimators` and `tf.feature_columns`, and it has changed considerably. In particular, there is no `infer_real_valued_columns_from_input()` function or `SKCompat` class.
```
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
feature_cols = [tf.feature_column.numeric_column("X", shape=[28 * 28])]
dnn_clf = tf.estimator.DNNClassifier(hidden_units=[300,100], n_classes=10,
feature_columns=feature_cols)
input_fn = tf.estimator.inputs.numpy_input_fn(
x={"X": X_train}, y=y_train, num_epochs=40, batch_size=50, shuffle=True)
dnn_clf.train(input_fn=input_fn)
test_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"X": X_test}, y=y_test, shuffle=False)
eval_results = dnn_clf.evaluate(input_fn=test_input_fn)
eval_results
y_pred_iter = dnn_clf.predict(input_fn=test_input_fn)
y_pred = list(y_pred_iter)
y_pred[0]
```
## Using plain TensorFlow
```
import tensorflow as tf
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
def neuron_layer(X, n_neurons, name, activation=None):
with tf.name_scope(name):
n_inputs = int(X.get_shape()[1])
stddev = 2 / np.sqrt(n_inputs)
init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
W = tf.Variable(init, name="kernel")
b = tf.Variable(tf.zeros([n_neurons]), name="bias")
Z = tf.matmul(X, W) + b
if activation is not None:
return activation(Z)
else:
return Z
with tf.name_scope("dnn"):
hidden1 = neuron_layer(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = neuron_layer(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = neuron_layer(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 40
batch_size = 50
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Batch accuracy:", acc_batch, "Val accuracy:", acc_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt") # or better, use save_path
X_new_scaled = X_test[:20]
Z = logits.eval(feed_dict={X: X_new_scaled})
y_pred = np.argmax(Z, axis=1)
print("Predicted classes:", y_pred)
print("Actual classes: ", y_test[:20])
from tensorflow_graph_in_jupyter import show_graph
show_graph(tf.get_default_graph())
```
## Using `dense()` instead of `neuron_layer()`
Note: previous releases of the book used `tensorflow.contrib.layers.fully_connected()` rather than `tf.layers.dense()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.dense()`, because anything in the contrib module may change or be deleted without notice. The `dense()` function is almost identical to the `fully_connected()` function, except for a few minor differences:
* several parameters are renamed: `scope` becomes `name`, `activation_fn` becomes `activation` (and similarly the `_fn` suffix is removed from other parameters such as `normalizer_fn`), `weights_initializer` becomes `kernel_initializer`, etc.
* the default `activation` is now `None` rather than `tf.nn.relu`.
* a few more differences are presented in chapter 11.
```
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
y_proba = tf.nn.softmax(logits)
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 20
n_batches = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Batch accuracy:", acc_batch, "Validation accuracy:", acc_valid)
save_path = saver.save(sess, "./my_model_final.ckpt")
show_graph(tf.get_default_graph())
```
# Exercise solutions
## 1. to 8.
See appendix A.
## 9.
_Train a deep MLP on the MNIST dataset and see if you can get over 98% precision. Just like in the last exercise of chapter 9, try adding all the bells and whistles (i.e., save checkpoints, restore the last checkpoint in case of an interruption, add summaries, plot learning curves using TensorBoard, and so on)._
First let's create the deep net. It's exactly the same as earlier, with just one addition: we add a `tf.summary.scalar()` to track the loss and the accuracy during training, so we can view nice learning curves using TensorBoard.
```
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
loss_summary = tf.summary.scalar('log_loss', loss)
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
accuracy_summary = tf.summary.scalar('accuracy', accuracy)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
Now we need to define the directory to write the TensorBoard logs to:
```
from datetime import datetime
def log_dir(prefix=""):
now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "tf_logs"
if prefix:
prefix += "-"
name = prefix + "run-" + now
return "{}/{}/".format(root_logdir, name)
logdir = log_dir("mnist_dnn")
```
Now we can create the `FileWriter` that we will use to write the TensorBoard logs:
```
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())
```
Hey! Why don't we implement early stopping? For this, we are going to need to use the validation set.
```
m, n = X_train.shape
n_epochs = 10001
batch_size = 50
n_batches = int(np.ceil(m / batch_size))
checkpoint_path = "/tmp/my_deep_mnist_model.ckpt"
checkpoint_epoch_path = checkpoint_path + ".epoch"
final_model_path = "./my_deep_mnist_model"
best_loss = np.infty
epochs_without_progress = 0
max_epochs_without_progress = 50
with tf.Session() as sess:
if os.path.isfile(checkpoint_epoch_path):
# if the checkpoint file exists, restore the model and load the epoch number
with open(checkpoint_epoch_path, "rb") as f:
start_epoch = int(f.read())
print("Training was interrupted. Continuing at epoch", start_epoch)
saver.restore(sess, checkpoint_path)
else:
start_epoch = 0
sess.run(init)
for epoch in range(start_epoch, n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val, loss_val, accuracy_summary_str, loss_summary_str = sess.run([accuracy, loss, accuracy_summary, loss_summary], feed_dict={X: X_valid, y: y_valid})
file_writer.add_summary(accuracy_summary_str, epoch)
file_writer.add_summary(loss_summary_str, epoch)
if epoch % 5 == 0:
print("Epoch:", epoch,
"\tValidation accuracy: {:.3f}%".format(accuracy_val * 100),
"\tLoss: {:.5f}".format(loss_val))
saver.save(sess, checkpoint_path)
with open(checkpoint_epoch_path, "wb") as f:
f.write(b"%d" % (epoch + 1))
if loss_val < best_loss:
saver.save(sess, final_model_path)
best_loss = loss_val
else:
epochs_without_progress += 5
if epochs_without_progress > max_epochs_without_progress:
print("Early stopping")
break
os.remove(checkpoint_epoch_path)
with tf.Session() as sess:
saver.restore(sess, final_model_path)
accuracy_val = accuracy.eval(feed_dict={X: X_test, y: y_test})
accuracy_val
```
| github_jupyter |
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
```
## Define a function for which we'd like to find the roots
```
def function_for_roots(x):
a = 1.01
b = -3.04
c = 2.07
return a*x**2 + b*x + c #get the roots of ax^2 + bx + c
```
## We need a function to check whether our initial values are valid
```
def check_initial_values(f, x_min, x_max, tol):
#check our initial guesses
y_min = f(x_min)
y_max = f(x_max)
#check that x_min and x_max contain a zero crossing
if(y_min*y_max>=0.0):
print("No zero crossing found in the range = ",x_min,x_max)
s = "f(%f) = %f, f(%f) = %f" % (x_min,y_min,x_max,y_max)
print(s)
return 0
#if x_min is a root, then return flag == 1
if(np.fabs(y_min)<tol):
return 1
#if x_max is a root, then return flag == 2
if(np.fabs(y_max)<tol):
return 2
#if we reach this point, the bracket is valid
#and we will return 3
return 3
```
## Now we will define the main work function that actually performs the iterative search
```
def bisection_root_finding(f, x_min_start, x_max_start, tol):
#this function uses bisection search to find a root
x_min = x_min_start #minimum x in bracket
x_max = x_max_start #maximum x in bracket
x_mid = 0.0 #mid point
y_min = f(x_min) #function value at x_min
y_max = f(x_max) #function value at x_max
y_mid = 0.0 #function value at mid point
imax = 10000 #set a maximum number of iterations
i = 0 #iteration counter
#check the initial values
flag = check_initial_values(f,x_min,x_max,tol)
if(flag==0):
print("Error in bisection_root_finding().")
raise ValueError('Intial values invalid',x_min,x_max)
elif(flag==1):
#lucky guess
return x_min
elif(flag==2):
#another lucky guess
return x_max
#if we reach here, then we need to conduct the search
#set a flag
flag = 1
#enter a while loop
while(flag):
x_mid = 0.5*(x_min+x_max) #mid point
y_mid = f(x_mid) #function value at x_mid
#check if x_mid is a root
if(np.fabs(y_mid)<tol):
flag = 0
else:
#x_mid is not a root
#if the product of the functio at the midpoint
#and at one of the end points is greater than
#zero, replace this end point
if(f(x_min)*f(x_mid)>0):
#replace x_min with x_mid
x_min = x_mid
else:
#repalce x_max with x_mid
x_max = x_mid
#print out the iteration
print(x_min,f(x_min),x_max,f(x_max))
#count the iteration
i += 1
#if we have exceeded the max number
#of iterations, exit
if(i>=imax):
print("Exceeded max number of iterations = ",i)
s = "Min bracket f(%f) = %f" % (x_min,f(x_min))
print(s)
s = "Max bracket f(%f) = %f" % (x_max,f(x_max))
print(s)
s = "Mid bracket f(%f) = %f" % (x_mid,f(x_mid))
print(s)
raise StopIteration('Stopping iterations after ',i)
#we are done!
return x_mid
x_min = 0.0
x_max = 1.5
tolerance = 1.0e-6
#print the initial guess
print(x_min,function_for_roots(x_min))
print(x_max,function_for_roots(x_max))
x_root = bisection_root_finding(function_for_roots,x_min,x_max,tolerance)
y_root = function_for_roots(x_root)
s = "Root found with y(%f) = %f" % (x_root,y_root)
print(s)
```
| github_jupyter |
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
*No changes were made to the contents of this notebook from the original.*
<!--NAVIGATION-->
< [Density and Contour Plots](04.04-Density-and-Contour-Plots.ipynb) | [Contents](Index.ipynb) | [Customizing Plot Legends](04.06-Customizing-Legends.ipynb) >
# Histograms, Binnings, and Density
A simple histogram can be a great first step in understanding a dataset.
Earlier, we saw a preview of Matplotlib's histogram function (see [Comparisons, Masks, and Boolean Logic](02.06-Boolean-Arrays-and-Masks.ipynb)), which creates a basic histogram in one line, once the normal boiler-plate imports are done:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
data = np.random.randn(1000)
plt.hist(data);
```
The ``hist()`` function has many options to tune both the calculation and the display;
here's an example of a more customized histogram:
```
plt.hist(data, bins=30, normed=True, alpha=0.5,
histtype='stepfilled', color='steelblue',
edgecolor='none');
```
The ``plt.hist`` docstring has more information on other customization options available.
I find this combination of ``histtype='stepfilled'`` along with some transparency ``alpha`` to be very useful when comparing histograms of several distributions:
```
x1 = np.random.normal(0, 0.8, 1000)
x2 = np.random.normal(-2, 1, 1000)
x3 = np.random.normal(3, 2, 1000)
kwargs = dict(histtype='stepfilled', alpha=0.3, normed=True, bins=40)
plt.hist(x1, **kwargs)
plt.hist(x2, **kwargs)
plt.hist(x3, **kwargs);
```
If you would like to simply compute the histogram (that is, count the number of points in a given bin) and not display it, the ``np.histogram()`` function is available:
```
counts, bin_edges = np.histogram(data, bins=5)
print(counts)
```
## Two-Dimensional Histograms and Binnings
Just as we create histograms in one dimension by dividing the number-line into bins, we can also create histograms in two-dimensions by dividing points among two-dimensional bins.
We'll take a brief look at several ways to do this here.
We'll start by defining some data—an ``x`` and ``y`` array drawn from a multivariate Gaussian distribution:
```
mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T
```
### ``plt.hist2d``: Two-dimensional histogram
One straightforward way to plot a two-dimensional histogram is to use Matplotlib's ``plt.hist2d`` function:
```
plt.hist2d(x, y, bins=30, cmap='Blues')
cb = plt.colorbar()
cb.set_label('counts in bin')
```
Just as with ``plt.hist``, ``plt.hist2d`` has a number of extra options to fine-tune the plot and the binning, which are nicely outlined in the function docstring.
Further, just as ``plt.hist`` has a counterpart in ``np.histogram``, ``plt.hist2d`` has a counterpart in ``np.histogram2d``, which can be used as follows:
```
counts, xedges, yedges = np.histogram2d(x, y, bins=30)
```
For the generalization of this histogram binning in dimensions higher than two, see the ``np.histogramdd`` function.
### ``plt.hexbin``: Hexagonal binnings
The two-dimensional histogram creates a tesselation of squares across the axes.
Another natural shape for such a tesselation is the regular hexagon.
For this purpose, Matplotlib provides the ``plt.hexbin`` routine, which will represents a two-dimensional dataset binned within a grid of hexagons:
```
plt.hexbin(x, y, gridsize=30, cmap='Blues')
cb = plt.colorbar(label='count in bin')
```
``plt.hexbin`` has a number of interesting options, including the ability to specify weights for each point, and to change the output in each bin to any NumPy aggregate (mean of weights, standard deviation of weights, etc.).
### Kernel density estimation
Another common method of evaluating densities in multiple dimensions is *kernel density estimation* (KDE).
This will be discussed more fully in [In-Depth: Kernel Density Estimation](05.13-Kernel-Density-Estimation.ipynb), but for now we'll simply mention that KDE can be thought of as a way to "smear out" the points in space and add up the result to obtain a smooth function.
One extremely quick and simple KDE implementation exists in the ``scipy.stats`` package.
Here is a quick example of using the KDE on this data:
```
from scipy.stats import gaussian_kde
# fit an array of size [Ndim, Nsamples]
data = np.vstack([x, y])
kde = gaussian_kde(data)
# evaluate on a regular grid
xgrid = np.linspace(-3.5, 3.5, 40)
ygrid = np.linspace(-6, 6, 40)
Xgrid, Ygrid = np.meshgrid(xgrid, ygrid)
Z = kde.evaluate(np.vstack([Xgrid.ravel(), Ygrid.ravel()]))
# Plot the result as an image
plt.imshow(Z.reshape(Xgrid.shape),
origin='lower', aspect='auto',
extent=[-3.5, 3.5, -6, 6],
cmap='Blues')
cb = plt.colorbar()
cb.set_label("density")
```
KDE has a smoothing length that effectively slides the knob between detail and smoothness (one example of the ubiquitous bias–variance trade-off).
The literature on choosing an appropriate smoothing length is vast: ``gaussian_kde`` uses a rule-of-thumb to attempt to find a nearly optimal smoothing length for the input data.
Other KDE implementations are available within the SciPy ecosystem, each with its own strengths and weaknesses; see, for example, ``sklearn.neighbors.KernelDensity`` and ``statsmodels.nonparametric.kernel_density.KDEMultivariate``.
For visualizations based on KDE, using Matplotlib tends to be overly verbose.
The Seaborn library, discussed in [Visualization With Seaborn](04.14-Visualization-With-Seaborn.ipynb), provides a much more terse API for creating KDE-based visualizations.
<!--NAVIGATION-->
< [Density and Contour Plots](04.04-Density-and-Contour-Plots.ipynb) | [Contents](Index.ipynb) | [Customizing Plot Legends](04.06-Customizing-Legends.ipynb) >
| github_jupyter |
```
import pandas as pd
import numpy as np
import os
import prody
import math
from pathlib import Path
import pickle
import sys
from sklearn.externals import joblib
from sklearn.metrics import r2_score,mean_squared_error
from abpred.Pipeline import PreparePredictions
def Kd_2_dG(Kd):
if Kd == 0:
deltaG = np.log(Kd+1)*(8.314/4184)*(298.15)
else:
deltaG = np.log(Kd)*(8.314/4184)*(298.15)
return deltaG
def deltaG_to_Kd(delg):
Kd_value = math.exp((delg)/((8.314/4184)*298.15))
return Kd_value
```
The effect of a given mutation on antibody binding was represented by apparent affinity (avidity) relative to those for wild-type (WT) gp120, calculated with the formula ([(EC50_WT/EC50_mutant)/(EC50_WT for 2G12/EC50_mutant for 2G12)] × 100)
```
# Test data
VIH_final = pd.read_csv('../data/VIH_Test15.csv',index_col=0)
# original info data
vih_data = pd.read_csv("../data/HIV_escape_mutations.csv",sep="\t")
#vih_data["pred_ddg2EC50"] = vih_data["mCSM-AB_Pred"].apply(deltaG_to_Kd)*100
vih_original = vih_data.loc[vih_data["Mutation_type"]=="ORIGINAL"].copy()
vih_reverse = vih_data.loc[vih_data["Mutation_type"]=="REVERSE"]
#sort values to appedn to prediction data table
vih_original.loc[:,"mut_code"] = (vih_reverse["Chain"]+vih_reverse["Mutation"].str[1:]).values
vih_original.sort_values(by='mut_code',inplace=True)
vih_original["Mutation_original"] = vih_original["Mutation"].str[-1]+vih_original["Mutation"].str[1:-1]+vih_original["Mutation"].str[0]
vih_original.loc[(vih_original['Exptal'] <= 33 ),"mutation-effect"] = "decreased"
vih_original.loc[(vih_original['Exptal'] > 300 ),"mutation-effect"] = "increased"
vih_original.loc[(vih_original['Exptal'] < 300 )&(vih_original['Exptal'] > 33 ),"mutation-effect"] = "neutral"
vih_reverse.loc[(vih_reverse['Exptal'] <= 33 ),"mutation-effect"] = "decreased"
vih_reverse.loc[(vih_reverse['Exptal'] > 300 ),"mutation-effect"] = "increased"
vih_reverse.loc[(vih_reverse['Exptal'] < 300 )&(vih_reverse['Exptal'] > 33 ),"mutation-effect"] = "neutral"
#
#xgbr = XGBRegressor()
#xgbr.load_model(fname='xgb_final_400F_smote_032019.sav')
#xgbr_borderline = XGBRegressor()
#xgbr_borderline.load_model(fname='xgb_final_400F_borderlinesmote_032019.sav')
# X and y data transformed to delta G
X = VIH_final.drop("Exptal",axis=1)
y_energy = (VIH_final["Exptal"]/1000).apply(Kd_2_dG)
y_binding = VIH_final["Exptal"].values
PreparePredictions(X).run()
X.ddg.sort_values().head(10)
vih_original.loc[vih_original["mutation-effect"]=="increased"]
461
197
#ridge_model = joblib.load('ridgeLinear_train15skempiAB_FINAL.pkl')
lasso_model = joblib.load('Lasso_train15skempiAB_FINAL.pkl')
elasticnet_model = joblib.load('elasticNet_train15skempiAB_FINAL.pkl')
svr_model = joblib.load('rbfSVRmodel_train15skempiAB_FINAL.pkl')
poly_model = joblib.load("poly2SVRmodel_train15skempiAB_FINAL.pkl")
#rf_model = joblib.load('RFmodel_train15skempiAB_FINAL.pkl')
gbt_model = joblib.load('GBTmodel_train15skempiAB_FINAL.overf.pkl')
#xgb_model = joblib.load('XGBmodel_train15skempiAB_FINAL.pkl')
#ridge_pred = ridge_model.predict(X)
lasso_pred = lasso_model.predict(X)
elasticnet_pred = elasticnet_model.predict(X)
svr_pred = svr_model.predict(X)
poly_pred = poly_model.predict(X)
#rf_pred = rf_model.predict(X)
gbt_pred = gbt_model.predict(X)
#xgb_pred = xgb_model.predict(X)
pred_stack = np.hstack([vih_original[["mutation-effect","mCSM-AB_Pred","Exptal"]].values,
lasso_pred.reshape((-1,1)),gbt_pred.reshape((-1,1)),svr_pred.reshape((-1,1)),poly_pred.reshape((-1,1))])
pred_data = pd.DataFrame(pred_stack,columns=["mutation-effect","mCSM-AB_Pred","Exptal","Lasso_pred","gbt_pred","svr_pred","poly_pred"])
# transform prediction score to relative to kd , refered in paper
#pred_data_binding = pred_data.applymap(deltaG_to_Kd)*100
pred_data["mean-pred"] = pred_data.loc[:,["Lasso_pred","gbt_pred","svr_pred"]].mean(axis=1)
pred_data
pred_data.loc[pred_data["mutation-effect"]=="increased"]
pred_data.loc[(pred_data["mean-pred"].abs() > 0.1)]
pred_data["True"] = y_energy.values
pred_data_binding["True"] = y_binding
#pred_data_converted.corr()
pred_data_binding.corr()
pred_data
average_pred_binding = pred_data_binding.drop("True",axis=1).loc[:,["gbt_pred","elasticnet_pred"]].mean(axis=1)
average_pred_energy = pred_data.drop("True",axis=1).loc[:,["gbt_pred","elasticnet_pred"]].mean(axis=1)
r2score = r2_score(y_energy,average_pred_energy)
rmse = mean_squared_error(y_energy,average_pred_energy)
print("R2 score:", r2score)
print("RMSE score:", np.sqrt(rmse))
np.corrcoef(y["Exptal"],average_pred)
# Corr mCSM-AB with converted mCSM AB data
np.corrcoef(y_binding,vih_reverse["pred_ddg2EC50"])
# Corr mCSM-AB with converted VIH paper data
np.corrcoef(y_energy,vih_reverse["mCSM-AB_Pred"])
# Corr FoldX feature alone
np.corrcoef(y["Exptal"],VIH_final["dg_change"].apply(deltaG_to_Kd)*100)
import seaborn as sns
#rmse_test = np.round(np.sqrt(mean_squared_error(y_test, y_pred_test)), 3)
df_pred = pd.DataFrame({"Predicted ddG(kcal/mol)": pred_data["gbt_pred"], "Actual ddG(kcal/mol)": y_energy.values})
pearsonr_test = round(df_pred.corr().iloc[0,1],3)
g = sns.regplot(x="Actual ddG(kcal/mol)", y="Predicted ddG(kcal/mol)",data=df_pred)
plt.title("Predicted vs Experimental ddG (Independent set: 123 complexes)")
plt.text(-2,3,"pearsonr = %s" %pearsonr_test)
#plt.text(4.5,-0.5,"RMSE = %s" %rmse_test)
#plt.savefig("RFmodel_300_testfit.png",dpi=600)
PredictionError?
```
| github_jupyter |
# Example of extracting features from dataframes with Datetime indices
Assuming that time-varying measurements are taken at regular intervals can be sufficient for many situations. However, for a large number of tasks it is important to take into account **when** a measurement is made. An example can be healthcare, where the interval between measurements of vital signs contains crucial information.
Tsfresh now supports calculator functions that use the index of the timeseries container in order to calculate the features. The only requirements for these function is that the index of the input dataframe is of type `pd.DatetimeIndex`. These functions are contained in the new class TimeBasedFCParameters.
Note that the behaviour of all other functions is unaffected. The settings parameter of `extract_features()` can contain both index-dependent functions and 'regular' functions.
```
import pandas as pd
from tsfresh.feature_extraction import extract_features
# TimeBasedFCParameters contains all functions that use the Datetime index of the timeseries container
from tsfresh.feature_extraction.settings import TimeBasedFCParameters
```
# Build a time series container with Datetime indices
Let's build a dataframe with a datetime index. The format must be with a `value` and a `kind` column, since each measurement has its own timestamp - i.e. measurements are not assumed to be simultaneous.
```
df = pd.DataFrame({"id": ["a", "a", "a", "a", "b", "b", "b", "b"],
"value": [1, 2, 3, 1, 3, 1, 0, 8],
"kind": ["temperature", "temperature", "pressure", "pressure",
"temperature", "temperature", "pressure", "pressure"]},
index=pd.DatetimeIndex(
['2019-03-01 10:04:00', '2019-03-01 10:50:00', '2019-03-02 00:00:00', '2019-03-02 09:04:59',
'2019-03-02 23:54:12', '2019-03-03 08:13:04', '2019-03-04 08:00:00', '2019-03-04 08:01:00']
))
df = df.sort_index()
df
```
Right now `TimeBasedFCParameters` only contains `linear_trend_timewise`, which performs a calculation of a linear trend, but using the time difference in hours between measurements in order to perform the linear regression. As always, you can add your own functions in `tsfresh/feature_extraction/feature_calculators.py`.
```
settings_time = TimeBasedFCParameters()
settings_time
```
We extract the features as usual, specifying the column value, kind, and id.
```
X_tsfresh = extract_features(df, column_id="id", column_value='value', column_kind='kind',
default_fc_parameters=settings_time)
X_tsfresh.head()
```
The output looks exactly, like usual. If we compare it with the 'regular' `linear_trend` feature calculator, we can see that the intercept, p and R values are the same, as we'd expect – only the slope is now different.
```
settings_regular = {'linear_trend': [
{'attr': 'pvalue'},
{'attr': 'rvalue'},
{'attr': 'intercept'},
{'attr': 'slope'},
{'attr': 'stderr'}
]}
X_tsfresh = extract_features(df, column_id="id", column_value='value', column_kind='kind',
default_fc_parameters=settings_regular)
X_tsfresh.head()
```
# Writing your own time-based feature calculators
Writing your own time-based feature calculators is no different from usual. Only two new properties must be set using the `@set_property` decorator:
1) `@set_property("input", "pd.Series")` tells the function that the input of the function is a `pd.Series` rather than a numpy array. This allows the index to be used.
2) `@set_property("index_type", pd.DatetimeIndex)` tells the function that the input is a DatetimeIndex, allowing it to perform calculations based on time datatypes.
For example, if we want to write a function that calculates the time between the first and last measurement, it could look something like this:
```python
@set_property("input", "pd.Series")
@set_property("index_type", pd.DatetimeIndex)
def timespan(x, param):
ix = x.index
# Get differences between the last timestamp and the first timestamp in seconds, then convert to hours.
times_seconds = (ix[-1] - ix[0]).total_seconds()
return times_seconds / float(3600)
```
| github_jupyter |
```
import yfinance as yf
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from cloudmesh.common.StopWatch import StopWatch
from tensorflow import keras
from pandas.plotting import register_matplotlib_converters
from sklearn.metrics import mean_squared_error
import pathlib
from pathlib import Path
cryptoName = input('Please enter the name of the crypto to predict.\nExamples include "EOS-USD", "DOGE-USD",\n"ETH-USD", and "BTC-USD" without double quotes')
print(cryptoName+' selected')
StopWatch.start("Overall time")
# Creating desktop path to save figures to the desktop
desktop = pathlib.Path.home() / 'Desktop'
desktop2 = str(Path(desktop))
fullpath = desktop2 + "\\"+cryptoName+"-prediction-model.png"
fullpath2 = desktop2 + "\\"+cryptoName+"-prediction-model-zoomed.png"
fullpath3 = desktop2 + "\\"+cryptoName+"-price.png"
fullpath4 = desktop2 + "\\"+cryptoName+"-training-loss.png"
pdfpath = desktop2 + "\\"+cryptoName+"-prediction-model.pdf"
pdfpath2 = desktop2 + "\\"+cryptoName+"-prediction-model-zoomed.pdf"
pdfpath3 = desktop2 + "\\"+cryptoName+"-price.pdf"
pdfpath4 = desktop2 + "\\"+cryptoName+"-training-loss.pdf"
register_matplotlib_converters()
ticker = yf.Ticker(cryptoName)
data = ticker.history(period = "max", interval = "1d")
#print(data)
# Sort the dataframe according to the date
data.sort_values('Date', inplace=True, ascending=True)
# Print the dataframe top
data.head()
# Visualization of data. Plotting the price close.
plt.figure(num=None, figsize=(7, 4), dpi=300, facecolor='w', edgecolor='k')
data['Close'].plot()
plt.tight_layout()
plt.grid()
plt.ylabel('Close Price in USD')
plt.xlabel('Date')
plt.tight_layout()
#plt.savefig(fullpath3, dpi=300, facecolor="#FFFFFF")
plt.savefig(pdfpath3, dpi=300)
plt.show()
print(data.index[0])
firstDate = data.index[0]
firstDateFormatted = pd.to_datetime(data.index[0], utc=False)
print(firstDateFormatted)
date_time_obj = firstDateFormatted.to_pydatetime()
trueFirstDate = date_time_obj.strftime('%m/%d/%Y')
print(trueFirstDate)
print(data.head())
# Get Close data
df = data[['Close']].copy()
# Split data into train and test
train, test = df.iloc[0:-200], df.iloc[-200:len(df)]
print(len(train), len(test))
train_max = train.max()
train_min = train.min()
# Normalize the dataframes
train = (train - train_min)/(train_max - train_min)
test = (test - train_min)/(train_max - train_min)
def create_dataset(X, y, time_steps=1):
Xs, ys = [], []
for i in range(len(X) - time_steps):
v = X.iloc[i:(i + time_steps)].values
Xs.append(v)
ys.append(y.iloc[i + time_steps])
return np.array(Xs), np.array(ys)
time_steps = 10
X_train, y_train = create_dataset(train, train.Close, time_steps)
X_test, y_test = create_dataset(test, test.Close, time_steps)
StopWatch.start("Training time")
model = keras.Sequential()
model.add(keras.layers.LSTM(250, input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(keras.layers.Dropout(0.2))
model.add(keras.layers.Dense(1))
model.compile(loss='mae', optimizer='adam')
model.summary()
history = model.fit(
X_train, y_train,
epochs=50,
batch_size=32,
shuffle=False
)
StopWatch.stop("Training time")
# Plotting the loss
plt.plot(history.history['loss'], label='train')
plt.legend();
plt.ylabel('Model Loss')
plt.xlabel('Number of Epochs')
plt.savefig(pdfpath4, dpi=300)
plt.show()
StopWatch.start("Prediction time")
y_pred = model.predict(X_test)
StopWatch.stop("Prediction time")
# Rescale the data back to the original scale
y_test = y_test*(train_max[0] - train_min[0]) + train_min[0]
y_pred = y_pred*(train_max[0] - train_min[0]) + train_min[0]
y_train = y_train*(train_max[0] - train_min[0]) + train_min[0]
# Plotting the results
plt.plot(np.arange(len(y_train), len(y_train) + len(y_test)), y_test.flatten(), marker='.', markersize=1, label="true")
plt.plot(np.arange(len(y_train), len(y_train) + len(y_test)), y_pred.flatten(), 'r', marker='.', markersize=1, label="prediction")
plt.plot(np.arange(0, len(y_train)), y_train.flatten(), 'g', marker='.', markersize=1, label="history")
plt.ylabel('Close Price in USD')
plt.xlabel('Days Since '+trueFirstDate)
leg = plt.legend()
leg_lines = leg.get_lines()
leg_texts = leg.get_texts()
plt.setp(leg_lines, linewidth=1)
plt.setp(leg_texts, fontsize='x-large')
plt.savefig(pdfpath, dpi=300)
#doge plt.axis([1350, 1450, 0.14, 0.35])
#btc plt.axis([2490, 2650, 34000, 73000])
#eth plt.axis([1370, 1490, 2200, 5800])
plt.axis([1370, 1490, 2200, 5800])
plt.savefig(pdfpath2, dpi=300)
plt.show()
print(y_test.shape)
print(y_pred.shape)
## Outputs error in United States Dollars
mean_squared_error(y_test, y_pred)
## Create a table of the error against the number of epochs
StopWatch.stop("Overall time")
StopWatch.benchmark()
```
| github_jupyter |
# TalkingData: Fraudulent Click Prediction
In this notebook, we will apply various boosting algorithms to solve an interesting classification problem from the domain of 'digital fraud'.
The analysis is divided into the following sections:
- Understanding the business problem
- Understanding and exploring the data
- Feature engineering: Creating new features
- Model building and evaluation: AdaBoost
- Modelling building and evaluation: Gradient Boosting
- Modelling building and evaluation: XGBoost
## Understanding the Business Problem
<a href="https://www.talkingdata.com/">TalkingData</a> is a Chinese big data company, and one of their areas of expertise is mobile advertisements.
In mobile advertisements, **click fraud** is a major source of losses. Click fraud is the practice of repeatedly clicking on an advertisement hosted on a website with the intention of generating revenue for the host website or draining revenue from the advertiser.
In this case, TalkingData happens to be serving the advertisers (their clients). TalkingData cover a whopping **approx. 70% of the active mobile devices in China**, of which 90% are potentially fraudulent (i.e. the user is actually not going to download the app after clicking).
You can imagine the amount of money they can help clients save if they are able to predict whether a given click is fraudulent (or equivalently, whether a given click will result in a download).
Their current approach to solve this problem is that they've generated a blacklist of IP addresses - those IPs which produce lots of clicks, but never install any apps. Now, they want to try some advanced techniques to predict the probability of a click being genuine/fraud.
In this problem, we will use the features associated with clicks, such as IP address, operating system, device type, time of click etc. to predict the probability of a click being fraud.
They have released <a href="https://www.kaggle.com/c/talkingdata-adtracking-fraud-detection">the problem on Kaggle here.</a>.
## Understanding and Exploring the Data
The data contains observations of about 240 million clicks, and whether a given click resulted in a download or not (1/0).
On Kaggle, the data is split into train.csv and train_sample.csv (100,000 observations). We'll use the smaller train_sample.csv in this notebook for speed, though while training the model for Kaggle submissions, the full training data will obviously produce better results.
The detailed data dictionary is mentioned here:
- ```ip```: ip address of click.
- ```app```: app id for marketing.
- ```device```: device type id of user mobile phone (e.g., iphone 6 plus, iphone 7, huawei mate 7, etc.)
- ```os```: os version id of user mobile phone
- ```channel```: channel id of mobile ad publisher
- ```click_time```: timestamp of click (UTC)
- ```attributed_time```: if user download the app for after clicking an ad, this is the time of the app download
- ```is_attributed```: the target that is to be predicted, indicating the app was downloaded
Let's try finding some useful trends in the data.
```
import numpy as np
import pandas as pd
import sklearn
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn import metrics
import xgboost as xgb
from xgboost import XGBClassifier
from xgboost import plot_importance
import gc # for deleting unused variables
%matplotlib inline
import os
import warnings
warnings.filterwarnings('ignore')
```
#### Reading the Data
The code below reads the train_sample.csv file if you set testing = True, else reads the full train.csv file. You can read the sample while tuning the model etc., and then run the model on the full data once done.
#### Important Note: Save memory when the data is huge
Since the training data is quite huge, the program will be quite slow if you don't consciously follow some best practices to save memory. This notebook demonstrates some of those practices.
```
# reading training data
# specify column dtypes to save memory (by default pandas reads some columns as floats)
dtypes = {
'ip' : 'uint16',
'app' : 'uint16',
'device' : 'uint16',
'os' : 'uint16',
'channel' : 'uint16',
'is_attributed' : 'uint8',
'click_id' : 'uint32' # note that click_id is only in test data, not training data
}
# read training_sample.csv for quick testing/debug, else read the full train.csv
testing = True
if testing:
train_path = "train_sample.csv"
skiprows = None
nrows = None
colnames=['ip','app','device','os', 'channel', 'click_time', 'is_attributed']
else:
train_path = "train.csv"
skiprows = range(1, 144903891)
nrows = 10000000
colnames=['ip','app','device','os', 'channel', 'click_time', 'is_attributed']
# read training data
train_sample = pd.read_csv(train_path, skiprows=skiprows, nrows=nrows, dtype=dtypes, usecols=colnames)
# length of training data
len(train_sample.index)
# Displays memory consumed by each column ---
print(train_sample.memory_usage())
# space used by training data
print('Training dataset uses {0} MB'.format(train_sample.memory_usage().sum()/1024**2))
# training data top rows
train_sample.head()
```
### Exploring the Data - Univariate Analysis
Let's now understand and explore the data. Let's start with understanding the size and data types of the train_sample data.
```
# look at non-null values, number of entries etc.
# there are no missing values
train_sample.info()
# Basic exploratory analysis
# Number of unique values in each column
def fraction_unique(x):
return len(train_sample[x].unique())
number_unique_vals = {x: fraction_unique(x) for x in train_sample.columns}
number_unique_vals
# All columns apart from click time are originally int type,
# though note that they are all actually categorical
train_sample.dtypes
```
There are certain 'apps' which have quite high number of instances/rows (each row is a click). The plot below shows this.
```
# # distribution of 'app'
# # some 'apps' have a disproportionately high number of clicks (>15k), and some are very rare (3-4)
plt.figure(figsize=(14, 8))
sns.countplot(x="app", data=train_sample)
# # distribution of 'device'
# # this is expected because a few popular devices are used heavily
plt.figure(figsize=(14, 8))
sns.countplot(x="device", data=train_sample)
# # channel: various channels get clicks in comparable quantities
plt.figure(figsize=(14, 8))
sns.countplot(x="channel", data=train_sample)
# # os: there are a couple commos OSes (android and ios?), though some are rare and can indicate suspicion
plt.figure(figsize=(14, 8))
sns.countplot(x="os", data=train_sample)
```
Let's now look at the distribution of the target variable 'is_attributed'.
```
# # target variable distribution
100*(train_sample['is_attributed'].astype('object').value_counts()/len(train_sample.index))
```
Only **about 0.2% of clicks are 'fraudulent'**, which is expected in a fraud detection problem. Such high class imbalance is probably going to be the toughest challenge of this problem.
### Exploring the Data - Segmented Univariate Analysis
Let's now look at how the target variable varies with the various predictors.
```
# plot the average of 'is_attributed', or 'download rate'
# with app (clearly this is non-readable)
app_target = train_sample.groupby('app').is_attributed.agg(['mean', 'count'])
app_target
```
This is clearly non-readable, so let's first get rid of all the apps that are very rare (say which comprise of less than 20% clicks) and plot the rest.
```
frequent_apps = train_sample.groupby('app').size().reset_index(name='count')
frequent_apps = frequent_apps[frequent_apps['count']>frequent_apps['count'].quantile(0.80)]
frequent_apps = frequent_apps.merge(train_sample, on='app', how='inner')
frequent_apps.head()
plt.figure(figsize=(10,10))
sns.countplot(y="app", hue="is_attributed", data=frequent_apps);
```
You can do lots of other interesting ananlysis with the existing features. For now, let's create some new features which will probably improve the model.
## Feature Engineering
Let's now derive some new features from the existing ones. There are a number of features one can extract from ```click_time``` itself, and by grouping combinations of IP with other features.
### Datetime Based Features
```
# Creating datetime variables
# takes in a df, adds date/time based columns to it, and returns the modified df
def timeFeatures(df):
# Derive new features using the click_time column
df['datetime'] = pd.to_datetime(df['click_time'])
df['day_of_week'] = df['datetime'].dt.dayofweek
df["day_of_year"] = df["datetime"].dt.dayofyear
df["month"] = df["datetime"].dt.month
df["hour"] = df["datetime"].dt.hour
return df
# creating new datetime variables and dropping the old ones
train_sample = timeFeatures(train_sample)
train_sample.drop(['click_time', 'datetime'], axis=1, inplace=True)
train_sample.head()
# datatypes
# note that by default the new datetime variables are int64
train_sample.dtypes
# memory used by training data
print('Training dataset uses {0} MB'.format(train_sample.memory_usage().sum()/1024**2))
# lets convert the variables back to lower dtype again
int_vars = ['app', 'device', 'os', 'channel', 'day_of_week','day_of_year', 'month', 'hour']
train_sample[int_vars] = train_sample[int_vars].astype('uint16')
train_sample.dtypes
# space used by training data
print('Training dataset uses {0} MB'.format(train_sample.memory_usage().sum()/1024**2))
```
### IP Grouping Based Features
Let's now create some important features by grouping IP addresses with features such as os, channel, hour, day etc. Also, count of each IP address will also be a feature.
Note that though we are deriving new features by grouping IP addresses, using IP adress itself as a features is not a good idea. This is because (in the test data) if a new IP address is seen, the model will see a new 'category' and will not be able to make predictions (IP is a categorical variable, it has just been encoded with numbers).
```
# number of clicks by count of IP address
# note that we are explicitly asking pandas to re-encode the aggregated features
# as 'int16' to save memory
ip_count = train_sample.groupby('ip').size().reset_index(name='ip_count').astype('int16')
ip_count.head()
```
We can now merge this dataframe with the original training df. Similarly, we can create combinations of various features such as ip_day_hour (count of ip-day-hour combinations), ip_hour_channel, ip_hour_app, etc.
The following function takes in a dataframe and creates these features.
```
# creates groupings of IP addresses with other features and appends the new features to the df
def grouped_features(df):
# ip_count
ip_count = df.groupby('ip').size().reset_index(name='ip_count').astype('uint16')
ip_day_hour = df.groupby(['ip', 'day_of_week', 'hour']).size().reset_index(name='ip_day_hour').astype('uint16')
ip_hour_channel = df[['ip', 'hour', 'channel']].groupby(['ip', 'hour', 'channel']).size().reset_index(name='ip_hour_channel').astype('uint16')
ip_hour_os = df.groupby(['ip', 'hour', 'os']).channel.count().reset_index(name='ip_hour_os').astype('uint16')
ip_hour_app = df.groupby(['ip', 'hour', 'app']).channel.count().reset_index(name='ip_hour_app').astype('uint16')
ip_hour_device = df.groupby(['ip', 'hour', 'device']).channel.count().reset_index(name='ip_hour_device').astype('uint16')
# merge the new aggregated features with the df
df = pd.merge(df, ip_count, on='ip', how='left')
del ip_count
df = pd.merge(df, ip_day_hour, on=['ip', 'day_of_week', 'hour'], how='left')
del ip_day_hour
df = pd.merge(df, ip_hour_channel, on=['ip', 'hour', 'channel'], how='left')
del ip_hour_channel
df = pd.merge(df, ip_hour_os, on=['ip', 'hour', 'os'], how='left')
del ip_hour_os
df = pd.merge(df, ip_hour_app, on=['ip', 'hour', 'app'], how='left')
del ip_hour_app
df = pd.merge(df, ip_hour_device, on=['ip', 'hour', 'device'], how='left')
del ip_hour_device
return df
train_sample = grouped_features(train_sample)
train_sample.head()
print('Training dataset uses {0} MB'.format(train_sample.memory_usage().sum()/1024**2))
# garbage collect (unused) object
gc.collect()
```
## Modelling
Let's now build models to predict the variable ```is_attributed``` (downloaded). We'll try the several variants of boosting (adaboost, gradient boosting and XGBoost), tune the hyperparameters in each model and choose the one which gives the best performance.
In the original Kaggle competition, the metric for model evaluation is **area under the ROC curve**.
```
# create x and y train
X = train_sample.drop('is_attributed', axis=1)
y = train_sample[['is_attributed']]
# split data into train and test/validation sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=101)
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
# check the average download rates in train and test data, should be comparable
print(y_train.mean())
print(y_test.mean())
```
### AdaBoost
```
# adaboost classifier with max 600 decision trees of depth=2
# learning_rate/shrinkage=1.5
# base estimator
tree = DecisionTreeClassifier(max_depth=2)
# adaboost with the tree as base estimator
adaboost_model_1 = AdaBoostClassifier(
base_estimator=tree,
n_estimators=600,
learning_rate=1.5,
algorithm="SAMME")
# fit
adaboost_model_1.fit(X_train, y_train)
# predictions
# the second column represents the probability of a click resulting in a download
predictions = adaboost_model_1.predict_proba(X_test)
predictions[:10]
# metrics: AUC
metrics.roc_auc_score(y_test, predictions[:,1])
```
### AdaBoost - Hyperparameter Tuning
Let's now tune the hyperparameters of the AdaBoost classifier. In this case, we have two types of hyperparameters - those of the component trees (max_depth etc.) and those of the ensemble (n_estimators, learning_rate etc.).
We can tune both using the following technique - the keys of the form ```base_estimator_parameter_name``` belong to the trees (base estimator), and the rest belong to the ensemble.
```
# parameter grid
param_grid = {"base_estimator__max_depth" : [2, 5],
"n_estimators": [200, 400, 600]
}
# base estimator
tree = DecisionTreeClassifier()
# adaboost with the tree as base estimator
# learning rate is arbitrarily set to 0.6, we'll discuss learning_rate below
ABC = AdaBoostClassifier(
base_estimator=tree,
learning_rate=0.6,
algorithm="SAMME")
# run grid search
folds = 3
grid_search_ABC = GridSearchCV(ABC,
cv = folds,
param_grid=param_grid,
scoring = 'roc_auc',
return_train_score=True,
verbose = 1)
# fit
grid_search_ABC.fit(X_train, y_train)
# cv results
cv_results = pd.DataFrame(grid_search_ABC.cv_results_)
cv_results
# plotting AUC with hyperparameter combinations
plt.figure(figsize=(16,6))
for n, depth in enumerate(param_grid['base_estimator__max_depth']):
# subplot 1/n
plt.subplot(1,3, n+1)
depth_df = cv_results[cv_results['param_base_estimator__max_depth']==depth]
plt.plot(depth_df["param_n_estimators"], depth_df["mean_test_score"])
plt.plot(depth_df["param_n_estimators"], depth_df["mean_train_score"])
plt.xlabel('n_estimators')
plt.ylabel('AUC')
plt.title("max_depth={0}".format(depth))
plt.ylim([0.60, 1])
plt.legend(['test score', 'train score'], loc='upper left')
plt.xscale('log')
```
The results above show that:
- The ensemble with max_depth=5 is clearly overfitting (training auc is almost 1, while the test score is much lower)
- At max_depth=2, the model performs slightly better (approx 95% AUC) with a higher test score
Thus, we should go ahead with ```max_depth=2``` and ```n_estimators=200```.
Note that we haven't experimented with many other important hyperparameters till now, such as ```learning rate```, ```subsample``` etc., and the results might be considerably improved by tuning them. We'll next experiment with these hyperparameters.
```
# model performance on test data with chosen hyperparameters
# base estimator
tree = DecisionTreeClassifier(max_depth=2)
# adaboost with the tree as base estimator
# learning rate is arbitrarily set, we'll discuss learning_rate below
ABC = AdaBoostClassifier(
base_estimator=tree,
learning_rate=0.6,
n_estimators=200,
algorithm="SAMME")
ABC.fit(X_train, y_train)
# predict on test data
predictions = ABC.predict_proba(X_test)
predictions[:10]
# roc auc
metrics.roc_auc_score(y_test, predictions[:, 1])
```
### Gradient Boosting Classifier
Let's now try the gradient boosting classifier. We'll experiment with two main hyperparameters now - ```learning_rate``` (shrinkage) and ```subsample```.
By adjusting the learning rate to less than 1, we can regularize the model. A model with higher learning_rate learns fast, but is prone to overfitting; one with a lower learning rate learns slowly, but avoids overfitting.
Also, there's a trade-off between ```learning_rate``` and ```n_estimators``` - the higher the learning rate, the lesser trees the model needs (and thus we usually tune only one of them).
Also, by subsampling (setting ```subsample``` to less than 1), we can have the individual models built on random subsamples of size ```subsample```. That way, each tree will be trained on different subsets and reduce the model's variance.
```
# parameter grid
param_grid = {"learning_rate": [0.2, 0.6, 0.9],
"subsample": [0.3, 0.6, 0.9]
}
# adaboost with the tree as base estimator
GBC = GradientBoostingClassifier(max_depth=2, n_estimators=200)
# run grid search
folds = 3
grid_search_GBC = GridSearchCV(GBC,
cv = folds,
param_grid=param_grid,
scoring = 'roc_auc',
return_train_score=True,
verbose = 1)
grid_search_GBC.fit(X_train, y_train)
cv_results = pd.DataFrame(grid_search_GBC.cv_results_)
cv_results.head()
# # plotting
plt.figure(figsize=(16,6))
for n, subsample in enumerate(param_grid['subsample']):
# subplot 1/n
plt.subplot(1,len(param_grid['subsample']), n+1)
df = cv_results[cv_results['param_subsample']==subsample]
plt.plot(df["param_learning_rate"], df["mean_test_score"])
plt.plot(df["param_learning_rate"], df["mean_train_score"])
plt.xlabel('learning_rate')
plt.ylabel('AUC')
plt.title("subsample={0}".format(subsample))
plt.ylim([0.60, 1])
plt.legend(['test score', 'train score'], loc='upper left')
plt.xscale('log')
```
It is clear from the plot above that the model with a lower subsample ratio performs better, while those with higher subsamples tend to overfit.
Also, a lower learning rate results in less overfitting.
### XGBoost
Let's finally try XGBoost. The hyperparameters are the same, some important ones being ```subsample```, ```learning_rate```, ```max_depth``` etc.
```
# fit model on training data with default hyperparameters
model = XGBClassifier()
model.fit(X_train, y_train)
# make predictions for test data
# use predict_proba since we need probabilities to compute auc
y_pred = model.predict_proba(X_test)
y_pred[:10]
# evaluate predictions
roc = metrics.roc_auc_score(y_test, y_pred[:, 1])
print("AUC: %.2f%%" % (roc * 100.0))
```
The roc_auc in this case is about 0.95% with default hyperparameters. Let's try changing the hyperparameters - an exhaustive list of XGBoost hyperparameters is here: http://xgboost.readthedocs.io/en/latest/parameter.html
Let's now try tuning the hyperparameters using k-fold CV. We'll then use grid search CV to find the optimal values of hyperparameters.
```
# hyperparameter tuning with XGBoost
# creating a KFold object
folds = 3
# specify range of hyperparameters
param_grid = {'learning_rate': [0.2, 0.6],
'subsample': [0.3, 0.6, 0.9]}
# specify model
xgb_model = XGBClassifier(max_depth=2, n_estimators=200)
# set up GridSearchCV()
model_cv = GridSearchCV(estimator = xgb_model,
param_grid = param_grid,
scoring= 'roc_auc',
cv = folds,
verbose = 1,
return_train_score=True)
# fit the model
model_cv.fit(X_train, y_train)
# cv results
cv_results = pd.DataFrame(model_cv.cv_results_)
cv_results
# convert parameters to int for plotting on x-axis
#cv_results['param_learning_rate'] = cv_results['param_learning_rate'].astype('float')
#cv_results['param_max_depth'] = cv_results['param_max_depth'].astype('float')
cv_results.head()
# # plotting
plt.figure(figsize=(16,6))
param_grid = {'learning_rate': [0.2, 0.6],
'subsample': [0.3, 0.6, 0.9]}
for n, subsample in enumerate(param_grid['subsample']):
# subplot 1/n
plt.subplot(1,len(param_grid['subsample']), n+1)
df = cv_results[cv_results['param_subsample']==subsample]
plt.plot(df["param_learning_rate"], df["mean_test_score"])
plt.plot(df["param_learning_rate"], df["mean_train_score"])
plt.xlabel('learning_rate')
plt.ylabel('AUC')
plt.title("subsample={0}".format(subsample))
plt.ylim([0.60, 1])
plt.legend(['test score', 'train score'], loc='upper left')
plt.xscale('log')
```
The results show that a subsample size of 0.6 and learning_rate of about 0.2 seems optimal.
Also, XGBoost has resulted in the highest ROC AUC obtained (across various hyperparameters).
Let's build a final model with the chosen hyperparameters.
```
# chosen hyperparameters
# 'objective':'binary:logistic' outputs probability rather than label, which we need for auc
params = {'learning_rate': 0.2,
'max_depth': 2,
'n_estimators':200,
'subsample':0.6,
'objective':'binary:logistic'}
# fit model on training data
model = XGBClassifier(params = params)
model.fit(X_train, y_train)
# predict
y_pred = model.predict_proba(X_test)
y_pred[:10]
```
The first column in y_pred is the P(0), i.e. P(not fraud), and the second column is P(1/fraud).
```
# roc_auc
auc = sklearn.metrics.roc_auc_score(y_test, y_pred[:, 1])
auc
```
Finally, let's also look at the feature importances.
```
# feature importance
importance = dict(zip(X_train.columns, model.feature_importances_))
importance
# plot
plt.bar(range(len(model.feature_importances_)), model.feature_importances_)
plt.show()
```
## Predictions on Test Data
Since this problem is hosted on Kaggle, you can choose to make predictions on the test data and submit your results. Please note the following points and recommendations if you go ahead with Kaggle:
Recommendations for training:
- We have used only a fraction of the training set (train_sample, 100k rows), the full training data on Kaggle (train.csv) has about 180 million rows. You'll get good results only if you train the model on a significant portion of the training dataset.
- Because of the size, you'll need to use Kaggle kernels to train the model on full training data. Kaggle kernels provide powerful computation capacities on cloud (for free).
- Even on the kernel, you may need to use a portion of the training dataset (try using the last 20-30 million rows).
- Make sure you save memory by following some tricks and best practices, else you won't be able to train the model at all on a large dataset.
```
# # read submission file
#sample_sub = pd.read_csv(path+'sample_submission.csv')
#sample_sub.head()
# # predict probability of test data
# test_final = pd.read_csv(path+'test.csv')
# test_final.head()
# # predictions on test data
# test_final = timeFeatures(test_final)
# test_final.head()
# test_final.drop(['click_time', 'datetime'], axis=1, inplace=True)
# test_final.head()
# test_final[categorical_cols]=test_final[categorical_cols].apply(lambda x: le.fit_transform(x))
# test_final.info()
# # number of clicks by IP
# ip_count = test_final.groupby('ip')['channel'].count().reset_index()
# ip_count.columns = ['ip', 'count_by_ip']
# ip_count.head()
# merge this with the training data
# test_final = pd.merge(test_final, ip_count, on='ip', how='left')
# del ip_count
# test_final.info()
# # predict on test data
# y_pred_test = model.predict_proba(test_final.drop('click_id', axis=1))
# y_pred_test[:10]
# # # create submission file
# sub = pd.DataFrame()
# sub['click_id'] = test_final['click_id']
# sub['is_attributed'] = y_pred_test[:, 1]
# sub.head()
# sub.to_csv('kshitij_sub_03.csv', float_format='%.8f', index=False)
# # model
# dtrain = xgb.DMatrix(X_train, y_train)
# del X_train, y_train
# gc.collect()
# watchlist = [(dtrain, 'train')]
# model = xgb.train(params, dtrain, 30, watchlist, maximize=True, verbose_eval=1)
# del dtrain
# gc.collect()
# # Plot the feature importance from xgboost
# plot_importance(model)
# plt.gcf().savefig('feature_importance_xgb.png')
# # Load the test for predict
# test = pd.read_csv(path+"test.csv")
# test.head()
# # number of clicks by IP
# ip_count = train_sample.groupby('ip')['channel'].count().reset_index()
# ip_count.columns = ['ip', 'count_by_ip']
# ip_count.head()
# test = pd.merge(test, ip_count, on='ip', how='left', sort=False)
# gc.collect()
# test = timeFeatures(test)
# test.drop(['click_time', 'datetime'], axis=1, inplace=True)
# test.head()
# print(test.columns)
# print(train_sample.columns)
# test = test[['click_id','ip', 'app', 'device', 'os', 'channel', 'day_of_week',
# 'day_of_year', 'month', 'hour', 'count_by_ip']]
# dtest = xgb.DMatrix(test.drop('click_id', axis=1))
# # Save the predictions
# sub = pd.DataFrame()
# sub['click_id'] = test['click_id']
# sub['is_attributed'] = model.predict(dtest, ntree_limit=model.best_ntree_limit)
# sub.to_csv('xgb_sub.csv', float_format='%.8f', index=False)
# sub.shape
```
| github_jupyter |
# Topic 2: Neural network
## Lesson 1: Introduction to Neural Networks
### 1. AND perceptron
Complete the cell below:
```
import pandas as pd
# TODO: Set weight1, weight2, and bias
weight1 = 0.0
weight2 = 0.0
bias = 0.0
# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
correct_outputs = [False, False, False, True]
outputs = []
# Generate and check output
for test_input, correct_output in zip(test_inputs, correct_outputs):
linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
output = int(linear_combination >= 0)
is_correct_string = 'Yes' if output == correct_output else 'No'
outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
if not num_wrong:
print('Nice! You got it all correct.\n')
else:
print('You got {} wrong. Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))
```
My answer:
```
import pandas as pd
# TODO: Set weight1, weight2, and bias
k = 100
weight1 = k * 1.0
weight2 = k * 1.0
bias = k * (-2.0)
# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
correct_outputs = [False, False, False, True]
outputs = []
# Generate and check output
for test_input, correct_output in zip(test_inputs, correct_outputs):
linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
output = int(linear_combination >= 0)
is_correct_string = 'Yes' if output == correct_output else 'No'
outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
if not num_wrong:
print('Nice! You got it all correct.\n')
else:
print('You got {} wrong. Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))
```
### 2. OR Perceptron
Complete the cell below:
```
import pandas as pd
# TODO: Set weight1, weight2, and bias
weight1 = 0.0
weight2 = 0.0
bias = 0.0
# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
correct_outputs = [False, True, True, True]
outputs = []
# Generate and check output
for test_input, correct_output in zip(test_inputs, correct_outputs):
linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
output = int(linear_combination >= 0)
is_correct_string = 'Yes' if output == correct_output else 'No'
outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
if not num_wrong:
print('Nice! You got it all correct.\n')
else:
print('You got {} wrong. Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))
```
My answer:
```
import pandas as pd
# TODO: Set weight1, weight2, and bias
k = 100
weight1 = k * 1.0
weight2 = k * 1.0
bias = k * (-1.0)
# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
correct_outputs = [False, True, True, True]
outputs = []
# Generate and check output
for test_input, correct_output in zip(test_inputs, correct_outputs):
linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
output = int(linear_combination >= 0)
is_correct_string = 'Yes' if output == correct_output else 'No'
outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
if not num_wrong:
print('Nice! You got it all correct.\n')
else:
print('You got {} wrong. Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))
```
2 ways to transform AND perceptron to OR perceptron:
* Increase the weights $w$
* Decrease the magnitude of the bias $|b|$
### 3. NOT Perceptron
Complete the code below:
Only consider the second number in ```test_inputs``` is the input, ignore the first number.
```
import pandas as pd
# TODO: Set weight1, weight2, and bias
weight1 = 0.0
weight2 = 0.0
bias = 0.0
# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
correct_outputs = [True, False, True, False]
outputs = []
# Generate and check output
for test_input, correct_output in zip(test_inputs, correct_outputs):
linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
output = int(linear_combination >= 0)
is_correct_string = 'Yes' if output == correct_output else 'No'
outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
if not num_wrong:
print('Nice! You got it all correct.\n')
else:
print('You got {} wrong. Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))
```
My answer:
```
import pandas as pd
# TODO: Set weight1, weight2, and bias
k = 100
weight1 = 0.0
weight2 = k * (-1.0)
bias = 0.0
# DON'T CHANGE ANYTHING BELOW
# Inputs and outputs
test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
correct_outputs = [True, False, True, False]
outputs = []
# Generate and check output
for test_input, correct_output in zip(test_inputs, correct_outputs):
linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
output = int(linear_combination >= 0)
is_correct_string = 'Yes' if output == correct_output else 'No'
outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
# Print output
num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
if not num_wrong:
print('Nice! You got it all correct.\n')
else:
print('You got {} wrong. Keep trying!\n'.format(num_wrong))
print(output_frame.to_string(index=False))
```
### 4. XOR Perceptron
an XOR Perceptron can be built by an AND Perceptron, an OR Perceptron and a NOT Perceptron.
<img src="../../imgs/xor.png" width="50%">
(image source: Udacity)
```NAND``` consists of an AND perceptron and a NON perceptron.
### 5. Perceptron algorithm
Complete the cell below:
```
import numpy as np
# Setting the random seed, feel free to change it and see different solutions.
np.random.seed(42)
def stepFunction(t):
if t >= 0:
return 1
return 0
def prediction(X, W, b):
return stepFunction((np.matmul(X,W)+b)[0])
# TODO: Fill in the code below to implement the perceptron trick.
# The function should receive as inputs the data X, the labels y,
# the weights W (as an array), and the bias b,
# update the weights and bias W, b, according to the perceptron algorithm,
# and return W and b.
def perceptronStep(X, y, W, b, learn_rate = 0.01):
# Fill in code
return W, b
# This function runs the perceptron algorithm repeatedly on the dataset,
# and returns a few of the boundary lines obtained in the iterations,
# for plotting purposes.
# Feel free to play with the learning rate and the num_epochs,
# and see your results plotted below.
def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 25):
x_min, x_max = min(X.T[0]), max(X.T[0])
y_min, y_max = min(X.T[1]), max(X.T[1])
W = np.array(np.random.rand(2,1))
b = np.random.rand(1)[0] + x_max
# These are the solution lines that get plotted below.
boundary_lines = []
for i in range(num_epochs):
# In each epoch, we apply the perceptron step.
W, b = perceptronStep(X, y, W, b, learn_rate)
boundary_lines.append((-W[0]/W[1], -b/W[1]))
return boundary_lines
```
This is data.csv:
```
0.78051,-0.063669,1
0.28774,0.29139,1
0.40714,0.17878,1
0.2923,0.4217,1
0.50922,0.35256,1
0.27785,0.10802,1
0.27527,0.33223,1
0.43999,0.31245,1
0.33557,0.42984,1
0.23448,0.24986,1
0.0084492,0.13658,1
0.12419,0.33595,1
0.25644,0.42624,1
0.4591,0.40426,1
0.44547,0.45117,1
0.42218,0.20118,1
0.49563,0.21445,1
0.30848,0.24306,1
0.39707,0.44438,1
0.32945,0.39217,1
0.40739,0.40271,1
0.3106,0.50702,1
0.49638,0.45384,1
0.10073,0.32053,1
0.69907,0.37307,1
0.29767,0.69648,1
0.15099,0.57341,1
0.16427,0.27759,1
0.33259,0.055964,1
0.53741,0.28637,1
0.19503,0.36879,1
0.40278,0.035148,1
0.21296,0.55169,1
0.48447,0.56991,1
0.25476,0.34596,1
0.21726,0.28641,1
0.67078,0.46538,1
0.3815,0.4622,1
0.53838,0.32774,1
0.4849,0.26071,1
0.37095,0.38809,1
0.54527,0.63911,1
0.32149,0.12007,1
0.42216,0.61666,1
0.10194,0.060408,1
0.15254,0.2168,1
0.45558,0.43769,1
0.28488,0.52142,1
0.27633,0.21264,1
0.39748,0.31902,1
0.5533,1,0
0.44274,0.59205,0
0.85176,0.6612,0
0.60436,0.86605,0
0.68243,0.48301,0
1,0.76815,0
0.72989,0.8107,0
0.67377,0.77975,0
0.78761,0.58177,0
0.71442,0.7668,0
0.49379,0.54226,0
0.78974,0.74233,0
0.67905,0.60921,0
0.6642,0.72519,0
0.79396,0.56789,0
0.70758,0.76022,0
0.59421,0.61857,0
0.49364,0.56224,0
0.77707,0.35025,0
0.79785,0.76921,0
0.70876,0.96764,0
0.69176,0.60865,0
0.66408,0.92075,0
0.65973,0.66666,0
0.64574,0.56845,0
0.89639,0.7085,0
0.85476,0.63167,0
0.62091,0.80424,0
0.79057,0.56108,0
0.58935,0.71582,0
0.56846,0.7406,0
0.65912,0.71548,0
0.70938,0.74041,0
0.59154,0.62927,0
0.45829,0.4641,0
0.79982,0.74847,0
0.60974,0.54757,0
0.68127,0.86985,0
0.76694,0.64736,0
0.69048,0.83058,0
0.68122,0.96541,0
0.73229,0.64245,0
0.76145,0.60138,0
0.58985,0.86955,0
0.73145,0.74516,0
0.77029,0.7014,0
0.73156,0.71782,0
0.44556,0.57991,0
0.85275,0.85987,0
0.51912,0.62359,0
```
My answer:
```
import numpy as np
X = np.array([
[0.78051,-0.063669],
[0.28774,0.29139],
[0.40714,0.17878],
[0.2923,0.4217],
[0.50922,0.35256],
[0.27785,0.10802],
[0.27527,0.33223],
[0.43999,0.31245],
[0.33557,0.42984],
[0.23448,0.24986],
[0.0084492,0.13658],
[0.12419,0.33595],
[0.25644,0.42624],
[0.4591,0.40426],
[0.44547,0.45117],
[0.42218,0.20118],
[0.49563,0.21445],
[0.30848,0.24306],
[0.39707,0.44438],
[0.32945,0.39217],
[0.40739,0.40271],
[0.3106,0.50702],
[0.49638,0.45384],
[0.10073,0.32053],
[0.69907,0.37307],
[0.29767,0.69648],
[0.15099,0.57341],
[0.16427,0.27759],
[0.33259,0.055964],
[0.53741,0.28637],
[0.19503,0.36879],
[0.40278,0.035148],
[0.21296,0.55169],
[0.48447,0.56991],
[0.25476,0.34596],
[0.21726,0.28641],
[0.67078,0.46538],
[0.3815,0.4622],
[0.53838,0.32774],
[0.4849,0.26071],
[0.37095,0.38809],
[0.54527,0.63911],
[0.32149,0.12007],
[0.42216,0.61666],
[0.10194,0.060408],
[0.15254,0.2168],
[0.45558,0.43769],
[0.28488,0.52142],
[0.27633,0.21264],
[0.39748,0.31902],
[0.5533,1],
[0.44274,0.59205],
[0.85176,0.6612],
[0.60436,0.86605],
[0.68243,0.48301],
[1,0.76815],
[0.72989,0.8107],
[0.67377,0.77975],
[0.78761,0.58177],
[0.71442,0.7668],
[0.49379,0.54226],
[0.78974,0.74233],
[0.67905,0.60921],
[0.6642,0.72519],
[0.79396,0.56789],
[0.70758,0.76022],
[0.59421,0.61857],
[0.49364,0.56224],
[0.77707,0.35025],
[0.79785,0.76921],
[0.70876,0.96764],
[0.69176,0.60865],
[0.66408,0.92075],
[0.65973,0.66666],
[0.64574,0.56845],
[0.89639,0.7085],
[0.85476,0.63167],
[0.62091,0.80424],
[0.79057,0.56108],
[0.58935,0.71582],
[0.56846,0.7406],
[0.65912,0.71548],
[0.70938,0.74041],
[0.59154,0.62927],
[0.45829,0.4641],
[0.79982,0.74847],
[0.60974,0.54757],
[0.68127,0.86985],
[0.76694,0.64736],
[0.69048,0.83058],
[0.68122,0.96541],
[0.73229,0.64245],
[0.76145,0.60138],
[0.58985,0.86955],
[0.73145,0.74516],
[0.77029,0.7014],
[0.73156,0.71782],
[0.44556,0.57991],
[0.85275,0.85987],
[0.51912,0.62359]
])
y = np.array([
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0]
])
print(X.shape)
print(y.shape)
import numpy as np
# Setting the random seed, feel free to change it and see different solutions.
np.random.seed(42)
def stepFunction(t):
if t >= 0:
return 1
return 0
def prediction(X, W, b):
return stepFunction((np.matmul(X,W)+b)[0])
# TODO: Fill in the code below to implement the perceptron trick.
# The function should receive as inputs the data X, the labels y,
# the weights W (as an array), and the bias b,
# update the weights and bias W, b, according to the perceptron algorithm,
# and return W and b.
def perceptronStep(X, y, W, b, learn_rate = 0.01):
# Fill in code
for i in range(len(y)):
true_label = y[i]
pred = prediction(X[i], W, b)
if true_label == pred:
continue
else:
if pred == 1 and true_label == 0:
# the point is classified positive, but it has a negative label
W -= learn_rate * X[i].reshape(-1, 1)
b -= learn_rate
elif pred == 0 and true_label == 1:
# the point is classified negative, but it has a positive label
W += learn_rate * X[i].reshape(-1, 1)
b += learn_rate
return W, b
# This function runs the perceptron algorithm repeatedly on the dataset,
# and returns a few of the boundary lines obtained in the iterations,
# for plotting purposes.
# Feel free to play with the learning rate and the num_epochs,
# and see your results plotted below.
def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 25):
x_min, x_max = min(X.T[0]), max(X.T[0])
y_min, y_max = min(X.T[1]), max(X.T[1])
W = np.array(np.random.rand(2,1))
b = np.random.rand(1)[0] + x_max
# These are the solution lines that get plotted below.
boundary_lines = []
for i in range(num_epochs):
# In each epoch, we apply the perceptron step.
W, b = perceptronStep(X, y, W, b, learn_rate)
boundary_lines.append((-W[0]/W[1], -b/W[1]))
return boundary_lines
```
Solution:
```
def perceptronStep(X, y, W, b, learn_rate = 0.01):
for i in range(len(X)):
y_hat = prediction(X[i],W,b)
if y[i]-y_hat == 1:
W[0] += X[i][0]*learn_rate
W[1] += X[i][1]*learn_rate
b += learn_rate
elif y[i]-y_hat == -1:
W[0] -= X[i][0]*learn_rate
W[1] -= X[i][1]*learn_rate
b -= learn_rate
return W, b
```
### 6. Softmax
Complete the code below:
```
import numpy as np
# Write a function that takes as input a list of numbers, and returns
# the list of values given by the softmax function.
def softmax(L):
pass
```
My answer:
```
import numpy as np
# Write a function that takes as input a list of numbers, and returns
# the list of values given by the softmax function.
def softmax(L):
return [(np.exp(L[i]) / np.sum(np.exp(L))) for i in range(len(L))]
L = [0, 2, 1]
softmax(L)
```
### 7. Cross-Entropy
Formula:
$$
Cross Entropy = - \sum_{i=1}^{|X|}y_i log(p_i) + (1 - y_i) log(1 - p_i)
$$
where
* $y_i$ is the true label for $i^{th}$ instance
* $p_i$ is the probability of the $i^{th}$ instance is positive.
Complete the code below
```
import numpy as np
# Write a function that takes as input two lists Y, P,
# and returns the float corresponding to their cross-entropy.
def cross_entropy(Y, P):
pass
```
My answer:
```
import numpy as np
# Write a function that takes as input two lists Y, P,
# and returns the float corresponding to their cross-entropy.
def cross_entropy(Y, P):
return -np.sum([Y[i] * np.log(P[i]) + (1 - Y[i]) * np.log(1 - P[i]) for i in range(len(Y))])
Y = np.array([1, 0, 1, 1])
P = np.array([0.4, 0.6, 0.1, 0.5])
assert float(format(cross_entropy(Y, P), '.10f')) == 4.8283137373
```
| github_jupyter |
```
# lab1.py
#You should start here when providing the answers to Problem Set 1.
#Follow along in the problem set, which is at:
#http://ai6034.mit.edu/fall12/index.php?title=Lab_1
# Import helper objects that provide the logical operations
# discussed in class.
from production import IF, AND, OR, NOT, THEN, forward_chain
## Section 1: Forward chaining ##
# Problem 1.2: Multiple choice
# Which part of a rule may change the data?
# 1. the antecedent
# 2. the consequent
# 3. both
ANSWER_1 = 'your answer here'
# A rule-based system about Monty Python's "Dead Parrot" sketch
# uses the following rules:
#
# rule1 = IF( AND( '(?x) is a Norwegian Blue parrot',
# '(?x) is motionless' ),
# THEN( '(?x) is not dead' ) )
#
# rule2 = IF( NOT( '(?x) is dead' ),
# THEN( '(?x) is pining for the fjords' ) )
#
# and the following initial data:
#
# ( 'Polly is a Norwegian Blue parrot',
# 'Polly is motionless' )
#
# Will this system produce the datum 'Polly is pining for the
# fjords'? Answer 'yes' or 'no'.
ANSWER_2 = 'your answer here'
# Which rule contains a programming error? Answer '1' or '2'.
ANSWER_3 = 'your answer here'
# If you're uncertain of these answers, look in tests.py for an
# explanation.
# In a completely different scenario, suppose we have the
# following rules list:
#
# ( IF( AND( '(?x) has feathers', # rule 1
# '(?x) has a beak' ),
# THEN( '(?x) is a bird' ),
# IF( AND( '(?y) is a bird', # rule 2
# '(?y) cannot fly',
# '(?y) can swim' ),
# THEN( '(?y) is a penguin' ) ) )
#
# and the following list of initial data:
#
# ( 'Pendergast is a penguin',
# 'Pendergast has feathers',
# 'Pendergast has a beak',
# 'Pendergast cannot fly',
# 'Pendergast can swim' )
#
# In the following questions, answer '0' if neither rule does
# what is asked. After we start the system running, which rule
# fires first?
ANSWER_4 = 'your answer here'
# Which rule fires second?
ANSWER_5 = 'your answer here'
# Problem 1.3.1: Poker hands
# You're given this data about poker hands:
poker_data = ( 'two-pair beats pair',
'three-of-a-kind beats two-pair',
'straight beats three-of-a-kind',
'flush beats straight',
'full-house beats flush',
'straight-flush beats full-house' )
# Fill in this rule so that it finds all other combinations of
# which poker hands beat which, transitively. For example, it
# should be able to deduce that a three-of-a-kind beats a pair,
# because a three-of-a-kind beats two-pair, which beats a pair.
transitive_rule = IF( AND('(?x) beats (?y)','(?y) beats (?z)'),
THEN('(?x) beats (?z)') )
# You can test your rule like this:
# print forward_chain([transitive_rule], poker_data)
# Here's some other data sets for the rule. The tester uses
# these, so don't change them.
TEST_RESULTS_TRANS1 = forward_chain([transitive_rule],
[ 'a beats b', 'b beats c' ])
TEST_RESULTS_TRANS2 = forward_chain([transitive_rule],
[ 'rock beats scissors',
'scissors beats paper',
'paper beats rock' ])
# Problem 1.3.2: Family relations
# First, define all your rules here individually. That is, give
# them names by assigning them to variables. This way, you'll be
# able to refer to the rules by name and easily rearrange them if
# you need to.
# Then, put them together into a list in order, and call it
# family_rules.
family_rules = [ ] # fill me in
# Some examples to try it on:
# Note: These are used for testing, so DO NOT CHANGE
simpsons_data = ("male bart",
"female lisa",
"female maggie",
"female marge",
"male homer",
"male abe",
"parent marge bart",
"parent marge lisa",
"parent marge maggie",
"parent homer bart",
"parent homer lisa",
"parent homer maggie",
"parent abe homer")
TEST_RESULTS_6 = forward_chain(family_rules,
simpsons_data,verbose=False)
# You can test your results by uncommenting this line:
# print forward_chain(family_rules, simpsons_data, verbose=True)
black_data = ("male sirius",
"male regulus",
"female walburga",
"male alphard",
"male cygnus",
"male pollux",
"female bellatrix",
"female andromeda",
"female narcissa",
"female nymphadora",
"male draco",
"parent walburga sirius",
"parent walburga regulus",
"parent pollux walburga",
"parent pollux alphard",
"parent pollux cygnus",
"parent cygnus bellatrix",
"parent cygnus andromeda",
"parent cygnus narcissa",
"parent andromeda nymphadora",
"parent narcissa draco")
# This should generate 14 cousin relationships, representing
# 7 pairs of people who are cousins:
black_family_cousins = [
x for x in
forward_chain(family_rules, black_data, verbose=False)
if "cousin" in x ]
# To see if you found them all, uncomment this line:
# print black_family_cousins
# To debug what happened in your rules, you can set verbose=True
# in the function call above.
# Some other data sets to try it on. The tester uses these
# results, so don't comment them out.
TEST_DATA_1 = [ 'female alice',
'male bob',
'male chuck',
'parent chuck alice',
'parent chuck bob' ]
TEST_RESULTS_1 = forward_chain(family_rules,
TEST_DATA_1, verbose=False)
TEST_DATA_2 = [ 'female a1', 'female b1', 'female b2',
'female c1', 'female c2', 'female c3',
'female c4', 'female d1', 'female d2',
'female d3', 'female d4',
'parent a1 b1',
'parent a1 b2',
'parent b1 c1',
'parent b1 c2',
'parent b2 c3',
'parent b2 c4',
'parent c1 d1',
'parent c2 d2',
'parent c3 d3',
'parent c4 d4' ]
TEST_RESULTS_2 = forward_chain(family_rules,
TEST_DATA_2, verbose=False)
TEST_RESULTS_6 = forward_chain(family_rules,
simpsons_data,verbose=False)
## Section 2: Goal trees and backward chaining ##
# Problem 2 is found in backchain.py.
from backchain import backchain_to_goal_tree
##; Section 3: Survey ##
# Please answer these questions inside the double quotes.
HOW_MANY_HOURS_THIS_PSET_TOOK = ''
WHAT_I_FOUND_INTERESTING = ''
WHAT_I_FOUND_BORING = ''
```
| github_jupyter |
# AHDB wheat lodging risk and recommendations
This example notebook was inspired by the [AHDB lodging practical guidelines](https://ahdb.org.uk/knowledge-library/lodging): we evaluate the lodging risk for a field and output practical recommendations. We then adjust the estimated risk according to the Leaf Area Index (LAI) and Green Cover Fraction (GCF) obtained using the Agrimetrics GraphQL API.
## AHDB lodging resistance score
AHDB's guidelines show how a lodging resistance score can be calculated based on:
- the crop variety's natural resistance to lodging without Plant Growth Regulators (PGR)
- the soil Nitrogen Suply (SNS) index, a higher supply increases lodging risk
- the sowing date, an earlier sowing increases lodging risk
- the sowing density, higher plant density increases lodging risk
The overall lodging resistance score is the sum of the individual scores. AHDB practical advice on reducing the risk of lodging is given for 4 resistance score categories:
| Lodging resistance category | Lodging risk |
|---|---|
| below 5 | very high |
| 5-6.8 | high |
| 7-8.8 | medium |
| 9-10 | low |
| over 10 | very low |
[Table image](img/lodging/ahdb_risk_categories.png)
```
# Input AHDB factors for evaluating lodging risks
def sns_index_score(sns_index):
return 3 - 6 * sns_index / 4
# Sowing dates and associated lodging resistance score
sowing_date_scores = {'Mid Sept': -2, 'End Sept': -1, 'Mid Oct': 0, 'End Oct': 1, 'Nov onwards': 2}
# Density ranges and associated lodging resistance score
sowing_density_scores = {'<150': 1.5, '200-150': +0.75, '300-200': 0, '400-300': -1, '>400': -1.75}
# AHDB resistance score categories
def score_category(score):
if score < 5:
return 'below 5'
if score < 7:
return '5-6.8'
if score < 9:
return '7-8.8'
if score < 10:
return '9-10'
return 'over 10'
# Combine individual factor scores
def lodging_resistance_category(resistance_score, sns_index, sowing_date, sowing_density):
score = resistance_score + sns_index_score(sns_index) + sowing_date_scores[sowing_date] + sowing_density_scores[sowing_density]
return score_category(score)
```
## AHDB practical advice
AHDB provides practical advice for managing the risk of stem and root lodging. This advice depends on the resistance score calculated specifically for a field. AHDB recommends fertilizer and PGR actions for managing stem lodging risk. For root lodging, AHDB also advises if the crop needs to be rolled (before the crop has reached stage "GS30").
```
# Nitrogen fertiliser advice for stem risk
stem_risk_N_advice = {
'below 5': 'Delay & reduce N',
'5-6.8': 'Delay & reduce N',
'7-8.8': 'Delay N',
}
# PGR advice for stem risk
stem_risk_PGR_advice = {
'below 5': 'Full PGR',
'5-6.8': 'Full PGR',
'7-8.8': 'Single PGR',
'9-10': 'PGR if high yield forecast'
}
# Nitrogen fertiliser advice for root risk
root_risk_N_advice = {
'below 5': 'Reduce N',
'5-6.8': 'Reduce N',
}
# PGR advice for root risk
root_risk_PGR_advice = {
'below 5': 'Full PGR',
'5-6.8': 'Full PGR',
'7-8.8': 'Single PGR',
'9-10': 'PGR if high yield forecast'
}
# Spring rolling advice for root risk
root_risk_Roll_advice = {
'below 5': 'Roll',
'5-6.8': 'Roll',
'7-8.8': 'Roll',
}
```
## AHDB standard lodging risk management recommendations
Using the definitions above, we can calculate the AHDB recommendation according to individual factors:
```
import pandas as pd
from ipywidgets import widgets
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
style = {'description_width': 'initial'}
def ahdb_lodging_recommendation(resistance_score, sns_index, sowing_date, sowing_density):
category = lodging_resistance_category(resistance_score, sns_index, sowing_date, sowing_density)
return pd.DataFrame(index=['Fertiliser nitrogen', 'Plant growth regulators', 'Spring rolling'], data={
'Stem lodging': [stem_risk_N_advice.get(category, ''), stem_risk_PGR_advice.get(category, ''), '' ],
'Root lodging': [root_risk_N_advice.get(category, ''), root_risk_PGR_advice.get(category, ''), root_risk_Roll_advice.get(category, '')]
})
widgets.interact(ahdb_lodging_recommendation,
resistance_score = widgets.IntSlider(description='Resistance score without PGR', min=1, max=9, style=style),
sns_index = widgets.IntSlider(description='SNS index', min=0, max=4, style=style),
sowing_date = widgets.SelectionSlider(description='Sowing date', options=sowing_date_scores.keys(), style=style),
sowing_density = widgets.SelectionSlider(description='Sowing density', options=sowing_density_scores.keys(), style=style),
)
```
[Widget image](img/lodging/recommendations_slider.png)
## Adjusting recommendations based on remote sensing information
The same practical guidelines from AHDB explains that crop conditions in Spring can indicate future lodging risk. In particular, Green Area Index (GAI) greater than 2 or Ground Cover Fraction (GCF) above 60% are indicative of increased stem lodging risk. For adjusting our practical advice, we will retrieve LAI and GCF from Agrimetrics GraphQL API.
### Using Agrimetrics GraphQL API
An Agrimetrics API key must be provided with each GraphQL API in a custom request header Ocp-Apim-Subscription-Key. For more information about how to obtain and use an Agrimetrics API key, please consult the [Developer portal](https://developer.agrimetrics.co.uk). To get started with GraphQL, see [Agrimetrics Graph Explorer](https://app.agrimetrics.co.uk/#/graph-explorer) tool.
```
import os
import requests
GRAPHQL_ENDPOINT = "https://api.agrimetrics.co.uk/graphql/v1/"
if "API_KEY" in os.environ:
API_KEY = os.environ["API_KEY"]
else:
API_KEY = input("Query API Subscription Key: ").strip()
```
We will also need a short function to help catch and report errors from making GraphQL queries.
```
def check_results(result):
if result.status_code != 200:
raise Exception(f"Request failed with code {result.status_code}.\n{result.text}")
errors = result.json().get("errors", [])
if errors:
for err in errors:
print(f"{err['message']}:")
print( " at", " and ".join([f"line {loc['line']}, col {loc['column']}" for loc in err['locations']]))
print( " path", ".".join(err['path']))
print(f" {err['extensions']}")
raise Exception(f"GraphQL reported {len(errors)} errors")
```
A GraphQL query is posted to the GraphQL endpoint in a json body. With our first query, we retrieve the Agrimetrics field id at a given location.
```
graphql_url = 'https://api.agrimetrics.co.uk/graphql'
headers = {
'Ocp-Apim-Subscription-Key': API_KEY,
'Content-Type': "application/json",
'Accept-Encoding': "gzip, deflate, br",
}
centroid = (-0.929365345, 51.408374978)
response = requests.post(graphql_url, headers=headers, json={
'query': '''
query getFieldAtLocation($centroid: CoordinateScalar!) {
fields(geoFilter: {location: {type: Point, coordinates: $centroid}, distance: {LE: 10}}) {
id
}
}
''',
'variables': {
'centroid': centroid
}
})
check_results(response)
field_id = response.json()['data']['fields'][0]['id']
print('Agrimetrics field id:', field_id)
```
GraphQL API supports filtering by object ids. Here, we retrieve the sowing crop information associated to the field id obtained in our first query.
```
# Verify field was a wheat crop in 2018
response = requests.post(graphql_url, headers=headers, json={
'query': '''
query getSownCrop($fieldId: [ID!]!) {
fields(where: {id: {EQ: $fieldId}}) {
sownCrop {
cropType
harvestYear
}
}
}
''',
'variables': {
'fieldId': field_id
}
})
check_results(response)
print(response.json()['data']['fields'][0]['sownCrop'])
```
It is necessary to register for accessing Verde crop observations on our field of interest. LAI is a crop-specific attribute, so it is necessary to provide `cropType` when registering.
```
# Register for CROP_SPECIFIC verde data on our field
response = requests.post(graphql_url, headers=headers, json={
'query': '''
mutation registerCropObservations($fieldId: ID!) {
account {
premiumData {
addCropObservationRegistrations(registrations: {fieldId: $fieldId, layerType: CROP_SPECIFIC, cropType: WHEAT, season: SEP2017TOSEP2018}) {
id
}
}
}
}
''',
'variables': {'fieldId': field_id}
})
check_results(response)
```
GCF is not crop specific, so we need to register as well for accessing non crop-specific attributes.
```
# Register for NON_CROP_SPECIFIC verde data on our field
response = requests.post(graphql_url, headers=headers, json={
'query': '''
mutation registerCropObservations($fieldId: ID!) {
account {
premiumData {
addCropObservationRegistrations(registrations: {fieldId: $fieldId, layerType: NON_CROP_SPECIFIC, season: SEP2017TOSEP2018}) {
id
}
}
}
}
''',
'variables': {'fieldId': field_id}
})
check_results(response)
```
Once Verde data for this field is available, we can easily retrieve it, for instance:
```
response = requests.post(graphql_url, headers=headers, json={
'query': '''
query getCropObservations($fieldId: [ID!]!) {
fields(where: {id: {EQ: $fieldId}}) {
cropObservations {
leafAreaIndex { dateTime mean }
}
}
}
''',
'variables': {'fieldId': field_id}
})
check_results(response)
```
The data can be loaded as a pandas DataFrame:
```
results = response.json()
leafAreaIndex = pd.io.json.json_normalize(
results['data']['fields'],
record_path=['cropObservations', 'leafAreaIndex'],
)
leafAreaIndex['date_time'] = pd.to_datetime(leafAreaIndex['dateTime'])
leafAreaIndex['value'] = leafAreaIndex['mean']
leafAreaIndex = leafAreaIndex[['date_time', 'value']]
leafAreaIndex.head()
```
[Table image](img/lodging/lai_for_field.png)
We proceed to a second similar query to obtain green vegetation cover fraction:
```
response = requests.post(graphql_url, headers=headers, json={
'query': '''
query getCropObservations($fieldId: [ID!]!) {
fields(where: {id: {EQ: $fieldId}}) {
cropObservations {
greenVegetationCoverFraction { dateTime mean }
}
}
}
''',
'variables': {'fieldId': field_id}
})
check_results(response)
results = response.json()
greenCoverFraction = pd.io.json.json_normalize(
results['data']['fields'],
record_path=['cropObservations', 'greenVegetationCoverFraction'],
)
greenCoverFraction['date_time'] = pd.to_datetime(greenCoverFraction['dateTime'])
greenCoverFraction['value'] = greenCoverFraction['mean']
greenCoverFraction = greenCoverFraction[['date_time', 'value']]
```
A year of observations was retrieved:
```
import matplotlib.pyplot as plt
plt.plot(leafAreaIndex['date_time'], leafAreaIndex['value'], label='LAI')
plt.plot(greenCoverFraction['date_time'], greenCoverFraction['value'], label='GCF')
plt.legend()
plt.show()
```
[Graph image](img/lodging/lai_gfc.png)
## Adjusting recommendation
GS31 marks the beginning of the stem elongation and generally occurs around mid April. Let's filter our LAI and GCF around this time of year:
```
from datetime import datetime, timezone
from_date = datetime(2018, 4, 7, tzinfo=timezone.utc)
to_date = datetime(2018, 4, 21, tzinfo=timezone.utc)
leafAreaIndex_mid_april = leafAreaIndex[(leafAreaIndex['date_time'] > from_date) & (leafAreaIndex['date_time'] < to_date)]
greenCoverFraction_mid_april = greenCoverFraction[(greenCoverFraction['date_time'] > from_date) & (greenCoverFraction['date_time'] < to_date)]
```
Check if LAI or GCF are above their respective thresholds:
```
(leafAreaIndex_mid_april['value'] > 2).any() | (greenCoverFraction_mid_april['value'] > 0.6).any()
```
Our field has an LAI below 2 in the 2 weeks around mid April and no GCF reading close enough to be taken into account. But we have now the basis for adjusting our recommendation by using Agrimetrics Verde crop observations. Let's broaden our evaluation to nearby Agrimetrics fields with a wheat crop in 2018.
```
response = requests.post(graphql_url, headers=headers, json={
'query': '''
query getFieldsWithinRadius($centroid: CoordinateScalar!, $distance: Float!) {
fields(geoFilter: {location: {type: Point, coordinates: $centroid}, distance: {LE: $distance}}) {
id
sownCrop {
cropType
harvestYear
}
}
}
''',
'variables': { 'centroid': centroid, 'distance': 2000 } # distance in m
})
check_results(response)
results = response.json()
nearby_fields = pd.io.json.json_normalize(
results['data']['fields'],
record_path=['sownCrop'],
meta=['id'],
)
nearby_wheat_fields = nearby_fields[(nearby_fields['cropType'] == 'WHEAT')
& (nearby_fields['harvestYear'] == 2018)]
available_fields = nearby_wheat_fields['id']
available_fields.head()
```
Using the same approach as above, we implement the retrieval of Verde LAI and GCF for the selected fields:
```
def register(field_id):
# Register for CROP_SPECIFIC verde data on our field
response = requests.post(graphql_url, headers=headers, json={
'query': '''
mutation registerCropObservations($fieldId: ID!) {
account {
premiumData {
addCropObservationRegistrations(registrations: {
fieldId: $fieldId, layerType: CROP_SPECIFIC, season: SEP2017TOSEP2018, cropType: WHEAT
}) {
id
}
}
}
}
''',
'variables': {'fieldId': field_id}
})
check_results(response)
# Register for NON_CROP_SPECIFIC verde data on our field
response = requests.post(graphql_url, headers=headers, json={
'query': '''
mutation registerCropObservations($fieldId: ID!) {
account {
premiumData {
addCropObservationRegistrations(registrations: {
fieldId: $fieldId, layerType: NON_CROP_SPECIFIC, season: SEP2017TOSEP2018
}) {
id
}
}
}
}
''',
'variables': {'fieldId': field_id}
})
check_results(response)
def crop_observations(field_id, attribute):
response = requests.post(graphql_url, headers=headers, json={
'query': '''
query getCropObservations($fieldId: [ID!]!) {{
fields(where: {{id: {{EQ: $fieldId}}}}) {{
cropObservations {{
{attribute} {{ mean dateTime }}
}}
}}
}}
'''.format(attribute=attribute),
'variables': {'fieldId': field_id}
})
check_results(response)
results = response.json()
data = pd.io.json.json_normalize(
results['data']['fields'],
record_path=['cropObservations', attribute],
)
data['date_time'] = pd.to_datetime(data['dateTime'])
data['value'] = data['mean']
return data[['date_time', 'value']]
def has_high_LAI(field_id, leafAreaIndex):
if not leafAreaIndex.empty:
leafAreaIndex_mid_april = leafAreaIndex[(leafAreaIndex['date_time'] > from_date) & (leafAreaIndex['date_time'] < to_date)]
return (leafAreaIndex_mid_april['value'] > 2).any()
return False
def has_high_GCF(field_id, greenCoverFraction):
if not greenCoverFraction.empty:
greenCoverFraction_mid_april = greenCoverFraction[(greenCoverFraction['date_time'] > from_date) & (greenCoverFraction['date_time'] < to_date)]
return (greenCoverFraction_mid_april['value'] > 0.6).any()
return False
```
We then revisit the recommendation algorithm:
```
def adjusted_lodging_recommendation(field_id, resistance_score, sns_index, sowing_date, sowing_density):
register(field_id)
leafAreaIndex = crop_observations(field_id, 'leafAreaIndex')
greenCoverFraction = crop_observations(field_id, 'greenVegetationCoverFraction')
high_LAI = has_high_LAI(field_id, leafAreaIndex)
high_GCF = has_high_GCF(field_id, greenCoverFraction)
plt.plot(leafAreaIndex['date_time'], leafAreaIndex['value'], label='LAI')
plt.plot(greenCoverFraction['date_time'], greenCoverFraction['value'], label='GCF')
plt.legend()
plt.show()
if high_LAI and high_GCF:
print('High LAI and GCF were observed around GS31 for this crop, please consider adjusting the recommendation')
elif high_LAI:
print('High LAI was observed around GS31 for this crop, please consider adjusting the recommendation')
elif high_GCF:
print('High GCF was observed around GS31 for this crop, please consider adjusting the recommendation')
else:
print('High LAI and GCF were not observed around GS31 for this crop')
return ahdb_lodging_recommendation(resistance_score, sns_index, sowing_date, sowing_density)
widgets.interact(adjusted_lodging_recommendation,
field_id=widgets.Dropdown(description='Agrimetrics field id', options=available_fields, style=style),
resistance_score=widgets.IntSlider(description='Resistance score without PGR', min=1, max=9, style=style),
sns_index=widgets.IntSlider(description='SNS index', min=0, max=4, style=style),
sowing_date=widgets.SelectionSlider(description='Sowing date', options=sowing_date_scores.keys(), style=style),
sowing_density=widgets.SelectionSlider(description='Sowing density', options=sowing_density_scores.keys(), style=style),
)
```
[Widget image: Low LAI](img/lodging/output_1.png) [Widget image: High LAI](img/lodging/output_2_high_lai.png)
| github_jupyter |
```
import pandas as pd
import numpy as np
from scipy.io import arff
from scipy.stats import iqr
import os
import math
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import seaborn as sns
import datetime
import calendar
from numpy import mean
from numpy import std
from sklearn.preprocessing import normalize
from sklearn.preprocessing import scale
from sklearn.feature_selection import f_regression
from sklearn.feature_selection import f_classif
from sklearn.feature_selection import mutual_info_classif
from sklearn.feature_selection import mutual_info_regression
from sklearn.feature_selection import RFE
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import learning_curve
import joblib
cancer = pd.read_csv('dataR2.csv')
print(cancer.shape)
cancer.head(2)
def print_unique(df):
for col in df.columns:
print(col, '\n', df[col].sort_values().unique(), '\n')
print_unique(cancer)
def snapshot(df):
n_missing = pd.DataFrame(df.isnull().sum(), columns = ['n_missing'])
pct_missing = pd.DataFrame(round(df.isnull().sum() / df.shape[0], 2), columns = ['pct_missing'])
dtype = pd.DataFrame(df.dtypes, columns = ['dtype'])
n_unique = []
for col in df.columns:
n_unique.append(df[col].nunique())
return pd.DataFrame(n_unique, index = df.columns, columns = ['n_unique']).join(dtype).join(n_missing).join(pct_missing)
snapshot = snapshot(cancer)
snapshot
np.sort(snapshot['n_unique'].unique())
features = cancer.columns.drop('Classification')
def plot_single_categorical(df, col):
plt.figure(figsize = (4, 4))
df[col].value_counts().plot.bar(color = mcolors.TABLEAU_COLORS)
sns.despine(top = True)
n_level = df[col].nunique()
for x_coor in range(n_level):
plt.annotate(df[col].value_counts().iloc[x_coor],
xy = (x_coor,
df[col].value_counts().iloc[x_coor] + df[col].value_counts().iloc[0]/50))
plt.xticks(rotation = 0)
plt.grid()
plt.title(col)
plt.show()
plot_single_categorical(cancer, 'Classification')
def feat_significance(X, y, n_feat_data_type, features):
mi_df = pd.DataFrame(mutual_info_classif(X, y, random_state = 42), index = X.columns, columns = ['score'])
mi_df = mi_df.sort_values(by = 'score', ascending = False)
def color_cell(s):
background = []
for i in range(len(s.index)):
if s.index[i] in features:
background.append('background-color: yellow')
else:
background.append('')
return background
if n_feat_data_type == 1:
return mi_df
else:
return mi_df.style.apply(color_cell, axis = 0)
feat_score = feat_significance(cancer[features], cancer['Classification'], 1, '')
feat_score
X_scaled = pd.DataFrame(scale(cancer[features]), columns = features)
y = cancer['Classification']
lr = LogisticRegression(random_state = 42)
knn = KNeighborsClassifier()
svc = SVC(random_state = 42)
tree = DecisionTreeClassifier(max_features = 'auto', random_state = 42)
alg_dict = {lr: 'lr', svc: 'svc', knn: 'knn', tree: 'tree'}
def num_feat_perform(algorithm, feat_ordered, X_ordered, y, metric):
scores = []
for i in range(1, len(feat_ordered)+1):
pred_data = X_ordered.iloc[:, 0:i]
score = mean(cross_val_score(algorithm, pred_data, y, scoring = metric, cv = 5))
scores.append(score)
n_features = len(feat_ordered)
plt.plot(np.arange(n_features), scores, marker = 'x')
plt.xticks(np.arange(n_features), np.arange(1, n_features + 1))
for i in range(n_features):
plt.text(i, scores[i], s = round(scores[i], 2))
plt.grid()
plt.xlabel('no. of features')
plt.ylabel('score')
def num_feat_multi_alg(alg_dict, feat_ordered, X_ordered, y, metric):
n_algorithm = len(alg_dict)
algorithms = list(alg_dict.keys())
alg_names = list(alg_dict.values())
if n_algorithm <= 2:
nrows = 1
ncols = n_algorithm
fig = plt.figure(figsize = (ncols * 6, 4))
else:
nrows = math.ceil(n_algorithm / 2)
ncols = 2
fig = plt.figure(figsize = (12, nrows * 4))
for n in range(n_algorithm):
ax = fig.add_subplot(nrows, ncols, n + 1)
ax = num_feat_perform(algorithms[n], feat_ordered, X_ordered, y, metric)
plt.title(f"'{alg_names[n]}' performance by '{metric}'")
plt.tight_layout()
plt.show()
num_feat_multi_alg(alg_dict, feat_score.index, X_scaled[feat_score.index], y, 'f1')
def plot_learning_curve(train_scores, test_scores, train_sizes):
train_scores = pd.DataFrame(train_scores, index = train_sizes, columns = ['split1', 'split2', 'split3', 'split4', 'split5'])
train_scores = train_scores.join(pd.Series(train_scores.mean(axis = 1), name = 'mean'))
test_scores = pd.DataFrame(test_scores, index = train_sizes, columns = ['split1', 'split2', 'split3', 'split4', 'split5'])
test_scores = test_scores.join(pd.Series(test_scores.mean(axis = 1), name = 'mean'))
plt.plot(train_scores['mean'], label = 'train_scores')
plt.plot(test_scores['mean'], label = 'test_scores')
plt.legend()
plt.grid()
plt.xlabel('no. of training samples')
def two_metric_graph(algorithm, X, y):
train_sizes = np.linspace(start = 20, stop = X.shape[0] * 0.8, num = 6, dtype = int)
fig = plt.figure(figsize = (10, 4))
for i, metric in enumerate(['f1', 'balanced_accuracy']):
train_sizes_abs, train_scores, test_scores = learning_curve(algorithm, X, y, train_sizes = train_sizes,
scoring = metric, cv = 5, shuffle = True,
random_state = 42)
ax = fig.add_subplot(1, 2, i + 1)
ax = plot_learning_curve(train_scores, test_scores, train_sizes)
plt.title(f"'performance by '{metric}'")
plt.tight_layout()
plt.show()
two_metric_graph(svc, X_scaled[feat_score.index[0:3]], y)
svc.fit(X_scaled[feat_score.index[0:3]], y)
joblib.dump(svc, 'svc.joblib')
```
| github_jupyter |
# Settings
```
%load_ext autoreload
%autoreload 2
%env TF_KERAS = 1
import os
sep_local = os.path.sep
import sys
sys.path.append('..'+sep_local+'..')
print(sep_local)
os.chdir('..'+sep_local+'..'+sep_local+'..'+sep_local+'..'+sep_local+'..')
print(os.getcwd())
import tensorflow as tf
print(tf.__version__)
```
# Dataset loading
```
dataset_name='Dstripes'
images_dir = 'C:\\Users\\Khalid\\Documents\projects\\Dstripes\DS06\\'
validation_percentage = 20
valid_format = 'png'
from training.generators.file_image_generator import create_image_lists, get_generators
imgs_list = create_image_lists(
image_dir=images_dir,
validation_pct=validation_percentage,
valid_imgae_formats=valid_format
)
inputs_shape= image_size=(200, 200, 3)
batch_size = 32
latents_dim = 32
intermediate_dim = 50
training_generator, testing_generator = get_generators(
images_list=imgs_list,
image_dir=images_dir,
image_size=image_size,
batch_size=batch_size,
class_mode=None
)
import tensorflow as tf
train_ds = tf.data.Dataset.from_generator(
lambda: training_generator,
output_types=tf.float32 ,
output_shapes=tf.TensorShape((batch_size, ) + image_size)
)
test_ds = tf.data.Dataset.from_generator(
lambda: testing_generator,
output_types=tf.float32 ,
output_shapes=tf.TensorShape((batch_size, ) + image_size)
)
_instance_scale=1.0
for data in train_ds:
_instance_scale = float(data[0].numpy().max())
break
_instance_scale
import numpy as np
from collections.abc import Iterable
if isinstance(inputs_shape, Iterable):
_outputs_shape = np.prod(inputs_shape)
_outputs_shape
```
# Model's Layers definition
```
units=20
c=50
menc_lays = [
tf.keras.layers.Conv2D(filters=units//2, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(filters=units*9//2, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latents_dim)
]
venc_lays = [
tf.keras.layers.Conv2D(filters=units//2, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(filters=units*9//2, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latents_dim)
]
dec_lays = [
tf.keras.layers.Dense(units=units*c*c, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(c , c, units)),
tf.keras.layers.Conv2DTranspose(filters=units, kernel_size=3, strides=(2, 2), padding="SAME", activation='relu'),
tf.keras.layers.Conv2DTranspose(filters=units*3, kernel_size=3, strides=(2, 2), padding="SAME", activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(filters=3, kernel_size=3, strides=(1, 1), padding="SAME")
]
```
# Model definition
```
model_name = dataset_name+'VAE_Convolutional_reconst_1ell_1psnr'
experiments_dir='experiments'+sep_local+model_name
from training.autoencoding_basic.autoencoders.VAE import VAE as AE
inputs_shape=image_size
variables_params = \
[
{
'name': 'inference_mean',
'inputs_shape':inputs_shape,
'outputs_shape':latents_dim,
'layers': menc_lays
}
,
{
'name': 'inference_logvariance',
'inputs_shape':inputs_shape,
'outputs_shape':latents_dim,
'layers': venc_lays
}
,
{
'name': 'generative',
'inputs_shape':latents_dim,
'outputs_shape':inputs_shape,
'layers':dec_lays
}
]
from utils.data_and_files.file_utils import create_if_not_exist
_restore = os.path.join(experiments_dir, 'var_save_dir')
create_if_not_exist(_restore)
_restore
#to restore trained model, set filepath=_restore
ae = AE(
name=model_name,
latents_dim=latents_dim,
batch_size=batch_size,
variables_params=variables_params,
filepath=None
)
from evaluation.quantitive_metrics.peak_signal_to_noise_ratio import prepare_psnr
from statistical.losses_utilities import similarty_to_distance
from statistical.ae_losses import expected_loglikelihood_with_lower_bound as ellwlb
ae.compile(loss={'x_logits': lambda x_true, x_logits: ellwlb(x_true, x_logits)+similarity_to_distance(prepare_psnr([ae.batch_size]+ae.get_inputs_shape()))(x_true, x_logits)})
```
# Callbacks
```
from training.callbacks.sample_generation import SampleGeneration
from training.callbacks.save_model import ModelSaver
es = tf.keras.callbacks.EarlyStopping(
monitor='loss',
min_delta=1e-12,
patience=12,
verbose=1,
restore_best_weights=False
)
ms = ModelSaver(filepath=_restore)
csv_dir = os.path.join(experiments_dir, 'csv_dir')
create_if_not_exist(csv_dir)
csv_dir = os.path.join(csv_dir, ae.name+'.csv')
csv_log = tf.keras.callbacks.CSVLogger(csv_dir, append=True)
csv_dir
image_gen_dir = os.path.join(experiments_dir, 'image_gen_dir')
create_if_not_exist(image_gen_dir)
sg = SampleGeneration(latents_shape=latents_dim, filepath=image_gen_dir, gen_freq=5, save_img=True, gray_plot=False)
```
# Model Training
```
ae.fit(
x=train_ds,
input_kw=None,
steps_per_epoch=int(1e4),
epochs=int(1e6),
verbose=2,
callbacks=[ es, ms, csv_log, sg, gts_mertics, gtu_mertics],
workers=-1,
use_multiprocessing=True,
validation_data=test_ds,
validation_steps=int(1e4)
)
```
# Model Evaluation
## inception_score
```
from evaluation.generativity_metrics.inception_metrics import inception_score
is_mean, is_sigma = inception_score(ae, tolerance_threshold=1e-6, max_iteration=200)
print(f'inception_score mean: {is_mean}, sigma: {is_sigma}')
```
## Frechet_inception_distance
```
from evaluation.generativity_metrics.inception_metrics import frechet_inception_distance
fis_score = frechet_inception_distance(ae, training_generator, tolerance_threshold=1e-6, max_iteration=10, batch_size=32)
print(f'frechet inception distance: {fis_score}')
```
## perceptual_path_length_score
```
from evaluation.generativity_metrics.perceptual_path_length import perceptual_path_length_score
ppl_mean_score = perceptual_path_length_score(ae, training_generator, tolerance_threshold=1e-6, max_iteration=200, batch_size=32)
print(f'perceptual path length score: {ppl_mean_score}')
```
## precision score
```
from evaluation.generativity_metrics.precision_recall import precision_score
_precision_score = precision_score(ae, training_generator, tolerance_threshold=1e-6, max_iteration=200)
print(f'precision score: {_precision_score}')
```
## recall score
```
from evaluation.generativity_metrics.precision_recall import recall_score
_recall_score = recall_score(ae, training_generator, tolerance_threshold=1e-6, max_iteration=200)
print(f'recall score: {_recall_score}')
```
# Image Generation
## image reconstruction
### Training dataset
```
%load_ext autoreload
%autoreload 2
from training.generators.image_generation_testing import reconstruct_from_a_batch
from utils.data_and_files.file_utils import create_if_not_exist
save_dir = os.path.join(experiments_dir, 'reconstruct_training_images_like_a_batch_dir')
create_if_not_exist(save_dir)
reconstruct_from_a_batch(ae, training_generator, save_dir)
from utils.data_and_files.file_utils import create_if_not_exist
save_dir = os.path.join(experiments_dir, 'reconstruct_testing_images_like_a_batch_dir')
create_if_not_exist(save_dir)
reconstruct_from_a_batch(ae, testing_generator, save_dir)
```
## with Randomness
```
from training.generators.image_generation_testing import generate_images_like_a_batch
from utils.data_and_files.file_utils import create_if_not_exist
save_dir = os.path.join(experiments_dir, 'generate_training_images_like_a_batch_dir')
create_if_not_exist(save_dir)
generate_images_like_a_batch(ae, training_generator, save_dir)
from utils.data_and_files.file_utils import create_if_not_exist
save_dir = os.path.join(experiments_dir, 'generate_testing_images_like_a_batch_dir')
create_if_not_exist(save_dir)
generate_images_like_a_batch(ae, testing_generator, save_dir)
```
### Complete Randomness
```
from training.generators.image_generation_testing import generate_images_randomly
from utils.data_and_files.file_utils import create_if_not_exist
save_dir = os.path.join(experiments_dir, 'random_synthetic_dir')
create_if_not_exist(save_dir)
generate_images_randomly(ae, save_dir)
from training.generators.image_generation_testing import interpolate_a_batch
from utils.data_and_files.file_utils import create_if_not_exist
save_dir = os.path.join(experiments_dir, 'interpolate_dir')
create_if_not_exist(save_dir)
interpolate_a_batch(ae, testing_generator, save_dir)
```
| github_jupyter |
# Modeling and Simulation in Python
Case study.
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
```
### Electric car
[Olin Electric Motorsports](https://www.olinelectricmotorsports.com/) is a club at Olin College that designs and builds electric cars, and participates in the [Formula SAE Electric](https://www.sae.org/attend/student-events/formula-sae-electric) competition.
The goal of this case study is to use simulation to guide the design of a car intended to accelerate from standing to 100 kph as quickly as possible. The [world record for this event](https://www.youtube.com/watch?annotation_id=annotation_2297602723&feature=iv&src_vid=I-NCH8ct24U&v=n2XiCYA3C9s), using a car that meets the competition requirements, is 1.513 seconds.
We'll start with a simple model that takes into account the characteristics of the motor and vehicle:
* The motor is an [Emrax 228 high voltage axial flux synchronous permanent magnet motor](http://emrax.com/products/emrax-228/); according to the [data sheet](http://emrax.com/wp-content/uploads/2017/01/emrax_228_technical_data_4.5.pdf), its maximum torque is 240 Nm, at 0 rpm. But maximum torque decreases with motor speed; at 5000 rpm, maximum torque is 216 Nm.
* The motor is connected to the drive axle with a chain drive with speed ratio 13:60 or 1:4.6; that is, the axle rotates once for each 4.6 rotations of the motor.
* The radius of the tires is 0.26 meters.
* The weight of the vehicle, including driver, is 300 kg.
To start, we will assume no slipping between the tires and the road surface, no air resistance, and no rolling resistance. Then we will relax these assumptions one at a time.
* First we'll add drag, assuming that the frontal area of the vehicle is 0.6 square meters, with coefficient of drag 0.6.
* Next we'll add rolling resistance, assuming a coefficient of 0.2.
* Finally we'll compute the peak acceleration to see if the "no slip" assumption is credible.
We'll use this model to estimate the potential benefit of possible design improvements, including decreasing drag and rolling resistance, or increasing the speed ratio.
I'll start by loading the units we need.
```
radian = UNITS.radian
m = UNITS.meter
s = UNITS.second
minute = UNITS.minute
hour = UNITS.hour
km = UNITS.kilometer
kg = UNITS.kilogram
N = UNITS.newton
rpm = UNITS.rpm
```
And store the parameters in a `Params` object.
```
params = Params(r_wheel=0.26 * m,
speed_ratio=13/60,
C_rr=0.2,
C_d=0.5,
area=0.6*m**2,
rho=1.2*kg/m**3,
mass=300*kg)
```
`make_system` creates the initial state, `init`, and constructs an `interp1d` object that represents torque as a function of motor speed.
```
def make_system(params):
"""Make a system object.
params: Params object
returns: System object
"""
init = State(x=0*m, v=0*m/s)
rpms = [0, 2000, 5000]
torques = [240, 240, 216]
interpolate_torque = interpolate(Series(torques, rpms))
return System(params, init=init,
interpolate_torque=interpolate_torque,
t_end=3*s)
```
Testing `make_system`
```
system = make_system(params)
system.init
```
### Torque and speed
The relationship between torque and motor speed is taken from the [Emrax 228 data sheet](http://emrax.com/wp-content/uploads/2017/01/emrax_228_technical_data_4.5.pdf). The following functions reproduce the red dotted line that represents peak torque, which can only be sustained for a few seconds before the motor overheats.
```
def compute_torque(omega, system):
"""Maximum peak torque as a function of motor speed.
omega: motor speed in radian/s
system: System object
returns: torque in Nm
"""
factor = (1 * radian / s).to(rpm)
x = magnitude(omega * factor)
return system.interpolate_torque(x) * N * m
compute_torque(0*radian/s, system)
omega = (5000 * rpm).to(radian/s)
compute_torque(omega, system)
```
Plot the whole curve.
```
xs = linspace(0, 525, 21) * radian / s
taus = [compute_torque(x, system) for x in xs]
plot(xs, taus)
decorate(xlabel='Motor speed (rpm)',
ylabel='Available torque (N m)')
```
### Simulation
Here's the slope function that computes the maximum possible acceleration of the car as a function of it current speed.
```
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object
t: time
system: System object
returns: sequence of derivatives
"""
x, v = state
r_wheel, speed_ratio = system.r_wheel, system.speed_ratio
mass = system.mass
# use velocity, v, to compute angular velocity of the wheel
omega2 = v / r_wheel
# use the speed ratio to compute motor speed
omega1 = omega2 / speed_ratio
# look up motor speed to get maximum torque at the motor
tau1 = compute_torque(omega1, system)
# compute the corresponding torque at the axle
tau2 = tau1 / speed_ratio
# compute the force of the wheel on the ground
F = tau2 / r_wheel
# compute acceleration
a = F/mass
return v, a
```
Testing `slope_func` at linear velocity 10 m/s.
```
test_state = State(x=0*m, v=10*m/s)
slope_func(test_state, 0*s, system)
```
Now we can run the simulation.
```
results, details = run_ode_solver(system, slope_func)
details
```
And look at the results.
```
results.tail()
```
After 3 seconds, the vehicle could be at 40 meters per second, in theory, which is 144 kph.
```
v_final = get_last_value(results.v)
v_final.to(km/hour)
```
Plotting `x`
```
def plot_position(results):
plot(results.x, label='x')
decorate(xlabel='Time (s)',
ylabel='Position (m)')
plot_position(results)
```
Plotting `v`
```
def plot_velocity(results):
plot(results.v, label='v')
decorate(xlabel='Time (s)',
ylabel='Velocity (m/s)')
plot_velocity(results)
```
### Stopping at 100 kph
We'll use an event function to stop the simulation when we reach 100 kph.
```
def event_func(state, t, system):
"""Stops when we get to 100 km/hour.
state: State object
t: time
system: System object
returns: difference from 100 km/hour
"""
x, v = state
# convert to km/hour
factor = (1 * m/s).to(km/hour)
v = magnitude(v * factor)
return v - 100
results, details = run_ode_solver(system, slope_func, events=event_func)
details
```
Here's what the results look like.
```
subplot(2, 1, 1)
plot_position(results)
subplot(2, 1, 2)
plot_velocity(results)
savefig('figs/chap11-fig02.pdf')
```
According to this model, we should be able to make this run in just over 2 seconds.
```
t_final = get_last_label(results) * s
```
At the end of the run, the car has gone about 28 meters.
```
state = results.last_row()
```
If we send the final state back to the slope function, we can see that the final acceleration is about 13 $m/s^2$, which is about 1.3 times the acceleration of gravity.
```
v, a = slope_func(state, 0, system)
v.to(km/hour)
a
g = 9.8 * m/s**2
(a / g).to(UNITS.dimensionless)
```
It's not easy for a vehicle to accelerate faster than `g`, because that implies a coefficient of friction between the wheels and the road surface that's greater than 1. But racing tires on dry asphalt can do that; the OEM team at Olin has tested their tires and found a peak coefficient near 1.5.
So it's possible that our no slip assumption is valid, but only under ideal conditions, where weight is distributed equally on four tires, and all tires are driving.
**Exercise:** How much time do we lose because maximum torque decreases as motor speed increases? Run the model again with no drop off in torque and see how much time it saves.
### Drag
In this section we'll see how much effect drag has on the results.
Here's a function to compute drag force, as we saw in Chapter 21.
```
def drag_force(v, system):
"""Computes drag force in the opposite direction of `v`.
v: velocity
system: System object
returns: drag force
"""
rho, C_d, area = system.rho, system.C_d, system.area
f_drag = -np.sign(v) * rho * v**2 * C_d * area / 2
return f_drag
```
We can test it with a velocity of 20 m/s.
```
drag_force(20 * m/s, system)
```
Here's the resulting acceleration of the vehicle due to drag.
```
drag_force(20 * m/s, system) / system.mass
```
We can see that the effect of drag is not huge, compared to the acceleration we computed in the previous section, but it is not negligible.
Here's a modified slope function that takes drag into account.
```
def slope_func2(state, t, system):
"""Computes the derivatives of the state variables.
state: State object
t: time
system: System object
returns: sequence of derivatives
"""
x, v = state
r_wheel, speed_ratio = system.r_wheel, system.speed_ratio
mass = system.mass
omega2 = v / r_wheel * radian
omega1 = omega2 / speed_ratio
tau1 = compute_torque(omega1, system)
tau2 = tau1 / speed_ratio
F = tau2 / r_wheel
a_motor = F / mass
a_drag = drag_force(v, system) / mass
a = a_motor + a_drag
return v, a
```
And here's the next run.
```
results2, details = run_ode_solver(system, slope_func2, events=event_func)
details
```
The time to reach 100 kph is a bit higher.
```
t_final2 = get_last_label(results2) * s
```
But the total effect of drag is only about 2/100 seconds.
```
t_final2 - t_final
```
That's not huge, which suggests we might not be able to save much time by decreasing the frontal area, or coefficient of drag, of the car.
### Rolling resistance
Next we'll consider [rolling resistance](https://en.wikipedia.org/wiki/Rolling_resistance), which the force that resists the motion of the car as it rolls on tires. The cofficient of rolling resistance, `C_rr`, is the ratio of rolling resistance to the normal force between the car and the ground (in that way it is similar to a coefficient of friction).
The following function computes rolling resistance.
```
system.set(unit_rr = 1 * N / kg)
def rolling_resistance(system):
"""Computes force due to rolling resistance.
system: System object
returns: force
"""
return -system.C_rr * system.mass * system.unit_rr
```
The acceleration due to rolling resistance is 0.2 (it is not a coincidence that it equals `C_rr`).
```
rolling_resistance(system)
rolling_resistance(system) / system.mass
```
Here's a modified slope function that includes drag and rolling resistance.
```
def slope_func3(state, t, system):
"""Computes the derivatives of the state variables.
state: State object
t: time
system: System object
returns: sequence of derivatives
"""
x, v = state
r_wheel, speed_ratio = system.r_wheel, system.speed_ratio
mass = system.mass
omega2 = v / r_wheel * radian
omega1 = omega2 / speed_ratio
tau1 = compute_torque(omega1, system)
tau2 = tau1 / speed_ratio
F = tau2 / r_wheel
a_motor = F / mass
a_drag = drag_force(v, system) / mass
a_roll = rolling_resistance(system) / mass
a = a_motor + a_drag + a_roll
return v, a
```
And here's the run.
```
results3, details = run_ode_solver(system, slope_func3, events=event_func)
details
```
The final time is a little higher, but the total cost of rolling resistance is only 3/100 seconds.
```
t_final3 = get_last_label(results3) * s
t_final3 - t_final2
```
So, again, there is probably not much to be gained by decreasing rolling resistance.
In fact, it is hard to decrease rolling resistance without also decreasing traction, so that might not help at all.
### Optimal gear ratio
The gear ratio 13:60 is intended to maximize the acceleration of the car without causing the tires to slip. In this section, we'll consider other gear ratios and estimate their effects on acceleration and time to reach 100 kph.
Here's a function that takes a speed ratio as a parameter and returns time to reach 100 kph.
```
def time_to_speed(speed_ratio, params):
"""Computes times to reach 100 kph.
speed_ratio: ratio of wheel speed to motor speed
params: Params object
returns: time to reach 100 kph, in seconds
"""
params = Params(params, speed_ratio=speed_ratio)
system = make_system(params)
system.set(unit_rr = 1 * N / kg)
results, details = run_ode_solver(system, slope_func3, events=event_func)
t_final = get_last_label(results)
a_initial = slope_func(system.init, 0, system)
return t_final
```
We can test it with the default ratio:
```
time_to_speed(13/60, params)
```
Now we can try it with different numbers of teeth on the motor gear (assuming that the axle gear has 60 teeth):
```
for teeth in linrange(8, 18):
print(teeth, time_to_speed(teeth/60, params))
```
Wow! The speed ratio has a big effect on the results. At first glance, it looks like we could break the world record (1.513 seconds) just by decreasing the number of teeth.
But before we try it, let's see what effect that has on peak acceleration.
```
def initial_acceleration(speed_ratio, params):
"""Maximum acceleration as a function of speed ratio.
speed_ratio: ratio of wheel speed to motor speed
params: Params object
returns: peak acceleration, in m/s^2
"""
params = Params(params, speed_ratio=speed_ratio)
system = make_system(params)
a_initial = slope_func(system.init, 0, system)[1] * m/s**2
return a_initial
```
Here are the results:
```
for teeth in linrange(8, 18):
print(teeth, initial_acceleration(teeth/60, params))
```
As we decrease the speed ratio, the peak acceleration increases. With 8 teeth on the motor gear, we could break the world record, but only if we can accelerate at 2.3 times the acceleration of gravity, which is impossible without very sticky ties and a vehicle that generates a lot of downforce.
```
23.07 / 9.8
```
These results suggest that the most promising way to improve the performance of the car (for this event) would be to improve traction.
| github_jupyter |
# Python Solution for Hackerrank By Viraj Shetty
## Hello World
```
print("Hello, World!")
```
## Python If-Else
```
if __name__ == '__main__':
n = int(input().strip())
if(n%2==1):
print("Weird")
if(n%2==0):
if (n in range(2,5)):
print("Not Weird")
if (n in range(6,21)):
print("Weird")
if (n>20):
print("Not Weird")
```
## Print Function
```
if __name__ == '__main__':
n = int(input())se
x = ""
for i in range (1,n+1):
x += str(i)
print(x)
```
## Leap Year Function
```
def is_leap(year):
leap = False
if year % 4 == 0 and year % 100 != 0:
leap = True
elif year % 400 ==0:
leap = True
elif year % 100 == 0:
leap = False
else:
leap = False
return leap
year = int(input())
print(is_leap(year))
```
## String Validators
```
if __name__ == '__main__':
s = input()
an = a = d = l = u = 0
for c in s:
if(c.isalnum() == True):
an += 1
if(c.isalpha() == True):
a += 1
if(c.isdigit() == True):
d += 1
if(c.islower() == True):
l += 1
if(c.isupper() == True):
u += 1
if(an !=0):
print("True")
else:
print("False")
if(a !=0):
print("True")
else:
print("False")
if(d !=0):
print("True")
else:
print("False")
if(l !=0):
print("True")
else:
print("False")
if(u !=0):
print("True")
else:
print("False")
```
## Runner Up
```
if __name__ == '__main__':
n = int(input())
arr = map(int, input().split())
def dup(dupl):
fl = []
for num in dupl:
if num not in fl:
fl.append(num)
return fl
arr1 = dup(arr)
arr1.sort()
print(arr1[-2])
```
## What’s your Name
```
def print_full_name(a, b):
print("Hello "+a+" "+b+"! You just delved into python." )
if __name__ == '__main__':
first_name = input()
last_name = input()
print_full_name(first_name, last_name)
```
## String Split and Join
```
def split_and_join(line):
line = line.split(" ")
line = "-".join(line)
return line
if __name__ == '__main__':
line = raw_input()
result = split_and_join(line)
print result
```
## Project Euler #173
```
import math
count = 0
n = int(input())
for i in range(2,int(math.sqrt(n)),2):
b = int(((n/i) - i)/2)
if b > 0:
count+=b
print(count)
```
## List Comprehension
```
x, y, z, n = (int(input()) for _ in range(4))
print ([[a,b,c] for a in range(0,x+1) for b in range(0,y+1) for c in range(0,z+1) if a + b + c != n ])
```
## Lists
```
n_of_commands = int(input())
list_of_commands = []
for command in range(n_of_commands):
x = input()
list_of_commands.append(x)
list_elements = []
for command in list_of_commands:
if command == "print":
print(list_elements)
elif command[:3]=="rem":
x = command.split()
remove_elem = int(x[1])
list_elements.remove(remove_elem)
elif command[:3]=="rev":
list_elements.reverse()
elif command == "pop":
list_elements.pop()
elif command[:3]=="app":
x = command.split()
append_elem = int(x[1])
list_elements.append(append_elem)
elif command == "sort":
list_elements.sort()
elif command[:3]=="ins":
x = command.split()
index = int(x[1])
insert_elem = int(x[2])
list_elements.insert(index,insert_elem)
else:
Break
```
## Solve Me First!
```
def solveMeFirst(a,b):
m = a+b
return m
num1 = int(input())
num2 = int(input())
sum = solveMeFirst(num1,num2)
print(sum)
```
## Simple Array Sum
```
import os
import sys
def simpleArraySum(ar):
Sum = sum(ar)
return Sum
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
ar_count = int(input())
ar = list(map(int, input().rstrip().split()))
result = simpleArraySum(ar)
fptr.write(str(result) + '\n')
fptr.close()
```
## Compare The Triplets
```
import math
import os
import random
import re
import sys
def compareTriplets(a, b):
counta = 0
countb = 0
for i in range (0,3):
if(a[i]>b[i]):
counta += 1
if(a[i]<b[i]):
countb += 1
return counta,countb
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
a = list(map(int, input().rstrip().split()))
b = list(map(int, input().rstrip().split()))
result = compareTriplets(a, b)
fptr.write(' '.join(map(str, result)))
fptr.write('\n')
fptr.close()
```
## A Very Big Sum
```
import math
import os
import random
import re
import sys
#function is same since python deals with
def aVeryBigSum(ar):
Sum = sum(ar)
return Sum
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
ar_count = int(input())
ar = list(map(int, input().rstrip().split()))
result = aVeryBigSum(ar)
fptr.write(str(result) + '\n')
fptr.close()
```
## Find the Point (Maths Based Problems)
```
import os
def findPoint(px, py, qx, qy):
rx = (qx-px) + qx
ry = (qy-py) + qy
return (rx,ry)
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input())
for n_itr in range(n):
pxPyQxQy = input().split()
px = int(pxPyQxQy[0])
py = int(pxPyQxQy[1])
qx = int(pxPyQxQy[2])
qy = int(pxPyQxQy[3])
result = findPoint(px, py, qx, qy)
fptr.write(' '.join(map(str, result)))
fptr.write('\n')
fptr.close()
```
## Power of A to B and mod C
```
if __name__ == '__main__':
import math as ms
c = []
while True:
try:
line = input()
except EOFError:
break
c.append(line)
a = int(c[0])
b = int(c[1])
m = int(c[2])
x = ms.pow(a,b)
c = (x%m)
print(int(x))
print(int(c))
```
## Map and Lambda
```
cube = lambda x: x**3
a = []
def fibonacci(n):
first = 0
second = 1
for i in range(n):
a.append(first)
t = first + second
first = second
second = t
return a
if __name__ == '__main__':
n = int(input())
print(list(map(cube, fibonacci(n))))
```
## Company Logo
```
from collections import Counter
for letter, counts in sorted(Counter(raw_input()).most_common(),key = lambda x:(-x[1],x[0]))[:3]:
print letter, counts
```
## Merge the Tools!
```
def merge_the_tools(string,k):
num_subsegments = int(len(string)/k)
for index in range(num_subsegments):
t = string[index * k : (index + 1) * k]
u = ""
for c in t:
if c not in u:
u += c
print(u)
if __name__ == '__main__':
string, k = input(), int(input())
merge_the_tools(string, k)
```
## Check SuperScript
```
main_set = set(map(int,input().split()))
n = int(input())
output = []
for i in range(n):
x = set(map(int,input().split()))
if main_set.issuperset(x):
output.append(True)
else:
output.append(False)
print(all(output))
```
## Check Subset
```
def common (A,B):
a_set = set(A)
b_set = set(B)
if (a_set & b_set):
answer.append("True")
else:
answer.append("False")
n = int(input())
answer = []
for i in range(0,n):
alen = int(input())
A = list(map(int,input().split()))
blen = int(input())
B = list(map(int,input().split()))
common(A,B)
for i in answer:
print(i)
```
## Formated Sorting ortingS
```
l = []
u = []
o = []
e = []
s = input()
all_list = list(s)
for i in all_list:
if i.islower():
l.append(i)
if i.isupper():
u.append(i)
if i.isnumeric():
if (int(i)%2==0):
e.append(i)
else:
o.append(i)
lower = sorted(l)
upper = sorted(u)
odd = sorted(o)
even = sorted(e)
tempr = lower+upper
tempr1 = tempr + odd
last = tempr1 + even
s = "".join(last)
print(s)
```
## Exceptions
```
import re
n = int(input())
for i in range(n):
x = input()
try:
if re.compile(x):
value = True
except:
value = False
print(value)
```
## Iterables and Iterators
```
from itertools import combinations
N = int(input())
S = raw_input().split(' ')
K = int(input())
num = 0
den = 0
for c in combinations(S,K):
den+=1
num+='a' in c
print float(num)/den
```
## Day of Any MM/DD/YYYY
```
import calendar as c
d = list(map(int,input().split()))
ans = c.weekday(d[2],d[0],d[1])
if (ans == 0):
print("MONDAY")
elif (ans == 1):
print("TUESDAY")
elif (ans == 2):
print("WEDNESDAY")
elif (ans == 3):
print("THURSDAY")
elif (ans == 4):
print("FRIDAY")
elif (ans == 5)
print("SATURDAY")
else:
print("SUNDAY")
```
## No idea!
```
main_set = set(map(int,input().split()))
n = int(input())
output = []
for i in range(n):
x = set(map(int,input().split()))
if main_set.issuperset(x):
output.append(True)
else:
output.append(False)
print(all(output))
```
## Collections.Counter()
```
n = int(input())
arr = list(map(int, input().split()))
l = int(input())
x=0
for i in range(l):
size,price = map(int,input().split())
if (size in arr):
x += price
arr.remove(size)
print(x)
```
## sWAP cASE
```
def swap_case(s):
for i in s:
if (i.islower()):
a.append(i.upper())
elif(i.isupper()):
a.append(i.lower())
else:
a.append(i)
b = ''.join(a)
return b
a = []
if __name__ == '__main__':
s = input()
result = swap_case(s)
print(result)
```
## Set discard and pop
```
n = int(input())
list_of_int = list(map(int,input().split()))
n_of_commands = int(input())
list_of_commands = []
for command in range(n_of_commands):
x = input()
list_of_commands.append(x)
set1 = set(list_of_int)
for command in list_of_commands:
if command == "pop":
set1.pop()
elif command.startswith('d'):
discard_num = int(command[-1])
set1.discard(discard_num)
else:
remove_num = int(command[-1])
set1.remove(remove_num)
print(sum(set1))
```
## Find a String
```
def count_substring(string, sub_string):
c=0
for i in range(len(string)):
if string[i:].startswith(sub_string):
c +=1
return c
if __name__ == '__main__':
string = input().strip()
sub_string = input().strip()
count = count_substring(string, sub_string)
print(count)
```
## Introduction to Sets
```
def average(arr):
for i in arr:
if i not in a:
a.append(i)
x = float(sum(a)/len(a))
return x
a = []
if __name__ == '__main__':
n = int(input())
arr = list(map(int, input().split()))
result = average(arr)
print(result)
```
### Set .symmetric_difference : Symmetric Difference can be changed to difference, union and intersection
```
n = int(input())
e = list(map(int,input().split()))
m = int(input())
f = list(map(int,input().split()))
a = set(e)
b = set(f)
c = 0
res = a.symmetric_difference(b)
for i in res:
c += 1
print(c)
```
## Div-mod
```
a = int(input())
b = int(input())
print(a//b)
print(a%b)
print(divmod(a,b))
```
## Symmetric Difference
```
n = int(input())
list1 = list(map(int,input().split()))
n1 = int(input())
list2 = list(map(int,input().split()))
[print(i) for i in sorted(set(list1).difference(set(list2)).union(set(list2).difference(set(list1))))]
```
## Collections.deque
```
from collections import deque
n = int(input())
d = deque()
list_of_commands = []
for i in range(n):
x = input()
list_of_commands.append(x)
for command in list_of_commands:
print(command[:7])
if command[:7]=="append":
x = command.split()
d.append(int(x[1]))
print(d)
elif command[:7]=="appendl":
x = command.split()
d.appendleft(int(x[1]))
print(d)
elif command[:4]=="pop":
d.pop()
print(d)
else:
d.popleft()
print(d)
```
| github_jupyter |
<figure>
<IMG SRC="https://raw.githubusercontent.com/pastas/pastas/master/doc/_static/Art_logo.jpg" WIDTH=250 ALIGN="right">
</figure>
# Menyanthes File
*Developed by Ruben Caljé*
Menyanthes is timeseries analysis software used by many people in the Netherlands. In this example a Menyanthes-file with one observation-series is imported, and simulated. There are several stresses in the Menyanthes-file, among which are three groundwater extractions with a significant influence on groundwater head.
```
# First perform the necessary imports
import matplotlib.pyplot as plt
import pastas as ps
%matplotlib notebook
```
## 1. Importing the Menyanthes-file
Import the Menyanthes-file with observations and stresses. Then plot the observations, together with the diferent stresses in the Menyanthes file.
```
# how to use it?
fname = '../data/MenyanthesTest.men'
meny = ps.read.MenyData(fname)
# plot some series
f1, axarr = plt.subplots(len(meny.IN)+1, sharex=True)
oseries = meny.H['Obsevation well']["values"]
oseries.plot(ax=axarr[0])
axarr[0].set_title(meny.H['Obsevation well']["Name"])
for i, val in enumerate(meny.IN.items()):
name, data = val
data["values"].plot(ax=axarr[i+1])
axarr[i+1].set_title(name)
plt.tight_layout(pad=0)
plt.show()
```
## 2. Run a model
Make a model with precipitation, evaporation and three groundwater extractions.
```
# Create the time series model
ml = ps.Model(oseries)
# Add precipitation
IN = meny.IN['Precipitation']['values']
IN.index = IN.index.round("D")
IN2 = meny.IN['Evaporation']['values']
IN2.index = IN2.index.round("D")
ts = ps.StressModel2([IN, IN2], ps.Gamma, 'Recharge')
ml.add_stressmodel(ts)
# Add well extraction 1
# IN = meny.IN['Extraction 1']
# # extraction amount counts for the previous month
# ts = ps.StressModel(IN['values'], ps.Hantush, 'Extraction_1', up=False,
# settings="well")
# ml.add_stressmodel(ts)
# Add well extraction 2
IN = meny.IN['Extraction 2']
# extraction amount counts for the previous month
ts = ps.StressModel(IN['values'], ps.Hantush, 'Extraction_2', up=False,
settings="well")
ml.add_stressmodel(ts)
# Add well extraction 3
IN = meny.IN['Extraction 3']
# extraction amount counts for the previous month
ts = ps.StressModel(IN['values'], ps.Hantush, 'Extraction_3', up=False,
settings="well")
ml.add_stressmodel(ts)
# Solve the model (can take around 20 seconds..)
ml.solve()
```
## 3. Plot the decomposition
Show the decomposition of the groundwater head, by plotting the influence on groundwater head of each of the stresses.
```
ax = ml.plots.decomposition(ytick_base=1.)
ax[0].set_title('Observations vs simulation')
ax[0].legend()
ax[0].figure.tight_layout(pad=0)
```
| github_jupyter |
# Refactor: Wine Quality Analysis
In this exercise, you'll refactor code that analyzes a wine quality dataset taken from the UCI Machine Learning Repository [here](https://archive.ics.uci.edu/ml/datasets/wine+quality). Each row contains data on a wine sample, including several physicochemical properties gathered from tests, as well as a quality rating evaluated by wine experts.
The code in this notebook first renames the columns of the dataset and then calculates some statistics on how some features may be related to quality ratings. Can you refactor this code to make it more clean and modular?
```
import pandas as pd
df = pd.read_csv('winequality-red.csv', sep=';')
df.head(10)
```
### Renaming Columns
You want to replace the spaces in the column labels with underscores to be able to reference columns with dot notation. Here's one way you could've done it.
```
new_df = df.rename(columns={'fixed acidity': 'fixed_acidity',
'volatile acidity': 'volatile_acidity',
'citric acid': 'citric_acid',
'residual sugar': 'residual_sugar',
'free sulfur dioxide': 'free_sulfur_dioxide',
'total sulfur dioxide': 'total_sulfur_dioxide'
})
new_df.head()
```
And here's a slightly better way you could do it. You can avoid making naming errors due to typos caused by manual typing. However, this looks a little repetitive. Can you make it better?
```
labels = list(df.columns)
labels[0] = labels[0].replace(' ', '_')
labels[1] = labels[1].replace(' ', '_')
labels[2] = labels[2].replace(' ', '_')
labels[3] = labels[3].replace(' ', '_')
labels[5] = labels[5].replace(' ', '_')
labels[6] = labels[6].replace(' ', '_')
df.columns = labels
df.head()
```
### Analyzing Features
Now that your columns are ready, you want to see how different features of this dataset relate to the quality rating of the wine. A very simple way you could do this is by observing the mean quality rating for the top and bottom half of each feature. The code below does this for four features. It looks pretty repetitive right now. Can you make this more concise?
You might challenge yourself to figure out how to make this code more efficient! But you don't need to worry too much about efficiency right now - we will cover that more in the next section.
```
median_alcohol = df.alcohol.median()
for i, alcohol in enumerate(df.alcohol):
if alcohol >= median_alcohol:
df.loc[i, 'alcohol'] = 'high'
else:
df.loc[i, 'alcohol'] = 'low'
df.groupby('alcohol').quality.mean()
median_pH = df.pH.median()
for i, pH in enumerate(df.pH):
if pH >= median_pH:
df.loc[i, 'pH'] = 'high'
else:
df.loc[i, 'pH'] = 'low'
df.groupby('pH').quality.mean()
median_sugar = df.residual_sugar.median()
for i, sugar in enumerate(df.residual_sugar):
if sugar >= median_sugar:
df.loc[i, 'residual_sugar'] = 'high'
else:
df.loc[i, 'residual_sugar'] = 'low'
df.groupby('residual_sugar').quality.mean()
median_citric_acid = df.citric_acid.median()
for i, citric_acid in enumerate(df.citric_acid):
if citric_acid >= median_citric_acid:
df.loc[i, 'citric_acid'] = 'high'
else:
df.loc[i, 'citric_acid'] = 'low'
df.groupby('citric_acid').quality.mean()
```
| github_jupyter |
# A Whale off the Port(folio)
---
In this assignment, you'll get to use what you've learned this week to evaluate the performance among various algorithmic, hedge, and mutual fund portfolios and compare them against the S&P TSX 60 Index.
```
# Initial imports
import pandas as pd
import numpy as np
import datetime as dt
from pathlib import Path
%matplotlib inline
```
# Data Cleaning
In this section, you will need to read the CSV files into DataFrames and perform any necessary data cleaning steps. After cleaning, combine all DataFrames into a single DataFrame.
Files:
* `whale_returns.csv`: Contains returns of some famous "whale" investors' portfolios.
* `algo_returns.csv`: Contains returns from the in-house trading algorithms from Harold's company.
* `sp_tsx_history.csv`: Contains historical closing prices of the S&P TSX 60 Index.
## Whale Returns
Read the Whale Portfolio daily returns and clean the data.
```
# Set file path for CSV
file_path = Path("Resources/whale_returns.csv")
# Read in the CSV into a DataFrame
whale_returns_csv = pd.read_csv(file_path)
whale_returns_csv.head()
# Inspect the first 10 rows of the DataFrame
whale_returns_csv.head(10)
# Inspect the last 10 rows of the DataFrame
whale_returns_csv.tail(10)
# View column data types by using the 'dtypes' attribute to list the column data types
whale_returns_csv.dtypes
# Identify data quality issues
# Identify the number of rows
whale_returns_csv.count()
# Count nulls
whale_returns_csv.isnull()
# Determine the number of nulls
whale_returns_csv.isnull().sum()
# Determine the percentage of nulls for each column
whale_returns_csv.isnull().sum() / len(whale_returns_csv) * 100
# Drop nulls
whale_returns_csv.dropna()
# Check for duplicated rows
whale_returns_csv.duplicated()
# Use the dropna function to drop the whole records that have at least one null value
whale_returns_csv.dropna(inplace=True)
```
## Algorithmic Daily Returns
Read the algorithmic daily returns and clean the data.
```
#Calculate and plot daily return
# Calculate and plot cumulative return
# Confirm null values have been dropped 1
whale_returns_csv.isnull()
# Confirm null values have been dropped 2
whale_returns_csv.isnull().sum()
# Reading algorithmic returns
# Count nulls
# Drop nulls
```
## S&P TSX 60 Returns
Read the S&P TSX 60 historic closing prices and create a new daily returns DataFrame from the data.
```
# Reading S&P TSX 60 Closing Prices
sp_tsx_path = Path("Resources/sp_tsx_history.csv")
# Check Data Types
sp_tsx_df = pd.read_csv(sp_tsx_path)
sp_tsx_df.head()
sp_tsx_df.tail()
# Use the 'dtypes' attribute to list the column data types
sp_tsx_df.dtypes
# Use the 'info' attribute to list additional infor about the column data types
sp_tsx_df.info()
# Use the 'as_type' function to convert 'Date' from 'object' to 'datetime64'
sp_tsx_df['Date'] = sp_tsx_df['Date'].astype('datetime64')
sp_tsx_df
# Sort datetime index in ascending order (past to present)
sp_tsx_df.sort_index(inplace = True)
sp_tsx_df.head()
# Confirm datetime64 conversion was proccesed correctly
sp_tsx_df.dtypes
# Set the date as the index to the Dataframe
sp_tsx_df.set_index(pd.to_datetime(sp_tsx_df['Date'], infer_datetime_format=True), inplace=True)
sp_tsx_df.head()
# Drop the extra date column
sp_tsx_df.drop(columns=['Date'], inplace=True)
sp_tsx_df.head()
sp_tsx_df.dtypes
sp_tsx_df['Close'] = sp_tsx_df.to_numeric('Close')
sp_tsx_df
daily_returns = sp_tsx_df.pct_change()
sp_tsx_df()
# Plot daily close
sp_tsx_df.plot()
# Calculate Daily Returns
# Drop nulls
# Rename `Close` Column to be specific to this portfolio.
```
## Combine Whale, Algorithmic, and S&P TSX 60 Returns
```
# Join Whale Returns, Algorithmic Returns, and the S&P TSX 60 Returns into a single DataFrame with columns for each portfolio's returns.
```
---
# Conduct Quantitative Analysis
In this section, you will calculate and visualize performance and risk metrics for the portfolios.
## Performance Anlysis
#### Calculate and Plot the daily returns.
```
# Plot daily returns of all portfolios
```
#### Calculate and Plot cumulative returns.
```
# Calculate cumulative returns of all portfolios
# Plot cumulative returns
```
---
## Risk Analysis
Determine the _risk_ of each portfolio:
1. Create a box plot for each portfolio.
2. Calculate the standard deviation for all portfolios.
4. Determine which portfolios are riskier than the S&P TSX 60.
5. Calculate the Annualized Standard Deviation.
### Create a box plot for each portfolio
```
# Box plot to visually show risk
```
### Calculate Standard Deviations
```
# Calculate the daily standard deviations of all portfolios
```
### Determine which portfolios are riskier than the S&P TSX 60
```
# Calculate the daily standard deviation of S&P TSX 60
# Determine which portfolios are riskier than the S&P TSX 60
```
### Calculate the Annualized Standard Deviation
```
# Calculate the annualized standard deviation (252 trading days)
```
---
## Rolling Statistics
Risk changes over time. Analyze the rolling statistics for Risk and Beta.
1. Calculate and plot the rolling standard deviation for all portfolios using a 21-day window.
2. Calculate the correlation between each stock to determine which portfolios may mimick the S&P TSX 60.
3. Choose one portfolio, then calculate and plot the 60-day rolling beta for it and the S&P TSX 60.
### Calculate and plot rolling `std` for all portfolios with 21-day window
```
# Calculate the rolling standard deviation for all portfolios using a 21-day window
# Plot the rolling standard deviation
```
### Calculate and plot the correlation
```
# Calculate the correlation
# Display de correlation matrix
```
### Calculate and Plot Beta for a chosen portfolio and the S&P 60 TSX
```
# Calculate covariance of a single portfolio
# Calculate variance of S&P TSX
# Computing beta
# Plot beta trend
```
## Rolling Statistics Challenge: Exponentially Weighted Average
An alternative way to calculate a rolling window is to take the exponentially weighted moving average. This is like a moving window average, but it assigns greater importance to more recent observations. Try calculating the [`ewm`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.ewm.html) with a 21-day half life for each portfolio, using standard deviation (`std`) as the metric of interest.
```
# Use `ewm` to calculate the rolling window
```
---
# Sharpe Ratios
In reality, investment managers and thier institutional investors look at the ratio of return-to-risk, and not just returns alone. After all, if you could invest in one of two portfolios, and each offered the same 10% return, yet one offered lower risk, you'd take that one, right?
### Using the daily returns, calculate and visualize the Sharpe ratios using a bar plot
```
# Annualized Sharpe Ratios
# Visualize the sharpe ratios as a bar plot
```
### Determine whether the algorithmic strategies outperform both the market (S&P TSX 60) and the whales portfolios.
Write your answer here!
---
# Create Custom Portfolio
In this section, you will build your own portfolio of stocks, calculate the returns, and compare the results to the Whale Portfolios and the S&P TSX 60.
1. Choose 3-5 custom stocks with at last 1 year's worth of historic prices and create a DataFrame of the closing prices and dates for each stock.
2. Calculate the weighted returns for the portfolio assuming an equal number of shares for each stock.
3. Join your portfolio returns to the DataFrame that contains all of the portfolio returns.
4. Re-run the performance and risk analysis with your portfolio to see how it compares to the others.
5. Include correlation analysis to determine which stocks (if any) are correlated.
## Choose 3-5 custom stocks with at last 1 year's worth of historic prices and create a DataFrame of the closing prices and dates for each stock.
```
# Reading data from 1st stock
# Reading data from 2nd stock
# Reading data from 3rd stock
# Combine all stocks in a single DataFrame
# Reset Date index
# Reorganize portfolio data by having a column per symbol
# Calculate daily returns
# Drop NAs
# Display sample data
```
## Calculate the weighted returns for the portfolio assuming an equal number of shares for each stock
```
# Set weights
weights = [1/3, 1/3, 1/3]
# Calculate portfolio return
# Display sample data
```
## Join your portfolio returns to the DataFrame that contains all of the portfolio returns
```
# Join your returns DataFrame to the original returns DataFrame
# Only compare dates where return data exists for all the stocks (drop NaNs)
```
## Re-run the risk analysis with your portfolio to see how it compares to the others
### Calculate the Annualized Standard Deviation
```
# Calculate the annualized `std`
```
### Calculate and plot rolling `std` with 21-day window
```
# Calculate rolling standard deviation
# Plot rolling standard deviation
```
### Calculate and plot the correlation
```
# Calculate and plot the correlation
```
### Calculate and Plot the 60-day Rolling Beta for Your Portfolio compared to the S&P 60 TSX
```
# Calculate and plot Beta
```
### Using the daily returns, calculate and visualize the Sharpe ratios using a bar plot
```
# Calculate Annualized Sharpe Ratios
# Visualize the sharpe ratios as a bar plot
```
### How does your portfolio do?
Write your answer here!
| github_jupyter |
# Saying the same thing multiple ways
What happens when someone comes across a file in our file format? How do they know what it means?
If we can make the tag names in our model globally unique, then the meaning of the file can be made understandable
not just to us, but to people and computers all over the world.
Two file formats which give the same information, in different ways, are *syntactically* distinct,
but so long as they are **semantically** compatible, I can convert from one to the other.
This is the goal of the technologies introduced this lecture.
## The URI
The key concept that underpins these tools is the URI: uniform resource **indicator**.
These look like URLs:
`www.turing.ac.uk/rsd-engineering/schema/reaction/element`
But, if I load that as a web address, there's nothing there!
That's fine.
A UR**N** indicates a **name** for an entity, and, by using organisational web addresses as a prefix,
is likely to be unambiguously unique.
A URI might be a URL or a URN, or both.
## XML Namespaces
It's cumbersome to use a full URI every time we want to put a tag in our XML file.
XML defines *namespaces* to resolve this:
```
%%writefile system.xml
<?xml version="1.0" encoding="UTF-8"?>
<system xmlns="http://www.turing.ac.uk/rsd-engineering/schema/reaction">
<reaction>
<reactants>
<molecule stoichiometry="2">
<atom symbol="H" number="2"/>
</molecule>
<molecule stoichiometry="1">
<atom symbol="O" number="2"/>
</molecule>
</reactants>
<products>
<molecule stoichiometry="2">
<atom symbol="H" number="2"/>
<atom symbol="O" number="1"/>
</molecule>
</products>
</reaction>
</system>
from lxml import etree
with open("system.xml") as xmlfile:
tree = etree.parse(xmlfile)
print(etree.tostring(tree, pretty_print=True, encoding=str))
```
Note that our previous XPath query no longer finds anything.
```
tree.xpath("//molecule/atom[@number='1']/@symbol")
namespaces = {"r": "http://www.turing.ac.uk/rsd-engineering/schema/reaction"}
tree.xpath("//r:molecule/r:atom[@number='1']/@symbol", namespaces=namespaces)
```
Note the prefix `r` used to bind the namespace in the query: any string will do - it's just a dummy variable.
The above file specified our namespace as a default namespace: this is like doing `from numpy import *` in python.
It's often better to bind the namespace to a prefix:
```
%%writefile system.xml
<?xml version="1.0" encoding="UTF-8"?>
<r:system xmlns:r="http://www.turing.ac.uk/rsd-engineering/schema/reaction">
<r:reaction>
<r:reactants>
<r:molecule stoichiometry="2">
<r:atom symbol="H" number="2"/>
</r:molecule>
<r:molecule stoichiometry="1">
<r:atom symbol="O" number="2"/>
</r:molecule>
</r:reactants>
<r:products>
<r:molecule stoichiometry="2">
<r:atom symbol="H" number="2"/>
<r:atom symbol="O" number="1"/>
</r:molecule>
</r:products>
</r:reaction>
</r:system>
```
## Namespaces and Schema
It's a good idea to serve the schema itself from the URI of the namespace treated as a URL, but it's *not a requirement*: it's a URN not necessarily a URL!
```
%%writefile reactions.xsd
<xs:schema xmlns:xs="http://www.w3.org/2001/XMLSchema"
targetNamespace="http://www.turing.ac.uk/rsd-engineering/schema/reaction"
xmlns:r="http://www.turing.ac.uk/rsd-engineering/schema/reaction">
<xs:element name="atom">
<xs:complexType>
<xs:attribute name="symbol" type="xs:string"/>
<xs:attribute name="number" type="xs:integer"/>
</xs:complexType>
</xs:element>
<xs:element name="molecule">
<xs:complexType>
<xs:sequence>
<xs:element ref="r:atom" maxOccurs="unbounded"/>
</xs:sequence>
<xs:attribute name="stoichiometry" type="xs:integer"/>
</xs:complexType>
</xs:element>
<xs:element name="reactants">
<xs:complexType>
<xs:sequence>
<xs:element ref="r:molecule" maxOccurs="unbounded"/>
</xs:sequence>
</xs:complexType>
</xs:element>
<xs:element name="products">
<xs:complexType>
<xs:sequence>
<xs:element ref="r:molecule" maxOccurs="unbounded"/>
</xs:sequence>
</xs:complexType>
</xs:element>
<xs:element name="reaction">
<xs:complexType>
<xs:sequence>
<xs:element ref="r:reactants"/>
<xs:element ref="r:products"/>
</xs:sequence>
</xs:complexType>
</xs:element>
<xs:element name="system">
<xs:complexType>
<xs:sequence>
<xs:element ref="r:reaction" maxOccurs="unbounded"/>
</xs:sequence>
</xs:complexType>
</xs:element>
</xs:schema>
```
Note we're now defining the target namespace for our schema.
```
with open("reactions.xsd") as xsdfile:
schema_xsd = xsdfile.read()
schema = etree.XMLSchema(etree.XML(schema_xsd))
parser = etree.XMLParser(schema=schema)
with open("system.xml") as xmlfile:
tree = etree.parse(xmlfile, parser)
print(tree)
```
Note the power of binding namespaces when using XML files addressing more than one namespace.
Here, we can clearly see which variables are part of the schema defining XML schema itself (bound to `xs`)
and the schema for our file format (bound to `r`)
## Using standard vocabularies
The work we've done so far will enable someone who comes across our file format to track down something about its significance, by following the URI in the namespace. But it's still somewhat ambiguous. The word "element" means (at least) two things: an element tag in an XML document, and a chemical element. (It also means a heating element in a toaster, and lots of other things.)
To make it easier to not make mistakes as to the meaning of **found data**, it is helpful to use
standardised namespaces that already exist for the concepts our file format refers to.
So that when somebody else picks up one of our data files, the meaning of the stuff it describes is obvious. In this example, it would be hard to get it wrong, of course, but in general, defining file formats so that they are meaningful as found data should be desirable.
For example, the concepts in our file format are already part of the "DBPedia ontology",
among others. So, we could redesign our file format to exploit this, by referencing for example [https://dbpedia.org/ontology/ChemicalCompound](https://dbpedia.org/ontology/ChemicalCompound):
```
%%writefile chemistry_template3.mko
<?xml version="1.0" encoding="UTF-8"?>
<system xmlns="https://www.turing.ac.uk/rsd-engineering/schema/reaction"
xmlns:dbo="https://dbpedia.org/ontology/">
%for reaction in reactions:
<reaction>
<reactants>
%for molecule in reaction.reactants.molecules:
<dbo:ChemicalCompound stoichiometry="${reaction.reactants.molecules[molecule]}">
%for element in molecule.elements:
<dbo:ChemicalElement symbol="${element.symbol}"
number="${molecule.elements[element]}"/>
%endfor
</dbo:ChemicalCompound>
%endfor
</reactants>
<products>
%for molecule in reaction.products.molecules:
<dbo:ChemicalCompound stoichiometry="${reaction.products.molecules[molecule]}">
%for element in molecule.elements:
<dbo:ChemicalElement symbol="${element.symbol}"
number="${molecule.elements[element]}"/>
%endfor
</dbo:ChemicalCompound>
%endfor
</products>
</reaction>
%endfor
</system>
```
However, this won't work properly, because it's not up to us to define the XML schema for somebody
else's entity type: and an XML schema can only target one target namespace.
Of course we should use somebody else's file format for chemical reaction networks: compare [SBML](http://sbml.org) for example. We already know not to reinvent the wheel - and this whole lecture series is just reinventing the wheel for pedagogical purposes. But what if we've already got a bunch of data in our own format. How can we lock down the meaning of our terms?
So, we instead need to declare that our `r:element` *represents the same concept* as `dbo:ChemicalElement`. To do this formally we will need the concepts from the next lecture, specifically `rdf:sameAs`, but first, let's understand the idea of an ontology.
## Taxonomies and ontologies
An Ontology (in computer science terms) is two things: a **controlled vocabulary** of entities (a set of URIs in a namespace), the definitions thereof, and the relationships between them.
People often casually use the word to mean any formalised taxonomy, but the relation of terms in the ontology to the concepts they represent, and the relationships between them, are also critical.
Have a look at another example: [https://dublincore.org/documents/dcmi-terms/](https://dublincore.org/documents/dcmi-terms/#terms-creator)
Note each concept is a URI, but some of these are also stated to be subclasses or superclasses of the others.
Some are properties of other things, and the domain and range of these verbs are also stated.
Why is this useful for us in discussing file formats?
One of the goals of the **semantic web** is to create a way to make file formats which are universally meaningful
as found data: if I have a file format defined using any formalised ontology, then by tracing statements
through *rdf:sameAs* relationships, I should be able to reconstruct the information I need.
That will be the goal of the next lecture.
| github_jupyter |
# Basic Python
Introduction to some basic python data types.
```
x = 1
y = 2.0
s = "hello"
l = [1, 2, 3, "a"]
d = {"a": 1, "b": 2, "c": 3}
```
Operations behave as per what you would expect.
```
z = x * y
print(z)
# Getting item at index 3 - note that Python uses zero-based indexing.
print(l[3])
# Getting the index of an element
print(l.index(2))
# Concatenating lists is just using the '+' operator.
print(l + l)
```
Dictionaries are essentially key-value pairs
```
print(d["c"]) # Getting the value associated with "c"
```
# Numpy and scipy
By convention, numpy is import as np and scipy is imported as sp.
```
import numpy as np
import scipy as sp
```
An array is essentially a tensor. It can be an arbitrary number of dimensions. For simplicity, we will stick to basic 1D vectors and 2D matrices for now.
```
x = np.array([[1, 2, 3],
[4, 7, 6],
[9, 4, 2]])
y = np.array([1.5, 0.5, 3])
print(x)
print(y)
```
By default, operations are element-wise.
```
print(x + x)
print(x * x)
print(y * y)
print(np.dot(x, x))
print(np.dot(x, y))
```
Or you can use the @ operator that is available in Python 3.7 onwards.
```
print(x @ x)
print(x @ y)
```
Numpy also comes with standard linear algebra operations, such as getting the inverse.
```
print(np.linalg.inv(x))
```
Eigen values and vectors
```
print(np.linalg.eig(x))
```
Use of numpy vectorization is key to efficient coding. Here we use the Jupyter %time magic function to demonstrate the relative speeds to two methods of calculation the L2 norm of a very long vector.
```
r = np.random.rand(10000, 1)
%time sum([i**2 for i in r])**0.5
%time np.sqrt(np.sum(r**2))
%time np.linalg.norm(r)
```
Scipy has all the linear algebra functions as numpy and more. Moreover, scipy is always compiled with fast BLAS and LAPACK.
```
import scipy.linalg as linalg
linalg.inv(x)
import scipy.constants as const
print(const.e)
print(const.h)
import scipy.stats as stats
dist = stats.norm(0, 1) # Gaussian distribution
dist.cdf(1.96)
```
# Pandas
pandas is one of the most useful packages that you will be using extensively during this course. You should become very familiar with the Series and DataFrame objects in pandas. Here, we will read in a csv (comma-separated value) file downloaded from figshare. While you can certainly manually download the csv and just called pd.read_csv(filename), we will just use the request method to directly grab the file and read it in using a StringIO stream.
```
import pandas as pd
from io import StringIO
import requests
from IPython.display import display
# Get the raw text of the data directly from the figshare url.
url = "https://ndownloader.figshare.com/files/13007075"
raw = requests.get(url).text
# Then reads in the data as a pandas DataFrame.
data = pd.read_csv(StringIO(raw))
display(data)
```
Here, we will get one column from the DataFrame - this is a Pandas Series object.
```
print(data["Enorm (eV)"])
df = data[data["Enorm (eV)"] >= 0]
df.describe()
```
Pandas dataframes come with some conveience functions for quick visualization.
```
df.plot(x="Enorm (eV)", y="E_raw (eV)", kind="scatter");
```
# Seaborn
Here we demonstrate some basic statistical data visualization using the seaborn package. A helpful resource is the [seaborn gallery](https://seaborn.pydata.org/examples/index.html) which has many useful examples with source code.
```
import seaborn as sns
%matplotlib inline
sns.distplot(df["Enorm (eV)"], norm_hist=False);
sns.scatterplot(x="Enorm (eV)", y="E_raw (eV)", data=df);
```
# Materials API using pymatgen
The MPRester.query method allows you to perform direct queries to the Materials Project to obtain data. What is returned is a list of dict of properties.
```
from pymatgen.ext.matproj import MPRester
mpr = MPRester()
data = mpr.query(criteria="*-O", properties=["pretty_formula", "final_energy", "band_gap", "elasticity.K_VRH"])
# What is returned is a list of dict. Let's just see what the first item in the list looks out.
import pprint
pprint.pprint(data[0])
```
The above is not very friendly for manipulation and visualization. Thankfully, we can easily convert this to a pandas DataFrame since the DataFrame constructor takes in lists of dicts as well.
```
df = pd.DataFrame(data)
display(df)
```
Oftentimes, you only want the subset of data with valid values. In the above data, it is clear that some of the entries do not have elasticity.K_VRH data. So we will use the dropna method of the pandas DataFrame to get a new DataFrame with just valid data. Note that a lot of Pandas methods returns a new DataFrame. This ensures that you always have the original object to compare to. If you want to perform the operation in place, you can usually supply `inplace=True` to the method.
```
valid_data = df.dropna()
print(valid_data)
```
Seaborn works very well with Pandas DataFrames...
```
sns.scatterplot(x="band_gap", y="elasticity.K_VRH", data=valid_data);
```
| github_jupyter |
# Python programming for beginners
[email protected]
## Agenda
1. Background, why Python, [installation](#installation), IDE, setup
2. Variables, Boolean, None, numbers (integers, floating point), check type
3. List, Set, Dictionary, Tuple
4. Text and regular expressions
5. Conditions, loops
6. Objects and Functions
7. Special functions (range, enumerate, zip), Iterators
8. I/O working with files, working directory, projects
9. Packages, pip, selected packages (xmltodict, biopython, xlwings, pyautogui, sqlalchemy, cx_Oracle, pandas)
10. Errors and debugging (try, except)
11. virtual environments
## What is a Programming language?

## Why Python
### Advantages:
* Opensource/ free - explanation
* Easy to learn
* Old
* Popular
* All purpose
* Simple syntaxis
* High level
* Scripting
* Dynamically typed
### Disadvantages:
* Old
* Dynamically typed
* Inconsistent development
<a id="installation"></a>
## Installation
[Python](http://python.org/)
[Anaconda](https://www.anaconda.com/products/individual)
## Integrated Development Environment (IDE)
* IDLE – comes with Python
* [Jupiter notebook](https://jupyter.org/install)
* [google colab](https://colab.research.google.com/notebooks/basic_features_overview.ipynb#scrollTo=KR921S_OQSHG)
* Spyder – comes with Anaconda
* [Visual Studio Code](https://code.visualstudio.com/)
* [PyCharm community](https://www.jetbrains.com/toolbox-app/)
## Python files
Python files are text files with .py extension
### Comments
Comments are pieces of code that are not going to be executed. In python everything after hashtag (#) on the same line is comment.
Comments are used to describe code: what is this particular piece of code doing and why you have created it.
```
# this is a comment it will be ignored when running the python file
```
## Variables
Assigning value to a variable
```
my_variable = 3
print(my_variable)
```
### Naming variables
Variable names cannot start with the number, cannot contain special characters or space except _
Should not be name of python function.
* variable1 -> <font color=green>this is OK</font>
* 1variable -> <font color=red>this is not OK</font>
* Important-variable! -> <font color=red>this is not OK</font>
* myVariable -> <font color=green>this is OK</font>
* my_variable -> <font color=green>this is OK</font>
## Data types
### Numbers
#### 1. integers (whole numbers)
```
var2 = 2
my_variable + var2
print(my_variable + 4)
my_variable = 6
print(my_variable +4)
```
we can assign the result to another variable
```
result = my_variable + var2
print(result)
```
#### 2. Doubles (floating point number)
```
double = 2.05
print(double)
```
#### Mathematical operations
<font color= #00B19C>- Additon and substraction</font>
```
2 + 3
5 - 2
```
<font color= #00B19C>- Multiplication and division</font>
```
2 * 3
6 / 2
```
<font color=red>Note: the result of division is float not int!</font>
<font color= #00B19C>- Exponential</font>
```
2 ** 4
# 2**4 is equal to 2*2*2*2
```
<font color= #00B19C>- Floor division</font>
```
7 // 3
```
7/3 is 2.3333 the floor division is giving the whole number 2 (how many times you can fit 3 in 7)
<font color= #00B19C>- Modulo</font>
```
7.0 % 2
```
7//3 is 2, modulo is giving the remainder of the operation (what is left when you fit 2 times 3 in 7 ; 7 =2*3 + 1)
<font color= red>Note: Floor division and modulo results are inegers if integers are used as arguments and float if one of the arguments is float</font>
### Special variables
#### 1. None
None means variable without data type, nothing
```
var = None
print(var)
```
#### 2. Bolean
<font color= red>Note: Bolean is type of integer that can take only values of 0 or 1</font>
```
var = True # or 1
var2 = False # or 0
print(var)
print(var+1)
```
### Check variable type
#### 1. type() function
```
print(type(True))
print(type(1))
print(type(my_variable))
```
#### 2. isinstance() function
```
print(isinstance(True, bool))
print(isinstance(False, int))
print(isinstance(1, int))
```
## Comparing variables
```
print(1 == 1)
print(1 == 2)
print(1 != 2)
print(1 < 2)
print(1 > 2)
my_variable = None
print(my_variable == None)
print(my_variable is None)
my_variable = 1.5
print(my_variable == 1.5)
print(my_variable is 1.5)
print(my_variable is not None)
```
<font color= red>Note as a general rule of thumb use "is" "is not" when checking if variable is **None**, **True** or **False** in all other cases use "=="</format>
### Converting Int to Float and vs versa
#### 1. float() function
```
float(3)
```
#### 2. int() function
<font color= red>Note the int() conversion is taking in to account only the whole number int(2.9) = 2!</font>
```
int(2.9)
```
## Tuple
tuple is a collection which is ordered and unchangeable.
```
my_tuple = (3, 8, 5, 7, 5)
```
access tuple items by index
<font color= red>Note Python is 0 indensing language = it starts to count from 0!</font>

```
print(my_tuple[0])
print(my_tuple[2:4])
print(my_tuple[2:])
print(my_tuple[:2])
print(my_tuple[-1])
print(my_tuple[::3])
print(my_tuple[1::2])
print(my_tuple[::-1])
print(my_tuple[-2::])
```
### Tuple methods
Methods are functions inside an object (every variable in Python is an object)
#### 1.count() method - Counts number of occurrences of item in a tuple
```
my_tuple.count(6)
```
#### 2.index() method - Returns the index of first occurence of an item in a tuple
```
my_tuple.index(5)
```
#### Other operations with tuples
Adding tuples
```
my_tuple + (7, 2, 1)
```
Nested tuples = tuples containing tuples
```
tuple_of_tuples = ((1,2,3),(3,4,5))
print(tuple_of_tuples)
print(tuple_of_tuples[0])
print(tuple_of_tuples[1][2])
```
## List
List is a collection which is ordered and changeable.
```
my_list = [3, 8, 5, 7, 5]
```
Accesing list members is exactly the same as accesing tuple members, .count() and .index() methods work the same way with lists.
The difference is that list members can be changed
```
my_list[1] = 9
print(my_list)
my_tuple[1] = 9
```
Lists are having more methods than tuples
#### 1.count() method
same as with tuple
#### 2.index() method
same as with tuple
#### 3.reverse() method
inverting the list same as my_list[::-1]
```
my_list.reverse()
print(my_list)
my_list = my_list[::-1]
print(my_list)
```
#### 4.sort() method
sorting the list from smallest to largest or alphabetically in case of text
```
my_list.sort()
print(my_list)
my_list.sort(reverse=True)
print(my_list)
```
#### 5.clear() method
removing everything from a list, equal to my_list = []
```
my_list.clear()
print(my_list)
```
#### 6.remove() method
Removes the first item with the specified value
```
my_list = [3, 8, 5, 7, 5]
my_list.remove(7)
print(my_list)
```
#### 7.pop() method
Removes the element at the specified position
```
my_list.pop(0)
print(my_list)
```
#### 8.copy() method
Returns a copy of the list
```
my_list_copy = my_list.copy()
print(my_list_copy)
```
what is the problem with my_other_list = my_list?
```
my_other_list = my_list
print(my_other_list)
my_list.pop(0)
print(my_list)
print(my_list_copy)
print(my_other_list)
my_other_list.pop(0)
print(my_list)
print(my_list_copy)
print(my_other_list)
```
#### 9.insert() method
Adds an element at the specified position, displacing the following members with 1 position
```
my_list = [3, 8, 5, 7, 5]
my_list.insert(3, 1)
print(my_list)
```
#### 10.append() method
Adds an element at the end of the list
```
my_list.append(6)
print(my_list)
my_list.append([6,7])
print(my_list)
```
#### 11.extend() method
dd the elements of a list (or any iterable), to the end of the current list
```
another_list = [2, 6, 8]
my_list.extend(another_list)
print(my_list)
another_tuple = (2, 6, 8)
my_list.extend(another_tuple)
print(my_list)
```
## <font color= red>End of first session</font>
#### Set
Set is an unordered collection of unique objects.
```
my_set = {3, 8, 5, 7, 5}
print(my_set)
print(my_set)
```
### Set methods
.add() - Adds an element to the set
.clear() - Removes all the elements from the set
.copy() - Returns a copy of the set
.difference() - Returns a set containing the difference between two or more sets
.difference_update() - Removes the items in this set that are also included in another, specified set
.discard() - Remove the specified item
.intersection() - Returns a set, that is the intersection of two other sets
.intersection_update() - Removes the items in this set that are not present in other, specified set(s)
.isdisjoint() - Returns whether two sets have a intersection or not
.issubset() - Returns whether another set contains this set or not
.issuperset() - Returns whether this set contains another set or not
.pop() - Removes an element from the set
.remove() - Removes the specified element
.symmetric_difference() - Returns a set with the symmetric differences of two sets
.symmetric_difference_update() - Inserts the symmetric differences from this set and another
.union() - Return a set containing the union of sets
.update() - Update the set with the union of this set and others
```
set_a = {1,2,3,4,5}
set_b = {4,5,6,7,8}
print(set_a.union(set_b))
print(set_a.intersection(set_b))
```
## Converting tuple to list to set
we can convert any tuple or set to list with **list()** function
we can convert any list or set to tuple with **tuple()** function
we can convert any tuple or list to set with **set()** function
```
my_list = [3, 8, 5, 7, 5]
print(my_list)
my_tuple = tuple(my_list)
print(my_tuple)
my_set =set(my_list)
print(my_set)
my_list2 = list(my_set)
print(my_list2)
```
this functions can be nested
```
my_unique_list = list(set(my_list))
print(my_unique_list)
```
### Checking if something is in a list, set, tuple
```
print(3 in my_set)
print(9 in my_set)
print(3 in my_list)
print(9 in my_tuple)
```
## Dictionary
dictionary is a collection which is unordered, changeable and indexed as a key-value pair
```
my_dict = {1: 2.3,
2: 8.6}
print(my_dict[2])
print(my_dict[3])
print(my_dict.keys())
print(my_dict.values())
print(1 in my_dict.keys())
print(2.3 in my_dict.values())
print(my_dict.items())
```
## Strings
strings are ordered sequence of characters, strings are unchangable
```
print(my_dict.get(2))
my_string = 'this is string'
other_string = "this is string as well"
multilane_string = '''this is
a multi lane
string'''
print(my_string)
print(other_string)
print(multilane_string)
my_string = 'this "word" is in quotes'
my_other_string = "This is Maria's book"
print(my_string)
print(my_other_string)
my_string = "this \"word\" is in quotes"
my_other_string = 'This is Maria\'s book'
print(my_string)
print(my_other_string)
my_number = 9
my_string = '9'
print(my_number+1)
print(my_string+1)
print(my_string+'1')
print(int(my_string)+1)
print(my_number+int('1'))
```
Accesing list members is exactly the same as with lists and tuples
```
print(other_string)
print(other_string[0])
print(other_string[::-1])
```
## String methods
.capitalize() - Converts the first character to upper case
.casefold() - Converts string into lower case
.center() - Returns a centered string
.count() - Returns the number of times a specified value occurs in a string
.encode() - Returns an encoded version of the string
.endswith() - Returns true if the string ends with the specified value
.expandtabs() - Sets the tab size of the string
.find() - Searches the string for a specified value and returns the position of where it was found
.format() - Formats specified values in a string
.format_map() - Formats specified values in a string
.index() - Searches the string for a specified value and returns the position of where it was found
.isalnum() - Returns True if all characters in the string are alphanumeric
.isalpha() - Returns True if all characters in the string are in the alphabet
.isdecimal() - Returns True if all characters in the string are decimals
.isdigit() - Returns True if all characters in the string are digits
.isidentifier() - Returns True if the string is an identifier
.islower() - Returns True if all characters in the string are lower case
.isnumeric() - Returns True if all characters in the string are numeric
.isprintable() - Returns True if all characters in the string are printable
.isspace() - Returns True if all characters in the string are whitespaces
.istitle() - Returns True if the string follows the rules of a title
.isupper() - Returns True if all characters in the string are upper case
.join() - Joins the elements of an iterable to the end of the string
.ljust() - Returns a left justified version of the string
.lower() - Converts a string into lower case
.lstrip() - Returns a left trim version of the string
.maketrans() - Returns a translation table to be used in translations
.partition() - Returns a tuple where the string is parted into three parts
.replace() - Returns a string where a specified value is replaced with a specified value
.rfind() - Searches the string for a specified value and returns the last position of where it was found
.rindex() - Searches the string for a specified value and returns the last position of where it was found
.rjust() - Returns a right justified version of the string
.rpartition() - Returns a tuple where the string is parted into three parts
.rsplit() - Splits the string at the specified separator, and returns a list
.rstrip() - Returns a right trim version of the string
.split() - Splits the string at the specified separator, and returns a list
.splitlines() - Splits the string at line breaks and returns a list
.startswith() - Returns true if the string starts with the specified value
.strip() - Returns a trimmed version of the string
.swapcase() - Swaps cases, lower case becomes upper case and vice versa
.title() - Converts the first character of each word to upper case
.translate() - Returns a translated string
.upper() - Converts a string into upper case
.zfill() - Fills the string with a specified number of 0 values at the beginning
```
my_string = ' string with spaces '
print(my_string)
my_stripped_string = my_string.strip()
print(my_stripped_string)
print('ABC' == 'ABC')
print('ABC' == ' ABC ')
list_of_words = my_string.split()
print(list_of_words)
text = 'id1, id2, id3, id4'
ids_list = text.split(', ')
print(ids_list)
new_text = ' / '.join(ids_list)
print(new_text)
xml_text = 'this is <body>text</body> with xml tags'
xml_text.find('<body>')
xml_body = xml_text[xml_text.find('<body>')+len('<body>'):xml_text.find('</body>')]
print(xml_body)
```
### Other operations with strings
combinig (adding) strings
```
text = 'text1'+'text2'
print(text)
text = 'text1'*4
print(text)
```
row and formated string
```
file_location = 'C:\Users\U6047694\Documents\job\Python_Projects\file.txt'
file_location = r'C:\Users\U6047694\Documents\job\Python_Projects\file.txt'
print(file_location)
var1 = 5
var2 = 6
print(f'Var1 is: {var1}, var2 is: {var2} and the sum is: {var1+var2}')
# this is the same as
print('Var1 is: '+str(var1)+', var2 is: '+str(var2)+' and the sum is: '+str(var1+var2))
```
## Regular expressions in Python
The regular expressions in python are stored in separate package **re** this package should be imported in order to access its functionality (methods).
### Methods in re package
* re.search() - Check if given pattern is present anywhere in input string. Output is a re.Match object, usable in conditional expressions
* re.fullmatch() - ensures pattern matches the entire input string
* re.compile() - Compile a pattern for reuse, outputs re.Pattern object
* re.sub() - search and replace
* re.escape() - automatically escape all metacharacters
* re.split() - split a string based on RE text matched by the groups will be part of the output
* re.findall() - returns all the matches as a list
* re.finditer() - iterator with re.Match object for each match
* re.subn() - gives tuple of modified string and number of substitutions
### re characters
'.' - Match any character except newline
'^' - Match the start of the string
'$' - Match the end of the string
'*' - Match 0 or more repetitions
'+' - Match 1 or more repetitions
'?' - Match 0 or 1 repetitions
### re set of characters
'[]' - Match a set of characters
'[a-z]' - Match any lowercase ASCII letter
'[lower-upper]' - Match a set of characters from lower to upper
'[^]' - Match characters NOT in a set
<a href="https://cheatography.com/davechild/cheat-sheets/regular-expressions/" >Cheet Sheet</a>
<a href="https://docs.python.org/3/library/re.html">re reference</a>
```
text = 'this is a sample text for re testing'
t_words = re.findall('t[a-z]* ', text)
print(t_words)
new_text = re.sub('t[a-z]* ', 'replace ', text)
print(new_text)
```
## Conditions
### IF, ELIF, ELSE conditions
if condition sintacsis:
```
a = 3
if a == 2:
print('a is 2')
if a == 3:
print('a is 3')
else:
print('a is not 2')
if a == 2:
pring('a is 2')
elif a == 3:
print('a is 3')
else:
print('a is not 2 or 3')
if a == 2:
pring('a is 2')
if a == 3:
print('a is 3')
else:
print('a is not 2 or 3')
if a > 2:
print('a is bigger than 2')
if a < 4:
print('a is smaller than 4')
else:
print('a is something else')
if a > 2:
print('a is bigger than 2')
elif a < 4:
print('a is smaller than 4')
else:
print('a is something else')
```
#### OR / AND in conditional statement
```
b = 4
if a > 2 or b < 2:
print(f'a is: {a} b is: {b}.')
```
#### Nested conditional statements
```
a = 2
if a == 2:
if b > a:
print('b is bigger than a')
else:
print('b is not bigger than a')
else:
print(f'a is {a}')
```
## Loops
### FOR loop
```
my_list = [1, 3, 5]
for item in my_list:
print(item)
```
### WHILE loop
```
a = 0
while a < 5:
a = a + 1 # or alternatively a += 1
print(a)
```
You can put else statement in the while loop as well
```
a = 3
while a < 5:
a = a + 1 # or alternatively a += 1
print(a)
else:
print('This is the end!')
```
Loops can be nested as well
```
columns = ['A', 'B', 'C']
rows = [1, 2, 3]
for column in columns:
print(column)
for row in rows:
print(row)
```
Break and Continue. Break is stopping the loop, continue is skipping to the next item in the loop
```
for column in columns:
print(column)
if column == 'B':
break
```
If we have nested loops break will stop only the loop in which is used
```
columns = ['A', 'B', 'C']
rows = [1, 2, 3]
for column in columns:
print(column)
for row in rows:
print(row)
if row == 2:
break
i = 0
while i < 6:
i += 1
if i == 3:
continue
print(i)
```
## Objects
Everything in Python is Object

```
class Player:
def __init__(self, name):
self.name = name
print(f'{self.name} is a Player')
def run(self):
return f'{self.name} is running'
player1 = Player('Messi')
player1.run()
```
### Inheritance
Inheritance allows us to define a class that inherits all the methods and properties from another class.
Parent class is the class being inherited from, also called base class.
Child class is the class that inherits from another class, also called derived class.
```
class Futbol_player(Player):
def kick_ball(self):
return f'{self.name} is kicking the ball'
class Basketball_player(Player):
def catch_ball(self):
return f'{self.name} is catching the ball'
player2 = Futbol_player('Leo Messi')
player2.kick_ball()
player2.run()
player3 = Basketball_player('Pau Gasol')
player3.catch_ball()
player3.kick_ball()
class a_list(list):
def get_3_element(self):
return self[3]
my_list = ['a', 'b', 'c', 'd']
my_a_list = a_list(['a', 'b', 'c', 'd'])
my_a_list.get_3_element()
my_list.get_3_element()
my_a_list.count('a')
```
## Functions
A function is a block of code which only runs when it is called.
You can pass data, known as arguments or parameters, into a function.
A function can return data as a result or not.
```
def my_func(n):
'''this is power function'''
result = n*n
return result
```
You can assign the result of a function to another variable
```
power5 = my_func(5)
print(power5)
```
multiline string (Docstrings) can be used to describe the functions, can be accessed by \__doc\__ method
```
print(my_func.__doc__)
```
One function can return more than one value
```
def my_function(a):
x = a*2
y = a+2
return x, y
variable1 = my_function(5)
print(variable1)
print(variable2)
```
One function can have between 0 and many arguments
```
def my_formula(a, b, c):
y = (a*b) + c
return y
```
#### Positional arguments
```
my_formula(2,3,4)
```
#### Keyword arguments
```
my_formula(c=4, a=2, b=3)
```
You can pass both positional and keyword arguments to a function but the positional should always come first
```
my_formula(4, c=4, b=3)
```
#### Default arguments
This are arguments that are assigned when declaring the function and if not specified will take the default data
```
def my_formula(a, b, c=3):
y = (a*b) + c
return y
my_formula(2, 3, c=6)
```
#### Arbitrary Arguments, \*args:
If you do not know how many arguments that will be passed into your function, add a * before the argument name in the function definition.
The function will receive a tuple of arguments, and they can be access accordingly:
```
def greeting(*args):
greeting = f'Hi to {", ".join(args[:-1])} and {args[-1]}'
print(greeting)
greeting('Joe', 'Ben', 'Bobby')
```
#### Arbitrary Keyword Arguments, \**kwargs
If you do not know how many keyword arguments that will be passed into your function, add two asterisk: ** before the parameter name in the function definition.
This way the function will receive a dictionary of arguments, and can access the items accordingly
```
def list_names(**kwargs):
for key, value in kwargs.items():
print(f'{key} is: {value}')
list_names(first_name='Jonny', family_name='Walker')
list_names(primer_nombre='Jose', segundo_nombre='Maria', primer_apellido='Peréz', segundo_apellido='García')
```
### Scope of the function
Scope of the function is what a function can see and use.
The function can use all global variables if there is no local assigned
```
a = 'Hello'
def my_function():
print(a)
my_function()
```
If we have local variable with the same name the function will use the local.
```
a = 'Hello'
def my_function():
a = 'Hi'
print(a)
my_function()
a = 'Hello'
def my_function():
print(a)
a = 'Hi'
my_function()
```
This is important as this is preventing us from changing global variables inside function
```
a = 'Hello'
def change_a():
a = a + 'Hi'
change_a()
print(a)
```
A function cannot access local variables from another function.
```
def my_function():
b = 'Hi'
print(a)
def my_other_function():
print(b)
my_other_function()
```
Local variables cannot be accessed from global environment
```
print(b)
```
Similar to variables you can use functions from the global environment or define them inside a parent function
```
def add_function(a, b):
result = a + b
return result
def formula_function(a, b, c):
result = add_function(a, b) * c
return result
print(formula_function(2,3,4))
```
We can use the result from one function as argument for another
```
print(formula_function(add_function(4,5), 3, 2))
```
We can use function as argument for another function or return function from another function, we have Anonymous/Lambda Function in Python as well.
#### Recursive functions
Recursive function is function that is using (calling) itself
```
def factorial(x):
"""This is a recursive function
to find the factorial of an integer (factorial(4) = 4*3*2*1)"""
if x == 1:
return 1
else:
result = x * factorial(x-1)
return result
factorial(5)
def extract('http..'):
result = request('http..')
if request = None:
time.sleep(360)
result = extract()
```
## Special functions (range, enumerate, zip)
### range() function - is creating sequence
```
my_range = range(5)
print(my_range)
my_list = list(range(2, 10, 2))
my_list
my_list = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h']
for i in range(3, len(my_list), 2):
print(my_list[i])
range_list = list(range(10))
print(range_list)
```
### enumerate() function is creating index for iterables
```
import time
my_list = list(range(10))
my_second_list = []
for index, value in enumerate(my_list):
time.sleep(1)
my_second_list.append(value+2)
print(f'{index+1} from {len(my_list)}')
print(my_second_list)
print(my_second_list)
```
### zip() function is aggregating items into tuples
```
list1 = [2, 4, 6, 7, 8]
list2 = ['a', 'b', 'c', 'd', 'e']
for item1, item2 in zip(list1, list2):
print(f'item1 is:{item1} and item2 is: {item2}')
```
### Iterator objects
```
string = 'abc'
it = iter(string)
it
next(it)
```
## I/O working with files, working directory, projects
I/O = Input / Output. Loading data to python, getting data out of python
### Keyboard input
#### input() function
```
str = input("Enter your input: ")
print("Received input is : "+ str)
```
### Console output
#### print() function
```
print('Console output')
```
### Working with text files
#### open() function
open(file_name [, access_mode][, buffering])
file_name = string with format 'C:/temp/my_file.txt'
access_mode = string with format: 'r', 'rb', 'w' etc
1. r = Opens a file for reading only. The file pointer is placed at the beginning of the file. This is the default mode.
2. rb = Opens a file for reading only in binary format.
3. r+ = Opens a file for both reading and writing.
4. rb = Opens a file for both reading and writing in binary format.
5. w = Opens a file for writing only. Overwrites the file if the file exists. If the file does not exist, creates a new file for writing.
6. wb = Opens a file for writing only in binary format. Overwrites the file if the file exists. If the file does not exist, creates a new file for writing.
7. w+ = Opens a file for both writing and reading. Overwrites the existing file if the file exists. If the file does not exist, creates a new file for reading and writing.
8. wb+ = Opens a file for both writing and reading in binary format. Overwrites the existing file if the file exists. If the file does not exist, creates a new file for reading and writing.
9. a = Opens a file for appending. The file pointer is at the end of the file if the file exists. That is, the file is in the append mode. If the file does not exist, it creates a new file for writing.
10. ab = Opens a file for appending in binary format. The file pointer is at the end of the file if the file exists. That is, the file is in the append mode. If the file does not exist, it creates a new file for writing.
11. a+ = Opens a file for both appending and reading. The file pointer is at the end of the file if the file exists. The file opens in the append mode. If the file does not exist, it creates a new file for reading and writing.
12. ab+ = Opens a file for both appending and reading in binary format. The file pointer is at the end of the file if the file exists. The file opens in the append mode. If the file does not exist, it creates a new file for reading and writing.
```
txt_file = open('C:/temp/python test/txt_file.txt', 'w')
txt_file.write('some text')
txt_file.close()
txt_file = open('C:/temp/python test/txt_file.txt', 'r')
text = txt_file.read()
txt_file.close()
print(text)
txt_file = open('C:/temp/python test/txt_file.txt', 'a')
txt_file.write('\nsome more text')
txt_file.close()
txt_file = open('C:/temp/python test/txt_file.txt', 'r')
txt_lines = txt_file.readlines()
print(type(txt_lines))
txt_file.close()
print(txt_lines)
txt_file = open('C:/temp/python test/txt_file.txt', 'r')
txt_line = txt_file.readline()
print(txt_line)
txt_line2 = txt_file.readline()
print(txt_line2)
```
### Deleting files
requires os library this library is part of Python but is not loaded by default so to use it we should import it
```
import os
os.remove('C:/temp/python test/txt_file.txt')
if os.path.exists('C:/temp/python test/txt_file.txt'):
os.remove('C:/temp/python test/txt_file.txt')
else:
print('The file does not exist')
```
### Removing directories with os.rmdir()
To delete the directory with os.rmdir() the directory should be empty we can check what is inside the directory with os.listdir() or os.walk()
```
os.listdir('C:/temp/python test/')
os.walk('C:/temp/python test/')
for item in os.walk('C:/temp/python test/'):
print(item[0])
print(item[1])
print(item[2])
```
### Rename file or directory
```
os.rename('C:/temp/python test/test file.txt', 'C:/temp/python test/test file renamed.txt')
os.listdir('C:/temp/python test/')
```
### Open folder or file in Windows with the associated program
```
os.startfile('C:/temp/python test/test file renamed.txt')
```
## Working directory
```
import os
os.getcwd()
os.chdir('C:/temp/python test/')
os.getcwd()
os.listdir()
```
### Projects
Project is a folder organising your files, the top level is your working directory.
Good practices of organising your projects:
1. Create separate folder for your python(.py) files, name this folder without space (eg. py_files or python_files)
2. Add in your py_files fodler a file called \_\_init\_\_.py, this is an empty python file that will allow you to import all files in this folder as packages.
3. is a good idea to make your project folder a git repository so you can track your changes.
4. put all your source files and result files in your project directory.
## Packages
Packages (or libraries) are python files with objects and functions that you can use, some of them are installed with python and are part of the programming language, others should be installed.
### Package managers
Package managers are helping you to install, update and uninstall packages.
#### pip package manager
This is the default python package manager
* pip install package_name=version - installing a package
* pip freeze - get the list of installed packages
* pip freeze > requirements.txt - saves the list of installed packages as requirements.txt file
* pip install -r requirements.txt - install all packages from requirements.txt file
#### conda package manager
This is used by anaconda distributions of python
### The Python Standard Library - packages included in python
[Full list](https://docs.python.org/3/library/)
* os - Miscellaneous operating system interfaces
* time — Time access and conversions
* datetime — Basic date and time types
* math — Mathematical functions
* random — Generate pseudo-random numbers
* statistics — Mathematical statistics functions
* shutil — High-level file operations
* pickle — Python object serialization
* logging — Logging facility for Python
* tkinter — Python interface to Tcl/Tk (creating UI)
* venv — Creation of virtual environments
* re - Regular expression operations
#### time package examples
```
import time
print('start')
time.sleep(3)
print('stop')
time_now = time.localtime()
print(time_now)
```
convert time to string with form dd-mm-yyyy
```
date = time.strftime('%d-%m-%Y', time_now)
print(date)
month = time.strftime('%B', time_now)
print(f'month is {month}')
```
convert string to time
```
as_time = time.strptime("30 Nov 2020", "%d %b %Y")
print(as_time)
```
#### datatime package examples
```
import datetime
today = datetime.date.today()
print(today)
print(type(today))
week_ago = today - datetime.timedelta(days=7)
print(week_ago)
today_string = today.strftime('%Y/%m/%d')
print(today_string)
print(type(today_string))
```
#### shutil package examples
functions for file copying and removal
* shutil.copy(src, dst)
* shutil.copytree(src, dst)
* shutil.rmtree(path)
* shutil.move(src, dst)
### How to import packages and function from packages
* Import the whole package - in this case you can use all the functions of the package including the functions in the modules of the package, you can rename the package when importing
```
import datetime
today = datetime.date.today()
print(today)
import datetime as dt
today = dt.date.today()
print(today)
```
* import individual modules or individual functions - in this case you can use the functions direktly as if they are defined in your script. <font color=red>Important: be aware of function shadowing - when you import functions with the same name from different packages or you have defined function with the same name!</font>
```
from datetime import date # importing date class
today = date.today()
print(today)
# Warning this is replacing date class with string!!!
date = '25/06/2012'
today = date.today()
print(today)
```
When importing individual functions or classes from the same package you can import them together
```
from datetime import date, time, timedelta
```
## Selected external packages
If you are using pip package manager all the packages available are installed from [PyPI](https://pypi.org/)
* [Biopython](https://biopython.org/) - contains parsers for various Bioinformatics file formats (BLAST, Clustalw, FASTA, Genbank,...), access to online services (NCBI, Expasy,...) and more
* [SQLAlchemy](https://docs.sqlalchemy.org/en/13/) - connect to SQL database and query the database
* [cx_Oracle](https://oracle.github.io/python-cx_Oracle/) - connect to Oracle database
* [xmltodict](https://github.com/martinblech/xmltodict) - convert xml to Python dictionary with xml tags as keys and the information inside the tags as values
```
import xmltodict
xml = """
<root xmlns="http://defaultns.com/"
xmlns:a="http://a.com/"
xmlns:b="http://b.com/">
<x>1</x>
<a:y>2</a:y>
<b:z>3</b:z>
</root>"""
xml_dict = xmltodict.parse(xml)
print(xml_dict.keys())
print(xml_dict['root'].keys())
print(xml_dict['root'].values())
```
### Pyautogui
[PyAutoGUI](https://pyautogui.readthedocs.io/en/latest/index.html) lets your Python scripts control the mouse and keyboard to automate interactions with other applications.
```
import pyautogui as pa
screen_width, screen_height = pa.size() # Get the size of the primary monitor.
print(f'screen size is {screen_width} x {screen_height}')
mouse_x, mouse_y = pa.position() # Get the XY position of the mouse.
print(f'mouse position is: {mouse_x}, {mouse_y}')
pa.moveTo(600, 500, duration=5) # Move the mouse to XY coordinates.
import time
time.sleep(3)
pa.moveTo(600, 500)
pa.click()
pa.write('Hello world!', interval=0.25)
pa.alert('Script finished!')
pa.screenshot('C:/temp/python test/my_screenshot.png', region=(0,0, 300, 400))
location = pa.locateOnScreen('C:/temp/python test/python.PNG')
print(location)
image_center = pa.center(location)
print(image_center)
pa.moveTo(image_center, duration=3)
```
### Pandas
[Pandas](https://pandas.pydata.org/docs/user_guide/index.html) - is providing high-performance, easy-to-use data structures and data analysis tools for Python
[Pandas cheat sheet](https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf)
Is providing 2 new data structures to Python
1. Series - is a one-dimensional labeled (indexed) array capable of holding any data type
2. DataFrame - is a 2-dimensional labeled data structure with columns of potentially different types. You can think of it like a spreadsheet or SQL table
```
import pandas as pd
d = {'b': 1, 'a': 0, 'c': 2}
my_serie = pd.Series(d)
print(my_serie['a'])
print(type(my_serie))
list1 = [1, 2, 3]
list2 = [5, 6, 8]
list3 = [10, 12, 13]
df = pd.DataFrame({'b': list1, 'a': list2, 'c': list3})
df
print(df.index)
print(df.columns)
print(df.shape)
df.columns = ['column1', 'column2', 'column3']
# alternative df.rename({'a':'column1'}) in case you dont want to rename all the columns
df
df.index = ['a', 'b', 'c']
df
```
#### selecting values from dataframe
* select column
```
df['column1']
```
* select multiple columns
```
df[['column3', 'column2']]
```
* selecting row
```
row1 = df.iloc[1]
row1
df.loc['a']
df.loc[['a', 'c']]
```
* selecting values from single cell
```
df['column1'][2]
df.iloc[1:2, 0:2]
```
* selecting by column only rows meeting criteria (filtering the table)
```
df[df['column1'] > 1]
```
* select random columns by number (n) or as a fraction (frac)
```
df.sample(n=2)
```
#### adding new data to Data Frame
* add new column
```
df['column4'] = [24, 12, 16]
df
df['column5'] = df['column1'] + df['column2']
df
df['column6'] = 7
df
```
* add new row
```
df = df.append({'column1':4, 'column2': 8, 'column3': 5, 'column4': 7, 'column5': 8, 'column6': 11}, ignore_index=True)
df
```
* add new dataframe on the bottom (columns should have the same names in both dataframes)
```
new_df = df.append(df, ignore_index=True)
new_df
```
* merging data frames (similar to joins in SQL), default ‘inner’
```
df2 = pd.DataFrame({'c1':[2, 3, 4, 5], 'c2': [4, 7, 11, 3]})
df2
merged_df = df.merge(df2, left_on='column1', right_on='c1', how='left')
merged_df
merged_df = pd.merge(df, df2, left_on='column1', right_on='c1')
merged_df
```
* copy data frames - this is important to prevent warnings and artefacts
```
df1 = pd.DataFrame({'a':[1,2,3,4,5], 'b':[6,7,8,9,10]})
df2 = df1[df1['a'] > 2].copy()
df2.iloc[0, 0] = 56
df2
```
* change the data type in a column
```
print(type(df1['a'][0]))
df1['a'] = df1['a'].astype('str')
print(type(df1['a'][0]))
df1
```
* value counts - counts the number of appearances of a value in a column
```
df1.iloc[0, 0] = '5'
df1
df1['a'].value_counts()
```
* drop duplicates - removes duplicated rows in a data frame
```
df1.iloc[0, 1] = 10
df1
df1.drop_duplicates(inplace=True)
df1
```
#### Pandas I/O
* from / to excel file
```
excel_sheet = pd.read_excel('C:/temp/python test/example.xlsx', sheet_name='Sheet1')
excel_sheet.head()
print(excel_sheet.shape)
print(excel_sheet['issue'][0])
excel_sheet = excel_sheet[~excel_sheet['keywords'].isna()]
print(excel_sheet.shape)
excel_sheet.to_excel('C:/temp/python test/example_1.xlsx', index=False)
```
To create excel file with multiple sheets pandas ExcelWriter method shoyld be used and sheets assigned to it
```
writer = pd.ExcelWriter('C:/temp/python test/example_2.xlsx')
df1.to_excel(writer, 'Sheet1', index = False)
excel_sheet.to_excel(writer, 'Sheet2', index = False)
writer.save()
```
* from html page
pandas read_html method is reading the whole page and is creating list of dataframes, one for every html table in the webpage
```
codons = pd.read_html('https://en.wikipedia.org/wiki/DNA_codon_table')
codons[2]
```
* from SQL database
```
my_data = pd.read_sql('select column1, column2 from table1', connection)
```
* from CSV file
```
my_data = pd.read_csv('data.csv')
```
### XLWings
Working with excel files
[Documentation](https://docs.xlwings.org/en/stable/)
```
import xlwings as xw
workbook = xw.Book()
new_sht = workbook.sheets.add('new_sheet')
new_sht.range('A1').value = 'Hi from Python'
new_sht.range('A1').column_width = 30
new_sht.range('A1').color = (0,255,255)
a2_value = new_sht.range('A2').value
print(a2_value)
workbook.save('C:/temp/python test/new_file.xlsx')
workbook.close()
```
## Errors an debugging
### Escaping errors in Python with try: except:
```
a = 7/0
import sys
try:
a = 7/0
except:
print(f'a cannot be calculated, {sys.exc_info()[0]}!')
a = None
try:
'something'
except:
try:
'something else'
except:
'and another try'
finally:
print('Nothing is working :(')
```
### Debugging in PyCharm
## Virtual environments
You can create new virtual environment for every Python project, the virtual environment is an indipendant instalation of Python and you can install packages indipendantly of your System Python.
| github_jupyter |
# AMATH 515 Homework 2
**Due Date: 02/08/2019**
* Name: Tyler Chen
* Student Number:
*Homework Instruction*: Please follow order of this notebook and fill in the codes where commented as `TODO`.
```
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
```
## Please complete the solvers in `solver.py`
```
import sys
sys.path.append('./')
from solvers import *
```
## Problem 3: Compressive Sensing
Consier the optimization problem,
$$
\min_x~~\frac{1}{2}\|Ax - b\|^2 + \lambda\|x\|_1
$$
In the following, please specify the $f$ and $g$ and use the proximal gradient descent solver to obtain the solution.
```
# create the data
np.random.seed(123)
m = 100 # number of measurements
n = 500 # number of variables
k = 10 # number of nonzero variables
s = 0.05 # measurements noise level
#
A_cs = np.random.randn(m, n)
x_cs = np.zeros(n)
x_cs[np.random.choice(range(n), k, replace=False)] = np.random.choice([-1.0, 1.0], k)
b_cs = A_cs.dot(x_cs) + s*np.random.randn(m)
#
lam_cs = 0.1*norm(A_cs.T.dot(b_cs), np.inf)
# define the function, prox and the beta constant
def func_f_cs(x):
# TODO: complete the function
return norm(A_cs@x-b_cs)**2/2
def func_g_cs(x):
# TODO: complete the gradient
return lam_cs*norm(x,ord=1)
def grad_f_cs(x):
# TODO: complete the function
return A_cs.T@(A_cs@x-b_cs)
def prox_g_cs(x, t):
# TODO: complete the prox of 1 norm
leq = x <= -lam_cs*t # boolean array of coordinates where x_i <= -lam_cs * t
geq = x >= lam_cs*t # boolean array of coordinates where x_i >= lam_cs * t
# (leq + geq) gives components where x not in [-1,1]*lam_cs*t
return (leq+geq) * x + leq * lam_cs*t - geq * lam_cs*t
# TODO: what is the beta value for the smooth part
beta_f_cs = norm(A_cs,ord=2)**2
```
### Proximal gradient descent on compressive sensing
```
# apply the proximal gradient descent solver
x0_cs_pgd = np.zeros(x_cs.size)
x_cs_pgd, obj_his_cs_pgd, err_his_cs_pgd, exit_flag_cs_pgd = \
optimizeWithPGD(x0_cs_pgd, func_f_cs, func_g_cs, grad_f_cs, prox_g_cs, beta_f_cs)
# plot signal result
plt.plot(x_cs)
plt.plot(x_cs_pgd, '.')
plt.legend(['true signal', 'recovered'])
plt.title('Compressive Sensing Signal')
plt.show()
# plot result
fig, ax = plt.subplots(1, 2, figsize=(12,5))
ax[0].plot(obj_his_cs_pgd)
ax[0].set_title('function value')
ax[1].semilogy(err_his_cs_pgd)
ax[1].set_title('optimality condition')
fig.suptitle('Proximal Gradient Descent on Compressive Sensing')
plt.show()
# plot result
fig, ax = plt.subplots(1, 3, figsize=(18,5))
ax[0].plot(x_cs)
ax[0].plot(x_cs_pgd, '.')
ax[0].legend(['true signal', 'recovered'])
ax[0].set_title('Compressive Sensing Signal')
ax[1].plot(obj_his_cs_pgd)
ax[1].set_title('function value')
ax[2].semilogy(err_his_cs_pgd)
ax[2].set_title('optimality condition')
#fig.suptitle('Proximal Gradient Descent on Compressive Sensing')
plt.savefig('img/cs_pgd.pdf',bbox_inches="tight")
```
### Accelerate proximal gradient descent on compressive sensing
```
# apply the proximal gradient descent solver
x0_cs_apgd = np.zeros(x_cs.size)
x_cs_apgd, obj_his_cs_apgd, err_his_cs_apgd, exit_flag_cs_apgd = \
optimizeWithAPGD(x0_cs_apgd, func_f_cs, func_g_cs, grad_f_cs, prox_g_cs, beta_f_cs)
# plot signal result
plt.plot(x_cs)
plt.plot(x_cs_apgd, '.')
plt.legend(['true signal', 'recovered'])
plt.title('Compressive Sensing Signal')
plt.show()
# plot result
fig, ax = plt.subplots(1, 2, figsize=(12,5))
ax[0].plot(obj_his_cs_apgd)
ax[0].set_title('function value')
ax[1].semilogy(err_his_cs_apgd)
ax[1].set_title('optimality condition')
fig.suptitle('Accelerated Proximal Gradient Descent on Compressive Sensing')
plt.show()
# plot result
fig, ax = plt.subplots(1, 3, figsize=(18,5))
ax[0].plot(x_cs)
ax[0].plot(x_cs_apgd, '.')
ax[0].legend(['true signal', 'recovered'])
ax[0].set_title('Compressive Sensing Signal')
ax[1].plot(obj_his_cs_apgd)
ax[1].set_title('function value')
ax[2].semilogy(err_his_cs_apgd)
ax[2].set_title('optimality condition')
#fig.suptitle('Proximal Gradient Descent on Compressive Sensing')
plt.savefig('img/cs_apgd.pdf',bbox_inches="tight")
```
## Problem 4: Logistic Regression on MINST Data
Now let's play with some real data, recall the logistic regression problem,
$$
\min_x~~\sum_{i=1}^m\left\{\log(1 + \exp(\langle a_i,x \rangle)) - b_i\langle a_i,x \rangle\right\} + \frac{\lambda}{2}\|x\|^2.
$$
Here our data pair $\{a_i, b_i\}$, $a_i$ is the image and $b_i$ is the label.
In this homework problem, let's consider the binary classification problem, where $b_i \in \{0, 1\}$.
```
# import data
mnist_data = np.load('mnist01.npy')
#
A_lgt = mnist_data[0]
b_lgt = mnist_data[1]
A_lgt_test = mnist_data[2]
b_lgt_test = mnist_data[3]
#
# set regularizer parameter
lam_lgt = 0.1
#
# beta constant of the function
beta_lgt = 0.25*norm(A_lgt, 2)**2 + lam_lgt
# plot the images
fig, ax = plt.subplots(1, 2)
ax[0].imshow(A_lgt[0].reshape(28,28))
ax[1].imshow(A_lgt[7].reshape(28,28))
plt.show()
# define function, gradient and Hessian
def lgt_func(x):
# TODO: complete the function of logistic regression
return np.sum(np.log(1+np.exp(A_lgt@x))) - b_lgt@A_lgt@x + lam_lgt*x@x/2
#
def lgt_grad(x):
# TODO: complete the gradient of logistic regression
return A_lgt.T@ ((np.exp(A_lgt@x)/(1+np.exp(A_lgt@x))) - b_lgt) + lam_lgt*x
#
def lgt_hess(x):
# TODO: complete the hessian of logistic regression
return A_lgt.T @ np.diag( np.exp(A_lgt@x)/(1+np.exp(A_lgt@x))**2 ) @ A_lgt + lam_lgt * np.eye(len(x))
```
### Gradient decsent on logistic regression
```
# apply the gradient descent
x0_lgt_gd = np.zeros(A_lgt.shape[1])
x_lgt_gd, obj_his_lgt_gd, err_his_lgt_gd, exit_flag_lgt_gd = \
optimizeWithGD(x0_lgt_gd, lgt_func, lgt_grad, beta_lgt)
# plot result
fig, ax = plt.subplots(1, 2, figsize=(12,5))
ax[0].plot(obj_his_lgt_gd)
ax[0].set_title('function value')
ax[1].semilogy(err_his_lgt_gd)
ax[1].set_title('optimality condition')
fig.suptitle('Gradient Descent on Logistic Regression')
plt.savefig('img/lr_gd.pdf',bbox_inches="tight")
```
### Accelerate Gradient decsent on logistic regression
```
# apply the accelerated gradient descent
x0_lgt_agd = np.zeros(A_lgt.shape[1])
x_lgt_agd, obj_his_lgt_agd, err_his_lgt_agd, exit_flag_lgt_agd = \
optimizeWithAGD(x0_lgt_agd, lgt_func, lgt_grad, beta_lgt)
# plot result
fig, ax = plt.subplots(1, 2, figsize=(12,5))
ax[0].plot(obj_his_lgt_agd)
ax[0].set_title('function value')
ax[1].semilogy(err_his_lgt_agd)
ax[1].set_title('optimality condition')
fig.suptitle('Accelerated Gradient Descent on Logistic Regression')
plt.savefig('img/lr_agd.pdf',bbox_inches="tight")
plt.show()
```
### Accelerate Gradient decsent on logistic regression
```
# apply the accelerated gradient descent
x0_lgt_nt = np.zeros(A_lgt.shape[1])
x_lgt_nt, obj_his_lgt_nt, err_his_lgt_nt, exit_flag_lgt_nt = \
optimizeWithNT(x0_lgt_nt, lgt_func, lgt_grad, lgt_hess)
# plot result
fig, ax = plt.subplots(1, 2, figsize=(12,5))
ax[0].plot(obj_his_lgt_nt)
ax[0].set_title('function value')
ax[1].semilogy(err_his_lgt_nt)
ax[1].set_title('optimality condition')
fig.suptitle('Newton\'s Method on Logistic Regression')
plt.savefig('img/lr_nm.pdf',bbox_inches="tight")
plt.show()
```
### Test Logistic Regression
```
# define accuracy function
def accuracy(x, A_test, b_test):
r = A_test.dot(x)
b_test[b_test == 0.0] = -1.0
correct_count = np.sum((r*b_test) > 0.0)
return correct_count/b_test.size
print('accuracy of the result is %0.3f' % accuracy(x_lgt_nt, A_lgt_test, b_lgt_test))
```
| github_jupyter |
# Start with simplest problem
I feel like clasification is the easiest problem catogory to start with.
We will start with simple clasification problem to predict survivals of titanic https://www.kaggle.com/c/titanic
# Contents
1. [Basic pipeline for a predictive modeling problem](#1)
1. [Exploratory Data Analysis (EDA)](#2)
* [Overall survival stats](#2_1)
* [Analysis features](#2_2)
1. [Sex](#2_2_1)
1. [Pclass](#2_2_2)
1. [Age](#2_2_3)
1. [Embarked](#2_2_4)
1. [SibSip & Parch](#2_2_5)
1. [Fare](#2_2_6)
* [Observations Summary](#2_3)
* [Correlation Between The Features](#2_4)
1. [Feature Engineering and Data Cleaning](#4)
* [Converting String Values into Numeric](#4_1)
* [Convert Age into a categorical feature by binning](#4_2)
* [Convert Fare into a categorical feature by binning](#4_3)
* [Dropping Unwanted Features](#4_4)
1. [Predictive Modeling](#5)
* [Cross Validation](#5_1)
* [Confusion Matrix](#5_2)
* [Hyper-Parameters Tuning](#5_3)
* [Ensembling](#5_4)
* [Prediction](#5_5)
1. [Feature Importance](#6)
## **Basic Pipeline for predictive modeling problem**[^](#1)<a id="1" ></a><br>
**<left><span style="color:blue">Exploratory Data Analysis</span> -> <span style="color:blue">Feature Engineering and Data Preparation</span> -> <span style="color:blue">Predictive Modeling</span></left>.**
1. First we need to see what the data can tell us: We call this **<span style="color:blue">Exploratory Data Analysis(EDA)</span>**. Here we look at data which is hidden in rows and column format and try to visualize, summarize and interprete it looking for information.
1. Next we can **leverage domain knowledge** to boost machine learning model performance. We call this step, **<span style="color:blue">Feature Engineering and Data Cleaning</span>**. In this step we might add few features, Remove redundant features, Converting features into suitable form for modeling.
1. Then we can move on to the **<span style="color:blue">Predictive Modeling</span>**. Here we try basic ML algorthms, cross validate, ensemble and Important feature Extraction.
---
## Exploratory Data Analysis (EDA)[^](#2)<a id="2" ></a><br>
With the objective in mind that this kernal aims to explain the workflow of a predictive modelling problem for begginers, I will try to use simple easy to understand visualizations in the EDA section. Kernals with more advanced EDA sections will be mentioned at the end for you to learn more.
```
# Python 3 environment comes with many helpful analytics libraries installed
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
import os
# Read data to a pandas data frame
data=pd.read_csv('../input/train.csv')
# lets have a look on first few rows
display(data.head())
# Checking shape of our data set
print('Shape of Data : ',data.shape)
```
* We have 891 data points (rows); each data point has 12 columns.
```
#checking for null value counts in each column
data.isnull().sum()
```
* The Age, Cabin and Embarked have null values.
### Lets look at overall survival stats[^](#2_1)<a id="2_1" ></a><br>
```
f,ax=plt.subplots(1,2,figsize=(13,5))
data['Survived'].value_counts().plot.pie(explode=[0,0.05],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Survived')
ax[0].set_ylabel('')
sns.countplot('Survived',data=data,ax=ax[1])
ax[1].set_title('Survived')
plt.show()
```
* Sad Story! Only 38% have survived. That is roughly 340 out of 891.
---
### Analyse features[^](#2_2)<a id="2_2" ></a><br>
#### Feature: Sex[^](#3_2_1)<a id="2_2_1" ></a><br>
```
f,ax=plt.subplots(1,3,figsize=(18,5))
data[['Sex','Survived']].groupby(['Sex']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Fraction of Survival with respect to Sex')
sns.countplot('Sex',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Survived vs Dead counts with respect to Sex')
sns.barplot(x="Sex", y="Survived", data=data,ax=ax[2])
ax[2].set_title('Survival by Gender')
plt.show()
```
* While survival rate for female is around 75%, same for men is about 20%.
* It looks like they have given priority to female passengers in the rescue.
* **Looks like Sex is a good predictor on the survival.**
---
#### Feature: Pclass[^](#2_2_2)<a id="2_2_2" ></a><br>
**Meaning :** Ticket class : 1 = 1st, 2 = 2nd, 3 = 3rd
```
f,ax=plt.subplots(1,3,figsize=(18,5))
data['Pclass'].value_counts().plot.bar(color=['#BC8F8F','#F4A460','#DAA520'],ax=ax[0])
ax[0].set_title('Number Of Passengers with respect to Pclass')
ax[0].set_ylabel('Count')
sns.countplot('Pclass',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Survived vs Dead counts with respect to Pclass')
sns.barplot(x="Pclass", y="Survived", data=data,ax=ax[2])
ax[2].set_title('Survival by Pclass')
plt.show()
```
* For Pclass 1 %survived is around 63%, for Pclass2 is around 48% and for Pclass2 is around 25%.
* **So its clear that higher classes had higher priority while rescue.**
* **Looks like Pclass is also an important feature.**
---
#### Feature: Age[^](#2_2_3)<a id="2_2_3" ></a><br>
**Meaning :** Age in years
```
# Plot
plt.figure(figsize=(25,6))
sns.barplot(data['Age'],data['Survived'], ci=None)
plt.xticks(rotation=90);
```
* Survival rate for passenegers below Age 14(i.e children) looks to be good than others.
* So Age seems an important feature too.
* Rememer we had 177 null values in the Age feature. How are we gonna fill them?.
#### Filling Age NaN
Well there are many ways to do this. One can use the mean value or median .. etc.. But can we do better?. Seems yes. [EDA To Prediction(DieTanic)](https://www.kaggle.com/ash316/eda-to-prediction-dietanic#EDA-To-Prediction-(DieTanic)) has used a wonderful method which I would use here too. There is a name feature. First lets extract the initials.
```
data['Initial']=0
for i in data:
data['Initial']=data.Name.str.extract('([A-Za-z]+)\.') #lets extract the Salutations
pd.crosstab(data.Initial,data.Sex).T.style.background_gradient(cmap='summer_r') #Checking the Initials with the Sex
```
Okay so there are some misspelled Initials like Mlle or Mme that stand for Miss. Lets replace them.
```
data['Initial'].replace(['Mlle','Mme','Ms','Dr','Major','Lady','Countess','Jonkheer','Col','Rev','Capt','Sir','Don'],['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mr'],inplace=True)
data.groupby('Initial')['Age'].mean() #lets check the average age by Initials
## Assigning the NaN Values with the Ceil values of the mean ages
data.loc[(data.Age.isnull())&(data.Initial=='Mr'),'Age']=33
data.loc[(data.Age.isnull())&(data.Initial=='Mrs'),'Age']=36
data.loc[(data.Age.isnull())&(data.Initial=='Master'),'Age']=5
data.loc[(data.Age.isnull())&(data.Initial=='Miss'),'Age']=22
data.loc[(data.Age.isnull())&(data.Initial=='Other'),'Age']=46
data.Age.isnull().any() #So no null values left finally
```
---
#### Feature: Embarked[^](#2_2_4)<a id="2_2_4" ></a><br>
**Meaning :** Port of Embarkation. C = Cherbourg, Q = Queenstown, S = Southampton
```
f,ax=plt.subplots(1,2,figsize=(12,5))
sns.countplot('Embarked',data=data,ax=ax[0])
ax[0].set_title('No. Of Passengers Boarded')
sns.countplot('Embarked',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Embarked vs Survived')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
```
* Majority of passengers borded from Southampton
* Survival counts looks better at C. Why?. Could there be an influence from sex and pclass features we already studied?. Let's find out
```
f,ax=plt.subplots(1,2,figsize=(12,5))
sns.countplot('Embarked',hue='Sex',data=data,ax=ax[0])
ax[0].set_title('Male-Female Split for Embarked')
sns.countplot('Embarked',hue='Pclass',data=data,ax=ax[1])
ax[1].set_title('Embarked vs Pclass')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
```
* We guessed correctly. higher % of 1st class passegers boarding from C might be the reason.
#### Filling Embarked NaN
```
f,ax=plt.subplots(1,1,figsize=(6,5))
data['Embarked'].value_counts().plot.pie(explode=[0,0,0],autopct='%1.1f%%',ax=ax)
plt.show()
```
* Since 72.5% passengers are from Southampton, So lets fill missing 2 values using S (Southampton)
```
data['Embarked'].fillna('S',inplace=True)
data.Embarked.isnull().any()
```
---
#### Features: SibSip & Parch[^](#2_2_5)<a id="2_2_5" ></a><br>
**Meaning :**
SibSip -> Number of siblings / spouses aboard the Titanic
Parch -> Number of parents / children aboard the Titanic
SibSip + Parch -> Family Size
```
f,ax=plt.subplots(2,2,figsize=(15,10))
sns.countplot('SibSp',hue='Survived',data=data,ax=ax[0,0])
ax[0,0].set_title('SibSp vs Survived')
sns.barplot('SibSp','Survived',data=data,ax=ax[0,1])
ax[0,1].set_title('SibSp vs Survived')
sns.countplot('Parch',hue='Survived',data=data,ax=ax[1,0])
ax[1,0].set_title('Parch vs Survived')
sns.barplot('Parch','Survived',data=data,ax=ax[1,1])
ax[1,1].set_title('Parch vs Survived')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
```
* The barplot and factorplot shows that if a passenger is alone onboard with no siblings, he have 34.5% survival rate. The graph roughly decreases if the number of siblings increase.
Lets combine above and analyse family size.
```
data['FamilySize'] = data['Parch'] + data['SibSp']
f,ax=plt.subplots(1,2,figsize=(15,4.5))
sns.countplot('FamilySize',hue='Survived',data=data,ax=ax[0])
ax[0].set_title('FamilySize vs Survived')
sns.barplot('FamilySize','Survived',data=data,ax=ax[1])
ax[1].set_title('FamilySize vs Survived')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
```
* This looks interesting! looks like family sizes of 1-3 have better survival rates than others.
---
#### Fare[^](#2_2_6)<a id="2_2_6" ></a><br>
**Meaning :** Passenger fare
```
f,ax=plt.subplots(1,1,figsize=(20,5))
sns.distplot(data.Fare,ax=ax)
ax.set_title('Distribution of Fares')
plt.show()
print('Highest Fare:',data['Fare'].max(),' Lowest Fare:',data['Fare'].min(),' Average Fare:',data['Fare'].mean())
data['Fare_Bin']=pd.qcut(data['Fare'],6)
data.groupby(['Fare_Bin'])['Survived'].mean().to_frame().style.background_gradient(cmap='summer_r')
```
* It is clear that as Fare Bins increase chances of survival increase too.
#### Observations Summary[^](#2_3)<a id="2_3" ></a><br>
**Sex:** Survival chance for female is better than that for male.
**Pclass:** Being a 1st class passenger gives you better chances of survival.
**Age:** Age range 5-10 years have a high chance of survival.
**Embarked:** Majority of passengers borded from Southampton.The chances of survival at C looks to be better than even though the majority of Pclass1 passengers got up at S. All most all Passengers at Q were from Pclass3.
**Family Size:** looks like family sizes of 1-3 have better survival rates than others.
**Fare:** As Fare Bins increase chances of survival increases
#### Correlation Between The Features[^](#2_4)<a id="2_4" ></a><br>
```
sns.heatmap(data.corr(),annot=True,cmap='RdYlGn',linewidths=0.2) #data.corr()-->correlation matrix
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()
```
---
## Feature Engineering and Data Cleaning[^](#4)<a id="4" ></a><br>
Now what is Feature Engineering? Feature engineering is the process of using domain knowledge of the data to create features that make machine learning algorithms work.
In this section we will be doing,
1. Converting String Values into Numeric
1. Convert Age into a categorical feature by binning
1. Convert Fare into a categorical feature by binning
1. Dropping Unwanted Features
#### Converting String Values into Numeric[^](#4_1)<a id="4_1" ></a><br>
Since we cannot pass strings to a machine learning model, we need to convert features Sex, Embarked, etc into numeric values.
```
data['Sex'].replace(['male','female'],[0,1],inplace=True)
data['Embarked'].replace(['S','C','Q'],[0,1,2],inplace=True)
data['Initial'].replace(['Mr','Mrs','Miss','Master','Other'],[0,1,2,3,4],inplace=True)
```
#### Convert Age into a categorical feature by binning[^](#4_2)<a id="4_2" ></a><br>
```
print('Highest Age:',data['Age'].max(),' Lowest Age:',data['Age'].min())
data['Age_cat']=0
data.loc[data['Age']<=16,'Age_cat']=0
data.loc[(data['Age']>16)&(data['Age']<=32),'Age_cat']=1
data.loc[(data['Age']>32)&(data['Age']<=48),'Age_cat']=2
data.loc[(data['Age']>48)&(data['Age']<=64),'Age_cat']=3
data.loc[data['Age']>64,'Age_cat']=4
```
#### Convert Fare into a categorical feature by binning[^](#4_3)<a id="4_3" ></a><br>
```
data['Fare_cat']=0
data.loc[data['Fare']<=7.775,'Fare_cat']=0
data.loc[(data['Fare']>7.775)&(data['Fare']<=8.662),'Fare_cat']=1
data.loc[(data['Fare']>8.662)&(data['Fare']<=14.454),'Fare_cat']=2
data.loc[(data['Fare']>14.454)&(data['Fare']<=26.0),'Fare_cat']=3
data.loc[(data['Fare']>26.0)&(data['Fare']<=52.369),'Fare_cat']=4
data.loc[data['Fare']>52.369,'Fare_cat']=5
```
#### Dropping Unwanted Features[^](#4_4)<a id="4_4" ></a><br>
Name--> We don't need name feature as it cannot be converted into any categorical value.
Age--> We have the Age_cat feature, so no need of this.
Ticket--> It is any random string that cannot be categorised.
Fare--> We have the Fare_cat feature, so unneeded
Cabin--> A lot of NaN values and also many passengers have multiple cabins. So this is a useless feature.
Fare_Bin--> We have the fare_cat feature.
PassengerId--> Cannot be categorised.
Sibsp & Parch --> We got FamilySize feature
```
#data.drop(['Name','Age','Ticket','Fare','Cabin','Fare_Range','PassengerId'],axis=1,inplace=True)
data.drop(['Name','Age','Fare','Ticket','Cabin','Fare_Bin','SibSp','Parch','PassengerId'],axis=1,inplace=True)
data.head(2)
sns.heatmap(data.corr(),annot=True,cmap='RdYlGn',linewidths=0.2) #data.corr()-->correlation matrix
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()
```
---
## Predictive Modeling[^](#5)<a id="5" ></a><br>
Now after data cleaning and feature engineering we are ready to train some classification algorithms that will make predictions for unseen data. We will first train few classification algorithms and see how they perform. Then we can look how an ensemble of classification algorithms perform on this data set.
Following Machine Learning algorithms will be used in this kernal.
* Logistic Regression Classifier
* Naive Bayes Classifier
* Decision Tree Classifier
* Random Forest Classifier
```
#importing all the required ML packages
from sklearn.linear_model import LogisticRegression #logistic regression
from sklearn.ensemble import RandomForestClassifier #Random Forest
from sklearn.naive_bayes import GaussianNB #Naive bayes
from sklearn.tree import DecisionTreeClassifier #Decision Tree
from sklearn.model_selection import train_test_split #training and testing data split
from sklearn import metrics #accuracy measure
from sklearn.metrics import confusion_matrix #for confusion matrix
#Lets prepare data sets for training.
train,test=train_test_split(data,test_size=0.3,random_state=0,stratify=data['Survived'])
train_X=train[train.columns[1:]]
train_Y=train[train.columns[:1]]
test_X=test[test.columns[1:]]
test_Y=test[test.columns[:1]]
X=data[data.columns[1:]]
Y=data['Survived']
data.head(2)
# Logistic Regression
model = LogisticRegression(C=0.05,solver='liblinear')
model.fit(train_X,train_Y.values.ravel())
LR_prediction=model.predict(test_X)
print('The accuracy of the Logistic Regression model is \t',metrics.accuracy_score(LR_prediction,test_Y))
# Naive Bayes
model=GaussianNB()
model.fit(train_X,train_Y.values.ravel())
NB_prediction=model.predict(test_X)
print('The accuracy of the NaiveBayes model is\t\t\t',metrics.accuracy_score(NB_prediction,test_Y))
# Decision Tree
model=DecisionTreeClassifier()
model.fit(train_X,train_Y)
DT_prediction=model.predict(test_X)
print('The accuracy of the Decision Tree is \t\t\t',metrics.accuracy_score(DT_prediction,test_Y))
# Random Forest
model=RandomForestClassifier(n_estimators=100)
model.fit(train_X,train_Y.values.ravel())
RF_prediction=model.predict(test_X)
print('The accuracy of the Random Forests model is \t\t',metrics.accuracy_score(RF_prediction,test_Y))
```
### Cross Validation[^](#5_1)<a id="5_1" ></a><br>
Accuracy we get here higlhy depends on the train & test data split of the original data set. We can use cross validation to avoid such problems arising from dataset splitting.
I am using K-fold cross validation here. Watch this short [vedio](https://www.youtube.com/watch?v=TIgfjmp-4BA) to understand what it is.
```
from sklearn.model_selection import KFold #for K-fold cross validation
from sklearn.model_selection import cross_val_score #score evaluation
from sklearn.model_selection import cross_val_predict #prediction
kfold = KFold(n_splits=10, random_state=22) # k=10, split the data into 10 equal parts
xyz=[]
accuracy=[]
std=[]
classifiers=['Logistic Regression','Decision Tree','Naive Bayes','Random Forest']
models=[LogisticRegression(solver='liblinear'),DecisionTreeClassifier(),GaussianNB(),RandomForestClassifier(n_estimators=100)]
for i in models:
model = i
cv_result = cross_val_score(model,X,Y, cv = kfold,scoring = "accuracy")
xyz.append(cv_result.mean())
std.append(cv_result.std())
accuracy.append(cv_result)
new_models_dataframe2=pd.DataFrame({'CV Mean':xyz,'Std':std},index=classifiers)
new_models_dataframe2
```
Now we have looked at cross validation accuracies to get an idea how those models work. There is more we can do to understand the performances of the models we tried ; let's have a look at confusion matrix for each model.
### Confusion Matrix[^](#5_2)<a id="5_2" ></a><br>
A confusion matrix is a table that is often used to describe the performance of a classification model. read more [here](https://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/)
```
f,ax=plt.subplots(2,2,figsize=(10,8))
y_pred = cross_val_predict(LogisticRegression(C=0.05,solver='liblinear'),X,Y,cv=10)
sns.heatmap(confusion_matrix(Y,y_pred),ax=ax[0,0],annot=True,fmt='2.0f')
ax[0,0].set_title('Matrix for Logistic Regression')
y_pred = cross_val_predict(DecisionTreeClassifier(),X,Y,cv=10)
sns.heatmap(confusion_matrix(Y,y_pred),ax=ax[0,1],annot=True,fmt='2.0f')
ax[0,1].set_title('Matrix for Decision Tree')
y_pred = cross_val_predict(GaussianNB(),X,Y,cv=10)
sns.heatmap(confusion_matrix(Y,y_pred),ax=ax[1,0],annot=True,fmt='2.0f')
ax[1,0].set_title('Matrix for Naive Bayes')
y_pred = cross_val_predict(RandomForestClassifier(n_estimators=100),X,Y,cv=10)
sns.heatmap(confusion_matrix(Y,y_pred),ax=ax[1,1],annot=True,fmt='2.0f')
ax[1,1].set_title('Matrix for Random-Forests')
plt.subplots_adjust(hspace=0.2,wspace=0.2)
plt.show()
```
* By looking at above matrices we can say that, if we are more concerned on making less mistakes by predicting survived as dead, then Naive Bayes model does better.
* If we are more concerned on making less mistakes by predicting dead as survived, then Decision Tree model does better.
### Hyper-Parameters Tuning[^](#5_3)<a id="5_3" ></a><br>
You might have noticed there are few parameters for each model which defines how the model learns. We call these hyperparameters. These hyperparameters can be tuned to improve performance. Let's try this for Random Forest classifier.
```
from sklearn.model_selection import GridSearchCV
n_estimators=range(100,1000,100)
hyper={'n_estimators':n_estimators}
gd=GridSearchCV(estimator=RandomForestClassifier(random_state=0),param_grid=hyper,verbose=True,cv=10)
gd.fit(X,Y)
print(gd.best_score_)
print(gd.best_estimator_)
```
* Best Score for Random Forest is with n_estimators=100
### Ensembling[^](#5_4)<a id="5_4" ></a><br>
Ensembling is a way to increase performance of a model by combining several simple models to create a single powerful model.
read more about ensembling [here](https://www.analyticsvidhya.com/blog/2018/06/comprehensive-guide-for-ensemble-models/).
Ensembling can be done in ways like: Voting Classifier, Bagging, Boosting.
I will use voting method in this kernal
```
from sklearn.ensemble import VotingClassifier
estimators=[('RFor',RandomForestClassifier(n_estimators=100,random_state=0)),
('LR',LogisticRegression(C=0.05,solver='liblinear')),
('DT',DecisionTreeClassifier()),
('NB',GaussianNB())]
ensemble=VotingClassifier(estimators=estimators,voting='soft')
ensemble.fit(train_X,train_Y.values.ravel())
print('The accuracy for ensembled model is:',ensemble.score(test_X,test_Y))
cross=cross_val_score(ensemble,X,Y, cv = 10,scoring = "accuracy")
print('The cross validated score is',cross.mean())
```
### Prediction[^](#5_5)<a id="5_5" ></a><br>
We can see that ensemble model does better than individual models. lets use that for predictions.
```
Ensemble_Model_For_Prediction=VotingClassifier(estimators=[
('RFor',RandomForestClassifier(n_estimators=200,random_state=0)),
('LR',LogisticRegression(C=0.05,solver='liblinear')),
('DT',DecisionTreeClassifier(random_state=0)),
('NB',GaussianNB())
],
voting='soft')
Ensemble_Model_For_Prediction.fit(X,Y)
```
We need to do some preprocessing to this test data set before we can feed that to the trained model.
```
test=pd.read_csv('../input/test.csv')
IDtest = test["PassengerId"]
test.head(2)
test.isnull().sum()
# Prepare Test Data set for feeding
# Construct feature Initial
test['Initial']=0
for i in test:
test['Initial']=test.Name.str.extract('([A-Za-z]+)\.') #lets extract the Salutations
test['Initial'].replace(['Mlle','Mme','Ms','Dr','Major','Lady','Countess','Jonkheer','Col','Rev','Capt','Sir','Don','Dona'],['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mr','Other'],inplace=True)
# Fill Null values in Age Column
test.loc[(test.Age.isnull())&(test.Initial=='Mr'),'Age']=33
test.loc[(test.Age.isnull())&(test.Initial=='Mrs'),'Age']=36
test.loc[(test.Age.isnull())&(test.Initial=='Master'),'Age']=5
test.loc[(test.Age.isnull())&(test.Initial=='Miss'),'Age']=22
test.loc[(test.Age.isnull())&(test.Initial=='Other'),'Age']=46
# Fill Null values in Fare Column
test.loc[(test.Fare.isnull()) & (test['Pclass']==3),'Fare'] = 12.45
# Construct feature Age_cat
test['Age_cat']=0
test.loc[test['Age']<=16,'Age_cat']=0
test.loc[(test['Age']>16)&(test['Age']<=32),'Age_cat']=1
test.loc[(test['Age']>32)&(test['Age']<=48),'Age_cat']=2
test.loc[(test['Age']>48)&(test['Age']<=64),'Age_cat']=3
test.loc[test['Age']>64,'Age_cat']=4
# Construct feature Fare_cat
test['Fare_cat']=0
test.loc[test['Fare']<=7.775,'Fare_cat']=0
test.loc[(test['Fare']>7.775)&(test['Fare']<=8.662),'Fare_cat']=1
test.loc[(test['Fare']>8.662)&(test['Fare']<=14.454),'Fare_cat']=2
test.loc[(test['Fare']>14.454)&(test['Fare']<=26.0),'Fare_cat']=3
test.loc[(test['Fare']>26.0)&(test['Fare']<=52.369),'Fare_cat']=4
test.loc[test['Fare']>52.369,'Fare_cat']=5
# Construct feature FamilySize
test['FamilySize'] = test['Parch'] + test['SibSp']
# Drop unwanted features
test.drop(['Name','Age','Ticket','Cabin','SibSp','Parch','Fare','PassengerId'],axis=1,inplace=True)
# Converting String Values into Numeric
test['Sex'].replace(['male','female'],[0,1],inplace=True)
test['Embarked'].replace(['S','C','Q'],[0,1,2],inplace=True)
test['Initial'].replace(['Mr','Mrs','Miss','Master','Other'],[0,1,2,3,4],inplace=True)
test.head(2)
# Predict
test_Survived = pd.Series(ensemble.predict(test), name="Survived")
results = pd.concat([IDtest,test_Survived],axis=1)
results.to_csv("predictions.csv",index=False)
```
## Feature Importance[^](#6)<a id="6" ></a><br>
Well after we have trained a model to make predictions for us, we feel curiuos on how it works. What are the features model weights more when trying to make a prediction?. As humans we seek to understand how it works. Looking at feature importances of a trained model is one way we could explain the decisions it make. Lets visualize the feature importances of the Random forest model we used inside the ensemble above.
```
f,ax=plt.subplots(1,1,figsize=(6,6))
model=RandomForestClassifier(n_estimators=500,random_state=0)
model.fit(X,Y)
pd.Series(model.feature_importances_,X.columns).sort_values(ascending=True).plot.barh(width=0.8,ax=ax)
ax.set_title('Feature Importance in Random Forests')
plt.show()
```
**If You Like the notebook and think that it helped you, please upvote to It keep motivate me**
| github_jupyter |
# ディープラーニングに必要な数学と NumPy の操作
# 1. NumPy の基本
## NumPy のインポート
```
import numpy as np
```
## ndarray による1次元配列の例
```
a1 = np.array([1, 2, 3]) # 1次元配列を生成
print('変数の型:',type(a1))
print('データの型 (dtype):', a1.dtype)
print('要素の数 (size):', a1.size)
print('形状 (shape):', a1.shape)
print('次元の数 (ndim):', a1.ndim)
print('中身:', a1)
```
## ndarray による1次元配列の例
```
a2 = np.array([[1, 2, 3],[4, 5, 6]], dtype='float32') # データ型 float32 の2次元配列を生成
print('データの型 (dtype):', a2.dtype)
print('要素の数 (size):', a2.size)
print('形状 (shape):', a2.shape)
print('次元の数 (ndim):', a2.ndim)
print('中身:', a2)
```
# 2. ベクトル(1次元配列)
## ベクトル a の生成(1次元配列の生成)
```
a = np.array([4, 1])
```
## ベクトルのスカラー倍
```
for k in (2, 0.5, -1):
print(k * a)
```
## ベクトルの和と差
```
b = np.array([1, 2]) # ベクトル b の生成
print('a + b =', a + b) # ベクトル a とベクトル b の和
print('a - b =', a - b) # ベクトル a とベクトル b の差
```
# 3. 行列(2次元配列)
## 行列を2次元配列で生成
```
A = np.array([[1, 2], [3 ,4], [5, 6]])
B = np.array([[5, 6], [7 ,8]])
print('A:\n', A)
print('A.shape:', A.shape )
print()
print('B:\n', B)
print('B.shape:', B.shape )
```
## 行列Aの i = 3, j = 2 にアクセス
```
print(A[2][1])
```
## A の転置行列
```
print(A.T)
```
## 行列のスカラー倍
```
print(2 * A)
```
## 行列の和と差
```
print('A + A:\n', A + A) # 行列 A と行列 A の和
print()
print('A - A:\n', A - A) # 行列 A と行列 A の差
```
## 行列 A と行列 B の和
```
print(A + B)
```
## 行列の積
```
print(np.dot(A, B))
```
## 積 BA
```
print(np.dot(B, A))
```
## アダマール積 A $\circ$ A
```
print(A * A)
```
## 行列 X と行ベクトル a の積
```
X = np.array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
a = np.array([[1, 2, 3, 4, 5]])
print('X.shape:', X.shape)
print('a.shape:', a.shape)
print(np.dot(X, a))
```
## 行列 X と列ベクトル a の積
```
X = np.array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
a = np.array([[1],
[2],
[3],
[4],
[5]])
print('X.shape:', X.shape)
print('a.shape:', a.shape)
Xa = np.dot(X, a)
print('Xa.shape:', Xa.shape)
print('Xa:\n', Xa)
```
## NumPy による行列 X と1次元配列の積
```
X = np.array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
a = np.array([1, 2, 3, 4, 5]) # 1次元配列で生成
print('X.shape:', X.shape)
print('a.shape:', a.shape)
Xa = np.dot(X, a)
print('Xa.shape:', Xa.shape)
print('Xa:\n', Xa)
import numpy as np
np.array([1, 0.1])
```
# 4. ndarray の 軸(axis)について
## Aの合計を計算
```
np.sum(A)
```
## axis = 0 で A の合計を計算
```
print(np.sum(A, axis=0).shape)
print(np.sum(A, axis=0))
```
## axis = 1 で A の合計を計算
```
print(np.sum(A, axis=1).shape)
print(np.sum(A, axis=1))
```
## np.max 関数の利用例
```
Y_hat = np.array([[3, 4], [6, 5], [7, 8]]) # 2次元配列を生成
print(np.max(Y_hat)) # axis 指定なし
print(np.max(Y_hat, axis=1)) # axix=1 を指定
```
## argmax 関数の利用例
```
print(np.argmax(Y_hat)) # axis 指定なし
print(np.argmax(Y_hat, axis=1)) # axix=1 を指定
```
# 5. 3次元以上の配列
## 行列 A を4つ持つ配列の生成
```
A_arr = np.array([A, A, A, A])
print(A_arr.shape)
```
## A_arr の合計を計算
```
np.sum(A_arr)
```
## axis = 0 を指定して A_arr の合計を計算
```
print(np.sum(A_arr, axis=0).shape)
print(np.sum(A_arr, axis=0))
```
## axis = (1, 2) を指定して A_arr の合計を計算
```
print(np.sum(A_arr, axis=(1, 2)))
```
| github_jupyter |
<a href="https://colab.research.google.com/github/mohameddhameem/TensorflowCertification/blob/main/Natural%20Language%20Processing%20in%20TensorFlow/Lesson%203/NLP_Course_Week_3_Exercise_Question.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import json
import tensorflow as tf
import csv
import random
import numpy as np
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import regularizers
embedding_dim = 100
max_length = 16
trunc_type='post'
padding_type='post'
oov_tok = "<OOV>"
training_size= 160000#Your dataset size here. Experiment using smaller values (i.e. 16000), but don't forget to train on at least 160000 to see the best effects
test_portion=.1
corpus = []
# Note that I cleaned the Stanford dataset to remove LATIN1 encoding to make it easier for Python CSV reader
# You can do that yourself with:
# iconv -f LATIN1 -t UTF8 training.1600000.processed.noemoticon.csv -o training_cleaned.csv
# I then hosted it on my site to make it easier to use in this notebook
!wget --no-check-certificate \
https://storage.googleapis.com/laurencemoroney-blog.appspot.com/training_cleaned.csv \
-O /tmp/training_cleaned.csv
num_sentences = 0
with open("/tmp/training_cleaned.csv") as csvfile:
reader = csv.reader(csvfile, delimiter=',')
for row in reader:
# Your Code here. Create list items where the first item is the text, found in row[5], and the second is the label. Note that the label is a '0' or a '4' in the text. When it's the former, make
# your label to be 0, otherwise 1. Keep a count of the number of sentences in num_sentences
list_item=[]
list_item.append(row[5])
this_label=row[0]
if this_label == '0':
list_item.append(0)
else:
list_item.append(1)
# YOUR CODE HERE
num_sentences = num_sentences + 1
corpus.append(list_item)
print(num_sentences)
print(len(corpus))
print(corpus[1])
# Expected Output:
# 1600000
# 1600000
# ["is upset that he can't update his Facebook by texting it... and might cry as a result School today also. Blah!", 0]
sentences=[]
labels=[]
random.shuffle(corpus)
for x in range(training_size):
sentences.append(corpus[x][0])
labels.append(corpus[x][1])
tokenizer = Tokenizer(oov_token=oov_tok)
tokenizer.fit_on_texts(sentences)# YOUR CODE HERE
word_index = tokenizer.word_index
vocab_size=len(word_index)
sequences = tokenizer.texts_to_sequences(sentences)# YOUR CODE HERE
padded = pad_sequences(sequences,maxlen=max_length, padding=padding_type,truncating=trunc_type)# YOUR CODE HERE
split = int(test_portion * training_size)
print(split)
test_sequences = padded[0:split]
training_sequences = padded[split:training_size]
test_labels = labels[0:split]
training_labels = labels[split:training_size]
print(vocab_size)
print(word_index['i'])
# Expected Output
# 138858
# 1
!wget http://nlp.stanford.edu/data/glove.6B.zip
!unzip /content/glove.6B.zip
# Note this is the 100 dimension version of GloVe from Stanford
# I unzipped and hosted it on my site to make this notebook easier
#### NOTE - Below link is not working. So download and zip on your own
#!wget --no-check-certificate \
# https://storage.googleapis.com/laurencemoroney-blog.appspot.com/glove.6B.100d.txt \
# -O /tmp/glove.6B.100d.txt
embeddings_index = {};
with open('/content/glove.6B.100d.txt') as f:
for line in f:
values = line.split();
word = values[0];
coefs = np.asarray(values[1:], dtype='float32');
embeddings_index[word] = coefs;
embeddings_matrix = np.zeros((vocab_size+1, embedding_dim));
for word, i in word_index.items():
embedding_vector = embeddings_index.get(word);
if embedding_vector is not None:
embeddings_matrix[i] = embedding_vector;
print(len(embeddings_matrix))
# Expected Output
# 138859
training_padded = np.asarray(training_sequences)
training_labels_np = np.asarray(training_labels)
testing_padded = np.asarray(test_sequences)
testing_labels_np = np.asarray(test_labels)
print(training_labels)
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size+1, embedding_dim, input_length=max_length, weights=[embeddings_matrix], trainable=False),
# YOUR CODE HERE - experiment with combining different types, such as convolutions and LSTMs
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Conv1D(64, 5, activation='relu'),
tf.keras.layers.MaxPooling1D(pool_size=4),
#tf.keras.layers.LSTM(64),
tf.keras.layers.Bidirectional(tf.keras.layers.GRU(32)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])# YOUR CODE HERE
model.summary()
num_epochs = 50
history = model.fit(training_padded, training_labels_np, epochs=num_epochs, validation_data=(testing_padded, testing_labels_np), verbose=2)
print("Training Complete")
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc=history.history['accuracy']
val_acc=history.history['val_accuracy']
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=range(len(acc)) # Get number of epochs
#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot(epochs, acc, 'r')
plt.plot(epochs, val_acc, 'b')
plt.title('Training and validation accuracy')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["Accuracy", "Validation Accuracy"])
plt.figure()
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(epochs, loss, 'r')
plt.plot(epochs, val_loss, 'b')
plt.title('Training and validation loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(["Loss", "Validation Loss"])
plt.figure()
# Expected Output
# A chart where the validation loss does not increase sharply!
```
| github_jupyter |
# 01.2 Scattering Compute Speed
**NOT COMPLETED**
In this notebook, the speed to extract scattering coefficients is computed.
```
import sys
import random
import os
sys.path.append('../src')
import warnings
warnings.filterwarnings("ignore")
import torch
from tqdm import tqdm
from kymatio.torch import Scattering2D
import time
import kymatio.scattering2d.backend as backend
###############################################################################
# Finally, we import the `Scattering2D` class that computes the scattering
# transform.
from kymatio import Scattering2D
```
# 3. Scattering Speed Test
```
# From: https://github.com/kymatio/kymatio/blob/0.1.X/examples/2d/compute_speed.py
# Benchmark setup
# --------------------
J = 3
L = 8
times = 10
devices = ['cpu', 'gpu']
scattering = Scattering2D(J, shape=(M, N), L=L, backend='torch_skcuda')
data = np.concatenate(dataset['img'],axis=0)
data = torch.from_numpy(data)
x = data[0:batch_size]
%%time
#mlflow.set_experiment('compute_speed_scattering')
for device in devices:
#with mlflow.start_run():
fmt_str = '==> Testing Float32 with {} backend, on {}, forward'
print(fmt_str.format('torch', device.upper()))
if device == 'gpu':
scattering.cuda()
x = x.cuda()
else:
scattering.cpu()
x = x.cpu()
scattering.forward(x)
if device == 'gpu':
torch.cuda.synchronize()
t_start = time.time()
for _ in range(times):
scattering.forward(x)
if device == 'gpu':
torch.cuda.synchronize()
t_elapsed = time.time() - t_start
fmt_str = 'Elapsed time: {:2f} [s / {:d} evals], avg: {:.2f} (s/batch)'
print(fmt_str.format(t_elapsed, times, t_elapsed/times))
# mlflow.log_param('M',M)
# mlflow.log_param('N',N)
# mlflow.log_param('Backend', device.upper())
# mlflow.log_param('J', J)
# mlflow.log_param('L', L)
# mlflow.log_param('Batch Size', batch_size)
# mlflow.log_param('Times', times)
# mlflow.log_metric('Elapsed Time', t_elapsed)
# mlflow.log_metric('Average Time', times)
###############################################################################
# The resulting output should be something like
#
# .. code-block:: text
#
# ==> Testing Float32 with torch backend, on CPU, forward
# Elapsed time: 624.910853 [s / 10 evals], avg: 62.49 (s/batch)
# ==> Testing Float32 with torch backend, on GPU, forward
```
| github_jupyter |
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [nbpages](https://jckantor.github.io/nbpages) by Jeffrey Kantor (jeff at nd.edu). The text is released under the
[CC-BY-NC-ND-4.0 license](https://creativecommons.org/licenses/by-nc-nd/4.0/legalcode).
The code is released under the [MIT license](https://opensource.org/licenses/MIT).*
<!--NAVIGATION-->
< [2.3 Heirarchical Tagging](https://jckantor.github.io/nbpages/02.03-Heirarchical-Tagging.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.5 Lint](https://jckantor.github.io/nbpages/02.05-Lint.html) ><p><a href="https://colab.research.google.com/github/jckantor/nbpages/blob/master/docs/02.04-Working-with-Data-and-Figures.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/nbpages/02.04-Working-with-Data-and-Figures.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
```
# IMPORT DATA FILES USED BY THIS NOTEBOOK
import os, requests
file_links = [("data/Stock_Data.csv", "https://jckantor.github.io/nbpages/data/Stock_Data.csv")]
# This cell has been added by nbpages. Run this cell to download data files required for this notebook.
for filepath, fileurl in file_links:
stem, filename = os.path.split(filepath)
if stem:
if not os.path.exists(stem):
os.mkdir(stem)
if not os.path.isfile(filepath):
with open(filepath, 'wb') as f:
response = requests.get(fileurl)
f.write(response.content)
```
# 2.4 Working with Data and Figures
## 2.4.1 Importing data
The following cell reads the data file `Stock_Data.csv` from the `data` subdirectory. The name of this file will appear in the data index.
```
import pandas as pd
df = pd.read_csv("data/Stock_Data.csv")
df.head()
```
## 2.4.2 Creating and saving figures
The following cell creates a figure `Stock_Data.png` in the `figures` subdirectory. The name of this file will appear in the figures index.
```
%matplotlib inline
import os
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("darkgrid")
fig, ax = plt.subplots(2, 1, figsize=(8, 5))
(df/df.iloc[0]).drop('VIX', axis=1).plot(ax=ax[0])
df['VIX'].plot(ax=ax[1])
ax[0].set_title('Normalized Indices')
ax[1].set_title('Volatility VIX')
ax[1].set_xlabel('Days')
fig.tight_layout()
if not os.path.exists("figures"):
os.mkdir("figures")
plt.savefig("figures/Stock_Data.png")
```
<!--NAVIGATION-->
< [2.3 Heirarchical Tagging](https://jckantor.github.io/nbpages/02.03-Heirarchical-Tagging.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.5 Lint](https://jckantor.github.io/nbpages/02.05-Lint.html) ><p><a href="https://colab.research.google.com/github/jckantor/nbpages/blob/master/docs/02.04-Working-with-Data-and-Figures.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/nbpages/02.04-Working-with-Data-and-Figures.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
| github_jupyter |
# Homework #4
These problem sets focus on list comprehensions, string operations and regular expressions.
## Problem set #1: List slices and list comprehensions
Let's start with some data. The following cell contains a string with comma-separated integers, assigned to a variable called `numbers_str`:
```
numbers_str = '496,258,332,550,506,699,7,985,171,581,436,804,736,528,65,855,68,279,721,120'
```
In the following cell, complete the code with an expression that evaluates to a list of integers derived from the raw numbers in `numbers_str`, assigning the value of this expression to a variable `numbers`. If you do everything correctly, executing the cell should produce the output `985` (*not* `'985'`).
```
values = numbers_str.split(",")
numbers = [int(i) for i in values]
# numbers
max(numbers)
```
Great! We'll be using the `numbers` list you created above in the next few problems.
In the cell below, fill in the square brackets so that the expression evaluates to a list of the ten largest values in `numbers`. Expected output:
[506, 528, 550, 581, 699, 721, 736, 804, 855, 985]
(Hint: use a slice.)
```
#test
print(sorted(numbers))
sorted(numbers)[10:]
```
In the cell below, write an expression that evaluates to a list of the integers from `numbers` that are evenly divisible by three, *sorted in numerical order*. Expected output:
[120, 171, 258, 279, 528, 699, 804, 855]
```
[i for i in sorted(numbers) if i%3 == 0]
```
Okay. You're doing great. Now, in the cell below, write an expression that evaluates to a list of the square roots of all the integers in `numbers` that are less than 100. In order to do this, you'll need to use the `sqrt` function from the `math` module, which I've already imported for you. Expected output:
[2.6457513110645907, 8.06225774829855, 8.246211251235321]
(These outputs might vary slightly depending on your platform.)
```
import math
from math import sqrt
[math.sqrt(i) for i in sorted(numbers) if i < 100]
```
## Problem set #2: Still more list comprehensions
Still looking good. Let's do a few more with some different data. In the cell below, I've defined a data structure and assigned it to a variable `planets`. It's a list of dictionaries, with each dictionary describing the characteristics of a planet in the solar system. Make sure to run the cell before you proceed.
```
planets = [
{'diameter': 0.382,
'mass': 0.06,
'moons': 0,
'name': 'Mercury',
'orbital_period': 0.24,
'rings': 'no',
'type': 'terrestrial'},
{'diameter': 0.949,
'mass': 0.82,
'moons': 0,
'name': 'Venus',
'orbital_period': 0.62,
'rings': 'no',
'type': 'terrestrial'},
{'diameter': 1.00,
'mass': 1.00,
'moons': 1,
'name': 'Earth',
'orbital_period': 1.00,
'rings': 'no',
'type': 'terrestrial'},
{'diameter': 0.532,
'mass': 0.11,
'moons': 2,
'name': 'Mars',
'orbital_period': 1.88,
'rings': 'no',
'type': 'terrestrial'},
{'diameter': 11.209,
'mass': 317.8,
'moons': 67,
'name': 'Jupiter',
'orbital_period': 11.86,
'rings': 'yes',
'type': 'gas giant'},
{'diameter': 9.449,
'mass': 95.2,
'moons': 62,
'name': 'Saturn',
'orbital_period': 29.46,
'rings': 'yes',
'type': 'gas giant'},
{'diameter': 4.007,
'mass': 14.6,
'moons': 27,
'name': 'Uranus',
'orbital_period': 84.01,
'rings': 'yes',
'type': 'ice giant'},
{'diameter': 3.883,
'mass': 17.2,
'moons': 14,
'name': 'Neptune',
'orbital_period': 164.8,
'rings': 'yes',
'type': 'ice giant'}]
```
Now, in the cell below, write a list comprehension that evaluates to a list of names of the planets that have a radius greater than four earth radii. Expected output:
['Jupiter', 'Saturn', 'Uranus']
```
earth_diameter = planets[2]['diameter']
#earth radius is = half diameter. In a multiplication equation the diameter value can be use as a parameter.
[i['name'] for i in planets if i['diameter'] >= earth_diameter*4]
```
In the cell below, write a single expression that evaluates to the sum of the mass of all planets in the solar system. Expected output: `446.79`
```
mass_list = []
for planet in planets:
outcome = planet['mass']
mass_list.append(outcome)
total = sum(mass_list)
total
```
Good work. Last one with the planets. Write an expression that evaluates to the names of the planets that have the word `giant` anywhere in the value for their `type` key. Expected output:
['Jupiter', 'Saturn', 'Uranus', 'Neptune']
```
[i['name'] for i in planets if 'giant' in i['type']]
```
*EXTREME BONUS ROUND*: Write an expression below that evaluates to a list of the names of the planets in ascending order by their number of moons. (The easiest way to do this involves using the [`key` parameter of the `sorted` function](https://docs.python.org/3.5/library/functions.html#sorted), which we haven't yet discussed in class! That's why this is an EXTREME BONUS question.) Expected output:
['Mercury', 'Venus', 'Earth', 'Mars', 'Neptune', 'Uranus', 'Saturn', 'Jupiter']
```
#Done in class
```
## Problem set #3: Regular expressions
In the following section, we're going to do a bit of digital humanities. (I guess this could also be journalism if you were... writing an investigative piece about... early 20th century American poetry?) We'll be working with the following text, Robert Frost's *The Road Not Taken*. Make sure to run the following cell before you proceed.
```
import re
poem_lines = ['Two roads diverged in a yellow wood,',
'And sorry I could not travel both',
'And be one traveler, long I stood',
'And looked down one as far as I could',
'To where it bent in the undergrowth;',
'',
'Then took the other, as just as fair,',
'And having perhaps the better claim,',
'Because it was grassy and wanted wear;',
'Though as for that the passing there',
'Had worn them really about the same,',
'',
'And both that morning equally lay',
'In leaves no step had trodden black.',
'Oh, I kept the first for another day!',
'Yet knowing how way leads on to way,',
'I doubted if I should ever come back.',
'',
'I shall be telling this with a sigh',
'Somewhere ages and ages hence:',
'Two roads diverged in a wood, and I---',
'I took the one less travelled by,',
'And that has made all the difference.']
```
In the cell above, I defined a variable `poem_lines` which has a list of lines in the poem, and `import`ed the `re` library.
In the cell below, write a list comprehension (using `re.search()`) that evaluates to a list of lines that contain two words next to each other (separated by a space) that have exactly four characters. (Hint: use the `\b` anchor. Don't overthink the "two words in a row" requirement.)
Expected result:
```
['Then took the other, as just as fair,',
'Had worn them really about the same,',
'And both that morning equally lay',
'I doubted if I should ever come back.',
'I shall be telling this with a sigh']
```
```
[line for line in poem_lines if re.search(r"\b\w{4}\b\s\b\w{4}\b", line)]
```
Good! Now, in the following cell, write a list comprehension that evaluates to a list of lines in the poem that end with a five-letter word, regardless of whether or not there is punctuation following the word at the end of the line. (Hint: Try using the `?` quantifier. Is there an existing character class, or a way to *write* a character class, that matches non-alphanumeric characters?) Expected output:
```
['And be one traveler, long I stood',
'And looked down one as far as I could',
'And having perhaps the better claim,',
'Though as for that the passing there',
'In leaves no step had trodden black.',
'Somewhere ages and ages hence:']
```
```
[line for line in poem_lines if re.search(r"(?:\s\w{5}\b$|\s\w{5}\b[.:;,]$)", line)]
```
Okay, now a slightly trickier one. In the cell below, I've created a string `all_lines` which evaluates to the entire text of the poem in one string. Execute this cell.
```
all_lines = " ".join(poem_lines)
```
Now, write an expression that evaluates to all of the words in the poem that follow the word 'I'. (The strings in the resulting list should *not* include the `I`.) Hint: Use `re.findall()` and grouping! Expected output:
['could', 'stood', 'could', 'kept', 'doubted', 'should', 'shall', 'took']
```
[item[2:] for item in (re.findall(r"\bI\b\s\b[a-z]{1,}", all_lines))]
```
Finally, something super tricky. Here's a list of strings that contains a restaurant menu. Your job is to wrangle this plain text, slightly-structured data into a list of dictionaries.
```
entrees = [
"Yam, Rosemary and Chicken Bowl with Hot Sauce $10.95",
"Lavender and Pepperoni Sandwich $8.49",
"Water Chestnuts and Peas Power Lunch (with mayonnaise) $12.95 - v",
"Artichoke, Mustard Green and Arugula with Sesame Oil over noodles $9.95 - v",
"Flank Steak with Lentils And Tabasco Pepper With Sweet Chilli Sauce $19.95",
"Rutabaga And Cucumber Wrap $8.49 - v"
]
```
You'll need to pull out the name of the dish and the price of the dish. The `v` after the hyphen indicates that the dish is vegetarian---you'll need to include that information in your dictionary as well. I've included the basic framework; you just need to fill in the contents of the `for` loop.
Expected output:
```
[{'name': 'Yam, Rosemary and Chicken Bowl with Hot Sauce ',
'price': 10.95,
'vegetarian': False},
{'name': 'Lavender and Pepperoni Sandwich ',
'price': 8.49,
'vegetarian': False},
{'name': 'Water Chestnuts and Peas Power Lunch (with mayonnaise) ',
'price': 12.95,
'vegetarian': True},
{'name': 'Artichoke, Mustard Green and Arugula with Sesame Oil over noodles ',
'price': 9.95,
'vegetarian': True},
{'name': 'Flank Steak with Lentils And Tabasco Pepper With Sweet Chilli Sauce ',
'price': 19.95,
'vegetarian': False},
{'name': 'Rutabaga And Cucumber Wrap ', 'price': 8.49, 'vegetarian': True}]
```
```
menu = []
for dish in entrees:
match = re.search(r"^(.*) \$(.*)", dish)
vegetarian = re.search(r"v$", match.group(2))
price = re.search(r"(?:\d\.\d\d|\d\d\.\d\d)", dish)
if vegetarian == None:
vegetarian = False
else:
vegetarian = True
if match:
dish = {
'name': match.group(1), 'price': price.group(), 'vegetarian': vegetarian
}
menu.append(dish)
menu
```
Great work! You are done. Go cavort in the sun, or whatever it is you students do when you're done with your homework
| github_jupyter |
Used https://github.com/GoogleCloudPlatform/cloudml-samples/blob/master/xgboost/notebooks/census_training/train.py as a starting point and adjusted to CatBoost
```
#Google Cloud Libraries
from google.cloud import storage
#System Libraries
import datetime
import subprocess
#Data Libraries
import pandas as pd
import numpy as np
#ML Libraries
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
import xgboost as xgb
from catboost import CatBoostClassifier, Pool, cv
from catboost import CatBoost, Pool
from catboost.utils import get_gpu_device_count
print('I see %i GPU devices' % get_gpu_device_count())
# Fill in your Cloud Storage bucket name
BUCKET_ID = "mchrestkha-demo-env-ml-examples"
census_data_filename = 'adult.data.csv'
# Public bucket holding the census data
bucket = storage.Client().bucket('cloud-samples-data')
# Path to the data inside the public bucket
data_dir = 'ai-platform/census/data/'
# Download the data
blob = bucket.blob(''.join([data_dir, census_data_filename]))
blob.download_to_filename(census_data_filename)
# these are the column labels from the census data files
COLUMNS = (
'age',
'workclass',
'fnlwgt',
'education',
'education-num',
'marital-status',
'occupation',
'relationship',
'race',
'sex',
'capital-gain',
'capital-loss',
'hours-per-week',
'native-country',
'income-level'
)
# categorical columns contain data that need to be turned into numerical values before being used by XGBoost
CATEGORICAL_COLUMNS = (
'workclass',
'education',
'marital-status',
'occupation',
'relationship',
'race',
'sex',
'native-country'
)
# Load the training census dataset
with open(census_data_filename, 'r') as train_data:
raw_training_data = pd.read_csv(train_data, header=None, names=COLUMNS)
# remove column we are trying to predict ('income-level') from features list
X = raw_training_data.drop('income-level', axis=1)
# create training labels list
#train_labels = (raw_training_data['income-level'] == ' >50K')
y = raw_training_data['income-level']
# Since the census data set has categorical features, we need to convert
# them to numerical values.
# convert data in categorical columns to numerical values
X_enc=X
encoders = {col:LabelEncoder() for col in CATEGORICAL_COLUMNS}
for col in CATEGORICAL_COLUMNS:
X_enc[col] = encoders[col].fit_transform(X[col])
y_enc=LabelEncoder().fit_transform(y)
X_train, X_validation, y_train, y_validation = train_test_split(X_enc, y_enc, train_size=0.75, random_state=42)
print(type(y))
print(type(y_enc))
%%time
#model = CatBoost({'iterations':50})
model=CatBoostClassifier(
od_type='Iter'
#iterations=5000,
#custom_loss=['Accuracy']
)
model.fit(
X_train,y_train,eval_set=(X_validation, y_validation),
verbose=50)
# # load data into DMatrix object
# dtrain = xgb.DMatrix(train_features, train_labels)
# # train model
# bst = xgb.train({}, dtrain, 20)
# Export the model to a file
fname = 'catboost_census_model.onnx'
model.save_model(fname, format='onnx')
# Upload the model to GCS
bucket = storage.Client().bucket(BUCKET_ID)
blob = bucket.blob('{}/{}'.format(
datetime.datetime.now().strftime('census/catboost_model_dir/catboost_census_%Y%m%d_%H%M%S'),
fname))
blob.upload_from_filename(fname)
!gsutil ls gs://$BUCKET_ID/census/*
```
| github_jupyter |
```
import requests
import csv
import pandas as pd
import feedparser
import re
file = open("newfeed3.csv","w",encoding="utf-8")
writer = csv.writer(file)
writer.writerow(["Title","Description","Link","Year","Month"])
feed = open("FinalUrl.txt","r")
urls = feed.read()
urls = urls.split("\n")
df = pd.DataFrame(columns=["Title","Description","Link","Year","Month"])
item_dicts = {}
for url in urls:
try:
f = feedparser.parse(url)
except Exception as e:
print('Could not parse the xml: ', url)
print(e)
for item in f.entries:
r = re.compile(r"<[^>]*>")
try:
items_dicts = {'Title':item.title,'Description':r.sub(r"",item.summary),'Link':item.link,'Year':item.published_parsed[0],'Month':item.published_parsed[1]}
except:
pass
f = csv.DictWriter(file, items_dicts.keys())
f.writerow(items_dicts)
import nltk
from nltk.tokenize import sent_tokenize, word_tokenize
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from sklearn.feature_extraction.text import TfidfVectorizer
import yake
df = pd.read_csv("newfeed3.csv")
df.dropna(inplace=True)
df.isna().sum()
df
desc_1 = []
for text in df["Description"]:
desc_1.append(re.sub("\s+"," ",text).lower())
desc_2 = []
for text in desc_1:
desc_2.append(re.sub("\[.+\]","",text))
desc_3 = []
for text in desc_2:
desc_3.append(re.sub("&.+;","",text))
desc_4 = []
for text in desc_3:
desc_4.append(re.sub(r'http\S+', '',text))
clean_desc = []
for text in desc_4:
clean_desc.append(re.sub(r'[^\w\s]',"",text))
stop_words=set(stopwords.words("english"))
wnet = WordNetLemmatizer()
port = PorterStemmer()
stop_words_2 = []
condition = ['not','nor','no']
for words in stop_words:
if words not in condition:
stop_words_2.append(words)
def lemmatize_text(text):
words = word_tokenize(text)
words_2 = []
lemm_2 = ""
for word in words:
if word not in stop_words_2:
words_2.append(word)
for word in words_2:
lemm = wnet.lemmatize(word)
lemm_2+=lemm+" "
return lemm_2
#lemm_desc = []
lemm_desc = ""
for text in clean_desc:
#lemm_desc.append(lemmatize_text(text))
lemm_desc+=lemmatize_text(text)+" "
language = "en"
max_ngram_size = 2
deduplication_thresold = 0.9
deduplication_algo = 'seqm'
windowSize = 1
numOfKeywords = 100
custom_kw_extractor = yake.KeywordExtractor(lan=language, n=max_ngram_size, dedupLim=deduplication_thresold, dedupFunc=deduplication_algo, windowsSize=windowSize, top=numOfKeywords, features=None)
keywords = custom_kw_extractor.extract_keywords(lemm_desc)
for kw in keywords:
print(kw)
kw = pd.DataFrame(keywords,columns=['keywords','tf idf'])
kw
import matplotlib.pyplot as plt
%matplotlib inline
fig ,ax = plt.subplots(figsize=(20,10))
ax.bar(kw['keywords'],kw['tf idf'])
plt.xticks(rotation='vertical')
plt.xlabel('keywords')
plt.ylabel('tf idf');
from nltk.sentiment.vader import SentimentIntensityAnalyzer
nltk.download('vader_lexicon')
def sentiment_analyse(text):
score = SentimentIntensityAnalyzer().polarity_scores(text)
pos = 1000 * score['pos']
return pos
lemm_desc2 = []
for text in clean_desc:
lemm_desc2.append(lemmatize_text(text))
p_score = []
for text in lemm_desc2:
score = sentiment_analyse(text)
p_score.append(score)
df["Popularity Score"] = p_score
df
```
| github_jupyter |
Final models with hyperparameters tuned for Logistics Regression and XGBoost with selected features.
```
#Import the libraries
import pandas as pd
import numpy as np
from tqdm import tqdm
from sklearn import linear_model, metrics, preprocessing, model_selection
from sklearn.preprocessing import StandardScaler
import xgboost as xgb
#Load the data
modeling_dataset = pd.read_csv('/content/drive/MyDrive/prediction/frac_cleaned_fod_data.csv', low_memory = False)
#All columns - except 'HasDetections', 'kfold', and 'MachineIdentifier'
train_features = [tf for tf in modeling_dataset.columns if tf not in ('HasDetections', 'kfold', 'MachineIdentifier')]
#The features selected based on the feature selection method earlier employed
train_features_after_selection = ['AVProductStatesIdentifier', 'Processor','AvSigVersion', 'Census_TotalPhysicalRAM', 'Census_InternalPrimaryDiagonalDisplaySizeInInches',
'Census_IsVirtualDevice', 'Census_PrimaryDiskTotalCapacity', 'Wdft_IsGamer', 'Census_IsAlwaysOnAlwaysConnectedCapable', 'EngineVersion',
'Census_ProcessorCoreCount', 'Census_OSEdition', 'Census_OSInstallTypeName', 'Census_OSSkuName', 'AppVersion', 'OsBuildLab', 'OsSuite',
'Firewall', 'IsProtected', 'Census_IsTouchEnabled', 'Census_ActivationChannel', 'LocaleEnglishNameIdentifier','Census_SystemVolumeTotalCapacity',
'Census_InternalPrimaryDisplayResolutionHorizontal','Census_HasOpticalDiskDrive', 'OsBuild', 'Census_InternalPrimaryDisplayResolutionVertical',
'CountryIdentifier', 'Census_MDC2FormFactor', 'GeoNameIdentifier', 'Census_PowerPlatformRoleName', 'Census_OSWUAutoUpdateOptionsName', 'SkuEdition',
'Census_OSVersion', 'Census_GenuineStateName', 'Census_OSBuildRevision', 'Platform', 'Census_ChassisTypeName', 'Census_FlightRing',
'Census_PrimaryDiskTypeName', 'Census_OSBranch', 'Census_IsSecureBootEnabled', 'OsPlatformSubRelease']
#Define the categorical features of the data
categorical_features = ['ProductName',
'EngineVersion',
'AppVersion',
'AvSigVersion',
'Platform',
'Processor',
'OsVer',
'OsPlatformSubRelease',
'OsBuildLab',
'SkuEdition',
'Census_MDC2FormFactor',
'Census_DeviceFamily',
'Census_PrimaryDiskTypeName',
'Census_ChassisTypeName',
'Census_PowerPlatformRoleName',
'Census_OSVersion',
'Census_OSArchitecture',
'Census_OSBranch',
'Census_OSEdition',
'Census_OSSkuName',
'Census_OSInstallTypeName',
'Census_OSWUAutoUpdateOptionsName',
'Census_GenuineStateName',
'Census_ActivationChannel',
'Census_FlightRing']
#XGBoost
"""
Best parameters set:
alpha: 1.0
colsample_bytree: 0.6
eta: 0.05
gamma: 0.1
lamda: 1.0
max_depth: 9
min_child_weight: 5
subsample: 0.7
"""
#XGBoost
def opt_run_xgboost(fold):
for col in train_features:
if col in categorical_features:
#Initialize the Label Encoder
lbl = preprocessing.LabelEncoder()
#Fit on the categorical features
lbl.fit(modeling_dataset[col])
#Transform
modeling_dataset.loc[:,col] = lbl.transform(modeling_dataset[col])
#Get training and validation data using folds
modeling_datasets_train = modeling_dataset[modeling_dataset.kfold != fold].reset_index(drop=True)
modeling_datasets_valid = modeling_dataset[modeling_dataset.kfold == fold].reset_index(drop=True)
#Get train data
X_train = modeling_datasets_train[train_features_after_selection].values
#Get validation data
X_valid = modeling_datasets_valid[train_features_after_selection].values
#Initialize XGboost model
xgb_model = xgb.XGBClassifier(
alpha= 1.0,
colsample_bytree= 0.6,
eta= 0.05,
gamma= 0.1,
lamda= 1.0,
max_depth= 9,
min_child_weight= 5,
subsample= 0.7,
n_jobs=-1)
#Fit the model on training data
xgb_model.fit(X_train, modeling_datasets_train.HasDetections.values)
#Predict on validation
valid_preds = xgb_model.predict_proba(X_valid)[:,1]
valid_preds_pc = xgb_model.predict(X_valid)
#Get the ROC AUC score
auc = metrics.roc_auc_score(modeling_datasets_valid.HasDetections.values, valid_preds)
#Get the precision score
pre = metrics.precision_score(modeling_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
#Get the Recall score
rc = metrics.recall_score(modeling_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
return auc, pre, rc
#LR
"""
'penalty': 'l2',
'C': 49.71967742639108,
'solver': 'lbfgs'
max_iter: 300
"""
#Function for Logistic Regression Classification
def opt_run_lr(fold):
#Get training and validation data using folds
cleaned_fold_datasets_train = modeling_dataset[modeling_dataset.kfold != fold].reset_index(drop=True)
cleaned_fold_datasets_valid = modeling_dataset[modeling_dataset.kfold == fold].reset_index(drop=True)
#Initialize OneHotEncoder from scikit-learn, and fit it on training and validation features
ohe = preprocessing.OneHotEncoder()
full_data = pd.concat(
[cleaned_fold_datasets_train[train_features_after_selection],cleaned_fold_datasets_valid[train_features_after_selection]],
axis = 0
)
ohe.fit(full_data[train_features_after_selection])
#transform the training and validation data
x_train = ohe.transform(cleaned_fold_datasets_train[train_features_after_selection])
x_valid = ohe.transform(cleaned_fold_datasets_valid[train_features_after_selection])
#Initialize the Logistic Regression Model
lr_model = linear_model.LogisticRegression(
penalty= 'l2',
C = 49.71967742639108,
solver= 'lbfgs',
max_iter= 300,
n_jobs=-1
)
#Fit model on training data
lr_model.fit(x_train, cleaned_fold_datasets_train.HasDetections.values)
#Predict on the validation data using the probability for the AUC
valid_preds = lr_model.predict_proba(x_valid)[:, 1]
#For precision and Recall
valid_preds_pc = lr_model.predict(x_valid)
#Get the ROC AUC score
auc = metrics.roc_auc_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds)
#Get the precision score
pre = metrics.precision_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
#Get the Recall score
rc = metrics.recall_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
return auc, pre, rc
#A list to hold the values of the XGB performance metrics
xg = []
for fold in tqdm(range(10)):
xg.append(opt_run_xgboost(fold))
#Run the Logistic regression model for all folds and hold their values
lr = []
for fold in tqdm(range(10)):
lr.append(opt_run_lr(fold))
xgb_auc = []
xgb_pre = []
xgb_rc = []
lr_auc = []
lr_pre = []
lr_rc = []
#Loop to get each of the performance metric for average computation
for i in lr:
lr_auc.append(i[0])
lr_pre.append(i[1])
lr_rc.append(i[2])
for j in xg:
xgb_auc.append(i[0])
xgb_pre.append(i[1])
xgb_rc.append(i[2])
#Dictionary to hold the basic model performance data
final_model_performance = {"logistic_regression": {"auc":"", "precision":"", "recall":""},
"xgb": {"auc":"","precision":"","recall":""}
}
#Calculate average of each of the lists of performance metrics and update the dictionary
final_model_performance['logistic_regression'].update({'auc':sum(lr_auc)/len(lr_auc)})
final_model_performance['xgb'].update({'auc':sum(xgb_auc)/len(xgb_auc)})
final_model_performance['logistic_regression'].update({'precision':sum(lr_pre)/len(lr_pre)})
final_model_performance['xgb'].update({'precision':sum(xgb_pre)/len(xgb_pre)})
final_model_performance['logistic_regression'].update({'recall':sum(lr_rc)/len(lr_rc)})
final_model_performance['xgb'].update({'recall':sum(xgb_rc)/len(xgb_rc)})
final_model_performance
#LR
"""
'penalty': 'l2',
'C': 49.71967742639108,
'solver': 'lbfgs'
max_iter: 100
"""
#Function for Logistic Regression Classification - max_iter = 100
def opt_run_lr100(fold):
#Get training and validation data using folds
cleaned_fold_datasets_train = modeling_dataset[modeling_dataset.kfold != fold].reset_index(drop=True)
cleaned_fold_datasets_valid = modeling_dataset[modeling_dataset.kfold == fold].reset_index(drop=True)
#Initialize OneHotEncoder from scikit-learn, and fit it on training and validation features
ohe = preprocessing.OneHotEncoder()
full_data = pd.concat(
[cleaned_fold_datasets_train[train_features_after_selection],cleaned_fold_datasets_valid[train_features_after_selection]],
axis = 0
)
ohe.fit(full_data[train_features_after_selection])
#transform the training and validation data
x_train = ohe.transform(cleaned_fold_datasets_train[train_features_after_selection])
x_valid = ohe.transform(cleaned_fold_datasets_valid[train_features_after_selection])
#Initialize the Logistic Regression Model
lr_model = linear_model.LogisticRegression(
penalty= 'l2',
C = 49.71967742639108,
solver= 'lbfgs',
max_iter= 100,
n_jobs=-1
)
#Fit model on training data
lr_model.fit(x_train, cleaned_fold_datasets_train.HasDetections.values)
#Predict on the validation data using the probability for the AUC
valid_preds = lr_model.predict_proba(x_valid)[:, 1]
#For precision and Recall
valid_preds_pc = lr_model.predict(x_valid)
#Get the ROC AUC score
auc = metrics.roc_auc_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds)
#Get the precision score
pre = metrics.precision_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
#Get the Recall score
rc = metrics.recall_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
return auc, pre, rc
#Run the Logistic regression model for all folds and hold their values
lr100 = []
for fold in tqdm(range(10)):
lr100.append(opt_run_lr100(fold))
lr100_auc = []
lr100_pre = []
lr100_rc = []
for k in lr100:
lr100_auc.append(k[0])
lr100_pre.append(k[1])
lr100_rc.append(k[2])
sum(lr100_auc)/len(lr100_auc)
sum(lr100_pre)/len(lr100_pre)
sum(lr100_rc)/len(lr100_rc)
"""
{'logistic_regression': {'auc': 0.660819451656712,
'precision': 0.6069858170181643,
'recall': 0.6646704904969867},
'xgb': {'auc': 0.6583717792973377,
'precision': 0.6042291042291044,
'recall': 0.6542422535211267}}
"""
```
| github_jupyter |
# Dealing with errors after a run
In this example, we run the model on a list of three glaciers:
two of them will end with errors: one because it already failed at
preprocessing (i.e. prior to this run), and one during the run. We show how to analyze theses erros and solve (some) of them, as described in the OGGM documentation under [troubleshooting](https://docs.oggm.org/en/latest/faq.html?highlight=border#troubleshooting).
## Run with `cfg.PARAMS['continue_on_error'] = True`
```
# Locals
import oggm.cfg as cfg
from oggm import utils, workflow, tasks
# Libs
import os
import xarray as xr
import pandas as pd
# Initialize OGGM and set up the default run parameters
cfg.initialize(logging_level='WARNING')
# Here we override some of the default parameters
# How many grid points around the glacier?
# We make it small because we want the model to error because
# of flowing out of the domain
cfg.PARAMS['border'] = 80
# This is useful since we have three glaciers
cfg.PARAMS['use_multiprocessing'] = True
# This is the important bit!
# We tell OGGM to continue despite of errors
cfg.PARAMS['continue_on_error'] = True
# Local working directory (where OGGM will write its output)
WORKING_DIR = utils.gettempdir('OGGM_Errors')
utils.mkdir(WORKING_DIR, reset=True)
cfg.PATHS['working_dir'] = WORKING_DIR
rgi_ids = ['RGI60-11.00897', 'RGI60-11.01450', 'RGI60-11.03295']
# Go - get the pre-processed glacier directories
gdirs = workflow.init_glacier_directories(rgi_ids, from_prepro_level=4)
# We can step directly to the experiment!
# Random climate representative for the recent climate (1985-2015)
# with a negative bias added to the random temperature series
workflow.execute_entity_task(tasks.run_random_climate, gdirs,
nyears=150, seed=0,
temperature_bias=-1)
```
## Error diagnostics
```
# Write the compiled output
utils.compile_glacier_statistics(gdirs); # saved as glacier_statistics.csv in the WORKING_DIR folder
utils.compile_run_output(gdirs); # saved as run_output.nc in the WORKING_DIR folder
# Read it
with xr.open_dataset(os.path.join(WORKING_DIR, 'run_output.nc')) as ds:
ds = ds.load()
df_stats = pd.read_csv(os.path.join(WORKING_DIR, 'glacier_statistics.csv'), index_col=0)
# all possible statistics about the glaciers
df_stats
```
- in the column *error_task*, we can see whether an error occurred, and if yes during which task
- *error_msg* describes the actual error message
```
df_stats[['error_task', 'error_msg']]
```
We can also check which glacier failed at which task by using [compile_task_log]('https://docs.oggm.org/en/latest/generated/oggm.utils.compile_task_log.html#oggm.utils.compile_task_log').
```
# also saved as task_log.csv in the WORKING_DIR folder - "append=False" replaces the existing one
utils.compile_task_log(gdirs, task_names=['glacier_masks', 'compute_centerlines', 'flowline_model_run'], append=False)
```
## Error solving
### RuntimeError: `Glacier exceeds domain boundaries, at year: 98.08333333333333`
To remove this error just increase the domain boundary **before** running `init_glacier_directories` ! Attention, this means that more data has to be downloaded and the run takes more time. The available options for `cfg.PARAMS['border']` are **10, 40, 80 or 160** at the moment; the unit is number of grid points outside the glacier boundaries. More about that in the OGGM documentation under [preprocessed files](https://docs.oggm.org/en/latest/input-data.html#pre-processed-directories).
```
# reset to recompute statistics
utils.mkdir(WORKING_DIR, reset=True)
# increase the amount of gridpoints outside the glacier
cfg.PARAMS['border'] = 160
gdirs = workflow.init_glacier_directories(rgi_ids, from_prepro_level=4)
workflow.execute_entity_task(tasks.run_random_climate, gdirs,
nyears=150, seed=0,
temperature_bias=-1);
# recompute the output
# we can also get the run output directly from the methods
df_stats = utils.compile_glacier_statistics(gdirs)
ds = utils.compile_run_output(gdirs)
# check again
df_stats[['error_task', 'error_msg']]
```
Now `RGI60-11.00897` runs without errors!
### Error: `Need a valid model_flowlines file.`
This error message in the log is misleading: it does not really describe the source of the error, which happened earlier in the processing chain. Therefore we can look instead into the glacier_statistics via [compile_glacier_statistics](https://docs.oggm.org/en/latest/generated/oggm.utils.compile_glacier_statistics.html) or into the log output via [compile_task_log](https://docs.oggm.org/en/latest/generated/oggm.utils.compile_task_log.html#oggm.utils.compile_task_log):
```
print('error_task: {}, error_msg: {}'.format(df_stats.loc['RGI60-11.03295']['error_task'],
df_stats.loc['RGI60-11.03295']['error_msg']))
```
Now we have a better understanding of the error:
- OGGM can not work with this geometry of this glacier and could therefore not make a gridded mask of the glacier outlines.
- there is no way to prevent this except you find a better way to pre-process the geometry of this glacier
- these glaciers have to be ignored! Less than 0.5% of glacier area globally have errors during the geometry processing or failures in computing certain topographical properties by e.g. invalid DEM, see [Sect. 4.2 Invalid Glaciers of the OGGM paper (Maussion et al., 2019)](https://gmd.copernicus.org/articles/12/909/2019/#section4) and [this tutorial](preprocessing_errors.ipynb) for more up-to-date numbers
## Ignoring those glaciers with errors that we can't solve
In the run_output, you can for example just use `*.dropna` to remove these. For other applications (e.g. quantitative mass change evaluation), more will be needed (not available yet in the OGGM codebase):
```
ds.dropna(dim='rgi_id') # here we can e.g. find the volume evolution
```
## What's next?
- read about [preprocessing errors](preprocessing_errors.ipynb)
- return to the [OGGM documentation](https://docs.oggm.org)
- back to the [table of contents](welcome.ipynb)
| github_jupyter |
<a href="https://colab.research.google.com/github/Tessellate-Imaging/monk_v1/blob/master/study_roadmaps/2_transfer_learning_roadmap/6_freeze_base_network/2.2)%20Understand%20the%20effect%20of%20freezing%20base%20model%20in%20transfer%20learning%20-%202%20-%20pytorch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Goals
### In the previous tutorial you studied the role of freezing models on a small dataset.
### Understand the role of freezing models in transfer learning on a fairly large dataset
### Why freeze/unfreeze base models in transfer learning
### Use comparison feature to appropriately set this parameter on custom dataset
### You will be using lego bricks dataset to train the classifiers
# What is freezing base network
- To recap you have two parts in your network
- One that already existed, the pretrained one, the base network
- The new sub-network or a single layer you added
-The hyper-parameter we can see here: Freeze base network
- Freezing base network makes the base network untrainable
- The base network now acts as a feature extractor and only the next half is trained
- If you do not freeze the base network the entire network is trained
# Table of Contents
## [Install](#0)
## [Freeze Base network in densenet121 and train a classifier](#1)
## [Unfreeze base network in densenet121 and train another classifier](#2)
## [Compare both the experiment](#3)
<a id='0'></a>
# Install Monk
## Using pip (Recommended)
- colab (gpu)
- All bakcends: `pip install -U monk-colab`
- kaggle (gpu)
- All backends: `pip install -U monk-kaggle`
- cuda 10.2
- All backends: `pip install -U monk-cuda102`
- Gluon bakcned: `pip install -U monk-gluon-cuda102`
- Pytorch backend: `pip install -U monk-pytorch-cuda102`
- Keras backend: `pip install -U monk-keras-cuda102`
- cuda 10.1
- All backend: `pip install -U monk-cuda101`
- Gluon bakcned: `pip install -U monk-gluon-cuda101`
- Pytorch backend: `pip install -U monk-pytorch-cuda101`
- Keras backend: `pip install -U monk-keras-cuda101`
- cuda 10.0
- All backend: `pip install -U monk-cuda100`
- Gluon bakcned: `pip install -U monk-gluon-cuda100`
- Pytorch backend: `pip install -U monk-pytorch-cuda100`
- Keras backend: `pip install -U monk-keras-cuda100`
- cuda 9.2
- All backend: `pip install -U monk-cuda92`
- Gluon bakcned: `pip install -U monk-gluon-cuda92`
- Pytorch backend: `pip install -U monk-pytorch-cuda92`
- Keras backend: `pip install -U monk-keras-cuda92`
- cuda 9.0
- All backend: `pip install -U monk-cuda90`
- Gluon bakcned: `pip install -U monk-gluon-cuda90`
- Pytorch backend: `pip install -U monk-pytorch-cuda90`
- Keras backend: `pip install -U monk-keras-cuda90`
- cpu
- All backend: `pip install -U monk-cpu`
- Gluon bakcned: `pip install -U monk-gluon-cpu`
- Pytorch backend: `pip install -U monk-pytorch-cpu`
- Keras backend: `pip install -U monk-keras-cpu`
## Install Monk Manually (Not recommended)
### Step 1: Clone the library
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
### Step 2: Install requirements
- Linux
- Cuda 9.0
- `cd monk_v1/installation/Linux && pip install -r requirements_cu90.txt`
- Cuda 9.2
- `cd monk_v1/installation/Linux && pip install -r requirements_cu92.txt`
- Cuda 10.0
- `cd monk_v1/installation/Linux && pip install -r requirements_cu100.txt`
- Cuda 10.1
- `cd monk_v1/installation/Linux && pip install -r requirements_cu101.txt`
- Cuda 10.2
- `cd monk_v1/installation/Linux && pip install -r requirements_cu102.txt`
- CPU (Non gpu system)
- `cd monk_v1/installation/Linux && pip install -r requirements_cpu.txt`
- Windows
- Cuda 9.0 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu90.txt`
- Cuda 9.2 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu92.txt`
- Cuda 10.0 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu100.txt`
- Cuda 10.1 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu101.txt`
- Cuda 10.2 (Experimental support)
- `cd monk_v1/installation/Windows && pip install -r requirements_cu102.txt`
- CPU (Non gpu system)
- `cd monk_v1/installation/Windows && pip install -r requirements_cpu.txt`
- Mac
- CPU (Non gpu system)
- `cd monk_v1/installation/Mac && pip install -r requirements_cpu.txt`
- Misc
- Colab (GPU)
- `cd monk_v1/installation/Misc && pip install -r requirements_colab.txt`
- Kaggle (GPU)
- `cd monk_v1/installation/Misc && pip install -r requirements_kaggle.txt`
### Step 3: Add to system path (Required for every terminal or kernel run)
- `import sys`
- `sys.path.append("monk_v1/");`
## Dataset - LEGO Classification
- https://www.kaggle.com/joosthazelzet/lego-brick-images/
```
! wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1MRC58-oCdR1agFTWreDFqevjEOIWDnYZ' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1MRC58-oCdR1agFTWreDFqevjEOIWDnYZ" -O skin_cancer_mnist_dataset.zip && rm -rf /tmp/cookies.txt
! unzip -qq skin_cancer_mnist_dataset.zip
```
# Imports
```
#Using pytorch backend
# When installed using pip
from monk.pytorch_prototype import prototype
# When installed manually (Uncomment the following)
#import os
#import sys
#sys.path.append("monk_v1/");
#sys.path.append("monk_v1/monk/");
#from monk.pytorch_prototype import prototype
```
<a id='1'></a>
# Freeze Base network in densenet121 and train a classifier
## Creating and managing experiments
- Provide project name
- Provide experiment name
- For a specific data create a single project
- Inside each project multiple experiments can be created
- Every experiment can be have diferent hyper-parameters attached to it
```
gtf = prototype(verbose=1);
gtf.Prototype("Project", "Freeze_Base_Network");
```
### This creates files and directories as per the following structure
workspace
|
|--------Project
|
|
|-----Freeze_Base_Network
|
|-----experiment-state.json
|
|-----output
|
|------logs (All training logs and graphs saved here)
|
|------models (all trained models saved here)
## Set dataset and select the model
## Quick mode training
- Using Default Function
- dataset_path
- model_name
- freeze_base_network
- num_epochs
## Sample Dataset folder structure
parent_directory
|
|
|------cats
|
|------img1.jpg
|------img2.jpg
|------.... (and so on)
|------dogs
|
|------img1.jpg
|------img2.jpg
|------.... (and so on)
## Modifyable params
- dataset_path: path to data
- model_name: which pretrained model to use
- freeze_base_network: Retrain already trained network or not
- num_epochs: Number of epochs to train for
```
gtf.Default(dataset_path="skin_cancer_mnist_dataset/images",
path_to_csv="skin_cancer_mnist_dataset/train_labels.csv",
model_name="densenet121",
freeze_base_network=True, # Set this param as true
num_epochs=5);
#Read the summary generated once you run this cell.
```
## From the summary above
- Model Params
Model name: densenet121
Use Gpu: True
Use pretrained: True
Freeze base network: True
## Another thing to notice from summary
Model Details
Loading pretrained model
Model Loaded on device
Model name: densenet121
Num of potentially trainable layers: 242
Num of actual trainable layers: 1
### There are a total of 242 layers
### Since we have freezed base network only 1 is trainable, the final layer
## Train the classifier
```
#Start Training
gtf.Train();
#Read the training summary generated once you run the cell and training is completed
```
### Best validation Accuracy achieved - 74.77 %
(You may get a different result)
<a id='2'></a>
# Unfreeze Base network in densenet121 and train a classifier
## Creating and managing experiments
- Provide project name
- Provide experiment name
- For a specific data create a single project
- Inside each project multiple experiments can be created
- Every experiment can be have diferent hyper-parameters attached to it
```
gtf = prototype(verbose=1);
gtf.Prototype("Project", "Unfreeze_Base_Network");
```
### This creates files and directories as per the following structure
workspace
|
|--------Project
|
|
|-----Freeze_Base_Network (Previously created)
|
|-----experiment-state.json
|
|-----output
|
|------logs (All training logs and graphs saved here)
|
|------models (all trained models saved here)
|
|
|-----Unfreeze_Base_Network (Created Now)
|
|-----experiment-state.json
|
|-----output
|
|------logs (All training logs and graphs saved here)
|
|------models (all trained models saved here)
## Set dataset and select the model
## Quick mode training
- Using Default Function
- dataset_path
- model_name
- freeze_base_network
- num_epochs
## Sample Dataset folder structure
parent_directory
|
|
|------cats
|
|------img1.jpg
|------img2.jpg
|------.... (and so on)
|------dogs
|
|------img1.jpg
|------img2.jpg
|------.... (and so on)
## Modifyable params
- dataset_path: path to data
- model_name: which pretrained model to use
- freeze_base_network: Retrain already trained network or not
- num_epochs: Number of epochs to train for
```
gtf.Default(dataset_path="skin_cancer_mnist_dataset/images",
path_to_csv="skin_cancer_mnist_dataset/train_labels.csv",
model_name="densenet121",
freeze_base_network=False, # Set this param as false
num_epochs=5);
#Read the summary generated once you run this cell.
```
## From the summary above
- Model Params
Model name: densenet121
Use Gpu: True
Use pretrained: True
Freeze base network: False
## Another thing to notice from summary
Model Details
Loading pretrained model
Model Loaded on device
Model name: densenet121
Num of potentially trainable layers: 242
Num of actual trainable layers: 242
### There are a total of 242 layers
### Since we have unfreezed base network all 242 layers are trainable including the final layer
## Train the classifier
```
#Start Training
gtf.Train();
#Read the training summary generated once you run the cell and training is completed
```
### Best Val Accuracy achieved - 81.33 %
(You may get a different result)
<a id='3'></a>
# Compare both the experiment
```
# Invoke the comparison class
from monk.compare_prototype import compare
```
### Creating and managing comparison experiments
- Provide project name
```
# Create a project
gtf = compare(verbose=1);
gtf.Comparison("Compare-effect-of-freezing");
```
### This creates files and directories as per the following structure
workspace
|
|--------comparison
|
|
|-----Compare-effect-of-freezing
|
|------stats_best_val_acc.png
|------stats_max_gpu_usage.png
|------stats_training_time.png
|------train_accuracy.png
|------train_loss.png
|------val_accuracy.png
|------val_loss.png
|
|-----comparison.csv (Contains necessary details of all experiments)
### Add the experiments
- First argument - Project name
- Second argument - Experiment name
```
gtf.Add_Experiment("Project", "Freeze_Base_Network");
gtf.Add_Experiment("Project", "Unfreeze_Base_Network");
```
### Run Analysis
```
gtf.Generate_Statistics();
```
## Visualize and study comparison metrics
### Training Accuracy Curves
```
from IPython.display import Image
Image(filename="workspace/comparison/Compare-effect-of-freezing/train_accuracy.png")
```
### Training Loss Curves
```
from IPython.display import Image
Image(filename="workspace/comparison/Compare-effect-of-freezing/train_loss.png")
```
### Validation Accuracy Curves
```
from IPython.display import Image
Image(filename="workspace/comparison/Compare-effect-of-freezing/val_accuracy.png")
```
### Validation loss curves
```
from IPython.display import Image
Image(filename="workspace/comparison/Compare-effect-of-freezing/val_loss.png")
```
## Accuracies achieved on validation dataset
### With freezing base network - 74.77 %
### Without freezing base network - 81.33 %
#### For this classifier, keeping the base network trainable seems to be a good option. Thus for other data it may result in overfitting the training data
(You may get a different result)
| github_jupyter |
## 使用TensorFlow的基本步骤
以使用LinearRegression来预测房价为例。
- 使用RMSE(均方根误差)评估模型预测的准确率
- 通过调整超参数来提高模型的预测准确率
```
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
# 加载数据集
california_housing_df = pd.read_csv("https://download.mlcc.google.cn/mledu-datasets/california_housing_train.csv", sep=",")
# 将数据打乱
california_housing_df = california_housing_df.reindex(np.random.permutation(california_housing_df.index))
# 替换房价的单位为k
california_housing_df['median_house_value'] /=1000.0
print("california house dataframe: \n", california_housing_df) # 根据pd设置,只显示10条数据,以及保留小数点后一位
```
### 检查数据
```
# 使用pd的describe方法来统计一些信息
california_housing_df.describe()
```
### 构建模型
我们将在这个例子中预测中位房价,将其作为学习的标签,使用房间总数作为输入特征。
#### 第1步:定义特征并配置特征列
为了把数据导入TensorFlow,我们需要指定每个特征包含的数据类型。我们主要使用以下两种类型:
- 分类数据: 一种文字数据。
- 数值数据:一种数字(整数或浮点数)数据或希望视为数字的数据。
在TF中我们使用**特征列**的结构来表示特征的数据类型。特征列仅存储对特征数据的描述,不包含特征数据本身。
```
# 定义输入特征
kl_feature = california_housing_df[['total_rooms']]
# 配置房间总数为数值特征列
feature_columns = [tf.feature_column.numeric_column('total_rooms')]
```
#### 第2步: 定义目标
```
# 定义目标标签
targets = california_housing_df['median_house_value']
```
**梯度裁剪**是在应用梯度值之前设置其上限,梯度裁剪有助于确保数值稳定性,防止梯度爆炸。
#### 第3步:配置线性回归器
```
# 使用Linear Regressor配置线性回归模型,使用GradientDescentOptimizer优化器训练模型
kl_optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.0000001)
# 使用clip_gradients_by_norm梯度裁剪我们的优化器,梯度裁剪可以确保我们的梯度大小在训练期间不会变得过大,梯度过大会导致梯度下降失败。
kl_optimizer = tf.contrib.estimator.clip_gradients_by_norm(kl_optimizer, 5.0)
# 使用我们的特征列和优化器配置线性回归模型
house_linear_regressor = tf.estimator.LinearRegressor(feature_columns=feature_columns, optimizer=kl_optimizer)
```
#### 第4步:定义输入函数
要将数据导入LinearRegressor,我们需要定义一个输入函数,让它告诉TF如何对数据进行预处理,以及在模型训练期间如何批处理、随机处理和重复数据。
首先我们将Pandas特征数据转换成NumPy数组字典,然后利用Dataset API构建Dataset对象,拆分数据为batch_size的批数据,以按照指定周期数(num_epochs)进行重复,**注意:**如果默认值num_epochs=None传递到repeat(),输入数据会无限期重复。
shuffle: Bool, 是否打乱数据
buffer_size: 指定shuffle从中随机抽样的数据集大小
```
def kl_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""使用单个特征训练房价预测模型
Args:
features: 特征DataFrame
targets: 目标DataFrame
batch_size: 批大小
shuffle: Bool. 是否打乱数据
Return:
下一个数据批次的元组(features, labels)
"""
# 把pandas数据转换成np.array构成的dict数据
features = {key: np.array(value) for key, value in dict(features).items()}
# 构建数据集,配置批和重复次数、
ds = Dataset.from_tensor_slices((features, targets)) # 数据大小 2GB 限制
ds = ds.batch(batch_size).repeat(num_epochs)
# 打乱数据
if shuffle:
ds = ds.shuffle(buffer_size=10000) # buffer_size指随机抽样的数据集大小
# 返回下一批次的数据
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
```
**注意:** 更详细的输入函数和Dataset API参考:[TF Developer's Guide](https://www.tensorflow.org/programmers_guide/datasets)
#### 第5步:训练模型
在linear_regressor上调用train()来训练模型
```
_ = house_linear_regressor.train(input_fn=lambda: kl_input_fn(kl_feature, targets), steps=100)
```
#### 第6步:评估模型
**注意:**训练误差可以衡量训练的模型与训练数据的拟合情况,但**不能**衡量模型泛化到新数据的效果,我们需要拆分数据来评估模型的泛化能力。
```
# 只做一次预测,所以把epoch设为1并关闭随机
prediction_input_fn = lambda: kl_input_fn(kl_feature, targets, num_epochs=1, shuffle=False)
# 调用predict进行预测
predictions = house_linear_regressor.predict(input_fn=prediction_input_fn)
# 把预测结果转换为numpy数组
predictions = np.array([item['predictions'][0] for item in predictions])
# 打印MSE和RMSE
mean_squared_error = metrics.mean_squared_error(predictions, targets)
root_mean_squared_error = math.sqrt(mean_squared_error)
print("均方误差 %0.3f" % mean_squared_error)
print("均方根误差: %0.3f" % root_mean_squared_error)
min_house_value = california_housing_df['median_house_value'].min()
max_house_value = california_housing_df['median_house_value'].max()
min_max_diff = max_house_value- min_house_value
print("最低中位房价: %0.3f" % min_house_value)
print("最高中位房价: %0.3f" % max_house_value)
print("中位房价最低最高差值: %0.3f" % min_max_diff)
print("均方根误差:%0.3f" % root_mean_squared_error)
```
由此结果可以看出模型的效果并不理想,我们可以使用一些基本的策略来降低误差。
```
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
calibration_data.describe()
# 我们可以可视化数据和我们学到的线,
sample = california_housing_df.sample(n=300) # 得到均匀分布的sample数据df
# 得到房屋总数的最小最大值
x_0 = sample["total_rooms"].min()
x_1 = sample["total_rooms"].max()
# 获得训练后的最终权重和偏差
weight = house_linear_regressor.get_variable_value('linear/linear_model/total_rooms/weights')[0]
bias = house_linear_regressor.get_variable_value('linear/linear_model/bias_weights')
# 计算最低最高房间数(特征)对应的房价(标签)
y_0 = weight * x_0 + bias
y_1 = weight * x_1 +bias
# 画图
plt.plot([x_0,x_1], [y_0,y_1],c='r')
plt.ylabel('median_house_value')
plt.xlabel('total_rooms')
# 画出散点图
plt.scatter(sample["total_rooms"], sample["median_house_value"])
plt.show()
```
### 模型调参
以上代码封装调参
```
def train_model(learning_rate, steps, batch_size, input_feature="total_rooms"):
"""Trains a linear regression model of one feature.
Args:
learning_rate: A `float`, the learning rate.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
input_feature: A `string` specifying a column from `california_housing_df`
to use as input feature.
"""
periods = 10
steps_per_period = steps / periods
my_feature = input_feature
my_feature_data = california_housing_df[[my_feature]]
my_label = "median_house_value"
targets = california_housing_df[my_label]
# Create feature columns.
feature_columns = [tf.feature_column.numeric_column(my_feature)]
# Create input functions.
training_input_fn = lambda:kl_input_fn(my_feature_data, targets, batch_size=batch_size)
prediction_input_fn = lambda: kl_input_fn(my_feature_data, targets, num_epochs=1, shuffle=False)
# Create a linear regressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
# Set up to plot the state of our model's line each period.
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.title("Learned Line by Period")
plt.ylabel(my_label)
plt.xlabel(my_feature)
sample = california_housing_df.sample(n=300)
plt.scatter(sample[my_feature], sample[my_label])
colors = [cm.coolwarm(x) for x in np.linspace(-1, 1, periods)]
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
root_mean_squared_errors = []
for period in range (0, periods):
# Train the model, starting from the prior state.
linear_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period
)
# Take a break and compute predictions.
predictions = linear_regressor.predict(input_fn=prediction_input_fn)
predictions = np.array([item['predictions'][0] for item in predictions])
# Compute loss.
root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(predictions, targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, root_mean_squared_error))
# Add the loss metrics from this period to our list.
root_mean_squared_errors.append(root_mean_squared_error)
# Finally, track the weights and biases over time.
# Apply some math to ensure that the data and line are plotted neatly.
y_extents = np.array([0, sample[my_label].max()])
weight = linear_regressor.get_variable_value('linear/linear_model/%s/weights' % input_feature)[0]
bias = linear_regressor.get_variable_value('linear/linear_model/bias_weights')
x_extents = (y_extents - bias) / weight
x_extents = np.maximum(np.minimum(x_extents,
sample[my_feature].max()),
sample[my_feature].min())
y_extents = weight * x_extents + bias
plt.plot(x_extents, y_extents, color=colors[period])
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.subplot(1, 2, 2)
plt.ylabel('RMSE')
plt.xlabel('Periods')
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(root_mean_squared_errors)
# Output a table with calibration data.
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
display.display(calibration_data.describe())
print("Final RMSE (on training data): %0.2f" % root_mean_squared_error)
```
**练习1: 使RMSE不超过180**
```
train_model(learning_rate=0.00002, steps=500, batch_size=5)
```
### 模型调参的启发法
> 不要死循规则
- 训练误差应该稳步减小,刚开始是急剧减小,最终应随着训练收敛达到平稳状态。
- 如果训练尚未收敛,尝试运行更长的时间。
- 如果训练误差减小速度过慢,则提高学习速率也许有助于加快其减小速度。
- 但有时如果学习速率过高,训练误差的减小速度反而会变慢。
- 如果训练误差变化很大,尝试降低学习速率。
- 较低的学习速率和较大的步数/较大的批量大小通常是不错的组合。
- 批量大小过小也会导致不稳定情况。不妨先尝试 100 或 1000 等较大的值,然后逐渐减小值的大小,直到出现性能降低的情况。
**练习2:尝试其他特征**
我们使用population特征替代。
```
train_model(learning_rate=0.00005, steps=500, batch_size=5, input_feature="population")
```
| github_jupyter |
# test note
* jupyterはコンテナ起動すること
* テストベッド一式起動済みであること
```
!pip install --upgrade pip
!pip install --force-reinstall ../lib/ait_sdk-0.1.7-py3-none-any.whl
from pathlib import Path
import pprint
from ait_sdk.test.hepler import Helper
import json
# settings cell
# mounted dir
root_dir = Path('/workdir/root/ait')
ait_name='eval_metamorphic_test_tf1.13'
ait_version='0.1'
ait_full_name=f'{ait_name}_{ait_version}'
ait_dir = root_dir / ait_full_name
td_name=f'{ait_name}_test'
# (dockerホスト側の)インベントリ登録用アセット格納ルートフォルダ
current_dir = %pwd
with open(f'{current_dir}/config.json', encoding='utf-8') as f:
json_ = json.load(f)
root_dir = json_['host_ait_root_dir']
is_container = json_['is_container']
invenotory_root_dir = f'{root_dir}\\ait\\{ait_full_name}\\local_qai\\inventory'
# entry point address
# コンテナ起動かどうかでポート番号が変わるため、切り替える
if is_container:
backend_entry_point = 'http://host.docker.internal:8888/qai-testbed/api/0.0.1'
ip_entry_point = 'http://host.docker.internal:8888/qai-ip/api/0.0.1'
else:
backend_entry_point = 'http://host.docker.internal:5000/qai-testbed/api/0.0.1'
ip_entry_point = 'http://host.docker.internal:6000/qai-ip/api/0.0.1'
# aitのデプロイフラグ
# 一度実施すれば、それ以降は実施しなくてOK
is_init_ait = True
# インベントリの登録フラグ
# 一度実施すれば、それ以降は実施しなくてOK
is_init_inventory = True
helper = Helper(backend_entry_point=backend_entry_point,
ip_entry_point=ip_entry_point,
ait_dir=ait_dir,
ait_full_name=ait_full_name)
# health check
helper.get_bk('/health-check')
helper.get_ip('/health-check')
# create ml-component
res = helper.post_ml_component(name=f'MLComponent_{ait_full_name}', description=f'Description of {ait_full_name}', problem_domain=f'ProbremDomain of {ait_full_name}')
helper.set_ml_component_id(res['MLComponentId'])
# deploy AIT
if is_init_ait:
helper.deploy_ait_non_build()
else:
print('skip deploy AIT')
res = helper.get_data_types()
model_data_type_id = [d for d in res['DataTypes'] if d['Name'] == 'model'][0]['Id']
dataset_data_type_id = [d for d in res['DataTypes'] if d['Name'] == 'dataset'][0]['Id']
res = helper.get_file_systems()
unix_file_system_id = [f for f in res['FileSystems'] if f['Name'] == 'UNIX_FILE_SYSTEM'][0]['Id']
windows_file_system_id = [f for f in res['FileSystems'] if f['Name'] == 'WINDOWS_FILE'][0]['Id']
# add inventories
if is_init_inventory:
inv1_name = helper.post_inventory('train_image', dataset_data_type_id, windows_file_system_id,
f'{invenotory_root_dir}\\mnist_dataset\\mnist_dataset.zip',
'MNIST_dataset are train image, train label, test image, test label', ['zip'])
inv2_name = helper.post_inventory('mnist_model', dataset_data_type_id, windows_file_system_id,
f'{invenotory_root_dir}\\mnist_model\\model_mnist.zip',
'MNIST_model', ['zip'])
else:
print('skip add inventories')
# get ait_json and inventory_jsons
res_json = helper.get_bk('/QualityMeasurements/RelationalOperators', is_print_json=False).json()
eq_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '=='][0])
nq_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '!='][0])
gt_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '>'][0])
ge_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '>='][0])
lt_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '<'][0])
le_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '<='][0])
res_json = helper.get_bk('/testRunners', is_print_json=False).json()
ait_json = [j for j in res_json['TestRunners'] if j['Name'] == ait_name][-1]
inv_1_json = helper.get_inventory(inv1_name)
inv_2_json = helper.get_inventory(inv2_name)
# add teast_descriptions
helper.post_td(td_name, ait_json['QualityDimensionId'],
quality_measurements=[
{"Id":ait_json['Report']['Measures'][0]['Id'], "Value":"0.25", "RelationalOperatorId":lt_id, "Enable":True}
],
target_inventories=[
{"Id":1, "InventoryId": inv_1_json['Id'], "TemplateInventoryId": ait_json['TargetInventories'][0]['Id']},
{"Id":2, "InventoryId": inv_2_json['Id'], "TemplateInventoryId": ait_json['TargetInventories'][1]['Id']}
],
test_runner={
"Id":ait_json['Id'],
"Params":[
{"TestRunnerParamTemplateId":ait_json['ParamTemplates'][0]['Id'], "Value":"10"},
{"TestRunnerParamTemplateId":ait_json['ParamTemplates'][1]['Id'], "Value":"500"},
{"TestRunnerParamTemplateId":ait_json['ParamTemplates'][2]['Id'], "Value":"train"}
]
})
# get test_description_jsons
td_1_json = helper.get_td(td_name)
# run test_descriptions
helper.post_run_and_wait(td_1_json['Id'])
res_json = helper.get_td_detail(td_1_json['Id'])
pprint.pprint(res_json)
# generate report
res = helper.post_report(td_1_json['Id'])
```
| github_jupyter |
```
%load_ext rpy2.ipython
%matplotlib inline
import logging
logging.getLogger('fbprophet').setLevel(logging.ERROR)
import warnings
warnings.filterwarnings("ignore")
```
## Python API
Prophet follows the `sklearn` model API. We create an instance of the `Prophet` class and then call its `fit` and `predict` methods.
The input to Prophet is always a dataframe with two columns: `ds` and `y`. The `ds` (datestamp) column should be of a format expected by Pandas, ideally YYYY-MM-DD for a date or YYYY-MM-DD HH:MM:SS for a timestamp. The `y` column must be numeric, and represents the measurement we wish to forecast.
As an example, let's look at a time series of the log daily page views for the Wikipedia page for [Peyton Manning](https://en.wikipedia.org/wiki/Peyton_Manning). We scraped this data using the [Wikipediatrend](https://cran.r-project.org/package=wikipediatrend) package in R. Peyton Manning provides a nice example because it illustrates some of Prophet's features, like multiple seasonality, changing growth rates, and the ability to model special days (such as Manning's playoff and superbowl appearances). The CSV is available [here](https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv).
First we'll import the data:
```
import pandas as pd
from fbprophet import Prophet
df = pd.read_csv('../examples/example_wp_log_peyton_manning.csv')
df.head()
```
We fit the model by instantiating a new `Prophet` object. Any settings to the forecasting procedure are passed into the constructor. Then you call its `fit` method and pass in the historical dataframe. Fitting should take 1-5 seconds.
```
m = Prophet()
m.fit(df)
```
Predictions are then made on a dataframe with a column `ds` containing the dates for which a prediction is to be made. You can get a suitable dataframe that extends into the future a specified number of days using the helper method `Prophet.make_future_dataframe`. By default it will also include the dates from the history, so we will see the model fit as well.
```
future = m.make_future_dataframe(periods=365)
future.tail()
```
The `predict` method will assign each row in `future` a predicted value which it names `yhat`. If you pass in historical dates, it will provide an in-sample fit. The `forecast` object here is a new dataframe that includes a column `yhat` with the forecast, as well as columns for components and uncertainty intervals.
```
forecast = m.predict(future)
forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail()
```
You can plot the forecast by calling the `Prophet.plot` method and passing in your forecast dataframe.
```
fig1 = m.plot(forecast)
```
If you want to see the forecast components, you can use the `Prophet.plot_components` method. By default you'll see the trend, yearly seasonality, and weekly seasonality of the time series. If you include holidays, you'll see those here, too.
```
fig2 = m.plot_components(forecast)
```
An interactive figure of the forecast and components can be created with plotly. You will need to install plotly 4.0 or above separately, as it will not by default be installed with fbprophet. You will also need to install the `notebook` and `ipywidgets` packages.
```
from fbprophet.plot import plot_plotly, plot_components_plotly
plot_plotly(m, forecast)
plot_components_plotly(m, forecast)
```
More details about the options available for each method are available in the docstrings, for example, via `help(Prophet)` or `help(Prophet.fit)`. The [R reference manual](https://cran.r-project.org/web/packages/prophet/prophet.pdf) on CRAN provides a concise list of all of the available functions, each of which has a Python equivalent.
## R API
In R, we use the normal model fitting API. We provide a `prophet` function that performs fitting and returns a model object. You can then call `predict` and `plot` on this model object.
```
%%R
library(prophet)
```
First we read in the data and create the outcome variable. As in the Python API, this is a dataframe with columns `ds` and `y`, containing the date and numeric value respectively. The ds column should be YYYY-MM-DD for a date, or YYYY-MM-DD HH:MM:SS for a timestamp. As above, we use here the log number of views to Peyton Manning's Wikipedia page, available [here](https://github.com/facebook/prophet/blob/master/examples/example_wp_log_peyton_manning.csv).
```
%%R
df <- read.csv('../examples/example_wp_log_peyton_manning.csv')
```
We call the `prophet` function to fit the model. The first argument is the historical dataframe. Additional arguments control how Prophet fits the data and are described in later pages of this documentation.
```
%%R
m <- prophet(df)
```
Predictions are made on a dataframe with a column `ds` containing the dates for which predictions are to be made. The `make_future_dataframe` function takes the model object and a number of periods to forecast and produces a suitable dataframe. By default it will also include the historical dates so we can evaluate in-sample fit.
```
%%R
future <- make_future_dataframe(m, periods = 365)
tail(future)
```
As with most modeling procedures in R, we use the generic `predict` function to get our forecast. The `forecast` object is a dataframe with a column `yhat` containing the forecast. It has additional columns for uncertainty intervals and seasonal components.
```
%%R
forecast <- predict(m, future)
tail(forecast[c('ds', 'yhat', 'yhat_lower', 'yhat_upper')])
```
You can use the generic `plot` function to plot the forecast, by passing in the model and the forecast dataframe.
```
%%R -w 10 -h 6 -u in
plot(m, forecast)
```
You can use the `prophet_plot_components` function to see the forecast broken down into trend, weekly seasonality, and yearly seasonality.
```
%%R -w 9 -h 9 -u in
prophet_plot_components(m, forecast)
```
An interactive plot of the forecast using Dygraphs can be made with the command `dyplot.prophet(m, forecast)`.
More details about the options available for each method are available in the docstrings, for example, via `?prophet` or `?fit.prophet`. This documentation is also available in the [reference manual](https://cran.r-project.org/web/packages/prophet/prophet.pdf) on CRAN.
| github_jupyter |
## TensorFlow 2 Complete Project Workflow in Amazon SageMaker
### Data Preprocessing -> Code Prototyping -> Automatic Model Tuning -> Deployment
1. [Introduction](#Introduction)
2. [SageMaker Processing for dataset transformation](#SageMakerProcessing)
3. [Local Mode training](#LocalModeTraining)
4. [Local Mode endpoint](#LocalModeEndpoint)
5. [SageMaker hosted training](#SageMakerHostedTraining)
6. [Automatic Model Tuning](#AutomaticModelTuning)
7. [SageMaker hosted endpoint](#SageMakerHostedEndpoint)
8. [Workflow Automation with the Step Functions Data Science SDK](#WorkflowAutomation)
1. [Add an IAM policy to your SageMaker role](#IAMPolicy)
2. [Create an execution role for Step Functions](#CreateExecutionRole)
3. [Set up a TrainingPipeline](#TrainingPipeline)
4. [Visualizing the workflow](#VisualizingWorkflow)
5. [Creating and executing the pipeline](#CreatingExecutingPipeline)
6. [Cleanup](#Cleanup)
9. [Extensions](#Extensions)
### ***Prerequisite: To run the Local Mode sections of this example, use a SageMaker Notebook Instance; otherwise skip those sections (for example if you're using SageMaker Studio instead).***
## Introduction <a class="anchor" id="Introduction">
If you are using TensorFlow 2, you can use the Amazon SageMaker prebuilt TensorFlow 2 container with training scripts similar to those you would use outside SageMaker. This feature is named Script Mode. Using Script Mode and other SageMaker features, you can build a complete workflow for a TensorFlow 2 project. This notebook presents such a workflow, including all key steps such as preprocessing data with SageMaker Processing, code prototyping with SageMaker Local Mode training and inference, and production-ready model training and deployment with SageMaker hosted training and inference. Automatic Model Tuning in SageMaker is used to tune the model's hyperparameters. Additionally, the [AWS Step Functions Data Science SDK](https://aws-step-functions-data-science-sdk.readthedocs.io/en/latest/readmelink.html) is used to automate the main training and deployment steps for use in a production workflow outside notebooks.
To enable you to run this notebook within a reasonable time (typically less than an hour), this notebook's use case is a straightforward regression task: predicting house prices based on the well-known Boston Housing dataset. This public dataset contains 13 features regarding housing stock of towns in the Boston area. Features include average number of rooms, accessibility to radial highways, adjacency to the Charles River, etc.
To begin, we'll import some necessary packages and set up directories for local training and test data. We'll also set up a SageMaker Session to perform various operations, and specify an Amazon S3 bucket to hold input data and output. The default bucket used here is created by SageMaker if it doesn't already exist, and named in accordance with the AWS account ID and AWS Region.
```
import os
import sagemaker
import tensorflow as tf
sess = sagemaker.Session()
bucket = sess.default_bucket()
data_dir = os.path.join(os.getcwd(), 'data')
os.makedirs(data_dir, exist_ok=True)
train_dir = os.path.join(os.getcwd(), 'data/train')
os.makedirs(train_dir, exist_ok=True)
test_dir = os.path.join(os.getcwd(), 'data/test')
os.makedirs(test_dir, exist_ok=True)
raw_dir = os.path.join(os.getcwd(), 'data/raw')
os.makedirs(raw_dir, exist_ok=True)
```
# SageMaker Processing for dataset transformation <a class="anchor" id="SageMakerProcessing">
Next, we'll import the dataset and transform it with SageMaker Processing, which can be used to process terabytes of data in a SageMaker-managed cluster separate from the instance running your notebook server. In a typical SageMaker workflow, notebooks are only used for prototyping and can be run on relatively inexpensive and less powerful instances, while processing, training and model hosting tasks are run on separate, more powerful SageMaker-managed instances. SageMaker Processing includes off-the-shelf support for Scikit-learn, as well as a Bring Your Own Container option, so it can be used with many different data transformation technologies and tasks.
First we'll load the Boston Housing dataset, save the raw feature data and upload it to Amazon S3 for transformation by SageMaker Processing. We'll also save the labels for training and testing.
```
import numpy as np
from tensorflow.python.keras.datasets import boston_housing
from sklearn.preprocessing import StandardScaler
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
np.save(os.path.join(raw_dir, 'x_train.npy'), x_train)
np.save(os.path.join(raw_dir, 'x_test.npy'), x_test)
np.save(os.path.join(train_dir, 'y_train.npy'), y_train)
np.save(os.path.join(test_dir, 'y_test.npy'), y_test)
s3_prefix = 'tf-2-workflow'
rawdata_s3_prefix = '{}/data/raw'.format(s3_prefix)
raw_s3 = sess.upload_data(path='./data/raw/', key_prefix=rawdata_s3_prefix)
print(raw_s3)
```
To use SageMaker Processing, simply supply a Python data preprocessing script as shown below. For this example, we're using a SageMaker prebuilt Scikit-learn container, which includes many common functions for processing data. There are few limitations on what kinds of code and operations you can run, and only a minimal contract: input and output data must be placed in specified directories. If this is done, SageMaker Processing automatically loads the input data from S3 and uploads transformed data back to S3 when the job is complete.
```
%%writefile preprocessing.py
import glob
import numpy as np
import os
from sklearn.preprocessing import StandardScaler
if __name__=='__main__':
input_files = glob.glob('{}/*.npy'.format('/opt/ml/processing/input'))
print('\nINPUT FILE LIST: \n{}\n'.format(input_files))
scaler = StandardScaler()
for file in input_files:
raw = np.load(file)
transformed = scaler.fit_transform(raw)
if 'train' in file:
output_path = os.path.join('/opt/ml/processing/train', 'x_train.npy')
np.save(output_path, transformed)
print('SAVED TRANSFORMED TRAINING DATA FILE\n')
else:
output_path = os.path.join('/opt/ml/processing/test', 'x_test.npy')
np.save(output_path, transformed)
print('SAVED TRANSFORMED TEST DATA FILE\n')
```
Before starting the SageMaker Processing job, we instantiate a `SKLearnProcessor` object. This object allows you to specify the instance type to use in the job, as well as how many instances. Although the Boston Housing dataset is quite small, we'll use two instances to showcase how easy it is to spin up a cluster for SageMaker Processing.
```
from sagemaker import get_execution_role
from sagemaker.sklearn.processing import SKLearnProcessor
sklearn_processor = SKLearnProcessor(framework_version='0.20.0',
role=get_execution_role(),
instance_type='ml.m5.xlarge',
instance_count=2)
```
We're now ready to run the Processing job. To enable distributing the data files equally among the instances, we specify the `ShardedByS3Key` distribution type in the `ProcessingInput` object. This ensures that if we have `n` instances, each instance will receive `1/n` files from the specified S3 bucket. It may take around 3 minutes for the following code cell to run, mainly to set up the cluster. At the end of the job, the cluster automatically will be torn down by SageMaker.
```
from sagemaker.processing import ProcessingInput, ProcessingOutput
from time import gmtime, strftime
processing_job_name = "tf-2-workflow-{}".format(strftime("%d-%H-%M-%S", gmtime()))
output_destination = 's3://{}/{}/data'.format(bucket, s3_prefix)
sklearn_processor.run(code='preprocessing.py',
job_name=processing_job_name,
inputs=[ProcessingInput(
source=raw_s3,
destination='/opt/ml/processing/input',
s3_data_distribution_type='ShardedByS3Key')],
outputs=[ProcessingOutput(output_name='train',
destination='{}/train'.format(output_destination),
source='/opt/ml/processing/train'),
ProcessingOutput(output_name='test',
destination='{}/test'.format(output_destination),
source='/opt/ml/processing/test')])
preprocessing_job_description = sklearn_processor.jobs[-1].describe()
```
In the log output of the SageMaker Processing job above, you should be able to see logs in two different colors for the two different instances, and that each instance received different files. Without the `ShardedByS3Key` distribution type, each instance would have received a copy of **all** files. By spreading the data equally among `n` instances, you should receive a speedup by approximately a factor of `n` for most stateless data transformations. After saving the job results locally, we'll move on to prototyping training and inference code with Local Mode.
```
train_in_s3 = '{}/train/x_train.npy'.format(output_destination)
test_in_s3 = '{}/test/x_test.npy'.format(output_destination)
!aws s3 cp {train_in_s3} ./data/train/x_train.npy
!aws s3 cp {test_in_s3} ./data/test/x_test.npy
```
## Local Mode training <a class="anchor" id="LocalModeTraining">
Local Mode in Amazon SageMaker is a convenient way to make sure your code is working locally as expected before moving on to full scale, hosted training in a separate, more powerful SageMaker-managed cluster. To train in Local Mode, it is necessary to have docker-compose or nvidia-docker-compose (for GPU instances) installed. Running the following commands will install docker-compose or nvidia-docker-compose, and configure the notebook environment for you.
```
!wget -q https://raw.githubusercontent.com/aws-samples/amazon-sagemaker-script-mode/master/local_mode_setup.sh
!wget -q https://raw.githubusercontent.com/aws-samples/amazon-sagemaker-script-mode/master/daemon.json
!/bin/bash ./local_mode_setup.sh
```
Next, we'll set up a TensorFlow Estimator for Local Mode training. Key parameters for the Estimator include:
- `train_instance_type`: the kind of hardware on which training will run. In the case of Local Mode, we simply set this parameter to `local` to invoke Local Mode training on the CPU, or to `local_gpu` if the instance has a GPU.
- `git_config`: to make sure training scripts are source controlled for coordinated, shared use by a team, the Estimator can pull in the code from a Git repository rather than local directories.
- Other parameters of note: the algorithm’s hyperparameters, which are passed in as a dictionary, and a Boolean parameter indicating that we are using Script Mode.
Recall that we are using Local Mode here mainly to make sure our code is working. Accordingly, instead of performing a full cycle of training with many epochs (passes over the full dataset), we'll train only for a small number of epochs just to confirm the code is working properly and avoid wasting full-scale training time unnecessarily.
```
from sagemaker.tensorflow import TensorFlow
git_config = {'repo': 'https://github.com/aws-samples/amazon-sagemaker-script-mode',
'branch': 'master'}
model_dir = '/opt/ml/model'
train_instance_type = 'local'
hyperparameters = {'epochs': 5, 'batch_size': 128, 'learning_rate': 0.01}
local_estimator = TensorFlow(git_config=git_config,
source_dir='tf-2-workflow/train_model',
entry_point='train.py',
model_dir=model_dir,
instance_type=train_instance_type,
instance_count=1,
hyperparameters=hyperparameters,
role=sagemaker.get_execution_role(),
base_job_name='tf-2-workflow',
framework_version='2.2',
py_version='py37',
script_mode=True)
```
The `fit` method call below starts the Local Mode training job. Metrics for training will be logged below the code, inside the notebook cell. You should observe the validation loss decrease substantially over the five epochs, with no training errors, which is a good indication that our training code is working as expected.
```
inputs = {'train': f'file://{train_dir}',
'test': f'file://{test_dir}'}
local_estimator.fit(inputs)
```
## Local Mode endpoint <a class="anchor" id="LocalModeEndpoint">
While Amazon SageMaker’s Local Mode training is very useful to make sure your training code is working before moving on to full scale training, it also would be useful to have a convenient way to test your model locally before incurring the time and expense of deploying it to production. One possibility is to fetch the TensorFlow SavedModel artifact or a model checkpoint saved in Amazon S3, and load it in your notebook for testing. However, an even easier way to do this is to use the SageMaker Python SDK to do this work for you by setting up a Local Mode endpoint.
More specifically, the Estimator object from the Local Mode training job can be used to deploy a model locally. With one exception, this code is the same as the code you would use to deploy to production. In particular, all you need to do is invoke the local Estimator's deploy method, and similarly to Local Mode training, specify the instance type as either `local_gpu` or `local` depending on whether your notebook is on a GPU instance or CPU instance.
Just in case there are other inference containers running in Local Mode, we'll stop them to avoid conflict before deploying our new model locally.
```
!docker container stop $(docker container ls -aq) >/dev/null
```
The following single line of code deploys the model locally in the SageMaker TensorFlow Serving container:
```
local_predictor = local_estimator.deploy(initial_instance_count=1, instance_type='local')
```
To get predictions from the Local Mode endpoint, simply invoke the Predictor's predict method.
```
local_results = local_predictor.predict(x_test[:10])['predictions']
```
As a sanity check, the predictions can be compared against the actual target values.
```
local_preds_flat_list = [float('%.1f'%(item)) for sublist in local_results for item in sublist]
print('predictions: \t{}'.format(np.array(local_preds_flat_list)))
print('target values: \t{}'.format(y_test[:10].round(decimals=1)))
```
We only trained the model for a few epochs and there is much room for improvement, but the predictions so far should at least appear reasonably within the ballpark.
To avoid having the SageMaker TensorFlow Serving container indefinitely running locally, simply gracefully shut it down by calling the `delete_endpoint` method of the Predictor object.
```
local_predictor.delete_endpoint()
```
## SageMaker hosted training <a class="anchor" id="SageMakerHostedTraining">
Now that we've confirmed our code is working locally, we can move on to use SageMaker's hosted training functionality. Hosted training is preferred for doing actual training, especially large-scale, distributed training. Unlike Local Mode training, for hosted training the actual training itself occurs not on the notebook instance, but on a separate cluster of machines managed by SageMaker. Before starting hosted training, the data must be in S3, or an EFS or FSx for Lustre file system. We'll upload to S3 now, and confirm the upload was successful.
```
s3_prefix = 'tf-2-workflow'
traindata_s3_prefix = '{}/data/train'.format(s3_prefix)
testdata_s3_prefix = '{}/data/test'.format(s3_prefix)
train_s3 = sess.upload_data(path='./data/train/', key_prefix=traindata_s3_prefix)
test_s3 = sess.upload_data(path='./data/test/', key_prefix=testdata_s3_prefix)
inputs = {'train':train_s3, 'test': test_s3}
print(inputs)
```
We're now ready to set up an Estimator object for hosted training. It is similar to the Local Mode Estimator, except the `train_instance_type` has been set to a SageMaker ML instance type instead of `local` for Local Mode. Also, since we know our code is working now, we'll train for a larger number of epochs with the expectation that model training will converge to an improved, lower validation loss.
With these two changes, we simply call `fit` to start the actual hosted training.
```
train_instance_type = 'ml.c5.xlarge'
hyperparameters = {'epochs': 30, 'batch_size': 128, 'learning_rate': 0.01}
git_config = {'repo': 'https://github.com/aws-samples/amazon-sagemaker-script-mode',
'branch': 'master'}
estimator = TensorFlow(git_config=git_config,
source_dir='tf-2-workflow/train_model',
entry_point='train.py',
model_dir=model_dir,
instance_type=train_instance_type,
instance_count=1,
hyperparameters=hyperparameters,
role=sagemaker.get_execution_role(),
base_job_name='tf-2-workflow',
framework_version='2.2',
py_version='py37',
script_mode=True)
```
After starting the hosted training job with the `fit` method call below, you should observe the training converge over the longer number of epochs to a validation loss that is considerably lower than that which was achieved in the shorter Local Mode training job. Can we do better? We'll look into a way to do so in the **Automatic Model Tuning** section below.
```
estimator.fit(inputs)
```
As with the Local Mode training, hosted training produces a model saved in S3 that we can retrieve. This is an example of the modularity of SageMaker: having trained the model in SageMaker, you can now take the model out of SageMaker and run it anywhere else. Alternatively, you can deploy the model into a production-ready environment using SageMaker's hosted endpoints functionality, as shown in the **SageMaker hosted endpoint** section below.
Retrieving the model from S3 is very easy: the hosted training estimator you created above stores a reference to the model's location in S3. You simply copy the model from S3 using the estimator's `model_data` property and unzip it to inspect the contents.
```
!aws s3 cp {estimator.model_data} ./model/model.tar.gz
```
The unzipped archive should include the assets required by TensorFlow Serving to load the model and serve it, including a .pb file:
```
!tar -xvzf ./model/model.tar.gz -C ./model
```
## Automatic Model Tuning <a class="anchor" id="AutomaticModelTuning">
So far we have simply run one Local Mode training job and one Hosted Training job without any real attempt to tune hyperparameters to produce a better model, other than increasing the number of epochs. Selecting the right hyperparameter values to train your model can be difficult, and typically is very time consuming if done manually. The right combination of hyperparameters is dependent on your data and algorithm; some algorithms have many different hyperparameters that can be tweaked; some are very sensitive to the hyperparameter values selected; and most have a non-linear relationship between model fit and hyperparameter values. SageMaker Automatic Model Tuning helps automate the hyperparameter tuning process: it runs multiple training jobs with different hyperparameter combinations to find the set with the best model performance.
We begin by specifying the hyperparameters we wish to tune, and the range of values over which to tune each one. We also must specify an objective metric to be optimized: in this use case, we'd like to minimize the validation loss.
```
from sagemaker.tuner import IntegerParameter, CategoricalParameter, ContinuousParameter, HyperparameterTuner
hyperparameter_ranges = {
'learning_rate': ContinuousParameter(0.001, 0.2, scaling_type="Logarithmic"),
'epochs': IntegerParameter(10, 50),
'batch_size': IntegerParameter(64, 256),
}
metric_definitions = [{'Name': 'loss',
'Regex': ' loss: ([0-9\\.]+)'},
{'Name': 'val_loss',
'Regex': ' val_loss: ([0-9\\.]+)'}]
objective_metric_name = 'val_loss'
objective_type = 'Minimize'
```
Next we specify a HyperparameterTuner object that takes the above definitions as parameters. Each tuning job must be given a budget: a maximum number of training jobs. A tuning job will complete after that many training jobs have been executed.
We also can specify how much parallelism to employ, in this case five jobs, meaning that the tuning job will complete after three series of five jobs in parallel have completed. For the default Bayesian Optimization tuning strategy used here, the tuning search is informed by the results of previous groups of training jobs, so we don't run all of the jobs in parallel, but rather divide the jobs into groups of parallel jobs. There is a trade-off: using more parallel jobs will finish tuning sooner, but likely will sacrifice tuning search accuracy.
Now we can launch a hyperparameter tuning job by calling the `fit` method of the HyperparameterTuner object. The tuning job may take around 10 minutes to finish. While you're waiting, the status of the tuning job, including metadata and results for invidual training jobs within the tuning job, can be checked in the SageMaker console in the **Hyperparameter tuning jobs** panel.
```
tuner = HyperparameterTuner(estimator,
objective_metric_name,
hyperparameter_ranges,
metric_definitions,
max_jobs=15,
max_parallel_jobs=5,
objective_type=objective_type)
tuning_job_name = "tf-2-workflow-{}".format(strftime("%d-%H-%M-%S", gmtime()))
tuner.fit(inputs, job_name=tuning_job_name)
tuner.wait()
```
After the tuning job is finished, we can use the `HyperparameterTuningJobAnalytics` object from the SageMaker Python SDK to list the top 5 tuning jobs with the best performance. Although the results vary from tuning job to tuning job, the best validation loss from the tuning job (under the FinalObjectiveValue column) likely will be substantially lower than the validation loss from the hosted training job above, where we did not perform any tuning other than manually increasing the number of epochs once.
```
tuner_metrics = sagemaker.HyperparameterTuningJobAnalytics(tuning_job_name)
tuner_metrics.dataframe().sort_values(['FinalObjectiveValue'], ascending=True).head(5)
```
The total training time and training jobs status can be checked with the following lines of code. Because automatic early stopping is by default off, all the training jobs should be completed normally. For an example of a more in-depth analysis of a tuning job, see the SageMaker official sample [HPO_Analyze_TuningJob_Results.ipynb](https://github.com/awslabs/amazon-sagemaker-examples/blob/master/hyperparameter_tuning/analyze_results/HPO_Analyze_TuningJob_Results.ipynb) notebook.
```
total_time = tuner_metrics.dataframe()['TrainingElapsedTimeSeconds'].sum() / 3600
print("The total training time is {:.2f} hours".format(total_time))
tuner_metrics.dataframe()['TrainingJobStatus'].value_counts()
```
## SageMaker hosted endpoint <a class="anchor" id="SageMakerHostedEndpoint">
Assuming the best model from the tuning job is better than the model produced by the individual Hosted Training job above, we could now easily deploy that model to production. A convenient option is to use a SageMaker hosted endpoint, which serves real time predictions from the trained model (Batch Transform jobs also are available for asynchronous, offline predictions on large datasets). The endpoint will retrieve the TensorFlow SavedModel created during training and deploy it within a SageMaker TensorFlow Serving container. This all can be accomplished with one line of code.
More specifically, by calling the `deploy` method of the HyperparameterTuner object we instantiated above, we can directly deploy the best model from the tuning job to a SageMaker hosted endpoint. It will take several minutes longer to deploy the model to the hosted endpoint compared to the Local Mode endpoint, which is more useful for fast prototyping of inference code.
```
tuning_predictor = tuner.deploy(initial_instance_count=1, instance_type='ml.m5.xlarge')
```
We can compare the predictions generated by this endpoint with those generated locally by the Local Mode endpoint:
```
results = tuning_predictor.predict(x_test[:10])['predictions']
flat_list = [float('%.1f'%(item)) for sublist in results for item in sublist]
print('predictions: \t{}'.format(np.array(flat_list)))
print('target values: \t{}'.format(y_test[:10].round(decimals=1)))
```
To avoid billing charges from stray resources, you can delete the prediction endpoint to release its associated instance(s).
```
sess.delete_endpoint(tuning_predictor.endpoint_name)
```
## Workflow Automation with the AWS Step Functions Data Science SDK <a class="anchor" id="WorkflowAutomation">
In the previous parts of this notebook, we prototyped various steps of a TensorFlow project within the notebook itself. Notebooks are great for prototyping, but generally are not used in production-ready machine learning pipelines. For example, a simple pipeline in SageMaker includes the following steps:
1. Training the model.
2. Creating a SageMaker Model object that wraps the model artifact for serving.
3. Creating a SageMaker Endpoint Configuration specifying how the model should be served (e.g. hardware type and amount).
4. Deploying the trained model to the configured SageMaker Endpoint.
The AWS Step Functions Data Science SDK automates the process of creating and running these kinds of workflows using AWS Step Functions and SageMaker. It does this by allowing you to create workflows using short, simple Python scripts that define workflow steps and chain them together. Under the hood, all the workflow steps are coordinated by AWS Step Functions without any need for you to manage the underlying infrastructure.
To begin, install the Step Functions Data Science SDK:
```
import sys
!{sys.executable} -m pip install --quiet --upgrade stepfunctions
```
### Add an IAM policy to your SageMaker role <a class="anchor" id="IAMPolicy">
**If you are running this notebook on an Amazon SageMaker notebook instance**, the IAM role assumed by your notebook instance needs permission to create and run workflows in AWS Step Functions. To provide this permission to the role, do the following.
1. Open the Amazon [SageMaker console](https://console.aws.amazon.com/sagemaker/).
2. Select **Notebook instances** and choose the name of your notebook instance
3. Under **Permissions and encryption** select the role ARN to view the role on the IAM console
4. Choose **Attach policies** and search for `AWSStepFunctionsFullAccess`.
5. Select the check box next to `AWSStepFunctionsFullAccess` and choose **Attach policy**
If you are running this notebook in a local environment, the SDK will use your configured AWS CLI configuration. For more information, see [Configuring the AWS CLI](https://docs.aws.amazon.com/cli/latest/userguide/cli-chap-configure.html).
### Create an execution role for Step Functions <a class="anchor" id="CreateExecutionRole">
You also need to create an execution role for Step Functions to enable that service to access SageMaker and other service functionality.
1. Go to the [IAM console](https://console.aws.amazon.com/iam/)
2. Select **Roles** and then **Create role**.
3. Under **Choose the service that will use this role** select **Step Functions**
4. Choose **Next** until you can enter a **Role name**
5. Enter a name such as `StepFunctionsWorkflowExecutionRole` and then select **Create role**
Select your newly create role and attach a policy to it. The following steps attach a policy that provides full access to Step Functions, however as a good practice you should only provide access to the resources you need.
1. Under the **Permissions** tab, click **Add inline policy**
2. Enter the following in the **JSON** tab
```json
{
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Action": [
"sagemaker:CreateTransformJob",
"sagemaker:DescribeTransformJob",
"sagemaker:StopTransformJob",
"sagemaker:CreateTrainingJob",
"sagemaker:DescribeTrainingJob",
"sagemaker:StopTrainingJob",
"sagemaker:CreateHyperParameterTuningJob",
"sagemaker:DescribeHyperParameterTuningJob",
"sagemaker:StopHyperParameterTuningJob",
"sagemaker:CreateModel",
"sagemaker:CreateEndpointConfig",
"sagemaker:CreateEndpoint",
"sagemaker:DeleteEndpointConfig",
"sagemaker:DeleteEndpoint",
"sagemaker:UpdateEndpoint",
"sagemaker:ListTags",
"lambda:InvokeFunction",
"sqs:SendMessage",
"sns:Publish",
"ecs:RunTask",
"ecs:StopTask",
"ecs:DescribeTasks",
"dynamodb:GetItem",
"dynamodb:PutItem",
"dynamodb:UpdateItem",
"dynamodb:DeleteItem",
"batch:SubmitJob",
"batch:DescribeJobs",
"batch:TerminateJob",
"glue:StartJobRun",
"glue:GetJobRun",
"glue:GetJobRuns",
"glue:BatchStopJobRun"
],
"Resource": "*"
},
{
"Effect": "Allow",
"Action": [
"iam:PassRole"
],
"Resource": "*",
"Condition": {
"StringEquals": {
"iam:PassedToService": "sagemaker.amazonaws.com"
}
}
},
{
"Effect": "Allow",
"Action": [
"events:PutTargets",
"events:PutRule",
"events:DescribeRule"
],
"Resource": [
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForSageMakerTrainingJobsRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForSageMakerTransformJobsRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForSageMakerTuningJobsRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForECSTaskRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForBatchJobsRule"
]
}
]
}
```
3. Choose **Review policy** and give the policy a name such as `StepFunctionsWorkflowExecutionPolicy`
4. Choose **Create policy**. You will be redirected to the details page for the role.
5. Copy the **Role ARN** at the top of the **Summary**
### Set up a TrainingPipeline <a class="anchor" id="TrainingPipeline">
Although the AWS Step Functions Data Science SDK provides various primitives to build up pipelines from scratch, it also provides prebuilt templates for common workflows, including a [TrainingPipeline](https://aws-step-functions-data-science-sdk.readthedocs.io/en/latest/pipelines.html#stepfunctions.template.pipeline.train.TrainingPipeline) object to simplify creation of a basic pipeline that includes model training and deployment.
The following code cell configures a `pipeline` object with the necessary parameters to define such a simple pipeline:
```
import stepfunctions
from stepfunctions.template.pipeline import TrainingPipeline
# paste the StepFunctionsWorkflowExecutionRole ARN from above
workflow_execution_role = "<execution-role-arn>"
pipeline = TrainingPipeline(
estimator=estimator,
role=workflow_execution_role,
inputs=inputs,
s3_bucket=bucket
)
```
### Visualizing the workflow <a class="anchor" id="VisualizingWorkflow">
You can now view the workflow definition, and visualize it as a graph. This workflow and graph represent your training pipeline from starting a training job to deploying the model.
```
print(pipeline.workflow.definition.to_json(pretty=True))
pipeline.render_graph()
```
### Creating and executing the pipeline <a class="anchor" id="CreatingExecutingPipeline">
Before the workflow can be run for the first time, the pipeline must be created using the `create` method:
```
pipeline.create()
```
Now the workflow can be started by invoking the pipeline's `execute` method:
```
execution = pipeline.execute()
```
Use the `list_executions` method to list all executions for the workflow you created, including the one we just started. After a pipeline is created, it can be executed as many times as needed, for example on a schedule for retraining on new data. (For purposes of this notebook just execute the workflow one time to save resources.) The output will include a list you can click through to access a view of the execution in the AWS Step Functions console.
```
pipeline.workflow.list_executions(html=True)
```
While the workflow is running, you can check workflow progress inside this notebook with the `render_progress` method. This generates a snapshot of the current state of your workflow as it executes. This is a static image. Run the cell again to check progress while the workflow is running.
```
execution.render_progress()
```
#### BEFORE proceeding with the rest of the notebook:
Wait until the workflow completes with status **Succeeded**, which will take a few minutes. You can check status with `render_progress` above, or open in a new browser tab the **Inspect in AWS Step Functions** link in the cell output.
To view the details of the completed workflow execution, from model training through deployment, use the `list_events` method, which lists all events in the workflow execution.
```
execution.list_events(reverse_order=True, html=False)
```
From this list of events, we can extract the name of the endpoint that was set up by the workflow.
```
import re
endpoint_name_suffix = re.search('endpoint\Wtraining\Wpipeline\W([a-zA-Z0-9\W]+?)"', str(execution.list_events())).group(1)
print(endpoint_name_suffix)
```
Once we have the endpoint name, we can use it to instantiate a TensorFlowPredictor object that wraps the endpoint. This TensorFlowPredictor can be used to make predictions, as shown in the following code cell.
#### BEFORE running the following code cell:
Go to the [SageMaker console](https://console.aws.amazon.com/sagemaker/), click **Endpoints** in the left panel, and make sure that the endpoint status is **InService**. If the status is **Creating**, wait until it changes, which may take several minutes.
```
from sagemaker.tensorflow import TensorFlowPredictor
workflow_predictor = TensorFlowPredictor('training-pipeline-' + endpoint_name_suffix)
results = workflow_predictor.predict(x_test[:10])['predictions']
flat_list = [float('%.1f'%(item)) for sublist in results for item in sublist]
print('predictions: \t{}'.format(np.array(flat_list)))
print('target values: \t{}'.format(y_test[:10].round(decimals=1)))
```
Using the AWS Step Functions Data Science SDK, there are many other workflows you can create to automate your machine learning tasks. For example, you could create a workflow to automate model retraining on a periodic basis. Such a workflow could include a test of model quality after training, with subsequent branches for failing (no model deployment) and passing the quality test (model is deployed). Other possible workflow steps include Automatic Model Tuning, data preprocessing with AWS Glue, and more.
For a detailed example of a retraining workflow, see the AWS ML Blog post [Automating model retraining and deployment using the AWS Step Functions Data Science SDK for Amazon SageMaker](https://aws.amazon.com/blogs/machine-learning/automating-model-retraining-and-deployment-using-the-aws-step-functions-data-science-sdk-for-amazon-sagemaker/).
### Cleanup <a class="anchor" id="Cleanup">
The workflow we created above deployed a model to an endpoint. To avoid billing charges for an unused endpoint, you can delete it using the SageMaker console. To do so, go to the [SageMaker console](https://console.aws.amazon.com/sagemaker/). Then click **Endpoints** in the left panel, and select and delete any unneeded endpoints in the list.
## Extensions <a class="anchor" id="Extensions">
We've covered a lot of content in this notebook: SageMaker Processing for data transformation, Local Mode for prototyping training and inference code, Automatic Model Tuning, and SageMaker hosted training and inference. These are central elements for most deep learning workflows in SageMaker. Additionally, we examined how the AWS Step Functions Data Science SDK helps automate deep learning workflows after completion of the prototyping phase of a project.
Besides all of the SageMaker features explored above, there are many other features that may be applicable to your project. For example, to handle common problems during deep learning model training such as vanishing or exploding gradients, **SageMaker Debugger** is useful. To manage common problems such as data drift after a model is in production, **SageMaker Model Monitor** can be applied.
| github_jupyter |
# Paralelizacion de entrenamiento de redes neuronales con TensorFlow
En esta seccion dejaremos atras los rudimentos de las matematicas y nos centraremos en utilizar TensorFlow, la cual es una de las librerias mas populares de arpendizaje profundo y que realiza una implementacion mas eficaz de las redes neuronales que cualquier otra implementacion de Numpy.
TensorFlow es una interfaz de programacion multiplataforma y escalable para implementar y ejecutar algortimos de aprendizaje automatico de una manera mas eficaz ya que permite usar tanto la CPU como la GPU, la cual suele tener muchos mas procesadores que la CPU, los cuales, combinando sus frecuencias, presentan un rendimiento mas potente. La API mas desarrollada de esta herramienta se presenta para Python, por lo cual muchos desarrolladores se ven atraidos a este lenguaje.
## Primeros pasos con TensorFlow
https://jakevdp.github.io/PythonDataScienceHandbook/02.01-understanding-data-types.html
```
# Creando tensores
# =============================================
import tensorflow as tf
import numpy as np
np.set_printoptions(precision=3)
a = np.array([1, 2, 3], dtype=np.int32)
b = [4, 5, 6]
t_a = tf.convert_to_tensor(a)
t_b = tf.convert_to_tensor(b)
print(t_a)
print(t_b)
# Obteniendo las dimensiones de un tensor
# ===============================================
t_ones = tf.ones((2, 3))
print(t_ones)
t_ones.shape
# Obteniendo los valores del tensor como array
# ===============================================
t_ones.numpy()
# Creando un tensor de valores constantes
# ================================================
const_tensor = tf.constant([1.2, 5, np.pi], dtype=tf.float32)
print(const_tensor)
matriz = np.array([[2, 3, 4, 5], [6, 7, 8, 8]], dtype = np.int32)
matriz
matriz_tf = tf.convert_to_tensor(matriz)
print(matriz_tf, end = '\n'*2)
print(matriz_tf.numpy(), end = '\n'*2)
print(matriz_tf.shape)
```
## Manipulando los tipos de datos y forma de un tensor
```
# Cambiando el tipo de datos del tensor
# ==============================================
print(matriz_tf.dtype)
matriz_tf_n = tf.cast(matriz_tf, tf.int64)
print(matriz_tf_n.dtype)
# Transponiendo un tensor
# =================================================
t = tf.random.uniform(shape=(3, 5))
print(t, end = '\n'*2)
t_tr = tf.transpose(t)
print(t_tr, end = '\n'*2)
# Redimensionando un vector
# =====================================
t = tf.zeros((30,))
print(t, end = '\n'*2)
print(t.shape, end = '\n'*3)
t_reshape = tf.reshape(t, shape=(5, 6))
print(t_reshape, end = '\n'*2)
print(t_reshape.shape)
# Removiendo las dimensiones innecesarias
# =====================================================
t = tf.zeros((1, 2, 1, 4, 1))
print(t, end = '\n'*2)
print(t.shape, end = '\n'*3)
t_sqz = tf.squeeze(t, axis=(2, 4))
print(t_sqz, end = '\n'*2)
print(t_sqz.shape, end = '\n'*3)
print(t.shape, ' --> ', t_sqz.shape)
```
## Operaciones matematicas sobre tensores
```
# Inicializando dos tensores con numeros aleatorios
# =============================================================
tf.random.set_seed(1)
t1 = tf.random.uniform(shape=(5, 2), minval=-1.0, maxval=1.0)
t2 = tf.random.normal(shape=(5, 2), mean=0.0, stddev=1.0)
print(t1, '\n'*2, t2)
# Producto tipo element-wise: elemento a elemento
# =================================================
t3 = tf.multiply(t1, t2).numpy()
print(t3)
# Promedio segun el eje
# ================================================
t4 = tf.math.reduce_mean(t1, axis=None)
print(t4, end = '\n'*3)
t4 = tf.math.reduce_mean(t1, axis=0)
print(t4, end = '\n'*3)
t4 = tf.math.reduce_mean(t1, axis=1)
print(t4, end = '\n'*3)
# suma segun el eje
# =================================================
t4 = tf.math.reduce_sum(t1, axis=None)
print('Suma de todos los elementos:', t4, end = '\n'*3)
t4 = tf.math.reduce_sum(t1, axis=0)
print('Suma de los elementos por columnas:', t4, end = '\n'*3)
t4 = tf.math.reduce_sum(t1, axis=1)
print('Suma de los elementos por filas:', t4, end = '\n'*3)
# Desviacion estandar segun el eje
# =================================================
t4 = tf.math.reduce_std(t1, axis=None)
print('Suma de todos los elementos:', t4, end = '\n'*3)
t4 = tf.math.reduce_std(t1, axis=0)
print('Suma de los elementos por columnas:', t4, end = '\n'*3)
t4 = tf.math.reduce_std(t1, axis=1)
print('Suma de los elementos por filas:', t4, end = '\n'*3)
# Producto entre matrices
# ===========================================
t5 = tf.linalg.matmul(t1, t2, transpose_b=True)
print(t5.numpy(), end = '\n'*2)
# Producto entre matrices
# ===========================================
t6 = tf.linalg.matmul(t1, t2, transpose_a=True)
print(t6.numpy())
# Calculando la norma de un vector
# ==========================================
norm_t1 = tf.norm(t1, ord=2, axis=None).numpy()
print(norm_t1, end='\n'*2)
norm_t1 = tf.norm(t1, ord=2, axis=0).numpy()
print(norm_t1, end='\n'*2)
norm_t1 = tf.norm(t1, ord=2, axis=1).numpy()
print(norm_t1, end='\n'*2)
```
## Partir, apilar y concatenar tensores
```
# Datos a trabajar
# =======================================
tf.random.set_seed(1)
t = tf.random.uniform((6,))
print(t.numpy())
# Partiendo el tensor en un numero determinado de piezas
# ======================================================
t_splits = tf.split(t, num_or_size_splits = 3)
[item.numpy() for item in t_splits]
# Partiendo el tensor segun los tamaños definidos
# ======================================================
tf.random.set_seed(1)
t = tf.random.uniform((6,))
print(t.numpy())
t_splits = tf.split(t, num_or_size_splits=[3, 3])
[item.numpy() for item in t_splits]
print(matriz_tf.numpy())
# m_splits = tf.split(t, num_or_size_splits = 0, axis = 1)
matriz_n = tf.reshape(matriz_tf, shape = (8,))
print(matriz_n.numpy())
m_splits = tf.split(matriz_n, num_or_size_splits = 2)
[item.numpy() for item in m_splits]
# Concatenando tensores
# =========================================
A = tf.ones((3,))
print(A, end ='\n'*2)
B = tf.zeros((2,))
print(B, end ='\n'*2)
C = tf.concat([A, B], axis=0)
print(C.numpy())
# Apilando tensores
# =========================================
A = tf.ones((3,))
print(A, end ='\n'*2)
B = tf.zeros((3,))
print(B, end ='\n'*2)
S = tf.stack([A, B], axis=1)
print(S.numpy())
```
Mas funciones y herramientas en:
https://www.tensorflow.org/versions/r2.0/api_docs/python/tf.
<div class="burk">
EJERCICIOS</div><i class="fa fa-lightbulb-o "></i>
1. Cree dos tensores de dimensiones (4, 6), de numeros aleatorios provenientes de una distribucion normal estandar con promedio 0.0 y dsv 1.0. Imprimalos.
2. Multiplique los anteriores tensores de las dos formas vistas, element-wise y producto matricial, realizando las dos transposiciones vistas.
3. Calcule los promedios, desviaciones estandar y suma de sus elementos para los dos tensores.
4. Redimensione los tensores para que sean ahora de rango 1.
5. Calcule el coseno de los elementos de los tensores (revise la documentacion).
6. Cree un tensor de rango 1 con 1001 elementos, empezando con el 0 y hasta el 30.
7. Realice un for sobre los elementos del tensor e imprimalos.
8. Realice el calculo de los factoriales de los numero del 1 al 30 usando el tensor del punto 6. Imprima el resultado como un DataFrame
# Creación de *pipelines* de entrada con tf.data: la API de conjunto de datos de TensorFlow
Cuando entrenamos un modelo NN profundo, generalmente entrenamos el modelo de forma incremental utilizando un algoritmo de optimización iterativo como el descenso de gradiente estocástico, como hemos visto en clases anteriores.
La API de Keras es un contenedor de TensorFlow para crear modelos NN. La API de Keras proporciona un método, `.fit ()`, para entrenar los modelos. En los casos en que el conjunto de datos de entrenamiento es bastante pequeño y se puede cargar como un tensor en la memoria, los modelos de TensorFlow (que se compilan con la API de Keras) pueden usar este tensor directamente a través de su método .fit () para el entrenamiento. Sin embargo, en casos de uso típicos, cuando el conjunto de datos es demasiado grande para caber en la memoria de la computadora, necesitaremos cargar los datos del dispositivo de almacenamiento principal (por ejemplo, el disco duro o la unidad de estado sólido) en trozos, es decir, lote por lote.
Además, es posible que necesitemos construir un *pipeline* de procesamiento de datos para aplicar ciertas transformaciones y pasos de preprocesamiento a nuestros datos, como el centrado medio, el escalado o la adición de ruido para aumentar el procedimiento de entrenamiento y evitar el sobreajuste.
Aplicar las funciones de preprocesamiento manualmente cada vez puede resultar bastante engorroso. Afortunadamente, TensorFlow proporciona una clase especial para construir *pipelines* de preprocesamiento eficientes y convenientes. En esta parte, veremos una descripción general de los diferentes métodos para construir un conjunto de datos de TensorFlow, incluidas las transformaciones del conjunto de datos y los pasos de preprocesamiento comunes.
## Creando un Dataset de TensorFlow desde tensores existentes
Si los datos ya existen en forma de un objeto tensor, una lista de Python o una matriz NumPy, podemos crear fácilmente un conjunto de datos usando la función `tf.data.Dataset.from_tensor_slices()`. Esta función devuelve un objeto de la clase Dataset, que podemos usar para iterar a través de los elementos individuales en el conjunto de datos de entrada:
```
import tensorflow as tf
# Ejemplo con listas
# ======================================================
a = [1.2, 3.4, 7.5, 4.1, 5.0, 1.0]
ds = tf.data.Dataset.from_tensor_slices(a)
print(ds)
for item in ds:
print(item)
for i in ds:
print(i.numpy())
```
Si queremos crear lotes a partir de este conjunto de datos, con un tamaño de lote deseado de 3, podemos hacerlo de la siguiente manera:
```
# Creando lotes de 3 elementos cada uno
# ===================================================
ds_batch = ds.batch(3)
for i, elem in enumerate(ds_batch, 1):
print(f'batch {i}:', elem)
```
Esto creará dos lotes a partir de este conjunto de datos, donde los primeros tres elementos van al lote n° 1 y los elementos restantes al lote n° 2. El método `.batch()` tiene un argumento opcional, `drop_remainder`, que es útil para los casos en los que el número de elementos en el tensor no es divisible por el tamaño de lote deseado. El valor predeterminado de `drop_remainder` es `False`.
## Combinar dos tensores en un Dataset
A menudo, podemos tener los datos en dos (o posiblemente más) tensores. Por ejemplo, podríamos tener un tensor para características y un tensor para etiquetas. En tales casos, necesitamos construir un conjunto de datos que combine estos tensores juntos, lo que nos permitirá recuperar los elementos de estos tensores en tuplas.
Suponga que tenemos dos tensores, t_x y t_y. El tensor t_x contiene nuestros valores de características, cada uno de tamaño 3, y t_y almacena las etiquetas de clase. Para este ejemplo, primero creamos estos dos tensores de la siguiente manera:
```
# Datos de ejemplo
# ============================================
tf.random.set_seed(1)
t_x = tf.random.uniform([4, 3], dtype=tf.float32)
t_y = tf.range(4)
print(t_x)
print(t_y)
# Uniendo los dos tensores en un Dataset
# ============================================
ds_x = tf.data.Dataset.from_tensor_slices(t_x)
ds_y = tf.data.Dataset.from_tensor_slices(t_y)
ds_joint = tf.data.Dataset.zip((ds_x, ds_y))
for example in ds_joint:
print('x:', example[0].numpy(),' y:', example[1].numpy())
ds_joint = tf.data.Dataset.from_tensor_slices((t_x, t_y))
for example in ds_joint:
#print(example)
print('x:', example[0].numpy(), ' y:', example[1].numpy())
ds_joint
# Operacion sobre el dataset generado
# ====================================================
ds_trans = ds_joint.map(lambda x, y: (x*2-1.0, y))
for example in ds_trans:
print(' x:', example[0].numpy(), ' y:', example[1].numpy())
```
## Mezclar, agrupar y repetir
Para entrenar un modelo NN usando la optimización de descenso de gradiente estocástico, es importante alimentar los datos de entrenamiento como lotes mezclados aleatoriamente. Ya hemos visto arriba como crear lotes llamando al método `.batch()` de un objeto de conjunto de datos. Ahora, además de crear lotes, vamos a mezclar y reiterar sobre los conjuntos de datos:
```
# Mezclando los elementos de un tensor
# ===================================================
tf.random.set_seed(1)
ds = ds_joint.shuffle(buffer_size = len(t_x))
for example in ds:
print(' x:', example[0].numpy(), ' y:', example[1].numpy())
```
donde las filas se barajan sin perder la correspondencia uno a uno entre las entradas en x e y. El método `.shuffle()` requiere un argumento llamado `buffer_size`, que determina cuántos elementos del conjunto de datos se agrupan antes de barajar. Los elementos del búfer se recuperan aleatoriamente y su lugar en el búfer se asigna a los siguientes elementos del conjunto de datos original (sin mezclar). Por lo tanto, si elegimos un tamaño de búfer pequeño, es posible que no mezclemos perfectamente el conjunto de datos.
Si el conjunto de datos es pequeño, la elección de un tamaño de búfer relativamente pequeño puede afectar negativamente el rendimiento predictivo del NN, ya que es posible que el conjunto de datos no esté completamente aleatorizado. En la práctica, sin embargo, por lo general no tiene un efecto notable cuando se trabaja con conjuntos de datos relativamente grandes, lo cual es común en el aprendizaje profundo.
Alternativamente, para asegurar una aleatorización completa durante cada época, simplemente podemos elegir un tamaño de búfer que sea igual al número de ejemplos de entrenamiento, como en el código anterior (`buffer_size = len(t_x)`).
Ahora, creemos lotes a partir del conjunto de datos ds_joint:
```
ds = ds_joint.batch(batch_size = 3, drop_remainder = False)
print(ds)
batch_x, batch_y = next(iter(ds))
print('Batch-x:\n', batch_x.numpy())
print('Batch-y: ', batch_y.numpy())
```
Además, al entrenar un modelo para múltiples épocas, necesitamos mezclar e iterar sobre el conjunto de datos por el número deseado de épocas. Entonces, repitamos el conjunto de datos por lotes dos veces:
```
ds = ds_joint.batch(3).repeat(count = 2)
for i,(batch_x, batch_y) in enumerate(ds):
print(i, batch_x.numpy(), batch_y.numpy(), end = '\n'*2)
```
Esto da como resultado dos copias de cada lote. Si cambiamos el orden de estas dos operaciones, es decir, primero lote y luego repetimos, los resultados serán diferentes:
```
ds = ds_joint.repeat(count=2).batch(3)
for i,(batch_x, batch_y) in enumerate(ds):
print(i, batch_x.numpy(), batch_y.numpy(), end = '\n'*2)
```
Finalmente, para comprender mejor cómo se comportan estas tres operaciones (batch, shuffle y repeat), experimentemos con ellas en diferentes órdenes. Primero, combinaremos las operaciones en el siguiente orden: (1) shuffle, (2) batch y (3) repeat:
```
# Orden 1: shuffle -> batch -> repeat
tf.random.set_seed(1)
ds = ds_joint.shuffle(4).batch(2).repeat(3)
for i,(batch_x, batch_y) in enumerate(ds):
print(i, batch_x, batch_y.numpy(), end = '\n'*2)
# Orden 2: batch -> shuffle -> repeat
tf.random.set_seed(1)
ds = ds_joint.batch(2).shuffle(4).repeat(3)
for i,(batch_x, batch_y) in enumerate(ds):
print(i, batch_x, batch_y.numpy(), end = '\n'*2)
# Orden 2: batch -> repeat-> shuffle
tf.random.set_seed(1)
ds = ds_joint.batch(2).repeat(3).shuffle(4)
for i,(batch_x, batch_y) in enumerate(ds):
print(i, batch_x, batch_y.numpy(), end = '\n'*2)
```
## Obteniendo conjuntos de datos disponibles de la biblioteca tensorflow_datasets
La biblioteca tensorflow_datasets proporciona una buena colección de conjuntos de datos disponibles gratuitamente para entrenar o evaluar modelos de aprendizaje profundo. Los conjuntos de datos están bien formateados y vienen con descripciones informativas, incluido el formato de características y etiquetas y su tipo y dimensionalidad, así como la cita del documento original que introdujo el conjunto de datos en formato BibTeX. Otra ventaja es que todos estos conjuntos de datos están preparados y listos para usar como objetos tf.data.Dataset, por lo que todas las funciones que cubrimos se pueden usar directamente:
```
# pip install tensorflow-datasets
import tensorflow_datasets as tfds
print(len(tfds.list_builders()))
print(tfds.list_builders()[:5])
# Trabajando con el archivo mnist
# ===============================================
mnist, mnist_info = tfds.load('mnist', with_info=True, shuffle_files=False)
print(mnist_info)
print(mnist.keys())
ds_train = mnist['train']
ds_train = ds_train.map(lambda item:(item['image'], item['label']))
ds_train = ds_train.batch(10)
batch = next(iter(ds_train))
print(batch[0].shape, batch[1])
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(15, 6))
for i,(image,label) in enumerate(zip(batch[0], batch[1])):
ax = fig.add_subplot(2, 5, i+1)
ax.set_xticks([]); ax.set_yticks([])
ax.imshow(image[:, :, 0], cmap='gray_r')
ax.set_title('{}'.format(label), size=15)
plt.show()
```
# Construyendo un modelo NN en TensorFlow
## La API de TensorFlow Keras (tf.keras)
Keras es una API NN de alto nivel y se desarrolló originalmente para ejecutarse sobre otras bibliotecas como TensorFlow y Theano. Keras proporciona una interfaz de programación modular y fácil de usar que permite la creación de prototipos y la construcción de modelos complejos en solo unas pocas líneas de código. Keras se puede instalar independientemente de PyPI y luego configurarse para usar TensorFlow como su motor de backend. Keras está estrechamente integrado en TensorFlow y se puede acceder a sus módulos a través de tf.keras.
En TensorFlow 2.0, tf.keras se ha convertido en el enfoque principal y recomendado para implementar modelos. Esto tiene la ventaja de que admite funcionalidades específicas de TensorFlow, como las canalizaciones de conjuntos de datos que usan tf.data.
La API de Keras (tf.keras) hace que la construcción de un modelo NN sea extremadamente fácil. El enfoque más utilizado para crear una NN en TensorFlow es a través de `tf.keras.Sequential()`, que permite apilar capas para formar una red. Se puede dar una pila de capas en una lista de Python a un modelo definido como tf.keras.Sequential(). Alternativamente, las capas se pueden agregar una por una usando el método .add().
Además, tf.keras nos permite definir un modelo subclasificando tf.keras.Model.
Esto nos da más control sobre la propagacion hacia adelante al definir el método call() para nuestra clase modelo para especificar la propagacion hacia adelante explicitamente.
Finalmente, los modelos construidos usando la API tf.keras se pueden compilar y entrenar a través de los métodos .compile() y .fit().
## Construyendo un modelo de regresion lineal
```
X_train = np.arange(10).reshape((10, 1))
y_train = np.array([1.0, 1.3, 3.1, 2.0, 5.0, 6.3, 6.6, 7.4, 8.0, 9.0])
X_train, y_train
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(X_train, y_train, 'o', markersize=10)
ax.set_xlabel('x')
ax.set_ylabel('y')
import tensorflow as tf
X_train_norm = (X_train - np.mean(X_train))/np.std(X_train)
ds_train_orig = tf.data.Dataset.from_tensor_slices((tf.cast(X_train_norm, tf.float32),tf.cast(y_train, tf.float32)))
for i in ds_train_orig:
print(i[0].numpy(), i[1].numpy())
```
Ahora, podemos definir nuestro modelo de regresión lineal como $𝑧 = 𝑤x + 𝑏$. Aquí, vamos a utilizar la API de Keras. `tf.keras` proporciona capas predefinidas para construir modelos NN complejos, pero para empezar, usaremos un modelo desde cero:
```
class MyModel(tf.keras.Model):
def __init__(self):
super(MyModel, self).__init__()
self.w = tf.Variable(0.0, name='weight')
self.b = tf.Variable(0.0, name='bias')
def call(self, x):
return self.w * x + self.b
model = MyModel()
model.build(input_shape=(None, 1))
model.summary()
```
| github_jupyter |
```
import safenet
safenet.setup_logger(file_level=safenet.log_util.WARNING)
myApp = safenet.App()
myAuth_,addData=safenet.safe_utils.AuthReq(myApp.ffi_app.NULL,0,0,id=b'crappy_chat_reloaded',scope=b'noScope'
,name=b'i_love_it',vendor=b'no_vendor',app_container=True,ffi=myApp.ffi_app)
encodedAuth = myApp.encode_authentication(myAuth_)
encodedAuth
grantedAuth = myApp.sysUri.quickSetup(myAuth_,encodedAuth)
grantedAuth
grantedAuth='bAEAAAADIADW4EAAAAAAAAAAAAAQAAAAAAAAAAAEFNJ53ABPX5QW524YYAMEN7T4MJJVIYH656RYZ4FCSZ4TUT7DX3AQAAAAAAAAAAADZO24ITUIIFUWNIUPYODCATWPRBZIBHLD4B6DGFUJDNASIIFYX5MQAAAAAAAAAAAG7B6WQXKW3UPQET62ZWDRY3U7NEYKRWBPQHLYJHTOOYIPPGOWKFFAAAAAAAAAAAACGBOVXSSUKP2Z7YMG5JJDC7BNTUU3YD4SBOBYN3CWRJXGCXLOSFTPQ7LILVLN2HYCJ7NM3BY4N2PWSMFI3AXYDV4ETZXHMEHXTHLFCSIAAAAAAAAAAAAJDOR7QCDWE2VXANINUIE4NYFTIAT66JFQN7B7ALHOV3QYVIYSGQIAAAAAAAAAAABK6S5AF4FRXH4AOBERKM65IJZZNGEILVD3GSDMQBIV4GP2XE5JHQGIAAAAAAAAAAAIAAAAAAAAAAABRG44C4NRSFY3TMLRYHI2TIOBTCMAAAAAAAAAAAMJTHAXDMOBOGE4DKLRSGE4DUNJUHAZREAAAAAAAAAAAGEZTQLRWHAXDCOBRFY2TOORVGQ4DGEQAAAAAAAAAAAYTGOBOGY4C4MJYGEXDMMB2GU2DQMYSAAAAAAAAAAADCMZYFY3DQLRRHAYS4OBWHI2TIOBTCIAAAAAAAAAAAMJTHAXDMOBOGE4DCLRYG45DKNBYGMJQAAAAAAAAAABRGM4C4NRYFYYTQMJOGE3DQORVGQ4DGEYAAAAAAAAAAAYTGOBOGY4C4MJYGEXDCNZWHI2TIOBTCMAAAAAAAAAAAMJTHAXDMOBOGE4DCLRRG44TUNJUHAZRGAAAAAAAAAAAGEZTQLRWHAXDCOBRFYYTQMB2GU2DQMYTAAAAAAAAAAADCMZYFY3DQLRRHAYS4MJYGI5DKNBYGMJQAAAAAAAAAABRGM4C4NRYFYYTQMJOGI2DEORVGQ4DGEYAAAAAAAAAAAYTGOBOGY4C4MJYGEXDENBTHI2TIOBTCMAAAAAAAAAAAMJTHAXDMOBOGE4DCLRSGQ4TUNJUHAZREAAAAAAAAAAAGEZTQLRWHAXDCOBZFYYTIORVGQ4DGEQAAAAAAAAAAAYTGOBOGY4C4MJYHEXDCNJ2GU2DQMYSAAAAAAAAAAADCMZYFY3DQLRRHA4S4MJXHI2TIOBTCIAAAAAAAAAAAMJTHAXDMOBOGE4DSLRRHA5DKNBYGMJAAAAAAAAAAABRGM4C4NRYFYYTQOJOGE4TUNJUHAZREAAAAAAAAAAAGEZTQLRWHAXDCOBZFYZTCORVGQ4DGEQAAAAAAAAAAAYTGOBOGY4C4MJYHEXDGNB2GU2DQMYSAAAAAAAAAAADCMZYFY3DQLRRHA4S4MZWHI2TIOBTCIAAAAAAAAAAAMJTHAXDMOBOGE4DSLRTHA5DKNBYGMJAAAAAAAAAAABRGM4C4NRYFYYTQOJOGM4TUNJUHAZRCAAAAAAAAAAAGQ3C4MJQGEXDKLRRG44TUNJUHAZQC2YVAAAAAAAAAEDQAAAAAAAAAADBNRYGQYK7GIAOWVHBIXIX3YGQAZIQREUXG4475KAEQOJARMHK5Z3DWBIVRXPEAVMYHIAAAAAAAAABQAAAAAAAAAAAIDF2MO3P472PTSCK3IIOW43ZICJR4Q4P5ZR6UWABAAAAAAAAAAABIAAAAAAAAAAAMFYHA4ZPORSXG5CQOJXWO4TBNVHGC3LFO7DUGA44PHQPW2LQGIPOFH34XS3SO3V3X6S3LX7ETSBIRY3TCAHJQOQAAAAAAAAAAEQAAAAAAAAAAAEIJOL5UDCOQRO3N2G6CFLCDF4ACW3LH2ON27YBAOOC7G4YGV25S4MAAAAAAAAAAAGJ6FXG5Y7A2Z5GTAO7H5APZ2ALENSBY2J7T4QNKAAFAAAAAAAAAAAAAAAAAAAQAAAAAIAAAAADAAAAABAAAAAAA'
myApp.setup_app(myAuth_,grantedAuth)
signKey = myApp.get_pub_key_handle()
signKey
```
---
### now we have an app and can start doing stuff
---
### creating a mutable Object
```
myMutable = myApp.mData()
```
### define Entries and drop them onto Safe
```
import datetime
now = datetime.datetime.utcnow().strftime('%Y-%m-%d - %H:%M:%S')
myName = 'Welcome to the SAFE Network'
text = 'free speech and free knowledge to the world!'
timeUser = f'{now} {myName}'
entries={timeUser:text}
```
entries={'firstkey':'this is awesome',
'secondKey':'and soon it should be',
'thirdKey':'even easier to use safe with python',
'i love safe':'and this is just the start',
'thisWasUploaded at':datetime.datetime.utcnow().strftime('%Y-%m-%d - %H:%M:%S UTC'),
'additionalEntry':input('enter your custom value here: ')}
```
infoData = myMutable.new_random_public(777,signKey,entries)
print(safenet.safe_utils.getXorAddresOfMutable(infoData,myMutable.ffi_app))
additionalEntries={'this wasnt here':'before'}
additionalEntries={'baduff':'another entry'}
myMutable.insertEntries(infoData,additionalEntries)
with open('testfile','wb') as f:
f.write(myMutable.ffi_app.buffer(infoData)[:])
with open('testfile','rb') as f:
infoData= safenet.safe_utils.getffiMutable(f.read(),myMutable.ffi_app)
myMutable.ffi_app.buffer(infoData)[:]
mutableBytes = b'H\x8f\x08x}\xc5D]U\xeeW\x08\xe0\xb4\xaau\x94\xd4\x8a\x0bz\x06h\xe3{}\xd1\x06\x843\x01P[t\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x007\xdbNV\x00\x00'
infoData= safenet.safe_utils.getffiMutable(mutableBytes,myMutable.ffi_app)
infoData
def getNewEntries(lastState,newState):
newEntries = {}
for additional in [item for item in newState if item not in lastState]:
newEntries[additional]=newState[additional]
return newEntries, newState
```
lastState={}
additionalEntries, lastState = getNewEntries(lastState,myMutable.getCurrentState(infoData))
additionalEntries
```
import queue
import time
from threading import Thread
import datetime
import sys
from PyQt5.QtWidgets import (QWidget, QPushButton, QTextBrowser,QLineEdit,
QHBoxLayout, QVBoxLayout, QApplication)
class Example(QWidget):
def __init__(self):
super().__init__()
self.lineedit1 = QLineEdit("anon")
self.browser = QTextBrowser()
self.lineedit = QLineEdit("Type a message and press Enter")
self.lineedit.selectAll()
self.setWindowTitle("crappychat_reloaded")
vbox = QVBoxLayout()
vbox.addWidget(self.lineedit1)
vbox.addWidget(self.browser)
vbox.addWidget(self.lineedit)
self.setLayout(vbox)
self.setGeometry(300, 300, 900, 600)
self.show()
self.lineedit.setFocus()
self.lineedit.returnPressed.connect(self.updateUi)
self.messageQueue = queue.Queue()
t = Thread(name='updateThread', target=self.updateBrowser)
t.start()
def updateUi(self):
try:
now = datetime.datetime.utcnow().strftime('%Y-%m-%d - %H:%M:%S')
myName = self.lineedit1.text()
text = self.lineedit.text()
timeUser = f'{now} {myName}'
additionalEntries={timeUser:text}
self.messageQueue.put(additionalEntries)
#self.browser.append(f"<b>{timeUser}</b>: {text}")
self.lineedit.clear()
except:
self.browser.append("<font color=red>{0} is invalid!</font>"
.format(text))
def updateBrowser(self):
lastState={}
while True:
try:
if not self.messageQueue.empty():
newEntries = self.messageQueue.get()
myMutable.insertEntries(infoData,newEntries)
additionalEntries, lastState = getNewEntries(lastState,myMutable.getCurrentState(infoData))
for entry in additionalEntries:
entry_string = entry.decode()
value_string = additionalEntries[entry].decode()
self.browser.append(f"<b>{entry_string}</b>: {value_string}")
self.browser.ensureCursorVisible()
except:
pass
time.sleep(2)
if __name__ == '__main__':
app = QApplication(sys.argv)
ex = Example()
sys.exit(app.exec_())
```
| github_jupyter |
# Tutorial 13: Skyrmion in a disk
> Interactive online tutorial:
> [](https://mybinder.org/v2/gh/ubermag/oommfc/master?filepath=docs%2Fipynb%2Findex.ipynb)
In this tutorial, we compute and relax a skyrmion in a interfacial-DMI material in a confined disk like geometry.
```
import oommfc as oc
import discretisedfield as df
import micromagneticmodel as mm
```
We define mesh in cuboid through corner points `p1` and `p2`, and discretisation cell size `cell`.
```
region = df.Region(p1=(-50e-9, -50e-9, 0), p2=(50e-9, 50e-9, 10e-9))
mesh = df.Mesh(region=region, cell=(5e-9, 5e-9, 5e-9))
```
The mesh we defined is:
```
%matplotlib inline
mesh.k3d()
```
Now, we can define the system object by first setting up the Hamiltonian:
```
system = mm.System(name='skyrmion')
system.energy = (mm.Exchange(A=1.6e-11)
+ mm.DMI(D=4e-3, crystalclass='Cnv')
+ mm.UniaxialAnisotropy(K=0.51e6, u=(0, 0, 1))
+ mm.Demag()
+ mm.Zeeman(H=(0, 0, 2e5)))
```
Disk geometry is set up be defining the saturation magnetisation (norm of the magnetisation field). For that, we define a function:
```
Ms = 1.1e6
def Ms_fun(pos):
"""Function to set magnitude of magnetisation: zero outside cylindric shape,
Ms inside cylinder.
Cylinder radius is 50nm.
"""
x, y, z = pos
if (x**2 + y**2)**0.5 < 50e-9:
return Ms
else:
return 0
```
And the second function we need is the function to definr the initial magnetisation which is going to relax to skyrmion.
```
def m_init(pos):
"""Function to set initial magnetisation direction:
-z inside cylinder (r=10nm),
+z outside cylinder.
y-component to break symmetry.
"""
x, y, z = pos
if (x**2 + y**2)**0.5 < 10e-9:
return (0, 0, -1)
else:
return (0, 0, 1)
# create system with above geometry and initial magnetisation
system.m = df.Field(mesh, dim=3, value=m_init, norm=Ms_fun)
```
The geometry is now:
```
system.m.norm.k3d_nonzero()
```
and the initial magnetsation is:
```
system.m.plane('z').mpl()
```
Finally we can minimise the energy and plot the magnetisation.
```
# minimize the energy
md = oc.MinDriver()
md.drive(system)
# Plot relaxed configuration: vectors in z-plane
system.m.plane('z').mpl()
# Plot z-component only:
system.m.z.plane('z').mpl()
# 3d-plot of z-component
system.m.z.k3d_scalar(filter_field=system.m.norm)
```
Finally we can sample and plot the magnetisation along the line:
```
system.m.z.line(p1=(-49e-9, 0, 0), p2=(49e-9, 0, 0), n=20).mpl()
```
## Other
More details on various functionality can be found in the [API Reference](https://oommfc.readthedocs.io/en/latest/).
| github_jupyter |
# Reader - Implantação
Este componente utiliza um modelo de QA pré-treinado em Português com o dataset SQuAD v1.1, é um modelo de domínio público disponível em [Hugging Face](https://huggingface.co/pierreguillou/bert-large-cased-squad-v1.1-portuguese).<br>
Seu objetivo é encontrar a resposta de uma ou mais perguntas de acordo com uma lista de contextos distintos.
A tabela de dados de entrada deve possuir uma coluna de contextos, em que cada linha representa um contexto diferente, e uma coluna de perguntas em que cada linha representa uma pergunta a ser realizada. Note que para cada pergunta serão utilizados todos os contextos fornecidos para realização da inferência, e portanto, podem haver bem mais contextos do que perguntas.
Obs: Este componente utiliza recursos da internet, portanto é importante estar conectado à rede para que este componente funcione corretamente.<br>
### **Em caso de dúvidas, consulte os [tutoriais da PlatIAgro](https://platiagro.github.io/tutorials/).**
## Declaração de Classe para Predições em Tempo Real
A tarefa de implantação cria um serviço REST para predições em tempo-real.<br>
Para isso você deve criar uma classe `Model` que implementa o método `predict`.
```
%%writefile Model.py
import joblib
import numpy as np
import pandas as pd
from reader import Reader
class Model:
def __init__(self):
self.loaded = False
def load(self):
# Load artifacts
artifacts = joblib.load("/tmp/data/reader.joblib")
self.model_parameters = artifacts["model_parameters"]
self.inference_parameters = artifacts["inference_parameters"]
# Initialize reader
self.reader = Reader(**self.model_parameters)
# Set model loaded
self.loaded = True
print("Loaded model")
def class_names(self):
column_names = list(self.inference_parameters['output_columns'])
return column_names
def predict(self, X, feature_names, meta=None):
if not self.loaded:
self.load()
# Convert to dataframe
if feature_names != []:
df = pd.DataFrame(X, columns = feature_names)
df = df[self.inference_parameters['input_columns']]
else:
df = pd.DataFrame(X, columns = self.inference_parameters['input_columns'])
# Predict answers #
# Iterate over dataset
for idx, row in df.iterrows():
# Get question
question = row[self.inference_parameters['question_column_name']]
# Get context
context = row[self.inference_parameters['context_column_name']]
# Make prediction
answer, probability, _ = self.reader([question], [context])
# Save to df
df.at[idx, self.inference_parameters['answer_column_name']] = answer[0]
df.at[idx, self.inference_parameters['proba_column_name']] = probability[0]
# Retrieve Only Best Answer #
# Initializate best df
best_df = pd.DataFrame(columns=df.columns)
# Get unique questions
unique_questions = df[self.inference_parameters['question_column_name']].unique()
# Iterate over each unique question
for question in unique_questions:
# Filter df
question_df = df[df[self.inference_parameters['question_column_name']] == question]
# Sort by score (descending)
question_df = question_df.sort_values(by=self.inference_parameters['proba_column_name'], ascending=False).reset_index(drop=True)
# Append best ansewer to output df
best_df = pd.concat((best_df,pd.DataFrame(question_df.loc[0]).T)).reset_index(drop=True)
if self.inference_parameters['keep_best'] == 'sim':
return best_df.values
else:
return df.values
```
| github_jupyter |
# Estimator validation
This notebook contains code to generate Figure 2 of the paper.
This notebook also serves to compare the estimates of the re-implemented scmemo with sceb package from Vasilis.
```
import pandas as pd
import matplotlib.pyplot as plt
import scanpy as sc
import scipy as sp
import itertools
import numpy as np
import scipy.stats as stats
from scipy.integrate import dblquad
import seaborn as sns
from statsmodels.stats.multitest import fdrcorrection
import imp
pd.options.display.max_rows = 999
pd.set_option('display.max_colwidth', -1)
import pickle as pkl
import time
import matplotlib as mpl
mpl.rcParams['pdf.fonttype'] = 42
mpl.rcParams['ps.fonttype'] = 42
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'x-small',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'xx-small',
'ytick.labelsize':'xx-small'}
pylab.rcParams.update(params)
import sys
sys.path.append('/data/home/Github/scrna-parameter-estimation/dist/schypo-0.0.0-py3.7.egg')
import schypo
import schypo.simulate as simulate
import sys
sys.path.append('/data/home/Github/single_cell_eb/')
sys.path.append('/data/home/Github/single_cell_eb/sceb/')
import scdd
data_path = '/data/parameter_estimation/'
fig_path = '/data/home/Github/scrna-parameter-estimation/figures/fig3/'
```
### Check 1D estimates of `sceb` with `scmemo`
Using the Poisson model. The outputs should be identical, this is for checking the implementation.
```
data = sp.sparse.csr_matrix(simulate.simulate_transcriptomes(100, 20))
adata = sc.AnnData(data)
size_factors = scdd.dd_size_factor(adata)
Nr = data.sum(axis=1).mean()
_, M_dd = scdd.dd_1d_moment(adata, size_factor=scdd.dd_size_factor(adata), Nr=Nr)
var_scdd = scdd.M_to_var(M_dd)
print(var_scdd)
imp.reload(estimator)
mean_scmemo, var_scmemo = estimator._poisson_1d(data, data.shape[0], estimator._estimate_size_factor(data))
print(var_scmemo)
df = pd.DataFrame()
df['size_factor'] = size_factors
df['inv_size_factor'] = 1/size_factors
df['inv_size_factor_sq'] = 1/size_factors**2
df['expr'] = data[:, 0].todense().A1
precomputed_size_factors = df.groupby('expr')['inv_size_factor'].mean(), df.groupby('expr')['inv_size_factor_sq'].mean()
imp.reload(estimator)
expr, count = np.unique(data[:, 0].todense().A1, return_counts=True)
print(estimator._poisson_1d((expr, count), data.shape[0], precomputed_size_factors))
```
### Check 2D estimates of `sceb` and `scmemo`
Using the Poisson model. The outputs should be identical, this is for checking the implementation.
```
data = sp.sparse.csr_matrix(simulate.simulate_transcriptomes(1000, 4))
adata = sc.AnnData(data)
size_factors = scdd.dd_size_factor(adata)
mean_scdd, cov_scdd, corr_scdd = scdd.dd_covariance(adata, size_factors)
print(cov_scdd)
imp.reload(estimator)
cov_scmemo = estimator._poisson_cov(data, data.shape[0], size_factors, idx1=[0, 1, 2], idx2=[1, 2, 3])
print(cov_scmemo)
expr, count = np.unique(data[:, :2].toarray(), return_counts=True, axis=0)
df = pd.DataFrame()
df['size_factor'] = size_factors
df['inv_size_factor'] = 1/size_factors
df['inv_size_factor_sq'] = 1/size_factors**2
df['expr1'] = data[:, 0].todense().A1
df['expr2'] = data[:, 1].todense().A1
precomputed_size_factors = df.groupby(['expr1', 'expr2'])['inv_size_factor'].mean(), df.groupby(['expr1', 'expr2'])['inv_size_factor_sq'].mean()
cov_scmemo = estimator._poisson_cov((expr[:, 0], expr[:, 1], count), data.shape[0], size_factor=precomputed_size_factors)
print(cov_scmemo)
```
### Extract parameters from interferon dataset
```
adata = sc.read(data_path + 'interferon_filtered.h5ad')
adata = adata[adata.obs.cell_type == 'CD4 T cells - ctrl']
data = adata.X.copy()
relative_data = data.toarray()/data.sum(axis=1)
q = 0.07
x_param, z_param, Nc, good_idx = schypo.simulate.extract_parameters(adata.X, q=q, min_mean=q)
imp.reload(simulate)
transcriptome = simulate.simulate_transcriptomes(
n_cells=10000,
means=z_param[0],
variances=z_param[1],
corr=x_param[2],
Nc=Nc)
relative_transcriptome = transcriptome/transcriptome.sum(axis=1).reshape(-1, 1)
qs, captured_data = simulate.capture_sampling(transcriptome, q=q, q_sq=q**2+1e-10)
def qqplot(x, y, s=1):
plt.scatter(
np.quantile(x, np.linspace(0, 1, 1000)),
np.quantile(y, np.linspace(0, 1, 1000)),
s=s)
plt.plot(x, x, lw=1, color='m')
plt.figure(figsize=(8, 2));
plt.subplots_adjust(wspace=0.2);
plt.subplot(1, 3, 1);
sns.distplot(np.log(captured_data.mean(axis=0)), hist=False, label='Simulated')
sns.distplot(np.log(data[:, good_idx].toarray().var(axis=0)), hist=False, label='Real')
plt.xlabel('Log(mean)')
plt.subplot(1, 3, 2);
sns.distplot(np.log(captured_data.var(axis=0)), hist=False)
sns.distplot(np.log(data[:, good_idx].toarray().var(axis=0)), hist=False)
plt.xlabel('Log(variance)')
plt.subplot(1, 3, 3);
sns.distplot(np.log(captured_data.sum(axis=1)), hist=False)
sns.distplot(np.log(data.toarray().sum(axis=1)), hist=False)
plt.xlabel('Log(total UMI count)')
plt.savefig(figpath + 'simulation_stats.png', bbox_inches='tight')
```
### Compare datasets generated by Poisson and hypergeometric processes
```
_, poi_captured = simulate.capture_sampling(transcriptome, q=q, process='poisson')
_, hyper_captured = simulate.capture_sampling(transcriptome, q=q, process='hyper')
q_list = [0.05, 0.1, 0.2, 0.3, 0.5]
plt.figure(figsize=(8, 2))
plt.subplots_adjust(wspace=0.3)
for idx, q in enumerate(q_list):
_, poi_captured = simulate.capture_sampling(transcriptome, q=q, process='poisson')
_, hyper_captured = simulate.capture_sampling(transcriptome, q=q, process='hyper')
relative_poi_captured = poi_captured/poi_captured.sum(axis=1).reshape(-1, 1)
relative_hyper_captured = hyper_captured/hyper_captured.sum(axis=1).reshape(-1, 1)
poi_corr = np.corrcoef(relative_poi_captured, rowvar=False)
hyper_corr = np.corrcoef(relative_hyper_captured, rowvar=False)
sample_idx = np.random.choice(poi_corr.ravel().shape[0], 100000)
plt.subplot(1, len(q_list), idx+1)
plt.scatter(poi_corr.ravel()[sample_idx], hyper_corr.ravel()[sample_idx], s=1, alpha=1)
plt.plot([-1, 1], [-1, 1], 'm', lw=1)
# plt.xlim([-0.3, 0.4])
# plt.ylim([-0.3, 0.4])
if idx != 0:
plt.yticks([])
plt.title('q={}'.format(q))
plt.savefig(figpath + 'poi_vs_hyp_sim_corr.png', bbox_inches='tight')
```
### Compare Poisson vs HG estimators
```
def compare_esimators(q, plot=False, true_data=None, var_q=1e-10):
q_sq = var_q + q**2
true_data = schypo.simulate.simulate_transcriptomes(1000, 1000, correlated=True) if true_data is None else true_data
true_relative_data = true_data / true_data.sum(axis=1).reshape(-1, 1)
qs, captured_data = schypo.simulate.capture_sampling(true_data, q, q_sq)
Nr = captured_data.sum(axis=1).mean()
captured_relative_data = captured_data/captured_data.sum(axis=1).reshape(-1, 1)
adata = sc.AnnData(sp.sparse.csr_matrix(captured_data))
sf = schypo.estimator._estimate_size_factor(adata.X, 'hyper_relative', total=True)
good_idx = (captured_data.mean(axis=0) > q)
# True moments
m_true, v_true, corr_true = true_relative_data.mean(axis=0), true_relative_data.var(axis=0), np.corrcoef(true_relative_data, rowvar=False)
rv_true = v_true/m_true**2#schypo.estimator._residual_variance(m_true, v_true, schypo.estimator._fit_mv_regressor(m_true, v_true))
# Compute 1D moments
m_obs, v_obs = captured_relative_data.mean(axis=0), captured_relative_data.var(axis=0)
rv_obs = v_obs/m_obs**2#schypo.estimator._residual_variance(m_obs, v_obs, schypo.estimator._fit_mv_regressor(m_obs, v_obs))
m_poi, v_poi = schypo.estimator._poisson_1d_relative(adata.X, size_factor=sf, n_obs=true_data.shape[0])
rv_poi = v_poi/m_poi**2#schypo.estimator._residual_variance(m_poi, v_poi, schypo.estimator._fit_mv_regressor(m_poi, v_poi))
m_hyp, v_hyp = schypo.estimator._hyper_1d_relative(adata.X, size_factor=sf, n_obs=true_data.shape[0], q=q)
rv_hyp = v_hyp/m_hyp**2#schypo.estimator._residual_variance(m_hyp, v_hyp, schypo.estimator._fit_mv_regressor(m_hyp, v_hyp))
# Compute 2D moments
corr_obs = np.corrcoef(captured_relative_data, rowvar=False)
# corr_obs = corr_obs[np.triu_indices(corr_obs.shape[0])]
idx1 = np.array([i for i,j in itertools.combinations(range(adata.shape[1]), 2) if good_idx[i] and good_idx[j]])
idx2 = np.array([j for i,j in itertools.combinations(range(adata.shape[1]), 2) if good_idx[i] and good_idx[j]])
sample_idx = np.random.choice(idx1.shape[0], 10000)
idx1 = idx1[sample_idx]
idx2 = idx2[sample_idx]
corr_true = corr_true[(idx1, idx2)]
corr_obs = corr_obs[(idx1, idx2)]
cov_poi = schypo.estimator._poisson_cov_relative(adata.X, n_obs=adata.shape[0], size_factor=sf, idx1=idx1, idx2=idx2)
cov_hyp = schypo.estimator._hyper_cov_relative(adata.X, n_obs=adata.shape[0], size_factor=sf, idx1=idx1, idx2=idx2, q=q)
corr_poi = schypo.estimator._corr_from_cov(cov_poi, v_poi[idx1], v_poi[idx2])
corr_hyp = schypo.estimator._corr_from_cov(cov_hyp, v_hyp[idx1], v_hyp[idx2])
corr_poi[np.abs(corr_poi) > 1] = np.nan
corr_hyp[np.abs(corr_hyp) > 1] = np.nan
mean_list = [m_obs, m_poi, m_hyp]
var_list = [rv_obs, rv_poi, rv_hyp]
corr_list = [corr_obs, corr_poi, corr_hyp]
estimated_list = [mean_list, var_list, corr_list]
true_list = [m_true, rv_true, corr_true]
if plot:
count = 0
for j in range(3):
for i in range(3):
plt.subplot(3, 3, count+1)
if i != 2:
plt.scatter(
np.log(true_list[i][good_idx]),
np.log(estimated_list[i][j][good_idx]),
s=0.1)
plt.plot(np.log(true_list[i][good_idx]), np.log(true_list[i][good_idx]), linestyle='--', color='m')
plt.xlim(np.log(true_list[i][good_idx]).min(), np.log(true_list[i][good_idx]).max())
plt.ylim(np.log(true_list[i][good_idx]).min(), np.log(true_list[i][good_idx]).max())
else:
x = true_list[i]
y = estimated_list[i][j]
print(x.shape, y.shape)
plt.scatter(
x,
y,
s=0.1)
plt.plot([-1, 1], [-1, 1],linestyle='--', color='m')
plt.xlim(-1, 1);
plt.ylim(-1, 1);
# if not (i == j):
# plt.yticks([]);
# plt.xticks([]);
if i == 1 or i == 0:
print((np.log(true_list[i][good_idx]) > np.log(estimated_list[i][j][good_idx])).mean())
count += 1
else:
return qs, good_idx, estimated_list, true_list
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'small',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'xx-small',
'ytick.labelsize':'xx-small'}
pylab.rcParams.update(params)
```
```
true_data = schypo.simulate.simulate_transcriptomes(n_cells=10000, means=z_param[0], variances=z_param[1], Nc=Nc)
q = 0.025
plt.figure(figsize=(4, 4))
plt.subplots_adjust(wspace=0.5, hspace=0.5)
compare_esimators(q, plot=True, true_data=true_data)
plt.savefig(fig_path + 'poi_vs_hyper_scatter_rv_2.5.png', bbox_inches='tight', dpi=1200)
q = 0.4
plt.figure(figsize=(4, 4))
plt.subplots_adjust(wspace=0.5, hspace=0.5)
compare_esimators(q, plot=True, true_data=true_data)
plt.savefig(fig_path + 'poi_vs_hyper_scatter_rv_40.png', bbox_inches='tight', dpi=1200)
def compute_mse(x, y, log=True):
if log:
return np.nanmean(np.abs(np.log(x)-np.log(y)))
else:
return np.nanmean(np.abs(x-y))
def concordance(x, y, log=True):
if log:
a = np.log(x)
b = np.log(y)
else:
a = x
b = y
cond = np.isfinite(a) & np.isfinite(b)
a = a[cond]
b = b[cond]
cmat = np.cov(a, b)
return 2*cmat[0,1]/(cmat[0,0] + cmat[1,1] + (a.mean()-b.mean())**2)
m_mse_list, v_mse_list, c_mse_list = [], [], []
# true_data = schypo.simulate.simulate_transcriptomes(n_cells=10000, means=z_param[0], variances=z_param[1],
# Nc=Nc)
q_list = [0.01, 0.025, 0.1, 0.15, 0.3, 0.5, 0.7, 0.99]
qs_list = []
for q in q_list:
qs, good_idx, est, true = compare_esimators(q, plot=False, true_data=true_data)
qs_list.append(qs)
m_mse_list.append([concordance(x[good_idx], true[0][good_idx]) for x in est[0]])
v_mse_list.append([concordance(x[good_idx], true[1][good_idx]) for x in est[1]])
c_mse_list.append([concordance(x, true[2], log=False) for x in est[2]])
m_mse_list, v_mse_list, c_mse_list = np.array(m_mse_list), np.array(v_mse_list), np.array(c_mse_list)
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'small',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'small',
'ytick.labelsize':'small'}
pylab.rcParams.update(params)
plt.figure(figsize=(8, 3))
plt.subplots_adjust(wspace=0.5)
plt.subplot(1, 3, 1)
plt.plot(q_list[1:], m_mse_list[:, 0][1:], '-o')
# plt.legend(['Naive,\nPoisson,\nHG'])
plt.ylabel('CCC log(mean)')
plt.xlabel('overall UMI efficiency (q)')
plt.subplot(1, 3, 2)
plt.plot(q_list[2:], v_mse_list[:, 0][2:], '-o')
plt.plot(q_list[2:], v_mse_list[:, 1][2:], '-o')
plt.plot(q_list[2:], v_mse_list[:, 2][2:], '-o')
plt.legend(['Naive', 'Poisson', 'HG'], ncol=3, loc='upper center', bbox_to_anchor=(0.4,1.15))
plt.ylabel('CCC log(variance)')
plt.xlabel('overall UMI efficiency (q)')
plt.subplot(1, 3, 3)
plt.plot(q_list[2:], c_mse_list[:, 0][2:], '-o')
plt.plot(q_list[2:], c_mse_list[:, 1][2:], '-o')
plt.plot(q_list[2:], c_mse_list[:, 2][2:], '-o')
# plt.legend(['Naive', 'Poisson', 'HG'])
plt.ylabel('CCC correlation')
plt.xlabel('overall UMI efficiency (q)')
plt.savefig(fig_path + 'poi_vs_hyper_rv_ccc.pdf', bbox_inches='tight')
plt.figure(figsize=(1, 1.3))
plt.plot(q_list, v_mse_list[:, 0], '-o', ms=4)
plt.plot(q_list, v_mse_list[:, 1], '-o', ms=4)
plt.plot(q_list, v_mse_list[:, 2], '-o', ms=4)
plt.savefig(fig_path + 'poi_vs_hyper_ccc_var_rv_inset.pdf', bbox_inches='tight')
plt.figure(figsize=(1, 1.3))
plt.plot(q_list, c_mse_list[:, 0], '-o', ms=4)
plt.plot(q_list, c_mse_list[:, 1], '-o', ms=4)
plt.plot(q_list, c_mse_list[:, 2], '-o', ms=4)
plt.savefig(fig_path + 'poi_vs_hyper_ccc_corr_inset.pdf', bbox_inches='tight')
```
| github_jupyter |
# TRTR and TSTR Results Comparison
```
#import libraries
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
pd.set_option('precision', 4)
```
## 1. Create empty dataset to save metrics differences
```
DATA_TYPES = ['Real','GM','SDV','CTGAN','WGANGP']
SYNTHESIZERS = ['GM','SDV','CTGAN','WGANGP']
ml_models = ['RF','KNN','DT','SVM','MLP']
```
## 2. Read obtained results when TRTR and TSTR
```
FILEPATHS = {'Real' : 'RESULTS/models_results_real.csv',
'GM' : 'RESULTS/models_results_gm.csv',
'SDV' : 'RESULTS/models_results_sdv.csv',
'CTGAN' : 'RESULTS/models_results_ctgan.csv',
'WGANGP' : 'RESULTS/models_results_wgangp.csv'}
#iterate over all datasets filepaths and read each dataset
results_all = dict()
for name, path in FILEPATHS.items() :
results_all[name] = pd.read_csv(path, index_col='model')
results_all
```
## 3. Calculate differences of models
```
metrics_diffs_all = dict()
real_metrics = results_all['Real']
columns = ['data','accuracy_diff','precision_diff','recall_diff','f1_diff']
metrics = ['accuracy','precision','recall','f1']
for name in SYNTHESIZERS :
syn_metrics = results_all[name]
metrics_diffs_all[name] = pd.DataFrame(columns = columns)
for model in ml_models :
real_metrics_model = real_metrics.loc[model]
syn_metrics_model = syn_metrics.loc[model]
data = [model]
for m in metrics :
data.append(abs(real_metrics_model[m] - syn_metrics_model[m]))
metrics_diffs_all[name] = metrics_diffs_all[name].append(pd.DataFrame([data], columns = columns))
metrics_diffs_all
```
## 4. Compare absolute differences
### 4.1. Barplots for each metric
```
metrics = ['accuracy', 'precision', 'recall', 'f1']
metrics_diff = ['accuracy_diff', 'precision_diff', 'recall_diff', 'f1_diff']
colors = ['tab:blue', 'tab:orange', 'tab:green', 'tab:red', 'tab:purple']
barwidth = 0.15
fig, axs = plt.subplots(nrows=1, ncols=4, figsize=(15, 2.5))
axs_idxs = range(4)
idx = dict(zip(metrics + metrics_diff,axs_idxs))
for i in range(0,len(metrics)) :
data = dict()
y_pos = dict()
y_pos[0] = np.arange(len(ml_models))
ax = axs[idx[metrics[i]]]
for k in range(0,len(DATA_TYPES)) :
generator_data = results_all[DATA_TYPES[k]]
data[k] = [0, 0, 0, 0, 0]
for p in range(0,len(ml_models)) :
data[k][p] = generator_data[metrics[i]].iloc[p]
ax.bar(y_pos[k], data[k], color=colors[k], width=barwidth, edgecolor='white', label=DATA_TYPES[k])
y_pos[k+1] = [x + barwidth for x in y_pos[k]]
ax.set_xticks([r + barwidth*2 for r in range(len(ml_models))])
ax.set_xticklabels([])
ax.set_xticklabels(ml_models, fontsize=10)
ax.set_title(metrics[i], fontsize=12)
ax.legend(DATA_TYPES, ncol=5, bbox_to_anchor=(-0.3, -0.2))
fig.tight_layout()
#fig.suptitle('Models performance comparisson Boxplots (TRTR and TSTR) \n Dataset F - Indian Liver Patient', fontsize=18)
fig.savefig('RESULTS/MODELS_METRICS_BARPLOTS.svg', bbox_inches='tight')
metrics = ['accuracy_diff', 'precision_diff', 'recall_diff', 'f1_diff']
colors = ['tab:orange', 'tab:green', 'tab:red', 'tab:purple']
fig, axs = plt.subplots(nrows=1, ncols=4, figsize=(15,2.5))
axs_idxs = range(4)
idx = dict(zip(metrics,axs_idxs))
for i in range(0,len(metrics)) :
data = dict()
ax = axs[idx[metrics[i]]]
for k in range(0,len(SYNTHESIZERS)) :
generator_data = metrics_diffs_all[SYNTHESIZERS[k]]
data[k] = [0, 0, 0, 0, 0]
for p in range(0,len(ml_models)) :
data[k][p] = generator_data[metrics[i]].iloc[p]
ax.plot(data[k], 'o-', color=colors[k], label=SYNTHESIZERS[k])
ax.set_xticks(np.arange(len(ml_models)))
ax.set_xticklabels(ml_models, fontsize=10)
ax.set_title(metrics[i], fontsize=12)
ax.set_ylim(bottom=-0.01, top=0.28)
ax.grid()
ax.legend(SYNTHESIZERS, ncol=5, bbox_to_anchor=(-0.4, -0.2))
fig.tight_layout()
#fig.suptitle('Models performance comparisson Boxplots (TRTR and TSTR) \n Dataset F - Indian Liver Patient', fontsize=18)
fig.savefig('RESULTS/MODELS_METRICS_DIFFERENCES.svg', bbox_inches='tight')
```
| github_jupyter |
# Generating Simpson's Paradox
We have been maually setting, but now we should also be able to generate it more programatically. his notebook will describe how we develop some functions that will be included in the `sp_data_util` package.
```
# %load code/env
# standard imports we use throughout the project
import numpy as np
import pandas as pd
import seaborn as sns
import scipy.stats as stats
import matplotlib.pyplot as plt
import wiggum as wg
import sp_data_util as spdata
from sp_data_util import sp_plot
```
We have been thinking of SP hrough gaussian mixture data, so we'll first work wih that. To cause SP we need he clusters to have an opposite trend of the per cluster covariance.
```
# setup
r_clusters = -.6 # correlation coefficient of clusters
cluster_spread = .8 # pearson correlation of means
p_sp_clusters = .5 # portion of clusters with SP
k = 5 # number of clusters
cluster_size = [2,3]
domain_range = [0, 20, 0, 20]
N = 200 # number of points
p_clusters = [1.0/k]*k
# keep all means in the middle 80%
mu_trim = .2
# sample means
center = [np.mean(domain_range[:2]),np.mean(domain_range[2:])]
mu_transform = np.repeat(np.diff(domain_range)[[0,2]]*(mu_trim),2)
mu_transform[[1,3]] = mu_transform[[1,3]]*-1 # sign flip every other
mu_domain = [d + m_t for d, m_t in zip(domain_range,mu_transform)]
corr = [[1, cluster_spread],[cluster_spread,1]]
d = np.sqrt(np.diag(np.diff(mu_domain)[[0,2]]))
cov = np.dot(d,corr).dot(d)
# sample a lot of means, just for vizualization
# mu = np.asarray([np.random.uniform(*mu_domain[:2],size=k*5), # uniform in x
# np.random.uniform(*mu_domain[2:],size=k*5)]).T # uniform in y
mu = np.random.multivariate_normal(center, cov,k*50)
sns.regplot(mu[:,0], mu[:,1])
plt.axis(domain_range);
# mu
```
However independent sampling isn't really very uniform and we'd like to ensure the clusters are more spread out, so we can use some post processing to thin out close ones.
```
mu_thin = [mu[0]] # keep the first one
p_dist = [1]
# we'll use a gaussian kernel around each to filter and only the closest point matters
dist = lambda mu_c,x: stats.norm.pdf(min(np.sum(np.square(mu_c -x),axis=1)))
for m in mu:
p_keep = 1- dist(mu_thin,m)
if p_keep > .99:
mu_thin.append(m)
p_dist.append(p_keep)
mu_thin = np.asarray(mu_thin)
sns.regplot(mu_thin[:,0], mu_thin[:,1])
plt.axis(domain_range)
```
Now, we can sample points on top of that, also we'll only use the first k
```
sns.regplot(mu_thin[:k,0], mu_thin[:k,1])
plt.axis(domain_range)
```
Keeping only a few, we can end up with ones in the center, but if we sort them by the distance to the ones previously selected, we get them spread out a little more
```
# sort by distance
mu_sort, p_sort = zip(*sorted(zip(mu_thin,p_dist),
key = lambda x: x[1], reverse =True))
mu_sort = np.asarray(mu_sort)
sns.regplot(mu_sort[:k,0], mu_sort[:k,1])
plt.axis(domain_range)
# cluster covariance
cluster_corr = np.asarray([[1,r_clusters],[r_clusters,1]])
cluster_std = np.diag(np.sqrt(cluster_size))
cluster_cov = np.dot(cluster_std,cluster_corr).dot(cluster_std)
# sample from a GMM
z = np.random.choice(k,N,p_clusters)
x = np.asarray([np.random.multivariate_normal(mu_sort[z_i],cluster_cov) for z_i in z])
# make a dataframe
latent_df = pd.DataFrame(data=x,
columns = ['x1', 'x2'])
# code cluster as color and add it a column to the dataframe
latent_df['color'] = z
sp_plot(latent_df,'x1','x2','color')
```
We might not want all of the clusters to have the reveral though, so we can also sample the covariances
```
# cluster covariance
cluster_std = np.diag(np.sqrt(cluster_size))
cluster_corr_sp = np.asarray([[1,r_clusters],[r_clusters,1]]) # correlation with sp
cluster_cov_sp = np.dot(cluster_std,cluster_corr_sp).dot(cluster_std) #cov with sp
cluster_corr = np.asarray([[1,-r_clusters],[-r_clusters,1]]) #correlation without sp
cluster_cov = np.dot(cluster_std,cluster_corr).dot(cluster_std) #cov wihtout sp
cluster_covs = [cluster_corr_sp, cluster_corr]
# sample the[0,1] k times
c_sp = np.random.choice(2,k,p=[p_sp_clusters,1-p_sp_clusters])
# sample from a GMM
z = np.random.choice(k,N,p_clusters)
x = np.asarray([np.random.multivariate_normal(mu_sort[z_i],cluster_covs[c_sp[z_i]]) for z_i in z])
# make a dataframe
latent_df = pd.DataFrame(data=x,
columns = ['x1', 'x2'])
# code cluster as color and add it a column to the dataframe
latent_df['color'] = z
sp_plot(latent_df,'x1','x2','color')
[p_sp_clusters,1-p_sp_clusters]
c_sp
```
We'll call this construction of SP `geometric_2d_gmm_sp` and it's included in the `sp_data_utils` module now, so it can be called as follows. We'll change the portion of clusters with SP to 1, to ensure that all are SP.
```
type(r_clusters)
type(cluster_size)
type(cluster_spread)
type(p_sp_clusters)
type(domain_range)
type(p_clusters)
p_sp_clusters = .9
sp_df2 = spdata.geometric_2d_gmm_sp(r_clusters,cluster_size,cluster_spread,
p_sp_clusters, domain_range,k,N,p_clusters)
sp_plot(sp_df2,'x1','x2','color')
```
With this, we can start to see how the parameters control a little
```
# setup
r_clusters = -.4 # correlation coefficient of clusters
cluster_spread = .8 # pearson correlation of means
p_sp_clusters = .6 # portion of clusters with SP
k = 5 # number of clusters
cluster_size = [4,4]
domain_range = [0, 20, 0, 20]
N = 200 # number of points
p_clusters = [.5, .2, .1, .1, .1]
sp_df3 = spdata.geometric_2d_gmm_sp(r_clusters,cluster_size,cluster_spread,
p_sp_clusters, domain_range,k,N,p_clusters)
sp_plot(sp_df3,'x1','x2','color')
```
We might want to add multiple views, so we added a function that takes the same parameters or lists to allow each view to have different parameters. We'll look first at just two views with the same parameters, both as one another and as above
```
many_sp_df = spdata.geometric_indep_views_gmm_sp(2,r_clusters,cluster_size,cluster_spread,p_sp_clusters,
domain_range,k,N,p_clusters)
sp_plot(many_sp_df,'x1','x2','A')
sp_plot(many_sp_df,'x3','x4','B')
many_sp_df.head()
```
We can also look at the pairs of variables that we did not design SP into and see that they have vey different structure
```
# f, ax_grid = plt.subplots(2,2) # , fig_size=(10,10)
sp_plot(many_sp_df,'x1','x4','A')
sp_plot(many_sp_df,'x2','x4','B')
sp_plot(many_sp_df,'x2','x3','B')
sp_plot(many_sp_df,'x1','x3','B')
```
And we can set up the views to be different from one another by design
```
# setup
r_clusters = [.8, -.2] # correlation coefficient of clusters
cluster_spread = [.8, .2] # pearson correlation of means
p_sp_clusters = [.6, 1] # portion of clusters with SP
k = [5,3] # number of clusters
cluster_size = [4,4]
domain_range = [0, 20, 0, 20]
N = 200 # number of points
p_clusters = [[.5, .2, .1, .1, .1],[1.0/3]*3]
many_sp_df_diff = spdata.geometric_indep_views_gmm_sp(2,r_clusters,cluster_size,cluster_spread,p_sp_clusters,
domain_range,k,N,p_clusters)
sp_plot(many_sp_df_diff,'x1','x2','A')
sp_plot(many_sp_df_diff,'x3','x4','B')
many_sp_df.head()
```
And we can run our detection algorithm on this as well.
```
many_sp_df_diff_result = wg.detect_simpsons_paradox(many_sp_df_diff)
many_sp_df_diff_result
```
We designed in SP to occur between attributes `x1` and `x2` with respect to `A` and 2 & 3 in grouby by B, for portions fo the subgroups. We detect other occurences. It can be interesting to exmine trends between the deisnged and spontaneous occurences of SP, so
```
designed_SP = [('x1','x2','A'),('x3','x4','B')]
des = []
for i,r in enumerate(many_sp_df_diff_result[['attr1','attr2','groupbyAttr']].values):
if tuple(r) in designed_SP:
des.append(i)
many_sp_df_diff_result['designed'] = 'no'
many_sp_df_diff_result.loc[des,'designed'] = 'yes'
many_sp_df_diff_result.head()
r_clusters = -.9 # correlation coefficient of clusters
cluster_spread = .6 # pearson correlation of means
p_sp_clusters = .5 # portion of clusters with SP
k = 5 # number of clusters
cluster_size = [5,5]
domain_range = [0, 20, 0, 20]
N = 200 # number of points
p_clusters = [1.0/k]*k
many_sp_df_diff = spdata.geometric_indep_views_gmm_sp(3,r_clusters,cluster_size,cluster_spread,p_sp_clusters,
domain_range,k,N,p_clusters)
sp_plot(many_sp_df_diff,'x1','x2','A')
sp_plot(many_sp_df_diff,'x3','x4','B')
sp_plot(many_sp_df_diff,'x3','x4','A')
many_sp_df_diff.head()
```
| github_jupyter |
# A Scientific Deep Dive Into SageMaker LDA
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Data Exploration](#DataExploration)
1. [Training](#Training)
1. [Inference](#Inference)
1. [Epilogue](#Epilogue)
# Introduction
***
Amazon SageMaker LDA is an unsupervised learning algorithm that attempts to describe a set of observations as a mixture of distinct categories. Latent Dirichlet Allocation (LDA) is most commonly used to discover a user-specified number of topics shared by documents within a text corpus. Here each observation is a document, the features are the presence (or occurrence count) of each word, and the categories are the topics. Since the method is unsupervised, the topics are not specified up front, and are not guaranteed to align with how a human may naturally categorize documents. The topics are learned as a probability distribution over the words that occur in each document. Each document, in turn, is described as a mixture of topics.
This notebook is similar to **LDA-Introduction.ipynb** but its objective and scope are a different. We will be taking a deeper dive into the theory. The primary goals of this notebook are,
* to understand the LDA model and the example dataset,
* understand how the Amazon SageMaker LDA algorithm works,
* interpret the meaning of the inference output.
Former knowledge of LDA is not required. However, we will run through concepts rather quickly and at least a foundational knowledge of mathematics or machine learning is recommended. Suggested references are provided, as appropriate.
```
%matplotlib inline
import os, re, tarfile
import boto3
import matplotlib.pyplot as plt
import mxnet as mx
import numpy as np
np.set_printoptions(precision=3, suppress=True)
# some helpful utility functions are defined in the Python module
# "generate_example_data" located in the same directory as this
# notebook
from generate_example_data import (
generate_griffiths_data,
match_estimated_topics,
plot_lda,
plot_lda_topics,
)
# accessing the SageMaker Python SDK
import sagemaker
from sagemaker.amazon.common import RecordSerializer
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import JSONDeserializer
```
# Setup
***
*This notebook was created and tested on an ml.m4.xlarge notebook instance.*
We first need to specify some AWS credentials; specifically data locations and access roles. This is the only cell of this notebook that you will need to edit. In particular, we need the following data:
* `bucket` - An S3 bucket accessible by this account.
* Used to store input training data and model data output.
* Should be withing the same region as this notebook instance, training, and hosting.
* `prefix` - The location in the bucket where this notebook's input and and output data will be stored. (The default value is sufficient.)
* `role` - The IAM Role ARN used to give training and hosting access to your data.
* See documentation on how to create these.
* The script below will try to determine an appropriate Role ARN.
```
from sagemaker import get_execution_role
role = get_execution_role()
bucket = sagemaker.Session().default_bucket()
prefix = "sagemaker/DEMO-lda-science"
print("Training input/output will be stored in {}/{}".format(bucket, prefix))
print("\nIAM Role: {}".format(role))
```
## The LDA Model
As mentioned above, LDA is a model for discovering latent topics describing a collection of documents. In this section we will give a brief introduction to the model. Let,
* $M$ = the number of *documents* in a corpus
* $N$ = the average *length* of a document.
* $V$ = the size of the *vocabulary* (the total number of unique words)
We denote a *document* by a vector $w \in \mathbb{R}^V$ where $w_i$ equals the number of times the $i$th word in the vocabulary occurs within the document. This is called the "bag-of-words" format of representing a document.
$$
\underbrace{w}_{\text{document}} = \overbrace{\big[ w_1, w_2, \ldots, w_V \big] }^{\text{word counts}},
\quad
V = \text{vocabulary size}
$$
The *length* of a document is equal to the total number of words in the document: $N_w = \sum_{i=1}^V w_i$.
An LDA model is defined by two parameters: a topic-word distribution matrix $\beta \in \mathbb{R}^{K \times V}$ and a Dirichlet topic prior $\alpha \in \mathbb{R}^K$. In particular, let,
$$\beta = \left[ \beta_1, \ldots, \beta_K \right]$$
be a collection of $K$ *topics* where each topic $\beta_k \in \mathbb{R}^V$ is represented as probability distribution over the vocabulary. One of the utilities of the LDA model is that a given word is allowed to appear in multiple topics with positive probability. The Dirichlet topic prior is a vector $\alpha \in \mathbb{R}^K$ such that $\alpha_k > 0$ for all $k$.
# Data Exploration
---
## An Example Dataset
Before explaining further let's get our hands dirty with an example dataset. The following synthetic data comes from [1] and comes with a very useful visual interpretation.
> [1] Thomas Griffiths and Mark Steyvers. *Finding Scientific Topics.* Proceedings of the National Academy of Science, 101(suppl 1):5228-5235, 2004.
```
print("Generating example data...")
num_documents = 6000
known_alpha, known_beta, documents, topic_mixtures = generate_griffiths_data(
num_documents=num_documents, num_topics=10
)
num_topics, vocabulary_size = known_beta.shape
# separate the generated data into training and tests subsets
num_documents_training = int(0.9 * num_documents)
num_documents_test = num_documents - num_documents_training
documents_training = documents[:num_documents_training]
documents_test = documents[num_documents_training:]
topic_mixtures_training = topic_mixtures[:num_documents_training]
topic_mixtures_test = topic_mixtures[num_documents_training:]
print("documents_training.shape = {}".format(documents_training.shape))
print("documents_test.shape = {}".format(documents_test.shape))
```
Let's start by taking a closer look at the documents. Note that the vocabulary size of these data is $V = 25$. The average length of each document in this data set is 150. (See `generate_griffiths_data.py`.)
```
print("First training document =\n{}".format(documents_training[0]))
print("\nVocabulary size = {}".format(vocabulary_size))
print("Length of first document = {}".format(documents_training[0].sum()))
average_document_length = documents.sum(axis=1).mean()
print("Observed average document length = {}".format(average_document_length))
```
The example data set above also returns the LDA parameters,
$$(\alpha, \beta)$$
used to generate the documents. Let's examine the first topic and verify that it is a probability distribution on the vocabulary.
```
print("First topic =\n{}".format(known_beta[0]))
print(
"\nTopic-word probability matrix (beta) shape: (num_topics, vocabulary_size) = {}".format(
known_beta.shape
)
)
print("\nSum of elements of first topic = {}".format(known_beta[0].sum()))
```
Unlike some clustering algorithms, one of the versatilities of the LDA model is that a given word can belong to multiple topics. The probability of that word occurring in each topic may differ, as well. This is reflective of real-world data where, for example, the word *"rover"* appears in a *"dogs"* topic as well as in a *"space exploration"* topic.
In our synthetic example dataset, the first word in the vocabulary belongs to both Topic #1 and Topic #6 with non-zero probability.
```
print("Topic #1:\n{}".format(known_beta[0]))
print("Topic #6:\n{}".format(known_beta[5]))
```
Human beings are visual creatures, so it might be helpful to come up with a visual representation of these documents.
In the below plots, each pixel of a document represents a word. The greyscale intensity is a measure of how frequently that word occurs within the document. Below we plot the first few documents of the training set reshaped into 5x5 pixel grids.
```
%matplotlib inline
fig = plot_lda(documents_training, nrows=3, ncols=4, cmap="gray_r", with_colorbar=True)
fig.suptitle("$w$ - Document Word Counts")
fig.set_dpi(160)
```
When taking a close look at these documents we can see some patterns in the word distributions suggesting that, perhaps, each topic represents a "column" or "row" of words with non-zero probability and that each document is composed primarily of a handful of topics.
Below we plots the *known* topic-word probability distributions, $\beta$. Similar to the documents we reshape each probability distribution to a $5 \times 5$ pixel image where the color represents the probability of that each word occurring in the topic.
```
%matplotlib inline
fig = plot_lda(known_beta, nrows=1, ncols=10)
fig.suptitle(r"Known $\beta$ - Topic-Word Probability Distributions")
fig.set_dpi(160)
fig.set_figheight(2)
```
These 10 topics were used to generate the document corpus. Next, we will learn about how this is done.
## Generating Documents
LDA is a generative model, meaning that the LDA parameters $(\alpha, \beta)$ are used to construct documents word-by-word by drawing from the topic-word distributions. In fact, looking closely at the example documents above you can see that some documents sample more words from some topics than from others.
LDA works as follows: given
* $M$ documents $w^{(1)}, w^{(2)}, \ldots, w^{(M)}$,
* an average document length of $N$,
* and an LDA model $(\alpha, \beta)$.
**For** each document, $w^{(m)}$:
* sample a topic mixture: $\theta^{(m)} \sim \text{Dirichlet}(\alpha)$
* **For** each word $n$ in the document:
* Sample a topic $z_n^{(m)} \sim \text{Multinomial}\big( \theta^{(m)} \big)$
* Sample a word from this topic, $w_n^{(m)} \sim \text{Multinomial}\big( \beta_{z_n^{(m)}} \; \big)$
* Add to document
The [plate notation](https://en.wikipedia.org/wiki/Plate_notation) for the LDA model, introduced in [2], encapsulates this process pictorially.

> [2] David M Blei, Andrew Y Ng, and Michael I Jordan. Latent Dirichlet Allocation. Journal of Machine Learning Research, 3(Jan):993–1022, 2003.
## Topic Mixtures
For the documents we generated above lets look at their corresponding topic mixtures, $\theta \in \mathbb{R}^K$. The topic mixtures represent the probablility that a given word of the document is sampled from a particular topic. For example, if the topic mixture of an input document $w$ is,
$$\theta = \left[ 0.3, 0.2, 0, 0.5, 0, \ldots, 0 \right]$$
then $w$ is 30% generated from the first topic, 20% from the second topic, and 50% from the fourth topic. In particular, the words contained in the document are sampled from the first topic-word probability distribution 30% of the time, from the second distribution 20% of the time, and the fourth disribution 50% of the time.
The objective of inference, also known as scoring, is to determine the most likely topic mixture of a given input document. Colloquially, this means figuring out which topics appear within a given document and at what ratios. We will perform infernece later in the [Inference](#Inference) section.
Since we generated these example documents using the LDA model we know the topic mixture generating them. Let's examine these topic mixtures.
```
print("First training document =\n{}".format(documents_training[0]))
print("\nVocabulary size = {}".format(vocabulary_size))
print("Length of first document = {}".format(documents_training[0].sum()))
print("First training document topic mixture =\n{}".format(topic_mixtures_training[0]))
print("\nNumber of topics = {}".format(num_topics))
print("sum(theta) = {}".format(topic_mixtures_training[0].sum()))
```
We plot the first document along with its topic mixture. We also plot the topic-word probability distributions again for reference.
```
%matplotlib inline
fig, (ax1, ax2) = plt.subplots(2, 1)
ax1.matshow(documents[0].reshape(5, 5), cmap="gray_r")
ax1.set_title(r"$w$ - Document", fontsize=20)
ax1.set_xticks([])
ax1.set_yticks([])
cax2 = ax2.matshow(topic_mixtures[0].reshape(1, -1), cmap="Reds", vmin=0, vmax=1)
cbar = fig.colorbar(cax2, orientation="horizontal")
ax2.set_title(r"$\theta$ - Topic Mixture", fontsize=20)
ax2.set_xticks([])
ax2.set_yticks([])
fig.set_dpi(100)
%matplotlib inline
# pot
fig = plot_lda(known_beta, nrows=1, ncols=10)
fig.suptitle(r"Known $\beta$ - Topic-Word Probability Distributions")
fig.set_dpi(160)
fig.set_figheight(1.5)
```
Finally, let's plot several documents with their corresponding topic mixtures. We can see how topics with large weight in the document lead to more words in the document within the corresponding "row" or "column".
```
%matplotlib inline
fig = plot_lda_topics(documents_training, 3, 4, topic_mixtures=topic_mixtures)
fig.suptitle(r"$(w,\theta)$ - Documents with Known Topic Mixtures")
fig.set_dpi(160)
```
# Training
***
In this section we will give some insight into how AWS SageMaker LDA fits an LDA model to a corpus, create an run a SageMaker LDA training job, and examine the output trained model.
## Topic Estimation using Tensor Decompositions
Given a document corpus, Amazon SageMaker LDA uses a spectral tensor decomposition technique to determine the LDA model $(\alpha, \beta)$ which most likely describes the corpus. See [1] for a primary reference of the theory behind the algorithm. The spectral decomposition, itself, is computed using the CPDecomp algorithm described in [2].
The overall idea is the following: given a corpus of documents $\mathcal{W} = \{w^{(1)}, \ldots, w^{(M)}\}, \; w^{(m)} \in \mathbb{R}^V,$ we construct a statistic tensor,
$$T \in \bigotimes^3 \mathbb{R}^V$$
such that the spectral decomposition of the tensor is approximately the LDA parameters $\alpha \in \mathbb{R}^K$ and $\beta \in \mathbb{R}^{K \times V}$ which maximize the likelihood of observing the corpus for a given number of topics, $K$,
$$T \approx \sum_{k=1}^K \alpha_k \; (\beta_k \otimes \beta_k \otimes \beta_k)$$
This statistic tensor encapsulates information from the corpus such as the document mean, cross correlation, and higher order statistics. For details, see [1].
> [1] Animashree Anandkumar, Rong Ge, Daniel Hsu, Sham Kakade, and Matus Telgarsky. *"Tensor Decompositions for Learning Latent Variable Models"*, Journal of Machine Learning Research, 15:2773–2832, 2014.
>
> [2] Tamara Kolda and Brett Bader. *"Tensor Decompositions and Applications"*. SIAM Review, 51(3):455–500, 2009.
## Store Data on S3
Before we run training we need to prepare the data.
A SageMaker training job needs access to training data stored in an S3 bucket. Although training can accept data of various formats we convert the documents MXNet RecordIO Protobuf format before uploading to the S3 bucket defined at the beginning of this notebook.
```
# convert documents_training to Protobuf RecordIO format
recordio_protobuf_serializer = RecordSerializer()
fbuffer = recordio_protobuf_serializer.serialize(documents_training)
# upload to S3 in bucket/prefix/train
fname = "lda.data"
s3_object = os.path.join(prefix, "train", fname)
boto3.Session().resource("s3").Bucket(bucket).Object(s3_object).upload_fileobj(fbuffer)
s3_train_data = "s3://{}/{}".format(bucket, s3_object)
print("Uploaded data to S3: {}".format(s3_train_data))
```
Next, we specify a Docker container containing the SageMaker LDA algorithm. For your convenience, a region-specific container is automatically chosen for you to minimize cross-region data communication
```
from sagemaker.image_uris import retrieve
region_name = boto3.Session().region_name
container = retrieve("lda", boto3.Session().region_name)
print("Using SageMaker LDA container: {} ({})".format(container, region_name))
```
## Training Parameters
Particular to a SageMaker LDA training job are the following hyperparameters:
* **`num_topics`** - The number of topics or categories in the LDA model.
* Usually, this is not known a priori.
* In this example, howevever, we know that the data is generated by five topics.
* **`feature_dim`** - The size of the *"vocabulary"*, in LDA parlance.
* In this example, this is equal 25.
* **`mini_batch_size`** - The number of input training documents.
* **`alpha0`** - *(optional)* a measurement of how "mixed" are the topic-mixtures.
* When `alpha0` is small the data tends to be represented by one or few topics.
* When `alpha0` is large the data tends to be an even combination of several or many topics.
* The default value is `alpha0 = 1.0`.
In addition to these LDA model hyperparameters, we provide additional parameters defining things like the EC2 instance type on which training will run, the S3 bucket containing the data, and the AWS access role. Note that,
* Recommended instance type: `ml.c4`
* Current limitations:
* SageMaker LDA *training* can only run on a single instance.
* SageMaker LDA does not take advantage of GPU hardware.
* (The Amazon AI Algorithms team is working hard to provide these capabilities in a future release!)
Using the above configuration create a SageMaker client and use the client to create a training job.
```
session = sagemaker.Session()
# specify general training job information
lda = sagemaker.estimator.Estimator(
container,
role,
output_path="s3://{}/{}/output".format(bucket, prefix),
instance_count=1,
instance_type="ml.c4.2xlarge",
sagemaker_session=session,
)
# set algorithm-specific hyperparameters
lda.set_hyperparameters(
num_topics=num_topics,
feature_dim=vocabulary_size,
mini_batch_size=num_documents_training,
alpha0=1.0,
)
# run the training job on input data stored in S3
lda.fit({"train": s3_train_data})
```
If you see the message
> `===== Job Complete =====`
at the bottom of the output logs then that means training sucessfully completed and the output LDA model was stored in the specified output path. You can also view information about and the status of a training job using the AWS SageMaker console. Just click on the "Jobs" tab and select training job matching the training job name, below:
```
print("Training job name: {}".format(lda.latest_training_job.job_name))
```
## Inspecting the Trained Model
We know the LDA parameters $(\alpha, \beta)$ used to generate the example data. How does the learned model compare the known one? In this section we will download the model data and measure how well SageMaker LDA did in learning the model.
First, we download the model data. SageMaker will output the model in
> `s3://<bucket>/<prefix>/output/<training job name>/output/model.tar.gz`.
SageMaker LDA stores the model as a two-tuple $(\alpha, \beta)$ where each LDA parameter is an MXNet NDArray.
```
# download and extract the model file from S3
job_name = lda.latest_training_job.job_name
model_fname = "model.tar.gz"
model_object = os.path.join(prefix, "output", job_name, "output", model_fname)
boto3.Session().resource("s3").Bucket(bucket).Object(model_object).download_file(fname)
with tarfile.open(fname) as tar:
tar.extractall()
print("Downloaded and extracted model tarball: {}".format(model_object))
# obtain the model file
model_list = [fname for fname in os.listdir(".") if fname.startswith("model_")]
model_fname = model_list[0]
print("Found model file: {}".format(model_fname))
# get the model from the model file and store in Numpy arrays
alpha, beta = mx.ndarray.load(model_fname)
learned_alpha_permuted = alpha.asnumpy()
learned_beta_permuted = beta.asnumpy()
print("\nLearned alpha.shape = {}".format(learned_alpha_permuted.shape))
print("Learned beta.shape = {}".format(learned_beta_permuted.shape))
```
Presumably, SageMaker LDA has found the topics most likely used to generate the training corpus. However, even if this is case the topics would not be returned in any particular order. Therefore, we match the found topics to the known topics closest in L1-norm in order to find the topic permutation.
Note that we will use the `permutation` later during inference to match known topic mixtures to found topic mixtures.
Below plot the known topic-word probability distribution, $\beta \in \mathbb{R}^{K \times V}$ next to the distributions found by SageMaker LDA as well as the L1-norm errors between the two.
```
permutation, learned_beta = match_estimated_topics(known_beta, learned_beta_permuted)
learned_alpha = learned_alpha_permuted[permutation]
fig = plot_lda(np.vstack([known_beta, learned_beta]), 2, 10)
fig.set_dpi(160)
fig.suptitle("Known vs. Found Topic-Word Probability Distributions")
fig.set_figheight(3)
beta_error = np.linalg.norm(known_beta - learned_beta, 1)
alpha_error = np.linalg.norm(known_alpha - learned_alpha, 1)
print("L1-error (beta) = {}".format(beta_error))
print("L1-error (alpha) = {}".format(alpha_error))
```
Not bad!
In the eyeball-norm the topics match quite well. In fact, the topic-word distribution error is approximately 2%.
# Inference
***
A trained model does nothing on its own. We now want to use the model we computed to perform inference on data. For this example, that means predicting the topic mixture representing a given document.
We create an inference endpoint using the SageMaker Python SDK `deploy()` function from the job we defined above. We specify the instance type where inference is computed as well as an initial number of instances to spin up.
With this realtime endpoint at our fingertips we can finally perform inference on our training and test data.
We can pass a variety of data formats to our inference endpoint. In this example we will demonstrate passing CSV-formatted data. Other available formats are JSON-formatted, JSON-sparse-formatter, and RecordIO Protobuf. We make use of the SageMaker Python SDK utilities `CSVSerializer` and `JSONDeserializer` when configuring the inference endpoint.
```
lda_inference = lda.deploy(
initial_instance_count=1,
instance_type="ml.m4.xlarge", # LDA inference may work better at scale on ml.c4 instances
serializer=CSVSerializer(),
deserializer=JSONDeserializer(),
)
```
Congratulations! You now have a functioning SageMaker LDA inference endpoint. You can confirm the endpoint configuration and status by navigating to the "Endpoints" tab in the AWS SageMaker console and selecting the endpoint matching the endpoint name, below:
```
print("Endpoint name: {}".format(lda_inference.endpoint_name))
```
We pass some test documents to the inference endpoint. Note that the serializer and deserializer will atuomatically take care of the datatype conversion.
```
results = lda_inference.predict(documents_test[:12])
print(results)
```
It may be hard to see but the output format of SageMaker LDA inference endpoint is a Python dictionary with the following format.
```
{
'predictions': [
{'topic_mixture': [ ... ] },
{'topic_mixture': [ ... ] },
{'topic_mixture': [ ... ] },
...
]
}
```
We extract the topic mixtures, themselves, corresponding to each of the input documents.
```
inferred_topic_mixtures_permuted = np.array(
[prediction["topic_mixture"] for prediction in results["predictions"]]
)
print("Inferred topic mixtures (permuted):\n\n{}".format(inferred_topic_mixtures_permuted))
```
## Inference Analysis
Recall that although SageMaker LDA successfully learned the underlying topics which generated the sample data the topics were in a different order. Before we compare to known topic mixtures $\theta \in \mathbb{R}^K$ we should also permute the inferred topic mixtures
```
inferred_topic_mixtures = inferred_topic_mixtures_permuted[:, permutation]
print("Inferred topic mixtures:\n\n{}".format(inferred_topic_mixtures))
```
Let's plot these topic mixture probability distributions alongside the known ones.
```
%matplotlib inline
# create array of bar plots
width = 0.4
x = np.arange(10)
nrows, ncols = 3, 4
fig, ax = plt.subplots(nrows, ncols, sharey=True)
for i in range(nrows):
for j in range(ncols):
index = i * ncols + j
ax[i, j].bar(x, topic_mixtures_test[index], width, color="C0")
ax[i, j].bar(x + width, inferred_topic_mixtures[index], width, color="C1")
ax[i, j].set_xticks(range(num_topics))
ax[i, j].set_yticks(np.linspace(0, 1, 5))
ax[i, j].grid(which="major", axis="y")
ax[i, j].set_ylim([0, 1])
ax[i, j].set_xticklabels([])
if i == (nrows - 1):
ax[i, j].set_xticklabels(range(num_topics), fontsize=7)
if j == 0:
ax[i, j].set_yticklabels([0, "", 0.5, "", 1.0], fontsize=7)
fig.suptitle("Known vs. Inferred Topic Mixtures")
ax_super = fig.add_subplot(111, frameon=False)
ax_super.tick_params(labelcolor="none", top="off", bottom="off", left="off", right="off")
ax_super.grid(False)
ax_super.set_xlabel("Topic Index")
ax_super.set_ylabel("Topic Probability")
fig.set_dpi(160)
```
In the eyeball-norm these look quite comparable.
Let's be more scientific about this. Below we compute and plot the distribution of L1-errors from **all** of the test documents. Note that we send a new payload of test documents to the inference endpoint and apply the appropriate permutation to the output.
```
%%time
# create a payload containing all of the test documents and run inference again
#
# TRY THIS:
# try switching between the test data set and a subset of the training
# data set. It is likely that LDA inference will perform better against
# the training set than the holdout test set.
#
payload_documents = documents_test # Example 1
known_topic_mixtures = topic_mixtures_test # Example 1
# payload_documents = documents_training[:600]; # Example 2
# known_topic_mixtures = topic_mixtures_training[:600] # Example 2
print("Invoking endpoint...\n")
results = lda_inference.predict(payload_documents)
inferred_topic_mixtures_permuted = np.array(
[prediction["topic_mixture"] for prediction in results["predictions"]]
)
inferred_topic_mixtures = inferred_topic_mixtures_permuted[:, permutation]
print("known_topics_mixtures.shape = {}".format(known_topic_mixtures.shape))
print("inferred_topics_mixtures_test.shape = {}\n".format(inferred_topic_mixtures.shape))
%matplotlib inline
l1_errors = np.linalg.norm((inferred_topic_mixtures - known_topic_mixtures), 1, axis=1)
# plot the error freqency
fig, ax_frequency = plt.subplots()
bins = np.linspace(0, 1, 40)
weights = np.ones_like(l1_errors) / len(l1_errors)
freq, bins, _ = ax_frequency.hist(l1_errors, bins=50, weights=weights, color="C0")
ax_frequency.set_xlabel("L1-Error")
ax_frequency.set_ylabel("Frequency", color="C0")
# plot the cumulative error
shift = (bins[1] - bins[0]) / 2
x = bins[1:] - shift
ax_cumulative = ax_frequency.twinx()
cumulative = np.cumsum(freq) / sum(freq)
ax_cumulative.plot(x, cumulative, marker="o", color="C1")
ax_cumulative.set_ylabel("Cumulative Frequency", color="C1")
# align grids and show
freq_ticks = np.linspace(0, 1.5 * freq.max(), 5)
freq_ticklabels = np.round(100 * freq_ticks) / 100
ax_frequency.set_yticks(freq_ticks)
ax_frequency.set_yticklabels(freq_ticklabels)
ax_cumulative.set_yticks(np.linspace(0, 1, 5))
ax_cumulative.grid(which="major", axis="y")
ax_cumulative.set_ylim((0, 1))
fig.suptitle("Topic Mixutre L1-Errors")
fig.set_dpi(110)
```
Machine learning algorithms are not perfect and the data above suggests this is true of SageMaker LDA. With more documents and some hyperparameter tuning we can obtain more accurate results against the known topic-mixtures.
For now, let's just investigate the documents-topic mixture pairs that seem to do well as well as those that do not. Below we retreive a document and topic mixture corresponding to a small L1-error as well as one with a large L1-error.
```
N = 6
good_idx = l1_errors < 0.05
good_documents = payload_documents[good_idx][:N]
good_topic_mixtures = inferred_topic_mixtures[good_idx][:N]
poor_idx = l1_errors > 0.3
poor_documents = payload_documents[poor_idx][:N]
poor_topic_mixtures = inferred_topic_mixtures[poor_idx][:N]
%matplotlib inline
fig = plot_lda_topics(good_documents, 2, 3, topic_mixtures=good_topic_mixtures)
fig.suptitle("Documents With Accurate Inferred Topic-Mixtures")
fig.set_dpi(120)
%matplotlib inline
fig = plot_lda_topics(poor_documents, 2, 3, topic_mixtures=poor_topic_mixtures)
fig.suptitle("Documents With Inaccurate Inferred Topic-Mixtures")
fig.set_dpi(120)
```
In this example set the documents on which inference was not as accurate tend to have a denser topic-mixture. This makes sense when extrapolated to real-world datasets: it can be difficult to nail down which topics are represented in a document when the document uses words from a large subset of the vocabulary.
## Stop / Close the Endpoint
Finally, we should delete the endpoint before we close the notebook.
To do so execute the cell below. Alternately, you can navigate to the "Endpoints" tab in the SageMaker console, select the endpoint with the name stored in the variable `endpoint_name`, and select "Delete" from the "Actions" dropdown menu.
```
sagemaker.Session().delete_endpoint(lda_inference.endpoint_name)
```
# Epilogue
---
In this notebook we,
* learned about the LDA model,
* generated some example LDA documents and their corresponding topic-mixtures,
* trained a SageMaker LDA model on a training set of documents and compared the learned model to the known model,
* created an inference endpoint,
* used the endpoint to infer the topic mixtures of a test input and analyzed the inference error.
There are several things to keep in mind when applying SageMaker LDA to real-word data such as a corpus of text documents. Note that input documents to the algorithm, both in training and inference, need to be vectors of integers representing word counts. Each index corresponds to a word in the corpus vocabulary. Therefore, one will need to "tokenize" their corpus vocabulary.
$$
\text{"cat"} \mapsto 0, \; \text{"dog"} \mapsto 1 \; \text{"bird"} \mapsto 2, \ldots
$$
Each text document then needs to be converted to a "bag-of-words" format document.
$$
w = \text{"cat bird bird bird cat"} \quad \longmapsto \quad w = [2, 0, 3, 0, \ldots, 0]
$$
Also note that many real-word applications have large vocabulary sizes. It may be necessary to represent the input documents in sparse format. Finally, the use of stemming and lemmatization in data preprocessing provides several benefits. Doing so can improve training and inference compute time since it reduces the effective vocabulary size. More importantly, though, it can improve the quality of learned topic-word probability matrices and inferred topic mixtures. For example, the words *"parliament"*, *"parliaments"*, *"parliamentary"*, *"parliament's"*, and *"parliamentarians"* are all essentially the same word, *"parliament"*, but with different conjugations. For the purposes of detecting topics, such as a *"politics"* or *governments"* topic, the inclusion of all five does not add much additional value as they all essentiall describe the same feature.
| github_jupyter |
```
from skempi_utils import *
from scipy.stats import pearsonr
df = skempi_df
df_multi = df[~np.asarray([len(s)>8 for s in df.Protein])]
s_multi = set([s[:4] for s in df_multi.Protein])
s_groups = set([s[:4] for s in G1 + G2 + G3 + G4 + G5])
len(s_multi & s_groups), len(s_multi), len(s_groups)
df_multi.head()
from sklearn.preprocessing import StandardScaler
from itertools import combinations as comb
from sklearn.externals import joblib
import numpy as np
def evaluate(group_str, y_true, y_pred, ix):
y_pred_pos = y_pred[ix == 0]
y_pred_neg = y_pred[ix == 1]
y_true_pos = y_true[ix == 0]
y_true_neg = y_true[ix == 1]
cor_all, _ = pearsonr(y_true, y_pred)
cor_pos, _ = pearsonr(y_true_pos, y_pred_pos)
cor_neg, _ = pearsonr(y_true_neg, y_pred_neg)
print("[%s:%d] cor_all:%.3f, cor_pos:%.3f, cor_neg:%.3f" % (group_str, len(y_true), cor_all, cor_pos, cor_neg))
return cor_all, cor_pos, cor_neg
def run_cv_test(X, y, ix, get_regressor, modelname, normalize=1):
gt, preds, indx, cors = [], [], [], []
groups = [G1, G2, G3, G4, G5]
prots = G1 + G2 + G3 + G4 + G5
for i, pair in enumerate(comb(range(NUM_GROUPS), 2)):
group = groups[pair[0]] + groups[pair[1]]
g1, g2 = np.asarray(pair) + 1
indx_tst = (ix[:, 0] == g1) | (ix[:, 0] == g2)
indx_trn = np.logical_not(indx_tst)
y_trn = y[indx_trn]
y_true = y[indx_tst]
X_trn = X[indx_trn]
X_tst = X[indx_tst]
if normalize == 1:
scaler = StandardScaler()
scaler.fit(X_trn)
X_trn = scaler.transform(X_trn)
X_tst = scaler.transform(X_tst)
regressor = get_regressor()
regressor.fit(X_trn, y_trn)
joblib.dump(regressor, 'models/%s%s.pkl' % (modelname, i))
regressor = joblib.load('models/%s%s.pkl' % (modelname, i))
y_pred = regressor.predict(X_tst)
cor, pos, neg = evaluate("G%d,G%d" % (g1, g2), y_true, y_pred, ix[indx_tst, 1])
cors.append([cor, pos, neg])
indx.extend(ix[indx_tst, 1])
preds.extend(y_pred)
gt.extend(y_true)
return [np.asarray(a) for a in [gt, preds, indx, cors]]
def run_cv_test_ensemble(X, y, ix, alpha=0.5, normalize=1):
gt, preds, indx, cors = [], [], [], []
groups = [G1, G2, G3, G4, G5]
prots = G1 + G2 + G3 + G4 + G5
for i, pair in enumerate(comb(range(NUM_GROUPS), 2)):
group = groups[pair[0]] + groups[pair[1]]
g1, g2 = np.asarray(pair) + 1
indx_tst = (ix[:, 0] == g1) | (ix[:, 0] == g2)
indx_trn = (ix[:, 0] != 0) & ((ix[:, 0] == g1) | (ix[:, 0] == g2))
y_trn = y[indx_trn]
y_true = y[indx_tst]
X_trn = X[indx_trn]
X_tst = X[indx_tst]
svr = joblib.load('models/svr%d.pkl' % i)
rfr = joblib.load('models/rfr%d.pkl' % i)
if normalize == 1:
scaler = StandardScaler()
scaler.fit(X_trn)
X_trn = scaler.transform(X_trn)
X_tst = scaler.transform(X_tst)
y_pred_svr = svr.predict(X_tst)
y_pred_rfr = rfr.predict(X_tst)
y_pred = alpha * y_pred_svr + (1-alpha) * y_pred_rfr
cor, pos, neg = evaluate("G%d,G%d" % (g1, g2), y_true, y_pred, ix[indx_tst, 1])
cors.append([cor, pos, neg])
indx.extend(ix[indx_tst, 1])
preds.extend(y_pred)
gt.extend(y_true)
return [np.asarray(a) for a in [gt, preds, indx, cors]]
def records_to_xy(skempi_records, load_neg=True):
data = []
for record in tqdm(skempi_records, desc="records processed"):
r = record
assert r.struct is not None
data.append([r.features(True), [r.ddg], [r.group, r.is_minus]])
if not load_neg: continue
rr = reversed(record)
assert rr.struct is not None
data.append([rr.features(True), [rr.ddg], [rr.group, rr.is_minus]])
X, y, ix = [np.asarray(d) for d in zip(*data)]
return X, y, ix
def get_temperature_array(records, agg=np.min):
arr = []
pbar = tqdm(range(len(skempi_df)), desc="row processed")
for i, row in skempi_df.iterrows():
arr_obs_mut = []
for mutation in row["Mutation(s)_cleaned"].split(','):
mut = Mutation(mutation)
res_i, chain_id = mut.i, mut.chain_id
t = tuple(row.Protein.split('_'))
skempi_record = records[t]
res = skempi_record[chain_id][res_i]
temps = [a.temp for a in res.atoms]
arr_obs_mut.append(np.mean(temps))
arr.append(agg(arr_obs_mut))
pbar.update(1)
pbar.close()
return arr
skempi_records = load_skempi_structs(pdb_path="../data/pdbs_n", compute_dist_mat=False)
temp_arr = get_temperature_array(skempi_records, agg=np.min)
skempi_structs = load_skempi_structs("../data/pdbs", compute_dist_mat=False)
skempi_records = load_skempi_records(skempi_structs)
# X_pos, y_pos, ix_pos = records_to_xy(skempi_records)
# X_pos.shape, y_pos.shape, ix_pos.shape
X_, y_, ix_ = records_to_xy(skempi_records)
X = X_[:, :]
# X = np.concatenate([X.T, [temp_arr]], axis=0).T
y = y_[:, 0]
ix = ix_
X.shape, y.shape, ix.shape
print("----->SVR")
from sklearn.svm import SVR
def get_regressor(): return SVR(kernel='rbf')
gt, preds, indx, cors = run_cv_test(X, y, ix, get_regressor, 'svr', normalize=1)
cor1, _, _ = evaluate("CAT", gt, preds, indx)
print(np.mean(cors, axis=0))
print("----->RFR")
from sklearn.ensemble import RandomForestRegressor
def get_regressor(): return RandomForestRegressor(n_estimators=50, random_state=0)
gt, preds, indx, cors = run_cv_test(X, y, ix, get_regressor, 'rfr', normalize=1)
cor2, _, _ = evaluate("CAT", gt, preds, indx)
print(np.mean(cors, axis=0))
# alpha = cor1/(cor1+cor2)
alpha = 0.5
print("----->%.2f*SVR + %.2f*RFR" % (alpha, 1-alpha))
gt, preds, indx, cors = run_cv_test_ensemble(X, y, ix, normalize=1)
cor, _, _ = evaluate("CAT", gt, preds, indx)
print(np.mean(cors, axis=0))
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
def run_holdout_test_ensemble(X, y, ix, alpha=0.5, normalize=1):
indx_tst = ix[:, 0] == 0
indx_trn = np.logical_not(indx_tst)
y_trn = y[indx_trn]
y_true = y[indx_tst]
X_trn = X[indx_trn]
X_tst = X[indx_tst]
svr = SVR(kernel='rbf')
rfr = RandomForestRegressor(n_estimators=50, random_state=0)
if normalize == 1:
scaler = StandardScaler()
scaler.fit(X_trn)
X_trn = scaler.transform(X_trn)
X_tst = scaler.transform(X_tst)
svr.fit(X_trn, y_trn)
rfr.fit(X_trn, y_trn)
y_pred_svr = svr.predict(X_tst)
y_pred_rfr = rfr.predict(X_tst)
y_pred = alpha * y_pred_svr + (1-alpha) * y_pred_rfr
cor, pos, neg = evaluate("holdout", y_true, y_pred, ix[indx_tst, 1])
return cor, pos, neg
alpha = 0.5
run_holdout_test_ensemble(X, y, ix, alpha=0.5, normalize=1)
```
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.