question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
number-of-ways-to-reorder-array-to-get-same-bst | Clear Explanation of an Easy Recursive Combinatorics Solution | clear-explanation-of-an-easy-recursive-c-683n | Intuition\n Describe your first thoughts on how to solve this problem. \nAs with most tree problems, we repeatedly explore the left and right subtrees of the tr | bigbullboy | NORMAL | 2023-06-17T17:15:44.341860+00:00 | 2023-06-18T07:28:01.212372+00:00 | 130 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs with most tree problems, we repeatedly explore the left and right subtrees of the tree to arrive at our solution. In this case, we look at how many permutations of a subtree array correspond to the same subtree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAfter noting that the first element in the array is the root of the (sub)tree, we can also conclude that all the elements in num[1:] which are smaller than the root will be in the left subtree and all the elements in nums[1:] which are greater than the root will be in the right subtree. \n\nFor example, if the BST array is [3, 2, 1, 4, 5], then the root is 3 and the left subtree is [2, 1] with root node 2 and the right subtree is [4, 5] with root node 4. Notice that the subarray [2, 3] can be permuted in any position in nums[1:] as along as their relative permutation to each other is the same. For example, the array [3, 4, 2, 5, 1] will also give us the left subtree [2, 1] and the right subtree [4, 5]. Let $m$ be the length of the array, and let $k$ be the number of nodes in the left subtree. We need to choose $k$ spots out of $m-1$ positions to place our left subtree nodes in the array. This can done in $\\binom{m-1}{k}$ ways where $\\binom{x}{y}$ is the binomial coefficient which is equal to $\\frac{x!}{y!(x-y!)}$. \n\nHowever, our final answer is not $\\binom{m-1}{k}$. This only tells us the number of ways the children of the current root node can be permuted in the array. It does not tell us about the children nodes of the current root node\'s children i.e. it does not tell us about deeper subtrees. For example, consider the BST array [3, 1, 5, 2, 4, 7]. The left subtree here is [1, 2] and the right subtree is [5, 4, 7]. Notice how the right subtree can be [5, 7, 4] or [5, 4, 7] and still correspond to the same BST. This implies that we must traverse each subtree and calculate the valid permutations for its children node as well. The final answer will be the valid permutation of the left subtree multiplied by the valid permutations of the right subtree multiplied by the valid permutations of the current tree. \n\n# Complexity\n- Time complexity: $O(n^2)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThis is because we are calling the dfs function twice for each node in the tree. \n\n- Space complexity:$O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nFirst, we are storing the left and right subtrees which have linear space. Next, our recursive call stack can have at most $n-1$ calls.\n\n# Code\n```\n\nclass Solution:\n\tdef numOfWays(self, nums: List[int]) -> int:\n\t\t"""\n\t\tCalculates the number of ways an array can be rearranged and\n\t\tstill correspond to the same BST. \n\n\t\tArgs:\n\t\t\tnums: List[int] = array of integers which correspond to a BST \n\n\t\tReturns:\n\t\t\tcount: int = number of ways the array can be rearranged and \n\t\t\t\t\t\t still correspond to the same BST\n\t\t"""\n\n\t\t# Since the answer might be very large, we return it modulo 10**9 + 7\n\t\tmod = 10 ** 9 + 7 \n\n\t\t# define a recursive function which repeatedly calculates the answer\n\t\t# for each level of the binary search tree\n\n\t\tdef dfs(arr):\n\n\t\t\t# if the length of the current subtree is less than or equal to\n\t\t\t# two, then we can\'t rearrange the array in more ways since the \n\t\t\t# first element is the root of the subtree\n\n\t\t\tlength = len(arr)\n\t\t\tif length <= 2:\n\t\t\t\treturn 1 \n\n\t\t\t# we collect the array representation of the left subtree and the\n\t\t\t# right subtree\n\t\t\tleft_nodes = [num for num in arr if num < arr[0]]\n\t\t\tright_nodes = [num for num in arr if num > arr[0]]\n\n\t\t\t# at this current level, we can permute the left and right subtree\n\t\t\t# nodes by choosing len(left_nodes) spots from the arr[1:]\n\t\t\tcurrent_level_permutation = comb(length-1, len(left_nodes))\n\n\t\t\t# we have calculated the permutations for the current level of the BST,\n\t\t\t# we need to calculate the permutations for the left subtree and the right\n\t\t\t# subtree. We multiply all the factors together and return the final answer.\n\t\t\treturn dfs(left_nodes) * dfs(right_nodes) *current_level_permutation\n\n\t\t# we call the function for the BST, subtract one since the argument passed in is\n\t\t# not considered, and return the answer modulo 10 ** 9 + 7\n\t\treturn (dfs(nums) - 1) % mod \n``` | 1 | 0 | ['Tree', 'Recursion', 'Combinatorics', 'Python3'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | 🔥🔥🔥C++ | neat and clean code | rare solution | must watch🔥🔥🔥 | c-neat-and-clean-code-rare-solution-must-axxu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Algo-Messihas | NORMAL | 2023-06-17T13:21:38.893124+00:00 | 2023-06-17T13:21:38.893157+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nconst int mod = 1e9+7;\nvector<int> pascals[1000];\nclass Solution {\nprivate:\n int solver(vector<int> nums, vector<int> pascals[]){\n int n = nums.size();\n if(n < 3) return 1;\n\n vector<int> left;\n vector<int> right;\n\n for(int i=1; i<n; i++){\n if(nums[i] < nums[0]) left.push_back(nums[i]);\n else right.push_back(nums[i]);\n }\n\n int left_ways = solver(left,pascals);\n int right_ways = solver(right,pascals);\n\n return ((1LL * pascals[n-1][left.size()] * left_ways%mod)%mod * right_ways%mod)%mod;\n }\npublic:\n int numOfWays(vector<int>& nums) {\n if(pascals[0].size() == 0){\n for(int i=0; i<1000; i++){\n vector<int> temp(i+1,1);\n pascals[i] = temp;\n for(int j=1; j<i; j++){\n pascals[i][j] = (pascals[i-1][j-1]%mod + pascals[i-1][j]%mod)%mod;\n }\n }\n }\n return solver(nums,pascals) - 1;\n }\n};\n``` | 1 | 0 | ['Array', 'Math', 'Divide and Conquer', 'Binary Search Tree', 'C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | The Competitive Programming Solution [C++] | the-competitive-programming-solution-c-b-ml5t | This is not a typical DSA solution, and leans more towards CP. Please don\'t downvote -- I already warned you :)\n\n# Approach\n-> Fix the root and then think a | jaintle | NORMAL | 2023-06-16T20:09:05.330080+00:00 | 2023-06-16T20:09:05.330101+00:00 | 89 | false | This is not a typical DSA solution, and leans more towards CP. Please don\'t downvote -- I already warned you :)\n\n# Approach\n-> Fix the root and then think about combinations.\n-> Every node has two sides; left and right\n-> At the top most level, we cannot change the order ordering among the left side elements or the right side elements, but we can change the ordering of how a combination of these left side and right side element is present.\n```\n-> For eg: [3,4,5,1,2]\n-> root is 3\n-> Left side: [1,2]\n-> Right side: [4,5]\n-> Now we cant change the ordering among (1 and 2) and (4 and 5)\n-> But we can change between their combination (1,2,4,5), (1,4,2,5), (4,5,1,2) etc.\n```\n\n-> For each node we will see combinations this way i.e. left side and right side.\n-> With some observation you\'ll understand that if the number of elements on the right side is denoted by `l[node]` and right side `r[node]`, there can be a total of \n\n$$\\Large~~~~~~~~~~~~~~~~~{l[node]+r[node]-1 \\choose l[node]} + {l[node]+r[node]-1 \\choose r[node]}$$ \n\n\ncombinations are possible corresponding to this node. \n***[** ASK IF YOU DON\'T UNDERSTAND THIS, I CAN EXPLAIN WITH A DIAGRAM **]***\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n unordered_map<int,int> l;\n unordered_map<int,int> r;\n\nint modMul(int a, int b,int mod)\n{\n int res = 0; \n \n a %= mod;\n \n while (b) {\n if (b & 1)\n res = (res + a) % mod;\n \n a = (2 * a) % mod;\n \n b >>= 1; \n }\n \n return res;\n}\n \n\n int power(int x, int y, int p)\n{\n int res = 1;\n \n x = x % p; \n \n while (y > 0)\n {\n \n if (y & 1)\n res = modMul(res,x,p);\n \n y = y >> 1; \n x = modMul(x, x, p);\n }\n return res;\n}\n \nint modInverse(int n, int p)\n{\n return power(n, p - 2, p);\n}\n \n\nint nCr(int n, int r, int p)\n{\n if (n < r)\n return 0;\n if (r == 0)\n return 1;\n \n\n int fac[n + 1];\n fac[0] = 1;\n for (int i = 1; i <= n; i++)\n fac[i] = modMul(fac[i - 1],i,p);\n \n return modMul(modMul(fac[n],modInverse(fac[r], p),p),modInverse(fac[n - r], p),p);\n}\n\n void createBST(vector<vector<int>>& v, int root, int num){\n if(num<root){\n l[root]++;\n if(v[root][0]==0){\n v[root][0]=num;\n }\n else createBST(v,v[root][0],num);\n }\n else{\n r[root]++;\n if(v[root][1]==0){\n v[root][1]=num;\n }\n else createBST(v,v[root][1],num);\n }\n }\n int numOfWays(vector<int>& nums) {\n // l.clear();\n // r.clear();\n vector<vector<int>> v(nums.size()+1, vector<int>(2,0));\n for(int i = 1; i<nums.size(); i++){\n createBST(v,nums[0],nums[i]);\n }\n int count = 1;\n int mod = 1e9+7;\n for(int i = 1; i<nums.size()+1; i++){\n if((l[i]!=0)&&(r[i]!=0))count = modMul(count,(nCr(l[i]+r[i]-1,l[i],1e9+7)+nCr(l[i]+r[i]-1,r[i],1e9+7))%(mod),mod);\n }\n return count-1;\n }\n};\n``` | 1 | 0 | ['Math', 'Divide and Conquer', 'Combinatorics', 'C++'] | 2 |
number-of-ways-to-reorder-array-to-get-same-bst | [ C++ / Java ] ✅ Easy and Clean Code 🔥 Divide and Conquer 🔥 Beats 💯✅✅ | c-java-easy-and-clean-code-divide-and-co-6z7m | Please Upvote if you like my Solution \uD83E\uDD17\uD83E\uDD17\n\n# Complexity \n- Time complexity: O(N^2) \n Add your time complexity here, e.g. O(n) \n\n- Spa | sunny8080 | NORMAL | 2023-06-16T18:30:45.032283+00:00 | 2023-06-16T18:35:17.835560+00:00 | 348 | false | # Please Upvote if you like my Solution \uD83E\uDD17\uD83E\uDD17\n\n# Complexity \n- Time complexity: $$O(N^2)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N^2)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# C++ Code\n```\n#define ll long long\n\nclass Solution {\n int mod = 1e9+7;\n vector<vector<ll>> pascal;\n \n ll numOfWaysHelp(vector<int>& nums) {\n if(nums.size() <= 2) return 1;\n\n vector<int> leftSubtree, rightSubtree;\n int n = nums.size();\n for(int i=1; i<n; i++){\n if( nums[i] < nums[0] ) leftSubtree.push_back(nums[i]);\n else rightSubtree.push_back(nums[i]);\n }\n\n ll leftWays = numOfWaysHelp(leftSubtree), rightWays = numOfWaysHelp(rightSubtree);\n int leftLen = leftSubtree.size(), rightLen = rightSubtree.size();\n return (pascal[n-1][leftLen] * ((leftWays * rightWays)%mod))%mod;\n }\npublic:\n int numOfWays(vector<int>& nums) {\n // calculate pascal triangle for calculating nCr in O(1)\n int n = nums.size();\n pascal.resize(n+1);\n for(int i=0; i<n+1; i++){\n pascal[i] = vector<ll>(i+1, 1);\n for(int j=1; j<i; j++)\n pascal[i][j] = (pascal[i-1][j-1] + pascal[i-1][j] )%mod;\n }\n \n return numOfWaysHelp(nums)%mod - 1;\n }\n};\n```\n\n---\n\n# Java Code\n```\nclass Solution {\n int mod = (int)1e9+7;\n\n private long numOfWaysHelp(List<Integer> nums, List<List<Integer>> pascal ) {\n if(nums.size() <= 2) return 1;\n\n List<Integer> leftSubtree = new ArrayList<>(), rightSubtree = new ArrayList<>();\n int n = nums.size();\n for(int i=1; i<n; i++){\n if( nums.get(i) < nums.get(0) ) leftSubtree.add(nums.get(i));\n else rightSubtree.add(nums.get(i));\n }\n\n long leftWays = numOfWaysHelp(leftSubtree, pascal), rightWays = numOfWaysHelp(rightSubtree, pascal);\n int leftLen = leftSubtree.size(), rightLen = rightSubtree.size();\n return (pascal.get(n-1).get(leftLen) * ((leftWays * rightWays)%mod))%mod;\n }\n\n public int numOfWays(int[] nums) {\n // calculate pascal triangle for calculating nCr in O(1)\n int n = nums.length;\n List<List<Integer>> pascal = new ArrayList<>();\n\n for(int i=0; i<n+1; i++){\n Integer row[] = new Integer[i+1];\n Arrays.fill(row, 1);\n pascal.add(Arrays.asList(row));\n for(int j=1; j<i; j++)\n pascal.get(i).set(j, (pascal.get(i-1).get(j-1) + pascal.get(i-1).get(j) )%mod);\n }\n\n List<Integer> tmp = new ArrayList<>();\n for(int x : nums) tmp.add(x);\n return (int)numOfWaysHelp(tmp, pascal) - 1;\n }\n}\n```\n\n\n | 1 | 0 | ['Divide and Conquer', 'Dynamic Programming', 'Tree', 'C++', 'Java'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | combination + recursion | combination-recursion-by-mr_stark-isk3 | \nclass Solution {\npublic:\n vector<vector<long long int >> comb;\n int mod = 1e9+7;\n \n long long int solve(vector<int>& v)\n {\n int n | mr_stark | NORMAL | 2023-06-16T16:20:28.376231+00:00 | 2023-06-16T16:20:28.376253+00:00 | 90 | false | ```\nclass Solution {\npublic:\n vector<vector<long long int >> comb;\n int mod = 1e9+7;\n \n long long int solve(vector<int>& v)\n {\n int n = v.size();\n if(n<=2)\n return 1;\n \n vector<int > l ,r;\n for(int i=1;i<n;i++){\n if(v[i]<v[0])\n l.push_back(v[i]);\n else\n r.push_back(v[i]);\n }\n \n \n long long int lans = solve(l)%mod;\n long long int rans = solve(r)%mod;\n \n int llen = l.size();\n return ((((comb[n-1][llen] * lans ) %mod)*rans)%mod);\n }\n \n int numOfWays(vector<int>& v) {\n \n int n = v.size();\n comb.resize(n+1);\n for(int i=0;i<n+1;i++)\n {\n comb[i] = vector<long long int>(i+1,1);\n for(int j=1;j<i;j++)\n {\n comb[i][j] = (comb[i-1][j-1]+comb[i-1][j]) %mod;\n }\n }\n \n long long int ans = solve(v);\n return ans%mod - 1;\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Go 22ms Solution | go-22ms-solution-by-mjmtg-elv3 | Approach\nRecursive function (compute): This function divides the given array into two sub-arrays (namely \'smaller\' and \'larger\') based on the first element | MJMTG | NORMAL | 2023-06-16T15:16:42.735321+00:00 | 2023-06-16T15:16:42.735358+00:00 | 95 | false | # Approach\nRecursive function (compute): This function divides the given array into two sub-arrays (namely \'smaller\' and \'larger\') based on the first element, simulating the creation of a BST. If there is only one or no element left, it simply returns 1 (base case of recursion). It then recursively calculates the number of ways for both the \'smaller\' and \'larger\' sub-arrays and multiplies them together. Lastly, it multiplies the result by the number of ways to choose the elements for the sub-arrays (calculated by the choose function), which gives the total number of ways to reorder the given array.\n\nChoosing function (choose): This function calculates the number of ways to choose k elements from n elements (i.e., binomial coefficient). It does this using the [multiplicative inverse](https://en.wikipedia.org/wiki/Modular_multiplicative_inverse) method, which is a common way to handle large factorials while avoiding overflow. Here, the multiplicative inverse is calculated using the ModInverse function from the math/big package in Go.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ Each call to compute triggers $$O(n)$$ calls to itself.and this could happen up to n times \n\n- Space complexity:\n$$O(n)$$ as there would be $$n$$ recursive calls.\n\n# Code\n```\nconst mod = 1e9 + 7\nvar cache = make([][]int, 1001)\n\nfunc init() {\n for i := range cache {\n cache[i] = make([]int, 1001)\n }\n}\n\nfunc numOfWays(nums []int) int {\n return compute(nums) - 1\n}\n\nfunc compute(nums []int) int {\n if len(nums) <= 1 {\n return 1\n }\n\n smaller, larger := splitNums(nums)\n\n n := len(nums) - 1\n k := len(larger)\n \n kn := choose(n, k)\n small := compute(smaller) % mod\n large := compute(larger) % mod\n\n res := ((small * large % mod) * kn) % mod\n return res\n}\n\nfunc splitNums(nums []int) (smaller, larger []int) {\n for _, x := range nums[1:] {\n if x > nums[0] {\n larger = append(larger, x)\n }\n if x < nums[0] {\n smaller = append(smaller, x)\n }\n }\n return smaller, larger\n}\n\nfunc choose(n, k int) int {\n if k == 0 || k == n {\n return 1\n }\n if cache[n][k] != 0 {\n return cache[n][k]\n }\n\n a, b := 1, 1\n\n for x := n; x > k; x-- {\n a = (a * x) % mod\n }\n for x := n - k; x > 1; x-- {\n b = (b * x) % mod\n }\n\n inv := big.NewInt(int64(b)).ModInverse(big.NewInt(int64(b)), big.NewInt(int64(mod)))\n modinv := inv.Int64()\n\n cache[n][k] = (a * int(modinv)) % mod\n return cache[n][k]\n}\n\n``` | 1 | 0 | ['Go'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Easy and simple solution with explanation | easy-and-simple-solution-with-explanatio-pwk2 | If you not understand problem clearly then here is explanation\nLet\'s suppose we have given array [3,4,5,1,2] and empty tree\nthen we have to place element in | Ashwini_Tiwari | NORMAL | 2023-06-16T12:37:19.921343+00:00 | 2023-06-16T12:37:19.921378+00:00 | 64 | false | **If you not understand problem clearly then here is explanation**\nLet\'s suppose we have given *array* [3,4,5,1,2] and empty tree\nthen we have to place element in tree by order they comes i.e.\nwe get first element 3 make it root then we have element 4 make it to right child of 3,now element 5 come make it to right child of 4 then element 1 come make it to left child of 3 which is its correct position according to BST rule (i.e. smaller element left side and larger element right side) now 2 come make it to right child of 1.\nNow we have to find how many arrangements of give permutation give same BST.```\n\ni.e. 3 as root, 4 is right child of 3,5 is right child of 4, 1 is left child of 3 and 2 is right child of 1.\nHint: writes all arrangement of array try to find pattern in this.\n(Sorry for poor English).\n\n```\nint mode=1e9+7;\nclass Solution {\npublic:\n vector<vector<long long>> bio;\n long long dfs(vector<int> &nums){\n if(nums.size()<3){\n return 1;\n }\n vector<int> left,right;\n int n=nums.size();\n for(int i=1;i<n;i++){\n if(nums[i]<nums[0]){\n left.push_back(nums[i]);\n }else{\n right.push_back(nums[i]);\n }\n }\n int k=left.size();\n return bio[n][k]*dfs(left)%mode *dfs(right)%mode;\n }\n int numOfWays(vector<int>& nums) {\n int n=nums.size();\n bio.resize(0);\n bio.resize(n+4);\n bio[1]={1};\n bio[2]={1,1};\n for(int i=3;i<=n;i++){\n bio[i].resize(i,1);\n for(int j=1;j<i-1;j++){\n bio[i][j]=(bio[i-1][j-1]+bio[i-1][j])%mode;\n }\n }\n return (dfs(nums)-1)%mode;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | EASY WELL EXPLAINED DP || COMBINATION SOLUTION | easy-well-explained-dp-combination-solut-5l7s | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the solution is to recursively divide the array into two parts, a | Syankita-_- | NORMAL | 2023-06-16T12:31:27.224711+00:00 | 2023-06-16T12:31:27.224732+00:00 | 225 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the solution is to recursively divide the array into two parts, a left part and a right part. The left part contains numbers smaller than the first element of the array,i.e root of the tree, and the right part contains numbers greater than or equal to the first element. The number of ways to split the array can be calculated by multiplying the number of ways to split the left part and the right part with the total number of combinations possible for the remaining elements.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe numOfWays function takes an input array nums and returns the number of ways to split the array as described above.\nIt initializes a variable mod with the value 1e9 + 7, which will be used for modular arithmetic.\nIt creates a 2D vector dp of size (n + 1) x (n + 1), where n is the size of the input array. This vector will be used to store precomputed values of binomial coefficients.\nIt then calls a helper function sol with the input array nums and the dp vector.\nInside the sol function, if the size of the input array is less than or equal to 2, it returns 1 since there is only one way to split such arrays.\nOtherwise, it initializes two vectors left and right to store the numbers that are smaller and greater than or equal to the first element of the array, respectively.\nIt recursively calculates the number of ways to split the left and right parts by calling sol with the respective vectors.\nFinally, it returns the result by multiplying the number of ways to split the left and right parts with the binomial coefficient calculated using the dp vector. It uses modular arithmetic to avoid integer overflow.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code initializes the dp vector with binomial coefficients in O(n^2) time, where n is the size of the input array.\nThe sol function is called recursively, and at each recursion level, it splits the array into two parts, which takes O(n) time.\nOverall, the time complexity of the code is O(n^3) because the sol function is called recursively for each element in the array, and calculating binomial coefficients takes O(n^2) time.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe code uses a 2D vector dp of size (n + 1) x (n + 1), which requires O(n^2) space.\nThe recursion depth of the sol function is at most n, so the space complexity of the recursion stack is O(n).\nOverall, the space complexity of the code is O(n^2) due to the dp vector.dp\n# Code\n```\nclass Solution {\npublic:\nlong long mod=1e9+7;\nint sol(vector<int>&num,vector<vector<long long>> &dp){\n int n=num.size();\n if(n<=2) return 1;\n vector<int> left,right;\n for(int i=1;i<n;i++){\n if(num[i]<num[0]) left.push_back(num[i]);\n else right.push_back(num[i]);\n }\n return (((dp[n-1][left.size()]*(sol(left,dp)))%mod)*(sol(right,dp)))%mod;//nCr-->dp\n}\n int numOfWays(vector<int>& nums) {\n int n=nums.size();\n vector<vector<long long>> dp(n + 1, vector<long long>(n + 1, 0));\n for (int i=0;i<=n;i++){\n dp[i][0]=1;\n dp[i][i]=1;\n for (int j=1;j<i;j++)\n dp[i][j]=(dp[i-1][j-1] + dp[i-1][j])%mod;\n }\n return sol(nums,dp)-1;\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Tree', 'Binary Search Tree', 'Combinatorics', 'C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Easy to understand code with nCr || C++ || Recursion || Fastest🔥 | easy-to-understand-code-with-ncr-c-recur-tapn | Approach\nAs mention in the problem we have to find the number of ways to reorder the given array which generates the same tree.\nThe first element can not be r | kunal_asatkar | NORMAL | 2023-06-16T12:26:05.062531+00:00 | 2023-06-16T12:30:05.557027+00:00 | 44 | false | # Approach\nAs mention in the problem we have to find the number of ways to reorder the given array which generates the same tree.\nThe first element can not be rearranged because if we change its position the tree will change.\n\nThe dfs function is a recursive helper function that takes in the nums array and a 2D vector comb as input. It performs a depth-first search to calculate the number of different reorderings.\n\nThe base case for the recursion is when the size of the nums array is less than or equal to 2. In this case, there is only one way to reorder the elements, so the function returns 1.\n\nIf the size of the nums array is greater than 2, the function continues with the recursive approach. It splits the nums array into two parts: left and right. The left array contains all the elements smaller than the first element of nums, and the right array contains all the elements greater than the first element.\n\n# Complexity\n- Time complexity:\nO(n<sup>2</sup>)\ndfs(nums) recursively calls itself. In each call it find the number of elements greater than the first element which require O(n) time.\n Since the total call will be n. Thus the total time complexity of the recursive solution is O(n<sup>2</sup>)\n\n\n- Space complexity:\nO(n<sup>2</sup>)\nAs we vector of vector to store the combinations\n\n# If find usefull please upvote |\n\n# Code\n```\nclass Solution {\npublic:\n\n int dfs(vector<int>& nums,vector<vector<int>>&comb) {\n int n = nums.size(),md=1e9+7;\n if (n <= 2) return 1;\n vector<int> left, right;\n for (int i = 1; i < n; ++i) {\n if (nums[i] < nums[0]) left.push_back(nums[i]);\n else right.push_back(nums[i]);\n }\n long long res = comb[n - 1][left.size()];\n res = res * dfs(left,comb) % md;\n res = res * dfs(right,comb) % md;\n return (int)res;\n }\n\n int numOfWays(vector<int>& nums) {\n int n = nums.size();\n int md=1e9+7;\n vector<vector<int>> comb(n + 1, vector<int>(n + 1));\n comb[0][0] = 1;\n for (int i = 1; i <= n; ++i) {\n comb[i][0] = 1;\n for (int j = 1; j <= i; ++j) {\n comb[i][j]=(comb[i-1][j-1]+comb[i-1][j]) % md;\n }\n }\n \n return dfs(nums,comb) - 1;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Combinations, Modular Inverse using Fermat's Little Theorem | combinations-modular-inverse-using-ferma-uqqy | Intuition\n Describe your first thoughts on how to solve this problem. \nThe position for the root is fixed at the first position, the left and the right sub-tr | CHIYOI | NORMAL | 2023-06-16T11:51:20.801062+00:00 | 2023-06-16T11:51:20.801082+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe position for the root is fixed at the first position, the left and the right sub-trees can be mixed with each other but without changing the order in each sub-tree.\n\nWe can get an initial answer, which is the number of combinations $$C^n_k$$, where $$n$$ is the length of the array and $$k$$ is the number of nodes in either the left sub-tree or the right sub-tree (the result should be the same because $$C^n_k = C^n_{n-k}$$).\n\nFor the order of each sub-tree, we can use a recursive approach and multiplying them into the initial answer we can get the final answer.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. `inverse`: Get the modular inverse using *Fermat\'s Little Theorem*: $$a^{-1} = a^{M - 2}\\mod M$$\n - `power`: Get the power efficiently.\n2. `c`: Calculate $$C^n_k$$. Use `inverse` to convert division to multiply so that we can perform the modulo.\n - `numerator`: The numerator is the product from `n - k + 1` to `n` inclusively.\n - `denominator`: The denominator is the product from `1` to `k` inclusively.\n\n# Complexity\nComplexity is calculated in average occasions, for dividing into two parts and recursively solve each part.\n\nIn each iteration, we used $$O(n)$$ to get each sub-tree and $$O(n)$$ to calculate the number of combinations (with $$log_2M$$ to get the power), so $$O(n)$$ is the answer.\n\nWe perform recursions based on the input, if the numbers of nodes in the left and right sub-trees are approximetely equal, we can get a recursion depth of $$O(log_2n)$$.\n- Time complexity: $$O(n\\log_2n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n\\log_2n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nconst int mod = 1e9+7;\n\nstatic int power(int x, int y) { return y == 0 ? 1 : (y % 2 == 0 ? power((long)x * x % mod, y / 2) : (long)x * power(x, y - 1) % mod); }\nint inverse(int a) { return power(a, mod - 2); }\n\nstatic int numerator(int i, int n) { return i <= n ? (long)numerator(i + 1, n) * i % mod : 1; }\nstatic int denominator(int i, int k) { return i <= k ? (long)denominator(i + 1, k) * i % mod : 1; }\nint c(int n, int k) { return (long)numerator(n - k + 1, n) * inverse(denominator(1, k)) % mod; }\n\nstatic void count(int i, int n, int *cg, int *cl, int *nums) { i < n ? ((nums[i] > nums[0] ? (*cg)++ : (*cl)++), count(i+1, n, cg, cl, nums)) : (void)0; }\nstatic void subs(int i, int n, int *g, int ig, int *l, int il, int *nums) { i < n ? ((nums[i] > nums[0] ? (g[ig++] = nums[i]) : (l[il++] = nums[i])), subs(i+1, n, g, ig, l, il, nums)) : (void)0; }\nint numOfWays(int *nums, int numsSize)\n{\n int *g, cg = 0, *l, cl = 0;\n int ans, i;\n\n return count(1, numsSize, &cg, &cl, nums),\n g = (cg > 0 ? calloc(cg, sizeof *g) : NULL),\n l = (cl > 0 ? calloc(cl, sizeof *l) : NULL),\n subs(1, numsSize, g, 0, l, 0, nums),\n ans = (long)c(numsSize-1, cg) * (cg > 2 ? numOfWays(g, cg) + 1 : 1) % mod * (cl > 2 ? numOfWays(l, cl) + 1 : 1) % mod,\n free(g),\n free(l),\n (ans - 1) % mod;\n} \n``` | 1 | 0 | ['C'] | 1 |
number-of-ways-to-reorder-array-to-get-same-bst | [Python 3] Solution with real BST | python-3-solution-with-real-bst-by-deimv-ly6g | Code\n\nfrom math import comb\n\nMOD = 10**9+7\n\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n root = self._build_bst(nums)\n | deimvis | NORMAL | 2023-06-16T10:31:59.690859+00:00 | 2023-06-16T10:31:59.690877+00:00 | 18 | false | # Code\n```\nfrom math import comb\n\nMOD = 10**9+7\n\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n root = self._build_bst(nums)\n return self.perms(root)[1] - 1\n\n def perms(self, node):\n """ returns (size, perms) """\n if node is None:\n return 0, 1\n \n left_size, left_perms = self.perms(node.left)\n right_size, right_perms = self.perms(node.right)\n size = left_size + right_size + 1\n\n res = comb(size-1, left_size) * left_perms * right_perms\n \n return size, res % MOD\n \n def _build_bst(self, nums):\n bst = BST()\n for x in nums:\n bst.insert(x)\n return bst.root\n\n\nclass BST:\n def __init__(self):\n self.root = None\n \n def insert(self, val):\n self.root = self._insert(self.root, val)\n \n def _insert(self, node, val):\n if node is None:\n return TreeNode(val)\n\n if val < node.val:\n node.left = self._insert(node.left, val)\n else:\n node.right = self._insert(node.right, val)\n return node\n\n\nclass TreeNode:\n def __init__(self, val):\n self.val = val\n self.left = None\n self.right = None\n``` | 1 | 0 | ['Python3'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Most Complicated (But faster than 93% users) C++ Approach | most-complicated-but-faster-than-93-user-znei | Intuition\n Describe your first thoughts on how to solve this problem. \n\nI dare you to find the intuition in this programme.\n\nUsed (dp + divide and conquer | Vraj109 | NORMAL | 2023-06-16T08:38:37.155195+00:00 | 2023-06-16T08:44:09.326866+00:00 | 53 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nI dare you to find the intuition in this programme.\n\nUsed (dp + divide and conquer + combinatorics + Tree + dfs + math).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nExtremely Complicated Approach consisting of making of the BST then\nsolving the problme with the help of divide and conquer approch and to solve for one segment use the the combinatorics with finding all the nCr\'s int only O(n)(for all combined).\n\n\n# Complexity\n- Time complexity: O(nlogn).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> fac;\n int MOD = 1e9 + 7;\n long long power(long long a, long long b,int m)\n{\n if(b == 0) return 1;\n\n a = a % m;\n long long temp = power(a, b/2,m);\n if(b&1)\n return (((temp * temp) % m) * a) % m;\n else\n return (temp * temp) % m;\n}\n\nlong long modInverse(long long n, int p)\n{\n return power(n, p - 2, p);\n}\nlong long mul(long long x,\n long long y, int p)\n{\n return x * 1ull * y % p;\n}\nlong long divide(long long x,\n long long y, int p)\n{\n return mul(x, modInverse(y, p), p);\n}\n class bst{\n public:\n int val;\n bst* l;\n bst* r;\n bst(int v){\n val = v;\n l = NULL;\n r = NULL;\n }\n };\n pair<int,long long> dfs(bst* root){\n if(!root) return {0,1};\n pair<int,long long> a = dfs(root->l);\n pair<int,long long> b = dfs(root->r);\n long long ans = divide(fac[a.first+b.first],mul(fac[b.first],fac[a.first],MOD),MOD);\n ans = mul(ans,a.second,MOD);\n ans = mul(ans,b.second,MOD);\n return {(a.first+b.first+1),ans};\n }\n int numOfWays(vector<int>& arr) {\n bst* root = new bst(arr[0]);\n fac.push_back(1);\n for(int i = 1;i<arr.size();i++){\n fac.push_back((fac[i-1]*i)%MOD);\n int a = arr[i];\n bst* node = root;\n bst* t = new bst(a);\n while(1){\n if(a > node->val){\n if(node->r == NULL){\n node->r = t;\n break;\n }\n node = node->r;\n }\n else{\n if(node->l == NULL){\n node->l = t;\n break;\n }\n node = node->l;\n }\n }\n }\n return (int)(dfs(root).second - 1);\n }\n};\n``` | 1 | 0 | ['Math', 'Divide and Conquer', 'Binary Search Tree', 'Combinatorics', 'C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Editorial Solution / Typescript / Pascal Triangle | editorial-solution-typescript-pascal-tri-e9po | \n\nfunction numOfWays(nums: number[]): number {\n const mod = BigInt(10 ** 9 + 7);\n const table: number[][] = [];\n\n // Fill Pascal Table\n for (let i = | bakunovdo | NORMAL | 2023-06-16T08:09:02.411581+00:00 | 2023-06-16T08:09:02.411610+00:00 | 128 | false | # \n```\nfunction numOfWays(nums: number[]): number {\n const mod = BigInt(10 ** 9 + 7);\n const table: number[][] = [];\n\n // Fill Pascal Table\n for (let i = 0; i < nums.length; i++) {\n table[i] = new Array(i + 1).fill(1);\n for (let j = 1; j < nums.length; j++) {\n if (j > i) continue;\n const a = table[i - 1][j - 1] ?? 0;\n const b = table[i - 1][j] ?? 0;\n table[i][j] = (a + b) % Number(mod);\n }\n }\n\n function getWaysHelper(nums: number[]): bigint {\n const m = nums.length;\n if (m < 3) return 1n;\n\n const leftNodes: number[] = [];\n const rightNodes: number[] = [];\n\n for (let i = 1; i < m; i++) {\n if (nums[i] < nums[0]) leftNodes.push(nums[i]);\n else rightNodes.push(nums[i]);\n }\n\n const leftWays = getWaysHelper(leftNodes) % mod;\n const rightWays = getWaysHelper(rightNodes) % mod;\n\n return (((leftWays * rightWays) % mod) * BigInt(table[m - 1][leftNodes.length])) % mod;\n }\n\n const ways = getWaysHelper(nums) - 1n; // -1 original order\n\n return Number(ways % mod);\n}\n``` | 1 | 0 | ['TypeScript'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Lets make it easy. Its really easy! | lets-make-it-easy-its-really-easy-by-cod-l4o5 | \n\n# Approach\nStep 1\nWe split the array into root, leftsubtree elements, rightsubtree elements.\nA simple filter loop would do that.\n\nWhy?\n We know | codshashank_1 | NORMAL | 2023-06-16T06:29:28.552016+00:00 | 2023-06-16T06:29:28.552034+00:00 | 230 | false | \n\n# Approach\nStep 1\nWe split the array into root, leftsubtree elements, rightsubtree elements.\nA simple filter loop would do that.\n\nWhy?\n We know the fundamentals of Binary Search Tree.\n 1. All the elements in Left SubTree(lst) are smaller than Right SubTree(rst) elements.\n So the ordering of those elements in the array which belong to different subtree would be independent.\n 2. Ordering of the elements in the same subtree matters and will be the same relativLY.\n Say a, b, c belong to lst, and d, e, f belong to rst. and the root of the tree is z\n So z, a,b,c,d,e,f will do fine and so will z, d,e,f,a,b,c.\n z, a,d,e,f,b,c will do fine (notice the relative orders)\n z, a,d,b,e,c,f will too be fine.\n These two sets are independent. Hence ordering wont affect the subtree\'s invariant property.\n Now is the time to realize why ordering affects within the same subtree? (Take pen and paper to prove;)\n\n So the problem turns out to be Leetcode Hard -> Leetcode easy naa?\n\n Step 2:(Recursive thinking ;) )\n After splitting, we compute recursivel the same for left subtree and right subtree.\n We obtain the the no of orderings possiblefrom left subtree by abstracting a leftsubtree(a subproblem) into a tree itself.\n We obtain the the no of orderings possiblefrom right subtree by abstracting the right subtree(a subproblem) into a tree itself.\n\n\n Step3 : Conquer your subproblems!! ;) Understand the combinatorics very carefully.\n By Fundamental theorem of counting the total possible orderings are \n sl = size_of_left_subtree, sr = size_of_right_subtree;\n n = sl + sr + 1(root) w here n is total size of the tree. \n table[n - 1][left_subtree_size] * left_recusrsion_result * right_recursion_result;\n since pascal table is zero index based, ncr = table[n][r];\n where out of n - 1 places left_subtree_size places are fixed so we choose to maintain order. And \n left_recusrsion_result * right_recursion_result orderings can be places in such choices of arrangements.\n\n\n Side Note: \n To access ncr effectively, we use the pascals table and retrieve table[n + 1][r + 1]\n If we wish to compute say 4c2 then table[5][3] would return us the computation in O(1) time.Its necessary to use O(1) time instead of O(n) by the brute force approach which involves the computation over factorials.\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\nprivate:\n vector<vector<long long>> table;\n long long mod;\n int solve(vector<int> &nums) {\n int n = nums.size();\n if(n <= 2) return 1;\n\n vector<int> right, left;\n for(int i = 1; i < n; ++i) {\n if(nums[i] < nums[0]) left.push_back(nums[i]);\n else right.push_back(nums[i]);\n } \n\n long long left_size = left.size(), right_size = right.size();\n\n int left_orderings = solve(left) ;\n int right_orderings = solve(right) ;\n\n return (((table[n - 1][left_size] * left_orderings) % mod) * right_orderings) % mod ; \n }\n \npublic:\n int numOfWays(vector<int>& nums) { \n\n int n = nums.size();\n mod = 1e9 + 7;\n for(int i = 0; i < n; ++i) {\n vector<long long> row(i + 1, 1);\n for(int j = 1; j < i; ++j) {\n row[j] = (table[i - 1][j] + table[i - 1][j - 1]) % mod; \n }\n table.push_back(row);\n }\n \n return solve(nums) - 1;\n \n\n \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | C++ | Dynamic Programming | Divide and Conquer | Combinational | Easy to Understand | <100ms | c-dynamic-programming-divide-and-conquer-hk3m | \nclass Solution {\npublic:\nconst long long mod = 1e9+7;\nvector<long long>fact;\nvoid calcFact(){\n fact[0] =1;\n fact[1] =1;\n for(long long i=2;i<1 | pspraneetsehra08 | NORMAL | 2023-06-16T06:06:49.176949+00:00 | 2023-06-16T06:06:49.176975+00:00 | 76 | false | ```\nclass Solution {\npublic:\nconst long long mod = 1e9+7;\nvector<long long>fact;\nvoid calcFact(){\n fact[0] =1;\n fact[1] =1;\n for(long long i=2;i<1001;i++)\n fact[i] = (fact[i-1]*i)%mod;\n}\n\nlong long modInv(long long n,long long p){\n if(p==0)\n return 1LL;\n long long ans = modInv(n,p/2);\n if(p&1)\n return (((ans*ans)%mod)*n)%mod;\n else\n return (ans*ans)%mod;\n}\n\nlong long help(vector<int>&nums){\n if(nums.size()<=2)\n return 1LL;\n vector<int>small,large;\n for(int i=1;i<nums.size();i++){\n if(nums[i]>nums[0])\n large.push_back(nums[i]);\n else\n small.push_back(nums[i]);\n }\n long long ans =1;\n ans = (ans*fact[(int)nums.size()-1])%mod;\n ans =(ans*modInv(fact[(int)nums.size()-(int)small.size()-1],mod-2))%mod;\n ans = (ans*modInv(fact[(int)small.size()],mod-2))%mod;\n ans = (ans*help(small))%mod;\n ans = (ans*help(large))%mod;\n return ans;\n}\n int numOfWays(vector<int>& nums) {\n fact = vector<long long>(1001);\n calcFact();\n long long ans = help(nums);\n ans--;\n ans = (ans+mod)%mod;\n return ans;\n }\n};\n``` | 1 | 0 | ['Divide and Conquer', 'Dynamic Programming', 'C', 'C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | C++ Easy Understanding | | Recursion | c-easy-understanding-recursion-by-rhythm-1hj6 | \nclass Solution {\n const int mod = 1e9 + 7;\n long inverse(long num) {\n if (num == 1) {\n return 1;\n }\n return mod - | rhythm_jain_ | NORMAL | 2023-06-16T04:32:00.760687+00:00 | 2023-06-16T04:32:00.760714+00:00 | 176 | false | ```\nclass Solution {\n const int mod = 1e9 + 7;\n long inverse(long num) {\n if (num == 1) {\n return 1;\n }\n return mod - mod / num * inverse(mod % num) % mod;\n }\n\n int dfs(vector<int>& nums) {\n int N = nums.size();\n if (N <= 2) return 1;\n \n vector<int> left, right;\n for (int i = 1; i < N; i++) \n {\n if (nums[i] < nums[0]) \n left.push_back(nums[i]);\n else \n right.push_back(nums[i]);\n }\n\n int a = left.size();\n int b = right.size();\n long res = 1;\n for (int i = b+1; i <= a + b; i++) res = res * i % mod;\n \n for (int i = 1; i <= a; i++) res = res * inverse(i) % mod;\n \n return res * dfs(left) % mod * dfs(right) % mod;\n }\n \npublic:\n int numOfWays(vector<int>& nums) {\n return dfs(nums) - 1;\n }\n};\n``` | 1 | 0 | ['Recursion', 'C'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | DP + COMBINATRICS + RECURSION (C++) | dp-combinatrics-recursion-c-by-ankit1072-5fsw | Trick to find nCr using dp is nCr = n-1Cr-1 + n-1Cr\n\nlets suppose that we know the answer to rearrange the elements of left subtree and of the right subtre | ankit1072 | NORMAL | 2023-06-16T04:16:38.125765+00:00 | 2023-06-16T04:33:24.304737+00:00 | 184 | false | **Trick to find nCr using dp is** nCr = n-1Cr-1 + n-1Cr\n\nlets suppose that we know the answer to rearrange the elements of left subtree and of the right subtree and now we want to construct our final answer for current root\n\nout of ```n-1``` places we need to choose ```left.size( ) ``` places and put left subtree elements permutation on those places and right subtree elements in the remaining places.\n\n**so, ans = (n-1) C ( left.size( ) ) * left * right**\n\nleft is numbers of ways to rearrange the elements of left subree so that it generates the same bst as the left subtree of the original bst and similarly for the right.\nbasically left is the answer for our recursion call for left subtree and right is the answer for recursion call on right subtree.\n\n```\nclass Solution {\npublic:\n \n int mod = 1e9 + 7;\n long long dp[1001][1001] = {};\n \n int helper(vector<int> & nums){\n if(nums.size() <= 2)\n return 1;\n \n int n = nums.size(); \n vector<int> left, right;\n for(int i = 1; i<n; i++){\n if(nums[i] < nums[0])\n left.push_back(nums[i]);\n else right.push_back(nums[i]);\n }\n \n int leftAns = helper(left), rightAns = helper(right);\n \n return (((dp[n-1][left.size()] * leftAns)%mod) * rightAns)%mod;\n \n }\n \n \n int numOfWays(vector<int>& nums) {\n for(int n = 0; n <= 1000; n++){\n dp[n][0] = 1;\n }\n for(int n = 1; n <= 1000; n++){\n for(int r = 1; r <= n; r++){\n\t\t\t\t// nCr = n-1Cr-1 + n-1Cr\n dp[n][r] = (dp[n-1][r-1] + dp[n-1][r])%mod;\n }\n }\n \n int res = (helper(nums) - 1 + mod)%mod;\n \n return res;\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'C', 'Combinatorics'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Editorial solution | C# | 100% efficient | editorial-solution-c-100-efficient-by-ba-7p78 | Intuition\n Describe your first thoughts on how to solve this problem. \nFollowing the steps from the \'Editorial\' of the problem.\nhttps://leetcode.com/proble | Baymax_ | NORMAL | 2023-06-16T03:15:49.992718+00:00 | 2023-06-16T03:22:40.439375+00:00 | 261 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n*Following the steps from the \'Editorial\' of the problem.*\nhttps://leetcode.com/problems/number-of-ways-to-reorder-array-to-get-same-bst/editorial/\n\n***We can either implement a function to form Pascal Triangle..\n[or]\nDefine a function to calculate nCr -> n! / ((n-r)! * r!) with help of caching to avoid TLE due to same function being called over-and-over again during recursion***\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N ^ 2) - as we form Pascal Triangle\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N ^ 2) - as we form Pascal Triangle\n\n# Code\n```\npublic class Solution {\n Dictionary<long, double> cache = new Dictionary<long, double>();\n int mod = 1000000007;\n long[][] table;\n\n public int NumOfWays(int[] nums) {\n FormPascalTriagle(nums.Length);\n return (int)DFS(nums.ToList()) - 1;\n }\n\n private long DFS(List<int> nums)\n {\n int n = nums.Count;\n if (n <= 2)\n return 1;\n \n List<int> smaller = new List<int>();\n List<int> greater = new List<int>();\n\n for (int i = 1; i < n; i++)\n {\n if (nums[i] < nums[0])\n smaller.Add(nums[i]);\n else\n greater.Add(nums[i]);\n }\n\n //apply mod after every product to avoid overflow\n return (table[n - 1][smaller.Count] * \n (DFS(smaller) % mod) % mod) *\n DFS(greater) % mod;\n\n }\n\n //Either form a Pascal triangle in the beginning..\n //or\n //implement a function to calculate nCr = n!/ ((n-r)! * r!)\n\n //For the second approach, we\'ll have to have Cache in place...\n //...to avoid TLE due to recursion calling same methods over and over again\n private void FormPascalTriagle(int n) {\n table = new long[n][];\n for (int i = 0; i < n; i++)\n table[i] = new long[n];\n\n for (int i = 0; i < n; i++)\n {\n table[i][0] = 1;\n table[i][i] = 1;\n }\n\n for (int i = 2; i < n; i++)\n {\n for (int j = 1; j < i; j++)\n {\n table[i][j] = (table[i - 1][j] + table[i - 1][j - 1]) % mod;\n }\n }\n }\n}\n``` | 1 | 0 | ['Array', 'Math', 'Dynamic Programming', 'Binary Search Tree', 'C#'] | 1 |
number-of-ways-to-reorder-array-to-get-same-bst | Rust | rust-by-unknown-cj4r | When computing (a / b) % m in function Combination(a, b), we cannot treat it as a % m / (b % m), we can only apply % m to the final result, but overflow may hap | unknown- | NORMAL | 2023-06-16T03:14:03.171445+00:00 | 2023-06-16T15:26:15.980250+00:00 | 47 | false | When computing `(a / b) % m` in function `Combination(a, b)`, we cannot treat it as `a % m / (b % m)`, we can only apply `% m` to the final result, but overflow may happen when multiplying.\nWe can use `mod inserse` to transform it into `a * mod_inverse(b) % m`, then apply `% m` anywhere as we want.\n\n```\nimpl Solution {\n pub fn num_of_ways(nums: Vec<i32>) -> i32 {\n Self::count(nums) as i32 - 1\n }\n\n fn count(nums: Vec<i32>) -> usize {\n if nums.len() <= 2 {\n return 1;\n }\n\n let mut left = vec![];\n let mut right = vec![];\n let root = nums[0];\n for n in nums.into_iter().skip(1) {\n if n > root {\n right.push(n);\n } else {\n left.push(n);\n }\n }\n let m = 1_000_000_007;\n let mut ret = Self::foo(left.len(), right.len());\n if ret == 0 {\n ret = 1;\n }\n let left = Self::count(left);\n let right = Self::count(right);\n ret = ret * left % m * right % m;\n ret\n }\n\n // for example:\n // n is 2: [1, 2]\n // m is 2: [3, 4]\n // merge m array into a array, keep themselies order\n // [3, 4, 1, 2], [1, 3, 4, 2], [1, 2, 3, 4]\n // [3, 1, 4, 2], [3, 1, 2, 4], [1, 3, 2, 4]\n fn foo(mut n: usize, mut m: usize) -> usize {\n Self::C(n + m, n)\n }\n\n // Combination number, pick r from n\n fn C(n: usize, r: usize) -> usize {\n (1..=r.min(n - r)).fold(1, |acc, i| acc * (n - i + 1) % 1_000_000_007 * Self::mod_inverse(i) % 1_000_000_007)\n }\n\n // modular inverse, use Fermat\'s little theorem\n // a^(M - 1) === 1 (mod M) => a^-1 === a^(M - 2) (mod M)\n fn mod_inverse(mut a: usize) -> usize {\n Self::power(a, 1_000_000_005)\n }\n\n // a ^ b % M\n fn power(mut a: usize, mut b: usize) -> usize {\n let mut ret = 1;\n let m = 1_000_000_007;\n while b > 0 {\n if b & 1 == 1 {\n ret = (ret * a) % m;\n }\n a = (a * a) % m;\n b >>= 1;\n }\n ret\n }\n}\n``` | 1 | 0 | ['Rust'] | 1 |
number-of-ways-to-reorder-array-to-get-same-bst | Ruby From Editorial, (somewhat) easy to understand | ruby-from-editorial-somewhat-easy-to-und-qh1l | \nMOD = 10 ** 9 + 7\n\ndef factorial (n)\n n.downto(1).inject(:*) || 1\nend \n\ndef comb (n, k)\n return factorial(n) / (factorial(k) * factorial(n - k))\ | pharmac1st | NORMAL | 2023-06-16T03:13:32.390325+00:00 | 2023-06-16T03:13:32.390343+00:00 | 34 | false | ```\nMOD = 10 ** 9 + 7\n\ndef factorial (n)\n n.downto(1).inject(:*) || 1\nend \n\ndef comb (n, k)\n return factorial(n) / (factorial(k) * factorial(n - k))\nend\n\ndef dfs(nums)\n return 1 if (nums.length < 3)\n left_nodes = nums.filter {|a| a < nums[0]}\n right_nodes = nums.filter {|a| a > nums[0]}\n return dfs(left_nodes) * dfs(right_nodes) * comb(nums.length - 1, left_nodes.length) % MOD\nend \n\ndef num_of_ways(nums)\n (dfs(nums) - 1) % MOD\nend\n``` | 1 | 0 | ['Ruby'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | C++ || Recursion + Combinatorics using Pascal table || Great Question | c-recursion-combinatorics-using-pascal-t-q5az | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rajat0301tajar | NORMAL | 2023-06-16T03:03:31.261140+00:00 | 2023-06-16T03:03:31.261159+00:00 | 371 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n typedef long long int64;\n vector<vector<int64>> table;\n const int MOD = (int)1e9 + 7;\n \n // ways(nums) = ways(leftNodes) * ways(rightNodes) * (nums.size() - 1)C(leftNodes.size())\n // (nums.size() - 1)C(leftNodes.size()) = num of ways to keep leftNodes in same order keeping the root\'s position unchanged.\n\n int64 solve(vector<int> &nums) {\n int n = nums.size();\n if(n <= 2) {\n return 1;\n }\n vector<int> leftNodes, rightNodes;\n for(int i = 1; i < n; i++) {\n if(nums[i] < nums[0]) {\n leftNodes.push_back(nums[i]);\n } else {\n rightNodes.push_back(nums[i]);\n }\n }\n int64 leftWays = solve(leftNodes) % MOD;\n int64 rightWays = solve(rightNodes) % MOD;\n return ((leftWays * rightWays) % MOD) * table[n - 1][leftNodes.size()] % MOD;\n }\n\n int numOfWays(vector<int>& nums) {\n int n = nums.size();\n table.resize(n + 1); // pascal triangle\n for(int i = 0; i < (n + 1); i++) {\n table[i] = vector<int64> (i + 1, 1);\n for(int j = 1; j < i; j++) {\n // nCr + nCr-1 = n+1Cr\n table[i][j] = (table[i - 1][j] + table[i - 1][j - 1]) % MOD;\n }\n }\n\n return (solve(nums) - 1) % MOD;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | C solution | c-solution-by-jerrychiang87-jqoz | Code\n\n#define MOD 1000000007\nlong long dfs(int *nums, int numsSize, int **combination_table)\n{\n if(numsSize<3)\n return 1;\n int *large = (int*)malloc | JerryChiang87 | NORMAL | 2023-06-16T02:15:26.637458+00:00 | 2023-06-16T02:15:26.637477+00:00 | 172 | false | # Code\n```\n#define MOD 1000000007\nlong long dfs(int *nums, int numsSize, int **combination_table)\n{\n if(numsSize<3)\n return 1;\n int *large = (int*)malloc(sizeof(int)*10000);\n int *small = (int*)malloc(sizeof(int)*10000);\n int lidx=0, sidx=0;\n for(int i=1;i<numsSize;i++)\n {\n if(nums[i]>nums[0])\n large[lidx++] = nums[i];\n else\n small[sidx++] = nums[i];\n }\n large = realloc(large, sizeof(int)*lidx);\n small = realloc(small, sizeof(int)*sidx);\n long long largeway = dfs(large, lidx, combination_table)%MOD;\n long long smallway = dfs(small, sidx, combination_table)%MOD;\n\n return ((largeway*smallway)%MOD)*(combination_table[numsSize-1][lidx])%MOD;\n}\n\n\nint numOfWays(int* nums, int numsSize){\n int i, j;\n\n int **combination_table = (int**)malloc(sizeof(int*)*numsSize);\n for(i=0;i<numsSize;i++)\n combination_table[i] = (int*)malloc(sizeof(int)*numsSize);\n \n for(i=0;i<numsSize;i++)\n {\n for(j=0;j<=i;j++)\n {\n if(j==0 || i==j)\n combination_table[i][j] = 1;\n else\n combination_table[i][j] = (combination_table[i-1][j] + combination_table[i-1][j-1])%MOD;\n }\n }\n\n return (dfs(nums, numsSize, combination_table)-1)%MOD;\n}\n``` | 1 | 0 | ['C'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | Python3 Solution | python3-solution-by-motaharozzaman1996-7xpm | \n\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n mod=10**9+7\n \n def f(nums):\n n=len(nums)\n | Motaharozzaman1996 | NORMAL | 2023-06-16T01:33:33.448132+00:00 | 2023-06-16T01:45:39.051352+00:00 | 562 | false | \n```\nclass Solution:\n def numOfWays(self, nums: List[int]) -> int:\n mod=10**9+7\n \n def f(nums):\n n=len(nums)\n if n<=1:\n return len(nums) \n\n left=[i for i in nums if i<nums[0]]\n right=[i for i in nums if i>nums[0]]\n\n Left=f(left)\n Right=f(right)\n\n if not Left or not Right :\n return Left or Right\n ans=comb(len(right)+len(left),len(right))\n return ans*Left*Right\n\n return (f(nums)-1)%mod \n\n return (f(nums)-1)%mod \n``` | 1 | 0 | ['Python', 'Python3'] | 1 |
number-of-ways-to-reorder-array-to-get-same-bst | Easiest JAVA solution using BigInteger class of Java 🙌🙌 | easiest-java-solution-using-biginteger-c-jsq5 | Intuition\nFirst element is always fixed , now take rest elements and divide array in two arrays and repeat same process for each array. \n Describe your first | Vatsal_04V | NORMAL | 2023-06-16T01:09:01.654820+00:00 | 2023-06-16T01:09:01.654837+00:00 | 122 | false | # Intuition\nFirst element is always fixed , now take rest elements and divide array in two arrays and repeat same process for each array. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTake first element as root, not divide array in two parts which contains lesser elments and greater elements than the root node respectively and put in new array in same order. \nNow except first place we can use rest all places to put the elements, we will find this by taking any required place ant put it in order, now we repeat the same operation for the two divided arrays. \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.math.BigInteger;\nclass Solution {\n int ans = 0;\n BigInteger[] b = new BigInteger[1001];\n BigInteger m = new BigInteger("1000000007");\n BigInteger m2 = factorial(1000);\n public int numOfWays(int[] nums) {\n b[0] = BigInteger.ONE;\n b[1] = BigInteger.ONE;\n int n = nums.length;\n if(n<=2) return 0;\n return (solve(nums).subtract(BigInteger.ONE)).mod(m).intValue();\n }\n public BigInteger solve(int[] nums){\n int n = nums.length;\n if(n<=2) return BigInteger.ONE;;\n int[] ar , br;\n int l = 0, h = 0;\n for(int i=1;i<nums.length;i++){\n if(nums[i]>nums[0]){\n h++;\n }else{\n l++;\n }\n }\n ar = new int[h];\n br = new int[l];\n h = 0;\n l = 0;\n for(int i=1;i<nums.length;i++){\n if(nums[i]>nums[0]){\n ar[h] = nums[i];\n h++;\n }else{\n br[l] = nums[i];\n l++;\n }\n }\n return ((b[n-1].divide(b[h]).divide(b[n-1-h]).mod(m).multiply(solve(ar)).multiply(solve(br)).mod(m))).mod(m);\n }\n public BigInteger factorial(int num){\n if (num<=1)\n return BigInteger.ONE;\n else\n return b[num] = factorial(num-1).multiply(BigInteger.valueOf(num));\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
number-of-ways-to-reorder-array-to-get-same-bst | Ruby solution with memoization and explanation (100%/100%) | ruby-solution-with-memoization-and-expla-3lew | Intuition\nUse recursion: for each tree, split it into the left subtree and the right subtree, then calculate the number of ways based on the length and structu | dtkalla | NORMAL | 2023-06-16T00:59:41.276298+00:00 | 2023-06-18T01:39:31.832306+00:00 | 53 | false | # Intuition\nUse recursion: for each tree, split it into the left subtree and the right subtree, then calculate the number of ways based on the length and structure of each subtree.\n\n# Approach\n0. Create a class memo to return the number of arrangements of normalized arrays. (Normalized here means it uses the numbers 1-n.)\n\nFind the number of ways to form a tree from the original array with a helper function, subtract 1, and do modulo.\n\nMain helper function:\n1. Return a memoized version if it\'s stored.\n\n2. Divide the elements other than the root into the left subtree and right subtree, keeping them in the same order.\n3. Normalize the right subtree (e.g., if it\'s [5,7,6], convert it to [1,3,2]). We do this with a helper function. (Note that we don\'t have to normalize the left; since it\'s the smaller section of a normalized array, it will always go 1-n.)\n4. Find the number of ways to arrange each subtree.\n\n5. Multiply the number of ways to arrange each subtree for result.\n6. Multiply this result by the orderings helper function.\n\nAs an example, if the left subtree had 3 elements and the right subtree had 5 elements, they would have 8 elements in total. The left elements have to keep relative order, as do the right elements, but we can changes when we do left elements versus right elements. Essentially, we have 8 spots and want to find how many ways we can choose 3 of them to be elements from the left subtree. This is just combinations, which we can calculate with factorials. (Look up combinations/factorials if this part doesn\'t make sense.)\n\n7. Mod the result, memoize, and return.\n\n# Complexity\n- Time complexity:\nThis is pretty from quick sort, but it divides the array the same way in the recursive step, so time complexity is the same: $$O(n *log(n))$$ average case, $$O(n^2)$$ worst case.\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\n@memo = {[] => 1, [1] => 1, [1,2] => 1}\n\ndef num_of_ways(nums)\n (num_ways(nums) - 1) % 1000000007\nend\n\ndef num_ways(nums)\n return @memo[nums] if @memo[nums]\n\n left = nums.select { |num| num < nums[0] }\n right = nums.select { |num| num > nums[0] }\n right = normalize(right)\n left_ways,right_ways = num_ways(left),num_ways(right)\n\n res = left_ways * right_ways\n res *= orderings(left.length,right.length)\n\n @memo[nums] = res % 1000000007\nend\n\ndef orderings(a,b)\n fact(a+b) / fact(a) / fact(b)\nend\n\ndef fact(n)\n return 1 if n < 2\n i = 1\n (2..n).each { |k| i *= k }\n i\nend\n``` | 1 | 0 | ['Ruby'] | 0 |
number-of-ways-to-reorder-array-to-get-same-bst | C++ || DFS | c-dfs-by-_biranjay_kumar-5ox1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | _Biranjay_kumar_ | NORMAL | 2023-06-16T00:36:27.761491+00:00 | 2023-06-16T00:36:27.761514+00:00 | 851 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n int mod = 1e9+7;\n vector<vector<long long>> table;\n\n void insert(TreeNode *root, int num){\n \n if(root->val == -1){\n root->val = num;\n }\n else{\n if(root->val < num){\n if(!root->right)root->right = new TreeNode(-1);\n insert(root->right, num);\n }\n else{\n if(!root->left)root->left = new TreeNode(-1);\n insert(root->left, num);\n }\n }\n\n }\n\n pair<int, int> dp(TreeNode *root){\n if(!root)return {0, 1};\n else{\n\n auto l = dp(root->left);\n auto r = dp(root->right);\n\n pair<int, int> p;\n p.first = l.first + r.first + 1;\n p.second = ((( table[p.first - 1][l.first] * l.second) % mod) * r.second) % mod;\n \n return p;\n }\n }\n\n int numOfWays(vector<int>& nums) {\n \n int n = nums.size();\n if(n>2){\n TreeNode *root = new TreeNode(-1);\n for(int x: nums){\n insert(root, x);\n }\n\n table.resize(n + 1);\n for(int i = 0; i < n + 1; ++i){\n table[i] = vector<long long>(i + 1, 1);\n for(int j = 1; j < i; ++j){\n table[i][j] = (table[i-1][j-1] + table[i-1][j]) % mod;\n }\n }\n\n return dp(root).second - 1;\n }\n else return 0;\n }\n};\n``` | 1 | 0 | ['Divide and Conquer', 'Dynamic Programming', 'Tree', 'Union Find', 'C++'] | 0 |
russian-doll-envelopes | Java NLogN Solution with Explanation | java-nlogn-solution-with-explanation-by-gq7yc | Sort the array. Ascend on width and descend on height if width are same.\n 2. Find the [longest increasing subsequence][1] based on height. \n\n\n----------\n\n | AyanamiA | NORMAL | 2016-06-07T06:40:32+00:00 | 2018-10-23T07:13:03.686918+00:00 | 91,670 | false | 1. Sort the array. Ascend on width and descend on height if width are same.\n 2. Find the [longest increasing subsequence][1] based on height. \n\n\n----------\n\n - Since the width is increasing, we only need to consider height. \n - [3, 4] cannot contains [3, 3], so we need to put [3, 4] before [3, 3] when sorting otherwise it will be counted as an increasing number if the order is [3, 3], [3, 4]\n\n\n----------\n\n\n public int maxEnvelopes(int[][] envelopes) {\n if(envelopes == null || envelopes.length == 0 \n || envelopes[0] == null || envelopes[0].length != 2)\n return 0;\n Arrays.sort(envelopes, new Comparator<int[]>(){\n public int compare(int[] arr1, int[] arr2){\n if(arr1[0] == arr2[0])\n return arr2[1] - arr1[1];\n else\n return arr1[0] - arr2[0];\n } \n });\n int dp[] = new int[envelopes.length];\n int len = 0;\n for(int[] envelope : envelopes){\n int index = Arrays.binarySearch(dp, 0, len, envelope[1]);\n if(index < 0)\n index = -(index + 1);\n dp[index] = envelope[1];\n if(index == len)\n len++;\n }\n return len;\n }\n\n\n [1]: https://leetcode.com/problems/longest-increasing-subsequence/ | 707 | 4 | ['Dynamic Programming', 'Java'] | 73 |
russian-doll-envelopes | [C++,Java, Python]Best Explanation with Pictures | cjava-pythonbest-explanation-with-pictur-73bl | If you like this solution or find it useful, please upvote this post.\n\n\tPrerequisite\n\t\n\tBefore moving on to the solution, you should know how can we find | rhythm_varshney | NORMAL | 2022-05-25T03:34:26.472184+00:00 | 2022-05-30T07:00:18.268844+00:00 | 31,252 | false | **If you like this solution or find it useful, please upvote this post.**\n<details>\n\t<summary>Prerequisite</summary>\n\t<br>\n\tBefore moving on to the solution, you should know how can we find the length of <strong>Longest Increasing Subsequence</strong> unsing <strong>Binary Search</strong>. You can find the detailed explanation of the logic on the below link. \n\t</br>\n\t<br></br>\n\t<a href="https://leetcode.com/problems/longest-increasing-subsequence/discuss/1636162/java-binary-search-stepwise-explanation">Longest Increasing Subsequence Using Binary Search</a>\n</details>\n<br></br>\n\n#### Why we need to sort?\n* In these types of problem when we are dealing with two dimensions, we need to reduce the problem from two-dimensional array into a one-dimensional array in order to improve time complexity. \n* **"Sort first when things are undecided"**, sorting can make the data orderly, reduce the degree of confusion, and often help us to sort out our thinking. the same is true with this question. Now, after doing the correct sorting, we just need to find Longest Increasing Subsequence of that one dimensional array.\n**Now, you may be wondered what correct sorting actually is?**\nIt is the sorting which we do to order to achieve the answer. Like, increasing, non-increasing sorting. Without any further discussion, let\'s dig into Intuition followed by algorithm.\n\n##### Algorithm\n* We sort the array in increasing order of width. And if two widths are same, we need to sort height in decreasing order. \n* Now why we need to sort in decreasing order if two widths are same. By this practice, we\'re assuring that no width will get counted more than one time. Let\'s take an example\nenvelopes=`[[3, 5], [6, 7], [7, 13], [6, 10], [8, 4], [7, 11]]`\n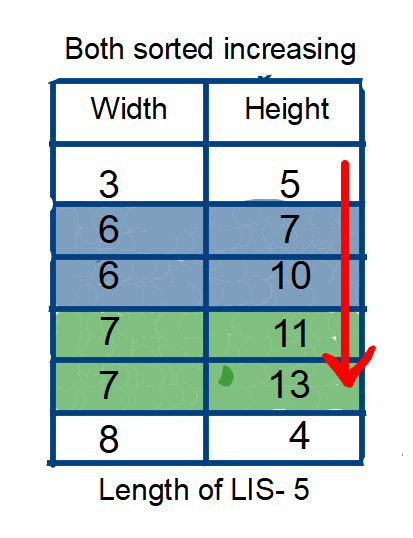\nNow, if you see for a while, **6 and 7** is counted twice while we\'re calculating the length of LIS, which will give the wrong ans. As question is asking, if any width/height are less than or equal, then, it is not possible to russian doll these envelopes. \nNow, we know the problem. So, how can we tackle these conditions when two width are same, so that it won\'t affect our answer. We can simple **reverse sort the height if two width are equal, to remove duplicacy.**\nNow, you may question, how reverse sorting the height would remove duplicacy? As the name itself says, Longest Increasing Subsequnce, the next coming height would be less than the previous one. Hence, forbidding it to increase length count.\n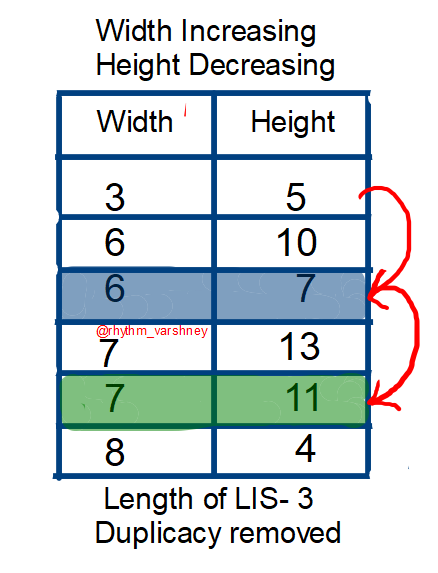\nIf you don\'t understand how LIS is calculated here, I strongly refer you to follow the prerequisite.\nNow, we have **sucessfully reduced the problem to LIS!** All you need to apply classical LIS on heights, to calculate the ans. This would be the maximum number of envelopes can be russian doll.\n\n**Code**\n\n```\nclass Solution {\n public int binarySearch(int[] dp, int val){\n int lo=0,hi=dp.length-1,res=0;\n while(lo<=hi){\n int mid=(lo+hi)/2;\n if(dp[mid]<val){\n res=mid;\n lo=mid+1;\n }else{\n hi=mid-1;\n }\n }\n return res+1;\n }\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes,(a,b)->a[0]==b[0]?b[1]-a[1]:a[0]-b[0]);\n int[] LIS=new int[envelopes.length+1];\n Arrays.fill(LIS,Integer.MAX_VALUE);\n LIS[0]=Integer.MIN_VALUE;\n int ans=0;\n for(int i=0;i<envelopes.length;i++){\n int val=envelopes[i][1];\n int insertIndex=binarySearch(LIS,val);\n ans=Math.max(ans,insertIndex);\n if(LIS[insertIndex]>=val){\n LIS[insertIndex]=val;\n }\n }\n return ans;\n }\n}\n```\n\nNow, if you compare the code of this problem with the classical LIS, it is very similar. Infact, we have added only one line to get the maximum Russian Doll.\n\n`Arrays.sort(envelopes,(a,b)->a[0]==b[0]?b[1]-a[1]:a[0]-b[0]);`\n\nLanguage Used- **JAVA**\nTime Complexity- **O(nlogn)**\nSpace Complexity- **O(n)**\n\n**Python Solution-**\n```class Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n LIS = []\n size = 0\n for (w, h) in envelopes:\n if not LIS or h > LIS[-1]:\n LIS.append(h)\n size += 1\n else:\n l, r = 0, size\n while l < r:\n m = l + (r - l) // 2\n if LIS[m] < h:\n l = m + 1\n else:\n r = m\n LIS[l] = h\n return size\n```\nby @bettercoder168\n\nC++ Code\n```\nclass Solution {\npublic:\n static bool comp(vector<int> &a, vector<int> &b){\n if(a[0]==b[0]){\n return a[1]>b[1];\n }\n return a[0]<b[0];\n }\n \n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(), envelopes.end(), comp);\n int i, j, n=envelopes.size();\n vector<int>lis;\n \n for(i=0; i<n; i++){\n auto it = lower_bound(lis.begin(), lis.end(), envelopes[i][1]);\n if(it==lis.end()){lis.push_back(envelopes[i][1]);}\n else{\n *it = envelopes[i][1];\n }\n }\n return lis.size();\n }\n};\n```\nby @uttarandas501\n\t\t\n##### If you like this solution or find it useful, please upvote this post.\n | 410 | 0 | ['C', 'Binary Tree', 'Python', 'Java'] | 26 |
russian-doll-envelopes | JS, Python, Java, C++ | Easy LIS Solution w/ Explanation | js-python-java-c-easy-lis-solution-w-exp-wvra | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-03-30T09:13:56.954030+00:00 | 2021-03-30T10:29:45.595458+00:00 | 13,320 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nThe naive approach here would be to try every single permutation of our envelope array (**E**), but that would be a **time complexity** of **O(N!)** which is frankly an incomprehensible number when **N** goes up to **5000**.\n\nAs the naive approach would involve repeating many of the same individual comparisons over and over again, we can quickly see that a **dynamic programming** (**DP**) solution would be beneficial.\n\nIn order for a DP solution to be effective, however, we\'d need to find a way to progress from the easiest subsolution and build from there for each successively more complex subsolution. The best way to do this would be to sort **E** first by **width** (**E[i][0]**), and then by **height** (**E[i][1]**).\n\nThen we could start with the smallest envelope and work our way up, storing in our DP array (**dp**) the result of how many smaller envelopes it is possible to fit in the corresponding envelope. That way we could simplify each iteration to checking to see which of the entries in **dp** corresponding to smaller envelopes is the largest. This would drop the time complexity to **O(N^2)**, which is a definite improvement.\n\nBut it should also be apparent that if we were to define a **subsequence** of **E** that was the ideal nesting order of envelopes for the solution, then that array would be strictly increasing in *both* width and height.\n\nIf we\'ve already sorted **E** primarily by width, we should then be able to consider a corresponding array of just the heights and realize that the solution would be defined as the [**longest increasing subsequence**](https://en.wikipedia.org/wiki/Longest_increasing_subsequence) of that.\n\nThe only difficulty would be for consecutive envelopes with the *same* sorted width. To avoid that, we can simply make sure that our sort function sorts height in descending order so that the first envelope encountered for any given width would be the largest one.\n\nAt the end of the longest increasing subsequence algorithm, the length of **dp** is equal to the length of the subsequence. Due to the sort function and the binary searches required for the algorithm, the time complexity now shrinks to **O(N log N)**.\n\n---\n\n#### ***Implementation:***\n\nPython has a built-in binary search function, **bisect()**.\n\nJava has a built-in binary search function as well (**Arrays.binarySearch()**), but in order to use the more performant **int[]** rather than a **List< Integer >**, we\'ll need to specify a max length for **dp** and then keep track of the current index of the longest subsequence separately in **ans**.\n\nC++ has a built-in binary search function, **lower_bound()**.\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **80ms / 40.8MB** (beats 100% / 90%).\n```javascript\nvar maxEnvelopes = function(E) {\n E.sort((a,b) => a[0] === b[0] ? b[1] - a[1] : a[0] - b[0])\n let len = E.length, dp = []\n for (let i = 0; i < len; i++) {\n let height = E[i][1], left = 0, right = dp.length \n while (left < right) {\n let mid = (left + right) >> 1\n if (dp[mid] < height) left = mid + 1\n else right = mid\n }\n dp[left] = height\n }\n return dp.length\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **140ms / 16.4MB** (beats 97% / 85%).\n```python\nclass Solution:\n def maxEnvelopes(self, E: List[List[int]]) -> int:\n E.sort(key=lambda x: (x[0], -x[1]))\n dp = []\n for _,height in E:\n left = bisect_left(dp, height)\n if left == len(dp): dp.append(height)\n else: dp[left] = height\n return len(dp)\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **7ms / 39.5MB** (beats 100% / 95%).\n```java\nclass Solution {\n public int maxEnvelopes(int[][] E) {\n Arrays.sort(E, (a,b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);\n int[] dp = new int[E.length];\n int ans = 0;\n for (int[] env : E) {\n int height = env[1];\n int left = Arrays.binarySearch(dp, 0, ans, height);\n if (left < 0) left = -left - 1;\n if (left == ans) ans++;\n dp[left] = height;\n }\n return ans;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **32ms / 15.9MB** (beats 99% / 99%).\n```c++\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& E) {\n sort(E.begin(), E.end(), [](vector<int>& a, vector<int>& b) \n -> bool {return a[0] == b[0] ? b[1] < a[1] : a[0] < b[0];});\n vector<int> dp;\n for (auto& env : E) {\n int height = env[1];\n int left = lower_bound(dp.begin(), dp.end(), height) - dp.begin();\n if (left == dp.size()) dp.push_back(height);\n dp[left] = height;\n }\n return dp.size();\n }\n};\n``` | 168 | 9 | ['C', 'Python', 'Java', 'JavaScript'] | 5 |
russian-doll-envelopes | C++ | O(NlogN) approach | LIS | Explaination with Comments | c-onlogn-approach-lis-explaination-with-r80np | \nclass Solution {\n static bool cmp(vector<int>& a, vector<int>& b){\n if(a[0]==b[0]) return a[1] > b[1];\n return a[0] < b[0];\n }\npublic | sahil_d70 | NORMAL | 2022-05-25T03:25:52.029727+00:00 | 2022-05-25T03:44:54.166626+00:00 | 19,214 | false | ```\nclass Solution {\n static bool cmp(vector<int>& a, vector<int>& b){\n if(a[0]==b[0]) return a[1] > b[1];\n return a[0] < b[0];\n }\npublic:\n int maxEnvelopes(vector<vector<int>>& env) {\n int n = env.size();\n \n // sorting by height & if we encounter same height\n // sort by descending order of width\n sort(env.begin(), env.end(), cmp);\n \n // e.g. -> env => (3,8) (4,5) (2,1) (2,6) (7,8) (5,3) (5,7)\n // sorted version => (2,6) (2,1) (3,8) (4,5) (5,7) (5,3) (7,8)\n \n // Now, we only need to care about width\n // So, as of now we only need to look upon v[i][1]\n // [ 6, 1, 8, 5, 7, 3, 8 ]\n \n // Now, we can only put envolop a in envolop b another if width of a is\n // less than width of b, or we can say we need an envolop whose width\n // is just greater than envolop a ( height we have already handled )\n // So, we can think of lower_bound and Longest Increasing Subsequence\n \n // because we have sorted all envolopes of a particular height\n // by descending order of width, one envolope will not interfare with \n // another envolop of same height, if we apply lower_bound\n // i.e. first elem greater than equal to itself in lis\n \n vector<int> lis;\n \n for(int i = 0;i<env.size();i++){\n int ele = env[i][1];\n \n int idx = lower_bound(lis.begin(), lis.end(), ele) - lis.begin();\n \n if(idx >= lis.size()) lis.push_back(ele);\n else lis[idx] = ele;\n }\n \n return lis.size();\n }\n};\n```\nPlease upvote if the concept is clear :) | 140 | 1 | ['C', 'Binary Tree'] | 10 |
russian-doll-envelopes | C++ 9-line Short and Clean O(nlogn) solution (plus classic O(n^2) dp solution). | c-9-line-short-and-clean-onlogn-solution-4thf | ///O(nlogn)\n\n struct Solution {\n int maxEnvelopes(vector<pair<int, int>>& es) {\n sort(es.begin(), es.end(), [](pair<int, int> a, pair<i | fentoyal | NORMAL | 2016-06-09T19:12:31+00:00 | 2018-09-29T15:58:15.073519+00:00 | 19,276 | false | ///O(nlogn)\n\n struct Solution {\n int maxEnvelopes(vector<pair<int, int>>& es) {\n sort(es.begin(), es.end(), [](pair<int, int> a, pair<int, int> b){\n return a.first < b.first || (a.first == b.first && a.second > b.second);});\n vector<int> dp;\n for (auto e : es)\n {\n auto iter = lower_bound(dp.begin(), dp.end(), e.second);\n if (iter == dp.end())\n dp.push_back(e.second);\n else if (e.second < *iter)\n *iter = e.second;\n }\n return dp.size();\n }\n };\n\n ///DP\n \n struct Solution {\n int maxEnvelopes(vector<pair<int, int>>& envelopes) {\n if (envelopes.empty()) return 0;\n sort(envelopes.begin(), envelopes.end());\n vector<int> dp(envelopes.size(), 1);\n for (int i = 0; i < envelopes.size(); ++i)\n for (int j = 0; j < i; ++j)\n if (envelopes[j].first < envelopes[i].first && envelopes[j].second < envelopes[i].second)\n dp[i] = max(dp[i] , dp[j] + 1);\n return *max_element(dp.begin(), dp.end());\n }\n }; | 99 | 4 | [] | 7 |
russian-doll-envelopes | Simple DP solution | simple-dp-solution-by-larrywang2014-hcx2 | public int maxEnvelopes(int[][] envelopes) {\n if ( envelopes == null\n || envelopes.length == 0\n || envelopes[0] | larrywang2014 | NORMAL | 2016-06-06T22:12:14+00:00 | 2018-10-20T11:27:23.290897+00:00 | 34,990 | false | public int maxEnvelopes(int[][] envelopes) {\n if ( envelopes == null\n || envelopes.length == 0\n || envelopes[0] == null\n || envelopes[0].length == 0){\n return 0; \n }\n \n Arrays.sort(envelopes, new Comparator<int[]>(){\n @Override\n public int compare(int[] e1, int[] e2){\n return Integer.compare(e1[0], e2[0]);\n }\n });\n \n int n = envelopes.length;\n int[] dp = new int[n];\n \n int ret = 0;\n for (int i = 0; i < n; i++){\n dp[i] = 1;\n \n for (int j = 0; j < i; j++){\n if ( envelopes[i][0] > envelopes[j][0]\n && envelopes[i][1] > envelopes[j][1]){\n dp[i] = Math.max(dp[i], 1 + dp[j]); \n }\n }\n \n ret = Math.max(ret, dp[i]);\n }\n return ret;\n } | 83 | 10 | [] | 20 |
russian-doll-envelopes | [Python] 4 lines solution, explained | python-4-lines-solution-explained-by-dba-8vob | There is solution, if we use similar idea of Problems 300 (Longest Increading subsequence), because we want to find the longest increasing sub-sequence. Check | dbabichev | NORMAL | 2021-03-30T11:49:35.375233+00:00 | 2021-03-30T11:49:35.375267+00:00 | 5,126 | false | There is solution, if we use similar idea of Problems **300** (Longest Increading subsequence), because we want to find the longest increasing sub-sequence. Check my solution https://leetcode.com/problems/longest-increasing-subsequence/discuss/667975/Python-3-Lines-dp-with-binary-search-explained\n\nActually we can done exactly the same as in 300,\nbut when we sort we put envelopes with equal first elements [6,8], [6,7] it this opposite order\nin this way we make sure that or longest increasing subsequence works like it is and we put into our dp table the second elements. For example if we have envelopes [1,3],[3,5],[6,8],[6,7],[8,4],[9,5], we work with [3,5,8,7,4,5] and look for longest increasing sequence here.\n\n```python\nclass Solution:\n def maxEnvelopes(self, envelopes):\n nums = sorted(envelopes, key = lambda x: [x[0], -x[1]]) \n dp = [10**10] * (len(nums) + 1)\n for elem in nums: dp[bisect_left(dp, elem[1])] = elem[1] \n return dp.index(10**10)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 67 | 1 | [] | 6 |
russian-doll-envelopes | Python O(nlogn) O(n) solution, beats 97%, with explanation | python-onlogn-on-solution-beats-97-with-exwsg | class Solution(object):\n def maxEnvelopes(self, envs):\n def liss(envs):\n def lmip(envs, tails, k):\n b, e | agave | NORMAL | 2016-06-14T15:16:15+00:00 | 2018-08-23T05:36:46.414509+00:00 | 20,016 | false | class Solution(object):\n def maxEnvelopes(self, envs):\n def liss(envs):\n def lmip(envs, tails, k):\n b, e = 0, len(tails) - 1\n while b <= e:\n m = (b + e) >> 1\n if envs[tails[m]][1] >= k[1]:\n e = m - 1\n else:\n b = m + 1\n return b\n \n tails = []\n for i, env in enumerate(envs):\n idx = lmip(envs, tails, env)\n if idx >= len(tails):\n tails.append(i)\n else:\n tails[idx] = i\n return len(tails)\n \n \n def f(x, y):\n return -1 if (x[0] < y[0] or x[0] == y[0] and x[1] > y[1]) else 1\n \n envs.sort(cmp=f)\n return liss(envs)\n\n # Runtime: 100ms\n\nThe idea is to order the envelopes and then calculate the longest increasing subsequence (LISS). We first sort the envelopes by width, and we also make sure that when the width is the same, the envelope with greater height comes first. Why? This makes sure that when we calculate the LISS, we don't have a case such as [3, 4] [3, 5] (we could increase the LISS but this would be wrong as the width is the same. It can't happen when [3, 5] comes first in the ordering).\n\nWe could calculate the LISS using the standard DP algorithm (quadratic runtime), but we can just use the tails array method with a twist: we store the index of the tail, and we do leftmost insertion point as usual to find the right index in `nlogn` time. Why not rightmost? Think about the case [1, 1], [1, 1], [1, 1]. | 56 | 2 | ['Binary Tree', 'Python'] | 9 |
russian-doll-envelopes | Two solutions in C++, well-explained | two-solutions-in-c-well-explained-by-lhe-jth4 | Solutions\n\n#### DP\nIt's quite intuitive to adopt DP to solve this problem: \n\n- sorting the envelopes first via its first value (width)\n- allocating an arr | lhearen | NORMAL | 2016-08-18T02:30:44.535000+00:00 | 2018-10-19T06:30:52.727491+00:00 | 8,730 | false | ### Solutions\n\n#### DP\nIt's quite intuitive to adopt DP to solve this problem: \n\n- sorting the envelopes first via its first value (width)\n- allocating an array to record the maximal amount for each envelope (the maximal amount we can get ending with the current envelope)\n\nDirectly the time cost here will be o(nlogn+n^2) which is o(n^2) and meantime taking up o(n) extra space.\n\n```\nint maxenvelopes(vector<pair<int, int>>& envelopes) \n{\n\tint size = envelopes.size();\n\tif(!size) return 0;\n\tsort(envelopes.begin(), envelopes.end());\n\tint maxrolls[size]{0}, maxroll = 1;\n\tmaxrolls[0] = 1;\n\tfor(int i = 1; i < size; ++i)\n\t{\n\t\tmaxrolls[i] = 1;\n\t\tfor(int j = i-1; j >= 0; --j)\n\t\t\tif(envelopes[i].first>envelopes[j].first && envelopes[i].second>envelopes[j].second)\n\t\t\t\tmaxrolls[i] = max(maxrolls[i], maxrolls[j]+1);\n\t\tmaxroll = max(maxroll, maxrolls[i]);\n\t}\n\treturn maxroll;\n}\n```\n\n#### LIS\nActually here we are counting the **longest increasing sequence** as well except there are two dimensions we need to consider. And also we should remember the o(nlogn) solution in LIS, where the essential greedy concept is trying to \n\n1. make the all the elements in the collector as small as possible, especially the last one which is the gate to control the size of the collector - the longest length;\n2. append the bigger ones to the collector;\n\nBut here we need to make some modifications since there are two dimensions to consider. To ensure the two dimensions array can be compressed into one dimension and meantime the requirements of the two conditions above are also properly met, just sorting is not enough here.\n\n- we need to convert this 2-dimentsion problem to a 1-dimension LIS: first sort the array via the width in ascending order and then sort the sub-array with the same width in descending order (the height) then the two conditions in LIS will also be met traversing from the smallest width to the biggest: and the height will be used as that in LIS - the last element will be updated to be as smaller as possible and meantime maintain the envelopes constraint since its width order will always be valid, furthermore the condition 2 is also met just as that in LIS.\n\n> **Note** if we do not sort the sub-arrays (with the same width) in descending order, the LIS in the height is then invalid. Suppose the sub-arrays are also sorted in ascending order, the height in the same width will be appended in our LIS method, wrong result. To sort the heights in the same width in descending order will avoid this case by updating the height in the same width since we are using `lower_bound`.\n\nTime complexity now becomes O(nlogn) taking up O(n) space.\n\n```\nint maxEnvelopes(vector<pair<int, int>>& envelopes) \n{\n\tint size = envelopes.size();\n\tsort(envelopes.begin(), envelopes.end(), [](pair<int, int> a, pair<int, int>b){\n\t\treturn a.first<b.first || (a.first==b.first && a.second>b.second);\n\t});\n\tvector<int> collector;\n\tfor(auto& pair: envelopes)\n\t{\n\t\tauto iter = lower_bound(collector.begin(), collector.end(), pair.second);\n\t\tif(iter == collector.end()) collector.push_back(pair.second);\n\t\telse if(*iter > pair.second) *iter = pair.second;\n\t}\n\treturn collector.size();\n}\n```\n\n##### lower_bound\n- On random-access iterators, logarithmic in the distance between first and last: Performs approximately log2(N)+1 element comparisons (where N is this distance).\n- On non-random-access iterators, the iterator advances produce themselves an additional linear complexity in N on average.\nAlways welcome new ideas and `practical` tricks, just leave them in the comments! | 55 | 2 | [] | 6 |
russian-doll-envelopes | The best answer your'e looking for. RECURSION|MEMOIZATION|TABULATION|1D OPTIMIZATION| BINARY SEARCH | the-best-answer-youre-looking-for-recurs-fytg | Recursion (gives TLE at test 57)\n\nclass Solution {\npublic:\n int f(int curr,int prev,vector<vector<int>>& envelopes){\n if(curr==envelopes.size()){ | Akashsb | NORMAL | 2023-02-22T14:09:02.443800+00:00 | 2023-02-22T14:09:02.443842+00:00 | 2,827 | false | # Recursion (gives TLE at test 57)\n```\nclass Solution {\npublic:\n int f(int curr,int prev,vector<vector<int>>& envelopes){\n if(curr==envelopes.size()){\n return 0;\n }\n int notTake=0+f(curr+1,prev,envelopes);\n int take=-1e9;\n if(prev==-1 or (envelopes[prev][0]<envelopes[curr][0] and envelopes[prev][1] <envelopes[curr][1])){\n take=1+f(curr+1,curr,envelopes);\n }\n return max(take,notTake);\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end());\n return f(0,-1,envelopes);\n }\n};\n```\n\n# Memoization (gives TLE at test 83)\n```\nclass Solution {\npublic:\n int f(int curr,int prev,vector<vector<int>>& envelopes,vector<vector<int>> &dp){\n if(curr==envelopes.size()){\n return 0;\n }\n if(dp[curr][prev+1]!=-1){\n return dp[curr][prev+1];\n }\n int notTake=0+f(curr+1,prev,envelopes,dp);\n int take=-1e9;\n if(prev==-1 or (envelopes[prev][0]<envelopes[curr][0] and envelopes[prev][1] <envelopes[curr][1])){\n take=1+f(curr+1,curr,envelopes,dp);\n }\n return dp[curr][prev+1]=max(take,notTake);\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end());\n int n=envelopes.size();\n vector<vector<int>> dp(n+1,vector<int>(n+1,-1));\n return f(0,-1,envelopes,dp);\n }\n};\n```\n\n# Tabulation (gives TLE at test 85)\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end());\n int n=envelopes.size();\n vector<vector<int>> dp(n+1,vector<int>(n+1,0));\n for(int curr=n-1;curr>=0;curr--){\n for(int prev=curr-1;prev>=-1;prev--){\n int notTake=0+dp[curr+1][prev+1];\n int take=-1e9;\n if(prev==-1 or (envelopes[prev][0]<envelopes[curr][0] and envelopes[prev][1]<envelopes[curr][1])){\n take=1+dp[curr+1][curr+1];\n }\n dp[curr][prev+1]=max(take,notTake); \n }\n }\n return dp[0][0];\n \n }\n};\n```\n\n# 1D array optimization (gives TLE at test 85)\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end());\n int n=envelopes.size();\n vector<int>next(n+1,0),currr(n+1,0);\n for(int curr=n-1;curr>=0;curr--){\n for(int prev=curr-1;prev>=-1;prev--){\n int notTake=0+next[prev+1];\n int take=-1e9;\n if(prev==-1 or (envelopes[prev][0]<envelopes[curr][0] and envelopes[prev][1]<envelopes[curr][1])){\n take=1+next[curr+1];\n }\n currr[prev+1]=max(take,notTake); \n }\n next=currr;\n }\n return currr[-1+1];\n }\n};\n```\n\n# Binary Search (Final asnwer)\n```\nclass Solution {\npublic:\n static bool comp(vector<int> &a,vector<int>&b){\n if(a[0]==b[0]){\n return a[1]>b[1];\n }\n else{\n return a[0]<b[0];\n }\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end(),comp);\n vector<int> temp;\n temp.push_back(envelopes[0][1]);\n for(int i=1;i<envelopes.size();i++){\n if(temp.back()<envelopes[i][1]){\n temp.push_back(envelopes[i][1]);\n }\n else{\n auto ind=lower_bound(temp.begin(),temp.end(),envelopes[i][1])-temp.begin();\n temp[ind]=envelopes[i][1];\n }\n }\n return temp.size();\n }\n};\n``` | 53 | 0 | ['Binary Search', 'Recursion', 'Memoization', 'C++'] | 4 |
russian-doll-envelopes | Russian Doll Envelopes | JS, Python, Java, C++ | Easy LIS Solution w/ Explanation | russian-doll-envelopes-js-python-java-c-cpzri | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-03-30T09:14:34.934563+00:00 | 2021-03-30T10:29:39.002260+00:00 | 2,621 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nThe naive approach here would be to try every single permutation of our envelope array (**E**), but that would be a **time complexity** of **O(N!)** which is frankly an incomprehensible number when **N** goes up to **5000**.\n\nAs the naive approach would involve repeating many of the same individual comparisons over and over again, we can quickly see that a **dynamic programming** (**DP**) solution would be beneficial.\n\nIn order for a DP solution to be effective, however, we\'d need to find a way to progress from the easiest subsolution and build from there for each successively more complex subsolution. The best way to do this would be to sort **E** first by **width** (**E[i][0]**), and then by **height** (**E[i][1]**).\n\nThen we could start with the smallest envelope and work our way up, storing in our DP array (**dp**) the result of how many smaller envelopes it is possible to fit in the corresponding envelope. That way we could simplify each iteration to checking to see which of the entries in **dp** corresponding to smaller envelopes is the largest. This would drop the time complexity to **O(N^2)**, which is a definite improvement.\n\nBut it should also be apparent that if we were to define a **subsequence** of **E** that was the ideal nesting order of envelopes for the solution, then that array would be strictly increasing in *both* width and height.\n\nIf we\'ve already sorted **E** primarily by width, we should then be able to consider a corresponding array of just the heights and realize that the solution would be defined as the [**longest increasing subsequence**](https://en.wikipedia.org/wiki/Longest_increasing_subsequence) of that.\n\nThe only difficulty would be for consecutive envelopes with the *same* sorted width. To avoid that, we can simply make sure that our sort function sorts height in descending order so that the first envelope encountered for any given width would be the largest one.\n\nAt the end of the longest increasing subsequence algorithm, the length of **dp** is equal to the length of the subsequence. Due to the sort function and the binary searches required for the algorithm, the time complexity now shrinks to **O(N log N)**.\n\n---\n\n#### ***Implementation:***\n\nPython has a built-in binary search function, **bisect()**.\n\nJava has a built-in binary search function as well (**Arrays.binarySearch()**), but in order to use the more performant **int[]** rather than a **List< Integer >**, we\'ll need to specify a max length for **dp** and then keep track of the current index of the longest subsequence separately in **ans**.\n\nC++ has a built-in binary search function, **lower_bound()**.\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **80ms / 40.8MB** (beats 100% / 90%).\n```javascript\nvar maxEnvelopes = function(E) {\n E.sort((a,b) => a[0] === b[0] ? b[1] - a[1] : a[0] - b[0])\n let len = E.length, dp = []\n for (let i = 0; i < len; i++) {\n let height = E[i][1], left = 0, right = dp.length \n while (left < right) {\n let mid = (left + right) >> 1\n if (dp[mid] < height) left = mid + 1\n else right = mid\n }\n dp[left] = height\n }\n return dp.length\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **140ms / 16.4MB** (beats 97% / 85%).\n```python\nclass Solution:\n def maxEnvelopes(self, E: List[List[int]]) -> int:\n E.sort(key=lambda x: (x[0], -x[1]))\n dp = []\n for _,height in E:\n left = bisect_left(dp, height)\n if left == len(dp): dp.append(height)\n else: dp[left] = height\n return len(dp)\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **7ms / 39.5MB** (beats 100% / 95%).\n```java\nclass Solution {\n public int maxEnvelopes(int[][] E) {\n Arrays.sort(E, (a,b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);\n int[] dp = new int[E.length];\n int ans = 0;\n for (int[] env : E) {\n int height = env[1];\n int left = Arrays.binarySearch(dp, 0, ans, height);\n if (left < 0) left = -left - 1;\n if (left == ans) ans++;\n dp[left] = height;\n }\n return ans;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **32ms / 15.9MB** (beats 99% / 99%).\n```c++\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& E) {\n sort(E.begin(), E.end(), [](vector<int>& a, vector<int>& b) \n -> bool {return a[0] == b[0] ? b[1] < a[1] : a[0] < b[0];});\n vector<int> dp;\n for (auto& env : E) {\n int height = env[1];\n int left = lower_bound(dp.begin(), dp.end(), height) - dp.begin();\n if (left == dp.size()) dp.push_back(height);\n dp[left] = height;\n }\n return dp.size();\n }\n};\n``` | 37 | 9 | [] | 2 |
russian-doll-envelopes | Python LIS based approach | python-lis-based-approach-by-constantine-f3n4 | The prerequisite for this problem is to understand and solve Longest Increasing Subsequence. So if you are familiar with LIS and have solved it, the difficulty | constantine786 | NORMAL | 2022-05-25T04:55:42.837316+00:00 | 2022-05-25T17:41:48.286978+00:00 | 5,498 | false | The prerequisite for this problem is to understand and solve [Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/). So if you are familiar with LIS and have solved it, the difficulty of this problem is reduced.\n\nNow, before we can start implementing LIS for this problem, we need to determine the sort order of the input `envelopes`. You can read this post which explains how the sort order is determined -> [Explanation on which sort order to choose](https://leetcode.com/problems/russian-doll-envelopes/discuss/2071477/Best-Explanation-with-Pictures)\n\n**Time - O(nlogn)** - Time required for sorting and performing LIS\n**Space - O(n)** - space required for `res`.\n\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n \n res = []\t\t\n\t\t# Perform LIS\n for _, h in envelopes:\n l,r=0,len(res)-1\n\t\t\t# find the insertion point in the Sort order\n while l <= r:\n mid=(l+r)>>1\n if res[mid]>=h:\n r=mid-1\n else:\n l=mid+1 \n idx = l\n if idx == len(res):\n res.append(h)\n else:\n res[idx]=h\n return len(res)\n \n```\n\nWe can make the above code more concise by using a python library `bisect_left` to locate the insertion point in the sort order. \n\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1])) \n res = []\n for _, h in envelopes:\n idx = bisect_left(res, h)\n if idx == len(res):\n res.append(h)\n else:\n res[idx]=h\n return len(res) \n```\n\n---\n\n***Please upvote if you find it useful*** | 32 | 0 | ['Python', 'Python3'] | 3 |
russian-doll-envelopes | C++ Time O(NlogN) Space O(N) , similar to LIS nlogn solution | c-time-onlogn-space-on-similar-to-lis-nl-43y2 | bool cmp (pair<int, int> i, pair<int, int> j) {\n if (i.first == j.first)\n return i.second > j.second;\n return i.first < j.first;\n | jordandong | NORMAL | 2016-06-07T06:12:40+00:00 | 2016-06-07T06:12:40+00:00 | 4,855 | false | bool cmp (pair<int, int> i, pair<int, int> j) {\n if (i.first == j.first)\n return i.second > j.second;\n return i.first < j.first;\n }\n \n class Solution {\n public:\n int maxEnvelopes(vector<pair<int, int>>& envelopes) {\n int N = envelopes.size();\n vector<int> candidates;\n sort(envelopes.begin(), envelopes.end(), cmp);\n for (int i = 0; i < N; i++) {\n int lo = 0, hi = candidates.size() - 1;\n while (lo <= hi) {\n int mid = lo + (hi - lo)/2;\n if (envelopes[i].second > envelopes[candidates[mid]].second)\n lo = mid + 1;\n else\n hi = mid - 1;\n }\n if (lo == candidates.size())\n candidates.push_back(i);\n else\n candidates[lo] = i;\n }\n return candidates.size();\n }\n }; | 30 | 1 | [] | 2 |
russian-doll-envelopes | O(Nlog(N)) python solution explained | onlogn-python-solution-explained-by-erjo-evcs | Sort the envelopes first by increasing width. For each block of same-width envelopes, sort by decreasing height.\n\nThen find the longest increasing subsequence | erjoalgo | NORMAL | 2017-11-24T01:53:08.144000+00:00 | 2018-10-11T00:03:26.019057+00:00 | 3,029 | false | Sort the envelopes first by increasing width. For each block of same-width envelopes, sort by decreasing height.\n\nThen find the longest increasing subsequence of heights.\n\nSince each same-width subarray is non-increasing in height, we can never pick more than one height within each width (otherwise heights would be non-increasing)\n\nThus, the resulting longest increasing heights subsequence is also increasing in width.\n\nExample:\n\n**input**\n\n [[5,4],[6,4],[6,7],[2,3]]\n\nsort by increasing widths, then decreasing heights:\n\n [[2,3],[5,4],[6,7],[6,4]]\n\nGet the heights:\n\n [3,4,7,4]\n\nFind the length longest increasing subsequence:\n\n [3,4,7]\n\n(Note that we could not have picked more than one evelope with width 6)\n\nAnswer: 3\n```\nclass Solution(object):\n def maxEnvelopes(self, envs):\n """\n :type envelopes: List[List[int]]\n :rtype: int\n """\n # sort first by increasing width\n # within each subarray of same-width envelopes\n # sort by decreasing height\n envs.sort(key=lambda (w,h): (w,-h))\n \n # now find the length of the longest increasing subsequence of heights.\n # Since each same-width block was sorted non-increasing, \n # we can only pick at most one height within each block\n # otherwise, the sequence would be non-increasing\n tails=[]\n for (w,h) in envs:\n idx=bisect.bisect_left(tails, h)\n if idx==len(tails):\n tails.append(h) \n elif idx==0 or tails[idx-1]<h:\n tails[idx]=h\n return len(tails) \n``` | 28 | 3 | [] | 5 |
russian-doll-envelopes | Short and simple Java solution (15 lines) | short-and-simple-java-solution-15-lines-lallh | \n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a, b) -> a[0] - b[0]);\n int max = 0;\n int dp [] = new int [e | chern_yee | NORMAL | 2016-06-08T17:44:04+00:00 | 2018-09-07T08:40:28.724542+00:00 | 6,493 | false | \n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a, b) -> a[0] - b[0]);\n int max = 0;\n int dp [] = new int [envelopes.length];\n for(int i = 0; i < envelopes.length; i++){\n dp[i] = 1;\n for(int j = 0; j < i; j++){\n if(envelopes[j][0] < envelopes[i][0] && envelopes[j][1] < envelopes[i][1])\n dp[i] = Math.max(dp[i], dp[j] + 1);\n }\n max = Math.max(dp[i], max);\n }\n return max;\n } | 24 | 2 | ['Java'] | 4 |
russian-doll-envelopes | 95% faster | C++ | N log N using Binary Search | LIS(concept) | 95-faster-c-n-log-n-using-binary-search-7vbzv | \nclass Solution {\npublic:\n static bool compare(vector<int>&a , vector<int>& b)\n {\n return a[0]==b[0]?a[1]>b[1]:a[0]<b[0];\n }\n int maxEnv | crag | NORMAL | 2021-03-31T11:35:14.361999+00:00 | 2021-03-31T11:35:14.362037+00:00 | 2,495 | false | ```\nclass Solution {\npublic:\n static bool compare(vector<int>&a , vector<int>& b)\n {\n return a[0]==b[0]?a[1]>b[1]:a[0]<b[0];\n }\n int maxEnvelopes(vector<vector<int>>&a) {\n sort(a.begin(),a.end(),compare);\n vector<int>dp;\n for(auto i:a)\n {\n auto it=lower_bound(dp.begin(),dp.end(),i[1]);\n if(it==dp.end())\n dp.push_back(i[1]);\n else\n *it=i[1];\n }\n return dp.size();\n }\n};\n```\n**Upvote if this help you** | 19 | 0 | ['Dynamic Programming', 'C', 'Binary Tree'] | 3 |
russian-doll-envelopes | [C++] - Classic DP problem variant | c-classic-dp-problem-variant-by-morning_-3b3a | Variant of Classic DP - LIS problem :\nTime Complexity - O(n^2)\nSpace Complexity - O(n)\n\n\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int> | morning_coder | NORMAL | 2021-03-30T07:44:14.656352+00:00 | 2021-03-31T06:28:06.307908+00:00 | 3,654 | false | **Variant of Classic DP - LIS problem :**\nTime Complexity - O(n^2)\nSpace Complexity - O(n)\n\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(begin(envelopes),end(envelopes),[]\n (const vector<int> &a,const vector<int> &b){\n return (a[0]==b[0] ? a[1]<b[1] : a[0]<b[0]);\n });\n\t\t\t \n vector<int> dp(envelopes.size(),1);\n\t\t\n for(int i=1;i<envelopes.size();i++){\n for(int j=0;j<i;j++){\n if(envelopes[j][0]<envelopes[i][0] && envelopes[j][1]<envelopes[i][1]){\n if(dp[i]<dp[j]+1)\n dp[i]=dp[j]+1;\n }\n }\n }\n return *max_element(begin(dp),end(dp));\n }\n};\n```\n\nEdit1 :- It can be done in O(nlogn) as well. Will include that approach later. | 15 | 3 | ['Dynamic Programming', 'C', 'C++'] | 4 |
russian-doll-envelopes | Binary Search (T.C=O(nlogn),S.C=O(n)) Approach || Beats 98% | binary-search-tconlognscon-approach-beat-rfjq | \n\n# Approach: \n Describe your approach to solving the problem. \n1. Sorting:\n\n- First, sort the envelopes by their width in ascending order. If two envelop | prayashbhuria931 | NORMAL | 2024-08-08T20:52:42.892013+00:00 | 2024-08-08T20:52:42.892030+00:00 | 1,448 | false | \n\n# Approach: \n<!-- Describe your approach to solving the problem. -->\n1. Sorting:\n\n- First, sort the envelopes by their width in ascending order. If two envelopes have the same width, sort them by height in descending order. This ensures that when processing envelopes with the same width, you only consider the heights to maintain a strictly increasing sequence of heights.\n2. Finding Longest Increasing Subsequence (LIS):\n\n- After sorting, the problem reduces to finding the Longest Increasing Subsequence (LIS) based on the heights of the envelopes. This is because the widths are already sorted, so you only need to focus on the heights to find the maximum nesting.\n\n3. Binary Search:\n\n- Use a dynamic array ans to keep track of the smallest possible ending height of increasing subsequences of different lengths. For each envelope, use binary search to determine the position where the current height fits into this array, updating the array as needed. This ensures that the ans array always maintains the smallest possible values at each length, which helps in achieving the LIS efficiently.\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\nstatic bool cmp(vector<int> &a, vector<int> &b)\n {\n // If the widths are equal, sort in descending order of heights\n if (a[0] == b[0])\n {\n return a[1] > b[1];\n }\n\n // Sort in ascending order of widths\n return a[0] < b[0];\n }\n\nint solveBS(int n,vector<vector<int>>& nums)\n {\n sort(nums.begin(),nums.end(),cmp);\n\n vector<int> ans;\n ans.push_back(nums[0][1]);\n\n for(int i=1;i<n;i++)\n {\n if(nums[i][1]>ans.back()) ans.push_back(nums[i][1]);\n else\n {\n //find index of just bada element in ans\n int index=lower_bound(ans.begin(),ans.end(),nums[i][1])-ans.begin();\n ans[index]=nums[i][1];\n }\n }\n\n return ans.size();\n } \npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n int n=envelopes.size();\n return solveBS(n,envelopes); \n }\n};\n```\n\n\n | 14 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
russian-doll-envelopes | [Java] LIS Revisited | Binary Search Best Explanation | java-lis-revisited-binary-search-best-ex-ygzg | Please upvote if you like the soltion\n\n\tPrerequisite\n\t\n\tBefore moving on to the solution, you should know how can we find the length of Longest Increasin | rhythm_varshney | NORMAL | 2022-01-31T15:30:31.333261+00:00 | 2022-05-25T03:31:01.474718+00:00 | 1,183 | false | **Please upvote if you like the soltion**\n<details>\n\t<summary>Prerequisite</summary>\n\t<br>\n\tBefore moving on to the solution, you should know how can we find the length of <strong>Longest Increasing Subsequence</strong> unsing <strong>Binary Search</strong>. You can find the detailed explanation of the logic on the below link. \n\t</br>\n\t<br></br>\n\t<a href="https://leetcode.com/problems/longest-increasing-subsequence/discuss/1636162/java-binary-search-stepwise-explanation">Longest Increasing Subsequence Using Binary Search</a>\n</details>\n<br></br>\n\n#### Why we need to sort?\n* In these types of problem when we are dealing with two dimensions, we need to reduce the problem from two-dimensional array into a one-dimensional array in order to improve time complexity. \n* **"Sort first when things are undecided"**, sorting can make the data orderly, reduce the degree of confusion, and often help us to sort out our thinking. the same is true with this question. Now, after doing the correct sorting, we just need to find Longest Increasing Subsequence of that one dimensional array.\n**Now, you may be wondered what correct sorting actually is?**\nIt is the sorting which we do to order to achieve the answer. Like, increasing, non-increasing sorting. Without any further discussion, let\'s dig into Intuition followed by algorithm.\n\n##### Algorithm\n* We sort the array in increasing order of width. And if two widths are same, we need to sort height in decreasing order. \n* Now why we need to sort in decreasing order if two widths are same. By this practice, we\'re assuring that no width will get counted more than one time. Let\'s take an example\nenvelopes=`[[3, 5], [6, 7], [7, 13], [6, 10], [8, 4], [7, 11]]`\n\nNow, if you see for a while, **6 and 7** is counted twice while we\'re calculating the length of LIS, which will give the wrong ans. As question is asking, if any width/height are less than or equal, then, it is not possible to russian doll these envelopes. \nNow, we know the problem. So, how can we tackle these conditions when two width are same, so that it won\'t affect our answer. We can simple **reverse sort the height if two width are equal, to remove duplicacy.**\nNow, you may question, how reverse sorting the height would remove duplicacy? As the name itself says, Longest Increasing Subsequnce, the next coming height would be less than the previous one. Hence, forbidding it to increase length count.\n\nIf you don\'t understand how LIS is calculated here, I strongly refer you to follow the prerequisite.\nNow, we have **sucessfully reduced the problem to LIS!** All you need to apply classical LIS on heights, to calculate the ans. This would be the maximum number of envelopes can be russian doll.\n\n**Code**\n\n```\nclass Solution {\n public int binarySearch(int[] dp, int val){\n int lo=0,hi=dp.length-1,res=0;\n while(lo<=hi){\n int mid=(lo+hi)/2;\n if(dp[mid]<val){\n res=mid;\n lo=mid+1;\n }else{\n hi=mid-1;\n }\n }\n return res+1;\n }\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes,(a,b)->a[0]==b[0]?b[1]-a[1]:a[0]-b[0]);\n int[] LIS=new int[envelopes.length+1];\n Arrays.fill(LIS,Integer.MAX_VALUE);\n LIS[0]=Integer.MIN_VALUE;\n int ans=0;\n for(int i=0;i<envelopes.length;i++){\n int val=envelopes[i][1];\n int insertIndex=binarySearch(LIS,val);\n ans=Math.max(ans,insertIndex);\n if(LIS[insertIndex]>=val){\n LIS[insertIndex]=val;\n }\n }\n return ans;\n }\n}\n```\n\nNow, if you compare the code of this problem with the classical LIS, it is very similar. Infact, we have added only one line to get the maximum Russian Doll.\n\n`Arrays.sort(envelopes,(a,b)->a[0]==b[0]?b[1]-a[1]:a[0]-b[0]);`\n\nTime Complexity- **O(nlogn)**\nSpace Complexity- **O(n)**\n\n##### If you like the explanation, please upvote\n\n | 14 | 0 | ['Binary Tree'] | 2 |
russian-doll-envelopes | 10 lines Python code beats %96. | 10-lines-python-code-beats-96-by-geeti-rpyv | \nclass Solution(object):\n def maxEnvelopes(self, envelopes):\n des_ht = [a[1] for a in sorted(envelopes, key = lambda x: (x[0], -x[1]))]\n dp | geeti | NORMAL | 2016-07-29T00:18:43.484000+00:00 | 2016-07-29T00:18:43.484000+00:00 | 3,384 | false | ```\nclass Solution(object):\n def maxEnvelopes(self, envelopes):\n des_ht = [a[1] for a in sorted(envelopes, key = lambda x: (x[0], -x[1]))]\n dp, l = [0] * len(des_ht), 0\n for x in des_ht:\n i = bisect.bisect_left(dp, x, 0, l)\n dp[i] = x\n if i == l:\n l+=1\n return l\n``` | 14 | 0 | [] | 4 |
russian-doll-envelopes | ✅C++ || Recursion->Memoization->BinarySearch | c-recursion-memoization-binarysearch-by-n8pdx | Method -1 [Recursion] Gives TLE!\n\n\n\tclass Solution {\n\tpublic:\n\t// LIS\n\t\tint f(int i,int prev,vector>& env,int n){\n\t\t\tif(i==n) return 0;\n\t\t | abhinav_0107 | NORMAL | 2022-09-06T06:53:27.590424+00:00 | 2022-09-06T06:54:35.519748+00:00 | 2,070 | false | # Method -1 [Recursion] Gives TLE!\n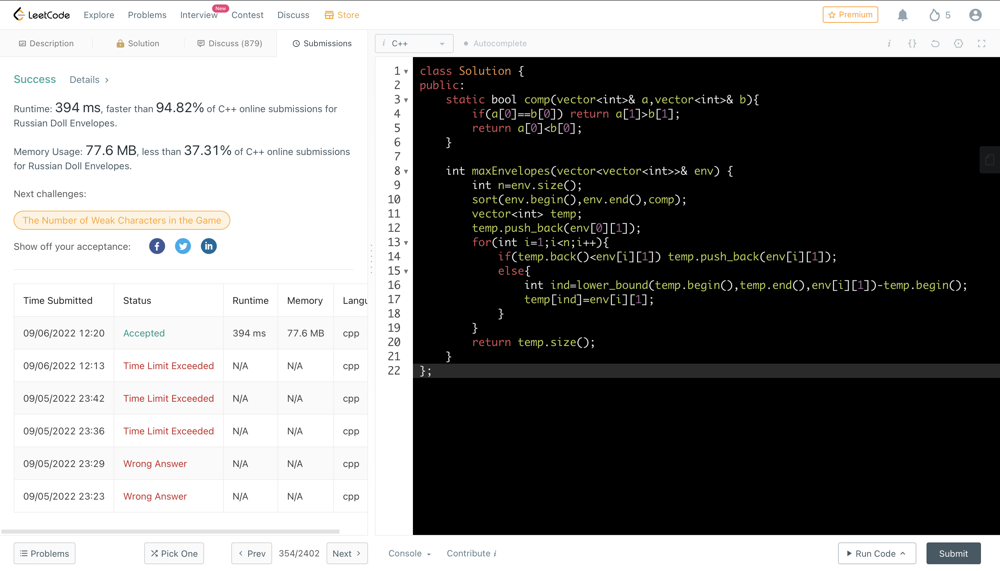\n\n\tclass Solution {\n\tpublic:\n\t// LIS\n\t\tint f(int i,int prev,vector<vector<int>>& env,int n){\n\t\t\tif(i==n) return 0;\n\t\t\tint pick=INT_MIN;\n\t\t\tif(prev==-1 || env[prev][0]<env[i][0] && env[prev][1]<env[i][1]) pick=1+f(i+1,i,env,n);\n\t\t\tint notpick=f(i+1,prev,env,n);\n\t\t\treturn max(pick,notpick);\n\t\t}\n\n\t\tint maxEnvelopes(vector<vector<int>>& env) {\n\t\t\tint n=env.size();\n\t\t\tsort(env.begin(),env.end()); \n\t\t\treturn f(0,-1,env,n);\n\t\t}\n\t};\n\n# Method - 2 [Memoization] Gives TLE!!\n\n\n\tclass Solution {\n\tpublic:\n\t// LIS\n\t\tint f(int i,int prev,vector<vector<int>>& env,int n,vector<vector<int>>& dp){\n\t\t\tif(i==n) return 0;\n\t\t\tif(dp[i][prev+1]!=-1) return dp[i][prev+1];\n\t\t\tint pick=INT_MIN;\n\t\t\tif(prev==-1 || (env[prev][0]<env[i][0] && env[prev][1]<env[i][1])) pick=1+f(i+1,i,env,n,dp);\n\t\t\tint notpick=f(i+1,prev,env,n,dp);\n\t\t\treturn dp[i][prev+1]=max(pick,notpick);\n\t\t}\n\n\t\tint maxEnvelopes(vector<vector<int>>& env) {\n\t\t\tint n=env.size();\n\t\t\tsort(env.begin(),env.end()); \n\t\t\tvector<vector<int>> dp(n,vector<int>(n+1,-1));\n\t\t\treturn f(0,-1,env,n,dp);\n\t\t}\n\t};\t\n\t\n***Since we can not reduce the TC further by Tabulation thus we have to apply Binary Search!**\n\n# Method - 3 [Binary Search] \n\n\n\n\n**T->O(nlogn) && S->O(n)**\n\n\tclass Solution {\n\tpublic:\n\t\tstatic bool comp(vector<int>& a,vector<int>& b){\n\t\t\tif(a[0]==b[0]) return a[1]>b[1];\n\t\t\treturn a[0]<b[0];\n\t\t}\n\n\t\tint maxEnvelopes(vector<vector<int>>& env) {\n\t\t\tint n=env.size();\n\t\t\tsort(env.begin(),env.end(),comp); \n\t\t\tvector<int> temp;\n\t\t\ttemp.push_back(env[0][1]);\n\t\t\tfor(int i=1;i<n;i++){\n\t\t\t\tif(temp.back()<env[i][1]) temp.push_back(env[i][1]);\n\t\t\t\telse{\n\t\t\t\t\tint ind=lower_bound(temp.begin(),temp.end(),env[i][1])-temp.begin();\n\t\t\t\t\ttemp[ind]=env[i][1];\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn temp.size();\n\t\t}\n\t};\n | 13 | 0 | ['Binary Search', 'Recursion', 'Memoization', 'C', 'Sorting', 'C++'] | 0 |
russian-doll-envelopes | Backtracking solution that you will be expected to provide in interviews [ACCEPTED] | backtracking-solution-that-you-will-be-e-zgc4 | The O(nlogn) solution is unreasonable for an interviewer to expect. The solution below should be more than sufficient for you to pass the interview:\n\n\nclass | topologicallysorted | NORMAL | 2020-01-30T17:52:59.531466+00:00 | 2020-02-01T07:47:30.930062+00:00 | 826 | false | The O(nlogn) solution is unreasonable for an interviewer to expect. The solution below should be more than sufficient for you to pass the interview:\n\n```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n // Sort in increasing order by\n // any dimension.\n // This is an optimization.\n if (envelopes.length == 0) return 0;\n Arrays.sort(envelopes, (a,b) -> { \n if (a[0] != b[0])\n return a[0] - b[0];\n return a[1] - b[1];\n });\n \n // We will cache hits\n HashMap<Integer, Integer> cache = new HashMap<>();\n return maxEnvelopes(envelopes, 0, -1, cache);\n }\n \n int maxEnvelopes(int[][] envelopes, int index, int prevIndex, HashMap<Integer, Integer> cache) {\n if (index == envelopes.length)\n return 0;\n \n int included = 0;\n // included\n if (prevIndex == -1 || (envelopes[index][0] > envelopes[prevIndex][0] \n && envelopes[index][1] > envelopes[prevIndex][1])){\n if (cache.containsKey(index)){\n included = cache.get(index);\n } else {\n included = 1 + maxEnvelopes(envelopes, index + 1, index, cache);\n // Note that hits are only cached for an index\n // when we know that the condition that prev is\n // less than current is satisifed\n cache.put(index, included);\n }\n }\n \n int skipped = maxEnvelopes(envelopes, index + 1, prevIndex, cache);\n \n return Math.max(skipped, included);\n }\n}\n``` | 12 | 1 | [] | 7 |
russian-doll-envelopes | C++ | DP | LIS | c-dp-lis-by-iashi_g-ejtf | \nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n if (envelopes.empty()) return 0;\n sort(envelopes.begin(), e | iashi_g | NORMAL | 2021-09-23T04:41:50.123565+00:00 | 2021-09-23T04:41:50.123607+00:00 | 1,007 | false | ```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n if (envelopes.empty()) return 0;\n sort(envelopes.begin(), envelopes.end());\n vector<int> dp(envelopes.size(), 1);\n for (int i = 0; i < envelopes.size(); ++i)\n for (int j = 0; j < i; ++j)\n if (envelopes[j][0] < envelopes[i][0] && envelopes[j][1] < envelopes[i][1])\n dp[i] = max(dp[i] , dp[j] + 1);\n return *max_element(dp.begin(), dp.end());\n }\n};\n``` | 11 | 1 | ['Dynamic Programming', 'C'] | 3 |
russian-doll-envelopes | JAVA || LIS Application | java-lis-application-by-himanshuchhikara-5q51 | Explanation:\nBasically its an 2-D version of longest-increasing-subsequence and there is a 3-D version also which is very popular interview problem of Codenati | himanshuchhikara | NORMAL | 2021-03-30T13:28:09.424719+00:00 | 2021-03-30T13:28:09.424749+00:00 | 1,348 | false | **Explanation:**\nBasically its an 2-D version of [longest-increasing-subsequence](https://leetcode.com/problems/longest-increasing-subsequence/) and there is a 3-D version also which is very popular interview problem of Codenation and Google [Box-stacking] .\n\nNote: `One envelope can fit into another if and only if both the width and height of one envelope is greater than the width and height of the other envelope.`\neg : envelope = [[5,4],[6,4],[6,7],[2,3]]\nAfter sorting\n```\n\n2 5 6 6\n3 4 7 4\n[6,7] is placed before [6,4] because if we select 7 we have to discard 4 as they both have width same.\n```\n**Approch 1: Comparable Based**\n**CODE:**\n```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Pair[] arr=new Pair[envelopes.length];\n for(int i=0;i<arr.length;i++){\n int[] nums=envelopes[i];\n int w=nums[0];\n int h=nums[1];\n Pair np=new Pair(w,h);\n arr[i]=np;\n }\n Arrays.sort(arr);\n \n return LIS(arr);\n }\n \n private int LIS(Pair[] arr){\n int ans=0;\n int[] minele=new int[arr.length];\n for(int i=0;i<arr.length;i++){\n int val=arr[i].h;\n int lo=0, hi=ans;\n \n while(lo<hi){\n int mid=(lo + hi)/2;\n if(minele[mid]<val){\n lo=mid+1;\n }else{\n hi=mid;\n }\n }\n minele[lo]=val;\n \n if(lo==ans){\n ans++;\n }\n }\n return ans;\n }\n \n public static class Pair implements Comparable<Pair>{\n int w;\n int h;\n \n Pair(int w,int h){\n this.w=w;\n this.h=h;\n }\n \n @Override\n public int compareTo(Pair other){\n if(this.w==other.w) return other.h -this.h;\n return this.w-other.w;\n }\n }\n}\n```\n**Complexity :**\n`Time : O(nlogn) and Space:O(n)`\n\n**Approch2 : Comparator Based\nCODE:**\n```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes,new EnvelopeComparator());\n return LIS(envelopes);\n }\n \n private int LIS(int[][] arr){\n int ans=0;\n int[] minele=new int[arr.length];\n for(int i=0;i<arr.length;i++){\n int val=arr[i][1];\n int lo=0, hi=ans;\n \n while(lo<hi){\n int mid=(lo + hi)/2;\n if(minele[mid]<val){\n lo=mid+1;\n }else{\n hi=mid;\n }\n }\n minele[lo]=val;\n \n if(lo==ans){\n ans++;\n }\n }\n return ans;\n }\n \n public class EnvelopeComparator implements Comparator<int[]>{\n @Override\n public int compare(int[] one,int[] two){\n if(one[0]==two[0]) return two[1]-one[1];\n return one[0]-two[0];\n }\n }\n}\n```\n**COMPLEXITY:** `TIME:O(NLOGN) AND SPACE:O(N)(minele array space)`\n\nPlease **UPVOTE** if found it helpful and feel free to reach out to me or comment down if you have any doubt.\n\n | 11 | 2 | ['Dynamic Programming', 'Binary Tree', 'Java'] | 3 |
russian-doll-envelopes | Clean and short nlogn solution | clean-and-short-nlogn-solution-by-jwzh-jd7x | See more explanation in [Longest Increasing Subsequence Size (N log N)][1]\n\n def maxEnvelopes(self, envelopes):\n def bin_search(A, key):\n | jwzh | NORMAL | 2016-06-07T04:18:30+00:00 | 2016-06-07T04:18:30+00:00 | 4,468 | false | See more explanation in [Longest Increasing Subsequence Size (N log N)][1]\n\n def maxEnvelopes(self, envelopes):\n def bin_search(A, key):\n l, r = 0, len(A)\n while l < r:\n mid = (l+r)/2\n if A[mid][1] < key[1]:\n l = mid + 1\n else:\n r = mid\n return l\n envelopes.sort(\n cmp = lambda x,y: x[0]-y[0] if x[0] != y[0] else y[1]-x[1])\n n = len(envelopes)\n tails = []\n for i in range(n):\n e = envelopes[i]\n p = bin_search(tails, e)\n if p == len(tails):\n tails.append(e)\n else:\n tails[p] = e\n return len(tails)\n\n\n [1]: http://www.geeksforgeeks.org/longest-monotonically-increasing-subsequence-size-n-log-n/ | 11 | 2 | ['Python'] | 4 |
russian-doll-envelopes | Russian Doll Envelopes || simple c++ solution || dynamic programming | russian-doll-envelopes-simple-c-solution-ne56 | Simple C++ solution \nUsing dynamic programming\n\n\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n sort(envelopes.begin(), envelopes.end(), | rawat_abhi33 | NORMAL | 2022-05-25T03:59:37.075083+00:00 | 2022-05-25T03:59:37.075122+00:00 | 3,663 | false | Simple C++ solution \nUsing dynamic programming\n\n``` \n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n sort(envelopes.begin(), envelopes.end(), [](vector<int>& a, vector<int>& b) \n -> bool {return a[0] == b[0] ? b[1] < a[1] : a[0] < b[0];});\n vector<int> dp;\n for (auto& env : envelopes) {\n int height = env[1];\n int left = lower_bound(dp.begin(), dp.end(), height) - dp.begin();\n \n if (left == dp.size()) dp.push_back(height);\n dp[left] = height;\n }\n return dp.size();\n }\n\t\n\t``` | 10 | 0 | ['Dynamic Programming', 'C'] | 0 |
russian-doll-envelopes | JAVA SOLUTION | 10 Lines | java-solution-10-lines-by-ghrushneshr25-iwfc | \nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a,b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);\n | ghrushneshr25 | NORMAL | 2022-05-25T02:44:12.799221+00:00 | 2022-05-25T02:44:12.799252+00:00 | 3,095 | false | ```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a,b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);\n int[] dp = new int[envelopes.length];\n int ans = 0;\n for (int[] env : envelopes) {\n int height = env[1];\n int left = Arrays.binarySearch(dp, 0, ans, height);\n if (left < 0) left = -left - 1;\n if (left == ans) ans++;\n dp[left] = height;\n }\n return ans;\n }\n}\n``` | 10 | 0 | ['Dynamic Programming', 'Binary Tree', 'Java'] | 1 |
russian-doll-envelopes | Python [Reduce to 1D] | python-reduce-to-1d-by-gsan-wknc | Reduce the problem to 1D and then it becomes Leetcode Problem 300 - Longest Increasing Subsequence.\nOnce the letters are sorted in increasing width, we only ne | gsan | NORMAL | 2021-03-30T11:10:00.934440+00:00 | 2021-03-31T00:07:17.575332+00:00 | 484 | false | Reduce the problem to 1D and then it becomes Leetcode Problem 300 - Longest Increasing Subsequence.\nOnce the letters are sorted in increasing width, we only need to sort based on height. Same width envelopes can be traversed in decreasing height because they will never be included in the same sequence.\n\nIf all the letter widths are distinct it would be much easier to see that this is Longest Increasing Subsequence.\n\nBut the reduction in this case is not trivial. Even if you find it, you need the binary search solution for Longest Increasing Subsequence, that one is not trivial either. In fact, I found this question to be one of the hardest.\n\nAlso the "vanilla" DP would work perfectly fine for sequences of smaller length (typically less than 1000 on Leetcode platform), which is `O(N^2)`.\n\nTime: `O(N logN)` due to sort and longest increasing subsequence computation\nSpace: `O(N)`\n\n\n```python\nclass Solution:\n def maxEnvelopes(self, A):\n #sort A\n A.sort(key = lambda x: (x[0], -x[1]))\n #reduce to 1D\n A1 = [y for _,y in A]\n #Now this is Leetcode 300\n return self.lengthOfLIS(A1)\n \n #Leetcode 300\n def lengthOfLIS(self, A1):\n L = 0\n DP = []\n for x in A1:\n i = bisect.bisect_left(DP, x)\n if i == len(DP):\n DP.append(x)\n else:\n DP[i] = x\n if i == L:\n L += 1\n return L \n``` | 10 | 2 | [] | 1 |
russian-doll-envelopes | C++ N log N solution | c-n-log-n-solution-by-wuyang-a0b4 | \nclass Solution {\npublic:\n // Dynamic Programming with Binary Search\n // Time complexity : O(nlogn). Sorting and binary search both take nlogn time.\n | wuyang | NORMAL | 2021-02-01T15:32:49.361269+00:00 | 2021-02-01T15:32:49.361311+00:00 | 1,240 | false | ```\nclass Solution {\npublic:\n // Dynamic Programming with Binary Search\n // Time complexity : O(nlogn). Sorting and binary search both take nlogn time.\n // Space complexity : O(n). dp array of size n is used.\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n // For each envelope, sorted by envelope[0] first, so envelope[1] is the the longest increasing\n // sequence(LIS) problem. When envelope[0] tie, we reverse sort by envelope[1] because bigger\n // envelope[1] can\'t contain the previous one.\n sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] == b[0] ? a[1] > b[1] : a[0] < b[0];\n });\n // dp keeps some of the visited element in a sorted list, and its size is length Of LIS sofar.\n // It always keeps the our best chance to build a LIS in the future.\n vector<int> dp;\n for (auto envelope: envelopes) {\n auto it = lower_bound(dp.begin(), dp.end(), envelope[1]);\n if (it == dp.end()){\n // If envelope[1] is the biggest, we should add it into the end of dp.\n dp.push_back(envelope[1]);\n } else {\n // If envelope[1] is not the biggest, we should keep it in dp and replace the previous\n // envelope[1] in this position. Because even if envelope[1] can\'t build longer LIS\n // directly, it can help build a smaller dp, and we will have the best chance to build\n // a LIS in the future. All elements before this position will be the best(smallest) LIS\n // sor far.\n *it = envelope[1];\n }\n }\n // dp doesn\'t keep LIS, and only keep the length Of LIS.\n return dp.size();\n }\n};\n``` | 10 | 1 | ['Dynamic Programming', 'C', 'Binary Tree'] | 1 |
russian-doll-envelopes | C++ DP version, Time O(N^2) Space O(N) | c-dp-version-time-on2-space-on-by-jordan-exvg | bool cmp (pair<int, int> i, pair<int, int> j) {\n if (i.first == j.first)\n return i.second < j.second;\n return i.first | jordandong | NORMAL | 2016-06-06T22:18:46+00:00 | 2016-06-06T22:18:46+00:00 | 2,554 | false | bool cmp (pair<int, int> i, pair<int, int> j) {\n if (i.first == j.first)\n return i.second < j.second;\n return i.first < j.first;\n }\n \n class Solution {\n public:\n int maxEnvelopes(vector<pair<int, int>>& envelopes) {\n int N = envelopes.size();\n vector<int> dp(N, 1);\n int mx = (N == 0) ? 0 : 1;\n sort(envelopes.begin(), envelopes.end(), cmp);\n for (int i = 0; i < N; i++) {\n for (int j = i - 1; j >= 0; j--) {\n if (envelopes[i].first > envelopes[j].first && envelopes[i].second > envelopes[j].second) {\n dp[i] = max(dp[i], dp[j] + 1);\n mx = max(dp[i], mx);\n }\n }\n }\n return mx;\n }\n }; | 10 | 1 | [] | 3 |
russian-doll-envelopes | No DP| Using Binary Search & LIS| CPP| Java| C| Python| Intuition| Approach | no-dp-using-binary-search-lis-cpp-java-c-7epf | Intuition\nThe problem of Russian doll envelopes is a variation of the longest increasing subsequence problem (LIS). The goal is to find the largest set of enve | vaib8557 | NORMAL | 2024-06-25T11:15:18.917090+00:00 | 2024-06-25T11:15:18.917109+00:00 | 1,439 | false | # Intuition\nThe problem of Russian doll envelopes is a variation of the longest increasing subsequence problem (LIS). The goal is to find the largest set of envelopes such that each envelope can fit into the next one in the set. To do this, we need to sort the envelopes and then find the LIS based on their dimensions.\n\n# Approach\n1. Sort the Envelopes: First, sort the envelopes by their width in ascending order. If two envelopes have the same width, sort them by height in descending order. Sorting by height in descending order for equal widths ensures that we don\'t consider envelopes with the same width but different heights as a valid sequence in the LIS step.\n\n2. Extract Heights: After sorting, extract the heights of the envelopes into a separate list.\n\n3. Longest Increasing Subsequence (LIS): Apply the LIS algorithm on the heights list. The LIS will give the maximum number of envelopes you can Russian doll.\n\n# Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n\n# CPP Code\n```\nclass Solution {\npublic:\n int maxEnvelopes(std::vector<std::vector<int>>& envelopes) {\n // Sort envelopes by width in ascending order. \n // If two envelopes have the same width, sort by height in descending order.\n std::sort(envelopes.begin(), envelopes.end(), [](const std::vector<int>& a, const std::vector<int>& b) {\n if (a[0] == b[0]) return a[1] > b[1];\n return a[0] < b[0];\n });\n\n // Extract the heights into a separate list.\n std::vector<int> heights;\n for (const auto& envelope : envelopes) {\n heights.push_back(envelope[1]);\n }\n\n // The \'ans\' vector will store the increasing subsequence of heights.\n std::vector<int> ans;\n\n for (const int height : heights) {\n // Find the position where \'height\' can be placed in \'ans\' using binary search.\n auto it = std::lower_bound(ans.begin(), ans.end(), height);\n\n // If \'height\' is greater than all elements in \'ans\', append it.\n if (it == ans.end()) {\n ans.push_back(height);\n } \n // Otherwise, replace the element at the found position with \'height\'.\n else {\n *it = height;\n }\n }\n\n // The size of \'ans\' represents the length of the longest increasing subsequence.\n return ans.size();\n }\n};\n```\n\n# Java Code\n```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n // Sort envelopes by width in ascending order. \n // If two envelopes have the same width, sort by height in descending order.\n Arrays.sort(envelopes, (a, b) -> {\n if (a[0] == b[0]) return b[1] - a[1];\n return a[0] - b[0];\n });\n\n // Extract the heights into a separate list.\n int[] heights = new int[envelopes.length];\n for (int i = 0; i < envelopes.length; i++) {\n heights[i] = envelopes[i][1];\n }\n\n // The \'ans\' list will store the increasing subsequence of heights.\n List<Integer> ans = new ArrayList<>();\n\n for (int height : heights) {\n // Find the position where \'height\' can be placed in \'ans\' using binary search.\n int pos = binarySearch(ans, height);\n\n // If \'height\' is greater than all elements in \'ans\', append it.\n if (pos == ans.size()) {\n ans.add(height);\n } \n // Otherwise, replace the element at the found position with \'height\'.\n else {\n ans.set(pos, height);\n }\n }\n\n // The size of \'ans\' represents the length of the longest increasing subsequence.\n return ans.size();\n }\n\n private int binarySearch(List<Integer> list, int target) {\n int left = 0, right = list.size();\n while (left < right) {\n int mid = (left + right) / 2;\n if (list.get(mid) < target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n return left;\n }\n}\n```\n# C Code\n```\nint compare(const void *a, const void *b) {\n int *envelopeA = *(int **)a;\n int *envelopeB = *(int **)b;\n if (envelopeA[0] == envelopeB[0]) {\n return envelopeB[1] - envelopeA[1];\n }\n return envelopeA[0] - envelopeB[0];\n}\n\nint lower_bound(int* array, int size, int value) {\n int left = 0, right = size;\n while (left < right) {\n int mid = (left + right) / 2;\n if (array[mid] < value) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n return left;\n}\n\nint maxEnvelopes(int** envelopes, int envelopesSize, int* envelopesColSize) {\n // Sort envelopes by width in ascending order. \n // If two envelopes have the same width, sort by height in descending order.\n qsort(envelopes, envelopesSize, sizeof(int*), compare);\n\n // Extract the heights into a separate list.\n int heights[envelopesSize];\n for (int i = 0; i < envelopesSize; i++) {\n heights[i] = envelopes[i][1];\n }\n\n // The \'ans\' array will store the increasing subsequence of heights.\n int ans[envelopesSize];\n int ansSize = 0;\n\n for (int i = 0; i < envelopesSize; i++) {\n int height = heights[i];\n // Find the position where \'height\' can be placed in \'ans\' using binary search.\n int pos = lower_bound(ans, ansSize, height);\n\n // If \'height\' is greater than all elements in \'ans\', append it.\n if (pos == ansSize) {\n ans[ansSize++] = height;\n } \n // Otherwise, replace the element at the found position with \'height\'.\n else {\n ans[pos] = height;\n }\n }\n\n // The size of \'ans\' represents the length of the longest increasing subsequence.\n return ansSize;\n}\n```\n# Python Code\n```\nclass Solution(object):\n def maxEnvelopes(self, envelopes):\n # Sort envelopes by width in ascending order.\n # If two envelopes have the same width, sort by height in descending order.\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n\n # Extract the heights into a separate list.\n heights = [envelope[1] for envelope in envelopes]\n\n # The \'ans\' list will store the increasing subsequence of heights.\n ans = []\n\n for height in heights:\n # Find the position where \'height\' can be placed in \'ans\' using binary search.\n pos = bisect_left(ans, height)\n\n # If \'height\' is greater than all elements in \'ans\', append it.\n if pos == len(ans):\n ans.append(height)\n # Otherwise, replace the element at the found position with \'height\'.\n else:\n ans[pos] = height\n\n # The size of \'ans\' represents the length of the longest increasing subsequence.\n return len(ans)\n``` | 9 | 0 | ['Binary Search', 'Dynamic Programming', 'C', 'Python', 'C++', 'Java'] | 1 |
russian-doll-envelopes | 354: Space 98.16%, Solution with step by step explanation | 354-space-9816-solution-with-step-by-ste-zo7g | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. We first sort the envelopes based on width in ascending order, and if | Marlen09 | NORMAL | 2023-03-02T06:14:26.844165+00:00 | 2023-03-02T06:14:26.844196+00:00 | 2,559 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. We first sort the envelopes based on width in ascending order, and if the widths are equal, we sort them based on height in descending order. This is because when we are trying to find the maximum number of envelopes we can Russian doll, we only care about the heights of the envelopes that have the same width as the current envelope, and we want to sort them in descending order so that we can maintain the largest possible doll set.\n\n2. We then initialize an array called doll_set to store the heights of the envelopes in the Russian doll set.\n\n3. We iterate through each envelope in the sorted envelopes list.\n\n4. For each envelope, we get its height and use binary search to find the index where we can insert the current height to maintain the sorted order of the doll set.\n\n5. If the index is beyond the length of the doll set, we add the height to the end of the doll set.\n\n6. Otherwise, we replace the height at that index with the current height, since it can fit inside the previous envelope.\n\n7. After iterating through all the envelopes, the length of the doll_set array is the maximum number of envelopes we can Russian doll, so we return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n # Same as 300. Longest Increasing Subsequence\n ans = 0\n dp = [0] * len(envelopes)\n\n for _, h in envelopes:\n l = 0\n r = ans\n while l < r:\n m = (l + r) // 2\n if dp[m] >= h:\n r = m\n else:\n l = m + 1\n dp[l] = h\n if l == ans:\n ans += 1\n\n return ans\n\n``` | 9 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'Python', 'Python3'] | 2 |
russian-doll-envelopes | java easy to understand | dynamic programming | longest increasing sub sequence | java-easy-to-understand-dynamic-programm-pps8 | \n\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n \n int omax = 0;\n Arrays.sort(envelopes,(a,b)->(a[0]-b[0]));\n | rmanish0308 | NORMAL | 2021-10-28T14:55:28.800721+00:00 | 2021-10-28T14:55:28.800772+00:00 | 700 | false | ```\n\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n \n int omax = 0;\n Arrays.sort(envelopes,(a,b)->(a[0]-b[0]));\n int[] dp = new int[envelopes.length];\n for(int i=0;i<envelopes.length;i++)\n {\n dp[i] = 1; \n for(int j=0;j<i;j++)\n {\n if(envelopes[i][0] > envelopes[j][0] && envelopes[i][1] > envelopes[j][1])\n {\n dp[i] = Math.max(dp[i],1+dp[j]);\n }\n }\n omax = Math.max(omax,dp[i]);\n }\n \n \n return omax;\n }\n}\n```\nPlease upvote if u find my code easy to understand | 9 | 2 | ['Dynamic Programming', 'Java'] | 1 |
russian-doll-envelopes | Gives TLE | Longest Increasing Subsequence variant | With explaination | gives-tle-longest-increasing-subsequence-7wtu | I know this solution gives TLE but for me it seems more intuitive. It may not pass all the cases of this question but you can definitely share it with the inter | iashi_g | NORMAL | 2023-06-06T04:45:05.917980+00:00 | 2024-01-05T09:28:10.934216+00:00 | 2,473 | false | # I know this solution gives TLE but for me it seems more intuitive. It may not pass all the cases of this question but you can definitely share it with the interviewer in actual interview.\n\n**Note - Despite two test cases exceeding the time limit, I am sharing the following code as it is more intuitive. You can give this approach in your interview; it sounds more realistic and intuitive.**\n\n# Intuition\nThe problem asks us to find the maximum number of envelopes we can Russian doll, which means we need to find the longest increasing subsequence based on both width and height. To solve this problem efficiently, we can use dynamic programming.\n\n# Approach\n1. Sort the given input array envelopes based on the width of the envelopes in ascending order. Sorting the envelopes based on width ensures that if envelopes[i] can be nested inside envelopes[j], then envelopes[j] will always appear before envelopes[i] in the sorted array.\n2. Create a vector vec of size n, where n is the number of envelopes. Each element of vec will store the length of the longest increasing subsequence that ends at the corresponding envelope.\n3. Iterate through each envelope in envelopes using the outer loop. For each envelope at index i, iterate through all the previous envelopes using the inner loop (from 0 to i-1).\n4. Check if the width and height of envelope envelopes[i] are strictly greater than the width and height of envelope envelopes[j]. If both conditions are satisfied and the length of the subsequence ending at envelopes[j] plus one is greater than the current length of the subsequence ending at envelopes[i], update the length of the subsequence at vec[i] to be one plus the length of the subsequence at vec[j].\n5. After the inner loop, the length of the longest increasing subsequence ending at envelopes[i] will be stored in vec[i].\n6. Iterate through vec and find the maximum length of the subsequence. This represents the maximum number of envelopes that can be Russian dolled.\n7. Return the maximum length.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(n^2), where n is the number of envelopes. The outer loop runs for n iterations, and the inner loop also runs for a maximum of n iterations.\n\n- Space complexity:\nThe space complexity is O(n) since we are using an additional vector vec of size n to store the lengths of subsequences.\n\n# Code\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end()); // based on width of envelope\n int n = envelopes.size();\n vector<int> vec(n,1);\n for(int i = 0; i < n; i++)\n {\n for(int j = 0 ; j < i; j++)\n {\n if(envelopes[j][0] < envelopes[i][0] && envelopes[j][1] < envelopes[i][1] && vec[j]+1 > vec[i])\n {\n vec[i] = 1+ vec[j];\n }\n }\n }\n int ans = 1;\n for(auto i:vec) ans = max(ans,i);\n return ans;\n }\n};\n``` | 8 | 0 | ['C++'] | 2 |
russian-doll-envelopes | C++ | Simple binary search solution | c-simple-binary-search-solution-by-nimes-w76q | Note : Sort hight in decreasing order when width is same.\n\nclass Solution {\npublic:\n int bSearch(vector<int>& vec, int maxVal, vector<vector<int>>& envel | Nimesh-Srivastava | NORMAL | 2022-05-25T01:08:11.473854+00:00 | 2022-05-25T01:08:11.473884+00:00 | 4,075 | false | **Note :** Sort `hight` in decreasing order when `width` is same.\n```\nclass Solution {\npublic:\n int bSearch(vector<int>& vec, int maxVal, vector<vector<int>>& envelopes, int i){\n int l = 0;\n int r = maxVal;\n \n int temp = maxVal;\n \n while(l <= r){\n int mid = l + (r - l) / 2;\n \n if(vec[mid] < envelopes[i][1])\n l = mid + 1;\n \n else {\n temp = mid;\n r = mid - 1;\n }\n }\n \n return temp;\n }\n \n // to sort in decreasing order\n static bool decSort(vector<int>& v1, vector<int>& v2) {\n if(v1[0] == v2[0])\n return v1[1] > v2[1];\n \n return v1[0] < v2[0];\n }\n \n int maxEnvelopes(vector<vector<int>>& envelopes) {\n int siz = envelopes.size();\n \n if(siz == 0)\n return 0;\n \n sort(envelopes.begin(), envelopes.end(), decSort);\n \n vector<int> vec(siz, 0);\n int maxVal = 0;\n \n for(int i = 0; i < siz; i++) {\n int pos = bSearch(vec, maxVal, envelopes, i);\n \n vec[pos] = envelopes[i][1];\n \n if(pos == maxVal)\n maxVal++;\n }\n \n return maxVal;\n }\n};\n``` | 8 | 2 | ['Dynamic Programming', 'C', 'Binary Tree', 'C++'] | 6 |
russian-doll-envelopes | Golang N log N solution | golang-n-log-n-solution-by-wuyang-9qmo | \n// Dynamic Programming with Binary Search\n// Time complexity : O(nlogn). Sorting and binary search both take nlogn time.\n// Space complexity : O(n). dp arra | wuyang | NORMAL | 2021-02-01T15:58:53.084034+00:00 | 2021-02-01T15:58:53.084068+00:00 | 410 | false | ```\n// Dynamic Programming with Binary Search\n// Time complexity : O(nlogn). Sorting and binary search both take nlogn time.\n// Space complexity : O(n). dp array of size n is used.\nfunc maxEnvelopes(envelopes [][]int) int {\n\t// For each envelope, sorted by envelope[0] first, so envelope[1] is the the longest\n\t// increasing sequence(LIS) problem. When envelope[0] tie, we reverse sort by envelope[1]\n\t// because bigger envelope[1] can\'t contain the previous one.\n\tsort.Slice(envelopes,func(i, j int) bool {\n\t\tif envelopes[i][0] == envelopes[j][0] {\n\t\t\treturn envelopes[i][1] > envelopes[j][1]\n\t\t} else {\n\t\t\treturn envelopes[i][0] < envelopes[j][0]\n\t\t}\n\t})\n\t// dp keeps some of the visited element in a sorted list, and its size is\n\t// length Of LIS sofar. It always keeps the our best chance to build a LIS in the future.\n\tdp := []int{}\n\tfor _, envelope := range envelopes {\n\t\ti := sort.SearchInts(dp, envelope[1])\n\t\tif (i == len(dp)) {\n\t\t\t// If envelope[1] is the biggest, we should add it into the end of dp.\n\t\t\tdp = append(dp, envelope[1])\n\t\t} else {\n\t\t\t// If envelope[1] is not the biggest, we should keep it in dp and replace\n\t\t\t// the previous envelope[1] in this position. Because even if envelope[1]\n\t\t\t// can\'t build longer LIS directly, it can help build a smaller dp, and\n\t\t\t// we will have the best chance to build a LIS in the future. All elements\n\t\t\t// before this position will be the best(smallest) LIS sor far. \n\t\t\tdp[i] = envelope[1];\n\t\t}\n\t}\n\t// dp doesn\'t keep LIS, and only keep the length Of LIS.\n\treturn len(dp) \n}\n``` | 8 | 1 | ['Dynamic Programming', 'Binary Tree', 'Go'] | 1 |
russian-doll-envelopes | Python 5 lines short code | python-5-lines-short-code-by-rudy-mpbx | python\nclass Solution:\n def maxEnvelopes(self, es):\n es.sort(key=lambda x: (x[0], -x[1]))\n heights = [0x3f3f3f3f] * len(es)\n for _, | rudy__ | NORMAL | 2019-12-31T12:48:53.461537+00:00 | 2019-12-31T13:19:50.957023+00:00 | 784 | false | ```python\nclass Solution:\n def maxEnvelopes(self, es):\n es.sort(key=lambda x: (x[0], -x[1]))\n heights = [0x3f3f3f3f] * len(es)\n for _, h in es:\n heights[bisect.bisect_left(heights, h)] = h\n return bisect.bisect_right(heights, 0x3f3f3f3f - 1)\n\n``` | 8 | 1 | [] | 1 |
russian-doll-envelopes | Python solution based on LIS | python-solution-based-on-lis-by-giiia-arp7 | It's a problem based on LIS. \nDP solution for LIS is N^2 which will TLE here.\nUsing Binary Search approach will get accepted.\n\nhttps://leetcode.com/problem | giiia | NORMAL | 2016-07-15T18:54:40.784000+00:00 | 2016-07-15T18:54:40.784000+00:00 | 2,308 | false | It's a problem based on LIS. \nDP solution for LIS is N^2 which will TLE here.\nUsing Binary Search approach will get accepted.\n\nhttps://leetcode.com/problems/longest-increasing-subsequence/\n\n def maxEnvelopes(self, envelopes):\n """\n :type envelopes: List[List[int]]\n :rtype: int\n """\n if not envelopes:\n return 0\n \n l = len(envelopes)\n if l == 1:\n return 1\n \n envelopes.sort(\n cmp = lambda x, y: x[0] - y[0] if x[0] != y[0] else y[1] - x[1]) \n # sort the envelopes by width because they need to be inorder before consider the heigths or versa\n \n width = []\n for i in envelopes:\n width.append(i[1])\n \n res = self.longestSubsequence(width)\n # the problem became LIS after sort(width)\n \n return res\n \n \n \n def longestSubsequence(self, nums):\n """\n return type: int (number of longest subsequence)\n """\n if not nums:\n return 0\n l = len(nums)\n res = []\n \n for num in nums:\n pos = self.binarySearch(num, res)\n if pos >= len(res):\n res.append(num)\n else:\n res[pos] = num\n \n return len(res)\n \n \n \n def binarySearch(self, target, nums):\n """\n return type: int (ceiling of the insert position)\n """\n if not nums:\n return 0\n \n l = len(nums)\n start = 0\n end = l - 1\n \n while start <= end:\n half = start + (end - start) // 2\n if nums[half] == target:\n return half\n elif nums[half] < target:\n start = half + 1\n else:\n end = half - 1\n \n return start\n''' | 8 | 1 | ['Python'] | 3 |
russian-doll-envelopes | C++ solutions || easy to solve | c-solutions-easy-to-solve-by-infox_92-p3bp | \nclass Solution {\npublic:\n static bool compare(vector<int>&a , vector<int>& b)\n {\n return a[0]==b[0]?a[1]>b[1]:a[0]<b[0];\n }\n int maxEnv | Infox_92 | NORMAL | 2022-11-02T09:28:47.328991+00:00 | 2022-11-02T09:28:47.329032+00:00 | 1,888 | false | ```\nclass Solution {\npublic:\n static bool compare(vector<int>&a , vector<int>& b)\n {\n return a[0]==b[0]?a[1]>b[1]:a[0]<b[0];\n }\n int maxEnvelopes(vector<vector<int>>&a) {\n sort(a.begin(),a.end(),compare);\n vector<int>dp;\n for(auto i:a)\n {\n auto it=lower_bound(dp.begin(),dp.end(),i[1]);\n if(it==dp.end())\n dp.push_back(i[1]);\n else\n *it=i[1];\n }\n return dp.size();\n }\n};\n``` | 7 | 0 | ['C', 'C++'] | 0 |
russian-doll-envelopes | LIS | run time : O(n logn) | space : O(n) | lis-run-time-on-logn-space-on-by-lowkeyi-7jby | \nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a, b) -> a[0] != b[0] ? a[0] - b[0] : b[1] - a[1]);\n | lowkeyish | NORMAL | 2022-05-26T16:23:46.875796+00:00 | 2022-05-26T16:23:46.875823+00:00 | 848 | false | ```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a, b) -> a[0] != b[0] ? a[0] - b[0] : b[1] - a[1]);\n List<Integer> result = new ArrayList<>();\n result.add(envelopes[0][1]);\n for (int i = 1; i < envelopes.length; ++i) {\n if (result.get(result.size() - 1) < envelopes[i][1])\n result.add(envelopes[i][1]);\n else {\n int idx = Collections.binarySearch(result, envelopes[i][1]);\n result.set(idx < 0 ? -idx - 1 : idx, envelopes[i][1]);\n }\n }\n return result.size();\n }\n}\n``` | 7 | 0 | ['Dynamic Programming', 'Binary Tree', 'Java'] | 0 |
russian-doll-envelopes | python O(NlogN) solution, DP, binary search is not used | python-onlogn-solution-dp-binary-search-v5rv0 | \nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n # sort the width by ascending order, the height by descending order\n | shun6096tw | NORMAL | 2022-05-13T08:00:28.063887+00:00 | 2022-05-13T08:00:28.063911+00:00 | 908 | false | ```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n # sort the width by ascending order, the height by descending order\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n tops = []\n for e in envelopes:\n if tops and tops[-1][0] < e[0] and tops[-1][1] < e[1]: \n # To speed up, if height and width is bigger than the envelope in our piles, create a new pile\n tops.append(e)\n continue\n\n for i in range(len(tops)):\n if tops[i][1] >= e[1]: \n # if envelope is smaller than top envelope of pile, update top envelope of pile\n tops[i] = e\n break\n else:\n # not trigger break (height and width is bigger than the envelope in our piles, create a new pile)\n tops.append(e)\n return len(tops)\n``` | 7 | 0 | ['Dynamic Programming', 'Python'] | 1 |
russian-doll-envelopes | Java Simple and easy solution, 8 ms, faster than 98.48%, T O nlogn, clean code with comments | java-simple-and-easy-solution-8-ms-faste-v7uw | PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n //sort the enevelope\n //as incr | satyaDcoder | NORMAL | 2021-03-31T09:09:51.701825+00:00 | 2021-03-31T09:09:51.701855+00:00 | 468 | false | **PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n //sort the enevelope\n //as increasing of width, when both width is same, then sort by decreasing order heights\n Arrays.sort(envelopes, (a, b) -> (a[0] == b[0]) ? (b[1] - a[1]) : (a[0] - b[0]));\n \n //just extarct the height\n int[] heights = new int[envelopes.length];\n for(int i = 0; i < heights.length; i++){\n heights[i] = envelopes[i][1];\n }\n \n //find the longest increasing subsequen on heights\n return getLIS(heights);\n }\n \n private int getLIS(int[] nums){\n int[] dp = new int[nums.length];\n int len = 0;\n \n for(int num : nums){\n int index = Arrays.binarySearch(dp, 0, len, num);\n \n if(index < 0){\n index = -(index + 1);\n }\n \n dp[index] = num;\n \n if(index == len)\n len++;\n }\n \n return len;\n }\n}\n``` | 7 | 0 | ['Java'] | 1 |
russian-doll-envelopes | Python O(nlogn) - a tricky sorting to solve the 2-D dilemma | python-onlogn-a-tricky-sorting-to-solve-w4yny | On the first look of this problem, we should be able to come up with sorting the envelopes from small to large. Something like sort(envelopes). Firstly sort by | hammer001 | NORMAL | 2019-05-08T23:15:58.134180+00:00 | 2019-05-08T23:15:58.134246+00:00 | 692 | false | On the first look of this problem, we should be able to come up with sorting the envelopes from small to large. Something like `sort(envelopes)`. Firstly **sort by the first dimension (let\'s say width), then use the second dimension data (height) to solve the LIS problem**. However, without carefully modifying your sort criteria, you could be wrong. The reason is: For one doll to cover another , both dimension have to be strictly greater. It means you cannot have something like `[[1,2], [1, 3]]` in your final doll list. \n\nHere is a tricky data set that better explain the bug in normal patient sort. \n`A = [[1,4], [2,5], [3,1], [3,2], [3,3]]`\n\nThe correct answer is to select `lst = [[1,4], [2,5]]` and answer is 2. But if you go over `[[3,1], [3,2], [3,3]]` and leverage the binary search to do the overwrite, you could end up with answer 3. \n\nThen you might be conservative and say: **Ok, I only pick one for the dolls with same width.** Then the previous example ends with answer 2, because after considering `[3,1]`, you will directly ignore `[[3,2], [3,3]]`. However, this is still wrong. \n\nConsider `B = [[1, 2], [2, 1], [2, 3]]`. The correct answer should be 2. However, if you just consider the first `width=2` doll, which is `[2, 1]`, you will miss the chance to take `[2, 3]`. \n\nSo the dilemma is: when you have a group of dolls with the **same width**, you really don\'t know which of the following you should do\n1. Pick one with smaller height and overwrite the `lst`\n2. Pick one with greater height and expand the `lst`\n\nThe right pick is depending on the upcoming dolls. If you do 1, it is possible that you miss the chance to expand the current `lst` and you get answer that is smaller than right answer. If you do 2, it is possible that the doll you pick has too large height, and you will miss more chances to expand later. \n\nActually, the correct solution is: when you sort the doll, it should be sorted like `envelopes.sort(key = lambda x: (x[0], -x[1]))`. The first dimension is sorted from small to larget. The **second dimension is sorted reversely**. Then, you do not need to worry about "Only pick one" for each width. The sorted order would take care of dedupl for you. \n\nHere is the solution\n\n```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n envelopes.sort(key = lambda x : (x[0], -x[1]))\n \n #print(envelopes)\n \n lst = []\n \n for start, end in envelopes:\n lo, hi = 0, len(lst)\n \n while lo < hi:\n mid = (lo + hi) // 2\n \n if end > lst[mid]:\n lo = mid + 1\n else:\n hi = mid\n \n if lo == len(lst):\n lst.append(end)\n else:\n lst[lo] = end\n \n return len(lst)\n``` | 7 | 0 | [] | 2 |
russian-doll-envelopes | Python 6 lines bisect solution | python-6-lines-bisect-solution-by-cenkay-853y | I don\'t go much into details. \n The method is all over the discussion, "longest increasing subsequence" tail method.\n We simply catch the minimum height for | cenkay | NORMAL | 2018-10-19T10:51:26.456095+00:00 | 2018-10-22T20:17:32.966354+00:00 | 579 | false | * I don\'t go much into details. \n* The method is all over the discussion, "longest increasing subsequence" tail method.\n* We simply catch the minimum height for specified number of dolls or length of tails in other words.\n* We reversed heights of same widths in envelopes array because it would continue adding another doll onto same width.\n```\nclass Solution:\n def maxEnvelopes(self, envelopes):\n tails = []\n for w, h in sorted(envelopes, key = lambda x: (x[0], -x[1])):\n i = bisect.bisect_left(tails, h)\n if i == len(tails): tails.append(h)\n else: tails[i] = h\n return len(tails)\n``` | 7 | 1 | [] | 1 |
russian-doll-envelopes | LIS - 💯🚀 single pattern to solve all LIS problems | lis-single-pattern-to-solve-all-lis-prob-kcw5 | 300. Longest Increasing Subsequence\n213. House Robber II\n198. House Robber\n740. Delete and Earn\n\n\n\n# Code\njava []\nimport java.util.Arrays;\n\npublic cl | Dixon_N | NORMAL | 2024-09-15T18:04:15.219169+00:00 | 2024-09-15T18:04:15.219208+00:00 | 1,570 | false | [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/solutions/5574584/longest-increasing-subsequence-one-stop-template/)\n[213. House Robber II](https://leetcode.com/problems/house-robber-ii/solutions/5791343/house-robber-i-ii-beats-100/)\n[198. House Robber](https://leetcode.com/problems/house-robber/solutions/5791346/house-robber-pattern-and-variation-all-approaches/)\n[740. Delete and Earn](https://leetcode.com/problems/delete-and-earn/solutions/5791351/house-robber-variation/)\n\n\n\n# Code\n```java []\nimport java.util.Arrays;\n\npublic class Solution {\n public int maxEnvelopes(int[][] envelopes) {\n int n = envelopes.length;\n if (n == 0) return 0;\n\n // Sort envelopes by width. If two envelopes have the same width, sort by height in ascending order.\n Arrays.sort(envelopes, (a, b) -> {\n if (a[0] == b[0]) return a[1] - b[1]; // Sort by height if width is the same\n return a[0] - b[0]; // Sort by width otherwise\n });\n\n // DP array to store the maximum number of envelopes ending at each index\n int[] dp = new int[n];\n Arrays.fill(dp, 1); // Every envelope is a standalone valid sequence, so initialize to 1\n\n int maxEnvelopes = 1; // To store the maximum number of envelopes\n\n // Loop through each envelope\n for (int i = 1; i < n; i++) {\n for (int j = 0; j < i; j++) {\n // Check if envelope[j] can fit into envelope[i]\n if (envelopes[j][0] < envelopes[i][0] && envelopes[j][1] < envelopes[i][1]) {\n dp[i] = Math.max(dp[i], dp[j] + 1); // Update dp[i] if we found a larger sequence\n }\n }\n maxEnvelopes = Math.max(maxEnvelopes, dp[i]); // Update the maximum envelopes found so far\n }\n\n return maxEnvelopes; // Return the maximum number of envelopes\n }\n}\n```\n```java []\npublic class Solution {\n public int maxEnvelopes(int[][] envelopes) {\n int n = envelopes.length;\n if (n == 0) return 0;\n\n // Step 1: Sort the envelopes by width in ascending order and by height in descending order\n Arrays.sort(envelopes, (a, b) -> {\n if (a[0] == b[0]) {\n return b[1] - a[1]; // If widths are equal, sort by height in descending order\n } else {\n return a[0] - b[0]; // Otherwise, sort by width in ascending order\n }\n });\n\n // Step 2: Extract the heights and apply LIS on them\n int[] heights = new int[n];\n for (int i = 0; i < n; i++) {\n heights[i] = envelopes[i][1];\n }\n\n // Find the length of LIS on heights using binary search approach\n return lengthOfLIS(heights);\n }\n\n // Helper function to find the length of LIS using binary search (efficient approach)\n private int lengthOfLIS(int[] nums) {\n List<Integer> lis = new ArrayList<>();\n for (int num : nums) {\n if (lis.isEmpty() || lis.get(lis.size() - 1) < num) {\n lis.add(num);\n } else {\n // Find the position to replace in the LIS list\n int pos = binarySearch(lis, num);\n lis.set(pos, num);\n }\n }\n return lis.size();\n }\n\n // Binary search to find the correct position to replace in the list\n private int binarySearch(List<Integer> lis, int target) {\n int low = 0, high = lis.size() - 1;\n while (low <= high) {\n int mid = low + (high - low) / 2;\n if (lis.get(mid) == target) {\n return mid;\n } else if (lis.get(mid) < target) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n return low;\n }\n}\n\n``` | 6 | 0 | ['Dynamic Programming', 'Java'] | 7 |
russian-doll-envelopes | Sort + LIS | C++ | sort-lis-c-by-tusharbhart-kwaf | \nclass Solution {\n static bool cmp(vector<int> &a, vector<int> &b) {\n return a[0] == b[0] ? a[1] > b[1] : a[0] < b[0];\n }\npublic:\n int max | TusharBhart | NORMAL | 2023-04-29T14:18:32.731244+00:00 | 2023-04-29T14:18:32.731281+00:00 | 1,734 | false | ```\nclass Solution {\n static bool cmp(vector<int> &a, vector<int> &b) {\n return a[0] == b[0] ? a[1] > b[1] : a[0] < b[0];\n }\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(), envelopes.end(), cmp);\n\n vector<int> v;\n for(auto e : envelopes) {\n if(!v.size() || v.back() < e[1]) v.push_back(e[1]);\n else {\n int pos = lower_bound(v.begin(), v.end(), e[1]) - v.begin();\n v[pos] = e[1];\n }\n }\n return v.size();\n }\n};\n\n\n``` | 6 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
russian-doll-envelopes | C# || NLogN || Binary search || DP | c-nlogn-binary-search-dp-by-cdev-p7xg | \n public int MaxEnvelopes(int[][] envelopes)\n {\n Array.Sort(envelopes, (a, b) => a[0] == b[0] ? b[1].CompareTo(a[1]) : a[0].CompareTo(b[0]));\n\ | CDev | NORMAL | 2022-05-25T01:39:59.552786+00:00 | 2022-05-25T01:39:59.552820+00:00 | 430 | false | ```\n public int MaxEnvelopes(int[][] envelopes)\n {\n Array.Sort(envelopes, (a, b) => a[0] == b[0] ? b[1].CompareTo(a[1]) : a[0].CompareTo(b[0]));\n\n int[] dp = new int[envelopes.Length];\n int len = 0;\n foreach(int[] envelope in envelopes){\n int index = Array.BinarySearch(dp, 0, len, envelope[1]);\n if(index< 0)\n index = ~index;\n dp[index] = envelope[1];\n if(index == len)\n len++;\n }\n return len;\n }\n``` | 6 | 0 | ['Binary Search', 'Dynamic Programming'] | 1 |
russian-doll-envelopes | Russian Doll Envelopes | Easy DP solution | simple trick explained !!! | russian-doll-envelopes-easy-dp-solution-s0n0z | The trick is, we first sort the envolopes based on their width, Then the problem now turned into finding longest Increasing subsequence(LIS), so we just need to | srinivasteja18 | NORMAL | 2021-03-30T07:53:30.093498+00:00 | 2021-03-30T08:45:41.933645+00:00 | 416 | false | The trick is, we first sort the envolopes based on their width, Then the problem now turned into finding **longest Increasing subsequence(LIS**), so we just need to find **LIS on heights of envolopes** but including some edges cases. \nLets see the edge cases to understand it more..\nconsider, `envolope = [[2,3],[5,8],[3,6],[5,7]]`, if we sort based on `compare function`, we get `[[2,3],[3,6],[5,7],[5,8]]`\nNow, if perform LIS on heights, **LIS=4, but answer should be 3**, to tackle this we take `en[i][0] > en[j][0] && en[i][1]>en[j][1]` as our condition instead of `en[i][1]>en[j][1]` inorder to make sure both width and height increasing.\n\n**Do Upvote** if you like the code and comment down if you are facing some difficulty or having some queries.\nGo through the code below for better understanding !!!\n\n\n```\nclass Solution {\npublic:\n static bool compare(vector<int>a,vector<int>b){\n if(a[0] == b[0]) return a[1]<b[1];\n return a[0]<b[0];\n }\n int maxEnvelopes(vector<vector<int>>& en) {\n sort(en.begin(),en.end(),compare);\n int n = en.size(),res=1;\n vector<int>dp(n,1);\n for(int i=0;i<n;i++){\n for(int j=i-1;j>=0;j--){\n if(en[i][0] > en[j][0] && en[i][1]>en[j][1]){\n dp[i] = max(dp[i],dp[j]+1);\n res = max(res,dp[i]);\n }\n }\n }\n return res;\n }\n};\n``` | 6 | 1 | [] | 0 |
russian-doll-envelopes | Python N Log N solution | python-n-log-n-solution-by-wuyang-i99t | \nclass Solution:\n # Dynamic Programming with Binary Search\n # Time complexity : O(nlogn). Sorting and binary search both take nlogn time.\n # Space | wuyang | NORMAL | 2021-02-01T15:51:42.197222+00:00 | 2021-02-01T15:51:42.197248+00:00 | 566 | false | ```\nclass Solution:\n # Dynamic Programming with Binary Search\n # Time complexity : O(nlogn). Sorting and binary search both take nlogn time.\n # Space complexity : O(n). dp array of size n is used.\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n # For each envelope, sorted by envelope[0] first, so envelope[1] is the the longest\n # increasing sequence(LIS) problem. When envelope[0] tie, we reverse sort by envelope[1]\n # because bigger envelope[1] can\'t contain the previous one.\n envelopes.sort(key=lambda e: (e[0], -e[1]))\n # dp keeps some of the visited element in a sorted list, and its size is length Of LIS\n # sofar. It always keeps the our best chance to build a LIS in the future.\n dp = []\n for envelope in envelopes:\n i = bisect.bisect_left(dp, envelope[1])\n if i == len(dp):\n # If envelope[1] is the biggest, we should add it into the end of dp.\n dp.append(envelope[1])\n else:\n # If envelope[1] is not the biggest, we should keep it in dp and replace the\n # previous envelope[1] in this position. Because even if envelope[1] can\'t build\n # longer LIS directly, it can help build a smaller dp, and we will have the best\n # chance to build a LIS in the future. All elements before this position will be\n # the best(smallest) LIS sor far. \n dp[i] = envelope[1]\n # dp doesn\'t keep LIS, and only keep the length Of LIS.\n return len(dp)\n``` | 6 | 0 | ['Dynamic Programming', 'Binary Tree', 'Python'] | 1 |
russian-doll-envelopes | [Python] Simple DP NlogN solution | python-simple-dp-nlogn-solution-by-101le-r1x5 | \nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n ## RC ##\n ## APPROACH : DP ##\n ## Similar to Leetcode | 101leetcode | NORMAL | 2020-06-21T22:42:58.191758+00:00 | 2020-06-21T22:42:58.191794+00:00 | 1,096 | false | ```\nclass Solution:\n def maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n ## RC ##\n ## APPROACH : DP ##\n ## Similar to Leetcode : 300 Longest Increasing Subsequence ##\n \n\t\t## TIME COMPLEXITY : O(NlogN) ##\n\t\t## SPACE COMPLEXITY : O(N) ##\n\n ## LIS : replace larger number with small one, append larger numbers ##\n ## NUMS [100, 89, 53, 68, 45, 81] ##\n ## DP ##\n # [100]\n # [89]\n # [53]\n # [53, 68]\n # [45, 68]\n # [45, 68, 81]\n \n def lis(nums):\n # print(nums)\n dp = []\n for i in range(len(nums)):\n idx = bisect_left(dp, nums[i])\n if idx == len(dp):\n dp.append(nums[i])\n else:\n dp[idx] = nums[i]\n # print(dp)\n return len(dp)\n \n # sort increasing in first dimension and decreasing on second\n # take a moment and think why ? ( we want to perform LIS on second dimension, think in terms when a set of boxes have same first dimension)\n envelopes.sort(key=lambda x: (x[0], -x[1]))\n \n # extract the second dimension and run the LIS\n return lis([envelope[1] for envelope in envelopes]) \n``` | 6 | 0 | ['Python', 'Python3'] | 0 |
russian-doll-envelopes | easy peasy python O(nlogn) solution with comments | easy-peasy-python-onlogn-solution-with-c-1s7w | \tdef maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n # sort in one property and find the longest increasing subsequence\n # in the other | lostworld21 | NORMAL | 2019-09-19T16:50:18.287688+00:00 | 2019-09-19T16:50:18.287738+00:00 | 1,536 | false | \tdef maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n # sort in one property and find the longest increasing subsequence\n # in the other property, that\'s it\n # to avoid cases such as [(3, 4), (3, 6)] - output should be 1\n # sort the (w) in ascending and (h) in descending\n \n #let\'s sort in second property(h) and then find LIS using first property(w)\n ln = len(envelopes)\n if ln <= 1:\n return ln\n \n envelopes = sorted(envelopes, key=lambda x:(x[1], -x[0]))\n #now find the LIS\n q = [envelopes[0][0]]\n \n for i in range(1, ln):\n num = envelopes[i][0]\n if q[-1] < num:\n q.append(num)\n elif q[-1] > num:\n # use binary search \n idx = self.upperbound(q, num)\n q[idx] = num\n \n return len(q)\n \n def upperbound(self, ls, num):\n ln = len(ls)\n s, e = 0, ln-1\n while s <= e:\n mid = (e-s)//2 + s\n if ls[mid] == num:\n #we can or we don\'t have to replace this\n return mid\n elif ls[mid] < num:\n if mid+1 < ln and ls[mid+1] > num:\n return mid+1\n s = mid + 1\n else:\n if mid == 0:\n return mid\n e = mid-1 | 6 | 0 | ['Binary Tree', 'Python', 'Python3'] | 0 |
russian-doll-envelopes | beat 99.78% user with cpp|| LIS reference || well commented code | beat-9978-user-with-cpp-lis-reference-we-3hux | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | gyuyul | NORMAL | 2024-09-02T11:24:35.120032+00:00 | 2024-09-15T14:32:29.190672+00:00 | 455 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n static bool comp(vector<int> &a , vector<int> &b){\n if(a[0] == b[0]){\n return a[1]>b[1];\n }\n else{\n return a[0]<b[0];\n }\n return false;\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n /// just for fast input and output\n int fast_io = [](){\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return 0;\n }(); \n\n // just a combination of lis\n // why beacuse in LIS - you have to maintain two \n // things first you can only take current element \n // if its index greater then previous taken index\n // and second its values \n // the first was taken care by the property of array\n // beacuse the indexes are always increasing when \n // go forward in the array \n // we can imitates this property by just sorting the \n // element on the basis of the envelope[i][0]\n // after sorting just care about the second paramenter envelope[i][1]\n\n\n // there is problem when you sort index just on the basis \n // envelope[i][0] beacause it might happen that two\n // same envelope[i][0] .. then in simple sorting \n // then it will go to second element and use that to find\n // order ... but it in that case you may use same envelopes[i][0]\n // to update the current anwser ..\n /// this will not happen if you just reverse the order for second element\n sort(envelopes.begin() , envelopes.end(), comp);\n \n // here we only care about how many no are smaller than this no \n // by how much we don\'t care\n vector<int> temp;\n temp.push_back(envelopes[0][1]);\n\n for(int i = 1 ; i< envelopes.size(); i++){\n // if(envelopes[i][0] == envelopes[i-1][0]) continue;\n if(envelopes[i][1]> temp.back()){\n temp.push_back(envelopes[i][1]);\n }\n else{\n // here some confusion may arise why are we replacing \n // beacause we want minmum possible value at particular \n // index-> just dry run se how it is working\n int ind = lower_bound(temp.begin() , temp.end() , envelopes[i][1]) - temp.begin();\n temp[ind] = envelopes[i][1];\n }\n }\n return temp.size();\n\n\n\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
russian-doll-envelopes | using dynamic programming (binary search on LIS) | using-dynamic-programming-binary-search-l9npb | Intuition\nTo find the maximum number of envelopes that can be nested (Russian-dolled), we need to treat it like finding the Longest Increasing Subsequence (LIS | saivishal87 | NORMAL | 2024-06-13T12:02:27.306561+00:00 | 2024-06-13T12:02:27.306583+00:00 | 784 | false | # Intuition\nTo find the maximum number of envelopes that can be nested (Russian-dolled), we need to treat it like finding the Longest Increasing Subsequence (LIS), but in two dimensions (width and height). By sorting and then applying a modified LIS algorithm, we can efficiently solve the problem.\n\n# Approach\nSorting:\nSort the envelopes by width in ascending order. If two envelopes have the same width, sort them by height in descending order. This ensures that when we consider heights, we only need to find increasing sequences.\n\nLIS with Binary Search:\nAfter sorting, extract the heights of the envelopes and find the length of the LIS using a dynamic programming approach combined with binary search.\nUse a vector dp to store the current LIS. For each height, use lower_bound to find its position in dp. If it\'s greater than all elements, append it. Otherwise, replace the existing element.\n\n\n# Complexity\n- Time complexity:\nSorting the envelopes take O(nlogn).\nFinding the LIS with binary search for each height takes O(nlogn).\nThus, the overall time complexity is O(nlogn).\n\n- Space complexity:\nThe dp vector used to store the heights takes O(n) space in the worst case.\nHence, the space complexity is O(n).\n\n# Code\n```\nclass Solution {\npublic:\nstatic bool comp(vector<int>&p1,vector<int>&p2){\n if(p1[0]==p2[0])\n return p1[1]>p2[1];\n return p1[0]<p2[0];\n}\n int maxEnvelopes(vector<vector<int>>& en) {\n int n=en.size();\n sort(en.begin(),en.end(),comp);\n vector<int>dp;\n int maxi=1;\n for(int i=0;i<n;i++){\n int height=en[i][1];\n auto it=lower_bound(dp.begin(),dp.end(),height);\n if(it==dp.end())\n dp.push_back(height);\n else\n *it=height;\n }\n return dp.size();\n }\n};\n``` | 5 | 0 | ['Binary Search', 'Dynamic Programming', 'C++'] | 0 |
russian-doll-envelopes | [C++] Binary Search | c-binary-search-by-harsh__18-r4sg | \tclass Solution {\n\t\tprivate:\n\n\t\t\tint solve(int n,vector &nums){\n\n\t\t\t\tvector ans;\n\t\t\t\tans.push_back(nums[0]);\n\n\t\t\t\tfor(int i = 1; i < n | Harsh__18 | NORMAL | 2022-08-13T04:45:09.545165+00:00 | 2022-08-13T04:45:09.545211+00:00 | 906 | false | \tclass Solution {\n\t\tprivate:\n\n\t\t\tint solve(int n,vector<int> &nums){\n\n\t\t\t\tvector<int> ans;\n\t\t\t\tans.push_back(nums[0]);\n\n\t\t\t\tfor(int i = 1; i < n; i++){\n\t\t\t\t\tif(nums[i] > ans.back()){\n\t\t\t\t\t\tans.push_back(nums[i]);\n\t\t\t\t\t}else{\n\t\t\t\t\t\tint index = lower_bound(ans.begin(),ans.end(),nums[i]) - ans.begin();\n\t\t\t\t\t\tans[index] = nums[i];\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\treturn ans.size();\n\n\t\t\t}\n\tpublic:\n\t\tint maxEnvelopes(vector<vector<int>>& envelopes) {\n\n\t\t\tint n = envelopes.size();\n\n\t\t\tif(n == 0) return 0;\n\n\t\t\tsort(envelopes.begin(),envelopes.end(),[](vector<int> &a, vector<int> &b){\n\t\t\t\tif(a[0] == b[0]){ \n\t\t\t\t\treturn a[1] > b[1];\n\t\t\t\t}\n\t\t\t\treturn a[0] < b[0];\n\t\t\t});\n\n\n\t\t\tvector<int> nums;\n\n\t\t\tfor(int i = 0; i < n; i++){\n\t\t\t\tnums.push_back(envelopes[i][1]);\n\t\t\t}\n\n\t\t\treturn solve(n,nums);\n\t\t}\n\t}; | 5 | 0 | ['Dynamic Programming', 'C', 'Sorting', 'C++'] | 1 |
russian-doll-envelopes | LIS | O(NlogN) | Easy to understand | Intuitive | lis-onlogn-easy-to-understand-intuitive-r0p4k | Longest Increasing Subsequence in 2 dimension!\nFirstly, if you have solved the Longest Increasing Subsequence (LIS) question, you\'ve perhaps related this ques | deepjyotide13 | NORMAL | 2022-07-10T21:58:53.621024+00:00 | 2022-07-26T19:26:39.395882+00:00 | 944 | false | # Longest Increasing Subsequence in 2 dimension!\nFirstly, if you have solved the `Longest Increasing Subsequence (LIS)` question, you\'ve perhaps related this question to LIS in some way or the other, if so, you\'re in the right track. In LIS we found the longest increasing subsequence in an 1D array but in this question the ask is to find the LIS in 2D array *(for both the width and the height, since an envelope can get inside another envelope iff both its height and width are smaller than the other one)*. The trick is to **sort the array according to its width**. That makes life easier as now we only need to deal with the height since width is already sorted. So **the LIS of height will automatically be the LIS of both width and height**.\n\n**Input:** ```[[5,4],[6,4],[6,7],[2,3]]```\n**After sorting:** ```[[2,3],[5,4],[6,7],[6,4]]```\nNow an LIS on height i.e., ```[3,4,7,4]``` will give 3 as the length since ```[3,4,7]``` is the LIS.\nAnd now if you bring the width into the picture ```[[2,3],[5,4],[6,7]]``` is the LIS of both width and height, which means an envelope ```[2,3]``` can be put inside an envelope ```[5,4]``` which in turn can be put inside an envelope ```[6,7]```. Hope the requirement of the concept of LIS is no more a question here.\n\nWe need to take care of certain scenarios where width may be same for 2 or more envelopes, say, `[6,5]` & `[6,7]`. In such scenarios we can not take both `5` and `7` in our LIS *(of height)* since the envelope of same width can not get inside the other. To skip this scenario and only take one envelope we better configure our code to sort the height in reverse order only when 2 or more width of envelopes are same. Now in the sorted array, `[6,7]` will appear before `[6,5]` so the LIS of height won\'t take both `7` & `5` into calculation.\n\n**Code:**\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n int N = envelopes.size();\n sort(envelopes.begin(), envelopes.end(), [](vector<int>& a, vector<int>& b) {\n if(a[0]==b[0]) return a[1]>b[1];\n return a[0]<b[0];\n });\n // for(int i=0; i<N; i++) cout<<envelopes[i][0]<<" "<<envelopes[i][1]<<endl;\n vector<int> dp;\n dp.push_back(envelopes[0][1]);\n int l=1;\n for(int i=1; i<N; i++) {\n if(envelopes[i][1]>dp.back()) {\n dp.push_back(envelopes[i][1]);\n l++;\n }\n else {\n int index = lower_bound(dp.begin(), dp.end(), envelopes[i][1]) - dp.begin();\n dp[index] = envelopes[i][1];\n }\n }\n return l;\n }\n};\n```\n**Time complexity:** `O(NlogN)` *(for sorting)* + `O(NlogN)` *(for inserting into the DP vector * for finding the lower bound)* ~ `O(NlogN)`\n**Space complexity:** `O(N)` *(size of the DP vector)*\n\nDo hit a like if you like the explanation. Thank you. | 5 | 0 | ['Dynamic Programming', 'C', 'Binary Tree'] | 1 |
russian-doll-envelopes | C++ || Sorting and LIS || | c-sorting-and-lis-by-pandeyji2023-20fz | \nclass Solution {\npublic:\n \n int find_bound(vector<int> &dp,int target){\n \n int pos = dp.size();\n \n int low = 0;\n int | pandeyji2023 | NORMAL | 2022-05-25T17:20:27.033220+00:00 | 2022-05-25T17:25:34.171309+00:00 | 538 | false | ```\nclass Solution {\npublic:\n \n int find_bound(vector<int> &dp,int target){\n \n int pos = dp.size();\n \n int low = 0;\n int high = dp.size()-1;\n \n while(low<=high){\n \n int mid = low + (high-low)/2;\n \n if(dp[mid]>=target){\n pos = mid;\n high = mid-1;\n }\n else{\n low = mid+1;\n }\n \n }\n \n return pos;\n \n } \n \n \n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n sort(envelopes.begin(),envelopes.end());\n \n for(int i=0;i<envelopes.size();){\n int start = i;\n int num = envelopes[i][0];\n \n \n while(i<envelopes.size() && envelopes[i][0]==num){\n i++;\n }\n \n int end = i-1;\n \n reverse(envelopes.begin()+start,envelopes.begin()+end+1);\n \n }\n \n \n vector<int> height;\n \n for(int i=0;i<envelopes.size();i++){\n int h = envelopes[i][1];\n height.push_back(h);\n \n }\n \n vector<int> dp;\n \n for(int i=0;i<height.size();i++){\n int sz = dp.size();\n \n if(sz == 0){\n dp.push_back(height[i]);\n }\n else if(dp[sz-1]<height[i]){\n dp.push_back(height[i]);\n }\n else{\n // here upper-bound will not work for the test-case--> \n // [[15,8],[2,20],[2,14],[4,17],[8,19],[8,9],[5,7],[11,19],[8,11],[13,11],[2,13],[11,19],[8,11], [13,11],[2,13],[11,19],[16,1],[18,13],[14,17],[18,19]] \n \n // So, here we create custom function for find the exact position for height[i] element in dp array... \n int pos = find_bound(dp,height[i]);\n if(pos >= dp.size()) continue;\n dp[pos] = height[i];\n \n }\n }\n \n\t return dp.size();\n }\n};\n``` | 5 | 0 | [] | 0 |
russian-doll-envelopes | C++ || LIS || Binary Search || with detailed comments | c-lis-binary-search-with-detailed-commen-weqx | c++\nclass Solution {\npublic:\n static bool my_comp(vector<int> &a, vector<int> &b){\n if (a[0] == b[0]) {\n return (a[1] > b[1]);\n | dha72 | NORMAL | 2022-05-25T16:54:19.402997+00:00 | 2022-05-25T16:54:19.403034+00:00 | 434 | false | ```c++\nclass Solution {\npublic:\n static bool my_comp(vector<int> &a, vector<int> &b){\n if (a[0] == b[0]) {\n return (a[1] > b[1]);\n }\n return a[0] < b[0];\n }\n \n int maxEnvelopes(vector<vector<int>>& envelopes) {\n /* Sort envelopes in increasing order of width and decreasing order of height.\n * Then, apply LIS on heights.\n * LIS:\n * Create a tmp_arr to save sequence.\n * If curr_elem in arr is greater than tmp_arr.back(), append curr_elem to tmp_arr.\n * Else, replace elem in tmp_arr such that,\n * curr_elem < tmp_elem and it should not break incerasing nature of tmp_arr.\n * (Binary search for curr_elem in tmp_arr will give you the proper index)\n * Finally return len of tmp_arr.\n */\n \n sort(envelopes.begin(), envelopes.end(), my_comp);\n\n vector<int> tmp;\n tmp.push_back(envelopes[0][1]);\n for (int i = 1; i < envelopes.size(); i++){\n int curr_elem = envelopes[i][1];\n if (tmp.back() < curr_elem)\n {\n tmp.push_back(curr_elem);\n }\n else \n {\n int idx = lower_bound(tmp.begin(), tmp.end(), curr_elem) - tmp.begin();\n tmp[idx] = curr_elem;\n }\n \n }\n return tmp.size();\n }\n};\n``` | 5 | 0 | ['C'] | 0 |
russian-doll-envelopes | 4 line of code in c++ using dp | 4-line-of-code-in-c-using-dp-by-kkg2002-ghr1 | ```\n// please upvote if you like it\nclass Solution {\npublic:\n int maxEnvelopes(vector>& E) {\n sort(E.begin(), E.end(), \n -> bool {r | kkg2002 | NORMAL | 2022-05-25T00:38:55.298863+00:00 | 2022-05-25T00:39:25.589288+00:00 | 961 | false | ```\n// please upvote if you like it\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& E) {\n sort(E.begin(), E.end(), [](vector<int>& a, vector<int>& b) \n -> bool {return a[0] == b[0] ? b[1] < a[1] : a[0] < b[0];});\n vector<int> dp;\n for (auto& env : E) {\n int height = env[1];\n int left = lower_bound(dp.begin(), dp.end(), height) - dp.begin();\n if (left == dp.size()) dp.push_back(height);\n dp[left] = height;\n }\n return dp.size();\n }\n}; | 5 | 1 | ['Dynamic Programming'] | 0 |
russian-doll-envelopes | TREESET || JAVA | treeset-java-by-flyroko123-8mcs | \n \n class Solution {\n\tpublic int maxEnvelopes(int[][] envelopes) {\n\t\n //sorting the array width wise but when equal sorting in descending ord | flyRoko123 | NORMAL | 2022-01-03T11:49:01.262757+00:00 | 2022-01-03T11:49:01.262803+00:00 | 141 | false | \n \n class Solution {\n\tpublic int maxEnvelopes(int[][] envelopes) {\n\t\n //sorting the array width wise but when equal sorting in descending order of the heights\n Arrays.sort(envelopes,(a,b)-> a[0]!=b[0] ? a[0]-b[0] : b[1]-a[1]);\n \n //implementing treeset which implements bst interface\n TreeSet<Integer> s=new TreeSet<>();\n \n //code for finding LIS of the height values in O(nlogn) time\n for(int i=0;i<envelopes.length;i++){\n Integer higher_value=s.ceiling(envelopes[i][1]);\n \n if(higher_value==null){\n s.add(envelopes[i][1]);\n }\n \n else{\n s.remove(higher_value);\n s.add(envelopes[i][1]);\n }\n \n }\n return s.size();\n }\n} | 5 | 0 | [] | 0 |
russian-doll-envelopes | Easy to understand || Sorting technique || LIS || D.P | easy-to-understand-sorting-technique-lis-xk0p | class Solution {\npublic:\n\n int maxEnvelopes(vector>& envelopes) {\n \n int n = envelopes.size();\n if(n==0)\n return 0;\n | luciferraturi | NORMAL | 2021-12-16T09:45:55.753900+00:00 | 2021-12-16T09:46:09.379721+00:00 | 327 | false | class Solution {\npublic:\n\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n int n = envelopes.size();\n if(n==0)\n return 0;\n \n sort(envelopes.begin(),envelopes.end());\n vector<int> dp(n+1,1);\n int max = 1;\n for(int i=1;i<n;++i)\n {\n for(int j=0;j<i;++j)\n {\n if(envelopes[i][0]>envelopes[j][0]\n && envelopes[i][1]>envelopes[j][1]\n && 1+dp[j]>dp[i])\n dp[i] = 1 + dp[j];\n if(max<dp[i])\n max = dp[i];\n }\n }\n return max;\n }\n}; | 5 | 0 | ['Dynamic Programming', 'C', 'Sorting'] | 0 |
russian-doll-envelopes | Rust solution | rust-solution-by-sugyan-8xw2 | rust\nuse std::cmp::Reverse;\n\nimpl Solution {\n pub fn max_envelopes(envelopes: Vec<Vec<i32>>) -> i32 {\n let mut envelopes = envelopes\n | sugyan | NORMAL | 2021-03-30T14:18:58.731615+00:00 | 2021-03-30T14:18:58.731655+00:00 | 122 | false | ```rust\nuse std::cmp::Reverse;\n\nimpl Solution {\n pub fn max_envelopes(envelopes: Vec<Vec<i32>>) -> i32 {\n let mut envelopes = envelopes\n .iter()\n .map(|envelope| (envelope[0], Reverse(envelope[1])))\n .collect::<Vec<_>>();\n envelopes.sort_unstable();\n let mut dp = Vec::new();\n for &(_, Reverse(h)) in &envelopes {\n if let Some(i) = dp.binary_search(&h).err() {\n if i < dp.len() {\n dp[i] = h;\n } else {\n dp.push(h);\n }\n }\n }\n dp.len() as i32\n }\n}\n``` | 5 | 1 | ['Rust'] | 1 |
russian-doll-envelopes | simple DP recursive solution easy to understand (1D dp) | simple-dp-recursive-solution-easy-to-und-0xsf | \nps:- you can make it more faster by sorting the array of envelopes\n\n\nclass Solution {\n static int n;\n static int dp[];\n public int maxEnvelopes | ankitsingh9164 | NORMAL | 2020-12-11T06:44:48.150159+00:00 | 2020-12-11T06:48:32.816979+00:00 | 344 | false | \nps:- you can make it more faster by sorting the array of envelopes\n\n```\nclass Solution {\n static int n;\n static int dp[];\n public int maxEnvelopes(int[][] a) {\n n=a.length;\n dp=new int[n+1];\n Arrays.fill(dp,-1);\n return dfs(a,n); \n }\n \n private static int dfs(int a[][],int prev){\n if(dp[prev]!=-1) return dp[prev];\n \n int x=0,y=0;\n if(prev!=n) {\n x=a[prev][0];\n y=a[prev][1];\n }\n int ans=0;\n for(int i=0;i<n;i++){\n if(a[i][0]>x && a[i][1]>y){\n ans=Math.max(ans,1+dfs(a,i));\n }\n }\n return dp[prev]=ans;\n }\n}\n``` | 5 | 1 | [] | 1 |
russian-doll-envelopes | C++ | LIS Based | (N * logN) | With Explanation | c-lis-based-n-logn-with-explanation-by-d-2gxq | We have to find the envelopes with fit inside each other. It is very intuitive to think that the envelopes which fit inside each other would have dimensions in | d_ankit | NORMAL | 2020-09-18T11:07:25.084065+00:00 | 2023-08-27T17:49:03.489183+00:00 | 431 | false | We have to find the envelopes with fit inside each other. It is very intuitive to think that the envelopes which fit inside each other would have dimensions in ascending order. So, in the first step, we would arrange the input in increasing order by sorting them on basis of width. \n\nInput : [[5,4],[6,4],[6,7],[2,3]]\nAfter sorting: [[2,3],[5,4],[6,4],[6,7]]\n\nAfter sorting the width, now we have to take care of the heights as well. Again, to make sure that one envelops exactly fit in another the height too has to be in increasing order. Basically now are just left with a subproblem, to find the largest increasing subsequence of height. \n\nFor the above example, we are left with finding find LIS of [3,4,4,7]. \nHere LIS would be 3 -> 4 -> 7, which gives the answer 3.\n\n**Notes:**\n1. Comparator functions have been used to handle caes when widgth are same.\n2. Please go through Leetcode 300( Longest Increasing Subsequence) in order to understand the approach used for finding LIS.\n\n\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(), envelopes.end(), [](auto a, auto b){return (a[0]==b[0])?a[1]>b[1]:a[0]<b[0];}); \n\t\t// sort in increasing order of width\n \n vector<vector<int>> lis;\n auto comp=[](auto a, auto b){return (a[1]<b[1])&&(a[0]<b[0]);};\n\t\t//custom comparator for comparing lengths\n \n for(int i =0; i < envelopes.size(); i++){ // find LIS of heights \n auto it = lower_bound(lis.begin(), lis.end(), envelopes[i], comp);\n \n if(it == lis.end()){\n lis.emplace_back(envelopes[i]);\n } else{\n *it = envelopes[i];\n }\n }\n \n return lis.size();\n }\n};\n``` | 5 | 1 | ['Binary Search', 'C', 'C++'] | 1 |
russian-doll-envelopes | C++ easy dp solution in O(nlogn) time and O(n) space with explanation | c-easy-dp-solution-in-onlogn-time-and-on-4by0 | This question is a varation of Longest increasing subsequence problem. We need to find the largest number of rectangles which can be russian doll. So, we need t | ashish8950 | NORMAL | 2020-08-01T07:28:08.747098+00:00 | 2020-08-01T07:28:08.747154+00:00 | 1,014 | false | This question is a varation of Longest increasing subsequence problem. We need to find the largest number of rectangles which can be russian doll. So, we need to first sort the numbers with respect to height or width. I have sorted the number according to width. Also, it is given that the height and width should be strictly greater so, to for that while sorting we need to take care that when the width are equal, then we must sort them according to decreaing height. This is done so that we don\'t include the equal heights sequence in the answer.\n\n```\nclass Solution {\npublic:\n static bool func(vector<int>& e1, vector<int>& e2){\n return (e1[0]==e2[0])?e1[1]>e2[1]:e1[0]<e2[0];\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n sort(envelopes.begin(),envelopes.end(),func);\n vector<int> v;\n for(int i=0;i<envelopes.size();i++)\n {\n if(i==0 || envelopes[i][1]>v[v.size()-1])\n {\n v.push_back(envelopes[i][1]);\n }\n else\n {\n int index=binarysearch(v,envelopes[i][1]);\n v[index]=envelopes[i][1];\n }\n }\n return v.size(); \n }\n \n int binarysearch(vector<int> &v,int x)\n {\n int i=0;\n int j=v.size()-1;\n int ans=0;\n while(i<=j)\n {\n int mid=(i+(j-i)/2);\n if(v[mid]==x)\n return mid;\n else if(v[mid]>x)\n {\n ans=mid;\n j=mid-1;\n }\n else\n i=mid+1;\n }\n return ans;\n }\n \n};\n``` | 5 | 0 | ['Binary Search', 'Dynamic Programming', 'C', 'C++'] | 0 |
russian-doll-envelopes | Solution using lambda in python | solution-using-lambda-in-python-by-aayuu-yja5 | IDEA:\n1. Sort envelopes according to width or you can sort height also.\n2. Now , find Longest Increasing Subsequence of height or width(if you sort envelopes | aayuu | NORMAL | 2020-06-27T07:11:55.054375+00:00 | 2020-06-27T07:11:55.054422+00:00 | 629 | false | IDEA:\n1. Sort envelopes according to width or you can sort height also.\n2. Now , find Longest Increasing Subsequence of height or width(if you sort envelopes according to height).\n3. Your answer will be length of Longest Increasing Subsequence.\n\n***Note**: I have used DP to find LIS with complexity O(n^2) you can also use binary approach which leads to O(nlogn).*\n```\ndef maxEnvelopes(self, envelopes: List[List[int]]) -> int:\n if not envelopes:\n return 0\n envelopes = sorted(envelopes,key=lambda envelop:(envelop[0],-1*envelop[1]))\n return self.LIS(envelopes)\n\n def LIS(self,envelopes):\n lis = [1]*len(envelopes)\n res = 1\n for i in range(1,len(envelopes)):\n for j in range(0,i):\n if(envelopes[j][1] < envelopes[i][1] and lis[i]<lis[j]+1):\n lis[i] = lis[j]+1\n if res < lis[i]:\n res = lis[i]\n return res\n```\nStill facing difficulties, comment below.\nYou can upvote too. :) | 5 | 1 | ['Array', 'Dynamic Programming', 'Sorting', 'Python3'] | 2 |
russian-doll-envelopes | Java 8-liner using TreeSet | java-8-liner-using-treeset-by-yubad2000-enab | \nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a, b)-> a[0]==b[0]? b[1]-a[1]: a[0]-b[0]);\n TreeSe | yubad2000 | NORMAL | 2020-02-16T20:03:42.820478+00:00 | 2020-02-16T20:03:42.820529+00:00 | 229 | false | ```\nclass Solution {\n public int maxEnvelopes(int[][] envelopes) {\n Arrays.sort(envelopes, (a, b)-> a[0]==b[0]? b[1]-a[1]: a[0]-b[0]);\n TreeSet<Integer> sortedSet = new TreeSet<>();\n for (int[] env : envelopes) {\n Integer ceiling = sortedSet.ceiling(env[1]); \n if (ceiling != null && ceiling.intValue() != env[1]) sortedSet.remove(ceiling);\n sortedSet.add(env[1]);\n } \n return sortedSet.size();\n }\n}\n``` | 5 | 0 | [] | 2 |
russian-doll-envelopes | C++ nlogn solution | c-nlogn-solution-by-louis1992-m044 | class Solution {\n public:\n int maxEnvelopes(vector<pair<int, int>>& envelopes) {\n auto Cmp = [](const pair<int, int> &a, const pair<int, | louis1992 | NORMAL | 2016-06-07T19:01:23+00:00 | 2016-06-07T19:01:23+00:00 | 1,303 | false | class Solution {\n public:\n int maxEnvelopes(vector<pair<int, int>>& envelopes) {\n auto Cmp = [](const pair<int, int> &a, const pair<int, int> &b) { \n if(a.first < b.first) return true;\n if(a.first == b.first && a.second > b.second) return true;\n return false;\n };\n auto Cmp2 = [](const pair<int, int> &a, const pair<int, int> &b) { \n return a.second < b.second;\n };\n sort(envelopes.begin(), envelopes.end(), Cmp);\n \n vector<pair<int, int>> res;\n for(int i=0; i<envelopes.size(); i++) {\n auto it = std::lower_bound(res.begin(), res.end(), envelopes[i], Cmp2);\n if(it == res.end()) res.push_back(envelopes[i]);\n else *it = envelopes[i];\n }\n return res.size();\n }\n }; | 5 | 0 | ['Binary Tree', 'C++'] | 0 |
russian-doll-envelopes | Russian Doll Envelopes C++ solution | russian-doll-envelopes-c-solution-by-ris-30ep | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rissabh361 | NORMAL | 2023-09-07T22:06:30.435061+00:00 | 2023-09-07T22:06:30.435087+00:00 | 719 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n static bool comp(vector<int> &a, vector<int> &b){\n if(a[0] == b[0])\n return a[1]>b[1];\n\n return a[0]<b[0];\n }\n int solveOptimal(int n, vector<vector<int>>& envelopes){\n if(n==0)\n return 0;\n vector<int> ans;\n ans.push_back(envelopes[0][1]);\n for(int i=1; i<n; i++){\n if(envelopes[i][1]>ans.back())\n ans.push_back(envelopes[i][1]);\n else{\n int index = lower_bound(ans.begin(),ans.end(),envelopes[i][1]) - ans.begin();\n ans[index] = envelopes[i][1];\n }\n }\n return ans.size();\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n int n = envelopes.size();\n sort(envelopes.begin(),envelopes.end(), comp);\n\n return solveOptimal(n,envelopes);\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
russian-doll-envelopes | Easy C++ solution DP+binary search approach Beat 99.61%✅✅ | easy-c-solution-dpbinary-search-approach-l0um | \n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) O(nlogn)\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) O(n) | Harshit-Vashisth | NORMAL | 2023-07-28T19:29:18.027342+00:00 | 2023-07-28T19:29:18.027376+00:00 | 986 | false | \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(n)\n\n# Code\n```\nclass Solution {\npublic:\n static bool compare(vector<int>& a, vector<int>& b){\n if(a[0]==b[0])\n return a[1]>b[1];\n return a[0]<b[0];\n }\n int mostOptimal(vector<vector<int>>& envelopes){\n \n vector<int> ans;\n ans.push_back(envelopes[0][1]);\n for(int i=1;i<envelopes.size();i++){\n if(envelopes[i][1]>ans.back())\n ans.push_back(envelopes[i][1]);\n else{\n int index=lower_bound(ans.begin(),ans.end(),envelopes[i][1])-ans.begin();\n ans[index]=envelopes[i][1];\n }\n }\n return ans.size();\n }\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n sort(envelopes.begin(),envelopes.end(),compare);\n int prev=-1;\n int curr=0;\n return mostOptimal(envelopes);\n\n \n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
russian-doll-envelopes | DP + BINARY SEARCH Solution | dp-binary-search-solution-by-2005115-twim | \n# Approach\nSort the envelopes based on their widths in ascending order. If two envelopes have the same width, sort them in descending order of their heights. | 2005115 | NORMAL | 2023-07-13T15:59:28.901626+00:00 | 2023-07-13T15:59:28.901655+00:00 | 955 | false | \n# Approach\nSort the envelopes based on their widths in ascending order. If two envelopes have the same width, sort them in descending order of their heights. This sorting is done using a custom comparator function passed to the sort function.\n\nExtract the heights of the sorted envelopes and store them in the ans vector.\n\nDefine a helper function lis that takes the ans vector and its size n as input and returns the length of the longest increasing subsequence.\n\nInitialize a result vector and push the first element of ans into it.\n\nIterate through the remaining elements of ans starting from index 1.\n\nIf the current element is greater than the last element in the result vector, it can be nested inside the envelopes encountered so far. Hence, push the current element to the result vector.\n\nIf the current element is not greater, find the index where it can be placed in the result vector using the lower_bound function. Update the element at that index with the current element.\n\nFinally, return the size of the result vector, which represents the length of the longest increasing subsequence.\n\nIn the maxEnvelopes function, call the lis function with the ans vector and its size, and return the result.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(NLOGN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int lis(vector<int>& ans, int n) {\n if (n == 0) {\n return 0;\n }\n \n vector<int> result;\n result.push_back(ans[0]);\n \n for (int i = 1; i < n; i++) {\n if (ans[i] > result.back()) {\n result.push_back(ans[i]);\n }\n else {\n int index = lower_bound(result.begin(), result.end(), ans[i]) - result.begin();\n result[index] = ans[i];\n }\n }\n \n return result.size();\n }\n \n int maxEnvelopes(vector<vector<int>>& envelopes) {\n // SORT THE VECTOR\n sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);\n });\n \n vector<int> ans;\n for (auto i : envelopes) {\n ans.push_back(i[1]);\n }\n \n int n = ans.size();\n return lis(ans, n);\n }\n};\n\n``` | 4 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'C++'] | 1 |
russian-doll-envelopes | Highly Intutive and Using Comparator | highly-intutive-and-using-comparator-by-924iy | \nclass Solution {\n\tpublic int maxEnvelopes(int[][] envelopes) {\n\t\tint n = envelopes.length;\n\t\tArrays.sort(envelopes, new Comparator<int[]>() {\n\t\t\tp | Aditya_jain_2584550188 | NORMAL | 2022-07-17T05:45:36.545114+00:00 | 2022-07-17T05:45:36.545154+00:00 | 401 | false | ```\nclass Solution {\n\tpublic int maxEnvelopes(int[][] envelopes) {\n\t\tint n = envelopes.length;\n\t\tArrays.sort(envelopes, new Comparator<int[]>() {\n\t\t\tpublic int compare(int[] a, int[] b) {\n\t\t\t\treturn a[0] == b[0] ? b[1] - a[1] : a[0] - b[0];\n\t\t\t}\n\t\t});\n\t\tint[] height = new int[n];\n\t\tfor (int i = 0; i < n; i++)\n\t\t\theight[i] = envelopes[i][1];\n\n\t\treturn lengthOfLIS(height);\n\t}\n\n\tpublic int lengthOfLIS(int[] arr) {\n\t\tint piles = 0, n = arr.length;\n\t\tint[] top = new int[n];\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tint poker = arr[i];\n\t\t\tint left = 0, right = piles;\n\t\t\twhile (left < right) {\n\t\t\t\tint mid = (left + right) / 2;\n\t\t\t\tif (top[mid] >= poker)\n\t\t\t\t\tright = mid;\n\t\t\t\telse\n\t\t\t\t\tleft = mid + 1;\n\t\t\t}\n\t\t\tif (left == piles)\n\t\t\t\tpiles++;\n\t\t\ttop[left] = poker;\n\t\t}\n\t\treturn piles;\n\t}\n}\n``` | 4 | 0 | ['Java'] | 0 |
russian-doll-envelopes | C++ Using Lower Bound | LIS | c-using-lower-bound-lis-by-vaibhavshekha-4znf | ```\nstatic bool cmp(vector&a,vector&b){\n if(a[0]!=b[0]) return a[0]b[1];\n }\n int maxEnvelopes(vector>& e) {\n sort(e.begin(),e.end(),cmp | vaibhavshekhawat | NORMAL | 2022-02-04T07:15:30.562798+00:00 | 2022-02-04T16:53:15.373559+00:00 | 397 | false | ```\nstatic bool cmp(vector<int>&a,vector<int>&b){\n if(a[0]!=b[0]) return a[0]<b[0];\n return a[1]>b[1];\n }\n int maxEnvelopes(vector<vector<int>>& e) {\n sort(e.begin(),e.end(),cmp);\n int n=e.size();\n vector<int> dp;\n for(int i=0;i<n;i++){\n auto it=lower_bound(dp.begin(),dp.end(),e[i][1]);\n if(it==dp.end()) dp.push_back(e[i][1]);\n else *it=e[i][1];\n }\n return dp.size();\n } | 4 | 1 | ['C'] | 0 |
russian-doll-envelopes | C++ | LIS-IMPLEMENTATION | COMPARATOR-TRICK | c-lis-implementation-comparator-trick-by-1m0k | PLEASE UPVOTE IF U LIKE MY SOLUTION AND EXPLANATION.\n\n\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n / | chikzz | NORMAL | 2022-01-03T12:54:21.205050+00:00 | 2022-01-03T14:29:32.623426+00:00 | 159 | false | **PLEASE UPVOTE IF U LIKE MY SOLUTION AND EXPLANATION.**\n\n```\nclass Solution {\npublic:\n int maxEnvelopes(vector<vector<int>>& envelopes) {\n \n //sort the given vector in non-decreasing manner onb basis of either height or width\n //HERE I HAVE SORTED ON THE BASIS OF HEIGHT\n \n //we then sort the other parameter in non-increasing manner for similar heights.(i.e., for a pair of\n //envelop if their heights are same then the one with greater width should come at first than the \n //lesser one in the sorted array)\n \n //we do this because we know that we can only consider one envelop from a group of similar-height\n //envelops but we cannot claim that we should take the envelop with (minimum of their widths) \n //as their might be a case [h,w]-->[H,W] where h<H but w>W or that we take the maximum of their \n //widths) for case like [H,W]-->[h,w] where H<h and W>w.\n \n //so we need an optimal sequence which provide us with longest possible length of envelopes\n //considering the above cases.\n \n \n //HENCE WE PERFORM LIS ON THE OTHER PARAMETER AFTER SORTING IT IN THE MANNER MENTIONED ABOVE\n //FOR ENSURING --->[h,w]-->[H,W] for which the W is just greater than w \n //in the set of [H]->[W1,W2,W3...]\n \n\t\t//counter case:if we arrange the width in non-decreasing order then we will have a sequence where\n\t\t//width will be in increasing order but we will include similar heights in this case.\n\t\t//eg:[[1,2],[1,3],[2,4],[2,5]]--->if we follow the above method we will get the entire seq (length=4)\n\t\t//as ans but the correct ans is 2.\n\t\t\n sort(envelopes.begin(),envelopes.end(),[&](const vector<int>& v1,const vector<int>& v2){return v1[0]==v2[0]?v1[1]>v2[1]:v1[0]<v2[0];});\n \n vector<int>LIS;\n for(auto &x:envelopes)\n {\n if(LIS.empty()||LIS.back()<x[1])\n LIS.push_back(x[1]);\n else\n {\n int idx=lower_bound(LIS.begin(),LIS.end(),x[1])-LIS.begin();\n LIS[idx]=x[1];\n }\n }\n return LIS.size();\n }\n};\n``` | 4 | 1 | [] | 1 |
russian-doll-envelopes | Python, Clean LIS | python-clean-lis-by-warmr0bot-i4xf | Idea \nThe idea is to apply LIS algorithm, please solve question 300 first, if you are unfamiliar with it, because this problem adds a level of complexity to th | warmr0bot | NORMAL | 2021-03-31T08:43:36.646324+00:00 | 2021-03-31T08:43:36.646352+00:00 | 449 | false | # Idea \nThe idea is to apply LIS algorithm, please solve question 300 first, if you are unfamiliar with it, because this problem adds a level of complexity to that problem. The key idea here is to make sure to sort the elements in ascending order by the first element and descending order by the second element.\n```\ndef maxEnvelopes(self, envelopes):\n\ttails = []\n\tfor _, b in sorted(envelopes, key = lambda x: (x[0], -x[1])): \n\t\tidx = bisect.bisect_left(tails, b)\n\t\ttails[idx:idx+1] = [b]\n\treturn len(tails)\n``` | 4 | 1 | ['Python', 'Python3'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.