question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
ipo | Golang | Priority Queue | golang-priority-queue-by-yfw13-2mw8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n- golang implementation | tw13 | NORMAL | 2023-02-23T00:59:31.859210+00:00 | 2023-02-23T00:59:31.859246+00:00 | 542 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- golang implementation of official solution https://leetcode.com/problems/ipo/solutions/2959870/ipo/?orderBy=most_votes\n\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntype Project struct {\n profit, capital int\n}\n\ntype IntHeap []int\nfunc (h IntHeap) Len() int { return len(h) }\nfunc (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }\nfunc (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\nfunc (h *IntHeap) Push(x interface{}) { *h = append(*h, x.(int)) }\nfunc (h *IntHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\tx := old[n-1]\n\t*h = old[0 : n-1]\n\treturn x\n}\n\nfunc findMaximizedCapital(k int, w int, profits []int, capital []int) int {\n n := len(profits)\n projects := make([]Project, n)\n for i := range profits {\n projects[i] = Project{profits[i], capital[i]}\n }\n sort.Slice(projects, func (i, j int) bool {\n return projects[i].capital < projects[j].capital\n })\n \n q := &IntHeap{}\n heap.Init(q)\n\n ptr := 0\n for i := 0; i < k; i++ {\n for ptr < n && projects[ptr].capital <= w {\n heap.Push(q, projects[ptr].profit)\n ptr++\n }\n if q.Len() == 0 {\n break\n }\n w += heap.Pop(q).(int)\n }\n return w\n}\n``` | 3 | 0 | ['Go'] | 1 |
ipo | ✅easiest-soln | Goldman Sachs🔥| well-explained👁️ | easiest-soln-goldman-sachs-well-explaine-mfqy | If you found my answer helpful, please consider giving it an upvote\uD83D\uDE0A\nReviseWithArsh #6Companies30Days Challenge 2023\nChallenge Company 2 : Goldman | nandini-gangrade | NORMAL | 2023-01-11T13:50:55.694704+00:00 | 2023-01-11T13:50:55.694741+00:00 | 623 | false | ## If you found my answer helpful, please consider giving it an upvote\uD83D\uDE0A\n**ReviseWithArsh #6Companies30Days Challenge 2023\nChallenge Company 2 : Goldman Sachs\nQ9. IPO**\n\n### Approach\n\n\n\n\n### Complexity\n- **Time complexity of O(nlogn)** where n is the number of projects. Because of the sorting and priority queue operations\n- **Space complexity of O(n)** is due to the usage of priority queue and project array\n\n# Code\n```\nclass Solution {\npublic:\n int findMaximizedCapital(int investmentOpportunities, int initialCapital, vector<int>& profits, vector<int>& capitalRequirements) {\n // Create an array of pairs, where each pair contains the capital required and its corresponding profit for a project\n vector <pair <int,int>> projects;\n for(int i = 0; i<profits.size(); i++) projects.push_back({capitalRequirements[i],profits[i]});\n // Sort the array by capital required\n sort(projects.begin(),projects.end());\n \n // Use a priority queue to store the profits of projects with capital requirements less than or equal to the current capital\n priority_queue <int> pq;\n int currentCapital = initialCapital, i=0;\n // Continue until no more investments are available or all projects have been considered\n while(i<projects.size() && investmentOpportunities) {\n // If the current capital is greater than or equal to the capital requirement of a project\n if(currentCapital >= projects[i].first) {\n // add the project to priority queue\n pq.push(projects[i++].second); \n } else {\n // if there is a project in priority queue with lower capital requirement than current capital, \n // we extract the project with highest profit\n if(!pq.empty()){\n currentCapital += pq.top();\n pq.pop();\n investmentOpportunities--;\n }\n else return currentCapital; // no investment opportunities remaining\n }\n }\n // Add remaining projects to the current capital\n while(!pq.empty() && investmentOpportunities > 0) {\n currentCapital += pq.top();\n pq.pop();\n investmentOpportunities--;\n }\n // Return the final capital\n return currentCapital;\n }\n};\n\n```\n- This code finds the maximum final capital that a company can obtain by investing in k projects.\n- It takes an initial capital, and for each project, an array of profits and an array of capital requirements.\n- It first creates a pair of capital requirements and profits for each project, sorts it by capital requirements, and then uses a priority queue to keep track of the maximum profits for projects that have capital requirements less than or equal to the current capital.\n- For each new capital requirement that is less than or equal to the current capital, it is added to the priority queue. When the current capital is less than the capital requirement of a project, it pops the project with the highest profit from the priority queue, adds its profit to the current capital, and decrements the number of investments available. | 3 | 0 | ['C++'] | 0 |
ipo | Priority-Queue||C++ | priority-queuec-by-ivr_turbo-e64y | \nclass Solution {\npublic:\n int findMaximizedCapital(int k, int W, vector<int>& Profits, vector<int>& Capital) {\n priority_queue<int>pq; // top ele | ivr_turbo | NORMAL | 2021-01-09T20:06:44.559795+00:00 | 2021-01-09T20:08:30.812207+00:00 | 411 | false | ```\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int W, vector<int>& Profits, vector<int>& Capital) {\n priority_queue<int>pq; // top element = max profit among all projects with Capital<=W; \n vector<pair<int,int>>v; // to store index of projects\n for(int i = 0;i<Capital.size();i++){\n v.push_back({Capital[i],i});\n }\n sort(v.begin(),v.end());\n int ans = W;\n int j = 0;\n while(k){\n //push values\n while(j<Capital.size() && v[j].first<=W){\n pq.push(Profits[v[j].second]);// push all profits for which capital<=W\n j++;\n }\n if(!pq.empty()){\n ans+=pq.top();// take the max profit among them\n W = W+pq.top();// new capital\n pq.pop();\n \n }\n k--;\n \n }\n return ans;\n \n }\n};\n``` | 3 | 0 | ['C', 'Heap (Priority Queue)'] | 2 |
ipo | greedy solution using 2 priority queue | greedy-solution-using-2-priority-queue-b-bq1j | \n//pair defined\ntypedef pair<int,int> p;\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int W, vector<int>& Profits, vector<int>& Capital) {\ | mohit_chau | NORMAL | 2020-09-23T20:25:06.154937+00:00 | 2020-09-23T20:25:06.154987+00:00 | 402 | false | ```\n//pair defined\ntypedef pair<int,int> p;\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int W, vector<int>& Profits, vector<int>& Capital) {\n\t //create minHeap to sort on the basis of capital\n priority_queue<p, vector<p>, greater<p>> minHeap;\n\t\t//create maxHeap to sort on the basis of profit\n priority_queue<p> maxHeap;\n\t\t//push all the capitals and profit to capital priority queue\n for(int i=0;i<Profits.size();i++){\n minHeap.push(make_pair(Capital[i], Profits[i]));\n }\n\t\t//push suitable profits and capital to profit priority queue from capital priority queue\n for(int i=0;i<k;i++){\n while(minHeap.size()>0 and minHeap.top().first<=W){\n pair<int,int> p=minHeap.top();\n maxHeap.push(make_pair(p.second,p.first));\n minHeap.pop();\n }\n if(maxHeap.size()>0){\n W+=maxHeap.top().first;\n maxHeap.pop();\n }\n }\n return W;\n }\n};\n``` | 3 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 1 |
ipo | Python Greedy | python-greedy-by-wangqiuc-x4d5 | The heuristic is, for each investment, we choose the largest profit from current doable projects, where doable means project\'s requested capital is no higher t | wangqiuc | NORMAL | 2019-04-15T03:11:50.193395+00:00 | 2019-07-26T18:32:06.141196+00:00 | 393 | false | The heuristic is, for each investment, we choose the largest profit from current doable projects, where doable means project\'s requested capital is no higher than current ```W```. \nAnd our ```W``` should keep increasing as capital doesn\'t decrease when we invest. Therefore, a greedy search can solve the problem by one-pass scan for each project with order of project\'s capital.\nTo implement it, we first sort project pair (profit, capital) by capital. \nThen for each investment, we push all doable projects (project\'s capital < W) into a max heap ordered by project\'s profit. Then we just pop the project with the highest project and add its profit to our capital ```W```. \nWe do it for ```k``` times and the maximum capital will be stored in ```W```.\n```\ndef findMaximizedCapital(k, W, Profit, Capital):\n\theap, projects = [], sorted(zip(Profit, Capital), key=lambda x:x[1])\n\ti, n = 0, len(projects)\n\tfor _ in range(k):\n\t\twhile i < n and projects[i][1] <= W:\n\t\t\theapq.heappush(heap, (-projects[i][0]))\n\t\t\ti += 1\n\t\tif heap: W -= heapq.heappop(heap)\n\t\telse: break\n\treturn W\n``` | 3 | 0 | [] | 0 |
ipo | Sorting + One O(k)-size Priority Queue Solution | sorting-one-ok-size-priority-queue-solut-d7lc | There are many excellent solutions based on two priority queue solution, however, we do not need to maintain two priority queues that contain all projects. \n I | wangxinbo | NORMAL | 2017-02-15T22:49:03.314000+00:00 | 2017-02-15T22:49:03.314000+00:00 | 1,757 | false | There are many excellent solutions based on two priority queue solution, however, we do not need to maintain two priority queues that contain all projects. \n* If we sort the Capital in increasing order, we can insert "doable" project into the pq until we meet an "undoable" project. \n\n* We need only one priority queue (multiset) to maintain the "doable" projects. Here the key observation is: we can only pop k times. So we do not need to maintain a large priority queue. Every time we find the size of PQ is larger than k (k is shrinking!!!), we just erase the project with least profit from the PQ.\n\n* Note that the worst case time complexity is still O(NlogN), because we need to sort : )\n\n```\nclass Solution {\npublic:\n struct Node {int profit, capital;};\n\n int findMaximizedCapital(int k, int W, vector<int>& Profits, vector<int>& Capital) {\n if(Profits.empty() || Capital.empty()) return W;\n vector<Node*> projects;\n for(int i = 0; i < Profits.size(); i++) \n projects.push_back(new Node({Profits[i], Capital[i]}));\n multiset<int> pq;\n sort(projects.begin(), projects.end(), [&](Node* n1, Node* n2) {return n1->capital < n2->capital;});\n for(auto start = projects.begin(); k > 0; k--) {\n for(; start != projects.end() && (*start)->capital <= W; start++) {\n pq.insert((*start)->profit);\n if(pq.size() > k) pq.erase(pq.begin());\n } \n if(pq.empty()) break;\n W += *pq.rbegin();\n pq.erase(prev(pq.end()));\n }\n return W;\n }\n};\n``` | 3 | 1 | [] | 2 |
ipo | KOTLIN and JAVA solution using 2 PriorityQueues | kotlin-and-java-solution-using-2-priorit-zuyd | \u2618\uFE0F\u2618\uFE0F\u2618\uFE0F If this solution was helpful, please consider upvoting! \u2705\n\n# Intuition\nTo maximize capital, we should always select | anlk | NORMAL | 2024-11-15T21:58:51.308775+00:00 | 2024-11-15T21:58:51.308805+00:00 | 20 | false | \u2618\uFE0F\u2618\uFE0F\u2618\uFE0F If this solution was helpful, please consider upvoting! \u2705\n\n# Intuition\nTo maximize capital, we should always select the most profitable project that we can afford with the current capital. \n\nThis approach combines sorting by capital (to ensure we only pick feasible projects) and prioritizing profits (to maximize returns).\n\nTo efficiently manage this process:\n\n- Use a min-heap to sort projects by their capital requirement.\n- Use a max-heap to keep track of the most profitable projects that can be undertaken given the current capital.\n\n\n# Approach\n- Pair the projects as (capital[i], profits[i]) and sort them by the capital requirement.\n- Use a min-heap to hold the sorted projects.\n- Use a max-heap to hold the profits of projects that are feasible with the current capital.\n- Iterate up to k times:\n - Push all feasible projects (those with capital requirement \u2264 current capital) into the max-heap.\n - If the max-heap is not empty, pick the most profitable project, add its profit to the current capital, and remove it from the heap.\n - If the max-heap is empty, break early (no more feasible projects).\n- Return the final capital.\n\n\n# Code\n```Kotlin []\nclass Solution {\n fun findMaximizedCapital(k: Int, w: Int, profits: IntArray, capital: IntArray): Int {\n val n = profits.size\n\n // Pairing and sorting by capital requirement\n val minCapital = PriorityQueue(compareBy<Pair<Int, Int>> { it.first })\n for (i in profits.indices) {\n minCapital.offer(Pair(capital[i], profits[i]))\n }\n\n val maxProfit = PriorityQueue<Int>(compareByDescending { it })\n var currentCapital = w\n\n // Selecting up to k projects\n repeat(k) {\n // Push all feasible projects into max-heap\n while (minCapital.isNotEmpty() && minCapital.peek().first <= currentCapital) {\n maxProfit.offer(minCapital.poll().second)\n }\n\n // If no feasible projects, break\n if (maxProfit.isEmpty()) return currentCapital\n\n // Select the most profitable project\n currentCapital += maxProfit.poll()\n }\n\n return currentCapital\n }\n}\n```\n\n\n```Java []\nclass Solution {\n public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {\n int n = profits.length;\n\n // Pairing and sorting by capital requirement\n PriorityQueue<int[]> minCapital = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));\n for (int i = 0; i < n; i++) {\n minCapital.offer(new int[]{capital[i], profits[i]});\n }\n\n // Max-heap for profits\n PriorityQueue<Integer> maxProfit = new PriorityQueue<>(Comparator.reverseOrder());\n\n // Selecting up to k projects\n while (k-- > 0) {\n // Push all feasible projects into max-heap\n while (!minCapital.isEmpty() && minCapital.peek()[0] <= w) {\n maxProfit.offer(minCapital.poll()[1]);\n }\n\n // If no feasible projects, break\n if (maxProfit.isEmpty()) break;\n\n // Select the most profitable project\n w += maxProfit.poll();\n }\n\n return w;\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Java', 'Kotlin'] | 0 |
ipo | Easy and Right approach with details | easy-and-right-approach-with-details-by-zqeam | Intuition\nYou are given n projects where the ith project has a pure profit profits[i] and a minimum capital of capital[i] is needed to start it.\n\nInitially, | anand_shukla1312 | NORMAL | 2024-06-15T07:00:24.807943+00:00 | 2024-06-15T07:00:24.807965+00:00 | 418 | false | # Intuition\nYou are given n projects where the ith project has a pure profit profits[i] and a minimum capital of capital[i] is needed to start it.\n\nInitially, you have w capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.\n\nPick a list of at most k distinct projects from given projects to maximize your final capital, and return the final maximized capital.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n-> you can use a greedy approach with the help of a max-heap (priority queue) to efficiently maximize the capital. Here\'s the step-by-step plan:\n\n1): Sort Projects by Capital: First, sort the projects based on their required capital in ascending order.\n2): Use a Max-Heap: Use a max-heap to keep track of the most profitable projects that can be completed with the current available capital.\n3): Iterate Over Projects: Iterate over the projects, and for each project that can be completed with the current capital, add its profit to the max-heap.\n4): Select k Projects: Pick the k most profitable projects by repeatedly extracting the maximum profit from the heap and adding it to the current capital.\n\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- **Time complexity**: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn) + O(nlogn) + O(klogn) = O(nlogn+klogn)\n\nSorting the Projects + Iterating Over Projects + Extracting from the Heap \n\n\n- **Space complexity**: \n*Storing Projects*: We use an additional list to store the sorted projects, which requires: O(n) space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nfrom heapq import heappush, heappop\nfrom typing import List\n\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n # Create a list of projects where each project is (capital, profit)\n projects = list(zip(capital, profits))\n \n # Sort projects by the required capital\n projects.sort()\n \n max_heap = []\n current_capital = w\n i = 0\n n = len(projects)\n \n for _ in range(k):\n # Push all projects that can be started with the current capital to the max-heap\n while i < n and projects[i][0] <= current_capital:\n heappush(max_heap, -projects[i][1]) # Use negative profit to simulate max-heap\n i += 1\n \n # If there are no projects that can be done, break\n if not max_heap:\n break\n \n # Choose the project with the maximum profit\n current_capital += -heappop(max_heap)\n \n return current_capital\n\n``` | 2 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Iterator', 'Python3'] | 2 |
ipo | Easy Explained Solution with comments||C++||Java | easy-explained-solution-with-commentscja-5do8 | Approach\n here are the key points explaining the code:\n\nClass and Comparator Function:\n\nThe Solution class contains the logic to maximize capital after sel | Ashutosh_Kumar_0506 | NORMAL | 2024-06-15T06:22:29.564549+00:00 | 2024-06-15T06:22:29.564577+00:00 | 206 | false | # Approach\n here are the key points explaining the code:\n\nClass and Comparator Function:\n\nThe Solution class contains the logic to maximize capital after selecting projects.\nA static comparator function cmp sorts pairs of capital and profits.\nSorts primarily by ascending capital.\nIf capitals are equal, sorts by descending profit.\nInput Parameters for findMaximizedCapital:\n\nk: Maximum number of projects to select.\nw: Initial capital.\nprofits: Vector of project profits.\ncapital: Vector of capital required for each project.\nSetup and Population of Vector:\n\nn: Number of projects.\nA vector v is created to store pairs of capital and profits.\nThe vector v is populated by iterating through profits and capital.\nSorting:\n\nThe vector v is sorted using the custom comparator cmp.\nPriority Queue (Max-Heap):\n\nA max-heap pq is initialized to store profits of feasible projects.\nj is used to track the current position in the sorted vector v.\nMain Loop:\n\nIterates k times to select up to k projects.\nInner While Loop:\nAdds projects to the max-heap if their capital requirement is \u2264 current capital w.\nMax-Heap Operation:\nIf the max-heap is not empty, the project with the highest profit is selected.\nThe profit is added to w, and the project is removed from the heap.\nBreak Condition:\nIf the max-heap is empty, no more feasible projects can be selected, and the loop breaks.\nReturn Statement:\n\nReturns the final capital w after selecting up to k projects.\nMain Function:\n\nDemonstrates the usage of findMaximizedCapital.\nDefines example vectors profits and capital.\nCalls the function with example parameters.\nPrints the result, showing the maximum capital after selecting projects.\nThis breakdown highlights the structure and logic of the code step-by-step.\n\n# Complexity\n\n- Time complexity:\n\nThe space complexity is O(n), primarily due to the storage of pairs in a vector and elements in a priority queue.\n\n- Space complexity:\n\nThe overall time complexity is O(n log n), dominated by the sorting step. The detailed breakdown is:\nCreating pairs: O(n)\nSorting the pairs: O(n log n)\nInserting and managing elements in the priority queue: O(n log n)\nSelecting up to k projects: O(k log n)\nGiven that k is typically much smaller than n, the dominant term remains O(n log n).\n\n# Code\n```\nclass Solution {\n // Comparator function to sort pairs based on capital in ascending order\n // If capital is the same, sort based on profits in descending order\n static bool cmp(pair<int,int>&a, pair<int,int>&b) {\n if (a.first < b.first) {\n return true;\n } else if (a.first == b.first && a.second > b.second) {\n return true;\n }\n return false;\n }\npublic:\n // Function to find the maximized capital after selecting k projects\n int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n int n = profits.size(); // Get the number of projects\n vector<pair<int, int>> v; // Vector to store pairs of capital and profits\n \n // Populate the vector with pairs of capital and profits\n for (int i = 0; i < n; i++) {\n v.push_back({capital[i], profits[i]});\n }\n \n // Sort the vector based on capital (ascending) and profits (descending)\n sort(v.begin(), v.end(), cmp);\n \n // Max-heap (priority queue) to store the profits of feasible projects\n priority_queue<int> pq;\n int j = 0; // Index to track the position in the sorted vector\n \n // Iterate k times to select k projects\n for (int i = 0; i < k; i++) {\n // Add all feasible projects to the max-heap\n while (j < n && v[j].first <= w) {\n pq.push(v[j].second);\n j++;\n }\n \n // If the max-heap is not empty, add the maximum profit project to w\n if (!pq.empty()) {\n w += pq.top();\n pq.pop();\n } else {\n // Break if no more feasible projects can be selected\n break;\n }\n }\n\n // Return the maximized capital after selecting k projects\n return w;\n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
ipo | Easy to understand | 💯 Fast | maxHeap | Sorting 🔥 🔥 🔥 | easy-to-understand-fast-maxheap-sorting-giygq | Intuition\nThe intuition behind this code is to maximize the available capital after selecting up to k projects, by strategically choosing the projects with the | deleted_user | NORMAL | 2024-06-15T05:16:11.933790+00:00 | 2024-06-15T05:16:11.933825+00:00 | 11 | false | # Intuition\nThe intuition behind this code is to maximize the available capital after selecting up to k projects, by strategically choosing the projects with the highest profit that can be started within the current capital constraints. It does this by sorting projects by their capital requirements to quickly find the most affordable ones, then using a max-heap to efficiently select the highest-profit projects that are currently affordable, updating the available capital with each project\'s profit. This greedy approach ensures that at each step, the most beneficial project within financial reach is selected to optimize the total capital.\n# Approach\n**Sort Projects by Capital:** Begin by sorting the projects based on the capital required to ensure you look at the cheapest projects first.\n\n**Use Max-Heap for Profits:** Employ a max-heap (inverted to a min-heap using negative values) to always have quick access to the project with the highest available profit.\n\n**Process Projects Within Capital:** As long as there are projects you can afford, add their profits (negatively) to the heap.\n\n**Select Top Profit Projects:** For up to k iterations, choose the most profitable project you can afford by popping from the heap, increasing your capital.\n\n**Resulting Capital:** After potentially choosing k projects, the resulting capital is the maximum capital achieved.\n# Complexity\n- Time complexity:\nO(NLogN+KLogN)\n\n- Space complexity:\nO(N)\n\n# Code\n```.python\nclass Solution:\n def findMaximizedCapital(\n self, k: int, w: int, profits: List[int], capital: List[int]\n ) -> int:\n n = len(profits)\n projects = [(capital[i], profits[i]) for i in range(n)]\n projects.sort()\n maxHeap = []\n i = 0\n for _ in range(k):\n while i < n and projects[i][0] <= w:\n heapq.heappush(maxHeap, -projects[i][1])\n i += 1\n if not maxHeap:\n break\n w -= heapq.heappop(maxHeap)\n\n return w\n``` | 2 | 0 | ['Python3'] | 0 |
ipo | Easy to understand c++ solution using priority_queue && sorting | easy-to-understand-c-solution-using-prio-0lxy | Intuition\n Describe your first thoughts on how to solve this problem. \npush the elements in array in sorted order till it is less than current ans then pick t | prathameshmg0205 | NORMAL | 2024-06-15T05:12:39.178883+00:00 | 2024-06-15T05:12:39.178924+00:00 | 185 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\npush the elements in array in sorted order till it is less than current ans then pick the top elements till it does not become greater than top element\nbreak according to condition\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:(2*NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:(N+sizeof(pq))~(2*N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n \n vector<pair<int,int>> vp;\n int n=profits.size();\n\n for(int i=0;i<n;i++)\n {\n \n vp.push_back({capital[i],profits[i]});\n\n }\n\n sort(vp.begin(),vp.end());\n int ans=w;\n int i=0;\n int m=vp.size();\n priority_queue<int> pq;\n\n\n while(i<m && k)\n {\n\n if(vp[i].first<=ans)\n {\n pq.push(vp[i].second);\n }else\n {\n while(!pq.empty()&& k && vp[i].first>ans)\n {\n ans=ans+pq.top();\n pq.pop();\n k--;\n }\n if(!k || ans<vp[i].first)\n {\n break;\n }\n else \n {\n pq.push(vp[i].second);\n }\n \n }\n i++;\n\n }\n\n while(!pq.empty() && k)\n {\n ans=ans+pq.top();\n pq.pop();\n k--;\n\n }\n \n\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
ipo | Easy Segment Tree Solution :) | easy-segment-tree-solution-by-user20222-eapo | Code\n\nclass SegmentTree{\n vector<int>tree;\n public:\n vector<int>nodes;\n SegmentTree(vector<int>v){\n int n = v.size();\n nodes = | user20222 | NORMAL | 2024-06-15T05:07:39.831978+00:00 | 2024-06-15T05:07:39.832010+00:00 | 243 | false | # Code\n```\nclass SegmentTree{\n vector<int>tree;\n public:\n vector<int>nodes;\n SegmentTree(vector<int>v){\n int n = v.size();\n nodes = v;\n tree.resize(4*n);\n build(1,0,n-1);\n }\n int build(int node,int l,int r){\n if(l==r){\n tree[node] = l;\n return l;\n }\n int mid = l+(r-l)/2;\n int left = build(2*node,l,mid);\n int right = build(2*node+1,mid+1,r);\n return tree[node] = nodes[left]>nodes[right]?left:right;\n }\n int query(int node,int l,int r,int ql,int qr){\n if(ql==l&&qr==r){\n return tree[node];\n }\n if(ql>r||qr<l){\n return -1;\n }\n int mid = l+(r-l)/2;\n int left = query(2*node,l,mid,ql,min(mid,qr));\n int right = query(2*node+1,mid+1,r,max(ql,mid+1),qr);\n if(left==-1)return right;\n if(right==-1)return left;\n return nodes[left]>nodes[right]?left:right;\n }\n int update(int node,int l,int r,int tr){ \n if(l==tr&&r==tr){\n nodes[tr] = -1;\n return l;\n }\n if(tr>r||tr<l)return tree[node];\n int mid = l+(r-l)/2;\n int left = update(2*node,l,mid,tr);\n int right = update(2*node+1,mid+1,r,tr); \n if(left==-1)tree[node] = right;\n if(right==-1)tree[node] = left;\n return tree[node] = nodes[left]>nodes[right]?left:right;\n }\n};\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n vector<pair<int,int>>vp;\n int n = profits.size();\n for(int i=0;i<n;i++){\n vp.push_back({capital[i],profits[i]});\n }\n sort(vp.begin(),vp.end());\n for(int i=0;i<n;i++){\n profits[i] = vp[i].second;\n capital[i] = vp[i].first;\n }\n SegmentTree* sg = new SegmentTree(profits);\n if(k>n)k = n;\n while(k){\n auto it= upper_bound(capital.begin(),capital.end(),w);\n if(it==capital.begin())return w;\n it--;\n int ind = it-capital.begin();\n int pro = sg->query(1,0,n-1,0,ind);\n if(sg->nodes[pro]==-1)return w;\n w+=profits[pro];\n sg->update(1,0,n-1,pro);\n k--;\n }\n return w;\n }\n};\n``` | 2 | 0 | ['Segment Tree', 'C++'] | 0 |
ipo | Easy to Understand | Beats 99% | easy-to-understand-beats-99-by-gameboey-pm9z | Intuition\nUsing max heap for profits we can easily maximize our capital after k projects.\n\n# Approach\n- Create pairs of profits[i] and capital[i].`\n- Sort | gameboey | NORMAL | 2024-06-15T01:45:41.926742+00:00 | 2024-06-15T01:45:41.926765+00:00 | 677 | false | # Intuition\nUsing max heap for `profits` we can easily maximize our capital after k projects.\n\n# Approach\n- Create pairs of profits[i] and capital[i].`\n- Sort pairs by required capital.\n- MaxHeap: While iterating:\n1. Push profits of affordable projects into a max heap.\n2. Pop and add top profit to capital.\n- Repeat k times.\n\n# Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n\n# Code\n```C++ []\n#define pi pair<int, int>\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);\n int j = 0, n = profits.size();\n vector<pi> temp;\n priority_queue<int> maxHeap;\n\n for(int i = 0; i < n; ++i) {\n temp.push_back({capital[i], profits[i]});\n }\n\n sort(begin(temp), end(temp));\n while(k--) {\n while(j < n && w >= temp[j].first) {\n maxHeap.push(temp[j++].second);\n }\n\n if(maxHeap.empty()) break;\n w += maxHeap.top();\n maxHeap.pop();\n }\n\n return w;\n }\n};\n```\n```java []\nclass Solution {\n class Pair {\n int first;\n int second;\n \n Pair(int first, int second) {\n this.first = first;\n this.second = second;\n }\n }\n \n public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {\n int j = 0;\n int n = profits.length;\n List<Pair> temp = new ArrayList<>();\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());\n\n for (int i = 0; i < n; ++i) {\n temp.add(new Pair(capital[i], profits[i]));\n }\n\n Collections.sort(temp, Comparator.comparingInt(p -> p.first));\n \n while (k-- > 0) {\n while (j < n && w >= temp.get(j).first) {\n maxHeap.offer(temp.get(j++).second);\n }\n\n if (maxHeap.isEmpty()) break;\n w += maxHeap.poll();\n }\n\n return w;\n }\n}\n```\n```python []\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n n = len(profits)\n temp = [(capital[i], profits[i]) for i in range(n)]\n temp.sort()\n\n maxHeap = []\n j = 0\n\n while k > 0:\n while j < n and w >= temp[j][0]:\n heapq.heappush(maxHeap, -temp[j][1])\n j += 1\n \n if not maxHeap:\n break\n \n w -= heapq.heappop(maxHeap)\n k -= 1\n \n return w\n```\n```Go []\ntype Pair struct {\n\tfirst, second int\n}\n\ntype PairList []Pair\n\nfunc (p PairList) Len() int { return len(p) }\nfunc (p PairList) Less(i, j int) bool { return p[i].first < p[j].first }\nfunc (p PairList) Swap(i, j int) { p[i], p[j] = p[j], p[i] }\n\ntype MaxHeap []int\n\nfunc (h MaxHeap) Len() int { return len(h) }\nfunc (h MaxHeap) Less(i, j int) bool { return h[i] > h[j] }\nfunc (h MaxHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *MaxHeap) Push(x interface{}) {\n\t*h = append(*h, x.(int))\n}\n\nfunc (h *MaxHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\tx := old[n-1]\n\t*h = old[0 : n-1]\n\treturn x\n}\n\nfunc findMaximizedCapital(k int, w int, profits []int, capital []int) int {\n\tn := len(profits)\n\ttemp := make(PairList, n)\n\tmaxHeap := &MaxHeap{}\n\n\tfor i := 0; i < n; i++ {\n\t\ttemp[i] = Pair{capital[i], profits[i]}\n\t}\n\n\tsort.Sort(temp)\n\tj := 0\n\n\tfor k > 0 {\n\t\tfor j < n && w >= temp[j].first {\n\t\t\theap.Push(maxHeap, temp[j].second)\n\t\t\tj++\n\t\t}\n\n\t\tif maxHeap.Len() == 0 {\n\t\t\tbreak\n\t\t}\n\n\t\tw += heap.Pop(maxHeap).(int)\n\t\tk--\n\t}\n\n\treturn w\n}\n```\n\\\n | 2 | 0 | ['C++', 'Java', 'Go', 'Python3', 'JavaScript'] | 2 |
ipo | [Swift] built-in Heap | swift-built-in-heap-by-iamhands0me-5rmp | \n\n# Code\n\nimport Collections\n\nclass Solution {\n func findMaximizedCapital(_ k: Int, _ w: Int, _ profits: [Int], _ capital: [Int]) -> Int {\n va | iamhands0me | NORMAL | 2024-06-15T01:29:55.790249+00:00 | 2024-06-15T01:29:55.790269+00:00 | 76 | false | \n\n# Code\n```\nimport Collections\n\nclass Solution {\n func findMaximizedCapital(_ k: Int, _ w: Int, _ profits: [Int], _ capital: [Int]) -> Int {\n var projects = zip(profits, capital).map(Project.init).sorted { $0.capital > $1.capital }\n var hp: Heap<Project> = []\n var currentCapital = w\n\n for _ in 1...k {\n while let minCapitalProject = projects.last, minCapitalProject.capital <= currentCapital {\n hp.insert(projects.removeLast())\n }\n\n guard let maxProfitProject = hp.popMax() else { break }\n\n currentCapital += maxProfitProject.profit\n }\n\n return currentCapital\n }\n}\n\nstruct Project: Comparable {\n let profit: Int\n let capital: Int\n\n static func <(lhs: Project, rhs: Project) -> Bool {\n lhs.profit < rhs.profit\n }\n}\n``` | 2 | 0 | ['Swift', 'Sorting', 'Heap (Priority Queue)'] | 0 |
ipo | Swift💯 | swift-by-upvotethispls-80mg | Greedy (accepted answer)\n\nimport Collections\n\nclass Solution {\n func findMaximizedCapital(_ k: Int, _ w: Int, _ profits: [Int], _ capital: [Int]) -> Int | UpvoteThisPls | NORMAL | 2024-06-15T01:06:10.015422+00:00 | 2024-06-15T01:18:56.205248+00:00 | 78 | false | **Greedy (accepted answer)**\n```\nimport Collections\n\nclass Solution {\n func findMaximizedCapital(_ k: Int, _ w: Int, _ profits: [Int], _ capital: [Int]) -> Int {\n var indices = capital.indices.sorted {capital[$0] > capital[$1]}\n var heap = Heap<Int>()\n\n return (0 ..< k).reduce(into: w) { assets, _ in\n while !indices.isEmpty, capital[indices.last!] <= assets {\n heap.insert(profits[indices.popLast()!])\n }\n assets += heap.popMax() ?? 0\n }\n }\n}\n``` | 2 | 0 | ['Swift'] | 0 |
ipo | Dart using PriorityQueues | dart-using-priorityqueues-by-dartist-o4jh | Code\n\nimport \'package:collection/collection.dart\';\n\ntypedef proCap = ({int capital, int profit});\n\nclass Solution {\n int findMaximizedCapital(int k, i | Dartist | NORMAL | 2024-05-21T16:28:19.717211+00:00 | 2024-05-21T16:30:15.344684+00:00 | 14 | false | # Code\n```\nimport \'package:collection/collection.dart\';\n\ntypedef proCap = ({int capital, int profit});\n\nclass Solution {\n int findMaximizedCapital(int k, int w, List<int> profits, List<int> capital) {\n final pqCap = PriorityQueue<proCap>((a, b) => a.capital - b.capital);\n final pqPro = PriorityQueue<proCap>((a, b) => b.profit - a.profit);\n\n for (int i = 0; i < profits.length; i++) {\n pqCap.add((capital: capital[i], profit: profits[i]));\n }\n\n for (int i = 0; i < k; i++) {\n while (pqCap.isNotEmpty && pqCap.first.capital <= w) {\n pqPro.add(pqCap.removeFirst());\n }\n\n if (pqPro.isEmpty) break;\n\n w += pqPro.removeFirst().profit;\n }\n\n return w;\n }\n}\n``` | 2 | 0 | ['Dart'] | 0 |
ipo | SIMPLEST SOLUTION | simplest-solution-by-hcmus-hqhuy-bfnc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\nUse a pointer to test | HCMUS-HQHuy | NORMAL | 2024-04-20T09:29:25.718939+00:00 | 2024-04-20T09:29:25.718972+00:00 | 167 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nUse a pointer to test what you can push when you have capital equals w, because w always increases so p increase(sorted array).\n\n# Complexity\n- Time complexity: $$O(nlog)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\tint findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n\t\tpriority_queue<int> heap;\t\t\n\t\tvector<int> id(profits.size(), 0); iota(id.begin(), id.end(), 0);\n\t\tsort(id.begin(), id.end(), [&](int x, int y) {\n\t\t\t\treturn capital[x] < capital[y];\n\t\t});\n\t\tint p = 0;\n\t\twhile (k--) {\n\t\t\twhile (p < capital.size() && capital[id[p]] <= w) heap.push(profits[id[p++]]);\n if (heap.empty()) break;\n\t\t\tw += heap.top(); heap.pop();\n\t\t}\n\t\treturn w;\t\n\t}\n};\n\n``` | 2 | 0 | ['C++'] | 3 |
ipo | [Java] Easy solution using max heap | java-easy-solution-using-max-heap-by-ytc-zmm7 | java\nclass Solution {\n public int findMaximizedCapital(int k, int w, final int[] profits, final int[] capital) {\n final int n = profits.length;\n | YTchouar | NORMAL | 2024-04-01T04:55:13.923454+00:00 | 2024-04-01T04:55:13.923491+00:00 | 587 | false | ```java\nclass Solution {\n public int findMaximizedCapital(int k, int w, final int[] profits, final int[] capital) {\n final int n = profits.length;\n final int[][] projects = new int[n][2];\n\n for(int i = 0; i < n; ++i) {\n projects[i][0] = capital[i];\n projects[i][1] = profits[i];\n }\n\n Arrays.sort(projects, (a, b) -> a[0] - b[0]);\n\n final PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());\n\n int idx = 0;\n\n while(k-- > 0) {\n while(idx < n && projects[idx][0] <= w)\n maxHeap.offer(projects[idx++][1]);\n\n if(maxHeap.isEmpty())\n break;\n\n w += maxHeap.poll();\n }\n\n return w;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
ipo | 3D Dynamic Programming || C++ | 3d-dynamic-programming-c-by-dalwadiharsh-j67q | Intuition\n Describe your first thoughts on how to solve this problem. \nThere is more suitable ways through using heap, but tried using 3d DP and it worked, bu | dalwadiharsh09 | NORMAL | 2023-12-22T21:46:41.757384+00:00 | 2023-12-22T21:46:41.757414+00:00 | 299 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere is more suitable ways through using heap, but tried using 3d DP and it worked, but has exceeded memory problem for large test cases.\n\n# Code\n```\nclass Solution {\npublic:\n int f(int index, int w, int k, vector<int>& c, vector<int>& p) {\n int n = c.size();\n if (index >= n || k == 0) return w;\n\n if (w >= 0 && dp[index][w][k] != -1) return dp[index][w][k];\n\n int y = f(index + 1, w, k, c, p);\n\n int x = 0;\n if (w - c[index] >= 0)\n x = f(index + 1, w + p[index], k - 1, c, p);\n\n return dp[index][w][k] = max(x, y);\n }\n\n int findMaximizedCapital(int k, int w, vector<int>& p, vector<int>& c) {\n int n = c.size();\n dp.resize(n + 1, vector<vector<int>>(100005, vector<int>(k + 1, -1)));\n return f(0, w, k, c, p);\n }\n\nprivate:\n vector<vector<vector<int>>> dp;\n};\n``` | 2 | 0 | ['Array', 'Dynamic Programming', 'C++'] | 4 |
ipo | Best Java Solution || Priority Queue || Sorting | best-java-solution-priority-queue-sortin-m4b2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-12-22T19:05:22.618610+00:00 | 2023-12-22T19:05:22.618638+00:00 | 413 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findMaximizedCapital(int k, int w, int[] pf, int[] cp) {\n \n int n = pf.length;\n int arr[][] = new int[n][2];\n for(int i=0; i<n; i++){\n arr[i] = new int[]{pf[i],cp[i]};\n }\n\n Arrays.sort(arr,(a,b)->(a[1]-b[1]));\n\n PriorityQueue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());\n\n int i=0;\n\n while(k>0){\n while(i<n && w>=arr[i][1]){\n pq.add(arr[i][0]);\n i++;\n }\n if(pq.size()!=0){\n w = w+pq.remove();\n }\n k--;\n }\n return w;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
ipo | PriorityQueue Optimize Solution | priorityqueue-optimize-solution-by-shree-ekwf | Complexity\n- Time complexity:O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(N*2)\n Add your space complexity here, e.g. O(n) \n\n# Co | Shree_Govind_Jee | NORMAL | 2023-10-30T13:37:10.897681+00:00 | 2023-10-30T13:37:10.897704+00:00 | 17 | false | # Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N*2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {\n int [][] proj = new int[profits.length][2];\n for(int i=0; i<profits.length; i++){\n proj[i][0]=capital[i];\n proj[i][1]=profits[i];\n }\n Arrays.sort(proj, (a, b)->Integer.compare(a[0], b[0]));\n\n int i=0;\n PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());\n while(k-->0){\n while(i<profits.length && proj[i][0]<=w){\n pq.offer(proj[i][1]);\n i++;\n }\n\n if(pq.isEmpty()){\n break;\n }\n w+=pq.poll();\n }\n\n return w;\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 1 |
ipo | O(klogn) | oklogn-by-pathaksanjeev38-o686 | \n\n# Code\n\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n maxProfit = [] # onl | pathaksanjeev38 | NORMAL | 2023-08-29T19:31:35.718185+00:00 | 2023-08-29T19:31:35.718203+00:00 | 111 | false | \n\n# Code\n```\nclass Solution:\n def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:\n maxProfit = [] # only projects we can afford\n minCapital = [(c,p) for c,p in zip(capital,profits)]\n heapq.heapify(minCapital) # sort on the bases of capital\n\n for i in range(k):\n while minCapital and minCapital[0][0] <= w:\n c,p = heapq.heappop(minCapital)\n heapq.heappush(maxProfit,-1*p)\n\n if not maxProfit:\n break\n w += -1*heapq.heappop(maxProfit)\n return w\n\n``` | 2 | 0 | ['Heap (Priority Queue)', 'Python3'] | 0 |
ipo | Easy C++|| Heap || Clean code | easy-c-heap-clean-code-by-harshit_patel2-nd0f | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Harshit_Patel2002 | NORMAL | 2023-06-14T06:34:49.120399+00:00 | 2023-06-14T06:34:49.120437+00:00 | 56 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {\n priority_queue<pair<int,int>> pq;\n priority_queue<int> pq2;\n\n for(int i=0;i<profits.size();i++){\n pq.push({-1*capital[i],profits[i]}); \n }\n\n for(int i=0;i<k;i++){\n\n while (!pq.empty() && -1*pq.top().first <= w ) {\n pair<int,int> temp = pq.top();\n pq.pop();\n pq2.push(temp.second);\n }\n if(!pq2.empty()){\n w += pq2.top();\n pq2.pop();}\n else break;\n \n }\n return w;\n \n }\n};\n``` | 2 | 0 | ['C++'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++/Java Track Direction | cjava-track-direction-by-votrubac-5om0 | Based on the problem description, we have a tree, and node zero is the root. \n\nHowever, the direction can point either from a parent to a child (positive), or | votrubac | NORMAL | 2020-05-31T04:02:03.530046+00:00 | 2020-06-02T01:51:02.009096+00:00 | 37,864 | false | Based on the problem description, we have a tree, and node zero is the root. \n\nHowever, the direction can point either from a parent to a child (positive), or from a child to its parent (negative). To solve the problem, we traverse the tree and count edges that are directed from a parent to a child. Direction of those edges need to be changed to arrive at zero node.\n\nIn the code below, I am using the adjacency list, and the sign indicates the direction. If the index is positive - the direction is from a parent to a child and we need to change it (`change += (to > 0)`).\n\n> Note that we cannot detect the direction for zero (`-0 == 0`), but it does not matter as we start our traversal from zero.\n\n**C++**\n```cpp\nint dfs(vector<vector<int>> &al, vector<bool> &visited, int from) {\n auto change = 0;\n visited[from] = true;\n for (auto to : al[from])\n if (!visited[abs(to)])\n change += dfs(al, visited, abs(to)) + (to > 0);\n return change; \n}\nint minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<int>> al(n);\n for (auto &c : connections) {\n al[c[0]].push_back(c[1]);\n al[c[1]].push_back(-c[0]);\n }\n return dfs(al, vector<bool>(n) = {}, 0);\n}\n```\n**Java**\nTried to do one-line initialization using `Collections.nCopies`, but got TLE. Accepted for same old `for` loop in < 30 milliseconds. \n```java\nint dfs(List<List<Integer>> al, boolean[] visited, int from) {\n int change = 0;\n visited[from] = true;\n for (var to : al.get(from))\n if (!visited[Math.abs(to)])\n change += dfs(al, visited, Math.abs(to)) + (to > 0 ? 1 : 0);\n return change; \n}\npublic int minReorder(int n, int[][] connections) {\n List<List<Integer>> al = new ArrayList<>();\n for(int i = 0; i < n; ++i) \n al.add(new ArrayList<>());\n for (var c : connections) {\n al.get(c[0]).add(c[1]);\n al.get(c[1]).add(-c[0]);\n }\n return dfs(al, new boolean[n], 0);\n}\n```\n**Complexity Analysis**\n- Time: O(n). We visit each node once.\n- Memory: O(n). We store *n* nodes in the adjacency list, with *n - 1* edges in total.\n\n**Bonus: Minimalizm Version**\nInstead of `visited`, we can just pass the previous index to prevent going back, as suggested by [zed_b](https://leetcode.com/zed_b). This is possible because every node has only one parent in the tree.\n```cpp\nint dfs(vector<vector<int>> &al, int prev, int node) {\n return accumulate(begin(al[node]), end(al[node]), 0, [&](int sum, int to) {\n return sum + (abs(to) == prev ? 0 : dfs(al, node, abs(to)) + (to > 0));\n }); \n}\nint minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<int>> al(n);\n for (auto &c : connections) {\n al[c[0]].push_back(c[1]);\n al[c[1]].push_back(-c[0]);\n }\n return dfs(al, 0, 0);\n}\n``` | 410 | 13 | [] | 49 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Simple Explanation | DFS with edge deletion | Idea | Code | Comments | Q & A | simple-explanation-dfs-with-edge-deletio-1xg0 | Key Idea\nThe base case that we know is - All outgoing edges from 0 must be reversed. So add the count into our final result. \nAt this stage, we can say all ed | interviewrecipes | NORMAL | 2020-05-31T04:03:09.879086+00:00 | 2020-06-05T03:51:45.972667+00:00 | 22,935 | false | **Key Idea**\nThe base case that we know is - All outgoing edges from 0 must be reversed. So add the count into our final result. \nAt this stage, we can say all edges are coming into node 0. What is the next thing we need to do?\nMake sure that all nodes that are connected to 0 have all edges coming into them.\nE.g. if nodes x and y are connected to 0. After first step, there will be edges from x to 0 and y to 0. Now we want to make sure that all nodes that are directly connected to x, must have an edge coming into x. Similarly for y. If we keep on doing this recursively, we will get the answer at the end. Along the way, we will keep counting the edges that we reversed.\n\n**Implementation**\nFor the ease of implementation, I have created two separate graph, one for outgoing edges and another for incoming. Everytime an edge is traversed, I erase the opposite edge so that I don\u2019t hit the same node twice.\n\n**Time Complexity** \nO(n) where n is number of nodes in the tree.\n\n**Thanks**\nIs there anything that is still unclear? Let me know and I can elaborate. \nPlease upvote if you find this helpful, it will be encouraging.\n\n**Q&A**\n```\nQ1. \n\n// Why we need to traverse both incoming as well as outgoing edges?\n// Ans. \n// We want all edges to come towards 0. Reversing outgoing edges\n// from 0 is necessary - you can understand this easily.\n// Then you need to recursively orient all outgoing edges from \n// those connected nodes too.\n// But why do we need to recursively call dfs() even for incoming\n// edges? \n// The answer is, we don\'t know the orientation of edges that are \n// connected to that neighbor node.\n// For example - say 0 has an incoming edge from 1 and 1 has one other\n// outgoing edge to 2. i.e. graph is like 0 <-- 1 --> 2.\n// Although, you don\'t need to reverse 0 <-- 1 edge, you still have to \n// make sure that all other edges are coming towards 1. When you call\n// dfs with node 1, you will then recognize the incorrect orientation\n// of 1 --> 2 edge. This is why traversing incoming edges is important.\n```\n```\nQ2.\n\n// Why do we need to erase edges?\n// Ans.\n// To avoid double counting. \n// We increment the count everytime we see an outgoing edge. We don\'t \n// increment for incoming. However, an incoming edge for one node is \n// the outgoing edge for the other.\n// In the previous example, 0 <-- 1 --> 2.\n// For node 0, we won\'t increment the count because there are no outgoing\n// edges. But when we are at 1, there are two outgoing edges. But 1 --> 0 \n// is already oriented towards 0 and we don\'t want to reverse that. How \n// will we distiguish between correctly oriented edges vs incorrectly \n// oriented ones in general? Easier approach is to remove those correctly \n// oriented edges immediately when we know their orientation is correct.\n```\n\n\n\n**Code**\nC++\n```\nclass Solution {\npublic:\n unordered_map<int, unordered_set<int>> out, in;\n int ans = 0;\n \n void dfs(int node) {\n \n // Why we need to traverse both incoming as well as outgoing edges?\n // Ans. \n // We want all edges to come towards 0. Reversing outgoing edges\n // from 0 is necessary - you can understand this easily.\n // Then you need to recursively orient all outgoing edges from \n // those connected nodes too.\n // But why do we need to recursively call dfs() even for incoming\n // edges? \n // The answer is, we don\'t know the orientation of edges that are \n // connected to that neighbor node.\n // For example - say 0 has an incoming edge from 1 and 1 has one other\n // outgoing edge to 2. i.e. graph is like 0 <-- 1 --> 2.\n // Although, you don\'t need to reverse 0 <-- 1 edge, you still have to \n // make sure that all other edges are coming towards 1. When you call\n // dfs with node 1, you will then recognize the incorrect orientation\n // of 1 --> 2 edge. This is why traversing incoming edges is important.\n \n // Why do we need to erase edges?\n // Ans.\n // To avoid double counting. \n // We increment the count everytime we see an outgoing edge. We don\'t \n // increment for incoming. However, an incoming edge for one node is \n // the outgoing edge for the other.\n // In the previous example, 0 <-- 1 --> 2.\n // For node 0, we won\'t increment the count because there are no outgoing\n // edges. But when we are at 1, there are two outgoing edges. But 1 --> 0 \n // is already oriented towards 0 and we don\'t want to reverse that. How \n // will we distiguish between correctly oriented edges vs incorrectly \n // oriented ones in general? Easier approach is to remove those correctly \n // oriented edges immediately when we know their orientation is correct.\n \n for (int x: out[node]) {\n // There is an edge (node->x). We must reverse it.\n ans++; \n\t\t\t// delete, edge (x <- node)\n in[x].erase(node);\n\t\t\t// recurse.\n dfs(x);\n }\n for (int x:in[node]) {\n\t\t // The edge is (x <- node). So delete (node -> x).\n\t\t\tout[x].erase(node);\n\t\t\t// recurse.\n dfs(x);\n }\n }\n \n int minReorder(int n, vector<vector<int>>& connections) {\n ans = 0;\n\t\t// make graph.\n for (auto x: connections) {\n out[x[0]].insert(x[1]);\n in[x[1]].insert(x[0]);\n }\n\t\t// start with node 0.\n dfs(0);\n return ans;\n }\n};\n```\n\n**Did you check the visuals of the other problem in the contest?**\nhttps://leetcode.com/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts/discuss/661995/\n | 224 | 9 | ['Depth-First Search'] | 17 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Python3] Easy Short DFS | python3-easy-short-dfs-by-localhostghost-1xbb | Start from node 0 (the capital) and dfs on the path and see if the path is \nin the same direction as the traversal. If it is on the same direction that \nmeans | localhostghost | NORMAL | 2020-05-31T04:06:50.800461+00:00 | 2020-09-06T17:06:27.779992+00:00 | 14,758 | false | Start from `node 0` (the capital) and dfs on the path and see if the path is \nin the same direction as the traversal. If it is on the same direction that \nmeans we need to reverse it because it can never get to the capital.\n\n```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n self.res = 0 \n roads = set()\n graph = collections.defaultdict(list)\n for u, v in connections:\n roads.add((u, v))\n graph[v].append(u)\n graph[u].append(v)\n def dfs(u, parent):\n self.res += (parent, u) in roads\n for v in graph[u]:\n if v == parent:\n continue\n dfs(v, u) \n dfs(0, -1)\n return self.res\n```\nDon\'t forget to upvote if you found this useful. Thank you. | 186 | 9 | [] | 20 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | straightforward c++ solution || bfs | straightforward-c-solution-bfs-by-helloi-b1uj | We put outward facing edges in one vector, and keep the reverse in another. \n\nStarting from the city, we switch edges that are facing away from us. \n\nIf t | helloisabelle | NORMAL | 2020-09-04T00:05:29.028218+00:00 | 2020-09-04T17:32:03.952627+00:00 | 9,670 | false | We put outward facing edges in one vector, and keep the reverse in another. \n\nStarting from the city, we switch edges that are facing away from us. \n\nIf there is a node that faces inward to us that we haven\'t visited yet, it would be in our back vector. \nWe need to add inward facing nodes to the queue as well, since they might have neighbors that need to be flipped.\n\n```\n\tint minReorder(int n, vector<vector<int>>& connections) {\n vector<int> visited(n);\n vector<vector<int>> adj(n), back(n);\n queue<int> q;\n q.push(0);\n int ans = 0;\n \n for (auto c : connections){\n adj[c[0]].push_back(c[1]);\n back[c[1]].push_back(c[0]);\n }\n \n while (!q.empty()){\n int curr = q.front();\n q.pop();\n visited[curr] = 1;\n\n // change dir for all arrows facing out\n for (auto a: adj[curr]){\n if (!visited[a]){\n ans++;\n q.push(a);\n }\n }\n // push other nodes so we visit everything\n for (auto b: back[curr]){\n if (!visited[b]) q.push(b);\n }\n }\n return ans;\n }\n``` | 159 | 3 | ['Breadth-First Search', 'C'] | 16 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | 🔥Easy Solutions with Exaplanation in Java 📝, Python 🐍, and C++ 🖥️🧐Look at once 💻 | easy-solutions-with-exaplanation-in-java-h49p | Intuition\nWe can use DFS to traverse the tree and change the direction of edges if needed.\n\n# Approach\nFirst, we create an adjacency list to represent the t | Vikas-Pathak-123 | NORMAL | 2023-03-24T00:51:45.613216+00:00 | 2023-03-24T01:39:55.522181+00:00 | 21,789 | false | # Intuition\nWe can use DFS to traverse the tree and change the direction of edges if needed.\n\n# Approach\nFirst, we create an adjacency list to represent the tree. Each node in the list contains a list of its neighbors.\n\nTo change the direction of edges, we assign a direction to each edge. If an edge goes from node i to node j, we represent it as i -> j. If an edge goes from node j to node i, we represent it as j -> -i.\n\nThen, we start DFS from node 0. We mark visited nodes to avoid revisiting them. If we reach a node i that has not been visited before, it means we need to change the direction of the edge that leads to node i. We do this by adding 1 to the result if the edge is directed from node j to node i (i.e., j -> i), and 0 otherwise (i.e., j -> -i).\n\nWe repeat this process until all nodes have been visited.\n\nFinally, we return the total number of edges that we have changed.\n\n# Complexity\n- Time complexity: O(n), where n is the number of nodes in the tree. We traverse the tree once using DFS.\n\n- Space complexity: O(n), where n is the number of nodes in the tree. We use a boolean array to keep track of visited nodes. Also, we use an adjacency list to represent the tree, which requires O(n) space.\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n```\n# Code\n``` Java []\nclass Solution {\n int dfs(List<List<Integer>> al, boolean[] visited, int from) {\n int change = 0;\n visited[from] = true;\n for (var to : al.get(from))\n if (!visited[Math.abs(to)])\n change += dfs(al, visited, Math.abs(to)) + (to > 0 ? 1 : 0);\n return change; \n }\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> al = new ArrayList<>();\n for(int i = 0; i < n; ++i) \n al.add(new ArrayList<>());\n for (var c : connections) {\n al.get(c[0]).add(c[1]);\n al.get(c[1]).add(-c[0]);\n }\n return dfs(al, new boolean[n], 0);\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int dfs(vector<vector<int>> &al, vector<bool> &visited, int from) {\n auto change = 0;\n visited[from] = true;\n for (auto to : al[from])\n if (!visited[abs(to)])\n change += dfs(al, visited, abs(to)) + (to > 0);\n return change; \n }\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<int>> al(n);\n for (auto &c : connections) {\n al[c[0]].push_back(c[1]);\n al[c[1]].push_back(-c[0]);\n }\n return dfs(al, vector<bool>(n) = {}, 0);\n }\n};\n```\n``` Python []\nclass Solution:\n def dfs(self, al, visited, from_node):\n change = 0\n visited[from_node] = True\n for to_node in al[from_node]:\n if not visited[abs(to_node)]:\n change += self.dfs(al, visited, abs(to_node)) + (1 if to_node > 0 else 0)\n return change\n\n def minReorder(self, n, connections):\n al = [[] for _ in range(n)]\n for c in connections:\n al[c[0]].append(c[1])\n al[c[1]].append(-c[0])\n visited = [False] * n\n return self.dfs(al, visited, 0)\n\n```\n# Please Comment\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution comment below if you like it.\uD83D\uDE0A\n``` | 152 | 8 | ['Depth-First Search', 'Graph', 'Python', 'C++', 'Java'] | 12 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java Simple BFS from Origin | java-simple-bfs-from-origin-by-hobiter-c0cm | Could be solved by DFS or BFS. BFS is easy to debug, and not causing stackoverflow.\n\n public int minReorder(int n, int[][] cs) {\n Set<String> st = | hobiter | NORMAL | 2020-05-31T04:02:25.643790+00:00 | 2020-05-31T18:12:35.037268+00:00 | 9,532 | false | Could be solved by DFS or BFS. BFS is easy to debug, and not causing stackoverflow.\n```\n public int minReorder(int n, int[][] cs) {\n Set<String> st = new HashSet<>();\n Map<Integer, Set<Integer>> map = new HashMap<>();\n for (int[] c : cs) {\n st.add(c[0] + "," + c[1]);\n map.computeIfAbsent(c[0], k -> new HashSet<>());\n map.computeIfAbsent(c[1], k -> new HashSet<>());\n map.get(c[0]).add(c[1]);\n map.get(c[1]).add(c[0]);\n }\n \n Queue<Integer> q = new LinkedList<>();\n q.add(0);\n int res = 0;\n boolean[] vs = new boolean[n];\n vs[0] = true;\n while (!q.isEmpty()) {\n int c = q.poll();\n for (int next : map.getOrDefault(c, new HashSet<>())) {\n if (vs[next]) continue;\n vs[next] = true;\n if (!st.contains(next + "," + c)) res++;\n q.offer(next);\n }\n }\n return res;\n }\n``` | 77 | 9 | [] | 11 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Image Explanation🏆- [Complete Intuition - DFS] - C++/Java/Python | image-explanation-complete-intuition-dfs-5fuh | Video Solution (Aryan Mittal)\nReorder Routes to Make All Paths Lead to the City Zero by Aryan Mittal\n\n\n\n\n# Approach & Intution\n\n\n\n\n\n\n\n\n\n# Code\n | aryan_0077 | NORMAL | 2023-03-24T02:10:25.595152+00:00 | 2023-03-24T05:18:46.387219+00:00 | 12,451 | false | # Video Solution (`Aryan Mittal`)\n`Reorder Routes to Make All Paths Lead to the City Zero` by `Aryan Mittal`\n\n\n\n\n# Approach & Intution\n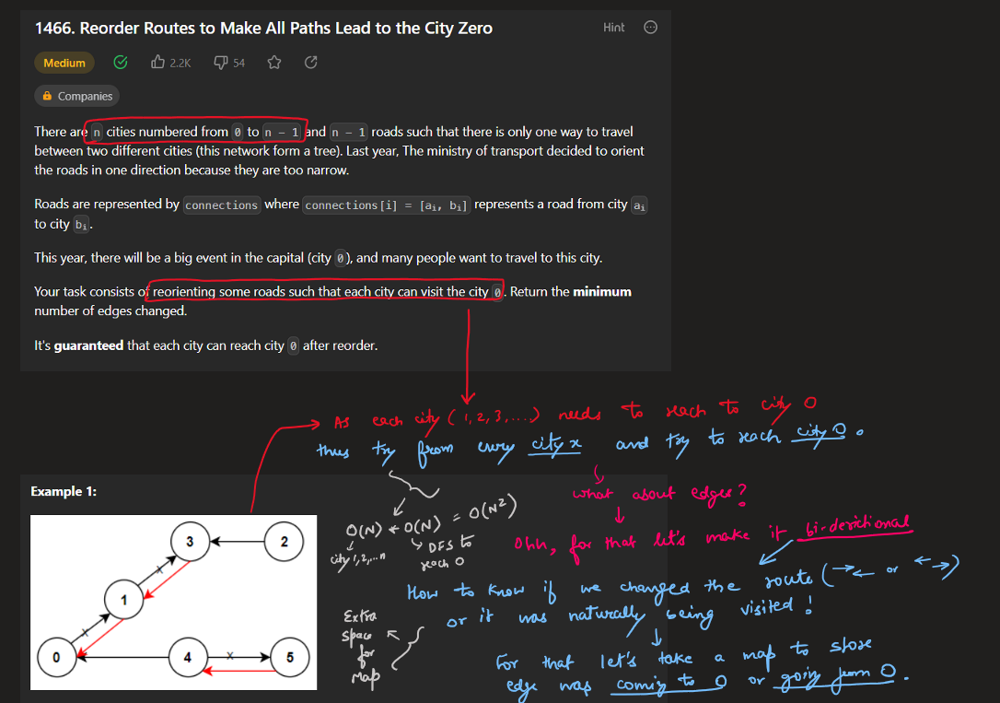\n\n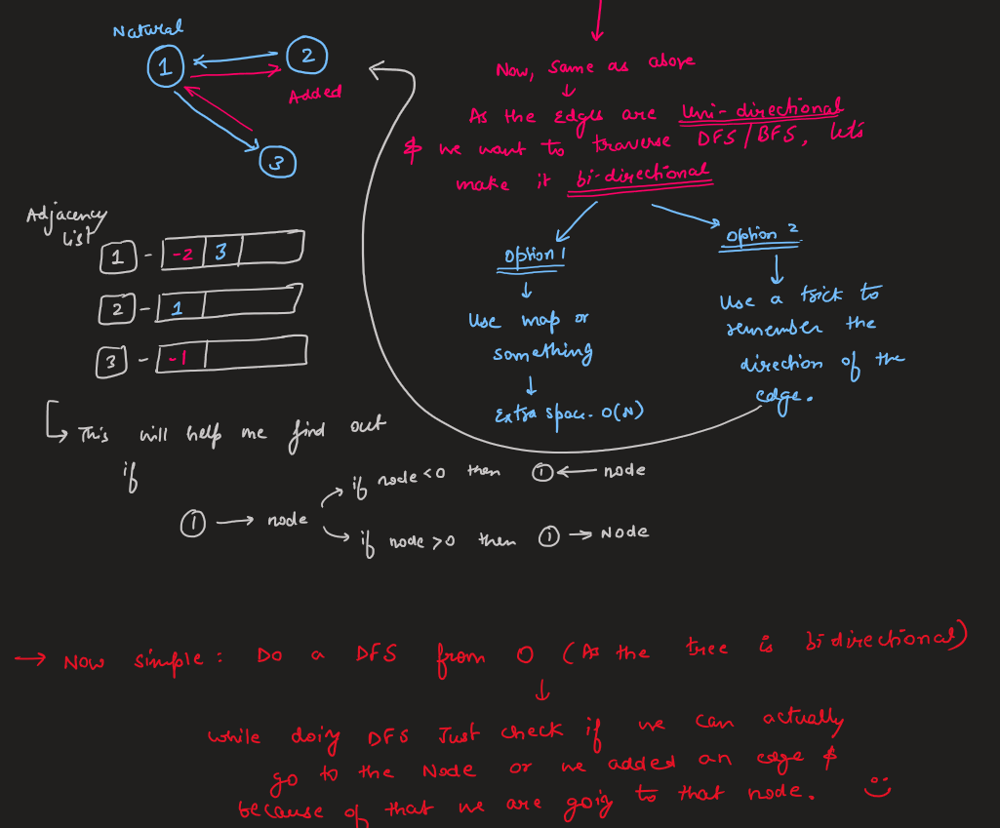\n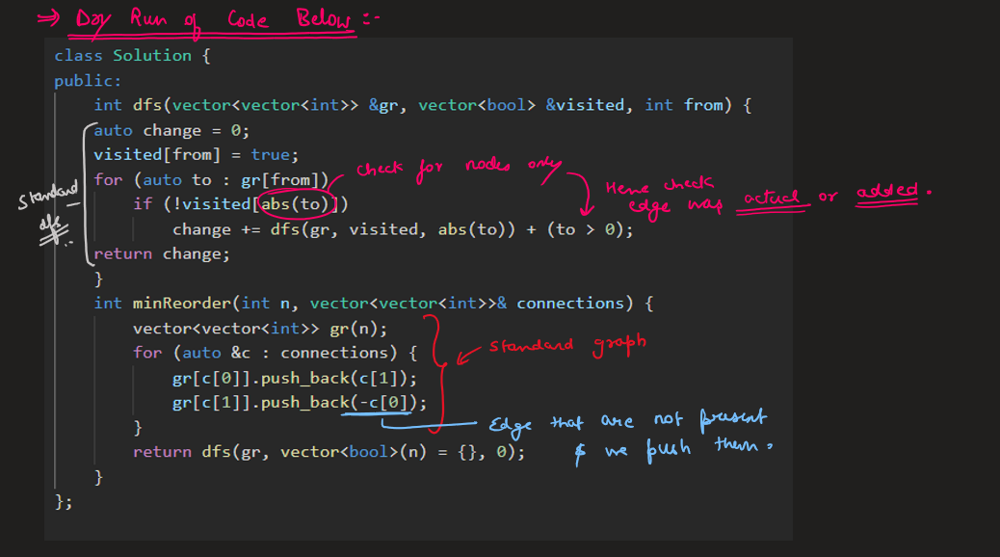\n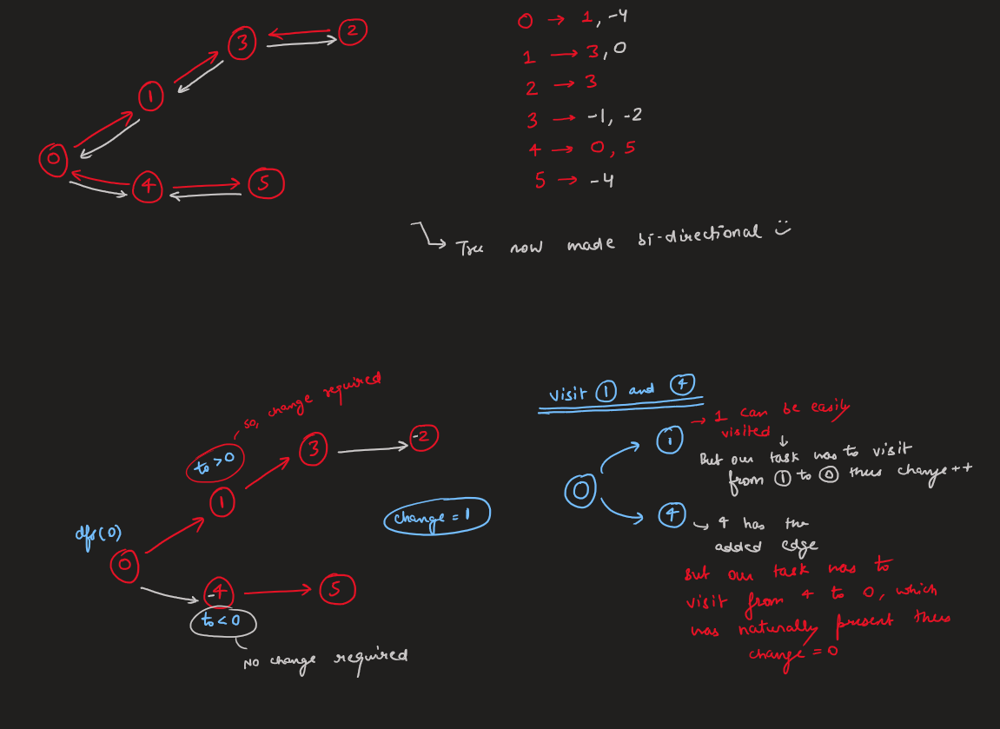\n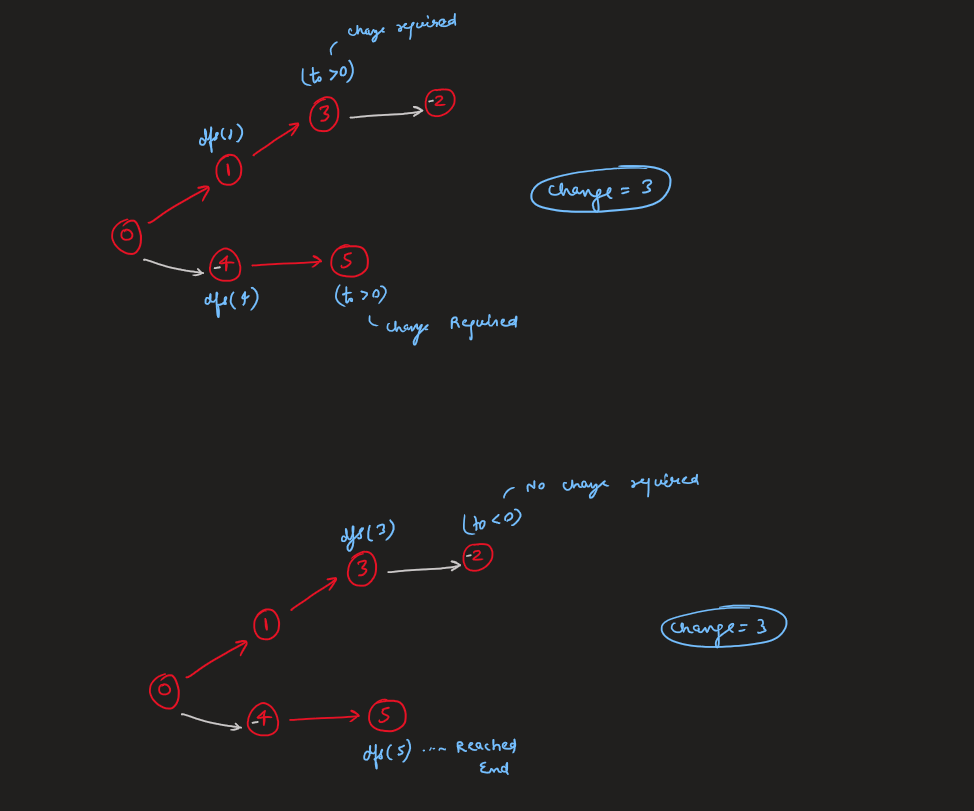\n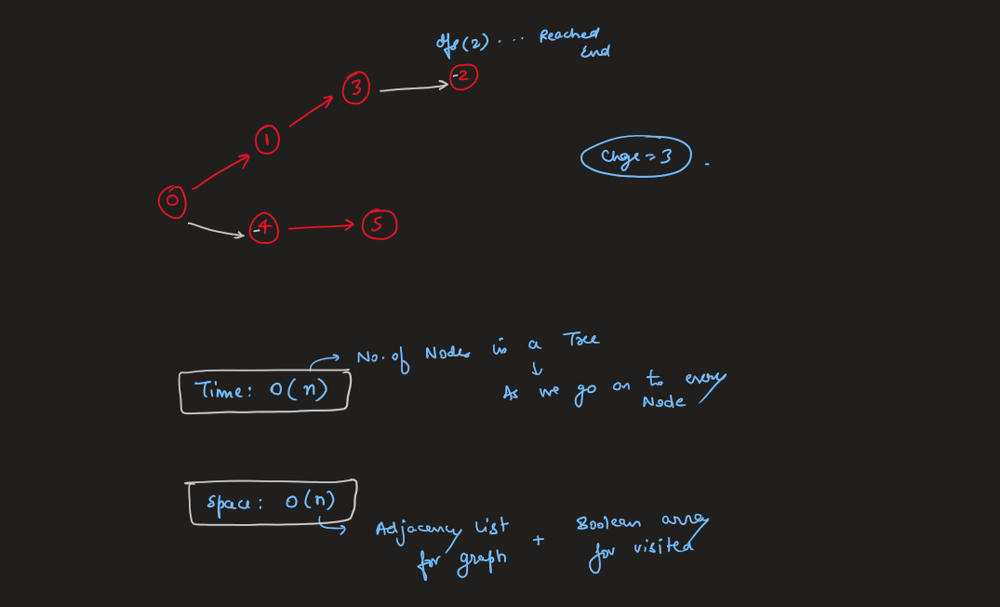\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int dfs(vector<vector<int>> &gr, vector<bool> &visited, int from) {\n auto change = 0;\n visited[from] = true;\n for (auto to : gr[from])\n if (!visited[abs(to)])\n change += dfs(gr, visited, abs(to)) + (to > 0);\n return change; \n }\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<int>> gr(n);\n for (auto &c : connections) {\n gr[c[0]].push_back(c[1]);\n gr[c[1]].push_back(-c[0]);\n }\n return dfs(gr, vector<bool>(n) = {}, 0);\n }\n};\n```\n```Java []\nclass Solution {\n int dfs(List<List<Integer>> gr, boolean[] visited, int from) {\n int change = 0;\n visited[from] = true;\n for (var to : gr.get(from))\n if (!visited[Math.abs(to)])\n change += dfs(gr, visited, Math.abs(to)) + (to > 0 ? 1 : 0);\n return change; \n }\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> gr = new ArrayList<>();\n for(int i = 0; i < n; ++i) \n gr.add(new ArrayList<>());\n for (var c : connections) {\n gr.get(c[0]).add(c[1]);\n gr.get(c[1]).add(-c[0]);\n }\n return dfs(gr, new boolean[n], 0);\n }\n}\n```\n```Python []\nclass Solution:\n def dfs(self, gr, visited, from_node):\n change = 0\n visited[from_node] = True\n for to_node in gr[from_node]:\n if not visited[abs(to_node)]:\n change += self.dfs(gr, visited, abs(to_node)) + (1 if to_node > 0 else 0)\n return change\n\n def minReorder(self, n, connections):\n gr = [[] for _ in range(n)]\n for c in connections:\n gr[c[0]].append(c[1])\n gr[c[1]].append(-c[0])\n visited = [False] * n\n return self.dfs(gr, visited, 0)\n```\n | 73 | 2 | ['Depth-First Search', 'Graph', 'Python', 'C++', 'Java'] | 7 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Easy C++ DFS solution || commented | easy-c-dfs-solution-commented-by-saiteja-yo98 | \nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n \n //for every city store the adjacent city along wit | saiteja_balla0413 | NORMAL | 2021-07-02T06:34:43.457944+00:00 | 2021-07-02T06:34:43.457983+00:00 | 4,056 | false | ```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n \n //for every city store the adjacent city along with direction \n //to store the direction we use positive indicating a road from a to b for a\n //we use negative indicating there is a road from b to a for a\n \n vector<vector<int>> adjCities(n);\n vector<bool> visited(n,false);\n for(int i=0;i<connections.size();i++)\n {\n int city1=connections[i][0];\n int city2=connections[i][1];\n adjCities[city1].push_back(city2);\n adjCities[city2].push_back(-city1);\n }\n \n //start dfs from city 0 \n //when ever you found a positive then it need to be reversed\n int count=0;\n reorderPaths(0,adjCities,count,visited);\n return count;\n\n }\n void reorderPaths(int currCity,vector<vector<int>>& adjCities,int& count,vector<bool>& visited)\n {\n visited[currCity]=true;\n for(auto city:adjCities[currCity])\n {\n \n if(!visited[abs(city)])\n {\n if(city>0) //reorder the path \n count++;\n reorderPaths(abs(city),adjCities,count,visited);\n }\n }\n }\n};\n```\n**Upvote if this helps you :)** | 61 | 1 | ['C'] | 7 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Python3] Simple BFS solution with explanation | python3-simple-bfs-solution-with-explana-rdiw | The key idea is to recognize that the given graph is directed and it may not be possible to visit every node starting from 0. In order to traverse the graph, we | redsand | NORMAL | 2020-10-07T11:31:20.525502+00:00 | 2020-10-11T13:31:46.037804+00:00 | 3,087 | false | The key idea is to recognize that the given graph is directed and it may not be possible to visit every node starting from 0. In order to traverse the graph, we need to make sure that every node is reachable from 0.\n\nSo turn the graph into an undirected one while noting down the original direction. Here, I have used a variable called cost. If the original direction was from source to destination, we need to reverse it and this has a cost of 1 and 0 otherwise. Perform BFS starting from 0 and add the cost to the result.\n\n```\nfrom collections import defaultdict, deque\n\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n graph = defaultdict(list)\n for src, dest in connections:\n graph[src].append((dest, 1))\n graph[dest].append((src, 0))\n \n q = deque([0])\n visited = set([0])\n num_changes = 0\n \n while q:\n curr = q.popleft()\n for child, cost in graph[curr]:\n if child not in visited:\n visited.add(child)\n num_changes += cost\n q.append(child)\n \n return num_changes\n``` | 61 | 0 | ['Breadth-First Search', 'Graph', 'Python'] | 7 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Python] Clean dfs with explanations | python-clean-dfs-with-explanations-by-db-teel | Let us put all the edges into adjacency list twice, one with weight 1 and one with weight -1 with oppisite direction. Then what we do is just traverse our graph | dbabichev | NORMAL | 2020-05-31T04:07:27.335840+00:00 | 2020-05-31T04:26:40.113053+00:00 | 3,618 | false | Let us put all the edges into adjacency list twice, one with weight `1` and one with weight `-1` with oppisite direction. Then what we do is just traverse our graph using usual dfs, and when we try to visit some neighbour, we check if this edge is usual or reversed.\n\n**Complexity** is `O(V+E)`, because we traverse our graph only once.\n\n```\nclass Solution:\n def dfs(self, start):\n self.visited[start] = 1\n for neib in self.adj[start]:\n if self.visited[neib[0]] == 0:\n if neib[1] == 1:\n self.count += 1\n self.dfs(neib[0])\n \n def minReorder(self, n, connections):\n self.visited = [0] * n\n self.adj = defaultdict(list) \n self.count = 0\n for i, j in connections:\n self.adj[i].append([j,1])\n self.adj[j].append([i,-1])\n\n self.dfs(0)\n return self.count\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote**! | 57 | 5 | [] | 6 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [C++] Concise & Easy to understand DFS Solution | With Explanation | c-concise-easy-to-understand-dfs-solutio-60hv | The idea is to do a DFS traversal starting from node 0. For nodes other than 0, we check the parent who called DFS on it, and if it doesn\'t have an outgoing ed | anandthegreat | NORMAL | 2020-05-31T05:15:20.767560+00:00 | 2020-05-31T16:40:49.782685+00:00 | 3,032 | false | The idea is to do a DFS traversal starting from node 0. For nodes other than 0, we check the parent who called DFS on it, and if it doesn\'t have an outgoing edge to the parent, we increment the answer. We don\'t really need to reverse any edge. \n```\nvoid dfs(int idx,int caller,vector<vector<int>> &adjList,vector<vector<int>> &outgoing,vector<bool> &visited,int &ans){\n visited[idx]=true;\n if(caller!=-1){ //if the city number is not 0\n //check if there is an outgoing edge from current node to it\'s parent node (who called dfs on this node)\n //if there is no outgoing edge, we\'ll have to reorient this edge\n if(find(outgoing[idx].begin(),outgoing[idx].end(),caller)==outgoing[idx].end())\n ans++;\n }\n for(auto i: adjList[idx]){\n if(!visited[i]){\n dfs(i,idx,adjList,outgoing,visited,ans);\n }\n }\n }\nint minReorder(int n, vector<vector<int>>& connections) {\n int ans=0;\n vector<vector<int>> adjList(n); //doesn\'t cares about direction\n vector<vector<int>> outgoing(n); //list of outgoing nodes from a node\n vector<bool> visited(n,false); \n for(auto i: connections){\n adjList[i[0]].push_back(i[1]);\n adjList[i[1]].push_back(i[0]);\n outgoing[i[0]].push_back(i[1]);\n }\n dfs(0,-1,adjList,outgoing,visited,ans); //start dfs from node 0 \n return ans;\n }\n```\nThe caller argument in the dfs function denotes the node who called dfs on the current node, i.e. it\'s parent. We intially call dfs on node 0 with caller=-1 as it doesn\'t have any parent to which it wants to reach. Upvote if you found it helpful. | 39 | 2 | ['Depth-First Search', 'C'] | 4 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java O(n) dfs with explanation | java-on-dfs-with-explanation-by-renato4-7jvb | Explanation: Since the problem states that we will always have n-1 connections and we will always be able to reorder so that every city can reach 0, we can conc | renato4 | NORMAL | 2020-05-31T04:18:36.688217+00:00 | 2020-06-01T02:13:42.499741+00:00 | 3,486 | false | Explanation: Since the problem states that we will always have `n-1` connections and we will always be able to reorder so that every city can reach 0, we can conclude that no cycles will exist. If you are not conviced, try to think about a case where you have `n-1` edges and a cycle. You will notice that if you do that, you will make some cities unable to reach the city 0 even after reordering.\n\nHaving this in mind, you can use the following approach to calculate the answer:\n1. Transform each edge in a bi-directional edge, so that when you go on the right (original) direction, it costs you 1, and when you go on the not original direction, it costs you 0.\n2. Start a dfs from city 0 and go to its neighbors, and always add the cost of going to that direction.\n3. Because of what you did on (1), if the direction is correct, it means that that edge needs to be reversed, hence it will cost one.\n\nCommented code presented below. Complexity is O(n).\n\n```\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n\t\t//ajdacency list where int[] will be [dest,cost]\n List<int[]>[] cons = new List[n];\n for(int[] con : connections) {\n if (cons[con[0]] == null) cons[con[0]] = new ArrayList<int[]>();\n if (cons[con[1]] == null) cons[con[1]] = new ArrayList<int[]>();\n cons[con[0]].add(new int[]{con[1],1});//original direction, costs 1\n cons[con[1]].add(new int[]{con[0],0});//oposite directions, costs 0\n }\n return dfs(0,cons,new boolean[n]);\n }\n private int dfs(int curr, List<int[]>[] cons, boolean[] visited) {\n int cost = 0;\n visited[curr]=true;\n for(int[] neigh : cons[curr]) {\n if (!visited[neigh[0]]) {\n cost += neigh[1];\n cost += dfs(neigh[0],cons,visited);\n }\n }\n return cost;\n }\n}\n``` | 31 | 3 | [] | 4 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Day 83 || DFS || Easiest Beginner Friendly Sol | day-83-dfs-easiest-beginner-friendly-sol-2vps | NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.\n\n# Intuitio | singhabhinash | NORMAL | 2023-03-28T16:50:03.967201+00:00 | 2023-03-28T16:50:03.967240+00:00 | 5,789 | false | **NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Create an adjacency list \'adj\' to represent the connections between cities. For each connection in the input list \'connections\', add two entries in \'adj\' - one for the city away from 0 and another for the city towards 0.\n2. Define a DFS function \'dfs\' that takes \'adj\', \'visited\', \'minChange\', and \'currCity\' as inputs.\n3. Mark the current city as visited.\n4. Iterate through all the neighbour cities of the current city in the adjacency list.\n5. If a neighbour city is not visited, check the direction of the connection (1 or -1).\n6. If the direction is 1, increment the \'minChange\' counter.\n7. Call the DFS function recursively with the neighbour city as the current city.\n8. In the main function, initialize a boolean vector \'visited\' of size \'n\' to keep track of visited cities, and set \'minChange\' to 0.\n9. Call the DFS function with inputs \'adj\', \'visited\', \'minChange\', and 0 (starting city).\n10. Return the value of \'minChange\'.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\nclass Solution {\npublic:\n void dfs(vector<vector<pair<int, int>>>& adj, vector<bool>& visited, int& minChange, int currCity) {\n visited[currCity] = true;\n for (auto neighbourCity : adj[currCity]) {\n if (!visited[neighbourCity.first]) {\n if (neighbourCity.second == 1)\n minChange++;\n dfs(adj, visited, minChange, neighbourCity.first);\n }\n }\n }\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int, int>>> adj(n);\n for (auto connection : connections) {\n adj[connection[0]].push_back({connection[1], 1}); // city away from 0\n adj[connection[1]].push_back({connection[0], -1}); // city toward 0\n }\n vector<bool> visited(n, false);\n int minChange = 0;\n dfs(adj, visited, minChange, 0);\n return minChange;\n }\n};\n```\n```Java []\nclass Solution {\n public void dfs(List<List<Pair<Integer, Integer>>> adj, boolean[] visited, int[] minChange, int currCity) {\n visited[currCity] = true;\n for (Pair<Integer, Integer> neighbourCity : adj.get(currCity)) {\n if (!visited[neighbourCity.getKey()]) {\n if (neighbourCity.getValue() == 1) {\n minChange[0]++;\n }\n dfs(adj, visited, minChange, neighbourCity.getKey());\n }\n }\n }\n \n public int minReorder(int n, int[][] connections) {\n List<List<Pair<Integer, Integer>>> adj = new ArrayList<>();\n for (int i = 0; i < n; i++) {\n adj.add(new ArrayList<>());\n }\n for (int[] connection : connections) {\n adj.get(connection[0]).add(new Pair<>(connection[1], 1));\n adj.get(connection[1]).add(new Pair<>(connection[0], -1));\n }\n boolean[] visited = new boolean[n];\n int[] minChange = new int[1];\n dfs(adj, visited, minChange, 0);\n return minChange[0];\n }\n}\n\n```\n```Python []\nclass Solution:\n def dfs(self, adj: List[List[Tuple[int, int]]], visited: List[bool], minChange: List[int], currCity: int) -> None:\n visited[currCity] = True\n for neighbourCity in adj[currCity]:\n if not visited[neighbourCity[0]]:\n if neighbourCity[1] == 1:\n minChange[0] += 1\n self.dfs(adj, visited, minChange, neighbourCity[0])\n \n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n adj = [[] for _ in range(n)]\n for connection in connections:\n adj[connection[0]].append((connection[1], 1))\n adj[connection[1]].append((connection[0], -1))\n visited = [False] * n\n minChange = [0]\n self.dfs(adj, visited, minChange, 0)\n return minChange[0]\n\n```\n\n# Time Complexity and Space Complexity:\n- **Time complexity :**\n\nThe adjacency list representation of the graph is constructed in O(E) time as we iterate through the given connections vector and add the edges to the corresponding vertices\' adjacency lists.\n\nThe depth-first search traversal is performed on each connected component of the graph, which is O(V) in the worst case when the graph is a complete graph. Within each connected component, each vertex is visited at most twice, once for marking it as visited and once for traversing its neighbors. Thus, the overall time complexity of the depth-first search traversal is O(V + E).\n\nTherefore, **the total time complexity of the solution is O(E + V + V + E) = O(2E + 2V) = O(E + V).**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity :**\n\nThe adjacency list representation of the graph is stored in memory, which takes O(E + V) space, where each vertex is stored once, and each edge is stored once in the adjacency list of its endpoints.\n\nThe visited array used to mark vertices as visited or not visited also takes O(V) space.\n\nIn the worst case, when the depth-first search traversal visits all vertices, the recursion stack could contain all the vertices in the connected component, which would take O(V) space.\n\nTherefore, **the total space complexity of the solution is O(E + V + V) = O(E + 2V) = O(E + V).**\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 30 | 1 | ['Depth-First Search', 'Graph', 'C++', 'Java', 'Python3'] | 4 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Visual Explanation | Simple Python DFS Solution | Idea | Comments | visual-explanation-simple-python-dfs-sol-t0ba | \n\nThought Process ...\n We want all directions towards city 0\n We know that we can reach to every city from 0 if its bidirectional\n Then we assume that we v | hanjo108 | NORMAL | 2021-12-07T05:10:24.558728+00:00 | 2021-12-07T18:46:13.431740+00:00 | 1,524 | false | 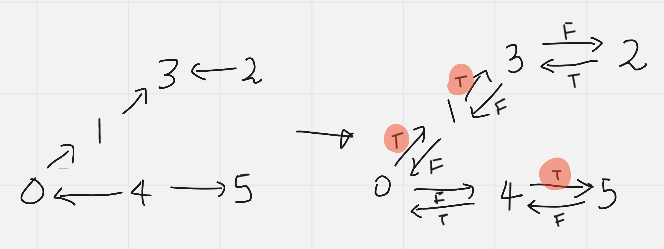\n\n**Thought Process ...**\n* We want all directions towards city 0\n* We know that we can reach to every city from 0 if its bidirectional\n* Then we assume that we visit every city starting from 0, and whenever direction toward to visiting city from 0 is equal to the given direction from input -> meaning that we need to swap the direction\n* total number of needs of swapping of direction is what the problem is looking for\n\n**Approach ...**\n* Let\'s build our own \'undirected\' graph so we can travel from 0 to all cities (from left to right on the image)\n* While we build our graph, let\'s mark down if the direction from 0 is equal to the direction given by the input with True or False (T, F marks on the image)\n* let us make sure that we mark down the visited cities so we don\'t go backward\n* When we traverse our \'undirected\' graph DFS, if the path I am using is same as the given input (which in this case True) and count the number of paths that we need to invert. (because we are traversing from 0 to cities, and problem want all cities can travel to 0)\n\n**Time and Space Complexity ... -> O(n), O(n)**\n* We visit all cities only once; therefore, time complexity -> O(n) where n is number of cities. (notice we can ignore the number of path because number of path is always n-1 in this problem)\n* We use space to build graph, recursive call stack, and visited set. All are O(n); therefore, O(3n) -> O(n)\n\n```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n graph = defaultdict(list)\n visited = set()\n # building undirected graph\n for s, e in connections:\n graph[s].append((e, True))\n graph[e].append((s, False))\n \n def dfs(currCity):\n count = 0\n if currCity in visited:\n return\n visited.add(currCity)\n for neigh, orig in graph[currCity]:\n if neigh not in visited:\n\t\t\t\t\t# if current path is same as original path that were given from input, \n\t\t\t\t\t# we know that we need to invert the path\n if orig == True:\n count += 1\n count += dfs(neigh)\n return count\n\t\t\t\n return dfs(0)\n```\n**Please correct me if I am wrong !\nPlease UPVOTE if you find this solution helpful !\nHappy algo!** | 26 | 0 | ['Depth-First Search', 'Python'] | 3 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Easy BFS Solution in JAVA in Depth | easy-bfs-solution-in-java-in-depth-by-_n-uzjp | Key Idea\nSo the basic idea is to make the whole graph bidirectional , with an exception that the other edge will be a fake one (reverse of the edge given in co | _nakul_30 | NORMAL | 2020-09-13T09:19:20.394935+00:00 | 2020-09-13T09:20:50.534304+00:00 | 1,436 | false | **Key Idea**\nSo the basic idea is to make the whole graph bidirectional , with an exception that the other edge will be a fake one (*reverse of the edge given in connections list*) as shown below : \n\n\n\n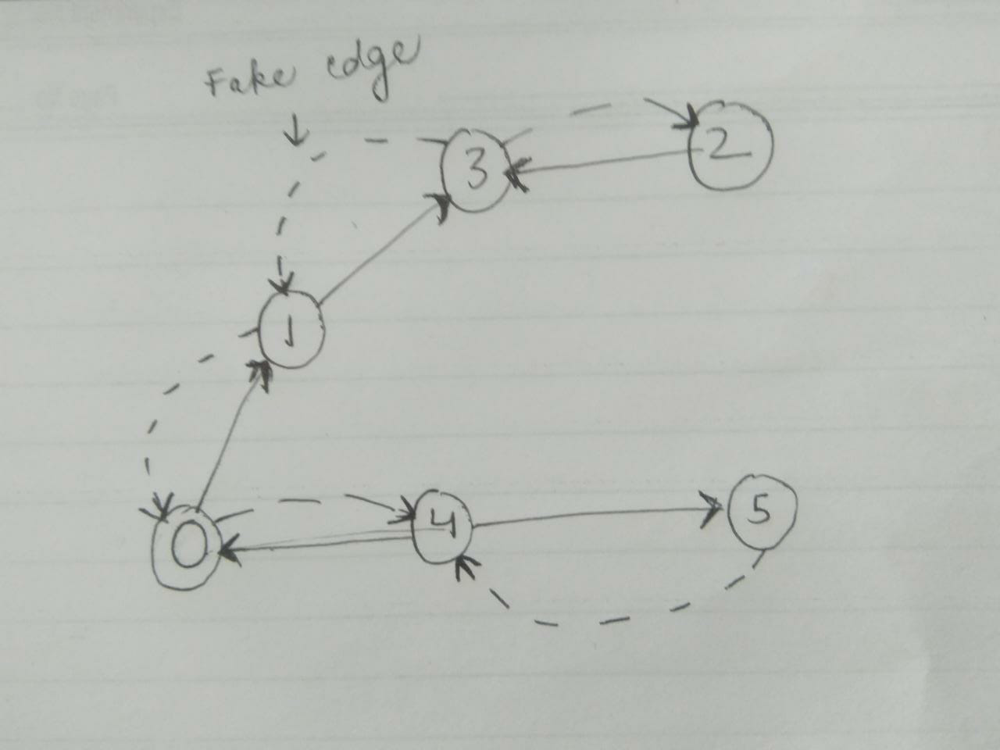\n\n\n\n\nAnd then perfom basic bfs operation on the graph with root as 0 and count the edge which is not Fake and going away from 0 **OR** going away from the nodes connected to 0 :\n\n\n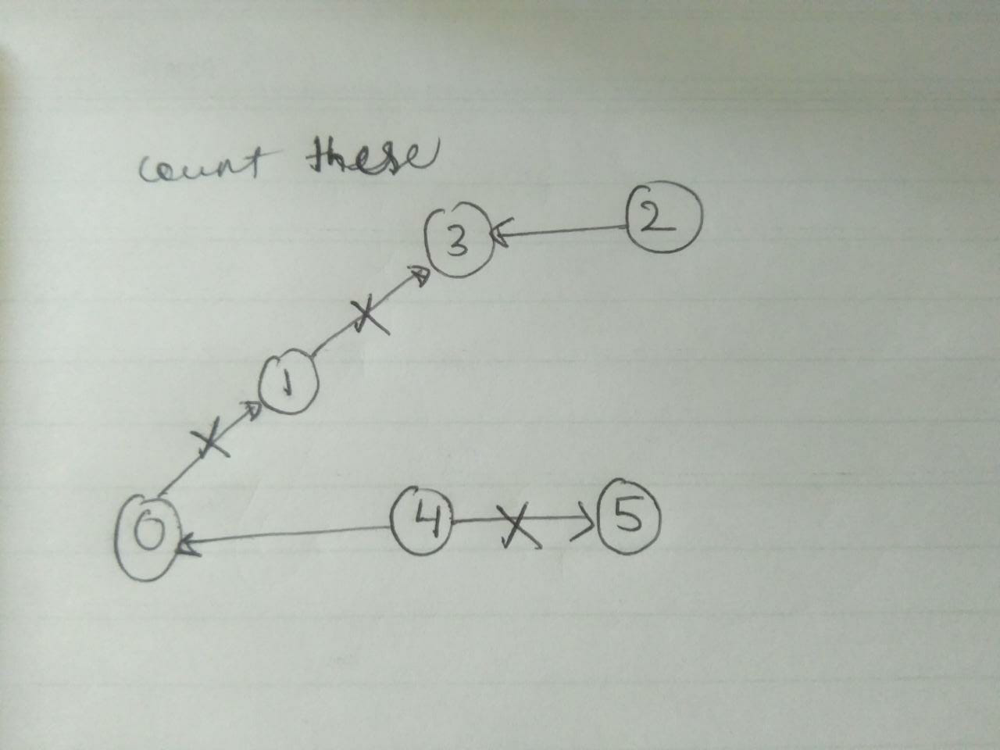\n\n\n\n**Algorithm**\n1. Make the whole graph bidirectional with fake edges.\n2. Start bfs with the root as 0.\n3. count the edge which is not fake and going away from 0 **OR** going away from nodes connected to 0.\n4. return count\n\n\n\n\n**Implementation**\n\n\n```\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n ArrayList<ArrayList<Pair>> adj = new ArrayList<>();\n \n for(int i = 0 ;i<n; i++){\n adj.add(new ArrayList<Pair>());\n }\n \n for(int ar[] : connections){\n addEdge(adj, ar[0], ar[1]);\n }\n \n return bfs(adj, n);\n }\n \n \n int bfs(ArrayList<ArrayList<Pair>> adj, int n){\n boolean visited[] = new boolean[n];\n \n Queue<Integer> q = new LinkedList<>();\n int count = 0;\n q.add(0);\n \n while(!q.isEmpty()){\n int temp = q.remove();\n visited[temp] = true;\n \n for(Pair p : adj.get(temp)){\n if(!visited[p.v]){\n // if the edge going away from zero/ nodes connected to 0 and is not fake then count ++\n if(p.isFake == false) count++; \n q.add(p.v);\n }\n }\n }\n \n return count;\n }\n \n \n void addEdge(ArrayList<ArrayList<Pair>> adj, int u, int v){\n adj.get(u).add(new Pair(v, false)); // this is the true edge \n\n adj.get(v).add(new Pair(u, true)); // this is the fake edge\n }\n}\n\n\nclass Pair{\n int v; // the other node\n boolean isFake = false; // is the edge fake or not\n Pair(int v, boolean isFake){\n this.v = v;\n this.isFake = isFake;\n }\n}\n```\n\n\n\n\n | 24 | 0 | ['Breadth-First Search'] | 5 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++ || line by line explanation | c-line-by-line-explanation-by-amankatiya-hnj6 | Intuition\nWe need find the number of road to rearrange in other words number of roads to reverse to reach 0 from each and every node.\n\n# Approach\nWe are go | amankatiyar783597 | NORMAL | 2023-03-24T03:35:31.457041+00:00 | 2023-03-24T03:42:13.489834+00:00 | 6,470 | false | # Intuition\nWe need find the number of road to rearrange in other words number of roads to reverse to reach 0 from each and every node.\n\n# Approach\nWe are going to use concept of incoming and out-going edges in node.\n\n\nLet\'s start solving this problem along with code and explanaion of logic behiend each step.....\n\nfirst we are going to find adjency list without making changes and one with reverse all the direction of edges. logic behind doing this ... if i could visite some cities/nodes from "A" (Node 0) given city/node that means we can\'t visit "A" (Node 0) from all visited cities and we need to reverse the direction of each road/edges to visit "A" (node 0).\n```\nfor(auto a : con){\n adj[a[0]].push_back(a[1]); // this is correce adjency list\n bk[a[1]].push_back(a[0]); // this is reverse adjencct list\n}\n```\nWe need a visited array that is for record of visted city/node\n```\nvector<int> vis(n,0);\n```\nNow start traversing by DFS/BFS and find number of cities/node you can visit from node 0 (these are the node which are not coming to node 0) these will be part of our answer.\n```\nqueue<int> q;\n q.push(0);\n while(!q.empty()){\n int a = q.front();\n vis[a] =1;\n q.pop();\n for( int no : adj[a]){\n if(!vis[no]){\n ans++;\n q.push(no);\n }\n }\n for( int no : bk[a]){\n if(!vis[no]){\n q.push(no);\n }\n }\n }\n```\nbelow part of code is to visit all outgoing rodes that will be part of our answer\n```\nfor( int no : adj[a]){\n if(!vis[no]){\n ans++;\n q.push(no);\n }\n}\n```\nthis part of code to visit all the incoming roads . city/nodes that are incoming and marking them visited so that not to reapetaion of visiting...\n```\nfor( int no : bk[a]){\n if(!vis[no]){\n q.push(no);\n }\n}\n```\n\n==========================================================\n```\nREAD IT ? VOTE UP .... give us motivation to continue.\n```\n==========================================================\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& con) {\n vector<vector<int>> adj(n) , bk(n);\n vector<int> vis(n,0);\n vis[0] =1;\n for(auto a : con){\n adj[a[0]].push_back(a[1]);\n bk[a[1]].push_back(a[0]);\n }\n int ans=0;\n queue<int> q;\n q.push(0);\n while(!q.empty()){\n int a = q.front();\n vis[a] =1;\n q.pop();\n for( int no : adj[a]){\n if(!vis[no]){\n ans++;\n q.push(no);\n }\n }\n for( int no : bk[a]){\n if(!vis[no]){\n q.push(no);\n }\n }\n }\n return ans;\n }\n};\n``` | 22 | 0 | ['C++'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [C++] Basic DFS Solution | No erasing required | Mark direction of Edges | c-basic-dfs-solution-no-erasing-required-dit8 | \nclass Solution {\npublic:\n // Correct Solution\n // We are just making an undirected graph, where we are giving (+ve) sign to outgoing\n // edges an | debanjan2002 | NORMAL | 2021-12-18T12:12:04.871171+00:00 | 2021-12-18T12:12:04.871199+00:00 | 1,991 | false | ```\nclass Solution {\npublic:\n // Correct Solution\n // We are just making an undirected graph, where we are giving (+ve) sign to outgoing\n // edges and pretending that there is also the same incoming edge (or in general the opposite edge)\n // and inserting it into the adj[] list as (-ve) elements.\n // This is done so that the DFS doesn\'t stop when there are no outgoing edges \n // (+ve edges) from the current edge. (Because there might be more outgoing edges afterwards)\n // Without the above idea, the basic idea fails in this test case : [[1,2],[2,0]].\n \n // Link to not fully correct code is given below\n // https://leetcode.com/submissions/detail/603533278/\n // This approach gets 72/76 test cases correct, but is not logically correct.\n // The below implementation corrects that.\n void makeGraph(vector<vector<int>>& connections,vector<int> adj[]){\n for(int i=0; i<connections.size(); i++){\n adj[connections[i][0]].push_back(connections[i][1]);\n adj[connections[i][1]].push_back(-connections[i][0]);\n }\n }\n void dfs(vector<int> adj[],vector<bool>& visited,int src,int &ans){\n visited[src] = true;\n for(int &v : adj[src]){\n if(!visited[abs(v)]){\n if(v > 0)\n ans++;\n dfs(adj,visited,abs(v),ans);\n }\n }\n }\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<int> adj[n];\n vector<bool> visited(n,false);\n int ans = 0;\n makeGraph(connections,adj);\n \n dfs(adj,visited,0,ans);\n return ans;\n }\n};\n``` | 20 | 2 | ['Depth-First Search', 'C', 'C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java beats 96% just a few lines | java-beats-96-just-a-few-lines-by-tomeri-02rk | \n public int minReorder(int n, int[][] connections) {\n int res = 0;\n Set<Integer> s = new HashSet<>();\n int u, v;\n s.add(0);\n | tomerittah | NORMAL | 2020-09-04T16:32:49.360723+00:00 | 2020-09-04T16:32:49.360794+00:00 | 1,584 | false | ```\n public int minReorder(int n, int[][] connections) {\n int res = 0;\n Set<Integer> s = new HashSet<>();\n int u, v;\n s.add(0);\n \n while (s.size() != n) {\n for (int i = 0; i < connections.length; i++) {\n u = connections[i][0];\n v = connections[i][1];\n \n if (s.contains(u) && !s.contains(v)) {\n s.add(v);\n res += 1;\n } else if (s.contains(v) && !s.contains(u)) {\n s.add(u);\n }\n }\n }\n \n return res;\n }\n``` | 20 | 0 | [] | 3 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | ✅ Java | Easy | BFS | java-easy-bfs-by-kalinga-fee9 | \nclass Solution {\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> adj=new ArrayList<>();\n for(int i=0;i<n;i++){\n | kalinga | NORMAL | 2023-03-24T02:32:50.129720+00:00 | 2023-03-24T02:32:50.129764+00:00 | 3,786 | false | ```\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> adj=new ArrayList<>();\n for(int i=0;i<n;i++){\n adj.add(new ArrayList<>());\n }\n for(int i=0;i<connections.length;i++){\n adj.get(connections[i][0]).add(connections[i][1]);\n adj.get(connections[i][1]).add(-connections[i][0]);\n }\n boolean vis[]=new boolean[n];\n int cnt=0;\n Queue<Integer> qu=new LinkedList<>();\n qu.add(0);\n vis[0]=true;\n while(!qu.isEmpty()){\n int curr=qu.poll();\n for(int it:adj.get(Math.abs(curr))){\n if(!vis[Math.abs(it)]){\n qu.add(it);\n vis[Math.abs(it)]=true;\n if(it>0)\n cnt++;\n }\n }\n }\n return cnt;\n }\n}\n```\n\n | 19 | 1 | ['Breadth-First Search', 'Graph', 'Java'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Python| Easy and fast | Beats 99% | python-easy-and-fast-beats-99-by-slavahe-8v9x | Time complexity: O(n)\n\nShort description:\nIn this solution, we add cities one by one to the country map. This addition follows 3 rules:\n1)If the first city | slavaherasymov | NORMAL | 2021-02-18T11:46:39.167848+00:00 | 2021-02-18T11:47:42.331111+00:00 | 2,888 | false | Time complexity: O(n)\n\nShort description:\nIn this solution, we add cities one by one to the country map. This addition follows 3 rules:\n1)If the first city of the road is already on the map, we need to change direction of this road and add a new city to the map.\n2)If the second city of the road is already on the map, we only add a new city to the map.\n3) If both cities are not on the map, we postpone this road and select next one. \n\nSolution:\n```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n cmap = {0}\n count = 0\n dq = deque(connections)\n while dq:\n u, v = dq.popleft()\n if v in cmap:\n cmap.add(u)\n elif u in cmap:\n cmap.add(v)\n count += 1\n else:\n dq.append([u, v])\n return count\n \n``` | 19 | 0 | ['Python', 'Python3'] | 4 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JAVA | Easy Solution Using Adjacency List | java-easy-solution-using-adjacency-list-9bgzw | \nclass Solution {\n List<Integer>[] incoming, outgoing;\n HashSet<Integer> visited;\n int ans;\n public int minReorder(int n, int[][] connections){ | onefineday01 | NORMAL | 2020-06-07T12:18:45.815982+00:00 | 2020-06-07T12:18:45.816013+00:00 | 1,957 | false | ```\nclass Solution {\n List<Integer>[] incoming, outgoing;\n HashSet<Integer> visited;\n int ans;\n public int minReorder(int n, int[][] connections){\n ans = 0;\n incoming = new ArrayList[n];\n outgoing = new ArrayList[n];\n for(int i = 0; i < n; i++){\n incoming[i] = new ArrayList();\n outgoing[i] = new ArrayList();\n }\n for(int edge[] : connections){\n incoming[edge[1]].add(edge[0]);\n outgoing[edge[0]].add(edge[1]);\n }\n visited = new HashSet();\n dfs(0);\n return ans;\n }\n void dfs(int v){\n visited.add(v);\n for(int i : outgoing[v])\n if(!visited.contains(i)){\n ans++;\n dfs(i);\n }\n for(int i: incoming[v])\n if(!visited.contains(i))\n dfs(i);\n }\n}\n```\n## DO UPVOTE IF YOU LIKE THE SOLUTION | 17 | 0 | ['Depth-First Search', 'Graph', 'Java'] | 4 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Java] Straight Forward DFS (Generic Solution) with Detail Explanation | java-straight-forward-dfs-generic-soluti-c07u | The idea which I have tried to implement through code is as follows. \nThe code will automatically handle the directions. Don\'t worry much about them yet.\nThe | manrajsingh007 | NORMAL | 2020-05-31T06:06:33.985636+00:00 | 2020-05-31T07:29:05.979956+00:00 | 1,310 | false | The idea which I have tried to implement through code is as follows. \nThe code will automatically handle the directions. Don\'t worry much about them yet.\nThere is no cycle in the graph.\nOnce you start traversing from 0, you start doing a dfs, all the nodes which you have visited traversing the edges were the wrong esdges which you will be inverting later on, so why not just count them.\nFor those nodes which have not been visited yet, again start with a DFS.\nFor instance in the first test case of the problem after doing dfs with node 0, you have visited node 0, node 1 and node 3. Now you again start DFS from the node 2(next unvisited node) but when you reach 3, you realise that 3 has already been visited implying that you have taken care of having a route from 3 to 0 somehow. Moreover you reached 3 from 2 so indirectly there is a path now from 2 to 0 as well. So no need to worry about 2. Now in future if there is a node say x whose dfs when done you reach 2, you will not have worry about x as well since then there would be a path from x to 0 indirectly.\nNow talking about node 4 and node 5, you start DFS from the next unvisited node that is 4. You can reach node 0 and node 5 but node 0 was visited so nothing will get added to the total edges due to that but since 5 was unvisited we will have to invert the edge connecting node 4 and node 5, in other words we add the contribution of the edge connecting node 4 and node 5 to our total no. of edges we need to invert.\n\nUpvote if you like the idea!!\n```\nclass Solution {\n public static int dfs(List<List<Integer>> g, int curr, boolean[] visited) {\n visited[curr] = true;\n List<Integer> adj = g.get(curr);\n int ans = 0;\n for(int i = 0; i < adj.size(); i++) if(!visited[adj.get(i)]) ans += 1 + dfs(g, adj.get(i), visited);\n return ans;\n }\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> g = new ArrayList<>();\n for(int i = 0; i < n; i++) g.add(new ArrayList<>());\n int m = connections.length;\n for(int i = 0; i < m; i++) {\n int sv = connections[i][0], ev = connections[i][1];\n g.get(sv).add(ev);\n }\n boolean[] visited = new boolean[n];\n int ans = 0;\n for(int i = 0; i < n; i++) if(!visited[i]) ans += dfs(g, i, visited);\n return ans;\n }\n} | 16 | 8 | [] | 7 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Using 0-1 BFS!!! Easy C++ Solution!!🔥🔥🔥 | using-0-1-bfs-easy-c-solution-by-vrishav-zl1j | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nHere, we are using 0-1 | vrishav28 | NORMAL | 2023-03-24T04:00:26.168653+00:00 | 2023-03-24T04:00:26.168686+00:00 | 2,208 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere, we are using 0-1 BFS. We will treat every edge which is already given hav weight 1 and the opposite of that edge as 0. Then we will apply BFS and find the total weight to reach the leaf nodes.\n\nNote: Here we are treating normal edges as weight 1 as we are applying the BFS from 0 to leaf nodes rather than leaf nodes to 0.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int,int>>> graph(n);\n for(auto &v: connections){\n graph[v[0]].push_back({v[1],1});\n graph[v[1]].push_back({v[0],0});\n }\n queue<pair<int,int>> q;\n q.push({0,0});\n vector<bool> vis(n,false);\n int ans=0;\n while(!q.empty()){\n auto p=q.front();\n q.pop();\n vis[p.first]=true;\n ans+=p.second;\n for(auto &x: graph[p.first]){\n if(vis[x.first])continue;\n // cout<<p.first<<\' \'<<p.second<<\' \'<<x.first<<" "<<x.second<<endl;\n q.push(x);\n }\n }\n return ans;\n }\n};\n``` | 14 | 0 | ['C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Complete Explanation with intuition || Simple DFS || Easy to understand | complete-explanation-with-intuition-simp-65ka | \n\n\nclass Solution {\npublic:\n void dfs(vector<vector<pair<int, int>>>&adj, vector<bool>& visited, int& ans, int currNode)\n {\n visited[currNod | mohakharjani | NORMAL | 2023-03-24T00:34:00.032450+00:00 | 2023-03-24T10:06:05.352698+00:00 | 2,364 | false | \n\n```\nclass Solution {\npublic:\n void dfs(vector<vector<pair<int, int>>>&adj, vector<bool>& visited, int& ans, int currNode)\n {\n visited[currNode] = true;\n for (pair<int, int>adjNode : adj[currNode])\n {\n //Curr = source, Next = adjNode.first\n if (visited[adjNode.first]) continue;\n \n //adjNode.second == 1 means that there is a real edge from \'Curr\' to \'Next\'\n bool isEdgeOutward = (adjNode.second == 1); \n if (isEdgeOutward) ans++; //but we want edge to come from \'Next\' to \'Curr\', so change direction \n dfs(adj, visited, ans, adjNode.first);\n }\n }\n int minReorder(int n, vector<vector<int>>& connections) \n {\n vector<vector<pair<int, int>>>adj(n);\n for(vector<int>connection : connections)\n {\n adj[connection[0]].push_back({connection[1], 1}); //real edge \n adj[connection[1]].push_back({connection[0], -1}); //false edge made for traversal\n }\n //===========================================================\n vector<bool>visited(n, false);\n int ans = 0;\n dfs(adj, visited, ans, 0);\n return ans;\n }\n};\n``` | 14 | 1 | ['Depth-First Search', 'Graph', 'C', 'C++'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | My Java DFS Solution with thought process | my-java-dfs-solution-with-thought-proces-0ey5 | \n/* \nMy thought process\nSo here we can first actually build the graph and I uses a List<List<integer>> for it.\nHere if we are having parent->child, then we | vrohith | NORMAL | 2020-09-30T05:38:43.952805+00:00 | 2020-09-30T05:38:43.952847+00:00 | 1,989 | false | ```\n/* \nMy thought process\nSo here we can first actually build the graph and I uses a List<List<integer>> for it.\nHere if we are having parent->child, then we take the sign as +ve and if vice versa we consider it as negative.\nFor traditional dfs, we need to keep track of the visited node thus we declare a boolean array for it.\nNow do the dfs from node 0.\n\nSo the dfs function actually looks for the parent->child relation node and this has to be reversed. So count of parent->child relation is tracked here and the count is returned.\n\nSo we looks for the neighbours of the current node and traverse throught it. Then we check whether we already visited it, if no then update the count + do the dfs with the current child + add 1 if the child > 0, ie from parent -> child or 0 ie then it will be child -> parent.\n\nFinally return the count and thats the problem.\n*/\n\n\n// 1. Convert the given into graph\n// 2. Do the dfs and look for the forward direction.\n// 3. Count of forward direction will give our answer.\n\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> adj = new ArrayList<>();\n for (int i=0; i<n; i++) {\n adj.add(new LinkedList<>());\n }\n for (int [] c:connections) {\n adj.get(c[0]).add(c[1]);\n adj.get(c[1]).add(-c[0]);\n }\n boolean [] visited = new boolean[n];\n return dfs(adj, visited, 0);\n }\n public int dfs(List<List<Integer>>adj, boolean [] visited, int v) {\n int reOrderCount = 0;\n visited[v] = true;\n List<Integer> children = adj.get(v);\n for (Integer child: children) {\n if (!visited[Math.abs(child)])\n reOrderCount += dfs(adj, visited, Math.abs(child)) + (child > 0 ? 1:0);\n }\n return reOrderCount;\n }\n}\n``` | 14 | 1 | ['Depth-First Search', 'Graph', 'Java'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Easy C++ Solution without Graphs | easy-c-solution-without-graphs-by-gazal1-yaik | I am inserting those nodes into the set from which we are having a path to 0. say -\neg- n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]\nnow I add 0 to th | gazal1199 | NORMAL | 2020-05-31T04:05:22.012482+00:00 | 2020-05-31T05:09:43.999945+00:00 | 693 | false | I am inserting those nodes into the set from which we are having a path to 0. say -\neg- n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]\nnow I add 0 to the set , now connection[0] represents a path from 0 to 1, but i want this from 1 to 0, so I increased the count by 1.\nNow this means I have reversed this path , therefore there is a path from 1 to 0 , so I insert 1 to the set,\nand so on...\nif there is already a path , so i am just inserting that node to the set without increasing the count.\n```\n\n int minReorder(int n, vector<vector<int>>& connections) {\n \n int count = 0;\n \n unordered_set<int>st;\n st.insert(0);\n \n for( int i = 0 ; i < connections.size() ; i++ ){\n \n if( st.find(connections[i][1]) == st.end() ){\n st.insert(connections[i][1]);\n count++;\n }\n \n else\n st.insert( connections[i][0]);\n }\n \n return count;\n }\n``` | 14 | 8 | [] | 5 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Simple Python Solution | simple-python-solution-by-sanatanmishra4-1q5j | \n# Code\n\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n dt = defaultdict(list)\n for a,b in connecti | sanatanmishra42 | NORMAL | 2023-03-24T04:45:42.505564+00:00 | 2023-03-24T04:45:42.505606+00:00 | 3,439 | false | \n# Code\n```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n dt = defaultdict(list)\n for a,b in connections:\n dt[a].append((b,True))\n dt[b].append((a,False))\n ans = 0\n q = [0]\n vis = set()\n while(q):\n node = q.pop()\n vis.add(node)\n for nd,st in dt[node]:\n if nd not in vis:\n q.append(nd)\n if st: ans+=1\n return ans\n``` | 12 | 0 | ['Python3'] | 7 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [ Without Graph ] Simple Solution using Set, faster than 100.00% of C++ online submissions | without-graph-simple-solution-using-set-doj94 | \nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n set <int > vv;\n int c=0;\n int l=connections. | lazerx | NORMAL | 2020-05-31T04:19:43.578514+00:00 | 2020-05-31T05:16:35.153041+00:00 | 688 | false | ```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n set <int > vv;\n int c=0;\n int l=connections.size();\n for(int i=0;i<l;i++)\n {\n if(connections[i][1]==0 || connections[i][0]==0)\n {\n if(connections[i][0]==0)\n {\n c++;\n }\n vv.insert(connections[i][1]);\n vv.insert(connections[i][0]);\n break;\n }\n }\n for(int i=0;i<l;i++)\n {\n if(vv.find(connections[i][1]) == vv.end())\n {\n c++;\n vv.insert(connections[i][1]);\n }\n else{\n vv.insert(connections[i][0]);\n }\n }\n return c;\n }\n};\n``` | 11 | 8 | ['C', 'Ordered Set'] | 3 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java | DFS Solution With Explanation | Cost of Moving Forward In Case of Bidirectional Roads | java-dfs-solution-with-explanation-cost-ro9hj | Problem Intuition-\nClearly, We need roads that take us to zero.\nIf Start a dfs from the zero, It will follow forward edges. The forward edges will take us far | asthakri50 | NORMAL | 2022-07-04T18:37:14.913459+00:00 | 2022-07-04T18:37:44.322658+00:00 | 937 | false | **Problem Intuition-**\nClearly, We need roads that take us to zero.\nIf Start a dfs from the zero, It will follow forward edges. The forward edges will take us far from zero, So you need to reverse those edges.\n\n\n**Code Explanation-**\nConsider the graph to be birectional, (rather make it directional) , such that the the cost of forward edges( original edges) is 1 and the cost of reversed edges is 0. \nStore them in the adjacency list such that adj[0] -> [1,1] means that there is a forward edge from 0 to 1.\nStart dfs from 0. Count whenever you traverse thorugh a forward edge. Return count.\n\n*Note- The edges are given in the forward manner (out degrees) only. Thats why we are considering cost of original edges as 1.*\n\n*Please feel free to ask any doubts. Also please upvote if you find it helpful.*\n\n\n```\nclass Solution {\n int count = 0 ;\n \n public int minReorder(int n, int[][] connections) {\n ArrayList<ArrayList< int[]> > adj = new ArrayList<ArrayList<int[]> >() ;\n \n for(int i = 0 ; i < n ; i++){\n adj.add(new ArrayList<int[]>() );\n }\n \n for(int i = 0 ; i < connections.length ; i++){\n int u = connections[i][0] ;\n int v = connections[i][1] ;\n \n adj.get(u).add(new int[]{v , 1} );\n adj.get(v).add(new int[]{u , 0}) ;\n }\n \n int[] visited = new int[n] ;\n Arrays.fill(visited , -1) ;\n \n \n dfs(0 , adj , visited) ;\n \n \n return count ;\n }\n \n private void dfs(int src , ArrayList<ArrayList<int[]>> adj , int[] visited){\n visited[src] = 1 ;\n \n for(int[] arr : adj.get(src) ){\n \n int num = arr[0] ;\n \n if(visited[num] == -1){\n count += arr[1] ;\n dfs(num , adj , visited) ;\n }\n }\n \n \n \n return ;\n }\n}\n``` | 10 | 0 | ['Depth-First Search', 'Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JavaScript Solution - DFS Approach? | javascript-solution-dfs-approach-by-dead-qm0d | I am not sure if this is a good way of doing it, but I thought I would post and get your guys\' opinions. Thank you.\n\n\nvar minReorder = function(n, connectio | Deadication | NORMAL | 2020-10-11T21:46:43.414249+00:00 | 2020-10-11T21:46:43.414312+00:00 | 1,117 | false | I am not sure if this is a good way of doing it, but I thought I would post and get your guys\' opinions. Thank you.\n\n```\nvar minReorder = function(n, connections) {\n const graph = [];\n const set = new Set();\n \n for (let i = 0; i < n; i++) {\n graph[i] = [];\n }\n \n for (const [u, v] of connections) {\n graph[u].push(v);\n graph[v].push(u);\n set.add(`${u}#${v}`);\n }\n \n let count = 0;\n \n dfs(0, -1)\n \n return count;\n \n \n function dfs(node, parent) {\n \n if (set.has(`${parent}#${node}`)) count++;\n \n for (const nei of graph[node]) {\n if (nei === parent) continue;\n \n dfs(nei, node);\n }\n }\n}; \n``` | 10 | 0 | ['Depth-First Search', 'JavaScript'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Clean Python 3, BFS O(N) | clean-python-3-bfs-on-by-lenchen1112-p97w | Make an undirected graph and perform BFS start from 0.\nThen just check reverse roads while BFS.\nTime: O(N)\nSpace: O(N)\n\nimport collections\nclass Solution: | lenchen1112 | NORMAL | 2020-05-31T04:02:35.460190+00:00 | 2020-05-31T04:02:41.586532+00:00 | 664 | false | Make an undirected graph and perform BFS start from 0.\nThen just check reverse roads while BFS.\nTime: `O(N)`\nSpace: `O(N)`\n```\nimport collections\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n graph = collections.defaultdict(list)\n visited = set([0])\n for u, v in connections:\n graph[u].append(v)\n graph[v].append(u)\n connections = set(map(tuple, connections))\n queue = collections.deque([0])\n changes = 0\n while queue:\n u = queue.popleft()\n for v in graph[u]:\n if v not in visited:\n changes += (u, v) in connections\n queue.append(v)\n visited.add(v)\n return changes\n``` | 10 | 6 | [] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | MOST INTUITIVE C++ SOLUTION !! | most-intuitive-c-solution-by-binarywizar-warf | \n\n# Intuition\nWe Need To Reach Capital City. For This, We Need To Run A DFS Traversal From Capital City (Node 0) To All The Cities. For This, We Need To Main | BinaryWizard_8 | NORMAL | 2024-05-04T16:57:30.526024+00:00 | 2024-05-04T17:03:17.197375+00:00 | 427 | false | ****\n\n# Intuition\nWe Need To Reach Capital City. For This, We Need To Run A DFS Traversal From Capital City (Node 0) To All The Cities. For This, We Need To Maintain An Adjacency List And Visited Array.\n\n\nNow, We Basically Need To Count The Number Of Edges Which Are Not Leading To Capital City Directly And Indirectly.\n\nHere Is Where The Slight Modification To Adjacency List Comes To Play. Read The Approach And Comments For Better Understanding.\n\n\n\n# Approach\n1. Prepare A Boolean Array For Visited Nodes And 2D Adjacency List.\n\n2. Push Destination Node To List Of Source Node And **Negative Of Source Node** To Adjacency List Of Destination Node.\n\n3. Initialise Count Of Edges To Be Reversed = 0.\n\n4. Start DFS Traversal From Capital City (Node 0).\n\n - **Base Case** : Current City Is Already Visited.\n - Mark Current City Visited.\n - Run A Loop For Adjacent Cities.\n - Check For Visited Neighbor.\n - In Case Of Positive Neighboring City: **Edge Needs To Be Reversed**.\n - Increase Count.\n - Recursive Call For DFS From Current Neighboring City.\n\n5. Return Count.\n\n# Complexity\n- Time complexity: **O (V + E)**\n\n- Space complexity: **O (V + E)**\n\n# Code\n```\n// DFS Traversal.\n\nclass Solution {\npublic:\n\n // Whenever A City With Positive Value Is Encountered.\n // Edge Needs To Be Reversed.\n\n void reverseEdge(int curr, vector<vector<int>> &adj, int &count, vector<bool> &vis) {\n \n // Base Case.\n if (vis[curr] == true) return;\n\n // Mark Current City As Visited.\n vis[curr] = true;\n\n for (auto neighborCity : adj[curr]) {\n\n // Reversing The Edge In Case Of Adjacent City With Positive Value.\n // City With Positive Value Implies There Is An Edge To Current City (Not From Current City).\n\n if (vis[abs(neighborCity)] == false) \n if (neighborCity > 0) count++;\n \n // Recursive Call For The Neighboring City.\n reverseEdge(abs(neighborCity), adj, count, vis);\n }\n }\n\n int minReorder(int n, vector<vector<int>> &connections) {\n \n vector<vector<int>> adj (n);\n vector<bool> vis (n, false);\n\n for (int i = 0; i < connections.size(); ++i) {\n\n int u = connections[i][0]; // Source City.\n int v = connections[i][1]; // Destination City.\n\n // Modification To Standard Approach.\n // In Adjacency List Of Destination City, Append Negative Value Of Source City.\n\n adj[u].push_back(v);\n adj[v].push_back(-u);\n }\n\n int count = 0;\n \n // Start DFS Traversal From Capital City.\n reverseEdge(0, adj, count, vis);\n\n return count;\n }\n}; | 9 | 0 | ['Depth-First Search', 'Graph', 'C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JAVA || Easy Solution with Explanation || 100% Faster code | java-easy-solution-with-explanation-100-prazj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shivrastogi | NORMAL | 2023-03-24T02:22:44.286871+00:00 | 2023-03-24T02:22:44.286901+00:00 | 1,544 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nPLEASE UPVOTE IF YOU LIKE..\n```\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n List<List<Edge>> graph = new ArrayList<>();\n for(int i = 0; i < n; i++) {\n graph.add(new ArrayList<>());\n }\n \n for(int i = 0; i < connections.length; i++) {\n // 1 denotes original edge\n graph.get(connections[i][0]).add(new Edge(connections[i][1], 1));\n \n // 0 denotes reversed edge\n graph.get(connections[i][1]).add(new Edge(connections[i][0], 0));\n }\n \n // Run a dfs from 0 and dissolve(mark) the edges that can be reached from zero, thereby increasing the count\n // Because if an edge is directly reachable from 0, it actually needs to get reversed\n return dfs(graph, 0, new boolean[n]);\n }\n \n // DFS\n private int dfs(List<List<Edge>> graph, int source, boolean[] isVisited) {\n int cost = 0;\n isVisited[source] = true;\n \n for(Edge neighbour : graph.get(source)) {\n if(!isVisited[neighbour.vertex]) {\n cost += neighbour.count + dfs(graph, neighbour.vertex, isVisited);\n }\n }\n return cost;\n }\n \n private class Edge {\n int vertex, count;\n public Edge(int vertex, int count) {\n this.vertex = vertex;\n this.count = count;\n }\n }\n}\n``` | 9 | 0 | ['Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Python 3 95% speed | python-3-95-speed-by-very_drole-hh9l | \n\n# Code\n\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n graph = defaultdict(set)\n for a, b in con | very_drole | NORMAL | 2022-09-30T20:58:01.983812+00:00 | 2022-09-30T20:58:01.983849+00:00 | 1,199 | false | \n\n# Code\n```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n graph = defaultdict(set)\n for a, b in connections:\n graph[a].add((b, True))\n graph[b].add((a, False))\n \n queue = deque([(0, False)])\n ans = 0\n visited = set()\n while queue:\n city, needs_flipped = queue.popleft()\n visited.add(city)\n if needs_flipped:\n ans += 1\n for neighbour in graph[city]:\n if neighbour[0] not in visited:\n queue.append(neighbour)\n return ans\n\n\n``` | 9 | 0 | ['Python3'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Python3] Simple DFS Solution. No set required, faster than 92%. | python3-simple-dfs-solution-no-set-requi-3kjs | To start we create out grid:\n\ngrid = defaultdict(list)\nfor a, b in connections:\n grid[a].append((b, 1))\n grid[b].append((a, 0))\n\nFor each connectio | Tommyd27 | NORMAL | 2023-03-24T09:59:55.580818+00:00 | 2023-03-24T09:59:55.580845+00:00 | 776 | false | To start we create out grid:\n```\ngrid = defaultdict(list)\nfor a, b in connections:\n grid[a].append((b, 1))\n grid[b].append((a, 0))\n```\nFor each connection we have, there is a road from A to B. We add a road in both directions, so to speak, but store the direction in the second element of the tuple, with 1 meaning we are travelling in the same direction as the road, and 0 meaning we are pathing the opposite direction.\n\nNext we have our depth first search, which we will start at 0/ the capital city:\n```\ndef dfs(location, parent):\n ans = 0\n for connection, direction in grid[location]:\n if connection == parent: continue\n ans += direction + dfs(connection, location)\n return ans\n```\nWe path through each road at our location in the grid, we avoid backtracking through the same path as our parent. This is sufficient as opposed to a visited variable, as due to the fact that there are n - 1 roads, there are no loops and only one way to path through the entire graph.\n\nAs we start our dfs at the capital/ node 0, if we travel down any road in its intended direction, it is pointed/ travelling away from the capital, thus needs to be flipped, so we add 1 to our answer. If we travel down a road in the other direction than its intended one, it is orientated before the capital and we can ignore it.\n\nThus now we just need to start our dfs at 0 and return the answer.\n```\nreturn dfs(0, -1)\n```\n# Solution\n```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n grid = defaultdict(list)\n for a, b in connections:\n grid[a].append((b, 1))\n grid[b].append((a, 0))\n\n def dfs(location, parent):\n ans = 0\n for connection, direction in grid[location]:\n if connection == parent: continue\n ans += direction + dfs(connection, location)\n return ans\n return dfs(0, -1)\n\n```\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$ | 8 | 0 | ['Depth-First Search', 'Python3'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Easy to understand code with detailed explanation | easy-to-understand-code-with-detailed-ex-qx64 | The problem asks us to reorient some roads such that each city can visit the capital city (city 0) and return the minimum number of roads changed. We are given | emmakuen | NORMAL | 2023-03-24T08:27:51.437149+00:00 | 2023-03-24T08:27:51.437177+00:00 | 641 | false | The problem asks us to reorient some roads such that each city can visit the capital city (city 0) and return the minimum number of roads changed. We are given n cities numbered from 0 to n-1 and n-1 roads that form a tree structure.\n\nTo solve this problem, we need to identify which roads need to be reversed to reach the capital city from every other city. We can start from the capital city (city 0) and traverse the tree structure to identify the required reversals. We can use a Depth-First Search (DFS) algorithm for the traversals.\n\nFirst, we initialize an object called `neighbors` to store the neighboring cities for each city, and a boolean array called `isZeroReachable` to track the cities that can reach the capital city.\n\nThen, we iterate over the connections array and populate the neighbors object with the neighboring cities for each city. For each connection, we add both the source city and the destination city to each other\'s neighboring list, with an indication of whether the direction of the connection needs to be reversed or not.\n\nNext, we start the DFS from the capital city (city 0) and then recursively traverse its neighbors and mark them as reachable, while counting the number of connections that need to be reversed.\n\nFinally, we return the total number of connections that need to be reversed.\n\n# JavaScript Code\n```\nvar minReorder = function (n, connections) {\n // Create an object to store the neighbors of each city\n let neighbors = {};\n // Create an array to keep track of which cities can reach city 0\n const isZeroReachable = Array(n).fill(false);\n // City 0 can reach itself\n isZeroReachable[0] = true;\n\n // Initialize an empty array for each city in neighbors\n for (let city = 0; city < n; city++) neighbors[city] = [];\n\n for (const [sourceCity, destinationCity] of connections) {\n // Add the destination city to the array for the source city with the boolean value false\n // boolean tracks the direction of the connection\n neighbors[sourceCity].push([destinationCity, false]);\n // Add the source city to the array for the destination city with the boolean value true\n neighbors[destinationCity].push([sourceCity, true]);\n }\n\n // Initialize the reorder count to 0 and call traverseCities with city 0\n let reorderCount = 0;\n traverseCities(0);\n\n // Return the reorder count\n return reorderCount;\n\n /**\n * @param {number} zeroReachableCity\n */\n function traverseCities(zeroReachableCity) {\n // Iterate over each neighbor of zeroReachableCity\n for (const [neighborCity, isSourceCity] of neighbors[zeroReachableCity]) {\n // If the neighbor is already reachable, continue to the next neighbor\n if (isZeroReachable[neighborCity]) continue;\n // If the connection is outgoing, increment reorderCount\n if (!isSourceCity) reorderCount++;\n // Mark the neighbor as reachable\n isZeroReachable[neighborCity] = true;\n // Recursively call traverseCities with the neighbor city as the new zeroReachableCity\n traverseCities(neighborCity);\n }\n }\n};\n\n``` | 8 | 0 | ['JavaScript'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JavaScript : Detailed explanation | javascript-detailed-explanation-by-jaypo-8a2v | Code\n\nvar minReorder = function(n, connections) {\n // from: (<from city>, [<to cities>])\n // to: (<to city>, [<from cities>])\n const from = new Ma | JayPokale | NORMAL | 2023-03-24T03:34:03.819336+00:00 | 2023-03-24T03:34:03.819382+00:00 | 1,176 | false | # Code\n```\nvar minReorder = function(n, connections) {\n // from: (<from city>, [<to cities>])\n // to: (<to city>, [<from cities>])\n const from = new Map(), to = new Map();\n\n // Function to insert in values in map\n const insert = (map, key, value) => {\n if(map.has(key)){\n const arr = map.get(key);\n arr.push(value);\n map.set(key, arr);\n } else {\n map.set(key, [value]);\n }\n }\n\n // Set all values in both maps\n for(const [a,b] of connections){\n insert(from, a, b);\n insert(to, b, a);\n }\n\n // Queue: cities to visit\n const queue = [0], visited = new Set();\n let count = 0;\n\n while(queue.length) {\n const cur = queue.shift(); // First element in queue\n\n // Check values in first map\n if(from.has(cur)){\n for(const x of from.get(cur)){\n // If visited, do nothing else add to queue\n if(visited.has(x)) continue;\n queue.push(x);\n count++; // Change direction of this path\n }\n }\n\n if(to.has(cur)){\n // If visited, do nothing else add to queue\n for(const x of to.get(cur)){\n if(visited.has(x)) continue;\n queue.push(x);\n }\n }\n\n visited.add(cur); // Mark city as visited\n }\n\n return count\n};\n``` | 8 | 0 | ['JavaScript'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Python][Explanation] Approach with "virtual" nodes beats 85% with DFS | pythonexplanation-approach-with-virtual-s6xfu | Okay, we have to reorient the roads for making our event successful. Let\'s go!\n\nFirst of all, let\'s think about the building graph and traversal. \n\nQ & A: | nahirniak | NORMAL | 2020-11-19T22:20:05.741118+00:00 | 2020-11-19T22:20:05.741161+00:00 | 527 | false | Okay, we have to reorient the roads for making our event successful. Let\'s go!\n\nFirst of all, let\'s think about the building graph and traversal. \n\n**Q & A:**\n\nQ: How will we traverse this one?\nA: Let\'s build connections in opposite direction!\n\nQ: What the traversal will give us?\nA: We will able to reach out to all nodes and count nodes that we added.\n\n**Stop.**\n\nQ: How will we understand that node has been added by us? \nA: Let\'s mark such nodes as "virtual" during building the graph.\n\nOkay, so we just need to make a DFS and compare if the connection between the current node and prev is virtual?\nYes! Just increment your counter, dude.\n\nTC: O(V + E) for DFS\nSC: O(V + E) for graph + O(E) for making opposite connections\n\n```\nclass Solution:\n \n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n if not connections: return 0\n \n graph = collections.defaultdict(dict)\n \n for fr,to in connections:\n graph[fr][to] = \'existing\'\n graph[to][fr] = \'virtual\'\n \n visited = [False] * n\n \n self.result = 0\n \n self.dfs(graph, 0, -1, visited)\n \n return self.result\n\n def dfs(self, graph, vertex, prev, visited):\n visited[vertex] = True\n \n if graph[vertex].get(prev, \'N/A\') == \'virtual\':\n self.result += 1\n \n for nei, type in graph[vertex].items():\n if not visited[nei]:\n self.dfs(graph, nei, vertex, visited)\n``` | 8 | 0 | [] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java NO BFS/DFS. Only use Set O(V*E), Beat 100% Time, 100% Space. | java-no-bfsdfs-only-use-set-ove-beat-100-jbf3 | Use set to contains node, and remove the node which can connect to 0.\nthere are 3 situtions: since edge is a -> b\n1. from 0 start edge, should reverse for su | flyatcmu | NORMAL | 2020-05-31T05:58:15.924221+00:00 | 2020-06-01T01:05:48.163803+00:00 | 480 | false | Use set to contains node, and remove the node which can connect to 0.\nthere are 3 situtions: since edge is a -> b\n1. from 0 start edge, should reverse for sure, count++;\n2. a - > b, if set NOT contains a, means a can connect to 0, and this edge a->b should reverse. count++;\n3. a -> b, if set NOT contains b, means b is connect to 0, and a is point to b, so nothing to do. continue scan.\n\n```\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n HashSet<Integer> set = new HashSet<>();\n for(int i = 0; i < n; i++) {\n set.add(i);\n }\n set.remove(0);\n int count = 0;\n while(!set.isEmpty()) {\n for(int[] connection: connections) {\n // a -> b;\n int a = connection[0];\n int b = connection[1];\n \n // if a, b both don\'t contains, means we already checked before.\n if(!set.contains(a) && !set.contains(b)) {\n continue;\n }\n \n if(a == 0) {\n // if start from 0 to other city, this edge should reverse;\n count++;\n set.remove(b);\n } else if(!set.contains(a)) {\n // if a is connect to 0, b is not, this edge should reverse;\n count++;\n set.remove(b);\n } else if(!set.contains(b)) {\n // if b is connect to 0, and a -> b, nothing to do, continue;\n set.remove(a);\n } \n }\n }\n return count;\n }\n}\n``` | 8 | 4 | [] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [BFS + DFS] Use DFS to explore and hashset to tracking old road orientation and trick | bfs-dfs-use-dfs-to-explore-and-hashset-t-lo0w | idea: traverse tree(or rode network) and count reversing\nTime Complexity: O(N)\nSpace Complexity: O(N)\nAlthough I solved 700+ leetcode problems, I am still r | codedayday | NORMAL | 2020-05-31T04:29:36.705757+00:00 | 2020-06-04T03:54:58.656293+00:00 | 1,419 | false | idea: traverse tree(or rode network) and count reversing\nTime Complexity: O(N)\nSpace Complexity: O(N)\nAlthough I solved 700+ leetcode problems, I am still rusty about some grammer. So I honestly documented all the bugs before deriving the final accepted solution. Wish it is helpful to the community. \n\n\n```\n// idea: traverse tree(or rode network) and count reversing\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n G_ = vector<vector<int>>(n);\n for(auto& e: connections){\n G_[e[0]].push_back(e[1]);\n G_[e[1]].push_back(e[0]);\n //paths_.insert(e);\n paths_.insert(e[0] << 16 | e[1]);\n }\n \n seen_ = vector<int> (n, 0);\n seen_[0]=1;\n ans_ = 0;\n dfs(0);\n return ans_;\n }\n \nprivate:\n int ans_;\n vector<int> seen_;\n //unordered_set<vector<int>> paths_; // bug2\n //set<vector<int>> paths_; // bug1\n unordered_set<int> paths_; //Note1:\n vector<vector<int>> G_;\n void dfs(int cur){ \n for(auto nxt: G_[cur]){ \n if(seen_[nxt]) continue;\n seen_[nxt] = 1;\n dfs(nxt);\n //if(paths_.count({cur, nxt})) ans_++;\n if(paths_.count(cur << 16 | nxt)) ans_++;\n }\n }\n};\n//Note1:this is a trick to compress state: key is (from_i << 16 | to_i)\n//without this, it will give TLE error\n```\n\nSolution 2: BFS (Bugged version, please help me to debug)\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& conn) {\n vector<vector<int>> G(n, vector<int>()); \n for(const auto& e: conn)\n G[e[0]].push_back(e[1]);\n \n queue<int> q;\n vector<bool> vis(n, false);\n \n int count = 0;\n for(int i = 0; i < n;i++){\n if(vis[i]) continue;\n vis[i] = 1;\n q.push(i); \n while(!q.empty()) \n for(int j = q.size(); j >0; j--){\n auto u = q.front(); q.pop(); \n for(auto v: G[u]){\n if(vis[v]) continue; \n vis[v] = true; \n q.push(v); \n count++;\n }\n } \n }\n return count;\n }\n};\n```\n\nNotes about BFS approach:\nExample 1: 5<--4-->0-->1-->3<--2\n\nI will try to explain using the example 1 (given in the question). We would be always starting from node 0 (as given) and if there is any outgoing edge from 0th node then we should count, so this can be done using the BFS as in BFS all edges at level 1 of 0th node will be visited and marked as visited (this are the all wrong path we need to correct, so count this edges for answer). So in 1st iteration 1st node will be visited, now its nearby nodes are visited and count its outgoing edges (so 3rd node will be visited). Now visited array will have visited entry for nodes 0, 1, and 3. The outer loop will insert 2 the queue but it will just mark It as visited(nearby already visited). Now 4 is inserted in the queue and its nearby are 0 and 5 but the key thing to note here is 0 will be not be inserted as it is already visited only 5 will be visited and its wrong direction is counted as answer. I hope this might help you to understand intuition behind the logic.\n\nBased on Example 1, I provide two more variations to provide some more intuition to clear some potetnial doubts I once had:\nExample 1: 5<--4-->0-->1-->3<--2\nExample 4: 0-->1-->3<--2<--4-->5\nExample 5: 0-->1-->3<--2-->4-->5\nNote, the only difference between Example 4 and 5 is direction between city 2 and 4.\n\nThe point in performing BFS is aggregating the count of all unvisited outging edges. That is it! Or is it? Here is my prove:\nFor all visited nodes/cities, you can simply treat them as one city: city 0. Any city point to city 0 is in right direction and no reverse operation is needed. If you are in univsited City i, and one of your next unvisited cities is j, that means j must be further away from city 0 than i, otherwise, j were already visited before i. In another word, you must visit i first before j.\n\nCredit:\nBFS is modified version of:\nhttps://leetcode.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/discuss/661783/C%2B%2B-Simple-BFS-solution\n\nThanks for warning from: @streamcslive \nThe above soltuion will fail in: \n3\n[[1,2],[2,0]]\n\nSo I provide a new version:\nBFS: (no bug version):\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n int answer=0;\n vector<vector<int>> G(n);\n //set<vector<int>> set1; \n unordered_set<int> set1;\n vector<bool> possible(n,false);\n for(auto i:connections){\n G[i[0]].push_back(i[1]);\n G[i[1]].push_back(i[0]);\n //set1.insert(i); \n set1.insert(i[0]<<16 | i[1]); \n }\n queue<int> q{{0}};\n while(!q.empty()){\n int cur=q.front(); q.pop();\n if(!possible[cur]){\n possible[cur]=true;\n for(auto i:G[cur]){\n //if(set1.find({cur,i})!=set1.end()&&!possible[i]){\n if(set1.count(cur << 16 | i) && !possible[i]){\n answer++;\n q.push(i);\n continue;\n }\n q.push(i);\n } \n } \n }\n return answer;\n }\n};\n```\nIt is a modified version from (I mainly speed up the code):\nhttps://leetcode.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/discuss/669037/C%2B%2B-Using-BFS-easy-explanation | 8 | 1 | ['Depth-First Search', 'Breadth-First Search', 'C'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | python dfs (actually simple not like the cringe overly short solutions) | python-dfs-actually-simple-not-like-the-ifjos | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | bruh50 | NORMAL | 2023-08-27T07:51:30.603616+00:00 | 2023-08-27T07:51:30.603632+00:00 | 823 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildAdj(self, matrix, n):\n adj = [[] for _ in range(n)]\n\n for a,b in matrix:\n adj[a].append((b, True))\n adj[b].append((a, False))\n \n return adj\n\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n count = 0\n adj = self.buildAdj(connections, n)\n visit = set()\n\n def dfs(node):\n nonlocal count\n visit.add(node)\n\n for nei, outgoing in adj[node]:\n if nei not in visit:\n if outgoing:\n count += 1\n \n dfs(nei)\n \n dfs(0)\n return count\n``` | 7 | 0 | ['Python3'] | 3 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Concise DFS | C++ | concise-dfs-c-by-tusharbhart-lc6c | \nclass Solution {\n int dfs(int node, int prnt, vector<pair<int, int>> adj[]) {\n int cnt = 0;\n for(auto ad : adj[node]) {\n if(ad | TusharBhart | NORMAL | 2023-03-24T01:00:52.820692+00:00 | 2023-03-24T01:00:52.820719+00:00 | 2,023 | false | ```\nclass Solution {\n int dfs(int node, int prnt, vector<pair<int, int>> adj[]) {\n int cnt = 0;\n for(auto ad : adj[node]) {\n if(ad.first == prnt) continue;\n cnt += ad.second + dfs(ad.first, node, adj);\n }\n return cnt;\n }\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<pair<int, int>> adj[n];\n for(auto e : connections) {\n adj[e[0]].push_back({e[1], 1});\n adj[e[1]].push_back({e[0], 0});\n }\n return dfs(0, -1, adj);\n }\n};\n``` | 7 | 0 | ['Depth-First Search', 'C++'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Go] [Golang] DFS, Adjacency List | go-golang-dfs-adjacency-list-by-f1rstmeh-6ej1 | Since we know that graph is sparse we\'ll use Adjacency List to represent graph.\nn : number of cities\nm: number of roads\nSpace and Time complexity for Adjace | f1rstmehul | NORMAL | 2022-03-09T10:44:12.942812+00:00 | 2022-03-16T03:01:08.128908+00:00 | 1,225 | false | Since we know that graph is sparse we\'ll use Adjacency List to represent graph.\n**n : number of cities**\n**m: number of roads**\n*Space* and *Time* complexity for *Adjacency List* will be: **O(n + m)** [only if graph is sparse]\nIn worst case(i.e. when graph is dense) *space* and *time* complexity will be **n^2.**\n\n### 1. Build an Adjacency List:\nTime to build an Adjacency List will be **O(m)**\n\n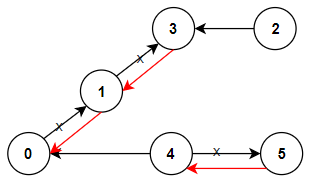\n\nWe\'ll use `[[0,1],[1,3],[2,3],[4,0],[4,5]]` edges to build list.\n```\nadList := make(map[int][]int)\n\nfor _, con := range connections {\n\t// Append the outgoing road to the city\n\tadList[con[0]] = append(adList[con[0]], con[1])\n\n\t// Append incoming road to the city. Here we need a way to differenciate between \n\t// incoming and outgoing road So we can mark this edge negetive. \n\tadList[con[1]] = append(adList[con[1]], -con[0])\n}\n```\n\n<details>\n <summary>Important Details</summary>\n \n> **Note that in case of the city `0` negative of `0` will be `0` itself So here we can\'t sure about the direction of the edge. But this won\'t create any issue when we\'ll traverse the graph because we\'re starting DFS from city `0` and marking it as visited.**\n\n</details>\n\n\nAfter building Adjacency List it will look like this: \n```\nmap[\n\t0:[1 -4] \n\t1:[0 3] \n\t2:[3] \n\t3:[-1 -2] \n\t4:[0 5] \n\t5:[-4]\n]\n```\n\n### 2. Keep track of visited nodes:\nTo keep track of visited cities we\'re using a slice. Because the city\'s names are simply from 0 to n-1 so we can directly map these with the slice index. If cities had some name like in the real world then we had to use a map.\n```\nvisited := make([]bool, n)\n```\n\n### 3. Use DFS to traverse the graph:\nHere we\'re using closure to avoid passing the `cities` and count parameters.\n```\nvar dfs func(start int)\ndfs = func(start int) {\n\tvisited[start] = true\n\tfor _, nb := range adList[start] {\n\t\t// incoming edge\n\t\tif nb < 0 { // nb -> neighbor\n\t\t\tnb = abs(nb)\n\t\t\tif !visited[nb] {\n\t\t\t\tdfs(nb)\n\t\t\t}\n\t\t} else {\n\t\t\t// outgoing edge that needs to be reoriented\n\t\t\tif !visited[nb] {\n\t\t\t\tcount++\n\t\t\t\tdfs(nb)\n\t\t\t}\n\t\t}\n\t}\n}\n// start with city `0`\ndfs(0)\n```\n\n## Complete Code\n```\nfunc minReorder(n int, connections [][]int) int {\n\tadList := make(map[int][]int)\n\n\tfor _, con := range connections {\n\t\tadList[con[0]] = append(adList[con[0]], con[1])\n\t\tadList[con[1]] = append(adList[con[1]], -con[0])\n\t}\n\n\tcount := 0\n visited := make([]bool, n)\n\n\tvar dfs func(start int)\n\tdfs = func(start int) {\n\t\tvisited[start] = true\n\t\tfor _, nb := range adList[start] {\n\t\t\tif nb < 0 {\n\t\t\t\tnb = abs(nb)\n\t\t\t\tif !visited[nb] {\n\t\t\t\t\tdfs(nb)\n\t\t\t\t}\n\t\t\t} else {\n\t\t\t\tif !visited[nb] {\n\t\t\t\t\tcount++\n\t\t\t\t\tdfs(nb)\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\tdfs(0)\n\treturn count\n}\n\nfunc abs(a int) int {\n\tif a < 0 {\n\t\treturn -a\n\t}\n\treturn a\n}\n``` | 7 | 0 | ['Depth-First Search', 'Go'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Video solution | Intuition explained in detail | C++ | DFS | video-solution-intuition-explained-in-de-01m1 | Video\nHey everyone i have created a video solution for this problem (its in hindi), it involves intuitive explanation with code, this video is part of my playl | _code_concepts_ | NORMAL | 2024-10-24T10:00:43.001455+00:00 | 2024-10-24T10:00:43.001487+00:00 | 420 | false | # Video\nHey everyone i have created a video solution for this problem (its in hindi), it involves intuitive explanation with code, this video is part of my playlist "Master Graphs"\nVideo link : https://www.youtube.com/watch?v=1aQPv0yDihs\nPlaylist link: : https://www.youtube.com/playlist?list=PLICVjZ3X1AcZ5c2oXYABLHlswC_1LhelY\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int count=0;\n\n void dfs(vector<vector<int>>& adj, int src, vector<bool>& visited){\n visited[src]=true;\n for(auto connectedCity: adj[src]){\n if(!visited[abs(connectedCity)]){\n if(connectedCity>0){\n count++;\n }\n dfs(adj,abs(connectedCity),visited);\n }\n }\n \n\n }\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<int>> adj(n);\n\n vector<bool> visited(n,false);\n\n for(int i=0;i<connections.size();i++){\n adj[connections[i][0]].push_back(connections[i][1]);\n adj[connections[i][1]].push_back(-connections[i][0]);\n\n }\n dfs(adj, 0, visited);\n\n return count;\n \n }\n};\n``` | 6 | 0 | ['C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | DFS (with explanation) | dfs-with-explanation-by-angielf-m20l | Approach\nThis solution uses a depth-first search (DFS) algorithm to determine the minimum number of edges that need to be changed to direct each city towards c | angielf | NORMAL | 2024-05-17T05:24:59.818040+00:00 | 2024-05-17T05:24:59.818074+00:00 | 937 | false | # Approach\nThis solution uses a depth-first search (DFS) algorithm to determine the minimum number of edges that need to be changed to direct each city towards city 0. Here is an overview of the approach:\n\n1. **Building the Graph**: The function first constructs a graph representation using an adjacency list. For each connection (road) between cities u and v, two entries are added to the adjacency list: one indicating a road from u to v with a direction of 1, and the other indicating a reverse road from v to u with a direction of 0.\n2. **Depth-First Search (DFS)**: The function then performs a DFS traversal starting from city 0 (the capital city) to count the number of edges that need to be changed. The dfs function recursively visits each city\'s neighbors, tracking the direction of the edges and incrementing the change_count based on the direction of the edge.\n3. **Counting Edge Changes**: At each step in the DFS traversal, the algorithm checks if the neighbor being visited is not the parent node to avoid revisiting the parent node. It then increments the change_count based on whether the edge needs to be changed (0 for reverse road, 1 for normal road).\n4. **Returning the Result**: The function returns the final count of edge changes needed to direct each city towards city 0 after completing the DFS traversal.\n\n# Complexity\n- Time complexity:\n$$O(n)$$, where n is the number of cities in the network. This complexity arises from the DFS traversal that visits each city once and explores its neighboring cities. Since the network is represented as a tree, the DFS traversal will have a maximum of n nodes to visit.\n\n- Space complexity:\n$$O(n)$$, where n is the number of cities in the network. This space is primarily used for storing the adjacency list representation of the graph, which can have up to n nodes in the case of a fully connected tree. Additionally, the recursive DFS function consumes space on the call stack proportional to the depth of the tree, which can be up to n in the worst case for a linear tree structure.\n\n# Code\n``` python3 []\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n graph = defaultdict(list)\n\n for u, v in connections:\n # Road from u to v\n graph[u].append((v, 1))\n # Reverse road from v to u\n graph[v].append((u, 0))\n\n def dfs(node, parent):\n change_count = 0\n for neighbor, direction in graph[node]:\n if neighbor != parent:\n # Count the edges that need to be changed\n change_count += direction\n change_count += dfs(neighbor, node)\n return change_count\n\n return dfs(0, -1)\n```\n``` javascript []\n/**\n * @param {number} n\n * @param {number[][]} connections\n * @return {number}\n */\nvar minReorder = function(n, connections) {\n const graph = new Array(n).fill(null).map(() => []);\n \n for (const [u, v] of connections) {\n // Road from u to v\n graph[u].push([v, 1]);\n // Reverse road from v to u\n graph[v].push([u, 0]);\n }\n\n function dfs(node, parent) {\n let changeCount = 0;\n for (const [neighbor, direction] of graph[node]) {\n if (neighbor !== parent) {\n // Count the edges that need to be changed\n changeCount += direction;\n changeCount += dfs(neighbor, node);\n }\n }\n return changeCount;\n }\n\n return dfs(0, -1);\n};\n```\n``` php []\nclass Solution {\n function dfs($node, $parent, $graph) {\n $changeCount = 0;\n foreach ($graph[$node] as list($neighbor, $direction)) {\n if ($neighbor !== $parent) {\n // Count the edges that need to be changed\n $changeCount += $direction;\n $changeCount += $this->dfs($neighbor, $node, $graph);\n }\n }\n return $changeCount;\n }\n\n /**\n * @param Integer $n\n * @param Integer[][] $connections\n * @return Integer\n */\n function minReorder($n, $connections) {\n $graph = array_fill(0, $n, []);\n \n foreach ($connections as $connection) {\n list($u, $v) = $connection;\n // Road from u to v\n $graph[$u][] = [$v, 1];\n // Reverse road from v to u\n $graph[$v][] = [$u, 0];\n }\n\n return $this->dfs(0, -1, $graph);\n }\n}\n``` | 6 | 0 | ['Depth-First Search', 'PHP', 'Python3', 'JavaScript'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [C++]/DFS CODE WITH DETAILED EXPLAINATION AND MINIMUM TIME COMPLEXITY ✅✅✅ | cdfs-code-with-detailed-explaination-and-bxs0 | Intuition\n- First, we can think of counting the total number of edges that are not pointing towards zero because that will give us our final answer.\n- However | tushar_1290 | NORMAL | 2023-06-28T03:36:45.517643+00:00 | 2023-06-28T03:36:45.517662+00:00 | 683 | false | # Intuition\n- First, we can think of counting the total number of edges that are not pointing towards zero because that will give us our final answer.\n- However, the question here is how to count these edges? Let\'s discuss the approach. Before proceeding i will suggest to think once again with this intuition.\n\n# Approach\n- First, we create an adjacency list, similar to what we do for an undirected graph.\n- Now, we can store the directions of all the edges in a map. For example, if there is an edge from u to v (u -> v), we can set map[{u, v}] = 1. We will use this map to determine the direction of each edge as we proceed further.\n- Now, we start a depth-first search (DFS) from 0 and count the edges that are directed from the parent to the child. These edges are pointing in the opposite direction of the 0 node, whether it is the direct or indirect parent of the current node.\n- Once the DFS traversal is completed, we will have the count of edges that are not pointing towards 0. This count represents our final answer.\n\n# Complexity\n- Time complexity: O(V*log(E)) V=no of vertices,E=no of edges,\nO(V) is for dfs and log(E) time for checking the direction of edge in map in dfs.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int ans=0;\n void dfs(vector<int> gr[],map<pair<int,int>,int> &direction,int node,int par){\n for(auto it: gr[node]){\n if(it==par) continue;\n if(direction.find({node,it})!=direction.end()) ans++;\n dfs(gr,direction,it,node);\n }\n }\n int minReorder(int n, vector<vector<int>>& conn) {\n vector<int> gr[n];\n map<pair<int,int>,int> direction;\n for(auto it: conn){\n gr[it[0]].push_back(it[1]);\n gr[it[1]].push_back(it[0]);\n direction[{it[0],it[1]}]=1;\n }\n\n dfs(gr,direction,0,-1);\n return ans;\n }\n};\n```\n# **PLEASE UPVOTE THE SOLUTION**\n\n | 6 | 0 | ['C++'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++ ✅ || BFS || Easy to Understand🔥 | c-bfs-easy-to-understand-by-snowflakes17-sn82 | \n# Approach\n Describe your approach to solving the problem. \n\n\n Create an adjacency list to represent the connections between the cities. \n We initialise | snowflakes17 | NORMAL | 2023-03-27T21:37:37.731688+00:00 | 2023-03-27T21:37:37.731737+00:00 | 246 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n* Create an adjacency list to represent the connections between the cities. \n* We initialise the given directed edge with `weight 1` and create an opposite edge corresponding to the same with `weight 0`.\n\n* Initialize a queue to perform BFS, a vector to keep track of visited cities, and a variable to store the answer.\n\n* Add the city 0 to the queue with a weight of 0 since we don\'t need to reverse any roads to reach city 0 from itself.\n\n* While `q.empty()!=0`, take the front element of the queue and mark it as visited. Also, add the weight of the current element to the answer.\n\n* For each neighbor of the current city, if it has not been visited yet, add it to the queue with the corresponding weight. If it has already been visited, skip it.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n\n int minReorder(int n, vector<vector<int>>& connections) {\n \n vector<vector<pair<int,int>>>adj(n);\n for(auto it: connections){\n adj[it[0]].push_back({it[1],1});\n adj[it[1]].push_back({it[0],0});\n }\n\n queue<pair<int,int>>q;\n vector<int>vis(n,-1);\n q.push({0,0});\n int ans=0;\n\n while(!q.empty()){\n int node=q.front().first;\n int wt=q.front().second;\n q.pop();\n vis[node]=1;\n \n ans+=wt;\n\n for(auto it: adj[node]){\n if(vis[it.first]==-1) q.push(it);\n else continue;\n }\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['C++'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Easy & Clear Solution Python 3 | easy-clear-solution-python-3-by-moazmar-livi | Intuition\nThe problem requires us to reorient some edges in a tree such that all cities can visit the capital city, and we need to return the minimum number of | moazmar | NORMAL | 2023-03-24T03:29:39.768153+00:00 | 2023-03-24T03:29:39.768197+00:00 | 1,150 | false | # Intuition\nThe problem requires us to reorient some edges in a tree such that all cities can visit the capital city, and we need to return the minimum number of edges that need to be changed. To solve this, we can use a DFS algorithm to traverse the tree and count the number of edges that need to be reversed.\n# Approach\nYour code initializes an empty adjacency list adj with n empty lists for each node in the graph. Then, it populates the adjacency list with the edges given in the connections list by adding the destination node with a value of 1 to the source node\'s list and adding the source node with a value of 0 to the destination node\'s list. Here, the value of 1 indicates that the edge needs to be reversed to reach the capital city, and 0 indicates that it doesn\'t need to be reversed.\n\nAfter setting up the adjacency list, the code implements a depth-first search algorithm dfs to traverse the tree. The dfs function takes two parameters: child and parent, where child represents the current node being traversed, and parent represents the parent of the current node.\n\nIn the dfs function, we iterate through each child node of the current node in the adjacency list. If the child node is not the parent node, it means that we need to reverse the edge between the current node and the child node. We increment the res variable by 1 if the value of the edge is 1, indicating that it needs to be reversed. Then, we call the dfs function recursively with the child node as the new current node and the current node as the new parent node.\n\nFinally, the code calls the dfs function with the capital city (node 0) as the current node and -1 as the parent node to start the traversal. It returns the res variable, which holds the number of edges that need to be reversed to reach the capital city.\n\n# Complexity\n- Time complexity:\nThe code iterates through each node in the tree once, so the time complexity is O(n), where n is the number of nodes in the tree.\n\n- Space complexity:\nThe code uses an adjacency list to store the edges, which takes O(n) space. The DFS algorithm uses a recursive stack, which can have at most n nodes in the worst case, so the space complexity is O(n). Overall, the space complexity of the code is O(n).\n\n# Code\n```\nclass Solution:\n res=0\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n adj=[]\n for i in range(n):\n adj.append([])\n for i in connections:\n adj[i[0]].append([i[1],1])\n adj[i[1]].append([i[0],0])\n def dfs(child,parent):\n for [c, s] in adj[child]:\n if c!=parent:\n self.res+=s\n dfs(c,child)\n dfs(0,-1)\n return self.res\n \n\n``` | 6 | 0 | ['Python3'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++ || BFS || Graph || Commented & clean code | c-bfs-graph-commented-clean-code-by-kr_s-v06l | \n // Intuition -> we have to make all the edges going towards 0\n \n // so we will start from 0 , all the nodes which are going away from\n // 0 , w | KR_SK_01_In | NORMAL | 2022-08-02T13:32:53.956896+00:00 | 2022-08-02T13:32:53.957244+00:00 | 838 | false | ```\n // Intuition -> we have to make all the edges going towards 0\n \n // so we will start from 0 , all the nodes which are going away from\n // 0 , we will take into count \n \n // Now the thing is , there is mixup of the all the edges , is it \n // sure that we will reach every nodes edge in that way \n \n // What extra we have to do we have to also make reversed edges \n // & we have to iterate the curr_edges of node & also reversed edges\n // of that node , & if not visited then push in the the queue\n \n // Lets code this BFS \n int minReorder(int n, vector<vector<int>>& edges) {\n \n vector<int> adj[n];\n vector<int> back_adj[n];\n \n for(int i=0;i<edges.size();i++)\n {\n int u=edges[i][0];\n int v=edges[i][1];\n \n adj[u].push_back(v);\n back_adj[v].push_back(u);\n }\n \n queue< int> q;\n q.push(0);\n \n vector<bool> visited(n , false);\n visited[0]=true;\n \n int ans=0;\n \n while(!q.empty())\n {\n int node=q.front();\n q.pop();\n \n // traverse all the nodes which are going away\n // from 0 \n \n for(auto x : adj[node])\n {\n if(visited[x]==false)\n {\n q.push(x);\n visited[x]=true;\n ans++;\n }\n }\n \n // Now which are not reachable , reached to it \n // means they are in directional edges , means towards 0\n // but we have to visit it , as it may occurs some edges\n // which are away from 0 , so for that we have to visit \n \n // all the nodes\n \n for(auto x : back_adj[node])\n {\n if(visited[x]==false)\n {\n q.push(x);\n visited[x]=true;\n \n }\n }\n }\n \n return ans;\n \n \n }\n``` | 6 | 0 | ['Breadth-First Search', 'Graph', 'C', 'C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Very Simple Explanation with diagram (just form new edges with weight = 0) | very-simple-explanation-with-diagram-jus-cwnx | \n\n\n the basic thing to note here is in this tree, whenever a parent is pointing to the child, that route needs to \n be inverted\n | uttu_dce | NORMAL | 2021-08-20T14:12:10.068840+00:00 | 2022-08-08T08:44:39.593432+00:00 | 214 | false | \n\n\n the basic thing to note here is in this tree, whenever a parent is pointing to the child, that route needs to \n be inverted\n so we have to make all the roads from children to parent (assuming that 0 is the root)\n so whenever the edge is from the parent to child, which means we can reach the child, \n\t\t\twe need to invert the edge\n \n so what i will do is i will assign a weight u to the original edges \n and also i will create a reverse edge which will have a weight v\n \n so now i will start from the root and keep traversing and sum all the weights \n at the end the total weight will be total = mu + nv (here i have used m original edges and n edges which i created)\n also when i use an oringinal edge to reach a child from a parent it means that from that node \n\t\t\tthe edge was pointing to the child, which is want we want to reverse \n so the answer is the total number of parent to child edges, which is equal to m\n \n so i will make u = 1 and v = 0\n```\n\nclass Solution {\npublic:\n vector<vector<pair<int, int>>> g;\n int ans = 0;\n void dfs(int u, int parent) {\n for(auto &[v, w] : g[u]) {\n if(v != parent) {\n ans+=w;\n dfs(v, u);\n }\n }\n }\n int minReorder(int n, vector<vector<int>>& edges) {\n g.resize(n);\n \n for(auto e : edges) {\n g[e[0]].push_back({e[1], 1});\n g[e[1]].push_back({e[0], 0});\n }\n dfs(0, -1);\n return ans;\n }\n};\n\nSame Solution Using BFS\n\nclass Solution {\n public :\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int,int>>> graph(n);\n for(auto e : connections) {\n graph[e[0]].push_back({e[1] ,1});\n graph[e[1]].push_back({e[0], 0});\n }\n int ans = 0;\n queue<pair<int,int>> q;\n q.push({0,0});\n vector<bool> vis(n,false);\n while(!q.empty()) {\n int cur = q.front().first;\n q.pop();\n // int wt = q.front().second;\n if(vis[cur]) continue;\n \n vis[cur] = true;\n for(auto nbrs : graph[cur]) {\n if(!vis[nbrs.first]) {\n ans+=nbrs.second;\n q.push(nbrs);\n } \n }\n }\n return ans;\n }\n};\n\n``` | 6 | 0 | [] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [2 Minute Read] Easy BFS | 2-minute-read-easy-bfs-by-dead_lock-flag | The trick we are going to apply here is that we would add some extra edges to our given Tree (if you are thinking, how it\'s a tree, then a graph having n nodes | dead_lock | NORMAL | 2021-07-19T16:39:53.728984+00:00 | 2021-09-04T18:00:50.398474+00:00 | 819 | false | The trick we are going to apply here is that we would add some extra edges to our given Tree (if you are thinking, how it\'s a tree, then a graph having `n` nodes and `n - 1` edges such that there is only one path between any 2 pair of vertices is sure to be a Tree). \n\n**The TRICK**\n1. Reverse the direction of edges in which it\'s originally given.\n2. For every edge of step 1, add it\'s reverse also, and mark it somehow so it\'s identifiable differently. (Let\'s call it `artificial` edge)\n\n**Algorithm**\n1. Maintain a `count` variable.\n2. Start BFS from node `0` and visit every node of the graph.\n3. If to visit a node, you use an `artificial` edge, increase your count by `1`.\n\n<br>\n\n**CONTEXT**\n- Firstly, we are storing the edges in a reverse order than that giving by `connections` because we wan\'t to be able to be able to reach from node `0` to every other node, since simulating the process of reaching from one node to every other node is easier than simulating to reach from every other node to `0` (which is demanded in the problem). \n- Secondly, we add a reverse edge for every edge which we added in the first step, to make sure that if there is an edge from, say node `a` to node `b`, then we now also have an edge from `b` to `a`, which helps us simulate as if we are rotating an edge. It signifies that if we choose the former edge, then we are not rotating this edge, but if we choose the latter one, then we are rotating this edge. Also, to recognize the latter edge we can use a `boolean` value to signify if it\'s an `artificial` edge or not.\n- Thirdly, we perform a Simple BFS, starting from node `0`, and move to the next node iteratively level by level, using the edge taking us from the current node to the next node. If this edge is a normal one, then we would simply continue with our BFS. If this edge is an `artificial` edge, then we would increase our `count` by `1`, and then continue with our BFS.\n\n<br>\n\nBelow is the code for the above algorithm in JAVA.\n\n```java\nclass Solution {\n\n\t// custom class for keeping the destination from a source \n class Dest {\n int v;\n\t\tboolean artificial; // true if this edge was added artificially and was not in the original Tree\n public Dest(int v, boolean artificial) {\n this.v = v;\n this.artificial = artificial;\n }\n }\n public int minReorder(int n, int[][] connections) {\n Map<Integer, ArrayList<Dest>> map = new HashMap<>();\n for(int i = 0; i < n; i++) {\n map.put(i, new ArrayList<>());\n }\n for(int e[] : connections) {\n int u = e[0], v = e[1];\n map.get(v).add(new Dest(u, false));\n map.get(u).add(new Dest(v, true));\n }\n \n int cost = 0;\n Queue<Integer> q = new LinkedList<>();\n q.add(0);\n boolean visited[] = new boolean[n];\n visited[0] = true;\n while(!q.isEmpty()) {\n int temp = q.poll();\n for(Dest i : map.get(temp)) {\n if(visited[i.v]) continue;\n if(i.artificial) cost++; // if this is the artificially added node, then increase cost\n q.add(i.v);\n visited[i.v] = true;\n }\n }\n return cost;\n }\n}\n``` | 6 | 0 | ['Breadth-First Search', 'Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Python | BFS | Directed Graph + Undirected Graph | Explained with comments | python-bfs-directed-graph-undirected-gra-uccn | \nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n from collections import defaultdict\n \n undire | underoos16 | NORMAL | 2020-05-31T04:22:17.315136+00:00 | 2020-05-31T05:11:47.632540+00:00 | 641 | false | ```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n from collections import defaultdict\n \n undirected_graph = defaultdict(list)\n actual_graph = defaultdict(set) # for faster lookup\n\n for a,b in connections:\n undirected_graph[a].append(b) #Figure out which cities are connected to each other (i.e a road exists between the two) \n undirected_graph[b].append(a)\n actual_graph[a].add(b) #Figure out which cities have "valid" roads (i.e you are allowed to go from a to b)\n\n queue = [(node, 0) for node in undirected_graph[0]] #All neighbours of 0 #(node, destination_node) \n res = 0\n visited = set([0])# Mark 0 as visited\n \n while queue:\n node, destination_node = queue.pop()\n visited.add(node) #Mark node as visited \n\n if not (destination_node in actual_graph[node]): #If there is no "valid" road which lets you travel from node to destination_node, you\'ll have to reverse the road\n res += 1\n\n for neighb in undirected_graph[node]: #For all unvisited neighbours, you\'ll have to continue exploring\n if neighb not in visited:\n queue.append((neighb, node))\n \n return res\n```\n\nTime: O(N)\nSpace: O(N)\n\nYou\'ll have to explore all N-1 edges to make the graphs anyway\nWorst case, you\'ll have to store all nodes (except 0) in the queue. | 6 | 0 | ['Breadth-First Search', 'Graph', 'Python'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | BFS | 94 % Beats | Java - Simple Explanation | bfs-94-beats-java-simple-explanation-by-4xmg7 | \n\n# Approach\n Describe your approach to solving the problem. \nFirst thing is making the graph bidirectional.\nIf an edge is given from a -> b, then we shoul | eshwaraprasad | NORMAL | 2024-09-01T11:29:31.903851+00:00 | 2024-09-01T11:29:31.903871+00:00 | 501 | false | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst thing is making the graph bidirectional.\nIf an edge is given from a -> b, then we should build the graph\nby edges a -> b and b -> -a .\nHere minus sign indicates that we have created this new edge and it\'s not the given directed edge.\n\n\n\n# Code\n```java []\nclass Solution {\n int dfs(List<List<Integer>> adj, boolean[] visited, int src) {\n int change = 0;\n visited[src] = true;\n for(int node : adj.get(src)) {\n if(!visited[Math.abs(node)]) {\n change += (node > 0 ? 1 : 0);\n change += dfs(adj, visited, Math.abs(node));\n }\n }\n return change;\n }\n public int minReorder(int n, int[][] connections) {\n List<List<Integer>> adj = new ArrayList<>();\n for(int i = 0; i < n; i++) adj.add(new ArrayList<>());\n\n for(int conn[] : connections) {\n int src = conn[0];\n int dest = conn[1];\n adj.get(src).add(dest);\n adj.get(dest).add(-src);\n }\n\n return dfs(adj, new boolean[n], 0);\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | BEATS 99% in time and 78% in space C# solution. DFS and BFS solution. Well commented. | beats-99-in-time-and-78-in-space-c-solut-g43t | General intuition\nThe logic is the same as that from the editorial solution. I just thought I\'d made this C# code much more readable and easy to understand. \ | Aadityakiran_S | NORMAL | 2023-09-08T04:35:24.087035+00:00 | 2023-09-08T10:07:24.604572+00:00 | 272 | false | # General intuition\nThe logic is the same as that from the editorial solution. I just thought I\'d made this C# code much more readable and easy to understand. \n\nWe\'re basically doing a traversal. Since **all roads** need to **lead from other cities to 0**, if we traverse using an original edge away from zero, that edge should be removed => all original edges should have a weight of 1 and fake edges (edges in reverse that we add for the express purpose of traversing the tree) should have a weight of 0.\n\n# Approach 1: DFS\nNothing fancy, just regular DFS. No need for any seen data stracture since it\'s a tree anyway.\n\n# Algorithm\n- Use an adjList to store the graph. Put `ai -> bi` as the original road and give it a weight of 1. \n- Put `bi -> ai` also in the list with a weight of 0.\n- DFS from 0 and at every step keep incrementing count using sign.\n- No need for any seen/cache data structure to prevent looping. Since it\'s given that the input is a tree like structure, only need to make sure we don\'t loop between parent and child => just skip over DFS when we encounter parent in the connection list of child.\n\n# Complexity\n- Time complexity: `O(n)` since we visit each node once to explore it\n\n- Space complexity: `O(h)` at max height of the tree will be in the stack at any one time.\n\n# Code\n```\npublic class Solution {\n public int MinReorder(int n, int[][] roads) {\n //graph is defined as an adjList with sign to denote if original (1) or fake (0) road\n // and connection to denote which city that road leads to\n List<List<(int sign, int conn)>> adj = new(); int count = 0;\n\n //Initialization\n for(int i = 0; i < n; i++){ adj.Add(new List<(int sign, int conn)>()); }\n\n //Populating\n foreach(int[] road in roads){\n adj[road[0]].Add((1, road[1])); //Adding original road\n adj[road[1]].Add((0, road[0])); //Adding fake road\n }\n\n DFS(0, -1); //DFS from 0. \n\n return count;\n\n void DFS(int curr, int par){ \n foreach((int sign, int conn) nei in adj[curr]){\n if(nei.conn == par) continue; //Don\'t want to go in a loop => skip parent in child\n\n count += nei.sign; //Keep adding sign\n DFS(nei.conn, curr); //Do DFS on child using curr as parent\n }\n }\n }\n}\n```\n\n# Approach 2: BFS\nSimple, bare-bones BFS traversal. Simply count the number of nodes going away from the 0 (original nodes) each time we explore. That\'s it.\n\n# Algorithm\n- Use an adjList to store the graph. Put `ai -> bi` as the original road and give it a weight of 1. \n- Put `bi -> ai` also in the list with a weight of 0.\n- The queue in the BFS traversal should have the current and the parent node so that we can know what the parent is of the current node to prevent looping.\n\n# Complexity\n- Time complexity: `O(n)` since we visit each node once to explore it\n\n- Space complexity: `O(w)` at max width of the tree will be in the queue at any one time.\n\n# Code\n```\npublic class Solution {\n public int MinReorder(int n, int[][] roads) {\n List<List<(int sign, int conn)>> adj = new(); int count = 0;\n\n for(int i = 0; i < n; i++){ adj.Add(new List<(int sign, int conn)>()); }\n foreach(int[] pair in roads){\n adj[pair[0]].Add((1, pair[1])); //Original road is given a weight of 1\n adj[pair[1]].Add((0, pair[0])); //Fake/Aritifical road is given a weight of 0\n }\n\n //Doing BFS\n //Need to keep track of parent to prevent infinite loop\n Queue<(int node, int par)> queue = new(); queue.Enqueue((0, -1));\n while(queue.Count > 0){\n int size = queue.Count;\n for(int i = 0; i < size; i++){\n (int curr, int par) = queue.Dequeue();\n foreach(var entry in adj[curr]){\n if(entry.conn == par) continue; //Skipping parent\n \n count += entry.sign; //Keeping count of all roads leading away from 0\n queue.Enqueue((entry.conn, curr)); //Adding in queue for further processing\n }\n }\n }\n\n return count;\n }\n}\n```\n# Approach 3: DFS and BFS variation\nThis is a variation that BingChat gave me to this question. It involves setting the value of the real edge as +ve and the fake edge as -ve rather than attach another flag to it. Pretty compact. Same complexities. \n\n```\npublic class Solution {\n public int MinReorder(int n, int[][] roads) {\n //Adjacency List declaration\n List<int>[] adj = new List<int>[n];\n for(int i = 0 ; i < n; i++){ adj[i] = new List<int>(); }\n\n //Original and fake roads should be differentiated.\n // Put +ve for original road and -ve for fake road\n foreach(int[] road in roads){ \n adj[road[0]].Add(road[1]); adj[road[1]].Add(-road[0]); \n }\n\n //Perform BFS\n Queue<(int curr, int par)> queue = new(); queue.Enqueue((0, -1));\n int count = 0;\n while(queue.Count > 0){\n int size = queue.Count;\n for(int i = 0; i < size; i++){\n (int curr, int par) = queue.Dequeue();\n\n foreach(int entry in adj[curr]){\n if(Math.Abs(entry) == par) continue;\n\n if(entry > 0) { count++; }\n queue.Enqueue((Math.Abs(entry), curr));\n }\n }\n }\n\n return count; //Comment from line 13-30 and you can get the DFS approach\n\n return DFS(0, -1); //Start DFS from 0 to count roads leading away from zero\n\n int DFS(int curr, int par){\n int count = 0; //Keep count of how many nodes from this node need to be changed\n foreach(int nei in adj[curr]){\n if(Math.Abs(nei) == par) continue; //Skip over parent to prevent self loop\n\n if(nei > 0){ count++; } //If edge is original => add count\n count += DFS(Math.Abs(nei), curr); //Incrementing node count\n }\n return count;\n }\n }\n}\n``` | 5 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Graph', 'C#'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | 1466. Reorder Routes to Make All Paths Lead to the City Zero | 1466-reorder-routes-to-make-all-paths-le-xuzs | ***\n# Code\n\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& con) {\n vector<vector<int>> adj(n) , bk(n);\n vector<int | tusharsingh102003 | NORMAL | 2023-03-24T16:21:03.241102+00:00 | 2023-03-24T16:21:03.241139+00:00 | 901 | false | ***\n# Code\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& con) {\n vector<vector<int>> adj(n) , bk(n);\n vector<int> v(n,0);\n v[0] =1;\n for(auto a : con){\n adj[a[0]].push_back(a[1]);\n bk[a[1]].push_back(a[0]);\n }\n int answer=0;\n queue<int> q;\n q.push(0);\n while(!q.empty()){\n int a = q.front();\n v[a] =1;\n q.pop();\n for( int no : adj[a]){\n if(!v[no]){\n answer++;\n q.push(no);\n }\n }\n for( int no : bk[a]){\n if(!v[no]){\n q.push(no);\n }\n }\n }\n return answer;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | 🔥 Java || Simple BFS Solution with Explanation ✅ | java-simple-bfs-solution-with-explanatio-iq9m | \uD83D\uDCCC\uD83D\uDCCC The idea is simple : Perform Breadth First Traversal from the starting vertex , move BREADTH-WISE and keep on counting the edges needs | Yash_kr | NORMAL | 2022-03-28T05:06:38.152222+00:00 | 2022-03-28T05:14:23.966643+00:00 | 236 | false | \uD83D\uDCCC\uD83D\uDCCC **The idea is simple** : *Perform Breadth First Traversal from the starting vertex , move BREADTH-WISE and keep on counting the edges needs to be reversed. Outdegree Edges will be reversed while Indegree edges will be not*\uD83D\uDC4D\uD83C\uDFFB\n\nNow Lets say in BFS Traversal we reached some vertex **3** and from this we can reach to **0**.\nYou have 2 types of edges on vertex **3**, either going outwards \uD83D\uDC49\uD83C\uDFFB( outdegree ) or inwards \uD83D\uDC48\uD83C\uDFFB( indegree ).\n\nCase 1\uFE0F\u20E3 : Now since, you can already reach \'0\' from \'3\' so you can also reach \'0\' from indegree vertices of \'3\' (i.e. vertices from which an edge comes to \'3\'). So you dont need to reverse any edge . Just simply add indegree neighbours to the queue for further BFS exploration.\n\nCase 2\uFE0F\u20E3 : The edges which are outdegree of \'3\' , you need to reverse them all. So for every outdegree vertex ( i.e. vertices to which \'3\' has an edge going to it) , add 1 (one) to your count variable and add the neighbour to the queue for furthur exploration.\n\nAfter processing any vertex mark it visited \u2705\n\n\uD83D\uDED1 Point to Note --> In Case 01 , where you are adding all the indegree vertices of the current vertex to the queue, you need to also need to remove those indegree ( incoming ) edges otherwise the current vertex will become as outdegree of the neighbour and it will be counted in the answer even when it is already processed.\n\nFor Example : Lets say the graph is like this \n 0--> 1 --> 10 <--4\n\t\t\t\t\t\tand you are currenlty at vertex 10 in BFS ( means 10 can reach 0 )\n\t\t\t\t\t\tYou know that 10 has one indegree vertex \'4\' so you will \n\t\t\t\t\t\tadd \'4\' to the queue ( no need to reverse this edge ). But Before adding \'4\' to the queue you also remove the indegree edge coming to \'10\' from \'4\' otherwise in future when we will be processing \'4\' we will see the outdegree edge going towards \'10\' and we will increase the count by 1 which was not even required \u203C\uFE0F. \n\n\n```\nclass Solution {\n \n public int minReorder(int n, int[][] connections) {\n \n HashSet<Integer>[] outdegree = new HashSet[n]; //outdegree of every vertex\n HashSet<Integer>[] indegree = new HashSet[n]; //indegree of every vertex\n for(int i=0;i<n;i++){\n outdegree[i] = new HashSet<>();\n indegree [i] = new HashSet<>();\n }\n \n int l = connections.length;\n for(int i=0;i<l;i++)\n {\n int x = connections[i][0];\n int y = connections[i][1];\n \n outdegree[x].add(y);\n indegree[y].add(x);\n }\n \n int[] vis = new int[n]; // visited array to store already processed vertices\n Queue<Integer> queue = new LinkedList<>();\n queue.add(0);\n \n int ans = 0;\n while(!queue.isEmpty())\n {\n int vtx = queue.remove();\n if(vis[vtx]==1) continue;\n\t\t\t\n\t\t\t//for every outdegree neighbour of current vertex\n for(Integer nbr : outdegree[vtx]) \n {\n ans+=1;\n queue.add(nbr);\n }\n \n\t\t\t// for every in-degree neighbour , add to the queue and remove that indegree edge \n for(Integer nbr : indegree[vtx]) \n { \n outdegree[nbr].remove(vtx);\n queue.add(nbr);\n }\n\t\t\t\n\t\t\t// and finally mark this vertex as visited/processed\n vis[vtx]=1; \n }\n \n return ans; \n }\n}\n```\n\n\uD83D\uDCCC Upvote If you Liked The Approach \uD83D\uDE04\uD83D\uDE0A | 5 | 0 | ['Breadth-First Search'] | 2 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C# solution (DFS) | c-solution-dfs-by-newbiecoder1-saik | Intuition\nStarting from city 0, traverse the graph by using DFS\nWhen encountering a foward path, we need to reverse it.\n\nComplexity\n- Time: O(n)\n- Space: | newbiecoder1 | NORMAL | 2022-03-21T16:38:02.928564+00:00 | 2024-09-28T05:22:13.321524+00:00 | 216 | false | **Intuition**\nStarting from city ```0```, traverse the graph by using DFS\nWhen encountering a foward path, we need to reverse it.\n\n**Complexity**\n- Time: O(n)\n- Space: O(n)\n\n**Implementation**\n```\npublic class Solution {\n public int MinReorder(int n, int[][] connections) {\n \n List<int>[] graph = new List<int>[n];\n for(int i = 0; i < n; i++)\n {\n graph[i] = new List<int>();\n }\n\n HashSet<(int,int)> directedEdges = new HashSet<(int,int)>();\n \n for(int i = 0; i < connections.Length; i++)\n {\n graph[connections[i][0]].Add(connections[i][1]);\n graph[connections[i][1]].Add(connections[i][0]);\n\n directedEdges.Add((connections[i][0], connections[i][1]));\n }\n\n int res = 0;\n HashSet<int> visited = new HashSet<int>();\n\n dfs(graph, directedEdges, 0, visited, ref res);\n\n return res;\n }\n\n public void dfs(List<int>[] graph, HashSet<(int,int)> directedEdges, int curr, HashSet<int> visited, ref int res)\n {\n visited.Add(curr);\n\n foreach(var next in graph[curr])\n {\n if(!visited.Contains(next))\n {\n if(directedEdges.Contains((curr,next)))\n res++; \n dfs(graph, directedEdges, next, visited, ref res); \n } \n }\n } \n}\n``` | 5 | 0 | ['Depth-First Search', 'Graph', 'C#'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JAVA | BFS | Explained Solution | java-bfs-explained-solution-by-siddhantg-whpc | Here we\'ll simply construct out graph and also maintain a hashset where we\'ll store the original edges given to us. So when we\'ll start our normal BFS with 0 | siddhantgupta792000 | NORMAL | 2022-02-23T02:04:01.508508+00:00 | 2022-02-23T02:04:01.508560+00:00 | 563 | false | Here we\'ll simply construct out graph and also maintain a hashset where we\'ll store the original edges given to us. So when we\'ll start our normal BFS with 0 as starting node whenever we find a edge that is taking as away from our parent we\'ll check if that exits in our hashset and if yes then we\'ll increase our answer count. \n\n```\nclass Solution {\n public int minReorder(int n, int[][] connections) {\n HashSet<String> set = new HashSet<>();\n ArrayList<Integer>[] graph = new ArrayList[n];\n for(int i = 0 ; i < n ; i++) {\n graph[i] = new ArrayList<>();\n }\n for(int[] e : connections) {\n int u = e[0], v = e[1];\n graph[u].add(v);\n graph[v].add(u);\n set.add(u + "->" + v);\n }\n Queue<Integer> q = new LinkedList<>();\n q.add(0);\n int res = 0;\n boolean[] vis = new boolean[n];\n while(!q.isEmpty()) {\n int size = q.size();\n while(size-- > 0) {\n int rem = q.remove();\n vis[rem] = true;\n for(int e : graph[rem]) {\n if(!vis[e]) {\n if(set.contains(rem + "->" + e)) res++;\n q.add(e); \n }\n }\n }\n }\n return res;\n }\n}\n``` | 5 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Simple, clean and self-explanatory solution | simple-clean-and-self-explanatory-soluti-0i66 | If you know any city x != 0that reaches 0, then you know 0 can be reached (eventually) if you reach the city x. Create a set to keep track of the cities that ca | aswin2 | NORMAL | 2020-09-07T17:22:31.267943+00:00 | 2020-09-07T17:22:31.267999+00:00 | 460 | false | If you know any city `x != 0 `that reaches 0, then you know 0 can be reached (eventually) if you reach the city x. Create a set to keep track of the cities that can reach 0. As you traverse the connection array, keep adding those cities which has connection to any city that is in the set. If you found any city which is in the set, and has a connection a city "x" which is not in the set, then that connection has to rerouted, so increment the count. Repeat this process, until the set size has reached n.\n\n```\npublic int minReorder(int n, int[][] conn) { \n HashSet<Integer> set = new HashSet<>();\n set.add(0);\n int ans = 0;\n while(set.size() < n){\n for(int i=0; i<conn.length; i++){\n if(set.contains(conn[i][1])){\n set.add(conn[i][0]);\n }else if(set.contains(conn[i][0]) && !set.contains(conn[i][1])){\n set.add(conn[i][1]);\n ans++;\n }\n }\n }\n return ans;\n }\n```\n | 5 | 2 | [] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Java] Runtime: 4 ms, faster than 99.21% | java-runtime-4-ms-faster-than-9921-by-10-vpsn | Runtime: 4 ms, faster than 99.21%\uFF0CMemory Usage: 53.9 MB, less than 100.00% of Java online submissions\n\n\npublic int minReorder(int n, int[][] roads) {\n\ | 103style | NORMAL | 2020-05-31T04:03:59.067521+00:00 | 2020-06-03T01:58:06.799175+00:00 | 471 | false | **Runtime: 4 ms, faster than 99.21%\uFF0CMemory Usage: 53.9 MB, less than 100.00% of Java online submissions**\n\n```\npublic int minReorder(int n, int[][] roads) {\n\tint res = 0;\n\t//find the first i make roads[i][0] =0 or roads[i][1] = 0, and swap roads[i] and roads[0]\n\tupdateZeroCityInHead(roads);\n\tint sortedIndex = 0, moveIndex = 1;\n\t//record the road\n\tint[] record = new int[n];\n\trecord[roads[0][0]] = 1;\n\trecord[roads[0][1]] = 1;\n\n\t//sort the roads array, to make the roads[i][0] or roads[i][1] (i>0)is exist in {roads[0][0] roads[0][1] .... roads[i-1][0] roads[i-1][1]}\u3002\n\twhile (sortedIndex + 1 >= n) {\n\t\tboolean swap = false;\n\t\tif (record[roads[moveIndex][0]] == 1\n\t\t\t\t|| record[roads[moveIndex][1]] == 1) {\n\t\t\trecord[roads[moveIndex][0]] = 1;\n\t\t\trecord[roads[moveIndex][1]] = 1;\n\t\t\tsortedIndex++;\n\t\t\tif (sortedIndex != moveIndex) {\n\t\t\t\tswap(roads, sortedIndex, moveIndex);\n\t\t\t\tswap = true;\n\t\t\t}\n\t\t}\n\t\tif (!swap) {\n\t\t\tmoveIndex++;\n\t\t}\n\t\tif (moveIndex >= n) {\n\t\t\tmoveIndex = sortedIndex + 1;\n\t\t}\n\t}\n\t//because roads[i][0] or roads[i][1] (i>0)is exist in S = {roads[0][0] roads[0][1] .... roads[i-1][0] roads[i-1][1]}, \n\t//if roads[i][1] is not in S, so we should change it, let res++;\n\tint[] t = new int[n];\n\tt[0] = 1;\n\tfor (int[] c : roads) {\n\t\tif (t[c[1]] == 0) {\n\t\t\tres++;\n\t\t}\n\t\tt[c[0]] = 1;\n\t\tt[c[1]] = 1;\n\t}\n\treturn res;\n}\n\n\n/**\n * find the first i make roads[i][0] =0 or roads[i][1] = 0, and swap roads[i] and roads[0]\n */\nprivate void updateZeroCityInHead(int[][] t) {\n\tint zeroIndex = -1;\n\tfor (int i = 0; i < t.length; i++) {\n\t\tif (t[i][0] == 0 || t[i][1] == 0) {\n\t\t\tzeroIndex = i;\n\t\t\tbreak;\n\t\t}\n\t}\n\tif (zeroIndex == -1) {\n\t\tthrow new IllegalArgumentException("connections is illegal!");\n\t}\n\tif (zeroIndex != 0) {\n\t\tswap(t, 0, zeroIndex);\n\t}\n}\n\nprivate void swap(int[][] t, int src, int des) {\n\tint[] f = t[src];\n\tt[src] = t[des];\n\tt[des] = f;\n}\n```\n\nIf the test case satisfies **roads[i][0] or roads[i][1] (i>0)is exist in S = {roads[0][0] roads[0][1] .... roads[i-1][0] roads[i-1][1]}**,\n**not like:**\n```\n3\n[[1,2],[2,0]]\n6\n[[2,3],[3,1],[1,0],[4,0],[4,5]]\n```\n**just use the following code , it can pass all test cases of leetcode, otherwise sort it first.**\n\n```\npublic int minReorder(int n, int[][] roads) {\n\tint res = 0;\n\tint[] t = new int[n];\n\tt[0] = 1;\n\tfor (int[] c : roads) {\n\t\tif (t[c[1]] == 0) {\n\t\t\tres++;\n\t\t}\n\t\tt[c[0]] = 1;\n\t\tt[c[1]] = 1;\n\t}\n\treturn res;\n}\n```\n | 5 | 5 | ['Java'] | 7 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JS/TS Solution DFS Approach | jsts-solution-dfs-approach-by-giogokul13-o14w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n## Time | giogokul13 | NORMAL | 2024-09-17T16:40:51.481640+00:00 | 2024-09-17T16:40:51.481672+00:00 | 303 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n## Time complexity: O(N)\n- The time complexity of this solution is O(n), where n is the number of cities. This is because we are performing a DFS traversal on the graph, which visits each city only once.\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n## Space complexity: O(N)\n- The space complexity is O(n), where n is the number of cities. This is because we are storing the adjacency list for each city, as well as the visited array to keep track of visited cities during the DFS traversal.\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number} n\n * @param {number[][]} connections\n * @return {number}\n */\nvar minReorder = function (n, connections) {\n let adjList = {};\n let reverseRoads = 0;\n let visited = Array(n).fill(false);\n\n for (let i = 0; i < n; i++) {\n adjList[i] = [];\n }\n\n // Step 1: Build a bidirectional graph\n for (let [a, b] of connections) {\n // Store forward and reverse roads\n adjList[a].push([b, 1]); // road goes from a to b, so 1 means road is directed away from 0\n adjList[b].push([a, 0]); // road goes from b to a (reverse connection), 0 means road is directed towards 0\n\n }\n\n // Step 2: DFS Traversal\n let dfs = (node) => {\n visited[node] = true;\n\n for (let [neighbor, isReversed] of adjList[node]) {\n if (!visited[neighbor]) {\n reverseRoads += isReversed; // Count if the road is directed away from city 0\n dfs(neighbor);\n }\n }\n }\n\n // Step 3: Start DFS from city 0\n dfs(0);\n\n return reverseRoads;\n}; \n``` | 4 | 0 | ['Depth-First Search', 'Graph', 'TypeScript', 'JavaScript'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Beats 93%🔥|| DFS🔥|| easy JAVA Solution✅ | beats-93-dfs-easy-java-solution-by-priya-b290 | Code\n\nclass Solution {\n class Pair{\n int val;\n boolean f;\n Pair(int val,boolean f){\n this.val=val;\n this.f | priyanshu1078 | NORMAL | 2024-03-18T16:44:37.604402+00:00 | 2024-03-18T16:44:37.604438+00:00 | 394 | false | # Code\n```\nclass Solution {\n class Pair{\n int val;\n boolean f;\n Pair(int val,boolean f){\n this.val=val;\n this.f=f;\n }\n }\n int ans;\n public int minReorder(int n, int[][] mat) {\n List<List<Pair>> adj=new ArrayList<>();\n for(int i=0;i<n;i++) adj.add(new ArrayList<>());\n for(int[] arr:mat){\n adj.get(arr[0]).add(new Pair(arr[1],true));\n adj.get(arr[1]).add(new Pair(arr[0],false));\n }\n boolean[] vis=new boolean[n];\n ans=0;\n sol(adj,vis,0);\n return ans;\n }\n public void sol(List<List<Pair>> adj,boolean[] vis,int idx){\n vis[idx]=true;\n for(Pair x:adj.get(idx)){\n if(!vis[x.val]){\n if(x.f) ans++;\n sol(adj,vis,x.val);\n }\n }\n }\n}\n``` | 4 | 0 | ['Depth-First Search', 'Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java | DFS | BSF | Beats 92% | java-dfs-bsf-beats-92-by-mcihan7-cxr3 | Approach\n- minus(-) represents opposite direction. \n\n# Time Complexity\n \nO(n)\n\n\n\n# 1.DFS\njava\nclass Solution {\n int count =0;\n\n public int m | mcihan7 | NORMAL | 2024-02-11T00:16:03.453406+00:00 | 2024-02-11T00:17:47.086877+00:00 | 279 | false | # Approach\n- minus(-) represents opposite direction. \n\n# Time Complexity\n \n$$O(n)$$\n\n\n\n# 1.DFS\n```java\nclass Solution {\n int count =0;\n\n public int minReorder(int n, int[][] connections) {\n boolean visit[] = new boolean[n];\n List<List<Integer>> graph = new ArrayList<>();\n\n for (int i = 0; i < n; i++) \n graph.add(i, new ArrayList<>());\n \n for (int[] nums : connections) {\n graph.get(nums[0]).add(nums[1]);\n graph.get(nums[1]).add(-nums[0]);\n }\n dfs(graph, visit, 0);\n return count;\n }\n\n private void dfs(List<List<Integer>> graph, boolean[] visit, int i) {\n if (!visit[i]) {\n visit[i] = true;\n for (int num : graph.get(i)) {\n int absNum = Math.abs(num);\n if (!visit[absNum]) {\n if (num > 0) \n count++; \n dfs(graph, visit, absNum);\n }\n }\n }\n }\n\n}\n```\n\n# 2. BFS\n\n```java\nclass Solution { \n public int minReorder(int n, int[][] connections) {\n boolean[] visit = new boolean[n];\n List<List<Integer>> graph = new ArrayList<>();\n\n for (int i = 0; i < n; i++) {\n graph.add(i, new ArrayList<>());\n }\n\n for (int[] nums : connections) {\n graph.get(nums[0]).add(nums[1]);\n graph.get(nums[1]).add(-nums[0]);\n }\n\n int count = 0;\n\n visit[0] = true;\n Deque<Integer> queue = new LinkedList<>();\n queue.offer(0);\n\n while (!queue.isEmpty()) {\n int pop = Math.abs(queue.pop());\n for (Integer num : graph.get(pop)) {\n if (!visit[Math.abs(num)]) {\n if (num > 0) {\n count++;\n }\n visit[Math.abs(num)] = true;\n queue.offer(num);\n }\n }\n }\n\n return count;\n }\n}\n```\n\n\n<br/>\n\n<img src="https://assets.leetcode.com/users/images/085853ae-9586-479f-acf2-ec3ce30fd0e7_1703932262.0024223.png" style="width:400px;height:auto;">\n\n<br/> | 4 | 0 | ['Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Clean DFS + BFS Solution With Explanation (O(n^2) || O(n) time) | clean-dfs-bfs-solution-with-explanation-27kmy | Idea\n- The main idea of both solutions is that we will necessarily traverse from zero, visiting the node closest to it (even if we cannot reach it from zero) a | vltvdnl | NORMAL | 2024-02-04T16:20:00.181477+00:00 | 2024-02-04T16:20:00.181512+00:00 | 230 | false | # Idea\n- The main idea of both solutions is that we will necessarily traverse from zero, visiting the node closest to it (even if we cannot reach it from zero) and so on. If a node is directed to zero, ans is not incremented, otherwise ans++.\n- First we convert the given array into an adjacent list with a specific feature. It is important for us to store for each node not only where we can go from it, but also how we can visit it. But how do we figure out which node we can come to from a given node, and which leads to this node? We will add those nodes that we can visit with +, others with -\n\n```\ngraph := make([][]int, n)\n for _, val := range connection{\n graph[val[0]] = append(graph[val[0]], val[1]) // where we can go\n graph[val[1]] = append(graph[val[1]], -val[0]) //where we can come from\n }\n```\n- Then create a **visited-array**, in which we will store those nodes that we have already visited. The answer will be stored in the **ans** variable\n ```\nvisited := make([]bool, n)\nans := 0\n```\n\n# First Approach (DFS)\n- Let\'s create a classic DFS for graph traversal with a slight modification. We pass the current Node to the function, immediately write its values to visited[node] = true. \n- Next, we traverse all nodes that are related to the data in one way or another. \n- If it hasn\'t been visited yet, we run recursively dfs from its value. If the value was negative, then ans unchanged, otherwise ans++ (Node direction). \n```\nvar dfs func(number int)\n dfs = func(number int){\n visited[number] = true \n for i:=0; i<len(graph[number]); i++{\n if !visited[abs(graph[number][i])]{\n dfs(abs(graph[number][i]))\n if graph[number][i] >0{ // check node direction\n ans++\n }\n }\n }\n }\n```\n- Then iteratively go through all nodes in the graph. If it has not been visited yet, run dfs from it\n\n\n#### Full Code (DFS)\n```\nfunc minReorder(n int, con [][]int) int {\n visited := make([]bool, n)\n graph := make([][]int, n)\n for _, val := range con{\n graph[val[0]] = append(graph[val[0]], val[1])\n graph[val[1]] = append(graph[val[1]], -val[0])\n }\n ans:=0\n var dfs func(number int)\n dfs = func(number int){\n visited[number] = true\n for i:=0; i<len(graph[number]); i++{\n if !visited[abs(graph[number][i])]{\n dfs(abs(graph[number][i]))\n if graph[number][i] >0{\n ans++\n }\n }\n }\n }\n for i:=0; i<len(graph); i++{\n if !visited[i]{\n dfs(i)\n }\n }\n return ans\n}\n\nfunc abs(a int) int{\n if a>=0{\n return a\n }\n return -a\n}\n```\n# Second solution (BFS)\n- The idea of the solution is the same as in the first one (looking at the node direction). We create a queue to which we sequentially add all nodes that are somehow related to the given node. Depending on the value of the node (positive or negative) we increase ans or leave it as it is. Mark this Node as visited. \n## Full code (BFS)\n```\nfunc minReorder(n int, con [][]int) int {\n visited := make([]bool, n)\n graph := make([][]int, n)\n for _, val := range con{\n graph[val[0]] = append(graph[val[0]], val[1])\n graph[val[1]] = append(graph[val[1]], -val[0])\n }\n queue := []int{}\n for _, val := range graph[0]{\n queue = append(queue, val)\n }\n\n ans:=0\n for len(queue) > 0{\n size := len(queue)\n for i:=0; i<size; i++{\n cur := queue[0]\n queue = queue[1:]\n if cur > 0 && !visited[abs(cur)]{\n ans++\n }\n if len(graph[abs(cur)]) > 0 && !visited[abs(cur)]{\n for _, val := range graph[abs(cur)]{\n queue = append(queue, val)\n }\n }\n visited[abs(cur)] = true\n }\n\n }\n return ans\n\n}\nfunc abs(a int) int{\n if a>=0{\n return a\n }\n return -a\n}\n```\n## If you hava any question, feel free to ask. If you like the solution or the explaination, Please UPVOTE! | 4 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Graph', 'Go'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | JavaScript Solution | javascript-solution-by-davinderpalrehal-w7jl | Intuition\nBuild an adjacency list with distances between the cities, where distance is 0 if incoming and 1 if outgoing.\n\n# Approach\nTraversing through the l | davinderpalrehal | NORMAL | 2023-12-22T18:54:57.724840+00:00 | 2023-12-22T18:54:57.724870+00:00 | 163 | false | # Intuition\nBuild an adjacency list with distances between the cities, where distance is 0 if incoming and 1 if outgoing.\n\n# Approach\nTraversing through the list just adding distances to cities that haven\'t been visited\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number[][]} connections\n * @return {number}\n */\nvar minReorder = function(n, connections) {\n const adjList = {}\n\n for (let c of connections) {\n const [src, dest] = c\n if (!adjList.hasOwnProperty(src)) adjList[src] = []\n if (!adjList.hasOwnProperty(dest)) adjList[dest] = []\n adjList[src].push({\n city: dest,\n distance: 1\n })\n adjList[dest].push({\n city: src,\n distance: 0\n })\n }\n\n const visited = new Set()\n const queue = []\n queue.push(0)\n let changes = 0\n\n while (queue.length) {\n const curr = queue.shift()\n\n if (visited.has(curr)) continue\n visited.add(curr)\n\n for (let n of adjList[curr]) {\n if (visited.has(n.city)) continue\n changes += parseInt(n.distance)\n queue.push(n.city)\n }\n }\n\n return changes\n};\n``` | 4 | 0 | ['JavaScript'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | DFS || C++ | dfs-c-by-deepakvrma-xqfa | \n# Code\n\nclass Solution {\npublic:\nint ans=0;\n void dfs(unordered_map<int,vector<int>>&mp ,unordered_map<int,bool>&vis,int m){\n vis[m]=true;\n | DeepakVrma | NORMAL | 2023-10-11T18:30:48.216321+00:00 | 2023-10-11T18:30:48.216358+00:00 | 89 | false | \n# Code\n```\nclass Solution {\npublic:\nint ans=0;\n void dfs(unordered_map<int,vector<int>>&mp ,unordered_map<int,bool>&vis,int m){\n vis[m]=true;\n for(auto i:mp[m]){\n if(i>=0){\n if(!vis[i]){ \n dfs(mp,vis,i);\n }\n }\n else{\n i=abs(i);\n if(!vis[i]){ \n ans++; \n dfs(mp,vis,i);\n }\n }\n }\n }\n // ans++\n // void sol(unordered_map<int,vector<int>>&mp ,unordered_map<int,bool>&vis,int m){\n // for(auto i:mp[m]) {\n // if(!vis[i]){\n // dfs(mp,vis,i);\n // ans++;\n // }\n // }\n // }\n int minReorder(int n, vector<vector<int>>& c) {\n int s=c.size();\n unordered_map<int,vector<int>>mp;\n unordered_map<int,bool>vis;\n for(int i=0;i<s;i++){\n mp[c[i][1]].push_back(c[i][0]);\n mp[c[i][0]].push_back(-c[i][1]);\n }\n dfs(mp,vis,0);\n if(ans==0)return ans;\n return ans;\n }\n};\n``` | 4 | 0 | ['Depth-First Search', 'C++'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | BFS C++ Bidirectional easy approach | bfs-c-bidirectional-easy-approach-by-ann-i3o4 | \n\n# Code\n\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int, bool>>> adj_list(n);\n | annupriy | NORMAL | 2023-03-25T10:37:44.074189+00:00 | 2023-03-25T10:37:44.074218+00:00 | 1,581 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int, bool>>> adj_list(n);\n int count = 0;\n for(int i=0; i<connections.size(); i++){\n adj_list[connections[i][0]].push_back({connections[i][1], false});\n adj_list[connections[i][1]].push_back({connections[i][0], true});\n }\n queue<pair<int, bool>> q;\n q.push({0, true});\n vector<bool> vis(n, false);\n vis[0] = true;\n while(!q.empty()){\n int node = q.front().first;\n q.pop();\n for(int i=0; i<adj_list[node].size(); i++){\n if(!vis[adj_list[node][i].first] && adj_list[node][i].second == false){\n count++;\n }\n if(!vis[adj_list[node][i].first]) {\n q.push(adj_list[node][i]);\n vis[adj_list[node][i].first] = true;\n }\n }\n }\n return count;\n }\n};\n``` | 4 | 0 | ['Breadth-First Search', 'C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java || DFS Solution || Explained Intuition and Approach | java-dfs-solution-explained-intuition-an-rh17 | ```\nclass Solution {\n int count=0;\n public int minReorder(int n, int[][] edges) {\n // the graph which is provided is directed in different dirn | kurmiamreet44 | NORMAL | 2023-03-25T07:50:06.448409+00:00 | 2023-03-25T07:50:06.448456+00:00 | 190 | false | ```\nclass Solution {\n int count=0;\n public int minReorder(int n, int[][] edges) {\n // the graph which is provided is directed in different dirn\'s so we cannot reach all nodes if we start \n // traversing the graph from zero node.\n // to overcome this we make the graph directed in both ways , and new directed edge made by us will be marked\n // by some value like 0(false), so that we know that this is not the actual directed edge but made by us\n \n List<List<int[]>> graph= new ArrayList<>();\n \n for(int i=0;i<n;i++)\n {\n graph.add(new ArrayList<>());\n }\n \n for(int i=0;i<edges.length;i++)\n {\n int edge[] = edges[i];\n // we add 1 in pair which represents that the edge actually exists \n graph.get(edge[0]).add(new int[]{edge[1],1});\n // we add 0 in pair which represents that the edge actually does not exist and we have created it \n graph.get(edge[1]).add(new int[]{edge[0],0});\n }\n \n // we will apply dfs \n boolean [] visited = new boolean[n];\n visited[0] = true;\n dfs(graph, 0, visited);\n \n return count;\n \n }\n \n // dfs traversal \n public void dfs( List<List<int[]>> graph, int vtx, boolean [] visited)\n {\n List<int[]> list = graph.get(vtx);\n for(int [] pair : list)\n {\n if(visited[pair[0]]== false)\n {\n visited[pair[0]] = true;\n // during dfs if we get the pair direction as 1 then it was original edge pointing away from 0\n // hence we increase the count as we would need to reverse it to reach 0 node\n if(pair[1] == 1)\n {\n count++;\n }\n dfs(graph, pair[0], visited);\n }\n }\n }\n} | 4 | 0 | ['Depth-First Search', 'Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | simple bfs solution | simple-bfs-solution-by-tawfik_045-bxls | \n\n# Code\n\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int,int>>>adj(n);\n fo | tawfik_045 | NORMAL | 2023-03-24T14:30:46.795268+00:00 | 2023-03-24T14:30:46.795312+00:00 | 1,477 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<vector<pair<int,int>>>adj(n);\n for(auto x:connections){\n adj[x[0]].push_back({x[1],1});\n adj[x[1]].push_back({x[0],0});\n }\n queue<int>qu;\n vector<int>vis(n,-1);\n qu.push(0);\n vis[0]=0;\n int ans=0;\n while(!qu.empty()){\n int cur=qu.front();\n qu.pop();\n for(auto x: adj[cur]){\n if(vis[x.first]==-1){\n vis[x.first]=vis[cur]+1;\n ans+=x.second;\n qu.push(x.first);\n }\n }\n }\n return ans;\n \n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | [Kotlin] Dfs | kotlin-dfs-by-dzmtr-9qcv | First, create adjacency list. The trick is to mark in directed roads with minus.\nThis will help us to distinguish them from out directed roads on our way.\n\nT | dzmtr | NORMAL | 2023-03-24T14:28:04.643230+00:00 | 2023-03-24T14:28:04.643281+00:00 | 30 | false | First, create adjacency list. The trick is to mark `in` directed roads with minus.\nThis will help us to distinguish them from `out` directed roads on our way.\n\nThen do dfs and count how many of the roads are `out`.\n\n```\nclass Solution {\n fun minReorder(n: Int, connections: Array<IntArray>): Int {\n val adj = mutableMapOf<Int, MutableList<Int>>()\n\n for ((a, b) in connections) {\n adj.getOrPut(a, { mutableListOf() }) += b\n adj.getOrPut(b, { mutableListOf() }) += (-a)\n }\n\n val vis = mutableSetOf<Int>()\n vis += 0\n\n fun dfs(a: Int): Int {\n var cnt = 0\n\n for (b in adj[a]!!) {\n if (vis.add(Math.abs(b))) {\n cnt += dfs(Math.abs(b))\n if (b > 0) cnt++\n }\n }\n\n return cnt\n }\n\n return dfs(0)\n }\n}\n``` | 4 | 0 | ['Kotlin'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++|| Graph || DFS || O(n) || 100% Faster | c-graph-dfs-on-100-faster-by-coder_0503-2gjm | Intuition\nConsider the graph as undirected graph and then do a DFS considering the src node as 0 and we need to reverse all the forward pointing edges.\nTo kee | Coder_0503 | NORMAL | 2023-03-24T12:29:48.480243+00:00 | 2023-03-24T12:29:48.480274+00:00 | 158 | false | # Intuition\nConsider the graph as undirected graph and then do a DFS considering the src node as 0 and we need to reverse all the forward pointing edges.\nTo keep track of real edges I have made adjacency list as the vector<pair<int,int>> so if a real edge is present from a to b then i am inserting it like:-\na -> {b,1}\nb -> {a,0}\n\nbecause b to a is a vitual edge.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIn the DFS traversal since we are starting from 0 and for all the nodes while traversing its adj list if we come accross a node which is unvisited and the edge to it is real edge then we surely need to reverse that edge so i incremented the count.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$ -> For DFS traversal \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n) -> $$ for visited array $$O(n) -> $$ stack space\n $$total space = O(n)+O(n) = O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int c=0;\n void find(vector<pair<int,int>>adj[],int i,vector<int>&vis){\n vis[i]=1;\n for(auto it:adj[i]){\n if(!vis[it.first]){\n c+=it.second;\n find(adj,it.first,vis);\n }\n }\n }\n int minReorder(int n, vector<vector<int>>& connections) {\n vector<pair<int,int>>adj[n];\n for(auto it:connections){\n adj[it[0]].push_back({it[1],1});\n adj[it[1]].push_back({it[0],0});\n }\n vector<int>vis(n,0);\n find(adj,0,vis);\n return c;\n } \n};\n``` | 4 | 0 | ['Depth-First Search', 'Graph', 'C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Easy JavaScript Solution using Queue and Insverse Graph. 92% faster then others. | easy-javascript-solution-using-queue-and-tnzr | Intuition\n1. Create Inverse Graph and Graph\n2. Take Queue with 0\n3. Loop through Queue and visit Inserve Geaph AND Graph\n4. IF Visited Through Graph ANSWER | rishabhthakkar7 | NORMAL | 2023-03-24T07:51:46.381907+00:00 | 2023-03-24T07:51:46.381938+00:00 | 375 | false | # Intuition\n1. Create Inverse Graph and Graph\n2. Take Queue with 0\n3. Loop through Queue and visit Inserve Geaph AND Graph\n4. IF Visited Through Graph ANSWER++ AND VISITED\n5. SAME PROCESSS TILL Queue is not empty\n6. NOTE: this approach works her because we do have n-1 roads\n\n\n**PLEASE UPVOTE!!!**\n```\nvar minReorder = function(n, connections) {\n let ans = 0;\n let graph = new Array(n).fill().map(_=>new Array());\n let inverse = new Array(n).fill().map(_=>new Array());\n let visited = new Array(n).fill(0);\n for(let i=0;i<connections.length;i++) {\n let [from,to] = connections[i];\n graph[from].push(to);\n inverse[to].push(from);\n }\n\n let q =[0];\n \n visited[0]=1;\n while(q.length>0) {\n let val = q.pop();\n visited[val]=1;\n for(let i=0;i<inverse[val].length;i++) {\n let node = inverse[val][i];\n if(visited[node] !== 1) {\n q.push(node);\n visited[node]=1\n }\n };\n for(let i=0;i<graph[val].length;i++) {\n let node = graph[val][i];\n if(visited[node] !== 1) {\n q.push(node);\n visited[node]=1\n ans++;\n }\n }; \n }\n\n return ans\n \n \n\n\n};\n``` | 4 | 0 | ['JavaScript'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Java | DFS | Clean code | O(n) time | java-dfs-clean-code-on-time-by-judgement-yln3 | Intuition\n Describe your first thoughts on how to solve this problem. \nSince there are n cities and n-1 roads, and the graph is connected, there are bound to | judgementdey | NORMAL | 2023-03-24T04:57:37.840339+00:00 | 2023-03-24T22:11:21.677768+00:00 | 278 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince there are `n` cities and `n-1` roads, and the graph is connected, there are bound to be no cycles in the graph. We can construct an adjacency list of the roads assuming they are bidirectional, but remembering the order of the roads in the list. Now we can run a DFS traversal starting from city 0 and visit all other cities. During the traversal we can count the number of roads that need to be re-ordered.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n List<Pair<Integer, Boolean>>[] adj;\n int cnt = 0;\n\n private void dfs(int city, int parent) {\n for (var a : adj[city]) {\n var neighbor = a.getKey();\n var needsReOrder = a.getValue();\n\n if (neighbor != parent) {\n if (needsReOrder) cnt++;\n dfs(neighbor, city);\n }\n }\n }\n\n public int minReorder(int n, int[][] connections) {\n adj = new ArrayList[n];\n\n for (var i=0; i<n; i++)\n adj[i] = new ArrayList<>();\n\n for (var con : connections) {\n adj[con[0]].add(new Pair(con[1], true));\n adj[con[1]].add(new Pair(con[0], false));\n }\n dfs(0, -1);\n\n return cnt;\n }\n}\n```\nIf you like my solution, please upvote it! | 4 | 0 | ['Depth-First Search', 'Graph', 'Recursion', 'Java'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Kotlin DFS | kotlin-dfs-by-kotlinc-tlia | \nclass Solution {\n fun minReorder(n: Int, connections: Array<IntArray>): Int {\n val g = Array<MutableList<Pair<Int, Boolean>>>(n) { mutableListOf<Pair<In | kotlinc | NORMAL | 2023-03-24T01:03:44.488251+00:00 | 2023-03-24T01:03:44.488295+00:00 | 111 | false | ```\nclass Solution {\n fun minReorder(n: Int, connections: Array<IntArray>): Int {\n val g = Array<MutableList<Pair<Int, Boolean>>>(n) { mutableListOf<Pair<Int, Boolean>>() }\n for ((a, b) in connections) {\n g[a].add(Pair(b, true)) // this edge is provided\n g[b].add(Pair(a, false)) // this edge is imagined\n }\n\n fun dfs(parent: Int, node: Int): Int {\n var res = 0\n for ((next, provided) in g[node]) {\n if (next == parent) continue\n if (provided) // we need to reverse it\n res++\n res += dfs(node, next)\n }\n return res\n }\n return dfs(-1, 0)\n }\n}\n``` | 4 | 0 | ['Kotlin'] | 1 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++ Fast and Intuitive Approach | c-fast-and-intuitive-approach-by-divyans-u9ec | Intuition\nUse DFS and a reverse graph to traverse.\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nWe create two adjacency lists. | divyansh-xz | NORMAL | 2023-01-11T05:29:58.385844+00:00 | 2023-01-11T05:29:58.385892+00:00 | 1,215 | false | # Intuition\nUse DFS and a reverse graph to traverse.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe create two adjacency lists. One of original graph and other of reverse of that graph(all edges direction reversed).\nWe create a queue from which we start dfs.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n void dfs(vector<vector<int>> & gr, vector<vector<int>> & gr2, vector<bool> &vis, int s, int &ans, queue<int> &q)\n {\n if(vis[s]) return;\n vis[s] = true;\n // cout<<"dfs "<<s<<endl;\n\n for(int adj: gr2[s])\n {\n q.push(adj);\n // cout<<"push "<<adj<<endl;\n }\n\n for(int e:gr[s])\n {\n if(!vis[e])\n {\n ans++;\n dfs(gr, gr2, vis, e, ans, q);\n }\n }\n }\n\n int minReorder(int n, vector<vector<int>>& connections) {\n int ans = 0;\n vector<bool> vis(n, false);\n vector<vector<int>> gr(n);\n vector<vector<int>> gr2(n);\n\n for(auto v:connections)\n {\n gr[v[0]].push_back(v[1]);\n gr2[v[1]].push_back(v[0]);\n }\n\n queue<int> q;\n q.push(0);\n\n while(q.size())\n {\n int x = q.front();\n q.pop();\n dfs(gr, gr2, vis, x, ans, q);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Depth-First Search', 'Graph', 'Queue', 'C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | C++ Solution | c-solution-by-pranto1209-8qxm | Approach\n Describe your approach to solving the problem. \n DFS\n\n# Code\n\nclass Solution {\npublic:\n vector<pair<int, int>> g[50005];\n int ans, v | pranto1209 | NORMAL | 2022-12-14T18:35:38.194428+00:00 | 2023-03-24T10:51:23.086382+00:00 | 456 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n DFS\n\n# Code\n```\nclass Solution {\npublic:\n vector<pair<int, int>> g[50005];\n int ans, vis[50005];\n void dfs(int u) {\n vis[u] = 1;\n for(auto v: g[u]) {\n if(!vis[v.first]) {\n ans += v.second;\n dfs(v.first);\n }\n }\n }\n int minReorder(int n, vector<vector<int>>& connections) {\n for(auto x: connections) {\n g[x[0]].push_back({x[1], 1});\n g[x[1]].push_back({x[0], 0});\n }\n ans = 0;\n dfs(0);\n return ans;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
reorder-routes-to-make-all-paths-lead-to-the-city-zero | Simple python solution using BFS traversal | simple-python-solution-using-bfs-travers-bajl | \nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n visited=[0]*n\n indegree=[[] for _ in range(n)]\n | beneath_ocean | NORMAL | 2022-10-24T12:31:53.799646+00:00 | 2022-10-24T12:31:53.799732+00:00 | 1,544 | false | ```\nclass Solution:\n def minReorder(self, n: int, connections: List[List[int]]) -> int:\n visited=[0]*n\n indegree=[[] for _ in range(n)]\n outdegree=[[] for _ in range(n)]\n for frm,to in connections:\n indegree[to].append(frm)\n outdegree[frm].append(to)\n lst=[0]\n visited[0]=1\n ct=0\n while lst:\n x=lst.pop(0)\n for i in indegree[x]:\n if visited[i]==0:\n lst.append(i)\n visited[i]=1\n for i in outdegree[x]:\n if visited[i]==0:\n lst.append(i)\n visited[i]=1\n # here we have to change the direction of edge\n ct+=1\n return ct\n``` | 4 | 0 | ['Breadth-First Search', 'Graph', 'Python', 'Python3'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.