question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
smallest-string-with-a-given-numeric-value | Simple + Intuitive|| Beginner Friendly || | simple-intuitive-beginner-friendly-by-pr-dita | \n\t string ans="";\n while(k)\n {\n\t\t\t int t=n-1; //remaining letters\n\t\t\t int t2=k-t; //finding t | prajjwal333 | NORMAL | 2022-03-22T04:19:46.628825+00:00 | 2022-03-22T04:26:54.267133+00:00 | 47 | false | ```\n\t string ans="";\n while(k)\n {\n\t\t\t int t=n-1; //remaining letters\n\t\t\t int t2=k-t; //finding the max value after removing the remaining letter\n int rem=t2/26; // checking for the max value\n char add;\n\t\t\t if(rem>=1) // if rem>=1 the max value is Z\n {\n add=\'z\';\n k=k-26;\n }\n else // else the remaining value is the max\n {\n add=\'a\'+t2-1;\n k=k-t2;\n }\n \n ans+=add;\n n=n-1;\n \n }\n reverse(ans.begin(),ans.end());\n return ans;\n\t\t\n\t```\n\t\n\t**All The Best\uD83D\uDC4D\uD83C\uDFFB** | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | Smallest String easy to understand JAVA solution | smallest-string-easy-to-understand-java-wc8cy | class Solution {\n public String getSmallestString(int n, int k) {\n //initializing array with size n\n char arr[]=new char[n]; \n //f | Sanku2906X | NORMAL | 2022-03-22T03:38:48.342259+00:00 | 2022-03-22T03:38:48.342299+00:00 | 64 | false | class Solution {\n public String getSmallestString(int n, int k) {\n //initializing array with size n\n char arr[]=new char[n]; \n //filling whole array with a\n Arrays.fill(arr,\'a\'); \n //for the a in array\n k-=n; \n //turn the character into z from the last element till k become smaller than 25\n for(int i=n-1;i>=0 && k>0;i--){\n arr[i]+=Math.min(k,25); \n k-=Math.min(k,25); }\n return String.valueOf(arr);\n }\n} | 2 | 0 | ['Array', 'Java'] | 1 |
smallest-string-with-a-given-numeric-value | Explaination || Greedy with proof | explaination-greedy-with-proof-by-ishubh-64bf | Since the constraints on k are suitable, we need not worry about edge cases.\nIntuition:\nlets say we have n spaces and k sum\n____________\nlets fill i=0, for | iShubhamRana | NORMAL | 2022-03-22T02:15:13.884543+00:00 | 2022-03-22T03:51:49.043623+00:00 | 58 | false | Since the constraints on k are suitable, we need not worry about edge cases.\n**Intuition**:\nlets say we have **n spaces and k sum**\n____________________________________________________________\nlets **fill i=0**, for every position **we have to fill the smallest alphabet possible such that after filling that alphabet we can still reach k**. In short after filling i=0, the maximum reachable sum should be gr**eater than or equal to k.**\nlet the value of character filled be **\'x\'** , after filling this the length left with us is **n-i-1**; so acc to prev statement\n\n>**x + 26*(n-i-1) >= k*\n> **x >= k - 26*(n-i-1)* \n\nWe will always pick equality condition since we need lexicographically smalles characters\n**if we get RHS<1, we will take 1 as we have > inequality.**\n\nHope it helps Do upvote :)\n```\nclass Solution {\npublic:\nstring getSmallestString(int n, int k) {\n\tstring ans = "";\n\tfor (int i = 0; i < n; i++) {\n\t\tint val = max(k - 26 * (n-i-1) ,1);\n\t\tans.push_back(val -1 + \'a\');\n\t\tk -= val;\n\t}\n\treturn ans;\n}\n\n};\n``` | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | Greedy O(n) Solution with Image Explanation | greedy-on-solution-with-image-explanatio-edgx | Leetcode 1663. Smallest String With A Given Numeric Value\n\nBy Frank Luo\n\n# Greedy\n\nAs we want to minimize the lexicographical order of the constructed str | longluo | NORMAL | 2022-03-22T02:06:15.058968+00:00 | 2022-11-15T02:33:26.589417+00:00 | 259 | false | [Leetcode](https://leetcode.com/) [1663. Smallest String With A Given Numeric Value](https://leetcode.com/problems/smallest-string-with-a-given-numeric-value/)\n\n***By Frank Luo***\n\n# Greedy\n\nAs we want to minimize the **lexicographical** order of the constructed string, let\'s start from the **beginning** of the string, select the **smallest** letter that satisfies the requirements each time, then we get the final answer.\n\nSuppose we are currently constructed to a certain position, as the picture below shows.\n\n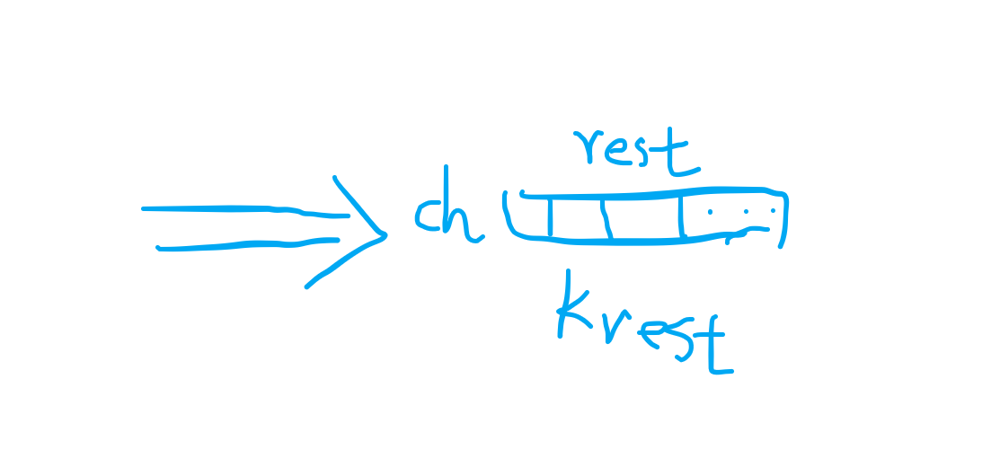\n\nIncluding this position, there are still $n_{rest}$ left to fill in, the remaining sum of these rest positions is $k_{rest}$.\n \nIf we put a letter $\\textit{ch}$, and so the remaining $n_{rest} - 1$ positions with the sum is $k_{rest}$ must satisfy:\n\n$$\n1 \\times (n_{rest}-1) \\leq k_{rest}-ch \\leq 26 \\times (n_{rest}-1)\n$$\n\ncan be:\n\n$$\nk_{rest}-26 \\times (n_{rest}-1 ) \\leq ch \\leq k_{rest}-1 \\times (n_{rest}-1)\n$$\n\nSo $\\textit{ch}$ \n\n1. $k_{rest} - 26 \\times (n_{rest}-1) \\leq 0$, we choose the character $a$;\n2. $k_{rest} - 26 \\times (n_{rest}-1) \\gt 0$, we choose the character corresponding to this value.\n \nLet\'s write the code:\n \n```java\n public String getSmallestString_greedy(int n, int k) {\n StringBuilder sb = new StringBuilder(n);\n for (int rest = n; rest >= 1; rest--) {\n int bound = k - 26 * (rest - 1);\n if (bound > 0) {\n char ch = (char) (bound + \'a\' - 1);\n sb.append(ch);\n k -= bound;\n } else {\n sb.append(\'a\');\n k--;\n }\n }\n\n return sb.toString();\n }\n```\n \n## Analysis\n\n- **Time Complexity**: $O(n)$\n- **Space Complexity**: $O(n)$\n\n--------------------------\n\nAll suggestions are welcome. \nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97 it. Thank you:-)\n\nExplore More [Leetcode Solutions](https://leetcode.com/discuss/general-discussion/1868912/My-Leetcode-Solutions-All-In-One). \uD83D\uDE09\uD83D\uDE03\uD83D\uDC97\n\n | 2 | 0 | ['Greedy', 'Java'] | 0 |
smallest-string-with-a-given-numeric-value | py: smallest string with a given numeric val, easy | py-smallest-string-with-a-given-numeric-hpfbx | \nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n ans = []\n for i in range(1, n+1):\n j = max(1, k-(26*(n-i | snalli | NORMAL | 2021-09-17T07:42:34.375583+00:00 | 2021-09-17T07:42:34.375617+00:00 | 107 | false | ```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n ans = []\n for i in range(1, n+1):\n j = max(1, k-(26*(n-i)))\n ans.append(chr(ord(\'a\')+j-1))\n k -= j\n \n return \'\'.join(ans)\n``` | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | PYTHON FOR BEGINNERS | python-for-beginners-by-msustar-oznv | \tclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n cantZ,rest,cantA,ch,backZ,digits=0,0,0,0,0,n\n cantZ=k//26\n r | msustar | NORMAL | 2021-09-03T14:11:31.727564+00:00 | 2021-09-03T14:11:31.727591+00:00 | 73 | false | \tclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n cantZ,rest,cantA,ch,backZ,digits=0,0,0,0,0,n\n cantZ=k//26\n rest=k%26\n if rest>digits-cantZ:\n cantA=digits - cantZ-1\n ch=rest-cantA\n return "a"*cantA +chr(ch+96)+"z"*(cantZ) \n if rest==digits-cantZ:\n cantA=digits - cantZ\n return "a"*cantA +"z"*(cantZ) \n else:\n if rest==0 and cantZ==n:\n return "z"*cantZ\n else:\n while True:\n backZ=((digits-cantZ-rest)//26)+1\n cantZ=cantZ-backZ\n rest=rest+backZ*26\n cantA=digits - cantZ-1 \n ch=rest-cantA \n if ch>0 and ch<26:\n break \n return "a"*cantA +chr(ch+96)+"z"*(cantZ) | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | JAVA | beats 96% | java-beats-96-by-shwetali_ps-s3a9 | \npublic String getSmallestString(int n, int k) {\n char[] alphabets = new char[]{\'a\',\'b\',\'c\',\'d\',\'e\',\'f\',\n | shwetali_ps | NORMAL | 2021-04-09T19:27:59.456679+00:00 | 2021-04-09T19:27:59.456712+00:00 | 74 | false | ```\npublic String getSmallestString(int n, int k) {\n char[] alphabets = new char[]{\'a\',\'b\',\'c\',\'d\',\'e\',\'f\',\n \'g\',\'h\',\'i\',\'j\',\'k\',\'l\',\n \'m\',\'n\',\'o\',\'p\',\'q\',\'r\',\n \'s\',\'t\',\'u\',\'v\',\'w\',\'x\',\'y\',\'z\'};\n char[] c = new char[n];\n Arrays.fill(c , \'a\');\n \n int i=n-1;\n int reqSum = k-n;\n while(reqSum>0)\n {\n if (reqSum <= 25)\n {\n c [i] = alphabets[reqSum];\n break;\n }\n \n else\n {\n c[i]=\'z\';\n i--;\n reqSum-=25;\n }\n }\n \n return String.valueOf(c);\n }\n\t``` | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | Python O(logn) Binary Search solution, faster than 91%, explained. | python-ologn-binary-search-solution-fast-a3te | If you think it through or see enough cases, you\'ll find this important pattern: \nThe solution is always formed by a bunch of \'a\'s, a bunch of \'z\'s and AT | G5-Qin | NORMAL | 2021-01-28T14:18:04.277094+00:00 | 2021-01-28T14:18:04.277134+00:00 | 128 | false | If you think it through or see enough cases, you\'ll find this important pattern: \n**The solution is always formed by a bunch of \'a\'s, a bunch of \'z\'s and AT MOST ONE character that is neither \'a\' or \'z\'.**\nIf you could not think it through, just do it reversely, if you have a solution for some case which contains two characters that is neither \'a\' or \'z\', you can either transform these two characters to a \'a\'-and-\'z\' combination or a \'some character less than before\'-and-\'z\' combination, either way the solution is better than the previous one.\n\nAccordingly, the problem is transformed to finding the most \'a\' we can put into the solution, then for the remaining empty positions we fill them with \'z\'s until we couldn\'t, then fill the last one with proper character if needed.\n\nSo the algorithm is done in 3 steps:\n1. find how many (most) \'a\'s we can have with binary search, let\'s say the number is ```x```.\n2. calculate how many (most) \'z\'s we can have to fill ```k - x```, let\'s say this number is ```y```.\n3. if ```x + 26 * y``` doesn\'t add up to k (which also means there is an extra position in the solution), fill the character ```k - (x + 26 * y)``` in the middle.\n\n(Feel free to leave comments if there\'s anything confusing. If you like my solution, please upvote!~)\n\n```python\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n l, r = 0, n\n while l <= r:\n mid = l + (r - l) // 2\n if k - mid > 26 * (n - mid):\n r = mid - 1\n elif k - mid == 26 * (n - mid):\n return \'a\' * mid + \'z\' * (n - mid)\n elif k - mid < 26 * (n - mid):\n l = mid + 1\n \n if l - 1 >= n:\n return \'a\' * n\n l = l - 1\n \n num_z = (k - l) // 26\n c = chr(ord(\'a\') - 1 + k - l - num_z * 26)\n return \'a\' * l + c + \'z\' * num_z\n``` | 2 | 1 | [] | 1 |
smallest-string-with-a-given-numeric-value | [Java] Smallest String With A Given Numeric Value | easy explanation | java-smallest-string-with-a-given-numeri-vmjg | \n\nProblem disection and solution approach\nSince there is a total order on the set of strings (as defined in task), a greedy approach constructing the solutio | fdokic | NORMAL | 2021-01-28T09:00:05.602325+00:00 | 2021-01-28T10:43:31.422964+00:00 | 232 | false | \n\n**Problem disection and solution approach**\nSince there is a total order on the set of strings (as defined in task), a greedy approach constructing the solution is sufficient, as for each index i of a string of length n, choosing the optimal character according to the order is possible because of it (can compare lex. order of any two strings). Since for the lexicographic order only considers the characters up until the first inequal one, and we must reach a total character value, a greedy approach using the largest possible character from behind is optimal.\n\n**Implementation**\nAs we need a lookup for value - character, we can use a static array (initialization at compile time), where the index holds the character value. Since we have to use at least n value to create a string of length n (all a\'s), we deduce this from k before starting. This way, we can directly use the array indices 0 indexed. We now fill the solution string from behind, always trying to take the maximal character our budget and the length of the alphabet allows (min 25, avail), and deduce the used value from the goal. As the size of the solution is known, we can directly initialize an array of the right size, saving time not having to append & collect characters, as String construction can use the char array in const time.\n\nTime: O(n) | 10ms, 85%\nMemory: O(max(len alphabet, n)) | 39.4 MB, 30%\n\nHope everything is clear now, if you liked it please leave an upvote for others to profit as well :) \n\n\n```\n public String getSmallestString(int n, int k) {\n char[] sol = new char[n];\n final char[] chr = {\'a\',\'b\',\'c\',\'d\',\'e\',\'f\',\'g\',\'h\',\'i\',\'j\',\'k\',\'l\',\'m\',\'n\',\'o\',\'p\',\'q\',\'r\',\'s\',\'t\',\'u\',\'v\',\'w\',\'x\',\'y\',\'z\'};\n int avail = k - n;\n for(int i=0; i < n; i++){\n int c = Math.min(25, avail);\n sol[n-i-1] = chr[c];\n avail -= c;\n }\n \n return new String(sol);\n }\n``` | 2 | 0 | ['Array', 'Java'] | 1 |
smallest-string-with-a-given-numeric-value | 6 Line C++ & Python Solution O(1) Time (Better than 100%) | 6-line-c-python-solution-o1-time-better-gldi2 | We first take x as k - n as we need to have space for all the n characters in the string.\nSince we need to get the lexicographically smallest string we need t | sainikhilreddy | NORMAL | 2020-11-23T05:09:45.501817+00:00 | 2020-11-24T07:11:08.690674+00:00 | 197 | false | We first take **x** as **k - n** as we need to have space for all the **n** characters in the string.\nSince we need to get the lexicographically smallest string we need to get the value of **x** below 25 by inserting all **z**\'s at the end.\nOnce we get the **x** below 25 we insert the character corresponding to it and then insert all **a**\'s in the beginning.\n**C++ Solution:**\n```\nclass Solution {\npublic:\n string getSmallestString(int n, int k) {\n int x = k - n;\n string ans = string(x / 25, \'z\');\n x %= 25;\n if (x) \n ans = (char)(\'a\' + x) + ans;\n return string(n - ans.length(), \'a\') + ans;\n }\n};\n```\n\n**Python Solution:**\n```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n x = k - n\n ans = \'z\'*(x // 25)\n x %= 25\n if x:\n ans = chr(ord(\'a\') + x) + ans\n return \'a\'*(n - len(ans)) + ans\n``` | 2 | 0 | ['C', 'Python', 'Python3'] | 0 |
smallest-string-with-a-given-numeric-value | C# | c-by-pramodr-cmp6 | \npublic class Solution {\n public string GetSmallestString(int n, int k) {\n char[] ans = new char[n];\n Array.Fill(ans,\'a\');\n k = k | pramodr | NORMAL | 2020-11-22T05:29:49.529640+00:00 | 2020-11-22T05:29:49.529675+00:00 | 115 | false | ```\npublic class Solution {\n public string GetSmallestString(int n, int k) {\n char[] ans = new char[n];\n Array.Fill(ans,\'a\');\n k = k-n;\n \n for(int i=n-1;i>=0;i--){\n int diff = Math.Min(k,25);\n ans[i]=(char)(\'a\'+diff);\n k=k-diff;\n }\n return new string(ans);\n }\n}\n``` | 2 | 0 | [] | 1 |
smallest-string-with-a-given-numeric-value | Unexpected TLE !! Can Anyone Explain | unexpected-tle-can-anyone-explain-by-aas-9dqn | \n\nclass Solution {\npublic:\n string getSmallestString(int n, int k) {\n string s = "";\n for(int i=0; i=0){\n s[n-i-1] += 25; | aashraya18 | NORMAL | 2020-11-22T05:08:52.306132+00:00 | 2020-11-22T05:11:12.136637+00:00 | 109 | false | ```\n\n```class Solution {\npublic:\n string getSmallestString(int n, int k) {\n string s = "";\n for(int i=0; i<n; i++){\n s = s + \'a\'; \n }\n int i=0;\n int rem = k - n;\n while(rem!=0){\n if(rem -25 >=0){\n s[n-i-1] += 25;\n rem-=25;\n }else{\n s[n-i-1] += rem;\n rem = 0;\n }\n i++;\n }\n return s;\n \n\n }\n}; | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | Java, O(n) | java-on-by-knownothingg-xiqe | \n\nclass Solution {\n\tpublic String getSmallestString(int n, int k) {\n\t// create a char array with length of n\n\t\tchar[] arr = new char[n];\n\t\t// imagin | KnowNothingg | NORMAL | 2020-11-22T04:43:59.484954+00:00 | 2020-11-22T04:43:59.484983+00:00 | 62 | false | \n```\nclass Solution {\n\tpublic String getSmallestString(int n, int k) {\n\t// create a char array with length of n\n\t\tchar[] arr = new char[n];\n\t\t// imagine arr is filled with \'a\', \'a\' value is 1, so subtract n from k\n k -= n;\n\t\tfor(int i = n-1; i >= 0; i--) {\n\t\t\tint cur = Math.min(k, 25);\n\t\t\t// update arr[i] with the value\n\t\t\tarr[i] = (char) (\'a\'+ cur);\n\t\t\tk -= cur;\n\t\t}\n \t\t\n\t\treturn new String(arr);\n\t}\n} \n``` | 2 | 1 | [] | 0 |
smallest-string-with-a-given-numeric-value | Python 1 liner | python-1-liner-by-user0571rf-asla | answer is in the form of aaaa?zzz. initially all chars are \'a\' and we need to add k-n more. the number of \'z\' is (k-n)//25 and the ? char is (k-n)%25 the r | user0571rf | NORMAL | 2020-11-22T04:11:50.372949+00:00 | 2021-01-29T21:59:42.902917+00:00 | 115 | false | answer is in the form of aaaa?zzz. initially all chars are \'a\' and we need to add k-n more. the number of \'z\' is (k-n)//25 and the ? char is (k-n)%25 the rest is \'a\'s\n\n```\n def getSmallestString(self, n: int, k: int) -> str:\n return \'a\'*(n-(k-n)//25-((k-n)%25>0))+chr((k-n)%25+ord(\'a\'))*((k-n)%25>0)+\'z\'*((k-n)//25)\n``` | 2 | 1 | ['Python', 'Python3'] | 1 |
smallest-string-with-a-given-numeric-value | Java, O(n), Greedy try smallest character from left to right | java-on-greedy-try-smallest-character-fr-gc7h | \nclass Solution {\n public String getSmallestString(int n, int k) {\n StringBuilder res = new StringBuilder();\n for(int i = 0; i < n; i++){\n | toffeelu | NORMAL | 2020-11-22T04:00:36.014238+00:00 | 2020-11-22T04:00:36.014278+00:00 | 111 | false | ```\nclass Solution {\n public String getSmallestString(int n, int k) {\n StringBuilder res = new StringBuilder();\n for(int i = 0; i < n; i++){\n int left = n - i - 1;\n //check if we put a \'a\' here, it\'s still possible to satisfy the requirement\n if(k <= left * 26){\n res.append("a");\n k -= 1;\n }\n else{\n int cur = k - left * 26;\n res.append((char)(\'a\' - 1 + cur));\n k -= cur;\n }\n }\n return res.toString();\n }\n}\n``` | 2 | 0 | [] | 0 |
smallest-string-with-a-given-numeric-value | beats 85% || simple cpp || greedy | beats-85-simple-cpp-greedy-by-yaswanth09-45v4 | Code\n\nclass Solution {\npublic:\n string getSmallestString(int n, int k) {\n string res(n,\'a\');\n k-=n;\n for(int i = n-1 ; i >= 0 a | yaswanth0901 | NORMAL | 2024-05-24T09:06:16.614700+00:00 | 2024-05-24T09:06:16.614723+00:00 | 14 | false | # Code\n```\nclass Solution {\npublic:\n string getSmallestString(int n, int k) {\n string res(n,\'a\');\n k-=n;\n for(int i = n-1 ; i >= 0 and k ; i--) {\n int x = min(25,k);\n res[i]+=x;\n k-=x;\n }\n return res;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-string-with-a-given-numeric-value | Easy and Straightforward Code | easy-and-straightforward-code-by-jeet_sa-ree3 | Intuition\n Describe your first thoughts on how to solve this problem. \nWe try to assign \'a\' to the starting characters of strings and \'z\' to the last part | jeet_sankala | NORMAL | 2024-01-06T21:14:19.194243+00:00 | 2024-01-06T21:14:19.194273+00:00 | 50 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe try to assign \'a\' to the starting characters of strings and \'z\' to the last part of string so that we could possibly get the lexicographical smallest string .\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst of all assign characher \'a\' to every string character then we could have to modify k=k-n , as we already assign 1 value . now iterate from the last and assign z to last characters.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(int n, int k) {\n k=k-n;\n string ans="";\n for(int i=0;i<n;i++){\n ans+=\'a\';\n }\n int j=n-1;\n while(k>25){\n ans[j]=\'z\';\n j--;\n k=k-25;\n }\n char ch=k+\'a\';\n ans[j]=ch;\n return ans;\n }\n};\n``` | 1 | 0 | ['Greedy', 'C++'] | 1 |
smallest-string-with-a-given-numeric-value | Best Java Solution || Beats 100% | best-java-solution-beats-100-by-ravikuma-8ofn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-10-07T06:20:46.574269+00:00 | 2023-10-07T06:20:46.574292+00:00 | 125 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n/*\n static String helper(int n, int k){\n StringBuilder s = new StringBuilder();\n s.append("a".repeat(n));\n if(n==k) return s.toString();\n\n k=k-n;\n for(int i=0; i<n; i++){\n if(k>=25){\n s.replace(i,i+1,"z");\n k=k-25;\n if(k==0) break;\n }\n else{\n char ch = (char)(k+97);\n s.replace(i,i+1,ch+"");\n break;\n }\n }\n\n return s.reverse().toString();\n }\n */\n public String getSmallestString(int n, int k) {\n char arr[] = new char[n];\n Arrays.fill(arr,\'a\');\n\n k=k-n;\n\n while(k>0){\n n--;\n arr[n] += Math.min(25,k);\n k = k-Math.min(25,k);\n }\n\n return String.valueOf(arr);\n }\n}\n``` | 1 | 1 | ['Java'] | 0 |
smallest-string-with-a-given-numeric-value | very easy python solution | very-easy-python-solution-by-a-fr0stbite-fgi0 | Approach\ndon\'t care about n, get most optimal, and split up\n\n# Complexity\n- Time complexity: ay, space-man i bet u don\'t know ur complexity\n\n- Space com | a-fr0stbite | NORMAL | 2023-09-14T02:01:31.067332+00:00 | 2023-10-04T05:41:20.328595+00:00 | 3 | false | # Approach\ndon\'t care about `n`, get most optimal, and split up\n\n# Complexity\n- Time complexity: ay, space-man i bet u don\'t know ur complexity\n\n- Space complexity: OH YEAH I DO\n\n- Time complexity: Then what is it?\n\n- Space complexity: well... uh... i... i think its $$O(n+k)$$...\n\n- Time complexity: sus... ok. mine is technically $$O(n)$$\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, n: int, k: int) -> str:\n firstRes = ""\n alpha = "abcdefghijklmnopqrstuvwxyz"\n prev = {}\n for i in range(1, 26):\n prev[alpha[i]] = alpha[i-1]\n while k > 0:\n place = 26\n while place > k:\n place -= 1\n firstRes = alpha[place-1] + firstRes\n k -= place\n i = 0\n while i < len(firstRes) and firstRes[i] == "a":\n i += 1\n while i < len(firstRes) and len(firstRes) < n:\n firstRes = "a" + firstRes[:i] + prev[firstRes[i]] + firstRes[i+1:]\n i += 1\n if firstRes[i] == "a":\n i += 1\n return firstRes\n``` | 1 | 0 | ['Python3'] | 0 |
smallest-string-with-a-given-numeric-value | Java Backtracking O(n) Easy | java-backtracking-on-easy-by-peekaboo682-o4t0 | Intutition\n- Backtracking - Keep decreasing the value of start so that the sum always remains equal to target k and length always remains n.\n\n\n# Approach\n | peekaboo682 | NORMAL | 2023-09-04T16:49:48.304978+00:00 | 2023-09-04T17:36:37.616104+00:00 | 214 | false | # Intutition\n- Backtracking - Keep decreasing the value of start so that the sum always remains equal to target k and length always remains n.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Set start value to z and buf value to n.\n- Start is used to store the character to be appended and buf is\n used to keep reference of the length required.\n- Initialize array to store resultant string.\n- If k is less than index value of start + buffer value\n then decrement start till condition is satisfied\n- Add start value to resultant array ch[].\n \n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n\n\n# Code\n```\nclass Solution {\n public String getSmallestString(int n, int k) \n {\n char start=\'z\';\n\n String ans="";\n\n int buf=n;\n int c=n-1;\n\n char ch[] = new char[n];\n\n while(k>0)\n {\n // System.out.print(start);\n if(k<(start-96)+buf)\n {\n \n while(k!=(start-96)+buf-1)\n {\n start--;\n }\n // System.out.print(start);\n }\n // System.out.println(start);\n ch[c--]=start;\n k-=(start-96);\n buf--;\n \n }\n\n ans= new String(ch);\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
smallest-string-with-a-given-numeric-value | Briefly explained C++ Solution || Detailed | briefly-explained-c-solution-detailed-by-5d8o | Intuition\nDont get in n instead just declare the string of size n and reverse fill it .\n# Approach\nHelloo ! \nI will break this question in two simple parts | Sakettiwari | NORMAL | 2023-08-31T21:30:19.767395+00:00 | 2023-08-31T21:30:19.767421+00:00 | 196 | false | # Intuition\nDont get in n instead just declare the string of size n and reverse fill it .\n# Approach\nHelloo ! \nI will break this question in two simple parts and I hope it will make the question more easier.\n\nFirst **tackle n**\ndeclare a string of size n with all a\'s;\nDONE!\n\nNow **tackle k**\nWe know for any value of k <= 26 we have an alphabet right??\nSo loop it with this condition just insert z and substract 27?\n27=z+a(which was present earlier)...\n\nAs the k reaches down the 26 just insert the charecter of that value!\n\n**HAPPY CODING UPVOTE IF HELPED !!!**\n\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(int n, int k) {\n int index=1;\n string s(n,\'a\');\n k-=n;\n int i;\n for( i=s.size()-1;i>=0 && k>=26;i--){\n s[i]=\'z\';\n k+=1;\n k-=26;\n }\n s[i]=char(97+k);\n return s;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-average-pass-ratio | C++ Greedy Max Heap O(m log n) | c-greedy-max-heap-om-log-n-by-votrubac-d0q9 | How much of profit in score can we get if we add one extra student to a particular class? Send an extra student to the class with the most profit; repeat till y | votrubac | NORMAL | 2021-03-14T04:01:37.755500+00:00 | 2021-03-14T06:24:37.121902+00:00 | 10,961 | false | How much of profit in score can we get if we add one extra student to a particular class? Send an extra student to the class with the most profit; repeat till you run out of students.\n\nLet\'s track profits for all classes in a max heap. While we still have extra students, we pick a class that gives us the maximum profit, add a student, calculate new profit and put it back to the heap.\n\nTo avoid iterating through the max heap in the end, we can track the total score as we go.\n\n**C++**\n```cpp\ndouble maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n auto profit = [&](double pass, double total) {\n return (pass + 1) / (total + 1) - pass / total;\n };\n double total = 0;\n priority_queue<pair<double, array<int, 2>>> pq;\n for (auto &c : classes) {\n total += (double) c[0] / c[1];\n pq.push({profit(c[0], c[1]), {c[0], c[1]}});\n }\n while (extraStudents--) {\n auto [added_profit, c] = pq.top(); pq.pop();\n total += added_profit;\n pq.push({profit(c[0] + 1, c[1] + 1), {c[0] + 1, c[1] + 1}});\n }\n return total / classes.size();\n}\n```\n**Complexity Analysis**\n- Time: O(m log n), where n and m are the number of classes and extra students.\n\t- Caveat: the complexity for the code above is O((n + m) log n). To achieve O(m log n), we need construct the heap in O(n), e.g. by using `make_heap`.\n\t- For the purpose of complexity analsyis, I assume that we build the initial heap in O(n).\n- Memory: O(n) to hold the information about classes.\n | 121 | 2 | [] | 26 |
maximum-average-pass-ratio | [Python/Java] Max Heap - Clean & Concise | pythonjava-max-heap-clean-concise-by-hie-fnu1 | Idea\n- How much profit we can get if we add one extraStudents to a particular class (pass, total)? This profit can be defined as: (pass+1)/(total+1) - pass/tot | hiepit | NORMAL | 2021-03-14T04:00:37.367789+00:00 | 2021-03-14T05:01:44.000819+00:00 | 7,531 | false | **Idea**\n- How much profit we can get if we add one `extraStudents` to a particular class `(pass, total`)? This profit can be defined as: `(pass+1)/(total+1) - pass/total`.\n- For each student from `extraStudents`, we try to add to a class which will increase its profit maximum.\n- We can use `maxHeap` structure which can give us the class which has maximum profit after adding.\n\n**Complexity:**\n- Time: \n\t- Python: `O(M*logN + N)`, where `M` is `extraStudents` and `N` is number of classes.\n\t- Java: `O(M*logN + N*logN)`\n- Space: `O(N)`\n\n**Python**\n```python\nclass Solution(object):\n def maxAverageRatio(self, classes, extraStudents):\n def profit(a, b):\n return (a + 1) / (b + 1) - a / b\n\n maxHeap = []\n for a, b in classes:\n a, b = a * 1.0, b * 1.0 # Convert int to double\n maxHeap.append((-profit(a, b), a, b))\n heapq.heapify(maxHeap) # Heapify maxHeap cost O(N)\n\n for _ in range(extraStudents):\n d, a, b = heapq.heappop(maxHeap)\n heapq.heappush(maxHeap, (-profit(a + 1, b + 1), a + 1, b + 1))\n\n return sum(a / b for d, a, b in maxHeap) / len(classes)\n```\n\n**Java**\n```java\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<double[]> maxHeap = new PriorityQueue<>(Comparator.comparingDouble(o -> -o[0])); // Max heap compared by first value in decreasing order.\n for (int[] c : classes) {\n double a = c[0], b = c[1];\n maxHeap.offer(new double[]{profit(a, b), a, b});\n }\n while (extraStudents-- > 0) {\n double[] top = maxHeap.poll();\n double a = top[1], b = top[2];\n maxHeap.offer(new double[]{profit(a+1, b+1), a+1, b+1});\n }\n double ans = 0.0d;\n while (!maxHeap.isEmpty()) {\n double[] top = maxHeap.poll();\n double a = top[1], b = top[2];\n ans += a/b;\n }\n return ans / classes.length;\n }\n double profit(double a, double b) {\n return (a + 1) / (b + 1) - a / b;\n }\n}\n```\n | 109 | 7 | [] | 12 |
maximum-average-pass-ratio | [C++] Explained Priority Queue | Greedy Solution | Find the Delta | c-explained-priority-queue-greedy-soluti-p0xj | There are few incorrect approaches:\n1. Choosing the smallest class size\n2. Choosing the smallest pass size\n3. Choosing the least pass ratio\n\nInstead, the c | vector_long_long | NORMAL | 2021-03-14T04:06:03.977339+00:00 | 2021-06-18T22:23:24.738221+00:00 | 4,824 | false | There are few incorrect approaches:\n1. Choosing the smallest class size\n2. Choosing the smallest pass size\n3. Choosing the least pass ratio\n\nInstead, the correct approach is:\n**Find the difference**, namely the delta. \n\nFor example, even though `1/2` and `10/20` has the same ratio. However, `1/2`\'s delta is equal to `(1+1)/(2+1)-1/2`, which is much greater than `(10+1)/(20+1)-10/20`. \n\nTherefore, we always greedily select the one with the greatest delta.\n\nWe can acheive this using a max heap. In C++, we can use the **priority queue**.\n\n[C++]: \n\n```\nstruct cmp{\n bool operator()(pair<int,int> a, pair<int,int> b){\n double ad = (a.first+1)/(double)(a.second+1) - (a.first)/(double)a.second;\n double bd = (b.first+1)/(double)(b.second+1) - (b.first)/(double)b.second;\n return ad < bd;\n }\n};\n\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n double acc = 0;\n priority_queue<pair<int,int>, vector<pair<int,int>>, cmp> que;\n for(vector<int> i: classes)\n que.push(make_pair(i[0],i[1]));\n while(extraStudents--){\n pair<int,int> cur = que.top(); que.pop();\n cur.first++, cur.second++;\n que.push(cur);\n }\n while(!que.empty()){\n pair<int,int> cur = que.top(); que.pop();\n acc += cur.first / (double) cur.second;\n }\n return acc / (double) classes.size();\n }\n};\n```\n | 81 | 2 | ['C', 'Heap (Priority Queue)', 'C++'] | 6 |
maximum-average-pass-ratio | Greedy+make_heap vs 2nd largest||251ms beats 100% | greedymake_heap251ms-beats-100-by-anwend-cmr7 | IntuitionTo compute the increment for each pair (p,q)
q+1p+1−qp=q(q+1)q−p
Then use Greedy to deploy the extraStudents for the pair (p,q) with the most increm | anwendeng | NORMAL | 2024-12-15T01:36:31.702128+00:00 | 2024-12-15T11:56:44.427859+00:00 | 11,460 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo compute the increment for each pair $(p, q)$\n$$ \n\\frac{p+1}{q+1}-\\frac{p}{q}=\\frac{q-p}{q(q+1)}\n$$\nThen use Greedy to deploy the extraStudents for the pair $(p, q)$ with the most increment at each time; that is done by using `make_heap`. Python code is done by using `heapify` & `heapreplace`.\n\n2nd approach is using the observation by @Sergei. If the largest increment is much bigger than the 2nd one, there is a way to reduce the number of heap operations.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Let `sum` denote the sum of ratio.\n2. Let `A` be the array containing the tuple `(increment, p, q)` which is using C-array & declared as global variable.\n3. Use a loop to add `p/q` to `sum` & compute the increment $$ \n\\frac{p+1}{q+1}-\\frac{p}{q}=\\frac{q-p}{q(q+1)}\n$$. Set `A[i]=(inc, p, q)`. It costs O(n) of TC.\n4. Apply `make_heap` to `A[0:n]`; TC:O(n)\n5. Use a loop from `i=0` to `k-1` do the following\n```\npop_heap(A, A+n);// make the max inc to A[n-1]; TC: O(log n)\nauto [r, p, q] = A[n-1];\nif (r==0) break;// early stop\n \n// Add the current inc to the sum; each ratio has the same weight\nsum += r;\n\n// Compute the new increment r2 for the pair (p+1, q+1)\ndouble r2= (double)(q - p) / ((q +1.0)* (q + 2.0));\n\nA[n-1]={ r2, p+1, q+1};// just update A[n-1] without push or pop\n\n// update the heap after changing value for A[n-1]; TC:O(log n)\npush_heap(A, A+n);\n```\n6. return `sum/n`\n7. Python is done. But Python has **min heap by using heapq**. The changing sign trick is used. heapify & heapreplace are used. `heapreplace` is more efficient than heappop & heappush\n8. C++ priority_queue is done, please ref the link in th comments\n9. 2nd approach is using the observation by @Sergei. If the largest increment is much bigger than the 2nd one, there is a way to reduce the number of heap operations. The main idea is to find 1st largest 1, to make heap from other elements. Then 2nd largest one will be on the top. Between 1st& 2nd ones there are many operations for numerator+1 & denominator+1 without any heap operations such as pop & push. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(n+k\\log n)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(n)$\n# Code ||C++ using make_heap 251ms beats 100%|Python 897ms Beats 96.67%\n```cpp []\nusing info = tuple<double, int, int>;\ninfo A[100000];\nclass Solution {\npublic:\n static double maxAverageRatio(vector<vector<int>>& classes, int k) {\n const int n = classes.size();\n double sum = 0.0;\n int i = 0;\n for (auto& pq : classes) {\n int p = pq[0], q = pq[1];\n sum += (double)p/q;\n double inc=(double)(q - p) / (q * (q + 1.0));\n A[i++]={inc, p, q};\n }\n \n make_heap(A, A+n);\n \n for (int i = 0; i < k; i++) {\n pop_heap(A, A+n);\n auto [r, p, q] = A[n-1];\n if (r==0) break;// early stop\n \n // Add the current inc to the sum\n sum += r;\n double r2= (double)(q - p) / ((q +1.0)* (q + 2.0));\n A[n-1]={ r2, p+1, q+1};\n push_heap(A, A+n);\n }\n \n return sum / n;\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n\n```\n``` Python []\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], k: int) -> float:\n n=len(classes)\n sum=0\n A=[]\n for p,q in classes:\n sum+=p/q\n A.append(((p-q)/(q*(q+1)), p, q)) # change sign\n\n heapify(A)\n\n for _ in range(k):\n (r, p, q)=A[0]\n if r==0: break\n sum-=r # change sign\n r2=(p-q)/((q +1.0)* (q + 2.0))\n heapreplace(A, (r2, p+1, q+1))\n return sum/n\n```\n# C++ finds the 1st, 2nd largest increments\n```\nusing info = tuple<double, int, int>;\nvector<info> A;\nclass Solution {\npublic:\n static inline double incr(int p, int q) {\n return (q - p) / (q * (q + 1.0));\n }\n static double maxAverageRatio(vector<vector<int>>& classes, int k) {\n const int n = classes.size();\n A.resize(n);\n double sum = 0.0;\n for (int i = n - 1; i >= 0; i--) {\n int p = classes[i][0], q = classes[i][1];\n sum += (double)p / q;\n A[i] = {incr(p, q), p, q};\n if (A[i]>A[n-1]) swap(A[i], A[n-1]);//keep A[n-1] largest\n }\n make_heap(A.begin(), A.end()-1);\n\n while (k>0) {\n pop_heap(A.begin(), A.end()-1);\n auto [r1, p1, q1]=A[n-1];\n double r2=get<0>(A[n-2]);\n sum+=r1;\n int s=1;\n double rr;\n for(; s<k; s++){\n rr=incr(p1+s, q1+s);\n if (rr<r2) break;\n else sum+=rr;// add rr to sum\n }\n k-=s; //decrease k by s\n if (k==0) break;\n A[n-1]=A[n-2];\n A[n-2]={rr, p1+s, q1+s};\n // if (A[n-1]<A[n-2]) swap(A[n-2], A[n-1]);\n push_heap(A.begin(), A.end()-1);\n }\n\n return sum / n;\n }\n};\n\n``` | 48 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'C++', 'Python3'] | 11 |
maximum-average-pass-ratio | [Python] Greedy Solution using Priority Queue | python-greedy-solution-using-priority-qu-gwfq | Explanation\nGreedily take the best current choice using priority queue.\n\n\n# Prove\nFor each class, the delta is decreasing when we add extra students.\nThe | lee215 | NORMAL | 2021-03-14T04:08:03.710314+00:00 | 2021-03-14T08:57:29.034800+00:00 | 4,655 | false | # **Explanation**\nGreedily take the best current choice using priority queue.\n<br>\n\n# **Prove**\nFor each class, the delta is decreasing when we add extra students.\nThe best local option is always the best.\nIt\'s a loss if we don\'t take it.\n<br>\n\n# **Complexity**\nTime `O(n + klogn)`\nSpace `O(n)`\n<br>\n\n**Python3**\n```py\n def maxAverageRatio(self, A, k):\n h = [(a / b - (a + 1) / (b + 1), a, b) for a, b in A]\n heapify(h)\n while k:\n v, a, b = heapq.heappop(h)\n a, b = a + 1, b + 1\n heapq.heappush(h, (-(a + 1) / (b + 1) + a / b, a, b))\n k -= 1\n return sum(a / b for v, a, b in h) / len(h)\n```\n | 45 | 2 | [] | 8 |
maximum-average-pass-ratio | Java PriorityQueue | java-priorityqueue-by-vikrant_pc-lpwp | \nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<int[]> queue = new PriorityQueue<>(new Cmp()) | vikrant_pc | NORMAL | 2021-03-14T04:00:31.762661+00:00 | 2021-03-14T04:14:29.487547+00:00 | 2,221 | false | ```\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<int[]> queue = new PriorityQueue<>(new Cmp());\n for(int[] c: classes) queue.offer(c); // add all to priority queue\n for(;extraStudents > 0;extraStudents--) { // add extra student to class that will max increase the average\n int[] c = queue.poll();\n c[0]++; c[1]++;\n queue.offer(c);\n }\n double result =0;\n while(!queue.isEmpty()) { // Calculate sum of pass ratios\n int[] c = queue.poll();\n result += (double)c[0]/c[1];\n }\n return result/classes.length; // return average\n }\n}\nclass Cmp implements Comparator<int[]> { // to sort in descending order of diff when 1 is added to class\n public int compare(int[] x, int[] y) {\n double xDiff = (double)(x[0]+1)/(x[1]+1) - (double)x[0]/x[1], yDiff = (double)(y[0]+1)/(y[1]+1) - (double)y[0]/y[1];\n return xDiff > yDiff? -1 : 1;\n }\n}\n``` | 28 | 0 | [] | 8 |
maximum-average-pass-ratio | Priority queue O((m+n)log n) Solution 100% Beats | simple-queue-omn-solution-100-beats-by-s-oshz | 🧠 Intuition 🤔The problem is about maximizing the overall average ratio by distributing extra students across the classes. The key idea is to identify which clas | Sumeet_Sharma-1 | NORMAL | 2024-12-15T01:50:05.778806+00:00 | 2024-12-15T04:15:18.316228+00:00 | 7,479 | false | # \uD83E\uDDE0 Intuition \uD83E\uDD14 \nThe problem is about maximizing the overall average ratio by distributing extra students across the classes. The key idea is to identify which class benefits the most from each extra student. This can be achieved by calculating the improvement, or "gain," for adding a student to each class and prioritizing those with the highest gain.\n\n---\n\n# \uD83D\uDEE0\uFE0F Approach \uD83D\uDCDA \n\n1. **Gain Calculation**: \n - Calculate the improvement in ratio by adding one extra student to a class. \n - The gain is the difference between the new ratio and the current ratio of a class. \n\n2. **Prioritize with a Max-Heap**: \n - Use a max-heap to track which class yields the highest gain from an extra student. \n - Each entry in the heap contains the current gain and the class\'s pass and total values. \n\n3. **Distribute Extra Students**: \n - Remove the class with the highest gain from the heap. \n - Update the pass and total counts for that class by adding one student. \n - Recalculate its gain and reinsert it into the heap. \n - Repeat this process for all extra students.\n\n4. **Calculate Final Average**: \n - Sum the updated ratios of all classes and divide by the total number of classes to get the final average. \n\n---\n\n# \u23F1\uFE0F Complexity Analysis \uD83D\uDE80 \n\n- **Time Complexity**: \n - Building the max-heap takes O(n log n). \n - Each student distribution involves extracting the max and reinserting into the heap, which takes O(log n). \n - For `extraStudents`, the total complexity is O(extraStudents * log n). \n\n- **Space Complexity**: \n - The space complexity is O(n) for the heap. \n\n---\n\n# Code\n```C# []\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution {\n public double MaxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<(double gain, int pass, int total), double> maxHeap = new PriorityQueue<(double, int, int), double>(Comparer<double>.Create((a, b) => b.CompareTo(a)));\n double sum = 0.0;\n\n foreach (var cls in classes) {\n int pass = cls[0], total = cls[1];\n sum += (double)pass / total;\n maxHeap.Enqueue((Gain(pass, total), pass, total), Gain(pass, total));\n }\n\n for (int i = 0; i < extraStudents; i++) {\n var top = maxHeap.Dequeue();\n int pass = top.pass, total = top.total;\n sum -= (double)pass / total;\n pass++;\n total++;\n sum += (double)pass / total;\n maxHeap.Enqueue((Gain(pass, total), pass, total), Gain(pass, total));\n }\n\n return sum / classes.Length;\n }\n\n private double Gain(int pass, int total) {\n return (double)(pass + 1) / (total + 1) - (double)pass / total;\n }\n}\n```\n```Python3 []\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n import heapq\n\n def gain(pass_, total):\n return (pass_ + 1) / (total + 1) - pass_ / total\n\n max_heap = []\n sum_ = 0.0\n\n for pass_, total in classes:\n sum_ += pass_ / total\n heapq.heappush(max_heap, (-gain(pass_, total), pass_, total))\n\n for _ in range(extraStudents):\n current_gain, pass_, total = heapq.heappop(max_heap)\n sum_ -= pass_ / total\n pass_ += 1\n total += 1\n sum_ += pass_ / total\n heapq.heappush(max_heap, (-gain(pass_, total), pass_, total))\n\n return sum_ / len(classes)\n\n```\n```Java []\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n // Lambda-like comparator for calculating gain in Java\n PriorityQueue<double[]> maxHeap = new PriorityQueue<>((a, b) -> Double.compare(b[0], a[0]));\n double sum = 0.0;\n\n // Initialize the heap with gains and add the initial ratios to sum\n for (int[] cls : classes) {\n int pass = cls[0], total = cls[1];\n double currentRatio = (double) pass / total;\n double gain = ((double) (pass + 1) / (total + 1)) - currentRatio;\n sum += currentRatio;\n maxHeap.offer(new double[]{gain, pass, total});\n }\n\n // Distribute extra students to maximize the average ratio\n for (int i = 0; i < extraStudents; i++) {\n double[] top = maxHeap.poll();\n double gain = top[0];\n int pass = (int) top[1];\n int total = (int) top[2];\n\n // Update the sum by removing the old ratio and adding the new one\n sum -= (double) pass / total;\n pass++;\n total++;\n sum += (double) pass / total;\n\n // Recalculate the gain and push back into the heap\n double newGain = ((double) (pass + 1) / (total + 1)) - ((double) pass / total);\n maxHeap.offer(new double[]{newGain, pass, total});\n }\n\n // Return the final average\n return sum / classes.length;\n }\n}\n\n```\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n auto gain = [](double pass, double total) {\n return (pass + 1) / (total + 1) - pass / total;\n };\n\n priority_queue<pair<double, pair<int, int>>> maxHeap;\n\n double sum = 0.0;\n\n for (const auto& cls : classes) {\n int pass = cls[0], total = cls[1];\n sum += (double)pass / total; \n maxHeap.push({gain(pass, total), {pass, total}});\n }\n\n for (int i = 0; i < extraStudents; ++i) {\n auto [currentGain, data] = maxHeap.top(); maxHeap.pop();\n int pass = data.first, total = data.second;\n\n sum -= (double)pass / total;\n pass += 1;\n total += 1;\n sum += (double)pass / total;\n\n maxHeap.push({gain(pass, total), {pass, total}});\n }\n\n return sum / classes.size();\n }\n};\n\n``` | 24 | 2 | ['Array', 'Heap (Priority Queue)', 'C++', 'Java', 'Python3', 'C#'] | 6 |
maximum-average-pass-ratio | Easy C++ solution || commented fully & explained | easy-c-solution-commented-fully-explaine-r9ul | \nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n \n //among all classes i choose the one | saiteja_balla0413 | NORMAL | 2021-06-18T06:49:37.856993+00:00 | 2021-06-18T06:49:37.857034+00:00 | 1,645 | false | ```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n \n //among all classes i choose the one which will have a larger growth in the pass ratio if i add one student to the class\n \n //add one student to the each class and store the growth (difference) in the pass ratio to a max heap\n using pi=pair<double,pair<int,int>>;\n priority_queue<pair<double,pair<int,int>>> pq;\n //double is used to store the difference\n //pair.first stores the pass students in the class\n //pair.second stores the total students in the class\n for(int i=0;i<classes.size();i++)\n {\n int pass=classes[i][0];\n int total=classes[i][1];\n \n //calculate the growth\n long double growth=(double)(pass+1)/(total+1) - (double)(pass)/(total);\n pq.push({growth,{pass,total}});\n }\n \n //now i have not added any students to any class and the number of students still remains the same\n //i have just want to know which class would have more growth if i add one \n //so i pushed all the classes growth to max heap\n \n while(extraStudents)\n {\n pi top= pq.top();\n pq.pop();\n extraStudents--;\n //calculate the growth again if i add one student to the class at the top\n int pass=top.second.first;\n int total=top.second.second;\n pass++;\n total++;\n long double growth=(double)(pass+1)/(total+1) - (double)(pass)/(total);\n pq.push({growth,{pass,total}});\n }\n \n //now pop out the elements from pq and calculate the pass ratio\n double res=0;\n while(!pq.empty())\n {\n //calculate the pass/total;\n res+=(double)(pq.top().second.first)/(pq.top().second.second);\n pq.pop();\n }\n return (double)res/(classes.size());\n \n }\n};\n```\n**Upvote if this helps you :)** | 23 | 0 | ['C', 'Heap (Priority Queue)'] | 3 |
maximum-average-pass-ratio | [Python] 100% Efficient solution, easy to understand with comments and explanation | python-100-efficient-solution-easy-to-un-nwpy | Key Idea: We need to keep assigning the remaining extra students to the class which can experience the greatest impact. \n\nLet see an example below, if we have | captainx | NORMAL | 2021-03-14T04:36:33.573517+00:00 | 2021-03-14T05:31:48.216744+00:00 | 2,333 | false | **Key Idea:** We need to keep assigning the remaining extra students to the class which can experience the greatest impact. \n\nLet see an example below, if we have following clasess - [[2,4], [3,9], [4,5], [2,10]], then the impact of assignment students to each class can be defined as,\n\n```\n# In simple terms it can be understood as follows,\n\ncurrentRatio = passCount/totalCount\nexpectedRatioAfterUpdate = (passCount+1)/(totalCount+1)\nimpact = expectedRatioAfterUpdate - currentRatio\n\t\t\t\nOR\n\n# Formula to calculate impact of assigning a student to a class\nimpacts[i] = (classes[i][0]+1) / (classes[i][1]+1) - classes[i][0]/classes[i][1]\ni.e.\nimpacts[0] -> (4+1)/(2+1)-4/2 \nimpacts[1] -> (3+1)/(9+1)-3/9 \n.\n.\netc.\n```\n\nAnd, once we assign a student to a class, then we need the class with "next" greatest impact. We know that heap is perfect candidate for scenarios in which you need to pick the least/greatest of all the collections at any point of time.\n\nHence, we can leverage that to fetch the greatest impacts in all the cases. \n\n**Note:** in below code we have negated (observe `-` sign ), because by default python heaps are min heaps. Hence, it\'s sort of a workaround to make our logic work :)\n\n```\nclass Solution:\n\tdef maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n\t\t\n\t\tn = len(classes)\n\t\t\n\t\timpacts = [0]*n\n\t\tminRatioIndex = 0\n\t\t\n\t\t# calculate and store impacts for each class in form of tuples -> (-impactValue, passCount, totalCount)\n\t\tfor i in range(n):\n\t\t\tpassCount = classes[i][0]\n\t\t\ttotalCount = classes[i][1]\n\t\t\t\n\t\t\t# calculate the impact for class i\n\t\t\tcurrentRatio = passCount/totalCount\n\t\t\texpectedRatioAfterUpdate = (passCount+1)/(totalCount+1)\n\t\t\timpact = expectedRatioAfterUpdate - currentRatio\n\t\t\t\n\t\t\timpacts[i] = (-impact, passCount, totalCount) # note the - sign for impact\n\t\t\t\n\t\theapq.heapify(impacts)\n\t\t\n\t\twhile(extraStudents > 0):\n\t\t\t# pick the next class with greatest impact \n\t\t\t_, passCount, totalCount = heapq.heappop(impacts)\n\t\t\t\n\t\t\t# assign a student to the class\n\t\t\tpassCount+=1\n\t\t\ttotalCount+=1\n\t\t\t\n\t\t\t# calculate the updated impact for current class\n\t\t\tcurrentRatio = passCount/totalCount\n\t\t\texpectedRatioAfterUpdate = (passCount+1)/(totalCount+1)\n\t\t\timpact = expectedRatioAfterUpdate - currentRatio\n\t\t\t\n\t\t\t# insert updated impact back into the heap\n\t\t\theapq.heappush(impacts, (-impact, passCount, totalCount))\n\t\t\textraStudents -= 1\n\t\t\n\t\tresult = 0\n\t\t\t\n\t\t# for all the updated classes calculate the total passRatio \n\t\tfor _, passCount, totalCount in impacts:\n\t\t\tresult += passCount/totalCount\n\t\t\t\n\t\t# return the average pass ratio\n\t\treturn result/n\n``` | 22 | 2 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 2 |
maximum-average-pass-ratio | Python | Greedy Algorithm Pattern & Priority Queue (Heap) | python-greedy-algorithm-pattern-priority-tq0w | see the Successfully Accepted SubmissionCodeKey InsightsImpact of an Extra StudentAdding one extra student to a class will increase its pass ratio. The key is t | Khosiyat | NORMAL | 2024-12-15T00:27:24.657569+00:00 | 2024-12-15T00:27:24.657569+00:00 | 2,662 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1478957269/?envType=daily-question&envId=2024-12-15)\n\n# Code\n```python3 []\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n # Function to calculate the gain in pass ratio for adding a student to a class\n def pass_ratio_gain(passi, totali):\n return (passi + 1) / (totali + 1) - passi / totali\n \n # Max-heap to store the gain, -gain because heapq is a min-heap by default\n heap = []\n for passi, totali in classes:\n gain = pass_ratio_gain(passi, totali)\n heappush(heap, (-gain, passi, totali))\n \n # Distribute the extra students\n for _ in range(extraStudents):\n # Pop the class with the maximum gain\n gain, passi, totali = heappop(heap)\n # Add one student to this class\n passi += 1\n totali += 1\n # Recalculate gain and push back into heap\n new_gain = pass_ratio_gain(passi, totali)\n heappush(heap, (-new_gain, passi, totali))\n \n # Calculate the final average pass ratio\n total_ratio = 0\n for _, passi, totali in heap:\n total_ratio += passi / totali\n \n return total_ratio / len(classes)\n\n```\n\n# Key Insights\n\n## Impact of an Extra Student\nAdding one extra student to a class will increase its pass ratio. The key is to calculate the **gain in pass ratio** when an extra student is added to a class. This can help prioritize which class should get the next extra student.\n\n## Priority Queue (Max-Heap)\nTo efficiently determine which class benefits the most from an extra student, use a **max-heap** where the priority is the gain in pass ratio for adding an extra student to a class.\n\n\n\n## Iterative Allocation\n1. Start by calculating the **initial gain** for all classes and insert them into the heap.\n2. Iteratively assign the extra students to the class with the **maximum gain**, updating the heap as you go.\n\n# Explanation of Code\n\n## Heap Initialization\n1. Compute the gain for each class and insert it into the max-heap.\n2. Store \\(-\\text{gain}\\) because Python\'s `heapq` is a min-heap, and we need max behavior.\n\n## Allocate Extra Students\n1. Extract the class with the **highest potential gain**.\n2. Add one extra student to this class and recalculate its gain.\n3. Reinsert the updated class into the heap.\n\n## Compute Average\nAfter distributing all extra students, compute the final average pass ratio by:\n1. Summing the pass ratios of all classes.\n2. Dividing by the total number of classes.\n\n# Complexity\n\n## Heap Operations\n- **Push and Pop Operations**: Each push and pop from the heap takes \\(O(\\log k)\\), where \\(k\\) is the number of classes.\n\n## Total Time\n- **Initial Heap Construction**: \\(O(k \\log k)\\).\n- **Extra Student Allocation**: \\(O(n \\log k)\\), where \\(n\\) is the number of extra students.\n- **Overall Time Complexity**: \\(O((n + k) \\log k)\\).\n\n\n\n\n\n | 17 | 1 | ['Python3'] | 2 |
maximum-average-pass-ratio | Faster Convergence | Heavy Math | C++ 64-91 ms 100% | faster-convergence-heavy-math-c-100-ms-1-w5xa | IntuitionWe have an array of up to 105 classes containing class population (105, which is quite a large class) and the number of studends who are going to pass | sergei99 | NORMAL | 2024-12-15T15:31:50.177122+00:00 | 2024-12-16T12:53:15.476655+00:00 | 720 | false | # Intuition\nWe have an array of up to $10^5$ classes containing class population ($10^5$, which is quite a large class) and the number of studends who are going to pass a forthcoming exam successfully. We need to distribute up to $10^5$ extra studends across classes so as to maximize the average pass ratio, which is computed as the arithmetic average of pass ratios of individual classes.\n\nThere is a pretty obvious solution replicated all over the site and consisting of the following steps:\n1. Push all elements to a heap queue, using the influence factor to the class\'es pass ratio of adding one brillian student to it as a sort key. The influence factor is computed as $\\frac {p + 1} {t + 1} - \\frac p t = \\frac {t - p} {t \\times (t + 1)}$ where $t$ is the class population (number of students), and $p$ is the number of studends to pass the exam.\nSince it\'s not an integral number, a floating point type is typically used to hold it, along with the two initial class parameters (population and number of studends to pass the exam).\n2. Add studends one by one to the class whose ratio they would influence most. Since that would reduce the influence factor (the denominator grows with the numerator staying the same), the class should be repushed into some other position of the queue.\n3. Once there are no extra studends remaining, return the average pass ratio, which could be computed as the classes are being processed.\n\nThis ultimately results in some $O(n + s \\times log(n)))$ or even $O((n + s) \\times log(n)))$ time complexity where $s$ is the number of extra studends, and $n$ is the number of classes.\n\n# Approach\n\nGenerally we follow the same logic as described above, but not so blindly. Lets go through the steps and consider improvements.\n\n## Step 1 - Dump the Dead Weight\n\nAn unordered array can be converted into a heap in $O(n)$ time if we first populate it and then heapify it all at once. This is opposed to one-by-one element addition to a heap, resulting in some $O(n \\times log(n))$ asymptotic time.\n\nDo we really need to compute and store ratios, resulting in 128-bit tuples for queue elements (64 bit for rating and 32 bit for each of the two class parameters)? There is enough information for rating in the input data, and usually the memory access is a bottleneck, not the computation. The heap can run without storing ratios if we provide a comparator. Consider e.g. two elements $(p, t)$ and $(v, u)$ where $p$, $v$ are numbers of passing students, and $t$, $u$ are the total class populations. Then the expression $\\frac {t - p} {t \\times (t + 1)} < \\frac {u - v} {u \\times (u + 1)}$ can be converted to $(t - p) \\times v \\times (u + 1) < (u - v) \\times t \\times (t + 1)$, which is integer and does not require costly divisions to compute it. The max bit size of the expressions is somewhere around 50, therefore we have to allocate a 64-bit integer for it and not to forget to expand intermediate results.\n\nWe can also skip adding classes with 100% ratios ($p == t$) because their ratios won\'t be affected by extra studends. We still need to reflect them in the overall ratio, but don\'t have to place them onto our heap queue.\n\nSo we have lowered the queue\'s memory size more than twice, thus improving the memory locality.\n\nWe can also handle edge cases separately. E.g. if all classes are already brilliant, we can simply return 100% without any further processing. Also, if there is only one non-brilliant class, we end up adding all students to it and returning the resultant ratio (averaged out with the other rocket scientist 100% classes if any).\n\n## Step 2 - Improve Convergence\n\nDo we really need to process extra students one by one? Consider we have two classes $(p, t)$ and $(v, u)$, the first one being at the top of the queue, and the second one next to it. How many brilliant studends can we add to the first class so that its influence factor becomes barely lower than that of the second class? Let $d$ be the number of students to add.\n$\\frac {t - p} {(t + d) \\times (t + d + 1)} \\le \\frac {u - v} {u \\times (u + 1)}$\nThis can be transformed into a square inequality with regard to $d$:\n$d^2 + (2t + 1) \\times d + t \\times (t + 1) - \\frac {(t - p) \\times u \\times (u + 1)} {u - v} > 0$\nDespite a horrible appearance, its discriminant is computed relatively simply:\n$D = 4 \\times \\frac {(t - p) \\times u \\times (u + 1)} {u - v} + 1$\nThis expression is always positive, and we need the larger equation root as the minimal possible $d$ to add, applying the math rounding it (add $0.5$ and take the integer floor value).\n\nSo we can avoid twitching the top queue element back and forth if we have a hundred of studends to add to the class with a top influence factor. However this would work out only once on its own. If the numbers are large enough, once we add $d$ students to the first class, we engage into distributing students one at a time between the first and the second top classes, and may be other classes, because the factor difference becomes too small. What if we still have some $99000$ more students to distribute?\n\nWe are employing another trick to mitigate that. If the remaining number of the extra studends is high enough, we can try to compute a "fair share" $f$ to give it to the top class. Generally that should be in the order of $\\frac s m$ where $s$ is the remaining number of extra studends, and $m$ is the number of classes in the queue ($m \\le n$, see Step 1). The exact useful value of the "fair share", however, is smaller, because students could be distributed unevenly. We put it as $f = \\frac 1 4 \\times \\lceil \\frac s m \\rceil$, which is based on pure heuristic.\n\nOnce we have computed $d$ and $f$, we choose the larger one of them and ensure we always give at least one student to the top-influenced class. This way we improve the convergence time to an average of $m \\times log(s) \\times log(m)$, though with a high constant multiplier (since we cut only about $\\frac 1 {4m}$ off the remaining count). For a really small $s$ or large $m$, the convergence time degrates to $O(s \\times log(m))$.\n\n## Addition to Step 2\n\nAs pointed out by @yjian012, the "fair share" factor can be larger. $\\frac 1 2$ doesn\'t pass some tests, but $\\frac 1 3$ works and gives better convergence speed and execution time than $\\frac 1 4$. Some tuning around TC#87 shows that the value of $0.33744$ is about the max value being accepted. For further calculation speedup we represent it as a binary fraction $\\frac {44229} {2^{17}} \\approx 0.337440491$. However TC#87 operates relatively small values (class populations less than 1000), while we are interested in faster convergence for larger values in the first place. So we could put $\\frac 1 2$ or $\\frac 5 8$, or even $\\frac {21} {32}$ for larger populations.\n\nWe have also tried to exclude the square inequality solution, and the outcome it turned out to be even faster.\n\nThese manipulations don\'t affect the overall time complexity, but significantly reduce its constant multiplier.\n\n## Micro-Optimisations\n\nC++ offers a great level of control to the developer. E.g. if we have a vector of vectors (typically 24-byte values consisting of 3 pointers each: begin, end of size, end of capacity), we can reinterpret it as a vector of integers. This is what we do in the code example below, build a fully in-place $O(1)$ space solution.\n\nHowever once we have spoiled the pointer data, we should prevent the calling code from calling destructors on the small vectors. So we clear the large vector via an integer vector reference on return. This produces a leaky code (small vectors\' storage is not released), which does not matter for a one-off run of a student program, but in a production app the original vectors should be cleared and their allocation reset to 0 before writing over their pointer data. We skip that step to save processing time.\n\n# Complexity\n- Time complexity: $O(n + min(m \\times log(s), s) \\times log(m))$\nwhere $n$ is the number of classes, and $s$ is the number of extra students\n\n- Space complexity: $O(1)$\n\n# Measurements\n\nThe indicators are clickable, referring to the relevant submission.\n\n|Language|Algorithm|Time, ms|Beating|Memory, Mb|Beating|\n|-|-|-|-|-|-|\n|C++|Square ineq + $\\frac 1 4$ share|[91](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1479497122)|100%|[83.74](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1479497122)|100%|\n|C++|Square ineq + $\\frac 1 3$ share|[84](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1480148450)|100%|[83.80](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1480148450)|100%|\n|C++|$\\frac {44229} {2^{17}}$ vs $\\frac 1 2$ share|[69](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1480194625)|100%|[83.95](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1480194625)|100%|\n|C++|$\\frac {44229} {2^{17}}$ vs $\\frac {21} {32}$ share|[64](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1480210858)|100%|[83.75](https://leetcode.com/problems/maximum-average-pass-ratio/submissions/1480210858)|100%|\n\n# Code\n```cpp [C++ 91 ms]\nclass Solution {\nprivate:\n static constexpr uint8_t VSH = 17;\n static constexpr uint VMASK = (1u << VSH) - 1u;\n\npublic:\n static double maxAverageRatio(vector<vector<int>>& classes, uint s) {\n const uint n = classes.size();\n if (n == 1) {\n const auto &x = classes.front();\n const uint p = x[0], t = x[1];\n return (double)(p + s) / (t + s);\n }\n vector<uint64_t> &qvec = (vector<uint64_t>&)classes;\n uint64_t *const qdata = qvec.data();\n const auto cmp = [](const uint64_t a, const uint64_t b) {\n const uint t = a >> VSH, p = a & VMASK, u = b >> VSH, v = b & VMASK;\n return (t - p) * (u + 1ull) * u < (u - v) * (t + 1ull) * t;\n };\n uint m = 0;\n double res = 0.;\n for (const auto &x : classes) {\n const uint p = x[0], t = x[1];\n if (p != t)\n qdata[m++] = (uint64_t(t) << VSH) + p;\n res += (double)p / t;\n }\n switch (m) {\n case 0:\n qvec.clear();\n return 1.;\n case 1: {\n const auto x = *qdata;\n qvec.clear();\n const uint p = x & VMASK, t = x >> VSH;\n return (double)(p + s) / (t + s);\n }\n }\n make_heap(qdata, qdata + m, cmp);\n while (true) {\n const uint64_t x = *qdata;\n const uint t = x >> VSH, p = x & VMASK, l = t - p;\n pop_heap(qdata, qdata + m--, cmp);\n const uint64_t y = *qdata;\n const uint u = y >> VSH, v = y & VMASK;\n const uint z = floor(sqrt((t - p) * (u + 1ull) * u / double(u - v) + 0.75)),\n f = (s + m) / (m + 1u) / 4u,\n d = max(z, t + f + !f) - t,\n e = min(d, s);\n res += (p + e) / double(t + e) - p / (double) t;\n s -= e;\n if (!s) break;\n qdata[m++] = x + e + (uint64_t(e) << VSH);\n push_heap(qdata, qdata + m, cmp);\n }\n qvec.clear();\n return res / n;\n }\n};\n```\n``` cpp [C++ 84 ms]\nclass Solution {\nprivate:\n static constexpr uint8_t VSH = 17;\n static constexpr uint VMASK = (1u << VSH) - 1u;\n\npublic:\n static double maxAverageRatio(vector<vector<int>>& classes, uint s) {\n const uint n = classes.size();\n if (n == 1) {\n const auto &x = classes.front();\n const uint p = x[0], t = x[1];\n return (double)(p + s) / (t + s);\n }\n vector<uint64_t> &qvec = (vector<uint64_t>&)classes;\n uint64_t *const qdata = qvec.data();\n const auto cmp = [](const uint64_t a, const uint64_t b) {\n const uint t = a >> VSH, p = a & VMASK, u = b >> VSH, v = b & VMASK;\n return (t - p) * (u + 1ull) * u < (u - v) * (t + 1ull) * t;\n };\n uint m = 0;\n double res = 0.;\n for (const auto &x : classes) {\n const uint p = x[0], t = x[1];\n if (p != t)\n qdata[m++] = (uint64_t(t) << VSH) + p;\n res += (double)p / t;\n }\n switch (m) {\n case 0:\n qvec.clear();\n return 1.;\n case 1: {\n const auto x = *qdata;\n qvec.clear();\n const uint p = x & VMASK, t = x >> VSH;\n return (double)(p + s) / (t + s);\n }\n }\n make_heap(qdata, qdata + m, cmp);\n while (true) {\n const uint64_t x = *qdata;\n const uint t = x >> VSH, p = x & VMASK, l = t - p;\n pop_heap(qdata, qdata + m--, cmp);\n const uint64_t y = *qdata;\n const uint u = y >> VSH, v = y & VMASK;\n const uint z = floor(sqrt((t - p) * (u + 1ull) * u / double(u - v) + 0.75)),\n f = (s + m) / (m + 1u) / 3u,\n d = max(z, t + f + !f) - t,\n e = min(d, s);\n res += (p + e) / double(t + e) - p / (double) t;\n s -= e;\n if (!s) break;\n qdata[m++] = x + e + (uint64_t(e) << VSH);\n push_heap(qdata, qdata + m, cmp);\n }\n qvec.clear();\n return res / n;\n }\n};\n```\n``` cpp [C++ 69 ms]\nclass Solution {\nprivate:\n static constexpr uint8_t VSH = 17;\n static constexpr uint VMASK = (1u << VSH) - 1u;\n\npublic:\n static double maxAverageRatio(vector<vector<int>>& classes, uint s) {\n const uint n = classes.size();\n if (n == 1) {\n const auto &x = classes.front();\n const uint p = x[0], t = x[1];\n return (double)(p + s) / (t + s);\n }\n vector<uint64_t> &qvec = (vector<uint64_t>&)classes;\n uint64_t *const qdata = qvec.data();\n const auto cmp = [](const uint64_t a, const uint64_t b) {\n const uint t = a >> VSH, p = a & VMASK, u = b >> VSH, v = b & VMASK;\n return (t - p) * (u + 1ull) * u < (u - v) * (t + 1ull) * t;\n };\n uint m = 0;\n double res = 0.;\n bool bigt = false;\n for (const auto &x : classes) {\n const uint p = x[0], t = x[1];\n if (p != t) {\n qdata[m++] = (uint64_t(t) << VSH) + p;\n bigt |= t > 1000;\n }\n res += (double)p / t;\n }\n switch (m) {\n case 0:\n qvec.clear();\n return 1.;\n case 1: {\n const auto x = *qdata;\n qvec.clear();\n const uint p = x & VMASK, t = x >> VSH;\n return (double)(p + s) / (t + s);\n }\n }\n const uint fmul = bigt ? 1u : 44229u;\n const uint8_t fsh = bigt ? 1 : 17;\n make_heap(qdata, qdata + m, cmp);\n while (true) {\n const uint64_t x = *qdata;\n const uint t = x >> VSH, p = x & VMASK, l = t - p;\n pop_heap(qdata, qdata + m--, cmp);\n const uint64_t y = *qdata;\n const uint u = y >> VSH, v = y & VMASK;\n const uint f = (s + m) / (m + 1u) * fmul >> fsh,\n e = min(f + !f, s);\n res += (p + e) / double(t + e) - p / (double) t;\n s -= e;\n if (!s) break;\n qdata[m++] = x + e + (uint64_t(e) << VSH);\n push_heap(qdata, qdata + m, cmp);\n }\n qvec.clear();\n return res / n;\n }\n};\n```\n``` cpp [C++ 64 ms]\nclass Solution {\nprivate:\n static constexpr uint8_t VSH = 17;\n static constexpr uint VMASK = (1u << VSH) - 1u;\n\npublic:\n static double maxAverageRatio(vector<vector<int>>& classes, uint s) {\n const uint n = classes.size();\n if (n == 1) {\n const auto &x = classes.front();\n const uint p = x[0], t = x[1];\n return (double)(p + s) / (t + s);\n }\n vector<uint64_t> &qvec = (vector<uint64_t>&)classes;\n uint64_t *const qdata = qvec.data();\n const auto cmp = [](const uint64_t a, const uint64_t b) {\n const uint t = a >> VSH, p = a & VMASK, u = b >> VSH, v = b & VMASK;\n return (t - p) * (u + 1ull) * u < (u - v) * (t + 1ull) * t;\n };\n uint m = 0;\n double res = 0.;\n bool bigt = false;\n for (const auto &x : classes) {\n const uint p = x[0], t = x[1];\n if (p != t) {\n qdata[m++] = (uint64_t(t) << VSH) + p;\n bigt |= t > 1000;\n }\n res += (double)p / t;\n }\n switch (m) {\n case 0:\n qvec.clear();\n return 1.;\n case 1: {\n const auto x = *qdata;\n qvec.clear();\n const uint p = x & VMASK, t = x >> VSH;\n return (double)(p + s) / (t + s);\n }\n }\n const uint fmul = bigt ? 21u : 44229u;\n const uint8_t fsh = bigt ? 5 : 17;\n make_heap(qdata, qdata + m, cmp);\n while (true) {\n const uint64_t x = *qdata;\n const uint t = x >> VSH, p = x & VMASK, l = t - p;\n pop_heap(qdata, qdata + m--, cmp);\n const uint64_t y = *qdata;\n const uint u = y >> VSH, v = y & VMASK;\n const uint f = (s + m) / (m + 1u) * fmul >> fsh,\n e = min(f + !f, s);\n res += (p + e) / double(t + e) - p / (double) t;\n s -= e;\n if (!s) break;\n qdata[m++] = x + e + (uint64_t(e) << VSH);\n push_heap(qdata, qdata + m, cmp);\n }\n qvec.clear();\n return res / n;\n }\n};\n``` | 12 | 0 | ['Array', 'Math', 'Greedy', 'Heap (Priority Queue)', 'C++'] | 8 |
maximum-average-pass-ratio | Solution for waifujahat | C# 119ms 100% / C++ 164ms 100% | Max Heap | solution-for-waifujahat-c-119ms-100-max-4nntc | C# SubmissionsC++ SubmissionsHow to SolvePersonally I think this task is hard, rather than medium. I need to maximizing the average pass ratio after distributin | waifujahat | NORMAL | 2024-12-15T05:49:05.520960+00:00 | 2024-12-15T08:07:32.817594+00:00 | 1,374 | false | # C# Submissions\n\n\n---\n\n# C++ Submissions\n\n\n---\n\n# How to Solve\n\nPersonally I think this task is hard, rather than medium. I need to maximizing the average pass ratio after distributing extra students across multiple classes. Each class has a pass ratio defined as `pass i / total i`. Assigning an extra student increases both `pass i` and `total i` by 1, but the extent of this improvement varies between classes. So, after watch some other people solutions, I think I know how to maximizing the overall average pass ratio, here :\n1. Just focus on classes where an extra student results in the largest improvement to the pass ratio\n2. Repeate selecting the class with the highest potential improvement or profit from assigning an extra student\n\nThe profit of adding a student to a class is the difference between the new pass ratio `pass i + 1` / `total i + 1` and the current pass ratio `pass i` / `total i`. So I decide to use `Max Heap` for selecting the class with the largest profit and every extra student assigned, I update the selected class and re-insert it into the heap with the new profit, ensuring the heap remains sorted by maximum profit. Pop the class with the highest profit and update `pass i` and `total i`, re-compute profit and re-insert it into the heap. I repeat until all extra students are assigned or no more improvement is possible. After assigning all extra students, compute the average pass ratio by summing the pass ratios of all classes and dividing by the number of classes.\n\nI need to be careful, with `The Constraints`, the result must be accurate within `10\u207B\u2075`. So, with up to `10\u2075` classes and students, I need to code carefully, every time a student is assigned, the heap must be update heapify operations. If the heap isn\'t updated correctly after recalculating profits, I may select suboptimal classes or fail to converge on the correct result, for example, recalculating profits in a suboptimal way or using recursive heapify operations for large inputs can lead TLE. \n\nThanks to those who have breakdown the logic and calculations, so I just need to find a way to coding my code much better. I wil explain my code :\n\n1. Create a heap to store the profit for each class along with the current pass and total student counts\n2. Populate initial values and heap\nCompute the initial pass ratio and calculate the profit of adding one student to that class using `CalculateProfit` then insert the class into the heap with the calculated profit.\n3. Build Max Heap\n4. Distribute extra students\nExtract the class with the maximum profit root of the heap, add one student to that class and update its pass ratio, recalculate the profit for this class after the addition of a student and update the heap with the new values and repeat this until all extra students are assigned.\n5. The heap is maintained using a simple binary heap structure and `HeapifyDown` ensures that the heap property is maintained by comparing parent and child nodes.\n6. Finally, the average pass ratio is computed by dividing the total pass ratio by the number of classes.\n\nSorry if I\'m bad at explaining, leave comments if you have any questions, I will reply. Please up vote.\n\n---\n# Code\n```csharp []\npublic class Solution {\n public double MaxAverageRatio(int[][] classes, int extraStudents) {\n\n int n = classes.Length;\n double total = 0;\n // Create a heap to store the profit for each class along with the current pass and total student counts\n var heap = new (double Increment, int Passes, int Total)[n];\n int heap_size = 0;\n\n // Populate the heap with initial values and calculate the total pass ratio\n for (int i = 0; i < n; i++) \n {\n int pass = classes[i][0], totalStudents = classes[i][1];\n // Add the pass ratio for the current class to the total\n total += (double)pass / totalStudents;\n // Calculate the potential increment in pass ratio by adding 1 extra student\n heap[heap_size++] = (CalculateProfit(pass, totalStudents), pass, totalStudents);\n }\n\n // Build the heap to prioritize the class with the highest profit\n BuildHeap(heap, heap_size);\n\n // Assign extra students to the classes with the highest potential profit\n while (extraStudents-- > 0) \n {\n var (maxIncrement, pass, totalStudents) = heap[0];\n\n // If there is no increment possible, break\n if (maxIncrement <= 0) \n break;\n\n total += maxIncrement;\n pass++;\n totalStudents++;\n // Recalculate the new increment profit after adding a student\n heap[0] = (CalculateProfit(pass, totalStudents), pass, totalStudents);\n // Reheapify the heap to maintain the heap property\n HeapifyDown(heap, 0, heap_size);\n }\n // Calculate and return the average pass ratio across all classes\n return total / n;\n }\n\n // Calculate the profit, increase in pass ratio when adding a student to a class\n private double CalculateProfit(int pass, int total) {\n \n double current_pass = (double)pass / total;\n double new_pass = (double)(pass + 1) / (total + 1);\n \n return new_pass - current_pass;\n }\n\n // Build the max heap by reheapifying from the bottom to the top\n private void BuildHeap((double Increment, int Passes, int Total)[] heap, int size) {\n\n // Start from the last non leaf node and heapify upwards\n for (int i = size / 2 - 1; i >= 0; i--) \n {\n HeapifyDown(heap, i, size);\n }\n }\n\n // Heapify the heap from index i downwards to ensure the heap property is maintained\n private void HeapifyDown((double Increment, int Passes, int Total)[] heap, int i, int size) {\n\n // Repeat until the heap property is satisfied\n while (true) \n {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n\n // If left child exists and has larger increment\n if (left < size && heap[left].Increment > heap[largest].Increment) \n {\n largest = left;\n }\n // If right child exists and has larger increment\n if (right < size && heap[right].Increment > heap[largest].Increment) \n {\n largest = right;\n }\n // If the largest value is already at i, the heap property is satisfied\n if (largest == i) \n break;\n\n // Swap the current node with the largest child\n (heap[i], heap[largest]) = (heap[largest], heap[i]);\n // Move to the child\n i = largest;\n }\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n\n int n = classes.size();\n double total = 0;\n // Create a heap to store the profit for each class along with the current pass and total student counts\n vector<tuple<double, int, int>> heap;\n\n // Populate the heap with initial values and calculate the total pass ratio\n for (int i = 0; i < n; i++) \n {\n int pass = classes[i][0], totalStudents = classes[i][1];\n // Add the pass ratio for the current class to the total\n total += (double)pass / totalStudents;\n // Calculate the potential increment in pass ratio by adding 1 extra student\n heap.push_back(make_tuple(CalculateProfit(pass, totalStudents), pass, totalStudents));\n }\n\n // Build the heap to prioritize the class with the highest profit\n MakeHeap(heap);\n\n // Assign extra students to the classes with the highest potential profit\n while (extraStudents-- > 0) \n {\n auto [maxIncrement, pass, totalStudents] = heap[0];\n\n // If there is no increment possible, break\n if (maxIncrement <= 0)\n break;\n\n total += maxIncrement;\n pass++;\n totalStudents++;\n // Recalculate the new increment profit after adding a student\n heap[0] = make_tuple(CalculateProfit(pass, totalStudents), pass, totalStudents);\n // Reheapify the heap to maintain the heap property\n HeapifyDown(heap, 0);\n }\n\n // Calculate and return the average pass ratio across all classes\n return total / n;\n }\n\nprivate:\n // Calculate the profit, increase in pass ratio when adding a student to a class\n double CalculateProfit(int pass, int total) {\n\n double current_pass = (double)pass / total;\n double new_pass = (double)(pass + 1) / (total + 1);\n\n return new_pass - current_pass;\n }\n\n // Build the max heap by reheapifying from the bottom to the top\n void MakeHeap(vector<tuple<double, int, int>>& heap) {\n\n // Start from the last non-leaf node and heapify upwards\n for (int i = heap.size() / 2 - 1; i >= 0; i--) \n {\n HeapifyDown(heap, i);\n }\n }\n\n // Heapify the heap from index i downwards to ensure the heap property is maintained\n void HeapifyDown(vector<tuple<double, int, int>>& heap, int i) {\n\n int size = heap.size();\n\n while (true) \n {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n\n // If left child exists and has a larger increment\n if (left < size && get<0>(heap[left]) > get<0>(heap[largest])) \n {\n largest = left;\n }\n // If right child exists and has a larger increment\n if (right < size && get<0>(heap[right]) > get<0>(heap[largest])) \n {\n largest = right;\n }\n // If the largest value is already at i, the heap property is satisfied\n if (largest == i)\n break;\n\n // Swap the current node with the largest child\n swap(heap[i], heap[largest]);\n // Move to the child\n i = largest;\n }\n }\n};\n``` | 12 | 1 | ['Greedy', 'Heap (Priority Queue)', 'C++', 'C#'] | 0 |
maximum-average-pass-ratio | [C++] why using vector<int> in priority_queue got TLE? | c-why-using-vectorint-in-priority_queue-5vmd1 | I used vector in priority_queue then I got TLE. \nBut if I replace the vector with pair in priority_queue, it passes all test cases.\nJust wonder why it happens | dannini_ | NORMAL | 2021-03-14T04:13:29.586316+00:00 | 2021-03-14T04:16:51.320852+00:00 | 941 | false | I used vector<int> in priority_queue then I got TLE. \nBut if I replace the vector<int> with pair<int, int> in priority_queue, it passes all test cases.\nJust wonder why it happens?\n\nHere\'s my code:\n```\nclass Solution {\npublic:\n static double cal(vector<int>& v) {\n return (double) (v[1] - v[0]) / (double) (v[1] * (v[1] + 1));\n }\n \n struct compare {\n bool operator() (vector<int>& a, vector<int>& b) {\n return cal(b) > cal(a);\n }\n };\n \n double maxAverageRatio(vector<vector<int>>& cs, int es) {\n priority_queue<vector<int>, vector<vector<int>>, compare> q;\n for (auto& c : cs) {\n q.emplace(c);\n }\n \n while (es > 0) {\n auto maxn = q.top();\n q.pop();\n maxn[0]++;\n maxn[1]++;\n q.push(maxn);\n es--;\n }\n double total = 0;\n while (!q.empty()) {\n auto& c = q.top();\n total += (double)(c[0]) / (double)(c[1]);\n q.pop();\n }\n return total / (double) cs.size();\n }\n\n};\n``` | 12 | 0 | [] | 5 |
maximum-average-pass-ratio | C++ using priority queue | c-using-priority-queue-by-code_time-wb29 | initial ratio for one class=x/y\nafter adding 1 child=(x+1)/(y+1)\nchange in ratio by adding one child=(y-x)/(y*(y+1))\nkeep removing and adding this ratio from | code_time | NORMAL | 2021-03-14T04:02:49.326967+00:00 | 2021-03-14T07:57:31.068895+00:00 | 870 | false | initial ratio for one class=x/y\nafter adding 1 child=(x+1)/(y+1)\nchange in ratio by adding one child=(y-x)/(y*(y+1))\nkeep removing and adding this ratio from priority queue for all the extra students\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& c, int e) {\n priority_queue<pair<double,int>> pq;\n int n=c.size();\n for(int i=0;i<n;i++){\n double v=(c[i][1]-c[i][0])*1.0/(((c[i][1])*1.0)*(c[i][1]+1));\n if(v<1){\n pq.push({v,i});}\n }\n while(e!=0){\n auto p=pq.top();\n pq.pop();\n int id=p.second;\n c[id][0]++;\n c[id][1]++;\n double v=(c[id][1]-c[id][0])*1.0/(((c[id][1])*1.0)*(c[id][1]+1));\n if(v<1){\n pq.push({v,id});}\n e--;\n \n }\n double ans=0;\n for(int i=0;i<n;i++){\n ans+=((c[i][0]*1.0)/c[i][1]);\n }\n ans/=n;\n return ans;\n \n }\n};\n``` | 10 | 0 | [] | 1 |
maximum-average-pass-ratio | C++ MaxHeap | No Lambda Nonsense | Comparator Class / Functor | Explained with comments | c-maxheap-no-lambda-nonsense-comparator-od60d | I was more familiar with Comparator Classes / Functors and completely clueless about auto []()\nSo here\'s one without Lambda functions.\n\nExplaination:\nIt is | isthisdp | NORMAL | 2021-03-23T10:48:11.219447+00:00 | 2021-03-23T10:53:59.184310+00:00 | 856 | false | I was more familiar with Comparator Classes / Functors and completely clueless about `auto []()`\nSo here\'s one without Lambda functions.\n\n**Explaination:**\nIt is not sufficient to pick out the class with the least pass ratio, add a brilliant kid (extraStudent), and recalculate the average. Although that might seem the best way to solve this "greedily", there may be another class which would have a greater increase/spike in the pass ratio when adding a brilliant kid (this depends on the size of the class). \n\nI define `spike` as the difference between the current Pass Ratio and the expected increase of the pass ratio in the event an `extraStudent` is added.\n\nSo all you have to do is to add a brilliant kid to the class which would have the greatest spike in the pass ratio by "sorting" the Max heap of `studentClasses` with respect to the spike/impact. The class with the highest spike is the one we\'d want to greedily add a student to.\n\n```\n// Trust me this isn\'t Java Lol\nclass studentClass {\npublic:\n int total,passed; // total strength of the class and number of students that passed\n double passRatio; \n\tdouble expectedIncreaseInPassRatio; // incase an extraStudent / brilliant kid is added\n studentClass(int passed, int total)\n {\n this->passed = passed;\n this->total = total;\n passRatio = (double)passed/total;\n expectedIncreaseInPassRatio = (double)(passed+1)/(total+1); // If an extra studen were to be added\n }\n};\n\n// The following class helps the priorty queue in prioritizing its elements\nclass PassRatioComparator {\npublic:\n\t// This as good as passing a comparator into a built in sorting function\n bool operator()(studentClass a, studentClass b) // Overloading the fucntion `()` operator. This is called a Fucntion Object or a Functor.\n {\n double spikeA = a.expectedIncreaseInPassRatio - a.passRatio;\n double spikeB = b.expectedIncreaseInPassRatio - b.passRatio;\n return spikeA < spikeB; \n\t\t// ^^ This makes sure that the class with Highest spike is infront of the Priority queue\n }\n};\n\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<studentClass, vector<studentClass>, PassRatioComparator> maxHeap;\n // ^^ Standard way of declaring a max heap with a comparator class \n \n for(auto c: classes)\n {\n studentClass x(c[0],c[1]); \n maxHeap.push(x);\n }\n \n while(extraStudents--)\n {\n studentClass x = maxHeap.top(); \n\t\t\t// ^^ This class has the highest spike/impact on adding an extra student\n maxHeap.pop();\n studentClass y(x.passed+1,x.total+1); \n\t\t\t// ^^ So create a new class with one extra student. \n\t\t\t\n\t\t\t// Now y has a better pass ratio such that:\n\t\t\t// y.passRatio == x.expectedIncreaseInPassRatio\n \n maxHeap.push(y);\n }\n \n int n = maxHeap.size();\n double sum=0;\n while(maxHeap.size()>0)\n {\n sum+=maxHeap.top().passRatio;\n maxHeap.pop();\n }\n return sum/n;\n }\n};\n```\nThis is my first ever post on Leetcode Discussions.\nUpvote for more! | 9 | 1 | ['Greedy', 'C', 'Heap (Priority Queue)'] | 2 |
maximum-average-pass-ratio | using heaps | c++ 🏆🔥 | using-heaps-c-by-shyyshawarma-2g6h | Intuitionin this problem in order to maximise the average pass ratio you need to maximise the pass ratio
the maximum change in the pass ration is checked acc to | Shyyshawarma | NORMAL | 2024-12-15T05:41:47.325801+00:00 | 2024-12-15T05:44:51.382949+00:00 | 1,056 | false | # Intuition\n\nin this problem in order to maximise the average pass ratio you need to maximise the pass ratio\nthe maximum change in the pass ration is checked acc to how much the ratio of any class changes if any student is added into it.\nfor this we will maintain a heap\nin this the change is already present at the top of the priority queue for the next addition of student.\nthen again the top value is taken and a student is added and then the change that will be done for it.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double,pair<int,int>>> pq;\n for(int i=0;i<classes.size();i++){\n int n=classes[i][0];\n int d=classes[i][1];\n double change=(double)(n+1)/(d+1)-(double)n/d;\n pq.push({change,{n,d}});\n }\n for(int i=0;i<extraStudents;i++){\n auto [change,p]=pq.top();\n pq.pop();\n int n=p.first;\n int d=p.second;\n n++;\n d++;\n double newchange=(double)(n+1)/(d+1)-(double)n/d;\n pq.push({newchange,{n,d}});\n }\n double passratio=0;\n while(!pq.empty()){\n auto [a,b]=pq.top();\n pq.pop();\n int n=b.first;\n int d=b.second;\n passratio+=(double)n/d;\n }\n return passratio/classes.size();\n \n }\n};\n``` | 8 | 0 | ['C++'] | 2 |
maximum-average-pass-ratio | Most Optimal Heap(Priority Queue) O(k + m logk) Approach 👀 | most-optimal-heappriority-queue-approach-g4ka | IntuitionTo maximize the average pass ratio, we should allocate extra students to classes where the gain (improvement in pass ratio) is largest. By focusing on | JK_01 | NORMAL | 2024-12-15T02:25:13.359156+00:00 | 2024-12-15T07:32:08.017585+00:00 | 2,462 | false | # Intuition\nTo maximize the average pass ratio, we should allocate extra students to classes where the gain (improvement in pass ratio) is largest. By focusing on the classes that benefit the most from an extra student, we maximize the overall pass ratio.\n\n# Approach\n1. **Gain Function:** Calculate the gain for adding one student to a class:\n```\n gain = (p + 1) / (t + 1) - (p) / (t)\n```\nwhere `p` is the number of passed students and `t` is the total number of students.\n\n2. **Max-Heap:** Use a max-heap (priority queue) to prioritize classes by their gain. Store negative gains to make the heap behave like a max-heap.\n\n3. **Allocate Extra Students:** For each extra student, pop the class with the highest gain, update its values, and push it back into the heap.\n\n4. **Final Average:** After distributing all extra students, compute the final average pass ratio by averaging the pass ratios of all classes.\n# Complexity\n**Time complexity:**\n- Heap operations (`push` and `pop`) take $$O(log k)$$, where `k` is the number of classes.\n- Distributing $$m$$ extra students involves $$m$$ heap operations.\n- Overall complexity: $$O(k + mlogk)$$.\n\n**Space complexity:** \n- The heap requires $$O(k)$$ space.\n\n\n# Code\n```python3 []\nclass Solution:\n def maxAverageRatio(self, cls: List[List[int]], extra: int) -> float:\n cls = [(p/t - (p+1)/(t+1), p, t) for p, t in cls]\n heapify(cls)\n\n if cls[0][0] == 0:\n return 1\n\n for _ in range(extra):\n _, p, t = heappop(cls)\n heappush(cls, ((p+1)/(t+1) - (p+2)/(t+2), p+1, t+1))\n\n return sum(p/t for _, p, t in cls) / len(cls)\n\n```\n```C++ []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& cls, int extra) {\n // Lambda function to calculate the gain of adding one student\n auto gain = [](int p, int t) {\n return (double)(p + 1) / (t + 1) - (double)p / t;\n };\n\n // Max-heap to store the classes by the gain in descending order\n priority_queue<pair<double, pair<int, int>>> pq;\n\n // Push all classes into the heap, prioritize by the gain\n for (auto& c : cls) {\n pq.push({gain(c[0], c[1]), {c[0], c[1]}});\n }\n\n // Distribute the extra students\n while (extra--) {\n auto [g, pt] = pq.top();\n pq.pop();\n int p = pt.first, t = pt.second;\n pq.push({gain(p + 1, t + 1), {p + 1, t + 1}});\n }\n\n // Compute the final average pass ratio\n double sum = 0;\n while (!pq.empty()) {\n auto [g, pt] = pq.top();\n pq.pop();\n sum += (double)pt.first / pt.second;\n }\n\n return sum / cls.size();\n }\n};\n```\n```Java []\nclass Solution {\n public double maxAverageRatio(int[][] cls, int extra) {\n // Gain calculation\n PriorityQueue<double[]> pq = new PriorityQueue<>((a, b) -> Double.compare(b[0], a[0]));\n\n for (int[] c : cls) {\n int p = c[0], t = c[1];\n pq.offer(new double[]{gain(p, t), p, t});\n }\n\n // Distribute extra students\n while (extra-- > 0) {\n double[] top = pq.poll();\n double g = top[0];\n int p = (int) top[1], t = (int) top[2];\n pq.offer(new double[]{gain(p + 1, t + 1), p + 1, t + 1});\n }\n\n // Compute the final average pass ratio\n double sum = 0;\n for (double[] c : pq) {\n sum += c[1] / c[2];\n }\n\n return sum / cls.length;\n }\n\n // Helper to calculate gain\n private double gain(int p, int t) {\n return (double) (p + 1) / (t + 1) - (double) p / t;\n }\n}\n\n```\n\n\n | 7 | 0 | ['Heap (Priority Queue)', 'C++', 'Java', 'Python3'] | 4 |
maximum-average-pass-ratio | Clean Python 3, greedy with heap | clean-python-3-greedy-with-heap-by-lench-4jie | Greedy add genius students into most benefit class.\n\nTime: O(N + ElogN)\nSpace: O(N)\n\nimport heapq\nclass Solution:\n def maxAverageRatio(self, classes: | lenchen1112 | NORMAL | 2021-03-14T04:02:07.028096+00:00 | 2021-03-14T04:02:07.028122+00:00 | 364 | false | Greedy add genius students into most benefit class.\n\nTime: `O(N + ElogN)`\nSpace: `O(N)`\n```\nimport heapq\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n total = sum(p / t for p, t in classes)\n heap = [(p / t - (p + 1) / (t + 1), p, t) for p, t in classes]\n heapq.heapify(heap)\n for _ in range(extraStudents):\n increase, p, t = heapq.heappop(heap)\n total -= increase\n p, t = p + 1, t + 1\n heapq.heappush(heap, ((p / t - (p + 1) / (t + 1), p, t)))\n return total / len(classes)\n``` | 7 | 0 | [] | 2 |
maximum-average-pass-ratio | PriorityQueue | Solution for LeetCode#1792 | priorityqueue-solution-for-leetcode1792-mrgti | IntuitionThe problem requires maximizing the average pass ratio across all classes by optimally allocating extra students. The key insight is that we should pri | samir023041 | NORMAL | 2024-12-15T07:15:42.278114+00:00 | 2024-12-15T19:11:37.036346+00:00 | 783 | false | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires maximizing the average pass ratio across all classes by optimally allocating extra students. The key insight is that we should prioritize adding students to classes where the increase in pass ratio is the highest.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use a max heap (priority queue) to store the potential increase in pass ratio for each class if we add one student.\n2. Initialize the sum of current pass ratios.\n3. For each extra student:\n\t- Remove the class with the highest potential increase from the heap.\n\t- Update the sum of pass ratios with this increase.\n\t- Update the class\'s pass/total counts.\n\t- Recalculate the new potential increase and add it back to the heap.\n4. Return the final average pass ratio.\n\n# Complexity\n- Time complexity: O((n + m) log n), where n is the number of classes and m is the number of extra students. We perform m heap operations, each taking O(log n) time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) for the priority queue.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) { \n int n=classes.length;\n PriorityQueue<double[]> pq=new PriorityQueue<>((a,b)->Double.compare(b[0], a[0]));\n\n\n double sumVal=0; \n\n for(int i=0; i<n; i++){\n double val1=(double)classes[i][0]/classes[i][1];\n double val2=(double)(classes[i][0]+1)/(classes[i][1]+1);\n double val=val2-val1;\n pq.add(new double[]{val, i});\n sumVal +=val1;\n }\n\n \n\n for(int j=0; j<extraStudents; j++){\n double[] que=pq.poll();\n double val=que[0];\n int i=(int)que[1];\n \n sumVal +=val;\n classes[i][0]+=1;\n classes[i][1]+=1;\n\n double val1=(double)classes[i][0]/classes[i][1];\n double val2=(double)(classes[i][0]+1)/(classes[i][1]+1);\n val=val2-val1;\n pq.add(new double[]{val, i});\n\n }\n\n return sumVal/n;\n }\n}\n``` | 6 | 0 | ['Heap (Priority Queue)', 'Java'] | 1 |
maximum-average-pass-ratio | Beginner Friendly - Hinglish-Comments-Intuition- Approach -easy to understand | beginner-friendly-hinglish-comments-intu-vc9d | Intuition
Humare paas classes hain, jisme pass aur total students ka ratio diya hai.
Hume extraStudents dene hain taaki pass ratio ko maximize kiya ja sake.
Har | mr_unknown_19 | NORMAL | 2024-12-15T03:28:37.402218+00:00 | 2024-12-15T03:28:37.402218+00:00 | 748 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Humare paas classes hain, jisme pass aur total students ka ratio diya hai.\n2. Hume extraStudents dene hain taaki pass ratio ko maximize kiya ja sake.\n3. Har class ke liye hum ek delta (improvement) calculate karte hain, jo batata hai ki ek extra student add karne se ratio me kitna improvement hoga.\n4. Hum priority queue (max heap) ka use karte hain taaki har baar wo class select ho jisme sabse zyada improvement ho.\n5. Fir extraStudents ko classes par apply karte hain, aur finally average pass ratio nikalte hain.\n\n# Step-by-Step:\nDelta Calculation: Har class ka delta (improvement) calculate karo.\nPriority Queue: Delta ke basis par classes ko queue me store karo.\nApply Extra Students: Har step me top class ko select kar ke uske pass aur total ko increment karo.\nFinal Average: Sab classes ka updated pass/total ratio ka average calculate karo.\nDry Run Example:\nGiven:\nclasses = [[1, 2], [3, 5], [2, 2]]\nextraStudents = 2\nInitial delta calculation:\n\nClass 1: delta = 0.1667 // ye wala max heap me top pr aayega \nClass 2: delta = 0.0667\nClass 3: delta = 0\nApply extra students:\n\nApply to Class 1 (max delta) \u2192 becomes (2 pass, 3 total).\nApply again to Class 1 \u2192 becomes (3 pass, 4 total).\nFinal average:\n\nClass 1: 3/4 = 0.75\nClass 2: 3/5 = 0.6\nClass 3: 2/2 = 1\nFinal average = (0.75 + 0.6 + 1) / 3 = 0.7833.\n\nResult:\nAverage pass ratio = 0.7833\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n log n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```cpp []\nclass Solution {\npublic:\n // Function to pass ratio improvement cal. krne k liye \ndouble getDelta(int pass, int total) {\n return (double)(pass + 1) / (total + 1) - (double)pass / total;\n}\n\ndouble maxAverageRatio(vector<vector<int>>& classes, int k) {\n priority_queue<pair<double, pair<int, int>>> pq;\n\n int pass , total ;\n for(int i =0 ; i<classes.size();i++){\n int pass = classes[i][0];\n int total = classes[i][1];\n // yha pr sab me 1 add krke unka increasing ratio kitna hai vo aur pair store kr diye \n pq.push({getDelta(pass,total),{pass,total}}) ;\n }\n\n // abb assign krenge extra wale ko \n while(k--){\n // top wal me increment jyda hoga iske pass and total value ko increse krenge \n int pass = pq.top().second.first ; \n int total = pq.top().second.second ; \n pass++ ;\n total++ ; \n // top ko remove krke new increment ratio wala value re-insert krenge \n pq.pop();\n pq.push({getDelta(pass,total),{pass,total}}) ; \n\n }\n\n double avg = 0.0 ; \n while(!pq.empty()){\n int pass = pq.top().second.first ; \n int total = pq.top().second.second ; \n avg += (double)pass / total ; // double value k liye type caste kiye hai \n pq.pop() ; \n }\nreturn avg/classes.size() ; \n}\n};\n``` | 6 | 0 | ['Greedy', 'Heap (Priority Queue)', 'C++'] | 1 |
maximum-average-pass-ratio | JAVA || Easiest Code || Simple Approach || Beginner Friendly 🔥🚀 | java-easiest-code-simple-approach-beginn-n9a7 | IntuitionThe goal is to maximize the average pass ratio after assigning extraStudents to the classes. The pass ratio for each class is defined as the number of | user6791FW | NORMAL | 2024-12-15T12:38:04.709380+00:00 | 2024-12-15T12:38:04.709380+00:00 | 330 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe goal is to maximize the average pass ratio after assigning `extraStudents` to the classes. The pass ratio for each class is defined as the number of passing students divided by the total number of students in that class. By assigning extra students to classes that will benefit the most (i.e., where the improvement in pass ratio is the largest), we maximize the average pass ratio. This requires calculating the improvement in pass ratio after adding one student and distributing the `extraStudents` accordingly.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initial Setup**:\n - We initialize a priority queue (`pq`) that stores classes, prioritized by the potential improvement in pass ratio after adding an extra student.\n - Each class is represented by an array of three values: the improvement after adding one student, the current number of passing students (`pass`), and the total number of students (`total`).\n \n2. **Priority Queue Operations**:\n - For each class, we compute the improvement if one student is added (i.e., the difference between the pass ratio after adding one student and the current pass ratio).\n - We then push this information into the priority queue, where the class with the maximum improvement is given higher priority.\n \n3. **Distributing Extra Students**:\n - While there are still extra students to assign, we repeatedly:\n - Pop the class with the maximum potential improvement from the queue.\n - Assign one student to this class.\n - Recompute the improvement (since adding a student affects the pass ratio) and push the updated class back into the queue.\n \n4. **Final Calculation**:\n - After all extra students are assigned, we compute the total pass ratio for all classes by summing their pass ratios and then dividing by the number of classes to get the average.\n\n# Complexity\n- Time complexity: - **O(n log n)**:\n - The priority queue operations (`offer` and `poll`) take `O(log n)` time, where `n` is the number of classes.\n - We perform a constant number of operations (each involving a `poll`, an update, and a `offer`) for each extra student, so the complexity due to extra students is `O(extraStudents log n)`.\n - The final loop that calculates the total pass ratio also takes `O(n)` time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: - **O(n)**:\n - We store the class information (pass, total, and improvement) in the priority queue. The maximum number of elements in the queue at any time is equal to the number of classes, so the space complexity is `O(n)`.\n - No other significant data structures are used that would contribute to additional space usage.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n // Priority queue to store classes by their potential improvement in pass ratio\n PriorityQueue<double[]> pq = new PriorityQueue<>((a, b) -> Double.compare(b[0], a[0]));\n\n // Calculate the initial improvement and add classes to the queue\n for (int[] c : classes) {\n int pass = c[0], total = c[1];\n double improvement = ((double)(pass + 1) / (total + 1)) - ((double) pass / total);\n pq.offer(new double[]{improvement, pass, total});\n }\n\n // Distribute extra students\n while (extraStudents > 0) {\n // Extract the class with the largest improvement\n double[] top = pq.poll();\n double improvement = top[0];\n int pass = (int) top[1];\n int total = (int) top[2];\n\n // Assign one extra student\n pass++;\n total++;\n\n // Recalculate the improvement and push back to the queue\n double newImprovement = ((double)(pass + 1) / (total + 1)) - ((double) pass / total);\n pq.offer(new double[]{newImprovement, pass, total});\n extraStudents--;\n }\n\n // Calculate the final average pass ratio\n double totalRatio = 0;\n while (!pq.isEmpty()) {\n double[] top = pq.poll();\n int pass = (int) top[1];\n int total = (int) top[2];\n totalRatio += (double) pass / total;\n }\n\n return totalRatio / classes.length;\n }\n}\n``` | 5 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'Java'] | 1 |
maximum-average-pass-ratio | Simple Solution Using MinPriorityQueue | simple-solution-using-minpriorityqueue-b-ye32 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | tavvfikk | NORMAL | 2024-12-15T06:09:39.984038+00:00 | 2024-12-15T06:09:39.984038+00:00 | 441 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n\n * @param {number[][]} classes\n\n * @param {number} extraStudents\n\n * @return {number}\n\n */\n\nconst maxAverageRatio = (classes, extraStudents) => {\n\n const pq = new MinPriorityQueue({priority: ([avg, pass, total]) => {\n const new_avg = (pass + 1) / (total + 1);\n return avg - new_avg;\n }});\n \n let total_avg = 0;\n for(const [pass, total] of classes) {\n \n const avg = pass / total;\n pq.enqueue([avg, pass, total]);\n total_avg += avg;\n \n }\n\n while(extraStudents--) {\n let [min_avg, min_pass, min_total] = pq.dequeue().element;\n\n total_avg -= min_avg;\n ++min_pass;\n ++min_total;\n\n const avg = min_pass / min_total;\n pq.enqueue([avg, min_pass, min_total]);\n \n total_avg += avg;\n }\n\n return total_avg / classes.length;\n\n};\n``` | 5 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'JavaScript'] | 0 |
maximum-average-pass-ratio | Greedy Proof | greedy-proof-by-yingyangme-hwei | Hi Guys, this is kinda my first post on leetcode, applogies for bad grammer and formatting. Also it\'s been ages since I\'ve written a mathematical proof, so it | yingyangme | NORMAL | 2022-01-23T07:00:41.777274+00:00 | 2022-01-23T08:28:56.844755+00:00 | 242 | false | Hi Guys, this is kinda my first post on leetcode, applogies for bad grammer and formatting. Also it\'s been ages since I\'ve written a mathematical proof, so it might not be very accurate but hopefully it should be intutive. Hope this can help one of you. \n\n### Greedy Algorithm\nIteratively each brilient student is added to the class with the maximum delta pass ratio and pass ratio of this class is updated. \n\nFor a class `class_i` with `pass_i` students passing and `total_i` being the total number of students. The pass ratio is `pass_i/total_i` When a brilliant student is added, the pass ratio changes to `(pass_i+1)/(total_i+1)`. Therefore, the pass ratio increased by `(total_i-pass_i)/(pass_i*(pass_i+1))` which we call as delta pass ratio.\n\n#### Lemma 1. The delta pass ratio decreases as we keep on adding new brilliant student \nIn the above equation of the pass ratio, the Numerator is constant as we keep adding brilliant students, but the Denominator keeps decreasing. Hence, the benefits of adding a new brilliant student keeps decreasing for the `class_i` .\n\n\n#### Algorithm Proof - Proof by contradiction\n- Say at step 1 `class_i` has the highest delta pass ratio.\n- Now if we are picking `class_i` at step 1, then we are good.\n- If we are not picking `class_i` at step\n\t- If we pick `class_i` eventually at `step_x`, then simply swap the steps `step_1` and `step_x`. \n\t- If `class_i` is never picked up, \n\t\t- let `class_k` be the class where last student `s_n` was added\n\t\t- delta pass ratio of `class_k` at step `s_(n-1)` will be less than delta pass ratio for `class_i` \n\t\t\t- since `class_i` has the highest delta pass ratio at `step_0` itself and delta pass ratio decreases with more steps \n\t\t- Hence this is a contradtion, as by changing `step_n` by choose `class_i` instead of `class_k`, the total ratio sum will increase. \n\n\n### Python code for reference \n\n``` python\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n def delta(p, t):\n return -(t-p)/(t*(t+1))\n \n ans = 0\n heap = []\n for class_i in classes:\n heap.append((delta(*class_i), class_i))\n ans += class_i[0]/class_i[1]\n \n heapq.heapify(heap)\n for i in range(extraStudents):\n delta_i, class_i = heapq.heappop(heap)\n ans -= delta_i\n class_i[0]+=1\n class_i[1]+=1\n heapq.heappush(heap, (delta(*class_i), class_i))\n return ans/len(classes)\n```\n | 5 | 0 | ['Greedy'] | 0 |
maximum-average-pass-ratio | [Python] Greedy Heap | python-greedy-heap-by-rowe1227-g74a | \n\nhtml5\n<b>Time Complexity: O((m+n)·log(n))</b> where m = extraStudents and n = classes.length ∵ we perform m operations on a length n heap\n<b | rowe1227 | NORMAL | 2021-03-14T04:00:23.747233+00:00 | 2021-03-14T08:39:41.429257+00:00 | 406 | false | \n\n```html5\n<b>Time Complexity: O((m+n)·log(n))</b> where m = extraStudents and n = classes.length ∵ we perform m operations on a length n heap\n<b>Space Complexity: O(n)</b> ∵ every class must be stored in the heap.\n```\n\n**Approach:**\n\nGreedily select the most needy class to receive a brilliant student.\nThe most needy class will be the class whose ratio increases the\nmost by giving it a brilliant student.\n\n>i.e. 5/10 = 50% and 10/20 = 50% but the first class will \n>benefit more because 6/11 = 54.5% and 11/21 = 52.4%\n\nStore all of the classes and their neediness in a heap so that the\nmost needy class is at `h[0]`.\n\nThen pop the most needy class, give it a brilliant student and update the heap.\nRepeat this step `m` times for `m` brilliant students and return the average class ratio.\n\n<hr>\n\n```python\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n \n # 1. Heapify classes according to how much they will benefit from getting a brilliant student\n h = []\n for p, t in classes:\n delta = ((p+1) / (t+1)) - (p / t)\n heapq.heappush(h, (-delta, p, t))\n \n # 2. Pop the most needy class and give it a brilliant student\n # Then insert the class back into the heap.\n for _ in range(extraStudents):\n d, p, t = heapq.heappop(h)\n p += 1\n t += 1\n delta = ((p+1) / (t+1)) - (p / t)\n heapq.heappush(h, (-delta, p, t))\n \n total_ratio = sum(p/t for d, p, t in h)\n return total_ratio / len(h)\n``` | 5 | 0 | [] | 1 |
maximum-average-pass-ratio | ✨Max Heap Explained Simply 🔑 |🔄 Beginner-Friendly 🔝 | Achieves 100% Success 🎯🔥 | max-heap-explained-simply-beginner-frien-7uub | Intuition 🤔✨We want to maximize the average pass ratio 🤓. To do this:
1️⃣ Focus on the class that benefits the most 📈 when we add a student.
2️⃣ Repeat this for | mansimittal935 | NORMAL | 2024-12-15T14:22:26.242733+00:00 | 2024-12-15T14:22:26.242733+00:00 | 194 | false | # Intuition \uD83E\uDD14\u2728\nWe want to maximize the average pass ratio \uD83E\uDD13. To do this:\n1\uFE0F\u20E3 Focus on the class that benefits the most \uD83D\uDCC8 when we add a student.\n2\uFE0F\u20E3 Repeat this for every extraStudent \uD83D\uDC69\u200D\uD83C\uDF93\uD83D\uDC68\u200D\uD83C\uDF93.\n3\uFE0F\u20E3 The idea is to greedily improve the ratio of the most impactful class each time \uD83D\uDCA1.\n\n---\n\n# Approach \uD83D\uDEE0\uFE0F\uD83D\uDE80\n1\uFE0F\u20E3 Calculate Benefit: For each class, compute the increase in pass ratio if one student is added \uD83D\uDCCA.\n2\uFE0F\u20E3 Use a Max Heap \uD83C\uDFD4\uFE0F: Push all classes into a heap based on their benefit, so the class with the highest potential improvement is on top.\n3\uFE0F\u20E3 Add Students: \n\n While extraStudents > 0 \uD83D\uDC69\u200D\uD83C\uDF93:\n\n- Remove the top class from the heap \uD83D\uDC46.\n- Add one student to it \uD83E\uDDD1\u200D\uD83C\uDFEB.\n- Recompute its benefit and push it back into the heap \uD83D\uDD04.\n\n4\uFE0F\u20E3 Compute Final Average: After distributing all students, sum up the final ratios of all classes and divide by the total number of classes \uD83E\uDDEE.\n\n---\n\n# Complexity \u23F1\uFE0F\uD83D\uDCBE\n## Time: \n- *$$O(nlogn)$$* to build the heap initially. \n- *$$O(klogn)$$* for processing k students.\n- Total: *$$O((n+k)logn)$$* \uD83D\uDE80.\n## Space: *$$O(n)$$* for the heap storage \uD83D\uDDC2\uFE0F.\n\n---\n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) { \n priority_queue<tuple<double, int, int>> maxHeap;\n\n for(vector<int> cls: classes) {\n int pass = cls[0], total = cls[1];\n double diff = (double) (pass + 1)/(total + 1) - (double) pass /total;\n maxHeap.push({diff, pass, total});\n } \n\n while(extraStudents > 0) {\n auto [diff, pass, total] = maxHeap.top();\n maxHeap.pop();\n\n pass ++;\n total++;\n double change = (double) (pass + 1)/(total + 1) - (double) pass /total;\n\n maxHeap.push({change, pass, total});\n extraStudents--;\n }\n\n double ans = 0;\n while(!maxHeap.empty()) {\n auto [ratio, pass, total] = maxHeap.top();\n ans += (double) pass/total;\n maxHeap.pop();\n }\n return (double) ans / classes.size();\n }\n};\n```\n```java []\nimport java.util.PriorityQueue;\n\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<double[]> maxHeap = new PriorityQueue<>((a, b) -> Double.compare(b[0], a[0]));\n\n for (int[] cls : classes) {\n int pass = cls[0], total = cls[1];\n double diff = (double) (pass + 1) / (total + 1) - (double) pass / total;\n maxHeap.offer(new double[]{diff, pass, total});\n }\n\n while (extraStudents > 0) {\n double[] top = maxHeap.poll();\n double diff = top[0];\n int pass = (int) top[1];\n int total = (int) top[2];\n \n pass++;\n total++;\n diff = (double) (pass + 1) / (total + 1) - (double) pass / total;\n\n maxHeap.offer(new double[]{diff, pass, total});\n extraStudents--;\n }\n\n double ans = 0;\n while (!maxHeap.isEmpty()) {\n double[] top = maxHeap.poll();\n ans += (double) top[1] / top[2];\n }\n return ans / classes.length;\n }\n}\n\n```\n```python []\nimport heapq\n\nclass Solution:\n def maxAverageRatio(self, classes, extraStudents):\n maxHeap = []\n for passed, total in classes:\n diff = (passed + 1) / (total + 1) - passed / total\n heapq.heappush(maxHeap, (-diff, passed, total))\n\n while extraStudents > 0:\n diff, passed, total = heapq.heappop(maxHeap)\n passed += 1\n total += 1\n diff = (passed + 1) / (total + 1) - passed / total\n heapq.heappush(maxHeap, (-diff, passed, total))\n extraStudents -= 1\n\n return sum(passed / total for _, passed, total in maxHeap) / len(classes)\n\n```\n```javascript []\nvar maxAverageRatio = function(classes, extraStudents) {\n const maxHeap = new MaxPriorityQueue({ priority: x => x.diff });\n\n for (let [pass, total] of classes) {\n const diff = (pass + 1) / (total + 1) - pass / total;\n maxHeap.enqueue({ diff, pass, total });\n }\n\n while (extraStudents > 0) {\n const { pass, total } = maxHeap.dequeue();\n const newPass = pass + 1;\n const newTotal = total + 1;\n const newDiff = (newPass + 1) / (newTotal + 1) - newPass / newTotal;\n maxHeap.enqueue({ diff: newDiff, pass: newPass, total: newTotal });\n extraStudents--;\n }\n\n let sum = 0;\n while (!maxHeap.isEmpty()) {\n const { pass, total } = maxHeap.dequeue();\n sum += pass / total;\n }\n return sum / classes.length;\n};\n\n```\n```ruby []\nrequire \'priority_queue\'\n\ndef max_average_ratio(classes, extra_students)\n max_heap = PriorityQueue.new\n \n classes.each do |pass, total|\n diff = (pass + 1).to_f / (total + 1) - pass.to_f / total\n max_heap.push([pass, total], -diff)\n end\n\n while extra_students > 0\n pass, total = max_heap.pop\n pass += 1\n total += 1\n diff = (pass + 1).to_f / (total + 1) - pass.to_f / total\n max_heap.push([pass, total], -diff)\n extra_students -= 1\n end\n\n sum = 0.0\n until max_heap.empty?\n pass, total = max_heap.pop\n sum += pass.to_f / total\n end\n sum / classes.size\nend\n\n```\n```rust []\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn max_average_ratio(classes: Vec<Vec<i32>>, extra_students: i32) -> f64 {\n let mut max_heap = BinaryHeap::new();\n\n for cls in classes {\n let (pass, total) = (cls[0], cls[1]);\n let diff = (pass + 1) as f64 / (total + 1) as f64 - pass as f64 / total as f64;\n max_heap.push((diff, pass, total));\n }\n\n let mut extra = extra_students;\n while extra > 0 {\n let (diff, mut pass, mut total) = max_heap.pop().unwrap();\n pass += 1;\n total += 1;\n let new_diff = (pass + 1) as f64 / (total + 1) as f64 - pass as f64 / total as f64;\n max_heap.push((new_diff, pass, total));\n extra -= 1;\n }\n\n let mut sum = 0.0;\n while let Some((_, pass, total)) = max_heap.pop() {\n sum += pass as f64 / total as f64;\n }\n sum / classes.len() as f64\n }\n}\n\n```\n```go []\nimport (\n "container/heap"\n)\n\nfunc maxAverageRatio(classes [][]int, extraStudents int) float64 {\n h := &MaxHeap{}\n heap.Init(h)\n\n for _, class := range classes {\n pass, total := class[0], class[1]\n diff := float64(pass+1)/float64(total+1) - float64(pass)/float64(total)\n heap.Push(h, []float64{diff, float64(pass), float64(total)})\n }\n\n for extraStudents > 0 {\n top := heap.Pop(h).([]float64)\n pass, total := top[1]+1, top[2]+1\n diff := float64(pass+1)/float64(total+1) - float64(pass)/float64(total)\n heap.Push(h, []float64{diff, pass, total})\n extraStudents--\n }\n\n var sum float64\n for h.Len() > 0 {\n top := heap.Pop(h).([]float64)\n sum += top[1] / top[2]\n }\n return sum / float64(len(classes))\n}\n\ntype MaxHeap [][]float64\n\nfunc (h MaxHeap) Len() int { return len(h) }\nfunc (h MaxHeap) Less(i, j int) bool { return h[i][0] > h[j][0] }\nfunc (h MaxHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\nfunc (h *MaxHeap) Push(x interface{}) { *h = append(*h, x.([]float64)) }\nfunc (h *MaxHeap) Pop() interface{} {\n old := *h\n n := len(old)\n x := old[n-1]\n *h = old[:n-1]\n return x\n}\n\n```\n```c# []\nusing System;\nusing System.Collections.Generic;\n\npublic class Solution {\n public double MaxAverageRatio(int[][] classes, int extraStudents) {\n var maxHeap = new PriorityQueue<(double diff, int pass, int total), double>();\n \n foreach (var cls in classes) {\n int pass = cls[0], total = cls[1];\n double diff = (double)(pass + 1) / (total + 1) - (double)pass / total;\n maxHeap.Enqueue((diff, pass, total), -diff);\n }\n\n while (extraStudents > 0) {\n var (diff, pass, total) = maxHeap.Dequeue();\n pass++;\n total++;\n diff = (double)(pass + 1) / (total + 1) - (double)pass / total;\n maxHeap.Enqueue((diff, pass, total), -diff);\n extraStudents--;\n }\n\n double sum = 0;\n while (maxHeap.Count > 0) {\n var (_, pass, total) = maxHeap.Dequeue();\n sum += (double)pass / total;\n }\n return sum / classes.Length;\n }\n}\n\n```\n```typescript []\nfunction maxAverageRatio(classes: number[][], extraStudents: number): number {\n const maxHeap = new MaxPriorityQueue<{ diff: number, pass: number, total: number }>({ priority: x => x.diff });\n\n for (const [pass, total] of classes) {\n const diff = (pass + 1) / (total + 1) - pass / total;\n maxHeap.enqueue({ diff, pass, total });\n }\n\n while (extraStudents > 0) {\n const { pass, total } = maxHeap.dequeue();\n const newPass = pass + 1;\n const newTotal = total + 1;\n const newDiff = (newPass + 1) / (newTotal + 1) - newPass / newTotal;\n maxHeap.enqueue({ diff: newDiff, pass: newPass, total: newTotal });\n extraStudents--;\n }\n\n let sum = 0;\n while (!maxHeap.isEmpty()) {\n const { pass, total } = maxHeap.dequeue();\n sum += pass / total;\n }\n return sum / classes.length;\n}\n\n```\n```dart []\nimport \'dart:collection\';\n\nclass Solution {\n double maxAverageRatio(List<List<int>> classes, int extraStudents) {\n var maxHeap = PriorityQueue<List<double>>((a, b) => b[0].compareTo(a[0]));\n\n for (var cls in classes) {\n int pass = cls[0], total = cls[1];\n double diff = (pass + 1) / (total + 1) - pass / total;\n maxHeap.add([diff, pass.toDouble(), total.toDouble()]);\n }\n\n while (extraStudents > 0) {\n var top = maxHeap.removeFirst();\n var pass = top[1] + 1;\n var total = top[2] + 1;\n var diff = (pass + 1) / (total + 1) - pass / total;\n maxHeap.add([diff, pass, total]);\n extraStudents--;\n }\n\n double sum = 0;\n while (maxHeap.isNotEmpty) {\n var top = maxHeap.removeFirst();\n sum += top[1] / top[2];\n }\n return sum / classes.length;\n }\n}\n\n```\n```swift []\nimport Foundation\n\nfunc maxAverageRatio(_ classes: [[Int]], _ extraStudents: Int) -> Double {\n var maxHeap = Heap { (a: (Double, Int, Int), b: (Double, Int, Int)) in a.0 > b.0 }\n\n for cls in classes {\n let pass = cls[0], total = cls[1]\n let diff = Double(pass + 1) / Double(total + 1) - Double(pass) / Double(total)\n maxHeap.insert((diff, pass, total))\n }\n\n var extra = extraStudents\n while extra > 0 {\n let (diff, pass, total) = maxHeap.remove()!\n let newPass = pass + 1, newTotal = total + 1\n let newDiff = Double(newPass + 1) / Double(newTotal + 1) - Double(newPass) / Double(newTotal)\n maxHeap.insert((newDiff, newPass, newTotal))\n extra -= 1\n }\n\n var sum = 0.0\n while let (_, pass, total) = maxHeap.remove() {\n sum += Double(pass) / Double(total)\n }\n return sum / Double(classes.count)\n}\n\nstruct Heap<T> {\n var nodes = [T]()\n let comparator: (T, T) -> Bool\n\n init(comparator: @escaping (T, T) -> Bool) {\n self.comparator = comparator\n }\n\n mutating func insert(_ value: T) {\n nodes.append(value)\n siftUp(from: nodes.count - 1)\n }\n\n mutating func remove() -> T? {\n guard !nodes.isEmpty else { return nil }\n if nodes.count == 1 { return nodes.removeLast() }\n let value = nodes[0]\n nodes[0] = nodes.removeLast()\n siftDown(from: 0)\n return value\n }\n\n private mutating func siftUp(from index: Int) {\n var child = index\n var parent = (child - 1) / 2\n while child > 0 && comparator(nodes[child], nodes[parent]) {\n nodes.swapAt(child, parent)\n child = parent\n parent = (child - 1) / 2\n }\n }\n\n private mutating func siftDown(from index: Int) {\n var parent = index\n while true {\n let left = 2 * parent + 1, right = 2 * parent + 2\n var candidate = parent\n if left < nodes.count && comparator(nodes[left], nodes[candidate]) { candidate = left }\n if right < nodes.count && comparator(nodes[right], nodes[candidate]) { candidate = right }\n if candidate == parent { return }\n nodes.swapAt(parent, candidate)\n parent = candidate\n }\n }\n}\n\n```\n | 4 | 1 | ['Swift', 'Heap (Priority Queue)', 'Python', 'C++', 'Java', 'Go', 'Rust', 'Ruby', 'C#', 'Dart'] | 0 |
maximum-average-pass-ratio | 251 ms -> 100% | 97.74 MB -> 56.39% | Simple as it gets with explanation. | 251-ms-100-9774-mb-5639-simple-as-it-get-ycd2 | Code | Ununheks | NORMAL | 2024-12-15T13:38:16.015858+00:00 | 2024-12-15T13:38:16.015858+00:00 | 177 | false | \n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n int classesLen = classes.size();\n \n // pq to know which class will increase the avg the most\n priority_queue<pair<double, int>> valueQueue;\n double finalAvg = 0.0;\n double localAvg = 0.0;\n\n\n // going through all classes adding them to finalAvg and\n // placing their avg increase into the pq if we were to add\n // an extra student there\n for (int i = 0; i < classesLen; ++i) {\n localAvg = static_cast<double>(classes[i][0]) / classes[i][1];\n valueQueue.push({(static_cast<double>(classes[i][0] + 1) / (classes[i][1] + 1)) - localAvg, i});\n finalAvg += localAvg;\n }\n\n // devide the avg once after the loop\n finalAvg /= classesLen;\n\n\n // while there are students to distribute we go through the pq\n while (extraStudents > 0) {\n // we take the class with highest avg inc value\n auto top = valueQueue.top();\n valueQueue.pop();\n\n // add the value / classLen to the finalAvg\n finalAvg += top.first / classesLen;\n\n // we add a student to that class\n ++classes[top.second][0];\n ++classes[top.second][1];\n\n // recalculate that class avg inc if we were to add an\n // extra student\n localAvg = static_cast<double>(classes[top.second][0]) / classes[top.second][1];\n valueQueue.push({(static_cast<double>(classes[top.second][0] + 1) / (classes[top.second][1] + 1)) - localAvg, top.second});\n \n // decrement the extraStudents left\n --extraStudents;\n }\n\n return finalAvg;\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
maximum-average-pass-ratio | Simple py,JAVA code explaine din detail!! HEAP(Priority Queue) || Greedy | simple-pyjava-code-explaine-din-detail-h-mgjb | Problem understanding
They have given a list of list classes which contains pass and total of a class.idx[0] denotes the no of students who have passed the gina | arjunprabhakar1910 | NORMAL | 2024-12-15T04:13:35.521284+00:00 | 2024-12-15T04:13:35.521284+00:00 | 567 | false | # Problem understanding\n- They have given a list of list `classes` which contains `pass` and `total` of a class.`idx[0]` denotes the no of students who have passed the ginal exam and `idx[1]` total number of students in the the given ***class<sub>idx</sub>***.\n- They also given `extraStudents` which are *genius* students who are always capable of passing an exam.\n- we should add these `extraStudents` into `classes` such that the **avg pass ratio** is maximum.\n - Note that `pass ratio` is ***pass<sub>i</sub>/total<sub>i</sub>***\n - maximising class ratio is equivalent to that of maximising the average class ratio.\n--- \n# Hints\n- Read the 5 hints provided in the question!\n- Then try solving the problem on your own,if u still didn\'t get the hints properly try reading the solution.\n---\n# Approach:Heap+greedy\n<!-- Describe your approach to solving the problem. -->\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- what we should observe is the `increase in pass ratio` or `gain` for each class after addition of 1 extra student.The one with highest `gain` gets the `1-extraStudent.`\n- This is calculated by `calculate_Increase_In_Pass_Ratio()` function,which tells what happen if current `pass`,`total` has the `1-extraStudent`.This is the *greedy startergy*.\n- We maintain a max-heap `heap` to manage this `gain`.The one with maximum `gain` gets the `extraStudent`.\n- So we allocate students`(extraStudent)` for the `class` with maximum `incInPassratio`.\n- First we have populated `heap` then we handled the above logic for 1-extraStudent per turn.\n- In the end we have calculate the totalSum named as `avg`(typo),then this total is divided by `classes` length to get the `maxAvg`.\n- This `maxAvg` is returned.\n\n# Complexity\n- Time complexity:$O(N)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(N)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Python3 []\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n def calculate_Increase_In_Pass_Ratio(passes,total):\n return ((passes+1)/(total+1))-(passes/total)\n heap=[]\n for p,t in classes:\n heapq.heappush(heap,(-calculate_Increase_In_Pass_Ratio(p,t),p,t))\n #print(list(heap))\n for i in range(extraStudents):\n _,p,t=heapq.heappop(heap)\n heapq.heappush(heap,(-calculate_Increase_In_Pass_Ratio(p+1,t+1),p+1,t+1))\n avg=0\n #print(list(heap))\n while heap:\n _,p,t=heapq.heappop(heap)\n avg+=p/t\n return avg/len(classes)\n```\n```java []\nclass Solution {\n public double calculateIncreaseInPassRatio(double pass,double total){\n return ((double)(pass+1)/(total+1))-((double)pass/total);\n }\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<double[]> heap=new PriorityQueue<>((a,b)->Double.compare(b[0],a[0]));\n for(int[] cl:classes){\n double pass=cl[0],total=cl[1];\n heap.offer(new double[]{calculateIncreaseInPassRatio(pass,total),pass,total});\n }\n for(int i=0;i<extraStudents;i++){\n double[] top=heap.poll();\n double pass=top[1],total=top[2];\n heap.offer(new double[]{calculateIncreaseInPassRatio(pass+1,total+1),pass+1,total+1});\n }\n double avg=0;\n while(!heap.isEmpty()){\n double[] top=heap.poll();\n double pass=top[1],total=top[2];\n avg+=((double)pass)/total;\n }\n return avg/classes.length;\n }\n}\n``` | 4 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'Python', 'Java'] | 1 |
maximum-average-pass-ratio | simple and intutive approach with comments | simple-and-intutive-approach-with-commen-j52f | Intuition\nadd a single student in class which enhance the average maximum among them.\nthen update its new enhancment after adding a passed student\n\n# Approa | Ghost1818 | NORMAL | 2024-01-13T10:22:36.002170+00:00 | 2024-01-13T10:26:08.310007+00:00 | 205 | false | # Intuition\nadd a single student in class which enhance the average maximum among them.\nthen update its new enhancment after adding a passed student\n\n# Approach\nstore the profit of every class in max heap with its index\nupdate the profit of particular class where a student is added and\nupdate classes vector as well\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int k) {\n double ans=0, n=classes.size(), i=0;\n priority_queue<pair<double,int>> pq;\n for(auto x:classes) \n pq.push({((double)(x[0]+1)/(x[1]+1))-((double)(x[0])/(x[1])),i++});\n // har class mi 1 pass student daal ke max heap mi arrange kar rahe hai \n // ki kismi profit ho raha hai , WITH ITS INDEX;\n while(k--)\n {\n int i=pq.top().second;\n int p=classes[i][0]++, t=classes[i][1]++; //add 1 student in that class\n pq.pop();\n // ab uska new profit on adding a passes student daal denge\n pq.push({((double)(p+2)/(t+2))-((double)(p+1)/(t+1)),i}); \n }\n for(auto x:classes)\n {\n ans+=((double)x[0])/x[1];\n }\n return ans/n;\n }\n};\n``` | 4 | 0 | ['Greedy', 'Heap (Priority Queue)', 'C++'] | 1 |
maximum-average-pass-ratio | Max Heap , C++ Easy Beats 90% ✅✅ | max-heap-c-easy-beats-90-by-deepak_5910-vfbk | Approach\n Describe your approach to solving the problem. \nWhat do you think about extra students, in which class do you add extra students.\nAfter adding a st | Deepak_5910 | NORMAL | 2023-06-27T09:43:12.866478+00:00 | 2023-10-12T19:37:02.662605+00:00 | 401 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nWhat do you think about **extra students**, in which class do you add extra students.\nAfter adding a student to all class keep **track of difference** but actually we will add that one student in class which has **maximum difference.**\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& c, int es) {\n\n int n = c.size();\n double avg = 0,ans = 0;\n priority_queue<pair<double,int>> pq;\n\n for(int i = 0;i<n;i++)\n {\n double diff =(double)(c[i][0]+1)/(double)(c[i][1]+1)-(double)c[i][0]/(double)c[i][1];\n pq.push({diff,i});\n }\n while(es--)\n {\n int i = pq.top().second;\n pq.pop();\n c[i][0]+=1;\n c[i][1]+=1;\n double diff = (double)(c[i][0]+1)/(double)(c[i][1]+1)-(double)c[i][0]/(double)c[i][1];\n pq.push({diff,i});\n }\n\n for(int i = 0;i<n;i++)\n {\n avg = (double)c[i][0]/(double)c[i][1];\n ans+=avg;\n }\n return ans/(double)n;\n }\n};\n```\n | 4 | 0 | ['Heap (Priority Queue)', 'C++'] | 1 |
maximum-average-pass-ratio | max heap | C++ | Commented code || Greedy | max-heap-c-commented-code-greedy-by-lazy-l7n5 | \n\ndouble maxAverageRatio(vector<vector<int>>& classes, int extra) {\n priority_queue<pair<double,pair<int,int>>>pq;\n int n=classes.size();\n | lazy_buddy | NORMAL | 2021-08-25T08:12:43.230484+00:00 | 2021-08-25T08:12:43.230514+00:00 | 329 | false | ```\n\ndouble maxAverageRatio(vector<vector<int>>& classes, int extra) {\n priority_queue<pair<double,pair<int,int>>>pq;\n int n=classes.size();\n //calculating the difference between the previous ration and new ratio\n //here I will increament student and pass student of each class by one and will chaeck where difference is maximum\n //thats why I am using preiority queue so that my max profit will be on top;\n for(int i=0;i<n;i++)\n {\n int pass=classes[i][0];\n int stud=classes[i][1];\n double diff=(double)(pass+1)/(stud+1)-(double)(pass)/(stud);\n pq.push({diff,{pass,stud}});\n }\n //now keep adding one by one new students to the class untill extra will not become zero\n while(extra--)\n {\n auto x=pq.top();\n pq.pop();\n \n int pass=x.second.first;\n int stud=x.second.second;\n pass++;\n stud++;\n //chck your new difference and reassign to the priority queue after popping the previous one\n double newdiff=(double)(pass+1)/(stud+1)-(double)(pass)/(stud);\n pq.push({newdiff,{pass,stud}});\n \n }\n //till here you have successfully assinged the student in optimal class\n //just take the avarage and this is your ans;\n double ans=0.0;\n while(!pq.empty())\n {\n auto x=pq.top();\n pq.pop();\n ans+=(double)(x.second.first)/(x.second.second);\n }\n return ans/n;\n }\n\n``` | 4 | 0 | [] | 0 |
maximum-average-pass-ratio | C++ || Not Very Simple | c-not-very-simple-by-tagarwal_be18-13hs | \nclass node\n{\n public:\n int x, y;\n double z;\n \n node(int x, int y, double z)\n {\n this -> x = x;\n this -> y = y;\n | tagarwal_be18 | NORMAL | 2021-05-24T19:22:18.017575+00:00 | 2021-05-24T19:22:18.017620+00:00 | 548 | false | ```\nclass node\n{\n public:\n int x, y;\n double z;\n \n node(int x, int y, double z)\n {\n this -> x = x;\n this -> y = y;\n this -> z = z;\n }\n};\n\nclass cmp\n{\n public:\n bool operator()(node a, node b)\n {\n return a.z < b.z;\n }\n};\n\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n int n = classes.size();\n priority_queue<node, vector<node>, cmp> pq;\n for(auto x : classes)\n {\n double prev = x[0] / (double)x[1];\n double next = (x[0] + 1) / (double)(x[1] + 1);\n node nodes(x[0], x[1], next - prev);\n pq.push(nodes);\n }\n while(extraStudents--)\n {\n auto temp = pq.top();\n pq.pop();\n temp.x++;\n temp.y++;\n double prev = temp.x / (double)temp.y;\n double next = (temp.x + 1) / (double)(temp.y + 1);\n node nodes(temp.x, temp.y, next - prev);\n pq.push(nodes);\n }\n double ans = 0;\n while(pq.size() != 0)\n {\n auto temp = pq.top();\n pq.pop();\n ans += temp.x / (double)temp.y;\n }\n return ans / n;\n }\n};\n``` | 4 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 2 |
maximum-average-pass-ratio | [JavaScript] Max Heap Approach O(N logN) Time | javascript-max-heap-approach-on-logn-tim-eb0c | Time: O((N + M) * logN) where N is # of classes and M is # of extraStudents\nSpace: O(N)\njavascript\nvar maxAverageRatio = function(classes, extraStudents) {\ | control_the_narrative | NORMAL | 2021-04-19T10:51:34.796053+00:00 | 2021-04-19T10:51:34.796084+00:00 | 382 | false | Time: `O((N + M) * logN)` where `N` is # of `classes` and `M` is # of `extraStudents`\nSpace: `O(N)`\n```javascript\nvar maxAverageRatio = function(classes, extraStudents) {\n const heap = new MaxPriorityQueue({priority: x => x[2]});\n \n for(let [pass, total] of classes) {\n const before = pass/total;\n const after = (pass+1)/(total+1)\n heap.enqueue([pass, total, after-before]);\n }\n \n while(extraStudents--) {\n let [pass, total] = heap.dequeue().element;\n pass++;\n total++;\n const before = pass/total;\n const after = (pass+1)/(total+1);\n heap.enqueue([pass, total, after-before]);\n }\n \n let sum = 0;\n \n while(!heap.isEmpty()) {\n const [pass, total] = heap.dequeue().element;\n sum += (pass/total);\n }\n return sum/classes.length;\n};\n``` | 4 | 0 | ['Heap (Priority Queue)', 'JavaScript'] | 0 |
maximum-average-pass-ratio | Python3 greedy algorithm | python3-greedy-algorithm-by-otoc-h0lj | Greedy algorithm: for each step of adding a student, maximize the increment of average score\n\n\n def maxAverageRatio(self, classes: List[List[int]], extraS | otoc | NORMAL | 2021-03-14T04:02:41.928471+00:00 | 2021-03-14T16:58:44.206034+00:00 | 253 | false | Greedy algorithm: for each step of adding a student, maximize the increment of average score\n\n```\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n heap = [[-(p + 1) / (t + 1) + p / t, p / t, p, t] for p, t in classes]\n heapq.heapify(heap)\n while extraStudents:\n neg_inc, ratio, p, t = heapq.heappop(heap)\n p += 1\n t += 1\n heapq.heappush(heap, [-(p + 1) / (t + 1) + p / t, p / t, p, t])\n extraStudents -= 1\n return sum(ele[1] for ele in heap) / len(heap)\n``` | 4 | 0 | [] | 0 |
maximum-average-pass-ratio | [Java] 🎄 Priority Queue ✨ Inline comments for clarity 😍 | java-priority-queue-inline-comments-for-7byf4 | IntuitionGreedily increase the pass rate for the classes where adding just 1 student increases the pass rate more than in others.Complexity
Time complexity:
O( | kesshb | NORMAL | 2024-12-15T11:22:31.239849+00:00 | 2024-12-15T11:22:31.239849+00:00 | 206 | false | # Intuition\nGreedily increase the pass rate for the classes where adding just 1 student increases the pass rate more than in others.\n\n# Complexity\n- Time complexity:\n$$O(n log n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```java []\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n // we will be greedily picking the class with the largest possible increase in a pass rate\n Queue<int[]> pq = new PriorityQueue<>((a, b) -> Double.compare(diff(b), diff(a)));\n for (int[] cl: classes) {\n pq.add(cl);\n }\n // so now we are putting the extra students every time to the class \n // where they will contribute to the pass rate mostly. See diff(int[] a) for details\n for (int i = 0; i < extraStudents; i++) {\n int[] next = pq.poll();\n next[0]++;\n next[1]++;\n // so we added an extra student and returned the class back to the PriorityQueue\n // in the next move it may be another class that needs our contribution in a form of an ideal student :)\n pq.add(next);\n }\n double sum = 0.0;\n // we can also define the number of classes as just classes.length\n int count = pq.size();\n while (!pq.isEmpty()) {\n int[] next = pq.poll();\n sum += (double) next[0] / (double) next[1];\n }\n return sum / count;\n }\n\n // calculate how the pass rate will increase for the class if we add an ideal student\n // that is, (pass + 1) / (total + 1) - pass / total\n private double diff(int[] a) {\n double aCurr = (double)a[0] / (double) a[1];\n double aAdd = (double)(a[0] + 1) / (double) (a[1] + 1);\n return aAdd - aCurr; \n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-average-pass-ratio | Best Solution You will ever see in Hinenglish | best-solution-you-will-ever-see-in-hinen-jhap | SochDekho Question keh rha hain ki har ek student kaisa add kara taka avergae max ho jai. Toh agr sum max kar denga toh avg bhi max ho jaiga
Aur sum max ke lia | jastegsingh007 | NORMAL | 2024-12-15T04:51:57.393613+00:00 | 2024-12-15T04:55:12.923957+00:00 | 330 | false | # Soch\nDekho Question keh rha hain ki har ek student kaisa add kara taka avergae max ho jai. Toh agr sum max kar denga toh avg bhi max ho jaiga \nAur sum max ke lia unn ratio mein students add karo jo sum ko maximize karai\nPehla thought aayga DP karloo jissa ya toh iss student pe dalo ya mat daloo\nBut constraints dekho pta chalaga ki not possible DP \nSo kooch greedy hoga\nOkay ab ratios ke term mein socho\nagr a/b ratio mein apan ek student ko add karta hain toh ratio (a+1)/(b+1) hoga.\nAur jo humara sum hain voh (a+1)/(b+1)-a/b se increase karaga toh agr apan har sami iss ko max kara with priority queue then humara final ratio bhi max hoga.\nHence bas itna sochna tha iss lia greedy work karaga.\n\n# Code\n```python3 []\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n temp=[]\n for a,b in classes:\n ratio=(a-b)/((b)*(b+1))\n heapq.heappush(temp,[ratio,a,b])\n while extraStudents>0:\n ratio,a,b=heapq.heappop(temp)\n a=a+1\n b=b+1\n extraStudents-=1\n ratio=(a-b)/((b)*(b+1))\n heapq.heappush(temp,[ratio,a,b])\n ans=0.00000\n #print(temp)\n while temp:\n _,a,b=heapq.heappop(temp)\n ans+=a/b\n return ans/len(classes)\n\n``` | 3 | 0 | ['Python3'] | 0 |
maximum-average-pass-ratio | C# - Fast - 962ms - PriorityQueue of improvement of pass ratio | c-fast-962ms-priorityqueue-of-improvemen-ws9w | Intuition / ApproachThe thing to figure out is which one class would be made better by the most by adding a brilliant student. That would be the one that would | hafthor | NORMAL | 2024-12-15T01:49:41.842734+00:00 | 2024-12-16T11:57:55.747695+00:00 | 119 | false | \n\n# Intuition / Approach\nThe thing to figure out is which one class would be made better by the most by adding a brilliant student. That would be the one that would make the biggest impact on the pass ratio for her class. So we calculate this with (pass+1)/(total+1) - pass/total. Our first instinct might be to sort by this, but then for every extraStudent, we would have to resort the list. In cases like that, the answer is to use a heap. We just add all the classes to the min heap using the negative of our biggest impact calculation, then for each extra student, get the lowest value item, adjust it by adding the brilliant student and put it back on the queue. Then we finally calculate the average.\n\nAs a minor optimization, we use .Peek and .DequeueEnqueue which are an O(1) and an O(log n) operation respectively, rather than a .Dequeue and .Enqueue which would each be an O(log n) operation.\n\nAs another optimization, we use .UnorderedItems to access the current items in the heap rather than using .Dequeue to get each item, making the final averaging operation O(n) rather than O(n log n).\n\n# Complexity\n- Time complexity: $$O(n log n + m log n)$$ where n is the number of classes and m is the number of extra students\n- Space complexity: $$O(n)$$\n\n# Code\n```csharp []\npublic class Solution {\n public double MaxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<(int p,int t),double> pq=new(classes.Select(c=>((c[0],c[1]), 1d*c[0]/c[1]-(c[0]+1d)/(c[1]+1))));\n while(extraStudents-- > 0) {\n var cl=pq.Peek();\n pq.DequeueEnqueue((cl.p+1,cl.t+1), (cl.p+1d)/(cl.t+1)-(cl.p+2d)/(cl.t+2));\n }\n return pq.UnorderedItems.Average(c=>1d*c.Item1.p/c.Item1.t);\n }\n}\n``` | 3 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'C#'] | 2 |
maximum-average-pass-ratio | go heap | go-heap-by-dynasty919-10ja | \nfunc maxAverageRatio(classes [][]int, extraStudents int) float64 {\n h := &maxheap{}\n for _, c := range classes {\n heap.Push(h, [2]int{c[0], c[ | dynasty919 | NORMAL | 2021-12-21T12:07:09.912398+00:00 | 2021-12-21T12:07:42.360165+00:00 | 175 | false | ```\nfunc maxAverageRatio(classes [][]int, extraStudents int) float64 {\n h := &maxheap{}\n for _, c := range classes {\n heap.Push(h, [2]int{c[0], c[1]})\n }\n \n for extraStudents > 0 {\n c := heap.Pop(h).([2]int)\n extraStudents--\n c[0]++\n c[1]++\n heap.Push(h, c)\n }\n var res float64\n for _, v := range *h {\n res += float64(v[0]) / float64(v[1])\n }\n return res / float64(len(classes))\n}\n\ntype maxheap [][2]int\n\nfunc (h maxheap) Len() int {\n return len(h)\n}\n\nfunc (h maxheap) Less(i int, j int) bool {\n return float64(h[i][0] + 1) / float64(h[i][1] + 1) - float64(h[i][0]) / float64(h[i][1]) >\n float64(h[j][0] + 1) / float64(h[j][1] + 1) - float64(h[j][0]) / float64(h[j][1])\n}\n\nfunc (h maxheap) Swap(i int, j int) {\n h[i], h[j] = h[j], h[i]\n}\n\nfunc (h *maxheap) Push(a interface{}) {\n *h = append(*h, a.([2]int))\n}\n\nfunc (h *maxheap) Pop() interface{} {\n l := len(*h)\n res := (*h)[l - 1]\n *h = (*h)[:l - 1]\n return res\n}\n``` | 3 | 0 | ['Go'] | 1 |
maximum-average-pass-ratio | C# SortedSet | c-sortedset-by-venki07-x6wv | \npublic class Solution {\n public double MaxAverageRatio(int[][] classes, int extraStudents) {\n \n var set = new SortedSet<(double delta, int | venki07 | NORMAL | 2021-08-04T14:45:29.014344+00:00 | 2021-08-04T14:45:29.014394+00:00 | 162 | false | ```\npublic class Solution {\n public double MaxAverageRatio(int[][] classes, int extraStudents) {\n \n var set = new SortedSet<(double delta, int index, double pass, double total)>();\n int index = 0;\n \n double avg = 0.0;\n foreach(var cl in classes)\n {\n double a = cl[0], b = cl[1];\n avg += a/b; \n set.Add((GetDeltaGain(a, b), index++, a + 1, b + 1)); //gotcha\n }\n \n while(extraStudents-- > 0)\n { \n var max = set.Max;\n set.Remove(set.Max); \n avg += max.delta;\n set.Add((GetDeltaGain(max.pass, max.total), index++, max.pass + 1, max.total + 1)); \n } \n \n return avg/classes.Length;\n }\n \n private double GetDeltaGain(double a, double b)\n {\n return (a + 1)/(b + 1) - a/b; //gotcha gotcha gotcha -- BRACKETS\n }\n}\n``` | 3 | 1 | [] | 1 |
maximum-average-pass-ratio | Java | O(mlogn) | Heap, Greedy | Small code | java-omlogn-heap-greedy-small-code-by-av-xdsn | \nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n double sum=0;\n PriorityQueue<int[]> pq = new Priori | avishekde | NORMAL | 2021-07-23T11:17:59.001706+00:00 | 2021-07-23T11:17:59.001741+00:00 | 447 | false | ```\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n double sum=0;\n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->Double.compare((double)(b[0]+1)/(b[1]+1)-(double)b[0]/b[1],(double)(a[0]+1)/(a[1]+1)-(double)a[0]/a[1]));\n for(int[] c: classes){\n pq.add(c);\n sum+=(double)c[0]/c[1];\n }\n \n while(extraStudents > 0){\n int[] c = pq.poll();\n pq.add(new int[]{c[0]+1,c[1]+1});\n double change = (double)(c[0]+1)/(c[1]+1)-(double)c[0]/c[1];\n sum += change;\n extraStudents--;\n }\n return sum/classes.length;\n }\n}\n``` | 3 | 0 | ['Greedy', 'Heap (Priority Queue)'] | 0 |
maximum-average-pass-ratio | JavaScript and TypeScript Solution | javascript-and-typescript-solution-by-me-fxsf | JavaScript AC (932 ms, 69.7 MB)\njs\n/**\n * @param {number[][]} classes\n * @param {number} extraStudents\n * @return {number}\n */\nvar maxAverageRatio = func | menheracapoo | NORMAL | 2021-03-16T14:41:39.760711+00:00 | 2021-03-16T14:41:39.760751+00:00 | 163 | false | JavaScript AC (932 ms, 69.7 MB)\n```js\n/**\n * @param {number[][]} classes\n * @param {number} extraStudents\n * @return {number}\n */\nvar maxAverageRatio = function(classes, extraStudents) {\n const q = new MaxPriorityQueue({\n priority: i => (classes[i][0] + 1) / (classes[i][1] + 1) - \n classes[i][0] / classes[i][1],\n });\n classes.forEach((_, i) => {\n q.enqueue(i);\n });\n \n let es = extraStudents;\n while (es) {\n const i = q.dequeue().element;\n \n classes[i][0] += 1;\n classes[i][1] += 1;\n q.enqueue(i);\n \n es -= 1;\n }\n \n let sum = 0;\n classes.forEach(([p, t]) => {\n sum += p / t;\n });\n \n return sum / classes.length;\n};\n```\n\nTypeScript AC (924 ms\t71.6 MB)\n```ts\nfunction maxAverageRatio(classes: number[][], extraStudents: number): number {\n const q = new MaxPriorityQueue({\n priority: i => (classes[i][0] + 1) / (classes[i][1] + 1) - \n classes[i][0] / classes[i][1],\n });\n classes.forEach((_, i) => {\n q.enqueue(i);\n });\n \n let es = extraStudents;\n while (es) {\n const i = q.dequeue().element;\n \n classes[i][0] += 1;\n classes[i][1] += 1;\n q.enqueue(i);\n \n es -= 1;\n }\n \n let sum = 0;\n classes.forEach(([p, t]) => {\n sum += p / t;\n });\n \n return sum / classes.length;\n};\n``` | 3 | 0 | [] | 0 |
maximum-average-pass-ratio | Java || PriorityQueue || O(mlogn+nlogn) | java-priorityqueue-omlognnlogn-by-legend-i23r | \n\t// O(mlogn+nlogn)\n\t// PriorityQueue\n\tpublic double maxAverageRatio(int[][] classes, int extraStudents) {\n\n\t\tPriorityQueue heap = new PriorityQueue(n | LegendaryCoder | NORMAL | 2021-03-15T12:32:32.466056+00:00 | 2021-03-15T12:32:32.466094+00:00 | 172 | false | \n\t// O(m*logn+n*logn)\n\t// PriorityQueue\n\tpublic double maxAverageRatio(int[][] classes, int extraStudents) {\n\n\t\tPriorityQueue<double[]> heap = new PriorityQueue<double[]>(new Comparator<double[]>() {\n\t\t\t@Override\n\t\t\tpublic int compare(double[] o1, double[] o2) {\n\t\t\t\treturn Double.compare(o2[0], o1[0]);\n\t\t\t}\n\t\t});\n\t\tfor (int[] clas : classes) {\n\t\t\tdouble delta = profit(clas[0], clas[1]);\n\t\t\theap.offer(new double[] { delta, clas[0], clas[1] });\n\t\t}\n\n\t\twhile (extraStudents >= 1) {\n\t\t\tdouble[] temp = heap.poll();\n\t\t\tdouble pass = temp[1] + 1, total = temp[2] + 1;\n\t\t\tdouble delta = profit(pass, total);\n\t\t\theap.offer(new double[] { delta, pass, total });\n\t\t\textraStudents--;\n\t\t}\n\n\t\tdouble average = 0d;\n\t\twhile (!heap.isEmpty()) {\n\t\t\tdouble[] temp = heap.poll();\n\t\t\taverage += temp[1] / temp[2];\n\t\t}\n\n\t\treturn average / classes.length;\n\t}\n\n\t// O(1)\n\tpublic double profit(double a, double b) {\n\t\treturn (a + 1) / (b + 1) - a / b;\n\t}\n | 3 | 0 | [] | 0 |
maximum-average-pass-ratio | [Python] Clear Greedy+Heap Solution with Video Explanation | python-clear-greedyheap-solution-with-vi-09uu | Video with clear visualization and explanation:\nhttps://youtu.be/TIn0wbbJDVs\n\n\n\nIntuition: Greedy+Heap\n \n\nCode\n\nfrom heapq import *\n\nclass Solution: | iverson52000 | NORMAL | 2021-03-14T20:36:43.965789+00:00 | 2021-03-14T20:36:43.965828+00:00 | 220 | false | Video with clear visualization and explanation:\nhttps://youtu.be/TIn0wbbJDVs\n\n\n\nIntuition: Greedy+Heap\n \n\n**Code**\n```\nfrom heapq import *\n\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n heap = []\n \n for p, t in classes:\n delta = ((p+1)/(t+1))-(p/t)\n heappush(heap, (-delta, p, t))\n \n for _ in range(extraStudents):\n delta, p, t = heappop(heap)\n p += 1\n t += 1\n delta_new = ((p+1)/(t+1))-(p/t)\n heappush(heap, (-delta_new, p, t))\n \n res = sum(p/t for delta, p, t in heap)/len(heap)\n return res\n```\n\n\n\nTime: O(n+klogn) / Space: O(n)\n\n\nFeel free to subscribe to my channel. More LeetCoding videos coming up! | 3 | 2 | ['Python'] | 0 |
maximum-average-pass-ratio | So beat 100% is meaningless (at least for C++) | so-beat-100-is-meaningless-at-least-for-htnk2 | Basically, I submitted twice using C++ in contest, one got TLE, and one got AC, but they both passed after contest, and beat 100%. Shown as below:\n\nTLE one:\n | acmer29 | NORMAL | 2021-03-14T08:35:56.896256+00:00 | 2021-03-14T08:39:49.865422+00:00 | 195 | false | Basically, I submitted twice using C++ in contest, one got TLE, and one got AC, but they both passed after contest, and beat 100%. Shown as below:\n\nTLE one:\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<heapNode, vector<heapNode>, less<heapNode>> heap;\n for(auto item : classes) {\n heap.push(heapNode(item[0], item[1]));\n }\n for(int i = 0; i < extraStudents; ++i) {\n auto tmp = heap.top();\n // tmp.print();\n heap.pop();\n heap.push(heapNode(tmp.pass + 1, tmp.all + 1));\n }\n // cout << "-----" << endl;\n double res = 0;\n while(heap.size()) {\n heapNode tmp = heap.top();\n // tmp.print();\n heap.pop();\n res += tmp.pass / tmp.all;\n }\n res = res / (double(classes.size()));\n return res;\n }\nprivate:\n struct heapNode {\n double pass, all;\n double foreseen;\n heapNode(double x, double y) : pass(x), all(y) {\n foreseen = (pass + 1) / (all + 1) - pass / all;\n }\n const bool operator < (const heapNode &p) const {\n return this->foreseen < p.foreseen;\n }\n void print() {\n cout << pass << " " << all << endl;\n }\n };\n};\n```\n\nAC one:\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<heapNode, vector<heapNode>, less<heapNode>> heap;\n for(auto item : classes) {\n heap.push(heapNode(item[0], item[1]));\n }\n for(int i = 0; i < extraStudents; ++i) {\n auto tmp = heap.top();\n // tmp.print();\n heap.pop();\n heap.push(heapNode(tmp.pass + 1, tmp.all + 1));\n }\n // cout << "-----" << endl;\n double res = 0;\n while(heap.size()) {\n heapNode tmp = heap.top();\n // tmp.print();\n heap.pop();\n res += tmp.pass / tmp.all;\n }\n res = res / (double(classes.size()));\n return res;\n }\nprivate:\n struct heapNode {\n double pass, all;\n double foreseen;\n heapNode(double x, double y) : pass(x), all(y), foreseen((pass + 1) / (all + 1) - pass / all) {}\n const bool operator < (const heapNode &p) const {\n return this->foreseen < p.foreseen;\n }\n };\n};\n```\n\nAnd during the contest it took 1464ms to AC, I submitted a third time using the AC code and ACed in 1884ms. (Very likely the time threshold is 2000ms)\n\nAs you can see there is **no** optimization between the two solution. And just before I re-submitted the above two pieces of code, **both** of them got AC, and with 996 - 984ms and told me the solution beats 100% of C++ submission, what a nice satire, leetcode! The unchanged pre-TLE code is actually a p100 level solution! \n\nOK backing to reasoning I can assume that it probably because of the spike of submission during the contest period impacted the judger\'s performance. And it is reasonable that as lc got hotter, more and more people join the contest, the service quality may deterioate. But this is the first time I experienced that this issue impact the submission status, and I don\'t think this should happen because the wrong submission status is greatly misleading especially during the contest. Feel really bad on this. | 3 | 0 | ['C'] | 0 |
maximum-average-pass-ratio | [Python] Simple solution, explained, priority queue | python-simple-solution-explained-priorit-27gs | \nimport heapq\n\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n \n # Organize the heap | scornz | NORMAL | 2021-03-14T04:12:05.939282+00:00 | 2021-03-14T04:12:05.939329+00:00 | 336 | false | ```\nimport heapq\n\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n \n # Organize the heap based on the "ratio improvement factor"\n # i.e. The (new ratio) - (old ratio), the one that will improve the largest should be the one added to\n # Add a negative since all heaps are minimum-oriented in python\n classes = [[-((p+1)/(t+1) - (p/t)), p, t] for p, t in classes]\n heapq.heapify(classes)\n \n # Go through the amount of students we need to add\n for _ in range(extraStudents):\n # Remove the next largest opportunity\n c = heapq.heappop(classes)\n \n # Change all of the values\n c[1] += 1\n c[2] += 1\n # Update ratio factor\n c[0] = -((c[1]+1)/(c[2]+1) - (c[1]/c[2]))\n # Push this back on to the heap\n heapq.heappush(classes, c)\n \n # Calculate the total pass ratio after doing this\n total_ratio = 0\n n = 0\n for c in sorted(classes):\n n += 1\n total_ratio += (c[1] / c[2])\n \n return total_ratio / n\n``` | 3 | 0 | ['Heap (Priority Queue)', 'Python3'] | 0 |
maximum-average-pass-ratio | C++ Use set to track the most effective at the end | c-use-set-to-track-the-most-effective-at-dsww | ~~~\nclass Solution {\npublic:\n double maxAverageRatio(vector>& c, int extraStudents) {\n set> s;\n int n = c.size();\n for (int i = 0; | xiaoping3418 | NORMAL | 2021-03-14T04:03:36.854141+00:00 | 2021-03-14T04:04:10.088563+00:00 | 181 | false | ~~~\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& c, int extraStudents) {\n set<pair<double, int>> s;\n int n = c.size();\n for (int i = 0; i < n; ++i) {\n double d = 1.0 * (c[i][0] + 1) / (c[i][1] + 1) - 1.0 * c[i][0] / c[i][1];\n s.insert({d, i});\n }\n \n while (extraStudents > 0) {\n auto it = s.rbegin();\n int i = it->second;\n s.erase(*it);\n c[i][0] = c[i][0] + 1; \n c[i][1] = c[i][1] + 1; \n double d = 1.0 * (c[i][0] + 1) / (c[i][1] + 1) - 1.0 * c[i][0] / c[i][1];\n s.insert({d, i});\n --extraStudents;\n }\n \n double res = 0.0;\n for (int i = 0; i < n; ++i) {\n res += 1.0 * c[i][0] / c[i][1];\n }\n return res/n;\n }\n};\n~~~\n | 3 | 0 | [] | 1 |
maximum-average-pass-ratio | [Java] Greedy solution using priority queue (with trick for early termination) | java-greedy-solution-using-priority-queu-0o01 | Use a max heap: the comparator compares the passing ratio with adding one more student.\nFor a class, if number of passing sutdents is equal to total number of | ninjavic | NORMAL | 2021-03-14T04:01:58.043054+00:00 | 2021-03-14T04:24:19.320656+00:00 | 168 | false | Use a max heap: the comparator compares the passing ratio with adding one more student.\nFor a class, if number of passing sutdents is equal to total number of students, it\'s passing ratio is already 1 and adding more passing students doesn\'t help further.\nThus, only add those with potential to increase the passing ratio to the priority queue. \n If priority queue is empty, we can terminate early, because we know adding more passing students won\'t help further. \n\n```\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n int n = classes.length;\n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->Double.compare(ratioIncr(b),ratioIncr(a))); // max pq\n double currRating = 0.0;\n for (int[] rating : classes) {\n currRating += (double)rating[0] / rating[1];\n if (rating[0] != rating[1]) { // only add those with potential to increase the passing ratio\n pq.offer(rating);\n }\n }\n currRating /= n;\n if (pq.isEmpty()) // early termination\n return currRating;\n while (extraStudents-- > 0) {\n int[] item = pq.poll();\n currRating += ratioIncr(item)/n;\n item[0]++; item[1]++;\n pq.offer(item);\n }\n return currRating;\n }\n\n private double ratioIncr(int[] item) {\n double ratio1 = (double)item[0] / item[1];\n double ratio2 = (double)(item[0]+1) / (item[1]+1);\n return ratio2 - ratio1;\n }\n}\n``` | 3 | 1 | [] | 0 |
maximum-average-pass-ratio | [Python3] Simple | Fastest | python3-simple-fastest-by-sushanthsamala-pa8k | Logic: We need to pick the class whose pass ratio will increase the most when we add 1 extraStudent. We need to repeat this for every extraStudent\n\nclass Solu | sushanthsamala | NORMAL | 2021-03-14T04:01:21.034047+00:00 | 2021-03-14T04:01:21.034076+00:00 | 252 | false | Logic: We need to pick the class whose pass ratio will increase the most when we add 1 extraStudent. We need to repeat this for every extraStudent\n```\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n h = []\n ones = 0\n for a,b in classes:\n if a==b:\n ones += 1\n continue\n heapq.heappush(h, [-(((a+1)/(b+1)) - (a/b)), b, a])\n \n # Base case average pass ratio is 1.0\n if not h: return 1.0\n \n for _ in range(extraStudents):\n _, y,x = heappop(h)\n heapq.heappush(h, [-(((x+2)/(y+2)) - ((x+1)/(y+1))), y+1, x+1])\n \n return (sum(x/y for _, y, x in h)+ones) / len(classes)\n``` | 3 | 1 | [] | 0 |
maximum-average-pass-ratio | Greedy, use priority queue to get the maximum increasement. O(nLogn), binary serach doesn't work | greedy-use-priority-queue-to-get-the-max-vf2s | \n\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double, pair<int, int> | chejianchao | NORMAL | 2021-03-14T04:00:43.582651+00:00 | 2021-03-14T04:00:43.582680+00:00 | 304 | false | \n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double, pair<int, int> > > pq;\n for(auto &cls : classes) {\n int t = cls[1], p = cls[0];\n double add = (p + 1) * 1.0 / (t + 1) - (p * 1.0 / t);\n pq.push({add, {p, t}});\n }\n while(extraStudents--) {\n auto p = pq.top(); pq.pop();\n int &t = p.second.second;\n int &pa = p.second.first;\n ++t; ++pa;\n p.first = (pa + 1) * 1.0 / (t + 1) - pa * 1.0 / t;\n pq.push(p);\n }\n double res = 0;\n while(pq.size()) {\n res += pq.top().second.first * 1.0 / pq.top().second.second; pq.pop();\n }\n return res / classes.size();\n }\n};\n``` | 3 | 0 | [] | 1 |
maximum-average-pass-ratio | CPP || easy to understand || best in world | cpp-easy-to-understand-best-in-world-by-gcblf | IntuitionWe can use nested pair for it pair<increased_differnce,pair<value_at_subarray[0],value_at_subarray[1]>>Complexity
Time complexity:O(N)
Space complexit | apoorvjain7222 | NORMAL | 2024-12-15T18:05:18.306983+00:00 | 2024-12-15T18:05:18.306983+00:00 | 99 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can use nested pair for it pair<increased_differnce,pair<value_at_subarray[0],value_at_subarray[1]>>\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double,pair<int,int>>>pq;\n int n = classes.size();\n for(int i=0;i<n;i++){\n pq.push(make_pair((double)(classes[i][0]+1)/(double)(classes[i][1]+1) - (double)(classes[i][0])/(double)(classes[i][1]),make_pair(classes[i][0],classes[i][1])));\n }\n while(extraStudents--){\n auto topa = pq.top();\n topa.second.first = topa.second.first + 1;\n topa.second.second = topa.second.second + 1;\n topa.first = (double)(topa.second.first+1)/(double)(topa.second.second+1)-(double)(topa.second.first)/(double)(topa.second.second);\n pq.pop();\n pq.push(topa);\n }\n double avga = 0;\n while(!pq.empty()){\n auto topa = pq.top();\n avga += (double)(topa.second.first)/(double)(topa.second.second);\n pq.pop();\n }\n return (double)avga/(double)(n);\n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-average-pass-ratio | Priority Queue Approach ||O(NlogN) ||Beats 89% Users|| Brief Desciption of Time and Space Complexity | priority-queue-approach-onlogn-beats-89-54fee | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Heisenberg_wc | NORMAL | 2024-12-15T13:38:25.470926+00:00 | 2024-12-15T13:38:25.470926+00:00 | 98 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic://Create a Max Heap and look for the max ration change \n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double,pair<double,double>>>pq;\n int no_of_class=classes.size();\n for(int i=0;i<no_of_class;i++){//O(n)\n double pass=classes[i][0];\n double total=classes[i][1];\n double average=(double)(pass/total)-(double)((pass+1)/(total+1));\n pq.push({abs(average),{pass,total}});//O(logn)\n }\n //O(nlogn)\n while(extraStudents!=0){//O(ExtraStudents)\n auto min_average=pq.top();\n pq.pop();//O(logn)\n double pass=min_average.second.first;\n double total=min_average.second.second;\n double new_ration=(double)((pass+1)/(total+1))-(double)(pass+2)/(total+2);\n pq.push({abs(new_ration),{pass+1,total+1}});//o(logn)\n extraStudents--;\n }\n //O(class_size*log(class_size)+Extra_students*(2*log(Extra_Students)))\n double ans;\n double sum=0;\n while(!pq.empty()){\n auto front=pq.top();\n pq.pop();\n double average=front.second.first/front.second.second;\n cout<<"Av"<<average<<endl;\n sum+=average;\n }\n cout<<sum<<" ";\n ans=sum/(double)(no_of_class);\n return ans;\n\n //Overall TC;O(2*class_size*log(class_size)+Extra_students*(2*log(Extra_Students)))\n //Simpel TC:O(2nlogn+2elogn);n=no of classes;e=no of Extra students \n //Space Complexity:O(1);\n \n }\n};\n\nPLZZ upvote \n\n``` | 2 | 0 | ['C++'] | 0 |
maximum-average-pass-ratio | Beats 100% Users With 160ms Runtime || MAX HEAP. | beats-100-users-with-160ms-runtime-max-h-3ex0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Yash-8055 | NORMAL | 2024-12-15T11:58:36.373688+00:00 | 2024-12-15T11:58:36.373688+00:00 | 83 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n\n int n = classes.size();\n double total = 0;\n // Create a heap to store the profit for each class along with the current pass and total student counts\n vector<tuple<double, int, int>> heap;\n\n // Populate the heap with initial values and calculate the total pass ratio\n for (int i = 0; i < n; i++) \n {\n int pass = classes[i][0], totalStudents = classes[i][1];\n // Add the pass ratio for the current class to the total\n total += (double)pass / totalStudents;\n // Calculate the potential increment in pass ratio by adding 1 extra student\n heap.push_back(make_tuple(CalculateProfit(pass, totalStudents), pass, totalStudents));\n }\n\n // Build the heap to prioritize the class with the highest profit\n MakeHeap(heap);\n\n // Assign extra students to the classes with the highest potential profit\n while (extraStudents-- > 0) \n {\n auto [maxIncrement, pass, totalStudents] = heap[0];\n\n // If there is no increment possible, break\n if (maxIncrement <= 0)\n break;\n\n total += maxIncrement;\n pass++;\n totalStudents++;\n // Recalculate the new increment profit after adding a student\n heap[0] = make_tuple(CalculateProfit(pass, totalStudents), pass, totalStudents);\n // Reheapify the heap to maintain the heap property\n HeapifyDown(heap, 0);\n }\n\n // Calculate and return the average pass ratio across all classes\n return total / n;\n }\n\nprivate:\n // Calculate the profit, increase in pass ratio when adding a student to a class\n double CalculateProfit(int pass, int total) {\n\n double current_pass = (double)pass / total;\n double new_pass = (double)(pass + 1) / (total + 1);\n\n return new_pass - current_pass;\n }\n\n // Build the max heap by reheapifying from the bottom to the top\n void MakeHeap(vector<tuple<double, int, int>>& heap) {\n\n // Start from the last non-leaf node and heapify upwards\n for (int i = heap.size() / 2 - 1; i >= 0; i--) \n {\n HeapifyDown(heap, i);\n }\n }\n\n // Heapify the heap from index i downwards to ensure the heap property is maintained\n void HeapifyDown(vector<tuple<double, int, int>>& heap, int i) {\n\n int size = heap.size();\n\n while (true) \n {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n\n // If left child exists and has a larger increment\n if (left < size && get<0>(heap[left]) > get<0>(heap[largest])) \n {\n largest = left;\n }\n // If right child exists and has a larger increment\n if (right < size && get<0>(heap[right]) > get<0>(heap[largest])) \n {\n largest = right;\n }\n // If the largest value is already at i, the heap property is satisfied\n if (largest == i)\n break;\n\n // Swap the current node with the largest child\n swap(heap[i], heap[largest]);\n // Move to the child\n i = largest;\n }\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-average-pass-ratio | Beat 99%|C++ solution| easy to understand | beat-99c-solution-easy-to-understand-by-yemoy | Intuitionwe need to maximise average.so for this we have to find the maximum growth rate of each class.ApproachComplexity
Time complexity: O (N logN)
Space | anandupadhyay042 | NORMAL | 2024-12-15T11:30:11.041049+00:00 | 2024-12-15T11:30:11.041049+00:00 | 161 | false | # Intuition\nwe need to maximise average.so for this we have to find the maximum growth rate of each class.\n\n# Approach\n\n# Complexity\n- Time complexity: O (N logN)\n\n\n- Space complexity:O(N)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& nums, int ex) {\n priority_queue<pair<double,int>>q;\n int n=nums.size();\n double ans=0;\n for(int i=0;i<nums.size();i++){\n double w=(double)(nums[i][0]+1)/(double)(nums[i][1]+1);\n double y=(double)nums[i][0]/(double)nums[i][1];\n ans+=y/n;\n q.push({w-y,i});\n }\n while(ex--){\n auto d=q.top().second;\n ans+=q.top().first/n;\n q.pop();\n nums[d][0]++;\n nums[d][1]++;\n double w=(double)(nums[d][0])/(double)(nums[d][1]);\n double x=(double)(nums[d][0]+1)/(double)(nums[d][1]+1);\n q.push({x-w,d}); \n\n }\n return ans;}\n};\n```\n\n | 2 | 0 | ['C++'] | 0 |
maximum-average-pass-ratio | ✅ Easy to Understand | Greedy | Priority Queue | Detailed Video Explanation🔥 | easy-to-understand-greedy-priority-queue-s0k6 | IntuitionTo maximize the average pass ratio across all classes, we need to distribute the extra students strategically. Intuitively, adding a student to a class | sahilpcs | NORMAL | 2024-12-15T09:29:52.934394+00:00 | 2024-12-15T09:29:52.934394+00:00 | 364 | false | # Intuition\nTo maximize the average pass ratio across all classes, we need to distribute the extra students strategically. Intuitively, adding a student to a class where it has the maximum impact on the pass ratio is the optimal approach. By focusing on the marginal gain in pass ratio for each class, we can prioritize classes that yield the most significant improvement.\n\n# Approach\n1. **Understand the Gain in Pass Ratio**: For each class, calculate the current pass ratio and the new pass ratio if one student is added. The difference between the new and current pass ratios represents the gain.\n\n2. **Use a Priority Queue**: Employ a max-heap (priority queue) to keep track of classes based on their potential gain in pass ratio. The class with the highest gain is at the top.\n\n3. **Distribute Extra Students**: Repeatedly add an extra student to the class with the highest gain (the top of the priority queue). Update the class\'s pass ratio and reinsert it into the queue after adjusting its parameters.\n\n4. **Calculate the Final Average**: After all extra students have been distributed, calculate the average pass ratio by summing up the pass ratios of all classes and dividing by the total number of classes.\n\n# Complexity\n- **Time complexity**:\n - Initializing the priority queue: $$O(n \\log n)$$ (for inserting all classes).\n - Processing extra students: $$O(k \\log n)$$ (where \\(k\\) is the number of extra students, and \\(n\\) is the number of classes).\n - Overall: $$O((n + k) \\log n)$$.\n\n- **Space complexity**:\n - The priority queue stores all classes: $$O(n)$$.\n\n\n\n# Code\n```java []\nclass Solution {\n\n // Comparator method to compare the gain in pass ratio when an extra student is added\n private static int compare(int[] c1, int[] c2){\n // Current pass ratios\n double pr1 = c1[0] * 1.0 / c1[1];\n double pr2 = c2[0] * 1.0 / c2[1];\n\n // New pass ratios if one student is added\n double npr1 = (c1[0] + 1.0) / (c1[1] + 1.0);\n double npr2 = (c2[0] + 1.0) / (c2[1] + 1.0);\n\n // Gain in pass ratios\n double d1 = npr1 - pr1;\n double d2 = npr2 - pr2;\n\n // Compare based on the higher gain in pass ratio\n return Double.compare(d2, d1);\n }\n\n // Helper method to calculate the pass ratio of a class\n private double passRatio(int[] c){\n return c[0] * 1.0 / c[1];\n }\n\n // Method to maximize the average pass ratio after distributing extra students\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n int n = classes.length;\n\n // Priority queue to store classes, ordered by the comparator\n PriorityQueue<int[]> pq = new PriorityQueue<>(Solution::compare);\n\n double totalPR = 0.0; // To keep track of the total pass ratio\n\n // Add all classes to the priority queue and calculate the initial total pass ratio\n for(int i = 0; i < n; i++){\n int[] curr = classes[i];\n pq.offer(new int[]{curr[0], curr[1]});\n totalPR += passRatio(curr);\n }\n\n // Distribute the extra students\n while(extraStudents > 0){\n // Poll the class that has the highest gain in pass ratio when an extra student is added\n int[] bestClass = pq.poll();\n\n // Update the total pass ratio by removing the old ratio and adding the new one\n totalPR -= passRatio(bestClass);\n bestClass[0]++; // Increment the number of passes\n bestClass[1]++; // Increment the total number of students\n totalPR += passRatio(bestClass);\n\n // Re-add the updated class back to the priority queue\n pq.offer(bestClass);\n extraStudents--; // Decrease the count of extra students\n }\n\n // Return the average pass ratio after distributing all extra students\n return totalPR / n;\n }\n}\n\n```\n```c++ []\n#include <vector>\n#include <queue>\n#include <functional>\n\nusing namespace std;\n\nclass Solution {\npublic:\n // Comparator function to compare the gain in pass ratio\n static bool compare(const vector<int>& c1, const vector<int>& c2) {\n double pr1 = c1[0] * 1.0 / c1[1];\n double pr2 = c2[0] * 1.0 / c2[1];\n\n double npr1 = (c1[0] + 1.0) / (c1[1] + 1.0);\n double npr2 = (c2[0] + 1.0) / (c2[1] + 1.0);\n\n double d1 = npr1 - pr1;\n double d2 = npr2 - pr2;\n\n return d1 < d2; // Max-heap based on gain in pass ratio\n }\n\n double passRatio(const vector<int>& c) {\n return c[0] * 1.0 / c[1];\n }\n\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<vector<int>, vector<vector<int>>, function<bool(const vector<int>&, const vector<int>&)>> pq(compare);\n\n double totalPR = 0.0;\n\n for (const auto& c : classes) {\n pq.push(c);\n totalPR += passRatio(c);\n }\n\n while (extraStudents > 0) {\n auto bestClass = pq.top();\n pq.pop();\n\n totalPR -= passRatio(bestClass);\n bestClass[0]++;\n bestClass[1]++;\n totalPR += passRatio(bestClass);\n\n pq.push(bestClass);\n extraStudents--;\n }\n\n return totalPR / classes.size();\n }\n};\n\n```\n```python []\nimport heapq\n\nclass Solution:\n def passRatio(self, c):\n return c[0] / c[1]\n\n def maxAverageRatio(self, classes, extraStudents):\n # Comparator function to calculate gain in pass ratio\n def compare(c):\n pr = c[0] / c[1]\n npr = (c[0] + 1) / (c[1] + 1)\n return pr - npr\n\n # Use a max-heap, so invert the comparator value for heapq\n pq = []\n for c in classes:\n heapq.heappush(pq, (-compare(c), c))\n\n totalPR = sum(self.passRatio(c) for c in classes)\n\n while extraStudents > 0:\n _, bestClass = heapq.heappop(pq)\n totalPR -= self.passRatio(bestClass)\n bestClass[0] += 1\n bestClass[1] += 1\n totalPR += self.passRatio(bestClass)\n heapq.heappush(pq, (-compare(bestClass), bestClass))\n extraStudents -= 1\n\n return totalPR / len(classes)\n\n```\n\n\nLeetCode 1792 Maximum Average Pass Ratio | Greedy | Heap | Asked in Amazon\nhttps://youtu.be/rQZSm61A4N4\n\n\n\n\n\n\n\n\n\n\n\n\n | 2 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'Python', 'C++', 'Java'] | 0 |
maximum-average-pass-ratio | Question is poorly asked | Key point here is marginal gain | Easy to read | question-is-poorly-asked-key-point-here-zn4bt | IntuitionApproachComplexity
Time complexity:
O(n * log(n))
logn (Enqueqe an element to pq)
Space complexity:
O(n)
Code | vivek781113 | NORMAL | 2024-12-15T06:43:07.297117+00:00 | 2024-12-15T06:43:07.297117+00:00 | 57 | false | # Intuition\n - the key here is, we want to maximize the avg.\n - what are the candiates which will give max avg, this will be calculated by marginal gain\n - Marginal Gain = (pass + 1) / (total + 1) - pass / total;\n# Approach\n - we will iterate through each class, find the candiated which will give max marginal gain.\n - Remember we are not incrementing pass or total here while adding to PQ\n - Now process extra student, at this point we will increase pass & total count\n\n# Complexity\n- Time complexity:\n - O(n * log(n))\n - logn (Enqueqe an element to pq)\n\n- Space complexity:\n - O(n)\n# Code\n```csharp []\npublic class Solution \n{\n public double MaxAverageRatio(int[][] classes, int extraStudents) \n {\n /*\n the problem is poorly described\n we ahve to add a student to class in suuch a way that marginal gain increases\n marginal gain = newGain - oldGain\n newGain = pass + 1 / total + 1 - pass / total\n so focus on the classes which is giving more gain not on the classes with least gain\n */ \n\n var pq = new PriorityQueue<(int pass, int total), double>();\n foreach (var c in classes) \n {\n int pass = c[0];\n int total = c[1];\n pq.Enqueue((pass, total), -Gain(pass, total));\n }\n\n while (extraStudents-- > 0) \n {\n (int pass, int total) = pq.Dequeue();\n ++pass; //1 student added here\n ++total; // 1 student added to overall class\n pq.Enqueue((pass, total), -Gain(pass, total));\n }\n\n double avg = 0;\n while (pq.Count > 0) \n {\n (int pass, int total) = pq.Dequeue();\n avg += (double)pass/total;\n }\n\n return (double)avg / classes.Length;\n }\n\n double Gain(int pass, int total) => (double) (pass + 1) / (total + 1) - (double) pass / total;\n}\n``` | 2 | 0 | ['Greedy', 'Heap (Priority Queue)', 'C#'] | 0 |
maximum-average-pass-ratio | Simple and Beginner friendly || Priority Queue || Clean code | simple-and-beginner-friendly-priority-qu-0uj3 | Intuition
To maximize the average ratio of passed to total students in multiple classes after applying a given number of operations, we use a greedy strategy w | hamza_18 | NORMAL | 2024-12-15T06:37:10.563336+00:00 | 2024-12-15T06:37:10.563336+00:00 | 181 | false | # Intuition\n1. To maximize the average ratio of passed to total students in multiple classes after applying a given number of operations, we use a greedy strategy with a priority queue (max-heap).\n\n2. Key Idea: Each operation adds 1 to both the passed and total students of a class. The impact of this operation is bigger when the class has fewer passed students compared to total students. Therefore, we want to prioritize classes where this gain is largest.\n\n\n# Approach\nGreedy Approach:\n\n1. Calculate the initial ratio for each class (passed[i] / total[i]).\n2. Use a priority queue to keep track of the class with the largest potential gain (difference in ratio before and after the operation).\n3. For each operation, apply it to the class with the largest gain and update its ratio.\n4. Final Calculation: After applying all operations, calculate the average ratio of passed students to total students across all classes\n\n\n# Complexity\n- Time complexity:\nO(n log n) - to build the max-heap for the initial ratios.\nO(es log n) - to process the operations and update the heap.\nO(n) - to compute the final average ratio.\nTotal time complexity: O((n + es) log n).\n\n- Space complexity:\n O(n) \n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int es) {\n priority_queue<pair<double, int>> maxheap;\n vector<vector<int>> temp = classes;\n double ans = 0.0;\n \n for (int i = 0; i < classes.size(); i++) {\n double ratio1 = (double)classes[i][0] / classes[i][1];\n double ratio2 = (double)(classes[i][0] + 1) / (classes[i][1] + 1);\n maxheap.push({ratio2 - ratio1, i});\n }\n \n while (es--) {\n int idx = maxheap.top().second;\n maxheap.pop();\n \n temp[idx][0]++;\n temp[idx][1]++; \n double newchange1 = (double)temp[idx][0] / temp[idx][1];\n double newchange2 = (double)(temp[idx][0] + 1) / (temp[idx][1] + 1);\n \n maxheap.push({newchange2 - newchange1, idx});\n }\n \n double totratio = 0.0;\n for (auto it : temp) {\n totratio += (double)it[0] / it[1];\n } \n ans = totratio / temp.size();\n return ans;\n }\n};\n\n``` | 2 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-average-pass-ratio | C++ | Greedy | Priority Queue | greedy-by-ahmedsayed1-8660 | Code | AhmedSayed1 | NORMAL | 2024-12-15T05:30:38.322902+00:00 | 2024-12-15T05:31:47.831146+00:00 | 53 | false | # Code\n```cpp []\ndouble calc(int a,int b){\n return (a+1) / double(b+1) - (a) / double(b);\n}\n\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double, pair<int, int>>>pq;\n for(auto i : classes)pq.push({calc(i[0],i[1]), {i[0], i[1]}});\n\n while(extraStudents--){\n auto[cost, p] = pq.top(); pq.pop();\n\n p.first++, p.second++;\n pq.push({calc(p.first, p.second), {p.first, p.second}});\n }\n\n double ans = 0;\n while(pq.size())\n ans += pq.top().second.first / double(pq.top().second.second), pq.pop();\n\n return ans/classes.size();\n }\n};\n``` | 2 | 0 | ['Greedy', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-average-pass-ratio | c++ | c-by-shashwat1915-nx22 | Code | shashwat1915 | NORMAL | 2024-12-15T04:05:59.952385+00:00 | 2024-12-15T04:05:59.952385+00:00 | 242 | false | # Code\n```cpp []\nclass Solution {\npublic:\ndouble rate_checker(int student,int total){\nreturn (double) (student+1)/(total+1)- (double) student/total;\n}\n double maxAverageRatio(vector<vector<int>>& c, int e) {\n double ans=0.0;\n priority_queue<pair<double,pair<int,int>>>q;\n for(auto x:c) q.push({rate_checker(x[0],x[1]),{x[0],x[1]}});\n while(e){\n auto topu=q.top();\n q.pop();\n int first=topu.second.first;\n int second=topu.second.second;\n first++;\n second++;\n q.push({rate_checker(first,second),{first,second}});\n e--;\n }\n while(!q.empty()){\n auto tope=q.top();\n q.pop();\n ans+=(double) tope.second.first/tope.second.second;\n }\n return ans/c.size();\n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-average-pass-ratio | The CHEATCODE to solving this problem! | the-cheatcode-to-solving-this-problem-by-zfsr | IntuitionWe have an integer extraStudents to disperse among classes. Naturally, while we still have an extraStudent we want to assign them to the class that wil | zachross | NORMAL | 2024-12-15T03:45:46.697128+00:00 | 2024-12-15T03:45:46.697128+00:00 | 106 | false | # Intuition\nWe have an integer *extraStudents* to disperse among classes. Naturally, while we still have an *extraStudent* we want to assign them to the class that will benefit the most. \n\nBut how do we know which class will benefit most? There is no obvious greedy heuristic that works. Here is where the CHEAT comes in, we don\'t need a greedy strategy to inform us which class will benefit most. We can just compute ourselves. Calculate the difference between a classes ratio after adding an extra student vs before. This is objectively how much the ratio will increase if a student is added.\n\nNow that we know how to determine which class will benefit most we should consider how to find the class that will benefit most after each extra student is added. \n\nIn essense we just need to find the min of all class ratios. This is a common pattern. It can be done effeceintly using a heap to find the min in logarithmic time.\n\n# Approach\n\nFirst compute the initial ratio gain each class will have from adding an extra student (ie. (passing+1/total+1) / (passing/total)). We will use this as the index of our heap. We negate it because heap is a min heap by default (this way biggest ratio gain becomes the min element). We also store the current counts of passing and total students per class so we can update the ratio gain if we add an additonal student to the class.\n\nAssigning extra students will never decrease the average ratio so we want to assign all of them. Thus we iterate for each extra student. We find the top of the heap (the class with the most to gain) and add a student. We the push the class back on the heap with an updated ratio, pass, and total counts.\n\nOnce we have iterated for all extra students we simply compute the average of the ratios by iterating through our list of classes, computing the ratios, summing them, and diving by the number of classes.\n\n# Complexity\n- Time complexity:\nO(Elog(c))\n\n- Space complexity:\nO(C)\n\n# Code\n```python3 []\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n ratios = [(-(((x+1)/(y+1))-(x/y)), x, y) for x, y in classes]\n heapify(ratios)\n for _ in range(extraStudents):\n mn = heappop(ratios)\n heappush(ratios, (-(((mn[1]+2)/(mn[2]+2)-(mn[1]+1)/(mn[2]+1))), mn[1] + 1, mn[2] + 1))\n return sum([x/y for _, x, y in ratios]) / len(ratios)\n``` | 2 | 0 | ['Greedy', 'Heap (Priority Queue)', 'Python3'] | 0 |
maximum-average-pass-ratio | easy heap solution C | Runtime Beats 100.00% | Memory Beats 100.00% | easy-heap-solution-c-runtime-beats-10000-fj5r | Complexity
Time complexity: O(nlogn)
Space complexity: O(n)
Code | JoshDave | NORMAL | 2024-12-15T02:55:41.917663+00:00 | 2024-12-15T04:43:47.048847+00:00 | 184 | false | # Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(n)\n\n# Code\n```c []\nstruct node {\n double value;\n int index;\n};\n\n#define get_parent(index) ((index - 1)>>1)\n#define get_left_child(index) ((index<<1) + 1)\n#define get_right_child(index) ((index<<1) + 2)\n\nvoid swap(struct node* a, struct node* b) {\n struct node temp = *a;\n *a = *b;\n *b = temp;\n}\n\nvoid heap_sort(struct node* stack, int* size, int index) {\n // moves up\n int parent = get_parent(index);\n while (index && stack[parent].value < stack[index].value) {\n swap(stack + parent, stack + index);\n index = parent;\n parent = get_parent(index);\n }\n // moves down\n int left = get_left_child(index);\n int right = get_right_child(index);\n while (left < *size && (stack[left].value > stack[index].value || stack[right].value > stack[index].value)) {\n if (*size <= right) right = left;\n if (stack[left].value > stack[right].value) right = left;\n swap(stack + right, stack + index);\n index = right;\n left = get_left_child(index);\n right = get_right_child(index);\n }\n}\n\nvoid heap_insert(struct node* stack, int* size, struct node input) {\n stack[*size] = input;\n heap_sort(stack, size, *size);\n ++(*size);\n}\n\nstruct node heap_pop(struct node* stack, int* size) {\n struct node result = stack[0];\n stack[0] = stack[*size - 1];\n --(*size);\n heap_sort(stack, size, 0);\n return result;\n}\n\ndouble maxAverageRatio(int** classes, int classesSize, int* classesColSize, int extraStudents) {\n struct node heap[classesSize];\n int heap_size = 0;\n for (int i = 0; i < classesSize; ++i) {\n struct node current;\n current.value = (double)(classes[i][0] + 1) / (classes[i][1] + 1);\n current.value -= (double)(classes[i][0]) / (classes[i][1]);\n current.index = i;\n heap_insert(heap, &heap_size, current);\n }\n \n while (extraStudents) {\n struct node current = heap_pop(heap, &heap_size);\n ++classes[current.index][0];\n ++classes[current.index][1];\n current.value = (double)(classes[current.index][0] + 1) / (classes[current.index][1] + 1);\n current.value -= (double)(classes[current.index][0]) / (classes[current.index][1]);\n heap_insert(heap, &heap_size, current);\n --extraStudents;\n }\n\n double total = 0;\n for (int i = 0; i < classesSize; ++i) total += (double)classes[i][0] / classes[i][1];\n total /= classesSize;\n return total;\n}\n``` | 2 | 0 | ['C'] | 0 |
maximum-average-pass-ratio | beats 97% 🎯✅✅✅ easy to understand | beats-97-easy-to-understand-by-ritik6g-ops0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ritik6g | NORMAL | 2024-12-15T02:01:48.993044+00:00 | 2024-12-15T02:01:48.993044+00:00 | 641 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n auto profit = [&](double pass, double total) {\n return (pass + 1) / (total + 1) - pass / total;\n };\n\n double total = 0;\n priority_queue<pair<double, array<int, 2>>> pq;\n for (int i = 0; i < classes.size(); i++) {\n total += (double)classes[i][0] / classes[i][1];\n pq.push({profit(classes[i][0], classes[i][1]),\n {classes[i][0], classes[i][1]}});\n }\n\n while (extraStudents--) {\n auto [pfit, arr] = pq.top();\n pq.pop();\n total += pfit;\n pq.push({profit(arr[0] + 1, arr[1] + 1), {arr[0] + 1, arr[1] + 1}});\n }\n return total / classes.size();\n }\n};\n``` | 2 | 0 | ['C++'] | 2 |
maximum-average-pass-ratio | Java & Python3 Solution | java-python3-solution-by-bleu_2-z2mt | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Bleu_2 | NORMAL | 2024-12-15T01:28:31.777530+00:00 | 2024-12-15T01:28:31.777530+00:00 | 482 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nimport java.util.PriorityQueue;\n\npublic class Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n // Create a max-heap to store the classes based on the potential increase in pass ratio\n PriorityQueue<ClassInfo> maxHeap = new PriorityQueue<>((a, b) -> {\n // Compare based on the potential increase in pass ratio\n return Double.compare(b.increase, a.increase);\n });\n\n // Calculate the initial pass ratios and their potential increases\n for (int[] classInfo : classes) {\n int passi = classInfo[0];\n int totali = classInfo[1];\n double currentRatio = (double) passi / totali;\n double newRatio = (double) (passi + 1) / (totali + 1);\n double increase = newRatio - currentRatio;\n maxHeap.offer(new ClassInfo(passi, totali, increase));\n }\n\n // Distribute the extra students\n for (int i = 0; i < extraStudents; i++) {\n ClassInfo classInfo = maxHeap.poll();\n classInfo.passi += 1;\n classInfo.totali += 1;\n double currentRatio = (double) classInfo.passi / classInfo.totali;\n double newRatio = (double) (classInfo.passi + 1) / (classInfo.totali + 1);\n classInfo.increase = newRatio - currentRatio;\n maxHeap.offer(classInfo);\n }\n\n // Calculate the final average pass ratio\n double totalPassRatio = 0;\n for (ClassInfo classInfo : maxHeap) {\n totalPassRatio += (double) classInfo.passi / classInfo.totali;\n }\n\n return totalPassRatio / classes.length;\n }\n\n // Helper class to store class information\n private static class ClassInfo {\n int passi;\n int totali;\n double increase;\n\n ClassInfo(int passi, int totali, double increase) {\n this.passi = passi;\n this.totali = totali;\n this.increase = increase;\n }\n }\n\n // Example usage\n public static void main(String[] args) {\n Solution solution = new Solution();\n \n int[][] classes1 = {{1, 2}, {3, 5}, {2, 2}};\n int extraStudents1 = 2;\n System.out.println(solution.maxAverageRatio(classes1, extraStudents1)); // Output: 0.78333\n\n int[][] classes2 = {{2, 4}, {3, 9}, {4, 5}, {2, 10}};\n int extraStudents2 = 4;\n System.out.println(solution.maxAverageRatio(classes2, extraStudents2)); // Output: 0.53485\n }\n}\n```\n```python3 []\nimport heapq\n\nclass Solution:\n def maxAverageRatio(self, classes, extraStudents):\n # Create a max-heap based on the potential increase in pass ratio\n max_heap = []\n \n # Populate the heap with the initial classes and their potential increases\n for passi, totali in classes:\n # Calculate the current pass ratio and the potential increase\n current_ratio = passi / totali\n # Calculate the increase in pass ratio if we add one extra student\n increase = (passi + 1) / (totali + 1) - current_ratio\n # Push the negative of the increase to create a max-heap\n heapq.heappush(max_heap, (-increase, passi, totali))\n \n # Assign extra students\n for _ in range(extraStudents):\n # Get the class with the maximum increase in pass ratio\n increase, passi, totali = heapq.heappop(max_heap)\n increase = -increase # Convert back to positive\n # Assign one extra student to this class\n passi += 1\n totali += 1\n # Recalculate the new increase and push it back into the heap\n new_increase = (passi + 1) / (totali + 1) - (passi / totali)\n heapq.heappush(max_heap, (-new_increase, passi, totali))\n \n # Calculate the final average pass ratio\n total_pass_ratio = 0\n for _, passi, totali in max_heap:\n total_pass_ratio += passi / totali\n \n return total_pass_ratio / len(classes)\n\n# Example usage\nsolution = Solution()\nclasses1 = [[1, 2], [3, 5], [2, 2]]\nextraStudents1 = 2\nprint(solution.maxAverageRatio(classes1, extraStudents1)) # Output: 0.78333\n\nclasses2 = [[2, 4], [3, 9], [4, 5], [2, 10]]\nextraStudents2 = 4\nprint(solution.maxAverageRatio(classes2, extraStudents2)) # Output: 0.53485\n```\n | 2 | 0 | ['Array', 'Java', 'Python3'] | 0 |
maximum-average-pass-ratio | [Kotlin] Heap / Priority Queue solution (with comments) | kotlin-heap-priority-queue-solution-with-bkjx | Intuition / ApproachThe key to this problem is to greedily add students to the class which would benefit the most (i.e. would see the highest increase in pass r | ZennY24 | NORMAL | 2024-12-15T01:15:47.633569+00:00 | 2024-12-15T01:16:52.194095+00:00 | 51 | false | # Intuition / Approach\n\nThe key to this problem is to greedily add students to the class which would benefit the most (i.e. would see the highest increase in pass ratio with this student) until no extra students remain. We can keep track of which class would see the highest increase by maintaining a heap / priority queue containing the indices of each class, sorted in descending order based on the delta in pass ratio after adding an extra student to that class.\n\n# Complexity\n- Time complexity: $$O((m+n)logn)$$, where $$m$$ is equal to `extraStudents` and $$n$$ is the size of `classes`\n\n- Space complexity: $$O(n)$$\n\n# Code\n```kotlin []\nclass Solution {\n fun maxAverageRatio(classes: Array<IntArray>, extraStudents: Int): Double {\n\n // Computes the positive delta in pass ratio after adding an extra student to classes[index]\n fun computeDelta(index: Int): Double {\n val pass: Int = classes[index][0]; val total: Int = classes[index][1]\n return (pass + 1.0) / (total + 1.0) - (pass + 0.0) / (total + 0.0)\n }\n\n // Initialize PriorityQueue containing the indices of each class, sorted in descending order based \n // on the delta in pass ratio after adding an extra student to that class.\n val priorityQueue = PriorityQueue<Int>() { c1, c2 -> if (computeDelta(c2) < computeDelta(c1)) -1 else 1 }\n for (index in classes.indices) {\n priorityQueue.offer(index)\n }\n\n // Add students to the class which would benefit the most (i.e. would see the highest increase in \n // pass ratio with this student) until no extra students remain.\n var studentsRemaining: Int = extraStudents\n while (studentsRemaining > 0) {\n val head = priorityQueue.poll()\n\n // Add extra student to this class\n classes[head][0]++\n classes[head][1]++\n\n priorityQueue.offer(head)\n studentsRemaining--\n }\n\n return priorityQueue.map({ index -> \n classes[index][0].toDouble() / classes[index][1].toDouble() }).average()\n }\n}\n``` | 2 | 0 | ['Greedy', 'Heap (Priority Queue)', 'Kotlin'] | 0 |
maximum-average-pass-ratio | C++ || Priority Queue || Beats 95% | c-priority-queue-beats-95-by-vikalp_07-5lyl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vikalp_07 | NORMAL | 2023-08-15T06:58:07.627831+00:00 | 2023-08-15T06:58:07.627860+00:00 | 577 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int k) {\n priority_queue<pair<double,int>> pq;\n for(int i=0;i<classes.size();i++)\n {\n int curr_n = classes[i][0];\n int curr_d = classes[i][1];\n double curr_f = (double)curr_n/(double)curr_d;\n int new_n = curr_n+1;\n int new_d = curr_d+1;\n double new_f = (double)new_n/(double)new_d;\n\n pq.push({new_f-curr_f,i});\n }\n\n while(k)\n {\n pair<double,int> p = pq.top();\n pq.pop();\n int index = p.second;\n classes[index][0]+=1;\n classes[index][1]+=1;\n\n int new_n = classes[index][0]+1;\n int new_d = classes[index][1]+1;\n double new_f = (double)new_n/(double)new_d;\n double curr_f = (double)classes[index][0]/(double)classes[index][1];\n\n pq.push({new_f-curr_f,index});\n k--;\n }\n double sum = 0;\n for(int i=0;i<classes.size();i++)\n {\n sum+=(double)classes[i][0]/(double)classes[i][1];\n }\n return sum/(double)classes.size();\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-average-pass-ratio | C++| Priority Queue | Greedy | c-priority-queue-greedy-by-ayushmanshivh-6uts | What the question ask? so we have to assign ExtraStudent in such class that we"ll get maximum possible ratio . so How we"ll do this . We have to send ExtraStude | AyushmanShivhare | NORMAL | 2022-07-08T12:49:54.285764+00:00 | 2022-07-08T12:49:54.285797+00:00 | 336 | false | What the question ask? so we have to assign ExtraStudent in such class that we"ll get maximum possible ratio . so How we"ll do this . We have to send ExtraStudents to classes 1 by 1 according to their ratio(calculate the difference of all classes for 1 student) where we get more difference we"ll send the student to that particular class. and again check the difference for the next student .\n```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double,pair<int,int>>>pq;\n for(int i=0;i<classes.size();i++){\n int var1 = classes[i][0] , var2 = classes[i][1];\n double diff = (double)(var1+1)/(var2+1) - (double)(var1)/(var2);\n pq.push({diff,{var1,var2}});\n }\n \n while(extraStudents!=0){\n int var1 = pq.top().second.first , var2 = pq.top().second.second;\n var1++;\n var2++;\n double newdiff = (double)(var1+1)/(var2+1) - (double)(var1)/(var2);\n pq.pop();\n pq.push({newdiff,{var1,var2}});\n extraStudents--;\n \n }\n double ans = 0;\n while(!pq.empty()){\n ans += (double)(pq.top().second.first) /(pq.top().second.second);\n pq.pop();\n }\n \n return ans/classes.size();\n \n }\n};\n``` | 2 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
maximum-average-pass-ratio | Java Priority Queue Clean Code Solution | java-priority-queue-clean-code-solution-h1h6h | \nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<double[]> pq = new PriorityQueue<>(new Compar | Superman-Qiang | NORMAL | 2022-05-05T03:28:10.185045+00:00 | 2022-05-05T03:28:10.185093+00:00 | 529 | false | ```\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n PriorityQueue<double[]> pq = new PriorityQueue<>(new Comparator<double[]>(){\n public int compare(double[] a, double[] b){\n double adiff = (a[0]+1)/(a[1]+1) - (a[0]/a[1]); \n double bdiff = (b[0]+1)/(b[1]+1) - (b[0]/b[1]);\n if(adiff==bdiff) return 0;\n return adiff>bdiff? -1:1;\n }\n });\n \n for(int[] c:classes) pq.add(new double[]{c[0],c[1]});\n \n for(int i =0;i<extraStudents;i++){\n double[] curr = pq.poll();\n pq.add(new double[]{curr[0]+1,curr[1]+1});\n }\n \n double sum = 0;\n while(!pq.isEmpty()){\n double[] curr = pq.poll();\n sum+=curr[0]/curr[1];\n }\n \n return sum/classes.length;\n }\n}\n``` | 2 | 0 | ['Heap (Priority Queue)', 'Java'] | 2 |
maximum-average-pass-ratio | C++ Solution Explanation | priority_queue | [1792] | c-solution-explanation-priority_queue-17-7dmo | How priority_queue (max heap) came into picture-->\nWe have to return maximum average pass ratio which is equal to sum of all pass ratios / number of classes. W | SameerNITW | NORMAL | 2022-03-02T17:50:13.786329+00:00 | 2022-03-03T11:13:45.924036+00:00 | 203 | false | **How priority_queue (max heap) came into picture-->**\nWe have to return maximum average pass ratio which is equal to sum of all pass ratios / number of classes. Where number of classes is constant so we need to increase the sum of all pass ratios.\nIn each class there is a pass ratio before adding extra students, as we need to increase the pass ratio of a class so we will maintain the increase in ratio if a student is added into a class.\nSuppose a class is given as [p,t], it\'s original pass ratio is p/t so initially we will add p/t to our total sum of ratios then if a student is added to this class the new ratio is (p+1)/(t+1) which means the increase in the ratio is : new ratio - old ratio which is [(p+1)/(t+1) - p/t].\nSo to maintain the profit (increase in ratio) in desc\nending order we use priority_queue here.\nAs the extra students are limited we need to add each student to the class which gives us the more profit (increase). Soon after adding the student we will increment our sum of ratios and also now the new ratio for this class will also be changed that should be added back to the queue.\n```\nclass Solution {\npublic:\n double nextProfit(double p,double t){\n return ((p+1)/(t+1) - p/t);\n }\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n double sumOfRatios = 0,p,t,profit;\n priority_queue<pair<double,pair<double,double>>>pq;\n for(vector<int>& v : classes){\n p = v[0]; t = v[1];\n sumOfRatios += p/t;\n profit = nextProfit(p,t);\n pq.push({profit,{p,t}});\n }\n pair<double,pair<double,double>>temp;\n while(extraStudents--){\n temp = pq.top(); pq.pop();\n profit = temp.first; p = temp.second.first; t = temp.second.second;\n sumOfRatios += profit;\n p++; t++; profit = nextProfit(p,t);\n pq.push({profit,{p,t}});\n }\n return (sumOfRatios/(double)classes.size());\n }\n};\n```\nFeel free to comment your queries if any\n**Upvote** if found useful\n**Thank you :)** | 2 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
maximum-average-pass-ratio | C++ Solution | c-solution-by-mk_kr_24-tgtd | \ndouble precise(double a)\n{\n double intpart;\n double fractpart = modf (a, &intpart);\n fractpart = roundf(fractpart * 100000.0)/100000.0; // Round t | mk_kr_24 | NORMAL | 2021-09-22T04:54:36.925688+00:00 | 2021-09-22T04:54:36.925716+00:00 | 192 | false | ```\ndouble precise(double a)\n{\n double intpart;\n double fractpart = modf (a, &intpart);\n fractpart = roundf(fractpart * 100000.0)/100000.0; // Round to 5 decimal places\n double b = intpart + fractpart;\n return b;\n}\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n int min_index= 0;\n double min_ratio= 0.00000, sum= 0.0;\n double cur_ratio= 0.0, new_ratio= 0.0;\n vector<double> ratio;\n int l= classes.size();\n multimap<double, int> mp;\n setprecision(5);\n for(int i= 0; i<l ;i++)\n {\n mp.insert({((double)classes[i][1]-(double)classes[i][0])/((double)classes[i][1]*((double)classes[i][1]+1)), i});\n ratio.push_back((double)classes[i][0]/(double)classes[i][1]);\n }\n for(int i= 0;i< extraStudents; i++)\n {\n int j= (--mp.end())->second;\n classes[j][0]+= 1;\n classes[j][1]+= 1;\n ratio[j]= (double)classes[j][0]/(double)classes[j][1];\n mp.erase(--mp.end());\n mp.insert({((double)classes[j][1]-(double)classes[j][0])/((double)classes[j][1]*((double)classes[j][1]+1)), j});\n }\n for(int i= 0;i< l;i++)\n {\n sum+= ratio[i];\n cout<<ratio[i]<<\'\\n\';\n }\n int k= (sum/l)*1e5;\n min_ratio= k/1e5;\n return min_ratio;\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-average-pass-ratio | Python solution with Heap - With the idea | python-solution-with-heap-with-the-idea-abaj6 | The idea is add each student such that their addition increases the particular class average more.\n\nFor this, I maintained a heap in which i keep adding what | ravinamani15 | NORMAL | 2021-07-04T13:54:59.328253+00:00 | 2021-07-04T13:54:59.328299+00:00 | 142 | false | The idea is add each student such that their addition increases the particular class average more.\n\nFor this, I maintained a heap in which i keep adding what will be the change in average with addition of one student to that particular class. i.e., `x/y - (x+1)/(y+1)` will be the negative value of change in average with addition of one student in it.\n\n```\nimport heapq\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n \n heap=[]\n for x,y in classes:\n heapq.heappush(heap, (x/y -(x+1)/(y+1) ,x,y))\n \n while extraStudents:\n extraStudents-=1\n perc,x,y =heapq.heappop(heap)\n x+=1\n y+=1\n heapq.heappush(heap, (x/y -(x+1)/(y+1) ,x,y))\n\n #print(heap)\n \n return sum(y/z for x,y,z in heap)/len(heap)\n```\n | 2 | 0 | [] | 1 |
maximum-average-pass-ratio | python solution | heap | | python-solution-heap-by-abhishen99-dbkl | \nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n h = []\n n=len(classes)\n \n | Abhishen99 | NORMAL | 2021-06-28T19:32:03.068609+00:00 | 2021-06-28T19:32:03.068635+00:00 | 367 | false | ```\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:\n h = []\n n=len(classes)\n \n \n for i in classes:\n currpassration = i[0]/i[1]\n ifaddthan = (i[0]+1)/ (i[1]+1)\n \n increase = ifaddthan - currpassration\n heappush(h,(-increase, currpassration,i[0],i[1]))\n \n heapify(h)\n \n while extraStudents:\n\n a,curr,pas, tot = heappop(h)\n a=-a \n curr +=a\n ifaddthan = (pas+2)/(tot+2)\n \n increase = ifaddthan - curr\n heappush(h, (-increase, curr, pas+1,tot+1))\n \n extraStudents-=1\n \n ps=0\n tot=0\n \n while h:\n a=h.pop()\n ps+=a[1]\n return ps/n\n \n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
maximum-average-pass-ratio | python heap solution | python-heap-solution-by-heisenbarg-gbmy | ```\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], e: int) -> float:\n heap=[]\n for i,j in classes:\n diff= | heisenbarg | NORMAL | 2021-06-18T08:25:25.788007+00:00 | 2021-06-18T08:25:25.788036+00:00 | 270 | false | ```\nclass Solution:\n def maxAverageRatio(self, classes: List[List[int]], e: int) -> float:\n heap=[]\n for i,j in classes:\n diff=(i+1)/(j+1)-(i/j)\n heapq.heappush(heap,(-diff,i,j))\n while(e>0):\n diff,i,j=heapq.heappop(heap)\n i+=1\n j+=1\n diff=(i+1)/(j+1)-(i/j)\n heapq.heappush(heap,(-diff,i,j))\n e-=1\n ans=0\n for diff,i,j in heap:\n ans+=(i/j)\n return ans/len(classes)\n | 2 | 0 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 0 |
maximum-average-pass-ratio | C++ clean solution | c-clean-solution-by-nishchhal-f5dw | \nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double,int>> q;\n | nishchhal | NORMAL | 2021-04-05T19:58:36.084894+00:00 | 2021-04-05T19:58:36.084939+00:00 | 311 | false | ```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<double,int>> q;\n \n for(int i=0;i<classes.size();i++){\n double a=(float)(classes[i][0]+1)/(float)(classes[i][1]+1)-(float)classes[i][0]/(float)classes[i][1];\n q.push(make_pair(a,i));\n }\n for(int j=0;j<extraStudents;j++){\n int i=q.top().second;\n classes[i][0]++;\n classes[i][1]++;\n double a=(float)(classes[i][0]+1)/(float)(classes[i][1]+1)-(float)classes[i][0]/(float)classes[i][1];\n q.pop();\n q.push(make_pair(a,i));\n }\n \n double ans=0;\n for (int i=0;i<classes.size();i++){\n ans+=(float)classes[i][0]/(float)classes[i][1];\n }\n return ans/classes.size();\n }\n};\n``` | 2 | 0 | ['Greedy', 'C', 'Heap (Priority Queue)'] | 0 |
maximum-average-pass-ratio | Java Simple and easy solution, using max heap and faster than 100%, clean code with comments. | java-simple-and-easy-solution-using-max-nkb5j | PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n //max heap\n | satyaDcoder | NORMAL | 2021-03-20T01:57:01.866337+00:00 | 2021-03-20T01:57:01.866365+00:00 | 211 | false | **PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n```\nclass Solution {\n public double maxAverageRatio(int[][] classes, int extraStudents) {\n //max heap\n //here we are using Max Heap, whaich has maximum element in root\n PriorityQueue<Class> maxHeap = new PriorityQueue<Class>(Comparator.comparingDouble(o -> -o.gainPassRatio));\n \n \n for(int[] eachClass : classes){\n int pass = eachClass[0];\n int total = eachClass[1];\n \n maxHeap.add(new Class(pass, total, getGainPassRatio(pass, total)));\n }\n \n \n while(extraStudents --> 0){\n //we are using Gready Approach \n //get the class, which will have a maximum \n //gain in passing ratio, if we add a student\n Class c = maxHeap.remove();\n \n //this class will have maximum gain in passing ratio\n //so add 1 extra student (who always pass)\n c.pass = c.pass + 1;\n c.total = c.total + 1;\n c.gainPassRatio = getGainPassRatio(c.pass + 1, c.total + 1);\n \n maxHeap.add(c);\n }\n \n double passRatioSum = 0.0d;\n while(!maxHeap.isEmpty()){\n Class c = maxHeap.remove();\n passRatioSum += ((double)c.pass / c.total);\n }\n \n \n return passRatioSum / classes.length;\n }\n \n private double getGainPassRatio(int pass, int total){\n double passRatio = (double)pass / total;\n \n //add 1 student, \n pass++;\n total++;\n \n double passRatioAfterAdding = (double)pass / total;\n \n //find gain in passing ratio, if we add 1 student\n return passRatioAfterAdding - passRatio; \n }\n}\n\nclass Class {\n int pass;\n int total;\n double gainPassRatio;\n \n public Class(int pass, int total, double gainPassRatio){\n this.pass = pass;\n this.total = total;\n this.gainPassRatio = gainPassRatio;\n }\n}\n``` | 2 | 0 | ['Heap (Priority Queue)'] | 0 |
maximum-average-pass-ratio | Simple C++ Solution Priority Queue | simple-c-solution-priority-queue-by-arya-7dg5 | \nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<long double,pair<long lo | aryan29 | NORMAL | 2021-03-15T10:52:28.624706+00:00 | 2021-03-15T10:52:28.624731+00:00 | 117 | false | ```\nclass Solution {\npublic:\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<long double,pair<long long int,long long int>>>pq;\n for(auto it:classes)\n {\n long long int z=(it[1]);\n z=z*(it[1]+1);\n long double pt=1.0*(it[1]-it[0])/z;\n pq.push({pt,{it[0],it[1]}});\n }\n for(int i=0;i<extraStudents;i++)\n {\n long long int t1=pq.top().second.first+1;\n long long int t2=pq.top().second.second+1;\n long long int z=t2;\n z=z*(t2+1);\n long double g=1.0*(t2-t1)/z;\n pq.pop();\n pq.push({g,{t1,t2}});\n } \n long double avg=0;\n while(!pq.empty())\n {\n avg+=1.0*(pq.top().second.first)/(pq.top().second.second);\n pq.pop();\n }\n return 1.0*avg/classes.size();\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-average-pass-ratio | [Java] PriorityQueue Solution beats 100% | java-priorityqueue-solution-beats-100-by-e1ys | \npublic double maxAverageRatio(int[][] classes, int extraStudents) {\n\tQueue<double[]> pq = new PriorityQueue<>((a,b) -> {\n\t\tdouble ratioDiffA = (a[0] + 1) | jerrywusa | NORMAL | 2021-03-14T18:01:06.548487+00:00 | 2021-03-14T18:01:06.548529+00:00 | 123 | false | ```\npublic double maxAverageRatio(int[][] classes, int extraStudents) {\n\tQueue<double[]> pq = new PriorityQueue<>((a,b) -> {\n\t\tdouble ratioDiffA = (a[0] + 1) / (a[1] + 1) - a[0] / a[1];\n\t\tdouble ratioDiffB = (b[0] + 1) / (b[1] + 1) - b[0] / b[1];\n\t\treturn Double.compare(ratioDiffB, ratioDiffA);\n\t});\n\tfor (int[] c : classes) {\n\t\tpq.add(new double[]{c[0], c[1]});\n\t}\n\twhile (extraStudents-- > 0) {\n\t\tdouble[] c = pq.poll();\n\t\tc[0]++;\n\t\tc[1]++;\n\t\tpq.add(c);\n\t}\n\tdouble ratioSum = 0;\n\tfor (double[] c : pq) {\n\t\tratioSum += c[0] / c[1];\n\t}\n\treturn ratioSum / classes.length;\n}\n``` | 2 | 0 | [] | 1 |
maximum-average-pass-ratio | [C++] Simple Heap solution. [Detailed Explanation] | c-simple-heap-solution-detailed-explanat-oxrl | \n/*\n https://leetcode.com/problems/maximum-average-pass-ratio/\n \n At a glance the obvious choice seems like picking the class with least pass\n | cryptx_ | NORMAL | 2021-03-14T06:47:10.878453+00:00 | 2021-03-14T06:47:10.878501+00:00 | 254 | false | ```\n/*\n https://leetcode.com/problems/maximum-average-pass-ratio/\n \n At a glance the obvious choice seems like picking the class with least pass\n ratio each time and adding a genius student. But this only brings the lower \n ratio scores near the avg, doesn\'t try to increase the max observed score or\n decide where to add a student in case two classes have the same pass ratio.\n So to answer the above ques, we use the delta change increment in avg ratio score.\n The class that can show the max change is picked and a student is added there.\n This way a class with max promise is always picked.\n \n TC: O(nlogn + klogn + nlogn) ~ O((n+k)logn), n: no. of classes\n*/\n\nclass Solution {\npublic:\n // Computes the change seen when a new student is added to current class strength\n double delta_increment(int &pass, int &total) {\n return (double) (pass + 1) / (total + 1) - (double)pass / total; \n }\n \n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n // Max heap wrt to the delta increment each class pass ratio can achieve\n priority_queue< tuple<double, int, int>, vector< tuple<double, int, int> >> max_heap;\n \n for(auto class_score: classes) \n max_heap.emplace(make_tuple(delta_increment(class_score[0], class_score[1]),\n class_score[0], class_score[1]));\n \n // Add the genius students to those classes where the ratio increment is max\n while(extraStudents--) {\n auto max_delta_class = max_heap.top();\n max_heap.pop();\n auto [delta, pass, total] = max_delta_class;\n ++pass, ++total;\n max_heap.emplace(make_tuple(delta_increment(pass, total), pass, total));\n }\n \n // Find the total avg class pass ratio\n double avg_pass = 0;\n while(!max_heap.empty()) {\n auto max_delta_class = max_heap.top();\n max_heap.pop();\n avg_pass += (double)get<1>(max_delta_class) / get<2>(max_delta_class);\n }\n return avg_pass / classes.size();\n }\n};\n``` | 2 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-average-pass-ratio | Ruby - Greedy, Priority Queue. | ruby-greedy-priority-queue-by-shhavel-w6pw | Observation\n\nIf there is a class with pass equeals p and total students equals t then pass ration equals p / t.\nAdding an extra student who passed exam incre | shhavel | NORMAL | 2021-03-14T05:17:41.964887+00:00 | 2021-03-15T13:44:15.309406+00:00 | 94 | false | ### Observation\n\nIf there is a class with pass equeals `p` and total students equals `t` then pass ration equals `p / t`.\nAdding an extra student who passed exam increases ration by:\n\n```\np + 1 p (p + 1) * t - p * (t + 1) t - p\n----- - - = -------------------------- = -----------\nt + 1 t t * (t + 1) t * (t + 1) \n```\n\n### Solution\n\nIgnore classed where all students pass the exam (pass ration `1` cannot be increased).\nAll other store in a priority queue. Sort the queue by the increase ratio we can obtain by adding one extra student.\n\n```ruby\ndef max_average_ratio(classes, extra_students)\n pq = classes.select { |p, t| p < t }.map { |p, t| [(t - p).to_f / (t * (t + 1)), p, t] }.sort\n while pq.any? && (extra_students -= 1) >= 0\n dr, p, t = pq.pop\n ndr = dr * t / (t + 2) # new ratio increase. Same as (t - p) / ((t + 1) * (t + 2))\n\n idx = pq.bsearch_index { |dr, _, _| dr >= ndr } || pq.size\n pq.insert(idx, [ndr, p + 1, t + 1])\n end\n (pq.sum { |_, p, t| p.fdiv t } + classes.size - pq.size) / classes.size\nend\n``` | 2 | 0 | ['Ruby'] | 1 |
maximum-average-pass-ratio | C++ priority queue | c-priority-queue-by-lisongsun-wu2n | The minute the contest is over, I realized the solution was so simple. Wasted the whole time working on a totally wrong path. Sad.\nKey points:\n Calculate rati | lisongsun | NORMAL | 2021-03-14T05:04:51.875442+00:00 | 2021-03-14T05:22:53.402752+00:00 | 151 | false | The minute the contest is over, I realized the solution was so simple. Wasted the whole time working on a totally wrong path. Sad.\n**Key points:**\n* Calculate ratio gain for inserting a student to each class. Use that ratio gain as key in a priority queue. Bundle class id in the queue with ratio gain.\n* Each time, insert a student into the highest ratio gain class. Recalculate that class\'s ratio gain after and maintain the queue. Repeat until all good students are inserted.\n* Do the ratio average calculation at the end.\n```\n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n std::priority_queue<std::pair<double, int>> q;\n for (int i=0; i<classes.size(); ++i)\n q.push({(classes[i][0]+1.0)/(classes[i][1]+1.0) - double(classes[i][0])/double(classes[i][1]), i});\n for (int i=0; i<extraStudents; ++i) {\n auto p = q.top();\n q.pop();\n ++classes[p.second][0];\n ++classes[p.second][1];\n q.push({(classes[p.second][0]+1.0)/(classes[p.second][1]+1.0) - double(classes[p.second][0])/double(classes[p.second][1]), p.second});\n }\n double ratios = 0;\n for (int i=0; i<classes.size(); ++i)\n ratios += double(classes[i][0])/double(classes[i][1]);\n return ratios/classes.size();\n }\n``` | 2 | 1 | ['C', 'Heap (Priority Queue)'] | 1 |
maximum-average-pass-ratio | C++ | using priority_queue | simple and sort | c-using-priority_queue-simple-and-sort-b-ytjf | \nclass Solution {\npublic:\n double mx(double a,double b)\n {\n return (a+1)/(b+1)-a/b;\n }\n \n double maxAverageRatio(vector<vector<int | sonusharmahbllhb | NORMAL | 2021-03-14T04:58:17.774879+00:00 | 2021-03-14T05:01:18.560033+00:00 | 163 | false | ```\nclass Solution {\npublic:\n double mx(double a,double b)\n {\n return (a+1)/(b+1)-a/b;\n }\n \n double maxAverageRatio(vector<vector<int>>& cls, int extra) {\n priority_queue<pair<double,pair<double,double>>> pq;\n \n for(auto v:cls)\n pq.push({mx(v[0],v[1]),{v[0],v[1]}});\n \n while(extra--)\n {\n pair<double,pair<double,double>> p=pq.top();\n \n p.first=mx(p.second.first+1,p.second.second+1);\n pq.pop();\n p.second.first+=1;\n p.second.second+=1;\n pq.push(p);\n }\n double ans=0;\n while(!pq.empty())\n {\n pair<double,pair<double,double>> p=pq.top();\n pq.pop();\n ans+=p.second.first/p.second.second;\n }\n \n return ans/cls.size();\n \n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 0 |
maximum-average-pass-ratio | [C++]- Simple and easy to understand solution | c-simple-and-easy-to-understand-solution-3d46 | Ques : How we are arranging in priority queue ? Based on what factor comparator will arrange ?\n--> Based upon the gain of average after incrementing the existi | morning_coder | NORMAL | 2021-03-14T04:45:20.842172+00:00 | 2021-03-14T04:46:13.198885+00:00 | 353 | false | **Ques : How we are arranging in priority queue ? Based on what factor comparator will arrange ?**\n--> Based upon the gain of average after incrementing the existing values of {pass,total}. Gain should be maximum.\n\n```\nclass comparator{\n public : \n int operator()(pair<int,int> &v1,pair<int,int> &v2){\n double new_val1=(double)(v1.first+1)/(v1.second+1);\n double old_val1=(double)v1.first/v1.second;\n \n double new_val2=(double)(v2.first+1)/(v2.second+1);\n double old_val2=(double)v2.first/v2.second;\n \n double diff1=new_val1-old_val1;\n double diff2=new_val2-old_val2;\n \n return (diff1<=diff2);\n \n }\n};\nclass Solution {\npublic:\n \n double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {\n priority_queue<pair<int,int>, vector<pair<int,int> >,comparator> pq;\n int count=0;\n for(int i=0;i<classes.size();i++){\n if(classes[i][0]!=classes[i][1])\n pq.push(make_pair(classes[i][0],classes[i][1]));\n else //if class with 100% pass average\n count++;\n }\n while(extraStudents>0 && !pq.empty()){\n pair<int,int> v=pq.top();pq.pop();\n v.first++,v.second++;\n pq.push(v);\n extraStudents--;\n }\n \n double pass=0,total=0;\n double ans=0;\n while(!pq.empty()){\n pair<int,int> v=pq.top();pq.pop();\n pass=v.first,total=v.second;\n ans+=pass/total;\n }\n ans+=count;\n return ans/classes.size();\n }\n};\n```\n\nPS - Same code will give TLE on 2 cases if we use vector instead of pair. | 2 | 0 | ['Greedy', 'C', 'Heap (Priority Queue)', 'C++'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.