question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
base-7 | ☑️ Converting number to it's Base 7 form. ☑️ | converting-number-to-its-base-7-form-by-5isg7 | Code | Abdusalom_16 | NORMAL | 2025-02-14T04:16:45.582478+00:00 | 2025-02-14T04:16:45.582478+00:00 | 128 | false | # Code
```dart []
class Solution {
String convertToBase7(int num) {
return num.toRadixString(7);
}
}
``` | 1 | 0 | ['Math', 'Dart'] | 0 |
base-7 | Easy solution | easy-solution-by-koushik_55_koushik-z8ky | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Koushik_55_Koushik | NORMAL | 2025-02-05T14:00:16.045814+00:00 | 2025-02-05T14:00:16.045814+00:00 | 241 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def convertToBase7(self, num: int) -> str:
if num == 0:
return '0'
is_negative = num < 0
num = abs(num)
result = ""
while num > 0:
digit = num % 7
result = str(digit) + result
num //= 7
if is_negative:
result = "-" + result
return result
``` | 1 | 0 | ['Python3'] | 0 |
base-7 | Beats 100% || Efficient Solution || Simple Logic | beats-100-efficient-solution-simple-logi-699n | ApproachObtaining every digit from the int(abs) and form a string ; Reverse it to obtain the result.Complexity
Time complexity:
Space complexity:
Code | AbhayForCodes | NORMAL | 2025-01-23T05:38:16.700067+00:00 | 2025-01-23T05:38:16.700067+00:00 | 250 | false | # Approach
Obtaining every digit from the int(abs) and form a string ; Reverse it to obtain the result.
# Complexity
- Time complexity:
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string str;
char sign;
string convertToBase7(int num) {
if(num < 0) {num *= -1; sign='n';}
if(num == 0){ return to_string(0);}
while(num > 0)
{
str.push_back( '0' + (num%7) );
num = num/7;
}
if(sign=='n') str.push_back('-');
std::reverse(str.begin(), str.end());
return str ;
}
};
``` | 1 | 0 | ['C++'] | 0 |
base-7 | W solution using c | w-solution-using-c-by-akash_mac-fzlo | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Akash_mac | NORMAL | 2025-01-08T04:37:44.082810+00:00 | 2025-01-08T04:37:44.082810+00:00 | 182 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string convertToBase7(int num) {
int nn=0,mul=1;
while(num!=0)
{
nn+=mul*(num%7);
num/=7;
mul*=10;
}
return to_string(nn);
}
};
``` | 1 | 0 | ['C++'] | 0 |
base-7 | Beginner's logic ( 0 ms) | beginners-logic-0-ms-by-dinhvanphuc-r0x4 | IntuitionApproachJust convert num mod 7 to string and append it to the first place by using the '+', then check if negative then append '-'. Remember that u hav | DinhVanPhuc | NORMAL | 2024-12-31T04:10:41.480268+00:00 | 2024-12-31T04:10:41.480268+00:00 | 336 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
Just convert num mod 7 to string and append it to the first place by using the '+', then check if negative then append '-'. Remember that u have to make the num positive or else it will append a lot of negative sign. That simple :>
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string convertToBase7(int num) {
if (num == 0) return "0";
string result;
bool isNegative = (num < 0);
num = abs(num);
while (num > 0) {
result = to_string(num % 7) + result;
num /= 7;
}
return (isNegative)? '-' + result : result;
}
};
``` | 1 | 0 | ['C++'] | 0 |
base-7 | BRUTE FORCE APPROACH | brute-force-approach-by-varun_balakrishn-cc2c | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Varun_Balakrishnan | NORMAL | 2024-12-28T17:24:43.158399+00:00 | 2024-12-28T17:24:43.158399+00:00 | 455 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String convertToBase7(int num) {
int temp = num;
int sign = 0;
String ans = "";
if(num < 0){
temp = -num;
sign = 1;
}
while(temp >= 7){
ans = (temp % 7) + ans ;
temp = temp / 7 ;
}
ans = temp + ans;
if(sign == 0){
return ans;
}
else{
ans = "-" + ans;
return ans;
}
}
}
``` | 1 | 0 | ['Java'] | 0 |
base-7 | ✅0ms python3 solution || beats 100% | 0ms-python3-solution-beats-100-by-rajesh-cd5l | Beats 100% 0ms in python3converting to base 7 is of the form1.check if the number is zero (base condition) then return 02.take a list, l to store the remainders | Rajesh_uda | NORMAL | 2024-12-24T19:08:15.859801+00:00 | 2024-12-24T19:08:15.859801+00:00 | 455 | false | # Beats 100% 0ms in python3
## converting to base 7 is of the form
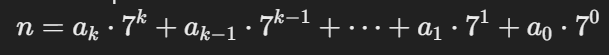
1.check if the number is zero (base condition) then return 0
2.take a list, l to store the remainders after division
3.append the remainder into l.
4.reduce the number to num//7
5.at num becomes zero, print the result to get the output
# Code
```python3 []
class Solution:
def convertToBase7(self, num: int) -> str:
if num == 0:
return "0"
l = []
sign = 1 if num >= 0 else -1
num = abs(num)
while num > 0:
l.append(str(num % 7))
num //= 7
result = ''.join(reversed(l))
return '-' + result if sign == -1 else result
``` | 1 | 0 | ['Python3'] | 0 |
base-7 | SINGLE LINE JAVA SOLUTION -TWO APPROACHES | single-line-java-solution-two-approaches-ulvr | APPROACH 1\n\nclass Solution {\n public String convertToBase7(int num) {\n return Integer.toString(num, 7); \n }\n}\n\nAPPROACH 2\n# Code\njava []\n | THANMAYI01 | NORMAL | 2024-11-09T10:33:44.760551+00:00 | 2024-11-09T10:33:44.760594+00:00 | 483 | false | APPROACH 1\n```\nclass Solution {\n public String convertToBase7(int num) {\n return Integer.toString(num, 7); \n }\n}\n```\nAPPROACH 2\n# Code\n```java []\nclass Solution {\n public String convertToBase7(int num) {\n if(num<0) return "-"+convertToBase7(-num);\n if(num<7) return Integer.toString(num);\n return convertToBase7(num/7)+Integer.toString(num%7);\n }\n}\n``` | 1 | 0 | ['Math', 'Java'] | 1 |
base-7 | Best solution for Base Conversion | best-solution-for-base-conversion-by-paw-v46o | Intuition\n Describe your first thoughts on how to solve this problem. \nTo convert an integer to base 7, I need to repeatedly divide the number by 7, collectin | pawan_leel | NORMAL | 2024-11-01T17:09:44.558994+00:00 | 2024-11-01T17:09:44.559021+00:00 | 80 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo convert an integer to base 7, I need to repeatedly divide the number by 7, collecting the remainders. These remainders represent the digits in the new base, starting from the least significant digit.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Handle Negative Numbers:** Since the output should be a string, check if the number is negative. If it is, work with its absolute value and append a "-" at the end.\n2. **Base Conversion:** Use a loop to divide the number by 7, storing the remainders. The remainders give the digits of the base 7 representation.\n3. **Construct the Result:** Since the remainders are collected in reverse order, reverse the string before returning it.\n\n# Complexity\n- Time complexity: O(log7n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(log7n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public String convertToBase7(int num) {\n return baseX(num,7);\n }\n private String baseX(int num,int base){\n if(num==0) return "0";\n StringBuilder sb = new StringBuilder();\n int temp = num;\n num = Math.abs(num);\n while(num>=base){\n int rem = num%base;\n sb.append(rem);\n num /= base;\n }\n sb.append(num);\n if(temp<0)\n sb.append("-");\n sb.reverse();\n return sb.toString();\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
base-7 | Easy and Simple code to solve Base 7. | easy-and-simple-code-to-solve-base-7-by-bg7wl | Intuition\nTo convert a number to base 7, we continuously divide the number by 7 and store the remainder at each step. These remainders represent the digits in | vijay_s_11335 | NORMAL | 2024-09-05T14:02:46.044692+00:00 | 2024-09-05T14:02:46.044714+00:00 | 53 | false | # Intuition\nTo convert a number to base 7, we continuously divide the number by 7 and store the remainder at each step. These remainders represent the digits in base 7, starting from the least significant digit. If the number is negative, we simply append a minus sign at the end.\n\n# Approach\n1. Handle the base case where the number is 0.\n2. Check if the number is negative and record the sign.\n3. Convert the number to its absolute value and divide it repeatedly by 7. \n4. Collect the remainders at each step, which represent the digits in base 7.\n5. Reverse the collected digits since they are generated in reverse order.\n6. If the number was negative, append a minus sign before returning the result.\n\n# Complexity\n- Time complexity:\nEach division reduces the number by a factor of 7, so the number of divisions is proportional to log7(n). Therefore, the time complexity is O(log7(n)).\n\n- Space complexity:\nSince the string result stores the base 7 representation, the space complexity is O(log7(n)) because that\u2019s the maximum number of digits needed to represent the number in base 7.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n string convertToBase7(int num) {\n if (num==0) return "0";\n bool isNegative = num<0;\n num = abs(num);\n string result = "";\n \n while(num>0){\n int remainder = num % 7;\n result += to_string(remainder);\n num /= 7;\n }\n \n if (isNegative) result += \'-\';\n reverse(result.begin(), result.end());\n return result;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
base-7 | Cpp Solution | cpp-solution-by-dileep_gampala-3bkj | Code\n\nclass Solution {\npublic:\n string convertToBase7(int num) {\n string ans="";\n int i;\n if(num==0)\n {\n retu | Dileep_Gampala | NORMAL | 2024-07-29T20:25:31.979758+00:00 | 2024-07-29T20:25:31.979778+00:00 | 20 | false | # Code\n```\nclass Solution {\npublic:\n string convertToBase7(int num) {\n string ans="";\n int i;\n if(num==0)\n {\n return "0";\n }\n if (num < 0)\n {\n return "-" + convertToBase7(-num);\n }\n while(num!=0)\n {\n ans=ans+to_string(num % 7);\n num=num/7;\n }\n reverse(ans.begin(),ans.end());\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
base-7 | 100% beat - very simple solution in C++ | 100-beat-very-simple-solution-in-c-by-ja-vnw7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | jainam1512 | NORMAL | 2024-05-27T06:25:10.180417+00:00 | 2024-05-27T06:25:10.180444+00:00 | 347 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string convertToBase7(int num) {\n string ans="";\n int c=0;\n if(num<0){\n num=num*-1;\n c=1;\n }\n while(true){\n if(num>=7){\n int t=num%7;\n num=num/7;\n ans=to_string(t)+ans;\n }\n\n if(num<7){\n ans=to_string(num)+ans;\n break;\n }\n }\n if(c==1){\n ans="-"+ans;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
base-7 | beats 99.31%|| easy python solution | beats-9931-easy-python-solution-by-md__j-1be2 | \nclass Solution:\n def convertToBase7(self, num: int) -> str:\n if num == 0:\n return "0"\n \n res = ""\n is_negative | MD__JAKIR1128__ | NORMAL | 2024-04-25T09:35:30.438403+00:00 | 2024-04-25T09:35:30.438437+00:00 | 1 | false | ```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n if num == 0:\n return "0"\n \n res = ""\n is_negative = num < 0\n num = abs(num)\n \n while num > 0:\n remainder = num % 7\n res = str(remainder) + res\n num //= 7\n \n if is_negative:\n res = "-" + res\n \n return res\n\n``` | 1 | 0 | [] | 0 |
base-7 | ✅ 1 Line Solution Beats 100% with Java ✅ | 1-line-solution-beats-100-with-java-by-k-gx9q | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kien-dev | NORMAL | 2024-04-14T09:45:11.409464+00:00 | 2024-04-14T09:45:11.409495+00:00 | 499 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String convertToBase7(int num) {\n return Integer.toString(num, 7);\n }\n}\n``` | 1 | 0 | ['Java'] | 2 |
base-7 | the best solution | the-best-solution-by-a-fr0stbite-zwxq | Intuition\nP.S. the title is a serious exagration\n\nsplit it up, see what each digit is, add the negative sign when needed.\n\n# some stuff\nAlso, if you like | a-fr0stbite | NORMAL | 2024-03-05T06:01:38.187001+00:00 | 2024-03-05T06:01:38.187030+00:00 | 18 | false | # Intuition\nP.S. the title is a serious exagration\n\nsplit it up, see what each digit is, add the negative sign when needed.\n\n# some stuff\nAlso, if you like the 2nd code snippet or just appreciat the short explanation and 1st code, plz upvote!\n\n# Code\nmy real code\n```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n res = ""\n if num < 0: res += "-"\n num = abs(num)\n for endPow in range(0, 10):\n if num // (7**endPow) < 7:\n break\n for i in range(endPow, -1, -1):\n char = str(num // (7**i))\n res += char\n num -= (7**i) * (num // (7**i))\n return res\n```\n\nmy totally ridiculous unexplainable code\n```\nclass Solution:\n def convertToBase7(self, num: int) -> str:\n someString = ""\n if num < 0 and ((num * 2) + 99 - 99) / 2 == num: \n num = abs(num)\n someString += "-"\n num = abs(num)\n for endPow in range(0, 10):\n n = num / (7**endPow)\n realN = ""\n for char in str(n):\n if char == ".": break\n realN += char\n if int(realN) <= 6:\n break\n for i in range(endPow, -1, -1):\n char = str(num // (7**i))\n someString += char\n num -= (7**i) * (num // (7**i))\n return someString\n``` | 1 | 0 | ['Python3'] | 0 |
base-7 | Convert to Base | Time: O(log(N)) | Space: O(log(N)) | convert-to-base-time-ologn-space-ologn-b-22va | Complexity\n- Time complexity: $O(\log{N})$\n- Space complexity: $O(\log{N})$\n\n# Code 1: Number.toString\nUses the built-in base conversion feature of Number. | rojas | NORMAL | 2023-10-26T16:48:24.215389+00:00 | 2023-11-04T18:54:40.311153+00:00 | 38 | false | # Complexity\n- Time complexity: $O(\\log{N})$\n- Space complexity: $O(\\log{N})$\n\n# Code 1: Number.toString\nUses the built-in base conversion feature of [Number.toString](https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Number/toString). It can convert a number to a string in any base from 2 to 36.\n\n```Typescript\nfunction convertToBase7(num: number): string {\n return num.toString(7);\n};\n```\n \n# Code 2: Custom\nManually converts the number to base 7. Works for bases from 2 to 10.\n```Typescript\nfunction convertToBase7(num: number): string {\n return toBase(num, 7);\n};\n\nfunction toBase(num: number, base: number): string {\n const res: number[] = [];\n const sign = Math.sign(num);\n num *= sign;\n while (num >= base) {\n const digit = num % base;\n num = (num - digit) / base;\n res.push(digit);\n }\n res.push(sign * num);\n return res.reverse().join("");\n}\n```\n\n# Code 3: Custom Extended\nManually converts the number to base 7. Works for bases from 2 to 36. It can be easily extended for higher bases and/or for custom mappings.\n\n```Typescript\nconst SYMBOLS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";\n\nfunction convertToBase7(num: number): string {\n return toBase(num, 7);\n};\n\nfunction toBase(num: number, base: number, symbols = SYMBOLS): string {\n const res: string[] = [];\n const sign = Math.sign(num);\n num *= sign;\n do {\n const digit = num % base;\n num = (num - digit) / base;\n res.push(symbols[digit]);\n } while (num > 0);\n (sign < 0) && res.push("-");\n return res.reverse().join("");\n}\n``` | 1 | 0 | ['TypeScript', 'JavaScript'] | 1 |
base-7 | Simple java Solution Beats 100% | simple-java-solution-beats-100-by-bhush9-dvmy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | bhush9699 | NORMAL | 2023-10-17T07:02:04.882898+00:00 | 2023-10-17T07:02:04.882926+00:00 | 752 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String convertToBase7(int num) \n {\n int base=1;\n int ans=0;\n while(num!=0)\n {\n int rem=num%7;\n ans+=base*rem;\n base*=10;\n num/=7;\n } \n return Integer.toString(ans);\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
base-7 | Best Java Solution | best-java-solution-by-ravikumar50-n90s | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-09-19T20:51:53.999987+00:00 | 2023-09-19T20:51:54.000014+00:00 | 330 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.math.*;\nclass Solution {\n\n // taken help\n public String convertToBase7(int num) {\n BigInteger m = new BigInteger(""+num);\n return m.toString(7);\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
base-7 | 504. Base 7 💻 💻|| 🔥🔥 JAVA code... | 504-base-7-java-code-by-jayakumar__s-hziz | Code\n\nclass Solution {\n public String convertToBase7(int num) {\n String str = "";\n int a = 0;\n if(num == 0){\n return " | Jayakumar__S | NORMAL | 2023-06-25T14:45:16.438001+00:00 | 2023-06-25T14:45:27.265014+00:00 | 573 | false | # Code\n```\nclass Solution {\n public String convertToBase7(int num) {\n String str = "";\n int a = 0;\n if(num == 0){\n return "0"+str;\n }\n if(num<0){\n num = num * (-1);\n a++;\n }\n\n while(num>0){\n str= num%7+ str;\n num = num/7;\n }\n if(a>0){\n return "-"+str;\n }\n return str;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
base-7 | 1 Liner Java Code Beats 100% || Easy to Understand | 1-liner-java-code-beats-100-easy-to-unde-anqa | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | jashan_pal_singh_sethi | NORMAL | 2023-06-22T12:20:33.675286+00:00 | 2023-06-22T12:21:06.674730+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String convertToBase7(int num) {\n return Integer.toString(num, 7);\n }\n}\n``` | 1 | 0 | ['String', 'Java'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ (Backtrack : C++ users, please pass string by reference to PASS) | c-backtrack-c-users-please-pass-string-b-uojg | My YouTube Channel - https://www.youtube.com/@codestorywithMIK\n\n/*\nSimple explanation :\nif you notice I am trying all three possibilities :-\n\n 1) I pic | mazhar_mik | NORMAL | 2021-09-12T04:25:36.422823+00:00 | 2023-04-15T03:47:14.659947+00:00 | 9,065 | false | My YouTube Channel - https://www.youtube.com/@codestorywithMIK\n```\n/*\nSimple explanation :\nif you notice I am trying all three possibilities :-\n\n 1) I pick s[i] for s1 but don\'t pick s[i] for s2 (because they should be disjoint)\n - I explore this path and find the result (and then backtrack)\n\n 2) I pick s[i] for s2 but don\'t pick s[i] for s1 (because they should be disjoint)\n - I explore this path and find the result (and then backtrack)\n\n 3) I don\'t pick s[i] at all - I explore this path and find the result\n (and then backtrack)\n\nIn any of the path, if I get s1 and s2 both as palindrome we update our\nresult with maximum length. It\'s like a classic Backtrack approach.\n*/\n```\n```\nclass Solution {\npublic:\n int result = 0;\n bool isPalin(string& s){\n int i = 0;\n int j = s.length() - 1;\n \n while (i < j) {\n if (s[i] != s[j]) return false;\n i++;\n j--;\n }\n \n return true;\n }\n \n void dfs(string& s, int i, string& s1, string& s2){\n \n if(i >= s.length()){\n if(isPalin(s1) && isPalin(s2))\n result = max(result, (int)s1.length()*(int)s2.length());\n return;\n }\n \n s1.push_back(s[i]);\n dfs(s, i+1, s1, s2);\n s1.pop_back();\n \n s2.push_back(s[i]);\n dfs(s, i+1, s1, s2);\n s2.pop_back();\n \n dfs(s, i+1, s1, s2);\n }\n \n int maxProduct(string s) {\n string s1 = "", s2 = "";\n dfs(s, 0, s1, s2);\n \n return result;\n }\n};\n``` | 209 | 6 | [] | 24 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Mask DP | mask-dp-by-votrubac-6q82 | We have 2^n possible palindromes, and each of them can be represented by a mask [1 ... 4096] (since n is limited to 12).\n\nFirst, we check if a mask represents | votrubac | NORMAL | 2021-09-12T04:00:48.115219+00:00 | 2021-09-12T21:49:48.836244+00:00 | 12,725 | false | We have `2^n` possible palindromes, and each of them can be represented by a mask `[1 ... 4096]` (since `n` is limited to `12`).\n\nFirst, we check if a mask represents a valid palindrome, and if so, store the length (or, number of `1` bits) in `dp`.\n\nThen, we check all non-zero masks `m1` against all non-intersecting masks `m2` (`m1 & m2 == 0`), and track the largest product.\n\n>Update1: as suggested by [Gowe](https://leetcode.com/Gowe/), we can use more efficient enumeration for `m2` to only go through "available" bits (`mask ^ m1`). This speeds up C++ runtime from 44 to 22 ms!\n\n> Update 2: we can do pruning to skip masks with no potential to surpass the current maximum. The runtime is now reduced to 4ms!\n\n> Update 3: an alternative solution (proposed by [LVL99](https://leetcode.com/LVL99/)) is to not check all submasks, but instead run "Largest Palindromic Subsequence" algo for all unused bits. This potentially can reduce checks from `2 ^ n` to `n ^ 2`. It\'s a longer solution, so posted it as a comment.\n\n**C++**\n```cpp\nint palSize(string &s, int mask) {\n int p1 = 0, p2 = s.size(), res = 0;\n while (p1 <= p2) {\n if ((mask & (1 << p1)) == 0)\n ++p1;\n else if ((mask & (1 << p2)) == 0)\n --p2;\n else if (s[p1] != s[p2])\n return 0;\n else\n res += 1 + (p1++ != p2--);\n }\n return res;\n}\nint maxProduct(string s) {\n int dp[4096] = {}, res = 0, mask = (1 << s.size()) - 1;\n for (int m = 1; m <= mask; ++m)\n dp[m] = palSize(s, m);\n for (int m1 = mask; m1; --m1)\n if (dp[m1] * (s.size() - dp[m1]) > res)\n for(int m2 = mask ^ m1; m2; m2 = (m2 - 1) & (mask ^ m1))\n res = max(res, dp[m1] * dp[m2]);\n return res;\n}\n```\n**Java**\nJava version courtesy of [amoghtewari](https://leetcode.com/amoghtewari/).\n```java\npublic int maxProduct(String s) {\n int[] dp = new int[4096];\n int res = 0, mask = (1 << s.length()) - 1;\n for (int m = 1; m <= mask; ++m)\n dp[m] = palSize(s, m);\n for (int m1 = mask; m1 > 0; --m1)\n if (dp[m1] * (s.length() - dp[m1]) > res)\n for(int m2 = mask ^ m1; m2 > 0; m2 = (m2 - 1) & (mask ^ m1))\n res = Math.max(res, dp[m1] * dp[m2]);\n return res;\n}\nprivate int palSize(String s, int mask) {\n int p1 = 0, p2 = s.length(), res = 0;\n while (p1 <= p2) {\n if ((mask & (1 << p1)) == 0)\n ++p1;\n else if ((mask & (1 << p2)) == 0)\n --p2;\n else if (s.charAt(p1) != s.charAt(p2))\n return 0;\n else\n res += 1 + (p1++ != p2-- ? 1 : 0);\n }\n return res;\n}\n``` | 118 | 6 | ['C', 'Java'] | 23 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Java - Simple Recursion | java-simple-recursion-by-shreyash1-oh8i | \nclass Solution {\n \n int max = 0;\n public int maxProduct(String s) {\n \n char[] c = s.toCharArray();\n dfs(c, 0, "", "");\n | shreyash1 | NORMAL | 2021-09-12T04:03:01.702257+00:00 | 2021-09-12T13:45:14.249066+00:00 | 6,627 | false | ```\nclass Solution {\n \n int max = 0;\n public int maxProduct(String s) {\n \n char[] c = s.toCharArray();\n dfs(c, 0, "", "");\n \n return max;\n }\n \n public void dfs(char[] c, int i, String s1, String s2){\n \n if(i >= c.length){\n \n if(isPalin(s1) && isPalin(s2))\n max = Math.max(max, s1.length()*s2.length());\n return;\n }\n \n dfs(c, i+1, s1+c[i], s2);\n dfs(c, i+1, s1, s2+c[i]);\n dfs(c, i+1, s1, s2);\n }\n \n public boolean isPalin(String str){\n \n int i = 0, j = str.length() - 1;\n \n while (i < j) {\n \n if (str.charAt(i) != str.charAt(j))\n return false;\n i++;\n j--;\n }\n \n return true;\n }\n}\n``` | 72 | 12 | ['Backtracking', 'Recursion', 'Java'] | 19 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [Python] Clean & Simple, bitmask | python-clean-simple-bitmask-by-yo1995-q42m | python\nclass Solution:\n def maxProduct(self, s: str) -> int:\n # n <= 12, which means the search space is small\n n = len(s)\n arr = [ | yo1995 | NORMAL | 2021-09-12T04:43:29.298317+00:00 | 2021-09-12T04:47:47.141843+00:00 | 4,032 | false | ```python\nclass Solution:\n def maxProduct(self, s: str) -> int:\n # n <= 12, which means the search space is small\n n = len(s)\n arr = []\n \n for mask in range(1, 1<<n):\n subseq = \'\'\n for i in range(n):\n # convert the bitmask to the actual subsequence\n if mask & (1 << i) > 0:\n subseq += s[i]\n if subseq == subseq[::-1]:\n arr.append((mask, len(subseq)))\n \n result = 1\n for (mask1, len1), (mask2, len2) in product(arr, arr):\n # disjoint\n if mask1 & mask2 == 0:\n result = max(result, len1 * len2)\n return result\n```\n\nA slightly improved version, to break early when checking the results\n\n```python\nclass Solution:\n def maxProduct(self, s: str) -> int:\n # n <= 12, which means the search space is small\n n = len(s)\n arr = []\n \n for mask in range(1, 1<<n):\n subseq = \'\'\n for i in range(n):\n # convert the bitmask to the actual subsequence\n if mask & (1 << i) > 0:\n subseq += s[i]\n if subseq == subseq[::-1]:\n arr.append((mask, len(subseq)))\n \n arr.sort(key=lambda x: x[1], reverse=True)\n result = 1\n for i in range(len(arr)):\n mask1, len1 = arr[i]\n # break early\n if len1 ** 2 < result: break\n for j in range(i+1, len(arr)):\n mask2, len2 = arr[j]\n # disjoint\n if mask1 & mask2 == 0 and len1 * len2 > result:\n result = len1 * len2\n break\n \n return result\n``` | 39 | 0 | ['Python'] | 7 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ Backtracking Solution [EXPLAINED] [ACCEPTED} | c-backtracking-solution-explained-accept-z85j | APPROACH:\nBy seeing the constraints, it can be inferred that brute force approach should work fine.\nTo make disjoint subsequence we\'ll use 2 strings . Now, a | rishabh_devbanshi | NORMAL | 2021-09-13T06:21:02.225537+00:00 | 2021-09-13T06:22:30.247686+00:00 | 2,720 | false | **APPROACH:**\nBy seeing the constraints, it can be inferred that brute force approach should work fine.\nTo make disjoint subsequence we\'ll use 2 strings . Now, at everry character i in string we have 3 choices:\n1) include that char in first string\n2) include that char in second string\n3) exclude that char from both strings\n\nto achieve this we\'ll use **backtracking** to generate all disjoint subsequences.\nNow of these subsequences , we consider only those which are pallindromic and leave the rest. For the pallindromic subsequence pair we calculate product eachtime and comapre with our ans calculated so far and update it if the latter product is greater.\n\n**NOTE :**\nMany code got TLE in same approach, that is because we have to pass every string by reference instead of pass by value, as in pass by value a copy of original string is made which takes time. So , to reduce that time and make ourcode faster we use backtracking instead of recursion + pass by value.\n\n**CODE:**\nThe code is given below and is pretty much self explanatory.\n\n```\nlong long ans = 0;\n \n bool isPal(string &s)\n {\n int start=0, end = s.length()-1;\n while(start < end)\n {\n if(s[start] != s[end]) return false;\n start++; end--;\n }\n return true;\n }\n \n void recur(string &s,int idx,string &s1,string &s2)\n {\n if(idx == s.size())\n {\n if(isPal(s1) and isPal(s2))\n {\n long long val =(int) s1.length() * s2.length();\n ans = max(ans , val);\n }\n return;\n }\n \n s1.push_back(s[idx]);\n recur(s,idx+1,s1, s2);\n s1.pop_back();\n \n s2.push_back(s[idx]);\n recur(s,idx+1,s1,s2);\n s2.pop_back();\n \n recur(s,idx+1,s1,s2);\n }\n\t\n\tint maxProduct(string s) {\n string s1="", s2 = "";\n recur(s,0,s1,s2);\n return ans;\n }\n```\n\nDo upvote if it heps :) | 31 | 0 | ['Backtracking', 'C'] | 5 |
maximum-product-of-the-length-of-two-palindromic-subsequences | c++ solution (lcs) | c-solution-lcs-by-dilipsuthar60-vuhr | https://leetcode.com/problems/longest-palindromic-subsequence/\n\nclass Solution {\npublic:\n int lps(string &s)\n {\n int n=s.size();\n str | dilipsuthar17 | NORMAL | 2021-09-12T04:11:42.663594+00:00 | 2023-01-14T09:52:22.923919+00:00 | 3,237 | false | [https://leetcode.com/problems/longest-palindromic-subsequence/](http://)\n```\nclass Solution {\npublic:\n int lps(string &s)\n {\n int n=s.size();\n string s1=s;\n string s2=s;\n reverse(s2.begin(),s2.end());\n int dp[s.size()+1][s.size()+1];\n memset(dp,0,sizeof(dp));\n for(int i=1;i<=n;i++)\n {\n for(int j=1;j<=n;j++)\n {\n dp[i][j]=(s1[i-1]==s2[j-1])?1+dp[i-1][j-1]:max(dp[i][j-1],dp[i-1][j]);\n }\n }\n return dp[n][n];\n }\n int maxProduct(string s) \n {\n int ans=0;\n int n=s.size();\n for(int i=1;i<(1<<n)-1;i++)\n {\n string s1="",s2="";\n for(int j=0;j<n;j++)\n {\n if(i&(1<<j))\n {\n s1.push_back(s[j]);\n }\n else\n {\n s2.push_back(s[j]);\n }\n }\n ans=max(ans,lps(s1)*lps(s2));\n }\n return ans;\n }\n \n};\n``` | 30 | 2 | ['C', 'Bitmask', 'C++'] | 4 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [Python] True O(2^n) dp on subsets solution, explained | python-true-o2n-dp-on-subsets-solution-e-r0xl | I saw several dp solution, which states that they have O(2^n) complexity, but they use bit manipulations, such as looking for first and last significant bit, wh | dbabichev | NORMAL | 2021-09-12T10:34:57.187179+00:00 | 2021-09-12T10:34:57.187212+00:00 | 2,930 | false | I saw several `dp` solution, which states that they have `O(2^n)` complexity, but they use bit manipulations, such as looking for first and last significant bit, which we can not say is truly `O(1)`. So I decided to write my own **true** `O(2^n)` solution.\n\nLet `dp(mask)` be the maximum length of palindrome if we allowed to use only non-zero bits from `mask`. In fact, this means, if we have `s = leetcode` and `mask = 01011001`, we can use only `etce` subsequence. How to evaluate `dp(mask)`?\n\n1. First option is we do not take last significant one, that is we work here with `01011000` and ask what is answer for this mask.\n2. Second option is we do not take first significant bit, that is we work here with `00011001` mask here.\n3. Final option is to take both first and last significant bits but it is allowed only if we have equal elements for them, that is we have mase `00011000` here and because `s[1] = s[7]` we can take this option.\n\nAlso what I calclate all first and last significant bits for all numbers in range `1, 1<<n`.\n\n#### Complexity\nTime complexity is `O(2^n)`, space complexity also `O(2^n)` to keep `dp` cache and `last` and `first` arrays.\n\n```python\nclass Solution:\n def maxProduct(self, s):\n n = len(s)\n \n first, last = [0]*(1<<n), [0]*(1<<n)\n \n for i in range(n):\n for j in range(1<<i, 1<<(i+1)):\n first[j] = i\n\n for i in range(n):\n for j in range(1<<i, 1<<n, 1<<(i+1)):\n last[j] = i\n \n @lru_cache(None)\n def dp(m):\n if m & (m-1) == 0: return m != 0\n l, f = last[m], first[m]\n lb, fb = 1<<l, 1<<f\n return max(dp(m-lb), dp(m-fb), dp(m-lb-fb) + (s[l] == s[f]) * 2)\n \n ans = 0\n for m in range(1, 1<<n):\n ans = max(ans, dp(m)*dp((1<<n) - 1 - m))\n \n return ans\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!** | 28 | 0 | ['Dynamic Programming'] | 6 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python 3 || 5 lines, greedy || T/S: 95% / 42% | python-3-5-lines-greedy-ts-95-42-by-spau-by53 | Here\'s the plan:\n1. We generate all subsequences of s as lists of characters.\n\n2. We filter that list for palindromes.\n3. We compare each pair of palindrom | Spaulding_ | NORMAL | 2024-08-03T03:29:56.752651+00:00 | 2024-08-03T05:13:22.455894+00:00 | 532 | false | Here\'s the plan:\n1. We generate all subsequences of `s` as lists of characters.\n\n2. We filter that list for palindromes.\n3. We compare each pair of palindromes, first to see whether they are disjoint, and if so, determine the product of their lengths.\n4. We determine the maximum product and return it as the answer to the problem.\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n\n n, d = len(s), defaultdict(int)\n\n for mask in range(1<<n): # <-- 1\n sub = [s[i] for i in range(n) if mask & (1<<i)] #\n\n if sub == sub[::-1]: d[mask] = len(sub) # <-- 2\n\n return max(d[mask1] * d[mask2] for mask1, mask2 # <-- 3\n in combinations(d,2) if mask1 & mask2 == 0) # <-- 4\n```\n[https://leetcode.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/submissions/1342459895/](https://leetcode.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/submissions/1342459895/)\n\nI could be wrong, but I think that time complexity is *O*(*N* * 2^ *N*) and space complexity is *O*(*N*^2), in which *N* ~ `len(s)`.\n\n\n\n | 14 | 0 | ['Python3'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python Bitmask | python-bitmask-by-colwind-a6fb | \ndef maxProduct(self, s: str) -> int:\n mem = {}\n n = len(s)\n for i in range(1,1<<n):\n tmp = ""\n for j in range( | colwind | NORMAL | 2021-09-12T04:09:33.371950+00:00 | 2021-09-12T04:09:33.371985+00:00 | 921 | false | ```\ndef maxProduct(self, s: str) -> int:\n mem = {}\n n = len(s)\n for i in range(1,1<<n):\n tmp = ""\n for j in range(n):\n if i>>j & 1 == 1:\n tmp += s[j]\n if tmp == tmp[::-1]:\n mem[i] = len(tmp)\n res = 0\n for i,x in mem.items():\n for j,y in mem.items():\n if i&j == 0:\n res = max(res,x*y)\n return res\n``` | 13 | 3 | [] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Video solution | Intuition and Approach explained in detail | C++ | Backtracking | video-solution-intuition-and-approach-ex-381u | Video\nHello every one i have created a video solution for this problem and solved this video by developing intutition for backtracking (its in hindi), i am pre | _code_concepts_ | NORMAL | 2024-05-06T06:36:28.363331+00:00 | 2024-07-06T21:12:17.480871+00:00 | 589 | false | # Video\nHello every one i have created a video solution for this problem and solved this video by developing intutition for backtracking (its in hindi), i am pretty sure you will never have to look for solution for this video ever again after watching this.\n\n\nThis video is the part of my playlist "Master backtracking".\nVideo Link: \n\nhttps://www.youtube.com/watch?v=Dk3QDMRc8vQ\n\n# Code\n```\nclass Solution {\n long ans = 0;\n\n bool isPal(string &s)\n {\n int start=0, end = s.length()-1;\n while(start < end)\n {\n if(s[start] != s[end]) return false;\n start++; end--;\n }\n return true;\n }\n void helper(string &s,int idx,string &s1,string &s2){\n if(isPal(s1) && isPal(s2)){\n long temp= (int) s1.length() * s2.length();\n ans= max(ans, temp); \n }\n for(int i=idx;i<s.size();i++){\n s1.push_back(s[i]);\n helper(s,i+1,s1,s2);\n s1.pop_back();\n\n s2.push_back(s[i]);\n helper(s,i+1,s1,s2);\n s2.pop_back();\n }\n return;\n }\n\npublic:\n int maxProduct(string s) {\n string s1="";\n string s2="";\n helper(s,0,s1,s2);\n return ans;\n }\n};\n``` | 12 | 0 | ['C++'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Easy Understand | Simple Method | Java | Python ✅ | easy-understand-simple-method-java-pytho-mde0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nUse mask to save all co | czshippee | NORMAL | 2023-04-08T05:08:00.671870+00:00 | 2023-04-21T02:26:53.087128+00:00 | 2,251 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse mask to save all combination in hashmap and use "&" bit manipulation to check if two mask have repeated letter.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O((2^n)^2)$ => $O(4^n)$ \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe worst case is need save every combination, for example the string of length 12 that only contains one kind of letter.\n$O(2^n)$\n\n# Code\nMathod using bit mask\n``` java []\nclass Solution {\n public int maxProduct(String s) {\n char[] strArr = s.toCharArray();\n int n = strArr.length;\n Map<Integer, Integer> pali = new HashMap<>();\n // save all elligible combination into hashmap\n for (int mask = 0; mask < 1<<n; mask++){\n String subseq = "";\n for (int i = 0; i < 12; i++){\n if ((mask & 1<<i) > 0)\n subseq += strArr[i];\n }\n if (isPalindromic(subseq))\n pali.put(mask, subseq.length());\n }\n // use & opertion between any two combination\n int res = 0;\n for (int mask1 : pali.keySet()){\n for (int mask2 : pali.keySet()){\n if ((mask1 & mask2) == 0)\n res = Math.max(res, pali.get(mask1)*pali.get(mask2));\n }\n }\n\n return res;\n }\n\n public boolean isPalindromic(String str){\n int j = str.length() - 1;\n char[] strArr = str.toCharArray();\n for (int i = 0; i < j; i ++){\n if (strArr[i] != strArr[j])\n return false;\n j--;\n }\n return true;\n }\n}\n```\n``` python3 []\nclass Solution:\n def maxProduct(self, s: str) -> int:\n n, pali = len(s), {} # bitmask : length\n for mask in range(1, 1 << n):\n subseq = ""\n for i in range(n):\n if mask & (1 << i):\n subseq += s[i]\n if subseq == subseq[::-1]: # valid is palindromic\n pali[mask] = len(subseq)\n res = 0\n for mask1, length1 in pali.items():\n for mask2, length2 in pali.items():\n if mask1 & mask2 == 0: \n res = max(res, length1 * length2)\n return res\n```\n\nThere is another method using recursion\n``` java []\nclass Solution {\n int res = 0;\n \n public int maxProduct(String s) {\n char[] strArr = s.toCharArray();\n dfs(strArr, 0, "", "");\n return res;\n }\n\n public void dfs(char[] strArr, int i, String s1, String s2){\n if(i >= strArr.length){\n if(isPalindromic(s1) && isPalindromic(s2))\n res = Math.max(res, s1.length()*s2.length());\n return;\n }\n dfs(strArr, i+1, s1 + strArr[i], s2);\n dfs(strArr, i+1, s1, s2 + strArr[i]);\n dfs(strArr, i+1, s1, s2);\n }\n\n public boolean isPalindromic(String str){\n int j = str.length() - 1;\n char[] strArr = str.toCharArray();\n for (int i = 0; i < j; i ++){\n if (strArr[i] != strArr[j])\n return false;\n j--;\n }\n return true;\n }\n}\n```\n\n**Please upvate if helpful!!**\n\n | 11 | 0 | ['Bit Manipulation', 'Bitmask', 'Python', 'Java', 'Python3'] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ Backtrack Solution | c-backtrack-solution-by-anubhvshrma18-ien5 | \nclass Solution {\npublic:\n int ans = 0;\n bool ispal(string &n){\n int i=0,j=n.length()-1;\n while(i<j){\n if(n[i]!=n[j]){\n | anubhvshrma18 | NORMAL | 2021-09-12T05:57:13.667924+00:00 | 2021-09-12T05:57:13.667967+00:00 | 618 | false | ```\nclass Solution {\npublic:\n int ans = 0;\n bool ispal(string &n){\n int i=0,j=n.length()-1;\n while(i<j){\n if(n[i]!=n[j]){\n return false;\n }\n i++,j--;\n }\n return true;\n }\n \n void temp(string &ori,int i,string a,string b){\n if(i==ori.length()){\n if(ispal(a) && ispal(b)){\n ans = max(ans,(int)(a.length()*b.length()));\n }\n return;\n }\n \n temp(ori,i+1,a+ori[i],b);\n temp(ori,i+1,a,b+ori[i]);\n temp(ori,i+1,a,b);\n \n \n }\n \n int maxProduct(string s) {\n temp(s,0,"","");\n return ans;\n }\n};\n``` | 11 | 2 | ['Backtracking', 'C'] | 3 |
maximum-product-of-the-length-of-two-palindromic-subsequences | 15 Lines of Code Easy Brutal Force Java Solution O(3^12 *12) Backtrack Solution | 15-lines-of-code-easy-brutal-force-java-w9oic | As long as I see the constraint is 0<len<12, I try to use brutal force which is backtrack.\nSo each position char can be either:\n1) pick by s1\n2) pick by s2\n | davidluoyes | NORMAL | 2021-09-12T04:04:35.158082+00:00 | 2021-09-12T04:05:40.419993+00:00 | 840 | false | As long as I see the constraint is 0<len<12, I try to use brutal force which is backtrack.\nSo each position char can be either:\n1) pick by s1\n2) pick by s2\n3) pick by nobody.\n```\nclass Solution {\n int max = 0;\n public int maxProduct(String s) {\n backtrack(s,0,"","");\n return max;\n }\n \n private void backtrack(String s, int i,String s1, String s2){\n if(i == s.length()){\n if(isValid(s1) && isValid(s2)){\n max = Math.max(max, s1.length()*s2.length());\n }\n return;\n }\n backtrack(s,i+1,s1,s2);\n backtrack(s,i+1,s1+s.charAt(i),s2);\n backtrack(s,i+1,s1,s2+s.charAt(i));\n }\n private boolean isValid(String s){\n if(s == null) return false;\n for(int i = 0,j=s.length() - 1;i<j;i++,j--){\n if(s.charAt(i) != s.charAt(j)) return false;\n }\n return true;\n }\n}\n``` | 11 | 3 | [] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [Java] Backtracking Solution | java-backtracking-solution-by-abhijeetma-3bod | \nclass Solution {\n public int maxProduct(String s) {\n return dfs(s.toCharArray(),"","",0,0);\n }\n \n public int dfs(char[] arr,String s,S | abhijeetmallick29 | NORMAL | 2021-09-12T05:06:42.758182+00:00 | 2021-09-12T05:54:09.321356+00:00 | 1,312 | false | ```\nclass Solution {\n public int maxProduct(String s) {\n return dfs(s.toCharArray(),"","",0,0);\n }\n \n public int dfs(char[] arr,String s,String p,int pos,int max){\n if(pos == arr.length){\n if(isValid(s) && isValid(p))max = Math.max(max,s.length() * p.length());\n return max;\n }\n return Math.max(dfs(arr,s + arr[pos],p,pos + 1,max),Math.max(dfs(arr,s,p + arr[pos],pos+1,max),dfs(arr,s,p,pos+1,max)));\n }\n \n public boolean isValid(String s){\n int i = 0,j = s.length()-1;\n while(i < j)if(s.charAt(i++) != s.charAt(j--))return false;\n return true;\n }\n}\n``` | 10 | 0 | ['Java'] | 3 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Bit Masking | bit-masking-by-kira3018-uuft | \nclass Solution {\npublic:\n int maxProduct(string s) {\n int n = s.length();\n int p = pow(2,n);\n vector<pair<int,int> > vec;\n | kira3018 | NORMAL | 2021-09-12T04:10:54.057618+00:00 | 2021-09-12T04:10:54.057644+00:00 | 850 | false | ```\nclass Solution {\npublic:\n int maxProduct(string s) {\n int n = s.length();\n int p = pow(2,n);\n vector<pair<int,int> > vec;\n for(int i = 1;i < p;i++){\n int a = isPalindrome(s,i);\n if(a != -1)\n vec.push_back({i,a}); \n }\n int ans = 1;\n for(int i = 0;i < vec.size();i++)\n for(int j = i+1;j < vec.size();j++)\n if((vec[i].first & vec[j].first) == 0)\n ans = max(ans,vec[i].second * vec[j].second); \n return ans;\n \n }\n int isPalindrome(string& s,int p){\n vector<int> vec;\n for(int i = 0;i < s.length();i++)\n if(p & (1<<i))\n vec.push_back(i); \n int index = vec.size()-1;\n for(int i = 0;i <= index;i++,index--)\n if(s[vec[i]] != s[vec[index]])\n return -1;\n return vec.size();\n }\n};\n``` | 10 | 1 | [] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ || Backtracking Solution || Intuition Explained | c-backtracking-solution-intuition-explai-h6qq | Intuition:\n\nIdea is to form all combinations of subsequences that are palindromic, that are not overlapping i.e first string and second string should not have | i_quasar | NORMAL | 2021-09-12T10:52:16.522842+00:00 | 2021-09-12T10:52:37.060662+00:00 | 498 | false | **Intuition:**\n\nIdea is to form all combinations of subsequences that are palindromic, that are not overlapping i.e *first* string and *second* string should not have any common element from main string. Out of all possible *first* and *second* strings, we find product of `first.size() * second.size()` . In the end we return the maximum product. \n\nNext, looking at the size of given string i.e `1 <= n <= 12`. We can do a brute force over it and use **Backtracking** to get all possible combinations of *first* and *second* string that are subsequences of original string. \n\nNow, lets see how can we form *first* and *second* string? Think of possible choices at every index of the original string. What can we pick and what we can skip. Since, we are given that both the palindromic should not have any common element (non-overlapping and disjoint). Thus, we cannot include current element in both strings simultaneously.\n\nSo, we have actually 3 choices at every index.\n1. Exclude the current element from both *first* and *second* string. \n\n2. Include the current element into *first* string -> Backtracking, **include -> use -> remove**\n\n3. Include the current element into *second* string. -> Backtracking, **include -> use -> remove**\n\n**Base Condition :** : When we reach the end of string, check if first and second string are palindrome or not. \n* If not then return \n* Else calculate the product of lengths `first.size() * second.size()` and update maximumProduct accordingly\n \nGo through the code, it is self explainatory and easy to understand. Just simple backtracking logic, nothing complex. \n\nNote: We are passing first and second strings by **reference**, so that in every function call new copies of string is not created. If we do not consider this, it will give a TLE. \n\n# Code : \n```\nint maxProd = 1, n;\n bool isPalindrome(const string& s)\n {\n int n = s.size();\n for(int i=0; i<n/2; i++)\n if(s[i] != s[n-1-i]) return false;\n return true;\n }\n \n void solve(string& s, string& first, string& second, int idx)\n {\n if(idx == n) \n {\n\t\t\t// Check if both strings are palindrome or not\n\t\t\t// If yes, then find product or their lengths\n if(isPalindrome(first) && isPalindrome(second)) \n {\n maxProd = max(maxProd, (int)(first.size() * second.size()));\n }\n return;\n }\n \n // Choice 1 : Exclude current element from both strings\n solve(s, first, second, idx+1);\n \n // Choice 2 : Include current element into first string\n first.push_back(s[idx]);\n solve(s, first, second, idx+1);\n first.pop_back();\n \n // Choice 3 : Include current element into second string\n second.push_back(s[idx]);\n solve(s, first, second, idx+1);\n second.pop_back();\n }\n \n int maxProduct(string s) {\n n = s.size();\n string first = "", second = "";\n solve(s, first, second, 0); // Start from 0th index\n return maxProd;\n }\n```\n\n**Time : O(n * 3^n)** \n* In each recursive call we have 3 choices so total **O(3^n)**\n* and **O(n)** to check if both strings are palindrome or not \n\n***If you find this solution helpful, do give it an upvote :)*** | 9 | 0 | ['Backtracking', 'Recursion'] | 3 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ DP from O(3^N) to O(2^N) | c-dp-from-o3n-to-o2n-by-lzl124631x-bek7 | See my latest update in repo LeetCode\n\n## Solution 1. Bitmask DP\n\nLet dp[mask] be the length of the longest palindromic subsequence within the subsequence r | lzl124631x | NORMAL | 2021-09-12T06:25:42.433990+00:00 | 2021-09-12T06:43:56.700016+00:00 | 1,261 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Bitmask DP\n\nLet `dp[mask]` be the length of the longest palindromic subsequence within the subsequence represented by `mask`.\n\nThe answer is `max( dp[m] * dp[(1 << N) - 1 - m] | 1 <= m < 1 << N )`. (`(1 << N) - 1 - m)` is the complement subset of `m`.\n\nFor `dp[m]`, we can brute-forcely enumerate each of its subset, and compute the maximum length of its palindromic subsets.\n\n```\ndp[m] = max( bitcount( sub ) | `sub` is a subset of `m`, and `sub` forms a palindrome )\n```\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/\n// Author: github.com/lzl124631x\n// Time: O(N * 2^N + 3^N)\n// Space: O(2^N)\nclass Solution {\n bool isPalindrome(string &s, int mask) {\n vector<int> index;\n for (int i = 0; mask; mask >>= 1, ++i) {\n if (mask & 1) index.push_back(i);\n }\n for (int i = 0, j = index.size() - 1; i < j; ++i, --j) {\n if (s[index[i]] != s[index[j]]) return false;\n }\n return true;\n }\npublic:\n int maxProduct(string s) {\n int N = s.size();\n vector<int> dp(1 << N), pal(1 << N);\n for (int m = 1; m < 1 << N; ++m) {\n pal[m] = isPalindrome(s, m);\n }\n for (int m = 1; m < 1 << N; ++m) { // `m` is a subset of all the characters\n for (int sub = m; sub; sub = (sub - 1) & m) { // `sub` is a subset of `m`\n if (pal[sub]) dp[m] = max(dp[m], __builtin_popcount(sub)); // if this subset forms a palindrome, update the maximum length\n }\n }\n int ans = 0;\n for (int m = 1; m < 1 << N; ++m) {\n ans = max(ans, dp[m] * dp[(1 << N) - 1 - m]);\n }\n return ans;\n }\n};\n```\n\n## Solution 2. Bitmask DP\n\nIn Solution 1, filling the `pal` array takes `O(N * 2^N)` time. We can reduce the time to `O(2^N)` using DP.\n\n```\npal[m] = s[lb] == s[hb] && pal[x]\n where `lb` and `hb` are the indexes of the lowest and highest bits of `m`, respectively,\n and `x` equals `m` removing the lowest and highest bits.\n```\n\n```cpp\nvector<bool> pal(1 << N);\npal[0] = 1;\nfor (int m = 1; m < 1 << N; ++m) {\n int lb = __builtin_ctz(m & -m), hb = 31 - __builtin_clz(m); \n pal[m] = s[lb] == s[hb] && pal[m & ~(1 << lb) & ~(1 << hb)];\n}\n```\n\nUsing the same DP idea, we can reduce the time complexity for filling the `dp` array from `O(3^N)` to `O(2^N)`, and we don\'t even need the `pal` array.\n\n```\n// if `m` is only a single bit 1\ndp[m] = 1 \n\n// otherwise\ndp[m] = max( \n dp[m - (1 << lb)], // if we exclude `s[lb]`\n dp[m - (1 << hb)], // if we exclude `s[hb]`\n dp[m - (1 << lb) - (1 << hb)] + (s[lb] == s[hb] ? 2 : 0) // If we exclude both `s[lb]` and `s[hb]` and plus 2 if `s[lb] == s[hb]`\n )\n```\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/\n// Author: github.com/lzl124631x\n// Time: O(2^N)\n// Space: O(2^N)\nclass Solution {\npublic:\n int maxProduct(string s) {\n int N = s.size();\n vector<int> dp(1 << N);\n for (int m = 1; m < 1 << N; ++m) {\n if (__builtin_popcount(m) == 1) dp[m] = 1; \n else {\n int lb = __builtin_ctz(m & -m), hb = 31 - __builtin_clz(m);\n dp[m] = max({ dp[m - (1 << lb)], dp[m - (1 << hb)], dp[m - (1 << lb) - (1 << hb)] + (s[lb] == s[hb] ? 2 : 0) });\n }\n }\n int ans = 0;\n for (int m = 1; m < 1 << N; ++m) {\n ans = max(ans, dp[m] * dp[(1 << N) - 1 - m]);\n }\n return ans;\n }\n};\n``` | 9 | 1 | [] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [C++] Simple Solution using Backtracking | c-simple-solution-using-backtracking-by-t5fpj | \n2 Cases at each pos, \n1. Not Pick that char in any string\n2. Pick that char, here 2 sub cases\n\ta. Pick in 1st String\n\tb. Pick in 2nd String\n\nbool is | sahilgoyals | NORMAL | 2021-09-12T04:45:53.216784+00:00 | 2021-09-12T05:01:35.831392+00:00 | 935 | false | \n**2 Cases at each pos**, \n1. Not Pick that char in any string\n2. Pick that char, here 2 sub cases\n\ta. Pick in 1st String\n\tb. Pick in 2nd String\n```\nbool isPalin(string &s) {\n\tint i = 0, j = s.length() - 1;\n\twhile(i < j) {\n\t\tif(s[i] != s[j]) return false;\n\t\ti++;\n\t\tj--;\n\t}\n\treturn true;\n}\n\nvoid dfs(string &s, int p, string &s1, string &s2, int &ans) {\n\tif(p >= s.length()) {\n\t\tif(isPalin(s1) && isPalin(s2)) {\n\t\t\tint tmp = s1.length() * s2.length();\n\t\t\tans = max(ans, tmp);\n\t\t}\n\t\treturn;\n\t}\n\t// Case 1: Not Pick\n\tdfs(s, p + 1, s1, s2, ans);\n\t\n\t// Case 2: Pick -> 2 cases\n\t// 2(a): Pick in 1st string\n\ts1.push_back(s[p]);\n\tdfs(s, p + 1, s1, s2, ans);\n\ts1.pop_back();\n\n\t// 2(b): Pick in 2nd string\n\ts2.push_back(s[p]);\n\tdfs(s, p + 1, s1, s2, ans);\n\ts2.pop_back();\n}\n\nint maxProduct(string s) {\n\tint ans = 0;\n\tstring s1 = "", s2 = "";\n\tdfs(s, 0, s1, s2, ans);\n\treturn ans;\n}\n``` | 9 | 1 | ['Backtracking', 'C', 'C++'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python DFS solution | python-dfs-solution-by-abkc1221-bco5 | We have 3 possibilities i.e, \n1) not considering the current char for either subsequence \n2) considering it for first one \n3) considering it for second subse | abkc1221 | NORMAL | 2021-09-12T06:08:50.869739+00:00 | 2021-09-12T06:18:36.629351+00:00 | 880 | false | We have 3 possibilities i.e, \n1) not considering the current char for either subsequence \n2) considering it for first one \n3) considering it for second subsequence\n[Follow here](https://leetcode.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/discuss/1458482/PYTHON-Simple-solution-backtracking)\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n self.res = 0\n def isPalindrome(word):\n l, r = 0, len(word)-1\n while l < r:\n if word[l] != word[r]:\n return False\n l += 1; r -= 1\n return True\n \n @functools.lru_cache(None)\n def dfs(i, word1, word2):\n if i >= len(s):\n if isPalindrome(word1) and isPalindrome(word2):\n self.res = max(self.res, len(word1) * len(word2))\n return\n \n\t\t\tdfs(i + 1, word1, word2) # 1st case \n dfs(i + 1, word1 + s[i], word2) # 2nd case\n dfs(i + 1, word1, word2 + s[i]) # 3rd case\n \n dfs(0, \'\', \'\')\n\t\t\n return self.res\n``` | 7 | 0 | ['Depth-First Search', 'Recursion', 'Memoization', 'Python'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ Bitmask DP Time: O(n * 3^n), Space: O(2^n) | c-bitmask-dp-time-on-3n-space-o2n-by-fel-llfr | dp[mask]represent the maximum length of palindrome if we used these characters.\nThere are two cases:\n1) If mask represent a palindrome subsequence, dp[mask]= | felixhuang07 | NORMAL | 2021-09-12T04:00:40.139680+00:00 | 2021-09-12T05:06:51.717071+00:00 | 1,016 | false | ```dp[mask]```represent the maximum length of palindrome if we used these characters.\nThere are two cases:\n1) If mask represent a palindrome subsequence, ```dp[mask]```= the length of that subsequence.\n2) If mask is not a palindrome subsequence, we iterate through all its submasks and find the longest palindrome length\n\nFinally, we iterate through all masks and find the maximum product of ```dp[mask]``` and ```dp[~mask]```, which sums up to the whole string.\n```\nbool ispalin(const string& s) {\n int l = 0, r = s.size() - 1;\n while(l < r) {\n if(s[l] != s[r])\n return false;\n ++l, --r;\n }\n return true;\n}\n\nclass Solution {\npublic:\n int maxProduct(string s) {\n const int N = s.size();\n vector<int> dp(1 << N);\n for(int mask = 1; mask < (1 << N); ++mask) {\n string cur;\n for(int i = 0; i < N; ++i)\n if(mask & (1 << i))\n cur += s[i];\n if(ispalin(cur))\n dp[mask] = cur.size();\n else {\n for(int sub = mask; sub; sub = (sub - 1) & mask)\n dp[mask] = max(dp[mask], dp[sub]);\n }\n }\n int ans = 0;\n for(int mask = 0; mask < (1 << N); ++mask) {\n int a = dp[mask];\n int other = 0;\n for(int i = 0; i < N; ++i)\n if(!(mask & (1 << i)))\n other |= 1 << i;\n int b = dp[other];\n ans = max(ans, a * b);\n }\n return ans;\n }\n};\n``` | 6 | 2 | ['Dynamic Programming', 'C', 'Bitmask'] | 4 |
maximum-product-of-the-length-of-two-palindromic-subsequences | MOST SIMPLE KNAPSACK SOLUTION EVER ON INTERNET: most of you thought, must be a hard question but see | most-simple-knapsack-solution-ever-on-in-dwqr | Intuition\njust simple knapsack : make two empty string s1 and s2 and at each element you have three options :\n1. add element to s1 \n2. add element to s2\n3. | aniket_kumar_ | NORMAL | 2024-10-31T09:16:44.422388+00:00 | 2024-10-31T09:16:44.422420+00:00 | 163 | false | # Intuition\njust simple knapsack : make two empty string s1 and s2 and at each element you have three options :\n1. add element to s1 \n2. add element to s2\n3. add element to none of them \n\nat the base case: if(index==s.size()){\n if(s1.size() and s2.size() and ispalindrome(s1) and ispalindrome(s2)){\n return s1.size()*s2.size();\n }\n return 0;\n }\n\n# Approach\nknapsack\n\n# Complexity\n- Time complexity:\nO(n^2) even after memoization\n\n- Space complexity:\no(n);\n\n# Code\n# whatsapp me if it worked: 6209554569\n```cpp []\nclass Solution {\npublic:\n bool ispalindrome(string s1){\n string a=s1;;\n reverse(s1.begin(),s1.end());\n \n return a==s1;\n }\n unordered_map<string,int>maps;\n int find(string&s,int index,string s1,string s2){\n if(index==s.size()){\n if(s1.size() and s2.size() and ispalindrome(s1) and ispalindrome(s2)){\n return s1.size()*s2.size();\n }\n return 0;\n }\n string key=to_string(index)+","+s1+","+s2;\n if(maps.find(key)!=maps.end()){\n return maps[key];\n }\n // go with s1 \n int a=find(s,index+1,s1+s[index],s2);\n // go with s2\n int b=find(s,index+1,s1,s2+s[index]);\n // go with none \n int c=find(s,index+1,s1,s2);\n return maps[key]=max(a,max(b,c));\n }\n int maxProduct(string&s) {\n \n return find(s,0,"","");\n }\n};\n``` | 4 | 0 | ['Dynamic Programming', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ bitmask, hashmap | c-bitmask-hashmap-by-brandonnjosa4-ahxd | If the string is n chars long, every possible string can be created in a loop from 0-2^n,\nthe same way you generate all subsets. \n\nCreate the strings and rev | BrandonNjosa4 | NORMAL | 2022-07-26T23:57:00.794681+00:00 | 2022-07-26T23:58:03.447275+00:00 | 594 | false | If the string is n chars long, every possible string can be created in a loop from 0-2^n,\nthe same way you generate all subsets. \n\nCreate the strings and reverse them, if its equal its a palidrome.\n\nThe binary version of the numbers in the loop from 0-2^n represents the char positions of each string created, store the palidromes with the outer loop number being the key, and the amount of bits being the value.\n\nLoop through the map in, and \'&\' each key value, if its 0, then they dont have any same bits, multiply them and keep track od the maximum.\n\n\n```\nclass Solution {\npublic:\n int maxProduct(string s) {\n unordered_map <int, int> map;\n int n = s.size();\n for (int i = 0; i < (1 << n); i++) {\n string str = "";\n for (int j = 0; j < n; j++) {\n if ((i & (1 << j))) {\n str += s[j];\n }\n }\n string str1(str); \n reverse(str.begin(), str.end());\n if (str == str1) {\n map[i] = __builtin_popcount(i);\n }\n }\n int maxNum = 0;\n for (pair<int,int> i: map) {\n for (pair<int, int> j : map) {\n if (i != j) {\n if ((i.first & j.first) == 0) {\n maxNum = max((i.second * j.second), maxNum);\n }\n }\n }\n }\n return maxNum;\n }\n};\n``` | 4 | 0 | ['Bit Manipulation', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Memoized DP | memoized-dp-by-ayushganguli1769-3o5i | We recursively generate two strings string_a , string_b from s.\nIn this quetion at every index i of string s, we have 3 choices:\n1.add s[i] to string_a\n2.add | ayushganguli1769 | NORMAL | 2021-09-12T08:15:28.334291+00:00 | 2021-09-12T08:15:28.334331+00:00 | 356 | false | We recursively generate two strings string_a , string_b from s.\nIn this quetion at every index i of string s, we have 3 choices:\n1.add s[i] to string_a\n2.add s[i] to string_b\n3.Do not add s[i] to string_a or string_b\nWe take max of every 3 choices at every step.\nWhen we i == length of s, we check is string_a and string_b generated are palindrome. If palindrome, return product of the length of two strings else return 0\nOn careful observation it is found that recursively generated i,string_a, string_b are repeating and hence we memoize them.\n```\nmemo = {}\ndef is_palindrome(string):\n (i,j) = (0,len(string)-1)\n while i < j:\n if string[i] != string[j]:\n return False\n i += 1\n j -= 1\n return True\ndef recurse(s,i,string_a,string_b):\n global memo\n if i >= len(s):\n if is_palindrome(string_a) and is_palindrome(string_b):\n return len(string_a) * len(string_b)\n else:\n return 0\n elif (i,string_a,string_b) in memo:\n return memo[(i,string_a,string_b)]\n ans1 = recurse(s,i+1,string_a+ s[i],string_b)\n ans2 = recurse(s,i+1,string_a,string_b+ s[i])\n ans3 = recurse(s,i+1,string_a,string_b)\n ans = max(ans1,ans2,ans3)\n memo[(i,string_a,string_b)] = ans\n return ans\n \nclass Solution:\n def maxProduct(self, s: str) -> int:\n global memo\n memo = {}\n return recurse(s,0,"","")\n``` | 4 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python - Bruteforce | python-bruteforce-by-ajith6198-k67p | \nclass Solution:\n def maxProduct(self, s: str) -> int:\n subs = []\n n = len(s)\n def dfs(curr, ind, inds):\n if ind == n:\ | ajith6198 | NORMAL | 2021-09-12T04:23:30.847028+00:00 | 2021-09-12T04:35:30.897772+00:00 | 717 | false | ```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n subs = []\n n = len(s)\n def dfs(curr, ind, inds):\n if ind == n:\n if curr == curr[::-1]:\n subs.append((curr, inds))\n return\n dfs(curr+s[ind], ind+1, inds|{ind})\n dfs(curr, ind+1, inds)\n \n dfs(\'\', 0, set())\n \n res = 0\n n = len(subs)\n for i in range(n):\n s1, i1 = subs[i]\n for j in range(i+1, n):\n s2, i2 = subs[j]\n if len(i1 & i2) == 0:\n res = max(res, len(s1)*len(s2))\n return res\n``` | 4 | 0 | ['Python', 'Python3'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Recursion [C++] Explanation | recursion-c-explanation-by-suraj013-fgva | I think the commented code is enough for the explanation.\nfor n <= 12:\n we have 3 option for every position\nso we can simply use recursion with a Time-Comple | suraj013 | NORMAL | 2021-09-12T04:00:45.575824+00:00 | 2021-09-30T11:29:09.312097+00:00 | 419 | false | I think the commented code is enough for the explanation.\nfor n <= 12:\n* we have 3 option for every position\nso we can simply use recursion with a Time-Complexity of **O(n * 3^n)**\n\n* we have maximum of (length(a)+length(b)) length string in any path in the recursion\nso Space Complexity: **O(n)**\n\n**Note**: Don\'t mess up with pass by reference(&)\n\n```\nclass Solution {\npublic:\n bool isPalindrome(string &a) {\n int i = 0, j = a.length()-1;\n while(i <= j) {\n if(a[i++] != a[j--]) return false;\n }\n return true;\n }\n \n void solve(string &s, int i, int n, string &a, string &b, int &res) {\n if(isPalindrome(a) && isPalindrome(b)) { // both subsequences are palindrome\n res = max(res, (int)a.length()*(int)b.length()); // take maximum of product of their length\n }\n if(i >= n) return ; // base case\n \n // case I: if we don\'t choose to add the current char to any of the subsequences\n solve(s, i+1, n, a, b, res);\n \n // case II: if we choose to add the current char to a\n a += s[i];\n solve(s, i+1, n, a, b, res);\n a.pop_back(); // backtrack\n \n // case III: if we choose to add the current char to b\n b += s[i];\n solve(s, i+1, n, a, b, res); \n b.pop_back(); // backtrack\n }\n \n int maxProduct(string s) {\n int n = s.length();\n string a = "", b = "";\n int res = 1;\n solve(s, 0, n, a, b, res);\n return res;\n }\n};\n``` | 4 | 1 | ['Backtracking', 'Recursion'] | 3 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Simplest Solution With Explanation | simplest-solution-with-explanation-by-ve-qwc4 | \n\n# Code\n\nclass Solution {\npublic:\n // To check whether a string is palindrome or not.\n bool isPalindrome(string s) {\n int n = s.size();\n | Venugopal_Reddy20 | NORMAL | 2023-08-03T13:36:12.823383+00:00 | 2023-08-03T13:36:12.823411+00:00 | 194 | false | \n\n# Code\n```\nclass Solution {\npublic:\n // To check whether a string is palindrome or not.\n bool isPalindrome(string s) {\n int n = s.size();\n for (int i = 0; i < n / 2; i++) {\n if (s[i] != s[n-i-1]) {\n return false;\n }\n }\n return true;\n }\n int maxProduct(int i, string s1, string s2, string &s) {\n // If we have traversed the whole string, we check the two strings picked on the way whether they are\n // palindrome or not. If they are, we can return their product.\n if (i == s.size()) {\n\n if (isPalindrome(s1) && isPalindrome(s2)) {\n return (s1.size()) * (s2.size());\n }\n return 0;\n }\n\n // We have two options for every index either not pick it or pick it.\n // If we want to pick it we can add it to string1 or string2 but not both simultaneously.\n int notTake = maxProduct(i + 1, s1, s2, s); \n int take1 = maxProduct(i + 1, s1 + s[i], s2, s);\n int take2 = maxProduct(i + 1, s1, s2 + s[i], s);\n\n // Finally we take max of all options.\n return max({notTake, take1, take2});\n }\n int maxProduct(string s) {\n return maxProduct(0, "", "", s); // [index, string1, string2, string]\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | bitmask | hashing | C++ | bitmask-hashing-c-by-_shant_11-gu36 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | _shant_11 | NORMAL | 2023-07-24T19:09:09.589817+00:00 | 2023-07-24T19:09:09.589836+00:00 | 322 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n priority_queue<int, vector<int>, greater<int>> pq;\npublic:\n bool isPalindrome(string& s){\n int l=0, r = s.size()-1;\n while(l <= r){\n if(s[l] != s[r]) return false;\n l++;\n r--;\n }\n return true;\n }\n int maxProduct(string s) {\n int n = s.size();\n unordered_map<int, int> mp;\n for(int i=1; i<(1<<n); i++){\n string t;\n for(int j=0; j<n; j++){\n if(i&(1<<j))t.push_back(s[j]);\n }\n if(isPalindrome(t)) mp[i] = t.size();\n }\n int res = 0;\n for(auto& x : mp){\n for(auto& y : mp){\n if((x.first & y.first) == 0) res = max(res, x.second* y.second);\n }\n }\n return res;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ (Backtrack : C++ users, please pass string by reference to PASS) | c-backtrack-c-users-please-pass-string-b-r0l9 | \nclass Solution {\npublic:\nint ans=INT_MIN;\nint maxProduct(string s) \n{\n\t//im trying to get all the disjoint subsequences\n\t\n //the ith char can be i | akshat0610 | NORMAL | 2022-10-21T10:01:41.788149+00:00 | 2022-10-21T10:01:41.788183+00:00 | 884 | false | ```\nclass Solution {\npublic:\nint ans=INT_MIN;\nint maxProduct(string s) \n{\n\t//im trying to get all the disjoint subsequences\n\t\n //the ith char can be in none of the string\n\t//the ith char can be in the first string\n\t//the ith cahr can be in the second string\n\t\n\tint idx=0;\n\tstring s1="";\n\tstring s2="";\n fun(s,idx,s1,s2);\n\treturn ans;\n}\nvoid fun(string &s,int idx,string &s1,string &s2)\n{\n\tif(idx >= s.length())\n\t{\n\t\tif(ispalin(s1)==true and ispalin(s2)==true)\n\t\t{\n\t\t\tint temp = s1.length() * s2.length();\n\t\t\tans=max(ans,temp);\n\t\t}\n\t\treturn;\n\t}\n\t\n\tchar ch = s[idx];\n\t\n\t//if the currchar got include in the first string s1\n\ts1.push_back(ch);\n\tfun(s,idx+1,s1,s2);\n\ts1.pop_back();\n\t\n\ts2.push_back(ch);\n\tfun(s,idx+1,s1,s2);\n s2.pop_back();\n\t\n\tfun(s,idx+1,s1,s2);\n}\nbool ispalin(string &s)\n{\n\tint i = 0;\n int j = s.length() - 1;\n \n while (i < j) {\n if (s[i] != s[j]) return false;\n i++;\n j--;\n }\n \n return true;\n}\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'C', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [C++] Simple C++ Code | c-simple-c-code-by-prosenjitkundu760-mtav | \n\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n | _pros_ | NORMAL | 2022-08-16T12:33:40.914456+00:00 | 2022-08-16T12:33:40.914498+00:00 | 573 | false | \n\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n int n, ans = -1;\n bool isPalindrome(string &p)\n {\n int i = 0, j = p.size()-1;\n while(i <= j)\n {\n if(p[i] == p[j])\n {\n i++;\n j--;\n }\n else\n return false;\n }\n return true;\n }\n void dfs(string &s, string &a, string &b, int idx)\n {\n if(idx == n)\n {\n if(isPalindrome(a) && isPalindrome(b)){\n int val = a.size()*b.size();\n ans = max(val, ans);\n }\n return;\n }\n a.push_back(s[idx]);\n dfs(s, a, b, idx+1);\n a.pop_back();\n b.push_back(s[idx]);\n dfs(s, a, b, idx+1);\n b.pop_back();\n dfs(s, a, b, idx+1);\n }\npublic:\n int maxProduct(string s) {\n n = s.size();\n string a = "", b = "";\n dfs(s, a, b, 0);\n return ans;\n }\n};\n``` | 3 | 1 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'C'] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Java - Bit Mask | java-bit-mask-by-mathew1234-imxd | \nclass Solution {\n public int maxProduct(String s) {\n HashMap<Integer,Integer> map=new HashMap<>(); // KEY=bit mask , VALUE= length of the string g | Mathew1234 | NORMAL | 2022-08-10T21:38:28.951169+00:00 | 2022-08-10T21:38:28.951235+00:00 | 366 | false | ```\nclass Solution {\n public int maxProduct(String s) {\n HashMap<Integer,Integer> map=new HashMap<>(); // KEY=bit mask , VALUE= length of the string generated from that mask\n int n=s.length();\n for(int mask=0;mask<(1<<n);mask++){// generate bitmask from 1 to 2^n \n String temp="";\n for(int i=0;i<n;i++){ \n if((mask & (1<<i)) !=0) // generate the string from the mask \n temp+=s.charAt(i);\n }\n \n if(isPali(temp)){ // check if its a palindrome\n map.put(mask,temp.length()); \n }\n }\n \n int res=0;\n for(int i: map.keySet()){\n for(int j :map.keySet()){\n if((i&j)==0){ // if AND of two bitmask is zero means they are disjoint\n res=Math.max(res, map.get(i)*map.get(j));\n }\n }\n }\n \n return res;\n \n \n \n \n }\n \n private boolean isPali(String s){\n int i=0;\n int j=s.length()-1;\n while(i<j){\n if(s.charAt(i)!=s.charAt(j))\n return false;\n i++;\n j--;\n }\n return true;\n }\n}\n``` | 3 | 0 | ['Bitmask'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Easy C++ Backtracking Solution | easy-c-backtracking-solution-by-harshset-mxh6 | \nclass Solution {\npublic:\n int ans=0;\n bool pal(string &s){\n int l=s.length();\n for(int i=0;i<l-1-i;i++) \n if(s[i]!=s[l-1- | harshseta003 | NORMAL | 2022-07-08T07:17:17.920976+00:00 | 2022-07-08T07:17:17.921012+00:00 | 447 | false | ```\nclass Solution {\npublic:\n int ans=0;\n bool pal(string &s){\n int l=s.length();\n for(int i=0;i<l-1-i;i++) \n if(s[i]!=s[l-1-i]) return false;\n return true;\n }\n void dfs(int curr,string &s1,string &s2,int l, string &s){\n if(curr==l){\n if(pal(s1) && pal(s2)){\n ans=max(ans,(int)s1.length()*(int)s2.length());\n }\n return;\n }\n s1.push_back(s[curr]);\n dfs(curr+1,s1,s2,l,s);\n s1.pop_back();\n \n s2.push_back(s[curr]);\n dfs(curr+1,s1,s2,l,s);\n s2.pop_back();\n \n dfs(curr+1,s1,s2,l,s);\n }\n int maxProduct(string &s) {\n int l=s.length();\n string s1,s2;\n dfs(0,s1,s2,l,s);\n return ans;\n }\n};\n``` | 3 | 0 | ['Backtracking', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ || LPS and Brute Force | c-lps-and-brute-force-by-_mhmd_noor-oq5t | upvote if you find it helpful :)\n\nclass Solution {\npublic:\n \n int LPS(string s){ //To find the longest palindrome of a given string\n \n | _mhmd_noor | NORMAL | 2022-06-15T19:52:26.275735+00:00 | 2022-06-15T19:54:06.193553+00:00 | 312 | false | ***upvote if you find it helpful :)***\n```\nclass Solution {\npublic:\n \n int LPS(string s){ //To find the longest palindrome of a given string\n \n if( s.size() == 1 ) return 1;\n int n = s.size();\n int dp[n][n];\n memset(dp,0,sizeof(dp));\n \n for(int i = 0; i < n; i++) dp[i][i]=1;\n \n for(int i = 1; i < n; i++){\n for(int j = 0,k = i; j < n-i; j++){\n k = i+j;\n if( s[j] == s[k] )\n dp[j][k] = dp[j+1][k-1]+2;\n else\n dp[j][k] = max(dp[j][k-1],dp[j+1][k]);\n }\n }\n \n return dp[0][n-1];\n }\n int maxProduct(string s) {\n int ans = 0, len = s.size();\n // Generate all subsequences of the String\n for(int i = 1; i < pow(2,len-1); i++){\n string p = "", q = "";\n for(int j = 0; j < len; j++){\n if( i & 1<<j ) p+=s[j];\n else q+=s[j];\n }\n ans = max(ans, LPS(p)*LPS(q));\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Simple BitMasking, Smart BruteForce 75ms (Java) | simple-bitmasking-smart-bruteforce-75ms-2vx3p | Total possible subsequence n = 1 << string.length()-1\n\nFor each possible subsequence check if the string is palindrome or not. If it\'s palindrome then store | 1_piece | NORMAL | 2021-09-12T05:32:58.860666+00:00 | 2021-09-12T05:39:10.317779+00:00 | 411 | false | Total possible subsequence n = 1 << string.length()-1\n\nFor each possible subsequence check if the string is palindrome or not. If it\'s palindrome then store it in a list. \nNow Iterate through the each pair and check if this pair gives us the maximum result. \n\nBoth pair need to be disjoint to achieve it, we will store the binary representation of the subsequnce and use `&` to check if both palindrome has any same char index or not. \n\n\n\n\n\n public int maxProduct(String s) {\n char[] chars = s.toCharArray();\n int n = 1 << chars.length;\n List<int[]> list = new ArrayList<int[]>();\n\t\t// each number from 1 to n represent a unique subsequence \n for (int i = 1; i < n; i++) {\n\t\t\t// get the string for current subsequence and check if it\'s palindrom\n if (isPalindrom(getString(i, chars))) {\n\t\t\t\t// if it\'s palindrome then store the binary representation fo the sequence and number of 1\'s \n\t\t\t\t// as it will be required to calculate the product of the two subsequence\n list.add(new int[]{i, countOnes(i)});\n }\n }\n\n int max = 0;\n for (int i = list.size() - 1; i >= 0; i--) {\n int[] first = list.get(i);\n int v = first[1];\n for (int j = i - 1; j >= 0; j--) {\n\t\t\t\t// check if both subsequence has any common char index or not\n if ((first[0] & list.get(j)[0]) == 0) {\n max = Math.max(max, v * list.get(j)[1]);\n }\n }\n }\n\n return max;\n }\n\n private String getString(int num, char[] chars) {\n StringBuilder sb = new StringBuilder();\n for (int i = 0; i < chars.length; i++) {\n if ((num & (1 << i)) != 0) {\n sb.append(chars[i]);\n }\n }\n return sb.toString();\n }\n\n private boolean isPalindrom(String s) {\n int i = 0, j = s.length() - 1;\n while (i < j) {\n if (s.charAt(i++) != s.charAt(j--)) {\n return false;\n }\n }\n return true;\n }\n\n private int countOnes(int v) {\n int i = 0;\n while (v != 0) {\n i++;\n v &= v - 1;\n }\n return i;\n } | 3 | 0 | ['Bitmask', 'Java'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [PYTHON] - Simple solution, backtracking✅ | python-simple-solution-backtracking-by-j-hngx | \nclass Solution:\n def maxProduct(self, s: str) -> int:\n self.answer = 0\n \n def dfs(i, word, word2):\n if i >= len(s):\n | just_4ina | NORMAL | 2021-09-12T04:22:47.360283+00:00 | 2021-09-17T23:35:45.486526+00:00 | 876 | false | ```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n self.answer = 0\n \n def dfs(i, word, word2):\n if i >= len(s):\n if word == word[::-1] and word2 == word2[::-1]:\n self.answer = max(len(word) * len(word2), self.answer)\n return\n \n dfs(i + 1, word + s[i], word2)\n dfs(i + 1, word, word2 + s[i])\n dfs(i + 1, word, word2)\n \n dfs(0, \'\', \'\')\n \n return self.answer\n``` | 3 | 1 | ['Backtracking', 'Recursion', 'Python', 'Python3'] | 4 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python [DP on subsequences] | python-dp-on-subsequences-by-gsan-4qrs | Let dp(sub) be a DP that finds longest palindromic subsequence on a given string sub. Caching intermediate results, this is done in linear time.\n\nWe need to s | gsan | NORMAL | 2021-09-12T04:09:20.283467+00:00 | 2021-09-12T05:28:17.702212+00:00 | 503 | false | Let `dp(sub)` be a DP that finds longest palindromic subsequence on a given string `sub`. Caching intermediate results, this is done in linear time.\n\nWe need to split into all possible subsets, on top of which we can apply DP. There are `2**12 = 4096` such splits at most, so we can cache the substrings.\n\nWe find the substrings using bitmask.\nGo only half length as the remaining is covered by symmetry. This cuts runtime in half.\n\n```python\nclass Solution:\n def maxProduct(self, s):\n @lru_cache(None)\n def dp(sub):\n if not sub:\n return 0\n if len(sub) == 1:\n return 1\n if len(sub) == 2:\n return 2 if sub[0] == sub[1] else 1\n if sub[0] == sub[-1]:\n return 2 + dp(sub[1:-1])\n return max(dp(sub[1:]), dp(sub[:-1]))\n \n ans = 0\n for mask in range(2**len(s) // 2):\n sub1 = \'\'\n sub2 = \'\'\n for j in range(len(s)):\n if (mask >> j) & 1:\n sub1 += s[j]\n else:\n sub2 += s[j]\n ans = max(ans, dp(sub1) * dp(sub2))\n return ans\n``` | 3 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [Python] Binary | python-binary-by-davidli-q18f | Binary\n- Step 1: find all palindromic subsequences\n- Step 2: for each pair of palindromic string, if there is no disjoint, calculate the product, update the m | davidli | NORMAL | 2021-09-12T04:02:41.000928+00:00 | 2021-09-12T04:10:28.610755+00:00 | 315 | false | Binary\n- Step 1: find all palindromic subsequences\n- Step 2: for each pair of palindromic string, if there is no disjoint, calculate the product, update the max product value\n\nTips to improve performance:\nUse binary to generate all possible subsequences,\ncache both the binary represent and length of the word\nif two word binary and is zero, there is no overlap\n\nfor exampe: for word "abcd"\n\n0100 means "b"\n0010 means "c"\n\n0100 & 0010 = 0, therefore, there is no overlap\n\nsame logic\n0100 means "b"\n0110 means "bc"\n0100 & 0110 != 0, thereforem, there is overlap\n\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n all_palindromic_subsequences = []\n \n n = len(s)\n \n def isPalindromic(word):\n l, r = 0, len(word) - 1\n while l <= r:\n if word[l] != word[r]:\n return False\n l += 1\n r -= 1\n return True\n \n for i in range(1 << n):\n cur = ""\n for j in range(n):\n if i & (1 << j) != 0:\n cur += s[j]\n if cur and isPalindromic(cur):\n all_palindromic_subsequences.append((i, len(cur)))\n \n mx = 0\n n = len(all_palindromic_subsequences)\n for i in range(n):\n for j in range(i + 1, n):\n b1, len1 = all_palindromic_subsequences[i]\n b2, len2 = all_palindromic_subsequences[j]\n if b1 & b2 == 0: \n cur_prod = len1 * len2\n mx = max(mx, cur_prod)\n return mx\n \n```\n | 3 | 2 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [C++] Brute force + DP explanation | c-brute-force-dp-explanation-by-code_rel-d3ss | Approach: \nstep1: Generate all subsequence in O(2^n) time (Note: we are storing indices not the characters while generating subsequence)\nstep2: Suppose one of | code_reload | NORMAL | 2021-09-12T04:01:20.244964+00:00 | 2021-09-12T04:10:47.744676+00:00 | 396 | false | **Approach:** \n*step1:* Generate all subsequence in O(2^n) time (Note: we are storing indices not the characters while generating subsequence)\n*step2:* Suppose one of the above subsequence is X. now first check if X is palindrome or not\n*step3:* If X is palindrome. Then get the remaining string i.e by deleting characters included in X from original string s in O(n) (as we know indices of character in X)\n*step 4:* from remaining string calculated above, find the length of longest palindromic subsequence present in it, which can be done in O(n^2) using Dynamic programming.\n\nOverall Time complexity is : O(2^n *n^2) \nwhich is good enough for n=12. \n\n```\nclass Solution {\n private:\n int ans; //to store final ans\n \n int max (int x, int y) { return (x > y)? x : y; }\n \n //find longest palindromic subsequence [Time:(O(n^2))]\n int lps(string& str)\n {\n int n = str.length();\n if(n<=1)return n;\n int i, j, cl;\n int L[n][n]; // Create a table to store results of subproblems\n\n // Strings of length 1 are palindrome of length 1\n for (i = 0; i < n; i++)\n L[i][i] = 1;\n for (cl=2; cl<=n; cl++){\n for (i=0; i<n-cl+1; i++){\n j = i+cl-1;\n if (str[i] == str[j] && cl == 2)\n L[i][j] = 2;\n else if (str[i] == str[j])\n L[i][j] = L[i+1][j-1] + 2;\n else\n L[i][j] = max(L[i][j-1], L[i+1][j]);\n }\n }\n\n return L[0][n-1];\n }\n \n \n bool isPal(string &x,vector<int>&v){ //check using indices present in v if they represent a palindromic sequence \n int l=0,h=v.size()-1;\n while(l<=h){\n if(x[v[l]]!=x[v[h]])return false;\n l++;\n h--;\n }\n return true;\n }\n \n \n void check(string &s,vector<int>&v){\n if((v.size()>0)&&(v.size()<s.size())&&!isPal(s,v))return; //return if indices present in vector v doesn\'t form a palindrome\n \n string res=""; //in res store all characters which are not included in vector v\n unordered_map<int,int> mp;\n for(auto i:v)mp[i]++;\n for(int i=0;i<s.length();i++){\n if(mp.count(i)==0)res+=s[i];\n }\n \n int l1=v.size(); \n int l2=lps(res); //get the length of longest palindromic subsequence present in res\n int currAns=l1*l2;\n ans=max(ans,currAns); //update ans\n }\n \n \n //Get all possible subsequence indicies in vector v [Time:(O(2^n))]\n void generateSequence(string &s,int i,vector<int> v){\n if(i==s.length()){\n check(s,v); //check for possible result\n return;\n }\n \n generateSequence(s,i+1,v); //don\'t include current character \n v.push_back(i);\n generateSequence(s,i+1,v); //include current character\n \n }\n \npublic:\n int maxProduct(string s) {\n ans=0; //initialize ans\n vector<int> v;\n generateSequence(s,0,v);\n return ans;\n }\n};\n``` | 3 | 2 | ['Dynamic Programming', 'Recursion', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Backtracking | backtracking-by-astha-poih | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | astha_ | NORMAL | 2025-01-03T08:43:37.204776+00:00 | 2025-01-03T08:43:37.204776+00:00 | 177 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isPal(string s){
int n=s.size();
for(int i=0;i<n/2;i++){
if(s[i]!=s[n-i-1]){
return false;
}
}
return true;
}
void recurse(string s,string s1,string s2,int ind,int& maxi,int n){
if(ind==n){
if(isPal(s1) && isPal(s2)){
maxi=max(maxi,(int)(s1.size()*s2.size()));
}
return;
}
//choice 1 no selection
recurse(s,s1,s2,ind+1,maxi,n);
//choice 2 include in s1
s1.push_back(s[ind]);
recurse(s,s1,s2,ind+1,maxi,n);
s1.pop_back(); //Backtracking
//choice 3 include in s2
s2.push_back(s[ind]);
recurse(s,s1,s2,ind+1,maxi,n);
s2.pop_back();
}
int maxProduct(string s) {
string s1="",s2="";
int maxi=0,n=s.size();
recurse(s,s1,s2,0,maxi,n); //Staring from 0 th index
return maxi;
}
};
``` | 2 | 0 | ['C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Bit Masking|| Dynamic Programming|| Faster then 94% of C++ users | bit-masking-dynamic-programming-faster-t-ai9i | Complexity\n- Time complexity:O(2^(2N))\n Add your time complexity here, e.g. O(n) \n\n# Code\n\nclass Solution {\npublic:\n bool palindrome(string &s) {\n | baarsh2307 | NORMAL | 2024-07-10T09:01:38.661435+00:00 | 2024-07-10T09:01:38.661474+00:00 | 124 | false | # Complexity\n- Time complexity:O(2^(2N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool palindrome(string &s) {\n int i = 0;\n int j = s.length() - 1;\n while (i < j) {\n if (s[i] != s[j])\n return false;\n i++;\n j--;\n }\n return true;\n }\n\n int maxProduct(string s) {\n int n = s.length();\n int mask = 1 << n;\n vector<pair<string, int>> pSubs;\n \n // Generate all subsequences and check if they are palindromes\n for (int i = 0; i < mask; i++) {\n string s2 = "";\n for (int j = 0; j < n; j++) {\n if ((1 << j) & i) {\n s2.push_back(s[j]);\n }\n }\n if (palindrome(s2)) {\n pSubs.push_back({s2, i});\n }\n }\n \n int x = pSubs.size();\n int maxProduct = 0;\n \n \n for (int i = 0; i < x; i++) {\n for (int j = i + 1; j < x; j++) {\n int mask1 = pSubs[i].second;\n int mask2 = pSubs[j].second;\n \n if ((mask1 & mask2) == 0) {\n int product = pSubs[i].first.size() * pSubs[j].first.size();\n maxProduct = max(maxProduct, product);\n }\n }\n }\n \n return maxProduct;\n }\n};\n\n``` | 2 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'C++'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [Java] DP with clear explanation - O(n*2^n) beats 89% | java-dp-with-clear-explanation-on2n-beat-gxqd | Intuition\nThere are multiple ways to approach this problem:\n1. Find all subsequences, then for any 2, check if they overlap, get get product. Time complexity | zttttt | NORMAL | 2023-04-16T04:30:32.425646+00:00 | 2023-04-16T04:30:32.425689+00:00 | 913 | false | # Intuition\nThere are multiple ways to approach this problem:\n1. Find all subsequences, then for any 2, check if they overlap, get get product. Time complexity O(2^n * 2^n * n) = O(n * 4^n).\n2. Divide s to 2 subsequences - for each character, either assign to seq1, or seq2, or discard. now for seq1 and seq2 check if they are palindrome and get product. Time complexity O(n * 3^n). We have 3^n because each character can be in seq1, seq2, or discarded.\n3. Go through all 2^n subsequences. Everytime, for the remaining unpicked characters, treat them as string, then apply DP solution in LC516 "Longest Palindromic Subsequence". Time complexity is O(n^2 * 2^n).\n4. Consolidate solving "Longest Palindromic Subsequence" of all 2^n subsequences together using DP (as a preprocessing). Then from this result we can easily get max product. Time complexity is O(n * 2^n). See details below.\n\n# Approach\nFor all 2^n subsequences, calculate the longest palindromic subsequence of each.\n\nThis can be done with dynamic programming. For example, for s = "leetcode", for sequence 01100101, i.e. "eeoe", we have **recursive relationship**:\n```\npalSubSeq(01100101) = max{\n 2 + palSubSeq(00100100),\n palSubSeq(00100101),\n palSubSeq(01100100),\n}\n```\n\nAfter we have palSubSeq[] for all 2^n subsequences, we can calculate max product in this way: go through all seq1 (from 0000000 to 1111111), note its flip-sequence is seq2 = 2^n - 1 - seq1. So product is `palSubSeq[seq1] * palSubSeq[2^n - 1 - seq1]`\n\nCoding-wise, mean challenge is to calculate the DP table palSubSeq[]. We use recursion + memoization here. First we use backtrack to get to all 2^n subsequences. Then for each subsequence, we apply the recursive relationship, and use memoization to avoid duplicate calculation.\n\n# Complexity\n- Time complexity: `O(n * 2^n)`\n\n- Space complexity: `O(2^n)`\n\n# Code\n```\nclass Solution {\n public int maxProduct(String s) {\n // 2^n total possible subsequences\n // first calculate longest palindrome subseq for each possible subsequence\n // then calculate product\n\n int length = s.length(); // this is n\n int count = (int)(Math.pow(2, length)); // this is 2^n\n\n // the memoization table to store longest palindrome subseq, of all possible subseq\n // for example, for s="leetcode", palSubSeq[00001011] stores the longest palindrome subseq of sequence "cde"\n // because there are totally 2^n possible subsequences, the table size is 2^n (note n<=12 so this size <= 4096)\n int[] palSubSeq = new int[count];\n // base case: single characters\n for (int bitIndex = 1; bitIndex < count; bitIndex *= 2) {\n palSubSeq[bitIndex] = 1;\n }\n\n // use bitmask to do backtracking\n boolean[] bitmask = new boolean[length];\n for (int i = 0; i < length; i++) {\n bitmask[i] = false;\n }\n // calculate the palSubSeq[] table\n palSubSeqBacktrack(s, bitmask, 0, palSubSeq);\n\n // get max product using palSubSeq[]\n // for any subsequence mask, its flip is 2^n - 1 - mask\n // for example, 00001011\'s flip is 11110100\n int maxProduct = 0;\n for (int i = 0; i < count / 2; i++) {\n int product = palSubSeq[i] * palSubSeq[count - i - 1];\n if (product > maxProduct) {\n maxProduct = product;\n }\n }\n return maxProduct;\n }\n\n // 2 stages of recursion calls\n // stage 1. use backtracking just to get to all 2^n subsequences\n private static void palSubSeqBacktrack(String s, boolean[] bitmask, int processingIndex, int[] palSubSeq) {\n if (processingIndex < bitmask.length) {\n // backtrack to bottom\n bitmask[processingIndex] = true;\n palSubSeqBacktrack(s, bitmask, processingIndex + 1, palSubSeq);\n bitmask[processingIndex] = false;\n palSubSeqBacktrack(s, bitmask, processingIndex + 1, palSubSeq);\n return;\n }\n\n // at bottom, call stage 2\n palSubSeqRecur(s, bitmask, palSubSeq);\n }\n\n // stage 2, for all subsequences, do recursion call + memoization. this could be changed to iterative\n private static int palSubSeqRecur(String s, boolean[] bitmask, int[] palSubSeq) {\n int bitIndex = bitmaskToIndex(bitmask);\n if (bitIndex == 0) {\n return 0;\n }\n if (palSubSeq[bitIndex] != 0) {\n return palSubSeq[bitIndex];\n }\n\n // all-0\'s should be handled above\n // single characters should have been filled in as base case\n // starting here it should have at least 2 characters (2 one\'s in the bitmask)\n int firstOneIndex;\n for (firstOneIndex = 0; firstOneIndex < bitmask.length; firstOneIndex++) {\n if (bitmask[firstOneIndex]) {\n break;\n }\n }\n int lastOneIndex;\n for (lastOneIndex = bitmask.length - 1; lastOneIndex >= 0; lastOneIndex--) {\n if (bitmask[lastOneIndex]) {\n break;\n }\n }\n\n int max = 0;\n // maxPalSubseq(001110011) = max{\n // 2 + maxPalSubseq(000110010) if s[2]==s[8],\n // maxPalSubseq(000110011),\n // maxPalSubseq(001110010),\n // }\n if (s.charAt(firstOneIndex) == s.charAt(lastOneIndex)) {\n bitmask[firstOneIndex] = false;\n bitmask[lastOneIndex] = false;\n max = 2 + palSubSeqRecur(s, bitmask, palSubSeq);\n }\n\n bitmask[firstOneIndex] = false;\n bitmask[lastOneIndex] = true;\n int altMax1 = palSubSeqRecur(s, bitmask, palSubSeq);\n\n bitmask[firstOneIndex] = true;\n bitmask[lastOneIndex] = false;\n int altMax2 = palSubSeqRecur(s, bitmask, palSubSeq);\n\n bitmask[firstOneIndex] = true;\n bitmask[lastOneIndex] = true;\n if (altMax1 > max) {\n max = altMax1;\n }\n if (altMax2 > max) {\n max = altMax2;\n }\n palSubSeq[bitIndex] = max;\n return max;\n }\n\n private static int bitmaskToIndex(boolean[] bitmask) {\n int length = bitmask.length;\n int number = 0;\n for (int i = 0; i < length; i++) {\n number = bitmask[i] ? (number * 2 + 1) : (number * 2);\n }\n return number;\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Backtracking', 'Java'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | ✔ C++ Beginner Friendly Recursive Solution ✔ Explained in Detail | c-beginner-friendly-recursive-solution-e-cqn1 | Time Taken : 1732ms Faster than 28.54%\nNOTE : Please someone help me detrmine the time complexity of the given code\n\nAPPROACH :\n Generating all possible pal | ayushman_sinha | NORMAL | 2023-04-14T06:11:57.285078+00:00 | 2023-04-14T06:17:33.468596+00:00 | 1,642 | false | **Time Taken : 1732ms Faster than 28.54%**\nNOTE : Please someone help me detrmine the time complexity of the given code\n\n**APPROACH :**\n* Generating all possible palindromic subsequence of the given string BUT instead of storing the string, I am storing the index of the subsequence thus formed into a vector.\n* For checking whether the subsequence is a PALINDROME or not , I can just use the index from the vector.\n* Storing the vector [ containing index of palindromic subsequence] into a 2D vector.\n* All possible cases are generated.\n* If two subsequences are valid and their product are greater than our maxProduct then we update our maxProduct.\n\n```\nclass Solution {\npublic:\n vector<vector<int>>ar;\n bool check(vector<int>&a,vector<int>&b){ \n for(int i=0;i<a.size();i++)\n for(int j=0;j<b.size();j++)\n if(a[i]==b[j]) return false;\n return true;\n }\n bool isPalin(string &s,vector<int>&ans){\n int a=0,b=ans.size()-1;\n while(a<=b){\n if(s[ans[a]]!=s[ans[b]]) return false;\n a++;\n b--;\n }\n return true; \n }\n void calc(string &s,vector<int>&ans,int i){\n if(isPalin(s,ans))\n ar.push_back(ans);\n \n if(i>=s.length()) return;\n ans.push_back(i);\n calc(s,ans,i+1);\n ans.pop_back();\n calc(s,ans,i+1);\n }\n int maxProduct(string s) {\n int ans=0;\n vector<int>a;\n calc(s,a,0);\n for(int i=0;i<ar.size();i++){\n for(int j=i+1;j<ar.size();j++){ \n int x=(int)ar[i].size()*ar[j].size();\n if(x>ans&&check(ar[i],ar[j])) \n ans=x;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Backtracking', 'Recursion', 'C', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | JAVA || Memoization || Optimal Solution || Easy Soltion | java-memoization-optimal-solution-easy-s-pjnd | \n\nclass Solution {\n \n int ans = 1;\n \n public int maxProduct(String s) {\n \n int[][] dp = new int[s.length() + 1][s.length() + | saswati10 | NORMAL | 2023-01-20T13:55:13.127734+00:00 | 2023-01-20T13:55:13.127788+00:00 | 541 | false | \n```\nclass Solution {\n \n int ans = 1;\n \n public int maxProduct(String s) {\n \n int[][] dp = new int[s.length() + 1][s.length() + 1];\n \n for(int[] d: dp)\n Arrays.fill(d, -1);\n \n int res = solve(s, "", "", 0, dp);\n \n return res;\n \n }\n public int solve(String s, String s1, String s2, int i, int[][] dp)\n {\n int s1l = s1.length();\n int s2l = s2.length();\n \n \n\n if(isPali(s1) && isPali(s2))\n {\n ans = Math.max(ans, s1.length()*s2.length());\n }\n \n dp[s1l][s2l] = ans;\n \n \n if(i >= s.length())\n {\n return dp[s1l][s2l];\n }\n \n int op1 = solve(s, s1 + s.charAt(i), s2, i + 1, dp);\n int op2 = solve(s, s1, s2 + s.charAt(i), i + 1, dp);\n int op3 = solve(s, s1, s2, i + 1, dp);\n \n return dp[s1l][s2l];\n }\n public boolean isPali(String s)\n {\n int i = 0;\n int j = s.length() - 1;\n while(i < j)\n {\n if(s.charAt(i) != s.charAt(j))\n return false;\n i++;\n j--;\n }\n return true;\n }\n}\n``` | 2 | 0 | ['Java'] | 2 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ Backtrack | c-backtrack-by-rishabhsinghal12-8u1o | \nclass Solution {\npublic:\n int ans;\n void dfs(int i, string& s, string& s1, string& s2){\n \n if(i == size(s)){\n \n | Rishabhsinghal12 | NORMAL | 2023-01-07T13:53:22.929548+00:00 | 2023-01-07T13:53:22.929589+00:00 | 484 | false | ```\nclass Solution {\npublic:\n int ans;\n void dfs(int i, string& s, string& s1, string& s2){\n \n if(i == size(s)){\n \n ans = max(ans, (isPal(s1) * isPal(s2)) );\n \n return;\n }\n \n // choose ith character for s1 (not for s2)\n \n s1.push_back(s[i]);\n dfs(i+1, s, s1, s2);\n \n //backtrack\n \n s1.pop_back();\n \n // choose ith character for s2 (not for s1)\n \n s2.push_back(s[i]);\n dfs(i+1, s, s1, s2);\n s2.pop_back();\n dfs(i+1, s, s1, s2);\n }\n int maxProduct(string& s) {\n \n ans = 0;\n string s1 = "",s2 = "";\n dfs(0, s, s1, s2);\n \n return ans;\n \n }\n private:\n int isPal(string& s) {\n \n int n = size(s);\n int i = 0, j = n-1;\n \n while(i <= j){\n \n if(s[i++] != s[j--]){\n \n return 0;\n }\n }\n \n return n;\n }\n};\n``` | 2 | 0 | ['Backtracking', 'C', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Java Bitmask + HashMap solution | java-bitmask-hashmap-solution-by-aasthas-fqi3 | \nclass Solution {\n\n //using bitmask\n public int maxProduct(String s) {\n \n if(s.length() == 2) {\n return 1;\n }\n \n | aasthasmile | NORMAL | 2022-09-25T23:47:30.469556+00:00 | 2022-09-25T23:47:30.469590+00:00 | 698 | false | ```\nclass Solution {\n\n //using bitmask\n public int maxProduct(String s) {\n \n if(s.length() == 2) {\n return 1;\n }\n \n int n = s.length();\n char[] ch = s.toCharArray();\n \n //bitmask to the length map\n Map<Integer, Integer> bitMasktoLengthMap = new HashMap<>();\n \n //using bitmask , calculate all the bitmask for 1 to 2^N\n // 1, 2, 3,............2024 ( 2 ^ 11 )\n for(int bitmask = 1 ; bitmask< Math.pow(2, n) ;bitmask++){\n \n //find all the subsequence(s) in the string using bitmask\n StringBuilder subsequence = new StringBuilder();\n for(int j = 0; j < n; j++ ){\n \n //if one of the bit is set to 1, then append that character to the subsequence.\n if(( bitmask & (1 << j ) ) != 0) { \n subsequence.append(ch[j]); //constructing subsequence of different length\n }\n }\n \n //if the sequence constructed above is a palindrome,\n // then store the mask and its length .\n if(isPalindrome(subsequence.toString().toCharArray())){\n bitMasktoLengthMap.put(bitmask, subsequence.length());\n }\n }\n \n Set<Integer> allBitMasks = bitMasktoLengthMap.keySet();\n \n int maxProduct = Integer.MIN_VALUE;\n for( int mask1 : allBitMasks){\n \n for( int mask2 : allBitMasks){\n \n //product of lengths of 2 disjoint palindromic subsequence(s)\n //if product of AND operation is 0 then subsequnce(s) are DIS-JOINT\n if(( mask1 & mask2 ) == 0){\n int product = bitMasktoLengthMap.get(mask1) * bitMasktoLengthMap.get(mask2);\n maxProduct = Math.max(maxProduct, product);\n }\n }\n }\n \n \n return maxProduct;\n }\n \n private boolean isPalindrome( char[] chars ) {\n \n int i = 0;\n int j = chars.length - 1;\n \n if(i == j)\n return true;\n \n while(i < j){\n if(chars[i] != chars[j]){\n return false;\n }\n i++;\n j--;\n }\n \n return true;\n }\n}\n```\n\nSteps :\n\n1. In order to find all the subsequence , we will use the bitmask from 1 to 2^ N .\n2. We will do AND operation to find the bit which is set ( bitmask & (1 << j ) ) != 0) then it means bit is SET.\n3. We will construct all the subsequence in this way for a sting of lengt N.\n4. Then we will check if the string is palindrome ( same from backward and forward ).\n5. If string is palindrome, then add the "bitmask" and its length to the map.\n6. At end , we need to check ( key1 & key2 ) gives a zero , which means palindromic subsequence is disjoint i.e. they have no bit in common to each other. \n7. If ( key1 & key2 ) == 0 , then we calculate product of their length ( value1 * value 2 ).\n8. We find the maximum value from multiple set(s) of ( value1 * value 2 ).\n | 2 | 0 | ['Bit Manipulation', 'Bitmask', 'Java'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python 3 without Bitmask, Simple Backtracking + DP approach | python-3-without-bitmask-simple-backtrac-zd6x | \nclass Solution:\n def maxProduct(self, s: str) -> int:\n sz, ans, s1, s2 = len(s), 0, \'\', \'\'\n \n @lru_cache(None)\n def so | hemantdhamija | NORMAL | 2022-09-21T11:43:50.052074+00:00 | 2022-09-21T11:43:50.052119+00:00 | 410 | false | ```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n sz, ans, s1, s2 = len(s), 0, \'\', \'\'\n \n @lru_cache(None)\n def solve(i: int, s1: str, s2: str) -> None:\n nonlocal ans, s\n if i >= sz:\n if s1 == s1[::-1] and s2 == s2[::-1]:\n ans = max(ans, len(s1) * len(s2))\n return\n solve(i + 1, s1, s2)\n s1_pick, s2_pick = s1 + s[i], s2 + s[i]\n solve(i + 1, s1_pick, s2)\n solve(i + 1, s1, s2_pick)\n \n solve(0, s1, s2)\n return ans\n``` | 2 | 0 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'Python'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | c++|bitmasking | cbitmasking-by-priyanshudeep-d7tt | class Solution {\npublic:\n int maxProduct(string s) {\n map m; //\n int n=s.length();\n \n for(int mask=1;mask<(1<<n);ma | priyanshudeep | NORMAL | 2022-07-13T14:34:47.555316+00:00 | 2022-07-13T14:34:47.555373+00:00 | 137 | false | class Solution {\npublic:\n int maxProduct(string s) {\n map<int ,int> m; //<bitmask,length>\n int n=s.length();\n \n for(int mask=1;mask<(1<<n);mask++)\n {\n string subseq="";\n for(int i=0;i<n;i++)\n {\n if(mask & (1<<i))\n {\n subseq+=s[i];\n }\n }\n string chk=subseq;\n reverse(chk.begin(),chk.end());\n if((subseq)==chk)\n {\n m[mask]=subseq.length();\n }\n \n }\n int ans=0;\n for(auto m1:m)\n {\n for(auto m2:m)\n {\n if(((m1.first)&(m2.first))==0)\n ans=max(ans,(m1.second)*(m2.second));\n \n }\n }\n return ans;\n }\n}; | 2 | 0 | ['Bitmask'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | ✅✅ C++ || BACKTRACKING || EXPLAINED | c-backtracking-explained-by-bhomik23-wbzb | ```\n/\nwe will try out all possibilities through recursion \nbase condition will be where we would have \ntraversed through the whole string , \nthis is the po | bhomik23 | NORMAL | 2022-07-09T09:26:32.334754+00:00 | 2022-08-22T13:14:06.194624+00:00 | 170 | false | ```\n/*\nwe will try out all possibilities through recursion \nbase condition will be where we would have \ntraversed through the whole string , \nthis is the point where we will check whether\nour 2 subsequences are palindromic , and \nif yes , then we will compare the product \nof the lengths of 2 strings with our ans\n\n\nrecurrence realation will contain three recursive calls , \nfirst for not inlcuding s[i] in both the strings \nsecond for inlcuding s[i] in the string s1\nthird for inlcuding s[i] in the string s2\n\nand we will get our ans recursively\n\n*/\nclass Solution {\npublic:\n bool ispalindrome(string s){\n int i = 0,j = s.size()-1;\n while(i<j){\n if(s[i]!=s[j]) return false;\n i++;\n j--;\n }\n return true;\n}\n \n void solve(string &s , string &s1 , string &s2 , int i , int &ans){\n if(i>=s.size()){\n if(ispalindrome(s1) && ispalindrome(s2)){\n int x=s1.size()*s2.size();\n ans=max(ans,x);\n \n }\n return ;\n }\n \n//******************************************************************************* \n \n // here we have not used backtracking , \n //but here we will not able to use &s1/&s2 ,\n //ie reference based addressing , and \n //therefore a new copy of s1 and s2 will be made each time\n //, resulting in TLE\n \n// // we dont add in either of the strings\n// solve(s,s1,s2,i+1,ans);\n \n// // adding in s1;\n// solve(s,s1+s[i],s2,i+1,ans);\n \n// // adding in s2\n// solve(s,s1,s2+s[i],i+1,ans);\n//******************************************************************************* \n\n // we dont add in either of the strings\n solve(s,s1,s2,i+1,ans);\n \n //pic in first string s1\n s1.push_back(s[i]);\n solve(s,s1,s2,i+1,ans);\n s1.pop_back();\n\n //pic in second string s2\n s2.push_back(s[i]);\n solve(s,s1,s2,i+1,ans);\n s2.pop_back();\n \n }\n\n int maxProduct(string s) {\n string s1="";\n string s2="";\n int ans=0;\n solve(s,s1,s2,0,ans);\n return ans;\n }\n}; | 2 | 0 | ['Backtracking', 'Recursion', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python | Dynamic Programming | Memoization | python-dynamic-programming-memoization-b-ng4s | \nclass Solution:\n def maxProduct(self, s: str) -> int:\n \n N = len(s)\n memo = {}\n \n def isValidPalindrom(word):\n | k1729g | NORMAL | 2022-04-21T07:33:39.244124+00:00 | 2022-04-21T07:33:39.244153+00:00 | 388 | false | ```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n \n N = len(s)\n memo = {}\n \n def isValidPalindrom(word):\n left, right = 0, len(word)-1\n while (left < right):\n if word[left] != word[right]: return False\n left += 1\n right -= 1\n \n return True\n \n def backTrack(i, word1, word2):\n \n if i > N: return float(\'-inf\')\n \n if i == N:\n isBothValidPalindrome = isValidPalindrom(word1) and isValidPalindrom(word2)\n return len(word1)*len(word2) if isBothValidPalindrome else float(\'-inf\')\n \n key = (i,word1, word2)\n \n if key in memo: return memo[key]\n \n memo[key] = max([\n backTrack(i+1, word1+s[i], word2),\n backTrack(i+1, word1, word2+s[i]), \n backTrack(i+1, word1, word2)\n ])\n \n return memo[key]\n \n return backTrack(0,"","")\n\n``` | 2 | 1 | ['Dynamic Programming', 'Memoization', 'Python'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | All 3 Solutions | Brute | Optimizations | Clean and Concise | Bits | all-3-solutions-brute-optimizations-clea-pyi8 | 1. Using Bits as a visitied array total brute force\n\n\nclass Solution {\npublic:\n bool check(string &s){\n int i=0,j=s.size()-1;\n \n | njcoder | NORMAL | 2022-03-18T11:17:13.398009+00:00 | 2022-03-18T11:22:59.460459+00:00 | 314 | false | #### **1. Using Bits as a visitied array total brute force**\n\n```\nclass Solution {\npublic:\n bool check(string &s){\n int i=0,j=s.size()-1;\n \n while(i < j){\n if(s[i] != s[j]) return false;\n i++;\n j--;\n }\n return true;\n }\n int fun2(int i,int vis_,int vis,string &s){\n \n if(i == s.size()){\n \n string tmp;\n \n for(int i=0;i<s.size();i++){\n int mask = (1 << i);\n if((mask & vis_) != 0){\n tmp.push_back(s[i]);\n }\n }\n if(check(tmp)) return tmp.size();\n return 0;\n }\n \n \n int mask = (1 << i);\n \n if((mask & vis) == 0){\n int left = fun2(i+1,vis_|mask,vis|mask,s);\n int right = fun2(i+1,vis_,vis,s);\n return max(left,right);\n }\n return fun2(i+1,vis_,vis,s);\n }\n \n int fun1(int i,int vis,string &s){\n \n int n = s.size();\n if(i == n){\n \n int len = fun2(0,0,vis,s);\n \n string tmp;\n \n for(int i=0;i<s.size();i++){\n int mask = (1 << i);\n if((mask & vis) != 0){\n tmp.push_back(s[i]);\n }\n }\n if(check(tmp)){\n return (len)*(tmp.size()); \n }\n return 0;\n } \n \n \n int mask = (1 << i);\n int left = fun1(i+1,mask | vis,s);\n int right = fun1(i+1,vis,s);\n \n return max(left,right);\n \n }\n \n int maxProduct(string s) {\n return fun1(0,0,s);\n \n }\n\t\n```\n\n### 2. Using Longest Common Subsequence\n\n```\n\tclass Solution {\npublic:\n vector<vector<int>> dp;\n int LCS(int i,int j,string &s1,string &s2){\n \n int n1 = s1.size();\n int n2 = s2.size();\n \n if(i == n1 or j == n2){\n return 0;\n }\n if(dp[i][j] != -1) return dp[i][j];\n if(s1[i] == s2[j]){\n return dp[i][j] = 1 + LCS(i+1,j+1,s1,s2);\n }\n \n return dp[i][j] = max(LCS(i+1,j,s1,s2),LCS(i,j+1,s1,s2));\n \n }\n \n int LPS(string &s){\n string t = s;\n reverse(s.begin(),s.end());\n dp = vector<vector<int>> (s.size(),vector<int> (s.size(),-1));\n return LCS(0,0,s,t);\n }\n\n int fun1(int i,int vis,string &s){\n \n int n = s.size();\n if(i == n){\n string s1,s2;\n for(int j=0;j<n;j++){\n int mask = (1 << j);\n if((vis & mask ) == 0){\n s2.push_back(s[j]);\n }else{\n s1.push_back(s[j]);\n }\n } \n return LPS(s1)*LPS(s2);\n } \n \n int mask = (1 << i);\n int left = fun1(i+1,mask | vis,s);\n int right = fun1(i+1,vis,s);\n \n return max(left,right);\n \n }\n \n int maxProduct(string s) {\n int n = s.size();\n return fun1(0,0,s);\n }\n};\n\n```\n\n### 3. Using Longest Palindromic Subsequence\n\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n \n int LPS_(int i,int j,string &s){\n \n if(i > j) return 0;\n if(i==j) return 1;\n if(dp[i][j] != -1) return dp[i][j];\n if(s[i] == s[j]){\n return dp[i][j] = 2 + LPS_(i+1,j-1,s);\n }\n return dp[i][j] = max(LPS_(i+1,j,s),LPS_(i,j-1,s));\n }\n \n int LPS(string &s){\n dp = vector<vector<int>> (s.size(),vector<int> (s.size(),-1));\n return LPS_(0,s.size()-1,s);\n }\n\n int fun1(int i,int vis,string &s){\n \n int n = s.size();\n if(i == n){\n string s1,s2;\n for(int j=0;j<n;j++){\n int mask = (1 << j);\n if((vis & mask ) == 0){\n s2.push_back(s[j]);\n }else{\n s1.push_back(s[j]);\n }\n } \n return LPS(s1)*LPS(s2);\n } \n \n int mask = (1 << i);\n int left = fun1(i+1,mask | vis,s);\n int right = fun1(i+1,vis,s);\n \n return max(left,right);\n \n }\n \n int maxProduct(string s) {\n int n = s.size();\n return fun1(0,0,s);\n }\n};\n\t\n}; | 2 | 0 | ['Dynamic Programming', 'Recursion'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | DFS C++| backtracking | dfs-c-backtracking-by-sameer_111-d61c | class Solution {\npublic:\n void dfs(string &s,int i,string &s1,string &s2,int &c){ \n \n\t if(i>=s.size()){\n if(ispalindrome(s1) && ispa | Sameer_111 | NORMAL | 2022-02-12T06:19:16.115705+00:00 | 2022-02-12T06:19:16.115737+00:00 | 198 | false | class Solution {\npublic:\n void dfs(string &s,int i,string &s1,string &s2,int &c){ \n \n\t if(i>=s.size()){\n if(ispalindrome(s1) && ispalindrome(s2)){\n int x = s1.size()*s2.size();\n c = max(x,c);\n }\n return;\n }\n //not pic any \n dfs(s,i+1,s1,s2,c);\n \n //pic in first string s1\n s1.push_back(s[i]);\n dfs(s,i+1,s1,s2,c);\n s1.pop_back();\n \n //pic in second string s2\n s2.push_back(s[i]);\n dfs(s,i+1,s1,s2,c);\n s2.pop_back();\n \n }\n bool ispalindrome(string s){\n int i = 0,j = s.size()-1;\n while(i<j){\n if(s[i]!=s[j]) return false;\n i++;\n j--;\n }\n return true;\n }\n int maxProduct(string s) {\n string s1 = "",s2 = "";\n int c = 0;\n dfs(s,0,s1,s2,c);\n return c;\n }\n}; | 2 | 0 | ['Backtracking', 'Depth-First Search', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | My Java Solution using recursion | my-java-solution-using-recursion-by-vroh-5m59 | \nclass Solution {\n \n private int maxProduct = -1;\n \n public int maxProduct(String s) {\n if (s == null || s.length() <= 1) {\n | vrohith | NORMAL | 2021-09-28T18:38:55.727832+00:00 | 2021-09-28T18:38:55.727877+00:00 | 360 | false | ```\nclass Solution {\n \n private int maxProduct = -1;\n \n public int maxProduct(String s) {\n if (s == null || s.length() <= 1) {\n return 0;\n }\n int length = s.length();\n if (length == 1) {\n return 1;\n }\n List<Character> word1 = new ArrayList<>();\n List<Character> word2 = new ArrayList<>();\n recursionHelper(s, 0, word1, word2);\n return maxProduct;\n }\n \n public void recursionHelper(String s, int currentIndex, List<Character> word1, List<Character> word2) {\n if (currentIndex >= s.length()) {\n // update the maxProduct by checking the palindrome\n if (isPalindrome(word1) && isPalindrome(word2)) {\n int length1 = word1.size();\n int length2 = word2.size();\n maxProduct = Math.max(maxProduct, length1 * length2);\n }\n return;\n }\n // otherwise consider other cases\n word1.add(s.charAt(currentIndex));\n recursionHelper(s, currentIndex + 1, word1, word2);\n // undo\n word1.remove(word1.size() - 1);\n // try the other possiblity with word2\n word2.add(s.charAt(currentIndex));\n recursionHelper(s, currentIndex + 1, word1, word2);\n // undo\n word2.remove(word2.size() - 1);\n // try possiblity without adding the char at index to both word1 and word2\n recursionHelper(s, currentIndex + 1, word1, word2);\n }\n \n public boolean isPalindrome(List<Character> word) {\n int size = word.size();\n int left = 0;\n int right = size - 1;\n while (left < right) {\n if (word.get(left++) != word.get(right--)) {\n return false;\n }\n }\n return true;\n }\n}\n``` | 2 | 1 | ['Recursion', 'Java'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | c++ backtracking solution | c-backtracking-solution-by-divkr98-te0e | \n\n#include<bits/stdc++.h>\nusing namespace std;\nint ans;\n\nbool ispal(string &s)\n{\n int i = 0 , j = s.length() - 1;\n while(i < j){\n if(s[i] | divkr98 | NORMAL | 2021-09-26T12:52:04.331586+00:00 | 2021-09-26T12:52:04.331621+00:00 | 264 | false | ```\n\n#include<bits/stdc++.h>\nusing namespace std;\nint ans;\n\nbool ispal(string &s)\n{\n int i = 0 , j = s.length() - 1;\n while(i < j){\n if(s[i] != s[j]) return false;\n ++i;\n --j;\n }\n return true;\n}\n\nvoid solve(int index , string &s , string &s1, string &s2)\n{\n\n /// add this char to s1 or s2 or skip.\n if(ispal(s1) and ispal(s2))\n {\n int len1 = s1.length();\n int len2 = s2.length();\n int len = len1 * len2;\n ans = max(ans , len);\n }\n if(index == s.length()) return;\n s1 = s1 + s[index];\n solve(index + 1 , s , s1 , s2);\n s1.pop_back();\n s2 = s2 + s[index];\n solve(index + 1, s , s1 , s2);\n s2.pop_back();\n solve(index + 1 , s , s1 , s2);\n}\n\nclass Solution {\npublic:\n int maxProduct(string s) {\n ans = 0;\n string s1 = "" , s2 = "" ;\n solve(0 , s, s1 , s2);\n return ans; \n }\n};\n\n``` | 2 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Backtracking | explained solution | c++ | backtracking-explained-solution-c-by-cra-jn7b | just see the constraint for this question its very small so this signifies that this will be a backtracking question.\n\nlets assume my s1 will have the 1st pal | crabbyD | NORMAL | 2021-09-14T19:37:25.867016+00:00 | 2021-09-14T19:37:25.867049+00:00 | 151 | false | just see the constraint for this question its very small so this signifies that this will be a backtracking question.\n\nlets assume my s1 will have the 1st palindrome string and s2 will have the second one.\n\ni am finding the max of a,b,c where a denotes when i am not not adding any values.\nb denotes i am pushing value in s1 \nc denotes i am pushing value in s2;\n\nthe required answer will be the max of (a,b,c)\n\n\n\n\n```\n int palinlen (string &a)\n {\n int i=0;\n int j=a.length()-1;\n while(i<j)\n {\n if(a[i]!=a[j])return 0;\n i++;\n j--;\n }\n return a.length();\n }\n \n \n int helper(string &a,string &b,string &s,int i)\n {\n if(i>=s.length())return palinlen(a)*palinlen(b);\n \n int x=helper(a,b,s,i+1);\n \n a.push_back(s[i]);\n int y=helper(a,b,s,i+1);\n a.pop_back();\n \n b.push_back(s[i]);\n int z=helper(a,b,s,i+1);\n b.pop_back();\n return max(x,max(y,z));\n \n }\n int maxProduct(string s) {\n string a="";\n string b="";\n return helper(a,b,s,0);\n }\n```\n\n\nplease upvote if you liked my solution.\n#happy_coding | 2 | 0 | ['Backtracking', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | a few solutions | a-few-solutions-by-claytonjwong-p7wm | Let A and B be the first and second candidate palindrome strings correspondingly. Perform DFS + BT considering all possibilities for each character s[i]:\n\n1. | claytonjwong | NORMAL | 2021-09-13T13:35:11.381646+00:00 | 2021-09-14T22:35:55.331352+00:00 | 57 | false | Let `A` and `B` be the first and second candidate palindrome strings correspondingly. Perform DFS + BT considering all possibilities for each character `s[i]`:\n\n1. `s[i]` is included in `A`\n2. `s[i]` is included in `B`\n3. `s[i]` is *not* included in `A` or `B`\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun maxProduct(s: String): Int {\n var best = 0\n var ok = { A: MutableList<Char> -> A == A.reversed() }\n fun go(i: Int = 0, A: MutableList<Char> = mutableListOf<Char>(), B: MutableList<Char> = mutableListOf<Char>()) {\n if (ok(A) && ok(B))\n best = Math.max(best, A.size * B.size)\n if (i == s.length)\n return\n A.add(s[i])\n go(i + 1, A, B)\n A.removeAt(A.lastIndex)\n B.add(s[i])\n go(i + 1, A, B)\n B.removeAt(B.lastIndex)\n go(i + 1, A, B)\n }\n go()\n return best\n }\n}\n```\n\n*Javascript*\n```\nlet maxProduct = (s, best = 0) => {\n let ok = A => A.join(\'\') == [...A].reverse().join(\'\');\n let go = (i = 0, A = [], B = []) => {\n if (ok(A) && ok(B))\n best = Math.max(best, A.length * B.length);\n if (i == s.length)\n return;\n A.push(s[i]);\n go(i + 1, A, B);\n A.pop();\n B.push(s[i]);\n go(i + 1, A, B);\n B.pop();\n go(i + 1, A, B);\n };\n go();\n return best;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def maxProduct(self, s: str, best = 0) -> int:\n ok = lambda A: A == A[::-1]\n def go(i = 0, A = [], B = []):\n nonlocal best\n if ok(A) and ok(B):\n best = max(best, len(A) * len(B))\n if i == len(s):\n return\n A.append(s[i])\n go(i + 1, A, B)\n A.pop()\n B.append(s[i])\n go(i + 1, A, B)\n B.pop()\n go(i + 1, A, B)\n go()\n return best\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using fun = function<void(int, string&&, string&&)>;\n int maxProduct(string s, int best = 0) {\n auto ok = [](auto& s) {\n int N = s.size(),\n i = 0,\n j = N - 1;\n while (i < j && s[i] == s[j])\n ++i, --j;\n return j <= i;\n };\n fun go = [&](auto i, auto&& A, auto&& B) {\n if (ok(A) && ok(B))\n best = max(best, int(A.size() * B.size()));\n if (i == s.size())\n return;\n A.push_back(s[i]);\n go(i + 1, move(A), move(B));\n A.pop_back();\n B.push_back(s[i]);\n go(i + 1, move(A), move(B));\n B.pop_back();\n go(i + 1, move(A), move(B));\n };\n go(0, {}, {});\n return best;\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ || Recursion + Backtracking || Easy To Understand ✔ | c-recursion-backtracking-easy-to-underst-p06c | \nclass Solution {\npublic:\n\tint ans = 0;\n\tint n;\n\t//function for checking is given string is Palindrome\n\tbool palindrome(string s)\n\t{\n\t\tint i = 0; | AJAY_MAKVANA | NORMAL | 2021-09-12T09:56:17.313587+00:00 | 2021-09-13T07:33:42.926834+00:00 | 147 | false | ```\nclass Solution {\npublic:\n\tint ans = 0;\n\tint n;\n\t//function for checking is given string is Palindrome\n\tbool palindrome(string s)\n\t{\n\t\tint i = 0;\n\t\tint j = s.size() - 1;\n\t\twhile (i <= j)\n\t\t{\n\t\t\tif (s[i++] != s[j--])\n\t\t\t{\n\t\t\t\treturn false;\n\t\t\t}\n\t\t}\n\t\treturn true;\n\t}\n\n\tvoid solve(int index, string &s, string &s1, string &s2)\n\t{\n\t\t//If index >= n (where n = s.size()) then return\n\t\tif (index >= n)\n\t\t{\n\t\t\t//If both s1 and s2 are palindrome then this is as required in problem\n\t\t\t//so update ans with ans = max(ans, s1.size() * s2.size());\n\t\t\tif (palindrome(s1) && palindrome(s2))\n\t\t\t{\n\t\t\t\tans = max(ans, (int)s1.size() * (int)s2.size());\n\t\t\t}\n\t\t\treturn;\n\t\t}\n\n\t\t//1. include s[index]\n\t\t\t//1.(i) adding s[index] in string s1\n\t\t\ts1.push_back(s[index]);\n\t\t\tsolve(index + 1, s, s1, s2);\n\t\t\ts1.pop_back();\n\t\t\t//1.(ii) adding s[index] in string s2\n\t\t\ts2.push_back(s[index]);\n\t\t\tsolve(index + 1, s, s1, s2);\n\t\t\ts2.pop_back();\n\n\t\t//2. not including s[index] in string generation\n\t\tsolve(index + 1, s, s1, s2);\n\t}\n\n\tint maxProduct(string s) {\n\t\tint index = 0;\n\t\tn = s.size();\n\t\tstring s1 = "";\n\t\tstring s2 = "";\n\t\tsolve(index, s, s1, s2);\n\t\treturn ans;\n\t}\n};\n```\n\n**If find Helpful *Upvote It* \uD83D\uDC4D** | 2 | 0 | ['Backtracking', 'Recursion', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Java Solution - Standard Recursion and Backtracking | java-solution-standard-recursion-and-bac-j3h1 | Idea\nFirst you need to find the first pallin subsequence string then you need to remove that string from the original string and finding the another pallin sub | pgthebigshot | NORMAL | 2021-09-12T04:46:49.961744+00:00 | 2021-09-12T04:59:21.312433+00:00 | 277 | false | **Idea**\nFirst you need to find the first pallin subsequence string then you need to remove that string from the original string and finding the another pallin subsequence string.\n```\nclass Solution {\n\tint max=Integer.MIN_VALUE;\n\tvoid recur(String str,int n,int ind,String s,List<Integer> list)\n\t{\n\t\tif(ind==n)\n { \n if(isPallin(str))\n {\n\t \tString st="";\n\t \tfor(int i=0;i<n;i++)\n\t \t\tif(!list.contains(i))\n\t \t\t\tst+=s.charAt(i);\n recur1("", st.length(), 0, st,str);\n }\n return;\n }\n\t\trecur(str,n,ind+1,s,new ArrayList(list));\n\t\tstr+=s.charAt(ind);\n\t\tlist.add(ind);\n\t\trecur(str,n,ind+1,s,new ArrayList(list));\n\t}\n\tvoid recur1(String str,int n,int ind,String s,String st)\n\t{\n\t\tif(ind==n)\n {\n if(isPallin(str))\n max=Math.max(max,st.length()*str.length());\n return;\n }\n\t\trecur1(str,n,ind+1,s,st);\n\t\tstr+=s.charAt(ind);\n\t\trecur1(str,n,ind+1,s,st);\n\t}\n\tboolean isPallin(String s)\n\t{\n\t\tint i=0,j=s.length()-1;\n\t\twhile(i<j)\n\t\t{\n\t\t\tif(s.charAt(i)!=s.charAt(j))\n\t\t\t\treturn false;\n i++;\n j--;\n\t\t}\n\t\treturn true;\n\t}\n public int maxProduct(String s) {\n \t\n recur("",s.length(),0,s,new ArrayList());\n return max;\n }\n}\n```\nAny Questions??\nelse\nPlease do upvote:)) | 2 | 1 | ['Backtracking', 'Java'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Dp in Python | dp-in-python-by-pisces311-8jo1 | We may use dp to enumerate the first palindromic sequence. Since the maximum length of the original string is only 12 - the iteration goes up to 2**12=4096 time | Pisces311 | NORMAL | 2021-09-12T04:43:56.590720+00:00 | 2021-09-12T04:58:51.201943+00:00 | 187 | false | We may use dp to enumerate the first palindromic sequence. Since the maximum length of the original string is only 12 - the iteration goes up to `2**12=4096` times. Actually, small sized problem should always remind you to think about brute force.\n\nAfter that, just try to find the longest palindromic subsequence in the rest characters. That\'s a classic problem. You can find the exact same problem here https://leetcode.com/problems/longest-palindromic-subsequence/.\n```\nclass Solution:\n def maxPalindrome(self, s):\n n = len(s)\n dp = [[0] * n for _ in range(n)]\n for i in range(n):\n dp[i][i] = 1\n for i in range(n - 1, -1, -1):\n for j in range(i + 1, n):\n if s[i] == s[j]:\n dp[i][j] = dp[i+1][j-1]+2\n else:\n dp[i][j] = max(dp[i+1][j], dp[i][j-1])\n return dp[0][n-1]\n\n def maxProduct(self, s: str) -> int:\n ans = 1\n for i in range(1, 2**len(s)+1):\n first = \'\'\n remain = \'\'\n for j in range(len(s)):\n if i & (2**j):\n first += s[j]\n else:\n remain += s[j]\n if first != first[::-1] or not remain:\n continue\n ans = max(ans, len(first) * self.maxPalindrome(remain))\n return ans\n``` | 2 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Simple Java DP Solution - Top Down Recursion | simple-java-dp-solution-top-down-recursi-m216 | \nclass Solution {\n public int maxProduct(String s) {\n return maxProduct(s, 0, "","");\n }\n Map<String, Integer> dp = new HashMap<>();\n p | vathsalyabhupathi | NORMAL | 2021-09-12T04:23:48.037141+00:00 | 2021-09-12T04:23:48.037168+00:00 | 310 | false | ```\nclass Solution {\n public int maxProduct(String s) {\n return maxProduct(s, 0, "","");\n }\n Map<String, Integer> dp = new HashMap<>();\n public int maxProduct(String s, int ci, String s1, String s2) {\n int max = 0;\n String key = ci+"_"+s1 +"_"+s2;\n \n if(dp.containsKey(key))\n return dp.get(key);\n if(ci==s.length()){\n if(s1.length()>0 && s2.length()>0 && isPalindrome(s1) && isPalindrome(s2)){\n return s1.length()*s2.length();\n }\n return max;\n }\n max = Math.max(Math.max(maxProduct(s, ci+1, s1+s.charAt(ci), s2),\n maxProduct(s, ci+1, s1, s2+s.charAt(ci))), maxProduct(s, ci+1, s1, s2));\n dp.put(key, max);\n return max;\n }\n boolean isPalindrome(String s){\n int start = 0, end = s.length()-1;\n while(start<end){\n if(s.charAt(start)!=s.charAt(end))\n return false;\n start++;\n end--;\n }\n return true;\n }\n}\n``` | 2 | 0 | [] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [C++] Backtracking Solution | c-backtracking-solution-by-manishbishnoi-4ipn | \nclass Solution {\n int ans;\n // Check for palindrome\n bool isPalindrome(string& temp){\n int i=0,j = temp.length() - 1;\n while(i<j){ | manishbishnoi897 | NORMAL | 2021-09-12T04:16:00.742005+00:00 | 2021-09-12T04:20:14.720798+00:00 | 156 | false | ```\nclass Solution {\n int ans;\n // Check for palindrome\n bool isPalindrome(string& temp){\n int i=0,j = temp.length() - 1;\n while(i<j){\n if(temp[i]!=temp[j]){\n return false;\n }\n i++,j--;\n }\n return true;\n }\n \n void helper(int i,string& str,string temp,int prev,vector<bool> &vis){\n if(i==str.length()){\n if(isPalindrome(temp)){\n\t\t\t\t// If we have already found 1 palindromic subsequence\n if(prev!=-1){\n int s = temp.length();\n ans=max(ans,prev*s);\n }\n else{ // Search for another palindromic subsequence\n helper(0,str,"",temp.length(),vis);\n }\n }\n return ; \n }\n helper(i+1,str,temp,prev,vis);\n if(!vis[i]){\n vis[i]=true;\n helper(i+1,str,temp+str[i],prev,vis);\n vis[i]=false;\n }\n }\n \npublic:\n int maxProduct(string s) {\n ans = 0;\n vector<bool> vis(s.length(),false);\n helper(0,s,"",-1,vis);\n return ans;\n }\n};\n``` | 2 | 1 | ['Backtracking', 'C'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Python Simple Soln(Brute Force) | python-simple-solnbrute-force-by-atul_ii-njyj | \n def maxProduct(self, s: str) -> int:\n def largestP(s):\n n = len(s)\n dp = [1] * n\n for j in range(1, len(s)):\n | atul_iitp | NORMAL | 2021-09-12T04:06:24.194510+00:00 | 2021-09-12T06:23:23.661225+00:00 | 143 | false | ```\n def maxProduct(self, s: str) -> int:\n def largestP(s):\n n = len(s)\n dp = [1] * n\n for j in range(1, len(s)):\n pre = dp[j]\n for i in reversed(range(0, j)):\n tmp = dp[i]\n if s[i] == s[j]:\n dp[i] = 2 + pre if i + 1 <= j - 1 else 2\n else:\n dp[i] = max(dp[i + 1], dp[i])\n pre = tmp\n return dp[0]\n \n l = len(s)\n output = 1\n for i in range(1, (2**(l-1)):\n r = \'\'\n m = \'\'\n for j in range(l):\n if i & (1<< j):\n r += s[j]\n else:\n m += s[j]\n output = max((largestP(r) * largestP(m)), output)\n return output\n \n``` | 2 | 1 | ['Dynamic Programming', 'Iterator'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Easy brute force solution in c++ | easy-brute-force-solution-in-c-by-adithy-kh9d | \n\n\n\nclass Solution {\npublic:\n bool isPalindrome(string str)\n {\n // Start from leftmost and rightmost corners of str\n int l = 0;\n | adithya_u_bhat | NORMAL | 2021-09-12T04:06:20.115534+00:00 | 2021-09-12T04:10:17.219389+00:00 | 92 | false | \n\n```\n\nclass Solution {\npublic:\n bool isPalindrome(string str)\n {\n // Start from leftmost and rightmost corners of str\n int l = 0;\n int h = str.size()-1;\n\n // Keep comparing characters while they are same\n while (h > l)\n {\n if (str[l++] != str[h--])\n {\n return false;\n }\n }\n return true;\n }\n int maxProduct(string s) {\n vector<pair<string,long long>> v;\n \n long long n = s.size();\n long long power = pow(2,n);\n\t\t\n\t\t\n for(int i=0;i<power;i++){\n string ans="";\n for(int j=0;j<n;j++){\n if(i&1<<j){\n ans = ans + s[j];\n }\n }\n if(isPalindrome(ans)){\n v.push_back({ans,i});\n }\n }\n long long val=1;\n for(int i=0;i<v.size()-1;i++){\n for(int j=1;j<v.size();j++){\n if((v[i].second & v[j].second)==0){\n \n long long ik = v[i].first.size();\n long long jk = v[j].first.size();\n \n if(ik*jk>val){\n val = ik*jk;\n }\n \n }\n }\n }\n return val;\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Java Solution with Explanation | java-solution-with-explanation-by-goals_-zfmp | Intuition\nRecursion to get all possible subsequence for consideration\nSimilar working as- all_possible_subsequence_of_string_problem\n\n# Approach\n1) conside | Goals_7 | NORMAL | 2024-09-04T07:29:17.928396+00:00 | 2024-09-04T07:29:17.928428+00:00 | 175 | false | # Intuition\nRecursion to get all possible subsequence for consideration\nSimilar working as- [all_possible_subsequence_of_string_problem](https://takeuforward.org/data-structure/power-set-print-all-the-possible-subsequences-of-the-string/)\n\n# Approach\n1) consider current char for S1\n2) consider current char for S2\n3) Don\'t consider current char for either\n\nNote- current char cannot be inclue in both at the same time\n\n# Complexity\n- Time complexity:\nO(3^n)\n\n- Space complexity:\nO(n) where n is char array\n\n# Code\n```java []\nclass Solution {\n int res = 0;\n \n public int maxProduct(String s) {\n char[] strArr = s.toCharArray();\n dfs(strArr, 0, "", "");\n return res;\n }\n\n public void dfs(char[] strArr, int i, String s1, String s2){\n if(i >= strArr.length){\n if(isPalindromic(s1) && isPalindromic(s2))\n res = Math.max(res, s1.length()*s2.length());\n return;\n }\n dfs(strArr, i+1, s1 + strArr[i], s2);\n dfs(strArr, i+1, s1, s2 + strArr[i]);\n dfs(strArr, i+1, s1, s2);\n }\n\n public boolean isPalindromic(String str){\n int j = str.length() - 1;\n char[] strArr = str.toCharArray();\n for (int i = 0; i < j; i ++){\n if (strArr[i] != strArr[j])\n return false;\n j--;\n }\n return true;\n }\n}\n``` | 1 | 0 | ['Recursion', 'Java'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Easy to understand Solution | Bitmask | Brute force | easy-to-understand-solution-bitmask-brut-nmox | Intuition\nThe problem is asking for the maximum product of the lengths of two non-overlapping palindromic subsequences. The key observation is that palindromic | Harsh-1510 | NORMAL | 2024-08-23T07:36:04.140967+00:00 | 2024-08-23T07:36:04.141001+00:00 | 24 | false | # Intuition\nThe problem is asking for the maximum product of the lengths of two non-overlapping palindromic subsequences. The key observation is that palindromic subsequences can be generated using bitmasks, and if we check for all possible pairs of subsequences, we can identify those that are non-overlapping and have the largest product of their lengths.\n\n# Approach\n1. **Bitmask Representation for Subsequence Generation:**\nEach subsequence of the given string can be represented using a bitmask. For a string of length n, there are \n2^n possible subsequences. Each bit in the bitmask represents whether a character at a particular position is included in the subsequence or not.\n\n2. **Generating Subsequences and Checking Palindromes:**\nFor each bitmask, generate the corresponding subsequence. Then, check if this subsequence is a palindrome by comparing it with its reverse. Store the length of this palindromic subsequence using the bitmask as the key in a map.\n\n3. **Checking Non-Overlapping Subsequences:**\nFor each pair of palindromic subsequences, check if they are non-overlapping by ensuring that the bitwise AND of their bitmasks is 0. If they are non-overlapping, compute the product of their lengths and update the result if it\u2019s the maximum found so far.\n\n# Complexity\n- Time complexity:\n * Generating all subsequences takes \uD835\uDC42((2^\uD835\uDC5B).\uD835\uDC5B), where \uD835\uDC5B is the length of the string.\n * Checking each pair of subsequences for overlap takes \n\uD835\uDC42((2^\uD835\uDC5B).(2^\uD835\uDC5B))in the worst case.\n * Therefore, the overall time complexity is \uD835\uDC42((4^\uD835\uDC5B)+(2^\uD835\uDC5B)\u22C5\uD835\uDC5B), which is feasible for small strings (e.g., \uD835\uDC5B\u226412).\n\n- Space complexity:\nThe space complexity is \uD835\uDC42(2\uD835\uDC5B) due to the storage of subsequences in the map.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxProduct(string s) {\n unordered_map<int, int> mp;\n int n = s.size();\n\n // Generate all subsequences using bitmasks\n for(int i = 0; i < (1 << n); i++){\n string subseq;\n for(int j = 0; j < n; j++){\n if(i & (1 << j)){\n subseq.push_back(s[j]);\n } \n }\n string rev = subseq;\n reverse(rev.begin(), rev.end());\n\n // If the subsequence is a palindrome, store its length\n if(subseq == rev){\n mp[i] = subseq.size();\n }\n }\n\n int res = 0;\n\n // Iterate over all pairs of subsequences\n for(auto& i : mp){\n for(auto& j : mp){\n // Ensure the two subsequences don\'t overlap\n if((i.first & j.first) == 0){\n res = max(res, i.second * j.second);\n }\n }\n }\n\n return res;\n }\n};\n\n``` | 1 | 0 | ['Hash Table', 'Bitmask', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Well defined with bitmask. Beats 100%. O(N^2 * 2^N). | well-defined-with-bitmask-beats-100-on2-xyn0h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nFind all subpalindromes | alexanderwsz | NORMAL | 2024-07-03T11:53:02.562963+00:00 | 2024-07-03T21:22:37.689483+00:00 | 109 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind all subpalindromes.\nTraverse subpalindromes\n---- if pair.isDisjoint\n-------- currentProduct = length1 * length2\n-------- currentMax = (maxProduct, currentProduct)\nreturn maxProduct\n\n\n# Complexity\n- Time complexity: O(N^2 * 2^N).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nUpvotes appreciated. Happy coding.\n# Code\n```\nclass Solution {\n func maxProduct(_ s: String) -> Int {\n func areDisjoint(_ mask1: Int, _ mask2: Int) -> Bool { mask1 & mask2 == 0 }\n\n func subPalindromes(_ characters: [Character]) -> [(Int, Int)] {\n func isPalindrome(_ array: [Character]) -> Bool {\n for i in 0..<(array.count / 2) where array[i] != array[array.count - 1 - i] { return false }\n return true\n }\n\n var palindromicSubsequences = [(Int, Int)]()\n let number = characters.count\n (1..<(1 << number)).forEach { mask in\n var subWord = [Character]()\n for i in 0..<number where (mask & (1 << i)) != 0 { subWord.append(characters[i]) }\n if isPalindrome(subWord) {\n palindromicSubsequences.append((mask, subWord.count)) \n }\n }\n return palindromicSubsequences\n }\n\n let characters = Array(s)\n var maxProduct = 0\n guard !characters.isEmpty else { return maxProduct }\n let palindromicSubsequences = subPalindromes(characters)\n let count = palindromicSubsequences.count\n (0..<count).forEach { i in\n ((i + 1)..<count).forEach { j in\n let (mask1, lenght1) = palindromicSubsequences[i]\n let (mask2, lenght2) = palindromicSubsequences[j]\n if areDisjoint(mask1, mask2) { maxProduct = max(maxProduct, lenght1 * lenght2) }\n }\n }\n \n return maxProduct\n }\n}\n\n``` | 1 | 0 | ['Swift'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | MOST OPTIMIZED C++ SOLUTION | most-optimized-c-solution-by-tin_le-e9vd | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | tin_le | NORMAL | 2024-04-17T00:31:34.417217+00:00 | 2024-04-17T00:31:34.417239+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->image.png\n\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(string s) {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n int n = s.size();\n int target = 1 << n;\n unordered_map<int, int> mp;\n string temp;\n for(int mask = 0; mask < target; mask++)\n {\n temp = "";\n for(int i = 0; i < n; i++)\n {\n if(mask & (1 << i))\n {\n temp += s[i];\n }\n }\n if(temp == string(temp.rbegin(), temp.rend()))\n { \n mp[mask] = temp.size();\n } \n }\n int res = 0;\n for(auto first = mp.begin(); first != mp.end(); first++)\n {\n for(auto second = next(first); second != mp.end(); second++)\n {\n if((first->first & second->first) == 0)\n {\n res = max(res, first->second * second->second);\n }\n }\n }\n return res;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Explained approach with time and space complexities. 🔥 | explained-approach-with-time-and-space-c-v1vj | Intuition \n Describe your first thoughts on how to solve this problem. \nUtilize bitmasking to efficiently generate all possible subsequences of the string and | sirsebastian5500 | NORMAL | 2024-02-27T03:03:19.535262+00:00 | 2024-02-27T03:03:19.535292+00:00 | 165 | false | # Intuition \n<!-- Describe your first thoughts on how to solve this problem. -->\nUtilize bitmasking to efficiently generate all possible subsequences of the string and to verify if two strings are disjoint.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGenerate all subsequences using bitmasking, store lengths of palindromic ones. Compute max product by iterating over pairs of these subsequences, ensuring they\'re disjoint (bitmasks don\'t overlap).\n\n# Complexity\n- Time complexity: O(4^n) time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n) space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nNote: Time complexity is from nested iteration over 2^n size dict.\n\n# Code\n```\nclass Solution:\n def is_palindrome(self, s: str) -> bool:\n L, R = 0, len(s) - 1\n while L < R:\n if s[L] != s[R]:\n return False\n L += 1\n R -= 1\n return True\n\n def maxProduct(self, s: str) -> int:\n n = len(s)\n length_pal = dict()\n\n # Generate every possible subsequence\n for bitmask in range(1, 2 ** n):\n sequence = ""\n for i in range(n):\n if bitmask & (1 << i):\n sequence += s[i]\n\n if self.is_palindrome(sequence):\n length_pal[bitmask] = len(sequence)\n \n # Compute the max product \n max_product = 0\n for bitmask1 in length_pal:\n for bitmask2 in length_pal:\n # Check if masks are disjoint\n if bitmask1 & bitmask2 == 0: \n max_product = max(max_product, length_pal[bitmask1] * length_pal[bitmask2])\n\n return max_product \n\n# O(4^n) time\n# O(2^n) space\n\n``` | 1 | 0 | ['Python3'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Simple find all subarray approach | simple-find-all-subarray-approach-by-aan-rjgk | Intuition\nInstead of storing the char we are storing the indices of all subarray\nIt will be easier to find duplicate. if we store char it can be duplicate\n\n | aanya_969 | NORMAL | 2024-01-11T14:11:35.463303+00:00 | 2024-01-11T14:11:35.463327+00:00 | 14 | false | # Intuition\nInstead of storing the char we are storing the indices of all subarray\nIt will be easier to find duplicate. if we store char it can be duplicate\n\n# Complexity\n- Time complexity:\nO(2^n * n^2)\n\n- Space complexity:\n(2^n * n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>>allSubarr;\n bool check(vector<int>&a,vector<int>&b){ \n for(int i=0;i<a.size();i++)\n for(int j=0;j<b.size();j++)\n //if from the same index return false\n if(a[i]==b[j]) return false;\n return true;\n }\n bool isPalin(string &s,vector<int>&ans){\n int a=0,b=ans.size()-1;\n while(a<=b){\n if(s[ans[a]]!=s[ans[b]]) return false;\n a++;\n b--;\n }\n return true; \n }\n void findStr(string& s, vector<int>&temp, int idx){\n //if at any point string is palindrome \n //store it in ans\n if(isPalin(s, temp)){\n allSubarr.push_back(temp);\n }\n //idx is greater than length return\n if(idx>=s.length()) return;\n //take that char\n temp.push_back(idx);\n findStr(s, temp, idx+1);\n //leave the char\n temp.pop_back();\n findStr(s, temp, idx+1);\n }\n int maxProduct(string s) {\n int ans=0;\n vector<int>temp;\n //find all possible substring in allSubarr\n findStr(s, temp, 0);\n //check for all subarray if any 2 gives the max product value\n for(int i=0; i<allSubarr.size(); i++){\n for(int j=i+1; j<allSubarr.size(); j++){\n //store the product\n int x=(int)allSubarr[i].size()*allSubarr[j].size();\n //check if selected 2 strings char are not from the same index\n if(check(allSubarr[i], allSubarr[j])){\n //store max value of x\n ans=max(ans, x);\n }\n }\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Bitmask approach in TypeScript | bitmask-approach-in-typescript-by-teoyuq-ryju | Approach\n1. Use bit mask to get all possible subsequences.\n2. If subsequence is palindrome, add [bitmask, length] pair to array.\n3. Iterate through all pairs | teoyuqi | NORMAL | 2024-01-01T12:11:26.269036+00:00 | 2024-01-01T12:11:26.269069+00:00 | 132 | false | # Approach\n1. Use bit mask to get all possible subsequences.\n2. If subsequence is palindrome, add `[bitmask, length]` pair to array.\n3. Iterate through all pairs in array. If two bitmasks are disjoint, `(bitmask1 & bitmask2) === 0`.\n4. Return max length product.\n\n# Complexity\nIn worst case, we have 2^n `[subseq, length]` pairs in `subseqLengthPairs`\n- Time complexity\n`O((2^n)^2) = O(4^n)`\n\n- Space complexity:\n`O(2^n)`\n\n# Code\n```TypeScript\nconst palindromeMemo = {};\nfunction maxProduct(s: string): number {\n // all [ palindromic subseq, length ] pairs\n const subseqLengthPairs: Array<Array<number>> = []\n for (let i = 0; i < 1 << s.length; i++) {\n const subseq = bitmaskToSubseq(s, i);\n if (isPalindrome(subseq)) {\n subseqLengthPairs.push([i, subseq.length]);\n }\n }\n\n let res = 0\n for (const [bitmask1, length1] of subseqLengthPairs) {\n for (const [bitmask2, length2] of subseqLengthPairs) {\n if ((bitmask1 & bitmask2) === 0) {\n // two subeq are disjoint\n res = Math.max(res, length1 * length2);\n }\n }\n }\n return res;\n};\n\nconst bitmaskToSubseq = (s: string, bitmask: number): string => {\n let subseq = "";\n for (let i = 0; i < s.length; i++) {\n if (((1 << i) & bitmask) !== 0) {\n subseq += s.charAt(i);\n }\n }\n return subseq;\n}\n\nconst isPalindrome = (s: string): boolean => {\n if (palindromeMemo?.[s] !== undefined) {\n return palindromeMemo[s];\n }\n let l = 0;\n let r = s.length - 1;\n while (l < r) {\n if (s.charAt(l) !== s.charAt(r)) {\n palindromeMemo[s] = false;\n return false;\n }\n l++; r--;\n }\n palindromeMemo[s] = true;\n return true\n}\n``` | 1 | 0 | ['Bit Manipulation', 'Bitmask', 'TypeScript'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | DP || Bitmask || Recurssion || C++|| ✅94.18% Beats✅|| | dp-bitmask-recurssion-c-9418-beats-by-fi-ho0j | Intuition\n Describe your first thoughts on how to solve this problem. \n- Initially check all LCS in the string.\n- Create a mask of every LCS possible.\n- Usi | FishBum | NORMAL | 2023-09-28T09:37:20.193627+00:00 | 2023-09-28T09:37:20.193653+00:00 | 88 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Initially check all LCS in the string.\n- Create a mask of every LCS possible.\n- Using the mask take the LCS of unset indexes.\n- Then take the maximum of the product of both for each LCS. \n\n# Code\n```\nclass Solution {\npublic:\n int ans = 0;\n int dp[1<<12][12][12];\n int help(string &s, int i, int j, int mask){\n if(i >= j){\n if(i == j && !(mask&(1<<i)))\n return 1;\n return 0;\n }\n \n if(dp[mask][i][j] != -1)\n return dp[mask][i][j];\n\n int a = 0;\n if((mask&(1<<i)) || (mask&(1<<j))){\n if((mask&(1<<i)))\n a = max(a, help(s, i+1, j, mask));\n if(mask&(1<<j))\n a = max(a, help(s, i, j-1, mask));\n }\n else{\n if(s[i] == s[j])\n a = max(a, help(s, i+1, j-1, mask) + 2); \n a = max(a, help(s, i+1, j, mask));\n a = max(a, help(s, i, j-1, mask));\n }\n\n return dp[mask][i][j] = a;\n }\n void solve(string &s, int i, int j, int len, int mask){\n if(i >= j){\n int a = 0, n = 0;\n if(i == j){\n a = 1;\n n = n | (1<<i);\n }\n if((mask | n) != (1<<s.length())-1)\n ans = max(ans, (len + a)*help(s, 0, s.length()-1, mask|n));\n if(mask != (1<<s.length())-1)\n ans = max(ans, len*help(s, 0, s.length()-1, mask));\n\n return ;\n }\n \n if(s[i] == s[j]){\n int n = 0;\n n = n | (1<<i);\n n = n | (1<<j);\n solve(s, i+1, j-1, len+2, mask | n);\n }\n\n solve(s, i+1, j, len, mask);\n solve(s, i, j-1, len, mask);\n\n return;\n }\n int maxProduct(string s) {\n int mask = 0;\n memset(dp, -1, sizeof dp);\n solve(s, 0, s.length()-1, 0, mask);\n return ans;\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'Bitmask', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Easy Detailed Sol || C++ Backtracking | easy-detailed-sol-c-backtracking-by-yeah-blc0 | Intuition\nas the constraints are too small we can look for generating all possible subsequences and then check whether they are distinct or not and calculate t | yeah_boi123 | NORMAL | 2023-07-13T11:14:52.043133+00:00 | 2023-07-13T11:14:52.043158+00:00 | 55 | false | # Intuition\nas the constraints are too small we can look for generating all possible subsequences and then check whether they are distinct or not and calculate the answer \n\n# Approach\nso what i did was to first i made all subsequences using bitmask and then i pushed the bitmask of the string which is a palindrome in a vector v after that i iterated over v vector and checked every pair which are distinct and updated the ans\n\n# Complexity\n- Time complexity:\nThe time complexity of the given code is O(2^N * N^2), where N is the length of the input string \'s\'.\n\n- Space complexity:\nThe space complexity of the given code is O(2^N * N), where N is the length of the input string \'s\'.\n\n# Code\n```\nclass Solution {\npublic:\n bool check(string &s){\n if(s.size()==0){\n return false;\n }\n int i=0;\n int n=s.size();\n int j=n-1;\n while(i<j){\n if(s[i]!=s[j]){\n return false;\n }\n i++;\n j--;\n }\n return true;\n }\n int maxProduct(string s) {\n int n=s.size();\n int tot=(1<<n)-1;\n vector<int> v;\n for(int bitmask=0; bitmask<=tot; bitmask++){\n string temp="";\n for(int j=0;j<n; j++){\n if(bitmask & (1<<j)){\n temp+=s[j];\n }\n }\n if(check(temp)){\n v.push_back(bitmask);\n }\n }\n int ans=0;\n for(int i=0; i<v.size(); i++){\n for(int j=i+1; j<v.size(); j++){\n if((v[i] & v[j])==0){\n int a=__builtin_popcount(v[i]);\n int b=__builtin_popcount(v[j]);\n ans=max(ans,a*b);\n }\n }\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Bit Manipulation', 'Bitmask', 'C++'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Javascript with bit mask | javascript-with-bit-mask-by-vwxyz-pefe | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vwxyz | NORMAL | 2023-04-07T09:31:33.849757+00:00 | 2023-04-07T09:31:33.849791+00:00 | 124 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {string} s\n * @return {number}\n */\nvar maxProduct = function(s) {\n const len = s.length\n const m = {} // hashmap for palindrome, ex: { 1: 1, 2:1, ... , 128: 1, 130, 2 }\n\n for (let mask=1;mask<(1<<len);mask++) { // iterate all cases \n let subseq = "" // temporary palindrome subsequence string\n for (let i=0;i<len;i++) { // iterate the total length of string\n if (mask & (1 << i)) { // if true, found a character index for the mask\n subseq += s[i] // append the character to the subsequence\n }\n }\n if (subseq == [...subseq].reverse().join(\'\')) { // check whether or not subseq is palindrome string\n m[mask] = subseq.length // if it\'s palindrome, add it to the hashmap\n }\n }\n \n let res = 0\n // iterate nested loop to find the max product\n for (const [m1,] of Object.entries(m)) { \n for (const [m2,] of Object.entries(m)) {\n if ((+m1 & +m2) == 0) { // found disjoint subseq\n res = Math.max(res, m[m1] * m[m2])\n }\n }\n }\n return res\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | Brute Force Appro | brute-force-appro-by-sanjeevkrpathak-8isx | \n\n# Code\n\nclass Solution:\n def maxProduct(self, s: str) -> int:\n N,pali = len(s),{} # bitmask = length\n\n for mask in range(1,1<<N): # 1 | sanjeevkrpathak | NORMAL | 2023-03-22T18:17:32.284176+00:00 | 2023-03-22T18:17:32.284218+00:00 | 225 | false | \n\n# Code\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n N,pali = len(s),{} # bitmask = length\n\n for mask in range(1,1<<N): # 1 << N == 2**N\n subseq = ""\n for i in range(N):\n if mask & (1<<i):\n subseq+=s[i]\n\n if subseq == subseq[::-1]:\n pali[mask] = len(subseq)\n\n \n res = 0\n for m1 in pali:\n for m2 in pali:\n if m1 & m2 == 0:\n res = max(res,pali[m1]*pali[m2])\n\n return res\n\n\n``` | 1 | 0 | ['Python3'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | [python 3] Bitmask | python-3-bitmask-by-gabhay-so81 | \tclass Solution:\n\t\tdef maxProduct(self, s: str) -> int:\n\t\t\tdef create_string(v):\n\t\t\t\tres=[]\n\t\t\t\tfor i in range(n):\n\t\t\t\t\tif 1<<i&v:\n\t\t | gabhay | NORMAL | 2022-11-24T11:30:40.735651+00:00 | 2022-11-24T11:30:40.735691+00:00 | 108 | false | \tclass Solution:\n\t\tdef maxProduct(self, s: str) -> int:\n\t\t\tdef create_string(v):\n\t\t\t\tres=[]\n\t\t\t\tfor i in range(n):\n\t\t\t\t\tif 1<<i&v:\n\t\t\t\t\t\tres.append(s[i])\n\t\t\t\tif res==res[::-1]:\n\t\t\t\t\tpal[v]=len(res)\n\t\t\tpal=dict()\n\t\t\tn=len(s)\n\t\t\tfor i in range(1,pow(2,n)):\n\t\t\t\tcreate_string(i)\n\t\t\tres=0\n\t\t\tfor x in pal:\n\t\t\t\tfor y in pal:\n\t\t\t\t\tif not x&y:\n\t\t\t\t\t\tres=max(res,pal[x]*pal[y])\n\t\t\treturn res | 1 | 0 | ['Bitmask', 'Python3'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ || NOT sure How DP is used in my soln. | c-not-sure-how-dp-is-used-in-my-soln-by-1nvgd | TC: O( 3 ^N )\nSC: O(1) + Auxiliary Stack Space O(N)\n\nclass Solution {\npublic:\n bool isPalindrome(string &str){\n int i=0,j=str.size()-1;\n | rohitraj13may1998 | NORMAL | 2022-08-31T18:57:15.552994+00:00 | 2022-08-31T18:57:15.553040+00:00 | 527 | false | TC: O( 3 ^N )\nSC: O(1) + Auxiliary Stack Space O(N)\n```\nclass Solution {\npublic:\n bool isPalindrome(string &str){\n int i=0,j=str.size()-1;\n while(i<j){\n if(str[i]!=str[j])\n return false;\n i++;\n j--;\n }\n return true;\n }\n void solve(int i,string &s1,string &s2,string &s,int &ans){\n //base case\n if(i>=s.size()){\n if(isPalindrome(s1) && isPalindrome(s2)){\n int prod=s1.size()*s2.size();\n ans= max(ans,prod);\n }\n return;\n }\n //dont pick\n solve(i+1,s1,s2,s,ans);\n \n //pick\n s1+=s[i];\n solve(i+1,s1,s2,s,ans);\n s1.pop_back();\n s2+=s[i];\n solve(i+1,s1,s2,s,ans);\n s2.pop_back();\n }\n \n int maxProduct(string s) {\n int n=s.size();\n int ans=0;\n string s1="",s2="";\n solve(0,s1,s2,s,ans);\n return ans;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'C++'] | 1 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++||Backtracking|| Easy to Understand | cbacktracking-easy-to-understand-by-retu-tfkp | ```\nclass Solution {\npublic:\n long long res;\n bool ispal(string &s)\n {\n int start=0,end=s.size()-1;\n while(start=s.size())\n | return_7 | NORMAL | 2022-07-21T15:29:24.161905+00:00 | 2022-07-21T15:29:24.161948+00:00 | 118 | false | ```\nclass Solution {\npublic:\n long long res;\n bool ispal(string &s)\n {\n int start=0,end=s.size()-1;\n while(start<end)\n {\n if(s[start]!=s[end])\n return false;\n start++;\n end--;\n }\n return true;\n }\n void backtrack(string s,int idx,string &s1,string &s2)\n {\n if(idx>=s.size())\n {\n if(ispal(s1)&&ispal(s2))\n {\n long long val=s1.size()*s2.size();\n res=max(val,res);\n }\n return ;\n }\n s1.push_back(s[idx]);\n backtrack(s,idx+1,s1,s2);\n s1.pop_back();\n \n s2.push_back(s[idx]);\n backtrack(s,idx+1,s1,s2);\n s2.pop_back();\n \n backtrack(s,idx+1,s1,s2);\n }\n int maxProduct(string s)\n {\n string s1="",s2="";\n backtrack(s,0,s1,s2);\n return res;\n \n }\n};\n// if you like the solution plz upvote. | 1 | 0 | ['Backtracking', 'C'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | eayc C++ code o(n^2*2^n) | eayc-c-code-on22n-by-gurmeet2000-30xp | \n int maxProduct(string s) {\n int n=s.length();\n int ans=0;\n for(int k=1;k<pow(2,n)-1;k++)\n {\n string unused="";\n | gurmeet2000 | NORMAL | 2022-06-20T07:17:52.407686+00:00 | 2022-06-20T07:22:39.086767+00:00 | 160 | false | ```\n int maxProduct(string s) {\n int n=s.length();\n int ans=0;\n for(int k=1;k<pow(2,n)-1;k++)\n {\n string unused="";\n string used="";\n for(int j=0;j<n;j++)\n {\n if(k&1<<j)\n {\n used+=s[j];\n }\n else \n {\n unused+=s[j];\n }\n }\n \n int check=1;\n for(int j=0;j<used.length()/2;j++)\n {\n if(used[j]!=used[used.length()-j-1])\n {\n check=0;\n break;\n }\n }\n \n if(!check)continue;\n int m=unused.length();\n vector<vector<int>>dp(m+1,vector<int>(m+1,0));\n \n for(int i=0;i<m;i++)dp[i][i]=1;\n for(int i=0;i<m-1;i++)\n {\n if(unused[i]==unused[i+1])dp[i][i+1]=2;\n else dp[i][i+1]=1;\n }\n for(int j=3;j<=m;j++)\n {\n for(int i=0;i<=m-j;i++)\n {\n if(unused[i]==unused[i+j-1])dp[i][i+j-1]=dp[i+1][i+j-2]+2;\n else dp[i][i+j-1]=max(dp[i][i+j-2],dp[i+1][i+j-1]);\n }\n }\n int u=used.length(); \n ans=max(ans,u*dp[0][m-1]);\n }\n return ans;\n }\n``` | 1 | 0 | ['Dynamic Programming', 'Bitmask'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | c++|dp with bitamask +longest palindromic subsequence | cdp-with-bitamask-longest-palindromic-su-jo8m | \nclass Solution {\npublic:\n bool check_palindrom(int m,string s){\n int i=0;\n string temp="";\n while(m>0){\n if(m&1){\n | deepak_pal8790 | NORMAL | 2022-06-09T03:29:10.082508+00:00 | 2022-06-09T03:29:37.836716+00:00 | 138 | false | ```\nclass Solution {\npublic:\n bool check_palindrom(int m,string s){\n int i=0;\n string temp="";\n while(m>0){\n if(m&1){\n temp+=s[i];\n }\n m=m>>1;\n i++;\n }\n int start=0;\n int end=temp.length()-1;\n while(start<=end){\n if(temp[start]!=temp[end])return false;\n start++;\n end--;\n }\n return true;\n }\n int find_ans(int m,string s){\n int n=s.length();\n string temp="";\n for(int i=0;i<n;i++){\n if((m&(1<<i))==0){\n temp+=s[i];\n }\n }\n int l=temp.length();\n if(l==0)return 0;\n vector<vector<int>>dp(l,vector<int>(l,0));\n for(int i=0;i<l;i++)dp[i][i]=1;\n for(int len=2;len<=l;len++){\n for(int i=0;i+len-1<l;i++){\n int j=i+len-1;\n if(len==2){\n if(temp[i]==temp[j])dp[i][j]=2;\n else dp[i][j]=1;\n }\n else{\n if(temp[i]==temp[j])dp[i][j]=2+dp[i+1][j-1];\n else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);\n }\n }\n }\n return dp[0][l-1];\n \n }\n int maxProduct(string s) {\n int n=s.length();\n int ans=0;\n\t\t//firstly finding each subsequence of string s \n for(int i=1;i<(1<<n);i++){\n bool flag=check_palindrom(i,s); //checking the current subsequence is palindrome \n if(!flag)continue;//if it is not palindrome continue to remaining subsequence\n int len1=__builtin_popcount(i);\n int len2=find_ans(i,s);//finding the maximum length subsequence which is palindrome in remaining string \n ans=max(len1*len2,ans);\n \n }\n return ans;\n }\n};\n\n``` | 1 | 0 | ['Dynamic Programming', 'Bitmask'] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ || Bactracking || Easy to understand | c-bactracking-easy-to-understand-by-abhi-kr6t | \nint ans=0;\n bool isPal(string& s)\n {\n int i=0,j=s.length()-1;\n while(i<=j)\n {\n if(s[i]!=s[j])\n return | abhishek_iiitp | NORMAL | 2022-05-20T05:30:14.714556+00:00 | 2022-05-20T05:30:14.714602+00:00 | 112 | false | ```\nint ans=0;\n bool isPal(string& s)\n {\n int i=0,j=s.length()-1;\n while(i<=j)\n {\n if(s[i]!=s[j])\n return false;\n i++;\n j--;\n }\n return true;\n }\n void helper(string& s,string& s1,string& s2,int i)\n {\n if(i>=s.size())\n {\n if(isPal(s1)&&isPal(s2))\n {\n ans=max(ans,(int)(s1.size())*(int)(s2.size()));\n \n }\n return;\n }\n \n s1+=s[i];\n helper(s,s1,s2,i+1);\n s1.pop_back();\n \n s2+=s[i];\n helper(s,s1,s2,i+1);\n s2.pop_back();\n \n helper(s,s1,s2,i+1);\n }\n int maxProduct(string s) \n {\n string s1="",s2="";\n int i=0;\n helper(s,s1,s2,i);\n return ans;\n }\n\t``` | 1 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | C++ || EASY TO UNDERSTAND || Simple Solution Using BackTracking | c-easy-to-understand-simple-solution-usi-y79o | \nclass Solution {\npublic:\n int ans=0;\n bool isPalin(string& s)\n {\n int i=0,j=s.length()-1;\n while(i<=j)\n {\n if | aarindey | NORMAL | 2022-04-08T11:59:39.734908+00:00 | 2022-04-08T11:59:39.734936+00:00 | 105 | false | ```\nclass Solution {\npublic:\n int ans=0;\n bool isPalin(string& s)\n {\n int i=0,j=s.length()-1;\n while(i<=j)\n {\n if(s[i]!=s[j])\n return false;\n i++;\n j--;\n }\n return true;\n }\n void dfs(string& s,string& s1,string& s2,int i)\n {\n if(i>=s.length())\n {\n if(isPalin(s1)&&isPalin(s2))\n {\n ans=max(ans,((int)s1.length())*((int)s2.length()));\n }\n return;\n }\n s1+=s[i];\n dfs(s,s1,s2,i+1);\n s1.pop_back();\n \n s2+=s[i];\n dfs(s,s1,s2,i+1);\n s2.pop_back();\n \n dfs(s,s1,s2,i+1);\n }\n int maxProduct(string s) {\n string s1="",s2="";\n int i=0;\n dfs(s,s1,s2,i);\n return ans;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome** | 1 | 0 | [] | 0 |
maximum-product-of-the-length-of-two-palindromic-subsequences | JS - slow but simple (without bitmask) | js-slow-but-simple-without-bitmask-by-ge-t2yg | Only possible since s.length <= 12 and we can basically check every possible variant.\n\nBased on this Python solution:\nhttps://leetcode.com/problems/maximum-p | georgiiperepechko | NORMAL | 2022-03-20T15:11:15.402017+00:00 | 2022-03-20T15:11:58.657100+00:00 | 199 | false | Only possible since s.length <= 12 and we can basically check every possible variant.\n\nBased on this Python solution:\nhttps://leetcode.com/problems/maximum-product-of-the-length-of-two-palindromic-subsequences/discuss/1458751/Python-DFS-solution\n\n```\nconst isPalindrome = (str) => {\n for (let i = 0, j = str.length - 1; i < j; i++, j--) {\n if (str[i] !== str[j]) return false;\n }\n return true;\n}\n\nfunction maxProduct(s) {\n function cb(letterIndex, word1, word2) {\n if (letterIndex > s.length) {\n return isPalindrome(word1) && isPalindrome(word2)\n ? word1.length * word2.length\n : 0;\n }\n \n const char = s[letterIndex];\n const newIndex = letterIndex + 1;\n \n return Math.max(\n cb(newIndex, word1, word2),\n cb(newIndex, `${word1}${char}`, word2),\n cb(newIndex, word1, `${word2}${char}`)\n );\n }\n \n return cb(0, \'\', \'\');\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.